苏教版小学数学六年级课课练习题 (93)

六年级数学分层练习（13）
1.把一个六面都涂上颜色的正方体木块，切成125块大小相同的小正方体。

（1）三面涂色的小正方体有多少块？
（2）二面涂色的小正方体有多少块？
（3）一面涂色的小正方体有多少块？
2．24块棱长是1厘米的正方体木块，摆成不同的长方体，可以摆出几种？表面积最大是多少？最小是多少？
3、甲乙两数的差和商都等于5，求甲乙两数的和是多少？
4.如图，这是一个铁皮出水管，每平方
米5元。

李师傅做20个这样的出水管，
需要用材料费多少元？（单位：厘米）
5.一个长方体铁块，长6厘米，宽5厘
米，高4厘米，如果把它车成一个最大
的正方体，这个正方体铁块的体积是（ ）立方厘米；如果把它熔铸成一个最大的正方体，这个正方体的体积是（ ）立方厘米。

（车是冷加工，而煅造和熔铸是热加工。

）
6. 一个棱长为1分米的正方体，按图中所示切了三刀，分成了大小不等的6个长方体。

这6个长方体的表面积之和是多少平方分米？
7. 一个小数，它的小数部分是整数部分的14
，这个小数可能是多少？。

【苏教版】六年级数学上册全册课时练习(每课一练)苏教版六年级数学上册第一单元课时练习第1课时长方体和正方体的认识（1）一、长方体有（）个面、（）个棱和（）个顶点，（）的面完全相同。

二、正方体是由（）个完全相同的（）围成的立体图形，正方体有（）条棱，它们的长度都（），正方体有（）个顶点。

三、先观察，再填空。

这是一个（），长（）、这是一个（），棱长是（）。

宽（）、高（）。

答案：一、6 12 8 相对二、6 正方形 12 相等 8三、长方体 6厘米 4厘米 8厘米正方体 2分米第2课时长方体和正方体的认识（2）四、下面的平面图，能围成正方体的有（）。

五、下面是一个长方体的展开图，说一说哪些面是相对的。

（ A ）——（）（）——（）（）——（）六、求出下面长方体或正方体中涂色面的面积。

答案：一、1 2 4二、A——F B——D C——E三、120平方厘米 20平方分米 49平方厘米第3课时长方体和正方体的表面积（1）七、看图做一做。

（1）右图中长方体前面的面积是（）平方厘米；左面的面积是（）平方厘米；下面的面积是（）平方厘米。

（2）这个长方体的表面积是多少平方厘米？八、一个正方体礼盒，棱长是2.5分米，想要在它的6个面上贴上包装纸，至少需要多少平方分米的包装纸？九、一种感冒药外盒包装的形状是长方体，长和宽都是4厘米，高是8厘米，制作这个包装盒至少需要硬纸板多少平方厘米？答案：一、（1）36 15 60 （2）（36+15+60）×2=222（平方厘米）二、2.5×2.5×6=37.5（平方分米）三、160平方厘米第4课时长方体和正方体的表面积（2）十、做一个长方体形状的金鱼缸（无盖），长8分米、宽4分米、高6分米，至少需要多少平方分米的玻璃？如果每平方分米的玻璃需要4元，那么至少需要多少元买玻璃？十一、一个正方体包装盒，棱长4.5分米，底面是木板，四周和上面用的是硬纸板。

做这个包装盒至少要用多少平方分米的木板和都是平方分米的硬纸板？十二、一个长6米、宽3.5米、高3米的房间，其中门窗的面积是8平方米。

第一单元扇形统计图第1课时扇形统计图1．如果只表示各种数量的多少，可以选用（）统计图表示；如果想要表示出数量增减变化的情况，可以选用（）统计图表示；如果要清楚地了解各部分数量同总数之间的关系，可以用（）统计图表示。

2．右图是一件毛衣各种毛占总重量的统计图，根据右图回答问题。

（1）棉的含量占这件衣服的（）％。

（2）（）的含量最多，（）的含量最少。

（3）兔毛含量比涤纶少占总数的（）％。

（4）这件毛衣重400克，羊毛有（）克，兔毛有（）克。

5．下图是某学校教师喜欢看的电视节目统计图（1）实验小学喜欢《走进科学》栏目的老师占百分之几？（2）喜欢的《大风车》的老师比喜欢《焦点访谈》的多20人，实验小学一共有多少老师？（3）喜欢《新闻联播》的和喜欢《走进科学》的一共有多少人？第2课时选择统计图1．下面数据分别用哪种统计图表示比较合适？（1）某地2010～2014年的年降雨量变化情况如下表。

（2）某服装广2014年5月某个星期销售衬衫情况如下表。

2．某班参加兴趣小组的情况如图。

（1）这是一个（）统计图。

（2）（）类活动最受欢迎。

（3）（）类活动占全班人数的五分之一。

（4）如果这个班有80人，美术组有（）人，歌咏组有（）人，书法组有（）人，科技组有（）。

第二单元圆柱与圆锥年份2010 2011 2012 2013 2014 降雨量（毫米）920 860 1005 670 704星期一二三四五六日销售量（件）120 110 145- 135 140 155 165第1课时圆柱和圆锥的认识一、在是圆柱的下面画“√”，不是圆柱的下面画“×”。

（）（）（）（）（）二、指出下面圆柱体的底面、侧面和高，并用直尺量一量它的底面直径和高各是多少。

三、在我们观察圆柱的时候，可以得到这样两幅图（如下图），这两幅图分别是从哪个角度观察得到的?（）（）四、图①是一枚跳棋的棋子。

从哪个角度观察这枚棋子，可以得到下面的图②、图③和图④?（）（）（）第2课时圆柱的侧面积和表面积一、元元把一个圆柱形易拉罐的侧面沿高剪开，得到的图形如下：1.这个圆柱形易拉罐的侧面积是（）cm2。

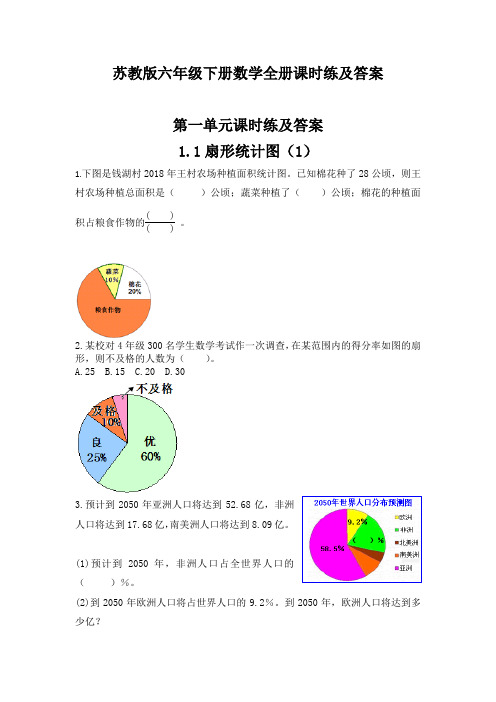
苏教版六年级下册数学全册课时练及答案第一单元课时练及答案1.1扇形统计图（1）1.下图是钱湖村2018年王村农场种植面积统计图。

已知棉花种了28公顷，则王村农场种植总面积是（ ）公顷；蔬菜种植了（ ）公顷；棉花的种植面积占粮食作物的( )( )。

2.某校对4年级300名学生数学考试作一次调查，在某范围内的得分率如图的扇形，则不及格的人数为（ ）。

A.25B.15C.20D.303.预计到2050年亚洲人口将达到52.68亿，非洲人口将达到17.68亿，南美洲人口将达到8.09亿。

(1)预计到2050年，非洲人口占全世界人口的（ ）％。

(2)到2050年欧洲人口将占世界人口的9.2％。

到2050年，欧洲人口将达到多少亿？(3)将各大洲按照人口数量从多到少排列。

答案1.140，14，107。

2. B 。

3. 3.（1）33.6，（2）4.85（3）亚洲＞非洲＞南美洲＞欧洲＞北美洲1.2选择统计图1. 如果只表示各种数量的多少，可以选用( )统计图表示；如果想要表示出数量增减变化的情况，可以选用( )统计图表示；如果要清楚地了解各部分数量同总数之间的关系，可以用( )统计图表示。

2．选择题。

（1）主要很容易看出各种数量的多少，应选择（）统计图。

A、条形B、折线C、扇形（2）灯塔村去年上半年总收入中农业收入占55%，副业收入占35%，其它收入占10%。

将此制成一个扇形统计图，其中扇形面积最大的是（）。

A、农业收入B、副业收入C、其它收入（3）某班在一次考试中，得优的有20人，得良的有15人，及格的有12人，不及格的有3人。

得优的占全班总人数的（）。

A、40%B、30%C、24%（4）扇形统计图甲中女生占56%，扇形统计图乙中女生占45%，甲乙两个统计图中所表示的女生人数（）。

A、甲比乙多B、甲比乙少C、不能确定3.如右图是养禽专业户李大叔2016年养的鸡、鸭、鹅收入情况统计图。

（1）去年李大叔养鹅收入是48000元，他去年养禽总收入是多少元？(2）已知他家去年用于购买禽苗、饲料及其它成本共花费62000元，另据有关规定他还要缴纳相关税收24000元，李大叔去年全年纯收入多少元？答案1. 条形折线扇形2．（1）A （2）A （3）A （4）C 3．（1）48000÷20％=240000（元）答：他去年养禽总收入是240000元。

新苏教版小学六年级下册数学《课课练》全部参考答案年级教研组资料一、扇形统计图【点击课堂】第1页一、 1. 各部分数量总数 2. (1)62.5(2)16 8二、 (1)骑自行车20 (2)15 10 (3)略第2页一、 1. 扇形折线条形 2. 1200 240 480 480二、 1－25%－45%－10%＝20%1200×45%－1200×25%＝240(平方米)第3页一、 48 18 24 30二、 1. B 2. A二、圆柱和圆锥【点击课堂】第7页一、 1. 底面侧面距离 2. 圆扇形顶点圆心 3. 略 4. 略 5. 略二、 1. √ 2. × 3. √ 4. √第9页一、 1. 侧面底面 2. 矩形底面周长高二、 3.14×22×2＋2×3.14×2×5＝87.92(平方厘米)3.14×12×2＋2×3.14×1×6＝43.96(平方米)三、 1. 2×3.14×0.6×2×5＝37.68(平方米)2. 3.14×22＋2×3.14×2×5＝75.36(平方米)3. 2×3.14×3×14＝263.76(平方厘米)263.76＋3.14×32＝273.18(平方厘米)第10页一、 1. 169.56 2. 62.8 314 3. 6004. 侧面积5. 150.72平方厘米3768平方厘米50.24平方米二、 1. 3.14×0.1×1.2×10＝3.768(平方米)2. 3.14×2×8×0.6＝30.144(千克)第11页一、 1. 相等底面积高底面积高底面积高 2. 略 3. 略二、 1. 15×10＝150(立方厘米)2. 3.14×202×50＝62800立方厘米＝62.8(升)3. 3.14×1.62×2×720＝11575.296(千克)第12页一、 1. 3.14×2.52×10＝196.25(立方厘米)3.14×22×12＝150.72(立方厘米)2. (1)r＝18.84÷2÷3.14÷3＝1(米)3.14×12×3＝9.42(立方米)(2)9.42×545＝5134(千克)3. (1)12×20＝240(平方厘米)(2)表面积：12×20＋3.14×62＋3.14×6×20＝729.84(平方厘米)体积：（1/2）×3.14×62×20＝1130.4(立方厘米)第13页一、 125.6立方厘米 2. 942 314 1570 47103. 24. 135二、 (1)3.14×52×3＝235.5(立方分米)(2)3.14×22×1＝12.56(立方米)(3)3.14×22×4＝50.24(立方厘米)(4)80×50＝4000(立方分米)三、 1. 3.14×22×200＝2512(立方厘米)2512×7.8＝19594(千克)2. 9.42÷3.14÷1＝3(米)3. (1)3.14×22＋3.14×2×2×6＝87.92(平方分米)(2)3.14×2²×6＝75.36(立方分米)＝75(升)4. 3.14×22×4＝50.24(立方分米)5. (1)3.14×12＝3.14(平方米)(2)3.14×12×3＝9.42(立方米)6. 3.14×2×2×(12－10)＝25.12(立方米)7. 80×（2/5）÷10＝3.2(分米)8. 3.14×0.1×0.1×5×60＝9.42(立方米)第16页一、 1. (1)6 (2)362. 3.14 9.423. 12二、 1. (1) （1/3）×3.14×32×4＝37.68(立方分米)(2) （1/3）×3.14×52×12＝314(立方厘米)2. （1/3）×3.14×32×1.5＝14.13(立方米)3. （1/3）×3.14×32×6＝56.52(立方厘米)4. （1/3）×15×4＝20(立方厘米)5. (1) （1/3）×3.14×62×9＝339.12(立方厘米)(2)339.12÷(3×3.14×62)＝1(厘米)第18页一、 1. B 2. A二、 1. 2/3 2 2. 28.26 169.56三、 1. （1/3）×12.56×1.5×1.25＝7.85(吨)2. 20÷[（1/3）×30]＝2(厘米)第19页一、略二、 1. × 2. √ 3. × 4. × 5. √三、略四、 1. （1/3）×3.14×12×1.5＝1.57(立方米)2厘米＝0.02米1.57÷0.02÷5＝15.7(米)2. 12×（3/2）＝18(立方米)3. 3.14×202＋2×3.14×20×45＝6908(平方厘米)3.14×202×45＝56520(立方厘米)＝56.52＞50能装50升水4. 0.6平方米＝60平方分米60×(5－0.5)＝270(立方分米)＝270(升)270×0.8＝216(千克)5. 3.14×0.42×16＝8.0384(立方厘米)2×3.14×0.4×16＝40.192(平方厘米)6. 9.42×10＝94.2(平方分米)94.2＋94.2×(1－80%)＝113.04(立方分米)第22－24页一、 1. 25.12 25.12 2. 9 3. 3 3 9 94. 125. 5二、 1. × 2. × 3. × 4. × 5. √三、 1. D 2. C 3. C 4. B 5. C四、略年级教研组资料一、扇形统计图【点击课堂】第1页一、 1. 各部分数量总数 2. (1)62.5(2)16 8二、 (1)骑自行车20 (2)15 10 (3)略第2页一、 1. 扇形折线条形 2. 1200 240 480 480二、 1－25%－45%－10%＝20%1200×45%－1200×25%＝240(平方米)第3页一、 48 18 24 30二、 1. B 2. A二、圆柱和圆锥【点击课堂】第7页一、 1. 底面侧面距离 2. 圆扇形顶点圆心 3. 略 4. 略 5. 略二、 1. √ 2. × 3. √ 4. √第9页一、 1. 侧面底面 2. 矩形底面周长高二、 3.14×22×2＋2×3.14×2×5＝87.92(平方厘米)3.14×12×2＋2×3.14×1×6＝43.96(平方米)三、 1. 2×3.14×0.6×2×5＝37.68(平方米)2. 3.14×22＋2×3.14×2×5＝75.36(平方米)3. 2×3.14×3×14＝263.76(平方厘米)263.76＋3.14×32＝273.18(平方厘米)第10页一、 1. 169.56 2. 62.8 314 3. 6004. 侧面积5. 150.72平方厘米3768平方厘米50.24平方米二、 1. 3.14×0.1×1.2×10＝3.768(平方米)2. 3.14×2×8×0.6＝30.144(千克)第11页一、 1. 相等底面积高底面积高底面积高 2. 略 3. 略二、 1. 15×10＝150(立方厘米)2. 3.14×202×50＝62800立方厘米＝62.8(升)3. 3.14×1.62×2×720＝11575.296(千克)第12页一、 1. 3.14×2.52×10＝196.25(立方厘米)3.14×22×12＝150.72(立方厘米)2. (1)r＝18.84÷2÷3.14÷3＝1(米)3.14×12×3＝9.42(立方米)(2)9.42×545＝5134(千克)3. (1)12×20＝240(平方厘米)(2)表面积：12×20＋3.14×62＋3.14×6×20＝729.84(平方厘米)体积：（1/2）×3.14×62×20＝1130.4(立方厘米)第13页一、 125.6立方厘米 2. 942 314 1570 47103. 24. 135二、 (1)3.14×52×3＝235.5(立方分米)(2)3.14×22×1＝12.56(立方米)(3)3.14×22×4＝50.24(立方厘米)(4)80×50＝4000(立方分米)三、 1. 3.14×22×200＝2512(立方厘米)2512×7.8＝19594(千克)2. 9.42÷3.14÷1＝3(米)3. (1)3.14×22＋3.14×2×2×6＝87.92(平方分米)(2)3.14×2²×6＝75.36(立方分米)＝75(升)4. 3.14×22×4＝50.24(立方分米)5. (1)3.14×12＝3.14(平方米)(2)3.14×12×3＝9.42(立方米)6. 3.14×2×2×(12－10)＝25.12(立方米)7. 80×（2/5）÷10＝3.2(分米)8. 3.14×0.1×0.1×5×60＝9.42(立方米)第16页一、 1. (1)6 (2)362. 3.14 9.423. 12二、 1. (1) （1/3）×3.14×32×4＝37.68(立方分米)(2) （1/3）×3.14×52×12＝314(立方厘米)2. （1/3）×3.14×32×1.5＝14.13(立方米)3. （1/3）×3.14×32×6＝56.52(立方厘米)4. （1/3）×15×4＝20(立方厘米)5. (1) （1/3）×3.14×62×9＝339.12(立方厘米)(2)339.12÷(3×3.14×62)＝1(厘米)第18页一、 1. B 2. A二、 1. 2/3 2 2. 28.26 169.56三、 1. （1/3）×12.56×1.5×1.25＝7.85(吨)2. 20÷[（1/3）×30]＝2(厘米)第19页一、略二、 1. × 2. √ 3. × 4. × 5. √三、略四、 1. （1/3）×3.14×12×1.5＝1.57(立方米)2厘米＝0.02米1.57÷0.02÷5＝15.7(米)2. 12×（3/2）＝18(立方米)3. 3.14×202＋2×3.14×20×45＝6908(平方厘米)3.14×202×45＝56520(立方厘米)＝56.52＞50能装50升水4. 0.6平方米＝60平方分米60×(5－0.5)＝270(立方分米)＝270(升)270×0.8＝216(千克)5. 3.14×0.42×16＝8.0384(立方厘米)2×3.14×0.4×16＝40.192(平方厘米)6. 9.42×10＝94.2(平方分米)94.2＋94.2×(1－80%)＝113.04(立方分米)第22－24页一、 1. 25.12 25.12 2. 9 3. 3 3 9 94. 125. 5二、 1. × 2. × 3. × 4. × 5. √三、 1. D 2. C 3. C 4. B 5. C四、略年级教研组资料一、扇形统计图【点击课堂】第1页一、 1. 各部分数量总数 2. (1)62.5(2)16 8二、 (1)骑自行车20 (2)15 10 (3)略第2页一、 1. 扇形折线条形 2. 1200 240 480 480二、 1－25%－45%－10%＝20%1200×45%－1200×25%＝240(平方米)第3页一、 48 18 24 30二、 1. B 2. A二、圆柱和圆锥【点击课堂】第7页一、 1. 底面侧面距离 2. 圆扇形顶点圆心 3. 略 4. 略 5. 略二、 1. √ 2. × 3. √ 4. √第9页一、 1. 侧面底面 2. 矩形底面周长高二、 3.14×22×2＋2×3.14×2×5＝87.92(平方厘米)3.14×12×2＋2×3.14×1×6＝43.96(平方米)三、 1. 2×3.14×0.6×2×5＝37.68(平方米)2. 3.14×22＋2×3.14×2×5＝75.36(平方米)3. 2×3.14×3×14＝263.76(平方厘米)263.76＋3.14×32＝273.18(平方厘米)第10页一、 1. 169.56 2. 62.8 314 3. 6004. 侧面积5. 150.72平方厘米3768平方厘米50.24平方米二、 1. 3.14×0.1×1.2×10＝3.768(平方米)2. 3.14×2×8×0.6＝30.144(千克)第11页一、 1. 相等底面积高底面积高底面积高 2. 略 3. 略二、 1. 15×10＝150(立方厘米)2. 3.14×202×50＝62800立方厘米＝62.8(升)3. 3.14×1.62×2×720＝11575.296(千克)第12页一、 1. 3.14×2.52×10＝196.25(立方厘米)3.14×22×12＝150.72(立方厘米)2. (1)r＝18.84÷2÷3.14÷3＝1(米)3.14×12×3＝9.42(立方米)(2)9.42×545＝5134(千克)3. (1)12×20＝240(平方厘米)(2)表面积：12×20＋3.14×62＋3.14×6×20＝729.84(平方厘米)体积：（1/2）×3.14×62×20＝1130.4(立方厘米)第13页一、 125.6立方厘米 2. 942 314 1570 47103. 24. 135二、 (1)3.14×52×3＝235.5(立方分米)(2)3.14×22×1＝12.56(立方米)(3)3.14×22×4＝50.24(立方厘米)(4)80×50＝4000(立方分米)三、 1. 3.14×22×200＝2512(立方厘米)2512×7.8＝19594(千克)2. 9.42÷3.14÷1＝3(米)3. (1)3.14×22＋3.14×2×2×6＝87.92(平方分米)(2)3.14×2²×6＝75.36(立方分米)＝75(升)4. 3.14×22×4＝50.24(立方分米)5. (1)3.14×12＝3.14(平方米)(2)3.14×12×3＝9.42(立方米)6. 3.14×2×2×(12－10)＝25.12(立方米)7. 80×（2/5）÷10＝3.2(分米)8. 3.14×0.1×0.1×5×60＝9.42(立方米)第16页一、 1. (1)6 (2)362. 3.14 9.423. 12二、 1. (1) （1/3）×3.14×32×4＝37.68(立方分米)(2) （1/3）×3.14×52×12＝314(立方厘米)2. （1/3）×3.14×32×1.5＝14.13(立方米)3. （1/3）×3.14×32×6＝56.52(立方厘米)4. （1/3）×15×4＝20(立方厘米)5. (1) （1/3）×3.14×62×9＝339.12(立方厘米)(2)339.12÷(3×3.14×62)＝1(厘米)第18页一、 1. B 2. A二、 1. 2/3 2 2. 28.26 169.56三、 1. （1/3）×12.56×1.5×1.25＝7.85(吨)2. 20÷[（1/3）×30]＝2(厘米)第19页一、略二、 1. × 2. √ 3. × 4. × 5. √三、略四、 1. （1/3）×3.14×12×1.5＝1.57(立方米)2厘米＝0.02米1.57÷0.02÷5＝15.7(米)2. 12×（3/2）＝18(立方米)3. 3.14×202＋2×3.14×20×45＝6908(平方厘米)3.14×202×45＝56520(立方厘米)＝56.52＞50能装50升水4. 0.6平方米＝60平方分米60×(5－0.5)＝270(立方分米)＝270(升)270×0.8＝216(千克)5. 3.14×0.42×16＝8.0384(立方厘米)2×3.14×0.4×16＝40.192(平方厘米)6. 9.42×10＝94.2(平方分米)94.2＋94.2×(1－80%)＝113.04(立方分米)第22－24页一、 1. 25.12 25.12 2. 9 3. 3 3 9 94. 125. 5二、 1. × 2. × 3. × 4. × 5. √三、 1. D 2. C 3. C 4. B 5. C四、略。

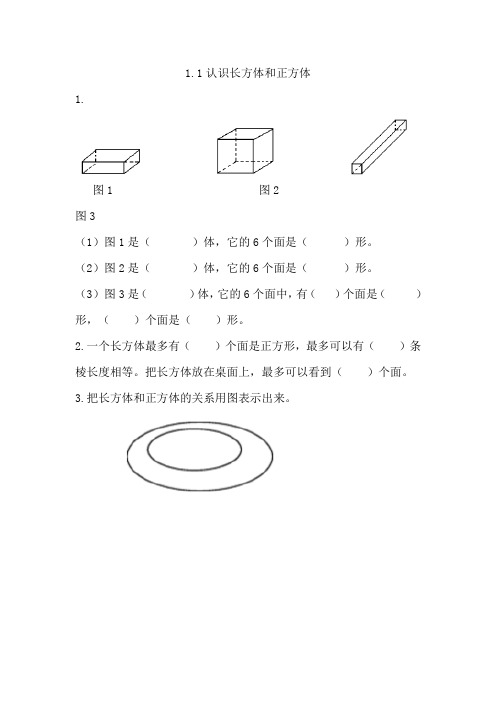
1.1认识长方体和正方体1.图1 图2图3（1）图1是（）体，它的6个面是（）形。

（2）图2是（）体，它的6个面是（）形。

（3）图3是（）体，它的6个面中，有（）个面是（）形，（）个面是（）形。

2.一个长方体最多有（）个面是正方形，最多可以有（）条棱长度相等。

把长方体放在桌面上，最多可以看到（）个面。

3.把长方体和正方体的关系用图表示出来。

答案：1.（1）长方长方（2）正方正方（3）长方 4 长方 2 正方2.2 8 33.正方体长方体1.2 长方体和正方体的展开图一、下面哪些图形沿线折叠后能围成一个长方体？（能围成的画“√”，不能围成的画“×”。

）（）（）（）二、下面哪个图形沿线折叠后能围成一个正方体（）。

A B C D三、如图是一个长方形展开图，每个图都画有一个数字，如果将这个展开图恢复成长方体，与“5”相对的面是（）答案：一、√×√二、B三、31.3 练习一一、填空。

1.长方体有（）个顶点，（）条棱，包含（）组相对的棱，相对的棱的长度（），长方体有（）个面，都是（）形，【也可能有两个相对的面是（）形】，相对的面有（）组，相对的面的面积（），相较于同一个顶点的三条棱的长度分别叫做长方体的（），（），（）。

2.一个长方体的棱长总和是48厘米，长5厘米，宽是4厘米，它的高是（）厘米。

二、一个立方体六个面上分别标着 1 2 3 4 5 6 ，下图是这个立方体的展开图，写出相对面标注的数字分别是（）和（）、（）和（）、（）和（）。

三、下面哪个图形不是长方体的展开图。

A B C D答案：一、 1. 8 12 3 相等 6 长方正方 3 相等长宽高 2. 3二、1和4 2和5 3和6三、C1.4 长方体和正方体的表面积一、填空。

1. 长宽高分别是6分米、5分米、4分米的长方体，它的表面积是（）平方分米。

2. 一个正方体的棱长是3厘米，它的占地面积是（）平方厘米。

它的表面积是（）平方米。

1.1扇形统计图（1）1.下图是钱湖村2018年王村农场种植面积统计图。

已知棉花种了28公顷，则王村农场种植总面积是（ ）公顷；蔬菜种植了（ ）公顷；棉花的种植面积占粮食作物的( )( )。

2.某校对4年级300名学生数学考试作一次调查，在某范围内的得分率如图的扇形，则不及格的人数为（ ）。

A.25B.15C.20D.303.预计到2050年亚洲人口将达到52.68亿，非洲人口将达到17.68亿，南美洲人口将达到8.09亿。

(1)预计到2050年，非洲人口占全世界人口的（ ）％。

(2)到2050年欧洲人口将占世界人口的9.2％。

到2050年，欧洲人口将达到多少亿？(3)将各大洲按照人口数量从多到少排列。

答案1.140，14，107。

2. B 。

3.（1）33.6，（2）4.85（3）亚洲＞非洲＞南美洲＞欧洲＞北美洲1.2选择统计图1. 如果只表示各种数量的多少，可以选用( )统计图表示；如果想要表示出数量增减变化的情况，可以选用( )统计图表示；如果要清楚地了解各部分数量同总数之间的关系，可以用( )统计图表示。

2．选择题。

（1）主要很容易看出各种数量的多少，应选择（）统计图。

A、条形B、折线C、扇形（2）灯塔村去年上半年总收入中农业收入占55%，副业收入占35%，其它收入占10%。

将此制成一个扇形统计图，其中扇形面积最大的是（）。

A、农业收入B、副业收入C、其它收入（3）某班在一次考试中，得优的有20人，得良的有15人，及格的有12人，不及格的有3人。

得优的占全班总人数的（）。

A、40%B、30%C、24%（4）扇形统计图甲中女生占56%，扇形统计图乙中女生占45%，甲乙两个统计图中所表示的女生人数（）。

A、甲比乙多B、甲比乙少C、不能确定3.如右图是养禽专业户李大叔2016年养的鸡、鸭、鹅收入情况统计图。

（1）去年李大叔养鹅收入是48000元，他去年养禽总收入是多少元？(2）已知他家去年用于购买禽苗、饲料及其它成本共花费62000元，另据有关规定他还要缴纳相关税收24000元，李大叔去年全年纯收入多少元？答案1. 条形折线扇形2．（1）A （2）A （3）A （4）C3．（1）48000÷20％=240000（元）答：他去年养禽总收入是240000元。

分层练习（32）一、填空题。

1.如果y x =34，那么yx 43=（ ）。

2.两个比的比值都是34，组成的比例的内项积是24，这个比例是（ ）。

3.把5×51=4×41改写成比例，一共能改写成（ ）个比例。

4.在6：8=3：4中，如果第一个外项增加12，第一个内项应增加（ ），才能组成比例。

二、解比例。

15%：52=x:16 22.4 x =12.6:6 6.5:x=3.25:4三、应用题。

1.一批零件，按3：2的比分给甲乙两人加工。

当甲完成一半时，乙已做了2400个。

已知甲乙两人的工效比是5：4，求这批零件有多少个？2.甲乙两人步行的速度比是13：11，如果甲乙分别由A 、B 两地同时出发相向而行0.5小时相遇；如果他们同向而行，甲追到乙要几小时？3．在含有镍245克和铝150克的合金中，增加多少铝，可使镍和铝的比是7：5？4.一个直角梯形的周长是120厘米，两底之和与两腰之和的比是5：3，且其中一腰长是另一腰的32，则这个直角梯形的面积是多少平方厘米？分层练习（33）一、填空题。

1.a ×6.5= b ×2.4，改写成比例是（ ）。

2.在2：0.6=10:3中,如果第一个外项减去0.4,第二个内项减去( ),比例才成立。

3.如果a:b=2:3,b:c=1:2,并且a+b+c=44。

那么a=( ),b=( ),c=( )。

4.根据b 2=ac 改写出来的比例式是（ ）。

5.一个三角形的三条边的长度比是3：4：5，对应于这三条边上的高的比是（ ）。

二、应用题。

1.在一幅比例尺为1：200的地图上测得一块三角形地的图上面积是6平方厘米，这块地的实际面积是多少公顷？2.一个圆锥形零件,画在一张图纸上,图上距离如图所示。

这个零件的实际体积是多少立方厘米.(图上单位:厘米)3.广场大钟4点钟敲4下用6秒，12点时敲12下要用多少秒？4.小明家到姥姥家德路程平时要走40分。

1.1认识长方体和正方体1.图1 图2图3（1）图1是（）体，它的6个面是（）形。

（2）图2是（）体，它的6个面是（）形。

（3）图3是（）体，它的6个面中，有（）个面是（）形，（）个面是（）形。

2.一个长方体最多有（）个面是正方形，最多可以有（）条棱长度相等。

把长方体放在桌面上，最多可以看到（）个面。

3.把长方体和正方体的关系用图表示出来。

答案：1.（1）长方长方（2）正方正方（3）长方 4 长方 2 正方2.2 8 33.正方体长方体1.2 长方体和正方体的展开图一、下面哪些图形沿线折叠后能围成一个长方体？（能围成的画“√”，不能围成的画“×”。

）（）（）（）二、下面哪个图形沿线折叠后能围成一个正方体（）。

A B C D三、如图是一个长方形展开图，每个图都画有一个数字，如果将这个展开图恢复成长方体，与“5”相对的面是（）答案：一、√×√二、B三、31.3 练习一一、填空。

1.长方体有（）个顶点，（）条棱，包含（）组相对的棱，相对的棱的长度（），长方体有（）个面，都是（）形，【也可能有两个相对的面是（）形】，相对的面有（）组，相对的面的面积（），相较于同一个顶点的三条棱的长度分别叫做长方体的（），（），（）。

2.一个长方体的棱长总和是48厘米，长5厘米，宽是4厘米，它的高是（）厘米。

二、一个立方体六个面上分别标着 1 2 3 4 5 6 ，下图是这个立方体的展开图，写出相对面标注的数字分别是（）和（）、（）和（）、（）和（）。

三、下面哪个图形不是长方体的展开图。

A B C D答案：一、 1. 8 12 3 相等 6 长方正方 3 相等长宽高 2. 3二、1和4 2和5 3和6三、C1.4 长方体和正方体的表面积一、填空。

1. 长宽高分别是6分米、5分米、4分米的长方体，它的表面积是（）平方分米。

2. 一个正方体的棱长是3厘米，它的占地面积是（）平方厘米。

它的表面积是（）平方米。

第七课时整理与练习（1）教学内容：课本109-111页“回顾与整理、练习与应用第1～8题”。

教学目标：A类：知识与技能：通过“回顾与整理”、“练习与运用”等活动，让学生进一步加深对百分数意义的理解，巩固百分数与小数、分数互化的方法，提高应用所学知识解决简单的求一个数是另一个的百分之几的实际问题的能力。

数学思考：使学生在利用百分数的的有关知识解决简单实际问题的过程中，进一步体会数学知识的内在联系，增强思维的深刻性，发展学生的数感。

解决问题：能在求一个数是另一个数的百分之几的基础上有所拓展。

从现实生活中发现并提出一些问题，并能应用百分数的知识解决问题，发展学生的应用意识。

如：甲数是乙数的80%，乙数是甲数的（）%，甲数比乙数少（）%，乙数比甲数多（）%。

B类：知识与技能：通过“回顾与整理”、“练习与运用”等活动，让学生进一步加深对百分数意义的理解，巩固百分数与小数、分数互化的方法，提高应用所学知识解决简单的求一个数是另一个的百分之几的实际问题的能力。

数学思考：使学生在利用百分数的的有关知识解决简单实际问题的过程中，进一步体会数学知识的内在联系，增强思维的深刻性，发展学生的数感。

解决问题：能解决教材的109—111页的1-8题以及平行性试题。

C类：知识与技能：通过“回顾与整理”、“练习与运用”等活动，让学生进一步加深对百分数意义的理解，巩固百分数与小数、分数互化的方法，提高应用所学知识解决简单的求一个数是另一个的百分之几的实际问题的能力。

解决问题：能基本解决教材的109—111页的1-8题。

第八课时 整理与练习（2）教学内容：课本111-112页探索与实践第9～13题和评价与反思。

教学目标： A 类： 知识与技能：让学生进一步感受百分数在实际生活中的广泛应用，加深对百分数意义以及求一个数是另一个数的百分之几的方法的理解。

数学思考：使学生在用百分数表达和交流生活现象、解决简单实际问题的过程中，体会数学与科学的联系，感受数学学习的价值。

苏教版小学数学6年级数学上册课课练参考答案苏教版小学数学6年级数学上册课课练参考答案
数学课课练参考答案
1. 表格填空题
1）填空。

在草原上，1只羊需要___kg草料，1只羊需要___升水。

答案：1只羊需要1kg草料，1只羊需要0.5升水。

2）填空。

360÷___×___=40。

答案：360÷9×5=200。

3）填空。

2m÷___=10cm。

答案：2m÷200=0.01m。

2. 计算题
1）计算。

（1）3500÷25×21=2940
（2）70.8÷0.9=78.67
2）算式的计算结果为60，算式中的数字分别为10，6，n，请求出n 的值。

答案：10-6+n=60，n=56。

3）从100米外的地方投掷铅球，一次跳远的成绩为11米，比赛开始前需要进行热身，小明跑了20圈，每圈距离为400米，小明把投掷铅球和跳远两项的距离加起来作为整体得分，请问小明的得分是多少？
答案：小明的得分为111米（20×400+100+11）。

3. 应用题
1）面积计算
某地区一个水库的水位标线为200米，水库面积为6平方公里，顶部长约为2000米（仅作参考），那么水库的深度大约为多少？
参考答案：水库的深度为30米。

2）单项选择题
某数值转化成分数后，分子和分母之和为40，分子是分母的3/5，则该数值是：（）
A.1/2
B.2/5
C.1/3
D.3/8
参考答案：B.该数值是2/5。

苏教版六年级数学下册全册课时练习第1课时扇形统计图基础训练1、牛奶里含有许多成分，每100克牛奶含成分如图。

（1）牛奶中哪种营养成分含量最多？是多少？（2）200克牛奶中含有乳糖多少克？2、空气的成分按体积含量各占总体积的百分比情况如下图。

（1）按体积含量计算，空气中氧气占（）％。

（2）按体积含量计算，（）占空气体积的含量最多，它比氧气多占空气体积的（）％。

（3）500升空气中含氧气多少升？3、育红小学六年级一班同学参加各种兴趣小组人数如下：文学组8人，数学组6人，美术组10人，音乐组8人，体育组8人，生物组2人王红根据上面的数据制成了下面的统计图。

育红小学六年级一班同学参加兴趣小组人数情况统计图2019年8月王红制作的统计图对吗？为什么？4、下图是六年级三班一次测验成绩的扇形统计图，下面是与之相对的统计表，请把扇形统计图和统计表补充完整。

成绩优良及格待及格人数18 95、下面是师大附小六年级同学在植树节植树情况的统计图。

三班和四班平均每班植树280棵，一班植树多少棵？6、下面是六年级一次测验成绩的扇形统计图，下面是与之相对应的统计表，请把统计表补充完整。

成绩优良及格待及格合计人数12提高训练1、看图回答问题。

你能根据统计图算出这两个年级学生每天上课和睡眠的时间吗？（结果保留整数）2、根据统计图回答问题。

（1）若许乐家的所有支出及储蓄总额是4500元，则他家这个月的伙食费是多少元？（2）若许乐家四月份的伙食费共花了800元，许乐家的支出及储蓄总共是多少元？3、明艺小学与明伦小学开展“争当奥运会志愿者”活动，下图展示了两个学校部分年级志愿者申报的情况。

小华：我们明艺小学五年级的志愿者比明伦小学五年级的志愿者多！他说的对吗？为什么？4、下面是六（1）班同学参加课外兴趣小组的统计图。

（1）六（1）班有多少人参加兴趣小组？（2）有多少人参加体育组？（3）音乐组的人数比体育组的多百分之几？第2课时选择合适的统计图1、下面是育光小学图书室的故事书、科技书和连环画这三类图书的统计图，已知这三类图书共有360本，先求出这三类图书各有多少本，再制成能描述这三类图书数量的统计图。

分层练习261.在比例尺是1：5000000的地图上，量得甲、乙两地距离8厘米，A、B两车分别从甲乙两地相对开出4小时相遇。

已知A、B两车的速度比是3:2，求A车速度。

2、小明买了一件上衣和两条同样的裤子，小华也买了与小明同样的一件上衣和同样的一条裤子，结果他们俩所用去钱数的比是3：2，已知一件上衣的价钱是35元，那么一条裤子价钱是多少元？3、商场的自动扶梯以匀速由下往上行驶。

两个孩子在行驶的扶梯上上下走动，同一时刻，女孩由下往上走，男孩由上往下走。

当女孩走了40级到达楼上时，男孩走了80级到达楼下，如果男孩在同一时间内走的楼梯级数是女孩的2倍，则当扶梯静止时，扶梯可看到的梯级共有多少级？4、时钟显示4时整以后，经过多少分，分针与时针重合？5、如下图，在三角形ABC中，BC=8厘米，AD=6厘米，E、F分别是AB、AC的中点。

那么三角形EBF的面积是多少平方厘米？6、某班学生做游戏，每人分得同样多个弹子，弹子就多12颗，如果再增加12颗，那么每人就分到12颗，问这个班有多少人？原来有弹子多少个？7、某年级同学春游，如果租有35个座位汽车需要4辆，如果租有42个座位的汽车要3辆，到达景点后要分组活动，且分的组数与每组人数相等，参加春游的有多少人？8、如图，已知正方形ABCD 的边长为4厘米，A E ＝52AB ，G 是DE 与AC 的交点。

求三角形GCD 的面积。

9、甲、乙两车同时从A 、B 两地相对开出，当甲车行了全程的85时和乙车相遇，已知乙车行完全程要12小时，求甲车行完全程要几小时？10、参加数学竞赛，女生人数时男生的90%，如果女生再有9人参加，则女生人数比男生多51，参加竞赛的女生有多少人？11、把3千克水加到盐水中，得到浓度为10%的盐水，再把1千克盐加到所得到的盐水中，这时盐水浓度为20%。

原来盐水浓度是多少？12、如图，一个长方形长是18厘米，宽是10厘米，一只小虫P 从A 点出发，沿长方形的四边逆时针运动再回到A 点，已知小虫每秒运动2厘米，经过多少秒后，线段AP 把长方形分成两部分，这两个部分面积的比是4：5？13、一艘船在静水中的速度为每分钟60米，船在水速为每分钟20米的河中从A 地到B 地，又从B 地返回A 地，共用了3.5小时，求A 、B 两地之间的距离。

苏教版数学六年级上册练习册答案苏教版数学六年级上册的练习册答案涵盖了多个章节，以下是部分章节的答案示例：第一章：分数的加减法1. 计算下列各题，并写出计算过程：- 1/2 + 3/4 = 5/4- 2/3 - 1/6 = 3/6 - 1/6 = 2/6 = 1/32. 解决实际问题：- 一个班级有40名学生，其中3/5是男生，求女生人数。

解：女生人数= 40 × (1 - 3/5) = 40 × 2/5 = 16（人）第二章：分数的乘除法1. 计算下列各题，并写出计算过程：- 1/2 × 3/4 = 3/8- 3/4 ÷ 1/2 = 3/4 × 2 = 3/22. 解决实际问题：- 一个长方形的长是10米，宽是长的2/5，求长方形的面积。

解：宽= 10 × 2/5 = 4（米）面积 = 长× 宽= 10 × 4 = 40（平方米）第三章：小数的加减乘除1. 计算下列各题，并写出计算过程：- 0.75 + 0.85 = 1.60- 1.2 - 0.95 = 0.252. 解决实际问题：- 一个水果店有苹果和香蕉两种水果，苹果每千克5元，香蕉每千克3元。

如果买了2千克苹果和3千克香蕉，需要支付多少钱？解：苹果总价= 5 × 2 = 10（元）香蕉总价= 3 × 3 = 9（元）总支付 = 10 + 9 = 19（元）第四章：比和比例1. 计算下列各题，并写出计算过程：- 比值：4:8 = 1:2- 比例：3:6 = 1:22. 解决实际问题：- 一个班级有男生20人，女生30人，求男生和女生的比。

解：男生和女生的比 = 20:30 = 2:3第五章：几何初步1. 计算下列各题，并写出计算过程：- 一个正方形的边长是5厘米，求它的周长。

解：周长= 5 × 4 = 20（厘米）2. 解决实际问题：- 一个圆形花坛的直径是10米，求它的面积。

苏教版小学数学六年级下册《课课练》答案苏教版小学数学六年级下册《课课练》答案一、扇形统计图1.各部分数量总数：62.5和168.2.骑自行车的数量分别为20和1510，第三部分数量未给出。

一、扇形、折线和条形统计图中，各部分所占比例分别为12%、24%、48%和48%。

2.已知总面积为1200平方米，去掉其中25%和45%的面积后，剩余240平方米。

一、已知扇形的弧长分别为48、18和24，求扇形的面积。

2.选择题答案为B和A。

二、圆柱和圆锥1.已知圆柱的底面半径和高分别为1.5厘米和10厘米，求圆柱的侧面积、底面积和全面积。

2.已知圆锥的底面半径为2厘米，高为6厘米，求圆锥的侧面积、全面积和体积。

3.已知圆锥的底面半径为3厘米，高为14厘米，求圆锥的侧面积、全面积和体积。

1.已知圆柱的底面周长为22厘米，高为5厘米，求圆柱的侧面积和全面积。

2.已知圆柱的底面半径为8厘米，高为6厘米，求圆柱的侧面积和全面积。

3.已知圆柱的侧面积为264平方厘米，高为10厘米，求圆柱的底面半径和全面积。

1.已知圆锥的底面半径为10厘米，高为12厘米，求圆锥的体积。

2.已知圆锥的底面半径为2厘米，高为8厘米，密度为2克/立方厘米，求圆锥的重量。

3.已知圆锥的底面半径为6厘米，高为720厘米，密度为1克/立方厘米，求圆锥的重量。

1.已知圆锥的底面半径为2.5厘米，高为10厘米，求圆锥的体积。

2.已知圆锥的底面半径为8厘米，高为6厘米，求圆锥的体积。

3.已知圆锥的底面半径为12厘米，高为20厘米，求圆锥的体积和全面积。

1.已知圆柱的底面积为150平方厘米，高为10厘米，求圆柱的体积。

2.已知圆柱的底面半径为20厘米，高为50厘米，求圆柱的体积。

3.已知圆柱的底面半径为1.6米，高为720厘米，求圆柱的重量。

1.已知圆柱的底面半径为2.5厘米，高为10厘米，求圆柱的体积。

2.已知圆柱的底面半径为8厘米，高为6厘米，求圆柱的体积。

六年级下册数学课一课一练正比例和反比例苏教版 例1、判别下面相关联的量成什么比例关系。

（1）圆的面积和半径。

〔 〕（2）做50道口算题，已做的题数和剩下的题数。

〔 〕（3）比的前项一定，后项和比值。

〔 〕（4）出米率一定，出米的质量和稻谷的质量。

〔 〕（5）在同一幅地图上，两地的图上距离和实践距离。

〔 〕（6）人的身高和体重。

〔 〕（7）圆锥的体积一定时，底面积和高。

〔 〕（8）等边三角形的周长和恣意一边的长度。

〔 〕（9）正方体的棱长一定时，体积和外表积。

〔 〕例2、下表中a 与b 是两种相关联的量。

（1）当x=200时，a 和b 成〔 〕比例。

（2）当x=〔 〕时，a 和b 成正比例。

例3、某人走12千米的路程，他行走的速度与所用时间的关系如下表：（2）假设以2.5千米/时的速度行进，大约需用〔〕时才干走完。

（3）假设想用5时走完，速度应到达〔 〕千米/时。

（4）观察上图，你发现了什么？例4、配制一种农药，其中生石灰、硫磺粉和水的质量比是1:2:12。

如今要配制这种农药2700千克，各种原料区分需求多少千克？例5、为庆贺六一儿童节，四〔2〕班的同窗分红两个小组停止演出。

第一小组与第二小组的人数之比是7:8，假设将第二小组的4名同窗调到第一小组，那么第一小组与第二小组的人数之比是3:2。

四〔2〕班共有多少人？例6、小华预备用60cm 长的铁丝围成一个长方形，假定围成的长方形的长与宽的比是3:2，那么这个长方形的面积是多少平方厘米？例7、在比例尺是1:5000000的地图上量得两个城市相距4.5厘米，一辆客车和一辆货车同时从两个城市相对开出，212小时相遇。

货车速度和客车速度的比是9:11，那么客车平均每小时行多少千米？例8、一艘轮船所带的柴油最多可用6小时，驶出时顺风，每小时行驶30千米；驶回时顺风，每小时行驶的路程时顺风是的54。

这艘轮船最多驶出多远就应前往了？随堂练习：1、假设x 与y 成正比例，那么表中的△是〔 〕；假设x 与y 成正比例，那么△是〔 〕。