第12章_磁场和它的源
- 格式:ppt
- 大小:2.43 MB
- 文档页数:56






第十二章稳恒磁场本章研究磁场的产生,磁场的基本规律,磁场与介质的相互作用。
磁感应强度是描述磁场的基本物理量。
“高斯定理”和安培环路定理是反映磁场性质的基本规律。
磁场对运动电荷的作用力——洛仑兹力——和磁场对载电流导线的作用——安培力和力矩,在许多领域均得到广泛应用。
在磁场作用下,磁介质发生磁化,磁化了的磁介质又会反过来影响磁场的分布。
我们还将讨论磁场和介质的这种相互作用规律并特别介绍有很大实用价值的铁磁质的特性。
§12-1磁场磁感应强度一、基本磁现象我国是世界上最早认识磁性和应用磁性的国家,早在战国时期(公元前300年),就已发现磁石吸铁的现象。
11世纪(北宋)时,我国科学家沈括创制了航海用的指南针,并发现了地磁偏角,地球的N极在地理南极附近百极在地理北极附近。
中国古代四大发明引为现代人的骄傲。
天然磁铁和人造磁铁都称永磁铁。
永磁铁不存在单一的磁极。
磁铁的两个磁极,不可能分割成为独立存在的N极和S极。
但我们知道,有独立存在的正电荷或负电荷,这是磁极和电荷的基本区别。
这与磁产生的机理有关。
历史上很长一段时期,人们对磁现象和电现象的研究都是彼此独立进行的。
1820年丹麦物理学家奥斯特实验发现,放在通有电流的导线周围的磁针,会受到力的作用而发生偏转,如图图4-14-1所示,其转动方向与导线中电流的方向有关。
这就是历史上著名的奥斯特实验,它第一次指出了磁现象与电现象之间的联系。
同年法国科学家安培发现,放在磁铁附近的载流导线及载流线圈,也会受到力的作用而发生运动,如图4-2,其后实验还发现,载流导线之间或载流线圈之间也有相互作用力。
(a)(b)图4-2例如把两个线圈面对面挂在一起,当两电流的流向相同时,两线圈相互吸引,如图4-3(a),当两电流的流向相反时,两线圈相互排斥,如图4-3(b)。
(a ) (b )图4-3电子射线束在磁场中路径发生偏转的实验,进一步说明了通过磁场区域时运动电荷要受到力的作用,如图4-4所示。


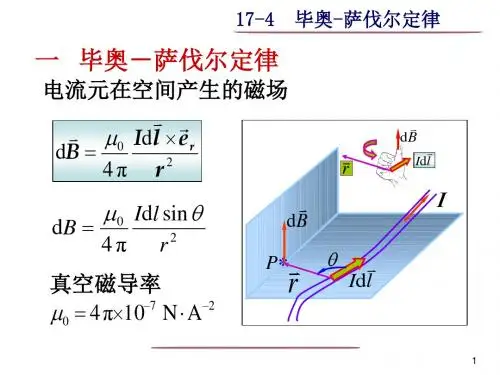
第十二章 大学物理辅导 磁场~64~ 第十二章磁场一、教材的安排与教学目的 1、教材安排本章的教材安排,按讲授顺序可归纳为以下五个方面: (1)磁感应强度,磁通量、磁场的高斯定理; (2)洛仑兹力;(3)安培定律与磁场对载流线圈的作用;(4)毕奥—沙伐尔定律与平行载流导线间的作用; (5)安培环路定律。
2、教学目的本章的主要教学目的是:(1)使学生正确理解并掌握安培定律; (2)使学生正确理解并掌握毕—沙定律; (3)使学生确切理解并掌握安培环路定律。
二、教学要求1、正确理解磁感应强度 B 的概念,明确B 是描述磁场性质的基本物理量;2、要明确理解磁场的高斯定理所表达的物理意义—磁场是无源场;3、正确理解并掌握洛仑兹力公式;4、正确理解并掌握安培定律,明确它和毕—沙定律一起构成研究磁场问题的基础,明确安培力是洛仑兹力的宏观表现。
5、正确理解并掌握毕—沙定律,明确它对所有的电流(包括稳恒和非稳恒的)都成立。
6、正确理解并掌握安培环路定律,它表明磁感应线是闭合的或者说明稳恒磁场是涡旋场,它与静电场不同。
三、内容提要1、磁感应强度定义大小方向:小磁针极所指方向意义:表达了磁场力的性质,为磁场本身的属性。
为一矢量::。
B F qv N =⎡⎣⎢⎢⎢⎡⎣⎢⎢⎢⎢⎢max2、磁场的高斯定理公式意义:表明磁场是无源场,或磁感应闭合成环。
说明:它对稳恒和非稳恒磁场均成立:。
φm B dS =⋅=⎡⎣⎢⎢⎢⎢⎰3、洛仑兹力定义运动电荷在磁场中运动所受的力公式:。
说明:洛仑兹力对运动电荷不作功,而只改变速度的方向:。
f qv B =⨯⎡⎣⎢⎢⎢第十二章 大学物理辅导 磁场~65~4、安培定律定义电流元在外磁场中所受的磁场作用力公式:。
说明:安培力是洛仑兹力的宏观表现:。
dF Idl BF Idl B =⨯=⨯⎰⎡⎣⎢⎡⎣⎢⎢⎢⎢⎢ 5、载流线圈在匀强磁场中受到的力矩(1)线圈的磁矩P NIS m =,S 为平面线框的面积。

1 磁场磁感线1.知道磁场的概念,知道磁体与磁体间、磁体与电流间、电流与电流间的作用是通过磁场发生的.2.理解磁感线的概念,知道磁感线的特点.3.理解安培定则,会用安培定则判断电流的磁场方向.一、电和磁的联系磁场1.磁体间的相互作用:同名磁极相互排斥,异名磁极相互吸引.2.奥斯特实验:把导线放置在指南针的上方,通电时磁针发生了转动.实验意义:奥斯特实验发现了电流的磁效应,即电流可以产生磁场,首次揭示了电与磁的联系.3.磁场:磁体与磁体之间、磁体与通电导体之间,以及通电导体与通电导体之间的相互作用,是通过磁场发生的,磁场是磁体或电流周围一种看不见、摸不着的特殊物质.二、磁感线1.磁场的方向:物理学规定,在磁场中的某一点,小磁针静止时N极所指方向就是这一点的磁场方向.2.磁感线(1)定义:在磁场中画出的一些有方向的曲线,曲线上每一点的切线方向都跟该点的磁场方向一致,这样的曲线就叫作磁感线.(2)特点①磁感线的疏密表示磁场的强弱.磁场强的地方,磁感线较密;磁场弱的地方,磁感线较疏.①磁感线某点的切线方向表示该点磁场的方向.三、安培定则1.直线电流的磁场安培定则:如图1甲所示,用右手握住导线,让伸直的拇指所指的方向与电流方向一致,弯曲的四指所指的方向就是磁感线环绕的方向.直线电流周围的磁感线环绕情况如图乙所示.图12.环形电流的磁场安培定则:如图2所示,让右手弯曲的四指与环形电流的方向一致,伸直的拇指所指的方向就是环形导线轴线上磁感线的方向.图23.通电螺线管的磁场安培定则:如图3所示,右手握住螺线管,让弯曲的四指与螺线管电流方向一致,伸直的拇指所指的方向就是螺线管轴线上磁场的方向或者说拇指所指的方向是它的北极的方向.图3一、磁场与磁感线1.磁场(1)磁场的客观性:磁场与电场一样,也是一种物质,是一种看不见而又客观存在的特殊物质.存在于磁体、通电导线、运动电荷、变化电场、地球的周围.(2)磁场的基本性质:对放入其中的磁极、电流、运动的电荷有力的作用,而且磁体与磁体、磁体与电流、电流与电流间的相互作用都是通过磁场发生的.2.磁感线(1)定义:磁感线是为了形象地描述磁场而人为假想的曲线,曲线上每一点的切线方向都跟该点的磁场方向相同.(2)特点:①在磁体外部,磁感线从N极发出,进入S极;在磁体内部由S极回到N极.①磁感线的疏密程度表示磁场的强弱,磁感线越密的地方磁场越强;磁场方向即过该点的磁感线的切线方向.①磁感线闭合而不相交,不相切,也不中断.①磁感线是人们为了形象描述磁场而假想的线,并不真实存在.(3)几种特殊磁体外部的磁感线分布(如图5所示):图5二、安培定则电流磁场的方向利用安培定则进行判断.1.直线电流的磁场(1)安培定则:用右手握住导线,让伸直的拇指所指的方向与电流方向一致,弯曲的四指所指的方向就是磁感线环绕的方向,如图6所示.图6(2)画法:如图7所示图7(3)特点:是非匀强磁场,距导线越远处磁场越弱.2.通电螺线管的磁场(1)安培定则:右手握住螺线管,让弯曲的四指所指的方向与电流的方向一致,伸直的拇指所指的方向就是螺线管轴线上磁感线的方向,如图8所示.图8(2)磁感线特点两端分别是N极和S极,管内是匀强磁场,管外是非匀强磁场,画法如图9所示.图93.环形电流的磁场(1)安培定则:让右手弯曲的四指与环形电流的方向一致,伸直的拇指所指的方向就是环形导线轴线上磁感线的方向,如图10所示.图10(2)磁感线的特点两侧分别是N极和S极,离圆环中心越远,磁场越弱,画法如图11所示.图11三、安培分子电流假说1.法国学者安培提出:在物质内部,存在着一种环形电流——分子电流.分子电流使每个物质微粒都成为微小的磁体,它的两侧相当于两个磁极.(如图12所示)图122.当铁棒中分子电流的取向大致相同时,铁棒对外显磁性;当铁棒中分子电流的取向变得杂乱无章时,铁棒对外不显磁性.1.在物理学史上,首先发现通电导线周围存在磁场的物理学家是()A.安培B.法拉第C.伏打D.奥斯特2.如图所示,把一条导线平行地放在磁针的上方附近,当导线中有电流通过时,磁针会发生偏转,首先观察到这个实验现象的物理学家是()A.奥斯特B.爱因斯坦C.伽利略D.法拉第3.下列说法正确的是()A.楞次最先发现了电流的磁效应B.奥斯特最早提出了分子电流假说C.安培最早发现通电导体周围存在磁场D.法拉第最早提出利用磁感线形象化地描述磁场4.如图所示,小磁针放置在螺线管轴线的正右侧。