Ppk与Cpk培训

2003年度质量培训SPC简介&CpPp——质保部内部交流目录一、spc概述二、spc包括的内容三、质量管理7个工具图四、控制图五、Cpk一、spc概述1.什么是SPC•SPC是英文Statistical Process Control的字首简称，即统计过程控制。

SPC就是应用统计技术对过程中的各个阶段进行监控，从而达到改进与保证质量的目的。

SPC强调全过程的预防。

•SPC给企业各类人员都带来好处。

对于生产第一线的操作者，可用SPC方法改进他们的工作，对于管理干部，可用SPC方法消除在生产部门与质量管理部门间的传统的矛盾，对于领导干部，可用SPC方法控制产品质量，减少返工与浪费，提高生产率，最终可增加上缴利税。

•SPC的特点是:（1）SPC是全系统的，全过程的，要求全员参加，人人有责。

这点与全面质量管理的精神完全一致。

(2) SPC强调用科学方法(主要是统计技术，尤其是控制图理论)来保证全过程的预防。

（3）SPC不仅用于生产过程，而且可用于服务过程和一切管理过程。

2.SPC发展简史过程控制的概念与实施过程监控的方法早在20世纪20年代就由美国的休哈特(W. A.Shewhart)提出。

今天的SPC与当年的休哈特方法并无根本的区别。

美国从20世纪80年代起开始推行SPC。

美国汽车工业已大规模推行了SPC，如福特汽车公司，通用汽车公司，克莱斯勒汽车公司等，上述美国三大汽车公司在ISO9000的基础上还联合制定了QS9000标准，在与汽车有关的行业中，颇为流行。

美国钢铁工业也大力推行了SPC，如美国LTV钢铁公司，内陆钢铁公司，伯利恒钢铁公司等等。

QS9000质量管理体系要求是由美国三大汽车公司--克莱斯勒、福特和通用汽车公司共同制订，于1994年颁布的一套完整的质量体系标准。

3.SPC的进行步骤进行SPC有下列步骤：步骤1：培训SPC。

培训内容主要有下列各项：SPC的重要性，正态分布等统计基本知识，质量管理七种工具，其中特别是要对控制图深入学习，两种质量诊断理论，如何制订过程控制网图，如何制订过程控制标准等等。

C ＰK 培訓教材一.Cpk 的定義某一制程在一定因素與正常管制狀態下的品質作業能力.二.Ｃｐk 的影響因素製程要因--—原料，机器設備,人員能力，測量儀器.製程條件-——常態分配,統計管制狀態。

三。

Cpk 的計算USL ：上限尺寸L ＳＬ：下限尺寸Ave ｒa ｇe:測量數据的平均值σ：標準差，其公式為: σ＝1/)(22--∑∑n n x xＣｐu=(USL —Average)/3σＣp ｌ=（Average-L ＳL ）/３σCpk=Min(Cpu,C ｐl) σ:其大小表示測量數据的離散程度， σ越小表示數据的離散程度越小,反之則數据的離散程度越大.C ｐu:其值表示測量數据偏離上限的程度, Cpu 越大表示測量數据偏離上限較遠； 反之則數据靠近上限。

Ｃpl: 其值表示測量數据偏離下限的程度, C ｐl 越大表示測量數据偏離下限較遠； 反之則數据靠近下限。

四．Cp ｋ的等級A ： 1.3３≦C ｐkA 級,製程能力滿足圖紙要求,生產中几乎沒有不良品產生。

B: １。

00≦Ｃｐｋ〈１．33Ｂ級，製程能力基本滿足圖紙要求，生產中約有０。

２7%不良品產生,必須加以注意,並設法維持不使其變坏。

Ｃ: Cpｋ<1.0０Ｃ級，製程能力不能滿足圖紙要求，生產中可能有較多不良品產生, 應採取緊急措施，全面檢討所有可能影響的因素,必要時得停止生產。

五.Cｐk 管制抽樣的基本原則管制方法取樣頻率管制圖查檢表高 1—-2小時1５——３0分鐘中 4-—8小時每小時低每班次 2小時六．CPＫ數据分析.1．數据均分布于中值兩旁, Ｃpk值一般大于1。

３3，見附圖1． 2。

數据离散地分布中值兩旁，Cｐｋ值一般小于1.33,見附圖2．3。

數据分布离散度小,但偏中值不遠,Cpk值大于1.33,見附圖3。

4.數据分布离散度小,但偏中值較遠,Cpｋ值小于１．33. 見附圖４.５。

數据絕大多數雖均分布于中值兩旁，但個別超差,將大大降低Cpk值，甚至Cpk值小于1。

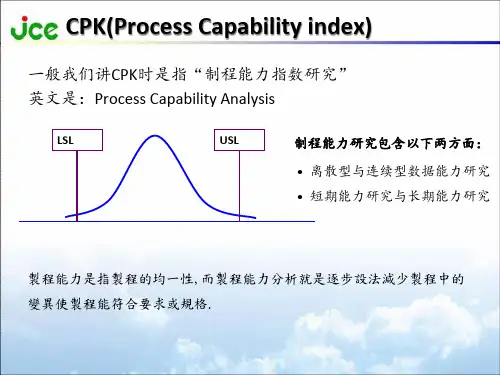
关于Ppk 与 Cpk区别1、PPK是没有检查过程是否稳定的情况下计算得到的。

通常在开始研究过程能力的时候，不去考虑过程是否稳定。

这样做简单。

考虑到数据中有可能存在特殊原因引起的变异，因此，在要求等于大于1.67。

不应当是连续抽样的原因，要求比CPK高。

2、如果不考虑过程是否稳定，不管是短期还是长期得到的数据计算得到的，只能叫Ppk，是过程性能指数，请注意，是性能指数，不是能力指数。

因为，数据中包含特殊原因引起的变异，只能叫性能指数。

如果性能指数和能力指数差异很大，说明改进的潜力很大。

3、Cpk计算之前，一定要检查过程是否稳定。

一般要求有100个数据，如果每个样本数是4的话，得到25个均值。

每个子样和子样之间可以定期间隔时间，譬如1小时。

连续取4个样本，计算均值。

再隔1小时，再连续取4个……。

通过极差控制图和均值控制图来检查过程是否稳定。

如果稳定，计算得到的是Cpk。

计算时候，标准差不是根据数据直接计算的。

而是根据极差均值计算估计的标准差。

对于特殊特性，要求大于等于1.33。

4、PPK的计算不要求检查过程是否稳定。

因为前面说的，这样时间很长。

那么，不关是否稳定，就用这100个数据，或者，干脆中间就不间隔1小时了。

就连续取100个数据。

通过均方差方法计算得到标准差，计算Ppk。

因为，PPK没有检查过过程是否稳定的，因为，为了保险，对特殊特性要求大于等于1.67。

因为，PPK中可能有特殊原因引起变差，因此，不叫过程能力指数，叫过程性能指数。

5、当过程稳定，Cpk又满足要求后，利用控制图来监视过程。

过程实际运行有可能发生特殊原因，一旦发现，就要查明后消除它。

使过程回到稳定。

6、有的不管长期的过程数据是否稳定，就用这些数据通过均方差方法计算得到标准差，再计算得到长期的PPK。

当然要比Cpk小了。

要注意，前面PPK比Cpk大是要求的数值，这里是实际的数值。

因为它有（可能有）特殊原因引起的变差在内。

通常把PPK叫过程性能指数，不是过程能力指数。

Cp、Cpk、Pp、Ppk 详解1. 背景Cp, Cpk, Pp 和 Ppk这几个概念在工业制造领域的应用已经很普遍了，但是这些概念往往被混淆。

网上的解释各执其词，而且错误百出（如下图）。

就连国外网站上的讨论也是众说不一⑥。

当这些概念用中文解释时，那就更复杂了。

比如这些概念里共有的"P" 是一个简单的英语词"process"，可被翻译成什么的都有，比如"过程，工艺，工序，制程…"等等。

可想而知加了其他词以后就更复杂了。

为了方便起见，以下process均采用"过程"。

笔者2003年在学校里就学习了这些概念，而且在之后的十几年的工作中也不断地在应用这些概念。

但始终觉得没有完全理解其本质区别。

多年下来一直都是在照猫画虎，套公式，得出结果，做出判断，完事。

更有甚者，现在有现成的计算机软件，点一点鼠标就可以得到结果。

更不用知道其后台是如何计算的了。

一般来说，能做到此，也就可以了。

所以下面的解析是为有意愿深入了解这些概念的差别的读者准备的。

Cp, Cpk, Pp 和 Ppk都是用来体现过程能力的指标①②，它们是用来测量过程能力的指数（process capability index），不是过程能力本身。

很多人只知道计算这些指数，却并不知道过程的固有能力到底是什么。

那什么是过程能力（process capability）？2. 过程能力的定义过程能力是指过程本身在没有外因干预、没有漂移（drift）（即统计学意义上可控under statistical control）的情况下其产出品的均一程度 (uniformity of product)②③。

不难理解，我们不可能直接测量过程本身，而只能通过测量其产出品的某个特性来体现其能力③。

通常用被测量的特性的离散程度，即标准方差，（西格玛），来表示过程能力。

而且过程能力被量化为，即其总宽度为6个西格玛。

Ppk 、Cpk ，还有Cmk 三者的定义是什么？有什么区别？如何计算？1、首先我们先说明Pp 、Cp 两者的定义及公式 Cp （Capability Indies of Process ）：稳定过程的能力指数，定义为容差宽度除以过程能力，不考虑过程有无偏移，一般表达式为：2^6d R LSL USL Cp σ-=Pp （Performance Indies of Process ）：过程性能指数，定义为不考虑过程有无偏移时，容差范围除以过程性能，一般表达式为：^6SLSL USL Pp σ-=（该指数仅用来与Cp 及Cpk 对比，或/和Cp 、Cpk 一起去度量和确认一段时间内改进的优先次序）CPU ：稳定过程的上限能力指数，定义为容差范围上限除以实际过程分布宽度上限，一般表达式为：^23d R X USL CPU σ-=CPL ：稳定过程的下限能力指数，定义为容差范围下限除以实际过程分布宽度下限，一般表达式为：^23d R LSL X CPL σ-=2、现在我们来阐述Cpk 、Ppk 的含义Cpk ：这是考虑到过程中心的能力（修正）指数，定义为CPU 与CPL 的最小值。

它等于过程均值与最近的规范界限之间的差除以过程总分布宽度的一半。

即：）（CPL CPU Min Cpk ,= Ppk ：这是考虑到过程中心的性能（修正）指数，定义为：^3SX USL σ-或^3SLSL X σ-的最小值。

即：）σ，σ（^^33SS LSLX X USL Min Ppk --= 其实，公式中的K 是定义分布中心μ与公差中心M 的偏离度，μ与M 的偏离为ε=| M-μ| ，则：2/T K ε=于是，Cp K Cpk ）（-=1 ， Pp K Ppk ）（-=1 3、公式中标准差的不同含义①在Cp 、Cpk 中，计算的是稳定过程的能力，稳定过程中过程变差仅由普通原因引起，公式中的标准差可以通过控制图中的样本平均极差R 估计得出：22^d R d R =σ因此，Cp 、Cpk 一般与控制图一起使用，首先利用控制图判断过程是否受控，如果过程不受控，要采取措施改善过程，使过程处于受控状态。

Ppk与Cpk培训Ppk 与CpkPpk 是针对一个初始过程，在人机物法环测等方面，包括规格都没有稳定的情况下进行研究得到的过程能力，称为初始过程能力；一个初始过程，加工零件数量为100Pcs ，用于过程能力研究的数据为50个，分别为X 1，X 2，X 3，……，X 50其平均值为X ?=X 1+X 2+?+X n n标准方差为Sigma=√∑(X i ?X ?n i=1)2n?1规格上限为S U ，规格下限为S L公差为T=S U –S LPpk=T 6 SigmaCpk 是针对一个稳定的过程，即在人机物法环测等方面相对稳定的情况下进行生产得到的产品进行通过能力研究，称为工程能力指数；针对一个稳定的生产过程，在其不同的生产阶段，分别取5组样品，每组样品数量为10pcs第一组样品中最大值与最小值的差为R1；第二组样品中最大值与最小值的差为R2；……第五组样品中最大值与最小值的差为R5；则这五组的平均极差R=(R1+R2+……+R5)/5标准差的计算则可简化为Sigma=R D 2，其中D2是一个统计学常数； CPK=T 6 SigmaPpK 、CpK 分别为1.33和1.67的意思对于一组确定的数据，其标准方差为Sigma ，若其规格的宽度为10Sigma ，则（PpK 、CpK ）=T 6 Sigma =10 Sigma 6 Sigma =1.67若其规格的宽度为8Sigma ，则（PpK 、CpK ）=T 6 Sigma =8Sigma 6 Sigma =1.33若其规格的宽度为6Sigma ，则（PpK 、CpK ）=T 6 Sigma =6 Sigma 6 Sigma =1.00也就是说，对于一组确定的数据而言，若规格越宽，则过程能力越大，越容易制作；对于一个确定的公差宽度而言，方差越小，过程能力越大；若要方差变小，则要求每个值与平均值越接近越好，对过程能力要求则越高；。

Ppk、Cpk，还有Cmk三者的定义是什么？有什么区别？如何计算？之答禄夫天创作1、首先我们先说明Pp、Cp两者的定义及公式Cp（Capability Indies of Process）：稳定过程的能力指数，定义为容差宽度除以过程能力，不考虑过程有无偏移，一般表达式为：Pp（Performance Indies of Process）：过程性能指数，定义为不考虑过程有无偏移时，容差范围除以过程性能，一般表达式为：（该指数仅用来与Cp及Cpk对比，或/和Cp、Cpk一起去度量和确认一段时间内改进的优先次序）CPU：稳定过程的上限能力指数，定义为容差范围上限除以实际过程分布宽度上限，一般表达式为：CPL：稳定过程的下限能力指数，定义为容差范围下限除以实际过程分布宽度下限，一般表达式为：2、现在我们来论述Cpk、Ppk的含义Cpk：这是考虑到过程中心的能力（修正）指数，定义为CPU与CPL的最小值。

它等于过程均值与最近的规范界限之间的差除以过程总分布宽度的一半。

即：Ppk：这是考虑到过程中心的性能（修正）指数，定义为：或的最小值。

即：其实，公式中的K是定义分布中心μ与公差中心M的偏离度，μ与M的偏离为ε=| Mμ| ，则：于是，，3、公式中尺度差的分歧含义①在Cp、Cpk中，计算的是稳定过程的能力，稳定过程中过程变差仅由普通原因引起，公式中的尺度差可以通过控制图中的样本平均极差估计得出：因此，Cp、Cpk一般与控制图一起使用，首先利用控制图判断过程是否受控，如果过程不受控，要采纳措施改善过程，使过程处于受控状态。

确保过程受控后，再计算Cp、Cpk。

②由于普通和特殊两种原因所造成的变差，可以用样本尺度差S 来估计，过程性能指数的计算使用该尺度差。

即：4、几个指数的比较与说明①无偏离的Cp暗示过程加工的均匀性（稳定性），即“质量能力”，Cp越大，这质量特性的分布越“苗条”，质量能力越强；而有偏离的Cpk暗示过程中心μ与公差中心M的偏离情况，Cpk越大，二者的偏离越小，也即过程中心对公差中心越“瞄准”。