当前位置：文档之家 › 热工基础第二讲

热工基础第二讲

  • 格式：pdf
  • 大小：868.56 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

热工基础

热工基础

【热辐射】
（2）特点： 可在真空中传播 能量传递同时伴随有能量的转换 任何物体只要在绝对零度以上，都能发射辐 射能，但是只有在物体温度较高时，热辐射才 能成为主要的传热方式。
（3）人站在火焰旁会感到热、太阳热量能传到 地球。
小结：
实际进行的传热过程，往往不是上述三 种基本方式单独出现，而是两种或三种传 热的组合，而又以其中一种或两种方式为 主。
【热对流(对流)】
（3）产生对流的原因 由于流体内部温度不同形成密度的差异，在浮力的 作用下产生流体质点的相对位移，使轻者上浮，重 者下沉，称为自然对流； 由于泵、风机或搅拌等外力作用而引起的质点强制 运动，称为强制对流。
流动的原因不同，热对流的规律也不同。 在强制对流的同时常常伴随有自然对流。
一般范围：2.3~427 W/m℃（纯银最大，其次为纯铜、铝等） 一般
温度T升高， λ下降
杂质含量增大, λ下降
2. 建材
一般范围：0.16~2.2 W/m℃，与材料结构、空隙率、 湿度、密度等有关 。 空气湿度增大， λ增大
3. 隔热材料（保温材料）
隔热材料：导热系数低于0.22 W/m℃的材料（多为 多孔结构）。
大多数金属：β<0 大多数非金属：β>0
湿度对导热系数有影响 因水的导热系数比气体大，所以湿物料 的导热系数比干物料的大
密度对导热系数有影响
密度小，导热系数小
傅立叶(Fourier, Jean Baptiste Joseph)(1768-1830)小传：法国数 学家、物理学家 。1768年3月21日生于法国欧塞尔 （Auxevre）,1830年5月16日卒于巴黎。因研究热传导理论而闻名于 世。 9岁父母双亡，被当地教堂收养。12岁由主教送于地方军事学 校读书。17岁（1785年）回乡教数学，1794年到巴黎，成为高等师 范学校的首批学员，次年到巴黎综合工科学校执教，1798年随拿破 仑远征埃及时，任军中秘书和埃及研究院秘书。1801年回国，1817 年当选为科学院院士，1822年任该院终身秘书。后又任法兰西学院 终身秘书和理工科大学校务委员会主席。 1807年向巴黎科学院提交“热的传播”论文，推导出著名的热传导 方程。并在求解该方程时发现解函数可以由三角函数构成的级数形式 表示，从而提出任意函数都可以展成三角函数的无穷级数。1822年 在代表作“热的分析理论”中解决了热在非均匀加热的固体中分布传 播问题，成为分析学在物理中应用的最早例证之一，对19世纪数学和 理论物理学的发展产生深远影响。傅立叶级数（三角级数）、傅立叶 分析等理论均由此创造。

热工基础__第二章能量转换的基本概念和基本定律.

热工基础__第二章能量转换的基本概念和基本定律.

(3) 、温度 • 物体冷热程度的标志；系统热平衡的物理特征量。 • 热力学第零定律： 当物体C同时与物体A和B接触而达到热平衡时,物体A 和B也一定热平衡。 这一事实说明物质具备某种宏观性质。若两个热力 系分别与第三个热力系热平衡，那么这两个热力彼此 处于热平衡。这一宏观物理性质称为温度。 • 温标： 热力学第零定律是温标的理论依据。 a、热力学温标: 水的三相点为 273.16 K,单位“开尔 文” 是水有三相点温度的1／273。16 T 单位 K， T = 273.15 + t b、摄氏温标 水的三相点为0.01 ℃，水的标准沸点为100 ℃。 t 单位 ℃ t = T - 273.15 ＊（有关温度热力学温标在第二定之后有严格证明）
dX 0
dX X
1
2
2
X1
• 强度量状态参数： 与系统内所含工质数量无关的状态参数。 • 广延量状态参数： 与系统内所含工质数量有关的状态参数。
3、基本状态参数 (1)、比体积
V v m
密度
单位 m3/kg
m V
v 1
(2)、压力（压强）
F p A
• 压力的国际制单位： 1 MPa = 103 kPa = 106 Pa
•以后在p－v图及T－s图中凡是用 实线画出的过程都表示可逆过程。
有用功Wu、无用功Wr和耗散功Wl
闭口系膨胀过程中用推动大所所消耗的功称为无用功Wr. 过程中由于耗散效应所消耗的功称为耗散功Wl ，则有用功Wu为 Wu＝ W－Wr－Wl Wr＝p0(V2 － V1) ＝ p0 ΔV (1－11) (1－12)
第二节
热力学第一定律
一 热力学第一定律的实质
热力学第一定律是能量守恒与转换定律在热现象中的应用。

热工基础课件

热工基础课件

根据受力平衡有：
pA p0 A ghA 0
化简得：
p p0 gh
h—静止流体中任意点在自由液面下的深度
这就是重力作用下的液体平衡方程，通常 称为流体静力学基本方程。——表达式之一
适用范围：重力作用下的平衡状态均质不可 压缩连通的流体。
热工基础 高职高专 ppt 高等职业教育 课件
若在静止液体中任取两 点 1 和 2 ，点 1 和点 2 压强各为 p1 和 p2, 位置坐标各为 z1 和 z2 ， 则有：
p1 p0 g ( z0 z1 ) p2 p0 g ( z0 z2 )
以上两式同除以g,整理后得
p1 p2 z2 两式联立得 z1 g g
a
g
热工基础 高职高专 ppt 高等职业教育 课件
3.常见的等压面
• 重力作用下同一静止液体中的水平面。重
力场中等压面判别条件：静止的连通的均 质的水平面。 • 气液分界面，即液体的自由表面，各点压 强均等于分界面上气体的压强，如处于大 气中的液体表面均为一个大气压。 • 互不掺混的两种液体的分界面，如水和水 银等。
在实验室研究中，由于压强比较小，或便于计
量和表达，也可用液柱高度作为压强的单位。
也有一些用标准大气压或工程大气压作为压强
单位的情况，计算时需要换算成标准单位。
热工基础 高职高专 ppt 高等职业教育 课件
计示压强
讨论思考题2-4
讨论思考题2-5
热工基础 高职高专 ppt 高等职业教育 课件
第三节 等压面及其性质
M点的绝对压强和相对压强为
1-2为等压面，则p1=p2
p pa 2 gh2 1 gh1
Pe= ρ2gh2－ ρ1gh1

热工基础第二章

热工基础第二章

13
对于单位质量工质， 对于单位质量工质，
1 2 q = ∆h + ∆ cf + g ∆z + ws 2
以上两式称为开口系统的稳定流动能量方程。 以上两式称为开口系统的稳定流动能量方程。 开口系统的稳定流动能量方程 对于微元过程 ，稳定流动能量方程写成
1 2 δQ = dH + mdcf + mgdz + δWs 2 1 2 δq = dh + dcf + gdz + δws 2
q = ∆h + ws
1. 热交换器
( wt = ws )
q = h2 − h1
2. 动力机械
( ws = 0 )
(q = 0)
21
ws = h1 − h2
3. 绝热节流
( q = 0 , ws = 0 )
h1 − h2 = 0
注意：绝热节流过程不是定焓过程 定焓过程。 注意：绝热节流过程不是定焓过程。 本质上存在摩擦和涡流， 不可逆过程， 本质上存在摩擦和涡流 ， 不可逆过程 ， 工质 处于非平衡状态，节流为不稳定流动。 处于非平衡状态，节流为不稳定流动。 22
5
2-3 闭口系统的热力学第一定律表达式 Q ∆U W
Q − W = ∆U = U 2 − U 1 Q = ∆U + W
对于微元过程， 对于微元过程，
δQ = d U + δW
6
对于可逆过程， 对于可逆过程，
δQ = dU + pdV
Q = ∆ U + ∫ pdV
1 2
对于单位质量工质, 对于单位质量工质,
3
2. 宏观动能 ：Ek ，单位为J或kJ 单位为J

热工基础-2-(3)热力学第二定律-

热工基础-2-(3)热力学第二定律-

热工基础—第2章
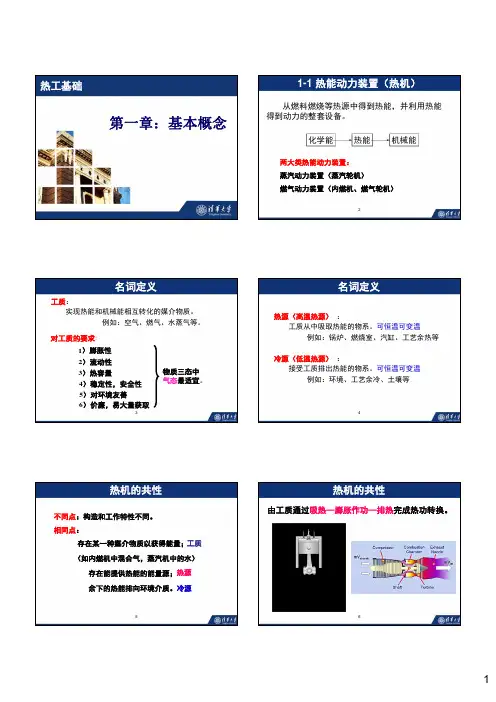
1、分析热力过程的方向性 （1）有限温差传热
只要Q=Q，B向 A传热并不违反第一
Q
Q'
定律（总热能不变）
（2） 功热转化
重物下落，水温升高是可行；
而反方向让水温下降，重物升高？ 只要使重物位能增加=水内能减少，不违 反第一定律。 △U＋W＝0
热工基础—第2章
（3） 电热转化
电流通过电阻，产生热量是可行；
温度为：
Te - Th - Tg
放热热源温度为：
Tg－TL－Te
在吸热和放热过程中，工质随时保持与热
源温度相等（进行无温差可逆传热）。
⑴对变温热源处理为——多热源可逆循环 变温热源——简化为无
穷多个宽度为ds的微元
可逆循环，（对每个小
循环可认为是温度相差
无限小的恒温吸热和恒 温放热，即组成多热源
可逆卡诺循环。
可逆过程熵变的计算：
设有一可逆过程12 ，其熵变及比熵变为：
2、热力学第二定律的数学表达式
克劳修斯积分等式 是循环可逆的 一种判据，那么如何判断循环不可逆呢?
（1）克劳修斯积分不等式
如图不可逆循环1－A－2－B－1, 其中虚线表示循环中的不可逆过 程。
用无数条可逆绝热过程线将循环分成无穷多
个微元循环。
但对电阻加热，电阻内产生电流？ 只要使产生的电能=加入的热能，不 违反第 一定律。
Q＝电能
除上述比较典型的例子外,还有许多例子可以 说明热力过程的方向性，如：气体自由膨胀、混
合过程等。
有些热力过程可以自动发生,有些则不能。 结论： 在自然界中,热力过程若要发生, ①必然遵循 热力学第一定律； ②但满足热力学第一定律的热
每一个不可逆微元循环，其热效率η t＜η

《热工基础》第二讲_193105270

《热工基础》第二讲_193105270

思考题
• 平衡状态与均匀状态之间的关系？ • 平衡状态与稳定状态之间的关系？
7
1-4 平衡状态、状态方程式、坐标图
1）平衡与均匀 2）平衡与稳定
1-4 平衡状态、状态方程式、坐标图
平衡状态与均匀状态之间的关系
平衡状态是相对时间而言的，均匀状态是相对空间而 言的 对于处于热力平衡态下的气体、液体（单相），如果 不计重力的影响，则系统内部各处的性质是均匀一致 的，各处的温度、压力、比体积等状态参数相同。如 果考虑重力影响，则系统中的压力和密度将沿高度而 有所差别。 对于气液两相并存的热力平衡系统，气相和液相的密 度不同，因而系统不是均匀的。 本书在未加特别说明之处，一律把平衡状态下的单相 物系当作是均匀的，各处的状态参数相同。
温度T(K) 54.3584 83.8058 234.3156 273.16 302.9146 429.7485 505.078 792.677
30
物质 O2 Ar Hg H2 O Ga In Sn Zn
状态 三相点 三相点 三相点 三相点 熔点 凝固点 凝固点 凝固点
29
5
序号 14 15 16 17
28
1. 定义固定点
序号 1 2 3 4 5 温度T(K) 0.65～5 13.8033 17 20.3 20.5561 物质 He e-H2 e-H2(或He) e-H2(或He) Ne 状态 蒸汽压与温度关系式 三相点 蒸汽压力点 (或气体温度测定点) 蒸汽压力点 (或气体温度测定点) 三相点
序号 6 7 8 9 10 11 12 13
热工基础
1-1 热能动力装置（热机）
从燃料燃烧等热源中得到热能，并利用热能 得到动力的整套设备。 化学能
两大类热能动力装置： 蒸汽动力装置（蒸汽轮机） 燃气动力装置（内燃机、燃气轮机）

热工基础课件2

热工基础课件2
系统储存能
内部储存能(微观) （热力学能即内能）
外部储存能(宏观) （宏观机械能）
一、热力学能(内能)
1、概念：热力学能是储存在系统内部的各 种微观能量的总称，它与系统内工质的 内部粒子的微观运动和粒子的空间位置 有关.
• 热力学能(内能)
符号：U，法定计量单位：焦耳（J）
• 比热力学能(比内能)（1kg物质的热力学能） ：
• 故热力学一定律也可表述为：“第一类永动机 是永远也造不成的”。
• 各种永动机问题长期困扰着科技界与社会。 • 第二类永动机—从单一热源取热，并将其全部
转变机械功的机器（或：热效率等于100%的 机器）（有关问题在第四章课中将详细讨论）。
• 长期以来一直有人在追求、研究各种形式的永 动机，无一有所收获。希望同学们树立正确的 思想方法，既要有怀疑精神，也不要误入歧途。
第一篇 工程热力学
本章主要内容
热力学第一定律的实质 系统储存能 闭口系能量方程 状态参数焓 开口系统能量方程及其应用
本章基本要求
1．掌握热力系储存能的概念，掌握状态参数热力 学能、焓的定义及物理意义；
2．深刻理解热力学第一定律的实质，并能熟练运 用热力学第一定律的数学表达式（即能量方程） 对闭口系能量交换进行分析及计算；
2-1 热力学第一定律的实质
• 实质：热力学第一定律是能量转换和守恒 定律在热力学上的应用。
• 意义：确定了热能和机械能之间的相互转 换的数量关系，是工程热力学的理论基础 之一，是热工分析与计算的理论依据。
• 表述：热可以变为功，功也可以变为热， 在相互转变时能的总量是不变的。热力学 第一定律又称为当量定律。
（细胞学说、达尔文进化论）
• 能量转换与守恒定律定律指出：一切物质都具 有能量。能量既不可能创造，也不能消灭，它 只能在一定的条件下从一种形式转变为另一种 形式。而在转换中，能量的总量恒定不变。

热工基础第二节 (1)

热工基础第二节 (1)
2
3
gl wl 2 重力 惯性力 重力 Ga Fr Re 2 ( ) w 惯性力 粘性力 粘性力
哥拉晓夫准数： Gr Ga t
其中

1 dV V dT
gl 3

2
t
为体积膨胀系数。
通常为定压过程，此时
1 T
物理意义：
Gr
gl3

2
2）、流体流动的状态的影响

3）、流体的物理性质的影响 影响流动速度、状态的物性参数等，都会影响对流换热。 如： 流体的密度ρ(kg／m3)、 动力粘度μ(kg/m.s)或运动粘度υ(=μ/ρ)， 比热容cp(kJ/kg· ℃）、 导热系数λ(W/m·℃） 导温系数a＝λ/（cpρ）(m2／s)。 4）相变的影响 流体的相变：凝结——凝结换热 沸腾——沸腾换热
影响对流换热的因素（与流体、固体都有关）
1）、流体发生运动的动力的影响 按动力的来源，流动分为两类：
受迫流动（强迫流动）：由外部的机械力作用导致流体的运动。
自然流动：由流体内部密度不同（浮升力作用）引起流体运动。

流体受迫流动时的换热称为受迫对流换热(或强制对流换热)， 流体自然流动时的换热称为自然对流换热。 层流: 流速较低，有规律的运动。对流换热时主要以导热为主 紊流 ：流体无规律运动，速度大。对流换热时主要以对流为主
• • • •
换热微分方程 流体的导热微分方程（能量微分方程） 连续性微分方程 流体的运动微分方程
求解微分方程组条件——单值条件
（一）、对流换热微分方程
n
理论求解对流换热问 题的思路: 对流换热量=
tf
w∞ w 边界层 层流底层
贴壁流体层的导热量

热工基础课件

热工基础课件

热与流体研究中心
24
热工基础
常用状态参数
压力P、温度T、体积V、热力学能U、 焓H和熵S，其中压力、温度和体积可直 接用仪器测量，称为基本状态参数。其余 状态参数可根据基本状态参数间接算得。
热与流体研究中心
27
热工基础
强度量与广延量
强度量：与系统质量无关，如P、T。强度 量不具有可加性。
广延量：与系统质量成正比，如V、U、H、 S。广延量具有可加性。广延量的比参数 （单位质量工质的体积、热力学能等）具有 强度量的性质，不具有可加性。
排入大气
热与流体研究中心
5
热工基础
燃气轮机装置示意图
热与流体研究中心
6
小型燃气轮机
热工基础
热与流体研究中心
7
热工基础
热与流体研究中心
8
热工基础
热与流体研究中心
9
热工基础
蒸汽动力装置（流程图）
热与流体研究中心
10
热工基础
比较上述两种热机
不同点：构造和工作特性不同。 相同点： 存在某一种媒介物质以获得能量；
（如内燃机中混合气，蒸汽机中的水） 存在能提供热能的能量源； 余下的热能排向环境介质。
结论：
各种形式的热机都存在以下几个相同的热力过 程：吸热、膨胀作功和排热。
热与流体研究中心
11
热工基础
名词定义：
工质（working substance; working medium ）:
实现热能和机械能相互转化的媒介物质。 ① 膨胀性；② 流动性；③ 热容量；④ 稳定性、安全性； ⑤ 环保性能；⑥价格。因此，物质三态中气体最合适。
热源（heat source; heat reservoir）:

北航热工基础2热工第二章

北航热工基础2热工第二章

cpdT cvdT RdT
c : 质量比热容
cp cv R
C’: 体积比热容 Cm: 摩尔比热容
c p cv 0 R c p,0 cv,0 M R R0
比热比k：定压比热与 定容比热的比值。
k c p cp c p,m cv cv cv,m
cv
R k 1
cp
kR k 1
(4) 定值比热，真实比热和平均比热
第二章 气体的热力性质
2.1理想气体与实际气体 2.2理想气体比热容 2.3实际气体状态方程 2.4对比态定律与压缩因子图
§2.4对比态定律与压缩因子图
压缩因子z 对比参数与对比态定律 压缩因子图
1) 压缩因子z的引入
实际气体状态方程 理想气体状态方程
复杂，不利于工程计算 简单，利于工程计算
为便于分析计算 理想气体（ideal gas）： 经过科学抽象的假想气体模型
假设条件 气体分子是弹性的、不占体积的质点 分子之间没有引力和斥力
理想气体可以用简单的状态方程描述，遵循克拉贝龙方程。
完全意义的理想气体是不存在的
2) 理想气体状态方程
Ideal-gas equation of state
工程热力学
Engineering Thermodynamics
北京航空航天大学
ቤተ መጻሕፍቲ ባይዱ
第二章 气体的热力性质
2.1理想气体与实际气体 2.2理想气体比热容 2.3实际气体状态方程 2.4对比态定律与压缩因子图
§2.1理想气体与实际气体
实际气体（real gas）：真实工质，热力状态不能用简单方程描述。
理想气体，忽略分子体积，分子自由运动空间为v
实际气体，考虑分子体积，分子自由运动空间为v－b

热工基础(2.2.1)--热力学第一定律(第2版)

热工基础(2.2.1)--热力学第一定律(第2版)

例例22 自自由由膨膨胀胀 如如抽抽去去隔隔板板，，分分析析△△UU
解：取气体为热力系
——闭口系？开口系？
0
0
Q = ∆U + W
∴ ∆U = 0 即U1 =U2
功,热量是穿过边界传递的能量
基本内容
2-2-1 热力学第一定律的实质 2-2-2 热力系的能量——热力学能 2-2-3 闭口系能量方程 2-2-4 稳定流动系统能量方程 2-2-5 稳流方程的应用
表述: 进入系统的能量－离开系统的能量
= 系统能量的变化∆E
能量1
能量2
∆Eiso = 0
∆E
E1
能量相互转换
E2
焦耳热功当量实验
James Joule (1818~1889)
基本内容
2-2-1 热力学第一定律的实质 2-2-2 热力系的能量——热力学能 2-2-3 闭口系能量方程 2-2-4 稳定流动系统能量方程 2-2-5 稳流方程的应用
分子尺度上 原子尺度上 原子尺度以下
…
U = U k + U p + U c + ...
2-2-2 热力系的能量－热力学能
3.热力学能是状态参数
U = Uk + Up = f1(T ) + f2 (V ) = f (T ,V )
Ñ∫ dU = 0
4.热力学能是一广延量
单位: J, kJ, kJ/kg
方法一：选房间作为研究对象
If we take the entire room-including
the air and the refrigerator-as the
system
0
闭口系 Q= ∆U +W

第二章 热能转换的基本概念和基本定律

第二章 热能转换的基本概念和基本定律

可逆过程：
W ( pV ) Wt Wf Wt
2
2
2
Wt W Wf 1
pdV ( pV ) 1
pdV d( pV ) 1
2
2
2
1 pdV (1 pdV 1 Vdp)
2
Wt 1 Vdp
或
2
wt 1 vdp
2
二、储存能 1、内部储存能——热力学能：工质微观粒子所具有的能量。
分子运动所具有的内动能
热力学能
分子间由于相互作用力所具有的内位能 维持一定分子结构的化学能和原子核内部的核能
热力学能U 是状态参数； 比热力学能 u＝U/m
热工基础与应用 第二章
2、外部储存能
Ek

1 mc2 2
或
ek

1 c2 2
出： e2m2 ,Wtot
e1m1
Wtot
e2m2
(E dE)sy
Q
增量： (Esy dEsy ) Esy dEsy
Q dEsy (e2m2 e1m1 ) Wtot
或
Q Esy (e2m2 e1m1) Wtot

热工基础与应用 第二章
式中：a,b, c 由630.74±0.2℃的银凝固点与金凝固点温度确定。 ③ 1064.43℃以上――由普朗克辐射定律定义，用1064.43℃作参考温度，取
c2 0.014388 m K 。
热工基础与应用 第二章
3、平衡状态
1、定义：一个热力系统，如果在不受外界影响的条件下， 系统的状态能够始终保持不变，则系统的这种状态称为平衡 状态。 2、实现条件：Δp=0 ΔT=0 (Δμ=0)。 4、状态参数坐标图和状态方程式
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

T2 T1

Q2 Q1
p1V1 T1

p2V2 T2
26
温标
国际温标：各国公认并执行的唯一法定温标 国际温标通常具备以下条件：
① 尽可能接近热力学温标； ② 复现精度高，各国均能以很高的准确度复现 同样的温标，确保温度量值的统一； ③ 用于复现温标的标准温度计，使用方便，性 能稳定。
27
国际温标（ITS-90）
1-5 工质的状态变化过程（热力过程）
1）膨胀性 2）流动性 3）热容量 4）稳定性，安全性 5）对环境友善 6）价廉，易大量获取
3
物质三态中 气态最适宜。
名词定义
热源（高温热源） ： 工质从中吸取热能的物系。可恒温可变温 例如：锅炉、燃烧室、汽缸、工艺余热等
冷源（低温热源） ： 接受工质排出热能的物系。可恒温可变温 例如：环境、工艺余冷、土壤等
温度T(K) 933.473 1234.93 1337.33 1357.77
物质 Al Ag Au Cu
状态 凝固点 凝固点 凝固点 凝固点
ITS-90 定义的固定点总共17个，这些固定点的准 确度为mK级；低温下限延伸了，按3He蒸汽压方程， 下限定到0.65K。
31
2. 标准仪器 将ITS-90的整个温标分为4个温区，其相应标
( K、℃、℉)
℉在我国不常用，而在欧美比较常用。国家相关标准 中规定，符号t表示摄氏度(℃)，符号T表示开尔文(K)。
C
=
5 9
(F
- 32)
F = 9 C + 32 5
33
温度单位
温度单位
1-3 工质的热力学状态及基本状态参数 2. 压力：
定义： 单位面积上所受的垂直作用力称为压力（即压强)
7
1-2 热力系统
为了研究方便，热力学常把分析对象从周围物体中分 割出来，研究它与周围物体之间的能量和物质的传递。
8
1-2 热力系统
汽缸-活塞装置
热力系统（热力系）： 人为分割出来作为热力学分析对象的有限物质系统
外界：热力系统以外的部分 边界：系统与外界之间的分界面
9
Tips：可以是固定的，也可以是移动的。
1-4 平衡状态、状态方程式、坐标图
需要注意：
自然界的物质实际上都处于非平衡状态，平 衡只是一种极限的理想状态
工程热力学通常只研究平衡状态
对于简单可压缩系统，两个独立的状态参数 即可确定一个状态
1-4 平衡状态、状态方程式、坐标图
思考题
• 平衡状态与均匀状态之间的关系？ • 平衡状态与稳定状态之间的关系？
28
1. 定义固定点
序号 1 2 3
温度T(K) 0.65～5 13.8033 17
4
20.3
5
20.5561
物质 He e-H2 e-H2(或He)
e-H2(或He)
Ne
状态 蒸汽压与温度关系式 三相点 蒸汽压力点 (或气体温度测定点) 蒸汽压力点 (或气体温度测定点) 三相点
29
序号 6 7 8 9 10 11 12 13
24
4
温标
摄氏温标：1740年瑞典的Celsius把冰点定为0 度，把水的沸点定为100度，用这两个固定点来 分度玻璃水银温度计，将两个固定点的距离等分 为 100份，每一份为1度记作℃。
25
温标
热力学温标 (单位:K)
根据热力学第二定律，由卡诺温介质的性 质无关，避免了经验温标因依附于测温介质特性而 产生随意性。最基本、最理想的温标。但复现装置 结构复杂，价格昂贵，使用不便。
平衡的观点。
19
温度的历史
十八世纪中叶，测温技术的发展，给热学研究带来 了深刻影响。 当时对温度计测量的物理量是什么，认识上存在 严重的模糊不清。 随着测温技术的研究和发展，提出了“潜热”和 “比热”等概念，奠定了热学的基础。
20
温标
温度不能直接测量，只能借助于冷热不同的物体 之间的热交换，以及物体的某些物理性质随着冷 热程度不同而变化的特性进行间接测量。
温度T(K) 54.3584 83.8058 234.3156 273.16 302.9146 429.7485 505.078 792.677
物质 O2 Ar Hg H2O Ga In Sn Zn
30
状态 三相点 三相点 三相点 三相点 熔点 凝固点 凝固点 凝固点
5
序号 14 15 16 17
1-3 工质的热力学状态及基本状态参数
3. 比体积和密度：
比体积： 单位质量物质所占的体积 单位：m3/kg
v

V m
密度： 单位体积物质的质量 单位：kg/m3


m V
v与ρ互成倒数，即：vρ＝1
1-4 平衡状态、状态方程式、坐标图
一、平衡状态（thermodynamic equilibrium state）
1-4 平衡状态、状态方程式、坐标图
二、状态方程式
对于简单可压缩热力系统，当它处于平衡状态时， 其压力、温度、比体积等参数服从一定的关系式，这样 的关系式叫做状态方程式。
状态方程式是平衡状态下基本状态参数p、v、T之间 的关系，状态方程式的具体形式取决于工质的性质。
1-4 平衡状态、状态方程式、坐标图
p,V ,T ,U , H , S
2．状态参数是系统的单值函数。 物理上—与过程无关； 数学上—其微量是全微分。
dx 0
dx dx
1a 2
1b 2
1-3 工质的热力学状态及基本状态参数
3．状态参数分类
广延量（extensive property）与系统质量成正比，有可加性 强度量（intensive property ）与系统质量无关，没有可加性
ITS-90的热力学温度记作T，单位为K；摄氏 温度记作t，单位为℃。T和t的关系(与IPTS-68 相同)为：
t = T-273.15
1990年国际温标，是以定义固定点温度指定 值以及在这些固定点上分度过的标准仪器来实 现热力学温标的，各固定点间的温度是依据内 插公式使标准仪器的示值与国际温标的温度相 联系。
一、准静态过程(quasi-static process) 或叫做准平衡过程 (quasi-equilibrium process)
定义：偏离平衡态无穷小，随时恢复平衡的状态变化过程。
进行条件： 破坏平衡的势— p, T 无穷小 气体工质和外界之间的压力差无穷小，温差无穷小
过程进行得无限缓慢，工质有恢复平衡的能力 “缓慢”是热力学意义上的缓慢，准平衡过程是实际过程的 理想化。工质与外界一旦出现不平衡，工质有足够时间得以恢复 平衡，就可以看作准平衡过程。
热力学温标是以热力学第二定律为基础的 一种理论温标，热力学温标确定的温度数值为 热力学温度。
22
温标
温标三要素：固定点定义、内插 公式和内插仪器(或称温度计/标准温度 计/标准仪器)，温标三要素的发展历史， 就是温标的发展历史。
23
温标
华氏温标：1714年荷兰的Fahrenheit以水银为测 温介质，以水银的体积随温度的变化为依据，制成 玻璃水银温度计。他规定水的沸腾温度为212度，冰 水的混合物温度为32度，这两个固定点中间等分为 180份,每一份为1度，记作F。
燃气动力装置——喷气发动机
Tips: 边界可以是实在的，也可以是假想的。
热力系统的类型 按系统与外界质量交换：
闭口系（closed system） （控制质量CM）
—没有质量越过边界
开口系（open system） （控制体积CV）
—通过边界与外界有质量交换
2
热力系统的类型
按能量交换：
绝热系(adiabatic system)：与外界无热量交换; 孤立系(isolated system)：与外界无任何形式的质能交换。
准仪器分别为(相互交叠)： ① 0.65～5.0K，3He 和4He蒸汽压温度计 ； ② 3.0～24.5561K，3He 、4He定容气体温度计 ③ 13.8033K～961.78℃，铂电阻温度计； ④ 961.78℃以上，光学或光电高温计。
3. 内插公式 分得非常细，可以跨范围或交叠使用。
32
温度单位
1-5 工质的状态变化过程（热力过程）
就热力系本身而言，热力学仅对平衡状态进行描述， “平衡”意味着宏观是静止的，而要实现能量交换， 热力系又必须通过状态的变化即过程来完成，“过 程”意味着变化，意味着平衡被破坏。
“平衡”和“过程”这两个矛盾的概念怎样统一起 来呢？这就需要引入准平衡过程。
1-5 工质的状态变化过程（热力过程）
为了定量地描述温度的高低，必须建立温度标尺 (温标－－用来衡量温度的标准尺度)，温标就是 温度的数值表示。各种温度计(传感器)的温度数 值均由温标确定。
标定－－温度计在使用前必须先进行分度。
21
温标
历史上提出过多种温标，如早期的经验温 标（摄氏温标和华氏温标）， 理论上的热力学 温标，当前世界通用的是国际温标。
压力计 测量工质压力的仪器
6
把绝对压力pab、环境大气压力patm 、表压pe 、真空度pv 、 差压△p的相互关系：
压力的单位 国际标准单位：帕斯卡(简称帕) 符号：Pa 1Pa=1N/m2
工程单位：
标准大气压（atm , 也称物理大气压） 巴（bar） 工程大气压（at） 毫米汞柱（mmHg) 毫米水柱（mmH2O)
Tips: 闭口系与系统内质量不变的区别。
Tips：孤立系与绝热系的关系。
1-3 工质的热力学状态及基本状态参数
状态： 工质在热力变化过程中某一瞬间呈现出来
的宏观物理状况，简称状态。
状态参数： 描述工质所处状态的宏观物理量。如温度、