ch9-三角

目录:1.原始种2.灰翅种3.蛋白石种4.派特(显派,隐派,亮飞行羽)5.肉桂翅6.鱼鳞种7.珍珠8.黄脸种9.黄/白化种（黄/白红眼）10.华乐种排名不分先后以下品种稀有度皆针对小虎。

☆为最低★★★★★★★为最高。

由于本文图片皆来自于网络，如果无意间触犯了您的权益1.原始种：（Base Color）：稀有度：☆原产于澳大利亚的内陆地区，在野外为群居生活。

是所有品种鸟的始祖。

具体特征：绿系：头羽和背羽一般呈黄色且有黑色条纹，毛色和条纹犹如虎皮一般，故称虎皮鹦鹉。

蓝系：头羽和背羽一般呈白且有黑色条纹，毛色和条纹犹如虎皮一般。

遗传方式：显性遗传。

对培育复合品种意义：无小编：原始和蛋白石属于比较相像的品种，原始的背部到头部全部是密集的条纹。

而蛋白石背部飞羽交集处有倒三角纯色斑块，绿鸟鸟的黄色花纹、蓝系鸟的白色花纹与身上本色相同。

[例图请参照介绍蛋白石的部分]2.灰翅种（Grewing or Dilution）：稀有度：紫色、深蓝色灰翅：★★★★黄绿色、浅天空蓝灰翅：★☆深受虎皮鹦鹉彩虹种爱好者的喜爱，是培育彩虹的基础材料。

鸟市里以浅天空蓝灰翅居多。

具体特征：身上的黑色斑块被替换成浅灰色。

遗传方式：隐性遗传。

对培育复合品种意义：可培育彩虹小编：鸟市里的灰翅以浅天空蓝灰翅居多，与原始、灰翅、隐派合称鸟市三霸，（鸟市里最多的品种之一，很常见），而深色灰翅相比之下就较为稀有和珍贵。

肉桂和灰翅极为相似，。

3. 蛋白石种（Opaline）稀有度：紫色、深蓝色：★★★天空蓝：★★绿色：★★蛋白石是培育各个复合品种的基础，例如培育彩虹珍珠都需要蛋白石，可以说是品种类基础鸟。

具体特征：背部飞羽交集处有倒三角纯色斑块，绿鸟鸟的黄色花纹、蓝系鸟的白色花纹与身上本色相同。

遗传方式：性连遗传。

对培育复合品种意义：可培育珍珠彩虹，培育品种基础鸟小编：蛋白石与原始最好区分的地方就是倒三角了~~下图介绍4派特（Dominant Pied、Recessive Pied、Clearflight Pied）派特又分为三类：显性派特、隐性派特、亮飞行羽派特隐派：蓝白色、黄绿色隐派稀有度：★★全名隐性派特，属于市场上常见鸟之一。

Ch9 镁、钛、铜及镍合金.ppt1、Ch9镁、钛、铜及镍合金简介本章主要内容：第一节镁及镁合金第二节钛及钛合金第三节铜及铜合金第四节镍及镍合金基本要求：了解镁、钛、铜及镍合金的分类，把握镁、钛、铜及镍合金的热处理，成份及性能特点和用处。

重点与难点：镁、钛、铜及镍合金的热处理、成分及性能特点；镁、钛、铜及镍合金细化晶粒和提高耐热性能的机理。

Chapter9镁、钛、铜及镍合金简介一、镁的性能特点及用处1.镁的性能特点低密度〔1.74g/cm3，约为铝的2/3〕，较高的电导率，很高的阻尼性能，高的化学活性。

以镁为基的合金有高的“强度/重量”比〔抗拉强度/密度〕。

8.1镁及镁合金9.1镁及镁合金Chapter9镁、钛、铜及镍合金简介2.镁的用处在整个镁的使用量中，有约一半是作为铝合金中的合金元素；在镍合金和铜合金2、的生产中用作脱氧剂和脱硫剂，在钢铁工业中用作脱氧剂和脱硫剂，在铍、钛、锆等金属的生产中用作还原剂；镁在球墨铸铁生产中是主要的石墨球化剂。

Chapter9镁、钛、铜及镍合金简介9.1镁及镁合金镁是有机化工反应物中的主要组分之一；高分散度的镁制作烟火剂；镁在金属防腐中起阴极爱护作用；由于镁具有高的、但可控的浸蚀倾向和低的密度，在光刻工艺中有重要作用。

Chapter9镁、钛、铜及镍合金简介9.1镁及镁合金二、镁合金的分类与合金化1.镁合金的分类镁合金按加工工艺通常可分为变形镁合金和铸造镁合金两大类。

其中在国家标准GB/T5153-1985中还列入了一号纯镁〔Mg1〕和二号纯镁〔Mg2〕。

另外，尚有部颁标准JB/T3070-1982给出了压铸镁合金的化学成分和力学性能。

Chap3、ter9镁、钛、铜及镍合金简介9.1镁及镁合金2.镁的合金化镁合金主要采纳固溶强化。

与镁形成固溶体的合金元素许多，主要有Al，Zn，Li，Ce，Zr，Th，Ag等。

Mg-Al-Zn系和Mg-Zn-Zr系是最常用的合金系。

第九章熱處理熱處理(Heat treatment)主要是用於改變金屬或合金材料的組織，因而獲得所預期改善的機械性質或物理性質。

處理的過程中，材料保持固態，藉由控制加熱和冷卻相互配合的操作來達到目的。

金屬材料的特性視其化學成分和結晶組織而定，對相同成分的金屬材料而言，可利用塑性加工或熱處理方法改變其組織，並因而得到不同的特性。

在機械製造業中，可以說重要的零件幾乎都要經過熱處理的步驟，才能使材料發揮其最佳特性與功能。

熱處理早已是機械加工的一項重要製程，配合其它的機械加工方法，得以生產更精良、可靠及耐用的零件。

熱處理程序進行包含加熱、冷卻及材料組織變化等條件。

所謂材料組織是指其晶粒的大小和晶粒內部的結晶構造。

要明瞭組織的變化，需先了解該材料的合金平衡狀態圖。

材料可以熱處理的必備條件是其組織會發生同素變態，例如鋼及鐵；或是有固溶限，才能使其中的某些元素藉由擴散析出而硬化，例如鋁銅合金。

熱處理進行的步驟依序為：1. 將工件加熱至適當溫度後，2. 保持一段適當的時間，3. 以適當的速率冷卻，4. 由於產生變態或擴散析出等作用，而改善材料之某些性質或加工性等。

欲獲得最佳的熱處理效果必須考慮：1. 待處理工件材料的化學成分和使用的場合，2. 工件材料的溫度、時間與組織變化曲線圖，3. 冷卻方式的選擇及材料因而產生的反應，4. 材料希望得到改善之機械性質為何，5. 工件幾何形狀、厚薄及尺寸等因素的影響。

熱處理的主要目的有：1. 增加材料的強度、硬度、耐磨耗及抗疲勞等性質。

2. 強化材料的韌性，以提高其耐衝擊性。

3. 使材料變軟，以增加其加工性。

4. 降低材料低溫脆化的轉換溫度，以擴展其使用溫度範圍。

5. 消除材料加工後之硬化作用或內部殘留應力，以利後續加工的進行。

6. 使成分元素分佈均勻化，因此得到均質化(Homogeneous)的組織。

7. 防止時效作用的變形。

熱處理的方法有很多種，大致可分為兩大類：1.一般熱處理指將整個工件一起施以加熱、冷卻等處理，使金屬材料整體得到性質上的改善。

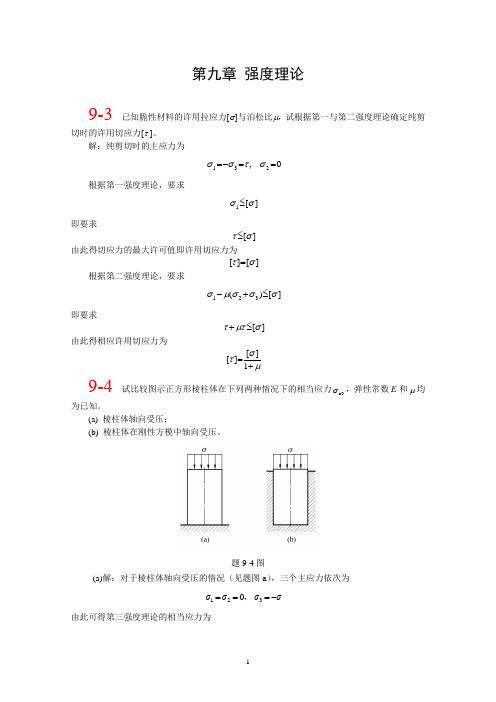
第九章 强度理论9-3 已知脆性材料的许用拉应力[σ]与泊松比μ，试根据第一与第二强度理论确定纯剪切时的许用切应力[τ ]。

解：纯剪切时的主应力为0 ,231==-=στσσ根据第一强度理论，要求 ][1σσ≤ 即要求][στ≤由此得切应力的最大许可值即许用切应力为][][στ= 根据第二强度理论，要求 ][)(321σσσμσ≤+-即要求][σμττ≤+由此得相应许用切应力为μστ+=1][][ 9-4 试比较图示正方形棱柱体在下列两种情况下的相当应力r3σ，弹性常数E 和μ均为已知。

(a) 棱柱体轴向受压；(b) 棱柱体在刚性方模中轴向受压。

题9-4图(a)解：对于棱柱体轴向受压的情况（见题图a ），三个主应力依次为ζζζζ-===321 0，由此可得第三强度理论的相当应力为ζζζζ=-=31r3(a)(b)解：对于棱柱体在刚性方模中轴向受压的情况（见题图b ），可先取受力微体及坐标如图9-4所示，然后计算其应力。

图9-4由图9-4可得ζζy -=根据刚性方模的约束条件，有 0)]([1=+-=z y x x ζζμζEε 即)(z y x ζζμζ+=注意到 x z ζζ=故有ζμμζζz x --==1 三个主应力依次为ζζζμμζζ-=--==3211， 由此可得其相当应力为ζμμζζζ--=-=12131r3 (b)按照第三强度理论，(a)与(b)两种情况相当应力的比值为1211)r3()r3(>--==μμζζr b a 这表明加刚性方模后对棱柱体的强度有利。

9-5 图示外伸梁，承受载荷F = 130 kN 作用，许用应力[σ]=170 MPa 。

试校核梁的强度。

如危险点处于复杂应力状态，采用第三强度理论校核强度。

题9-5图解：1.内力分析由题图可知，+B 截面为危险截面，剪力与弯矩均为最大，其值分别为m N 1080.7m 600.0N 10130 kN 130432S ⋅⨯=⨯⨯====Fl M F F ，2．几何性质计算34324max ,)(343)(343545433m 1090.2]m )0137.0140.0(0085.0211023.2[ 2m 1023.2)m 20137.0140.0(0137.0122.0 m 1005.5m 140.01007.7 m 1007.7]m 12)0137.02280.0()0085.0122.0(12280.0122.0[------⨯=-⨯⨯+⨯==⨯=-⨯⨯=⨯=⨯=⨯=⨯-⨯--⨯=z a z b z z z S S S W I式中：足标b 系指翼缘与腹板的交界点；足标a 系指上翼缘顶边中点。

Ch1：均变论、灾变论、太阳系、类地行星、类木行星、小行星Ch2：晶体、非晶体、条痕、硬度、光泽、解理、硅氧四面体Ch3:：岩浆、熔岩、玄武岩柱状节理、绳状熔岩、枕状熔岩、火山锥、火山口、岩浆房、环太平洋火山带、侵入岩、围岩、同化作用、混染作用、鲍文反应系列、岩脉、岩床、岩株、岩基、显晶质结构、隐晶质结构、非晶质结构、斑状结构、火成碎屑结构、气孔构造、杏仁构造、部分熔融Ch4：搬运作用、沉积作用、压固作用、胶结作用、成岩作用、分选、磨圆、层理、交错层理、层面、递变层理、波痕、泥裂、缝合线Ch5：变质作用、静压力、定向压力、化学活动流体、脱水反应、脱CO2反应、变晶、变晶结构、片理、片麻理、接触热变质、接触交代、区域变质、埋藏变质、混和岩化、混和花岗岩Ch6：物理风化、化学风化、差异风化、球形风化、风化壳、土壤、古风化壳、残积物Ch7；岩层的产状要素、褶曲要素（轴面、核、翼、枢纽）、背斜和向斜、断层要素（断层面、盘、断距），正断层、逆断层、走滑断层、逆掩断层、断层擦痕、拖曳褶曲、三角面山Ch8：地壳、地幔、地核、莫霍面、古登堡面、岩石圈、软流圈、大陆地壳、大洋地壳、均衡原理、震源、震中、海啸、地震波、纵波、横波、表面波、P波阴影带、S波阴影带、震级、地震烈度、环太平洋地震带、地中海-印尼地震带、洋中脊地震带、陨石Ch9：块体运动：山坡上块体的向下运动称为块体运动。

稳定角：倒石堆锥坡达33°-37°，是为稳定角。

因为碎屑堆积体只有达到这一坡角才能保持稳定。

滑坡：块体沿着上凹的弧形滑面下滑，同时绕水平轴向内旋转。

倒石锥：崩落与崩滑的碎屑落在山麓的堆积体呈顶端朝上的锥形，称为倒石堆。

泥石流：斜坡上或沟谷中松散碎屑物质被暴雨或积雪、冰川消融水所饱和，在重力作用下，沿斜坡或沟谷流动的一种特殊洪流。

特点是爆发突然，历时短暂，来势凶猛和巨大的破坏力。

蠕变：是粒流中运动速度极其缓慢的一种。

它出现在山坡的表层。

不等式整理目录Ch1. 伯努利不等式Ch2. 均值不等式Ch3. 幂均不等式Ch4. 柯西不等式Ch5. 切比雪夫不等式Ch6. 排序不等式Ch7. 琴生不等式Ch8. 波波维奇亚不等式Ch9. 加权不等式Ch10. 赫尔德不等式Ch11. 闵可夫斯基不等式Ch12. 牛顿不等式Ch13. 麦克劳林不等式Ch14. 定义多项式Ch15. 舒尔不等式Ch16. 定义序列Ch17. 缪尔海德不等式Ch18. 卡拉玛塔不等式Ch19. 单调函数不等式Ch20. 3个对称变量pqr法Ch21. 3个对称变量uvw 法 Ch22. ABC 法 Ch23. SOS 法 Ch24. SMV 法 Ch25. 拉格朗日乘数法 Ch26. 三角不等式 Ch27. 习题与习题解析Ch1. 伯努利不等式1.1若实数i x （i 12n ,,...,=）各项符号相同，且i x 1>-，则：12n 12n 1x 1x 1x 1x x x ()()...()...+++≥++++ 1()1()当12n x x x x ...====时，1()式变为：n 1x 1nx ()+≥+ 2() Ch2. 均值不等式2.1若12n a a a ,,...,为正实数，记：⑴n Q =，为平方平均数，简称平方均值；⑵ 12nn a a a A n...+++=，为算术平均数，简称算术均值；⑶n G =，为几何平均数，简称几何均值； ⑷ n 12nnH 111a a a ...=+++，为调和平均数，简称调和均值.则：n n n n Q A G H ≥≥≥ 3()iff 12n a a a ...===时，等号成立. （注：iff if and only if =当且仅当.）3()Ch3.幂均不等式3.1设12n a a a a (,,...,)=为正实数序列，实数r 0≠，则记：1r r rr12n r a a a M a n ...()⎛⎫+++= ⎪⎝⎭4()4()式的r M a ()称为幂平均函数.3.2若12n a a a a (,,...,)=为正实数序列，且实数r 0≠，则：r s M a M a ()()≤ 5()当r s ≤时，5()式对任何r 都成立，即r M a ()关于r 是单调递增函数.5()3.3设12n m m m m (,,...,)=为非负实数序列，且12n m m m 1...+++=，若12n a a a a (,,...,)=为正实数序列，且实数r 0≠，则：1m rrr rr1122n n M a m a m a m a ()(...)=+++ 6()6()式称为加权幂平均函数.3.4若12n a a a a (,,...,)=为正实数序列，且实数r 0≠，对m r M a ()则：m m r s M a M a ()()≤即：11rrr sss sr1122n n 1122n n m a m a m a m a m a m a (...)(...)+++≤+++ 7()当r s ≤时，7()式对任何r 都成立，即m r M a ()关于r 是单调递增函数.7()Ch4. 柯西不等式4.1若12n a a a ,,...,和12n b b b ,,...,均为实数，则：222222212n 12n 1122n n a a a b b b a b a b a b (...)(...)(...)++++++≥+++ 8()iffn 1212na a ab b b ...===时，等号成立.（注：iff if and only if =当且仅当.） 8()4.2柯西不等式还可以表示为：222222212n 12n 1122n n a a a b b b a b a b a b n n n.........()()()+++++++++≥ 9()简称：“平方均值两乘积，大于积均值平方” 我们将1122n na b a b a b n...+++简称为积均值，记：n D =则：224n n n Q a Q b D ab [()][()][()]≥n D ab ()≥ 10() 4.3推论1：若a b c x y z ,,,,,为实数，x y z 0,,>，则：2222n 12n 1212n 12na a a a a ab b b b b b (...)......++++++≥+++ 11() iffn 1212na a ab b b ...===时，等号成立. 11()式是柯西不等式的推论，称权方和不等式4.4推论2：若12n a a a ,,...,和12n b b b ,,...,均为实数，则：...+≥ 12()iffn 1212na a ab b b ...===时，等号成立. 4.5推论3：若a bc x y z ,,,,,为正实数，则：x y zb c c a a b y z z x x y()()()+++++≥+++ 13() Ch5. 切比雪夫不等式5.1若12n a a a ...≤≤≤；12n b b b ...≤≤≤，且均为实数.则：12n 12n 1122n n a a a b b b n a b a b a b (...)(...)(...)++++++≤+++ 14()iff 12n a a a ...===或12n b b b ...===时，等号成立.12()由于有12n a a a ...≤≤≤，12n b b b ...≤≤≤条件，即序列同调， 所以使用时，常采用WLOG 12n a a a ...≤≤≤…… (注：WLOG Without Loss Of Generality =不失一般性) 5.2切比雪夫不等式常常表示为：12n 12n 1122n na a ab b b a b a b a b n n n.........()()()+++++++++≤ 15()简称：“切比雪夫同调数，均值积小积均值”.即：两个序列数的均值之积不大于两个序列数各积之均值. 则：2n n n A a A b D ab ()()[()]≤n D ab ()≤ 16() Ch6. 排序不等式6.1若12n a a a ...≤≤≤；12n b b b ...≤≤≤为实数，对于12n a a a (,,...,)的任何轮换12n x x x (,,...,)，都有下列不等式：1122n n 1122n n n 1n 121n a b a b a b x b x b x b a b a b a b .........-+++≥+++≥+++ 17()17().其中，1122n n a b a b a b ...+++称正序和，n 1n 121n a b a b a b ...-+++称反序和，1122n n x b x b x b ...+++称乱序和. 故17()式可记为：18()6.2推论：若12n a a a ,,...,为实数，设12n x x x (,,...,)为12n a a a (,,...,)的一个排序，则：22212n 1122n n a a a a x a x a x ......+++≥+++ 19()Ch7. 琴生不等式7.1定义凸函数：对一切x y a b ,[,]∈，01(,)α∈，若函数f a b R :[,]→是向下凸函数，则：f x 1y f x 1f y (())()()()ααα+-≤+- 20() 20()式是向下凸函数的定义式.注：f a b R :[,]→表示区间a b [,]和函数f x ()在a b [,]区间都是实数.7.2若f a b R :(,)→对任意x a b (,)∈，存在二次导数f x 0''()≥，则f x ()在a b (,)区间为向下凸函数；iff x a b (,)∈时，若f x 0''()>，则f x ()在a b (,)区间为严格向下凸函数. 7.3若12n f f f ,,...,在a b (,)区间为向下凸函数，则函数1122n n c f c f c f ...+++在在a b (,)区间对任何12n c c c 0,,...,(,)∈∞也是向下凸函数.7.4若f a b R :(,)→是一个在a b (,)区间的向下凸函数，设n N ∈，12n 01,,...,(,)ααα∈为实数，且12n 1...ααα+++=，则对任何12n x x x a b ,,...,(,)∈，有：1122n n 1122n n f x x x f x f x f x (...)()()...()αααααα+++≤+++ 21()21()简称：“对于向下凸函数，均值的函数值不大于函数的均值”. Ch8. 波波维奇亚不等式8.1若f a b R :[,]→是一个在a b [,]区间的向下凸函数，则对一切x y z a b ,,[,]∈，有：x y z f x f y f z 2x y y z z xf f f f 333222()()()()[()()()]++++++++≥++ 22() 22()8.2波波维奇亚不等式可以写成：x y z f x f y f z x y y z z xf f f f 3322223()()()()()()()++++++++++≥23() 简称：“对于向下凸函数的三点情况，三点均值的函数与函数的均值之平均值，不小于两点均值的函数值之平均值”.8.3若f a b R :[,]→是一个在a b [,]区间的向下凸函数，12n a a a a b ,,...,[,]∈，则：12n 12n f a f a f a n n 2f a n 1f b f b f b ()()...()()()()[()()...()]++++-≥-+++ 24()其中：12n a a a a n...+++=，i j i j 1b a n 1≠=-∑（对所有的i ） 24()当1a x =，2a y =，3a z =，n 3=时，x y z a 3++=，1y z b 2+=，2z x b 2+=，3x yb 2+= 代入23()式得：x y z y z z x x y f x f y f z 3f 2f f f 3222()()()()[()()()]++++++++≥++ 即：x y z f x f y f z 2x y y z z xf f f f 333222()()()()[()()()]++++++++≥++ 25() 25()式正是22()式.Ch9. 加权不等式9.1若i a 0(,)∈∞，i 01[,]α∈（i 12n ,,...,=），且12n 1...ααα+++=，则：n 1212n 1122n n a a a a a a ......αααααα≤+++ 26()26()26()式形式直接理解为：几何均值不大于算术均值.Ch10. 赫尔德不等式10.1若实数a b 0,>，实数p q 1,>且111p q+=，则：p q a b ab p q ≤+ 27() iff p q a b =时，等号成立. 27()10.2若12n a a a ,,...和12n b b b ,,...为正实数，p q 1,>且111p q+=，则： 11p p p q q q pq1122n n 12n 12n a b a b a b a a a b b b ...(...)(...)+++≤++++++ 28()28()iff p p pn 12q q q 12na a ab b b ...===时，等号成立.10.3赫尔德不等式还可以写成：11p p p q q q p q1122n n 12n 12n a b a b a b a a a b b b n n n.........()()+++++++++≤ 29()即：2n p q D ab M a M b [()]()()≤n D ab ()≥ 30() 简称：“幂均值的几何均值不小于积均值”. （注：赫尔德与切比雪夫的不同点：赫尔德要求是111p q+=，切比雪夫要求是同调；赫尔德的积均值小，切比雪夫的积均值大.）10.4若12n a a a ,,...、12n b b b ,,...和12n m m m ,,...为三个正实数序列，p q 1,>且111p q+=，则：11nnnpqp qi i i i i i i i 1i 1i 1a b m a m b m ===⎛⎫⎛⎫≤ ⎪ ⎪⎝⎭⎝⎭∑∑∑ 31() 31()iff p p pn 12q q q 12na a ab b b ...===时，等号成立.10.5若ij a (i 12m ,,...,=;j 12n ,,...,=)，12n ,,...,ααα为正实数且...12n 1ααα+++=，则：()()jj m mnn ijij j 1j 1i 1i 1aa αα====≤∏∏∑∑ 32()32()10.6推论：若123a a a N ,,+∈，123b b b N ,,+∈，123c c c N ,,+∈，则：3333333333123123123111222333a a a b b b c c c a b c a b c a b c ()()()()++++++≥++ 33()简称：“立方和的乘积不小于乘积和的立方”. Ch11.闵可夫斯基不等式11.1若12n a a a ,,...,；12n b b b ,,...,为正实数，且p 1>，则：111nnnppppppi i i i i 1i 1i 1a b a b (())()()===+≤+∑∑∑ 34()iffn 1212na a ab b b ...===时，等号成立. 34()11.2若12n a a a ,,...,；12n b b b ,,...,为正实数，且p 1>，则：11nnn pp p p p p i i i i i 1i 1i 1a b a b ()()()===⎛⎫+≤+ ⎪⎝⎭∑∑∑ 35()iffn 1212na a ab b b ...===时，等号成立. 35()11.3若12n a a a ,,...,；12n b b b ,,...,；12n m m m ,,...,为三个正实数序列，且p 1>，则：111nnnp p p pppi i i i i i i i 1i 1i 1a b m a m b m (())()()===+≤+∑∑∑ 36()iffn 1212na a ab b b ...===时，等号成立. 36()Ch12.牛顿不等式12.1若12n a a a ,,...,为任意实数，考虑多项式：n n 112n 01n 1n P x x a x a x a c x c x c x c ()()()...()...--=+++=++++ 37()的系数01n c c c ,,...,作为12n a a a ,,...,的函数可表达为：0c 1=；112n c a a a ...=+++；21213n 1n i j c a a a a a a a a ...-=+++=∑；（i j n <≤） 3i j k c a a a =∑；（i j k n <<≤） ……n 12n c a a a ...=.对每个k 12n ,,...,=，我们定义k k k k n c k n k p c C n !()!!-== 38() 则37()式类似于二项式定理，系数为：kk nk c C p =. 12.2若12n a a a ,,...,为正实数，则对每个k 12n 1,,...,=-有：2k 1k 1k p p p -+≤ 39()iff 12k a a a ...===时，等号成立. 39()Ch13.麦克劳林不等式13.1若12n a a a ,,...,为正实数，按38()定义，则：111kn212k n p p p p ......≥≥≥≥ 40()iff 12k a a a ...===时，等号成立.40()Ch14.定义多项式14.1若12n x x x ,,...,为正实数序列，并设12n ,,...,ααα为任意实数.记：n 1212n 12n F x x x x x x (,,...,)...ααα=；12n T [,,...,]ααα为12n F x x x (,,...,)所有可能的积之和，遍及12n ,,...,ααα的所有轮换.14.2举例说明⑴ T 100[,,]：表示共有3个参数的所有积之和，共有36!=项.第1个参数的指数是1，第2和第3个参数的指数是0.故：[,,]()!()()100100100T 10031x y z y x z z y x 2x y z =-⋅++=++.⑵ T 11[,]：表示共有2个参数的所有积之和，共有22!=项.第1个和第2个参数的指数是1.故：[,]()!()11T 1121x y 2xy =-⋅=.⑶ T 12[,]：表示共有2个参数的所有积之和，共有22!=项.第1个参数的指数是1，第2个参数的指数是2.故：[,]()!()121222T 1221x y y x xy x y =-⋅+=+.⑷ T 121[,,]：表示共有3个参数的所有积之和，共有36!=项.第1个参数的指数是1，第2个参数的指数是2，第3个参数的指数是1.故：[,,]()222T 1212xy z x yz xyz =++.即：[,,][,,]T 121T 211=⑸ T 210[,,]：表示共有3个参数的所有积之和，共有36!=项.第1个参数的指数是2，第2个参数的指数是1，第3个参数的指数是0.故：222222T 210x y x z y x y z z x z y [,,]=+++++.⑹ T 300[,,]：表示共有3个参数的所有积之和，共有36!=项.第1个参数的指数是3，第2个和第3个参数的指数是0.故：333T 3002x y z [,,]()=++.⑺ [,,]T a b c ：表示共有3个参数的所有积之和，共有36!=项.第1个参数的指数是a ，第2个参数的指数是b ，第3个参数的指数是c .故：[,,]a b c a c b b c a b a c c a b c b a T a b c x y z x y z x y z x y z x y z x y z =+++++.由于[,,][,,][,,][,,][,,]...T a b c T b c a T c a b T c b a T b a c =====表达式比较多， 所以我们规定：[,,]T a b c （a b c ≥≥）.Ch15.舒尔不等式15.1若R α∈，且0β>，则：[,,][,,][,,]T 200T 2T 0αβαββαββ++≥+ ()41()4115.2 解析()41式[,,]()222T 2002x y z αβαβαβαβ++++=++；[,,]()T 2x y z x y z x y z αβββαβββααββ=++；[,,]T 0x y x y y z y z x z x z αβββαβαβββαββαβαββαββ+++++++=+++++将上式代入()41式得：222x y z x y z x y z x y z αβαβαβαβββαβββα++++++++x y x y y z y z x z x z αβββαβαβββαββαβαββ++++++≥+++++即：222y x y z z x y x z x y z αβααββαβαβββββα++++++++y x y y z x y x z 0z x z βαβββααββαβββαβαββ++++++------≥即：()()22x x y z x y x z y y x z x y y z αβββββββαβββββββ++--+--()2z z x y y z x z 0αβββββββ++-≥-即：()()()()()()x x y x z y y z y x z z x z y 0αββββαββββαββββ--+--+--≥ ()42()42式与()4115.3若实数,,x y z 0>，设t R ∈，则：()()()()()()t t t x x y x z y y z y x z z x z y 0--+--+--≥ ()43iff x y z ==或,x y z 0==及轮换，等号成立.按照()41式写法，即：t α=，1β=，则：[,,][,,][,,]T t 200T t 112T t 110++≥+ ()44()43式是我们最常见的舒尔不等式形式.15.4推论：设实数,,x y z 0>，实数,,a b c 0>且a b c ≥≥或a b c ≤≤，则：()()()()()()a x y x z b y z y x c z x z y 0--+--+--≥ ()45()43式中，t x a =，t y b =，t z c =，就得到()45式.15.5推论：设实数,,x y z 0>，则：[()()()]3333332223xyz x y z 2xy yz zx +++≥++ ()4615.6推论：若(,]k 03∈，则对于一切,,a b c R +∈，有：()()()2222k 3k k abc a b c 2ab bc ca -++++≥++ ()47Ch16. 定义序列16.1设存在两个序列()(,,...,)n i i 112n ββββ==和()(,,...,)n i i 112n αααα==，当满足下列条件：⑴ ......12n 12n βββααα+++=+++ ①⑵ ...12n βββ≥≥≥且...12n ααα≥≥≥ ②⑶ ......12s 12s βββααα+++≤+++ ③对一切[,]s 1n ∈，③式都成立.则：()n i i 1β=就是()n i i 1α=的优化值，记作：()()i i βα<.注：这里的序列只有定性的比较，没有定量的比较.Ch17.缪尔海德不等式17.1若,,...,12n x x x 为非负实数序列，设()i α和()i β为正实数序列，且()()i i βα<，则：[][]i i T T βα≤ ()48iff ()()i i αβ=或...12n x x x ===时，等号成立.()4817.2解析()48式若实数123a a a 0≥≥≥，实数123b b b 0≥≥≥，且满足11a b ≥，1212a a b b +≥+，123123a a a b b b ++=++；设,,x y z 0>，则：满足序列(,,)(,,)123123b b b a a a <条件， 则：[,,]333333121221211221b b b b b b b b b b b b b b b b b b 123T b b b x y z x y z x y z x y z x y z x y z =+++++[,,]333333121221211221a a a a a a a a a a a a a a a a a a 123T a a a x y z x y z x y z x y z x y z x y z =+++++ 即()48式为： [,,][,,]123123T b b b T a a a ≤用通俗的方法表达即：331212a b a a b b sym sym x y z x y z ≥∑∑ ()49()49.17.3例题：设(,,)x y z 为非负变量序列，考虑(,,)221和(,,)311.由16.1中的序列优化得：(,,)(,,)221311<由缪尔海德不等式()48式得：[,,][,,]T 221T 311< ①[,,]()222222T 2212x y z x yz xy z =++ ②[,,]()333T 3112x yz xy z xyz =++ ③将②③代入①得：222222333x y z x yz xy z x yz xy z xyz ++≤++即：222xy yz zx x y z ++≤++ ④由柯西不等式：()()()2222222x y z y z x xy yz zx ++++≥++即：()()22222x y z xy yz zx ++≥++即：222x y z xy yz zx ++≥++ ⑤ ⑤式④式等价，这就证明了④式是成立的，而缪尔海德不等式直接得到①式是成立的. ⑤式可以用[,,][,,]T 200T 110≥来表示，这正是缪尔海德不等式的()48式.Ch18.卡拉玛塔不等式18.1设在实数区间I R ∈的函数f 为向下凸函数，且当,i i a b I ∈（,,...,i 12n =）两个序列()n i i 1a =和()n i i 1b =满足()()i i a b >，则： ()()...()()()...()12n 12n f a f a f a f b f b f b +++≥+++ ()50()5018.2若函数f 为严格向下凸函数，即不等取等号，()()i i a b ≠，且()()i i a b >，则：()()...()()()...()12n 12n f a f a f a f b f b f b +++>+++ ()51若函数f 为严格向上凸函数，则卡拉玛塔不等式反向.Ch19.单调函数不等式19.1若实数函数:(,)f a b R →在区间(,)a b 对一切,(,)x y a b ∈为单调增函数，则当x y ≥时，有()()f x f y ≥；若f 在区间(,)a b 对一切,(,)x y a b ∈为严格单调增函数，当x y >时，有()()f x f y >.19.2若实数函数:(,)f a b R →在区间(,)a b 对一切,(,)x y a b ∈为单调减函数，则当x y ≥时，有()()f x f y ≤；若f 在区间(,)a b 对一切,(,)x y a b ∈为严格单调减函数，当x y >时，有()()f x f y <.19.3若实数函数:(,)f a b R →在区间(,)a b 为可导函数，当对一切(,)x a b ∈，'()f x 0≥，则f 在区间(,)a b 为单调递增函数；当对一切(,)x a b ∈，'()f x 0≤，则f 在区间(,)a b 为单调递减函数.19.4设两个函数:[,]f a b R →和:[,]g a b R →满足下列条件：⑴ 函数f 和g 在[,]a b 区间是连续的，且()()f a g a =；⑵ 函数f 和g 在[,]a b 区间可导；⑶ 导数'()'()f x g x >对一切(,)x a b ∈成立，则对一切(,)x a b ∈有：()()f x g x > ()52()52Ch20.3个对称变量pqr 法20.1设,,x y z R +∈，对于具有变量对称形式的不等式，采用下列变量代换：p x y z =++；q xy yz zx =++；r xyz =，则,,p q r R +∈.代换后的不等式(,,)f p q r ，很容易看出其满足的不等式关系，这样证明不等式的方法称为pqr 法.20.2常用的代换如下：⑴22cyc x p 2q =-∑ ⑵ ()32cycx p p 3q 3r =-+∑⑶ 222cycx y q 2pr =-∑⑷ ()()()x y y z z x pq r +++=-⑸()()2cyc x y y z p q ++=+∑ ⑹ ()cycxy x y pq 3r +=-∑⑺ ()()()1x 1y 1z 1p q r +++=+++⑻ ()()cyc1x 1y 32p q ++=++∑⑼()()2cyc cycx y z xy x y pq 3r +=+=-∑∑20.3常用的pqr 法的不等式若,,x y z 0≥，则：⑴ 3p qr 4pq +≥⑵ pq 9r ≥⑶ 2p 3q ≥⑷ 3p 27r ≥⑸ 32q 27r ≥⑹ 2q 3pr ≥⑺ 32p 9r 7pq +≥⑻ 322p 9r 7pqr +≥⑼ 22p q 3pr 4q +≥Ch21.3个对称变量uvw 法21.1在,,a b c R ∈的不等式中，采用下列变量代换：3u a b c =++；23v ab bc ca =++；3w abc =.上述变换强烈含有“平均”的意味：u 对应“算术平均值”；v 对应“积均值”；w 对应“几何平均值”. 21.2当,,a b c 0≥时，则：u v w ≥≥ ()53()53即：“算术平均值”≥“积均值”≥“几何平均值”.21.3若,,a b c 0≥，则,,23u v w 0≥ ()54()5421.4若,,23u v w R ∈，任给,,a b c R ∈，则当且仅当22u v ≥，且[32323w 3uv 2u 3uv 2u ∈---+时， 则：3u a b c =++，23v ab bc ca =++，3w abc =等式成立.这称为uvw 定理.Ch22.ABC 法22.1 ABC 法即Abstract Concreteness Method设p x y z =++；q xy yz zx =++；r xyz =.则函数(,,)f x y z 变换为(,,)f r q p .这与Ch20.3个对称变量pqr 法类似.22.2若函数(,,)f r q p 是单调的，则当()()()x y y z z x 0---=时，(,,)f r q p 达到极值. 22.3若函数(,,)f r q p 是凸函数，则当()()()x y y z z x 0---=时，(,,)f r q p 达到极值. 22.4若函数(,,)f r q p 是r 的线性函数，则当()()()x y y z z x 0---=时，(,,)f r q p 达到极值. 22.5若函数(,,)f r q p 是r 的二次三项式，则当()()()x y y z z x 0---=时，(,,)f r q p 达到极值.Ch23.SOS 法23.1 SOS 法即Sum Of Squares23.2本法的全部思想是将给出的不等式改写成以下形式：()()()222a b c S S b c S a c S a b =-+-+- ()55其中，,,a b c S S S 分别都是,,a b c 的函数.⑴ 若,,a b c S S S 0≥，则S 0≥；⑵ 若a b c ≥≥或a b c ≤≤，且,,b b a b c S S S S S 0++≥，则S 0≥； ⑶ 若a b c ≥≥或a b c ≤≤，且,,,a c a b c b S S S 2S S 2S 0++≥，则S 0≥； ⑷ 若a b c ≥≥，且,,22b c b a S S a S b S 0+≥，则S 0≥；⑸ 若a b S S 0+≥或b c S S 0+≥或c a S S 0+≥，且a b b c c a S S S S S S 0++≥，则S 0≥. 23.3 常用的形式⑴ ()22cyc cyc cyc1a ab a b 2-=-∑∑∑ ⑵ ()32cyc cyc cyc1a 3abc a a b 2-=⋅-∑∑∑ ⑶ ()223cyc cyccyc 1a b ab a b 3-=-∑∑∑ ⑷ ()()322cyc cyc cyc1a a b 2a b a b 3-=+-∑∑∑ ⑸()333cyc cyccyc cyc 1a b ab a b a 3-=⋅-∑∑∑∑ ⑹ ()()42222cyc cyc cyca ab 2a b a b -=+-∑∑∑ Ch24.SMV 法24.1 SMV 法即Strong Mixing Variables Method本法对多于2个变量的对称不等式非常有用.24.2 设(,,...,)12n x x x 为任意实数序列，⑴ 选择,{,,...,}i j 12n ∈使min{,,...,}i 12n x x x x =，max{,,...,}j 12n x x x x =；⑵ 用其平均数i j x x 2+代替i x 和j x ，经过多次代换后各项i x （,,...,i 12n =）都趋于相同的极限...12n x x x x n+++=. 24.3 设实数空间的函数F 是一个对称的连续函数，满足(,,...,)(,,...,)12n 12n F a a a F b b b ≥ ()56其中，(,,...,)12n b b b 序列是由(,,...,)12n a a a 序列经过预定义变换而得到的.预定义变换可根据当前的题目灵活采用，如a b2+. 24.4 例题说明例题：设实数,,a b c 0>，证明：a b c 3b c c a a b 2++≥+++. 解析：采用SMV 法. 设：(,,)a b c f a b c b c c a a b =+++++ ① 则：(,,)t t c 2t c f t t c t c c t t t t c 2t =++=+++++ ② 其中，a b t 2+=. 由②得：(,,)()()2t c 112t c t 113f t t c 2t c 2t 22t c 2t 222+=++-=+-≥-=++ 由()56式得：(,,)(,,)3f a b c f t t c 2≥≥证毕. Ch25.拉格朗日乘数法25.1 设函数(,,...,)12n f x x x 在实数空间的I R ∈连续可导，且(,,...,)i 12n g x x x 0=，其中（,,....i 12k =），即有k 个约束条件，则(,,...,)12n f x x x 的极值出现在I 区间的边界或偏导数（函数为ki i i 1L f g λ==-∑）全部为零的点上.Ch26.三角不等式26.1 设,,(,)0αβγπ∈，且αβγπ++=，则,,αβγ就是同一个三角形的内角. 26.2 若,,αβγ为同一个三角形的内角，则有下列不等式：⑴ sin sin sin αβγ++≤； ⑵ cos cos cos 32αβγ++≤；⑶ sin sin sin αβγ≤⑷ cos cos cos 18αβγ≤； ⑸ sin sin sin 22294αβγ++≤； ⑹ cos cos cos 22234αβγ++≥； ⑺ tan tan tan αβγ++≥；⑻ cot cot cot αβγ++≥；⑼ sinsin sin 32222αβγ++≤；⑽ coscos cos 222αβγ++≤； ⑾ sinsin sin 12228αβγ≤；⑿ cos cos cos 2228αβγ≤； ⒀ sin sin sin 22232224αβγ++≥； ⒁ cos cos cos 22292224αβγ++≤； ⒂ tan tan tan222αβγ++≥⒃cotcotcot222αβγ++≥Ch27.习题27.1 设,,...,(,]12n x x x 01∈，求证：()()...()321111x x x n 12n 1x 1x 1x 2+++≥.27.2 设,,...,12n x x x 0≥，且...12n 1x x x 2+++=，求证：()()...()12n 11x 1x 1x 2---≥. 27.3 设,,...,12n a a a R +∈，且...12n a a a 1=......12n a a a +≤+++. 27.4 设,,a b c 0>，且abc 1=，求证：333a b c ab bc ca ++≥++. 27.5 设,,,a b c d 0>，求证：a b c d 2b 2c 3d c 2d 3a d 2a 3b a 2b 3c 3+++≥++++++++.27.6 设,,a b c 0>，求证：222a bc b ca c aba b c b c c a a b+++++≥+++++. 27.7设,a b 0>，n N ∈，求证：()()n n n 1a b112b a++++≥.27.8 设,,...,12n x x x R +∈，且...22212n x x x 1+++=，若n N ∈，n 2≥，求(,,...,)...()()()555n 1212n nnni 1i 2i ni 1i 1i 1x x x f x x x x x x x x x ====+++---∑∑∑的最小值.27.9 设,,a b c R +∈，且a b c abc ++=32≤. 27.10 设,,a b c R ∈2. 27.11设,,a b c R +∈，且ab bc ca 3++=,求证：()()()2221a 1b 1c 8+++≥.27.12设,,a b c 0>，且a b c 1++=，求证：()()3332226a b c 15a b c +++≥++. 27.13设,,a b c 0≥，且a b c 2++=，求证：444333a b c abc a b c +++≥++. 27.14设,,a b c 0>，求证：()()()()3333338a b c a b b c c a ++≥+++++.27.15设,,a b c 0≥，求证：()33331a b c abc a b c 7+++≥++. 27.16设,,a b c 0>，且a b c 1++=，求证：2224a b c 3abc 9+++≥. 27.17设,,...,12n a a a 0>，求证：()()...()()()...()222n 1212n 231a a a 1a 1a 1a 111a a a +++≤+++.27.18设,,,a b c d 0>，且abcd 1=，求证：()()()()2222111111a 1b 1c 1d +++≥++++.27.19设,,,a b c d 0≥，且a b c d 4+++=，求证：()()()()2222abc bcd cda dab abc bcd cda dab 8+++++++≤.27.20设,,a b c 0≥，且222a b c 3++=，求证：222222a b b c c d a b c ++≤++.27.21设,,a b c R ∈，求证：()()()2222223333333a ab b b bc c c ca a a b b c c a -+-+-+≥++.27.22设,,,a b c d 0>，且a b c d abcd 5++++=，求证：11114a b c d+++≥.27.23设不等式：()()()()2222222222ab a b bc b c ca c a M a b c -+-+-≤++对一切实数,,a b c 都成立，求M 的最小值.27.24设,,a b c 0≥，且a b c 3++=，求证：()()222a b b c c a ab bc ca 9++++≤.Ch27.习题解析27.1 设,,...,(,]12n x x x 01∈，求证：()()...()321111x x x n 12n 1x 1x 1x 2+++≥.解析：设：n 11x x +=，则：因为i x 01(,]∈，所以i11x [,)∈+∞ （i 12n ,,...,=） 由伯努利不等式2()：当i x 1>-且i 1[,)α∈+∞时，i i i i 1x 1x ()αα+≥+ ①iff i x 0=或i 1α=时，①式等号成立.由均值不等式3()：i i 1x α+≥ ②iff i i x 1α=时，②式等号成立.由①②式得：i i 1x ()α+≥ ③iff i i x 1α==时， ③式等号成立.设：i i 11x α+=，则由③式得：i 11x i 1x ()++≥ ④则：21x 11x ()+≥31x 21x ()+≥11x n 1x ()+≥上面各式相乘得：321111x x x n 12n 1x 1x 1x 22()()...()+++≥=. 证毕.27.2 设,,...,12n x x x 0≥，且...12n 1x x x 2+++=，求证：()()...()12n 11x 1x 1x 2---≥. 解析：因为i x 0≥，ni i 11x 2==∑，所以i 1x 02[,]∈ 设i i y x =-，则i 1y 012[,]∈->-由伯努利不等式1()：12n 12n 1y 1y 1y 1y y y ()()...()(...)+++≥++++ ① 将i i y x =-代入①式，并代入...12n 1x x x 2+++=得： 12n 12n 111x 1x 1x 1x x x 122()()...()(...)---≥-+++=-=. 证毕.27.3 设12n a a a 0,,...,>，且...12n a a a 1=......12n a a a +≤+++. 解析：因为12n a a a 0,,...,>，且...12n a a a 1=，所以由均值不等式3()n ...++≥=1≥ ①iff 12n a a a 1...====时，①式等号成立.由柯西不等式8()：2222222111...](...)...++++++≥+ 即：212n a a a n (...)...+++⋅≥+即：12n a a a (...)...+++≥+ ②iff 12n a a a 1...====时，②式等号成立.将①式代入②式得：12n a a a ......+++≥+ ③iff 12n a a a 1...====时， ③式等号成立. 证毕.27.4 设,,a b c 0>，且abc 1=，求证：333a b c ab bc ca ++≥++. 解析：因为,,a b c 0>，且abc 1=，所以由均值不等式3()：222222222a b b c c a a b c ab bc ca 222+++++=++≥++ ① iff a b c 1===时，①式等号成立.由均值不等式3()：a b c 3++≥=，即：a b c13++≥ ② iff a b c 1===时，②式等号成立.WLOG ，设a b c ≤≤，则因为,,a b c 0>，所以222a b c ≤≤由切比雪夫不等式14()：222222a b c a b c 3a a b b c c ()()()++++≤⋅+⋅+⋅ 即：333222a b ca b c a b c 3()++++≥⋅++ ③ iff a b c 1===时，③式等号成立.将①②代入③式得：333a b c ab bc ca ++≥++ ④iff a b c 1===时， ④式等号成立. 证毕.27.5 设,,,a b c d 0>，求证：a b c d 2b 2c 3d c 2d 3a d 2a 3b a 2b 3c 3+++≥++++++++.解析：记A b 2c 3d =++，B c 2d 3a =++，C d 2a 3b =++，D a 2b 3c =++则：aA bB cC dD 4ab ac ad bc bd cd ()+++=+++++ ① 待证式为：a b c d 2A B C D 3+++≥ ② 由柯西不等式8()：2a b c daA bB cC dD a b c d A B C D()()()++++++≥+++ 即：2a b c d a b c d A B C D aA bB cC dD ()++++++≥+++ ③由②③式，只需证明2a b c d 2aA bB cC dD 3()+++≥+++ ④ 设多项式：P x x a x b x c x d ()()()()()=++++43201234c x c x c x c x c =++++则： 1c a b c d =+++ ⑤2c ab ac ad bc bd cd =+++++代入①式得：2aA bB cC dD 4c +++= ⑥ 根据定义38()：k k k nc p C =得：11114c c p C 4==，即：11c 4p =；22224c c p C 6==，即：22c 6p = 则：2221112222c 16p p 24c a b cd aA bB cC 6p 3D p d 4()==⋅++⋅+++=+ ⑦ 由麦克劳林不等式40()：1212p p ≥，即：212p 1p ≥代入⑦式得：2a b c d aA bB c dD 23C ()++++≥++，④式得证. iff a b c d ===时，等号成立. 证毕.27.6 设,,a b c 0>，求证：222a bc b ca c aba b c b c c a a b +++++≥+++++.解析：不等式左边=222a b c b c c b c c b c a c a a bba a ab +++++++++++ 不等式右边=()()()a c ab a bc b c a b c c a a b b c +++++=+++++222ab a ac b c c a b c c a a b b c ca b b =+++++++++++ 则不等式其实就是：222222a b c c a b b c c a a b b c c a a b++≥++++++++ ① 由于是对称不等式，WLOG ，假设a b c ≥≥，则222a b c ≥≥ ②且b c a c a b +≤+≤+，即：111b c c a a b≥≥+++ ③ 则有排序不等式()18：222222a b c c a b b c c a a b b c c a a b ++≥++++++++ 其中，222a b c b c c a a b +++++为正序和；222c a b b c c a a b+++++为乱序和. iff a b c ==时，等号成立. 证毕.27.7设,a b 0>，n N ∈证：()()n n n 1a b112b a++++≥.解析：当n 0=时，()()00a b112b a+++=，0122+=，不等式成立；当n 1=时，()()11a b a b1124b a b a+++=++≥，1124+=，不等式成立；当n 2≥时，构建函数()n f x x =. 则函数的导数'()n 1f x nx -=；二次导数''()()n 2f x n n 1x 0-=-≥，故在x 0>时函数为向下凸函数. 由琴生不等式()20：()()()1212f x f x x x f 22++≥ ①将()()n 1a f x 1b =+，()()n 2bf x 1a=+ ，()()()[][()]n n n 12b a 11x x 1b a a b f 12222a b++++==++≥ 带入①式得：()()n nn a b11b a 22+++≥，即：()()n n n 1a b 112b a ++++≥ 综上，当n 0=、n 1=和n 2≥时， ()()n n n 1a b112b a ++++≥都成立,即n N ∈时，()()n n n 1a b112b a++++≥成立. 证毕.27.8 设,,...,12n x x x R +∈，且...22212n x x x 1+++=，若n N ∈，n 2≥，求(,,...,)...()()()555n 1212n nnni 1i 2i ni 1i 1i 1x x x f x x x x x x x x x ====+++---∑∑∑的最小值.解析：记ni i 1S x ==∑，（,,...,i 12n =）.则(,,...,) (555)n 1212n 12nx x x f x x x S x S x S x =+++---①WLOG 假设...12n x x x ≥≥≥，则...44412n x x x ≥≥≥ ② 由于ni i 1S x ==∑，所以()nk i k i 1S x x x =-=-∑与k x 无关，则kkx S x -与k x 同单调性. 即：...n 1212nx x x S x S x S x ≥≥≥--- ③ 由切比雪夫不等式14()：若(,,...,)12n a a a 与(,,...,)12n b b b 同单调性，则有：12n 12n 1122n n a a a b b b n a b a b a b (...)(...)(...)++++++≤+++ ④设：4i i a x =，ni nx b S x =-，（,,...,i 12n =），则满足{}i a 与{}i b 同单调性.代入④式得：(...)(...)(...)4444n n 111n 1n 1n 1nx x x x x x n x x S x S x S x S x ++++≤⋅++⋅----即：......()(...)5445n 1n n 111n 1n x x x x x xf S x S x n S x S x ++=++≥⋅++---- ⑤由均值不等式()3：n n Q A ≥...221n x x 1n n ++=故：...441n 1x x n++≥ ⑥ 构建函数：()xg x S x=- ⑦ 则导函数：'()()2S g x S x =-，''()()32Sg x 0S x =>- 故()g x 为向下凸函数.由琴生不等式21()：(...)()()...()1122n n 1122n n g x x x g x g x g x αααααα+++≤+++ 取加权i 1nα=（,,...,i 12n =）时，上式变为： ...()()...()()12n 12n x x x g x g x g x g n n++++++≤⑧ 即：...()()...()()12n12n x x x g x g x g x n g n++++++≥⋅即：.........12n n 112n 1nx x x Sx x n n n n n x x x S S x S x n 1S S n n +++++≥⋅=⋅=+++-----⑨ 将⑥和⑨式代入⑤式得：...()55n 11n x x 11n 1f S x S x n n n 1n n 1=++≥⋅⋅=---- 故：(,,...,)12n f x x x 的最小值是()1n n 1-.27.9 设,,a b c R +∈，且a b c abc ++=32≤. 解析：在圆锥曲线里，椭圆方程为：2222x y 1ab+=时，常常采用的参数方程是：cos x a θ=，sin y b θ=，因为将它带入方程时满足cos sin 221θθ+=，这个三角函数的基本关系. 对于三角形的内角,,A B C ，同样有关系A B C π++=和tan tan tan tan tan tan A B C A B C ++=. 而本题初始条件a b c abc ++=.设tan a A =.tan b B =，tan c C =，因为,,a b c R +∈，所以,,(,)A B C 02π∈ ①则当,,A B C 为三角形的内角时，A B C π++=， tan tan tan tan tan tan A B C A B C ++=满足条件. 带入不等式左边得：+=cos cos cos A B C =++ ②构建函数()cos f x x =-，则在(,)x 02π∈区间函数()f x 为向下凸函数，故由琴生不等式21()得：函数值的均值不小于均值的函数值.1122n n 1122n n f x x x f x f x f x (...)()()...()αααααα+++≤+++ ③当加权...12n 1nααα====时，③式变为： ()()...()...()12n 12nf x f x f x x x x f n n++++++≥即：()()()()f A f B f C A B Cf 33++++≥ ④即：cos cos cos cos()cos A B C A B C 13332π++++-≥-=-=-即：cos cos cos 3A B C 2++≤ ⑤32+≤. 证毕.27.10 设,,a b c R ∈++≥.解析：因为,,a b c R ∈，由柯西不等式12()式...+≥++=≥2==.≥证毕. 27.11设,,a b c R +∈，且ab bc ca 3++=,求证：()()()2221a 1b 1c 8+++≥. 解析：对赫尔德不等式32()：jjm nn mijij i 1j 1j 1i 1aa ()()αα====≤∑∏∏∑ 32()当 n 4=，m 4=，123414αααα====时，32()式为： ()()()()1111444411121314212223243132333441424344a a a a a a a a a a a a a a a a +++[()()()()]1411213141122232421323334314243444a a a a a a a a a a a a a a a a ≤++++++++++++即：()()()()11213141122232421323334314243444a a a a a a a a a a a a a a a a ++++++++++++[()()()()]11114444411121314212223243132333441424344a a a a a a a a a a a a a a a a ≥+++ ①设：11a 1=，221a a =，231a b =，2241a a b =；12a 1=，2222a c a =，232a c =，242a a =； 13a 1=，223a c =，2233a b c =，243a b =；14a 1=，24a 1=，34a 1=，44a 1=.代入①式得：()()()()2222222222221a b a b 1c a c a 1c b c b 1111+++⋅+++⋅+++⋅+++[()()()()]1111222222222222444441111a c a c 1b c b c 1a b a b 1≥⋅⋅⋅+⋅⋅⋅+⋅⋅⋅+⋅⋅⋅ ()41ac bc ab =+++ ②②式就是赫尔德不等式.()()()2222221a 1b 1c +++()()()()()()2222221a 1b 1c 1a 1b 1c =++⋅++⋅++()()()2222222222221a b a b 1c a c a 1b c b c =+++⋅+++⋅+++()()()()222222222222222211a b a b 1c a c a 1b c b c 11114=+++⋅+++⋅+++⋅+++ ()()()()222222222222222211a b a b 1c a c a 1c b c b 11114=+++⋅+++⋅+++⋅+++ 将②式代入上式得：(())()()2222224111a 1b 1c 4ac bc ab ++++++≤开方出来即：()()()()222211a 1b 1c 21ac bc ab ++++++≤③ 将ab bc ca 3++=代入③式得：()()(())222211a 1b 1c 8213++++=≤. iff a b c 1===时等号成立. 证毕.27.12设,,a b c 0>，且a b c 1++=，求证：()()3332226a b c 15a b c +++≥++. 解析：采用pqr 法.设：p a b c =++，q ab bc ca =++，r abc =，则：p 1=⑴22cycx p 2q=-∑； ⑵ ()32cycx p p 3q 3r =-+∑则：2222a b c p 2q ++=-；()3332a b c p p 3q 3r 13q 3r ++=-+=-+于是，待证式变为：()()2613q 3r 15p 2q -++≥-即：28q 18r 0-+≥，即：14q 9r 0-+≥，即：3p 4pq 9r 0-+≥ ①⑴ 3p qr 4pq +≥，即：3p 4pq 9r 0-+≥ 故：①式成立，即待证式成立. 证毕.27.13设,,a b c 0≥，且a b c 2++=，求证：444333a b c abc a b c +++≥++. 解析：由舒尔不等式()43：()()()()()()t t t x x y x z y y z y x z z x z y 0--+--+--≥ ① 即：()()()t 2t 2t 2x x xy xz yz y y yz xy zx z z zx yz xy 0--++--++--+≥ 即：()()()()()()t 2t 2t 2t 1t 1t 1x x yz y y zx z z xy x y z y z x z x y ++++++++≥+++++ 即：()()()t 2t t 2t t 2t t 1t 1t 1x x yz y xy z z xyz x y z y z x z x y +++++++++++≥+++++ 即：()()()()t 2t 2t 2t 1t 1t 1t 1t 1t 1x y z x y z xyz x y z y z x z x y +++---++++++++≥+++++ 两边都加t 2t 2t 2x y z +++++得：()()()()t 2t 2t 2t 1t 1t 1t 1t 1t 12x y z x y z xyz x y z x y z +++---++++++++≥++++ ② ②式就是舒尔不等式.设t 2=，代入②式得：()()()()4443332x y z x y z xyz x y z x y z +++++≥++++ 将a b c 2++=代入上式得：()()4443332x y z 2xyz 2x y z +++≥++ 即：444333a b c abc a b c +++≥++ ③ ③式就是我们要证明的不等式. 证毕.27.14设,,a b c 0>，求证：()()()()3333338a b c a b b c c a ++≥+++++.解析：待证式化为：()()()3333332222228a b c 2a b c 3a b ab b c bc c a ca ++≥++++++++。

课题：第二节分子的立体构型第1课时价层电子对互斥理论授课班级课时教学目的知识与技能1.认识共价分子的多样性和复杂性2.初步认识价层电子对互斥模型；3.能用VSEPR模型预测简单分子或离子的立体结构；过程与方法情感态度价值观培养学生严谨认真的科学态度和空间想象能力重点分子的立体结构；利用价层电子对互斥模型预测分子的立体结构难点价层电子对互斥理论知识结构与板书设计第二节分子的立体构型一、形形色色的分子1.三原子分子立体结构：有直线形C02、CS2等，V形如H2O、S02等。

2.四原子分子立体结构：平面三角形：如甲醛(CH20)分子等，三角锥形：如氨分子等。

3.五原子分子立体结构：正四面体形如甲烷、P4等。

4.测分子体结构：红外光谱仪→吸收峰→分析。

二、价层电子对互斥模型1.价层电子互斥模型2.价层电子对互斥理论：对ABn型的分子或离子，中心原子A价层电子对（包括用于形成共价键的共用电子对和没有成键的孤对电子）之间存在排斥力，将使分子中的原子处于尽可能远的相对位置上，以使彼此之间斥力最小，分子体系能量最低。

3.价层电子对互斥模型：(1)中心原子上的价电子都用于形成共价键：分子中的价电子对相互排斥的结果(2)中心原子上有孤对电子：孤对电子也要占据中心原子周围的空间，并参与互相排斥，使分子的空间结构发生变化。

4. 价层电子对互斥理论的应用(1)确定中心原子A价层电子对数目(2) 价电子对数计算方法(3)确定价层电子对的空间构型(4) 分子空间构型确定教学过程教学步骤、内容教学方法、手段、师生活动[复习]共价键的三个参数。

[过渡]我们知道许多分子都具有一定的空间结构，如：……，是什么原因导致了分子的空间结构不同，与共价键的三个参数有什么关系？我们开始研究分子的立体结构。

[板书]第二节分子的立体构型一、形形色色的分子[讲]大多数分子是由两个以上原子构成的，于是就有了分子中的原子的空间关系问题，这就是所谓“分子的立体结构”。

Ch1：均变论、灾变论、太阳系、类地行星、类木行星、小行星Ch2：晶体、非晶体、条痕、硬度、光泽、解理、硅氧四面体Ch3:：岩浆、熔岩、玄武岩柱状节理、绳状熔岩、枕状熔岩、火山锥、火山口、岩浆房、环太平洋火山带、侵入岩、围岩、同化作用、混染作用、鲍文反应系列、岩脉、岩床、岩株、岩基、显晶质结构、隐晶质结构、非晶质结构、斑状结构、火成碎屑结构、气孔构造、杏仁构造、部分熔融Ch4：搬运作用、沉积作用、压固作用、胶结作用、成岩作用、分选、磨圆、层理、交错层理、层面、递变层理、波痕、泥裂、缝合线Ch5：变质作用、静压力、定向压力、化学活动流体、脱水反应、脱CO2反应、变晶、变晶结构、片理、片麻理、接触热变质、接触交代、区域变质、埋藏变质、混和岩化、混和花岗岩Ch6：物理风化、化学风化、差异风化、球形风化、风化壳、土壤、古风化壳、残积物Ch7；岩层的产状要素、褶曲要素（轴面、核、翼、枢纽）、背斜和向斜、断层要素（断层面、盘、断距），正断层、逆断层、走滑断层、逆掩断层、断层擦痕、拖曳褶曲、三角面山Ch8：地壳、地幔、地核、莫霍面、古登堡面、岩石圈、软流圈、大陆地壳、大洋地壳、均衡原理、震源、震中、海啸、地震波、纵波、横波、表面波、P波阴影带、S波阴影带、震级、地震烈度、环太平洋地震带、地中海-印尼地震带、洋中脊地震带、陨石Ch9：块体运动：山坡上块体的向下运动称为块体运动。

稳定角：倒石堆锥坡达33°-37°，是为稳定角。

因为碎屑堆积体只有达到这一坡角才能保持稳定。

滑坡：块体沿着上凹的弧形滑面下滑，同时绕水平轴向内旋转。

倒石锥：崩落与崩滑的碎屑落在山麓的堆积体呈顶端朝上的锥形，称为倒石堆。

泥石流：斜坡上或沟谷中松散碎屑物质被暴雨或积雪、冰川消融水所饱和，在重力作用下，沿斜坡或沟谷流动的一种特殊洪流。

特点是爆发突然，历时短暂，来势凶猛和巨大的破坏力。

蠕变：是粒流中运动速度极其缓慢的一种。

它出现在山坡的表层。

氨气空间结构三角锥知乎
氨气（NH3）的空间结构是一个三角锥形。

氨气分子由一个氮原
子和三个氢原子组成，氮原子位于分子的中心，而三个氢原子则均
位于氮原子周围。

氮原子的电子排布为2s²2p³，其中一个2s轨道和三个2p轨
道参与了共价键的形成。

氮原子与每个氢原子之间形成了共价键，
共享了电子对。

氮原子的2s轨道和一个2p轨道形成了一个杂化轨道，称为sp³杂化轨道。

这四个sp³杂化轨道朝向空间的四个不同
方向，分别与三个氢原子的1s轨道重叠，形成了三个氮-氢共价键。

由于氮原子的sp³杂化轨道朝向四个不同方向，氨气分子的空
间结构呈现出三角锥形。

氮原子位于三个氢原子的中心，而三个氢
原子则均位于氮原子周围，形成了一个平衡稳定的结构。

这种三角锥形的空间结构使得氨气分子呈现出一定的极性。

由
于氮原子比氢原子的电负性更高，氮原子带有部分负电荷，而氢原
子则带有部分正电荷。

因此，氨气分子在空间中呈现出一个部分正
电荷和一个部分负电荷的极性分布。

总结起来，氨气的空间结构是一个三角锥形，氮原子位于分子的中心，而三个氢原子则均位于氮原子周围。

这种结构使得氨气分子呈现出一定的极性。

hclo- 分子构型
HClO-分子构型
HClO-分子是一种含有氢、氯和氧原子的共价分子，化学式为HClO-。

在这种分子中，氢原子和氯原子共用一对电子，氧原子和氯原子共用一对电子，氧原子上有三对孤对电子。

HClO-分子的构型是三角锥型，氧原子位于分子的中心，氢原子和氯原子分别位于氧原子的两侧。

HClO-分子的构型对于其化学性质有很大的影响。

由于氧原子上有孤对电子，可以与其他离子或分子形成氢键或配位键，因此HClO-分子具有很强的亲电性和配位能力。

此外，由于HClO-分子的构型中氢原子和氯原子的距离相对较近，因此HClO-分子可以通过氢键相互作用形成分子间或分子内的氢键键合物。

HClO-分子的构型也对于其物理性质有影响。

由于HClO-分子的构型是三角锥型，因此其分子极性较大，导致其在水中的溶解度较高。

此外，由于HClO-分子中含有氢键和氧键，因此其分子间作用力也比较强，使得HClO-分子的沸点和熔点较高。

在生物体内，HClO-分子也具有重要的作用。

HClO-分子是一种强氧化剂，可以通过氧化作用杀死细菌和病毒。

人体免疫系统中的白细胞可以产生HClO-分子来消灭入侵的病原体。

此外，HClO-分子也可以参与身体对抗炎症和感染的过程。

HClO-分子的构型是三角锥型，具有很强的亲电性和配位能力，分子极性较大，溶解度较高，沸点和熔点较高，可以通过氧化作用杀死细菌和病毒，在生物体内具有重要的作用。