大学 机械振动 课后习题和答案
- 格式:doc
- 大小:1.39 MB
- 文档页数:57
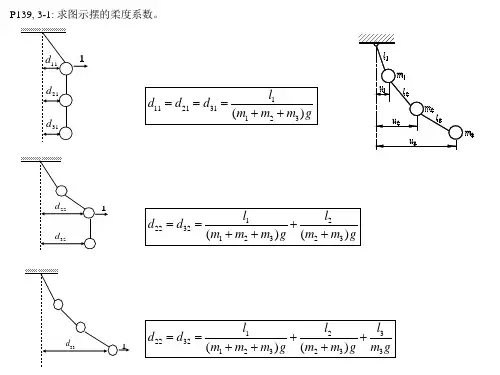

1.1试举出振动设计'系统识别和环境预测的实例。
1.2如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?1.3设有两个刚度分别为心,心的线性弹簧如图T-1.3所示,试证明:1)它们并联时的总刚度k eq为:k eq = k x+ k22)它们串联时的总刚度匕满足:丿-畔+ 土keq & k2解:1)对系统施加力P,则两个弹簧的变形相同为X,但受力不同,分别为: P x = k x x<由力的平衡有:P = ^ + P,=(k1+k2)xp故等效刚度为:k eq^- = k1+k2x2)对系统施加力P,则两个弹簧的变形为:P%i=r 111,弹簧的总变形为:x = x}+x2= P(——I ---- )故等效刚度为:k =—Xk x k2k,2+ k、1 1=—l-------k、k21.4求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为心, 解:对系统施加扭矩T,则两轴的转角为:VTrx系统的总转角为:0 = G + g = Hy- + T-)褊k,i故等效刚度为:犒=二+二1.5两只减振器的粘性阻尼系数分别为q, C2,试计算总粘性阻尼系数"在两只减振器并联时,2)在两只减振器串联时。
解:1)对系统施加力P,则两个减振器的速度同为厂受力分别为:P{ - c x x<P2=C2X由力的平衡有:P=£ + E =(q+C2)Xp故等效刚度为:c eq=- = c]+c2X2)对系统施加力P,则两个减振器的速度为:p 1 1故等效刚度为:c eq=- = - + -1.6 一简谐运动,振幅为0. 5cm,周期为0.15s,求最大速度和加速度。
解:简谐运动的a>n= — = /5),振幅为5x10 3m ;= 5x10-cos(^_ 2/r即:—5x10'丽fsin(丽血/s)*610=(話讥。
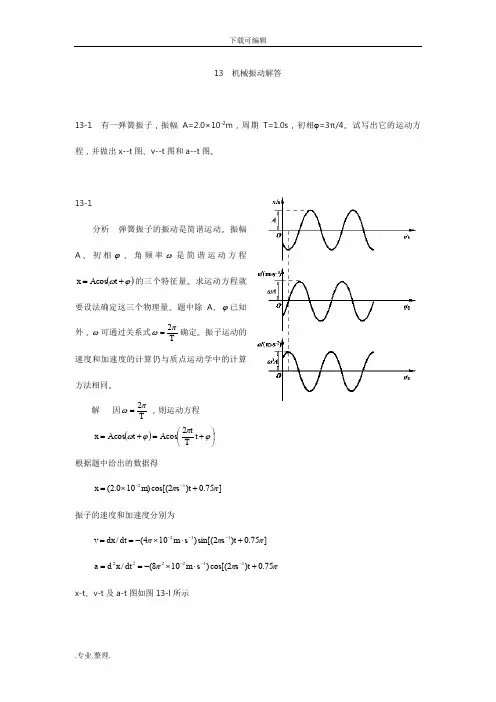
13 机械振动解答13-1 有一弹簧振子,振幅A=2.0×10-2m ,周期T=1.0s ,初相ϕ=3π/4。
试写出它的运动方程,并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外,ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
解 因Tπω2=,则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ,求:(1)振幅、频率、角频率、周期和初相;(2)t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较,即可求得各特征量。
运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t 值后,即可求得结果。
解 (l )将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得:振幅A= 0.10 m ,角频率120-=s πω,初相πϕ25.0=,则周期 s T 1.0/2==ωπ,频率Hz T 10/1==ν。
(2)t= 2s 时的位移、速度、加速度分别为m m x 21007.7)25.040cos()10.0(-⨯=+=ππ )25.040sin()2(/1πππ+⋅-==-s m dt dx v )25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体,密度ρ5.5×103kg •m -3。
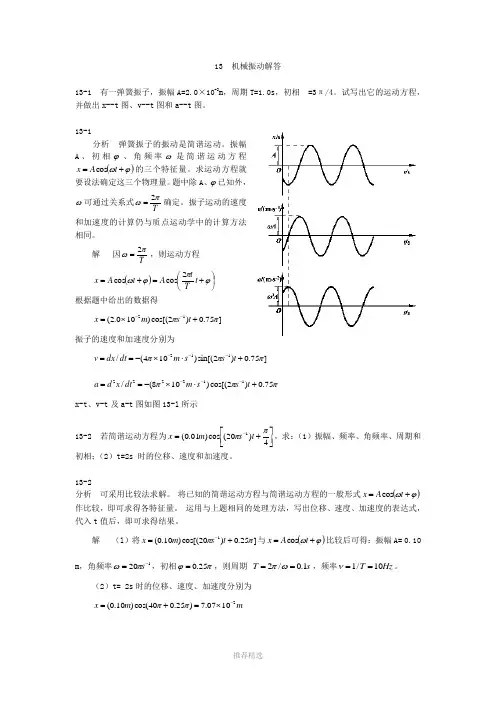
13 机械振动解答13-1 有一弹簧振子,振幅A=2.0×10-2m ,周期T=1.0s ,初相=3π/4。
试写出它的运动方程,并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外,ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
解 因Tπω2=,则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ,求:(1)振幅、频率、角频率、周期和初相;(2)t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较,即可求得各特征量。
运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t 值后,即可求得结果。
解 (l )将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得:振幅A= 0.10 m ,角频率120-=s πω,初相πϕ25.0=,则周期 s T 1.0/2==ωπ,频率Hz T 10/1==ν。
(2)t= 2s 时的位移、速度、加速度分别为mm x 21007.7)25.040cos()10.0(-⨯=+=ππ)25.040sin()2(/1πππ+⋅-==-s m dt dx v )25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体,密度ρ5.5×103kg •m -3。
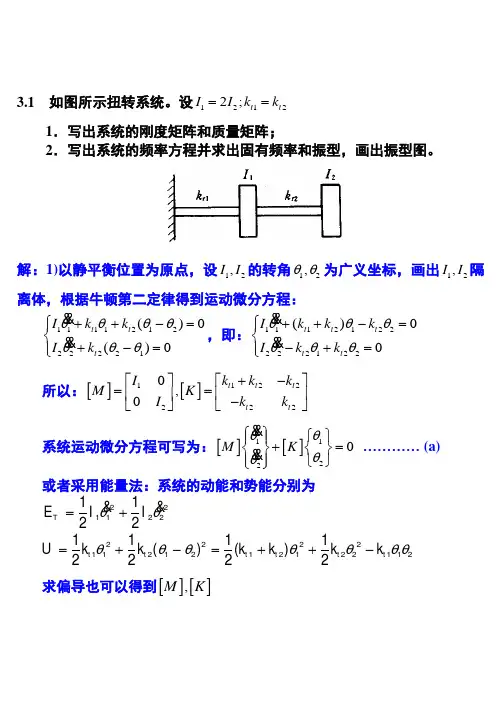
3.1 如图所示扭转系统。
设12122;t t I I k k ==1.写出系统的刚度矩阵和质量矩阵;2.写出系统的频率方程并求出固有频率和振型,画出振型图。
解:1)以静平衡位置为原点,设12,I I 的转角12,θθ为广义坐标,画出12,I I 隔离体,根据牛顿第二定律得到运动微分方程:111121222221()0()0t t t I k k I k θθθθθθθ⎧++-=⎪⎨+-=⎪⎩ ,即:1112122222122()00t t t t t I k k k I k k θθθθθθ⎧++-=⎪⎨-+=⎪⎩所以:[][]12212220,0t t t t t k k k I M K k k I +-⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦系统运动微分方程可写为:[][]11220M K θθθθ⎧⎫⎧⎫⎪⎪+=⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭………… (a)或者采用能量法:系统的动能和势能分别为θθ=+2211221122T E I I θθθθθθθ=+-=++-222211212121221121111()()2222t t t t t t U k k k k k k求偏导也可以得到[][],M K由于12122;t t I I k k ==,所以[][]212021,0111t M I K k -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦2)设系统固有振动的解为: 1122cos u t u θωθ⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭,代入(a )可得:[][]122()0u K M u ω⎧⎫-=⎨⎬⎩⎭………… (b)得到频率方程:22121211222()0t t t t k I k k k I ωωω--==--即:224222121()240t t I k I k ωωω=-+=解得:21,222ω==所以:1ω=2ω= ………… (c)将(c )代入(b )可得:112121211122(22220(22t t t t t t k k I k I u u k k k I I ⎡⎤±--⎢⎥⎧⎫⎢⎥=⎨⎬⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦解得:11212u u =-;12222u u =令21u ,得到系统的振型为:-0.70710.70713.2 求图所示系统的固有频率和振型。

一、选择题:1.3001:把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ [ ]2.3002:两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处。
则第二个质点的振动方程为:(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x [ ]3.3007:一质量为m 的物体挂在劲度系数为k 的轻弹簧下面,振动角频率为ω。
若把此弹簧分割成二等份,将物体m 挂在分割后的一根弹簧上,则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 [ ]4.3396:一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述,则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 v 与a5.3552期分别为T 1和T 2。
将它们拿到月球上去,相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >'[ ] 6.5178:一质点沿x 轴作简谐振动,振动方程为)312cos(1042π+π⨯=-t x (SI)。
从t = 0时刻起,到质点位置在x = -2 cm 处,且向x 轴正方向运动的最短时间间隔为(A) s 81 (B) s 61 (C) s 41 (D) s 31 (E)[ ]7.5179:一弹簧振子,重物的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动。

1.1 试举出振动设计、系统识别和环境预测的实例。
1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?1.3 设有两个刚度分别为1k ,2k 的线性弹簧如图T —1.3所示,试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 满足:21111k k k eq +=解:1)对系统施加力P ,则两个弹簧的变形相同为x ,但受力不同,分别为:1122P k xP k x=⎧⎨=⎩由力的平衡有:1212()P P P k k x =+=+故等效刚度为:12eq Pk k k x ==+2)对系统施加力P ,则两个弹簧的变形为: 1122Px k Px k ⎧=⎪⎪⎨⎪=⎪⎩,弹簧的总变形为:121211()x x x P k k =+=+故等效刚度为:122112111eq k k P k x k k k k ===++1.4 求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为1t k ,2t k 。
解:对系统施加扭矩T ,则两轴的转角为: 1122t t Tk T k θθ⎧=⎪⎪⎨⎪=⎪⎩系统的总转角为:121211()t t T k k θθθ=+=+,12111()eq t t k T k k θ==+故等效刚度为:12111eq t t k k k =+1.5 两只减振器的粘性阻尼系数分别为1c ,2c ,试计算总粘性阻尼系数eq c1)在两只减振器并联时,2)在两只减振器串联时。
解:1)对系统施加力P ,则两个减振器的速度同为x &,受力分别为:1122P c x P c x =⎧⎨=⎩&& 由力的平衡有:1212()P P P c c x =+=+&故等效刚度为:12eq P c c c x ==+& 2)对系统施加力P ,则两个减振器的速度为: 1122P x c P x c ⎧=⎪⎪⎨⎪=⎪⎩&&,系统的总速度为:121211()x x x P c c =+=+&&& 故等效刚度为:1211eq P c x c c ==+&1.6 一简谐运动,振幅为0.5cm,周期为0.15s,求最大速度和加速度。

第5章 机械振动一、选择题5-1 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为2A-,且向x 轴的正方向运动,代表这个简谐振动的旋转矢量图为[ ]分析与解 图中旋转矢量投影点的运动方向指向Ox 轴正向,同时矢端在x 轴投影点的位移为2A-,满足题意,因而选(D)。
5-2 作简谐振动的物体,振幅为A ,由平衡位置向x 轴正方向运动,则物体由平衡位置运动到32Ax =处时,所需的最短时间为周期的几分之几[ ] (A) 1 /2 (B) 1/4 (C) 1/6 (D) 1/12分析与解 设1t 时刻物体由平衡位置向x 轴正方向运动,2t 时刻物体第一次运动到32A x =处,可通过旋转矢量图,如图5-2所示,并根据公式2t T ϕπ∆∆=得31226t T T T ϕπππ∆∆===,,因而选(C)。
5-3 两个同周期简谐振动曲线如图5-3(a)所示,1x 的相位比2x 的相位[ ] O O OO A Axxx(A) (B)(D)(C)A /2-A /2 A /2 -A /2A Aωωωωx习题5-1图习题5-2图(A) 落后2π (B) 超前2π(C) 落后π (D) 超前π分析与解 可通过振动曲线作出相应的旋转矢量图(b ),正确答案为(B )。
5-4 一弹簧振子作简谐振动,总能量为E ,若振幅增加为原来的2倍,振子的质量增加为原来的4倍,则它的总能量为[ ](A) 2E (B) 4E (C) E (D) 16E 分析与解 因为简谐振动的总能量2p k 12E E E kA =+=,因而当振幅增加为原来的2倍时,能量变为原来的4倍,因而答案选(B)。
5-5 两个同振动方向、同频率、振幅均为A 的简谐振动合成后,振幅仍为A ,则这两个简谐振动的相位差为[ ](A) 60 (B) 90 (C) 120 (D) 180分析与解 答案(C )。
由旋转矢量图可知两个简谐振动的相位差为120时,合成后的简谐运动的振幅仍为A 。


2.1 弹簧下悬挂一物体,弹簧静伸长为δ。
设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:设物体质量为m ,弹簧刚度为k ,则:mg k δ=,即:n ω==取系统静平衡位置为原点0x =,系统运动方程为: δ⎧+=⎪=⎨⎪=⎩00020mx kx x x (参考教材P14)解得:δω=()2cos n x t t2.2 弹簧不受力时长度为65cm ,下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。
解:由题可知:弹簧的静伸长0.850.650.2()m =-= 所以:9.87(/)0.2n g rad s ω=== 取系统的平衡位置为原点,得到:系统的运动微分方程为:20n x x ω+=其中,初始条件:(0)0.2(0)0x x =-⎧⎨=⎩ (参考教材P14) 所以系统的响应为:()0.2cos ()n x t t m ω=-弹簧力为:()()cos ()k n mg F kx t x t t N ω===-因此:振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。
2.3 重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2m 从高度为h 处自由落到1m 上而无弹跳,如图所示,求其后的运动。
解:取系统的上下运动x 为坐标,向上为正,静平衡位置为原点0x =,则当m 有x 位移时,系统有: 2121()2T E m m x =+ 212U kx =由()0T d E U +=可知:12()0m m x kx ++= 即:12/()n k m m ω=+系统的初始条件为:⎧=⎪⎨=-⎪+⎩2020122m gx k m x gh m m (能量守恒得:221201()2m gh m m x =+) 因此系统的响应为:01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩200021122n m g A x k x m g ghk A k m m即:ωω=-2()(cos )n n m g x t t t k2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆心受到一弹簧k 约束,如图所示,求系统的固有频率。

13机械振动解答13-1 有一弹簧振子,振幅A=2.0 X 10-2m,周期T=1.Os ,初相=3 π /4。
试写岀它的运动方程,并做岀x--t图、v--t图和a--t图。
13-1分析弹簧振子的振动是简谐运动。
振幅A、初相「、角频率•■是简谐运动方程X=ACoSlQt亠。
的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A、「已知外,2 Tr-■ ■可通过关系式•=—确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
解因.=Z ,则运动方程TX=ACOS讥=ACOS i2 t t : !■ I1W尸I T丿根据题中给出的数据得X =(2.0 10 ^m)cos[( 2":S A)t 0.75二]振子的速度和加速度分别为V =dχ∕dt - 10^m s1)sin[(2∏s')t 亠0.75二]a =d2χ∕dt2二2 10 2m S 丄)cos[(2二S 丄)t 0.75二x-t、v-t及a-t图如图13-1所示13-2 若简谐运动方程为X =(0.01m)cos(20:s」)t ',求:(1)振幅、频率、角频率、周期和- 4初相;(2) t=2s时的位移、速度和加速度。
13-2分析可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式X=ACOS ∙∙t ■作比较,即可求得各特征量。
运用与上题相同的处理方法,写岀位移、速度、加速度的表达式,代入t值后,即可求得结果。
解 (l )将X =(0.10m)cos[(20 7s ^)t • 0.25 二]与X=ACOS lU t w]比较后可得:振幅A= 0.10m 角频率• =20二S1,初相=0.25二,则周期T =2TJ=0∙1s ,频率=1∕T =10Hz。
(2) t= 2s时的位移、速度、加速度分别为X =(0.10m)cos(40 二0.25 二)=7.07 10i mV =dx∕dt - -(2~'m S^)Sin(40,亠0.25二)a =d2x∕dt2 = J40 二2m s?)cos(40 ;亠0.25二)13-3设地球是一个半径为R的均匀球体,密度P 5.5 X 103kg? m3。
弹簧下悬挂一物体,弹簧静伸长为δ。
设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:设物体质量为m ,弹簧刚度为k ,则:mg k δ=,即:n ω== 取系统静平衡位置为原点0x =,系统运动方程为:δ⎧+=⎪=⎨⎪=⎩00020mx kx x x (参考教材P14)解得:δω=()2cos n x t t弹簧不受力时长度为65cm ,下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。
解:由题可知:弹簧的静伸长0.850.650.2()m =-= 所以:9.87(/)0.2n g rad s ω=== 取系统的平衡位置为原点,得到:系统的运动微分方程为:20n x x ω+=其中,初始条件:(0)0.2(0)0x x =-⎧⎨=⎩(参考教材P14) 所以系统的响应为:()0.2cos ()n x t t m ω=-弹簧力为:()()cos ()k n mg F kx t x t t N ω===- 因此:振幅为、周期为2()7s π、弹簧力最大值为1N 。
重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2m 从高度为h 处自由落到1m 上而无弹跳,如图所示,求其后的运动。
解:取系统的上下运动x 为坐标,向上为正,静平衡位置为原点0x =,则当m 有x 位移时,系统有:2121()2T E m m x =+212U kx =由()0T d E U +=可知:12()0m m x kx ++= 即:12/()n k m m ω=+系统的初始条件为:⎧=⎪⎨=-⎪+⎩2020122m gx k m x gh m m (能量守恒得:221201()2m gh m m x =+) 因此系统的响应为:01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩200021122n m g A x k x m g ghk A k m m即:ωω=-2()(cos )n n m g x t t t k一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆心受到一弹簧k 约束,如图所示,求系统的固有频率。
5-1有一弹簧振子,振幅 A 2.0 10 2m ,周期T 1.0s ,初相 3 / 4.试写出它的振 动位移、速度和加速度方程。
分析根据振动的标准形式得出振动方程,通过求导即可求解速度和加速度方程。
一 2解:振动方程为: x Acos[ t ] Acos[ t ] 一 3代入有关数据得: x 0.02 cos[2 t ]( SI ) 4振子的速度和加速度分别是:3 v dx/dt 0.04 sin[2 t ](SI ) 4a d 2x/dt 20.08 2 cos[2 t —](SI )45-2若简谐振动方程为 x 0.1cos[20 t /4]m ,求: (1) 振幅、频率、角频率、周期和初相; (2) t=2s 时的位移、速度和加速度.分析 通过与简谐振动标准方程对比,得出特征参量。
解:(1)可用比较法求解.根据x Acos[ t ]0.1cos[20 t /4](1)t=0时,作用于质点的力的大小;(2 )作用于质点的力的最大值和此时质点的位置分析 根据振动的动力学特征和已知的简谐振动方程求解,位移最大时受力最大。
得:振幅A 0.1m ,角频率20 rad / s ,频率/2 10s 1,周期T 1/0.1s ,/4rad(2) t 2s 时,振动相位为20 t/4(40/ 4) rad 由 x A cos ,A sin ,a A 2 cos2x 得x 0.0707m, 4.44m/s,a279m/s 25-3质量为2 kg 的质点,按方程x0.2sin[5t ( /6)](SI)沿着 x 轴振动.求:解:(1)跟据f ma m 2x,x 0.2sin[5t ( /6)]将t 0代入上式中,得:f 5.0N(2)由f m 2x可知,当x A 0.2m时,质点受力最大,为f 10.0N5-4为了测得一物体的质量 m 将其挂到一弹簧上并让其自由振动,测得振动频率1.0Hz ;而当将另一已知质量为 m'的物体单独挂到该弹簧上时,测得频率为22.0Hz .设振动均在弹簧的弹性限度内进行,求被测物体的质量分析根据简谐振动频率公式比较即可。
N O1机械振动答案本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March《大学物理AII 》作业 机械振动一、选择题:1.假设一电梯室正在自由下落,电梯室天花板下悬一单摆(摆球质量为m ,摆长为l ) 。
若使单摆摆球带正电荷,电梯室地板上均匀分布负电荷,那么摆球受到方向向下的恒定电场力F 。
则此单摆在该电梯室内作小角度摆动的周期为:[ C ] (A) Fm l π2 (B) Flmπ2(C) Fmlπ2 (D) mlF π2 解: 2.图(a)、(b)、(c)为三个不同的简谐振动系统。
组成各系统的各弹簧的原长、各弹簧的劲度系数及重物质量均相同。
(a)、(b)、(c)三个振动系统的2(为固有角频率)值之比为[ B ] (A) 2∶1∶21(B)1∶2∶4(C) 2∶2∶1 (D) 1∶1∶2解:由弹簧的串、并联特征有三个简谐振动系统的等效弹性系数分别为:2k,k ,k 2 则由m k=2ω可得三个振动系统的2(为固有角频率)值之比为:m k 2 :m k :m k2,即1∶2∶4 故选B 3.两个同周期简谐振动曲线如图所示。
则x 1的相位比x 2的相位 [ A ] (A) 超前/2 (B) 落后 (C) 落后 解:由振动曲线画出旋转矢量图可知x 1的相位比x 2的相位超前k m m mk k k k (b) (c) t x O x 1 x 2x 2A1A ω4.一物体作简谐振动,振动方程为)21cos(π+=t A x ω。
则该物体在t = T /8(T 为振动周期)时刻的动能与t = 0时刻的动能之比为: [ B ] (A) 1:4 (B) 1:2 (C) 1:1 (D) 2:1 (E) 4:1解:由简谐振动系统的动能公式:)21(sin 2122πω+=t kA E k有t = 0时刻的动能为:22221)2102(sin 21kA T kA =+⋅ππt = T /8时刻的动能为:22241)2182(sin 21kA T T kA =+⋅ππ,则在t = T /8时刻的动能与t = 0时刻的动能之比为:1:2二、填空题:1.用40N 的力拉一轻弹簧,可使其伸长10cm 。
t (s )v (m.s -1)12m v m vo1.3题图题图 第三章 机械振动一、选择题1.质点作简谐振动,距平衡位置2。
0cm 时,加速度a=4.0cm 2/s ,则该质点从一端运动到另一端的时间为(一端运动到另一端的时间为( C )A:1.2s B: 2.4s C:2.2s D:4.4s 解:解:s T t T xax a 2.2422,2222,22===\=====p pw pw w2.一个弹簧振子振幅为2210m -´,当0t =时振子在21.010m x -=´处,且向正方向运动,则振子的振动方程是:[ A ] A :2210cos()m3x t p w -=´-;B :2210cos()m 6x t pw -=´-;C :2210cos()m 3xt pw -=´+ ;D :2210cos()m 6x t pw -=´+;解:由旋转矢量可以得出振动的出现初相为:3p-3.用余弦函数描述一简谐振动,若其速度与时间(v —t )关系曲线如图示,则振动的初相位为:[ A ] A :6p ;B :3p ;C :2p ;D :23p ;E :56p解:振动速度为:max 0sin()v v t w j =-+0t =时,01sin2j =,所以06p j =或056p j = 由知1.3图,0t =时,速度的大小是在增加,由旋转矢量图知,旋转矢量在第一象限内,对应质点的运动是由正最大位移向平衡位置运动,速度是逐渐增加的,旋转矢量在第二象限内,对应质点的运动是由平衡位置向负最大位移运动,速度是逐渐减小的,所以只有06pj =是符合条件的。
符合条件的。
4.某人欲测钟摆摆长,将钟摆摆锤上移1毫米,测得此钟每分快0。
1秒,则此钟摆的摆长为(长为( B )A:15cm B:30cm C:45cm D:60cm 解:单摆周期解:单摆周期 ,2glT p=两侧分别对T ,和l 求导,有:求导,有:cm m m T dT dl l l dl T dT 3060)1.0(2121,21=-´-==\= 1.2题图题图xyoxy二、填空题1.有一放置在水平面上的弹簧振子。
一、选择题:1.3001:把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ [ ]2.3002:两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处。
则第二个质点的振动方程为:(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x [ ]3.3007:一质量为m 的物体挂在劲度系数为k 的轻弹簧下面,振动角频率为ω。
若把此弹簧分割成二等份,将物体m 挂在分割后的一根弹簧上,则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 [ ]4.3396:一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述,则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 v 与a5.3552期分别为T 1和T 2。
将它们拿到月球上去,相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >'[ ] 6.5178:一质点沿x 轴作简谐振动,振动方程为)312cos(1042π+π⨯=-t x (SI)。
从t = 0时刻起,到质点位置在x = -2 cm 处,且向x 轴正方向运动的最短时间间隔为(A) s 81 (B) s 61 (C) s 41 (D) s 31 (E)[ ]v v 217.5179:一弹簧振子,重物的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动。
试举出振动设计、系统识别和环境预测的实例。
如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?设有两个刚度分别为1k ,2k 的线性弹簧如图T —所示,试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 满足:21111k k k eq +=解:1)对系统施加力P ,则两个弹簧的变形相同为x ,但受力不同,分别为:1122P k xP k x=⎧⎨=⎩由力的平衡有:1212()P P P k k x =+=+故等效刚度为:12eq Pk k k x ==+2)对系统施加力P ,则两个弹簧的变形为: 1122Px k P x k ⎧=⎪⎪⎨⎪=⎪⎩,弹簧的总变形为:121211()x x x P k k =+=+故等效刚度为:122112111eq k k P k x k k k k ===++求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为1t k ,2t k 。
解:对系统施加扭矩T ,则两轴的转角为: 1122t t T k T k θθ⎧=⎪⎪⎨⎪=⎪⎩系统的总转角为:121211()t t T k k θθθ=+=+,12111()eq t t k T k k θ==+ 故等效刚度为:12111eq t t k k k =+两只减振器的粘性阻尼系数分别为1c ,2c ,试计算总粘性阻尼系数eq c1)在两只减振器并联时,2)在两只减振器串联时。
解:1)对系统施加力P ,则两个减振器的速度同为x &,受力分别为:1122P c x P c x =⎧⎨=⎩&& 由力的平衡有:1212()P P P c c x =+=+&故等效刚度为:12eq P c c c x ==+& 2)对系统施加力P ,则两个减振器的速度为: 1122P x c P x c ⎧=⎪⎪⎨⎪=⎪⎩&&,系统的总速度为:121211()x x x P c c =+=+&&& 故等效刚度为:1211eq P c x c c ==+&一简谐运动,振幅为,周期为,求最大速度和加速度。
解:简谐运动的22(/)0.15nrad sTππω==,振幅为3510m-⨯;即:333222510cos()()0.1522510sin()(/)0.150.1522510()cos()(/)0.150.15x t mx t t m sx t t m sπππππ---⎧=⨯⎪⎪⎪=-⨯⨯⎨⎪⎪=-⨯⨯⎪⎩&&&所以:3max322 max2510(/)0.152510()(/)0.15x m sx m sππ--⎧=⨯⨯⎪⎪⎨⎪=⨯⨯⎪⎩&&&一加速度计指示出结构振动频率为82Hz ,并具有最大加速度50g ,求振动的振幅。
解:由 2max n x A ω=⨯&&可知:2max max 22222509.8/9.8(2)(225)1/50n x x m s A m f s ωπππ⨯====⨯&&&&证明:两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动,即:)cos()cos(cos θωϕωω-=-+t C t B t A ,并讨论0=ϕ,2/π,π三种特例。
证明:cos cos()cos cos cos sin sin (cos )cos sin sin ))cos()A tB t A t B t B t A B t B tt t C t ωωϕωωϕωϕϕωϕωωθωθωθ+-=++=++=-=-=-其中:sin ()cos B arctg A B C ϕθϕ⎧=⎪+⎨⎪=⎩1)当0ϕ=时:0;C A B θ==+;2)当2πϕ=时:(/);arctg B A C θ=3)当ϕπ=时:0;C A B θ==-;把复数4+5i 表示为指数形式。
解:i 4+5i=Ae θ,其中:A =,5()4arctg θ=证明:一个复向量用i相乘,等于把它旋转2/π。
证明:i ii i22 Ae Ae e Aeiππθθθ+⨯=⨯=证明:梯度算子∇是线性微分算子,即),,(),,()],,(),,([z y x g b z y x f a z y x bg z y x af ∇+∇=+∇这里,a ,b 是与x 、y 、z 无关的常数。
求函数t q B t p A t g ωωcos cos )(+=的均方值。
考虑p 与q 之间的如下三种关系:① np q =,这里n 为正整数;② p q /为有理数;③ p q /为无理数。
汽车悬架减振器机械式常规性能试验台,其结构形式之一如图T —所示。
其激振器为曲柄滑块机构,在导轨下面垂向连接被试减振器。
试分析减振器试验力学的基本规律(位移、速度、加速度、阻尼力)。
图 T —汽车悬架减振器机械式常规性能试验台的另一种结构形式如图T —所示。
其激振器采用曲柄滑块连杆机构,曲柄被驱动后,通过连杆垂向带动与滑块连接的被试减振器。
试分析在这种试验台上的减振器试验力学的基本规律,并与前题比较。
图 T —弹簧下悬挂一物体,弹簧静伸长为δ。
设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:设物体质量为m ,弹簧刚度为k ,则: mg k δ=,即:n ω== 取系统静平衡位置为原点0x =,系统运动方程为:δ⎧+=⎪=⎨⎪=⎩&&&00020mx kx x x (参考教材P14)解得:δω=()2cos n x t t弹簧不受力时长度为65cm ,下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。
解:由题可知:弹簧的静伸长0.850.650.2()m =-=V所以:7(/)n rad s ω=== 取系统的平衡位置为原点,得到:系统的运动微分方程为:20n x x ω+=&& 其中,初始条件:(0)0.2(0)0x x =-⎧⎨=⎩& (参考教材P14)所以系统的响应为:()0.2cos ()n x t t m ω=-弹簧力为:()()cos ()k n mgF kx t x t t N ω===-V因此:振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。
重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2m 从高度为h 处自由落到1m 上而无弹跳,如图所示,求其后的运动。
解:取系统的上下运动x 为坐标,向上为正,静平衡位置为原点0x =,则当m 有x 位移时,系统有:2121()2T E m m x=+& 212U kx =由()0T d E U +=可知:12()0m m x kx ++=&&即:n ω=系统的初始条件为:⎧=⎪⎨=-⎪⎩&20012m gx x (能量守恒得:221201()2m gh m m x =+&)因此系统的响应为:01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==⎪⎩&2001n m gA x x A即:ωω=-2()(cos )n n m g x t t t k一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆心受到一弹簧k 约束,如图所示,求系统的固有频率。
解:取圆柱体的转角θ为坐标,逆时针为正,静平衡位置时0θ=,则当m 有θ转角时,系统有:2222111()()222T E I m r I mr θθθ=+=+&&& 21()2U k r θ=由()0T d E U +=可知:22()0I mr kr θθ++=&&即:n ω= (rad/s )均质杆长L、重G,用两根长h的铅垂线挂成水平位置,如图所示,试求此杆相对铅垂轴OO微幅振动的周期。
求如图所示系统的周期,三个弹簧都成铅垂,且21312,k k k k ==。
解:取m 的上下运动x 为坐标,向上为正,静平衡位置为原点0x =,则当m 有x 位移时,系统有:212T E mx =& 22211115226U kx k x k x =+= (其中:1212k k k k k =+)由()0T d E U +=可知:1503mx k x +=&&即:n ω=rad/s ),2T =(s )如图所示,半径为r 的均质圆柱可在半径为R 的圆轨面内无滑动地、以圆轨面最低位置O 为平衡位置左右微摆,试导出柱体的摆动方程,求其固有频率。
解:设物体重量W ,摆角坐标θ如图所示,逆时针为正,当系统有θ摆角时,则: θθ=--≈-2()(1cos )()2U W R r W R r设ϕ&为圆柱体转角速度,质心的瞬时速度: ()c R r r υθϕ=-=&&,即:()R r rϕθ-=&& 记圆柱体绕瞬时接触点A 的转动惯量为A I ,则:=+=+22212A C W W W I I r r r g g gϕθθ-===-&&&222221133()()()2224T A W R r W E I r R r g r g(或者理解为:ϕθ=+-&&22211()22T c W E I R r g ,转动和平动的动能) 由()0T d E U +=可知:θθ-+-=&&23()()02W R r W R r g即:ω=n rad/s )横截面面积为A ,质量为m 的圆柱形浮子静止在比重为γ的液体中。
设从平衡位置压低距离x (见图),然后无初速度地释放,若不计阻尼,求浮子其后的运动。
解:建立如图所示坐标系,系统平衡时0x =,由牛顿第二定律得:()0mx Ax g γ+=&&,即:n ω=有初始条件为:{==&000x x x所以浮子的响应为:()sin()2x t x π=+求如图所示系统微幅扭振的周期。
图中两个摩擦轮可分别绕水平轴O 1,O 2转动,它们相互啮合,不能相对滑动,在图示位置(半径O 1A 与O 2B 在同一水平线上),弹簧不受力。
摩擦轮可以看做等厚均质圆盘,质量分别为m 1,m 2。
解:两轮的质量分别为12,m m ,因此轮的半径比为:12r r = 由于两轮无相对滑动,因此其转角比为:121212r r θθθθ==&&取系统静平衡时10θ=,则有:222222111222121111111()()()22224T E m r m r m m r θθθ=+=+&&& 2221112221211111()()()()222U k r k r k k r θθθ=+=+由()0T d E U +=可知:222121112111()()02m m r k k r θθ+++=&&即:n ω=rad/s ),=2T (s )如图所示,轮子可绕水平轴转动,对转轴的转动惯量为I ,轮缘绕有软绳,下端挂有重量为P 的物体,绳与轮缘之间无滑动。