安徽省淮南四中2012届高三第六次月考理科数学试卷2012-2-26

主视图俯视图左视图2222012届第四次六校联考 高三数学（理科）试题本试卷共4页，21小题，满分150分．考试用时120分钟．参考公式：锥体体积公式13V Sh =，其中S 为锥体的底面积，h 为锥体的高．第 Ⅰ 卷一．选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知,A B 是非空集合，命题甲：A B B = ，命题乙：A B ⊂≠，那么 （ ） A.甲是乙的充分不必要条件 B. 甲是乙的必要不充分条件C.甲是乙的充要条件D. 甲是乙的既不充分也不必要条件 2.复数21i i =- （ ）A . 1i - B. 1i -+ C. 1i + D. 1i --3.已知点(,)N x y 在由不等式组002x y x y x +≥⎧⎪-≥⎨⎪≤⎩确定的平面区域内，则(,)N x y 所在平面区域的面积是 （ ）A ．1B ．2C ．4D ．84.等差数列{a n }中，已知35a =，2512a a +=，29n a =，则n 为 （ ）A. 13B. 14C. 15D. 165. 函数21log 1x y x+=-的图像 （ ）A ． 关于原点对称 B. 关于主线y x =-对称C. 关于y 轴对称D. 关于直线y x =对称6.若某空间几何体的三视图如图所示，则该几何体的体积是 （ ）A. 42B.22C.423D.2237.已知平面,,αβγ，直线,m l ，点A ，有下面四个命题：A . 若l α⊂，m A α= 则l 与m 必为异面直线； B. 若,l l m α 则m α ；C. 若 , , ,l m l m αββα⊂⊂ 则 αβ ；D. 若 ,,,m l l m αγγαγβ⊥==⊥ ，则l α⊥.其中正确的命题是 （ ）8.某种游戏中，黑、黄两个“电子狗”从棱和为1的正方体ABCD -A 1B 1C 1D 1的顶点A 出发沿棱向前爬行，每爬完一条棱称为“爬完一段”，黑“电子狗”爬行的路线是AA 1→A 1D 1→…，黄“电子狗”爬行的路线是AB →BB 1→…，它们都遵循如下规则：所爬行的第i +2段与第i 段所在直线必须异面直线(其中i 是正整数).设黑“电子狗”爬完2012段、黄“电子狗”爬完2011段后各自停止在正方体的某个顶点处，这时黑、黄“电子狗”间的距离是 （ ） A. 0B. 1C. 2D. 3第 Ⅱ 卷二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分． （一）必做题：第9、10、11、12、13题是必做题，每道试题考生都必须做答． 9. 0211x dx --=⎰ .10.函数2()sin cos 2f x x x =+,x R ∈的最小正周期为ABC ∆中，90=∠C ，11.在直角30=∠A ，1=BC ，中点，则 CD AB ⋅= .D 为斜边AB 的22219x ya-=(0)a >的一条渐近12.若双曲线320x y -=，则以双曲线的顶点线方程为和焦点分别为焦点和顶点的椭圆的离心率为__________. 13.将“杨辉三角”中的数从左到右、从上到下排 成一数列：1，1，1，1，2，1，1，3，3，1，1，4，6，4，1，…， 右图所示程序框图用来输出此数列的前若干项并求其和，若输入m=4则相应最后的输出S 的值是__________.ADCEECADON M BA（二）选做题：第14、15题是选做题，考生只能从中选做一题．14．（坐标系与参数方程选做题）已知曲线1C 、2C 的极坐标方程分别为2cos()2πρθ=-+，2cos()104πρθ-+=，则曲线1C 上的点与曲线2C 上的点的最远距离为________.15．（几何证明选讲选做题）如图，点M 为O 的弦A B 上的一点，连接MO .MN OM ⊥，MN 交圆于N ，若2M A =，4M B =，则MN = .三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分） 在ABC ∆中，角,,A B C 的对边分别为,,a b c ，S 是该三角形的面积，（1）若(2s i nc o s ,s i n c o s )2Ba B B B=- ，(sin cos ,2sin )2B b B B =+ ，//a b，求角B 的度数；（2）若8a =，23B π=，83S =，求b 的值.17 （本小题满分12分）甲、乙两人各射击一次，击中目标的概率分别是32和43假设两人射击是否击中目标，相互之间没有影响；每人各次射击是否击中目标，相互之间也没有影响⑴求甲射击3次，至少1次未击中．．．目标的概率； ⑵假设某人连续2次未击中．．．目标，则停止射击，问：乙恰好射击4次后，被中止射击的概率是多少？⑶设甲连续射击3次，用ξ表示甲击中目标时射击的次数，求ξ的数学期望E ξ. （结果可以用分数表示）18. （本小题满分14分）如图，四边形ABCD 中（图1），E 是BC 的中点，2D B =，1,D C =5BC =， 2.AB AD ==将（图1）沿直QPOYX线B D 折起，使二面角A BD C --为060（如图2） （1）求证：A E ⊥平面BDC ；（2）求异面直线A B 与CD 所成角的余弦值； （3）求点B 到平面ACD 的距离.19（本小题满分14分）已知函数()241(12)ln(21)22xa f x a x x +=-+++ .（1）设1a =时，求函数()f x 极大值和极小值; （2）a R ∈时讨论函数()f x 的单调区间.20.（本小题满分l4分）如图，P 是抛物线C ：212y x =上横坐标大于零的一点，直线l 过点P 并与抛物线C 在点P 处的切线垂直，直线l与抛物线C 相交于另一点Q .（1）当点P 的横坐标为2时，求直线l 的方程；（2）若0O P O Q ⋅=，求过点,,P Q O 的圆的方程.21. （本小题满分l4分）已知数列{}n a 的前n 项和为n S ，正数数列{}n b 中 ,2e b = (e 为自然对数的底718.2≈)且*N n ∈∀总有12-n 是n S 与n a 的等差中项，1 1++n n n b b b 与是的等比中项.(1) 求证: *N n ∈∀有nn n a a 21<<+； (2) 求证：*N n ∈∀有13ln ln ln )1(2321-<+++<-n n n a b b b a .高三数学（理科）试题答案一．选择题：1、B ；2、A ；3、C ；4、C ；5、A ；6、B ；7、D ；8、D二、填空题：9.4π； 10. π ； 11. -1 ； 12.21313； 13. 15；选做题：14. 21+ 15. 22三、解答题：16.解：（1）//a b 24cos sincos 202BB B ∴⋅+= 21cos 4cos 2cos 102BB B -∴⋅+-= 1cos 2B ∴=(0,180)B ∠∈ 60B ∴∠=……………………6分（2）83S = 1sin 832ac B ∴=……………………7分得 4c =……………………8分2222cos b a c ac B =+-2284284cos120=+-⋅⋅……………………10分47b ∴=……………………12分17.解：（1）记“甲连续射击3次，至少1次未击中目标”为事件A 1，由题意，射击3次，相当于3次独立重复试验，故P （A 1）=1- P （1A ）=1-32()3=1927答：甲射击3次，至少1次未击中目标的概率为1927；……………………4分(2) 记“乙恰好射击4次后，被中止射击”为事件A 2，由于各事件相互独立，故P （A 2）=41×41×43×41+41×41×43×43 =364，答：乙恰好射击4次后，被中止射击的概率是364……………………8分（3）根据题意ξ服从二项分布，2323E ξ=⨯=……………………12分（3）方法二：03311(0)()327p C ξ==⋅=123216(1)()()3327p C ξ==⋅⋅=22132112(2)()()3327p C ξ==⋅⋅=3303218(1)()()3327p C ξ==⋅⋅=161280123227272727E ξ=⨯+⨯+⨯+⨯=……………………12分 说明：（1），（2）两问没有文字说明分别扣1分，没有答，分别扣1分。

寿县一中2012届高三第六次月考数学试题（理科）温馨提示：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.满分150分，考试时间120分钟.2.答题前，考生在答题卡上务必用黑色墨水签字笔将自己的班级、姓名、准考号填写清楚.3.请将试卷答案填在答题卡上.必须在题号所指示的答题区域作答，超出答题区域书写．．．．．．．．的答案．．．无效，在试题卷、草稿纸上答题无效．．．．．．．．．．．．．．．．. 第Ⅰ卷（选择题，共50分）一、选择题：本大题共10个小题，每小题5分，共50分.每小题给出的四个选项中，只有一项是符合题目要求的. 请把答案填在答题卡的相应位置.1.设全集为U ,用集合,A B 的交、并、补集符号表示图中的阴影部分为（ ） A.A B ⋂ B.()U C A B ⋂ C.()U A C B ⋂ D.()U C A B ⋂2.“2a =”是“直线20ax y +=平行于直线1x y +=”的（ ）A.充分必要条件B.充分非必要条件C.必要非充分条件D.既非充分又非必要条件3.一个几何体由若干单位正方体组成，其正视图和侧视图相同（如图所示），则组成该几何体的小正方体的个数最少有（ ）A.5个B.7个C.8个D.9个4.定义运算,,a a b a b b a b≤⎧*=⎨>⎩，如121*=，令()22x xf x -=*，则()f x 为（ ）A.奇函数，值域(0,1]B.偶函数，值域(0,1]C.非奇非偶函数，值域(0,1]D.偶函数，值域(0,)+∞5.右图为计算20个数据的平均数的程序，则在横线上应填的语句是（ ） A.20i > B.20i >= C.20i < D.20i <=6.已知函数()sin()(0,0)f x A x A ωϕω=+>>在区间00[,]x x πω+上单调递减则函数()cos()g x A x ωϕ=+在同一区间上为（ ）A.增函数B.减函数C.先增后减函数D.先减后增函数 7.已知直线,m n 及平面,αβ，则下列选项正确的是（ ）A.若//,//m m αβ，则//αβB.若//m α，//m n ，则//n αC.若,m ααβ⊥⊥，则//m βD.若m α⊥,//m β，则αβ⊥8.关于x 的方程2()50x a b x a b -++-+=的两根12,x x 满足12012x x <<<<，则3ba +的取值 范围是（ ）A.(0,3)B.(1,3)C.7(1,)3D.7(,3)39.在ABC ∆中，2sin sin cos sin sin cos sin sin cos A B C A C B B C A =+，则内角C （ ）A.最大为60B.最小为60C.最大为90D.最小为9010.已知,A B 为双曲线222(0)x y a a -=>的两个顶点，P 为双曲线在第一象限内任意一点，令,,PAB PBA APB αβγ∠=∠=∠=,则有（ ）A.tan tan tan 0αβγ++=；B.tan tan tan 0αβγ+-=；C.tan tan 2tan 0αβγ++=；D.tan tan 2tan 0αβγ+-=.第Ⅱ卷（非选择题，共100分）二、填空题:本大题共5小题，每小题5分，共25分. 请把答案填在答题卡的相应位置. 11.已知4(s i n ,1),(c o s ,)3θθ-a =b =且0θπ<<，若//a b，则s i n 2c θθ+= ．12.三棱锥P ABC -的棱2PA PB PC ===且两两垂直，则该三棱锥的内切球半径是 ．13.已知函数()f x 对定义域内任意,x y ,有()()()1()()f x f y f x y f x f y ++=-且(1)1f =,则(2011)f = .14.椭圆22221x y a b +=与双曲线22221x y b c-=有相同的焦点12,F F ,P 为两曲线的一个交点，且12PF PF ⊥,则两曲线的离心率之积是 15.以下一组命题:①若A 为随机事件，则0()1P A <<；②由一组变量(,)i i x y 产生的回归直线必经过(,)x y ； ③一组变量{}i x 的平均数为6,方差为1,另一组变量{}i y 满足21i i y x =+,则变量{}i y 的平均数为13,方差为4；④利用秦九韶算法求532()5321f x x x x =-+-，需经过10次计算. 其中正确的命题有 （填写所有正确命题的序号）三、解答题：本大题共6个小题，满分75分，解答应写出必要的文字说明、证明过程或演算步骤．请将解答过程写在答题卡的相应位置． 16.（本小题12分）2011年寿县一中某班t 名学生在一次百米测试中，成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组,第一组[13,14);第二组[14,15);第三组[15,16);第四组[16,17);第五组[17,18].下表是按上述分组方式得到的频率分布表：（Ⅰ）求频率分布表中x 、y 的值，并估计该次测试的平均成绩；（Ⅱ）设,m n 是从第一组或第五组中任意抽取的两名学生的百米测试成绩， 求事件“1m n ->”的概率.17.（本小题12分）已知集合23{|20},{|1}1A x x x tB x x =++<=≥-，全集U R =.（Ⅰ）若8t =-，求()U A C B ⋃；（Ⅱ）若A B ⋂≠∅，求实数t 的取值范围.18.（本小题12分）已知椭圆2222:1(0)x y C a b a b+=>>和两点(4,1),(3,2)A B ，且椭圆右焦点与上顶点的连线平行于AB .（Ⅰ）若椭圆经过A 点，求椭圆C 的方程；（Ⅱ）若椭圆C 与线段AB 有公共点，求实数a 的取值范围.19.（本小题13分）设函数2()sin cos 1()f x x x x x R =+∈. （Ⅰ）求函数()f x 的最小正周期及单调递增区间； （Ⅱ）若[0,]2x π∈，求函数()f x 的最大值和最小值；（Ⅲ）若把函数()f x 的图象按向量a 平移后所得函数为奇函数,求使得a 最小的a .20.（本小题13分）如图,四棱锥P ABCD -中,底面ABCD 为等腰梯形,//AB DC ,AC BD ⊥, O 为,AC BD 的交点，且PO ⊥底面ABCD,2,1,OB OD OP ===（Ⅰ）求异面直线PD 与BC 所成角的余弦值； （Ⅱ）求二面角P AB C --的大小； （Ⅲ）设点M 在棱PC 上,PMMCλ=,问λ为何值时,PC ⊥平面BMD .PACBDO21.（本小题13分）已知圆224x y +=，点(1,0),(4,0)M N .（Ⅰ）若P 为圆上动点.（1）求PMN ∆重心的轨迹方程；（2）求证：MPN ∠的平分线恒过定点，并求该点坐标；（Ⅱ）过M 作相互垂直的直线分别与圆交于,,,A C B D 四点，求四边形ABCD 的面积的最大值 和最小值.参考答案及评分标准一、选择题：本大题共10小题，每小题5分，共50分.二、填空题：本大题共5个小题，每小题5分，共25分.11.1-； 13.1- 14.； 15.②③④三、解答题：本大题共6个小题,满分75分． 16.（本小题12分） 【解】：（Ⅰ）由表可知，4500.08t ==，1(0.040.180.320.08)0.38y =-+++=………2分 则500.042x =⨯=………………………………………………………………………………4分该次测试的平均成绩为：13.50.0414.50.1815.50.3816.50.3217.50.0815.72⨯+⨯+⨯+⨯+⨯=…………………6分（Ⅱ）由题设可知，第一组[13,14)中有2名学生，百米测试成绩设为,x y ； 第五组[17,18]中有4名学生，百米测试成绩设为,,,A B C D ，则,m n 可能的结果为： (,),(,),(,),(,),(,),(,),(,),(,),(,)x y x A x B x C x D y A y B y C y D ,(,),(,),(,),A B A C A D(,),(,),(,)B C B D C D ,共15种,使1m n ->成立的有(,),(,),(,),(,),(,),x y x A x B x C x D (,),(,),(,),(,)y A y B y C y D ，共8种.8(1)15P m n ∴->=. ……………………………12分17.（本小题12分）【解】：（Ⅰ）当8t =-时，2{|280}(4,2)A x x x =+-<=-，………………………… 2分3{|1}(1,4]1B x x =≥=-，()(,1](4,)UC B =-∞⋃+∞ ……………………………………4分故()(,2)(4,)U A C B ⋃=-∞⋃+∞ ……………………………………………………………6分（Ⅱ）若A B ⋂≠∅，则A ≠∅,此时4401t t ∆=->⇒<…………………………………7分解不等式220x x t ++<得11x -<-(11A =--若A B ⋂≠∅，则需满足113t ->⇒<- 综上，实数t的取值范围是3t <-.…………………………………………………………………12分18.（本小题12分） 【解】：（Ⅰ）21134AB k -==--,因为椭圆右焦点与上顶点的连线平行于AB ,则1bc-=-………2分 2222,2b c a b c b ∴=∴=+=，故椭圆C可化简为2222x y a += …………………………………4分又椭圆经过A 点，则224218a =+=，故椭圆C 的方程为221189x y += …………………………6分 （Ⅱ）可求得线段AB所在直线方程为5y x =-+（34x ≤≤） …………………………………7分 由（Ⅰ）知椭圆C 为2222x y a +=，联立22225x y a y x ⎧+=⎨=-+⎩，消去y 并整理得：22320500x x a -+-=……………………………（＆）由于椭圆C 与线段AB 有公共点，即方程（＆）在[3,4]x ∈上有解（＆）式可变形为2232050a x x =-+，令2()32050g x x x =-+，[3,4]x ∈ 则只需2a 在函数()g x 的值域之内，易知1050()[(),(4)][,18]33g x g g ∈=， 故250[,18]3a ∈a ⇒∈.…………………………………………………………………12分19.（本小题13分）【解】：21cos 2()sin cos 12122x f x x x x x -=+=++1332cos 2sin(2)2262x x x π=-+=-+……………………………………2分 （Ⅰ）函数()f x 的最小正周期22T ππ== ………………………………………………………3分 令22226263k x k k x k πππππππππ-≤-≤+⇒-≤≤+即函数()f x 的单调递增区间为[,]()63k k k Z ππππ-+∈. …………………………………5分 （Ⅱ）5[0,],2[,]2666x x ππππ∈∴-∈-，1sin(2)[,1]62x π∴-∈-，所以函数()f x 的最小值为1，最大值为52………………………………………………………9分 （Ⅲ）令26x k ππ-=212k x ππ⇒=+()k Z ∈，即函数图象对称中心为3(,)2122k ππ+ 0k =时距原点最近，则满足条件3(,)122π=--a ……………………………………………13分 20.（本小题13分）【解】:（Ⅰ）由题设CD AB ==BC =,取AB 中点E ， 连接,DE PE ,则有四边形BCDE 为平行四边形，则//BC DE 故PDE ∠为异面直线PD 与BC 所成角（或其补角）……………3分2PD DE PE ===，由余弦定理求得:222cos 2PD DE PE PDE PD DE +-∠==⋅………………………………………………………5分（Ⅱ）连接OE ，则OE AB ⊥，AB ⊥平面POE ， ∴PEO∠即为所求二面角的平面角，易求得45PEO ∠= ……………………………………9分（Ⅲ）连接OM ，由题设,PC BD ⊥, 若PC ⊥平面BMD ，只须PC OM ⊥即可, 在Rt POC∆中，223PO PM PC PC ===,2λ=…………………………………………13分21.（本小题13分）【解】：（Ⅰ）设重心00(,),(,)G x y P x y ，则00001(14)353313x x x x y y y y⎧=++⎪=-⎧⎪⇒⎨⎨=⎩⎪=⎪⎩，又00(,)P x y 为圆上的点，则22004x y +=，则22(35)(3)4x y -+=PACBDOEM化简并整理得：2254()39x y -+=…………………………………………………………………4分（Ⅱ）0000,14PM PN y yk k x x ==--，可得直线000:(1)0,PM y x x y y ---= 000:(4)40PN y x x y y ---=，设MPN ∠的平分线与x 轴交与(,0)Q t ，=2t =，即知必过(2,0)Q ……………………………8分（Ⅲ）设弦,AC BD 的中点分别为,E F ,则22222221,4OE OF OM OE CE OF DF +==+=+= 222222(4)(4)8()7CE DF OE OF OE OF +=-+-=-+=,22224()28AC BD CE DF +=+=[]22222211(28),12,1644S AC BD AC AC AC =⨯=⨯-∈求得7S ≤≤.…………………………………………………………………………………………13分。

2012届淮南四中一模练习卷六一、选择题1．若2{|,}x x a a ⊂∅≤∈≠R ，则a 的取值范围是（ ）A ．[0,)+∞B ．(0,)+∞C ．(,0]-∞D ．(,0)-∞2．已知定义在R 上的奇函数)(x f 满足,1)1(,0)()2(=-=--f x f x f 且则)2()1(f f +)2010()3(f f +++ 的值为 （ ） A ．-1 B ．0 C ．1 D ．23．已知△ABC 所在平面上的动点M 满足222AM BC AC AB ⋅=-，则M 点的轨迹过△ABC 的（ ）A ．内心B ．垂心C ．重心D ．外心 4．满足不等式2|2||1|≤++-y x 的图形的面积为 （ ）A ．2B ．2C ．4D ．8 5．“x + y >2”是“x >1且y >1”的 （ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 6．如图，平面内有三个向量,, ,其中与 的夹角为60°,与、与的夹角都为30°,1==32=,若μλ+=,则λμ+的值为（ ）A ．2B ．．．47．已知y =()x f 是定义在（–2，2）上的偶函数，且()x f在[0，2]上是增函数，若()()012<+--m f m f ，则实数m 的取值范围是（ ）A ．（0，1）B ．（12，1）C ．（0，12）D ．（12，2）8．已知a >0且a ≠1，若函数()x f = log a （ax 2– x ）在[3， 4]是增函数，则a 的取值范围是A ．（1，+∞） B ．11[,)(1,)64+∞ C ．11[,)(1,)84+∞ D ．11[,)649．在△ABC 中，60,A a b =︒==B 等于 （ ） A ．45°或135° B ．135° C ．45° D ．以上答案都不对10．在等差数列{}n a 中，前n 项和n n S m =，前m 项和m mS n=，其中m n ≠，则m n S +的值（ ）A ．大于4B ．等于4C ．小于4D ．大于2且小于4 二填空题11．已知椭圆22)(y c x +-10)(22=+++y c x 的短轴长为b 2，那么直线03=++cy bx 截圆122=+y x 所得的弦长等于12. 在ABC ∆中，角,,A B C 所对的边分别是,,a b c ，已知点D 是BC 边的中点，且21()2AD BC a ∙=，则角B =13.不等式)1(||+≥x a x 对任意的实数x 都成立，则实数a 的取值范围是14．已知双曲线()222211,0x y a b a b -=>>的焦距为2c ，离心率为e ，若点（-1,0）与（1,0）到直线1x y a b -= 的距离之和45s c ≥，则e 的取值范围是15.已知数列{}n a 满足133a =，12n n a a n +-=，则na n的最小值为 ；三．解答题16.已知向量),2cos 2sin 3()2cos ,1(y xx b x a +==→→与共线，且有函数)(x f y =．（Ⅰ）若1)(=x f ，求)232cos(x -π的值； （Ⅱ）在ABC ∆中，角C B A ,,的对边分别是c b a ,,，且满足b c C a 2cos 2=+，求函数)(B f 的取值范围.17. 已知函数xxx f ln )(=(0,1x x >≠)． （1）求函数)(x f 的极值;（2）若不等式xe x >对任意实数x 恒成立，求实数a 的取值范围．练习六答案 一、选择题答案 AADCBBBACA 二、填空题答案11.8/5；12. 30o；13. [-1,0]；14. ⎣；15.212 三、解答题16．解：（Ⅰ）∵→a 与→b 共线 ∴ )2cos 2sin 3(2cosxx x y += 21)6sin()cos 1(21sin 23++=++=πx x x …………………………3分 ∴121)6sin()(=++=πx x f ，即21)6s i n (=+πx …………………………………………4分 211)6(sin 21)3(cos 2)3(2cos )232cos(22-=-+=--=-=-ππππx x x x…………………………………………6分（Ⅱ）已知b c C a 2cos 2=+ 由正弦定理得：CA C A C C A C ABC C A sin cos 2cos sin 2sin cos sin 2)sin(2sin 2sin cos sin 2+=++==+∴21cos =A ， ∴在ABC ∆中 ∠3π=A . ……………………………8分21)6sin()(++=πB B f∵∠3π=A ∴320π<<B ,6566πππ<+<B …………………………………………10分∴1)6sin(21≤+<πB ,23)(1≤<B f ∴函数)(B f 的取值范围为]23,1( . …………………………………………12分17. 解：（1）函数x xx f ln )(=的定义域为),1()1,0(+∞ ， 2ln 1()ln x f x x-'=，……………3分 令()0f x '=，解得e x =，列表)； 所以极小值为)(e f ＝e ，无极大值.（2）当0x ≤时，对任意0a ≠，不等式恒成立；当0x >时，在x ae x >两边取自然对数，得ln xx a>， 1当01x <≤时，ln 0x ≤，当0a >，不等式恒成立；如果0a <，ln 0x <， ln 0a x >，不等式等价于ln xa x<， 由(1)得，此时(,0)ln xx∈-∞，不等式不恒成立. 2当1x >时，ln 0x >，则0a >,不等式等价于ln xa x<,由(1)得，此时ln xx的最小值为e ，得0a e <<.…………14分综上：a 的取值范围是0a e <<.【说明】本题考查用导数判断函数单调性、求极值、对数函数的性质、转化化归思想、分类讨论思想、不等式的性质、恒成立问题处理方法.。

2012年普通高等学校招生全国统一考试（安徽卷）数学理科一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的1.复数满足，则为 ( )A. B. C. D.【测量目标】复数代数形式的四则运算.【考查方式】给出代数式，求复数.【难易程度】容易【参考答案】D【试题解析】设，则，所以可得，故.2.下列函数中，不满足等于的是（）A. B. C. D.【测量目标】函数相等.【考查方式】给出一系列函数解析式，计算两函数值，得到答案.【难易程度】容易【参考答案】C【试题解析】令，则，其中C不满足，故答案为C.3．如图所示，程序框图（算法流程图）的输出结果是 ( )A.3B.4C.5D.8第3题图【测量目标】循环结构的程序框图.【考查方式】理解程序框图中的计算关系，求值.【难易程度】容易【参考答案】B【试题解析】第一次循环后：；第二次循环后：；第三次循环后：，跳出循环，输出 .4. 公比为2的等比数列{} 的各项都是正数，且=16，则 ( )A.4B.5C.6D.7【测量目标】等比数列的性质，对数的求值.【考查方式】给出等比数列两项乘积，求出等比中项，根据公比求出再求对数的值.【难易程度】中等【参考答案】B【试题解析】设等比数列的公比为，，则，所以，故.5.甲、乙两人在一次射击比赛中各射靶5次，两人成绩的条形统计图如图所示，则( )第5题图A.甲的成绩的平均数小于乙的成绩的平均数B.甲的成绩的中位数等于乙的成绩的中位数C.甲的成绩的方差小于乙的成绩的方差D.甲的成绩的极差小于乙的成绩的极差【测量目标】频率直方图.【考查方式】给出频率直方图，通过图比较两者的中位数，平均数，以及方差和极差.【难易程度】容易【参考答案】C【试题解析】由条形图易知甲的平均数为，中位数为，(步骤1)方差为，极差为；（步骤2）乙的平均数为，中位数为5，（步骤3）方差为，极差为，（步骤4）故，甲乙中位数不相等且.（步骤5）6.设平面与平面相交于直线m，直线a在平面内,直线b在平面内，且，则“”是“”的 ( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【测量目标】充分，必要条件.【参考方式】判断充分必要条件.【难易程度】容易【参考答案】A【试题解析】判断本题条件命题为“”条件命题，命题“”为结论命题，当时，由线面垂直的性质定理可得，所以条件具有充分性；但当时，如果，就得不出，所以条件不具有必要性，故条件是结论的充分不必要条件.7.()的展开式的常数项是 ( )A. B. C. D.【测量目标】二项式定理.【考查方式】整理所给的方程，直接利用二项式定理求展开式常数项.【难易程度】容易【参考答案】D【试题解析】因为，所以要找原二项式展开式中的常数项，（步骤1）只要找展开式中的常数项和含项即可.通项公式（步骤2）8.在平面直角坐标系中，点（0，0），点，将向量绕点按逆时针方向旋转后得向量，则点的坐标是（）A. B. C. D.【测量目标】三角函数的定义和求值，两角和的正切.【考查方式】根据题意得到正切值，将向量转动后再利用两角和的正切公式求解.【难易程度】中等【参考答案】A【试题解析】设，因为，所以，（步骤1）可得，（步骤2）验证可知只有当点坐标为时满足条件，（步骤3）故答案为A；法二：估算.设，因为，所以，可得，，所以点在第三象限，排除B，D选项，又，故答案为A.9.过抛物线的焦点的直线交该抛物线于A，B两点，为坐标原点.若，则的面积为（）第9题A. B. C. D.【测量目标】直线的方程，直线和抛物线的位置关系.【考查方式】给出抛物线方程求出直线方程，根据直线与抛物线的位置关系求三角形面积.【难易程度】较难【参考答案】C【试题解析】如图，设，由抛物线方程，可得抛物线焦点，(步骤1)抛物线准线方程为，故.(步骤2)可得，，故，直线的斜率为，(步骤3)直线的方程为，（步骤4）联立直线与抛物线方程可得，(步骤5)因为两点横坐标之积为，所以点的横坐标为，(步骤6)可得，，(步骤7)点到直线的距离为，所以.（步骤8）10.6位同学在毕业聚会活动中进行纪念品的交换，任意两位同学之间最多交换一次，进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换，则收到4份纪念品的同学人数为 ` ( )A.1或3B.1或4C.2或3D.2或4【测量目标】简单的计数，排列组合的应用.【考查方式】通过实际的问题，利用简单的计数原理和排列组合求值.【难易程度】较难【参考答案】D【试题解析】任意两个同学之间交换纪念品共要交换次，如果都完全交换，每个人都要交换5次，也就是得到5份纪念品，现在6个同学总共交换了13次，少交换了2次，这2次如果不涉及同一个人，则收到4份纪念品的同学人数有4人；如果涉及同一个人，则收到4份纪念品的同学人数有2人，答案为D.2012年普通高等学校招生全国统一考试（安徽卷）数学（理科）第Ⅱ卷（非选择题共100分）请用0.5毫米海瑟墨水签字笔在答题卡上作答，在试卷上答题无效.二、填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡的相应位置.11.若满足约束条件则的取值范围是______.第11 题图【测量目标】二元线性规划求目标函数的范围.【考查方式】直接给出约束条件，画出可行域，求目标函数的的取值范围.【难易程度】容易【参考答案】【试题解析】法一：画出可行域是如图所示的的边界及内部，令.易知当直线经过点时，直线在轴上截距最大，目标函数取得最小值，即；当直线经过点时，直线在轴上截距最小，目标函数取得最大值，即，所以.法二：界点定值，同法一先画出可行域，令，把边界点代入目标函数可得，，比较可得.12.某几何体的三视图如图所示，该几何体的表面积是______.第12题图【测量目标】三视图求几何体的表面积.【考查方式】观察三视图，通过空间想象得出几何体，求几何体表面积.【难易程度】中等【参考答案】【试题解析】如图，根据三视图还原的实物图为底面是直角梯形的直四棱柱，其表面积为.第12题图13.在极坐标系中，圆的圆心到直线的距离是____________.【测量目标】点到直线的距离，坐标系和参数方程.【考查方式】将参数方程化为一般方程，利用点到直线的距离公式求值.【难易程度】容易【参考答案】【试题解析】圆，即化为直角坐标为，（步骤1）直线的方程也就是直线，即为，（步骤2）圆心到直线的距离为.（步骤3）14.若平面向量，满足，则的最小值是___________.【测量目标】绝对值，均值不等式，向量的异向性.【考查方式】给出绝对值不等式，利用均值不等式求两向量的最值.【难易程度】中等【参考答案】【试题解析】由，有，（步骤1），可得，所以，（步骤2）故当且方向相反时，的最小值为.（步骤3）15.设的内角所对边的长分别为，则下列命题正确的是_____________（写出所有正确命题的编号）.①若，则；②若，则；③若，则；④若，则；⑤若，则.【测量目标】正余弦定理判断三角形角的大小，均值不等式，命题之间的关系.【考查方式】根据三角形的边角关系，通过均值不等式以及正余弦定理判断角的大小从而确定命题间的关系.【难易程度】较难【参考答案】①②③【试题解析】对于①，由得，（步骤1）则，因为，所以，故①正确；（步骤2）对于②，由得，即，则，（步骤3）因为，所以，故②正确；（步骤4）对于对于③，可变为，可得，（步骤4）所以，所以，故，③正确；（步骤5）对于④，可变为，可得，所以，（步骤6）因为，所以，④错误；（步骤7）对于⑤，可变为，即，（步骤8）所以，所以，所以，故⑤错误. （步骤9）答案为①②③三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.16.(本小题满分12分)设函数.（I）求函数的最小正周期；（II）设函数对任意，有，且当时，，求函数在上的解析式.【测量目标】两角和与差的三角函数公式，二倍角公式，三角函数的性质，求分段函数解析式.【考查方式】给出函数解析式，根据三角函数的性质得到周期，利用两角和与差的三角公式以及二倍角公式求分段函数解析式.【难易程度】中等【试题解析】.（步骤1）（1）函数的最小正周期.（步骤2）（2）当时，，（步骤3）当时，，当时， .（步骤4）得：函数在上的解析式为（步骤5）17.（本小题满分12分）某单位招聘面试，每次从试题库随机调用一道试题，若调用的是类型试题，则使用后该试题回库，并增补一道类试题和一道类型试题入库，此次调题工作结束；若调用的是类型试题，则使用后该试题回库，此次调题工作结束.试题库中现共有道试题，其中有道类型试题和道类型试题，以表示两次调题工作完成后，试题库中类试题的数量.（Ⅰ）求的概率；（Ⅱ）设，求的分布列和均值（数学期望）.【测量目标】基本事件概率，条件概率，离散型随机变量及其分布列均值.【考查方式】通过实际问题考查基本事件的的概率以及分布列和数学期望.【难易程度】中等【试题解析】（I）表示两次调题均为类型试题，概率为.（步骤1）（Ⅱ）时，每次调用的是类型试题的概率为，随机变量可取.，，.（步骤2）.（步骤4）答：（Ⅰ）的概率为；（Ⅱ）的均值为.（步骤5）18.（本小题满分12分）平面图形，其中是矩形，，，．现将该平面图形分别沿和折叠，使与所在平面都与平面垂直，再分别连接,得到如图空间图形，对此空间图形解答下列问题．第18题图（1）证明：；（2）求的长；（3）求二面角的余弦值．【测量目标】空间中线线、线面、面面的位置关系，空间中的距离以及二面角.【考查方式】线线，线面，面面的垂直的相互转化，证明线线垂直；根据证明得到三角关系求距离；分析所求二面角所形成的三角形，解三角形，求角.【难易程度】中等【试题解析】（1）取的中点为点，连接，则，∴，∵平面平面，∴平面，（步骤1）同理：平面，得，∴共面，（步骤2）又∵，∴平面，∴．（步骤3）（2）延长到，使，得，（步骤4），平面平面∴平面，∴平面，（步骤5）．（3），∴是二面角的平面角．（步骤6）在中，，在中，，∴二面角的余弦值为．（步骤7）19.（本小题满分13分）设.（I）求在上的最小值；（II）设曲线在点的切线方程为，求的值.【测量目标】函数、导数的基础知识，运用导数研究函数性质，导数的几何性质.【考查方式】给出含参的函数解析式，利用导数对参数进行分类讨论求函数的最值；根据导数的几何性质，得到切点方程联立该点函数方程求值.【难易程度】中等【试题解析】（I）设，则.（步骤1）①当时，在上是增函数，得：当时，的最小值为.（步骤2）②当时，，当且仅当时，的最小值为.（步骤3）（II），（步骤4）由题意得：20. （本小题满分13分）如图，分别是椭圆的左，右焦点，过点作轴的垂线交椭圆的上半部分于点，过点作直线的垂线交直线于点；（I）若点的坐标为，求椭圆的方程；（II）证明：直线与椭圆只有一个交点.第20 题图【测量目标】椭圆方程和椭圆几何性质，直线与椭圆的位置关系. 【考查方式】通过图形以及已知条件求椭圆方程；根据直线与圆的位置关系进行证明.【难易程度】中等【试题解析】（I）点代入，得：.（步骤1）.①又. ②.③（步骤2）由①②③得：，即椭圆的方程为.（步骤3）（II）设，则.（步骤4）得：，（步骤5）.（步骤6）过点与椭圆相切的直线斜率.（步骤7）得：直线与椭圆只有一个交点.21.（本小题满分13分）数列满足：.（I）证明：数列是单调递减数列的充分必要条件是；（II）求的取值范围，使数列是单调递增数列.【测量目标】数列概念及其性质，不等式及其性质，充要条件.【考查方式】给出数列关系式，分步骤证明充分，必要条件；分类讨论，归纳求参数的取值范围使得数列单调递增.【难易程度】较难【试题解析】（I）必要条件当时，数列是单调递减数列；（步骤1）充分条件数列是单调递减数列.（步骤2）得：数列是单调递减数列的充分必要条件是.（II）由（I）得：.①当时，，不合题意；（步骤3）②当时，，，（步骤4）.（步骤5）当时，与同号，由，.（步骤6）当时，存在，使与异号.（步骤7）与数列是单调递减数列矛盾得：当时，数列是单调递增数列.（步骤8）。

保密★启用前淮南一中六安一中蒙城一中颍上一中2012届高三“四校”联考第二次考试理科综合试题命题学校：蒙城一中2012-04-06本试卷分第I卷（选择题）和第II卷（非选择题）两部分。

第I卷第1至20题，第II卷第21至31题。

全卷满分300分，考试时间150分钟。

本试题可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na -23 Cl-35.5考生注意事项：1.答题前，务必在答题卡．．．上．规定的地方填写自己的姓名、班级、座位号。

2.答第I卷时，每小题选出答案后，用0.5毫米的黑色签字笔把对应题目的答案填写在答题卡上。

如需改动，用橡皮擦干净后，再选填其他答案。

3.答第II卷时，必须用0.5毫米的黑色墨水签字笔在答题．．卡上．．书写，要求字体工整、笔迹清晰。

必须在题号所指示的答题方框内作答，超出答题方框书写的答案无效。

第I卷选择题（本部分共20小题，每题6分，共120分）1.研究表明生物膜在结构和功能上具有一定的联系。

高尔基体具有极性，靠近细胞核的一面称为形成面，接近细胞膜的一面称为成熟面。

从形成面到成熟面，膜的厚度和化学成分发生逐渐改变，下列叙述正确的是A.形成面似核膜，成熟面似内质网B.形成面似内质网，成熟面似细胞膜C.形成面似核膜，成熟面似细胞膜D.形成面似内质网，成熟面似核膜2.右图为基因型AABb的某动物进行细胞分裂的示意图。

相关判断错误的是A．此细胞可能为为次级精母细胞B．此细胞中基因a来源于基因突变或者四分体时期的交叉互换C．此细胞可能形成两种精子或一种卵细胞D．此动物体细胞内最多含有四个染色体组3.当呼吸底物不是糖时，有氧呼吸消耗的O2和产生的CO2的体积并不相等.利用如下图所示装置两套，设为甲、乙，测定单位质量小麦种子呼吸时CO2释放量与O2消耗量的比值，下列构思可以达到实验目的的是( ）A．甲装置烧杯中盛放清水，在光照下测定O2释放量，乙装置在黑暗下测定CO2释放量B．甲装置烧杯中盛放清水，测定CO2释放量，乙装置换成CO2吸收剂测定O2消耗量C．甲装置烧杯中盛放清水，测定气体体积变化量，乙装置换成CO2吸收剂，测定O2消耗量D．甲装置烧杯中盛放CO2缓冲剂（可吸收和放出CO2），测定氧气消耗量，乙装置放死亡种子作对照4.激素作为一种化学信使，能把某种调节的信息由内分泌细胞携带至靶细胞。

2012年安徽省普通高等学校招生统一考试试题、参考答案
(理科数学)
本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分．第I 卷1至2页，第II 卷3至4页，共150分．
第I 卷
考生注意：
1．答题前，考生务必将自己的准考证号、姓名填写在答题卡上．考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致．
2．第I 卷每小题选出答案后，用2Ｂ铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．第II 卷用黑色墨水签字笔在答题卡上书写作答．若在试题卷上作答，答案无效．
3．考试结束，监考员将试题卷、答题卡一并收回．
参考公式：
如果事件A B ，互斥，那么 球的表面积公式
()()()P A B P A P B +=+ 24πS R =
如果事件A B ，相互独立，那么 其中R 表示球的半径
()()()P A B P A P B =g g 球的体积公式
如果事件A 在一次试验中发生的概率是P ，那么 34π3V R =
n 次独立重复试验中恰好发生k 次的概率 ()(1)k k n k n n P k C P P -=-
其中R 表示球的半径。

2012年普通高等学校招生全国统一考试（安徽卷）数学（理科）答案1-5 DCBBC 6-10 ADACD 11. [3,0]- 12. 92 13. 3 14. 98- 15. ①②③16【解析】22111()cos(2)sin cos 2sin 2(1cos 2)24222f x x x x x x π=++=-+-11sin 222x =-（I ）函数()f x 的最小正周期22T ππ== （2）当[0,]2x π∈时，11()()sin 222g x f x x =-=当[,0]2x π∈-时，()[22x ππ+∈11()()sin 2()sin 22222g x g x x x ππ=+=+=-当[,)2x ππ∈--时，()[2x ππ+∈11()()sin 2()sin 222g x g x x x ππ=+=+=得：函数()g x 在[,0]π-上的解析式为1sin 2(0)22()1sin 2()22x x g x x x πππ⎧--≤≤⎪⎪=⎨⎪-≤<⎪⎩17【解析】（I ）2X n =+表示两次调题均为A 类型试题，概率为12n n m n m n +⨯+++ （Ⅱ）m n =时，每次调用的是A 类型试题的概率为12p =随机变量X 可取,1,2n n n ++21()(1)4P X n p ==-=，1(1)2(1)2P X n p p =+=-=，21(2)4P X n p =+== X n1n + 2n +P1412 14111(1)(2)1424EX n n n n =⨯++⨯++⨯=+答：（Ⅰ）2X n =+的概率为12n n m n m n +⨯+++（Ⅱ）求X 的均值为1n +18【解析】（I ）取11,BC B C 的中点为点1,O O ，连接1111,,,AO OO AO AO 则AB AC AO BC =⇒⊥，面ABC ⊥面11BB C C AO ⇒⊥面11BB C C 同理：11AO ⊥面11BB C C 得：1111//,,,AO AO A O A O ⇒共面 又11,OO BC OO AO O ⊥=⇒ BC ⊥面111AOO A AA BC ⇒⊥（Ⅱ）延长11AO 到D ，使1O D OA = 得：11////O D OA AD OO ⇒ 1O O B C ⊥，面111A BC ⊥面11BB C C 1OO ⇒⊥面111A B C ⇒AD ⊥面111A B C 222214(21)5A A A D D A =+=++= （Ⅲ）11,AO BC AO BC AOA ⊥⊥⇒∠是二面角1A BC A --的平面角 在11Rt OO A ∆中，222211114225A O OO AO =+=+=在1Rt OAA ∆中，22211115cos 25AO AO AA AOA AO AO +-∠==-⨯ 得：二面角1A BC A --的余弦值为55-。

安徽省淮南四中二月高三数学试题（理科）一、选择题：本大题共12个小题. 每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的 1．若z 是复数，且i z 432+-=，则z 的一个值为A ．1-2iB ．1+2iC ．2-iD ．2+i2．若以连续掷两次骰子分别得到的点数m ，n 作为点P 的横、纵坐标，则点P 在直线x+y=5下方的概率为（ ）A ．61 B ．41 C ．121D ．913．下列有关命题的说法正确的是 ( )．A ．命题“若21x =，则1=x ”的否命题为：“若21x =，则1x ≠”． B ．“1x =-”是“2560x x --=”的必要不充分条件．C ．命题“x R ∃∈，使得210x x ++<”的否定是：“x R ∀∈， 均有210x x ++<”． D ．命题“若x y =，则sin sin x y =”的逆否命题为真命题． 4．已知函数]3,3[sin ππω-=在x y 上是减函数，则实数的ω的取值范围是 （ ）A ．]23,(--∞B ．)0,23[-C ．]23,0(D ．),23[+∞5. 已知m 是平面α的一条斜线，点A α∉，l 为过点A 的一条动直线，那么下列情形可能 出现的是（ ）A ．//l m ，l α⊥B ．l m ⊥，l α⊥C ．l m ⊥，//l αD ．//l m ，//l α 6．已知集合(21){|sin ,,}2k A y y x x k Z π+===∈，2{|20}B x x ax b =-+=， 若B ≠∅，A B A =，则满足条件的实数对(,)a b 共有 （ ）A ．0对B ．1对C ．2对D ．3对7．若21()(*,100)nx n N n x+∈≤展开式中一定存在常数项，则n 的最大值为 ( )A ．90B ．96C ．99D ．1008．如果直线l ：10y kx =-与圆22240x y mx y +++-=交于M ．N 两点，且M ．N 关于直线20x y +=对称，则直线l 截圆所得的弦长为（）A 5B ．5C ．2D ．49．数列{}n a 满足11(*)2n n a a n N ++=∈，11a =，n S 是{}n a 的前n 项和，则21S ＝（ ） A ．4B ．6C ．92D ．11210．若关于x ，y 的不等式组1212x y x y ax y -≤⎧⎪+≥⎨⎪+≤⎩表示的平面区域是一个三角形，则a 的取值范围是A ．12a -<<B ．1a <-或2a >C ．21a -<<D ．2a <-或1a >11．已知）（x f 是以2为周期的偶函数，当[0,1]x ∈时，()f x x =，那么在区间[1,3]-内，关于x 的方程()1f x kx k =++（k R ∈且1k ≠-）有4个不同的根，则k 的取值范围是A ．1(,0)4-B ．(1,0)-C ．1(,0)2-D ．1(,0)3- 12．如图， AB是抛物线22(0)y px p =>的一条经过焦点F 的弦，AB 与两坐标轴不垂直，已知点M （－1，0）， ∠AMF ＝∠BMF ，则p 的值是A ．12B ．1C ．2D ．4第II 卷（非选择题 共90分）二、填空题：本大题共4个小题，每小题4分，共16分， 13．观察下列式子： ,474131211,3531211,2321122222<+++<++<+，则可以猜想：当2≥n 时，有 .14．已知数列{}n a 中，11a =，1n n a a +=+，利用如图示的程序框图计算该数列的第10项，则判断框中应填的语句 是________________． 15．=-⎰-dx x 0224 .16．在△ABC 中，已知15AB AC ⋅=，6AB BC ⋅=，14AC BC ⋅=，则△ABC 的面积为AB O F M xy（第12题图）开始 n=1,S=1n=n+1 S=S+n 结束输出S是否（第14题图）三．解答题(本大题共6小题，满分74分．解答须写出文字说明，证明过程和演算步骤．)淮南四中二月高三 数学（理科）试题答题卷一：选择题（每小题5分，共计60分）题号 1 2 3 4 5 6 7 89 10 11 12 答案二：填空题（每小题4分，共计16分） 13． ； 14． ； 15． ； 16． ；三：解答题……………………………………密…………………………封……………………………………线…………………………………………班级 姓名 学号 .17．（本小题满分12分）已知向量)3,cos 2(2x a =→-，)2sin ,1(x b =→-， 函数→-→-⋅=b a x f )(，2)(→-=b x g ．（Ⅰ）求函数)(x g 的最小正周期； （Ⅱ）在∆ABC 中，c b a ,,分别是角C B A ,,的对边，且3)(=C f ，1=c ，32=ab ，且b a >，求b a ,的值． 18．（本小题满分12分）参考答案一、选择题.1-5BADBC6-10DCDBADC 二、填空题 13．n n n12131211222-<++++14．n<10（或n≤9） 15.π 16.3 三、解答题17．（本小题满分12分） 解：（Ⅰ）234cos 2124cos 112sin 1)(22+-=-+=+==→-x x x bx g ---------2分 ∴函数)(x g 的最小周期242ππ==T ----------4分 （Ⅱ）x x x x b a x f 2sin 3cos 2)2sin ,1()3,cos 2()(22+=⋅=⋅=→-→- 1)62sin(22sin 312cos ++=++=πx x x -------------6分31)62sin(2)(=++=πC C f ∴1)62sin(=+πC ------------7分C 是三角形内角 ∴)613,6(62πππ∈+C ， ∴262ππ=+C 即：6π=C -------------8分 ∴232cos 222=-+=ab c a b C 即：722=+b a ----------------10分将32=ab 可得：71222=+aa 解之得：432或=a ∴23或=a ∴32或=bb a >， ∴2=a 3=b ------------12分18、【解析】：1）ξ的取值：6、2、1、-2………（1分）P （ξ=6）=126200=0.63；P （ξ=2）=50200=0.25；P （ξ=1）=20200=0.1；P （ξ=-2）=4200=0.02； ………（4分）ξ 6 2 1 －２ P 0.63 0.25 0.1 0.02E ξ0.02=4.34………（6分）2ξ 6 2 1 －２P 0.7 0.29-xx 0.01………（9分）E ξ=6×0.7+2×（0.29-x ）+1×x+（-2）×0.01≥4.73∴x ≤0.03C 1B 1DC BOyxz∴三等品率最多为300………（12分）19、解：（Ⅰ）当D 为AC 中点时,有//1AB 平面1BDC ……2分证明:连结1B C 交1BC 于O ,连结DO ∵四边形11BCC B 是矩形 ∴O 为1B C 中点又D 为AC 中点,从而1//DO AB ………………………4分 ∵1AB ⊄平面1BDC ,DO ⊂平面1BDC∴//1AB 平面1BDC ……………………………………6分 （Ⅱ）建立空间直角坐标系B xyz -如图所示, 则(0,0,0)B ,3,1,0)A ,(0,2,0)C ,33(,0)22D ,1(0,2,23)C …………7分 所以33(,0)2BD =,1(0,2,23)BC =. …………………8分 设),,(1z y x n =为平面1BDC 的法向量,则有330222230x y y z +=⎪⎨⎪+=⎩,即33x zy z =⎧⎪⎨=-⎪⎩ 令1=z ,可得平面1BDC 的一个法向量为1(3,3,1)n =-,而平面1BCC 的一个法向量为2(1,0,0)n =……………11分 所以1212123313cos ,13||||13n n n n n n ⋅<>=== 所以二面角D BC C --1的余弦值为13133…………………………12分 20、解：（Ⅰ）当1=a 时，x x x f ln 21)(2+=，x x x x x f 11)(2+=+='；……………2分对于∈x [1，e]，有0)(>'x f ，∴)(x f 在区间[1，e]上为增函数，…………3分∴21)()(2max e e f x f +==，21)1()(min ==f x f .……………………………4分（Ⅱ）令x ax x a ax x f x g ln 2)21(2)()(2+--=-=，则)(x g 的定义域为（0，+∞）.……………………………………………5分在区间（1，+∞）上，函数)(x f 的图象恒在直线ax y 2=下方等价于0)(<x g 在区间（1，+∞）上恒成立.∵xx a x x ax x a x a x a x g ]1)12)[(1(12)12(12)12()(2---=+--=+--='① 若21>a ，令0)(='x g ，得极值点11=x ，1212-=a x ，………………6分当112=>x x ，即121<<a 时，在（2x ，+∞)上有0)(>'x g ， 此时)(x g 在区间(2x ，+∞)上是增函数，并且在该区间上有)(x g ∈()(2x g ，+∞)，不合题意；…………………7分当112=<x x ，即1≥a 时，同理可知，)(x g 在区间(1，+∞)上，有)(x g ∈()1(g ，+∞)，也不合题意；………………………………………8分② 若21≤a ，则有012≤-a ，此时在区间(1，+∞)上恒有0)(<'x g ， 从而)(x g 在区间(1，+∞)上是减函数；……………………………………9分 要使0)(<x g 在此区间上恒成立，只须满足021)1(≤--=a g 21-≥⇒a ， 由此求得a 的范围是[21-，21]. 综合①②可知，当a ∈[21-，21]时，函数)(x f 的图象恒在直线ax y 2=下方.………………………………………………12分21、解：（I ）设),(),,(2211y x B y x A由.0844222=--⎩⎨⎧=+=my y xy my x 得.8,42121-==+∴y y m y y ………………………………………………2分又),,2()2,(,),2,0(111111y x my x AT MA n M --=+=-λλ即.21,211111my y m y --=-=+∴λλ得同理，由.21,222my BT MB --==λλ得………………………………4分.1882)(22)11(2221212121-=+-=+--=+--=+∴mmy my y y y y m λλ…………6分 （II ）方法一：当m=0时，A （2，22），B （2，－2），D （n ，22），E （n ，－22）. ∵ABED 为矩形，∴直线AE 、BD 的交点N 的坐标为（).0,22+n ………………8分当),,22(),,22(),,(),,(,021121y n NE y x n AN y n E y n D m -=--+=≠ 时(*))2(28)2(2)(2222)222(22)22(2112121121n m m n m y my y y n y n y my n y n y x n +=+-=-+-=-+--+=-+-+则 同理，对BN 、ND 进行类似计算也得（*）式.………………………………12分即n=－2时，N 为定点（0，0）.反之，当N 为定点，则由（*）式等于0，得n=－2.…………………………14分 方法二：首先n=－2时，则D （－2，y 1），A （),,2(),,2(),,222211y my B y E y my +-+ )2(4:2121++-=-x my y y y y l DB ① )2(4:1212++-=-x my y y y y l EA ②…………………………………………8分 ①－②得,).4141)()(2(12121212y y my my y y x y y ≠+++-+=- .04884241411222121212=+-=++=-+++=∴my m m my y my y y m my my x.)0,0(为定点N ∴…………………………………………………………10分反之，若N 为定点N （0，0），设此时),,(),,(21y n E y n D 则).,2(),,(221y my NB y n ND +==由D 、N 、B 三点共线，.022121=-+∴ny y y my ③同理E 、N 、A 三点共线，.021221=-+∴ny y y my ④………………12分③+④得,0)()(22212121=+-++y y n y y y my即－16m+8m －4m=0，m(n+2)=0. 故对任意的m 都有n=－2.……………………………………………………13分22、【解析】（Ⅰ）∵ 33332123n n a a a a S ++++=，∴ 3333212311n n a a a a S --++++=， ∴322111()()()n n n n n n n n n n n a S S S S S S a S S a ---=-=-+=+-，∴ 22nn n a S a =-。

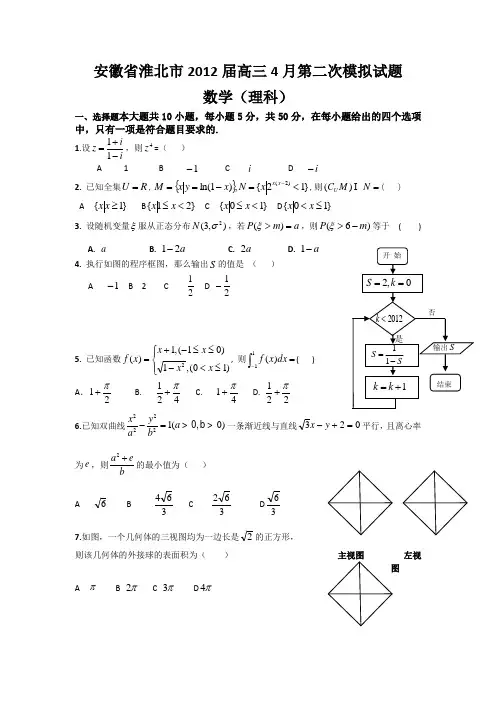
安徽省淮北市2012届高三4月第二次模拟试题数学（理科）一、选择题本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.设iiz -+=11，则4z =（ ）A 1B 1-C iD i -2. 已知全集R U =,{}}12{,)1ln()2(<=-==-x x x N x y x M ,则=N M C U )(( ) A }1{≥x x B }21{<≤x x C }10{<≤x x D }10{≤<x x3. 设随机变量ξ服从正态分布),3(2σN ，若a m P =>)(ξ，则)6(m P ->ξ等于 ( ) A. aB. a 21-C. a 2D. a -1 4. 执行如图的程序框图，那么输出S 的值是 （ ） A 1- B 2 C 21 D 21- 5. 已知函数⎪⎩⎪⎨⎧≤<-≤≤-+=)10(,1)01(,1)(2x x x x x f , 则⎰-=11)(dx x f ( )A ．21π+ B. 421π+ C. 41π+ D. 221π+6.已知双曲线22221(0)x y a a b -=>0,b >一条渐近线与直线023=+-y x 平行，且离心率为e ，则2a eb+的最小值为（ ）A6 B364 C 362 D 367.如图，一个几何体的三视图均为一边长是2的正方形，则该几何体的外接球的表面积为（ ） 主视图 左视Aπ B π2 C π3 D π4第12题俯视图8．动点(,)P x y 满足的区域为：⎪⎩⎪⎨⎧≤--≥-+≥+-0420501y x y x y x ，若幂函数(),(f x x αα=为常数）的图像与动点P 所在的区域有公共点，则α的取值范围是（ ） A ),3[log 2+∞ B ]3log ,2[log 23 C ),2[log 3+∞ D),3[log ]2log ,(23+∞⋃-∞9．已知函数()f x 对任意x R ∈都有(4)()2(2)f x f x f +-=，若(1)y f x =-的图象关于直线1x =对称，且(1)2f =，则=)1003(f （ ）A ．2B ．3C ．4D ．610．已知C 为线段AB 上一点，P 为直线AB 外一点，I 为PC 上一点，满足104=-=-,=，且)0(>++=λλBA BI ,）A 2B 4C 3D 5二、填空题本大题共5小题，每小题5分，共25分.把答案填在答题卡的相应位置.11．设二项式6)(xa x -的展开式中2x 的系数为A ,常数项为B ,若A B 4=,则=a12. 如图，正方体1111ABCD A B C D -的棱长为1，线段11B D 上有两个动点E ，F ，且1EF =，则四面体A EFB -的体积13．已知n n T S ,分别是等差数列}{},{n n b a 的前n 项和，且)(,2412+∈-+=N n n n T S n n 则=+++1561118310b b a b b a14．已知过定点(1,0)P -的直线⎪⎪⎩⎪⎪⎨⎧=-=t y t x l 22122: (其中t 为参数)与圆222440x y x y +--+=交于,M N 两点，则PM PN ⋅=15．设()sin2cos2f x a x b x ＝＋，其中,,0a b R ab ∈≠. 若()6f x f π⎛⎫≤⎪⎝⎭对一切x R ∈ 恒成立，则 ① 11012f π⎛⎫=⎪⎝⎭； ② 7125f f ππ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭；③ ()f x 既不是奇函数也不是偶函数； ④ ()f x 的单调递增区间是()2,63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦； ⑤ 经过点(),a b 的所有直线均与函数()f x 的图象相交．以上结论正确的是__________________（写出所有正确结论的编号）．三、解答题16．一笼子中装有2只白猫，3只黑猫，笼门打开每次出来一只猫，每次每只猫都有可能出来。

绝密★启用前2012年普通高等学校招生全国统一考试(安徽卷)数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷第1至第3页,第Ⅱ卷第4至第6页.全卷满分150分,考试时间120分钟. 考生注意事项：1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致.务必在答题卡背面规定的地方填写姓名和座位号后两位.2.答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3.答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上．．．．书写,要求字体工整、笔迹清晰.作图题可先用铅笔在答题卡．．．规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚.必须在题号所指示的答题区域作答,超出答题区域书写的答案无效．．．．．．．．．．．．．,．在．答题卷、草稿纸上答题无效．．．．．．．．．．．．. 4.考试结束,务必将试题卷和答题卡一并上交. 参考公式：如果事件A 与B 互斥；则()()()P A B P A P B +=+ 如果事件A 与B 相互独立；则()()()P AB P A P B = 如果A 与B 是事件,且()0P B >；则()()()P AB P A B P B =第Ⅰ卷(选择题共50分)一、选择题：本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数z 满足：(i)(2i)5z --=；则z =（ ）A .22i --B .22i -+C .2-2iD .2+2i2.下列函数中,不满足(2)2()f x f x =的是 （ ）A .()||f x x =B .()||f x x x =-C .()1f x x =+D .()f x x =-3.如图所示,程序框图（算法流程图）的输出结果是（ ）A .3B .4C .5D .84.公比为2的等比数列{}n a 的各项都是正数,且31116a a =,则210log =a （ ）A .4B .5C .6D .75.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则 （ ）A .甲的成绩的平均数小于乙的成绩的平均数B .甲的成绩的中位数等于乙的成绩的中位数C .甲的成绩的方差小于乙的成绩的方差D .甲的成绩的极差小于乙的成绩的极差6.设平面α与平面β相交于直线m ,直线a 在平面α内,直线b 在平面β内,且b m ⊥ 则“αβ⊥”是“a b ⊥”的（ ）A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件7.2521(2)(1)x x +-的展开式的常数项是（ ）A .3-B .2-C .2D .38.在平面直角坐标系中,(0,0),(6,8)O P ,将向量OP 绕点O 按逆时针旋转3π4后得到向量OQ ,则点Q 的坐标是（ ）A.(- B.(- C.(2)--D.(-9.过抛物线24y x =的焦点F 的直线交抛物线于,A B 两点,O 为是坐标原点.若3AF =,则AOB ∆的面积为 （ ）ABCD.10.6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为 （ ）A .1或3B .1或4C .2或3D .2或4姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无------------------------------------第Ⅱ卷(非选择题 共100分)二、填空题：本大题共5小题,每小题5分,共25分.把答案填在题中的横线上.11.若,x y 满足约束条件：0,23,23,x x y x y ⎧⎪+⎨⎪+⎩≥≥≤则x y -的取值范围为______.12.某几何体的三视图如图所示,该几何体的表面积是______.13.在极坐标系中,圆4sin ρθ=的圆心到直线π()6R θρ=∈的距离是______. 14.若平面向量a,b 满足：|2|3-≤a b ；则⋅a b 的最小值是______.15.设ABC ∆的内角,,A B C 所对的边为,,a b c ,则下列命题正确的是______（写出所有正确命题的编号）.①若2ab c >；则π3C <②若2a b c +>；则π3C <③若333a b c +=；则π2C <④若()2a b c ab +<；则π2C >⑤若22222()2a b c a b +<；则π3C >三、解答题：本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤. 16.（本小题满分12分）设函数2π())sin 24f x x x =++ （Ⅰ）求函数()f x 的最小正周期；（Ⅱ）设函数()g x 对任意x ∈R ,有π()()2g x g x +=,且当π[0,]2x ∈时,1()()2g x f x =-.求()g x 在区间[π,0]-上的解析式.17.（本小题满分12分）某单位招聘面试,每次从试题库随机调用一道试题,若调用的是A 类型试题,则使用后该试题回库,并增补一道A 类试题和一道B 类型试题入库,此次调题工作结束；若调用的是B 类型试题,则使用后该试题回库,此次调题工作结束.试题库中现共有n m +道试题,其中有n 道A 类型试题和m 道B 类型试题,以X 表示两次调题工作完成后,试题库中A 类试题的数量.（Ⅰ）求2X n =+的概率；（Ⅱ）设m n =,求X 的分布列和均值（数学期望）.18.（本小题满分12分）平面图形111ABB AC C 如图1所示,其中11BB C C 是矩形,12,4BC BB ==,AB AC =1111A B A C ==.现将该平面图形分别沿BC 和11B C 折叠,使ABC ∆与111A B C ∆所在平面都与平面11BB C C 垂直,再分别连接111,,A A A B AC ,得到如图2所示的空间图形.对此空间图形解答下列问题. （Ⅰ）证明：1AA BC ⊥； （Ⅱ）求1AA 的长；（Ⅲ）求二面角1A BC A --的余弦值.19.（本小题满分13分）设1()(0)x x f x ae b a ae =++>.（Ⅰ）求()f x 在[0,)+∞内的最小值；（Ⅱ）设曲线()y f x =在点(2,(2))f 的切线方程为32y x =；求a,b 的值.20.（本小题满分13分）如图,12(,0),(,0)F c F c -分别是椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,过点1F 作x轴的垂线交椭圆C 的上半部分于点P ,过点2F 作直线2PF 的垂线交直线2a x c=于点Q .（Ⅰ）若点Q 的坐标为(4,4)；求此时椭圆C 的方程； （Ⅱ）证明：直线PQ 与椭圆C 只有一个交点.21.（本小题满分13分）数列{}n x 满足：2*110,()n n n x x x x c n +==-++∈N（Ⅰ）证明：数列{}n x 是单调递减数列的充分必要条件是0c <； （Ⅱ）求c 的取值范围,使{}n x 是单调递增数列.2012年普通高等学校招生全国统一考试（安徽卷）数学(理科)答案解析【解析】{}n a 是等比数列，且，又等比数列4=，16a ∴=log 32=log 【解析】1(45x =甲甲的成绩的平均数等于乙的成绩的平均数；甲的成绩的中位数甲的成绩的方差为甲的成绩的极差【解析】αβ⊥，”的充分条件，m ，则a ⊥故选A ．【解析】第一个因式取【解析】(0,0)O ，设(10cos OP =5，又OP按旋转OQ，10cos OQ θ⎡=+⎢⎝⎭⎦∴【提示】由点，知(6,8)OP =，设(10cos OP =，由向量OP 绕点逆时针方向旋转后得向量OQ ，由此能求出结果．【考点】平面向量的坐标运算，||3AF =，即点)=a θ-，∴【解析】2613C -=丙、丁、戍、己6①设仅有甲与乙，丙没交换纪念品，则甲收到得最大值0；当0 x =，3y =时，取得最小值3-．|2|3a b -≤，22494a b a b ∴+≤+，又2244||||4a b a b a b +≥≥-，44a b a b ≥-，98a b -∴≥，a b ∴的最小值是98-．示】由平面向量a ，b 满足|2|3a b -≤，知22494a b a b +≤+，故22224244||||4a b a b a b a b +≥=≥-，由此能求出a b 的最小值．【考点】平面向量数量积【解析】①2ab c >，②2a b c +>，cos ∴③33a b +=2cos a C =确；④2a b ==以例27o sa C +=，又71082>-放大为ab ，再结合均值定理即可证明（Ⅰ）()f x =12=（Ⅱ）当 AB AC =面ABC AO ∴⊥面共面，又1OO BC ⊥1AO O =，BC ⊥面BC ；（Ⅱ）延长D OA =，连接，1AO AO ∥1O D OA ∴∥AD OO ∴∥1OO BC ⊥1OO ∴⊥面AD ∴⊥面（Ⅲ）AO BC ⊥1AOA 是二面角11Rt OO A ∆中，51AO O =，（Ⅱ）()f x a =，2PF QF ⊥244b a c c -⨯--又24a c=②，22a b =-由①②③解得：，则2PF QF ⊥，解得2y =又2222x y a b +2y b =-过点1n n x x +-。

2012届淮南四中一模选择题、填空题专项卷三2012-1一．选择题1．已知"03",2成立则<-∈x x R x 是“0)2)(1(≤--x x 成立”的 （ ） A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 2．命题“若0,,,022==∈=+b a R b a b a 则”是逆否命题是 （ ）A ．若0),,(022≠+∈≠≠b a R b a b a 则B ．若0),,(022≠+∈≠=b a R b a b a 则C ．若0),,(0022≠+∈≠≠b a R b a b a 则且D ．若0),,(0022≠+∈≠≠b a R b a b a 则或3．已知函数,2cos )4(sin 22x x y -+=π则它的周期T 和图象的一条对称轴方程是（ ）A ．8,2ππ==x T B ．83,2ππ==x T C ．8,ππ==x T D ．83,ππ==x T4．已知向量与则若,25)(,5||),4,2(),2,1(=⋅+=--==的夹角为 （ ）A ．30°或150°B ．60°或120°C ．120° D.150°5、 系数为非零实数的关于x 的不等式a 1 x 2+b 1 x +c 1＜0和a 2 x 2+b 2 x +c 2＜0的解集分别是M 、N ，则“a 1a 2＝b 1b 2＝c 1c 2”是“M ＝N ”成立的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也非必要条件6．已知P 是双曲线116922=-y x 的右支上一点，M 、N 分别是圆4)5(22=++y x 和1)5(22=++y x 上的点，则||||PN PM -的最大值为（ ） A ．6 B ．7 C ．8 D ．9 7．已知函数c b a x x f x,,,log )21()(3正实数-=是公差为负实数的等差数列，且满足0)()(<⋅c f a f ；已知命题P ：实数0)(=x f d 是方程的一个解；则下列四个命题： ①a d <；②b d >；③c d <；④c d >中是命题P 的必要不充分条件的命题个数为（ ）A ．1B ．2C ．3D ．48．若}{n a 是等差数列，n S 是其前n 项和，083>+a a ，09<S ，则1S ，2S ，3S ，…，n S 中最小的是（ ）A ．4S ；B ．5S ；C ．6S ；D ．9S .9.已知函数)0)(sin(2)(>+=ωϕωx x f 的导数()f x '的最大值为π，且对任意R x ∈，都有12()()()f x f x f x '''≤≤成立，则||21x x -的最小值为 ( ) A.π B.1 C.2 D.410．已知平面内一点},16)sin 2()cos 2(|),{(22R y x y x P ∈=-+-∈ααα，则满足条件的点P 在平面内所组成的图形的面积是（ ）A ．36πB ．32πC ．16πD ．4π二．填空题11.若函数()(01)xxf x ka aa a -=->≠且在(,)-∞+∞上既是奇函数又是减函数，则函数)22(log )(g 2k a a x x x a --=，则使0)(<x f 的x 的取值范围是12.已知函数22log (2),0(),026x x f x x x x +>⎧⎪=⎨≤⎪+⎩,()2f a =，则a =13.函数log (1)1(0,1)a y x a a =-+>≠的图象恒过定点M ,且点M 在直线y mx n =+上，其中0mn >，则11m n+的最小值为_____14．在中，，则的最大值为 。

淮南市2012届高三第二次模拟考试理科综合能力测试考生注意事项：1．本试卷分第1卷（选择题）和第Ⅱ卷（非选择题）两部分，全卷满分300分，时间150分钟。

2．答题前，务必在答题卷规定的地方填写清楚自己的姓名、座位号、准考证号、贴好条形码。

3．在答题卷中题号所指示的答题区域作答，超出区域的答案无效。

第1卷（选择题，共120分）可能用到的相对原子质量：H-1 C-l2 0-16 Na-23 S-32 Zn-65一、选择题（本大题包括20小题，每小题6分，共120分。

每一小题只有一个选项最符合题意）1. 2011年11月25日nature杂志在线发表了德国研究人员的最新研究成果：癌变前的衰老肝细胞能被由肿瘤抗原引导的免疫反应清除。

利用这一成果，可以对癌变前衰老细胞进行抗原特异性免疫监测。

下列有关叙述中，不正确的是A．衰老肝细胞的细胞膜通透性改变，使物质运输功能降低B．癌变以后的肝细胞容易向其他组织转移C．在免疫系统被抑制的患者肝脏中，衰老肝细胞不会积累D．由肿瘤抗原引导的免疫反应清除癌变前的衰老肝细胞属于细胞免疫2．关于下图的相关说法中，正确的是A．若曲线1表示酵母菌C02释放量随02浓度的变化，则e点是无氧呼吸消失点B．曲线2可以表示质壁分离过程中细胞液浓度的变化C．pH由10到2的过程中，胃蛋白酶的活性变化如曲线2D．若曲线3表示在密闭装置中酵母菌种群数量的变化，则be段种内斗争最弱，cd段种内斗争最激烈3．若右图表示的是原核细胞中DNA的复制和转录过程，下列有关叙述正确的是A．核仁与图中rRNA的合成以及核糖体的形成有关B．中心法则中的遗传信息传递指的是B过程C．每种tRNA能识别并转运一种氨基酸D．图中A过程一定会发生基因突变4．调查人员对一患有某种单基因遗传病的女性家系成员进行调查后，记录如下（“+”代表患者，“-”代表正常）。

下列有关分析正确的是A．该遗传病属于伴X染色体显性遗传病B．调查该病的发病方式应在自然人群中随机取样调查C．该女性与其祖母基因型相同的概率为2/3D．该女性的父母再生一个正常孩子的概率为1/45．如图表示GA（赤霉素）、ETH(乙烯)和IAA（吲哚乙酸）的关系，“+”表示促进，“-”表示抑制，下列有关说法不正确的是A．GA和IAA均可促进生长，表现为协同作用B．GA可以通过抑制IAA氧化酶的活性来降低IAA浓度C．由图推测，IAA两重性可能与ETH有关D．束缚态IAA可能具有平衡植物体内IAA水平的作用6．细菌外毒素是一类蛋白质，能刺激宿主产生免疫应答，形成能中和外毒素毒性的抗毒素。

安徽省淮南市数学高三上学期理数 12 月月考试卷姓名:________班级:________成绩:________一、 单选题 (共 12 题；共 24 分)1. （2 分） 复数 A.1 B.2，且， 则 的值为（ ）C.D. 2. （2 分） 设 A={x|﹣1≤x＜2}，B={x|x＜a}，若 A∩B≠∅，则 a 的取值范围是（ ） A . a＜2 B . a＞﹣2 C . a＞﹣1 D . ﹣1＜a≤23. （2 分） (2019 高二下·富阳月考) 若方程 （）存在 3 个实数根，则实数 的取值范围是A. B. C. D. 4. （2 分） 已知 a>0，函数 f(x)=ax2+bx+c，向量第 1 页 共 14 页与向量垂直时，则下列选项的命题中为假命题的是（ ） A. B. C. D.5. （2 分） 椭圆 A.3上有一点 P 到左焦点的距离是 4，则点 p 到右焦点的距离是（ ）．B.4C.5D.66. （ 2 分 ） (2017 高 二 下 · 深 圳 月 考 ) 在中，内角，，则的面积是（ ）所对的边分别是，若A.B.C. D. 7. （2 分） (2016 高三上·平罗期中) 已知数列{an}是等差数列，若 a4+2a6+a8=12，则该数列前 11 项的和为 （） A . 10 B . 12第 2 页 共 14 页C . 24 D . 33 8. （2 分） 已知直线 l1：x﹣2y﹣1=0，直线 l2：ax﹣by+1=0，其中 a，b∈{1，2，3，4，5，6，}．则直线 l1 与 l2 的交点位于第一象限的概率为（ ）A.B.C.D. 9. （2 分） 四面体 ABCD 中，E、F 分别为 AC、BD 中点，若 CD=2AB，EF⊥AB，则 EF 与 CD 所成的角等于（ ） A . 30° B . 45° C . 60° D . 90°10. （2 分） (2019 高一下·蛟河月考) 已知函数别是函数取得零点和最小值点横坐标，且在A.3B.5C.7D.9，和分单调，则 的最大值是（ ）11. （2 分） (2019 高三上·通州期中) 设函数则实数 的取值范围是（ ）第 3 页 共 14 页若方程有且只有一个根，A. B. C. D.12. （2 分） 已知 零点个数为（ ）为 R 上的可导函数，当 时，A.1B.2C.0D . 0或2二、 填空题 (共 4 题；共 4 分)， 则函数的13. （1 分） (2018·吉林模拟) 若曲线 ________的一条切线是直线，则实数 b 的值为14. （1 分） (2017 高一下·汽开区期末) 如图，在中，上，且，，则________．，点 D 在线段 AC15. （1 分） (2019 高一上·郑州期中) 已知函数，则关于 的不等式的解集是________.16. （1 分） (2017·东城模拟) 如图，在棱长为 2 的正方体 ABCD﹣A1B1C1D1 中，E 为对角线 B1D 上的一点， M，N 为对角线 AC 上的两个动点，且线段 MN 的长度为 1．第 4 页 共 14 页⑴当 N 为对角线 AC 的中点且 DE= 时，则三棱锥 E﹣DMN 的体积是________；⑵当三棱锥 E﹣DMN 的体积为 时，则 DE=________．三、 解答题 (共 7 题；共 85 分)17. （15 分） (2019 高二上·湖南期中) 已知数列 的前 项和为 ，且对任意的都有，数列 满足…（1） 求数列 ， 的通项公式；，函数 .（2） 若数列 满足， 是数列 的前 项和，是否存在正实数 ，对于任意，不等式，恒成立？若存在，请求出 的取值范围；若不存在，请说明理由.18. （10 分） (2019 高三上·上海月考) 已知点，，动点满足直线与的斜率之积为，记 的轨迹为曲线 .（1） 求 的方程，并说明 是什么曲线；（2） 过坐标原点的直线交 于 、 两点，点 在第一象限， 延长交 于点 ，轴，垂足为 ，连结 并①证明：是直角三角形；②求面积的最大值.19. （15 分） (2013·江西理) 小波以游戏方式决定是参加学校合唱团还是参加学校排球队，游戏规则为：以 0 为起点，再从 A1 ， A2 ， A3 ， A4 ， A5 ， A6 ， A7 ， A8（如图）这 8 个点中任取两点分别为终点得到两 个向量，记这两个向量的数量积为 X．若 X=0 就参加学校合唱团，否则就参加学校排球队．第 5 页 共 14 页（1） 求小波参加学校合唱团的概率； （2） 求 X 的分布列和数学期望． 20. （15 分） (2015 高一上·福建期末) 如图，在四棱锥 P﹣ABCD 中，PA⊥底面 ABCD，AD⊥AB，AB∥DC， AD=DC=AP=2，AB=1，点 E 为棱 PC 的中点．（1） 证明：BE∥平面 ADP； （2） 求直线 BE 与平面 PDB 所成角的正弦值．21. （10 分） (2020·阜阳模拟) 设函数，，其中（1） 若的图象总在函数的图象的下方，求实数 的取值范围；， 为正实数.（2） 设，证明：对任意，都有.22. （10 分） (2019·贵州模拟) 选修 4-4：坐标系与参数方程在直角坐标系中，直线 的方程为，曲线 ：（ 为参数，），在以原点 为极点， 轴正半轴为极轴的极坐标系中，曲线 ：.第 6 页 共 14 页（1） 求曲线 的普通方程和曲线 的直角坐标方程；（2）若直线 与曲线 有公共点，且直线 与曲线 含边界）内，求 的取值范围.的交点 恰好在曲线与 轴围成的区域（不23. （10 分） (2017·山西模拟) 设函数 f（x）=2|x+1|+|x﹣3|．（1） 求不等式 f（x）＜5 的解集；（2） 设 g（x）=kx，若 f（x）≥g（x）恒成立，求 k 的取值范围．第 7 页 共 14 页一、 单选题 (共 12 题；共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题；共 4 分)13-1、 14-1、 15-1、参考答案第 8 页 共 14 页16-1、三、 解答题 (共 7 题；共 85 分)17-1、17-2、第 9 页 共 14 页18-1、18-2、第 10 页 共 14 页19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、23-1、23-2、。