数学八年级上华东师大版13.1幂的运算-13.1 .3积的乘方课件
- 格式：ppt
- 大小：283.50 KB
- 文档页数：9
下载文档原格式
合集下载
数学华师大版八年级上《幂的运算》课件ppt(共18张PPT)
同底数幂相乘 m n m+n a · a =a
指数相加 底数不变 指数相乘
其中m , n都是 正整数
m n mn （a ） =a
幂的乘方
练习一
2. 计算：
①(10m· 10m－1 ).100= 102m+1 ②3×27×9×3m=
15 (m － n) =
3m＋6
③(m－n)4· (m－n) 5· (n－m)6
幂的运算 3 积的乘方
积的乘方
回忆: 同底数幂的乘法法则：
m n m+n a · a =a
其中m , n都是正整数
语言叙述： 同底数幂相乘，底数 不变，指数相加
回忆: 幂的乘方法则：
m n mn （a ） =a
其中m , n都是正整数
语言叙述： 幂的乘方，底数不变， 指数相乘
想一想：同底数 幂的乘法法则与 幂的乘方法则有 什么相同点和不 同点？
（C）(x7)7
（D ）x 3x 4x 5x 2
3．计算(-32)5-(-35)2的结果是（ B ）
（A ）0
（C）2×310
（B） -2×310
（D） -2×37
积的乘方
（1）(ab)2 = (ab) • (ab) = (aa) • (bb) = a (2 )b( 2 ) (ab) • (ab) • (ab) （2）（ab）3＝__________________________
(aaa) • (bbb) ＝__________________________
＝ a ( 3 )b( 3 ) (ab) • (ab) • (ab) • (ab) （3）（ab）4＝__________________________ (aaaa) • (bbbb) ＝__________________________ ＝a
华师大版八年级数学上册《积的乘方》精品课件
(－4×0.25)2005
用 法 则
＝ ＝1 (3)－82000×(－0.125)＝2001
－1
进
行 ＝ －82000×(－0.125)2000× (－0.125)
计
算 ＝ －82000×0.1252000× (－0.125)
＝ －（8×0.125）2000× (－0.125)
＝ －1× (－0.125) ＝ 0.125
（2） (105)6 (1030 )
（4） (a7)3 ( a21 )
（6） (x5)5
（ x25 ）
（8）(y3)2·(y2)3
（ y 12 ）
9、要学生做的事，教职员躬亲共做； 要学生 学的知 识，教 职员躬 亲共学 ；要学 生守的 规则， 教职员 躬亲共 守。2021/7/292021/7/29Thur sday, July 29, 2021
10、阅读一切好书如同和过去最杰出的人谈话。2021/7/292021/7/292021/7/297/29/2021 12:44:48 PM
11、一个好的教师，是一个懂得心理学和教育学的人。2021/7/292021/7/292021/7/29Jul-2129-Jul-21
12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/7/292021/7/292021/7/29Thursday, July 29, 2021
＝__(_a_a_a_)_•_(_b_b_b_)______________ ＝ a ( 3 )b( 3 ) （3）（ab）4＝___(a_b_)_•__(a_b_)_•_(_a_b_)_•_(_a_b_)______ ＝__(_a_a_a_a_)_•_(_b_b_b_b_)____________ ＝ a ( 4)b(4)
华东师大版八年级数学上册12.幂的乘方课件
议一议
同底数幂的乘法法则与幂的乘方法则有什么 相同点和不同点？
符号表示
相同点 不同点
同底数幂
相乘 am an amn
底 数
指数相加
不
幂的乘方 am n amn
变 指数相乘
共同之处：
同底数幂相乘
幂的乘方
底数不变
指数相加
指数相乘
其中m、n都是正整数
1.幂的乘方的法则 语言叙述 幂的乘方，底数不变，指数相乘.
(2)a2m =( a2 ) m =( am)2 （m为正整数）.
例1. 计算. (1) (103)5
(2) (b5)4
(3) (am)2
(4) -(x4)3
1.口算
(1)(102)3； (3)(an)3； (5) -(x4)3 ；
(2)(b7)5； (4) (y2)6 ； (6) (-y3)2;
求：（1）a2m ，a3n的值； （2） am+n 的值. （3） a2m+3n 的值.
2.已知 44×83=2x，求x的值.
解：∵44×83 = (22)4×(23)3 = 28×29 = 217
∴x=17.
互动探究
3.已知 2a 5，3b 7，求 22a3b 的值 .
4. 已知a3n=5，b2n=3，求：a6nb4n的值．
2 a6 a2
3 x2 x3 x4 4 (x)3 (x)5
5 (x)3 x6 6 a2 a3 a4 a
12.1.2 幂的乘方
(am )n ?
学习目标
1. 理解幂的乘方的运算性质，进一步体会和 巩固幂的意义. 2.掌握幂的乘方法则的推导过程，并能灵活应用.
问题探究一：幂的乘方的法则
华东师大版数学八年级上册12.1.3积的乘方课件
(a a a a) (b b b b) a（4）b（4）
比较等式两边底数与指数的变化，这几道题的计算有 什么共同特点，从中你能发现什么规律? 思考:若（3）中的指数变为正整数n时， ( ab )n= ？
abn ab ab ab( ab )n表示n个ab 相乘
n个
n个 n个
a a a b b b 乘法交换律与结合律
1·要注意，积的乘方运算中，括号内是积，不是和
2、运用积的乘方运算性质时，先看积中有哪些因式， 再将每个因式分别乘方，尤其是字母的系数，不要 漏掉乘方 3、因式可以为单项式，也可以为多项式. 4、三个或三个以上的积的乘方 5·出现正负号时：奇负偶正，先进行符号判断，再进 行幂的运算
达标检测，当堂反馈（5分钟）
3 (x + y)2
4 （2a2b）7
5 a b2
判断题 1.下列各式哪些能用积的乘方运算？
1 (3a)2
2 (-3ab)2
4 （2a2b）7
可以
注意：
1、积的乘方是指底数是乘积形式的乘方，积的 乘方运算中，括号内是积，不是和。
巩固练习1
写出下列幂的运算中底数的所有因式
(1)（2b）2 底数的所有因式 。 (2)(2ab)3 底数的所有因式 。 (3)(3ab2)3 底数的所有因式 。 (4)(-3x)2 底数的所有因式 。
巩固练习
判断下列计算是否正确，错误的并改正。
(1)（2b）2=2b2。 (2)(3ab)3=27ab3 (3)(-3x)2=3x2 (4)(2ab)3=6a3b3 (5)(abc)2=a2b2c2
巩固练习
判断下列计算是否正确，错误的并改正。
(1)（2b）2=2b2。×（2b）2=4b2。 (2)(3ab)3=27ab3 × (3ab)3=27a3b3 (3)(-3x)2=3x2 × (-3x)2=9x2 (4)(2ab)3=6a3b3 × (2ab)3=8a3b3 (5)(abc)2=a2b2c2 √
比较等式两边底数与指数的变化，这几道题的计算有 什么共同特点，从中你能发现什么规律? 思考:若（3）中的指数变为正整数n时， ( ab )n= ？
abn ab ab ab( ab )n表示n个ab 相乘
n个
n个 n个
a a a b b b 乘法交换律与结合律
1·要注意，积的乘方运算中，括号内是积，不是和
2、运用积的乘方运算性质时，先看积中有哪些因式， 再将每个因式分别乘方，尤其是字母的系数，不要 漏掉乘方 3、因式可以为单项式，也可以为多项式. 4、三个或三个以上的积的乘方 5·出现正负号时：奇负偶正，先进行符号判断，再进 行幂的运算
达标检测，当堂反馈（5分钟）
3 (x + y)2
4 （2a2b）7
5 a b2
判断题 1.下列各式哪些能用积的乘方运算？
1 (3a)2
2 (-3ab)2
4 （2a2b）7
可以
注意：
1、积的乘方是指底数是乘积形式的乘方，积的 乘方运算中，括号内是积，不是和。
巩固练习1
写出下列幂的运算中底数的所有因式
(1)（2b）2 底数的所有因式 。 (2)(2ab)3 底数的所有因式 。 (3)(3ab2)3 底数的所有因式 。 (4)(-3x)2 底数的所有因式 。
巩固练习
判断下列计算是否正确，错误的并改正。
(1)（2b）2=2b2。 (2)(3ab)3=27ab3 (3)(-3x)2=3x2 (4)(2ab)3=6a3b3 (5)(abc)2=a2b2c2
巩固练习
判断下列计算是否正确，错误的并改正。
(1)（2b）2=2b2。×（2b）2=4b2。 (2)(3ab)3=27ab3 × (3ab)3=27a3b3 (3)(-3x)2=3x2 × (-3x)2=9x2 (4)(2ab)3=6a3b3 × (2ab)3=8a3b3 (5)(abc)2=a2b2c2 √
华东师大版八年级上12.1《积的乘方》课件(共12张PPT)
例题讲解
【例1】计算： (1)(2b)3 ; (2)(2a3)2 ; (3)(-a)3; (4)(-3x)4 .
解：(1) (2b)3 =23b3 = 8b3 (2) (2a3)2 = 22×(a3)2 = 4a6 (3) (-a)3 = (-1)3 ·a3 = -a3 (4) (-3x)4 = (-3)4 ·x4 = 81x4
12.1 幂的运算
积的乘方
目 Contents 录
01 旧知回顾 02 新知探究
03 例题讲解
04 拓展提升
05 课堂小结
旧知回顾
幂的乘方法则
幂
(am)n=amn (m,n都是正整数)
的
意 义 同底数幂乘法的运算性质：
am ·an= am+n （m,n都是正整数）
新知探究
计算
(2×3)2 ＝(2×3)(2×3)＝6×6＝36 22×32 ＝4×9＝36
(1) 23×53 = (2×5)3 = 103 (2) 28×58 = (2×5)8 = 108 (3) (-5)16 × (-2)15
= (-5)×[(-5)×(-2)]15 = -5×1015 (4) 24 × 44 ×(-0.125)4 = [2×4×(-0.125)]4 = 14 = 1
课堂小结
22×32= (2×3)2
你能发 现什么?
(ab)2与a2b2是否相等?
探索 & 交流
(ab)3= ab·ab·ab =a·a·a ·b·b·b =a3·b3
猜想 (ab)n= anbn
(ab)n = an·bn
n个ab
(ab)n = ab·ab·……·ab
n个a
n个b
=(a·a·……·a) (b·b·……·b)
华东师大版八年级数学上册《幂的运算》课件
（3）(ab)4＝______(a_b_)_•__(a_b_)__• _(a_b_)__• _(a_b_)___ ＝______(_a_a_a_a_)_•_(_b_b_b_b_)________ ＝ a (4)b( 4)
积的乘方 试猜想：
（ab）n=？ 其中 n 是正整数
概括：
（ab）n＝ (ab) (ab) (ab)
n个( )
＝(a a a）• (b b b）
n个
n个
＝ anbn ∴（ab）n ＝ a nbn （n为正整数）
积的乘方，等于各因数乘方的积.
例 计算：
解（1）（2b）3
＝23b3 ＝8b3
（2）（2×a3）2
＝22×（a3）2 ＝4a6
（3）（－a）3
＝（－1）3 •a3 ＝ －a3
am·an =am+n（m，n都是正整数）.
同底数幂相乘， 底数不变，指数相加.
计算：
（1）（－3）7×（ －3）6；
（2） －x3 • x5；
（3）b2m • b2m+1.
解： （1）（－3）7×（ －3）6
= （－3）7+6 = （－3）13；
（2） －x3 • x5 = －x3+5 = －x8； （3）b2m • b2m+1 = b2m+2m+1 = b4m +1.
(am)n＝ am·n (m、n是正整数)
幂的乘方，底数不变，指数相乘.
例 计算： (1) (103)5 (2) (b5)4
下列计算过程是否正确？ (1) x2·x6·x3＋x5·x4·x＝x11＋x10＝x2l
(2) (x4)2＋(x5)3＝x8＋x15＝x23
积的乘方 试猜想：
（ab）n=？ 其中 n 是正整数
概括：
（ab）n＝ (ab) (ab) (ab)
n个( )
＝(a a a）• (b b b）
n个
n个
＝ anbn ∴（ab）n ＝ a nbn （n为正整数）
积的乘方，等于各因数乘方的积.
例 计算：
解（1）（2b）3
＝23b3 ＝8b3
（2）（2×a3）2
＝22×（a3）2 ＝4a6
（3）（－a）3
＝（－1）3 •a3 ＝ －a3
am·an =am+n（m，n都是正整数）.
同底数幂相乘， 底数不变，指数相加.
计算：
（1）（－3）7×（ －3）6；
（2） －x3 • x5；
（3）b2m • b2m+1.
解： （1）（－3）7×（ －3）6
= （－3）7+6 = （－3）13；
（2） －x3 • x5 = －x3+5 = －x8； （3）b2m • b2m+1 = b2m+2m+1 = b4m +1.
(am)n＝ am·n (m、n是正整数)
幂的乘方，底数不变，指数相乘.
例 计算： (1) (103)5 (2) (b5)4
下列计算过程是否正确？ (1) x2·x6·x3＋x5·x4·x＝x11＋x10＝x2l
(2) (x4)2＋(x5)3＝x8＋x15＝x23
12.幂的乘方课件华东师大版八年级数学上册
62 相乘.a3表示
3 个
6 相乘，(62)4表示
a 相乘，(a2)3表示 3 个
a2 相乘.
2.计算:(1)(23)2＝ 23 ×
anm)＝
23 ＝
23＋3 (根据an·am＝
26 ；
(2)(33)5＝ 33 ×
33 ×
33 ×
33＋3＋3＋3＋3 (根据an·am＝anm)＝
33 ×
315 ；
33 ＝
(2a)2＋(3b)3＝52＋73＝368.
方法归纳交流 注意公式(am)n＝amn(m、n都是正整数)的
逆运用，即amn＝
(am)n .
合作探究
1.计算:[(x－y)2·(x－y)n－1]2＝
(x－y)2n＋2 .
2.已知|x|＝1，|y|＝ ，则(x20)3－x3y2的值等于
A.－或－
B.或
[变式训练1]已知2a＝5，2b＝7，求22a＋3b的值.
解:22a＋3b＝22a×23b＝(2a)2×(2b)3＝52×73＝25×343＝
8575.
合作探究
[变式训练2]已知2a＋1＝10，3b＝7，求22a＋33b的值.
解:因为2a＋1＝10，所以2×2a＝10，即2a＝5，22a＋33b＝
底数
不变 ，指数
相乘 .
合作探究
计算:(1)x2·(x3)4；(2)(xn)2·(x3)m.
解:(1)x2·(x3)4＝x2·x3×4＝x2＋3×4＝x14；
(2)(xn)2·(x3)m＝x2n·x3m＝x2n＋3m.
方法归纳交流 一般地，幂的运算顺序和数字一样，先算
乘方 ，再算乘除，最后算
加减 .
华东师大版数学八年级上册《积的乘方》课件
一、幂的乘方法则
(am)n= amn (m、n都是正整数)
二、幂的乘方法则的拓展延伸
[(am)n]p =am·n·p （m、n、p都是正整数）
三、幂的乘方的逆运算
amn = (am)n (m、n都是正整数)
It's your turn
1.判断下列计算是否正确，并简要说明理由：
① (a3)5=a8
(×)
(1)(-4xmyzn)3
小试牛刀
例3、计算
(1) (2a2)3+(-3a3)2+(a2)2·a2
解：原式 = 23(a2)3+(-3)2(a3)2+a4·a2 =8a6+9a6+a6 =18a6
It's your turn
练习3、计算
(1) (2x2)3-(3x3)2
(2) a·a5+(-2a3)2+(-3a2)3
1.判断下列计算是否正确，并简要说明理由：
(1)（ab2)3=ab6 (2) (3xy)3=9x3y3 (3) (-2a2)2=-4a4 (4) -(-ab2)2=a2b4
(×) (× ) (× ) (× )
It's your turn
2.计算 (1) (ab)8 ; (4) (5ab2)3 ; 3×103)3.
5 32021 来自3 22021
小结
一、积的乘方法则 二、积的乘方法则的拓展延伸 三、积的乘方法则的逆运算
小结
运算 种类
同底数 幂乘法
幂的 乘方
积的 乘方
公式
法则 中运算
计算结果
底数
指数
乘法 不变
指数 相加
乘方 不变
指数 相乘
(am)n= amn (m、n都是正整数)
二、幂的乘方法则的拓展延伸
[(am)n]p =am·n·p （m、n、p都是正整数）
三、幂的乘方的逆运算
amn = (am)n (m、n都是正整数)
It's your turn
1.判断下列计算是否正确，并简要说明理由：
① (a3)5=a8
(×)
(1)(-4xmyzn)3
小试牛刀
例3、计算
(1) (2a2)3+(-3a3)2+(a2)2·a2
解：原式 = 23(a2)3+(-3)2(a3)2+a4·a2 =8a6+9a6+a6 =18a6
It's your turn
练习3、计算
(1) (2x2)3-(3x3)2
(2) a·a5+(-2a3)2+(-3a2)3
1.判断下列计算是否正确，并简要说明理由：
(1)（ab2)3=ab6 (2) (3xy)3=9x3y3 (3) (-2a2)2=-4a4 (4) -(-ab2)2=a2b4
(×) (× ) (× ) (× )
It's your turn
2.计算 (1) (ab)8 ; (4) (5ab2)3 ; 3×103)3.
5 32021 来自3 22021
小结
一、积的乘方法则 二、积的乘方法则的拓展延伸 三、积的乘方法则的逆运算
小结
运算 种类
同底数 幂乘法
幂的 乘方
积的 乘方
公式
法则 中运算
计算结果
底数
指数
乘法 不变
指数 相加
乘方 不变
指数 相乘
2020年秋华东师 大版八年级上册数学课件 12.1 幂的运算幂的乘方
A．4
B．3
C．2
D．1
4.判断下面计算是否正确？正确的说出理由，不正确的 请改正.
（1）(x3)3=x6 × 原式=x3×3=x9. （2）x3. x3=x9 × 原式=x3+3=x6.
（3）x3+ x3=x9 × 原式=2x3.
5.已知am=2，an=3，求： （1）a2m ，a3n的值； （2） am+n 的值； （3） a2m+3n 的值.
6.已知44×83=2x，求x的值.
解：∵44×83 = (22)4×(23)3 = 28×29 = 217,
∴x=17.
课堂总结
法则
（am）n=amn (m,n为正整数） 幂的乘方，底数不变，指数相乘
幂的乘方
注意
幂的乘方与同底数幂的乘法的区别： (am)n=amn;am ﹒an=am+n
幂的乘方法则的逆用： amn=(am)n=(an)m
[(x5)m]n=_(_x_5m_)_n_=__x_5_m_n_.
随堂即练
1．(x4)2等于 A．x6
(B ) B．x8
C．x16
D．2x4
2.下列各式的括号内，应填入b4的是( C )
A．b12＝( )8
B．b12＝( )6
C．b12＝( )3
D．b12＝( )2
3．如果(9n)2＝312，那么n的值是( B )
解：(1) ∵am=2，an=3， ∴a2m= (am)2= 22 = 4，a3n= (an)3= 33= 27.
(2) ∵am=2，an=3， ∴am+n= am.an=2×3=6.
(3) ∵am=2，an=3， ∴a2m+3n= a2m. a3n= (am)2. (an)3= 4×27 = 108.
华东师大版数学八年级上册3.积的乘方PPT
2 ( 1 2)8 22
2
逆用幂的乘方 的运算性质
幂的乘方的运 算性质
逆用同底数幂的 乘法运算性质
逆用积的乘方 的运算性质
4
【根据最新版数学教材编写】 16
一个圆柱形的储油罐内壁半
20m
径r是 20m，高h是40m.
(1) 它的容积是多少L ？
(1m3 ＝103 L）
解：V ＝ πr 2h
≈3.14×(2×10)2×(4×10)
你能用文字语言叙述这个性质吗？
【根据最新版数学教材编写】 7
积的乘方的运算性质： ((aabb))nn==___a__n_b___n_..((nn为为正正整整数数))
积的乘方,把积的每一个因式分别乘 方,再把所得的幂相乘.
例1 计算：
(1)（5m)3 (2) (-xy2)3 (3)(3×103)2
逆用积 的乘方 的运算
(1)4 24 2
原式 （1 2）4 2
性质
( 1 )100 2100 2
原式 （1 2）100 2
1
1
【根据最新版数学教材编写】 15
试一试 ( 1)4 210 4
解：原式 [( 1 )2 ]4 210 2
( 1 )8 210 ( 12)8 28 22
【根据最新版数学教材编写】 22
课后作业
1.从教材习题中选取， 2.完成练习册本课时的习题.
【根据最新版数学教材编写】 23
同学们下课啦
授课老师：xxx
同学们下课啦
授课老师：xxx
积的乘方的运算性质： ((aabb))nn==__a___n__b___n..((nn为为正正整整数数))
请你推广: 1(abc)n = anbncn (n为正整数)
2
逆用幂的乘方 的运算性质
幂的乘方的运 算性质
逆用同底数幂的 乘法运算性质
逆用积的乘方 的运算性质
4
【根据最新版数学教材编写】 16
一个圆柱形的储油罐内壁半
20m
径r是 20m，高h是40m.
(1) 它的容积是多少L ？
(1m3 ＝103 L）
解：V ＝ πr 2h
≈3.14×(2×10)2×(4×10)
你能用文字语言叙述这个性质吗？
【根据最新版数学教材编写】 7
积的乘方的运算性质： ((aabb))nn==___a__n_b___n_..((nn为为正正整整数数))
积的乘方,把积的每一个因式分别乘 方,再把所得的幂相乘.
例1 计算：
(1)（5m)3 (2) (-xy2)3 (3)(3×103)2
逆用积 的乘方 的运算
(1)4 24 2
原式 （1 2）4 2
性质
( 1 )100 2100 2
原式 （1 2）100 2
1
1
【根据最新版数学教材编写】 15
试一试 ( 1)4 210 4
解：原式 [( 1 )2 ]4 210 2
( 1 )8 210 ( 12)8 28 22
【根据最新版数学教材编写】 22
课后作业
1.从教材习题中选取， 2.完成练习册本课时的习题.
【根据最新版数学教材编写】 23
同学们下课啦
授课老师：xxx
同学们下课啦
授课老师：xxx
积的乘方的运算性质： ((aabb))nn==__a___n__b___n..((nn为为正正整整数数))
请你推广: 1(abc)n = anbncn (n为正整数)
八年级数学上册 第22章整式的乘除电子教材 华东师大版
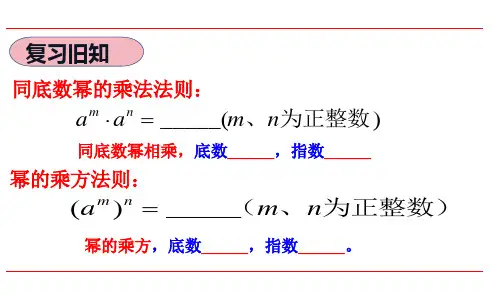
第13章整式的乘除§13.1幂的运算1. 同底数幂的乘法2. 幂的乘方3. 积的乘方4. 同底数幂的除法§13.2整式的乘法1. 单项式与单项式相乘2. 单项式与多项式相乘3. 多项式与多项式相乘§13.3乘法公式1. 两数和乘以这两数的差2. 两数和的平方阅读材料贾宪三角§13.4整式的除法1. 单项式除以单项式2. 多项式除以单项式§13.5因式分解阅读材料你会读吗小结复习题课题学习面积与代数恒等式第13章整式的乘除某地区在退耕还林期间，将一块长m米、宽a米的长方形林区的长、宽分别增加n米和b米．用两种方法表示这块林区现在的面积，可得到：〔m＋n〕〔a＋b〕＝ma＋mb＋na＋nb你知道上面的等式蕴含着什么样的运算法那么吗?·§13.1 幂的运算1. 同底数幂的乘法试一试〔1〕23×２4＝〔２×２×２〕×〔２×２×２×２〕＝２()；〔2〕53×５4＝5()；〔3〕a3·a4＝a()．概括a m·a n＝〔a·a·…·a〕〔a·a·…·a〕＝a·a·…·a＝a n m+．可得a m·a n＝a n m+〔m、n为正整数〕．这就是说，同底数幂相乘，底数不变，指数相加．例1计算：〔1〕103×１０4；〔2〕a·a3；〔3〕a·a3·a5．解〔1〕103×１０4＝１０43+＝１０7．〔2〕a·a3＝a31+＝a4．〔3〕a·a3·a5＝a4·a5＝a9．练习1. 判断以下计算是否正确，并简要说明理由：〔1〕a·a2＝a2；〔2〕a＋a2＝a3；〔3〕a3·a3＝a9；〔4〕a3＋a3＝a6．2. 计算：〔1〕102×105；〔2〕a3·a7；〔3〕x·x5·x7．2. 幂的乘方试一试根据乘方的意义及同底数幂的乘法填空：〔1〕〔23〕2＝23×２3＝２()；〔2〕〔32〕3＝32×３2×３2＝３()；〔3〕〔a3〕4＝a3·a3·a3·a3＝a()．概括〔a m〕n＝a m·a m·…·a m〔n个〕＝a m+...〔n个〕+m+m=a mn可得〔a m〕n＝a mn〔m、n为正整数〕．这就是说，幂的乘方，底数不变，指数相乘．例2计算：（1）〔103〕5；〔2〕〔b3〕4．解〔1〕〔103〕5＝105*3＝１０15．（2）〔b3〕4＝b4*3＝b12．练习1. 判断以下计算是否正确，并简要说明理由：〔1〕〔a3〕5＝a8；〔2〕a5·a5＝a15；〔3〕〔a2〕3·a4＝a9．2. 计算：〔1〕〔22〕2；〔2〕〔y2〕5；〔3〕〔x4〕3；〔4〕〔y3〕2·〔y2〕3．3. 积的乘方试一试〔1〕〔ab〕2＝〔ab〕·〔ab〕＝〔aa〕·〔bb〕＝a()b()；〔2〕〔ab〕3＝＝＝a()b()；〔3〕〔ab〕4＝＝＝a()b()．概括〔ab〕n＝〔ab〕·〔ab〕·…·〔ab〕〔n个〕＝〔a·a·…·a〕·〔b·b·…·b〕＝a n b n．可得〔ab〕n＝a n b n〔n为正整数〕．这就是说，积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘．例3计算：〔1〕〔2b〕3；〔2〕〔2a3〕2；〔3〕〔－a〕3；〔4〕〔－3x〕4．解〔1〕〔2b〕3＝23b3＝8b3．〔2〕〔2a3〕2＝22×〔a3〕2＝4a6．〔3〕〔－a〕3＝〔－1〕3·a3＝－a3．〔4〕〔－3x〕4＝〔－3〕4·x4＝81x4．练习1. 判断以下计算是否正确，并说明理由：〔1〕〔xy3〕2＝xy6；〔2〕〔－2x〕3＝－2x3．2. 计算：〔1〕〔3a〕2；〔2〕〔－3a〕3；〔3〕〔ab2〕2；〔4〕〔－2×１０3〕3．4. 同底数幂的除法我们已经知道同底数幂的乘法法那么：a m·a n＝a n m+，那么同底数幂怎么相除呢?试一试用你熟悉的方法计算：〔1〕25÷２2＝；〔2〕107÷103＝；〔3〕a7÷a3＝〔a≠0〕．概括由上面的计算，我们发现：25÷２2＝23＝225-；107÷103＝104＝1037-；a7÷a3＝a4＝a37-．一般地，设m、n为正整数，m＞n，a≠0，有a m÷a n＝a n m-．这就是说，同底数幂相除，底数不变，指数相减．我们可以利用除法的意义来说明这个法那么的道理：因为除法是乘法的逆运算，a m ÷a n 实际上是要求一个式子〔〕，使 a n ·〔〕＝a m ．而由同底数幂的乘法法那么，可知a n · a n m -＝a )(n m n -+＝a m ，所以要求的式子〔〕，就是a n m -，从而有a m ÷a n ＝a n m -．例4计算：〔1〕 a 8÷a 3；〔2〕 〔－a 〕10÷〔－a 〕3；〔3〕 〔2a 〕7÷〔2a 〕4．解〔1〕 a 8÷a 3＝a 38-＝a 5．〔2〕 〔－a 〕10÷〔－a 〕3＝〔－a 〕310-＝〔－a 〕7＝－a 7． 〔3〕 〔2a 〕7÷〔2a 〕4＝〔2a 〕47-＝〔2a 〕3＝8a 3． 思 考你会计算〔a ＋b 〕4÷〔a ＋b 〕2吗?练习1. 填空：〔1〕 a 5·〔〕＝a 9；〔2〕 〔〕·〔－b 〕2＝〔－b 〕7； 〔3〕 x 6÷〔〕＝x ；〔4〕 〔〕÷〔－y 〕3＝〔－y 〕7．2. 计算：〔1〕 a 10÷a 2；〔2〕 〔－x 〕9÷〔－x 〕3；〔3〕 m 8÷m 2·m 3；〔4〕 〔a 3〕2÷a 6．习题13.11. 计算〔以幂的形式表示〕：〔1〕93×95；〔2〕a7·a8；〔3〕35×２7；〔4〕x2·x3·x4．2. 计算〔以幂的形式表示〕：〔1〕〔103〕3；〔2〕〔a3〕7；〔3〕〔x2〕4；〔4〕〔a2〕3·a5．3. 判断以下等式是否正确，并说明理由：〔1〕a2·a2＝〔2a〕2；〔2〕a2·b2＝〔ab〕4；〔3〕a12＝〔a2〕6＝〔a3〕4＝〔a5〕7．4. 计算〔以幂的形式表示〕：〔1〕〔3×１０5〕2；〔2〕〔2x〕2；〔3〕〔－2x〕3；〔4〕a2·〔ab〕3；〔5〕〔ab〕3·〔ac〕4．5. 计算：〔1〕x12÷x4；〔2〕〔－a〕6÷〔－a〕4；〔3〕〔p3〕2÷p5；〔4〕a10÷〔－a2〕3．6. 判断以下计算是否正确，错误的给予纠正：〔1〕〔a2b〕2＝a2b2；〔2〕a5÷b2＝a3b；〔3〕〔3xy2〕2＝6x2y4；〔4〕〔－m〕7÷〔－m〕2＝m5．7. 计算：〔1〕〔a3〕3÷〔a4〕2；〔2〕〔x2y〕5÷〔x2y〕3；〔3〕x2·〔x2〕3÷x5；〔4〕〔y3〕3÷y3÷〔－y2〕2．8. 用多少张边长为a的正方形硬纸卡片，能拼出一个新的正方形?试写出三个答案，并用不同的方法表示新正方形的面积．从不同的表示方法中，你能发现什么?§13.2 整式的乘法1. 单项式与单项式相乘计算：2x3·5x2．例1计算：〔1〕3x2y·〔－2xy3〕；〔2〕〔－5a2b3〕·〔－４b2c〕．解〔1〕3x2y·〔－2xy3〕＝［３·〔－２〕］·〔x2·x〕·〔y·y3〕〔2〕〔－5a2b3〕·〔－４b2c〕＝［〔－５〕·〔－４〕］·a2·〔b3·b2〕·c ＝20a2b5c．概括单项式与单项式相乘，只要将它们的系数、相同字母的幂分别相乘，对于只在一个单项式中出现的字母，那么连同它的指数一起作为积的一个因式．例2卫星绕地球外表做圆周运动的速度〔即第一宇宙速度〕约为7.9×１０3米/秒，那么卫星运行3×１０2秒所走的路程约是多少?解7.9×１０3×３×１０2＝23.7×１０5＝２.３７×１０6〔米〕．答：卫星运行3×１０2秒所走的路程约是2.37×１０6米．讨论你能说出a·b,3a·2a,以及3a·5ab的几何意义吗?练习1. 计算：〔1〕3a2·2a3；〔2〕〔－9a2b3〕·8ab2；〔3〕〔－3a2〕3·〔－2a3〕2；〔4〕－3xy2z·〔x2y〕2．2. 光速约为３×１０8米/秒，太阳光射到地球上的时间约为５×１０2秒，那么地球与太阳的距离约是多少米?3. 小明的步长为a厘米，他量得一间屋子长15步，宽14步，这间屋子的面积有多少平方厘米?2. 单项式与多项式相乘试一试计算：2a2·〔3a2－5b〕．例3计算：〔－2a2〕·〔３ab2－5ab3〕．解〔－2a2〕·〔３ab2－5ab3〕＝〔－2a2〕·3ab2＋〔－2a2〕·〔－５ab3〕＝－6a3b2＋10a3b3．概括单项式与多项式相乘，只要将单项式分别乘以多项式的每一项，再将所得的积相加．练习1. 计算：〔1〕3x3y·〔2xy2－3xy〕；〔2〕2x·〔3x2－xy＋y2〕．2. 化简：x〔x2－1〕＋2x2〔x＋1〕－3x〔2x－5〕．3. 多项式与多项式相乘回忆我们再来看一看本章导图中的问题：图13.2.1某地区在退耕还林期间，将一块长m米、宽a米的长方形林区的长、宽分别增加n米和b米．用两种方法表示这块林区现在的面积．这块林区现在长为〔m＋n〕米，宽为〔a＋b〕米，因而面积为〔m＋n〕〔a＋b〕米2．也可以这样理解：如图13.2.1所示，这块地由四小块组成，它们的面积分别为ma米2、mb米2、na米2、nb米2，故这块地的面积为〔ma＋mb＋na＋nb〕米2．由于〔m＋n〕〔a＋b〕和〔ma＋mb＋na＋nb〕表示同一块地的面积，故有〔m＋n〕〔a＋b〕＝ma＋mb＋na＋nb．实际上，把〔m＋n〕看成一个整体，有〔m＋n〕〔a＋b〕＝〔m＋n〕a＋〔m＋n〕b＝ma＋mb＋na＋nb．如下式所示，等式的右边可以看作左边用线相连各项乘积的和：〔m+n〕〔a+b〕=ma+mb+na+nb概括这个等式实际上给出了多项式乘以多项式的法那么：多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加．例4计算：〔1〕〔x＋2〕〔x－3〕；〔2〕〔3x－1〕〔2x＋1〕．解〔1〕〔x＋2〕〔x－3〕＝x2－3x＋2x－6＝x2－x－6．〔2〕〔3x－1〕〔2x＋1〕＝6x2＋3x－2x－1＝6x2＋x－1．例5计算：〔1〕〔x－3y〕〔x＋7y〕；〔2〕〔2x＋5y〕〔3x－2y〕．解〔1〕〔x－3y〕〔x＋7y〕＝x2＋7xy－3yx－21y2＝x2＋4xy－21y2．（3）〔2x＋5y〕〔3x－2y〕＝6x2－4xy＋15yx－10y2＝6x2＋11xy－10y2．练习1. 计算：〔1〕〔x＋5〕〔x－7〕；〔2〕〔x＋5y〕〔x－7y〕；〔3〕〔2m＋3n〕〔2m－3n〕；〔4〕〔2a＋3b〕〔2a＋3b〕．2. 小东找来一张挂历纸包数学课本．课本长a厘米，宽b厘米，厚c厘米，小东想将课本封面与封底的每一边都包进去m厘米．问小东应在挂历纸上裁下一块多大面积的长方形?习题13.21. 计算：〔1〕5x3·8x2；〔2〕11x12·〔－12x11〕；〔3〕2x2·〔－3x〕4；〔4〕〔－8xy2〕·－(1/2x)3．2. 世界上最大的金字塔——胡夫金字塔高达146.6米，底边长230.4米，用了约2.3×１０6块大石块，每块重约2.5×１０3千克．请问：胡夫金字塔总重约多少千克?3. 计算：〔1〕－3x·〔2x2－x＋4〕；〔2〕5/2xy·(－x3y2＋4/5x2y3)．4. 化简：〔1〕x(1/2x＋1)－3x(3/2x－2)；〔2〕x2〔x－1〕＋2x〔x2－2x＋3〕．5. 一块边长为xcm的正方形地砖，被裁掉一块2cm宽的长条．问剩下局部的面积是多少?6. 计算：〔1〕〔x＋5〕〔x＋6〕；〔2〕〔3x＋4〕〔3x－4〕；〔3〕〔2x＋1〕〔2x＋3〕；〔4〕〔9x＋4y〕〔9x－4y〕．7. 一块长a厘米、宽b厘米的玻璃，长、宽各减少c厘米后恰好能铺盖一张办公桌台面〔玻璃与台面一样大小〕．问台面面积是多少? §13.3 乘法公式1.两数和乘以这两数的差做一做计算：〔a＋b〕〔a－b〕．这两个特殊的多项式相乘，得到的结果特别简洁：〔a＋b〕〔a－b〕＝a2－b2．这就是说，两数和与这两数差的积，等于这两数的平方差．试一试图13.3.1先观察图13.3.1，再用等式表示以下图中图形面积的运算：＝－．例1计算：〔1〕〔a＋3〕〔a－3〕；〔2〕〔2a＋3b〕〔2a－3b〕；〔3〕〔1＋2c〕〔1－2c〕；〔4〕〔－2x－y〕〔2x－y〕．解〔1〕〔a＋3〕〔a－3〕＝a2－32＝a2－9．〔2〕〔2a＋3b〕〔2a－3b〕＝〔2a〕2－〔3b〕2＝4a2－9b2．〔3〕〔1＋2c〕〔1－2c〕＝12－〔2c〕2＝1－4c2．〔4〕〔－2x－y〕〔2x－y〕＝〔－y－2x〕〔－y＋2x〕＝〔－y〕2－〔2x〕2＝y2－4x2．例2计算：1998×２００２．解1998×２００２＝〔2000－2〕×〔2000＋2〕＝200０2－22＝4000000－4＝3999996．例3街心花园有一块边长为a米的正方形草坪，经统一规划后，南北向要加长2米，而东西向要缩短2米．问改造后的长方形草坪的面积是多少?解〔a＋2〕〔a－2〕＝a2－4〔平方米〕．答：改造后的长方形草坪的面积是〔a2－4〕平方米．练习1. 计算：〔1〕〔2x＋1/2〕〔2x－1/2〕；〔2〕〔－x＋2〕〔－x－2〕；〔3〕〔－2x＋y〕〔2x＋y〕；〔4〕〔y－x〕〔－x－y〕．2. 计算：〔1〕498×502；〔2〕999×1001．3. 用一定长度的篱笆围成一个矩形区域，小明认为围成一个正方形区域时面积最大，而小亮认为不一定．你认为如何?2.两数和的平方做一做计算：〔a＋b〕2．经计算，我们又得到一个漂亮的结果：〔a＋b〕2＝a2＋2ab＋b2．这就是说，两数和的平方，等于它们的平方和加上这两数积的2倍．试一试先观察图13.3.2，再用等式表示以下图中图形面积的运算：图＝＋＋．例4计算：〔1〕〔2a＋3b〕2；〔2〕〔2a＋b/2〕2．解〔1〕〔2a＋3b〕2＝〔2a〕2＋2·２a·3b＋〔3b〕2＝4a2＋12ab＋9b2．（2）〔2a＋b/2〕2＝〔2a〕2＋2·2a·b/2＋b/22＝4a2＋2ab＋b2/4．例5计算：〔1〕〔a－b〕2；〔2〕〔2x－3y〕2．解〔1〕〔a－b〕2＝［a＋〔－b〕］2＝a2＋2·a·〔－b〕＋〔－b〕2＝a2－2ab＋b2．〔2〕〔2x－3y〕2＝［２x＋〔－3y〕］2＝〔2x〕2＋2·〔2x〕·〔－3y〕＋〔－3y〕2＝4x2－12xy＋9y2．此题也可直接运用小题〔1〕的结果〔两数差的平方公式〕来计算：〔2x－3y〕2＝〔2x〕2－2·〔2x〕·〔3y〕＋〔3y〕2＝ 4x 2－12xy ＋9y 2．图13.3.3讨 论你能从图13.3.3中的面积关系来解释小题〔1〕的结果吗?练习1. 计算：〔1〕 〔x ＋3〕2；〔2〕 〔2x ＋y 〕2． 2. 计算：〔1〕 〔x －3〕2；〔2〕 〔2m －n 〕2． 3. 计算：〔1〕 〔－2m ＋n 〕2；〔2〕 〔－2m －n 〕2．4. 要给一边长为a 米的正方形桌子铺上正方形的桌布，桌布的四周均超出桌面0.1米，问需要多大面积的桌布?习题13.31. 计算：〔1〕 〔a ＋2b 〕〔a －2b 〕；〔2〕 〔2a ＋5b 〕〔2a －5b 〕； 〔3〕 〔－2a －3b 〕〔－2a ＋3b 〕；〔4〕 〔－31a ＋21b 〕〔31a ＋21b 〕． 2. 计算：〔1〕 〔3a ＋b 〕2；〔2〕 〔2a ＋31b 〕2；〔3〕 〔2a ＋1〕〔－2a －1〕． 3. 计算：〔1〕 〔2a －4b 〕2；〔2〕〔21a －31b 〕2． 4. 填空：〔1〕a2＋6a＋＝〔a＋〕2；〔2〕4x2－20x＋＝〔2x－〕2；〔3〕a2＋b2＝〔a－b〕2＋；〔4〕〔x－y〕2＋＝〔x＋y〕2．5. 有一块边长为a米的正方形空地，现准备将这块空地四周均留出b 米宽修筑围坝，中间修建喷泉水池．你能计算出喷泉水池的面积吗?阅读材料贾宪三角贾宪三角〔如图1〕最初于11世纪被发现，原图载于我国北宋时期数学家贾宪图1的?黄帝九章算法细草?一书中，原名“开方作法根源图〞，用来作开方运算，在数学史上占有领先地位．我国南宋时期数学家杨辉对此有着记载之功，他于1261年写下的?详解九章算法?一书中记载着这一图表．因此，后人把这个图表称作贾宪三角或杨辉三角．在欧洲，贾宪三角那么被人们称为“帕斯卡三角〞，这是因为法国数学家帕斯卡于1654年发表了此“三角〞，并且影响较大．但这比我国已经迟了近600年．其实，数学史上有不少人各自独立地绘制过类似图表，如1427年阿拉伯的数学家阿尔·卡西，1527年德国的阿皮亚纳斯，1544年德国的施蒂费尔，1545年法国的薛贝尔等．贾宪三角在历史上被不同时代的人绘制出来，是有着不同的应用趋向的．贾宪将它应用于开方运算，注重增乘方法并把这种方法推向求高次方根；帕斯卡关心数字三角阵的性质探讨以及把这种性质推广到组合数的性质上；而施蒂费尔那么注重二项展开式系数间的关系；还有我国元代数学家朱世杰于13世纪巧妙地利用贾宪三角得出了一系列级数求和的重要公式，并且利用这些公式求出许多更为复杂的级数之和，这在当时世界上也处于领先水平．与我们现在的学习联系最紧密的是二项式乘方展开式的系数规律．如图2，在贾宪三角中，第三行的三个数〔1，2，1〕恰好对应着两数和的平方公式〔a＋b〕2的展开式a2＋2ab＋b2的系数．类似地，通过计算可以发现：第四行的四个数〔1，3，3，1〕恰好对应着两数和的立方〔a＋b〕3的展开式a3＋３a2b＋3ab2＋b3的系数，第五行的五个数〔1，4，6，4，1〕恰好对应着两数和的四次方〔a＋b〕4的展开式a4＋4a3b＋6a2b2＋4ab3＋b4的系数，等等．由此可见，贾宪三角可以看作是对我们现在学习的两数和的平方公式的推广而得到的．〔a＋b〕0 (1)〔a＋b〕1………… 1 1〔a＋b〕2………… 1 2 1〔a＋b〕3………… 1 3 3 1〔a＋b〕4………… 1 4 6 4 1〔a＋b〕5………… 1 5 10 10 5 1〔a＋b〕6………… 1 6 15 20 15 6 1图2同学们，贾宪三角告诉了我们二项式乘方展开式的系数规律，你发现其中的字母及字母指数的排列规律了吗?如果发现了，请你试着写出〔a＋b〕5、〔a＋b〕6与〔a＋b〕7的展开式．§13.4 整式的除法1. 单项式除以单项式计算：12a5c2÷３a2．根据除法的意义，上式就是要求一个单项式，使它与３a2相乘的积等于12a5c2．∵〔4a3c2〕·３a2＝12a5c2，∴12a5c2÷３a2＝4a3c2．概括单项式相除，把系数、同底数幂分别相除作为商的因式，对于只在被除式中出现的字母，那么连同它的指数一起作为商的一个因式．例1计算：〔1〕24a3b2÷３ab2；〔2〕－21a2b3c÷３ab；〔3〕〔６xy2〕2÷３xy．解〔1〕24a3b2÷3ab2＝〔24÷３〕〔a3÷a〕〔b2÷b2〕＝8a13 ·１＝8a2．〔2〕－21a2b3c÷３ab＝〔－21÷３〕a12-b13-c＝－7ab2c．〔3〕〔6xy2〕2÷３xy＝36x2y4÷３xy＝12xy3．思考你能用〔a－b〕的幂表示下式的结果吗?12〔a－b〕5÷３〔a－b〕2．例2地球的质量约为5.98×１０24千克，木星的质量约为1.9×１０27千克．问木星的质量约是地球的多少倍?〔结果保存三个有效数字〕分析此题只需做一个除法运算：〔1.9×１０27〕÷〔５.９８×１０24〕，我们可以先将1.9除以5.98，再将１０27除以１０24，最后将商相乘．27-解〔1.9×１０27〕÷〔5.98×１０24〕＝〔1.9÷５.９８〕×１０24≈0.318×１０3＝３１８．答：木星的质量约是地球的318倍．练习1. 填表：2. 下雨时，常常是“先见闪电，后闻雷鸣〞，这是由于光速比声速快的缘故．光在空气中的传播速度约为3×１０8米/秒，而声音在空气中的传播速度约为3.4×１０2米/秒．请计算一下，光速是声速的多少倍?〔结果保存两个有效数字〕2. 多项式除以单项式试一试计算：〔1〕〔ax＋bx〕÷x；〔2〕〔ma＋mb＋mc〕÷m．根据除法的意义，容易探索、计算出结果．以小题〔2〕为例，〔ma＋mb＋mc〕÷m就是要求一个多项式，使它与m的积是ma ＋mb＋mc．∵m〔a＋b＋c〕＝ma＋mb＋mc，∴〔ma＋mb＋mc〕÷m＝a＋b＋c．概括多项式除以单项式，先把这个多项式的每一项除以这个单项式，再把所得的商相加．例3计算：〔1〕〔9x4－15x2＋6x〕÷３x；〔2〕〔28a3b2c＋a2b3－14a2b2〕÷〔－7a2b〕．解〔1〕〔9x4－15x2＋6x〕÷３x＝9x4÷３x－15x2÷３x＋6x÷３x＝3x3－5x＋2．（2）〔28a3b2c＋a2b3－14a2b2〕÷〔－7a2b〕＝28a3b2c÷〔－7a2b〕＋a2b3÷〔－7a2b〕－14a2b2÷〔－7a2b〕＝－4abc－1/7b2＋2b．练习1. 计算：〔1〕〔3ab－2a〕÷a；〔2〕〔5ax2＋15x〕÷5x；〔3〕〔12m2n＋15mn2〕÷6mn；〔4〕〔x3－2x2y〕÷〔－x2〕．2. 计算：〔1〕〔4a3b3－6a2b3c－2ab5〕÷〔－２ab2〕；〔2〕x2y3－1/2x3y2＋2x2y2÷1/2xy2．习题13.41.计算：〔1〕－21a2b3÷7a2b；〔2〕7a5b2c3÷〔－3a3b〕；〔3〕－1/2a4x4÷－1/6a3x2；〔4〕〔16x3－8x2＋4x〕÷〔－2x〕．2.计算：〔1〕〔6a3b－9a2c〕÷３a2；〔2〕〔4a3－6a2＋9a〕÷〔－2a〕〔3〕〔－4m4＋20m3n－m2n2〕÷〔－4m2〕；〔4〕x2y－1/2xy2－2xy÷1/2xy．3.计算：〔1〕〔12p3q4＋20p3q2r－6p4q3〕÷〔－2pq〕2；〔2〕［４y〔2x－y〕－2x〔2x－y〕］÷〔2x－y〕．4. 一颗人造地球卫星的速度是８×１０3米/秒，一架喷气式飞机的速度是5×１０2米/秒，试问：这颗人造地球卫星的速度是这架喷气式飞机的速度的多少倍?5. 聪聪在一次数学课外活动中发现了一个奇特的现象：他随便想一个非零的有理数，把这个数平方，再加上这个数，然后把结果除以这个数，最后减去这个数，所得结果总是1．你能说明其中的道理吗? §13.5 因式分解回忆运用前面所学的知识填空：〔1〕m〔a＋b＋c〕＝；〔2〕〔a＋b〕〔a－b〕＝；〔3〕〔a＋b〕2＝．试一试填空：〔1〕ma＋mb＋mc＝〔〕〔〕；〔2〕a2－b2＝〔〕〔〕；〔3〕a2＋2ab＋b2＝〔〕2．概括我们“回忆〞的是已熟悉的整式乘法运算，而“试一试〞中的问题，其过程正好与整式的乘法相反，它是把一个多项式化为几个整式的积的形式．把一个多项式化为几个整式的积的形式，叫做多项式的因式分解〔factorization〕．多项式ma＋mb＋mc中的每一项都含有一个相同的因式m，我们称之为公因式〔common factor〕．把公因式提出来，多项式ma＋mb＋mc就可以分解成两个因式m和〔a＋b＋c〕的乘积了．像这种因式分解的方法，叫做提公因式法．“试一试〞中的〔2〕、〔3〕小题，实际上是将乘法公式反过来用，对多项式进行因式分解的，这种因式分解的方法称为公式法．做一做把以下多项式分解因式：〔1〕3a＋3b＝；〔2〕5x－5y＋5z＝；〔3〕x2－4y2＝；〔4〕m2＋6mn＋9n2＝．例1把以下多项式分解因式：〔1〕－5a2＋25a；〔2〕3a2－9ab；〔3〕25x2－16y2；〔4〕x2＋4xy＋4y2．解〔1〕－5a2＋25a＝－5a〔a－5〕．〔2〕3a2－9ab＝3a〔a－3b〕．〔3〕25x2－16y2＝〔5x〕2－〔4y〕2＝〔5x＋4y〕〔5x－4y〕．〔4〕x2＋4xy＋4y2＝x2＋2·x·2y＋〔2y〕2＝〔x＋2y〕2．例2把以下多项式分解因式：〔1〕4x3y＋4x2y2＋xy3；〔2〕3x3－12xy2．解〔1〕4x3y＋4x2y2＋xy3＝xy〔4x2＋4xy＋y2〕＝xy〔2x＋y〕2．（2）3x3－12xy2＝3x〔x2－4y2〕＝3x［x2－〔2y〕2］＝3x〔x＋2y〕〔x－2y〕．练习1. 判断以下因式分解是否正确，并简要说明理由．如果不正确，请写出正确答案．〔1〕4a2－4a＋1＝4a〔a－1〕＋1；〔2〕x2－4y2＝〔x＋4y〕〔x－4y〕．2. 把以下多项式分解因式：〔1〕a2＋a；〔2〕4ab－2a2b；〔3〕9m2－n2；〔4〕2am2－8a；〔5〕2a2＋4ab＋2b2．3. 丁丁和冬冬分别用橡皮泥做了一个长方体和圆柱体，放在一起，恰好一样高．丁丁和冬冬想知道哪一个体积较大，但身边又没有尺子，只找到了一根短绳，他们量得长方体底面的长正好是3倍绳长，宽是2倍绳长，圆柱体的底面周长是10倍绳长．你知道哪一个体积较大吗?大多少?〔提示：可设绳长为a厘米，长方体和圆柱体的高均为h厘米〕习题13.51. 把以下多项式分解因式：〔1〕3x＋3y；〔2〕－24m2x－16n2x；〔3〕x2－1；〔4〕〔xy〕2－1；〔5〕a4x2－a4y2；〔6〕3x2＋6xy＋3y2；〔7〕〔x－y〕2＋4xy；〔8〕4a2－3b〔4a－3b〕．2. 先将以下代数式分解因式，再求值：2x〔a－2〕－y〔2－a〕，其中a＝0.5，x＝1.5，y＝－2．3. 在一块边长为a＝6.6米的正方形空地的四角均留出一块边长为b ＝1.7米的正方形修建花坛，其余的地方种草坪．问草坪的面积有多大?4. 一块边长为a米的正方形广场，扩建后的正方形边长比原来长2米，问扩建后的广场面积增大了多少?你会读吗阅读材料你会读吗数学中有不少运算符号与记号，如何用英语准确地表达这些符号与记号呢?读一读，看看你能读懂多少?A ＋B ＝C ……A plus B equals CA －B ＝C ……A minus B equals CA ×B ＝C ……A multiplied by B equals C……A times B equals CA ÷B ＝C ……A divided by B equals C 21……one half 32……two thirdsA 2……A squared A 3……A cubedA ……the square root of AA ＞B ……A is greater than BA ∶B ……the ratio of A to Bl ∥m ……l is parallel to m 小结一、 知识结构二、概括1. 本章主要研究整式的乘法与除法运算，其运算法那么从根本上说是运用了数的运算律，最终都可以归结为单项式乘以单项式与单项式除以单项式，其中幂的运算是它们的根底．2. 在多项式乘以多项式中，有一些特殊形式的乘法运算结果较为简洁，在计算中可以作为乘法公式直接运用．学习中要注意掌握这些公式的结构特点，以便能准确地运用公式．3. 因式分解与因数分解类似，它与整式乘法的过程恰好相反，我们可以运用整式的乘法得到因式分解的方法，也可以运用整式乘法来检验因式分解的正确性．复习题A组1. 计算：〔1〕a10·a8；〔2〕〔xy〕2·〔xy〕3；〔3〕［〔－x〕3］2；〔4〕［〔－x〕2］3；〔5〕〔－2mn2〕3；〔6〕〔y3〕2·〔y2〕4．2. 计算：〔1〕〔4×１０4〕×〔２×１０3〕；〔2〕2a·３a2；〔3〕〔－3xy〕·〔－４yz〕；〔4〕〔－2a2〕2·〔－５a3〕；〔5〕〔－3x〕·〔2x2－x－1〕；〔6〕〔x＋2〕〔x＋6〕；〔7〕〔x－2〕〔x－6〕；〔8〕〔2x－1〕〔3x＋2〕．3. 计算：〔1〕〔x＋2〕〔x－2〕；〔2〕〔m＋n〕〔m－n〕；〔3〕〔－m－n〕〔－m＋n〕；〔4〕〔－m－n〕〔m＋n〕；〔5〕〔－m＋n〕〔m－n〕；〔6〕2/3x＋3/4y2．4. 计算：〔1〕20222－2022×2000；〔2〕〔2x＋5〕2－〔2x－5〕2；〔3〕－12xy·３x2y－x2y·〔－3xy〕；〔4〕2x·1/2x－1－3x1/3x＋2/3；〔5〕〔－2x2〕·〔－y〕＋3xy·1－1/3x；〔6〕〔－6x2〕2＋〔－3x〕3·x．5. 计算：〔1〕a·a4÷a3；〔2〕〔－x〕6÷〔－x〕2·〔－x〕3；〔3〕27x8÷3x4；〔4〕－12m3n3÷4m2n3；〔5〕〔6x2y3z2〕2÷4x3y4；〔6〕〔－6a2b5c〕÷〔－2ab2〕2．6. 计算：〔1〕〔6a4－4a3－2a2〕÷〔－2a2〕；〔2〕〔4x3y＋6x2y2－xy3〕÷２xy；〔3〕〔x4＋2x3－1/2x2〕÷〔－1/2x〕2；〔4〕〔2ab2－b3〕2÷２b3．7. 计算：［〔x－2y〕2＋〔x－2y〕〔x＋2y〕－2x〔2x－y〕］÷2x．8. 把以下多项式分解因式：〔1〕x2－25x；〔2〕2x2y2－4y3z；〔3〕am－an＋ap；〔4〕x3－25x；〔5〕1－4x2；〔6〕25x2＋20xy＋4y2；〔7〕x3＋4x2＋4x．9. 先化简，再求值：〔1〕3a〔2a2－4a＋3〕－2a2〔3a＋4〕，其中a＝－2；〔2〕〔a－3b〕2＋〔3a＋b〕2－〔a＋5b〕2＋〔a－5b〕2，其中a＝－8，b＝－6．10. 一个正方形的边长增加3cm，它的面积增加了45cm2．求这个正方形原来的边长．假设边长减少3cm，它的面积减少了45cm2，这时原来边长是多少呢?11. 1千克镭完全蜕变后，放出的热量相当于3.75×１０5千克煤放出的热量，据估计地壳里含1×１０10千克镭．试问这些镭完全蜕变后放出的热量相当于多少千克煤放出的热量．B组12. 求以下各式的值：〔1〕〔3x4－2x3〕÷〔－x〕－〔x－x2〕·３x，其中x＝－1/2；〔2〕［〔ab＋1〕〔ab－2〕－2a2b2＋2］÷〔－ab〕，其中a＝3/2，b＝－4/3．13. 〔x＋y〕2＝1，〔x－y〕2＝49，求x2＋y2与xy的值．14. a＋b＝3，ab＝2，求a2＋b2的值．15. a－b＝1，a2＋b2＝25，求ab的值．16. 把以下各式分解因式：〔1〕x〔x＋y〕－y〔x＋y〕；〔2〕〔a＋b〕2＋2〔a＋b〕＋1；〔3〕4x4－4x3＋x2；〔4〕x2－16ax＋64a2；〔5〕〔x－1〕〔x－3〕＋1；〔6〕〔ab＋a〕＋〔b＋1〕．C组17. 一个长方形的长增加4cm，宽减少1cm，面积保持不变；长减少2cm，宽增加1cm，面积仍保持不变．求这个长方形的面积．18. 当整数k取何值时，多项式x2＋4kx＋4恰好是另一个多项式的平方?19. 试判断以下说法是否正确，并说明理由:〔1〕两个连续整数的平方差必是奇数；〔2〕假设a为整数，那么a3－a能被6整除．课题学习面积与代数恒等式在前面的学习中，我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释这些代数恒等式．例如，图1可以用来解释图2可以用来解释2222a++b+．=)a(bab还有很多代数恒等式可以用硬纸片拼成的图形面积来说明其正确性．现在让我们一起参加下面的实践与探索活动．〔1〕尽可能多地做一些如图3所示的正方形与长方形的硬纸片．〔2〕利用制作的硬纸片拼成一些长方形或正方形，并用所拼成的图形面积来说明所学的乘法公式及某些幂的运算公式的正确性．图４〔3〕根据图4，利用面积的不同表示方法写出一个代数恒等式来．〔4〕试写出一个代数恒等式，比方〔a＋2b〕〔2a－b〕＝2a2＋3ab－2b2，然后用上述方法来说明它的正确性．。
华东师大版八年级数学上册1《同底数幂的乘法》教学课件
≈3.80×1013（千米）
答：比邻星与地球的距离约为 3.80×1013千米.
试一试
1、判断对与错： (-2)8(-2)7
= 28＋7＝215
错
x3·x5 =x3 ·5=x15 错
2、计算: a8+a2=
不能再计算啦！
a8+a8= 2a8
想一想 am ·an ·ap 等于什么？
am·an·ap = am+n+p
12.1 幂的运算
同底数幂的乘法
目 Contents 录
01 情境引入 02 新知探究
03 知识运用
04 练习提升
05 课堂小结
情境引入
光在真空中的速度大约是3×105 千米/秒，太阳系 以外距离地球最近的恒星是比邻星，它发出的光到达 地球大约需要4.22年。
？
比邻星
速度×时间=距离
地球
3×105 ×3×107 × 4.22 = 37.98 ×（105 × 107 ）
课堂小结
结论：am·an=am+n(m,n都是正整数） 同底数幂相乘，底数不变，指数相加。
注：（1）只实用于同底数幂相乘； （2）运用该性质一定是底数不变，指数相加。
注意： 不能忽视指数为1的情况；
运算结果的底数一般应为正数． 若底数不同，先化为相同，后运用法则．
看谁计算又对又快（结果用幂的情势表示）
（1） 3×33
（2） 105 ·105 （3）（－3）2 ·（－3）3 （4） b5 ·b2 ·b
3４ 1010
－35
b8
判断（正确的打“√”，错误的打“×”）
=a·aห้องสมุดไป่ตู้… ·a
m+n个a
答：比邻星与地球的距离约为 3.80×1013千米.
试一试
1、判断对与错： (-2)8(-2)7
= 28＋7＝215
错
x3·x5 =x3 ·5=x15 错
2、计算: a8+a2=
不能再计算啦！
a8+a8= 2a8
想一想 am ·an ·ap 等于什么？
am·an·ap = am+n+p
12.1 幂的运算
同底数幂的乘法
目 Contents 录
01 情境引入 02 新知探究
03 知识运用
04 练习提升
05 课堂小结
情境引入
光在真空中的速度大约是3×105 千米/秒，太阳系 以外距离地球最近的恒星是比邻星，它发出的光到达 地球大约需要4.22年。
？
比邻星
速度×时间=距离
地球
3×105 ×3×107 × 4.22 = 37.98 ×（105 × 107 ）
课堂小结
结论：am·an=am+n(m,n都是正整数） 同底数幂相乘，底数不变，指数相加。
注：（1）只实用于同底数幂相乘； （2）运用该性质一定是底数不变，指数相加。
注意： 不能忽视指数为1的情况；
运算结果的底数一般应为正数． 若底数不同，先化为相同，后运用法则．
看谁计算又对又快（结果用幂的情势表示）
（1） 3×33
（2） 105 ·105 （3）（－3）2 ·（－3）3 （4） b5 ·b2 ·b
3４ 1010
－35
b8
判断（正确的打“√”，错误的打“×”）
=a·aห้องสมุดไป่ตู้… ·a
m+n个a
华师大版初中数学八年级上册电子课本
试一试
（1） 144 的平方根是什么? （2） 0 的平方根是什么?
4
（3） 25 的平方根是什么? （4） －４有没有平方根?为什么? 请你自己也编三道求平方根的题目，并给出解答．
概括
一个正数如果有平方根数的范围从有理数扩充到实数以后（本章 第２节），每一个正实数必定有两个平方根．，那么必定有两个，它们 互为相反数．显然，如果我们知道了这两个平方根中的一个，那么立 即可以得到它的另一个平方根．
本章主要研究整式的乘法与除法运算其运算法则从根本上说是幂的运算amananm?amananm?amnamnabnanbn单项式乘以单项式单项式乘以多项式多项式乘以多项式因式分解提公因式法公式法单项式除以单项式多项式除以单项式乘法公式ababa2b2ab2a22abb2第44页共132页运用了数的运算律最终都可以归结为单项式乘以单项式与单项式除以单项式其中幂的运算是它们的基础
华东师大版八年级数学上册教材
目录 第 12 章 数的开方 §12.1 平方根与 立方根 1.平方根 2.立方根 §12.2 实 数 与 数 轴 阅 读 材料 为 什么 说 2 不是有理数
5 的算法 小结
复习题
第 13 章整式的乘除
§13.1 幂的运算 1. 同底数幂的乘法 2. 幂的乘方 3. 积的乘方 4. 同底数幂的除法
思考
负数有平方根吗?
求一个非负数的平方根的运算，叫做开平方．将一个正数开平方，
关键是找出它的一个算术平方根．
在例 1 中，100 的算术平方根是 100＝10，100 的平方根是±100
＝±１０．
例 2 将下列各数开平方：
（1）49；
（2）1.69
ቤተ መጻሕፍቲ ባይዱ
解（1） 因为 7 2 ＝49，所以 49 ＝7，因此 49 的平方根为±７；
（1） 144 的平方根是什么? （2） 0 的平方根是什么?
4
（3） 25 的平方根是什么? （4） －４有没有平方根?为什么? 请你自己也编三道求平方根的题目，并给出解答．
概括
一个正数如果有平方根数的范围从有理数扩充到实数以后（本章 第２节），每一个正实数必定有两个平方根．，那么必定有两个，它们 互为相反数．显然，如果我们知道了这两个平方根中的一个，那么立 即可以得到它的另一个平方根．
本章主要研究整式的乘法与除法运算其运算法则从根本上说是幂的运算amananm?amananm?amnamnabnanbn单项式乘以单项式单项式乘以多项式多项式乘以多项式因式分解提公因式法公式法单项式除以单项式多项式除以单项式乘法公式ababa2b2ab2a22abb2第44页共132页运用了数的运算律最终都可以归结为单项式乘以单项式与单项式除以单项式其中幂的运算是它们的基础
华东师大版八年级数学上册教材
目录 第 12 章 数的开方 §12.1 平方根与 立方根 1.平方根 2.立方根 §12.2 实 数 与 数 轴 阅 读 材料 为 什么 说 2 不是有理数
5 的算法 小结
复习题
第 13 章整式的乘除
§13.1 幂的运算 1. 同底数幂的乘法 2. 幂的乘方 3. 积的乘方 4. 同底数幂的除法
思考
负数有平方根吗?
求一个非负数的平方根的运算，叫做开平方．将一个正数开平方，
关键是找出它的一个算术平方根．
在例 1 中，100 的算术平方根是 100＝10，100 的平方根是±100
＝±１０．
例 2 将下列各数开平方：
（1）49；
（2）1.69
ቤተ መጻሕፍቲ ባይዱ
解（1） 因为 7 2 ＝49，所以 49 ＝7，因此 49 的平方根为±７；
华师大版八年级上册数学课件 12.1 幂的运算(第3课时)积的乘方 (15张PPT)
解：原式= -8x9·x4 =-8x13.
注意：运算顺序 是先乘方，再乘 除，最后加减.
12
5.如果（an·bm·b)3=a9b15，求m，n的值. 解：∵（an·bm·b)3=a9b15， （an）3·（bm）3·b3=a9b15， a3n ·b3m·b3=a9b15， a3n ·b3m+3=a9b15， 3n=9，3m+3=15. n=3，m=4.
注意：逆用积的乘法法则，有时可使运算更加简便快捷！
9
随堂即练
1.判断：
(1)（ab2)3=ab6
( ×)
(2) (3xy)3=9x3y3
(×)
(3) (-2a2)2=-4a4 (4) -(-ab2)2=a2b4
(× ) ( ×)
2.下列运算正确的是（ C ）
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
10
3.计算： (1) (ab)8 ; (4) (5ab2)3 ;
(2) (2m)3 ;
(3) (-xy)5;
(5) (2×102)2 ; (6) (-3×103)3.
解：(1)原式=a8·b8. (2)原式= 23 ·m3=8m3. (3)原式=(-x)5 ·y5=-x5y5. (4)原式=53 ·a3 ·(b2)3=125a3b6. (5)原式=22×(102)2=4×104. (6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
14
15
n个a n个b =(a·a·····a)·(b·b·····b)
=anbn.
由此可得：(ab)n=anbn (n为正整数).
4
(ab)n = anbn （n为正整数）
注意：运算顺序 是先乘方，再乘 除，最后加减.
12
5.如果（an·bm·b)3=a9b15，求m，n的值. 解：∵（an·bm·b)3=a9b15， （an）3·（bm）3·b3=a9b15， a3n ·b3m·b3=a9b15， a3n ·b3m+3=a9b15， 3n=9，3m+3=15. n=3，m=4.
注意：逆用积的乘法法则，有时可使运算更加简便快捷！
9
随堂即练
1.判断：
(1)（ab2)3=ab6
( ×)
(2) (3xy)3=9x3y3
(×)
(3) (-2a2)2=-4a4 (4) -(-ab2)2=a2b4
(× ) ( ×)
2.下列运算正确的是（ C ）
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
10
3.计算： (1) (ab)8 ; (4) (5ab2)3 ;
(2) (2m)3 ;
(3) (-xy)5;
(5) (2×102)2 ; (6) (-3×103)3.
解：(1)原式=a8·b8. (2)原式= 23 ·m3=8m3. (3)原式=(-x)5 ·y5=-x5y5. (4)原式=53 ·a3 ·(b2)3=125a3b6. (5)原式=22×(102)2=4×104. (6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
14
15
n个a n个b =(a·a·····a)·(b·b·····b)
=anbn.
由此可得：(ab)n=anbn (n为正整数).
4
(ab)n = anbn （n为正整数）
华东师大版八年级上册数学课件华师大版八年级数学上册12-1幂的运算-积的乘方课件3
你能发 现什么?
(ab)2与a2b2是否相等?
灿若寒星
(ab)3 (ab) (ab) (ab) （乘方的意义）
(aaa) (bbb)（乘法交换律、结合律）
a3b3
同理：
（同底数幂相乘的法则）
(ab)4 (ab) (ab) (ab) (ab)
(aaaa) (bbbb)
灿若寒星
该你出手了： (a b)n an bn
(1) (3a)3
(2) (ab2 )2
(3) (2 103 )2
(4) (2x 2 y 3 )3
灿若寒星
灿若寒星
A.（xy）3 2 xy6
B. (2x)3 8x3
C. (a2b)4 a8b4 D. (3mn)3 9m3n3
反向使用: an·bn=(ab)n
试用简便方法计算: (1)23×53; =(2×5)3 =103 (2)28×58; =(2×5)8 =108
灿若寒星
1、在手工课上,小军制作了一个正 方形的模具,其边长是4×103㎝,问 该模具的体积是多少?
解：（4×103）3
=43×（103）3 =64×109 =6.4×1010
初中数学课件
金戈铁骑整理制作
灿若寒星
复习
1：同底数幂相乘的运算性质？
一般形式还 记得吗？
同底数幂相乘，底数不变，指数相加。
一般形式： a n
am
an
m （m，n为正整数)
2：幂的乘方的运算性质？
幂的乘方，底数不变，指数相乘
一般形式： (am )n amn
(m,n为正整数)
灿若寒星
3、计算下列各式：
积的乘方=. 每个因式分别乘方后的积
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
12.1 .3 积的乘方
情景引入
小明和小华今年都上初二了, 他们两 1 个进行了一场比赛,看谁先算出 2 ( 2 ) 谁就胜,小明用了三分钟,小华一下子 就写出了正确答案,你知道小华用了什 么灵丹妙药吗?
10 11
同学们你们想拥有这种灵丹妙药吗?
一填空 : : 2 ( 2) ( 2 ) (1)( ab) (ab) (ab) (aa) (bb) a b 3 ( 3) ( 3 ) （ 2 ） (ab) ______ ____ a b 4 ( 4) ( 4) (3)( ab) ______ _____ a b
5 (2) ( ) 13
2004
3 2003 .( 2 ) 5
15 3
(3) (0.125) .( 2 )
15
能力拓展
一.填空： 6 3 3 (1)a y ( ) ； 3 2 n 8 (2)若(a ym） a y ，则m ___，n ___ . 1 2004 2004 (3)3 ( ) ________. 3
n n n
(abc) a b c
(n为正整数 )
例3 计算
探究2
3 2 3
(1)( 2b) ; (2)(2a ) ; (3)(-a) ; 4 3 4 (4)( 3 x) ; (5)(ab) (ac)
3
看谁做的又对 又快!
1.计算:
巩固练习
2 3
(1)(3a) ； (2)(-3a) ； 2 2 3 3 (3)(ab ) ； (4)( 2 10 ) .
2.判断下列计算是否正确,并说明理由 3 2 6 3
1( xy ) xy ；• 2（ 2x） 2x ； 2 3 3 5 6 3 3 3 3（ x y） x y ； 4（ a b） b a
3
探究三
1 11 小华怎么那么快计算出 210 （ ） 呢？ 2
二.思考: (1)观察上面几道题的计算结果,你能发现什么 规律? n n n (2)你能猜测到,当n为正整数时, (ab) ___? ab 你能用上面类似的方法说明为什么吗?
探究1
积的乘方法则
(ab) a b (n为正整数 )
即:积的乘方,等于把积的每个因式 分别乘方,再把所得的幂相乘. n n n n
利用了a b
10
n
n
abn （n为正整数）
现在你能迅速的解答出 下列题吗？ 16 17 （ 1 ） （ 0.125) . (8)
1 11 解： 2 ( ) 2 1 10 1 10 2 ( ) 2 2 1 1 [2 ( )]1 0 2 2 1 1 2 1 2
二.计算： 2 3 2 (1)( xy z ) ； 2 3 （ 2 ） [ቤተ መጻሕፍቲ ባይዱ4 （x y） ] ； 3 4 （ 3 ） (t s ) ( s t )
课堂小结
本节课我们学习了积的乘方,等于积中每个 因式分别乘方,并把所得的幂相乘. 由特殊到一般的归纳方法再次在我们者节 课中出现,同学们在学习中要善于从特殊中 去发现规律,总结规律.
情景引入
小明和小华今年都上初二了, 他们两 1 个进行了一场比赛,看谁先算出 2 ( 2 ) 谁就胜,小明用了三分钟,小华一下子 就写出了正确答案,你知道小华用了什 么灵丹妙药吗?
10 11
同学们你们想拥有这种灵丹妙药吗?
一填空 : : 2 ( 2) ( 2 ) (1)( ab) (ab) (ab) (aa) (bb) a b 3 ( 3) ( 3 ) （ 2 ） (ab) ______ ____ a b 4 ( 4) ( 4) (3)( ab) ______ _____ a b
5 (2) ( ) 13
2004
3 2003 .( 2 ) 5
15 3
(3) (0.125) .( 2 )
15
能力拓展
一.填空： 6 3 3 (1)a y ( ) ； 3 2 n 8 (2)若(a ym） a y ，则m ___，n ___ . 1 2004 2004 (3)3 ( ) ________. 3
n n n
(abc) a b c
(n为正整数 )
例3 计算
探究2
3 2 3
(1)( 2b) ; (2)(2a ) ; (3)(-a) ; 4 3 4 (4)( 3 x) ; (5)(ab) (ac)
3
看谁做的又对 又快!
1.计算:
巩固练习
2 3
(1)(3a) ； (2)(-3a) ； 2 2 3 3 (3)(ab ) ； (4)( 2 10 ) .
2.判断下列计算是否正确,并说明理由 3 2 6 3
1( xy ) xy ；• 2（ 2x） 2x ； 2 3 3 5 6 3 3 3 3（ x y） x y ； 4（ a b） b a
3
探究三
1 11 小华怎么那么快计算出 210 （ ） 呢？ 2
二.思考: (1)观察上面几道题的计算结果,你能发现什么 规律? n n n (2)你能猜测到,当n为正整数时, (ab) ___? ab 你能用上面类似的方法说明为什么吗?
探究1
积的乘方法则
(ab) a b (n为正整数 )
即:积的乘方,等于把积的每个因式 分别乘方,再把所得的幂相乘. n n n n
利用了a b
10
n
n
abn （n为正整数）
现在你能迅速的解答出 下列题吗？ 16 17 （ 1 ） （ 0.125) . (8)
1 11 解： 2 ( ) 2 1 10 1 10 2 ( ) 2 2 1 1 [2 ( )]1 0 2 2 1 1 2 1 2
二.计算： 2 3 2 (1)( xy z ) ； 2 3 （ 2 ） [ቤተ መጻሕፍቲ ባይዱ4 （x y） ] ； 3 4 （ 3 ） (t s ) ( s t )
课堂小结
本节课我们学习了积的乘方,等于积中每个 因式分别乘方,并把所得的幂相乘. 由特殊到一般的归纳方法再次在我们者节 课中出现,同学们在学习中要善于从特殊中 去发现规律,总结规律.