华理通信原理、第七章(正弦载波数字调制系统2)
- 格式:ppt
- 大小:585.00 KB
- 文档页数:25
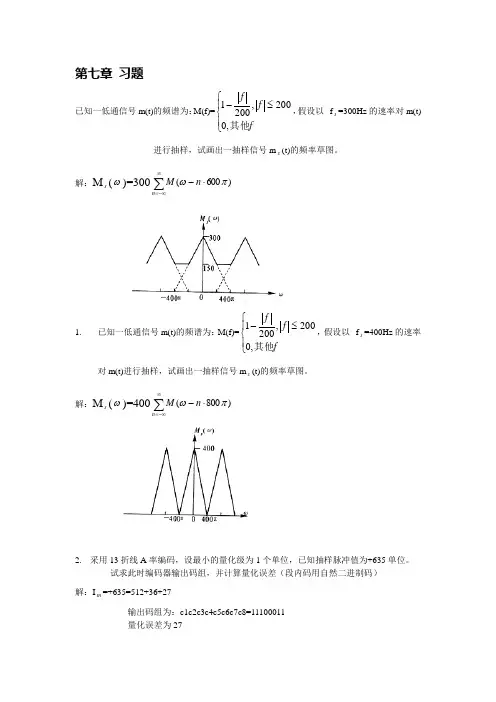
第七章 习题已知一低通信号m(t)的频谱为:M(f)=⎪⎩⎪⎨⎧≤-f f f其他,0200,2001,假设以f s =300Hz 的速率对m(t)进行抽样,试画出一抽样信号m s (t)的频率草图。
解:M s (ω)=300∑∞-∞=⋅-n n M )600(πω1.已知一低通信号m(t)的频谱为:M(f)=⎪⎩⎪⎨⎧≤-f f f其他,0200,2001,假设以f s =400Hz 的速率对m(t)进行抽样,试画出一抽样信号m s (t)的频率草图。
解:M s (ω)=400∑∞-∞=⋅-n n M )800(πω2. 采用13折线A 率编码,设最小的量化级为1个单位,已知抽样脉冲值为+635单位。
试求此时编码器输出码组,并计算量化误差(段内码用自然二进制码) 解:I m =+635=512+36+27输出码组为:c1c2c3c4c5c6c7c8=11100011 量化误差为273. 采用13折线A 率编码,设最小的量化级为1个单位,已知抽样脉冲值为-95单位。
试求此时编码器输出码组,并计算量化误差(段内码用折叠二进制码) 解:-95= -(64+74⨯+3) c5c6c7c8=0000输出码组为:c1c2c3c4c5c6c7c8=00110000 量化误差为74. 采用13折线A 率编码器电路,设接收端收到的码组为“01010011”,最小量化单位为1个单位,并已知段内码为折叠二进码。
试问译码器输出为多少单位。
解:I 0= -(256+4.5⨯16)=-3285. 采用13折线A 率编码器电路,设接收端收到的码组为“01010011”,最小量化单位为1个单位,并已知段内码为自然二进码。
试问译码器输出为多少单位 解:I 0= -(256+3.5⨯16)=-3126. 单路话音信号的最高频率为4KHz ,抽样速率为8kHz ,将所得的脉冲由PAM 方式或PCM方式传输。
设传输信号的波形为矩形脉冲,其宽度为τ,且占空比为1。


载波调制原理载波调制原理是一种常见的调制方式,用于在通信系统中将基带信号转换为可以传输的高频信号。
通过将基带信号与一个高频载波信号相乘,可以实现信号的传输和调制。
本文将对载波调制原理进行详细介绍。
在通信系统中,基带信号是指未经过调制的信号,通常是来自于声音、视频或数据等信息。
为了将这些信息传输到远距离的接收端,我们需要将基带信号转换为高频信号,以便在信道中传输。
这就是载波调制的作用。
载波调制的原理是通过将基带信号与一个高频载波信号相乘,来实现信号的调制。
在这个过程中,基带信号被叠加到载波信号上,形成了一个新的调制信号。
这个调制信号的频率通常远高于基带信号,从而可以通过天线等设备传输到接收端。
载波调制的过程可以分为两个主要步骤:调制和解调。
在调制过程中,基带信号与载波信号相乘,形成调制信号。
而在解调过程中,接收端将接收到的调制信号分离出基带信号和载波信号,以便恢复原始信息。
载波调制有许多不同的类型,包括调幅调制(AM)、调频调制(FM)和调相调制(PM)等。
每种调制方式都有其特定的优点和应用场景。
例如,调幅调制通常用于广播领域,而调频调制则常用于音频传输。
在实际应用中,载波调制技术已经被广泛应用于无线通信、广播、电视等领域。
通过将基带信号转换为高频信号,我们可以实现远距离、高质量的信号传输,从而满足人们日益增长的通信需求。
总的来说,载波调制原理是一种重要的调制方式,通过将基带信号与高频载波信号相乘,实现信号的传输和调制。
在通信领域,载波调制技术发挥着重要作用,为人们的通信需求提供了有效的解决方案。
希望本文的介绍能够帮助读者更好地理解载波调制原理及其应用。


辅修班通信原理复习考点:第一章1.数字通信系统的组成:信源:电信号,可以使模拟的也可以是数字的。
信源编码器:对模拟信号数字化处理(抽样)、去除冗余,提高传输效率信道编码器:对以上处理的信号再进行编码,以实现一定范围内的检错纠错能力,提高信息传输的准确性。
数字调制器:将数字序列变换成某种信号的形式,以适合在特定的信道传播。
信道:传送信号的物理媒介。
数字解调器:将不同的信号波形恢复成数字序列。
信道译码器:实现检错、纠错能力。
信源解码器:将信源完全或近似的恢复出来。
信宿2.数字通信系统的基本性能指标及测量参数:1.码元与比特率(信息速率)的转换--------M进制。
注:符号/s= bauds/s2.带宽利用率:或3.信噪比:或(4.误码率出错的码元数量发送的码元数量5.误码率出错的比特数量发送的比特数量注:6.能量信号7.功率信号.8.信源、信道特点:可靠性、有效性第二章希尔伯特变换:希尔伯特反变换:性质:1.对函数f(t)进行希尔伯特变换后,在进行希尔伯特反变换,则恢复原来的函数。
2.对函数f(t)进行两次希尔伯特变换等效于取函数f(t)的负值函数-f(t)3.函数f(t)与其希尔伯特变换有相同的能量。
4.若f(t)为偶函数,则其希尔伯特变换为奇函数;若f(t)为奇函数,则其希尔伯特变换为偶函数。
5.函数f(t)与其希尔伯特变换相互正交。
匹配滤波器性质:1.使信噪比最大。
2.冲激响应为其自身信号反转后延时T的信号。
(t)=x(T-t)第三章信源编码抽样定理:1.低通抽样2.带通抽样其中相关结论:无论信号的最高频率取值多大,都可将无失真恢复的原来信号的抽样频率限定在2W~4W的范围内。
(W为原信号的带宽)均匀量化:1.量化噪声为量化的正负动态范围为量化精度2.量化精度N每增加一位,量化信噪比有6dB的改善。
非均匀量化:A率量化:国际标准A取87.56结论:A率的压缩变换对小信号在这一区域SNR有24dB的提升。
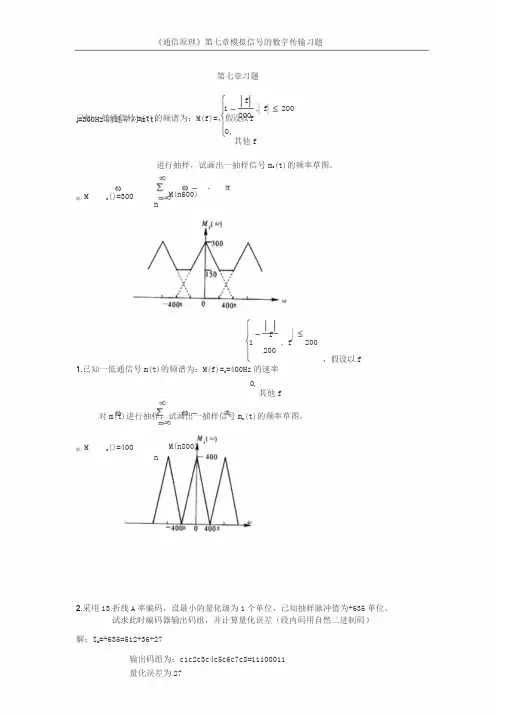
《通信原理》第七章模拟信号的数字传输习题第七章习题1f200, f 200已知一低通信号m(t)的频谱为:M(f)=,假设以fs=300Hz的速率对m(t)0,其他f进行抽样,试画出一抽样信号m s(t)的频率草图。
解:M s()=300 nM(n600)1f200, f 200,假设以f1.已知一低通信号m(t)的频谱为:M(f)=s=400Hz的速率0,其他f 对m(t)进行抽样,试画出一抽样信号m s(t)的频率草图。
解:M s()=400M(n800) n2.采用13折线A率编码,设最小的量化级为1个单位,已知抽样脉冲值为+635单位。
试求此时编码器输出码组,并计算量化误差(段内码用自然二进制码)解:I m=+635=512+36+27输出码组为:c1c2c3c4c5c6c7c8=11100011量化误差为271《通信原理》第七章模拟信号的数字传输习题3.采用13折线A率编码,设最小的量化级为1个单位,已知抽样脉冲值为-95单位。
试求此时编码器输出码组,并计算量化误差(段内码用折叠二进制码)解:-95=-(64+74+3)c5c6c7c8=0000输出码组为:c1c2c3c4c5c6c7c8=00110000量化误差为74.采用13折线A率编码器电路,设接收端收到的码组为“01010011”,最小量化单位为1个单位,并已知段内码为折叠二进码。
试问译码器输出为多少单位。
解:I0=-(256+4.516)=-3285.采用13折线A率编码器电路,设接收端收到的码组为“01010011”,最小量化单位为1个单位,并已知段内码为自然二进码。
试问译码器输出为多少单位解:I0=-(256+3.516)=-3126.单路话音信号的最高频率为4KHz,抽样速率为8kHz,将所得的脉冲由PAM方式或PCM方式传输。
设传输信号的波形为矩形脉冲,其宽度为,且占空比为1。
(1)计算PAM系统的最小带宽。
(2)在PCM系统中,抽样后信号按8级量化,求PCM系统的最小带宽。





第七章习题参考答案7- 1采用图P7-1(a)、(b)所示调制信号进行角度调制时,试分别画出调频波和调相波的瞬时频率与瞬时相位变化波形图及已调波的波形图。
图P7-1解:(a))0II I - 1图P7-1J7 — 2有一调角波数学表示式v = 12sin( 108t-0.03cos10°t)V,试问这是调频波求中心角频率,调制角频率以及最大角频偏?[参考答案:As m = 300rad/s]解:一个角度调制波既可以是调频波又可以是调相波,关键是看已调波中瞬时相位厶惟)的表达式与调制信号的关系,与调制信号成正比为调相波,与调制信号的积分成正比为调频波。
由调角波的表达式v = 12sin(108t — 0.03cos104t)得知△惟)=—0.03cos104t,若调制信号v Q = V m sin st,则v = 12sin(10*t— 0.03cos10°t)为调频波。
中心频率为C 108 rad/s,调制角频率为Q = 104 rad/s,最大角频偏4△ s m = M f Q = 0.03 X10 rad/s = 300rad/s 7求调制指数。
若调制频率降为20Hz,求调制指数。
[参考答案:M fi =20 ,M f2 = 104]解: 由于调制频率为10kHz,属于单音调制。
k f V Qm . 3M f = _ ,又△ s m = k f V Qm = 2 n X200 X10 ,32 nX200 X10 所以M竹=3 = 202 nX10 X102 nX200 X1034当调制频率为20Hz时,M f2 - 3 =1042 nX207 — 4 一个调相波的载波频率是7~10MHz,调制指数是20。
调制频率同上题, 求角频偏。
[参考答案:As mi = 1.26 X106rad/s , △如?= 2.5 X103rad/s]解:同样属于单音调制。
M p二k p V Q m = 20△s p = k p Q V Qm = 2 7lFk p V Qm = 2 7T FM p所以当调制信号的频率为10kHz时,△s m1 = 2 nX10 X10 X20rad/s = 1.26 X10 rad/s当调制信号的频率为20kHz时,△s m2 = 2 nX20 X203 X20rad/s = 2.51 X103rad/s7 — 5 某调角波v = 4sin(2 nX107t + 2(cos2 nX103t)V(1)试求在t = 0,t = 0.25ms时刻的瞬时频率。