物理课后答案

一牛顿环的各环是否等宽?密度是否均匀?解释原因?因为环是由空气劈上下表面反射的两束光叠加干涉形成的。

劈的上表面变化在横向是不均匀的，故光程差也不是均匀变化的。

所以各环是不等宽的环的密度也不是均匀的。

各环不等宽，半径小的环宽，越到外边越窄，密度是不均匀的,牛顿环的半径公式是：半径r等于根号下(m+1/2)λR，其中m为环的级数。

从公式可以看出，半径和环数并不是线性关系，这样环自然不均匀。

计算可以知道，越往外环越密。

二牛顿环的干涉圆环是由哪两束相干光干涉产生的?半凸透镜下表面和下底面上表面的两束反射光三电桥由哪几部分组成?电桥平衡的条件?由电源、开关、检流计桥臂电阻组成。

平衡条件是Rx=(R1/R2)R3四接通电源后,检流计指针始终向一边偏转,试分析出现这种情况的原因?指针向一侧偏转就说明发生了电子的定向移动了，这个应该没问题。

指针不偏转，有2种情况吧，其1呢是整个电路发生了断路或其他故障，还1种情况则是流过的电流太小，不足于使电表发生偏转或其偏转的角度肉眼根本看不到。

无论如何调节，检流计指针都不动，电路中可能出现故障是调节臂电阻断路或短路。

无论如何调节，检流计指针始终像一边偏而无法平衡，电路中有可能出现故障是有一个臂（非调节臂）的电阻坏了。

（断路或短路）五什么叫铁磁材料的磁滞现象?铁磁物质经外磁场磁化到饱和以后，把磁场去掉。

这些物质仍保留有剩余磁化强度。

需要反方向加磁场才能把这剩余磁化强度变为零。

这种现象称为铁磁的磁滞现象。

也是说，铁磁材料的磁状态，不仅要看它现在所处的磁场条件；而且还要看它过去的状态。

六如何判断铁磁材料属于软.硬材料?软磁材料的特点是：磁导率大，矫顽力小，磁滞损耗小，磁滞回线呈长条状；硬磁材料的特点是：剩磁大，矫顽力也大用光栅方程进行测量的条件是什么?条件是一束平行光垂直射入光栅平面上，光波发生衍射，即可用光栅方程进行计算。

如何实现：使用分光计，光线通过平行光管射入，当狭缝位于透镜的焦平面上时，就能使射在狭缝上的光经过透镜后成为平行光用光栅方程进行测量,当狭缝太窄或者太宽会怎么样?为什么?缝太窄，入射光的光强太弱，缝太宽，根据光的空间相干性可以知道，条纹的明暗对比度会下降！区别是，太窄了，亮纹会越来越暗，暗纹不变，直到一片黑暗！太宽，暗条纹会逐渐加强，明纹不变，直到一片光明！(1) 校正电流表时，如果发现改装的毫安表读数总是高于标准表的读数，分流电阻应调大还是调小?为什么?答：应调小。

第九章振动9-1一个质点作简谐运动，振幅为A，在起始时刻质点的位移为-A，且向x 轴正方向运2动，代表此简谐运动的旋转矢量为（）题９-１图分析与解（b）图中旋转矢量的矢端在x 轴上投影点的位移为－A/2，且投影点的运动方向指向O x轴正向，即其速度的x 分量大于零，故满足题意．因而正确答案为（b）．9-2已知某简谐运动的振动曲线如图（a）所示，则此简谐运动的运动方程为（）(A)x = 2cos⎡2πt -2 π⎤(cm)(C)x = 2cos⎡2 πt +2 π⎤(cm)⎢⎣3 3 ⎥⎦ ⎢⎣3 3 ⎥⎦(B)x = 2cos⎡4πt -2 π⎤(cm)(D)x = 2cos⎡4 πt +2 π⎤(cm)⎢⎣3 3 ⎥⎦ ⎢⎣3 3 ⎥⎦题９-２图分析与解由振动曲线可知，初始时刻质点的位移为–A/2，且向x 轴负方向运动．图（ｂ）是其相应的旋转矢量图，由旋转矢量法可知初相位为2π / 3 ．振动曲线上给出质点从–A/2 处运动到+A 处所需时间为 1 s，由对应旋转矢量图可知相应的相位差∆ϕ=4π3 ，则角频率ω=∆ϕ/ ∆t =(4π/ 3)s-1 ，故选（D）．本题也可根据振动曲线所给信息，逐一代入方程来找出正确答案．9-3两个同周期简谐运动曲线如图（a）所示，x1 的相位比x2 的相位（）（A）落后π2（B）超前π2（C）落后π（D）超前π分析与解由振动曲线图作出相应的旋转矢量图（b）即可得到答案为（b）．题９-３图9-4当质点以频率ν作简谐运动时，它的动能的变化频率为（）（A）v（B）v （C）2v2（D）4v分析与解质点作简谐运动的动能表式为E k=1mω2 A 2sin2 (ωt2+ϕ)，可见其周期为简谐运动周期的一半，则频率为简谐运动频率ν 的两倍．因而正确答案为（C）．9-5图（a）中所画的是两个简谐运动的曲线，若这两个简谐运动可叠加，则合成的余弦振动的初相位为（）3（A）π21（B）π2（C）π（D）0分析与解由振动曲线可以知道，这是两个同振动方向、同频率简谐运动，它们的相位差是π（即反相位）．运动方程分别为x1=A cosωt 和x2=Acos(ωt +π)．它们的振幅不同．对2于这样两个简谐运动，可用旋转矢量法，如图（b）很方便求得合运动方程为x1 =而正确答案为（D）．Acosωt ．因2题９-５图9-6 有一个弹簧振子，振幅A = 2.0 ⨯10-2 m ，周期T = 1.0 s ，初相ϕ出它的运动方程，并作出x -t 图、v -t 图和a -t 图．=3π / 4 ．试写题９-6 图分析弹簧振子的振动是简谐运动．振幅 A 、初相ϕ、角频率ω是简谐运动方程m / k 外， ω 可通过关系式ω = 2π / T 确定．振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同．解 因ω = 2π / T ，则运动方程x = A cos (ωt + ϕ ) = A ⎛ 2πt + ϕ ⎫cos ⎪ ⎝ T⎭根据题中给出的数据得x = 2.0 ⨯ 10-2 cos (2πt + 0.75π ) (m )振子的速度和加速度分别为v = d x / d y a = d 2x / d 2y = -4π ⨯ 10-2sin (2πt = -8π ⨯ 10-2cos (2πt + 0.75π) ( m ⋅ s-1 )+ 0.75π) ( m ⋅ s -1)x - t 、 v - t 及 a - t 图如图所示．9-7 若简谐运动方程为 x = 0.10 cos (20πt + 0.25π)(m )，求：（1） 振幅、频率、角频率、周期和初相；（2） t = 2s 时的位移、速度和加速度．分析 可采用比较法求解．将已知的简谐运动方程与简谐运动方程的一般形式x = A cos (ωt + ϕ )作比较，即可求得各特征量．运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果．解 （1） 将 x = 0.10 cos (20πt + 0.25π)(m )与 x = A cos (ωt + ϕ )比较后可得：振幅 A ＝ 0.10m ，角频率ω = 20π s -1，初相ϕ ＝0.25 π ，则周期T = 2π / ω = 0.1 s ，频率 v = 1/ T Hz ．（２） t = 2s 时的位移、速度、加速度分别为x = 0.10 cos (40πt + 0.25π) = 7.07 ⨯10-2 mv = d x / d t = -2πsin (40π + 0.25π) = -4.44m ⋅ s -1a = d 2 x / d 2t = -40π2cos (40π + 0.25π) = -2.79 ⨯102 m ⋅ s -29-8 一远洋货轮，质量为 m ，浮在水面时其水平截面积为 S ．设在水面附近货轮的水平截面积近似相等，水的密度为 ρ，且不计水的粘滞阻力，证明货轮在水中作振幅较小的竖直自由运动是简谐运动，并求振动周期．分析 要证明货轮作简谐运动，需要分析货轮在平衡位置附近上下运动时，它所受的合外力 F 与位移 x 间的关系，如果满足 F = -kx ，则货轮作简谐运动．通过 F = -kx 即可求得振动 周期T = 2π / ω = 2π ．证 货轮处于平衡状态时［图（a ）］，浮力大小为 F ＝mg ．当船上下作微小振动时，取货轮处于力平衡时的质心位置为坐标原点 O ，竖直向下为 x 轴正向，如图（b ）所示．则当货轮向下偏移 x 位移时，受合外力为∑ F = P + F '其中 F ' 为此时货轮所受浮力，其方向向上，大小为F ' = F + ρgSx = mg + ρgSx则货轮所受合外力为题９-８图∑F=P -F '=-ρgSx =-kx式中k =ρgS 是一常数．这表明货轮在其平衡位置上下所作的微小振动是简谐运动．由∑F =m d2 x / d2t 可得货轮运动的微分方程为d2 x / d2t +ρgSx / m = 0令ω2 =ρgS / m ，可得其振动周期为T =2π / ω = 2π9-9设地球是一个半径为R 的均匀球体，密度ρ= 5.5 ⨯103 kg ⋅ m-3 ．现假定沿直径凿通一条隧道，若有一质量为m 的质点在此隧道内作无摩擦运动．（1）证明此质点的运动是简谐运动；（2）计算其周期．题９-９图分析证明方法与上题相似．分析质点在隧道内运动时的受力特征即可．证（1）取图所示坐标．当质量为m 的质点位于x 处时，它受地球的引力为m / ρgSm / k x xF = -Gm x m式中G 为引力常量， m 是以 x 为半径的球体质量，即 m = 4πρx 3/ 3 ．令 k = 4πρGm / 3 ，则质点受力F = 4πρGmx / 3 = -kx因此，质点作简谐运动．（2） 质点振动的周期为T = 2π = = 5.07 ⨯103 s9-10 如图（a ）所示，两个轻弹簧的劲度系数分别为 k 1 、k 2时．（1） 证明其运动仍是简谐运动；（2） 求系统的振动频率．．当物体在光滑斜面上振动题 9-10 图分析 从上两题的求解知道，要证明一个系统作简谐运动，首先要分析受力情况，然后看是否满足简谐运动的受力特征（或简谐运动微分方程）．为此，建立如图（b ）所示的坐标．设系统平衡时物体所在位置为坐标原点 O ，Ox 轴正向沿斜面向下，由受力分析可知，沿 Ox 轴， 物体受弹性力及重力分力的作用，其中弹性力是变力．利用串联时各弹簧受力相等，分析物体 在任一位置时受力与位移的关系，即可证得物体作简谐运动，并可求出频率υ ．证 设物体平衡时两弹簧伸长分别为 x 1 、 x 2 ，则由物体受力平衡，有mg sin θ = k 1x 1 = k 2 x 2按图（b ）所取坐标，物体沿 x 轴移动位移 x 时，两弹簧又分别被拉伸 x 1' 和 x 2' ，即物体受力为（1）x = x 1' + x 2' ．则 3π / Gρ1 2π(k + k )/ m 1 21 2F = mg si n θ - k 2 (x 2 + x 2' )= mg si n θ - k 1 (x 1 + x 1') 将式（1）代入式（2）得（２） F = -k 2 x 2' = -k 1x 1' 由式（3）得 x 1' = -F / k 1 、 x 2' = -F / k 2 ，而 x = x 1' + x 2' ，则得到（３）F = -[k k / (k + k )]x = -kx 1 2式中 k = k 1k 2 / (k 1 + k 2 )为常数，则物体作简谐运动，振动频率v = ω / 2π = 12π k / m = 讨论 （1） 由本题的求证可知，斜面倾角 θ 对弹簧是否作简谐运动以及振动的频率均不产生影响．事实上，无论弹簧水平放置、斜置还是竖直悬挂，物体均作简谐运动．而且可以证明它们的频率相同，均由弹簧振子的固有性质决定，这就是称为固有频率的原因．（2） 如果振动系统如图（c ）（弹簧并联）或如图（d ）所示，也可通过物体在某一位置的受力分析得出其 作简谐运动，且振动频率均为v = ，读者可以一试．通过这些例子可以知道，证明物体是否作简谐运动的思路是相同的．*9－11 在如图（a ）所示装置中，一劲度系数为 k 的轻弹簧，一端固定在墙上，另一端连接一质量为 m 1 的物体 A ，置于光滑水平桌面上．现通过一质量 m 、半径为 R 的定滑轮 B （可视为匀质圆盘）用细绳连接另一质量为 m 2 的物体 C ．设细绳不可伸长，且与滑轮间无相对滑动， 求系统的振动角频率．题 9-11 图分析 这是一个由弹簧、物体 A 、C 和滑轮 B 组成的简谐运动系统．求解系统的振动频率可采用两种方法．（1） 从受力分析着手．如图（b ）所示，设系统处于平衡状态时，与物体1 2πk k /(k + k )m1 2 1 2k 正向从原点 O 伸长 x 时，分析物体 A 、C 及滑轮 B 的受力情况，并分别列出它们的动力学方程，可解得系统作简谐运动的微分方程．（2）从系统机械能守恒着手．列出系统机械能守恒方 程，然后求得系统作简谐运动的微分方程．解 1 在图（b ）的状态下，各物体受力如图（c ）所示．其中 F = -k (x + x 0 )i ．考虑到绳 子不可伸长，对物体 A 、B 、C 分别列方程，有F T 1 = -k (x + x 0 ) = d 2 x m 1 d t 2 d 2 x（1）m 2 g - F T 2 = m 2 d t2 （2）( - ) = α = 1d 2 xF T 2 F T 1 R J2 mR d t 2（3） kx 0 = m 2 g （4）方程（3）中用到了 F = F ' 、F = F ' 、J = mR 2/ 2 及α = a / R ．联立式（1） ～式（4）T 2 T 2 可得T 1 T 1d 2 x k则系统振动的角频率为d t2+m 1 + m 2 + m / 2x = 0（5）ω = 解 2 取整个振动装置和地球为研究系统，因没有外力和非保守内力作功，系统机械能守恒．设物体平衡时为初始状态，物体向右偏移距离 x （此时速度为 v 、加速度为 a ）为末状态， 则由机械能守恒定律，有E = -m gx + 1 m v 2 + 1 m v 2 + 1 J ω2 + 1 k (x + x )20 2 2 1 2 2 2 2在列出上述方程时应注意势能（重力势能和弹性势能）零点的选取．为运算方便，选初始状态下物体 C 所在位置为重力势能零点；弹簧原长时为弹性势能的零点．将上述方程对时间求导得0 = -m gv + m v d v + m v d v + Jω d ω + k (x + x )d x2 1 d t 2 d t d t 0d t 将 J = mR 2 / 2 ， ωR = v ， d v / d t = d 2 x / d t 2和m g = kx 代入上式，可得d 2x + d t 2 m2 0+ m + m / 2 x = 0（6）12式（6）与式（5）相同，表明两种解法结果一致．9-12 一放置在水平桌面上的弹簧振子，振幅 A ＝2.0 ×10-2 m ，周期 T ＝0.50ｓ．当 t ＝0 时，（1） 物体在正方向端点；（2） 物体在平衡位置、向负方向运动；（3） 物体在 x ＝-1.0×10-2m 处， 向负方向运动； （4） 物体在 x ＝-1.0×10-2 m 处，向正方向运动．求以上各种情况的运动方程．分析 在振幅 A 和周期 T 已知的条件下，确定初相 φ 是求解简谐运动方程的关键．初相k / (m 1 + m 2 + m / 2)π π = 4π 的确定通常有两种方法．（1） 解析法：由振动方程出发，根据初始条件，即 t ＝0 时，x ＝x 0 和 v ＝v 0 来确定 φ 值．（2） 旋转矢量法：如图（a ）所示，将质点 P 在 Ox 轴上振动的初始位置 x 0 和速度 v 0 的方向与旋转矢量图相对应来确定 φ．旋转矢量法比较直观、方便，在分析中常采用．题 9-12 图解 由题给条件知 A ＝2.0 ×10-2 m ， ω = 2 / T = 4π s -1，而初相 φ 可采用分析中的两种不 同方法来求．解析法 ： 根据简 谐 运动方 程 x = A cos (ωt + ϕ ) ，当 t = 0 时有 x 0 = A cos (ωt + ϕ ) ，v 0 = - Aωsin ．当（1） x 0 = A 时， cos ϕ1 = 1，则ϕ1 = 0 ；π π（2） x 0 = 0 时， cos ϕ2 = 0 ，ϕ2 = ± ，因v 0 < 0 ，取ϕ2 = ；2 2（3） x 0 = 1.0 ⨯10-2 m 时， cos ϕ = 0.5 ，ϕ3 = ± π 3 ，由v 0 < 0 ，取ϕ3 = ； 3（4） x = -1.0 ⨯10-2m 时， cos ϕ = -0.5 ，ϕ = π ± ，由v > 0 ，取ϕ 4π 0 4 4 3 0 4 3旋转矢量法：分别画出四个不同初始状态的旋转矢量图，如图（b ）所示，它们所对应的初 相分别为ϕ1 = 0 ， ϕ2 =， ϕ3 =2， ϕ4 =．33振幅 A 、角频率 ω、初相 φ 均确定后，则各相应状态下的运动方程为（1） x = 2.0 ⨯10-2cos4πt(m )（2） x = 2.0 ⨯10-2 cos (4πt + π/2) (m ) （3） x = 2.0 ⨯10-2 cos (4πt + π/3) (m ) （4） x = 2.0 ⨯10-2 cos (4πt + 4π/3) (m )9-13 有一弹簧， 当其下端挂一质量为 m 的物体时， 伸长量为 9.8 ×10-2 m ．若使物体上、下振动，且规定向下为正方向．（1） 当 t ＝0 时，物体在平衡位置上方 8.0 ×10-2 ｍ 处，由静止开始向下运动，求运动方程．（2） 当 t ＝0 时，物体在平衡位置并以 0.6ｍ·s -1 的速度向上运动，求运动方程．π π 3．k / m g / ∆l x + ( 21010 v / ω )2⎝ 12 ⎭分析 求运动方程，也就是要确定振动的三个特征物理量 A 、ω 和 φ．其中振动的角频率是 由弹簧振子系统的固有性质（振子质量 m 及弹簧劲度系数 k ）决定的，即ω =k /m ，k 可根据物体受力平衡时弹簧的伸长来计算；振幅 A 和初相 φ 需要根据初始条件确定．题 9-13 图解 物体受力平衡时，弹性力 F 与重力 P 的大小相等，即 F ＝mg ．而此时弹簧的伸长量 Δl ＝9.8 ×10-2m ．则弹簧的劲度系数 k ＝F ／Δl ＝mg ／Δl ．系统作简谐运动的角频率为ω = = = 10 s -1（1） 设系统平衡时，物体所在处为坐标原点，向下为 x 轴正向．由初始条件 t ＝0 时， x 10 ＝8.0 ×10-2 m 、v 10 ＝0 可得振幅 A = = 8.0 ⨯10- 2m ；应用旋转矢量法可确定初相ϕ1 = π ［图（a ）］．则运动方程为x = 8.0 ⨯10-2cos (10t + π) (m ) （2）t ＝0 时，x 20 ＝0、v 20 ＝0.6 ｍ·s -1 ，同理可得 A 2 == 6.0 ⨯10- 2 m ； ϕ2 = π / 2 ［图（b ）］．则运动方程为x = 6.0 ⨯10-2cos (10t + 0.5π) (m ) 9-14 某振动质点的 x -t 曲线如图（a ）所示，试求：（1） 运动方程；（2） 点 P 对应的相位；（3） 到达点 P 相应位置所需的时间．分析 由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题．本题就是要通过 x －t 图线确定振动的三个特征量 A 、ω 和ϕ0 ，从而写出运动方程．曲线最大幅值即为振幅 A ；而 ω、ϕ0 通常可通过旋转矢量法或解析法解出，一般采用旋转矢量法比较方便． 解 （1） 质点振动振幅 A ＝0.10 ｍ．而由振动曲线可画出 t 0 ＝0 和 t 1 ＝4 ｓ时旋转矢 量，如图（ b ） 所 示．由图可见初相 ϕ0 = -π / 3 （或 ϕ0 = 5π / 3 ）， 而由 ω(t 1 - t 0 ) = π / 2 + π / 3 得ω = 5π / 24 s ，则运动方程为 -1x = 0.10 cos⎛ 5πt - π / 3⎫(m )24⎪ x + ( 220 20 v / ω)2ppp p题9-14 图（2）图（a）中点P 的位置是质点从A／2 处运动到正向的端点处．对应的旋转矢量图如图（c）所示．当初相取ϕ0 =-π / 3 时，点P 的相位为ϕp =ϕ0 +ω(t - 0)= 0 （如果初相取成=5π / 3 ，则点P 相应的相位应表示为ϕp =ϕ0 +ω(t -0)=2π ．（3）由旋转矢量图可得ω(t - 0)=π/ 3 ，则t =1.6 s ．9-15作简谐运动的物体，由平衡位置向x 轴正方向运动，试问经过下列路程所需的最短时间各为周期的几分之几？（1）由平衡位置到最大位移处；（2）由平衡位置到x ＝A/2 处；（3）由x ＝A/2 处到最大位移处．解采用旋转矢量法求解较为方便．按题意作如图所示的旋转矢量图，平衡位置在点O．（1））平衡位置x1到最大位移x3处，图中的旋转矢量从位置 1 转到位置 3 ，故∆ϕ1=π / 2 ，则所需时间∆t1=∆ϕ1 / ω=T / 4（2）从平衡位置x1到x2＝A/2 处，图中旋转矢量从位置1 转到位置2，故有∆ϕ2则所需时间=π / 6 ，∆t2=∆ϕ2 / ω=T / 12（3）从x2＝A/2 运动到最大位移x3处，图中旋转矢量从位置 2 转到位置3，有∆ϕ0=π / 3 ，则所需时间∆t3=∆ϕ3 / ω=T / 6N 题 9-15 图9-16 在一块平板下装有弹簧，平板上放一质量为 1.0 kg 的重物．现使平板沿竖直方向作上下简谐运动，周期为 0.50ｓ，振幅为 2.0×10-2 m ．求：（1） 平板到最低点时，重物对平板的作用力；（2） 若频率不变，则平板以多大的振幅振动时，重物会跳离平板？ （3） 若振幅不变，则平板以多大的频率振动时， 重物会跳离平板？题 9-16 图分析 按题意作示意图如图所示．物体在平衡位置附近随板作简谐运动，其间受重力 P 和板支持力 F N 作用，F N 是一个变力．按牛顿定律，有d 2 y F = mg - F N = m d t 2（1）由于物体是随板一起作简谐运动，因而有a 改写为 = d 2y d t 2 = -A ω 2 cos (ωt + ϕ ) ，则式（1）可 F N = mg + mA ω 2cos (ωt + ϕ ) （2）（1） 根据板运动的位置，确定此刻振动的相位ωt + ϕ ，由式（2）可求板与物体之间的作 用力．（2） 由式（2）可知支持力 F N 的值与振幅 A 、角频率 ω 和相位（ ωt + ϕ ）有关．在振 动过程中，当ωt + ϕ ＝ π 时 F N 最小．而重物恰好跳离平板的条件为 F N ＝0，因此由式（2）可 分别求出重物跳离平板所需的频率或振幅．解 （1） 由分析可知，重物在最低点时，相位ωt + ϕ ＝0，物体受板的支持力为F = mg + mA ω 2 = mg + mA (2π / t)2 = 12.96 N 重物对木块的作用力 F N ' 与 F N 大小相等，方向相反． （2） 当频率不变时，设振幅变为 A ′．根据分析中所述，将 F N ＝0 及ωt + ϕ 分析中式（2），可得= π 代入max max2A ' = mg / mω2 = gT 2 / 4π2 = 6.2 ⨯10-2 m（3） 当振幅不变时，设频率变为v ' ．同样将 F N ＝0 及ωt + ϕ 可得= π 代入分析中式（2）， v ' = ω = 2π = 3.52 Hz 9-17 两 质点作同 频率、同 振幅的简 谐运动． 第一个质 点的运动 方程 为x 1 = A cos (ωt + ϕ )，当第一个质点自振动正方向回到平衡位置时，第二个质点恰在振动正方 向的端点，试用旋转矢量图表示它们，并求第二个质点的运动方程及它们的相位差．题 9-17 图解 图示为两质点在时刻 t 的旋转矢量图，可见第一个质点 M 的相位比第二个质点 N 的相位超前π / 2 ，即它们的相位差 Δφ＝π/2．故第二个质点的运动方程应为x 2 = A cos (ωt + ϕ - π / 2)9-18 图（a ）为一简谐运动质点的速度与时间的关系曲线，且振幅为 2cm ，求（1） 振动周期；（2） 加速度的最大值；（3） 运动方程．分析 根据 v -t 图可知速度的最大值 v max ，由 v max ＝Aω 可求出角频率 ω，进而可求出周期 T 和加速度的最大值 a max ＝Aω2 ．在要求的简谐运动方程 x ＝A cos （ωt ＋φ）中，因为 A 和 ω 已得出，故只要求初相位 φ 即可．由 v －t 曲线图可以知道，当 t ＝0 时，质点运动速度v 0 ＝v max /2 ＝Aω/2，之后速度越来越大，因此可以判断出质点沿 x 轴正向向着平衡点运动．利用 v 0 ＝－Aωsinφ 就可求出 φ．解 （1） 由v = A ω 得ω =1.5 s -1 ，则 T = 2π / ω = 4.2 s （2） a = A ω 2 = 4.5 ⨯10-2 m ⋅ s -2 （3） 从分析中已知 v 0 = - Aωsin= Aω / 2 ，即 sin ϕ = -1 / 2= -π / 6,-5π / 6因为质点沿 x 轴正向向平衡位置运动，则取 = -5π / 6 ，其旋转矢量图如图（b ）所示．则运动 方程为 x = 2cos (1.5t - 5π / 6) (cm )1 mg / m A 2πg / l g / l max题 9-18 图9-19 有一单摆，长为 1.0m ，最大摆角为 5°，如图所示．（1） 求摆的角频率和周期；（2）设开始时摆角最大，试写出此单摆的运动方程；（3） 摆角为 3°时的角速度和摆球的线速度各为多少？题 9-19 图分析 单摆在摆角较小时（θ＜5°）的摆动，其角量 θ 与时间的关系可表示为简谐运动方程 θ = θmax co s (ωt + ϕ ) ，其中角频率 ω 仍由该系统的性质（重力加速度 g 和绳长 l ）决定，即 ω = ．初相 φ 与摆角 θ，质点的角速度与旋转矢量的角速度（角频率）均是不同的物理 概念，必须注意区分．解 （1） 单摆角频率及周期分别为ω = = 3.13 s -1; T = 2π / ω = 2.01 s（2） 由t = 0 时θ = θ = 5o可得振动初相ϕ = 0 ，则以角量表示的简谐运动方程为 θ = π cos3.13t 36（３） 摆角为 3°时，有cos (ωt + ϕ ) = θ / θmax = 0.6 ，则这时质点的角速度为J / mgl c maxE c M线速度的大小为d θ/d t = -θmax ωsi n (ωt + ϕ ) = -θmax ω = -0.80θ ω = -0.218 s -1 v = l d θ/d t = -0.218 s -1讨论 质点的线速度和角速度也可通过机械能守恒定律求解，但结果会有极微小的差别．这是因为在导出简谐运动方程时曾取sin θ ≈ θ ，所以，单摆的简谐运动方程仅在 θ 较小时成立．9-20 为了测月球表面的重力加速度，宇航员将地球上的“秒摆”（周期为 2.00ｓ），拿到月 球上去，如测得周期为 4.90ｓ，则月球表面的重力加速度约为多少？ （取地球表面的重力加速度 g = 9.80 m ⋅s-2 ） 解 由单摆的周期公式T = 2π 可知 g ∝ 1 / T 2 ，故有 g / g = T 2 / T 2 ，则月球的重力加速度为 g = (T/ T M )2g M E E M= 1.63 m ⋅ s - 29-21 一飞轮质量为 12kg ，内缘半径 r ＝0.6ｍ，如图所示．为了测定其对质心轴的转动惯量，现让其绕内缘刃口摆动，在摆角较小时，测得周期为 2.0s ，试求其绕质心轴的转动惯量．9-21 题图分析 飞轮的运动相当于一个以刃口为转轴的复摆运动，复摆振动周期为 T = 2π ，因此，只要知道复摆振动的周期和转轴到质心的距离l c ，其以刃口为转轴的 转动惯量即可求得．再根据平行轴定理，可求出其绕质心轴的转动惯量．解 由复摆振动周期T = 2π J / mgl ，可得 J = mgrT 2 / 4π2．则由平行轴定理得 J 0 = J - mr 2 = mgrT 2 / 4π 2 - mr 2 = 2.83 kg ⋅ m 29-22 如图（a ）所示，质量为 1.0 ×10-2kg 的子弹，以 500m·s -1 的速度射入木块，并嵌在木块中，同时使弹簧压缩从而作简谐运动，设木块的质量为 4.99 kg ，弹簧的劲度系数为 8.0 ×103 N·m -1 ，若以弹簧原长时物体所在处为坐标原点，向左为 x 轴正向，求简谐运动方程．1 - cos2 (ωt + ϕ ) l / g E E题 9-22 图分析 可分为两个过程讨论．首先是子弹射入木块的过程，在此过程中，子弹和木块组成的系统满足动量守恒，因而可以确定它们共同运动的初速度 v 0 ，即振动的初速度．随后的过程是以子弹和木块为弹簧振子作简谐运动．它的角频率由振子质量 m 1 ＋m 2 和弹簧的劲度系数 k 确定，振幅和初相可根据初始条件（初速度 v 0 和初位移 x 0 ）求得．初相位仍可用旋转矢量法求．解 振动系统的角频率为 ω == 40 s -1由动量守恒定律得振动的初始速度即子弹和木块的共同运动初速度 v 0 为v = m v (m + m ) = 1.0 m ⋅ s -10 1 1 2 又因初始位移 x 0 ＝0，则振动系统的振幅为A = = v 0/ ω = 2.5⨯10-2 m 图（b ）给出了弹簧振子的旋转矢量图，从图中可知初相位 0 = π / 2 ，则简谐运动方程为x = 2.5⨯10-2 cos (40t + 0.5π) (m )9-23 如图（a ）所示，一劲度系数为 k 的轻弹簧，其下挂有一质量为 m 1 的空盘．现有一质量为 m 2 的物体从盘上方高为 h 处自由落入盘中，并和盘粘在一起振动．问：（1） 此时的振动周期与空盘作振动的周期有何不同？ （2） 此时的振幅为多大？k / (m 1 + m 2 ) x + ( 2 0 0 v / ω) 2x + (v / ω) 2 20 0题 9-23 图分析 原有空盘振动系统由于下落物体的加入，振子质量由 m 1 变为 m 1 + m 2，因此新系统的角频率（或周期）要改变．由于 A = ，因此，确定初始速度 v 0 和初始位移 x 0 是求解振幅 A 的关键．物体落到盘中，与盘作完全非弹性碰撞，由动量守恒定律可确定盘与物体的共同初速度 v 0 ，这也是该振动系统的初始速度．在确定初始时刻的位移 x 0 时，应注意新振动系统的平衡位置应是盘和物体悬挂在弹簧上的平衡位置．因此，本题中初始位移 x 0 ，也就是空盘时的平衡位置相对新系统的平衡位置的位移．解 （1） 空盘时和物体落入盘中后的振动周期分别为T = 2π / ω = 2π T ' = 2π / ω' = 2π 可见 T ′＞T ，即振动周期变大了． （2） 如图（b ）所示，取新系统的平衡位置为坐标原点 O ．则根据分析中所述，初始位移为空盘时的平衡位置相对粘上物体后新系统平衡位置的位移，即x = l - l =m 1g - m 1 + m 2 g = - m 2 g 01 2 k k k式中 l 1 ＝m 1/k 为空盘静止时弹簧的伸长量，l 2 ＝（m 1 ＋m 2）/k 为物体粘在盘上后，静止时弹 簧的伸长量．由动量守恒定律可得振动系统的初始速度，即盘与物体相碰后的速度v 0 = m 2 v =m 1 + m 2 式中 v = 是物体由 h 高下落至盘时的速度．故系统振动的振幅为m 1 / k(m 1 + m 2 )/ km 2 m 1 + m 2 2gh2ghx +(2 v / ω ) ' 20 0x + 20 0( v/ ω) 211A ==本题也可用机械能守恒定律求振幅A．9-24如图所示，劲度系数为k 的轻弹簧，系一质量为m1的物体，在水平面上作振幅为A的简谐运动．有一质量为m2的粘土，从高度h 自由下落，正好在（a）物体通过平衡位置时，（b）物体在最大位移处时，落在物体上．分别求：（1）振动周期有何变化？（2）振幅有何变化？题9-24 图分析谐振子系统的周期只与弹簧的劲度系数和振子的质量有关．由于粘土落下前后，振子的质量发生了改变，因此，振动周期也将变化．至于粘土如何落下是不影响振动周期的．但是，粘土落下时将改变振动系统的初始状态，因此，对振幅是有影响的．在粘土落到物体上的两种不同情况中，系统在水平方向的动量都是守恒的．利用动量守恒定律可求出两种情况下系统的初始速度，从而利用机械能守恒定律（或公式A =）求得两种情况下的振幅．解（1）由分析可知，在（a）、（b）两种情况中，粘土落下前后的周期均为T =2π / ω =2πT '=2π / ω'=2π物体粘上粘土后的周期T′比原周期T 大．（2）（a）设粘土落至物体前后，系统振动的振幅和物体经过平衡位置时的速度分别为A、v 和A′、v′．由动量守恒定律和机械能守恒定律可列出如下各式kA'2 / 2 =m v2 / 2 （1）kA'2 / 2 =(m+m)v'2 / 22（2）联立解上述三式，可得m1v=(m1+m2)v'A'=（3）即A′＜A，表明增加粘土后，物体的振幅变小了．（b）物体正好在最大位移处时，粘土落在物体上．则由动量守恒定律知它们水平方向的共同速度v′＝m1v/（m1＋m2）＝0，因而振幅不变，即m2gk1 +2khm1+m2m1/ k(m1+m2)/ km1/(m1+m2)AA / a max max 0 max max 9-25 质量为 0.10kg 的物体，以振幅 1.0×10-2 m 作简谐运动，其最大加速度为 4.0 ｍ·s -1求：（1） 振动的周期；（2） 物体通过平衡位置时的总能量与动能；（3） 物体在何处其动能和势能相等？ （4） 当物体的位移大小为振幅的一半时，动能、势能各占总能量的多少？分析 在简谐运动过程中，物体的最大加速度 a = A ω 2，由此可确定振动的周期T ．另外，在简谐运动过程中机械能是守恒的，其中动能和势能互相交替转化，其总能量 E ＝kA 2/2．当动能与势能相等时，E k ＝E P ＝kA 2/4．因而可求解本题．解 （1） 由分析可得振动周期 T = 2π / ω = 2π = 0.314 s（2） 当物体处于平衡位置时，系统的势能为零，由机械能守恒可得系统的动能等于总能量，即 E = E = 1 mA 2ω 2 = 1 mAak 2 2max = 2.0 ⨯10-3 J（3） 设振子在位移 x 0 处动能与势能相等，则有kx 2 / 2 = kA 2 / 4得 x 0 = ± 2 A / 2 = ±7.07 ⨯10-3 m（４） 物体位移的大小为振幅的一半（即 x = A / 2 ）时的势能为 E = 1 kx 2 = 1 k ⎛ A ⎫ = E / 4 P 2 2 2 ⎪ ⎝ ⎭则动能为E K = E - E P = 3E / 4 9-26 一氢原子在分子中的振动可视为简谐运动．已知氢原子质量 m ＝1.68 ×10-27 Kg ，振动频率υ ＝1.0 ×1014 Hz ，振幅 A ＝1.0 ×10-11ｍ．试计算：（1） 此氢原子的最大速度；（2） 与此振动相联系的能量．解 （1） 简谐运动系统中振子运动的速度 v ＝－A ωsin （ωt ＋φ），故氢原子振动的最大速度为v = ωA = 2πvA = 6.28⨯102 m ⋅ s -1 （２） 氢原子的振动能量E = mv 2 / 2 = 3.31⨯10-20 J 9-27 质量 m ＝10g 的小球与轻弹簧组成一振动系统， 按 x = 0.5(8πt + π / 3) (cm )的规 律作自由振动，求（1） 振动的角频率、周期、振幅和初相；（2） 振动的能量 E ；（3） 一个周期内的平均动能和平均势能．解 （1） 将 x = 0.5(8πt + π / 3) (cm )与 x = A cos (ωt + ϕ )比较后可得：角频率ω = 8π s -1 ，振 幅 A ＝0.5cm ，初相 φ＝π/3，则周期 T ＝2π/ω＝0.25 ｓA + A + 2 A A cos ( 2 2 1 2 1 2 ϕ - ϕ ) 2 1（2） 简谐运动的能量 E = 1 mA 2ω 2 = 7.90 ⨯10-5 J （3） 简谐运动的动能和势能分别为 E = 1 mA 2ω 2sin 2 (ωt + ϕ ) K 2E = 1 mA 2ω 2cos 2 (ωt + ϕ ) P 2则在一个周期中，动能与势能对时间的平均值分别为E = 1 ⎰T 1 mA 2ω 2 sin 2 (ωt + ϕ )d t = mA 2ω 2 = 3.95 ⨯10-5 J T 0 2 4E = 1 ⎰T 1 mA 2ω 2 cos 2 (ωt + ϕ )d t = mA 2ω 2 = 3.95 ⨯10-5 J T 0 2 49-28已 知 两 同 方 向 、 同 频 率 的 简 谐 运 动 的 运 动 方 程 分 别 为 x 1= 0.05cos (10t + 0.75π) (m )； x 2 = 0.06cos (10t + 0.25π) (m ) ．求：（1） 合振动的振幅及初相；（2） 若有另一同方向、同频率的简谐运动 x 3 = 0.07co s (10t + ϕ3 ) (m )，则ϕ3 为多少时， x 1 ＋x 3 的振幅最大？ 又ϕ3 为多少时，x 2 ＋x 3 的振幅最小？题 9-28 图分析 可采用解析法或旋转矢量法求解.由旋转矢量合成可知，两个同方向、同频率简谐运动 的合成仍为一简谐运动，其角频率不变；合振动的振幅 A = ，其大小与两个分振动的初相差ϕ2 - ϕ1 相关．而合振动的初相位ϕ = arctan [(A s in ϕ + A sin ϕ ) / (A cos ϕ + A cos ϕ )] 1 1 2 2 1 1 2 2解 （1） 作两个简谐运动合成的旋转矢量图（如图）．因为∆ϕ 故合振动振幅为= ϕ2 - ϕ1 = -π / 2 ， A = 合振动初相位= 7.8 ⨯10-2 m ϕ = arctan [(A s in ϕ + A sin ϕ ) / (A cos ϕ + A cos ϕ )] 1 1 2 2 1 1 2 2= arctan11 = 1.48 rad （2） 要使 x 1 ＋x 3 振幅最大，即两振动同相，则由∆ϕ= 2k π 得 A + A + 2 A A cos ( 2 2 1 2 1 2 ϕ - ϕ ) 21 K PA 2 + A 2 + 2A 2cos (π + ϕ - ϕ ) 2 12ϕ3 = ϕ1 + 2k π = 2k π + 0.75π, k= 0,±1,±2,...要使 x 1 ＋x 3 的振幅最小，即两振动反相，则由()得 ϕ3 = ϕ2 + (2k + 1)π = 2k π + 1.25π, k = 0,±1,±2,...9-29 手电筒和屏幕质量均为 m ，且均被劲度系数为 k 的轻弹簧悬挂于同一水平面上，如 图所示．平衡时，手电筒的光恰好照在屏幕中心．设手电筒和屏幕相对于地面上下振动的表达式分别为 x 1 = A cos (ωt + ϕ1 )和 x 2 = A cos (ωt + ϕ2 )．试求在下述两种情况下，初相位 φ1 、φ2 应满足的条件：（1） 光点在屏幕上相对于屏静止不动；（2） 光点在屏幕上相对于屏作振幅 A ′＝2A 的振动．并说明用何种方式起动，才能得到上述结果．题 9-29 图分析 落在屏幕上的光点相对地面的运动和屏幕相对于地面的运动都已知道，且是两个简谐运动．因此由运动的合成不难写出光点相对屏的运动（实际上是两个同方向、同频率简谐运动的合成）．根据相对运动公式，有依题意x 光对地 = x 光对屏 + x 屏对地x 光对地 = x 1 = A cos (ωt + ϕ1 ) x 屏对地 = x 2 = A cos (ωt + ϕ2 ) 所以 x 光对屏 = x 1 - x 2 = x 1 + x 2'= A cos (ωt + ϕ1 ) + A cos (ωt + π + ϕ2 ) 可见光点对屏的运动就是两个同方向、同频率简谐运动 x 1 = A cos (ωt + ϕ1 ) 和 x 2' = A cos (ωt + π + ϕ2 )的合成．用与上题相同的方法即可求解本题．其中合运动振幅 A ' = ． 解 （1） 根据分析和参考上题求解，当要求任一时刻光点相对于屏不动，即 x 光对屏 = 0 ，就是 当π + ϕ2 - ϕ1 = (2k + 1)π 时，即ϕ = ϕ1 + 2k π 时（ k = 0,±1,±2,...），A ′＝0．当光点 相对于屏作振幅为 2A 的运动时，要求π + ϕ2 - ϕ1 = 2k π ，即ϕ2 = ϕ1 + (2k - 1)π ．（2） 由以上求解可知，要使光点相对于屏不动，就要求手电筒和屏的振动始终要同步， 即同相位，为此，把它们往下拉 A 位移后，同时释放即可；同理，要使光点对屏作振幅为 2A 的谐振动，两者必须相位相反，为此，让手电筒位于平衡点 0 上方的-A 处，而屏则位于+A 处同。

医⽤物理学课后习题参考答案医⽤物理学课后习题参考答案第⼀章1-1 ① 1rad/s ② 6.42m/s1-2 ① 3.14rad/s - ② 31250(3.9310)rad π? 1-3 3g =2l β 1-4 1W=g 2m l 1-5 ① 22k E 10.8(1.0710)J π=? ② -2M=-4.2410N m ??③ 22W 10.8(1.0710)J π=-?1-6 ① 26.28rad/s ② 314rad ③ 394J ④ 6.28N1-7 ①ω② 1g 2m l 1-8 ① =21rad/s ω② 10.5m/s1-9 ① =20rad/s ω② 36J ③ 23.6kg m /s ?1-10 ① 211=2ωω②1=-2k k1E E ? 1-11 =6rad/s ω 1-12 12F =398F 239NN = 1-13 ① 51.0210N ? ② 1.9%1-14 ① 42210/N m ? ② 52410/N m ?1-15 ① -65m(510)m µ? ② -31.2510J ?第三章3-1 -33V=5.0310m ?3-2 ① 12m/s ② 51.2610a P ?3-3 ① 9.9m/s ② 36.0m3-4 ①-221.510;3.0/m m s ? ② 42.7510a P ? ③粗处的压强⼤于51.2910a P ?时，细处⼩于P 0时有空吸作⽤。

3-5 主动脉内Re 为762～3558，Re <1000为层流，Re >1500为湍流， 1000< Re <1500为过渡流。

3-6 71.210J ? 3-7 0.77m/s3-8 ①3=5.610a P P ?? ②173=1.3810a P s m β-③-143Q=4.0610/m s ?3-9 0.34m/s 3-10 431.5210/J m ?第四章4-1 -23S=810cos(4t )m 2ππ?+ 或-2-2S=810cos(4t-)m=810sin 4t 2πππ??4-2 ① ?π?= ② 12t=1s S 0,S 0==当时， 4-3 ① S=0.1cos(t-)m 3ππ②5t (0.833)6s s ?= 4-4 ①-2S=810cos(2t-)m 2ππ? ② -2=-1610s in(2t-)m/s 2v πππ?;2-22a=-3210cos(2t-)m/s 2πππ?③k E =0.126J 0.13J;F=0≈.4-5 ①max =20(62.8)m/s v π②242max a =4000 3.9410m/s π=? ③22321E=m A =1.9710J=200J 2ωπ? 4-6 ①2A 5.010,=4,T=0.25,=1.25m Hz s m νλ-=?② -2S=5.010cos8(t-)0.5x m π?4-7 ①S=0.10cos (-)0.10cos 0.2(-)522x x t m t m ππ= ②S=-0.10m4-8 ①=60,=1.0Hz m νλ② -2S=5.010cos120(-)60x t m π? 4-9 ①1s ?π-=②2A 6.010,=20,T=0.1,=0.2,c 2.m s m m/s ωπλ-=?= 4-10 ①22-31=A =25.44J m 2ερω? ②328.4210W m -?? 4-11 ① 0 ② 2A4-12 ①-39.1210a P ? ②-9E=1.6510J ?4-13 ① 889.9 ② 0.54-14 ① -621.010W m -?? ② -61.010W ?4-15 2=0.054 5.410v m/s m/s -=?第五章5-1 ①71.110a P ? ②67.0810a P ?5-2 ① 2534.8310m -? ② -9=2.7310;9d m ?倍。

第十二章 导体电学【例题精选】例12-1 把A ，B 两块不带电的导体放在一带正电导体的电场中,如图所示. 设无限远处为电势零点，A 的电势为U A ，B 的电势为U B ，则 (A) U B > U A ≠0． (B) U B > U A = 0．(C) U B = U A ． (D) U B < U A ． [ D ]例12-2 选无穷远处为电势零点，半径为R 的导体球带电后，其电势为U 0，则球外离球心距离为r 处的电场强度的大小为(A) 302rU R ． (B) R U 0． (C) 20r RU ． (D) r U 0． [ C ] *例12-3 如图所示，封闭的导体壳A 内有两个导体B 和C 。

A 、C 不带电，B 带正电，则A 、B 、C 三导体的电势U A 、U B 、U C 的大小关系是（A ） U A = UB = UC （B ） U B > U A = U C （C ） U B > U C > U A （D ） U B > U A > U C例12-4 在一个不带电的导体球壳内，先放进一个电荷为 +q 的点电荷，点电荷不与球壳内壁接触。

然后使该球壳与地接触一下，再将点电荷+q 取走。

此时，球壳的电荷为 ；电场分布的范围是 ． -q 球壳外的整个空间例12-5 如图所示，A 、B 为靠得很近的两块平行的大金属平板，两板的面积均为S ，板间的距离为d ．今使A 板带电荷q A ，B 板带电荷q B ，且q A > q B ．则A 板的靠近B 的一侧所带电荷为 ；两板间电势差U = ．)(21B A q q - Sd q q B A 02)(ε- 例12-6 一空气平行板电容器，电容为C ，两极板间距离为d 。

充电后，两极板间相互作用力为F 。

则两极板间的电势差为 ；极板上的电荷为 。

C Fd /2 FdC 2例12-7 C 1和C 2两个电容器，其上分别标明200 pF （电容量）、500 V （耐压值） 和300 pF 、900 V ．把它们串连起来在两端加上1000 V 电压，则(A) C 1被击穿，C 2不被击穿． (B) C 2被击穿，C 1不被击穿．(C) 两者都被击穿． (D) 两者都不被击穿． [ C ]ABA C Bd例12-8 半径分别为1.0 cm 与2.0 cm 的两个球形导体，各带电荷 1.0³10-8 C ，两球相距很远．若用细导线将两球相连接．求：(1) 每个球所带电荷；(2) 每个球的电势．(22/C m N 1094190⋅⨯=πε) 解：两球相距很远，可视为孤立导体，互不影响．球上电荷均匀分布．设两球半径分别为r 1和r 2，导线连接后的电荷分别为q 1和q 2，而q 1 + q 1 = 2q ， 则两球电势分别是 10114r q U επ=， 20224r q U επ=两球相连后电势相等 21U U =，则有 21212122112r r qr r q q r q r q +=++== 由此得到 921111067.62-⨯=+=r r qr q C 92122103.132-⨯=+=r r qr q C两球电势 310121100.64⨯=π==r q U U ε V例12-9 如图所示，三个“无限长”的同轴导体圆柱面A 、B 和C ，半径分别为 R a 、 R b 、R c ．圆柱面B 上带电荷，A 和C 都接地．求Ｂ的内表面上电荷线密度λ1和外表面上电荷线密度λ2之比值λ1/ λ2．解：设B 上带正电荷，内表面上电荷线密度为λ1，外表面上电荷线密度为λ2，而A 、C 上相应地感应等量负电荷，如图所示．则A 、B 间场强分布为 E 1=λ1 / 2πε0r ，方向由B 指向AB 、C 间场强分布为E 2=λ2 / 2πε0r ，方向由B 指向CB 、A 间电势差 a b R R R R BA R R r r r E U ab a bln 2d 2d 0111ελελπ=π-=⋅=⎰⎰B 、C 间电势差 b c R R R R BC R R r r r E U cb cb ln 2d 2d 0222ελελπ=π-=⋅=⎰⎰ 因U BA ＝U BC ,得到()()a b b c R R R R /ln /ln 21=λλ 【练习题】*12-1 设地球半径R =6.4⨯106 m ，求其电容？解：C=4πε0R=7.12³10-4F12-2三块互相平行的导体板，相互之间的距离d 1和d 2比板面积线度小得多，外面二板用导线连接．中间板上带电，设左右两面上电荷面密度分别为σ1和σ2，如图所示．则比值σ1 / σ2为λ2(A) d 1 / d 2． (B) d 2 / d 1． (C) 1． (D) 2122/d d ． [ B ]12-3 充了电的平行板电容器两极板(看作很大的平板)间的静电作用力F 与两极板间的电压U 的关系：(A) F ∝U ． (B) F ∝1/U ． (C) F ∝1/U 2． (D) F ∝U 2． [ D ] 12-4 两个半径相同的金属球，一为空心，一为实心，把两者各自孤立时的电容值加以比较，则(A) 空心球电容值大． (B) 实心球电容值大．(C) 两球电容值相等． (D) 大小关系无法确定． [ C ] 12-5 一导体A ，带电荷Q 1，其外包一导体壳B ，带电荷Q 2，且不与导体A 接触．试证在静电平衡时，B 的外表面带电荷为Q 1 + Q 2．证明：在导体壳内部作一包围B 的内表面的闭合面,如图．设B 内表面上带电荷Q 2′，按高斯定理，因导体内部场强E 处处为零，故0/)(d 021='+=⎰⋅εQ Q S E S∴ 12Q Q -=' 根据电荷守恒定律，设B 外表面带电荷为2Q ''，则 222Q Q Q =''+' 由此可得 21222Q Q Q Q Q +='-='' 第十三章 电介质【例题精选】例13-1 一导体球外充满相对介电常量为εr 的均匀电介质，若测得导体表面附近场强为E ，则导体球面上的自由电荷面密度σ为(A) ε 0 E ． (B) ε 0 ε r E ． (C) ε r E ． (D) (ε 0 ε r - ε 0)E ． [ B ] 例13-2 C 1和C 2两空气电容器串联起来接上电源充电。

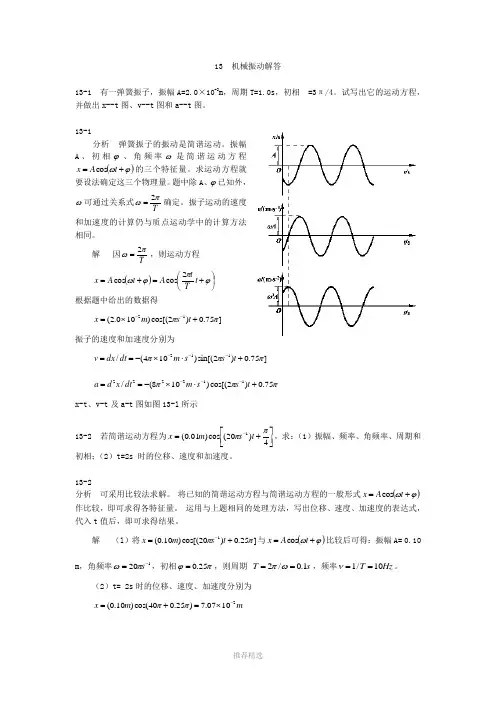
13 机械振动解答13-1 有一弹簧振子，振幅A=2.0×10-2m ，周期T=1.0s ，初相=3π/4。

试写出它的运动方程，并做出x--t 图、v--t 图和a--t 图。

13-1分析 弹簧振子的振动是简谐运动。

振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。

求运动方程就要设法确定这三个物理量。

题中除A 、ϕ已知外，ω可通过关系式Tπω2=确定。

振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。

解 因Tπω2=，则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ，求：（1）振幅、频率、角频率、周期和初相；（2）t=2s 时的位移、速度和加速度。

13-2分析 可采用比较法求解。

将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较，即可求得各特征量。

运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t 值后，即可求得结果。

解 （l ）将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得：振幅A= 0.10 m ，角频率120-=s πω，初相πϕ25.0=，则周期 s T 1.0/2==ωπ，频率Hz T 10/1==ν。

（2）t= 2s 时的位移、速度、加速度分别为mm x 21007.7)25.040cos()10.0(-⨯=+=ππ)25.040sin()2(/1πππ+⋅-==-s m dt dx v )25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体，密度ρ5.5×103kg •m -3。

第六章 自由电子论和电子的输运性质思 考 题1.如何理解电子分布函数)(E f 的物理意义是: 能量为E 的一个量子态被电子所占据的平均几率?[解答]金属中的价电子遵从费密-狄拉克统计分布, 温度为T 时, 分布在能级E 上的电子数目1/)(+=-Tk E E BF e gn ,g 为简并度, 即能级E 包含的量子态数目. 显然, 电子分布函数11)(/)(+=-Tk E E BF e E f是温度T 时, 能级E 的一个量子态上平均分布的电子数. 因为一个量子态最多由一个电子所占据, 所以)(E f 的物理意义又可表述为: 能量为E 的一个量子态被电子所占据的平均几率.2.绝对零度时, 价电子与晶格是否交换能量?[解答]晶格的振动形成格波，价电子与晶格交换能量，实际是价电子与格波交换能量. 格波的能量子称为声子, 价电子与格波交换能量可视为价电子与声子交换能量. 频率为i ω的格波的声子数11/-=Tk i B i e n ω .从上式可以看出, 绝对零度时, 任何频率的格波的声子全都消失. 因此, 绝对零度时, 价电子与晶格不再交换能量.3.你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?[解答]自由电子论只考虑电子的动能. 在绝对零度时, 金属中的自由(价)电子, 分布在费密能级及其以下的能级上, 即分布在一个费密球内. 在常温下, 费密球内部离费密面远的状态全被电子占据, 这些电子从格波获取的能量不足以使其跃迁到费密面附近或以外的空状态上, 能够发生能态跃迁的仅是费密面附近的少数电子, 而绝大多数电子的能态不会改变. 也就是说, 常温下电子的平均动能与绝对零度时的平均动能一定十分相近. 4.晶体膨胀时, 费密能级如何变化?[解答] 费密能级3/2220)3(2πn m E F=,其中n 是单位体积内的价电子数目. 晶体膨胀时, 体积变大, 电子数目不变, n 变小, 费密能级降低.5.为什么温度升高, 费密能反而降低?[解答]当0≠T 时, 有一半量子态被电子所占据的能级即是费密能级. 温度升高, 费密面附近的电子从格波获取的能量就越大, 跃迁到费密面以外的电子就越多, 原来有一半量子态被电子所占据的能级上的电子就少于一半, 有一半量子态被电子所占据的能级必定降低. 也就是说, 温度升高, 费密能反而降低.6.为什么价电子的浓度越大, 价电子的平均动能就越大?[解答]由于绝对零度时和常温下电子的平均动能十分相近，我们讨论绝对零度时电子的平均动能与电子浓度的关系.价电子的浓度越大价电子的平均动能就越大, 这是金属中的价电子遵从费密-狄拉克统计分布的必然结果. 在绝对零度时, 电子不可能都处于最低能级上, 而是在费密球中均匀分布. 由(6.4)式3/120)3(πn k F =可知, 价电子的浓度越大费密球的半径就越大,高能量的电子就越多, 价电子的平均动能就越大. 这一点从(6.5)和(6.3)式看得更清楚. 电子的平均动能E 正比与费密能0F E , 而费密能又正比与电子浓度3/2n:()3/222032πn mE F=,()3/2220310353πn mE EF ==.所以价电子的浓度越大, 价电子的平均动能就越大.7.对比热和电导有贡献的仅是费密面附近的电子, 二者有何本质上的联系?[解答]对比热有贡献的电子是其能态可以变化的电子. 能态能够发生变化的电子仅是费密面附近的电子. 因为, 在常温下, 费密球内部离费密面远的状态全被电子占据, 这些电子从格波获取的能量不足以使其跃迁到费密面附近或以外的空状态上, 能够发生能态跃迁的仅是费密面附近的电子, 这些电子吸收声子后能跃迁到费密面附近或以外的空状态上.对电导有贡献的电子, 即是对电流有贡献的电子, 它们是能态能够发生变化的电子. 由(6.79)式)(00ε⋅∂∂+=v τe E f f f可知, 加电场后,电子分布发生了偏移. 正是这偏移)(0ε⋅∂∂v τe E f部分才对电流和电导有贡献. 这偏移部分是能态发生变化的电子产生的. 而能态能够发生变化的电子仅是费密面附近的电子, 这些电子能从外场中获取能量, 跃迁到费密面附近或以外的空状态上. 而费密球内部离费密面远的状态全被电子占拒, 这些电子从外场中获取的能量不足以使其跃迁到费密面附近或以外的空状态上. 对电流和电导有贡献的电子仅是费密面附近电子的结论从(6.83)式xk Sxx ESv e j Fετπ∇=⎰d 4222和立方结构金属的电导率E S v e k S xF ∇=⎰d 4222τπσ看得更清楚. 以上两式的积分仅限于费密面, 说明对电导有贡献的只能是费密面附近的电子.总之, 仅仅是费密面附近的电子对比热和电导有贡献, 二者本质上的联系是: 对比热和电导有贡献的电子是其能态能够发生变化的电子, 只有费密面附近的电子才能从外界获取能量发生能态跃迁.8.在常温下, 两金属接触后, 从一种金属跑到另一种金属的电子, 其能量一定要达到或超过费密能与脱出功之和吗?[解答]电子的能量如果达到或超过费密能与脱出功之和, 该电子将成为脱离金属的热发射电子. 在常温下, 两金属接触后, 从一种金属跑到另一种金属的电子, 其能量通常远低于费密能与脱出功之和. 假设接触前金属1和2的价电子的费密能分别为1F E 和2F E , 且1F E >2F E , 接触平衡后电势分别为1V 和2V . 则两金属接触后, 金属1中能量高于11eV E F -的电子将跑到金属2中. 由于1V 大于0, 所以在常温下, 两金属接触后, 从金属1跑到金属2的电子, 其能量只小于等于金属1的费密能.9.两块同种金属, 温度不同, 接触后, 温度未达到相等前, 是否存在电势差? 为什么?[解答]两块同种金属, 温度分别为1T 和2T , 且1T >2T . 在这种情况下, 温度为1T 的金属高于0F E 的电子数目, 多于温度为2T 的金属高于0F E 的电子数目. 两块金属接触后, 系统的能量要取最小值, 温度为1T 的金属高于0F E 的部分电子将流向温度为2T 的金属. 温度未达到相等前, 这种流动一直持续. 期间, 温度为1T 的金属失去电子, 带正电; 温度为2T 的金属得到电子, 带负电, 二者出现电势差.10.如果不存在碰撞机制, 在外电场下, 金属中电子的分布函数如何变化?[解答]如果不存在碰撞机制, 当有外电场ε后, 电子波矢的时间变化率εe t -=d d k .上式说明, 不论电子的波矢取何值, 所有价电子在波矢空间的漂移速度都相同. 如果没有外电场ε时, 电子的分布是一个费密球, 当有外电场ε后, 费密球将沿与电场相反的方向匀速刚性漂移, 电子分布函数永远达不到一个稳定分布. 11.为什么价电子的浓度越高, 电导率越高?[解答]电导σ是金属通流能力的量度. 通流能力取决于单位时间内通过截面积的电子数(参见思考题18). 但并不是所有价电子对导电都有贡献, 对导电有贡献的是费密面附近的电子. 费密球越大, 对导电有贡献的电子数目就越多. 费密球的大小取决于费密半径3/12)3(πn k F =.可见电子浓度n 越高, 费密球越大, 对导电有贡献的电子数目就越多, 该金属的电导率就越高.12.电子散射几率与声子浓度有何关系? 电子的平均散射角与声子的平均动量有何关系?[解答]设波矢为k 的电子在单位时间内与声子的碰撞几率为),',(θΘk k , 则),',(θΘk k 即为电子在单位时间内与声子的碰撞次数. 如果把电子和声子分别看成单原子气体, 按照经典统计理论, 单位时间内一个电子与声子的碰撞次数正比与声子的浓度.若只考虑正常散射过程, 电子的平均散射角θ与声子的平均波矢q 的关系为由于F k k k ==', 所以F F k q k q 222sin==θ.在常温下, 由于q <<k , 上式可化成F F k q k q ==θ.由上式可见, 在常温下, 电子的平均散射角与声子的平均动量q 成正比.13.低温下, 固体比热与3T 成正比, 电阻率与5T 成正比, 2T 之差是何原因?[解答]按照德拜模型, 由(3.133)式可知, 在甚低温下, 固体的比热34)(512D B V T Nk C Θπ=.而声子的浓度⎰⎰-=-=mB mB T k pTk ce v eD V n ωωωωωωπωω0/2320/1d 231d )(1,作变量变换T k x B ω =,得到甚低温下333232T v Ak n p Bπ=,其中⎰∞-=021d xe x x A .可见在甚低温下, 固体的比热与声子的浓度成正比. 按照§6.7纯金属电阻率的统计模型可知, 纯金属的电阻率与声子的浓度和声子平均动量的平方成正比. 可见, 固体比热与3T 成正比, 电阻率与5T 成正比, 2T 之差是出自声子平均动量的平方上. 这一点可由(6.90)式得到证明. 由(6.90)可得声子平均动量的平方286220/240/3321d 1d )(T v v Bk e v e v q s p B T k s T k p D B DB =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎰⎰ωωωωωωωω ,其中⎰⎰∞∞--=02031d 1d x xe x x e x x B 。

大学物理学课后习题答案（下册）习题99.1 选择题(1)正方形的两对角线处各放置电荷Q，另两对角线各放置电荷q，若Q 所受到合力为零，则Q 与q 的关系为：（）（A ）Q=-2 3/2q (B) Q=2 3/2q (C) Q=-2q (D) Q=2q[答案：A](2)下面说法正确的是：（）（A ）若高斯面上的电场强度处处为零，则该面内必定没有电荷；（B ）若高斯面内没有电荷，则该面上的电场强度必定处处为零；（C）若高斯面上的电场强度处处不为零，则该面内必定有电荷；（D ）若高斯面内有电荷，则该面上的电场强度必定处处不为零。

[答案：D](3)一半径为R 的导体球表面的面点荷密度为σ，则在距球面R 处的电场强度（）（A ）σ/ε0（B）σ/2ε0（C）σ/4ε0（D ）σ/8ε0[答案：C](4)在电场中的导体内部的（）（A ）电场和电势均为零；（B）电场不为零，电势均为零；（C）电势和表面电势相等；（D）电势低于表面电势。

[答案：C]9.2 填空题(1)在静电场中，电势不变的区域，场强必定为。

[ 答案：相同](2)一个点电荷q 放在立方体中心，则穿过某一表面的电通量为，若将点电荷由中心向外移动至无限远，则总通量将。

[ 答案：q/6ε0, 将为零](3)电介质在电容器中作用（a）——（b）——。

[ 答案：(a)提高电容器的容量;(b) 延长电容器的使用寿命](4)电量Q 均匀分布在半径为R 的球体内，则球内球外的静电能之比。

[ 答案：5：6]9.3 电量都是q 的三个点电荷，分别放在正三角形的三个顶点．试问：(1) 在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡( 即每个电荷受其他三个电荷的库仑力之和都为零)?(2) 这种平衡与三角形的边长有无关系?解: 如题9.3 图示(1)以A 处点电荷为研究对象，由力平衡知：q 为负电荷2 14π0qcos30a 214π(qq3a)23解得(2)与三角形边长无关．q3q3题9.3 图题9.4 图9.4 两小球的质量都是m，都用长为l 的细绳挂在同一点，它们带有相同电量，静止时两线夹角为2 , 如题9.4 图所示．设小球的半径和线的质量都可以忽略不计，求每个小球所带的电量．解: 如题9.4 图示T sin T cosF emg14π 0 (2lq 2sin ) 2解得q2l sin 4 0 mg t an9.5 根据点电荷场强公式 Eq4 0 r，当被考察的场点距源点电荷很近(r→0)时，则场强→∞，这是没有物理意义的，对此应如何理解?q解: E4 π0rr0 仅对点电荷成立，当r0 时，带电体不能再视为点电荷，再用上式求场强是错误的，实际带电体有一定形状大小，考虑电荷在带电体上的分布求出的场强不会是无限大．9.6 在真空中有 A ，B 两平行板，相对距离为 d ，板面积为S ，其带电量分别为+ q 和- q ．则q 2 这两板之间有相互作用力 f ，有人说 f =4 d 2, 又有人说，因为 f = qE , Eq，所S222d2l l 22以 f =q ．试问这两种说法对吗 ?为什么 ? f 到底应等于多少 ?S解: 题中的两种说法均不对． 第一种说法中把两带电板视为点电荷是不对的，第二种说法把q合场强 E看成是一个带电板在另一带电板处的场强也是不对的．正确解答应为一个S板的电场为 E q，另一板受它的作用力fq q q2，这是两板间相互作用的电场力．2 0 S2 0 S2 0 S9.7 长 l =15.0cm 的直导线 AB 上均匀地分布着线密度=5.0x10 -9C 2 m-1的正电荷．试求：(1) 在导线的延长线上与导线B 端相距a 1 =5.0cm 处 P 点的场强； (2) 在导线的垂直平分线上与导线中点相距d 2 =5.0cm 处 Q 点的场强．解： 如题 9.7 图所示(1) 在带电直线上取线元dx ，其上电量dq 在 P 点产生场强为 dE PE P14 π 0 ( adE Pdxx) 22 dx题 9.7 图4π 02(a x) 2[ 11]4π 0a l al 2 2lπ 0 (4 al 2)用 l15 cm ，5.0 10 9 C m 1, a 12.5 cm 代入得(2) 同理2E P6.74 10 N CdE1 dx 1方向水平向右方向如题 9.7 图所示Q 4 π 0 x2由于对称性dE Qxl0 ，即 E Q 只有 y 分量，2d 220 l 1∵dE Qy1x d2 224 π 0 xd 2x22EdEd 2 2 dxQylQyl4π 2l 2(x23d 2 )22π 0 l4d2以5.0 10 9C cm , l 15 cm , d 2 5 cm 代入得E Q E Qy14.96 102 N C ，方向沿 y 轴正向9.8一个半径为 R 的均匀带电半圆环，电荷线密度为, 求环心处 O 点的场强．解: 如 9.8 图在圆上取 dl Rd题 9.8 图dqdl R d ，它在 O 点产生场强大小为Rd dE24π 0 R方向沿半径向外则dE xdE sinsin d 4π 0 RdE ydE cos()cos d 4π 0 R积 分 E xsin d4π 0 R2π 0 RE ycos d 04π 0 R∴E E x2π R，方向沿x 轴正向．122222 229.9均匀带电的细线弯成正方形，边长为 l ，总电量为 q ．(1) 求这正方形轴线上离中心为 r处的场强 E ； (2) 证明：在 rl 处，它相当于点电荷 q 产生的场强 E ．解: 如 9.9 图示，正方形一条边上电荷q在 P 点产生物强4dE P 方向如图，大小为dE Pcos 4π 0 1 cos 2 l2r24∵cos 1l22r 2l 2∴dE Pcos 2cos 1ll2l24π0 rr42dE P 在垂直于平面上的分量dE∴dEl dE P cosr4π 0 rlr 2lr2l424题 9.9 图由于对称性， P 点场强沿 OP 方向，大小为E P 4 dE∵4π 0(r 2q 4l4 lr l2l2) r 24222e ．e内r 0 内1∴E P4π 0 (r qrl) r 2l4 2方向沿OP9.10(1) 点电荷q 位于一边长为a的立方体中心，试求在该点电荷电场中穿过立方体的一个面的电通量；(2) 如果该场源点电荷移动到该立方体的一个顶点上，这时穿过立方体各面的电通量是多少?解: (1) 由高斯定理 E dS qs立方体六个面，当q 在立方体中心时，每个面上电通量相等∴各面电通量q 6 0(2) 电荷在顶点时，将立方体延伸为边长2a 的立方体，使q 处于边长2a 的立方体中心，则边长2a 的正方形上电通量q 6 0对于边长 a 的正方形，如果它不包含q 所在的顶点，则qe，24 0如果它包含q 所在顶点则 e 0 ．如题9.10 图所示．题9.10 图9.11均匀带电球壳内半径6cm，外半径10cm，电荷体密度为238cm ,12cm 各点的场强．10 5 C2 m-3 求距球心5cm，解: 高斯定理 E dSsq2q , E4πr0 0当r 5 cm时，q 0 , E 0r 8 cm 时，q4π3p (r r 3 ) 34πr 3 r 2∴ E34π 23.48 10 4 N C ，方向沿半径向外．22外3 r 3r 12 cm 时, q4π(r3 r 内）4π 3 外 ∴E33r 内 4.10 10 4N C1沿半径向外 .4π 0 r9.12半径为 R 1 和 R 2 ( R 2 ＞ R 1 ) 的两无限长同轴圆柱面，单位长度上分别带有电量 和-, 试求:(1)r ＜ R 1 ； (2) R 1 ＜ r ＜ R 2 ；(3) r ＞ R 2 处各点的场强．解: 高斯定理qE dSs取同轴圆柱形高斯面，侧面积则S E d S S2πrl E 2πrl对(1)r R 1 q 0, E 0(2)R 1rR 2q l∴E2π 0 r沿径向向外(3)∴r R 2q 0E题 9.13 图9.13 两个无限大的平行平面都均匀带电，电荷的面密度分别为 1 和 2 ，试求空间各处场强． 解:如题 9.13 图示，两带电平面均匀带电，电荷面密度分别为1 与2 ，两面间，E1( 2 02)n1 面外，E1 (1 2)n20 210 1 2 面外， E(12 02) nn ：垂直于两平面由1 面指为2 面．9.14半径为 R 的均匀带电球体内的电荷体密度为, 若在球内挖去一块半径为r ＜ R 的 小球体，如题 9.14图所示．试求：两球心 O 与 O 点的场强，并证明小球空腔内的电场是均匀的． 解:将此带电体看作带正电的均匀球与带电的均匀小球的组合，见题9.14 图 (a) ．(1)球在 O 点产生电场球在 O 点产生电场 E 10E 200，4 πr 33OO' 4π 0d∴O 点电场 E 0r33 d3OO '；4 d 3(2)在 O 产生电场 E 103 4π 0dOO '球在 O 产生电场 E 20∴ O 点电场E 0OO'3 0题 9.14 图(a)题 9.14 图 (b)(3) 设空腔任一点 P 相对 O 的位矢为 r ，相对 O 点位矢为 r ( 如 题 8-13(b) 图)r 则E PO，3r E PO,3 03 3q -8r0 6OO∴E PE PO E PO(r r )3 0 OO' d3 0 3 0∴腔内场强是均匀的．-69.15 一电偶极子由 =1.0 3 10 C 的两个异号点电荷组成，两电荷距离d=0.2cm ，把这电5-1偶极子放在 1.0 3 10 N2 C的外电场中，求外电场作用于电偶极子上的最大力矩．解:∵ 电偶极子 p 在外场 E 中受力矩Mp E∴M maxpE qlE 代入数字M max1.0 1062 1031.0 1052.0 10 4N m9.16 两点电荷1 =1.5 3 10 C ， -82 =3.03 10C ，相距 r 1 =42cm ，要把它们之间的距离变为r 2 =25cm ，需作多少功 ?解: Ar 2 F drr 2 q 1 q 2dr q 1q 2(11 ) r 1r 24π 24π 0 r 1r 26.55 10 J外力需作的功AA 6.55 106J题 9.17 图9.17 如题 9.17图所示，在 A ， B 两点处放有电量分别为+q ,- q 的点电荷， AB 间距离为2 R ，现将另一正试验点电荷q 0 从 O 点经过半圆弧移到 C 点，求移动过程中电场力作的功． 解:如题 9.17 图示U 1 ( q 4π 0 Rq) 0 RU 1 ( q q ) 4π 0 3 R Rq 6 π 0 Rq q4-31-19∴A q 0 (U O U C )q o q 6π 0 R9.18 如题 9.18图所示的绝缘细线上均匀分布着线密度为 的正电荷 , 两直导线的长度和半圆环的半径都等于R ．试求环中心 O 点处的场强和电势．解: (1) 由于电荷均匀分布与对称性， AB 和 CD 段电荷在 O 点产生的场强互相抵消，取dl Rd则 dqRd 产生 O 点 d E 如图，由于对称性， O 点场强沿 y 轴负方向题 9.18 图EdE2Rd cosy24π 0 R［ sin() 4 π 0 R2sin］22 π 0 R(2)AB 电荷在 O 点产生电势，以 UAdx 1B4 π 0 x2 R dxR4π 0 x4π 0ln 2同理 CD 产生半圆环产生U 24 π 0πR 3ln 24π 0 R4 0∴U O U 1 U 2 U 32π 0ln 24 09.19 一电子绕一带均匀电荷的长直导线以23 10 m 2 s 的匀速率作圆周运动． 求带电直线上的线电荷密度． ( 电子质量m 0 =9.1 3 10 kg ，电子电量 e =1.60 3 10 C)2U U -1E 解:设均匀带电直线电荷密度为 ，在电子轨道处场强E2π 0 r电子受力大小F eeEe 2 π 0 r∴e mv2π 0 rr2π 0 得mv 2 12.5 10 13 C m 1e-19.20 空气可以承受的场强的最大值为=30kV2 cm，超过这个数值时空气要发生火花放 电． 今有一高压平行板电容器，极板间距离为 d =0.5cm ，求此电容器可承受的最高电压． 解:平行板电容器内部近似为均匀电场UEd 1.5 104V9.21 证明：对于两个无限大的平行平面带电导体板 ( 题9.21 图) 来说， (1) 相向的两面上，电荷的面密度总是大小相等而符号相反； (2) 相背的两面上，电荷的面密度总是大小相等而符号相同． 证:如题 9.21 图所示，设两导体 A 、B 的四个平面均匀带电的电荷面密度依次为1 ，2 ，3 ，4题 9.21 图(1) 则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时，有E d S ( s3) S 0∴2 3说明相向两面上电荷面密度大小相等、符号相反；(2) 在 A 内部任取一点 P ，则其场强为零，并且它是由四个均匀带电平面产生的场强叠加而成的，即2212342 02222-77又∵2 3∴1 4说明相背两面上电荷面密度总是大小相等，符号相同．9.22 三个平行金属板 A ， B 和 C 的面积都是 200cm ， A 和 B 相距 4.0mm ， A 与 C 相距 2.0 mm ． B ， C 都接地，如题 9.22图所示．如果使 A 板带正电 3.0 3 10 C ，略去边缘效应，问 B 板和 C 板上的感应电荷各是多少 ?以地的电势为零，则 A 板的电势是多少 ? 解: 如题 9.22 图示，令 A 板左侧面电荷面密度为1 ，右侧面电荷面密度为2题 9.22 图(1) ∵U AC U AB ，即∴E AC d ACE AB d A B1E AC d AB ∴22E AB且1 +2q A23S d ACq A S2 q A 13S而qCS 2q 32 10 7Cq B2S1 10 C(2)U A E AC d A Cd AC2.3 103V9.23 两个半径分别为R 1 和 R 2 （ R 1 ＜ R 2 ) 的同心薄金属球壳，现给内球壳带电+ q ，试计算：(1) 外球壳上的电荷分布及电势大小；(2) 先把外球壳接地，然后断开接地线重新绝缘，此时外球壳的电荷分布及电势； *(3) 再使内球壳接地，此时内球壳上的电荷以及外球壳上的电势的改变量．得, 1A 1R 2解: (1) 内球带电q ；球壳内表面带电则为 q , 外表面带电为 q ，且均匀分布，其电势qdrq UE drRR4π r 2 4π R22题 9.23 图(2) 外壳接地时，外表面电荷 q 入地，外表面不带电，内表面电荷仍为 q ．所以球壳电势由内球q 与内表面 q 产生：Uq 4π 0 R 2q 04π 0 R 2(3) 设此时内球壳带电量为q ；则外壳内表面带电量为 q ，外壳外表面带电量为 q q( 电荷守恒 ) ，此时内球壳电势为零，且q' q' U Aq q' 04 π 0 R 14π 0 R 24π 0 R 2得外球壳上电势UqR 1 qR 2q' q'q q'R 1 R 2 qB4π 0 R 24π 0 R 24π 0 R 24π 0 29.24 半径为 R 的金属球离地面很远，并用导线与地相联，在与球心相距为一点电荷 + q ，试求：金属球上的感应电荷的电量． d3R 处有解:如题 9.24 图所示，设金属球感应电荷为q ，则球接地时电势 U O由电势叠加原理有：题 9.24 图q' q O4π 0 R4π 0 3 RUF 01223得qq 39.25 有三个大小相同的金属小球，小球1， 2带有等量同号电荷，相距甚远，其间的库仑力为 F 0 ．试求：(1) 用带绝缘柄的不带电小球3先后分别接触 1，2后移去，小球 1，2之间的库仑力；(2) 小球 3依次交替接触小球 1， 2很多次后移去，小球 1， 2之间的库仑力．解: 由题意知q 4π 0r2(1) 小球 3 接触小球 1后，小球 3 和小球 1均带电qq ,2小球 3 再与小球 2 接触后，小球 2 与小球 3 均带电q3 q 4∴此时小球 1与小球 2 间相互作用力3 q 2F q' q" 8 3 F 4π 0 r4π 0 r8(2) 小球 3 依次交替接触小球 1、 2 很多次后，每个小球带电量均为2q .3∴小球 1 、 2 间的作用力 F 22 23 q 3 q 40 4π 0r 299.26 在半径为R 1 的金属球之外包有一层外半径为R 2 的均匀电介质球壳， 介质相对介电常数为r ，金属球带电Q ．试求：(1) 电介质内、外的场强； (2) 电介质层内、外的电势； (3) 金属球的电势．解: 利用有介质时的高斯定理D dS qS(1) 介质内(R 1 rR 2 ) 场强DQr4 πr, E 内 Qr ;4 π 0 r r20 F 3r外 2介质外 (r R 2 ) 场强DQr 4πr 3, E 外Qr4 π 0 r(2) 介质外 (rR 2 ) 电势UE drrQ 4 π 0 r介质内(R 1 rR 2 ) 电势UE 内 dr rE 外 drrq1 ( 4π 0 r r 1 Q )R 2 4 π 0 R 2(3) 金属球的电势Q(1 r1 4π 0 r rR 2R 2 U E 内 drE 外 drR 1 R 2R 2 Qdr QdrR4π 0 r R 24 π 0rQ4π 0( 1 r1 rR 1R 29.27 如题 9.27图所示，在平行板电容器的一半容积内充入相对介电常数为 r 的电介质．试求：在有电介质部分和无电介质部分极板上自由电荷面密度的比值． 解: 如题 9.27 图所示，充满电介质部分场强为E 2 ，真空部分场强为 E 1 ，自由电荷面密度分别为2 与1由 D dSq 0 得D 11 ，D 22而D 1E 1 , D 20 rE 23)2)2E 1 E 2∴2 U d0 rE 2 r10 E 1题 9.27 图题 9.28 图9.28 两个同轴的圆柱面，长度均为l ，半径分别为 R 1 和 R 2 ( R 2 ＞ R 1 ) ， 且 l >> R 2 - R 1 ，两柱面之间充有介电常数的均匀电介质 . 当两圆柱面分别带等量异号电荷Q 和- Q 时，求：(1) 在半径 r 处(R 1 ＜ r ＜ R 2 ＝，厚度为 dr ，长为 l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量； (2) 电介质中的总电场能量； (3) 圆柱形电容器的电容．解: 取半径为 r 的同轴圆柱面(S)则D d S ( S)2πrlD当 (R 1 r∴R 2 ) 时，q QDQ 2 πrl D 2Q2 (1) 电场能量密度w2 8π2r 2l 2Q2 Q 2dr 薄壳中 dWwd8π2r 2l22πrdrl4π rl(2) 电介质中总电场能量WdWR 2 Q2drQ lnR 2VR 14πrl4πl R 1(3) 电容：∵WQ2C2Q 2 2πl∴C2W ln( R2 / R1 )题9.29 图9.29 如题9.29 图所示，C1 =0.25 F，C2 =0.15 F，C3 =0.20 F ．C1上电压为50V．求：U AB ．解: 电容C1 上电量Q1 C1U 1电容C2 与C3 并联C23 C2 C3其上电荷∴Q23 Q1Q232C1U 125 50UABC23U 1 U 2C2350(13525)3586 V9.30C1 和C2 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”，把它们串联起来后等值电容是多少?如果两端加上1000 V 的电压，是否会击穿?解: (1) C1 与C2 串联后电容C C1C2200 300 120pF(2) 串联后电压比C1 C2U 1 C2200 300 3U 2 C1，而U 1 U 221000∴U 1600 V , U 2400 V即电容C1 电压超过耐压值会击穿，然后C2 也击穿．9.31半径为R1 =2.0cm 的导体球，外套有一同心的导体球壳，壳的内、外半径分别为R2 =4.0cmU2222 2和 R 3 =5.0cm ，当内球带电荷 Q =3.0 3 10 C 时，求：(1) 整个电场储存的能量；(2) 如果将导体壳接地，计算储存的能量； (3) 此电容器的电容值．解: 如图，内球带电 Q ，外球壳内表面带电Q ，外表面带电 Q(1) 在 rR 1 和 R 2题 9.31 图r R 3 区域在 Rr R 时E 0E Qr 1214π 0 rrR 3 时Qr 24π 0 r∴在 R 1rR 2 区域W 1R 2 1 R 1 2Q( 2 4π 0 r) 24πr drR 2 Q drQ( 1 1 ) R 18π 0 r8π 0 R 1R 2在 rR 3 区域W 1 ( Q) 2 4πr 2drQ 1R 32 0 4π 0 r8π0 R 3∴ 总能量W W 1 W 2Q( 1 1 1 ) 8π 0 R 1R 2R 31.82 10 4J(2) 导体壳接地时，只有R 1rR 2 时 EQr , W 2 04π 0 r2 -83E 3 22312∴W W 1Q21( 8π 0 R 11 ) 1.01 R 210 4 J(3) 电容器电容C2W Q2 4 π 0 /(11 ) R 1R 24.49 10F习 题 1010.1 选择题(1) 对于安培环路定理的理解，正确的是：（ A ）若环流等于零，则在回路 L 上必定是 H 处处为零； （ B ）若环流等于零，则在回路 L 上必定不包围电流；（ C ）若环流等于零，则在回路L 所包围传导电流的代数和为零；（ D ）回路 L 上各点的 H 仅与回路 L 包围的电流有关。

人教版高中物理必修1 课后答案第一章机械基础习题1 回答1.一个物体的速度与时间的关系可以用速度公式来表示：速度 = 距离/时间。

根据题目给出的信息，可知速度为60千米/小时，时间为3小时，代入速度公式计算可得：60 = 距离/3，解方程得出距离为180千米。

2.物体的匀速运动可以用速度公式来表示：速度 = 距离/时间。

根据题目给出的信息，可知速度为80米/分钟，时间为10分钟，代入速度公式计算可得：80 = 距离/10，解方程得出距离为800米。

习题2 回答1.物体在匀加速直线运动中，位移与初速度、时间和加速度有关。

根据题目给出的信息，可知初速度为0，时间为5秒，加速度为6米/秒²，代入位移公式计算可得：位移 = 初速度 * 时间 + 1/2 * 加速度 * 时间²，代入数值计算后得出位移为75米。

2.物体在匀加速直线运动中，速度与初速度、时间和加速度有关。

根据题目给出的信息，可知初速度为20米/秒，时间为8秒，加速度为4米/秒²，代入速度公式计算可得：速度 = 初速度 + 加速度 * 时间，代入数值计算后得出速度为52米/秒。

第二章力的作用和运动习题1 回答1.牛顿第一定律也被称为惯性定律，它描述的是物体静止或匀速直线运动时所具有的性质。

根据牛顿第一定律，如果物体受到的合力为零，则物体将保持静止或匀速直线运动。

因此，如果在匀速直线运动中没有外力的作用，物体将保持原来的速度。

2.牛顿第二定律描述的是物体运动状态与作用力之间的关系。

根据牛顿第二定律，物体的加速度与作用在物体上的合力成正比，与物体的质量成反比。

即：合力 = 质量* 加速度。

因此，当给定物体的质量和加速度，就可以根据牛顿第二定律计算作用在物体上的合力。

3.牛顿第三定律描述的是相互作用力的特点。

根据牛顿第三定律，对于相互作用的两个物体，它们之间的作用力大小相等、方向相反。

例如，当一个人站在地面上时，他对地面施加了一个向下的力，而地面对他也施加了一个大小相等、方向相反的力，使他能够保持平衡。

第十八章 波 动1、一横波沿绳子传播，其波的表达式为 x)2- t 100050ππcos(.y = (SI) 求: (1) 波的振幅、波速、频率和波长。

(2) 绳子上各质点的最大振动速度和最大振动加速度。

(3) 在m .x 201=处和m .x 702=处二质点振动的位相差。

解：（1）)0.02 (100cos 05.0) 2 100cos(05.0x t x t y -=-=πππ m A 05.0=∴,υππω 2 100 ==502/100==⇒ππυ(HZ) )(501-⋅=s m u , )(15050m u===υλ(2) ) 2 100sin(10005.0πππ-⨯-==∂∂t v tY, )(7.15510005.01max -⋅==⨯=s m v ππ) 2 100cos()100(05.02 22x t a t Yπππ-⨯-==∂∂∴ 8.4934500)100(05.022m ax ==⨯=ππa )(2-⋅s m(3)ππλπϕ=-=-=∆12.07.022 12x x2、一平面简谐波沿ｘ轴正向传播，波的振幅cm A 10=，波的圆频率-1s rad 7 ⋅=πω，当s .t 01=时，cm x 10=处的a 质点正通过其平衡位置向ｙ轴负方向运动，而cm x 20=处的ｂ质点正通过cm y 5=点向ｙ轴正方向运动。

设该波波长10c m>λ，求该平面波的表达式。

解：设波动方程为：)2 7cos(1.0πϕπλ⋅-+=xt Yt=1(s)时， 05.0)2 7cos(1.0 ,0)2 7cos(1.02.01.0=⋅-+==⋅-+=πϕππϕπλλ b a Y Y∵0<a v ⇒ ππϕππλk 22 721.0+=⋅-+ ① ∵ 0>b v ， ⇒ ππϕππλk 22 732.0+-=⋅-+ ② 且m 1.0 >λ，故b a ,两质点的位相差π2<①-②得：5λ=1.2， 即 λ=0.24（m ） 代入①得：πϕ317-= 所以 波动方程为：) 7cos(1.031325πππ+-=x t Y 3、图示一平面简谐波在0=t 时刻的波形图，求： （1）该波的波动方程； （2）Ｐ处质点的振动方程。

习题七7-1下列表述是否正确?为什么?并将错误更正．（1）A E Q ∆+∆=∆ （2）⎰+=V p E Q d（3）121Q Q -≠η （4）121Q Q -<不可逆η 解：(1)不正确，A E Q +∆=(2)不正确，⎰+=Vp E Q d Δ(3)不正确，121Q Q -=η(4)不正确，121Q Q -=不可逆η7-2 V p -图上封闭曲线所包围的面积表示什么?如果该面积越大，是否效率越高?答：封闭曲线所包围的面积表示循环过程中所做的净功．由于1Q A 净=η，净A 面积越大，效率不一定高，因为η还与吸热1Q 有关．7-3 如题7-3图所示，有三个循环过程，指出每一循环过程所作的功是正的、负的，还是零，说明理由．解：各图中所表示的循环过程作功都为0．因为各图中整个循环分两部分，各部分面积大小相等，而循环方向一个为逆时针，另一个为顺时针，整个循环过程作功为0．题7-3图7-4 用热力学第一定律和第二定律分别证明，在V p -图上一绝热线与一等温线不能有两个交点．题7-4图解：1.由热力学第一定律有 A E Q +∆=若有两个交点a 和b ，则 经等温b a →过程有0111=-=∆A Q E 经绝热b a →过程012=+∆A E 022<-=∆A E从上得出21E E ∆≠∆，这与a ,b 两点的内能变化应该相同矛盾．2.若两条曲线有两个交点，则组成闭合曲线而构成了一循环过程，这循环过程只有吸热，无放热，且对外做正功，热机效率为%100，违背了热力学第二定律． 7-5 一循环过程如题7-5图所示，试指出： (1)ca bc ab ,,各是什么过程；(2)画出对应的V p -图； (3)该循环是否是正循环?(4)该循环作的功是否等于直角三角形面积?(5)用图中的热量ac bc ab Q Q Q ,,表述其热机效率或致冷系数． 解：(1) a b 是等体过程bc 过程：从图知有KT V =，K 为斜率 由vRT pV = 得 K vR p =故bc 过程为等压过程 ca 是等温过程(2)V p -图如题57'-图题57'-图(3)该循环是逆循环(4)该循环作的功不等于直角三角形面积，因为直角三角形不是V p -图中的图形．(5)ab ca bc abQ Q Q Q e -+=题7-5图 题7-6图7-6 两个卡诺循环如题7-6图所示，它们的循环面积相等，试问： (1)它们吸热和放热的差值是否相同； (2)对外作的净功是否相等； (3)效率是否相同?答：由于卡诺循环曲线所包围的面积相等，系统对外所作的净功相等，也就是吸热和放热的差值相等．但吸热和放热的多少不一定相等，效率也就不相同． 7-7 评论下述说法正确与否?(1)功可以完全变成热，但热不能完全变成功；(2)热量只能从高温物体传到低温物体，不能从低温物体传到高温物体．(3)可逆过程就是能沿反方向进行的过程，不可逆过程就是不能沿反方向进行的过程． 答：(1)不正确．有外界的帮助热能够完全变成功；功可以完全变成热，但热不能自动地完全变成功； (2)不正确．热量能自动从高温物体传到低温物体，不能自动地由低温物体传到高温物体．但在外界的帮助下，热量能从低温物体传到高温物体．(3)不正确．一个系统由某一状态出发，经历某一过程达另一状态，如果存在另一过程，它能消除原过程对外界的一切影响而使系统和外界同时都能回到原来的状态，这样的过程就是 可逆过程．用任何方法都不能使系统和外界同时恢复原状态的过程是不可逆过程．有些过程 虽能沿反方向进行，系统能回到原来的状态，但外界没有同时恢复原状态，还是不可逆过程． 7-8 热力学系统从初平衡态A 经历过程P 到末平衡态B ．如果P 为可逆过程，其熵变为：⎰=-BA AB T Q S S 可逆d ，如果P 为不可逆过程，其熵变为⎰=-B A A B T Q S S 不可逆d ，你说对吗？哪一个表述要修改，如何修改？答：不对．熵是状态函数，熵变只与初末状态有关，如果过程P 为可逆过程其熵变为：⎰=-BA AB T Q S S 可逆d ，如果过程P 为不可逆过程，其熵变为⎰>-B A A B T Q S S 不可逆d7-9 根据⎰=-B A A B T Q S S 可逆d 及⎰>-B A A B T Q S S 不可逆d ，这是否说明可逆过程的熵变大于不可逆过程熵变?为什么?说明理由．答：这不能说明可逆过程的熵变大于不可逆过程熵变，熵是状态函数，熵变只与初末状态有关，如果可逆过程和不可逆过程初末状态相同，具有相同的熵变．只能说在不可逆过程中，系统的热温比之和小于熵变．7-10 如题7-10图所示，一系统由状态a 沿acb 到达状态b 的过程中，有350 J 热量传入系统，而系统作功126 J ．(1)若沿adb 时，系统作功42 J ，问有多少热量传入系统?(2)若系统由状态b 沿曲线ba 返回状态a 时，外界对系统作功为84 J ，试问系统是吸热还是放热?热量传递是多少?题7-10图解：由abc 过程可求出b 态和a 态的内能之差 A E Q +∆=224126350=-=-=∆A Q E J abd 过程，系统作功42=A J26642224=+=+∆=A E Q J 系统吸收热量ba 过程，外界对系统作功84-=A J30884224-=--=+∆=A E Q J 系统放热7-11 1 mol 单原子理想气体从300 K 加热到350 K ，问在下列两过程中吸收了多少热量?增加了多少内能?对外作了多少功? (1)体积保持不变； (2)压力保持不变． 解：(1)等体过程由热力学第一定律得E Q ∆= 吸热)(2)(1212V T T R iT T C E Q -=-=∆=υυ25.623)300350(31.823=-⨯⨯=∆=E Q J对外作功 0=A (2)等压过程)(22)(1212P T T R i T T C Q -+=-=υυ吸热75.1038)300350(31.825=-⨯⨯=Q J )(12V T T C E -=∆υ内能增加 25.623)300350(31.823=-⨯⨯=∆E J对外作功 5.4155.62375.1038=-=∆-=E Q A J 7-12 一个绝热容器中盛有摩尔质量为mol M ，比热容比为γ的理想气体，整个容器以速度v 运动，若容器突然停止运动，求气体温度的升高量(设气体分子的机械能全部转变为内能)．解：整个气体有序运动的能量为221mu ，转变为气体分子无序运动使得内能增加，温度变化2V 21mu T C M m E =∆=∆ )1(211212mol V 2mol -==∆γu M R C u M T7-13 0.01 m 3氮气在温度为300 K 时，由0.1 MPa(即1 atm)压缩到10 MPa ．试分别求氮气经等温及绝热压缩后的(1)体积；(2)温度；(3)各过程对外所作的功． 解：(1)等温压缩 300=T K 由2211V p V p = 求得体积3211210101.0101-⨯=⨯==p V p V 3m对外作功21112ln lnp pV p V V VRT A ==01.0ln 01.010013.115⨯⨯⨯⨯=31067.4⨯-=J(2)绝热压缩R C 25V =57=γ由绝热方程 γγ2211V p V p =γγ/12112)(p V p V =1121/12112)()(V p pp V p V γγγ==3411093.101.0)101(-⨯=⨯=m由绝热方程γγγγ---=22111p T p T 得K 579)10(30024.04.1111212=⨯==--T p p T T γγγγ热力学第一定律A E Q +∆=，0=Q 所以)(12molT T C M MA V --=RT M MpV mol =，)(2512111T T R RT V p A --= 35105.23)300579(25300001.010013.1⨯-=-⨯⨯⨯⨯-=A J7-14 理想气体由初状态),(11V p 经绝热膨胀至末状态),(22V p ．试证过程中气体所作的功为12211--=γV p V p A ，式中γ为气体的比热容比.答：证明： 由绝热方程C V p V p pV ===γγγ2211 得γγV V p p 111=⎰=21d V V Vp A⎰-----==21)11(1d 11121111V V r V V V p v v V p A γγγγγ]1)[(112111---=-γγV VV p又 )(1111211+-+----=γγγγV V V p A 112221111--=+-+-γγγγγV V p V V p 所以 12211--=γV p V p A7-15 1 mol 的理想气体的T-V 图如题7-15图所示，ab 为直线，延长线通过原点O ．求ab过程气体对外做的功．题7-15图解：设KV T =由图可求得直线的斜率K 为002V T K =得过程方程V V T K 002=由状态方程 RT pV υ= 得VRTp υ=ab 过程气体对外作功⎰=002d V v Vp A⎰⎰⎰====000020002202d 2d 2d V V V v V V RTV V RT VV V T V R V V RT A7-16 某理想气体的过程方程为a a Vp ,2/1=为常数，气体从1V 膨胀到2V ．求其所做的功．解：气体作功⎰=21d V v Vp A⎰-=-==-2121)11()(d 2121222V V V VV V a V a V V a A7-17 设有一以理想气体为工质的热机循环，如题7-17图所示．试证其循环效率为1112121---=p p VV γη答：等体过程 吸热)(12V 1T T C Q -='υ)(1221V 11R V p R V p C Q Q -='= 绝热过程 03='Q等压压缩过程放热)(12p 2T T C Q -='υ)(2212P R V p R V p C -=循环效率 121Q Q-=η )1/()1/(1)()(1121212221V 2212p 12---=---=-=p p V p V p C V p V p C Q Q ννγηη题7-17图 题7-19图7-18 一卡诺热机在1000 K 和300 K 的两热源之间工作，试计算 (1)热机效率；(2)若低温热源不变，要使热机效率提高到80%，则高温热源温度需提高多少? (3)若高温热源不变，要使热机效率提高到80%，则低温热源温度需降低多少?解：(1)卡诺热机效率121T T -=η%7010003001=-=η(2)低温热源温度不变时，若%8030011=-=T η要求 15001=T K ，高温热源温度需提高500K(3)高温热源温度不变时，若%80100012=-=T η要求 2002=T K ，低温热源温度需降低100K7-19 如题7-19图所示是一理想气体所经历的循环过程，其中AB 和CD 是等压过程，BC 和DA 为绝热过程，已知B 点和C 点的温度分别为2T 和3T ．求此循环效率．这是卡诺循环吗?解：(1)热机效率121Q Q -=η AB 等压过程 )(12P 1T T C Q -='υ 吸热)(P mo 1A B lT T C M MQ -=CD 等压过程 )(12P 2T T vC Q -='放热)(P mol22D C T T C M MQ Q -='-=)/1()/1(12B A B C D C A B D C T T T T T T T T T T Q Q --=--=根据绝热过程方程得到AD 绝热过程 γγγγ----=D D A A T p T p 11 BC 绝热过程 γγγγ----=C C B B T p T p 111又B C D DC BA T T T T p p p p ===231T T -=η(2)不是卡诺循环，因为不是工作在两个恒定的热源之间． 7-20 （1）用一卡诺循环的致冷机从7℃的热源中提取1000 J 的热量传向27℃的热源，需要多少功?从-173℃向27℃呢?(2)一可逆的卡诺机，作热机使用时，如果工作的两热源的温度差愈大，则对于作功就愈有利．当作致冷机使用时，如果两热源的温度差愈大，对于致冷是否也愈有利?为什么? 解：(1)卡诺循环的致冷机2122T T T A Q e -==静 7℃→27℃时，需作功 4.71100028028030022211=⨯-=-=Q T T T A J173-℃→27℃时，需作功 2000100010010030022212=⨯-=-=Q T T T A J(2)从上面计算可看到，当高温热源温度一定时，低温热源温度越低，温度差愈大，提取同样的热量，则所需作功也越多，对致冷是不利的．7-21 如题7-21图所示，1 mol 双原子分子理想气体，从初态K 300,L 2011==T V 经历三种不同的过程到达末态K 300,L 4022==T V ． 图中1→2为等温线，1→4为绝热线，4→2为等压线，1→3为等压线，3→2为等体线．试分别沿这三种过程计算气体的熵变．题7-21图解：21→熵变等温过程 A Q d d = , V p A d d =，RT pV =⎰⎰==-21111221d 1d V V V V RT T T Q S S76.52ln ln!212===-R V V R S S J 1K -⋅321→→熵变⎰⎰+=-312312d d T QT Q S S32V 13p V p 12ln ln d d 2331T TC T T C T T C T TC S S T T T T +=+=-⎰⎰31→等压过程 31p p = 3211T V T V =1213V V T T = 23→等体过程 2233T p T p =3232p p T T = 1232p p T T =12V 12P 12ln ln p pC V V C S S +=-在21→等温过程中 2211V p V p =所以2ln ln ln ln1212V 12P 12R V VR V V C V V C S S ===-241→→熵变⎰⎰+=-412412d d T QT Q S S41p 42p p 12ln lnd 024T TC T T C TT C S S T T ==+=-⎰41→绝热过程111441144111----==γγγγV V T T V T V T γγγγ/121/141144411)()(,p pp p V V V p V p ===在21→等温过程中 2211V p V p =γγγ/112/121/14114)()()(V V p p p p V V ===γγ11241)(-=V V T T2ln ln 1ln12P 41P 12R V V C T T C S S =-==-γγ7-22 有两个相同体积的容器，分别装有1 mol 的水，初始温度分别为1T 和2T ，1T ＞2T ，令其进行接触，最后达到相同温度T ．求熵的变化，(设水的摩尔热容为mol C )． 解：两个容器中的总熵变⎰⎰+=-TT T T lT T C T T C S S 12d d mo mol 0 212mol 21mol ln)ln (ln T T T C T T T T C =+=因为是两个相同体积的容器，故)()(1mol 2mol T T C T T C -=- 得212T T T += 21212mol 04)(lnT T T T C S S +=-7-23 把0℃的0.5kg 的冰块加热到它全部溶化成0℃的水，问：(1)水的熵变如何?(2)若热源是温度为20 ℃的庞大物体，那么热源的熵变化多大? (3)水和热源的总熵变多大?增加还是减少?(水的熔解热334=λ1g J -⋅) 解：(1)水的熵变612273103345.031=⨯⨯==∆T Q S J 1K -⋅(2)热源的熵变570293103345.032-=⨯⨯-==∆T Q S J 1K -⋅(3)总熵变4257061221=-=∆+∆=∆S S S J 1K -⋅熵增加。