贝叶斯估计[一类资料]
- 格式:ppt
- 大小:582.00 KB
- 文档页数:29


贝叶斯估计与贝叶斯决策的概念贝叶斯估计和贝叶斯决策是概率论中重要的两个概念,它们在处理不确定性问题和统计推断中扮演着重要角色。
本文将介绍贝叶斯估计和贝叶斯决策的概念、原理以及应用。
一、贝叶斯估计贝叶斯估计是指在给定观测数据的条件下,利用贝叶斯定理来估计未知参数的方法。
在贝叶斯估计中,我们引入了先验概率和似然函数,并通过贝叶斯定理来更新我们对参数的估计。
贝叶斯估计的基本原理可以用以下公式表示:P(θ|X) = P(X|θ) * P(θ) / P(X)其中,P(θ|X) 表示在给定观测数据 X 的条件下,参数θ 的后验概率;P(X|θ) 是参数θ 给定观测数据 X 的似然函数;P(θ) 是参数θ 的先验概率;P(X) 是观测数据的边缘概率。
在贝叶斯估计中,先验概率可以通过领域知识或历史数据来确定,而似然函数则可以通过对观测数据的建模来获得。
通过不断地更新先验概率,我们可以得到后验概率,并将其作为参数的估计值。
贝叶斯估计在许多领域都有广泛的应用,例如机器学习、统计推断、信号处理等。
它能够有效地利用已知信息和数据,对未知参数进行准确的估计。
二、贝叶斯决策贝叶斯决策是一种基于贝叶斯准则的决策方法,它在已知观测数据的条件下,寻找一个决策规则来使得期望损失最小化。
贝叶斯决策的目标是选择一个最优的决策,使得在给定观测数据的条件下,使得期望损失最小。
贝叶斯决策的基本原理可以用以下公式表示:d* = argminΣL(d, a) * P(a|X)其中,d* 是最优决策,ΣL(d, a) 是决策 d 对于观测数据 X 情况下的期望损失,P(a|X) 是在观测数据 X 条件下决策 a 的后验概率。
贝叶斯决策需要利用先验概率和条件概率来对可能的决策进行评估,并选择最优的决策。
它能够充分考虑不确定性和风险,从而在决策问题中展现出优越性。
贝叶斯决策在许多实际问题中都有广泛的应用,例如医学诊断、金融风险评估、无人驾驶等。
通过考虑不确定性和风险,贝叶斯决策可以帮助我们做出最优的决策,提高决策的准确性和效果。

贝叶斯估计公式
贝叶斯估计公式是一种基于贝叶斯定理的统计学方法,用于估计未知参数的概率分布。
在实际应用中,贝叶斯估计公式被广泛应用于机器学习、数据挖掘、信号处理等领域。
贝叶斯估计公式的核心思想是将先验知识和观测数据结合起来,得到后验概率分布。
具体而言,假设我们有一个未知参数θ,我们希望通过观测数据D来估计θ的概率分布。
根据贝叶斯定理,我们可以得到:
P(θ|D) = P(D|θ)P(θ) / P(D)
其中,P(θ|D)表示θ在给定数据D的条件下的后验概率分布,P(D|θ)表示在给定θ的条件下,数据D的概率分布,P(θ)表示θ的先验概率分布,P(D)表示数据D的边缘概率分布。
在实际应用中,我们通常会选择一个合适的先验分布,然后通过观测数据来更新后验分布。
例如,在分类问题中,我们可以选择一个先验分布,然后通过观测数据来更新后验分布,从而得到分类结果。
贝叶斯估计公式的优点在于它可以利用先验知识来提高估计的准确性。
例如,在医学诊断中,医生可以利用先验知识来估计患者的疾病概率,从而更准确地进行诊断。
然而,贝叶斯估计公式也存在一些缺点。
首先,它需要选择一个合
适的先验分布,这可能会影响估计的准确性。
其次,计算后验分布通常需要进行复杂的积分计算,这可能会导致计算量过大。
贝叶斯估计公式是一种重要的统计学方法,它可以利用先验知识来提高估计的准确性。
在实际应用中,我们需要选择一个合适的先验分布,并通过观测数据来更新后验分布,从而得到更准确的估计结果。

- 贝叶斯近似算法介绍-概述说明以及解释1.引言1.1 概述在贝叶斯统计学中,贝叶斯近似算法是一种通过近似地求解贝叶斯推断问题的方法。
贝叶斯推断是一种基于贝叶斯定理的统计推断方法,旨在估计未知参数的后验分布。
然而,由于后验分布通常难以解析求解,因此需要采用近似算法来求解。
贝叶斯近似算法通过在后验分布中进行采样或使用近似的数值方法来估计参数的后验分布。
这些算法包括马尔可夫链蒙特卡洛方法(MCMC)、变分推断方法等。
本文将介绍贝叶斯近似算法的基本概念,探讨其原理及应用场景,并介绍一些常见的贝叶斯近似算法。
通过深入了解贝叶斯近似算法,读者可以更好地理解和应用这些方法于实际问题中。
1.2 文章结构文章结构部分的内容:本文将首先介绍贝叶斯推断的基本概念,包括其原理和应用场景。
接着,将详细讨论贝叶斯近似算法的概述,包括其核心思想和主要方法。
最后,将探讨贝叶斯近似算法在实际应用中的具体案例和效果。
通过深入了解贝叶斯近似算法的原理和应用,希望读者能够更好地理解其在数据分析和机器学习领域的重要性和价值。
1.3 目的本文旨在介绍贝叶斯近似算法,讨论其在贝叶斯推断中的应用以及其优势和局限性。
通过深入了解贝叶斯近似算法的工作原理和算法流程,读者将能够更好地理解该算法在实际问题中的应用场景和效果。
此外,本文还将探讨贝叶斯近似算法的发展趋势和未来可能的改进方向,为读者提供对该算法的全面认识和深入了解。
通过本文的阅读,读者将能够掌握贝叶斯近似算法的基本概念和原理,从而在实际问题中灵活运用该算法,提高问题求解的效率和精度。
2.正文2.1 贝叶斯推断简介贝叶斯推断是一种基于贝叶斯定理的统计推断方法。
在统计学中,我们通常需要根据收集到的数据来对未知参数进行推断。
贝叶斯推断通过将先验知识和数据信息结合起来,得出对参数的后验分布,从而对参数进行推断。
贝叶斯推断的核心思想是先验概率和后验概率之间的贝叶斯定理。
在贝叶斯推断中,我们首先给定一个先验分布,描述对参数的初始信念或者认识。


贝叶斯估计法
贝叶斯估计法是一种基于贝叶斯定理的统计学方法,用于估计未知参数的概率分布。
它是一种非常有用的方法,可以在许多领域中应用,例如医学、金融、工程等。
贝叶斯估计法的基本思想是,通过先验概率和观测数据来计算后验概率。
先验概率是指在没有观测数据的情况下,我们对未知参数的概率分布的估计。
观测数据是指我们已经获得的数据,用于更新我们对未知参数的估计。
后验概率是指在观测数据的情况下,我们对未知参数的概率分布的估计。
贝叶斯估计法的步骤如下:
1. 确定先验概率分布。
先验概率分布可以是任何分布,例如正态分布、均匀分布等。
2. 收集观测数据。
观测数据可以是任何数据,例如样本数据、实验数据等。
3. 计算似然函数。
似然函数是指在给定参数值的情况下,观测数据出现的概率。
4. 计算后验概率分布。
后验概率分布是指在观测数据的情况下,未知参数的概率分布。
5. 利用后验概率分布进行推断。
可以利用后验概率分布进行参数估
计、假设检验、置信区间估计等。
贝叶斯估计法的优点是可以利用先验知识来提高参数估计的准确性。
例如,在医学领域中,我们可以利用先验知识来估计某种疾病的患病率,从而更准确地估计某个人是否患有该疾病。
此外,贝叶斯估计法还可以处理小样本问题,因为它可以利用先验知识来提高参数估计的准确性。
贝叶斯估计法是一种非常有用的统计学方法,可以在许多领域中应用。
它的基本思想是利用先验概率和观测数据来计算后验概率,从而提高参数估计的准确性。


贝叶斯评估贝叶斯评估是一种基于贝叶斯定理的统计推断方法,用来估计未知参数的分布。
它的核心思想是将先验知识和实际观测数据结合起来,通过不断更新先验分布来获得后验分布,从而得到对未知参数的估计。
贝叶斯评估方法的基本步骤如下:1. 建立先验分布:在进行实际观测之前,需要根据已知的先验知识和经验,建立对未知参数的先验分布。
先验分布可以是任何合理的概率分布,比如均匀分布、正态分布等。
2. 收集观测数据:根据具体问题,收集一定数量的观测数据。
观测数据是贝叶斯评估的基础,通过分析观测数据可以获得对未知参数的更准确的估计。
3. 更新先验分布:利用贝叶斯定理,将先验分布和观测数据结合起来,得到后验分布。
后验分布是对未知参数的估计分布,在更新后的后验分布中,观测数据对参数的估计起到了重要作用。
4. 利用后验分布进行推断:根据后验分布,可以进行一系列的推断分析。
比如可以计算参数的平均值、方差等统计特征,进一步了解未知参数的分布情况。
贝叶斯评估方法具有以下优点:1. 能够将先验知识合理地引入推断过程中,在缺乏大量观测数据时,可以对未知参数进行有效的估计。
2. 能够灵活地处理不确定性,对于分布的尾部情况有更好的估计能力。
3. 能够随着观测数据的增加不断更新先验分布,获得更准确的估计结果。
贝叶斯评估方法也存在一些限制:1. 对于复杂的模型和参数,贝叶斯评估可能会变得非常困难,需要进行高维积分或者采样等复杂计算。
2. 先验分布的选择对结果影响较大,不同的先验分布可能会导致不同的推断结果。
3. 在处理大量、高维的数据时,贝叶斯评估可能会变得非常耗时。
总之,贝叶斯评估是一种有效的统计推断方法,能够结合先验知识和观测数据,对未知参数进行估计。
尽管存在一些限制,但在合适的问题设置和合理的先验分布选择下,贝叶斯评估可以得到准确和可靠的结果,对于决策和推断具有重要意义。
第五章贝叶斯统计5.1 简介到目前为止,我们已经知道了大量的不同的概率模型,并且我们前面已经讨论了如何用它们去拟合数据等等。
前面我们讨论了如何利用各种先验知识,计算MAP参数来估计θ=argmax p(θ|D)。
同样的,对于某种特定的请况,我们讨论了如何计算后验的全概率p(θ|D)和后验的预测概率密度p(x|D)。
当然在以后的章节我们会讨论一般请况下的算法。
5.2 总结后验分布后验分布总结关于未知变量θ的一切数值。
在这一部分,我们讨论简单的数,这些数是可以通过一个概率分布得到的,比如通过一个后验概率分布得到的数。
与全面联接相比,这些统计汇总常常是比较容易理解和可视化。
5.2.1最大后验估计通过计算后验的均值、中值、或者模型可以轻松地得到未知参数的点估计。
在5.7节,我们将讨论如何利用决策理论从这些模型中做出选择。
典型的后验概率均值或者中值是估计真实值的恰当选择,并且后验边缘分布向量最适合离散数值。
然而,由于简化了优化问题,算法更加高效,后验概率模型,又名最大后验概率估计成为最受欢迎的模型。
另外,通过对先验知识的取对数来正则化后,最大后验概率可能被非贝叶斯方法解释(详情参考6.5节)。
最大后验概率估计模型在计算方面该方法虽然很诱人,但是他有很多缺点,下面简答介绍一下。
在这一章我们将更加全面的学习贝叶斯方法。
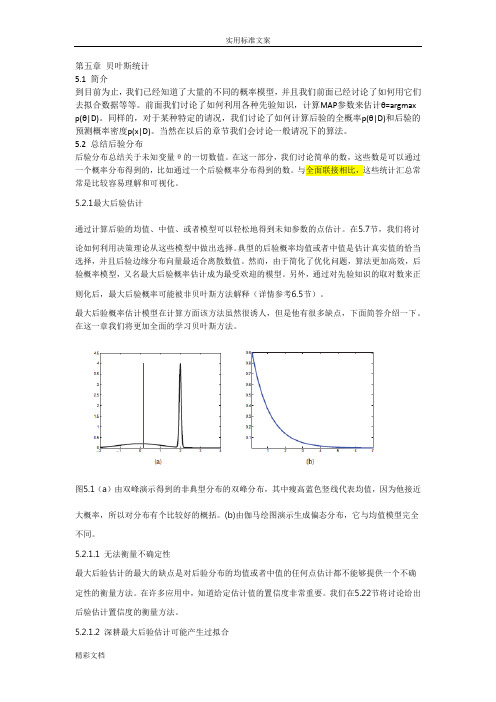
图5.1(a)由双峰演示得到的非典型分布的双峰分布,其中瘦高蓝色竖线代表均值,因为他接近大概率,所以对分布有个比较好的概括。
(b)由伽马绘图演示生成偏态分布,它与均值模型完全不同。
5.2.1.1 无法衡量不确定性最大后验估计的最大的缺点是对后验分布的均值或者中值的任何点估计都不能够提供一个不确定性的衡量方法。
在许多应用中,知道给定估计值的置信度非常重要。
我们在5.22节将讨论给出后验估计置信度的衡量方法。
5.2.1.2 深耕最大后验估计可能产生过拟合在机器学习中,相比于解释模型的参数,我们能够得到精确预测结果。


贝叶斯估计方法引言:贝叶斯估计方法是一种常用的统计学方法,用于通过已知的先验概率和观测到的证据来计算后验概率。
它在概率推理、机器学习、人工智能等领域都有广泛的应用。
本文将介绍贝叶斯估计方法的原理、应用场景以及常见的算法。
一、贝叶斯估计方法的原理贝叶斯估计方法基于贝叶斯定理,根据先验概率和观测到的证据来计算后验概率。
其基本思想是将不确定性表示为概率分布,并通过观测数据来更新这个分布。
具体而言,贝叶斯估计方法可以分为两个步骤:1. 先验概率的选择:根据领域知识或经验,选择合适的先验概率分布。
先验概率可以是均匀分布、正态分布等。
2. 观测数据的更新:根据观测到的证据,通过贝叶斯定理更新先验概率分布,得到后验概率分布。
二、贝叶斯估计方法的应用场景贝叶斯估计方法在各个领域都有广泛的应用,下面介绍几个常见的应用场景:1. 文本分类:在文本分类中,可以使用贝叶斯估计方法来计算给定文本属于某个类别的概率。
通过观测到的文本特征,可以更新先验概率分布,从而得到后验概率分布,进而进行分类。
2. 信号处理:在信号处理中,可以使用贝叶斯估计方法来估计信号的参数。
通过观测到的信号样本,可以更新先验概率分布,从而得到后验概率分布,进而估计信号的参数。
3. 异常检测:在异常检测中,可以使用贝叶斯估计方法来判断观测数据是否属于正常情况。
通过观测到的数据,可以更新先验概率分布,从而得到后验概率分布,进而进行异常检测。
三、常见的贝叶斯估计算法1. 最大似然估计法(MLE):最大似然估计法是贝叶斯估计方法的一种常见算法。
它通过最大化观测数据的似然函数,来估计参数的值。
最大似然估计法通常在先验概率分布为均匀分布时使用。
2. 最大后验估计法(MAP):最大后验估计法是贝叶斯估计方法的另一种常见算法。
它通过最大化后验概率函数,来估计参数的值。
最大后验估计法通常在先验概率分布为正态分布时使用。
3. 贝叶斯网络:贝叶斯网络是一种图模型,用于表示变量之间的依赖关系。



R贝叶斯包分类介绍(R task view ofBayesian)=========一般模型==================arm包: 包括使用lm,glm,mer,polr等对象进行贝叶斯推断的R函数BACCO: 随机函数的贝叶斯分析. 包含3个子包: emulator, calibrator, and approximator, 进行贝叶斯估计和评价计算机程序.bayesm: 市场与微经济分析模型的许多贝叶斯推断函数. 模型包括线性回归, 多项式logit, 多项式probit, 多元probit, 多元混合normals(包括聚类), 密度估计-使用有限混合正态模型与Dirichlet先验过程, 层次线性模型, 层次多元logit, 层次负二项回归模型, 线性工具变量模型(linear instrumental variable models). bayesSurv: 生存回归模型的贝叶斯推断.DPpackage: 贝叶斯非参数和半参数模型. 现在还包括密度估计, ROC曲线分析, 区间一致数据, 二项回归模型, 广义线性模型和IRT类型模型的半参数方法. MCMCpack: 特定模型的MCMC模拟算法, 广泛用于社会和行为科学. 拟合很多回归模型的R函数. 生态学模型推断. 还包括一个广义Metropolis采样器, 适合任何模型.mcmc: 随机行走Metropolis算法, 对于连续随机向量.==========特殊模型和方法=============AdMit: 拟合适应性混合t分布拟合目标密度使用核函数.bark: 实现(Bayesian Additive Regression Kernels)BayHaz: 贝叶斯估计smooth hazard rates, 通过Compound Poisson Process (CPP) 先验概率.bayesGARCH: 贝叶斯估计GARCH(1,1) 模型, 使用t分布.BAYSTAR: 贝叶斯估计threshold autoregressive modelsBayesTree: implements BART (Bayesian Additive Regression Trees) by Chipman, George, and McCulloch (2006).BCE: 从生物注释数据中估计分类信息.bcp: a Bayesian analysis of changepoint problem using the Barry and Hartigan product partition model.BMA:BPHO: 贝叶斯预测高阶相互作用, 使用slice 采样技术.bqtl: 拟合quantitative trait loci (QTL) 模型.可以估计多基因模型, 使用拉普拉斯近似. 基因座内部映射(interval mapping of genetic loci).bim: 贝叶斯内部映射, 使用MCMC方法.bspec: 时间序列的离散功率谱贝叶斯分析cslogistic: 条件特定的logistic回归模型(conditionally specified logistic regression model)的贝叶斯分析.deal: 逆运算网络分析: 当前版本覆盖离散和连续的变量, 在正态分布下.dlm: 贝叶斯与似然分析动态信息模型. 包括卡尔曼滤波器和平滑器的计算, 前向滤波后向采样算法.EbayesThresh: thresholding methods 的贝叶斯估计. 尽管最初的模型是在小波下开发的, 当参数集是稀疏的, 用户也可以受益.eco: 使用MCMC方法拟合贝叶斯生态学推断in two by two tables evdbayes: 极值模型的贝叶斯分析.exactLoglinTest: log-linear models 优度拟合检验的条件P值的MCMC估计. HI: transdimensional MCMC 方法几何途径, 和随机多元Adaptive Rejection Metropolis Sampling.G1DBN: 动态贝叶斯网络推断.Hmisc内的gbayes()函数, 当先验和似然都是正态分布, 导出后验(且最优)分布, 且当统计量来自2-样本问题.geoR包的krige.bayes()函数地理统计数据的贝叶斯推断, 允许不同层次的模型参数的不确定性.geoRglm 包的binom.krige.bayes() 函数进行贝叶斯后验模拟, 二项空间模型的空间预测.MasterBayes: MCMC方法整合家谱数据(由分子和形态数据得来的)lme4包的mcmcsamp()函数信息混合模型和广义信息混合模型采样.lmm: 拟合信息混合模型, 使用MCMC方法.MNP: 多项式probit模型, 使用MCMC方法.MSBV AR: 估计贝叶斯向量自回归模型和贝叶斯结构向量自回归模型.pscl: 拟合item-response theory 模型, 使用MCMC方法, 且计算beta分布和逆gamma分布的最高密度区域RJaCGH: CGH微芯片的贝叶斯分析, 使用hidden Markov chain models. 正态数目的选择根据后验概率, 使用reversible jump Markov chain Monte Carlo Methods 计算.sna: 社会网络分析, 包含函数用于从Butt's贝叶斯网络精确模型, 使用MCMC方法产生后验样本.tgp: 实现贝叶斯treed 高斯过程模型: 一个空间模型和回归包提供完全的贝叶斯MCMC后验推断, 对于从简单线性模型到非平稳treed高斯过程等都适合. Umacs: Gibbs采样和Metropolis algorithm的贝叶斯推断.vabaye1Mix: 高斯混合模型的贝叶斯推断, 使用多种方法.=Post-estimation tools=====BayesValidate: 实现了对贝叶斯软件评估的方法.boa: MCMC序列的诊断, 描述分析与可视化. 导入BUGS格式的绘图. 并提供Gelman and Rubin, Geweke, Heidelberger and Welch, and Raftery and Lewis 诊断. Brooks and Gelman 多元收缩因子.coda: (Convergence Diagnosis and Output Analysis) MCMC的收敛性分析, 绘图等. 可以轻松导入WinBUGS, OpenBUGS, and JAGS 软件的MCMC输出. 亦包括Gelman and Rubin, Geweke, Heidelberger and Welch, and Raftery and Lewis 诊断. mcgibbsit: 提供Warnes and Raftery MCGibbsit MCMC 诊断. 作用于mcmc对象上面.ramps: 高斯过程的贝叶斯几何分析, 使用重新参数化和边际化的后验采样算法. rv: 基于模拟的随机变量类, 后验模拟对象可以方便的作为随机变量来处理. scapeMCMC: 处理年龄和时间结构的人群模型贝叶斯工具. 提供多种MCMC诊断图形, 可以方便的修改参数===========学习贝叶斯的包===================BaM: Jeff Gill's book, "Bayesian Methods: A Social and Behavioral Sciences Approach, Second Edition" (CRC Press, 2007). 伴随的包Bolstad: 此书的包. Introduction to Bayesian Statistics, by Bolstad, W.M. (2007). 的包LearnBayes: 学习贝叶斯推断的很多的函数. 包括1个,2个参数后验分布和预测分布, MCMC算法来描述分析用户定义的后验分布. 亦包括回归模型, 层次模型. 贝叶斯检验, Gibbs采样的实例.贝叶斯包一般模型拟合Bayesian packages for general model fitting1.The arm package contains R functions for Bayesianinference using lm, glm, mer and polr objects. arm package 包含了用于使用lm,glm,mer 和polr对象的贝叶斯推理的R函数Install.packages(“arm”)Library(“arm”)Help(package=”arm”) Documentation for package …arm‟ version 1.5-08 DESCRIPTION file.Help PagesFunctions to compute the balance statistics函数来计算平衡统计balanceFunctions to compute the balance statistics函数来计算平衡统计balance-classbayesglm-class Bayesian generalized linear models. 贝叶斯广义线性模型。



贝叶斯估计法贝叶斯估计法是统计学中常用的一种方法,它是基于贝叶斯定理的推论而来的,可以用于估计一个未知参数的值。
其核心思想是先假设一个先验分布,然后根据已知的样本数据和假设的先验分布,通过贝叶斯定理计算后验分布,最终得到对未知参数的估计。
在使用贝叶斯估计法时,我们需要首先定义以下概念:先验分布:指在未观测到数据前,对参数的概率分布的估计。
常见的先验分布有均匀分布、正态分布等。
似然函数:指在已知参数下,给定样本的条件下所有样本出现的概率密度函数,是样本数据给出参数信息的度量。
后验分布:指在已知数据后,对参数的概率分布的估计。
它是在先验分布和似然函数的基础上,通过贝叶斯公式计算得到的。
在实际数据分析中,我们需要对先验分布做出适当的假设,通过先验分布的假设来反映我们对参数的先验认知。
然后根据已知数据和似然函数,计算出参数的后验分布,并用其来估计未知参数。
贝叶斯估计法与点估计法的区别贝叶斯估计法与点估计法是统计学中常用的两种估计方法,它们之间的区别在于:点估计法:通常是求得一个能代表总体参数未知数的值作为估计,例如样本的平均数、中位数等。
点估计法估计参数时,只考虑来自样本的信息。
贝叶斯估计法:将样本和先验信息结合在一起,通过后验分布对未知参数进行估计。
在贝叶斯估计法中,我们对参数的先验知识和数据信息进行综合考虑,最终得到一个更加准确的估计值。
因此,相比于点估计法,贝叶斯估计法更加具有弹性,它不仅可以考虑已知数据的影响,还可以利用专家知识或先验信息来修正估计值,从而提高估计的准确性。
为了说明贝叶斯估计法的实际应用,我们以估计某测试设备的故障率为例进行说明。
假设我们已经收集了100个设备的测试数据,其中有5个出现故障。
我们希望用贝叶斯估计法来估计设备的故障率。
首先,我们需要对故障率做出一个先验分布的估计。
由于我们缺乏关于该设备故障率的信息,因此我们选择假设故障率服从0到1之间的均匀分布,即先验分布为P(θ)=1。

贝叶斯方法预测是一种基于贝叶斯定理的预测方法,它结合了先验概率、给定假设下观察到不同数据的概率以及观察到的数据本身,来计算假设的贝叶斯概率。
这种方法在许多领域都有应用,如统计学、机器学习、数据科学等。
使用贝叶斯方法进行预测的一般步骤如下:
1. 收集数据:首先需要收集与预测相关的历史数据和先验信息。
这些数据可以来自不同的来源,如市场调查、专家意见、实验数据等。
2. 建立模型:根据收集到的数据和先验信息,建立一个合适的概率模型。
这个模型应该能够描述不同事件之间的概率关系,以及如何从已知的数据中推断出未知事件的概率。
3. 计算后验概率:使用贝叶斯定理,结合先验概率和观察到的数据,计算出各个假设的后验概率。
这个后验概率反映了在给定观察到的数据下,各个假设成立的概率。
4. 预测未来事件:根据计算出的后验概率,对未来事件进行预测。
通常情况下,会选择后验概率最大的假设作为预测结果。
5. 更新先验概率:根据预测结果和新的观察数据,更新先验概率,并重复以上步骤,以实现持续的预测和更新。
需要注意的是,贝叶斯方法是一种基于概率的方法,其预测结果具有一定的不确定性。
因此,在使用贝叶斯方法进行预测时,需要综
合考虑各种因素,如数据的可靠性、模型的精度和复杂度等,以获得更加准确的预测结果。