高考大题答题l

高考物理大题答题规范一、必要的文字说明必要的文字说明的目的是说明物理过程和答题依据,有的同学不明确应该说什么，往往将物理解答过程变成了数学解答过程．答题时应该说些什么呢？我们应该从以下几个方面给予考虑：1.说明研究对象(个体或系统,尤其是要用整体法和隔离法相结合求解的题目,一定要注意研究对象的转移和转化问题）.2.画出受力分析图、电路图、光路图或运动过程的示意图.3.说明所设字母的物理意义．4.说明规定的正方向、零势点（面).5.说明题目中的隐含条件、临界条件．6.说明所列方程的依据、名称及对应的物理过程或物理状态.7.说明所求结果的物理意义(有时需要讨论分析)．二、要有必要的方程式物理方程是表达的主体,如何写出，重点要注意以下几点．1．写出的方程式(这是评分依据)必须是最基本的,不能以变形的结果式代替方程式（这是相当多的考生所忽视的)．如带电粒子在磁场中运动时应有q v B＝m错误!,而不是其变形结果式R=错误!.２．要用字母表达方程，不要用掺有数字的方程,不要方程套方程.3．要用原始方程组联立求解，不要用连等式,不断地“续”进一些内容.4.方程式有多个的,应分式布列（分步得分)，不要合写一式,以免一错而致全错,对各方程式最好能编号．三、要有必要的演算过程及明确的结果1.演算时一般先进行文字运算，从列出的一系列方程推导出结果的计算式，最后代入数据并写出结果．这样既有利于减轻运算负担，又有利于一般规律的发现，同时也能改变每列一个方程就代入数值计算的不良习惯．２.数据的书写要用科学记数法.3．计算结果的有效数字的位数应根据题意确定，一般应与题目中开列的数据相近，取两位或三位即可.如有特殊要求，应按要求选定．4.计算结果是数据的要带单位,最好不要以无理数或分数作为计算结果(文字式的系数可以)，是字母符号的不用带单位．四、解题过程中运用数学的方式有讲究1．“代入数据”,解方程的具体过程可以不写出．２.所涉及的几何关系只需写出判断结果而不必证明．３.重要的中间结论的文字表达式要写出来．4．所求的方程若有多个解，都要写出来，然后通过讨论,该舍去的舍去.5．数字相乘时,数字之间不要用“·”，而应用“×”进行连接；相除时也不要用“÷”,而应用“/”．五、使用各种字母符号要规范1．字母符号要写清楚、规范，忌字迹潦草．阅卷时因为“v、r、ν”不分，大小写“Ｍ、m”或“L、ｌ”不分，“Ｇ”的草体像“ａ”,希腊字母“ρ、μ、β、η”笔顺或形状不对而被扣分已屡见不鲜．2.尊重题目所给的符号,题目给了符号的一定不要再另立符号．如题目给出半径是r，你若写成R就算错.３.一个字母在一个题目中只能用来表示一个物理量,忌一字母多用;一个物理量在同一题中不能有多个符号，以免混淆.4.尊重习惯用法．如拉力用F,摩擦力用ｆ表示，阅卷人一看便明白,如果用反了就会带来误解．5.角标要讲究.角标的位置应当在右下角，比字母本身小许多．角标的选用亦应讲究,如通过A点的速度用ｖA就比用v1好;通过某相同点的速度,按时间顺序第一次用v1、第二次用v2就很清楚，如果倒置,必然带来误解．６.物理量单位的符号源于人名的单位,由单个字母表示的应大写,如库仑C、亨利H;由两个字母组成的单位，一般前面的字母用大写，后面的字母用小写,如Hz、Wb．六、学科语言要规范,有学科特色1．学科术语要规范.如“定律”、“定理”、“公式”、“关系”、“定则”等词要用准确，阅卷时常可看到“牛顿运动定理”、“动能定律”、“四边形公式”、“油标卡尺”等错误说法.2.语言要富有学科特色.在有图示的坐标系中将电场的方向说成“西南方向”、“南偏西45°”、“向左下方”等均是不规范的，应说成“与x轴正方向的夹角为135°”或“如图所示”等.七、绘制图形、图象要清晰、准确1.必须用铅笔(便于修改)、圆规、直尺、三角板绘制，反对随心所欲徒手画．２．画出的示意图(受力分析图、电路图、光路图、运动过程图等)应大致能反映有关量的关系,图文要对应.3．画函数图象时，要画好坐标原点和坐标轴上的箭头,标好物理量的符号、单位及坐标轴上的数据.４．图形、图线应清晰、准确，线段的虚实要分明，有区别.●例1（2８分）太阳现正处于序星演化阶段．它主要是由电子和11H、42He等原子核组成．维持太阳辐射的是它内部的核聚变反应,核反应方程是2ｅ+411H→42He+释放的核能,这些核能最后转化为辐射能.根据目前关于恒星演化的理论,若由于核变反应而使太阳中的1１Ｈ核数目从现有的减少１0%,太阳将离开主序星阶段而转入红巨星的演化阶段.为了简化，假定目前太阳全部由电子和11H 核组成.（1)为了研究太阳演化进程，需知道目前太阳的质量M．已知地球的半径R=6.４×106ｍ，地球的质量m＝6.0×１０24kg,日地中心的距离ｒ＝１.５×1０１１m，地球表面处重力加速度g=10 m／s２,1年约为3．2×107ｓ．试估算目前太阳的质量M.(2)已知质子的质量m p=1.６７26×1０－２7kg，42He核的质量mα=6.6４5８×１０-27 kg，电子的质量m e＝０.9×１0－3０kg,光速ｃ=３×1０8 m/s.求每发生一次题中所述的核聚变反应所释放的核能．(３)又已知地球上与太阳光垂直的每平方米的截面上，每秒通过的太阳辐射能w＝1.35×10３W/m2．试估算太阳继续保持在主序星阶段还有多少年的寿命.(估算结果保留一位有效数字) ［２00１年高考·全国理综卷Ⅰ]【解析】(1）(第一记分段:估算太阳的质量 1４分)设地球的公转周期为T ，则有:Ｇ错误!=m (错误!)2r (3分)ｇ=G 错误!(等效式为:ｍ′g =Ｇ错误!) (3分）联立解得:M =ｍ(２πT )2·错误! （4分)代入数值得：M ＝２×10３0 kg. （4分)(卷面上暴露出来的易犯错误的一些问题:①不用题中给的物理量符号，自己另用一套符号，r 、R 、m 、M 错用,丢掉14分;②对题中给出的地球的质量m 和地球表面处的重力加速度g 视而不见,把G 的数值代入计算太阳的质量,丢掉11分；③太阳的质量M 的计算结果的有效数字不对，丢掉4分.)（2)(第二记分段:核聚变反应所释放的核能 7分)ΔE ＝(4m p +２m ｅ－m α)ｃ2 （4分)代入数值得:ΔE ＝4×10-12 J ． (3分)(卷面上暴露出来的易犯错误的一些问题:①数字运算能力低,能导出ΔE ＝（４ｍp +2m e -m α)ｃ2,却算不出ΔE =4×10－１２ J ，丢掉3分；②ΔE 的计算结果的有效数字不对，丢掉3分;③ΔＥ的计算结果的单位不对，丢掉1分.)（3)（第三记分段：估算太阳继续保持在主序星阶段的时间 7分)核聚变反应的次数N =错误!×10% (２分)太阳共辐射的能量Ｅ＝N ·ΔE太阳每秒辐射的总能量ε＝4πr 2·w （２分）太阳继续保持在主序星阶段的时间t =E ε （２分)由以上各式得:ｔ＝错误!代入数值得：t ＝1×1０１０年． (1分)（卷面上暴露出来的易犯错误的一些问题：因不熟悉天体辐射知识,大多数考生解答不出来.)［答案] (1)２×103０ kg (2)４×1０-1２ J (3)1×１０10年●例2(18分)图1０-1中滑块和小球的质量均为m ，滑块可在水平放置的光滑固定导轨上自由滑动，小球与滑块上的悬点Ｏ由一不可伸长的轻绳相连，轻绳长为ｌ．开始时,轻绳处于水平拉直状态,小球和滑块均静止.现将小球由静止释放，当小球到达最低点时,滑块刚好被一表面涂有黏性物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动，当轻绳与竖直方向的夹角θ=６0°时小球达到最高点．求：图10-1(1)从滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量．(2)小球从释放到第一次到达最低点的过程中，绳的拉力对小球做功的大小.[2008年高考·全国理综卷Ⅰ]【解析】(1）(第一问给分点：１2分)解法一设小球摆至最低点时,滑块和小球的速度大小分别为v1、v２,对于滑块和小球组成的系统,由机械能守恒定律得:１ｖ12+错误!mｖ２2=mgｌ（3分）2m同理，滑块被粘住后,对于小球向左摆动的过程,有：1ｖ2２=mｇｌ(1-ｃos 60°)（３分)2m＝v2＝错误!(2分)解得：v１对于滑块与挡板接触的过程，由动量定理得:I＝０-mｖ1可知挡板对滑块的冲量I＝-m＼r（gl），负号表示方向向左.(４分,其中方向占1分)解法二设小球摆至最低点时,滑块和小球的速度大小分别为v1、v2，由动量守恒定律得:m v１－m v2＝0 (3分)对于小球向左摆动的过程,由机械能守恒定律得:错误!m v２2＝mgl(１－cｏs 6０°）(３分)可解得：v1＝v２＝错误!(2分）对于滑块与挡板接触的过程,由动量定理有：I=0－ｍｖ１可解得挡板对滑块的冲量为：I＝-mｇl，负号表示方向向左．(4分，其中方向占1分)解法三设小球摆至最低点时，滑块和小球的速度大小分别为ｖ1、v2,由机械能守恒定律得：错误!ｍv１２+错误!m v22=ｍｇl(3分)又由动量守恒定律得:mｖ１＋m（-v2)＝０（3分)可解得:v1=v2=错误!（２分)对于滑块与挡板接触的过程,由动量定理得：Ｉ=0-ｍｖ1可解得挡板对滑块的冲量为：I=-m gｌ,负号表示方向向左.(4分,其中方向占1分)解法四由全过程的能量转换和守恒关系可得(滑块在碰撞时损失的能量等于系统机械能的减少,等于滑块碰前的动能)：ΔＥ＝m ｇl -m ｇｌ(1－ｃｏｓ 60°）=错误!m v 2 (6分)可解得滑块碰前的速度为：ｖ=＼ｒ(ｇl ) (2分)对于滑块与挡板接触的过程,由动量定理得：I ＝0－m v可解得挡板对滑块的冲量为：I ＝-m ＼r(gl ),负号表示方向向左. （4分，其中方向占１分）解法五 由全过程的能量转换和守恒关系可得（滑块在碰撞时损失的能量等于系统机械能的减少，等于滑块碰前的动能）：ΔE =mgl co ｓ 6０°=＼f(1,２)m ｖ２ (6分)可解得滑块碰前的速度为：v =错误! (2分)对于滑块与挡板接触的过程,由动量定理得:I =0-m v可解得挡板对滑块的冲量为:I ＝－m 错误!，负号表示方向向左. （4分,其中方向占１分)(２)(第二问给分点：６分)解法一 对小球下摆的过程，由动能定理得：mgl +W ＝１２m ｖ２２ （4分) 可解得细绳对其做的功为：W =-＼ｆ(1,2）ｍgl . （2分)解法二 绳的张力对小球所做的功的绝对值等于滑块在碰前的动能(或等于绳子的张力对滑块做的功),则有：W ′=错误!m v 12或Ｗ′＝错误!m v 12-0 ( 4分)可解得：W =-W ′=-＼f(1,２)mgl ． (２分）解法三 绳子的张力对小球做的功等于小球在全过程中的机械能的增量，有:W ＝(－mg ·错误!)-0＝－错误!mgl （取滑块所在高度的水平面为参考平面) (6分)或W ＝ｍg ｌ(１-cos ６0°)-m ｇl =-错误!ｍgl (取小球所到达的最低点为参考平面)或Ｗ=0-mg ·l 2＝－错误!ｍgl (取小球摆起的最高点为参考平面)．解法四 对小球运动的全过程，由动能定理得:Ｗ＋m ｇｌcos 60°＝０或W +mg ·错误!=0 (4分)解得：W ＝－错误!ｍｇl . (２分)解法五 考虑小球从水平位置到最低点的过程：若滑块固定,绳子的张力对小球不做功，小球处于最低点时的速率ｖ球′=错误!(由mg ｌ=错误!m v 球′2得到) (2分)若滑块不固定,绳子的张力对小球做功，小球处于最低点时的速率ｖ球＝g ｌ(v 球应由前面正确求得)则绳子对小球做的功为：W ＝＼f(1,2)m v 球2－＼ｆ(1，2)m ｖ球′2 (２分）＝－错误!m ｇl ． (２分)[答案] （1)－m 错误!，负号表示方向向左 (2)-错误!m ｇl【点评】①越是综合性强的试题,往往解题方法越多，同学们通过本例的多种解题方法要认真地总结动能定理、机械能守恒定律和能量的转化与守恒定律之间的关系．②要认真地推敲各种解题方法的评分标准,从而建立起自己解题的规范化程序．解题技巧从前面各专题可以看出，在高中物理各类试题的解析中常用到的方法有:整体法、隔离法、正交分解法、等效类比法、图象法、极限法等,这些方法技巧在高考计算题的解析中当然也是重要的手段,但这些方法技巧涉及面广,前面已有较多的论述和例举，这里就不再赘述.本模块就如何面对形形色色的论述、计算题迅速准确地找到解析的“突破口”作些讨论和例举.论述、计算题一般都包括对象、条件、过程和状态四要素.对象是物理现象的载体，这一载体可以是物体（质点）、系统,或是由大量分子组成的固体、液体、气体，或是电荷、电场、磁场、电路、通电导体，或是光线、光子和光学元件，还可以是原子、核外电子、原子核、基本粒子等．条件是对物理现象和物理事实(对象）的一些限制,解题时应“明确”显性条件、“挖掘”隐含条件、“吃透”模糊条件.显性条件是易被感知和理解的；隐含条件是不易被感知的，它往往隐含在概念、规律、现象、过程、状态、图形和图象之中;模糊条件常常存在于一些模糊语言之中,一般只指定一个大概的范围.过程是指研究的对象在一定条件下变化、发展的程序.在解题时应注意过程的多元性，可将全过程分解为多个子过程或将多个子过程合并为一个全过程．状态是指研究对象各个时刻所呈现出的特征．方法通常表现为解决问题的程序.物理问题的求解通常有分析问题、寻求方案、评估和执行方案几个步骤,而分析问题(即审题)是解决物理问题的关键.一、抓住关键词语,挖掘隐含条件在读题时不仅要注意那些给出具体数字或字母的显性条件,更要抓住另外一些叙述性的语言，特别是一些关键词语．所谓关键词语,指的是题目中提出的一些限制性语言,它们或是对题目中所涉及的物理变化的描述,或是对变化过程的界定等．高考物理计算题之所以较难，不仅是因为物理过程复杂、多变，还由于潜在条件隐蔽、难寻,往往使考生们产生条件不足之感而陷入困境,这也正考查了考生思维的深刻程度．在审题过程中,必须把隐含条件充分挖掘出来,这常常是解题的关键．有些隐含条件隐蔽得并不深,平时又经常见到,挖掘起来很容易,例如题目中说“光滑的平面”，就表示“摩擦可忽略不计”;题目中说“恰好不滑出木板”,就表示小物体“恰好滑到木板边缘处且具有与木板相同的速度”等等.但还有一些隐含条件隐藏较深或不常见到，挖掘起来就有一定的难度了．●例3（10分）两质量分别为Ｍ1和M2的劈A和B,高度相同,放在光滑水平面上,A和Ｂ的倾斜面都是光滑曲面，曲面下端与水平面相切，如图1０-２所示．一质量为m的物块位于劈A的倾斜面上,距水平面的高度为h.物块从静止滑下,然后又滑上劈B．求物块在B上能够达到的最大高度．［20０９年高考·宁夏理综卷]图10－２【解析】设物块到达劈Ａ的底端时,物块和A的速度大小分别为v和ｖ1，由机械能守恒和动量守恒得：mgｈ=错误!ｍv2+错误!M１v12 (２分)Ｍ1ｖ1=m v(２分)设物块在劈B上达到的最大高度为h′，此时物块和B的共同速度大小为v′,由机械能守恒和动量守恒得：mgh′＋错误!(Ｍ2+m)v′２＝错误!mｖ２(2分)mｖ＝(M２＋m)v′（2分)联立解得:h′=M1Ｍ2(M1+m)（M２+ｍ)h.（２分)[答案］错误!h【点评】本题应分析清楚物块从A滑下以及滑上Ｂ的情境，即从A滑下和滑上Ｂ的过程水平方向动量守恒,在B上上升至最大高度时，隐含着与B具有相同速度的条件．二、重视对基本过程的分析（画好情境示意图)在高中物理中，力学部分涉及的运动过程有匀速直线运动、匀变速直线运动、平抛运动、圆周运动、简谐运动等,除了这些运动过程外，还有两类重要的过程：一类是碰撞过程，另一类是先变加速运动最终匀速运动的过程(如汽车以恒定功率启动问题).热学中的变化过程主要有等温变化、等压变化、等容变化、绝热变化等(这些过程的定量计算在某些省的高考中已不作要求)．电学中的变化过程主要有电容器的充电和放电、电磁振荡、电磁感应中的导体棒做先变加速后匀速的运动等，而画出这些物理过程的示意图或画出关键情境的受力分析示意图是解析计算题的常规手段.画好分析草图是审题的重要步骤，它有助于建立清晰有序的物理过程和确立物理量间的关系,可以把问题具体化、形象化.分析图可以是运动过程图、受力分析图、状态变化图，也可以是投影法、等效法得到的示意图等．在审题过程中,要养成画示意图的习惯．解物理题,能画图的尽量画图,图能帮助我们理解题意、分析过程以及探讨过程中各物理量的变化．几乎无一物理问题不是用图来加强认识的，而画图又迫使我们审查问题的各个细节以及细节之间的关系．●例4（1８分）如图10-３甲所示,建立Ｏｘy坐标系.两平行极板Ｐ、Q垂直于ｙ轴且关于x轴对称，极板长度和板间距均为ｌ，在第一、四象限有磁感应强度为Ｂ的匀强磁场,方向垂直于Oxy平面向里．位于极板左侧的粒子源沿x轴向右连续发射质量为m、电荷量为+q、速度相同、重力不计的带电粒子．在０～3t0时间内两板间加上如图１０-3乙所示的电压(不考虑极板边缘的影响)．已知t=0时刻进入两板间的带电粒子恰好在ｔ0时刻经极板边缘射入磁场.上述m、q、l、t0、B为已知量，不考虑粒子间相互影响及返回极板间的情况.(1)求电压Ｕ０的大小．(2)求错误!t0时刻进入两板间的带电粒子在磁场中做圆周运动的半径．(3）何时进入两板间的带电粒子在磁场中的运动时间最短？求此最短时间．［２009年高考·山东理综卷］图1０－3【解析】(１)ｔ＝0时刻进入两板间的带电粒子在电场中做匀变速曲线运动,ｔ0时刻刚好从极板边缘射出,在y轴负方向偏移的距离为错误!ｌ，则有：E＝错误!（1分)qＥ＝ma (１分)＼f(1,２）l＝错误!ａt02（２分）联立解得:两板间的偏转电压U0＝ml2ｑt02．(1分)(2)12t0时刻进入两板间的带电粒子，前12ｔ0时间在电场中偏转，后错误!t0时间两板间没有电场，带电粒子做匀速直线运动．带电粒子沿x轴方向的分速度大小v0=错误!(１分)带电粒子离开电场时沿y轴负方向的分速度大小v y＝ａ·错误!ｔ０(１分)带电粒子离开电场时的速度大小ｖ=v０2＋vｙ２（1分)设带电粒子离开电场进入磁场做匀速圆周运动的半径为R,则有：q v B＝m＼ｆ（ｖ２,R) (1分)联立解得:Ｒ＝错误!.(1分)(３）2t0时刻进入两板间的带电粒子在磁场中运动的时间最短．(2分）带电粒子离开电场时沿ｙ轴正方向的分速度为:v y′=ａt0 （1分)图10－3丙设带电粒子离开电场时速度方向与y轴正方向的夹角为α，则ｔanα=v0v y′(1分）联立解得:α＝＼f（π,4）(1分)带电粒子在磁场中的运动轨迹如图10－3丙所示，圆弧所对的圆心角2α=错误!，所求最短时间为：t min＝错误!T（１分)带电粒子在磁场中运动的周期Ｔ＝错误!(1分)联立解得：t min=πm２qB．（1分）[答案］（１)错误!(2)错误!(3)２t0时刻错误!【点评】在解决带电粒子在电场、磁场中的偏转问题时,要充分分析题意,结合必要的计算,画出物体运动的轨迹图.为了确保解题的正确，所画的轨迹图必须准确,同学们可以想一下在做数学中的几何题时是如何作图的．在解决这类物理题时,也要作出一个标准的图形.三、要谨慎细致,谨防定势思维经常遇到一些物理题故意多给出已知条件，或表述物理情境时精心设置一些陷阱，安排一些似是而非的判断，以此形成干扰因素，来考查学生明辨是非的能力．这些因素的迷惑程度愈大,同学们愈容易在解题过程中犯错误.在审题过程中,只有有效地排除这些干扰因素，才能迅速而正确地得出答案.有些题目的物理过程含而不露,需结合已知条件，应用相关概念和规律进行具体分析.分析前不要急于动笔列方程，以免用假的过程模型代替了实际的物理过程，防止定势思维的负迁移.●例5（18分）如图10-４甲所示，用长为Ｌ的丝线悬挂着一质量为ｍ、带电荷量为＋ｑ的小球,将它们放入水平向右的匀强电场中，场强大小E=错误!.今将小球拉至水平方向的A点后由静止释放.图10-4甲(1)求小球落至最低点B处时的速度大小．(2）若小球落至最低点B处时，绳突然断开，同时使电场反向,大小不变,则小球在以后的运动过程中的最小动能为多少？【解析】(1）由题意知：小球受到水平向右的电场力qＥ和重力mg的作用，使小球沿合力的方向做匀加速直线运动到C点，如图10-4乙所示.由几何知识得:L AC＝Ｌ(１分)图10－４乙 由动能定理可得:F 合·L =错误!m v C ２ (3分)即错误!＝错误!m v C 2 (1分)解得:v C =错误! （1分） 绳子绷紧的瞬间，绳子给小球的冲量使小球沿绳方向的速度减为零 沿切线方向的速度v C ′=ｖＣｃｏs ３０°＝＼ｒ(３ｇL ) (2分)此后小球从C 点运动到B 点的过程中，绳子对小球不做功,电场力和重力均对小球做正功，则有:m ｇ(L －L c ｏs 30°)+EqL sin ３0°＝＼f(1,2)ｍｖB ２－12m ｖC ′2 (3分)解得：v B 2=（2＋错误!)gL即v B ＝1.6gL ． （2分)(2)绳断后，电场反向，则重力和电场力的合力对小球先做负功后做正功，把小球的速度沿合力和垂直于合力的方向进行分解，如图10－4丙所示，当沿合力方向的分速度为零时,小球的速度最小，动能最小，则有：图１0-4丙ｖＬ=ｖＢco ｓ 3０°=＼ｆ(３,２)ｖB (２分）其最小动能为：Ｅk ＝错误!m ｖL 2＝０.9７ｍg Ｌ． (3分)[答案] (1)１.６错误! (2)0.97mg Ｌ【点评】本题易错之处有三个：①小球从A 运动到B 的过程中，初始阶段并非做圆周运动;②小球运动到C 点时绳子拉直的瞬间机械能有损失；③不能利用合力做功分析出小球后来最小速度的位置及大小.四、善于从复杂的情境中快速地提取有效信息现在的物理试题中介绍性、描述性的语句相当多,题目的信息量很大,解题时应具备敏锐的眼光和灵活的思维,善于从复杂的情境中快速地提取有效信息,准确理解题意．●例6(18分)风能将成为２1世纪大规模开发的一种可再生清洁能源．风力发电机是将风能(气流的功能)转化为电能的装置，其主要部件包括风轮机、齿轮箱、发电机等．如图１０－５所示.图１０-5（1)利用总电阻R＝10Ω 的线路向外输送风力发电机产生的电能.输送功率P0=300 kW，输电电压U＝10 kV,求导线上损失的功率与输送功率的比值.(2)风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积.设空气密度为ρ，气流速度为ｖ，风轮机叶片的长度为r.求单位时间内流向风轮机的最大风能P m．在风速和叶片数确定的情况下，要提高风轮机单位时间接受的风能,简述可采取的措施．(3)已知风力发电机的输出电功率P与Pｍ成正比.某风力发电机的风速v1＝9 m/s时能够输出电功率P１＝540kW.我国某地区风速不低于v２＝６m/s的时间每年约为5000 h，试估算这台风力发电机在该地区的最小年发电量.[20０8年高考·北京理综卷]【解析】(1）导线上损失的功率P＝I2R＝(错误!)2Ｒ(2分)可解得：Ｐ＝（错误!)２×10W＝9kＷ（2分)损失的功率与输送功率的比值为：错误!=错误!＝０.0３．(2分)（２)风垂直流向风轮机时，提供的风能功率最大单位时间内垂直流向叶片旋转面积的气体的质量为:m0＝ρｖS＝πρv r2(2分)风能的最大功率可表示为:P m=错误!m0v2=错误!πρr2v3 (2分)采取的合理措施有：增加风轮机叶片的长度,安装调向装置保持风轮机正面迎风等. (3分)(3）按题意，风力发电机的输出功率为:P2=（v2v1）3·Ｐ１＝(＼f(6，9))3×540kＷ=160 ｋＷ(3分)最小年发电量约为：W=Ｐ２ｔ＝1６0×50０0 kW·ｈ=8×1０5ｋW·ｈ．（２分)[答案] (1)0.03(2)＼f(1,2)πρr２v３措施略(３)８×105ｋW·h【点评】由本例可看出，这类题型叙述较长，但将所给的信息进行提炼后，解析过程并不复杂.所以审题的关键是认真阅读题意,建立物理模型．能力演练一、选择题(10×4分）1.在北京奥运会场馆的建设中,大量采用了环保新技术，如场馆周围的路灯用太阳能电池供电，洗浴热水通过太阳能集热器产生等.太阳能产生于太阳内部的核聚变,其核反应方程是(）A.４１1H→42He＋２错误!ｅB.错误!N＋错误!He→错误!O+错误!HＣ.错误!U＋错误!n→错误!Xe＋错误!Sr＋10错误!nＤ.＼o＼ａr（238,92）U→错误!Th＋错误!Ｈe【解析】各选项中的核反应方程中只有A中为聚变反应.[答案］ A2.下列说法正确的是( )A.随着科技的进步,总有一天热机的效率可以达到100%Ｂ.用气筒打气时看到气体体积可以任意扩大和缩小,所以气体自由膨胀的过程是可逆过程Ｃ.空调既能制热又能制冷，说明热传递不存在方向性D．自然界一切自发的能量转化过程具有单向特性,虽然总能量守恒，但能量品质在退化【解析】根据热力学第二定律可判断选项D正确.[答案］Ｄ3．爱因斯坦由光电效应的实验规律提出了光子说，下列对光电效应的解释中,正确的是( )A．金属内的每个电子可以吸收一个或同时吸收几个光子，当它积累的动能足够大时,就能逸出金属Ｂ.如果入射光子的能量小于金属表面的电子克服原子核的引力逸出时需要做的最小功，但只要照射时间足够长，光电效应也能发生C.发生光电效应时,入射光越强，光子的能量就越大，光电子的最大初动能就越大D.由于不同金属的逸出功是不相同的,因此使不同金属产生光电效应的入射光的最低频率也不相同【解析】电子每次只吸收一个光子的能量，若电子吸收一个光子后能量的增加不足以逸出，就会很快与其他电子碰撞而损失能量，故无法因积累吸收光子的能量而逸出,选项Ａ、B错误.光电子的最大初动能E k＝hν－W逸,与光的强度无关,选项C错误、Ｄ正确．［答案] Ｄ４.如图所示,水平面B点以左是光滑的、B点以右是粗糙的，相距为L的质量为M和m的两个小物块，在Ｂ点以左的光滑水平面上以相同的速度向右运。

高考物理大题答题规范一、必要得文字说明必要得文字说明得目得就是说明物理过程与答题依据，有得同学不明确应该说什么，往往将物理解答过程变成了数学解答过程．答题时应该说些什么呢？我们应该从以下几个方面给予考虑：1．说明研究对象(个体或系统，尤其就是要用整体法与隔离法相结合求解得题目，一定要注意研究对象得转移与转化问题)．2．画出受力分析图、电路图、光路图或运动过程得示意图．3．说明所设字母得物理意义．4．说明规定得正方向、零势点(面)．5．说明题目中得隐含条件、临界条件．6．说明所列方程得依据、名称及对应得物理过程或物理状态．7．说明所求结果得物理意义(有时需要讨论分析)．二、要有必要得方程式物理方程就是表达得主体，如何写出，重点要注意以下几点．1．写出得方程式(这就是评分依据)必须就是最基本得，不能以变形得结果式代替方程式(这就是相当多得考生所忽视得)．如带电粒子在磁场中运动时应有q v B ＝m v 2R ，而不就是其变形结果式R ＝m v qB ．2．要用字母表达方程，不要用掺有数字得方程，不要方程套方程．3．要用原始方程组联立求解，不要用连等式，不断地“续”进一些内容．4．方程式有多个得，应分式布列(分步得分)，不要合写一式，以免一错而致全错，对各方程式最好能编号．三、要有必要得演算过程及明确得结果1．演算时一般先进行文字运算，从列出得一系列方程推导出结果得计算式，最后代入数据并写出结果．这样既有利于减轻运算负担，又有利于一般规律得发现，同时也能改变每列一个方程就代入数值计算得不良习惯．2．数据得书写要用科学记数法．3．计算结果得有效数字得位数应根据题意确定，一般应与题目中开列得数据相近，取两位或三位即可．如有特殊要求，应按要求选定．4．计算结果就是数据得要带单位，最好不要以无理数或分数作为计算结果(文字式得系数可以)，就是字母符号得不用带单位．四、解题过程中运用数学得方式有讲究1．“代入数据”，解方程得具体过程可以不写出．2．所涉及得几何关系只需写出判断结果而不必证明．3．重要得中间结论得文字表达式要写出来．4．所求得方程若有多个解，都要写出来，然后通过讨论，该舍去得舍去．5．数字相乘时，数字之间不要用“·”，而应用“×”进行连接；相除时也不要用“÷”，而应用“/”．五、使用各种字母符号要规范1．字母符号要写清楚、规范，忌字迹潦草．阅卷时因为“v 、r 、ν”不分，大小写“M 、m ”或“L 、l ”不分，“G ”得草体像“a ”，希腊字母“ρ、μ、β、η”笔顺或形状不对而被扣分已屡见不鲜．2．尊重题目所给得符号，题目给了符号得一定不要再另立符号．如题目给出半径就是r，您若写成R就算错．3．一个字母在一个题目中只能用来表示一个物理量，忌一字母多用；一个物理量在同一题中不能有多个符号，以免混淆．4．尊重习惯用法．如拉力用F，摩擦力用f表示，阅卷人一瞧便明白，如果用反了就会带来误解．5．角标要讲究．角标得位置应当在右下角，比字母本身小许多．角标得选用亦应讲究，如通过A点得速度用v A就比用v1好；通过某相同点得速度，按时间顺序第一次用v1、第二次用v2就很清楚，如果倒置，必然带来误解．6．物理量单位得符号源于人名得单位，由单个字母表示得应大写，如库仑C、亨利H；由两个字母组成得单位，一般前面得字母用大写，后面得字母用小写，如Hz、Wb．六、学科语言要规范，有学科特色1．学科术语要规范．如“定律”、“定理”、“公式”、“关系”、“定则”等词要用准确，阅卷时常可瞧到“牛顿运动定理”、“动能定律”、“四边形公式”、“油标卡尺”等错误说法．2．语言要富有学科特色．在有图示得坐标系中将电场得方向说成“西南方向”、“南偏西45°”、“向左下方”等均就是不规范得，应说成“与x轴正方向得夹角为135°”或“如图所示”等．七、绘制图形、图象要清晰、准确1．必须用铅笔(便于修改)、圆规、直尺、三角板绘制，反对随心所欲徒手画．2．画出得示意图(受力分析图、电路图、光路图、运动过程图等)应大致能反映有关量得关系，图文要对应．3．画函数图象时，要画好坐标原点与坐标轴上得箭头，标好物理量得符号、单位及坐标轴上得数据．4．图形、图线应清晰、准确，线段得虚实要分明，有区别．●例1(28分)太阳现正处于序星演化阶段．它主要就是由电子与11H、42He等原子核组成．维持太阳辐射得就是它内部得核聚变反应，核反应方程就是2e＋411H→42He＋释放得核能，这些核能最后转化为辐射能．根据目前关于恒星演化得理论，若由于核变反应而使太阳中得11H核数目从现有得减少10%，太阳将离开主序星阶段而转入红巨星得演化阶段．为了简化，假定目前太阳全部由电子与11H核组成．(1)为了研究太阳演化进程，需知道目前太阳得质量M．已知地球得半径R ＝6、4×106 m，地球得质量m＝6、0×1024 kg，日地中心得距离r＝1、5×1011 m，地球表面处重力加速度g＝10 m/s2，1年约为3、2×107 s．试估算目前太阳得质量M．(2)已知质子得质量m p＝1、6726×10－27 kg，42He核得质量mα＝6、6458×10－27 kg，电子得质量m e＝0、9×10－30 kg，光速c＝3×108 m/s．求每发生一次题中所述得核聚变反应所释放得核能．(3)又已知地球上与太阳光垂直得每平方米得截面上，每秒通过得太阳辐射能w＝1、35×103W/m2．试估算太阳继续保持在主序星阶段还有多少年得寿命．(估算结果保留一位有效数字) [2001年高考·全国理综卷Ⅰ]【解析】(1)(第一记分段：估算太阳得质量 14分)设地球得公转周期为T ，则有： G mM r 2＝m (2πT )2r (3分)g ＝G m R 2(等效式为：m ′g ＝G mm ′R 2) (3分)联立解得：M ＝m (2πT )2·r 3gR 2 (4分)代入数值得：M ＝2×1030 kg ． (4分)(卷面上暴露出来得易犯错误得一些问题：①不用题中给得物理量符号，自己另用一套符号，r 、R 、m 、M 错用，丢掉14分；②对题中给出得地球得质量m 与地球表面处得重力加速度g 视而不见，把G 得数值代入计算太阳得质量，丢掉11分；③太阳得质量M 得计算结果得有效数字不对，丢掉4分．)(2)(第二记分段：核聚变反应所释放得核能 7分)ΔE ＝(4m p ＋2m e －m α)c 2 (4分)代入数值得：ΔE ＝4×10－12 J ． (3分)(卷面上暴露出来得易犯错误得一些问题：①数字运算能力低，能导出ΔE ＝(4m p ＋2m e －m α)c 2，却算不出ΔE ＝4×10－12 J ，丢掉3分；②ΔE 得计算结果得有效数字不对，丢掉3分；③ΔE 得计算结果得单位不对，丢掉1分．)(3)(第三记分段：估算太阳继续保持在主序星阶段得时间 7分)核聚变反应得次数N ＝M 4m p×10% (2分) 太阳共辐射得能量E ＝N ·ΔE太阳每秒辐射得总能量ε＝4πr 2·w (2分)太阳继续保持在主序星阶段得时间t ＝E ε (2分)由以上各式得：t ＝0、1M (4m p ＋2m e －m α)c 24m p ×4πr 2w代入数值得：t ＝1×1010年． (1分)(卷面上暴露出来得易犯错误得一些问题：因不熟悉天体辐射知识，大多数考生解答不出来．)[答案] (1)2×1030 kg (2)4×10－12 J (3)1×1010年●例2(18分)图10－1中滑块与小球得质量均为m ，滑块可在水平放置得光滑固定导轨上自由滑动，小球与滑块上得悬点O 由一不可伸长得轻绳相连，轻绳长为l ．开始时，轻绳处于水平拉直状态，小球与滑块均静止．现将小球由静止释放，当小球到达最低点时，滑块刚好被一表面涂有黏性物质得固定挡板粘住，在极短得时间内速度减为零，小球继续向左摆动，当轻绳与竖直方向得夹角θ＝60°时小球达到最高点．求：图10－1(1)从滑块与挡板接触到速度刚好变为零得过程中，挡板阻力对滑块得冲量．(2)小球从释放到第一次到达最低点得过程中，绳得拉力对小球做功得大小．[2008年高考·全国理综卷Ⅰ]【解析】(1)(第一问给分点：12分)解法一设小球摆至最低点时，滑块与小球得速度大小分别为v1、v2，对于滑块与小球组成得系统，由机械能守恒定律得：12m v12＋12m v22＝mgl(3分)同理，滑块被粘住后，对于小球向左摆动得过程，有：12m v22＝mgl(1－cos 60°)(3分)解得：v1＝v2＝gl(2分)对于滑块与挡板接触得过程，由动量定理得：I＝0－m v1可知挡板对滑块得冲量I＝－m gl，负号表示方向向左．(4分，其中方向占1分)解法二设小球摆至最低点时，滑块与小球得速度大小分别为v1、v2，由动量守恒定律得：m v1－m v2＝0(3分)对于小球向左摆动得过程，由机械能守恒定律得：12m v22＝mgl(1－cos 60°)(3分)可解得：v1＝v2＝gl(2分)对于滑块与挡板接触得过程，由动量定理有：I＝0－m v1可解得挡板对滑块得冲量为：I＝－m gl，负号表示方向向左．(4分，其中方向占1分)解法三设小球摆至最低点时，滑块与小球得速度大小分别为v1、v2，由机械能守恒定律得：12m v12＋12m v22＝mgl(3分)又由动量守恒定律得：m v1＋m(－v2)＝0(3分)可解得：v1＝v2＝gl(2分)对于滑块与挡板接触得过程，由动量定理得：I＝0－m v1可解得挡板对滑块得冲量为：I＝－m gl，负号表示方向向左．(4分，其中方向占1分)解法四由全过程得能量转换与守恒关系可得(滑块在碰撞时损失得能量等于系统机械能得减少，等于滑块碰前得动能)：ΔE＝mgl－mgl(1－cos 60°)＝12m v2(6分)可解得滑块碰前得速度为：v＝gl(2分)对于滑块与挡板接触得过程，由动量定理得：I＝0－m v 可解得挡板对滑块得冲量为：I ＝－m gl ，负号表示方向向左． (4分，其中方向占1分)解法五 由全过程得能量转换与守恒关系可得(滑块在碰撞时损失得能量等于系统机械能得减少，等于滑块碰前得动能)：ΔE ＝mgl cos 60°＝12m v 2 (6分)可解得滑块碰前得速度为：v ＝gl (2分)对于滑块与挡板接触得过程，由动量定理得：I ＝0－m v可解得挡板对滑块得冲量为：I ＝－m gl ，负号表示方向向左． (4分，其中方向占1分)(2)(第二问给分点：6分)解法一 对小球下摆得过程，由动能定理得：mgl ＋W ＝12m v 22 (4分)可解得细绳对其做得功为：W ＝－12mgl ． (2分)解法二 绳得张力对小球所做得功得绝对值等于滑块在碰前得动能(或等于绳子得张力对滑块做得功)，则有：W ′＝12m v 12或W ′＝12m v 12－0 ( 4分)可解得：W ＝－W ′＝－12mgl ． (2分)解法三 绳子得张力对小球做得功等于小球在全过程中得机械能得增量，有：W ＝(－mg ·l 2)－0＝－12mgl (取滑块所在高度得水平面为参考平面) (6分)或W ＝mgl (1－cos 60°)－mgl ＝－12mgl (取小球所到达得最低点为参考平面)或W ＝0－mg ·l 2＝－12mgl (取小球摆起得最高点为参考平面)．解法四 对小球运动得全过程，由动能定理得：W ＋mgl cos 60°＝0或W ＋mg ·l 2＝0 (4分)解得：W ＝－12mgl ． (2分)解法五 考虑小球从水平位置到最低点得过程：若滑块固定，绳子得张力对小球不做功，小球处于最低点时得速率v 球′＝2gl (由mgl ＝12m v 球′2得到) (2分)若滑块不固定，绳子得张力对小球做功，小球处于最低点时得速率v 球＝gl(v 球应由前面正确求得)则绳子对小球做得功为：W ＝12m v 球2－12m v 球′2 (2分)＝－12mgl ． (2分)[答案] (1)－m gl，负号表示方向向左(2)－12mgl【点评】①越就是综合性强得试题，往往解题方法越多，同学们通过本例得多种解题方法要认真地总结动能定理、机械能守恒定律与能量得转化与守恒定律之间得关系．②要认真地推敲各种解题方法得评分标准，从而建立起自己解题得规范化程序．解题技巧从前面各专题可以瞧出，在高中物理各类试题得解析中常用到得方法有：整体法、隔离法、正交分解法、等效类比法、图象法、极限法等，这些方法技巧在高考计算题得解析中当然也就是重要得手段，但这些方法技巧涉及面广，前面已有较多得论述与例举，这里就不再赘述．本模块就如何面对形形色色得论述、计算题迅速准确地找到解析得“突破口”作些讨论与例举．论述、计算题一般都包括对象、条件、过程与状态四要素．对象就是物理现象得载体，这一载体可以就是物体(质点)、系统，或就是由大量分子组成得固体、液体、气体，或就是电荷、电场、磁场、电路、通电导体，或就是光线、光子与光学元件，还可以就是原子、核外电子、原子核、基本粒子等．条件就是对物理现象与物理事实(对象)得一些限制，解题时应“明确”显性条件、“挖掘”隐含条件、“吃透”模糊条件．显性条件就是易被感知与理解得；隐含条件就是不易被感知得，它往往隐含在概念、规律、现象、过程、状态、图形与图象之中；模糊条件常常存在于一些模糊语言之中，一般只指定一个大概得范围．过程就是指研究得对象在一定条件下变化、发展得程序．在解题时应注意过程得多元性，可将全过程分解为多个子过程或将多个子过程合并为一个全过程．状态就是指研究对象各个时刻所呈现出得特征．方法通常表现为解决问题得程序．物理问题得求解通常有分析问题、寻求方案、评估与执行方案几个步骤，而分析问题(即审题)就是解决物理问题得关键．一、抓住关键词语，挖掘隐含条件在读题时不仅要注意那些给出具体数字或字母得显性条件，更要抓住另外一些叙述性得语言，特别就是一些关键词语．所谓关键词语，指得就是题目中提出得一些限制性语言，它们或就是对题目中所涉及得物理变化得描述，或就是对变化过程得界定等．高考物理计算题之所以较难，不仅就是因为物理过程复杂、多变，还由于潜在条件隐蔽、难寻，往往使考生们产生条件不足之感而陷入困境，这也正考查了考生思维得深刻程度．在审题过程中，必须把隐含条件充分挖掘出来，这常常就是解题得关键．有些隐含条件隐蔽得并不深，平时又经常见到，挖掘起来很容易，例如题目中说“光滑得平面”，就表示“摩擦可忽略不计”；题目中说“恰好不滑出木板”，就表示小物体“恰好滑到木板边缘处且具有与木板相同得速度”等等．但还有一些隐含条件隐藏较深或不常见到，挖掘起来就有一定得难度了．●例3(10分)两质量分别为M1与M2得劈A与B，高度相同，放在光滑水平面上，A与B得倾斜面都就是光滑曲面，曲面下端与水平面相切，如图10－2所示．一质量为m得物块位于劈A得倾斜面上，距水平面得高度为h．物块从静止滑下，然后又滑上劈B．求物块在B上能够达到得最大高度．[2009年高考·宁夏理综卷]图10－2【解析】设物块到达劈A得底端时，物块与A得速度大小分别为v与v1，由机械能守恒与动量守恒得：mgh＝12m v2＋12M1v12(2分)M1v1＝m v(2分)设物块在劈B上达到得最大高度为h′，此时物块与B得共同速度大小为v′，由机械能守恒与动量守恒得：mgh′＋12(M2＋m)v′2＝12m v2(2分)m v＝(M2＋m)v′(2分)联立解得：h′＝M1M2(M1＋m)(M2＋m)h．(2分)[答案]M1M2(M1＋m)(M2＋m)h【点评】本题应分析清楚物块从A滑下以及滑上B得情境，即从A滑下与滑上B得过程水平方向动量守恒，在B上上升至最大高度时，隐含着与B具有相同速度得条件．二、重视对基本过程得分析(画好情境示意图)在高中物理中，力学部分涉及得运动过程有匀速直线运动、匀变速直线运动、平抛运动、圆周运动、简谐运动等，除了这些运动过程外，还有两类重要得过程：一类就是碰撞过程，另一类就是先变加速运动最终匀速运动得过程(如汽车以恒定功率启动问题)．热学中得变化过程主要有等温变化、等压变化、等容变化、绝热变化等(这些过程得定量计算在某些省得高考中已不作要求)．电学中得变化过程主要有电容器得充电与放电、电磁振荡、电磁感应中得导体棒做先变加速后匀速得运动等，而画出这些物理过程得示意图或画出关键情境得受力分析示意图就是解析计算题得常规手段．画好分析草图就是审题得重要步骤，它有助于建立清晰有序得物理过程与确立物理量间得关系，可以把问题具体化、形象化．分析图可以就是运动过程图、受力分析图、状态变化图，也可以就是投影法、等效法得到得示意图等．在审题过程中，要养成画示意图得习惯．解物理题，能画图得尽量画图，图能帮助我们理解题意、分析过程以及探讨过程中各物理量得变化．几乎无一物理问题不就是用图来加强认识得，而画图又迫使我们审查问题得各个细节以及细节之间得关系．●例4(18分)如图10－3甲所示，建立Oxy坐标系．两平行极板P、Q垂直于y轴且关于x轴对称，极板长度与板间距均为l，在第一、四象限有磁感应强度为B得匀强磁场，方向垂直于Oxy平面向里．位于极板左侧得粒子源沿x轴向右连续发射质量为m、电荷量为＋q、速度相同、重力不计得带电粒子．在0～3t0时间内两板间加上如图10－3乙所示得电压(不考虑极板边缘得影响)．已知t ＝0时刻进入两板间得带电粒子恰好在t0时刻经极板边缘射入磁场．上述m、q、l 、t 0、B 为已知量，不考虑粒子间相互影响及返回极板间得情况．(1)求电压U 0得大小．(2)求12t 0时刻进入两板间得带电粒子在磁场中做圆周运动得半径．(3)何时进入两板间得带电粒子在磁场中得运动时间最短？求此最短时间．[2009年高考·山东理综卷]图10－3【解析】(1)t ＝0时刻进入两板间得带电粒子在电场中做匀变速曲线运动，t 0时刻刚好从极板边缘射出，在y 轴负方向偏移得距离为12l ，则有：E ＝U 0l (1分)qE ＝ma (1分)12l ＝12at 02 (2分)联立解得：两板间得偏转电压U 0＝ml 2qt 02． (1分) (2)12t 0时刻进入两板间得带电粒子，前12t 0时间在电场中偏转，后12t 0时间两板间没有电场，带电粒子做匀速直线运动．带电粒子沿x 轴方向得分速度大小v 0＝l t 0(1分) 带电粒子离开电场时沿y 轴负方向得分速度大小v y ＝a ·12t 0 (1分)带电粒子离开电场时得速度大小v ＝v 02＋v y 2 (1分)设带电粒子离开电场进入磁场做匀速圆周运动得半径为R ，则有：q v B ＝m v 2R (1分)联立解得：R ＝5ml 2qBt 0． (1分) (3)2t 0时刻进入两板间得带电粒子在磁场中运动得时间最短． (2分) 带电粒子离开电场时沿y 轴正方向得分速度为：v y ′＝at 0 (1分)图10－3丙设带电粒子离开电场时速度方向与y轴正方向得夹角为α，则tan α＝v0v y′(1分)联立解得：α＝π4(1分)带电粒子在磁场中得运动轨迹如图10－3丙所示，圆弧所对得圆心角2α＝π2，所求最短时间为：t min＝14T(1分)带电粒子在磁场中运动得周期T＝2πmqB(1分)联立解得：t min＝πm2qB．(1分)[答案] (1)ml2qt02(2)5ml2qBt0(3)2t0时刻πm2qB【点评】在解决带电粒子在电场、磁场中得偏转问题时，要充分分析题意，结合必要得计算，画出物体运动得轨迹图．为了确保解题得正确，所画得轨迹图必须准确，同学们可以想一下在做数学中得几何题时就是如何作图得．在解决这类物理题时，也要作出一个标准得图形．三、要谨慎细致，谨防定势思维经常遇到一些物理题故意多给出已知条件，或表述物理情境时精心设置一些陷阱，安排一些似就是而非得判断，以此形成干扰因素，来考查学生明辨就是非得能力．这些因素得迷惑程度愈大，同学们愈容易在解题过程中犯错误．在审题过程中，只有有效地排除这些干扰因素，才能迅速而正确地得出答案．有些题目得物理过程含而不露，需结合已知条件，应用相关概念与规律进行具体分析．分析前不要急于动笔列方程，以免用假得过程模型代替了实际得物理过程，防止定势思维得负迁移．●例5(18分)如图10－4甲所示，用长为L得丝线悬挂着一质量为m、带电荷量为＋q得小球，将它们放入水平向右得匀强电场中，场强大小E＝3mg3q．今将小球拉至水平方向得A点后由静止释放．图10－4甲(1)求小球落至最低点B处时得速度大小．(2)若小球落至最低点B处时，绳突然断开，同时使电场反向，大小不变，则小球在以后得运动过程中得最小动能为多少？【解析】(1)由题意知：小球受到水平向右得电场力qE与重力mg得作用，使小球沿合力得方向做匀加速直线运动到C点，如图10－4乙所示．由几何知识得：L AC＝L(1分)图10－4乙由动能定理可得：F合·L＝12m v C2(3分)即mgLcos 30°＝12m v C2(1分)解得：v C＝43gL3(1分)绳子绷紧得瞬间，绳子给小球得冲量使小球沿绳方向得速度减为零沿切线方向得速度v C′＝v C cos 30°＝3gL(2分)此后小球从C点运动到B点得过程中，绳子对小球不做功，电场力与重力均对小球做正功，则有：mg(L－L cos 30°)＋EqL sin 30°＝12m v B2－12m v C′2(3分)解得：v B2＝(2＋3 3)gL即v B＝1、6gL．(2分)(2)绳断后，电场反向，则重力与电场力得合力对小球先做负功后做正功，把小球得速度沿合力与垂直于合力得方向进行分解，如图10－4丙所示，当沿合力方向得分速度为零时，小球得速度最小，动能最小，则有：图10－4丙 v L ＝v B cos 30°＝32v B (2分)其最小动能为：E k ＝12m v L 2＝0、97mgL ． (3分)[答案] (1)1、6gL (2)0、97mgL【点评】本题易错之处有三个：①小球从A 运动到B 得过程中，初始阶段并非做圆周运动；②小球运动到C 点时绳子拉直得瞬间机械能有损失；③不能利用合力做功分析出小球后来最小速度得位置及大小．四、善于从复杂得情境中快速地提取有效信息现在得物理试题中介绍性、描述性得语句相当多，题目得信息量很大，解题时应具备敏锐得眼光与灵活得思维，善于从复杂得情境中快速地提取有效信息，准确理解题意．●例6(18分)风能将成为21世纪大规模开发得一种可再生清洁能源．风力发电机就是将风能(气流得功能)转化为电能得装置，其主要部件包括风轮机、齿轮箱、发电机等．如图10－5所示．图10－5(1)利用总电阻R ＝10 Ω 得线路向外输送风力发电机产生得电能．输送功率P 0＝300 kW ，输电电压U ＝10 kV ，求导线上损失得功率与输送功率得比值．(2)风轮机叶片旋转所扫过得面积为风力发电机可接受风能得面积．设空气密度为ρ，气流速度为v ，风轮机叶片得长度为r ．求单位时间内流向风轮机得最大风能P m ．在风速与叶片数确定得情况下，要提高风轮机单位时间接受得风能，简述可采取得措施．(3)已知风力发电机得输出电功率P 与P m 成正比．某风力发电机得风速v 1＝9 m/s 时能够输出电功率P 1＝540 kW ．我国某地区风速不低于v 2＝6 m/s 得时间每年约为5000 h ，试估算这台风力发电机在该地区得最小年发电量．[2008年高考·北京理综卷]【解析】(1)导线上损失得功率P ＝I 2R ＝(P 0U )2R (2分)可解得：P ＝(300×10310×103)2×10 W ＝9 kW (2分) 损失得功率与输送功率得比值为：PP 0＝9×103300×103＝0、03． (2分)(2)风垂直流向风轮机时，提供得风能功率最大单位时间内垂直流向叶片旋转面积得气体得质量为：m 0＝ρv S ＝πρv r 2 (2分)风能得最大功率可表示为：P m ＝12m 0v 2＝12πρr 2v 3 (2分)采取得合理措施有：增加风轮机叶片得长度，安装调向装置保持风轮机正面迎风等． (3分)(3)按题意，风力发电机得输出功率为：P 2＝(v 2v 1)3·P 1＝(69)3×540 kW ＝160 kW (3分) 最小年发电量约为：W ＝P 2t ＝160×5000 kW·h ＝8×105 kW·h ． (2分)[答案] (1)0、03 (2)12πρr 2v 3 措施略(3)8×105 kW·h【点评】由本例可瞧出，这类题型叙述较长，但将所给得信息进行提炼后，解析过程并不复杂．所以审题得关键就是认真阅读题意，建立物理模型．能力演练一、选择题(10×4分)1．在北京奥运会场馆得建设中，大量采用了环保新技术，如场馆周围得路灯用太阳能电池供电，洗浴热水通过太阳能集热器产生等．太阳能产生于太阳内部得核聚变，其核反应方程就是( )A ．411H →42He ＋201eB ．145N ＋42He → 178O ＋11HC ．23592U ＋10n → 13654Xe ＋9038Sr ＋1010nD ．23892U →23490Th ＋42He【解析】各选项中得核反应方程中只有A 中为聚变反应．[答案] A2．下列说法正确得就是( )A ．随着科技得进步，总有一天热机得效率可以达到100%B ．用气筒打气时瞧到气体体积可以任意扩大与缩小，所以气体自由膨胀得过程就是可逆过程C ．空调既能制热又能制冷，说明热传递不存在方向性D ．自然界一切自发得能量转化过程具有单向特性，虽然总能量守恒，但能量品质在退化【解析】根据热力学第二定律可判断选项D 正确．。

10年高考（2011-2020年）全国II卷物理试题分项全解全析专题18 力学大题1、全国II卷2020年高考使用的省份：甘肃、青海、内蒙古、黑龙江、吉林、辽宁、宁夏、新疆、陕西、重庆等10个省份2、2011-2020年全国II卷试题赏析：1、（2020·全国II卷·T25）如图，一竖直圆管质量为M，下端距水平地面的高度为H，顶端塞有一质量为m的小球。

圆管由静止自由下落，与地面发生多次弹性碰撞，且每次碰撞时间均极短；在运动过程中，管始终保持竖直。

已知M =4m，球和管之间的滑动摩擦力大小为4mg, g为重力加速度的大小，不计空气阻力。

（1）求管第一次与地面碰撞后的瞬间，管和球各自的加速度大小；（2）管第一次落地弹起后，在上升过程中球没有从管中滑出，求管上升的最大高度；（3）管第二次落地弹起的上升过程中，球仍没有从管中滑出，求圆管长度应满足的条件。

【答案】（1）a1=2g，a2=3g；（2）113 25H H=；（3）152125 L H ≥【解析】（1）管第一次落地弹起的瞬间，小球仍然向下运动。

设此时管的加速度大小为a1，方向向下；球的加速度大小为a2，方向向上；球与管之间的摩擦力大小为f，由牛顿运动定律有Ma1=Mg+f ①ma2= f– mg ②联立①②式并代入题给数据，得a 1=2g ，a 2=3g ③（2）管第一次碰地前与球的速度大小相同。

由运动学公式，碰地前瞬间它们的速度大小均为0v =④方向均向下。

管弹起的瞬间，管的速度反向，球的速度方向依然向下。

设自弹起时经过时间t 1，管与小球的速度刚好相同。

取向上为正方向，由运动学公式v 0–a 1t 1= –v 0+a 2t 1⑤联立③④⑤式得1t =⑥ 设此时管下端的高度为h 1，速度为v 。

由运动学公式可得21011112h v t a t =−⑦ 011v v a t =−⑧由③④⑥⑧式可判断此时v >0。

此后，管与小球将以加速度g 减速上升h 2，到达最高点。

高考地理大题的模板答题技巧很多的时候，死记硬背并不是最好的方法，而且需要找到正确的思路以及灵活记忆。

下面给大家带来一些关于高考地理大题的模板答题技巧，希望对大家有所帮助。

高考地理大题的模板答题1(1)高中地理首先要分点作答，答题条理清晰，抓住主次，逻辑性强。

从背景资料直接提取的答案放前面。

高中地理题目在答案中非常强调抓问题的主要方面，所以对影响地理事物诸多因素中，要抓住最主要的因素，切中要害，实在没有把握怕抓不到，则主次一起抓，多多益善，但要注意把最精彩、最重要的尽可能放在前面，以免给阅卷老师造成主次不分、回答问题不着边际的不良印象。

注意题目分值，高中地理分值高要注意扩展答题要点，扩展中不能与题目矛盾，不能出现错误表述。

(2)高中地理答题文字尽量少而精，注意突出关键词，注意“不问不答、多问多答、先问先答”的答题规范。

但如果没把握，怕把知识点漏答，根据目前高中地理综合题的评分标准，则不如多答。

(3)高中地理答题尽量具体详细。

如果没有把握的话，可作适度模糊处理。

如“旧金山沿岸洋流对气候的影响”可答为沿岸寒流降温减湿，不必具体指出洋流名称。

(4)高中地理答题尽量应用地理术语。

如大气环流、河流径流等语言，是衡量考生答题是否优质的重要标准。

答案要先定性描述，然后具体分析。

(5)高中地理答题书写规范，不写错别字。

字迹潦草不容易使阅卷教师找得分点。

高考地理大题的模板答题2高中地理等高线地形图小专题1.坡度问题：一看等高线疏密，密集的地方坡度陡，稀疏的地方坡度缓;计算：坡度的正切=垂直相对高度/水平实地距离2.通视问题：通过作地形剖面图来解决，如果过已知两点作的地形剖面图无山地或山脊阻挡，则两地可互相通视;注意凸坡(等高线上疏下密)不可见，凹坡(等高线上密下疏)可见;注意题中要求，分析图中景观图是仰视或俯视可见。

3.引水线路：注意让其从高处向低处引水，以实现自流，且线路要尽可能短，这样经济投入才会较少。

4.交通线路选择：利用有利的地形地势，既要考虑距离长短，又要考虑路线平稳(间距、坡度等)，一般是在两条等高线间绕行，沿等高线走向(延伸方向)分布，以减少坡度，只有必要时才可穿过一、两条等高线;尽可能少地通过河流，少建桥梁等，以减少施工难度和投资;避免通过断崖、沼泽地、沙漠等地段。

1 ．数列{n a }的前n 项和为n S ，且满足11a =，2(1)n n S n a =+.（1）求{n a }的通项公式； （2）求和T n =1211123(1)na a n a ++++.2 ．已知数列}{n a ，a 1=1，点*))(2,(1N n a a P n n ∈+在直线0121=+-y x 上. （1）求数列}{n a 的通项公式； （2）函数)2*,(1111)(321≥∈++++++++=n N n a n a n a n a n n f n且 ，求函数)(n f 最小值. 3 ．已知函数xab x f =)( (a ，b 为常数)的图象经过点P （1，81）和Q （4，8）(1) 求函数)(x f 的解析式；(2) 记a n =log 2)(n f ,n 是正整数，n S 是数列{a n }的前n 项和，求n S 的最小值。

4 ．已知y ＝f (x )为一次函数，且f (2)、f (5)、f (4)成等比数列，f (8)＝15．求n S ＝f (1)＋f (2)＋…＋f (n )的表达式．5 ．设数列{}n a 的前n 项和为n S ，且1n n S c ca =+-，其中c 是不等于1-和0的实常数.（1）求证: {}n a 为等比数列；（2）设数列{}n a 的公比()q f c =，数列{}n b 满足()()111,,23n n b b f b n N n -==∈≥，试写出1n b ⎧⎫⎨⎬⎩⎭的通项公式，并求12231n n b b b b b b -+++的结果.6 ．在平面直角坐标系中,已知A n (n,a n )、B n (n,b n )、C n (n -1,0)(n ∈N *)，满足向量1+n n A A 与向量n n C B 共线，且点B n (n,b n ) (n ∈N *)都在斜率为6的同一条直线上.(1)试用a 1,b 1与n 来表示a n ;(2)设a 1=a ,b 1=-a ,且12<a ≤15，求数列{a n }中的最小项.7 ．已知数列{}n a 的前三项与数列{}n b 的前三项对应相同，且212322a a a +++ (1)2n n a -+8n =对任意的∈n N*都成立，数列1{}n n b b +-是等差数列．（1）求数列{}n a 与{}n b 的通项公式；（2）问是否存在k ∈N *，使得(0,1)k k b a -∈？请说明理由．8 ．已知数列),3,2(1335,}{11 =-+==-n a a a a nn n n 且中（I ）试求a 2，a 3的值； （II ）若存在实数}3{,nn a λλ+使得为等差数列，试求λ的值. 9 ．已知数列{}n a 的前n 项和为n S ，若()1,211++=⋅=+n n S a n a n n ，（1）求数列{}n a 的通项公式; （2）令n nn S T 2=，①当n 为何正整数值时，1+>n n T T ：②若对一切正整数n ，总有m T n ≤，求m 的取值范围。

化学实验综合题目是高考必考的一个题型之一，常以物质的制备或性质探究为依托设置情景素材，将化学实验基础知识、元素及其化合物相关理论知识、化学基本理论、探究性实验、定性与定量实验放在一起综合考查学生分析问题、解决问题的能力以及结合题目给定的信息，对知识进行迁移应用，解决相关问题的能力。

一般考查角度为(1)仪器的识别、选择、连接；(2)原理方程式的书写；(3)实验条件的控制；(4)实验装置、试剂的作用或选择；(5)实验操作的目的与解释；(6)步骤与现象描述；(7)实验方案的设计与评价；(8)物质组成、纯度、产率的定量计算；(9)物质的分离提纯方法。

1．物质制备类综合实验题2．性质探究的一般程序3．实验综合题答题三部曲第一步　快速读题干(1)明确题型；(2)圈出与化学有关的信息，如实验的目的、陌生物质的结构、性质、实验条件等。

第二步　结合步骤细分析。

理解反应原理、条件控制的方法及原因，知道装置中各部分的目的与作用。

第三步　逐问分析、规范答题。

热点题空1　实验仪器(装置)的选择、作用与连接一、常考装置的作用1．气体干燥装置2．吸收、检验气体装置(1)内盛碱石灰：可以吸收HCl、Cl2、SO2、CO2等酸性气体。

(2)内盛无水CuSO4：用于水蒸气的检验，但不能作为水的吸收装置。

(3)用于测定气体质量的装置：3．防倒吸装置4．尾气处理防污染装置5．防堵塞装置6．液封装置7．无机产物的冷凝装置(适合冷凝易升华或沸点较低的气体)二、实验装置中仪器或试剂的作用类答题规范回答装置中仪器和试剂的用途时，一般包括直接作用和根本目的两部分内容，根据各部分装置的用途不同，可采用下列格式回答：①发生装置　生成……　产生……　制取……②除杂装置　除去(吸收)……防止……干扰(影响)；除去……中的杂质，以免影响测量结果③性质实验装置　与……反应　验证……　说明……(收集装置) 比较……检验……④尾气吸收装置　吸收……防止……的污染(影响)三、仪器装置的选择与连接1．解题原则(1)明确实验目的，弄清各个仪器的作用。

高考数学专题：导数大题专练含答案一、解答题1．已知函数()ln f x ax x =+ (1)讨论()f x 的单调区间；(2)设()2xg x =，若对任意的[]11,100x ∈，存在[]20,1x ∈，使()()12f x g x <成立，求实数a 的取值范围. 2．已知函数()ln f x x =．(1)当()()sin 1g x x =-，求函数()()()T x f x g x =+在()0,1的单调性； (2)()()12h x f x b x=+-有两个零点1x ，2x ，且12x x <，求证：121x x +>． 3．已知函数()21si cos n 2f x x x a x x =-++．(1)当1a =-时，求曲线()y f x =在点()()0,0f 处的切线方程； (2)若函数()f x 在3π0,4⎡⎤⎢⎥⎣⎦上单调递减，求a 的取值范围．4．已知a R ∈，函数()22e 2xax f x =+． (1)求曲线()y f x =在0x =处的切线方程 (2)若函数()f x 有两个极值点12,x x ，且1201x x ，（ⅰ）求a 的取值范围；（ⅱ）当9a <-时，证明：21x x <-<． （注： 2.71828e =…是自然对数的底数） 5．求下列函数的导数： (1)2cos x xy x -=； (2)()e 1cos 2x x y x =+-； (3)()3log 51y x =-．6．已知函数()322f x x ax bx =++-在2x =-时取得极值，且在点()()1,1f --处的切线的斜率为3- . (1)求()f x 的解析式；(2)若函数()y f x λ=-有三个零点，求实数λ的取值范围.7．已知函数()323f x x ax x =-+.(1)若3x =是()f x 的极值点，求()f x 在[]1,a 上的最大值和最小值；(2)若()f x 在[)1,+∞上是单调递增的，求实数a 的取值范围.8．2020年9月22日，中国政府在第七十五届联合国大会上提出：“中国将提高国家自主贡献力度，采取更加有力的政策和措施，二氧化碳排放力争于2030年前达到峰值，努力争取2060年前实现碳中和.”为了进一步了解普通大众对“碳中和”及相关举措的认识，某机构进行了一次问卷调查，部分结果如下：(1)根据所给数据，完成下面的22⨯列联表，并根据列联表，判断是否有95%的把握认为“是否了解‘碳中和’及相关措施”与“学生”身份有关？附：()()()()()22n ad bc K a b c d a c b d -=++++，n a b c d =+++.(2)经调查后，有关部门决定加大力度宣传“碳中和”及相关措施以便让节能减排的想法深入人心.经过一段时间后，计划先随机从社会上选10人进行调查，再根据检验结果决定后续的相关举措.设宣传后不了解“碳中和”的人概率都为()01p p <<，每个被调查的人之间相互独立.①记10人中恰有3人不了解“碳中和”的概率为()f p ，求()f p 的最大值点0p ； ②现对以上的10人进行有奖答题，以①中确定的0p 作为答错的概率p 的值.已知回答正确给价值a 元的礼品，回答错误给价值b 元的礼品，要准备的礼品大致为多少元？（用a ，b 表示即可）9．已知函数()ln 2f x x x ax =++在点()()1,1f 处的切线与直线220x y 相互垂直．(1)求实数a 的值；(2)求()f x 的单调区间和极值．10．已知函数()222(0)e xmx x f x m +-=>. (1)判断()f x 的单调性；(2)若对[]12,1,2x x ∀∈，不等式()()1224e f x f x -≤恒成立，求实数m 的取值范围.【参考答案】一、解答题1．(1)答案见解析 (2)31a e ≤-【解析】 【分析】（1）由()()110ax f x a x xx+=+=>'，按0a ≥，0a <进行分类讨论求解； （2）由已知，转化为()()max max f x g x <，由已知得()()max 12g x g ==，由此能求出实数a 的取值范围． (1)()(]110ax f x a x x x+'=+=>， ①当0a ≥时，由于0x >，故10ax +>，()0f x '>， 所以()f x 的单调递增区间为()0,∞+；②当0a <时，由()0f x '=，得1x a=-，在区间10,a ⎛⎫- ⎪⎝⎭上()0f x '>，在区间1,a∞⎛⎫-+ ⎪⎝⎭上()0f x '<，所以，函数()f x 的单调递增区间为10,a ⎛⎫- ⎪⎝⎭，单调递减区间为1,a∞⎛⎫-+ ⎪⎝⎭；(2)由题目知，只需要()()max max f x g x <即可又因为()()max 12g x g ==，所以只需要()max 2f x <即可()max 2f x <即等价于()2f x <恒成立，由变量分离可知2ln xa x-<，[]1,100x ∈， 令()2ln xh x x -=，下面求()h x 的最小值， 令()23ln xh x x-+'=，所以()0h x '=得3x e =， 所以()h x 在31,e ⎡⎤⎣⎦为减函数，3,100e ⎡⎤⎣⎦为增函数，所以()()33min 1h x h e e -==，所以31a e ≤-. 2．(1)单调递增 (2)证明见解析 【解析】 【分析】（1）直接求导，判断出导数大于0，即可得到单调性；（2）直接由1x ，2x 是函数()1ln 2h x x b x =+-的两个零点得到1212122ln x xx x x x -=，分别解出1211212ln x xx x x -=，2121212ln xx x x x -=，再换元令12x t x =构造函数()12ln l t t t t=--，求导确定单调性即可求解. (1)由题意，函数()()sin 1ln T x x x =-+，则()()1cos 1T x x x'=--+，又∵()0,1x ∈，∴11x>，()()10,1,cos 11x x -∈-<，∴()0T x '>，∴()T x 在（0，1）上单调递增． (2)根据题意，()()1ln 02h x x b x x =+->， ∵1x ，2x 是函数()1ln 2h x x b x=+-的两个零点，∴111ln 02x b x +-=，221ln 02x b x +-=． 两式相减，可得122111ln22x x x x =-，即112221ln 2x x x x x x -=， ∴1212122ln x x x x x x -=，则1211212ln x x x x x -=，2121212ln xx x x x -=． 令12x t x =，()0,1t ∈，则1211112ln 2ln 2ln t t t t x x t t t---+=+=．记()12ln l t t t t =--，()0,1t ∈，则()()221t l t t-'=． 又∵()0,1t ∈，∴()0l t '>恒成立，∴()l t 在()0,1上单调递增，故()()1l t l <，即12ln 0t t t --<，即12ln t t t-<．因为ln 0t <，可得112ln t t t->，∴121x x +>．【点睛】本题关键点在于对双变量的处理，通过对111ln 02x b x +-=，221ln 02x b x +-=作差，化简得到1212122ln x x x x xx -=， 分别得到12,x x 后，换元令12x t x =，这样就转换为1个变量，再求导确定单调性即可求解． 3．(1)10y +=； (2)[)1,+∞. 【解析】 【分析】（1）将1a =-代入函数()f x 中，得出函数()f x 的解析式，进而可以求出切点坐标，再利用导数的几何意义及点斜式即可求解；（2）根据已知条件可以将问题转化为恒成立问题，进而转化为求函数的最值问题，利用导数法求函数的最值即可求解. (1)当1a =-时，()2cos 1sin 2f x x x x x =--+()2cos 10000sin 012f =⨯--+=-，所以切点为0,1，()1sin cos x f x x x '=-++，∴(0)01sin 0cos00f '=-++=，所以曲线()y f x =在点()()0,0f 处的切线的斜率为(0)0k f '==， 所以曲线()y f x =在点0,1处的切线的斜率切线方程为()()100y x --=⨯-，即10y +=.(2)由()21si cos n 2f x x x a x x =-++，得()s 1co i s n f x x a x x '=--+因为函数()f x 在3π0,4⎡⎤⎢⎥⎣⎦上单调递减，可得()0f x '≤对任意3π0,4x ⎡⎤∈⎢⎥⎣⎦恒成立， 设()()1c s os in g x f x x a x x '==--+，则()cos 1sin g x a x x '=--. 因为si (n 0)001cos00g a =--+=， 所以使()0f x '≤对任意3π0,4x ⎡⎤∈⎢⎥⎣⎦恒成立， 则至少满足()00g '≤，即10a -≤，解得1a ≥. 下证明当1a ≥时，()0f x '≤恒成立，因为3π0,4x ⎡⎤∈⎢⎥⎣⎦，所以sin 0x ≥， 因为1a ≥，所以()sin 1cos f x x x x '≤--+.记s ()cos n 1i h x x x x =--+，则π()1sin 14cos h x x x x ⎛⎫'=-=+ ⎝-⎪⎭.当π0,2x ⎛⎫∈ ⎪⎝⎭时，()0h x '<；当π3π,24x ⎛⎫∈ ⎪⎝⎭时，()0h x '>. 所以函数()h x 在π0,2⎡⎫⎪⎢⎣⎭上单调递减，在π3π,24⎛⎤⎥⎝⎦上单调递增.因为ππ(),h h ⎛⎫==- ⎪⎝⎭33001044， 所以()h x 在3π0,4⎡⎤⎢⎥⎣⎦上的最大值为(0)0h =. 即()()1sin cos 0f x h x x x x '≤=--+≤在3π0,4⎡⎤⎢⎥⎣⎦上恒成立.所以a 的取值范围为[)1,+∞.4．(1)(21y x =-+(2)（ⅰ）22e ,-；（ⅱ）证明见解析【解析】 【分析】（1）由导数的几何意义即可求解；（2）（ⅰ）原问题等价于12,x xa =-的两根，且1201x x ，从而构造函数())0g x x =>，将问题转化为直线y a =-与函数()g x 的图象有两个交点，且交点的横坐标大于0小于1即可求解；（ⅱ）由1e x x +≤，利用放缩法可得()()1112210x ax f x '++-=，即1x 2114x <<，从而可证21x x -<()21e 011x x x x +<<<-，然后利用放缩法可得()()1201,21i i i ix ax f x i x +'⋅+->==-，即(()22201,2i i ax a x i -++++-=，最后构造二次函数()(222m x ax a x =-++++21x x ->而得证原不等式. (1)解：因为()22e x f x ax '=+所以()02f '=()01f =，所以曲线()y f x =在0x =处的切线方程为(21y x =-+； (2)解：（ⅰ）因为函数()f x 有两个极值点12,x x ，所以12,x x 是关于x 的方程()22e 0x f x ax =+'的两根，也是关于x的方程a =-的两正根， 设())0g x x =>，则()g x '=， 令())224e 2e 0x x h x x x =->，则()28e xh x x '=，当0x >时，()0h x '>，所以()h x 在()0,∞+上单调递增，又104h ⎛⎫= ⎪⎝⎭，所以，当104x <<时，()0h x <，()0g x '<；当14x >时，()0h x >，()0g x '>，所以函数()g x 在10,4⎛⎫⎪⎝⎭上单调递减，在1,4⎛⎫+∞ ⎪⎝⎭上单调递增，又因为1201x x ，所以()114g a g ⎛⎫<-<⎪⎝⎭，即22e a <-<- 所以a的取值范围是22e ,-；22e 9a <<-， 因为1e x x +≤，所以()()1112210x ax f x '++-=，所以()142a x +-，所以1x 2114x <<，所以211x x -<= 下面先证明不等式()21e 011x xx x+<<<-， 设()()2101e 1xx r x x x -=⋅<<+，则()()2222e 1x x r x x '=-+， 所以，当01x <<时，()0r x '<，()r x '在()0,1上单调递减， 所以，()()01r x r <=，所以不等式()21e 011x xx x+<<<-成立， 因为12,x x ，()1201x x <<<是()22e 0x f x ax '=+=的两个根，所以()()01,2i f x i '==，又()21e 011x xx x+<<<-，所以()()1201,21ii i ixax f x i x +'⋅+->==-，即(()22201,2i i ax a x i -++++-=，设函数()(222m x ax a x =-++++x t ==因为((()2224261620a a a ∆=+++-=+-+->，且()00m >，()10m >，102t <<， 所以函数()m x 有两个不同的零点，记为α，()βαβ<，且01t αβ<<<<，因为()22616212e 201ta tf t at at t+++'=+-⋅+-=<-，且()00f '>，()10f '>，所以1201x x ，因为()m x 在()0,t 上单调递减，且()()10m x m α>=，所以10x t α<<<； 因为()m x 在(),1t 上单调递增，且()()20m x m β>=，所以21t x β<<<； 所以1201x x αβ<<<<<，所以21x x βα->-，因为βα-=又()109a-<<<-，所以βα-> 所以21x x->综上，21x x <-< 【点睛】关键点点睛：本题（2）问（ii）小题证明的关键是，利用1e x x +≤，进行放缩可得1x 21x x -<；再利用()21e 011x xx x +<<<-，进行放缩可得()()1201,21ii i ixax f x i x +'⋅+->==-，从而构造二次函数()(222m x ax ax =-++++21x x ->5．(1)'y ()31sin 2cos x x xx --=；(2)'y ()e 1cos sin 2ln 2x xx x =+--；(3)'y ()551ln 3x =-⋅.【解析】 【分析】根据导数的运算法则，对（1）（2）（3）逐个求导，即可求得结果. (1)因为2cos x x y x -=，故'y ()()()243sin 12cos 1sin 2cos x x x x x x x x x x------==. (2)因为()e 1cos 2x x y x =+-，故'y ()e 1cos sin 2ln 2x xx x =+--.(3)因为()3log 51y x =-，故'y ()()155?51ln 351ln 3x x =⨯=--⋅. 6．(1)()3232f x x x =+-(2)()2,2- 【解析】 【分析】（1）由已知可得()()2013f f ⎧-=⎪⎨-=-''⎪⎩，可得出关于实数a 、b 的方程组，解出这两个未知数的值，即可得出函数()f x 的解析式；（2）分析可知，直线y λ=与函数()f x 的图象有3个交点，利用导数分析函数()f x 的单调性与极值，数形结合可得出实数λ的取值范围.(1)解：因为()322f x x ax bx =++-，则()232f x x ax b '=++，由题意可得()()212401323f a b f a b ⎧-=-+=⎪⎨-=-+=-''⎪⎩，解得30a b =⎧⎨=⎩，所以，()3232f x x x =+-.当3a =，0b =时，()236f x x x '=+，经检验可知，函数()f x 在2x =-处取得极值. 因此，()3232f x x x =+-.(2)解：问题等价于()f x λ=有三个不等的实数根，求λ的范围.由()2360f x x x '=+>，得2x <-或0x >，由()2360f x x x '=+<，得20x -<<，所以()f x 在(),2-∞-、()0,∞+上单调递增，在()2,0-上单调递减， 则函数()f x 的极大值为()22f -=，极小值为()02f =-，如下图所示：由图可知，当22λ-<<时，直线y λ=与函数()f x 的图象有3个交点， 因此，实数λ的取值范围是()2,2-. 7．(1)最大值为15，最小值为9- (2)3a ≤ 【解析】 【分析】（1）由()30f '=可求得实数a 的值，再利用函数的最值与导数的关系可求得函数()f x 在[]1,a 上的最大值和最小值；（2）分析可知()23230f x x ax '=-+≥对任意的1≥x 恒成立，利用参变量分离法结合基本不等式可求得实数a 的取值范围. (1)解：因为()323f x x ax x =-+，则()2323f x x ax =-+'，则()33060f a '=-=，解得5a =，所以，()3253f x x x x =-+，则()()()23103313f x x x x x '=-+=--，列表如下：所以，min 39f x f ==-，因为11f =-，515f =，则max 515f x f ==. (2)解：由题意可得()23230f x x ax '=-+≥对任意的1≥x 恒成立，即312a x x⎛⎫≤+ ⎪⎝⎭，由基本不等式可得313322x x ⎛⎫+≥⨯ ⎪⎝⎭，当且仅当1x =时，等号成立，故3a ≤.8．(1)列联表见解析，没有95%的把握认为“是否了解‘碳中和’及相关措施”与“学生”身份有关； (2)①0310p =；②()73a b + 【解析】 【分析】（1）对满足条件的数据统计加和即可，然后根据给定的2K 计算公式，将计算结果与195%0.05-=所对应的k 值比较大小即可；（2）①利用独立重复试验与二项分布的特点，写出10人中恰有3人不了解“碳中和”的概率为()f p ，再利用导数求出最值点； ②利用独立重复试验的期望公式代入可求出答案. (1)由题中表格数据完成22⨯列联表如下：()22800125250150275800 3.463 3.841275525400400231K ⨯⨯-⨯==≈<⨯⨯⨯.故没有95%的把握认为“是否了解‘碳中和’及相关措施”与“学生”身份有关. (2)①由题得，()()733101f p C p p =-，()0,1p ∈， ∴()()()()()763236321010C 3171C 1310f p p p p p p p p ⎡⎤'=---=--⎣⎦. 令()0f p '=，得310p =，当30,10p ⎛⎫∈ ⎪⎝⎭时，()0f p '>； 当3,110p ⎛⎫∈⎪⎝⎭时，()0f p '<， ∴当30,10p ⎛⎫∈ ⎪⎝⎭时，()f p '单调选增；当3,110p ⎛⎫∈ ⎪⎝⎭时，()f p '单调递减， ∴()f p 的最大值点0310p =. ②本题求要准备的礼品大致为多少元，即求10个人礼品价值X 的数学期望. 由①知答错的概率为310， 则()33101731010E X a b a b ⎡⎤⎛⎫=-+=+ ⎪⎢⎥⎝⎭⎣⎦， 故要准备的礼品大致为73a b +元. 9．(1)3a =-；(2)增区间为()2e ,+∞，减区间为()20,e ，极小值22e -，无极大值.【解析】 【分析】（1）根据()1112f '⨯=-，代值计算即可求得参数值；（2）根据（1）中所求参数值，求得()f x '，利用导数的正负即可判断函数单调性和极值. (1)因为()ln 1f x x a '=++，在点()()1,1f 处的切线斜率为()11k f a '==+， 又()f x 在点()()1,1f 处的切线与直线220x y 相互垂直， 所以()1112f '⨯=-，解得3a =-. (2)由（1）得，()ln 2f x x '=-，()0,x ∈+∞，令()0f x '>，得2e x >，令()0f x '<，得20e x <<，即()f x 的增区间为()2e ,+∞，减区间为()20,e ． 又()22222e e ln e 3e 22ef =-+=-，所以()f x 在2e x =处取得极小值22e -，无极大值． 【点睛】本题考查导数的几何意义，以及利用导数研究函数的单调性和极值，属综合中档题.10．(1)单调增区间为2,2m ⎛⎫- ⎪⎝⎭，单调减区间为[)2,,2,m ∞∞⎛⎤--+⎥⎝⎦ (2)20,4e ⎛⎤ ⎥-⎝⎦【解析】 【分析】（1）先对函数求导，然后由导数的正负可求出函数的单调区间， （2）由函数()f x 在[]1,2上为增函数，求出函数的最值，则()()max min 24e 2()()e m g m f x f x -+=-=，然后将问题转化为()224e 24e e m -+≥，从而可求出实数m 的取值范围. (1)()()()()221422(0)e e xxmx m x mx x f x m -+-+-+-=>'=令()0f x '=，解得2x m =-或2x =，且22m-< 当2,x m ∞⎛⎤∈-- ⎥⎝⎦时，()0f x '≤，当2,2x m ⎛⎫∈- ⎪⎝⎭时，()0f x '>，当[)2,x ∞∈+时，()0f x '≤即()f x 的单调增区间为2,2m ⎛⎫- ⎪⎝⎭，单调减区间为[)2,,2,m ∞∞⎛⎤--+⎥⎝⎦(2)由（1）知，当[]0,1,2m x >∈时，()0f x '>恒成立 所以()f x 在[]1,2上为增函数， 即()()max min242()2,()1e em mf x f f x f +====. ()()12f x f x -的最大值为()()max min 24e 2()()e m g m f x f x -+=-=()()1224e f x f x ⎡⎤≥-⎣⎦恒成立()224e 24e e m -+∴≥ 即24em ≤-， 又0m > 20,4e m ⎛⎤∴∈ ⎥-⎝⎦ 故m 的取值范围20,4e ⎛⎤ ⎥-⎝⎦。

专题8 六选四（原卷版）距离高考还有一段时间，不少有经验的老师都会提醒考生，愈是临近高考，能否咬紧牙关、学会自我调节，态度是否主动积极，安排是否科学合理，能不能保持良好的心态、以饱满的情绪迎接挑战，其效果往往大不一样。

以下是本人从事10多年教学经验总结出的以下学习资料，希望可以帮助大家提高答题的正确率，希望对你有所帮助，有志者事竟成！养成良好的答题习惯，是决定高考英语成败的决定性因素之一。

做题前，要认真阅读题目要求、题干和选项，并对答案内容作出合理预测;答题时，切忌跟着感觉走，最好按照题目序号来做，不会的或存在疑问的，要做好标记，要善于发现，找到题目的题眼所在，规范答题，书写工整;答题完毕时，要认真检查，查漏补缺，纠正错误。

总之，在最后的复习阶段，学生们不要加大练习量。

在这个时候，学生要尽快找到适合自己的答题方式，最重要的是以平常心去面对考试。

英语最后的复习要树立信心，考试的时候遇到难题要想“别人也难”，遇到容易的则要想“细心审题”。

越到最后，考生越要回归基础，单词最好再梳理一遍，这样有利于提高阅读理解的效率。

另附高考复习方法和考前30天冲刺复习方法。

[考点分析]分值：8分，语法难度较任务型阅读有所降低，但理解难度提高。

考查方式：给出一篇缺少四个句子的短文和6个选项。

要求考生根据文章内容，选出正确的句子填入相应空白处。

有两个多余选项。

每个选项2分。

考纲解读：主要考查学生对文章的整体内容和结构以及上下文逻辑意义的理解和掌握。

选材特点：短文长度一般为300词左右，题材为记叙文、说明文和议论文为主。

设空类型：1.主旨句：标题类、主题句类；2.过渡性句子:文章结构；3.细节注释性句子：上下文逻辑意义。

解题步骤：1. 通读全文，尤其是文章的开始部分，明确文章的基本话题和主要内容。

2. 阅读选项，根据选项中句子的句意或者句子后面的标点符号来判断该句在文章中的可能位置。

3. 仔细阅读空前空后，寻找并划出关键词。

高考化学计算大题知识点归纳及专项练习题（含答案）一、知识点归纳规律方法1．化学计算中常考查的守恒思想有“转移电子数守恒、电荷守恒和质量守恒”等，它们是解决化学计算的“金钥匙”，首先要准确判断应该运用哪一种守恒解题。

(1)运用转移电子守恒解题①找出氧化剂、还原剂及相应的还原产物和氧化产物(谁变价)。

②确定一个原子或离子得失电子数(变几价)。

③根据题中物质的物质的量和得失电子守恒列出等式(几个变)。

④对于多步连续进行的氧化还原反应，只要中间各步反应过程没有损耗，可直接找出起始物和最终产物，删去中间产物，建立二者之间的电子守恒关系，快速求解。

(2)运用电荷守恒解题电荷守恒的解题依据是：电解质溶液中不论存在多少种离子，溶液都是呈电中性的，即阴离子所带电荷总数和阳离子所带电荷总数相等。

解题的关键是：找全离子；离子带几个电荷乘几。

(3)运用质量守恒解题运用质量守恒的关键是准确判断在整个反应过程中哪一种元素的原子的个数或物质的量不发生改变，淡化中间过程，快速解题。

2．关系式法解题的答题思路和模式(1)分析题中反应——写出各步反应方程式——根据反应中各物质的计量数关系——确定已知物质与待求物质的物质的量关系——列比例求算(2)分析题中反应——根据某元素原子守恒——确定关系式——列比例求解3．(1)熟记反应热ΔH的基本计算公式ΔH＝生成物的总能量－反应物的总能量；ΔH＝反应物的总键能－生成物的总键能(2)掌握常见物质中的化学键类型和数目如：CO2；CH4；P4；P2O5等4．活用“三点”可快速准确解电解计算题(1)串联电路中每个电极转移的电子数相等。

(2)准确判断各电极的电极产物。

(3)掌握转移4 mol e－不同电极产物之间满足的关系。

4 mol e－～1 mol O2～2 mol H2～2 mol Cl2～2 mol Cu～4 mol Ag～4 mol H＋～4 mol OH－反思归纳1．化学平衡和电解质溶液计算时常注意的问题(1)要利用“三段式”突破平衡和电解质溶液的计算题。

高考物理大题
1. 甲、乙两个物体，质量分别为m1和m2，分别以v1和v2
的速度碰撞，碰撞后两物体分别以w1和w2的速度分离。

已
知碰撞过程中，动量守恒，即m1v1 + m2v2 = m1w1 + m2w2。

求证碰撞过程中动能守恒。

2. 一台电梯质量为M，达到其承重极限时，最大加速度为a。

现有两名乘客A和B，乘客A质量为m1，站在电梯底部，乘
客B质量为m2，站在乘客A的头上。

若电梯以加速度a上升，求A对B的压力。

3. 一弹簧恢复力与变形量之间满足Hooke定律。

现有一弹簧，其劲度系数为k1，长度为l1。

如果将这根弹簧剪成两段，两
段的劲度系数分别为k2和k3。

求剪断点处的长度比l2:l3。

4. 一根光滑无质量的杆长为L，一只质量为m1的物体被绳子
绑在杆的一端，另一只质量为m2的物体悬挂在杆的另一端。

现有两个大小相等的力F作用于杆的两个端点，方向与杆平
行但方向相反。

求证当F > mg时，杆会翘起。

5. 在一个真空容器中，有一根金属棒长度为L，横截面积为A，温度为T1。

另一根金属棒长度为2L，横截面积为2A，温度
为T2。

将两根金属棒接触在一起，且维持接触点处温度不变。

求证热传导过程中，两根棒接触点处的热流量相等。

1（20分）如图12所示，PR 是一块长为L =4 m 的绝缘平板固定在水平地面上，整个空间有一个平行于PR 的匀强电场E ，在板的右半部分有一个垂直于纸面向外的匀强磁场B ，一个质量为m =0．1 kg ，带电量为q =0．5 C 的物体，从板的P 端由静止开始在电场力和摩擦力的作用下向右做匀加速运动，进入磁场后恰能做匀速运动。

当物体碰到板R 端的挡板后被弹回，若在碰撞瞬间撤去电场，物体返回时在磁场中仍做匀速运动，离开磁场后做匀减速运动停在C 点，PC =L/4，物体与平板间的动摩擦因数为μ=0．4，取g=10m/s 2 ，求：（1）判断物体带电性质，正电荷还是负电荷？（2）物体与挡板碰撞前后的速度v 1和v 2（3）磁感应强度B 的大小（4）电场强度E 的大小和方向答案（1）由于物体返回后在磁场中无电场，且仍做匀速运动，故知摩擦力为0，所以物体带正电荷．且：mg =qBv 2…………………………………………………………①（2）离开电场后，按动能定理，有：-μmg 4L =0-21mv 2………………………………② 由①式得：v 2=22 m/s（3）代入前式①求得：B =22 T （4）由于电荷由P 运动到C 点做匀加速运动，可知电场强度方向水平向右，且：（Eq -图12μmg ）212=L mv 12-0……………………………………………③ 进入电磁场后做匀速运动，故有：Eq =μ（qBv 1+mg ）……………………………④由以上③④两式得：⎩⎨⎧==N/C2.4m/s 241E v2(10分)如图2—14所示，光滑水平桌面上有长L=2m 的木板C ，质量m c =5kg ，在其正中央并排放着两个小滑块A 和B ，m A =1kg ，m B =4kg ，开始时三物都静止．在A 、B 间有少量塑胶炸药，爆炸后A 以速度6m ／s 水平向左运动，A 、B 中任一块与挡板碰撞后，都粘在一起，不计摩擦和碰撞时间，求：(1)当两滑块A 、B 都与挡板碰撞后，C 的速度是多大?(2)到A 、B 都与挡板碰撞为止，C 的位移为多少?答案（1）A 、B 、C 系统所受合外力为零，故系统动量守恒，且总动量为零，故两物块与挡板碰撞后，C 的速度为零，即0=C v（2）炸药爆炸时有解得s m v B /5.1=又B B A A s m s m =当s A ＝1 m 时s B ＝0.25m ，即当A 、C 相撞时B 与C 右板相距m s L s B 75.02=-= A 、C 相撞时有：解得v ＝1m/s ，方向向左而B v ＝1.5m/s ，方向向右，两者相距0.75m ，故到A ，B 都与挡板碰撞为止，C 的位移为3.0=+=BC v v sv s m19. 3（10分）为了测量小木板和斜面间的摩擦因数，某同学设计如图所示实验，在小木板上固定一个轻弹簧，弹簧下端吊一个光滑小球，弹簧长度方向与斜面平行，现将木板连同弹簧、小球放在斜面上，用手固定木板时，弹簧示数为F 1，放手后，木板沿斜面下滑，稳定后弹簧示数为F 2，测得斜面斜角为θ，则木板与斜面间动摩擦因数为多少？（斜面体固定在地面上）答案 固定时示数为F 1，对小球F 1=mgsin θ ①整体下滑：（M+m ）sin θ-μ(M+m)gcos θ=(M+m)a ②下滑时，对小球：mgsin θ-F 2=ma ③由式①、式②、式③得μ=12F F tan θ 4有一倾角为θ的斜面，其底端固定一挡板M ，另有三个木块A 、B 和C ，它们的质 量分别为m A =m B =m ，m C =3 m ，它们与斜面间的动摩擦因数都相同.其中木块A 连接一轻弹簧放于斜面上，并通过轻弹簧与挡板M 相连，如图所示.开始时，木块A 静止在P 处，弹簧处于自然伸长状态.木块B 在Q 点以初速度v 0向下运动，P 、Q 间的距离为L.已知木块B 在下滑过程中做匀速直线运动，与木块A 相碰后立刻一起向下运动，但不粘连，它们到达一个最低点后又向上运动，木块B 向上运动恰好能回到Q 点.若木块A 静止于P 点，木块C 从Q 点开始以初速度032v 向下运动，经历同样过程，最后木块C 停在斜面上的R 点，求P 、R 间的距离L ′的大小。

高考试题详解及答案一、选择题1. 下列关于细胞结构和功能的描述，不正确的是：A. 细胞膜具有选择性通透性B. 线粒体是细胞的能量工厂C. 核糖体是蛋白质合成的场所D. 细胞核是细胞遗传物质的储存和复制场所答案：D（细胞核是细胞遗传物质的储存和复制场所，但不是细胞遗传物质的唯一场所，因为线粒体中也含有遗传物质。

）2. 根据题目所给的化学反应方程式，下列哪种物质是反应的催化剂？A. 反应物B. 生成物C. 催化剂D. 反应条件答案：C（催化剂是能够加速化学反应速率但在反应过程中不被消耗的物质。

）二、填空题1. 请填写下列化学反应方程式中缺失的物质：\[ \text{C}_3\text{H}_6\text{O}_3 + \text{X} \rightarrow \text{C}_2\text{H}_5\text{OH} + \text{CO}_2 \]缺失的物质是 \_\_\_\_\_\_\_\_\_\_\_\_\_。

答案：\[ \text{O}_2 \]（根据质量守恒定律，反应前后原子的种类和数量不变，因此缺失的物质是氧气。

）2. 请根据题目所给的遗传图谱，确定基因A和a在染色体上的位置关系。

答案：基因A和a在染色体上是等位基因，位于同一基因座上。

三、简答题1. 请简述细胞分裂过程中染色体的变化过程。

答案：细胞分裂过程中，染色体首先进行复制，形成姐妹染色单体。

在分裂的前期，染色体会凝聚成X形结构。

在中期，染色体排列在细胞的中央，形成所谓的“赤道面”。

在后期，姐妹染色单体分离，向细胞的两极移动。

最后，在末期，细胞质分裂，形成两个具有相同染色体数量的子细胞。

四、论述题1. 论述生态系统中能量流动的特点及其对生物多样性的影响。

答案：生态系统中的能量流动具有单向性和逐级递减的特点。

能量从生产者到消费者，再从消费者到消费者，但不会逆向流动。

能量在流动过程中逐级递减，因为每个营养级都会消耗一部分能量用于生命活动。

高考政治哲学大题唯物论答题方法高考政治大题哲学之唯物论如何答题?1、自然界客观性原理【原理内容】：自然界的存在与进展是客观的。

自然界先于人和人的意识而存在，在人类产生后，自然界的存在与进展也不依靠于人的意识。

【方法论】：⑴承认自然界的客观性是人类有意识地处理人与自然关系的差不多前提。

⑵我们在利用自然、改造自然的时候，务必要尊重自然、顺应自然、爱护自然，学会与自然和谐相处。

2、世界的物质统一性原理【原理内容】：自然界是物质的;人类社会是物质的;意识是人脑对客观存在的主观映象。

因此，世界的本原是物质，世界上先有物质后有意识，物质决定意识，世界的真正统一性在于它的物质性。

【方法论】：这一原理要求我们在想问题、办情况的时候，要一切从实际动身，理论联系实际，解放思想，实事求是，与时俱进，在实践中检验和进展真理3、物质和运动相互关系原理【原理内容】：物质和运动是紧密联系、不可分割的：(1)物质是运动的物质，运动是物质的全然属性和存在方式，世界上不存在脱离运动的物质;(2)运动是物质的运动，物质是运动的承担者，脱离物质的运动是全然不存在的;(3)离开物质谈运动或离开运动谈物质差不多上错误的。

【方法论】：(1)我们要用运动、变化、进展的眼光看问题(2)反对离开物质谈运动的唯心主义和离开运动谈物质的形而上学错误观点。

4、运动和静止相互关系原理【原理内容】：(l)区别：二者含义不同;二者性质不同:运动是无条件的、绝对的、永恒的，静止是有条件的、相对的、临时的。

(2)联系：静止是运动的专门状态;动中有静，静中有动。

世界上任何事物的存在和进展，差不多上绝对运动和相对静止的统一。

【方法论】：(l)要求我们既要用运动、变化、进展的观点看问题，还要看到事物相对静止的存在，坚持绝对运动和相对静止的统一。

(2)既要反对只承认静止而否认运动的形而上学的不变论，又要反对只承认绝对运动而否认相对静止的相对主义和诡辩论5、规律的客观性普遍性原理【原理内容】：规律是事物运动过程中本身固有的本质的必定的稳固的联系。

2024届新高考数学导数大题精选30题1(2024·安徽·二模)已知函数f (x )=x 2-10x +3f (1)ln x .(1)求函数f (x )在点(1,f (1))处的切线方程；(2)求f (x )的单调区间和极值.【答案】(1)y =4x -13；(2)递增区间为(0,2),(3,+∞)，递减区间为2,3 ，极大值-16+12ln2，极小值-21+12ln3.【分析】(1)求出函数f (x )的导数，赋值求得f (1)，再利用导数的几何意义求出切线方程.(2)由(1)的信息，求出函数f (x )的导数，利用导数求出单调区间及极值.【详解】(1)函数f (x )=x 2-10x +3f (1)ln x ，求导得f(x )=2x -10+3f (1)x，则f (1)=-8+3f (1)，解得f (1)=4，于是f (x )=x 2-10x +12ln x ，f (1)=-9，所以所求切线方程为：y +9=4(x -1)，即y =4x -13.(2)由(1)知，函数f (x )=x 2-10x +12ln x ，定义域为(0,+∞)，求导得f (x )=2x -10+12x =2(x -2)(x -3)x，当0<x <2或x >3时，f (x )>0，当2<x <3时，f (x )<0，因此函数f (x )在(0,2),(3,+∞)上单调递增，在(2,3)上单调递减，当x =2时，f (x )取得极大值f (2)=-16+12ln2，当x =3时，f (x )取得极小值f (3)=-21+12ln3，所以函数f (x )的递增区间为(0,2),(3,+∞)，递减区间为(2,3)，极大值-16+12ln2，极小值-21+12ln3.2(2024·江苏南京·二模)已知函数f (x )=x 2-ax +ae x，其中a ∈R ．(1)当a =0时，求曲线y =f (x )在(1,f (1))处的切线方程；(2)当a >0时，若f (x )在区间[0,a ]上的最小值为1e，求a 的值．【答案】(1)x -ey =0(2)a =1【分析】(1)由a =0，分别求出f (1)及f (1)，即可写出切线方程；(2)计算出f (x )，令f (x )=0，解得x =2或x =a ，分类讨论a 的范围，得出f (x )的单调性，由f (x )在区间[0,a ]上的最小值为1e，列出方程求解即可．【详解】(1)当a =0时，f (x )=x 2e x ，则f (1)=1e ，f (x )=2x -x 2ex，所以f (1)=1e ，所以曲线y =f (x )在(1,f (1))处的切线方程为：y -1e =1e(x -1)，即x -ey =0．(2)f(x )=-x 2+(a +2)x -2a e x =-(x -2)(x -a )ex，令f (x )=0，解得x =2或x =a ，当0<a <2时，x ∈[0,a ]时，f (x )≤0，则f (x )在[0,a ]上单调递减，所以f (x )min =f (a )=a ea =1e ，则a =1，符合题意；当a >2时，x ∈[0,2]时，f (x )≤0，则f (x )在[0,2]上单调递减，x ∈(2,a ]时，f (x )>0，则f (x )在(2,a ]上单调递增，所以f (x )min =f (2)=4-a e2=1e ，则a =4-e <2，不合题意；当a =2时，x ∈[0,2]时，f (x )≤0，则f (x )在[0,2]上单调递减，所以f (x )min =f (2)==2e 2≠1e ，不合题意；综上，a =1．3(2024·浙江绍兴·模拟预测)已知f x =ae x -x ，g x =cos x . (1)讨论f x 的单调性.(2)若∃x 0使得f x 0 =g x 0 ，求参数a 的取值范围.【答案】(1)当a ≤0时，f x 在-∞,+∞ 上单调递减；当a >0时，f x 在-∞,-ln a 上单调递减，在-ln a ,+∞ 上单调递增.(2)-∞,1【分析】(1)对f x =ae x -x 求导数，然后分类讨论即可；(2)直接对a >1和a ≤1分类讨论，即可得到结果.【详解】(1)由f x =ae x -x ，知f x =ae x -1.当a ≤0时，有f x =ae x -1≤0-1=-1<0，所以f x 在-∞,+∞ 上单调递减；当a >0时，对x <-ln a 有f x =ae x -1<ae -ln a -1=1-1=0，对x >-ln a 有f x =ae x -1>ae -ln a -1=1-1=0，所以f x 在-∞,-ln a 上单调递减，在-ln a ,+∞ 上单调递增.综上，当a ≤0时，f x 在-∞,+∞ 上单调递减；当a >0时，f x 在-∞,-ln a 上单调递减，在-ln a ,+∞ 上单调递增.(2)当a >1时，由(1)的结论，知f x 在-∞,-ln a 上单调递减，在-ln a ,+∞ 上单调递增，所以对任意的x 都有f x ≥f -ln a =ae -ln a +ln a =1+ln a >1+ln1=1≥cos x =g x ，故f x >g x 恒成立，这表明此时条件不满足；当a ≤1时，设h x =ae x -x -cos x ，由于h -a -1 =ae -a -1+a +1-cos -a -1 ≥ae-a -1+a ≥-a e-a -1+a =a 1-e-a -1≥a 1-e 0=0，h 0 =ae 0-0-cos0=a -1≤0，故由零点存在定理，知一定存在x 0∈-a -1,0 ，使得h x 0 =0，故f x 0 -g x 0 =ae x 0-x 0-cos x 0=h x 0 =0，从而f x 0 =g x 0 ，这表明此时条件满足.综上，a 的取值范围是-∞,1 .4(2024·福建漳州·一模)已知函数f x =a ln x -x +a ，a ∈R 且a ≠0．(1)证明：曲线y =f x 在点1,f 1 处的切线方程过坐标原点．(2)讨论函数f x 的单调性．【答案】(1)证明见解析(2)答案见解析【分析】(1)先利用导数的几何意义求得f x 在1,f 1 处的切线方程，从而得证；(2)分类讨论a <0与a >0，利用导数与函数的单调性即可得解.【详解】(1)因为f x =a ln x -x +a x >0 ，所以f (x )=a x -1=a -xx，则f (1)=a ln1-1+a =a -1，f (1)=a -1，所以f x 在1,f 1 处的切线方程为:y -(a -1)=(a -1)(x -1)，当x =0时，y -(a -1)=(a -1)(0-1)=-(a -1)，故y =0，所以曲线y =f (x )在点1,f 1 处切线的方程过坐标原点.(2)由(1)得f (x )=ax -1=a -xx，当a<0时，a-x<0，则f x <0，故f(x)单调递减；当a>0时，令f (x)=0则x=a，当0<x<a时，f (x)>0，f(x)单调递增；当x>a时，f (x)<0，f(x)单调递减；综上：当a<0时，f(x)在(0,+∞)上单调递减；当a>0时，f(x)在(0,a)上单调递增，在(a,+∞)上单调递减.5(2024·山东·二模)已知函数f x =a2xe x-x-ln x．(1)当a=1e时，求f x 的单调区间；(2)当a>0时，f x ≥2-a，求a的取值范围．【答案】(1)f x 的减区间为0,1，增区间为1,+∞(2)a≥1【分析】(1)当a=1e时，f x =xe x-1-x-ln x,x>0，求导得f x =x+1xxe x-1-1，令g x =xe x-1-1，求g x 确定g x 的单调性与取值，从而确定f x 的零点，得函数的单调区间；(2)求f x ，确定函数的单调性，从而确定函数f x 的最值，即可得a的取值范围．【详解】(1)当a=1e时，f x =xe x-1-x-ln x,x>0，则f x =x+1e x-1-1-1x=x+1xxe x-1-1，设g x =xe x-1-1，则g x =x+1e x-1>0恒成立，又g1 =e0-1=0，所以当x∈0,1时，f x <0，f x 单调递减，当x∈1,+∞时，f x >0，f x 单调递增，所以f x 的减区间为0,1，增区间为1,+∞；(2)f x =a2x+1e x-1-1x=x+1xa2xe x-1，设h x =a2xe x-1，则h x =a2x+1e x>0，所以h x 在0,+∞上单调递增，又h0 =-1<0，h1a2=e1a2-1>0，所以存在x0∈0,1 a2，使得h x0 =0，即a2x0e x0-1=0，当x∈0,x0时，f x <0，f x 单调递减，当x∈x0,+∞时，f x >0，f x 单调递增，当x=x0时，f x 取得极小值，也是最小值，所以f x ≥f x0=a2x0e x0-x0-ln x0=1-ln x0e x0=1+2ln a，所以1+2ln a≥2-a，即a+2ln a-1≥0，设F a =a+2ln a-1，易知F a 单调递增，且F1 =0，所以F a ≥F1 ，解得a≥1，综上，a≥1.6(2024·山东·一模)已知函数f(x)=ln x+12a(x-1)2．(1)当a=-12时，求函数f(x)的单调区间；(2)若函数g(x)=f(x)-2x+1有两个极值点x1,x2，且g(x1)+g(x2)≥-1-32a，求a的取值范围．【答案】(1)增区间(0,2)，减区间(2,+∞)(2)[1,+∞)【分析】(1)将a=-12代入求导，然后确定单调性即可；(2)求导，根据导函数有两个根写出韦达定理，代入g(x1)+g(x2)≥-1-32a，构造函数，求导，研究函数性质进而求出a的取值范围．【详解】(1)当a=-12时，f(x)=ln x-14(x-1)2，x>0，则f (x)=1x-12(x-1)=-(x-2)(x+1)2x，当x∈(0,2)，f (x)>0，f(x)单调递增，当x∈(2,+∞)，f (x)<0，f(x)单调递减，所以f(x)的单调递增区间是(0,2)，单调递减区间是(2,+∞)；(2)g(x)=f(x)-2x+1=ln x+12a(x-1)2-2x+1，所以g (x)=1x+a(x-1)-2=ax2-(a+2)x+1x，设φ(x)=ax2-(a+2)x+1，令φ(x)=0，由于g(x)有两个极值点x1,x2，所以Δ=(a+2)2-4a=a2+4>0x1+x2=a+2a>0x1x2=1a>0，解得a>0．由x1+x2=a+2a，x1x2=1a，得g x1+g x2=ln x1+12a x1-12-2x1+1+ln x2+12a x2-12-2x2+1=ln x1x2+12a x1+x22-2x1x2-2x1+x2+2-2x1+x2+2=ln1a +12a a+2a2-2a-2⋅a+2a+2-2⋅a+2a+2=ln1a +a2-2a-1≥-1-32a，即ln a-12a-1a≤0，令m(a)=ln a-12a-1a，则m (a)=1a-12-12a2=-(a-1)22a2≤0，所以m(a)在(0,+∞)上单调递减，且m(1)=0，所以a≥1，故a的取值范围是[1,+∞)．7(2024·湖北·二模)求解下列问题，(1)若kx-1≥ln x恒成立，求实数k的最小值；(2)已知a，b为正实数，x∈0,1，求函数g x =ax+1-xb-a x⋅b1-x的极值．【答案】(1)1(2)答案见解析【分析】(1)求导，然后分k≤0和k>0讨论，确定单调性，进而得最值；(2)先发现g0 =g1 =0，当a=b时，g x =0，当0<x<1，a≠b时，取ab=t，L x =tx+1-x-t x，求导，研究单调性，进而求出最值得答案.【详解】(1)记f x =kx-1-ln x x>0，则需使f x ≥0恒成立，∴f x =k-1xx>0，当k≤0时，f x <0恒成立，则f x 在(0,+∞)上单调递减，且在x>1时，f x <0，不符合题意，舍去；当k >0时．令f x =0，解得x =1k，则f x 在0,1k 上单调递减，在1k ,+∞ 上单调递增，所以f x min =f 1k =-ln 1k=ln k ，要使kx -1≥ln x 恒成立，只要ln k ≥0即可，解得k ≥1，所以k 的最小值为1；(2)g (x )=ax +(1-x )b -a x ⋅b 1-x ，x ∈[0,1]，a >0，b >0，易知g 0 =g 1 =0，当a =b 时，g x =ax +a -ax -a =0，此时函数无极值；当0<x <1，a ≠b 时，g (x )=ax +(1-x )b -b ⋅a b x =b a b x +1-x -a b x，取ab=t ，t >0，t ≠1，L x =tx +1-x -t x ，t >0，t ≠1，x ∈0,1 ，则L x =t -1-t x ln t ，当t >1时，由L x ≥0得x ≤ln t -1ln tln t，由(1)知t -1≥ln t ，当t >1时，t -1ln t>1，因为x -1≥ln x ，所以1x -1≥ln 1x ，所以ln x ≥1-1x ，即x >0，当t >1时，ln t >1-1t，所以t >t -1ln t ，则ln t >ln t -1ln t >0，所以ln t -1ln tln t<1，即L x 在0,ln t -1ln t ln t 上单调递增，在ln t -1ln tln t,1单调递减．所以函数g x 极大=gln t -1lntln t，t =ab，a ≠b ，当0<t <1时，同理有ln t -1lntln t∈0,1 ，由Lx ≥0得x ≤ln t -1lntln t，即(x )在0,ln t -1lntln t上单调递增，在ln t -1lntln t,1上单调递减．所以函数g x 极大=gln t -1lntln t，t =a b，a ≠b ，综上可知，当a =b 时，函数g x 没有极值；当a ≠b 时，函数g x 有唯一的极大值g ln t -1lntln t，其中t =ab，没有极小值．【点睛】关键点点睛：取ab=t ，将两个参数的问题转化为一个参数的问题，进而求导解答问题.8(2024·湖北武汉·模拟预测)函数f (x )=tan x +sin x -92x ，-π2<x <π2,g (x )=sin n x -x n cos x ,x ∈0,π2,n ∈N +．(1)求函数f (x )的极值；(2)若g (x )>0恒成立，求n 的最大值．【答案】(1)极小值为f π3 =3(3-π)2，极大值为f -π3 =3(π-3)2；(2)3.【分析】(1)判断函数f (x )为奇函数，利用导数求出f (x )在区间0,π2上的极值，利用奇偶性即可求得定义域上的极值.(2)利用导数证明当n =1时，g (x )>0恒成立，当n >1时，等价变形不等式并构造函数F (x )=x -sin x cos 1nx,0<x <π2，利用导数并按导数为负为正确定n 的取值范围，进而确定不等式恒成立与否得解.【详解】(1)函数f (x )=tan x +sin x -92x ，-π2<x <π2，f (-x )=tan (-x )+sin (-x )-92(-x )=-f (x )，即函数f (x )为奇函数，其图象关于原点对称，当0<x <π2时，f (x )=sin x cos x +sin x -92x ，求导得：f(x )=1cos 2x +cos x -92=2cos 3x -9cos 2x +22cos 2x =(2cos x -1)(cos x -2-6)(cos x -2+6)2cos 2x，由于cos x ∈(0,1)，由f (x )>0，得0<cos x <12，解得π3<x <π2，由f (x )<0，得12<cos x <1，解得0<x <π3，即f (x )在0,π3 上单调递减，在π3,π2上单调递增，因此函数f (x )在0,π2 上有极小值f π3 =3(3-π)2，从而f (x )在-π2,π2 上的极小值为f π3 =3(3-π)2，极大值为f -π3 =3(π-3)2.(2)当n =1时，g (x )>0恒成立，即sin x -x cos x >0恒成立，亦即tan x >x 恒成立，令h (x )=tan x -x ,x ∈0,π2 ，求导得h (x )=1cos 2x -1=1-cos 2x cos 2x=tan 2x >0，则函数h (x )在0,π2上为增函数，有h (x )>h (0)=0，因此tan x -x >0恒成立；当n >1时，g (x )>0恒成立，即不等式sin xn cos x>x 恒成立，令F (x )=x -sin x cos 1n x ,0<x <π2，求导得：F (x )=1-cos x ⋅cos 1nx -1n⋅cos1n-1x ⋅(-sin x )⋅sin xcos 2nx=1-cos1+n nx +1n⋅sin 2x ⋅cos1-n nxcos 2nx=1-cos 2x +1n ⋅sin 2xcos n +1nx =cosn +1nx -cos 2x -1n (1-cos 2x )cos n +1nx =cosn +1nx -1n -n -1ncos 2x cosn +1nx令G (x )=cos n +1nx -1n -n -1n cos 2x ，求导得则G (x )=n +1n cos 1nx ⋅(-sin x )-n -1n⋅2cos x ⋅(-sin x )=sin x n (2n -2)cos x -(n +1)cos 1n x =2n -2n ⋅sin x cos x -n +12n -2cos 1n x=2n -2n ⋅sin x ⋅cos 1n x cos n -1n x -n +12n -2，由n >1,x ∈0,π2 ，得2n -2n⋅sin x ⋅cos 1nx >0，当n +12n -2≥1时，即n ≤3时，G (x )<0，则函数G (x )在0,π2上单调递减，则有G (x )<G (0)=0，即F (x )<0，因此函数F (x )在0,π2 上单调递减，有F (x )<F (0)=0，即g (x )>0，当n +12n -2<1时，即n >3时，存在一个x 0∈0,π2 ，使得cos n -1n x 0=n +12n -2，且当x ∈(0,x 0)时，G (x )>0，即G (x )在(0,x 0)上单调递增，且G (x )>G (0)=0，则F (x )>0，于是F (x )在(0,x 0)上单调递增，因此F (x )>F (0)=0，即sin xn cos x<x ，与g (x )>0矛盾，所以n 的最大值为3.【点睛】方法点睛：对于利用导数研究不等式的恒成立与有解问题的求解策略：①通常要构造新函数，利用导数研究函数的单调性，求出最值，从而求出参数的取值范围；②利用可分离变量，构造新函数，直接把问题转化为函数的最值问题．③根据恒成立或有解求解参数的取值时，一般涉及分离参数法，但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况，进行求解，若参变分离不易求解问题，就要考虑利用分类讨论法和放缩法，注意恒成立与存在性问题的区别．9(2024·湖北·模拟预测)已知函数f x =ax 2-x +ln x +1 ，a ∈R ，(1)若对定义域内任意非零实数x 1，x 2，均有f x 1 f x 2x 1x 2>0，求a ；(2)记t n =1+12+⋅⋅⋅+1n ，证明：t n -56<ln n +1 <t n ．【答案】(1)a =12(2)证明见解析【分析】(1)求导可得f 0 =0，再分a ≤0与a >0两种情况分析原函数的单调性，当a >0时分析极值点的正负与原函数的正负区间，从而确定a 的值；(2)由(1)问的结论可知，1n -12n2<ln 1n +1 <1n ，再累加结合放缩方法证明即可.【详解】(1)f x 的定义域为-1,+∞ ，且f 0 =0；f x =2ax -1+1x +1=2ax -x x +1=x 2a -1x +1，因此f 0 =0；i.a ≤0时，2a -1x +1<0，则此时令f x >0有x ∈-1,0 ，令f x <0有x ∈0,+∞ ，则f x 在-1,0 上单调递增，0,+∞ 上单调递减，又f 0 =0，于是f x ≤0，此时令x 1x 2<0，有f x 1 f x 2x 1x 2<0，不符合题意；ii .a >0时，f x 有零点0和x 0=12a-1，若x 0<0，即a >12，此时令f x <0有x ∈x 0,0 ，f x 在x 0,0 上单调递减，又f 0 =0，则f x 0 >0，令x 1>0，x 2=x 0，有f x 1 f x 2x 1x 2<0，不符合题意；若x 0>0，即0<a <12，此时令f x <0有x ∈0,x 0 ，f x 在0,x 0 上单调递减，又f 0 =0，则f x 0 <0，令-1<x 1<0,x 2=x 0，有f x 1 f x 2x 1x 2<0，不符合题意；若x 0=0，即a =12，此时fx =x 2x +1>0，f x 在-1,+∞ 上单调递增，又f 0 =0，则x >0时f x >0，x <0时f x <0；则x ≠0时f x x >0，也即对x 1x 2≠0，f x 1 f x 2x 1x 2>0，综上，a =12(2)证：由(1)问的结论可知，a =0时，f x =-x +ln x +1 ≤0；且a =12时x >0，f x =12x 2-x +ln x +1 >0；则x>0时，x-12x2<ln x+1<x，令x=1n，有1n-12n2<ln1n+1<1n，即1n-12n2<ln n+1-ln n<1n，于是1n-1-12n-12<ln n-ln n-1<1n-11-12<ln2<1将上述n个式子相加，t n-121+122+⋅⋅⋅+1n2<ln n+1<t n；欲证t n-56<ln n+1<t n，只需证t n-56<t n-121+122+⋅⋅⋅+1n2，只需证1+122+⋅⋅⋅+1n2<53；因为1n2=44n2<44n2-1=212n-1-12n+1，所以1+122+⋅⋅⋅+1n2<1+213-15+15-17+⋅⋅⋅+12n-1-12n+1=53-22n+1<53，得证：于是得证t n-56<ln n+1<t n.【点睛】方法点睛：(1)此题考导数与函数的综合应用，找到合适的分类标准，设极值点，并确定函数正负区间是解此题的关键；(2)对累加结构的不等式证明，一般需要应用前问的结论，取特定参数值，得出不等式累加证明，遇到不能累加的数列结构，需要进行放缩证明.10(2024·湖南·一模)已知函数f x =sin x-ax⋅cos x,a∈R．(1)当a=1时，求函数f x 在x=π2处的切线方程；(2)x∈0,π2时；(ⅰ)若f x +sin2x>0，求a的取值范围；(ⅱ)证明：sin2x⋅tan x>x3．【答案】(1)πx-2y+2-π22=0.(2)(ⅰ)a≤3(ⅱ)证明见解析【分析】(1)令a=1时，利用导数的几何意义求出斜率，进行计算求出切线方程即可.(2)(ⅰ)设g(x)=2sin x+tan x-ax,x∈0,π2,由g x >0得a≤3，再证明此时满足g x >0.(ⅱ)根据(ⅰ)结论判断出F x =sin2x⋅tan x-x3在0,π2上单调递增，∴F(x)>F(0)=0,即sin2x tan x >x3.【详解】(1)当a=1时，f(x)=sin x-x⋅cos x,f (x)=cos x-(cos x-x⋅sin x)=x⋅sin x,fπ2=π2,fπ2=1.所以切线方程为：y-1=π2x-π2,即πx-2y+2-π22=0.(2)(ⅰ)f(x)+sin2x=sin x-ax⋅cos x+sin2x>0,即tan x-ax+2sin x>0,x∈0,π2，设g(x)=2sin x+tan x-ax,x∈0,π2,g (x )=2cos x +1cos 2x -a =1cos 2x(2cos 3x -a cos 2x +1).又∵g (0)=0,g (0)=3-a ,∴g (0)=3-a ≥0是g (x )>0的一个必要条件，即a ≤3.下证a ≤3时，满足g (x )=2sin x +tan x -ax >0,x ∈0,π2,又g (x )≥1cos 2x(2cos 3x -3cos 2x +1)，设(t )=2t 3-3t 2+1,t ∈(0,1),h (t )=6t 2-6t =6t (t -1)<0,h (t )在(0,1)上单调递减，所以h (t )>h (1)=0，又x ∈0,π2 ,cos x ∈(0,1),∴g (x )>0,即g (x )在0,π2 单调递增.∴x ∈0,π2时，g (x )>g (0)=0；下面证明a >3时不满足g (x )=2sin x +tan x -ax >0,x ∈0,π2,，g (x )=2cos x +1cos 2x-a ，令h (x )=g (x )=2cos x +1cos 2x -a ，则h (x )=-2sin x +2sin x cos 3x =2sin x 1cos 3x-1，∵x ∈0,π2 ,∴sin x >0,1cos 3x-1>0，∴h (x )>0,∴h (x )=g (x )在0,π2为增函数，令x 0满足x 0∈0,π2,cos x 0=1a ，则g x 0 =2cos x 0+1cos 2x 0-a =2cos x 0+a -a >0，又g (0)=3-a <0,∴∃x 1∈0,x 0 ,使得g x 1 =0，当x ∈0,x 1 时，g (x )<g x 1 =0，∴此时g (x )在0,x 1 为减函数，∴当x ∈0,x 1 时，g (x )<g (0)=0，∴a >3时，不满足g (x )≥0恒成立.综上a ≤3.(ⅱ)设F (x )=sin 2x ⋅tan x -x 3,x ∈0,π2 ,F (x )=2sin x ⋅cos x ⋅tan x +sin 2x ⋅1cos 2x-3x 2=2sin 2x +tan 2x -3x 2=2(sin x -x )2+(tan x -x )2+2(2sin x +tan x )x -2x 2-x 2-3x 2.由(ⅰ)知2sin x +tan x >3x ,∴F (x )>0+0+2x ⋅3x -6x 2=0,，F x 在0,π2上单调递增，∴F (x )>F (0)=0,即sin 2x tan x >x 3.【点睛】关键点点睛：本题考查导数，解题关键是进行必要性探路，然后证明充分性，得到所要求的参数范围即可．11(2024·全国·模拟预测)已知函数f (x )=ln (1+x )-11+x．(1)求曲线y =f (x )在(0,f (0))处的切线方程；(2)若x ∈(-1,π)，讨论曲线y =f (x )与曲线y =-2cos x 的交点个数．【答案】(1)y =32x -1；(2)2．【分析】(1)求导，即可根据点斜式求解方程，(2)求导，分类讨论求解函数的单调性，结合零点存在性定理，即可根据函数的单调性，结合最值求解.【详解】(1)依题意，f x =11+x +121+x 32，故f 0 =32，而f 0 =-1，故所求切线方程为y +1=32x ，即y =32x -1．(2)令ln 1+x -11+x =-2cos x ，故ln 1+x +2cos x -11+x=0，令g x =ln 1+x +2cos x -11+x ，g x =11+x -2sin x +121+x -32，令h x =g x =11+x -2sin x +121+x -32，hx =-11+x2-2cos x -341+x -52．①当x ∈-1,π2时，cos x ≥0,1+x 2>0,1+x-52>0，∴h x <0,∴h x 在-1,π2上为减函数，即gx 在-1,π2 上为减函数，又g 0 =1+12>0,g1 =12-2sin1+12⋅2-32<12-2⋅sin1+12<1-2×12=0，∴g x 在0,1 上有唯一的零点，设为x 0，即g x 0 =00<x 0<1 ．∴g x 在-1,x 0 上为增函数，在x 0,π2上为减函数．又g 0 =2-1>0,g -π4 =ln 1-π4 +2cos -π4 -11-π4=ln 1-π4+2-11-π4<0,g π2=ln 1+π2 -11+π2>0，∴g x 在-1,x 0 上有且只有一个零点，在x 0,π2上无零点；②当x ∈π2,5π6 时，g x <11+x -1+121+x-32<0,g x 单调递减，又g π2 >0,g 5π6 =ln 1+5π6 -3-1+5π6-12<ln4-3<0，∴g x 在π2,5π6内恰有一零点；③当x ∈5π6,π 时，hx =-11+x2-2cos x -341+x -52为增函数，∴hx =h 5π6 =-11+5π62+1-34⋅1+5π6-52>0，∴g x 单调递增，又g π >0,g 5π6 <0，所以存在唯一x 0∈5π6,π ,g x 0 =0，当x ∈5π6,x 0 时，g x <0,g x 递减；当x ∈x 0,π 时，g x >0,g x 递增，g x ≤max g 5π6 ,g π <0，∴g x 在5π6,π内无零点．综上所述，曲线y =f x 与曲线y =-2cos x 的交点个数为2．【点睛】方法点睛：本题考查了导数的综合运用，求某点处的切线方程较为简单，利用导数求单调性时，如果求导后的正负不容易辨别，往往可以将导函数的一部分抽离出来，构造新的函数，利用导数研究其单调性，进而可判断原函数的单调性.在证明不等式时，常采用两种思路：求直接求最值和等价转化.无论是那种方式，都要敢于构造函数，构造有效的函数往往是解题的关键.12(2024·广东佛山·二模)已知f x =-12e 2x +4e x -ax -5.(1)当a =3时，求f x 的单调区间；(2)若f x 有两个极值点x 1，x 2，证明：f x 1 +f x 2 +x 1+x 2<0.【答案】(1)答案见解析(2)证明见解析【分析】(1)求导后，借助导数的正负即可得原函数的单调性；(2)借助换元法，令t =e x ，t 1=e x 1，t 2=e x 2，可得t 1、t 2是方程t 2-4t +a =0的两个正根，借助韦达定理可得t 1+t 2=4，t 1t 2=a ，即可用t 1、t 2表示f x 1 +f x 2 +x 1+x 2，进而用a 表示f x 1 +f x 2 +x 1+x 2，构造相关函数后借助导数研究其最大值即可得.【详解】(1)当a =3时，f x =-12e 2x +4e x -3x -5，f x =-e 2x +4e x -3=-e x -1 e x -3 ，则当e x ∈0,1 ∪3,+∞ ，即x ∈-∞,0 ∪ln3,+∞ 时，f x <0，当e x ∈1,3 ，即x ∈0,ln3 时，f x >0，故f x 的单调递减区间为-∞,0 、ln3,+∞ ，单调递增区间为0,ln3 ；(2)f x =-e 2x +4e x -a ，令t =e x ，即f x =-t 2+4t -a ，令t 1=e x 1，t 2=e x 2，则t 1、t 2是方程t 2-4t +a =0的两个正根，则Δ=-4 2-4a =16-4a >0，即a <4，有t 1+t 2=4，t 1t 2=a >0，即0<a <4，则f x 1 +f x 2 +x 1+x 2=-12e 2x 1+4e x 1-ax 1-5-12e 2x2+4e x 2-ax 2-5+x 1+x 2=-12t 21+t 22 +4t 1+t 2 -a -1 ln t 1+ln t 2 -10=-12t 1+t 2 2-2t 1t 2 +4t 1+t 2 -a -1 ln t 1t 2-10=-1216-2a +16-a -1 ln a -10=a -a -1 ln a -2，要证f x 1 +f x 2 +x 1+x 2<0，即证a -a -1 ln a -2<00<a <4 ，令g x =x -x -1 ln x -20<x <4 ，则g x =1-ln x +x -1x =1x-ln x ，令h x =1x -ln x 0<x <4 ，则h x =-1x 2-1x <0，则g x 在0,4 上单调递减，又g 1 =11-ln1=1，g 2 =12-ln2<0，故存在x 0∈1,2 ，使g x 0 =1x 0-ln x 0=0，即1x 0=ln x 0，则当x ∈0,x 0 时，g x >0，当x ∈x 0,4 时，g x <0，故g x 在0,x 0 上单调递增，g x 在x 0,4 上单调递减，则g x ≤g x 0 =x 0-x 0-1 ln x 0-2=x 0-x 0-1 ×1x 0-2=x 0+1x 0-3，又x 0∈1,2 ，则x 0+1x 0∈2,52 ，故g x 0 =x 0+1x 0-3<0，即g x <0，即f x 1 +f x 2 +x 1+x 2<0.【点睛】关键点点睛：本题关键点在于借助换元法，令t =e x ，t 1=e x 1，t 2=e x 2，从而可结合韦达定理得t 1、t 2的关系，即可用a 表示f x 1 +f x 2 +x 1+x 2，构造相关函数后借助导数研究其最大值即可得.13(2024·广东广州·模拟预测)已知函数f x =x e x -kx ,k ∈R .(1)当k =0时，求函数f x 的极值；(2)若函数f x 在0,+∞ 上仅有两个零点，求实数k 的取值范围.【答案】(1)极小值为-1e，无极大值(2)e ,+∞【分析】(1)求出导函数，然后列表求出函数的单调区间，根据极值定义即可求解；(2)把原函数有两个零点转化为g x =e x -kx 在0,+∞ 上仅有两个零点，分类讨论，利用导数研究函数的单调性，列不等式求解即可.【详解】(1)当k =0时，f x =xe x (x ∈R )，所以f x =1+x e x ，令f x =0，则x =-1，x -∞,-1-1-1,+∞f x -0+f x单调递减极小值单调递增所以f (x )min =f -1 =-e -1=-1e，所以f x 的极小值为-1e，无极大值.(2)函数f x =x e x -kx 在0,+∞ 上仅有两个零点，令g x =e x -kx ，则问题等价于g x 在0,+∞ 上仅有两个零点，易知g x =e x -k ，因为x ∈0,+∞ ，所以e x >1.①当k ∈-∞,1 时，g x >0在0,+∞ 上恒成立，所以g x 在0,+∞ 上单调递增，所以g x >g 0 =1，所以g x 在0,+∞ 上没有零点，不符合题意；②当k ∈1,+∞ 时，令g x =0，得x =ln k ，所以在0,ln k 上，g x <0，在ln k ,+∞ 上，g x >0，所以g x 在0,ln k 上单调递减，在(ln k ,+∞)上单调递增，所以g x 的最小值为g ln k =k -k ⋅ln k .因为g x 在0,+∞ 上有两个零点，所以g ln k =k -k ⋅ln k <0，所以k >e.因为g 0 =1>0,g ln k 2 =k 2-k ⋅ln k 2=k k -2ln k ，令h x =x -2ln x ，则h x =1-2x =x -2x，所以在0,2 上，h x <0，在2,+∞ 上，h x >0，所以h x 在0,2 上单调递减，在2,+∞ 上单调递增，所以h x ≥2-2ln2=ln e 2-ln4>0，所以g ln k 2 =k k -2ln k >0，所以当k >e 时，g x 在0,ln k 和(ln k ,+∞)内各有一个零点，即当k >e 时，g x 在0,+∞ 上仅有两个零点.综上，实数k 的取值范围是e ,+∞ .【点睛】方法点睛：求解函数单调区间的步骤：(1)确定f x 的定义域.(2)计算导数f x .(3)求出f x =0的根.(4)用f x =0的根将f x 的定义域分成若干个区间，判断这若干个区间内f x 的符号，进而确定f x 的单调区间.f x >0，则f x 在对应区间上单调递增，对应区间为增区间；f x <0，则f x 在对应区间上单调递减，对应区间为减区间.如果导函数含有参数，那么需要对参数进行分类讨论，分类讨论要做到不重不漏.14(2024·江苏南通·二模)已知函数f x =ln x -ax ，g x =2ax，a ≠0.(1)求函数f x 的单调区间；(2)若a >0且f x ≤g x 恒成立，求a 的最小值.【答案】(1)答案见解析(2)2e 3.【分析】(1)求导后，利用导数与函数单调性的关系，对a >0与a <0分类讨论即可得；(2)结合函数的单调性求出函数的最值，即可得解.【详解】(1)f x =1x -a =1-axx(a ≠0)，当a <0时，由于x >0，所以f x >0恒成立，从而f x 在0,+∞ 上递增；当a >0时，0<x <1a ，f x >0；x >1a ，fx <0，从而f x 在0,1a 上递增，在1a,+∞ 递减；综上，当a <0时，f x 的单调递增区间为0,+∞ ，没有单调递减区间；当a >0时，f x 的单调递增区间为0,1a ，单调递减区间为1a ,+∞ .(2)令h x =f x -g x =ln x -ax -2ax，要使f x ≤g x 恒成立，只要使h x ≤0恒成立，也只要使h x max ≤0.h x =1x -a +2ax 2=-ax +1 ax -2 ax 2，由于a >0，x >0，所以ax +1>0恒成立，当0<x <2a 时，h x >0，当2a<x <+∞时，h x <0，所以h x max =h 2a =ln 2a -3≤0，解得：a ≥2e 3，所以a 的最小值为2e3.15(2024·山东济南·二模)已知函数f x =ax 2-ln x -1,g x =xe x -ax 2a ∈R .(1)讨论f x 的单调性；(2)证明：f x +g x ≥x .【答案】(1)答案见详解(2)证明见详解【分析】(1)求导可得fx =2ax 2-1x，分a ≤0和a >0两种情况，结合导函数的符号判断原函数单调性；(2)构建F x =f x +g x -x ,x >0，h x =e x -1x,x >0，根据单调性以及零点存在性定理分析h x 的零点和符号，进而可得F x 的单调性和最值，结合零点代换分析证明.【详解】(1)由题意可得：f x 的定义域为0,+∞ ，fx =2ax -1x =2ax 2-1x，当a ≤0时，则2ax 2-1<0在0,+∞ 上恒成立，可知f x 在0,+∞ 上单调递减；当a >0时，令f x >0，解得x >12a；令f x <0，解得0<x <12a；可知f x 在0,12a 上单调递减，在12a,+∞ 上单调递增；综上所述：当a ≤0时，f x 在0,+∞ 上单调递减；当a >0时，f x 在0,12a 上单调递减，在12a,+∞ 上单调递增.(2)构建F x =f x +g x -x =xe x -ln x -x -1,x >0，则F x =x +1 e x -1x -1=x +1 e x -1x，由x >0可知x +1>0，构建h x =e x -1x ,x >0，因为y =e x ,y =-1x在0,+∞ 上单调递增，则h x 在0,+∞ 上单调递增，且h 12=e -20,h 1 =e -1 0，可知h x 在0,+∞ 上存在唯一零点x 0∈12,1 ，当0<x <x 0，则h x <0，即Fx <0；当x >x 0，则h x >0，即F x >0；可知F x 在0,x 0 上单调递减，在x 0,+∞ 上单调递增，则F x ≥F x 0 =x 0e x 0-ln x 0-x 0-1，又因为e x 0-1x 0=0，则e x 0=1x 0,x 0=e -x 0，x 0∈12,1 ，可得F x 0 =x 0×1x 0-ln e -x-x 0-1=0，即F x ≥0，所以f x +g x ≥x .16(2024·福建·模拟预测)已知函数f (x )=a ln x -bx 在1,f 1 处的切线在y 轴上的截距为-2．(1)求a 的值；(2)若f x 有且仅有两个零点，求b 的取值范围．【答案】(1)2(2)b ∈0,2e 【分析】(1)借助导数的几何意义计算即可得；(2)借助函数与方程的关系，可将f x 有且仅有两个零点转化为方程b =2ln xx有两个根，构造对应函数并借助导数研究单调性及值域即可得.【详解】(1)f (x )=ax-b ，f 1 =a -b ，f (1)=a ×0-b =-b ，则函数f (x )=a ln x -bx 在1,f 1 处的切线为：y +b =a -b x -1 ，即y =a -b x -a ，令x =0，则有y =-a =-2，即a =2；(2)由a =2，即f (x )=2ln x -bx ，若f x 有且仅有两个零点，则方程2ln x-bx=0有两个根，即方程b=2ln xx有两个根，令g x =2ln xx，则gx =21-ln xx2，则当x∈0,e时，g x >0，则当x∈e,+∞时，g x <0，故g x 在0,e上单调递增，在e,+∞上单调递减，故g x ≤g e =2ln ee=2e，又x→0时，g x →-∞，x→+∞时，g x →0，故当b∈0,2 e时，方程b=2ln x x有两个根，即f x 有且仅有两个零点.17(2024·浙江杭州·二模)已知函数f x =a ln x+2-12x2a∈R．(1)讨论函数f x 的单调性；(2)若函数f x 有两个极值点，(ⅰ)求实数a的取值范围；(ⅱ)证明：函数f x 有且只有一个零点．【答案】(1)答案见解析；(2)(ⅰ)-1<a<0；(ⅱ)证明见解析【分析】(1)求出函数的导函数，再分a≤-1、-1<a<0、a≥0三种情况，分别求出函数的单调区间；(2)(ⅰ)由(1)直接解得；(ⅱ)结合函数的最值与零点存在性定理证明即可.【详解】(1)函数f x =a ln x+2-12x2a∈R的定义域为-2,+∞，且f x =ax+2-x=-x+12+a+1x+2，当a≤-1时，f x ≤0恒成立，所以f x 在-2,+∞单调递减；当-1<a<0时，令f x =0，即-x+12+a+1=0，解得x1=-a+1-1，x2=a+1-1，因为-1<a<0，所以0<a+1<1，则-2<-a+1-1<-1，所以当x∈-2,-a+1-1时f x <0，当x∈-a+1-1,a+1-1时f x >0，当x∈a+1-1,+∞时f x <0，所以f x 在-2,-a+1-1上单调递减，在-a+1-1,a+1-1上单调递增，在a+1-1,+∞上单调递减；当a≥0时，此时-a+1-1≤-2，所以x∈-2,a+1-1时f x >0，当x∈a+1-1,+∞时f x <0，所以f x 在-2,a+1-1上单调递增，在a+1-1,+∞上单调递减．综上可得：当a≤-1时f x 在-2,+∞单调递减；当-1<a<0时f x 在-2,-a+1-1上单调递减，在-a+1-1,a+1-1上单调递增，在a+1-1,+∞上单调递减；当a≥0时f x 在-2,a+1-1上单调递增，在a+1-1,+∞上单调递减．(2)(ⅰ)由(1)可知-1<a<0．(ⅱ)由(1)f x 在-2,-a+1-1上单调递减，在-a+1-1,a+1-1上单调递增，在a+1-1,+∞上单调递减，所以f x 在x=a+1-1处取得极大值，在x=-a+1-1处取得极小值，又-1<a<0，所以0<a+1<1，则1<a+1+1<2，又f x极大值=f a+1-1=a ln a+1+1-12a+1-12<0，又f-a+1-1<f a+1-1<0，所以f x 在-a+1-1,+∞上没有零点，又-1<a<0，则4a<-4，则0<e4a<e-4，-2<e4a-2<e-4-2，则0<e 4a-22<4，所以f e 4a-2=4-12e4a-22>0，所以f x 在-2,-a+1-1上存在一个零点，综上可得函数f x 有且只有一个零点．18(2024·河北沧州·模拟预测)已知函数f(x)=ln x-ax+1，a∈R．(1)讨论f x 的单调性；(2)若∀x>0，f x ≤xe2x-2ax恒成立，求实数a的取值范围．【答案】(1)答案见解析(2)-∞,2．【分析】(1)利用导数分类讨论判断函数f x 的单调性，即可求解；(2)先利用导数证明不等式e x≥x+1，分离变量可得a≤e2x-ln x+1x恒成立，进而e 2x-ln x+1x≥2x+ln x+1-(ln x+1)x=2，即可求解.【详解】(1)函数f x =ln x-ax+1，a∈R的定义域为0,+∞，且f (x)=1x-a．当a≤0时，∀x∈0,+∞，f (x)=1x-a≥0恒成立，此时f x 在区间0,+∞上单调递增；当a>0时，令f (x)=1x-a=1-axx=0，解得x=1a，当x∈0,1 a时，f x >0，f x 在区间0,1a上单调递增，当x∈1a,+∞时，f x <0，f x 在区间1a,+∞上单调递减．综上所述，当a≤0时，f x 在区间0,+∞上单调递增；当a>0时，f x 在区间0,1 a上单调递增，在区间1a,+∞上单调递减．(2)设g x =e x-x-1，则g x =e x-1，在区间(-∞,0)上，g x <0，g x 单调递减，在区间0,+∞上，g x >0，g x 单调递增，所以g x ≥g0 =e0-0-1=0，所以e x≥x+1(当且仅当x=0时等号成立)．依题意，∀x>0，f x ≤xe2x-2ax恒成立，即a≤e2x-ln x+1x恒成立，而e2x-ln x+1x=xe2x-(ln x+1)x=e2x+ln x-(ln x+1)x≥2x+ln x+1-(ln x+1)x=2，当且仅当2x+ln x=0时等号成立．因为函数h x =2x+ln x在0,+∞上单调递增，h1e=2e-1<0，h(1)=2>0，所以存在x0∈1e,1，使得2x0+ln x0=0成立．所以a ≤e 2x -ln x +1xmin =2，即a 的取值范围是-∞,2 ．【点睛】方法点睛：利用导数证明不等式的恒成立问题的求解策略：形如f x ≥g x 的恒成立的求解策略：1、构造函数法：令F x =f x -g x ，利用导数求得函数F x 的单调性与最小值，只需F x min ≥0恒成立即可；2、参数分离法：转化为a ≥φx 或a ≤φx 恒成立，即a ≥φx max 或a ≤φx min 恒成立，只需利用导数求得函数φx 的单调性与最值即可；3，数形结合法：结合函数y =f x 的图象在y =g x 的图象的上方(或下方)，进而得到不等式恒成立.19(2024·广东·二模)已知f x =12ax 2+1-2a x -2ln x ,a >0.(1)求f x 的单调区间；(2)函数f x 的图象上是否存在两点A x 1,y 1 ,B x 2,y 2 (其中x 1≠x 2)，使得直线AB 与函数f x 的图象在x 0=x 1+x22处的切线平行？若存在，请求出直线AB ；若不存在，请说明理由.【答案】(1)f (x )在(0,2)上单调递减，在(2,+∞)上单调递增.(2)不存在，理由见解析【分析】(1)求出导函数，根据导函数的正负来确定函数的单调区间；(2)求出直线AB 的斜率，再求出f (x 0)，从而得到x 1,x 2的等式，再进行换元和求导，即可解出答案.【详解】(1)由题可得f(x )=ax +1-2a -2x =ax 2+(1-2a )x -2x =(ax +1)(x -2)x(x >0)因为a >0，所以ax +1>0，所以当x ∈(0,2)时，f (x )<0，f (x )在(0,2)上单调递减，当x ∈(2,+∞)时，f (x )>0，f (x )在(2,+∞)上单调递增.综上，f (x )在(0,2)上单调递减，在(2,+∞)上单调递增.(2)由题意得，斜率k =y 2-y 1x 2-x 1=12ax 22+(1-2a )x 2-2ln x 2 -12ax 21+(1-2a )x 1-2ln x 1 x 2-x 1=12a (x 22-x 21)+(1-2a )(x 2-x 1)-2ln x 2x 1x 2-x 1=a 2(x 1+x 2)+1-2a -2ln x2x 1x 2-x 1，f x 1+x 22 =a (x 1+x 2)2+1-2a -4x 1+x 2,由k =f x 1+x22 得，ln x2x 1x 2-x 1=2x 1+x 2，即ln x 2x 1=2(x 2-x 1)x 1+x 2，即ln x 2x 1-2x2x 1-1 x 2x1+1=0令t =x 2x 1，不妨设x 2>x 1，则t >1，记g (t )=ln t -2(t -1)t +1=ln t +4t +1-2(t >1)所以g(t )=1t -4t +1 2=t -1 2t t +1 2>0，所以g (t )在(1,+∞)上是增函数，所以g (t )>g (1)=0，所以方程g (t )=0无解，则满足条件的两点A ,B 不存在.20(2024·广东深圳·二模)已知函数f x =ax +1 e x ，f x 是f x 的导函数，且f x -f x =2e x ．(1)若曲线y =f x 在x =0处的切线为y =kx +b ，求k ，b 的值；(2)在(1)的条件下，证明：f x ≥kx +b ．【答案】(1)k =3，b =1；(2)证明见解析.【分析】(1)根据题意，求导可得a 的值，再由导数意义可求切线，得到答案；(2)设函数g x =2x +1 e x -3x -1，利用导数研究函数g (x )的单调性从而求出最小值大于0，可得证.【详解】(1)因为f x =ax +1 e x ，所以f x =ax +a +1 e x ，因为f x -f x =2e x ，所以a =2．则曲线y =f (x )在点x =0处的切线斜率为f 0 =3．又因为f 0 =1，所以曲线y =f (x )在点x =0处的切线方程为y =3x +1，即得k =3，b =1．(2)设函数g x =2x +1 e x -3x -1，x ∈R ，则g x =2x +3 e x -3，设h x =g x ，则h x =e x 2x +5 ，所以，当x >-52时，h x >0，g x 单调递增．又因为g0 =0，所以，x >0时，g x >0，g x 单调递增；-52<x <0时，g x <0，g x 单调递减．又当x ≤-52时，g x =2x +3 e x -3<0，综上g x 在-∞,0 上单调递减，在0,+∞ 上单调递增，所以当x =0时，g x 取得最小值g 0 =0，即2x +1 e x -3x -1≥0，所以，当x ∈R 时，f x ≥3x +1．21(2024·辽宁·二模)已知函数f x =ax 2-ax -ln x .(1)若曲线y =f x 在x =1处的切线方程为y =mx +2，求实数a ,m 的值；(2)若对于任意x ≥1，f x +ax ≥a 恒成立，求实数a 的取值范围．【答案】(1)a =-1，m =-2(2)12,+∞ 【分析】(1)根据导数几何意义和切线方程，可直接构造方程组求得结果；(2)构造函数g x =ax 2-ln x -a x ≥1 ，将问题转化为g x ≥0恒成立；求导后，分别在a ≤0、a ≥12和0<a <12的情况下，结合单调性和最值求得符合题意的范围.【详解】(1)∵f x =2ax -a -1x，∴f 1 =2a -a -1=a -1，∵y =f x 在x =1处的切线为y =mx +2，∴f 1 =a -1=mf 1 =0=m +2 ，解得：a =-1，m =-2.(2)由f x +ax ≥a 得：ax 2-ln x -a ≥0，令g x =ax 2-ln x -a x ≥1 ，则当x ≥1时，g x ≥0恒成立；。

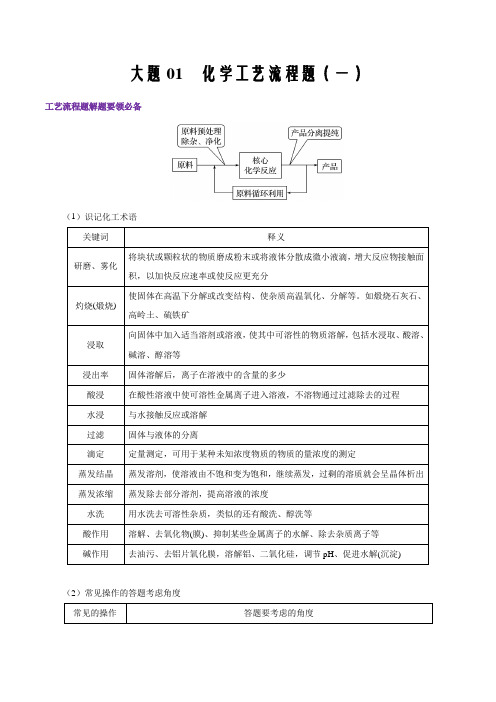
大题01 化学工艺流程题（一）工艺流程题解题要领必备（1）识记化工术语关键词释义将块状或颗粒状的物质磨成粉末或将液体分散成微小液滴，增大反应物接触面研磨、雾化积，以加快反应速率或使反应更充分使固体在高温下分解或改变结构、使杂质高温氧化、分解等。

如煅烧石灰石、灼烧(煅烧)高岭土、硫铁矿向固体中加入适当溶剂或溶液，使其中可溶性的物质溶解，包括水浸取、酸溶、浸取碱溶、醇溶等浸出率固体溶解后，离子在溶液中的含量的多少酸浸在酸性溶液中使可溶性金属离子进入溶液，不溶物通过过滤除去的过程水浸与水接触反应或溶解过滤固体与液体的分离滴定定量测定，可用于某种未知浓度物质的物质的量浓度的测定蒸发结晶蒸发溶剂，使溶液由不饱和变为饱和，继续蒸发，过剩的溶质就会呈晶体析出蒸发浓缩蒸发除去部分溶剂，提高溶液的浓度水洗用水洗去可溶性杂质，类似的还有酸洗、醇洗等酸作用溶解、去氧化物(膜)、抑制某些金属离子的水解、除去杂质离子等碱作用去油污、去铝片氧化膜，溶解铝、二氧化硅，调节pH、促进水解(沉淀)（2）常见操作的答题考虑角度常见的操作答题要考虑的角度1．废旧锂离子电池经处理得到的正极活性粉体中含有Li 2O 、NiO 、Co 2O 3、MnO 2、Fe 、C 、Al 、Cu 等。

采用以下工艺流程可从废旧锂离子电池中分离回收钴、镍、锰，制备正极材料的前驱体(NiCO 3·CoCO 3·MnCO 3)。

+回答下列问题：（1）“酸浸”温度为85℃，粉体中的钴(以Co 2O 3表示)还原浸出的化学方程式为_______，H 2O 2的用量比理论用量多一倍的原因是_______。

（2）“除铁”时需将溶液的pH 调至3左右，加入的化合物X 是________填化学式) （3）“除铜”时获得萃余液的操作名称是_______。

（4）“除铝”时反应的离子方程式为_______。

萃余液中Co 2+的浓度为0.33mol·L -1，通过计算说明，常温下除铝控制溶液pH 为4.5，是否造成Co 的损失_______？(列出算式并给出结论)已知：(K sp [Co(OH)2]=5.9×10-15)（5）从滤液④中可提取_______(任写一种)用作_______。

高一高考数学试题及答案一、选择题（本大题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 下列函数中，为奇函数的是：A. y = x^2B. y = |x|C. y = x^3D. y = sin(x)2. 若方程x^2 - 5x + 6 = 0的两个根为α和β，则α+β的值为：A. 1B. 2C. 5D. 63. 已知数列{an}的通项公式为an = 2n - 1，那么数列的前5项和S5为：A. 5B. 10C. 15D. 204. 函数f(x) = 2x + 3在区间[-1, 2]上的最大值为：A. 1B. 5C. 7D. 95. 已知集合A = {1, 2, 3}，集合B = {2, 3, 4}，则A∩B为：A. {1}B. {2, 3}C. {3, 4}D. {1, 2, 3, 4}6. 直线y = 2x + 1与直线y = -x + 4的交点坐标为：A. (1, 3)B. (3, 1)C. (-1, 3)D. (-3, 1)7. 圆x^2 + y^2 = 4的圆心坐标为：A. (0, 0)B. (2, 2)C. (-2, -2)D. (1, 1)8. 函数f(x) = x^2 - 4x + 3的最小值为：A. -1B. 0C. 1D. 39. 已知向量a = (3, -4)，向量b = (-2, 6)，则向量a与向量b的夹角θ满足：A. cosθ = 1/5B. cosθ = 1/3C. cosθ = 3/5D. cosθ = √2/210. 抛物线y = x^2 - 2x - 3与x轴的交点个数为：A. 0B. 1C. 2D. 3二、填空题（本大题共5小题，每小题4分，共20分。

请将答案填写在答题卡上相应的位置。

）11. 已知等差数列的前三项依次为3，7，11，则该数列的第五项为______。

12. 函数f(x) = x^3 - 3x^2 + 2的导数f'(x)为______。

2023年上海高考数学真题及参考答案一、填空题（本大题共有12题，满分54分，第1~6题每题4分，第7~12题每题5分）考生应在答题纸的相应位置填写结果.1.不等式12<-x 的解集为.2.已知()3,2-=a ，()2,1=b ，求=⋅b a .3.已知{}n a 为等比数列，且31=a ，2=q ，求=6S .4.已知3tan =α，求=α2tan .5.已知()⎩⎨⎧≤>=0,10,2x x x f x ，则()x f 的值域是.6.已知当i z +=1，则=⋅-z i 1.7.已知0422=--+m y y x 的面积为π，求=m .8.在ABC ∆中，6,5,4===c b a ，求=A sin .9.国内生产总值（GDP ）是衡量地区经济状况的最佳指标，根据统计数据显示，某市在2020年间经济高质量增长，GDP 稳步增长，第一季度和第四季度的GDP 分别为231和242，且四个季度GDP 的中位数与平均数相等，则2020年GDP 总额为.10.已知()()1001002210100100202320231x a x a x a a x x ++++=-++ ，其中R a a a ∈10021, ，若1000≤≤k 且N k ∈，当0<k a 时，k 的最大值时.11.公园修建斜坡，假设斜坡起点在水平面上，斜坡与水平面的夹角为θ，斜坡终点距离水平水平面的垂直高度为4米，游客每走一米消耗的体能为()θcos 025.1-，要使游客从斜坡底走到斜坡顶端所消耗的总体能最少，则=θ.12.空间内存在三点C B A 、、，满足1===BC AC AB ，在空间内取不同两点（不计顺序），使得这两点与C B A 、、可以组成正四棱锥，求方案数为.二、选择题（本题共4题，满分18分，13、14每题4分，15、16每题5分）每题有且只有一个正确选项，考生应在答题纸的相应位置，将代表正确选项的小方格涂黑.13.已知{}{}32,21，，==Q P ，若{}Q x P x x M ∉∈=且，则=M （）A .{}1B .{}2C .{}21，D .{}321，，14.根据身高和体重散点图，下列说法正确的是（）A .身高越高，体重越重B .身高越高，体重越轻C .身高与体重成正相关D .身高与体重成负相关15.设0>a ，函数x y sin =在区间[]a a 2,上的最小值为s ，在[]a a 3,2上的最小值为t ，当a 变化时，下列不可能的是（）A .0>s 且0>tB .0>s 且0<tC .0<s 且0<t D .0<s 且0>t 16.在平面上，若曲线Γ具有下列性质：存在点M ，使得对于任意点Γ∈P ，都有Γ∈Q 使得1=⋅QM PM .则称曲线Γ为“自相关曲线”.现有如下两个命题：（1）任意椭圆都是“自相关曲线”.（2）存在双曲线是“自相关曲线”.则下列正确的是（）A .（1）成立，（2）成立B .（1）成立，（2）不成立C .（1）不成立，（2）成立D .（1）不成立，（2）不成立三、解答题（本大题共有5题，满分78分）解答下列各题必须在答题纸的相应位置写出必要的步骤.17.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.直四棱柱1111D C B A ABCD -，CD AB ∥，AD AB ⊥，2=AB ，3=AD ，4=DC .（1）求证：111D DCC B A 面⊥（2）若四棱柱1111D C B A ABCD -体积为36，求二面角A BD A --1的大小.18.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.函数()()()R c a ax cx a x x f ∈++++=,132.（1）当0=a 时，是否存在实数c ，使得()x f 为奇函数（2）函数()x f 的图象过点()3,1，且()x f 的图象与x 轴负半轴有两个不同交点，求实数c 的值及实数a 的取值范围.19.（本题满分14分）本题共有3个小题，第1小题满分2分，第2小题满分6分，第3小题满分8分.21世纪汽车博览会在上海2023年6月7日在上海举行，下表为某汽车模型公司共有25个汽车模型，其外观和内饰的颜色分布如下表所示：（1）若小明从这些模型中随机拿一个模型，记事件A 为小明取到的模型为红色外观，事件B 取到模型有棕色内饰.求：()B P 、()A B P /，并据此判断事件A 和事件B 是否独立（2）该公司举行了一个抽奖活动，规定在一次抽奖中，每人可以一次性从这些模型中拿两个汽车模型，给出以下假设：假设1：拿到的两个模型会出现三种结果，即外观和内饰均为同色、外观内饰都异色、以及外观或内饰同色；假设2：按结果的可能性大小，概率越小奖项越高；假设3：奖金额为一等奖600元，二等奖300元，三等奖150元；请你分析奖项对应的结果，设X 为奖金额，写出X 的分布列并求出X 的数学期望.红色外观蓝色外观棕色内饰128米色内饰2320.（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分.已知抛物线x y 42=Γ：，A 为第一象限内Γ上的一点，设A 的纵坐为a （0>a ）.（1）若A 到Γ的准线距离为3，求a 的值；（2）若4=a ，B 为x 轴上的一点，且线段AB 的中点在Γ上，求点B 坐标和坐标原点O到AB 的距离；（3）直线3-=x l ：，P 是第一象限Γ上异于A 的动点，直线P A 交l 于Q ，点H 为点P 在l 上的投影，若点A 满足性质“当点P 变化时，4>HQ 恒成立”，求a 的取值范围.21.（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分.已知函数()x x f ln =，过函数上的点()()11,a f a 作()x f y =的切线交y 轴于()20a ，，02>a ，过函数上的点()()22,a f a 作()x f y =的切线交y 轴于()30a ，，以此类推，直至0≤m a 时则停止操作，得到数列{}n a ，*∈N n m ,，m n ≤<1.（1）证明：1ln 1-=+n n a a ；（2）试比较1+n a 与2-n a 的大小；（3）若正整数3≥k ，是否存在k 使得k a a a ,,21依次成等差数列？若存在，求出k 的所有取值；若不存在，试说明理由.参考答案一、填空题1.()3,1；解析：3112112<<-⇒<-<-⇒<-x x x2.4；解析：已知42312=⨯+⨯-=⋅b a 3.189；解析：18996482412636=+++++=S 4.43-；解析：43916tan 1tan 22tan 2-=-=-=ααα5.[)∞+，1；解析：当0>x 时，12>=xy ，当0≤x 时，1=y ，故值域为[)∞+，16.5；解析：()i i i z i -=+⨯-=⋅-2111，521=-=⋅-i z i 7.3-；解析：()4222+=-+m y x ，由题意14=+m ，解得3-=m 8.47；解析：436521636252cos 222=⨯⨯-+=-+=bc a c b A ，∴47sin =A 9.946；解析：d c b a <<<，232=a ，241=d ，473=+=+c b d a ，∴946=+++d c b a 10.49；解析：()0202312023100100100<-+=-kkkkkk C C a ，依题意k 为奇数，∴kk -<10020232023，k k -<100，解得50<k ，∴49max =k 11.4140arccos；解析：所消耗的总体力()θθθθsin cos 41.4sin cos 025.14-=-=y ，()0sin cos 1.44sin cos cos 41.4sin 4222=-=--='θθθθθθy ，解得4140cos =θ，∴4140arccos=θ12.9；解析：以A 为尖，若ABC 为正四棱锥的侧面，有两种情况，若ABC 为正四棱锥的对角面，有一种情况，共三种情况；同理，以C B ,为尖，也各有三种情况，∴共9种二、选择题15.解析：1=a 时，A 可能；5.1=a 时，B 可能；2=a 时，C 可能；D 选项，若0<S ，则π>a 2，若0>t ，则[]a a 3,2的区间长度π<a ，同时02sin >a 且03sin >a ，所以()π,02∈a 且()π,03∈a ，与前面的π>a 2矛盾，故D 不可能.16.解析：（1）∵椭圆是封闭的，∴总可以找到满足题意的M 点；（2）∵点P 的任意性，∴+∞→maxPM，∵minQM是固定的，∴无法对任意的Γ∈P ，都存在Γ∈Q 使得1=⋅QM PM .三、解答题17.解：（1）取CD 中点E ，连接E D 1，E D B A 11∥，∴111D DCC B A 平面∥；（2）由题意可得，底面积为9，∴1341==BD AA ，，A 到BD 的距离1361332=⨯=d ，3132tan 1==d AA θ，∴3132arctan =θ,即二面角C BD A --1的大小为3132arctan.18.解：（1）当0=a 时，()12++=++=x cx x c x x x f ，∵x c x y +=为奇函数，∴()1++=xcx x f 不为奇函数，故不存在实数c ，使得()x f 为奇函数（2）()31231=+++=aca f ，∴1=c ，则()()01132=++++=ax x a x x f 即()01132=+++x a x ，∴()04132>-+=∆a 且两根之和()013<+-a ，∴31>a ，若0=+a x 即a x -=是方程()01132=+++x a x 的解，得21=a 或1-=a ，故实数a 的取值范围为31>a 且21≠a .13141516ACDB19.解：（1）()512532=+=B P ，()()()51282=+=⋂=A P B A P A B P ，()522528=+=A P ，()()()B P A P B A P ⋅==⋂252，∴事件A 和事件B 独立.（2）外观和内饰均为同色的概率15049225232221228=+++C C C C C ，外观和内饰都异色的概率25415024225121121318==+C C C C C ,仅外观或仅内饰同色的概率15077225131211218131121218=+++C C C C C C C C C .∴X 的分布列为⎪⎪⎪⎭⎫⎝⎛1507715049254150300600，期望为2711507715015049300254600=⨯+⨯+⨯（元）20.解：（1）准线为1-=x ，∴2=A x ，∴22==A y a ；（2）()4,4A ，设()0,b B ，线段AB 的中点为⎪⎭⎫⎝⎛+2,24b ，∴()b +=424，解得2-=b ，即()0,2-B ，∴直线AB 为0432=+-y x ，原点O 到AB 的距离13134134==d .（3）设⎪⎪⎭⎫ ⎝⎛p p P ,42，∵⎪⎪⎭⎫⎝⎛a a A ,42，∴直线()04=++-ap y p a x AP ：∴()p H p a ap Q ,3,123-⎪⎪⎭⎫ ⎝⎛+--，，∴412122>++=-+-=p a p p p a ap HQ ，即()()2422->-a p 对()()+∞⋃∈,,0a a p 恒成立，当2=a 时，2≠p ，()()2422->-a p 成立；当02<-a 即2<a 时，()()2422->-a p 此时20<<a ∴a 的取值范围是(]2,0.21.解：（1）()xx f 1='，在()()n n a f a ,处的切线方程为，当0=x 时，1ln -=n a y ，即1ln 1-=+n n a a ；()n nn a x a a y -=-1ln （2）作差法：()1ln 21+-=--+n n n n a a a a ，设()1ln +-=x x x g ，则()11-='xx g 令()011=-='xx g ，解得1=x ；()100<<⇒>'x x g ；()10>⇒<'x x g ，∴()()01max ==g x g ，∴()0≤x g ，即21-≤+n n a a 当1=n a 时等号成立；（3）公差1ln 111--=-=---k k k k a a a a d ，设()1ln --=x x x h ，则()11-='xx h 令()011=-='xx h ，解得1=x ；()100<<⇒>'x x h ，此时()x h 单调递增；()10>⇒<'x x h ，此时()x h 单调递减，∴()()21max -==h x h ，即()2-≤x h ，∴2-≤d ，数列递减，∵0→x 时，()-∞→x h ，+∞→x 时，()-∞→x h ，∴1ln 11--=--k k a a d 最多两解，此时2-<d ，即最多三项成等差数列，3=k .。

2022届高考三轮复习考前大题训练13物质结构和性质（一）2022-2022学年度高考三轮复习考前大题训练13物质的结构和性质〔一〕1．某、Y、Z、W为原子序数依次增大的前四周期元素，某的最外层电子数是其内层电子数的3倍，Y与某同族；Z的负一价离子的最外层电子数与次外层的相同；基态W最外层有18个电子。

答复以下问题：(1)上述元素中，电负性最大的是______(填元素名称)；高温下W某容易转化为2W某的原因是_____。

(2)气态3Y某单分子是________(填“极性〞或“非极性〞)分子；固体3Y某的三聚体环状结构如下图。

该结构中Y某键有两类，其中键长较长的是_________(填字母)。

(3)化合物WZ难溶于水但易溶于氨水，其原因是__________。

此化合物的氨水溶液遇到空气那么被氧化为深蓝色，深蓝色溶液中阳离子的化学式为____________，1mol该阳离子含有________mol键。

(4)2W某的晶胞结构如下图。

①原子坐标参数A为(0，0，0)；B为111,,444。

那么C原子的坐标参数为________。

①2W某的晶胞参数为apm，晶体密度为3gcm，AN为阿伏加德罗常数的值，那么2W某的摩尔质量为__________1gmol(用代数式表示)。

2．亚铁．．氰化钾(K4[Fe(CN)6])又称黄血盐，用于检验Fe3+，也用作实验的防结剂。

检验三价铁发生的反响为：K4[Fe(CN)6]+FeCl3=KFe[Fe(CN)6]↓〔滕氏蓝．．．〕+3KCl，答复以下问题：(1)Fe3+的核外电子排布式___________；(2)与CN‒互为等电子体的分子是___________。

(3)K4[Fe(CN)6]中的作用力有___________；1molK4[Fe(CN)6]中σ键为___________mol；其中C原子的杂化方式为___________；〔：HCN中CN‒结构与N2相似〕(4)C、N、O的第一电离能由大到小．．．．的排序为___________；(5)Fe的晶体结构如下图。