2019届高三物理一轮复习专题练习：双星及多星问题

双星和多星问题1．考点及要求：(1)万有引力定律应用(Ⅱ)；(2)力合成与分解(Ⅱ)；(3)匀速圆周运动向心力(Ⅱ).2.方法与技巧：(1)“双星问题〞隐含条件是两者向心力一样、周期一样、角速度一样；双星中轨道半径与质量成反比；(2)多星问题中，每颗行星做圆周运动所需向心力是由它们之间万有引力合力提供，即F 合＝m v 2r，以此列向心力方程进展求解．1．(双星问题)(多项选择)宇宙中两颗相距很近恒星常常组成一个系统，它们以相互间万有引力彼此提供向心力，从而使它们绕着某一共同圆心做匀速圆周运动，假设它们运转周期为T ，两星到某一共同圆心距离分别为R 1和R 2，那么，系统中两颗恒星质量关系是( ) A ．这两颗恒星质量必定相等 B ．这两颗恒星质量之和为4π2R 1＋R 23GT 2C ．这两颗恒星质量之比为m 1∶m 2＝R 2∶R 1D ．其中必有一颗恒星质量为4π2R 1＋R 23GT 22．(多星问题)宇宙间存在一些离其他恒星较远三星系统，其中有一种三星系统如图1所示，三颗质量均为m 星位于等边三角形三个顶点，三角形边长为L ，忽略其他星体对它们引力作用，三星在同一平面内绕三角形中心O 做匀速圆周运动，引力常量为G ，以下说法正确是( ) 图1A ．每颗星做圆周运动角速度为 3GmL3B ．每颗星做圆周运动加速度与三星质量无关C ．假设距离L 和每颗星质量m 都变为原来2倍，那么周期变为原来2倍D ．假设距离L 和每颗星质量m 都变为原来2倍，那么线速度变为原来4倍3．(多项选择)宇宙间存在一个离其他星体遥远系统，其中有一种系统如图2所示，四颗质量均为m 星体位于正方形顶点，正方形边长为a ，忽略其他星体对它们引力作用，每颗都在同一平面内绕正方形对角线交点O 做匀速圆周运动，引力常量为G ，那么( ) 图2A ．每颗星做圆周运动线速度大小为1＋24GmaB ．每颗星做圆周运动角速度大小为Gm 2a3 C ．每颗星做圆周运动周期为2π2a3GmD ．每颗星做圆周运动加速度与质量m 有关4．2002年四月下旬，天空中出现了水星、金星、火星、木星、土星近乎直线排列“五星连珠〞奇观．假设火星和木星绕太阳做匀速圆周运动，周期分别是T 1和T 2，而且火星离太阳较近，它们绕太阳运动轨道根本上在同一平面内，假设某一时刻火星和木星都在太阳同一侧，三者在一条直线上排列，那么再经过多长时间将第二次出现这种现象( ) A.T 1＋T 22B.T 1T 2C.T 1T 2T 2－T 1D. T 21＋T 2225．宇宙中存在一些离其他恒星较远两颗星组成双星系统，通常可忽略其他星体对它们引力作用．双星系统中星体1质量为m ，星体2质量为2m ，两星体相距为L ，同时绕它们连线上某点做匀速圆周运动，引力常量为G .求该双星系统运动周期．6．宇宙中存在质量相等四颗星组成四星系统，这些系统一般离其他恒星较远，通常可忽略其他星体对它们引力作用．四星系统通常有两种构成形式：一是三颗星绕另一颗中心星运动(三绕一)，二是四颗星稳定地分布在正方形四个顶点上运动．假设每个星体质量均为m ，引力常量为G .(1)分析说明三绕一应该具有怎样空间构造模式．(2)假设相邻星球最小距离为a ，求两种构成形式下天体运动周期之比．答案解析1．BC [对m 1有：G m 1m 2R 1＋R 22＝m 1R 14π2T 2，解得m 2＝4π2R 1R 1＋R 22GT 2，同理可得m 1＝4π2R 2R 1＋R 22GT 2，故两者质量不相等，应选项A 错误；将两者质量相加得m 1＋m 2＝4π2R 1＋R 23GT 2，应选项B 正确；m 1∶m 2＝R 2∶R 1，应选项C 正确；两者质量之和为4π2R 1＋R 23GT 2，那么不可能其中一个质量为4π2R 1＋R 23GT 2，应选项D 错误．]2．C [任意两星间万有引力F ＝G m 2L2，对任一星受力分析，如下图．由图中几何关系和牛顿第二定律可得：3F ＝ma ＝mω2L3，联立可得：ω＝ 3GmL3，a ＝ω2L3＝3GmL 2，选项A 、B 错误；由周期公式可得：T ＝2πω＝2πL 33Gm ，当L 和m 都变为原来2倍，那么周期T ′＝2T ，选项C 正确；由速度公式可得：v ＝ωL3＝GmL，当L 和m 都变为原来2倍，那么线速度v ′＝v ，选项D 错误．]3．AD [由星体均围绕正方形对角线交点做匀速圆周运动可知，星体做匀速圆周运动轨道半径r ＝22a ，每颗星体在其他三个星体万有引力合力作用下围绕正方形对角线交点做匀速圆周运动，由万有引力定律和向心力公式得：Gm 22a2＋2G m 2a 2cos 45°＝m v 222a，解得v ＝1＋24Gm a ，角速度为ω＝vr ＝2＋22Gm a 3，周期为T ＝2πω＝2π2a34＋2Gm，加速度a ＝v 2r ＝22＋1Gm2a 2，应选项A 、D 正确，B 、C 错误．] 4．C [根据万有引力提供向心力得：GMm r 2＝m 4π2r T 2，解得T ＝2π r 3GM，火星离太阳较近，即轨道半径小，所以周期小．设再经过时间t 将第二次出现这种现象，此为两个做匀速圆周运动物体追及相遇问题，虽然不在同一轨道上，但是当它们相遇时，运动较快物体比运动较慢物体多运行2π弧度．所以2πT 1t －2πT 2t ＝2π，解得t ＝T 1T 2T 2－T 1，选项C 正确．]5．2πLL3Gm解析 双星系统围绕两星体间连线上某点做匀速圆周运动，设该点距星体1为R ，距星体2为r对星体1，有G 2mm L 2＝m 4π2T2R对星体2，有G 2mm L2＝2m 4π2T2r根据题意有R ＋r ＝L ，由以上各式解得T ＝2πLL 3Gm6．(1)见解析 (2) 4＋23－34解析 (1)三颗星绕另一颗中心星运动时，其中任意一个绕行星球受到另三个星球万有引力合力提供向心力，三个绕行星球向心力一定指向同一点，且中心星受力平衡，由于星球质量相等，具有对称关系，因此向心力一定指向中心星，绕行星一定分布在以中心星为中心等边三角形三个顶点上，如图甲所示．(2)对三绕一模式，三颗星绕行轨道半径均为a ，所受合力等于向心力，因此有2G m 23a 2cos 30°＋G m 2a 2＝m 4π2T 21a 解得T 21＝23－3π2a3Gm对正方形模式，如图乙所示，四星轨道半径均为22a ，同理有2G m 2a2cos 45°＋G m 22a2＝m 4π2T 22·22a 解得T 22＝44－2π2a37Gm故T 1T 2＝ 4＋23－34。

双星问题物理高三练习题双星问题是物理学中的一个重要问题，涉及到天体运动以及引力的影响。

在高三物理练习中，通常会出现与双星问题相关的题目，下面将介绍一道双星问题的物理练习题。

题目：一个双星系统由两颗质量分别为m₁和m₂的恒星组成。

它们之间的距离为d，两个恒星之间的引力为F。

已知m₁ = 2m₂，F =4G(m₁m₂/d²)（其中G为引力常数）。

求解这个双星系统的动能与势能之比。

解析：根据题目给出的信息，我们首先要计算出这个双星系统的动能和势能。

根据物理学的知识，动能和势能分别可以表示为以下公式：动能（Kinetic Energy）：KE = (1/2)mv²势能（Potential Energy）：PE = -G(m₁m₂/d)首先计算动能。

由于题目中没有给出速度v的具体数值，我们可以假设两颗星体的速度相同，即v₁ = v₂ = v。

那么，m₁和m₂的动能可以表示为：KE₁ = (1/2)m₁v²KE₂ = (1/2)m₂v²由于m₁ = 2m₂，可以将上述公式代入，得到：KE₁ = (1/2)(2m₂)v² = m₂v²KE₂ = (1/2)m₂v²接下来计算势能。

根据题目给出的公式可以得出：PE = -G(m₁m₂/d) = -2G(m₂²/d)因此，这个双星系统的总势能为：PE = PE₁ + PE₂ = -2G(m₂²/d) - 2G(m₂²/d) = -4G(m₂²/d)接下来求解动能与势能之比。

动能与势能之比可以表示为：KE/PE = (m₂v²)/(-4G(m₂²/d))化简上述式子，得到：KE/PE = -d(v²/4Gm₂)由题目可知，v²/4Gm₂ = F/(4Gm₂) = m₁/d²代入上式，得到最终的结果：KE/PE = -d(m₁/d²)KE/PE = -m₁/d综上所述，这个双星系统的动能与势能之比为-m₁/d。

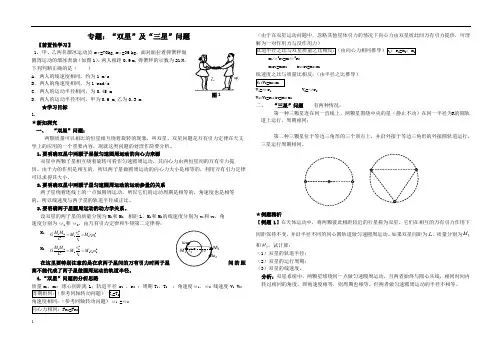
专题：“双星”及“三星”问题【前置性学习】1. 甲、乙两名溜冰运动员m 甲=70kg,m 乙=36 kg ，面对面拉着弹簧秤做圆周运动的溜冰表演（如图1），两人相距0.9 m ，弹簧秤的示数为21 N ，下列判断正确的是（ ）A ．两人的线速度相同，约为1 m/sB ．两人的角速度相同，为1 rad/sC ．两人的运动半径相同，为0.45 mD ．两人的运动半径不同，甲为0.6 m,乙为0.3 m ★学习目标 1. ★新知探究一、 “双星”问题：两颗质量可以相比的恒星相互绕着旋转的现象，叫双星。

双星问题是万有引力定律在天文学上的应用的一个重要内容，现就这类问题的处理作简要分析。

1.要明确双星中两颗子星做匀速圆周运动的向心力来源双星中两颗子星相互绕着旋转可看作匀速圆周运动，其向心力由两恒星间的万有引力提 供。

由于力的作用是相互的，所以两子星做圆周运动的向心力大小是相等的，利用万有引力定律可以求得其大小。

2.要明确双星中两颗子星匀速圆周运动的运动参量的关系两子星绕着连线上的一点做圆周运动，所以它们的运动周期是相等的，角速度也是相等 的，所以线速度与两子星的轨道半径成正比。

3.要明确两子星圆周运动的动力学关系。

设双星的两子星的质量分别为M 1和M 2，相距L ，M 1和M 2的线速度分别为v 1和v 2，角 速度分别为ω1和ω2，由万有引力定律和牛顿第二定律得：M 1： 22121111121M M v G M M r Lr ω==M 2： 22122222222M M v G M M r Lr ω==在这里要特别注意的是在求两子星间的万有引力时两子星间的距离不能代成了两子星做圆周运动的轨道半径。

4.“双星”问题的分析思路质量m 1，m 2；球心间距离L ；轨道半径 r 1 ，r 2 ；周期T 1，T 2 ；角速度ω1，ω2 线速度V 1 V 2；周期相同：（参考同轴转动问题） T 1=T 2 角速度相同：（参考同轴转动问题）ω1 =ω2 向心力相同：Fn 1=Fn 2（由于在双星运动问题中，忽略其他星体引力的情况下向心力由双星彼此间万有引力提供，可理解为一对作用力与反作用力）轨道半径之比与双星质量之比相反：（由向心力相同推导）r 1：r 2=m 2：m 1m 1ω2r 1=m 2ω2r 2m 1r 1=m 2r 2 r 1:r 2=m 2:m 1线速度之比与质量比相反：（由半径之比推导） V 1:V 2=m 2:m 1V 1=ωr 1 V 2=ωr 2 V 1:V 2=r 1:r 2=m 2:m 1二、 “三星”问题 有两种情况：第一种三颗星连在同一直线上，两颗星围绕中央的星（静止不动）在同一半径为R 的圆轨道上运行，周期相同；第二种三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的外接圆轨道运行，三星运行周期相同。

双星及多星问题一、双星问题1.模型构建：在天体运动中，将两颗彼此相距较近，且在相互之间万有引力作用下绕两者连线上的某点做角速度、周期相同的匀速圆周运动的恒星称为双星。

2．模型条件： (1)两颗星彼此相距较近。

(2)两颗星靠相互之间的万有引力提供向心力做匀速圆周运动。

(3)两颗星绕同一圆心做圆周运动。

3．模型特点: (1)“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供。

(2)“周期、角速度相同”——两颗恒星做匀速圆周运动的周期、角速度相等。

(3)三个反比关系：m1r1＝m2r2；m1v1＝m2v2；m1a1＝m2a2推导：根据两球的向心力大小相等可得，m1ω2r1＝m2ω2r2，即m1r1＝m2r2；等式m1r1＝m2r2两边同乘以角速度ω，得m1r1ω＝m2r2ω，即m1v1＝m2v2；由m1ω2r1＝m2ω2r2直接可得，m1a1＝m2a2。

(4)巧妙求质量和：Gm1m2L2＝m1ω2r1①Gm1m2L2＝m2ω2r2②由①＋②得：G m1＋m2L2＝ω2L ∴m1＋m2＝ω2L3G4. 解答双星问题应注意“两等”“两不等”(1)“两等”: ①它们的角速度相等。

②双星做匀速圆周运动向心力由它们之间的万有引力提供，即它们受到的向心力大小总是相等。

(2)“两不等”:①双星做匀速圆周运动的圆心是它们连线上的一点，所以双星做匀速圆周运动的半径与双星间的距离是不相等的，它们的轨道半径之和才等于它们间的距离。

②由m1ω2r1＝m2ω2r2知由于m1与m2一般不相等，故r1与r2一般也不相等。

二、多星模型(1)定义：所研究星体的万有引力的合力提供做圆周运动的向心力，除中央星体外，各星体的角速度或周期相同．(2)三星模型：①三颗星位于同一直线上，两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示)．②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)．(3)四星模型：①其中一种是四颗质量相等的恒星位于正方形的四个顶点上，沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙)．②另一种是三颗恒星始终位于正三角形的三个顶点上，另一颗位于中心O，外围三颗星绕O做匀速圆周运动(如图丁所示)．三、卫星的追及相遇问题1、某星体的两颗卫星从相距最近到再次相距最近遵从的规律：内轨道卫星所转过的圆心角与外轨道卫星所转过的圆心角之差为2π的整数倍。

双星及多星、天体追及问题1.双星问题知识点(1)运动模型：远离其他天体的两星在相互间的万有引力作用下绕两星连线上某点O各自做匀速圆周运动。

（2)几个结论：①两星彼此间的万有引力提供向心力，即＝m 1r1，＝m 2r2。

1②两星绕行方向、周期及角速度都相同，即T1＝T2，ω1＝ω2。

③两星的轨道半径与它们之间的距离关系为r1+r2＝L。

④两星做圆周运动的半径r1、r2与星体质量成反比，即。

⑤两星的运动周期为T＝2π。

⑥两星的总质量为m＝m1+m2＝。

22.多星问题类型三星模型四星模型3结构图2.多星问题类型三星模型四星模型结构图结论：1、每颗星做圆周运动的向心力均由系统内其余星对它万有引力的合力提供42、每颗星做圆周运动转动的方向、周期、角速度、线速度的大小均相同活动一、宇宙双星及多星模型1.宇宙双星模型2017年，人类第一次直接探测到来自双中子星合并的引力波。

根据科学家们复原的过程，在两颗中子星合并前约100 s时，它们相距约400 km，绕二者连线上的某点每秒转动12圈。

将两颗中子星都看作是质量均匀分布的球体，由这些数据、万有引力常量并利用牛顿力学知识，可以估算出这一时刻两颗中子星(BC)A．质量之积B．质量之和C．速率之和D．各自的自转角速度2. 宇宙三星模型三颗质量均为M的星球(可视为质点)位于边长为L的等边三角形的三个顶点上。

如图所示，如果它们中的每一颗都在相互的引力作用下沿等边三角形的外接圆轨道运行，引力常量为G，下列说法正确的是(BD)A．其中一颗星球受到另外两颗星球的万有引力的合力大小为3GM 2 2L2B．其中一颗星球受到另外两颗星球的万有引力的合力指向圆心OC．它们运行的轨道半径为3 2LD．它们运行的速度大小为GML56【习练】宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引力作用。

设四星系统中每个星体的质量均为m ，半径均为R ，四颗星稳定分布在边长为a 的正方形的四个顶点上。

双星、多星系统问题宇宙中不存在孤立的天体，常见的情况是两个或多个天体组成一个相对独立的系统。

高中物理中常常处理一些相对简单的天体系统，其中最简单的是双星系统，相对复杂的有三星、四星系统等。

一、稳定双星系统1、基本模型如图2-14-1所示，质量分别为m 1、m 2的两个天体在万有引力的相互作用下，绕着二者连线上的某个点（公共圆心O ）以相同的角速度做圆周运动，构成一个稳定的双星系统。

在这个系统中，两天体的运动存在如下三个基本关系：（1）向心力大小相同：2212n 1n L m m GF F ==；（2）速度大小相同：ωωω==21；（3）轨道半径之和等于两天体的间距：L r r =+21。

2、基本结论（1）轨道半径关系：2211r m r m =由牛顿第二定律，有天体1：121221r m L m Gm ω=，天体2：222221r m Lm Gm ω=；两式联立，有2211r m r m =，即两天体的轨道半径与各自的质量成反比，质量大的天体轨道半径小，质量小的天体轨道半径大；联立L r r =+21，可得L m m m r 2121+=，L m m m r 2112+=。

（2）系统的周期：)(π2213m m G L T +=把L m m m r 2121+=代入121221r m L m m G ω=，可得321)(Lm m G +=ω，则双星系统的周期为)(π2π2213m m G L T +==ω；即两天体间距越小，总质量越大，系统的周期越小，角速度越大。

（3）线速度关系：2211v m v m =，且Lm m G L v v )(2121+==+ω在2211r m r m =式两边乘以共同的角速度ω，得2211r m r m ωω=，也就是2211v m v m =，即两天体的线速度大小与各自的质量成反比，质量大的天体线速度小，质量小的天体线速度大。

联立321)(Lm m G +=ω,2211r v r v ωω==，，L r r =+21，可得两天体的线速度大小之和为：L m m G L v v v )(2121+==+=ω。

考点突破每日一练（23）双星和多星问题、动量能量的综合问题1．一个国际研究小组借助于智利的“甚大望远镜”，观测到了一组双星系统，它们绕两者连线上的某点O 做匀速圆周运动，如图1所示，此双星系统中体积较小的星体能“吸食”另一颗体积较大星体表面的物质，达到质量转移的目的，假设在“吸食”过程中两者球心之间的距离保持不变，则在该过程中( )A ．它们之间的万有引力保持不变B ．它们做圆周运动的角速度不断变大C ．体积较大的星体做圆周运动的半径变大，线速度也变大D ．体积较大的星体做圆周运动的半径变大，线速度变小2．宇宙空间有一些星系与其它星体的距离非常遥远，可以忽略其它星系对它们的作用．如图所示，今有四颗星体组成一稳定星系，在万有引力作用下运行，其中三颗星体A 、B 、C 位于边长为a 的正三角形的三个顶点上，沿外接圆轨道做匀速圆周运动，第四颗星体D 位于三角形外接圆圆心，四颗星体的质量均为m ，万有引力常量为G ，则下列说法正确的是( )A ．星体A 受到的向心力为()3＋3Gm2a 2B ．星体A 受到的向心力为()3＋23Gm 2aC ．星体B 运行的周期为2πaa1＋33GmD ．星体B 运行的周期为2πaa3＋3Gm3．(多选)宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引力作用．设四星系统中每个星体质量均为m ，半径均为R ，四颗星稳定分布在边长为a 的正方形的四个顶点上，其中a 远大于R .已知引力常量为G .关于四星系统，下列说法正确的是( )A ．四颗星围绕正方形对角线的交点做匀速圆周运动B ．四颗星的线速度均为v ＝Gm a 2＋24 C ．四颗星表面的重力加速度均G m R2D ．四颗星的周期均为2πa 2a 4＋2Gm4．如图所示，质量均为m 的小车和木箱紧挨着静止在光滑的水平冰面上，质量为2m 的小孩站在小车上用力向右迅速推出木箱，木箱相对于冰面运动的速度为v ，木箱运动到右侧时与竖直墙壁发生弹性碰撞，反弹后能被小孩接住，求：(1)小孩接住箱子后共同速度的大小；(2)若小孩接住箱子后再次以相对于冰面的速度v 将木箱向右推出，木箱仍与竖直墙壁发生弹性碰撞，判断小孩能否再次接住木箱．参考答案1．C [设体积较小的星体质量为m 1，轨道半径为r 1，体积较大的星体质量为m 2，轨道半径为r 2，双星之间的距离为L ，转移的质量为Δm ，则质量发生转移后两星体之间的万有引力为F＝Gm 1＋Δmm 2－ΔmL 2，由数学知识可知，随着Δm 的增大，两星体之间的万有引力将发生变化，选项A 错误；对体积较小的星体有G m 1＋Δmm 2－ΔmL2＝(m 1＋Δm )ω2r 1，对体积较大的星体有Gm 1＋Δmm 2－ΔmL2＝(m 2－Δm )ω2r 2，所以ω＝G m 1＋m 2L 3，因两星体的总质量不变，距离也不变，所以质量发生转移前后的角速度不变，选项B 错误；由Gm 1＋Δm L＝ω2r 2可知，随着Δm 的增大，r 2增大，即体积较大的星体做圆周运动的半径变大，由v ＝ωr 2可知线速度也变大，选项C 正确，D 错误． ]2．A [每颗星体做匀速圆周运动，靠另外三颗星体万有引力的合力提供向心力，故：F n ＝F AB cos 30°＋F AD ＋F AC cos 30°＝Gm 2a 2×32＋Gm 223×32a2＋Gm 2a 2×32＝(3＋3)Gm 2a 2① 故A 正确，B 错误；万有引力提供向心力，故：F n ＝m4π2T 2(23×32a )② 联立①②解得：T ＝2πaa31＋3Gm，故C 、D 错误．]3．ACD [四颗星均围绕正方形的中心旋转，每颗星受到的三个力的合力为F ＝2G m 2a 2＋G m 22a2，轨道半径为r ＝22a ，根据牛顿第二定律有F ＝m v 2r ＝m ω2r ＝m 4π2r T2，解得v ＝Gm a 1＋24，T ＝2πa 2a 4＋2Gm，故A 、D 对，B 错；对星体表面质量为m 0的物体，其受到的重力等于万有引力，即m 0g ＝Gmm 0R 2，故重力加速度g ＝G mR2，C 对．] 4．(1)v2(2)无法再次接住木箱解析 (1)取向左为正方向，根据动量守恒定律 推出木箱的过程中0＝(m ＋2m )v 1－mv接住木箱的过程中mv ＋(m ＋2m )v 1＝(m ＋m ＋2m )v 2v 2＝v 2(2)若小孩第二次将木箱推出，根据动量守恒定律 4mv 2＝3mv 3－mvv 3＝v故无法再次接住木箱．。

高中物理双星和多星问题一、选择题1. 如图，“食双星”是指在相互引力作用下绕连线上O点做匀速圆周运动，彼此掩食（像月亮挡住太阳）而造成亮度发生周期性变化的两颗恒星．在地球上通过望远镜观察这种双星，视线与双星轨道共面．已知两颗恒星A、B间距为d，运动周期为T，万有A.4π2d3GT2引力常量为G，则可推算出双星的总质量为（）B.π2d2GT2C.2π2d2GT2D.π2d3GT22. 宇宙中两颗相距较近的天体称为“双星”，它们以二者连线上的某一点为圆心做匀速圆周运动，而不至因为万有引力的作用而吸引到一起，如图所示，某双星系统中A、B 两颗天体绕O点做匀速圆周运动，它们的轨道半径之比r A:r B=1:2，则两颗天体的（） A.质量之比m A:m B=2:1B.角速度之比ωA:ωB=1:2C.线速度大小之比v A:v B=2:1D.向心力大小之比F A:F B=2:13. 人类已直接探测到来自双中子星合并的引力波．根据科学家们复原的过程，在两颗中子星合并前的某一时刻，他们相距L，绕二者连线上的某点每秒转动n圈．将两颗中子星都看作是质量均匀分布的球体，已知万有引力常量为G，结合牛顿力学知识可算出这一时刻两颗中子星的质量之和为（）A.4π2n2L3G B.8π2n2L3GC.G4π2n2L3D.G8πn2L34. 2017年，人类第一次直接探测到来自双中子星合并的引力波．根据科学家们复原的过程，在两颗中子星A和B合并前它们相距L，绕二者连线上的某点每秒转动n圈．合并前将两颗中子星都看作是质量均匀分布的球体，A和B的质量之比为k，并且它们各自的运动都看做是匀速圆周运动，下列说法中正确的是（）A.中子星A和B的运动周期均为nB.中子星A和B的角速度大小之比为1:1C.中子星A和B的向心力大小之比为1kD.中子星A和B的线速度大小之和为πnL5. 月球与地球质量之比约为1:80，有研究者认为月球和地球可视为一个由两质点构成的双星系统，他们都围绕地球与月球连线上某点O做匀速圆周运动．据此观点，可知月球与地球绕O点运动线速度大小之比约为（）A.1:6400B.1:80C.80:1D.6400:16. 2017年，人类第一次直接探测到来自双中子星的引力波．根据科学家们复原的过程，在两颗中子星合并前约100s时，它们相距约400km，绕二者连线上的某点每秒转动12圈．将两颗中子星都看做质量均匀分布的球体，且合并前两颗中子星的质量均保持不变．估算一下，当两颗中子星相距100km 时，绕二者连线上的某点每秒转动（ ） A.6圈B.24圈C.48圈D.96圈7. 银河系的恒量中大约有四分之一是双星，某双星由质量分别为M 和m(M >m) 的两个星体构成，两星体在相互之间的万有引力作用下绕两者连线上某一定点O 做匀速圆周运动，若该双星运行的周期为T ，引力常量为G ，不考虑其他星体的影响，则两星体之间的距离为（ ） A.√GT 2(M+m)4π23B.√GT 2(M−m)4π23C.√GT 24π2(M+m)3 D.√GT 24π2(M−m)38. 双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动．研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化．若某双星系统中两星做圆周运动的周期为T ，经过一段时间演化后，两星总质量变为原来的k 倍，两星之间的距离变为原来的n 倍，则此时圆周运动的周期为（ ） A.√nkTB.√n 2kT C.√n 3kT D.√n 3k 2T二、 多选题9. 引力波探测于2017年获得诺贝尔物理学奖．双星的运动是产生引力波的来源之一，假设宇宙中有一双星系统由P 、Q 两颗星体组成，这两颗星绕它们连线的某一点在二者万有引力作用下做匀速圆周运动，测得P 星的周期为T ，P 、Q 两颗星的距离为L ，P 、Q 两颗星的轨道半径之差为Δr(P 星的轨道半径大于Q 星的轨道半径），万有引力常量为G ，则（ ）A.Q 、P 两颗星的质量之和为4π2l 3GT 2B.P 、Q 两颗星的运动半径之比为ll−Δr C.P 、Q 两颗星的线速度大小之差为2πΔr TD.P 、Q 两颗星的质量之比为l−Δrl+Δr10. 双星系统如图所示，已知恒星A 、B 间的距离恒为L ，恒星A 和恒星B 的总质量为4M ，恒星A 与恒星B 的转动半径之比为3:1，引力常量为G ，下列说法正确的是（ ） A.恒星的角速度为√GM4L 3 B.恒星A 的质量为MC.恒星A 与恒星B 的向心力大小之比为1:1D.恒星A 与恒星B 的线速度大小之比为1:4参考答案一、选择题1.A解：设A、B两天体的轨道半径分别为r1、r2，两者做圆周运动的周期都为T，万有引力提供向心力，由牛顿第二定律可得Gm A m Bd2=m A(2πT)2r1，Gm A m Bd2=m B(2πT)2r2，其中d=r1+r2，解得M=m A+m B=4π2d3GT2．故选A．2.A解：双星都绕O点做匀速圆周运动，两者之间的万有引力提供向心力，角速度相等，设为ω，对A星：G m A m BL2=m Aω2r A，对B星：G m A m BL2=m Bω2r B，故m A:m B=r B:r A=2:1，角速度之比ωA:ωB=1:1，由v=ωr得线速度大小之比v A:v B=r A:r B=1:2，向心力大小之比F A:F B=1:1，故A正确，BCD错误．故选A．3.A解：设两颗星的质量分别为m1、m2，轨道半径分别为r1、r2，根据万有引力提供向心力可知：G m1m2L2=m14π2T2r1=m24π2T2r2，解得质量之和m1+m2=4π2L3GT2，而周期T=1n ，联立解得m1+m2=4π2n2L3G，故A正确．故选：A．4.B解：A．A、B两颗星的周期均为T=1n，故A错误；B．A、B两颗星的周期相同，所以角速度之比为1:1，故B正确；C．因为两星之间的万有引力提供向心力，所以两星的向心力相同，故C错误；D．两星的向心力相同，根据F向=mω2r得，m1ω2r1=m2ω2r2，即m1r1=m2r2，A、B质量之比为k，故r1r2=1k，其中r1+r2=L、v=ωr，解得A和B的线速度大小之和为2πnL，故D错误．故选B．5.C解：月球和地球绕O做匀速圆周运动，它们之间的万有引力提供各自的向心力，则地球和月球的向心力相等，且月球和地球和O始终共线，说明月球和地球有相同的角速度和周期，因此有：mω2r =Mω2R ， 又由于v =ωr ， 所以v 月v 地=M m =801．故选C ．6.D 解：设两颗星的质量分别为m 1、m 2，轨道半径分别为r 1、r 2，相距L ＝400km ， 根据万有引力提供向心力可知：Gm 1m 2L 2=m 1r 1ω12， Gm 1m 2L 2=m 2r 2ω12，r 1+r 2＝L ， 联立可得：r1r 2=m 2m 1，合并前两颗中子星的质量均保持不变，则它们的轨道半径的比值不变；当两颗中子星相距：L ′＝100km =L4时，r 1′=14r 1，由于：Gm 1m 2L ′2=m 1r 1′ω22，则可得：ω2＝8ω1，开始时两颗星绕二者连线上的某点每秒转动12圈，角速度增大为8倍后，则两颗星绕二者连线上的某点每秒转动的速度增大为8倍，为每秒96圈，故ABC 错误，D 正确． 故选D ．7.A 解：设星体S 1和S 2的质量分别为M 、m ，两星间距离为L ， 星体S 1做圆周运动的向心力由万有引力提供得：GMm L 2=Mω2r 1， 星体S 2做圆周运动的向心力由万有引力提供得：GMm L 2=mω2r 2，r 1+r 2=L ， 联立解得：L =√GT 2(M+m)4π3．故选：A ．8.C 解：设m 1的轨道半径为R 1，m 2的轨道半径为R 2，两星之间的距离为L ，由于它们之间的距离恒定，因此双星在空间的绕向一定相同，同时角速度和周期也都相同，由向心力公式可得： 对m 1:G m 1m 2L 2=m 14π2T 2R 1， 对m 2:Gm 1m 2L 2=m 24π2T 2R 2，又因为R 1+R 2=L ，m 1+m 2=M ， 联立可得：T =2π√L 3GM ，所以当两星总质量变为原来的k 倍，两星之间的距离变为原来的n 倍，圆周运动的周期为：T ′=2π√(nL)3GkM =√n 3k T ． 故选C ．二、多选题9.A,C,D解：ABD．双星系统靠相互间的万有引力提供向心力，角速度大小相等，则周期相等，所以Q星的周期为T，根据题意可知，r P+r Q=l，r P−r Q=Δr，解得：r P=l+Δr 2，r Q=l−Δr2，则P、Q两颗星的运动半径之比为l+Δrl−Δr，根据G m p m Ql2=m pω2r P=m Qω2r Q，可得m P=ω2r Q l2G ，m Q=ω2r P l2G，则质量和为：m P+m Q=ω2r Q l2G +ω2r P l2G=4π2l2GT2(r Q+r P)=4π2l2GT2，质量比为：m Pm Q=r Qr P=l−Δrl+Δr，故AD正确，B错误；C．P星的线速度大小v P=2πr PT =π(l+Δr)T，Q星的线速度大小v Q=2πr QT=π(l−Δr)T，则PQ两颗星的线速度大小之差为Δv=2πΔrT，故C正确．故选ACD．10.B,C解：B．设恒星A的质量为m A、运动的半径为r A，恒星B的质量为m B，运动的半径为r B，由于双星的角速度相同，故有Gm A m BL2=m Aω2r A=m Bω2r B，解得m A r A=m B r B，即m A=M，选项B正确；A．r A=34L，代入Gm A m BL2=m Aω2r A，解得ω=√4GML3，选项A错误；C．恒星A与恒星B的向心力都由万有引力提供，且都为Gm A m BL2，选项C正确；D．由于双星的角速度相同，恒星A与恒星B的线速度之比为半径之比，即为3:1，选项D错误．故选BC．。

高考重点难点热点快速突破1．双星模型(1)定义：绕公共圆心转动的两个星体组成的系统，我们称之为双星系统，如图所示．(2)特点：①各自所需的向心力由彼此间的万有引力相互提供，即Gm 1m 2L 2＝m 1ω 21r 1，Gm 1m 2L2＝m 2ω 22r 2 ②两颗星的周期及角速度都相同，即T 1＝T 2，ω1＝ω2③两颗星的半径与它们之间的距离关系为：r 1＋r 2＝L (3)两颗星到圆心的距离r 1、r 2与星体质量成反比，即m 1m 2＝r 2r 1. 2．多星模型(1)定义：所研究星体的万有引力的合力提供做圆周运动的向心力，除中央星体外，各星体的角速度或周期相同．(2)三星模型：①三颗星位于同一直线上，两颗环绕星围绕中央星在同一半径为R 的圆形轨道上运行(如图3甲所示)．②三颗质量均为m 的星体位于等边三角形的三个顶点上(如图乙所示)．(3)四星模型：①其中一种是四颗质量相等的恒星位于正方形的四个顶点上，沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙所示)．②另一种是三颗恒星始终位于正三角形的三个顶点上，另一颗位于中心O ，外围三颗星绕O 做匀速圆周运动(如图丁所示)．典例分析【例1】 (多选)(2017年昆明模拟)宇宙中两颗相距很近的恒星常常组成一个系统，它们以相互间的万有引力彼此提供向心力，从而使它们绕着某一共同的圆心做匀速圆周运动，若已知它们的运转周期为T ，两星到某一共同圆心的距离分别为R 1和R 2，那么，系统中两颗恒星的质量关系是( )A ．这两颗恒星的质量必定相等B ．这两颗恒星的质量之和为4π2R 1＋R 23GT 2C ．这两颗恒星的质量之比为m 1∶m 2＝R 2∶R 1D ．其中必有一颗恒星的质量为4π2R 1＋R 23GT 2【答案】 BC【例2】：2016年2月11日，美国科学家宣布探测到引力波的存在，引力波的发现将为人类探索宇宙提供新视角，这是一个划时代的发现．在如图所示的双星系统中，A、B两个恒星靠着相互之间的引力正在做匀速圆周运动，已知恒星A的质量为太阳质量的29倍，恒星B的质量为太阳质量的36倍，两星之间的距离L＝2×105 m，太阳质量M＝2×1030 kg，引力常量G＝6.67×10－11N·m2/kg2，π2＝10.若两星在环绕过程中会辐射出引力波，该引力波的频率与两星做圆周运动的频率具有相同的数量级，则根据题目所给信息估算该引力波频率的数量级是( )A．102 Hz B．104 Hz C．106 Hz D．108 Hz【答案】 A【例3】：．经过用天文望远镜长期观测，人们在宇宙中已经发现了许多双星系统，通过对它们的研究，使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识，双星系统由两个星体组成，其中每个星体的线度都远小于两星体之间的距离，一般双星系统距离其他星体很远，可以当成孤立系统来处理．现根据对某一双星系统的测量确定，该双星系统中每个星体的质量都是M，两者相距L，它们正围绕两者连线的中点做圆周运动．(1)计算出该双星系统的运动周期T；(2)若该实验中观测到的运动周期为T 观测，且T 观测∶T ＝1∶N (N >1)．为了理解T 观测与T 的不同，目前有一种流行的理论认为，在宇宙中可能存在一种望远镜观测不到的暗物质．作为一种简化模型，我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质．若不考虑其他暗物质的影响，根据这一模型和上述观测结果确定该星系间这种暗物质的密度．【答案】 (1)πL2L GM (2)3N －1M2πL3 【解析】 (1)双星均绕它们连线的中点做圆周运动，万有引力提供向心力，则G M 2L 2＝M ⎝⎛⎭⎪⎫2πT 2·L 2，解得T ＝πL2L GM.【例4】：由三颗星体构成的系统，忽略其他星体对它们的作用，存在着一种运动形式，三颗星体在相互之间的万有引力作用下，分别位于等边三角形的三个顶点上，绕某一共同的圆心O 在三角形所在的平面内做相同角速度的圆周运动(图为A 、B 、C 三颗星体质量不相同时的一般情况)．若A 星体质量为2m 、B 、C 两星体的质量均为m ，三角形的边长为a ，求：(1)A 星体所受合力大小F A ； (2)B 星体所受合力大小F B ； (3)C 星体的轨道半径R C ； (4)三星体做圆周运动的周期T .【答案 】 (1)23G m 2a 2 (2)7G m 2a 2 (3)74a (4)πa 3Gm【解析】(1)由万有引力定律，A 星体所受B 、C 星体引力大小为F BA ＝G m A m B r 2＝G 2m 2a2＝F CA方向如图所示则合力大小为F A ＝F BA ·cos 30°＋F CA ·cos 30°＝23G m 2a2(3)由于m A ＝2m ，m B ＝m C ＝m通过分析可知，圆心O 在BC 的中垂线AD 的中点 则R C ＝⎝ ⎛⎭⎪⎫34a 2＋⎝ ⎛⎭⎪⎫12a 2＝74a (4)三星体运动周期相同，对C 星体，由F C ＝F B ＝7G m 2a 2＝m (2πT)2R C ，可得T ＝πa 3Gm. 专题练习1：宇宙间存在一些离其他恒星较远的三星系统，其中有一种三星系统如图所示，三颗质量均为m 的星位于等边三角形的三个顶点，三角形边长为R ，忽略其他星体对它们的引力作用，三星在同一平面内绕三角形中心O 做匀速圆周运动，万有引力常量为G ，则( )A ．每颗星做圆周运动的线速度为 Gm RB ．每颗星做圆周运动的角速度为 3GmR 3C ．每颗星做圆周运动的周期为2πR 33GmD ．每颗星做圆周运动的加速度与三星的质量无关 【答案】 ABC【解析】由图可知，每颗星做匀速圆周运动的半径r ＝R2cos 30°＝33R .由牛顿第二定律得Gm 2R 2·2cos 30°＝m v 2r ＝mω2r ＝m 4π2T2r ＝ma ，可解得v ＝GmR，ω＝ 3GmR 3，T ＝2πR 33Gm ，a ＝3GmR2，故A 、B 、C 均正确，D 错误． 2.宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引力作用．设四星系统中每个星体的质量均为m ，半径均为R ，四颗星稳定分布在边长为a 的正方形的四个顶点上．已知引力常量为G.关于宇宙四星系统，下列说法错误的是( )A ． 四颗星围绕正方形对角线的交点做匀速圆周运动B ． 四颗星的轨道半径均为C ． 四颗星表面的重力加速度均为D ． 四颗星的周期均为2πa【答案】B3.宇宙中存在一些离其他恒星较远，由质量相等的三个星体组成的三星系统，通常可忽略其他星体对它们的引力作用．已观测到稳定的三星系统存在的一种形式是三个星体位于等边三角形的三个顶点上，并沿外接于等边三角形的圆形轨道运行，如图所示．设每个星体的质量均为m，相邻的两个星体之间的距离为L，引力常量为G，则( )A．该圆形轨道的半径为3 2 LB．每个星体的运行周期均为3πL3 2GmC．每个星体做圆周运动的线速度均为Gm LD．每个星体做圆周运动的加速度均与星体的质量无关【答案】：C4．双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动，研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化，若某双星系统中两星做圆周运动的周期为T ，经过一段时间演化后，两星总质量变为原来的k 倍，两星之间的距离变为原来的n 倍，则此时圆周运动的周期为( )A.n 3k 2B.n 3k T C.n 2kT D.n kT 【答案】：B【解析】：设m 1的轨道半径为r 1，m 2的轨道半径为r 2，由于它们之间的距离恒定，因此双星在空间的绕向一定相同，同时角速度和周期也都相同，两星之间的万有引力提供两星做圆周运动的向心力，即Gm 1m 2r 1＋r 22＝m 1r 1⎝⎛⎭⎪⎫2πT 2，Gm 1m 2r 1＋r 22＝m 2r 2⎝ ⎛⎭⎪⎫2πT 2，可得T ＝2πr 1＋r 23G m 1＋m 2，故当两恒星总质量变为原来的k倍，两星间距变为原来的n 倍时，圆周运动的周期变为n 3kT ，B 正确． 5．经长期观测，人们在宇宙中已经发现了“双星系统”，“双星系统”由两颗相距较近的恒星组成，每个恒星的直径远小于两个星体之间的距离，而且双星系统一般远离其他天体．如图所示，两颗星球组成的双星，在相互之间的万有引力作用下，绕连线上的O 点做周期相同的匀速圆周运动．现测得两颗星之间的距离为L ，质量之比为m 1∶m 2＝3∶2.则可知( )A ．m 1、m 2做圆周运动的角速度之比为2∶3B ．m 1、m 2做圆周运动的线速度之比为3∶2C ．m 1做圆周运动的半径为r 1＝25LD ．m 2做圆周运动的半径为r 2＝25L【答案：】C6. (多选)宇宙中，两颗靠得比较近的恒星，只受到彼此之间的万有引力作用互相绕转，称之为双星系统．在浩瀚的银河系中，多数恒星都是双星系统．设某双星系统P、Q绕其连线上的O点做匀速圆周运动，如图所示．若PO>OQ，则( )A．星球P的质量一定大于Q的质量B．星球P的线速度一定大于Q的线速度C．双星间距离一定，双星的质量越大，其转动周期越大D．双星的质量一定，双星之间的距离越大，其转动周期越大【答案】BD7. (多选)宇宙中两个相距较近的星球可以看成双星，它们只在相互间的万有引力作用下，绕两球心连线上的某一固定点做周期相同的匀速圆周运动．根据宇宙大爆炸理论，双星间的距离在不断缓慢增加，设双星仍做匀速圆周运动，则下列说法正确的是( ) A．双星相互间的万有引力不变B．双星做圆周运动的角速度均增大C．双星做圆周运动的速度均减小D．双星做圆周运动的半径均增大【答案】CD【解析】双星间的距离在不断缓慢增加，由万有引力定律，F＝G，知万有引力减小，A错误；根据万有引力提供向心力得G＝m1r1ω2＝m2r2ω2，可知m1r1＝m2r2，知轨道半径比等于质量之反比，双星间的距离变大，则双星的轨道半径都变大，B 错误，D 正确；根据G＝m 1v 1ω＝m 2v 2ω，可得线速度减小，C 正确8. (多选)双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动．若某双星系统中两星做圆周运动的周期为T ，两星总质量为M ，两星之间的距离为r ，两星质量分别为m 1、m 2，做圆周运动的轨道半径分别为r 1、r 2，则下列关系式中正确的是( )A ． M ＝B ． r 1＝rC ． T ＝2πD ． ＝【答案】AC【解析】由于它们之间的距离恒定，因此双星在空间的绕向一定相同，同时角速度和周期也都相同．由向心力公式可得：对m 1：＝m 1ω2r 1① 对m 2：＝m 2ω2r 2②；由①②式可得：m 1r 1＝m 2r 2 ，即＝，D 错误．r 1＋r 2＝r ，得：r 1＝r ＝r ，B 错误．将ω＝，r 1＝r 代入①式，可得：＝m 1·r，得：T ＝2π，M ＝，A 、C 正确．9．宇宙中存在由质量相等的四颗星组成的四星系统，四星系统离其他恒星较远，通常可忽略其他星体对四星系统的引力作用．已观测到稳定的四星系统存在两种基本的构成形式：一种是四颗星稳定地分布在边长为a 的正方形的四个顶点上，均围绕正方形对角线的交点做匀速圆周运动，其运动周期为T 1；另一种形式是有三颗星位于边长为a 的等边三角形的三个顶点上，并沿外接于等边三角形的圆形轨道运行，其运动周期为T 2，而第四颗星刚好位于三角形的中心不动．试求两种形式下，星体运动的周期之比T 1T 2.【答案】T 1T 2＝6＋634＋2【解析】：对于第一种形式，一个星体在其它三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动，其轨道半径为：r1＝22a.。

微专题25 双星与多星问题【核心要点提示】(1)核心问题是“谁”提供向心力的问题．(2)“双星问题”的隐含条件是两者的向心力相同、周期相同、角速度相同；双星中轨道半径与质量成反比；(3)多星问题中，每颗行星做圆周运动所需的向心力是由它们之间的万有引力的合力提供，即F 合＝m v 2r ，以此列向心力方程进行求解．【微专题训练】“双星体系”由两颗相距较近的恒星组成，每个恒星的半径远小于两个星球之间的距离，而且双星系统一般远离其他天体．如图1所示，相距为L 的A 、B 两恒星绕共同的圆心O 做圆周运动，A 、B 的质量分别为m 1、m 2，周期均为T .若有间距也为L 的双星C 、D ，C 、D 的质量分别为A 、B 的两倍，则( )A ．A 、B 运动的轨道半径之比为m 1m 2B ．A 、B 运动的速率之比为m 1m 2C ．C 运动的速率为A 的2倍D ．C 、D 运动的周期均为22T 【解析】对于双星A 、B ，有G m 1m 2L 2＝m 1(2πT )2r 1＝m 2(2πT )2r 2，r 1＋r 2＝L ，得r 1＝m 2m 1＋m 2L ，r 2＝m 1m 1＋m 2L ，T ＝2πL L G m 1＋m 2，A 、B 运动的轨道半径之比为r 1r 2＝m 2m 1，A 错误；由v＝2πr T 得，A 、B 运动的速率之比为v 1v 2＝r 1r 2＝m 2m 1，B 错误；C 、D 运动的周期T ′＝2πL L G 2m 1＋2m 2＝22T ，D 正确；C 的轨道半径r 1′＝2m 22m 1＋2m 2L ＝r 1，C 运动的速率为v 1′＝2πr 1′T ′＝2v 1，C 错误．【答案】D(2013·山东理综)双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动．研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化．若某双星系统中两星做圆周运动的周期为T ，经过一段时间演化后，两星总质量变为原来的k 倍，两星之间的距离变为原来的n 倍，则此时圆周运动的周期为( ) A.n 3k 2T B.n 3kT C.n 2kT D.n kT 【解析】双星靠彼此的引力提供向心力，则有 G m 1m 2L 2＝m 1r 14π2T 2 G m 1m 2L 2＝m 2r 24π2T 2 并且r 1＋r 2＝L 解得T ＝2πL 3G (m 1＋m 2)当两星总质量变为原来的k 倍，两星之间距离变为原来的n 倍时 T ′＝2πn 3L 3Gk (m 1＋m 2)＝n 3k·T 故选项B 正确． 【答案】B(多选)宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引力作用．设四星系统中每个星体的质量均为m ，半径均为R ，四颗星稳定分布在边长为a 的正方形的四个顶点上．已知引力常量为G .关于四星系统，下列说法正确的是( )A ．四颗星围绕正方形对角线的交点做匀速圆周运动B ．四颗星的轨道半径均为a2C ．四颗星表面的重力加速度均为GmR 2D ．四颗星的周期均为2πa2a(4＋2)Gm【解析】其中一颗星体在其他三颗星体的万有引力作用下，合力方向指向对角线的交点，围绕正方形对角线的交点做匀速圆周运动，由几何知识可得轨道半径均为22a ，故A 正确，B 错误；在星体表面，根据万有引力等于重力，可得G mm ′R 2＝m ′g ，解得g ＝GmR2，故C 正确；由万有引力定律和向心力公式得Gm 2(2a )2＋2Gm 2a 2＝m 4π2T 2·2a2，T ＝2πa2a(4＋2)Gm，故D正确． 【答案】ACD(2016·河南省郑州市高三月考)宇宙中有这样一种三星系统，系统由两个质量为m 的小星体和一个质量为M 的大星体组成，两个小星体围绕大星体在同一圆形轨道上运行，轨道半径为r 。

⾼考物理计算题复习《双星问题》（解析版）《双星问题》⼀、计算题1.神奇的⿊洞是近代引⼒理论所预⾔的⼀种特殊天体，探寻⿊洞的⽅案之⼀是观测双星系统的运动规律。

天⽂学家观测河外星系⼈麦析伦云时，发现了双星系统，它由可见星A和不可见的暗星B构成，两星视为质点，不考虑其它星体的影响，A、B围绕两者连线上的O点做匀速圆周运动，它们之间的距离保持不变，如图所⽰。

引⼒常量为G，由观测能够得到可见星A的速率v和运⾏周期T。

可见星A所受暗星B的引⼒FA可等效为位于O点处质量为的星体可视为质点对它的引⼒，设A和B的质量分别为，，试求⽤、表⽰求暗星B的的质量与可见星A的速率v、运⾏周期T和质量之间的关系式。

要求等号左边只含有和，，等号右边为其它量2.众多的恒星组成不同层次的恒星系统，最简单的恒星系统是两颗互相绕转的双星，如下图所⽰，两星各以⼀定速率绕其连线上某⼀点匀速转动，这样才不⾄于因万有引⼒作⽤⽽吸引在⼀起，已知双星质量分别为、，它们间的距离始终为L，引⼒常数为G，求：双星旋转的中⼼O到的距离；双星的转动周期。

3.天⽂观测中发现宇宙中存在着“双星”，所谓双星，是两颗质量相近，分别为和的恒星，它们的距离为r，⽽r远远⼩于它们跟其它天体之间的距离，这样的双星将绕着它们的连线上的某点O作匀速圆周运动．求：这两颗星到O点的距离、各是多⼤双星的周期．4.现代观测表明，由于引⼒的作⽤，恒星有“聚焦”的特点，众多的恒星组成不同层次的恒星系统，最简单的恒星系统是两颗互相绕转的双星．它们以两者连线上的某点为圆⼼做匀速圆周运动，这样就不⾄于由于万有引⼒的作⽤⽽吸引在⼀起．如图所⽰，设某双星系统中的两星、的质量分别为m和2m，两星间距为L，在相互间万有引⼒的作⽤下，绕它们连线上的某点O转动．已知引⼒常量G，求：、两星之间的万有引⼒⼤⼩；星到O点的距离；它们运动的周期．5.⿊洞是宇宙空间内存在的⼀种天体。

⿊洞的引⼒很⼤，使得视界内的逃逸速度⼤于光速。

36 双星与多星问题[方法点拨] (1)核心问题是“谁”提供向心力的问题．(2)“双星问题”的隐含条件是两者的向心力相同、周期相同、角速度相同；双星中轨道半径与质量成反比；(3)多星问题中，每颗行星做圆周运动所需的向心力是由它们之间的万有引力的合力提供，即F 合＝m v 2r，以此列向心力方程进行求解．1．(2019·四川泸州一检)“双星体系”由两颗相距较近的恒星组成，每个恒星的半径远小于两个星球之间的距离，而且双星系统一般远离其他天体．如图1所示，相距为L 的A 、B 两恒星绕共同的圆心O 做圆周运动，A 、B 的质量分别为m 1、m 2，周期均为T .若有间距也为L 的双星C 、D ，C 、D 的质量分别为A 、B 的两倍，则( )图1A ．A 、B 运动的轨道半径之比为m 1m 2B ．A 、B 运动的速率之比为m 1m 2C ．C 运动的速率为A 的2倍D ．C 、D 运动的周期均为22T 2．(多选)太空中存在一些离其他恒星很远的、由三颗星体组成的三星系统，可忽略其他星体对它们的引力作用．已观测到稳定的三星系统存在两种基本的构成形式：一种是直线三星系统——三颗星体始终在一条直线上；另一种是三角形三星系统——三颗星体位于等边三角形的三个顶点上．已知某直线三星系统A 每颗星体的质量均为m ，相邻两颗星中心间的距离都为R ；某三角形三星系统B 的每颗星体的质量恰好也均为m ，且三星系统A 外侧的两颗星体做匀速圆周运动的周期和三星系统B 每颗星体做匀速圆周运动的周期相等．引力常量为G ，则( )A ．三星系统A 外侧两颗星体运动的线速度大小为v ＝Gm RB ．三星系统A 外侧两颗星体运动的角速度大小为ω＝12R5GmRC ．三星系统B 的运动周期为T ＝4πRR 5GmD ．三星系统B 任意两颗星体中心间的距离为L ＝3125R3．(多选)(2019·福建龙岩3月质检)冥王星和其附近的星体卡戎的质量分别为M 、m (m <M )，两星相距L ，它们只在相互间的万有引力作用下，绕球心连线的某点O 做匀速圆周运动．冥王星与星体卡戎到O 点的距离分别为R 和r .则下列说法正确的是( ) A ．可由G Mm R2＝MR ω2计算冥王星做圆周运动的角速度B ．可由G Mm L 2＝M v 2L 计算冥王星做圆周运动的线速度C ．可由G Mm L2＝mr (2πT)2计算星体卡戎做圆周运动的周期D ．冥王星与星体卡戎绕O 点做圆周运动的动量大小相等4．(2019·山东枣庄一模)2019年12月17日我国发射了“悟空”探测卫星，这期间的观测使人类对暗物质的研究又进了一步．宇宙空间中两颗质量相等的星球绕其连线中心转动时，理论计算的周期与实际观测周期不符，且T 理论T 观测＝k (k >1)；因此，科学家认为，在两星球之间存在暗物质．假设以两星球球心连线为直径的球体空间中均匀分布着暗物质，两星球的质量均为m ，那么，暗物质的质量为( )A.k 2－14mB.k 2－28mC ．(k 2－1)mD ．(2k 2－1)m5．(2019·广西南宁一模)2019年2月11日，科学家宣布“激光干涉引力波天文台(LIGO)”探测到由两个黑洞合并产生的引力波信号，这是在爱因斯坦提出引力波概念100周年后，引力波被首次直接观测到．在两个黑洞合并过程中，由于彼此间的强大引力作用，会形成短时间的双星系统．如图2所示，黑洞A 、B 可视为质点，它们围绕连线上O 点做匀速圆周运动，且AO 大于BO ，不考虑其他天体的影响．下列说法正确的是( )图2A ．黑洞A 的向心力大于B 的向心力 B ．黑洞A 的线速度大于B 的线速度C ．黑洞A 的质量大于B 的质量D ．两黑洞之间的距离越大，A 的周期越小6．(多选)(2019·陕西商洛模拟)宇宙中两颗相距很近的恒星常常组成一个系统，它们以相互间的万有引力彼此提供向心力，从而使它们绕着某一共同的圆心做匀速圆周运动，若已知它们的运转周期为T ，两星到某一共同圆心的距离分别为R 1和R 2，那么，系统中两颗恒星的质量关系是( )A ．这两颗恒星的质量必定相等B ．这两颗恒星的质量之和为4π2(R 1＋R 2)3GT 2C ．这两颗恒星的质量之比为m 1∶m 2＝R 2∶R 1D ．其中必有一颗恒星的质量为4π2(R 1＋R 2)3GT2答案精析1．D [对于双星A 、B ，有Gm 1m 2L 2＝m 1(2πT )2r 1＝m 2(2πT )2r 2，r 1＋r 2＝L ，得r 1＝m 2m 1＋m 2L ，r 2＝m 1m 1＋m 2L ，T ＝2πLL G (m 1＋m 2)，A 、B 运动的轨道半径之比为r 1r 2＝m 2m 1，A 错误；由v ＝2πrT得，A 、B 运动的速率之比为v 1v 2＝r 1r 2＝m 2m 1，B 错误；C 、D 运动的周期T ′＝2πL L G (2m 1＋2m 2)＝22T ，D 正确；C 的轨道半径r 1′＝2m 22m 1＋2m 2L ＝r 1，C 运动的速率为v 1′＝2πr 1′T ′＝2v 1，C 错误．]2．BCD [三星系统A 中，三颗星体位于同一直线上，两颗星体围绕中央星体在同一半径为R 的圆轨道上运行．其中外侧的一颗星体由中央星体和另一颗外侧星体的合万有引力提供向心力，有：G m 2R 2＋G m 2(2R )2＝m v 2R，解得v ＝5Gm 4R ，A 错误；三星系统A 中，周期T ＝2πRv ＝4πRR 5Gm ，则其角速度为ω＝2πT ＝12R5GmR，B 正确；由于两种系统周期相等，则三星系统B 的运行周期为T ＝4πRR5Gm，C 正确；三星系统B 中，三颗星体位于等边三角形的三个顶点上，并沿外接于等边三角形的圆形轨道运行，如图所示，对某颗星体，由万有引力定律和牛顿第二定律得：2Gm 2L 2cos 30°＝m L 2cos 30°·4π2T 2，解得L ＝3125R ，D 正确．]3．CD [冥王星与星体卡戎之间的万有引力提供各自做圆周运动的向心力：可由GMm(R ＋r )2＝MR ω2计算冥王星做圆周运动的角速度，故A 错误；同理，可由G Mm L 2＝M v 2R计算冥王星做圆周运动的线速度，故B 错误；冥王星与其附近的星体卡戎可视为双星系统．所以冥王星和星体卡戎做圆周运动的周期是相等的，可由G Mm L 2＝mr (2πT)2计算星体卡戎做圆周运动的周期，故C 正确；因GMm (R ＋r )2＝MR ω2＝mr ω2，由于它们的角速度的大小是相等的，所以：MR ω＝mr ω，又：v m ＝ωr ，v M ＝ωR ，p m ＝mv m ，p M ＝Mv M ，所以冥王星与星体卡戎绕O 点做圆周运动的动量大小相等，故D 正确．]4．A [两星球均绕它们的连线的中点做圆周运动，设它们之间的距离为L ，由万有引力提供向心力得：G m 2L 2＝m 4π2T 理论2·L2，解得：T理论＝πL2LGm.根据观测结果，星体的运动周期T 理论T 观测＝k ，这种差异是由两星球之间均匀分布的暗物质引起的，均匀分布在两星球之间的暗物质对双星系统的作用与一质量等于暗物质的总质量m ′、位于中点O 处的质点的作用相同．则有：G m 2L 2＋Gmm ′(L 2)2＝m 4π2T 观测2·L 2，解得：T 观测＝πL2L G (m ＋4m ′)，又T 理论T 观测＝k ，所以：m ′＝k 2－14m ，故A 正确，B 、C 、D 错误．]5．B [两黑洞靠相互间的万有引力提供向心力，根据牛顿第三定律可知，A 对B 的作用力与B 对A 的作用力大小相等、方向相反，则黑洞A 的向心力等于B 的向心力，故A 错误；两黑洞靠相互间的万有引力提供向心力，具有相同的角速度，由题图可知A 的轨道半径比较大，根据v ＝ωr 可知，黑洞A 的线速度大于B 的线速度，故B 正确；由于m A ω2r A ＝m B ω2r B ，由于A 的轨道半径比较大，所以A 的质量小，故C 错误；两黑洞靠相互间的万有引力提供向心力，所以G m A m B L 2＝m A 4π2T 2r A ＝m B 4π2T 2r B ，又：r A ＋r B ＝L ，得r A ＝m B Lm A ＋m B ，L 为二者之间的距离，所以得：G m A m B L 2＝m A 4π2T 2·m B L m A ＋m B ，即：T 2＝4π2L 3G (m A ＋m B )，则两黑洞之间的距离越小，A 的周期越小，故D 错误．]6．BC [设两星质量分别为m 1、m 2.对m 1有：G m 1m 2(R 1＋R 2)2＝m 1R 14π2T 2，解得m 2＝4π2R 1(R 1＋R 2)2GT 2，同理可得m 1＝4π2R 2(R 1＋R 2)2GT2，故两者质量不相等，故选项A 错误；将两者质量相加得m 1＋m 2＝4π2(R 1＋R 2)3GT 2，则不可能其中一个的质量为4π2(R 1＋R 2)3GT 2，故选项D 错误，选项B 正确；m 1∶m 2＝R 2∶R 1，故选项C 正确．]。

专题17 双星或多星模型一、单选题1.双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动.研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化.若某双星系统中两星做圆周运动的周期为T ，经过一段时间演化后，两星总质量变为原来的k 倍，两星之间的距离变为原来的n 倍，则此时圆周运动的周期为（ ）【答案】B【解析】两恒星之间的万有引力提供各自做圆周运动的向心力，则有：2121122()m m Gm r L T π= 2122222()m m G m r L T π=又12L r r =+，12M m m =+联立以上各式可得T =故当两恒星总质量变为kM ，两星间距变为nL 时，圆周运动的周期T '，B 正确，ACD 错误。

故选B 。

2.经长期观测发现，A 行星运行的轨道半径为R 0，周期为T 0，但其实际运行的轨道与圆轨道总存在一些偏离，且周期性地每隔t 0时间发生一次最大的偏离.如图所示，天文学家认为形成这种现象的原因可能是A 行星外侧还存在着一颗未知行星B ，则行星B 的运行轨道半径为（ ）A.R ＝R 0B.R ＝R 000t t T -C.R ＝R 0D.R ＝R 0【答案】A【解析】A 行星运行的轨道发生最大偏离，必是B 对A 的引力引起的，B 行星在此时刻对A 有最大的力，故A 、B 行星与恒星在同一直线上且位于恒星同一侧.设行星B 的运行周期为T ，半径为R ，则有02T πt 0－2Tπt 0＝2π，所以T ＝0000t T t T -，由开普勒第三定律得33220R R T T =，得R ＝R，所以A 正确. 3.银河系的恒星中有一些是双星.某双星由质量不等的星体S 1和S 2构成，两星在相互之间的万有引力作用下绕两者连线上某一定点O 做匀速圆周运动，由天文观测测得其周期为T ，S 1到O 点的距离为r 1，S 1和S 2间的距离为r ，已知万有引力常量为G .则S 2的质量为（ ）A.22124()r r r GTπ- B.23124r GT π C.22124r r GT π D.2324r GTπ 【答案】C【解析】设星体S 1和S 2的质量分别为m 1、m 2，星体S 1做圆周运动的向心力由万有引力提供得：21211224 Gm m m r r T π=，即221224r r m GTπ=.故C 正确，ABD 错误. 4.太空中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其它星体对它们的引力作用。

⼈教版⾼中物理天体运动（双星及多星）专项练习双星及多星1.“双星体系”由两颗相距较近的恒星组成，每个恒星的半径远⼩于两个星球之间的距离，⽽且双星系统⼀般远离其他天体．如图1所⽰，相距为L的A、B两恒星绕共同的圆⼼O做圆周运动，A、B的质量分别为m1、m2，周期均为T.若有间距也为L的双星C、D，C、D的质量分别为A、B的两倍，则()A．A、B运动的轨道半径之⽐为m1m2B．A、B运动的速率之⽐为m1 m2C．C运动的速率为A的2倍D．C、D运动的周期均为2 2T2.双星系统由两颗恒星组成，两恒星在相互引⼒的作⽤下，分别围绕其连线上的某⼀点做周期相同的匀速圆周运动．研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发⽣变化．若某双星系统中两星做圆周运动的周期为T，经过⼀段时间演化后，两星总质量变为原来的k倍，两星之间的距离变为原来的n倍，则此时圆周运动的周期为()A.n3k2T B.n3k T C.n2k T D.nk T3.(多选)宇宙中存在⼀些质量相等且离其他恒星较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引⼒作⽤．设四星系统中每个星体的质量均为m，半径均为R，四颗星稳定分布在边长为a 的正⽅形的四个顶点上．已知引⼒常量为G.关于四星系统，下列说法正确的是()A．四颗星围绕正⽅形对⾓线的交点做匀速圆周运动B．四颗星的轨道半径均为a 2C．四颗星表⾯的重⼒加速度均为GmR2D．四颗星的周期均为2πa2a(4＋2)Gm4. (多)宇宙中有这样⼀种三星系统，系统由两个质量为m的⼩星体和⼀个质量为M的⼤星体组成，两个⼩星体围绕⼤星体在同⼀圆形轨道上运⾏，轨道半径为r。

关于该三星系统的说法中正确的是()A．在稳定运⾏的情况下，⼤星体提供两⼩星体做圆周运动的向⼼⼒B．在稳定运⾏的情况下，⼤星体应在⼩星体轨道中⼼，两⼩星体在⼤星体相对的两侧C．⼩星体运⾏的周期为T＝4πr32G（4M＋m）D．⼤星体运⾏的周期为T＝4πr32G（4M＋m）5.如图所⽰，质量分别为m和M的两个星球A和B在引⼒作⽤下都绕O点做匀速圆周运动，星球A 和B两者中⼼之间的距离为L.已知A、B的中⼼和O点始终共线，A和B分别在O点的两侧．引⼒常量为G. (1)求两星球做圆周运动的周期；(2)在地⽉系统中，若忽略其他星球的影响，可以将⽉球和地球看成上述星球A和B，⽉球绕其轨道中⼼运⾏的周期记为T1.但在近似处理问题时，常常认为⽉球是绕地⼼做圆周运动的，这样算得的运⾏周期为T2.已知地球和⽉球的质量分别为5.98×1024 kg和7.35×1022 kg.求T2与T1两者的平⽅之⽐．(结果保留3位⼩数) 【答案】(1)2πL3G(M＋m)(2)1.0126.宇宙中存在⼀些离其他恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其他星体对他们的引⼒作⽤．已观测到稳定的三星系统存在两种基本的构成形式：⼀种是三颗星位于同⼀直线上，两颗星围绕中央星在同⼀半径为R的圆轨道上运⾏；另⼀种形式是三颗星位于等边三⾓形的三个顶点上，并沿外接于等边三⾓形的圆轨道运⾏．设每个星体的质量均为m.(1)试求第⼀种形式下，星体运动的线速度和周期；(2)假设两种形式星体的运动周期相同，第⼆种形式下星体之间的距离应为多少？【答案】(1)v＝5GmR2R，T＝4πR35Gm(2)r＝(125)13R7.神奇的⿊洞是近代引⼒理论所预⾔的⼀种特殊天体，探寻⿊洞的⽅案之⼀是观测双星系统的运动规律．天⽂学家观测河外星系⼤麦哲伦云时，发现了LMCX－3双星系统，它由可见星A和不可见的暗星B构成．两星视为质点，不考虑其他天体的影响，A、B围绕两者连线上的O点做匀速圆周运动，它们之间的距离保持不变，如图所⽰，引⼒常量为G，由观测能够得到可见星A的速率v和运⾏周期T.(1)可见星A所受暗星B的引⼒F A可等效为位于O点处质量为m′的星体(视为质点)对它的引⼒，设A和B的质量分别为m1、m2，试求m′(⽤m1、m2表⽰)；(2)求暗星B的质量m2与可见星A的速率v、运⾏周期T和质量m1之间的关系式．(3)恒星演化到末期，如果其质量⼤于太阳质量m s的2倍，它将有可能成为⿊洞．若可见星A的速率v＝2.7×105 m/s，运⾏周期T＝4.7π×104 s，质量m1＝6m s，试通过估算来判断暗星B有可能是⿊洞吗？(G＝6.67×10－11 N·m2/kg2，m s＝2.0×1030 kg)【答案】(1)m′＝m32m1＋m22；(2)m32m1＋m22＝v3T2πG；(3)暗星B有可能是⿊洞．。

高三物理双星问题试题1.经长期观测人们在宇宙中已经发现了“双星系统”．“双星系统”是由两颗相距较近的恒星组成，每个恒星的线度远小于两个星体之间的距离，而且双星系统一般远离其他天体．如右图所示，两颗星球组成的双星，在相互之间的万有引力的作用下，绕连线上的O点做周期相同的匀速圆周运动．现测得两颗星之间的距离为L，质量之比为m1∶m2＝3∶2.则可知()A．m1、m2做圆周运动的线速度之比为3∶2B．m1、m2做圆周运动的角速度之比为3∶2C．m1做圆周运动的半径为D．m2做圆周运动的半径为【答案】C【解析】双星靠相互间的万有引力提供向心力，具有相同的角速度，对：，对：．得：，．所以．C正确，D错误；又，所以线速度之比．故A错误．根据公式可得1:1，B错误故选C【考点】双星问题．点评：解决本题的关键知道双星靠相互间的万有引力提供向心力，具有相同的角速度．以及会用万有引力提供向心力进行求解2.(15分)天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。

双星系统在银河系中很普遍。

利用双星系统中两颗恒星的运动特征可推算出它们的总质量。

已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T，两颗恒星之间的距离为r，试推算这个双星系统的总质量。

（引力常量为G）【答案】【解析】设两颗恒星的质量分别为m1、m2，做圆周运动的半径分别为r1、r2，角速度分别为w1,w2。

根据题意有w1=w2①（1分）r 1+r2=r ②（1分）根据万有引力定律和牛顿定律，有G③（3分）G④（3分）联立以上各式解得⑤（2分）根据解速度与周期的关系知⑥（2分）联立③⑤⑥式解得（3分）本题考查天体运动中的双星问题，两星球间的相互作用力提供向心力，周期和角速度相同，由万有引力提供向心力列式求解3.冥王星与其附近的另一星体卡戎可视为双星系统，质量比约为7∶1，同时绕它们连线上某点O 做匀速圆周运动，由此可知，冥王星绕O点运动的A．轨道半径约为卡戎的B．角速度大小约为卡戎的C．线速度大小约为卡戎的7倍D．向心力大小约为卡戎的7倍【答案】A【解析】由m1r1= m2r2，可得冥王星绕O点运动的轨道半径约为卡戎的，选项A正确；冥王星与另一星体卡戎绕它们连线上某点O做匀速圆周运动角速度相同，向心加速度大小相等，选项BD错误；由v=ωr可知线速度大小约为卡戎的，选项C错误。

高中物理双星问题例题1. 两个不同质量的天体组成双星系统，它们以它们之间的连线上的某一点为圆心做匀速圆周运动。

正确的说法是：A. 质量大的天体线速度较大B. 质量小的天体角速度较大C. 两个天体的向心力大小相等2. 月球和地球的质量之比约为1：80，有研究者认为月球和地球可视为一个由两个质点构成的双星系统，它们围绕地球和月球之间的连线上的某一点O做匀速圆周运动。

根据这种观点，我们可以知道月球和地球绕O点运动的线速度大小之比约为：3. 经过长期观测，人们在宇宙中已经发现了许多“双星系统”。

双星系统由两颗相距较近的恒星组成，每个恒星的大小远小于两个星体之间的距离。

双星系统一般远离其他天体。

如图所示，两颗星球组成的双星，在它们之间的万有引力作用下，绕连线上的O点做周期相同的匀速圆周运动。

现在已经测得两颗星之间的距离为L，它们的质量之比为m1：m2=2：3。

正确的说法是：A. m1、m2做圆周运动的线速度之比为3：2B. m1、m2做圆周运动的角速度之比为3：26. 我们的银河系中大约四分之一的恒星是___。

某个双星由质量不等的星体S1和S2构成，它们在相互之间的万有引力作用下绕两者连线上的某一定点C做匀速圆周运动。

由天文观察测得它们的运动周期为T，S1到C点的距离为r1，S1和S2的距离为r，已知引力常量为G。

由此可以求出S1的质量为：A. (r1+r)³T²G/4π²B. r1³T²G/4π²C. (r1+r)T²G/4π²。