苏教版八年级下册数学[二次根式的加减(基础)知识点整理及重点题型梳理]

苏教版八年级下册数学重难点突破知识点梳理及重点题型巩固练习二次根式（提高）知识讲解【学习目标】1、理解二次根式的概念，了解被开方数是非负数的理由.2、理解并掌握下列结论： a ≥0，（a ≥0），（a ≥0），（a ≥0），并利用它们进行计算和化简．【要点梳理】 要点一、二次根式及代数式的概念1.二次根式：一般地，式子(a ≥0)叫做二次根式，“”称为二次根号，a 叫做被开方数．要点诠释：二次根式的两个要素：①根指数为2；②被开方数为非负数.2.代数式：形如5，a ，a+b ，ab ，，x 3，这些式子，用基本的运算符号(基本运算包括加、减、乘、除、乘方、开方)把数和表示数的字母连接起来的式子，我们称这样的式子为代数式.要点二、二次根式的性质1.a ≥0，（a ≥0）；2. （a ≥0）；3.. 要点诠释：1.二次根式(a ≥0)的值是非负数。

一个非负数可以写成它的算术平方根的形式， 即2()(0a a a =≥）.2a 2()a 要注意区别与联系：（1）a 的取值范围不同，2)a 中a ≥02a a 为任意值.（2）a ≥0时，2)a 2a a ；a <0时，2)a 2a a -.【典型例题】类型一、二次根式的概念 1．（2015•启东）若x 、y 为实数，且224412x x y x -+-+=+，求x y x y +-的值．【答案与解析】∵y=，∴x 2﹣4=0，x+2≠0，解得：x=2，∴y=， ∴1137372244224x y x y +-=+⨯-=⨯=． 【总结升华】主要考查了二次根式有意义的条件，得出x ，y 的值是解题关键． 举一反三：【变式】方程480x x y m -+--=，当0y >时，m 的取值范围是（ ）.A ．01m << B.m ≥2 C.2m < D.m ≤2【答案】C类型二、二次根式的性质2.根据下列条件，求字母x 的取值范围：(1)； (2). 【答案与解析】解：(1)(2)【总结升华】二次根式性质的运用.举一反三：【二次根式及其乘除法（上）例1(1)(2)】【变式1】x 取何值时，下列函数在实数范围内有意义？（1）y=x -－11+x ,__________；（2）y=222+-x x ，___________.【答案】(1)01001x x x x -+≠∴≠-≥，≤且（2）2222(1)10,x x x x -+=-+>∴为任意实数. 【变式2】问题探究： 因为，所以， 因为，所以 请你根据以上规律，结合你的以验化简下列各式：（1）；（2）．【答案】解：（1）==； （2）==． 3.（2016春•濮阳期末）先阅读，后解答：（1）由根式的性质计算下列式子得：①=3，②=，③=，④=5，⑤=0．由上述计算，请写出的结果（a 为任意实数）．（2）利用（1）中的结论，直接写出下列问题的结果：①= ； ②化简：（x ＜2）= ．（3）应用：若+=3，则x 的取值范围是 ． 【思路点拨】（1）将a 分为正数、0、负数三种情况得出结果；（2）①当a=3，14﹣π＜0时，根据（1）中的结论可知，得其相反数﹣a ，即得π﹣3.14；②先将被开方数化为完全平方式，再根据公式得结果；（3）根据（1）式得：+=|x﹣5|+|x﹣8|，然后分三种情况讨论：①当x＜5时，②当5≤x≤8时，③当x＞8时，分别计算，哪一个结果为3，哪一个就是它的取值．【答案与解析】解：（1）=|a|=；（2）①=|3.14﹣π|=π﹣3.14，②（x＜2），=，=|x﹣2|，∵x＜2，∴x﹣2＜0，∴=2﹣x；故答案为：①π﹣3.14，②2﹣x；（3）∵+=|x﹣5|+|x﹣8|，①当x＜5时，x﹣5＜0，x﹣8＜0，所以原式=5﹣x+8﹣x=13﹣2x．②当5≤x≤8时，x﹣5≥0，x﹣8≤0．所以原式=x﹣5+8﹣x=3，③当x＞8时，x﹣5＞0，x﹣8＞0，所以原式=x﹣5+x﹣8=2x﹣13．∵+=3，所以x的取值范围是5≤x≤8，故答案为：5≤x≤8．【总结升华】本题考查了二次根式的性质和化简，明确二次根式的两个性质：①（）2=a（a ≥0）（任何一个非负数都可以写成一个数的平方的形式）；②=|a|=；尤其是第2个性质的运用，注意被开方数是完全平方式时，如第（3）小题，要分情况进行讨论．【二次根式及其乘除法（上）例4】4.已知c b a ,,为三角形的三边， 则222)()()(a c b a c b c b a -++--+-+= ．【思路点拨】三角形三边关系：任意两边之和大于第三边．【答案】a b c ++【解析】c b a ,,为三角形的三边,0,0,0a b c b c a b c a ∴+->--<+->即原式=a b c a c b b c a +-++-++-=a b c ++【总结升华】重点考查二次根式的性质：的同时，复习了三角形三边的性质.。

八年级二次根式必考知识点在八年级数学中，二次根式作为一个重要的知识点，经常出现在考试中。

二次根式是关于代数和几何的一种基本概念和运算方法。

了解和掌握二次根式的基本性质和运算规律是十分重要的，下面我们来看看八年级二次根式必考知识点：一、二次根式基本定义二次根式就是形如“根号下a”的式子，其中a为一个正实数。

二次根式也可以写成下面的形式：根号下a = a^1/2二次根式可以用于求解各种几何题目，但是在运算中，二次根式的拆分、合并和化简则是必须掌握的核心知识。

二、二次根式的加减法二次根式的加减法的运算规律是，对于任意的正实数a和b，有：根号下a ±根号下b = 根号下(a ± b)例如，根号下2 + 根号下3 = 根号下5，根号下8 - 根号下2 = 2根号下2。

三、二次根式的乘法二次根式的乘法的运算规律是，对于任意的正实数a和b，有：根号下a ×根号下b = 根号下ab例如，根号下2 ×根号下3 = 根号下6，根号下8 ×根号下2 =4 × 2 = 8。

四、二次根式的除法二次根式的除法的运算规律比较特殊，要求分子和分母中只有二次根式。

对于任意的正实数a和b，有：根号下a ÷根号下b = 根号下(a ÷ b)例如，根号下6 ÷根号下2 = 根号下(6 ÷ 2) = 根号下3。

五、二次根式的化简在运算中，二次根式的化简是必须掌握的核心知识。

化简的原则是数字尽可能取出平方因子，变成整数或者分数的形式，同时尽量消去根号。

下面是一些常见的化简方法：1. 合并同类项根号下2 + 3根号下2 = 4根号下22. 有理化分母根号下2 ÷根号下3 = 根号下6 ÷ 3 = （根号下6 ÷根号下9） ×根号下9 = （根号下6 ÷ 3） × 3 = （1 ÷根号下3） × 3 = 3 ÷根号下33. 分离出平方因子根号下8 = 根号下4 × 2 = 2根号下24. 二次根式的除法（根号下7 + 根号下5） ÷（根号下7 - 根号下5） = （根号下7 + 根号下5）×（根号下7 + 根号下5） ÷（根号下7 - 根号下5）×（根号下7 + 根号下5） = （7 + 2根号下35 + 5）÷2 = 6 + 根号下35以上就是八年级二次根式必考的知识点，要想在考试中得高分，必须要掌握这些知识。

课题：二次根式一、【知识积累】1.二次根式：式子a （a ≥0）叫做二次根式。

2.最简二次根式：必须同时满足下列条件：⑴被开方数中不含开方开的尽的因数或因式； ⑵被开方数中不含分母； ⑶分母中不含根式。

3.同类二次根式：二次根式化成最简二次根式后，若被开方数相同，则这几个二次根式就是同类二次根式。

4.二次根式的性质：（1）（a ）2=a （a ≥0）； （2）5.二次根式的运算：（1）因式的外移和内移：如果被开方数中有的因式能够开得尽方，那么，就可以用它的算术根代替而移到根号外面；如果被开方数是代数和的形式，那么先解因式，•变形为积的形式，再移因式到根号外面，反之也可以将根号外面的正因式平方后移到根号里面．（2）二次根式的加减法：先把二次根式化成最简二次根式再合并同类二次根式． （3）二次根式的乘除法：二次根式相乘（除），将被开方数相乘（除），所得的积（商）仍作积（商）的被开方数并将运算结果化为最简二次根式．ab =a ·b （a≥0，b≥0）；b ba a=（b≥0，a>0）． （4）有理数的加法交换律、结合律，乘法交换律及结合律，•乘法对加法的分配律以及多项式的乘法公式，都适用于二次根式的运算． 二、【典例引领】类型一：考查二次根式的概念（求自变量取值范围） 1、下列各式中，不是二次根式的是（ ）A ．45 B ．3π- C ．14 D ．122、二次根式4122--x x 有意义时的x 的取值范围是 。

3、已知： 122+--++=x x y ，则2001)(y x += 。

类型二：考查二次根式的性质（非负性、化简）（图1）a （a ＞0）==a a 2a -（a ＜0）0 （a =0）；4、代数式243x --的最大值是 。

5、实数在数轴上的位置如图1所示，化简|a-1|+2)2(-a = 。

6、把34-的根号外的因式移到根号内得 ；625-的平方根是 。

7、化简：=--x x 1 ；=-+-+-222)72()57(2)73( 。

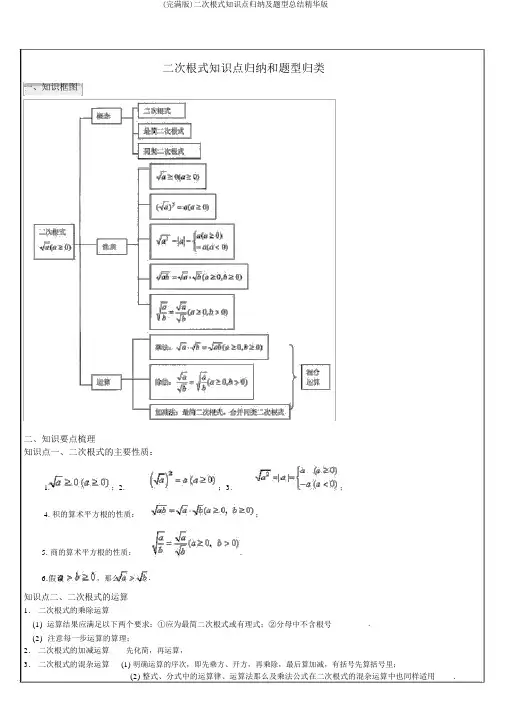
二次根式知识点归纳和题型归类一、知识框图二、知识要点梳理知识点一、二次根式的主要性质：1.；2.；3.；4.积的算术平方根的性质：；5. 商的算术平方根的性质：.6.假设，那么.知识点二、二次根式的运算1．二次根式的乘除运算(1) 运算结果应满足以下两个要求：①应为最简二次根式或有理式；②分母中不含根号.(2)注意每一步运算的算理；2．二次根式的加减运算先化简，再运算，3．二次根式的混杂运算(1) 明确运算的序次，即先乘方、开方，再乘除，最后算加减，有括号先算括号里；(2) 整式、分式中的运算律、运算法那么及乘法公式在二次根式的混杂运算中也同样适用.一. 利用二次根式的双重非负性来解题〔a0 〔a≥0〕，即一个非负数的算术平方根是一个非负数。

〕1.〕。

A、3；B、x ；C、x21；D、x1以下各式中必然是二次根式的是〔2．等式(x 1)2＝1－ x 成立的条件是 _____________ ．3．当 x____________ 时，二次根式2x 3 有意义．4.x 取何值时，以下各式在实数范围内有意义。

〔 1〕〔 2〕1〔3〕5x 2 x1x4〔 4〕假设x( x1)x x1，那么 x 的取值范围是〔 5〕假设x3x3，那么 x 的取值范围是。

x1x16.假设3m 1 有意义，那么m能取的最小整数值是；假设 20m 是一个正整数，那么正整数m的最小值是________．7.当 x 为何整数时，10x11有最小整数值，这个最小整数值为。

8. 假设2004 a a2005a ，那么a2004 2=_____________；假设y x33x 4 ，那么x y9．设 m、n 满足n m299m22mn =。

m 3，那么10. 假设三角形的三边a、 b、 c 满足a24a 4 b 3 =0，那么第三边c的取值范围是11. 假设|4x8 |x y m0 ，且 y 0 时，那么〔〕 A 、0m1 B 、m2C、m 2 D、 m 2利用二次根式的性质2a(a b)(即一个数的平方的算术平方根等于这个数的绝对值)来解题二． a =|a|=0(a0)a(a0)1.x33x2＝－x x 3 ，那么〔〕 A.x≤0 B. x≤－ 3Ｃ. x≥－ 3 D.－ 3≤x≤ 02.． a<b，化简二次根式 a 3b 的正确结果是〔〕A．a ab B ．a ab C． a ab D ．a ab3.假设化简 | 1-x |-28x16 的结果为2x-5 那么〔〕 A 、 x 为任意实数B、1≤ x≤ 4C、 x≥1 D 、x≤ 4 x4. a， b， c 为三角形的三边，那么(a b c)2(b c a) 2(b c a) 2=5.当 -3<x<5 时，化简26921025 =。

《二次根式的加减》考点分析中考考点知道什么是同类二次根式（能判断几个二次根式是否为同类二次根式，并把同类二次根式的概念与方程或方程组相联系，同时考查二次根式的加减法运算，即合并同类二次根式）会进行二次根式的加减法运算.考点讲解1．同类二次根式的概念：几个二次根式都化成最简二次根式以后，如果被开方数相同，这几个二次根式就叫做同类二次根式.同类二次根式的定义和判断，是学好二次根式加减运算的基础和关键.判断几个二次根式是否是同类二次根式，必须满足以下两个条件：（1）它们都是最简二次根式；（2）它们的被开方数必须完全相同.需要强调的是：同类二次根式与根号前面的数或式无关.另外，对尚未化为最简二次根式的几个根式，被开方数不相同，并不能判定为不同类二次根式.如：与-2，它们分别可化为6、-，故它们仍为同类二次根式.2．二次根式的加减法是学习本节内容的重点.二次根式的加减，实质上就是对二次根式进行化简与合并.合并“同类二次根式”与合并“同类项”类同，因此合并同类二次根式时，只把根号外的因式（数）相加，根指数和被开方数保持不变.这就是对二次根式进行加减运算.其步骤是：（1）对每个二次根式化简，一般先化为最简二次根式；（2）对同类二次根式进行合并、整理即得结果.3．原来在学习整式加减法中运用的交换律、分配律及去括号、添括号法则在二次根式的加减法中仍然适用.4．二次根式的加减运算结果应写成最简形式，这结果或是单个最简二次根式，或是几个不同类最简二次根式的和、差.5．考查本节的知识，要求能判断几个二次根式是否为同类二次根式，并能熟练地进行二次根式的加、减运算.考题评析1．（福州市）下列二次根式中与是同类二次根式的是（）.（A）（B）（C）（D）考点：同类二次根式.评析：要判断同类二次根式，首先明确最简二次根式及化简二次根式的方法.然后看被开方数是否相同（技巧：将各二次根式被开方数均除以作判断标准的最简二次根式的被开方数，结果能写成完全平方数即是，如300÷3=100=102，故选D）.2．（江西省）计算：= .考点：无理数的加减评析：运算是减法，首先化成最简二次根式，再合并，要正确运用法则.3．（西安市）已知a =2+，b =-2，求下式的值：（a4-b4）÷考点：运用二次根式和差求代数式的值（分式运算及无理数）评析：由于代数式比较复杂，首先要化简该代数式，即分式运算要注意因式分解和约分，其次观察所给的字母的值代入计算是否简单，若计算繁琐，则利用其较简单代数式的值整体代入.如该题可知： a-b=4故代数式化简成与a+b和a-b有关的式子.（ab=-1等）计算.注：此方法是常用的一种技巧，要理解掌握.2。

二次根式是数学中的一种特殊形式的根式表达方式，通常是指在根号下的表达式中含有一个变量的平方。

二次根式在数学中非常重要，涉及到数学中许多的基本概念和应用。

下面将详细介绍八年级数学中与二次根式有关的基础知识点。

一、二次根式的定义二次根式是形如√a的表达式，其中a可以是一个正实数，也可以是一个变量的平方。

当a是正实数时，√a表示使x²=a的非负实数x。

例如，√4=2，√9=3当a是变量的平方时，√a表示使x²=a的非负实数x的情况。

例如，√x²=x，√(x+1)²=x+1二、二次根式的化简与提取1.化简二次根式当二次根式内没有可以约分的因子时，可以使用下列公式进行化简：√(a×b)=√a×√b√(a/b)=√a/√b例如，√12可以化简为√4×√3，其中√4=2，因此√12=2√32.提取二次根式当二次根式内有可以提取的因子时，可以使用下列公式进行提取：√(a×a×b)=a√b√(a×a×a×b)=a²√b例如，√(16×5)可以提取为4√5三、二次根式的运算1.二次根式的加减运算当两个二次根式的根号内的表达式一样时，可以进行加减运算。

例如，√5+√5=2√5，√3-√3=0。

2.二次根式的乘法运算两个二次根式相乘时，将根号内的表达式相乘，并进行化简。

例如，√2×√3=√(2×3)=√63.二次根式的除法运算两个二次根式相除时，将根号内的表达式相除，并进行化简。

例如，√8/√2=√(8/2)=√4=2四、二次根式的应用1.二次根式的几何意义二次根式可以用来表示几何中的长度、面积等概念。

例如，一个边长为a的正方形的对角线长度可以表示为√2×a。

2.二次根式的解方程二次根式可以用来解决一些方程问题。

例如，方程x²+3x+2=0的解可以表示为√1和√23.二次根式的化简与提取在一些运算或应用问题中，需要对二次根式进行化简或提取，以便得到更简洁的表达式或结果。

初二数学二次根式的加减运算在数学中，二次根式是一种特殊的代数表达式，可以用来表示平方根。

初二学生在学习数学时会接触到二次根式的加减运算，这是一项基础且重要的运算。

本文将详细介绍初二数学中二次根式的加减运算，并提供相关的例题和解析，以帮助同学们更好地理解和掌握这一知识点。

一、二次根式的基本概念二次根式是指形如√a的数表达式，其中a为非负实数。

当a为正实数时，√a表示其平方根；当a为零时，√a等于0；当a为负实数时，√a无意义，记为不存在。

二、二次根式的加减运算规则1.同类项相加减：当二次根式的底数和指数均相同时，可以进行加减运算。

2.不同类项的加减：当二次根式的底数或指数不同，或者二次根式与常数项相加减时，无法进行加减运算，需要进行化简或转换为同类项后再进行运算。

三、二次根式的加减运算步骤与例题分析下面通过具体的例题来说明二次根式的加减运算步骤及注意事项：例题1：计算√5 + √20 - 2√5。

解析：首先将√5和2√5视为同类项，合并得到3√5；然后将√20展开为√4 × √5，进一步化简为2√5；最后进行合并，得到5√5。

例题2：计算√3 - (√2+ √5) 。

解析：这是一个不同类项的减法运算，无法直接计算，需要进行化简。

先将√2 + √5展开为√(2×5) = √10，然后再进行减法运算：√3 - √10 。

由于二次根式√3和√10的底数不同，无法继续进行加减运算，但可以保留原样。

所以最终结果为√3 - √10。

例题3：计算3√(5 + 2√3) - √(5 - 2√3) 。

解析：这是一个较为复杂的二次根式加减运算，需要仔细观察。

首先，要注意括号内的二次根式是一个整体。

我们将5 + 2√3 视为一个二次根式，记为A，将 5 - 2√3 视为另一个二次根式，记为B，然后根据加减运算规则进行计算：3√A - √B 。

将A展开：√(2√3 × 2√3) = √(4×3) = √12 = 2√3 。

第十二章二次根式一、二次根式的概念一般地，我们把形如 a （a≥0）的式子叫做二次根式，“”称为二次根号。

★正确理解二次根式的概念，要把握以下五点：（1）二次根式的概念是从形式上界定的，必须含有二次根号“”，“”的根指数为2，即“2”，我们一般省略根指数2，写作“”。

如25 可以写作 5 。

（2）二次根式中的被开方数既可以是一个数，也可以是一个含有字母的式子。

（3）式子 a 表示非负数a的算术平方根，因此a≥0， a ≥0。

其中a≥0是 a 有意义的前提条件。

（4）在具体问题中，如果已知二次根式 a ，就意味着给出了a≥0这一隐含条件。

（5）形如b a （a≥0）的式子也是二次根式，b与 a 是相乘的关系。

要注意当b是分数时不能写成带分数，例如832 可写成8 23，但不能写成2232 。

二、二次根式的性质：★（ a ）2（a≥0）与a2的区别与联系：三、代数式用基本运算符号（基本运算包括加、减、乘、除、乘方和开方）把数或表示数的字母连接起来的式子叫代数式。

例：3，x，x+y，3x （x≥0），-ab，st（t≠0，x3都是代数式注（1）单独一个数或字母也是代数式；（2）代数式中不能含有关系符号（＞，＜，=等）（1）将两个代数式用关系符号（＞，＜，=等）连接起来的式子叫关系式，方程和不等式都是关系式。

如2x+3＞3x-5是关系式。

列代数式的常用方法：（1）直接法：根据问题的语言叙述直接写出代数式。

（2）公式法：根据公式列出代数式。

（3）探究规律法：将蕴含在一组数或一组图形中的排列规律用代数式表示出来。

四、二次根式的乘除1、单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式。

2、单项式与单项式相除，把系数与同底数幂分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式。

五、二次根式的乘法法则a ．b =ab （a≥0，b≥0）即：二次根式相乘，把被开方数相乘，根指数不变（1）进行二次根式的乘法运算时，一定不能忽略其被开方数a，b均为非负数这一条件。

八年级数学二次根式知识点在八年级数学中，二次根式是比较基础的一个知识点，也是初学者需要特别掌握的内容之一。

本文将详细介绍二次根式的定义、性质、运算方法和解题技巧，希望能够帮助大家更好地掌握这个知识点。

1. 二次根式的定义二次根式是指如下形式的算式：$\sqrt{a}$其中，a是一个非负实数，$\sqrt{a}$表示a的平方根。

例如，$\sqrt{4}$等于2，$\sqrt{9}$等于3。

2. 二次根式的性质（1）二次根式的值不超过其被开方数的值。

即，对于任意非负实数a和b，当a≥b时，有$\sqrt{a}≥\sqrt{b}$。

这是因为，平方根函数$\sqrt{x}$在x≥0的范围内是单调递增的。

（2）二次根式的值域为非负实数。

即，对于任意非负实数a，有$\sqrt{a}≥0$。

这是因为，平方根函数$\sqrt{x}$在x≥0的范围内是非负的。

（3）二次根式可以转化为分数形式。

即，对于任意非负实数a和正整数b，有$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$。

这是因为，分子、分母分别乘以$\sqrt{b}$，可以得到等式右边的形式。

3. 二次根式的运算方法（1）二次根式的加减法对于相同根式$\sqrt{a}$和$\sqrt{b}$，有：$\sqrt{a}±\sqrt{b}=\sqrt{a±b}$例如，$\sqrt{2}+\sqrt{8}=\sqrt{2}+2\sqrt{2}=3\sqrt{2}$。

（2）二次根式的乘法对于非负实数a和b，有：$\sqrt{a}·\sqrt{b}=\sqrt{ab}$例如，$\sqrt{2}·\sqrt{8}=\sqrt{16}=4$。

（3）二次根式的除法对于非负实数a和b（b≠0），有：$\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$例如，$\frac{\sqrt{8}}{\sqrt{2}}=\sqrt{4}=2$。

八年级下册：二次根式的详细计算专题二次根式是数学中的一个重要概念，掌握了二次根式的计算方法对于学习代数和解决实际问题非常有帮助。

本文将详细介绍二次根式的计算方法和相关技巧。

1. 二次根式的定义二次根式是指形如$\sqrt{a}$ 的数，其中$a$ 为一个非负实数。

如果 $a$ 的平方为一个有理数，则二次根式是一个有理数；否则，二次根式是一个无理数。

2. 二次根式的基本运算2.1. 二次根式的加减运算对于同样的二次根式，可以进行加减运算。

例如：$\sqrt{2} + \sqrt{3} = \sqrt{2} + \sqrt{3}$$\sqrt{5} - \sqrt{2} = \sqrt{5} - \sqrt{2}$2.2. 二次根式的乘法运算对于两个二次根式，可以进行乘法运算。

例如：$\sqrt{2} \times \sqrt{3} = \sqrt{6}$$\sqrt{5} \times \sqrt{2} = \sqrt{10}$2.3. 二次根式的除法运算对于两个二次根式，可以进行除法运算。

例如：$\frac{\sqrt{6}}{\sqrt{2}} = \sqrt{3}$$\frac{\sqrt{10}}{\sqrt{5}} = \sqrt{2}$3. 二次根式的化简有时候，我们需要将二次根式化简为最简形式。

化简的方法有：3.1. 提取公因数如果一个二次根式可以被一个数整除，那么可以将这个数提取出来。

例如：$2\sqrt{3} = \sqrt{12}$$3\sqrt{6} = \sqrt{54}$3.2. 有理化分母如果二次根式的分母是一个二次根式，可以通过有理化分母将其化简为最简形式。

例如：$\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$$\frac{3}{\sqrt{5}} = \frac{3\sqrt{5}}{5}$4. 二次根式的应用二次根式在解决实际问题中经常会用到。

八年级二次根式知识点梳理在初中数学学习中，二次根式是一个重要的知识点，掌握好二次根式的运算和化简方法，对于后续的数学学习和应用都有着非常重要的作用。

本文将从基础概念、运算法则、化简方法和解题思路四个方面来进行二次根式知识点的梳理。

一、基础概念1. 二次根式的定义二次根式是指形如“a√b”的式子，其中a和b都是实数，a为系数，b为被开方数，√为根号符号。

2. 根式的运算符号根式的运算符号有加号、减号、乘号、除号，分别表示根式的加减、乘和除。

二、运算法则1. 二次根式的加减对于同类项，即被开方数相同的二次根式，其系数相加减即可，例如：3√2 + 5√2 = 8√24√3 - 2√3 = 2√3对于不同类项，则需要先化简为同类项后再进行加减运算，例如：2√3 + 5√2 - 3√3 = -√3 + 5√22. 二次根式的乘法二次根式的乘法可以使用分配律进行运算，例如：(3√2)(2√3) = 6√(2×3) = 6√63. 二次根式的除法二次根式的除法可以将被除数和除数同时乘以并分别化简为整数或同类项的二次根式，然后将化简后的结果进行相除，例如：(6√5) ÷ (2√5) = (6÷2)√(5÷5) = 34. 二次根式的混合运算二次根式的混合运算可以按照运算法则的顺序进行，先进行括号内的运算，然后进行乘除运算，最后进行加减运算，例如：(5√2 - 2√3) × 2√6 = 10√12 - 4√18 = 10√4√3 - 4√9√2 = 20√3 - 12√2三、化简方法1. 化简平方数根如√4、√9、√16等都是平方数根，可以直接化为整数，例如：√4 = 2√9 = 3√16 = 42. 分解因数将被开方数分解成若干个因子的积，然后再进行化简，例如：√32 = √16×2 = 4√2√75 = √25×3 = 5√33. 有理化分母二次根式的有理化分母可以将分母乘以分母的共轭形式，即将分母的加减号改为相反数的加减号，例如：(2+√3)÷(1-√3) = (2+√3)(1+√3)÷(1-√3)(1+√3) = 2√3 + 5四、解题思路1. 直观感受对于不确定的二次根式，可以通过估算其大小来判断其范围，例如：1 < √2 < 22 < √5 < 33 < √10 < 42. 转化为同类项将不同类项的二次根式转化为同类项后再进行加减运算，例如：√48 + √75 - √27 = 4√3 + 5√3 - 3√3 = 6√33. 有理化分母和化简将二次根式中的分母有理化并将其化简为整数或同类项的二次根式，然后再进行计算，例如：(1+√7)÷(1-√7) + √28 = (1+√7)(1+√7) ÷ (1-√7)(1+√7) +2√7 =8+2√7以上就是本文对八年级二次根式知识点的梳理，希望能够对大家的数学学习有所帮助。

八年级下册：二次根式的详细计算专题一、引言本文档将详细介绍八年级下册关于二次根式的计算知识点。

二次根式是数学中的一个重要内容，它涉及到了平方根和一些基本的运算法则。

通过研究本专题，学生将能够掌握二次根式的计算方法，并能够灵活运用于解决实际问题。

二、基本概念1. 二次根式的定义二次根式是指形如√a (a≥0) 的表达式，其中√表示平方根，a表示被开方数。

例如√4表示对4开方，即2。

2. 二次根式的运算法则- 二次根式的加减法：对于同一个被开方数的二次根式，可以直接进行相加或相减。

例如√2+ √2 = 2√2。

- 二次根式的乘法：将二次根式的被开方数相乘，系数相乘。

例如√2 × √3 = √6。

- 二次根式的除法：将二次根式的被开方数相除，系数相除。

例如√6 ÷ √2 = √3。

三、计算示例1. 加减法示例计算以下二次根式的和与差：- √5 + √3- √8 - √22. 乘法与除法示例计算以下二次根式的乘积与商：- √7 × √2- √20 ÷ √5四、解决实际问题二次根式在实际问题中的应用非常广泛，例如在几何中的勾股定理、物理中的速度计算等。

通过研究二次根式的计算方法，我们可以灵活运用于解决这些实际问题。

以下是一个例子：例题：小明骑自行车以每小时10公里的速度行驶，他行驶了t小时后，所行驶的距离可以表示为√(100t)（单位：千米）。

求小明行驶了多少千米？解答：根据题意，小明行驶的距离为√(100t)。

我们可以将该式子化简为10√t。

因此，小明行驶了10√t千米。

五、总结通过本专题的研究，我们学会了二次根式的定义、运算法则以及如何将其应用于解决实际问题。

掌握二次根式的计算方法对于我们的数学研究和实际生活都具有重要意义。

在今后的研究中，我们应该加强练，熟练掌握二次根式的计算技巧，为进一步研究数学打下坚实的基础。

二次根式的运算法则归纳与总结二次根式是数学中的一个重要概念，它在代数运算中扮演着重要的角色。

为了能够更好地进行二次根式的运算，我们需要归纳和总结相应的运算法则。

本文将带领读者一起来探索二次根式的运算法则及其应用。

一、加减运算法则对于形如√a ± √b的二次根式，可以应用以下加减运算法则：1. 当根内无理数部分相同时，即a = b，可进行如下加减运算：√a ± √b = √2a（±1）例如：√5 + √5 = 2√52. 当根内无理数部分不同时，即a ≠ b，需将二次根式化简后再进行加减运算：√a ± √b = √(a ± b ± 2√ab)例如：√7 + √3 = √(7 + 3 + 2√(7 × 3)) = √10 + √21二、乘法运算法则对于形如√a × √b的二次根式，可以应用以下乘法运算法则：√a × √b = √(ab)例如：√2 × √3 = √(2 × 3) = √6三、除法运算法则对于形如√a ÷ √b的二次根式，可以应用以下除法运算法则：√a ÷ √b = √(a ÷ b)例如：√8 ÷ √2 = √(8÷ 2) = √4 = 2四、合并同类项法则对于形如k√a ± m√b的二次根式，其中k和m为常数，a和b为非负实数，可以应用以下合并同类项法则进行化简：k√a ± m√b = √(ka) ± √(mb)例如：3√2 + 2√3 = √(3 × 2) + √(2 × 3) = √6 + √6 = 2√6五、有理化分母法则当二次根式的分母是二次根式时，我们需要进行有理化分母操作，具体步骤如下：1. 分母乘以其共轭形式，即将分母中二次根式的正负号取反；2. 分子分母同时化简；3. 化简后的二次根式无分母，得到最终结果。

【1】八年级下册数学二次根式的加减在八年级下册数学教材中，二次根式的加减是一个重要的知识点。

对于许多学生来说，二次根式的加减可能是一个比较难以理解的概念。

然而，只要我们能够掌握一定的技巧和方法，就能够轻松地解决二次根式的加减运算。

本文将以从简到繁、由浅入深的方式来探讨八年级下册数学二次根式的加减，以帮助读者更深入地理解这一知识点。

【2】二次根式的概念让我们来回顾一下二次根式的概念。

在数学中，二次根式是指形如√a 的数，其中a为非负实数。

对于二次根式的加减，我们需要掌握一些基本的运算规则，例如同类项相加减、合并同类项等。

这些规则将帮助我们在解决二次根式的加减问题时更加得心应手。

【3】二次根式的加减规则接下来，让我们来了解一下二次根式的加减规则。

当我们在进行二次根式的加减运算时，需要注意以下几点：1. 同类项相加减：只有当根号内的数相同，即根号下的被开方数相等时，才能进行加减运算。

2. 合并同类项：在进行二次根式的加减运算时，需要将根号内的数合并成一个根号。

【4】举例说明为了更加直观地理解二次根式的加减运算，让我们通过举例进行说明。

假设我们要计算√8 + 2√8的结果。

我们可以发现这两个二次根式是同类项，因为它们的根号内的被开方数都是8。

根据加法的运算规则，我们可以将这两个二次根式相加，得到3√8。

【5】深入探讨除了简单的加减运算外，二次根式的加减也涉及到更深入的探讨。

当我们需要进行多项式的二次根式加减运算时，就需要运用更多的技巧和方法。

在解决这类问题时，我们可以考虑将多项式展开，然后按照同类项的规则进行合并，最终得到简化的结果。

【6】总结回顾通过本文的讨论，我们对八年级下册数学二次根式的加减有了更深入的了解。

在实际的学习和应用中，我们可以通过大量的练习来提高自己的计算能力和思维能力。

对于一些复杂的问题，我们也可以寻求老师和同学的帮助，共同探讨解决方法。

【7】个人观点和理解在我个人看来，二次根式的加减是数学中的一道重要课题，它不仅考验了我们的计算能力，也锻炼了我们的逻辑思维能力。

“三步六字”围攻二次根式的加减二次根式加减时，必须先将所给式子中的每个二次根式化成最简二次根式，再将被开方数相同的二次根式进行合并，所以进行二次根式的加减运算时，可以分成“三步六字”围攻，智取其值.一、运算过程解读第一步：化简-—把每一个根式化简成“最简二次根式”所谓“最简二次根式”就是二次根式必须符合如下的两个特征：（1）被开方数不含分母。

如果被开方数是分式或分数，可以利用)0,0(>≥=b a b a b a ，然后再分母有理化得到)0,0(>≥=b a b ab b a 。

如93271271==. (2）被开方数中不含能开得尽方的因数或因式.也就是说应该把能开得尽方的因数或因式开出来.如222282=⨯=第二步：观察—-观察被开方数相同的项.在第一步化简的基础上，观察寻找出被开方数相同的项,将它们分别聚集在一起,特别要注意一定是化简后再识别，防止出现认为12与31，8与5.0被开方数是不相同错误现象. 第三步:合并-—合并同类二次根式（即被开方数相同二次根式）与整式的合并同类项相似,合并同类二次根式时，只是把被开方数相同的二次根式外面的因数或因式进行加减,根式内部的被开方数（或式）保持不变.二、典型案例剖析【例1】(临沂）27－1831－12 分析：因为题中的二次根式都不是最简二次根式，因此必须对每个二次根式先进行化简. 解：原式=332⨯－23312⨯－322⨯=33－2－23=（33－23)－2 =3－2【例2】（新疆乌鲁木齐市）计算：⎛÷ ⎝ 分析：本题是加减乘除的混合运算，根据运算顺序应当先算有括号内的，事实上括号内就是二次根式的加减，可用“三步六字”去解决。

解：原式⎛=÷ ⎝143==．【例302)+ 分析:本题是一个较为复杂的“二次根式的加减"运算问题,需要搞清两个性质，一个就是“任何不等于0的数的零次幂都等于1"，另一个就是二次根式的性质：||2a a =，还要掌握一个去括号法则：去掉括号和括号前的“－"时,括号内各项都要变号.02)+(11|1=++-．111=-+．1= 创新展台：【例4】（邵阳市）阅读下列材料，然后回答问题. 在进行二次根式运算时，我们有时会碰上如35，32，132+一样的式子，其实我们还可以将其进一步化简:35＝5535553＝⨯⨯；……① 32＝363332＝⨯⨯……② 132+＝））（（）－（1313132-+⨯＝131313222---＝）（）（ ……③ 以上这种化简的步骤叫做分母有理化.132+还可以用以下方法化简: 132+＝131313131313131322-+-++-+-＝））（（＝）（＝……④ （1)请用不同的方法化简352+. 参照③式得352+＝_________________________； 参照④式得352+＝___________________________。