解三角形大题经典练习(优.选)

1.在△ABC中，角A，B，C的对边分别为a，b，c，已知．（Ⅰ）求cosA的值；（Ⅱ）的值．2.在△ABC中，角A，B，C的对边分别为a，b，c．已知．（1）求的值；（2）若cosB=，△ABC的周长为5，求b的长．3.△ABC的三个角A、B、C所对的边分别为a、b、c，asinAsinB+bcos2A=a．（Ⅰ）求；（Ⅱ）若C2=b2+a2，求B．4.在△ABC中，角A，B，C的对边是a，b，c，已知3acosA=ccosB+bcosC （1）求cosA的值（2）若a=1，，求边c的值．5.在△ABC中，角A、B、C的对边分别为a，b，c（1）若，求A的值；（2）若，求sinC的值．6.△ABC的角A、B、C所对的边分别为a、b、c，已知a=1，b=2，cosC= （I）求△ABC的周长；（II）求cos（A﹣C）的值．7.在△ABC中，角A、B、C所对的边分别为a，b，c，已知cos2C=．（I）求sinC的值；（Ⅱ）当a=2，2sinA=sinC时，求b及c的长．8.设△ABC的角A、B、C的对边长分别为a、b、c，且3b2+3c2﹣3a2=4bc．（Ⅰ）求sinA的值；（Ⅱ）求的值．9.在△ABC中，a，b，c分别为角A，B，C的对边，且2asinA=（2b+c）sinB+（2c+b）sinC．（Ⅰ）求A的大小；（Ⅱ）求sinB+sinC的最大值．10.在锐角△ABC中，a，b，c分别为角A，B，C所对的边，且．（1）确定角C的大小；（2）若，且△ABC的面积为，求a+b的值．11.在△ABC中，角A，B，C的对边分别为，．（Ⅰ）求sinC的值；（Ⅱ）求△ABC的面积．12.设△ABC的角A，B，C的对边分别为a，b，c，且A=60°，c=3b．求：（Ⅰ）的值；（Ⅱ）cotB+cot C的值．13.△ABC的角A，B，C的对边分别为a，b，c．已知，求：（Ⅰ）A的大小；（Ⅱ）2sinBcosC﹣sin（B﹣C）的值．（Ⅱ）求sinB 的最大值．15.在△ABC 中，角A ，B ，C 对边的边长分别是a ，b ，c ．已知．（1）若△ABC 的面积等于，求a ，b ；（2）若sinC+sin （B ﹣A ）=2sin2A ，求△ABC 的面积．16.设ABC △的角A B C ，，所对的边长分别为a b c ，，，且cos 3a B =，sin 4b A =．（Ⅰ）求边长a ；（Ⅱ）若ABC △的面积10S =，求ABC △的周长222（Ⅱ）2sin cos sin()B C B C --的值.18. 在ABC △中,角,,A B C 对边的边长分别是,,a b c .已知2,3c C π==.⑴若ABC △求,a b ;⑵若sin sin()2sin 2C B A A +-=,求ABC △的面积.答案与评分标准一．选择题（共2小题）1．（2009•）已知锐角△ABC的面积为，BC=4，CA=3，则角C的大小为（）A．75°B．60°C．45°D．30°考点：解三角形。

大题 解三角形(精选30题)1(2024·江苏·一模)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ，已知2cos B +1=c a.(1)证明：B =2A ；(2)若sin A =24,b =14，求△ABC 的周长.2(2024·湖南常德·三模)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且sin 2A +sin 2B +sin A sin B =sin 2C ．(1)求角C ；(2)若a ，b ，c 成等差数列，且△ABC 的面积为1534，求△ABC 的周长．3(2024·江苏·一模)在△ABC 中，sin B -A +2sin A =sin C ．(1)求B 的大小；(2)延长BC 至点M ，使得2BC =CM ．若∠CAM =π4，求∠BAC 的大小．4(2024·浙江温州·二模)记△ABC的内角A,B,C所对的边分别为a,b,c，已知2c sin B=2b．(1)求C；(2)若tan A=tan B+tan C，a=2，求△ABC的面积．5(2024·浙江嘉兴·二模)在△ABC中，内角A,B,C所对的边分别是a,b,c，已知2cos A-3cos2A= 3.(1)求cos A的值；(2)若△ABC为锐角三角形，2b=3c，求sin C的值.6(2023·福建福州·模拟预测)在△ABC中，角A,B,C的对边分别是a,b,c，且a sin C=c sin B,C= 2π3．(1)求B；(2)若△ABC面积为334，求BC边上中线的长．7(2024·山东淄博·一模)如图，在△ABC中，∠BAC=2π3,∠BAC的角平分线交BC于P点，AP=2.(1)若BC=8，求△ABC的面积;(2)若CP=4，求BP的长.8(2024·安徽·模拟预测)如图，在平面四边形ABCD中，AB=AD=4，BC=6．(1)若A=2π3，C=π3，求sin∠BDC的值；(2)若CD=2，cos A=3cos C，求四边形ABCD的面积．9(2024·浙江·一模)在△ABC中，内角A,B,C所对的边分别是a,b,c，已知c2b2+c2-a2=sin Csin B．(1)求角A；(2)设边BC的中点为D，若a=7，且△ABC的面积为334，求AD的长．10(2024·湖北·一模)在△ABC中，已知AB=22,AC=23,C=π4．(1)求B的大小；(2)若BC>AC，求函数f x =sin2x-B-sin2x+A+C在-π,π上的单调递增区间．11(2024·福建厦门·二模)定义：如果三角形的一个内角恰好是另一个内角的两倍，那么这个三角形叫做倍角三角形.如图，△ABC的面积为S，三个内角A、B、C所对的边分别为a,b,c，且sin C=2Sc2-b2.(1)证明：△ABC是倍角三角形；(2)若c=9，当S取最大值时，求tan B.12(2024·福建漳州·模拟预测)如图，在四边形ABCD中，∠DAB=π2，B=π6，且△ABC的外接圆半径为4.(1)若BC=42，AD=22，求△ACD的面积；(2)若D=2π3，求BC-AD的最大值.13(2024·山东济南·二模)如图，在平面四边形ABCD中，BC⊥CD，AB=BC=2，∠ABC=θ，120°≤θ<180°.(1)若θ=120°，AD=3，求∠ADC的大小；(2)若CD=6，求四边形ABCD面积的最大值.14(2024·湖北武汉·模拟预测)已知锐角△ABC的三内角A，B，C的对边分别是a，b，c，且b2+c2 -(b⋅cos C+c⋅cos B)2=bc，(1)求角A的大小；(2)如果该三角形外接圆的半径为3，求bc的取值范围．15(2024·湖南邵阳·模拟预测)在△ABC中，角A,B,C的对边分别为a,b,c，且△ABC的周长为a sin Bsin A+sin B-sin C．(1)求C；(2)若a=2，b=4，D为边AB上一点，∠BCD=π6，求△BCD的面积．16(2024·广东梅州·二模)在△ABC中，角A，B，C所对应的边分别为a，b，c，3a cos B-b sin A= 3c，c=2，(1)求A的大小：(2)点D在BC上，(Ⅰ)当AD⊥AB，且AD=1时，求AC的长；(Ⅱ)当BD=2DC，且AD=1时，求△ABC的面积S△ABC．17(2024·广东广州·一模)记△ABC的内角A，B，C的对边分别为a，b，c，△ABC的面积为S.已知S=-34(a2+c2-b2).(1)求B；(2)若点D在边AC上，且∠ABD=π2，AD=2DC=2，求△ABC的周长.18(2024·广东佛山·模拟预测)在△ABC中，角A,B,C所对的边分别为a,b,c，其中a=1，cos A= 2c-12b．(1)求角B的大小；(2)如图，D为△ABC外一点，AB=BD，∠ABC=∠ABD，求sin∠CABsin∠CDB的最大值．19(2024·河北石家庄·二模)在△ABC中，角A，B，C所对的边分别为a，b，c，设向量m=(2sin A,3sin A+3cos A)，n =(cos A,cos A-sin A),f(A)=m ⋅n ,A∈π6,2π3.(1)求函数f A 的最大值;(2)若f(A)=0,a=3,sin B+sin C=62，求△ABC的面积.20(2024·广东·一模)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c，已知b-c cos A= 2a cos B cos C．(1)求cos B；(2)若点D在AC上(与A,C不重合)，且C=π4,∠ADB=2∠CBD，求CDAD的值．21(2024·辽宁·二模)在△ABC中，D为BC边上一点，DC=CA=1，且△ACD面积是△ABD面积的2倍．(1)若AB=2AD，求AB的长；(2)求sin∠ADBsin B的取值范围．22(2024·黑龙江齐齐哈尔·一模)记△ABC的内角A,B,C的对边分别为a,b,c，已知B=π4,4b cos C=2c+2a.(1)求tan C；(2)若△ABC的面积为32，求BC边上的中线长.23(2024·重庆·模拟预测)如图，某班级学生用皮尺和测角仪(测角仪的高度为1.7m )测量重庆瞰胜楼的高度，测角仪底部A 和瞰胜楼楼底O 在同一水平线上，从测角仪顶点C 处测得楼顶M 的仰角，∠MCE =16.5°(点E 在线段MO 上)．他沿线段AO 向楼前进100m 到达B 点，此时从测角仪顶点D 处测得楼顶M 的仰角∠MDE =48.5°，楼尖MN 的视角∠MDN =3.5°(N 是楼尖底部，在线段MO 上)．(1)求楼高MO 和楼尖MN ；(2)若测角仪底在线段AO 上的F 处时，测角仪顶G 测得楼尖MN 的视角最大，求此时测角仪底到楼底的距离FO ．参考数据：sin16.5°sin48.5°sin32°≈25，tan16.5°≈827，tan48.5°≈87，40×35≈37.4,24(2024·重庆·模拟预测)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ．已知b =2b cos 2π12-A 2 -a sin B 2cos B 2 ．(1)求角A 的大小；(2)若BP =PC ，且b +c =2，求AP 的最小值．25(2024·山西朔州·一模)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ，向量m =a +b ,c ,n =sin A -sin C ,sin A -sin B ，且m ⎳n ．(1)求B ；(2)求b 2a 2+c2的最小值．26(2024·河南开封·二模)记△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b cos A =2a sin B ．(1)求sin A ；(2)若a =3，再从条件①，条件②，条件③中选择一个条件作为已知，使其能够确定唯一的三角形，并求△ABC 的面积．条件① ：b =6c ；条件② ：b =6；条件③ ：sin C =13．注：如果选择的条件不符合要求，第(2)问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．27(2024·河南·一模)△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且满足b 2-a 2=ac .(1)求证：B =2A ；(2)若△ABC 为锐角三角形，求sin (C -A )-sin B sin A的取值范围.28(2023·河南·三模)在锐角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知a c =a 2+b 2-c 2b2，且a ≠c ．(1)求证：B =2C ；(2)若∠ABC 的平分线交AC 于D ，且a =12，求线段BD 的长度的取值范围．29(2024·湖北·二模)已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c a <b ，c =2a cos A cos B -b cos2A ．(1)求A ；(2)者BD =13BC ，AD =2，求b +c 的取值范围．30(2024·河北·二模)若△ABC 内一点P 满足∠PAB =∠PBC =∠PCA =θ，则称点P 为△ABC 的布洛卡点，θ为△ABC 的布洛卡角．如图，已知△ABC 中，BC =a ，AC =b ，AB =c ，点P 为的布洛卡点，θ为△ABC 的布洛卡角．(1)若b =c ，且满足PB PA=3，求∠ABC 的大小．(2)若△ABC 为锐角三角形．(ⅰ)证明：1tan θ=1tan ∠BAC +1tan ∠ABC +1tan ∠ACB ．(ⅱ)若PB 平分∠ABC ，证明：b 2=ac ．。

大题 解三角形(精选30题)1(2024·江苏·一模)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ，已知2cos B +1=ca.(1)证明：B =2A ；(2)若sin A =24,b =14，求△ABC 的周长.【答案】(1)证明见解析(2)7+14【分析】(1)利用正弦定理边化角结合角范围可证；(2)利用倍角公式求得sin C ，然后利用正弦定理可得【详解】(1)2cos B +1 sin A =sin C =sin A +B =sin A cos B +cos A sin B ⇒sin A =sin B cos A -cos B sin A =sin B -A 因为A ,B ∈0,π ,∴B -A ∈-π,π∴A =B -A 或A +B -A =π(舍)，∴B =2A .(2)由sin A =24，结合(1)知A +B =3A ∈0,π ，则A ∈0,π3 ，得cos A =1-sin 2A =1-242=144sin B =sin2A =2sin A cos A =2×24×144=74，cos B =cos2A =1-2sin 2A =1-2×18=34，∴sin C =sin A +B =sin A cos B +cos A sin B =24×34+144×74=10216=528，由正弦定理得a sin A=b sin B =c sin C ⇒a 24=1474=c528⇒a =2c =5 ∴△ABC 的周长为a +b +c =7+14.2(2024·湖南常德·三模)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且sin 2A +sin 2B +sin A sin B =sin 2C ．(1)求角C ；(2)若a ，b ，c 成等差数列，且△ABC 的面积为1534，求△ABC 的周长．【答案】(1)2π3(2)15【分析】(1)先利用正弦定理角化边得出a 2+b 2+ab =c 2；再结合余弦定理得出cos C =-12即可求解.(2先根据a ，b ，c 成等差数列得出a +c =2b ；再利用三角形的面积公式得出ab =15；最后结合(1)中的a 2+b 2+ab =c 2，求出a ，b ，c 即可解答.【详解】(1)因为sin 2A +sin 2B +sin A sin B =sin 2C ，由正弦定理a sin A=b sin B =csin C 可得：a 2+b 2+ab =c 2.由余弦定理可得：cos C =a 2+b 2-c 22ab =a 2+b 2-(a 2+b 2+ab )2ab=-12.又因为C ∈(0,π)，所以C =2π3.(2)由a ,b ,c 成等差数列可得：a +c =2b ①.因为三角形ABC 的面积为1534，C =2π3，∴12ab sin C =1534，即ab =15②.由(1)知：a 2+b 2+ab =c 2③由①②③解得：a =3,b =5,c =7.∴a +b +c =15，故三角形ABC 的周长为15.3(2024·江苏·一模)在△ABC 中，sin B -A +2sin A =sin C ．(1)求B 的大小；(2)延长BC 至点M ，使得2BC =CM ．若∠CAM =π4，求∠BAC 的大小．【答案】(1)B =π4；(2)∠BAC =π12或5π12．【分析】(1)由sin C =sin A +B ，代入已知等式中，利用两角和与差的正弦公式化简得cos B =22，可得B 的大小；(2)设BC =x ，∠BAC =θ，在△ABC 和△ACM 中，由正弦定理表示边角关系，化简求∠BAC 的大小.【详解】(1)在△ABC 中，A +B +C =π，所以sin C =sin A +B ．因为sin B -A +2sin A =sin C ，所以sin B -A +2sin A =sin A +B ，即sin B cos A -cos B sin A +2sin A =sin B cos A +cos B sin A 化简得2sin A =2cos B sin A ．因为A ∈0,π ，所以sin A ≠0，cos B =22．因为0<B <π，所以B =π4．(2)法1：设BC =x ，∠BAC =θ，则CM =2x ．由(1)知B =π4，又∠CAM =π4，所以在△ABM 中，∠AMC =π2-θ．在△ABC 中，由正弦定理得BC sin ∠BAC =AC sin B ，即x sin θ=ACsin π4①．在△ACM 中，由正弦定理得CM sin ∠CAM =AC sin M ，即2x sin π4=ACsin π2-θ②．①÷②，得222sin θ=cos θ22，即2sin θcos θ=12，所以sin2θ=12．因为θ∈0,3π4，2θ∈0,3π2，所以2θ=π6或5π6，故θ=π12或5π12．法2：设BC=x，则CM=2x，BM=3x．因为∠CAM=π4=B，所以△ACM∽△BAM，因此AMBM=CMAM，所以AM2=BM⋅CM=6x2，AM=6x．在△ABM中，由正弦定理得BMsin∠BAM=AMsin B，即3xsin∠BAM=6x22，化简得sin∠BAM=3 2．因为∠BAM∈0,3π4，所以∠BAM=π3或2π3，∠BAC=∠BAM-π4，故∠BAC=π12或5π12．4(2024·浙江温州·二模)记△ABC的内角A,B,C所对的边分别为a,b,c，已知2c sin B=2b．(1)求C；(2)若tan A=tan B+tan C，a=2，求△ABC的面积．【答案】(1)C=π4或3π4(2)43【分析】(1)根据正弦定理，边化角，结合三角形中角的取值范围，可得sin C，从而确定角C.(2)根据条件求角求边，再结合三角形面积公式求面积.【详解】(1)由2c sin B=2b 得2sin C sin B=2sin B，而B为三角形内角，故sin B>0,得sin C=22，而C为三角形内角，∴C=π4或3π4(2)由tan A=-tan B+C=tan B+tan C得-tan B+tan C1-tan B tan C=tan B+tan C，又tan B+tan C≠0，∴tan B tan C=2， ，故B,C∈0,π2，由(1)得tan C=1，故tan B=2，∴tan A=tan B+tan C=3，而A为三角形内角，∴sin A=31010.又asin A=csin C即231010=c22⇒c=203，又tan B=2，而B为三角形内角，故sin B=255，∴S=12ac sin B=12×2×203×255=43.5(2024·浙江嘉兴·二模)在△ABC中，内角A,B,C所对的边分别是a,b,c，已知2cos A-3cos2A= 3.(1)求cos A的值；(2)若△ABC为锐角三角形，2b=3c，求sin C的值.【答案】(1)cos A=13或cos A=0；(2)429.【分析】(1)根据题意，利用二倍角余弦公式化简求解；(2)解法一，由2b =3c ，利用正弦定理边化角得2sin B =3sin C ，结合sin A +C =sin B 和cos A =13，化简运算并结合平方关系求得答案；解法二，根据条件利用余弦定理可得c =23a ，再利用正弦定理边化角并结合条件求得答案.【详解】(1)由题可得2cos A -32cos 2A -1 =3，即3cos 2A -cos A =0，解得cos A =13或cos A =0.(2)解法一：因为2b =3c ，由正弦定理得2sin B =3sin C ，即2sin A +C =3sin C ，即2sin A cos C +2sin C cos A =3sin C ，因为cos A =13，所以sin A =223；所以423cos C +23sin C =3sin C ，又sin 2C +cos 2C =1，且△ABC 为锐角三角形，解得sin C =429.解法二：由余弦定理得cos A =b 2+c 2-a 22bc=13，因为2b =3c ，所以9c 24+c 2-a 23c2=13，即c 2=49a 2，所以c =23a ，所以sin C =23sin A ，又cos A =13，所以sin A =223，所以sin C =23sin A =429.6(2023·福建福州·模拟预测)在△ABC 中，角A ,B ,C 的对边分别是a ,b ,c ，且a sin C =c sin B ,C =2π3．(1)求B ；(2)若△ABC 面积为334，求BC 边上中线的长．【答案】(1)B =π6(2)212【分析】(1)由正弦定理边化角即可得到角B ；(2)根据A =B ，得a =b ，结合三角形面积公式即可得到a =b =3，再由正弦定理得边c ，以及2AD =AB +AC ，即可得到答案．【详解】(1)∵a sin C =c sin B ，由正弦定理边化角得sin A sin C =sin C sin B ，∵sin C ≠0，∴sin A =sin B ，∴A =B 或A +B =π(舍)，又∵C =2π3，∴B =π6；(2)∵B =π6，C =2π3，A =π6，∴a =b ，∴S △ABC =12ab sin C ，即334=12a 2⋅32，解得a =b =3，由正弦定理a sin A=csin C ，得c =a sin Csin A=3，设BC 边的中点为D ，连接AD ，如下图：∵2AD =AB +AC ，即(2AD )2=(AB +AC)2，即4AD 2=c 2+b 2+2bc cos A =9+3+2×3×3×32，解得AD =212．7(2024·山东淄博·一模)如图，在△ABC 中，∠BAC =2π3,∠BAC 的角平分线交BC 于P 点，AP =2.(1)若BC =8，求△ABC 的面积;(2)若CP =4，求BP 的长.【答案】(1)3+1952(2)2+2133【分析】(1)利用余弦定理和三角形面积公式即可求出答案；(2)首先利用余弦定理求出AC =1+13，再利用正弦定理求出sin C ，再根据三角恒变换求出sin B ，最后再根据正弦定理即可.【详解】(1)△ABC 中，设角A 、B 、C 的对边分别为a 、b 、c ，在△ABC 中由余弦定理得BC 2=AB 2+AC 2-2AB ⋅AC ⋅cos ∠CAB ，即64=c 2+b 2+b ⋅c ①因S △ABC =S △MBP +S △MCP ，即bc 2⋅32=2c 2⋅32+2b 2⋅32，整理得b ⋅c =2b +2c ②①②解得b ⋅c =2+265，所以S △ABC =12bc sin ∠BAC =3+1952.(2)因为AP =2,CP =4,∠PAC =π3，所以在△APC 中由余弦定理可得CP 2=AP 2+AC 2-2AP ⋅AC ⋅cos ∠CAP ，所以16=4+AC 2-2AC解得AC =1+13，由正弦定理得APsin C =PCsin ∠CAP，即2sin C=432，解得sin C =34，所以cos C =1-sin 2C =134，sin B =sin (∠BAC +C )=sin ∠BAC cos C +cos ∠BAC sin C =39-38,△ABC 中由正弦定理得AC sin B =BC sin ∠BAC，则1+1339-38=BC32，解得BC =14+2133，所以PB =BC -PC =14+2133-4=2+2133.8(2024·安徽·模拟预测)如图，在平面四边形ABCD 中，AB =AD =4，BC =6．(1)若A =2π3，C =π3，求sin ∠BDC 的值；(2)若CD =2，cos A =3cos C ，求四边形ABCD 的面积．【答案】(1)34(2)162+853【分析】(1)△ABD 中求出BD ，在△BCD 中，由正弦定理求出sin ∠BDC 的值；(2)△ABD 和△BCD 中，由余弦定理求出cos A 和cos C ，得sin A 和sin C ，进而可求四边形ABCD 的面积．【详解】(1)在△ABD 中，AB =AD =4，A =2π3，则∠ADB =π6，BD =2AD cos ∠ADB =2×4×cos π6=43，在△BCD 中，由正弦定理得BC sin ∠BDC =BDsin C ，sin ∠BDC =BC sin C BD =6sin π343=34.(2)在△ABD 和△BCD 中，由余弦定理得BD 2=AB 2+AD 2-2AB ⋅AD cos A =42+42-2×4×4×cos A =32-32cos A ，BD 2=CB 2+CD 2-2CB ⋅CD cos C =62+22-2×6×2×cos C =40-24cos C ，得4cos A -3cos C =-1，又cos A =3cos C ，得cos A =-13,cos C =-19，则sin A =223，sin C =459，四边形ABCD 的面积S =S △ABD +S △BCD =12AB ⋅AD ⋅sin A +12CB ⋅CD ⋅sin C=12×4×4×223+12×6×2×459=162+853.9(2024·浙江·一模)在△ABC 中，内角A ,B ,C 所对的边分别是a ,b ,c ，已知c 2b 2+c 2-a2=sin Csin B ．(1)求角A ；(2)设边BC 的中点为D ，若a =7，且△ABC 的面积为334，求AD 的长．【答案】(1)A =π3(2)132【分析】(1)根据正弦定理和题中所给式子化简计算得到b 2+c 2-a 2=bc ，再结合余弦定理即可求出角A ；(2)根据三角形面积公式得到bc =3和b 2+c 2=10，再结合中线向量公式计算即可.【详解】(1)在△ABC 中，由正弦定理得，sin C sin B =cb，因为c 2b 2+c 2-a 2=sin C sin B ，所以c 2b 2+c 2-a 2=cb ，化简得，b 2+c 2-a 2=bc ，在△ABC 中，由余弦定理得，cos A =b 2+c 2-a 22bc=12，又因为0<A <π，所以A =π3(2)由S △ABC =12bc sin A =34bc =334，得bc =3，由a 2=b 2+c 2-2bc cos A ，得7=b 2+c 2-3，所以b 2+c 2=10．又因为边BC 的中点为D ，所以AD =12AB +AC，所以AD =12(AB +AC )2=12b 2+c 2+2bc cos A =12×10+2×3×12=13210(2024·湖北·一模)在△ABC 中，已知AB =22,AC =23,C =π4．(1)求B 的大小；(2)若BC >AC ，求函数f x =sin 2x -B -sin 2x +A +C 在-π,π 上的单调递增区间．【答案】(1)B =π3或B =2π3(2)-π,-7π12 ,-π12,5π12 ,11π12,π【分析】(1)利用正弦定理及三角函数的特殊值对应特殊角即可求解；(2)利用大边对大角及三角形的内角和定理，再利用诱导公式及三角函数的性质即可求解.【详解】(1)在△ABC 中，由正弦定理可得：AB sin C=AC sin B ，即2222=23sin B ，解得sin B =32，又0<B <π，故B =π3或B =2π3．(2)由BC >AC ，可得A >B ，故B =π3,A +C =2π3.f x =sin 2x -π3 -sin 2x +2π3 =sin 2x -π3 -sin 2x +π-π3=2sin 2x -π3,令-π2+2k π≤2x -π3≤π2+2k π,k ∈Z ,解得-π12+k π≤x ≤5π12+k π，k ∈Z .由于x∈-π,π，取k=-1，得-π≤x≤-7π12；取k=0，得-π12≤x≤5π12；取k=1，得11π12≤x≤π，故f x 在-π,π上的单调递增区间为-π,-7π12,-π12,5π12,11π12,π．11(2024·福建厦门·二模)定义：如果三角形的一个内角恰好是另一个内角的两倍，那么这个三角形叫做倍角三角形.如图，△ABC的面积为S，三个内角A、B、C所对的边分别为a,b,c，且sin C=2Sc2-b2.(1)证明：△ABC是倍角三角形；(2)若c=9，当S取最大值时，求tan B.【答案】(1)证明见解析(2)23-3【分析】(1)由三角形面积公式化简条件，结合余弦定理及正弦定理进一步化简即可证明；(2)由正弦定理结合题中条件得到a=9sin3Bsin2B，结合三角形面积公式S=12×ac sin B化为关于tan B的表达式，构造函数，利用导数求得最大值即可.【详解】(1)因为sin C=2Sc2-b2=2×12ab sin Cc2-b2=ab sin Cc2-b2，又sin C≠0,所以abc2-b2=1，则b2=c2-ab，又由余弦定理知，b2=a2+c2-2ac cos B，故可得2c cos B=a+b，由正弦定理，2sin C cos B=sin A+sin B,又sin A=sin B+C=sin B cos C+cos B sin C,代入上式可得sin C cos B=sin B cos C+sin B,即sin C cos B-sin B cos C=sin B，sin C-B=sin B，则有C-B=B,C=2B,故△ABC是倍角三角形.(2)因为C=2B，所以A=π-B-C=π-3B>0,故0<B<π3，则tan B∈0,3，又c=9，又asin A=csin C，则a=9sin Asin C=9sinπ-3Bsin2B=9sin3Bsin2B,则S=12×ac sin B=92a sin B=92×9sin3Bsin2B×sin B=814⋅sin3Bcos B,=814⋅sin2B cos B+cos2B sin Bcos B=814×sin2B+cos2B tan B=8142tan B1+tan2B+1-tan2B1+tan2B⋅tan B=814×3tan B-tan3B1+tan2B设x=tan B∈0,3，f x =3x-x31+x2，则f x =3-3x21+x2-3x-x3⋅2x1+x22=-x4-6x2+31+x22令f x =0得x2=23-3或者x2=-23-3(舍)，且当0<x2<23-3时，f x >0，当23-3<x2<3时，f x <0，则f x 在0,23-3上单调递增，在23-3,3上单调递减，故当x=23-3时，f x 取最大值，此时S也取最大值，故tan B=23-3为所求.12(2024·福建漳州·模拟预测)如图，在四边形ABCD中，∠DAB=π2，B=π6，且△ABC的外接圆半径为4.(1)若BC=42，AD=22，求△ACD的面积；(2)若D=2π3，求BC-AD的最大值.【答案】(1)4；(2)833.【分析】(1)在三角形ABC中，根据正弦定理求得AC,∠CAB，再在三角形ADC中，利用三角形面积公式即可求得结果；(2)设∠DAC=θ，在三角形ADC,ABC中分别用正弦定理表示BC,AD，从而建立BC-AD关于θ的三角函数，进而求三角函数的最大值，即可求得结果.【详解】(1)因为B=π6，△ABC的外接圆半径为4，所以ACsin B=8，解得AC=4.在△ABC中，BC=42，则BCsin∠CAB=42sin∠CAB=8，解得sin∠CAB=22.又∠CAB∈0,π2，所以∠CAB=π4；在△ACD中，AC=4，∠DAC=π2-∠CAB=π4，AD=22，所以SΔACD=12×4×22×22=4.(2)设∠DAC=θ，θ∈0,π3.又D=2π3，所以∠ACD=π3-θ.因为∠DAB=π2，所以∠CAB=π2-θ.在△DAC中，AC=4，由正弦定理得ACsin D=ADsin∠ACD，即432=ADsinπ3-θ，解得AD=833sinπ3-θ=83332cosθ-12sinθ=4cosθ-433sinθ.在△ABC中，AC=4，由正弦定理得ACsin B=BCsin∠CAB，即412=BCsinπ2-θ，解得BC=8sinπ2-θ=8cosθ，所以BC-AD=4cosθ+33sinθ=833sinθ+π3.又θ∈0,π3，所以θ+π3∈π3,2π3，当且仅当θ+π3=π2，即θ=π6时，sinθ+π3取得最大值1，所以BC-AD的最大值为83 3.13(2024·山东济南·二模)如图，在平面四边形ABCD中，BC⊥CD，AB=BC=2，∠ABC=θ，120°≤θ<180°.(1)若θ=120°，AD=3，求∠ADC的大小；(2)若CD=6，求四边形ABCD面积的最大值.【答案】(1)∠ADC=45°(2)3+2【分析】(1)在△ABC中，利用余弦定理可得AC=6，由等腰三角形可得∠BCA=30°，然后在△ADC中利用正弦定理即可求解；(2)利用勾股定理求得BD=22，然后四边形面积分成S△BCD+S△ABD即可求解.【详解】(1)在△ABC中，AB=BC=2，θ=120°，所以∠BCA=30°，由余弦定理可得，AC2=22+22-2×2×2×-1 2=6，即AC=6，又BC⊥CD，所以∠ACD=60°，公众号：慧博高中数学最新试题在△ADC中，由正弦定理可得3sin60°=6sin∠ADC，得sin∠ADC=22，因为AC<AD，所以0°<∠ADC<60°，所以∠ADC=45°.(2)在Rt△BCD中，BC=2,CD=6，所以BD=22，所以，四边形ABCD的面积S=S△BCD+S△ABD=12×2×6+12×2×22sin∠ABD=3+2sin∠ABD，当∠ABD =90°时，S max =3+2，即四边形ABCD 面积的最大值为3+2.14(2024·湖北武汉·模拟预测)已知锐角△ABC 的三内角A ，B ，C 的对边分别是a ，b ，c ，且b 2+c 2-(b ⋅cos C +c ⋅cos B )2=bc ，(1)求角A 的大小；(2)如果该三角形外接圆的半径为3，求bc 的取值范围．【答案】(1)π3(2)6,9【分析】(1)由余弦定理将cos B ,cos C 化成边，化简再结合余弦定理可求得答案；(2)利用正弦定理，将边化角，再利用角的范围即可得出结果.【详解】(1)∵b 2+c 2-b cos C +c cos B 2=bc ，由余弦定理可得b 2+c 2-b ⋅a 2+b 2-c 22ab+c ⋅a 2+c 2-b 22ac 2=bc ，化简整理得b 2+c 2-a 2=bc ，又b 2+c 2-a 2=2bc cos A ，∴cos A =12，又0<A <π2，所以A =π3.(2)因为三角形外接圆半径为R =3，所以b =23sin B ，c =23sin C ，∴bc =12sin B sin C ，由(1)得B +C =2π3，所以bc =12sin B sin C =12sin B sin 2π3-B =12sin B 32cos B +12sin B =63sin B cos B +6sin 2B =33sin2B +31-cos2B=632sin2B -12cos2B +3=6sin 2B -π6+3，因为△ABC 是锐角三角形，且B +C =2π3，所以π6<B <π2，∴π6<2B -π6<5π6，∴12<sin 2B -π6≤1，∴6<6sin 2B -π6+3≤9，即6<bc ≤9.所以bc 的取值范围为6,9 .15(2024·湖南邵阳·模拟预测)在△ABC 中，角A ,B ,C 的对边分别为a ,b ,c ，且△ABC 的周长为a sin Bsin A +sin B -sin C ．(1)求C ；(2)若a =2，b =4，D 为边AB 上一点，∠BCD =π6，求△BCD 的面积．【答案】(1)C =2π3；(2)235.【分析】(1)根据给定条件，利用正弦定理角化边，再利用余弦定理求解即得.(2)由(1)的结论，利用三角形面积公式，结合割补法列式求出CD ，再求出△BCD 的面积.【详解】(1)在△ABC 中，a +b +c =a sin B sin A +sin B -sin C，由正弦定理得a +b +c =aba +b -c ，整理得a 2+b 2-c 2=-ab ，由余弦定理得cos C =a 2+b 2-c 22ab=-12，而0<C <π，所以C =2π3.(2)由D 为边AB 上一点，∠BCD =π6及(1)得∠ACD =π2，且S △ACD +S △BCD =S △ABC ，即有12b ⋅CD sin π2+12a ⋅CD sin π6=12ab sin 2π3，则4CD +CD =43，解得CD =435，所以△BCD 的面积S △BCD =12a ⋅CD sin π6=14×2×435=235.16(2024·广东梅州·二模)在△ABC 中，角A ，B ，C 所对应的边分别为a ，b ，c ，3a cos B -b sin A =3c ，c =2，(1)求A 的大小：(2)点D 在BC 上，(Ⅰ)当AD ⊥AB ，且AD =1时，求AC 的长；(Ⅱ)当BD =2DC ，且AD =1时，求△ABC 的面积S △ABC ．【答案】(1)A =2π3(2)AC =83+411；S △ABC =32+34【分析】(1)利用正弦定理，三角函数恒等变换的应用化简已知等式可得tan A 的值，结合A ∈(0,π)即可求解A 的值；(2)(Ⅰ)根据锐角三角函数和差角公式可得cos ∠ABC =AB BD =25,sin ∠ABC =AD BD =15,sin C =-510+155正弦定理即可求解.(Ⅱ)采用面积分割的方法以及正弦定理即可解决．【详解】(1)因为3a cos B -b sin A =3c ，所以由正弦定理可得3sin A cos B -sin B sin A =3sin C ，又sin C =sin (A +B )=sin A cos B +cos A sin B ，所以-sin B sin A =3cos A sin B ，因为B 为三角形内角，sin B >0，所以-sin A =3cos A ，可得tan A =-3，因为A ∈(0,π)，所以A =2π3；(2)(Ⅰ)此时AB =2=2AD ，AD ⊥AB ，所以DB =AB 2+AD 2=5，所以cos ∠ABC =AB BD =25,sin ∠ABC =AD BD =15,sin C =sin B +2π3 =15×-12 +25×32=-510+155，在△ABC 中，由正弦定理可得AC sin ∠ABC =AB sin C ⇒AC =AB sin ∠ABC sin C =2×15-510+155=83+411；(Ⅱ)设∠CAD =α，由S △ABC =S △BAD +S △CAD ，可得3b =2sin 2π3-α +b sin α，化简可得3b -b sin α=2sin 2π3-α 有b sin ∠ADC =CD sin α,2sin ∠ADB =BDsin 2π3-α，由于BD =2DC ，所以b sin αsin ∠ADC ×sin ∠ADB 2sin 2π3-α =12，所以b =sin 2π3-α sin α=12×3b -b sin αsin α⇒sin α=33,b =6+12，则S △ABC =12bc sin A =32+34．17(2024·广东广州·一模)记△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，△ABC 的面积为S .已知S =-34(a 2+c 2-b 2).(1)求B ；(2)若点D 在边AC 上，且∠ABD =π2，AD =2DC =2，求△ABC 的周长.【答案】(1)2π3；(2)3+23【分析】(1)根据三角形面积公式和余弦定理，化简已知条件，结合B 的范围，即可求得结果；(2)利用平面向量的线性运算及数量积运算，求得AB ,BC ，即可求得三角形周长.【详解】(1)由S =-34(a 2+c 2-b 2)，则12ac ⋅sin B =-34×2ac ⋅cos B ，tan B =-3又B ∈0,π ，故B =2π3.(2)由(1)可知，B =2π3，又∠ABD =π2，则∠CBD =π6；由题可知，AD =2DC =2，故BD =BC +CD =BC +13CA =BC +13BA -BC =23BC+13BA ，所以BA ⋅BD =BA ⋅23BC +13BA =13c 2-13ac =0，因为c ≠0，所以a =c ，A =C =π6，在Rt △ABD 中，c =AD ⋅cos π6=3，故△ABC 的周长为AB +BC +AC =3+3+3=3+2 3.18(2024·广东佛山·模拟预测)在△ABC 中，角A ,B ,C 所对的边分别为a ,b ,c ，其中a =1，cos A =2c -12b．(1)求角B 的大小；(2)如图，D 为△ABC 外一点，AB =BD ，∠ABC =∠ABD ，求sin ∠CABsin ∠CDB的最大值．【答案】(1)B =π3(2)3【分析】(1)根据题意，由正弦定理将边化为角，可得角的方程，化简计算，即可得到结果；(2)根据题意，由正弦定理可得sin ∠CAB sin ∠CDB =CDAC，再由余弦定理分别得到AC 2,CD 2，再由基本不等式代入计算，即可得到结果.【详解】(1)因为a =1，所以cos A =2c -a2b，由正弦定理a sin A=b sin B =c sin C ，可得cos A =2sin C -sin A2sin B ，整理可得2sin B cos A =2sin C -sin A ，又因为sin C =sin A +B =sin A cos B +sin B cos A ，化简可得sin A =2sin A cos B ，而sin A ≠0，则cos B =12，又B ∈0,π ，则B =π3(2)在△BCD 中，由BC sin ∠CDB =CDsin ∠CBD 可得sin ∠CDB =sin 23πCD，在△ABC 中，由BC sin ∠CAB =AC sin ∠ABC 可得sin ∠CAB =sin π3AC，所以sin ∠CAB sin ∠CDB =CD AC ，设AB =BD =t t >0 ，由余弦定理CD 2=BA 2+BC 2-2BA ⋅BC ⋅cos ∠CBD ，AC 2=BA 2+BC 2-2BA ⋅BC ⋅cos ∠CBA ，可得CD 2=t 2+1+t ，AC 2=t 2+1-t ，因此CD 2AC 2=t 2+1+t t 2+1-t =1+2t t 2+1-t ≤1+22t ⋅1t -1=3，当且仅当t =1t时，即t =1等号成立，所以sin ∠CAB sin ∠CDB的最大值为3，此时AB =BD =1.19(2024·河北石家庄·二模)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，设向量m=(2sin A ,3sin A +3cos A )，n =(cos A ,cos A -sin A ),f (A )=m ⋅n ,A ∈π6,2π3.(1)求函数f A 的最大值;(2)若f (A )=0,a =3,sin B +sin C =62，求△ABC 的面积.【答案】(1)3(2)S △ABC =34【分析】(1)由平面向量的数量积与三角恒等变换知识计算可得f (x )=2sin 2A +π3，再结合三角函数的值域计算即可求得；(2)由题中条件计算可得A =π3，再由正弦定理得b +c =6，由余弦定理可得bc =1，再由三角形的面积公式计算即可求得．【详解】(1)f (x )=m ⋅n=2sin A cos A +(3sin A +3cos A )(cos A -sin A )=sin2A +3(cos 2A -sin 2A )=sin2A +3cos2A =2sin 2A +π3因为A ∈π6,2π3 ，所以2A +π3∈2π3,5π3，所以当2A +π3=2π3，即A =π6时，f (x )有最大值2×32=3；(2)因为f A =0，所以2sin 2A +π3 =0，所以2A +π3=k π,k ∈Z ，因为A ∈π6,23A ，所以A =π3，由正弦定理得：2R =a sin A =332=2，所以sin B =b 2R =b 2，sin C =c 2R=c2，又因为sin B +sin C =62，所以b 2+c 2=62，所以b +c =6，由余弦定理有：a 2=b 2+c 2-2bc cos A ，即3=(b +c )2-3bc ，所以bc =1，所以S △ABC =12bc sin A =12×1×32=34．20(2024·广东·一模)设锐角三角形ABC 的内角A ,B ,C 的对边分别为a ,b ,c ，已知b -c cos A =2a cos B cos C ．(1)求cos B ；(2)若点D 在AC 上(与A ,C 不重合)，且C =π4,∠ADB =2∠CBD ，求CD AD的值．【答案】(1)12(2)2+3【分析】(1)根据条件，边转角得到sin B -sin C cos A =2sin A cos B cos C ，再利用sin B =sin A cos C +cos A sin C 即可求出结果；(2)根据题设得到∠DBC =C =π4，进而可求得A =5π12，∠ABD =π12，再利用CDAD=S △BCD S △ABD ，即可求出结果.【详解】(1)由b -c cos A =2a cos B cos C ，得到sin B -sin C cos A =2sin A cos B cos C ，又sin B =sin (π-A -C )=sin (A +C )=sin A cos C +cos A sin C ，所以cos C sin A=2sin A cos B cos C，又三角形ABC为锐角三角形，所以sin A≠0,cos C≠0，得到1=2cos B，即cos B=1 2 .(2)因为∠ADB=2∠CBD，又∠ADB=∠ACB+∠CBD，所以∠ACB=∠CBD，则BD=CD，所以∠DBC =C=π4，由(1)知，B=π3，则A=π-π3-π4=5π12，∠ABD=π-π2-5π12=π12，则CDAD=S△BCDS△ABD=12BC⋅BD sinπ412AB⋅BD sinπ12=sin A⋅sinπ4sin C⋅sinπ12=sin5π12⋅sinπ4sinπ4⋅sinπ12=cosπ12sinπ12=1tanπ12，又tan π12=tanπ4-π3=1-331+33=3-33+3，所以CDAD=3+33-3=2+ 3.21(2024·辽宁·二模)在△ABC中，D为BC边上一点，DC=CA=1，且△ACD面积是△ABD面积的2倍．(1)若AB=2AD，求AB的长；(2)求sin∠ADBsin B的取值范围．【答案】(1)1(2)54,+∞【分析】(1)根据三角形面积公式，结合余弦定理进行求解即可；(2)根据余弦定理、二倍角的余弦公式求出AB,AD的表达式，最后根据正弦定理求出sin∠ADBsin B的表达式，利用余弦函数的最值性质进行求解即可.公众号：慧博高中数学最新试题【详解】(1)设BC边上的高为AE，垂足为E，因为△ACD面积是△ABD面积的2倍，所以有S△ACDS△ABD=12CD⋅AE12BD⋅AE=2⇒BD=12⇒BC=32，设AB=2AD=x⇒AD=22x，由余弦定理可知：cos C=AC2+BC2-AB22AC⋅BC =AC2+DC2-AD22AC⋅DC⇒1+94-x22×1×32=1+1-12x22×1×1，解得x=1或x=-1舍去，即AB=1；(2)由(1)可知BD=12,BC=32，设∠ADC=θ，由DC=CA⇒∠DAC=∠ADC=θ⇒C=π-2θ且θ∈0,π2，由余弦定理可得：AD=12+12-2×1×1⋅cosπ-2θ=2+2cos2θ=2+22cos 2θ-1 =2cos θ，AB =12+32 2-2×1×32⋅cos π-2θ =134+3cos2θ=134+32cos 2θ-1 =6cos 2θ+14，在△ABD 中，因为θ∈0,π2 ，所以由正弦定理可知：AB sin ∠ADB =AD sin B ⇒sin ∠ADB sin B =ABAD =6cos 2θ+142cos θ=14×24cos 2θ+1cos 2θ=14×24+1cos 2θ，因为θ∈0,π2，所以cos θ∈0,1 ⇒cos 2θ∈0,1 ⇒1cos 2θ>1⇒24+1cos 2θ>25⇒24+1cos 2θ>5，于是有sin ∠ADB sin B >54，因此sin ∠ADB sin B的取值范围为54,+∞ ..22(2024·黑龙江齐齐哈尔·一模)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ，已知B =π4,4b cos C =2c +2a .(1)求tan C ；(2)若△ABC 的面积为32，求BC 边上的中线长.【答案】(1)tan C =12(2)52.【分析】(1)利用正弦定理以及三角恒等变换的知识求得tan C .(2)根据三角形ABC 的面积求得ac ，根据同角三角函数的基本关系式求得sin A ,cos A ，利用正弦定理、向量数量积运算来求得BC 边上的中线长.【详解】(1)由正弦定理可得c sin C=bsin B ，所以4sin B cos C =2sin C +2sin A ，即22cos C =2sin C +2sin A ，又A +B +C =π，所以22cos C =2sin C +2sin π4+C =22sin C +2cos C ，整理得2cos C =22sin C ，解得tan C =12；(2)依题意，12ac sin B =12ac ×22=32，解得ac =32，又tan A =tan 3π4-C =-1-tan C1-tan C =-3，所以A 为钝角，所以由sin A cos A=-3sin 2A +cos 2A =1 ,解得sin A =310,cos A =-110，由正弦定理可得c a =sin C sin A=15310=23，又ac =32，所以a =3,c =2,b =c sin Bsin C=2×2215=5，设BC 的中点为D ，则AD =12AB +AC，所以AD 2=14(AB +AC )2=b 2+c 2+2bc cos A 4=2+5+2×2×5×-1104=54，所以BC 边上的中线长为52.23(2024·重庆·模拟预测)如图，某班级学生用皮尺和测角仪(测角仪的高度为1.7m )测量重庆瞰胜楼的高度，测角仪底部A 和瞰胜楼楼底O 在同一水平线上，从测角仪顶点C 处测得楼顶M 的仰角，∠MCE =16.5°(点E 在线段MO 上)．他沿线段AO 向楼前进100m 到达B 点，此时从测角仪顶点D 处测得楼顶M 的仰角∠MDE =48.5°，楼尖MN 的视角∠MDN =3.5°(N 是楼尖底部，在线段MO 上)．(1)求楼高MO 和楼尖MN ；(2)若测角仪底在线段AO 上的F 处时，测角仪顶G 测得楼尖MN 的视角最大，求此时测角仪底到楼底的距离FO ．参考数据：sin16.5°sin48.5°sin32°≈25，tan16.5°≈827，tan48.5°≈87，40×35≈37.4,【答案】(1)41.7m ，5m (2)FO 为37．4m【分析】(1)法一：在△CDM 中，由正弦定理得，可得CM =100sin48.5°sin32°，进而求得ME ，MO ，进而求得CE ，计算可求得楼离MO 和楼尖MN ；法二：利用CE =ME tan ∠MCE，DE =MEtan ∠MDE ，可求得ME ，进而计算可求得楼离MO 和楼尖MN ；(2)设FO =xm ，tan ∠MGE =40x ，tan ∠NGE =35x，进而可得tan ∠MGN =tan ∠MGE -∠NGE =40x -35x1+40x ⋅35x，利用基本不等式可求得楼尖MN 的视角最大时x 的值．【详解】(1)法一：∠MCE =16.5°，∠MDE =48.5°，∴∠DMC =32°．在△CDM 中，由正弦定理得，CM =CD sin ∠CDMsin ∠DMC，又CD =100m ，∴CM =100sin 180°-48.5° sin32°=100sin48.5°sin32°．∴ME =CM sin ∠MCE =100sin48.5°sin16.5°sin32°=40m ，∴MO =ME +EO =40m +1.7m =41.7m ．CE =ME tan ∠MCE =40tan16.5°=40827=135(m )．∴DE =CE -CD =35m ．∵∠NDE =∠MDE -∠MDN =45°，∴NE =DE =35m ，MN =ME -NE =5m ．法二：CE =ME tan ∠MCE，DE =MEtan ∠MDE ，∴CE -DE =ME tan ∠MCE-MEtan ∠MDE =100，即ME ×278-78=100，∴ME =40m ，∴MO =ME +EO =40m +1.7m =41.7m ．CE =ME tan ∠MCE =40tan16.5°=40827=135m ．∴DE =CE -CD =35m ．∵∠NDE =∠MDE -∠MDN =45°，∴NE =DE =35m ，MN =ME -NE =5m ．(2)设FO =xm ，tan ∠MGE =40x ，tan ∠NGE =35x，∴tan ∠MGN =tan ∠MGE -∠NGE =tan ∠MGE -tan ∠NGE1+tan ∠MGE ⋅tan ∠NGE=40x -35x1+40x ⋅35x =5x +40×35x ≤52x ⋅40×35x =5240×35，当且仅当x =40×35x，即x ≈37.4时，等号成立．∴测角仪底到楼底的距离FO 为37．4m 处时，测得楼尖MN 的视角最大．24(2024·重庆·模拟预测)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ．已知b =2b cos 2π12-A 2 -a sin B 2cos B 2 ．(1)求角A 的大小；(2)若BP =PC ，且b +c =2，求AP 的最小值．【答案】(1)A =π3；(2)32．【分析】(1)根据题意，由正弦定理代入计算，结合三角恒等变换公式代入计算，即可得到结果；(2)根据题意，由平面向量数量积的运算律代入计算，结合基本不等式代入计算，即可得到结果.【详解】(1)在△ABC 中，由正弦定理a sin A=bsin B ，可得a sin B =b sin A又由b =2b cos 2π12-A 2 -a sin B 2cos B 2 知2a sin B 2cos B 2=b ⋅2cos 2π12-A 2-1 ，即a sin B =b cos π6-A ，得b sin A =b cos π6-A ，得sin A =cos π6-A =32cos A +12sin A ，得12sin A =32cos A ，所以tan A =3；又因为A ∈0,π ，所以A =π3．(2)由BP =PC ，得AP =12AB +12AC ，所以AP 2=12AB +12AC 2=14AB 2+14AC2+12AB ⋅AC=14c 2+14b 2+12bc cos A =14c 2+14b 2+14bc =14b +c 2-bc ≥14b +c 2-b +c 2 2 =316b +c 2=34，当且仅当b =c b +c =2 ，即b =c =1时等号成立，故AP 的最小值为32．25(2024·山西朔州·一模)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ，向量m =a +b ,c ,n=sin A -sin C ,sin A -sin B ，且m ⎳n ．(1)求B ；(2)求b 2a 2+c2的最小值．【答案】(1)B =π3(2)12【分析】(1)利用向量共线的坐标形式可得a 2+c 2-b 2=ac ，结合余弦定理可求B ；(2)利用基本不等式可求最小值.【详解】(1)因为m ⎳n，所以a +b sin A -sin B =c sin A -sin C ，由正弦定理可得a +b a -b =c a -c 即a 2-b 2=ac -c 2，故a 2+c 2-b 2=ac ，所以cos B =a 2+c 2-b 22ac =12，而B 为三角形内角，故B =π3.(2)结合(1)可得：b 2a 2+c 2=a 2+c 2-ac a 2+c 2=1-aca 2+c2,1-ac a 2+c2≥1-ac 2ac =1-12=12，当且仅当a =c 时等号成立，故b 2a 2+c2的最小值为12.26(2024·河南开封·二模)记△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b cos A =2a sin B ．(1)求sin A ；(2)若a =3，再从条件①，条件②，条件③中选择一个条件作为已知，使其能够确定唯一的三角形，并求△ABC 的面积．条件① ：b =6c ；条件② ：b =6；条件③ ：sin C =13．注：如果选择的条件不符合要求，第(2)问得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分．【答案】(1)sin A =33；(2)答案见解析.【分析】(1)利用正弦定理边化角，结合同角公式计算即得.(2)选择条件①，利用余弦定理及三角形面积公式计算求解；选择条件②，利用正弦定理计算判断三角形不唯一；选择条件③，利用正弦定理计算判断，再求出三角形面积.【详解】(1)由b cos A =2a sin B 得：sin B cos A =2sin A sin B ，而sin B ≠0，则cos A =2sin A >0，A 为锐角，又sin 2A +cos 2A =1，解得sin A =33，所以sin A =33且A 为锐角.(2)若选条件①，由sin A =33，A 为锐角，得cos A =63，由余弦定理得a 2=b 2+c 2-2bc cos A ，又b =6c ，则3=6c 2+c 2-4c 2，解得c =1,b =6,△ABC 唯一确定，所以S △ABC =12bc sin A =22.若选条件②，由正弦定理得a sin A =b sin B ，则sin B =6×333=63<1，由b =6>a =3，得B >A ，因此角B 有两解，分别对应两个三角形，不符合题意.若选条件③，由sin A =33，A 为锐角，得cos A =63，又sin A =33>sin C =13，得a >c ，A >C ，则cos C =223，因此sin B =sin (A +C )=sin A cos C +cos A sin C =63,△ABC 唯一确定，由正弦定理得a sin A=c sin C ，则c =3×1333=1，所以S △ABC =12ac sin B =22.27(2024·河南·一模)△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且满足b 2-a 2=ac .(1)求证：B =2A ；(2)若△ABC 为锐角三角形，求sin (C -A )-sin Bsin A的取值范围.【答案】(1)证明见解析(2)(-2,0)【分析】(1)用正弦定理边化角，再利用和差化积公式与诱导公式进行化简，得sin (B -A )=sin A ，从而用等量关系即可得证；(2)由(1)知，锐角三角形△ABC 中B =2A ，利用角A ,B ,C 关系求得角A 的范围，再把式子sin (C -A )-sin Bsin A用角A 的三角函数来表示并利用两角和差的正弦公式进行化简，进而用三角函数的取值范围即可求解.【详解】(1)证明：由条件b 2-a 2=ac ，根据正弦定理可得sin 2B -sin 2A =sin A sin C ，1-cos2B 2-1-cos2A2=sin A sin C ，即cos2A -cos2B =2sin A sin C ，cos2A -cos2B =cos A +B +A -B -cos A +B -A -B =-2sin (A +B )sin (A -B )=2sin A sin C ，又△ABC 中sin (A +B )=sin π-C =sin C ≠0，进行化简得sin (B -A )=sin A ，所以B -A =A ，即B =2A 或B -A =π-A ，即B =π(舍去)，所以B =2A .(2)若△ABC 为锐角三角形，根据(1)B =2A ，则B =2A <π2C =π-A -B <π2 ⇒2A <π2π-3A <π2 ，得π6<A <π4，式子sin (C -A )-sin B sin A =sin (π-A -B -A )-sin B sin A =sin4A -sin2Asin A ，=sin (3A +A )-sin (3A -A )sin A=2cos3A ，由π6<A <π4得π2<3A <3π4，又易知函数y =cos x 在π2,3π4内单调递减，所以cos3A ∈-22,0，因此sin (C -A )-sin B sin A =2cos3A ∈(-2,0).28(2023·河南·三模)在锐角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知a c =a 2+b 2-c 2b 2，且a ≠c ．(1)求证：B =2C ；(2)若∠ABC 的平分线交AC 于D ，且a =12，求线段BD 的长度的取值范围．【答案】(1)证明见解析(2)(43,62)【分析】(1)根据正余弦定理边角互化可得sin B =sin2C ，即可利用三函数的性质求解，(2)根据正弦定理以及角的范围即可利用三角函数的范围求解.【详解】(1)证明：由余弦定理可得a c =2ab cos C b 2=2a cos Cb ， 故b =2c cos C ，由正弦定理得sin B =2sin C cos C =sin2C ．所以在△ABC 中，B =2C 或B +2C =π．若B +2C =π，又B +A +C =π，故A =C ，因为a ≠c ，所以A ≠C ，故B +2C =π不满足题意，舍去，所以B =2C ．(2)在△BCD 中，由正弦定理可得a sin ∠BDC =BD sin C ，即12sin ∠BDC =BDsin C所以BD =12sin C sin ∠BDC =12sin C sin2C =6cos C因为△ABC 是锐角三角形，且B =2C ，所0<C <π20<2C <π20<π-3C <π2 得π6<C <π4，22<cos C <32 所以43<BD <62．所以线段BD 长度的取值范围是(43,62)．29(2024·湖北·二模)已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c a <b ，c =2a cos A cos B -b cos2A ．(1)求A ；(2)者BD =13BC ，AD =2，求b +c 的取值范围．【答案】(1)A =π3(2)1277<b +c <6【分析】(1)借助正弦定理、三角形内角和与两角差的正弦公式计算即可得；(2)借助向量的模长与平方的关系，结合数量积公式计算可得(b +c )2+3c 2=36，借助三角函数的性质，可令b +c =6cos α，3c =6sin α，结合余弦定理计算可得1277<6cos α<6，即可得解.【详解】(1)由正弦定理得sin C =2sin A cos A cos B -sin B cos2A ，则sin C =sin2A cos B -sin B cos2A ，则sin C =sin 2A -B ，∵C =π-A +B ，∴sin A +B =sin 2A -B ．即A +B =2A -B 或A +B =π-2A -B ，解得A =2B 或A =π3．因为a <b ，所以A <B ，所以A =2B 舍去，即A =π3；(2)由BD =13BC 得AD -AB =13AC -AB ，则AD =13AC +23AB ，则|AD |2=19b 2+49c 2+49bc cos A ，则4=19b 2+49c 2+29bc ，则b 2+4c 2+2bc =36，即(b +c )2+3c 2=36．令b +c =6cos α，3c =6sin α，因为c >0，b +c >0，所以0<α<π2．因为b =6cos α-23sin α>0，所以tan α<3，解得0<α<π3．由(1)得A =π3，则a 2=b 2+c 2-2bc cos A =b 2+c 2-bc ，又因为a <b ．所以a 2<b 2，所以7b 2+c 2-bc <b 2，解得c <b ，所以23sin α<6cos α-23sin α，解得tan α<32，所以0<tan α<32．令tan α1=32，则0<α<α1<π3，则cos α1<cos α<1．因为cos α1=277，所以1277<6cos α<6，即1277<b +c <6．30(2024·河北·二模)若△ABC 内一点P 满足∠PAB =∠PBC =∠PCA =θ，则称点P 为△ABC 的布洛卡点，θ为△ABC 的布洛卡角．如图，已知△ABC 中，BC =a ，AC =b ，AB =c ，点P 为的布洛卡点，θ为△ABC 的布洛卡角．。

解三角形解答题题型一 基础题型：求边求角+边角互化1．在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c ，已知cos cos sin sin 1A B A B C -=.（1）求角C 的大小；（2）若ABC ∆的面积为c =，求+a b 的值.2．在ABC △中，角,,A B C 所对的边分别为,,a b c ，且cos25A =，6b c +=，2ABC S ∆=. （1）求sin A 的值；（2）求a 的值.11．在ABC ∆中，内角A ，B ，C 的对边分别为a ，b ，c ，且()2sin cos sin sin 22A CB a b cC a A π+-+=-. （1）求角C 的大小； （2）若7c =，()13cos 14A C +=-，求ABC ∆的面积.15．锐角ABC ∆的内角A 、B ，C 的对边分别为a ，b ，c ，2sin (cos cos )A a B b A +=. (1)求角C 的大小；(2)若c =，ABC ∆的面积为ABC ∆的周长.题型二 三角形中的最值问题3．已知ABC ∆的内角A 、B 、C 所对的边分别为a 、b 、c .且cos 2sin cos 6B C A π⎛⎫=-⋅ ⎪⎝⎭. （1）求角A ；（2）若ABC ∆的面积为23，求ABC ∆周长的最小值.7．已知ABC △的内角A ，B ，C 所对的边分别为a ，b ，c ，若向量(,)m a b c =+与(cos 3sin ,1)n C C =+-相互垂直.（Ⅰ）求角A 的大小；（Ⅱ）若3a =，求ABC △周长的最大值.12．在锐角三角形ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，且2sin 2cos 3cos()A A B C -+sin 330A --=.（1）求A 的大小；（2）若2a =，求ABC ∆的周长L 的取值范围.题型三 平面几何中的应用4．如图所示，ABC ∆中，6BC =，60ABC ︒∠=，在ABC ∆内存在一点P ，满足2PA =，23PB =，PAB ∆外接圆的半径为2.（1）求PBC ∠，APB ∠；（2）求PC 的长及APC ∆的面积.5．ABC ∆的内角,,A B C 的对边分别为,,a b c 。

解三角形高考大题，带答案1. （宁夏17）（本小题满分12分）如图，ACD △是等边三角形，ABC △是等腰直角三角形，90ACB =∠，BD 交AC 于E ，2AB =．（Ⅰ）求cos CAE ∠的值； （Ⅱ）求AE ．解：（Ⅰ）因为9060150BCD =+=∠，CB AC CD ==，所以15CBE =∠．所以6cos cos(4530)4CBE =-=∠． ···················································· 6分 （Ⅱ）在ABE △中，2AB =， 由正弦定理2sin(4515)sin(9015)AE =-+．故2sin 30cos15AE=124⨯== 12分2. （江苏17）（14分） 某地有三家工厂，分别位于矩形ABCD 的顶点A 、B 及CD 的中点P 处，已知AB=20km ，BC=10km ，为了处理三家工厂的污水，现要在矩形ABCD 的区域上（含边界），且A 、B 与等距离的一点O 处建造一个污水处理厂，并铺设排污管道AO 、BO 、OP ，设排污管道的总长为ykm 。

（1）按下列要求写出函数关系式：①设∠BAO=θ(rad )，将y 表示成θ的函数关系式； ②设OP=x (km )，将y 表示成x 的函数关系式；（2）请你选用（1）中的一个函数关系式，确定污水处理厂的位置，使三条排污管道总长度最短。

专题解三角形大题(含答案)靠自己打拼出来的天下，才是最美的；靠自己获得的一切，才是最珍贵的。

今天，你，做数学题了吗？1.在△ABC中，已知bcosA+a=c，求B的大小和△ABC的面积。

根据正弦定理和余弦定理，可以得到sinBcosA+sinA=sinC和cosB=（c-a2-b2）/2ab。

代入已知条件，解得B=π/3，S△ABC=absinB=√3/4.2.在△ABC中，已知（b-a）sinB+asinA=csinC，且c=2，求角C的度数和△ABC面积的最大值。

同样利用正弦定理和余弦定理，可以得到a2+b2-c2=ab和cosB=(c-a2-b2)/2ab。

解得C=π/3，S△ABC=absinC=√3.3.在△ABC中，已知a+b+c=2，求sinC和如果△ABC是钝角三角形，求其面积。

根据余弦定理，可以得到cosC=(a2+b2-c2)/2ab。

代入已知条件，解得sinC=√3/2，若△ABC是钝角三角形，面积为0.4.在△ABC中，已知2cosC（acosB+bcosA）=c，求角C和如果c=2，求△ABC面积的最大值。

根据余弦定理，可以得到cosC=(a2+b2-c2)/2ab。

代入已知条件，解得C=π/3，S△ABC=absinC=√3.当c=2时，代入面积公式，解得S△ABC=√3.5.在四边形ABCD中，已知∠D=2∠B，且AD=2，CD=6，cosB=1/3，求△ACD的面积和AB的长。

根据余弦定理，可以得到AC2=40-24cosB=32，再根据海龙公式和正弦定理，可以解得S△ACD=8√3和AB=2√7.6.在△ABC中，已知bsin（A+C）=asinC，且a=2c，求sinB和△ABC的周长。

代入正弦定理和已知条件，解得sinB=1/2，周长为3c。

1.由$a^2+b^2-c^2=ab$，得到$ab+4=a^2+b^2$。

由不等式$a^2+b^2\geq 2ab$，得到$ab+4\geq 2ab$，因此$ab\leq 4$。

解三角形测试题一、选择题：1、ΔABC中,a=1,b=3, ∠A=30°,则∠B等于〔〕A．60°B．60°或120°C．30°或150°D．120°2、符合以下条件的三角形有且只有一个的是〔〕A．a=1,b=2 ,c=3 B．a=1,b=2,∠A=30°C．a=1,b=2,∠A=100°D．b=c=1, ∠B=45°3、在锐角三角形ABC中，有〔〕A．cosA>sinB且cosB>sinA B．cosA<sinB且cosB<sinAC．cosA>sinB且cosB<sinA D．cosA<sinB且cosB>sinA4、假设(a+b+c)(b+c－a)=3abc,且sinA=2sinBcosC, 那么ΔABC是〔〕A．直角三角形B．等边三角形C．等腰三角形D．等腰直角三角形5、设A、B、C为三角形的三内角,且方程(sinB－sinA)x2+(sinA－sinC)x +(sinC－sinB)=0有等根，那么角B 〔〕A．B>60°B．B≥60°C．B<60°D．B ≤60°6、满足A=45,c=6,a=2的△ABC的个数记为m,则a m的值为〔〕A．4 B．2 C．1 D．不定7、如图：D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点仰角分别是β,ABα(α<β),则A 点离地面的高度AB 等于 〔 〕A ．)sin(sin sin αββα-a B ．)cos(sin sin βαβα-⋅aC ．)sin(cos sin αββα-a D ．)cos(sin cos βαβα-a8、两灯塔A,B 与海洋观察站C 的距离都等于a(km), 灯塔A 在C 北偏东30°,B 在C 南 偏东60°,则A,B 之间的相距 〔 〕A ．a (km)B ．3a(km)C ．2a(km)D ．2a (km)二、填空题：9、A 为ΔABC 的一个内角,且sinA+cosA=127, 则ΔABC 是______三角形. 10、在ΔABC 中，A=60°, c:b=8:5,内切圆的面积为12π,则外接圆的半径为_____.11、在ΔABC 中，假设S ΔABC =41 (a 2+b 2－c 2),那么角∠C=______. 12、在ΔABC 中，a =5,b = 4,cos(A －B)=3231,则cosC=_______.三、解答题：13、在ΔABC 中,求分别满足以下条件的三角形形状： ①B=60°,b 2=ac ； ②b 2tanA=a 2tanB ； ③sinC=BA BA cos cos sin sin ++④ (a 2－b 2)sin(A+B)=(a 2+b 2)sin(A －B).D Cα β14、已知ΔABC 三个内角A 、B 、C 满足A+C=2B,A cos 1+ C cos 1 =－B cos 2 , 求2cosCA 的值.15、二次方程ax 2－2bx+c=0,其中a 、b 、c 是一钝角三角形的三边,且以b 为最长.①证明方程有两个不等实根； ②证明两个实根α,β都是正数； ③假设a=c,试求|α－β|的变化范围.16、海岛O 上有一座海拨1000米的山,山顶上设有一个观察站A,上午11时,测得一轮船在岛北60°东C 处,俯角30°,11时10分,又测得该船在岛的北60°西B 处,俯角60°.①这船的速度每小时多少千米？②如果船的航速不变,它何时到达岛的正西方向？此时所在点E离岛多少千米？一、BDBBD AAC 二、〔9〕钝角 〔10〕3314 〔11〕4π 〔12〕81三、〔13〕分析：化简已知条件，找到边角之间的关系，就可判断三角形的形状. ①由余弦定理ac ac c a ac b c a ac b c a =-+⇒=-+⇒-+=︒22222222212260cos 0)(2=-∴c a ，c a =∴. 由a=c 及B=60°可知△ABC 为等边三角形. ②由AAb B a A b cos sin tan tan 222⇒=,2sin 2sin ,cos sin cos sin sin sin cos sin cos sin cos sin 22222B A B B A A AB a b B A A B B B a =∴=∴==⇒=∴A=B 或A+B=90°，∴△ABC 为等腰△或Rt △. ③BA B A C cos cos sin sin sin ++= ，由正弦定理：,)cos (cos b a B A c +=+再由余弦定理：b a acb c a c bc c b a c +=-+⨯+-+⨯22222222∆∆∴+=∴=--+∴Rt ABC b a c b a c b a 为,,0))((222222. ④由条件变形为2222)sin()sin(ba b a B A B A +-=+-︒=+=∴=∴=⇒=--+-++∴90,2sin 2sin sin sin sin cos cos sin ,)sin()sin()sin()sin(2222B A B A B A BA B A B A b a B A B A B A B A 或. ∴△ABC 是等腰△或Rt △. 点评：这类判定三角形形状的问题的一般解法是：由正弦定理或余弦定理将已知条件转化为只含边的式子或只含角的三角函数式，然后化简考察边或角的关系，从而确定三角形的形状. 有时一个条件既可用正弦定理也可用余弦定理甚至可以混用. 如本例的②④也可用余弦定理，请同学们试试看.〔14〕分析：︒=+︒=∴=+120,60,2C A B B C A 再代入三角式解得A 或 C. 解：︒=+︒=∴=-︒∴=+120.60,2180,2C A B B B B C A .∴由已知条件化为：22cos )120cos(.22)120cos(1cos 1-=+-︒∴-=-︒+A A A A),120cos(cos A A -︒设ααα-︒=+︒==-60,60,2C A CA 则.代入上式得：)60cos(α-︒ )60cos()60cos(22)60cos(ααα-︒+︒-=+︒+.化简整理得023cos 2cos 242=-+αα222cos ,22cos ,0)3cos 22)(2cos 2(=+=∴=+-⇒C A 即ααα. 注：此题有多种解法. 即可以从上式中消去B 、C 求出cosA ，也可以象本例的解法.还可以用和、差化积的公式，同学们可以试一试.〔15〕分析：证明方程有两个不等实根，即只要验证△＞0即可.要证α，β为正数，只要证明αβ＞0，α+β＞0即可. 解：①在钝角△ABC 中，b 边最长.ac b ac b B ac c a b B 424)2(,cos 20cos 122222-=--=∆-+=<<-∴且.0cos 4)(24)cos 2(2222>--=--+=B ac c a ac B ac c a 〔其中0cos 40)(22>-≥-B ac c a 且∴方程有两个不相等的实根. ②,0,02>=>=+aca b αββα ∴两实根α、β都是正数. ③a=c 时，=-=-+=-+=-∴⎪⎪⎩⎪⎪⎨⎧===+424)(2)(,12222222a b a a c a bαββααβββααββα2||0,4cos 40,0cos 1,cos 44)cos 2(22222<-<<-<∴<<--=--+βα因此B B B aa B ac c a . 〔16〕分析：这是一个立体的图形，要注意画图和空间的简单感觉.解：①如图：所示. OB=OA 3330tan =(千米)，3=OC 〔千米〕 则313120cos 222=︒⋅-+=OC OB OC OB BC 〔千米〕3926010313=÷=∴v 船速〔千米/小时〕 ②由余弦定理得：=∠=∠∴=⨯-+=∠OBC EBO BC OB OC BC OB OBC sin sin ,261352cos 222 =︒+∠-︒=∠-=∠=-)]30(180sin[sin ,26135cos ,26393)26135(12EBO OEB EBO .131330sin cos 30cos sin )30sin(=︒⨯∠+︒⨯∠=︒+∠EBO EBO EBO 再由正弦定理，得OE=1.5〔千米〕，5),(639==vBEBE 千米〔分钟〕. 答：船的速度为392千米/小时；如果船的航速不变，它5分钟到达岛的正西方向，此时所在点E 离岛1.5千米.。

1．（2013大纲）设的内角的对边分别为,.(I)求(II)若,求. 2．（2013四川）在中,角的对边分别为,且. (Ⅰ)求的值;(Ⅱ)若,,求向量在方向上的投影.3．（2013山东）设△的内角所对的边分别为,且,,. (Ⅰ)求的值; (Ⅱ)求的值.4．（2013湖北）在中,角,,对应的边分别是,,.已知.(I)求角的大小;(II)若的面积,,求的值.5．（2013新课标）△在内角的对边分别为,已知.(Ⅰ)求;(Ⅱ)若,求△面积的最大值.6．（2013新课标1）如图,在△ABC 中,∠ABC=90°,AB=3,BC=1,P 为△ABC 内一点,∠BPC=90°(1)若PB=12,求PA;(2)若∠APB=150°,求tan ∠PBA[7．（2013江西）在△ABC 中,角A,B,C 所对的边分别为a,b,c,已知cosC+(conA-√3sinA)cosB=0.ABC ∆,,A B C ,,a b c ()()a b c a b c ac ++-+=B sin sin AC =C ABC ∆,,A B C ,,a b c 232cos cos sin()sin cos()25A B B A B B A C ---++=-cosA a =5b =BA BC ABC ,,ABC ,,a b c 6a c +=2b =7cos 9B =,a c sin()A B -ABC ∆A B C a b c ()cos23cos 1A B C -+=A ABC∆S =5b =sin sin B C(1) 求角B 的大小;(2)若a+c=1,求b 的取值范围33．（2013大纲）设的内角的对边分别为,.(I)求(II)若,求. 【答案】4．（2013年高考四川卷（理））在中,角的对边分别为,且. (Ⅰ)求的值;(Ⅱ)若,,求向量在方向上的投影.【答案】解:由,得 , 即, 则,即 ABC ∆,,A B C ,,a b c ()()a b c a b c ac ++-+=B sin sin AC =C ABC ∆,,A B C ,,a b c 232cos cos sin()sin cos()25A B B A B B A C ---++=-cosA a =5b =BA BC ()I ()()232cos cos sin sin cos 25A B B A B B A C ---++=-()()3cos 1cos sin sin cos 5A B B A B B B -+---=-⎡⎤⎣⎦()()3cos cos sin sin 5A B B A B B ---=-()3cos 5A B B -+=-3cos 5A =-由,得, 由正弦定理,有,所以,. 由题知,则,故.根据余弦定理,有,解得或(舍去).故向量在方向上的投影为 35．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））设△的内角所对的边分别为,且,,. (Ⅰ)求的值; (Ⅱ)求的值.【答案】解:(Ⅰ)由余弦定理,得,又,,,所以,解得,.(Ⅱ)在△中,,由正弦定理得,因为,所以为锐角,所以因此.36．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））已知函数的最小正周期为.()II 3cos ,05A A π=-<<4sin 5A =sin sin a bA B=sin sin 2b A B a ==a b >A B >4B π=(22235255c c ⎛⎫=+-⨯⨯- ⎪⎝⎭1c =7c =-BABC cos BA B =ABC ,,A B C ,,a b c 6a c +=2b =7cos 9B =,a c sin()A B -2222cos b a c ac B =+-()222(1cos )b ac ac B =+-+6a c +=2b =7cos 9B =9ac =3a =3c =ABC sin 9B ==sin sin 3a B A b ==a c=A 1cos 3A ==sin()sin cos cos sin A B A B A B -=-=()4cos sin (0)4f x x x πϖϖϖ⎛⎫=⋅+> ⎪⎝⎭π(Ⅰ)求的值; (Ⅱ)讨论在区间上的单调性.【答案】解:(Ⅰ).所以 (Ⅱ)所以37．（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））已知函数的周期为,图像的一个对称中心为,将函数图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移个单位长度后得到函数的图像. (1)求函数与的解析式;(2)是否存在,使得按照某种顺序成等差数列?若存在,请确定的个数;若不存在,说明理由(3)求实数与正整数,使得在内恰有2013个零点. 【答案】解:(Ⅰ)由函数的周期为,,得又曲线的一个对称中心为,故,得,所以将函数图象上所有点的横坐标伸长到原来的倍(纵坐标不变)后可得的图象,再将的图象向右平移个单位长度后得到函数ϖ()f x []0,22)42sin(2)12cos 2(sin 2)cos (sin cos 22++=++=+⇒πωωωωωωx x x x x x 122=⇒=⇒ωπωπ1,2)42sin(2)(=++=ωπx x f ；解得，令时，当8242]4,4[)42(]2,0[ππππππππ==++∈+∈x x x x .]28[]8,0[)(上单调递减，上单调递增；在在πππx f y =(Ⅱ)当时,,所以问题转化为方程在内是否有解设,则因为,所以,在内单调递增又,且函数的图象连续不断,故可知函数在内存在唯一零点,即存在唯一的满足题意(Ⅲ)依题意,,令当,即时,,从而不是方程的解,所以方程等价于关于的方程,现研究时方程解的情况令,则问题转化为研究直线与曲线在的交点情况,令,得或当变化时,和变化情况如下表当且趋近于时,趋向于 当且趋近于时,趋向于 当且趋近于时,趋向于 当且趋近于时,趋向于故当时,直线与曲线在内有无交点,在内有个交点; 当时,直线与曲线在内有个交点,在内无交点;当时,直线与曲线在内有个交点,在内有个交点 由函数的周期性,可知当时,直线与曲线在内总有偶数个交点,从而不存在正整数,使得直线与曲线在内恰有个交点;当时,直线与曲线在内有个交点,由周期性,,所以综上,当,时,函数在内恰有个零点38．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分14分.已知,. (1)若,求证:;(2)设,若,求的值.【答案】解:(1)∵ ∴ 即,又∵,∴∴∴(cos ,sin )(cos ,sin )a b ααββ=＝，παβ<<<0||2a b -=a b ⊥(0,1)c =a b c +=βα,2||=-b a 2||2=-b a ()22222=+-=-b b a a b a 1sin cos ||2222=+==ααa a 1sin cos ||2222=+==ββb b 222=-b a 0=b a b ⊥a(2)∵∴即两边分别平方再相加得: ∴ ∴ ∵ ∴ 39．（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））已知函数,.(Ⅰ) 求的值; (Ⅱ) 若,,求.【答案】(Ⅰ); (Ⅱ) 因为,,所以, 所以, 所以. 40．（2013年高考湖南卷（理））已知函数.(I)若是第一象限角,且.求的值; (II)求使成立的x 的取值集合.【答案】解: (I))1,0()sin sin ,cos (cos b a =++=+βαβα⎩⎨⎧=+=+1sin sin 0cos cos βαβα⎩⎨⎧-=-=βαβαsin 1sin cos cos βsin 221-=21sin =β21sin =απαβ<<<0πβπα61,65==()12f x x π⎛⎫=- ⎪⎝⎭x ∈R 6f π⎛⎫- ⎪⎝⎭3cos 5θ=3,22πθπ⎛⎫∈ ⎪⎝⎭23f πθ⎛⎫+ ⎪⎝⎭1661244f πππππ⎛⎫⎛⎫⎛⎫-=--=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭222cos 2sin 233124f ππππθθθθθ⎛⎫⎛⎫⎛⎫+=+-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3cos 5θ=3,22πθπ⎛⎫∈⎪⎝⎭4sin 5θ=-24sin 22sin cos 25θθθ==-227cos 2cos sin 25θθθ=-=-23f πθ⎛⎫+⎪⎝⎭cos2sin 2θθ=-72417252525⎛⎫=---= ⎪⎝⎭2()sin()cos().()2sin 632x f x x x g x ππ=-+-=α()f α=()g α()()f x g x ≥.(II) 41．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分16分.如图,游客从某旅游景区的景点处下山至处有两种路径.一种是从沿直线步行到,另一种是先从沿索道乘缆车到,然后从沿直线步行到.现有甲.乙两位游客从处下山,甲沿匀速步行,速度为.在甲出发后,乙从乘缆车到,在处停留后,再从匀速步行到.假设缆车匀速直线运动的速度为,山路长为,经测量,,. (1)求索道的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在处互相等待的时间不超过分钟,乙步行的速度应控制在什么范围内?【答案】解:(1)∵, ∴∴,∴ 根据得 533sin 3)(sin 3sin 23cos 21cos 21sin 23)(==⇒=++-=ααf x x x x x x f 51cos 12sin 2)(,54cos )2,0(,53sin 2=-===⇒∈=⇒ααααπααg 且21)6sin(cos 21sin 23cos 1sin 3)()(≥+=+⇒-≥⇒≥πx x x x x x g x f Z k k k x k k x ∈+∈⇒++∈+⇒],322,2[]652,62[6ππππππππA C A C AB BC A AC min /50m min 2A B B min 1C min /130m AC m 12601312cos =A 53cos =C AB C 31312cos =A 53cos =C ），（、20π∈C A 135sin =A 54sin =C []6563sin cos cos sin sin sin sin =+=+=+-=C A C A C A C A B ）（）（πsinB sinC AC AB =m C AC AB 1040sin sinB==CBA(2)设乙出发t 分钟后,甲.乙距离为d,则∴ ∵即 ∴时,即乙出发分钟后,乙在缆车上与甲的距离最短. (3)由正弦定理得(m) 乙从B 出发时,甲已经走了50(2+8+1)=550(m),还需走710 m 才能到达C 设乙的步行速度为V ,则∴∴ ∴为使两位游客在处互相等待的时间不超过分钟,乙步行的速度应控制在范围内法二:解:(1)如图作BD ⊥CA 于点D , 设BD =20k ,则DC =25k ,AD =48k , AB =52k ,由AC =63k =1260m, 知:AB =52k =1040m.(2)设乙出发x 分钟后到达点M , 此时甲到达N 点,如图所示. 则:AM =130x ,AN =50(x +2),由余弦定理得:MN 2=AM 2+AN 2-2 AM ·AN cos A =7400 x 2-14000 x +10000,其中0≤x ≤8,当x =3537(min)时,MN 最小,此时乙在缆车上与甲的距离最短.(3)由(1)知:BC =500m,甲到C 用时:126050=1265(min).若甲等乙3分钟,则乙到C 用时:1265+3=1415 (min),在BC 上用时:865 (min) .此时乙的速度最小,且为:500÷865=125043m/min. 1312)50100(1302)50100()130(222⨯+⨯⨯-++=t t t t d )507037(20022+-=t t d 13010400≤≤t 80≤≤t 3735=t 3735sinBsinA ACBC =50013565631260sin sinB ===A AC BC min /m 350710500≤-v 3507105003≤-≤-v 14625431250≤≤v C 3⎥⎦⎤⎢⎣⎡14625,431250若乙等甲3分钟,则乙到C 用时:1265-3=1115 (min),在BC 上用时:565 (min) .此时乙的速度最大,且为:500÷565=62514m/min. 故乙步行的速度应控制在[125043,62514]范围内.42．（2013年高考湖北卷（理））在中,角,,对应的边分别是,,.已知.(I)求角的大小;(II)若的面积,,求的值.【答案】解:(I)由已知条件得:,解得,角 (II),由余弦定理得:, 43．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））△在内角的对边分别为,已知.(Ⅰ)求;(Ⅱ)若,求△面积的最大值.【答案】ABC ∆A B C a b c ()cos23cos 1A B C -+=A ABC∆S =5b =sin sin B C cos23cos 1A A +=22cos 3cos 20A A ∴+-=1cos 2A =60A =︒1sin 2S bc A ==4c ⇒=221a =()222228sin a R A ==25sin sin 47bc B C R ∴==CBADMN44．（2013年高考新课标1（理））如图,在△ABC 中,∠ABC=90°,AB=3,BC=1,P 为△ABC 内一点,∠BPC=90°(1)若PB=12,求PA;(2)若∠APB=150°,求tan ∠PBA [【答案】(Ⅰ)由已知得,∠PBC=,∴∠PBA=30o ,在△PBA 中,由余弦定理得==,∴PA=;(Ⅱ)设∠PBA=,由已知得,PB=,在△PBA 中,由正弦定理得,,化简得,,∴=,∴=.45．（2013年上海市春季高考数学试卷(含答案)）本题共有2个小题,第一小题满分4分,第二小题满分9分.在平面直角坐标系中,点在轴正半轴上,点在轴上,其横坐标为,且 是首项为1、公比为2的等比数列,记,.(1)若,求点的坐标; (2)若点的坐标为,求的最大值及相应的值.[解](1)(2) 【答案】[解](1)设,根据题意,.由,知, 而, 所以,解得或. 故点的坐标为或. (2)由题意,点的坐标为,. 因为所以, xOy A y n P x n x {}n x 1nn n P AP θ+∠=n N *∈31arctan 3θ=A A (0n θn (0 )A t ，12n n x -=31arctan 3θ=31tan 3θ=3443343223443()4tan tan()321x x t x x t t t OAP OAP x x t x x t t tθ--=∠-∠===+⋅++⋅241323t t =+4t =8t =A (0 4)，(0 8)，n P 1(2 0)n -，1tan n n OAP -∠=111212tan tan()12n n n n n n n n OAP OAP θ--+-=∠-∠===2n n ≥tan 4n θ≤=当且仅当,即时等号成立. 易知在上为增函数, 因此,当时,最大,其最大值为. 46．（2013年高考江西卷（理））在△ABC 中,角A,B,C 所对的边分别为a,b,c,已知cosC+(conA-√3sinA)cosB=0.(1) 求角B 的大小;若a+c=1,求b 的取值范围【答案】解:(1)由已知得 即有因为,所以,又,所以, 又,所以. (2)由余弦定理,有.因为,有. 又,于是有,即有.2nn =4n =0 tan 2n y x πθ<<=，(0 )2π，4n =nθarctan4cos()cos cos cos 0A B A B A B -++=sin sin cos 0A B A B =sin 0A≠sin 0B B =cos 0B≠tan B =0B π<<3B π=2222cos b a c ac B =+-11,cos 2a c B +==22113()24b a =-+01a <<2114b ≤<112b ≤<。

解三角形高考大题，带答案1. （宁夏17）（本小题满分12分）如图，ACD △是等边三角形，ABC △是等腰直角三角形，90ACB =∠，BD 交AC 于E ，2AB =．（Ⅰ）求cos CAE ∠的值； （Ⅱ）求AE ．解：（Ⅰ）因为9060150BCD =+=∠，CB AC CD ==， 所以15CBE =∠．所以62cos cos(4530)4CBE +=-=∠． ··············································································· 6分 （Ⅱ）在ABE △中，2AB =， 由正弦定理2sin(4515)sin(9015)AE =-+．故2sin 30cos15AE =122624⨯=+62=-． 12分2. （江苏17）（14分）某地有三家工厂，分别位于矩形ABCD 的顶点A 、B 及CD 的中点P 处，已知AB=20km ，BC=10km ，为了处理三家工厂的污水，现要在矩形ABCD 的区域上（含边界），且A 、B 与等距离的一点O 处建造一个污水处理厂，并铺设排污管道AO 、BO 、OP ，设排污管道的总长为ykm 。

初中数学专项练习《解直角三角形》100道计算题包含答案一、计算题(共100题)1、先化简再求值：其中.2、计算：|﹣|+ ﹣4sin45°﹣．3、先化简，再求值：，其中a=2sin60°+3tan45°．4、计算5、先化简，再求值：÷（﹣x﹣3），其中x=sin45°﹣4cos60°．6、先化简再求值：÷（a﹣），其中a＝2cos30°+1，b＝tan45°．7、计算：| ﹣2|+3tan30°+（）﹣1﹣（3﹣π）0﹣．8、计算：．9、计算：|﹣2|+2﹣1﹣cos60°﹣（1﹣）0．10、计算：2cos230°﹣sin30°+ ．11、计算：（﹣）﹣1+3tan30°﹣+（﹣1）2016．12、计算：13、计算：4sin45°+3tan230°- .14、计算：﹣4cos45°+（）﹣1+|﹣2|．15、计算：4cos30°+（π﹣1）0﹣+| ﹣2|．16、先化简，再求值：（﹣）÷ ，其中x=2sin30°+2cos45°．17、计算:18、计算：-2|+ 3 tan 30 ° - 2 cos 45 ° ．19、计算：.20、先化简，再求值：，其中．21、计算：（π﹣3.14）0﹣| sin60°﹣4|+（）﹣1．22、计算：23、计算：2sin45°+| |﹣（π﹣2016）0+（）﹣2．24、先化简，再求值：，其中.25、计算：3tan30°﹣（﹣）﹣1+20190+| ﹣2|．26、计算：|﹣2 |+（﹣1）0﹣4sin60°﹣（﹣2）2.27、计算：20150﹣3tan30°+（﹣）﹣2﹣| ﹣2|．28、计算：29、计算：30、先化简，再求值的值，其中x=4sin45°-2cos60°。

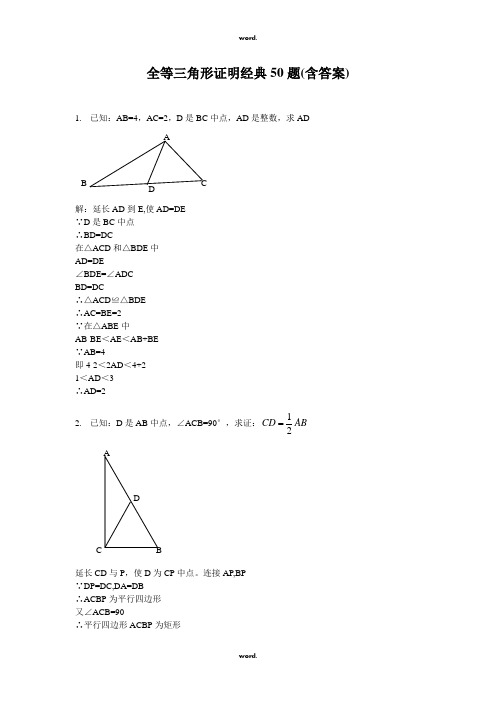
全等三角形证明经典50题(含答案)1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE ＜AE ＜AB+BE∵AB=4即4-2＜2AD ＜4+21＜AD ＜3∴AD=22. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB延长CD 与P ，使D 为CP 中点。

连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形AD BC∴AB=CP=1/2AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。

∴ ∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ，可得，∠EFD ＝CGDDE ＝DC∠FDE ＝∠GDC （对顶角）B ACDF21 E∴△EFD≌△CGDEF＝CG∠CGD＝∠EFD又，EF∥AB∴，∠EFD＝∠1∠1=∠2∴∠CGD＝∠2∴△AGC为等腰三角形，AC＝CG又EF＝CG∴EF＝AC5.已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠CA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明：在AE 上取F ，使EF ＝EB ，连接CF∵CE ⊥AB∴∠CEB ＝∠CEF ＝90°∵EB ＝EF ，CE ＝CE ，∴△CEB ≌△CEF∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180°∴∠D ＝∠CFA∵AC 平分∠BAD∴∠DAC ＝∠FAC∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD解：延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD BCAD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE＜AE＜AB+BE ∵AB=4即4-2＜2AD＜4+21＜AD＜3∴AD=28.已知：D是AB中点，∠ACB=90°，求证：12 CD AB9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

专题精选习题----解三角形1.在 ABC 中，内角A, B, C 的对边分别为 a , b, c ，已知cosA 2 cosCcosB = 2c a b.(2) 若 cosB =,b = 2 ，求 ABC 的面积 S .42.在ABC 中，角A, B, C 的对边分别是 a, b, c ，已知sin C + cosC = 1 sin2 .(1) 求sin C 的值；(2) 若a 2 + b 2= 4(a + b) 8 ，求边 c 的值.3.在ABC 中，角A, B, C 的对边分别是 a, b, c .(1) 若 sin(A + ) = 2 cosA ，求 A 的值； 6 (2) 若 cosA = ,b = 3c ，求sin C 的值. 34.ABC 中， D 为边 BC 上的一点， BD = 33, sin B = , cos 三ADC= ，求 AD .13 55 31 C (1) 求sin CsinA的值；15.在ABC 中，角A, B, C 的对边分别是 a, b, c ，已知 a = 1,b = 2, cosC = (1) 求 ABC 的周长；(2) 求cos(A 一 C) 的值.6.在 ABC 中，角 A, B, C 的对边分别是 a, b, c . 已知sin A+ sin C = psin B(p R) ，且 ac = 1b 2 .45(1) 当 p = 4, b = 1时，求 a , c 的值； (2)若角 B 为锐角，求 p 的取值范围 .7.在ABC 中，角 A, B, C 的对边分别是 a, b, c .且 2asin A = (2b + c)sin B + (2c + b)sin C .(1) 求 A 的值；(2) 求sin B +sin C 的最大值.8.在ABC 中，角A, B, C 的对边分别是 a, b, c ，已知cos2C = 一 (1) 求sin C 的值；(2) 当 a = 2,2sin A = sin C 时，求b, c 的长.14 .14 .9.在ABC 中，角A, B, C 的对边分别是 a, b, c ，且满足cos = , AB . AC = 32 5 .(1) 求ABC 的面积；(2) 若b + c = 6 ，求 a 的值.10.在 ABC 中，角A, B, C 的对边分别是 a, b, c ， cos(C + 几 ) + cos(C 几 ) = 2 . 4 4 2(1) 求角 C 的大小；(2) 若 c = 2 3， sin A = 2sin B ，求 a, b .11.在 ABC 中，角 A, B, C 的对边分别是 a, b, c ，且.(1)求角 A 的大小； (2) 若a = 1 ，求ABC 的周长l 的取值范围.a cosC + c =b 212.在ABC 中，角 A, B, C 的对边分别是 a, b, c ，且满足 (2b c) cosA a cosC = 0 .(1)求角 A 的大小；(2) 若 a = 3， S ABC =3 34 ， ABC 的形状，并说明理由 .A 2 5 试判断113.在ABC中，角A, B, C 的对边分别是a, b, c ，且2(a2 + b2 c2 ) = 3ab.(1) 求sin 2 ；(2) 若c = 2 ，求ABC面积的最大值 .14.在ABC中，角A, B, C 的对边分别是a, b, c ，且满足4a2 cosB 2accosB = a2 + b2 c2 .(1)求角B 的大小；(2) 设m = (sin 2A,cos2C),n = ( 3,1) ，求m .n 的取值范围 .15.已知m = (sin x, cos x),n = (cos x,cos x)( > 0)，若函数f (x) = m . n 1的最小正周期为2 4几.(1)求函数y = f (x) 取最值时x 的取值集合；(2) 在ABC中，角A, B, C 的对边分别是a, b, c，且满足(2a c) cosB = bcosC，求f (A) 的取值范围.16.如图，ABC中，(1)求BC 的长；(2)求DBC 的面积. sin = , AB = 2 ，点D 在线段AC 上，且AD = 2DC , BD = .2 3 3ADC 三ABC 3 4 3B17.已知向量 a = (cosa , sin a ), b = (cos b , sin b ), a 一 b =5 .(1) 求cos(a 一 b ) 的值； (2) 若 0 想 a 想几,一 几 想 b 想 0， sin b = 一 5，求sin a . 2 2 1318.在 编ABC 中， 角 A, B, C 的对边分别是 a, b, c ， 已知 sin 2 2C + sin 2C . sin C + cos2C = 1， 且a +b = 5，c = 7 .(1)求角 C 的大小； (2) 求 编ABC 的面积.19.在 编ABC 中，角A, B, C 的对边分别是 a, b, c ，且满足 cosA . ( 3 sin A 一 cosA) = (1)求角 A 的大小；(2) 若 a = 2 2, S 编ABC = 2 3 ，求b, c 的长.20.已知函数 f (x) =sin 几x + cos 几x, (x 仁 R) ，当 x 仁 [一1,1] 时，其图象与 x 轴交于 M , N 两点，2 2最高点为 P .(1) 求 PM, PN 夹角的余弦值；(2)将函数 f (x) 的图象向右平移 1 个单位， 再将所得图像上每点的横坐标扩大为原来的 2 倍，而得2 83 3到函数 y = g(x) 的图象，试画出函数 y = g(x) 在[ , ] 上的图象.3 1 12 .2 521.已知函数 f (x) = 2asin 2 x + 2 sinx cosx 一 a (a 为常数)在x = 3处取得最大值 .8(1) 求 a 的值；(2) 求 f (x) 在[0, ]上的增区间.22.在ABC 中，角A, B, C 的对边分别是 a, b, c ，且b 2 + c 2 一 a 2 = bc .(1)求角 A 的大小； (2)若函数 f (x) = sin 2xcos 2x + cos 2 2x，当 f (B) = 22+1 时，若 a = 3 ，求b 的值.23.在ABC 中， 角 A, B, C 的对边分别是 a, b, c ， 已知. B = , sin A = ,b =3 5(1) 求sin C 的值； (2) 求 ABC 的面积.24.在ABC 中，角 A, B, C 的对边分别是 a, b, c ，且b cosC = (3a 一 c) cosB .(1) 求sin B 的值；(2) 若b = 2 ，且a = c ，求ABC 的面积.3 325.已知函数 f (x) = 3 sin xcos x+ cos 2 x + 12 2 2 2 .(1)求 f (x) 的单调区间； (2)在锐角三角形ABC 中， 角 A, B, C 的对边分别是a, b, c ， 且满足(2b a) cosC = c .cosA ，求 f (A) 的取值范围 .26.在ABC 中，角A, B, C 的对边分别是 a, b, c ， a sin Asin B + b cos 2 A = 2a .(1) 求； a(2) 若 c 2 = b 2 + 3a 2 ，求角 B .27.港口 A 北偏东 30O 方向的 C 处有一检查站， 港口正东方向的 B 处有一轮船， 距离检查站为31海里， 该轮船从 B 处沿正西方向航行 20 海里后到达 D 处观测站，已知观测站与检查站距离为 21 海里，问 此时轮船离港口 A 还有多远？b28.某巡逻艇在A 处发现在北偏东45o距A 处 8 海里的B 处有一走私船，正沿东偏南15o的方向以 12 海里/小时的速度向我岸行驶，巡逻艇立即以12 3 海里/小时的速度沿直线追击，问巡逻艇最少需要多长时间才能追到走私船，并指出巡逻艇航行方向 .29.在海岛A 上有一座海拔1km 的山峰，山顶设有一个观察站 P.有一艘轮船按一固定方向做匀速直线航行，上午 11:00 时，测得此船在岛北偏东15o 、俯角为30o 的B 处，到 11:10 时，又测得该船在岛北偏西45o、俯角为60o的C 处.(1)求船航行速度；(2) 求船从 B 到 C 行驶过程中与观察站 P 的最短距离 .30.如图所示，甲船由 A 岛出发向北偏东45o的方向做匀速直线航行，速度为15 2 海里/小时，在甲1船从 A 到出发的同时，乙船从 A 岛正南 40 海里处的 B 岛出发，朝北偏东9 ( tan9 = )的方向做2匀速直线航行，速度为 m 海里/小时.(1) 求 4 小时后甲船到 B 岛的距离为多少海里；(2)若两船能相遇，求 m.。

解三角形大题经典练习高考大题练习（解三角形1）1、在ABC ∆中，内角C B A ,,的对边分别为c b a ,,，已知bac B C A -=-2cos cos 2cos ． （1）求A C sin sin 的值； （2）若2,41cos ==b B ，求ABC ∆的面积S ． 2、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，已知2sin 1cos sin CC C -=+． （1）求C sin 的值；（2）若224()8a b a b +=+-，求边c 的值．3、在ABC ∆中，角C B A ,,的对边分别是c b a ,,．（1）若A A cos 2)6sin(=+π，求A 的值；（2）若c b A 3,31cos ==，求C sin 的值．4、ABC ∆中，D 为边BC 上的一点，53cos ,135sin ,33=∠==ADC B BD ，求AD ．高考大题练习（解三角形1、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，已知41cos ,2,1===C b a ． （1）求ABC ∆的周长； （2）求)cos(C A -的值．2、在ABC ∆中，角C B A ,,的对边分别是c b a ,,．已知)(sin sin sin R p B p C A ∈=+，且241b ac =．（1）当5,14p b ==时，求c a ,的值； （2）若角B 为锐角，求p 的取值范围．3、在ABC ∆中，角C B A ,,的对边分别是c b a ,,．且C b c B c b A a sin )2(sin )2(sin 2+++=． （1）求A 的值； （2）求C B sin sin +的最大值．4、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，已知412cos -=C ．（1）求C sin 的值； （2）当C A a sin sin 2,2==时，求c b ,的长．高考大题练习（解三角形3）1、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，且满足25cos 32A AB AC =⋅=u u ur u u u r ．1、在ABC ∆中，角A ，B ，C 对应的边分别是a ，b ，c ．已知()cos23cos 1A B C -+=． (I)求角A 的大小； (II)若ABC ∆的面积53S =，5b =，求sin sin B C 的值．2、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，已知12cos sin 2sin 2sin 2=+⋅+C C C C ，且5=+b a ，7=c ．（1）求角C 的大小； （2）求ABC ∆的面积．3、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，且满足21)cos sin 3(cos =-⋅A A A ． （1）求角A 的大小； （2）若32,22==∆ABC S a ，求c b ,的长．4、设ABC ∆的内角,,A B C 的对边分别为,,a b c ，()()a b c a b c ac ++-+=． （1）求B ； （2）若31sin sin A C -=，求C ．高考大题练习（解三角形6）1、△ABC 在内角,,A B C 的对边分别为,,a b c ，已知cos sin a b C c B =+． (Ⅰ)求B ； (Ⅱ)若2b =，求△ABC 面积的最大值．2、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，且bc a c b =-+222． （1）求角A 的大小；（2）若函数2()sin cos cos 222x x xf x =+，当212)(+=B f 时，若3=a ，求b 的值．3、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，已知3,sin ,335B A b π===． （1）求C sin 的值； （2）求ABC ∆的面积．4、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，且B c a C b cos )3(cos -=．（1）求B sin 的值； （2）若2=b ，且c a =，求ABC ∆的面积． （2）高考大题练习（解三角形7）1、已知函数212cos 2cos 2sin 3)(2++=x x x x f ．（1）求)(x f 的单调区间；（2）在锐角三角形ABC ∆中，角C B A ,,的对边分别是c b a ,,，且满足A c C a b cos cos )2(⋅=-，求)(A f 的取值范围．2、在ABC ∆中，角C B A ,,的对边分别是c b a ,,，a A b B A a 2cos sin sin 2=+．（1）求ab； （2）若2223a b c +=，求角B ．3、港口A 北偏东︒30方向的C 处有一检查站，港口正东方向的B 处有一轮船，距离检查站为31海里，该轮船从B 处沿正西方向航行20海里后到达D 处观测站，已知观测站与检查站距离为21海里，问此时轮船离港口A 还有多远？4、某巡逻艇在A 处发现在北偏东︒45距A 处8海里的B 处有一走私船，正沿东偏南︒15的方向以12海里/小时的速度向我岸行驶，巡逻艇立即以312海里/小时的速度沿直线追击，问巡逻艇最少需要多长时间才能追到走私船，并指出巡逻艇航行方向．高考大题练习（解三角形8）1、如图，ACD △是等边三角形，ABC △是等腰直角三角形，90ACB =o ∠，BD 交AC 于E ，2AB =．（Ⅰ）求cos CAE ∠的值； （Ⅱ）求AE ．2、（辽宁17）在ABC △中，内角A B C ，，对边的边长分别是a b c ，，，已知2c =，3C π=． （Ⅰ）若ABC △的面积等于3，求a b ，； （Ⅱ）若sin 2sin B A =，求ABC △的面积．BAC D E3、设ABCa B=，sin4，，，且cos3b A=．，，所对的边长分别为a b c△的内角A B C（Ⅰ）求边长a；（Ⅱ）若ABC△的周长l．△的面积10S=，求ABC4、在△ABC中，a=3，b6，∠B=2∠A．（1）求cos A的值；（2）求c的值．。

解三角形高考大题，带答案1. （宁夏17）（本小题满分12分）如图，ACD △是等边三角形，ABC △是等腰直角三角形，90ACB =∠，BD 交AC 于E ，2AB =．（Ⅰ）求cos CAE ∠值； （Ⅱ）求AE ．解：（Ⅰ）因为9060150BCD =+=∠，CB AC CD ==，所以15CBE =∠．所以6cos cos(4530)4CBE =-=∠． ···················································· 6分 （Ⅱ）在ABE △中，2AB =， 由正弦定理2sin(4515)sin(9015)AE =-+．故= 12分2. （江苏17）（14分）某地有三家工厂，分别位于矩形ABCD 顶点A 、B 及CD 中点P 处，已知AB=20km ，BC=10km ，为了处理三家工厂污水，现要在矩形ABCD 区域上（含边界），且A 、B 及等距离一点O 处建造一个污水处理厂，并铺设排污管道AO 、BO 、OP ，设排污管道总长为ykm 。

（1）按下列要求写出函数关系式：①设∠BAO=θ(rad )，将y 表示成θ函数关系式； ②设OP=x (km )，将y 表示成x 函数关系式； （2）请你选用（1）中一个函数关系式，确定污水处理厂位置，使三条排污管道总长度最短。

2021届高三（新高考）数学大题优练 解三角形例1．ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知()2cos cos b a C c A -=．（1）求角C 的大小； （2）若2a =，()2cos cos c a B b A b -=，求ABC △的面积．【答案】（1）π4；（2）12．【解析】（1）由已知及正弦定理，得2sin cos sin cos sin cos B C A C C A -=， ∴()2sin cos sin cos cos sin sin B C A C A C A C =+=+，∵πA C B +=-，∴()sin sin A C B +=，∴2sin cos sin B C B =． 又∵sin 0B ≠，∴2cos 2C =． ∵()0,πC ∈，∴π4C =． （2）由已知及余弦定理，得222222222a c b b c a ac bc b ac bc +-+-⋅-⋅=，222222222a cb bc a b +-+--=，化简，得222a b =． 又∵2a =，∴1b =，∴ABC △的面积1121sin 212222ABC ab C S ==⨯⨯⨯=△． 例2．设函数2()12cos 43sin cos 5f x x x x =--． （1）求()f x 的最小正周期和值域；（2）在锐角ABC △中，角A ､B ､C 的对边长分别为a ､b ､c ．若()5f A =-，3a =，求ABC △周长的取值范围．【答案】（1）πT =，值域为431,431⎡⎤-++⎣⎦；（2）(3]3,33+． 【解析】（1）()2212cos 43sin cos 512cos 23sin 25x x x f x x x =--=--π6cos 223sin 2143cos 216x x x ⎛⎫=-+=++ ⎪⎝⎭，πT ∴=，值域为431,431⎡⎤-++⎣⎦．优选例题（2）由()5f A =-，可得212cos cos A A A =，因为三角形为锐角ABC △sin A A =，即tan A =π3A =， 由正弦定理sin sin sin a b c A B C ==，得2sin b B =，2π2sin 2sin()3c C B ==-，所以2π12sin sin()2(sin cos sin )322a b c B B B B B ⎡⎤++=+-=++⎢⎥⎣⎦32(sin ))2π6B B B =+=++因为ABC △为锐角三角形，所以0π2B <<，0π2C <<， 即022π3π02πB B ⎧<<⎪⎪⎨⎪<-<⎪⎩，解得π6π2B <<，所以ππ2π363B <+<sin()16πB <+≤，即3)6πB ++≤，所以周长的取值范围为(3+．例3．在锐角ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，()2,a c b =-m ，()cos ,cos B A =n 且⊥m n ．（1）求角B ；（2）若2b =，求ABC △的面积的最大值． 【答案】（1）π3；（2【解析】（1）因为⊥m n ，所以()2cos cos 0a c B b A -+=， 由2sin sin sin a b cR A B C===，得2sin a R A =⋅，2sin b R B =⋅，2sin c R C =⋅， 所以()sin 2sin cos sin cos 0A C B B A -+=，所以()sin 2sin cos 0A B C B +-=，即sin 2sin cos C C B =， 又因为sin 0C ≠，1cos 2B =， 所以π0,2B ⎛⎫∈ ⎪⎝⎭，π3B =．（2）因为2222cos b a c ac B =+-，且2b =，π3B =， 又因为2242a c ac ac +=+≥，4ac ≤(当且仅当2a c ==时等号成立)，所以11sin 422ABC S ac B =⋅≤⨯=△ 即ABC S △ 例4．已知ABC △中，cos cA b<． （1）求证：B 是钝角；（2）若ABC △同时满足下列四个条件中的三个：①sin 2A =；②2a =；③c =sin 2C =．请指出这三个条件，说明理由，并求出b 的值．【答案】（1）证明见解析；（2）只有满足①②③时，1b =． 【解析】（1）因为cos c A b <，由正弦定理可得sin cos sin CA B<， 在三角形中，sin sin()sin cos cos sin C A B A B A B =+=+，且sin 0B >， 所以不等式整理为sin cos cos sin sin cos A B A B B A +<， 即sin cos 0A B <，在三角形中可得sin 0A >，所以cos 0B <，所以得证B 为钝角． （2）（i ）若满足①②③，则正弦定理可得sin sin a cA C=，2=，所以1sin 2C =， 又a c >，所以A C >，在三角形中，sin 2A =，所以π4A =或3π4A =，而由（1）可得π4A =，所以可得π6C =，π7πππ4612πB A C =--=--=，所以1b ===． （ii ）若满足①②④，由（1）B 为钝角，A ，C 为锐角，及sin 2A =，sin 2C =可得π4A =，π3C =，所以5π12B=不符合B为钝角，故这种情况不成立．（iii）若满足②③④，由B为钝角，sin2C=，所以π3C=，而a c>，所以A C>，这时π3B<，不符合B为钝角的情况，所以这种情况不成立．综上所述：只有满足①②③时，1b=．1．ABC△的内角A，B，C的对边分别为a，b，c．已知()()sin cos cos sinc A A a C C-=-．（1）记AC边上的高为h，求bh；（2）若5c=，1a=，求b．2．如图，在ABC△中，6AB=，3cos4B=，点D在BC边上，4AD=，ADB∠为锐角．（1）若62AC=，求线段DC的长度；（2）若2BAD DAC∠=∠，求sin C的值．3．在ABC△中，已知角A，B，C的对边分别为a，b，c，若2b=，3cos sinB b B=-．（1）求角B的大小；（2）若BAC∠的平分线AD交BC于点D，ACD△的面积为3，求线段BD的长度．模拟优练4．已知ABC △的三个内角A ，B ，C 的对边分别是a ，b ，c ，且cos cos 2cos b C c B a A +=． （1）求角A ；（2）若a =ABC △的面积为bc +的值．5．在ABC △中，内角A ，B ，C 的对边分别为a ，b ，c ，且()sin sin sin sin a A B b B c C -+=． （1）求角C ；（2）若3c =，6a b +=，求ABC △的面积．6．ABC △的内角A ，B ，C 的对边为a ，b ，c ，且223(sin sin )3sin ()8sin sin B C B C B C +-+=． （1）求cos A 的值；（2）若ABC △的面积为a b c ++的最小值．7．在ABC △中，内角A ，B ，C 所对的边分别为a ，b ，c ，且满足2cos cos cos b A a C c A -=．（1）求角A 的大小；（2）若2a =，求b c +的最大值．8．在ABC △中，内角A ，B ，C 所对的边分别为a ，b ，c ，且sin sin sin sin B C aA C b c+=--．（1）求B ；（2）若ABC △是锐角三角形，且ABC △的面积为c 的取值范围．9．已知ABC △同时满足下列四个条件中的三个： ①π3A =；②2cos 3B =-；③7a =；④3b =．（1）请指出这三个条件，并说明理由； （2）求ABC △的面积．10．在△ABC 中，a 、b 、c 分别为角A 、B 、C 所对的边，且22()b a a c c -=-． （1）求角B ； （2）若b =2ac +的最大值．1．【答案】（1）2；（2）2b =或2．【解析】（1）()()sin cos cos sin c A A a C C -=-，由正弦定理可得()()sin sin cos sin cos sin C A A A C C -=-， 化为()2sin sin sin cos cos sin sin sin C A A C A C A C B =+=+=， ∴2sin c A b =， ∵sin h c A =，∴2sin b bh c A==． （2）由（1）有2sin sin sin C A B =，∴2sin a C b =，即sin 22b b C a ==． 由余弦定理可得2222cosc a b ab C =+-，∴2512cos b b C =+-，可得24cos 2b C b-=，∴222224sin cos 122b b C C b ⎛⎫-⎛⎫+=+= ⎪ ⎪⎝⎭⎝⎭，化为42680b b -+=，解得22b =或4， 解得2b =或2．2．【答案】（1）7；（2）71432． 【解析】（1）在ABD △中，由余弦定理得22223616312co 24s AB BD AD B AB B BD D BD +-⋅⋅=+-==，∴5BD =或4BD =． 当4BD =时，161636cos 0244ADB +-∠=<⨯⨯，则π2ADB ∠>，不合题意，舍去；当5BD =时，162536cos 0245ADB +-∠=>⨯⨯，则π2ADB ∠<，符合题意，∴5BD =．在ABC △中，22223672312co 24s AB BC AC B AB B BC C BC +-⋅⋅=+-==，∴12BC =或3BC =-（舍）， ∴7DC BC BD =-=．（2）记DAC ∠θ=，则2BAD θ∠=．在ABD △中，2229cos cos 2216AB AD BD BAD AB AD θ+-∠===⋅，∴2θ为锐角，参考答案得21cos 27sin232θθ-==，sin 216θ=，即sin 8θ=，cos 8θ=．法一：sin 3sin 2cos cos 2sin 64θθθθθ=+=，同理cos364θ=． 由3cos 4B =，知sin B =， ∴()()sin sin π3sin 3sin cos3cos sin 332C B B B B θθθθ=--=+=+=． 法二：2221625361cos 22458AD BD AB BDA AD BD +-+-∠===⋅⨯⨯，sin BDA ∠=， ∴()sin sin sin cos cos sin 32C BDA BDA BDA θθθ=∠-=∠-∠= 3．【答案】（1）π6B =；（2）BD = 【解析】（1）由2b =sin B b B =-，∴sin 2B B =，即1sin cos 122B B +=，得πsin 13B ⎛⎫+= ⎪⎝⎭，又()0,πB ∈，∴ππ4π,333B ⎛⎫+∈ ⎪⎝⎭，可知ππ23B +=，解得π6B =． （2）设BAD θ∠=，由AD 是BAC ∠的平分线，有CAD θ∠=， 在ABD △中，由正弦定理得πsin sin 6BD AD θ=，所以1sin 2AD BD θ⋅=． 又ACD △1sin sin 2b AD AD θθ⋅==，∴12BD =BD = 4．【答案】（1）π3A =；（2）6． 【解析】（1）因为cos cos 2cos b C c B a A +=， 由正弦定理得sin cos sin cos 2sin cos B C C B A A +=， 所以()sin sin 2sin cos B C A A A +==， 因为0πA <<，所以，sin 0A ≠，所以1cos 2A =，所以π3A =．（2）因为ABC △的面积为1sin 2bc A =因为π3A =，所以1πsin 23bc =8bc =． 由余弦定理得2222cos a b c bc A =+-， 因为a =π3A =， 所以()()2222π122cos3243b c bc b c bc b c =+-=+-=+-，所以6b c +=．5．【答案】（1）π3；（2． 【解析】（1）由正弦定理，得sin 2a A R =，sin 2b B R =，sin 2c C R =， 又()sin sin sin sin a A B b B c C -+=，所以222a b c ab +-=． 由余弦定理，得222cos 22a b c ab C ab ab+-==，故1cos 2C =． 又()0,πC ∈，所以π3C =． （2）由余弦定理，得229a b ab +-=．联立方程组，得2296a b ab a b ⎧=+-⎨+=⎩，化简得96ab a b =⎧⎨+=⎩，解得33a b =⎧⎨=⎩，所以ABC △的面积1sin 2S ab C ==．6．【答案】（1）13；（2）4+ 【解析】（1）由223(sin sin )3sin ()8sin sin B C B C B C +-+=， ∵πA B C ++=，所以228(sin sin )sin sin sin 3B C A B C +=+， 由正弦定理可得228()3b c a bc +=+，则22223b c a bc +-=， 由余弦定理可得2221cos 23b c a A bc +-==．（2）由1cos 3A =，得sin A =，∵1sin 2ABC S bc A ==△12bc =，由22223b c a bc +-=，得222224216333a b c bc bc bc bc =+-≥-==， ∴4a ≥，当且仅当b c ==又b c +≥=b c ==∴4a b c ++≥+b c == 即a b c ++的最小值为4+7．【答案】（1）π3A =；（2）4． 【解析】（1）由正弦定理得2sin cos sin cos sin cosB A AC C A -=， 则()2sin cos sin cos cos sin sin sin B A A C A C A C B =+=+=， 0πB <<，则sin 0B >，于是1cos 2A =， 又0πA <<，故π3A =． （2）根据余弦定理222222cos a b c bc A b c bc =+-=+-，则()()2224332b c b c bc b c +⎛⎫=+-≥+- ⎪⎝⎭， 即()216b c +≤，当且仅当b c =时等号成立． 所以b c +的最大值为4．8．【答案】（1）π3B =；（2）24c <<． 【解析】（1）由正弦定理以及sin sin sin sin B C a A C b c +=--，得b c a a c b c +=--， 即222a c b ac +-=，在ABC △中，由余弦定理得2221cos 222a cb ac B ac ac +-===， 又0πB <<，所以π3B =． （2）因为ABC △是锐角三角形，所以π022ππ032A A ⎧<<⎪⎪⎨⎪<-<⎪⎩，所以ππ62A <<．因为11πsin sin 2234ABC S ac B ac ac ====△8ac =． 由正弦定理得sin sin a C c A=，所以212π8sin 8sin 2sin 8sin 34sin sin sin sin tan A A A ac C C c A A A A A⎫⎛⎫+⎪- ⎪⎝⎭⎝⎭=====+． 因为ππ62A <<，所以tan >A，所以10tan A <<4416<+<， 所以2416c <<，所以24c <<．9．【答案】（1）ABC △同时满足①，③，④．理由见解析；（2）【解析】（1）ABC △同时满足①，③，④．理由如下： 若ABC △同时满足①，②． 因为21cos 32B =-<-，且(0,π)B ∈，所以2π3B >， 所以πA B +>，矛盾．所以ABC △只能同时满足③，④．所以a b >，所以A B >，故ABC △不满足②．故ABC △满足①，③，④．（2）因为2222cos a b c bc A +-=，所以222173232c c =+-⨯⨯⨯， 解得8c =，或5c =-（舍），所以ABC △的面积1sin 2S bc A ==．10．【答案】（1）π3；（2）． 【解析】（1）22()b a a c c -=-，即222b a c ac =+-． ∵2222cos b a c ac B =+-，∴1cos 2B =， 又(0,π)B ∈，∴π3B =． （2）由sin sin 2a c A C==，可得2sin a A =，2sin c C =， ∵24sin 2sin a c A C +=+，2+π3A C =，∴2π3C A =-，∴2π24sin 2sin()5sin )3a c A A A A A ϕ+=+-==+ (其中tan 5ϕ=)， ∵2π03A <<，∴2a c +的最大值为。

解三角形高考大题，带答案1. （宁夏17）（本小题满分12分）如图，ACD △是等边三角形，ABC △是等腰直角三角形，90ACB =∠，BD 交AC 于E ，2AB =．（Ⅰ）求cos CAE ∠的值； （Ⅱ）求AE ．解：（Ⅰ）因为9060150BCD =+=∠，CB AC CD ==，所以15CBE =∠．所以62cos cos(4530)4CBE +=-=∠． ···················································· 6分 （Ⅱ）在ABE △中，2AB =， 由正弦定理2sin(4515)sin(9015)AE=-+．故2sin 30cos15AE =122624⨯=+62=-． 12分2. （江苏17）（14分） 某地有三家工厂，分别位于矩形ABCD 的顶点A 、B 及CD 的中点P 处，已知AB=20km ，BC=10km ，为了处理三家工厂的污水，现要在矩形ABCD 的区域上（含边界），且A 、B 与等距离的一点O 处建造一个污水处理厂，并铺设排污管道AO 、BO 、OP ，设排污管道的总长为ykm 。

（1）按下列要求写出函数关系式：①设∠BAO=θ(rad )，将y 表示成θ的函数关系式； ②设OP=x (km )，将y 表示成x 的函数关系式；（2）请你选用（1）中的一个函数关系式，确定污水处理厂的位置，使三条排污管道总长度最短。