江苏省苏北四市高三数学上学期期末统考试题苏教版

江苏省苏北四市（徐州市、淮安市、宿迁市、连云港市）2022届高三（上）期末数学试卷一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）设全集U＝R，集合A＝{x|1＜x＜4}，集合B＝{x|0＜x＜2}，则集合A∩（∁U B）＝（）A．（1，2）B．（1，2〗C．（2，4）D．〖2，4）2．（5分）已知复数z满足z（1+i）＝4i，则|z|＝（）A．1B．C．2D．23．（5分）不等式成立的一个充分条件是（）A．x＜﹣1B．x＞﹣1C．﹣1＜x＜0D．0＜x＜14．（5分）某地元旦汇演有2男3女共5名主持人站成一排，则舞台站位时男女间隔的不同排法共有（）A．12种B．24种C．72种D．120种5．（5分）已知向量＝（x，1），＝（2，y），＝（1，﹣2），且∥，⊥，则|2﹣|＝（）A．3B．C．D．6．（5分）已知抛物线C1：y2＝2px（p＞0）的焦点F为椭圆C2：＝1（a＞b＞0）的右焦点，且C1与C2的公共弦经过F，则椭圆的离心率为（）A．B．C．D．7．（5分）如图，一个装有某种液体的圆柱形容器固定在墙面和地面的角落内，容器与地面所成的角为30°，液面呈椭圆形，椭圆长轴上的顶点M，N到容器底部的距离分别是12和18，则容器内液体的体积是（）A．15πB．36πC．45πD．48π8．（5分）记〖x〗表示不超过实数x的最大整数，记a n＝〖log8n〗，则的值为（）A．5479B．5485C．5475D．5482二、选择题：本题共4小题，每小题5分，共20分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得5分，有选错的得0分，部分选对的得2分。

9．（5分）已知的展开式中共有7项，则（）A．所有项的二项式系数和为64B．所有项的系数和为1C．二项式系数最大的项为第4项D．有理项共4项10．（5分）将函数f（x）＝A sin（ωx+φ）的图象向左平移个单位长度后得到y＝g（x）的图象如图，则（）A．f（x）为奇函数B．f（x）在区间上单调递增C．方程f（x）＝1在（0，2π）内有4个实数根D．f（x）的解析式可以是11．（5分）在平面直角坐标系xOy中，若对于曲线y＝f（x）上的任意点P，都存在曲线y＝f（x）上的点Q，使得＝0成立，则称函数f（x）具备“⊗性质”．则下列函数具备“⊗性质”的是（）A．y＝x+1B．y＝cos2x C．y＝D．y＝e x﹣212．（5分）如图，一张长、宽分别为，1的矩形纸，A，B，C，D分别是其四条边的中点．现将其沿图中虚线折起，使得P1，P2，P3，P4四点重合为一点P，从而得到一个多面体．则（）A．在该多面体中，B．该多面体是三棱锥C．在该多面体中，平面BAD⊥平面BCDD．该多面体的体积为三、填空题：本题共4小题，每小题5分，共20分。

2022～2023学年高三年级模拟试卷数 学（答案在最后）(满分：150分 考试时间：120分钟)2023．1一、 选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 若非空且互不相等的集合M ，N ，P 满足M ∩N ＝M ，N ∪P ＝P ，则M ∪P ＝( ) A. M B. N C. P D. ∅2. 已知i 5＝a ＋b i(a ，b ∈R )，则a ＋b 的值为( ) A. －1 B. 0 C. 1 D. 23. 设p ：4x －3＜1；q ：x －(2a ＋1)＜0，若p 是q 的充分不必要条件，则( ) A. a ＞0 B. a ＞1 C. a ≥0 D. a ≥14. 已知点Q 在圆C ：x 2－4x ＋y 2＋3＝0上，点P 在直线y ＝x 上，则PQ 的最小值为( ) A. 2 －1 B. 1 C. 2 D. 25. 某次足球赛共8支球队参加，分三个阶段进行．(1) 小组赛：经抽签分成甲、乙两组，每组4队进行单循环比赛，以积分和净胜球数取前两名；(2) 半决赛：甲组第一名与乙组第二名，乙组第一名与甲组第二名进行主、客场交叉淘汰赛(每两队主、客场各赛1场)，决出胜者；(3) 决赛：两个胜队参加，比赛1场，决出胜负． 则全部赛程共需比赛的场数为( )A. 15B. 16C. 17D. 186. 若f (x )＝sin (2x ＋π6 )在区间[－t ，t ]上单调递增，则实数t 的取值范围是( )A. [π6 ，π2 ]B. (0，π3 ]C. [π6 ，π3 ]D. (0，π6]7. 足球是由12个正五边形和20个正六边形组成的．如图，将足球上的一个正六边形和它相邻的正五边形展开放平，若正多边形边长为a ，A ，B ，C 分别为正多边形的顶点，则AB → ·AC →＝( )A. (3＋3 cos 18°)a 2B. (3 ＋cos 18°)a 2C. (3＋2 cos 18°)a 2D. (33 ＋3cos 18°)a 28. 在某次数学节上，甲、乙、丙、丁四位同学分别写下了一个命题：甲：ln 3＜3 ln 2；乙：ln π＜πe；丙：212＜12；丁：3eln 2＞42 .所写为真命题的是( )A. 甲和乙B. 甲和丙C. 丙和丁 D ．甲和丁二、 多选题：本题共4小题，每小题5分，共计20分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．9. 连续抛掷一枚骰子2次，记事件A 表示“2次结果中正面向上的点数之和为奇数”，事件B 表示“2次结果中至少一次正面向上的点数为偶数”，则( )A. 事件A 与事件B 不互斥B. 事件A 与事件B 相互独立C. P (AB )＝34D. P (A |B )＝2310. 在长方体ABCDA 1B 1C 1D 1中，AA 1＝3，底面ABCD 是边长为2的正方形，底面A 1B 1C 1D 1的中心为M ，则( )A. C 1D 1∥平面ABMB. 向量AM → 在向量AC →上的投影向量为12 AC →C. 棱锥MABCD 的内切球的半径为31010D. 直线AM 与BC 所成角的余弦值为111111. 公元前6世纪，古希腊的毕达哥拉斯学派把5－12 (5－12≈0.618)称为黄金数．离心率等于黄金数的倒数的双曲线称为黄金双曲线．若黄金双曲线E ：x 2a 2 －y 2＝1(a ＞0)的左、右顶点分别为A 1，A 2，虚轴的上端点为B ，左焦点为F ，离心率为e ，则( )A. a 2e ＝1B. A 2B ·FB →＝0C. 顶点到渐近线的距离为eD. △A 2FB 的外接圆的面积为2＋54π 12. 设函数f (x )的定义域为R ，f (2x ＋1)为奇函数，f (x ＋2)为偶函数，当x ∈[0，1]时，f (x )＝a x ＋b ，若f (0)＋f (3)＝－1，则( )A. b ＝－2B. f (2 023)＝－1C. f (x )为偶函数D. f (x )的图象关于点(12，0)对称三、 填空题：本题共4小题，每小题5分，共计20分．13. 若(1－2x )5(x ＋2)＝a 0＋a 1x ＋…＋a 6x 6，则a 3＝________． 14. 某学校组织1 200名学生进行“防疫知识测试”．测试后统计分析如下：学生的平均成绩为x ＝80，方差为s 2＝25.学校要对成绩不低于90分的学生进行表彰．假设学生的测试成绩X 近似服从正态分布N (μ，σ2)，其中μ近似为平均数x ，σ2近似为方差s 2，则估计获表彰的学生人数为________．(四舍五入，保留整数)参考数据：随机变量X 服从正态分布N (μ，σ2)，则P (μ－σ＜X ＜μ＋σ)＝0.682 7， P (μ－2σ＜X ＜μ＋2σ)＝0.954 5，P (μ－3σ＜X ＜μ＋3σ)＝0.997 3.15. 已知抛物线y 2＝2x 与过点T (6，0)的直线相交于A ，B 两点，且OB ⊥AB (O 为坐标原点)，则△OAB 的面积为________．16. 已知函数f (x )＝⎩⎪⎨⎪⎧e x －1，x ≤1，|ln （x －1）|，x ＞1，则函数F (x )＝f (f (x ))－2f (x )－12 的零点个数为________．四、 解答题：本题共6小题，共计70分．解答时应写出必要的文字说明、证明过程或演算步骤．17. (本小题满分10分)已知△ABC 为锐角三角形，内角A ，B ，C 的对边分别为a ，b ，c ，且a cos B ＋b cos A ＝2c cos C .(1) 求角C 的大小；(2) 若c ＝2，求△ABC 的周长的取值范围．18.(本小题满分12分)已知等比数列{a n }的前n 项和为S n ，S 3＝14，S 6＝126. (1) 求数列{a n }的通项公式；(2) 当n ∈N *时，a n b 1＋a n －1b 2＋…＋a 1b n ＝4n －1，求数列{b n }的通项公式．19.(本小题满分12分)如图，在四棱锥SABCD 中，侧面SAD ⊥底面ABCD ，SA ⊥AD ，且四边形ABCD 为平行四边形，AB ＝1，BC ＝2，∠ABC ＝π3，SA ＝3.(1) 求二面角SCDA 的大小；(2) 若点P 在线段SD 上且满足SP → ＝λSD →，试确定实数λ的值，使得直线BP 与平面PCD 所成的角最大．20.(本小题满分12分)设椭圆E ：x 2a 2 ＋y 2b 2 ＝1(a ＞b ＞0)的左、右焦点分别为F 1(－c ，0)，F 2(c ，0)，离心率为33 ，若椭圆E 上的点到直线l ：x ＝a 2c的最小距离为3－3 .(1) 求椭圆E 的方程；(2) 过F 1作直线交椭圆E 于A ，B 两点，设直线AF 2，BF 2与直线l 分别交于C ，D 两点，线段AB ，CD 的中点分别为M ，N ，O 为坐标原点，若M ，O ，N 三点共线，求直线AB 的方程．21.(本小题满分12分)第22届世界杯于2022年11月21日到12月18日在卡塔尔举办．在决赛中，阿根廷队通过点球战胜法国队获得冠军．(1) 扑点球的难度一般比较大，假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门，门将也会等可能地随机选择球门的左、中、右三个方向来扑点球，而且门将即使方向判断正确也有23 的可能性扑不到球．不考虑其它因素，在一次点球大战中，求门将在前三次扑到点球的个数X 的分布列和数学期望．(2) 好成绩的取得离不开平时的努力训练，甲、乙、丙三名前锋队员在某次传接球的训练中，球从甲脚下开始，等可能地随机传向另外2人中的1人，接球者接到球后再等可能地随机传向另外2人中的1人，如此不停地传下去，假设传出的球都能接住．记第n 次传球之前球在甲脚下的概率为p n ，易知p 1＝1，p 2＝0.① 试证明：{p n －13}为等比数列；② 设第n 次传球之前球在乙脚下的概率为q n ，比较p 10与q 10的大小．22. (本小题满分12分)已知函数f (x )＝a e x ＋cos x ＋12 x 2，其中a 为实数，e 是自然对数的底数．(1) 当a ＝0时，求曲线f (x )在点(π2 ，f (π2))处的切线方程；(2) 若g (x )为f (x )的导数，g (x )在(0，π)上有两个极值点，求a 的取值范围．2022～2023学年高三年级模拟试卷(苏北四市)数学参考答案及评分标准1. C2. C3. A4. A5. C6. D7. A8. B9. AD 10. ABD 11. ABD 12. AC 13. －120 14. 27 15. 152 16. 517. 解：(1) 由正弦定理，得sin A cos B ＋sin B cos A ＝2sin C cos C ， 即sin (A ＋B )＝2sin C cos C ，即sin C ＝ 2sin C cos C ．(2分) 又C ∈(0，π)，所以sin C ≠0， 所以cos C ＝12 ，故C ＝π3.(4分)(2) 由正弦定理，得a ＝c sin A sin C ＝43 sin A ，b ＝43 sin B ，(5分)所以△ABC 的周长L ＝a ＋b ＋c ＝43 (sin A ＋sin B )＋2＝43[sin A ＋sin (2π3 －A )]＋2＝4(32 sin A ＋12 cos A )＋2＝4sin (A ＋π6)＋2.(8分) 由△ABC 为锐角三角形可知，⎩⎨⎧0<A <π2，0＜B ＝2π3－A ＜π2，得π6 ＜A ＜π2 ，所以π3 ＜A ＋π6 ＜2π3 ，所以sin (A ＋π6 )∈(32 ，1]，所以△ABC 的周长的取值范围是(2＋23 ，6].(10分) 18. 解：(1) 设数列{a n }的公比为q .⎩⎪⎨⎪⎧S 3＝a 1＋a 2＋a 3＝14 ①，S 6－S 3＝a 4＋a 5＋a 6＝112 ②， ②① 得q 3＝8，所以q ＝2，(3分) 有S 3＝a 1＋a 2＋a 3＝a 1＋2a 1＋4a 1＝14，得a 1＝2， 则数列{a n }的通项公式为a n ＝2n .(注：若使用等比求和公式没有讨论公比q ＝1，扣1分)(5分)(2) 由2n b 1＋2n －1b 2＋…＋2b n ＝4n －1，n ＝1时2b 1＝3，得b 1＝32 ，(6分)所以n ≥2时，2n －1b 1＋2n －2b 2＋…＋2b n －1＝4n －1－1.(8分)2n b 1＋2n －1b 2＋…＋2b n ＝2(2n －1b 1＋2n －2b 2＋…＋2b n －1)＋2b n ＝4n －1，(10分) 有2(4n －1－1)＋2b n ＝4n －1，得n ≥2时，b n ＝4n －1＋12 ，(11分)又b 1＝32 ，故b n ＝4n －1＋12.(12分)19. 解：(1) 连接AC ，在△ABC 中，AB ＝1，BC ＝2，∠ABC ＝π3 ，由余弦定理得AC ＝3 ，所以∠BAC ＝π2.(2分)因为侧面SAD ⊥底面ABCD ，平面SAD ∩底面ABCD ＝AD ，SA ⊥AD ， 所以SA ⊥平面ABCD ，所以SA ⊥AC .(4分)(解法1)以A 为原点建立如图所示的空间直角坐标系．则B (1，0，0)，C (0，3 ，0)，S (0，0，3)，D (－1，3 ，0)，CD → ＝(－1，0，0)，SC →＝(0，3 ，－3).设平面SCD 的法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·CD →＝0，n ·SC →＝0， 得⎩⎨⎧x ＝0，3y －3z ＝0， 可取n ＝(0，3 ，1).易知m ＝(0，0，1)为平面ABCD 的一个法向量．(6分)所以cos θ＝n ·m |n ||m | ＝11＋3 ＝12 .因为二面角SCDA 为锐角，所以θ＝π3 ，即二面角SCDA 的大小为π3.(8分)(解法2)因为SA ⊥平面ABCD ，所以SA ⊥CD .因为四边形ABCD 为平行四边形，所以AC ⊥CD ， 又SA ∩AC ＝A ，所以CD ⊥平面SAC ，所以CD ⊥SC .又平面ACD ∩平面SCD ＝CD ，所以∠ACS 为二面角SCDA 的平面角．(6分)因为tan ∠ACS ＝33 ＝3 ，二面角SCDA 为锐角，所以θ＝π3 ，即二面角SCDA 的大小为π3.(8分)(2) 设P (x 1，y 1，z 1)，SP → ＝λSD →， 得(x 1，y 1，z 1－3)＝λ(－1，3 ，－3)，x 1＝－λ，y 1＝3 λ，z 1＝3－3λ，所以P (－λ，3 λ，3－3λ) ，所以BP →＝(－λ－1，3 λ，3－3λ).(10分)由(1)知平面PCD 的一个法向量为n ＝(0，3 ，1).因为cos α＝BP →·n |BP →||n | ＝3λ＋3－3λ2（λ＋1）2＋（3λ）2＋（3－3λ）2 ＝3213λ2－16λ＋10 ， 所以当λ＝813 时，cos α最大， 即当λ＝813时，BP 与平面PCD 所成的角最大．(12分)20. 解：(1) 由条件知⎩⎨⎧c a ＝33，a2c －a ＝3－3，解得⎩⎨⎧a ＝3，c ＝1，所以b 2＝a 2－c 2＝2，所以椭圆E 的方程为x 23 ＋y 22＝1.(4分)(2) 由(1)知，F 1(－1，0)，F 2(1，0)，由题意知，直线AB 的斜率不为0.设直线AB 的方程为x ＝my －1，联立⎩⎪⎨⎪⎧x 23＋y 22＝1，x ＝my －1，消去x 并整理得(2m 2＋3)y 2－4my －4＝0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝4m2m 2＋3 ，y 1y 2＝－42m 2＋3 .(6分)所以y M ＝2m2m 2＋3 ，x M ＝my M －1＝－32m 2＋3 ，所以直线OM 的斜率为k OM ＝y M x M ＝－2m3. 直线AF 2的方程为y ＝y 1x 1－1 (x －1)，直线l 的方程为x ＝3，则C (3，2y 1x 1－1 ).直线BF 2的方程为y ＝y 2x 2－1 (x －1)，同理有D (3，2y 2x 2－1).(8分)所以y N ＝y 1x 1－1 ＋y 2x 2－1 ＝y 1my 1－2 ＋y 2my 2－2 ＝y 1（my 2－2）＋y 2（my 1－2）（my 1－2）（my 2－2）＝2my 1y 2－2（y 1＋y 2）m 2y 1y 2－2m （y 1＋y 2）＋4 ＝2m ·－42m 2＋3－2×4m2m 2＋3m 2·－42m 2＋3－2m ·4m2m 2＋3＋4 ＝4mm 2－3 ，(10分) 所以直线ON 的斜率为k ON ＝y N x N ＝4m3（m 2－3）.由M ，O ，N 三点共线可得k OM ＝k ON ，即－2m 3 ＝4m3（m 2－3） ，所以m ＝0或m ＝±1.故直线AB 的方程为x ＝－1或x －y ＋1＝0或x ＋y ＋1＝0.(12分)21. (1) 解：依题意可得，门将每次可以扑到点球的概率为p ＝13 ×13 ＝19 ，(1分)门将在前三次扑到点球的个数X 可能的取值为0，1，2，3，易知X ～B (3，19 )，所以P (X ＝k )＝C k 3 ×(19 )k ×(89 )3－k，k ＝0，1，2，3，(2分) 故X 的分布列为所以X 的数学期望E (X )＝3×19 ＝13.(6分)(2) ① 证明：第n 次传球之前球在甲脚下的概率为p n ，则当n ≥2时，第n －1次传球之前球在甲脚下的概率为p n －1， 第n －1次传球之前球不在甲脚下的概率为1－p n －1， 则p n ＝p n －1×0＋(1－p n －1)×12 ＝－12 p n －1＋12 ，(8分)所以{p n －13 }是以23 为首项， 公比为－12的等比数列. (10分)② 解：由①可知p n ＝23 (－12 )n －1＋13 ，所以p 10＝23 (－12 )9＋13 ＜13 ，所以q 10＝12 (1－p 10)＝12 [23 －23 (－12 )9]＞13，故p 10＜q 10.(12分)22. 解：(1) 当a ＝0时，f (x )＝cos x ＋12 x 2，则f ′(x )＝－sin x ＋x ，所以f ′(π2 )＝π2 －1.(1分)又f (π2 )＝π28 ，所以曲线y ＝f (x )在点(π2 ，f (π2 ))处的切线方程为y ＝(π2 －1)x －π28 ＋π2 .(3分)(2) 因为g (x )＝a e x －sin x ＋x ，所以g ′(x )＝a e x －cos x ＋1，g (x )在(0，π)上有两个极值点，即g ′(x )在(0，π)内有两个变号零点． 令g ′(x )＝0得a e x －cos x ＋1＝0，所以a －cos x －1e x＝0.(5分)设h (x )＝a －cos x －1e x ，则h ′(x )＝sin x ＋cos x －1e x ＝2sin （x ＋π4）－1e x， 当x ∈(0，π2 )时，sin (x ＋π4 )∈(22，1]，所以h ′(x )＞0，所以h (x )单调递增；当x ∈(π2 ，π)时，sin (x ＋π4 )∈(－22 ，22)，所以h ′(x )＜0，所以h (x )单调递减，(7分)所以h (0)＝a ，h (π2)＝a ＋e －π2 ，h (π)＝a ＋2e －π.当－e－π2＜a ＜－2e－π时，h (0)＜0，h (π2)＞0，h (π)＜0，所以∃x 1∈(0，π2 )，x 2∈(0，π)，使h (x 1)＝h (x 2)＝0.(9分)当x ∈(0，x 1)时，h (x )＜0，g ′(x )＜0，g (x )单调递减； 当x ∈(x 1，x 2)时，h (x )＞0，g ′(x )＞0，g (x )单调递增； 当x ∈(x 2，π)时，h (x )＜0，g ′(x )＜0，g (x )单调递减； 即－e －π2＜a ＜－2e－π时，g (x )在(0，π)上有两个极值点．(12分)。

江苏省苏北四市2020届高三上学期期末考试(满分160分，考试时间120分钟)参考公式：1. 样本数据x 1，x 2，…，x n 的方差s 2＝1n ∑n i ＝1(x i －x)2，其中x ＝1n ∑ni ＝1x i ； 2. 圆锥的体积V ＝13Sh ，其中S 是圆锥的底面圆面积，h 是圆锥的高．一、 填空题：本大题共14小题，每小题5分，共70分．1. 已知集合A ＝{x|0<x<2}，B ＝{x|－1<x<1)，则A ∪B ＝________．S←0 I←1While I ＜6 I←I ＋1 S←S ＋I End While Print S2. 已知复数z 满足z 2＝－4，且z 的虚部小于0，则z ＝________．3. 若一组数据7，x ，6，8，8的平均数为7，则该组数据的方差是________．4. 执行如图所示的伪代码，则输出的结果为________．5. 函数f(x)＝log 2x －2的定义域为________．6. 某学校高三年级有A ，B 两个自习教室，甲、乙、丙3名学生各自随机选择其中一个教室自习，则甲、乙两人不在同一教室上自习的概率为________．7. 若关于x 的不等式x 2－mx ＋3<0的解集是(1，3)，则实数m 的值为________． 8. 在平面直角坐标系xOy 中，双曲线x 23－y 2＝1的右准线与渐近线的交点在抛物线y 2＝2px上，则实数p 的值为________．9. 已知等差数列{a n }的前n 项和为S n ，a 2＋a 9＝8，S 5＝－5，则S 15的值为________． 10. 已知函数y ＝3sin 2x 的图象与函数y ＝cos 2x 的图象相邻的三个交点分别是A ，B ，C ，则△ABC 的面积为________．11. 在平面直角坐标系xOy 中，已知圆M ：x 2＋y 2－4x －8y ＋12＝0，圆N 与圆M 外切于点(0，m)，且过点(0，－2)，则圆N 的标准方程为______________．12. 已知函数f(x)是定义在R 上的奇函数，其图象关于直线x ＝1对称，当x ∈(0，1]时，f(x)＝－e ax (其中e 是自然对数的底数)．若f(2 020－ln 2)＝8，则实数a 的值为________． 13. 如图，在△ABC 中，D ，E 是BC 上的两个三等分点，AB →·AD →＝2AC →·AE →，则cos ∠ADE 的最小值为________．(第13题)14. 设函数f(x)＝|x 3－ax －b|，x ∈[－1，1]，其中a ，b ∈R .若f(x)≤M 恒成立，则当M 取得最小值时，a ＋b 的值为________．二、 解答题：本大题共6小题，共90分. 解答时应写出必要的文字说明、证明过程或演算步骤．15. (本小题满分14分)如图，在三棱锥PABC 中，AP ＝AB ，点M ，N 分别为棱PB ，PC 的中点，平面PAB ⊥平面PBC.求证：(1) BC ∥平面AMN ；(2) 平面AMN ⊥平面PBC.16. (本小题满分14分)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且cos A ＝55. (1) 若a ＝5，c ＝25，求b 的值； (2) 若B ＝π4，求tan 2C 的值．如图，在圆锥SO中，底面半径R为3，母线长l为5.用一个平行于底面的平面去截圆锥，截面圆的圆心为O1，半径为r.现要以截面为底面，圆锥底面圆心O为顶点挖去一个倒立的小圆锥OO1，记圆锥OO1的体积为V.(1) 将V表示成r的函数；(2) 求V的最大值．在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a>b>0)的右顶点为A ，过点A 作直线l 与圆O ：x 2＋y 2＝b 2相切，与椭圆C 交于另一点P ，与右准线交于点Q.设直线l 的斜率为k.(1) 用k 表示椭圆C 的离心率；(2) 若OP →·OQ →＝0，求椭圆C 的离心率．已知函数f(x)＝(a －12)ln x(a ∈R )．(1) 若曲线y ＝f(x)在点(1，f(1))处的切线方程为x ＋y －1＝0，求a 的值； (2) 若f(x)的导函数f′(x)存在两个不相等的零点，求实数a 的取值范围；(3) 当a ＝2时，是否存在整数λ，使得关于x 的不等式f(x)≥λ恒成立？若存在，求出λ的最大值；若不存在，请说明理由．已知数列{a n }的首项a 1＝3，对任意的n ∈N *，都有a n ＋1＝ka n －1(k≠0)，数列{a n －1}是公比不为1的等比数列．(1) 求实数k 的值；(2) 设b n ＝⎩⎪⎨⎪⎧4－n ，n 为奇数，a n－1，n 为偶数，数列{b n }的前n 项和为S n ，求所有正整数m 的值，使得S 2mS 2m －1恰好为数列{b n }中的项．2020届高三模拟考试试卷(四)数学附加题(满分40分，考试时间30分钟)21. 【选做题】 在A ，B ，C 三小题中只能选做两题，每小题10分，共20分．若多做，则按作答的前两题计分．解答时应写出必要的文字说明、证明过程或演算步骤．A. (选修42：矩阵与变换)已知矩阵M ＝⎣⎢⎡⎦⎥⎤23t 1的一个特征值为4，求矩阵M 的逆矩阵M －1.B. (选修44：坐标系与参数方程)在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρ(cos θ＋sin θ)＝12，曲线C 的参数方程为⎩⎨⎧x ＝23cos θ，y ＝2sin θ(θ为参数，θ∈R )．在曲线C 上求点M ，使点M 到l 的距离最小，并求出最小值．C. (选修45：不等式选讲)已知正数x ，y ，z 满足x ＋y ＋z ＝1，求1x ＋2y ＋1y ＋2z ＋1z ＋2x的最小值．【必做题】 第22，23题，每小题10分，共20分．解答时应写出必要的文字说明、证明过程或演算步骤． 22. 如图，在三棱柱ABCA 1B 1C 1中，侧面AA 1B 1B 为正方形，侧面BB 1C 1C 为菱形，∠BB 1C 1＝60°，平面AA 1B 1B ⊥平面BB 1C 1C.(1) 求直线AC 1与平面AA 1B 1B 所成角的正弦值； (2) 求二面角BAC 1C 的余弦值．23. 已知n 为给定的正整数，设(23＋x)n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，x ∈R .(1) 若n ＝4，求a 0，a 1的值；(2) 若x ＝13，求∑n k ＝0(n －k)a k x k 的值．2020届高三模拟考试试卷(四)(苏北四市)数学参考答案及评分标准1. {x|－1<x<2}2. －2i3. 454. 205. [4，＋∞)6. 127. 48. 149. 135 10. 32π11. (x ＋2)2＋y 2＝8 12. 3 13. 47 14. 3415. 证明：(1) 在△PBC 中，因为点M ，N 分别为棱PB ，PC 的中点，所以MN ∥BC.(3分)又MN ⊂平面AMN ，BC ⊄平面AMN ，所以BC ∥平面AMN.(6分)(2) 在△PAB 中，因为AP ＝AB ，点M 为棱PB 的中点，所以AM ⊥PB.(8分)因为平面PAB ⊥平面PBC ，平面PAB∩平面PBC ＝PB ，AM ⊂平面PAB ，所以AM ⊥平面PBC.(12分)又AM ⊂平面AMN ，所以平面AMN ⊥平面PBC.(14分) 16. 解：(1) 在△ABC 中，由余弦定理b 2＋c 2－2bccos A ＝a 2，得b 2＋20－2×25×55b ＝25，即b 2－4b －5＝0，(4分) 解得b ＝5或b ＝－1(舍)，所以b ＝5.(6分) (2) 由cos A ＝55及0<A<π，得sin A ＝1－cos 2A ＝1－（55）2＝255，(8分) 所以cos C ＝cos[π－(A ＋B)]＝－cos(A ＋π4)＝－22(cos A －sin A)＝1010.因为0<C<π，所以sin C ＝1－cos 2C ＝1－（1010）2＝31010， 从而tan C ＝sin Ccos C ＝310101010＝3，(12分)所以tan 2C ＝2tan C 1－tan 2C ＝2×31－32＝－34.(14分)17. 解：(1) 在△SAO 中，SO ＝SA 2－AO 2＝52－32＝4.(2分)由△SNO 1∽△SAO 可知SO 1SO ＝r R ，所以SO 1＝43r ，(4分)所以OO 1＝4－43r ，所以V(r)＝13πr 2(4－43r)＝49π(3r 2－r 3)，0<r<3.(7分)(2) 由(1)得V(r)＝49π(3r 2－r 3)，0<r<3，所以V′(r)＝49π(6r －3r 2)，令V′(r)＝0，得r ＝2，(9分)当r ∈(0，2)时，V′(r)>0，所以V(r)在(0，2)上单调递增； 当r ∈(2，3)时，V′(r)<0，所以V(r)在(2，3)上单调递减． 所以当r ＝2时，V(r)取得最大值V(2)＝16π9.答：小圆锥的体积V 的最大值为16π9.(14分)18. 解：(1) 直线l 的方程为y ＝k(x －a)，即kx －y －ak ＝0.因为直线l 与圆O ：x 2＋y 2＝b 2相切，所以|－ak|k 2＋1＝b ，故k 2＝b 2a 2－b 2.所以椭圆C 的离心率e ＝1－b 2a2＝1k 2＋1.(4分) (2) 设椭圆C 的焦距为2c ，则右准线方程为x ＝a 2c.由⎩⎪⎨⎪⎧y ＝k （x －a ），x ＝a 2c 得y ＝k(a 2c －a)＝k a 2－ac c ，所以Q(a 2c ，k （a 2－ac ）c )．(6分)由⎩⎪⎨⎪⎧x 2a 2＋y 2b 2＝1，y ＝k （x －a ）得(b 2＋a 2k 2)x 2－2a 3k 2x ＋a 4k 2－a 2b 2＝0， 解得x P ＝a 3k 2－ab 2b 2＋a 2k 2，则y P ＝k(a 3k 2－ab 2b 2＋a 2k 2－a)＝－2ab 2k b 2＋a 2k 2，所以P(a 3k 2－ab 2b 2＋a 2k 2，－2ab 2kb 2＋a 2k2)．(10分)因为OP →·OQ →＝0，所以a 2c ·a 3k 2－ab 2b 2＋a 2k 2＋k （a 2－ac ）c ·－2ab 2k b 2＋a 2k 2＝0，即a(a 2k 2－b 2)＝2b 2k 2(a －c)．(12分) 由(1)知k 2＝b 2a 2－b 2，所以a(a 2b 2a 2－b 2－b 2)＝2b 4（a －c ）a 2－b 2， 所以a ＝2a －2c ，即a ＝2c ，所以c a ＝12，故椭圆C 的离心率为12.(16分)19. 解：(1) f′(x)＝1x 2ln x ＋(a －1x )1x.因为曲线y ＝f(x)在点(1，f(1))处的切线方程为x ＋y －1＝0，所以f′(1)＝a －1＝－1，解得a ＝0.(2分)(2) 因为f′(x)＝ax －1＋ln xx 2存在两个不相等的零点，所以g(x)＝ax －1＋ln x 存在两个不相等的零点，则g′(x)＝1x ＋a.①当a≥0时，g′(x)>0，所以g(x)单调递增，至多有一个零点．(4分) ②当a<0时，因为当x ∈(0，－1a )时，g′(x)>0，g(x)单调递增；当x ∈(－1a ，＋∞)时，g′(x)<0，g(x)单调递减，所以x ＝－1a 时，g(x)max ＝g(－1a )＝ln(－1a)－2.(6分)因为g(x)存在两个零点，所以ln(－1a )－2>0，解得－e －2<a<0.(7分)因为－e －2<a<0，所以－1a>e 2>1.因为g(1)＝a －1<0，所以g(x)在(0，－1a )上存在一个零点．(8分)因为－e －2<a<0，所以(－1a )2>－1a.因为g((－1a )2)＝ln(－1a )2＋1a －1，设t ＝－1a ，则y ＝2ln t －t －1(t>e 2)．因为y′＝2－tt<0，所以y ＝2ln t －t －1(t>e 2)单调递减， 所以y<2ln(e 2)－e 2－1＝3－e 2<0，所以g((－1a )2)＝ln(－1a )2＋1a －1<0，所以g(x)在(－1a，＋∞)上存在一个零点．综上可知，实数a 的取值范围是(－e －2，0)．(10分)(3) 当a ＝2时，f(x)＝(2－1x )ln x ，f′(x)＝1x 2ln x ＋(2－1x )1x ＝2x －1＋ln xx 2，设g(x)＝2x －1＋ln x ，则g′(x)＝1x ＋2>0，所以g(x)单调递增，且g(12)＝ln 12<0，g(1)＝1>0，所以存在x 0∈(12，1)使得g(x 0)＝0.(12分)因为当x ∈(0，x 0)时，g(x)<0，即f′(x)<0，所以f(x)单调递减； 当x ∈(x 0，＋∞)时，g(x)>0，即f′(x)>0，所以f(x)单调递增， 所以x ＝x 0时，f(x)取得极小值，也是最小值，此时f(x 0)＝(2－1x 0)ln x 0＝(2－1x 0)(1－2x 0)＝－(4x 0＋1x 0)＋4.(14分)因为x 0∈(12，1)，所以f(x 0)∈(－1，0)．因为f(x)≥λ，且λ为整数，所以λ≤－1，即λ的最大值为－1.(16分) 20. 解：(1) 由a n ＋1＝ka n －1，a 1＝3可知，a 2＝3k －1，a 3＝3k 2－k －1.因为{a n －1}为等比数列，所以(a 2－1)2＝(a 1－1)(a 3－1)，即(3k －2)2＝2×(3k 2－k －2)，即3k 2－10k ＋8＝0，解得k ＝2或k ＝43.(2分)当k ＝43时，a n ＋1－3＝43(a n －3)，所以a n ＝3，则a n －1＝2，所以数列{a n －1}的公比为1，不符合题意；当k ＝2时，a n ＋1－1＝2(a n －1)，所以数列{a n －1}的公比q ＝a n ＋1－1a n －1＝2，所以实数k 的值为2.(4分) (2) 由(1)知a n －1＝2n ，所以b n ＝⎩⎪⎨⎪⎧4－n ， n 为奇数，2n ， n 为偶数，则S 2m ＝(4－1)＋4＋(4－3)＋42＋…＋[4－(2m －1)]＋4m＝(4－1)＋(4－3)＋...＋[4－(2m －1)]＋4＋42＋ (4)＝m(4－m)＋4m ＋1－43，(6分)则S 2m －1＝S 2m －b 2m ＝m(4－m)＋4m －43.因为b 2m ＋b 2m ＋1＝3－2m ＋4m ，又(b 2m ＋2＋b 2m ＋3)－(b 2m ＋b 2m ＋1)＝3×4m －2>0， 且b 2＋b 3＝5>0，b 1＝3>0，所以S 2m －1>0，则S 2m >0. 设S 2mS 2m －1＝b t >0，t ∈N *，(8分) 则t ＝1，3或t 为偶数，因为b 3＝1不可能，所以t ＝1或t 为偶数．①当S 2mS 2m －1＝b 1时，m （4－m ）＋4m ＋1－43m （4－m ）＋4m －43＝3，化简得6m 2－24m ＋8＝－4m ≤－4， 即m 2－4m ＋2≤0，所以m 可能取值为1，2，3，验证S 2S 1＝73，S 4S 3＝3，S 6S 5＝8723，得当m ＝2时，S 4S 3＝b 1成立．(12分)②当t 为偶数时，S 2m S 2m －1＝m （4－m ）＋4m ＋1－43m （4－m ）＋4m －43＝1＋3－3m 2＋12m －44m ＋1， 设c m ＝－3m 2＋12m －44m ，则c m ＋1－c m ＝9m 2－42m ＋214m ＋1. 由①知m>3，当m ＝4时，c 5－c 4＝－345<0；当m>4时，c m ＋1－c m >0，所以c 4>c 5<c 6<…，所以c m 的最小值为c 5＝－191 024，所以0<S 2m S 2m －1<1＋3－191 024＋1<5.令S 2m S 2m －1＝4＝b 2，则1＋3－3m 2＋12m －44m＋1＝4，即－3m 2＋12m －4＝0，无整数解． 综上，正整数m 的值2.(16分)2020届高三模拟考试试卷(苏北四市) 数学附加题参考答案及评分标准21. A. 解：矩阵M 的特征多项式为f(λ)＝⎪⎪⎪⎪⎪⎪λ－2－3－t λ－1＝(λ－2)(λ－1)－3t.(2分) 因为矩阵M 的一个特征值为4，所以f(4)＝6－3t ＝0，所以t ＝2.(5分)所以M ＝⎣⎢⎡⎦⎥⎤2321，所以M －1＝⎣⎢⎢⎡⎦⎥⎥⎤12×1－3×2－32×1－3×2－22×1－3×222×1－3×2＝⎣⎢⎡⎦⎥⎤－14 34 12－12.(10分) B. 解：由l ：ρcos θ＋ρsin φ－12＝0，及x ＝ρcos θ，y ＝ρsin θ，所以l 的直角坐标方程为x ＋y －12＝0. (2分)在曲线C 上取点M(23cos φ，2sin φ)，则点M 到l 的距离 d ＝|23cos φ＋2sin φ－12|2＝⎪⎪⎪⎪4sin （φ＋π3）－122＝12－4sin （φ＋π3）2，(6分)当φ＝π6时，d 取最小值42，(8分)此时点M 的坐标为(3，1)．(10分)C. 解：因为x ，y ，z 都为正数，且x ＋y ＋z ＝1，所以由柯西不等式，得3(1x ＋2y ＋1y ＋2z ＋1z ＋2x)＝(1x ＋2y ＋1y ＋2z ＋1z ＋2x )·[(x ＋2y)＋(y ＋2z)＋(z ＋2x)](5分) ≥(1x ＋2y·x ＋2y ＋1y ＋2z·y ＋2z ＋1z ＋2x·z ＋2x)2＝9， 当且仅当x ＝y ＝z ＝13时等号成立，所以1x ＋2y ＋1y ＋2z ＋1z ＋2x的最小值为3.(10分)22. 解：(1) 因为四边形AA 1B 1B 为正方形，所以AB ⊥BB 1.因为平面AA 1B 1B ⊥平面BB 1C 1C ，平面AA 1B 1B∩平面BB 1C 1C ＝BB 1， AB ⊂平面AA 1B 1B ，所以AB ⊥平面BB 1C 1C. (2分)以点B 为坐标原点，分别以BA ，BB 1所在的直线为x ，y 轴，以过点B 且垂直于平面AA 1B 1B 的直线为z 轴，建立如图所示的空间直角坐标系Bxyz.不妨设正方形AA 1B 1B 的边长为2， 则A(2，0 ，0)，B 1(0，2，0)．在菱形BB 1C 1C 中，因为∠BB 1C 1＝60°，所以C 1(0，1，3)，所以AC 1→＝(－2，1，3)． 因为平面AA 1B 1B 的一个法向量为n ＝(0，0，1)， 设直线AC 1与平面AA 1B 1B 所成角为α， 则sin α＝|cos 〈AC 1→，n 〉|＝|3|22×1＝64，即直线AC 1与平面AA 1B 1B 所成角的正弦值为64.(6分) (2) 由(1)可知，C(0，－1，3)，所以CC 1→＝(0，2，0)． 设平面ACC 1的一个法向量为n 1＝(x 1，y 1，z 1)，因为⎩⎪⎨⎪⎧n 1·AC 1→＝0，n 1·CC 1→＝0，即⎩⎨⎧（x 1，y 1，z 1）·（－2，1，3）＝0，（x 1，y 1，z 1）·（0，2，0）＝0，取x 1＝32，y 1＝0，z 1＝1，即n 1＝(32，0，1)． 设平面ABC 1的一个法向量为n 2＝(x 2，y 2，z 2)， 因为BA →＝(2，0，0)，BC 1→＝(0，1, 3)，所以⎩⎨⎧（x 2，y 2，z 2）·（2，0，0）＝0，（x 2，y 2，z 2）·（0，1，3）＝0，取n 2＝(0，3，－1)．(8分)设二面角BAC 1C 的平面角为θ，则cos θ＝－cos 〈n 1，n 2〉＝－n 1·n 2|n 1|·|n 2|＝－－134＋1·3＋1＝77， 所以二面角BAC 1C 的余弦值为77.(10分) 23. 解：(1) 因为n ＝4，所以a 0＝C 04(23)4＝1681，a 1＝C 14(23)3＝3227.(2分) (2) 当x ＝13时，a k x k ＝C k n (23)n －k (13)k， 因为kC k n ＝k n ！k ！（n －k ）！＝n （n －1）！（k －1）！（n －k ）！＝nC k －1n －1，(4分)＝n －13n(23＋13)n －1＝23n ，当n ＝1时，也符合． 所以(n －k)a k x k 的值为23n.(10分)。

江苏省苏北四市2020届高三数学上学期期末考试试题(满分160分，考试时间120分钟)2020．1 参考公式：1. 样本数据x 1，x 2，…，x n 的方差s 2＝1n ∑n i ＝1(x i －x)2，其中x ＝1n ∑n i ＝1x i ；2. 圆锥的体积V ＝13Sh ，其中S 是圆锥的底面圆面积，h 是圆锥的高．一、 填空题：本大题共14小题，每小题5分，共70分．1. 已知集合A ＝{x|0<x<2}，B ＝{x|－1<x<1)，则A∪B＝________． S←0 I ←1While I ＜6 I←I＋1 S←S＋I End While Print S(第4题)2. 已知复数z 满足z 2＝－4，且z 的虚部小于0，则z ＝________．3. 若一组数据7，x ，6，8，8的平均数为7，则该组数据的方差是________．4. 执行如图所示的伪代码，则输出的结果为________．5. 函数f(x)＝log 2x －2的定义域为________．6. 某学校高三年级有A ，B 两个自习教室，甲、乙、丙3名学生各自随机选择其中一个教室自习，则甲、乙两人不在同一教室上自习的概率为________．7. 若关于x 的不等式x 2－mx ＋3<0的解集是(1，3)，则实数m 的值为________．8. 在平面直角坐标系xOy 中，双曲线x 23－y 2＝1的右准线与渐近线的交点在抛物线y 2＝2px 上，则实数p 的值为________．9. 已知等差数列{a n }的前n 项和为S n ，a 2＋a 9＝8，S 5＝－5，则S 15的值为________． 10. 已知函数y ＝3sin 2x 的图象与函数y ＝cos 2x 的图象相邻的三个交点分别是A ，B ，C ，则△ABC 的面积为________．11. 在平面直角坐标系xOy 中，已知圆M ：x 2＋y 2－4x －8y ＋12＝0，圆N 与圆M 外切于点(0，m)，且过点(0，－2)，则圆N 的标准方程为______________．12. 已知函数f(x)是定义在R 上的奇函数，其图象关于直线x ＝1对称，当x∈(0，1]时，f(x)＝－e ax(其中e 是自然对数的底数)．若f(2 020－ln 2)＝8，则实数a 的值为________．(第13题)13. 如图，在△ABC 中，D ，E 是BC 上的两个三等分点，AB →·AD →＝2AC →·AE →，则cos ∠ADE 的最小值为________．14. 设函数f(x)＝|x 3－ax －b|，x ∈[－1，1]，其中a ，b ∈R .若f(x)≤M 恒成立，则当M 取得最小值时，a ＋b 的值为________．二、 解答题：本大题共6小题，共90分. 解答时应写出必要的文字说明、证明过程或演算步骤．15. (本小题满分14分) 如图，在三棱锥PABC 中，AP ＝AB ，点M ，N 分别为棱PB ，PC 的中点，平面PAB⊥平面PBC.求证：(1) BC∥平面AMN ；(2) 平面AMN⊥平面PBC.16. (本小题满分14分)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且cos A ＝55. (1) 若a ＝5，c ＝25，求b 的值；(2) 若B ＝π4，求tan 2C 的值．如图，在圆锥SO中，底面半径R为3，母线长l为5.用一个平行于底面的平面去截圆锥，截面圆的圆心为O1，半径为r.现要以截面为底面，圆锥底面圆心O为顶点挖去一个倒立的小圆锥OO1，记圆锥OO1的体积为V.(1) 将V表示成r的函数；(2) 求V的最大值．在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y2b 2＝1(a>b>0)的右顶点为A ，过点A 作直线l 与圆O ：x 2＋y 2＝b 2相切，与椭圆C 交于另一点P ，与右准线交于点Q.设直线l 的斜率为k.(1) 用k 表示椭圆C 的离心率；(2) 若OP →·OQ →＝0，求椭圆C 的离心率．已知函数f(x)＝(a －12)ln x (a∈R )．(1) 若曲线y ＝f(x)在点(1，f(1))处的切线方程为x ＋y －1＝0，求a 的值； (2) 若f(x)的导函数f′(x)存在两个不相等的零点，求实数a 的取值范围；(3) 当a ＝2时，是否存在整数λ，使得关于x 的不等式f(x)≥λ恒成立？若存在，求出λ的最大值；若不存在，请说明理由．已知数列{a n }的首项a 1＝3，对任意的n∈N *，都有a n ＋1＝ka n －1(k≠0)，数列{a n －1}是公比不为1的等比数列．(1) 求实数k 的值；(2) 设b n ＝⎩⎪⎨⎪⎧4－n ，n 为奇数，a n －1，n 为偶数，数列{b n }的前n 项和为S n ，求所有正整数m 的值，使得S 2mS 2m －1恰好为数列{b n }中的项．2020届高三模拟考试试卷(四)数学附加题(满分40分，考试时间30分钟)21. 【选做题】 在A ，B ，C 三小题中只能选做两题，每小题10分，共20分．若多做，则按作答的前两题计分．解答时应写出必要的文字说明、证明过程或演算步骤．A. (选修42：矩阵与变换)已知矩阵M ＝⎣⎢⎡⎦⎥⎤23t 1的一个特征值为4，求矩阵M 的逆矩阵M －1.B. (选修44：坐标系与参数方程)在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρ(cos θ＋sin θ)＝12，曲线C 的参数方程为⎩⎨⎧x ＝23cos θ，y ＝2sin θ(θ为参数，θ∈R )．在曲线C 上求点M ，使点M 到l 的距离最小，并求出最小值．C. (选修45：不等式选讲)已知正数x ，y ，z 满足x ＋y ＋z ＝1，求1x ＋2y ＋1y ＋2z ＋1z ＋2x的最小值．【必做题】 第22，23题，每小题10分，共20分．解答时应写出必要的文字说明、证明过程或演算步骤．22. 如图，在三棱柱ABCA 1B 1C 1中，侧面AA 1B 1B 为正方形，侧面BB 1C 1C 为菱形，∠BB 1C 1＝60°，平面AA 1B 1B ⊥平面BB 1C 1C.(1) 求直线AC 1与平面AA 1B 1B 所成角的正弦值； (2) 求二面角BAC 1C 的余弦值．23. 已知n 为给定的正整数，设(23＋x)n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n，x ∈R .(1) 若n ＝4，求a 0，a 1的值；(2) 若x ＝13，求∑nk ＝0(n －k)a k x k的值．2020届高三模拟考试试卷(四)(苏北四市)数学参考答案及评分标准1. {x|－1<x<2}2. －2i3. 454. 205. [4，＋∞)6. 127. 48. 14 9. 13510.32π 11. (x ＋2)2＋y 2＝8 12. 3 13. 47 14. 3415. 证明：(1) 在△PBC 中，因为点M ，N 分别为棱PB ，PC 的中点，所以MN∥BC.(3分) 又MN ⊂平面AMN ，BC ⊄平面AMN ，所以BC∥平面AMN.(6分)(2) 在△PAB 中，因为AP ＝AB ，点M 为棱PB 的中点，所以AM⊥PB.(8分) 因为平面PAB⊥平面PBC ，平面PA B∩平面PBC ＝PB ，AM ⊂平面PAB ，所以AM⊥平面PBC.(12分)又AM ⊂平面AMN ，所以平面AMN⊥平面PBC.(14分)16. 解：(1) 在△ABC 中，由余弦定理b 2＋c 2－2bccos A ＝a 2，得 b 2＋20－2×25×55b ＝25，即b 2－4b －5＝0，(4分) 解得b ＝5或b ＝－1(舍)，所以b ＝5.(6分) (2) 由cos A ＝55及0<A<π，得sin A ＝1－cos 2A ＝1－（55）2＝255，(8分) 所以cos C ＝cos [π－(A ＋B)]＝－cos(A ＋π4)＝－22(cos A －sin A)＝1010.因为0<C<π，所以sin C ＝1－cos 2C ＝1－（1010）2＝31010， 从而tan C ＝sin Ccos C ＝310101010＝3，(12分)所以tan 2C ＝2tan C 1－tan 2C ＝2×31－32＝－34.(14分) 17. 解：(1) 在△SAO 中，SO ＝SA 2－AO 2＝52－32＝4.(2分)由△SNO 1∽△SAO 可知SO 1SO ＝r R ，所以SO 1＝43r ，(4分)所以OO 1＝4－43r ，所以V(r)＝13πr 2(4－43r)＝49π(3r 2－r 3)，0<r<3.(7分)(2) 由(1)得V(r)＝49π(3r 2－r 3)，0<r<3，所以V′(r)＝49π(6r －3r 2)，令V′(r)＝0，得r ＝2，(9分)当r∈(0，2)时，V ′(r)>0，所以V(r)在(0，2)上单调递增； 当r∈(2，3)时，V ′(r)<0，所以V(r)在(2，3)上单调递减．所以当r ＝2时，V(r)取得最大值V(2)＝16π9.答：小圆锥的体积V 的最大值为16π9.(14分)18. 解：(1) 直线l 的方程为y ＝k(x －a)，即kx －y －ak ＝0.因为直线l 与圆O ：x 2＋y 2＝b 2相切，所以|－ak|k 2＋1＝b ，故k 2＝b 2a 2－b 2.所以椭圆C 的离心率e ＝1－b2a2＝1k 2＋1.(4分) (2) 设椭圆C 的焦距为2c ，则右准线方程为x ＝a2c.由⎩⎪⎨⎪⎧y ＝k （x －a ），x ＝a 2c得y ＝k(a 2c －a)＝k a 2－ac c ，所以Q(a 2c ，k （a 2－ac ）c )．(6分)由⎩⎪⎨⎪⎧x 2a 2＋y 2b 2＝1，y ＝k （x －a ）得(b 2＋a 2k 2)x 2－2a 3k 2x ＋a 4k 2－a 2b 2＝0， 解得x P ＝a 3k 2－ab 2b 2＋a 2k 2，则y P ＝k(a 3k 2－ab 2b 2＋a 2k 2－a)＝－2ab 2k b 2＋a 2k 2，所以P(a 3k 2－ab 2b 2＋a 2k 2，－2ab 2kb 2＋a 2k2)．(10分)因为OP →·OQ →＝0，所以a 2c ·a 3k 2－ab 2b 2＋a 2k 2＋k （a 2－ac ）c ·－2ab 2k b 2＋a 2k 2＝0，即a(a 2k 2－b 2)＝2b 2k 2(a －c)．(12分)由(1)知k 2＝b 2a 2－b 2，所以a(a 2b 2a 2－b 2－b 2)＝2b 4（a －c ）a 2－b2， 所以a ＝2a －2c ，即a ＝2c ，所以c a ＝12，故椭圆C 的离心率为12.(16分)19. 解：(1) f′(x)＝1x 2ln x ＋(a －1x )1x.因为曲线y ＝f(x)在点(1，f(1))处的切线方程为x ＋y －1＝0，所以f′(1)＝a －1＝－1，解得a ＝0.(2分)(2) 因为f′(x)＝ax －1＋ln xx2存在两个不相等的零点， 所以g(x)＝ax －1＋ln x 存在两个不相等的零点，则g′(x)＝1x ＋a.①当a≥0时，g ′(x)>0，所以g(x)单调递增，至多有一个零点．(4分) ②当a<0时，因为当x∈(0，－1a )时，g ′(x)>0，g(x)单调递增；当x∈(－1a ，＋∞)时，g ′(x)<0，g(x)单调递减，所以x ＝－1a 时，g(x)max ＝g(－1a )＝ln(－1a)－2.(6分)因为g(x)存在两个零点，所以ln(－1a )－2>0，解得－e －2<a<0.(7分)因为－e －2<a<0，所以－1a>e 2>1.因为g(1)＝a －1<0，所以g(x)在(0，－1a )上存在一个零点．(8分)因为－e －2<a<0，所以(－1a )2>－1a.因为g((－1a )2)＝ln(－1a )2＋1a －1，设t ＝－1a ，则y ＝2ln t －t －1(t>e 2)．因为y′＝2－t t<0，所以y ＝2ln t －t －1(t>e 2)单调递减，所以y<2ln(e 2)－e 2－1＝3－e 2<0，所以g((－1a )2)＝ln(－1a )2＋1a －1<0，所以g(x)在(－1a，＋∞)上存在一个零点．综上可知，实数a 的取值范围是(－e －2，0)．(10分)(3) 当a ＝2时，f(x)＝(2－1x )ln x ，f ′(x)＝1x 2ln x ＋(2－1x )1x ＝2x －1＋ln xx 2， 设g(x)＝2x －1＋ln x ，则g′(x)＝1x ＋2>0，所以g(x)单调递增，且g(12)＝ln 12<0，g(1)＝1>0，所以存在x 0∈(12，1)使得g(x 0)＝0.(12分)因为当x∈(0，x 0)时，g(x)<0，即f′(x)<0，所以f(x)单调递减； 当x∈(x 0，＋∞)时，g(x)>0，即f′(x)>0，所以f(x)单调递增， 所以x ＝x 0时，f(x)取得极小值，也是最小值，此时f(x 0)＝(2－1x 0)ln x 0＝(2－1x 0)(1－2x 0)＝－(4x 0＋1x 0)＋4.(14分)因为x 0∈(12，1)，所以f(x 0)∈(－1，0)．因为f(x)≥λ，且λ为整数，所以λ≤－1，即λ的最大值为－1.(16分)20. 解：(1) 由a n ＋1＝ka n －1，a 1＝3可知，a 2＝3k －1，a 3＝3k 2－k －1.因为{a n －1}为等比数列，所以(a 2－1)2＝(a 1－1)(a 3－1)，即(3k －2)2＝2×(3k 2－k －2)，即3k 2－10k ＋8＝0，解得k ＝2或k ＝43.(2分)当k ＝43时，a n ＋1－3＝43(a n －3)，所以a n ＝3，则a n －1＝2，所以数列{a n －1}的公比为1，不符合题意；当k ＝2时，a n ＋1－1＝2(a n －1)，所以数列{a n －1}的公比q ＝a n ＋1－1a n －1＝2，所以实数k 的值为2.(4分)(2) 由(1)知a n －1＝2n，所以b n ＝⎩⎪⎨⎪⎧4－n ， n 为奇数，2n ， n 为偶数，则S 2m ＝(4－1)＋4＋(4－3)＋42＋…＋[4－(2m －1)]＋4m＝(4－1)＋(4－3)＋...＋[4－(2m －1)]＋4＋42＋ (4)＝m(4－m)＋4m ＋1－43，(6分) 则S 2m －1＝S 2m －b 2m ＝m(4－m)＋4m－43.因为b 2m ＋b 2m ＋1＝3－2m ＋4m，又(b 2m ＋2＋b 2m ＋3)－(b 2m ＋b 2m ＋1)＝3×4m－2>0， 且b 2＋b 3＝5>0，b 1＝3>0，所以S 2m －1>0，则S 2m >0. 设S 2m S 2m －1＝b t >0，t ∈N *，(8分) 则t ＝1，3或t 为偶数，因为b 3＝1不可能，所以t ＝1或t 为偶数． ①当S 2m S 2m －1＝b 1时，m （4－m ）＋4m ＋1－43m （4－m ）＋4m－43＝3，化简得6m 2－24m ＋8＝－4m≤－4， 即m 2－4m ＋2≤0，所以m 可能取值为1，2，3，验证S 2S 1＝73，S 4S 3＝3，S 6S 5＝8723，得当m ＝2时，S 4S 3＝b 1成立．(12分)②当t 为偶数时，S 2m S 2m －1＝m （4－m ）＋4m ＋1－43m （4－m ）＋4m －43＝1＋3－3m 2＋12m －44m＋1， 设c m ＝－3m 2＋12m －44m ，则c m ＋1－c m ＝9m 2－42m ＋214m ＋1. 由①知m>3，当m ＝4时，c 5－c 4＝－345<0；当m>4时，c m ＋1－c m >0，所以c 4>c 5<c 6<…，所以c m 的最小值为c 5＝－191 024，所以0<S 2m S 2m －1<1＋3－191 024＋1<5.令S 2m S 2m －1＝4＝b 2，则1＋3－3m 2＋12m －44m＋1＝4，即－3m 2＋12m －4＝0，无整数解． 综上，正整数m 的值2.(16分)2020届高三模拟考试试卷(苏北四市) 数学附加题参考答案及评分标准21. A. 解：矩阵M 的特征多项式为f(λ)＝⎪⎪⎪⎪⎪⎪λ－2－3－t λ－1＝(λ－2)(λ－1)－3t.(2分)因为矩阵M 的一个特征值为4，所以f(4)＝6－3t ＝0，所以t ＝2.(5分)所以M ＝⎣⎢⎡⎦⎥⎤2321，所以M －1＝⎣⎢⎢⎡⎦⎥⎥⎤12×1－3×2－32×1－3×2－22×1－3×222×1－3×2＝⎣⎢⎢⎡⎦⎥⎥⎤－1434 12－12.(10分) B. 解：由l ：ρcos θ＋ρsin φ－12＝0，及x ＝ρcos θ，y ＝ρsin θ， 所以l 的直角坐标方程为x ＋y －12＝0. (2分)在曲线C 上取点M(23cos φ，2sin φ)，则点M 到l 的距离d ＝|23cos φ＋2sin φ－12|2＝⎪⎪⎪⎪⎪⎪4sin （φ＋π3）－122＝12－4sin （φ＋π3）2，(6分)当φ＝π6时，d 取最小值42，(8分)此时点M 的坐标为(3，1)．(10分)C. 解：因为x ，y ，z 都为正数，且x ＋y ＋z ＝1， 所以由柯西不等式，得3(1x ＋2y ＋1y ＋2z ＋1z ＋2x)＝(1x ＋2y ＋1y ＋2z ＋1z ＋2x )·[(x＋2y)＋(y ＋2z)＋(z ＋2x)](5分) ≥(1x ＋2y·x ＋2y ＋1y ＋2z·y ＋2z ＋1z ＋2x·z ＋2x)2＝9， 当且仅当x ＝y ＝z ＝13时等号成立，所以1x ＋2y ＋1y ＋2z ＋1z ＋2x的最小值为3.(10分)22. 解：(1) 因为四边形AA 1B 1B 为正方形，所以AB⊥BB 1.因为平面AA 1B 1B ⊥平面BB 1C 1C ，平面AA 1B 1B ∩平面BB 1C 1C ＝BB 1， AB ⊂平面AA 1B 1B ，所以AB⊥平面BB 1C 1C. (2分)以点B 为坐标原点，分别以BA ，BB 1所在的直线为x ，y 轴，以过点B 且垂直于平面AA 1B 1B 的直线为z 轴，建立如图所示的空间直角坐标系Bxyz.不妨设正方形AA 1B 1B 的边长为2， 则A(2，0 ，0)，B 1(0，2，0)．在菱形BB 1C 1C 中，因为∠BB 1C 1＝60°，所以C 1(0，1，3)，所以AC 1→＝(－2，1，3)． 因为平面AA 1B 1B 的一个法向量为n ＝(0，0，1)， 设直线AC 1与平面AA 1B 1B 所成角为α， 则sin α＝|cos 〈AC 1→，n 〉|＝|3|22×1＝64，即直线AC 1与平面AA 1B 1B 所成角的正弦值为64.(6分) (2) 由(1)可知，C(0，－1，3)，所以CC 1→＝(0，2，0)． 设平面ACC 1的一个法向量为n 1＝(x 1，y 1，z 1)，因为⎩⎪⎨⎪⎧n 1·AC 1→＝0，n 1·CC 1→＝0，即⎩⎨⎧（x 1，y 1，z 1）·（－2，1，3）＝0，（x 1，y 1，z 1）·（0，2，0）＝0，取x 1＝32，y 1＝0，z 1＝1，即n 1＝(32，0，1)． 设平面ABC 1的一个法向量为n 2＝(x 2，y 2，z 2)， 因为BA →＝(2，0，0)，BC 1→＝(0，1, 3)，所以⎩⎨⎧（x 2，y 2，z 2）·（2，0，0）＝0，（x 2，y 2，z 2）·（0，1，3）＝0，取n 2＝(0，3，－1)．(8分)设二面角BAC 1C 的平面角为θ，则cos θ＝－cos 〈n 1，n 2〉＝－n 1·n 2|n 1|·|n 2|＝－－134＋1·3＋1＝77， 所以二面角BAC 1C 的余弦值为77.(10分) 23. 解：(1) 因为n ＝4，所以a 0＝C 04(23)4＝1681，a 1＝C 14(23)3＝3227.(2分)(2) 当x ＝13时，a k x k ＝C k n (23)n －k (13)k，因为kC kn ＝kn ！k ！（n －k ）！＝n （n －1）！（k －1）！（n －k ）！＝nC k －1n －1，(4分)＝n －13n(23＋13)n －1＝23n ，当n ＝1时，也符合． 所以(n －k)a k x k的值为23n.(10分)。

江苏省苏北四市2017届高三第一学期期末考试数学试题数学Ⅰ答案1． }3,0,2{- 2．2 3． 14 4． 20 5．316．1 75π 8． 12-9． 2 10． (,3]-∞- 11． 8 12． 5713． [7,13]14． {20,16}--二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答．．．．．．．．．．，解答时应写出文字说明、证明过程或计算步骤．15．（1）由正弦定理可知，2cos (sin cos sin cos )sin A B C C B A +=，…………2分 即2cos sin sin A A A =，因为(0,π)A ∈，所以sin 0A ≠，所以2cos 1A =，即1cos 2A =， ………………………………………………4分 又(0,π)A ∈，所以π3A =． ……………………………………………………6分 （2）因为3cos 5B =，(0,π)B ∈，所以4sin 5B =，…………………8分 所以24sin22sin cos 25B B B ==，27cos212sin 25B B =-=-， ……………10分 所以2π2πsin()sin[()]sin(2)33B C B B B -=--=- 2π2πsin 2cos cos2sin 33B B =-………………………………12分2417()()25225=⨯---= ……………14分 16．（1）取BE 中点F ，连结CF ，MF ，又M 是AE 的中点，所以12MF AB =∥．因为N 是矩形ABCD 的边CD 的中点， 所以12NC AB =∥．所以MF NC =∥， 所以四边形MNCF 是平行四边形．……4分所以MN CF ∥，又MN ⊄平面EBC ，CF ⊂平面EBC ，所以直线MN ∥平面EBC ．………………………………………………7分 （2）在矩形ABCD 中，AB BC ⊥．又平面⊥EAB 平面ABCD ，平面 ABCD 平面AB EAB =，BC ⊂平面ABCD ，ABCDEMN(第16题)F所以BC ⊥平面EAB ．………………………………………………………10分 又EA ⊂平面EAB ，所以EA BC ⊥． 又EB EA ⊥，BCEB B =，EB ，BC ⊂平面EBC ，所以直线⊥EA 平面EBC ．…………………………………………………14分 17．（1）过B 作MN 的垂线，垂足为D ． 在Rt ABD △中，3tan tan 4BD BAD BAN AD ∠=∠==， 所以43AD BD =．在Rt BCD △中，tan tan 1BDBCD BCN CD∠=∠==， 所以CD BD =．则41133AC AD CD BD BD BD =-=-==，所以3BD =，则3CD =，4AD =． …………………………………………2分由勾股定理得，5AB (km)．所以A ，B 两镇间的距离为5km ． ……………………………………………4分 （2）方案①：沿线段AB 在水下铺设时，总铺设费用为5420⨯=(万元)．…6分 方案②：设BPD θ∠=，则0π(,)2θθ∈，其中0BAN θ=∠． 在Rt BDP △中，3tan tan BD DP θθ==，3sin sin BD BP θθ==， 所以344tan AP DP θ=-=-． 则总铺设费用为6122cos 24886tan sin sin AP BP θθθθ-+=-+=+⋅．…………8分 设2cos ()sin f θθθ-=，则222sin (2cos )cos 12cos '()sin sin f θθθθθθθ---==，令'()0f θ=，得π3θ=，列表如下：(第17题)所以()f θ的最小值为()3f =所以方案②的总铺设费用最低为8+(万元)，此时4AP =．……12分 而820+<，所以应选择方案②进行铺设，点P 选在A 的正西方向(4km 处，总铺设费用最低．…………………………………………………………………………14分18．（1）由题意，得2c a a c c ⎧=⎪⎪⎨⎪+=⎪⎩解得4,a c =⎧⎪⎨=⎪⎩ 则b = 所以椭圆C 的标准方程为221168x y +=．………………………………………4分（2）由题可设直线PA 的方程为(4)y k x =+，0k >，则(0,4)M k ， 所以直线FN 的方程为y x =-，则2(0,)N k-． (i)当直线PA 的斜率为12，即12k =时，(0,2)M ，(0,4)N -，F ， 因为MF FN ⊥，所以圆心为(0,1)-，半径为3，所以FMN △的外接圆的方程为22(1)9x y ++=．……………………………8分(ii)联立22(4),1,168y k x x y =+⎧⎪⎨+=⎪⎩ 消去y 并整理得，2222(12)1632160k x k x k +++-=，解得14x =-或2224812k x k -=+，所以222488(,)1212k kP k k -++，……………………10分 直线AN 的方程为1(4)2y x k=-+，同理可得，222848(,)1212k k Q k k --++，所以P ，Q 关于原点对称，即PQ 过原点． 所以APQ △的面积211632()212122P Q k S OA y y k k k=⋅-=⨯=++≤14分 当且仅当12k k =，即k ==”． 所以APQ △的面积的最大值为16分19．（1）当0a =时，2()2ex f x =，所以()0f x ≤的解集为{0}；当0a ≠时，()()2exf x x a =-， 若0a >，则()0f x ≤的解集为[0,2e ]a ； 若0a <，则()0f x ≤的解集为[2e ,0]a ． 综上所述，当0a =时，()0f x ≤的解集为{0}； 当0a >时，()0f x ≤的解集为[0,2e ]a ；当0a <时，()0f x ≤的解集为[2e ,0]a ．……………………4分（2）设2()()()ln 2e x h x f x g x x =-=-，则21e'()e e x x h x x x-=-=．令'()0h x =，得x所以2()ln 02ex h x x =-≥，即()()f x g x ≥．…………………………………8分（3）假设存在常数a ，b 使得()()f x ax b g x +≥≥对任意的0x >恒成立，即22ln 2ex ax b x +≥≥对任意的0x >恒成立．而当x 21ln 2e 2x x ==，所以11222b ≥≥，所以122b =，则122b =-所以2212220(*)2e 2e 2x x ax b ax --=-+≥恒成立，①当0a ≤时，1202<，所以(*)式在(0,)+∞上不恒成立；②当0a >时，则2214(2)0e 2a -≤，即2(20a ≤， 所以a =12b =-．……………………………………………………12分令1()ln2x x x ϕ=+，则'()x ϕ='()0x ϕ=，得x当0x <'()0x ϕ>，()x ϕ在上单调增；当x '()0x ϕ<，()x ϕ在)+∞上单调减．所以()x ϕ的最大值0ϕ=．所以1ln 02x -+≤恒成立． 所以存在a =12b =-符合题意．………………………………………16分20．（1）当1n 时，121(1)(1)6(1)a a S ，故25a ；当2n ≥时，11(1)(1)6(1)nnna a S n ， 所以+111(1)(+1(1)(1)6()6(1)n n n nnna a a a S n S n ），即11(1)()6(1)n n n n a a a a ，又0na ，所以116nn a a ，………………………………………………3分 所以216(1)66k a a k ka，25+6(1)61ka kk，*kN ，故**33, ,,31, ,.nn a n n a n n n N N 为奇数为偶数 …………………………………………5分（2）当n 为奇数时，1(32)(33)6nS n a nn ，由(31)n S n n ≤得，23321n n a n ≤恒成立，令2332()1n n f n n ，则2394(1)()0(2)(1)n n f n f n n n ，所以(1)4a f ≤．……………………………………………………………8分当n 为偶数时，13(3+1)6nS n n a n ，由(31)n S n n ≤得，3(1)a n ≤恒成立，所以9a ≤． 又10a a，所以实数a 的取值范围是(0,4]．……………………………10分（3）当2a时，若n 为奇数，则31na n ，所以31na n ．解法1：令等比数列{}n b 的公比*4()m q m N ，则1(1)154nm n n b b q ．设(1)km n ，因为214114443kk ，所以(1)21545[3(1444)1]m nk ，213[5(144+4)2]1k ，…………………………14分 因为215(144+4)2k 为正整数，所以数列{}n b 是数列{}n a 中包含的无穷等比数列， 因为公比*4()m qm N 有无数个不同的取值，对应着不同的等比数列，故无穷等比数列{}n b 有无数个．………………………………………………16分 解法2：设222231(3)k b a k k ≥，所以公比2315k q． 因为等比数列{}n b 的各项为整数，所以q 为整数， 取*252()k mm N ，则31qm ，故15(31)n nb m ，由1315(31)n n k m 得，11[5(31)1]()3n n k m n N ，而当2n ≥时，12215[(31)(31)]5(31)3n n n n nk k m m m m ，即215(31)n nnk k m m ，…………………………………………………14分又因为12k ，25(31)n m m 都是正整数，所以n k 也都是正整数，所以数列{}n b 是数列{}n a 中包含的无穷等比数列， 因为公比*31()qm m N 有无数个不同的取值，对应着不同的等比数列，故无穷等比数列{}n b 有无数个．………………………………………………16分数学Ⅱ(附加题)答案A ．因为D 为弧BC 的中点， 所以DBC DAB ∠=∠，DC DB =，因为AB 为半圆O 的直径，所以90ADB ∠=︒， 又E 为BC 的中点，所以EC EB =，所以DE BC ⊥， 所以ABD △∽BDE △， 所以2AB BD BDAD BE BC==，所以2AB BC AD BD ⋅=⋅．……………………………10分B ．由条件知，2=A αα，即1222111a b ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦， 即2422a b +⎡⎤⎡⎤=⎢⎥⎢⎥-+⎣⎦⎣⎦，……………6分 所以24,22,a b +=⎧⎨-+=⎩解得2,4.a b =⎧⎨=⎩所以a ，b 的值分别为2，4．…………………………………………………10分 C ．直线l 的直角坐标方程为0x y m -+=，圆C 的普通方程为22(1)(2)9x y -++=，………………………………………5分 圆心C 到直线l=1m =-或5m =-．…………10分 D．因为a，b ，0c >，所以3331112727abc abc a b c +++≥327abcabc=+18≥，（第21(A)题）当且仅当a b c ====”， 所以18m =．…………………………………………………………………6分 所以不等式12x x m +-<即1218x x +<+， 所以2181218x x x --<+<+，解得193x >-， 所以原不等式的解集为19(,)3-+∞．…………………………………………10分 【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．22．（1）设“甲选做D 题，且乙、丙都不选做D 题”为事件E ．甲选做D 题的概率为1113C 1C 3=，乙，丙不选做D 题的概率都是2324C 1C 2=．则1111()32212P E =⨯⨯=．答：甲选做D 题，且乙、丙都不选做D 题的概率为112．…………………3分 （2）X 的所有可能取值为0，1，2，3． …………………………………4分1112(0)(1)32212P X ==-⨯⨯=，212111115(1)()(1)C (1)()3232212P X ==⨯+-⨯-⨯=， 12222111114(2)C (1)()(1)C (1)3223212P X ==⨯-⨯+-⨯-=， 222111(3)C (1)3212P X ==⨯-=． ……………………………………………8分 所以X 的概率分布为X 的数学期望15114()01236123123E X =⨯+⨯+⨯+⨯=．…………………10分23．（1）21(1)n x -+的展开式中含n x 的项的系数为21C n n ，……………………1分 由1011101111(1)(1)(C C C )(C C C )n nn n n nnn n n n n x x x x xx 可知，1(1)(1)n n x x -++的展开式中含n x 的项的系数为01111111C C C C C C nnn n n n nn n ．所以0111111121C C C C C C C n n n nn n n n n n n ------+++=．…………………………………4分（2）当*k N 时，!!C !()!(1)!()!k nn n k kk n k k nk11(1)!C (1)!()!k n n nn k n k ．……………………………6分所以12222211111(C )2(C )(C )[(C )](C C )(C C )n nnn k k k k knnnnn nn n k k k n k k n11111(CC )(C C )nnk kn k kn nn n k k nn．………8分由（1）知0111111121C C C CC C Cnn n n n n n nn n n ------+++=，即1211(C C )C nn k knn n n k ，所以1222221(C )2(C )(C )C n n n n n n n n -+++=． …………………………………10分。

徐州市2019～2020学年度高三年级第一次质量检测数 学一、填空题：本大题共14小题，每小题5分，共70分.请把答案直接填写在答题卡相应位置上．．．．．．．．. 1.已知集合{}02A x x =<<，{}11B x x =-<<，则A B =U _________.2.已知复数z 满足24z =-，且z 的虚部小于0，则z =_________.3.若一组数据7，x ，6，8，8的平均数为7，则该组数据的方差是______.4.执行如图所示的伪代码，则输出的结果为_________.5.函数2()log 2f x x -的定义域是 ．6.某学校高三年级有A 、B 两个自习教室，甲、乙、丙3名学生各自随机选择其中一个教室自习，则甲、乙两人不在同一教室上自习的概率为________.7.若关于x 的不等式230x mx -+<的解集是()1,3，则实数m 的值为_____.8.在平面直角坐标系xOy 中，双曲线2213x y -=的右准线与渐近线的交点在抛物线22y px =上，则实数p 的值为________.9.已知等差数列{}n a 前n 项和为n S ，298a a +=，55S =-，则15S 的值为_________. 10.已知函数32y x =的图象与函数cos 2y x =的图象相邻的三个交点分别是A 、B 、C ，则ABC ∆的面积为________.11.在平面直角坐标系xOy 中，已知圆22:48120M x y x y +--+=，圆N 与圆M 外切于点()0,m ，且过点()0,2-，则圆N 标准方程为_________.12.已知函数()f x 是定义在R 上的奇函数，其图象关于直线1x =对称，当(]0,1x ∈时，()ax f x e =-（其中e 是自然对数的底数，若()2020ln 28f -=，则实数a 的值为_____.13.如图，在ABC ∆中，D 、E 是BC 上的两个三等分点，2AB AD AC AE ⋅=⋅u u u r u u u r u u u r u u u r ，则cos ADE ∠的最小值为________.14.设函数()3f x x ax b =--，[]1,1x ∈-，其中a 、b ∈R .若()f x M ≤恒成立，则当M 取得最小值时，+a b 的值为______.二、解答题：本大题共6小题，共90分.请在答题卡指定区域．．．．．．．内作答.解答时应写出文字说明、证明过程或演算步骤.15.如图，在三棱锥P ABC -中，PA AB =，,M N 分别为棱,PB PC 的中点，平面PAB ⊥平面PBC . 求证：（1）BC ∥平面AMN ；（2）平面AMN ⊥平面PBC .16.在ABC ∆中，角A 、B 、C 对边分别为a 、b 、c ，且5cos A =. （1）若5a =，25c =，求b 的值；（2）若4B π=，求tan 2C 值.17.如图，在圆锥SO 中，底面半径R 为3，母线长l 为5.用一个平行于底面的平面去截圆锥，截面圆的圆心为1O ，半径为r ，现要以截面为底面，圆锥底面圆心O 为顶点挖去一个倒立的小圆锥1OO ，记圆锥1OO 体积为V .（1）将V 表示成r 的函数；（2）求V 的最大值.18.在平面直角坐标系xOy 中，已知椭圆2222:1(0)x y C a b a b+=>>的右顶点为A ，过点A 作直线l 与圆222:O x y b +=相切，与椭圆C 交于另一点P ，与右准线交于点Q .设直线l 的斜率为k .（1）用k 表示椭圆C 的离心率；（2）若0OP OQ ⋅=u u u r u u u r，求椭圆C 的离心率. 19.已知函数1()ln ()f x a x a x ⎛⎫=-∈ ⎪⎝⎭R . （1）若曲线()y f x =在点(1,(1))f 处的切线方程为10x y +-=，求a 的值；（2）若()f x 的导函数()f x '存在两个不相等的零点，求实数a 的取值范围；（3）当2a =时，是否存在整数λ，使得关于x 的不等式()f x λ≥恒成立？若存在，求出λ的最大值；若。

江苏省苏北四市2022届高三数学上学期第一次质量检测（期末）试题（含解析）一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1.已知集合{|02}A x x =<<，{|11}B x x =-<<，则A B =_____.答案：{12}x x -<< 解：由题意直接求解即可得AB ={12}x x -<<2.已知复数z 满足24z =-，且z 的虚部小于0，则z =_____. 答案：2i -解: 24z =-,则2z i =±，又因为z 的虚部小于0，则2z i =- 3.若一组数据7,,6,8,8x 的平均数为7，则该组数据的方差是_____. 答案：45解：7++6+8+875x = 解得6x =，222222(77)(67)(67)(87)(87)455S -+-+-+-+-==4.执行如图所示的伪代码，则输出的结果为_____. 答案：205.函数2()log 2f x x =-的定义域为_____. 答案：[4,+)∞解：由题意得：2log 2x x >⎧⎨≥⎩，解得4x ≥，所以函数的定义域为[4,+)∞6.某学校高三年级有,A B 两个自习教室，甲、乙、丙3名学生各自随机选择其中一个教室自习，则甲、乙两人不在同一教室上自习的概率为______. 答案：12解：22222222212..A P A A A ==7.若关于x 的不等式230x mx -+<的解集是(1,3)，则实数m 的值为______. 答案：4解：由题意得：221303330m m ⎧-+=⎪⎨-+=⎪⎩，解得4m =8.在平面直角坐标系xOy 中，双曲线2213x y -=的右准线与渐近线的交点在抛物线22y px =上，则实数p 的值为______. 答案：14解：由题意得：双曲线右准线与渐近线的交点为33(,)22±，代入22y px =得：14p =9.已知等差数列{}n a 的前n 项和为n S ，298a a +=，55S =-，则15S 的值为_____. 答案：135解：298a a +=，55S =-，则388a a +=，355a =-，解得：31a =-，89a = 因为158********S a ==⨯=10.已知函数3sin 2y x =的图象与函数cos2y x =的图象相邻的三个交点分别是,,A B C ，则ABC ∆的面积为_____. 答案：3π211.在平面直角坐标系xOy 中，已知圆22:48120M x y x y +--+=，圆N 与圆M 外切与点(0,)m ，且过点(0,2)-，则圆N 的标准方程为______.答案：22(2)8x y ++=12.已知函数()f x 是定义在R 上的奇函数，其图象关于直线1x =对称，当(0,1]x ∈时，()ax f x e =-（其中e 是自然对数的底数），若(2020ln 2)8f -=，则实数a 的值为_____. 答案：3解：由题意得：4T = ，ln 2(2020ln 2)(ln 2)(ln 2)28a a f f f e -=-=-===，解得：3a =13.如图，在ABC ∆中，,D E 是BC 上的两个三等分点，2AB AD AC AE ⋅=⋅，则cos ADE ∠的最小值为____.答案：47解：323(2)2(2)AB AD AC AE AB AB AC AC AB AC ⋅=⋅⇒⋅+=⋅+ 22222424c AB AC b AB AC c b =⋅+⇒⋅=- 222222()(2)2cos |||2|442AB AC AB AC c b AB ACADE AB AC AB AC c b AB AC b c AB AC-⋅+--⋅∠==-⋅+++⋅⋅+-⋅2222247(45)(3)b c b c b =≥--+14.设函数3()||f x x ax b =--，[1,1]x ∈-，其中,a b R ∈.若()f x M ≤恒成立，则当M 取得最小值时，a b +的值为______.答案：34方法一：(1)|1|111()||282111()||282M f a b M f a b M f a b ⎧⎪≥=--⎪⎪≥=--⎨⎪⎪≥-=-+-⎪⎩所以111111362(1)()3()2|1|||3||2282822M f f f a b a b a b ≥+-+≥--+-+-+--≥当且仅当0b =，34a =时，上述等号成立，所以M 取最小值时，34a b +=. 方法二：由对称性可知，M 最小时，0b =，且3min ()1x ax a -=-(,(0,1))a x ∈ 所以3+1(1)x a x ≥+，即2min 3(1)4a x x =-+=，则34a b += 二、解答题：本大题共6小题，共计90分．请在答题卡指定区域．．．．．．．内作答．解答时应写出文字说明、证明过程或演算步骤15. （本小题满分14分）如图，在三棱锥P ABC -中，AP AB =，,M N 分别为棱,PB PC 的中点，平面PAB ⊥平面PBC . （1）求证：BC ∥平面AMN ； （2）求证：平面AMN ⊥平面PBC .解：（1）在PBC △中，因为M ，N 分别为棱PB ，PC 的中点，所以MN // BC ． ………………………………3分 又MN ⊂平面AMN ，BC ⊄平面AMN ，所以BC //平面AMN ．…………………………6分 （2）在PAB △中，因为AP AB =，M 为棱PB 的中点，所以AM PB ⊥．………………………………8分又因为平面PAB ⊥平面PBC ，平面PAB 平面PBC PB =，AM ⊂平面PAB ， 所以AM ⊥平面PBC ．…………………………………………………………12分 又AM ⊂平面AMN ，所以平面AMN ⊥平面PBC ． …………………………14分16. （本小题满分14分）在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且5cos A =. （1）若5a =，25c =b 的值； （2）若4B π=，求tan2C 的值.解：（1）在ABC △中，由余弦定理2222cos b c bc A a +-=得，252022525b +-⨯=，即2450b b --=， …………………………4分 解得5b =或1b =-（舍），所以5b =． ………………………………………6分（2）由5cos 5A =及0A <<π得，22525sin 1cos 1()55A A =-=-=，…8分 所以210cos cos(())cos()(cos sin )4210C A B A A A π=π-+=-+=--=， 又因为0C <<π，所以2210310sin 1cos 1()1010C C =-=-=， 从而310sin 10tan 3cos 1010C C C ===，………………………………………………12分所以222tan 233tan 21tan 134C C C ⨯===---．………………………………………14分17. （本小题满分14分）如图，在圆锥SO 中，底面半径R 为3，母线长l 为5.用一个平行于底面的平面区截圆锥，截面圆的圆心为1O ，半径为r ，现要以截面为底面，圆锥底面圆心O 为顶点挖去一个倒立的小圆锥1OO ，记圆锥1OO 的体积为V . （1）将V 表示成r 的函数； （2）求V 得最大值.解：（1）在SAO △中，2222534SO SA AO =--=， …………………………2分由1SNO △∽SAO △可知，1SO r SO R=，所以143SO r =，……………………4分所以1443OO r =-，所以223144()π(4)π(3),03339V r r r r r r =-=-<<．…7分（2）由（1）得234()π(3),039V r r r r =-<<，所以24()π(63)9V r r r '=-，令()0V r '=，得2r =，………………………9分当(0,2)r ∈时，()0V r '>，所以()V r 在(0,2)上单调递增； 当(2,3)r ∈时，()0V r '<，所以()V r 在(2,3)上单调递减．所以当2r =时，()V r 取得最大值16π(2)9V =．答：小圆锥的体积V 的最大值为16π9．………………………………………14分18. （本小题满分16分）在平面直角坐标系xOy 中，已知椭圆2222:1x y C a b +=(0)a b >>的右顶点为A ,过点A 作直线l 与圆222:O x y b +=相切，与椭圆C 交于另一点P ，与右准线交于点Q .设直线l 的斜率为k .（1）用k 表示椭圆C 的离心率；（2）若0OP OQ ⋅=,求椭圆C 的离心率.（1）直线l 的方程为)(a x k y -=，即0=--ak y kx ，因为直线l 与圆222b y x O =+：相切，所以b k ak=+-12，故2222b a b k -=． 所以椭圆C 的离心率222111b e ak =-=+4分 （2）设椭圆C 的焦距为2c ，则右准线方程为2a x c=，由⎪⎩⎪⎨⎧=-=c ax a x k y 2)(得c ac a k a c a k y -=-=22)(，所以))(,(22c ac a k c a Q -，…6分 由⎪⎩⎪⎨⎧-==+)(12222a x k y b y a x 得02)(2224232222=-+-+b a k a x k a x k a b ， 解得222223k a b ab k a x p +-=，则22222222232)(k a b kab a k a b ab k a k y p +-=-+-=， 所以)2-2222222223ka b kab k a b ab k a P ++-，（，……………………………………………10分 因为0=⋅OQ OP ，所以02)(222222222232=+-⋅-++-⋅k a b kab c ac a k k a b ab k a c a ，即)(2)(22222c a k b b k a a -=-，………………………………………………12分由（1）知，2222b a b k -=，所以22422222)(2)(ba c ab b b a b a a --=--， 所以c a a 22-=，即c a 2=，所以21=a c ，故椭圆C 的离心率为21．……16分19. （本小题满分16分）已知函数1()()ln f x a x x=-()a R ∈.（1）若曲线()y f x =在点(1,(1))f 处的切线方程为10x y +-=，求a 的值； （2）若()f x 的导函数'()f x 存在两个不相等的零点，求实数a 的取值范围； （3）当2a =时，是否存在整数λ，使得关于x 的不等式()f x λ≥恒成立？若存在， 求出λ的最大值；若不存在，说明理由.解：（1）()2111()ln f x x a x x x'=+-，因为曲线()y f x =在点(1,(1))f 处的切线方程为10x y +-=，所以(1)11f a '=-=-，得0a =．……………………………………………2分（2）因为21ln ()ax x f x x-+'=存在两个不相等的零点． 所以()1ln g x ax x =-+存在两个不相等的零点，则1()g x a x'=+．①当0a ≥时，()0g x '>，所以()g x 单调递增，至多有一个零点．……4分②当0a <时，因为当1(0)x a∈-，时，()0g x '>，()g x 单调递增， 当1(+)x a∈-∞，时，()0g x '<，()g x 单调递减， 所以1x a =-时，max 11()()ln()2g x g a a=-=--． …………………………6分因为()g x 存在两个零点，所以1ln()20a-->，解得2e 0a --<<．………7分因为2e 0a --<<，所以21e 1a->>．因为(1)10g a =-<，所以()g x 在1(0)a-，上存在一个零点． …………8分 因为2e 0a --<<，所以211()a a->-．因为22111[()]ln()1g a a a-=-+-，设1t a =-，则22ln 1(e )y t t t =-->，因为20t y t-'=<，所以22ln 1(e )y t t t =-->单调递减，所以()2222ln e e 13e 0y <--=-<，所以22111[()]ln()10g a a a-=-+-<，所以()g x 在1()a-+∞，上存在一个零点． 综上可知，实数a 的取值范围为2(e ,0)--．…………………………………10分（3）当2a =时，1()(2)ln f x x x =-，()2211121ln ()ln 2x x f x x x x x x-+'=+-=， 设()21ln g x x x =-+，则1()20g x x'=+>．所以()g x 单调递增，且11()ln 022g =<，(1)10g =>，所以存在01(1)2x ∈，使得0()0g x =，……12分 因为当0(0)x x ∈，时，()0g x <，即()0f x '<，所以()f x 单调递减；当0(+)x x ∈∞，时，()0g x >，即()0f x '>，所以()f x 单调递增，所以0x x =时，()f x 取得极小值，也是最小值，此时()0000000111()(2)ln (2)12(4)4f x x x x x x x =-=--=-++，……………14分因为01(1)2x ∈，，所以0()(10)f x ∈-，， 因为()f x λ≥，且λ为整数，所以1λ-≤，即λ的最大值为1-．………16分20. （本小题满分16分）已知数列{}n a 的首项13a =，对任意的*n N ∈,都有11n n a ka +=-(0)k ≠，数列{1}n a -是公比不为1的等比数列.（1）求实数k 的值；（2）设4,1,n n n n b a n -⎧⎪=⎨-⎪⎩为奇数为偶数，数列{}n b 的前n 项和为n S ，求所有正整数m 的值，使得221m m S S -恰好为数列{}n b 中的项.解：（1）由11n n a ka +=-，13a =可知，231a k =-，2331a k k =--，因为{1}n a -为等比数列，所以2213(1)(1)(1)a a a -=--，即22(32)2(32)k k k -=⨯--，即231080k k -+=，解得2k =或43k =，…2分当43k =时，143(3)3n n a a +-=-，所以3n a =，则12n a -=，所以数列{1}n a -的公比为1，不符合题意；当2k =时，112(1)n n a a +-=-，所以数列{1}n a -的公比1121n n a q a +-==-，所以实数k 的值为2． …………………………………………………………4分（2）由（1）知12n n a -=，所以4n n n n b n - , ⎧⎪=⎨2, ⎪⎩为奇数,为偶数,则22(41)4(43)4[4(21)]4m m S m =-++-+++--+2(41)(43)[4(21)]444mm =-+-++--++++144(4)3m m m +-=-+，……………………………………………………6分 则212244(4)3m m m m S S b m m --=-=-+，因为22+1324mm m b b m +=-+，又222+322+1()()3420m m m m m b b b b ++-+=⨯->，且2350b b +=>，130b =>，所以210m S ->，则20m S >，设2210,m t m Sb t S -=>∈*N ，…………………………………………………………8分 则1,3t =或t 为偶数，因为31b =不可能，所以1t =或t 为偶数，①当2121=m m S b S -时，144(4)3344(4)3m mm m m m +--+=--+，化简得2624844m m m -+=--≤， 即242m m -+≤0，所以m 可取值为1，2，3，验证624135787,3,323S S S S S S ===得，当2m =时，413S b S =成立．…………………12分②当t 为偶数时，1222144(4)331443124(4)134m m mm m m m SS m m m m +---+==+--+--++， 设231244m mm m c -+-=，则211942214m m m m m c c ++-+-=，由①知3m >，当4m =时，545304c c --=<；当4m >时，10m m c c +->，所以456c c c ><<，所以m c 的最小值为5191024c -=， 所以22130151911024m m S S -<<+<-+，令22214m m S b S -==，则2314312414mm m +=-+-+， 即231240m m -+-=，无整数解．综上，正整数m 的值2．………………………………………………………16分徐州市2022度高三年级第一次质量检测数学Ⅱ（附加题） 21．【选做题】本题包含A 、B 、C 小题，请选定其中两题，并在答题卡相应的答题区域内作答.若多做，则按作答的前两题评分，解答应写出文字说明、证明过程或演算步骤． A ．[选修4—2：矩阵与变换] （本小题满分10分）已知矩阵2M t ⎡=⎢⎣ 31⎤⎥⎦的一个特征值为4，求矩阵M 的逆矩阵1M -.解：矩阵M 的特征多项式为23()(2)(1)31f t t λλλλλ--==-----．…………2分 因为矩阵M 的一个特征值为4，所以(4)630f t =-=，所以2t =．…………5分所以2321⎡⎤=⎢⎥⎣⎦M ，所以11313213221324422112132213222--⎡⎤⎡⎤-⎢⎥⎢⎥⨯-⨯⨯-⨯==⎢⎥⎢⎥--⎢⎥⎢⎥⨯-⨯⨯-⨯⎣⎦⎣⎦M ．……10分（第22题）BACxyzB 1 A 1C 1 B ．[选修4—4：坐标系与参数方程] （本小题满分10分）在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为(cos sin )12ρθθ+=，曲线C 的参数方程为23cos 2sin x y θθ⎧=⎪⎨=⎪⎩（θ为参数，R θ∈）.在曲线C 上点M ,使点M 到l的距离最小，并求出最小值.解：由:cos sin 120l ρθρϕ+-=，及cos x ρθ=，sin y ρθ=，所以l 的直角坐标方程为120x y +-=． ………………………………………2分在曲线C 上取点()23cos 2sin M ϕϕ，，则点M 到l 的距离 ()()4sin 12124sin 23cos 2sin 1233222d ϕϕϕϕππ+--++-===，…………6分 当6ϕπ=时，d 取最小值42，…………………………………………………8分此时点M 的坐标为()3,1．………………………………………………………10分 C ．[选修4—5：不等式选讲] （本小题满分10分）已知正数,,x y z 满足1x y z ++=，求111+222x y y z z x++++的最小值. 解：因为x y z ，，都为正数，且1x y z ++=，所以由柯西不等式得，1113()222x y y z z x+++++111()[(2)(2)(2)]222x y y z z x x y y z z x=++⋅++++++++………………5分 2111(222)9222x y y z z x x y y z z x⋅++⋅++⋅+=+++≥， 当且仅当13x y z ===时等号成立，所以111222x y y z z x+++++的最小值为3．…………………………………10分第22题、第23题，每题10分，共计20分，请在答题卡指定区域内作答，解答应写出文字说明、证明过程或演算步骤． 22.（本小题满分10分）如图，在三棱柱111ABC A B C -中，侧面11AA B B 为正方形，侧面11BB C C 为菱形，1160BB C ∠=，平面11AA B B ⊥平面11BB C C .（1）求直线1AC 与平面11AA B B 所成角的正弦值； （2）求二面角1B AC C --的余弦值.解：（1）因为四边形11AA B B 为正方形，所以1AB BB ⊥，因为平面11AA B B ⊥平面11BB C C ，平面11AA B B平面111BB C C BB =，AB ⊂平面11AA B B ，所以AB ⊥平面11BB C C . ……………………………2分以点B 为坐标原点，分别以BA ,1BB 所在的直线为x ,y 轴，建立如图所示的空间直角坐标系B xyz -.不妨设正方形11AA B B 的边长为2，则()2 0 0A ，，，()10 2 0B ，，． 在菱形11BB C C 中，因为1160BB C ∠=︒，所以1(0 1 3)C ，，，所以1( 2 1 3)AC =-，，． 因为平面11AA B B 的法向量为()0 0 1=，，n ， 设直线1AC 与平面11AA B B 所成角为α， 则1|3|6sin |cos ,|221AC α=<>==⨯n ，即直线1AC 与平面11AA B B 64．………………………6分（2）由（1）可知，(0 1 3C -，，，所以()10 2 0CC =，，． 设平面1ACC 的一个法向量为()1111 x y z =，，n ， 因为11110,0,AC CC ⎧⋅=⎪⎨⋅=⎪⎩n n 即()(()()111111 2 1 30 0 2 00x y z x y z ⎧⋅-=⎪⎨⋅=⎪⎩，，，，，，，，，取13x =，10y =，11z =，即13 0 1⎫=⎪⎭，，n ． 设平面1ABC 的一个法向量为()2222 x y z =，，n ， 因为()2 0 0BA =，，，(10 1 3BC =，，， 所以()()()(222222 2 0 00 0 1 30x y z x y z ⋅=⎧⎪⎨⋅=⎪⎩，，，，，，，，，取()20 3 1=-，，n ．…………8分 设二面角1B AC C --的平面角为θ，则121212 71cos cos 31314θ⋅-=-<>=-==⋅+⋅+，n n n n n n所以二面角1B AC C --7．…………………………………10分23.（本小题满分10分）已知n 为给定的正整数，设20122()3n n n x a a x a x a x +=++++，x R ∈.（1）若4n =，求0a ，1a 的值；（2）若13x =，求0()nk k k n k a x =-∑的值.解：（1）因为4n =，所以0404216C ()=381a =，1314232C ()=327a =．……………………2分 （2）当13x =时，21C ()()33k k n k kk n a x -=， 又因为11!(1)!C C !()!(1)!()!k k n n n n k k n n k n k k n k ---===---，………………………4分当1n =时，011022()C ()33nk k k n k a x =-==∑； …………………………………5分 当2n ≥时，0021()()C ()()33n nkk n k k k n k k n k a x n k -==-=-∑∑ 012121C ()()C ()()3333n nk n k k k n k k n n k k n k --===-∑∑1112121()C ()()3333n n k n k kn k n n ---==+-∑ 1111121C ()()333n k n k k n k n n ----==-∑1121()333n n n -=-+23n =，当1n =时，也符合．所以0()nk k k n k a x =-∑的值为23n ．………………………………………………10分。

江苏省苏北四市(徐州、淮安、宿迁、连云港)2022届高三年级第一学期期末调研考试数学试题变式题1 知识点 交并补混合运算【正确答案】D1-1（基础） 已知集合{}5A x x =<，{}17B x x =<<，则() RA B ⋂=（）．A.[]5,7B.[)5,7C.(]5,7D.()5,7【正确答案】 B1-2（基础） 已知集合{}310A x x =≤<，{}13516B x x =<-<，则()A B =R （）A.{}23x x <<B.{}23x x <≤C.{}710x x <<D.{}210x x <<【正确答案】 A1-3（巩固） 已知集合{}{260,1A xx x B x x =--≤=≤-∣∣或}4x >，则RA B =（）A.{}21xx -≤≤-∣ B.{3xx ≤∣或}4x > C.{}24xx -≤≤∣ D.{}13xx -<≤∣ 【正确答案】 D1-4（巩固） 设全集U =R ,集合{}{}21,40M x x N x x =≤=-<,集合()U M N 等于（）A.[)1,2B.()1,2C.()2,1-D.[)2,1-【正确答案】 B1-5（提升） 设全集U =R ，集合{}21A x x =-<，{}240xB x =-≥，则集合()UA B =（）A.()1,2B.(]1,2C.[)1,2D.[]1,2【正确答案】 A已知全集为R ，集合{}2311,4302x A xB x x x x -⎧⎫=≥=-+≤⎨⎬-⎩⎭∣∣，则()R A B ⋂（） A.3,34⎡⎤⎢⎥⎣⎦ B.3,14⎡⎤⎢⎥⎣⎦C.[]2,3D.(]2,3【正确答案】 C2 知识点 求复数的模,复数的除法运算3i+A.5C.3【正确答案】 B2-2（基础） 复平面内表示复数62i2iz +=-，则z =（）A. B. C.4D.【正确答案】 A2-3（巩固） 已知i 是虚数单位，复数z 满足()2i 12i z +⋅=-+，则=z （） A.iB.1C.35D.53【正确答案】 B2-4（巩固） 若()()1i 12z +-=，则=z （）A.1B.2【正确答案】 D已知复数2i1iz -=+（其中i 为虚数单位），则||z z -=（） A.0B.1C.32D.3【正确答案】 D设i 为虚数单位，若复数z 满足()1i 2z +=，则i z -=（）A.1D.2【正确答案】 C3 知识点 分式不等式,充分条件的判定及性质【正确答案】C3-1（基础） 若x ∈R ，则使“22x x <”成立的一个必要不充分条件为（） A.01x << B.224x x >C.21x> D.0x >【正确答案】 D3-2（基础） 若p ：23x -≤，则p 成立的一个充分不必要条件是（） A.16x -≤≤ B.25x -≤≤ C.15x -<≤ D.06x ≤≤【正确答案】 C3-3（巩固） “a b >”的一个充分条件是（） A.11a b < B.2ab b >C.110b a-<-<D.2a ab >【正确答案】 C3-4（巩固） 对于实数x ，规定[]x 表示不大于x 的最大整数，例如][1.22,1.51⎡⎤-=-=⎣⎦，那么不等式[]24[]1670x x -+<成立的充分不必要条件是（）A.1722x << B.13x ≤≤ C.14x ≤<D.14x ≤≤不等式20x x m -+>在R 上恒成立的一个必要不充分条件是（ ） A.14m >B.01m <<C.0m >D.1m >【正确答案】 C“ a b >”的一个充分条件是（） A.e 0a b -> B.ln0ab> C.a b a b >D.110a b<< 【正确答案】 D4 知识点 不相邻排列问题【正确答案】A4-1（基础） 高中数学新教材有必修一和必修二，选择性必修有一､二､三共5本书，把这5本书放在书架上排成一排，必修一､必修二不相邻的排列方法种数是（） A.72B.144C.48D.36【正确答案】 A4-2（基础） 现有10本书，其中有4本不同的英文读物，6本不同的中文读物，某学生计划一年看完这10本书，为了缓解疲劳，要求英文读物不能相邻阅读，则可以排出的阅读顺序总数为（） A.7476A A B.1646A AC.4467A AD.6467A A【正确答案】 D4-3（巩固） 某学校组织6×100接力跑比赛，某班级决定派出A ，B ，C ，D ，E ，F 等6位同学参加比赛．在安排这6人的比赛顺序时要保证A 要在B 之前，D 和F 的顺序不能相邻，则符合要求的安排共有（） A.240种 B.180种C.120种D.150种【正确答案】 A4-4（巩固） 自2020年“新冠”出现后，全国人民“众志成城，齐心抗疫”.许多志愿者挺身而出，现安排4名男性志愿者，3名女性志愿者站成一排将逐一进行核酸检测，要求男女相间且女性甲要在女性乙之前检测，则不同的安排方法的种数是（） A.36种B.72种C.108种D.144种某人根据自己爱好，希望从{},,,W X Y Z 中选2个不同字母，从{}0,2,6,8中选3个不同数字编拟车牌号，要求前3位是数字，后两位是字母，且数字2不能排在首位，字母Z 和数字2不能相邻，那么满足要求的车牌号有（） A.198个 B.180个 C.216个 D.234个【正确答案】 A援鄂医护人员A ，B ，C ，D ，E ，F 共6人（其中A 是队长）圆满完成抗击新冠肺炎疫情任务返回本地，他们受到当地群众与领导的热烈欢迎．当地媒体为了宣传他们的优秀事迹，让这6名医护人员和当地的一位领导共7人站成一排拍照，则领导和队长A 相邻且不站两端，B 与C 相邻，B 与D 不相邻的排法种数为（）． A.120B.240C.288D.360【正确答案】 B5 知识点 平面向量线性运算的坐标表示,由向量共线（平行）求参数,坐标计算向量的模,利用向量垂直求参数【正确答案】B5-1（基础） 已知向量()32a =-，，()1b x =，（0x >），若()()2a b a b +⊥-，则b =（）【正确答案】 B5-2（基础） 已知()3,4a =，(),1b t =，()a b a -⊥，则b =（）A.2B. C.1D.【正确答案】 B5-3（巩固） 已知平面向量(2,)a m =，(1,2)b =-，且|2||2|a b a b -=+，则||a b +=（） A.1B.2C.3D.4已知向量,a b 满足||1,||2,(3,2)a b a b ==-=，则|2|a b -等于（）A.D.【正确答案】 A已知直角梯形ABCD 中，AD ∥BC ，∠ADC ＝90，AD ＝4，BC ＝2，P 是腰DC 上的动点，则|2|PA PB +的最小值为（）A.8B.7C.6D.4【正确答案】 A（提升） 已知e 为单位向量，向量a 满足：()()50a e e a --⋅=，则a e +的最大值为（） A.4B.5C.6D.7【正确答案】 C6 题】 知识点 椭圆定义及辨析,求椭圆的离心率或离心率的取值范围,根据抛物线方程求焦点或准线,抛物线的对称性的应用22【正确答案】 B6-2（基础） 已知椭圆C ：22221x y a b +=与抛物线E ：()220y px p =>有公共焦点F ，椭圆C 与抛物线E 交于A ，B 两点，且A ，B ，F 三点共线，则椭圆C 的离心率为（）1 【正确答案】 A已知12F F 、是椭圆22221(0)x ya b a b+=>>的左､右焦点，点P 为抛物线28(0)y ax a =->准线上一点，若12F PF △是底角为15︒的等腰三角形，则椭圆的离心率为（）1 1【正确答案】 A已知椭圆22122:1(0)x y C a b a b +=>>的右焦点F 与抛物线22:2(0)C y px p =>的焦点重合，P 为椭圆1C 与抛物线2C 的公共点，且PF x ⊥轴，那么椭圆1C 的离心率为（）1 C.21【正确答案】 A已知椭圆22221x y a b+=(0)a b >>的右焦点2(,0)F c ，此椭圆在第一象限交抛物线24y cx =于点P ，且232cPF =，则椭圆的离心率为( )【正确答案】 A已知椭圆()2222:10x y E a b a b+=>>的焦距为2c ，左焦点为F ，右顶点为A ，若抛物线()2158y a c x =+与椭圆交于B ，C 两点，且四边形ABFC 是菱形，则椭圆E 的离心率是（）A.815B.415C.23D.12【正确答案】 D7 题】 知识点 柱体体积的有关计算,椭圆的其他应用【正确答案】 C7-1（基础） 中国古代数学的瑰宝《九章第术》中记载了一种称为“曲池”的几何体，该几何体为上、下底面均为扇环形的柱体（扇环是指圆环被扇形截得的部分）．现有一个如下图所示的“曲池”，其高为3，1AA ⊥底面，底面扇环所对的圆心角为2π，AD 长度为BC 长度的3倍，且线段2AB CD ==，则该“曲池”的体积为（）A.92π B.5π C.112πD.6π【正确答案】 D7-2（基础） 陀螺是中国民间最早的娱乐工具之一，也称陀罗．图1是一种木陀螺，可近似地看作是一个圆锥和一个圆柱的组合体，其直观图如图2所示，其中,B C 分别是上、下底面圆的圆心，且3AC AB =，则该陀螺下半部分的圆柱与上半部分的圆锥的体积的比值是（）A.2B.3C.4D.6【正确答案】 D7-3（巩固） 图1中的机械设备叫做“转子发动机”，其核心零部件之一的转子形状是“曲侧面三棱柱”，图2是一个曲侧面三棱柱，它的侧棱垂直于底面，底面是“莱洛三角形”（如图3），莱洛三角形是以正三角形的三个顶点为圆心，正三角形的边长为半径画圆弧得到的，若曲侧面三棱柱的高为4，底面任意两顶点之间的距离为A.(2002π-B.(400πC. D.(4002π【正确答案】B7-4（巩固）2022年6月5日，我国三名航天员乘坐神舟十四号载入飞船成功升空．预计三名航天员在太空工作6个月，在轨期间将进行多个科学实验，任务完成后，乘返回舱返回地面．某自然科学博物馆为了青少年参观学习的需要，仿制了一个返回舱，如图所示，若仿制的返回舱的内腔轴截面曲线C近似由半椭圆：221(0)1612y xy+=>和弧：22(2)16(0)x y y+-=≤组成，曲线C内接一各边与坐标轴分别平行的矩形，满足水平方向矩形的边长为6，若由这个矩形绕y轴旋转，形成圆柱作为返回时载物及航天员座椅的空间，则这个空间的体积为（）A. B. C.36π D.【正确答案】B7-5（提升）《乌鸦喝水》是《伊索寓言》中的一个寓言故事，通过讲述一只乌鸦喝水的故事，告诉人们遇到困难要运用智慧、认真思考才能让问题迎刃而解的道理.如图所示，乌鸦想喝水，发现有一个锥形瓶，已知该锥形瓶上面的部分是圆柱体，下面的部分是圆台，瓶口的直径为3cm，瓶底的直径为9cm，瓶口距瓶颈.现将1颗石子投入瓶中，发现水位，时，乌鸦就能喝到水，则乌鸦共需要投入的石子数量至少是（石子体积均视为一致）（）A.2颗B.3颗C.4颗D.5颗【正确答案】 B7-6（提升） 如图，“十字歇山”是由两个直三棱柱重叠后的景象，重叠后的底面为正方形，直三棱柱的底面是顶角为120︒，腰为3的等腰三角形，则该几何体的体积为（）A.23B.24C.26D.27【正确答案】 D【原卷 8 题】 知识点 分组（并项）法求和【正确答案】B8-1（基础） 已知数列{}n a 的通项公式为cos 1),(n n a n n S π=-为数列的前n 项和，2021S =（） A.1008 B.1009C.1010D.1011【正确答案】 D数列()(){}121nn --的前2022项和等于（） A.1010- B.2022 C.2018- D.2019【正确答案】 B设数列{}n a 的通项公式为()()121cos12nn n a n π=--⋅-，其前n 项和为n S ，则2022S =（） A.4041 B.5- C.2021- D.4045-【正确答案】 D已知数列{}n a 的前n 项和为n S ，111012a =，1221012n n n n a a a +++++=，则2023S =（） A.138B.674C.675D.2023【正确答案】 C高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号.设x ∈R ，用[]x 表示不超过x 的最大整数，则()[]f x x =称为高斯函数.已知数列{}n a 满足21a =，且121(1)2n n n n a na +++-=，若[]lg n n b a =数列{}n b 的前n 项和为n T ，则2021T =（） A.3950 B.3953 C.3840 D.3845【正确答案】 D设数列{}n a 的通项公式为()()()*121cos1N 2nn n a n n π=--⋅+∈，其前n 项和为n S ，则120S =（） A.60-B.120-C.180D.240【正确答案】 D9 知识点 二项式的系数和,求有理项或其系数,二项展开式各项的系数和【正确答案】 A C D9-1（基础） 已知()22nx n⎛∈ ⎝N 的展开式中各项的二项式系数之和为64，则（）．A.6n =B.展开式中各项的系数和为1C.展开式中第3项或第4项的二项式系数最大D.展开式中有理项只有4项 【正确答案】 ABD在nx⎛⎝的展开式中，只有第4项的二项式系数最大，下列结论正确的是（）A.6n =B.各项二项式系数之和为128C.各项系数之和为0D.有理项共4项【正确答案】 ACD在72x⎛⎝的展开式中，下列说法正确的有（）A.所有项的二项式系数和为128B.所有项的系数和为1C.二项式系数最大的项为第4项D.有理项共3项【正确答案】 AB已知二项式12nx ⎫⎪⎭的展开式中各项系数之和是1128，则下列说法正确的有（）A.展开式共有7项B.二项式系数最大的项是第4项C.所有二项式系数和为128D.展开式的有理项共有4项【正确答案】 CD已知6112a x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则下列结论正确的有（）A.1a =B.展开式中常数项为160C.展开式系数的绝对值的和1458D.展开式中含2x 项的系数为240【正确答案】 ACD下列结论正确的是（）A.*023()nk k n n k C n N ==∈∑B.多项式621x x ⎛⎫+- ⎪⎝⎭展开式中3x 的系数为52 C.若1021001210(21),x a a x a x a x x R -=++++∈，则10012103a a a a ++++=D.012321221*22222222232()n n n n n n n n n C C C C C C n N --++++++=⋅∈ 【正确答案】 ACD10 知识点 由图象确定正（余）弦型函数解析式,求sinx 型三角函数的单调性,求正弦（型）函数的奇偶性π的是（）A.为了得到()sin 2g x x =的图象，只要将()f x 的图象向右平移6π个单位长度 B.函数()f x 的图象的一条对称轴为712x π=C.函数()f x 在区间0,10π⎛⎫⎪⎝⎭上单调递增D.方程()0f x =在区间[]0,2020上有1285个实数解 【正确答案】 AB已知()sin()0,||2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象关于点7,012π⎛⎫⎪⎝⎭对称，相邻两条对称轴的距离为2π，则下列说法正确的是（） A.2ω=，6πϕ=B.将函数()f x 的图象向右平移6π个单位长度后，得到的图象关于y 轴对称C.函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的单调递减区间为,32ππ⎡⎤⎢⎥⎣⎦D.为了得到()f x 的图象，可以将函数sin 2y x =的图象向右平移6π个单位 【正确答案】 BC已知函数()()sin f x A x ωϕ=+ (A ＞0，ω＞0，2πϕ<)的部分图象如图所示，下列说法正确的是（）A.函数f (x )的图象关于点(,0)6π-对称 B.函数f (x )的图象关于直线512x π=-对称 C.函数f (x )在2,36ππ⎡⎤--⎢⎥⎣⎦单调递增 D.该图象向右平移3π个单位可得y =2sin2x 的图象【正确答案】 AB10-4（巩固） 已知函数()()πsin 20,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的部分图象如图所示，则下列结论正确的是（）A.()f x 的图象关于点π,03⎛⎫- ⎪⎝⎭对称B.()f x 的图象向右平移π12个单位后得到sin2y x =的图象C.()f x 在区间π,2π⎡⎤--⎢⎥⎣⎦上单调递增D.π6f x ⎛⎫+ ⎪⎝⎭为偶函数【正确答案】 BD10-5（提升） 已知函数()()()sin 0,0,0πf x A x A ωϕωϕ=+>><<的部分图象如图所示，则下列说法正确的是（）．A.π2f ⎛⎫= ⎪⎝⎭B.()f x 在区间5π0,12⎛⎫⎪⎝⎭单调递减C.()f x 在区间π11π,1212⎛⎫- ⎪⎝⎭上有且仅有2个零点D.将()f x 的图象向右平移π12个单位长度后，可得到一个奇函数的图象 【正确答案】 BC10-6（提升） 已知函数π()sin()0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，下列说法正确的是（）A.函数()y f x =的周期为π2B.函数()y f x =的图象关于直线19π12x =对称 C.函数()y f x =在区间2ππ,36⎡⎤--⎢⎥⎣⎦上单调递增D.函数()1y f x =-在区间[]0,2π上有4个零点 【正确答案】 BD【原卷 11 题】 知识点 画出具体函数图象,垂直关系的向量表示,函数新定义【正确答案】 B D11-1（基础） 在数学中，布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理，它可应用到有限维空间，并构成一般不动点定理的基石，布劳威尔不动点定理得名于荷兰数学家鲁伊兹•布劳尔（L.E.J.Brouwer ），简单的讲就是对于满足一定条件的连续函数()f x 存在一个点0x ，使得()00f x x =，那么我们称该函数为“不动点函数”，下列为“不动点函数”的是（）A.()23f x x x =++B.()21xf x x =+-C.()221,12,1x x f x x x ⎧-≤⎪=⎨->⎪⎩D.()1f x x =-【正确答案】 BC11-2（基础） 已知函数=()y f x 的定义域为D ，若存在区间[,]a b D ⊆，使得{=(),[,]}=[,]yy f x x a b a b ∈∣，则称区间[,]a b 为函数=()y f x 的“和谐区间”.下列说法正确的是（） A.[1,0]-是函数2()2f x x x =-的一个“和谐区间” B.[1,3]-是函数2()2f x x x =-的一个“和谐区间” C.[0,2]是函数3()=12f x x -的一个“和谐区间” D.2,25⎡⎤⎢⎥⎣⎦是函数3()=12f x x -的一个“和谐区间”【正确答案】 BC对于定义在I 上的函数()y f x =，如果存在区间[,]m n I ⊆，同时满足下列两个条件：①()f x 在区间[],m n 上为增函数；②当[,]x m n ∈时，函数()f x 值域也为[,]m n ，则称[,]m n 是函数()y f x =的一个“递增黄金区间”．下列函数中存在“递增黄金区间”的是（） A.1y x =+ B.222y x x -=+ C.22x y =- D.lg y x =【正确答案】 BC定义一：关于一个函数()()f x x D ∈，若存在两条距离为d 的直线1y kx m =+和2y kx m =+，使得在x D ∈时，()12kx m f x kx m +≤≤+恒成立，则称函数()f x 在D 内有一个宽度为d 的通道.定义二：若一个函数()f x ，关于任意给定的正数ε，都存在一个实数0x ，使得函数()f x 在[)0,x ∞+内有一个宽度为ε的通道，则称()f x 在正无穷处有永恒通道.则下列在正无穷处有永恒通道的函数为（）A.()ln f x x =B.()sin xf x x=C.()f x =D.()e xf x -=【正确答案】 BCD对于定义域为D 的函数()y f x =，若同时满足：①()f x 在D 内单调递增或单调递减；②存在区间[,]a b D ⊆，使()f x 在[,]a b 上的值域为[,]a b ，则把()()y f x x D =∈称为闭函数.下列结论正确的是（） A.函数21y x =+是闭函数 B.函数3y x =-是闭函数 C.函数1xy x =+是闭函数D.若函数y k =是闭函数，则9,24k ⎛⎤∈-- ⎥⎝⎦【正确答案】 BD设R x ∈，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，也叫取整函数．如[1.2]1=，[2]2=，[ 1.2]2-=-．令()[]f x x x =-，以下结论正确的有（）A.( 1.1)0.9f -=B.1133f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭C.(1)()1f x f x +=+D.函数()f x 的值域为[0,1)【正确答案】 AD12 知识点 柱体体积的有关计算,证明面面垂直【正确答案】 B C D12-1（基础） 四面体ABCD 的每个顶点都在球O 的表面上，AB 是球O 的一条直径，且2AC =，4BC =，现有下面四个结论，其中所有正确结论的编号是（） A.球O 的表面积为20πB.若3AD =，则4BD =C.AC 上存在一点M ，使得//AD BMD.四面体ABCD 【正确答案】 AD12-2（基础） 如图，在多面体EFG ABCD -中，四边形ABCD ，CFGD ，ADGE 均是边长为1的正方形，点H 在棱EF 上，则（）A.该几何体的体积为23B.点D 在平面BEF 内的射影为BEF △的垂心C.GH BH +D.存在点H ，使得DH BF ⊥【正确答案】 BD12-3（巩固） 如图，平行六面体1111ABCD A B C D -中，以顶点A 为端点的三条棱长均为1，且它们彼此的夹角都是60°，则（）A.1ACB.1AC BD ⊥C.四边形11BDD BD.平行六面体1111ABCD A B C D -【正确答案】 ABD12-4（巩固） 如图，直三棱柱111ABCA B C 中，12AA =，1AB BC ==，90ABC ︒∠=，侧面11AA C C 中心为O ，点E 是侧棱1BB 上的一个动点，有下列判断，正确的是（）A.直三棱柱侧面积是4+ B.直三棱柱体积是13C.三棱锥1E AAO -的体积为定值D.1AE EC +的最小值为【正确答案】 ACD12-5（提升） 如图，已知三棱柱111ABCA B C 的侧棱垂直于底面，且底面ABC ∆为等腰直角三角形，2ACB π∠=，1AA =，M N ，分别是1BC BB ，的中点，P 是线段11A C 上的动点，则下列结论正确的是（）A.1A P MN ⊥B.直线MN 与直线11A BC.直线MN ⊥平面1A PND.若P 是线段11A C 的中点，则三棱锥1A PMN -的体积1V 与三棱柱111ABC A B C 的体积2V 之比为18【正确答案】 ACD12-6（提升） 正方体1111ABCD A B C D -的棱长为2，E ，F ，G 分别为BC ，1CC ，1BB 的中点．则（）A.正方体1111ABCD A B C D -体积是三棱锥D EFC -体积的24倍B.正方体1111ABCD A B C D -外接球的体积为C.平面DEF 截正方体所得的截面面积为32D.三棱锥C DEF -与三棱锥G DEF -的体积相等 【正确答案】 ABC【原卷 13 题】 知识点 直线与圆相交的性质——韦达定理及应用【正确答案】13-1（基础） 已知直线x y a +=与圆224x y +=交于A ，B 两点，O 为坐标原点，3OA OB OA OB +=-，则实数a 的值为___________.【正确答案】13-2（基础） 在直角坐标系xoy 中，直线122y x =-+与圆22:240C x y x y a +--+=（a R ∈）相交于A ，B 两点，且2AOB π∠=，则=a __________.1.613-3（巩固） 已知直线():0l y kx k =>与圆()22:14C x y ++=交于不同的两点A ，B ，点()2,1P ，则22PA PB +的最大值为______．【正确答案】 22或22+已知动点A 到()1,3P 的距离是到()4,0Q 的距离的2倍，记动点A 的轨迹为C ，直线l ：40x ty --=与C 交于E ，F 两点，若13OQF OQE S S =△△（点O 为坐标原点，S 表示面积），则t =___________．【正确答案】 1-已知直线:l y kx =与圆222210x y x y +--+=相交于A ，B 两点，存在点()0,M b ，()0b >，使得MA MB ⊥，则实数k 的取值范围是______. 【正确答案】 [1，+∞)（提升） 已知圆22(1)9x y ++=与直线3y tx =+交于A ，B 两点，点(,)P a b 在直线2y x =上，且PA PB =，则a 的取值范围为_____【正确答案】 ()()1,00,2-⋃14 题】 知识点 求函数值【正确答案】-214-1（基础） 设函数()f x 满足(3)2()3f x f x x -+=+，则(3)f =______. 【正确答案】 314-2（基础） 已知函数()y f x =，对任意x N ∈，满足(1)()2f x f x +=+，若(l)3f =，则(3)f =___________． 【正确答案】 714-3（巩固） 已知()f x 是定义在R 上的奇函数，()13f =，且()()()+1=2,-1,0f x f x x x ≠≠，则()3f -=___________. 【正确答案】 12-14-4（巩固） 定义在()1,+∞上的函数()f x 满足下列两个条件（1）对任意的()1,x ∈+∞恒有()()22f x f x =成立；（2）当(]1,2x ∈时，()2f x x =-．则()6f 的值是__________． 【正确答案】 2定义在R 上的函数()f x 满足()()f x f x -=-，()()22f x f x -=+，且()2,0x ∈-时，()212f x x =+，则()2017f =________________.14-6（提升） 已知函数()f x 为奇函数，且当0x >时，()ln f x x =，则21e f f ⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭___. 【正确答案】 ln 2-或1ln 215 题】 知识点 三角函数的化简、求值——同角三角函数基本关系,用和、差角的正切公式化简、求值sin cos 1αα⋅1【正确答案】 -115-2（基础） 已知()310,sin ,tan 253παααβ<<=-=-，则tan β=___________.15-3（巩固） 若0,2πα⎛⎫∈ ⎪⎝⎭，且sin 2cos αα+=，则tan 4πα⎛⎫+= ⎪⎝⎭________.【正确答案】 2-15-4（巩固） 设1tan 2α=，()4cos 5πβ+=-，()0,βπ∈，则()tan 2αβ-的值为____.,2πβπ⎛⎫∈ ⎪⎝⎭，sin 13β=，若()3sin 2sin αβα+=，则()tan αβ+=______．已知sin 2θ＝35，0＜2θ＜2π，则22cos sin 12)4θθπθ--+＝________．0.516 题】 知识点 棱柱的结构特征和分类,圆锥的结构特征辨析,多面体与球体内切外接问题,柱、锥、台体的轴截面【正确答案】16-1（基础） 已知圆锥的底面半径为若圆锥内某正方体的底面在圆锥的底面上，则该正方体的最大体积为______. 【正确答案】 116-2（基础） 四棱锥S ABCD -中，底面ABCD 是边长为2的正方形，侧面SAD 是以SD 为斜边的等腰直角三角形，若四棱锥S ABCD -的体积取值范围为83⎤⎥⎣⎦，则该四棱锥外接球表面积的取值范围是______.【正确答案】 28,203ππ⎡⎤⎢⎥⎣⎦.16-3（巩固） 已知四面体ABCD 的各棱长都为4，点E 是线段BD 的中点，若球O 是四面体ABCD 的外接球，过点E 作球O 的截面，则所得截面圆的面积取值范围是______. 【正确答案】 []4,6ππ16-4（巩固） 已知正三棱柱111ABCA B C 的各棱长均为2，D 为棱AB 的中点，则过点D 的平面截该三棱柱外接球所得截面面积的取值范围为___________. 【正确答案】 7,3ππ⎡⎤⎢⎥⎣⎦已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上．若该球的体积为36π，且23l ≤≤，则该正四棱锥体积的取值范围是______． 【正确答案】 12827,814⎡⎤⎢⎥⎣⎦已知球O 是正三棱锥A BCD -的外接球，3BC =，AB =点E 在线段BD 上，且6BD BE =，过点E 作球O 的截面，则所得截面圆面积的取值范围是___________. 【正确答案】 5,44ππ⎡⎤⎢⎥⎣⎦17 知识点 正弦定理边角互化的应用,三角形面积公式及其应用,求三角形中的边长或周长的最值或范围【正确答案】 （1）答案见解析 （2）（2，8）17-1（基础） 在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且()2cos cos 0b a C c B -+=请在①2b =，②c =a c =这三个条件中任选两个，将问题（1）补充完整，然后解答问题 1、已知______，计算ABC 的面积； 2、当5c =时，求ABC 的周长的最大值.注：如选择多种搭配方式分别解答，按第一个解答计分. 【正确答案】 1、答案见解析 2、1517-2（基础） 在①cos cos 2B bC a c =-+，②sin sin sin A b c B C a c+=-+，③2S BC =⋅三个条件中任选一个补充在下面的横线上，并加以解答．在ABC 中，ABC 的面积为S ，角A ，B ，C 的对边分别为a ，b ，c 且选条件：_____________．1、求B ∠；2、作AB AD ⊥，使得四边形ABCD 满足,4ACD AD π∠==BC 的取值范围．【正确答案】 1、条件选择见解析，23B π=；2、⎛ ⎝⎭.17-3（巩固） 在ABC 中，内角,,A B C 的对边分别为,,a b c ，且______．在①cos cos 2b C B π⎛⎫-= ⎪⎝⎭；②2ABC S BC =⋅△；③tan tan tan A C A C +=这三个条件中任选一个，补充在上面的问题中，并进行解答． 1、求角B 的大小；2、若角B 的内角平分线交AC 于D ，且1BD =，求4a c +的最小值． 【正确答案】 1、23B π= 2、917-4（巩固） 在①222)S a b c +-，②cos cos 2cos a B b A c C +=，请在这两个条件中任选一个，补充到下面问题中，并完成解答.在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，设S 为ABC 的面积，满足______________(填写序号即可)．1、求角C 的大小；2、若3c =，求ABC 周长的最大值．注：如果选择多个条件分别解答，按第一个解答计分. 【正确答案】 1、3C π=2、9在①sinsin 2A B b c B +=，②cos cos cos c a bC A B +=+，)cos sin c A b a C -=-这三个条件中任选一个，补充在下面的问题中，并解答.在锐角ABC 中，内角,,A B C 的对边分别为,,a b c ，且满足__________. 1、求角C 的大小；2、若c ，角A 与角B 的内角平分线相交于点D ，求ABD △面积的取值范围.注：如果选择多个条件分别解答，按第一个解答计分. 【正确答案】 1、3π2、⎝⎦在ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c ，记ABC 的面积为S .已知_________.从①2sin tan a C c A =，②2cos 2a B c b =-，③)2224S b c a =+-三个条件中选择一个填在上面的横线上，并解答下列问题.（注：如果选择多个条件分别解答，则按第一个解答计分） 1、求角A 的大小；2、若边长2a =，求ABC 的周长的取值范围. 【正确答案】 1、无论选择①②③，3A π=； 2、(]4,618 题】 知识点 累加法求数列通项,含绝对值的等差数列前n 项和,由递推关系证明等比数列【正确答案】18-1（基础） 已知在前n 项和为n S 的等差数列{}n a 中，42222a a -=，3102S =． 1、求数列{}n a 的通项公式； 2、求数列{}n a 的前20项和20T ． 【正确答案】 1、403n a n =-； 2、324.18-2（基础） 已知等差数列{}n a 的前n 项和为n S ，4228S S =+，21219n n a a +=+，*n ∈N ．1、求{}n a 的通项公式;2、设n n b a =，求数列{}n b 的前20项之和20T ． 【正确答案】 1、217n a n =- 2、208已知n S 是数列{}n a 的前n 项和，且214n S n n =-.1、求{}n a 的通项公式；2、若123n n T a a a a =++++，求n T .【正确答案】 1、152n a n =-2、2214,171498,7n n n n T n n n ⎧-≤≤=⎨-+>⎩已知等差数列{}n a 的公差为d ，数列{}n a 的前n 项和为n S ，且2510,20a S ==. 1、求数列{}n a 的通项公式； 2、求数列2{2}n a n a +的前n 项和n T ； 3、请直接写出n A =123||||||||n a a a a ++++的结果.【正确答案】 1、226n a n =-2、11212(1)81937n n T n n -=-+3、22193,3=31960,>3n n n n A n n n -≤-⎧⎨+⎩在等比数列{}n a 中，()0,n a n +>∈N ，公比()0,1q ∈，且3546392100a a a a a a ++=，又有4是3a 和7a 的等比中项．1、求数列{}n a 的通项公式；2、设2log n n b a =，求数列{}n b 的前21项和21S ．【正确答案】 1、72nn a -=2、126在数列{}n a 中，18a =，42a =，且满足212n n n a a a +++=. 1、求数列{}n a 的通项公式;2、设n S 是数列{}n a 的前n 项和，求n S . 【正确答案】 1、210n a n =-+；2、229,5940,6n n n n S n n n ⎧-+≤=⎨-+≥⎩.19 知识点 证明线面垂直,线面垂直证明线线垂直,已知面面角求其他量【正确答案】19-1（基础） 如图，在四棱锥P ABCD -中，平面PAD ⊥平面,,1,2,ABCD AD BC PA AB BC AD CD PA AD =====⊥∥，点E 在棱PC 上，设CE CP λ=.1、证明：CD AE ⊥.2、设二面角C AE D --的平面角为θ，且cos θ=，求λ的值. 【正确答案】 1、证明见解析； 2、34λ=.19-2（基础） 如图，四棱锥S ABCD -的底面ABCD 是直角梯形，且//AB CD ，AD DC ⊥，24CD AB ==，AD a =，正三角形SAD 所在平面与平面ABCD 相互垂直，E 、O 分别为SD 、AD 的中点.1、求证：SO BC ⊥；2、若二面角E AC D --，求a 的值. 【正确答案】 1、证明见解析； 2、6.19-3（巩固） 如图，在四面体ABCD 中，ABC 是正三角形，ACD 是直角三角形，,ABD CBD AB BD ∠=∠=．1、求证：AC BD ⊥；2、已知点E 在棱BD 上，且2AB =，设DE mDB =，若二面角D AC E --，求m ．【正确答案】 1、证明见解析； 2、13.如图，在三棱锥D ABC -中，二面角D AB C --是直二面角，AB BD ⊥，且,AB BD AC BC ==，P 为CD 上一点，且BP ⊥平面ACD ．,E F 分别为棱,DA DC 上的动点，且DE DFDA DCλ==．1、证明：AC BC ⊥；2、若平面EFB 与平面ABC λ的值． 【正确答案】 1、证明见解析 2、12λ=19-5（提升） 三棱锥-P ABC 中，PAB PAC ≅△△，2BC AB ，PA AB ⊥，直线PC 与平面ABC 所成的角为3π，点D 在线段PA 上.1、求证：BD AC ⊥；2、若点E 在PC 上，满足34PE PC =，点D 满足(01)AD AP λλ=<<，求实数λ使得二面角A BE D --的余弦值为25. 【正确答案】 1、证明见解析； 2、12λ=. 19-6（提升） 如图，四棱锥P ABCD -中，底面ABCD 是直角梯形，90AB DC BAD ∠=︒∥，，222PD DC BC PA AB =====，PD DC ⊥.1、求证：PA ⊥平面ABCD ；2、设(01)BM BD λλ=<<，当平面P AM 与平面PBD λ的值. 【正确答案】 1、证明见解析 2、12λ=【原卷 20 题】 知识点 由频率分布直方图计算频率、频数、样本容量、总体容量,由频率分布直方图估计平均数,指定区间的概率【正确答案】20-1（基础） 为了提高生产效率，某企业引进一条新的生产线，现要定期对产品进行检测.每次抽取100件产品作为样本，检测新产品中的某项质量指标数，根据测量结果得到如下频率分布直方图.1、指标数不在175.和22.5之间的产品为次等品，试估计产品为次等品的概率； 2、技术评估可以认为，这种产品的质量指标数X 服从正态分布()2,1.22N μ，其中μ近似为样本的平均数（同一组中的数据用该组区间的中点值为代表），计算μ值，并计算产品指标数落在()17.56,22.44内的概率. 参考数据：()2,XN μσ，则()0.6826P X μσμσ-<<+=，(22)0.9544P X μσμσ-<<+=.【正确答案】 1、0.04 2、20μ=，0.954420-2（基础） 2021年是“十四五”规划开局之年，也是建党100周年．为了传承红色基因，某学校开展了“学党史，担使命”的知识竞赛．现从参赛的所有学生中，随机抽取100人的成绩作为样本，得到成绩的频率分布直方图，如图．（1）求频率分布直方图中a 的值，并估计该校此次竞赛成绩的平均分x （同一组中的数据用该组区间中点值代表）；（2）在该样本中，若采用分层抽样的方法，从成绩高于75分的学生中随机抽取7人查看他们的答题情况，再从这7人中随机抽取3人进行调查分析，求这3人中至少有1人成绩在[]85,95内的概率； （3）假设竞赛成绩服从正态分布()2,N μσ，已知样本数据的方差为121，用平均分x 作为μ的近似值，用样本标准差s 作为σ的估计值，求该校本次竞赛的及格率（60分及以上为及格）．参考数据：()0.6827P μσξμσ-<+≈≤，()220.9545P μσξμσ-<+≈≤，()330.9973P μσξμσ-<≤+≈． 【正确答案】 （1）0.035a =；平均分为71分；（2）57；（3）0.84135．2022年北京冬季奥运会将在北京市和河北省张家口市联合举行，北京市延庆区张山营镇的2022北京冬奥森林公园于2020年4月22日正式启动了冬奥赛区的树木移植工作．本次移植的树木来自2022北京冬奥赛区树木假植区，包含暴马丁香、核桃楸、大叶白蜡等多个品种．现从冬奥赛区树木假植区中抽取300棵暴马丁香，并对树木高度H （单位：m ）进行测量，将测量结果绘制为如图所示的频率分布直方图．（1）估计抽取的300棵暴马丁香树木高度的平均值（同一组中的数据可用该区间的中点值为代表）； （2）北京冬奥赛区树木假植区内的暴马丁香的高度H （m ）服从正态分布()2,0.122N μ，其中μ近似为样本平均数x ．记X 为假植区内10000棵暴马丁香中高度位于区间()2.122,2.244的数量，求()E X ； （3）在树木移植完成后，采取施用生根粉、加挂营养液等方式确保了移植树木的成活率，经验收，单棵移植成活率达到了90%．假设各棵树木成活与否相互不影响，求移植五棵暴马丁香成活四棵及以上的概率．（保留三位小数）附：若()2~,H N μσ，则()0.6827-<<+=P H μσμσ，()220.9545-<<+=P H μσμσ．【正确答案】 （1）()2m ；（2）()1359E X =；（3）0.919．20-4（巩固） 某科技公司新研制生产一种特殊疫苗，为确保疫苗质量，定期进行质量检验．某次检验中，从产品中随机抽取100件作为样本，测量产品质量体系中某项指标值，根据测量结果得到如下频率分布直方图：。

江苏省苏北四市（徐州、淮安、连云港、宿迁）高三数学上学期期末联考试题一、填空题（本大题共14小题，每小题5分，共70分）1、已知集合{}{}2,0,2,3A B =-=-，则A B =U ．2、已知复数z 满足(1)2i z i -=，其中i 为虚数单位，则z 的模为 ．3、某次比赛甲得分的茎叶图如图所示，若去掉一个最高分，去掉一个最低分，则剩下4个 分数的方差为 ．4、根据如图所示的伪代码，则输出S 的值为 ．5、从1,2,3,4,5,6这六个数中一次随机地取2个数，则所取2个数的和能被3整除的概率 为 ．6、若抛物线28y x =的焦点恰好是双曲线2221(0)3x y a a -=>的右焦点，则实数a 的值为 ．7、已知圆锥的底面直径与高都是2，则该圆锥的侧面积为 ． 8、若函数()sin()(0)6f x x πωπω=->的最小正周期为15，则1()3f 的值为 ．9、已知等比数列{}n a 的前n 项和为n S ，若223323,23S a S a =+=+，则公比q 的值为 ．10、已知函数()f x 是定义R 在上的奇函数，当0x >时，()23xf x =-，则不等式()5f x -≤ 的解集为 ．11、若实数,x y 满足133(0)2xy x x +=<<，则313x y +-的最小值为 ． 12、已知非零向量,a b r r满足a b a b ==+r r r r ，则a r 与2a b -r r 夹角的余弦值为 ．13、已知,A B 是圆221:1C x y +=上的动点，AB =，P 是圆222:(3)(4)1C x y -+-=上的动点，则PA PB +u u u r u u u r的取值范围为 ．14、已知函数32sin ,1()925,1x x f x x x x a x <⎧=⎨-++⎩≥，若函数()f x 的图象与直线y x =有三个不同的公共点，则实数a 的取值集合为 ．二、解答题（本大题共6小题，共90分．解答应写出必要的文字说明、证明 或演算步骤）15、在ABC ∆中，角,,A B C 的对边分别为,,a b c ．已知2cos (cos cos )A b C c B a +=． （1）求角A 的值； （2）若3cos 5B =，求sin()BC -的值．16、如图，在四棱锥E ABCD -中，平面EAB ⊥平面ABCD ，四边形ABCD 为矩形，EA EB ⊥，点,M N 分别是,AE CD 的中点．求证：（1）直线MN ∥平面EBC ；（2）直线EA ⊥平面EBC ．17、如图，已知,A B 两镇分别位于东西湖岸MN 的A 处和湖中小岛的B 处，点C 在A 的 正西方向1km 处，3tan ,44BAN BCN π∠=∠=．现计划铺设一条电缆联通,A B 两镇，有两种铺设方案：①沿线段AB 在水下铺设；②在湖岸MN 上选一点P ，先沿线段AP 在地下铺设，再沿线段PB 在水下铺设，预算地下、水下的电缆铺设费用分别为2万元∕km 、4万元∕km ．（1）求,A B 两镇间的距离；（2）应该如何铺设，使总铺设费用最低？18、如图，在平面直角坐标系xOy中，已知椭圆2222:1(0)x yC a ba b+=>>的离心率为22，且右焦点F到左准线的距离为62．（1）求椭圆C的标准方程；（2）设A为椭圆C的左顶点，P为椭圆C上位于x轴上方的点，直线PA交y轴于点M，过点F作MF的垂线，交y轴于点N．（ⅰ）当直线的PA斜率为12时，求FMN∆的外接圆的方程；（ⅱ）设直线AN交椭圆C于另一点Q，求APQ∆的面积的最大值．19、已知函数2(),()ln ,2R x f x ax g x x ax a e=-=-∈． （1）解关于()R x x ∈的不等式()0f x ≤； （2）证明：()()f x g x ≥；（3）是否存在常数,a b ，使得()()f x ax b g x +≥≥对任意的0x >恒成立？若存在，求 出,a b 的值；若不存在，请说明理由．20、已知正项数列{}n a 的前n 项和为n S ，且11,(1)(1)6()n n n a a a a S n +=++=+，*∈N n ．（1）求数列{}n a 的通项公式；（2）若对于N n *∀∈ ，都有(31)n S n n +≤成立，求实数a 取值范围；（3）当2a =时，将数列{}n a 中的部分项按原的顺序构成数列{}n b ，且12b a =，证明： 存在无数个满足条件的无穷等比数列{}n b ．苏北四市高三年级第二次调研测试数学II(附加题)21．[选做题]本题包括A 、B 、C 、D 四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤． A.【选修4-1几何证明选讲】（本小题满分10分)如图，AB 为半圆O 的直径，D 为弧BC 的中点，E 为BC 的中点， 求证：AB ·BC=2AD ·BD ．B ．【选修4-2矩阵与变换】（本小题满分10分）已知矩阵A= 的一个特征值为2，其对应的一个特征向量为a = ，求实数a ，b 的值.C.【选修4-4：坐标系与参数方程】（本小题满分10分）在平面直角坐标系Oy 中，以O 为极点，轴的正半轴为极轴建立极坐标系．直线 l ：2ρsin （θ一4π）=m （m ∈R ），圆C 的参数方程为（t 为参数）．当圆心C 到直线l 的距离为2时，求m 的值。

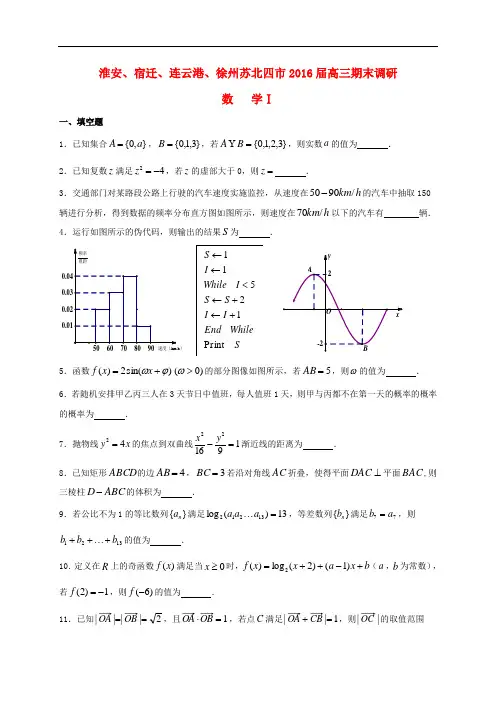
淮安、宿迁、连云港、徐州苏北四市2016届高三期末调研数 学Ⅰ一、填空题1．已知集合},0{a A =，}3,1,0{=B ，若}3,2,1,0{=B A Y ，则实数a 的值为 ． 2．已知复数z 满足42-=z ，若z 的虚部大于0，则=z ．3．交通部门对某路段公路上行驶的汽车速度实施监控，从速度在h km /9050-的汽车中抽取150辆进行分析，得到数据的频率分布直方图如图所示，则速度在h km /70以下的汽车有 辆． 4．运行如图所示的伪代码，则输出的结果S 为 ．）5．函数)sin(2)(ϕω+=x x f )0(>ω的部分图像如图所示，若5=AB ，则ω的值为 ． 6．若随机安排甲乙丙三人在3天节日中值班，每人值班1天，则甲与丙都不在第一天的概率的概率的概率为 ．7．抛物线x y 42=的焦点到双曲线191622=-y x 渐近线的距离为 ． 8．已知矩形ABCD 的边4=AB ，3=BC 若沿对角线AC 折叠，使得平面DAC ⊥平面BAC ,则三棱柱ABC D -的体积为 ．9．若公比不为1的等比数列}{n a 满足13)(log 13212=⋯a a a ，等差数列}{n b 满足77a b =，则1321b b b +⋯++的值为 ．10．定义在R 上的奇函数)(x f 满足当0≥x 时，b x a x x f +-++=)1()2(log )(2（a ，b 为常数），若1)2(-=f ，则)6(-f 的值为 ． 11．已知2||||==OB OA ，且1=⋅OB OA ，若点C 满足1||=+CB OA ，则||OC 的取值范围是 ． 12．已知函数⎩⎨⎧<-≥+=0)(0cos 2)(x x a x x x x x f ，若关于x 的不等式π<)(x f 的解集为)2,(π-∞，则实数a 的取值范围是 ．13．已知)1,0(A ，)0,1(B ，)0,(t C ，点D 是直线AC 上的动点，若BD AD 2≤恒成立，则最小正整数t 的值为 ．14．设c b a ,,是正实数，满足a c b ≥+，则ba cc b ++的最小值为 ． 二、解答题15．在锐角三角形ABC 中，角C B A ,,的对边为c b a ,,，已知53sin =A ，21)tan(-=-B A ， （1）求B tan ； （2）若5=b ，求c .16．如图，在四棱锥ABCD P -中，已知底面ABCD 为矩形，⊥PA 平面PDC ,点E 为棱PD 的中点，求证：（1）//PB 平面EAC ；（2）平面⊥PAD 平面ABCD .17．如图，OA 是南北方向的一条公路，OB 是北偏东045方向的一条公路，某风景区的一段边界为曲线C ．为方便游客光，拟过曲线C 上的某点分别修建与公路OA ,OB 垂直的两条道路PN PM ,，且PN PM ,的造价分别为5万元/百米，40万元/百米，建立如图所示的直角坐标系xoy ，则曲线符合函数)91(242≤≤+=x x x y 模型，设x PM =，修建两条道路PN PM ,的总造价为)(x f 万元，题中所涉及的长度单位均为百米. （1）求)(x f 解析式;（2）当x 为多少时，总造价)(x f 最低？并求出最低造价．OPABCDE18．已知各项均为正数的数列}{n a 的首项11=a ，n S 是数列}{n a 的前项和，且满足：).0(*1111N n a a a a S a S a n n n n n n n n ∈≠=-+-++++λλ.（1）若1a ，2a ，3a 成等比数列，求实数λ的值; （2）若21=λ，求n S .19. 如图，在平面直角坐标系xoy 中，已知椭圆C ：)0(12222>>=+b a b y a x 的离心率21=e ，左顶点为)0,4(-A ，过点A 作斜率为)0(≠k k 的直线l 交椭圆C 于点D ，交y 轴于点E . （1）求椭圆C 的方程;（2）已知P 为AD 的中点，是否存在定点Q ，对于任意的)0(≠k k 都有EQ OP ⊥，若存在，求出点Q 的坐标；若不存在说明理由;（3）若过O 点作直线l 的平行线交椭圆C 于点M ，求OMAEAD +的最小值.20．已知函数]42)4(231[)(23--++-=a x a x x e x f x，其中R a ∈，e 为自然对数的底数 （1）若函数)(x f 的图像在0=x 处的切线与直线0=+y x 垂直，求a 的值． （2）关于x 的不等式xe xf 34)(-<在)2,(-∞上恒成立，求a 的取值范围． （3）讨论)(x f 极值点的个数．x附加题部分21．【选做题】A ．[选修4—1：几何证明选讲]（本小题满分10分）如图，PAQ ∠是直角，圆O 与射线AP 相切于点T ，与射线AQ 相交于两点,B C ．求证：BT 平分OBA ∠．B ．[选修4—2：矩阵与变换]（本小题满分10分）已知矩阵1214A ⎡⎤=⎢⎥-⎣⎦，求矩阵A 的特征值和特征向量．C ．[选修4—4：坐标系与参数方程]（本小题满分10分） 在极坐标系中，圆C 的极坐标方程为28sin()1303πρρθ--+=，已知33(1,),(3,)22A B ππ，P 为圆C 上一点，求PAB ∆面积的最小值．D ．[选修4—5：不等式选讲]（本小题满分10分） 设,x y 均为正数，且x y >，求证：2212232x y x xy y +≥+-+．【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写 出文字说明、证明过程或演算步骤． 22.（本小题满分10分）如图，在直三棱柱111ABC A B C -中，底面ABC ∆是直角三角形，1AB AC ==，点P 是棱1BB 上一点，满足1(01)BP BB λλ=≤≤u u u r u u u r． （1）若13λ=，求直线PC 与平面1A BC 所成角的正弦值； （2）若二面角1P AC B --的正弦值为23，求λ的值．23.（本小题满分10分）已知数列{}n a 满足21211132,(),()()(1)n na n f n g n f n f n a a a =-=+++=--L ，*n N ∈． （1）求证：1(2)3g >；（2）求证：当3n ≥时，1()3g n >．数学I 参考答案及评分标准一、填空题1. 2；2. 2i ； 3．75； 4．9； 5．3π； 6.13； 7．35； 8. 245； 9．26； 10. 4； 11．； 12．()-∞+；13．4； 14.12．二、解答题15．（1）在锐角三角形ABC 中，由3sin 5A =，得4cos 5A ， …………2分所以sin 3tan cos 4A A A ==.……………………………………………………………4分由tan tan 1tan()1tan tan 2A B A B A B --==-+⋅，得tan 2B =. ………………7分（2）在锐角三角形ABC 中，由tan 2B =，得sin B =，cos B =9分所以sin sin()sin cos cos sin 25C A B A B A B =+=+=，…………………11分由正弦定理sin sin b cB C =，得sin 11sin 2b Cc B ==. ………………14分 16．(1) 连接BD 与AC 相交于点O ，连结OE ．………2分因为四边形ABCD 为矩形，所以O 为BD 中点． 因为E 为棱PD 中点，所以PB ∥OE ．………4分 因为PB ⊄平面EAC ，OE ⊂平面EAC ，所以直线PB ∥平面EAC ．……………………6分(2) 因为PA ⊥平面PDC ，CD ⊂平面PDC ，所以 PA ⊥CD ． …………………8分因为四边形ABCD 为矩形，所以AD ⊥CD ．…………………………………10分 因为 PA ∩AD ＝A ，PA ，AD ⊂平面PAD ，所以 CD ⊥平面PAD ．…………12分 因为CD ⊂平面ABCD ，所以 平面PAD ⊥平面ABCD ． …………………14分17． (1)在如图所示的直角坐标系中，因为曲线C的方程为)=19y x x ≤≤，PM x = 所以点P坐标为2,x x x ⎛+ ⎝⎭，直线OB 的方程为0x y -=， ……………………………………………………2分OPABCDE则点P 到直线0x y -=24x =，………………4分又PM 的造价为5万元／百米，PN 的造价为40万元／百米． 则两条道路总造价为()22432()540519f x x x x x x ⎛⎫=+⋅=+ ⎪⎝⎭≤≤． …………8分 (2) 因为22432()5405f x x x x x ⎛⎫=+⋅=+ ⎪⎝⎭， 所以 333645(64)()=51x f x x x -⎛⎫'-= ⎪⎝⎭， ………………………10分令()0f x '=，得4x =，列表如下：所以当4x =时，函数()f x 有最小值，最小值为()232454304f ⎛⎫=+= ⎪⎝⎭．……13分答：（1）两条道路PM ,PN 总造价()f x 为232()5f x x x ⎛⎫=+ ⎪⎝⎭()19x ≤≤；（2）当4x =时，总造价最低，最低造价为30万元． ……………………14分（注：利用三次均值不等式223232()5553022x x f x x x x ⎛⎫⎛⎫=+=++⨯= ⎪ ⎪⎝⎭⎝⎭≥，当且仅当23222x x x ==，即4x =时等号成立，照样给分．） 18.（1）令1n =，得221a λ=+．令2n =，得23322323a S a S a a a a λ--=+，所以()()324121a λλλ=+++．…………2分由2213a a a =，得()()22241121λλλλ⎛⎫= ⎪⎝⎭++++，因为0λ≠，所以1λ=．………4分（2）当12λ=时，111112n n n n n n n n a S a S a a a a ++++--=+， 所以11111112n n n n n n S S a a a a ++++--=+，即111112n n n n S S a a ++-=++，………………………6分 所以数列1n n S a ⎧⎫⎨⎬⎩⎭+是以2为首项，公差为12的等差数列，所以()11212n n S n a =-⋅++， ……………………………………………………8分 即3122n n n S a ⎛⎫= ⎪⎝⎭++，①当2n ≥时，113122n n n S a --⎛⎫= ⎪⎝⎭++，②①-②得，13222n n n n n a a a -=-++，……………………………………………10分 即()()112n n n a n a -=++，所以()1221n n a an n n -=++≥， ………………………12分所以2n a n ⎧⎫⎨⎬⎩⎭+是首项为13是常数列，所以()123n a n =+. ……………………14分代入①得2351226n n n n n S a +⎛⎫=-= ⎪⎝⎭+. ……………………16分19. （1）因为左顶点为(40)A -，，所以4a =，又12e =，所以2c =.…………………2分 又因为22212b a c =-=，所以椭圆C 的标准方程为2211612x y +=. ………………………………………4分（2）直线l 的方程为(4)y k x =+，由2211612(4),x y y k x ⎧+=⎪⎨⎪=+⎩，消元得，22[(4)]11612x k x ++=.化简得，22(4)[(43)1612)]0x k x k +++-=，所以14x =-，222161243k x k -+=+. ……………………………………………………6分当22161243k x k -+=+时，222161224(4)4343k k y k k k -+=+=++， 所以222161224,4343()D k k k k -+++.因为点P 为AD 的中点，所以P 的坐标为2221612,4343()k kk k -++，则3(0)4OP k k k-=≠.…………………………………………………………………………8分 直线l 的方程为(4)y k x =+，令0x =，得E 点坐标为(0,4)k ， 假设存在定点(,)(0)Q m n m ≠，使得OP EQ ⊥， 则1OP EQ k k =-，即3414n k k m--⋅=-恒成立， 所以(412)30m k n +-=恒成立，所以412030m n +=⎧⎨-=⎩，，即30m n =-⎧⎨=⎩，，因此定点Q 的坐标为(3,0)-. …………………………………………10分 （3）因为OM l P ，所以OM 的方程可设为y kx =，由2211612x y y kx⎧+=⎪⎨⎪=⎩，得M点的横坐标为x =12分由OM l P ，得2D A E A D AM Mx x x x x x AD AE OM x x -+--+==22216128k -++=…………………………………………………14分≥即k =所以当k =AD AE OM+的最小值为 …………………………16分 20. (1) 由题意，321()e 3x f x x x ax a ⎛⎫'=-+- ⎪⎝⎭， …………………………………………2分因为()f x 的图象在0x =处的切线与直线0x y +=垂直，所以(0)=1f '，解得1a =-. ……………………………4分(2) 法一：由4()e 3x f x <-，得3214e 2(4)24e 33x x x x a x a ⎡⎤-++--<-⎢⎥⎣⎦，即326(312)680x x a x a -++--<对任意(2)x ∈-∞，恒成立，……………………………6分即()32636128x a x x x ->-=-对任意(2)x ∈-∞，恒成立，因为2x <，所以()()322612812323x x x a x x -++>=----， ……………………………8分记()21()23g x x =--，因为()g x 在(2)-∞，上单调递增，且(2)0g =， 所以0a ≥，即a 的取值范围是[0)+∞，． ………………………………………10分法二：由4()e 3x f x <-，得3214e 2(4)24e 33x x x x a x a ⎡⎤-++--<-⎢⎥⎣⎦，即326(312)680x x a x a -++--<在(2)-∞，上恒成立，……………………………6分因为326(312)680x x a x a -++--<等价于2(2)(434)0x x x a --++<，①当0a ≥时，22434(2)30x x a x a -++=-+≥恒成立， 所以原不等式的解集为(2)-∞，，满足题意． …………………………………………8分 ②当0a <时，记2()434g x x x a =-++，有(2)30g a =<， 所以方程24340x x a -++=必有两个根12,x x ，且122x x <<，原不等式等价于12(2)()()0x x x x x ---<，解集为12()(2)x x -∞U ，，，与题设矛盾， 所以0a <不符合题意．综合①②可知，所求a 的取值范围是[0)+∞，．…………………………………………10分(3) 因为由题意，可得321()e 3x f'x x x ax a ⎛⎫=-+- ⎪⎝⎭，所以()f x 只有一个极值点或有三个极值点. ………………………………………11分令321()3g x x x ax a =-+-，①若()f x 有且只有一个极值点，所以函数()g x 的图象必穿过x 轴且只穿过一次， 即()g x 为单调递增函数或者()g x 极值同号．ⅰ）当()g x 为单调递增函数时，2()20g'x x x a =-+≥在R 上恒成立，得1a ≥…12分 ⅱ）当()g x 极值同号时，设12,x x 为极值点，则12()()0g x g x ⋅≥，由2()20g'x x x a =-+=有解，得1a <，且21120,x x a -+=22220x x a -+=， 所以12122,x x x x a +==，所以3211111()3g x x x ax a =-+-211111(2)3x x a x ax a =--+-11111(2)33x a ax ax a =---+-[]12(1)3a x a =--，同理，[]222()(1)3g x a x a =--，所以()()[][]121222(1)(1)033g x g x a x a a x a =--⋅--≥，化简得221212(1)(1)()0a x x a a x x a ---++≥，所以22(1)2(1)0a a a a a ---+≥，即0a ≥，所以01a <≤．所以，当0a ≥时，()f x 有且仅有一个极值点； …………………14分 ②若()f x 有三个极值点，所以函数()g x 的图象必穿过x 轴且穿过三次，同理可得0a <； 综上，当0a ≥时，()f x 有且仅有一个极值点，当0a <时，()f x 有三个极值点． …………………16分数学Ⅱ（附加题）参考答案及评分标准21．【选做题】本题包括A 、B 、C 、D 四小题，请选定其中两小题．．．．．．．．，并在相应的答题区域．．．．．．．．．内作答．．．，若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．21A ．连结OT ．因为AT 是切线，所以OT AP ⊥．………………………2分 又因为PAQ ∠是直角，即AQ AP ⊥， 所以AB OT P ，所以TBA BTO ∠=∠． ………………………………… 5分 又OT OB =，所以OTB OBT ∠=， …………………8分 所以OBT TBA ∠=∠，即BT 平分OBA ∠． …………………………………10分 21B ．矩阵A 的特征多项式为()2125614f λλλλλ--==--+， ……………2分 由()0f λ=，解得12λ=，23λ=．. …………………………………………4分当12λ=时，特征方程组为20,20,x y x y -=⎧⎨-=⎩故属于特征值12λ=的一个特征向量121α⎡⎤=⎢⎥⎣⎦；………………………………7分当23λ=时，特征方程组为220,0,x y x y -=⎧⎨-=⎩故属于特征值23λ=的一个特征向量211α⎡⎤=⎢⎥⎣⎦． …………………………10分21C ．圆C 的直角坐标方程为22434130x y x y ++-+=，即22(23)(2)3x y ++-=． ………………………………………………4分 又(0,1),(0,3)A B --,所以2AB =．……………………………………………6分P 到直线AB 距离的最小值为2333-=，………………………………8分所以PAB ∆面积的最小值为123=32⨯⨯．…………………………………10分21D ．因为x ＞0，y ＞0，x －y ＞0，22211222()2()x y x y x xy y x y +-=-+-+-，…………………………………4分=21()()()x y x y x y -+-+-23213()3()x y x y -=-≥， ……………………8分所以2212232x y x xy y ++-+≥． ……………………………………………10分【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写 出文字说明、证明过程或演算步骤．22.以A 为坐标原点O ，分别以AB ，AC ，1AA 所在直线为x 轴、y 轴、z 轴，建立空间直角坐标系O xyz -．因为=1AB AC =，12AA =，则(0,0,0)A ，(1,0,0)B ，(0,1,0)C ，1(0,0,2)A ，1(1,0,2)B ，(1,0,2)P λ．……………………………………………1分（1）由13λ=得，2(1,1,)3CP =-u u u r ，1(1,02)A B =u u u r ，-，1(0,1,2)A C =-u u u u r ， 设平面1A BC 的法向量为1111(,,)x y z =n ，由11110,0A B A C ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u u r ，n n 得111120,20.x z y z -=⎧⎨-=⎩ 不妨取11z =，则112x y ==，从而平面1A BC 的一个法向量为1(2,2,1)=n ．……………………………………3分 设直线PC 与平面1A BC 所成的角为θ，则111sin |cos ,|||||CP CP CP θ⋅=<>==⋅u u u r u u u r u u u r n n n ， 所以直线PC 与平面1A BC所成的角的正弦值为33．…………………………5分 （2）设平面1PAC 的法向量为2222(,,)x y z =n ， 1(1,022)A P λ=u u u r ，-， 由21210,0A C A P ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u r ，n n 得222220,(22)0.y z x z λ-=⎧⎨+-=⎩ 不妨取21z =，则22222x y λ=-=，，所以平面1PAC 的法向量为2(22,2,1)λ=-n ．……………………………………7分则12cos ,<>=n n ，又因为二面角1P AC B --的正弦值为23，，………………………………………………………9分 化简得2+890λλ-=，解得1λ=或9λ=-（舍去），故λ的值为1． …………………………10分23．（1）由题意知，32n a n =-,2121111()n n n n g n a a a a ++=++++L ， …………1分当2n =时，234111111691(2)47101403g a a a =++=++=>． ……………2分 （2）用数学归纳法加以证明： ①当3n =时，34591111(3)g a a a a =++++L 11111117101316192225=++++++1111111()()7101316192225=++++++ 1111111()()8161616323232>++++++133131181632816163=++>++>， 所以当3n =时，结论成立．………………………………………………4分②假设当n k =时，结论成立，即1()3g k >， 则1n k =+时，(1)g k +()g k =22212(1)1111()k k k k a a a a +++++++-L …………6分 22212(1)11111()3k k k k a a a a +++>++++-L 21(21)133(1)232k k k +>+-+-- 221(21)(32)[3(1)2]3[3(1)2][32]k k k k k +--+-=++--2213733[3(1)2][32]k k k k --=++--， 由3k ≥可知，23730k k -->，即1(1)3g k +>． 所以当1n k =+时，结论也成立．综合①②可得，当3n ≥时，1()3g n >． …………………10分。

高三数学试题参考答案一、选择题：1．D 2．C 3．C 4．A 5．B 6．A 7．C 8．B二、选择题：9．ACD 10．BC 11．BD 12．BCD三、填空题：13． 14．2- 15．7- 16．43 四、解答题：17．（1）选择①：条件即sin cos b C B ，由正弦定理可知，sin sin cos B C C B =，在△ABC 中，,(0,π)B C ∈，所以sin 0B ≠，sin 0C ≠，所以sin B B =，且cos 0B ≠，即tan B =所以B ＝π3．…3分选择②：条件即12sin cos 2ac B B ⨯=，即sin B B =，在△ABC 中，(0,π)B ∈，所以sin 0B ≠，则cos 0B ≠，所以tan B B ＝π3． ………………………………………3分选择③：条件即tan tan tan 1)A C A C +=-，所以tan tan tan tan()1tan tan A C B A C A C+=-+=--， 在△ABC 中，,(0,π)B C ∈，所以B ＝π3．……………………………3分 （2）由（1）知，B ＝π3，所以2ππ3A B C C =--=-，由正弦定理可知，2π4sin()sin 32sin sin C c A a C C -==+， …………………8分 由△ABC 是锐角三角形得，π0,22ππ0,32C A C ⎧<<⎪⎪⎨⎪<=-<⎪⎩所以ππ62C <<．所以tan C >，所以28a <<，故a 的取值范围为(2,8)．………………10分18．（1）由2154n n n a a a ++=-可知，2114()n n n n a a a a +++-=-，即14n n b b +=，………3分由13a =，215a =可知，12112b a a -==，所以{}n b 是以12为首项，4为公比的等比数列，所以{}n b 的通项公式为112434n n n b -=⨯=⨯． ………………………………6分（2）由（1）知，134n n n a a +-=⨯，所以112211()()()n n n n n a a a a a a a a ---=-+-++-+ 123(4441)n n --=++++3(14)4114n n -==--， ……………………9分 所以2lo 104102g n n c n =-=-，所以{|}|n c 的前20项和20864202430260T =++++++++=． ……12分19．（1）在直三棱柱111ABC A B C -中，1AA ⊥平面ABC ，又,AB AC ⊂平面ABC ，所以1AA AB ⊥，1AA AC ⊥，又1AB AA =，所以四边形11ABB A 是正方形．…………………………………2分 连接1AB ，则11AB A B ⊥，又11A B B C ⊥，11,AB B C ⊂平面1AB C ，所以1A B ⊥平面1AB C ， …………4分 又AC ⊂平面1AB C ，所以1A B AC ⊥，又1AA AC ⊥，11,A B AA ⊂平面11ABB A ，所以AC ⊥平面11ABB A ，又AB ⊂平面11ABB A ，所以AB AC ⊥．………………………………………6分（2）以1{,,}AB AC AA 为正交基底建立空间直角坐标系A xyz -，设1AB =，则(1,0,0)B ，(0,1,0)C ，1(0,0,1)A ，1(1,0,1)B则1(1,0,1)A M λ=-，1(0,1,1)AC =-，…………8设平面1A MC 的法向量为(,,)x y z =m ， 则110,0,A M A C ⎧⋅=⎪⎨⋅=⎪⎩m m 即(1)0,0,x z y z λ+-=⎧⎨-=⎩ 得(1),,x z y z λ=-⎧⎨=⎩，取1z =， 则平面1A MC 的一个法向量为(1,1,1)λ=-m 考虑向量(1,1,0)=n ，满足10,0,BB BC ⎧⋅=⎪⎨⋅=⎪⎩n n所以(1,1,0)=n 是平面11BCC B 的一个法向量，因为二面角11A MC C --的大小为π4， 所以|||cos ,|||||2⋅==m n m n m n ，解得12λ=．………12分 20．（1）由()10.09+0.220.330.240.081a a ⨯+++++=，解得0.02a =，…………2分样本中指标数不在17.5和22.5之间的频率为()0.02110.04⨯+=，所以产品为次等品的概率估计值为0.04． ……………………………………5分（2）依题意170.02180.09190.22200.33210.24220.08μ=⨯+⨯+⨯+⨯+⨯+⨯230.02+⨯20=．…………………………………………………………………8分所以()2~201.22X N ，， 所以()()17.5622.44202 1.22202 1.220.9544P x P x <<=-⨯<<+⨯=．…12分21．（1）要证()f x <，即证：当(0,)x ∈+∞时，不等式ln 0x 恒成立．令()ln F x x =，则()F x '=， ……………………………………2分 故当(0,4)x ∈，()0F x '>，()F x 单调递增；当(4,)x ∈+∞，()0F x '<，()F x 单调递减． 则max ()(2)ln 420F x F ==-<，故()f x <． …………………………4分（2）要使得函数()f x 的图象与()g x 的图象有两个不同的公共点，只需函数()()()G x f x g x =-在(0,)+∞上有两个不同的零点，222122()()()ax x G x f x g x a x x x -++'''=-=-+=， ①当0a ≤时，(0,)x ∈+∞时，()0G x '>，()G x 单调递增，所以()G x 不可能存在两个零点； ……………………………………………5分 ②当0a >时，方程220ax x -++=有两个异号的根，不妨设正根为0x ， 故0(0,)x x ∈时，()0G x '>，()G x 单调递增；0(,)x x ∈+∞时，()0G x '<，()G x 单调递减，要使得()G x 存在两个零点，则max 00002()()ln 50G x G x x ax x ==--+>， 又因为20020ax x -++=，故20012a x x =+， 则有max 0004()()ln 40G x G x x x ==-+>，解得01x >， 又因为20012a x x =+，故03a <<．……………………………………………8分 下证：当03a <<时，2()ln 5G x x ax x=--+存在两个零点． 取5552(e )e 0eG a ---=--<，又0()(1)30G x G a >=->， 且()G x 在0(0,)x 单调递增，所以()G x 在0(0,)x 上存在唯一零点． ………9分因为22()ln 555G x x ax ax ax x x=--+<--+<+， 取2814x a=，则2228181()()2044a a a -++<，所以02814x a >， 故281()4G a <981206350244a a a a --+=<， 又0()0G x >，且()G x 在0(,)x +∞上单调递减，所以()G x 在0(,)x +∞存在唯一零点．故03a <<时，2()ln 5G x x ax x=--+存在两个零点． 因此实数a 的取值范围是(0,3)． ……………………………………………12分22．（1）因为双曲线的虚轴长为4，且经过53(,)42， 所以2224,2591,164b a b =⎧⎪⎨-=⎪⎩ 解得1,2a b .=⎧⎨=⎩ 所以双曲线的标准方程为2214y x -=．…………………………………………2分 （2）联立1,2,x y x =-⎧⎨=-⎩ 得(1,2)T -，由题意知过T 点的直线斜率存在， 设过T 点的直线方程为()21y k x -=+，()11P x ,y ，()22Q x ,y ，联立()2221,1,4y k x y x -=+⎧⎪⎨-=⎪⎩ 得()()()2222424480k x k k x k k --+-++=， 则()()()22222444480k k k k k ∆=++-++>，得2k >-， 所以2122424k k x x k ++=-，()2122484k k x x k -++⋅=-， ……………………………4分 因为2(10)A ,，所以直线2A P 的方程为()1111y y x x =--， 联立112,(1),1y x y y x x =-⎧⎪⎨=-⎪-⎩ 解得()11121M y x y x =+-， 同理可得()22221N y x y x =+-， …………………………………………………6分 所以()()()()121211221222212122M N y y kx k kx k x x y x y x k x k k x k+++++=+=++-+-++++ ()()()()()()2121212222442222k k x x k k x x k k k x k k x k +++++++=++++⎡⎤⎡⎤⎣⎦⎣⎦，…………8分因为()()()()212122224422k k x x k k x x k k +++++++()()()()()()222222248244422244k k k k k k k k k k k k -+++++++++-=- ()()()()()22222248244404k k k k k k k k ⎡⎤-+++-++--⎣⎦==-， 即0M N x x +=．…………………………………………………………………10分 所以对角线MN 与12A A 互相平分，即四边形12A MA N 为平行四边形．……12分。

数学试卷答案 第 1 页(共 6 页)徐州市、连云港市2020届高三第一学期期末调研考试数学I 参考答案与评分标准一、填空题：1．{12}x x −<< 2．2i − 3．45 4．20 5．[4,+)∞ 6．127．4 8．14 9．135 1011．22(2)8x y ++= 12．3 13．4714．34二、解答题：15．（1）在PBC △中，因为M ，N 分别为棱PB ，PC 的中点，所以MN // BC ． ………………………………3分 又MN ⊂平面AMN ，BC ⊄平面AMN ，所以BC //平面AMN ．…………………………6分（2）在PAB △中，因为AP AB =，M 为棱PB 的中点， 所以AM PB ⊥．………………………………8分 又因为平面P AB ⊥平面PBC ，平面P AB 平面PBC PB =，AM ⊂平面P AB ， 所以AM ⊥平面PBC ．…………………………………………………………12分 又AM ⊂平面AMN ，所以平面AMN ⊥平面PBC ． …………………………14分16．（1）在ABC △中，由余弦定理2222cos b c bc A a +−=得，220225b +−⨯=，即2450b b −−=， …………………………4分 解得5b =或1b =−（舍），所以5b =． ………………………………………6分 （2）由cos A =及0A <<π得，sin A ，…8分 所以cos cos(())cos()sin )4C A B A A A π=π−+=−+=−=， 又因为0C <<π，所以sin C ===， 从而sin tan 3cos C C C ===，………………………………………………12分 所以222tan 233tan 21tan 134C C C ⨯===−−−．………………………………………14分 17．（1）在SAO △中，4SO ===， …………………………2分由1SNO △∽SAO △可知，1SO r SO R =，所以143SO r =，……………………4分 所以1443OO r =−，所以223144()π(4)π(3),03339V r r r r r r =−=−<<．…7分 （2）由（1）得234()π(3),039V r r r r =−<<， A P N M C B数学试卷答案 第 2 页(共 6 页) 所以24()π(63)9V r r r '=−，令()0V r '=，得2r =，………………………9分 当(0,2)r ∈时，()0V r '>，所以()V r 在(0,2)上单调递增；当(2,3)r ∈时，()0V r '<，所以()V r 在(2,3)上单调递减．所以当2r =时，()V r 取得最大值16π(2)9V =． 答：小圆锥的体积V 的最大值为16π9．………………………………………14分 18．（1）直线l 的方程为)(a x k y −=，即0=−−ak y kx ，因为直线l 与圆222b y x O =+：相切，所以b k ak =+−12，故2222b a b k −=． 所以椭圆C的离心率e =．………………………………4分 （2）设椭圆C 的焦距为2c ，则右准线方程为2a x c=， 由⎪⎩⎪⎨⎧=−=c a x a x k y 2)(得c ac a k a c a k y −=−=22)(，所以))(,(22c ac a k c a Q −，…6分 由⎪⎩⎪⎨⎧−==+)(12222a x k y b y a x 得02)(2224232222=−+−+b a k a x k a x k a b ， 解得222223k a b ab k a x p +−=，则22222222232)(k a b k ab a k a b ab k a k y p +−=−+−=， 所以)2-2222222223k a b k ab k a b ab k a P ++−，（，……………………………………………10分 因为0=⋅，所以02)(222222222232=+−⋅−++−⋅ka b k ab c ac a k k a b ab k a c a ， 即)(2)(22222c a k b b k a a −=−，………………………………………………12分由（1）知，2222b a b k −=，所以22422222)(2)(b a c a b b b a b a a −−=−−， 所以c a a 22−=，即c a 2=，所以21=a c ，故椭圆C 的离心率为21．……16分 19．（1）()2111()ln f x x a x x x'=+−， 因为曲线()y f x =在点(1,(1))f 处的切线方程为10x y +−=，所以(1)11f a '=−=−，得0a =．……………………………………………2分（2）因为21ln ()ax x f x x−+'=存在两个不相等的零点． 所以()1ln g x ax x =−+存在两个不相等的零点，则1()g x a x'=+． ①当0a ≥时，()0g x '>，所以()g x 单调递增，至多有一个零点．……4分数学试卷答案 第 3 页(共 6 页)②当0a <时，因为当1(0)x a ∈−，时，()0g x '>，()g x 单调递增， 当1(+)x a ∈−∞，时，()0g x '<，()g x 单调递减， 所以1x a =−时，max 11()()ln()2g x g a a =−=−−． …………………………6分 因为()g x 存在两个零点，所以1ln()20a−−>，解得2e 0a −−<<．………7分 因为2e 0a −−<<，所以21e 1a−>>． 因为(1)10g a =−<，所以()g x 在1(0)a−，上存在一个零点． …………8分 因为2e 0a −−<<，所以211()a a−>−． 因为22111[()]ln()1g a a a −=−+−，设1t a=−，则22ln 1(e )y t t t =−−>， 因为20t y t−'=<，所以22ln 1(e )y t t t =−−>单调递减， 所以()2222ln e e 13e 0y <−−=−<，所以22111[()]ln()10g a a a−=−+−<， 所以()g x 在1()a−+∞，上存在一个零点． 综上可知，实数a 的取值范围为2(e ,0)−−．…………………………………10分（3）当2a =时，1()(2)ln f x x x =−，()2211121ln ()ln 2x x f x x x x x x−+'=+−=， 设()21ln g x x x =−+，则1()20g x x'=+>．所以()g x 单调递增， 且11()ln 022g =<，(1)10g =>，所以存在01(1)2x ∈，使得0()0g x =，……12分 因为当0(0)x x ∈，时，()0g x <，即()0f x '<，所以()f x 单调递减；当0(+)x x ∈∞，时，()0g x >，即()0f x '>，所以()f x 单调递增，所以0x x =时，()f x 取得极小值，也是最小值， 此时()0000000111()(2)ln (2)12(4)4f x x x x x x x =−=−−=−++，……………14分 因为01(1)2x ∈，，所以0()(10)f x ∈−，， 因为()f x λ≥，且λ为整数，所以1λ−≤，即λ的最大值为1−．………16分20．（1）由11n n a ka +=−，13a =可知，231a k =−，2331a k k =−−，因为{1}n a −为等比数列，所以2213(1)(1)(1)a a a −=−−，即22(32)2(32)k k k −=⨯−−，即231080k k −+=，解得2k =或43k =，…2分 当43k =时，143(3)3n n a a +−=−，所以3n a =，则12n a −=， 所以数列{1}n a −的公比为1，不符合题意；当2k =时，112(1)n n a a +−=−，所以数列{1}n a −的公比1121n n a q a +−==−，数学试卷答案 第 4 页(共 6 页) 所以实数k 的值为2． …………………………………………………………4分（2）由（1）知12n n a −=，所以4n n n n b n − , ⎧⎪=⎨2, ⎪⎩为奇数,为偶数,则22(41)4(43)4[4(21)]4m m S m =−++−+++−−+2(41)(43)[4(21)]444m m =−+−++−−++++144(4)3m m m +−=−+，……………………………………………………6分 则212244(4)3m m m m S S b m m −−=−=−+， 因为22+1324m m m b b m +=−+，又222+322+1()()3420m m m m m b b b b ++−+=⨯−>， 且2350b b +=>，130b =>，所以210m S −>，则20m S >， 设2210,m t m S b t S −=>∈*N ，…………………………………………………………8分 则1,3t =或t 为偶数，因为31b =不可能，所以1t =或t 为偶数， ①当2121=m m S b S −时，144(4)3344(4)3m m m m m m +−−+=−−+，化简得2624844m m m −+=−−≤， 即242m m −+≤0，所以m 可取值为1，2，3， 验证624135787,3,323S S S S S S ===得，当2m =时，413S b S =成立．…………………12分 ②当t 为偶数时，1222144(4)331443124(4)134m m m m mm m S S m m m m +−−−+==+−−+−−++， 设231244m m m m c −+−=，则211942214m m m m m c c ++−+−=， 由①知3m >，当4m =时，545304c c −−=<； 当4m >时，10m m c c +−>，所以456c c c ><<，所以m c 的最小值为5191024c −=， 所以22130151911024m m S S −<<+<−+，令22214m m S b S −==，则2314312414mm m +=−+−+， 即231240m m −+−=，无整数解．综上，正整数m 的值2．………………………………………………………16分（第22题）数学Ⅱ参考答案与评分标准21．A ．矩阵M 的特征多项式为23()(2)(1)31f t t λλλλλ−−==−−−−−．…………2分 因为矩阵M 的一个特征值为4，所以(4)630f t =−=，所以2t =．…………5分 所以2321⎡⎤=⎢⎥⎣⎦M ，所以11313213221324422112132213222−−⎡⎤⎡⎤−⎢⎥⎢⎥⨯−⨯⨯−⨯==⎢⎥⎢⎥−−⎢⎥⎢⎥⨯−⨯⨯−⨯⎣⎦⎣⎦M ．……10分 B ．由:cos sin 120l ρθρϕ+−=，及cos x ρθ=，sin y ρθ=，所以l 的直角坐标方程为120x y +−=． ………………………………………2分在曲线C上取点()2sin M ϕϕ，，则点M 到l 的距离124sin 3d ϕπ−+===，…………6分 当6ϕπ=时，d 取最小值8分此时点M 的坐标为()3,1．………………………………………………………10分 C ．因为x y z ，，都为正数，且1x y z ++=，所以由柯西不等式得，1113()222x y y z z x+++++111()[(2)(2)(2)]222x y y z z x x y y z z x=++⋅++++++++………………5分29=≥， 当且仅当13x y z ===时等号成立，所以111222x y y z z x+++++的最小值为3．…………………………………10分22．（1）因为四边形11AA B B 为正方形，所以1AB BB ⊥，因为平面11AA B B ⊥平面11BB C C ，平面11AA B B平面111BB C C BB =，AB ⊂平面11AA B B ，所以AB ⊥平面11BB C C . 以点B 为坐标原点，分别以BA ,1BB 所在的直线为x ,y 轴，建立如图所示的空间直角坐标系B − 不妨设正方形11AA B B 的边长为2，则()2 0 0A ，，，()10 2 0B ，，． 在菱形11BB C C 中，因为1160BB C ∠=︒，所以1(0 1C ，，所以1(2 1 AC =−，．因为平面11AA B B 的法向量为()0 0 1=，，n ， 设直线1AC 与平面11AA B B 所成角为α，则1sin |cos ,|AC α=<>==n ，即直线1AC 与平面11AA B B………………………6分（2）由（1）可知，(0 1 C −，，所以()10 2 0CC =，，．设平面1ACC 的一个法向量为()1111 x y z =，，n ， 因为11110,0,AC CC ⎧⋅=⎪⎨⋅=⎪⎩n n 即()(()()111111 2 1 0 0 2 00x y z x y z ⎧⋅−=⎪⎨⋅=⎪⎩，，，，，，，，取1x ，10y =，11z =，即1 0 1⎫=⎪⎭，，n ．设平面1ABC 的一个法向量为()2222 x y z =，，n ， 因为()2 0 0BA =，，，(10 1 BC =，， 所以()()()(222222 2 0 00 0 1 0x y z x y z ⋅=⎧⎪⎨⋅=⎪⎩，，，，，，，，取()20 1=−，n ．…………8分设二面角1B AC C −−的平面角为θ，则121212 cos cos θ⋅=−<>=−==⋅，n n n n n n所以二面角1B AC C −−．…………………………………10分23．（1）因为4n =，所以0404216C ()=381a =，1314232C ()=327a =．……………………2分 （2）当13x =时，21C ()()33k k n k kk n a x −=， 又因为11!(1)!C C !()!(1)!()!k k n n n n k k n n k n k k n k −−−===−−−，………………………4分当1n =时，011022()C ()33nk k k n k a x =−==∑； …………………………………5分当2n ≥时，0021()()C ()()33n nk k n k kk n k k n k a x n k −==−=−∑∑012121C ()()C ()()3333n nk n k k k n k k n n k k n k −−===−∑∑1112121()C ()()3333n n k n k kn k n n −−−==+−∑ 1111121C ()()333n k n k k n k n n −−−−==−∑1121()333n n n −=−+23n =，当1n =时，也符合．所以0()nk k k n k a x =−∑的值为23n ．………………………………………………10分。