新湘教版七年级数学下册《4章 相交线与平行线 4.1 平面上两条直线的位置关系》教案_7
- 格式:doc
- 大小:73.00 KB
- 文档页数:3

第四章相交线与平行线4.1.1 1平面上两条直线的位置关系教学目标:知识与技能:1.了解同一平面内两条直线的位置关系,理解平行线的概念。
2.理解并掌握平行的基本事实及直线平行关系的传递性。
3.学会用直尺和三角板画平行线。
过程与方法:通过观察、动手操作、推断、合作交流等活动,进一步发展空间观念,培养识图能力,推理能力和表达能力。
情感态度与价值观:通过学生之间的交流讨论、师生互动,培养学生的合作意识及积极思考、勇于探索的理性思维习惯。
重点难点:重点:平行线的概念与平行的基本事实。
难点:对平行的基本事实及直线平行关系的传递性的理解。
教学过程一.新课导入利用多媒体导入新课。
现实生活中,各种各样的图形都是由平行线和相交线交织而成。
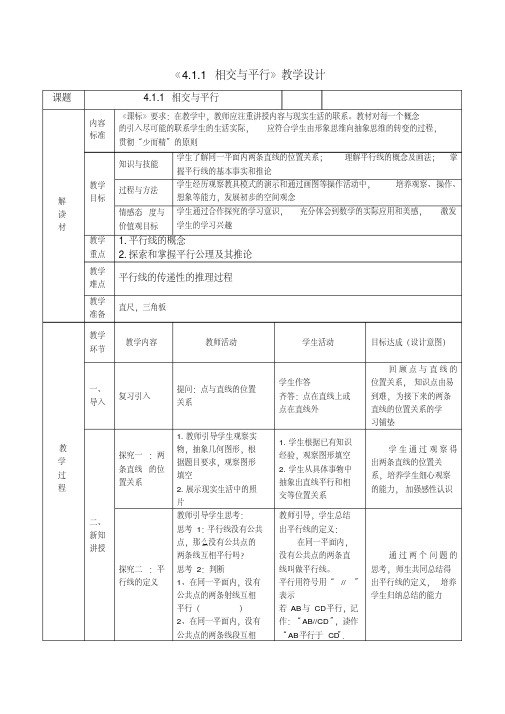
如图所示:多媒体播放PPT自学课文(8—10分钟)二、合作探究(一)平行线的概念:在,没有的两条直线叫做平行线。
(二)两直线平行的表示:直线AB与CD平行,记作__________,读作_____________学生合作交流得出答案。
【注意】①今后如果没有特殊说明,两条重合的直线只当做一条.②在每条直线上取定一个方向,两条直线平行也就是它们的方向相同或相反.③今后遇到线段、射线平行时,特指线段、射线所在的直线平行.(三)直线与直线的位置关系:在同一平面内,两条直线的位置关系只有两种:________ ,_________ (四)如何用直尺和三角板画平行线b∥a?(直线b要经过P点)方法为:①“落”(三角板的一边落在已知直线上),Pa②“靠”(用直尺紧靠三角板的另一边),③“推”(沿直尺移动三角板,直至落在已知直线上的三角板的一边经过已知点),④“画”(沿三角板过已知点的边画直线)。
学生先自己画,然后教师播放PPT演示(五)比一比谁是赢家?通过点C画直线AB的平行线,看能画出几条?平行线的基本事实:经过直线外一点有且只有一条直线与这条直线平行.(六)过点D画一条直线与直线AB平行,它与1中所画的直线平行吗?学生合作交流得出结论。









4.1.2 相交直线所成的角教学目标:1.理解相交直线所成的角意义,理解对顶角、同位角、内错角、同旁内角的概念。
能准确地找出三条直线相交所构成的八个角的关系。
2.理解对顶角相等的性质。
3.会运用对顶角相等及等量代换的性质得到三条直线相交所得8个角之间的等量关系及互补关系。
教学难点:准确找出三条直线相交所构成的八个角的关系,对顶角的性质及等量代换得到他们之间的等量关系教学重点:三条直线所构成的八个角的关系、对顶角的性质。
教学内容:一、对顶角【自主学习】(一)动手操作观察思考:要求学生拿出事先准备好的纸和剪刀,用剪刀剪开纸张的过程,随着两个把手之间的角逐渐变小,剪刀刃之间的角度也相应。
两把手之间的角逐渐变大,剪刀刃之间的角度也相应。
我们把剪刀的构成抽象为两条直线,就是我们要研究的两条相交直线所成的角的问题。
(二)自主探究问题1:两条相交直线相交形成的四个角有什么位置关系?(1)观察∠AOC 与∠BOC,它们的位置有什么关系?它们的数量有什么关系?(引出邻补角定义)(2)观察∠AOC 与∠BOD,它们的位置有什么关系?有什么特点?(引出对顶角定义)对顶角的定义:∠1和∠3有一个公共顶点O ,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角叫做对顶角.问题2:你所画的图形中还有哪些对顶角?问题3:判断下列图形中哪对角是对顶角?问题4:∠1与∠3有怎样的数量关系?你能说出∠1=∠3的道理吗?解:因为 ∠1与∠2互补,∠3与∠2互补(邻补角的定义)所以∠1=∠3(同角的补角相等)同理∠2=∠4 .【应用】如图,已知直线a 、b 相交。
∠1=40°,求∠2、∠3、∠4的度数。
1 2 1 2二、探究问题1:∠1与∠3有怎样的数量关系?比较它们的大小(用自己喜欢的方式)。
你能说出∠1=∠3的道理吗?解:因为∠1与∠2互补,∠3与∠2互补(补角的定义),所以∠1=∠3(同角的补角相等)同理∠2=∠4 .对顶角的性质:对顶角相等.三、探究“三线八角我们来探究:两条直线被第三条直线所截,所构成的角中没有公共顶点的角之间的关系。
《相交直线所成的角》教学设计
(第二课时)
教学目标
知识与技能:
1.理解相交直线所成的角意义,理解同位角、内错角、同旁内角的概念。
能准确地找出三条直线相交所构成的八个角的关系。
2.会运用对顶角相等及等量代换的性质得到三条直线相交所得8个角之间的等量关系及互补关系。
过程与方法:
通过动手、操作、推断、交流等活动,经历探索对同位角、内错角、同旁内角的过程,进一步发展空间观念,培养识图能力、推理能力和表达能力。
情感、态度与价值观
通过学生之间的交流讨论,师生互动,培养学生的合作意识及积极思考、勇于探索的理性思维习惯。
教学重点:1、区别“两条直线相交”和“两条直线被第三条直线所截”。
2、理解同位角、内错角、同旁内角的位置特征和结构特征。
教学难点:准确地找出三条直线构成的8个角之间的关系
教学过程:
一、温故知新
1、对顶角的概念①有公共顶点
②其中一个角的两边分别是另一个角两的反向延长线。
2、对顶角的性质:对顶角相等。
3、指出右图中的对顶角。
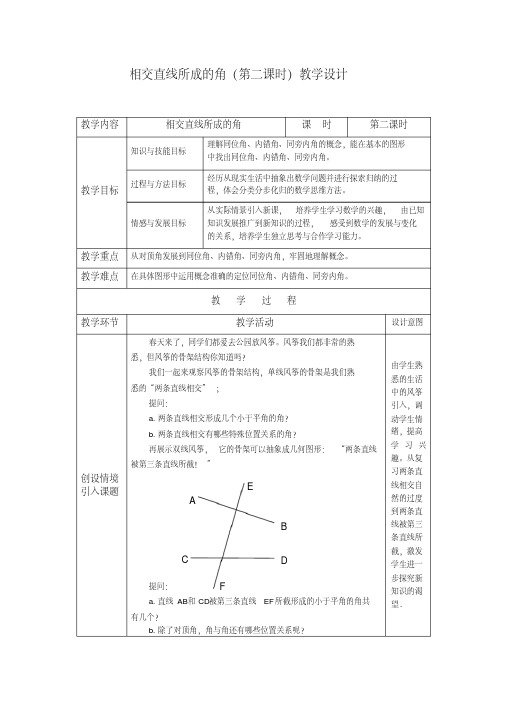
4、教师提问:“两直线相交”和“两条直线被
第三条直线所截”是同一个意思吗?请画图说明。
两直线相交两条直线被第三条直线所截
5、两条直线相交可以形成4个角,两条直线被第三条直线所截可形成几个角?
(8个)
二、讲授新课
今天我们所学的内容是“三线八角”。
即:两条直线被第三条直线所截所构成胡8个角之间的关系。
观察∠1和∠5的位置关系。
1、都在被截直线的同一方(上方)。
2、在截线的同侧(右侧)。
我们把具有∠1和∠5这种位位置关系的一对角叫做
知识点二:内错角
观察∠3和∠5的位置关系。
1、它们在被截直线之间(之内)。
2、在截线的两侧(一左、一右)。
我们把具有∠3和∠5这种位位置关系的一对角叫做
知识点三:同旁内角
观察∠4和∠5的位置关系
1、它们在两条被截直线之间(之内)。
2、在截线的同一旁(同侧)。
我们把具有∠4和∠5这种位位置关系的一对角叫做同旁内角;
你还能从上图中找出其他的同位角、内错角、同旁内角吗?
动手动脑
画一画在上图中如果去掉多余的线只保留其中两个角,那剩下的图形会是什么样子?
3
1 4
5 5 5
形如字母“F ”形如字母“Z ”形如字母“U”
三、巩固练习
例1 如图,直线EF与AB,CD相交,构成8个角. 指出
图中所有的同位角、内错角和同旁内角.
解:同位角有∠2和∠5,∠1和∠8,
∠3和∠6,∠4和∠7;
内错角有∠1和∠6,∠4和∠5;
同旁内角有∠1和∠5,∠4和∠6.
例2 如图,直线a,b被直线c所截,找出中所有的同位角、内错角、同旁内角.
解:
同位角:∠1与∠4,∠2与∠5
内错角:∠3与∠4
同旁内角:∠2与∠4
四、课堂小结
经过一节课的学习,相信同学们对这节课都有了一定的了解,
接下来,请同学们归纳本节课的重要知识;
角的名称位置特征结构特征
形如字母“F”
同位角在两条被截直线同一
方,在截线同侧
形如字母“Z”
内错角在两条被截直线之间,
在截线两侧(交错)
同旁内角在两条被截直线之间,
形如字母“U”
在截线同侧
五、布置作业
必做题:教材78页A组第6、7题;
选做题:教材78页B组第8、9题;
我及时反思教学过程,觉得学生对概念的理解不透,他们只是简单的记住了图形的结构“同位角形如字母F,内错角形如字母Z或N,同旁内角形如字母U”。
在找角时学生光记得找图形了,而忽略了在“三线八角”中,首先要确定截线,再结合图形特征(F,Z或N,U)在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,那么,如何确定图形中的截线呢?我及时调整课程为学生讲解截线的寻找办法。