近六年广东省中考数学试题各小题的考点分析

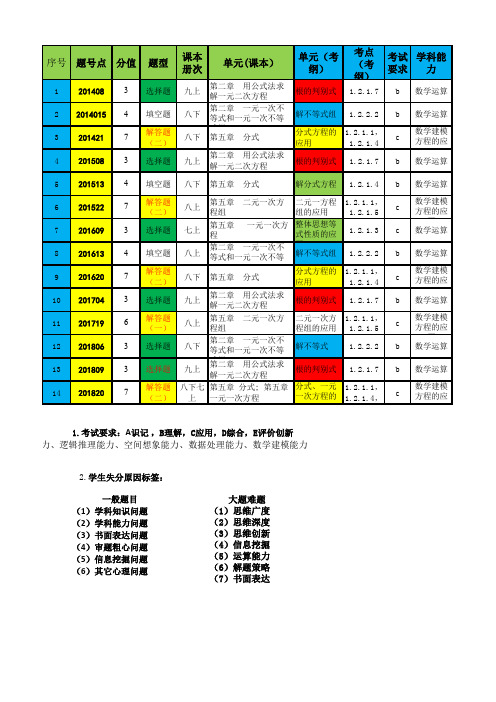
序号题号点分值题型课本册次单元(课本）单元（考纲）考点（考纲）考试要求学科能力12014083选择题九上第二章 用公式法求解一元二次方程根的判别式 1.2.1.7b数学运算220140154填空题八下第二章 一元一次不等式和一元一次不等式组解不等式组 1.2.2.2b数学运算32014217解答题（二）八下第五章 分式分式方程的应用1.2.1.1，1.2.1.4c数学建模方程的应用42015083选择题九上第二章 用公式法求解一元二次方程根的判别式 1.2.1.7b数学运算52015134填空题八下第五章 分式解分式方程 1.2.1.4b数学运算62015227解答题（二）八上第五章 二元一次方程组二元一方程组的应用1.2.1.1，1.2.1.5c数学建模方程的应用72016093选择题七上第五章 一元一次方程整体思想等式性质的应用1.2.1.3c数学运算82016134填空题八上第二章 一元一次不等式和一元一次不等式组解不等式组 1.2.2.2b数学运算92016207解答题（二）八下第五章 分式分式方程的应用1.2.1.1，1.2.1.4c数学建模方程的应用102017043选择题九上第二章 用公式法求解一元二次方程根的判别式 1.2.1.7b数学运算112017196解答题（一）八上第五章 二元一次方程组二元一次方程组的应用1.2.1.1，1.2.1.5c数学建模方程的应用122018063选择题八下第二章 一元一次不等式和一元一次不等式组解不等式 1.2.2.2b数学运算132018093选择题九上第二章 用公式法求解一元二次方程根的判别式 1.2.1.7b数学运算142018207解答题（二）八下七上第五章 分式; 第五章一元一次方程分式、一元一次方程的应用1.2.1.1，1.2.1.4，c数学建模方程的应用1.考试要求：A识记，B理解，C应用，D综合，E评价创新能力、逻辑推理能力、空间想象能力、数据处理能力、数学建模能力2.学生失分原因标签：一般题目（1）学科知识问题（2）学科能力问题（3）书面表达问题（4）审题粗心问题（5）信息挖掘问题（6）其它心理问题 大题难题（1）思维广度（2）思维深度（3）思维创新（4）信息挖掘（5）运算能力（6）解题策略（7）书面表达命题来源失分原因改编学科知识问题改编学科知识问题改编学科能力问题改编学科知识问题改编学科知识问题改编学科能力问题改编学科能力问题信息挖掘问题改编学科知识问题改编学科能力问题改编学科知识问题改编学科能力问题改编学科知识问题改编学科知识问题改编学科能力问题。

广东中考数学试卷分析初中毕业升学考试是学生结束义务教育阶段学习的一次重要考试，既是对学生学习水平的一次测试，又是对初中三年数学教学的一次终结性评价。

对于中考试卷的观察、分析和思考不仅对中考命题趋势的把握有益，而且有利于让将要参加中考的学生能及时的了解中考信息，调整自己的学习策略，以期将来能取得好成绩。

卷面分析：1、试卷结构：东莞市中考试卷满分120分，考试时间100分钟。

共五道大题，22道小题。

2011年和2012年“题型及相应分值”分析表大题及类型小题及分值总分值第一大题（选择题）5道题，每小题3分15分第二大题（填空题）5道题，每小题4分20分第三道题（解答题）5道题，每小题6分30分第四道题（解答题）4道题，每小题7分28分第五道题（解答题） 3道题，每小题9分27分2013年“题型及相应分值”分析表大题及类型小题及分值总分值第一大题（选择题）10道题，每小题3分30分第二大题（填空题）6道小题，每小题4分24分第三道题（解答题一）3道小题，每小题5分15分第四道题（解答题二）3道小题，每小题8分24分第五道题（解答题三） 3道小题，每小题9分27分2、考查知识点分析和难易程度从知识领域来看，试卷涉及《数学课程标准》规定的“数与代数”、“空间与图形”、“统计与概率”、“实践与应用”四大领域。

“知识领域”分析表①2011年中考试卷内容：知识点题号分值难度合计分值数与代数倒数1 3 易５７分科学计数法2 3 易反比例函数 6 4 易二次根式7 4 易实数运算11 6 易不等式12 6 中判别式15 6 中分式方程16 7 易找规律20 9 中二次函数22 9 难空间与图形相似图形 3.10 3.4 3333分正多边形内角 5 3 易全等三角形13 6 易圆的性质9.14 4.6 易易三角形13 6 易统计与概率概率 4 3 易10分统计18 7 中实践与应用程序8 4 易20分探究问题能力21 9 难三角函数17 7 中②2012年中考试卷内容：知识点题号分值难度合计分值数与代数绝对值１３易59分科学计数法 2 ３易混合运算12 6 中分解因式６４易有理数运算9 4 易解一元二次方程方程13 6 中不等式7 4 中三角函数解应用题18 ７中抛物线22 9 难反比例函数与直线关系17 7 中实数的运算11 6 中空间与图形36分三视图 4 ３易矩形的折叠问题21 9 中四边形10 4 中平行四边形的判定15 6 中圆的性质8 ４易基本作图和等腰三角形性质14 6 中三角形 5 3 易统计与概率概率20 9 难11分统计 3 3 易实践与应用归纳总结能力19 ７中14分探究问题能力16 7 难③2013年中考试卷内容：知识点题号分值难度合计分值数与代数相反数１３易５４分科学计数法 3 3 易数轴上解集的表示8 ３易代数式的化简18 5 中有理数运算7 3 易因式分解11 ４易二次函数及抛物线23 9 中一元二次方程组17 5 易一次函数与反函数象限问题10 3 易绝对值以及二次根式12 4 易不等式的运算 4 3 易空间与图形同位角 6 ３易３８分三视图 2 ３易作线段图及全等三角形求法19 5 易矩形面积以及三角形相似22 8 中圆的性质24 9 中轴对称图形9 3 易三角形14 ４易六边形内角和问题13 4 易四边形15 4 中四边形面积问题16 4 中统计与概率中位数 5 3 易１０分统计图与统计表20 8 易实践与应用归纳总结能力25 ９难１８分探究问题能力21 8 中二、试题特点分析1、试题源于教材、贴近学生实际试卷中绝大部分试题是考察基础知识的问题，许多试题选自课本的例题和习题或者是由课本的例题和习题经过适当的改编而成的，只经过了简单的改编。

2017--2019近几年广州中考数学情考点分析及建议近几年考情分析引言2019年广州中考数学试卷整体难度保持稳定，在稳定的基础上注重数学基础知识的考查，更加重视数学素养和数学方法。

选择填空题考法常规，考查范围以基础知识为主。

解答题部分，17-23题题型结构稳定，着重考查学生的“四基”。

24-25题着重考查学生的“代几”综合运用能力、作图探究能力、图形变换、数形结合思想的运用。

本次命题依据考试大纲,着力体现新课标的教学理念，突出对学生基本数学素养的评价，既考查了四基——基础知识、基本技能、基本数学思想方法和基本活动经验,又突出课本核心内容,关注学生研究的结果,也重视研究的过程。

2019广州中考数学命题，有利于培养学生对知识点的综合运用能力、动手作图能力与运算能力，有助于学生构建知识体系。

本次命题不设置偏题，确保了试题的科学性、公平性和严谨性。

一、整体评价试卷难度稳定，整体布局与往年的广州中考类似。

选择填空考法常规，但计算量增大；解答题梯度明显，区分度很高，注重知识接洽，请求学生具备计算本领、多个知识点灵活运用本领、作图本领等数学基本头脑和本领。

二、试卷特点试卷题型分为选择题、填空题、解答题，在分值分布和题型特征方面与往年相似。

今年函数部分分值降低，压轴题与以往同等，考查一题函数、一题几何的模式。

函数压轴题，考查含参问题、函数过定点的问题，注重初高衔接；另一道压轴题，以等边三角形为背景的翻折问题，通过构造“辅助圆”解决最值问题。

今年的试题主要特点：①重视基础，考查灵活运用知识点的本领；②突显学生作图本领，加强着手本领；③注重知识点交汇；④常规但不俗套；⑤注重学生计算本领的考查；⑥相比往年，今年减少了分类讨论头脑的考查。

今年第10题，难度不大，但涉及的知识点较多，考查一元二次方程根的判别式、根与系数的关系、平方差公式以及整体思想等知识点。

第16题，则是引入“半角模型”和“三垂直模型”的构造，以及利用函数求最值问题，强调了学生平时在研究过程中，对常见的典型几何模型的归纳，以及函数思想解决最值问题。

广州中考真题数学试卷分析中考是每一个初中生都要经历的一次重要考试，数学试卷是其中的一项主要内容。

本文将对广州中考的数学试卷进行分析，探讨试卷结构、考点分布以及解题技巧等方面的内容，旨在帮助考生更好地备考。

一、试卷结构分析广州中考数学试卷通常由选择题和解答题两部分组成。

选择题占据了试卷的大部分，考察基础知识的掌握程度。

选择题种类多样，包括单选题和多选题等。

其中，单选题主要考察基本概念、运算能力和问题解决能力；多选题要求考生辨别信息，运用数学方法解决实际问题。

解答题是试卷的较难部分，主要考察对知识点的理解和应用能力。

解答题的题目种类与选择题相似，但要求考生用文字、符号或图表等形式给出解答过程和结果，注重思维能力、创新能力和推理能力。

二、考点分布分析广州中考数学试卷的考点分布广泛，主要包括数与代数、几何与测量、函数与图像、统计与概率等方面。

1. 数与代数：包括整数、分数、小数、有理数、实数、代数式、方程和不等式等。

这些知识点的理解和掌握对于解决实际问题至关重要。

2. 几何与测量：主要涉及图形的性质、计算、相似、合同、判定等。

几何与测量是对生活中形状、大小和量度等方面的认识和应用，考察学生对几何概念的掌握和几何问题的解决能力。

3. 函数与图像：包括函数的定义、性质和运算以及函数图像的绘制和分析等。

函数与图像在数学中起着重要的作用，通过对函数的研究，可以更好地理解数学问题。

4. 统计与概率：主要涉及数据的收集、整理、分析和表示等统计方法，以及概率的计算和应用等。

统计与概率是对数据进行分析和预测的重要手段，也是日常生活中经常使用的数学方法。

三、解题技巧总结1. 熟练掌握基础知识：广州中考数学试卷考察的是学生对基本概念和运算方法的掌握程度，因此要通过大量的练习，熟悉并掌握基础知识。

2. 理解题意，注重分析：在解答题目时，要仔细阅读题目并理解其意思，注意提取有效信息，并进行合理的分析和推理。

3. 建立数学模型：对于较复杂的问题，可以尝试建立数学模型，将实际问题转化为数学问题，从而更好地解决问题。

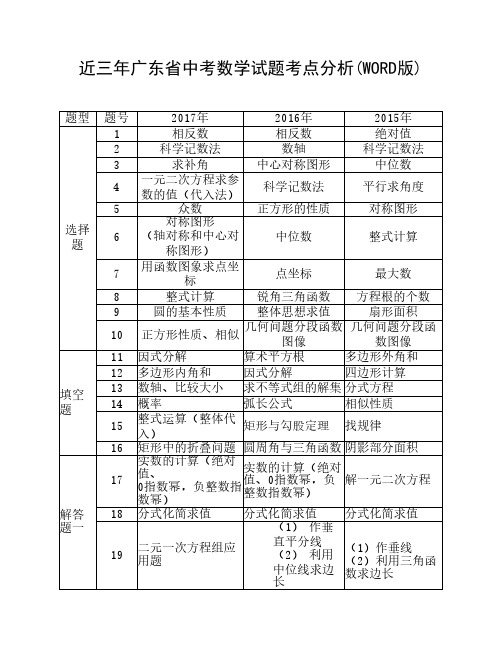
近三年广东省中考数学试题考点分析(WORD版)题型题号2017年2016年2015年选择题1相反数相反数绝对值2科学记数法数轴科学记数法3求补角中心对称图形中位数4一元二次方程求参数的值（代入法）科学记数法平行求角度5众数正方形的性质对称图形6对称图形（轴对称和中心对称图形）中位数整式计算7用函数图象求点坐标点坐标最大数8整式计算锐角三角函数方程根的个数9圆的基本性质整体思想求值扇形面积10正方形性质、相似几何问题分段函数图像几何问题分段函数图像填空题11因式分解算术平方根多边形外角和12多边形内角和因式分解四边形计算13数轴、比较大小求不等式组的解集分式方程14概率弧长公式相似性质15整式运算（整体代入）矩形与勾股定理找规律16矩形中的折叠问题圆周角与三角函数阴影部分面积解答题一17实数的计算（绝对值、0指数幂，负整数指数幂）实数的计算（绝对值、0指数幂，负整数指数幂）解一元二次方程18分式化简求值分式化简求值分式化简求值19二元一次方程组应用题（1）作垂直平分线（2）利用中位线求边长（1）作垂线（2）利用三角函数求边长解答题二20（1）作垂直平分线（2）利用外角求角度分式方程的应用（1）画树状图（2）求概率21几何证明与计算（菱形的性质、等腰三角和等边三角形的性质）解直角三角形几何证明与计算（折叠）22数据分析（频数分布图、扇形、估算）数据分析（条形、扇形、估算）（1）二元一次方程组应用（2）一元一次不等式应用解答题三23函数小综合（一次函数、二次函数、锐角三角函数）函数小综合（反比例函数、一次函数、二次函数）反比例函数与一次函数(最短路径问题)24（1）圆切线的性质、圆的基本性质、角平分线（2）切线的性质、平行和等腰三角形（3）全等、相似的证明和性质、求弧长（1）相似证明（2）三角形的性质（3）圆的切线的证明（1）角（圆的垂径定理）（2）特殊四边形的证明（3）垂直25图形变换，动态的问题、数形结合（1）求点的坐标（2）等腰三角形存在性讨论（3）二次函数、分类讨论、数形结合等求面积的最小值图形变换，动态的问题、数形结合（1）平行四边形的判定（2）全等三角形的性质和判定（3）二次函数、分类讨论、数形结合等求面积的最大值动点问题，数形结合（1）几何基本计算（2）三角函数计算边长（3）积，解直角三角形应用，二次函数求最值，二次根式计算。

近六年广东省中考数学试题各小题的考点分析（一）年年考的题型有（12点）1．数的简单计算（相反数、绝对值、算术平方根、倒数等，其中08年绝对值，09年算术平方根，10年相反数，11年倒数，12年绝对值，预测今年算术平方根、相反数）；以及数的综合计算（往往综合零指数、负指数、方根、特殊角的三角函数、绝对值化简等）。

通常是一大一小（3+6=9分）；2．科学记数法（都是与当年最热时事相关的数据，近几年都是以正整数指数为主，预测今年也是考正指数幂的科学记数法。

分值一般是3分或4分）3．式的简单计算（幂的计算、乘法公式、根式与分式等计算）；以及式的综合计算（有时还设计成化简求值的题，主要考查整式与分式的基本计算），分值一般是3分、4分或6分。

预测今年中考一小一大。

（2）[2010广东第2题]下列运算正确的是（ ）A ．abba 532=+B ．b a b a -=-4)2(2C ．22))((bab a b a -=-+D ．222)(bab a +=+（3）[2012广东第12题]先化简，再求值：（x+3）（x ﹣3）﹣x （x ﹣2），其中x=4． （4）[2009广东第2题] 计算23)(a 的结果是A. 6aB. 9aC.5aD. 8a4．作图题（用尺规作图或者方格纸中作图，纯作图的题已不太会出现，一般以三角形、四边形或圆等几何图形为背景，设计一、两问的回答）。

分值一般为6分。

07年作线段的垂直平分线并求线段的长；08年作中线并求线段的长；09年过点作已知线的垂线并证明边相等；10年作平移和旋转后的直角三角形；11年作平移后的圆并求面积。

12年角平分线，今年预测中线、垂直线的作法。

如：（1）[2012广东第14题]如图，在△ABC 中，AB=AC ，∠ABC=72°．（1）用直尺和圆规作∠ABC 的平分线BD 交AC 于点D （保留作图痕迹，不要求写作法）； （2）在（1）中作出∠ABC 的平分线BD 后，求∠BDC 的度数．5．探究规律（数的计算、式的计算、图形计数、图形计算等，往往设计在第10题和解答题，近三年都设计为一大一小。

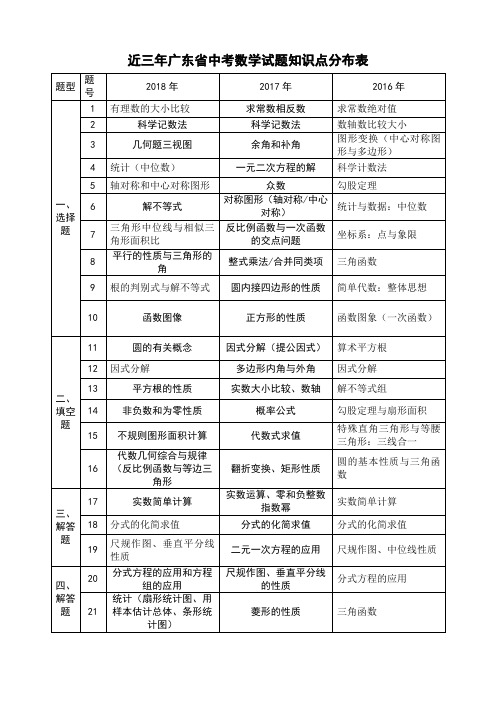
分析人：2018--2020广东省数学中考试卷分析目录C O N T E N T 01近三年试卷各考题和分数分配02每年考题的特点03今后复习的建议01 近三年试卷各考题和分数分配201820192020年份题号1实数大小比较绝对值 相反数2科学计数法 科学计数法中位数3三视图 三视图 关于x轴对称的点的坐标4中位数幂的运算 多边形内角和5二次根式有意义6不等式解法 中位数 中位线7相似比 实数大小比较 二次函数平移8角度计算 二次根式化简 不等式组解法9折叠求线段长度10函数图像综合 几何综合 二次函数图像综合201820192020年份题号实数运算 分解因式11圆心角、圆周角关系12分解因式 平行线性质 同类项概念13平方根 多边形内角和 二次根式、绝对值非负性14非负性 整体思想运算 整体思想计算15阴影部分面积 解直角三角形 运用菱形、等腰三角形等性质计算角度16圆锥侧面积公式17解直角三角形 函数图象综合 几何综合年份题号20182019202024待定系数法求函数解析式、函数图像性质综合 圆的性质、三角形、四边形性质等综合反比例函数、一次函数三角形等综合25旋转、二次函数最值，相似等综合 相似、三角形面积公式、二次函数最值一次函数、二次函数、相似等综合02 每年考题的特点2018年此部分内容作为文字排版占位显示 （建议使用主题字体）标题文本预设此部分内容作字排版占位显示 （建议使用主题字体）标题文本预设点击输入标题内容1、依据课标、紧扣考纲点击输入标题内容2、重视基础、体现常规点击输入标题内容难题主要有：16题（4分）、23题（3）小题（3分）、24题（3）小题（4分）、25题（3）小题（3分）（16题填空题4分）知识点：反比例函数、等边三角形、解一元二次方程、图形规律。

（25题解答题9分）代数、几何综合：双动点分析，分类讨论思想；图形的旋转；等边三角形；勾股定理；等面积法（或相似）求线段长；三角函数的定义；二次函数的最值；（24题解答题9分）圆的综合：平行线的判定；全等三角形的判定与性质；圆的切线判定；三角函数；直角三角形的性质；圆周角定理及其推论；相似三角形的判定与性质；3、突出能力、体现选拔（23题解答题9分）函数综合：一次函数与二次函数的交点问题、待定系数法求函数解析式、三角函数、分类讨论思想；4、力求创新、美中不足保持稳定、力求创新：（1） 试卷重视四基（基础知识、基本技能、基本数学思想方法和基本活动经验）的考查；（2）试卷重视对运算能力、推理能力、应用意识和综合能力的考查；（3）试卷体现数学思想方法，特别是：转换与化归、数形结合、方程与函数、分类讨论；（4）试卷力求创新，在题目设置上有不少想法（如16，23（3），24，25等）难度偏大、美中不足：(1）难题或中难题占比过大：如15、16、23（3）（2）试卷整体布局可以更加合理：如24、25题；（3）试卷梯度可以更加明显（三种题目最好都能从易到难）：如23（3）、24（1）（2）2019年此部分内容作为文字排版占位显示 （建议使用主题字体）标题文本预设此部分内容作字排版占位显示 （建议使用主题字体）标题文本预设点击输入标题内容1、整体分析：考察模块和难易度选择题基础题的特点：相当基础，大部分知识比较常规，与往年相差不大，是常考点，也是热门考点。

广东中考数学试题及答案分析作为广东中考数学试题的考生，备战考试需要对历年试题进行彻底的分析和掌握。

本文将就广东中考数学试题的难点和解题思路进行详尽解析，希望能够帮助同学们更好地备考。

一、选择题分析广东中考数学试卷中，选择题是考生最先接触到的部分。

这一部分的题目选自各个知识点，考查基础知识掌握情况以及对解题思路的应用能力。

以下是一道典型的选择题：题目：已知集合A={x|2x-1<5}，集合B={y|y^2-6*y+5>0}，则集合A∩B中元素的个数为（）。

A. 0B. 1C. 2D. 3解析：首先我们要分别解出集合A和集合B的元素范围。

对于集合A，我们可以将不等式2x-1<5进行变形得到x<3，即所有使得2x-1小于5的x的取值都小于3。

对于集合B，我们可以将不等式y^2-6*y+5>0进行因式分解得到(y-1)(y-5)>0，即函数图像在y轴上的零点为1和5，故y的取值范围为(负无穷，1) U (5，正无穷)。

取集合A和集合B的交集，我们可以将两个集合的取值范围进行比较，即小于3并且大于5的数是不存在的，所以集合A∩B中元素的个数为0，选项A 为正确答案。

二、填空题分析填空题是广东中考数学试卷中的重要组成部分，涵盖了各个知识点的应用和推理能力。

以下是一道典型的填空题：题目：若正数a和b满足a^2+b^2=17，且a+b≥4，则a的最小值为_____。

解析：根据题目已知条件，我们可以列出不等式组a^2+b^2=17以及a+b≥4。

为了求a的最小值，我们需要先将两个不等式进行化简。

由于a和b都为正数，根据柯西不等式，我们可以得出2(a^2+b^2)≥(a+b)^2，即2*17≥(a+b)^2，所以34≥(a+b)^2。

由于a+b≥4，所以(a+b)^2≥4^2=16，两个不等式组合起来，我们可以得出34≥(a+b)^2≥16，从而推导出a的最小值为根号16=4。

三、解答题分析解答题是广东中考数学试卷中较为考查学生问题解决能力和综合运用能力的一部分。

广东中考数学真题和答案解析及答案解析近年来，广东中考数学试卷一直备受瞩目。

无论是难度还是题目设计，都给考生们带来了一定的挑战。

本文将针对近几年的广东中考数学试题，对其中的几个经典题目进行解析，帮助考生们更好地应对考试。

一、面积题在广东中考数学试卷中，面积题常常出现，考查学生对图形的面积计算能力。

例如，以往一道比较经典的题目是：一块土地为长方形，长4m，宽3m。

上面种植了一片蔬菜，后来蔬菜不收成，又重新种植蔬菜。

新蔬菜的种植后，长方形土地的面积是原来的1.4倍，宽仍为原来的宽的一半。

求新蔬菜的种植面积。

解析：设新蔬菜的种植面积为S，根据题意可得新蔬菜的种植长为4m，种植宽为3/2m。

根据面积的计算公式S=长×宽，可以得到：S = 4 × 3/2 = 6因此，新蔬菜的种植面积为6平方米。

二、函数题函数题是广东中考数学试卷中的必考题型。

一个经典的函数题如下：已知函数y = f(x) = 2x + 1，求函数f(3)的值。

解析：函数y = f(x) = 2x + 1中，当x = 3时，可以计算得到：f(3) = 2 × 3 + 1 = 7因此，函数f(3)的值为7。

三、几何题几何题在广东中考数学试卷中也是常见的题型。

考生们需要掌握几何形状的性质，并能够根据题目要求进行推理和计算。

下面举例一道经典的几何题：如图，△ABC是等腰三角形，AB = AC，D为BC的中点，E为AB的中点，AD与BE交于点F。

已知AF:FD = 2:1，如果AB = 10cm，求△ABC的面积。

解析：首先，由已知条件可以得知BD = DC = 5cm，AE = EB =5cm。

因此，△ADE和△BFE都是等腰三角形。

根据题目中已知条件AF:FD = 2:1，可以得到AF = 6cm，FD =3cm。

再根据△ADE和△BFE是等腰三角形，可以得到DE = 4cm，BF =8cm。

根据△ABC的性质可知，△ABC是一个等腰直角三角形，AB = AC，∠ABC = 90度。

七，图形与变化19．（6分）（2019•广东）如图，在△ABC中，点D是AB边上的一点．（2）在（1）的条件下，若＝2，求的值．（1）请用尺规作图法，作19．（6分）（2018•广东）如图，BD是菱形ABCD的对角线，∠CBD＝75°，20．（7分）（2017•广东）如图，在△ABC中，∠A＞∠B．19．（6分）（2016•广东）如图，具体分析：2016—2019均考察了尺规作图，包括等角的作图，垂直平分线、中线、角平分线、垂线的作图等。

考查频次：7年4考，以解答题形式出现，20年之后没有再考查，这与20年后题型的调整相关。

考查角度：直接考查尺规作图，除2017年位置在解答题（二）外，其于年份均在解答题（一）的位置；均为两问，第一问考察尺规作图，第二问在第一问的基础上，考察所作角、线的性质，为递进关系。

（2）视图，展开图，命题和投影6．（3分）（2021•广东）下列图形是正方体展开图的个数为（）A．1个B．2个C．3个D．4个3．（3分）（2019•广东）如图，由4个相同正方体组合而成的几何体，它的左视图是（）A．B．C．D．A．B．C．D．具体分析：18-21年都有考察。

其中，2021-6考察正方体的展开图；19-3（左视图）和18-3（主视图）考察几何体的视图考，均以选择题形式出现，比较简单考查角度：①直接考查矩形/正方形/正三棱锥/圆柱/圆锥的展开图②考察规则图形或组合图形的三视图同类型的题有：图形的对称5．（3分）（2019•广东）下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（）A．B．C．D．具体分析：2016-2019年均考察了图形的对称性，17、18、19年考察了中心对称图形和轴对称图形，16年只考察了中心对称图形；其中19年直接用图形表达，和之前相比更加立体直观从20年开始，没有再考查过图形的对称和视图，只在21年考察了一次正方体的展开图。

考查角度：直接考查中心对称图形和轴对称图形的性质，比较简单专题：图形的折叠、平移和旋转①折叠后求线段的长度问题23．（8分）（2021•广东）如图，边长为1的正方形ABCD中，点E为AD的中点．连接BE，将△ABE沿BE折叠得到△FBE，BF交AC于点G，求CG的长．具体分析：延长BF交CD于H，连接EH．证明△EDH∽△BAE，推出＝＝，推出DH＝，CH＝，由CH∥AB，推出＝＝，可得结论．9．（3分）（2020•广东）如图，在正方形ABCD中，AB＝3，点E，F分别在边AB，CD 上，∠EFD＝60°．若将四边形EBCF沿EF折叠，点B′恰好落在AD边上，则BE的长度为（）A．1B．C．D．2具体分析：已知∠EFD＝∠BEF＝60＝∠FEB'＝60°，BE＝B'E设BE＝x，则B'E＝x，AE＝3﹣x，由直角三角形的性质可得：2（3﹣x）＝x，解方程求出x16．（4分）（2017•广东）如图，矩形纸片ABCD中，AB=5，BC=3，先按图（2）操作：将矩形纸片ABCD沿过点A的直线折叠，使点D落在边AB上的点E处，折痕为AF；再按图（3）操作，沿过点F的直线折叠，使点C落在EF上的点H 处，折痕为FG，则A、H两点间的距离为．具体分析：连接AH．由题意可知在Rt△AEH中，AE=AD=3，EH=EF﹣HF=3﹣2=1，根据AH=，计算即可．15．（4分）（2016•广东）如图，矩形ABCD中，对角线AC=2，E为BC边上一点，BC=3BE，将矩形ABCD沿AE所在的直线折叠，B点恰好落在对角线AC上的B′处，则AB=．具体分析：∵△EB′C是直角三角形，BC=3BE ∴EC=2B′E ∴∠ACB=30°∴AC=2AB 可求出AB的长．具体分析：2016-15、2017-16、2020-9、2021-23均考察了图形的折叠问题，均求折叠后线段的长度解题方法：①不存在特殊角的：做辅助线，证相似或全等，找出所求线段与已知线段之间的比例关系，可解（2021-23）②存在特殊角的：找出特殊角，并根据特殊角的性质可解（2016-15直接求解；2020-9借助一次方程求解）③直角三角形中，a,已知其他两边的长度，求第三边，利用勾股定理直接求（2017-16）B,已知三边的整式表达，利用勾股定理列一元方程求解考查角度：本类题综合考查矩形/正方形的性质和折叠问题、勾股定理、含30°角的直角三角形的性质等知识，明确翻折前后的图形全等、灵活运用所学知识解决问题是解题的关键，难度中等，属于中考常考题型。