江苏省13市高三上学期考试数学试题分类汇编:圆锥曲线 Word版含答案
- 格式:doc
- 大小:3.21 MB
- 文档页数:11

江苏省13大市2013届高三上学期期末数学试题分类汇编 导数及其应用 1、(南通市2013届高三期末)曲线在点(1,f(1))处的切线方程为 ▲ . 答案:. 2、(苏州市2013届高三期末)过坐标原点作函数图像的切线,则切线斜率为 . 答案: 3、(泰州市2013届高三期末)曲线y=2lnx在点(e,2)处的切线与y轴交点的坐标为 (0,0) 4、(扬州市2013届高三期末)已知函数()在区间上取得最小值4,则 ▲ . 5、(常州市2013届高三期末)第八届中国花博会将于2013年9月在常州举办,展览园指挥中心所用地块的形状是大小一定的矩形ABCD,,.a,b为常数且满足.组委会决定从该矩形地块中划出一个直角三角形地块建游客休息区(点E,F分别在线段AB,AD上),且该直角三角形AEF的周长为(),如图.设,△的面积为. (1)求关于的函数关系式; (2)试确定点E的位置,使得直角三角形地 块的面积最大,并求出的最大值. 解:(1)设,则,整理,得.………3分 ,. …………………………………4分 (2) 当时,,在递增,故当时,; 当时,在上,,递增,在上,,递减,故当时,. 6、(连云港市2013届高三期末)(连云港市2013届高三期末)某单位决定对本单位职工实行年医疗费用报销制度,拟制定医疗费用在2万元10万元2万元10万元方案报销医疗费用y(万元)随医疗总费用x(万元)增加而增加报销医疗费用不得低于医疗总费用的50%报销医疗费用不得超过万元. (1)请分析采用函数模型y0.05(x2+4x+8)作为报销方案; (2)若定采用函数模型y+a(a为常数)作为报销方案,请你确定整数的值.(1)函数y=0.05(x2+4x+8)在[2,10]上是增函数,满足条件①, ……………2分 当x=10时,y有最大值7.4万元,小于8万元,满足条件③. ………………………4分 但当x=3时,y=0得xb时由(1)知x1=b,x2=A(b,0)B 当a<b时 x1=,x2=b 同理可得a-b=(舍) 综上a-b=………………………………………………..………………………….7分 的减区间为即(b,b+1)(x)减区间为 ∴公共减区间为(b,b+)长度为…………………………….……………………10分 (3) 若,则左边是一个一次因式,乘以一个恒正(或恒负)的二次三项式,或者是三个一次因式的积,无论哪种情况,总有一个一次因式的指数是奇次的,这个因式的零点左右的符号不同,因此不可能恒非负。

2010-2011学年第一学期江苏省13市高三数学期末考试题分类汇编----圆锥曲线解答题【南京市】在直角坐标系xOy 中,中心在原点O ,焦点在x 轴上的椭圆C 上的点到两焦点的距离之和为(1)求椭圆C 的方程;(2)过椭圆C 的右焦点F 作直线l 与椭圆C 分别交于A 、B 两点,其中点A 在x 轴下方,且3AF FB .求过O 、A 、B 三点的圆的方程.【南通市】18.(本题满分15分)如图,已知椭圆22:11612x yC+=的左、右顶点分别为A、B,右焦点为F,直线l为椭圆的右准线,N为l上一动点,且在x轴上方,直线AN与椭圆交于点M.(1)若AM=MN,求∠AMB的余弦值;(2)设过A,F,N三点的圆与y轴交于P,Q两点,当线段PQ的中点坐标为(0,9)时,求这个圆的方程.【苏州市】 如图,椭圆22143x y +=的左焦点为F ,上顶点为A ,过点A 作直线AF 的垂线分别交椭圆、x 轴于B 、C 两点(1)若AB BC λ= ,求实数λ的值(2)设点P 为ACF ∆的外接圆上的任意一点,当PAB ∆面积最大时,求P 坐标【无锡市】已知椭圆2214xy+=的左顶点为A,过A作两条互相垂直的弦AM,AN交椭圆于M、N两点,(1)当直线AM的斜率为1时,求点M的坐标(2)当直线AN的斜率变化时,直线MN是否过x轴上的一定点,若过定点,请给证明,并求出定点;若不过,说明理由。
【常州市】在平面直角坐标系xoy 中,椭圆C :22221(0)x y a b a b+=>>的右焦点为F (4,0)m (0m >,m 为常数),离心率为0.8,过焦点F 、倾斜角为θ的直线l 交椭圆C 于M 、N 两点(1) 求椭圆C 的标准方程(2) 若2πθ=时,119MF NF +=,求实数m (3) 试问11MF NF+的值是否与θ得大小无关,并证明你的结论。
【镇江市】已知圆C 方程228(62)610x y mx m y m +--+++=(,0)m R m ∈≠,椭圆的中心在原点,焦点在x 轴上(1)证明圆C 恒过一定点M ,并求此定点M 的坐标(2)判断直线4330x y +-=与圆C 的位置关系,并证明你的结论(3)当2m =时,圆C 与椭圆的左准线相切,且椭圆过点M ,求此时椭圆方程;在x 轴上是否存在两个定点A 、B ,使得对椭圆上任意一点Q (异于长轴端点),直线QA ,QB 的斜率之积为定值?若有求出,没有说明理由。

各城区高三上学期期末圆锥曲线汇编及答案精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-圆锥曲线一.选填练习1.“10m >”是“”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件2.已知直线0-+=x y m 与圆22:1+=O x y 相交于,A B 两点,且∆OAB 为正三角形,则实数m 的值为(A )23 (B)2(C )23或23- (D )26或26- 3. 设a ∈R ,则“1a =”是 “直线10ax y +-=与直线10x ay ++=平行”的(A )充分不必要条件 (B )必要不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 4.在极坐标系Ox 中,方程sin ρθ=表示的曲线是(A) 直线(B) 圆(C) 椭圆(D)双曲线5.若x ,y 满足110x y x y x +≤⎧⎪-≤⎨⎪≥⎩,,, 则2z x y =-的最大值是(A) 2- (B) 1- (C) 1 (D) 26.设m 是不为零的实数,则“0m >”是“方程221x y m m-=表示双曲线”的(A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件 (D )既不充分也不必要条件7.已知直线0x y m -+=与圆O :221x y +=相交于A ,B 两点,且OAB ∆为正三角形,则实数m 的值为(A(B)(C或(D)8.已知a ∈R ,那么“直线1y ax =-与42y ax =-+垂直”是“12a =”的 A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件9.已知点()2,1A -,点),(y x P 满足线性约束条件20,10,24,x y x y +≥⎧⎪-≤⎨⎪-≥⎩O 为坐标原点,那么OP OA ⋅的最小值是A. 11B. 0C. 1-D. 5-10.在极坐标系中,已知点A 是以2,6π⎛⎫⎪⎝⎭为圆心,1为半径的圆上的点,那么点A 到极点的最大距离是_____.11.已知A ,B 是函数2x y =的图象上的相异两点.若点A ,B 到直线12y =的距离相等,则点A ,B 的横坐标之和的取值范围是 (A )(,1)-∞- (B )(,2)-∞- (C )(1,)-+∞ (D )(2,)-+∞12.已知M 为曲线C :3cos ,sin x y θθ=+⎧⎨=⎩(θ为参数)上的动点.设O 为原点,则OM 的最大值是(A )1 (B )2 (C )3(D )413.已知点F 为抛物线C :()220y px p =>的焦点,点K 为点F 关于原点的对称点,点M 在抛物线C 上,则下列说法错误..的是 (A )使得MFK ∆为等腰三角形的点M 有且仅有4个 (B )使得MFK ∆为直角三角形的点M 有且仅有4个(C )使得4MKF π∠=的点M 有且仅有4个 (D )使得6MKF π∠=的点M 有且仅有4个14.点(2,0)到双曲线2214x y -=的渐近线的距离是______________ .(11)设抛物线C :24y x =的顶点为O ,经过抛物线C 的焦点且垂直于x 轴的直线和抛物线C 交于A ,B 两点,则OA OB += .15.过双曲线22221(0x y a a b-=>,0)b >的一个焦点F 作一条与其渐近线垂直的直线,垂足为A ,O 为坐标原点,若OF OA 21=,则此双曲线的离心率为 (A) 2(B) 3(C) 2 (D) 516.能够说明“方程22(1)(3)(1)(3)m x m y m m -+-=--的曲线是椭圆”为假命题的一个m 的值是 .17. 已知圆22(2)9x y -+=的圆心为C .直线l 过点(2,0)M -且与x 轴不重合,l 交圆C 于,A B 两点,点A 在点M ,B 之间.过M 作直线AC 的平行线交直线BC 于点P ,则点P 的轨迹是A. 椭圆的一部分B. 双曲线的一部分C. 抛物线的一部分D. 圆的一部分18. 已知中心在原点,焦点在坐标轴上的双曲线C ,则双曲线C 的渐近线方程为 .19..已知双曲线C的中心在原点,对称轴为坐标轴,它的一个焦点与抛物线28y x=的焦点重合,一条渐近线方程为0x y+=,则双曲线C的方程是.20.若变量x,y满足约束条件40,540,540,x yx yx y+-≥⎧⎪-+≥⎨⎪--≤⎩则22x y+的最小值为.21.已知双曲线C:2221(0)yx bb-=>的一个焦点到它的一条渐近线的距离为1,则b= ;若双曲线1C与C不同,且与C有相同的渐近线,则1C的方程可以为.(写出一个答案即可)22.已知点(,)M x y的坐标满足条件10,10,10.xx yx y-⎧⎪+-⎨⎪-+⎩≤≥≥设O为原点,则OM的最小值是____.二.大题练习(本小题14分)已知椭圆22221(0)x yC a ba b+=>>:的离心率等于22,经过其左焦点(1,0)F-且与x轴不重合的直线l与椭圆C交于,M N两点.(Ⅰ) 求椭圆C的方程;(Ⅱ) O为原点,在x轴上是否存在定点Q,使得点F到直线QM,QN的距离总相等?若存在,求出点Q的坐标;若不存在,说明理由.2.本小题13分)已知椭圆的右焦点与短轴两个端点的连线互相垂直.(Ⅰ)求椭圆的标准方程; (Ⅱ)设点为椭圆的上一点,过原点且垂直于的直线与直线交于点,求面积的最小值.3.CY (本小题满分14分)已知椭圆2222:1(0)5x y C b b b+=>的一个焦点坐标为(2,0).(Ⅰ)求椭圆C 的方程;(Ⅱ)已知点(3,0)E ,过点(1,0)的直线l (与x 轴不重合)与椭圆C 交于,M N两点,直线ME 与直线5x =相交于点F ,试证明:直线FN 与x 轴平行. 4. (本小题满分14分)已知抛物线:C 24x y =的焦点为F ,过抛物线C 上的动点P (除顶点O 外)作C 的切线l 交x 轴于点T .过点O 作直线l 的垂线OM (垂足为M )与直线PF 交于点N .(Ⅰ)求焦点F 的坐标;(Ⅱ)求证:FT MN ;(Ⅲ)求线段FN 的长.(本小题13分)已知椭圆C :2229x y +=,点(2,0)P . (Ⅰ)求椭圆C 的短轴长与离心率;(Ⅱ)过(1,0)的直线l 与椭圆C 相交于M 、N 两点,设MN 的中点为T ,判断||TP 与||TM 的大小,并证明你的结论.6. (本小题14分)已知椭圆22:13+=x y C m m,直线:20+-=l x y 与椭圆C 相交于P ,Q 两点,与x 轴交于点B ,点,P Q 与点B 不重合. (Ⅰ)求椭圆C 的离心率;(Ⅱ)当2∆=OPQ S 时,求椭圆C 的方程;(Ⅲ)过原点O 作直线l 的垂线,垂足为.N 若λ=PN BQ ,求λ的值.7.SJS (本小题共14分)已知椭圆2222:1(0)x y C a b a b +=>>离心率等于12,(2,3)P 、(2,3)Q -是椭圆上的两点.(Ⅰ)求椭圆C 的方程;(Ⅱ),A B 是椭圆上位于直线PQ 两侧的动点.当,A B 运动时,满足APQ BPQ ∠=∠,试问直线AB 的斜率是否为定值?如果为定值,请求出此定值;如果不是定值,请说明理由.8.(本小题共14分)已知椭圆2222:1(0)x y C a b a b +=>>离心率等于12,(2,3)P 、(2,3)Q -是椭圆上的两点.(Ⅰ)求椭圆C 的方程;(Ⅱ),A B 是椭圆上位于直线PQ 两侧的动点,若直线AB 的斜率为12,求四边形APBQ 面积的最大值.9.(本小题满分14分)已知椭圆2222:1(0)x y C a b a b+=>>过点(2,0)A .(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线y kx =C 交于,M N 两点.若直线3x =上存在点P ,使得四边形PAMN 是平行四边形,求k 的值.10.(本小题满分14分)已知椭圆2222:1(0)x y C a b a b+=>>过(2,0)A ,(0,1)B 两点.(Ⅰ)求椭圆C 的方程及离心率;(Ⅱ)设点Q 在椭圆C 上.试问直线40x y +-=上是否存在点P ,使得四边形PAQB 是平行四边形?若存在,求出点P 的坐标;若不存在,说明理由.11.(本题满分13分)已知椭圆()222210x y a b a b+=>>过点()0,1-,离心率2e =.(Ⅰ)求椭圆的方程;(Ⅱ)已知点(),0P m ,过点()1,0作斜率为()0k k ≠直线l ,与椭圆交于M ,N 两点,若x 轴平分MPN ∠ ,求m 的值.圆锥曲线答案一.选填练习1. A2. D3. C4. B5. D6. A7. D8. B9. C 10. 3 11 B 12. D 13. C 14.2 15. C 16. (,1]{2}[3,)m ∈-∞+∞17. B 18. y x =± 19. 22122x y -= 20. 8 21. 1,222x y -=等二.大题练习1.(本题满分共14分)解:(I)由题意得221 1.a ab ⎧=⎪⎨⎪=+⎩解得 1.a b ⎧=⎪⎨=⎪⎩ 故椭圆C 的方程为2212x y +=.(II )当直线MN 斜率存在时,设直线MN 的方程为(1)(0)y k x k =+≠.由22(1),1,2y k x x y =+⎧⎪⎨+=⎪⎩消去y 得2222(12)4(22)0k x k x k +++-=. 易得0∆>.设1122(,),(,)M x y N x y ,则2122212241222.12k x x k k x x k ⎧-+=⎪⎪+⎨-⎪=⎪+⎩, 设(,0)Q t .由点,M N 在x 轴异侧,则问题等价于“QF 平分MQN ∠”,且12,x t x t ≠≠,又等价于“12120QM QN y yk k x t x t+=+=--”,即1221()()0y x t y x t -+-=. 将1122(1),(1)y k x y k x =+=+代入上式,整理得12122()(1)20x x x x t t ++--=. 将①②代入上式,整理得20t +=,即2t =-, 所以(20)Q -,.当直线MN 的斜率不存在时,存在(20)Q -,也使得点F 到直线QM ,QN 的距离相等.故在x 轴上存在定点(20)Q -,,使得点F 到直线QM ,QN 的距离总相等.2(共13分)解:(Ⅰ)由题意,得解得.所以椭圆的方程为.(Ⅱ)设,,则. 当时,点,点坐标为或,. ① ②当时,直线的方程为.即,直线的方程为.点到直线的距离为,.所以,.又,所以且, 当且仅当,即时等号成立,综上,当时,取得最小值1.3. (本小题满分14分)解:(Ⅰ)由题意可知222,5.c a b =⎧⎨=⎩所以225,1a b ==.所以椭圆C 的方程为2215x y +=. (Ⅱ)①当直线l 的斜率不存在时,此时MN x ⊥轴.设(1,0)D ,直线5x =与x 轴相交于点G ,易得点(3,0)E 是点(1,0)D 和点(5,0)G 的中点,又因为||||MD DN =,所以||||FG DN =.所以直线//FN x 轴.②当直线l 的斜率存在时,设直线l 的方程为(1)(0)y k x k =-≠,1122(,),(,)M x y N x y .因为点(3,0)E ,所以直线ME 的方程为11(3)3y y x x =--. 令5x =,所以11112(53)33F y y y x x =-=--. 由22(1),55y k x x y =-⎧⎨+=⎩消去y 得2222(15)105(1)0k x k x k +-+-=. 显然0∆>恒成立.所以22121222105(1),.5151k k x x x x k k -+==++ 因为1211211221112(3)2(1)(3)2(1)333F y y x y k x x k x y y y x x x -------=-==--- 22221212115(1)10[35][3()5]515133k k k k x x x x k k x x --⨯+-++++==--22221516510513k k k k k x --++=⋅=+- 所以2F y y =. 所以直线//FN x 轴.综上所述,所以直线//FN x 轴. 4. (本小题满分14分)解:(Ⅰ) (0,1)F ……………2分 (Ⅱ)设00(,)P x y .由24x y =,得214y x =,则过点P 的切线l 的斜率为0012x x k y x ='==.则过点P 的切线l 方程为2001124y x x x =-.令0y =,得012T x x =,即01(,0)2T x .又点P 为抛物线上除顶点O 外的动点,00x ≠,则02TF k x =-.而由已知得MN l ⊥,则02MN k x =-又00x ≠,即FT 与MN 不重合, 即FTMN .(Ⅲ)由(Ⅱ)问,直线MN 的方程为02y x x =-,00x ≠.直线PF 的方程为0011y y x x --=,00x ≠.设MN 和PF 交点N 的坐标为(,)N N N x y 则0002.........(1)11..........(2)NN NN y x x y y x x ⎧=-⎪⎪⎨-⎪=+⎪⎩由(1)式得,02NNx x y =-(由于N 不与原点重合,故0N y ≠).代入(2),化简得02NNy y y -=()0N y ≠.又2004x y =,化简得,22(1)1NN x y +-= (0N x ≠).即点N 在以F 为圆心,1为半径的圆上.(原点与()0,2除外) 即1FN =. …………14分 5. (本小题13分)解:(Ⅰ)C :221992x y +=,故29a =,292b =,292c =,有3a =,b c ==椭圆C的短轴长为2b =离心率为c e a ==.……………..5分(Ⅱ)方法1:结论是:||||TP TM <.当直线l 斜率不存在时,:1l x =,||0||2TP TM =<=……………..7分当直线l 斜率存在时,设直线l :(1)y k x =-,11(,)M x y ,22(,)N x y2229(1)x y y k x ⎧+=⎨=-⎩,整理得:2222(21)4290k x k x k +-+-= ……………..8分 22222(4)4(21)(29)64360k k k k ∆=-+-=+>故2122421k x x k +=+,21222921k x x k -=+ ……………..9分PM PN ⋅1212(2)(2)x x y y =--+ 21212(2)(2)(1)(1)x x k x x =--+-- 2221212(1)(2)()4k x x k x x k =+-++++2222222294(1)(2)42121k k k k k k k -=+⋅-+⋅++++226521k k +=-+ 0<……………..1 故90MPN ∠>︒,即点P 在以MN 为直径的圆内,故||||TP TM <(Ⅱ)方法2:结论是:||||TP TM <.当直线l 斜率不存在时,:1l x =,||0||2TP TM =<=……………..7分当直线l 斜率存在时,设直线l :(1)y k x =-,11(,)M x y ,22(,)N x y ,(,)T T T x y2229(1)x y y k x ⎧+=⎨=-⎩,整理得:2222(21)4290k x k x k +-+-= ……………..8分 22222(4)4(21)(29)64360k k k k ∆=-+-=+>故2122421k x x k +=+,21222921k x x k -=+ ……………..9分212212()221T k x x x k =+=+,2(1)21T T ky k x k =-=-+222242222222222222(22)494||(2)(2)()2121(21)(21)T Tk k k k k k TP x y k k k k ++++=-+=-+-==++++22222212121222224222222222111||(||)(1)()(1)()42441429(1)(169)16259(1)[()4]42121(21)(21)TM MN k x x k x x x x k k k k k k k k k k k ⎡⎤==+-=++-⎣⎦-++++=+-⋅==++++ 此时,424242222222221625949412165||||0(21)(21)(21)k k k k k k TM TP k k k ++++++-=-=>+++6. (本题共14分)解:(Ⅰ)m a 32=,m b =2,m c 22=, -------------32222==a c e ,故36=e . -----------------(Ⅱ)设()11,y x P ,()22,y x Q⎩⎨⎧=-+=+023322y x my x ,得到03122=-+m x x 12-4, 依题意,由2(12)44(123)0m ∆=--⨯⨯->得1m >.且有121231234x x m x x +=⎧⎪⎨-=⎪⎩, ------------------------6分12|PQ x x =-==, ------------------------7分原点到直线l 的距离2=d所以11||222OPQ S PQ d ∆=⋅== ------------------------9分解得 73m =>1, 故椭圆方程为223177x y +=. ------------------------1 (Ⅲ)直线l 的垂线为:ON y x =, ------------------------由20y xx y =⎧⎨+-=⎩解得交点)1,1(N , ------------------------12分因为PN BQ λ=,又123x x +=所以BQPN =λ=122212221=--=--x x x x ,故λ的值为1. ------------------------14分7.(本小题共14分)解:(Ⅰ)因为12c e a==,又222a b c =+,所以22224,3a c b c == ………2分设椭圆方程为2222143x y c c+=,代入(2,3),得2224,16,12c a b === ……4分椭圆方程为2211612x y +=…………5分(Ⅱ)当APQ BPQ ∠=∠时,,PA PB 斜率之和为0 …………6分 设PA 斜率为k ,则PB 斜率为k - …………7分设PA 方程为3(2)y k x -=-,与椭圆联立得223(2)3448y k x x y -=-⎧⎨+=⎩代入化简得:2222(34)8(32)4(4912)480k x k k x k k ++-++--=(2,3)P ,128(23)234k k x k-+=+ 同理228(23)234k k x k ++=+,2122161234k x x k -+=+,1224834kx x k --=+ 21122112()412AB y y k x x k k x x x x -+-===--即直线AB 的斜率为定值12.8.(本小题共14分)解:(Ⅰ)因为12c e a ==,又222a b c =+, 所以22224,3a c b c == ……… 2分设椭圆方程为2222143x y c c+=,代入(2,3),得2224,16,12c a b === ………4分椭圆方程为2211612x y += ……… 5分(Ⅱ)设1122(,),(,)A x y B x y ………6分设AB 方程为221211612y x t x y ⎧=+⎪⎪⎨⎪+=⎪⎩,代入化简得:22120x tx t ++-= ………8分 224(12)0t t ∆=-->,44t -<<1221212x x tx x t +=-⎧⎨=-⎩,又(2,3),(2,3)P Q - APBQ APQ BPQ S S S ∆∆=+1216||2x x =⨯⨯-==………13分 当0t =时,S最大为………14分 9.(本小题满分14分)解:(Ⅰ)由题意得2a =,c e a ==c =.[ 2分] 因为222a b c =+,[ 3分] 所以1b =,[ 4分]所以椭圆C 的方程为2214x y +=.[ 5分](Ⅱ)若四边形PAMN 是平行四边形,则 //PA MN ,且 ||||PA MN =.[ 6分] 所以 直线PA 的方程为(2)y k x =-, 所以 (3,)P k,||PA [ 7分] 设11(,)M x y ,22(,)N x y .由2244,y kx x y ⎧=+⎪⎨+=⎪⎩得22(41)80k x +++=, [ 8分]由0∆>,得 212k >.且12x x +=122841x x k =+.[ 9分]所以||MN=[10分]因为 ||||PA MN =, 所以= 整理得 421656330k k -+=,[12分]解得k =k =[13分] 经检验均符合0∆>,但k =PAMN 是平行四边形,舍去.所以 k ,或 k =[14分] 10.(本小题满分14分)解:(Ⅰ)由题意得,2a =,1b =.[ 2分]所以椭圆C 的方程为2214x y +=.[ 3分]设椭圆C 的半焦距为c ,则c =[ 4分]所以椭圆C 的离心率c e a ==[ 5分](Ⅱ)由已知,设(,4)P t t -,00(,)Q x y . [ 6分]若PAQB 是平行四边形,则 PA PB PQ +=,[ 8分]所以 00(2,4)(,3)(,4)t t t t x t y t --+--=--+, 整理得002, 3x t y t =-=-.[10分] 将上式代入220044x y +=,得 22(2)4(3)4t t -+-=,[11整理得2528360t t -+=, 解得185t =,或2t =.[13分]此时 182(,)55P ,或(2,2)P .经检验,符合四边形PAQB 是平行四边形,所以存在 182(,)55P ,或(2,2)P 满足题意.[14分11. 解:(Ⅰ)因为椭圆的焦点在x 轴上,过点()0,1-,离心率2e =,所以1b =,2c a =……………………2分 所以由222a b c =+,得2 2.a =……………………3分所以椭圆C 的标准方程是22 1.2x y +=……………………4分 (Ⅱ)因为过椭圆的右焦点F 作斜率为k 直线l ,所以直线l 的方程是(1)y k x =-.联立方程组()221,1,2y k x x y ⎧=-⎪⎨+=⎪⎩ 消去y ,得()2222124220.k x k x k +-+-= 显然0.∆>设点()11,M x y ,()22,N x y , 所以2122412k x x k +=+,212222.12k x x k -⋅=+……………………7分 因为x 轴平分MPN ∠,所以MPO NPO ∠=∠. 所以0.MP NP k k +=……………………9分 所以12120.y y x m x m+=--所以()()12210.y x m y x m -+-= 所以()()()()1221110.k x x m k x x m --+--= 所以()()1212220.k x x k km x x km ⋅-+++= 所以()2222224220.1212k k k k km km k k -⋅-++=++ 所以2420.12k km k-+=+……………………12分 所以420.k km -+=因为0k ≠,所以 2.m =……………………13分。

江苏省各地市 2020 年高考数学最新联考试题分类大汇编第 10 部分 : 圆锥曲线一、填空题:2. (2020 年 3 月苏、锡、常、镇四市高三数学教学情况调查一) 在平面直角坐标系xOy中,双曲线8kx2ky28的渐近线方程为;2.y22x 【解析】由题知 8x 2y 20 即 y2 2x .x 2y 21 a, b 0b2. (江苏省苏州市2020 年 1 月高三调研 )若双曲线a 2b2的离心率为 2 ,则a=▲.c1b 22,b 23,b3.2.3【解析】a22aaax 2y 2 1(a 0,b0)2020 届高三第一次模拟考试 )已知双曲线 C:a 2b29. (江苏省南京市的右顶点、右焦点分别为 A 、 F,它的左准线与x轴的交点为 B ,若 A 是线段 BF 的中点,则双曲线C 的离心率为.Ba 2 ,0 , A a,0 , F c,02ac a9.2 1【解析】由题意知:cc,则,即e 2 2e 1 0 ,解得 e21x 2y 2 1(a 0,b0))双曲线 a 2b 210.(江苏省徐州市 2020 届高三第一次调研考试的两条渐近线将平面划分为 “上、下、左、右 ”四个区域(不含边界) ,若点(1,2)在 “上”区域内,则双曲线离心率e的取值范围是▲.10.1,5x 2 y 2 1ybx 1,2a 2b 2a【解析】双曲线的一条渐近 线为,点 在该直线的上方,由线性规划知识,知:2b e21 ( b)2 5 e 1, 5a ,所以a ,故4. ( 江苏省苏北四市 2020 届高三第一次调研) 若抛物线的焦点坐标为(2,0) ,则抛物线的标准方程是▲.y 2p24.【解析】根据焦点坐标在x轴上,可设抛物线标准方程为2 px,有 2 ,p4,抛物线标准方2程为 y 8x2x 2y11. (江苏省泰州市 2020 届高三年级第一次模拟)双曲线3的离心率是 。
2 【解答】由题知a 21,b 2 3, c 24 于是离心率ec2 1.a 。

江苏省13大市2013届高三上学期期末数学试题分类汇编圆锥曲线一、填空题1、(常州市2013届高三期末)已知双曲线22221(0,0)x y a b a b -=>>的一条渐近线经过点(1,2),则该双曲线的离心率的值为 ▲ 答案2、(连云港市2013届高三期末)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2 = 4x 的准线交于A 、B 两点,AB =3,则C 的实轴长为 ▲ . 答案:13、(南京市、盐城市2013届高三期末)已知1F 、2F 分别是椭圆14822=+y x 的左、右焦点,点P 是椭圆上的任意一点, 则121||PF PF PF -的取值范围是 ▲ .答案:[0,2]+4、(南通市2013届高三期末)已知双曲线22221y x a b-=的一个焦点与圆x 2+y 2-10x =0的圆心,则该双曲线的标准方程为 ▲ .答案:221520y x -=. 5、(徐州、淮安、宿迁市2013届高三期末)已知双曲线)0,0(12222>>=-b a by ax 的右焦点为,F 若以F 为圆心的圆05622=+-+x y x 与此双曲线的渐近线相切,则该双曲线的离心率为 ▲ . 答案:56、(苏州市2013届高三期末)在平面直角坐标系xOy 中,双曲线2222:1(0,0)x y E a b a b-=>>的左顶点为A ,过双曲线E 的右焦点F 作与实轴垂直的直线交双曲线E 于B ,C 两点,若ABC ∆为直角三角形,则双曲线E 的离心率为 . 答案:27、(泰州市2013届高三期末)设双曲线22145x y -=的左、右焦点分别为1F ,2F ,点P 为双曲线上位于第一象限内一点,且12PF F V 的面积为6,则点P 的坐标为 答案:⎪⎪⎭⎫⎝⎛2,556 8、(无锡市2013届高三期末)如图,过抛物线y 2=2px (p>0)的焦点F 的直线L 交抛物线于点A 、B ,交其准线于点C ,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 。

一、填空题:10.(江苏省苏锡常镇四市2013年3月高三教学情况调研—)已知1F ,2F 是双曲线的两个焦点,以线段12F F 为边作正12MF F ∆,若边1MF 的中点在此双曲线上,则此双曲线的离心率为 ▲ . 【答案】31+11.(江苏省扬州市2013年3月高三第二次调研)在平面直角坐标系xOy 中,已知A 、B 分别是双曲线2213y x -=的左、右焦点,△ABC 的顶点C 在双曲线的右支上,则sin sin sin A B C-的值是 . 【答案】21-10. (江苏省无锡市2013年2月高三质量检测)椭圆x 22+y 2=1的左焦点为F ,直线x =m 与椭圆相交于点A 、B ,当△FAB 的周长最大时,△FAB 的面积为 ▲ . 【答案】 21、(常州市2013届高三期末)已知双曲线22221(0,0)x y a b a b -=>>的一条渐近线经过点(1,2),则该双曲线的离心率的值为 ▲ 答案:52、(连云港市2013届高三期末)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2 = 4x 的准线交于A 、B 两点,AB =3,则C 的实轴长为 ▲ .答案:13、(南京市、盐城市2013届高三期末)已知1F 、2F 分别是椭圆14822=+y x 的左、右焦点,点P 是椭圆上的任意一点,则121||PF PF PF -的取值范围是 ▲ .答案:[0,222]+6、(苏州市2013届高三期末)在平面直角坐标系xOy 中,双曲线2222:1(0,0)x y E a b a b-=>>的左顶点为A ,过双曲线E 的右焦点F 作与实轴垂直的直线交双曲线E 于B ,C 两点,若ABC ∆为直角三角形,则双曲线E 的离心率为 . 答案:27、(泰州市2013届高三期末)设双曲线22145x y -=的左、右焦点分别为1F ,2F ,点P 为双曲线上位于第一象限内一点,且12PF F 的面积为6,则点P 的坐标为 答案:⎪⎪⎭⎫⎝⎛2,556 8、(无锡市2013届高三期末)如图,过抛物线y 2=2px (p>0)的焦点F 的直线L 交抛物线于点A 、B ,交其准线于点C ,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 。

江苏省13市县2016届高三上学期期末考试数学试题分类汇编圆锥曲线一、填空题1、(常州市2016届高三上期末)已知双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线经过点P(1,-2),则该双曲线的离心率为2、(淮安、宿迁、连云港、徐州苏北四市2016届高三上期末)抛物线x y 42=的焦点到双曲线191622=-y x 渐近线的距离为 3、(南京、盐城市2016届高三上期末)在平面直角坐标系xOy 中,已知抛物线C 的顶点在坐标原点,焦点在x 轴上,若曲线C 经过点(1,3)P ,则其焦点到准线的距离为 ▲4、(南通市海安县2016届高三上期末)在平面直角坐标系xOy 中,已知双曲线)0,0(12222>>=-b a by a x 的一条渐近线的方程为x y 3=则该双曲线的离心率为 5、(苏州市2016届高三上期末)双曲线22145x y -=的离心率为 ▲ 6、(泰州市2016届高三第一次模拟)在平面直角坐标系xOy 中,双曲线2212x y -=的实轴长为 ▲ .7、(无锡市2016届高三上期末)设ABC ∆是等腰三角形,120ABC ∠= ,则以A 、B 为焦点且过点C 的双曲线的离心率为8、(扬州市2016届高三上期末)双曲线116922=-y x 的焦点到渐近线的距离为 ▲ 9、(镇江市2016届高三第一次模拟)以抛物线y 2=4x 的焦点为焦点,以直线y =±x 为渐近线的双曲线标准方程为________.填空题答案 1、5 2、35 3、92 4、2 5、326、227、132+ 8、49、【答案】x 212-y 212=1.【解析】由题意设双曲线的标准方程为22221x y a b-=,y 2=4x 的焦点为()1,0,则双曲线的焦点为()1,0;y =±x 为双曲线的渐近线,则1b a =,又因222a b c +=,所以2211,22a b ==,故双曲线标准方程为x 212-y 212=1.二、解答题1、(常州市2016届高三上期末)在平面直角坐标系xoy 中,设椭圆22221(0)x y a b a b+=>>的离心率是e ,定义直线b y e=±学科网为椭圆的“类准线”,已知椭圆C 的“类准线”方程为23y =±,长轴长为4。

江苏省13大市2013届高三上学期期末数学试题分类汇编导数及其应用1、(南通市2013届高三期末)曲线2(1)1()e (0)e 2x f f x f x x '=-+在点(1,f (1))处的切线方程为 ▲ . 答案:1e 2y x =-. 2、(苏州市2013届高三期末)过坐标原点作函数ln y x =图像的切线,则切线斜率为 . 答案:1e3、(泰州市2013届高三期末)曲线y=2lnx 在点(e,2)处的切线与y 轴交点的坐标为 (0,0)4、(扬州市2013届高三期末)已知函数xmx x f -=ln )((R m ∈)在区间],1[e 上取得最小值4,则=m ▲ . e 3-5、(常州市2013届高三期末)第八届中国花博会将于2013年9月在常州举办,展览园指挥中心所用地块的形状是大小一定的矩形ABCD ,BC a =,CD b =.a ,b 为常数且满足b a <.组委会决定从该矩形地块中划出一个直角三角形地块AEF 建游客休息区(点E ,F 分别在线段AB ,AD 上),且该直角三角形AEF 的周长为(2l b >),如图.设AE x =,△AEF 的面积为S .(1)求S 关于x 的函数关系式;(2)试确定点E 的位置,使得直角三角形地 块AEF 的面积S 最大,并求出S 的最大值.解:(1)设AF y =,则x y l ++=,整理,得222()l lxy l x -=-.………3分 2(2)4(12)l l x S lx x xy --==,](0,x b ∈. …………………………………4分(2)()()]22'22242,(0,44l x lx l l S x x x b x l x l ⎛⎫⎛⎫-+=⋅=-⋅∈ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭∴当b ≤时,'0S >,S 在](0,b 递增,故当x b =时,()()max 24bl b l S b l -=-;当b >时,在x ⎛⎫∈ ⎪ ⎪⎝⎭上,'0S >,S 递增,在,x b ⎫∈⎪⎪⎭上,'0S <,S 递减,故当x =时,2max S =.6、(连云港市2013届高三期末)(连云港市2013届高三期末)某单位决定对本单位职工实行年医疗费用报销制度,拟制定年医疗总费用在2万元至10万元(包括2万元和10万元)的报销方案,该方案要求同时具备下列三个条件:①报销的医疗费用y (万元)随医疗总费用x (万元)增加而增加;②报销的医疗费用不得低于医疗总费用的50%;③报销的医疗费用不得超过8万元.(1)请你分析该单位能否采用函数模型y =0.05(x 2+4x +8)作为报销方案;(2)若该单位决定采用函数模型y =x -2ln x +a (a 为常数)作为报销方案,请你确定整数a 的值.(参考数据:ln2≈0.69,ln10≈2.3)【解】(1)函数y =0.05(x 2+4x +8)在[2,10]上是增函数,满足条件①, ……………2分 当x =10时,y 有最大值7.4万元,小于8万元,满足条件③. ………………………4分但当x =3时,y =2920<32,即y ≥x2不恒成立,不满足条件②,故该函数模型不符合该单位报销方案. ………………………6分(2)对于函数模型y =x -2ln x +a ,设f (x )= x -2ln x +a ,则f ´(x )=1-2x =x -2x≥0.所以f (x )在[2,10]上是增函数,满足条件①,由条件②,得x -2ln x +a ≥x 2,即a ≥2ln x -x2在x ∈[2,10]上恒成立,令g (x )=2ln x -x 2,则g ´(x )=2x -12=4-x2x,由g ´(x )>0得x <4,∴g (x )在(0,4)上增函数,在(4,10)上是减函数.∴a ≥g (4)=2ln4-2=4ln2-2. ………………10分 由条件③,得f (10)=10-2ln10+a ≤8,解得a ≤2ln10-2. ……………………12分 另一方面,由x -2ln x +a ≤x ,得a ≤2ln x 在x ∈[2,10]上恒成立, ∴a ≤2ln2,综上所述,a 的取值范围为[4ln2-2,2ln2],所以满足条件的整数a 的值为1. ……………14分7、(南京市、盐城市2013届高三期末)对于定义在区间D 上的函数()f x , 若任给0x D ∈, 均有0()f x D ∈, 则称函数()f x 在区间D 上封闭.试判断()1f x x =-在区间[2,1]-上是否封闭, 并说明理由; 若函数3()1x ag x x +=+在区间[3,10]上封闭, 求实数a 的取值范围; 若函数3()3h x x x =-在区间[,](,)a b a b Z ∈上封闭, 求,a b 的值.解: (1)()1f x x =-在区间[2,1]-上单调递增,所以()f x 的值域为[-3,0]………2分 而[-1,0][2,1]⊄-,所以()f x 在区间[2,1]-上不是封闭的……………… 4分(2)因为33()311x a a g x x x +-==+++, ①当3a =时,函数()g x 的值域为{}3[3,10]⊆,适合题意……………5分 ②当3a >时,函数()g x 在区间[3,10]上单调递减,故它的值域为309[,]114a a++, 由309[,]114a a++[3,10]⊆,得303119104aa +⎧≥⎪⎪⎨+⎪≤⎪⎩,解得331a ≤≤,故331a <≤……………………7分③当3a <时,在区间[3,10]上有33()3311x a a g x x x +-==+<++,显然不合题意 …………………8分综上所述, 实数a 的取值范围是331a ≤≤……………………………9分 (3)因为3()3h x x x =-,所以2()333(1)(1)h x x x x '=-=+-, 所以()h x 在(,1)-∞-上单调递减,在(1,1)-上递增,在(1,)+∞上递增.①当1a b <≤-时,()h x 在区间[,]a b 上递增,所以()()h a ah b b ≥⎧⎨≤⎩,此时无解………10分②当111a b ≤--<≤且时,因max ()(1)2h x h b =-=>,矛盾,不合题意…………11分③当11a b ≤->且时,因为(1)2,(1)2h h -==-都在函数的值域内,故22a b ≤-⎧⎨≥⎩,又33()3()3a h a a a b h b b b ⎧≤=-⎨≥=-⎩,解得202202a a b b -≤≤≥⎧⎨≤≤≤⎩或或,从而22a b =-⎧⎨=⎩ ………12分 ④当11a b -≤<≤时,()h x 在区间[,]a b 上递减,()()h b ah a b ≥⎧⎨≤⎩(*),而,a b Z ∈,经检验,均不合(*)式……………………………13分⑤当111a b -<≤≥且时,因min ()(1)2h x h a ==-<,矛盾,不合题意…………14分⑥当1b a >≥时,()h x 在区间[,]a b 上递增,所以()()h a ah b b ≥⎧⎨≤⎩,此时无解 ……………15分综上所述,所求整数,a b 的值为2,2a b =-=…………………16分8、(南通市2013届高三期末)某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,()ABCD AB AD >为长方形薄板,沿AC 折叠后,AB '交DC 于点P .当△ADP的面积最大时最节能,凹多边形ACB PD '的面积最大时制冷效果最好. (1)设AB =x 米,用x 表示图中DP 的长度,并写出x 的取值范围; (2)若要求最节能,应怎样设计薄板的长和宽? (3)若要求制冷效果最好,应怎样设计薄板的长和宽?解:(1)由题意,AB x =,2BC x =-.因2x x >-,故12x <<. …………2分设DP y =,则PC x y =-.因△ADP ≌△CB P ',故PA PC x y ==-.由 222PA AD DP =+,得 2221()(2)2(1)x y x y y x -=-+⇒=-,12x <<.……5分(2)记△ADP 的面积为1S ,则11(1)(2)S x x=-- ………………………………………………………………6分23()2x x=-+≤-当且仅当x =(1,2)时,S 1取得最大值.……………………………………8分2米时,节能效果最好. ……………………9分 (3)记△ADP 的面积为2S ,则221114(2)(1)(2)3()22S x x x x x x=-+--=-+,12x <<.…………………………10分于是,3222142(2)02x S x x x x-+'=--==⇒=.……………………………11分 关于x 的函数2S在上递增,在上递减.所以当x =时,2S 取得最大值. …………………………13分宽为2制冷效果最好. ………………………14分9、(徐州、淮安、宿迁市2013届高三期末)已知函数).1,0(ln )(2≠>-+=a a a x x a x f x (1) 求函数)(x f 在点))0(,0(f 处的切线方程;(2) 求函数)(x f 单调区间;(3) 若存在]1,1[,21-∈x x ,使得e e x f x f (1)()(21-≥-是自然对数的底数),求实数a的取值范围.ABCD(第17题)B 'P⑴因为函数2()ln (0,1)x f x a x x a a a =->≠+,所以()ln 2ln x f x a a x a '=-+,(0)0f '=,…………………………………………2分 又因为(0)1f =,所以函数()f x 在点(0,(0))f 处的切线方程为1y =. …………4分 ⑵由⑴,()ln 2ln 2(1)ln x x f x a a x a x a a '=-=-++.因为当0,1a a >≠时,总有()f x '在R 上是增函数, ………………………………8分 又(0)0f '=,所以不等式()0f x '>的解集为(0,)∞+,故函数()f x 的单调增区间为(0,)∞+.………………………………………………10分 ⑶因为存在12,[1,1]x x ∈-,使得12()()e 1f x f x --≥成立, 而当[1,1]x ∈-时,12max min ()()()()f x f x f x f x --≤,所以只要max min ()()e 1f x f x --≥即可.……………………………………………12分 又因为x ,()f x ',()f x 的变化情况如下表所示:所以()f x 在[1,0]-上是减函数,在[0,1]上是增函数,所以当[1,1]x ∈-时,()f x 的最小值()()min 01f x f ==,()f x 的最大值()max f x 为()1f -和()1f 中的最大值.因为11(1)(1)(1ln )(1ln )2ln f f a a a a a aa--=--=--+++, 令1()2ln (0)g a a a a a =-->,因为22121()1(1)0g a a a a '=-=->+,所以1()2ln g a a a a=--在()0,a ∈+∞上是增函数.而(1)0g =,故当1a >时,()0g a >,即(1)(1)f f >-;当01a <<时,()0g a <,即(1)(1)f f <-.………………………………………14分 所以,当1a >时,(1)(0)e 1f f --≥,即ln e 1a a --≥,函数ln y a a =-在(1,)a ∈+∞上是增函数,解得e a ≥;当01a <<时,(1)(0)e 1f f ---≥,即1ln e 1a a+-≥,函数1ln y a a =+在(0,1)a ∈上是减函数,解得10ea <≤. 综上可知,所求a 的取值范围为1(0,][e,)ea ∈∞+U .………………………………16分10、(泰州市2013届高三期末)已知函数f(x)=(x-a)2()x b -,a,b 为常数, (1)若a b ≠,求证:函数f(x)存在极大值和极小值(2)设(1)中 f(x) 取得极大值、极小值时自变量的分别为12,x x ,令点A 11(,()x f x ),B 22(,()x f x ),如果直线AB 的斜率为12-,求函数f(x)和/()f x 的公共递减区间的长度 (3)若/()()f x mf x ≥对于一切x R ∈ 恒成立,求实数m,a,b 满足的条件解:(1)[])2(3)()(/b a x b x x f +--= …………………………………………………1分b a ≠Θ32b a b +≠∴0)(,=∴x f 有两不等 b 和32ba + ∴f (x )存在极大值和极小值 ……………………………….……………………………4分(2)①若a =b ,f (x )不存在减区间②若a >b 时由(1)知x 1=b ,x 2=32ba + ∴A (b ,0)B ⎪⎪⎭⎫⎝⎛--+9)(2,322b a b a 21329)(22-=-+-∴b b a b a ∴)(3)(22b a b a -=- 23=-∴b a○3当a <b 时 x 1=32ba +,x 2=b 。

江苏省12市2015届高三上学期期末考试数学试题分类汇编圆锥曲线一、填空题1、(常州市2015届高三)已知双曲线2241ax y -=a 的值为 ▲2、(连云港、徐州、淮安、宿迁四市2015届高三)已知椭圆)0(12222>>=+b a by a x ,点A ,1B ,2B ,F 依次为其左顶点、下顶点、上顶点和右焦点.若直线2AB 与直线1B F 的交点恰在该椭圆的右准线上,则该椭圆的离心率为 ▲3、(南京市、盐城市2015届高三)若双曲线222(0)x y a a -=>的右焦点与抛物线24y x =的焦点重合,则a = ▲ .4、(南通市2015届高三)在平面直角坐标系xOy 中,以直线2y x =±为渐近线,且经过抛物5、(苏州市2015届高三上期末)以抛物线24y x =的焦点为顶点,顶点为中心,离心率为2的双曲线标准方程为6、(泰州市2015届高三上期末)双曲线12222=-by a x 的右焦点到渐近线的距离是其到左顶点距离的一半,则双曲线的离心率e = ▲7、(无锡市2015届高三上期末)已知焦点在x 轴上的双曲线的渐近线方程为13y x ,则该双曲线的离心率为8、(扬州市2015届高三上期末)已知双曲线C :22221(0,0)x y a b a b -=>>的一条渐近线与直线l :x +=0垂直,且C 的一个焦点到l 的距离为2,则C 的标准方程为____二、解答题1、(常州市2015届高三)在平面直角坐标系xOy 中,已知椭圆C :22221(0)x y a b a b+=>>的离心率12e =,直线:10()l x my m --=∈R 学科网过椭圆C 的右焦点F ,且交椭圆C 于A ,B 两点.(1)求椭圆C 的标准方程;(2)已知点5(,0)2D ,连结BD ,过点A 作垂直于y 轴的直线1l ,设直线1l 与直线BD 交于点P ,试探索当m 变化时,是否存有一条定直线2l ,使得点P 恒在直线2l 上?若存有,请求出直线2l 的方程;若不存有,请说明理由.2、(连云港、徐州、淮安、宿迁四市2015届高三)在平面直角坐标系xOy 中,已知抛物线22(0)y px p的准线方程为14x,过点(0,2)M 作抛物线的切线MA ,切点为A (异于点O ),直线l 过点M 与抛物线交于两点B ,C ,与直线OA 交于点N .(1)求抛物线的方程; (2)试问:MN MNMB MC+的值是否为定值?若是,求出定值;若不是,说明理由.3、(南京市、盐城市2015届高三)在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的右准线方程为4x =,右顶点为A ,上顶点为B ,右焦点为F ,斜率为2的直线l 经过点A ,且点F 到直线l 的距离为255.(1)求椭圆C 的标准方程;(2)将直线l 绕点A 旋转,它与椭圆C 相交于另一点P ,当,,B F P 三点共线时,试确定直线l 的斜率.(第23题)xyO MBNClA4、(南通市2015届高三)如图,在平面直角坐标系xOy 中,12,F F 分别是椭圆22221(0)x y a b a b+=>>的左、右焦点,顶点B 的坐标为()0,b ,且∆12BF F 是边长为2的等边三角形.()1求椭圆的方程;()2过右焦点2F 的直线l 与椭圆交于,A C 两点,记∆2ABF ,∆2BCF 的面积分别为12,S S .若122S S =,求直线l 的斜率.5、(苏州市2015届高三上期末)如图,已知椭圆22:1124x y C +=,点B 是其下顶点,过点B 的直线交椭圆C 于另一点A (A 点在x 轴下方),且线段AB 的中点E 在直线y x =上.(1)求直线AB 的方程;(2)若点P 为椭圆C 上异于A 、B 的动点,且直线AP,BP 分别交直线y x =于点M 、N ,证明:OM ON 为定值.P NMBOAxyE6、(泰州市2015届高三上期末)如图,在平面直角坐标系xOy 中,离心率为22的椭圆:C 22221(0)x y a b a b+=>>的左顶点为A ,过原点O 的直线(与坐标轴不重合)与椭圆C 交于,P Q 两点,直线,PA QA 分别与y 轴交于,M N 两点.若直线PQ 斜率为22时,23PQ =. (1)求椭圆C 的标准方程;(2)试问以MN 为直径的圆是否经过定点(与直线PQ 的斜率无关)?请证明你的结论.7、(无锡市2015届高三上期末)已知椭圆22:142x y C 的上顶点为A ,直线:l y kx m交椭圆于,P Q 两点,设直线,AP AQ 的斜率分别为12,k k . (1)若0m 时,求12k k 的值;(2)若121k k 时,证明直线:l ykx m 过定点.N MQAOPxy8、(扬州市2015届高三上期末)如图,A ,B ,C 是椭圆M :22221(0)x y a b a b+=>>上的三点,其中点A 是椭圆的右顶点,BC 过椭圆M 的中心,且满足AC ⊥BC ,BC =2AC 。

广东省13大市2013届高三上期末考数学文试题分类汇编圆锥曲线 一、填空、选择题1、(潮州市2013届高三上学期期末)若抛物线22y px =的焦点与双曲线22122x y -=的右焦点重合,则p 的值为A .2-B .2C .4-D .4答案:D2、(东莞市2013届高三上学期期末)若抛物线22y px =的焦点与双曲线2213x y -=的右焦点重合,则常数p 的值等于 . 答案:43、(佛山市2013届高三上学期期末)已知双曲线的顶点与焦点分别是椭圆的22221y x a b+=(0a b >>)焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为 A .13 B .12 C .33 D .22答案:D4、(广州市2013届高三上学期期末)在区间15,⎡⎤⎣⎦和24,⎡⎤⎣⎦分别取一个数,记为a b ,, 则方程22221x y a b+=表示焦点在x 轴上且离心率小于32的椭圆的概率为A .12 B .1532C .1732D .3132 答案:B5、(惠州市2013届高三上学期期末)已知双曲线22221x y a b-=的一个焦点与抛物线2410y x =的焦点重合,且双曲线的离心率等于103,则该双曲线的方程为( ) A .2219y x -= B .221x y -= 5 C .2219x y -= D .22199x y -= 答案:C6、(江门市2013届高三上学期期末)已知双曲线12222=-by a x 的两个焦点分别为1F 、2F ,双曲线与坐标轴的两个交点分别为A 、B ,若||35||21AB F F =,则双曲线的离心率=eA .35B .45C .34D .38答案:A7、(茂名市2013届高三上学期期末)已知双曲线221(0)5x y m m -=>的右焦点F (3,o ),则此双曲线的离心率为( )A .6B .322C .32D .34答案:C8、(湛江市2013届高三上学期期末)椭圆2243x y +=1的左、右焦点分别为F 1、F 2,P 是椭圆上任一点则的取值范围是A 、(0,4]B 、(0,3]C 、[3,4)D 、[3,4] 答案:D9、(肇庆市2013届高三上学期期末)经过圆2220x y y ++=的圆心C ,且与直线2340x y +-=平行的直线方程为( )A .2330x y ++= B . 2330x y +-= C . 2320x y ++= D . 3220x y --=答案:A10、(中山市2013届高三上学期期末)直线2(1)10x ay +++=的倾斜角的取值范围是( ) A .[0,]4π B .3,4ππ⎡⎫⎪⎢⎣⎭C .[0,](,)42πππD .3,,424ππππ⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭答案:B 12、(珠海市2013届高三上学期期末)如图,F 1,F 2是双曲线C :22221x y a b-=(a >0,b >0)的左、右焦点,过F 1的直线与C 的左、右两支分别交于A ,B 两点.若 | AB | : |BF 2 | : | AF 2 |=3 : 4 : 5,则双曲线的离心率为 .xy OA BF 1F 2(第13题图)答案:13二、解答题1、(东莞市2013届高三上学期期末)在平面直角坐标系xoy 中,已知三点(0,0)O ,(1,1)A -,(1,1)B ,曲线C 上任意—点(,)M x y 满足:14()2MA MB OM OA OB +=-⋅+.(l )求曲线C 的方程;(2)设点P 是曲线C 上的任意一点,过原点的直线L 与曲线相交于M ,N 两点,若直线 PM ,PN 的斜率都存在,并记为PM k ,PN k .试探究PMPN k k ⋅的值是否与点P 及直线L 有关,并证明你的结论;(3)设曲线C 与y 轴交于D 、E 两点,点M (0,m )在线段DE 上,点P 在曲线C 上运动.若当点P 的坐标为(0,2)时,MP取得最小值,求实数m 的取值范围.解:(1)由题意可得, )22,2()1,1()1,1(y x y x y x MBMA --=--+---=+,…………1分 所以4844)22()2(||2222+-+=-+-=+y y x y x MB MA ,…………2分 又y y x OB OA OM -=⋅-=+⋅-4)2,0(),(214)(214, …………3分 所以y y y x -=+-+4484422,即14322=+y x . …………4分(2)因为过原点的直线L 与椭圆相交的两点N M ,关于坐标原点对称,所以可设),(),,(),,(0000y x N y x M y x P --. …………5分 因为N M P ,,在椭圆上,所以有14322=+y x , ………①1432200=+y x , ………② …6分①-②得 3422202-=--x x y y . 又00x x y y k PM--=,0x x y y k PN ++=, …………7分所以342022020000-=--=++⋅--=⋅x x y y x x y y x x y y k k PNPM , …………8分 故PN PMk k ⋅的值与点P 的位置无关,与直线L 也无关. …………9分(3)由于),(y x P 在椭圆C 上运动,椭圆方程为14322=+y x ,故22≤≤-y ,且22433y x -=. …………10分因为),(m y x MP -=,所以 3241)(||2222++-=-+=m my y m y x MP 33)4(4122+--=m m y . …………12分 由题意,点P 的坐标为)2,0(时,||MP 取得最小值,即当2=y 时,||MP 取得最 小值,而22≤≤-y ,故有24≥m ,解得21≥m . …………13分又椭圆C 与y 轴交于E D 、两点的坐标为)2,0(、)2,0(-,而点M 在线段DE 上, 即22≤≤-m ,亦即221≤≤m ,所以实数m 的取值范围是]2,21[.…………14分 2、(佛山市2013届高三上学期期末)已知(2,0)A -,(2,0)B ,(,)C m n . (1)若1m =,3n =,求ABC ∆的外接圆的方程;(2)若以线段AB 为直径的圆O 过点C (异于点,A B ),直线2x =交直线AC 于点R ,线段BR 的中点为D ,试判断直线CD 与圆O 的位置关系,并证明你的结论. 解析:(1)法1:设所求圆的方程为220xy Dx Ey F ++++=,由题意可得4204201330D F D F DEF ⎧-+=⎪++=⎨⎪++++=⎩,解得0,4D E F ===-,∴ABC ∆的外接圆方程为2240x y +-=,即224x y +=.-----------------6分法2:线段AC 的中点为13(,)22-,直线AC 的斜率为133k =,∴线段AC 的中垂线的方程为313()22y x -=-+, 线段AB 的中垂线方程为0x =,∴ABC ∆的外接圆圆心为(0,0),半径为2r =, ∴ABC ∆的外接圆方程为224x y +=.-----------------6分法3:22||(10)(30)2OC =-+-= ,而||||2OA OB ==,∴ABC ∆的外接圆是以O 为圆心,2为半径的圆, ∴ABC ∆的外接圆方程为224x y +=.-----------------6分法4:直线AC 的斜率为133k =,直线BC 的斜率为23k =-, ∴121k k ⋅=-,即AC BC ⊥,∴ABC ∆的外接圆是以线段AB 为直径的圆, ∴ABC ∆的外接圆方程为224x y +=.-----------------6分(2)由题意可知以线段AB 为直径的圆的方程为224x y +=,设点R 的坐标为(2,)t ,∵,,A C R 三点共线,∴//AC AR,----------------8分而(2,)AC m n =+ ,(4,)AR t =,则4(2)n t m =+,∴42nt m =+, ∴点R 的坐标为4(2,)2n m +,点D 的坐标为2(2,)2nm +,-----------------10分 ∴直线CD 的斜率为222(2)22244nn m n n mn m k m m m -+-+===---, 而224mn +=,∴224m n -=-,∴2mn mk n n==--,-----------------12分 ∴直线CD 的方程为()my n x m n-=--,化简得40mx ny +-=, ∴圆心O 到直线CD 的距离224424dr m n====+,所以直线CD 与圆O 相切.3、(广州市2013届高三上学期期末)已知椭圆()22122:10x y C a b a b+=>>的右焦点与抛物线22:4C yx =的焦点F 重合,椭圆1C 与抛物线2C 在第一象限的交点为P ,53PF =.(1)求椭圆1C 的方程;(2) 若过点()1,0A -的直线与椭圆1C 相交于M 、N 两点,求使FM FN FR +=成立的动点R 的轨迹方程;(3) 若点R 满足条件(2),点T 是圆()2211x y -+=上的动点,求RT 的最大值.(1)解法1:抛物线22:4C y x =的焦点F 的坐标为()1,0,准线为1x =-,设点P 的坐标为()00,x y ,依据抛物线的定义,由53PF=,得01x +53=, 解得023x =. …………… 1分∵ 点P 在抛物线2C 上,且在第一象限,∴ 202443y x ==⨯,解得0263y =.∴点P 的坐标为226,33⎛⎫⎪ ⎪⎝⎭. …………… 2分 ∵点P 在椭圆22122:1x y C a b+=上, ∴2248193a b +=. …………… 3分又1c =,且22221a b c b =+=+, …………… 4分解得224,3a b ==.∴椭圆1C 的方程为22143x y +=. …………… 5分 解法2: 抛物线22:4C yx =的焦点F 的坐标为()1,0,设点P 的坐标为()0x y ,,0000xy ,>>.∵53PF =,∴()2202519xy -+=. ① …………… 1分 ∵点P 在抛物线22:4C yx =上,∴204y x =. ②解①②得023x =,0263y =. ∴点P 的坐标为226,33⎛⎫⎪ ⎪⎝⎭. …………… 2分∵点P 在椭圆22122:1x y C a b+=上, ∴2248193a b +=. …………… 3分又1c =,且22221a b c b =+=+, …………… 4分解得224,3a b ==.∴椭圆1C 的方程为22143x y +=. …………… 5分 (2)解法1:设点M()11,x y 、()22,N x y 、(),R x y ,则()()()11221,,1,,1,FM x y FN x y FR x y =-=-=-. ∴()12122,FM FN x x y y +=+-+.∵ FM FN FR += ,∴121221,x x x y y y +-=-+=. ① …………… 6分∵M 、N 在椭圆1C 上, ∴222211221, 1.4343x y x y +=+= 上面两式相减得()()()()12121212043x x x x y y y y +-+-+=.②把①式代入②式得()()()12121043x x x y y y +--+=.当12x x ≠时,得()1212314x y y x x y+-=--. ③ …………… 7分 设FR 的中点为Q ,则Q 的坐标为1,22x y +⎛⎫ ⎪⎝⎭.∵M 、N 、Q 、A 四点共线,∴MNAQ k k =, 即121221312yy y yx x x x -==+-++. ④ …………… 8分 把④式代入③式,得()3134x yx y+=-+, 化简得()2243430yx x +++=. …………… 9分当12x x =时,可得点R 的坐标为()3,0-,经检验,点()3,0R-在曲线()2243430y x x +++=上.∴动点R 的轨迹方程为()2243430yx x +++=. …………… 10分解法2:当直线MN 的斜率存在时,设直线MN 的方程为()1yk x =+,由()221143y k x x y,,⎧=+⎪⎨+=⎪⎩消去y ,得()22223484120k x k x k +++-=. 设点M()11,x y 、()22,N x y 、(),R x y ,则2122834k x x k+=-+, ()()()1212122611234ky y k x k x k x x k +=+++=++=+.…6分∵()()()11221,,1,,1,FM x y FN x y FR x y =-=-=-. ∴()12122,FM FN x x y y +=+-+.∵ FM FN FR += ,∴121221,x x x y y y +-=-+=.∴21228134k x x x k+=+=-+, ① 2634kyk=+. ② …………… 7分 ①÷②得()314x k y+=-, ③ …………… 8分 把③代入②化简得()2243430yx x +++=. (*) …………… 9分当直线MN 的斜率不存在时,设直线MN 的方程为1x =-,依题意, 可得点R 的坐标为()3,0-,经检验,点()3,0R-在曲线()2243430y x x +++=上.∴动点R 的轨迹方程为()2243430y x x +++=. …………… 10分(3)解: 由(2)知点R()x y ,的坐标满足()2243430yx x +++=,即()224343y x x =-++,由20y ≥,得()23430x x -++≥,解得31x -≤≤-. (11)分 ∵圆()2211x y -+=的圆心为()10F ,,半径1r =,∴()221RF x y =-+()()2231434x x x =--++ ()21101052x =--. …………… 12分∴当3x =-时,4RF max =, (13)分此时,415RT max =+=. (14)分4、(惠州市2013届高三上学期期末)如图,椭圆y2222:1(0)x y M a b a b +=>>的离心率为32,直线x a =±和y b =±所围成的矩形ABCD 的面积为8.(1)求椭圆M 的标准方程;(2)设直线:()R l y x m m =+∈与椭圆M 有两个不同的交点,,P Q l 与矩形ABCD 有两个不同的交点,S T ,求||||PQ ST 的最大值及取得最大值时m 的值. 1)2223324c a b e a a -==⇒=……①…………1分矩形ABCD 面积为8,即228a b ⋅=……②…………2分 由①②解得:2,1a b ==, …………3分∴椭圆M 的标准方程是2214x y +=. ………………………4分(2)222244,58440,x y x mx m y x m ⎧+=⇒++-=⎨=+⎩,设1122(,),(,)P x y Q x y ,则21212844,55m x x m x x -+=-=, …………………7分由226420(44)0m m ∆=-->得55m -<<. ……………………8分22284442||245555m PQ m m -⎛⎫=--=- ⎪⎝⎭. ………………10分当l 过A 点时,1m =,当l 过C 点时,1m =-.……………11分①当51m -<<-时,有(1,1),(2,2),||2(3)S m T m ST m ---+=+,222||454461||5(3)5PQ m ST m t t-==-+-+, 其中3t m =+,由此知当134t =,即45,(5,1)33t m ==-∈--时,||||PQ ST 取得最大值255.②由对称性,可知若15m <<,则当53m =时,||||PQ ST 取得最大值255.③当11m -≤≤时,||22ST =,2||25||5PQ m ST =-, 由此知,当0m =时,||||PQ ST 取得最大值255. ………………13分 综上可知,当53m =±和0时,||||PQ ST 取得最大值255.………………14分5、(江门市2013届高三上学期期末)已知椭圆C 的焦点为)0 , 1(1-F 、)0 , 1(2F ,点)22, 1(-P 在椭圆上. ⑴求椭圆C 的方程;⑵若抛物线px y 22=(0>p )与椭圆C 相交于点M 、N ,当OMN ∆(O 是坐标原点)的面积取得最大值时,求p 的值.解:⑴依题意,设椭圆C 的方程为12222=+by a x ……1分,||||221PF PF a +=……2分,22=,所以2=a ……3分,1=c ,所以122=-=c a b ……4分,椭圆C 的方程为1222=+y x ……5分⑵根据椭圆和抛物线的对称性,设) , (00y x M 、) , (00y x N -(0 , 00>y x ) (6)分,OMN ∆的面积0000)2(21y x y x S =⨯=……7分,) , (00y x M 在椭圆上,122020=+y x ,所以002020202022221y x y x y x =⋅≥+=,等号当且仅当002y x=时成立……9分,解⎪⎪⎩⎪⎪⎨⎧==+002020212yx y x (0 , 00>y x )得⎪⎩⎪⎨⎧==22100y x ……10分,) , (00y x M 即)22 , 1(M 在抛物线px y 22=上,所以12)22(2⨯=p ……11分,解得41=p ……12分.6、(茂名市2013届高三上学期期末)已知椭圆1C :22221x y a b+= (0a b >>)过点(0,2)A 且它的离心率为33。
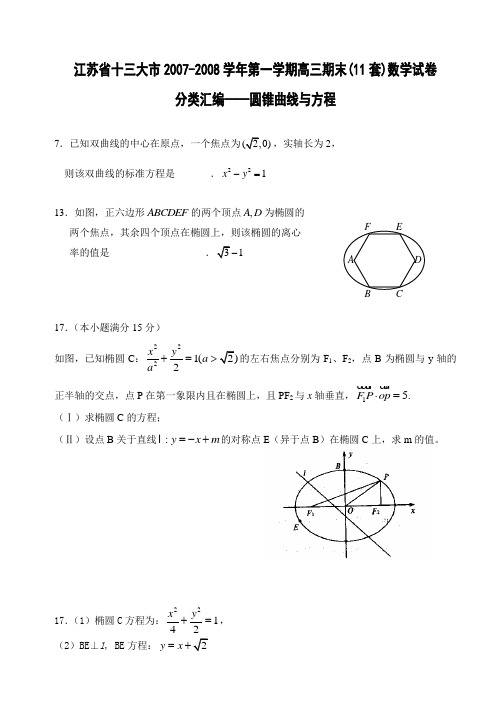
江苏省十三大市2007-2008学年第一学期高三期末(11套)数学试卷分类汇编——圆锥曲线与方程7.已知双曲线的中心在原点,一个焦点为,实轴长为2,则该双曲线的标准方程是_______.221x y-=13.如图,正六边形ABCDEF的两个顶点,A D为椭圆的两个焦点,其余四个顶点在椭圆上,则该椭圆的离心率的值是___________________117.(本小题满分15分)如图,已知椭圆C:2221(2x yaa+=>的左右焦点分别为F1、F2,点B为椭圆与y轴的正半轴的交点,点P在第一象限内且在椭圆上,且PF2与x轴垂直,15.F P op⋅=(Ⅰ)求椭圆C的方程;(Ⅱ)设点B关于直线:y x m=-+的对称点E(异于点B)在椭圆C上,求m的值。
17.(1)椭圆C方程为:221 42x y+=,(2)BE⊥l, BE方程:y x=由221,42y x x y ⎧=⎪⎨+=⎪⎩得0,3x x ==-或((3E BE y x m m ∴=-=-中点为代入得5.中心在原点,对称轴为坐标轴的双曲线的渐近线方程为y x =,且双曲线过点(2,1)P ,则双曲线的方程为 .2212x y -= 12.抛物线2:C y x =上两点M N 、满足12MN MP =,若(0,2)OP =-,则||MN = .2. 抛物线24x y =-的焦点坐标是 ▲ . (0,1)- 8. 若R ∈k ,试写出方程13322=+--k y k x 表示双曲线的一个充分不必要条件 ▲ . 答案不惟一,如3k >,或3k <-等11. 两个正数,m n 的等差中项是5,等比中项是4.若m n >,则椭圆221x y m n+=的离心率e 的大小为 ▲ .17. (本小题满分15分)已知圆C 与两坐标轴都相切,圆心C 到直线y x =-(Ⅰ)求圆C 的方程. (Ⅱ)若直线:1x yl m n+=(2,2)m n >>与圆C相切,求证:6mn ≥+ 17. 解:(I )设圆C 半径为r ,由已知得:a b r a⎧⎪=⎪⎪=⎨= ………………………………3分∴11a b r ==⎧⎨=⎩,或11a b r ==-⎧⎨=⎩ ………………………………5分∴圆C 方程为2222(1)(1)1,(1)(1)1x y x y -+-=+=或++. ………7分 (II)直线0l nx my mn +-=方程为,∵22:(1)(1)1l C x y -+-=直线与圆相切, ……………………8分1,= ………………………………10分∴222(),n m mn n m +-=+左边展开,整理得,22 2.mn m n =+- ………………………………12分 ∴2.2mn m n ++=∵0,0,m n m n >>+≥∴22mn +≥∴220,-≥22≥≤ ………………………14分 ∵2,2m n >>2≥∴6mm ≥+ ………………15分8.若抛物线22y px =的焦点与双曲线22122x y -=的右焦点重合,则p 的值为 ▲ .4 14.设P 是椭圆1162522=+y x 上任意一点,A 和F 分别是椭圆的左顶点和右焦点, 则⋅+⋅41的最小值为 ▲ . 9-4. 双曲线221916x y -=的渐近线方程为 ▲ .答案:43y x =±.12.设椭圆22221(0)x y a b a b+=>>的两个焦点分别为F 1,F 2,点P 在椭圆上,且120PF PF ⋅=,12tan 2PF F ∠=,则该椭圆的离心率等于 ▲ ..讲评建议:设PF 1=m ,则PF 2=2m ,,2a =3m ,22c e a=. 3.抛物线y 2=4x 的焦点坐标是 ▲ . (1,0);18.(本小题满分15分)已知圆O :222x y +=交x 轴于A ,B两点,曲线C 是以AB 为长轴,离心率为2的椭圆,其左焦点为F .若P 是圆O 上一点,连结PF ,过原点O 作直线PF的垂线交椭圆C 的左准线于点Q .(Ⅰ)求椭圆C 的标准方程;(5分)(Ⅱ)若点P 的坐标为(1,1),求证:直线PQ 与圆O 相切;(5分)(Ⅲ)试探究:当点P 在圆O 上运动时(不与A 、B 重合),直线PQ 与圆O 是否保持相切的位置关系?若是,请证明;若不是,请说明理由. (5分)18.(本小题满分15分)解:(Ⅰ)因为2a e ==,所以c=1……………………(3分) 则b=1,即椭圆C 的标准方程为2212x y +=……………………………………(5分) (Ⅱ)因为P (1,1),所以12PF k =,所以2OQ k =-,所以直线OQ 的方程为y=-2x(7分) 又椭圆的左准线方程为x=-2,所以点Q(-2,4) ……………………………………(8分) 所以1PQ k =-,又1OP k =,所以1k k PQ O P -=⊥,即OP PQ ⊥,故直线PQ 与圆O 相切………………………………………………………………(10分) (Ⅲ)当点P 在圆O 上运动时,直线PQ 与圆O 保持相切 (11))证明:设00(,)P x y(0x ≠则22002y x =-,所以001PF y k x =+,001OQ x k y +=-, 所以直线OQ 的方程为001x y x y +=- …………………………(13分)所以点Q(-2,0022x y +) ……………………………………… (14分) 所以002200000000000022(22)22(2)(2)PQ x y y y x x x x k x x y x y y +--+--====-+++,又00OP yk x =,所以1k k PQ O P -=⊥,即OP PQ ⊥,故直线PQ 始终与圆O 相切 …………(16分) 5.已知双曲线032122=+-=-y x ay x 的一条渐近线与直线垂直,则a= 4 18.(本题满分15分)若椭圆)0(12222>>=+b a by a x 过点(-3,2),离心率为33,⊙O 的圆心为原点,直径为椭圆的短轴,⊙M 的方程为4)6()8(22=-+-y x ,过⊙M 上任一点P 作⊙O 的切线PA 、PB ,切点为A 、B.(1)求椭圆的方程;(5分)(2)若直线PA 与⊙M 的另一交点为Q ,当弦PQ 最大时,求直线PA 的直线方程;(5分) (3)求OB OA ⋅的最大值与最小值.(5分)18.解:(1)由题意得:⎪⎩⎪⎨⎧==∴⎪⎪⎪⎩⎪⎪⎪⎨⎧+===+1015331492222222b a c b a a c b a 所以椭圆的方程为1101522=+y x (2)由题可知当直线PA 过圆M 的圆心(8,6)时,弦PQ 最大因为直线PA 的斜率一定存在, 设直线PA 的方程为:y-6=k(x-8)又因为PA 与圆O 相切,所以圆心(0,0)到直线PA 的距离为10即101|68|2=+-k k 可得91331==k k 或所以直线PA 的方程为:0509130103=--=+-y x y x 或 (3)设α=∠AOP 则α2,=∠∠=∠AOB BOP AOP 则1201)(21cos 2cos 222-=-=-=∠OP OP OA AOB α 8210||,12210||min max =-==+=OP OP 10200cos |||2-=∠⋅=⋅∴OP AOB OB 18155)(,855)(min max -=⋅-=⋅∴OB OA OB OA4.已知椭圆的中心在原点、焦点在y 轴上,若其离心率是12,焦距是8,则该椭圆的方程为 ★ .y 264 + x 248=1。

江苏省13大市2013年高三历次考试数学试题分类汇编:圆锥曲线一、填空题1.(扬州市2012-2013学年度第一学期期末检测高三数学试题)已知椭圆22221(0) x ya ba b+=>>的离心率e=,A、B是椭圆的左、右顶点,P是椭圆上不同于A、B的一点,直线PA、PB斜倾角分别为α、β,则cos()cos()αβαβ-+=____.【答案】352 .(苏州市2012-2013学年度第一学期高三期末考试数学试卷)在平面直角坐标系xOy中,双曲线2222:1(0,0)x yE a ba b-=>>的左顶点为A,过双曲线E的右焦点F作与实轴垂直的直线交双曲线E于B,C两点,若ABC∆为直角三角形,则双曲线E的离心率为_________.【答案】23 .(江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题)设双曲线22145x y-=的左、右焦点分别为1F,2F,点P为双曲线上位于第一象限内一点,且12PF F的面积为6,则点P的坐标为___________【答案】⎪⎪⎭⎫⎝⎛2,5564 .(镇江市2013届高三上学期期末考试数学试题)圆心在抛物线22x y=上,并且和抛物线的准线及y轴都相切的圆的标准方程为______.【答案】()121122=⎪⎭⎫⎝⎛-+±yx;5 .(江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷)在平面直角坐标系xOy中,抛物线22(0)x py p=>上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为______.【答案】46 .(南京市、盐城市2013届高三第三次模拟考试数学试卷)设点P是曲线y=x2上的一个动点,曲线y=x2在点P处的切线为l,过点P且与直线l垂直的直线与曲线y=x2的另一交点为Q,则PQ的最小值为________.【答案】3327 .(江苏省盐城市2013届高三年级第二次模拟考试数学试卷)椭圆12222=+by a x (0>>b a )的左焦点为F,直线m x =与椭圆相交于A,B 两点,若FAB ∆的周长最大时,FAB ∆的面积为ab ,则椭圆的离心率为________.【答案】28 .(南通市2013届高三第一次调研测试数学试卷)已知双曲线22221y x a b-=的一个焦点与圆x 2+y 2-10x =0的圆心重合,,则该双曲线的标准方程为________.【答案】答案:221520y x -=. 本题考查双曲线的标准方程、简单性质与圆的有关知识.对双曲线的讲评不宜过分引申9 .(苏北三市(徐州、淮安、宿迁)2013届高三第二次调研考试数学试卷)已知双曲线)0,0(12222>>=-b a b y a x 的右焦点为,F 若以F 为圆心的圆05622=+-+x y x 与此双曲线的渐近线相切,则该双曲线的离心率为_____.【答案】510.(扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷)在平面直角坐标系xOy 中,设椭圆与双曲线2233y x -=共焦点,且经过点)2,则该椭圆的离心率为____.【答案】11.(南京市、淮安市2013届高三第二次模拟考试数学试卷)在平面直角坐标系xOy 中,已知双曲线C:22143x y -=.设过点M(0,1)的直线与双曲线C 交于A 、B 两点,若2AM MB =,则直线的斜率为_____.【答案】12±12.(南京市、盐城市2013届高三第三次模拟考试数学试卷)在平面直角坐标系xOy 中,点F 是双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的右焦点,过F 作双曲线C 的一条渐近线的垂线,垂足为A ,延长FA 与另一条渐近线交于点B .若FB →=2FA →,则双曲线的离心率为________.【答案】213.(徐州、宿迁市2013届高三年级第三次模拟考试数学试卷)方程22115x y k k =-++表示双曲线的充要条件是k ∈____.【答案】(1,5)-;14.(南京市、盐城市2013届高三年级第一次模拟考试数学试题)已知1F 、2F 分别是椭圆14822=+y x 的左、右焦点, 点P 是椭圆上的任意一点, 则121||PF PF PF -的取值范围是 .【答案】[0,222]+15.(连云港市2012-2013学年度第一学期高三期末考试数学试卷)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2= 4x 的准线交于A 、B 两点,AB =3,则C 的实轴长为______. 【答案】1;16.(2012-2013学年度苏锡常镇四市高三教学情况调研(二)数学试题)若双曲线221(0)yx a a-=>的一个焦点到一条渐近线的距离等于3,则此双曲线方程为______.【答案】2213y x -= 17.(扬州市2012-2013学年度第一学期期末检测高三数学试题)已知圆C 的圆心为抛物线x y42-=的焦点,又直线4360x y --=与圆C 相切,则圆C 的标准方程为____.【答案】22(1)4x y ++=;18.(常州市2013届高三教学期末调研测试数学试题)已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线经过点(1,2),则该双曲线的离心率的值为______.【答案】519.(江苏省无锡市2013届高三上学期期末考试数学试卷)如图,过抛物线y 2=2px(p>0)的焦点F 的直线L交抛物线于点A 、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为_____________.【答案】23y x =20.(江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题)已知1F ,2F 是双曲线的两个焦点,以线段12F F 为边作正12MF F ∆,若边1MF 的中点在此双曲线上,则此双曲线的离心率为__________.【答案】31+21.(镇江市2013届高三上学期期末考试数学试题)设双曲线22221x y a b-=的左、右焦点分别为12,F F ,点P在双曲线的右支上,且124PF PF =,则此双曲线离心率的最大值为______.【答案】35; 二、解答题22.(江苏省盐城市2013届高三年级第二次模拟考试数学试卷)如图,圆O 与离心率为23的椭圆T:12222=+by a x (0>>b a )相切于点M )1,0(. ⑴求椭圆T 与圆O 的方程;⑵过点M 引两条互相垂直的两直线1l 、2l 与两曲线分别交于点A 、C 与点B 、D(均不重合). ①若P 为椭圆上任一点,记点P 到两直线的距离分别为1d 、2d ,求2221d d +的最大值; ②若MD MB MC MA ⋅=⋅43,求1l 与2l 的方程.【答案】解: (1)由题意知:222,1,23a b c b a c =+==解得3,1,2===c b a 可知: 椭圆C 的方程为1422=+y x 与圆O 的方程122=+y x (2)设),(00y x P 因为1l ⊥2l ,则202022221)1(++==+y x PM d d 因为142020=+y x 所以316)31(3)1(442020202221++-=++-=+y y y d d ,因为110≤≤-y 所以当310-=y 时2221d d +取得最大值为316,此时点)31,324(-±P (3)设1l 的方程为1+=kx y ,由⎩⎨⎧=++=1122y x kx y 解得)11,12(222k k k k A +-+-; 由⎪⎩⎪⎨⎧=++=14122y x kx y 解得)4141,148(222k k k k C +-+- 把C A ,中的k 置换成k 1-可得)11,12(222+-+k k k k B ,)44,48(222+-+k k k k D 12分 所以)12,12(222k k k k +-+-=,)418,148(222kk k k +-+- )12,12(22+-+=k k k ,)48,48(22+-+=k k k由34MA MC MB MD ⋅=⋅得44413222+=+k k k 解得2±=k 15分所以1l 的方程为12+=x y ,2l 的方程为122+-=x y 或1l 的方程为12+-=x y ,2l 的方程为122+=x y 16分 的情形:过定椭圆内的定点作两条斜率和为定值的动弦,则两动弦的中点所在直线过定值.此结论在抛物线中也成立.另外,也可以求过两中点所在直线的斜率的最值.近几年江苏高考解析几何大题的命题趋势:多考一点“算”,少考一点“想”.式方程为22200x x y y +-=)(3)设直线MA 的斜率为k ,()11,A x y ,()22,B x y ,由题直线MA 与MB 的斜率互为相反数,直线MB 的斜率为k -.联立直线MA 与椭圆方程:221364y kx x y ⎧=+-⎪⎨+=⎪⎩ ,整理得()()2229113162108180k x k x k k ++-+--=,得1x =-,所以2x =-,整理得21x x -=,21x x +=又()()212221y y kx kx k x x -=-++-+-=-++=3210891k k -+=+所以212113ABy y k x x -===-为定值方程为:220x y Dx Ey F ++++=,则圆心为(,22D E --),PQ 中点M (2,m m -), PQ 的垂直平分线的方程为:m x y 232--=,圆心(2,2E D --)满足m x y 232--=,所以322E D m -=-○2, 圆过定点(2,0),所以420D F ++=○3,圆过1122(,),(,)P x y Q x y , 则2211112222220,0,x y Dx Ey F x y Dx Ey F ++++=++++=⎧⎨⎩ 两式相加得: 22221212121220,x x y y Dx Dx Ey Ey F ++++++++=222212121212(1)(1)()()2044x x x x D x x E y y F ++-+-+++++=,12y y m +=, 5220mD mE F -++=∴○4因为动直线12y x m =+与椭圆C 交与P,Q (均不与A 点重合)所以1-≠m ,由○2○3○4解得:3(1)3335,,,42222m D E m F m -==+=--代入圆的方程为:223(1)3335()042222m x y x m y m -++++--=, 整理得:22335333()()0422422x y x y m x y +-+-++-=,所以:223350,4223330,422x y x y x y ⎧+-+-=⎪⎪⎨⎪+-=⎪⎩ 解得:0,1,x y =⎧⎨=⎩或2,0x y =⎧⎨=⎩(舍).所以圆过定点(0,1)(法二) 设圆的一般方程为:220x y Dx Ey F ++++=,将m x y +=21代入的圆的方程: 024522=+++⎪⎭⎫⎝⎛+++F mE m x E D m x ○5 方程○1与方程○5为同解方程.22122(1)542E m mE Fm D m m ++-+=+=,圆过定点(2,0),所以024=++F D ,因为动直线m x y +=21与椭圆C 交与P,Q(均不与A 点重合)所以1-≠m . 解得: 3(1)3335,,42222m D E m F m -==+=--, (以下相同) 【说明】本题考查圆锥曲线的基本量间关系、直线与圆锥曲线的位置关系;考查定点定值问题;考查运算求解能力和推理论证能力.23.(镇江市2013届高三上学期期末考试数学试题)斜率为1的直线与抛物线22y x =交于不同两点,A B ,求线段AB 中点M 的轨迹方程. .【答案】解:设直线方程:m x y +=,()()()y x M y x B y x A ,,,,,2211将m x y +=代入22y x =,得()02222=+-+m x m x ,所以()22122122240,22,,m m x x m x x m ⎧∆=-->⎪⎪+=-⎨⎪=⎪⎩∴21<m ,1,211221=+=>-=+=m x y m x x x , 线段AB 中点M 的轨迹方程为:⎪⎭⎫ ⎝⎛>=211x y24.(江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题)直角坐标系xOy 中,已知椭圆:C【答案】(1)P (53a ,54b ), 22B A K ·K OP =-1,∴4b 2=3a 2=4(a 2-c 2), ∴a 2=4c 2, ∴e=21① (2)MN=7214=22112b a +,∴1272222=+b a b a ②由①②得,a 2=4,b 2=3, ∴13422=+y x RQRF RQ RF ··11RQRF RQ RF ··22∴22000002200000)1(),)(,1()1(),)(,1(y x y t x y x y x y t x y x +-----=++-----化简得: ∴t =-31y 0 ∵0<y 0<3,t∈(-33,0) 25.(扬州市2012-2013学年度第一学期期末检测高三数学试题)如图,已知椭圆1E 方程为22221(0)x y a b a b+=>>,圆2E 方程为222x y a +=,过椭圆的左顶点A 作斜率为1k 直线1l 与椭圆1E 和圆2E 分别相交于B 、C.(Ⅰ)若11k =时,B 恰好为线段AC 的中点,试求椭圆1E 的离心率e ; (Ⅱ)若椭圆1E 的离心率e =12,2F 为椭圆的右焦点,当2||||2BA BF a +=时,求1k 的值; (Ⅲ)设D 为圆2E 上不同于A 的一点,直线AD 的斜率为2k ,当2122k b k a=时,试问直线BD 是否过定点?若过定点,求出定点坐标;若不过定点,请说明理由.【答案】解:(Ⅰ)当11k =时,点C 在y 轴上,且(0,)C a ,则(,)22a aB -,由点B 在椭圆上,得2222()()221a a a b -+=, ∴2213b a =,22222213c b e a a==-=,∴e =(Ⅱ)设椭圆的左焦点为1F ,由椭圆定义知,12||||2BF BF a +=, ∴1||||BF BA =,则点B 在线段1AF 的中垂线上,∴2B a cx +=-, 又12c e a ==,∴12c a =,b =,∴34B a x =-, 代入椭圆方程得B y==,∴1B B y k x a=+= (Ⅲ)法一:由12222(),1,y k x a x y ab =+⎧⎪⎨+=⎪⎩得2222122()0k x a x a a b +-+=, ∴x a =-,或22212221()a b k a x b a k -=+, ∵B x a ≠-,∴22212221()B a b k a x b a k -=+,则21122212()B B ab k y k x a b a k =+=+由2222(),,y k x a x y a =+⎧⎨+=⎩得22222()0x a k x a -++=, 得x a =-,或2222(1)1a k x k -=+,同理,得2222(1)1D a k x k -=+,22221D ak y k =+,当2122k b k a =时,422222222422222222()()B b a b k a a b k a x b a b k b k a--==++,2222222B ab k y a b k =+, 22222222222222222222222211()(1)1BDab k ak a b k k k k a a b k a k a b k k -++==----++,∴ BD⊥AD,∵2E 为圆, ∴ ∠ADB 所对圆2E 的弦为直径,从而直线BD 过定点(a ,0) 法二:直线BD 过定点(,0)a , 证明如下:设(,0)P a ,(,)B B B x y ,则:22221(0)B B x y a b a b +=>>22222212222222()1B B B AD PBPB B B B y y y a a a a b k k k k b b x a x a b x a b a ==⋅⋅=⋅=-=-+--, 所以PB AD ⊥,又PD AD ⊥所以三点,,P B D 共线,即直线BD 过定点(,0)P a26.(南通市2013届高三第一次调研测试数学试卷)解答时应写出文字说明、证明过程或演算步骤.如图,已知定点R (0,-3),动点P ,Q 分别在x 轴和y 轴上移动,延长PQ 至点M ,使12PQ QM =,且0PR PM ⋅=.(1)求动点M 的轨迹C 1;(2)圆C 2: 22(1)1x y +-=,过点(0,1)的直线l 依次交C 1于A ,D 两点(从左到右),交C 2于B ,C 两点(从左到右),求证:AB CD ⋅为定值.【答案】解:(1)法一:设M (x ,y ),P (x 1,0),Q (0,y 2),则由10,2PR PM PQ QM ⋅==及R (0,-3),得(第22题)11122()(3)0,1,211.22x x x y x x y y y ⎧⎪--+-=⎪⎪-=⎨⎪⎪=-⎪⎩化简,得24x y = 所以,动点M 的轨迹C 1是顶点在原点,开口向上的抛物线 法二:设M (x ,y ).由12PQ QM =,得 (,0),(0,)23x yP Q -.所以,3(,3),(,)22x xPR PM y =-=.由0PR PM =,得 3(,3)(,)022x x y -⋅=,即23304x y -=.化简得 24x y =所以,动点M 的轨迹C 1是顶点在原点,开口向上的抛物线(2)证明:由题意,得 AB CD AB CD ⋅=⋅,⊙C 2的圆心即为抛物线C 1的焦点F . 设11(,)A x y ,22(,)D x y ,则1111AB FA FB y y =-=+-= 同理 2CD y =.设直线的方程为 (1)x k y =-.由2(1),1,4x k y y x =-⎧⎪⎨=⎪⎩得221(1)4y k y =-,即2222(24)0k y k y k --+=.所以,121AB CD AB CD y y ⋅=⋅==27.(2012-2013学年度苏锡常镇四市高三教学情况调研(二)数学试题)已知抛物线21:1C y x =+和抛物线22:C y x a =--在交点处的两条切线互相垂直,求实数a 的值.【答案】28.(常州市2013届高三教学期末调研测试数学试题)如图,在平面直角坐标系xoy 中,已知12,F F 分别是椭圆E :22221(0)x y a b a b+=>>的左、右焦点,A ,B 分别是椭圆E 的左、右顶点,且2250AF BF +=.(1)求椭圆E 的离心率;(2)已知点()1,0D 为线段2OF 的中点,M 为椭圆E 上的动点(异于点A 、B ),连接1MF 并延长交椭圆E 于点N ,连接MD 、ND 并分别延长交椭圆E 于点P 、Q ,连接PQ ,设直线MN 、PQ 的斜率存在且分别为1k 、2k ,试问是否存在常数λ,使得120k k λ+=恒成立?若存在,求出λ的值;若不存在,说明理由.【答案】解:(1)2250AF BF +=,225AF F B ∴=.()5a c a c ∴+=-,化简得23a c =,故椭圆E 的离心率为23.(2)存在满足条件的常数λ,47=-.点()1,0D 为线段2OF 的中点,2c ∴=,从而3a =,b =,左焦点()12,0F -,椭圆E 的方程为22195x y +=.设()11,M x y ,()22,N x y ,()33,P x y ,()44,Q x y ,则直线MD的方程为1111x x y y -=+,代入椭圆方程22195x y +=,整理得,2112115140x x y y y y --+-=.()1113115y x y y x -+=-,13145y y x ∴=-.从而131595x x x -=-,故点1111594,55x y P x x ⎛⎫- ⎪--⎝⎭.同理,点2222594,55x y Q x x ⎛⎫- ⎪--⎝⎭.三点M 、1F 、N 共线,121222y y x x ∴=++,从而()1221122x y x y y y -=-.从而()()()()121221121234121212341212124457557595944455y y x y x y y y y y y y x x k k x x x x x x x x x x --+-----=====--------.故21407kk -=,从而存在满足条件的常数λ,47=-.29.(苏州市2012-2013学年度第一学期高三期末考试数学试卷)如图,在平面直角坐标系xOy 中,已知点F 是椭圆2222:1(0)x y E a b a b+=>>的左焦点,A ,B ,C 分别为椭圆E 的右、下、上顶点,满足5FC BA =,椭圆的离心率为12. (1)求椭圆的方程;(2)若P 为线段FC (包括端点)上任意一点,当PA PB 取得最小值时,求点P 的坐标;(3)设点M 为线段BC (包括端点)上的一个动点,射线MF 交椭圆于点N ,若NF FM λ=,求实数【答案】30.(徐州、宿迁市2013届高三年级第三次模拟考试数学试卷)如图,在平面直角坐标系xOy 中,已知椭圆E :22221(0)x y a b a b+=>>的离心率3e =,12,A A 分别是椭圆E 的左、右两个顶点,圆2A 的半径为a ,过点1A 作圆2A 的切线,切点为P ,在x 轴的上方交椭圆E 于点Q . ⑴求直线OP 的方程;⑵求1PQ QA 的值;⑶设a 为常数.过点O 作两条互相垂直的直线,分别交椭圆E 于点,B C ,分别交圆2A 于点,M N ,记OBC △和OMN △的面积分别为1S ,2S ,求12S S ⋅的最大值.【答案】⑴连结2A P ,则21A P A P ⊥,且2A P a =,又122A A a =,所以1260A A P ∠=.所以260POA ∠=,所以直线OP的方程为y = ⑵由⑴知,直线2A P的方程为)y x a =-,1A P的方程为)y x a =+, 联立解得2P a x =因为e ,即c a =所以2234c a =,2214b a =,故椭圆E 的方程为222241x y a a =+.由2222),41,y x a x y a a ⎧=+⎪⎪⎨⎪=⎪⎩+解得7Q a x =-, 所以1()3274()7a aPQ a QA a --==--- ⑶不妨设OM 的方程为(0)y kx k =>,联立方程组2222,41,y kx x y a a =⎧⎪⎨=⎪⎩+解得B ,所以OB =用1k-代替上面的k ,得OC =.同理可得,OM =,ON =(第18题图)所以41214S S OB OC OM ON a ⋅=⋅⋅⋅⋅=15=,当且仅当1k =时等号成立,所以12S S ⋅的最大值为45a31.(江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷)如图,在平面直角坐标系xOy 中,椭圆22221(0)y x a b a b+=>>的右焦点为(1 0)F ,,离心率为.分别过O ,F 的两条弦AB ,CD 相交于点E (异于A ,C 两点),且OE EF =.(1)求椭圆的方程;(2)求证:直线AC ,BD 的斜率之和为定值.【答案】(1)解:由题意,得1c =,c e a ==,故a =从而2221b a c =-=,所以椭圆的方程为2212x y +=. ① (2)证明:设直线AB 的方程为y kx =, ②直线CD 的方程为(1)y k x =--, ③ 由①②得,点A ,B的横坐标为由①③得,点C ,D记11( )A x kx ,,22( )B x kx ,,33( (1))C x k x -,,44( (1))D x k x -,, 则直线AC ,BD 的斜率之和为 13241324(1)(1)kx k x kx k x x x x x ----+-- 132413241324(1)()()(1)()()x x x x x x x x k x x x x +--+-+-=⋅--(第18题)1234123413242()()()()()x x x x x x x x k x x x x --+++=⋅--2222213242(1)2420212121()()k k k k k k x x x x -⎛⎫---+ ⎪+++⎝⎭=⋅-- 0=32.(2012-2013学年度苏锡常镇四市高三教学情况调研(二)数学试题)如图,设A ,B 分别为椭圆2222:1(0)x y E a b a b+=>>的右顶点和上顶点,过原点O 作直线交线段AB 于点M (异于点A ,B ),交椭圆于C ,D 两点(点C 在第一象限内),ABC ∆和ABD ∆的面积分别为1S 与2S . (1)若M 是线段AB 的中点,直线OM 的方程为13y x =,求椭圆的离心率; (2)当点M 在线段AB 上运动时,求12S S 的最大值.【答案】(注:可编辑下载,若有不当之处,请指正,谢谢!)。

江苏省13市2017高三上学期考试数学试题分类汇编数列一、填空题1、(南京市、盐城市2017届高三第一次模拟)设{}n a 是等差数列,若45621a a a ++=,则9S = ▲ .2、(苏北四市(淮安、宿迁、连云港、徐州)2017届高三上学期期中)设n S 是等差数列{}n a 的前n 项和,且23a =,416S =,则9S 的值为 ▲ .3、(苏北四市(徐州、淮安、连云港、宿迁)2017届高三上学期期末)已知等比数列{}n a 的前n 项和为n S ,若223323,23S a S a =+=+,则公比q 的值为.4、(苏州市2017届高三上学期期中调研)已知等比数列{}n a 的各项均为正数,且满足:194a a =,则数列2{log }n a 的前9项之和为 ▲ .5、(苏州市2017届高三上学期期中调研)已知数列{}n a 满足:111(1),1n n n a a a a ++=-=,数列{}n b 满足:1n n n b a a +=⋅,则数列{}n b 的前10项的和10S = ▲ .6、(苏州市2017届高三上期末调研测试)设n S 是等差数列{}n a 的前n 项和,若7772-==S a ,,则7a 的值为7、(无锡市2017届高三上学期期末)设公比不为1的等比数列{}n a 满足12318a a a =-,且243,,a a a 成等差数列,则数列{}n a 的前4项和为.8、(盐城市2017届高三上学期期中)在等比数列{}n a 中,已知121a a +=,342a a +=,则910a a += ▲9、(扬州市2017届高三上学期期末)在正项等比数列{}n a 中,若4321226a a a a +--=,则56a a +的最小值为▲.10、(镇江市2017届高三上学期期末)数列{}n a 为等比数列,且741531+++a a a ,,成等差数列,则公差=d11、(盐城市2017届高三上学期期中)在数列{}n a 中,10112a =-,且当2100n ≤≤时,102232n n n a a -+=⨯恒成立,则数列{}n a 的前100项和100S = ▲ .二、解答题1、(南京市、盐城市2017届高三第一次模拟)若存在常数*(,2)k k N k ∈≥、q 、d ,使得无穷数列{}n a 满足1,,,,n n n n a d N ka n qa N k *+*⎧+∉⎪⎪=⎨⎪∈⎪⎩则称数列{}n a 为“段比差数列”,其中常数k 、q 、d 分别叫做段长、段比、段差. 设数列{}n b 为“段比差数列”.(1)若{}n b 的首项、段长、段比、段差分别为1、3、q 、3.①当0q =时,求2016b ;②当1q =时,设{}n b 的前3n 项和为3n S ,若不等式133n n S λ-≤⋅对n N *∈恒成立,求实数λ的取值范围;(2)设{}n b 为等比数列,且首项为b ,试写出所有满足条件的{}n b ,并说明理由.2、(南通、泰州市2017届高三第一次调研测)已知等差数列{}n a 的公差d 不为0,且1k a ,2k a ,…,n k a ,…(12k k <<…n k <<…)成等比数列,公比为q .(1)若11k =,23k =,38k =,求1a d的值; (2)当1a d为何值时,数列{}n k 为等比数列; (3)若数列{}n k 为等比数列,且对于任意n *∈N ,不等式2n n k n a a k +>恒成立,求1a 的取值 范围.3、(苏北四市(淮安、宿迁、连云港、徐州)2017届高三上学期期中)在数列{}n a 中,已知113a =,111233n n n a a ++=-,*n ∈N ,设n S 为{}n a 的前n 项和. (1)求证:数列{3}nn a 是等差数列; (2)求n S ;(3)是否存在正整数p ,q ,r ()p q r <<,使,,p q r S S S 成等差数列?若存在,求出p ,q ,r 的值;若不存在,说明理由.4、(苏北四市(徐州、淮安、连云港、宿迁)2017届高三上学期期末)已知正项数列{}n a 的前n 项和为n S ,且11,(1)(1)6()n n n a a a a S n +=++=+,*∈N n .(1)求数列{}n a 的通项公式;(2)若对于N n *∀∈,都有(31)n S n n +≤成立,求实数a 取值范围;(3)当2a =时,将数列{}n a 中的部分项按原来的顺序构成数列{}n b ,且12b a =,证明: 存在无数个满足条件的无穷等比数列{}n b .5、(苏州市2017届高三上学期期中调研)已知等比数列{}n a 的公比1q >,且满足:23428a a a ++=,且32a +是24,a a 的等差中项.(1)求数列{}n a 的通项公式; (2)若12log n n n b a a =,12n n S b b b =+++,求使1262n n S n ++⋅>成立的正整数n 的最小值.6、(无锡市2017届高三上学期期末) 数列{}n a 的前n 项和为n S ,()12,,3n n n a S a r r R n N *⎛⎫==+∈∈ ⎪⎝⎭. (1)求r 的值及数列{}n a 的通项公式; (2)设()n nnb n N a *=∈,记{}n b 的前n 项和为n T . ①当n N *∈时,2n n T T λ<-恒成立,求实数λ的取值范围; ②求证:存在关于n 的整式()g n ,使得()()1111n nn i TT g n -=+=⋅-∑对一切2,n n N *≥∈都成立.7、(盐城市2017届高三上学期期中)若数列{}n a 中的项都满足21221n n n a a a -+=<(*n N ∈),则称{}n a 为“阶梯数列”.(1)设数列{}n b 是“阶梯数列”,且11b =,21219n n b b +-=(*n N ∈),求2016b ;(2)设数列{}n c 是“阶梯数列”,其前n 项和为n S ,求证:{}n S 中存在连续三项成等差数列,但不存在连续四项成等差数列;(3)设数列{}n d 是“阶梯数列”,且11d =,21212n n d d +-=+(*n N ∈),记数列21n n d d +⎧⎫⎨⎬⎩⎭的前n 项和为n T . 问是否存在实数t ,使得()10n n t T t T ⎛⎫-+< ⎪⎝⎭对任意的n N *∈恒成立?若存在,请求出实数t 的取值范围;若不存在,请说明理由.8、(扬州市2017届高三上学期期末)已知数列{}n a 与{}n b 的前n 项和分别为n A 和n B ,且对任意n *∈N ,112()n n n n a a b b ++-=-恒成立. (1)若21,2n A n b ==,求n B ;(2)若对任意n *∈N ,都有n n a B =及3124122334113n n n b b b ba a a a a a a a ++++++<成立,求正实数1b 的取值范围;(3)若12,a =2n n b =,是否存在两个互不相等的整数,s t (1)s t <<,使11,,s ts tA A AB B B 成等差数列?若存在,求出,s t 的值;若不存在,请说明理由.9、(镇江市2017届高三上学期期末)已知*∈N n ,数列{}n a 的各项均为正数,前n 项和为n S ,且2121==a a ,,设 n n n a a b 212+=-.(1)若数列{}n b 是公比为3的等比数列,求n S 2;(2)若对任意*∈N n ,22na S n n +=恒成立,求数列{}n a 的通项公式;(3)若)(1232-=nn S ,数列{}1+n n a a 也为等比数列,求数列的{}n a 通项公式.参考答案一、填空题1、632、813、24、95、10116、-137、588、16 9、48 10、3 11、-4二、解答题1、(1)①方法一:∵{}n b 的首项、段长、段比、段差分别为1、3、0、3,2014201300b b ∴=⨯=,2015201433b b ∴=+=,2016201536b b ∴=+=. ……………3分方法二:∵{}n b 的首项、段长、段比、段差分别为1、3、0、3,∴11b =,24b =,37b =,4300b b =⨯=,5433b b =+=,6536b b =+=,7600b b =⨯=,…∴当4n ≥时,{}n b 是周期为3的周期数列. ∴201666b b ==.……………3分②方法一:∵{}n b 的首项、段长、段比、段差分别为1、3、1、3,∴()()()32313131331313126n n n n n n n n b b b d b qb d b q b d d b d +-+-----=+-=+-=++-==⎡⎤⎣⎦,∴{}31n b -是以24b =为首项、6为公差的等差数列, 又()()32313313131313n n n n n n n b b b b d b b d b ------++=-+++=,()()()312345632313n n n n S b b b b b b b b b --∴=+++++++++()()2253113346932n n n b b b n n n--⎡⎤=++=+⨯=+⎢⎥⎣⎦,……………6分133n n S λ-≤⋅,313n n S λ-∴≤,设313nnn S c -=,则()max n c λ≥, 又()()()2221112322913193333n n n n n n n n n n n c c +-----++++-=-=, 当1n =时,23220n n --<,12c c <;当2n ≥时,23220n n -->,1n n c c +<, ∴123c c c <>>⋅⋅⋅,∴()2max 14n c c ==,……………9分∴14λ≥,得[)14,λ∈+∞. ……………10分 方法二:∵{}n b 的首项、段长、段比、段差分别为1、3、1、3,∴313n n b b +=,∴333333126n n n n b b b b d +++-=-==,∴{}3n b 是首项为37b =、公差为6的等差数列,∴()2363176342n n n b b b n n n -+++=+⨯=+, 易知{}n b 中删掉{}3n b 的项后按原来的顺序构成一个首项为1公差为3的等差数列,()21245323122121362n n n n b b b b b b n n n ---∴++++++=⨯+⨯=-, ()()222334693n S n n n n n n∴=++-=+,………………6分以下同方法一.(2)方法一:设{}n b 的段长、段比、段差分别为k 、q 、d ,则等比数列{}n b 的公比为1k kb q b +=,由等比数列的通项公式有1n n b bq -=, 当m N *∈时,21k m k m b b d ++-=,即()11k m k m k m b q b q b q q d +-=-=恒成立, ……………12分①若1q =,则0d =,n b b =;②若1q ≠,则()1kmd qq b=-,则kmq 为常数,则1q =-,k 为偶数,2d b =-,()11n n b b -=-;经检验,满足条件的{}n b 的通项公式为n b b=或()11n n b b -=-. ……………16分方法二:设{}n b 的段长、段比、段差分别为k 、q 、d ,①若2k =,则1b b =,2b b d =+,()3b b d q =+,()4b b d q d =++,由2132b b b =,得b d bq +=;由2243b b b =,得()()2b d q b d q d +=++,联立两式,得01d q =⎧⎨=⎩或21d b q =-⎧⎨=-⎩,则n b b =或()11n n b b -=-,经检验均合题意. …………13分②若3k ≥,则1b b =,2b b d =+,32b b d =+,由2132b b b =,得()()22b d b b d+=+,得0d =,则n b b =,经检验适合题意.综上①②,满足条件的{}n b 的通项公式为n b b =或()11n n b b -=-. ……………16分2、【解】(1)由已知可得:1a ,3a ,8a 成等比数列,所以2111(2)(7)a d a a d +=+,………2分整理可得:2143d a d =.因为0d ≠,所以143a d =.……………………………4分(2)设数列{}n k 为等比数列,则2213k k k =.又因为1k a ,2k a ,3k a 成等比数列,所以[][][]2111312(1)(1)(1)a k d a k d a k d +-+-=+-.整理,得21213132132(2)(2)a k k k d k k k k k k --=---+. 因为2213k k k =,所以1213213(2)(2)a k k k d k k k --=--. 因为2132k k k ≠+,所以1a d =,即11a d=.………………………………………6分当11a d=时,1(1)n a a n d nd =+-=,所以n k n a k d =. 又因为1111n n n k k a a q k dq --==,所以11n n k k q -=. 所以1111nn n n k k q q k k q+-==,数列{}n k 为等比数列. 综上,当11a d=时,数列{}n k 为等比数列.………………………………………8分(3)因为数列{}n k 为等比数列,由(2)知1a d =,11(1)n n k k q q -=>.1111111n n n n k k a a q k dq k a q ---===,11(1)n a a n d na =+-=.因为对于任意n *∈N ,不等式2n n k n a a k +>恒成立. 所以不等式1111112n n na k a q k q --+>,即111112n n k q a n k q -->+,111111110222n n nn k q q na k q k q --+<<=+恒成立.……………………10分下面证明:对于任意的正实数(01)εε<<,总存在正整数1n ,使得11n n εq <. 要证11n n εq <,即证11ln ln ln n n q ε<+. 因为11ln e 2x x x <≤,则1122111ln 2ln n n n =<,解不等式1211ln ln n n q ε<+,即1122211()ln ln 0n q n ε-+>,可得121n >21n >.不妨取201n ⎡⎤=+⎢⎥⎢⎥⎣⎦,则当10n n >时,原式得证.所以11102a <≤,所以12a ≥,即得1a 的取值范围是[)2+∞,.……………16分3、(1)证明:因为111233n n n a a ++=-,所以11332n n n n a a ++-=-,…………………2分 又因为113a =,所以113=1a ⋅, 所以{3}nn a 是首项为1,公差为2-的等差数列.…………………………4分(2)由(1)知31(1)(2)32n n a n n =+-⋅-=-,所以1(32)()3n n a n =-,………6分所以12311111()(1)()(3)()(32)()3333n n S n =⋅+-⋅+-⋅++-⋅…,所以23+1111111()(1)()(52)()+(32)()33333n n n S n n =⋅+-⋅+⋅⋅⋅+-⋅-⋅ ,两式相减得2312111112[()()()](32)()333333n n n S n +=-++⋯+--⋅1111()11132[](23)()139313n n n -+-=-⨯+-⋅-112()3n n +=⋅, 所以3n n nS =.…………………………………………………………………10分(3)假设存在正整数p ,q ,r ()p q r <<,使,,p q r S S S 成等差数列, 则2q p r S S S =+,即2333q p rq p r =+. 由于当2n ≥时,()132()03n n a n =-<,所以数列{}n S 单调递减.又p q <,所以1p q -≤且q 至少为2,所以1133p q p q --≥,………………12分1123333q q q q q q ----=. ①当3q ≥时,112333p q q p q q --≥≥,又03r r>,所以2333p r q p r q+>,等式不成立.…………………………………………14分②当2q =时,1p =,所以41933r r =+,所以139r r =,所以3r =({}n S 单调递减,解唯一确定).综上可知,p ,q ,r 的值为1,2,3.………………………………16分4、(1)当1n =时,121(1)(1)6(1)a a S ++=+,故25a =;当2n ≥时,11(1)(1)6(1)n n n a a S n --++=+-,所以+111(1)(+1(1)(1)6()6(1)n n n n n n a a a a S n S n )--+-++=+-+-, 即11(1)()6(1)n n n n a a a a +-+-=+,又0n a >,所以116n n a a +--=,………………………………………………3分 所以216(1)66k a a k k a -=+-=+-,25+6(1)61k a k k =-=-,*k N Î,故**33, ,,31, ,.n n a n n a n n n N N 为奇数为偶数ìï+-?ï=íï-?ïî…………………………………………5分 (2)当n 为奇数时,1(32)(33)6n S n a n n =+-+-,由(31)n S n n ≤+得,23321n n a n ≤+++恒成立,令2332()1n n f n n ++=+,则2394(1)()0(2)(1)n n f n f n n n +++-=>++, 所以(1)4a f ≤=.……………………………………………………………8分当n 为偶数时,13(3+1)6n S n n a n =?-, 由(31)n S n n ≤+得,3(1)a n ≤+恒成立,所以9a ≤.又10a a =>,所以实数a 的取值范围是(0,4].……………………………10分 (3)当2a =时,若n 为奇数,则31n a n =-,所以31n a n =-.解法1:令等比数列{}n b 的公比*4()m q m N =?,则1(1)154n m n n b b q --==?.设(1)k m n =-,因为214114443k k --++++=,所以(1)21545[3(1444)1]m n k --??++++,213[5(144+4)2]1k -=++++-,…………………………14分因为215(144+4)2k -++++为正整数,所以数列{}n b 是数列{}n a 中包含的无穷等比数列,因为公比*4()m q m N =?有无数个不同的取值,对应着不同的等比数列, 故无穷等比数列{}n b 有无数个.………………………………………………16分 解法2:设222231(3)k b a k k ≥==-,所以公比2315k q -=. 因为等比数列{}n b 的各项为整数,所以q 为整数, 取*252()k m m N =+?,则31q m =+,故15(31)n n b m -=?,由1315(31)n n k m --=?得,11[5(31)1]()3n n k m n N -*=++?, 而当2n ≥时,12215[(31)(31)]5(31)3n n n n n k k m m m m -----=+-+=+, 即215(31)n n n k k m m --=++,…………………………………………………14分 又因为12k =,25(31)n m m -+都是正整数,所以n k 也都是正整数, 所以数列{}n b 是数列{}n a 中包含的无穷等比数列,因为公比*31()q m m N =+?有无数个不同的取值,对应着不同的等比数列, 故无穷等比数列{}n b 有无数个.………………………………………………16分 5、解:(1)∵32a +是24,a a 的等差中项,∴3242(2)a a a +=+,..........1分代入23428a a a ++=,可得38a =,∴2420a a +=,∴21311820a q a q a q ⎧=⎪⎨+=⎪⎩,解之得122a q =⎧⎨=⎩或13212a q =⎧⎪⎨=⎪⎩,........4分 ∵1q >,∴122a q =⎧⎨=⎩,∴数列{}n a 的通项公式为2n n a =. ..........6分(2)∵1122log 2log 22n n n n n n b a a n ===-⋅,..........7分∴2(12222)n n S n =-⨯+⨯++⋅, ……① )22)1(2221(S 2132+⋅+⋅-++⨯+⨯-=n n n n n , ……②②-①得23122222n n n S n +=++++-⋅1112(12)222212n n n n n n +++-=-⋅=--⋅-...........12分 ∵1262n n S n ++⋅>,∴12262n +->,∴16n +>,5n >,..........13分∴使1262n n S n ++⋅>成立的正整数n 的最小值为6...........14分 6、7、解:(1)21219n n b b +-=,11b =,{}21n b -∴是以11b =为首项9为公比的等比数列,12221193n n n b b ---∴=⨯=,201420153b ∴=,∵数列{}n b 是“阶梯数列”,∴201420162015==3b b . (3)分(2)由数列{}n c 是“阶梯数列”得212n n c c -=,故2122221n n n n S S S S ----=-,∴{}n S 中存在连续三项()22212,,2n n n S S S n --≥成等差数列; ……………5分(注:给出具体三项也可)假设{}n S 中存在连续四项123,,,,k k k k S S S S +++成等差数列, 则12132k k k k k k S S S S S S +++++-=-=-,即123k k k c c c +++==,当*21,k m m N =-∈时, 22122m m m c c c ++==,① 当*2,k m m N =∈时, 212223m m m c c c +++==,②由数列{}n c 是“阶梯数列”得221m m c c +<2223m m c c ++=<,③①②与③都矛盾,故假设不成立,即{}n S 中不存在连续四项成等差数列. …………………8分(3)∵21212n n d d +-=+,11d =,{}21n d -∴是以11d =为首项2为公差的等差数列,()2111221n d d n n -∴=+-⨯=-,又数列{}n d 是“阶梯数列”,故21221n n d d n -==-,()()2222121111111212122121k k k k d d d d k k k k +-+⎛⎫∴===- ⎪-+-+⎝⎭, (1)0分①当()*2n k k N =∈时,2132435462121222111111n k k k k k T T d d d d d d d d d d d d -++⎛⎫⎛⎫⎛⎫==++++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭133521211112k k d d d d d d -+⎛⎫=+++ ⎪⎝⎭11111111221,1213352121213k k k ⎛⎫⎡⎫=⨯-+-++-=-∈ ⎪⎪⎢-++⎝⎭⎣⎭,13,12n T ⎡⎫∴-∈--⎪⎢⎣⎭,又()10n n t T t T ⎛⎫-+< ⎪⎝⎭恒成立,1nn t T T ∴-<<恒成立, 213t ∴-≤<. …………………13分 ②当()*21n k k N =-∈时,2122222221211111122121n k k k k k k k k T T T T T d d d d k k -+-+⎛⎫==-=-=-- ⎪-+⎝⎭1111,142423k k ⎡⎫=--∈⎪⎢-+⎣⎭,[)13,1n T ∴-∈--,又()10n n t T t T ⎛⎫-+< ⎪⎝⎭恒成立,1n n t T T ∴-<<恒成立, 113t ∴-≤<. …………………15分综上①②, 存在满足条件的实数t ,其取值范围是11,3⎡⎫-⎪⎢⎣⎭. …………………16分注:()()22, 2,,21421, 21,,2121n k n k k N k T k k n k k N k k ⎧=∈*⎪+⎪=⎨--⎪=-∈*-+⎪⎩也可写成nT =8、(1)因为2,n A n =,所以221,1(1),n 2n n a n n =⎧=⎨--≥⎩即21n a n =- --------------------------------------2分故111()12n n n n b b a a ++-=-=,所以数列{}n b 是以2为首项,1为公差的等差数列,所以21132(1)1222n B n n n n n =⋅+⋅⋅-⋅=+ --------------------------------------4分(2)依题意112()n n n n B B b b ++-=-,即112()n n n b b b ++=-,即12n nb b +=, 所以数列{}n b 是以1b 为首项,2为公比的等比数列,所以1112(21)12nn n n a B b b -==⨯=--,所以11112(21)(21)nn n n n n b a a b +++=-⋅- --------------------------5分 因为111111112111()(21)(21)2121n n n n n n n n b b a a b b b ++++⋅==--⋅--- --------------------------8分 所以31241112233411111()2121n n n n b b b b a a a a a a a a b +++++++=---,所以1111111()21213n b +-<--恒成立,即1113(1)21n b +>--,所以13b ≥。

江苏省13市县2016届高三上学期期末考试数学试题分类汇编圆锥曲线一、填空题1、(常州市2016届高三上期末)已知双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线经过点P (1,-2),则该双曲线的离心率为2、(淮安、宿迁、连云港、徐州苏北四市2016届高三上期末)抛物线x y 42=的焦点到双曲线191622=-y x 渐近线的距离为 3、(南京、盐城市2016届高三上期末)在平面直角坐标系xOy 中,已知抛物线C 的顶点在坐标原点,焦点在x 轴上,若曲线C 经过点(1,3)P ,则其焦点到准线的距离为 ▲ 4、(南通市海安县2016届高三上期末)在平面直角坐标系xOy 中,已知双曲线)0,0(12222>>=-b a b y a x 的一条渐近线的方程为x y 3=则该双曲线的离心率为 5、(苏州市2016届高三上期末)双曲线22145x y -=的离心率为 ▲6、(泰州市2016届高三第一次模拟)在平面直角坐标系xOy 中,双曲线2212x y -=的实轴长为 ▲ .7、(无锡市2016届高三上期末)设ABC ∆是等腰三角形,120ABC ∠=,则以A 、B 为焦点且过点C 的双曲线的离心率为8、(扬州市2016届高三上期末)双曲线116922=-y x 的焦点到渐近线的距离为 ▲ 9、(镇江市2016届高三第一次模拟)以抛物线y 2=4x 的焦点为焦点,以直线y =±x 为渐近线的双曲线标准方程为________.填空题答案12、35 3、924、25、32 6、 78、4 9、【答案】x 212-y212=1.【解析】由题意设双曲线的标准方程为22221x y a b-=,y 2=4x 的焦点为()1,0,则双曲线的焦点为()1,0;y =±x 为双曲线的渐近线,则1b a =,又因222a b c +=,所以2211,22a b ==,故双曲线标准方程为x 212-y212=1.二、解答题1、(常州市2016届高三上期末)在平面直角坐标系xoy 中,设椭圆22221(0)x y a b a b+=>>的离心率是e ,定义直线by e=±为椭圆的“类准线”,已知椭圆C的“类准线”方程为y =±,长轴长为4。

江苏省13市2020届高三上学期期中期末考试数学试题分类汇编圆锥曲线一、填空题1、(常州市2020届高三上学期期末考试)在平面直角坐标系xOy 中,双曲线2222:1(0,0)x y C a b a b-=>>的右顶点为A,过A 做x 轴的垂线与C 的一条渐近线交于点B,若2OB a =,则C 的离心率为2、(常州市2020届高三上学期期末考试)在平面直角坐标系xOy 中,圆222:22210C x ax y ay a -+-+-=上存在点P 到点(0,1)的距离为2,则实数a 的取值范围是3、(南京、盐城市2020届高三上学期期末考试)在平面直角坐标系 xOy 中, 若抛物线 y 2 = 4x 上的点 P 到其焦点的距离为 3,则点 P 到点O 的距离为________.4、(南通、泰州市2020届高三上学期期末)在平面直角坐标系 xOy 中, 已知点 A ,B 分别在双曲线C : x 2 - y 2 =1 的两条渐近线上, 且双曲线C 经过线段 AB 的中点.若点 A 的横坐标为 2 ,则点 B 的横坐标为______.5、(苏北四市(徐州、宿迁、淮安、连云港)2020届高三上学期期末考试)在平面直角坐标系xOy中,双曲线2213x y -=的右准线与渐近线的交点在抛物线22y px =上,则实数p 的值为______.6、(苏州市2020届高三上学期期末考试)在平面直角坐标系xOy 中,己知点F 1,F 2是双曲线22221x y a b-=(a >0,b >0)的左、右焦点,点P 的坐标为(0,b ),若∠F 1PF 2=120°,则该双曲线的离心率为 .7、(无锡市2020届高三上学期期末考试)双曲线22:143x y C -=的左右顶点为,A B ,以AB 为直径作圆O ,P 为双曲线右支上不同于顶点B 的任一点,连接PA 角圆O 于点Q ,设直线,PB QB 的斜率分别为12,k k ,若12k k λ=,则λ=_____.8、(徐州市2020届高三上学期期中考试)在平面直角坐标系xOy 中,若双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线的倾斜角为30º,期C 的离心率为 . 9、(扬州市2020届高三上学期期末考试)在平面直角坐标系xOy 中,顶点在原点且以双曲线2213y x -=的右准线为准线的抛物线方程是10、(扬州市2020届高三上学期期中考试)双曲线1422=-x y 的渐近线方程为 . 11、(扬州市2020届高三上学期期中考试)抛物线x y 42=上横坐标为4的点到焦点的距离为 .12、(镇江市2020届高三上学期期末考试)顶点在原点且以双曲线221124x y -=的右焦点为焦点的抛物线方程是 .参考答案:1、22、117117,01,⎡⎤⎡⎤-+⎢⎥⎢⎥⎣⎦⎣⎦U 3、23 4、12 5、146、26 7、34- 8、23 9、22y x =- 10、2y x =±11、5 12、216y x =二、解答题1、(常州市2020届高三上学期期末考试)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ,椭圆右顶点为A ,点2F 在圆22(2)1x y -+=上。

江苏省2013届高三最新数学(精选试题26套)分类汇编9:圆锥曲线一、填空题1 .(南京师大附中2013届高三模拟考试5月卷)在平面直角坐标系xOy 中,已知双曲线C :x 2a 2-y 2b2=1(a >b >0)的一条渐近线方程为 y =3x ,则该双曲线的离心率的值是_____.【答案】2 2 .(江苏省徐州市2013届高三考前模拟数学试题)已知双曲线与椭圆2212x y +=有相同的焦点,且它们的离心率互为倒数,则该双曲线的方程为________. 【答案】22221x y -=3 .(江苏省常州市金坛四中2013年高考数学冲刺模拟试卷doc )已知椭圆x 2sin α-y 2cosα=1 (0≤α<2π)的焦点在y 轴上,则α的取值范围是____【答案】⎝ ⎛⎭⎪⎫π2,3π44 .(江苏省常州市西夏墅中学2013年高考冲刺模拟试卷)如图,已知椭圆)0(12222>>=+b a b y a x 的左、右准线分别为21,l l ,且分别交x 轴于D C ,两点,从1l 上一点A 发出一条光线经过椭圆的左焦点F 被x 轴反射后与2l 交于点B ,若AF BF ⊥,且75ABD ∠=︒,则椭圆的离心率等于_________.【答案】226- 5 .(江苏省常州市奔牛高级中学2013年高考数学冲刺模拟试卷)以椭圆22221(0)x y a b a b +=>>的左焦点(,0)F c -为圆心,c 为半径的圆与椭圆的左准线交于不同的两点,则该椭圆的离心率的取值范围是______________.【答案】6 .(江苏省启东中学2013届高三综合训练(3))椭圆()222210x y a b a b=>>+的右焦点为1F ,右准线为1l ,若过点1F 且垂直于x 轴的弦的弦长等于点1F 到1l 的距离,则椭圆的离心率是_______. 【答案】217 .(江苏省常州高级中学2013年高考数学模拟试卷)在平面直角坐标系xOy 中,过点11( 0)A x ,、22( 0)A x ,分别作x 轴的垂线与抛物线22x y =分别交于点12A A ''、,直线12A A ''与 x 轴交于点33( 0)A x ,,这样就称12x x 、确定了3x .同样,可由23x x 、确定4x ,,若12x =,23x =,则5x =_________.【答案】 12;设()21 2n n n A x x ,、()21111 2n n n A x x +++,,则割线n A 1n A +的方程为:2212111122()2n n n nn nx x y x x x x x ++--=--, 令0y =得121n nn n nx x x x x +++=+,即21111n n n x x x ++=+,不难得到34515171266x x x ===,,;8 .(南京师大附中2013届高三模拟考试5月卷)在平面直角坐标系xOy 中, 抛物线方程为x 2=2py (p >0). 若直线x -y -2=0与该抛物线相切,则实数p 的值是_____. 【答案】49 .(武进区湟里高中2013高三数学模拟试卷)已知椭圆22221(0)x y a b a b+=>>的上、下顶点分别为,M N ,右顶点为A ,右焦点为F ,若0AN MF =,则椭圆的离心率为_________.【答案】解析:由题设得1b bc a-⨯=-即2b ac =,也就是220a ac c --=,210e e +-=,e =. 10.(江苏省常州市第五中学2013年高考数学文科)冲刺模拟试卷)已知双曲线过点(2,1)且一条渐近线方程为x -y =0,则该双曲线的标准方程为____.【答案】x 23 - y 23=111.(江苏省常州市金坛市第一中学2013年高考冲刺模拟试卷)椭圆15222=+y ax (a 为定值,且5>a )的左焦点为F,直线m x =与椭圆相交于点A.B,FAB ∆的周长的最大值是12,则该椭圆的离心率e 是_______________. 【答案】3212.(江苏省常州市第二中学2013年高考数学(文科)冲刺模拟试卷doc )如图,已知椭圆C 的方程为: 22221x y a b+=(0)a b >>,B 是它的下顶点,F 是其右焦 点,BF 的延长线与椭圆及其右准线分别交于P 、Q 两点, 若点P 恰好是BQ 的中点,则此椭圆的离心率是___.【答案】13.(江苏省常州高级中学2013年高考数学模拟试卷)在平面直角坐标系xOy 中,直角三角形ABC 的三个顶点都在椭圆222 1 (1)x y a a+=>上, 其中0 1A (,)为直角顶点.若该三角形的面积的最大值为278,则实数a 的值为_________.【答案】3 设AB 的方程为:1(0)y kx k =+>,则AC 的方程为:11y x k=-+,由22211y kx x y a =+⎧⎪⎨+=⎪⎩,得 2222(1)20a k x a kx ++=,解得22221B a k x a k -=+,用“1k -”替换“k ”得2222C a k x a k=+,故222222221a k a k AB AC a k a k ==++ 所以()()44222222242122(1)121(1)()1ABCa k a k k k S AB AC a k a k a k a k ∆++=⋅==+++++, 令12t k k=+≥,则4322222(1)1ABC a a S a a a t ∆=--+≤(当且仅当212a t a -=>时等号成立), 由322781a a =-得2(3)(839)0a a a ---=解得3a =,或a =(舍去),所以3a =.第12题14.(江苏省常州市横山桥中学2013年高考数学冲刺模拟试卷doc )已知双曲线x 2a 2-y 2b2=1(a >0,b >0) 的焦点到渐近线的距离是a ,则双曲线的离心率的值是_____. 【答案】215.(江苏省常州市金坛四中2013年高考数学冲刺模拟试卷doc )已知A(1,4),F 是双曲线x 24-y212=1的左焦点,P 是双曲线右支上的动点,则|PF|+|PA|的最小值为________ 【答案】916.(江苏省常州市武进高级中学2013年高考数学文科)冲刺模拟试卷doc )已知双曲线的顶点与焦点分别是椭圆的22221y x a b+=(0a b >>)焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为______17.(江苏省常州市金坛四中2013年高考数学冲刺模拟试卷doc )已知点P 是双曲线22221(0,0)x y a b a b-=>>右支上一点,1F 、2F 分别是双曲线的左、右焦点. I 为12PF F ∆内心,若121212IPF IPF IF F S S S ∆∆∆=+,则双曲线的离心率为________.【答案】218.(江苏省启东中学2013届高三综合训练(2))已知抛物线)0(22>=p px y ,过定点(p,0)作两条互相垂直的直线121,,l l l 与抛物线交于P 、Q 两点,l 2与抛物线交于M 、N 两点,l 1斜率为k.某同学已正确求得弦PQ 的中点坐标为(k p p k p ,2+),请你写出弦MN 的中点坐标:_____________. 【答案】),(2pk p pk -+19.(江苏省常州市金坛四中2013年高考数学冲刺模拟试卷doc )椭圆x 225+y29=1上一点M 到焦点F 1的距离为2,N 是MF 1的中点,则|ON|等于____ 【答案】420.(江苏省启东中学2013届高三综合训练(3))如图,用一块形状为半椭圆1422=+y x )0(≥y 的铁皮截取一个以短轴BC 为底的等腰梯形ABCD ,记所得等腰梯形ABCD 的面积为S ,则1S的最小值是___________.21.(江苏省西亭高级中学2013届高三数学终考卷)已知抛物线y 2=2px (p >0),过定点(p ,0)作两条互相垂直的直线l 1,l 2,l 1与抛物线交于P 、Q 两点,l 2与抛物线交于M 、N 两点,l 1斜率为k .某同学已正确求得弦PQ 的中点坐标为(p k 2+p ,pk),请你写出弦MN 的中点坐标: ▲ .【答案】),(2pk p pk -+22.(江苏省常州市戴埠高级中学2013年高考数学(文科)冲刺模拟试卷)已知点P 在抛物线24y x =上,那么点P 到点Q(2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为_________. 【答案】答案 1(,1)4-23.(江苏省常州市戴埠高级中学2013年高考数学(文科)冲刺模拟试卷)设椭圆2222+=1x y a b (>>0)a b 的左、右顶点分别为,A B ,点P 在椭圆上且异于,A B 两点,O 为坐标原点.若直线AP 与BP 的斜率之积为12-,求椭圆的离心率_________. 【答案】224.(江苏省常州市第二中学2013年高考数学(文科)冲刺模拟试卷doc )如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为60颗,以此实验数据为依据可以估计出椭圆的面积约为____________________.【答案】19.225.(江苏省常州市第二中学2013年高考数学(文科)冲刺模拟试卷doc )已知双曲线中x心在原点,渐近线方程为2xy ±=,一个焦点为)0,5(F ,抛物线)0(22>=p px y 的焦点为双曲线的一个顶点,则=p _______________. 【答案】5426.(江苏省扬州市2013届高三下学期5月考前适应性考试数学(理)试题)若抛物线28y x=的焦点与双曲线221x y m-=的右焦点重合,则双曲线的离心率为______.【答案】327.(江苏省南通市海门中学2013届高三下学期5月月考数学试卷)已知双曲线12222=-b y a x ()0,1>>b a 的焦距为c 2,离心率为e ,若点(-1,0)和(1,0)到直线1=-b y a x 的距离之和为S ≥c 54,则e 的取值范围是_________. 【答案】 ]5,25[28.(江苏省扬州中学2013届高三最后一次模拟考试数学试题)已知A ,B ,P 是双曲线22221x y a b -=上不同的三点,且A ,B 连线经过坐标原点,若直线PA ,PB 的斜率乘积12PA PB k k ⋅=,则该双曲线的离心率为_________.29.(江苏省常州市金坛四中2013年高考数学冲刺模拟试卷doc )已知F 1、F 2是椭圆的两个焦点,过F 1且与椭圆长轴垂直的直线交椭圆于A 、B 两点,若△ABF 2是等腰直角三角形,则这个椭圆的离心率是____ 【答案】2-130.(江苏省启东中学2013届高三综合训练(1))已知B 为双曲线22221(0,0)x y a b a b-=>>的左准线与x 轴的交点,点(0,)A b ,若满足2AP AB =的点P 在双曲线上,则该双曲线的离心率为__.31.(江苏省扬州市2013届高三下学期5月考前适应性考试数学(理)试题)在平面直角坐标系xOy 中,已知点A 是椭圆221259x y +=上的一个动点,点P 在线段OA 的延长线上,且72OA OP ⋅=,则点P 横坐标的最大值为______. 【答案】15提示:设(1)OP OA λλ=>,由272OA OP OA λ⋅=⋅=,得272OAλ=, 2272P A A A A x x x x y λ=⋅=⋅+=22729925A A A x x x ⋅-⋅+=27216925A A x x ⋅+⋅=7291625AA x x +⋅, 研究点P 横坐标的最大值,仅考虑05A x <≤,72151225P x ≤=⋅(当且仅当154A x =时取“=”). 32.(江苏省启东中学2013届高三综合训练(1))在平面直角坐标系xOy 中,抛物线y 2=2x的焦点为F . 设M 是抛物线上的动点,则MOMF的最大值为____..33.(江苏省常州市华罗庚高级中学2013年高考数学冲刺模拟试卷)设双曲线22145x y -=的左、右焦点分别为1F ,2F ,点P 为双曲线上位于第一象限内一点,且21F PF ∆的面积为6,则点P 的坐标为_________. 【答案】⎪⎪⎭⎫⎝⎛2,556 34.(江苏省常州市西夏墅中学2013年高考冲刺模拟试卷)等腰Rt ABC 中,斜边BC =一个椭圆以C 为其中一个焦点,另一个焦点在线段AB 上,且椭圆经过A,B两点,则该椭圆的离心率为____________.【答案】36-35.(江苏省常州市第五中学2013年高考数学文科)冲刺模拟试卷)已知椭圆x 2a 2+y 2b2=1(a >b >0)的两个焦点为F 1(-c ,0),F 2(c ,0),P 为该椭圆上一点,且→PF 1·→PF 2=c 2,则此椭圆离心率的取值范围是___________.【答案】[3236.(2013年江苏省高考数学押题试卷 )设一个椭圆的短轴长、焦距、长轴长成等差数列,则此椭圆的离心率e=_________.【答案】45. 由a +b =2c , a 2-b 2=c 2, 两式相除得a -b =12c , 与a +b =2c 相加得2a =52c ,从而e=c a =45. 二、解答题37.(江苏省常州市西夏墅中学2013年高考冲刺模拟试卷)已知椭圆221:12x C y +=和圆222:1C x y +=,A ,B ,F 分别为椭圆C 1左顶点、下顶点和右焦点. ⑴点P 是曲线C 2上位于第二象限的一点,若△APF的面积为12+求证:AP ⊥OP ; ⑵点M 和N 分别是椭圆C 1和圆C 2上位于y 轴右侧的动点,且直线BN 的斜率是直线BM 斜率的2倍,证明直线MN 恒过定点.【答案】38.(江苏省常州市武进高级中学2013年高考数学文科)冲刺模拟试卷doc)某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面2103米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.(1)求这条抛物线的解析式;(2)在某次试跳中,测得运动员在空中的运动路线是(Ⅰ)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为335米,问此次跳水会不会失误?并通过计算说明理由.【答案】解:(1)在给定的直角坐标系下,设最高点为A ,入水点为B , 抛物线的解析式为2y ax bx c =++. 由题意,知O (0,0),B (2,-10),且顶点A 的纵坐标为23. 22506421043342100a c ac b b a a b c c ⎧=-⎪=⎧⎪⎪-⎪⎪∴=⇒=⎨⎨⎪⎪++=-=⎪⎪⎩⎪⎩或3220a b c ⎧=-⎪⎪=-⎨⎪=⎪⎩∵抛物线对称轴在y 轴右侧,∴02ba->,又∵抛物线开口向下,∴a <0, 从而b >0,故有2510,,063a b c =-== ∴抛物线的解析式为2251063y x x =-+.(2)当运动员在空中距池边的水平距离为335米时,即3332155x =-=时,225810816()65353y =-⨯+⨯=-,∴此时运动员距水面的高为10-163=143<5,因此,此次跳水会失误.39.(江苏省2013届高三高考模拟卷(二)(数学) )已知椭圆C : x 2a + y 2b=1(a >b >0)的左焦点为F 1(-3,0),过点F 1作一条直线l 交椭圆于A ,B 两点,点A 关于坐标原点O 的对称点为A 1,两直线AB ,A 1B 的斜率之积为-1625.(1)求椭圆C 的方程;(2)已知D (m ,0)为F 1右侧的一点,连AD ,BD 分别交椭圆左准线于M ,N 两点,若以MN 为直径的圆恰好过点F 1,求m 的值.【答案】解:(1)设A (x 1,y 1),B (x 2,y 2),则A 1(-x 1,-y 1).所以,AB k =y 2-y 1x 2-x 1,1A B k =y 2+y 1x 2+x 1,于是AB k ·1A B k =y 22-y 12x 22-x 12,由⎩⎨⎧x 12a 2+ y 12b 2=1,x 22a 2+ y 22b2=1,得x 22-x 12a 2+ y 12-y 12b 2=0,所以AB k ·1A B k =-b 2a 2所以,b 2a 2=1625,所以b a =45.设b =4k ,a =5k ,其中k >0.由c =3,得25k 2-16k 2=9,所以k =1所以,椭圆C :x 225+ y 216=1(2)①若l 存在斜率k 时,设l :y =k (x +3),A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =k (x +3),x 225+ y 216=1消去y ,得(16+25k 2)x 2+150k 2x +225 k 2-400=0. 所以222212121212222150225400256,(3)(3)162516251625k k k x x x x y y k x x k k k -+=-=⇒=++=-+++设342525(,),(,)33M y N y --,由M 、A 、D 共线,得131(325)3()m y y m x +=-, 同理242(325)3()m y y m x +=-又131411111616(,),(,),033F M y F N y F M F N F M F N 由已知得=-=-⊥⇒∙=, 得212343412325)256,99()()m y y y y y y m x m x (而,即+=-=--222561625k k -+·212325)9()()m m x m x (+--=-2569,整理得 22(1)(16400)0k m +-=,所以m =±5,因为m >-3,所以m =540.(江苏省2013届高三高考压轴数学试题)抛物线y x 22-=上有两点),().,(2211y x B y x A 且)2,0(,0-==⋅(O 为坐标原点)(1)求证:∥ (2)若2-=,求AB 所在直线方程. 【答案】抛物线y x 22-=上有两点),().,(2211y x B y x A 且)2,0(,0-==⋅OM OB OA (O 为坐标原点)(1)求证:∥ (2)若2-=,求AB 所在直线方程.41.(南京师大附中2013届高三模拟考试5月卷)在平面直角坐标系xOy 中,椭圆C : x 2a 2+ y 2b2=1(a >b >0)的上顶点到焦点的距离为2,离心率为32. (1)求a ,b 的值.(2)设P 是椭圆C 长轴上的一个动点,过点P 作斜率为k 的直线l 交椭圆C 于A 、B 两点. (ⅰ)若k =1,求△OAB 面积的最大值;(ⅱ)若PA 2+PB 2的值与点P 的位置无关,求k 的值. 【答案】解(1)由题设可知a =2,e =c a =32,所以c =3,故b =1. 因此,a =2,b =1 (2)由(1)可得,椭圆C 的方程为 x 24+y 2=1.设点P (m ,0)(-2≤m ≤2),点A (x 1,y 1),点B (x 2,y 2). (ⅰ)若k =1,则直线l 的方程为y =x -m .联立直线l 与椭圆C 的方程,即⎩⎪⎨⎪⎧y =x -m x 24+y 2=1.将y 消去,化简得 54x 2-2mx +m 2-1=0.解之得x 1=2(2m - 1-m 2)5, x 2=2(2m + 1-m 2)5, 从而有,x 1+x 2=8m 5, x 1· x 2=4(m 2-1)5,而y 1=x 1-m ,y 2=x 2-m ,因此,∣AB |= (x 1-x 2)2+(y 1-y 2)2= 2(x 1-x 2)2= 2 (x 1+x 2)2-4 x 1·x 2 =452· 5-m 2,点O 到直线l 的距离d =∣m ∣2,所以,S △OAB =12×|AB |×d =255-m 2×|m |,因此,S 2△OAB =425( 5-m 2)×m 2≤425·(5-m 2+m 22)2=1.又-2≤m ≤2,即m 2∈[0,4].所以,当5-m 2=m 2,即m 2=52, m =±102时,S △OAB 取得最大值1.(ⅱ)设直线l 的方程为y =k (x -m ).将直线l 与椭圆C 的方程联立,即⎩⎪⎨⎪⎧y =k (x -m ) x 24+y 2=1. 将y 消去,化简得(1+4k 2)x 2-8mk 2x +4(k 2m 2-1)=0,解此方程,可得,x 1+x 2=8mk 2 1+4k 2,x 1·x 2=4(k 2m 2-1)1+4k 2 .所以,PA 2+PB 2=(x 1-m )2+y 12+(x 2-m )2+y 22=34(x 12+x 22)-2m (x 1+x 2)+2m 2+2 =m 2·(-8k 4-6k 2+2)+(1+4k 2)·(8k 2+8) (1+4k 2)2(*) 因为PA 2+PB 2的值与点P 的位置无关,即(*)式取值与m 无关,所以有-8k 4-6k 2+2=0,解得k =±12.所以,k 的值为±1242.(江苏省南通市通州区姜灶中学2013届高三5月高考模拟数学试题 )设椭圆2222+=1x y a b(>>0)a b 的左、右顶点分别为,A B ,点P 在椭圆上且异于,A B 两点,O 为坐标原点.(Ⅰ)若直线AP 与BP 的斜率之积为12-,求椭圆的离心率;(Ⅱ)若||=||AP OA ,证明直线OP 的斜率k 满足|k 【答案】法一:(1)取(0,)P b ,(,0),(,0)A aB a -;则221()22AP BP b b k k a b a a ⨯=⨯-=-⇔=222212a b e e a -==⇔=(2)设(cos ,sin )(02)P a b θθθπ≤<;则线段OP 的中点(cos ,sin )22a b Q θθ||=||AP OA 1AQ AQ OP k k ⇔⊥⇔⨯=- sin sin cos 22cos AQ AQ AQ b k b ak ak a a θθθθ=⇔-=+2AQ AQ ak k k ⇒≤⇔<⇔>方法二:依题意,直线OP 的方程为y kx =,可设点00(,)P x kx ,由点P 在椭圆上,有22200221x k x a b +=,因为00,0a b kx >>≠,所以22200221x k x a b+=即2220(1)k x a +<③ 由||||,(,0)AP OA A a =-,得222200()x a k x a ++=整理得2200(1)20k x ax ++=,于是0221a x k -=+,代入③得222224(1)3||1a k a k k k+⨯<⇒>⇒>+43.(江苏省常州市奔牛高级中学2013年高考数学冲刺模拟试卷)在平面直角坐标系xOy中,已知椭圆212222,)0(1F F b a by a x 的左右焦点为>>=+,M 是椭圆上任一点,21F MF Λ面积的最大值为1,椭圆的内接矩形(短形的边与椭圆的对称轴平行)面积的最大值为22. (1) 求椭圆的方程;(2) 设M 、A 、B是椭圆上异于顶点的三点,且存在锐角OB OA OM ⋅+⋅=θθθsin cos ,使得①求证:直线OA 与OB 斜率乘积为定值 ②求22OBOA +的值.【答案】44.(江苏省常州市华罗庚高级中学2013年高考数学冲刺模拟试卷)如图,已知抛物线M :()042>=p py x 的准线为l ,N 为l 上的一个动点,过点N 作抛物线M 的两条切线,切点分别为A ,B ,再分别过A ,B 两点作l 的垂线,垂足分别为C ,D . (1)求证:直线AB 必经过y 轴上的一个定点Q ,并写出点Q 的坐标;(2)若ANB BDN ACN ∆∆∆,,的面积依次构成等差数列,求此时点N 的坐标.【答案】45.(江苏省常州市西夏墅中学2013年高考冲刺模拟试卷)某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段.已知跳水板AB 长为2m,跳水板距水面CD 的高BC 为3m.为安全和空中姿态优美,训练时跳水曲线应在离起跳点A 处水平距h m(h ≥1)时达到距水面最大高度4m.规定:以CD 为横轴,BC 为纵轴建立直角坐标系. (1)当h =1时,求跳水曲线所在的抛物线方程;(2)若跳水运动员在区域EF 内入水时才能达到比较好的训练效果,求此时h 的取值范围.【答案】则⎥⎦⎤⎢⎣⎡∈34,1h ,答,此时h 的取值范围⎥⎦⎤⎢⎣⎡∈34,1h .46.(2013年江苏省高考数学押题试卷 )在平面上,给定非零向量b ,对任意向量c ,定义c =a -2(a ⋅b )|b |2b . (1)若a =(2,3), b =(-1,3), 求c ;(2)若b =(2,1),证明:若位置向量a 的终点在直线Ax +By +C =0上,则位置向量c 的终点也在一条直线上;(3)已知存在单位向量b ,当位置向量a 的终点在抛物线C :x 2=y 上时,位置向量c 终点总在抛物线C′: y 2=x 上,曲线C 和C′关于直线l 对称,问直线l 与向量b 满足什么关系? 【答案】(1) c =(2,3)-2(-2+9)10(-1,3)=(175,-65). (2)设a =(x ,y ), c =(x′,y′),则(x′,y′)=(x ,y )-25(x +2y )(2,1)=(-35x -45y , -45x +35y ),所以, ⎩⎨⎧x ′=-35x -45y ,y ′=-45x +35y .于是,⎩⎨⎧x =-35x ′-45y ′,y =-45x ′+35y ′.故A (-35x′-45y′)+B (-45x′+35y′)+C =0,从而, -15(3A +4B )x′+15(-4A +3B )y′+C =0.由于A , B 不同时为零,所以3A +4B , -4A +3B 也不同时为零.于是向量c 的终点在一条直线-15(3A +4B )x +15(-4A +3B )y +C =0上. (3)设b =(b 1, b 2), 则b 12+b 22=1,对任意实数t , 取a =(t ,t 2), 则 c =(t ,t 2)-(2(t ,t 2)⋅(b 1, b 2))(b 1, b 2)=(t ,t 2)-(2tb 1+2t 2b 2)(b 1, b 2)=((1-2b 22)t -2b 1b 2t 2, -2b 1b 2t +(1-2b 12)t 2).因为c 的终点在曲线C′上,所以((1-2b 22)t -2b 1b 2t 2)2=-2b 1b 2t +(1-2b 12)t 2. ○1 由于t 为任意实数,比较○1式两边t 的系数得 1-2b 22=0, (-2b 1b 2)2=-2b 1b 2, 1-2b 12=0, 从而, b 12=b 22=12, b 1b 2<0,所以, b =±(22,-22).对曲线C 中任意点(x 0,y 0),可知(y 0, x 0)在曲线C′上, 反之亦然. 故曲线C :x 2=y 与曲线C′:y 2=x 关于直线l :y =x 对称. l 的方向向量d =(1,1), 因为d ⋅b =0,所以d ⊥b , 即直线l 与向量b 垂直. 47.(江苏省扬州中学2013届高三最后一次模拟考试数学试题)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD 的三边AB 、BC 、CD 由长6分米的材料弯折而成,BC 边的长为2t 分米(312t ≤≤);曲线AOD 拟从以下两种曲线中选择一种:曲线1C 是一段余弦曲线(在如图所示的平面直角坐标系中,其解析式为cos 1y x =-),此时记门的最高点O 到BC 边的距离为1()h t ;曲线2C 是一段抛物线,其焦点到准线的距离为98,此时记门的最高点O 到BC 边的距离为2()h t .(1)试分别求出函数1()h t 、2()h t 的表达式;(2)要使得点O 到BC 边的距离最大,应选用哪一种曲线?此时,最大值是多少?【答案】解:(1)对于曲线1C ,因为曲线AOD 的解析式为cos 1y x =-,所以点D 的坐标为(,cos 1)t t -所以点O 到AD 的距离为1cos t -,而3AB DC t ==-,则第17题13()(3)(1cos )cos 4(1)2h t t t t t t =-+-=--+≤≤对于曲线2C ,因为抛物线的方程为294x y =-,即249y x =-,所以点D 的坐标为24(,)9t t -所以点O 到AD 的距离为249t ,而3AB DC t ==-,所以2243()3(1)92h t t t t =-+≤≤(2)因为1()1sin 0h t t '=-+<,所以1()h t 在3[1,]2上单调递减,所以当1t =时,1()h t 取得最大值为3cos1-又224939()()9816h t t =-+,而312t ≤≤,所以当32t =时,2()h t 取得最大值为52因为1cos1cos 32π>=,所以153cos1322-<-=, 故选用曲线2C ,当32t =时,点E 到BC 边的距离最大,最大值为52分米48.(江苏省启东中学2013届高三综合训练(3))已知椭圆C :x 2 a 2 +y 2b 2=1(a >b >0)的离心率为1 2 ,且经过点P (1,3 2). (I)求椭圆C 的方程;(II)设F 是椭圆C 的右焦点,M 为椭圆上一点,以M 为圆心,MF 为半径作圆M .问点M 满足什么条件时,圆M 与y 轴有两个交点?(Ⅲ)设圆M 与y 轴交于D 、E 两点,求点D 、E 距离的最大值.【答案】解:(Ⅰ)∵椭圆x 2 a 2 +y 2 b 2 =1(a >b >0)的离心率为1 2 ,且经过点P (1,32),∴⎩⎪⎨⎪⎧a 2-b 2 a =121a 2 +94b2=1,即 ⎩⎪⎨⎪⎧3a 2-4b 2=01 a 2 +9 4b 2 =1,解得 ⎩⎨⎧a 2=4b 2=3,∴椭圆C 的方程为x 2 4 +y 23=1(Ⅱ)易求得F (1,0).设M (x 0,y 0),则x 02 4 +y 023=1,圆M 的方程为(x -x 0)2+(y -y 0)2=(1-x 0)2+y 02,令x =0,化简得y 2-2y 0y +2x 0-1=0,⊿=4y 02-4(2x 0-1)2>0①.将y 02=3(1- x 024 )代入①,得3x 02+8x 0-16<0,解出 -4<x 0<4 3,又∵3422200<≤-∴≤≤-x x (Ⅲ)设D (0,y 1),E (0,y 2),其中y 1<y 2.由(2),得DE = y 2- y 1=4y 02-4(2x 0-1) =-3x 02-8x 0+16 =-3(x 0+4 3 )2+64 3, 当x 0=-4 3 时,DE 的最大值为338 49.(江苏省常州市金坛四中2013年高考数学冲刺模拟试卷doc )已知椭圆C 的方程为x 2a 2+y2b2=1 (a>b>0),双曲线x 2a 2-y2b2=1的两条渐近线为l 1,l 2,过椭圆C 的右焦点F 作直线l,使l ⊥l 1,又l 与l 2交于P 点,设l 与椭圆C 的两个交点由上至下依次为A,B.(1)当l 1与l 2夹角为60°,双曲线的焦距为4时,求椭圆C 的方程及离心率;(2)求|FA||AP|的最大值.【答案】解(1)双曲线的渐近线为y=±b a x,两渐近线夹角为60°,又ba <1,∴∠POx=30°,∴b a =tan 30°=33,∴a=3b.又a 2+b 2=22,∴3b 2+b 2=4, ∴b 2=1,a 2=3,∴椭圆C 的方程为x 23+y 2=1,∴离心率e=a 2-b 2a =63(2)由已知,l:y=a b (x-c)与y=b a x 联立,解方程组得P ⎝ ⎛⎭⎪⎫a 2c ,ab c设|FA||AP|=λ,则FA →=λAP →,∵F(c,0),设A(x 0,y 0),则(x 0-c,y 0)=λ⎝ ⎛⎭⎪⎫a 2c -x 0,ab c -y 0,∴x 0=c +λ·a 2c 1+λ,y 0=λ·ab c 1+λ.即A ⎝⎛⎭⎪⎪⎫c +λ·a 2c 1+λ,λ·ab c 1+λ 将A 点坐标代入椭圆方程,得(c 2+λa 2)2+λ2a 4=(1+λ)2a 2c 2,等式两边同除以a 4,(e 2+λ)2+λ2=e 2(1+λ)2,e ∈(0,1),∴λ2=e 4-e2e 2-2=-⎣⎢⎡⎦⎥⎤2-e 2+22-e 2+3≤-22-e2·22-e2+3=3-22=(2-1)2, ∴当2-e 2=2,即e 2=2-2时,λ有最大值2-1,即|FA||AP|的最大值为2-150.(2013年江苏省高考数学押题试卷 )已知椭圆C 的方程为22221(0)x y a b a b+=>>,点A B 、分别为其左、右顶点,点12F F 、分别为其左、右焦点,以点A 为圆心,1AF 为半径作圆A ;以点B 为圆心,OB 为半径作圆B ;若直线:l y x =被圆A 和圆B(1)求椭圆C 的离心率;(2)己知a =7,问是否存在点P ,使得过P 点有无数条直线被圆A 和圆B 截得的弦长之比为34;若存在,请求出所有的P 点坐标;若不存在,请说明理由.【答案】(1)由3l k =-,得直线l 的倾斜角为150︒, 则点A 到直线l 的距离1sin(180150)2a d a =︒-︒=, 故直线l 被圆A截得的弦长为1L ==直线l 被圆B截得的弦长为22cos(180150)L a =︒-︒,据题意有:12L L =6=化简得:2163270e e -+=,解得:74e =或14e =,又椭圆的离心率(0,1)e ∈; 故椭圆C 的离心率为14e =.(2)假设存在,设P 点坐标为(,)m n ,过P 点的直线为L ;当直线L 的斜率不存在时,直线L 不能被两圆同时所截; 故可设直线L 的方程为()y n k x m -=-,则点)0,7(-A 到直线L 的距离2117knkm k D ++--=,由(1)有14c e a ==,得34A a r a c =-==421, 故直线L 被圆A截得的弦长为1'L =则点)0,7(B 到直线L 的距离2217kn km k D ++-=,7=B r ,故直线L 被圆B截得的弦长为2'L =,据题意有:1234L L =,即有22221216()9()A B r D r D -=-,整理得1243D D =,2173knkm k ++-=,○1 所以4|―7k ―km +n |=3|7k -km +n |,即4(―7k ―km +n )=3(7k -km +n )或4(―7k ―km +n )=-3(7k -km +n ), 也就是(49+m )k -n =0或(1+m )k -n =0与k 无关.于是⎩⎨⎧49+m =0 n =0或⎩⎨⎧1+m =0 n =0,故所求点P 坐标为(-1,0)或(-49,0).方法二 对式○1两边平方整理成关于k 的一元二次方程得 07)14350()3433507(222=++-++n k mn m k m m ,关于k 的方程有无穷多解,故有:⎩⎨⎧-==⎩⎨⎧-==⇒⎪⎩⎪⎨⎧==+=++49010070143500343350722m n m n n m n n m m 或,故所求点P 坐标为(-1,0)或(-49,0).(注设过P 点的直线为m kx y +=后求得P 点坐标同样得分)51.(江苏省常州市第五中学2013年高考数学文科)冲刺模拟试卷)给定椭圆2222:1(0)x y C a b a b+=>>,称圆心在坐标原点O ,的圆是椭圆C 的“伴随圆”. 若椭圆C的一个焦点为20)F ,其短轴上的一个端点到2F(1)求椭圆C 及其“伴随圆”的方程;(2)若过点(0,)(0)P m m <的直线与椭圆C 只有一个公共点,且截椭圆C 的“伴随圆”所得的弦长为求m 的值;(3)过椭圆C “伴椭圆”上一动点Q 作直线12,l l ,使得12,l l 与椭圆C 都只有一个公共点,试判断直线12,l l 的斜率之积是否为定值,并说明理由. 【答案】解:(1)由题意得:a =半焦距c =则1b =, 椭圆C 方程为2213x y += , “伴随圆”方程为224x y +=(2)则设过点P 且与椭圆有一个交点的直线为:y kx m =+,则2213y kx m x y =+⎧⎪⎨+=⎪⎩整理得()222136(33)0k x kmx m +++-= 所以()()()2226413330km k m ∆=-+-=,解2231k m +=① 又因为直线截椭圆C 的“伴随圆”所得的弦长为22,则有=()2221m k =+ ② 联立①②解得,221,4k m ==,所以1k =±,2(0)m m =-<,则(0,2)P -(3)当12,l l 都有斜率时,设点00(,),Q x y 其中22004x y +=, 设经过点00(,),Q x y 与椭圆只有一个公共点的直线为00()y k x x y =-+,由0022()13y kx y kx x y =+-⎧⎪⎨+=⎪⎩,消去y 得到[]22003()30x kx y kx ++--= 即2220000(13)6()3()30k x k y kx x y kx ++-+--=,[]22200006()4(13)3()30k y kx k y kx ⎡⎤∆=--⋅+--=⎣⎦,经过化简得到:222000(3)210x k x y k y -++-=, 因为22004x y +=,所以有2220000(3)2(3)0x k x y k x -++-=, 设12,l l 的斜率分别为12,k k ,因为12,l l 与椭圆都只有一个公共点,所以12,k k 满足方程2220000(3)2(3)0x k x y k x -++-=,因而121k k ⋅=-,即直线12,l l 的斜率之积是为定值1-52.(江苏省常州高级中学2013年高考数学模拟试卷)如图,在平面直角坐标系xOy 中.椭圆22:12x C y +=的右焦点为F ,右准线为l . (1)过点F 作直线交椭圆C 于点,A B ,又直线OA 交l 于点T ,若2OT OA =,求线段AB 的长;(2)已知点M 的坐标为()000,,0x y x ≠,直线OM 交直线0012x xy y +=于点N ,且和椭圆C 的一个交点为点P ,是否存在实数λ,使得2?OP OM ON λ=⋅,若存在,求出实数λ;若不存在,请说明理由.【答案】解:(1)由题意可知1A F x x c ===,故将1A x =代入2212x y +=,可得||2A y =,从而AB =(2)假设存在实数λ满足题意. 由已知得0:y OM y x x =① 0012x xy y += ② 椭圆C :2212x y += ③ 由①②解得0220022N x x x y =+,0220022N y y x y =+.由①③解得220220022Px x x y =+,220220022P y y x y =+∴22222220000222222000000222()222P Px y x y OP x y x y x y x y +=+=+=+++, 2222000000222222000000222()222N N x y x y OM ON x x y y x y x y x y +⋅=+=+=+++. 故可得1λ=满足题意53.(江苏省徐州市2013届高三考前模拟数学试题)已知椭圆E :()222210x y a b a b =>>+的离心率为12,右焦点为F ,且椭圆E 上的点到点F 距离的最小值为2.⑴求椭圆E 的方程; ⑵设椭圆E 的左、右顶点分别为,A B ,过点A 的直线l 与椭圆E 及直线8x =分别相交于点,M N .(ⅰ)当过,,A F N 三点的圆半径最小时,求这个圆的方程;(ⅱ)若cos AMB ∠=,求ABM △的面积. 【答案】⑴由已知,12c a =,且2a c -=,所以4a =,2c =,所以22212b a c =-=,所以椭圆E 的方程为2211612x y =+ ⑵(ⅰ)由⑴,(4,0)A -,(2,0)F ,设(8,)N t .设圆的方程为220x y dx ey f =++++,将点,,A F N 的坐标代入,得21640,420,6480,d f d f t d et f ⎧-=⎪=⎨⎪=⎩+++++++解得2,72,8,d e t t f =⎧⎪⎪=--⎨⎪=-⎪⎩ 所以圆的方程为22722()80x y x t y t--=+++, 即222172172(1)[()]9()24x y t t t t-=+++++,因为2272()t t +≥,当且仅当72t t=±+,圆的半径最小,故所求圆的方程为22280x y x ±-=++ (ⅱ)由对称性不妨设直线l 的方程为(4)(0)y k x k =>+.由22(4),1,1612y k x x y =⎧⎪⎨=⎪⎩++得222121624(,)3434k k M k k -++,所以222424(,)3434kMA k k --=++,2223224(,)3434k k MB k k -=++,所以cos 24MA MB AMB MA MB∠===, 化简,得42164090k k --=,解得214k =,或294k =,即12k =,或32k =, 此时总有3M y =,所以ABM △的面积为183122⨯⨯=.54.(江苏省西亭高级中学2013届高三数学终考卷)如图,F 1,F 2是离心率为22的椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,直线l :x =-12将线段F 1F 2分成两段,其长度之比为1:3.设A ,B 是C 上的两个动点,线段AB 的中点M 在直线l 上,线段AB 的中垂线与C 交于P ,Q 两点. ①求椭圆C 的方程;②是否存在点M ,使以PQ 为直径的圆经过点F 2,若存在,求出M 点坐标,若不存在,请说明理由.【答案】解:(Ⅰ)设F 2(c ,0),∵直线l :x =﹣将线段F 1F 2分成两段,其长度之比为1:3,∴,解得c =1.∵离心率为e =,∴a =,∴椭圆C 的方程为.……4分(Ⅱ)当直线AB 垂直于x 轴时,直线AB 的方程为x =﹣, 此时P (﹣,0),Q (,0),=﹣1,不合题意.……6分当直线AB 不垂直于x 轴时,设存在点M (﹣,m ),m ≠0, 设直线AB 的斜率为k ,A (x 1,y 1),B (x 2,y 2),由,得,则﹣1+4mk =0,故k =,此时,直线PQ 的斜率为k 1=﹣4m ,PQ 的直线方程为y ﹣m =﹣4m (x +),即y =﹣4mx ﹣m .……8分联立,消去y ,整理,得(32m 2+1)x 2+16m 2x +2m 2﹣2=0.∴,x 1x 2=,……10分由题意=0,∴=(x 1﹣1)(x 2﹣1)+y 1y 2=x 1x 2﹣(x 1+x 2)+1+(4mx 1+m )(4mx 2+m )=(1+16m 2)x 1x 2+(4m 2﹣1)(x 1+x 2)+1+m 2=++1+m 2==0,∴m =.∵M 在椭圆内,∴,∴m =符合条件.……13分 综上所述,存在两点M 符合条件,坐标为M (﹣,﹣)和M (﹣,). (14)分55.(江苏省常州市金坛四中2013年高考数学冲刺模拟试卷doc )在平面直角坐标系中,已知点(1,1)P -,过点P 作抛物线20:T y x =的切线,其切点分别为11(,)M x y 、22(,)N x y (其中12x x <). (Ⅰ)求1x 与2x 的值;(Ⅱ)若以点P 为圆心的圆E 与直线MN 相切,求圆E 的面积;(Ⅲ)过原点(0,0)O 作圆E 的两条互相垂直的弦,AC BD ,求四边形ABCD 面积的最大值.【答案】解析:(Ⅰ)由2y x =可得,2y x '=∵直线PM 与曲线0T 相切,且过点(1,1)P -,∴2111121x x x +=-,即211210x x --=,∴1212x ==或11x =, 同理可得:21x =,或21x =∵12x x <,∴11x =21x =(Ⅱ)由(Ⅰ)知,122x x +=,121x x ⋅=-,则直线MN 的斜率221212121212y y x x k x x x x x x --===+--,--∴直线M 的方程为:1121()()y y x x x x -=+-,又211y x =,∴22112112()y x x x x x x x -=+--,即210x y -+=∵点P 到直线MN 的距离即为圆E 的半径,即r ==故圆E 的面积为216644455S r πππ==⋅= (Ⅲ)四边形ABCD 的面积为12S AC BD =g不妨设圆心E 到直线AC 的距离为1d ,垂足为1E ;圆心E 到直线BD 的距离为2d ,垂足为2E ;则AC BD ==由于四边形12EE OE 为矩形.且2222212(10)(10)2d d OE +==-+--=所以12S AC BD ==g 由基本不等式222ab a b ≤+可得222222212222()5S r d d ≤+=-+=,当且仅当12d d =时等号成立 注:(Ⅲ)解法较多,阅卷时可酌情给分.56.(江苏省常州市华罗庚高级中学2013年高考数学冲刺模拟试卷)已知椭圆C :22221x y a b+=(a >b >0)的上顶点为A ,左,右焦点分别为F 1,F 2,且椭圆C 过点P (43,b 3),以AP为直径的圆恰好过右焦点F 2.(1)求椭圆C 的方程;(2)若动直线l 与椭圆C 有且只有一个公共点,试问:在x 轴上是否存在两定点,使其到直线l 的距离之积为1?若存在,请求出两定点坐标;若不存在,请说明理由.【答案】解:(1)因为椭圆过点P (43,b 3),所以169a 2+19=1,解得a 2=2,又以AP 为直径的圆恰好过右焦点F 2.所以AF 2⊥F 2P ,即-b c ⋅b343-c =-1, b 2=c (4-3c )而b 2=a 2-c 2=2-c 2,所以c 2-2c +1=0,解得c 2=1, 故椭圆C 的方程是x 22+y 2=1(2)①当直线l 斜率存在时,设直线l 方程为y =kx +p ,代入椭圆方程得(1+2k 2)x 2+4kpx +2p 2-2=0.因为直线l 与椭圆C 有只有一个公共点,所以△=16k 2p 2-4(1+2k 2)(2p 2-2)=8(1+2k 2―p 2)=0,即 1+2k 2=p 2设在x 轴上存在两点(s ,0),(t ,0),使其到直线l 的距离之积为1,则|ks +p |k 2+1 ⋅ |kt +p |k 2+1=|k 2st +kp (s +t )+p 2|k 2+1=1,即(st +1)k +p (s +t )=0(*),或(st +3)k 2+(s +t )kp +2=0 (**).由(*)恒成立,得⎩⎨⎧st +1=0,s+t =0.解得⎩⎨⎧s =1t =-1,或⎩⎨⎧s =-1t =1,而(**)不恒成立.②当直线l 斜率不存在时,直线方程为x =±2时, 定点(-1,0)、F 2(1,0)到直线l 的距离之积d 1⋅ d 2=(2-1)(2+1)=1. 综上,存在两个定点(1,0),(-1,0),使其到直线l 的距离之积为定值1 57.(江苏省启东中学2013届高三综合训练(2))在平面直角坐标系xOy 中,已知点(1,1)A -,P是动点,且三角形POA 的三边所在直线的斜率满足k OP +k OA =k PA . (1)求点P 的轨迹C 的方程;(2)若Q 是轨迹C 上异于点P 的一个点,且PQ OA λ=,直线OP 与QA 交于点M ,问:是否存在点P 使得△PQA 和△PAM 的面积满足2PQA PSM S S ∆∆=?若存在,求出点P 的坐标;若不存在,说明理由.【答案】解:(1)设点(,)P x y 为所求轨迹上的任意一点,则由OP OA PA k k k +=得,(第18题图)(第18题图)1111y y x x -+=-+,整理得轨迹C 的方程为2y x =(0x ≠且1x ≠-) (2)设221122(,),(,),P x x Q x x由PQ OA λ=可知直线//PQ OA ,则PQ OA k k =,故2221211010x x x x --=---,即211x x =--, 直线OP 方程为:1y x x = ①;直线QA 的斜率为:2111(1)1211x x x ---=----+, ∴直线QA 方程为:11(2)(1)y x x -=--+, 即11(2)1y x x x =-+-- ②联立①②,得12x =-,∴点M 的横坐标为定值12-由2PQA PAM S S ∆∆=,得到2QA AM =,因为//PQ OA ,所以2OP OM =, 由2PO OM =,得11x =,∴P 的坐标为(1,1). ∴存在点P 满足2PQA PSM S S ∆∆=,P 的坐标为(1,1)58.(江苏省南通市海门中学2013届高三下学期5月月考数学试卷)已知椭圆22221(0)x y a b a b +=>>的焦距为4,设右焦点为1F ,离心率为e . (1)若2e =,求椭圆的方程; (2)设A 、B 为椭圆上关于原点对称的两点,1AF 的中点为M ,1BF 的中点为N ,若原点O 在以线段MN 为直径的圆上.①证明点A 在定圆上;②设直线AB 的斜率为k ,若k ≥求e 的取值范围. 【答案】解:(Ⅰ)由e =,c =2,得a =,b =2 , 所求椭圆方程为22184x y +=.。
江苏省13市2017高三上学期考试数学试题分类汇编圆锥曲线一、填空题1、(南京市、盐城市2017届高三第一次模拟)设双曲线2221(0)x y a a-=>的一条渐近线的倾斜角为30︒,则该双曲线的离心率为 ▲ .2、(南通、泰州市2017届高三第一次调研测)在平面直角坐标系xOy 中,直线20x y +=为双曲线22221(00)x y a b a b-=>>,的一条渐近线,则该双曲线的离心率为▲.3、(苏北四市(淮安、宿迁、连云港、徐州)2017届高三上学期期中)2017届高三上学期期末)如图,在平面直角坐标系xOy 中,已知A ,1B ,2B 分别为椭圆2222:1(0)x y C a b a b+=>>的右、下、上顶点,F 是椭圆C 的右焦点.若21B F AB ⊥,则椭圆C 的离心率是 ▲4、(苏北四市(徐州、淮安、连云港、宿迁)若抛物线28y x =的焦点恰好是双曲线2221(0)3x y a a -=>的右焦点,则实数a 的值为. 5、(苏州市2017届高三上学期期末调研)在平面直角坐标系xOy 中,双曲线16322=-y x 的离心率为6、(苏州市2017届高三上期末调研测试)在平面直角坐标系xOy 中,已知过点),(11M 的直线l 与圆52122=-++)()(y x 相切,且与直线01=-+y ax 垂直,则实数=a .7、(无锡市2017届高三上学期期末)设P 为有公共焦点12,F F 的椭圆1C 与双曲线2C 的一个交点,且12PF PF ⊥,椭圆1C 的离心率为1e ,双曲线2C 的离心率为2e ,若123e e =,则1e =.8、(扬州市2017届高三上学期期中)抛物线)0(22>=p py x 的准线方程为21-=y ,则抛物线方程为9、(扬州市2017届高三上学期期中)双曲线)0,0(12222>>=-b a by a x 的右焦点为F ,直线x y 34=与双曲线相交于A 、B 两点。
若BF AF ⊥,则双曲线的渐近线方程为。
10、(扬州市2017届高三上学期期末)已知抛物线216y x =的焦点恰好是双曲线222112x y b-=的右焦点,则双曲线的渐近线方程为▲. 11、(镇江市2017届高三上学期期末)双曲线),(0012222>>=-b a by a x 的焦点到相应准线的距离等于实轴长,则双曲线的离心率为.二、解答题 1、(南京市、盐城市2017届高三第一次模拟)在平面直角坐标系xOy 中,已知圆222:O x y b +=经过椭圆222:14x y E b+=(02)b <<的焦点.(1)求椭圆E 的标准方程;(2)设直线:l y kx m =+交椭圆E 于,P Q 两点,T 为弦PQ 的中点,(1,0),(1,0)M N -,记直线,TM TN 的斜率分别为12,k k ,当22221m k -=时,求12k k ⋅的值.2、(南通、泰州市2017届高三第一次调研测)如图,在平面直角坐标系xOy 中,已知椭圆22221x y a b+=(0)a b >>,焦点到 相应准线的距离为1. (1)求椭圆的标准方程;(2)若P 为椭圆上的一点,过点O 作OP 的垂线交直线y =于点Q ,求2211OP OQ +的值.3、(苏北四市(淮安、宿迁、连云港、徐州)2017届高三上学期期中)如图,在平面直角坐标系xOy 中,已知圆22:40C x y x +-=及点(1,0)A -,(1,2)B .(1)若直线l 平行于AB ,与圆C 相交于M ,N 两点,MN AB =,求直线l 的方程; (2)在圆C 上是否存在点P ,使得2212PA PB +=?若存在,求点P 的个数;若不存在,说明理由.4、(苏北四市(徐州、淮安、连云港、宿迁)2017届高三上学期期末)如图,在平面直角坐标系xOy 中,已知椭圆2222:1(0)x y C a b a b +=>>的离心率为2,且右焦点F 到左准线的距离为. (1)求椭圆C 的标准方程;(2)设A 为椭圆C 的左顶点,P 为椭圆C 上位于x 轴上方的点,直线PA 交y 轴于点M ,过点F 作MF 的垂线,交y 轴于点N .(ⅰ)当直线的PA 斜率为12时,求FMN ∆的外接圆的方程; (ⅱ)设直线AN 交椭圆C 于另一点Q ,求APQ ∆的面积的最大值.5、(无锡市2017届高三上学期期末)已知椭圆22143x y +=,动直线l 与椭圆B,C 两点(B在第一象限).(1)若点B 的坐标为3,2⎛⎫⎪⎝⎭,求OBC ∆面积的最大值; (2)设()()1122,,,B x y C x y ,且1230y y +=,求当OBC ∆面积最大时,直线l 的方程.6、(扬州市2017届高三上学期期中)已知椭圆C :)0(12222>>=+b a by a x 的右焦点为F ,过点F 的直线交y 轴于点N ,交椭圆C 于点A 、P (P 在第一象限),过点P 作y 轴的垂线交椭圆C 于另外一点Q 。
若2=。
(1)设直线PF 、QF 的斜率分别为k 、k ',求证:k k'为定值; (2)若=且APQ ∆的面积为51512,求椭圆C 的方程。
7、(扬州市2017届高三上学期期末)如图,椭圆2222:1(0)x y C a b a b+=>>,圆222:O x y b +=,过椭圆C 的上顶点A 的直线l :y kx b =+分别交圆O 、椭圆C 于不同的两点P 、Q ,设AP PQ λ=.(1)若点(3,0),P -点(4,1),Q --求椭圆C 的方程; (2)若3λ=,求椭圆C 的离心率e 的取值范围.8、(镇江市2017届高三上学期期末)已知椭圆)(:012222>>=+b a by a x C 的离心率为23,且点),(213-在椭圆C 上.(1)求椭圆C 的标准方程;(2)若直线l 交椭圆C 于Q P ,两点,线段PQ 的中点为H ,O 为坐标原点,且1=OH , 求POQ ∆面积的最大值.参考答案 一、填空题 1、3234、1 56、127、3 8、22x y = 9、2y x =± 10、y =11、1二、解答题 1、解:(1)因02b <<,所以椭圆E 的焦点在x 轴上,又圆222:O x y b +=经过椭圆E 的焦点,所以椭圆的半焦距c b =, ……………3分所以224b =,即22b =,所以椭圆E 的方程为22142x y +=. ……6分 (2)方法一:设11(,)P x y ,22(,)Q x y ,00(,)T x y ,联立22142x y y kx m ⎧+=⎪⎨⎪=+⎩,消去y ,得222(12)4240k x kmx m +++-=, 所以122412km x x k +=-+,又22221m k -=,所以12x x +2k m =-, 所以0k x m =-,012k y m k m m=-⋅=, ……………10分则1222221111122442(22)211m m k k k k k m m k m m⋅=⋅===-----+--. …………14分 方法二:设11(,)P x y ,22(,)Q x y ,00(,)T x y ,则22112222142142x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩, 两式作差,得()()()()12121212042x x x x y y y y +-+-+=,又1202x x x +=,1202y y y +=,∴()()01201202x x x y y y -+-=,∴()01201202y y y xx x -+=-, 又11(,)P x y ,22(,)Q x y 在直线y kx m =+上,∴1212y y k x x -=-,∴0020x ky +=,①又00(,)T x y 在直线y kx m =+上,∴00y kx m =+,② 由①②可得02212km x k =-+,0212my k=+. ……………10分 以下同方法一.2、【解】(1)由题意得,2c a =,21a c c-=,…………2分解得a =,1c =,1b =. 所以椭圆的方程为2212x y +=. …………………………………………………4分 (2)由题意知OP 的斜率存在.当OP 的斜率为0时,OP =OQ =22111OP OQ +=. (6)分当OP 的斜率不为0时,设直线OP 方程为y kx =.由2212x y y kx ⎧+=⎪⎨⎪=⎩,,得()22212k x +=,解得22221x k =+,所以222221k y k =+,所以2222221k OP k +=+.………………………………………………………………9分因为OP OQ ⊥,所以直线OQ 的方程为1y x k=-.由1y y xk ⎧=⎪⎨=-⎪⎩得x =,所以2222OQ k =+.………………………………12分所以222221*********k OP OQ k k ++=+=++. 综上,可知22111OP OQ +=.……………………………………………………14分3、(1)圆C 的标准方程为22(2)4x y -+=,所以圆心(2,0)C ,半径为2.因为l AB ∥,(1,0)A -,(1,2)B ,所以直线l 的斜率为2011(1)-=--,设直线l 的方程为0x y m -+=, ……………………………………………2分则圆心C 到直线l的距离为d ==4分因为MN AB =而222()2MN CM d =+,所以2(2)422m +=+, ……………………………6分 解得0m =或4m =-,故直线l 的方程为0x y -=或40x y --=.…………………………………8分 (2)假设圆C 上存在点P ,设(,)P x y ,则22(2)4x y -+=,222222(1)(0)(1)(2)12PA PB x y x y +=++-+-+-=,即22230x y y +--=,即22(1)4x y +-=, ………………………………10分因为|22|22-+,……………………………………12分 所以圆22(2)4x y -+=与圆22(1)4x y +-=相交,所以点P 的个数为2.…………………………………………………………14分4、(1)由题意,得2c a a c c ⎧=⎪⎪⎨⎪+=⎪⎩解得4,a c =⎧⎪⎨=⎪⎩则b =所以椭圆C 的标准方程为221168x y +=.………………………………………4分(2)由题可设直线PA 的方程为(4)y k x =+,0k >,则(0,4)M k ,所以直线FN的方程为4y x k =-,则2(0,)N k -. (i)当直线PA 的斜率为12,即12k =时,(0,2)M ,(0,4)N -,F ,因为MF FN ⊥,所以圆心为(0,1)-,半径为3,所以FMN △的外接圆的方程为22(1)9x y ++=.……………………………8分(ii)联立22(4),1,168y k x x y =+⎧⎪⎨+=⎪⎩消去y 并整理得,2222(12)1632160k x k x k +++-=,解得14x =-或2224812k x k -=+,所以222488(,)1212k kP k k -++,……………………10分直线AN 的方程为1(4)2y x k=-+,同理可得,222848(,)1212k kQ k k --++,所以P ,Q 关于原点对称,即PQ 过原点.所以APQ △的面积211632()212122P Q k S OA y y k k k=⋅-=⨯=++≤14分当且仅当12k k=,即2k ==”.所以APQ △的面积的最大值为.…………………………………………16分5、6、解:(1)设(,0)F c 且222c a b =-,00(,)P x y ,则00(,)Q x y -,所以00y k x c =-,00'y k x c =--,因为2NF FP =,所以02()c x c =-,即032x c =………3分 ∴0002y y k x c c ==-,0002'5y y k x c c ==---∴5'k k =-,即5'kk =-为定值………6分(2)若AN FP =,则3AF FP =,所以3AF FP =,解得:01(,3)2A c y --因为点A 、P 在椭圆C 上,则220222202291149124y c a b y c ab ⎧+=⎪⎪⎨⎪+=⎪⎩()(), (1)9(2)⨯-得:228084c a =,解得:2225c a =………10分则2223c b =,代入(1)得:22002213102y y c b ==,202320y c =因为0013462APQ S c y cy ∆=⨯⨯=且APQ S ∆=,解得:220125c y =,则24c =……14分所以椭圆方程为:221106x y +=. ………16分7、(1)由P 在圆222:O x y b +=上得3,b =又点Q 在椭圆C 上得2222(4)(1)1,3a --+=解得218,a = ∴椭圆C 的方程是221.189x y +=--------------------------------------5分(2)由222y kx b x y b=+⎧⎨+=⎩得0x =或221P kbx k =-+--------------------------------------7分 由22221y kx bx y a b =+⎧⎪⎨+=⎪⎩得0x =或22222Q kba x a k b =-+--------------------------------------9分 AP PQ λ= ,3λ=,34AP AQ ∴=, 2222223241kba kb k a b k ∴⋅=++即222223141a a k b k ⋅=++222223441a b k e a -∴==- 20k >241e ∴>,即12e >,又01e <<,11.2e ∴<<----16分 8、解:(1)由已知得c a =,221341a b +=, 解得24a =,12=b ,……2分椭圆C 的方程是2214x y +=. ……4分 (2)设l 与x 轴的交点为(,0)D n ,直线:l x my n =+,与椭圆交点为11(,)P x y ,22(,)Q x y ,联立x my n =+,2214x y +=,得222(4)240m y mny n +++-=,1,2y = ∴12224y y mn m+=-+,212244n y y m -=+, ∴12122()24224x x m y y n n m +++==+,即224(,)44n mn H m m -++, ……6分 由1OH =,得2222(4)16m n m +=+, ……10分 则S △POQ 121211||||||22OD y y n y y =-=-, 令22222121212224()[()4]1216(16)m T n y y n y y y y m +=-=+-=⋅⋅+, ……12分 设24(4)t m t =+…,则2222411144(16)241444824m t m t t t t +==+++++…,……14分 当且仅当144t t=,即12t =,S △POQ 1=, ……15分 所以△POQ 面积的最大值为1. ……16分。