专题01 三角形(专题详解)(解析版)

专题01等腰三角形的性质与判定（十六大题型+跟踪训练）题型1：等腰三角形的定义1．用刻度尺测量得出下图（）是等腰三角形．A ．B ．C ．D ．【答案】B【分析】分别量取各三角形的三边长，然后根据等腰三角形两腰相等，进行判断即可．【解析】解：A 中三边长分别为：1.8，2.6，2.9，不是等腰三角形，故不符合要求；B 中三边长分别为：2.2，2.2，2.2，是等腰三角形，故符合要求；C 中三边长分别为：3.4，3.2，2，不是等腰三角形，故不符合要求；D 中三边长分别为：3.3，1.8，3.7，不是等腰三角形，故不符合要求；故选：B ．【点睛】本题考查了等腰三角形的定义．解题的关键在于熟练掌握等腰三角形两腰相等．2．在ABC 中，若AB BC =，则ABC 是（）A ．不等边三角形B ．等边三角形C ．直角三角形D ．等腰三角形【答案】D【分析】由等腰三角形的定义：有两边相等的三角形，即可判断．【解析】解：在ABC 中，若AB BC =，则ABC 是等腰三角形．故选：D ．【点睛】本题考查等腰三角形，关键是掌握等腰三角形的定义．3．以下列线段为边不能组成等腰三角形的是（）A ．2，2，4B ．6，3，6C ．4，4，5D ．1，1，1【答案】A【分析】根据三角形三边关系和等腰三角形的判定对所给的四个选项逐一判断、解析即可．【解析】解：A ．∵224+=，∴以2，2，4为边不能组成三角形，更不可能组成等腰三角形，故此选项符合题意；B．∵以6，3，6为边能组成三角形，且有两边相等，∴以6，3，6为边能组成等腰三角形，故此选项不符合题意；C．∵以4，4，5为边能组成三角形，且有两边相等，∴以4，4，5为边能组成等腰三角形，故此选项不符合题意；D．∵以1，1，1为边能组成三角形，且有两边相等，∴以1，1，1为边能组成等腰三角形，故此选项不符合题意．故选：A．【点睛】本题考查三角形的三边关系、等腰三角形的判定等知识点及其应用问题．牢固掌握三角形的三边关系、等腰三角形的判定是解题的关键．4．等腰三角形两边长分别是2cm和3cm，则周长是（）A．7cm B．8cm C．7cm或8cm D．条件不足，无法求出【答案】C【分析】分两种情况讨论：①底边为3cm时；②底边为2cm时，分别求解即可得到答案．【解析】解：分两种情况讨论：①底边为3cm时，等腰三角形的周长为3227cm++=；②底边为2cm时，等腰三角形的周长为2338cm++=，∴等腰三角形的周长为7cm或8cm，故选C．【点睛】本题考查了等腰三角形的性质，利用分类讨论的思想解决问题是解题关键．5．已知等腰三角形的一边长为2cm，另一边长为4cm，则它周长是（）A．6cm B．8cm C．10cm D．8cm或10cm【答案】C【分析】根据等腰三角形的性质及三角形的三边关系进行分类讨论，即可得到答案．当AD AC+与BC+即115 22x x x⎛⎫+-+⎪⎝⎭解得：8x=，8，8，5能够组成三角形；当BC BD+与AD+∵BD AC ⊥，∴90ADB ∠=︒，∵46ABD ∠=︒，∴9044A ABD ∠︒-=︒=∠，∵BD AC ⊥，∴90ADB ∠=︒，∵46ABD ∠=︒，∴904644DAB ∠︒=︒-，【分析】根据轴对称的性质，得到ABC 是以AB 和AC 为腰的等腰三角形，再根据对称性可得结果．【解析】解：由题意可得：ABC 是以AB 和AC 为腰的等腰三角形，且不是等边三角形，∴AB AC =，∴ABC 的周长2AB AC BC AB BC =++=+，故选B ．【点睛】本题考查了等腰三角形的性质，轴对称图形，解题的关键是根据题意判断出ABC 是等腰三角形．13．如图，在ABC 中，90C ∠=︒，AC BC =，AD 平分CAB ∠交BC 于D ，DE AB ⊥于E ，若5cm AB =，则DBE 的周长是（）A ．5cmB ．6cmC ．7cmD ．8cm【答案】A 【分析】根据角平分线的定义和性质可得DE CD =，CAD EAD ∠=∠，推出CDA EDA ∠=∠，可得AC AE =，证明再根据等腰直角三角形的性质求出AC BC AE ==，然后求出DBE 的周长AB =，代入数据即可得解．【解析】解：AD 平分CAB ∠，DE AB ⊥，90C ∠=︒，DE CD ∴=，CAD EAD ∠=∠，CDA EDA ∴∠=∠，AC AE ∴=，又AC BC = ，AC BC AE ∴==，DBE ∴△的周长DE BD EB CD BD EB BC EB AE EB AB =++=++=+=+=，5cm AB = ，DBE ∴△的周长5cm =．故选：A ．A ．80︒B 【答案】C 【分析】根据等边对等角可得【解析】解：∵AB AC =∴B C ∠=∠，∵80B ∠=︒，∴80C ∠=︒，∵180A B C ∠+∠+∠=︒∴20A ∠=︒．故选：C ．【点睛】本题考查三角形内角和定理，等腰三角形的性质．解题的关键是掌握三角形的三个内角之和是180°．16．如图，在△ABC 中，AB =AD =DC ，∠C =35°，则∠B 的度数为（）A ．50︒B ．60︒C ．70︒D ．80︒【答案】C 【分析】首先利用等腰三角形的性质求得∠DAC 的度数，然后求得∠BDA 的度数，最后利用等腰三角形的性质求得∠B 的度数．【解析】解：∵AD =DC ，∴∠DAC =∠C ，∵∠C =35°，∴∠DAC =35°，∴∠BDA =∠C +∠DAC =70°，∵AB =AD ，∴∠BDA =∠B =70°．故选：C ．【点睛】本题考查了等腰三角形的性质：等腰三角形两底角相等．17．如图，在ABC 中，90BAC ∠= ，AB AC =，点D 在BC 上，且BD BA =，则CAD ∠的度数为（）A ．30︒B ．25︒C ．22.5︒D ．21︒【答案】C 【分析】利用ABC 是等腰直角三角形先求出B ∠，再利用BDA △是等腰三角形求出BAD ∠，最后利用直【答案】50︒/50度【分析】首先根据垂直平分线的性质得到据角的和差计算求解即可．∵80ACB ∠=︒∴803050BCE ACB ACE ∠=∠-∠=︒-︒=︒．故答案为：50︒．【点睛】此题考查了垂直平分线的性质，等边对等角性质，解题的关键是熟练掌握以上知识点．21．如图，直线a ∥b ，AB AC =，140 ∠=，则∠BAC 的度数是（）A ．100B ．110C ．120D ．130【答案】A 【分析】根据直线a ∥b ，140 ∠=，可知140ACB ∠=∠= ，由AB AC =，可得40ACB ABC ∠=∠= ，利用平行的性质即可求出∠BAC 的值．【解析】解：由题意得，∵直线a ∥b ，140 ∠=，∴140ACB ∠=∠= ，∵AB AC =，∴40ACB ABC ∠=∠= ，∴()180118080100BAC ABC ∠=︒-∠+∠=︒-︒=︒，故选：A ．【点睛】本题主要考查的是平行线的性质，熟练利用平行线进行角度转化时解题的关键．22．如图，在∠ECF 的边CE 上有两点A 、B ，边CF 上有一点D ，其中BC =BD =DA 且∠ECF =27°，则∠ADF 的度数为（）A ．54°B ．91°C ．81°D ．101°【答案】C【分析】根据等腰三角形的性质以及三角形外角和内角的关系，逐步推出∠ADF 的度数．【解析】解：∵BC =BD =DA ，∴∠C =∠BDC ，∠ABD =∠BAD ，∵∠ABD =∠C +∠BDC ，∠ECF =27°，∴∠ADF =∠C +∠BAD =3∠ECF =81°．故选：C ．【点睛】本题考查了等腰三角形的性质：等腰三角形的两个底角相等，三角形外角和内角的运用．23．如图，在ABC 中，DE 垂直平分BC ，若6428CDE A ∠=︒∠=︒，，则ABD ∠的度数为（）A ．100︒B ．128︒C ．108︒D ．98︒【答案】A 【分析】直接利用线段垂直平分线的性质结合三角形内角和定理得出答案．【解析】解：∵DE 垂直平分BC ，∴BD =DC ，∴∠BDE =∠CDE =64°，∴∠ADB =180°-64°-64°=52°，∵∠A =28°，∴∠ABD =180°-28°-52°=100°．故选：A ．【点睛】此题主要考查了线段垂直平分线的性质、三角形内角和定理，正确掌握相关定理是解题关键．24．如图，已知D 为ABC 边AB 的中点，E 在AC 上，将ABC 沿着DE 折叠，使A 点落在BC 上的F 处．若70B ∠=︒，则BDF ∠等于（）键．题型5：等边对等角的解答证明26．如图，在ABC 中，AB AC =，点D 、E 都在边BC 上，且BE CD =，求证：AD AE =．【答案】见详解【分析】利用等腰三角形的性质可得B C ∠=∠，再由SAS 证明()SAS ABE ACD ≌△△，从而得AD AE =．【解析】证明：∵AB AC =，∴B C ∠=∠，在ABE 和ACD 中，AB AC B C BE CD =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABE ACD ≌△△，∴AD AE =．【点睛】本题考查等腰三角形的性质，全等三角形的性质与判定，熟练掌握相关性质定理是解题的关键．27．如图，,∥DE AB AE 平分DAB ∠，点C 在线段AE 上，AC BC AD ==，求证：AE AB =．【答案】见解析【分析】根据平行和角平分线得出AD DE =，再证△ADE ≌△ACB 即可．【解析】证明：∵AE 平分DAB ∠，∴DAE CAB ∠=∠，∵DE AB ∥，∴E BAE ∠=∠，∵AC BC =，∴B BAE ∠=∠，∴E B ∠=∠,在△ADE 和△ACB 中，E B DAE CAB AD AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△ACB ，∴AE AB =．【点睛】本题考查了全等三角形的判定与性质，等腰三角形的性质，解题关键是熟练运用等腰三角形的性质得出角相等．28．如图，在ABC 中，AB AC =，点D 在BC 边上，点E 在AC 边上，连接AD ，DE ．已知12∠=∠，AD DE =．（1）求证：ABD △≌DCE △；（2）若3BD =，5CD =，求AE 的长．【答案】（1）见解析；（2）2【分析】（1）根据等边对等角可得：B C ∠=∠，利用全等三角形的判定定理证明即可；（2）根据全等三角形的性质可得5AB DC ==，3CE BD ==，由图形中各边的关系计算即可得出．【解析】（1）证明：∵AB AC =，∴B C ∠=∠，在ABD 和DCE 中，12B C AD DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ABD DCE ≅ ；（2）解：∵ABD DCE ≅ ，∴5AB DC ==，3CE BD ==，∵5AB AC ==，∴532AE AB CE =-=-=．【点睛】题目主要考查全等三角形及等腰三角形的性质，理解题意，结合图形，熟练运用各个性质是解题关键．29．如图，在ABC 中，AB AC =，延长BC 至D ，使得BD AC =，连接AD ，再延长AB 至E ，使得BE CD =，连接DE ．求证：≌BED CDA △△．【答案】见详解【分析】先证明,EBD ACD ∠=∠再根据SAS 判定证明即可．【解析】解：∵在ABC 中，AB AC =，ABC ACB ∴∠=∠，180,180,EBD ABC ACD ACB ∠=︒-∠∠=︒-∠ ,EBD ACD ∴∠=∠BE CD = ，BD AC =，(SAS)BED CDA ≌．【点睛】本题考查了等腰三角形的性质，全等三角形的判定，解题的关键是熟练掌握全等三角形的判定定理．题型6：等腰三角形的“三线合一”30．等腰三角形的“三线合一”指的是（）A ．中线，高线，角平分线互相重合B ．顶角的平分线，中线，高线三线互相重合C ．腰上的中线，腰上的高线，底角的平分线互相重合D ．顶角的平分线，底边上的中线及底边上的高线三线互相重合【答案】D【分析】根据等腰三角形的性质直接选取答案即可求解．【解析】解：三线合一，即在等腰三角形中顶角的角平分线，底边的中线，底边的高线，三条线相互重合．【点睛】本题考查等腰三角形的性质，解题的关键是熟练掌握等腰三角形的三线合一的性质，属于中考基础题．33．下列说法错误的是（）A ．等腰三角形两腰上的高相等B ．等腰三角形两腰上的中线相等C ．等腰三角形两底角的平分线相等D ．等腰三角形高、中线和角平分线重合【答案】D【分析】根据等腰三角形的性质依次判断．【解析】解：A 、等腰三角形两腰上的高相等，故正确；B 、等腰三角形两腰上的中线相等，故正确；C 、等腰三角形两底角的平分线相等，故正确；D 、等腰三角形底边上的高、底边上的中线和顶角的角平分线重合，故错误；故选：D ．【点睛】此题考查了等腰三角形的性质，熟记等腰三角形的性质是解题的关键．34．已知点P 到ABC 的两边AB ，AC 所在直线的距离相等，且PB PC =，则下列命题为假命题的是（）A ．若点P 在边BC 上，则AB AC=B ．若点P 在ABC 内部，则AB AC=C ．若点P 在ABC 外部，则AB AC=D ．若AB AC =，则点P 可能在边BC 上，可能在ABC 内部，也可能在ABC 外部【答案】C【分析】选项A 根据等腰三角形的性质判断；当点P 在ABC 内部时，分别作PE ，PF 垂直AB ，AC 于点E ，F ，先证明Rt Rt (HL)BEP CFP ≌ ，再证明(AAS)ABP ACP ≌可判断选项B ；若AB AC =，都有(SSS)ABP ACP ≌，可判断选项D ；选项C 有两种情况，具体见详解．【解析】∵点P 到ABC 的两边AB ，AC 所在直线的距离相等，∴点P 在BAC ∠的角平分线所在的直线上，即BAP CAP ∠=∠，如图1，当点P 在边BC 上时，即P 为BC 的中点，根据等腰三角形的“三线合一”，得到AB AC =，故选项A 是真命题；如图2，当点P 在ABC 内部时，分别作PE ，PF 垂直AB ，AC 于点E ，F ，,PE PF PB PC == ，Rt Rt (HL)BEP CFP ≌ ，得到EBP FCP ∠=∠，∵BAP CAP ∠=∠，AP AP =，(AAS)ABP ACP ∴ ≌，AB AC ∴=；故选项B 是真命题；若AB AC =，都有(SSS)ABP ACP ≌，故选项D 是真命题；当点P 在ABC 外部时，如图3所示，AB 与AC 不一定相等，故选：C ．【点睛】此题考查了等腰三角形的判定与性质以及直角三角形全等的判定与性质．本题的关键是注意数形结合思想的应用，注意掌握辅助线的作法．题型7：等腰三角形的“三线合一”有关的最值问题35．如图，在ABC 中，AB AC =，=4BC ，面积是10；AB 的垂直平分线ED 分别交AC ，AB 边于E 、D 两点，若点F 为BC 边的中点，点P 为线段ED 上一动点，则PBF △周长的最小值为（）A ．7B ．9C ．10D ．14【答案】A 【分析】连接AP ，根据线段垂直平分线性质得AP BP =，PBF △周长==BP PF BF AP PF BF AF BF ++++≥+，再根据等腰三角形的性质和三角形的面积求出AF ，BF ，即可得出答案．【解析】解：如图所示．连接AP ，∵DE 是AB 的垂直平分线，A．①②③【答案】D【分析】根据三线合一得到A．8cm B．【答案】B【分析】根据等腰三角形三线合一的性质，得【答案】见解析【分析】过点A 作AM BC ⊥于点M ，由等腰三角形的性质得出2BAC BAM ∠=∠，D E ∠=∠，由三角形外角的性质得出2BAC D ∠=∠，即可推出BAM D ∠=∠，最后根据平行线的判定和性质即可证明DE BC ⊥．【解析】证明：如图，过点A 作AM BC ⊥于点M ．AB AC = ，2BAC BAM ∠∠∴=，AD AE = ，D E ∴∠=∠，2BAC D E D ∠∠∠∠∴=+=，22BAC BAM D ∠∠∠∴==，BAM D ∠∠∴=，DE AM ∴∥，AM BC ⊥ ，DE BC ∴⊥．【点睛】本题主要考查了等腰三角形的性质，三角形外角的性质，平行线的判断和性质，正确作出辅助线，构建等腰三角形三线合一的性质是解题的关键．42．如图，在ABC 中，AB AC =，40BAC ∠︒=，AD 是BC 边上的高．线段AC 的垂直平分线交AD 于点E ，交AC 于点F ，连接BE ．(1)试问：线段AE 与BE 的长相等吗？请说明理由；(2)求EBD ∠的度数．【答案】(1)相等，理由见解析(2)50︒【分析】（1）连接CE ，根据中垂线的性质得到,AE CE BE CE ==，即可得到AE BE =；（2）利用等边对等角，求出ABC ∠的度数，三线合一，求出BAE ∠的度数，等边对等角得到ABE ∠的度数，利用EBD ABD ABE ∠=∠-∠，即可得解．【解析】（1）解：线段AE 与BE 的长相等，理由如下：连接CE ，∵AB AC =，AD 是BC 边上的高，∴BD CD =，∴AD 为BC 的垂直平分线，∵点E 在AD 上，∴BE CE =，又∵线段AC 的垂直平分线交AD 于点E ，交AC 于点F ，∴AE CE =，∴AE BE =；（2）∵AB AC =，40BAC ∠︒=，【答案】见解析【分析】作EF AC ⊥于点F EA EC = ，12AF FC AC ∴==．2AC AB = ，A．3【答案】A【分析】利用等腰三角形三线合一解题即可．∠=【解析】解：∵B【解析】解：如图，在AB 上截取BE BC =，连接DE ，∵BD 平分ABC ∠，∴ABD CBD ∠=∠，在CBD △和EBD △中，CB BE CBD DBE BD BD =⎧⎪∠=∠⎨⎪=⎩，∴CBD △≌EBD △()SAS ，∴CDB BDE ∠=∠，C DEB ∠=∠，∴2CDE CDB ∠=∠，∵2C CDB ∠=∠，∴CDE DEB C ∠=∠=∠，∴ADE AED ∠=∠，∴AD AE =，∴ABC 的周长＝27AD AE BE BC CD AB AB CD ++++=++=，故选：C ．【点睛】本题考查全等三角形的判定和性质以及等腰三角形的性质，注意掌握添加恰当辅助线构造全等三角形是解题的关键．题型11：等角对等边证明等腰三角形的解答证明48．已知：如图，在ABC 中，点D 在CA 边的延长线上，AE 平分DAB ∠，AE BC ∥．求证：ABC 为等腰三角形．【答案】见解析【分析】首先依据平行线的性质证明2B ∠=∠，1C ∠=∠，然后结合角平分线的定义可证明B C ∠=∠，故此可证明ABC 为等腰三角形．【解析】证明：∵AE BC ∥，∴2B ∠=∠，1C∠=∠∵AE 平分DAB ∠，∴12∠=∠∴B C∠=∠即ABC 为等腰三角形．【点睛】本题主要考查的是等腰三角形的判定，熟练掌握平行线的性质及等腰三角形的判定定理是解题的关键．49．如图，在ABD △和ACD 中，AB AC =，BD CD =．(1)求证：ABD ACD △≌△；(2)过点D 作∥DE AC 交AB 于点E ，求证：AED △是等腰三角形．【答案】(1)见解析(2)见解析【分析】（1）根据SSS 证明三角形全等即可；（2）证明EAD ADE ∠=∠即可证明AE DE =，进而得到AED △是等腰三角形．【解析】（1）证明：在ABD △和ACD 中，AB AC AD AD DB DC =⎧⎪=⎨⎪=⎩，∴()SSS ABD ACD ≌；（2）证明：∵ABD ACD △≌△，∴∠=∠DAB DAC ，∵∥DE AC ，∴ADE DAC ∠=∠，∴EAD EDA ∠=∠，∴AE DE =，∴AED △是等腰三角形．【点睛】本题考查全等三角形的判定和性质，平行线的性质，等腰三角形的判定等知识，解题的关键是掌握全等三角形的判定方法．50．已知ABC 中，AD 平分BAC ∠交BC 于点D ，且2B C ∠=∠．(1)如图1，求证：AB BD AC +=；(2)如图2，延长CB 至点E ，使BE AB =，连接AE ，若36C ∠=︒，直接写出图中所有的等腰三角形（ABC 和ADE V 除外）．【答案】(1)证明见解析(2)ABE 是等腰三角形，ACE △是等腰三角形，ADC △是等腰三角形，ABD △是等腰三角形；【分析】（1）如图所示，在AC 上取一点E ，使得AE AB =，连接DE ，证明()SAS ABD AED ≌△△得到BD ED B AED ==，∠∠，根据三角形外角的性质结合已知条件证明EDC C ∠=∠，得到ED EC BD ==，即可证明AC AE CE AB BD =+=+；（2）根据等腰三角形的判定条件结合三角形内角和定理进行推理即可．【解析】（1）证明：如图所示，在AC 上取一点E ，使得AE AB =，连接DE ，∵AD 平分BAC ∠，∴BAD EAD ∠=∠，又∵AB AE AD AD ==，，∴()SAS ABD AED ≌△△，∴BD ED B AED ==，∠∠，∵2B C ∠=∠，∴2AED C ∠=∠，∵AED C EDC ∠=∠+∠，∴EDC C ∠=∠，∴ED EC BD ==，∴AC AE CE AB BD =+=+；（2）解：∵BE AB =，∴BEA BAE ∠=∠，ABE 是等腰三角形，∵BEA BAE ABC +=∠∠∠，∴2ABC BEA =∠∠，又∵272ABE C ==︒∠∠，∴36BEA BAE C ===︒∠∠∠，∴AE AC =，即ACE △是等腰三角形，∵18072BAC C ABC =︒--=︒∠∠∠，AD 平分BAC ∠，∴36BAD CAD ∠=∠=︒，∴36DAC C ∠=∠=︒，∴72ADB C DAC =+=︒∠∠∠，ADC △是等腰三角形，∴72ADB ABD ∠∠==︒，∴ABD △是等腰三角形．【点睛】本题主要考查了等腰三角形的判定，全等三角形的性质与判定，三角形内角和定理，三角形外角的性质，角平分线的定义等，灵活运用所学知识是解题的关键．题型12：等角对等边证明边长相等、求边长51．如图，已知12∠=∠，B C ∠=∠，不正确的等式是（）A ．AB AC=B ．BAE CAD ∠=∠C ．BE DC =D ．BD DE=【答案】D 【分析】根据等腰三角形的判定和全等三角形的判定和性质定理即可得到结论．【解析】解：∵B C ∠=∠，∴AB AC =，故A 选项正确，不符合题意；在ABE 和ACD 中，12B C AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AAS ABE ACD ≌，∴BE CD =，BAE CAD ∠=∠，∵BE CD =，∴BE DE CD DE -=-，∴BD CE =，故B 选项、C 选项正确，D 选项错误，故选：D ．【点睛】本题考查等腰三角形的判定，全等三角形的判定和性质，掌握等腰三角形的判定是解题的关键．52．如图，ABC 中，BD 平分ABC ∠交AC 于点D ，过点D 作DE BC ∥交AB 于点E ，若12AB =，7DE =，则AE 的长为（）A ．5B ．6C ．7D ．8【答案】A【分析】由角平分线的定义和平行线的性质，得到ABD EDB ∠=∠，则7BE DE ==，即可求出答案．【解析】解：∵在ABC 中，BD 平分ABC ∠，∴ABD CBD ∠=∠，∵DE BC ∥，∴CBD EDB ∠=∠，∴ABD EDB ∠=∠，∴7BE DE ==，∴1275AE AB BE =-=-=；故选：A ．【点睛】本题考查了角平分线的定义和平行线的性质，解题的关键是掌握所学的知识进行计算．53．如图，点P 是AOB ∠的角平分线OC 上一点，点Q 是OA 上一点，且PQ OB ∥，若2PQ =，则线段OQ 的长是（）A ．1.8B ．2.5C ．3D ．2【答案】D 【分析】利用角平分线的定义以及平行线的性质推出QPO QOP ∠=∠，据此即可求解．【解析】解：∵点P 是AOB ∠的角平分线OC 上一点，∴QOP POB ∠=∠，∵PQ OB ∥，∴QPO POB ∠=∠，∴QPO QOP ∠=∠，∴2OQ PQ ==，故选：D ．【点睛】本题考查了平行线的性质，等角对等边，掌握“两直线平行内错角相等”是解题的关键．54．如图，在ABC 中，BE 平分ABC ∠，DE BC ∥．若8DE =，5AD =，则AB 的长为（）A ．13B ．12C ．10D ．9【答案】A 【分析】先根据平行线的性质和角平分线的定义证明DBE DEB ∠=∠，得到8DE DB ==，则13AB AD BD =+=．【解析】解：∵BE 平分ABC ∠，∴DBE CBE ∠=∠，∵DE BC ∥，∴DEB CBE ∠=∠，∴DBE DEB ∠=∠，∴8DE DB ==，∴8513AB AD BD =+=+=，故选A ．【点睛】本题主要考查了角平分线的定义，平行线的性质，等腰三角形的判定，证明DBE DEB ∠=∠是解题的关键．55．如图，在ABC 中，45AB AC ==，，ABC ∠和ACB ∠的平分线交于点E ，过点E 作MN BC ∥分别交AB AC ，于M ，N ，则AMN 的周长为（）A ．8B ．9C ．10D ．不确定【答案】B 【分析】根据角平分线的定义和MN BC ∥可以得出MB ME =，NC NE =，继而可以得出AMN 的周长AB AC =+，从而可以得出答案．【解析】解：∵MN BC ∥，∴∠∠=MEB EBC ．∵BE 平分ABC ∠，∴MBE EBC =∠∠，∴MEB MBE ∠=∠．∴MB ME =．同理，NC NE =，∴9AMN C AM ME EN AN AB AC =+++=+=△．故选：B ．【点睛】本题考查了等腰三角形的性质，等角对等边，利用角平分线及平行线的性质得出MEB MBE ∠=∠是解题的关键.56．如图，ABC DEF ≌△△，点E 在AC 上，B ，F ，C ，D 四点在同一条直线上．若40,35A CED ∠=︒∠=︒，则下列结论正确的是（）A ．,EF EC AB FC==B ．,EF EC AE FC ≠=C ．,EF EC AE FC=≠D ．,EF EC AE FC≠≠【答案】C 【分析】根据全等三角形的性质得到ACB DFE ∠=∠，40D A AC DF ==︒=∠∠，，则EF EC =，由于D CED ∠≠∠，则CE CD ≠，则AE CF ≠，由此即可得到答案．【解析】解：∵ABC DEF ≌△△，∴ACB DFE ∠=∠，40D A AC DF ==︒=∠∠，，∴EF EC =，∵4035D CED ∠=︒≠∠=︒，∴CE CD ≠，∴AE CF ≠，∴四个选项中只有C 选项符合题意，故选C ．【点睛】本题主要考查了全等三角形的性质，等腰三角形的判定，熟知全等三角形的性质是解题的关键．57．如图，在ABC 中，AB AC =，AD BC ⊥于点D ．(1)若37B ∠=︒，求CAD ∠的度数；(2)若点E 在边AC 上，EF AB ∥交AD 的延长线于点F ．求证：AE FE =．【答案】(1)53︒(2)见解析【分析】（1）根据等腰三角形底角相等，再根据直角三角形的性质即可求得CAD ∠；（2）根据两直线平行内错角相等，再根据AD 是BAC ∠的角平分线即可得到DAC F ∠=∠，从而证得AE FE =．【解析】（1）解：AB AC = ，AD BC ⊥，37B C ∴∠=∠=︒，90ADC ∠=︒，9053CAD C ∴∠=︒-∠=︒；（2）证明：E F A B ∥ ，BAF F ∴∠=∠，AB AC = ，AD BC ⊥，AD ∴是BAC ∠的角平分线，BAF DAC ∴∠=∠，DAC F ∴∠=∠，AE FE ∴=．【点睛】本题考查等腰三角形的性质、平行线的性质、直角三角形的性质，解题的关键是熟练掌握等腰三角形、平行线、直角三角形的相关知识．58．如图，在四边形ABCD 中，AD BC ∥，E 是AB 的中点，连接DE 并延长交CB 的延长线于点F ，点G 在边BC 上，且GDF ADF ∠=∠．连接EG ，判断EG 与DF 的位置关系，并说明理由．【答案】EG 与DF 的位置关系是EG DF ⊥；理由见解析【分析】证明()AAS ADE BFE ≌△△，得出DE EF =，证明GDF BFE ∠=∠，得出GD GF =，根据垂直平分线的判定得出GE 垂直平分DF ，即可得出答案．【解析】解：EG 与DF 的位置关系是EG DF ⊥；理由见如下：∵AD BC ∥，∴ADE BFE ∠=∠，E 是AB 的中点，AE BE ∴=，又∵FEB DEA ∠=∠，∴()AAS ADE BFE ≌△△，DE EF ∴=，∵GDF ADF ∠=∠，ADE BFE ∠=∠，∴GDF BFE ∠=∠，GD GF ∴=，DE EF = ，∴GE 垂直平分DF ，∴EG DF ⊥．【点睛】本题主要考查了全等三角形的判定和性质，等腰三角形的判定，垂直平分线的判定，解题的关键是熟练掌握三角形全等的判定方法，得出ADE BFE V V ≌．题型13：直线上与已知两点组成等腰三角形的点59．如图，ABC ，点P 为直线AC 上的一个动点，若使得ABP 是等腰三角形．则符合条件的点P 有（）A ．1个B ．2个C ．3个D ．4个【答案】D【分析】根据等腰三角形的判定定理即可得到结论．【解析】解：作AB 垂直平分线与AC 的交点，可得22P A P B =，以A 为圆心，AB 为半径画圆，交AC 有两个交点，13P A AB P A ==，以B 为圆心，AB 为半径画圆，交AC 有一个交点，4P B AB =，故选：D ．【点睛】本题考查了等腰三角形的判定来解决实际问题，其关键是根据等腰三角形的判定定理解答．60．如图，线段AB 的一个端点B 在直线m 上，直线m 上存在点C ，使ABC 为等腰三角形，这样的点C 有（）A ．2个B ．3个C ．4个D ．5个【答案】C 【分析】以A 为圆心，以BA 的长为半径画弧与直线m 交于点D ，此时BA AD =，同理以B 为圆心以BA 的长为半径画弧与直线m 交于E 、C ，此时BC BA =，BE BA =，再作BA 的垂直平分线与直线m 交于点F ，此时BF AF =，据此可得答案．【解析】解：如图所示，以A 为圆心，以BA 的长为半径画弧与直线m 交于点D ，此时BA AD =，同理以B 为圆心以BA 的长为半径画弧与直线m 交于E 、C ，此时BC BA =，BE BA =，再作BA 的垂直平分线与直线m 交于点F ，此时BF AF =，∴直线m 上存在4个点C ，使ABC 为等腰三角形，故选：C ．【点睛】本题考查了等腰三角形的定义，线段垂直平分线的性质，解题的关键在于能够熟练掌握等腰三角形的定义．61．如图，直线a b ，相交于点O ，150∠=︒，点A 在直线a 上，直线b 上存在点B ，使以点O A B 、、为顶点的三角形是等腰三角形，这样的B 点有（）A ．1个B ．2个C ．3个D ．4个【答案】D 【分析】分别以点O A B 、、为顶点的等腰三角形有3种情况，分别为OA OB =，OA AB =，OB AB =，从这三方面考虑点B 的位置即可；【解析】解：当OA OB =时；以点O 为圆心，OA 的长为半径作圆，与直线b 在O 点两侧各有一个交点，此时B 点有2个；当OA AB =时；以点A 为圆心，OA 的长为半径作圆，与直线b 有一个交点，此时B 点有1个；当OB AB =时；作OA的垂直平分线，与直线b有一个交点，此时B点有1个；∴满足条件的B点总共有4个；故选：D．【点睛】本题考查了等腰三角形的判定，两条边相等的三角形为等腰三角形，因此要注意分类讨论，由每种情况的特点选择合适的方法确定点B是解题的关键．题型14：等腰三角形有关的尺规作图62．如图，给出了尺规作等腰三角形的三种作法，认真观察作图痕迹，下面的已知分别对应作图顺序正确的是（）①已知等腰三角形的底边和底边上的高；②已知等腰三角形的底边和腰；③已知等腰三角形的底边和一底角．A．①②③B．②①③C．③①②D．②③①【答案】B【分析】根据等腰三角形的性质即可求解．【解析】解：图形①的作图依据是“②已知等腰三角形的底边和腰”；图形②的作图依据是“①已知等腰三角形的底边和底边上的高”；图形③的作图依据是“③已知等腰三角形的底边和一底角”．故选：B ．【点睛】本题主要考查尺规作图等腰三角形，掌握等腰三角形的性质，作图的方法是解题的关键．63．如图（1），锐角ABC 中，AB BC AC >>，要用尺规作图的方法在AB 边上找一点D ，使ACD 为等腰三角形，关于图（2）中的甲、乙、丙三种作图痕迹，下列说法正确的是（）A ．甲、乙、丙都正确B ．甲、丙正确，乙错误C ．甲、乙正确，丙错误D ．只有甲正确【答案】A【分析】根据圆、线段垂直平分线、角的尺规作图进行分析即可．【解析】解：甲图：以点A 为圆心，AC 为半径作弧，交AB 于点D ，∴AD AC =，∴ACD 为等腰三角形，乙图：作AC 的垂直平分线，交AB 于点D ，∴AD DC =，∴ACD 为等腰三角形，丙图：∵所作的A DCA ∠=∠，∴AD DC =，∴ADC △是等腰三角形，∴甲、乙、丙都正确，故选A ．【点睛】本题考查等腰三角形的定义、尺规作图−圆、角、垂直平分线，熟练掌握等腰三角形的判定与圆、角和线段垂直平分线的基本作图的方法是解题的关键．64．已知锐角40AOB ∠=︒，如图，按下列步骤作图：①在OA 边取一点D ，以O 为圆心，OD 长为半径画 MN，交OB 于点C ．②以D 为圆心，DO 长为半径画 GH， GH 与OB 交于点E ，连接DC 并延长，使DC 的延长【答案】见解析【分析】以AB为腰和底两种情况作图即可．【解析】如图，以AB为腰，AO为对称轴；如图，以AB为底作等腰三角形，CM为对称轴；【点睛】本题考查利用网格作图，掌握等腰三角形的判定定理是解题的关键．66．图1，图2均是44⨯的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，点A，B，C均为格点．只用无刻度的直尺，分别在给定的网格中找一格点M，按下列要求作图：=；(1)在图1中，连接MA，MB，使MA MB==．(2)在图2中，连接MA，MB，MC，使MA MB MC【答案】(1)见解析(2)见解析=；【分析】（1）根据勾股定理得MA MB==．（2）连接AC，取AC中点M，MA MB MC【解析】（1）解：如图1正确画图．（2）如图2正确画图．【点睛】本题主要考查尺规作图，熟练根据题意作出符合题意的图形是解题的关键．67．如图，在每个小正方形的边长均为方形的顶点上．(1)在方格纸中画出以AB为底的等腰ABC(2)在方格纸中画出以DE为一边的等腰DEF直接写出DC的长度．【答案】(1)图见解析；(2)图见解析，22DC ．（2）如图所示，DEF 即为所求；CD =【点睛】本题考查的是作图：应用与设计作图，根据题意找出符合条件的点是解题的关键．题型16：等腰三角形的性质和判定综合题68．如图，在ABC 中，90BAC ∠=︒，AB 90EDF ∠=︒，下列结论：①BED AFD △≌△积，则1211142S S S ≤≤；④EF AD =；所有正确的结论是（。

倍长中线模型模型讲解【结论】已知△ABC中，∠ACB＝∠DCE，AC＝BC，DC＝EC，且点A、D、E 在同一直线上，AE与BC相交于点F，连接BE．（1）△ACD≌△BCE（2）∠CAD＝∠CBE；∠AEB＝∠ACF【证明】（1）∵∠ACB＝∠DCE，CA＝CB，CD＝CE，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴∠CAD＝∠CBE，∵∠CF A＝∠BFE，∴∠AEB＝∠ACF△BCE可看成△ACD绕C点顺时针旋转一定角度而得到的；△ACD可看成△BCE绕C点逆时针旋转一定角度而得到的。

所以，通常用旋转的思想来构造全等三角形手拉手模型的关键：AC=BC（线段相等、有公共点且此三点不共线）那么，哪些图形满足这些特征呢？1【等边三角形类】等边△ABD、△BCE，则：（1）△ABC≌△BDE （2）∠ACB＝∠DEB已知等边△BCE，将△ABC绕B点旋转60°到△BDE，那么会得到一个新的△ABD也为等边三角形。

【等腰直角三角形类】等腰Rt△ABD、△BCE，则：（1）△ABC≌△BDE （2）∠ACB＝∠DEB已知等腰Rt△BCE，将△ABC绕B点旋转90°到△BDE，那么会得到一个新的△ABD也为等腰Rt△。

方法点拨例题演练1．（2021春•鄄城县期末）如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝（）A．55°B．50°C．45°D．60°【解答】解：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠1＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴∠2＝∠ABD＝30°，∵∠1＝25°，∴∠3＝∠1+∠ABD＝25°+30°＝55°，故选：A．2．（2016春•威海期末）如图，△ABC和△CDE均为等边三角形，且AB＝DE，AC⊥CD，连接AE，BD，分别交CD，AC于点G，连接FG，BE．下列结论：①AE＝BD＝BE；②BC平分∠DBE；③直线EC⊥AB；④FG∥BE．其中正确结论的个数为（）A．1个B．2个C．3个D．4个【解答】解：∵△ABC和△CDE均为等边三角形，且AB＝DE，∴∠ACB＝∠DCE＝60°，∵AC⊥CD，∴∠ACD＝90°，∴∠ACE＝∠BCD＝150°，∴∠BCE＝150°，在△ACE与△BCD与△BCE中，，∴△ACE≌△BCD≌△BCE，∴AE＝BD＝BE，故①正确，∠DBC＝∠EBC，故②正确；∴∠BEC＝∠AEC，∵BE＝AE，∴直线EC⊥AB；故③正确；在△BCF与△ECG中，，∴△BCF≌△ECG，∴BF＝EG，设AE，BD交于H，∵∠FBC＝∠GEC，∠CBE＝∠CEB，∴∠HBE＝∠HEB，∴BH＝EH，∴HF＝HG，∴，∴FG∥BE，故④正确，故选：D．3．（2018秋•海珠区校级期中）如图，在△ABC中，∠ABC＝45°，AD，BE分别为BC、AC边上的高，AD、BE相交于点F，下列结论：①∠FCD＝45°；②AE＝EC；③S△ABF：S△AFC＝BD：CD；④若BF＝2EC，则△FCD的周长等于AB的长，正确的有（）个．A．1B．2C．3D．4【解答】解：∵△ABC中，AD，BE分别为BC、AC边上的高，∴AD⊥BC，而△ABF和△ACF有一条公共边，∴S△ABF：S△AFC＝BD：CD，∴③正确；∵∠ABC＝45°，∴AD＝BD，∠DAC和∠FBD都是∠ACD的余角，而∠ADB＝∠ADC＝90°，∴△BDF≌△ADC，∴FD＝CD，∴∠FCD＝∠CFD＝45°，∴①正确；若AE＝EC，BE⊥AC，可得AB＝BC，与题意不符合，故②错误．若BF＝2EC，根据①得BF＝AC，∴AC＝2EC，即E为AC的中点，∴BE为线段AC的垂直平分线，∴AF＝CF，BA＝BC，∴AB＝BD+CD＝AD+CD＝AF+DF+CD＝CF+DF+CD，即△FDC周长等于AB的长，∴④正确．强化训练故选：C．1．（2021春•北碚区校级期末）如图，已知凸五边形ABCDE中，EC，EB为其对角线，EA ＝ED．（1）如图1，若∠A＝60°，∠CDE＝120°，且CD+AB＝BC．求证：EC平分∠BCD；（2）如图2，∠A与∠D互补，∠DEA＝2∠CEB，若凸五边形ABCDE面积为30，且CD ＝AB＝4．求点E到BC的距离．【解答】（1）证明：延长CD到T，使得DT＝BA，连接ET．∵∠CDE＝120°，∴∠EDT＝180°﹣120°＝60°，∵∠A＝60°，∴∠A＝∠EDT，在△EAB和△EDT中，，∴△EAB≌△EDT（SAS），∴EB＝ET，∴CB＝CD+BA＝CD+DT＝CT，在△ECB和△ECT中，，∴△ECB≌△ECT（SSS），∴∠ECB＝∠ECD．（2）解：延长CD到Q，使得∠QED＝∠AEB，过点E作EH⊥BC于H．∵∠A+∠CDE＝180°，∠CDE+∠EDQ＝180°，∴∠A＝∠EDQ，在△AEB和△DEQ中，，∴△AEB≌△DEQ（ASA），∴EB＝EQ，∵∠AED＝2∠BEC，∴∠AEB+∠CED＝∠BEC，∴∠CED+∠DEQ＝∠BEC，∴∠CEB＝∠CEQ，在△CEB和△CEQ中，，∴△ECB≌△ECQ（SAS），∵S五边形ABCDE＝S四边形EBCQ＝2S△EBC＝30，∴S△EBC＝15，∵CD＝AB＝4，∴AB＝6，CD＝4，∴BC＝CD+QD＝CD+AB＝10，∴×10×EH＝15，∴EH＝3，∴点E到BC的距离为3．2．（2021春•松江区期末）如图，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，点E、F分别在直线BC、CD上，且∠EAF＝∠BAD．（1）当点E、F分别在边BC、CD上时（如图1），请说明EF＝BE+FD的理由；（2）当点E、F分别在边BC、CD延长线上时（如图2），（1）中的结论是否仍然成立？若成立，请说明理由；若不成立，请写出EF、BE、FD之间的数量关系，并说明理由．【解答】解：（1）EF＝BE+DF，理由：延长EB至G，使BG＝DF，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABG＝180°，∴∠ADC＝∠ABG，在△ABG和△ADF中，，∴△ABG≌△ADF（SAS），∴AG＝AF，∠BAG＝∠DAF，∵∠EAF＝∠BAD，∴∠BAE+∠DAF＝∠BAE+∠BAG＝∠EAF，即∠EAG＝∠EAF，在△EAG和△EAF中，，∴△EAG≌△EAF（SAS），∴GE＝EF，∴EF＝BE+DF；（2）（1）中结论不成立，EF＝BE﹣FD，在BE上截取BM＝DF，连接AM，∵∠ABC+∠ADC＝180°，∠ADC+∠ADF＝180°，∴∠ABC＝∠ADF，在△ABM和△ADF中，，∴△ABM≌△ADF（SAS），∴AM＝AF，∠BAM＝∠DAF，∵∠BAM+∠MAD＝∠DAF+∠MAD，∴∠BAD＝∠MAF，∵∠EAF＝∠BAD，∴∠EAF＝∠MAF，∴∠EAF＝∠EAM，在△AME和△AFE中，，∴△AME≌△AFE（SAS），∴ME＝BE﹣BM＝BE﹣DF，∴EF＝BE﹣FD．3．（2017•南岸区二模）如图，已知等腰Rt△ABC，∠ACB＝90°，CA＝CB，以BC为边向外作等边△CBD，连接AD，过点C作∠ACB的角平分线与AD交于点E，连接BE．（1）若AE＝2，求CE的长度；（2）以AB为边向下作△AFB，∠AFB＝60°，连接FE，求证：F A+FB＝FE．【解答】解：（1）延长CE交AB于G，∵△BAC是等腰直角三角形，CE平分∠ACB，∴CG⊥AB，∴∠AGC＝90°，∵CA＝CB，∠ACB＝90°，∴∠CAB＝45°，∴△CAG是等腰直角三角形，∵△BCD是等边三角形，∴BC＝CD＝AC，∠BCD＝60°，∴∠CAD＝∠CDA，∴∠ACD＝∠ACB+∠BCD＝150°，∴∠CAD＝∠CDA＝15°，∴∠EAB＝∠CAB﹣∠CAD＝30°，在Rt△AEG中，∠EAG＝30°，AE＝2，∴AG＝，EG＝1，∵CG＝AG＝，∴CE＝CG﹣EG＝﹣1．（2）延长FB到H，使得BH＝AF，连接EH．作EI⊥BF于I．由（1）可知：AC＝BC，CE平分∠ACB，∴∠ACE＝∠BCE，∴△ACE≌△BCE，∴AE＝BE，∴∠EAB＝∠EBA＝30°，在△AFB中，∠AFB＝60°，∴∠F AB+∠FBA＝120°，∴∠F AE＝∠EAB+∠F AB＝30°+∠F AB，∠EBH＝180°﹣∠EBA﹣∠ABF＝150°﹣（120°﹣∠F AB）＝30°+∠F AB，∴∠EBH＝∠F AE，∴△AFE≌△BHE，∴∠AFE＝∠BHE，EF＝EH，∴∠EFB＝∠EHB＝∠AFE＝30°，∵EI⊥FH，∴EI＝IH，在Rt△FEI中，∠EFI＝30°，∴FI＝FE，∴FH＝BH+FB＝FE，∴F A+FB＝FE．4．（2021春•南岸区期末）如图，已知∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC．（1）△ABC与△ADE全等吗？请说明理由；（2）若AF⊥CB，垂足为F，请说明线段2CF＝CE；（3）在（2）的基础上，猜想线段BF，DE，CD存在的数量关系，并直接写出结论．【解答】解：（1）△ABC≌△ADE，理由如下：如图1，∵∠BAD＝∠CAE＝90°，∴∠BAC＝∠DAE＝90°﹣∠CAD，在△ABC和△ADE中，，∴△ABC≌△ADE（SAS）．（2）如图2，作AG⊥BC于点G，则∠AGC＝∠AGE＝90°，∵AC＝AE，AG＝AG，∴Rt△AGC≌Rt△AGE（HL），∴CG＝EG＝CE，∠CAG＝∠EAG＝∠CAE＝45°，∴∠ACG＝∠E＝45°，∵△ABC≌△ADE，∴∠ACF＝∠E＝45°，∵AF⊥CB，∴∠F＝90°，∴∠CAF＝45°，∵∠ACF＝∠ACG＝45°，AC＝AC，∠CAF＝∠CAG＝45°，∴△CAF≌△CAG，∴CF＝CG＝CE，∴2CF＝CE．（3）BF＝（CD﹣DE），理由如下：如图2，由（2）得，CF＝CG＝EG，∵△ABC≌△ADE，∴BC＝DE，∴CF﹣BC＝EG﹣DE，∴BF＝DG，∵DG＝EG﹣DE＝CE﹣DE＝（CD+DE）﹣DE＝（CD﹣DE），∴BF＝（CD﹣DE）．5．（2021春•沙坪坝区校级期末）如图，C为AB上一点，△ACD和△BCE为等边三角形，AE交CD于M，DB交CE于N．求证：（1）AE＝DB；（2）MN∥AB；（3）PC平分∠APB；（4）PC+PE＝PB．【解答】证明：（1）∵△ACD和△BCE是等边三角形，∴∠ACD＝∠BCE＝60°，AC＝DC，EC＝BC，∴∠ACD+∠DCE＝∠DCE+∠ECB，即∠ACE＝∠DCB，∴△ACE≌△DCB（SAS），∴AE＝BD；（2）∵△ACE≌△DCB，∴∠EAC＝∠BDC，∵∠ACD＝∠BCE＝60°，∴∠DCE＝60°，∴∠ACD＝∠MCN＝60°，且∠EAC＝∠BDC，AC＝DC，∴△ACM≌△DCN（ASA），∴CM＝CN，又∵∠MCN＝60°，∴△MCN是等边三角形，∴∠NMC＝∠ACD＝60°，∴MN∥AB；（3）如图，过点C作CG⊥AE于G，作CH⊥BD于H，∵∠EAC＝∠BDC，AC＝DC，∠AGC＝∠DHC＝90°，∴△AGC≌△DHC（AAS），∴CG＝CH，且CG⊥AE，CH⊥BD，∴PC平分∠APB；（4）如图，在PB上截取PF＝PC，连接CF，∵△ACE≌△DCB，∴∠CAE＝∠BDC，∠AEC＝∠DBC，∵∠ACD＝∠BDC+∠CBD＝60°，∴∠DOA＝∠CAE+∠CBD＝60°，∴∠APB＝120°，∵PC平分∠APB，∴∠CPF＝APB＝60°，∴△CPF为等边三角形，∴CF＝CP，∠CFP＝60°，∴∠CFB＝∠CPE＝120°，∴△CFB≌△CPE（AAS），∴BF＝PE，∴PB＝BF+PF＝PE+PC．6．（2013秋•沙坪坝区校级月考）如图，等边△ABC中，点E、F分别是AB、AC的中点，P为BC上一点，连接EP，作等边△EPQ，连接FQ，EF．（1）若等边△ABC的边长为20，且∠BPE＝45°，求等边△EPQ的边长；（2）求证：BP＝EF+FQ．【解答】（1）解：过点E作EM⊥BC于M∵等边△ABC，∴∠B＝60°，∵E为AB的中点，∴BE＝AB＝10，在Rt△BEM中，sin B＝，∴＝，∴EM＝5，在Rt△EMP中，sin∠EPM＝，∴＝，∴EP＝5，即等边△EPQ的边长为5；（2）证明：取BC的中点N，连接NE，∵等边△ABC，∴AB＝BC，∵E为AB的中点，F为AC的中点，N为BC的中点，∴EF＝BC，BE＝AB，BN＝BC，EF∥BC，∴EF＝BE＝BN，∵∠B＝60°，∴△EBN是等边三角形，∴EN＝BN＝EF，∠ENB＝60°，∵EF∥BC，∴∠FEN＝60°，∴∠1+∠2＝60°，∵等边△EPQ，∴EP＝EQ，∠PEQ＝60°，∴∠2+∠3＝60°，∴∠1＝∠3，在△ENP和△EFQ中，，∴△ENP≌△EFQ（SAS），∴NP＝FQ，∴BP＝BN+NP＝EF+FQ．7．（2020秋•斗门区校级期中）如图，在Rt△ABC中，∠A＝90°，AB＝AC，D、E分别在AB，AC上，且AD＝AE．若△ADE绕点A逆时针旋转，得到AD1E1，设旋转角为a（0°＜a≤180°），记直线BD1与CE1的交点为P．（1）求证：BD1＝CE1；（2）当∠CPD1＝2∠CAD1时，求旋转角为a的度数．【解答】解：（1）在△ABD1和△ACE1中，，∴△ABD1≌△ACE1 （SAS），∴BD1＝CE1；（2）设AC与BP交于点G，由（1）知△ABD1≌△ACE1，∴∠ABD1＝∠ACE1，∵∠AGB＝∠CGP，∴∠CPG＝∠BAG＝90°，∴∠CPD1＝90°，∵∠CPD1＝2∠CAD1，∴∠CAD1＝∠CPD1＝45°，∴旋转角α＝90°+∠CAD1＝135°．8．（2021春•渝中区校级期末）如图，△CAB与△CDE为等腰直角三角形，∠ACB＝∠DCE ＝90°，CA＝CB，CD＝CE，∠CAB＝∠CBA＝45°，∠CDE＝∠CED＝45°，连接AD、BE．（1）如图1，若∠CAD＝28°，∠DCB＝10°，则∠DEB的度数为27度；（2）如图2，若A、D、E三点共线，AE与BC交于点F，且CF＝BF，AD＝3，求△CEF 的面积；（3）如图3，BE与AC的延长线交于点G，若CD⊥AD，延长CD与AB交于点N，在BC上有一点M且BM＝CG，连接NM，请猜想CN、NM、BG之间的数量关系并证明你的猜想．【解答】解：（1）如图1中，∵△ACB，△CDE都是等腰直角三角形，∴∠ACB＝∠DCE＝90°，CA＝CB，CD＝CE，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴∠CAD＝∠CBE＝28°，∵∠DCB＝10°，∴∠ECB＝90°﹣10°＝80°，∴∠CEB＝180°﹣80°﹣28°＝72°，∵∠CED＝45°，∴∠DEB＝72°﹣45°＝27°．故答案为：27．（2）如图2中，过点C作CQ⊥DE于Q．∵△ACD≌△BCE，∴∠ADC＝∠CEB，AD＝BE＝3，∵∠CDE＝∠CED＝45°，∴∠ADC＝∠CEB＝135°，∴∠AEB＝90°，在△CFQ和∠BFE中，，∴△CQF≌△BEF（AAS），∴CQ＝BE＝3，QF＝EF，∵CQ＝EQ＝3，∴EF＝EQ＝，∴S△CEF＝•EF•CQ＝××3＝．（3）如图3中，结论：CN+MN＝BG．理由：如图过点B作BT⊥BC交CN的延长线于T∵AD⊥CD，∴∠ADC＝90°，∵△ACD≌△BCE，∴∠ADC＝∠BEC＝90°，∵∠BCT+∠ECB＝90°，∠ECB+∠CBG＝90°，∴BCT＝∠CBG，在△CBT和△BCG中，，∴△CBT≌△BCG（ASA），∴BT＝CG，CT＝BG，∵BM＝CG，∴BM＝BT，在△BNM和△BNT中，，∴△BNM≌△BNT（SAS），∴MN＝NT，∴CN+MN＝CN+NT＝CT＝BG．9．（2021春•楚雄州期末）已知△ABC中，∠ACB＝∠DCE＝α，AC＝BC，DC＝EC，且点A、D、E在同一直线上，AE与BC相交于点F，连接BE．（1）如图1，当α＝60°时，求出∠AEB的度数．（2）如图2，当α＝90°时，若∠CBE＝∠BAE，CF＝2，AB＝4+2，求△ABF的面积．【解答】解：（1）∵∠ACB＝∠DCE＝60°，CA＝CB，CD＝CE，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴∠CAD＝∠CBE，∵∠CF A＝∠BFE，∴∠AEB＝∠ACF＝60°．（2）同理可证△ACD≌△BCE，∴∠CAF＝∠CBE，∵∠CBE＝∠BAE，∴∠CAF＝∠BAE，∴AF平分∠CAB，∵FC⊥AC，CF＝2，∴点F到AB的距离＝CF＝2，∴S△ABF＝•AB•CF＝×（4+2）×2＝4+2．10．（2012秋•渝北区期末）如图，△ABC中，AC＝BC，∠ACB＝90°，点D在△ABC的外部，且AD⊥BD，AD交BC于点E，连接CD，过点C作CG⊥CD，交AD于点G．（1）若CG＝4，求DG的长；（2）若CG＝BD，求证：AB＝AC+CE．【解答】（1）解：∵AD⊥BD，∴∠ADB＝90°，∵∠ACB＝90°，而∠AEC＝∠BED，∴∠CAE＝∠EBD，∵CG⊥CD，∴∠GCD＝90°，即∠GCE+∠ECD＝90°，而∠GCE+∠ACG＝90°，∴∠ACG＝∠ECD，在△ACG和△BCD中，∴△ACG≌△BCD，∴CG＝CD，∴△CDG为等腰直角三角形，∴DG＝CG＝4；（2）证明：延长AC、BD，它们相交于点H，如图，∵CG＝BD，而CG＝CD，∴BD＝CD，∴∠DCB＝∠DBC，∵∠H+∠CBH＝90°，∠CHD+∠DCB＝90°，∴∠H＝∠HCD，∴CD＝HD，∴DH＝DB，而AD⊥BH，∴AB＝AH，在△ACE和△BCH中，∴△ACE≌△BCH，∴CE＝CH，∴AB＝AC+CH＝AC+CE．11．已知△BAC和△BDE都是等腰直角三角形，∠BAC＝∠BDE＝90°．（1）如图1，点E、B、C三点在一条直线上，连接AE，若∠AEC＝30°，BC＝4，求BE的长．（2）如图2，将△BDE以点B为旋转中心顺时针旋转，当C在ED延长线上时，EC交AB于点H．求证：∠BAE＝2∠BCH．【解答】（1）解：如图1中，作AH⊥BC于H．∵AB＝AC，∠BAC＝90°，AH⊥BC，∴AH＝BH＝HC＝2，在Rt△AEH中，∵∠AHE＝90°，AH＝2，∠AEH＝30°，∴EH＝＝2，∴BE＝EH﹣BH＝2﹣2．（2）证明：如图2中，连接AD．∵∠BDH＝∠HAC，∠BHD＝∠CHA，∴△BHD∽△CHA，∴＝，∴＝，∵∠AHD＝∠CHB，∴△AHD∽△CHB，∴∠ADH＝∠CBH＝45°，∠DAH＝∠BCH，∴∠ADB＝90°+45°＝135°，∴∠ADE＝360°﹣90°﹣135°＝135°，∴∠ADE＝∠ADB，在△ADE和△ADB中，，∴△ADE≌△ADB，∴∠DAE＝∠DAB，∵∠DAB＝∠BCH，∴∠BAE＝2∠BCH．12．（2021•鄂尔多斯）旋转是一种重要的图形变换，当图形中有一组邻边相等时往往可以通过旋转解决问题．（1）尝试解决：如图①，在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，点M是BC上的一点，BM＝1cm，CM＝2cm，将△ABM绕点A旋转后得到△ACN，连接MN，则AM ＝cm．（2）类比探究：如图②，在“筝形”四边形ABCD中，AB＝AD＝a，CB＝CD，AB⊥BC 于点B，AD⊥CD于点D，点P、Q分别是AB、AD上的点，且∠PCB+∠QCD＝∠PCQ，求△APQ的周长．（结果用a表示）（3）拓展应用：如图③，已知四边形ABCD，AD＝CD，∠ADC＝60°，∠ABC＝75°，AB＝2，BC＝2，求四边形ABCD的面积．【解答】解：（1）如图①，∵∠BAC＝90°，AB＝AC，∴∠B＝∠ACB＝45°，由旋转得：CN＝BM＝1，∠ACN＝∠B＝45°，∠MAN＝∠BAC＝90°，AM＝AN，∴∠MCN＝∠ACB+∠ACN＝45°+45°＝90°，△AMN是等腰直角三角形，∵CM＝2，∴MN＝＝，∴AM＝MN＝（cm）；故答案为：；（2）如图②，延长AB到E，使BE＝DQ，连接CE，∵AB⊥BC，AD⊥CD，∴∠ADC＝∠ABC＝90°，∴∠CBE＝∠CDQ＝90°，在△CDQ和△CBE中，，∴△CDQ≌△CBE（SAS），∴∠DCQ＝∠BCE，CQ＝CE，∵∠PCB+∠QCD＝∠PCQ，∴∠PCB+∠BCE＝∠PCQ＝∠PCE，在△QCP和△ECP中，，∴△QCP≌△ECP（SAS），∴PQ＝PE，∴△APQ的周长＝AQ+PQ+AP＝AQ+PE+AP＝AQ+BE+PB+AP＝AQ+DQ+AB＝2AB＝2a；（3）如图③，连接BD，由于AD＝CD，所以可将△BCD绕点D顺时针方向旋转60°，得到△DAB′，连接BB′，延长BA，作B′E⊥BA于E，由旋转得：△BCD≌△B′AD，∴BD＝B'D，∠BDB'＝60°，∠CBD＝∠AB'D，∴S四边形ABCD＝S四边形BDB′A，△BDB'是等边三角形，∵∠ABC＝75°，∠ADC＝60°，∴∠BAB′＝∠BDB'+∠AB'D+∠ABD＝135°，∴∠B′AE＝45°，∵B′A＝BC＝2，∴B′E＝AE＝，∴BE＝AB+AE＝2+＝3，∴BB′＝＝2，设等边三角形的高为h，则勾股定理得：h＝＝，∴S四边形ABCD ＝S四边形BDB′A＝S△BDB′﹣S△ABB′＝×2×﹣××＝5﹣2．。

期中考点专题01 三角形的基础重点突破三角形的概念：由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。

三角形特性三角形用符号“”表示，顶点是A、B、C的三角形记作“ABC”，读作“三角形ABC”。

三角形按边分类：等腰三角形：有两条边相等的三角形叫做等腰三角形，其中相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰与底边的夹角叫做底角。

等边三角形：底边与腰相等的等腰三角形叫做等边三角形，即三边都相等。

三角形三边的关系（重点（1）三角形的随意两边之和大于第三边。

三角形的随意两边之差小于第三边。

（这两个条件满意其中一个即可）用数学表达式表达就是：记三角形三边长分别是a，b，c，则a＋b＞c或c－b＜a。

（2）已知三角形两边的长度分别为a，b，求第三边长度的范围：|a－b|＜c＜a＋b三角形的分类：三角形按边的关系分类如下：三角形按角的关系分类如下：三角形的稳定性➢三角形具有稳定性➢四边形及多边形不具有稳定性要使多边形具有稳定性，方法是将多边形分成多个三角形，这样多边形就具有稳定性了。

考查题型考查题型一三角形的个数问题典例1．（2024·西林县期中）如图所示，其中三角形的个数是（）A．2个B．3个C．4个D．5个【答案】D【提示】依据三角形的定义解答即可，由不在同始终线上的三条线段首尾顺次相接所组成的图形叫做三角形.【详解】图中的三角形有：△ABC，△BCD，△BCE，△ABE，△CDE共5个.故选D.【名师点拨】本题考查了三角形的概念，由不在同始终线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边，相邻边的公共端点叫做三角形的顶点.相邻两条边组成的角，叫做三角形的内角，简称为三角形的角.变式1-1．（2024·秦皇岛市期中）图中三角形的个数是（）A．3个B．4个C．5个D．6个【答案】D【解析】图中的三角形有: △ABD, △ADE, △AEC, △ABE, △ADC, △ABC,共6个.故选D.变式1-2．（2024·洛阳市期末）图中三角形的个数是（）A．4个B．6个C．8个D．10个【答案】C【提示】依据三角形的定义即可得．【详解】图中的三角形是，共8个故选：C．【名师点拨】本题考查了三角形的定义，驾驭理解三角形的概念是解题关键．变式1-3．（2024·恩施市期中）如图，图中三角形的个数有（）A．6个B．8个C．10个D．12个【答案】B【解析】试题解析：以O为一个顶点的有△CBO、△CDO、△ABO、△ADO，不以O为顶点的三角形有△CAD、△CBA、△BCD、△BAD，共有8个．故选B.考查题型二三角形的分类典例2（2024·石家庄市期末）在△ABC中，∠A=20°，∠B=60°，则△ABC的形态是（）A．等边三角形 B．锐角三角形C．直角三角形 D．钝角三角形【答案】D【解析】试题提示：依据三角形的内角和定理求出∠C，即可判定△ABC的形态．解：∵∠A=20°，∠B=60°，∴∠C=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°，∴△ABC是钝角三角形．故选D．变式2-1．（2024·黄冈市期中）一个三角形三个内角的度数之比为1：2：3，则这个三角形肯定是（）A．锐角三角形B．直角三角形C．钝角三角形D．等腰直角三角形【答案】B【解析】试题提示：依据三角形的内角和为180°，可知最大角为90°，因式这个三角形是直角三角形.故选B.变式2-2．（2024·深圳市期中）在△ABC中，若∠A：∠B：∠C＝1：3：5，则△ABC是（）A．锐角三角形B．直角三角形C．钝角三角形D．形态不确定【答案】C【提示】依据∠A：∠B：∠C=1：3：5，可设∠A=x°，∠B=3x°，∠C=5x°，再依据三角形内角和为180°可得方程x+3x+5x=180，解方程算出x的值，即可推断出△ABC的形态．【详解】解：∵∠A：∠B：∠C=1：3：5，∴设∠A=x°，∠B=3x°，∠C=5x°，∴x+3x+5x=180，解得：x=20，∴∠C=5×20°=100°，∴△ABC是钝角三角形．故选：C．【名师点拨】本题考查三角形内角和定理，关键是利用方程思想列出三个角的关系式．变式2-3．（2024·石家庄市期末）下面给出的四个三角形都有一部分被遮挡，其中不能确定三角形类型的是（）A．B．C．D．【答案】A【提示】依据三角形按角分类的方法一一推断即可．【详解】视察图象可知：选项B，D的三角形是钝角三角形，选项C中的三角形是锐角三角形，选项A中的三角形无法判定三角形的类型．故选A．【名师点拨】本题考查了三角形的分类，解题的关键是娴熟驾驭基本学问，属于中考常考题型．考查题型三构成三角形的条件典例3．（2024·宜兴市期末）下列各组线段不能组成三角形的是 ( )A．4cm、4cm、5cm B．4cm、6cm、11cmC．4cm、5cm、6cm D．5cm、12cm、13cm【答案】B【提示】依据三角形的随意两边之和大于第三边对各选项提示推断后利用解除法求解.【详解】A 、4485+=>，∴445cm cm cm 、、能组成三角形，故本选项错误；B 、461011+=<，∴4611cm cm cm 、、不能组成三角形，故本选项正确；C 、5496+=>，∴456cm cm cm 、、能组成三角形，故本选项错误；D 、5121713+=>，∴51213cm cm cm 、、能组成三角形，故本选项错误.故选：B .【名师点拨】本题考查了三角形的三边关系，是基础题，熟记三边关系是解题的关键.变式3-1．（2024·太仓市）等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为（ ）A ．12B ．15C ．12或15D ．18【答案】B【解析】试题提示：依据题意，要分状况探讨：①、3是腰；②、3是底．必需符合三角形三边的关系，随意两边之和大于第三边．解：①若3是腰，则另一腰也是3，底是6，但是3+3=6，∴不构成三角形，舍去．②若3是底，则腰是6，6．3+6＞6，符合条件．成立．∴C=3+6+6=15．故选B ．变式3-2．（2024·兰州市期末）等腰三角形的一边长为4，另一边长为9，则这个三角形的周长为( )A ．22B ．17C ．13D ．17或22【答案】A【提示】分4是腰长和底边两种状况探讨求解即可．【详解】解：4是腰长时，三角形的三边分别为4、4、9，∵4+4=8＜9，∴不能组成三角形，4是底边时，三角形的三边分别为4、9、9，能组成三角形，周长=4+9+9=22，综上所述，该等腰三角形的周长为22．故选A ．【名师点拨】本题主要考查了三角形三边关系，难点在于分状况探讨并利用三角形的三边关系推断是否能组成三角形．cm cm长的两根木棒首尾相接成一个三角形的变式3-3．（2024·哈尔滨市期中）下列长度的四根木棒中，能与49，是（）A．4cm B．5cm C．9cm D．13cm【答案】C【提示】依据三角形三边关系：三角形随意两边之和大于第三边，逐一推断选项，即可.【详解】∵4+4<9，cm cm长的木棒首尾相接，不能组成三角形，∴4cm，49，∴A错误；∵5+4=9，cm cm长的木棒首尾相接，不能组成三角形，∴5cm，49，∴B错误；∵9+4>9，cm cm长的木棒能组成三角形，∴9cm，49，∴C正确；∵4+9=13，cm cm长的木棒，不能组成三角形，∴13cm，49，∴D错误；故选C.【名师点拨】本题主要考查三角形的三边关系，驾驭“三角形随意两边之和大于第三边”，是解题的关键.m-=，且m，n恰好是等腰△ABC的两条边的边长，变式3-4．（2024·濮阳市期末）若实数m，n满意20则△ABC的周长是( )A．12 B．8 C．10 D．10或8【答案】C【提示】依据非负数的性质求出,m n的值，依据等腰三角形的性质求解即可.m-=【详解】20m n∴==2,4,当三角形的腰长为2时，224+=，构不成三角形；++=.当三角形的腰长为4时，三角形的周长为：44210故答案选：C.【名师点拨】考查非负数的性质以及等腰三角形的性质，驾驭三角形的三边关系是解题的关键.考查题型四三角形第三边的取值范围典例4．（2024·三明市期末）已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）A．1 B．2 C．8 D．11【答案】C【提示】依据三角形两边之和大于第三边，两边之差小于第三边可确定出第三边的范围，据此依据选项即可推断. 【详解】设第三边长为x，则有7-3<x<7+3，即4<x<10，视察只有C选项符合，故选 C.【名师点拨】本题考查了三角形三边的关系，娴熟驾驭三角形三边之间的关系是解题的关键.a的三条线段能组成一个三角形，则a的值可以是（）变式4-1．（2024·龙岩市期中）若长度分别为,3,5A．1 B．2 C．3 D．8【答案】C【提示】依据三角形三边关系可得5﹣3＜a＜5+3，解不等式即可求解．【详解】由三角形三边关系定理得：5﹣3＜a＜5+3，即2＜a＜8，由此可得，符合条件的只有选项C，故选C．【名师点拨】本题考查了三角形三边关系，能依据三角形的三边关系定理得出5﹣3＜a＜5+3是解此题的关键，留意：三角形的两边之和大于第三边，三角形的两边之差小于第三边．变式4-2．（2024·齐齐哈尔市期末）已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为A．2 B．3 C．5 D．13【答案】B【提示】依据“三角形两边之和大于第三边, 两边之差小于第三边”，可得x的取值范围，一一推断可得答案. 【详解】解：依据“三角形两边之和大于第三边, 两边之差小于第三边”可得:13-2<x<13+2,即11<x<15,因为取正整数,故x的取值为12、13、14,即这样的三角形共有3个.故本题正确答案为B.【名师点拨】本题主要考查构成三角形的三边的关系.变式4-3．（2024·广州市期中）一个三角形的两边长为3和8，第三边长为奇数，则第三边长为（）A ．5或7B ．7或9C ．7D ．9【答案】B 【详解】依据三角形三边关系可得：5＜第三边＜11，依据第三边长为奇数，则第三边长为7或9．故选B.考查题型五 三角形三边关系的应用典例5．（2024·德州市期末）已知三角形的两边分别为1和4，第三边长为整数 ，则该三角形的周长为（ ）A ．7B ．8C ．9D ．10【答案】C【提示】依据三角形的三边关系“第三边大于两边之差，而小于两边之和”，求得第三边的取值范围；再依据第三边是整数，从而求得周长．【详解】设第三边为x ，依据三角形的三边关系，得：4-1＜x ＜4+1，即3＜x ＜5，∵x 为整数，∴x 的值为4．三角形的周长为1+4+4=9．故选C.【名师点拨】此题考查了三角形的三边关系．关键是正确确定第三边的取值范围．变式5-1．（2024·汕头市期中）已知a b c 、、是ABC ∆的三边长，化简a b c b a c +----的值是（ ）A ．2c -B ．22b c -C ．22a c -D ．22a b - 【答案】B【提示】依据三角形的三边关系“随意两边之和大于第三边，随意两边之差小于第三边”，得到a+b-c ＞0，b -a -c ＜0，再依据肯定值的性质进行化简计算.【详解】依据三角形的三边关系，得a+b-c>0，b -a -c <0.∴原式= a+b-c −(a +c −b)= 22b c -.故选择B 项.【名师点拨】本题考查三角形三边关系和肯定值，解题的关键是娴熟驾驭三角形三边关系.变式5-2．（2024·保定市期末）如图，为估计池塘岸边A ，B 的距离，小明在池塘的一侧选取一点O ，测得OA=15米，OB=10米，A ，B 间的距离可能是（ ）A．30米B．25米C．20米D．5米【答案】C【解析】设A，B间的距离为x．依据三角形的三边关系定理，得：15-10＜x＜15+10，解得：5＜x＜25，所以，A，B之间的距离可能是20m．故选C．变式5-3．（2024·滨州市期末）若（a﹣3）2+|b﹣6|＝0，则以a、b为边长的等腰三角形的周长为（）A．12 B．15 C．12或15 D．18【答案】B【提示】依据非负数的和为零，可得每个非负数同时为零，可得a、b的值，依据等腰三角形的判定，可得三角形的腰，依据三角形的周长公式，可得答案．【详解】由（a﹣3）2+|b﹣6|＝0，得a﹣3＝0，b﹣6＝0．则以a、b为边长的等腰三角形的腰长为6，底边长为3，周长为6+6+3＝15，故选B．【名师点拨】本题考查了非负数的性质，利用非负数的和为零得出每个非负数同时为零是解题关键．变式5-4．（2024·南开区期末）假如一等腰三角形的周长为27，且两边的差为12，则这个等腰三角形的腰长为（）A．13 B．5 C．5或13 D．1【答案】A【详解】设等腰三角形的腰长为x，则底边长为x﹣12或x+12，当底边长为x﹣12时，依据题意，2x+x﹣12=27，解得x=13，∴腰长为13；当底边长为x+12时，依据题意，2x+x+12=27，解得x=5，因为5+5＜17，所以构不成三角形，故这个等腰三角形的腰的长为13，故选A．考查题型六三角形的稳定性典例6．（2024·路北区期中）下列图形具有稳定性的是（）A．B．C．D．【答案】A【提示】依据三角形具有稳定性，四边形具有不稳定性进行推断即可得．【详解】A、具有稳定性，符合题意；B、不具有稳定性，故不符合题意；C、不具有稳定性，故不符合题意；D、不具有稳定性，故不符合题意，故选A．【名师点拨】本题考查了三角形的稳定性和四边形的不稳定性，正确驾驭三角形的性质是解题关键．变式6-1．（2024·乌鲁木齐市期末）为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，这样做的道理是（）A．两点之间，线段最短B．垂线段最短C．三角形具有稳定性D．两直线平行，内错角相等【答案】C【解析】试题提示：三角形具有稳定性，其它多边形不具有稳定性，把多边形分割成三角形则多边形的形态就不会变更．解：这样做的道理是三角形具有稳定性．故选：C．变式6-2．（2024·安阳市期末）王师傅用4根木条钉成一个四边形木架，如图．要使这个木架不变形，他至少还要再钉上几根木条？（）．A．0根B．1根C．2根D．3根【答案】B【解析】三角形具有稳定性，连接一条对角线，即可得到两个三角形，故选B变式6-3．（2024·济南市期末）如图，窗户打开后，用窗钩AB可将其固定，其所运用的几何原理是（）A．三角形的稳定性B．垂线段最短C．两点确定一条直线D．两点之间，线段最短【答案】A【提示】依据点A、B、O组成一个三角形，利用三角形的稳定性解答．【详解】解：一扇窗户打开后，用窗钩将其固定，正好形成三角形的形态，所以，主要运用的几何原理是三角形的稳定性．故答案选A.【名师点拨】本题考查三角形稳定性的实际应用．三角形的稳定性在实际生活中有着广泛的应用．变式6-4．（2024·深圳市期末）如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的依据是( )A．两点之间的线段最短B．长方形的四个角都是直角C．三角形有稳定性D．长方形是轴对称图形【答案】C【详解】用木条EF固定长方形门框ABCD，使其不变形的依据是三角形具有稳定性．故选：C．【名师点拨】本题考查了三角形具有稳定性在实际生活中的应用，是基础题．变式6-5．（2024·抚顺市期中）人字梯中间一般会设计一“拉杆”，这样做的道理是（）A．两点之间，线段最短B．垂线段最短C．两直线平行，内错角相等D．三角形具有稳定性【答案】D【提示】依据三角形的稳定性解答即可．【详解】解：人字梯中间一般会设计一“拉杆”，是为了形成三角形，利用三角形具有稳定性来增加其稳定性，故选：D．【名师点拨】此题考查三角形的性质，关键是依据三角形的稳定性解答．。

专题01 三角形章末重难点题型汇编【举一反三】【考点1 三角形的稳定性】【方法点拨】理解稳定性：“只要三角形三条边的长度固定，这个三角形的形状和大小也就完全确定，三角形的这种性质叫做“三角形的稳定性”.这就是说，三角形的稳定性不是“拉得动、拉不动”的问题，其实质应是“三角形边长确定，其形状和大小就确定了”.【例1】（2019春•永泰县期中）如图小方做了一个方形框架，发现很容易变形，请你帮他选择一个最好的加固方案（）A．B．C．D．【思路点拨】根据三角形的稳定性进行解答．【答案】解：根据三角形的稳定性可得C是最好的加固方案．故选：C．【方法总结】此题主要考查了三角形的稳定性，当三角形三边的长度确定后，三角形的形状和大小就能唯一确定下来，故三角形具有稳定性．【变式1-1】（2019秋•西陵区校级期中）将几根木条用钉子钉成如图的模型，其中在同一平面内不具有稳定性的是（）A．B．C．D．【思路点拨】根据三角形具有稳定性进行解答．【答案】解：根据三角形具有稳定性可得A、B、D都具有稳定性，C未曾构成三角形，因此不稳定，故选：C．【方法总结】此题主要考查了三角形的稳定性，是需要识记的内容．【变式1-2】（2018秋•桐梓县校级期中）图中的五角星是用螺栓将两端打有孔的5根木条连接而构成的，它的形状不稳定．如果用在图中木条交叉点打孔加装螺栓的办法来达到使其形状稳定的目的，且所加螺栓尽可能少，那么需要添加螺栓（）A．1个B．2个C．3个D．4个【思路点拨】用木条交叉点打孔加装螺栓的办法来达到使其形状稳定的目的，可用三角形的稳定性解释．【答案】解：如图：A点加上螺栓后，根据三角形的稳定性，原不稳定的五角星中具有了稳定的各边．故选：A．【方法总结】本题考查三角形稳定性的实际应用．三角形的稳定性在实际生活中有着广泛的应用，如钢架桥、房屋架梁等，因此要使一些图形具有稳定的结构，往往通过连接辅助线转化为三角形而获得．【变式1-3】（2019秋•安陆市期中）我们都有这样的生活经验，要想使多边形（三角形除外）木架不变形至少再钉上若干根木条，如图所示，四边形至少再钉上一根；五边形至少再钉上两根；六边形至少再钉上三根；…，按照此规律，十二边形至少再钉上（）A．11根B．10根C．9根D．8根【思路点拨】根据分成三角形个数与边数的关系，需要的木条数等于过多边形的一个顶点的对角线的条数，由此得出答案即可．【答案】解：过n边形的一个顶点可以作（n﹣3）条对角线，把多边形分成（n﹣2）个三角形，所以，要使一个十二边形木架不变形，至少需要12﹣3＝9根木条固定．故选：C．【方法总结】此题考查了图形的变化规律，考虑把多边形分成三角形是解题的关键．【考点2 判断三角形的高】【方法点拨】三角形任意一边上的高必须满足：(1)过该边所对的顶点；(2)垂足必须在该边或在该边的延长线上．【例2】（2019春•海州区期中）如图，△ABC中的边BC上的高是（）A．AF B．DB C．CF D．BE【思路点拨】根据三角形高的定义即可解答．【答案】解：△ABC中的边BC上的高是AF，故选：A．【方法总结】本题考查了三角形的角平分线、中线和高：过三角形的一个顶点引对边的垂线，这个点与垂足的连线段叫三角形的高．【变式2-1】（2019春•大丰区期中）要求画△ABC的边AB上的高，下列画法中，正确的是（）A．B．C．D．【思路点拨】作哪一条边上的高，即从所对的顶点向这条边或者条边的延长线作垂线即可．【答案】解：过点C作AB边的垂线，正确的是C．故选：C．【方法总结】本题是一道作图题，考查了三角形的角平分线、高、中线，是基础知识要熟练掌握．【变式2-2】（2019春•苏州期中）如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，那么这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．不能确定【思路点拨】根据直角三角形的性质即可直接得出结论．【答案】解：∵直角三角形的三条高的交点恰好是三角形的一个顶点，∴若三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是直角三角形；故选：B．【方法总结】本题考查的是三角形高的性质，熟知直角三角形的三条高的交点恰好是三角形的一个顶点是解答此题的关键．【变式2-3】（2018春•南岗区校级期中）如图，BD是△ABC的高，EF∥AC，EF交BD于G，下列说法正确的有（）①BG是△EBF的高；②CD是△BGC的高；③DG是△AGC的高；④AD是△ABG的高．A．1个B．2个C．3个D．4个【思路点拨】根据三角形的高的定义以及平行线的性质，即可解答．【答案】解：∵BD是△ABC的高，∴∠ADB＝∠CDB＝90°，∵EF∥AC，∴∠EGB＝∠ADB＝90°，∴BG是△EBF的高，①正确；∵∠CDB＝90°，∴CD是△BGC的高，②正确；∵∠ADG＝∠CDG＝90°，∴DG是△AGC的高，③正确；∵∠ADB＝90°，∴AD是△ABG的高，④正确．故选：D．【方法总结】本题考查了三角形的高的定义：从三角形的一个顶点向它的对边作垂线，垂足与顶点之间的线段叫做三角形的高，理解定义是关键．也考查了平行线的性质．【考点3 三角形边角关系的应用】【方法点拨】掌握三角形两边的和大于第三边，三角形两边的差小于第三边是解题关键.【例3】（2019春•福州期末）用一根长为10cm的绳子围成一个三角形，若所围成的三角形中一边的长为2cm，且另外两边长的值均为整数，则这样的围法有（）A．1种B．2种C．3种D．4种【思路点拨】根据三角形的两边之和大于第三边，根据周长是10厘米，可知最长的边要小于5厘米，进而得出三条边的情况．【答案】解：∵三角形中一边的长为2cm，且另外两边长的值均为整数，∴三条边分别是2cm、4cm、4cm．故选：A．【方法总结】本题主要考查了学生根据三角形三条边之间的关系解决问题的能力．在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．【变式3-1】（2019秋•银海区期末）a，b，c为△ABC的三边，化简|a+b+c|﹣|a﹣b﹣c|﹣|a﹣b+c|﹣|a+b﹣c|，结果是（）A．0B．2a+2b+2c C．4a D．2b﹣2c【思路点拨】首先根据：三角形两边之和大于第三边，去掉绝对值号，然后根据整式的加减法的运算方法，求出结果是多少即可．【答案】解：|a+b+c|﹣|a﹣b﹣c|﹣|a﹣b+c|﹣|a+b﹣c|＝（a+b+c）﹣（b+c﹣a）﹣（a﹣b+c）﹣（a+b﹣c）＝a+b+c﹣b﹣c+a﹣a+b﹣c﹣a﹣b+c＝0故选：A．【方法总结】此题主要考查了三角形的三边的关系，以及整式加减法的运算方法，要熟练掌握，解答此题的关键是要明确：三角形两边之和大于第三边．【变式3-2】（2019春•秦淮区期末）已知一个三角形中两条边的长分别是a、b，且a＞b，那么这个三角形的周长L的取值范围是（）A．3b＜L＜3a B．2a＜L＜2（a+b）C．a+2b＜L＜2a+b D．3a﹣b＜L＜3a+b【思路点拨】先根据三角形的三边关系求得第三边的取值范围，再确定这个三角形的周长l的取值范围即可．【答案】解：设第三边长x．根据三角形的三边关系，得a﹣b＜x＜a+b．∴这个三角形的周长L的取值范围是a﹣b+a+b＜L＜a+b+a+b，即2a＜L＜2a+2b．故选：B．【方法总结】考查三角形的三边关系，要注意三角形形成的条件：任意两边之和大于第三边，任意两边之差小于第三边．【变式3-3】（2019•孝感模拟）如图，用四个螺丝将四条不可弯曲的木条围成一个木框（形状不限），不计螺丝大小，其中相邻两螺丝的距离依次为3、4、5、7，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任意两个螺丝间的距离的最大值为（）A．6B．7C．8D．9【思路点拨】两个螺丝的距离最大，则此时这个木框的形状为三角形，可根据三条木棍的长来判断有几种三角形的组合，然后分别找出这些三角形的最长边即可．【答案】解：已知4条木棍的四边长为3、4、5、7；①选3+4、5、7作为三角形，则三边长为7、5、7，能构成三角形，此时两个螺丝间的最长距离为7；②选5+4、7、3作为三角形，则三边长为9、7、3，能构成三角形，此时两个螺丝间的最大距离为9；③选5+7、3、4作为三角形，则三边长为12、4、3；4+3＜12，不能构成三角形，此种情况不成立；④选7+3、5、4作为三角形，则三边长为10、5、4；而5+4＜10，不能构成三角形，此种情况不成立；综上所述，任两螺丝的距离之最大值为9．故选：D．【方法总结】本题考查的是三角形的三边关系定理，能够正确的判断出调整角度后三角形木框的组合方法是解答的关键．【考点4 多边形的相关概念】【方法点拨】了解凸多边形的定义，掌握多边形对角线与所分成三角形个数之间的关系：从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形.【例4】（2019春•道里区期末）下列选项中的图形，不是凸多边形的是（）A．B．C．D．【思路点拨】根据凸多边形的概念，如果多边形的边都在任何一条边所在的直线的同旁，该多边形即是凸多边形．否则即是凹多边形．【答案】解：图形不是凸多边形的是A．故选：A．【方法总结】本题主要考查了凸多边形的定义，正确理解凸多边形的定义是解决此类问题的关键．【变式4-1】（2019秋•德州校级月考）要使一个五边形具有稳定性，则需至少添加（）条对角线．A．1B．2C．3D．4【思路点拨】根据三角形具有稳定性，过一个顶点作出所有对角线即可得解．【答案】解：如图需至少添加2条对角线．故选：B．【方法总结】本题考查了三角形具有稳定性的应用，作出图形更形象直观．【变式4-2】（2018秋•南城县期末）从一个七边形的某个顶点出发，分别连接这个点与其余各顶点，可以把一个七边形分割成（）个三角形．A．6B．5C．8D．7【思路点拨】从n边形的一个顶点出发，连接这个点与其余各顶点，可以把一个四边形分割成（n﹣2）个三角形．【答案】解：从一个七边形的某个顶点出发，分别连接这个点与其余各顶点，可以把一个七边形分割成7﹣2＝5个三角形．故选：B．【方法总结】本题考查的知识点为：从n边形的一个顶点出发，可把n边形分成（n﹣2）个三角形．【变式4-3】（2018秋•绵阳期中）一个多边形截去一角后，变成一个八边形则这个多边形原来的边数是（）A．8或9B．7或8C．7或8或9D．8或9或10【思路点拨】根据截去一个角后边数增加1，不变，减少1讨论得解．【答案】解：∵截去一个角后边数可以增加1，不变，减少1，∴原多边形的边数是7或8或9．故选：C．【方法总结】本题考查了多边形，关键是理解多边形截去一个角后边数有增加1，不变，减少1三种情况．【考点5 多边形内角和与外角和的应用】【方法点拨】（1）掌握多边形内角和计算公式：(n-2) ×180 °(n ≥3的整数），多边形的外角和等于360°特别注意：与边数无关.【例5】（2019春•吴江区期中）一个多边形的每个内角都相等，并且它的一个外角与一个内角的比为1：3，则这个多边形为（）A．三角形B．四边形C．六边形D．八边形【思路点拨】此题要结合多边形的内角与外角的关系来寻求等量关系，构建方程求出每个外角．多边形外角和是固定的360°．【答案】解：设这个多边形的边数为n，依题意得（n﹣2）×180°＝3×360°，解得n＝8，∴这个多边形为八边形，故选：D．【方法总结】此题考查多边形的内角与外角的关系、方程的思想．关键是记住多边形一个内角与外角互补和外角和的特征．【变式5-1】（2018秋•桐梓县校级期中）如图，小明从A点出发，沿直线前进12米后向左转36°，再沿直线前进12米，又向左转36°…照这样走下去，他第一次回到出发地A点时，一共走了（）米．A．100B．120C．140D．60【思路点拨】根据多边形的外角和为360°，由题意得到小明运动的轨迹为正10边形的周长，求出即可．【答案】解：由题意得：360°÷36°＝10，则他第一次回到出发地A点时，一共走了12×10＝120（米）．故选：B．【方法总结】此题考查了多边形的内角与外角，熟练掌握多边形的外角和定理是解本题的关键．【变式5-2】（2019春•江都区期中）如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，则∠1+∠2+∠3等于（）A．180°B．90°C．210°D．270°【思路点拨】根据两直线平行，同旁内角互补得到以点B、点C为顶点的五边形的两个外角的度数之和等于180°，再根据多边形的外角和定理列式计算即可得解．【答案】解：延长AB，DC，∵AB∥CD，∴∠4+∠5＝180°，根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5＝360°，∴∠1+∠2+∠3＝360°﹣180°＝180°．故选：A．【方法总结】本题考查了平行线的性质，多边形的外角和定理，是基础题，理清求解思路是解题的关键．【变式5-3】（2019春•江阴市期中）如图，在六边形ABCDEF中，∠A+∠B+∠E+∠F＝α，CP、DP分别平分∠BCD、∠CDE，则∠P的度数是（）A．α﹣180°B．180°﹣αC．αD．360°﹣α【思路点拨】由多边形内角和定理求出∠A+∠B+∠E+∠F+∠CDE+∠BCD＝720°①，由角平分线定义得出∠BCP＝∠DCP，∠CDP＝∠PDE，根据三角形内角和定理得出∠P+∠PCD+∠PDE＝180°，得出2∠P+∠BCD+∠CDE＝360°②，由和②即可求出结果．【答案】解：在六边形ABCDEF中，∠A+∠B+∠E+∠F+∠CDE+∠BCD＝（6﹣2）×180°＝720°①，∵CP、DP分别平分∠BCD、∠CDE，∴∠BCP＝∠DCP，∠CDP＝∠PDE，∵∠P+∠PCD+∠PDE＝180°，∴2（∠P+∠PCD+∠PDE）＝360°，即2∠P+∠BCD+∠CDE＝360°②，①﹣②得：∠A+∠B+∠E+∠F﹣2∠P＝360°，即α﹣2∠P＝360°，∴∠P＝α﹣180°；故选：A．【方法总结】本题考查了多边形内角和定理、角平分线定义以及三角形内角和定理；熟记多边形内角和定理和三角形内角和定理是解题关键．【考点6 三角形内角和定理的应用】【方法点拨】三角形内角和等于180°.【例6】（2019春•石景山区期末）如图，BD平分∠ABC．∠ABD＝∠ADB．（1）求证：AD∥BC；（2）若BD⊥CD，∠BAD＝α，求∠DCB的度数（用含α的代数式表示）．【思路点拨】（1）想办法证明∠ADB＝∠DBC即可．（2）利用平行线的性质，三角形的内角和定理即可解决问题．【答案】（1）证明：∵BD平分∠ABC，∴∠ABD＝∠CBD∵∠ABD＝∠ADB，∴∠ADB＝∠DBC，∴AD∥BC．（2）解：∵AD∥BC，且∠BAD＝α，∴∠ABC＝180°﹣α，∴∠DBC＝∠ABC＝90°﹣α，∵BD⊥CD，∴∠BDC＝90°∴∠C＝90°﹣（90°﹣α）＝α．【方法总结】本题考查三角形内角和定理，角平分线的定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．【变式6-1】（2018秋•包河区期末）如图，△ABC中，∠ACB＞90°，AE平分∠BAC，AD⊥BC交BC的延长线于点D．（1）若∠B＝30°，∠ACB＝100°，求∠EAD的度数；（2）若∠B＝α，∠ACB＝β，试用含α、β的式子表示∠EAD，则∠EAD＝．（直接写出结论即可）【思路点拨】（1）根据垂直的定义得到∠D＝90°，根据邻补角的定义得到∠ACD＝180°﹣100°＝80°，根据三角形的内角和得到∠BAC＝50°，根据角平分线的定义得到∠CAE＝∠BAC＝25°，于是得到结论；（2）根据垂直的定义得到∠D＝90°，得到∠ACD＝180°﹣β，求得∠BAC＝90°﹣α﹣（β﹣90°）＝180°﹣α﹣β，根据角平分线的定义得到∠CAE＝∠BAC＝90°﹣（α+β），根据角的和差即可得到结论．【答案】解：（1）∵AD⊥BC，∴∠D＝90°，∵∠ACB＝100°，∴∠ACD＝180°﹣100°＝80°，∴∠CAD＝90°﹣80°＝10°，∵∠B＝30°，∴∠BAD＝90°﹣30°＝60°，∴∠BAC＝50°，∵AE平分∠BAC，∴∠CAE＝∠BAC＝25°，∴∠EAD＝∠CAE+∠CAD＝35°；（2）∵AD⊥BC，∴∠D＝90°，∵∠ACB＝β，∴∠ACD＝180°﹣β，∴∠CAD＝90°﹣∠ACD＝β﹣90°，∵∠B＝α，∴∠BAD＝90°﹣α，∴∠BAC＝90°﹣α﹣（β﹣90°）＝180°﹣α﹣β，∵AE平分∠BAC，∴∠CAE＝∠BAC＝90°﹣（α+β），∴∠EAD＝∠CAE+∠CAD＝90°﹣（α+β）+β﹣90°＝β﹣α．故答案为：β﹣α．【方法总结】本题考查了三角形的内角和，角平分线的定义，正确的识别图形是解题的关键．【变式6-2】（2019春•福州期末）如图，在△ABC中，∠ABC的平分线交AC于点D．作∠BDE＝∠ABD 交AB于点E．（1）求证：ED∥BC；（2）点M为射线AC上一点（不与点A重合）连接BM，∠ABM的平分线交射线ED于点N．若∠MBC ＝∠NBC，∠BED＝105°，求∠ENB的度数．【思路点拨】（1）利用角平分线的定义，进行等量代换，得出内错角相等，从而两直线平行；（2）分两种情况分别进行解答，根据每一种情况画出相应的图形，依据图形中，角之间的相互关系，转化到一个三角形中，利用三角形的内角和定理，设未知数，列方程求解即可．【答案】解：（1）∵BD平分∠ABC，∴∠ABD＝∠DBC，又∵∠BDE＝∠ABD，∴∠BDE＝∠DBC，∴ED∥BC；（2）∵BN平分∠ABM，∴∠ABN＝∠NBM，①当点M在线段AC上时，如图1所示：∵DE∥BC，∴∠ENB＝∠NBC，∵∠MBC＝∠NBC，∴∠NBM＝∠MBC＝∠NBC，设∠MBC＝x°，则∠EBN＝∠NBM＝x°，∠ENB＝∠NBC＝2x°，在△ENB中，由内角和定理得：x+2x+105°＝180°，解得：x＝25，∴∠ENB＝2x＝50°，②当点M在AC的延长线上时，如图2所示：∵DE∥BC，∴∠ENB＝∠NBC，∵∠MBC＝∠NBC，∴∠NBM＝3∠MBC，设∠MBC＝x°，则∠EBN＝∠NBM＝3x°，∠ENB＝∠NBC＝2x°，在△EMB中，由内角和定理得：3x+2x+105°＝180°，解得：x＝15，∴∠ENB＝2x＝30°，答：∠ENB的度数为50°或30°．【方法总结】综合考查角平分线的定义、平行线的性质、三角形的内角和定理等知识，分类讨论，分别画出相应的图形，利用等量代换和图形中角之间的关系布列方程是解决问题常用的方法．【变式6-3】（2018秋•丰城市期末）已知将一块直角三角板DEF放置在△ABC上，使得该三角板的两条直角边DE，DF恰好分别经过点B、C．（1）∠DBC+∠DCB＝度；（2）过点A作直线直线MN∥DE，若∠ACD＝20°，试求∠CAM的大小．【思路点拨】（1）在△DBC中，根据三角形内角和定理得∠DBC+∠DCB+∠D＝180°，然后把∠D＝90°代入计算即可；（2）在Rt△ABC中，根据三角形内角和定理得∠ABC+∠ACB+∠A＝180°，即，∴∠ABD+∠BAC＝90°﹣∠ACD＝70°，整体代入即可得出结论．【答案】解：（1）在△DBC中，∵∠DBC+∠DCB+∠D＝180°，而∠D＝90°，∴∠DBC+∠DCB＝90°；故答案为90；（2）在△ABC中，∵∠ABC+∠ACB+∠A＝180°，即∠ABD+∠DBC+∠DCB+∠ACD+∠BAC＝180°，而∠DBC+∠DCB＝90°，∴∠ABD+∠ACD＝90°﹣∠BAC，∴∠ABD+∠BAC＝90°﹣∠ACD＝70°．又∵MN∥DE，∴∠ABD＝∠BAN．而∠BAN+∠BAC+∠CAM＝180°，∴∠ABD+∠BAC+∠CAM＝180°，∴∠CAM＝180°﹣（∠ABD+∠BAC）＝110°．【方法总结】此题主要考查了三角形内角和定理，平行线的性质，解本题的关键是求出∠ABD+∠BAC＝70°．【考点7 三角形外角性质的应用】【方法点拨】三角形的外角等于与它不相邻的两个内角的和.【例7】（2019春•宝应县期中）如图，在Rt△ABC中，∠ACB＝90°，∠A＝34°，△ABC的外角∠CBD 的平分线BE交AC的延长线于点E．（1）求∠CBE的度数；（2）过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．【思路点拨】（1）根据三角形的外角的性质求出∠CBD，根据角平分线的定义计算，得到答案；（2）根据平行线的性质解答即可．【答案】解：（1）∵∠ACB＝90°，∠A＝34°，∴∠CBD＝124°，∵BE是∠CBD的平分线，∴∠CBE＝∠CBD＝62°；（2）∵∠ECB＝90°，∠CBE＝62°，∴∠CEB＝28°，∵DF∥BE，∴∠F＝∠CEB＝28°．【方法总结】本题考查的是三角形的外角的性质、平行线的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．【变式7-17】（2018春•岱岳区期中）如图，△ABC中，∠A＝30°，∠B＝62°，CE平分∠ACB，CD⊥AB 于D，DF⊥CE于F，求∠ACE和∠CDF的度数．【思路点拨】根据三角形内角和定理求出∠ACB，根据角平分线的定义求出∠ACE；根据垂直的定义、三角形内角和定理求出∠CDF．【答案】解：∵∠A＝30°，∠B＝62°，∴∠ACB＝180°﹣30°﹣62°＝88°；∵CE平分∠ACB，∴∠ACE＝∠BCE＝∠ACB＝44°，∵CD⊥AB，∴∠CDB＝90°，∴∠BCD＝90°﹣∠B＝28°，∴∠ECD＝∠ECB﹣∠BCD＝16°，∵DF⊥CE，∴∠CDF＝90°﹣∠DCF＝74°．【方法总结】本题考查的是三角形内角和定理、三角形的外角的性质以及角平分线的定义，掌握三角形内角和等于180°是解题的关键．【变式7-2】（2018春•商水县期末）如图，∠BAD＝∠CBE＝∠ACF，∠FDE＝64°，∠DEF＝43°，求△ABC各内角的度数．【思路点拨】根据三角形外角性质得到∠FDE＝∠BAD+∠ABD，而∠BAD＝∠CBE，则∠FDE＝∠BAD+∠CBE＝∠ABC＝64°；同理可得∠DEF＝∠ACB＝43°，然后根据三角形内角定理计算∠BAC＝180°﹣∠ABC﹣∠ACB即可．∠BAD＝∠CBE＝∠ACF，∠FDE＝48°，∠DEF＝64°，【答案】解：∵∠FDE＝∠BAD+∠ABD，∠BAD＝∠CBE∴∠FDE＝∠BAD+∠CBE＝∠ABC，∴∠ABC＝64°；同理∠DEF＝∠FCB+∠CBE＝∠FCB+∠ACF＝∠ACB，∴∠ACB＝43°；∴∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣64°﹣43°＝73°，∴△ABC各内角的度数分别为64°、43°、73°．【方法总结】本题考查了三角形的内角和定理：三角形的内角和为180°．也考查了三角形外角的性质，熟记：三角形的外角等于与它不相邻的两个内角之和是解题的关键．【变式7-3】（2019春•南开区校级月考）如图，在△ABC中，AD是高，∠DAC＝10°，AE是∠BAC外角的平分线，BF平分∠ABC交AE于点F，若∠ABC＝46°，求∠AFB的度数．【思路点拨】根据直角三角形的性质求出∠BAD的度数，得到∠BAC的度数，根据邻补角的性质求出∠CAM的度数，根据角平分线的定义求出∠MAE的度数，根据三角形的外角的性质计算即可．【答案】解：∵AD是高，∴∠ADB＝90°，∴∠BAD＝90°﹣∠ABC＝44°，又∠DAC＝10°，∴∠BAC＝54°，∴∠MAC＝126°，∵AE是∠BAC外角的平分线，∴∠MAE＝∠MAC＝63°，∵BF平分∠ABC，∴∠ABF＝∠ABC＝23°，∴∠AFB＝∠MAE﹣∠ABF＝40°．【方法总结】本题考查的是三角形的外角的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．【考点8 利用互余关系倒角】【方法点拨】直角三角形两锐角互余，通常利用这一结论进行倒角.【例8】（2019春•莲湖区期中）如图，在△ACB中，∠ACB＝90゜，CD⊥AB于D．（1）求证：∠ACD＝∠B；（2）若AF平分∠CAB分别交CD、BC于E、F，求证：∠CEF＝∠CFE．【思路点拨】（1）由于∠ACD与∠B都是∠BCD的余角，根据同角的余角相等即可得证；（2）根据直角三角形两锐角互余得出∠CF A＝90°﹣∠CAF，∠AED＝90°﹣∠DAE，再根据角平分线的定义得出∠CAF＝∠DAE，然后由对顶角相等的性质，等量代换即可证明∠CEF＝∠CFE．【答案】证明：（1）∵∠ACB＝90゜，CD⊥AB于D，∴∠ACD+∠BCD＝90°，∠B+∠BCD＝90°，∴∠ACD＝∠B；（2）在Rt△AFC中，∠CF A＝90°﹣∠CAF，同理在Rt△AED中，∠AED＝90°﹣∠DAE．又∵AF平分∠CAB，∴∠CAF＝∠DAE，∴∠AED＝∠CFE，又∵∠CEF＝∠AED，∴∠CEF＝∠CFE．【方法总结】本题考查了直角三角形的性质，三角形角平分线的定义，对顶角的性质，余角的性质，难度适中．【变式8-1】（2011春•越城区校级期中）如图，△ABC中，AD是BC边上的高线，BE是一条角平分线，它们相交于点P，已知∠EPD＝125°，求∠BAD的度数．【思路点拨】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CBE的度数，再根据角平分线的定义求出∠ABC的度数，然后利用直角三角形的两锐角互余列式计算即可得解．【答案】解：∵AD是BC边上的高线，∠EPD＝125°，∴∠CBE＝∠EPD﹣∠ADB＝125°﹣90°＝35°，∵BE是一条角平分线，∴∠ABD＝2∠CBE＝2×35°＝70°，在Rt△ABD中，∠BAD＝90°﹣∠ABD＝90°﹣70°＝20°．故答案为：20°．【方法总结】本题考查了直角三角形两锐角互余的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，准确识图，根据图形找出图中各角之间的关系是解题的关键．【变式8-2】在△ABC中，∠ACB＝90°，E是BC边上的一点，过C作CF⊥AE，垂足为F，过点B作BD ⊥BC，交CF的延长线于点D，若∠D＝65°，求∠EAC的度数．【思路点拨】根据直角三角形的两个锐角互余进行解答即可．【答案】解：在RT△DBC中，∠D＝65°，可得：∠DCB＝25°，在RT△ACE中，∠DCB＝25°，可得：∠ACF＝65°，在RT△ACF中，∠ACF＝65°，可得：∠EAC＝25°．【方法总结】此题考查直角三角形的性质，关键是根据直角三角形的两个锐角互余进行解答．【变式8-3】（1）如图①，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，∠ACD与∠B有什么关系？为什么？（2）如图②，在Rt△ABC中，∠C＝90°，D、E分别在AC，AB上，且∠ADE＝∠B，判断△ADE的形状是什么？为什么？（3）如图③，在Rt△ABC和Rt△DBE中，∠C＝90°，∠E＝90°，AB⊥BD，点C，B，E在同一直线上，∠A与∠D有什么关系？为什么？【思路点拨】（1）根据直角三角形的性质得出∠ACD+∠A＝∠B+∠DCB＝90°，再解答即可；（2）根据直角三角形的性质得出∠ADE+∠A＝∠A+∠B＝90°，再解答即可；（3）根据直角三角形的性质得出∠ABC+∠A＝∠ABC+∠DBE＝∠DBE+∠D＝90°，再解答即可．【答案】解：（1）∠ACD＝∠B，理由如下：∵在Rt△ABC中，∠ACB＝90°，CD⊥AB，∴∠ACD+∠A＝∠B+∠DCB＝90°，∴∠ACD＝∠B；（2）△ADE是直角三角形．∵在Rt△ABC中，∠C＝90°，D、E分别在AC，AB上，且∠ADE＝∠B，∠A为公共角，∴∠AED＝∠ACB＝90°，∴△ADE是直角三角新；（3）∠A+∠D＝90°．∵在Rt△ABC和Rt△DBE中，∠C＝90°，∠E＝90°，AB⊥BD，∴∠ABC+∠A＝∠ABC+∠DBE＝∠DBE+∠D＝90°，∴∠A+∠D＝90°．【方法总结】此题考查直角三角形的性质，关键是根据直角三角形的性质得出两锐角互余．。

专题01 等腰三角形三种压轴题型全攻略【基础知识点】性质：等腰三角形两个底角相等（简称：等边等角）；推论：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合（三线合一）判定：①有两边相等的三角形是等腰三角形；②有两个角相等的三角形是等腰三角形类型一、与等腰三角形有关最值问题例．如图，等腰Rt△ABC和等腰Rt△ADE的腰长分别为4和2，其中△BAC＝△DAE＝90°，点M为边DE的中点，若等腰Rt△ADE绕点A旋转，则点B到点M的距离最小值为__________．【答案】4【详解】解：连接AM，如下图所示：点M为边DE的中点，且Rt△ADE为等腰三角形，AM DE ∴⊥，12AM DE DM==，在Rt△ADE中，2AD=，由勾股定理可知：222AD AM DM=+，故有AM DM==当A、B、M三点不共线时，由三角形的三边关系可知：此时一定有BM AB AM>-，当三点共线且M点位于A、B之间时，此时有BM AB AM=-，∴4BM AB AM≥-=-4【变式训练1】如图，AD为等腰△ABC的高，其中△ACB=50°，AC=BC，E，F分别为线段AD，AC上的动点，且AE=CF，当BF＋CE取最小值时，△AFB的度数为（）A ．75°B ．90°C ．95°D ．105°【答案】C【详解】如图，作CH△BC ，且CH=BC ，连接HB ，交AC 于F ，此时△BCH 是等腰直角三角形且FH+BF 最小， △AC=BC ，△CH=AC ，△△HCB=90°，AD△BC ，△AD//CH ，△△ACB=50°，△△ACH=△CAE=40°，△△CFH△△AEC ，△FH=CE ，△FH+BF=CE+BF 最小， 此时△AFB=△ACB+△HBC=50°+45°=95°．故选：C ．【变式训练2】如图，C 是线段AB 上一动点，ACD △，CBE △都是等边三角形，M ，N 分别是CD ，BE 的中点，若6AB =，则线段MN 的最小值为______．【解析】连接CN ，△ACD △和BCE 为等边三角形，△AC CD =，BC CE =，60ACD BCE B ∠=∠=∠=︒ △18060DCE ACD BCE ∠=︒-∠-∠=︒， △N 是BE 的中点，△CN BE ⊥，302BCEECN BCN ∠∠=∠==∠︒，△90DCN DCE ECN ∠=∠+∠=∠︒， 设AC a =，△12CM a =△6AB =，△6BC a =- ，△cos )CN BCN BC a =∠⨯=-△MN==△当92a=时，MN的值最小为【变式训练3】在ABC中，90ACB∠=︒，60B∠=︒，4AB=，点D是直线BC上一动点，连接AD，在直线AD的右恻作等边ADE，连接CE，当线段CE的长度最小时，则线段CD 的长度为__________．【答案】3【详解】解：如图，以AC为边向左作等边三角形ACF，连接DF，△90ACB∠=︒，60B∠=︒，△30BAC∠=︒，△4AB=，△122BC AB==，△2223AC AB BC，△ACF是等边三角形，△CF AC AF===60FAC∠=︒，△ADE是等边三角形，△AD AE=，60DAE∠=︒，△FAC DAC DAE DAC∠-∠=∠-∠，△CAE FAD∠=∠，在ACE和AFD中，AC AFCAE FADAE AD=⎧⎪∠=∠⎨⎪=⎩，△()ACE AFD SAS≅，△CE DF=，当DF BC⊥时，DF的长是最小的，即CE的长最小，△906030FCD'∠=︒-︒=︒，Rt CFD'，△12D F CF'==3CD'=，△当线段CE的长度最小时，则线段CD的长度为3．故答案是：3．【变式训练4】如图所示，在△ABC中，AB＝AC＝BD、CE为△ABC的两条中线，且BD△CE于点N，M为线段BD上的动点，则AM+EM+BC的最小值为_____．【答案】【详解】解：连接DE ．△AB ＝AC ，△△ABC ＝△ACB ，△BE ＝12AB ，DC ＝12AC ，△BE ＝CD ，△BC ＝CB ，△△EBC △△DCB （SAS ），△△ECB ＝△DBC ，EC ＝BD ，△BN ＝CN ，△EN ＝DN ， △BD △EC ，△△EDM ，△BCN 都是等腰直角三角形， △AE ＝EB ，AD ＝DC ，△DE //BC ，DE ＝12BC ，△EN NC＝DE BC ＝12，△CN ＝2EN ，△BN ＝2EN ，△AE ＝BE ＝△EN ＝3，BN ＝6，△BN ＝CN ＝6，△BC ＝作点A 关于直线BD 的对称点H ，连接EH 交BD 于M ，连接AM ，此时AM +EM 的值最小，最小值＝线段EH 的长，过点H 作HT △AB 于T ，延长BD 交AH 于J ． △AJ//EN ，AE ＝EB ，△BN ＝NJ ＝6，△AJ ＝JH ＝2EN ＝6，△S △ABH ＝12•AB •HT ＝12•AH •BJ ，△HT △AT=△ET ＝AE ﹣AT ＝，△EH△AM +EM +BC 的最小值为．故答案为 类型二、等腰三形存在性问题例1．（几何图形种）如图，在矩形ABCD 中，=8AB ，=5AD ，点E 是线段CD 上的一点（不与点D ，C 重合），将△BCE 沿BE 折叠，使得点C 落在'C 处，当△'C CD 为等腰三角形时，CE 的长为___________．【答案】52或203【详解】解：△四边形ABCD 是矩形 △90C ∠=︒，8,5CD AB BC AD ====△将△BCE 沿BE 折叠，使得点C 落在'C 处，△BCE BC E '≌,90C E CE BC E BCE ''∴=∠=∠=︒，BC BC '=， 设CE x =，则8DE CD x x =-=- ①当C D C C ''=时，如图过点C '作,C F CD C G BC ''⊥⊥，则四边形C GCF '为矩形C D C C ''=，142C G DF FC CD '∴====，4EF x =-在Rt BC G '中，3BG =，532C F CG '∴==-= 在Rt C FE '中222C E C F EF ''=+，即()22224x x =+-，解得52x =，52CE ∴= ②当CC CD '=时，如图，设,CC BE '交于点O ，设OE y =,BC BC EC EC ''==，BE ∴垂直平分CC '，11422OC OC CC CD ''∴====3OB =在Rt OCE 中222OE OC CE +=，即2224y x += 在Rt BCE 中，222BE BC CE =+，即()2223+5y x =+ 联立()22222243+5y x y x ⎧+=⎪⎨=+⎪⎩，解得203163x y ⎧=⎪⎪⎨⎪=⎪⎩，203EC ∴= ③当DC DC '=时，如图，又BC BC '=，DB ∴垂直平分CC ',BC BC EC EC ''==，BE ∴垂直平分CC ' 此时,D E 重合，不符合题意 综上所述，203=EC 或52，故答案为：52或203例2．（坐标系中）在平面直角坐标系中，△ABC 的顶点A 、B 、C 的坐标分别为(0，3)、(4，0)、(0，0)，AB =5，点P 为x 轴上一点，若使得△ABP 为等腰三角形，那么点P 的坐标除点(78，0)外，还可以是_____．【答案】（1-，0）、（4-，0）、（9，0）【详解】设P （a ，0），△A （0，3），B （4，0），△PB =|a -4|，PA 2=a 2+9，AB =5，△△ABP 是等腰三角形，△①当PB =AB 时，△|a -4|=5，△a =-1或9，△P （-1，0）或（9，0）， ②当PA =PB 时，△（a -4）2=a 2+9，△a =78，P （78，0），③当PA =AB 时，△a 2+9=25，△a =4（舍）或a =-4，△P （-4，0）． 即：满足条件的点P 的坐标为（-1，0）、（-4，0）、（9，0）．【变式训练1】如图，正方形ABCO 的边OA 、OC 在坐标物上，点B 坐标为()3,3．将正方形ABCO 绕点A 顺时针旋转角度()090αα︒<<︒，得到正方形ADEF ，ED 交线段OC 于点G ，ED 的延长线交线段BC 于点P ．连AP 、AG ．（1）求证：AOG △ADG ；（2）求PAG ∠的度数；并判断线段OG 、PG 、BP 之间的数量关系，说明理由；（3）当12∠=∠时，求直线PE 的解析式（可能用到的数据：在Rt 中，30°内角对应的直角边等于斜边一半）．（4）在（3）的条件下，直线PE 上是否存在点M ，使以M 、A 、G 为顶点的三角形是等腰三角形？若存在，请直接写出M 点坐标；若不存在，请说明理由．【答案】（1）证明见解析；（2）45PAG ∠=︒，PG OG BP =+；（3）3y -；（4）(0,3)-或3)【详解】（1）证明：在Rt△AOG 和Rt△ADG 中，AO ADAG AG=⎧⎨=⎩，△AOG △ADG （HL ）．（2）在Rt △ADP 和Rt △ABP 中，AD ABAP AP =⎧⎨=⎩ΔΔADP ABP ∴≅（HL ），则DAP BAP ∠=∠；ΔΔAOG ADG ≅，1DAG ∴∠=∠； 又190DAG DAP BAP ∠+∠+∠+∠=︒，2290DAG DAP ∴∠+∠=︒，45DAG DAP ∴∠+∠=︒， PAG DAG DAP ∠=∠+∠，45∴∠=︒PAG ；ΔΔAOG ADG ≅，DG OG ∴=，ΔΔADP ABP ≅，DP BP ∴=，PG DG DP OG BP ∴=+=+． （3）解：ΔΔAOG ADG ≅，AGO AGD ∴∠=∠，又190AGO ∠+∠=︒，290PGC ∠+∠=︒，12∠=∠，AGO PGC ∴∠=∠， 又AGO AGD ∠=∠，AGO AGD PGC ∴∠=∠=∠，又180AGO AGD PGC ∠+∠+∠=︒，180360AGO AGD PGC ∴∠=∠=∠=︒÷=︒，12906030∴∠=∠=︒-︒=︒；△在Rt ΔAOG 中，2,3AG OG OA ==，222AG OG OA =+△222(2)3OG OG =+，解得OG =G ∴点坐标为0)，3CG = 在Rt ΔPCG 中，2PG CG =，222PG CG PC =+△222(2)CG CG PC =+，△3PC ==，P ∴点坐标为：(3，3)，设直线PE 的解析式为：y kx b =+，则033b k b +=+=⎪⎩，解得3k b ⎧=⎪⎨=-⎪⎩∴直线PE 的解析式为3y =-．（4）①如图1，当点M 在x 轴的负半轴上时，AG MG =，点A 坐标为(0,3)，∴点M 坐标为(0,3)-．②如图2，当点M 在EP 的延长线上时，由（3），可得60AGO PGC ∠=∠=︒，EP ∴与AB 的交点M ，满足AG MG =，A 点的横坐标是0，G M ∴的横坐标是3，∴点M 坐标为3)．综上，可得点M 坐标为(0,3)-或3)．【变式训练2】如图，一次函数y ＝﹣34x +3的图象与x 轴和y 轴分别交于点A 和点B ，将△AOB沿直线CD 对折，使点A 与点B 重合，直线CD 与x 轴交于点C ，与AB 交于点D ． （1）点A 的坐标为 ，点B 的坐标为 ； （2）求OC 的长度；（3）在x 轴上有一点P ，且△PAB 是等腰三角形，不需计算过程，直接写出点P 的坐标．【答案】（1）(4,0)，(0,3)；（2）78；（3）(4,0)-或(1,0)-或(9,0)或7(,0)8．【详解】解：（1）对应一次函数334y x =-+， 当0y =时，3304x -+=，解得4x =，即(4,0)A ，当0x =时，3y =，即(0,3)B ， 故答案为：(4,0)，(0,3)； （2）(4,0),(0,3)A B ，4,3OA OB ∴==，由折叠的性质得：AC BC =，设OC a =，则4BC AC OA OC a ==-=-，在Rt BOC 中，222OB OC BC +=，即2223(4)a a +=-，解得78a ，即OC 的长度为78；（3）设点P 的坐标为(,0)P m ，则4PA m =-，PB 5AB ，根据等腰三角形的定义，分以下三种情况：①当PB AB =时，PAB △5=，解得4m =±， 此时点P 的坐标为(4,0)P -或(4,0)P （与点A 重合，不符题意，舍去）； ②当PA AB =时，PAB △是等腰三角形，则45m -=，解得9m =或1m =-， 此时点P 的坐标为(1,0)P -或(9,0)P ；③当PA PB =时，PAB △是等腰三角形，则4m -=解得78m =，此时点P 的坐标为7(,0)8P ；综上，点P 的坐标为(4,0)-或(1,0)-或(9,0)或7(,0)8．【变式训练3】如图，在直角坐标系中，直线l ：y ＝43x +8与x 轴、y 轴分别交于点B ，点A ，直线x ＝﹣2交AB 于点C ，D 是直线x ＝﹣2上一动点，且在点C 的上方，设D （﹣2，m ） （1）求点O 到直线AB 的距离；（2）当四边形AOBD 的面积为38时，求点D 的坐标，此时在x 轴上有一点E （8，0），在y 轴上找一点M ，使|ME ﹣MD |最大，请求出|ME ﹣MD |的最大值以及M 点的坐标；（3）在（2）的条件下，将直线l ：y ＝43x +8左右平移，平移的距离为t （t ＞0时，往右平移；t ＜0时，往左平移）平移后直线上点A ，点B 的对应点分别为点A ′、点B ′，当△A ′B ′D 为等腰三角形时，求t 的值．【答案】（1）4.8；（2）当点M 的坐标为（0，403）时，|ME ﹣MD |取最大值（3）t的值为﹣2﹣、4、﹣或9．【详解】（1）当x ＝0时，y ＝43x +8＝8，△A （0，8），△OA ＝8；当y ＝43x +8＝0时，y ＝﹣6，△B （﹣6，0），△OB ＝6．△AB10，△点O 到直线AB 的距离＝OA OBOA⋅＝4.8． （2）当x ＝﹣2时，y ＝43x +8＝163，△C （﹣2，163），△S 四边形AOBD ＝S △ABD +S △AOB ＝12CD •（x A ﹣x B ）+12OA •OB ＝3m +8＝38，解得：m ＝10， △当四边形AOBD 的面积为38时，点D 的坐标为（﹣2，10）．在x 轴负半轴上找出点E 关于y 轴对称的点E ′（﹣8，0），连接E ′D 并延长交y 轴于点M ，连接DM ，此时|ME ﹣MD |最大，最大值为线段DE ′的长度，如图1所示．DE ′= 设直线DE ′的解析式为y ＝kx +b （k ≠0），将D （﹣2，10）、E ′（﹣8，0）代入y ＝kx +b ，21080k b k b -+=⎧⎨-+=⎩，解得：53403k b ⎧=⎪⎪⎨⎪=⎪⎩，△直线DE ′的解析式为y ＝53x +403，△点M 的坐标为（0，403）．故当点M 的坐标为（0，403）时，|ME ﹣MD |取最大值 （3）△A （0，8），B （﹣6，0），△点A ′的坐标为（t ，8），点B ′的坐标为（t ﹣6，0）， △点D （﹣2，10），△B ′D8116t -+，A ′B ′10，A ′D△A ′B ′D 为等腰三角形分三种情况：①当B ′D ＝A ′D8116t -+t ＝9； ②当B ′D ＝A ′B ′8116t -+＝10， 解得：t ＝4；③当A ′B ′＝A ′D 时，有10解得：t 1＝﹣2﹣，t 2＝﹣．综上所述：当△A ′B′D 为等腰三角形时，t 的值为﹣2﹣4、﹣或9．类型三、等腰三角形中的动点问题例1.如图，△ABC是边长为6cm的等边三角形，点P，Q分别从顶点A，B同时出发，点P 沿射线AB运动，点Q沿折线BC−CA运动，且它们的速度都为1cm/s．当点Q到达点A时，点P随之停止运动连接PQ，PC，设点P的运动时间为t(s)．（1）当点Q在线段BC上运动时，BQ的长为_______（cm），BP的长为_______（cm）（用含t的式子表示）；（2）当PQ与△ABC的一条边垂直时，求t的值；（3）在运动过程中，当△CPQ是等腰三角形时，直接写出t的值．【答案】（1）t；(6−t)；（2）当t=2或t=4或t=8时，PQ与△ABC的一条边垂直；（3）当t=3或t=9时，∆CPQ为等腰三角形．【详解】解：（1）点Q从点B出发，速度为1cm/s，点P从点A出发，速度为1cm/s，△BQ=tcm，AP=tcm，△BP=(6−t)cm，故答案为：t；(6−t)；（2）根据题意分三种情况讨论：①如图所示：当PQ⊥CB时，∠PQB=90°，△三角形ABC为等边三角形，△∠A=∠ACB=∠ABC=60°，△∠QPB=30°，△QB=12PB，由（1）可得：t=12(6−t)，解得：t=2；②如图所示：当PQ⊥AB时，∠QPB=90°，△∠ABC=60°，△∠BQP=30°，△QB=2PB，由（1）可得：t=2(6−t)，解得：t=4；③如图所示：当PQ⊥AC时，∠AQP=90°，△∠A=60°，△∠APQ=30°，△AP=2QA，由（1）可得：t=2(12−t)，解得：t=8；综上可得：当t=2或t=4或t=8时，PQ与△ABC的一条边垂直；（3）根据题意，分情况讨论：①当点Q在BC边上时，CQ=PQ时，如图所示：过点Q作QE⊥AB，△∠ABC=60°，△∠BQE=30°，△BE=12BQ=12t，△QE=√32t，CQ=6−t，PE=6−t−1 2t=6−32t，△PQ=√PE2+QE2=√(6−32t)2+(√32t)2△CQ=PQ，△(6−t)2=(6−32t)2+(√32t)2，解得：t=3或t=0（舍去）；②当点Q在BC边上时，CP=CQ时，如图所示：过点P作PF⊥AC，△∠CAB=60°，△∠APF=30°，△AF=12AP=12t，△PF=√32t，CQ=6−t，CF=6−12t，△CP=√PF2+CF2=12(√3 2△CP=CQ，△(6−t)2=(6−12t)2+(√32t)2，解得：t=0（舍去）；③当点Q在BC边上时，CP=PQ时，如图所示：由图可得：∠CQP>60°，∠QCP<60°，∠CQP≠∠QCP，△这种情况不成立；④当点Q在AC边上时，只讨论CP=PQ情况，如图所示：过点Q作QE⊥AB，过点C作CF⊥AB，△∠CAB=60°，∆ABC为等边三角形，△∠AQE =30°，AF =BF =3，△CF =3√3，AQ =12−t ， △AE =6−12t ，△QE =√32(12−t)，△EP =t −(6−12t)=32t −6，△PQ =√QE 2+EP 2=√34(12−t)2+(32t −6)2，△CF =3√3，PF =t −3，△PC =√CF 2+FP 2=√(3√3)2+(t −3)2，△PC =PQ ，△34(12−t)2+(32t −6)2=(3√3)2+(t −3)2，解得：t 1=9或t 2=6（舍去）， 综上可得：当t =3或t =9时，∆CPQ 为等腰三角形．【变式训练1】如图1，ABC ∆中，CD AB ⊥于D ，且::2:3:4BD AD CD =； （1）试说明ABC ∆是等腰三角形；（2）已知Δ40ABC S =cm 2，如图2，动点M 从点B 出发以每秒1cm 的速度沿线段BA 向点A 运动，同时动点N 从点A 出发以相同速度沿线段AC 向点C 运动，当其中一点到达终点时整个运动都停止．设点M 运动的时间为t (秒)． ①若DMN ∆的边与BC 平行，求t 的值；②在点N 运动的过程中，ADN ∆能否成为等腰三角形?若能，求出t 的值；若不能，请说明理由．【答案】（1）证明见解析；（2）①t 值为5或6；②点N 运动的时间为6s ，365s ，或5s 时，ΔADN 为等腰三角形. 【详解】解：（1）设BD ＝2x ，AD ＝3x ，CD ＝4x ，则AB ＝5x ，在Rt △ACD 中，AC 5x ，△AB ＝AC ，△△ABC 是等腰三角形； （2）①S △ABC ＝12×5x ×4x ＝40cm 2，而x ＞0，△x ＝2cm ， 则BD ＝4cm ，AD ＝6cm ，CD ＝8cm ，AC ＝10cm ．当MN △BC 时，AM ＝AN ，即10−t ＝t ，此时t ＝5，当DN △BC 时，AD ＝AN ，此时t ＝6， 综上所述，若△DMN 的边与BC 平行时，t 值为5或6； ②ΔADN 能成为等腰三角形，分三种情况： （△）若AD =AN =6，如图：则t =61=6s ；（△）若DA =DN ，如图：过点D 作DH AC ⊥于点H ，则AH =NH ， 由1122ACDSAD CD AC DH =⋅=⋅，得11681022DH ⨯⨯=⨯⨯，解得245DH =，在Rt ADH 中，185AH ===， 3625AN AH ∴==，3615AN t s ∴==； （△）若ND =NA ，如图：过点N 作NQ AB ⊥于点Q ，则AQ =DQ =3，142NQ CD ==，5AN ∴==，51ANt s ∴==； 综上，点N 运动的时间为6s ，365s ，或5s 时，ΔADN 为等腰三角形. 【变式训练2】在平面直角坐标系中，A （a ，0），B （b ，0），C （c ，0），a ≠0且a ，b ，c 满足条件()20a b +=．（1）直接写出△ABC 的形状 ；（2）点D 为射线BC 上一动点，E 为射线CO 上一点，且△ACB =120°，△ADE =60° ① 如图1，当点E 与点C 重合时，求AD 的长；② 如图2，当点D 运动到线段BC 上且CD =2BD ，求点E 的坐标；【答案】（1）等腰三角形，证明见解析；（2）①6；②0,7.E【详解】解：（1） ()20a b +=，030a b c 解得：3a bc∴ A （b -，0），B （b ，0），C （3，0），,OA OB ∴= 而,OC AB ⊥ ,AC BC ∴=ABC ∴是等腰三角形.（2）① △ACB =120°，△ADE =60°，,ACBD DAC 60,DACACD ∴是等边三角形，,AD CD AC,AC BC =30,ABCCAB 90,DAB ∴∠=︒2BD BC CD AD,AD DC BC ∴==3,,CO COAB 6,BC6.AD②在CE 上取点F ，使CF =CD ，连接DF ，记,AD CE 的交点为K ，如图所示：△AC =BC ，△ACB =120°， △△ACO =△BCO =60°， △△CDF 是等边三角形， △△CFD =60°，CD =FD ， △△EFD =120°， △△ACO =△ADE =60°，,AKCFKD △△CAD =△CED ，又△△ACD =△EFD =120°， △△ACD △△EFD （AAS ）， △AC =EF ， 由（1）得：c =3， △OC =3， △△AOC =90°，△ACO =60°， △△OAC =30°， △BC =AC =2OC =6，EF =AC =6，△CD =2BD ， △BD =2，CF =CD =4， △CE =EF +CF =6+4=10， △OE =CE -OC =1037-=， △0,7.E 【变式训练3】如图，在等边△ABC 中，AB ＝AC ＝BC ＝6cm ，现有两点M 、N 分别从点A 、B 同时出发，沿三角形的边运动，已知点M 的速度为1cm/s ，点N 的速度为2cm/s ．当点N 第一次回到点B 时，点M 、N 同时停止运动，设运动时间为ts ． （1）当t 为何值时，M 、N 两点重合；（2）当点M 、N 分别在AC 、BA 边上运动，△AMN 的形状会不断发生变化． ①当t 为何值时，△AMN 是等边三角形； ②当t 为何值时，△AMN 是直角三角形；（3）若点M 、N 都在BC 边上运动，当存在以MN 为底边的等腰△AMN 时，求t 的值．【答案】（1）当M 、N 运动6秒时，点N 追上点M ；（2）①2t =，△AMN 是等边三角形；②当32t =或125时，△AMN 是直角三角形；（3）8t =【详解】解：（1）设点M 、N 运动x 秒后，M 、N 两点重合，x ×1+6＝2x ，解得：x ＝6， 即当M 、N 运动6秒时，点N 追上点M ；（2）①设点M、N运动t秒后，可得到等边三角形△AMN，如图1，AM＝t，AN＝6﹣2t，△AB＝AC＝BC＝6cm，△△A＝60°，当AM＝AN时，△AMN是等边三角形，△t＝6﹣2t，解得t＝2，△点M、N运动2秒后，可得到等边三角形△AMN．②当点N在AB上运动时，如图2，若△AMN＝90°，△BN＝2t，AM＝t，△AN＝6﹣2t，△△A＝60°，△2AM＝AN，即2t＝6﹣2t，解得32t=；如图3，若△ANM＝90°，由2AN＝AM得2（6﹣2t）＝t，解得125t=．综上所述，当t为32或125s时，△AMN是直角三角形；（3）当点M、N在BC边上运动时，可以得到以MN为底边的等腰三角形，由（1）知6秒时M、N两点重合，恰好在C处，如图4，假设△AMN是等腰三角形，△AN＝AM，△△AMN＝△ANM，△△AMC＝△ANB，△AB＝BC＝AC，△△ACB是等边三角形，△△C＝△B，在△ACM和△ABN中，△△AMC＝△ANB，△C＝△B，AC＝AB，△△ACM△△ABN（AAS），△CM＝BN，△t﹣6＝18﹣2t，解得t＝8，符合题意．所以假设成立，当M、N运动8秒时，能得到以MN为底的等腰三角形．。

专题01 等腰三角形三种压轴题型全攻略(解析版)等腰三角形三种压轴题型全攻略(解析版)在数学中，等腰三角形是一种特殊的三角形，它具有两条边相等的性质。

在考试中，等腰三角形常常出现在各类题目中，而三种压轴题型更是考察学生对等腰三角形的理解和运用能力。

本文将为大家介绍三种常见的等腰三角形压轴题型，并给出详细的解析，帮助大家更好地掌握解题技巧。

一、等腰三角形的性质首先，我们回顾一下等腰三角形的性质。

等腰三角形有两条边相等，可以分为底边和两条等腰边。

其性质如下：1. 等腰三角形的底边上的两个底角相等。

2. 等腰三角形的两条等腰边上的两个顶角相等。

利用这些性质，我们可以解决以下三种常见的等腰三角形压轴题型。

二、题型一：等腰三角形边长第一种题型是给定一个等腰三角形，要求计算其边长。

这种题型通常会给出等腰三角形的底边长度或两条等腰边的长度，并要求计算等腰三角形的其他边长。

解题步骤如下：Step 1：根据已知条件，将等腰三角形的底边或两条等腰边的长度表示出来。

Step 2：利用等腰三角形的性质，根据已知条件得到其他边长的表达式。

Step 3：根据所得到的表达式，计算出未知边长的具体数值。

三、题型二：等腰三角形的面积第二种题型是给定一个等腰三角形，要求计算其面积。

这种题型通常会给出等腰三角形的底边长度和高，并要求计算面积。

解题步骤如下：Step 1：根据已知条件，将等腰三角形的底边长度和高表示出来。

Step 2：根据面积公式 S = (1/2) ×底边 ×高，计算出面积。

Step 3：得到等腰三角形的面积。

四、题型三：等腰三角形的角度第三种题型是给定一个等腰三角形，要求计算其顶角的度数。

这种题型通常会给出等腰三角形的顶角的度数，并要求计算其他角的度数。

解题步骤如下：Step 1：根据已知条件，将等腰三角形的某个顶角的度数表示出来。

Step 2：利用等腰三角形的性质，根据已知条件得到其他角度的表达式。

专题01三角形基础专项训练三角形的三边关系1．（2023春·江苏常州·七年级统考期中）三角形的三边长分别为3、6和a ，其中a 为奇数，那么这个三角形的周长是（）A ．14B ．15C ．16D ．14或16【答案】D【分析】先根据三角形三边之间的关系求出a 的值，再求出周长即可．【详解】解：∵三角形的三边长分别为3、6和a ，∴6363a ，即39a ，∵a 为奇数，∴5a 或7，∴这个三角形周长为35614 或36716 ，故选：D ．【点睛】本题主要考查了三角形三边之间的关系，解题的关键是掌握三角形任意两边之和大于第三边，两边之差小于第三边．2．（2023春·江苏盐城·七年级统考期中）已知a ，b ，c 为ABC 的三边长，b ，c 满足22(3)0b c ，且a 为方程51a 的解，则ABC 的周长为．【答案】9【分析】利用绝对值的性质以及偶次方的性质得出2b 、3c 的值，再解绝对值方程可得6a 或4a ，进而利用三角形三边关系得出a 的值，进而求出ABC 的周长．【详解】解：∵22(3)0b c ，∴20b 且30c ，∴2b 、3c ，∵a 为方程51a 的解，∴6a 或4a ，又236 ，∴4a ，则ABC 的周长为2349 ，故答案为：9．【点睛】此题主要考查了三角形三边关系以及绝对值的性质和偶次方的性质，得出a 的值是解题关键．3．（2023春·上海奉贤·七年级校考期中）已知一个三角形的两边长分别为3和7，且第三边长为整数，那么第三边长的最小值为．【答案】5【分析】根据三角形的三边关系“第三边大于两边之差，而小于两边之和”，求得第三边的取值范围；再根据第三边是整数，从而求得第三边长的最小值．【详解】解：设第三边为a ，根据三角形的三边关系，得：7337a ，即410a ，a ∵为整数，a 的最小值为5．故答案为：5．【点睛】此题考查了三角形的三边关系．注意第三边是整数的已知条件是解题的关键．4．（2022秋·湖南永州·八年级校考期中）若a ，b ，c 是三角形的三边长，a b c a c b c a b．【答案】3c a b【分析】根据绝对值的性质和三角形的三边关系即可求得答案．【详解】∵a b c ，∴ 0a b c a b c ．∴ a b c a b c a b c ．同理可得a cb ac b ，c a b c a b ．∴a b c a c b c a ba b c a c b c a ba b c a c b c a b 3c a b ．故答案为：3c a b ．【点睛】本题主要考查三角形的三边关系和绝对值的性质，牢记三角形的三边关系（三角形两边的和大于第三边）是解题的关键．由三角形的中线求面积5．（2023春·江苏盐城·七年级统考期中）如图，在ABC 中，D 是AC 的中点，E 是AB 上的一点，且3AE BE ，BD 与CE 相交于点F ，若CDF 的面积为3，则ABC 的面积为．【答案】10【分析】连接AF ，根据中点可得3ADF CDF S S ，根据3AE BE 可得3AEF BEF S S ，设BEF S x ，可得4BCF S x ，进而可得:4:1ACF AEF S S ，求出x 的值，进而可求解．【详解】解：连接AF ，如图所示：∵D 是AC 的中点，3CDF S ，3ADF CDF S S ，又3AE BE ∵，3AEF BEF S S ，设BEF S x ，则3AEF S x △，ABD BCD S S ∵，333BCF S x x ，4BCF S x ，:4:1CF EF ，:4:1ACF AEF S S ，332AEF S x ，解得：12x ，122(34)102ABC BCD S S \==´+´=，故答案为：10．【点睛】本题考查了根据三角形中线求面积，根据三角形面积等高模型得到:4:1ACF AEF S S 是解题的关键．6．（2022春·天津南开·七年级校联考期中）如图，正方形ABCD 的边长为4，E 、F 分别是BC 、CD 边上的中点，求图中阴影部分的面积．【答案】323/2103【分析】连接CG ，根据三角形中线的性质可得,GBE GCE GCF GDF S S S S ，通过证明4DFG BEG ECFG S S S 四边形，得出GBE GCE GCF GDF S S S S ，即可求解．【详解】解：如图，令,BF DE 相交于点G ，连接CG ，∵正方形ABCD 的边长为4，E 、F 分别是BC 、CD 边上的中点，∴,GE GF 分别是,BCG CDG 中线，2BE CE CF DF ，∴,GBE GCE GCF GDF S S S S ，∵12442BCF DCE S S ，∴4DFG BEG ECFG S S S 四边形，∴GBE GCE GCF GDF S S S S ，∴14433GBE GCE GCF GDF S S S S ，∴阴影部分的面积 43244433GBE GCE GCF GDF ABCD S S S S S 正方形，故答案为：323．【点睛】本题主要考查了三角形中线的性质，解题的关键是掌握三角形的中线将三角形面积分为相等是两部分．7．（2023春·黑龙江哈尔滨·七年级哈尔滨市第四十九中学校校考期中）如图，在ABC 中，点E 为AB的中点，点D 为BC 延长线上一点，连接DE ，DE 与AC 边交于点F ，23BC DC ，若DBE 的面积为4，则DFC △的面积为．【答案】95【分析】连接AD BF ，，由线段比转化得到面积比，设23BFC DFC S x S x ，，结合中线的性质得到关于面积的方程求解即可．【详解】解：连接AD BF ，，23BC DC ∵32DFC DAC BFC BAC S S S S 设23BFC DFC S x S x ，，∵点E 是AB 中点，∴DAE DBE FAE FBE S S S S ，，325DAF DBF S S x x x ，538DAC S x x x ，216833BAC S x x，1610233BAF S x x x，1523BEF BAF S S x ，52023433DEB S x x x x ，35x ，393355DFC S x ，故答案为：95．【点睛】本题主要考查三角形面积的计算，利用线段比转化为面积比并结合中线的性质列方程是解决本题的关键．8．（2023春·江苏无锡·七年级统考期中）如图，在ABC 中，8AB ，10AC ，3CD BD ，点E 是AC 的中点，BE 、AD 交于点F ，则四边形DCEF 的面积的最大值是（）A ．24B ．22C ．20D ．18【答案】D 【分析】连接CF ，设 BFD S a ，由三角形面积公式可得3CFD S a ，3ADC ABD S S ，由点E 是AC 的中点，得ABE CBE S S ，AFE CEF S S ，进而得4ABF CBF S S a ，5ABD S a ，15ADC S a ，12AFC S a ，20ABC S a ，6EFC S a ，得出9DCEF S a 四边形，通过讨论ABC 的面积最大值得四边形DCEF 的面积最大值．【详解】解：连接CF ，设 BFD S a ，3CD BD ∵，3CFD S a ，3ADC ABD S S ，∵点E 是AC 的中点，ABE CBE S S ，AFE CEF S S ，4BFD C ABF CB F F D S a S ，45ABF BFD ABD S a S a S a ，15ADC S a ，51520ABC ABD ADC S S S a a a204412ABC ABF C A B FC F a S S S a S a a ，126A EF FC C S a S ，639F DCE C F E C FD S a a S S a 四边形 ，920ABC DCEF S S 四边形 ，∵在ABC 中，8AB ，10AC ，1810402ABC S 的最大值 ， 四边形DCEF 的面积的最大值是18，故选：D ．【点睛】本题考查了三角形的面积，已知两边三角形面积的最大值等知识，解题关键是理解运用同高的两个三角形面积之比等于底边之比．由三角形中线求长度9．（2022秋·浙江杭州·八年级统考期中）已知等腰三角形的底边长为10cm ，一腰上的中线把其周长分成的两部分的差为6cm ，则腰长为．【答案】16cm /16厘米【分析】设腰长为cm x ，分腰长和腰长的一半长的和和腰长的一半和底边长的和进行讨论求解即可．【详解】解：设腰长为cm x ，依题意得，当腰长和腰长的一半长的和比腰长的一半和底边长的和大时，1110622x x x ，解得16cm x ，当腰长的一半和底边长的和比腰长和腰长的一半长的和大时，1110622x x x 骣琪+-+=琪桫，解得4cm x ，因为4410 ，所以4cm x 不符合题意舍弃．故答案为：16cm ．【点睛】本题考查了三角形的中线，等腰三角形的性质，掌握相关知识并分情况讨论是解题的关键．10．（2022春·陕西西安·七年级西安市曲江第一中学校考期中）在ABC 中，BC 边上的中线AD 将ABC 分成的两个新三角形的周长差为5cm ，AB 与AC 的和为11cm ，则AC 的长为．【答案】3cm 或8cm 【分析】根据三角形的中线的定义可得BD CD ，然后求出ABD △与ADC △的周长差是AB 与AC 的差或AC 与AB 的差，然后代入数据计算即可得解．【详解】如图1，图2，∵AD 是BC 边上的中线，∴BD CD ，∵中线AD 将ABC 分成的两个新三角形的周长差为5cm ，∴ 5AB BD AD AC CD AD 或 5AC CD AD AB BD AD ，∴5AB AC 或者5AC AB ，∵AB 与AC 的和为11cm ，∴11AB AC ，∴83AB AC 或38AB AC，故答案为：3cm 或8cm ．【点睛】本题考查了三角形的中线，熟记概念并求出两个三角形的周长的差等于两边长的差是解题的关键．11．（2022秋·安徽合肥·八年级统考期中）如图，在ABC 中AB BC （＞），2AC BC ＝，BC 边上的中线AD 把ABC 的周长分成70和50两部分，求AC 和AB 的长．【答案】5636AC AB ＝，＝【分析】先根据2AC BC 和三角形的中线列出方程求解，分类讨论①70AC CD ，②50AC CD ，注意答案是否满足条件，即是否满足题目给出的条件、是否满足三角形三边的关系．【详解】解：设BD CD x ，则24AC BC x ，∵BC 边上的中线AD 把ABC 的周长分成70和50两部分，AB BC ＞，①当7050AC CD AB BD ，时470x x ，解得：14x ，∴441456AC x ，14BD CD ，∴50501436AB BD ，∴3628AB BC ＞，满足条件∵36286456BC AB AC ＞，满足三边关系，∴5636AC AB ，；②当5070AC CD AB BD ，时，450x x ，解得：10x ，∴441040AC x ，∴10BD CD ，20BC ，70701060AB BD ，∵402060AC BC AB ，∴此时构不成三角形，∴舍去，∴5636AC AB ，．【点睛】本题考查了三角形中线的性质和三边的关系，解题的关键是找到等量关系，列出方程．12．（2022秋·海南省直辖县级单位·八年级统考期中）如图所示，在ABC 中，AB AC ，AC 边上的中线把三角形的周长分为24cm 和30cm 的两部分，求这个三角形的边BC 的长．【答案】14cm 或22cm【分析】方法1：设2cm AB AC x ，cm BC y ，进而得出1cm 2AD CD AC x，再分两种情况，建立方程组求解，最后判定能否构成三角形．方法2：设cm AD CD a ，进而表示出2cm AB AC a ， 544cm BC a ，再分两种情况，建立方程求解，即可得出结论．【详解】解法1：设2cm AB AC x ，cm BC y ，∵点D 是AC 的中点，∴1cm 2AD CD AC x ，∵AC 边上的中线把三角形的周长分为24cm 和30cm 的两部分，∴①22430x x x y，解得822x y ，∴22cm BC ，②23024x x x y，解得1014x y ，∴14cm BC ，解法2、∵BD 是ABC 的中线，∴2AC CD AD ，设cm AD CD a ，∴2cm AB AC a ，∵AC 边上的中线把三角形的周长分为24cm 和30cm 的两部分，∴ 24304544cm BC a a ，①当24cm AB AD 时，∴224a a ，∴8a ，∴544543222cm BC a ，②当30cm AB AD 时，∴230a a ，∴10a ，∴544544014cm BC a ，综上，BC 为14cm 或22cm ．【点睛】此题主要考查了等腰三角形的性质，三角形的周长，分类讨论的思想，解本题的关键是建立方程组求解．三角形的高线13．（2022秋·北京朝阳·八年级校考期中）如图，在Rt ABC △中，90ABC ，点D 沿BC 自点B 向点C 运动（点D 与点B ，C 不重合），作BE AD 于点E ，CF AD 的延长线于点F ，在点D 的运动过程中，BE CF 的值逐渐（填“增大”，“减小”或“不变”）．【答案】减小【分析】根据点D 沿BC 自点B 向点C 运动时，Rt ABC △的面积不变，但是AD 会增大，由面积公式可得BE CF 的值逐渐减小【详解】解：由ABC ABD ACD S S S △△得：1122ABC S AD BE AD CF△ 12AD BE CF ∵Rt ABC △的面积不变，但是点D 沿BC 自点B 向点C 运动时，AD 会增大，∴BE CF 的值逐渐减小，故答案为：减小【点睛】本题考查了三角形的动点问题，利用三角形的面积转换是解决问题的关键14．（2023春·辽宁大连·七年级统考期中）如果一个多边形的内角和为1260 ，那么这个多边形是边形．【答案】九【分析】设它的边数为n ，根据多边形的内角和公式列方程求解即可．【详解】解：设它的边数为n ，根据题意，得(2)1801260n ，解得9n ，所以这是一个九边形．故答案为：九．【点睛】本题考查多边形内角和与外角，掌握多边形的内角和公式是解决问题的关键．15．（2023春·湖北武汉·七年级统考期中）已知平面直角坐标系中， 3,4A ， 2,1B ， 1,0C ，延长AB 与x 轴交于一点P ，若13PBC ABC S S ，则P 点的坐标为．【答案】11,03【分析】过点A 作AD x 轴于点D ，过点B 作BE x ⊥轴于点E ，根据 3,4A ， 2,1B ， 1,0C ，求出7ABC S △，得出17733PBC S ，设点P 的坐标为 0m ,，得出 17123m ，求出m 的值，即可得出答案．【详解】解：过点A 作AD x 轴于点D ，过点B 作BE x ⊥轴于点E ，如图所示：∵ 3,4A ， 2,1B ， 1,0C ，∴1BE ， 123EC ，312CD ， 325DE ，4 AD ，∴ABC BCE ACDABED S S S S 梯形 11114513242227 ，∴17733PBC S ，设点P 的坐标为 0m ,，∵ 1,0C ，∴1CP m ，∴ 17123m ，解得：113m，∴点P 的坐标为11,03．故答案为：11,03．【点睛】本题主要考查了平面直角坐标系中三角形的面积计算，解题的关键是作出辅助线，利用割补法求出ABC 的面积．三角形的角平分线16．（2022秋·浙江绍兴·八年级校联考期中）如图，AE 是△ABC 的角平分线，AD ⊥BC 于点D .若∠BAC ＝128°，∠C ＝36°，则∠DAE 的度数是()A ．10°B ．12°C ．15°D ．18°【答案】A 【分析】根据角平分线定义求出∠EAC=64°,根据垂线定义求出∠CAD=54°,相减即可求解.【详解】解：∵AE 平分∠BAC,∠BAC ＝128°，∴∠EAC=64°,∵AD ⊥BC,∠C ＝36°，∴∠CAD=54°,∴∠DAE=∠EAC-∠DAC =64°-54°=10°,故选A.【点睛】本题考查了角平分线的定义,垂线的定义,属于简单题,表示出∠EAD=∠EAC-∠DAC 是解题关键.17．（2018秋·浙江杭州·八年级统考期中）如图，BF 是ABD 的平分线，CE 是ACD 的平分线，BF 与CE 交于点G ．若140BDC ，110BGC ，则A 的度数为（）A ．70B ．80C ．50D ．55【答案】B 【详解】解：如图，连接BC ．∵140BDC ，∴18014040DBC DCB ．∵110BGC ，∴18011070GBC GCB ．∵BF 是ABD 的平分线，CE 是ACD 的平分线，∴113022GBD GCD ABD ACD ，∴30240100ABC ACB ，∴18010080A ．故选B ．18．（2021秋·安徽安庆·八年级校考期中）如图，∠MAN ＝100°，点B ，C 是射线AM ，AN 上的动点，∠ACB 的平分线和∠MBC 的平分线所在直线相交于点D ，则∠BDC 的大小为()A ．40°B ．50°C ．80°D ．随点B ，C 的移动而变化【答案】B 【详解】试题解析：∵CD 平分∠ACB ，BE 平分∠MBC ，∴∠ACB=2∠DCB ，∠MBC=2∠CBE ，∵∠MBC=2∠CBE=∠A+∠ACB ，∠CBE=∠D+∠DCB ，∴2∠CBE=∠D+∠DCB ，∴∠MBC=2∠D+∠ACB ，∴2∠D+∠ACB=∠A+∠ACB ，∴∠A=2∠D ，∵∠A=100°，∴∠D=50°．故选B ．19．（2023春·江西萍乡·八年级统考期中）如图，在Rt △ABC 中，∠C ＝90°，AD 平分∠CAB ，CD ＝3，AB ＝12，则△ABD 的面积为．【答案】18【分析】过点D 作DE AB 于点E ，先根据角平分线的性质可得3DE CD ，再利用三角形的面积公式即可得．【详解】解：如图，过点D 作DE AB 于点E ，90C ∵，CD AC ，又AD ∵平分CAB ，3CD ，3DE CD ，12AB ∵，ABD 的面积是111231822AB DE ，故答案为：18．【点睛】本题考查了角平分线的性质，熟练掌握角平分线的性质是解题关键．三角形的角20．（2023春·山东烟台·七年级统考期中）例题再现：（1）如图1，五角星的顶角分别是,,,,A B C D E ，则A B C D E _________（直接写出答案）；知识链接n 边形的内角和等于 2180 n ．变式拓展：（2）如图2，将该五角星剪掉一个顶角A ．①求B C D E P Q 的度数；②若8B C D E A ，求P Q 的度数．【答案】（1）180 （2）①360 ②200【分析】（1）利用三角形的外角的性质和三角形的内角和进行求解即可；（2）①三角形的外角的性质得到QGF B D ，PFG C E ，进而得到42180360QGF PFG P Q ，即可得解；②根据180A B C D E 以及8B C D E A ，求出A ，进而求出B C D E ，再利用①中结论进行求解即可。

专题01 三角形的证明一、单选题1．（广东韶关·八年级期中）若三角形内一点到三边的距离相等,则这个点是（）A．三条边的垂直平分线的交点B．三条中线的交点C．三条高的交点D．三条角平分线的交点【答案】D【提示】根据角平分线的判定定理到角两边距离相等的点在角平分线上,得出到到三边的距离相等的点是三角形三个角的平分线交点即可．【解答】解：根据角平分线的判定定理：到角两边距离相等的点在角平分线上,∴到到三边的距离相等的点是三角形三个角的平分线交点．故选择D．【点睛】本题考查角平分线的判定,以及角平分线交点的性质,掌握角平分线的判定与性质是解题关键．2．（湖北省直辖县级单位·八年级期中）如图,Rt△ABC中,∠C＝90°,AD平分∠BAC,交BC于点D,AB ＝10,S△ABD＝15,则CD的长为（）A．3 B．4 C．5 D．6【答案】A【提示】过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后利用△ABD的面积列式计算即可得解．【解答】解：如图,过点D作DE⊥AB于E,∵∠C=90°,AD平分∠BAC, ∴DE=CD,∴S△ABD=12AB×DE=12×10×DE=15,解得DE=3,∴CD=DE=3,故选：A．【点睛】本题考查了三角形的面积和角平分线的性质,能熟记角平分线上的点到角两边的距离相等是解此题的关键．3．（黑龙江·牡丹江四中八年级期中）等腰三角形底边长为5,一腰上的中线把周长分成两部分的差为3cm,则腰长为（）A．8cm或2cm B．2cm C．8cm D．8cm或25cm【答案】C【提示】根据题意,画出图形,然后分两种情况讨论,即可求解．【解答】解：如图,CD为△ABC的中线,AB=AC,底边BC=5cm,∴AD=BD,根据题意得：当（AD+AC+CD）-（BD+BC+CD）=3cm时,则AC-BC=3cm,∴AB=AC=8cm；当（BD+BC+CD）-（AD+AC+CD）=3cm时,则BC -AC =3cm,∴AB=AC=2cm,∵4AB AC BC +=<,不合题意,舍去； 综上所述,腰长为8cm ． 故选：C 【点睛】本题主要考查了等腰三角形的性质,熟练掌握等腰三角形的两腰相等是解题的关键． 4．（山东济宁·八年级期中）如图,已知ABC 是等边三角形,点B ,C ,D ,E 在同一直线上,且CG CD =,DF DE =,则E ∠=（ ）A ．30°B ．20°C ．15°D ．10°【答案】C 【提示】由于△ABC 是等边三角形,那么∠B ＝∠1＝60°,而CD ＝CG ,那么∠CGD ＝∠2,而∠1是△CDG 的外角,可得∠1＝2∠2,同理有∠2＝2∠E ,等量代换有4∠E ＝60°,即可求得∠E ． 【解答】 解：如图所示,∵△ABC 是等边三角形, ∴∠B ＝∠1＝60°, ∵CD ＝CG , ∴∠CGD ＝∠2,∴∠1＝∠CGD +∠2=2∠2, ∵DF =DE , ∴∠DFE =∠E ,∴∠2＝∠DFE +∠E =2∠E , ∴4∠E ＝60°, ∴∠E ＝15°． 故选：C ． 【点睛】本题考查了等边三角形的性质、等腰三角形的性质、三角形外角的性质,解题的关键是利用外角性质得出∠1=2∠2,∠2=2∠E ．5．（辽宁·沈阳市第四十三中学八年级期中）如图,在△ABC 中,∠C =90°,∠B =15°,AB 的垂直平分线交BC 于D ,交AB 于E ,若DB =10cm,则CD 的长为（ ）A ．5B ．3C ．55D ．10【答案】B 【提示】利用线段垂直平分线的性质求得AD =BD =10 cm,及∠ADC =30°,再利用含30度角的直角三角形的性质以及勾股定理即可求解． 【解答】解：∵AB 的垂直平分线交BC 于D ,交AB 于E , ∴AD =BD =10 cm,∠DBA =∠BAD =15°, ∴∠ADC =30°, ∴AC =12AD =5（cm ）,CD 222210553AD AC --=cm ）． 故选：B 【点睛】本题考查了含30°角的直角三角形,勾股定理,解题的关键是：熟记含30°角的直角三角形的性质,线段垂直平分线的性质及三角形的外角性质．6．（重庆市凤鸣山中学八年级期中）如图,在ABC 中,AB AC =,36A ∠=︒,AB 的中垂线DE 交AC 于点D ,交AB 于点E ,下述结论中正确的是（ ）A ．点D 是线段AC 的中点B ．AD BD BC == C ．BDC 的周长等于AB CD + D ．BD 平分EDC ∠【答案】B 【提示】由在△ABC 中,AB ＝AC ,∠A ＝36°,根据等边对等角与三角形内角和定理,即可求得∠ABC 与∠C 的度数,又由AB 的垂直平分线是DE ,根据线段垂直平分线的性质,即可求得AD ＝BD ,继而求得∠ABD 的度数,则可知BD 平分∠ABC ；可得△BCD 的周长等于AB ＋BC ,又可求得∠BDC 的度数,求得AD ＝BD ＝BC ,则可求得答案；注意排除法在解选择题中的应用． 【解答】解：∵36A ∠=︒,AB AC =, ∴72ABC C ∠=∠=︒, ∵DE 垂直平分AB , ∴AD BD =, ∴36ABD A ∠=∠=︒, ∴36DBC ∠=︒, ∵C DBC ∠>∠, ∴BD ＞CD , ∴AD ＞CD ,∴点D 不是线段AC 的中点,故A 错误； ∵∠DBC ＝36°,∠C ＝72°,∴∠BDC ＝180°−∠DBC −∠C ＝72°, ∴∠BDC ＝∠C , ∴BD ＝BC ,∴AD ＝BD ＝BC ,故B 正确；∴△BCD 的周长为：BC ＋CD ＋BD ＝BC ＋CD ＋AD ＝BC ＋AC ＝BC ＋AB ,故C 错误； ∵在△ABC 中,AB ＝AC ,∠A ＝36°,∴∠ABC＝∠C＝180362︒-︒＝72°,∵AB的垂直平分线是DE,∴AD＝BD,∴∠ABD＝∠A＝36°,∴∠DBC＝∠ABC−∠ABD＝72°−36°＝36°,∴72BCD BDC∠=∠=︒,∵9054EDB ABD∠=︒-∠=︒,∴EDB BDC∠≠∠,故D错误；故选：B．【点睛】此题考查了等腰三角形的性质,线段垂直平分线的性质以及三角形内角和定理等知识．此题综合性较强,但难度不大,解题的关键是注意数形结合思想的应用,注意等腰三角形的性质与等量代换．7．（江苏苏州·八年级期中）如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC＝30°,AD＝4,BD＝6,则CD的长为（）A．25B．5 C．2 D．213【答案】A【提示】将△BCD绕点C顺时针旋转60°得到△ACE,连接CE,DE,由旋转的性质知DC=EC、∠DCE=∠ACB=60°、BD=AE=6,即可得△DCE为等边三角形,根据∠ADC=30°得到∠ADE=90°,根据勾股定理即可得到结论．【解答】解：如图所示,将△BCD绕点C顺时针旋转60°得到△ACE,连接CE,DE,由旋转的性质知DC =EC ,∠DCE =∠ACB =60°,BD =AE =6, 则△DCE 为等边三角形, ∵∠ADC =30°, ∴∠ADE =90°, ∴AD 2+DE 2=AE 2, ∴42+DE 2=62, ∴DE =CD =25． 故选：A ． 【点睛】本题考查旋转变换,熟练掌握旋转变换的性质、等边三角形的判定与性质、勾股定理,正确的作出辅助线是解题的关键．8．（福建·龙岩二中八年级期中）如图,在Rt ACB 中,90BAC ∠=︒,AD BC ⊥垂足为D ．ABD △与'ADB 关于直线AD 对称,点B 的对称点是点'B ,若'14B AC ∠=︒,则B 的度数为（ ）A ．38︒B ．48︒C ．52︒D ．54︒【答案】D 【提示】通过折叠角相等,∠BAD ＋∠B ´AD ＋∠B ´AC ＝90°计算得∠BAD ,进而用余角进行计算． 【解答】解：∵∠BAD ＋∠B ´AD ＋∠B ´AC ＝90°,且∠BAD ＝∠B ´AD ,∠B ´AC ＝14°, ∴∠BAD ＝38°, ∴∠B ＝90°−38°＝52°. 故选：D ． 【点睛】本题考查折叠以及直角三角形中角的转化与计算,属于中考常考题型．9．（福建师范大学附属中学初中部八年级期中）如图,直线m 是△ABC 中BC 边的垂直平分线,点P是直线m 上的一动点,若AB ＝5,AC ＝4,BC ＝6,则△APC 周长的最小值是（ ）A ．9B ．10C ．11D ．12.5【答案】A 【提示】根据垂直平分线的性质BP PC =,所以APC △周长9AC AP PC AC AP BP AC AB =++=++≥+=. 【解答】∵直线m 是ABC 中BC 边的垂直平分线, ∴BP PC =∴APC △周长AC AP PC AC AP BP =++=++ ∵两点之间线段最短 ∴AP BP AB +≥APC ∴的周长AC AP BP AC AB =++≥+ 4AC =,5AB =∴APC △周长最小为9AC AB += 故选：A 【点睛】本题主要考查线段垂直平分线的性质定理,以及两点之间线段最短.做本题的关键是能得出AP BP AB +≥,做此类题的关键在于能根据题设中的已知条件,联系相关定理得出结论,再根据结论进行推论．10．（2022·全国·八年级期中）如图,等腰ABC 中,AB AC =,120BAC ∠=︒,AD DC ⊥于D ,点O 是线段AD 上一点,点P 是BA 延长线上一点,若OP OC =,则下列结论：①30APO DCO ∠+∠=︒；②APO DCO ∠=∠；③POC △是等边三角形；④AB OA AP =+．其中正确的是（ ）A．①③④B．①②③C．②③④D．①②③④【答案】A【提示】①利用等边对等角得：∠APO＝∠ABO,∠DCO＝∠DBO,则∠APO+∠DCO＝∠ABO+∠DBO＝∠ABD,据此即可求解；②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断；③证明∠POC＝60°且OP＝OC,即可证得△OPC是等边三角形；④证明△OP A≌△CPE,则AO ＝CE,得AC＝AE+CE＝AO+AP．【解答】解：①如图1,连接OB,∵AB＝AC,AD⊥BC,∴BD＝CD,∠BAD＝12∠BAC＝12×120°＝60°,∴OB＝OC,∠ABC＝90°﹣∠BAD＝30°∵OP＝OC,∴OB＝OC＝OP,∴∠APO＝∠ABO,∠DCO＝∠DBO,∴∠APO+∠DCO＝∠ABO+∠DBO＝∠ABD＝30°,故①正确；②由①知：∠APO＝∠ABO,∠DCO＝∠DBO,∵点O是线段AD上一点,∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,故②不正确；③∵∠APC+∠DCP+∠PBC＝180°,∴∠APC+∠DCP＝150°,∵∠APO+∠DCO＝30°,∴∠OPC+∠OCP＝120°,∴∠POC＝180°﹣（∠OPC+∠OCP）＝60°, ∵OP＝OC,∴△OPC是等边三角形,故③正确；④如图2,在AC上截取AE＝P A,∵∠P AE＝180°﹣∠BAC＝60°,∴△APE是等边三角形,∴∠PEA＝∠APE＝60°,PE＝P A,∴∠APO+∠OPE＝60°,∵∠OPE+∠CPE＝∠CPO＝60°,∴∠APO＝∠CPE,∵OP＝CP,在△OP A和△CPE中,PA PEAPO CPEOP CP=⎧⎪∠=∠⎨⎪=⎩,∴△OP A≌△CPE（SAS）,∴AO＝CE,∴AC＝AE+CE＝AO+AP,∴AB＝AO+AP,故④正确；正确的结论有：①③④,故选：A．【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质等知识,正确作出辅助线是解决问题的关键．二、填空题11．（云南·弥勒市长君实验中学八年级期中）一个等腰三角形一腰上的高与另一腰的夹角为50°,则该等腰三角形的顶角度数为__________．【答案】40°或140°【提示】本题要分情况讨论．当等腰三角形的顶角是钝角或者等腰三角形的顶角是锐角两种情况．【解答】解：①当为锐角三角形时,如图1,∵∠ABD＝50°,BD⊥AC,∴∠A＝90°−50°＝40°,∴三角形的顶角为40°；②当为钝角三角形时,如图2,∵∠ABD＝50°,BD⊥AC,∴∠BAD＝90°−50°＝40°,∵∠BAD＋∠BAC＝180°,∴∠BAC＝140°∴三角形的顶角为140°,故答案为40°或140°．【点睛】本题主要考查了等腰三角形的性质及三角形内角和定理,做题时,考虑问题要全面,必要的时候可以做出模型帮助解答,进行分类讨论是正确解答本题的关键,难度适中．12．（上海市西南位育中学八年级期中）如图在△ABC中,AB＝AC,BF＝CD,BD＝CE,∠FDE＝70°,那么∠A＝_____．【答案】40°【提示】先证明△BDF≌△CED,得到∠BFD=∠CDE,根据三角形的内角和与平角的定义推出∠FDE与∠B相等,再利用三角内角和定理整理即可得出结论．【解答】解：∵AB=AC,∴∠B=∠C,在△BDF和△CED中,BF CDB CBD CE⎧⎪∠∠⎨⎪⎩＝＝＝,∴△BDF≌△CED（SAS）,∴∠BFD=∠CDE,∴∠FDE=180°-∠CDE-∠BDF=180°-∠BFD-∠BDF=∠B,∵∠FDE=70°,∴∠B=70°,∵∠B+∠C+∠A=180°,∴∠A=40°．故答案为：40°．【点睛】本题考查了三角形全等的性质与判定．解题的关键是通过三角形全等利用角的等量代换得到∠FDE =∠B ．13．（山东济宁·八年级期中）如图,AD 是ABC 中BAC ∠的角平分线,DE AB ⊥于点E ,7ABC S =△,2DE =,4AB =,则AC 长是______．【答案】3 【提示】作DF ⊥AC 于点F ,由角平分线的性质可得DF =DE =2,然后根据三角形的面积公式求解． 【解答】解：作DF ⊥AC 于点F ,∵AD 是ABC 中BAC ∠的角平分线,DE AB ⊥, ∴DF =DE =2, ∵11722AB DE AC DF ⋅+⋅=, ∴11422722AC ⨯⨯+⨯=, ∴AC =3, 故答案为：3．【点睛】本题考查了角平分线的性质,熟练掌握角平分线上的点到角两边的距离相等是解答本题的关键． 14．（北京市师达中学八年级期中）如图,BD 是∠ABC 的平分线,点P 是射线BD 上一点,PE ⊥BA 于点E ,2PE =,点F 是射线BC 上一个动点,则线段PF 的最小值为_________．【答案】2【提示】过P作PH⊥BC,根据垂线段最短得出此时PH的长最小,根据角平分线的性质得出PE=PH,再求出答案即可．【解答】解：过P作PH⊥BC,此时PH的长最小,∵BD是∠ABC的平分线,PH⊥BC,PE⊥BA,∴PE=PH,∵PE=2,∴PH=2,即PF的最小值是2,故答案为：2.【点睛】本题考查了垂线段最短和角平分线的性质,能找出当PF最小时点F的位置是解此题的关键．∠+∠+∠=______°．15．（浙江杭州·八年级期中）如图是单位长度为1的正方形网格,则123【答案】135如图,证明ABC≌AEF可得1390∠+∠=︒,根据等腰直角三角形的性质可得245∠=︒,进而即可求得答案．【解答】解：如图,在ABC与AEF 中AB AEB EBC FE=⎧⎪∠=∠⎨⎪=⎩∴ABC≌AEF∴4=3∠∠1490∠+∠=︒1390∴∠+∠=︒245∴∠=︒123135∴∠+∠+∠=︒故答案为：135【点睛】本题考查了全等三角形的性质与判定,等腰直角三角形的性质,掌握全等三角形的性质与判定是解题的关键．16．（江苏·无锡市江南中学八年级期中）已知直角三角形△ABC的三条边长分别为3,4,5,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画___条．【答案】6【提示】根据等腰三角形的性质分别利用AB,AC为底以及为腰得出符合题意的图形即可．解：如图所示：当BC 2=CC 2,AC 1=AC ,BC =BC 3,BC =CC 4,BC =CC 5,C 6A =C 6B 都能得到符合题意的等腰三角形． 故答案为：6． 【点睛】此题主要考查了等腰三角形的判定以及应用设计与作图等知识,正确利用图形分类讨论得出是解题关键．17．（福建·厦门市湖里中学八年级期中）如图,ABC 中,6AB =,4AC =,AD 平分∠BAC ,DE ⊥AB 于点E ,BF ⊥AC 于点F ,2DE =,则BF 的长为______．【答案】5 【提示】过点D 作DG AC ⊥,根据角平分线的性质可得2DG DE ==,结合图形得出6ABDS=,4ACDS=,10ABCS=,利用等面积法计算即可得出结果．【解答】解：如图所示：过点D 作DG AC ⊥,∵AD 平分BAC ∠,DG AC ⊥,DE AB ⊥,∴2DG DE ==, ∵6AB =,4AC =, ∴1·62ABDS AB DE ==,1·42ACDS AC DG ==, ∴10ABCABDACDS S S=+=,∴1·102ABCSAC BF ==, 即14?102BF ⨯=, 解得：5BF =, 故答案为：5． 【点睛】题目主要考查角平分线的性质及三角形等面积法求三角形的高,理解题意,熟练掌握运用角平分线的性质是解题关键．18．（云南·云大附中八年级期中）如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点G ,过点G 作EF //BC 交AB 于E ,交AC 于F ,过点G 作GD AC ⊥于D ,下列五个结论：①EF BE CF =+；②BE CF =；③1902BGC A ∠=︒+∠；④点G 到△ABC 各边的距离相等；⑤设GD m =,AE AF n +=,则AEF S mn =△．其中正确的结论是______（请填写序号）．【答案】①③④ 【提示】①根据BG 、CG 为角平分线,且EF ∥BC ,可得△BEG 和△CFG 为等腰三角形,从而得出结论； ②G 为角平分线交点,不能得到BE 和CF 相等；③先根据角平分线的性质得出∠GBC +∠GCB =12（∠ABC +∠ACB ）,再由三角形内角和定理即可得出结论；④根据角平分线定理即可得出答案；⑤连接AG,根据三角形面积公式即可得出答案． 【解答】解：①∵∠ABC 和∠ACB 的平分线相交于点G ； ∴∠EBG =∠CBG ,∠FCG =∠BCG ．∵EF ∥BC ,∴∠EGB =∠CBG ,∠FGC =∠BCG ； ∴∠EBG =∠EGB ,∠FGC =∠FCG , ∴EB =EG ,FG =FC ,∴EF =EG +FG =BE +CF ,故本小题正确；②G 点是角平分线的交点,G 不一定是EF 中点,故本小题错误； ③∵∠ABC 和∠ACB 的平分线相交于点G ； ∴∠GBC +∠GCB =12ABC ACB ∠+∠（）=18012A ︒-∠（）,∴∠BGC =180GBC GCB ︒-∠+∠（）=11180802A ︒-︒-∠（）=190+2A ︒∠,故本小题正确； ④∵CG 平分∠ACB ,∴G 到AC 、BC 的距离相等； ∵BG 平分∠ABC ,∴G 到AB 、BC 的距离相等； ∴G 到三边的距离都相等,故本小题正确；⑤连接AG ,∵点G 是角平分线的交点,GD m =,AE AF n +=, ∴1122AEF S AE GD AF GD =⋅+⋅△=()12AE AF GD +⋅=12nm ,故本小题错误． 答案为：①③④【点睛】本题主要考查的是等腰三角形的性质与判定、角平分线的性质、三角形内角和定理,熟练掌握相关内容是解题的关键． 三、解答题19．（广东·深圳市福田区第二实验学校八年级期中）如图,在△ABC 中,AB ＝4,BC 5点D 在AB 上,且BD ＝1,CD ＝2．(1)求证：CD ⊥AB ； (2)求AC 的长． 【答案】(1)见解析 13【提示】（1）根据勾股定理逆定理证明△BCD 是直角三角形,即可得证； （2）先求得AD ＝AB DB -3=,在Rt △ACD 中,勾股定理求解即可． (1)证明：∵在△BCD 中,BD ＝1,CD ＝2,BC 5∴BD 2＋CD 2＝12＋2252＝BC 2, ∴△BCD 是直角三角形,且∠CDB ＝90°, ∴CD ⊥AB ； (2)解：∵CD ⊥AB , ∴∠ADC ＝90°, ∵AB ＝4,DB ＝1, ∴AD ＝3,在Rt △ACD 中,∵CD ＝2,∴AC 22AD CD +2232+13∴AC 13 【点睛】本题考查了勾股定理以及勾股定理的逆定理,掌握勾股定理是解题的关键． 20．（天津·八年级期中）如图,AC BC ⊥,BD AD ⊥,AC 与BD 交于点O ,AC BD =．(1)求证：ΔΔADB BCA ≅； (2)求证：OAB ∆是等腰三角形． 【答案】(1)见解析 (2)见解析 【提示】根据AC BC ⊥,BD AD ⊥可证角相等并等于90度,进而可证Rt ABD Rt BAC ≌； 由（1）可知Rt ABD Rt BAC ≌,进而可证OA OB =,从而可证OAB 是等腰三角形． (1) 证明：AC BC ⊥,BD AD ⊥90D C ∴∠=∠=︒,在Rt ABD △和Rt BAC 中,AC BDAB BA =⎧⎨=⎩, ∴()Rt ABD Rt BAC HL ≌． (2)∵Rt ABD Rt BAC ≌DBA CAB ∴∠=∠,OA OB ∴=,即OAB 是等腰三角形． 【点睛】本题考查直角三角形的判定,全等三角形的性质,等腰三角形的证明,能够找到判定全等所需的条件进行全等判定是解决本题的关键．21．（重庆·八年级期中）点C 、D 都在线段AB 上,且AD BC =,AE BF =,A B ∠=∠,CE 与DF 相交于点G ．(1)求证：ΔΔACE BDF ≅； (2)若10CE =,4DG =,求EG 的长． 【答案】(1)见解析 (2)6 【提示】（ 1）由“SAS ”可证ΔΔACE BDF ≅；（ 2）由全等三角形的性质可得ACE BDF ∠=∠,可得4CG DG ==,即可求解． (1) 证明：AD BC =,AD DC BC DC ∴+=+,AC BD ∴=,在ACE ∆与BDF ∆中, AC BD A B AE BF =⎧⎪∠=∠⎨⎪=⎩, ()ΔΔACE BDF SAS ∴≅；(2)由（1）得：ΔΔACE BDF ≅,ACE BDF ∴∠=∠, 4CG DG ∴==,1046EG CE CG ∴=-=-=．【点睛】本题考查了全等三角形的判定和性质,等腰三角形的判定与性质,证明三角形全等是解题的关键． 22．（广东·珠海市文园中学八年级期中）如图,已知：E 是∠AOB 的平分线上一点,EC ⊥OB ,ED ⊥OA ,C 、D 是垂足,连接CD ,且交OE 于点F ．(1)求证：OE是CD的垂直平分线；(2)若∠AOB=60°,请直接写出OE与EF之间的数量关系．【答案】(1)见解析(2)OE=4EF【提示】（1）先根据E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA得出△ODE≌△OCE,可得出OD=OC,DE=CE,OE=OE,可得出△DOC是等腰三角形,由等腰三角形的性质即可得出OE是CD的垂直平分线；（2）先根据E是∠AOB的平分线,∠AOB=60°可得出∠AOE=∠BOE=30°,由直角三角形的性质可得出OE=2DE,同理可得出DE=2EF即可得出结论．(1)证明：∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,∴DE=CE,∵OE=OE,∴Rt△ODE≌Rt△OCE,∴OD=OC,∴△DOC是等腰三角形,∵OE是∠AOB的平分线,∴OE是CD的垂直平分线；(2)解：∵OE是∠AOB的平分线,∠AOB=60°,∴∠AOE=∠BOE=30°,∵EC⊥OB,ED⊥OA,∴OE=2DE,∠ODF=∠OED=60°,∴∠EDF=30°,∴OE=4EF．【点睛】本题考查的是角平分线的性质及直角三角形的性质、等腰三角形的判定与性质,熟知以上知识是解答此题的关键．23．（山东·昌乐县教学研究室八年级期中）△ABC中,AB＝AC,BD平分∠ABC交AC于点D,从点A作AE∥BC交BD的延长线于点E．（1）若∠BAC＝40°,求∠E的度数；（2）点F是BE上一点,且FE＝BD．取DF的中点H,请问AH⊥BE吗？试说明理由．【答案】（1）∠E＝35°；（2）AH⊥BE．理由见解析．【提示】（1）根据等腰三角形两底角相等,已知顶角,可以求出底角,再根据角平分线的定义求出∠CBD的度数,最后根据两直线平行,内错角相等求出；（2）由“SAS”可证△ABD≌△AEF,可得AD=AF,由等腰三角形的性质可求解．【解答】解：（1）∵AB=AC,∴∠ABC=∠ACB,∵∠BAC=40°,∴∠ABC=12（180°-∠BAC）=70°,∵BD平分∠ABC,∴∠CBD=12∠ABC=35°,∵AE∥BC,∴∠E=∠CBD=35°；（2）∵BD平分∠ABC,∠E=∠CBD, ∴∠CBD=∠ABD=∠E,在△ABD和△AEF中,AB AEE ABDBD EF=⎧⎪∠=∠⎨⎪=⎩,∴△ABD≌△AEF（SAS）,∴AD=AF,∵点H是DF的中点,∴AH⊥BE．【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,证明三角形全等是解题的关键．24．（广西柳州·八年级期中）如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M．（1）若∠B=70°,则∠NMA的度数是_________．（2）连接MB,若AB=8cm,BC=6cm．①求△MBC的周长；②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,直接写出△PBC的周长最小值；若不存在,说明理由．【答案】（1）50°；（2）①14cm；②存在,14cm．【提示】（1）根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案；（2）①根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案；②根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系．【解答】解：（1）∵∠B=70°,AB=AC,∴∠B=∠C=70°,∴∠A=180°-∠B-∠C=50°,∵MN⊥AB,∴∠ANM=90°,∴∠NMA=90°-∠A=50°,故答案为：50°；（2）如图：①∵MN垂直平分AB．∴MB=MA,又∵BC=6cm,AC=BC=8cm,∴△MBC的周长是MB+MC+BC= MA+MC+BC=AC+BC=14(cm)；②当点P与M重合时,△PBC周长的值最小,理由：∵PB+PC=P A+PC,P A+PC≥AC,∴P与M重合时,P A+PC=AC,此时PB+PC最小,∴△PBC周长的最小值=AC+BC=8+6=14(cm)．【点睛】本题主要考查了轴对称的性质,等腰三角形的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,熟记性质是解题的关键．25．（江苏盐城·八年级期中）如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高．（1）求证：AD垂直平分EF；（2）若AB+AC＝10,S△ABC＝15,求DE的长．【答案】（1）见解析；（2）3DE（1）由角平分线的性质得DE ＝DF ,再根据HL 证明Rt △AED ≌Rt △AFD ,得AE ＝AF ,从而证明结论； （2）根据DE ＝DF ,得111++()15222ABDACDS SAB ED AC DF DE AB AC ==+=,代入计算即可． 【解答】（1）证明：∵AD 是△ABC 的角平分线,DE 、DF 分别是△ABD 和△ACD 的高, ∴DE ＝DF ,在Rt △AED 与Rt △AFD 中,AD ADDE DF =⎧⎨=⎩, ∴Rt △AED ≌Rt △AFD （HL ）, ∴AE ＝AF , ∵DE ＝DF ,∴AD 垂直平分EF ； （2）解：∵DE ＝DF , ∴111++()15222ABDACDSSAB ED AC DF DE AB AC ==+=, ∵AB +AC ＝10, ∴DE ＝3． 【点睛】本题考查了全等三角形的判定与性质,角平分线的性质,解题的关键是掌握这些知识点．26．（湖北武汉·八年级期中）如图,在△ABC 中,∠ACB ＝90°,∠A =30°,D 为AB 上一点,以CD 为边在CD 右侧作等边△CDE ．（1）如图1,当点E 在边AC 上时,求证：DE ＝AE ；（2）如图2,当点E 在△ABC 内部时,猜想ED 和EA 数量关系；（3）当点E 在△ABC 外部时,过点E 作EH ⊥AB 点H ,EF ∥AB ,CF ＝2,AH ＝3．直接写出AB 的长为 ．【答案】（1）见解析；（2）ED =EA ,理由见解析；（3）16（1）根据等边三角形的性质、三角形的外角的性质得到∠EDA＝∠A,根据等腰三角形的判定定理证明；（2）取AB的中点O,连接CO、EO,分别证明△BCD≌△OCE和△COE≌△AOE,根据全等三角形的性质证明；（3）取AB的中点O,连接CO、EO、EA,根据（2）的结论得到△CEF≌△DCO,根据全等三角形的性质解答．【解答】（1）证明：∵△CDE是等边三角形,∴∠CED＝∠DCE=60°,∴∠EDA＝60°﹣∠A＝30°,∵∠A=30°,∴∠EDA=30°,∴∠EDA＝∠B,∴DE＝EA；（2）结论：ED＝EA,理由：如图2中,取AB的中点O、EO,∵∠ACB＝90°,∠BAC＝30°,∴∠B＝60°,OC＝OB,∴△BCO为等边三角形,∴CB＝CO=BO=AO,∵△CDE是等边三角形,∴∠BCD＝∠OCE,在△BCD和△OCE中,CB COBCD OCECD CE=⎧⎪∠=∠⎨⎪=⎩,∴∠COE＝∠B＝60°,∴∠AOE＝60°,在△COE和△AOE中,OC OACOE AOEOE OE=⎧⎪∠=∠⎨⎪=⎩,∴△COE≌△AOE（SAS）,∴EC＝EA,∴ED＝EA；（3）解：如图3中,取AB的中点O、连接EO,AE,由（2）得△BCD≌△OCE,∴∠COE＝∠B＝60°,∴∠AOE＝60°,同法可得△COE≌△AOE,∴EC＝EA,∴ED＝EA,∵EH⊥AB,∴DH＝AH＝5,∵EF∥AB,∴∠F＝180°﹣∠B＝120°,∵∠FCD＝∠FCE+60°＝∠CDB+60°,∴∠FCE＝∠CDB,在△CEF和△DCO中,F CODECF ODCCE CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴CF＝OD＝2,∴OA＝OD+AD＝2+6＝8,∴AB＝2OA＝16．【点睛】本题主要考查了等边三角形判定和性质,全等三角形的判定和性质,熟练掌握等边三角形判定和性质定理,全等三角形的判定和性质定理是解题的关键．27．（四川·成都外国语学校八年级期中）如图1,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,∠ACE＝45°．(1)求证：△AEF≌△CEB．(2)若G在BC的延长线上,连接GA,若GA＝GB,求证：AC平分∠DAG．(3)如图2,在（2）的条件下,H为AG的中点,连接DH交AC于M,连接EM、ED,若S△EMC＝4,∠BAD ＝15°,求AM的长．【答案】(1)见解析(2)见解析(3)6【提示】（1）先判断出AE=CE,再利用等角的余角相等判断出∠EAF=∠ECB,进而判断出AEF CEB△≌△,即可得出结论；（2）先利用三角形外角的性质得出∠AEF=45︒+∠CAD,进而得出∠B=45︒+∠CAD,而∠B=∠BAG,得出∠BAG=45︒+∠CAD,而∠BAG=45︒+∠CAG,即可得出结论；（3）先判断出ADH是等边三角形,进而利用含30度角的直角三角形的性质判断出AM=3CM,进而求出ACM的面积,即可求出AE,进而求出AC,即可得出结论．(1)证明：∵CE⊥AB,∴∠AEC ＝∠BEC ＝90°, ∵∠ACE ＝45°, ∴∠CAE ＝45°＝∠ACE , ∴AE ＝CE , ∵AD ⊥BC , ∴∠ADC ＝90°, ∴∠ECB +∠CFD ＝90°, ∵∠CFD ＝∠AFE , ∴∠ECB +∠AFE ＝90°, ∵∠EAF +∠AFE ＝90°, ∴∠EAF ＝∠ECB , 在AEF 和CEB 中,90EAF ECB AE CE AEF CEB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴AEF CEB △≌△（ASA ）； (2)∵AEF CEB △≌△, ∴∠AFE ＝∠B ,∵∠AFE ＝∠ACE +∠CAD ＝45°+∠CAD , ∴∠B ＝45°+∠CAD , ∵AG ＝BG , ∴∠B ＝∠BAG , ∴∠BAG ＝45°+∠CAD ,∵∠BAG ＝∠CAE +∠CAG ＝45°+∠CAG , ∴∠CAD ＝∠CAG , ∴AC 平分∠DAG ； (3)∵∠BAD ＝15°,∠CAE ＝45°, ∴∠CAD ＝∠CAE ﹣∠BAD ＝30°, ∵∠CAD ＝∠CAG ,∴∠DAG＝2∠CAD＝60°,在Rt△ADG中,点H是AG的中点,∴DH＝AH,∴△ADH是等边三角形,∴∠ADH＝60°,AD＝AH,∵∠CAD＝∠CAG,∴AC⊥DH,即：∠AMD＝∠DMC＝90°∵∠ADC＝90°,∴∠CDM＝30°,在Rt△DMC中,DM,在Rt△AMD中,AM＝3CM, ∴S△AEM＝3S△CEM＝3×4＝12,∴S△ACE＝S△CEM+S△AEM＝16,∵∠AEC＝90°,AE＝CE,∴S△ACE＝12AE2＝16,∴AE＝∴AC＝8,∴AM+CM＝8,∵AM＝3CM,∴3CM+CM＝8,∴CM＝2,∴AM＝3CM＝6．【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等角的余角相等,等边三角形的判定和性质,三角形外角的性质,含30度角的直角三角形的性质,求出AE是解本题的关键．。

专题01 三角形的三边、内外角、高线、中线及角平分线压轴题九种模型全攻略考点一三角形的稳定性考点二三角形的三边关系考点三三角形内角和定理的证明考点四与平行线有关的三角的内角和问题考点五三角形的高线、中线、角平分线考点六与角平分线有关的三角的内角和问题考点七三角形折叠中的角度问题考点八三角形内角和定理的应用考点九三角形外角的定义和性质考点一三角形的稳定性例题：（2021·广西·南宁十四中七年级期末）下列图形中没有运用三角形稳定性的是（）A．B．C．D．【答案】B【解析】【分析】利用三角形的稳定性解答即可．【详解】解：对于A、C、D选项，都含有三角形，故利用了三角形的稳定性；而B选项中，用到了四边形的不稳定性.故选B．【点睛】本题主要考查了三角形的稳定性，需理解稳定性在实际生活中的应用；明确能体现出三角形的稳定性，则说明物体中必然存在三角形是解题关键．【变式训练】1．（2022·吉林吉林·二模）如图，人字梯中间设计一“拉杆”，在使用梯子时，固定拉杆会增加安全性．这样做蕴含的数学道理是（）A．三角形具有稳定性B．两点之间线段最短C．经过两点有且只有一条直线D．垂线段最短【答案】A【解析】【分析】人字梯中间设计一“拉杆”后变成一个三角形，稳定性提高．【详解】三角形的稳定性如果三角形的三条边固定，那么三角形的形状和大小就完全确定了，三角形的这个特征，叫做三角形的稳定性.故选A【点睛】本题考查三角形的稳定性，理解这一点是本题的关键．2．（2022·广东·佛山市惠景中学七年级期中）如图所示的自行车架设计成三角形，这样做的依据是三角形具有___．【答案】稳定性【解析】【分析】根据是三角形的稳定性，即可求解．【详解】解：自行车的主框架采用了三角形结构，这样设计的依据是三角形具有稳定性，故答案为：稳定性．【点睛】本题考查的是三角形的性质，掌握三角形具有稳定性是解题的关键．考点二三角形的三边关系例题：（2022·黑龙江·哈尔滨市风华中学校七年级期中）下列各组长度的线段为边，能构成三角形的是（）．A．1，2，3B．3，4，5C．4，5，11D．6，3，3【答案】B【解析】【分析】比较三边中两较小边之和与较大边的大小即可得到解答．【详解】解：A、1+2=3，不符合题意；B、3+4>5，符合题意；C、4+5<11，不符合题意；D、3+3=6，不符合题意；故选B．【点睛】本题考查构成三角形的条件，熟练掌握三角形的三边关系是解题关键．【变式训练】1．（2022·黑龙江·哈尔滨市第六十九中学校七年级期中）下列各组长度的三条线段能够组成三角形的是（）A．3，4，8B．5，6，11C．5，6，10D．10，7，3【答案】C【解析】【分析】根据三角形三边关系可直接进行排除选项．【详解】解：A、3+4＜8，不符合三角形三边关系，故不能构成三角形；B、5+6=11，不符合三角形三边关系，故不能构成三角形；C、5+6＞10，符合三角形三边关系，故能构成三角形；D、3+7=10，不符合三角形三边关系，故不能构成三角形；故选C．【点睛】本题主要考查三角形三边关系，熟练掌握三角形三边关系是解题的关键．2．（2022·海南·海口市第十四中学七年级阶段练习）在△ABC中，三条边长分别为3和6，第三边长为奇数，那么第三边的长是()A．5或7B．7或9C．3或5D．9【答案】A【解析】【分析】先求出第三边长的取值范围，再根据条件具体确定符合条件的值即可．【详解】解：因为三条边长分别为3和6，所以6-3＜第三边＜6+3，所以3＜第三边＜9，因为第三边长为奇数，∴第三边的长为5或7，故选：A．【点睛】本题考查了三角形的三边关系，掌握三角形任意两边之和大于第三边，任意两边之差小于第三边是解题的关键．3．（2022·江苏·南师附中新城初中七年级期中）已知三角形三边长分别为3，x，14，若x为正整数，则这样的三角形个数为（）A．4B．5C．6D．7【答案】B【解析】【分析】直接根据三角形的三边关系求出x的取值范围，进而可得出结论．【详解】解：三角形三边长分别为3，x，14，x<<．∴-<<+，即1117x143143x为正整数，x=，13，14，15，16，即这样的三角形有5个．12故选：B．【点睛】本题考查的是三角形的三边关系，熟知三角形两边之和大于第三边，两边之差小于第三边是解答此题的关键．考点三 三角形内角和定理的证明例题：（2021·广西·靖西市教学研究室八年级期末）（1）如图①，直线DE 经过点A ，DE ∴BC ．若∴B ＝45°，∴C ＝58°，那么∴DAB ＝ ；∴EAC ＝ ；∴BAC ＝ ．(在空格上填写度数）（2）求证：在∴ABC 中，∴A +∴B +∴C ＝180°．【答案】（1）45°；58°；77°（2）见解析【解析】【分析】（1）通过平行线的性质，两直线平行，内错角相等，可分别求出：45DAB ∠=︒，58EAC ∠=︒．由图可知：180DAB BAC EAC ∠+∠+∠=︒，可求出：77BAC ∠=︒．（2）过点A 作//DE BC ，通过平行线的性质，可得：B DAB ∠=∠，C EAC ∠=∠所以180BAC B C BAC DAB EAC ∠+∠+∠=∠+∠+∠=︒．【详解】（1）解：//DE BC ，45B ∠=︒，58C ∠=︒∴45B DAB ∠=∠=︒，=58C EAC ∠=∠︒180BAC DAB EAC ∠+∠+∠=︒∴18077BAC DAB EAC ∠=︒-∠-∠=︒，故答案是：45°，58°，77°；（2）证明：过点A 作//DE BC//DE BC∴B DAB ∠=∠，C EAC ∠=∠180BAC DAB EAC ∠+∠+∠=︒∴180BAC B C BAC DAB EAC ∠+∠+∠=∠+∠+∠=︒【点睛】本题主要考查知识点为，平行线的性质．即：两直线平行，同位角相等，内错角相等，同旁内角互补．熟练掌握平行线的性质是解决本题的关键．【变式训练】1．（2022·全国·八年级专题练习）在小学，我们曾经通过动手操作，利用拼图的方法研究了三角形三个内角的数量关系．如图，把三角形ABC分成三部分，然后以某一顶点（如点B）为集中点，把三个角拼在一起，观察发现恰好构成了平角，从而得到了“三角形三个内角的和是180°”的结论．但是，通过本学期的学习我们知道：由观察、实验、归纳、类比、猜想得到的结论还需要通过证明来确认它的正确性．小聪认真研究了拼图的操作方法，形成了证明命题“三角形三个内角的和是180°”的思路：①画出命题对应的几何图形；②写出已知，求证；③受拼接方法的启发画出辅助线；④写出证明过程．请你参考小聪解决问题的思路，写出证明该命题的完整过程．【答案】见解析【解析】【分析】根据要求画出△ABC，写出已知，求证．构造平行线，利用平行线的性质解决问题即可．【详解】解：已知：△ABC．求证：∴A+∴B+∴C=180°．证明：如图，延长CB到F，过点B作BE∴AC．∴BE∴AC，∴∴1=∴4，∴5=∴3，∴∴2+∴4+∴5=180°，∴∴1+∴2+∴3=180°，即∴A +∴ABC +∴C =180°．【点睛】本题考查三角形内角和定理的证明，平行线的性质，平角的定义等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题．2．（2022·北京·中考真题）下面是证明三角形内角和定理的两种添加辅助线的方法，选择其中一种，完成证明． 三角形内角和定理：三角形三个内角和等于180°， 已知：如图，ABC ∆,求证：180.A B C ∠+∠+∠=方法一证明：如图，过点A 作.DE BC ∥方法二证明：如图，过点C 作.CD AB ∥【解析】【分析】 选择方法一，过点A 作//DE BC ，依据平行线的性质，即可得到B BAD ∠=∠，C EAC ∠=∠，再根据平角的定义，即可得到三角形的内角和为180︒．【详解】证明：过点A 作//DE BC ，则B BAD ∠=∠，C EAC ∠=∠．( 两直线平行，内错角相等）点D ，A ，E 在同一条直线上，180DAB BAC C ∴∠+∠+∠=︒．（平角的定义）180B BAC C ∴∠+∠+∠=︒．即三角形的内角和为180︒．【点睛】本题主要考查了平行线的性质以及三角形内角和定理的运用，熟练掌握平行线的性质是解题的关键．考点四 与平行线有关的三角的内角和问题例题：（2022·山东泰安·一模）如图，AB ∥CD ，EF 分别与AB ，CD 交于点B ，F ．若30E ∠=︒，130EFC ∠=︒，则A ∠=______．【答案】20︒【解析】【分析】通过两直线平行，同位角相等，求出∴ABE 的度数，再利用三角形内角和定理求解．【详解】解：//AB CD ，130ABE EFC ∠∠∴==︒，在∴ABE 中，30E ∠=︒，1801803013020A E ABE ∠∴=︒-∠-∠=︒-︒-︒=︒，20A ∠∴=︒．故答案为：20︒．【点睛】本题考查平行线的性质，三角形的内角和定理，灵活运用平行线的性质和三角形内角和定理是解题的关键．【变式训练】1．（2022·江西南昌·模拟预测）如图，直线AB ，CD 被直线BC ，EG 所截．若AB //CD ，176∠=︒，236∠=︒，则3∠的度数为（ ）A ．30B ．36︒C ．40︒D ．45︒【答案】C【解析】【分析】由两直线平行，同旁内角互补求出∴CGE的度数，再由三角形的内角和定理求得∴3的度数．【详解】∠=︒，解：∴AB//CD，176∴∴CGE＝180°－∴1＝104°，∴∴2＋∴3＋∴CGE＝180°，236∠=︒，∴∴3＝180°－∴2－∴CGE＝40°．故选：C【点睛】此题考查了平行线的性质、三角形的内角和定理，熟练掌握相关性质和定理是解题的关键．2．（2022·全国·八年级课时练习）如图所示，直线a b∥，直线c与直线a，b分别相交于点A、点B，AM∴b，垂足为点M，若∴1＝56°，则∴2＝______．【答案】34°##34度【解析】【分析】先根据平行线的性质得出∴ABM的度数，再由三角形内角和定理求出∴2的度数即可．【详解】∥，∴1＝56°，：解：∴直线a b∴∴ABM＝∴1＝56°，∴AM∴b，垂足为点M，∴∴AMB＝90°，∴∴2＝180°−∴AMB−∴ABM＝180°−56°−90°＝34°，故答案为：34°．【点睛】本题考查三角形中求角度问题，涉及到平行线的性质、三角形内角和定理，在求角度问题中，熟练运用三角形内角和是180°是解决问题的关键．考点五 三角形的高线 、中线、角平分线例题1：（2022·重庆市育才中学七年级阶段练习）下列各组图形中，BD 是ABC 的高的图形是（ ） A ． B ． C ． D ．【答案】B【解析】【分析】三角形的高即从三角形的顶点向对边引垂线，顶点和垂足间的线段．根据概念即可得到答案．【详解】解：根据三角形高的定义可知，只有选项B 中的线段BD 是∴ABC 的高，故选：B ．【点睛】考查了三角形的高的概念，掌握高的作法是解题的关键．例题2：（2021·广西·靖西市教学研究室八年级期中）如图，已知BD 是∴ABC 的中线，AB ＝5，BC ＝3，且∴ABD的周长为12，则∴BCD 的周长是_____．【答案】10【解析】【分析】先根据三角形的中线、线段中点的定义可得AD CD =，再根据三角形的周长公式即可求出结果．【详解】 解：BD 是ABC 的中线，即点D 是线段AC 的中点，AD CD ∴=，5AB =，ABD △的周长为12，12AB BD AD ∴++=，即512BD AD ++=，解得：7BD AD +=，7BD CD ∴+=，则BCD △的周长是3710BC BD CD ++=+=．故答案为：10．【点睛】本题主要考查了三角形的中线、线段中点的定义等知识点，掌握线段中点的定义是解题关键．例题3：（2022·全国·八年级）如图，在ABC 中，90CAB ∠=︒，AD 是高，CF 是中线，BE 是角平分线，BE 交AD 于G ，交CF 于H ，下列说法正确的是（ ）①AEG AGE ∠=∠；②BH CH =；③2EAG EBC ∠=∠；④ACF BCF S S =A ．①③B ．①②③C ．①③④D ．②③④【答案】C【解析】【分析】 ①根据∴CAB =90°，AD 是高，可得∴AEG =90°−∴ABE ，∴DGB =90°−∴DBG ，又因为BE 是角平分线，可得∴ABE =∴DBE ，故能得到∴AEG =∴DGB ，再根据对顶角相等，即可求证该说法正确；②因为CF 是中线，BE 是角平分线，得不到∴HCB =∴HBC ，故该说法错误；③∴EAG +∴DAB =90°，∴DBA +∴DAB =90°，可得∴EAG =∴DBA ，因为∴DBA =2∴EBC ，故能得到该说法正确； ④根据中线平分面积，可得该说法正确．【详解】解：①∴∴CAB =90°，AD 是高，∴∴AEG =90°−∴ABE ，∴DGB =90°−∴DBG ，∴BE 是角平分线，∴∴ABE =∴DBE ，∴∴AEG =∴DGB ，∴∴DGB =∴AGE ，∴∴AEG =∴AGE ，故该说法正确；②因为CF 是中线，BE 是角平分线，得不到∴HCB =∴HBC ，故该说法错误；③∴∴EAG +∴DAB =90°，∴DBA +∴DAB =90°，∴∴EAG =∴DBA ，∴∴DBA=2∴EBC，∴∴EAG=2∴EBC，故该说法正确；④根据中线平分面积，可得S△ACF=S△BCF，故该说法正确．故选：C．【点睛】本题考查了三角形的高，中线，角平分线的性质，解题的关键是熟练掌握各线的特点和性质．【变式训练】1．（2022·浙江杭州·中考真题）如图，CD∴AB于点D，已知∴ABC是钝角，则（）A．线段CD是ABC的AC边上的高线B．线段CD是ABC的AB边上的高线C．线段AD是ABC的BC边上的高线D．线段AD是ABC的AC边上的高线【答案】B【解析】【分析】根据高线的定义注意判断即可．【详解】∴ 线段CD是ABC的AB边上的高线，∴A错误，不符合题意；∴ 线段CD是ABC的AB边上的高线，∴B正确，符合题意；∴ 线段AD是ACD的CD边上的高线，∴C错误，不符合题意；∴线段AD是ACD的CD边上的高线，∴D错误，不符合题意；故选B．【点睛】本题考查了三角形高线的理解，熟练掌握三角形高线的相关知识是解题的关键．2．（2022·陕西·西安市曲江第一中学七年级期中）在ABC中，BC边上的中线AD将ABC分成的两个新三角形的周长差为5cm，AB与AC的和为11cm，则AC的长为________．【答案】3cm或8cm【解析】【分析】根据三角形的中线的定义可得BD CD =，然后求出ABD △与ADC 的周长差是AB 与AC 的差或AC 与AB 的差，然后代入数据计算即可得解．【详解】如图1，图2，∴AD 是BC 边上的中线，∴BD CD =，∴中线AD 将ABC 分成的两个新三角形的周长差为5cm ，∴()()5AB BD AD AC CD AD ++-++=或()()5AC CD AD AB BD AD ++-++=，∴5AB AC -=或者5AC AB -=，∴AB 与AC 的和为11cm ，∴11AB AC +=，∴83AB AC =⎧⎨=⎩或38AB AC =⎧⎨=⎩， 故答案为：3cm 或8cm ．【点睛】本题考查了三角形的中线，熟记概念并求出两个三角形的周长的差等于两边长的差是解题的关键． 3．（2021·全国·八年级课时练习）填空：（1）如图（1）,,AD BE CF 是ABC 的三条中线，则2AB =______，BD =______，12AE =______． （2）如图（2）,,AD BE CF 是ABC 的三条角平分线，则1∠=______，132∠=______，2ACB ∠=______．【答案】 AF 或BF CD AC 2∠ ABC ∠ 4∠【解析】【分析】（1）根据三角形的中线定义：三角形一边的中点与此边所对顶点的连线叫做三角形的中线可得E 、F 、D 分别是AC 、AB 、BC 上的中点，进而得到答案．（2）根据角平分线定义，从一个角的顶点出发，把这个角分成两个相等的角的射线，叫做这个角的平分线即可解答．【详解】解：（1）∴CF 是AB 边上的中线，∴AB ＝2AF ＝2BF ；∴AD 是BC 边上的中线，∴BD ＝CD ，∴BE 是AC 边上的中线，∴AE ＝12AC ，（2）∴AD 是BAC ∠的角平分线，∴12∠=∠ ，∴BE 是ABC ∠的角平分线， ∴132∠=ABC ∠， ∴CF 是ACB ∠的角平分线，∴2ACB ∠=4∠．故答案为：AF 或BF ；CD ；AC ；2∠；ABC ∠；4∠【点睛】此题主要考查了三角形的中线、角平分线，解题的关键是掌握三角形的中线及角平分线的定义．考点六 与角平分线有关的三角的内角和问题例题：（2022·江苏·南京市第十三中学七年级期中）在∴ABC 中，∴ABC 与∴ACB 的平分线相交于点P ，若∴P =125°，则∴A =_____°【答案】70【解析】【分析】依据BP 、CP 分别平分∴ABC 、∴ACB ，可得∴PBC =12∴ABC ，∴PCB =12∴ACB ，再根据三角形内角和定理，即可求得∴ABC +∴ACB =110°，即可求得∴A 的度数．【详解】 解：BP 、CP 分别平分∴ABC 、∴ACB ，∴∴PBC =12∴ABC ，∴PCB =12∴ACB ， =180=180125=55PBC PCB P ∠+∠︒-∠︒-︒︒，∴∴PBC +∴PCB =12∴ABC +12∴ACB =55°， ∴∴ABC +∴ACB =110°，()=180=180110=70ABC ACB A ∠∴∠︒-︒-︒+∠︒，故答案为：70．【点睛】本题考查了三角形内角和定理，角平分线定义，能正确运用定理进行推理是解此题的关键．【变式训练】1.（2022·福建省福州屏东中学七年级期末）如图，在ABC 中，AD 是高，AE 是角平分线．(1)若32B =︒∠，60C ∠=°，求DAE ∠的度数；(2)若18C B ∠-∠=︒，求DAE ∠的度数．【答案】(1)14°(2)9° 【解析】【分析】先求∴DAC =30°，再求∴BAC =180°-32°-60°=88°，根据角的平分线计算∴EAC =1442BAC ∠=︒，求得∴DAE =14°． (2)根据∴DAE =12BAC DAC ∠-∠=1(180)(90)2B C C -∠-∠--∠=11909022B C C -∠-∠-+∠=12()C B ∠-∠，代入计算即可．(1)∴AD 是高，AE 是角平分线，32B =︒∠，60C ∠=°，∴∴DAC =30°，∴BAC =180°-32°-60°=88°，∴∴EAC =1442BAC ∠=︒， ∴∴DAE =∴EAC -∴DAC =44°-30°=14°．(2)∴∴DAE =12BAC DAC ∠-∠ =1(180)(90)2B C C -∠-∠--∠ =11909022B C C -∠-∠-+∠ =12()C B ∠-∠，18C B ∠-∠=︒，∴∴DAE =9°．【点睛】本题考查了三角形内角和定理，直角三角形性质，角的平分线意义，熟练掌握三角形内角和定理，直角三角形性质是解题的关键．2．（2022·黑龙江·哈尔滨工业大学附属中学校七年级期中）如图，ABC 中，AD BC ⊥于点D ，E 为AC 上任意一点，连接BE 交AD 于点F ．(1)若4070ABD AFE ∠=︒∠=︒，，求证：BE 平分ABC ∠．(2)如图2，在（1）的条件下，若AFE AEF ∠=∠，请直接写出图中所有直角三角形．【答案】(1)证明见解析；(2)∴ABC 、∴ABE 、∴ABD 、∴ACD 、∴BDF 都是直角三角形．【解析】【分析】（1）AD ∴BC ，得∴ADB =90°，进而得∴DBF =20°，又由∴ABD =40°即可得∴DBF = 12ABD ∠，即可证明结论成立； （2）由AD ∴BC 得∴ABD 、∴ACD 、∴BDF 是直角三角形，另由∴ABE +∴AEF =20°+ 70°=90°，可得∴BAE =90°得∴ABE 、∴ABC 是直角三角形．(1)解： ∴AD ∴BC ，∴∴ADB =90°，∴在Rt ∴BDF 中，∴DBF +∴BFD =90°，∴∴BFD +∴AFE =70°，∴∴DBF =20°，∴∴ABD =40°，∴∴DBF = 12ABD ∠， ∴BE 平分∴ABC ；(2)解：∴AD ∴BC ，∴∴ABD 、∴ACD 、∴BDF 是直角三角形，∴∴ABE =∴CBE =20°，∴∴AEF =∴AFE =70°，∴∴ABE +∴AEF =20°+ 70°=90°，∴.在∴ABE 中，∴BAE =90°，∴∴ABC 、∴ABE 是直角三角形，综上所述∴ABC 、∴ABE 、∴ABD 、∴ACD 、∴BDF 都是直角三角形．【点睛】本题主要考查了直角三角形及角平分线与垂直，熟练掌握直角三角形的概念是解题的关键．考点七 三角形折叠中的角度问题例题：（2022·河南·南阳市第三中学七年级阶段练习）如图，在三角形纸片ABC 中，65A ∠=︒，75B ∠=︒，将纸片的一角折叠，使点C 落在ABC 外的点C '处．若225∠=︒，则1∠的度数为（ ）A．115°B．100°C．105°D．95°【答案】C【解析】【分析】在∴ABC中利用三角形内角和定理可求出∴C的度数，由折叠的性质，可知：∴CDE＝∴C′DE，∴CED＝∴C′ED，结合∴2的度数可求出∴CED的度数，在∴CDE中利用三角形内角和定理可求出∴CDE的度数，再由∴1＝180°﹣∴CDE﹣∴C′DE即可求出结论．【详解】解：在∴ABC中，∴A＝65°，∴B＝75°，∴∴C＝180°﹣∴A﹣∴B＝40°．由折叠，可知：∴CDE＝∴C′DE，∴CED＝∴C′ED，∴∴CED＝18022︒+∠＝102.5°，∴∴CDE＝180°﹣∴CED﹣∴C＝37.5°，∴∴1＝180°﹣∴CDE﹣∴C′DE＝180°﹣2∴CDE＝105°．故选：C．【点睛】本题考查了三角形内角和定理以及折叠的性质，利用三角形内角和定理及折叠的性质求出∴CDE的度数是解题的关键．【变式训练】1．（2022·全国·八年级课时练习）如图，在∴ABC中，∴A＝30°，∴B＝50°，将点A与点B分别沿MN和EF折叠，使点A、B与点C重合，则∴NCF的度数为（）.A．22°B．21°C．20°D．19°【答案】C【解析】【分析】根据三角形的内角和定理可得∴ACB ＝100°，再由折叠的性质可得∴ACN ＝∴A ＝30°，∴FCE ＝∴B ＝50°，即可求解．【详解】解：∴∴A ＝30°，∴B ＝50°，∴∴ACB ＝100°，∴将点A 与点B 分别沿MN 和EF 折叠，使点A 、B 与点C 重合，∴∴ACN ＝∴A ＝30°，∴FCE ＝∴B ＝50°，∴∴NCF ＝20°，故选：C ．【点睛】本题主要考查了图形的折叠的性质、三角形内角和定理、熟练掌握图形的折叠的性质、三角形内角和定理是解题的关键．2．（2022·江苏·南京市第十三中学七年级期中）如图 1，△ABC 中，D 是 AC 边上的点，先将 ABD 沿看 BD 翻折，使点 A 落在点A ＇处，且 A ′D ∴BC ，A ′B 交 AC 于点 E （如图 2），又将△BCE 沿着 A ′B 翻折，使点 C 落在点 C ′处，若点C ′恰好落在 BD 上（如图 3），且∴C ′EB =75°，则∴C = ___°【答案】80°##80度【解析】【分析】先由平行线性质得：A '∠=∴CBE ，再由折叠可得：∴A =∴A '，∴ABD =∴DBE =∴CBE ，BC E '∠=∴C ，则∴A =∴ABD =∴DBE =∴CBE ，由三角形内角和定理知180BC E C EB DBE ''∠+∠+∠=︒，而75C EB '∠=︒，可求得105C DBE ∠+∠=︒，然后由∴A +∴C +∴ACB =180°，则∴C +4∴DBE =180°，即可求出∴C 度数．【详解】解：∴A ′D ∴BC ，∴A '∠=∴CBE ，由折叠可得：∴A =∴A '，∴ABD =∴DBE =∴CBE ，BC E '∠=∴C ，∴∴A =∴ABD =∴DBE =∴CBE ，∴180BC E C EB DBE ''∠+∠+∠=︒，75C EB '∠=︒，∴105BC E DBE '∠+∠=︒，∴105C DBE ∠+∠=︒，∴∴A +∴C +∴ACB =180°，∴∴C +4∴DBE =180°，∴∴C =80°，故答案为：80°．【点睛】本题考查平行线的性质，折叠性质，三角形内角和定理，求出105C DBE ∠+∠=︒和∴C +4∴DBE =180°是解题的关键．考点八 三角形内角和定理的应用例题：（2022·河南南阳·二模）小明把一副三角板按如图所示方式摆放，直角边CD 与直角边AB 相交于点F ，斜边∥DE BC ，∴B ＝30°，∴E ＝45°，则∴CFB 的度数是（ ）A ．95°B ．115°C ．105°D ．125°【答案】C【解析】【分析】 根据等腰直角三角形的性质可得45D ∠=︒，再由平行线的性质得出45BCF ∠=︒，再由三角形的内角和定理进行求解即可．【详解】CDE ∆是直角三角形，∴E ＝45°，45D ∴∠=︒，∥DE BC ，45BCF D ∴∠=∠=︒，180,30B BCF BFC B ∠+∠+∠=︒∠=︒，105CFB ∴∠=︒，故选：C ．【点睛】本题考查了等腰直角三角形的性质，平行线的性质及三角形的内角和定理，熟练掌握知识点是解题的关键．【变式训练】1．（2022·福建省福州第十六中学七年级期中）如图，直线MN PQ ∥，点A 在直线MN 与PQ 之间，点B 在直线MN 上，连接AB ．ABM ∠的平分线BC 交PQ 于点C ，连接AC ，过点A 作AD PQ ⊥交PQ 于点D ，作AF AB ⊥交PQ 于点F ，AE 平分DAF ∠交PQ 于点E ，若45CAE ∠=︒，52ACB DAE ∠=∠，则ACD ∠的度数是（ ）A ．18︒B ．27︒C ．30D ．45︒【答案】B【解析】【分析】 设DAE α∠=，则EAF α∠=，52ACB α∠=，先求得180BCE CEA ∠+∠=︒，即可得到AE BC ∥，进而得出ACB CAE ∠=∠，即可得到18DAE ∠=︒，再依据Rt ACD △内角和即可得到∴ACD 的度数．【详解】设DAE α∠=，则EAF α∠=，52ACB α∠=， ∴,AD PQ AF AB ⊥⊥，∴90BAF ADE ∠=∠=︒，∴90BAE BAF EAF α∠=∠+∠=︒+，90CEA ADE DAE α∠=∠+∠=︒+，∴BAE CEA ∠=∠，∴MN PQ ∥，BC 平分∴ABM ，∴BCE CBM CBA ∠=∠=∠，又∴360ABC BCE CEA BAE ∠+∠+∠+∠=︒，∴180BCE CEA ∠+∠=︒，∴AE BC ∥，∴ACB CAE ∠=∠，即5452α=︒，∴18α=︒，∴18DAE ∠=︒，∴在Rt ACD △中，9090)451827(ACD CAD ∠=︒-∠=︒-︒+︒=︒，故答案为：B ．【点睛】此题考查平行线的性质，三角形内角和定理，解题关键在于得出ACB CAE ∠=∠．2．（江西省吉安市六校联谊联考2021-2022学年七年级下学期期中考试数学试题）如图，在ABC 中，点D 在边BC 上，点G 在边AB 上，点E 、F 在边AC 上，70AGF ABC ∠=∠=︒，12180∠+∠=︒(1)试判断BF 与DE 的位置关系，并说明理由；(2)若DE AC ⊥，30∠=︒CDE ，求A ∠的度数．【答案】(1)BF ∴DE ，理由见解析(2)50︒【解析】【分析】（1）先证FG CB ∥，得出∴1=∴3，进而得出23180∠+∠=︒，最后证得DE BF ；（2）由DE AC ⊥，可知∴DEC =90°，进而∴C =60°，根据三角形内角和定理最后求得∴A 的度数．(1)解：BF DE ，理由如下：∴70AGF ABC ∠=∠=︒，∴FG CB ∥，∴13∠=∠，又12180∠+∠=︒，∴23180∠+∠=︒，∴DE BF ．(2)解：∴DE AC ⊥，∴90CED ∠=︒，30CDE ∠=︒，60C ∴∠=︒，∴180180706050A ABC C ∠=︒-∠-∠=︒-︒-︒=︒．【点睛】本题考查了平行线的判定和性质，三角形内角和定理，熟练地掌握平行线的判定和性质是解决问题的关键．考点九 三角形外角的定义和性质例题：（2022·四川·成都七中七年级期中）如图，已知7AOB ∠=︒，一条光线从点A 出发后射向OB 边．若光线与OB 边垂直，则光线沿原路返回到点A ，此时90783A ∠=︒-︒=︒．当83A ∠<︒时，光线射到OB 边上的点1A 后，经OB 反射到线段AO 上的点2A ，易知12∠∠=．若12A A AO ⊥，光线又会沿21A A A →→原路返回到点A ，此时A ∠=______ °．若光线从A 点出发后，经若干次反射能沿原路返回到点A ，则锐角A ∠的最小值=______ °．【答案】 76 6【解析】【分析】根据入射角等于反射角得出1290783∠∠==︒-︒=︒，再由1∠是1AA O 的外角即可得A ∠度数；如图，当MN OA ⊥时，光线沿原路返回，分别根据入射角等于反射角和外角性质求出5∠、9∠的度数，从而得出与A ∠具有相同位置的角的度数变化规律，即可解决问题．【详解】解：12A A AO ⊥，7AOB ∠=︒，1290783∠∠∴==︒-︒=︒，176A AOB ∠∠∠∴=-=︒，如图：当MN OA ⊥时，光线沿原路返回，4390783∠∠∴==︒-︒=︒，654837769027AOB ∠∠∠∠∴==-=︒-︒=︒=︒-⨯︒，8767679037AOB ∠∠∠∠∴==-=︒-︒=︒-⨯︒，98697629047AOB ∠∠∠∴=-=︒-︒=︒=︒-⨯︒，由以上规律可知，9027A n ∠=︒-⋅︒，当6n =时，A ∠取得最小值，最小度数为6︒，故答案为：76，6．【点睛】本题主要考查直角三角形的性质和三角形的外角性质及入射角等于反射角，根据三角形的外角性质及入射角等于反射角得出与A ∠具有相同位置的角的度数变化规律是解题的关键．【变式训练】1．（2021·广西·靖西市教学研究室八年级期末）如图，∴BCD ＝145°，则∴A +∴B +∴D 的度数为_____．【答案】145°【解析】【分析】连接AC 并延长，延长线上一点为E ．由三角形外角的性质可得：DCE D DAC ∠=∠+∠，BCE E BAC ∠=∠+∠．所以可得：145DAB B D DAC BAC B D DCE BCE BCD ∠+∠+∠=∠+∠+∠+∠=∠+∠=∠=︒【详解】解：连接AC 并延长，延长线上一点为EDCE ∠是ACD △的外角∴DCE D DAC ∠=∠+∠同理可得：BCE B BAC ∠=∠+∠∴145DAB B D DAC BAC B D DCE BCE BCD ∠+∠+∠=∠+∠+∠+∠=∠+∠=∠=︒故答案为145︒．【点睛】本题主要考查知识点为，三角形中外角的性质．即：三角形的一个外角等于不相邻的两个内角的和．本题需根据已知和所求作出辅助线．掌握外角的性质是解决本题的关键．2．（2022·江苏·淮安市淮安区教师发展中心学科研训处七年级期中）平面内的两条直线有相交和平行两种位置关系．(1)如图1，AB∴CD，点P在AB、CD内部，∴B＝55°，∴D＝40°，则∴BPD＝°；(2)如图2，AB∴CD，点P在AB、CD外部（CD的下方），则∴BPD、∴B、∴D之间的数量关系为；(3)如图3，直接写出∴BPD、∴B、∴D、∴BQD之间的数量关系为；(4)如图4，计算∴A+∴B+∴C+∴D+∴E+∴F的度数是°．【答案】(1)95(2)∴BPD+∴D=∴B(3)∴BQD+∴QBP+∴PDQ=∴BPD(4)360【解析】【分析】（1）延长BP交CD于点E，根据平行线的性质、三角形外角的性质即可求解；（2）根据AB∴CD，得∴B=∴BOD，再由三角形外角的性质即可求证；（3）连接BD，由∴BQD+∴QBP+∴DBP+∴BDP+∴PDQ=180°，∴DBP+∴BDP+∴BPD=180°即可求解；（4）连接AD，由∴B+∴F=∴EHF，∴GAD+∴ADG=∴EGH，∴EHF+∴EGH+∴E=180°，∴CAD+∴ADC+∴C=180°，即可求解；(1)解：延长BP交CD于点E，∴AB∴CD，∴B＝55°，∴∴B=∴BED=55°，∴∴D＝40°，∴∴BPD＝∴D+∴BED＝95°．故答案为：95．(2)∴AB∴CD，∴∴B=∴BOD，∴∴BPD+∴D=∴BOD，∴∴BPD+∴D=∴B．故答案为：∴BPD+∴D=∴B．(3)连接BD，∴∴BQD+∴QBP+∴DBP+∴BDP+∴PDQ=180°，∴DBP+∴BDP+∴BPD=180°，∴∴BQD+∴QBP+∴PDQ-∴BPD=0，∴∴BQD+∴QBP+∴PDQ=∴BPD．故答案为：∴BQD+∴QBP+∴PDQ=∴BPD．(4)如图，连接AD，∴∴B+∴F=∴EHF，∴GAD+∴ADG=∴EGH，∴EHF+∴EGH+∴E=180°，∴∴B+∴F+∴GAD+∴ADG+∴E=180°，∴∴CAD+∴ADC+∴C=180°，∴∴B+∴F+∴GAD+∴ADG+∴CAD+∴ADC+∴C+∴E=360°．故答案为：360．【点睛】本题主要考查平行线的性质、三角形的内角和定理、三角形外角的性质，掌握相关知识并结合题意正确做出辅助线是解题的关键．一、选择题1．（2022·黑龙江·哈尔滨市风华中学校七年级期中）画ABC的BC边上的高，正确的是（）A．B．C．D．【答案】A【解析】【分析】利用三角形的高线的定义判断即可．【详解】解：画△ABC的BC边上的高，即过点A作BC边的垂线．∴只有选项A符合题意，故选：A．【点睛】本题考查了三角形高线的画法，从三角形的一个顶点向对边作垂线，顶点与垂足间的线段，叫做三角形的高线，锐角三角形的三条高线都在三角形的内部，钝角三角形的高有两条在三角形的外部．直角三角形的高线有两条是三角形的直角边．2．（2022·辽宁·沈阳市第七中学七年级阶段练习）在△ABC 中，2A B C ∠=∠=∠，则△ABC 的形状是（ ） A ．锐角三角形B ．钝角三角形C ．直角三角形D ．形状无法确定【答案】A【解析】【分析】利用∴A ，∴B ，∴C 的关系和三角形内角和定理，求出具体的度数，即可求解．【详解】解：∴∴A =∴B =2∴C ，∴A +∴B +∴C =180°，∴2∴C +2∴C +∴C =180°，∴∴C =36°，∴∴A =∴B =2∴C =72°，∴∴ABC 为锐角三角形，故选：A ．【点睛】本题考查三角形内角和定理，解题的关键是利用∴A ，∴B ，∴C 的关系求出具体度数．3．（2022·福建·漳州实验中学七年级阶段练习）如图，BC ∴AE 于点C ，CD ∥AB ，∴DCB =40°，则∴A 的度数是（ ）A ．70°B ．60°C ．50°D ．40°【答案】C【解析】【分析】 根据直角三角形两锐角互余可得90A B ∠+∠=︒，再根据两直线平行，内错角相等可得B 的度数，进而求A ∠即可．【详解】BC AE ⊥，90ACB ∴∠=︒，90∴∠+∠=︒，A B∥，∠=︒,40 CD AB DCB40B DCB ∴∠=∠=︒，9050A B ∴∠=︒-∠=︒，故选：C ．【点睛】本题考查了直角三角形两锐角互余及平行线的性质，熟练掌握知识点且灵活运用是解题关键． 4．（2022·全国·八年级课时练习）如图，将ABC ∆沿着平行于BC 的直线DE 折叠，点A 落在点A '处，若44B ∠=︒，则A DB '∠的度数是（ ）A ．108°B ．104°C ．96°D ．92°【答案】D【解析】【分析】 根据两直线平行，同位角相等可得∴ADE ＝∴B ，再根据翻折变换的性质可得∴A ′DE ＝∴ADE ，然后根据平角等于180°列式计算即可得解．【详解】解：∴∥DE BC ，∴∴ADE ＝∴B ＝44°，∴∴ABC 沿着平行于BC 的直线折叠，点A 落到点A ′，∴∴A ′DE ＝∴ADE ＝44°，∴∴A ′DB ＝180°﹣44°﹣44°＝92°．故选：D ．【点睛】本题考查了平行线的性质，翻折变换的性质，三角形的内角和定理，熟记性质并准确识图理清图中各角度之间的关系是解题的关键．5．（2022·山东青岛·七年级期末）如图，BD 是ABC 的边AC 上的中线，AE 是ABD △的边BD 上的中线，BF 是ABE △的边AE 上的中线，若ABC 的面积是32，则阴影部分的面积是（ ）A ．9B ．12C ．18D ．20【答案】B【解析】【分析】利用中线等分三角形的面积进行求解即可．【详解】∴BD 是ABC 的边AC 上的中线， ∴11321622ABD BCD ABC S S S ===⨯=△△， ∴AE 是ABD △的边BD 上的中线， ∴1116822ABE ADE ABD S S S ===⨯=， 又∴BF 是ABE △的边AE 上的中线，则CF 是ACE 的边AE 上的中线，∴118422BEF ABF ABE S S S ===⨯=，182CEF ACF ADE CED ACE S S S S S =====，则4812BEF CEF S SS =+=+=阴影，故选：B ．【点睛】 本题考查了中线的性质，清晰明确三角形之间的等量关系，进行等量代换是解题的关键．6．（2022·山西实验中学七年级期中）两束与地面平行的光线AB ，CD 经镜面a ，b 反射之后交于点G ，镜面a ，b 与地面的夹角分别为∴1，∴2，已知∴1=25°，∴2=40°（由光的反射性质可知入射光线与镜面的夹角等于反射光线与镜面的夹角），则两条反射光线的夹角（∴DGH ）的度数为（ ）。

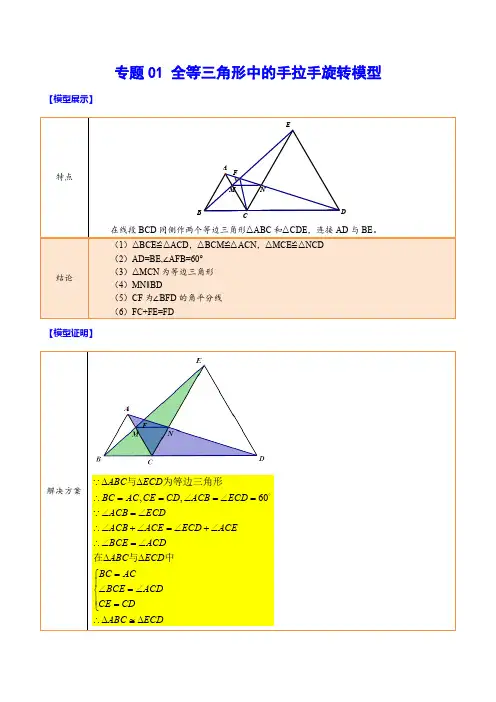
专题01 全等三角形中的手拉手旋转模型【模型展示】【模型证明】ECDABC CD CE ACD BCE AC BC ECD ABC ACD BCE ACE ECD ACE ACB ECDACB ECD ACB CD CE AC BC ECD ABC ∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆∠=∠∴∠+∠=∠+∠∴∠=∠=∠=∠==∴∆∆中与在为等边三角形与 60,,BDMN NCD MNC NCD MNC MCN MCN MCN CN CM ACN BCM AFB AFM BCM AFM BMC AMF MAF AFM BMC CBM BCM AFM AMF MAF BCM BMC CBM CADCBE ACD BCE ADBE ACD BCE //60606060,60)(180)(180180180∴∠=∠∴=∠=∠∴∆∆∴=∠=∴∆≅∆=∠=∠=∠∴∠=∠∠+∠-=∠∠+∠-=∠∴=∠+∠+∠=∠+∠+∠∠=∠∴∆≅∆=∴∆≅∆为等边三角形为等边三角形即P Q NMFECABD【模型拓展】【题型演练】一、单选题1．如图，在ABCV中，90ABC∠=°，分别以AB，AC为边作等边ABD△和等边ACEV，连结DE，若3AB=，5AC=，则ED=（）A．B．C．4D．【答案】C【分析】在Rt△ABC中可直接运用勾股定理求出BC，然后结合“手拉手”模型证得△ABC≌△ADE，即可得到DE=BC，从而求解即可．【详解】解：在Rt△ABC中，AB=3，AC=5，∴由勾股定理得：BC=4，∵ABD △和ACE V 均为等边三角形，∴AB =AD ，AC =AE ，∠BAD =∠CAE =60°，∴∠BAD -∠CAD =∠CAE -∠CAD ，即：∠BAC =∠DAE ，在△ABC 和△ADE 中，AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS )，∴DE =BC =4，故选：C ．【点睛】本题考查全等三角形的判定与性质，勾股定理的应用，掌握全等三角形的判定与性质，熟练运用勾股定理解三角形是解题关键．2．如图，C 为线段AE 上一动点（不与点A ，E 重合），在AE 同侧分别作等边三角形ABC 和等边三角形CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连结PQ ．以下结论错误的是（ ）A ．∠AOB =60°B ．AP =BQC ．PQ ∥AED ．DE =DP【答案】D【分析】利用等边三角形的性质，BC ∥DE ，再根据平行线的性质得到∠CBE =∠DEO ，于是∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°，得出A 正确；根据△CQB ≌△CPA （ASA ），得出B 正确；由△ACD ≌△BCE 得∠CBE =∠DAC ，加之∠ACB =∠DCE =60°，AC =BC ，得到△CQB ≌△CPA （ASA ），再根据∠PCQ =60°推出△PCQ 为等边三角形，又由∠PQC =∠DCE ，根据内错角相等，两直线平行，得出C 正确；根据∠CDE =60°，∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ，可知∠DQE ≠∠CDE ，得出D 错误．【详解】解：∵等边△ABC 和等边△CDE ，∴AC =BC ，CD =CE ，∠ACB =∠DCE =60°，∴∠ACB +∠BCD =∠DCE +∠BCD ，即∠ACD =∠BCE，在△ACD 与△BCE 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△BCE （SAS ），∴∠CBE =∠DAC ，又∵∠ACB =∠DCE =60°，∴∠BCD =60°，即∠ACP =∠BCQ ，又∵AC =BC ，在△CQB 与△CPA 中，ACP BCQ AC BCPAC CBQ ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△CQB ≌△CPA （ASA ），∴CP =CQ ，又∵∠PCQ =60°可知△PCQ 为等边三角形，∴∠PQC =∠DCE =60°，∴PQ ∥AE ，故C 正确，∵△CQB ≌△CPA ，∴AP =BQ ，故B 正确，∵AD =BE ，AP =BQ ，∴AD -AP =BE -BQ ，即DP =QE ，∵∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ，∠CDE =60°，∴∠DQE ≠∠CDE ，故D 错误；∵∠ACB =∠DCE =60°，∴∠BCD =60°，∵等边△DCE ，∠EDC=60°=∠BCD，∴BC∥DE，∴∠CBE=∠DEO，∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°，故A正确．故选：D．【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质，利用旋转不变性，解题的关键是找到不变量．3．如图，在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝90°，AB＝AC＝5，AD＝AE＝2，点P，Q，R分别是BC，DC，DE的中点．把△ADE绕点A在平面自由旋转，则△PQR的面积不可能是（）A．8B．6C．4D．2【答案】A【分析】连接BD、CE，BD的延长线交CE的延长线于O，AC交BO于H．证明△BAD≌△CAE,然后可推出△PQR是等腰直角三角形，S△PQR＝12•PQ2,由AB＝5，AD＝2可知3≤BD≤7，从而得到32≤PQ≤72，那么9 8≤12•PQ2≤498,即可得出答案．【详解】解：连接BD、CE，BD的延长线交CE的延长线于O，AC交BO于H．∵AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∴△BAD≌△CAE，∴BD＝CE，∠ABH＝∠OCH，∵∠AHB＝∠CHO，∴∠O＝∠BAH＝90°，∵点P ，Q ，R 分别是BC ，DC ，DE 的中点，∴PQ ＝12BD ，PQ ∥BO ，QR ＝12EC ，QR ∥CO ，∵BO ⊥OC ，∴PQ ⊥RQ ，PQ ＝QR ，∴△PQR 是等腰直角三角形，∴S △PQR ＝12•PQ 2，∵AB ＝5，AD ＝2，∴3≤BD ≤7，∴32≤PQ ≤72，∴98≤12•PQ 2≤498，∴△PQR 的面积不可能是8，故答案为：A ．【点睛】本题考查了旋转的性质，等腰直角三角形的性质，全等三角形的判定和性质，三角形的中位线定理，解题的关键是灵活运用所学知识解决问题．4．如图，在ABC V 中，AB AC =，点D 、F 是射线BC 上两点，且AD AF ⊥，若AE AD =，15BAD CAF ∠=∠=°；则下列结论中正确的有（ ）①CE BF ⊥；②ABD ACE △≌△；③ABC ADCE S S =四边形△；④122BC EF AD CF-=-A ．1个B ．2个C ．3个D ．4个【答案】D【分析】由AD ⊥AF ，∠BAD=∠CAF ，得出∠BAC=90°，由等腰直角三角形的性质得出∠B=∠ACB=45°，由SAS 证得△ABD ≌△ACE （SAS ），得出BD=CE ，∠B=∠ACE=45°，S △ABC =S 四边形ADCE ，则∠ECB=90°，即EC ⊥BF ，易证∠ADF=60°，∠F=30°，由含30°直角三角形的性质得出EF=2CE=2BD ，DF=2AD ，则BD=12EF ，由BC-BD=DF-CF ，得出BC-12EF=2AD-CF ，即可得出结果．【详解】∵AD ⊥AF ，∠BAD=∠CAF ，∴∠BAC=90°，∵AB=AC ，∴∠B=∠ACB=45°，在△ABD 和△ACE 中，AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩，∴△ABD ≌△ACE （SAS ），∴BD=CE ，∠B=∠ACE=45°，S △ABC =S 四边形ADCE ，∴∠ECB=90°，∴EC ⊥BF ，∵∠B=45°，∠BAD=15°，∴∠ADF=60°，∴∠F=30°，∴EF=2CE=2BD ，DF=2AD ，∴BD=12EF ，∵BC-BD=DF-CF ，∴BC-12EF=2AD-CF ，∴①、②、③、④正确．故选：D ．【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、含30°角直角三角形的性质、外角的定义等知识，熟练掌握直角三角形的性质、证明三角形全等是解题的关键．5．如图，正ABC V 和正CDE △中，B 、C 、D 共线，且3BC CD =，连接AD 和BE 相交于点F ，以下结论中正确的有（ ）个①60AFB ∠=° ②连接FC ，则CF 平分BFD ∠ ③3BF DF = ④BF AF FC=+A ．4B ．3C ．2D ．1【答案】A【分析】根据“手拉手”模型证明BCE ACD V V ≌，从而得到CBE CAD ∠=∠，再结合三角形的外角性质即可求解60AFB ACB ∠=∠=°，即可证明①；作CM BE ⊥于M 点，CN AD ⊥于N 点，证明CEM CDN V V ≌，结合角平分线的判定定理即可证明②；利用面积法表示BCF △和DCF V 的面积，然后利用比值即可证明③；利用“截长补短”的思想，在AD 上取点Q ，使得FC FQ =，首先判断出FCQ V 为等边三角形，再结合“手拉手”模型推出BCF ACQ V V ≌即可证明④．【详解】解：①∵ABC V 和CDE △均为等边三角形，∴60ACB ECD ∠=∠=°，AC BC =，EC DC =，∴ACB ACE ECD ACE ∠+∠=∠+∠，∴BCE ACD ∠=∠，在BCE V 和ACD △中，BC AC BCE ACDEC DC =⎧⎪∠=∠⎨⎪=⎩∴()BCE ACD SAS V V ≌，∴CBE CAD ∠=∠，∵AFB CBE CDA ∠=∠+∠，ACB CDA CAD ∠=∠+∠，∴60AFB ACB ∠=∠=°，故①正确；②如图所示，作CM BE ⊥于M 点，CN AD ⊥于N 点，则90CME CND ∠=∠=°，∵BCE ACD V V ≌，∴CEM CDN ∠=∠，在CEM V 和CDN △中，CME CND CEM CDNCE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CEM CDN AAS V V ≌，∴CM CN =，∴CF 平分BFD ∠，故②正确；③如图所示，作FP BD ⊥于P 点，∵1122BCF S BF CM BC FP ==V g g ，1122DCF S DF CN CD FP ==V g g ，∴11221122BCFDCF BF CM BC FP S S DF CN CD FP ==V V g g g g ，∵CM CN =，∴整理得：BF BC DF CD=，∵3BC CD =，∴33BF CD DF CD==，∴3BF DF =，故③正确；④如图所示，在AD 上取点Q ，使得FC FQ =，∵60AFB ACB ∠=∠=°，CF 平分BFD ∠，∴120BFD ∠=°，1602CFD BFD ∠=∠=°，∴FCQ V 为等边三角形，∴60FCQ ∠=°，CF CQ =，∵60ACB ∠=°，∴ACB ACF FCQ ACF ∠+∠=∠+∠，∴BCF ACQ ∠=∠，在BCF △和ACQ V 中，BC AC BCF ACQCF CQ =⎧⎪∠=∠⎨⎪=⎩∴()BCF ACQ SAS V V ≌，∴BF AQ =，∵AQ AF FQ =+，FQ FC =，∴BF AF FC =+，故④正确；综上，①②③④均正确；故选：A ．【点睛】本题考查等边三角形的判定与性质，全等三角形的判定与性质等，理解等边三角形的基本性质，掌握全等三角形中的辅助线的基本模型，包括“手拉手”模型，截长补短的思想等是解题关键．6．如图，点C 是线段AE 上一动点（不与A ，E 重合），在AE 同侧分别作等边三角形ABC 和等边三角形CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连接PQ ，有以下5个结论：①AD=BE ；②PQ ∥AE ；③AP=BQ ；④DE=DP ；⑤∠AOB=60°．其中一定成立的结论有（ ）个A ．1B ．2C ．3D ．4【答案】D 【分析】①由于△ABC 和△CDE 是等边三角形，可知AC=BC ，CD=CE ，∠ACB=∠DCE=60°，从而证出△ACD ≌△BCE ，可推知AD=BE；③由△ACD≌△BCE得∠CBE=∠DAC，加之∠ACB=∠DCE=60°，AC=BC，得到△ACP≌△BCQ（ASA），所以AP=BQ；故③正确；②根据②△CQB≌△CPA（ASA），再根据∠PCQ=60°推出△PCQ为等边三角形，又由∠PQC=∠DCE，根据内错角相等，两直线平行，可知②正确；④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ，∠CDE=60°，可知∠DQE≠∠CDE，可知④错误；⑤利用等边三角形的性质，BC∥DE，再根据平行线的性质得到∠CBE=∠DEO，于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°，可知⑤正确．【详解】①∵等边△ABC和等边△DCE，∴BC=AC,DE=DC=CE，∠DEC=∠BCA=∠DCE=60∘，∴∠ACD=∠BCE，在△ACD和△BCE中，AC=BC，∠ACD=∠BCE，DC=CE，∴△ACD≌△BCE(SAS)，∴AD=BE；故①正确；③∵△ACD≌△BCE(已证)，∴∠CAD=∠CBE，∵∠ACB=∠ECD=60°(已证)，∴∠BCQ=180°-60°×2=60°，∴∠ACB=∠BCQ=60°，在△ACP与△BCQ中，∠CAD=∠CBE，AC=BC，∠ACB=∠BCQ=60°，∴△ACP≌△BCQ(ASA)，∴AP=BQ；故③正确；②∵△ACP≌△BCQ，∴PC=QC，∴△PCQ是等边三角形，∴∠CPQ=60∘，∴∠ACB=∠CPQ ，∴PQ ∥AE ；故②正确；④∵AD=BE ，AP=BQ ，∴AD−AP=BE−BQ ，即DP=QE ，∠DQE=∠ECQ+∠CEQ=60°+∠CEQ ，∠CDE=60°，∴∠DQE≠∠CDE ，∴DE≠QE ，则DP≠DE ，故④错误；⑤∵∠ACB=∠DCE=60°，∴∠BCD=60°，∵等边△DCE ，∠EDC=60°=∠BCD ，∴BC ∥DE ，∴∠CBE=∠DEO ，∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.故⑤正确；综上所述，正确的结论有：①②③⑤，错误的结论只有④，故选D ．【点睛】本题考查全等三角形的判定和性质，以及等边三角形的判定和性质，此图形是典型的“手拉手”模型，熟练掌握此模型的特点是解题的关键．二、填空题7．如图，ABD △、CDE △是两个等边三角形，连接BC 、BE ．若30DBC ∠=°，6BD =，8BC =，则BE =________．【答案】BE =10【分析】连接AC ，根据题意易证△ACD ≌△BED(SAS)，根据全等三角形的性质可得AC=BE ，再根据勾股定理求出AC 的值即可得出结论．【详解】如图，连接AC ，∵ABD △、CDE △是两个等边三角形，∴AB=BD=AD=2，CD=DE ，∠ABD=∠ADB=∠CDE=60，∴∠ADB+∠BDC=∠CDE+∠BDC ，∴∠ADC=∠BDE ，在△ACD 与△BDE 中AD BD ADC BDE CD DE =⎧⎪=⎨⎪=⎩∠∠，∴△ACD ≌△BED （SAS ），∴AC=BE ，∵30DBC ∠=°，∴∠ABC=∠ABD+∠DBC=60°+30°=90°，在Rt △ABC 中，AB=6，BC=8，∴10=，∴BE=10，故答案为：10．【点睛】本题考查了等边三角形的性质，全等三角形的判定与性质，勾股定理，孰练的掌握知识点是解题关键．8．如图，△ABC 中，∠C ＝90°，AC ＝BC =△ABC 绕点A 顺时针方向旋转60°到△AB 'C '的位置，连接BC '，BC '的延长线交AB '于点D ，则BD 的长为 _____．【分析】连接BB ′，根据旋转的性质可得AB ＝AB ′，判断出△ABB ′是等边三角形，根据等边三角形的三条边都相等可得AB ＝BB ′，然后利用“边边边”证明△ABC ′和△B ′BC ′全等，根据全等三角形对应角相等可得∠ABC ′＝∠B ′BC ′，延长BC ′交AB ′于D ，根据等边三角形的性质可得BD ⊥AB ′，利用勾股定理列式求出AB ，然后根据等边三角形的性质和等腰直角三角形的性质求出BD ．【详解】解：如图，连接BB ′，∵△ABC 绕点A 顺时针方向旋转60°得到△AB ′C ′，∴AB ＝AB ′，∠BAB ′＝60°，∴△ABB ′是等边三角形，∴AB ＝BB ′，在△ABC ′和△B ′BC ′中，AB BB AC B C BC BC =¢⎧⎪¢=¢¢⎨⎪¢=¢⎩，∴△ABC ′≌△B ′BC ′（SSS ），∴∠ABC ′＝∠B ′BC ′30=° ，延长BC ′交AB ′于D ，则BD ⊥AB ′，∵∠C ＝90°，AC ＝BC ，∴AB 2=AB ’，∴AD =112AB =∴BD =，【点睛】本题考查了旋转的性质，全等三角形的判定与性质，等边三角形的判定与性质，等腰直角三角形的性质，作辅助线构造出全等三角形并求出BC ′在等边三角形的高上是解题的关键，也是本题的难点．9．如图，ABC V 是边长为5的等边三角形，BD CD =，120BDC ∠=°．E 、F 分别在AB 、AC 上，且60EDF ∠=°，则三角形AEF 的周长为______．【答案】10【分析】延长AB 到N ，使BN =CF ，连接DN ，求出∠FCD =∠EBD =∠NBD =90°，根据SAS 证△NBD ≌△FCD ，推出DN =DF ，∠NDB =∠FDC ，求出∠EDF =∠EDN ，根据SAS 证△EDF ≌△EDN ，推出EF =EN ，易得△AEF 的周长等于AB +AC ．【详解】解：延长AB 到N ，使BN =CF ，连接DN ，∵△ABC 是等边三角形，∴∠ABC =∠ACB =60°，∵BD =CD ，∠BDC =120°，∴∠DBC =∠DCB =30°，∴∠ACD =∠ABD =30°+60°=90°=∠NBD ，∵在△NBD 和△FCD 中，BD DC NBD FCD BN CF =⎧⎪∠=∠⎨⎪=⎩，∴△NBD ≌△FCD （SAS ），∴DN =DF ，∠NDB =∠FDC ，∵∠BDC =120°，∠EDF =60°，∴∠EDB +∠FDC =60°，∴∠EDB +∠BDN =60°，即∠EDF =∠EDN ，在△EDN 和△EDF 中，DE DE EDF EDN DN DF =⎧⎪∠=∠⎨⎪=⎩，∴△EDN ≌△EDF （SAS ），∴EF =EN =BE +BN =BE +CF ，即BE +CF =EF ．∵△ABC 是边长为5的等边三角形，∴AB =AC =5，∵BE +CF =EF ，∴△AEF 的周长为：AE +EF +AF =AE +EB +FC +AF =AB +AC =10，故答案为：10．【点睛】本题考查了等边三角形性质和判定，等腰三角形的性质，三角形的内角和定理，全等三角形的性质和判定的综合运用．注意掌握辅助线的作法，注意掌握数形结合思想的应用．10．如图，C 为线段AE 上一动点（不与点A 、E 重合），在AE 同侧分别作正△ABC 和正△CDE ，AD 与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：①AD=BE；②PQ P AE；③AP=BQ；④DE=DP；⑤∠AOB=60°．恒成立的结论有_____．（把你认为正确的序号都填上）【答案】①②③⑤为等边三角形，再证【分析】根据等边三角形的性质及SAS即可证明；根据全等三角形的性质证明MCN明△ACD≌△BCE即可求解．【详解】解：①△ABC和△DCE均是等边三角形，点A，C，E在同一条直线上，∴AC=BC，EC=DC，∠BCE=∠ACD=120°∴△ACD≌△ECB∴AD=BE，故本选项正确，符合题意；②∵△ACD≌△ECB∴∠CBQ=∠CAP，又∵∠PCQ=∠ACB=60°，CB=AC，∴△BCQ≌△ACP，∴CQ=CP，又∠PCQ=60°，∴△PCQ为等边三角形，∴∠QPC=60°=∠ACB，∴PQ P AE，故本选项正确，符合题意；③∵∠ACB=∠DCE=60°，∴∠BCD=60°，∴∠ACP=∠BCQ，∵AC=BC，∠DAC=∠QBC，∴△ACP≌△BCQ（ASA），∴CP=CQ，AP=BQ，故本选项正确，符合题意；④已知△ABC 、△DCE 为正三角形，故∠DCE =∠BCA =60°⇒∠DCB =60°，又因为∠DPC =∠DAC +∠BCA ，∠BCA =60°⇒∠DPC ＞60°，故DP 不等于DE ，故本选项错误，不符合题意；⑤∵△ABC 、△DCE 为正三角形，∴∠ACB =∠DCE =60°，AC =BC ，DC =EC ，∴∠ACB +∠BCD =∠DCE +∠BCD ，∴∠ACD =∠BCE ，∴△ACD ≌△BCE （SAS ），∴∠CAD =∠CBE ，∴∠AOB =∠CAD +∠CEB =∠CBE +∠CEB ，∵∠ACB =∠CBE +∠CEB =60°，∴∠AOB =60°，故本选项正确，符合题意．综上所述，正确的结论是①②③⑤．三、解答题11．如图，ACB △和ECD V 都是等腰直角三角形，,,CA CB CD CE ACB ==△的顶点A 在ECD V 的斜边DE 上，连接BD ．（1）求证：BD AE =．（2）若3cm,6cm AE AD ==，求AC 的长．【答案】（1）证明见解析；（2）AC =．【分析】（1）根据同角的余角相等得出∠BCD=∠ACE ，然后根据SAS 定理证明△BCD ≌△ACE ，从而得出结论；（2）根据全等三角形的性质得出∠BDC=∠AEC ，然后结合等腰直角三角形的性质求得∠BDA 是直角三角形，从而利用勾股定理求解．【详解】（1）∵ACB △和ECD V 都是等腰直角三角形，∴90ACB ECD ∠=∠=°，∴90,90ACD BCD ACD ACE ∠+∠=°∠+∠=°，∴BCD ACE ∠=∠，在BCD △和ACB △中，CB CA BCD ACECD CE =⎧⎪∠=∠⎨⎪=⎩∴()BCD ACE SAS V V ≌，∴BD AE =．（2）∵BCD ACE V V ≌，∴BDC AEC ∠=∠，又∵ECD V 是等腰直角三角形，∴45CDE CED ∠=∠=°，∴45BDC ∠=°，∴90BDC CDE ∠+∠=°，∴BDA ∠是直角三角形，∴22222223645AB BD AD AE AD =+=+=+=，在等腰直角三角形ACB 中，22222AB AC BC AC =+=，∴AC =【点睛】本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．12．如图，A 、B 、C 在同一直线上，且△ABD ，△BCE 都是等边三角形，AE 交BD 于点M ，CD 交BE 于点N ，MN ∥AC ，求证：（1）∠BDN=∠BAM ；（2）△BMN 是等边三角形．【答案】（1）证明过程见详解；（2）证明过程见详解。

2021年高考数学压轴必刷题（第三辑）专题01解三角形劣构性解答题突破A 辑1()cos cos sin A c B b C a A +=，②()cos2cos22sin sin sin A B C B C -=-，③()2cos cos b c A a C -=这三个条件中任选一个，补充到下面问题中，并解答问题．在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且______． （1）求A ；（2）若2a =，b c +=ABC 的面积． 注：如果选择多个条件分别解答，按第一个解答计分．【答案】（1）3A π=；（2（1）方案一：若选①．()2sin cos sin cos sin A C B B C A +=，()2sin sin A C B A +=，2sin sin A A A =， 又(0,)A π∈，所以sin 0A ≠，所以tan A =，所以3A π=． 方案二：若选②．由已知及倍角公式得()()()2212sin 12sin 2sin sin sin A B C B C ---=-，所以2222sin 2sin 2sin sin 2sin B A C B C -=-， 所以222sin sin sin sin sin B C A C B +-=， 由正弦定理得222b c a bc +-=，由余弦定理得2221cos 22b c a A bc +-==，又(0,)A π∈，所以3A π=． 方案三：若选③．由已知及正弦定理得()2sin sin cos sin cos B C A A C -=， 所以2sin cos sin()sin B A A C B =+=， 因为(0,)B π∈，所以sin 0B ≠，所以1cos 2A =， 又(0,)A π∈，所以3A π=． （2）由余弦定理2222cos a b c bc A =+-，2a =，3A π=，得224b c bc =+-， 即()234b c bc +-=．因为b c +=2bc =，所以1sin 22ABCSbc A ==．2．在①22()3a b c ab +=+，②sin cos a A a C =-，③(2)sin (2)sin 2sin a b A b a B c C -+-=，这三个条件中任选一个，补充在下列问题中，并解答.已知ABC 的内角,,A B C 的对边分别为,,a b c ，c =_____.（1）求C ∠；（2）求ABC 周长的最大值.【答案】（1）答案见解析，3C π=；（2）最大值为 （1）选①，把22()3a b c ab +=+，整理得222a b c ab +-=，由余弦定理得2221cos 222a b c ab C ab ab +-===，因为(0,)C π∈，所以3C π=.选②，因为sin cos a A a C =-，由正弦定理，可得sin sin sin cos A C A A C -，因为(0,)A π∈，则sin 0A ≠cos 1C C -=，可得1sin 62C π⎛⎫-= ⎪⎝⎭， 又0C π<<，所以5666C πππ-<-<，故66C ππ-=，即3C π=. 选③，因为(2)sin (2)sin 2sin a b A b a B c C -+-=，由正弦定理得：2(2)(2)2a b a b a b c -+-=，即222a b c ab+-=，所以2221cos 22a b c C ab +-==，因为0C π<<，所以3C π=.（2）由（1）可知，3C π=，在ABC 中，由余弦定理得222cos 3a b ab C +-=，即223a b ab +-=，所以223()()334a b a b ab ++-=≤，当且仅当a b =时取等号，所以a b +≤a b c ++≤即ABC 周长的最大值为 3．在①sinsin 2B Cc a C +=；②2cos cos co (s )A b C c B a +=；③()22sin sin sin sin sin B C A B C -=-中任选一个，补充在横线上，并回答下面问题.在△ABC 中，已知内角,,A B C 所对的边分别为,,a b c 若1)c b =，______. (1)求C 的值；(2)若△ABC 的面积为3，求b 的值. 【答案】（1）4π；（2）2. 选① (1)sinsin sin sin sin cos sin sin 222B C A Ac a C c a C C A C π+-=⇒=⇒= 0,sin 0C C π<<∴≠cos2sin 222A A A cos ∴=，0,cos 02AA π<<∴≠ 1sin 223A A π∴=⇒=21)sin 1)sin sin 1)sin()3c b C B C C π=⇒=⇒=- 化简得sin cos 4C C C π=⇒=(2) 21sin 1)324ABCScb A b === 2b ∴=选②2cos cos cos 2cos sin cos sin cos sin ()()A b C c B a A B C C B A +=⇒+=2cos si )n s (in ,A B C A ∴+=2cos sin sin ,A A A ∴= 0,sin 0A A π<<∴≠1cos 23A A π∴=⇒= 21)sin 1)sin sin 1)sin()3c b C B C C π=⇒=⇒=- 化简得sin cos 4C C C π=⇒=(2) 21sin 1)32ABCScb A b === 2b ∴=选③()22222sin sin sin sin sin sin sin sin sin sin B C A B C B C A B C -=-⇒+=+222b c a bc +=+ ，1cos 2A ∴=0,A π<<3A π∴=21)sin 1)sin sin 1)sin()3c b C B C C π=⇒=⇒=- 化简得sin cos 4C C C π=⇒=(2) 21sin 1)32ABCScb A b === 2b ∴=4．如图，在ABC 中，D 是BC 上的点，4,3AB BD C π===，再从条件①、条件②这两个条件中选择一个作为已知，求：（1）角B 的大小； （2）ACD △的面积．条件①：AD 3AC =．【答案】（1）6B π=，具体选择见解析；（2. 选择条件①：解：（1）在ABD △中4,AB BD AD === 由余弦定理，得222cos 2AB BD AD B AB BD +-=⋅==因为0B π<<， 所以6B π=.（2）由（1）知，6B π=，因为3C π=，所以2BAC π∠=.所以ABC 为直角三角形. 所以3AC =，6BC =.又因为4BD =，所以2CD =.所以1sin 2ACDSAC CD C =⋅⋅1322=⨯⨯=. 选择条件②：解：（1）在ABC 中,3,AC AB ==3C π=. 由正弦定理sin sin AC AB B C =，得1sin 2B =. 由题可知 BC π<<=03， 所以6B π=.（2）由（1）知，6B π=，因为3C π=，所以2BAC π∠=.所以ABC 为直角三角形， 得6BC =.又因为4BD =，所以2CD =.所以1sin 2ACDSAC CD C =⋅⋅1322=⨯⨯=. 5．在ABC 中，3cos 5A =，a =再从条件①、条件②这两个条件中选择一个作为已知.求： （Ⅰ）c 的值；（Ⅱ）sin C 和ABC 的面积.条件①：π4B =；条件②：5b =. 【答案】（Ⅰ）7c =；（Ⅱ）sin C =14ABCS=选①：π4B =，sin B =cos B =（Ⅰ）由3cos 5A =，则4sin 5A =，()sin sin sin cos cos sin C A B A B A B =+=+=在ABC 中，由正弦定理sin sin a cA C=，即4510=，解得7c =，（Ⅱ）由（Ⅰ）可得sin C =11sin 714222ABCSac B ==⨯⨯=. 选②：5b =（Ⅰ）在ABC 中，由余弦定理可得2222cos a b c bc A =+-，即233225255c c =+-⨯⨯， 解得7c =或1c =-（舍去）. 在ABC 中，由正弦定理sin sin a cA C=，解得sin C =11sin 5142210ABCSab C ==⨯⨯=.6()cos cos sin C a B b A c C +=，②sinsin 2A Ba c A +=，③()()2sin 2sin 2sin ab A b a Bc C -+-=这三个条件中任选一个，补充在下列问题中，并解答.已知ABC 的角A ，B ，C 对边分别为,,a b c ，c =___________.（1）求C ∠； （2）求ABC 周长的范围.【答案】条件选择见解析；（1）3π；（2）(. 解：（1）选①： 由正弦定理得()3cosC sinAcosB sinBcosA sinCsinC +=()A B sinCsinC +=因为0sinC tanC ≠∴=， 因为()03C C ππ∈∴=，，选②：由正弦定理得2CsinAsinsinCsinA π-=，因为02222c C CsinA cos sinC sin cos ≠∴==， 因为02Ccos ≠，所以122C sin =，因为()03C C ππ∈∴=，，选③：因为()()2sin 2sin 2sin a b A b a B c C -+-=，所以()()2222a b a b a b c -+-=，即222a b c ab +-=，所以2221cos 22a b c C ab +-==，因为0C π<<，所以3C π=；（2）由（1）可知：3C π=， 在ABC 中，由余弦定理得222cos 3a b ab C +-=，即223a b ab +-=，所以()()223334a b a b ab ++-=≤，所以a b +≤a b =时等号成立，所以a b c ++≤ABC 周长的最大值为又因为a b c +>=ABC 周长的取值范围为(7．已知ABC ，满足2a b =， ，求ABC 的面积 （1）3A π=（2）cos 7B =. 注：如果选择多个条件分别解答，按第一个解答计分【答案】若选（1），ABC S =△；若选（2），ABCS若选（1），由余弦定理得：2222cos a b c bc A =+-， 即2174222=+-⨯⨯⨯c c ，2230c c --=，解得3c =或1c =-（舍去）.所以11sin 232222ABC S bc A ==⨯⨯⨯=△. 若选（2）由余弦定理得：2222cos b a c ac B =+-，即24727=+-⨯c c ，即230c -+=，解得c =此时222a b c =+，即2A π=，所以11222△==⨯=ABC S bc 8．已知有条件①()2cos cos b c A a C -=，条件①25cos cos 24A A π⎛⎫++=⎪⎝⎭；请在上述两个条件中任选一个，补充在下面题目中，然后解答补充完整的题目.在锐角ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，a =5b c +=，且满足______.（2）求ABC 的面积.(注：如果选择多个条件分别解答，按第一个解答计分.)【答案】条件选择见解析；（1）3A π=；（2 （1）选择条件①()2cos cos b c A a C -=，法1：由正弦定理得()2sin sin cos sin cos B C A A C -=，所以()2sin cos sin sin B A A C B =+=， 因为sin 0B ≠， 所以1cos 2A =，又π0,2A ⎛⎫∈ ⎪⎝⎭，所以3A π=，法2：由余弦定理得()222222222b c a a b c b c abc ab+-+--=， 化简得222b c a bc +-=，则2221cos 22b c a A bc +-==，又π0,2A ⎛⎫∈ ⎪⎝⎭，所以3A π=.选择条件②25cos cos 24A A π⎛⎫++=⎪⎝⎭，因为cos sin 2A A π⎛⎫+=-⎪⎝⎭，所以25sin cos 4A A +=，因为22sin cos 1A A +=，所以251cos cos 4A A -+=， 化简得21cos 02A ⎛⎫-= ⎪⎝⎭，解得1cos 2A =，又()0,A π∈，所以3A π=.（2）由余弦定理2222cos3a b c bc π=+-，得()273b c bc =+-，所以()2763b c bc bc +-=⇒=，于是ABC 的面积11sin 622S bc A ==⨯=9．在cossin 2B Ca B +=，sin 3cos Bb A =这两个条件中任选一个，补充在下面问题中，然后解答补充完整的题.在ABC 中，6,cos BC B ==. （1）求AC 的长；【答案】条件选择见解析；（1）4AC =；（2）. 选择①（1cos sin sin 2B CB A B +=， 又sin 0B ≠，sin 2AA π-=，2sin cos 222A A A=，∴cos 22A =， 即26A π=，3A π=，由cos 3=B可得sin 3B ==，根据正弦定理sin sin BC ACA B== 4AC ∴=.（2）1sin sin()sin cos cos sin 23236C A B A B A B =+=+=+⨯=，11sin 46226S AC BC C =⋅⋅=⨯⨯⨯= 选择②（1sin 3cos B b A =sin 3sin cos A B B A =， 又sin 0B ≠，∴sin cos AA=tan A = ∴3A π=，又sin 3B == 结合正弦定理sin sin BC ACA B=，23=4AC ∴=.（2）1sin sin()sin cos cos sin 23236C A B A B A B =+=+=+⨯=，11sin 4622S AC BC C =⋅⋅=⨯⨯= 10．现给出两个条件：①22cos c a B =，②()2cos cos b A C =，从中选出一个条件补充在下面的问题中，并以此为依据求解问题.在ABC 中，a ，b ，c 分别为内角A ，B ，C 所对的边，______. （1）求A ； （2）若31a ，求ABC 周长的最大值.【答案】（1）6π；（2）1.若选择条件①22cos c a B =.（1）由余弦定理可得22222cos 22a c b c a B a ac+-==⋅，整理得222c b a +-=，可得222cos 2b c A bc a +===-. 因为()0,A π∈，所以6A π=.（2）由余弦定理2222cos a b c bc A =+-，得)222122b c bc =+-⋅，即()(22242b c b c bc -+=+-，亦即(()(224bc b c =+--，因为()24b c bc +≤，当且仅当b c =时取等号，所以()((()22424b c b c ++--≤⨯，解得b c +≤当且仅当b c ==.所以1a b c ++≤，即ABC 周长的最大值为1若选择条件②()2cos cos b A C =.（1）由条件得2cos cos cos b A C A =，由正弦定理得)()2sin cos sin cos sin cos B A A C C A A C B =+=+=.因为sin 0B ≠，所以cos A =， 因为()0,A π∈，所以6A π=.（2）由余弦定理2222cos a b c bc A =+-，得)22212b c bc =+-，即()(22242b c b c bc -+=+-，亦即(()(224bc b c =+--，因为()24b c bc +≤，当且仅当b c =时取等号，所以()((()22424b c b c ++--≤⨯，解得b c +≤当且仅当b c ==.所以1a b c ++≤，即ABC 周长的最大值为1 11．在①π6A ∠=，②3ABDS ，③1cos 2ABD ∠=-三个条件中任选一个，补充在以下问题的横线上，并解答.问题：在平面四边形ABCD 中，已知1AB BC CD ===，AD =，且满足________. （1）求sin BDC ∠的值； （2）求平面四边形ABCD 的面积.注：如果选择多个条件分别解答，按照第一个解答计分.【答案】（1（2（1）选①可知：在ABD △中，1,6AD AB A π==∠=，由余弦定理有213cos416BD π=+-=-=，所以1BD =，所以1BD BC CD ===， 所以3BDC π∠=，所以sin BDC ∠=选②可知：在ABD △中，1,4ABDAD AB S ===，所以1331sin 2ABDS A， 解得1sin 2A =，又0A π<<，所以6A π=或56π，当6Aπ=时，213cos4162BD π=+-=-=，所以1BD BC CD ===，所以3BDC π∠=，所以sin BDC ∠=当56Aπ=时，2513cos 76BD π=+-==，所以BD =而1BC CD ==，不满足2+>BC CD BD ==56A π=不成立， 综上得：sinBDC ∠=如选③：在ABD △中，11,cos 2AD AB ABD ==∠=-，又0ABD π<∠<，所以23ABD π∠=，由正弦定理得2sin sin 3ADAB ADB π=∠1sin sin 3ADB =∠，所以1sin 2ADB ∠=，又ADB ABD ∠<∠，所以6ADB π∠=，所以6ADB BAD π∠=∠=，所以1BD AB ==，所以1BD BC CD ===，所以3BDC π∠=，所以sin BDC ∠=（2）由（1）得111sin 23DBCSπ=⨯⨯⨯=11sin 26ABDS π=⨯=所以平面四边形ABCD 的面积为+DBC ABDS S S====12．在①sin sin sin sin A C A Bb a c--=+，②2cos cos cos c C a B b A =+这两个条件中任选一个，补充在下面问题中的横线上，并解答.在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ， . （1）求角C ；（2）若c =a b +=ABC 的面积. 注：如果选择多个条件分别解答，按第一个解答计分.【答案】（1）3C π=；（2（1）若选①： 由正弦定理得a c a bb a c--=+， 所以222a c ab b -=-，由余弦定理得2222cos c a b ab C =+-， 解得1cos 2C =， 因为()0,C π∈，所以3C π=.若选②：由正弦定理得sin cos sin cos 2sin cos A B B A C C +=， 即sin()2sin cos A B C C +=， 即sin 2sin cos C C C =，因为()0,C π∈，所以sin 0C ≠，所以1cos 2C =，所以3C π=.（2）由余弦定理得2222cos c a b ab C =+-， 得225a b ab =+-，即25()3a b ab =+-，解得2ab =，则ABC 的面积11sin 222ABCSab C ==⨯=故ABC 13．在b a =①2sin tan b A a B =②，()()sin sin sin a c A c A B b B -++=③这三个条件中任选一个，补充在下面的横线上，并加以解答.已知ABC 的内角A ，B ，C 所对的边分别是a ，b ，c ，满足______. （1）求角B ；（2）若2a c b +=，且ABC ∆外接圆的直径为2，求ABC ∆的面积.【答案】选择见解析；（1）3B π=；（2 1（）选①，由正弦定理得sinsin B A =sin 0A ≠，cos 1B B -=，即1sin 62B π⎛⎫-= ⎪⎝⎭，0B π<<，5666B πππ∴-<-<，66B ππ∴-=，3B π∴=；选②，2sin tan b A a B =，sin 2sin cos a Bb A B =，由正弦定理可得sin 2sin sin sin cos BB A A B=⋅，sin 0A ≠，1cos 2B ∴=，(0,)B π∈，3B π∴=选③，sin()sin()sin A B C C π+=-=，由已知结合正弦定理可得()22a c a cb -+=，222a cb ac ∴+-=，2221cos 222a cb ac B ac ac +-∴===， (0,)B π∈，3B π∴=.2（）设ABC 的外接圆半径为R ，则1R =，2sin b R B ==，由余弦定理得()22222cos33b ac ac a c ac π=+-=+-，即3123ac =-，所以3ac =，所以ABC的面积为：1sin 2S ac B == 14．在△ABC 中，sin cos()6b A a B π=-. （1）求B ； （2）若5c =，.求a . 从①7b =，②4Cπ这两个条件中任选一个，补充在上面问题中并作答. 【答案】（1）3π（2）7b =时，8a =；4Cπ时，535a （1）因为sin cos()6b A a B π=-，sin sin a bA B =，所以sin sin sin cos()6B A A B π.又因为sin 0A ≠，所以sin cos()6BBπ，即31sin cos sin 2B B B . 所以sin()03B π.又因为2333B πππ-<-<，所以03B π，所以3B π=.（2）若选①7b =，则在△ABC 中，由余弦定理2222cos b a c ac B =+-， 得25240a a --=，解得8a =或3a =-（舍）.所以8a =. 若选②4Cπ，则62sin sin()sin cos cos sin3434A B C ππππ，由正弦定理sin sin a cA C=， 622，解得535a . 所以535a. 15．①在函数1π()sin()(0,||)22f x x ωϕωϕ=+><的图像向右平移π12个单位长度得到()g x 的图像，()g x 的图像关于原点对称，②向量11(3sin,cos ),(cos ,),02224m x x n x ωωωω==>，()f x m n =⋅； ③函数π1()cos sin()(0)2264f x x x ωωω=+->这三个条件中任选一个，补充在下面问题中，并解答.已知_______，函数()f x 图像的相邻两条对称轴之间的距离为π2.（1）求π()6f 的值；（2）求函数()f x 在[0,π]上的单调递减区间. 注：如果选择多个条件分别解答，按第一个解答计分. 【答案】（1）π1()62f =；（2）π2,π63⎡⎤⎢⎥⎣⎦. （1）选择条件①：依题意，()f x 相邻两对称轴之间距离为π2，则周期为π，从而2ω=， 从而1()sin(2)2f x x ϕ=+，1π()sin(2)26g x x ϕ=+-，又()g x 的图像关于原点对称，则(0)0g =，由π||2ϕ<知π6ϕ=， 从而1π()sin(2)26f x x =+，π1()62f = 选择条件②： 依题意，31()sin cos cos 2224f x m n x x x ωωω=⋅=+即有：11π()cos =sin()426f x x x x ωωω=++ 又因为()f x 相邻两对称轴之间距离为π2，则周期为π，从而2ω=， 从而1π()sin(2)26f x x =+，π1()62f =选择条件③： 依题意，π1()cossin()2264f x x x ωω=+-即有：11()cos(cos )222224f x x x x ωωω=+-化简得：211()cos (cos )22224f x x x x ωωω=+-即有：11π()cos =sin()426f x x x x ωωω=++ 又因为()f x 相邻两对称轴之间距离为π2，则周期为π，从而2ω=， 从而1π()sin(2)26f x x =+，π1()62f =（2）1π()sin(2)26f x x =+，则其单调递减区间为ππ32π22ππ,262k x k k Z +≤+≤+∈，解得π2π,ππ,63x k k k Z ⎡⎤∈++∈⎢⎥⎣⎦，令0k =，得π2,π63x ⎡⎤∈⎢⎥⎣⎦， 从而()f x 在[]0,π上的单调递减区间为π2,π63⎡⎤⎢⎥⎣⎦.16．请从①6,sin()2b B π=-=42a c b +=+=,中，并解决问题.问题：在ABC 中，角、、A B C 所对的边分别为a b c 、、，已知sin sin sin c a c bB A C--=+ （1）求a ；（2）求ABC 的面积.（注：如果选择条件①和条件②分别解答，按第一个解答计分.） 【答案】选择条件①：（1）（2；选择条件②：（1）（2） 选择条件①：（1）sin sin sin c a c bB AC --=+， ∴由正弦定理可得：c a c bb a c--=+，整理可得：222b c a bc +-=，根据余弦定理可知22201cos ,6022b c a A A bc +==∴=- ABC中，6,sin()2b B π=-=即cos B =，则0,2B π⎛⎫∈ ⎪⎝⎭，所以3sin 4B =，由正弦定理得6sin 23sin 4b Aa B===（2）因为133sin sin()sin cos cos sin 248C A B A B A B =+=+=⨯=11sin 622ABCSab C ==⨯=选择条件②：（1）sin sin sin c a c bB AC --=+， ∴由正弦定理可得：c a c bb a c--=+，整理可得：222b c a bc +-=，又2b =，4a c +=+(()224424a a a ∴+---=+；化简整理可得：()(26444a a c =+--==（2）由（1）知222+=a b c ，故三角形为直角三角形，122ABCS∴=⨯⨯综上所述：ABCa S ==17．已知,,abc 分别为ABC 内角,,A B C 的对边，若ABC 是锐角三角形，需要同时满足下列四个条件中的三个： ①3A π=②13a = ③15c = ④1sin 3C =（1）条件①④能否同时满足，请说明理由；（2）以上四个条件，请在满足三角形有解的所有组合中任选一组，并求出对应的ABC 的面积.【答案】（1）不能，理由见解析；（2）同时满足①②③， 解：（1）ABC 不能同时满足①，④. 理由如下： 若ABC 同时满足①，④， 则在锐角ABC 中，11sin 32C =<，所以06C π<< 又因为3A π=，所以32A C ππ<+<所以2B π>，这与ABC 是锐角三角形矛盾所以ABC 不能同时满足①，④.（2）因为ABC 需同时满足三个条件，由（1）知不能同时满足①④，故只能同时满足①②③或②③④ 若同时满足②③④，因为c a >，所以C A >，则6A C π<<，则2B π>这与ABC 是锐角三角形矛盾.故ABC 不能同时满足②③④，只能同时满足①②③.因为2222cos a b c bc A =+-， 所以222113152152b b =+-⨯⨯⨯， 解得8b =或7b =.当7b =时，22271315cos 02713C +-=<⨯⨯，所以C 为钝角，与题意不符合，所以8b =.所以ABC 的面积1sin 2S bc A == 18．在ABC 中，1sin()1,sin 3C A B -==.（1）求sin A 的值；（2）若①AC =；②BC =请从以上两个条件中任选一个，求ABC 的面积.注：如果选择多种方案分别解答，那么按第一种方案解答计分.【答案】（1）32） （1）由(,)2πππ-∈-⇒-=C A C A .又21sin sin()sin(2)cos 212sin 23π=+=+==-=B A C A A A .因为(0,)sin π∈⇒=A A .（2）选①：由正弦定理可得sin ==ABC B.且sin sin()cos 2π=+===C A A .故11sin 22=⨯⨯=⨯=S BC AC C .选②：由正弦定理可得==AC且sin sin()cos 2π=+===C A A .故11sin22=⨯⨯=⨯=S BC AC C.19．在ABC中，a，b，c分别是角A，B，C的对边，3Bπ=，3a=.（1）若4Aπ=，求b；（2）若______，求c的值及ABC的面积.请从①b=sin2sinC A=，这两个条件中任选一个，将问题（2）补充完整，并作答.注意，只需选择其中的一种情况作答即可，如果选择两种情况作答，以第一种情况的解答计分.【答案】（1；（2）选①：4,ABCc S==6c=；ABCS =.（1）由3Bπ=，3a=，4Aπ=，由正弦定理可得sin sinb aB A=，则3b==（2）若选①：由余弦定理可得2222cosb c a ac B=+-，即21139232c c=+-⨯⨯，整理可得2340c c=--，解得4c=，-1c=（舍去），∴11sin3422ABCS ac B==⨯⨯=选②:sin2sinC A=，可得2c a=，3a=∴6c=∴11sin6322ABCS ac B==⨯⨯=20．在①()1cos C b B+=sin cosC a c B=-这两个条件中任选一个作为已知条件，补充到下面的横线上并作答.ABC的内角A、B、C的对边分别为a、b、c，已知______.（1）求C；（2）若7c=，13a b+=，求ABC的面积.【答案】（1）3π；（2）（1）选择条件①：()1cos sin C b B +=，由正弦定理可得()1cos sin sin C B C B +=，sin 0B ≠，1cos C C ∴+=，cos 1C C -=，即2sin 16C π⎛⎫-= ⎪⎝⎭，所以，1sin 62C π⎛⎫-= ⎪⎝⎭， 0C π<<，则5666C πππ-<-<，66C ππ∴-=，解得3C π=； 选择条件②：3sin cos 3b C a c B =-，由正弦定理得sin sin sin cos 3B C A C B =-， ()()sin sin sin sin cos cos sin A B C B C B C B C π=-+=+=+⎡⎤⎣⎦，∴上式可化简为sin sin cos 3B C B C =，sin 0B ≠，cos tan C C C =⇒=0C π<<，3C π∴=； （2）由余弦定理2222cos c a b ab C =+-，可得2249a b ab +-=，又由13a b +=，则()2349a b ab +-=，()249403a b ab +-∴==，因此，ABC 的面积为12sin ABCS ab C ==21．在ABC 中，3A π=，b = （Ⅰ）B 的大小； （Ⅱ）ABC 的面积 .条件①：222b a c =+； 条件②：cos sin a B b A =. 注：如果选择条件①和条件②分别解答，按第一个解答计分.【答案】（Ⅰ）4B π=若选择条件①：222b a c =+.（Ⅰ）因为222b a c =+，由余弦定理222cos 22a cb B ac +-==， 因为()0,B π∈，所以4B π=.（Ⅱ）由正弦定理sin sin a b A B=，得sin sin b Aa B===又因为()sin sin sin cos cos sin C A B A B A B =+=+12222=+⨯4=，所以11sin 22ABC S ab C ===△. 若选择条件②：cos sin a B b A =. （Ⅰ）由正弦定理sin sin a bA B=，得sin sin a B b A =. 又因为cos sin a B b A =，所以sin cos B B =， 又因为()0,B π∈，所以4B π=.（Ⅱ）由正弦定理sin sin a b A B=，得sin sin b Aa B===又因为()sin sin sin cos cos sin C A B A B A B =+=+12222=+⨯4=，所以11sin 22ABC S ab C ===△. 22．在锐角ABC中，a =，________， （1）求角A ；（2）求ABC 的周长l 的范围.注：在①cos,sin ,cos ,sin 2222A A A A m n ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭，且12m n ⋅=-，②cos (2)cos A b c a C -=，③11()cos cos ,()344f x x x f A π⎛⎫=--= ⎪⎝⎭这三个条件中任选一个，补充在上面问题中并对其进行求解.【答案】条件选择见解析，（1）3A π=；（2）(6+. （1）若选①，因为cos ,sin ,cos ,sin 2222A A A A m n ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭，且12m n ⋅=-， 所以221cossin 222A A -+=-，即1cos 2A =， 因为0,2A π⎛⎫∈ ⎪⎝⎭，所以3A π=. 若选②，因为cos (2)cos A b c a C -=，2cos cos cos b A a C c A =+， 所以2sin cos sin cos sin cos sin()sin B A A C C A A C B =+=+=， 因为sin 0B ≠，所以1cos 2A =. 又因为0,2A π⎛⎫∈ ⎪⎝⎭，所以3A π=.若选③，11()cos cos 24f x x x x ⎛⎫=- ⎪ ⎪⎝⎭21111cos 2sin 21cos sin 242224x x x x x +=-=⨯-111cos 22sin 22226x x x π⎛⎫⎛⎫=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭. 因为1()4f A =，所以1sin 262A π⎛⎫+= ⎪⎝⎭.又因为0,2A π⎛⎫∈ ⎪⎝⎭，72,666A πππ⎛⎫+∈ ⎪⎝⎭， 所以5266ππ+=A ，3A π=. （2）因为3A π=，所以23B C π+=，23C B π=-.4sin sin b CB C ===，所以4sin b B =，24sin 3c B π⎛⎫=- ⎪⎝⎭.214sin 4sin 4sin 4sin 32l B B B B B π⎫⎛⎫=-++=+++⎪ ⎪⎪⎝⎭⎝⎭6B π⎛⎫=++ ⎪⎝⎭因为锐角ABC 且3A π=，所以,62B ππ⎛⎫∈ ⎪⎝⎭所以2,633B πππ⎛⎫+∈ ⎪⎝⎭sin 16B π⎛⎫<+≤ ⎪⎝⎭，故(6l ∈+.23．在①cos cos 2cos c A a C b B +=，②222a c b ac +-=，③22cos 3cos 02BB -=这三个条件中任选一个，补充在下面问题中，并解答.在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且满足______. （1）求角B 的大小；（2）若b =ABC 面积的最大值. 【答案】条件选择见解析（1）3π；（2）4. 解：若选条件①：（1）因为cos cos 2cos c A a C b B +=，由正弦定理，得sin cos cos sin 2sin cos C A C A B B +=，即()sin 2sin cos A C B B +=.在ABC 中，A B C π++=，得()()sin sin sin A C B B π+=-=. 即sin 2sin cos B B B =，又()0,B π∈，所以1cos 2B =，所以3B π=. （2）因为b =2222232cos 2b a c ac B a c ac ac ac ac ==+-=+-≥-=(当且仅当a c =时等号成立)，结合三角形的面积公式得到11sin 322ABCSac B =≤⨯=，. 若选条件②：（1）结合余弦定理得到2221cos 22a cb B ac +-==，又()0,B π∈，所以3B π=.（2）由b =2222232cos 2b a c ac B a c ac ac ac ac ==+-=+-≥-=(当且仅当a c =时等号成立)，结合三角形的面积公式得到11sin 322ABCSac B =≤⨯=. 若选条件③： （1）因为22cos3cos 02BB -=，所以 1cos 3cos 0B B +-=，所以1cos 2B =. 又()0,B π∈，所以3B π=.（2）由b =2222232cos 2b a c ac B a c ac ac ac ac ==+-=+-≥-=(当且仅当a c =时等号成立)，结合三角形的面积公式得到11sin 322ABCSac B =≤⨯=. 24．已知ABC 的内角A ，B ，C 所对边分别为a ，b ，c ，2b =，2242c a c +-=-. （1）求A 的值；（2）从①a B =，②()1sin 2B C -=两个条件中选一个作为已知条件，求sin C 的值. 【答案】（1）23π；（2）答案见解析. （1）由2b =，2242c a c +-=-，∴22222421cos 22242b c a c a c A bc c c +-+--====-⋅，又因为0A π<<，所以23A π=. （2）选择①作为己知条件.在ABC中，由a B =，以及正弦定理sin sin a b A B=，2sin sin 3B =，解得21sin 2B =， 由23A π=，得B 为锐角， 所以4B π=，因为在ABC 中，A B C π++=，所以()sin sin sin cos cos sin C A B A B A B =+=+=22sincos cos sin 3434ππππ+，所以sin C =. 选择②作为已知条件，因为在ABC △中，A B C π++=，所以()1sin sin 232B C C π⎛⎫-=-=⎪⎝⎭， 所以2236C k πππ-=+或()52k 6k Z ππ+∈，所以12C π=，故sin 4C =. 25．在①22()3a b c ab +=+，①sin cos a A a C =-，①(2)sin (2)sin 2sin a b A b a B c C -+-=，这三个条件中任选一个，补充在下列问题中，并解答.已知ABC 的内角,,A B C 的对边分别为,,a b c，c =_____.（1）求C ∠；（2）求ABC 周长的最大值.注：如果选择多个条件分别解答，按第一个解答计分. 【答案】（1）条件选择见解析，3C π=；（2）最大值为 （1）选①，把22()3a b c ab +=+，整理得222a b c ab +-=，由余弦定理得2221cos 222a b c ab C ab ab +-===，因为(0,)C π∈，所以3C π=.选②，因为sin cos a A a C =-，由正弦定理，可得sin sin sin cos A C A A C -，因为(0,)A π∈，则sin 0A ≠cos 1C C -=， 可得1sin 62C π⎛⎫-= ⎪⎝⎭， 又0C π<<，所以5666C πππ-<-<，故66C ππ-=，即3C π=. 选③，因为(2)sin (2)sin 2sin a b A b a B c C -+-=，由正弦定理得：2(2)(2)2a b a b a b c -+-=，即222a b c ab +-=，所以2221cos 22a b c C ab +-==，因为0C π<<，所以3C π=. （2）由（1）可知，3C π=， 在ABC 中，由余弦定理得222cos 3a b ab C +-=，即223a b ab +-=，所以223()()334a b a b ab ++-=≤，当且仅当a b =时取等号，所以a b +≤a b c ++≤即ABC 周长的最大值为。

专题一直角三角形的存在性问题【考题研究】这类问题主要是已知直角三角形的一边（即直角三角形的两个点确定），求解第三点。

这类问题主要是和动点问题结合在一起，主要在于考查学生的探寻能力和分类研究的推理能力，也是近几年来各市地对学生能力提高方面的一个考查。

【解题攻略】解直角三角形的存在性问题，一般分三步走，第一步寻找分类标准，第二步列方程，第三步解方程并验根．一般情况下，按照直角顶点或者斜边分类，然后按照三角比或勾股定理列方程．有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便．解直角三角形的问题，常常和相似三角形、三角比的问题联系在一起．如果直角边与坐标轴不平行，那么过三个顶点作与坐标轴平行的直线，可以构造两个新的相似直角三角形，这样列比例方程比较简便．在平面直角坐标系中，两点间的距离公式常常用到．怎样画直角三角形的示意图呢？如果已知直角边，那么过直角边的两个端点画垂线，第三个顶点在垂线上；如果已知斜边，那么以斜边为直径画圆，直角顶点在圆上（不含直径的两个端点）．【解题类型及其思路】当直角三角形存在时可从三个角度进行分析研究：（1）当动点在直线上运动时，常用的方法是①121k k⋅=-，②三角形相似，③勾股定理；（2）当动点在曲线上运动时，情况分类如下，第一当已知点处作直角的方法①121k k⋅=-，②三角形相似，③勾股定理；第二是当动点处作直角的方法：寻找特殊角【典例指引】类型一【确定三角形的形状】典例指引1．（2019·辽宁中考模拟）已知，m，n是一元二次方程x2+4x+3=0的两个实数根，且|m|＜|n|，抛物线y=x2+bx+c 的图象经过点A（m，0），B（0，n），如图所示．（1）求这个抛物线的解析式；（2）设（1）中的抛物线与x轴的另一个交点为抛物线的顶点为D，求出点C，D的坐标，并判断△BCD的形状；（3）点P是直线BC上的一个动点（点P不与点B和点C重合），过点P作x轴的垂线，交抛物线于点M，点Q在直线BC上，距离点P为2个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．【答案】（1）223y x x=--；（2）C（3，0），D（1，﹣4），△BCD是直角三角形；（3）2213(03)2213(03)22t t tSt t t t⎧-+⎪⎪=⎨⎪-⎪⎩＜＜＜或＞【解析】试题分析：（1）先解一元二次方程，然后用待定系数法求出抛物线解析式；（2）先解方程求出抛物线与x轴的交点，再判断出△BOC和△BED都是等腰直角三角形，从而得到结论；（3）先求出QF=1，再分两种情况，当点P在点M上方和下方，分别计算即可．试题解析：解（1）∵2+430x x+=，∴11x=-，23x=-，∵m，n是一元二次方程2+430x x+=的两个实数根，且|m|＜|n|，∴m=﹣1，n=﹣3，∵抛物线223y x x=--的图象经过点A（m，0），B（0，n），∴10{3b cc-+==-，∴2{3bc=-=-，∴抛物线解析式为223y x x=--；（2）令y=0，则2230x x--=，∴11x=-，23x=，∴C（3，0），∵223y x x=--=2(1)4x--，∴顶点坐标D（1，﹣4），过点D作DE⊥y轴，∵OB=OC=3，∴BE=DE=1，∴△BOC和△BED都是等腰直角三角形，∴∠OBC=∠DBE=45°，∴∠CBD=90°，∴△BCD是直角三角形；（3）如图，∵B（0，﹣3），C（3，0），∴直线BC解析式为y=x﹣3，∵点P的横坐标为t，PM⊥x轴，∴点M的横坐标为t，∵点P在直线BC上，点M在抛物线上，∴P（t，t﹣3），M（t，223t t--），过点Q 作QF⊥PM，∴△PQF是等腰直角三角形，∵PQ2，∴QF=1．①当点P在点M上方时，即0＜t＜3时，PM=t﹣3﹣（223t t--）=23t t-+，∴S=12PM×QF=21(3)2t t-+=21322t t-+，②如图3，当点P在点M下方时，即t＜0或t＞3时，PM=223t t--﹣（t﹣3）=23t t-，∴S=12PM×QF=12（23t t-）=21322t t-．综上所述，S=2213(03)22{13(03)22t t tt t t t或-+<<-．【举一反三】（2019·淮滨县王店乡教育管理站中考模拟）如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A （﹣1，0）B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．（1）求抛物线的解析式和直线AC的解析式；（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．【答案】（1）抛物线解析式为y=﹣x2+2x+3；直线AC的解析式为y=3x+3；（2）点M的坐标为（0，3）；（3）符合条件的点P的坐标为（73，209）或（103，﹣139），【解析】分析：（1）设交点式y =a （x +1）（x -3），展开得到-2a =2，然后求出a 即可得到抛物线解析式；再确定C （0，3），然后利用待定系数法求直线AC 的解析式；（2）利用二次函数的性质确定D 的坐标为（1，4），作B 点关于y 轴的对称点B ′，连接DB ′交y 轴于M ，如图1，则B ′（-3，0），利用两点之间线段最短可判断此时MB +MD 的值最小，则此时△BDM 的周长最小，然后求出直线DB ′的解析式即可得到点M 的坐标；（3）过点C 作AC 的垂线交抛物线于另一点P ，如图2，利用两直线垂直一次项系数互为负倒数设直线PC 的解析式为y =-13x +b ，把C 点坐标代入求出b 得到直线PC 的解析式为y =-13x +3，再解方程组223133y x x y x ⎧-++⎪⎨-+⎪⎩＝＝得此时P 点坐标；当过点A 作AC 的垂线交抛物线于另一点P 时，利用同样的方法可求出此时P 点坐标．详解：（1）设抛物线解析式为y =a （x +1）（x ﹣3），即y =ax 2﹣2ax ﹣3a ，∴﹣2a =2，解得a =﹣1，∴抛物线解析式为y =﹣x 2+2x +3；当x =0时，y =﹣x 2+2x +3=3，则C （0，3），设直线AC 的解析式为y =px +q ，把A （﹣1，0），C （0，3）代入得03p q q -+=⎧⎨=⎩，解得33p q =⎧⎨=⎩， ∴直线AC 的解析式为y =3x +3；（2）∵y =﹣x 2+2x +3=﹣（x ﹣1）2+4，∴顶点D 的坐标为（1，4），作B 点关于y 轴的对称点B ′，连接DB ′交y 轴于M ，如图1，则B ′（﹣3，0），∵MB =MB′，∴MB+MD=MB′+MD=DB′，此时MB+MD的值最小，而BD的值不变，∴此时△BDM的周长最小，易得直线DB′的解析式为y=x+3，当x=0时，y=x+3=3，∴点M的坐标为（0，3）；（3）存在．过点C作AC的垂线交抛物线于另一点P，如图2，∵直线AC的解析式为y=3x+3，∴直线PC的解析式可设为y=﹣13x+b，把C（0，3）代入得b=3，∴直线PC的解析式为y=﹣13x+3，解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝，解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩，则此时P点坐标为（73，209）；过点A作AC的垂线交抛物线于另一点P，直线PC的解析式可设为y=﹣x+b，把A（﹣1，0）代入得13+b=0，解得b=﹣13，∴直线PC的解析式为y=﹣13x﹣13，解方程组223 1133y x xy x⎧-++⎪⎨--⎪⎩＝＝，解得1xy=-⎧⎨=⎩或103139xy⎧=⎪⎪⎨⎪=-⎪⎩，则此时P点坐标为（103，﹣139）.综上所述，符合条件的点P的坐标为（73，209）或（103，﹣139）.类型二【确定点的坐标】典例指引2．19．（2019·江西中考模拟）已知抛物线l：y=ax2+bx+c（a，b，c均不为0）的顶点为M，与y轴的交点为N，我们称以N为顶点，对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线，直线MN为抛物线l的衍生直线．（1）如图，抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是，衍生直线的解析式是；（2）若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1，求这条抛物线的解析式；（3）如图，设（1）中的抛物线y=x2﹣2x﹣3的顶点为M，与y轴交点为N，将它的衍生直线MN先绕点N 旋转到与x轴平行，再沿y轴向上平移1个单位得直线n，P是直线n上的动点，是否存在点P，使△POM 为直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．【答案】（1）y=﹣x2﹣3, y=﹣x﹣3；（2）y=2x2﹣4x+1；（3）存在，P为（1172+，﹣2）或（1172，﹣2）或（9，﹣2）或（﹣8，﹣2）．【解析】分析：（1）衍生抛物线顶点为原抛物线与y轴的交点，则可根据顶点设顶点式方程，由衍生抛物线过原抛物线的顶点则解析式易得，MN解析式易得．（2）已知衍生抛物线和衍生直线求原抛物线思路正好与（1）相反，根据衍生抛物线与衍生直线的两交点分别为衍生抛物线与原抛物线的交点，则可推得原抛物线顶点式，再代入经过点，即得解析式．（3）由N （0，﹣3），衍生直线MN绕点N旋转到与x轴平行得到y=﹣3，再向上平移1个单位即得直线y=﹣2，所以P点可设（x，﹣2）．在坐标系中使得△POM为直角三角形一般考虑勾股定理，对于坐标系中的两点，分别过点作平行于x轴、y轴的直线，则可构成以两点间距离为斜边的直角三角形，且直角边长都为两点横纵坐标差的绝对值．进而我们可以先算出三点所成三条线的平方，然后组合构成满足勾股定理的三种情况，易得P点坐标．本题解析：（1）∵抛物线y=x2﹣2x﹣3过（0，﹣3），∴设其衍生抛物线为y=ax2﹣3，∵y=x2﹣2x﹣3=x2﹣2x+1﹣4=（x﹣1）2﹣4，∴衍生抛物线为y=ax2﹣3过抛物线y=x2﹣2x﹣3的顶点（1，﹣4），∴﹣4=a•1﹣3，解得a=﹣1，∴衍生抛物线为y=﹣x2﹣3．设衍生直线为y=kx+b，∵y=kx+b过（0，﹣3），（1，﹣4），∴304bk b -=+⎧⎨-=+⎩，∴13 kb=-⎧⎨=-⎩，∴衍生直线为y=﹣x﹣3．（2）∵衍生抛物线和衍生直线两交点分别为原抛物线与衍生抛物线的顶点，∴将y=﹣2x2+1和y=﹣2x+1联立，得22121y xy x⎧=-+⎨=-+⎩，解得1xy=⎧⎨=⎩或11xy=⎧⎨=-⎩，∵衍生抛物线y=﹣2x2+1的顶点为（0，1），∴原抛物线的顶点为（1，﹣1）．设原抛物线为y=a（x﹣1）2﹣1，∵y=a（x﹣1）2﹣1过（0，1），∴1=a（0﹣1）2﹣1，∴原抛物线为y=2x2﹣4x+1．（3）∵N（0，﹣3），∴MN绕点N旋转到与x轴平行后，解析式为y=﹣3，∴再沿y轴向上平移1个单位得的直线n解析式为y=﹣2．设点P坐标为（x，﹣2），∵O（0，0），M（1，﹣4），∴OM2=（x M﹣x O）2+（y O﹣y M）2=1+16=17，OP2=（|x P﹣x O|）2+（y O﹣y P）2=x2+4，MP2=（|x P﹣x M|）2+（y P﹣y M）2=（x﹣1）2+4=x2﹣2x+5．①当OM2=OP2+MP2时，有17=x2+4+x2﹣2x+5，解得x=117+或x=117-，即P（117+，﹣2）或P（117-，﹣2）．②当OP2=OM2+MP2时，有x2+4=17+x2﹣2x+5，解得x=9，即P（9，﹣2）．③当MP2=OP2+OM2时，有x2﹣2x+5=x2+4+17，解得x=﹣8，即P（﹣8，﹣2）．综上所述，当P为（117+，﹣2）或（117-，﹣2）或（9，﹣2）或（﹣8，﹣2）时，△POM为直角三角形．【名师点睛】本题考查了一次函数、二次函数图象及性质，勾股定理及利用其表示坐标系中两点距离的基础知识，特别注意的是：利用其表示坐标系中两点距离，是近几年中考的热点,需学生熟练运用.如图，抛物线y =﹣x 2+bx +c 的图象与x 轴交于A （﹣5，0），B （1，0）两点，与y 轴交于点C ，抛物线的对称轴与x 轴交于点D ．（1）求抛物线的函数表达式；（2）如图1，点E （x ，y ）为抛物线上一点，且﹣5＜x ＜﹣2，过点E 作EF ∥x 轴，交抛物线的对称轴于点F ，作EH ⊥x 轴于点H ，得到矩形EHDF ，求矩形EHDF 周长的最大值；（3）如图2，点P 为抛物线对称轴上一点，是否存在点P ，使以点P ，A ，C 为顶点的三角形是直角三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由．【答案】（1）y =﹣x 2﹣4x +5．（2）372；（3）P 坐标为（﹣2，7）或（﹣2，﹣3）或（﹣2，6）或（﹣2，﹣1）．【解析】试题分析：（1）利用待定系数法即可解决问题；（2）构建二次函数利用二次函数的性质即可解决问题；（3）分三种情形分别求解①当90,ACP ∠=o 由222AC PC PA +=， 列出方程即可解决．②当90CAP ∠=︒时，由222AC PA PC +=， 列出方程即可解决．③当90APC ∠=︒ 时，由222PA PC AC +=，列出方程即可；试题解析：(1)把A (−5,0),B (1,0)两点坐标代入2y x bx c =-++， 得到255010b c b c --+=⎧⎨-++=⎩，解得45b c =-⎧⎨=⎩， ∴抛物线的函数表达式为24 5.y x x =--+(2)如图1中，∵抛物线的对称轴x =−2,2(,45)E x x x ，--+ ∴2452EH x x EF x =--+=--，，∴矩形EFDH 的周长225372()2(53)2().22EH EF x x x =+=--+=-++ ∵−2<0， ∴52x =-时,矩形EHDF 的周长最大,最大值为37.2 (3)如图2中,设P (−2,m )①当90,ACP ∠=o ∵222AC PC PA +=，∴22222(52)2(5)3m m ++-=+，解得m =7，∴P 1(−2,7).②当90CAP ∠=o 时,∵222AC PA PC +=，∴22222(52)32(5)m m ++=+-，解得m =−3，∴P 2(−2,−3).③当90APC ∠=o 时,∵222PA PC AC +=，∴2222232(5)(52)m m ，+++-=解得m=6或−1，∴P3(−2,6),P4(−2,−1)，综上所述,满足条件的点P坐标为(−2,7)或(−2,−3)或(−2,6)或(−2,−1).类型三【确定动点运动的时间】典例指引3．已知二次函数y＝ax2＋bx－2的图象与x轴交于A，B两点，与y轴交于点C，点A的坐标为(4，0)，且当x ＝－2和x＝5时二次函数的函数值y相等．(1)求实数a，b的值；(2)如图①，动点E，F同时从A点出发，其中点E以每秒2个单位长度的速度沿AB边向终点B运动，点F5AC方向运动．当点E停止运动时，点F随之停止运动．设运动时间为t秒．连接EF，将△AEF沿EF翻折，使点A落在点D处，得到△DEF.①是否存在某一时刻t，使得△DCF为直角三角形？若存在，求出t的值；若不存在，请说明理由；②设△DEF与△ABC重叠部分的面积为S，求S关于t的函数关系式．【解析】试题分析：（1）根据抛物线图象经过点A以及“当x=﹣2和x=5时二次函数的函数值y相等”两个条件，列出方程组求出待定系数的值．（2）①首先由抛物线解析式能得到点A、B、C三点的坐标，则线段OA、OB、OC的长可求，进一步能得出AB、BC、AC的长；首先用t表示出线段AD、AE、AF（即DF）的长，则根据AE、EF、OA、OC的长以及公共角∠OAC能判定△AEF、△AOC相似，那么△AEF也是一个直角三角形，及∠AEF是直角；若△DCF 是直角，可分成三种情况讨论：i）点C为直角顶点，由于△ABC恰好是直角三角形，且以点C为直角顶点，所以此时点B、D重合，由此得到AD的长，进而求出t的值；ii）点D为直角顶点，此时∠CDB与∠CBD恰好是等角的余角，由此可证得OB=OD，再得到AD的长后可求出t的值；iii）点F为直角顶点，当点F在线段AC上时，∠DFC是锐角，而点F在射线AC的延长线上时，∠DFC 又是钝角，所以这种情况不符合题意．②此题需要分三种情况讨论：i ）当点E 在点A 与线段AB 中点之间时，两个三角形的重叠部分是整个△DEF ；ii ）当点E 在线段AB 中点与点O 之间时，重叠部分是个不规则四边形，那么其面积可由大直角三角形与小钝角三角形的面积差求得；iii ）当点E 在线段OB 上时，重叠部分是个小直角三角形．试题解析：解：（1）由题意得： 16420{ 4222552a b a b a b +-=--=+-，解得：a =12，b =32-． （2）①由（1）知二次函数为213222y x x =--.∵A （4，0），∴B （﹣1，0），C （0，﹣2），∴OA =4，OB =1，OC =2，∴AB =5，AC =BC AC 2+BC 2=25=AB 2，∴△ABC 为直角三角形，且∠ACB =90°．∵AE =2t ，AF ，∴AF AB AE AC ==又∵∠EAF =∠CAB ，∴△AEF ∽△ACB ，∴∠AEF =∠ACB =90°，∴△AEF 沿EF 翻折后，点A 落在x 轴上点D 处；由翻折知，DE =AE ，∴AD =2AE =4t ，EF =12AE =t ． 假设△DCF 为直角三角形，当点F 在线段AC 上时： ⅰ）若C 为直角顶点，则点D 与点B 重合，如图2，∴AE =12AB =52t =52÷2=54； ⅱ）若D 为直角顶点，如图3．∵∠CDF =90°，∴∠ODC +∠EDF =90°．∵∠EDF =∠EAF ，∴∠OBC +∠EAF =90°，∴∠ODC =∠OBC ，∴BC =DC ．∵OC ⊥BD ，∴OD =OB =1，∴AD =3，∴AE =32，∴t =34； 当点F 在AC 延长线上时，∠DFC ＞90°，△DCF 为钝角三角形．综上所述，存在时刻t ，使得△DCF 为直角三角形，t =34或t =54． ②ⅰ）当0＜t ≤54时，重叠部分为△DEF ，如图1、图2，∴S =12×2t ×t =t 2； ⅱ）当54＜t ≤2时，设DF 与BC 相交于点G ，则重叠部分为四边形BEFG ，如图4，过点G 作GH ⊥BE 于H ，设GH =m ，则BH = 12m ，DH =2m ，∴DB =32m ． ∵DB =AD ﹣AB =4t ﹣5，∴ 32m =4t ﹣5，∴m =23（4t ﹣5），∴S =S △DEF ﹣S △DBG =12×2t ×t ﹣12（4t ﹣5）×23（4t ﹣5）=2134025333t t -+-； ⅲ）当2＜t ≤52时，重叠部分为△BEG ，如图5． ∵BE =DE ﹣DB =2t ﹣（4t ﹣5）=5﹣2t ，GE =2BE =2（5﹣2t ），∴S =12×（5﹣2t ）×2（5﹣2t ）=4t 2﹣20t +25． 综上所述： 2225(0)41340255{(2) 3334542025(2)2t t S t t t t t t <≤=-+-<≤-+<≤ ．【名师点睛】此题主要考查的是动点函数问题，涉及了函数解析式的确定、直角三角形以及相似三角形的判定和性质、等腰三角形的性质以及图形面积的解法等综合知识；第二题的两个小题涉及的情况较多，一定要根据动点的不同位置来分类讨论，抓住动点的关键位置来确定未知数的取值范围是解题的关键所在．【举一反三】（2018·河北中考模拟）如图，在平面直角坐标系xOy 中，A 、B 为x 轴上两点，C 、D 为y 轴上的两点，经过点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C 的坐标为（0，），点M 是抛物线C 2：2y mx 2mx 3m =--（m ＜0）的顶点．（1）求A 、B 两点的坐标；（2）“蛋线”在第四象限上是否存在一点P ，使得△PBC 的面积最大？若存在，求出△PBC 面积的最大值；若不存在，请说明理由；（3）当△BDM 为直角三角形时，求m 的值．【答案】（1）A （，0）、B （3，0）；（2）存在．S △PBC 最大值为2716；（3）2m 2=-或1m =-时，△BDM 为直角三角形．【解析】【分析】（1）在2y mx 2mx 3m =--中令y =0，即可得到A 、B 两点的坐标．（2）先用待定系数法得到抛物线C 1的解析式，由S △PBC = S △POC + S △BOP –S △BOC 得到△PBC 面积的表达式，根据二次函数最值原理求出最大值．（3）先表示出DM 2，BD 2，MB 2，再分两种情况：①∠BMD =90°时；②∠BDM =90°时，讨论即可求得m 的值．【详解】解：（1）令y =0，则2mx 2mx 3m 0--=，∵m ＜0，∴2x 2x 30--=，解得：1x 1=-，2x 3=．∴A （，0）、B （3，0）． （2）存在．理由如下：∵设抛物线C 1的表达式为()()y a x 1x 3=+-（a 0≠），把C （0，32-）代入可得，12a =．∴Ｃ1的表达式为：()()1y x 1x 32=+-，即213y x x 22=--． 设P （p ，213p p 22--）， ∴ S △PBC = S △POC + S △BOP –S △BOC =23327p 4216--+（）． ∵3a 4=-<0，∴当3p 2=时,S △PBC 最大值为2716． （3）由C 2可知： B （3，0），D （0，3m -），M （1，4m -），∴BD 2=29m 9+，BM 2=216m 4+，DM 2=2m 1+．∵∠MBD <90°, ∴讨论∠BMD =90°和∠BDM =90°两种情况：当∠BMD =90°时，BM 2+ DM 2= BD 2，即216m 4+＋2m 1+=29m 9+，解得：12m =22m =(舍去)． 当∠BDM =90°时，BD 2+ DM 2= BM 2，即29m 9+＋2m 1+=216m 4+，解得：1m 1=-，2m 1=(舍去) ．综上所述，2m =或1m =-时，△BDM 为直角三角形． 【新题训练】1．（2019·重庆实验外国语学校初三）如图1，已知抛物线y ＝﹣23384x +x +3与x 轴交于A 和B 两点，（点A 在点B 的左侧），与y 轴交于点C ．（1）求出直线BC 的解析式．（2）M 为线段BC 上方抛物线上一动点，过M 作x 轴的垂线交BC 于H ，过M 作MQ ⊥BC 于Q ，求出△MHQ 周长最大值并求出此时M 的坐标；当△MHQ 的周长最大时在对称轴上找一点R ，使|AR ﹣MR |最大，求出此时R 的坐标．（3）T 为线段BC 上一动点，将△OCT 沿边OT 翻折得到△OC ′T ，是否存在点T 使△OC ′T 与△OBC 的重叠部分为直角三角形，若存在请求出BT 的长，若不存在，请说明理由．【答案】（1）y ＝﹣34x +3；（2）R （1，92）；（3）BT ＝2或BT ＝165． 【详解】 解：（1）令y =0，即2333084x x -++=，解得122,4x x =-=， ∵点A 在点B 的左侧∴A （﹣2，0），B （4，0），令x =0解得y =3，∴C （0，3），设BC 所在直线的解析式为y =kx +3， 将B 点坐标代入解得k =34-∴BC 的解析式为y ＝-34x +3； （2）∵MQ ⊥BC ，M 作x 轴，∴∠QMH ＝∠CBO ，∴tan ∠QMH ＝tan ∠CBO ＝34， ∴QH ＝34QM ，MH ＝54MQ ， ∴△MHQ 周长＝MQ +QH +MH ＝34QM +QM +54MQ ＝3QM ， 则求△MHQ 周长的最大值，即为求QM 的最大值； 设M （m ，233384m m -++）， 过点M 与BC 直线垂直的直线解析式为243733812y x m m =--+， 直线BC 与其垂线相交的交点22972721,35025200100Q m m m m ⎛⎫+--+⎪⎝⎭， ∴()23=410MQ m m -+，∴当m＝2时，MQ有最大值65，∴△MHQ周长的最大值为185，此时M（2，3），函数的对称轴为x＝1，作点M关于对称轴的对称点M'（0，3），连接AM'与对称轴交于点R，此时|AR﹣MR|＝|AR﹣M'R|＝AM'，∴|AR﹣MR|的最大值为AM'；∵AM'的直线解析式为y＝32x+3，∴R（1，92）；（3）①当TC'∥OC时，GO⊥TC'，∵△OCT≌△OTC'，∴3412=55 OG⨯＝，∴12655 T⎛⎫ ⎪⎝⎭，∴BT＝2；②当OT⊥BC时，过点T作TH⊥x轴，OT＝125，∵∠BOT＝∠BCO，∴3=1255cOo BOTHs∠＝，∴OH＝36 25，∴36482525 T⎛⎫ ⎪⎝⎭，∴BT＝165；综上所述：BT＝2或BT＝165．2．（2019·福建师范大学附属中学初中部初三月考）如图，抛物线y＝mx2+nx﹣3（m≠0）与x轴交于A(﹣3，0)，B(1，0)两点，与y轴交于点C，直线y＝﹣x与该抛物线交于E，F两点．（1）求点C坐标及抛物线的解析式．（2）P是直线EF下方抛物线上的一个动点，作PH⊥EF于点H，求PH的最大值．（3）以点C为圆心，1为半径作圆，⊙C上是否存在点D，使得△BCD是以CD为直角边的直角三角形？若存在，直接写出D点坐标；若不存在，请说明理由．【答案】（1）y＝x2+2x﹣3；（2212；（3）点D的坐标为：310，﹣310)、(310﹣10)、(1，﹣3)【详解】 解：（1）∵抛物线与x 轴交于A (﹣3，0)，B (1，0)两点，∴抛物线的表达式为：()22(3)(1)23=23=+-=+-+-y a x x a x x ax ax a ，即﹣3a ＝﹣3，解得：a ＝1，故抛物线的表达式为：y ＝x 2+2x ﹣3；（2）过点P 作PM ∥y 轴交直线EF 于点M ，设点P (x ，x 2+2x ﹣3)、点M (x ，﹣x )，则PH ＝22PM ＝()2222321223=2228⎛⎫---+-++ ⎪⎝⎭x x x x ， 当x ＝﹣32时，PH 的最大值为2128； （3）①当∠BCD ＝90°时，如图2左侧图，当点D 在BC 右侧时，过点D 作DM ⊥y 轴于点M ，则CD ＝1，OB ＝1，OC ＝3，tan ∠BCO ＝13＝tan ∠CDM ＝tanα，则sinα10，cosα10x D ＝CDcosα＝310，同理y D ＝﹣3﹣10， 故点D (310，﹣3﹣1010)； 同理当点D （D ′）在BC 的左侧时，同理可得：点D ′(﹣310，﹣3+10)； ②当∠CDB ＝90°时，如右侧图，CD ＝OB ＝1，则点D (1，﹣3)；综上，点D 的坐标为：(310，﹣3﹣10)、(﹣310，﹣3+10)、(1，﹣3)． 3．（2019·四川中考真题）如图，顶点为(3,3)P 的二次函数图象与x 轴交于点(6,0)A ，点B 在该图象上，OB 交其对称轴l 于点M ，点M 、N 关于点P 对称，连接BN 、ON ．（1）求该二次函数的关系式．（2）若点B 在对称轴l 右侧的二次函数图象上运动，请解答下列问题：①连接OP ，当12OP MN =时，请判断NOB ∆的形状，并求出此时点B 的坐标． ②求证：BNM ONM ∠=∠．【答案】（1）二次函数的关系式为2211y (x 3)3x 2x 33=--+=-+；（2）①NOB ∆是等腰直角三角形，此时点B 坐标为(332,3)+-；②见解析【详解】解：（1）∵二次函数顶点为(3,3)P∴设顶点式2(3)3y a x =-+∵二次函数图象过点(6,0)A∴2(63)30a -+=，解得：13a =- ∴二次函数的关系式为2211y (x 3)3x 2x 33=--+=-+（2）设21(,2)(3)3B b b b b -+>∴直线OB 解析式为：1(2)3y b x =-+∵OB 交对称轴l 于点M∴当3M x =时，1(2)363M y b b =-+⨯=-+∴(3,6)M b -+∵点M 、N 关于点P 对称∴3(6)3NP MP b b ==--+=-，∴33N y b b =+-=，即(3,)N b ①∵12OP MN = ∴OP MP =3b =-解得：3b =+∴22112(32(3333b b -+=-⨯++⨯+=-∴(33)B +-，(3,3N +∴222(3(3)36OB =++-=+2223(336ON =++=+B 222(33)(3372BN =++---=+∴OB ON =，222OB ON BN +=∴NOB ∆是等腰直角三角形，此时点B 坐标为(33)+-．②证明：如图，设直线BN 与x 轴交于点D∵21(,2)3B b b b-+、(3,)N b设直线BN解析式为y kx d=+∴21233kb d b bk d b⎧+=-+⎪⎨⎪+=⎩解得：1k b3d2b⎧=-⎪⎨⎪=⎩∴直线BN：123y bx b=-+当0y=时，1203bx b-+=，解得：6x=∴(6,0)D∵(3,0)C，NC x⊥轴∴NC垂直平分OD∴ND NO=∴BNM ONM∠=∠4．（2018·贵州中考真题）如图，已知抛物线2(0)y ax bx c a=++≠的对称轴为直线1x=-，且抛物线与x 轴交于A、B两点，与y轴交于C点，其中(1,0)A，(0,3)C.（1）若直线y mx n=+经过B、C两点，求直线BC和抛物线的解析式；（2）在抛物线的对称轴1x=-上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M 的坐标；（3）设点P为抛物线的对称轴1x=-上的一个动点，求使BPC∆为直角三角形的点P的坐标.【答案】（1）抛物线的解析式为223y x x=--+，直线的解析式为3y x=+.（2）(1,2)M-；（3）P的坐标为(1,2)--或(1,4)-或317(1,)2+-或317(1,)2--.【详解】（1）依题意得：123baa b cc⎧-=-⎪⎪++=⎨⎪=⎪⎩，解得：123abc=-⎧⎪=-⎨⎪=⎩，∴抛物线的解析式为223y x x=--+.∵对称轴为1x=-，且抛物线经过()1,0A，∴把()3,0B-、()0,3C分别代入直线y mx n=+，得303m nn-+=⎧⎨=⎩，解之得：13mn=⎧⎨=⎩，∴直线y mx n=+的解析式为3y x=+.（2）直线BC与对称轴1x=-的交点为M，则此时MA MC+的值最小，把1x=-代入直线3y x=+得2y=，∴()1,2M-.即当点M到点A的距离与到点C的距离之和最小时M的坐标为()1,2-.（注：本题只求M坐标没说要求证明为何此时MA MC+的值最小，所以答案未证明MA MC+的值最小的原因）.（3）设()1,P t-，又()3,0B-，()0,3C，∴218BC =，()2222134PB t t =-++=+，()()222213610PC t t t =-+-=-+，①若点B 为直角顶点，则222BC PB PC +=，即：22184610t t t ++=-+解得：2t =-，②若点C 为直角顶点，则222BC PC PB +=，即：22186104t t t +-+=+解得：4t =， ③若点P 为直角顶点，则222PB PC BC +=，即：22461018t t t ++-+=解得： 1317t +=，2317t -=. 综上所述P 的坐标为()1,2--或()1,4-或3171,⎛⎫+- ⎪ ⎪⎝⎭或3171,⎛⎫-- ⎪ ⎪⎝⎭.5．（2018·四川中考真题）如图①,已知抛物线y =ax 2+bx +c 的图像经过点A （0，3)、B （1，0），其对称轴为直线l ：x =2，过点A 作AC ∥x 轴交抛物线于点C ，∠AOB 的平分线交线段AC 于点E ，点P 是抛物线上的一个动点，设其横坐标为m .（1）求抛物线的解析式；（2）若动点P 在直线OE 下方的抛物线上，连结PE 、PO ，当m 为何值时，四边形AOPE 面积最大，并求出其最大值；（3）如图②，F 是抛物线的对称轴l 上的一点，在抛物线上是否存在点P 使△POF 成为以点P 为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P 的坐标；若不存在，请说明理由.【答案】（1）y =x 2-4x +3.（2）当m =52时，四边形AOPE 面积最大，最大值为758.（3）P 点的坐标为 ：P 13+515-），P 235-，1+5），P 35+51+5），P 455-15-. 【详解】（1）如图1，设抛物线与x 轴的另一个交点为D ，由对称性得：D（3，0），设抛物线的解析式为：y=a（x-1）（x-3），把A（0，3）代入得：3=3a，a=1，∴抛物线的解析式；y=x2-4x+3；（2）如图2，设P（m，m2-4m+3），∵OE平分∠AOB，∠AOB=90°，∴∠AOE=45°，∴△AOE是等腰直角三角形，∴AE=OA=3，∴E（3，3），易得OE的解析式为：y=x，过P作PG∥y轴，交OE于点G，∴G（m，m），∴PG=m-（m2-4m+3）=-m2+5m-3，∴S四边形AOPE=S△AOE+S△POE，=12×3×3+12PG•AE，=92+12×3×（-m2+5m-3），=-32m2+152m，=32（m-52）2+758，∵-32＜0，∴当m=52时，S有最大值是758；（3）如图3，过P作MN⊥y轴，交y轴于M，交l于N，∵△OPF是等腰直角三角形，且OP=PF，易得△OMP≌△PNF，∴OM=PN，∵P（m，m2-4m+3），则-m2+4m-3=2-m，解得：m=5+52或552-∴P 5+51+555-15-）；如图4，过P作MN⊥x轴于N，过F作FM⊥MN于M，同理得△ONP ≌△PMF ， ∴PN =FM ，则-m 2+4m -3=m -2，解得：x =3+5或35-； P 的坐标为（3+5，152-）或（352-，1+52）； 综上所述，点P 的坐标是：（5+5，1+5）或（55-，15-）或（3+5，15-）或（35-，1+52）． 6．（2019·云南中考模拟）已知，抛物线y ＝﹣x 2+bx +c 经过点A （﹣1，0）和C （0，3）．（1）求抛物线的解析式；（2）在抛物线的对称轴上，是否存在点P ，使P A +PC 的值最小？如果存在，请求出点P 的坐标，如果不存在，请说明理由；（3）设点M 在抛物线的对称轴上，当△MAC 是直角三角形时，求点M 的坐标．【答案】（1）223y x x =-++；（2）当PA PC +的值最小时，点P 的坐标为()1,2；（3）点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,3⎛⎫- ⎪⎝⎭. 【详解】解：()1将()1,0A -、()0,3C 代入2y x bx c =-++中， 得：{103b c c --+==，解得：{23b c ==， ∴抛物线的解析式为223y x x =-++．()2连接BC 交抛物线对称轴于点P ，此时PA PC +取最小值，如图1所示．当0y =时，有2230x x -++=，解得：11x =-，23x =，∴点B 的坐标为()3,0．Q 抛物线的解析式为2223(1)4y x x x =-++=--+，∴抛物线的对称轴为直线1x =．设直线BC 的解析式为()0y kx d k =+≠，将()3,0B 、()0,3C 代入y kx d =+中，得：{303k d d +==，解得：{13k d =-=， ∴直线BC 的解析式为3y x =-+．Q 当1x =时，32y x =-+=，∴当PA PC +的值最小时，点P 的坐标为()1,2．()3设点M 的坐标为()1,m ，则22(10)(3)CM m =-+-，()22[01](30)10AC =--+-=，()22[11](0)AM m =--+-． 分三种情况考虑：①当90AMC ∠=o 时，有222AC AM CM =+，即22101(3)4m m =+-++，解得：11m =，22m =，∴点M 的坐标为()1,1或()1,2；②当90ACM ∠=o 时，有222AM AC CM =+，即224101(3)m m +=++-，解得：83m =， ∴点M 的坐标为81,3⎛⎫ ⎪⎝⎭； ③当90CAM ∠=o 时，有222CM AM AC =+，即221(3)410m m +-=++，解得：23m =-， ∴点M 的坐标为21,.3⎛⎫- ⎪⎝⎭综上所述：当MAC V 是直角三角形时，点M 的坐标为()1,1、()1,2、81,3⎛⎫⎪⎝⎭或21,.3⎛⎫- ⎪⎝⎭7．（2019·黑龙江中考模拟）如图，在平面直角坐标系中，抛物线y =ax 2+2x +c 与x 轴交于A （﹣1，0）B （3，0）两点，与y 轴交于点C ．（1）求抛物线y =ax 2+2x +c 的解析式:；（2）点D 为抛物线上对称轴右侧、x 轴上方一点，DE ⊥x 轴于点E ，DF ∥AC 交抛物线对称轴于点F ，求DE +DF 的最大值；（3）①在拋物线上是否存在点P ，使以点A ，P ，C 为顶点，AC 为直角边的三角形是直角三角形？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由；②点Q 在抛物线对称轴上，其纵坐标为t ，请直接写出△ACQ 为锐角三角形时t 的取值范围．【答案】（1）y =﹣x 2+2x +3；（2）DE +DF 有最大值为132；（3）①存在，P 的坐标为（73，209）或（103，139-）；②23-＜t ＜83． 【详解】解：（1）设抛物线解析式为y =a （x +1）（x ﹣3），即y =ax 2﹣2ax ﹣3a ，∴﹣2a =2，解得a =﹣1，∴抛物线解析式为y =﹣x 2+2x +3；（2）当x =0时，y =﹣x 2+2x +3=3，则C （0，3），设直线AC 的解析式为y =px +q ，把A （﹣1，0），C （0，3）代入得03p q q -+=⎧⎨=⎩，解得33p q =⎧⎨=⎩，∴直线AC 的解析式为y =3x +3，如答图1，过D 作DG 垂直抛物线对称轴于点G ，设D （x ，﹣x 2+2x +3），∵DF ∥AC ，∴∠DFG =∠ACO ，易知抛物线对称轴为x =1，∴DG =x -1，DF 10x -1），∴DE +DF =﹣x 2+2x 10（x -1）=﹣x 2+（10）x 10，∴当x =101+，DE +DF 有最大值为132；答图1 答图2（3）①存在；如答图2，过点C作AC的垂线交抛物线于另一点P1，∵直线AC的解析式为y=3x+3，∴直线PC的解析式可设为y=13-x+m，把C（0，3）代入得m=3，∴直线P1C的解析式为y=13-x+3，解方程组223133y x xy x⎧=-++⎪⎨=-+⎪⎩，解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩，则此时P1点坐标为（73，209）；过点A作AC的垂线交抛物线于另一点P2，直线AP2的解析式可设为y=13-x+n，把A（﹣1，0）代入得n=13 -，∴直线PC的解析式为y=1133x--，解方程组2231133y x xy x⎧=-++⎪⎨=--⎪⎩，解得1xy=-⎧⎨=⎩或103139xy⎧=⎪⎪⎨⎪=-⎪⎩，则此时P2点坐标为（103，139-），综上所述，符合条件的点P的坐标为（73，209）或（103，139-）；②23-＜t＜83．8．（2019·广西中考模拟）如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，抛物线与x轴的另一交点为B．（1）若直线y =mx +n 经过B 、C 两点，求直线BC 和抛物线的解析式；（2）设点P 为抛物线的对称轴x =﹣1上的一个动点，求使△BPC 为直角三角形的点P 的坐标．【答案】（1）y =x +3， y =﹣x 2﹣2x +3；（2）（﹣1，﹣2）或（﹣1，4）或（﹣1，3172） 或（﹣1，3172） 【详解】解：（1）∵抛物线y =ax 2+bx +c （a ≠0）的对称轴为直线x =﹣1，且抛物线经过A （1，0），抛物线与x 轴的另一交点为B ，∴B 的坐标为：（﹣3，0），设抛物线的解析式为：y =a （x ﹣1）（x +3），把C （0，3）代入，﹣3a =3，解得：a =﹣1，∴抛物线的解析式为：y =﹣（x ﹣1）（x +3）=﹣x 2﹣2x +3；把B （﹣3，0），C （0，3）代入y =mx +n 得： 30{3m n n -+==， 解得：1{3m n ==，∴直线y =mx +n 的解析式为：y =x +3；（2）设P （﹣1，t ），又∵B （﹣3，0），C （0，3），∴BC 2=18，PB 2=（﹣1+3）2+t 2=4+t 2，PC 2=（﹣1）2+（t ﹣3）2=t 2﹣6t +10，①若点B 为直角顶点，则BC 2+PB 2=PC 2，即：18+4+t 2=t 2﹣6t +10，解之得：t =﹣2；②若点C 为直角顶点，则BC 2+PC 2=PB 2，即：18+t2﹣6t+10=4+t2，解之得：t=4，③若点P为直角顶点，则PB2+PC2=BC2，即：4+t2+t2﹣6t+10=18，解之得：t1=3172+，t2=3172-；综上所述P的坐标为（﹣1，﹣2）或（﹣1，4）或（﹣1，3172+）或（﹣1，3172-）．9．（2019·山东中考模拟）如图，在平面直角坐标系中，∠ACB=90°，OC=2OB，tan∠ABC=2，点B的坐标为（1，0）．抛物线y=﹣x2+bx+c经过A、B两点．（1）求抛物线的解析式；（2）点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使PE=12 DE．①求点P的坐标；②在直线PD上是否存在点M，使△ABM为直角三角形？若存在，求出符合条件的所有点M的坐标；若不存在，请说明理由．【答案】（1）y=﹣x2﹣3x+4；（2）①P（﹣1，6），②存在，M（﹣1，111，311）或（﹣1，﹣1）或（﹣1，132）．【详解】解：（1）∵B（1，0），∴OB=1，∵OC=2OB=2，∴C（﹣2，0），Rt△ABC中，tan∠ABC=2，∴AC2BC=，∴AC23=，∴AC=6，∴A（﹣2，6），把A（﹣2，6）和B（1，0）代入y=﹣x2+bx+c得：42610b cb c--+=⎧⎨-++=⎩，解得：34bc=-⎧⎨=⎩，∴抛物线的解析式为：y=﹣x2﹣3x+4；（2）①∵A（﹣2，6），B（1，0），∴AB的解析式为：y=﹣2x+2，设P（x，﹣x2﹣3x+4），则E（x，﹣2x+2），∵PE=12 DE，∴﹣x2﹣3x+4﹣（﹣2x+2）=12（﹣2x+2），∴x=-1或1（舍），∴P（﹣1，6）；②∵M在直线PD上，且P（﹣1，6），设M（﹣1，y），∵B（1，0），A（﹣2，6）∴AM2=（﹣1+2）2+（y﹣6）2=1+（y﹣6）2，BM2=（1+1）2+y2=4+y2，AB2=（1+2）2+62=45，分三种情况：i）当∠AMB=90°时，有AM2+BM2=AB2，∴1+（y﹣6）2+4+y2=45，解得：y=311，∴M（﹣1，3+11）或（﹣1，3﹣11）；ii）当∠ABM=90°时，有AB2+BM2=AM2，∴45+4+y2=1+（y﹣6）2，∴y=﹣1，∴M（﹣1，﹣1），iii）当∠BAM=90°时，有AM2+AB2=BM2，∴1+（y﹣6）2+45=4+y2，∴y=132，∴M（﹣1，132）；综上所述，点M的坐标为：∴M（﹣1，3+11）或（﹣1，3﹣11）或（﹣1，﹣1）或（﹣1，132）．10．（2019·山东中考模拟）已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C （﹣2，0），点P是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时，△P AB的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．【答案】（1）抛物线解析式为y=﹣12x2+2x+6；（2）当t=3时，△P AB的面积有最大值；（3）点P（4，6）．【详解】（1）∵抛物线过点B （6，0）、C （﹣2，0），∴设抛物线解析式为y =a （x ﹣6）（x +2），将点A （0，6）代入，得：﹣12a =6，解得：a =﹣12， 所以抛物线解析式为y =﹣12（x ﹣6）（x +2）=﹣12x 2+2x +6； （2）如图1，过点P 作PM ⊥OB 与点M ，交AB 于点N ，作AG ⊥PM 于点G ，设直线AB 解析式为y =kx +b ， 将点A （0，6）、B （6，0）代入，得：660b k b =⎧⎨+=⎩， 解得：16k b =-⎧⎨=⎩， 则直线AB 解析式为y =﹣x +6， 设P （t ，﹣12t 2+2t +6）其中0＜t ＜6， 则N （t ，﹣t +6）， ∴PN =PM ﹣MN =﹣12t 2+2t +6﹣（﹣t +6）=﹣12t 2+2t +6+t ﹣6=﹣12t 2+3t ， ∴S △P AB =S △P AN +S △PBN=12PN •AG +12PN •BM =12PN •（AG +BM ） =12PN •OB =12×（﹣12t 2+3t ）×6=﹣32t 2+9t =﹣32（t ﹣3）2+272， ∴当t =3时，△P AB 的面积有最大值；（3）△PDE 为等腰直角三角形，则PE =PD ，点P （m ，-12m 2+2m +6）， 函数的对称轴为：x =2，则点E 的横坐标为：4-m ，则PE =|2m -4|，即-12m 2+2m +6+m -6=|2m -4|， 解得：m =4或-2或5+17或5-17（舍去-2和5+17）故点P 的坐标为：（4，6）或（5-17，317-5）．11．（2019·陕西中考模拟）如图，已知直线y kx 6=-与抛物线2y ax bx c =++相交于A ，B 两点，且点A （1，－4）为抛物线的顶点，点B 在x 轴上．（1）求抛物线的解析式；（2）在（1）中抛物线的第二象限图象上是否存在一点P ，使△POB 与△POC 全等？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若点Q 是y 轴上一点，且△ABQ 为直角三角形，求点Q 的坐标．【答案】解：（1）2y x 2x 3=--；（2）存在，P 1-1313-1）；（3）Q 点坐标为（0，-72）或（0，32）或（0，－1）或（0，－3）.。

专题01 解三角形中的角、边、面积、周长计算问题考点一 角的计算典例1．在ABC 中，角A ，B ，C 所对边分别为a ，b ，c ，已知()sin sin sin sin c C b B a A B -=-，b =6c =.（1）求角C 的大小； （2）求sin B 的值；（3）求cos 26B π⎛⎫- ⎪⎝⎭的值.【答案】（1）3π（2）14（3【分析】（1）利用正弦定理边角互化结合余弦定理即可求解； （2）利用正弦定理即可求解；（3）先求出cos B ，再利用三角恒等变换结合二倍公式即可求解. （1）解：()sin sin sin sin c C b B a A B -=- 由正弦定理将角化为边整理得：222a b c ab +-=所以2221cos 222a b c ab C ab ab +-=== 又()0,πC ∈ 所以3C π=（2）解：由（1）知，3C π=，又b =6c =由正弦定理得：sin sin b cB C=6sin3π=解得：1sin 4B =（3）解：由题知，b =6c = 即b c < 所以3B C π<=所以B 为锐角 由（2）知，1sin 4B =所以cos B ==所以1sin 22sin cos 24B B B ==⨯=217cos 212sin 12168B B =-=-⨯=所以7cos 2cos 2cos sin 2sin 612668B B B πππ⎛⎫-=+= ⎪⎝⎭=即cos 26B π⎛⎫=- ⎪⎝⎭. 变式1-1．在△ABC 中，角A,B,C 所对的边分别为a,b,c .已知b =1,c =√2，3cosC 4= （1）求a 的值； （2）求sin A 的值；（3）求cos 26A π⎛⎫- ⎪⎝⎭的值.【答案】 （1）2（2）√144（3）−3√38−√78【分析】（1）根据余弦定理解方程； （2）利用正弦定理即可得解；（3）求出cosA ，利用两角差的余弦公式求解. （1）由余弦定理可得：2=a 2+1−2a ×34，2a 2−3a −2=0,a >0 所以解得：a =2 （2）cos C =34,sinC =√74，由正弦定理可得：√2√74=2sinA解得：sinA =√144（3）由余弦定理cosA =2√2=−√24cos (2A −π6)=√32cos2A +12sin2A =√32(1−2sin 2A )+sinAcosA =−3√38−√78变式1-2．在ABC 中，角A ､B ､C 的对边分别为a ､b ､c ，已知()22332a c b ac -=- （1）求cos B 的值；（2）若53a b =，求sin A 的值. 【答案】 （1）23（2【分析】（1）化简原式，直接利用余弦定理求cos B 的值即可；（2）由（1）可得sin B =sin A =．（1）在ABC 中，由()22332a c b ac -=-，整理得222223a cb ac +-=，又由余弦定理，可得2cos 3B =； （2）()0,B π∈由（1）可得sin B =，又由正弦定理sin sin a bA B =，及已知53a b =，可得sin 3sin 5a B A b ===故sin A =. 变式1-3．已知ABC 的内角,,A B C 的对边分别为,,a b c ，满足sin 1sin sin b Ca c A B=-++ （1）求角A 的值（2）若3,a b ==sin(2)B A +的值 【答案】 （1）3A π=（2【分析】（1）根据已知条件，由正弦定理角化边，得到三边的关系，进而利用余弦定理求解；（2）由正弦定理求得sin B ,并根据边的大小关系判定B 为锐角，然后利用倍角公式和两角和的正弦公式计算. （1） 解：∵sin 1sin sin b C a c A B=-++， 由正弦定理得，1b ca c a b=-++. 化简得，222b c a bc +-=.由余弦定理得，2221cos 22b c a A bc +-==.又0A π<<， ∴3A π=.（2）解：由（1）知，3A π=，又3a =，b =，∴sin sin b A B a ⋅==. 又b a <，∴cos B ==∴sin 22sin cos B B B ==21cos 212sin 3B B =-=-，∴()sin 2sin 2sin 2cos cos 2sin 333B A B B B πππ⎛⎫+=+=+=⎪⎝⎭考点二 边的计算典例2．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且22cos c b a B +=． （1）求角A 的大小；（2）若1b =，2c =，点D 在边BC 上，且2CD BD =，求线段AD 的长． 【答案】 （1）23A π=（2）AD =【分析】（1）由正弦定理化边为角，然后由诱导公式、两角和的正弦公式化简可得A 角；（2）ABC 中由余弦定理求得a ，再由余弦定理求得cos B ，然后在ABD △中由余弦定理求得AD ． （1）在ABC 中，由正弦定理得2sin sin 2sin cos C B A B += 因为()()sin sin sin C A B A B π=--=+，代入得2sin cos 2cos sin sin 2sin cos A B A B B A B ++=即2cos sin sin 0A B B +=．又sin 0B ≠，所以1cos 2A =-． 又()0,A π∈，所以23A π=． （2）在ABC 中，由余弦定理得2222cos 7a b c bc A =+-=所以a =13BD a ==在ABC 中，由余弦定理得222cos 2a c b B ac +-==在ABD △中，由余弦定理得222132cos 9AD AB BD AB BD B =+-⨯⨯⨯=，所以AD =变式2-1．已知钝角ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且___________，4sin cos sin b A A a B =+，1a =，求c 的值.（1）从条件①sin A =，②sin C B =中选择一个填到横线上，并解决问题； （2）以（1）中结论为条件，若D 是边AC 上一点，且2AD DC =，求线段BD 的长度. 【答案】 （1）1（2【分析】（1）由正弦定理化边为角可得tan A =6A π=.选择条件①：求得b =可求出；选择条件②，由正弦定理可得b =，再由余弦定理即可求出； （2）利用余弦定理即可求出. （1）因为4sin cos sin b A A a B +，由正弦定理可得4sin sin cos sin sin A B B A B A =+，sin sin cos A B B A =，因为sin 0B ≠cos A A =，则tan A =， 又0A π<<，所以6A π=.选择条件①：由sin A =，得6b A π===由余弦定理得2222cos a b c bc A =+-，即2221cos 6c π=+-，解得1c =或2c =，当2c =时，222c a b =+，ABC 是直角三角形，不符合题意； 当1c =时，2,63A CB ππ===，ABC 是钝角三角形，符合题意；所以1c =. 选择条件②，因为sin C B =，由正弦定理可得b ， 由余弦定理可得2222cos a b c bc A =+-，即2221)cos6c c π=+-⋅⋅，解得1c =.（2）由（1）知，BAD 中，221,336BA AD AC A π=====， 由余弦定理可得2222cos BD BA AD BA AD A =+-⋅⋅，即22211213BD =+-⨯=⎝⎭，故BD . 变式2-2．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且sin 21sin A bB a=-. （1）判断三角形△ABC 的形状；（2）记线段AB 上靠近点A 的三等分点为D ，若CD =6b =，求c . 【答案】（1）等腰三角形； （2）6c =. 【分析】（1）由已知，结合正弦定理可得()()20a b a b +-=，根据20a b +>即可判断形状.（2）应用余弦定理，结合CDB CDA π∠=-∠有cos CDB ∠=cos CDA -∠求AD ，即可求c . （1）∵sin 21sin A b B a =-，由正弦定理得21a bb a=-，整理得()()20a b a b +-=. ∴由20a b +>，可得a b =，即三角形为等腰三角形. （2）设AD x =，则2BD x =，由余弦定理得：2cosCDB ∠=，2cos CDA ∠=，而CDB CDA π∠=-∠，22=，解得2x =，∴36c AB BD ===.变式2-3．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若cos sin 0a C C b c --=. （1）求A ；（2）若a =2，ABC b ，c 的值. 【答案】 （1）3A π=（2）2b c == 【分析】（1）先利用正弦定理将边变成角，然后利用()sin sin B A C =+以及两角和的正弦公式代入计算即可； （2）先利用面积公式求出bc ，再利用余弦定理求出22b c +，然后解方程组即可. （1）由cos sin 0a C C b c --=及正弦定理得sin cos sin sin sin 0A C A C B C --=.因为()()sin sin sin sin cos cos sin B A C A C A C A C π=--=+=+，sin cos sin sin 0A C A C C --=.由于sin 0C ≠，cos 10A A --= 所以1sin 62A π⎛⎫-= ⎪⎝⎭.又0A π<<，故3A π=.（2）由题得ABC 的面积1sin 2S bc A ==4bc =①. 而222a b c =+-2cos bc A ，且2a =，故228b c +=②， 由①②得2b c ==.考点三 面积的计算典例3．在ABC 中，角A ，B ，C 所对边分别为a ，b ，c ，2cos 1cos b BaA-=+．(1)证明：2a b c =+；(2)若4cos ,5A a ==ABC 的面积． 【答案】(1)证明见解析(2)6 【解析】 【分析】小问1：证法一：运用余弦定理可证，证法二：利用正弦定理可证； 小问2：由余弦定理求得20bc =，结合三角形面积公式可求结果． (1)（1）证法一：∵2cos 1cos b BaA-=+，∵cos 2cos b b A a a B +=-，由余弦定理可得222222222b c a a c b b b a a bc ac+-+-+⨯=-⨯．则()22222222222224,24bc b c a ac a c b bc b c a ac a c b ++-=-+-++-=--+，2224bc c ac +=，∵2a b c =+．证法二：∵2cos 1cos b B a A -=+，由正弦定理得sin 2cos sin 1cos B BA A-=+，∵2sin sin cos sin sin cos A A B B B A -=+，可得2sin sin sin cos sin cos sin sin()sin sin A B A B B A B A B B C =++=++=+， 所以由正弦定理可得2a b c =+． (2)（2）由余弦定理可得22222()2cos 22b c a b c bc a A bc bc+-+--== 222242323412225a bc a a bc a bc bc bc ---===-=．∵24325bc =，∵20bc =，∵4cos 5A =，A 为三角形内角，∵3sin 5A ==， ∵113sin 206225ABCSbc A ==⨯⨯=． 变式3-1．记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知221cos sin 02A A -+=.(1)求角A 的值；(2)若ABC 为锐角三角形，设a =5b =，求ABC 的面积. 【答案】(1)1π3A =或2π3【解析】 【分析】（1）利用三角恒等变换得到1cos 22A =-，进而求出22π3A =或4π3，故1π3A =或2π3；（2）利用余弦定理求出2c =或3，验证后得到3c =，进而利用三角形面积公式进行求解. (1)2211cos sin cos 2022A A A -+=+=，所以1cos 22A =-，因为(0,π)A ∈，所以2(0,2π)A ∈，故22π3A =或4π3，即1π3A =或2π3. (2)由第一问所求和ABC 为锐角三角形得1π3A =，由余弦定理可得2222cos a b c bc A =+-，化为2560c c -+=，解得2c =或3， 若2c =，则cos 0B =<，即B 为钝角，2c ∴=不成立，当3c =，经检验符合条件，ABC 的面积为11sin 5322S bc A ==⨯⨯=变式3-2．在ABC 中，7cos 8A =，3c =，且b c ≠，再从条件∵、条件∵中选择一个作为已知. 条件∵：sin 2sinB A =； 条件∵：sin sin 2sin A BC +=. (1)求b 的值； (2)求ABC 的面积.【答案】(1)选条件∵：4b =；选条件∵：4b =(2)选条件∵；选条件∵【解析】 【分析】（1）若选∵：在三角形ABC 中由正弦定理及余弦定理可得a ，b 关系式，解方程可得b 的值；若选∵：由正弦定理可得a ，b ，c 的关系，再由余弦定理可得a ，b ，c 的关系，再由A 角的余弦值可得b 的值． （2）结合（1），利用三角形面积公式即可求出三角形的面积； (1)选条件∵：sin 2sin B A =. 在ABC 中，因为sin sin b a B A =，所以sin 2sin a Bb a A ==. 因为222cos 2b c a A bc+-=，且3c =，7cos 8A =，2b a =，所以22497128a a a +-=， 化简得22760a a -+=，解得2a =或32a =. 当32a =时，23b ac ===，与题意矛盾， 所以2a =，所以4b =. 选条件∵：sin sin 2sin A B C +=.在ABC 中，因为sin sin sin abcA B C==，且3c =，所以由sin sin 2sin A B C +=，得26a b c +==.因为222cos 2b c a A bc+-=，且3c =，7cos 8A =，6a b =-，所以()2296768b b b +--=，解得4b =.(2)选条件∵：sin 2sin B A =.因为7cos 8A =，()0,πA ∈，所以sin A =所以11sin 4322ABC S bc A ==⨯⨯△.选条件∵：sin sin 2sin A B C +=. 由（1）知4b =，所以62a b =-=.因为7cos 8A =，()0,πA ∈，所以sin A =所以11sin 4322ABC S bc A ==⨯⨯△.变式3-3．在ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，3B π=，3a =.(1)若4A π=，求b .(2)若______，求c 的值及ABC 的面积.请从∵b =∵sin 2sin C A =，这两个条件中任选一个，将问题（2）补充完整，并作答.【答案】(2)选14ABCc S ==：，26ABCc S==：，【解析】 【分析】(1)根据正弦定理计算即可得出结果；(2)利用余弦定理或正弦定理求出c 的值，再结合三角形的面积公式计算即可. (1)334B a A ππ===，，，由正弦定理，得sin sin b aB A=，所以sin sin 2a b B A =⨯== (2)选∵：由余弦定理，得2222cos b a c ac B =+-，即21139232c c =+-⨯⨯，整理，得2340c c --=，由c >0，得c =4，所以11sin 3422ABCSac B ==⨯⨯= 选∵：因为sin 2sin C A =，由正弦定理，得c =2a ， 所以c =6，所以11sin 6322ABCSac B ==⨯⨯=考点四 周长的计算典例4．已知ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且满足22()b c a bc -=-. (1)求角A 的大小； (2)若a =ABC S =△，求ABC 的周长.【答案】(1)π3A =；(2)5 【解析】 【分析】（1）由已知可得222b c a bc +-=，由余弦定理求出cos A 的值，再结合()0,πA ∈即可得角A 的大小； （2）根据三角形的面积公式可得bc 的值，再由余弦定理即可求出b c +的值，进而可得ABC 的周长. (1)因为22()b c a bc -=-，所以222b c a bc +-=，由余弦定理可得：2221cos 222b c a bc A bc bc +-===， 又因为()0,πA ∈，所以π3A =. (2)由已知11sin 2222ABCSbc A bc ==⨯=所以6bc =， 由已知及余弦定理得2222222cos ()3a b c bc A b c bc b c bc =+-=+-=+-，即27()36b c =+-⨯，所以2()25b c +=，解得：5b c +=或5b c +=-（舍），所以ABC 的周长为5a b c ++=变式4-1．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ab=． (1)求角B ；(2)若c b ==，ABC 的周长l ． 【答案】(1)6B π=(2)3 【解析】 【分析】(1)ab=cos B B =，由此可求角B ；(2)由余弦定理可得2222cos b a c ac B =+-，解方程求a c ，，由此可得ABC 的周长l ．(1)ab=sin sin cos B A A B =．在ABC 中，sin 0A ≠cos B B =，所以tan B ． 又0B π<<，所以6B π=．(2)由余弦定理2222cos b a c ac B =+-，可得2232cos 6a c ac π=+-，即223a c +-=，又c =，解得3a c ==．故ABC 的周长33l a b c =++==变式4-2．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且()1cos cos a C c A -=． (1)证明：ABC 是等腰三角形；(2)若ABC ，且1cos 3C =，求ABC 的周长．【答案】(1)证明见解析；(2)【解析】 【分析】(1)根据给定条件利用三角形射影定理化简即可得解.(2)根据给定条件求出sin C ，再利用三角形面积定理及(1)的结论求出a ，b ，然后借助余弦定理求出c 即可计算作答. (1)在ABC 中，()1cos cos cos cos a C c A a a C c A -=⇔=+， 由射影定理cos cos b a C c A =+得，a b =， 所以ABC 是等腰三角形． (2)在ABC 中，因1cos 3C =且()0,πC ∈，则sin C =又1sin 2ABC S ab C ==△，即2ab =，由(1)知a b =，则有a b ==在ABC 中，由余弦定理得：222182cos 22233c a b ab C =+-=+-=，解得c =又a b ==a ，b ，c 能构成三角形，符合题意，a b c ++=+所以ABC 的周长为 变式4-3．在ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，满足2cos cos cos a A b C c B =+． (1)求A 的大小；(2)若a =ABC 的面积为ABC 的周长． 【答案】(1)3A π=(2)10+【解析】 【分析】（1）通过正弦定理将边化为角的关系，可得cos A ，进而可得结果； （2）由面积公式得24bc =，结合余弦定理得b c +，进而得结果. (1)∵2cos cos cos a A b C c B =+∵由正弦定理，得2sin cos sin cos sin cos A A B C C B =+ ∵2sin cos sin A A A =∵0A π<<，∵1cos 2A =，故3A π=(2)由（1）知，3A π=∵1sin 2ABCSbc A ==∵24bc =∵由余弦定理知，2222cos a b c bc A =+- ∵2228b c bc +-=， 故()2100b c +=∵10b c +=，故10a b c ++=+∵ABC的周长为10+巩固练习练习一 角的计算1．在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知1cos 3a C cb +=. （1）求cos A 的值； （2）求πsin 23A ⎛⎫- ⎪⎝⎭的值.【答案】 （1）13.（2. 【分析】（1）根据正弦定理进行边角互化，再由正弦的和角公式可求得答案； （2）由正弦的二倍角公式和正弦的差角公式可求得答案. （1）解：因为1cos 3a C c b +=，由正弦定理得1cos sin sin 3sin C C B A +=， 又sin sin()sin cos cos sin B A C A C +A C =+=，所以1sin sin cos 3C C A =， 因为sin 0C ≠，所以1cos 3A =. （2）解：由（1）得1cos 3A =，所以sin A ，所以sin 22sin cos A A A ==27cos 22cos 19A A =-=-，所以117sin(2)sin 22()3229A A A π-==-=，所以sin(2)3A π-=. 2．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且满足()22232cos b c b A a b c -=+-.（1）求cos A 的值；（2）求cos 23A π⎛⎫+ ⎪⎝⎭的值. 【答案】 （1）23（2【分析】（1）由余弦定理结合正弦定理化简可得；（2）由（1）求出sin 2A 和cos2A ，再利用和的余弦公式即可求出. （1）由已知结合余弦定理得()32cos 2cos b c b A ab C -=，∴()32cos 2cos b c A a C -=. 由正弦定理得()3sin 2sin cos 2sin cos B C A A C -= ∴()()3sin cos 2sin cos cos sin 2sin B A A C A C A C =+=+. ∵A B C π++=，∴3sin cos 2sin B A B =， ∵sin 0B >，∴2cos 3A =. （2）因为2cos 3A =，所以sin A =，则sin 22sin cos A A A ==， 则21cos 22cos 19A A =-=-，所以cos 2cos 2cos sin 2sin 333A A A πππ⎛⎫+=-=⎪⎝⎭3．在ABC 的内角A ，B ，C 所对边的长分别是a ，b ，c ，已知sin :sin :sin 2A B C =b = （1）求a 的值； （2）求cos C 的值；（3）求sin 26C π⎛⎫+ ⎪⎝⎭的值.【答案】（1）（2）34（3 【分析】（1）利用正弦定理和已知条件可求；（2）根据边的比例关系和余弦定理可求cos C ；（3）利用倍角公式求解sin 2,cos 2C C ，然后利用和角公式可求结果. （1）因为sin :sin :sin 2A B C =::2a b c =因为b =a = （2）由（1）可得2,c a ==2223cos24a b c C ab +-==. （3）因为a c >，所以C 为锐角，所以sin C =sin 22sin cos C C C ==，21cos 22cos 18C C =-=；所以111sin 22cos 26228C C C π⎛⎫++=⨯= ⎪⎝⎭4．在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且sin cos 0b A B =，2a c =，2b =. （1）求角B ； （2）求a ，c ； （3）求()cos 2A B -的值. 【答案】 （1）23B π=（2）c =a =（3）1314【分析】（1）根据题目条件，结合正弦定理，可以得到tan B =（2）2a c =，2b =，结合第一问求出的B ，列余弦定理方程求解；（3）直接利用两角差的余弦公式展开，分别求出展开式的每一项.（1）在ABC 中，由正弦定理sin sin a bA B=，得sin sin cos 0B A A B =.又因为在ABC 中sin 0A ≠，所以sin =B B . 因为0B π<<，所以sin 0B ≠，因而cos 0B ≠.所以sin tan cos B B B ==23B π=. （2）因为2a c =，2b =，由余弦定理得22242cos3a c ac π=+-，解得c =a =（3）由余弦定理得222cos 2b c a A bc +-==(0,)A π∈，则sin 0A >所以sin A ，所以sin 22sin cos A A A =21cos 22cos 17A A =-=，所以()cos 2cos2cos sin 2sin A B A B A B -=+11137214=⨯=.练习二 边的计算5．在ABC 中，角,,A B C 所对的边分别为,,a b c cos sin C c B =. （1）求角C ；（2）若2b =，ABC 的面积为c . 【答案】 （1）3C π=（2）c =【分析】（1cos sin sin B C C B =，进而得tan C = （2）由面积公式得8ab =，进而根据题意得2b =，4a =，再根据余弦定理求解即可. （1）cos sin C c B =，cos sin sin B C C B =， 因为()0,,sin 0B B π∈≠，sin C C =，即tan C = 因为()0,C π∈，所以3C π=.（2）解：因为ABC 的面积为3C π=，所以1sin 2S ab C ===8ab =， 因为2b =，所以4a =，所以2222201cos 2162a b c c C ab +--===，解得c =所以c =.6．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且a b c <<，三角形三边上的高之比为2:3:4. （1）求cos C 的值；（2）若E 为边AC 上一点，30CEB ∠=︒，3BC =，求BE 的长. 【答案】 （1）1124-（2 【分析】()1由于a b c <<，则三边a ，b ，c 上的高之比为123::4:3:2h h h =，根据123111222ABC S ah bh ch ===△，得出432a b c ==，并利用余弦定理求出cos C 的值； ()2利用()1中cos C 的值求出sin C 的值，进而利用正弦定理求出BE 的长.（1）解：由于a b c <<，则三边a ，b ，c 上的高之比为123::4:3:2h h h =. 又因为123111222ABC S ah bh ch ===△，则432a b c ==. 设43212a b c x ===，则3a x =，4b x ，6c x =. 在ABC 中，由余弦定理得222cos 2a b c C ba+-=222291636112424x x x x +-==-. （2） 解：将11cos 24C =-代入22sin cos 1C C +=，得2223513sin 1cos 24C C ⨯=-=，又()0,C π∈，则sin C ==在EBC 中，由正弦定理得sin sin BC BECEB C=∠，则6BE ==7．已知钝角ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且___________，4sin cos sin b A A a B +，1a =，求c 的值.从条件①sin A =，②sin C B =中选择一个填到横线上，并解决问题. 【答案】条件选择见解析，1c = 【分析】结合正弦定理化简已知条件，求得A .若选①，则利用余弦定理求得c ；若选②，则结合正弦定理、余弦定理求得c 的值. 【详解】依题意4sin cos sin b A A a B =+，由正弦定理得4sin sin cos sin sin B A B A A B =+, 在三角形ABC 中，sin 0,sin 0A B >>，所以4sin sin A A A =+，3sin ,tan A A A == 由于()0,A π∈，所以6A π=.若选①，则1,2b == 由余弦定理得2222cos a b c bc A =+-，即2213320c c c =+--+=， 解得1c =或2c =. 当1c =时，2,63A CB ππ===符合题意. 当2c =时，222c a b =+，则ABC 是直角三角形，不符合题意.若选②，sin C B =，由正弦定理得c =， 由余弦定理得2222cos a b c bc A =+-，即222112cos ,1,3b b A b b ⎫=+-⋅==⎪⎪⎝⎭，所以1c ==.8．在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且a （1）求角A 的大小；（2）若a =4B π=，求c .【答案】 （1）3A π=（2）c【分析】（1）根据余弦定理直接计算cos A 即可； （2）根据正弦定理直接计算即可. （1）因为a由余弦定理得：2222cos a b c bc A =+-⋅， 所以1cos 2A =，结合()0,A π∈， 故3A π=.（2）由（1）得：3A π=，于是53412C A B πππππ=--=--=， 由正弦定理得：sin sin a cA C=，于是sin sin a C c A ππ⎛⎫+ ⎪===，故c .练习三 面积的计算9．在ABC 中，角,,A B C 所对边分别为,,a b csin cos 3B bC π⎛⎫=- ⎪⎝⎭.(1)求角C 的大小；(2)若22223a c a b ==-，求ABC 的面积. 【答案】(1)6π；【解析】 【分析】（1）由正弦定理边角关系、三角形内角的性质可得tan C =，即可知C 的大小. （2）由余弦定理及已知条件可得1b =或2b =，再应用三角形面积公式求∵ABC 的面积. (1)sin sin cos 3C B B C π⎛⎫=- ⎪⎝⎭0B π<<，则sin 0B ≠，1cos 2C C C =，可得tan C =，又0C π<<， ∵6C π=.(2)由余弦定理：2222cos c a b ab C =+-且a =22126c b b =+-，222332c b a +=，则228c b =-，∵228126b b b -=+-，整理得2320b b -+=，解得1b =或2b =，∴∵当1b =时，c =1sin 2ABCSab C ==∵当2b =时，2c =，此时1sin 2ABC S ab C ==△∵∵ABC 10．已知ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且满足22()b c a bc -=-.(1)求角A 的大小；(2)若2a =，sin 2sin C B =，求ABC 的面积. 【答案】(1)3A π=【解析】 【分析】（1）由22()b c a bc -=-可得222b c a bc +-=，再利用余弦定理可求得角A ，（2）由sin 2sin C B =可得2c b =，再利用余弦定理可求出,b c 的值，然后利用三角形的面积公式可求得答案 (1)因为22()b c a bc -=-可得：222b c a bc +-=，由余弦定理可得，2221cos 22b c a A bc +-==又(0,)A π∈，所以3A π=(2)由sin 2sin C B =可得2c b =，由余弦定理知：2222cos a b c bc A =+-，22144222b b b b =+-⋅⨯，解得b =c =11sin 22ABCSbc A ===11．在ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c cos sin 0A a B +=. (1)求角A 的大小；(2)若a =2b c +=，求ABC 的面积. 【答案】(1)23π【解析】 【分析】（1）由正弦定理边化角即可求解角A 的大小；（2）结合余弦定理得2222cos a b c bc A =+-，由()2222b c b c bc +=+-代换可得bc ，联立正弦面积公式可求ABC 的面积.(1)cos sin sin 0B A A B +=，(0,)B π∈，sin 0B ≠sin 0A A +=，显然2A π≠，则tan A =(0,)A π∈23A π∴=； (2)由余弦定理得：22222cos ()22cos =+-=+--a b c bc A b c bc bc A ，将1cos 2A =-代入得22()a b c bc =+-，a =2b c +=代入得2,11sin bc S bc A ===12．在ABC 中，()2cos cos b A C =． (1)求A ∠的大小；(2)现在给出三个条件：∵=c ；∵4B π=；∵2a =．试从中选出两个条件，补充在下面的问题中，______，______，求ABC 的面积． 【答案】(1)6π(2)若选∵∵，S =∵∵，1S . 【解析】 【分析】（1）根据正弦定理进行边角互化，再利用两角和的正弦公式求解；（2）根据正弦定理可知，不能同时选∵∵，若选∵∵，由余弦定理可解得各边长及三角形的面积；若选∵∵，利用正弦定理可解得各边长及面积. (1)解：由正弦定理可得()2cos cos b A C =，即2sin cos cos cos B A C A A C =，即)()2sin cos sin cos cos sin B A A C A C A C B +=+，又在ABC 中，sin 0B ≠，所以cos A =()0,A π∠∈，所以6A π∠=；(2)若选∵∵，由4B π=，sin B又正弦定理c ，即sin C B ==不成立，所以不能同时选∵∵； 若选∵∵，由余弦定理得222cos 2b c a A bc +-=222b =，c =1sin 2A =，所以111sin 2222S bc A ==⨯⨯=若选∵∵，由cos A =1sin 2A =，且sin Bcos B ()sin sin sin cos cos sin C A B A B A B =+=+=sin sin a b A B =，即212=b =所以11sin 2122S ab C ==⨯⨯=.练习四 周长的计算13．在ABC 中，角,,A B C 的对边分别为,,a b c ，若sin sin sin sin a A b B c C a B +=+. (1)求角C ；(2)若ABC2c =，求ABC 的周长.【答案】(1)3π(2)6 【解析】 【分析】（1）、根据正弦定理和余弦定理求解即可；（2）、利用面积公式求出ab 的值，化简求出a b +的值，从而求出ABC 的周长. (1)sin sin sin sin a A b B c C a B +=+, sin ,sin ,sin ,222a b cA B C R R R=== 222a b c ab ∴+-=,2221cos 222a b c ab C ab ab +-∴===, 又0C π<<，3C π∴=.(2)由（1）可知3C π=.1sin 2ABCSab C ==,4ab ∴=, 222a b c ab +-=,2c =,228a b ∴+=,()222216a b a b ab ∴+=++=,4a b ∴+=，6a b c ∴++=.ABC 的周长为6.14．已知ABC 的三个内角A ，B ，C 所对的边为a ，b ，c .若11sin sin sin sin sin A 22c C a A b B a B b --=+. (1)求角C 的大小；(2)若ABC c =ABC 的周长. 【答案】(1)23C π= (2)6+【解析】 【分析】（1）利用正弦定理进行角化边的运算，结合余弦定理求出cos C ，根据角的范围可求出角C .（2）由三角形面积可求出4ab =，代入（1）中的等式结合完全平方式可求出()2a b +的值，进而求出三角形的周长. (1)解：由正弦定理得2221122c a b ab ab --=+则222a b c ab +-=-，由余弦定理得2221cos 222a b c ab C ab ab +--===-， 又由0C π<<，可得23C π=； (2)由12sin23ab π=4ab =， 又由2232a b ab +-=-，有2228a b +=，又由()222228836a b a ab b +=++=+=，有6a b +=，故ABC 的周长为6+15．已知ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，且()()sin sin a A B C c B C +-=+. (1)求角C 的值；(2)若26a b +=，且ABC ABC 的周长. 【答案】(1)3C π=(2)6或5【解析】 【分析】（1）利用正弦定理结合二倍角的正弦公式可求得cos C 的值，结合角C 的取值范围可求得角C 的值； （2）由三角形的面积公式可求得ab 的值，结合已知条件可得出关于a 、b 的方程组，解出这两边的长，利用余弦定理求出c 的值，即可得出ABC 的周长. (1)解：由正弦定理得()()sin sin 2sin sin sin sin A C C A C A ππ-=-=，()0,A π∈，则sin 0A >，所以，sin sin 22sin cos C C C C ==， ()0,C π∈，则sin 0C >，可得1cos 2C =，故3C π=.(2)解：由三角形的面积公式可得1sin 2ABC S ab C ===△4ab =， 由已知可得264a b ab +=⎧⎨=⎩，解得22a b =⎧⎨=⎩或14a b =⎧⎨=⎩. 当2a b ==时，则ABC 为等边三角形，其周长为6；当1a =且4b =时，由余弦定理可得c =此时，ABC 的周长为5a b c ++=综上所述，ABC 的周长为6或516．在ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，____．从∵22()3b c a bc +-=，∵sin sin 3a Bb A π⎛⎫=+ ⎪⎝⎭这两个条件中任选一个，补充在上面问题中并作答．(1)求角A 的大小；(2)若b =4，ABC 的面积ABC 的周长．【答案】(1)3π；(2)10+ 【解析】 【分析】（1）选∵，利用余弦定理化简即得解；选∵，利用正弦定理和三角恒等变换化简即得解；（2）由面积求出6,c =再利用余弦定理求出a =. (1) 解：选∵：222222221()3,,cos 22b c a b c a bc b c a bc A bc +-+-=∴+-=∴==，()0,,3A A ππ∈∴=；选∵：由正弦定理得：sin sin sin sin 3A B B A π⎛⎫=+⎪⎝⎭，在ABC 中，0,sin 0,sin sin 3B B A A ππ⎛⎫<<∴≠∴=+⎪⎝⎭，11sin sin ,sin 22A A A A A ∴=∴=，可得tan A =()0,,3A A ππ∈∴=.(2)解：由（1）知1,4,sin 632ABCA b Sbc A c π=====∴=，由余弦定理可得22212cos 1636246282a b c bc A =+-=+-⨯⨯⨯=，则a =因此，ABC 的周长为10a b c ++=+。

专题01 三角形的高线和角分线结合类型一 从一个顶点出发的高线和角分线1．如图，在ABC V 中，CD 、CE 分别是ABC V 的高和角平分线，,()BAC B Ða Ðb a b ==>．(1)若70,40a b =°=°，求DCE Ð的度数；(2)试用a 、b 的代数式表示DCE Ð的度数_________．【答案】(1)15DCE Ð=°(2)2a b-【解析】【分析】（1）根据三角形的内角和定理求出∠ACB 的值，再由角平分线的性质以及直角三角形的性质求出∠DCE ．（2）由（1）的解题思路即可得正确结果．(1)解：Q 70BAC Ð=°，40B Ð=°\()180()180704070ACB BAC B Ð=°-Ð+Ð=°-°+°=°，Q CE 是ACB Ð的平分线，\1352ACE ACB Ð=Ð=°．Q CD 是高线，\90ADC Ð=°，\9020ACD BAC Ð=°-Ð=°，\352015DCE ACE ACD Ð=Ð-Ð=°-=°°．(2)解：Q BAC a Ð=，B bÐ=\()180()180ACB BAC B a b Ð=°-Ð+Ð=°-+，Q CE 是ACB Ð的平分线，\()1118090222ACE ACB a b a b +Ð=Ð=´°-+=°-éùëû．Q CD 是高线，\90ADC Ð=°，\9090ACD BAC a Ð=°-Ð=°-，\909022DCE ACE ACD a b a b a +-Ð=Ð-Ð=°--°+=．【点睛】本题主要考查角平分线，高线以及角的转换，掌握角平分线，高线的性质是解题的关键．2．如图，在三角形ABC 中，AD BC ^，AE 平分∠BAC ，60B Ð=°，20C Ð=°．(1)∠BAE 的度数是______．(2)∠DAE 的度数是______．(3)探究：如果把条件60B Ð=°，20C Ð=°改成40B C Ð-Ð=°，你认为能得出∠DAE 的度数吗？若能，请你写出求解过程；若不能，请说明理由．【答案】(1)50°(2)20°(3)能，过程见解析【解析】【分析】(1)根据三角形内角和定理得∠BAC ，然后根据角平分线定义得∠BAE =12∠BAC ，即可；(2)由于AD ⊥BC ，则∠ADE =90°， 根据三角形外角性质得∠ADE = ∠B +∠BAD ，所以∠BAD =90°-∠B ，然后利用∠DAE = ∠BAE -∠BAD 进行计算；(3)根据三角形内角和定理得∠BAC ，再根据角平分线定义得∠BAE ，加上∠ADE =∠B +∠BAD =90°，则∠BAD =90°-∠B ，然后利用角的和差得∠DAE =∠BAE -∠BAD ，即可求得∠DAE 的度数等于∠B 与∠C 差的一半，即可求解；（本题方法不唯一）；(1)∵∠B +∠C +∠BAC = 180°∴∠BAC = 180°-∠B -∠C = 180°- 60°- 20°= 100°，∵ AE 平分∠BAC ，∴∠BAE =12∠BAC = 50°(2)∵AD ⊥BC∴∠ADE = 90°，而∠ADE =∠B +∠BAD ，∠BAD = 90°-∠B = 90°- 60°=30°∴∠DAE =∠BAE -∠BAD = 50°- 30°= 20°(3)能得出∠DAE 的度数．（解法1）设C x Ð=，则40B x Ð=°+，∴()180401402BAC x x x Ð=°-°--=°-．∵AE 平分∠BAC ，∴1702BAE BAC x Ð=Ð=°-．∵AD BC ^，40B x Ð=°+，∴50BAD x Ð=°-，∴()()705020DAE BAE BAD x x Ð=Ð-Ð=°--°-=°．（解法2）∵180BAC B C Ð+Ð+Ð=°，∴()180BAC B C Ð=°-Ð+Ð．∵AE 平分∠BAC ，∴()119022BAE BAC B C Ð=Ð=°-Ð+Ð．∵AD BC ^，∴90BAD B Ð=°-Ð，∴()()()11909022DAE BAE BAD B C B B C Ð=Ð-Ð=°-Ð+Ð-°-Ð=Ð-Ð．∵40B C Ð-Ð=°，∴20DAE Ð=°．【点睛】本题考查了三角形的内角和定理，三角形的角平分线的定义，角的和差，三角形的外角的性质，解题的关键是理解并熟悉三角形的内角和定义，以及掌握角三角形的角平分线的定义．3．如图，在ABC D 中，AD BC ^，AE 平分BAC Ð，若140Ð=°，220Ð=°，求B Ð的度数？【答案】30°【解析】【分析】根据AE 平分∠BAC ，可得∠BAE =∠EAC ，由∠1=40°，∠2=20°，可求得∠EAD 的度数，在直角三角形ABD 在利用两锐角互余，即可求解．【详解】解：∵AE 平分∠BAC ，∴∠1=∠EAC =∠EAD +∠2，∴∠EAD =∠1-∠2=40°-20°=20°，在Rt △ABD 中，∠B =90°-∠BAD =90°-40°-20°=30°．【点睛】本题考查了三角形的角平分线、中线和高的相关知识；求得∠EAD的度数是正确解答本题的关键．4．如图，AD、AE分别是△ABC的角平分线和高线.(1) 若∠B＝50°，∠C＝60°，求∠DAE的度数；（2）若∠C ＞∠B，猜想∠DAE与∠C-∠B之间的数量关系，并加以证明.(∠C-∠B). 证明见解析．【答案】（1）5°；（2）∠ DAE =12【解析】【分析】∠CAB=35°，（1）先根据三角形内角和得到∠CAB=180°-∠B-∠C=70°，再根据角平分线与高线的定义得到∠CAD=12∠AEC=90°，则∠CAE=90°-∠C=30°，然后利用∠DAE=∠CAD-∠CAE计算即可．（2）根据题意可以用∠B和∠C表示出∠CAD和∠CAE，从而可以得到∠DAE与∠C-∠B的关系．【详解】(1)在△ABC中,∵∠B=50°,∠C=60°,∴∠BAC=180°-50°-60°=70°.∵AD是∠BAC的角平分线,∠BAC=35°.∴∠BAD=∠DAC=12又∵AE是BC上的高,∴∠AEC=90°.在△CAE中,∠CAE=90°-∠C=90°-60°=30°,∴∠DAE=∠CAD-∠CAE=35°-30°=5°.(∠C-∠B).（2）∠ DAE =12证明如下：∵AE是△ABC的高，∴∠AEC=90°，∴∠EAC=90°-∠C ，∵AD 是△ABC 的角平分线，∴∠DAC=12∠BAC.∵∠BAC=180°-∠B-∠C ，∴∠DAC=12(180°-∠B-∠C) ，∴∠DAE=∠DAC-∠EAC =12(180°-∠B-∠C) - (90°-∠C)=12(∠C-∠B)【点睛】本题考查三角形内角和定理、角的平分线的性质、直角三角形的性质，解题的关键是明确题意，找出所求问题需要的条件．5．如图，在ABC V 中，AE 为边BC 上的高，点D 为边BC 上的一点，连接AD ．（1）当AD 为边BC 上的中线时，若6AE =，ABC V 的面积为30，求CD 的长；（2）当AD 为BAC Ð的角平分线时，若66C Ð=°，36B Ð=°，求DAE Ð的度数．【答案】（1）5；（2）15°【解析】【分析】（1）利用三角形的面积公式求出BC 即可解决问题；（2）先根据三角形内角和求得∠BAC 的度数，再根据AD 平分∠BAC ，AE ⊥BC ，求得∠BAE ，∠BAD 的度数，最后根据∠DAE =∠BAE -∠BAD 计算即可．【详解】解：（1）∵AE ⊥BC ，AE =6，△ABC 的面积为30，×BC×AE=30，∴12×BC×6=30，∴12∴BC=10，∵AD是△ABC的中线，BC=5；∴CD=12（2）∠BAC=180°-∠B-∠C=180°-36°-66°=78°∵AD平分∠BAC，∠BAC=39°，∴∠BAD=12∵AE⊥BC，∴∠AEB=90°，∴∠BAE=90°-∠B=54°，∴∠DAE=∠BAE-∠BAD=54°-39°=15°．【点睛】本题考查三角形的面积，三角形的中线与高等知识，解题的关键是熟练掌握基本知识，属于中基础题．6．如图，在△ABC中，AE为边BC上的高，点D为边BC上的一点，连接AD．（1）当AD为边BC上的中线时．若AE=4，△ABC的面积为24，求CD的长；（2）当AD为∠BAC的角平分线时．①若∠C =65°，∠B =35°，求∠DAE的度数；②若∠C-∠B =20°，则∠DAE = °．【答案】（1）6 ；（2）①15°；②10．【解析】【分析】（1）利用三角形的面积公式求出BC即可解决问题；（2）①根据三角形内角和求出∠BAC和∠CAE的度数，然后根据角平分线的定义求得∠CAD的度数，从而求解；②设∠C=x°，则∠B=（x+20）°，然后根据三角形内角和用含x的式子表示出∠BAC和∠CAE的度数，然后根据角平分线的定义求得∠CAD的度数，从而求解．【详解】解：（1）由题意可知：AE⊥BC，AE=4，△ABC的面积为24，∴12×BC×AE=24，∴12×BC×4=24，∴BC=12，∵AD是△ABC的中线，∴CD=12BC=6，（2）①在△ABC中，∠BAC=180°-∠C-∠B =80°，在△AEC中，∵AE⊥BC∴∠CAE=180°-90°-∠C=25°∵AD为∠BAC的角平分线∴∠CAD=140 2BACÐ=o∴∠DAE的度数为∠CAD -∠CAE =15°②设∠C=x°，则∠B=（x+20）°在△ABC中，∠BAC=180°-∠C-∠B =（160-2x）°，在△AEC中，∵AE⊥BC∴∠CAE=180°-90°-∠C=（90-x）°∵AD为∠BAC的角平分线∴∠CAD=1(80) 2BAC x Ð=-o∴∠DAE的度数为∠CAE- ∠CAD =10°故答案为：10．【点睛】本题考查三角形的面积，三角形的中线与高等知识，解题的关键是熟练掌握基本知识，属于中基础题．7．△ABC中，AD为∠BAC的平分线，AF为BC边上的高．（1）若∠B=38°，∠C=76°，求∠DAF 的度数．（2）若∠B=m°，∠C=n°，（m<n ）．求∠DAF 的度数（用含m 、n 的式子表示）．（3）若∠C-∠B=30°，则∠DAF=_________度．（填空）【答案】(1)19°；(2)11n -m 22°°；(3)15°【解析】【分析】（1）由三角形的内角和是180°，可求∠BAC=66°，因为AD 为∠BAC 的平分线，得∠BAD=33°；又由三角形的一个外角等于与它不相邻的两个内角的和，得∠ADC=∠BAD+∠B=71°；又已知AF 为BC 边上的高，所以∠DAF=90°-∠ADC=19°；（2）求出∠BAC 度数，求出∠DAC ，根据角平分线求出∠BAD ，根据三角形外角的性质求出∠ADC 的度数，即可求出∠DAF 度数；（3）利用（2）的结论即可求出答案．【详解】解：(1)∵∠BAC+∠B+∠C=180°,又∵∠B=38°，∠C=76°,∴∠BAC=66°．∵AD 为∠BAC 的平分线,∴∠BAD=33°,∴∠ADC=∠BAD+∠B=71°．又∵AF 为BC 边上的高,∴∠DAF=90°-∠ADC=19°．(2)∵∠BAC+∠B+∠C=180°,又∵∠B=m°，∠C=n°,∴∠BAC=180°- m°-n°．∵AD 为∠BAC 的平分线,∴∠BAD=111BAC=90-m n 222а°-°,∴∠ADC=∠BAD+∠B=1190+m n 22°°-°又∵AF 为BC 边上的高,∴∠DAF=90°-∠ADC=11n -m 22°°．(3)由（2）可知∠DAF=90°-∠ADC=11C-B 22ÐÐ∵∠C-∠B=30°∴∠DAF=15°故答案为：15°【点睛】本题考查三角形外角的性质及三角形的内角和定理，求角的度数常常要用到“三角形的内角和是180°这一隐含的条件；解答的关键是沟通外角和内角的关系．8．如图，在ABC V 中，AD 是高，AE 是角平分线，20B Ð=°，60C Ð=°．（1）求CAD Ð、AEC Ð和EAD Ð的度数．（2）若图形发生了变化，已知的两个角度数改为：当30B Ð=°，60C Ð=°，则EAD Ð=__________°．当50B Ð=°，C 60∠=°时，则EAD Ð=__________°．当60B Ð=°，60C Ð=°时，则EAD Ð=__________°．当70B Ð=°，60C Ð=°时，则EAD Ð=__________°．（3）若B Ð和C Ð的度数改为用字母a 和b 来表示，你能找到EAD Ð与a 和b 之间的关系吗？请直接写出你发现的结论．【答案】（1）30°，70°，20°；（2）15°，5°，0°，5°；（3）当a b <时，1()2EAD b a Ð=-；当a b >时，1()2EAD a b Ð=-．【解析】【分析】（1）先利用三角形内角和定理求出BAC Ð的度数，再根据角平分线和高的性质分别得出EAC Ð和DAC Ð的度数，进而可求AEC Ð和EAD Ð的度数；（2）先利用三角形内角和定理求出BAC Ð的度数，再根据角平分线和高的性质分别得出EAC Ð和DAC Ð的度数，则前三问利用EAD EAC DAC Ð=Ð-Ð即可得出答案，第4问利用EAD DAC EAC Ð=Ð-Ð即可得出答案；（3）按照（2）的方法，将相应的数换成字母即可得出答案．【详解】（1）∵20B Ð=°，60C Ð=°，∴180100BAC B C Ð=-Ð-Ð=°° ．∵AE 平分BAC Ð，∴1502EAC BAC Ð=Ð=°．∵AD 是高，90ADC ADE \Ð=Ð=° ，9030CAD C \Ð=°-Ð=° ，20EAD EAC CAD \Ð=Ð-Ð=° ，9070AEC EAD \Ð=°-Ð=° ．（2）当30B Ð=°，60C Ð=°时，∵30B Ð=°，60C Ð=°，∴18090BAC B C Ð=°-Ð-Ð=°．∵AE 平分BAC Ð，∴1452EAC BAC Ð=Ð=°．∵AD 是高，90ADC \Ð=° ，9030CAD C \Ð=°-Ð=° ，15EAD EAC CAD \Ð=Ð-Ð=° ；当50B Ð=°，60C Ð=°时，∵50B Ð=°，60C Ð=°，∴18070BAC B C Ð=-Ð-Ð=°° ．∵AE 平分BAC Ð，∴1352EAC BAC Ð=Ð=°．∵AD 是高，90ADC \Ð=° ，9030CAD C \Ð=°-Ð=° ，5EAD EAC CAD \Ð=Ð-Ð=° ；当60B Ð=°，60C Ð=°时，∵60B Ð=°，60C Ð=°，∴18060BAC B C Ð=°-Ð-Ð=°．∵AE 平分BAC Ð，∴1302EAC BAC Ð=Ð=°．∵AD 是高，90ADC \Ð=° ，9030CAD C \Ð=°-Ð=° ，0EAD EAC CAD \Ð=Ð-Ð=° ；当70B Ð=°，60C Ð=°时，∵70B Ð=°，60C Ð=°，∴18050BAC B C Ð=°-Ð-Ð=°．∵AE 平分BAC Ð，∴1252EAC BAC Ð=Ð=°．∵AD 是高，90ADC \Ð=° ，9030CAD C \Ð=°-Ð=° ，5EAD DAC EAC \Ð=Ð-Ð=° ．（3）当B C Ð<Ð 时，即a b <时，∵B a Ð=，C b Ð=，∴180180BAC B C a b Ð=°-Ð-Ð=°-- ．∵AE 平分BAC Ð，∴1111(180)902222EAC BAC a b a b Ð=Ð=°--=--．∵AD 是高，90ADC \Ð=° ，9090CAD C b \Ð=°-Ð=°- ，1()2EAD EAC CAD b a \Ð=Ð-Ð=- ；当B C Ð>Ð 时，即a b >时，∵B a Ð=，C b Ð=，∴180180BAC B C a b Ð=°-Ð-Ð=°-- ．∵AE 平分BAC Ð，∴1111(180)902222EAC BAC a b a b Ð=Ð=°--=--．∵AD 是高，90ADC \Ð=° ，9090CAD C b \Ð=°-Ð=°- ，1()2EAD DAC EAC a b \Ð=Ð-Ð=- ；综上所述，当a b <时，1()2EAD b a Ð=-；当a b >时，1()2EAD a b Ð=-．【点睛】本题主要考查三角形内角和定理和三角形的角平分线，高，掌握三角形内角和定理和直角三角形两锐角互余是解题的关键．9．已知ABC V 中，CD 是AB 边上的高，CE 平分ACB Ð．若A m Ð=°，B n Ð=°，m n ¹，则DCE Ð的度数等于（ ）A ．12m °B ．12n °C ．()12m n °-°D ．12m n °-°【答案】D【解析】【分析】题目由于在三角形中未确定A B ÐÐ、大小，所以需要进行分类讨论：（1）A B Ð<Ð，作出符合题意的相应图形，由图可得：DCE BCE BCD Ð=Ð-Ð，根据角平分线的性质得：()18022m n ACB BCE °-°+°ÐÐ==，在Rt BCD D 中，9090BCD B n Ð=°-Ð=°-°，故可得()12DCE n m Ð=°-°；（2）A B Ð>Ð时，由图可得：DCE ACE ACD Ð=Ð-Ð，()18022m n ACB ACE °-°+°ÐÐ==，在Rt ACD D 中，9090ACD A m Ð=°-Ð=°-°，故可得()12DCE m n Ð=°-°；综上可得：12DCE m n Ð=°-°．【详解】解：（1）如图1所示：A B Ð<Ð时，图1∵CD 是AB 边上的高，∴CD AB ^，90CDB Ð=°，∵A m Ð=°，B n Ð=°，∴()180ACB m n Ð=°-°+°，∵CE 平分ACB Ð，∴()18022m n ACB ACE BCE °-°+°ÐÐ=Ð==，在Rt BCD D 中，9090BCD B n Ð=°-Ð=°-°，∴()()()18019022m n DCE BCE BCD n n m °-°+°Ð=Ð-Ð=-°-°=°-°；（2）如图2所示：A B Ð>Ð时，图2∵CD 是AB 边上的高，∴CD AB ^，90CDB Ð=°，∵A m Ð=°，B n Ð=°，∴()180ACB m n Ð=°-°+°，∵CE 平分ACB Ð，∴()18022m n ACB ACE BCE °-°+°ÐÐ=Ð==，在Rt ACD D 中，9090ACD A m Ð=°-Ð=°-°，∴()()()18019022m n DCE ACE ACD m m n °-°+°Ð=Ð-Ð=-°-°=°-°；综合（1）（2）两种情况可得：12DCE m n Ð=°-°．故选：D ．【点睛】题目主要考查对三角形分类讨论、数形结合思想，主要知识点是三角形的角平分线、高线的基本性质及图形内角的运算，题目难点是在依据题意进行分类讨论的情况下，作出相应的三角形图形．类型二 高线和角分线结合进阶10．在ABC V 中，AD 是BAC Ð的角平分线，B C Ð<Ð，（1）如图1，AE 是ABC V 边BC 上的高，36,70B C Ð=°Ð=°，求DAE Ð的度数；（2）如图2，点E 在AD 上，EF BC ^于F ，猜想DEF Ð与B Ð、C Ð的数量关系，并证明你的结论．【答案】（1）17°（2）∠DEF ＝12（∠C −∠B ），证明见解析【解析】【分析】（1）依据角平分线的定义以及垂线的定义，即可得到∠CAD ＝12∠BAC ，∠CAE ＝90°−∠C ，进而得出∠DAE ＝12（∠C −∠B ），由此即可解决问题．（2）过A 作AG ⊥BC 于G ，依据平行线的性质可得∠DAG ＝∠DEF ，依据（1）中结论即可得到∠DEF ＝12（∠C −∠B ）．【详解】解答：解：（1）如图1，∵AD 平分∠BAC ，∴∠CAD ＝12∠BAC ，∵AE ⊥BC ，∴∠CAE ＝90°−∠C ，∴∠DAE ＝∠CAD −∠CAE ＝12∠BAC −（90°−∠C ）＝12（180°−∠B −∠C ）−（90°−∠C ）＝12∠C −12∠B ＝12（∠C −∠B ），∵36,70B C Ð=°Ð=°，∴∠DAE＝1（70°−36°）＝17°．2（∠C−∠B）．（2）结论：∠DEF＝12理由：如图2，过A作AG⊥BC于G，∵EF⊥BC，∴AG//EF，∴∠DAG＝∠DEF，（∠C−∠B），由（1）可得，∠DAG＝12∴∠DEF＝1（∠C−∠B）．2【点睛】此题主要考查了角平分线的性质、三角形内角和定理和直角三角形的性质，解题时注意：三角形内角和是180°．11．如图一，在△ABC中，AD是∠BAC的平分线，AE是BC边上的高，∠ABC＝30°，∠ACB＝70°．（1）求∠DAE的度数．（2）如图二，若点F为AD延长线上一点，过点F作FG⊥BC于点G，求∠AFG的度数．【答案】（1）20°；（2）20°．【解析】【分析】（1）先利用三角形内角和定理求出80BAC Ð=°，再利用角平分线求出40BAD Ð=°，进而求出70ADC BAD ABD Ð=Ð+Ð=°，最后用三角形的内角和定理 即可得出结论；（2）先判断出//FG AE ，即可得出结论．【详解】解：（1）在ABC D 中，30ABC =°ÐQ ，70ACB Ð=°，180180307080BAC ABC ACB \Ð=°-Ð-Ð=°-°-°=°AD Q 平分BAC Ð11804022BAD CAD BAC \Ð=Ð=Ð=´°=°，在ABD D 中，403070ADC BAD ABD Ð=Ð+Ð=°+°=°AE ∵为三角形的高，90AED \Ð=°．在AED D 中，180180709020DAE ADE AED Ð=°-Ð-Ð=°-°-°=°．（2）90FG BC FGD ^\Ð=°Q 90AED Ð=°Q FGD AED\Ð=Ð//FG AE\AFG DAE\Ð=Ð由（1）可知20DAE Ð=°20AFG \Ð=°．【点睛】此题主要考查了三角形的内角和定理，角平分线的定义，高线的定义，平行线的判定和性质，求出BAE Ð是解本题的关键．12．在△ABC 中，AD 是角平分线．B C Ð<Ð．(1)如图（1），AE 是高，35B Ð=°，65C =°∠，求∠DAE 的度数；(2)如图（2），点E 在AD 上，EF BC ^于F ，试探究∠DEF 与∠B 、∠C 的大小关系，并证明你的结论；(3)如图（3），点E 在AD 的延长线上．EF BC ^于F ，试探究∠DEF 与∠B 、∠C 的大小关系是___（直接写出结论，不需证明）．【答案】(1)15°(2)2DEF C B ÐÐÐ=-，证明见解析(3)2DFF C BÐÐÐ=-【解析】【分析】（1）根据AE 是高确定∠CEA 的度数，再结合三角形内角和定理确定∠BAC 和∠CAE 的度数，根据AD 是角平分线确定∠DAC 的度数，进而即可求出∠DAE 的度数．（2）过点A 作AG ⊥BC 于G ．根据两直线平行的判定定理和性质得到∠DEF =∠DAG ，根据AG ⊥BC 确定∠CGA 的度数，再结合三角形内角和定理用∠B 和∠C 表示∠BAC 和∠CAG ，根据AD 是角平分线得到∠DAC ，进而求出∠DAG ，即可得到∠DEF 与∠B 、∠C 的大小关系．（3）过点A 作AG ⊥BC 于G ．根据两直线平行的判定定理和性质得到∠DEF =∠DAG ，根据AG ⊥BC 确定∠CGA 的度数，再结合三角形内角和定理用∠B 和∠C 表示∠BAC 和∠CAG ，根据AD 是角平分线得到∠DAC ，进而求出∠DAG ，即可得到∠DEF 与∠B 、∠C 的大小关系．(1)解：∵∠B =35°，∠C =65°，∴∠BAC =180°-∠B -∠C =80°．∵AD 是角平分线，AE 是高，∴1402DAC BAC Ð=Ð=°，∠CEA =90°．∴∠CAE =180°-∠C -∠CEA =25°．∴∠DAE =∠DAC -∠CAE =15°．(2)解：如下图所示，过点A 作AG ⊥BC 于G ．∵EF ⊥BC 于F ，∴EF AG ∥．∴∠DEF =∠DAG ．∵∠B +∠C +∠BAC =180°，∴∠BAC =180°-∠B -∠C ．∵AD 是角平分线，AG ⊥BC ，∴11190222DAC BAC B C Ð=Ð=°-Ð-Ð，∠CGA =90°．∴∠CAG =180°-∠C -∠CGA =90°-∠C ．∴∠DAG =∠DAC -∠CAG =1122C B Ð-Ð．∴1122DEF C B Ð=Ð-Ð．∴2DEF C B ÐÐÐ=-．(3)解：如下图所示，过点A 作AG ⊥BC 于G ．∵EF ⊥BC 于F ，∴EF AG ∥．∴∠DEF =∠DAG ．∵∠B +∠C +∠BAC =180°，∴∠BAC =180°-∠B -∠C ．∵AD 是角平分线，AG ⊥BC ，∴11190222DAC BAC B C Ð=Ð=°-Ð-Ð，∠CGA =90°．∴∠CAG =180°-∠C -∠CGA =90°-∠C ．∴∠DAG =∠DAC -∠CAG =1122C B Ð-Ð．∴1122DEF C B Ð=Ð-Ð．∴2DEF C B ÐÐÐ=-．【点睛】本题考查了三角形内角和定理，两直线平行的判定定理和性质，角平分线的性质，综合应用这些知识点是解题关键．类型三 从不同顶点出发的高线和角分线13．如图，在△ABC 中，CE 平分∠ACB 交AB 于点E ，AD 是△ABC 边BC 上的高，AD 与CE 相交于点F ，且∠ACB ＝80°，求∠AFE 的度数．【答案】∠AFE =50°．【解析】【分析】根据CE 平分∠ACB ，∠ACB ＝80°，得出∠ECB =11804022ACB Ð=´°=°，根据高线性质得出∠ADC =90°，根据三角形内角和得出∠DFC =180°-∠ADC -∠ECB =180°-90°-40°=50°，利用对顶角性质得出∠AFE =∠DFC =50°即可．【详解】解：∵CE 平分∠ACB ，∠ACB ＝80°，∴∠ECB =11804022ACB Ð=´°=°，∵AD 是△ABC 边BC 上的高，AD ⊥BC ，∴∠ADC =90°，∴∠DFC =180°-∠ADC -∠ECB =180°-90°-40°=50°，∴∠AFE =∠DFC =50°．【点睛】本题考查角平分线定义，垂线性质，三角形内角和，对顶角性质，掌握角平分线定义，垂线性质，三角形内角和，对顶角性质是解题关键．14．在△ABC 中，AD 是高，AE 、BF 是角平分线，它们相交于点O ，∠BAC ＝50°，∠C ＝70°，求∠DAE 和∠AOB 的度数．【答案】∠DAE 的度数为 5°；∠AOB 的度数为125°【解析】【分析】根据三角形内角和定理求得ABC Ð，根据角平分线的性质求得1252CAE BAE BAC Ð=Ð=Ð=°，1302ABF CBF ABC Ð=Ð=Ð=°，进而根据高线的定义以及三角形内角和定理求得DAC Ð，根据DAE CAE CAD Ð=Ð-Ð，即可求得DAE Ð，根据180AOB BAO ABO Ð=°-Ð-Ð即可求得∠AOB ．【详解】解：Q ∠BAC ＝50°，∠C ＝70°，18060ABC BAC C \Ð=°-Ð-Ð=°Q AE 、BF 是△ABC 的角平分线，∠BAC ＝50°，1252CAE BAE BAC \Ð=Ð=Ð=°,1302ABF CBF ABC Ð=Ð=Ð=°\1801802530125AOB BAO ABO Ð=°-Ð-Ð=°-°-°=°Q AD 是高线，90ADC \Ð=°，18020DAC ADC C \Ð=°-Ð-Ð=°，25205DAE CAE CAD \Ð=Ð-Ð=°-°=°，【点睛】本题考查了角平分线的定义，高线的定义，三角形内角和定理，掌握以上知识是解题的关键．15．如图，在△ABC 中，AD ，AF 分别为△ABC 的中线和高，BE 为△ABD 的角平分线．（1）若∠BED =40°，∠BAD =25°，求∠BAF 的大小；（2）若△ABC 的面积为40，BD =5，求AF 的长．【答案】（1）60°；（2）8【解析】【分析】（1）先利用三角形的外角性质计算出∠ABE=15°，再利用角平分线定义得到∠ABC=2∠ABE=30°，然后根据高的定义和互余可求出∠BAF 的度数；（2）先根据中线定义得到BC=2BD=10，然后利用三角形面积公式求AF 的长．【详解】（1）∵∠BED=∠ABE+∠BAE ，∴∠ABE=40°-25°=15°，∵BE 平分∠ABC ，∴∠ABC=2∠ABE=30°，∵AF 为高，∴∠AFB=90°，∴∠BAF=90°-∠ABF=90°-30°=60°；（2）∵AD为中线，∴BD=CD=5，∵S△ABC=12AF•BC=40，∴AF=24010´=8．【点睛】本题考查了三角形内角和定理：三角形内角和是180°．也考查了三角形外角性质和三角形面积公式．本题的关键是充分应用三角形的角平分线、高和中线的定义．。

专题01 三角形六大重难题型一．中线分周长（分类讨论）1．如图，已知BD 是△ABC 的中线，AB ＝5，BC ＝3，且△ABD 的周长为12，则△BCD 的周长是 10　．试题分析：先根据三角形的中线、线段中点的定义可得AD ＝CD ，再根据三角形的周长公式即可求出结果．答案详解：解：∵BD 是△ABC 的中线，即点D 是线段AC 的中点，∴AD ＝CD．实战训练∵AB＝5，△ABD的周长为12，∴AB+BD+AD＝12，即5+BD+AD＝12．解得BD+AD＝7．∴BD+CD＝7．则△BCD的周长是BC+BD+CD＝3+7＝10．所以答案是：10．2．已知AD是△ABC的中线，若△ABD与△ACD的周长分别是17和15，△ABC的周长是22，则AD的长为　5　．试题分析：根据三角形的周长公式列式计算即可得解．答案详解：解：∵△ABD与△ACD的周长分别是17和15，∴AB+BC+AC+2AD＝17+15＝32，∵△ABC的周长是22，∴AB+BC+AC＝22，∴2AD＝32﹣22＝10，∴AD＝5．所以答案是：5．3．如图所示，AD是△ABC的中线．若AB＝7cm，AC＝5cm，则△ABD和△ADC的周长的差为　2　cm．试题分析：根据三角形中线的定义得到BD＝CD，求得△ABD和△ACD的周长差＝（AB+AD+BD）﹣（AC+AD+CD）＝AB﹣AC，于是得到结论．答案详解：解：∵AD是BC边上的中线，∴BD＝CD，∴△ABD和△ACD的周长差＝（AB+AD+BD）﹣（AC+AD+CD）＝AB﹣AC，∵AB＝7cm，AC＝5cm，∴△ABD和△ACD的周长差＝7﹣5＝2cm．所以答案是：2．二．中线之等分面积4．如图，已知△ABC 中，点D 、E 分别是边BC 、AB 的中点．若△ABC 的面积等于8，则△BDE 的面积等于（ ）A ．2B ．3C ．4D ．5试题分析：根据三角形的面积公式即可得到结论．答案详解：解：∵点D 是边BC 的中点，△ABC 的面积等于8，∴S △ABD =12S △ABC ＝4，∵E 是AB 的中点，∴S △BDE =12S △ABD =12×4＝2，所以选：A ．5．已知：如图所示，在△ABC 中，点D ，E ，F 分别为BC ，AD ，CE 的中点，且S △ABC ＝4cm 2，则阴影部分的面积为　1　cm 2．试题分析：易得△ABD ，△ACD 为△ABC 面积的一半，同理可得△BEC 的面积等于△ABC 面积的一半，那么阴影部分的面积等于△BEC 的面积的一半．答案详解：解：∵D 为BC 中点，根据同底等高的三角形面积相等，∴S △ABD ＝S △ACD =12S △ABC =12×4＝2（cm 2），同理S △BDE ＝S △CDE =12S △BCE =12×2＝1（cm 2），∴S △BCE ＝2（cm 2），∵F 为EC 中点，∴S △BEF =12S △BCE =12×2＝1（cm 2）．所以答案是1．三．三角形的高的辨别6．如图，△ABC中，AD⊥BC于D，点E在CD上，则图中以AD为高的三角形有　6　个．试题分析：由于AD⊥BC于D，图中共有6个三角形，它们都有一边在直线CB上，由此即可确定以AD为高的三角形的个数．答案详解：解：∵AD⊥BC于D，而图中有一边在直线CB上，且以A为顶点的三角形有6个，∴以AD为高的三角形有6个．所以答案是：6．7．如图，△ABC中，BC边所在直线上的高是线段　AD　．试题分析：根据三角形的高的概念解答即可．答案详解：解：△ABC中，BC边所在直线上的高是线段AD，所以答案是：AD四．多边形的内角和与外角和8．若一个多边形的内角和是540°，则这个多边形是　五　边形．试题分析：根据多边形的内角和公式求出边数即可．答案详解：解：设多边形的边数是n，则（n﹣2）•180°＝540°，解得n＝5，所以答案是：五．9．如图，∠A+∠B+∠C+∠D+∠E+∠F的值是（ ）A．240°B．360°C．540°D．720°试题分析：根据四边形的内角和及三角形的外角定理即可求解．答案详解：解：如图，AC、DF与BE分别相交于点M、N，在四边形NMCD中，∠MND+∠CMN+∠C+∠D＝360°，∵∠CMN＝∠A+∠E，∠MND＝∠B+∠F，∴∠A+∠B+∠C+∠D+∠E+∠F＝360°，所以选：B．10．一个多边形的内角和等于1260°，从它的一个顶点出发，可以作对角线的条数是（ ）A．4B．6C．7D．9试题分析：设这个多边形的边数为n，根据多边形的内角和定理得到（n﹣2）×180°＝1260°，然后解方程即可．答案详解：解：设这个多边形的边数为n，∴（n﹣2）×180°＝1260°，解得n＝9，∴这个多边形为九边形；从这个多边形的一个顶点出发共有：9﹣3＝6（条）．所以选：B．五．三角形的内角和11．如图，在△ABC中，D是AC上一点，E是AB上一点，BD，CE相交于点F，∠A＝60°，∠ABD＝20°，∠ACE＝35°，则∠EFD的度数是（ ）A．115°B．120°C．135°D．105°试题分析：由△ABD的内角和为180°，可以求∠ADB，由△AEC内角和为180°，可以求∠AEC，再根据四边形AEFD内角和为360°，可求∠EFD．答案详解：解：在△AEC中，∠A+∠ACE+∠AEC＝180°，∴∠AEC＝180°﹣∠A﹣∠ACE＝180°﹣60°﹣35°＝85°，在△ABD中，∠A+∠ABD+∠ADB＝180°，∴∠ADB＝180°﹣∠A﹣∠ABD＝180°﹣60°﹣20°＝100°，在四边形AEFD中，∠A+∠AEC+∠ADB+2∠EFD＝360°，∴∠EFD＝360°﹣∠A﹣∠AEC﹣∠ADB＝360°﹣60°﹣85°﹣100°＝115°，所以选：A．12．如图，△ABC中，∠BAC＞∠B，∠C＝70°，将△ABC折叠，使得点B与点A重合，折痕PD 分别交AB、BC于点D、P，当△APC中有两个角相等时，∠B的度数为（ ）A．35°或20°B．20°或27.5°C．35°或25°或32.5°D．35°或20°或27.5°试题分析：分三种情况，利用三角形的内角和定理、等腰三角形的性质先求出∠APC的度数，再利用折叠的性质和三角形的内角和定理求出∠B．答案详解：解：由折叠的性质知：∠BPD＝∠APD=12∠BPA，∠BDP＝∠ADP＝90°．当AP＝AC时，∠APC＝∠C＝70°，∵∠BPD=12（180°﹣∠APC）＝55°，∴∠B＝90°﹣55°＝35°；当AP＝PC时，∠PAC＝∠C＝70°，则∠APC＝40°．∵∠BPD=12（180°﹣∠APC）＝70°，∴∠B＝90°﹣70°＝20°；当PC＝AC时，∠APC＝∠PAC，则∠APC＝55°．∵∠BPD=12（180°﹣∠APC）＝62.5°，∴∠B＝90°﹣62.5°＝27.5°．所以选：D．13．如图，∠ABD，∠ACD的角平分线交于点P，若∠A＝48°，∠D＝10°，则∠P的度数为（ ）A．19°B．20°C．22°D．25°试题分析：延长PC交BD于E，根据角平分线的定义可得∠1＝∠2，∠3＝∠4，再根据三角形的内角和定理可得∠A+∠1＝∠P+∠3，然后根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠5，整理可得∠P=12（∠A﹣∠D），然后代入数据计算即可得解．答案详解：解：如图，延长PC交BD于E，∵∠ABD，∠ACD的角平分线交于点P，∴∠1＝∠2，∠3＝∠4，由三角形的内角和定理得，∠A+∠1＝∠P+∠3①，在△PBE中，∠5＝∠2+∠P，在△DCE中，∠5＝∠4﹣∠D，∴∠2+∠P＝∠4﹣∠D②，①﹣②得，∠A﹣∠P＝∠P+∠D，∴∠P=12（∠A﹣∠D），∵∠A＝48°，∠D＝10°，∴∠P=12（48°﹣10°）＝19°．所以选：A．14．如图，在△ABC中，∠B＝28°，将△ABC沿直线m翻折，点B落在点D的位置，则∠1﹣∠2的度数是（ ）A．42°B．46°C．52°D．56°试题分析：根据折叠得出∠D＝∠B＝28°，根据三角形的外角性质得出∠1＝∠B+∠BEF，∠BEF ＝∠2+∠D，求出∠1＝∠B+∠2+∠D即可．答案详解：解：∵∠B＝28°，将△ABC沿直线m翻折，点B落在点D的位置，∴∠D＝∠B＝28°，∵∠1＝∠B+∠BEF，∠BEF＝∠2+∠D，∴∠1＝∠B+∠2+∠D，∴∠1﹣∠2＝∠B+∠D＝28°+28°＝56°，所以选：D．15．如图，将△ABC沿DE、HG、EF翻折，三个顶点均落在点O处，若∠1＝131°，则∠2的度数为（ ）A．49°B．50°C．51°D．52°试题分析：先根据折叠性质得：∠HOG＝∠B，∠DOE＝∠A，∠EOF＝∠C，根据三角形内角和为180°和周角360°求出结论．答案详解：解：由折叠得：∠HOG＝∠B，∠DOE＝∠A，∠EOF＝∠C，∵∠A+∠B+∠C＝180°，∴∠HOG+∠DOE+∠EOF＝180°，∵∠1+∠2+∠HOG+∠DOE+∠EOF＝360°，∴∠1+∠2＝180°，∵∠1＝131°，∴∠2＝180°﹣131°＝49°，所以选：A．16．如图，在△ABC中，∠1＝100°，∠C＝80°，∠2=12∠3，BE平分∠ABC交AD于E，求∠4的度数．试题分析：首先根据三角形的外角的性质求得∠3，再根据已知条件求得∠2，进而根据三角形的内角和定理求得∠ABD，再根据角平分线的定义求得∠ABE，最后根据三角形的外角的性质求得∠4．答案详解：解：∵∠1＝∠3+∠C，∠1＝100°，∠C＝80°，∴∠3＝20°，∵∠2=12∠3，∴∠2＝10°，∴∠ABC＝180°﹣100°﹣10°＝70°，∵BE平分∠ABC，∴∠ABE＝35°，∵∠4＝∠2+∠ABE，∴∠4＝45°．17．如果在直角三角形中，一个锐角是另一个锐角的3倍，那么这个三角形中最小的一个角等于　22.5　度．试题分析：在直角三角形中，设最小的锐角的度数为x，则另一个锐角的度数则为3x．由“直角三角形的两个锐角互余”的性质知，x+3x＝90°．通过解方程即可求得x的值．答案详解：解：在直角三角形中，设最小的锐角的度数为x，则另一个锐角的度数则为3x．则x+3x＝90°，即4x＝90°，解得，x＝22.5°，即这个直角三角形中最小的一个角等于22.5°．所以答案是：22.5．六．新定义类18．新定义：在△ABC中，若存在最大内角是最小内角度数的n倍（n为大于1的正整数），则称△ABC为“n倍角三角形”．例如，在△ABC中，若∠A＝90°，∠B＝60°，则∠C＝30°，因为∠A最大，∠C最小，且∠A＝3∠C，所以△ABC为“3倍角三角形”．（1）在△DEF中，若∠E＝40°，∠F＝60°，则△DEF为“　2　倍角三角形”．（2）如图，在△ABC中，∠C＝36°，∠BAC、∠ABC的角平分线相交于点D，若△ABD为“6倍角三角形”，请求出∠ABD的度数．试题分析：（1）根据三角形内角和定理求出∠D，根据n倍角三角形的定义判断；（2）根据角平分线的定义、三角形内角和定理求出∠ADB，n倍角三角形的定义分情况讨论计算，得到答案．答案详解：解：（1）在△DEF中，∠E＝40°，∠F＝60°，则∠D＝180°﹣∠E﹣∠F＝80°，∴∠D＝2∠E，∴△DEF为“2倍角三角形”，所以答案是：2；（2）∵∠C＝36°，∴∠BAC+∠ABC＝180°﹣36°＝144°，∵∠BAC、∠ABC的角平分线相交于点D，∴∠DAB=12∠BAC，∠DBA=12∠ABC，∴∠DAB+∠DBA=12×144°＝72°，∴∠ADB＝180°﹣72°＝108°，∵△ABD为“6倍角三角形”，∴∠ADB＝6∠ABD或∠ADB＝6∠BAD，当∠ADB＝6∠ABD时，∠ABD＝18°，当∠ADB＝6∠BAD时，∠BAD＝18°，则∠ABD＝180°﹣108°﹣18°＝54°，综上所述，∠ABD的度数为18°或54°．19．在△ABC中，若存在一个内角角度是另外一个内角角度的n倍（n为大于1的正整数），则称△ABC为n倍角三角形．例如，在△ABC中，∠A＝80°，∠B＝75°，∠C＝25°，可知∠B＝3∠C，所以△ABC为3倍角三角形．（1）在△ABC中，∠A＝80°，∠B＝60°，则△ABC为　2　倍角三角形；（2）若锐角三角形MNP是3倍角三角形，且最小内角为α，请直接写出α的取值范围为　22.5°＜α＜30°　．（3）如图，直线MN与直线PQ垂直相交于点O，点A在射线OP上运动（点A不与点O重合），点B在射线OM上运动（点B不与点O重合）．延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线所在的直线分别相交于E、F，若△AEF为4倍角三角形，求∠ABO 的度数．试题分析：（1）由∠A＝80°，∠B＝60°，可求∠C的度数，发现内角之间的倍数关系，得出答案，（2）△DEF是3倍角三角形，必定有一个内角是另一个内角的3倍，然后根据这两个角之间的关系，分情况进行解答，（3）首先证明∠EAF＝90°，分两种情形分别求出即可．答案详解：解：（1）∵∠A＝80°，∠B＝60°，∴∠C＝180°﹣∠A﹣∠B＝40°，∴∠A＝2∠C，∴△ABC为2倍角三角形，所以答案是：2；（2）∵最小内角为α，∴3倍角为3α，由题意可得：3α＜90°，且180°﹣4α＜90°，∴最小内角的取值范围是22.5°＜α＜30°．所以答案是22.5°＜α＜30°．（3）∵AE平分∠BAO，AF平分∠AOG，∴∠EAB＝∠EAO，∠OAF＝∠FAG，∴∠EAF＝∠EAO+∠OAF=12（∠BAO+∠OAG）＝90°，∵△EAF是4倍角三角形，∠F显然大于∠E,∴∠E=14×90°或15×90°，∵AE平分∠BAO，OE平分∠BOQ，∴∠E=12∠ABO，∴∠ABO＝2∠E，∴∠ABO＝45°或36°．20．在△ABC中，若存在一个内角角度，是另外一个内角角度的n倍（n为大于1的正整数），则称△ABC为n倍角三角形．例如，在△ABC中，∠A＝80°，∠B＝75°，∠C＝25°，可知∠B＝3∠C，所以△ABC为3倍角三角形．（1）在△ABC中，∠A＝55°，∠B＝25°，则△ABC为　4　倍角三角形；（2）若△DEF是3倍角三角形，且其中一个内角的度数是另外一个内角的余角的度数的13，求△DEF的最小内角；（3）若△MNP是2倍角三角形，且∠M＜∠N＜∠P＜90°，请直接写出△MNP的最小内角的取值范围．试题分析：（1）由∠A＝55°，∠B＝25°，可求∠C的度数，发现内角之间的倍数关系，得出答案，（2）△DEF是3倍角三角形，必定有一个内角是另一个内角的3倍，然后根据这两个角之间的关系，分情况进行解答，（3）可设未知数表示2倍角三角形的各个内角，然后列不等式组确定最小内角的取值范围．答案详解：解：（1）∵∠A＝55°，∠B＝25°，∴∠C＝180°﹣∠A﹣∠B＝100°，∴∠C＝4∠B，所以答案是：4（2）设最小的内角为x°，则3倍角为3x°①当最小的内角的度数是3倍内角的余角的度数的13时，即：x=13（90°﹣3x），解得：x＝15°②3倍内角的度数是最小内角的余角的度数的13时，即：3x=13（90°﹣x），解得：x＝9°，因此，△DEF的最小内角是9°或15°．（3）设∠M的度数为x，则其它的两个角分别为2x，（180°﹣3x），由∠M＜∠N＜∠P＜90°可得：2x＜90°且180°﹣3x＜90°且2x≠180°﹣3x∴30°＜x＜45°且x≠36°．答：△MNP的最小内角的取值范围是30°＜x＜45°且x≠36°．21．若△ABC中刚好有∠B＝2∠C，则称此三角形为“可爱三角形”，并且∠A称作“可爱角”．现有一个“可爱且等腰的三角形”，那么聪明的同学们知道这个三角形的“可爱角”应该是（ ）A．45°或36°B．72°或36°C．45°或72°D．45°或36°或72°试题分析：分设三角形底角为α，顶角为2α或设三角形的底角为2α，顶角为α，根据三角形的内角和为180°，得出答案．答案详解：解：①设三角形底角为α，顶角为2α，则α+α+2α＝180°，解得：α＝45°，②设三角形的底角为2α，顶角为α，则2α+2α+α＝180°，解得：α＝36°，∴2α＝72°，∴三角形的“可爱角”应该是45°或72°，所以选：C．22．若三角形满足一个角α是另一个角β的3倍，则称这个三角形为“智慧三角形”，其中α称为“智慧角”．在有一个角为60°的“智慧三角形”中，“智慧角”是　60或90　度．试题分析：根据“智慧三角形”及“智慧角”的意义，列方程求解即可．答案详解：解：在有一个角为60°的三角形中，①当另两个角分别是100°、20°时，“智慧角”是60°；②α+β＝120°且α＝3β，∴α＝90°．，即“智慧角”是90°．所以答案是：60或90．。

专题01 三角形的证明【易错题型专项训练】易错点一：等腰三角形性质与判定1.已知三角形三个内角度数如图所示，试画一条直线MN ，将这个三角形分割成两个等腰三角形． 【难度】★★ 【解析】【总结】本题考查了等腰三角形的分割，注意从多个角度考虑．2.如图，在下列三角形中，若AB =AC ，则不能被一条直线分成两个小等腰三角形的是（ ）．【难度】★★ 【答案】B ．【解析】A 选项，作B ∠的角平分线即可；C 选项，作A ∠的角平分线即可；D 选项， 作72BAD ∠=︒交BC 于点D ．【总结】本题考查了等腰三角形的分割，注意从多个角度考虑．3.（1）如果等腰三角形中有一个角为120°，另外两个角的度数为________； （2）如果等腰三角形中有一个角为30°，另外两个角的度数为____________． 【难度】★★【答案】（1）30︒、30︒；（2）30︒、120︒或75︒、75︒．【解析】（1）120︒只能为等腰三角形的顶角，所以另外两个角的度数为30︒、30︒； （2）当30︒为等腰三角形的底角时，另外两个角的度数为30︒、120︒；当30︒为等腰三角形的顶角时，另外两个角的度数为75︒、75︒． 【总结】本题考查了等腰三角形的性质，注意要分类讨论．4.（1）等腰三角形的两边长分别为6厘米和12厘米，它的周长为________； （2）等腰三角形的两边长分别为8厘米和12厘米，它的周长为___________． 【难度】★★【答案】（1）30厘米；（2）28厘米或32厘米．【解析】（1）由三角形的存在性可知6厘米为底，12厘米为腰，所以周长为30厘米；（2）当8厘米为腰时，周长为28厘米；当12厘米为腰时，周长为32厘米．【总结】本题考查了三边关系的运用，注意考虑三角形的存在性问题．5.已知等腰三角形的周长为24 cm，其中一边长为7 cm ，则与它相邻的另一边长（）A．7 cm或10 cm B．8.5 cm或7 cmC．7 cm或10 cm或8.5 cm D．10 cm或8.5 cm.【难度】★【答案】C．【解析】当7 cm为腰时，底边为10 cm；当7 cm为底时，腰为8.5 cm，所以另一边长为7 cm或10 cm或8.5 cm.【总结】本题考查了等腰三角形的性质，注意分类讨论和考虑三角形的存在性问题．6.等腰三角形中，AB的长是BC长2倍，三角形的周长是40，求AB的长．【难度】★★【答案】16．【解析】设BC xx x xAB=；x=，∴16++=，解得：8=，当AB为腰时，2240=，则2AB x当AB为底时，2+=，∴三角形不存在．x x x【总结】本题考查了等腰三角形的周长的确定，注意分类讨论．7.已知下列语句：①有一个角为300，腰长相等的两个等腰三角形全等．②有一个角为1100的腰长相等的两个等腰三角形全等．③腰长相等，顶角相等的两个等腰三角形全等．④底角和底边对应相等的两个等腰三角形全等．⑤一腰和底边对应相等的两个等腰三角形全等．⑥顶角和底边对应相等的两个等腰三角形全等．⑦底和一腰上的高对应相等的两个等腰三角形全等．其中不能判断两个等腰三角形全等的方法有（）A．0个B．1个C．2个D．3个【难度】★★【答案】B．【解析】①30︒可以作为底角也可以作为顶角，所以不全等，其余正确．【总结】本题考查了等腰三角形的性质及三角形全等的判定，当给出的角是锐角时，注意分类讨论．8.如图，已知D是等边三角形ABC的边AB边延长线上一点，BD的垂直平分线HE交AC延长线于点E，那么CE与AD相等吗?试说明理由．【难度】★★【解析】//H HG BC AE G 过点作，交于点．60//6060,903018030,22ABC A ABC AB AC HG BC AHG ABC AHG A AHG HG AG AHHE BD AHE BH DHGHE AHE AHG GEH AHE A GHE GEH EG HG AG AHCE AE AC AG AC AH ∆∴∠=∠==∴∠=∠=︒∴∠=∠=︒∴∆∴==∴∠=︒=∴∠=∠-∠=︒∠=︒-∠-∠=︒∴∠=∠∴===∴=-=-=-是等边三角形，，，，为等边三角形，为的垂直平分线，，，，222.AC AB BH ACAB BH AB BH DH AD =+-=+=++=【总结】本题主要考查了等边三角形的判定和性质，注意辅助线的添加．9.如图，已知：在等边三角形ABC 中，D 、E 分别是AB 、AC 边上的点，且BD =AE ，EB 与CD 相交于点O ．EF 与CD 垂直于点F ，试说明OE =2OF ．【难度】★★【解析】60F OFG OE G ∠=︒过点作，交于点60(..)60609030ABC A ABC AB BC AB BCABE BCD A ABC AE BD ABE BCD S A S ABE BCDADO ABC BCD ADO BOD ABE BOD ABC EOF OFG OG OF GFEF CD OFE OEF ∆∴∠=∠=︒==⎧⎪∆∆∠=∠⎨⎪=⎩∴∆≅∆∴∠=∠∠=∠+∠∠=∠+∠∴∠=∠=︒∴∠=︒∴∆∴==⊥∴∠=︒∴∠=︒∠是等边三角形，，在与中，，，又为等，，，，边三，角，形，，302.GFE OEF GFE GE GF OF OE OG GE OF =︒∴∠=∠∴==∴=+=，，，【总结】本题主要考查了等边三角形的判定与性质的综合运用，注意对方法的选择． 易错点二:直角三角形的性质与判定1.（1）等腰三角形底角是75°，腰长为9，则此三角形的面积是_______；（2）等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的顶角的度数是_____________． 【难度】★★ 【答案】（1）481；（2）30°或150°． 【解析】（1）∵等腰三角形底角是75°，∴顶角为30度，则腰上的高为29，则三角形的面 积为48129921=⨯⨯；（2）注意分锐角三角形和钝角三角形两种情况分类讨论．【总结】考察直角三角形的性质．注意等腰三角形分为锐角等腰三角形和钝角等腰三角形． 2.（1）直角三角形两边长为3和4，则此三角形第三边长为_________； （2）直角三角形两直角边长为3和4，则此三角形斜边上的高为_________； （3）等腰三角形两边长是2、4，则它腰上的高是____________． 【难度】★★【答案】（1）5或7；（2）512；（3）215．【解析】（1）3和4可以是两直角边长，也可以是一个直角边和斜边； （2）由勾股定理可得：斜边长为5，则由等面积法可知：三角形斜边上的高为512543=⨯； （3）∵2、2、4不能构成三角形，所以三角形的三边长为4、4、2， 作等腰三角底边上的高，则由等腰三角形三线合一性质和勾股定理可得：底边上的高为15，则由等面积法可知：此三角形腰上的高为2154152=⨯． 【总结】考察等腰三角形的性质和勾股定理的应用，注意分类讨论．3.已知已直角三角形的周长为2，求这个直角三角形的面积．【难度】★★【答案】52．【解析】∵斜边上的中线为2，所以斜边长为4．∵直角三角形的周长为4+26，∴两直角边之和为26． ∵斜边长为4，则两直角边的平方和为16，∴设两直角边分别为x y ，，则有⎩⎨⎧=+=+261622y x y x ，解得：()()52222=+-+=y x y x xy ，∴直角三角形的面积为25． 【总结】考察勾股定理和直角三角形性质的应用，解题时注意方法的运用．4.如图，公路MN 和公里PQ 在点P 处交汇，且∠QPN =30°，点A 处有一所中学，AP =160米，假设拖拉机行驶时，周围100米以内会受到噪音的影响，那么拖拉机在MN 上沿PN 方向行驶时，学校是否会受到噪音的影响?请说明理由；如果受影响，已知拖拉机的速度是18千米/时，那么学校受影响的时间是多少秒?【难度】★★ 【答案】24秒．【解析】过A 做AB ⊥MN ，垂足为B ．在Rt △ABP 中，∠QPN =30°，160=AP ，∴8021==AP AB∵80<100，所以学校会受到噪音的影响．假设在C 处开始受到噪音影响，在D 处开始不受影响， ∴100100==AD CA ，由勾股定理可得：60==BD CB ∴受影响的路程为120米=0.12千米∴学校受影响的时间为秒2436001812.0=⨯． 【总结】考察勾股定理和直角三角形性质的应用，解题时注意对题意的分析．5.如图，在四边形ABCD 中，BC ＞BA ，AD=CD ，BD 平分∠ABC，求证：∠A+∠C=180°．【解析】解：过点D作DE⊥BC于E，过点D作DF⊥AB交BA的延长线于F，∵BD平分∠ABC，∴DE=DF，∠DEC=∠F=90°，在RtCDE和Rt△ADF中，，∴Rt△CDE≌Rt△ADF（HL），∴∠FAD=∠C，∴∠BAD+∠C=∠BAD+∠FAD=180°．6.如图，OC平分∠AOB，点D，E分别在OA，OB上，点P在OC上且有PD=PE．求证：∠PDO=∠PEB．【解析】证明：过点P作PF⊥OA，PH⊥OB，∵OC平分∠AOB，∴PF=PH，在Rt△PDF和Rt△PEH中，，∴△PDF≌△PEH（HL），∴∠PDO=∠PEB．易错点三：两外角角平分线模型应用1.如图，在△ABC中，∠ABC的外角平分线与∠ACB的外角平分线相交于点D，那么∠BDC与∠A的数量关系是_____________.【答案】90°-∠A．【解析】解：∵BD、CD是∠ABC和∠ACB外角的平分线，∴∠CBD=（∠A+∠ACB），∠BCD=（∠A+∠ABC），∵∠ABC+∠ACB=180°-∠A，∠BDC=180°-∠CBD-∠BCD=180°-（∠A+∠ACB+∠A+∠ABC）=180°-（2∠A+180°-∠A）=90°-∠A．即∠BDC=90°-∠A，故答案为：∠BDC=90°-∠A．2.如图，已知射线ox与射线oy互相垂直，B，A分别为ox、oy上一动点，∠ABx、∠BAy的平分线交于C．问：B、A在ox、oy上运动过程中，∠C的度数是否改变？若不改变，求出其值；若改变，说明理由．【解析】解：∠C的度数不会改变．∵∠ABN、∠BAM的平分线交于C，∴∠C=180°-（∠1+∠2）=180°-（∠ABN+∠BAM）=180°-（∠O+∠OAB+∠BAM）=90°-∠O=45°．3.如图，在△ABC中，分别作其内角∠ACB与外角∠DAC的角平分线，且两条角平分线所在的直线交于点E（1）填空：①如图1，若∠B=60°，则∠E=______；②如图2，若∠B=90°，则∠E=______；（2）如图3，若∠B=α，求∠E的度数；（3）如图4，仿照（2）中的方法，在（2）的条件下分别作∠EAB与∠ECB的角平分线，且两条角平分线交于点G，求∠G的度数．【解析】（1）①根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=60°，再根据角平分线的定义可得∠F AC﹣∠ACE=30°，可求∠E的度数；②根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=90°，再根据角平分线的定义可得∠F AC﹣∠ACE=45°，可求∠E的度数；（2）根据三角形的外角性质可得∠DAC﹣∠ACB=∠B=12α，再根据角平分线的定义可得∠F AC﹣∠ACE=12α，可求∠E的度数；（3）根据角平分线的定和义可得三角形的外角性质可得∠G=∠HAC﹣∠ACG=32∠F AC﹣32∠ACE=32（∠F AC﹣∠ACE），可求∠G的度数．【详解】（1）①∠DAC﹣∠ACB=∠B=60°．∵EA平分∠DAC，EC平分∠ACB，∴∠F AC=12∠DAC，∠ACE=12∠ACB，∴∠E=∠F AC﹣∠ACE=12∠B=30°；②∠DAC﹣∠ACB=∠B=60°．∵EA平分∠DAC，EC平分∠ACB，∴∠F AC=12∠DAC，∠ACE=12∠ACB，∴∠E=∠F AC﹣∠ACE=12∠B=45°；（2）∠DAC﹣∠ACB=∠B=α．∵EA平分∠DAC，EC平分∠ACB，∴∠F AC=12∠DAC，∠ACE=12∠ACB，∴∠E=∠F AC﹣∠ACE=12∠B=12α；易错点四：利用角平分线的性质求点到直线的距离1.如图，AB∥CD，O为∠BAC、∠ACD的平分线的交点，OE⊥AC于E，且OE＝2，则AB与CD间的距离为_______.【答案】4cm【解析】解：如图，过点O作OF⊥AB于F，作OG⊥CD于G，∵O是∠ACD与∠BAC的平分线的交点，OE⊥AC，∴OE=OF，OE=OG，∴OE=OF=OG=2 cm，∵AB//CD，∴AB与CD间的距离=OF+OG=2+2=4 cm.故答案为：4 cm.2.如图，已知在△ABC中，BD，CE分别平分∠ABC，∠ACB，且BD，CE交于点O，过O作OP⊥BC于P，OM⊥AB于M，ON⊥AC于N，则OP，OM，ON的大小关系为___________．【答案】OP=ON=OM．【解析】解：∵BD，CE分别平分∠ABC，∠ACB，OP⊥BC于P，OM⊥AB于M，ON⊥AC于N∴OP=ON，OP=OM∴OP=ON=OM．故填OP=ON=OM．易错点五：利用角平分线的性质求三角形的周长1.如图，在△ABC中，∠C＝90°，AC＝BC，DA平分∠CAB交BC于D，问能否在AB上确定一点E，使△BDE 的周长等于AB的长？若能，请作出点E，并给出证明；若不能，请说明理由.【解答】解：能，过点D作DE⊥AB于E，则△BDE的周长等于AB的长.理由：如图，∵CD⊥AC于C，DE⊥AB于E又∵AD平分∠BAC∴CD＝ED，AC＝AE在Rt△DEB中，∠B＝45°，∴DE＝BE△BOE的周长＝BD＋DE＋BE＝BD＋CD＋BE∴AC＝BC又∵BD＋CD＝BC∴BD＋CD＝AC∴BD＋CD＝AE∴△BOE的周长＝AE＋BE＝AB2.如图，在中,，分别是和的角平分线，且，，则的周长是_______.【答案】5．【解答】∵分别是和的角平分线，∴，.∵，，∴，，∴，，∴，∴的周长．易错点六：利用角平分线的性质证明线段相等1.已知：∠AOB=90°，OM是∠AOB的平分线，将三角板的直角顶点P在射线OM上滑动，两直角边分别与OA、OB交于C、D．（1）PC和PD有怎样的数量关系是．（2）请你证明（1）得出的结论．【解答】解：（1）PC=PD．（2）过P分别作PE⊥OB于E，PF⊥OA于F，∴∠CFP=∠DEP=90°，∵OM是∠AOB的平分线，∴PE=PF，∵∠1+∠FPD=90°，（直角三角板）又∵∠AOB=90°，∴∠FPE=90°，∴∠2+∠FPD=90°，∴∠1=∠2，在△CFP和△DEP中，∴△CFP≌△DEP（ASA），∴PC=PD．2.如图，为△ABC平分线上的一点，点D和E分别在AB和BC上，且PD＝PE，试探究∠BDP与∠BEP的数量关系，并给予证明.【解析】解：过P作PM⊥AB于M，PN⊥BC于N由角分线性质得PM＝PN在Rt△DPM和Rt△EPN中，PD＝PE，PM＝PN∴Rt△DPM≌Rt△EPN(HL)，∴∠ADP＝∠BEP，又∠BDP＋∠ADP＝180°∴∠BDP＋∠BED＝180°易错点七：利用角平分线的性质解决面积问题1.如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，△ABC的面积是_______．【答案】31.5．【解析】解：作OE⊥AC，OF⊥AB，垂足分别为E、F，连接OA，∵OB，OC分别平分∠ABC和∠ACB，OD⊥BC，∴OD=OE=OF，∴S△ABC=S△OBC+S△OAC+S△OAB=×OD×BC+×OE×AC+×OF×AB=×OD×（BC+AC+AB）=×3×21=31.5．故填31.5．2.如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC的面积是28cm2，AB＝20cm，AC＝8cm，则DE的长为______cm.【答案】2【解析】解：∵在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，∴DE=DF，∵△ABC面积是28cm2，AB=20cm，AC=8cm，∴S△ABC=AB•DE+AC•DF=28，即×20×DE+×8×DF=28，解得DE=2cm．故答案为：2易错点八：角平分线的判定应用1.如图，在△ABC中，点P是角平分线AD、BE的交点.求证：点P在∠C的平分线上.【解析】证明：如图，过点P作PM⊥AB，PN⊥BC，PQ⊥AC，垂足分别为M、N、Q，∵P在∠BAC的平分线AD上，∴PM=PQ，P在∠ABC的平分线BE上，∴PM=PN，∴PQ=PN，∴点P在∠C的平分线．2.如图：在△ABC中，∠B，∠C相邻的外角的平分线交于点D．求证：点D在∠A的平分线上．【解析】解：过D作DE⊥BC于E，DF⊥AB，交AB延长线于F，作DG⊥AC，交AC延长线于G，∵BD是∠CBF的角平分线，DE⊥BC，DF⊥AB，∴DE=DF，同理可得DE=DG，∴DF=DG，又∵DF⊥AB，DG⊥AC，∴点D在∠BAC的角平分线上．。

培优专题01 与三角形模型有关的角度计算◎模型一A字模型【条件】△ADE与△ABC.【结论】∠AED+∠ADE=∠B+C.【证明】根据三角形内角和可得，∠AED+∠ADE=180°-∠A，∠B+C=180°-∠A，∠∠AED+∠ADE=∠B+C，得证.1．（2022·湖北咸宁·七年级期中）如图，已知l1∥l2，∠A＝45°，∠2＝100°，则∠1的度数为（）A．50°B．55°C．45°D．60°【答案】B【分析】根据平角的定义得出∠ACB＝80°，根据三角形内角和得到∠ABC＝55°，再根据平行线的性质即可得解．【详解】解：∠∠2＝100°，∠∠ACB ＝180°−100°＝80°， ∠∠A ＝45°，∠∠ABC ＝180°−45°−80°＝55°， ∠l 1∥l 2，∠∠1＝∠ABC ＝55°， 故选：B ．【点睛】此题考查了平行线的性质，熟记“两直线平行，内错角相等”是解题的关键．2．（2022·全国·八年级课时练习）如图，ABC 中，65A ∠=︒，直线DE 交AB 于点D ，交AC 于点E ，则BDE CED ∠+∠=（ ）．A ．180︒B ．215︒C ．235︒D ．245︒【答案】D【分析】根据三角形内角和定理求出ADE AED ∠+∠，根据平角的概念计算即可． 【详解】解：65A ∠=︒，18065115ADE AED ∴∠+∠=︒-︒=︒， 360115245BDE CED ∴∠+∠=︒-︒=︒，故选：D ．【点睛】本题考查的是三角形内角和定理的应用，掌握三角形内角和等于180︒是解题的关键． 3．（2022·全国·八年级课时练习）如图是某建筑工地上的人字架，若1120∠=︒，那么32∠-∠的度数为_________．【答案】60︒【分析】根据平角的定义求出4，再利用三角形的外角的性质即可解决问题．【详解】解：如图14180∠+∠=︒，1120∠=︒， 460∴∠=︒，324，32460∴∠-∠=∠=︒，故答案为：60︒．【点睛】本题考查三角形外角的性质、平角的性质等知识，解题的关键是熟练掌握基本知识，属于中考基础题．4．（2020·湖南·常德市第二中学九年级期中）如图，在ABC ∆中，90C ∠=︒，6BC =，D ，E 分别在AB 、AC 上，将ADE ∆沿DE 折叠，使点A 落在点A '处，若A '为CE 的中点，则折痕DE 的长为__．DE BC ，故∆BC ．【详解】解：ABC ∆沿90DEA =∠'=︒，AED ∆∽，的中点，AE =∴=．ED2故答案为：2．【点睛】本题考查相似三角形的判定和性质，掌握“A ”字形三角形相似的判定和性质为解题关键． 5．（2022·全国·八年级课时练习）如图所示，DAE ∠的两边上各有一点,B C ，连接BC ，求证180DBC ECB A +∠=︒∠+∠．【答案】见解析【分析】根据三角形的外角等于与它不相邻的两个内角的和证明即可． 【详解】解：DBC ∠和ECB ∠是ABC 的外角， ,DBC A ACB ECB A ABC ∴∠=∠+∠∠=∠+∠．又180A ABC ACB ∠+∠+∠=︒，180DBC ECB A ACB ABC A A ∴∠+∠=∠+∠+∠+∠︒=+∠．【点睛】本题主要考查三角形外角的性质，熟知三角形的外角等于与它不相邻的两个内角的和是解题的关键．◎模型二 8字模型【条件】AD 、BC 相交于点O.【结论】∠A +∠B =∠C +∠D.(上面两角之和等于下面两角之和)【证明】在∠ABO 中，由内角和定理：∠A +∠B +∠BOA =180°，在∠CDO 中，∠C +∠D +∠COD =180°， ∠∠A +∠B +∠BOA =180°=∠C +∠D +∠COD ，由对顶角相等：∠BOA =∠COD ∠∠A +∠B =∠C +∠D ，得证.6．（2022·全国·八年级课时练习）如图，AB 和CD 相交于点O ，∠A ＝∠C，则下列结论中不能完全确定正确的是（）A．∠B＝∠D B．∠1＝∠A＋∠D C．∠2＞∠D D．∠C＝∠D【答案】D【分析】利用三角形的外角性质，对顶角相等逐一判断即可．【详解】∠∠A＋∠AOD＋∠D＝180°，∠C＋∠COB＋∠B＝180°，∠A＝∠C，∠AOD＝∠BOC，∠∠B＝∠D，∠∠1＝∠2＝∠A＋∠D，∠∠2＞∠D，故选项A，B，C正确，故选D．【点睛】本题考查了对顶角的性质，三角形外角的性质，熟练掌握并运用两条性质是解题的关键．7．（2022·全国·八年级课时练习）如图，∠1=60°，则∠A+∠B+∠C+∠D+∠E+∠F=（）A．240°B．280°C．360°D．540°【答案】A【分析】根据三角形内角和定理得到∠B与∠C的和，然后在五星中求得∠1与另外四个角的和，加在一起即可．【详解】解：由三角形外角的性质得：∠3=∠A+∠E，∠2=∠F+∠D，∠∠1+∠2+∠3=180°，∠1=60°，∠∠2+∠3=120°，即：∠A+∠E+∠F+∠D=120°，∠∠B+∠C=120°，∠∠A+∠B+∠C+∠D+∠E+∠F=240°．故选A．【点睛】本题考查了三角形的外角和三角形的内角和的相关知识，解决本题的关键是将题目中的六个角分成两部分来分别求出来，然后再加在一起．8．（2022·全国·八年级课时练习）如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I＝__．【答案】900°【分析】根据多边形的内角和，可得答案．【详解】解：连EF，GI，如图，∠6边形ABCDEFK的内角和＝（6－2）×180°＝720°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝720°－（∠1＋∠2），即∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋（∠1＋∠2）＝720°，∠∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F∠H＋（∠3＋∠4）＝900°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F（∠3＋∠4）＋∠5＋∠6＋∠H＝720°＋180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＝900°，故答案为：900°．【点睛】本题考查了n边形的内角和定理：n边形的内角和为（n－2）×180°（n≥3的整数）．9．（2022·全国·八年级课时练习）如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为__．【答案】1080°【分析】连KF，GI，根据n边形的内角和定理得到7边形ABCDEFK的内角和＝（7－2）×180°＝900°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠1＋∠2）＝900°，由三角形内角和定理可得到∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＋∠5＋∠6＋∠H＝900°＋180°，即可得到∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K的度数．【详解】解：连KF，GI，如图，∠7边形ABCDEFK的内角和＝（7－2）×180°＝900°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＝900°－（∠1＋∠2），即∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠1＋∠2）＝900°，∠∠1＋∠2＝∠3＋∠4，∠5＋∠6＋∠H＝180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＝900°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠K＋（∠3＋∠4）＋∠5＋∠6＋∠H＝900°＋180°，∠∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K＝1080°．故∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＋∠I＋∠K的度数为1080°．故答案为：1080°．【点睛】本题考查了n边形的内角和定理：n边形的内角和为（n－2）×180°（n≥3的整数）．10．（2022·全国·八年级课时练习）如图，OAB和OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC、BD交于M（1）如图1，当α＝90°时，∠AMD 的度数为 °； （2）如图2，当α＝60°时，求∠AMD 的度数；（3）如图3，当OCD 绕O 点任意旋转时，∠AMD 与α是否存在着确定的数量关系？如果存在，请你用α表示∠AMD ，并用图3进行证明；若不确定，说明理由． 【答案】（1）90；（2）120︒；（3）180α︒-【分析】（1）如图1，设OA 交BD 于K ，只要证明△≌△BOD AOC ，推出OBD OAC ∠=∠，由BKO AKM ∠=∠，可得90AMK BOK ∠=∠=︒；（2）如图2，设OA 交BD 于K ，只要证明△≌△BOD AOC ，推出OBD OAC ∠=∠，由BKO AKM ∠=∠，可得60AMK BOK ∠=∠=︒；（3）如图3，设OA 交BD 于K ，只要证明△≌△BOD AOC ，推出OBD OAC ∠=∠，由BKM AKO ∠=∠，可得BMK AOK α∠=∠=，可得180AMD α∠=︒-； 【详解】解：（1）如图1中，设OA 交BD 于K∠OA OB OC OD ==，，90AOB COD ∠=∠=︒ ∠BOD AOC ∠=∠ ∠△≌△()BOD AOC SAS ∠OBD OAC ∠=∠ ∠BKO AKM ∠=∠ ∠90AMK BOK ∠=∠=︒ ∠90AMD ∠=︒ 故答案为90︒（2）如图2，设OA 交BD 于K ，∠OA OB OC OD ==，，60AOB COD ∠=∠=︒ ∠BOD AOC ∠=∠ ∠△≌△()BOD AOC SAS ∠OBD OAC ∠=∠ ∠BKO AKM ∠=∠ ∠60AMK BOK ∠=∠=︒ ∠180120AMD AMK ∠=︒-∠=︒ 故答案为120︒（3）如图3，设OA 交BD 于K ，∠OA OB OC OD ==，，AOB COD α∠=∠= ∠BOD AOC ∠=∠ ∠△≌△()BOD AOC SAS ∠OBD OAC ∠=∠ ∠AKO BKM ∠=∠ ∠BMK AOK α∠=∠=∠180180AMD BMK α∠=︒-∠=︒- 故答案为180α︒-【点睛】本题考查了几何变换综合题，全等三角形的判定，三角形内角和性质，解题的关键是灵活运用所学知识解决问题，学会利用“8字型”证明角相等．◎模型三 飞镖模型【条件】四边形ABDC 如上左图所示.【结论】∠D =∠A +∠B +∠C.(凹四边形凹外角等于三个内角和) 【证明】如上右图，连接AD 并延长到E ，则：∠BDC =∠BDE +∠CDE =(∠B +∠1)+(∠2+∠C )=∠B +∠BAC +∠C.本质为两个三角形外角和定理证明. 11．（2022·全国·八年级课时练习）在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果52,25A B ︒︒∠=∠=，30,35,72C D E ︒︒︒∠=∠=∠=，那么F ∠的度数是（ ）．A ．72︒B ．70︒C ．65︒D ．60︒【答案】A【分析】延长BE 交CF 的延长线于O ，连接AO ，根据三角形内角和定理求出,BOC ∠再利用邻补角的性质求出DEO ∠，再根据四边形的内角和求出DFO ∠，根据邻补角的性质即可求出DFC ∠的度数． 【详解】延长BE 交CF 的延长线于O ，连接AO ，如图，∠180,OAB B AOB ∠+∠+∠=︒∠180,AOB B OAB ∠=︒-∠-∠ 同理得180,AOC OAC C ∠=︒-∠-∠ ∠360,AOB AOC BOC ∠+∠+∠=︒ ∠360BOC AOB AOC ∠=︒-∠-∠360(180)(180)B OAB OAC C =︒-︒-∠-∠-︒-∠-∠ 107,B C BAC =∠+∠+∠=︒ ∠72,BED ∠=︒∠180108,DEO BED ∠=︒-∠=︒ ∠360DFO D DEO EOF ∠=︒-∠-∠-∠36035108107110,=︒-︒-︒-︒=︒∠180********DFC DFO ∠=︒-∠=︒-︒=︒, 故选：A ．【点睛】本题考查三角形内角和定理，多边形内角和，三角形的外角的性质，邻补角的性质，解题关键是会添加辅助线，将已知条件联系起来进行求解．三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；邻补角性质：邻补角互补；多边形内角和：180(2)n ︒-．12．（2022·全国·八年级课时练习）如图，已知BE ，CF 分别为△ABC 的两条高，BE 和CF 相交于点H ，若△BAC=50°，则△BHC 为（ ）A ．115°B ．120°C ．125°D ．130°【答案】D【详解】∠BE 为∠ABC 的高，∠BAC=50°， ∠∠ABE=90°-50°=40°， ∠CF 为∠ABC 的高， ∠∠BFC=90°，∠∠BHC=∠ABE+∠BFC=40°+90°=130°．故选D．13．（2022·全国·八年级课时练习）如图，若115∠+∠+∠+∠+∠+∠=EOC∠=︒，则A B C D E F____________．【答案】230°【分析】根据三角形外角的性质，得到∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠EOC=∠1+∠F=115°，∠1=∠A+∠B，即可得到结论．【详解】解：如图∠∠EOC=∠E+∠2=115°，∠2=∠D+∠C，∠∠E+∠D+∠C=115°，∠∠EOC=∠1+∠F=115°，∠1=∠A+∠B，∠∠A+∠B+∠F=115°，∠∠A+∠B+∠C+∠D+∠E+∠F=230°，故答案为：230°．【点睛】本题主要考查三角形内角和定理和三角形外角的性质，解决本题的关键是要熟练掌握三角形外角性质．14．（2022·山东德州·七年级期末）如图，则∠A+∠B+∠C+∠D+∠E的度数是__．【答案】180°【分析】由三角形的一个外角等于与它不相邻的两个内角的和，得∠4＝∠A＋∠2，∠2＝∠D＋∠C，进而利用三角形的内角和定理求解．【详解】解：如图可知：∠∠4是三角形的外角，∠∠4＝∠A＋∠2，同理∠2也是三角形的外角，∠∠2＝∠D＋∠C，在∠BEG中，∠∠B＋∠E＋∠4＝180°，∠∠B＋∠E＋∠A＋∠D＋∠C＝180°．故答案为：180°．【点睛】本题考查三角形外角的性质及三角形的内角和定理，解答的关键是沟通外角和内角的关系．15．（2022·全国·八年级课时练习）模型规律：如图1，延长CO交AB于点D，则∠=∠+∠=∠+∠+∠．因为凹四边形ABOC形似箭头，其四角具有“BOC A B C 1BOC B A C B∠=∠+∠+∠”这个规律，所以我们把这个模型叫做“箭头四角形”．模型应用（1）直接应用：∠如图2，60,20,30A B C∠=︒∠=︒∠=︒，则BOC∠=__________︒；∠如图3，A B C D E F∠+∠+∠+∠+∠+∠=__________︒；（2）拓展应用：∠如图4，ABO∠、ACO∠的2等分线（即角平分线）1BO、1CO交于点1O，已知120BOC∠=︒，50BAC∠=︒，则1BO C∠=__________︒；∠如图5，BO、CO分别为ABO∠、ACO∠的10等分线1,2,3,,(,)89i=⋯．它们的交点从上到下依次为1O、2O、3O、…、9O．已知120BOC∠=︒，50BAC∠=︒，则7BO C∠=__________︒；∠如图6，ABO∠、BAC∠的角平分线BD、AD交于点D，已知120,44BOC C∠=︒∠=︒，则ADB=∠__________︒；∠如图7，BAC∠、BOC∠的角平分线AD、OD交于点D，则B、C∠、D∠之同的数量关系为__________．【详解】解：（1）∠∠BOC=∠A+∠B+∠C=60°+20°+30°=110°；◎模型四双垂直模型【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE，∠ACB=∠CED.【证明】∠∠B=∠D=∠ACE=90°；∠∠BAC+∠ACB=90°；又∠ECD+∠ACB=90°；∠∠BAC=∠DCE同理,∠ACB+∠DCE=90°，且∠CED+∠DCE=90°；∠∠ACB=∠CED，得证.16．（2021·青海海东·八年级期中）如图，已知∠ABC∠∠CDE，∠B＝90°，点C为线段BD上一点，则∠ACE的度数为（）A．94°B．92°C．90°D．88°【答案】C【分析】由全等三角形的性质得出∠ACB＝∠CED，则可得出答案．【详解】解：∠∠ABC∠∠CDE，∠∠ACB＝∠CED，∠B＝∠D＝90°，∠∠CED+∠ECD＝90°，∠∠ACB+∠ECD＝90°，∠∠ACB+∠ECD+∠ACE＝180°，∠∠ACE＝90°．故选：C．【点睛】本题考查了全等三角形的性质；熟练掌握三角形全等的性质定理是解题的关键．17．（2020·河南·郑州市第八中学模拟预测）如图所示，一副三角尺摆放置在矩形纸片的内部，三角形的三个顶点恰好在矩形的边上，若16FGC ∠=︒，则AEF ∠等于（ ）A ．106︒B ．114︒C ．126︒D ．134︒【答案】D【分析】根据矩形的性质可得∠C=90°，AD∠BC ，利用直角三角形的两个锐角互余求出∠GFC ，从而求出∠EFB ，然后根据平行线的性质可得∠AEF ＋∠EFB=180°，从而求出结论． 【详解】解：∠四边形ABCD 为矩形 ∠∠C=90°，AD∠BC ∠16FGC ∠=︒∠∠GFC=90°－∠FGC=74° 由三角尺可知：∠EFG=60° ∠∠EFB=180°－∠GFC －∠EFG=46° ∠AD∠BC∠∠AEF ＋∠EFB=180° ∠∠AEF=180°－∠EFB=134° 故选D ．【点睛】此题考查的是矩形的性质、直角三角形的性质和平行线的性质，掌握矩形的性质、直角三角形的两个锐角互余和平行线的性质是解决此题的关键．18．（2022·山东青岛·七年级期末）如图，小虎用10块高度都是4cm 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC BC =，90ACB ∠=︒），点C 在DE 上，点A 和B 分别与木墙的顶端重合，则两堵木墙之间的距离为______．【答案】40 cm【分析】根据题意可得AC＝BC，∠ACB＝90°，AD∠DE，BE∠DE，进而得到∠ADC＝∠CEB＝90°，再根据等角的余角相等可得∠BCE ＝∠DAC ，再证明∠ADC ∠∠CEB 即可，利用全等三角形的性质进行解答．【详解】解：由题意得：AC ＝BC ，∠ACB ＝90°，AD ∠DE ，BE ∠DE ， ∠∠ADC ＝∠CEB ＝90°，∠∠ACD ＋∠BCE ＝90°，∠ACD ＋∠DAC ＝90°， ∠∠BCE ＝∠DAC ， 在∠ADC 和∠CEB 中，ADC CEB DAC BCE AC BC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∠∠ADC ∠∠CEB （AAS ）；由题意得：AD ＝EC ＝12cm ，DC ＝BE ＝28cm ， ∠DE ＝DC ＋CE ＝40（cm ）， 答：两堵木墙之间的距离为40cm ， 故答案为：40 cm ．【点睛】此题主要考查了全等三角形的应用，涉及到垂直的定义、直角三角形的性质和连个三角形全等的判定与性质等知识点，解题的关键是正确找出证明三角形全等的条件．19．（2021·江苏盐城·七年级期中）将含有30角的直角三角板（30A ∠=︒）和直尺按如图方式摆放，已知136∠=︒，则2∠=______︒．【答案】24【分析】过点B 作BC //MN ，由平行线传递性，可得BC //KL ，再由平行线的性质可得1=LBC ∠∠ ，2=ABC ∠∠ ，最后由在直角三角形中两锐角互余的关系，求出2=24∠︒ ．【详解】解：过点B 作BC //MN ，如图所示：MN //KH∴ BC //KL1LBC ∴∠=∠又1=36∠︒=36LBC ∴∠︒又 BC //MN2=ABC ∴∠∠又=30A ∠︒=60ABL ∴∠︒又=ABL LBC ABC ∠∠+∠603624ABC ∴∠=︒-︒=︒224∴∠=︒故答案为：24【点睛】本题考查了平行线的判定与性质(两直线平行，内错角相等)，平行线传递性(如果两条直线都与第三条直线平行，那么这两条直线也互相平行)，直角三角形中两锐角互余，角的和差计算等综合知识点．难点是作已知直线的平行线．20．（2022·全国·八年级专题练习）如图1，已知ABC ∆中，90ACB ∠=︒，AC BC =，BE 、AD 分别与过点C 的直线垂直，且垂足分别为E ，D ．(1)猜想线段AD 、DE 、BE 三者之间的数量关系，并给予证明．(2)如图2，当过点C 的直线绕点C 旋转到ABC ∆的内部，其他条件不变，如图2所示，∠线段AD 、DE 、BE 三者之间的数量关系是否发生改变？若改变，请直接写出三者之间的数量关系，若不改变，请说明理由；∠若 2.8AD =， 1.5DE =时，求BE 的长． 【答案】(1)DE AD BE =+，证明见解析 (2)∠发生改变，DE AD BE =-；∠1.3【分析】（1）证明ACD CBE ∆≅∆，可得AD CE =，CD ＝BE ， 即可求解；（2）∠证明ACD CBE ∆≅∆，可得AD CE =，CD ＝BE ， 即可求解；∠由∠可得DE AD BE =-，从而得到BE AD DE =-，即可求解．（1）解：DE AD BE =+， 理由如下： ∠BE 、AD 分别与过点C 的直线垂直， ∠90BEC ADC ∠∠=︒＝， ∠90ACD CAD ∠∠+︒＝， ∠90ACB ∠=︒， ∠90ACD BCE ∠+∠=︒， ∠CAD BCE ∠=∠，在ACD ∆和CBE ∆中，ADC BECCAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ACD CBE AAS ∴∆≅∆，AD CE ∴=，CD ＝BE ，∠ DE ＝EC ＋CD ，DE AD BE ∴=+；（2）解：∠发生改变．∠BE 、AD 分别与过点C 的直线垂直，∠90BEC ADC ∠∠=︒＝，∠90ACD CAD ∠∠+︒＝， ∠90ACB ∠=︒， ∠90ACD BCE ∠+∠=︒， ∠CAD BCE ∠=∠，在ACD ∆和CBE ∆中，ADC BEC CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ACD CBE AAS ∴∆≅∆，AD CE ∴=，CD ＝BE ，∠ DE ＝CE -CD ， ∠DE AD BE=-； ∠由∠知：DE AD BE =-， ∠ 2.8 1.5 1.3BE AD DE =-=-=， ∠BE 的长为1.3.【点睛】本题主要考查了全等三角形的判定和性质、等角的余角相等，熟练掌握全等三角形的判定和性质是解题的关键．◎模型五 风筝模型【条件】四边形ABPC ，分别延长AB 、AC 于点D 、E ，如上左图所示. 【结论】∠PBD+∠PCE =∠A +∠P .【证明】如上右图，连接AP ，则：∠PBD =∠PAB +∠APB ，∠PCE =∠PAC +∠APC ，∴∠PBD+∠PCE=∠PAB +∠APB+∠PAC +∠APC=∠BAC +∠BPC ，得证.21．（2022·内蒙古赤峰·八年级期末）如图，将ABC 的一角折叠，若12130∠+∠=︒，则B C ∠+∠=（）A．50°B．65°C．115°D．130°【答案】C【分析】根据折叠性质证得∠3=∠4，∠5=∠6，再根据平角定义求得∠4+∠5=115°，然后根据三角形的内角和定理求解即可．【详解】解：如图，由折叠性质得：∠3=∠4，∠5=∠6，∠∠1+∠3+∠4=180°，∠5+∠6+∠2=180°，∠∠1+∠2+2∠4+2∠5=360°，∠∠1+∠2=130°，∠2∠4+2∠5=360°－130°=230°，∠∠4+∠5=115°，∠∠4+∠5+∠A=180°，∠A+∠B+∠C=180°，∠∠B+∠C=∠4+∠5=115°，故选：C．【点睛】本题考查三角形折叠中的角度问题，熟练掌握折叠性质是解答的关键.22．（2022·海南海口·七年级期末）如图，把∠ABC纸片沿MN折叠，使点C落在∠ABC内部点C′处，若∠C=36°，则∠1+∠2等于（）A ．54°B ．62°C ．72°D ．76°【答案】C【分析】根据折叠可知∠C =∠'C ，四边形内角和为360°，即可求出'CMC ∠+'CNC ∠，用平角的定义即可求出∠1+∠2【详解】∠∠CMN 折叠得到'C MN ∠∠C =∠'C∠∠1=180°-'CMC ∠，∠2=180°-'CNC ∠∠∠1+∠2=180°-'CMC ∠+180°-'CNC ∠=360°-（'CMC ∠+'CNC ∠） ∠'CMC ∠+'CNC ∠=360°-∠C -'C ∠=360°-36°-36°=288° ∠∠1+∠2=360°-288°=72° 故选：C【点睛】本题主要考查了折叠问题，掌握三角形的内角和定理，四边形的内角和以及平角的定义是解题的关键．23．（2022·山东烟台·七年级期中）如图，在三角形纸片ABC 中65A ∠=︒，75B ∠=︒，将纸片的一角折叠，使点C 落在∠ABC 内，若150∠=︒，则∠2的度数为_________.【答案】30°##30度【分析】根据题意，已知∠A =65°，∠B =75°，可结合三角形内角和定理和四边形内角和求解． 【详解】解：如图，设折痕为DE ；∠65A ∠=︒，75B ∠=︒，∠180180657540C A B ∠=︒-∠+∠=︒-︒+︒=︒（）（）， ∠180140CDE CED C ∠+∠=︒-∠=︒， 又∠150∠=︒，∠2360(1)36030030A B CED CDE ∠=︒-∠+∠+∠+∠+∠=︒-︒=︒， 故答案为：30°．【点睛】本题主要是考查了三角形、四边形内角和，即三角形的内角和为180°，四边形的内角和为360°；熟练掌握三角形的内角和定理是解题的关键．24．（2022·湖北恩施·一模）图，把等边ABC 沿直线DE 折叠，点A 落在'A 处，若150∠=︒，则2∠=______．【答案】40︒【分析】先求出AED ∠的度数，再根据折叠得到AED A ED '∠=∠，即可求出2∠的度数． 【详解】∠等边ABC 沿直线DE 折叠 ∠60A ∠=︒，AED A ED '∠=∠ ∠150∠=︒∠180170AED A ∠=︒-∠-∠=︒ ∠70AED A ED '∠=∠=︒∠420180AED A ED ∠=︒-'∠-∠=︒ 故答案为：40︒【点睛】此题考查翻折问题，折叠问题的实质是“轴对称”，解题关键是找出经轴对称变换所得的等量关系．25．（2022·江苏·扬州市竹西中学七年级期末）如图∠，把∠ABC纸片沿DE折叠，使点A落在四边形BCED内部点A′的位置，通过计算我们知道：2∠A＝∠1+∠2．请你继续探索：(1)如果把∠ABC纸片沿DE折叠，使点A落在四边形BCED的外部点A′的位置，如图∠，此时∠A与∠1、∠2之间存在什么样的关系？为什么？请说明理由．(2)如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图∠，你能求出∠A、∠D、∠1与∠2之间的关系吗？（直接写出关系式即可）（1）解：如图所示，连接AA'，◎模型六 两内角角平分线模型【条件】△ABC 中，BI 、CI 分别是∠ABC 和∠ACB 的角平分线，且相交于点I. 【结论】A I ∠+︒=∠2190 【证明】∵BI 是∠ABC 平分线，∴ABC ∠=∠212∵CI 是∠ACB 平分线，∴ACB ∠=∠213 由A →B →I →C →A 的飞镖模型可知： ∠I =∠A +∠2+∠3=∠A +ABC ∠21+ACB ∠21=∠A +)180(21A ∠-︒=A ∠+︒2190. 26．（2022·山东东营·七年级期末）如图，在△ABC 中，BF 平分△ABC ，CF 平分△ACB ，△BFC =125°，则△A 的度数为（ ）A ．60°B ．80°C ．70°D ．45°【答案】C【分析】先根据三角形内角和定理得出CBF BCF ∠+∠的度数，再由角平分线的性质得出ABC ACB ∠+∠的度数，根据三角形内角和定理即可得出结论． 【详解】解：∠125BFC ∠=︒， ∠18012555BCF CBF ∠+∠=︒︒=︒﹣． ∠BF 平分ABC ∠，CF 平分ACB ∠，∠()2110ABC ACB BCF CBF ∠+∠=∠+∠=︒， ∠180A ABC ACB ∠+∠+∠=︒，∠18011070﹣．A∠=︒︒=︒故选：C ．【点睛】本题考查的是三角形内角和定理，以及三角形角平分线的定义，熟知三角形内角和是180°是解答此题的关键．27．（2022·福建·泉州五中七年级期末）如图，在四边形ABCD 中，∠A +∠D ＝α，∠ABC 的平分线与∠BCD 的平分线交于点P ，则∠P ＝（ ）A ．90°﹣12α B ．12αC ．90°+12α D ．360°﹣α28．（2022·河南鹤壁·七年级期末）已知ABC 中，A α∠=．在图1中B 、C ∠的平分线交于点1O ，则可计算得11902BO C α∠=︒+；在图2中，设B 、C ∠的两条三等分角线分别对应交于2O 、3O ，则3BO C ∠=_______________．【详解】解：Aα∠=，180ACB=︒-B∠、C∠的两条三等分角线分别对应交于332 ( 3CBO BCO ABC ∴∠+=∠3(BO C CBO∴∠=-∠+故答案为：【点睛】本题考查三角形内角和定理，解题的关键是熟练运用三等分角线求解．29．（2022·江苏常州·七年级期中）如图，在∠MBC中，∠ABC、∠ACB的角平分线OB、OC交于点O，若∠O=m°，则∠A的度数是______________________________°（用含m的代数式表示）．【答案】（2m-180）【分析】先由角平分线的定义得到∠ABC=2∠OBC，∠ACB=2∠OCB，再利用三角形内角和定理求解即可．【详解】解：∠OB，OC分别是∠ABC和∠ACB的角平分线，∠∠ABC=2∠OBC，∠ACB=2∠OCB，∠∠O+∠OBC+∠OCB=180°，∠∠OBC+∠OCB=180°-∠O=180°-m°，∠∠ABC+∠ACB=2∠OBC+2∠OCB=360°-2m°，∠∠A=180°-∠ABC-∠ACB=2m°-180°，故答案为：（2m-180）．【点睛】本题主要考查了三角形内角和定理，角平分线的定义，熟知相关知识是解题的关键．30．（2021·重庆·垫江第八中学校七年级阶段练习）在∠ABC中，BD，CE是它的两条角平分线，且BD，CE相交于点M，MN∠BC于点N．将∠MBN记为∠1，∠MCN记为∠2，∠CMN记为∠3．(1)如图1，若∠A=110°，∠BEC=130°，则∠2= °，∠3－∠1= °；(2)如图2，猜想∠3－∠1与∠A的数量关系，并证明你的结论；(3)若∠BEC=α，∠BDC=β，用含α和β的代数式表示∠3－∠1的度数．（直接写出结果即可）∠BD平分∠ABD，【点睛】本题主要考查了三角形内角和定理，三角形外角的像这种，角平分线的定义，垂直的定义，熟知三角形内角和为180度是解题的关键．◎模型七 两外角角平分线模型【条件】△ABC 中，BI 、CI 分别是△ABC 的外角的角平分线，且相交于点O. 【结论】A O ∠-︒=∠2190. 【证明】∵BO 是∠EBC 平分线，∴EBC ∠=∠212，∵CO 是∠FCB 平分线，∴FCB ∠=∠215 由△BCO 中内角和定理可知：∠O =180°-∠2 -∠5 =180°-EBC ∠21 -FCB ∠21 =180°-)180(21ABC ∠-︒ -)180(21ACB ∠-︒=)(21ACB ABC ∠+∠=)180(21A ∠-︒=A O ∠-︒=∠2190. 31．（2022·江苏·江阴市祝塘第二中学七年级阶段练习）如图，在△ABC 中，设∠A ＝x °，∠ABC 与∠ACD 的平分线交于点A 1，得∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2；…；∠A 2021BC 与∠A 2021CD 的平分线相交于点A 2022，得∠A 2022，则∠A 2022是（ ）度．A ．202012x B ．202112x C ．202212x D ．202312x∠∠A＝∠ACD−∠ABC，∠A1＝∠A1CD−∠A1BC，∠BA1和CA1分别是∠ABC和∠ACD的角平分线，32．（2022·浙江·八年级专题练习）如图，ABC 中，56A ∠=︒，BD 平分ABC ∠，CD 平分ABC 的外角ACE ∠，BD 、CD 交于点D ，则D ∠的度数（ ）A ．28︒B ．56︒C ．30D ．26︒BD 平分平分ABC 的外角DBC ∴∠=12DCE ACE =∠根据外角性质：DBC D +∠28D DCE α∴∠=∠-=︒．故选：A ．33．（2022·陕西·西安博爱国际学校八年级期末）如图，在∠ABC中，∠ABC=75°，∠A=40°，∠ACD是∠ABC的外角，若∠ABC与∠ACD的平分线交于点P，则∠BPC的大小为_____．∠34．（2022·陕西·西安市曲江第一中学八年级期末）如图，在ABC中，ABC的内角CAB∠和外角CBD 的角平分线交于点P，已知42∠=︒，则CAPB∠的度数为____________．【答案】84︒##84度为ABC外角CBD=∠C+∠以求出答案．【详解】解：如下图，。

专题01三角形的高、中线、角平分线的八种常见应用【解题策略】 三角形的高、中线和角平分线是三角形中三种重要的线段,它们提供了重要的线段或角的关系,对我们以后深入研究三角形的一些特征有很大帮助,因此,我们需要从不同的角度认识这三种线段.在三角形的两条边和这两条边上的高这四个量中，已知其中的三个量，可用等面积法求第四个量.题型01三角形的高在求线段长中的应用【典例分析】【例1-1】（23-24八年级上·云南文山·期末）如图，90,8,10,ACB AC AB CD ∠=°==是斜边的高，则CD =（ ）A ．3B ．4.2C ．4.8D ．5【答案】C 【分析】本题考查等积法求线段的长与勾股定理．先由勾股定理计算出BC ，再根据等面积法求解即可，掌握等积法，是解题的关键．【详解】解：∵90,8,10ACB AC AB ∠=°==，∴6BC ，∵CD 是斜边的高， ∴1122ABC S AC BC AB CD =⋅=⋅ ， ∴8610CD ×=， ∴48 4.810CD ==； 故选C【例1-2】（23-24七年级下·辽宁鞍山·期中）如图，在ABC 中，90ACB ∠=°，5AB =，4AC =，3BC =，则点C 到AB 边距离为 ．【答案】125/225/2.4 【分析】本题考查与三角形有关的线段，三角形的高，根据题意可得ABC 是直角三角形，设点C 到AB 边距离为h ，由三角形面积公式计算即可求解．【详解】解：在ABC 中，90ACB ∠=°， ∴ABC 是直角三角形，设点C 到AB 边距离为h ，1122ABC S AC BC AB h ∴=⋅=⋅ ，即345h ×=，125h ∴=， 故答案为：125． 【例1-3】（22-23八年级上·河南·阶段练习）如图，在ABC 中，8AC =，4BC =，高3BD =．(1)作出BC 边上的高AE ；(2)求AE 的长．【答案】(1)见解析(2)6AE =【分析】（1）过点A 作BC 边的垂线，交BC 延长线于E 即可；（2）利用等积法求得AE 的长度即可．【详解】（1）解：如图， 过点A 作BC 边的垂线，交BC 延长线于E ，∴线段AE 即为BC 边上的高，（2）解：∵11S 22ABC BC AE AC BD =⋅=⋅ ，8AC =，4BC =，3BD =， ∴1148322AE ×=××， ∴6AE =．【点睛】本题考查了作三角形的高及求高，熟记三角形的面积公式即可解题，属于基础题【变式演练】【变式1-1】（23-24八年级上·四川成都·期末）如图，在Rt ABC △中，90ACB ∠=°，6AC =，8BC =，CD 是斜边的高，则CD 的长为（ ）A ．245B ．125C ．5D ．10【答案】A【分析】本题主要考查了勾股定理，三角形面积的计算，解题的关键是熟练掌握勾股定理，在一个直角三角形中，两条直角边分别为a 、b ，斜边为c ，那么222+=a b c ．先根据勾股定理求出10AB =，然后根据三角形面积进行计算即可．【详解】解：∵在Rt ABC △中，90ACB ∠=°，6AC =，8BC =，∴10AB =， ∵1122ABC S AC BC AB CD =⋅=⋅ ， ∴6824105AC BC CD AB ．故选：A【变式1-2】（23-24八年级上·四川泸州·阶段练习）如图，ABC 中，AD BC ⊥于D ，CE AB ⊥于E ，6,5,4AB AD BC ===，则CE 的长为 ．【答案】103/133【分析】本题考查了三角形的面积计算，根据1122ABC S AB CE BC AD =×=× ，即可求解． 【详解】解：∵AD BC ⊥，CE AB ⊥， ∴1122ABC S AB CE BC AD =×=× ， ∵6,5,4AB AD BC ===， ∴1164522CE ××=××， ∴103CE =． 故答案为：103【变式1-3】（21-22七年级下·江苏无锡·期中）如图，在ABC 中，AD 为边BC 上的高，连接AE ．(1)当AE 为边BC 上的中线时，若6AD =，ABC 的面积为24，求CE 的长；(2)当AE 为BAC ∠的平分线时，若66C ∠=°，36B ∠=°，求DAE ∠的度数．【答案】(1)4CE =(2)15DAE ∠=°【分析】本题考查三角形的面积，三角形的中线与高等知识，解题的关键是熟练掌握三角形的基本知识． （1）先根据三角形面积公式计算出8BC =，然后根据AE 为边BC 上的中线得到CE 的长；（2）先根据三角形内角和定理计算出78BAC ∠=°，再利用角平分线的定义得到39CAE ∠=°，接着计算出CAD ∠，然后计算CAE CAD ∠−∠即可．【详解】（1） AD 为边BC 上的高，ABC 的面积为24，1242BC AD ∴⋅=， 22486BC ×∴==， AE 为边BC 上的中线，142CE BC ∴==； （2） 66C ∠=°，36B ∠=°，∴180180663678BAC C B °−°°°°∠=∠−∠=−−=，∴AE 为BAC ∠的平分线， ∴1392CAE BAC ∠=∠=°，90ADC ∠=°，66C ∠=°， ∴906624CAD ∠°°=°=−，∴392415DAE CAE CAD ∠=∠−∠=°−°=°题型02三角形的高在求角的度数中的应用【典例分析】【例2-1】（23-24八年级上·湖北武汉·阶段练习）如图，在ABC 中，AD 是BC 边上的高，BE 平分ABC∠交AC 边于E ，60BAC ∠=°，22ABE ∠=°，则DAC ∠的大小是（ ）A ．10°B ．12°C ．14°D ．16°【答案】C 【分析】本题考查了三角形的内角和定理，角平分线的定义，准确识图理清图中各角度之间的关系是解题的关键．根据角平分线的定义可得2ABC ABE ∠=∠，再根据直角三角形两锐角互余求出BAD ∠，然后根据DAC BAC BAD ∠=∠−∠计算即可得解．【详解】解：BE 平分ABC ∠，222244ABC ABE ∴∠=∠=×°=°，AD 是BC 边上的高，90904446BAD ABC ∴∠=°−∠=°−°=°，604614DAC BAC BAD ∴∠=∠−∠=°−°=°．故选：C【例2-2】（23-24八年级上·黑龙江牡丹江·期末）已知ABC 中，50A ∠=°，AB ，AC 边上的高所在的直线交于H ，则BHC ∠=度． 【答案】130°或50°【分析】本题主要考查了三角形的内角和定理，三角形的高线，解题的关键是分ABC 是锐角三角形与钝角三角形两种情况进行讨论．分两种情况考虑：①ABC 是锐角三角形时，先根据高线的定义求出90ADB ∠=°，90BEC ∠=°，然后根据直角三角形两锐角互余求出ABD ∠的度数，再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解；②ABC 是钝角三角形时，根据直角三角形两锐角互余求出BHC A ∠=∠即可．【详解】解：①如图1，ABC 是锐角三角形时，BD 、CE 是ABC 的高线，90ADB ∴∠=°，90BEC ∠=°， 在ABD △中，50A ∠=° ，905040ABD ∴∠=°−°=°，4090130BHC ABD BEC ∴∠=∠+∠=°+°=°；②ABC 是钝角三角形时，BD 、CE 是ABC 的高线，90A ACE ∴∠+∠=°，90BHC ∠+∠=°，ACE HCD ∠=∠ ， 50BHC A ∴∠=∠=°，综上所述，BHC ∠的度数是130°或50°，故答案为：130°或50°【例2-3】（22-23七年级下·江苏常州·期中）如图，在ABC 中，50ABC ∠=°，CE 为AB 边上的高，AF 与CE 交于点G ．若80∠=°AFC ，求AGC ∠的度数．【答案】120°【分析】由高的定义可得90BEC ∠=°，由三角形内角和可得BCE ∠的度数，再根据三角形内角和可得出CGF ∠的度数，由平角的定义可得出AGC ∠的度数．本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键【详解】解：CE 是AB 边上的高，90BEC ∴∠=°，在ABC 中，50ABC ∠=°， 18040BCE ABC BEC ∴∠=°−∠−∠=°，80AFC ∠=° ，18060CGF AFC BCE ∴∠=°−∠−∠=°，180120AGC CGF ∴∠=°−∠=°【变式演练】【变式2-1】（22-23八年级上·安徽安庆·期末）如图，在ABC 中，5525B C AD ∠=°∠=°，，是BC 边的高，AE 平分BAC ∠，则DAE ∠的度数为（ ）A ．12.5°B ．15°C ．17.5°D ．20°【答案】B 【分析】本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键．先根据三角形内角和定理求出BAC ∠的度数，再根据AE 平分BAC ∠求出BAE ∠的度数，根据AD BC ⊥求出BAD ∠的度数，由DAE BAE BAD ∠=∠−∠即可得出结论．【详解】在ABC 中，55B ∠=°，25C ∠=°，1805525100BAC ∴∠=°−°−°=°．AE 平分BAC ∠，1502BAE BAC ∴°∠=∠=． AD 是边BC 上的高，90ADB ∴∠=°，90905535BAD B ∴∠=°−∠=°−°=°，503515DAE BAE BAD ∴∠=∠−∠=°−°=°．故选：B【变式2-2】（22-23）八年级上·安徽马鞍山·期末）如图，AD 、AE 分别是ABC 的高和角平分线，且38B ∠=°，74C ∠=°，则DAE ∠= ．【答案】18°【分析】本题主要考查了三角形内角和定理以及角平分线的性质定理，利用三角形内角和定理求出68BAC ∠=°，利用角平分线的性质得出34EAC ∠=°，再利用三角形内角和定理求出16DAC ∠=°，进一步即可求出DAE ∠．【详解】解：∵38B ∠=°，74C ∠=°∴18068BACB C ∠=°−∠−∠=°， ∵AE 是BAC ∠的平分线， ∴1342EAC BAC ∠=∠=°， ∵AD 是ABC 的高，∴90ADC ∠=°， ∴18016DAC C ADC ∠=°−∠−∠=°，∴341618DAE EAC DAC ∠=∠−∠=°−°=°，故答案为：18°【变式2-3】（23-24八年级上·海南省直辖县级单位·期中）如图所示，在ABC 中，AD 是高，AE 、BF 是角平分线，它们相交于点O ，60BAC °∠=，70C ∠=°．(1)求EAD ∠的度数；(2)求BOA ∠的度数．【答案】(1)10°(2)125°【分析】本题考查了角平分线的定义、三角形的内角和性质，直角三角形的两个锐角互余，正确掌握相关性质内容是解题的关键．（1）先由角平分线的定义得30CAE BAE ∠=∠=°，结合直角三角形的两个锐角互余，得20CAD ∠=°，即可作答．（2）先由角平分线的定义得55OAB OBA +=°∠∠，再运用三角形的内角和性质进行列式计算，即可作答． 【详解】（1）解：∵AE 是BAC ∠的平分线，60BAC ∠=° ∴30CAE BAE ∠=∠=° ∵AD 是高，70C ∠=°∴在Rt ACD △中，20CAD ∠=° ∴302010EAD CAE CAD ∠=∠−∠=°−°=°（2）解：∵AE BF 、是角平分线 ∴11 110552()2OAB OBA CAB CBA ∠+∠=∠+∠=×°=° ∴180125()BOAOAB OBA ∠=°−∠+∠=° 题型03三角形的高在求相关线段的比值中的应用【典例分析】【例3-1】（23-24八年级上·四川绵阳·期末）如图，,AE CD 是ABC 的高，5,3AE CD ==，则AB BC=（ ）A ．53B ．45C ．35D ．25【答案】A【分析】本题考查与三角形的高有关的计算，利用等积法列出比例式，进行求解即可．【详解】解：∵,AE CD 是ABC 的高， ∴1122ABC AB B S CD C AE ⋅=⋅= ，∴53AB AE BC CD ==； 故选：A【例3-2】（23-24八年级上·山东德州·阶段练习）如图，在ABC 中，AD BC ⊥，CE AB ⊥，垂足分别为D ，E ，AD 与CE 相交于点O ，连接BO 并延长交AC 于点F .若5AB =，4BC =，6AC =，则CE ：AD ：BF 的值为 .【答案】12:15:10【分析】本题主要考查三角形的高，由题意得：BF AC ⊥，再根据三角形的面积公式，可得5432ABCS AD CE BF === ，进而即可得到答案． 【详解】解： 在ABC 中，AD BC ⊥，CE AB ⊥，垂足分别为点D 和点E ，AD 与CE 交于点O ， BF AC ∴⊥，5AB = ，4BC =，6AC =，∴1122ABC S BC AD AB CE BF =⋅=⋅=⋅ ， ∴5432ABCS AD CE BF === ， CE ∴：AD ：BF =12:15:10，故答案是：12:15:10【例3-3】（23-24八年级上·广东东莞·阶段练习）如图，在ABC 中，AD 与CE 是ABC 的高．(1)若7cm,10cm,8cm AB BC CE ===，求AD ； (2)若2,3,AB BC ABC ==△的高AD 与CE 的比是多少？【答案】(1)28cm 5(2)12【分析】（1）利用三角形面积公式1122ABC S AB CE BC AD =⋅=⋅ ，即可求解； （2）利用三角形面积公式1122ABC S AB CE BC AD =⋅=⋅ 求解即可． 【详解】（1）解：∵1122ABC S AB CE BC AD =⋅=⋅ ， ∴1178=1022AD ××××， ∴285AD cm =； （2）解：∵1122ABC S AB CE BC AD =⋅=⋅ ， ∴112=422CE AD ××××， ∴12AD CE =． 【点睛】本题考查三角形的面积，利用同一个三角形的面积的两种表示列方程是解题的关键【变式演练】【变式3-1】（23-24八年级上·河北承德·期末）在ABC 中，高2,4AD CE ==．则边:AB BC 是（ ） A ．1:2 B ．2:1 C ．3:1 D ．1:3【答案】A【分析】本题考查的是三角形的高、三角形的面积公式，熟记三角形的面积公式是解题的关键．利用三角形的面积公式可得答案． 【详解】解：∵1122ABC S AB CE BC AD =⋅=⋅ ，2,4AD CE ==， ∴42AB BC =， ∴:2:41:2AB BC==， 故选：A ．【变式3-2】（23-24八年级上·福建厦门·期中）如图，在ABC 中，2AB =，4BC =，ABC 的高AD 与CE的比是 ．【答案】1:2【分析】本题考查了三角形高的定义．根据三角形的面积公式可得11=22ABC S AB CE BC AD ×=×△，即可求解．【详解】解：∵11=22ABC S AB CE BC AD ×=×△ ∴2142AD AB CE BC ===， 故答案为：1:2【变式3-3】（22-23八年级上·全国·课后作业）如图，AD 是ABC 的中线，DE AC DF AB ⊥⊥，，E ，F 分别是垂足．已知2AB AC =，求DE 与DF 的长度之比．【答案】2:1【分析】根据三角形面积法进行求解即可． 【详解】解：∵AD 是ABC 的中线， ∴ABD ACD S S ， ∵DE AC DF AB ⊥⊥，，∴1122ABD ACD S AB DF S AC DE =⋅=⋅△△，， ∴1122AB DF AC DE ⋅=⋅， ∵2AB AC =， ∴2:1DE ABDF AC==． 【点睛】本题主要考查了三角形中线的性质，三角形面积，熟知三角形中线平分三角形面积是解题的关键题型04三角形的高在求相关线段和的问题中的应用【典例分析】【例4-1】（2022八年级上·浙江·专题练习）如图，ABC ∆中，2ABAC ==，P 是BC 上任意一点，PE AB ⊥于点E ，PF AC ⊥于点F ，若1ABC S ∆=，则PE PF +值为（ ）A ．1B ．1.2C ．1.5D ．2【答案】A【分析】连接AP ，则ABC ACP ABP S S S ∆∆∆=+，依据Δ1=2ACP S AC PF ×，Δ1=2ABP S AB PE ×，代入计算即可得到1PE PF +=．【详解】解：如图所示，连接AP ，则ABCACP ABP S S S ∆∆∆=+，∵PE AB ⊥于点E ，PF AC ⊥于点F ， ∴Δ1=2ACP S AC PF ×，Δ1=2ABP S AB PE ×，又∵1ABC S ∆=，2ABAC ==， ∴111=+22AC PF AB PE ××， 即111=2+222PF PE ××××，∴1PE PF +=， 故选：A ．【点睛】本题主要考查了三角形的面积，解决问题的关键是作辅助线将等腰三角形分割成两个三角形，利用面积法进行计算【例4-2】（23-24八年级上·重庆北碚·期中）在等腰ABC 中，4ABAC ==，30BAC ∠=°，D 是BC 上任意一点，DE AB ⊥，DF AC ⊥，DE DF +=．【答案】2【分析】本题考查等腰三角形的性质，直角三角形30度的性质，三角形的面积等知识，解题的关键是学会利用面积法解决问题，属于中考常考题型．作BH AC ⊥于H ，利用含30度的直角三角形的性质得到122BH AB ==，根据ABCABD ACD S S S =+ ，DE AB ⊥，DF AC ⊥，列出等式，由此即可解决问题．【详解】解：过B 作BH AC ⊥于H ，30BAC ∠=° ，122BH AB ∴==， ∵DE AB ⊥，DF AC ⊥，ABCABD ACD S S S =+ ， ∴111222AC BH AB DE AC DF ⋅=⋅+⋅， 则111444222BH DE DF ×⋅=×⋅+×⋅， 则2BH DE DF =+=， 故答案为：2【例4-3】（23-24八年级上·四川自贡·阶段练习）如图，在ABC 中，2ABAC ==，P 是BC 边上的任意一点，PE AB ⊥于点E ，PF AC ⊥于点F ．若6ABC S = ，求PE PF +的长．【答案】6PE PF +=【分析】根据1122ABC ABP APC S S S AB PE AC PF =+=⋅+⋅ ，结合已知条件，即可求得PE PF +的值． 【详解】解：如图，连接AP ，PE AB ⊥于点E ，PF AC ⊥于点F ，1122ABC ABP APC S S S AB PE AC PF ∴=+=⋅+⋅ ， 2AB AC == ，6ABC S = ，∴1122AB PE AC PF ⋅+⋅6PE PF =+=【变式演练】【变式4-1】（23-24八年级上·广东广州·期中）Rt ABC △中，90C ∠=°，D 是BC 上一点，连接AD ，过B 、C 两点分别作直线AD 的垂线，垂足为E 、F ，若8BC =，6AC =，9AD =，则BE CF +的值是（ ）A ．6B ．163C ．8D ．203【答案】B【分析】本题考查三角形的面积，根据两种不同三角形的面积：12ABCS AC BC =⋅ ，ABCABD ACD S S S =+ ，建立等式是解决问题的关键．【详解】解：∵90C ∠=°，8BC =，6AC =， ∴11682422ABC AC B S C ⋅=××==， 又∵BE AD ⊥，CF AD ⊥，9AD =，∴ABC ABD ACD S S S =+ 即：()111924222AD BE AD CF BE CF ⋅+⋅=××+= ∴163BE CF +=， 故选：B ．【变式4-2】（23-24八年级上·黑龙江齐齐哈尔·期中）如图，在ABC 中，5ABAC ==，F 是BC 边上任意一点，过F 作FD AB ⊥于D ，FE AC ⊥于E ，若10ABC S =△，则FE FD +=．【答案】4【分析】连接AF ，根据ABC ABF ACF S S S =+ ，即可求解．熟练掌握等腰三角形的性质，正确理解题意，根据等面积法列出等式是解题的关键． 【详解】解：连接AF ，如图：则10ABF A ABC CF S S S =+= △△， 12ABFS AB FD =×△，12ACF S AC FE =×△， ∴111022AC FE AB FD ×+×=，∵5ABAC ==， ∴551022FE FD +=， ∴4FE FD += 故答案为：4题型05三角形的中线在求线段长中的应用【典例分析】【例5-1】（23-24八年级上·重庆·阶段练习）如图，ABC 中，159AB BC ==，，BD 是AC 边上的中线，若ABD △的周长为35，则BCD △的周长是（ ）A ．20B ．29C ．26D ．28【答案】B【分析】本题考查了中线的意义，根据BD 是AC 边上的中线，得到AD CD =，根据ABD △的周长为AB BD AD ++；BCD △的周长为BC BD CD ++，计算周长的差，得到()()1596AB BD AD BC BD CD BC ++−++=−=−=，结合ABD △的周长为35，计算35629−=即可． 【详解】∵BD 是AC 边上的中线， ∴AD CD =，∵ABD △的周长为AB BD AD ++；BCD △的周长为BC BD CD ++，∴()()1596AB BD AD BC BD CD AB BC ++−++=−=−=， ∵ABD △的周长为35， ∴BCD △的周长为35629−=, 故选B【例5-2】（23-24八年级上·全国·课后作业）如图，AD ，AE 分别是ABC 的高和中线，已知5cm AD =，6cm CE =，则ABC 的面积为 ．【答案】230cm【分析】本题主要考查了求三角形面积，熟知三角形高和中线的定义是解题的关键． 先根据中线的定义求出212BC CE cm ＝＝，再根据三角形面积公式求解即可． 【详解】解：AE 是ABC 的中线，6cm CE =，212cm BC CE ∴，AD 是ABC 的高，∴2130cm 2ABC S AD BC， 故答案为：230cm【例5-3】（23-24八年级上·陕西渭南·期中）已知ABC ，AD 是BC 边上的中线，且4AC =，若ABD △的周长比ACD 的周长大5，求AB 的长． 【答案】9AB =【分析】本题考查的是三角形的中线，掌握三角形的中线的概念是解题的关键．根据中线的性质得到BD CD =，根据三角形的周长公式计算得到答案．【详解】解：如图，∵AD 是BC 边上的中线， ∴BD CD =，∵ABD △的周长比ACD 的周长大5，∴()()5AB BD AD AC AD CD ++−++=， ∴5AB AC −=， ∵4AC =， ∴9AB =【变式演练】【变式5-1】（23-24八年级上·福建福州·期末）如图，在ABC 中，AD 是高，AE 是中线，若3AD =，6ABC S = ，则BE 的长为（ ）A ．1B ．2C ．3D ．4【答案】B【分析】本题考查了三角形的高线和中线的意义，根据高线求出4BC =，根据AE 是中线即可求解． 【详解】解：∵162ABC S BC AD =××=，3AD =， ∴4BC = ∵AE 是中线， ∴122BE BC == 故选：B【变式5-2】（23-24八年级上·重庆垫江·阶段练习）在ABC 中，AD 为BC 边的中线．若ABD △与ADC △的周长差为3,8AB =，则AC = ． 【答案】5或11AD 为BC 边上的中线，得BD CD =，根据题意，分类讨论进而即可求解，掌握中线的性质是解题的关键． 【详解】解：①当AB AC >时，∵ABD △与ADC △的周长差为3，∴()3AB BD AD AC CD AD ++−++=， ∵AD 为BC 边上的中线，∴BD CD =，∴()3AB BD AD AC CD AD AB AC ++−++=−=，∵8AB =，∴835AC =−=,②当AC AB >时，同理可得3AC AB −=，则8311AC =+= 故答案为：5或11【变式5-3】（21-22八年级上·湖北十堰·阶段练习）如图，在ABC 中()AB BC >，2AC BC =，BC 边上的中线AD 把ABC 的周长分成50和35两部分，求AC 和AB 的长．【答案】40AC =，25AB =【分析】本题主要考查了三角形中线的性质和三边的关系，先根据2AC BC =和三角形的中线列出方程求解，分类讨论①50AC CD +=，②35AC CD +=，注意答案是否满足条件，即是否满足题目给出的条件、是否满足三角形三边的关系．解题的关键是找到等量关系，列出方程．【详解】解：设BDCD x ==，则24AC BC x ==， BC 边上的中线AD 把ABC 的周长分成50和35两部分，AB BC >，①当50AC CD +=，35AB BD +=时， 450x x +=，解得：10x =，441040AC x ∴==×=，10BD CD ==，35351025AB BD ∴=−=−=，2520AB BC ∴=>=，满足条件；20254540BC AB AC +=+=>= ，满足三边关系，40AC ∴=，25AB =；②当35AC CD +=，50AB BD +=时， 435x x +=，解得：7x =，44728AC x ∴==×=，7BD CD ∴==，5050743AB BD =−=−=，28144243AC BC AB +=+=<= ，∴不满足三角形的三边关系，∴不合题意，舍去，综上：40AC =，25AB =题型06三角形的中线与高在证明线段相等中的应用【典例分析】【例6】如图，ABC ∆中，AD 为中线，D ，E 分别为BC ，AD 的中点，且40ABC S ∆=，CM AD ⊥于M ．（1）ABD S ∆= ；（2）若5AE =，求CM 的长；（3）若BN AD ⊥交AD 的延长线于N ，求证：CM BN =．【分析】（1）根据三角形中线的性质得出面积即可；（2）根据三角形面积公式得出CM 即可；（3）根据三角形面积公式进行证明解答．【解答】（1）解：AD 为中线，且40ABC S ∆=，11402022ABD ABC S S ∆∆∴==×=， 故答案为：20；（2）解：AD 为中线，D ，E 分别为BC ，AD 的中点，40ABC S ∆=， ∴111024AEC ACD ABC S S S ∆∆===，12AECS AE CM ∆=⋅， ∴15102CM ×⋅=， 4CM ∴=；（3）证明：AD 为中线，D ，E 分别为BC ，AD 的中点， ∴12ABD ACD ABC S S S ∆∆∆==， 12ABDS AD BN ∆=⋅，12ACD S AD CM ∆=⋅， ∴1122AD BN AD CM ⋅=⋅， CM BN ∴=．【点评】此题是三角形综合题，考查三角形中线的性质和三角形面积公式，关键是根据三角形中线的性质解答．题型07三角形的角平分线在解与平行线相关问题中的应用【典例分析】【例7-1】（22-23八年级上·湖北随州·期中）如图，在ABC 中，DE BC ∥，ABC ∠和ACB ∠的平分线分别交ED 于点G 、F ，若36FG DE ==，，则EB DC +的值为（ ）A ．6B ．7C ．9D ．10【答案】C 【分析】本题考查了角平分线，平行线的性质，等角对等边等知识．熟练掌握角平分线，平行线的性质，等角对等边是解题的关键．由角平分线，平行线的性质可得EGB CBG ABG DFC BCF ACF ∠=∠=∠∠=∠=∠，，则BE EG DC DF ==，，根据EB DC EG DF EF FG DE EF +=+=++−，计算求解即可．【详解】解：∵BG CF 、是ABC ∠和ACB ∠的平分线，∴ABG CBG ACF BCF ∠=∠∠=∠，， ∵DE BC ∥，∴EGB CBG ABG DFC BCF ACF ∠=∠=∠∠=∠=∠，， ∴BE EGDC DF ==，， ∴9EB DC EG DF EF FG DE EF +=+=++−=，故选：C【例7-2】（23-24八年级上·重庆渝北·期中）如图，在ABC 中，ED BC ∥，ABC ∠和ACB ∠的角平分线分别交ED 于点G ，F ，若4BE =，6CD =，3FG =．则ED 的长为 ．【答案】7【分析】本题考查了等腰三角形的判定与性质，平行线的性质，根据角平分线的定义和平行线的性质可证EBG 和DFC 是等腰三角形，从而可得4EB EG ==，6DC DF ==，然后利用线段的和差关系进行计算，即可解答．【详解】解：BG 平分ABC ∠，CF 平分ACB ∠，ABG CBG ∴∠=∠，ACF BCF ∠=∠，ED BC ∥，EGB CBG ∴∠=∠，DFC BCF ∠=∠，ABG EGB ∴∠=∠，ACF DFC ∠=∠，4EB EG ∴==，6DC DF ==，3FG = ，4637DE EG DF FG ∴=+−=+−=，故答案为：7【例7-3】（23-24八年级上·江苏徐州·期中）如图，BE 是ABC 的角平分线，在AB 上取点D ，使DB DE =．(1)求证：DE BC ∥；(2)若65A ∠=°，45AED ∠=°，求EBC ∠的度数． 【答案】(1)见解析(2)35°【分析】本题考查了角平分线的定义、平行线的判定与性质、等边对等角、三角形内角和定理，熟练掌握以上知识点并灵活运用是解此题的关键．（1）由角平分线的定义可得ABE CBE ∠=∠，由等边对等角可得DBE DEB ∠=∠，从而得出CBE DEB ∠=∠，即可得证；（2）由平行线的性质可得45ACB AED ∠=∠=°，由三角形内角和定理得出70ABC ∠=°，最后由角平分线的定义计算即可得出答案．【详解】（1）证明：BE 平分ABC ∠，ABE CBE ∴∠=∠，DB DE = ，DBE DEB ∴∠=∠，CBE DEB ∴∠=∠，DE BC ∴∥；（2）解：DE BC ∥，45ACB AED ∴∠=∠=°，18070ABC ACB A ∴∠=°−∠−∠=°，BE 平分ABC ∠，11703522EBC ABC ∴∠=∠=×°=°．【变式演练】【变式7-1】（23-24八年级上·内蒙古呼和浩特·期中）如图，在ABC 中，ED BC ∥，ABC ∠和ACB ∠的平分线分别交ED 于点G 、F ，若37FG ED ==，，则EB DC +的值为（ ）A ．9B ．10C ．11D ．12【答案】B 【分析】本题考查了角平分线，平行线的性质，等角对等边等知识．熟练掌握角平分线，平行线的性质，等角对等边是解题的关键．由角平分线、平行线的性质可得EGB GBC ABG DFC BCF ACF ∠=∠=∠∠=∠=∠，，则EB EG DF DC ==，，根据EB CD ED FG +=+，计算求解即可．【详解】解：∵BG 平分ABC ∠，CF 平分ACB ∠，∴ABG GBC ACF BCF ∠=∠∠=∠，， ∵ED BC ∥，∴EGB GBC ABG DFC BCF ACF ∠=∠=∠∠=∠=∠，， ∴EB EGDF DC ==，， ∴10EB CD EG DF EG FG DG ED FG +=+=++=+=．故选：B【变式7-2】（23-24八年级上·河北沧州·期中）如图，在ABC 中，ABC ∠和ACB ∠的平分线交于点E ，过点E 作MN BC ∥交AB 于M ，交AC 于N ，若9BM CN +=，则线段MN 的长为 ．【答案】9【分析】本题考查了角平分线的定义、平行线的性质、等角对等边，由角平分线的定义结合平行线的性质可得MBE MEB NEC ECN ∠=∠∠=∠，，由等角对等边得出BM ME EN CN ==，，再由MN BM CN =+，即可得解，熟练掌握角平分线的定义、平行线的性质、等角对等边，是解此题的关键．【详解】解：ABC ACB ∠∠ 、的平分线相交于点E ，MBE EBC ECN ECB ∴∠=∠∠=∠，，MN BC ，EBC MEB NEC ECB ∴∠=∠∠=∠，，MBE MEB NEC ECN ∴∠=∠∠=∠，，BM ME EN CN ∴==，，MN ME EN ∴=+，即MNBM CN =+， 9BM CN += ，9MN ∴=，故答案为：9【变式7-3】（23-24八年级上·河北保定·期末）如图，在ABC 中，46B ∠=°，54C ∠=°，AD 平分BAC ∠交BC 于点D ，点E 是边AC 上一点，若40ADE ∠=°，求证：DE AB ∥．【答案】见解析【分析】本题考查了三角形内角和定理、角平分线的定义、平行线的判定，由三角形内角和定理得出80BAC ∠=°，由角平分线的定义得出1402BAD BAC ∠=∠=°，从而得出40ADE BAD ∠=∠=°，即可得证． 【详解】证明：∵在ABC 中，46B ∠=°，54C ∠=°，∴180465480BAC ∠=°−°−°=°． ∵AD 平分BAC ∠， ∴1402BAD BAC ∠=∠=°． ∵40ADE BAD ∠=∠=°． ∴DE AB ∥题型08三角形的角平分线与高再求角的度数中的应用【典例分析】【例8-1】（22-23八年级上·新疆乌鲁木齐·期中）如图，ABC 中，AD BC ⊥，AE 平分BAC ∠，70B ∠=°，34C ∠=°，则DAE ∠=（ ）A ．18°B ．34°C ．20°D ．38°【答案】A 【分析】本题主要考查了与角平分线有关的三角形内角和问题．利用垂直求得9056DACC ∠=°−∠=°是正确解答本题的关键．在ABC 中，根据三角形内角和定理得到BAC ∠的度数，进而求出DAC ∠的度数，在直角ACD 中根据三角形内角和定理得到DAC ∠的度数，则DAE ∠的度数就可以求出．【详解】解：在ABC 中，70B ∠=°，34C ∠=°，∴18076BACB C ∠=°−∠−∠=°， 又∵AE 平分BAC ∠， ∴1382EAC BAC ∠=∠=°， 在直角ACD 中，9056DACC ∠=°−∠=°， ∴18DAE DAC EAC ∠=∠−∠=°．故选：A【例8-2】（23-24八年级上·浙江绍兴·阶段练习）如图,在ABC 中,AD 是高,AE 是角平分线,若60,16B DAE ∠=°∠=°,则C ∠= ．【答案】28?/28度【分析】本题考查了三角形的高、角平分线、三角形内角和等知识，解题的关键从已知条件入手，逐步推得待求的结论．先由AD 是高与=60B ∠°求得BAD ∠，再求得BAE ∠，再由角平分线AE 推得BAC ∠，最后由三角形的内角和求得C ∠的度数．【详解】∵AD 是高，∴90ADB ∠=°， ∵=60B ∠°，∴9030BADB °∠=−∠=°． ∵16DAE ∠=°， ∴46BAE BAD DAE =+=°∠∠∠． ∵AE 是角平分线，∴46CAEBAE ==°∠∠， ∴92BAC BAE CAE =+=°∠∠∠， 在ABC 中，180180609228CB BAC =°−−=°−°−°=°∠∠∠． 故答案为：28°【例8-3】（23-24八年级上·云南怒江·阶段练习）如图，在ABC 中，AD 是高，AE 、BF 是角平分线，它们相交于点O ，70C ∠=°，60ABC ∠=°，求DAE ∠的度数．【答案】5°【分析】本题考查了三角形的内角和定理、直角三角形的两个锐角互余、三角形的角平分线等知识，熟练掌握三角形的内角和定理是解题关键．先根据三角形的内角和定理求出50BAC ∠=°，再根据直角三角形的性质可得30BAD ∠=°，然后根据角平分线的定义可得1252BAE BAC ∠=∠=°，最后根据DAE BAD BAE ∠=∠−∠求解即可得．【详解】解：∵在ABC 中，70C ∠=°，60ABC ∠=°， ∴18050BACC ABC ∠=°−∠−∠=°， ∵在ABC 中，AD 是高，即AD BC ⊥，∴9030BADABC ∠=°−∠=°， ∵在ABC 中，AE 是角平分线，即AE 是BAC ∠的角平分线，∴1252BAE BAC ∠=∠=°， ∴5DAE BAD BAE ∠=∠−∠=°【变式演练】【变式8-1】（23-24八年级上·山东滨州·期末）如图，在ABC 中，AD 是高，AE 是角平分线．若60BAC ∠=°，70C ∠=°，则EAD ∠的大小为（ ）A ．5°B ．10°C ．15°D ．20°【答案】B 【分析】本题主要考查了三角形的内角和定理，角平分线，解答的关键是结合图形分析清楚角与角之间的数量关系．由AD 是高，70C ∠=°，可得20CAD ∠=°，再由AE 是BAC ∠的角平分线，60BAC ∠=°，从而得30CAE ∠=°，进而可求EAD ∠的度数． 【详解】解：AD 是ABC 的高，70C ∠=°，90ADC ∴∠=°，18020CAD ADC C ∴∠=°−∠−∠=°，AE 是BAC ∠的角平分线，60BAC ∠=°， 1302CAE BAC ∴∠=∠=°， 10EAD CAE CAD ∴∠=∠−∠=°．故选：B【变式8-2】（23-24八年级上·四川自贡·期末）如图，在ABC 中，AD 是高，角平分线AE ，BF 相交于点O ，30BAE ∠=°，20DAC ∠=°，则AOB ∠ 的度数是 ．【答案】125°【分析】本题考查的是三角形的高的含义，角平分线的含义，先计算70C ∠=°，60BAC ∠=°，50ABC ∠=°，25ABO ∠=°，再利用三角形的内角和定理可得答案．【详解】解：AD 是ABC 的高，90ADC ∴∠= ，180ADC C CAD ∠+∠+∠=° ，20DAC ∠=°，180902070C ∴∠=°−°−°=°，∵AE 平分BAC ∠，30BAE ∠=°， ∴60BAC ∠=°， 180ABC C CAB ∠+∠+∠°= ，180706050ABC ∴∠=°−°−°=°，BF 分别平分ABC ∠， ∴1252ABO ABC ∠=∠=°， 180ABO BAO AOB ∠+∠+∠= ，1802530125AOB °°°°∴∠=−−=．故答案为：125°【变式8-3】（23-24八年级上·北京·期中）如图，AD 是ABC 的高，AE 是ABC 的角平分线，若38B ∠=°，70C ∠=°．求AEC ∠和DAE ∠的度数．【答案】74AEC ∠=°，16DAE ∠=° 【分析】本题考查三角形的内角和定理及角平分线的性质，高线的性质，由三角形内角和定理可求得BAC ∠的度数，根据角平分线定义求出EAC ∠的度数，在Rt ADC 中，可求得DAC ∠的度数，最后根据角的和差关系求解即可．【详解】∵38B ∠=°，70C ∠=°，∴18072BACB C ∠=°−∠−∠=°， ∵AE 是角平分线，∴1362EAC BAC ∠=∠=°． ∵AD 是高，70C ∠=°， ∴9020DAC C ∠=°−∠=°， ∴362016EAD EAC DAC ∠=∠−∠=°−°=°， 901674AEC ∠=°−°=°。

专题01 用勾股定理解三角形一、单选题1．如图，在ABC 中，90C ∠=︒，13AB =，5AC =，D 、E 分别是AC 、AB 的中点，则DE 的长是（ ）A ．6.5B ．6C ．5.5D ．2【答案】B 【分析】根据勾股定理可先求出BC ，然后结合中位线定理得出结论． 【解析】由勾股定理得：12BC =，∵D 、E 分别是AC 、AB 的中点， ∵DE 是ABC 的中位线， 则162DE BC ==， 故选：B ． 【小结】本题考主要考查三角形的中位线定理，熟记并灵活运用基本定理是解题关键． 2．直角三角形的直角边长分别为3，4，则直角三角形的周长为（ ）A ．5B ．12C ．12或7D ．7【答案】B 【分析】先根据勾股定理求出直角三角形的斜边，继而即可求出三角形的周长． 【解析】根据勾股定理可知：斜边=5，∵三角形周长=3+4+5=12，故选：B．【小结】本题考查的是勾股定理的应用，难度适中，解题关键是根据勾股定理求出斜边的长．3．如图，在∵ABC中，∵ACB=90°，CD是高，∵A=30°，AB=4，则下列结论中不正确的是（）A．BC=2B．BD=1C．AD=3D．CD=2【答案】D【分析】根据含30°角的直角三角形的性质及勾股定理求出各线段的长度，即可判断．【解析】∵∵ACB=90°，∵A=30°，∵BC=12AB=2，∵B=60°，∵CD∵AB，∵∵CDB=∵CDA=90°，∵BCD=30°，∵BD=12BC=1，∵AD=AB-BD=4-1=3，CD==∵不正确的是D．故选：D．【小结】本题考查的是直角三角形的性质，勾股定理，掌握直角三角形中，30°角所对的直角边等于斜边的一半是解题的关键．4．如图是2002年8月在北京召开的国际数学大会的会标，它是由四个相同的直角三角形与中间一个小正方形拼成的一个大正方形，若大正方形的边长是13cm，每个直角三角形较短的一条直角边的长是5cm，则小正方形的边长为（）A．4cm B．5cm C．6cm D．7cm【答案】D【分析】先设直角三角形的两直角边分别是a cm、b cm（a＞b），斜边是c cm，于是有a2+b2=c2，即a2+52=132，易得a=12 cm，a-b即可得小正方形的边长．【解析】设大直角三角形的两直角边分别是a cm、b cm（a＞b），斜边是c cm，那么有a2+b2=c2，∵大正方形的边长是13cm，每个直角三角形较短的一条直角边的长是5cm，∵a2+52=132，解得a= 12（舍去负值），即a=12 cm，∵小正方形的边长为：a-b=12-5=7 cm．故选：D．【小结】本题考查了勾股定理，解题的关键是知道小正方形的边长等于直角三角形较长直角边减去较小直角边．5．已知一个直角三角形三边的平方和为800，则这个直角三角形的斜边长为（）A．20B．40C．80D．100【答案】A【分析】直角三角形中两直角边的平方和等于斜边的平方，已知三边的平方和可以求出斜边的平方，根据斜边的平方可以求出斜边长．【解析】∵在直角三角形中斜边的平方等于两直角边的平方和，又∵已知三边的平方和为800，则斜边的平方为三边平方和的一半，即斜边的平方为，800÷2=400，∵斜边长， 故选：A ． 【小结】本题考查了勾股定理在直角三角形中的灵活应用，考查了勾股定理的定义，本题中正确计算斜边长的平方是解题的关键．6．如图，O 的直径AB 垂直于弦,CD 垂足为,22.5,2E A OC ∠=︒=，则CD 的长为（ ）A B ．2C ．D ．4【答案】C 【分析】由垂径定理可得出CD=2CE ，∵CEO=90°，由∵A=22.5°，利用圆周角定理可求出∵COE=45°，进而可得出∵CEO 为等腰直角三角形，再利用等腰直角三角形的性质及OC=2可求出CE 的长（或通过解直角三角形求出CE 的长），结合CD=2CE 可求出CD 的长． 【解析】∵∵O 的直径AB 垂直于弦CD ， ∵CD=2CE ，∵CEO=90°， 又∵∵COE=2∵A=45°， ∵∵CEO 为等腰直角三角形，∵CD=2CE= 故选：C ． 【小结】本题考查了圆周角定理、垂径定理以及等腰直角三角形，利用等腰直角三角形的性质求出CE的长是解题的关键．7．菱形的边长是5cm，一条对角线的长为6cm，则另一条对角线的长为（）A．6cm B．C．8cm D．10cm【答案】C【分析】根据菱形性质得出OB＝OD＝3cm，OA＝OC，AC∵BD，由勾股定理求出OA，即可得出答案．【解析】如图所示：∵四边形ABCD是菱形，∵AB＝5cm，OB＝OD＝12BD＝3cm，AC∵BD，∵∵AOB＝90°，由勾股定理得：OA=4cm，∵AC＝2OA＝8cm，故选：C．【小结】本题考查了菱形的性质和勾股定理，熟练掌握菱形的对角线互相垂直平分是解题的关键．8．若直角三角形中，斜边的长为17，一条直角边长为15，则另一条直角边长为（）A．7B．8C．20D．65【答案】B【分析】根据勾股定理解答即可．【解析】∵直角三角形中，斜边的长为17，一条直角边长为15， ∵另一条直角边222171456=-=， ∵另外一边为8． 故选：B ． 【小结】此题主要考查了勾股定理，正确把握勾股定理是解题关键． 9．边长为2的正方形的对角线长是（ ）A B ．2C ．D ．4【答案】C 【分析】根据勾股定理，可得对角线的长，根据开方运算，可得答案． 【解析】对角线平方的长是8，边长为2的正方形的对角线长是 故选：C ． 【小结】本题考查了算术平方根，利用了开方运算．10．如图，菱形ABCD 的周长为32，60ABC ∠=，点E 、F 分别为AO 、AB 的中点，则EF 的长度为（ ）A ．B ．3C D ．4【答案】A 【分析】首先根据菱形的性质得出8,,AB AC BD =⊥1302ABO ABC =∠=∠︒，然后利用含30°的直角三角形的性质和勾股定理求出BO 的长度，最后利用三角形中位线的性质求解即可．【解析】∵菱形ABCD 的周长为32，60ABC ∠=︒8,,AB AC BD ∴=⊥1302ABO ABC =∠=∠︒． 142AO AB ∴==，BO ∴==．∵点E 、F 分别为AO 、AB 的中点，12EF BO ∴== 故选：A ． 【小结】本题主要考查菱形的性质，含30°的直角三角形的性质和三角形中位线的性质，熟练掌握这些性质是关键． 11．若直角三角形两边长分别是6，8，则它的斜边为（ ） A ．8 B ．10C ．8或10D ．以上都不正确【答案】C 【分析】分两种情况：∵6和8都是直角边，利用勾股定理求解即可；∵6是直角边，8是斜边，从而可确定答案． 【解析】∵6和810=； ∵8是斜边，综上所述，斜边为8或10， 故选：C ． 【小结】本题主要考查勾股定理，分情况讨论是关键．12．如图，长为12cm 的橡皮筋放置在水平面上，固定两端A 和B ，然后把中点C 垂直向上拉升4.5cm 至点D ，则拉升后橡皮筋伸长了（ ）A．2cm B．3cm C．4cm D．5cm【答案】B【分析】根据勾股定理，可求出AD、BD的长，则AD BD+即为拉长后橡皮筋的长，从而减去原来的长度即可得到答案．【解析】Rt△ACD中，16cm2AC AB==， 4.5cmCD=；根据勾股定理，得：7.5cmAD=；215cmAD BD AD∴+==；15123cm∴-=；故选：B．【小结】此题主要考查了等腰三角形的性质以及勾股定理的应用．关键是根据勾股定理，可求出AD、BD的长．13．如图，AB为∵O的直径，点C为∵O上一点，连接CO，作AD//OC，若CO＝52，AC＝2，则AD＝（）A．3B．C．72D．175【答案】D【分析】根据题意，作出合适的辅助线，然后可以求得OG的长，再利用勾股定理即可得到AG的长，从而可以得到AD的长．【解析】作AE∵OC于点E，作OF∵CA于点F，作OG∵AD于点G，则EA∵OG，∵AD∵OC，∵四边形OEAG是矩形，∵OG ＝EA ，∵OF ∵AC ，OA ＝OC ＝52，AC ＝2， ∵CF ＝1，∵OF2=， ∵22AC OF OC AE⋅⋅=，∵522222AE ⋅=，解得5AE =， ∵OG， ∵OG ∵AD ，∵AG1710==， ∵AD ＝2AG ＝175，故选：D ．【小结】本题考查圆的性质，矩形的判定与性质，勾股定理，面积等积式，掌握圆的性质，矩形的判定与性质，勾股定理，面积等积式是解题关键．14．如图，在正方形网格中，以格点为顶点的ABC 的面积等于3，则点A 到边BC 的距离为（ ）A B ．C ．4 D ．3【答案】D 【分析】根据勾股定理表示出BC 的长，再根据三角形的面积为3，求出BC ，即可求出点A 到边BC 的距离． 【解析】设单位方格的边长为a ，BC a ==，ABC 的面积等于3，()211222322a a a a a ∴-⨯⨯⨯-⨯⨯=，解得a =，2BC ===， ∴点A 到边BC 的距离为2632ABC S BC ==． 故答案为：D ． 【小结】此题考查了三角形的面积勾股定理的运用，关键是根据图形列出求三角形面积的算式． 15．等腰三角形底边上的高为4cm ，周长为16cm ，三角形的面积为（ ） A ．214cm B ．212cm C ．210cm D ．28cm【答案】B 【分析】设等腰三角形的底边长为2x ，则有腰长为8-x ，然后根据勾股定理可得()22248x x +=-，进而问题可求解．【解析】 如图，由题意得：AD =4cm ，设等腰三角形的底边长为2x cm ，由周长为16cm 可得()8cm AB x =-， ∵在Rt ∵ADB 中，由勾股定理得()22248x x +=-，解得：3x =， ∵6BC cm =， ∵21122ABCSBC AD cm =⋅=； 故选B ． 【小结】本题主要考查等腰三角形的性质及勾股定理，熟练掌握等腰三角形的性质及勾股定理是解题的关键． 16．在ABC 中，AB =AC =5，BC =6，M 是BC 的中点，MN ∵AC 于点N ．则MN =（ ） A ．125B ．61C ．6D ．11【答案】A 【分析】连接AM ，根据等腰三角形三线合一的性质得到AM ∵BC ，根据勾股定理求得AM 的长，再根据在直角三角形的面积公式即可求得MN 的长． 【解析】 如图，连接AM ，∵AB =AC ，点M 为BC 中点， ∵AM ∵CM ，BM =CM =12BC =3， 在Rt ∵ABM 中，AB =5，BM =3，∵AM4==，又∵S∵AMC=12MN•AC=12AM•MC，∵MN=AM CMAC=125故选：A．【小结】本题考查三角形的面积，等腰三角形的性质，勾股定理，掌握相关性质定理正确推理计算是解题关键．17．两个直角三角形拼成如图所示的图形，则2x的值为（）A B．3C D．5【答案】B【分析】可设直角边都是1的直角三角形的斜边为y，根据勾股定理可求出y2＝2，则再利用勾股定理可求出2x的值．【解析】在直角边都是1的直角三角形中，设斜边为y，则由勾股定理得：y2＝12+12＝2，同理可得：x2＝y2+12＝2+1＝3．故选：B．【小结】此题考查了勾股定理，掌握勾股定理的应用条件及方法是解题的关键．18．一直角三角形的斜边长比其中一直角边长大3，另一直角边长为9，则斜边长为（）A．15B．12C．10D．9【答案】A【分析】设斜边长为x，则一直角边长为x-3，再根据勾股定理求出x的值即可．【解析】设斜边长为x ，则一直角边长为x -3， 根据勾股定理得92+(x -3)2=x 2， 解得x=15． 故选：A ． 【小结】本题考查了勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．19．如图，在Rt ABC △中，90C ∠=︒，D 为AC 上一点．若12DA DB ==，ABD △的面积为60，则CD 的长是（ ）A ．5B ．C ．8D ．10【答案】B 【分析】根据Rt ∵ABC 中，∵C =90°，可证BC 是∵DAB 的高，然后利用三角形面积公式求出BC 的长，再利用勾股定理即可求出DC 的长． 【解析】∵∵C =90°，DA =12， ∵S ∵DAB =12DA BC ⋅=60， ∵BC =10，在Rt ∵BCD 中，CD ²+BC ²=BD ²，即CD ²+10²=12²，解得：CD =， 故选：B ． 【小结】本题主要考查勾股定理，解题的关键是掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．20．一等腰三角形底边长为10cm，腰长为13cm，则腰上的高为（）A．12cm B．60cm13C．12013cm D．13cm5【答案】C【分析】过点A作AD∵BC于D，过点B作BE∵AC于E，根据勾股定理求出AD，根据三角形的面积公式计算即可．【解析】如下图，在等腰三角形ABC中，底边长为BC=10cm，腰长为AB=13cm，过点A作AD∵BC于D，过点B作BE∵AC于E，∵AD∵BC于D，∵BD=DC，∵BC=10cm，∵BD=DC=5cm，在Rt∵ABD中，12AD==cm，由于1122BC AD AC BE⋅=⋅，∵10121201313BE⨯==cm，故选：C．【小结】本题考查的是勾股定理、等腰三角形的性质，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．21．如图，在长方形ABCD中，AB=3，BC=6，对角线AC的垂直平分线分别交AD、AC于点M，N，连接CM，则CM的长为（）A．154B．153C．-154D．-153【答案】A【分析】由线段垂直平分线的性质求出AM=CM，在Rt∵DMC中，由勾股定理得出DM2+DC2=CM2，得出方程（6-CM）2+32=CM2，求出CM即可．【解析】∵四边形ABCD是矩形，∵∵D=∵B=90°，AD=BC=6，AB=DC=3，∵MN是AC的垂直平分线，∵AM=CM，∵DM=AD-AM=AD-CM=6-CM，在Rt∵DMC中，由勾股定理得：DM2+DC2=CM2，（6-CM）2+32=CM2，解得：CM=154，故选：A．【小结】本题考查了矩形性质，勾股定理，线段垂直平分线性质的应用，关键是能得出关于CM的方程．22．如图，已知∵ABC中，∵ABC=90°，AB=BC，过∵ABC的顶点B作直线l，且点A到l的距离为2，点C到l的距离为3，则AC的长是()A B．C D．5【答案】C【分析】分别过A 、C 作AD ∵l 于D ，CE ∵l 于E ，根据锐角互余可得∵ABD =∵BCE ，∵DAB =∵CBE ，利用ASA 可证明∵ABD ∵∵CBE ，即可得BD =CE ，根据勾股定理可求出AB 的长，再利用勾股定理求出AC 的长即可． 【解析】作AD ∵l 于点D ，作CE ∵l 于点E ， ∵∵ABC =90°， ∵∵ABD +∵CBE =90°， 又∵DAB +∵ABD =90°， ∵∵BAD =∵CBE ， 在∵ABD 和∵BCE 中，ADB BEC BAD CBE AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，，， ∵∵ABD ∵∵BCE (AAS )， ∵BE =AD =2，DB =CE =3，在Rt ∵BCE 中，根据勾股定理，得BC在Rt ∵ABC 中，根据勾股定理，得AC=．故选：C ． 【小结】本题考查全等三角形的判定与性质及勾股定理，根据三角形全等得出BD =CE 是解题关键．23．如图1，点P 从ABC 的顶点A 出发，沿A B C →→匀速运动到点,C 图2是点P 运动时线段CP 的长度y 随时间x 变化的关系图象，其中点Q 为曲线部分的最低点，则ABC 的边AB 的长度为（ ）A ．12B ．8C ．10D ．13【答案】C 【分析】根据图2中的曲线可得，当点P 在∵ABC 的顶点A 处，运动到点B 处时，图1中的AC ＝BC ＝13，当点P 运动到AB 中点时，此时CP ∵AB ，根据图2点Q 为曲线部分的最低点，可得CP ＝12，根据勾股定理可得AP ＝5，再根据等腰三角形三线合一可得AB 的长． 【解析】根据图2中的曲线可知：当点P 在∵ABC 的顶点A 处，运动到点B 处时， 图1中的AC ＝BC ＝13， 当点P 运动到AB 中点时， 此时CP ∵AB ，根据图2点Q 为曲线部分的最低点， 得CP ＝12，所以根据勾股定理，得此时AP 5． 所以AB ＝2AP ＝10． 故选：C ． 【小结】本题考查了动点问题的函数图象，解决本题的关键是综合利用两个图形给出的条件．24．如图，在ABC 中，90C ∠=︒，D 是边BC 上一点，ADC 2B ∠=∠，5AD =，4AC =，则AB 的长为（ ）A ．B ．C ．6D ．8【答案】A 【分析】根据勾股定理求出CD ，根据三角形的外角的性质得到∵B ＝∵BAD ，求出BD ，计算即可． 【解析】∵∵C ＝90°，AC ＝4，AD ＝5， ∵CD ＝3，∵∵ADC ＝2∵B ，∵ADC ＝∵B +∵BAD ， ∵∵B ＝∵BAD ， ∵DB ＝AD ＝5， ∵BC ＝BD +CD ＝8，在Rt∵ABC 中，∵C ＝90°，AC ＝4，BC ＝8，∵AB ===故选：A ． 【小结】本题考查的是勾股定理、等腰三角形判定的应用，掌握如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2＝c 2是解题的关键．25．菱形CD AB 的边20AB =，面积为320，D 90∠BA <，∵O 与边AB 、D A 都相切，10AO =，则∵O 的半径长等于（ ）A ．5B ．6C ．D ．【答案】C 【分析】如图作DH∵AB 于H ，连接BD ，延长AO 交BD 于E ．利用菱形的面积公式求出DH ，再利用勾股定理求出AH ，BD ，由∵AOF∵∵DBH ，可得=OA OFBD BH，即可解决问题． 【解析】如图作DH∵AB 于H ，连接BD ，延长AO 交BD 于E ．∵菱形ABCD 的边AB=20，面积为320， ∵AB•DH=320， ∵DH=16，在Rt∵ADH 中，12=，∵HB=AB -AH=8，在Rt∵BDH 中，=设∵O 与AB 相切于F ，与AD 相切于J ，连接OF ，OJ ，则OF∵AB ，OJ∵AD ，OF=OJ ， ∵OA 平分∵DAB ， ∵AD=AB ， ∵AE∵BD ，∵∵OAF+∵ABE=90°，∵ABE+∵BDH=90°， ∵∵OAF=∵BDH ，∵∵AFO=∵DHB=90°， ∵∵AOF∵∵DBH ， ∵=OA OFBD BH，8OF=，∵OF= 故选：C ． 【小结】本题考查切线的性质、菱形的性质、勾股定理、相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．26．如图，在Rt ABC △中，90C ∠=︒，BD 平分,5cm,3cm ABC AB BC ∠==，则AD 的长等于（ ）A ．2.5cmB ．2cmC ．1.5cmD ．3cm【答案】A 【分析】如图（见解析），先根据角平分线的性质可得CD DE =，再根据直角三角形全等的判定定理与性质可得3cm BE BC ==，从而可得2cm AE =，然后利用勾股定理可得4cm AC =，最后在Rt ADE △中，利用勾股定理即可得． 【解析】如图，过点D 作DE AB ⊥于点E ，BD 平分ABC ∠，90C ∠=︒，DE AB ⊥， CD DE ∴=，在Rt BCD 和Rt BED 中，CD DEBD BD =⎧⎨=⎩，()Rt BCD Rt BED HL ∴≅，3cm BE BC ∴==， 5cm AB =，2cm AE AB BE ∴=-=，在Rt ABC 中，90,5cm,3cm C AB BC ∠=︒==，4cm AC ∴==，设cm AD x =，则(4)cm DE CD AC AD x ==-=-， 则在Rt ADE △中，222AE DE AD +=，即2222(4)x x +-=， 解得 2.5(cm)x =， 即 2.5cm AD =， 故选：A ． 【小结】本题考查了角平分线的性质、直角三角形全等的判定定理与性质、勾股定理等知识点，通过作辅助线，利用到角平分线的性质是解题关键．27．如图，∵ABCD 的对角线AC 与BD 相交于点O ，AB ∵AC ，若AB ＝4，AC ＝6，则BO 的长为（ ）A ．5B ．8C ．10D ．11【答案】A 【分析】根据平行四边形的性质可得AO ＝CO ＝12AC ＝3，再利用勾股定理可得BO 的长． 【解析】∵四边形ABCD 是平行四边形， ∵AO ＝CO ＝12AC ＝3， ∵AB ∵AC ，AB ＝4，∵BO 5， 故选：A ． 【小结】此题主要考查了平行四边形的性质和勾股定理，解题关键是掌握平行四边形的对角线互相平分．28．如图，在矩形ABCD 中，AB ＝5，AD ＝12，对角线BD 的垂直平分线分别与AD ，BC 边交于点E 、F ，则四边形BFDE 的面积为（ ）A．84524B．84512C．16912D．82513【答案】A【分析】根据矩形的性质和菱形的判定得出四边形BEDF是菱形，进而利用勾股定理和菱形的面积公式解答即可．【解析】∵四边形ABCD是矩形，∵AD∵BC，∵∵DEO＝∵BFO，∵EDO＝∵FBO，∵对角线BD的垂直平分线分别与AD，BC边交于点E、F，∵BO＝DO，EF∵BD，∵∵DEO∵∵BFO（AAS），∵EO＝FO，∵BO＝DO，∵四边形BEDF是平行四边形，∵EF∵BD，∵平行四边形BEDF是菱形，∵BE＝DE，∵AB＝5，AD＝12，∵A＝90°，∵BD＝13，设DE＝x，则AE＝12﹣x，在Rt∵AEB中，AB2+AE2＝BE2，即52+（12﹣x）2＝x2，∵x 16924=， ∵BE ＝DE 16924=，在Rt∵BEO 中，OE 6524===， ∵EF ＝2EO 6512=， ∵菱形BEDF 的面积116584513221224BD EF =⋅⋅=⨯⨯=， 故选：A ． 【小结】此题考查矩形的性质、菱形的性质和判定以及勾股定理，关键是根据矩形的性质和菱形的判定和性质解答． 29．如图，D 是ABC 内一点，BD CD ⊥，6AD =，4BD =，3CD =，E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点，则四边形EFGH 的周长是（ ）A ．7B ．9C ．10D ．11【答案】D 【分析】先根据勾股定理求出线段BC 的长度，再根据三角形中位线的性质定理求出 2.5EF HG ==，3EH GF ==，即可求出四边形的周长． 【解析】∵BD CD ⊥，4BD =，3CD =，由勾股定理得：5BC ==，∵E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点， ∵12HG BC EF ==，12EH FG AD ==，∵6AD =，∵ 2.5EF HG ==，3EH GF ==，∵四边形EFGH 的周长是()2 2.5311EF FG HG EH +++=⨯+=． 故选：D ． 【小结】此题考查勾股定理的应用，三角形中位线的性质定理，熟记定理并正确应用是解题的关键．30．如图，在∵ABC 中，∵ACB =90°，AC =3、BC =4、P 、Q 两点分别在AC 和AB 上．且CP =BQ =1，在平面上找一点M ．以A 、P 、Q 、M 为顶点画平行四边形，这个平行四边形的周长的最大值为（ ）A ．12B ．4C ．6+D ．8+【答案】D 【分析】先依据勾股定理以及相似三角形的性质，即可得到PQ 的长，再分三种情况，即可得到以A 、P 、Q 、M 为顶点的平行四边形的周长，进而得出周长的最大值． 【解析】由勾股定定理得：5AB =，则4AQ =； 过点Q 作QN AC ⊥，垂足为N ，则//QN BC ， 则::4AN NC AQ QB ==， 则125AN =， 122255PN ∴=-=， 由::NQ BC AQ AB =，得165NQ =，再由勾股定理得：PQ =如图1：周长2()4PA PQ =+= 如图2：周长2()12PA PM =+=；如图3：周长2()8AQ PQ =+=∵84>88>即814.412>>，故周长的最大值是8故选：D ． 【小结】本题主要考查了平行四边形的性质以及勾股定理的运用，关键是作辅助线构造直角三角形，利用勾股定理计算得到PQ 的长．31．如图，在Rt ABC ∆中，90,BAC BA CA ∠=︒==D 为BC 边的中点，点E 是CA 延长线上一点，把CDE ∆沿DE 翻折，点C 落在C '处，EC '与AB 交于点F ，连接BC '．当43FA EA =时，BC '的长为（ ）AB ．CD ．【答案】D 【分析】如图，连接CC ′，过点C ′作C ′H ∵EC 于H ．设AB 交DE 于N ，过点N 作NT ∵EF 于N ，过点D 作DM ∵EC 于M ．证明∵CC ′B =90°，求出CC ′，BC 即可解决问题． 【解析】如图，连接CC′，过点C′作C′H∵EC于H．设AB交DE于N，过点N作NT∵EF于N，过点D作DM∵EC 于M．∵∵F AE=∵CAB=90°，43 FAAE，∵EF：AF：AE=5：4：3，∵C′H∵AF，∵∵EAF∵∵EHC′，∵EC′：C′H：EH=EF：AF：AE=5：4：3，设EH=3k，C′H=4k，EC′=EC=5k，则CH=EC=EH=2k，由翻折可知，∵AEN=∵TEN，∵NA∵EA，NT∵ET，∵∵NAE=∵NTE，∵NE=NE，∵∵NEA∵∵NET（AAS），∵AN=NT，EA=ET，设AE=3m，AF=4m，EF=5m，AN=NT=x，则AE=ET=3m，TF=2m，在Rt∵FNT中，∵FN2=NT2+FT2，∵（4m-x）2=x2+（2m）2，解得x=32 m，∵AC=AB，∵CAB=90°，∵BC∵CD=BD∵DM∵CM，∵DCM=45°，∵CM=DM∵AN∵DM，∵AN EA DM EM=，∵31232mAN DMEA EM m===，∵EM，∵ECk，∵k=，∵CH C H'==，∵CC'===∵DC=DC′=DB，∵∵CC′B=90°，∵BC'===故选：D．【小结】本题考查翻折变换，解直角三角形，等腰直角三角形的性质，相似三角形的性质，全等三角形的性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程解决问题．32．如图，正方形ABCD的边长为a，点E在边AB上运动（不与点A，B重合），∵DAM＝45°，点F在射线AM上，且AFBE，CF与AD相交于点G，连接EC、EF、EG．则下列结论：∵∵ECF＝45°；∵∵AEG的周长为a；∵BE2+DG2＝EG2；∵∵EAF的面积的最大值是a2；∵当BE=a时，G是线段AD的中点．其中正确的结论是（）A．∵∵∵B．∵∵∵C．∵∵∵D．∵∵∵【答案】D【分析】∵正确：如图1中，在BC上截取BH=BE，连接EH．证明∵FAE∵∵EHC（SAS），即可解决问题；∵∵错误：如图2中，延长AD到H，使得DH=BE，则∵CBE∵∵CDH（SAS），再证明∵GCE∵∵GCH（SAS），即可解决问题；∵正确：设BE=x，则AE=a-x，，构建二次函数，利用二次函数的性质解决最值问题；∵正确：当BE=13a时，设DG＝x，则EG＝x13+a，利用勾股定理构建方程可得x2a=，即可解决问题．【解析】如图1中，在BC上截取BH＝BE，连接EH，∵BE＝BH，∵EBH＝90°，∵EH，∵AF=，∵AF＝EH，∵∵DAM＝∵EHB＝45°，∵BAD＝90°，∵∵FAE＝∵EHC＝135°，∵BA＝BC，BE＝BH，∵AE＝HC，∵∵FAE∵∵EHC（SAS），∵EF＝EC，∵AEF＝∵ECH，∵∵ECH+∵CEB＝90°，∵∵AEF+∵CEB＝90°，∵∵FEC＝90°，∵∵ECF＝∵EFC＝45°，故∵正确，如图2中，延长AD到H，使得DH＝BE，则∵CBE∵∵CDH（SAS），∵∵ECB＝∵DCH，∵∵ECH＝∵BCD＝90°，∵∵ECG＝∵GCH＝45°，∵CG＝CG，CE＝CH，∵∵GCE∵∵GCH（SAS），∵EG＝GH，∵GH＝DG+DH，DH＝BE，∵EG＝BE+DG，故∵错误，∵∵AEG的周长＝AE+EG+AG＝AE+AH＝AD+DH+AE＝AE+EB+AD＝AB+AD＝2a，故∵错误，设BE＝x，则AE＝a﹣x，AF=，∵S∵AEF=12•（a﹣x）×x=1-2x2+12ax=1-2（x2﹣ax14+a214-a2）=1-2（x1-2a）218+a2，∵12-<0，∵x=12a 时，∵AEF 的面积的最大值为218a ，故∵正确， 当BE=13a 时，设DG ＝x ，则EG ＝x 13+a ，在Rt∵AEG 中，则有（x 13+a ）2＝（a ﹣x ）2+（23a ）2，解得x 2a=， ∵AG ＝GD ，故∵正确， 综上，∵∵∵正确， 故选：D ． 【小结】本题考查正方形的性质，全等三角形的判定和性质，二次函数的应用等知识，熟练掌握并灵活运用是解题的关键．33．如图，在ABC 中，AC BC =，90ACB ∠=︒，AE 平分BAC ∠交BC 于E ，BD AE ⊥于D ，DM AC ⊥交AC 的延长线于M ，连接CD ，给出四个结论：∵45ADC ∠=︒；∵12BD AE =；∵AC BE AB +=；∵2AB BC MC -=；其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C 【分析】过E 作EQ ∵AB 于Q ，作∵ACN ＝∵BCD ，交AD 于N ，过D 作DH ∵AB 于H ，根据角平分线性质求出CE ＝EQ ，DM ＝DH ，根据勾股定理求出AC ＝AQ ，AM ＝AH ，根据等腰三角形的性质和判定求出BQ ＝QE ，进而可判断∵；根据三角形外角性质求出∵CND ＝45°，证∵ACN ∵∵BCD ，推出CD ＝CN ，进而可判断∵∵；证∵DCM ∵∵DBH ，得到CM ＝BH ，进一步变形即可判断∵，于是可得答案． 【解析】如图，过E 作EQ ∵AB 于Q ， ∵∵ACB ＝90°，AE 平分∵CAB ，∵CE＝EQ，∵∵ACB＝90°，AC＝BC，∵∵CBA＝∵CAB＝45°，∵EQ∵AB，∵∵EQA＝∵EQB＝90°，由勾股定理得：AC＝AQ，∵∵QEB＝45°＝∵CBA，∵EQ＝BQ，∵AB＝AQ+BQ＝AC+CE，∵BE＞EQ=CE，∵∵错误；作∵ACN＝∵BCD，交AD于N，∵∵CAD＝12∵CAB＝22.5°＝∵BAD，∵∵ABD＝90°﹣22.5°＝67.5°，∵∵DBC＝67.5°﹣45°＝22.5°＝∵CAD，∵∵DBC＝∵CAD，∵AC=BC，∵ACN＝∵BCD，∵∵ACN∵∵BCD（ASA），∵CN＝CD，AN＝BD，∵∵ACN+∵NCE＝90°，∵∵NCB+∵BCD＝90°，∵∵CND＝∵CDA＝45°，∵∵ACN＝45°﹣22.5°＝22.5°＝∵CAN，∵AN＝CN，∵∵NCE＝∵AEC＝67.5°，∵CN＝NE，∵DCB=90°－67.5°=22.5°，∵BD＝AN＝EN＝12AE，∵ADC=180°－∵DAC－∵ACD=180°－22.5°－112.5°=45°，∵∵正确，∵正确；过D作DH∵AB于H，∵∵MCD＝∵CAD+∵CDA＝67.5°，∵DBA＝67.5°，∵∵MCD＝∵DBA，∵AE平分∵CAB，DM∵AC，DH∵AB，∵DM＝DH，在∵DCM和∵DBH中90 M DHB MCD DBA DM DH ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩，∵∵DCM∵∵DBH，∵BH＝CM，由勾股定理得：AM＝AH，∵AC AB AC AH BH AC AM CMAM AM AM+++++==＝2AMAM＝2，∵AC+AB＝2AM，即AC+AB＝2AC+2CM，∵AB﹣AC＝2CM，∵AC＝CB，∵AB﹣CB＝2CM，∵∵正确．综上，正确的有3个．故选：C．【小结】本题主要考查了等腰直角三角形的判定和性质、三角形的外角性质、三角形的内角和定理、等腰三角形的性质和判定、全等三角形的性质和判定以及勾股定理等知识，正确添加辅助线、能综合运用所学知识进行推理是解此题的关键．34．如图，在Rt ABC △中，90,30,ACB ABC CD ︒∠︒=∠=平分ACB ∠．边AB 的垂直平分线DE 分别交,CD AB 于点,D E ．以下说法错误的是（ ）A ．60BAC ∠=︒B ．2CD BE =C ．DE AC =D 12BC AB =+【答案】B 【分析】利用直角三角形的性质、三角形内角和定理、勾股定理、全等三角形的判定与性质等知识对各选项的说法分别进行论证，即可得出结论． 【解析】如图，连接BD 、AD ，过点D 作DM∵BC 于M ，DN∵CA 的延长线于N ，A 、在Rt ABC △中，90ACB ∠=︒，30ABC ∠=︒， ∵60BAC ∠=︒．故此选项说法正确； B 、∵DM∵BC ，DN∵CA ∵∵DNC ＝∵DMC ＝90°， ∵CD 平分∵ACB ， ∵∵DCN ＝∵DCM ＝45°． ∵∵DCN ＝∵CDN ＝45°．∵CN=DN ．则∵CDN 是等腰直角三角形．同理可证：∵CDM 也是等腰直角三角形，．， ∵DM=DN= CM=CN ，∵MDN ＝90°． ∵DE 垂直平分AB ， ∵BD=AD ，AB=2BE ． ∵Rt∵BDM∵∵ADN ， ∵∵BDM=∵AND ．∵∵BDM+∵ADM =∵AND+∵ADM ＝∵MDN ． ∵∵ADB=90°．=．即．∵在Rt∵AND 中，AD 是斜边，DN 是直角边，∵AD ＞DN ． ∵2BE ＞CD ．故此选项说法错误． C 、∵BD=AD ，∵ADB=90°， ∵∵ABD 是等腰直角三角形． ∵DE=12AB ． 在Rt ABC △中，90ACB ∠=︒，30ABC ∠=︒， ∵AC=12AB ． ∵DE=AC ．故此选项说法正确． D 、∵Rt∵BDM∵∵ADN ， ∵BM=AN ．∵CN=AC+AN=AC+BM=CM ． ∵BC=BM+CM=AC+2BM ．，．∵AC=12 AB，12AB+BC．故此选项说法正确．故选：B．【小结】本题属于三角形综合题，考查了直角三角形的性质，全等三角形的判定与性质，勾股定理等知识，难度较大，准确作出辅助线并灵活运用所学知识是解题的关键．35．如图，在平面直角坐标系中，O为坐标原点，直线y x=-+x轴交于B点，与y轴交于A点，点C D，在线段AB上，且22CD AC BD==，若点P在坐标轴上，则满足7PC PD+=的点P的个数是（）A．4B．3C．2D．1【答案】A【分析】作点C关于y轴的对称点'C，根据直线y x=-+x轴交于B点，与y轴交于A点，求出A，B两点的坐标，然后利用勾股定理求得'C D=，即'PD PC C D<+，可判断点P在x轴上，使得7PC PD+=的点P的个数是两个；作点D关于x轴的对称点'D，同理可判断点P在y轴上，使得7PC PD+=的点P 的个数是两个，据此求解即可．【解析】如图示，作点C关于y轴的对称点'C，直线y x =-+x 轴交于B 点，与y 轴交于A 点，则当0x =时，y =A 点坐标是：（0，，当0y =时，x =B 点坐标是：（0），∵OA OB ==∵8AB ，∵22CD AC BD ==，AB CD AC BD =++ ∵4CD =，2==AC BD ，由勾股定理可得：CE AE ==DF AF ==∵OE =OF =∵C 点坐标是：，D 点坐标是：（ ，则'C 点坐标是：（，∵'CD <∵'7CD<， 即：'P D P C C D <+， ∵如下图示，点P 在y 轴上，使得7PC PD +=的点P 的个数是两个， 如图示，作点D 关于x 轴的对称点'D ，同理可以求得'CD = 即：'P D P C C D <+，∵点P 在y 轴上，使得7PC PD +=的点P 的个数是两个，综上所述，点P 在坐标轴上，满足7PC PD +=的点P 的个数是4个， 故选：A ．【小结】本题考查了一次函数的应用、轴对称的性质、勾股定理的应用，熟悉相关性质是解题的关键． 36．在∵ABC 中，∵BAC =90°，点D 在边BC 上，AD =AB ( )A ．若AC =2AB ，则∵C =30° B ．若AC =2AB ，则3BD =2CD C ．若∵B =2∵C ，则AC =2AB D ．若∵B =2∵C ，则S ∵ABD =2∵ACD 【答案】B 【分析】根据直角三角形30°角所对边是斜边的一半，可得BC =2AB ＞AC ，从而可判断选项A 、C ；作AE∵BC ，根据勾股定理和等面积法克求得BC 、BD 和DC ，从而得出BD 和CD 的关系，可判断选项B ； 可先得出AD 为中线，根据三角形中线平分三角形的面积可判断选项D ． 【解析】由题，∵BAC=90°，点D 在BC 边上，AD=AB ，A.若AC =2AB ，则BC ==，若∵C=30°，BC=2AB ，故A 错误；B. 若AC =2AB ，则BC ，作AE∵BC ，则1122ABCSAB AC BC AE =⋅=⋅，可得AB AC AE AB BC ⋅===， ∵AD=AB ，∵5BE DE AB ===，∵,55BD AB DC BC AB AB ==-=， ∵3BD =2CD ，故B 正确；C. 若∵B =2∵C ， ∵∵BAC=90°， ∵∵B+∵C=90°， ∵∵C=30°，∵B=60°，∵BC=2AB ，AC ＜2AB ，故C 错误；D. 若∵B =2∵C ，由选项C 可得∵C=30°，∵B=60°， ∵AD=AB ，∵∵ABD 为等边三角形， ∵∵ADB=60°，∵∵DAC=∵ADB -∵C=30°=∵C ，∵AD=DC=BD ，即AD 为∵ABC 的中线， ∵S ∵ABD =S ∵ACD ，故D 错误． 故选：B ． 【小结】本题考查等边三角形的性质和判定，勾股定理，含30°角的直角三角形．熟练掌握这些定理，能借助已知条件，选择合适的定理分析是解题关键．37．在Rt ∵ABC 中，∵C =90°，点P 在边AB 上．BC =6， AC =8， ( ) A ．若∵ACP=45°， 则CP=5 B ．若∵ACP=∵B ，则CP=5 C ．若∵ACP=45°，则CP=245 D ．若∵ACP=∵B ，则CP=245【答案】D【分析】四个选项，A、C选项CP为顶角的平分线，B、D选项CP为底边上的高线，根据直角三角形斜边上的中线可得斜边上的中线等于5，利用等面积法可得底边上的高线等于245，易得三角形不是等腰三角形，所以它斜边上的高线、中线和直角的角平分线不是同一条，可得正确的为D选项．【解析】∵∵C=90°，点P在边AB上．BC=6，AC=8，∵10AB==，当CP为AB的中线时，152CP AB==，若∵ACP=45°，如图1，则CP为直角∵ACB的平分线，∵BC≠AC，∵CP与中线、高线不重合，不等于5，故A选项错误；若∵ACP=∵B，如图2∵∵ACB=90°,∵∵A+∵B=90°，∵∵A+∵ACP =90°，∵∵APC=90°，即CP为AB的高线，∵BC≠AC，∵CP与中线不重合，不等于5，故B选项错误；当CP为AB的高线时，1122ABCS AC BC AB PC =⋅=⋅△,即11861022PC⨯⨯=⨯⋅，解得245PC=,故D选项正确，C选项错误．故选：D ． 【小结】本题考查直角三角形斜边上的中线，等腰三角形三线合一，勾股定理等．能根据等面积法算出斜边上的高线的长度是解题关键．38．如图，在等腰Rt ABC 中，90ACB ∠=︒，点P 是ABC 内一点，且1CP =，BP =2AP =，以CP 为直角边，点C 为直角顶点，作等腰Rt DCP ，下列结论：∵点A 与点D ∵AP PC ⊥；∵AB =∵2APBS=，其中正确结论有是（ ）A ．∵∵∵B ．∵∵C ．∵∵D ．∵∵∵【答案】C 【分析】连结AD ，由等腰Rt ABC ，可得AC=BC ，等腰Rt DCP ，可得CD=CP ，由余角性质可∵DCA=∵PCB ，可证∵ADC∵∵BPC （SAS ）AD BP ==∵，由勾股定理22222AD +DP =+=4=AP ，可证∵ADP 为等腰直角三角形，可判断∵，由PB 与PD 可求由勾股定理，可判断∵，由面积112122APBS PB AD ===可判断∵即可 【解析】 连结AD ，在等腰Rt ABC 中，90ACB ∠=︒， ∵AC=BC ，∵Rt DCP 是等腰三角形， ∵CD=CP ，∵∵ACD+ACP=90°，∵ACP+∵PCB=90°，。

专题01 三角形的基础（满分：100分时间：90分钟）班级_________ 姓名_________ 学号_________ 分数_________一、单选题(共12小题，每小题4分，共计48分)1．（2020·南山区期中）有下列长度的三条线段，其中能组成三角形的是( )A．3cm、6cm、10cm B．10cm、4cm、6cmC．3cm、1cm、1cm D．4cm、6cm、9cm【答案】D【详解】解：A、3+6＜10，不能组成三角形；B、4+6=10，不能组成三角形；C、1+1＜3，不能组成三角形；D、4+6＞9，9-6＜4，能组成三角形；故选D.2．（2020·汶川县期末）小颖用长度为奇数的三根木棒搭一个三角形，其中两根木棒的长度分别为7cm和3cm，则第三根木棒的长度是（）A．7cm B．8cm C．11cm D．13cm【答案】A【详解】解：设第三根木棒长为xcm,根据三角形的三边关系，得7-3<x<7+3，即4<x<10．又∵x为奇数，∴第三根木棒的长度可以为5cm，7cm，9cm．故选A．3．（2020·射阳县期中）如果三角形的两边长分别为5和7，第三边长为偶数，那么这个三角形的周长可以是（）A．10 B．11 C．16 D．26【答案】C【详解】设第三边为acm，根据三角形的三边关系知，2＜a＜12，由于第三边的长为偶数，则a 可以为4cm 或6cm 或8cm 或10cm ．∴三角形的周长是 5+7+4=16cm 或5+7+6=18cm 或5+7+8=20cm 或5+7+10=22cm ． 故选C ．4．（2020·铜仁市期末）在一次数学实践活动中，杨阳同学为了估计一池塘边,A B 两点间的距离，如下图，先在池塘边取一个可以直接到达A 点和B 点的点,C 连结,CA CB 、测得15,12CA m CB m ==，则,A B 间的距离不可能是（ ）A ．20mB ．24mC ．25mD ．28m【答案】D 【详解】 解：∵中，15,12CA m CB m ==∴15－12＜AB ＜15＋12 ∴3＜AB ＜27由各选项可知：只有D 选项不在此范围内 故选D ．5．（2019潍坊市期末）将一个三角形纸片剪开分成两个三角形，这两个三角形不可能是（ ） A ．都是锐角三角形 B ．都是直角三角形C ．都是钝角三角形D ．是一个直角三角形和一个钝角三角形【答案】A 【详解】如图，沿三角形一边上的高剪开即可得到两个直角三角形．如图，钝角三角形沿虚线剪开即可得到两个钝角三角形．如图，直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形．因为剪开的边上的两个角互补，故这两个三角形不可能都是锐角三角形．故选A．6．（2018·浦东新区期末）设M表示直角三角形，N表示等腰三角形，P表示等边三角形，Q表示等腰直角三角形．下列四个图中，能正确表示它们之间关系的是（）A．B．C．D．【答案】C【详解】解：根据各类三角形的概念可知，C可以表示它们彼此之间的包含关系．故选：C．7．（2020·长沙市期末）如图，ABCD中，对角线AC和BD交于点O，若AC=8，BD=6，则边AB长的取值范围是（）A．1＜AB＜7 B．2＜AB＜14 C．6＜AB＜8 D．3＜AB＜4【答案】A【详解】∵四边形ABCD是平行四边形，∴AO=12AC,BO=12BD，∵AC=8，BD=6，∴AO=4，BO=3，∴4−3<AB<4+3，解得：1<AB<7.故答案为：A8．（2020·周口市期末）下列说法：（1）一个等边三角形一定不是钝角三角形；（2）一个钝角三角形一定不是等腰三角形；（3）一个等腰三角形一定不是锐角三角形；（4）一个直角三角形一定不是等腰三角形．其中正确的有（）个A．1 B．2 C．3 D．4【答案】A【详解】解：（1）一个等边三角形一定不是钝角三角形，原命题是真命题；（2）一个钝角三角形不一定不是等腰三角形，原命题是假命题；（3）一个等腰三角形不一定不是锐角三角形，原命题是假命题；（4）一个直角三角形不一定不是等腰三角形，原命题是假命题；故选：A．9．（2020·南宁市期末）现有2cm，4 cm，5 cm，8 cm长的四根木棒，任选三根组成一个三角形，那么可以组成三角形的个数为（）A．1个B．2个C．3个D．4个【答案】B【解析】试题分析：其中的任意三条组合有2cm、4cm、5cm；2cm、4cm、8cm；4cm、5cm、8cm；2cm、5cm、8cm 共四种情况，根据三角形的三边关系，则2cm、4cm、5cm；4cm、5cm、8cm符合，故选B．10．（2019·大同市期中）如图，工人师傅做了一个长方形窗框ABCD，E，F，G，H分别是四条边上的中点，为了稳固，需要在窗框上钉一根木条，这根木条不应钉在( )A．G，H两点处B．A，C两点处C．E，G两点处D．B，F两点处【答案】C【详解】A选项：若钉在G、H两点处则构成了三角形，能固定窗框，故不符合题意；B选项：若钉在A、C两点处则构成了三角形，能固定窗框，故不符合题意；C选项：若钉在E、G两点处则构成了两个四边形，不能固定窗框，故符合题意；D选项：若钉在B、F两点处则构成了三角形，能固定窗框，故不符合题意；故选C.11．（2018·武昌区期中）下列图形中，不是运用三角形的稳定性的是（）A．房屋顶支撑架B．自行车三脚架C．拉闸门D．木门上钉一根木条【答案】C【详解】伸缩的拉闸门是利用了四边形的不稳定性，A、B、D都是利用了三角形的稳定性．故选C．12．（2020·赤峰市期末）下列图形中，不具有稳定性的是（）A．B．C．D．【答案】B【详解】A、可以看成两个三角形，而三角形具有稳定性，则这个图形一定具有稳定性，故本选项错误；B、可以看成一个三角形和一个四边形，而四边形不具有稳定性，则这个图形一定不具有稳定性，故本选项正确；C、可以看成三个三角形，而三角形具有稳定性，则这个图形一定具有稳定性，故本选项错误；D、可以看成6个三角形，而三角形具有稳定性，则这个图形一定具有稳定性，故本选项错误．故选：B．二、填空题(共5小题，每小题5分，共计20分)13．（2020·汶川县期末）若（a﹣4）2+|b﹣9|=0，则以a、b为边长的等腰三角形的周长为_______．【答案】22【详解】解：根据题意得，a -4=0，b -9=0， 解得a =4，b =9，① 若a =4是腰长，则底边为9，三角形的三边分别为4、4、9，不能组成三角形，② 若b =9是腰长，则底边为4，三角形的三边分别为9、9、4，能组成三角形， 周长=9+9+4=22． 14．（2020·菏泽市期末）三角形的两条边长分别是2cm ，8cm ，第三边为奇数，则其周长为________． 【答案】17cm 或19cm 【详解】解：8-2＜第三边＜8+2⇒6＜第三边＜10，这个范围的奇数是7和9，所以三角形的周长是2+8+7=17（cm ）或2+8+9=19（cm ） 故答案为：17cm 或19cm ．15．（2020·苏州市期末）等腰三角形的两边长分别是3和7，则其周长为 ． 【答案】17 【解析】试题分析：因为边为3和7，没明确是底边还是腰，所以有两种情况，需要分类讨论： 当3为底时，其它两边都为7，3、7、7可以构成三角形，周长为17； 当3为腰时，其它两边为3和7，3+3=6＜7，所以不能构成三角形，故舍去． ∴等腰三角形的周长为17．16．（2020·朝阳市期末）如果三条线段,,a b c 可组成三角形，且3a =，4b =，c 是奇数，则c =__________． 【答案】3或5 【详解】因为三条线段,,a b c 可组成三角形，且3a =，4b =， 所以b a c a b -<<+，即17c <<， 因为c 是奇数， 所以c =3或5， 故答案为：3或5．17．（2020·临沂市期末）如图所示，要使一个六边形木架在同一平面内不变形，至少还要再钉上 _____根木条．【答案】3 【详解】如图，过左上角的A 点分别钉三根木条AB 、AC 、AD 即可把六边形木架变成三个不重叠的三角形．故答案为3．三、解答题(共4小题，每小题8分，共计32分)18．（2018·邵阳市期末）小辉用7根木条钉成一个七边形的木架，他为了使该木架稳固，想在其中加上四根木条，请你在图1、2、3中画出你的三种想法，并说明加上木条后使该木架稳固所用的数学道理．【答案】答案见解析． 【解析】试题分析：根据三角形具有稳定性进行画图即可． 解：如图所示：19．（2020·钦州市期末）已知a ，b ，c 分别为△ABC 的三条边，且满足23a b c +=-，26a b c -=-，a b >． （1）求c 的取值范围．（2）若ABC ∆的周长为12，求c 的值． 【答案】（1）36c <<；（2）5c =． 【详解】解：（1）∵a ，b ，c 分别为ABC ∆的三条边，且23a b c +=-，26a b c -=-，∴23,26,c c c c ->⎧⎨-<⎩解得36c <<． 故答案为：36c <<．（2）∵ABC ∆的周长为12，23a b c +=-， ∴3312a b c c ++=-=， 解得5c =． 故答案为：5c =．20．（2020·赤峰市期末）平面内有四个点A ，B,C ，D ，用它们作顶点可以组成几个三角形？画出图形，并写出存在的三角形．（只写含已知字母的）【答案】详见解析，分别是：△ABC ，△ACD ，△ABD ； 【详解】答：按点共线分类，可分为三种情形：（1）四点共线． 四个点A 、B 、C 、D 在同一条直线上，不能组成三角形；（2）三点共线． 四个点A 、B 、C 、D 中有且仅有三个点（例如B 、C 、D ）在同一条直线上，如图1所示，可组成三个三角形,分别是：△ABC ，△ACD ，△ABD ；（3）任意三点不共线． 四个点A 、B 、C 、D 中任何三个点都不在同一条直线上，如图2所示，可组成四个三角形，分别是：△ABC ，△ABD ，△ACD ，△BCD ．21．（2020·十堰市期中）已知a 、b 、c 是三角形三边长，试化简：|b +c ﹣a |+|b ﹣c ﹣a |+|c ﹣a ﹣b |﹣|a ﹣b +c |． 【答案】2b新人教部编版初中数学“活力课堂”精编试题【详解】∵b+c-a>0, b-c-a<0. c-a-b<0, a-b+c>0，∴|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|=(b+c-a)-(b-c-a)-(c-a-b)-(a-b+c)=(b+c-a-b+c+a-c+a+b-a+b-c=2b。