方法第一章计算方法概论(2009-2010学年)
- 格式:pdf
- 大小:501.12 KB
- 文档页数:74



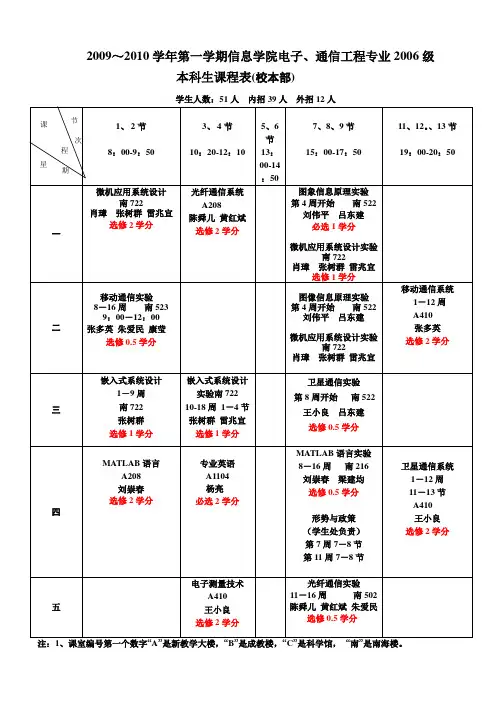
2009~2010学年第一学期信息学院电子、通信工程专业2006级
本科生课程表(校本部)
学生人数:51人内招39人外招12人
2、06级毕业实习一周(1学分),具体时间、地点由系通知,指导教师:杨恢东等现代电子教研室教师
2009~2010学年第一学期信息学院电子、通信工程专业2007级
本科生课程表(校本部)
学生人数:74人内招63人外招11人
注:课室编号第一个数字“A”是新教学大楼,“B”是成教楼,“C”是科学馆,“南”是南海楼。
2009~2010学年第一学期信息学院电子技术与科学专业2007级
本科生课程表(校本部)
学生人数:20人内招20人
2009~2010学年第一学期信息学院电子、通信工程专业2008级
本科生课程表(校本部)
2009~2010学年第一学期信息学院电子技术与科学专业2008级
本科生课程表(校本部)
注:2009级本科生从第二周周三(9月16日)开始上课。
2009~2010学年第一学期信息学院电子、通信、电科专业2009级本科生课程表 (珠海校区) 2009年7月20日第二版
预计学生人数:108人内招93人外招15人。

教材聂玉峰,王振海计算方法,西北工业大学版社,2009作业计算方法作业集(A、B)参考书¾封建湖,车刚明计算方法典型题分析解集(第三版)西北工业大学出版社,2001¾封建湖,聂玉峰,王振海数值分析导教导学导考(第二版)西北工业大学出版社,2006¾车刚明,聂玉峰,封建湖,欧阳洁数值分析典型题解析及自测试题(第二版)西北工业大学出版社,2003西北工业大学理学院欧阳洁2第一章绪论§1 引言§2 误差的度量与传播§3 选用算法时应遵循的原则西北工业大学理学院欧阳洁3§1 引言科学与工程领域中运用计算机求解问题的一般过程:1 实际问题的提出2 建立数学模型3 设计可靠、高效的数值方法4 程序设计5 上机实践计算结果6 数据处理及结果分析西北工业大学理学院欧阳洁4学习算法的意义科学计算(数值模拟)已经被公认为与理论分析、实验分析并列的科学研究三大基本手段之一。
计算方法课程的研究对象具有广泛的适用性,著名流行软件如Maple、Matlab、Mathematica 等已将其绝大多数内容设计成函数,简单调用之后便可以得到运行结果。
但由于实际问题的具体特征、复杂性, 以及算法自身的适用范围决定了应用中必须选择、设计适合于自己特定问题的算法,因而掌握数值方法的思想和内容至关重要。
西北工业大学理学院欧阳洁5计算方法的任务数学模型可算化(1)用有限维空间代替无限维空间(2)用有限过程代替无限过程(3)用简单问题替代复杂问题研究算法的可靠性收敛性、稳定性、误差估计研究算法的复杂度时间复杂度、空间复杂度、逻辑复杂度西北工业大学理学院欧阳洁6鉴于实际问题的复杂性,通常将其具体地分解为一系列子问题进行研究,本课程主要涉及如下几个方面问题的求解算法:¾非线性方程求根¾线性代数方程组求解¾函数插值¾曲线拟合¾数值积分与数值微分¾常微分方程初值问题的数值解法¾矩阵特征值与特征向量计算西北工业大学理学院欧阳洁7§2 误差的度量与传播一误差的来源与分类二绝对误差、相对误差、有效数字三误差的传播西北工业大学理学院欧阳洁8一误差的来源与分类模型误差:数学模型与实际问题的误差观测误差:观测结果与实际问题的误差截断误差:数学模型的理论解与数值计算问题的精确解之间的误差舍入误差:对超过某有限位数的数据进行舍入所产生的误差西北工业大学理学院欧阳洁9二绝对误差、相对误差、有效数字1.绝对误差与绝对误差限2. 相对误差与相对误差限3. 有效数字与有效数西北工业大学理学院欧阳洁11三误差的传播近似数参加运算后所得之值一般也是近似值,含有误差,将这一现象称为误差传播。



第一章绪论1.1 "数值分析"研究对象与特点"数值分析"是计算数学的一个主要部分.而计算数学是数学科学的一个分支,它研究用计算机求解数学问题的数值计算方法及其软件实现.计算数学几乎与数学科学的一切分支有联系,它利用数学领域的成果发展了新的更有效的算法及其理论,反过来很多数学分支都需要探讨和研究适用于计算机的数值方法.因此,"数值分析"内容十分广泛.但本书作为"数值分析"基础,只介绍科学与工程计算中最常用的基本数值方法,包括线性方程组与非线性方程求根、插值与最小二乘拟合、数值积分与常微分方程数值解法等.这些都是计算数学中最基础的内容.近几十年来由于计算机的发展及其在各技术科学领域的应用推广与深化,新的计算性学科分支纷纷兴起,如计算力学、计算物理、计算化学、计算经济学等等,不论其背景与含义如何,要用计算机进行科学计算都必须建立相应的数学模型,并研究其适合于计算机编程的计算方法.因此,计算数学是各种计算性科学的联系纽带和共性基础,是一门兼有基础性、应用性和边缘性的数学学科.计算数学作为数学科学的一个分支,当然具有数学科学的抽象性与严密科学性的特点,但它又具有广泛的应用性和边缘性特点.现代科学发展依赖于理论研究、科学实验与科学计算三种主要手段,它们相辅相成,互相独立,可以互相补充又都不可缺少,作为三种科学研究手段之一的科学计算是一门工具性、方法性、边缘性的新学科,发展迅速,它的物质基础是计算机(包括其软硬件系统),其理论基础主要是计算数学.计算数学与计算工具发展密切相关,在计算机出现以前,数值计算方法只能计算规模小的问题,并且也没形成单独的学科,只有在计算机出现以后,数值计算才得以迅速发展并成为数学科学中一个独立学科--计算数学.当代计算能力的大幅度提高既来自计算机的进步,也来自计算方法的进步,计算机与计算方法的发展是相辅相成、互相促进的.计算方法的发展启发了新的计算机体系结构,而计算机的更新换代也对计算方法提出了新的标准和要求.例如为在计算机上求解大规模的计算问题、提高计算效率,诞生并发展了并行计算机.自计算机诞生以来,经典的计算方法业已经历了一个重新评价、筛选、改造和创新的过程,与此同时,涌现了许多新概念、新课题和能充分发挥计算机潜力、有更大解题能力的新方法,这就构成了现代意义下的计算数学.这也是数值分析的研究对象与特点.概括地说,数值分析是研究适合于在计算机上使用的实际可行、理论可靠、计算复杂性好的数值计算方法.具体说就是:第一,面向计算机,要根据计算机特点提供实际可行的算法,即算法只能由计算机可执行的加减乘除四则运算和各种逻辑运算组成.第二,要有可靠的理论分析,数值分析中的算法理论主要是连续系统的离散化及离散型方程数值求解.有关基本概念包括误差、稳定性、收敛性、计算量、存储量等,这些概念是刻画计算方法的可靠性、准确性、效率以及使用的方便性.第三,要有良好的复杂性及数值试验,计算复杂性是算法好坏的标志,它包括时间复杂性(指计算时间多少)和空间复杂性(指占用存储单元多少).对很多数值问题使用不同算法,其计算复杂性将会大不一样,例如对20阶的线性方程组若用代数中的Cramer法则作为算法求解,其乘除法运算次数需要,若用每秒运算1亿次的计算机计算也要30万年,这是无法实现的,而用"数值分析"中介绍的Gauss消去法求解,其乘除法运算次数只需3 060次,这说明选择算法的重要性.当然有很多数值方法不可能事先知道其计算量,故对所有数值方法除理论分析外,还必须通过数值试验检验其计算复杂性.本课程虽然只着重介绍数值方法及其理论,一般不涉及具体的算法设计及编程技巧,但作为基本要求仍希望读者能适当做一些计算机上的数值试验,它对加深算法的理解是很有好处的.讲解:(1)计算数学是研究用计算机求解数学问题的数值计算方法及其软件实现,"数值分析"是计算数学的主要部分。

计算方法概论嘿,朋友们!今天咱就来唠唠计算方法这档子事儿。
你说计算方法,那可真是无处不在啊!就好比咱每天吃饭用筷子,这筷子就是一种工具,能帮咱把饭菜夹到嘴里。
那计算方法呢,就是咱解决各种问题的工具呀!想象一下,你面前有一堆数字,乱七八糟的,就像一团乱麻。
这时候计算方法就闪亮登场啦!它就像一把神奇的梳子,能把这团乱麻给理顺咯。
比如说简单的加减乘除,这是最基础的计算方法吧。
可别小瞧它们,没有它们,咱买东西咋算账呀?去菜市场跟大妈砍价都没底气呢!再比如解方程,那可真是个技术活。
有时候那些方程就像一个个小怪兽,张牙舞爪地等着咱去打败它们。
咱就得用合适的计算方法,一步步地把它们给制服喽。
还有那些高级点儿的计算方法,像什么微积分啦、线性代数啦。
哎呀,听着就觉得高大上吧?这些计算方法就像是武林高手的绝招,能解决那些特别难搞的问题。
你想想,要是遇到个超级复杂的工程问题或者科学难题,没有这些厉害的计算方法,那不就抓瞎啦?计算方法就像一把钥匙,能打开各种知识的大门。
学物理得用计算方法吧?研究经济也得靠它吧?就连咱平时玩个游戏,算个得分啥的,不也得用计算方法嘛!而且啊,计算方法还在不断发展呢!就跟咱人一样,得不断学习进步呀。
新的计算方法不断涌现,让我们解决问题的能力越来越强。
咱再说说那些数学家们,他们可真是计算方法的大师啊!他们绞尽脑汁,想出各种新奇的计算方法,为我们的生活带来了多大的便利呀!咱得感谢他们不是?总之,计算方法可太重要啦!它就像我们生活中的好朋友,默默地帮着我们解决各种难题。
我们可得好好学它,掌握它,让它为我们的生活增添更多的精彩!别等遇到问题了才后悔当初没好好学计算方法呀,那可就晚咯!所以呀,从现在开始,就跟计算方法好好打交道吧,让它成为我们的得力助手!你们说是不是这个理儿?。

计算方法主讲:廖福成计算方法主要参考书:1.张晓丹等, 《应用计算方法教程》 ,机械 工业出版社,2008。
2.杨大地,王开荣, 《数值分析》 ,科学出 版社,2006。
3.关治,陆金甫, 《数值分析基础》 ,高等 教育出版社,1998。
4.关治,陆金甫, 《数值方法》 ,清华大学 出版社,2006。
5.吴勃英, 《数值分析》 高等教育出版社, , 2007。
6.李庆扬,王能超,易大义, 《数值分析》 , 华中科技大学出版社,2006,第四版。
计算方法第一章计算方法概论计算方法又称数值分析, 是计算数学的一个重要组成部 分, 它主要研究来自科学和工程中的数学问题的算法设计与 相关理论.本章首先介绍计算方法的意义、 任务, 其次介绍计算数 学的一些基本概念, 包括算法与效率、 计算机中数的浮点运 算,误差、问题的性态以及算法的数值稳定性等.上述概念 将贯穿到本教程的全部内容中.计算方法1.11.1.1引言计算方法的意义计算机的发展极大地扩展了数学的应用范围与能力,使得科 学计算平行于理论分析和科学实验成为人类探索未知领域,研究 现代科学技术的第三种手段.对于理论或实验方法难于完成的研 究,计算机模拟可以大大增强对所研究问题的认识. 科学计算的成败不仅与计算工具的先进性有关,而且与所用 计算方法的效能密切相关,计算方法对于计算速度的提高与增强 计算结果的准确性来说,与计算机硬件同等重要.这就导致了计 算方法研究领域的空前活跃,并形成了一门以原来分散在数学各 分支的计算方法为基础的新的数学分支—计算数学. 一系列与计算 数学相关的边缘学科,如计算力学、计算物理、计算电磁学、计 算化学、计算生物、计算地质与计算经济学等,也都相继出现了.计算方法1.1.2 数值计算方法研究的对象与特点数值计算方法:研究适合计算机进行科学计算的方法。
使用计算机、离散。
用计算机解决科学技术和工程问题的步骤:实际问题建立数学模型算法设计程序设计上机计算求得结果其中算法设计是本课程的主要内容。
计算方法主讲:廖福成计算方法主要参考书:1.张晓丹等, 《应用计算方法教程》 ,机械 工业出版社,2008。
2.杨大地,王开荣, 《数值分析》 ,科学出 版社,2006。
3.关治,陆金甫, 《数值分析基础》 ,高等 教育出版社,1998。
4.关治,陆金甫, 《数值方法》 ,清华大学 出版社,2006。
5.吴勃英, 《数值分析》 高等教育出版社, , 2007。
6.李庆扬,王能超,易大义, 《数值分析》 , 华中科技大学出版社,2006,第四版。
计算方法第一章计算方法概论计算方法又称数值分析, 是计算数学的一个重要组成部 分, 它主要研究来自科学和工程中的数学问题的算法设计与 相关理论.本章首先介绍计算方法的意义、 任务, 其次介绍计算数 学的一些基本概念, 包括算法与效率、 计算机中数的浮点运 算,误差、问题的性态以及算法的数值稳定性等.上述概念 将贯穿到本教程的全部内容中.计算方法1.11.1.1引言计算方法的意义计算机的发展极大地扩展了数学的应用范围与能力,使得科 学计算平行于理论分析和科学实验成为人类探索未知领域,研究 现代科学技术的第三种手段.对于理论或实验方法难于完成的研 究,计算机模拟可以大大增强对所研究问题的认识. 科学计算的成败不仅与计算工具的先进性有关,而且与所用 计算方法的效能密切相关,计算方法对于计算速度的提高与增强 计算结果的准确性来说,与计算机硬件同等重要.这就导致了计 算方法研究领域的空前活跃,并形成了一门以原来分散在数学各 分支的计算方法为基础的新的数学分支—计算数学. 一系列与计算 数学相关的边缘学科,如计算力学、计算物理、计算电磁学、计 算化学、计算生物、计算地质与计算经济学等,也都相继出现了.计算方法1.1.2 数值计算方法研究的对象与特点数值计算方法:研究适合计算机进行科学计算的方法。
使用计算机、离散。
用计算机解决科学技术和工程问题的步骤:实际问题建立数学模型算法设计程序设计上机计算求得结果其中算法设计是本课程的主要内容。
计算方法又称数值 分析,它研究用计算机解决数学问题的数值算法及其结 论。
计算方法1.2算法与效率1.2.1 算 法解决某类数学问题的数值方法称为数值算法,它是 求解数学问题的过程的完整准确的描述。
为了使算法能 够在计算机上实现,必须将一个数学问题分解成为有限 次的四则运算。
计算方法算法常具有的基本特征:1、算法常表现为一个无穷过程的截断例1解计算 ln1.7 .ln x 在 x0 = 1 的幂级数展开为( −1)k + 1 ln x = ∑ ( x − 1)k , 0 < x ≤ 2 , k k =1∞从而( −1)k +1 ln1.7 = ∑ (0.7)k . k k =1∞计算方法这是一个无穷级数, 为计算它, 我们必须在适当的地方 “截断” ,使计算量不太大,精度又能满足要求。
( −1)k +1 令 Pn ( x ) = ∑ 我们希望对误差限 Tol 确 ( x − 1)k , k k =1n定 n ,使近似值 Pn (1.7 ) 满足ln 1.7 − Pn (1.7 ) < Tol .计算方法∞ ( −1)k +1 k 由级数理论,交错级数 ∑ (0.7 ) = ∑ ak 的余项满足 k k =1 k =1 ∞ln 1.7 − Pn (1.7 ) < an +1 ,当 an +1 < Tol 时,有 ln 1.7 − Pn (1.7 ) < Tol .基于上述讨论,给出如下算法计算方法%算法 x=0.7; tol=10^(-5); n=1; p=x; s=0; term=p; t=-1; while abs(term)>=tol n=n+1; t=-t; s=s+t*term; p=p*x; term=p/n; end disp(s); disp(n);计算方法% input 自变量 1.7, % 误差限 Tol = 10 ; % t 用来定义符号。
% abs( x ) 表示 x 的绝对值。
−5应用此算法求得: n =24, s= 0.530633026589034. (ln(1.7)=0.530628…) 用简化问题的解作为原来问题的近似解, 或构造迭代法 逼近问题的解, 涉及到方法的收敛性问题. 因此构造和分析 此类算法,必须讨论它的收敛性和误差估计.计算方法2、算法常表现为一个连续过程的离散化1 例 2. 计算积分 I = ∫ dx 0 1+ x1解、把区间 [0,1] 分成 4 等分,分别计算 4 个小曲边梯形的1 面 积 , 加 起 来 作 为 积 分 的 近 似 值 。
记 f ( x) = ,取 1+ x f ( xi ) + f ( x i + 1 ) 1 h h = , xi = ih, i = 0,1, 2, 3, 4 , Ti = 2 4则3 1 I=∫ dx ≈ ∑ Ti = 0.697024 0 1+ x i =0 1而精确值为 0.693147 ,可见精度不高。
如进一步划分区间,可 提高精度。
计算方法%a=0,b=1 a=0;b=1; n=input('输入区间等分数 n (n>0'); h=(b-a)/n; T=0; for i=0:n-1 T=T+(Hanshu_f(a+i*h)+Hanshu_f(a+(i+1)*h))*h/2; end disp(T);%函数 Hanshu_f.mfunction f=f(x); f=1/(1+x)计算方法3、算法常表现为“迭代”的形式“迭代”是指一简单算法的多次重复,后一次使用 前一次的结果。
这在程序中表现为“循环” ,易于编写 计算机程序。
例 3 计算多项式p( x ) = a n x + a n − 1 xnn −1++ a1 x + a0的值.计算方法解:用 t k 表示 x , uk 表示 ak x +k k+ a1 x + a0 ,作为初始值,令⎧ t0 = 1 ⎨ ⎩ u0 = a0对 k = 1, 2,, n ,反复执行 ⎧ t k = xt k −1 ⎨ ⎩ uk = uk −1 + ak t k (*)易见p( x ) = un式(*)是一个简单算法的多次循环。
计算方法p( x ) = a n x n + a n − 1 x n − 1 ++ a1 x + a0此算法程序 % inputx, n, a(1), a( 2), ,n +1, a( n + 1), 这里a(i ) = ai −1 , i = 1,% output u=p(x)t = 1; u = a(1) for i = 1 : n t = x * t; end u = u + a(i + 1)* t;计算方法此问题还有一种更好的迭代算法p( x ) = a n x n + a n − 1 x n − 1 + = ( an x n −1 + an −1 x n − 2 ++ a1 x + a0 + a1 ) x + a0 a2 ) x + a1 ) x + a0 + a1 ) x + a0= ((an x n − 2 + an −1 x n− 3 + = ( ( an x + an −1 ) x +令v0 = an ⎧ ⎨ ⎩ vk = xvk −1 + an− k于是 p( x ) = vn 。
后一算法计算量小。
计算方法(**)此算法程序 % input x, n, a(1), a( 2), 这里 a(i ) = ai −1 , i = 1,, a( n + 1), ,n +1%. output v(1)=p(x) 1. v(n+1)= a(n+1); 2. for k=n:-1:1 v(k)= x*v(k+1)+a(k); end计算方法例如,计算 p( x ) = 6 x + 90.6 x + 7.8 x + 2.5 x + 4 , x = 2.344 3 2n=4; a(1)=4;a(2)=2.5;a(3)=7.8; a(4)=90.6;a(5)=6;x=2.34; %. output v=p(x) v= a(n+1); for k=n:-1:1 v= x*v+a(k); end v计算方法例 4 不用开方计算 a (a > 0) 的值。
解:在高等数学里已学过,数列xk +11 a = ( xk + ), k = 0,1, 2, 2 xk收敛,且极限为 a 。
我们利用此式计算。
设 x0 是 a 的一个近似值, x0 > 0 ,则a 也是 a 的一个近 x0似值,且 x0 与a 中必有一个大于 a ,一个小于 a ,可以设想它 x0们的平均值应是 a 的一个更好的近似值。
于是有了以上算法。
计算方法例如计算 3 ,取 x0 = 2 ,有xk +1 =计算有1 3 ( xk + ), k = 0,1, 2, xk 2 x0 = 2 x1 = 1.75 x2 = 1.7321429 x3 = 1.7320508a=3;x=2; n=5; for k=1:n k, x=1/2*(x+a/x) end可见此算法收敛速度极快,只算三次就得到 8 位有效数字。
迭代法应用时要考虑是否收敛,收敛条件和收敛速度等。
计算方法1.2.2 算法的效率同一个数学问题可能有多种数值算法,我们要做出选 择.评价一个算法的好坏主要有两条标准:算法的计算效率 和计算结果的精度.我们自然应该选择计算效率高又能满足 精度要求的算法.算法的计算效率是由它的计算工作量体现 的.一般地,将计算机完成一次浮点加(减)法或乘(除) 法 运 算 称 为 一 次 浮 点 运 算 , 记 作 flop ( floating point operation).我们将一个算法所需四则浮点运算的总次数定义 为它的计算量,单位是 flop. 由于计算机做加减法比做乘除 法快得多,故在统计计算量时,可忽略算法所含加减法的运 算次数,将算法的计算量简化为该算法所需乘法和除法运算 的总次数.通常,算法的计算量越小,它的计算效率就越高.计算方法例 5 再次讨论多项式p( x ) = a n x n + a n − 1 x n − 1 +的计算问题.+ a1 x + a0⎧ t0 = 1 解:算法 1 ⎨ ⎩ u0 = a0 ⎧ t k = xt k −1 , ⎨ ⎩ uk = uk −1 + ak t k k = 1, 2, ,n (*)p( x ) = un计算量为 N=2nflop。
计算方法算法 2p( x ) = a n x n + a n − 1 x n − 1 + = ( an x n −1 + an−1 x n − 2 ++ a1 x + a0 + a1 ) x + a0 a2 ) x + a1 ) x + a0 + a1 ) x + a0= ((an x n− 2 + an−1 x n− 3 + = ( ( a n x + a n −1 ) x +令v 0 = an ⎧ ⎨ ⎩ vk = xv k −1 + an− k于是 p( x ) = vn 。