第10讲 正弦函数、余弦函数的性质(二)

1.4.2 正弦函数、余弦函数的性质（二）学习目标：1．借助图象理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等)．(重点) 2．能利用性质解决一些简单问题．(重点、难点)课前自主预习：一、教材梳理正、余弦函数的图象与性质________y＝cos x二、效果自测：(1)函数y ＝－12sin x ，x ∈⎣⎡⎦⎤0，π2的值域是_____________． (2)函数y ＝2＋2cos x 的单调递增区间是_______________．三、疑难点拨：1．解读正弦、余弦函数的单调性(1)理解正弦函数、余弦函数的单调性，通常作函数y ＝sin x ，x ∈⎣⎡⎦⎤－π2，3π2，y ＝cos x ，x ∈[－π，π]的简图． (2)单调区间要在定义域内求解．(3)求解或判断正弦函数、余弦函数的单调区间(或单调性)是求与之相关的复合函数值域(最值)关键的一步．(4)确定含有正弦函数或余弦函数的较复杂函数的单调性时，要注意使用复杂函数的判断方法来判断． 2．解析正弦函数、余弦函数的最值(1)明确正弦、余弦函数的有界性，即|sin x|≤1，|cos x|≤1.(2)对有些函数，其最值不一定就是1或－1，要依赖函数的定义域来决定． (3)形如y ＝Asin(ωx ＋φ)(A ＞0，ω＞0)的函数求最值时，通常利用“整体代换”，即令ωx ＋φ＝z ，将函数转化为y ＝Asin z 的形式求最值．课堂互动探究题型一：求三角函数的单调区间例1、求函数y ＝2sin ⎝⎛⎭⎫π4－x 的单调增区间．规律总结：求与正、余弦函数有关的单调区间的策略 (1)结合正、余弦函数的图象，熟记它们的单调区间；(2)形如y ＝Asin(ωx ＋φ)(A ＞0，ω＞0)的函数求单调区间时，应采用“换元法”整体代换，将“ωx ＋φ”看作一个整体“z”，即通过求y ＝Asin z 的单调区间而求出原函数的单调区间．求形如y ＝Acos(ωx ＋φ)(A ＞0，ω＞0)的函数的单调区间，方法同上．【互动探究】求函数y ＝2cos ⎝⎛⎭⎫π4－x 的单调增区间．题型二：比较三角函数值的大小问题例2、比较下列各组数的大小：(1)cos ⎝⎛⎭⎫－235π与cos ⎝⎛⎭⎫－174π； (2)sin 194°与cos 160°； (3)sin 1，sin 2，sin 3.规律总结：比较三角函数值大小的方法(1)通常利用诱导公式化为锐角三角函数值；(2)不同名的函数化为同名函数； (3)自变量不在同一单调区间化至同一单调区间． 活学活用：1．比较下列各组数的大小：)1(sin(－320°)与sin 700°； (2)cos 17π8与cos 379π. 题型三：正、余弦函数的值域与最值问题例3、求下列函数的最大值和最小值．(1)y ＝3＋2cos ⎝⎛⎭⎫2x ＋π3； (2)y ＝2sin ⎝⎛⎭⎫2x ＋π3⎝⎛⎭⎫－π6≤x ≤π6.规律总结：求正、余弦函数最值问题的关注点(1)形如y ＝asin x(或y ＝acos x)的函数的最值要注意对a 的讨论． (2)将函数式转化为y ＝Asin(ωx ＋φ)或y ＝Acos(ωx ＋φ)的形式． (3)换元后配方利用二次函数求最值． 活学活用2．求下列函数的最值：(1)y ＝3sin x －1sin x ＋2； (2)y ＝3－4cos ⎝⎛⎭⎫2x ＋π3，x ∈⎣⎡⎦⎤－π3，π6. 易错误区系列(六) 用换元法求三角函数最值中的常见错误典例：函数y ＝cos2 x －4cos x ＋5的值域是________．【即时演练】求函数y ＝1－2cos2 x ＋5sin x 的最大值和最小值．学业达标测试：1．函数y ＝－cos x 在区间⎣⎡⎦⎤－π2，π2上是( )A ．增函数B ．减函数C ．先减后增函数D ．先增后减函数 2．已知函数y ＝3cos(π－x )，则当x ＝____________时，函数取得最大值． 3．函数y ＝cos ⎝⎛⎭⎫x －π3的单调减区间是___________________________________．4．cos 1，cos 2，cos 3的大小关系是______________________________________ 5．求使下列函数取得最大值、最小值的自变量x 的集合，并分别写出最大值、最小值：(1)y ＝3－2sin x ； (2)y ＝cos x3.作业：1、设函数f (x )＝a cos x ＋b 的最大值是1，最小值是－3，试确定g (x )＝b sin ⎝⎛⎭⎫ax ＋π3的最大值．2、已知ω是正数，函数f (x )＝2sin ωx 在区间⎣⎡⎦⎤－π3，π4上是增函数，求ω的取值范围．。

1．4.2正弦函数、余弦函数的性质(二)学习目标1.掌握y＝sin x，y＝cos x的最大值与最小值，并会求简单三角函数的值域和最值.2.掌握y＝sin x，y＝cos x的单调性，并能利用单调性比较大小.3.会求函数y＝A sin(ωx＋φ)及y＝A cos(ωx＋φ)的单调区间．知识点一、正弦、余弦函数的定义域、值域观察下图中的正弦曲线和余弦曲线．正弦曲线：余弦曲线：可得如下性质：由正弦、余弦曲线很容易看出正弦函数、余弦函数的定义域都是实数集R ，值域都是[－1,1]． 对于正弦函数y ＝sin x ，x ∈R ，有：当且仅当x ＝π2＋2k π，k ∈Z 时，取得最大值1；当且仅当x ＝－π2＋2k π，k ∈Z 时，取得最小值－1.对于余弦函数y ＝cos x ，x ∈R ，有： 当且仅当x ＝2k π，k ∈Z 时，取得最大值1； 当且仅当x ＝(2k ＋1)π，k ∈Z 时，取得最小值－1. 知识点二、正弦、余弦函数的单调性当x ∈⎣⎡⎦⎤－π2，π2时，曲线逐渐上升，是增函数，sin x 的值由－1增大到1；当x ∈⎣⎡⎦⎤π2，3π2时，曲线逐渐下降，是减函数，sin x 的值由1减小到－1. 推广到整个定义域可得当x ∈⎣⎡⎦⎤－π2＋2k π，π2＋2k π(k ∈Z )时，正弦函数y ＝sin x 是增函数，函数值由－1增大到1； 当x ∈⎣⎡⎦⎤π2＋2k π，3π2＋2k π(k ∈Z )时，正弦函数y ＝sin x 是减函数，函数值由1减小到－1. 观察余弦函数y ＝cos x ，x ∈[－π，π]的图象．观察图象可知：当x ∈[－π，0]时，曲线逐渐上升，函数是增函数，cos x 的值由－1增大到1； 当x ∈[0，π]时，曲线逐渐下降，函数是减函数，cos x 的值由1减小到－1. 推广到整个定义域可得当x ∈[2k π－π，2k π]，k ∈Z 时，余弦函数y ＝cos x 是增函数，函数值由－1增大到1； 当x ∈[2k π，(2k ＋1)π]，k ∈Z 时，余弦函数y ＝cos x 是减函数，函数值由1减小到－1.·正弦函数、余弦函数的单调区间是什么？类型一、求正弦、余弦函数的单调区间 例1求函数y ＝2sin ⎝⎛⎭⎫π4－x 的单调递增区间．跟踪训练1求函数f (x )＝2cos ⎝⎛⎭⎫2x －π6的单调递增区间．类型二、正弦、余弦函数单调性的应用 命题角度1利用正、余弦函数的单调性比较大小 例2利用三角函数的单调性，比较下列各组数的大小．(1)sin 196°与cos 156°； (2)cos ⎝⎛⎭⎫－235π与cos ⎝⎛⎭⎫－174π.跟踪训练2cos 1，cos 2，cos 3的大小关系是________．(用“>”连接) 命题角度2已知三角函数的单调性求参数范围例3已知ω是正数，函数f (x )＝2sin ωx 在区间⎣⎡⎦⎤－π3，π4上是增函数，求ω的取值范围．跟踪训练3已知ω>0，函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4在⎝⎛⎭⎫π2，π上单调递减，则ω的取值范围是( ) A.⎣⎡⎦⎤12，54 B.⎣⎡⎦⎤12，34 C.⎝⎛⎦⎤0，12 D ．(0,2]类型三、正弦、余弦函数的值域或最值例4求函数f (x )＝2sin 2x ＋2sin x －12，x ∈⎣⎡⎦⎤π6，5π6的值域．跟踪训练4已知函数f (x )＝2a sin x ＋b 的定义域为⎣⎡⎦⎤－π3，2π3，函数的最大值为1，最小值为－5，求a 和b 的值．1．函数y ＝cos x －1的最小值是( ) A ．0 B ．1 C ．－2 D ．－12．函数y ＝sin 2x 的单调递减区间是( )A.⎣⎡⎦⎤π2＋2k π，3π2＋2k π(k ∈Z )B.⎣⎡⎦⎤k π＋π4，k π＋3π4(k ∈Z ) C.[]π＋2k π，3π＋2k π(k ∈Z ) D.⎣⎡⎦⎤k π－π4，k π＋π4(k ∈Z ) 3．下列不等式中成立的是( ) A ．sin ⎝⎛⎭⎫－π8>sin ⎝⎛⎭⎫－π10 B ．sin 3>sin 2 C ．sin 75π>sin ⎝⎛⎭⎫－25π D ．sin 2>cos 14．函数y ＝cos x 在区间[－π，a ]上为增函数，则a 的取值范围是________． 5．求函数y ＝3－2sin 12x 的最值及取到最值时的自变量x 的集合．1．求函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的单调区间的方法把ωx ＋φ看成一个整体，由2k π－π2≤ωx ＋φ≤2k π＋π2(k ∈Z )解出x 的范围，所得区间即为增区间，由2k π＋π2≤ωx ＋φ≤2k π＋3π2(k ∈Z )解出x 的范围，所得区间即为减区间．若ω<0，先利用诱导公式把ω转化为正数后，再利用上述整体思想求出相应的单调区间．2．比较三角函数值的大小，先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较，再利用单调性作出判断． 3．求三角函数值域或最值的常用方法将y 表示成以sin x (或cos x )为元的一次或二次等复合函数，再利用换元或配方或利用函数的单调性等来确定y 的范围.1．4.2正弦函数、余弦函数的性质(二)类型一 求正弦、余弦函数的单调区间 例1 求函数y ＝2sin ⎝⎛⎭⎫π4－x 的单调递增区间． 考点 正弦函数、余弦函数的单调性 题点 正弦函数、余弦函数单调性的判断 解 y ＝2sin ⎝⎛⎭⎫π4－x ＝－2sin ⎝⎛⎭⎫x －π4， 令z ＝x －π4，则y ＝－2sin z .因为z 是x 的一次函数，所以要求y ＝－2sin z 的单调递增区间，即求sin z 的单调递减区间， 即2k π＋π2≤z ≤2k π＋3π2(k ∈Z )．∴2k π＋π2≤x －π4≤2k π＋3π2(k ∈Z )，即2k π＋3π4≤x ≤2k π＋7π4(k ∈Z )，∴函数y ＝2sin ⎝⎛⎭⎫π4－x 的单调递增区间为⎣⎡⎦⎤2k π＋3π4，2k π＋7π4(k ∈Z )． 反思与感悟 用整体替换法求函数y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)的单调区间时，如果式子中x 的系数为负数，先利用诱导公式将x 的系数变为正数再求其单调区间．求单调区间时，需将最终结果写成区间形式．跟踪训练1 求函数f (x )＝2cos ⎝⎛⎭⎫2x －π6的单调递增区间．考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的判断解 令－π＋2k π≤2x －π6≤2k π，k ∈Z ， 解得－5π12＋k π≤x ≤π12＋k π，k ∈Z ， 所以函数f (x )的单调递增区间是⎣⎡⎦⎤－5π12＋k π，π12＋k π，k ∈Z .类型二 正弦、余弦函数单调性的应用命题角度1 利用正、余弦函数的单调性比较大小例2 利用三角函数的单调性，比较下列各组数的大小．(1)sin 196°与cos 156°；(2)cos ⎝⎛⎭⎫－235π与cos ⎝⎛⎭⎫－174π. 考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用解 (1)sin 196°＝sin(180°＋16°)＝－sin 16°，cos 156°＝cos(180°－24°)＝－cos 24°＝－sin 66°.∵0°<16°<66°<90°，且y ＝sin x 在[0°，90°]上是增函数，∴sin 16°<sin 66°，从而－sin 16°>－sin 66°，即sin 196°>cos 156°.(2)cos ⎝⎛⎭⎫－235π＝cos 235π＝cos ⎝⎛⎭⎫4π＋35π＝cos 35π， cos ⎝⎛⎭⎫－174π＝cos 174π＝cos ⎝⎛⎭⎫4π＋π4＝cos π4. ∵0<π4<35π<π，且y ＝cos x 在[0，π]上是减函数， ∴cos 35π<cos π4，即cos ⎝⎛⎭⎫－235π<cos ⎝⎛⎭⎫－174π. 反思与感悟 用正弦函数或余弦函数的单调性比较大小时，应先将异名化同名，把不在同一单调区间内的角用诱导公式转化到同一单调区间，再利用单调性来比较大小．跟踪训练2 cos 1，cos 2，cos 3的大小关系是________．(用“>”连接)考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用答案 cos 1>cos 2>cos 3解析 由于0<1<2<3<π，而y ＝cos x 在[0，π)上单调递减，所以cos 1>cos 2>cos 3. 命题角度2 已知三角函数的单调性求参数范围例3 已知ω是正数，函数f (x )＝2sin ωx 在区间⎣⎡⎦⎤－π3，π4上是增函数，求ω的取值范围． 考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用解 由－π2＋2k π≤ωx ≤π2＋2k π(k ∈Z )，ω>0，得 －π2ω＋2k πω≤x ≤π2ω＋2k πω，k ∈Z ， ∴f (x )的单调递增区间是⎣⎡⎦⎤－π2ω＋2k πω，π2ω＋2k πω，k ∈Z . 根据题意，得⎣⎡⎦⎤－π3，π4⊆⎣⎡⎦⎤－π2ω＋2k πω，π2ω＋2k πω(k ∈Z )， 从而有⎩⎨⎧－π2ω≤－π3，π2ω≥π4，ω>0，解得0<ω≤32. 故ω的取值范围是⎝⎛⎦⎤0，32. 反思与感悟 此类问题可先解出f (x )的单调区间，将问题转化为集合间的包含关系，然后列不等式组求出参数范围．跟踪训练3 已知ω>0，函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4在⎝⎛⎭⎫π2，π上单调递减，则ω的取值范围是( ) A.⎣⎡⎦⎤12，54B.⎣⎡⎦⎤12，34C.⎝⎛⎦⎤0，12 D ．(0,2]考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用答案 A解析 取ω＝54，f (x )＝sin ⎝⎛⎭⎫54x ＋π4， 其减区间为⎣⎡⎦⎤85k π＋π5，85k π＋π，k ∈Z ，显然⎝⎛⎭⎫π2，π⊆⎣⎡⎦⎤85k π＋π5，85k π＋π，k ∈Z ，排除B ，C. 取ω＝2，f (x )＝sin ⎝⎛⎭⎫2x ＋π4， 其减区间为⎣⎡⎦⎤k π＋π8，k π＋58π，k ∈Z ， 显然⎝⎛⎭⎫π2，π⊈⎣⎡⎦⎤k π＋π8，k π＋58π，k ∈Z ，排除D.类型三 正弦、余弦函数的值域或最值例4 求函数f (x )＝2sin 2x ＋2sin x －12，x ∈⎣⎡⎦⎤π6，5π6的值域． 考点 正弦函数、余弦函数的最大值与最小值题点 正弦函数的最大值与最小值解 令t ＝sin x ，因为x ∈⎣⎡⎦⎤π6，5π6，所以t ∈⎣⎡⎦⎤12，1，则f (x )可化为y ＝2t 2＋2t －12＝2⎝⎛⎭⎫t ＋122－1，t ∈⎣⎡⎦⎤12，1， 所以当t ＝12时，y min ＝1， 当t ＝1时，y max ＝72， 故f (x )的值域是⎣⎡⎦⎤1，72. 反思与感悟 一般函数的值域求法有：观察法、配方法、判别式法、反比例函数法等．三角函数是函数的特殊形式，一般方法也适用，但要结合三角函数本身的性质．常见的三角函数求值域或最值的类型有以下几种：(1)形如y ＝sin(ωx ＋φ)的三角函数，令t ＝ωx ＋φ，根据题中x 的取值范围，求出t 的取值范围，再利用三角函数的单调性、有界性求出y ＝sin t 的最值(值域)．(2)形如y ＝a sin 2x ＋b sin x ＋c (a ≠0)的三角函数，可先设t ＝sin x ，将函数y ＝a sin 2x ＋b sin x ＋c (a ≠0)化为关于t 的二次函数y ＝at 2＋bt ＋c (a ≠0)，根据二次函数的单调性求值域(最值)．(3)对于形如y ＝a sin x (或y ＝a cos x )的函数的最值还要注意对a 的讨论．跟踪训练4 已知函数f (x )＝2a sin x ＋b 的定义域为⎣⎡⎦⎤－π3，2π3，函数的最大值为1，最小值为－5，求a 和b 的值．考点 正弦函数、余弦函数的最大值与最小值题点 正弦函数的最大值与最小值解 ∵－π3≤x ≤2π3，∴－32≤sin x ≤1. 若a ＝0，不满足题意．若a ＞0，则⎩⎪⎨⎪⎧ 2a ＋b ＝1，－3a ＋b ＝－5，解得⎩⎪⎨⎪⎧ a ＝12－63，b ＝－23＋12 3.若a ＜0，则⎩⎪⎨⎪⎧ 2a ＋b ＝－5，－3a ＋b ＝1，解得⎩⎪⎨⎪⎧a ＝－12＋63，b ＝19－12 3. 故a ＝12－63，b ＝－23＋123或a ＝－12＋63，b ＝19－12 3.1．函数y ＝cos x －1的最小值是( )A ．0B ．1C ．－2D ．－1考点 正弦函数、余弦函数的最大值与最小值题点 余弦函数的最大值与最小值答案 C解析 cos x ∈[－1,1]，所以y ＝cos x －1的最小值为－2.2．函数y ＝sin 2x 的单调递减区间是( )A.⎣⎡⎦⎤π2＋2k π，3π2＋2k π(k ∈Z )B.⎣⎡⎦⎤k π＋π4，k π＋3π4(k ∈Z ) C.[]π＋2k π，3π＋2k π(k ∈Z )D.⎣⎡⎦⎤k π－π4，k π＋π4(k ∈Z ) 考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的判断答案 B解析 由2k π＋π2≤2x ≤2k π＋3π2，k ∈Z ，得k π＋π4≤x ≤k π＋3π4，k ∈Z ， ∴y ＝sin 2x 的单调递减区间是⎣⎡⎦⎤k π＋π4，k π＋3π4(k ∈Z )． 3．下列不等式中成立的是( )A ．sin ⎝⎛⎭⎫－π8>sin ⎝⎛⎭⎫－π10 B ．sin 3>sin 2 C ．sin 75π>sin ⎝⎛⎭⎫－25π D ．sin 2>cos 1考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用答案 D解析 ∵sin 2＝cos ⎝⎛⎭⎫π2－2＝cos ⎝⎛⎭⎫2－π2， 且0<2－π2<1<π，∴cos ⎝⎛⎭⎫2－π2>cos 1， 即sin 2>cos 1.故选D.4．函数y ＝cos x 在区间[－π，a ]上为增函数，则a 的取值范围是________．考点 正弦函数、余弦函数的单调性题点 正弦函数、余弦函数单调性的应用答案 (－π，0]解析 因为y ＝cos x 在[－π，0]上是增函数，在[0，π]上是减函数，所以只有－π<a ≤0时满足条件，故a ∈(－π，0]．5．求函数y ＝3－2sin 12x 的最值及取到最值时的自变量x 的集合． 考点 正弦函数、余弦函数的最大值与最小值题点 正弦函数的最大值与最小值解 ∵－1≤sin 12x ≤1，∴当sin 12x ＝－1，12x ＝2k π－π2，k ∈Z ， 即x ＝4k π－π，k ∈Z 时，y max ＝5，此时自变量x 的集合为{x |x ＝4k π－π，k ∈Z }；当sin 12x ＝1，12x ＝2k π＋π2，k ∈Z ， 即x ＝4k π＋π，k ∈Z 时，y min ＝1，此时自变量x 的集合为{x |x ＝4k π＋π，k ∈Z }．1．求函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的单调区间的方法把ωx ＋φ看成一个整体，由2k π－π2≤ωx ＋φ≤2k π＋π2(k ∈Z )解出x 的范围，所得区间即为增区间，由2k π＋π2≤ωx ＋φ≤2k π＋3π2(k ∈Z )解出x 的范围，所得区间即为减区间．若ω<0，先利用诱导公式把ω转化为正数后，再利用上述整体思想求出相应的单调区间．2．比较三角函数值的大小，先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较，再利用单调性作出判断．3．求三角函数值域或最值的常用方法将y 表示成以sin x (或cos x )为元的一次或二次等复合函数，再利用换元或配方或利用函数的单调性等来确定y 的范围.。

第2课时正弦函数、余弦函数的性质【教学目标】1．知识目标（1）认识正弦函数、余弦函数的周期性，了解正弦函数、余弦函数是描述自然界周期性变化的有力工具。

（2）理解周期函数与最小正周期的意义，会求三角函数的最小正周期。

2.能力目标理解并掌握正弦函数、余弦函数的周期性3.情感目标（1）通过本节的学习体会数形结合思想在探讨三角函数性质方面的应用。

【重点难点】重点正弦函数、余弦函数的周期性难点周期函数、最小正周期的意义案例（一）教学过程、对于所有的周期函数都有最小正周期吗？为什么？板书设计教学过程1、探究：“根据正弦和余弦函数的图象，你能说出它们具有哪些性质吗？”学生――观察正弦曲线、余弦曲线，说出正弦函数、余弦函数的一些性质。

教师――有意引导学生观察正弦函数的图象经过一段之后是否出现了“重复”现象（或“周而复始”的现象）。

使目标靠拢本节课题。

师生――共同讨论，正弦函数在[]π2,0内的图象，向左、向右经过 、、ππ42之后都会出现“重复”现象，这一点可以从正弦线的变化规律中看出，还可以从诱导公式)(,sin )2sin(Z k x k x ∈=+π中得到反映。

这种“重复”的性质通常用“周期”术语来刻画，这说明三角函数具有周期性。

2、什么是周期函数？教师――用数学语言如何描述函数具有周期性呢？引导分析，给出周期函数的定义，强调常数)()(,0x f T x f T =+≠在定义域内恒成立。

若T 为周期函数)(x f 的一个周期，则),(Z k kT ∈且)0≠k 均为)(x f 的周期。

进一步给出最小正周期的意义。

教师――提出问题：是不是所有的周期函数都有最小正周期？让学生思考并举例说明。

学生――思考，并举例说明。

师生――根据定义共同分析周期函数的性质，强调一个周期函数不一定存在最小正周期。

如：R k x f ∈=,2)(是周期函数，但无最小正周期。

3、你能根据周期函数的定义具体说明正弦函数、余弦函数的周期性吗？学生――根据定义，探究、验证正弦函数的周期性。

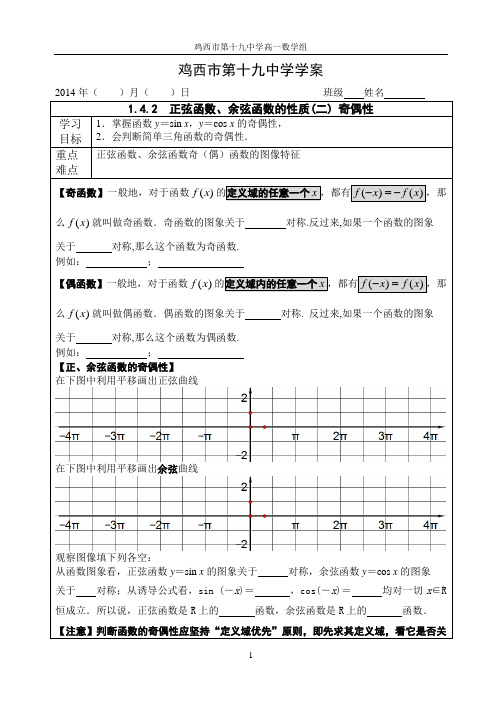
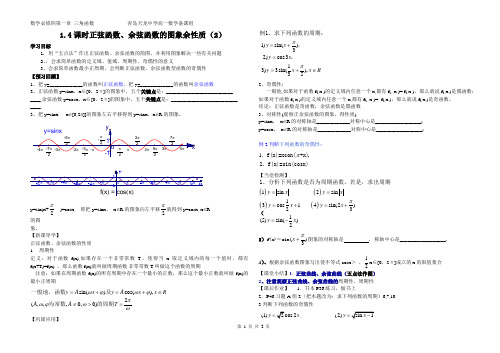
1.4课时正弦函数、余弦函数的图象余性质（2）学习目标1. 用“五点法”作出正弦函数、余弦函数的简图，并利用图象解决一些有关问题 2、，会求简单函数的定义域、值域、周期性、奇偶性的意义3、会求简单函数最小正周期，会判断正弦函数、余弦函数型函数的奇偶性 【预习回顾】1、把y=_____________的函数叫正弦函数、把y=_____________的函数叫余弦函数2、正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是：__________________________ ____,余弦函数y=cosx ，x ∈[0，2π]的图象中，五个关键点是：__________________________ ____,3、把y=sinx x ∈[0,2π]]的图象左右平移得到y=sinx ，x ∈R 的图象，y=sin(x+2π )=cosx, 即把y=sinx ， x ∈R 的图象向左平移2π就得到y=cosx, x ∈R 的图象。

【新课导学】正弦函数、余弦函数的性质 1. 周期性定义：对于函数f(x),如果存在一个非零常数T,，使得当x 取定义域内的每一个值时，都有f(x+T)=f(x) ，那么函数f(x)就叫做周期函数.非零常数T 叫做这个函数的周期.注意：如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.sin()cos(),2(,,,0,0)y A x y A x x R A A T ωϕωϕπωϕωω=+=+∈≠>=一般地，函数及为常数的周期【巩固应用】1)sin()32)cos3 1 3)3sin(),35y x y x y x x Rππ=+==+∈例1、求下列函数的周期：，，2、奇偶性：一般地,如果对于函数f( x )的定义域内任意一个x,都有f(- x )= f( x)，那么就说f( x )是偶函数；如果对于函数f( x )的定义域内任意一个x,都有f(- x )= -f( x)，那么就说f( x )是奇函数。