2018年北京高考卷数学(理科)试题及答案

2018年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回•第部分（选择题共40 分）一、选择题共 8小题，每小题 5分，共40分.1.已知集合Ax|x 2， B2,0,1,2，则 A B( )A 0,1 B. 1,0,1C. 2,0,1,2D.1,0,1,22.在复平面内， 复数- 1 11的共轭复数对应的点位于（）iA 第一象限B.第二象限C.第三象限D.第四象限3.执行如图所示的程序框图，输出的s 值为（ ）B.-C.-D.—124•“十二平均律”是通用的音律体系，明代朱载埴最早用数学方法计算出半音比例，为这个理论的发展做 出了重要贡献•十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一 个单音的频率与它的前一个单音的频率的比都等于 122 .若第一个单音的频率为 f ，则第八个单音的频率为（）A 32fB. 3 22 fC.12 25 fD.1227 f5.某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为值为（A.1B.2 D.46.设a , b 均为单位向量，则“ a 3b 3a b 是“ a 丄b ”的（A 充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件7.在平面直角坐标系中，记d 为点 P cos ,sin 到直线x my0的距离，当，m 变化时，d 的最大A1B.2C.3D.48.设集合A x, y | x y 1, ax y 4, x ay2，则（A 对任意实数a , 2,1 AC.当且仅当a 0时，2,1 AB.对任意实数a , 2,1 A3D.当且仅当a 时，2,1 A2侧〔左）规图、填空题共6小题，每小题5分，共30分.四个交点及椭圆 M 的两个焦点恰为一个正六边形的顶点，则椭圆 M 的离心率为 _________________ ;双曲线N 的 离心率为 ___________ .三、解答题共6小题，共80分。

2018年普通高等学校招生全国统一考试（北京卷）数学（理工类）第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，选出符合题目要求的一项.1．若集合{}2A x x =<，{}2,0,1,2B x =-，则A B =I （A ）{}01， （B ）{}-101，，（C ）{}-201，，（D ）{}-1012，，， 2.在复平面内，复数i1i-的共轭复数对应的点位于 （A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限3．执行如图所示的程序框图，输出的s 值为（ ）．A ．12 B ．56C ．76D ．7124．“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要的贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于第一个单音的频率为f ，则第八个单音的频率为（ ）．ABC ．D ．5．某四棱锥的三视图如图所示，在此三棱锥的侧面中，直角三角形的个数为（ ）． A ．1 B ．2 C ．3 D ．46.设a b ,均为单位向量，则“33a b a b -=+”是“a b ⊥”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件7. 在平面直角坐标系中，记d 为点()P cos ,sin θθ到直线20x my --=的距离.当,m θ变化时，d 的最大值为 （A ）1 （B ）2 （C ）3（D ）48. 设集合(){},|1,4,2A x y x y ax y x ay =-≥+>-≤，则()A 对任意实数a ，()2,1A ∈ ()B 对任意实数a ，()2,1A ∉()C 当且仅当0a <时，()2,1A ∉ ()D 当且仅当32a ≤时，()2,1A ∉二.填空（9）设{}n a 是等差数列，且13a =，2536a a +=，则{}n a 的通项公式为 。

2018年普通高等学校招生全国统一考试理科数学试题参考答案一、选择题1．A 2．D 3．B 4．D 5．C 6．C 7．CD 8．二、填空题212．．119．3 10．21?3?6n?a n3yx （答案不唯一）．14 =sin 13．2；13?三、解答题（15）（共13分）π1BABCBB=–，∴sin∈（解：（Ⅰ）在△，π），∴中，∵cos=2734．2?B?1cos78ab73A=，∴sin．= 由正弦定理得??34AsinsinABsin27πππAAB =，π），∴∈（．∈（0，∵），∴∠322ABBABCCABA=∵sin+sin=sin（+cos）=sincos（Ⅱ）在△中，3114333=．?)(???727214h3333hABCC== ，，=∵如图所示，在△中，sin∴CsinBC??7?BC214．33AC边上的高为．∴214分）（16）（共CABABC -解：（Ⅰ）在三棱柱中，111ABCCC∵⊥平面，1ACCA∴四边形为矩形．11CAEFAC，分别为的中点，，又11 EFAC．∴⊥BCAB．∵=BEAC∴，⊥BEFAC∴．⊥平面CCEFEFACBEAC，⊥∥，（Ⅱ）由（I）知⊥．1ABCABCEFCC，∴⊥平面又⊥平面．1BEABCBEEF，∴⊥．平面∵ xyzE如图建立空间直角坐称系-．BCDF，），1（1，（-1，0，0），由题意得0（0，2，），0G （0，2，1）．0，0，2），（uuuruur∴，0)2，CB=(1，，CD=(2，，01)BCD 的法向量为设平面，n?(bc)a，，uuur?2a?c?00n?CD???，∴，∴uur??a?2b?0?n?CB?0??abc=-4，=-1令，=2，则BCD的法向量∴平面，n?4)?(2，?1，uur CDC的法向量为又∵平面，0)，，2EB=(01uuruur21n?EB．∴=????cosn?EBruu21|n||EB|BCDCBCDC的由图可得二面角为钝角，所以二面角----1121．余弦值为?21GBCDF，（Ⅲ）平面的法向量为，2，1），∵（0，?1，?4)(2n?（0，0，2），uuuruuuruuur，∴与，∴不垂直，∴1)，，?2=(0GFGF?2?n GF?n GFBCDBCDGF与平面内，∴与平面不平行且不在平面∴BCD相交．（17）（共12分）解：（Ⅰ）由题意知，样本中电影的总部数是，140+50+300+200+800+510=2000．第四类电影中获得好评的电影部数是200×0.25=50．50．故所求概率为0.025?2000A为“从第四类电影中随机选出的电影获得好评”，设事件（Ⅱ）B为“从第五类电影中随机选出的电影获得好评”．事件PPP（）（）故所求概率为+（）=ABABAB?AB PAPBPAPB）．）（1–=（（（）（1–）（））+PAPB）估计为0.2．（（）估计为0.25，由题意知：故所求概率估计为0.25×0.8+0.75×0.2=0.35．（Ⅲ）>>=>>．??????DDDDDD142536（18）（共13分）解：（Ⅰ）因为=[]，)f(x23?x?4axa?(4a?1)x e f ′xaxaaxaxa+3］+1+［）–所以（4（=）［2+4–（4+1）］e x2xR）（∈e x axax+2］e–（2．+1）=［x2fa)e．–′(1)=(1faa=1．)e=0，解得由题设知′(1)=0，即(1–f (1)=3e≠0．此时a的值为1．所以f xaxax=ax–1］e（））–（=（Ⅱ）由（Ⅰ）得′（）［2+1+2x2x–2)e( ．x11xf ax)<0；(，若2)时，>，则当′∈(a2xf x)>0．()时，当′∈(2，+∞f xx=2处取得极小值．在( )<0所以11xxaxax–1<0，1≤2)时，，则当–若2<0，≤–∈(0，22f x)>0．所以′(f x)的极小值点．不是(所以21a，+∞）．的取值范围是（综上可知，2（19）（共14分）ypxP（1，2=2）经过点，解：（Ⅰ）因为抛物线2ppyx．，所以抛物线的方程为4=2 ，解得=4=2所以2l的斜率存在且不为0由题意可知直线，lykxk≠0）=．+1设直线（的方程为由得．220?4)x?k1xk?(2??y?kx?1?依题意，解得k<0或2??4yx0<k<1．22?0?1?k??(2k?4)?4PAPBlk≠．从而-2）y轴相交，故直线1不过点（又，，与-3．l斜率的取值范围是（-∞，-3）∪（-3，0）∪（0，1所以直线）．AxyBxy）．），，（（Ⅱ）设（，211214k?2．由（I）知，?xx?x??x 212122kk?2y yPA2= 直线–的方程为．1?1)2y?(x?1x?1?y?2?kx?1Mx．=0，得点令的纵坐标为112?y??2?M x?1x?111?kx?1N．同理得点的纵坐标为22?y?N x?12ruuuuuurruuuuuur由，得，．????QO=QNQOQM=y?=1?y1?MN所以22k?4?x?1x?12xx?(x?x)111111．211221????????=2?22kk1??1?y1?y(k?1)x(k?1)xk?1xxk?1221N1M2k11为定值．所以???（20）（共14分）αβ=（0，1，1，，0），1），所以解：（Ⅰ）因为=（11Mαα)= [(1+1?|1?1|)+(1+1?|1?1|)+(0+0(?，|0?0|)]=2，21M αβ）(1|)]=1．=，1|)+(0+1 [(1+0–|1?0|)+(1+1–|1––|0–2αxxxxBMααxxxx．+，则+(+（Ⅱ）设，=（，，），）∈= 41412323xxxxMαα)为奇数，(，∈{0，1}由题意知，且，，，4312xxxx中1的个数为1或，3．所以，，4213B?{(1，0，0，0），（0，1，0，0)，（所以0，0，1，0)，（0，0，0，1)，（0，1，1，1)，(1，0，1，1)，(1，1，0，1)，(1，1，1，0)}.将上述集合中的元素分成如下四组：（1，0，0，0)，(1，1，1，0)；（0，1，0，0)，(1，1，0，1)；（0，0，1，0)，（1，0，1，1)；（0，0，0，1)，（0，1，1，1).αβMαβ）=1. ，均有，经验证，对于每组中两个元素(，B的元素．所以每组中的两个元素不可能同时是集合B中元素的个数不超过4.所以集合又集合{（1，0，0，0），（0，1，0，0），（0，0，1，0），（0，0，0，1)}满足条件，B中元素个数的最大值为所以集合4.S xxx xxxAx =1∈，，，（Ⅲ）设=(，…，，…，，）|(）knnk2112xxxkn)，2，…，=0）（=1==…=，k121–S xxx xxx=0}，==={( ，= ，…，）|…nnn221+11ASSS．=∪…∪∪则n+111Sknαβ，经验证，，–（1=1，2，…，）中的不同元素对于k Mαβ)≥(，1.Skn–12 所以，…，（）中的两个元素不可能同时是=1，k B 的元素．集合Bn+1.所以中元素的个数不超过xxxSxxk=1，2，=…=（=0…，取e=(，，…，）∈且nknkk+112n–1）.BSSB的元素个数）∪，…，e（，ee∪，则集合令=nnn+1–112n.，且满足条件+1为B是一个满足条件且元素个数最多的集合．故。

2018年普通高等学校招生全国统一考试（北京卷）数学（理工类）第一部分（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，选出符合题目要求的一项.1．若集合{}2A x x =<，{}2,0,1,2B x =-，则A B =I （A ）{}01，（B ）{}-101，，（C ）{}-201，，（D ）{}-1012，，， 2.在复平面内，复数i1i-的共轭复数对应的点位于 （A ）第一象限（B ）第二象限 （C ）第三象限（D ）第四象限3．执行如图所示的程序框图，输出的s 值为（）．A ．12B ．56C ．76D ．7124．“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要的贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于．若第一个单音的频率为f ，则第八个单音的频率为（）．ABC ．D ．5．某四棱锥的三视图如图所示，在此三棱锥的侧面中，直角三角形的个数为（）． A ．1 B ．2 C ．3 D ．46.设a b r r ,均为单位向量，则“33a b a b -=+r r r r ”是“a b ⊥r r”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件7. 在平面直角坐标系中，记d 为点()P cos ,sin θθ到直线20x my --=的距离.当,m θ变化时，d 的最大值为 （A ）1 （B ）2 （C ）3（D ）48. 设集合(){},|1,4,2A x y x y ax y x ay =-≥+>-≤，则()A 对任意实数a ，()2,1A ∈()B 对任意实数a ，()2,1A ∉ ()C 当且仅当0a <时，()2,1A ∉()D 当且仅当32a ≤时，()2,1A ∉二.填空（9）设{}n a 是等差数列，且13a =，2536a a +=，则{}n a 的通项公式为。

2018年北京高考数学及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN2018年普通高等学校招生全国统一考试数 学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回.第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分.1. 已知集合{}2|<=x x A ，{}2,1,0,2-=B ，则=⋂B A ( ).A {}1,0 .B {}1,0,1- .C {}2,1,0,2- .D {}2,1,0,1-2. 在复平面内，复数i-11的共轭复数对应的点位于( ) .A 第一象限 .B 第二象限 .C 第三象限 .D 第四象限3. 执行如图所示的程序框图，输出的s 值为( ).A 21 .B 65 .C 67 .D 1274.“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122．若第一个单音的频率为f ，则第八个单音的频率为( ).A f 32 .B f 322 .C f 1252 .D f 12725. 某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为( ).A 1 .B 2 .C 3 .D 46. 设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的( ).A 充分而不必要条件 .B 必要而不充分条件 .C 充分必要条件 .D 既不充分也不必要条件7. 在平面直角坐标系中，记d 为点()θθsin ,cos P 到直线02=--my x 的距离，当m ,θ变化时，d 的最大值为( ) .A 1.B 2 .C 3.D 48. 设集合(){}2,4,1|,≤->+≥-=ay x y ax y x y x A ，则( ).A 对任意实数a ，()A ∈1,2.B 对任意实数a ，()A ∉1,2.C 当且仅当0<a 时，()A ∉1,2.D 当且仅当23≤a 时，()A ∉1,2第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分.9. 设{}n a 是等差数列，且31=a ，3652=+a a ，则{}n a 的通项公式为__________．10.在极坐标系中，直线()0sin cos >=+a a θρθρ与圆θρcos 2=相切，则=a _________．11. 设函数()()06cos >⎪⎭⎫ ⎝⎛-=ωπωx x f ，若()⎪⎭⎫⎝⎛≤4πf x f 对任意的实数x 都成立，则ω的最小值为__________．12.若x ，y 满足x y x 21≤≤+，则x y -2的最小值是__________．13.能说明“若()()0f x f >对任意的]2,0(∈x 都成立，则()x f 在[]2,0上是增函数”为假命题的一个函数是__________．14. 已知椭圆()01:2222>>=+b a b y a x M ，双曲线1:2222=-ny m x N ，若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为__________；双曲线N 的离心率为__________．三、解答题共6小题，共80分。

2018年普通高等学校招生全国统一考试（北京卷）数学（理工类）第一部分（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，选出符合题目要求的一项.1．若集合2A x x，2,0,1,2B x ，则A BI （A ）01，（B ）-101，，（C ）-201，，（D ）-1012，，，2.在复平面内，复数i 1i的共轭复数对应的点位于（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限3．执行如图所示的程序框图，输出的s 值为（）．A ．12B ．56C ．76D ．7124．“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要的贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122．若第一个单音的频率为f ，则第八个单音的频率为（）．A ．32fB．322fC．1252fD．1272f5．某四棱锥的三视图如图所示，在此三棱锥的侧面中，直角三角形的个数为（）．A．1B．2C．3D．4a b a b”是“a b”的6.设a b,均为单位向量，则“33（A）充分而不必要条件（B）必要而不充分条件（C）充分必要条件（D）既不充分也不必要条件7. 在平面直角坐标系中，记d为点P cos,sin到直线20x my的距离.当,m变化时，d的最大值为（A）1（B）2 （C）3 （D）4A x y x y ax y x ay，则8. 设集合,|1,4,2A对任意实数a，2,1A B对任意实数a，2,1AC 当且仅当0a 时，2,1AD 当且仅当32a时，2,1A二.填空（9）设n a 是等差数列，且13a ，2536a a ，则n a 的通项公式为。

（10）在极坐标系中，直线cossin(0)a a与圆2cos相切，则a。

（11）设函数cos6f xx0。

2018年高考北京卷理数试题及答案（1）已知集合A={x||x|<2}，B={–2，0，1，2}，则A B=（A）{0，1} （B）{–1，0，1}（C）{–2，0，1，2} （D）{–1，0，1，2}（2）在复平面内，复数11i的共轭复数对应的点位于（A）第一象限（B）第二象限（C）第三象限（D）第四象限（3）执行如图所示的程序框图，输出的s值为（A）12（B）56（C）76（D）712（4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122．若第一个单音的频率为f，则第八个单音的频率为（A32（B322（C）1252（D）1272（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ）1 （B ）2 （C ）3（D ）4（6）设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件（7）在平面直角坐标系中，记d 为点P （cos θ，sin θ）到直线20x my --=的距离，当θ，m 变化时，d 的最大值为 （A ）1 （B ）2 （C ）3（D ）4（8）设集合{(,)|1,4,2},A x y x y ax y x ay =-≥+>-≤则 （A ）对任意实数a ，(2,1)A ∈（B ）对任意实数a ，（2，1）A ∉（C ）当且仅当a <0时，（2，1）A ∉ （D ）当且仅当32a ≤时，（2，1）A ∉ 二、填空题共6小题，每小题5分，共30分。

（9）设{}n a 是等差数列，且a 1=3，a 2+a 5=36，则{}n a 的通项公式为__________．（10）在极坐标系中，直线cos sin (0)a a ρθρθ+=>与圆=2cos ρθ相切，则a =__________．（11）设函数f （x ）=πcos()(0)6x ωω->，若π()()4f x f ≤对任意的实数x 都成立，则ω的最小值为__________．（12）若x ，y 满足x +1≤y ≤2x ，则2y –x 的最小值是__________．（13）能说明“若f （x ）>f （0）对任意的x ∈（0，2］都成立，则f （x ）在［0，2］上是增函数”为假命题的一个函数是__________．（14）已知椭圆22221(0)x y M a b a b +=>>：，双曲线22221x y N m n-=：．若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为__________；双曲线N 的离心率为__________．三、解答题共6小题，共80分。

2018年普通高等学校招生全国统一考试（北京卷）数学（理工类）第一部分（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，选出符合题目要求的一项.1．若集合{}2A x x =<，{}2,0,1,2B x =-，则A B =I （A ）{}01，（B ）{}-101，，（C ）{}-201，，（D ）{}-1012，，， 2.在复平面内，复数i1i-的共轭复数对应的点位于 （A ）第一象限（B ）第二象限 （C ）第三象限（D ）第四象限3．执行如图所示的程序框图，输出的s 值为（）．A ．12B ．56C ．76D ．7124．“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要的贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于．若第一个单音的频率为f ，则第八个单音的频率为（）．ABC ．D ．5．某四棱锥的三视图如图所示，在此三棱锥的侧面中，直角三角形的个数为（）． A ．1 B ．2 C ．3 D ．46.设a b r r ,均为单位向量，则“33a b a b -=+r r r r ”是“a b ⊥r r”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件7. 在平面直角坐标系中，记d 为点()P cos ,sin θθ到直线20x my --=的距离.当,m θ变化时，d 的最大值为 （A ）1 （B ）2 （C ）3（D ）48. 设集合(){},|1,4,2A x y x y ax y x ay =-≥+>-≤，则()A 对任意实数a ，()2,1A ∈()B 对任意实数a ，()2,1A ∉ ()C 当且仅当0a <时，()2,1A ∉()D 当且仅当32a ≤时，()2,1A ∉二.填空（9）设{}n a 是等差数列，且13a =，2536a a +=，则{}n a 的通项公式为。

2018北京理一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1． 已知集合A ＝{x | |x |＜2}，B ＝{–2，0，1，2}，则A ∩B ＝A ． {0，1}B ． {–1，0，1}C ． {–2，0，1，2}D ． {–1，0，1，2}【解析】因|x |＜2，故－2＜x ＜2，因此A ∩B ＝{–2，0，1，2}∩(－2，2)＝{0，1}，选A ．2．在复平面内，复数11－i 的共轭复数对应的点位于 A ． 第一象限 B ． 第二象限 C ． 第三象限 D ． 第四象限【解析】11－i＝1＋i 2＝12＋12i ，其共轭复数为12－12i ，对应的点为(12，－12)，故选D ． 3． 执行如图所示的程序框图，输出的S 值为A ．12B ．56C ．76D ．712 【解析】初始化数值k ＝1，S ＝1，循环结果执行如下：第一次：S ＝1＋(－1)1•12＝12，k ＝2≥3不成立；第二次：S ＝12＋(－1)2•13＝56，k ＝3≥3成立，循环结束，输出S ＝56，故选B ． 4． “十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122．若第一个单音的频率为f ，则第八个单音的频率为A ．32fB ．322fC ．1225fD ．1227f【解析】从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122，第一个单音的频率为f ．由等比数列的定义知，这十三个单音的频率构成一个首项为f ，公比为122的等比数列，记为{a n }．则第八个单音频率为a 8＝f ·(122)8－1＝1227f ．5．某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为A ． 1B ． 2C ． 3D ． 4【解析】在正方体中作出该几何体的直观图，记为四棱锥P －ABCD ，如图，由图可知在此四棱锥的侧面中，直角三角形的个数为3，是△P AD ，△PCD ，△P AB ．6．设a ，b 均为单位向量，则“|a －3b |＝|3a ＋b |”是“a ⊥b ”的A ． 充分而不必要条件B ． 必要而不充分条件C ． 充分必要条件D ． 既不充分也不必要条件【解析】|a －3b |＝|3a ＋b |⇔|a －3b |2＝|3a ＋b |2⇔a 2－6a •b ＋9b 2＝9a 2＋6a •b ＋b 2，因a ，b 均为单位向量，故a •b ＝0，即a ⊥b ，即“|a －3b |＝|3a ＋b |”是“a ⊥b ”的充分必要条件．选C ．7．在平面直角坐标系中，记d 为点P (cos θ，sin θ)到直线x －my －2＝0的距离，当θ，m 变化时，d 的最大值为A ． 1B ． 2C ． 3D ． 4【解析】因cos 2θ＋sin 2θ＝1，故 P 为单位圆上一点，而直线x －my －2＝0过点A (2，0)，故d 的最大值为OA ＋1＝2＋1＝3，选C ．8．设集合A ＝{(x ，y )| x －y ≥1，ax ＋y ＞4，x －ay ≤2}，则A ．对任意实数a ，(2，1)∈AB ．对任意实数a ，(2，1)∉AC ．当且仅当a ＜0时，(2，1)∉AD ．当且仅当a ≤32时，(2，1)∉A 【解析】若(2，1)∈A ，则a ＞32且a ≥0，即若(2，1)∈A ，则a ＞32，此命题的逆否命题为：若a ≤32，则有(2，1)∉A ，故选D ．二、填空题共6小题，每小题5分，共30分。

绝密★启用前2018年普通高等学校招生全国统一考试数学（理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

学科:网第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合A={x||x|<2}，B={–2，0，1，2}，则A B=（A）{0，1} （B）{–1，0，1}（C）{–2，0，1，2} （D）{–1，0，1，2}（2）在复平面内，复数11i的共轭复数对应的点位于（A）第一象限（B）第二象限（C）第三象限（D）第四象限（3）执行如图所示的程序框图，输出的s值为（A）12（B）56（C）76（D）712（4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于f ，则第八个单音的频率为（A （B（C ）（D ）（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ）1 （B ）2 （C ）3（D ）4（6）设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件（7）在平面直角坐标系中，记d 为点P （cos θ，sin θ）到直线20x my --=的距离，当θ，m 变化时，d 的最大值为 （A ）1 （B ）2 （C ）3（D ）4（8）设集合{(,)|1,4,2},A x y x y ax y x ay =-≥+>-≤则 （A ）对任意实数a ，(2,1)A ∈（B ）对任意实数a ，（2，1）A ∉（C ）当且仅当a <0时，（2，1）A ∉ （D ）当且仅当32a ≤时，（2，1）A ∉ 第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

2018年普通高等学校招生全国统一考试数 学（理）（卷）一．选择题（共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项）1．已知集合{}|2A x x =<，{}2,0,1,2B =-，则AB =（ ）（A ）{}0,1 （B ）{}1,0,1- （C ）{}2,0,1,2- （D ）{}1,0,1,2-2．在复平面，复数11i-的共轭复数对应的点位于（ ） （A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限3．执行如图所示的程序框图，输出的s 值为（ ） （A ）12 （B ）56 （C ）76 （D ）7124．“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献。

十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122。

若第一个单音的频率为f ，则第八个单音的频率为（ ） （A ）32f （B ）322f （C ）1252f （D ）1272f5．某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（ ）（A ）1 （B ）2 （C ）3 （D ）46．设,a b 均为单位向量，则“|3||3|a b a b -=+”是“a b ⊥”的（ ） （A ）充分不必要条件 （B ）必要不充分条件（C ）充分必要条件 （D ）既不充分也不必要条件7．在平面直角坐标系中，记d 为点()cos ,sin P θθ到直线20x my --=的距离，当,m θ变化时，d 的最大值为（ ） （A ）1 （B ）2 （C ） 3 （D ）48．设集合(){},|1,4,2A x y x y ax y x ay =-≥+>-≤，则（ ）（A ）对任意实数a ，()2,1A ∈ （B ）对任意实数a ，()2,1A ∉（C ）当且仅当0a <时，()2,1A ∉ （D ）当且仅当32a ≤时，()2,1A ∉ 二．填空题（共6小题，每小题5分，共30分）9．设{}n a 是等差数列，且13a =，2536a a +=，则{}n a 的通项公式为__________。

绝密★启用前2018年普通高等学校招生全国统一考试数学(理）（北京卷）本试卷共5页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效.考试结束后，将本试卷和答题卡一并交回。

学科：网第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中,选出符合题目要求的一项。

（1）已知集合A={x|｜x｜〈2｝，B=｛–2，0，1，2｝，则A B=（A）｛0,1} (B)｛–1，0，1｝（C）｛–2，0,1,2｝（D）{–1，0，1，2｝（2）在复平面内,复数11i的共轭复数对应的点位于（A）第一象限（B)第二象限（C)第三象限（D）第四象限（3）执行如图所示的程序框图，输出的s值为（A）12（B）56（C)76（D）712(4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于122．若第一个单音的频率为f ，则第八个单音的频率为 （A)32f （B ）322f （C ）1252f（D ）1272f（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ）1 （B ）2 （C ）3（D ）4（6）设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的 （A)充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件(D ）既不充分也不必要条件（7）在平面直角坐标系中,记d 为点P （cos θ，sin θ)到直线20x my --=的距离，当θ，m 变化时，d 的最大值为 （A)1 （B)2 （C ）3（D ）4（8）设集合{(,)|1,4,2},A x y x y ax y x ay =-≥+>-≤则 （A)对任意实数a ,(2,1)A ∈（B ）对任意实数a ,（2，1）A ∉（C ）当且仅当a <0时，（2,1）A ∉ （D ）当且仅当32a ≤时，（2，1)A ∉ 第二部分(非选择题 共110分）二、填空题共6小题,每小题5分，共30分。

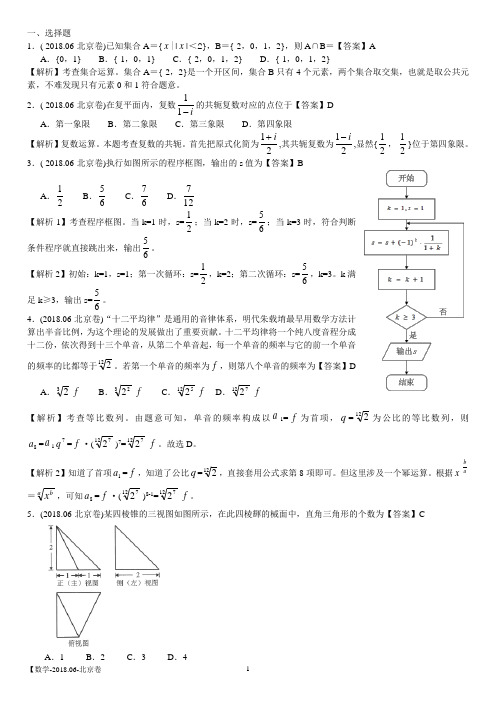
一、选择题1．( 2018.06-北京卷)已知集合A ＝{x |Ιx Ι＜2}，B ＝{-2，0，1，2}，则A ∩B ＝【答案】A A ．{0，1} B ．{-1，0，1} C ．{-2，0，1，2} D ．{-1，0，1，2}【解析】考查集合运算。

集合A ＝{-2，2}是一个开区间，集合B 只有4个元素，两个集合取交集，也就是取公共元素，不难发现只有元素0和1符合题意。

2．( 2018.06-北京卷)在复平面内，复数i-11的共轭复数对应的点位于【答案】D A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 【解析】复数运算。

本题考查复数的共轭。

首先把原式化简为21i +,其共轭复数为21i -,显然{21，-21}位于第四象限。

3．( 2018.06-北京卷)执行如图所示的程序框图，输出的s 值为【答案】BA ．21 B ．65 C ．67 D ．127 【解析1】考查程序框图。

当k=1时，s=21；当k=2时，s=65；当k=3时，符合判断条件程序就直接跳出来，输出65。

【解析2】初始：k=1，s=1；第一次循环：s=21，k=2；第二次循环：s=65，k=3。

k 满足k ≥3，输出s=65。

4．(2018.06-北京卷)“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献。

十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于122。

若第一个单音的频率为f ，则第八个单音的频率为【答案】D A ．32f B ．322f C ．1252f D ．1272f【解析】考查等比数列。

由题意可知，单音的频率构成以a 1=f 为首项，q =122为公比的等比数列，则8a =a 17q =f ²(1272)7=1272f 。

故选D 。

【解析2】知道了首项1a =f ，知道了公比q =122，直接套用公式求第8项即可。

绝密★启用前2018 年普通高等学校招生全国统一考试（北京卷）数学（理）本试卷共 150 分。

考试时长 120 分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题共40分）一、选择题共 8 小题，每小题 5 分，共 40 分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合A={x||x|<2}，B={–2，0，1，2}，则A B=（A）{0，1} （B）{–1，0，1}（C）{–2，0，1，2} （D）{–1，0，1，2}（2）在复平面内，复数1的共轭复数对应的点位于1 i（A）第一象限（B）第二象限（C）第三象限（D）第四象限（3）执行如图所示的程序框图，输出的s值为1577 （A）2（B）6（C）6（D）12（4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献．十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于 122 ．若第一个单音的频率为 f ，则第八个单音的频率为（A ） 32 f （B ）3 22f（C ）1225f（D ） 1227f（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（A ）1 （B ）2（C ）3（D ）4 （6）设 a ，b 均为单位向量，则“ a 3b 3a b”是“a ⊥b ”的（A ）充分而不必要条件（B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件（7）在平面直角坐标系中，记 d 为点 P （cos θ，sin θ）到直线 x my 2 0 的距离，当θ，m变化时，d 的最大值为（A ）1 （B ）2 （C ）3（D ）4（ ）设集合 A {(x , y ) | x y 1, ax y 4, x ay 2}, 则8 （ ）对任意实数 a ， (2,1) A （ ）对任意实数 a ，（，）AB2 1A （C ）当且仅当 a <0 时，（2，1） A（D ）当且仅当 a 3时，（2，1） A2第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。