基于时间序列分析的地表沉降数据分析处理

施工中的沉降观测与数据分析处理流程一、背景介绍在城市建设和基础设施建设的过程中，地面的沉降问题是一个常见的挑战。

沉降对建筑物和地下管线的稳定性和安全性有着重要影响，因此，在施工过程中对沉降进行观测和数据分析处理是至关重要的。

二、沉降观测的方法为了准确监测地面沉降情况，一般采用测点布设的方式进行观测。

常用的观测方法包括测点设置、仪器选择和数据采集等。

1. 测点设置首先，需要根据实际情况确定测点的布设范围和数量。

一般来说，测点应布置在建筑物或工程附近的地面上，以便实时监测地面沉降的变化。

测点的位置和数量应根据工程规模和地质条件进行合理选择。

2. 仪器选择根据沉降观测的需要，需要选择合适的仪器设备进行监测。

目前，常用的仪器包括测量仪器、自动化监测设备和全站仪等。

根据具体情况选择合适的仪器设备，以确保观测数据的准确性和稳定性。

3. 数据采集观测过程中，需要定期采集沉降数据。

为了保证数据的准确性，需要按照预定的时间间隔进行数据采集，并在数据采集后进行及时的记录和备份。

三、沉降数据的处理方法沉降观测结束后，需要对采集到的数据进行处理和分析。

这一步骤旨在分析地面沉降的变化趋势和规律，并提供相关参考数据。

1. 数据清洗在进行数据处理之前，需要对采集到的数据进行清洗，包括数据的筛选和去除异常值等。

在清洗过程中，需要注意保留关键数据，以便后续的分析和处理。

2. 数据分析通过对清洗后的数据进行分析，可以得到地面沉降的变化趋势和规律。

常用的分析方法包括统计分析、图表分析和回归分析等。

通过这些方法，可以获取各个测点的沉降速度、沉降趋势和沉降规律等重要参数。

3. 结果解读根据数据分析的结果，可以对地面沉降情况进行解读。

解读过程中，需要结合实际情况和工程要求，对沉降的影响程度和可能的风险进行评估和预测。

四、沉降观测与工程管理的关系沉降观测和数据处理在工程管理中起到重要的作用。

通过对地面沉降进行监测和分析，可以提前发现潜在的问题，及时采取措施进行调整和修复，从而确保工程的稳定性和安全性。

测绘技术地表沉陷监测方法与数据处理技巧地球的表面是一个复杂且动态的系统，不同地区的地表沉陷问题一直是我们关注的焦点。

地表沉陷不仅会给人们的生活和财产安全带来威胁，还会对环境和生态系统造成严重影响。

因此，准确监测和及时处理地表沉陷问题显得尤为重要。

在这篇文章中，我们将介绍一些测绘技术地表沉陷监测方法和数据处理技巧。

第一部分：测绘技术地表沉陷监测方法1. 卫星测量技术卫星测量技术是一种常用且有效的测绘技术，可以用来监测地表沉陷。

通过卫星遥感，我们可以获取大范围、高分辨率的地表形变数据。

卫星测量技术的优势在于覆盖范围大，时间分辨率高，可以实时监测地表沉陷情况。

同时，卫星测量技术还可以提供三维形变场信息，帮助我们深入了解地表沉陷的特征和机制。

2. 激光雷达技术激光雷达技术是一种近年来快速发展的测绘技术，被广泛应用于地表沉陷监测。

激光雷达可以通过发射激光脉冲并记录反射回来的时间来计算距离，进而获取地表形变信息。

与传统测量技术相比，激光雷达技术具有高精度、高效率、非接触等优点。

而且，激光雷达可以在夜晚和恶劣天气条件下进行测量，适用范围更广。

第二部分：地表沉陷数据处理技巧1. 数据预处理在进行地表沉陷数据处理之前，首先需要对原始数据进行预处理。

这包括去除噪声、补偿系统误差、检查和修复数据缺失等步骤。

数据预处理的目标是保证数据质量和准确性，为后续分析和处理提供可靠的基础。

2. 数据分析与建模地表沉陷数据的分析和建模是理解和解释地表沉陷机制的关键步骤。

通过对时间序列数据的分析，我们可以探索地表沉陷的特征、趋势和周期性。

同时，基于观测数据，可以建立数学模型来模拟地表沉陷的过程和机制。

地表沉陷数据的分析和建模可以帮助我们更好地理解地表沉陷的原因以及对策制定。

3. 数据可视化与结果呈现地表沉陷数据的可视化和结果呈现是将复杂数据转化为直观、易于理解的形式的重要手段。

通过绘制时空图、变形云图和等值面图等，可以直观地展示地表沉降的空间分布和变化趋势。

基于时序InSAR技术的常州市地面沉降监测与分析种亚辉;董少春;胡欢【摘要】城市地面沉降不仅会对居民生命安全造成影响,而且也会给当地的社会经济造成损失.常州市位于长江三角洲地面沉降区,也是我国经济最发达的地区之一.因此地面沉降监测是常州市掌握地面沉降的动态,为防灾减灾提供决策依据的重要举措.本文采用SBAS InSAR方法对2012-2013年23景TerraSAR-X高分辨率雷达影像数据进行了地表形变的反演,获取了该时间段常州地区年均沉降速率和时序地表累积形变图.结果表明,在整个观测期间,常州市呈现出\"全区基本保持稳定,武进区局部沉降严重\"的特点.为此,我们利用PS-InSAR技术对武进区的地面沉降进行了重点监测,发现该区多条重要交通线路存在不同程度的地面沉降.最后我们结合历史监测结果和水文地质背景,揭示了常州地区近50年地面沉降的时空变化特征和规律.综合分析表明,地下水全面禁采后研究区地面沉降的确得到了有效控制,沉降速率减缓,甚至出现了回弹.而武进地区的地面沉降虽然也在减缓,但仍然存在明显的地面沉降,一些重要交通线路的周边沉降已超过安全阈值,有必要在常规监测的同时,对这些沉降严重的区域进行重点监测,并建立预警预报机制,在城市基础设施选址和规划时提供决策依据.【期刊名称】《高校地质学报》【年(卷),期】2019(025)001【总页数】13页(P131-143)【关键词】地面沉降;小基线集方法;永久散射体方法;TerraSAR-X;道路精细监测;常州【作者】种亚辉;董少春;胡欢【作者单位】南京大学地球科学与工程学院,南京210023;南京大学地球科学与工程学院,南京210023;南京大学地球科学与工程学院,南京210023【正文语种】中文【中图分类】P2371 引言地面沉降是一种可由多种因素引起的地面标高缓慢降低的环境地质现象，严重时会成为一种地质灾害（薛禹群等，2003）。

时间序列 AR(p) 模型在沉降监测数据处理中的应用摘要：进入21世纪以来，我国加快了城市化进程，给人民生活带来了便利。

同时，近年来由于工程施工引起的地表沉降灾害也层出不穷。

随着变形监测技术的不断发展，现在已有很多的沉降监测预测模型。

本文以厦门第二西通道A3标基坑沉降监测工程为例，介绍了时间序列模型的基本原理，采用AR(p)模型进行沉降分析，分析模型的精度与适用度，可以为工程施工阶段的变形监测提供较为可靠和准确的信息，为后期设计与维护提供参考。

关键词：沉降监测；时间序列模型；AR(p)模型一、引言随着我国建设事业的快速发展，高频率的工程建设中使得地表承受能力逐渐下降，各种地表沉降灾害渐渐出现。

变形监测采取的办法主要是通过连续同周期的监测，得到实时准确的监测数据，并在数据处理后进行准确分析与判断，进而建立最适合的预测模型对沉降进行较为合理的预测。

通过预测提前获知危险沉降区域从而采取预防措施，可以提前防止沉降灾害的发生。

随着变形监测技术的不断发展，现在已有很多的沉降监测预测模型。

在这些预测模型中，沉降监测中使用较多的预测模型包括：灰色系统、线性回归与时间序列模型等。

本文主要是以厦门第二西通道工程A3标明挖I-1基坑为研究对象，先介绍了时间序列模型的基本建模流程，利用实际数据，结合时间序列模型中的AR（p）自回归模型确定函数模型，对实测数据进行分析，判断其沉降趋势，并对模型的精度进行分析，通过模拟并预测变形发展趋势，为工程施工阶段的变形监测提供较为可靠和准确的参考。

二、时间序列AR（p）的建立时间序列是一种依据时间发展，运用动态统计进行分析与预测的方法。

具体来说指通过随机过程理论与一定的数学统计法，预测事物将来的发展，可以有效解决现实生活生产问题。

时间序列分析主要是从单个的时间变量形成的序列，进行微分方程的建立，从而得到形变趋势项，然后采取自回归模型(AR模型）进行模型构造。

在时间序列的理论和科技一直发展和改进，及各类学科不同行业的相互深入与交叉，航天工程、军事建设及工农业等诸多领域应用，随着时代变化发展，该模型的越来越受到人们的重视，得到不同行业科研工作者越来越多的关注。

用时间序列分析法进行建筑物沉降观测数据处理的研究摘要：时间序列方法分析已经被广泛的运用在建筑沉降观测数据的处理过程中，实现对建筑物的沉降检测工作。

通过这项新技术的运用和处理有效的对沉降趋势进行科学化的预测和监控，提高了建筑沉降监测系统的工作效率，促进了动态沉降预测模型的建立和运行。

为选择科学的解决办法而做好充分的准备。

其中需要注意的是必须将沉降的总量控制在一定的范围内，确保其能正常的投入到工作中去，本文主要对几种主要的时间序列分析方法的形式和功能进行研究和分析。

关键字：时间序列；建筑沉降；数据处理；观测我国改革开发政策的实行带动着我国的经济发展不断进步和增长，在城市化的进程中，高层建筑成为城市发展的标志，具有现代化经济增长的象征意义。

在地基上建设高层建筑的发展趋势就对土层的负载承受提出了更高的要求，为了实现建筑的安全施工和建设必须将预防建筑物基础的沉降和倾斜作为重点的建设项目。

将沉降的观测数据处理的系统模型充分的运用在建筑物的施工中去，以便为建筑施工提供科学、准确的动态数据，出现异常，及时预警，从而确保建筑施工安全，根据这些数据再进行基础的地基处理方法的研究和设计，确保地基的沉降总量在一个规定的范围内。

一、时序分析法的概念在动态的领域研究中，时间序列分析法被广泛的运用在动态模型的数据建设中，通过多数据模型的科学分析来有效地判断，全面的掌握数据内部的结构特征和性能。

时间序列法的工作主要是针对固定时间内，连续变化数字之间的动态关系分析，在研究的对象中这些动态数字是普遍存在的，由于观测的数据形式背景存在差异，其具体的信息内容和所呈现的规律也不相同，造成人们的认识也存在一定的偏差，对于目前建筑陈沉降中的具体应用以自回归模型展开。

为了在有限的时间内，高效的解决动态数据处理并保证结果的精确，时序分析法就成为实现这项目的的科学分析方法，因为具备这样显著的特征而被工程和自然领域中广泛应用。

基于建筑物的沉降检测序列具有动态的特征，需要结合实例来具体分析时序分析法的作用和工作原理，以对同一检测项的观测序列来进行数据处理的模式开展工作，通过数学的表达式来反映检测项目的变化特征和趋势以及它们之间的数学关系。

SAR技术探讨地面沉降的监测与分析随着城市化进程的加剧，地面沉降已经成为一项日益引起人们关注的问题。

地面沉降不仅对城市建设和基础设施的稳定性造成影响，还可能导致房屋倾斜、管道爆裂等严重后果。

为了及时监测和分析地面沉降情况，科研人员提出了利用合成孔径雷达（SAR）技术进行地面沉降监测和分析的方法。

在利用SAR技术进行地面沉降监测和分析时，首先需要获取地表的SAR影像数据。

通过对时间序列的SAR影像数据进行处理，可以提取地面沉降的变化信息。

一般来说，地面沉降会引起地面物体的形变，这种形变会导致SAR影像中物体的相位差异。

通过相位差异的计算和分析，可以得到地面沉降的具体数据，比如沉降的速率、沉降的范围等。

在地面沉降监测中，除了利用SAR影像数据进行分析外，还可以结合地面监测数据进行综合分析。

比如，可以利用地面GPS监测站、地基雷达测量设备等设备获取地面变形的实时数据，然后与SAR影像数据进行对比，验证SAR技术监测结果的准确性。

另外，还可以利用地面观测数据进行地面沉降的趋势分析，预测未来的沉降情况。

在地面沉降分析中，需要考虑多种因素的影响。

比如，地质结构、地下水位、人类活动等因素都可能导致地面沉降。

通过结合这些因素，可以更准确地分析地面沉降的原因和机制。

在城市建设和规划中，也需要考虑地面沉降的影响因素，采取相应的措施避免地面沉降引起的问题。

通过利用SAR技术进行地面沉降的监测和分析，可以实现对地面沉降情况的实时监测和准确分析，为城市建设和基础设施的稳定性提供重要的数据支持。

未来随着技术的不断发展，SAR技术将在地面沉降监测和分析中发挥更重要的作用，为解决地面沉降问题提供更科学、更有效的方法。

基于时间序列分析的沉降数据的处理与分析孙鹏，张康康，马喜芳（山东科技大学泰安校区，泰安，271000）摘要：本文结合济南国奥城4#楼的沉降数据，介绍了时间序列分析对变形监测的数据拟合和预测具有良好的效果,能精确地反映监测点的变化规律。

关键词：时间序列分析；变形监测；ARMA 模型；AR 模型；变形预测众所周知，变形无处不在，对人的影响也是无处不在。

为此，需要对变形体进行变形监测。

通过在变形体上埋设监测点，通过重复观测获取一系列的包含变形信息的观测数据,通过对这些数据的处理、分析,才能获得变形体的形变信息。

时序分析法作为一种动态分析法,通过对同一监测项的平稳观测序列进行数据处理,找出监测项的变化特征、变化趋势,用某一代数式去描述监测序列前后之间的数学关系,进而利用这一关系式对未来某一时刻的监测值进行预报,为工程建设的可行性评估、施工,后期营运提供数据证材。

1 时间序列分析模型1.1 时间序列的类型最常用的时间序列是ARMA(Autorgressive Moving Average)序列，其特殊情况为AR(n ）序列和MA(m)序列。

用ARMA 模型去近似地描述动态数据在实际应用中有许多优点,例如它是线性模型，只要给出少量参数就可完全确定模型形式；另外,便于分析数据的结构和内在性质，也便于在最小方差意义下进行最佳预测和控制。

1.1.1 平稳自回归模型 [1]t p t p t t t a x x x x ++++=---ϕϕϕ 2211 （1）设 }{t x 是平稳时间序列，}{t a 是白噪声系列，式（1）称为p 阶平稳自回归模型，记作AR （p ）。

1.1.2 可逆滑动平均模型 [1]q t q t t t t a a a a x -------=θθθ 2211 （2）设}{t x 是平稳零均值时间序列，}{t a 是白噪声系列，式（2）为q 阶滑动平均模型，记作MA （q ）。

1.1.3 自回归滑动平均混合模型 [1]以上两种模型的综合，即为q t q t t t p t p t t t a a a a x x x x ----------=----θθθϕϕϕ 22112211 (3) 其中(1)j j p ϕ≤≤和(1)j j q θ≤≤为实参数，t a 是满足条件的白噪声。

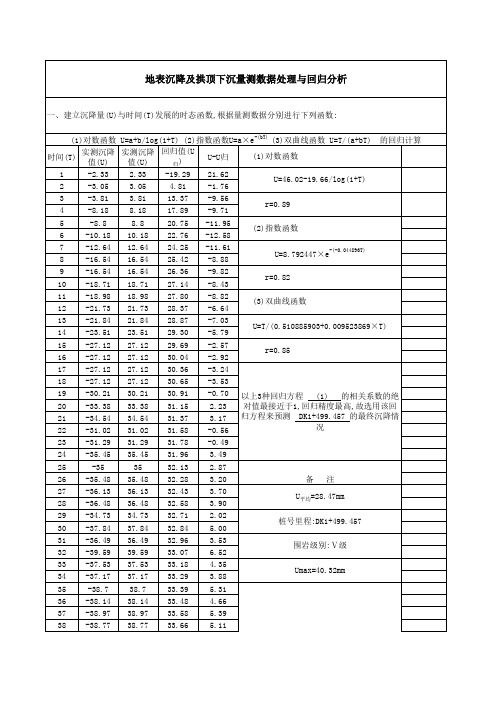
区域地面沉降监测及数据处理分析作者：王文生来源：《华夏地理中文版》2015年第06期摘要：文章详细介绍了区域地面沉降监测及数据处理，并依据等值线图对该区域地面沉降情况进行了分析，提出了对地面沉降监测的技术改进方法。

关键词：地面沉降；数据处理；数据分析；沉降分析地面沉降监测属于变形监测的范畴，通常采用的方法大致有高精度水准测量、GPS观测、精密全站仪三角高程测量等。

本文采用某区域地面沉降监测2010-2013年连续四年的实测数据，对该区域地面沉降情况进行分析，并提出了对地面沉降监测的技术改进方法。

一、沉降点布设和观测方法（一）沉降点布设某区域地面沉降监测共布设监测点86个，均匀分布在A、B、C、D区，控制面积约200平方公里，监测点利用C级点9个，利用旧水准点11，其余66个为新埋设。

起算点是两个相对稳定的国家一等基岩点，分别位于该区域的东西两侧，该位置符合二等水准网形的基本要求。

如图1所示。

（二）观测方法该区域的地面沉降监测采用国家二等水准观测方法，观测过程中的所有限差均符合国家二等水准的观测要求。

观测使用DINI03电子水准仪配合条码式因瓦标尺。

测站观测顺序：奇数站：后—前—前—后偶数站：前—后—后—前每測段均采用往返测观测。

观测尽量在观测条件较好时进行。

主要技术指标限差执行二等水准规范。

（三）数据处理数据处理时，按要求应对观测高差进行下列改正：1.水准标尺长度改正。

δ=f×h式中：δ—改正数（mm）；f—标尺改正系数（mm/ m）；h—往测或返测高差（m）。

2.正常水准面不平行改正。

ε=-（γi+1-γi）·Hm/γm式中：γm—两水准点正常重力平均值，10-5m/s2；γi.γi+1—分别为i点、i+1点椭球面上的正常重力值，10-5m/s2；Hm—两水准点概略高程平均值，单位为米（m）。

γm=（γi+γm+1）/2-0.154 3Hmγ=978 032（1+0.005 302 4sin2φ-0.000 005 8sin22φ）式中：φ—水准点纬度，γ值取至0.01×10-5m/ s2.3.环线闭合差改正（在水准平差程序里进行）。

基于时序InSAR技术的兰州市地表沉降监测与分析基于时序InSAR技术的兰州市地表沉降监测与分析摘要：地表沉降是由于自然和人为因素引起的地表向下的相对移动。

它是城市发展中普遍存在的问题之一，需要及时监测和分析，以便采取相应的措施进行修复和防控。

本文以兰州市为研究对象，利用时序InSAR技术对地表沉降进行监测与分析。

通过对遥感影像的处理和分析，得出了兰州市地表沉降的时空变化规律，并针对不同行政区域的沉降情况进行了对比分析。

研究结果表明，兰州市地表沉降主要集中在市区和其周边地区，且呈现出逐年加剧的趋势。

本研究为兰州市地表沉降的监测与修复提供了理论依据和参考。

关键词：地表沉降；时序InSAR技术；兰州市；监测；分析1. 引言兰州市位于中国西北地区，是甘肃省的省会城市。

近年来，随着城市的快速发展和人口的增加，地下水的不合理开采、地质构造和工程施工等因素导致了该地区地表沉降问题的加剧。

地表沉降会引发多种问题，包括地下管道破裂、建筑物倾斜、地面裂缝等，严重影响到城市的正常运行和居民的生活质量。

因此，及时监测和分析地表沉降的情况对于采取相应的治理和修复措施至关重要。

2. 数据和方法本研究采用时序InSAR技术对兰州市地表沉降进行监测与分析。

时序InSAR技术是一种利用合成孔径雷达干涉测量技术观测地表沉降的方法，具有高精度、高时空分辨率等优点。

本研究使用了ALOS、SENTINEL等多源遥感卫星影像数据，并应用SARscape软件进行相关处理和分析。

3. 结果与分析通过对时序InSAR数据的处理和分析，得出了兰州市地表沉降的时空变化规律。

研究结果显示，兰州市地表沉降主要集中在市区和其周边地区，且呈现出逐年加剧的趋势。

兰州市中心区域的地表沉降速率达到了每年10毫米以上，而市郊地区的地表沉降速率也超过了每年5毫米，远远超过了国家标准规定的安全范围。

4. 沉降原因分析通过对兰州市地表沉降原因的分析，主要包括自然因素和人为因素。

如何进行地表沉降监测数据分析与预测地表沉降是指由于地下水开采、地下排水、地下工程施工等原因引起的地表或地质体的下沉现象。

在城市化进程中，随着城市建设规模的扩大，地表沉降的问题越来越突出。

因此，进行地表沉降监测数据分析与预测，对于保障城市建设的安全和可持续发展具有重要意义。

本文将从数据收集、数据分析和预测模型建立三个方面进行探讨。

一、数据收集进行地表沉降监测数据的分析与预测，首先要收集相关的监测数据。

通常，地表沉降监测数据可以通过地面测量、遥感技术、卫星测量等多种手段获取。

其中，地面测量是常用的方法之一，包括全站仪、GPS等测量仪器。

此外，地表沉降的监测数据还可以通过地下水位观测井、沉降观测点等进行采集。

数据收集的过程中需要注意数据的准确性和完整性，确保数据的可靠性。

二、数据分析在进行地表沉降监测数据分析时，首先要进行数据的处理与清洗。

数据的处理包括数据缺失值的填充、异常值的排除等，以确保数据的完整性和准确性。

然后，可以利用统计学方法对数据进行分析，如计算数据的平均值、方差、标准差等，从中得到数据的特征和趋势。

此外，还可以使用地统计分析方法，探索数据的空间分布特点。

例如，通过空间插值方法将有限的监测点的数据推算到整个区域上，以获取更为全面的数据分析结果。

三、预测模型建立为了进行地表沉降的预测，可以根据历史的监测数据建立预测模型。

根据不同的情况，可以选择合适的模型，如趋势分析模型、回归模型等。

其中，趋势分析模型可以用来描述地表沉降的发展趋势，通过对历史数据的分析，可以预测未来一段时间内地表沉降的变化情况。

回归模型可以用来研究地表沉降与相关因素（如地下水开采量、地下排水量等）之间的关系，从而预测未来地表沉降的可能变化。

在进行地表沉降监测数据分析与预测时，还需要考虑一些其他因素。

首先，要考虑数据的时间尺度，根据具体情况选择合适的时间尺度进行分析与预测。

其次，要考虑地表沉降与其他地质灾害（如地震、地裂缝等）的关系，以综合考虑地质灾害的整体风险。

了解测绘技术中的地表沉降监测与分析方法地表沉降是指地下水开采、地下矿井开采、地下空腔涌湖以及地下水位变化等因素导致的地表下陷现象。

地表沉降对城市规划、土地利用以及基础设施建设等方面有着重要的影响。

为了及时掌握地表沉降的情况，科学家们开发出了一系列测绘技术中的地表沉降监测与分析方法。

一、遥感技术遥感技术是通过卫星、飞机等载体获取地表信息的一种技术。

在地表沉降监测中，遥感技术可以通过获取地表高程的变化来间接反映出地表沉降的情况。

遥感技术在地表沉降监测中的应用主要有以下几个方面：1. 激光雷达遥感技术：利用激光束与地表的反射和散射特性，可以获取地表的三维坐标信息，从而实现对地表沉降的监测与分析。

2. 合成孔径雷达遥感技术：通过合成孔径雷达的高分辨率成像能力，可以获取地表形变信息，进而推测地表沉降的情况。

3. 热红外遥感技术：热红外遥感技术可以通过测量地表的辐射温度来推测地表沉降的情况。

地表沉降导致地下水位下降后，地下水的上升速度会减缓，从而导致地表温度的降低。

利用热红外遥感技术，可以通过测量地表温度的变化来推测地表沉降的情况。

二、测量仪器技术测量仪器技术是直接测量地表沉降的一种方法。

常用的测量仪器包括全站仪、水准仪、GNSS等。

1. 全站仪：全站仪是一种测量仪器，可以通过测量地表的高程变化来推测地表沉降的情况。

全站仪通过测量地表上若干点的坐标高程，并将其与基准点的坐标高程进行比较来判断地表是否发生沉降。

2. 水准仪：水准仪是一种测量仪器，可以通过测量地表的高程变化来推测地表沉降的情况。

水准仪通过测量水准点的高程，并将其与基准点的高程进行比较来判断地表是否发生沉降。

3. GNSS：全球卫星定位系统（GNSS）是一种通过卫星信号获取地表坐标信息的技术。

通过在地表上布设多个GNSS接收器，可以实现对地表的实时监测与分析，从而判断地表是否发生沉降。

三、数学模型与分析方法除了遥感技术和测量仪器技术，数学模型与分析方法也是地表沉降监测与分析的重要手段。

地基沉降监测数据分析地基沉降是建筑工程中一个重要的技术指标，它直接关系到建筑物的安全性和使用寿命。

地基沉降监测数据的分析对于及时发现和解决地基沉降问题至关重要。

本文将通过对地基沉降监测数据进行分析，探讨其中的规律和相关因素，为工程项目提供科学的依据。

地基沉降数据搜集在建筑工程中，通常会通过在地基部位设置测点来进行地基沉降监测。

通过定期对这些测点数据进行采集和记录，将得到一系列地基沉降监测数据。

这些数据包括沉降量、沉降速率等指标，同时也可以获得不同季节、不同阶段的数据，为后续的分析提供数据基础。

地基沉降数据分析方法地基沉降数据一般呈现出曲线状的变化趋势，通过绘制变化曲线可以更直观地反映地基沉降的情况。

在分析地基沉降数据时，可以采用统计学方法，如均值、方差、标准差等指标，对数据进行描述性统计分析；同时也可以应用回归分析、时间序列分析等方法，从不同角度研究地基沉降的成因和规律。

地基沉降数据分析结果通过对地基沉降监测数据的分析，我们可以得出不同地点、不同时间段地基沉降的情况。

根据分析结果，可以评估地基沉降的速率、趋势和变化规律，判断是否存在异常情况和危险性。

同时还可以识别影响地基沉降的因素，如地质条件、地下水位等，为后续的工程设计和施工提供重要参考。

地基沉降数据分析应用地基沉降数据的分析可以应用于建筑工程的多个阶段，包括工程设计、施工监测和工程验收等环节。

通过对地基沉降监测数据的分析，可以及时发现问题、预测趋势，采取有效措施，保障建筑物的安全性和稳定性。

同时在工程验收阶段，地基沉降数据的分析也是判断工程质量和可靠性的重要依据。

结论地基沉降监测数据的分析是建筑工程中不可或缺的一环，通过科学的数据统计和分析，可以全面了解地基沉降的情况和规律，及时发现问题、预防风险，确保建筑物的安全性和可持续性发展。

希望通过本文的介绍和分析，能够对大家有所启发，提升对地基沉降数据分析的认识和应用能力。

如何进行地面形变监测和沉降观测的数据处理随着城市建设的不断发展和地质灾害的频繁发生，地面形变监测和沉降观测的重要性在日益凸显。

这项工作的核心在于对所采集到的数据进行合理有效的处理和分析，以便更好地了解地下结构的变化及其对土地利用和人类活动的影响。

本文将探讨如何进行地面形变监测和沉降观测的数据处理。

首先，数据处理的第一步是数据的预处理。

这意味着对原始数据进行噪声滤波和异常值剔除，以确保数据的准确性和可靠性。

噪声滤波是为了去除掉由于仪器误差或环境影响而引入的随机误差，使数据更加平滑和稳定。

异常值剔除则是为了排除掉可能由于系统故障或其他外部因素导致的数据异常，以免影响后续的分析结果。

其次，数据处理的第二步是数据的校正和校准。

在进行形变监测和沉降观测过程中，常常会遇到基准面的参考问题。

因此，需要对采集到的数据进行基准面的校正，以确保数据的可比性和一致性。

校正可以通过采集与基准面相关的参考点数据，并进行数学模型拟合和转换，从而实现对数据的校正。

另外，数据还需要进行时间校准，以解决数据采集的时间差异带来的问题，确保数据在时间序列上的连续性和可比性。

然后，在数据处理的第三步中，可以根据具体的研究目的和需求，选择合适的统计方法和模型对数据进行分析。

对于形变监测数据，常见的分析方法包括波动性分析、周期性分析和趋势分析等。

波动性分析可以帮助我们了解形变数据的波动情况和变化规律，周期性分析可以揭示数据中存在的周期性变化，而趋势分析则可以探究形变数据的整体变化趋势。

对于沉降观测数据，常见的分析方法包括累积沉降分析、速率分析和区域沉降分析等。

累积沉降分析可以帮助我们了解土地沉降的累积情况，速率分析可以计算出土地沉降的速率和变化率，而区域沉降分析则可以揭示不同地区土地沉降的空间分布。

最后，数据处理的第四步是结果的可视化和解释。

通过选择合适的图表和图形工具，将处理和分析后的数据结果进行可视化展示，以便更好地传达研究结论和发现。

用时间序列分析法进行建筑物沉降观测数据处理的探讨摘要：沉降观测是保证建筑物安全性、正常使用寿命的重要手段，高效正确的处理沉降观测数据至关重要。

因此，本文根据近几年来所观测过的不同建筑物的沉降观测实际经验，从不同角度入手客观探讨了时间序列分析法及其在建筑物沉降观测数据处理中的应用，在发挥时间序列分析法作用过程中保证处理质量，最大化提高建筑物沉降观测数据准确度与全面性。

关键词：时间序列分析法；建筑物；沉降观测；数据分析；探讨近年来，在现代化发展背景下，民用以及工业建筑工程建设频繁增加，尤其是高层建筑的大规模建设，深基坑工程也越来越多，建筑物安全问题日渐成为社会大众关注的焦点。

沉降观测是检查建筑工程质量的一大关键性依据，数据处理又是沉降观测工作开展中不可或缺的重要环节，在联系建筑物建设实际的基础上科学运用时间序列分析法，精准、快速、高效处理建筑物沉降观测中产生的海量数据，了解建筑物不同部位沉降变形具体情况，将其有效控制在允许范围内。

一、时间序列分析法概述时间序列分析法就是有序地处理繁杂化、动态化的随机数据，是一种简单而有效的方法。

在处理过程中，准确把握数据具有的相关性以及有序性特点，构建适宜的模型，了解一系列数据内部结构体系、相互关系[1]，辨别、分析数据呈现的变化规律。

以“地基沉降观测”为例，在时间序列分析法作用下，不需要全方位、系统化了解各类力学因素，深入剖析其对地基沉降观测数值产生的具体影响，只需要比较、分析在观测过程中收集的一系列地基沉降数据，明确数据具有的规律，构建与之对应的模型，通过立体空间模拟数据规律曲线，预测其动态变化、发展趋势，精准分析预测结果，科学处理各类隐患问题，在优化、完善的基础上提高地基的安全系数。

二、时间序列分析法在建筑物沉降观测数据处理中的应用1、建筑物沉降观测数据处理实例以某市某建筑工程为例，以时间序列分析法为切入点，针对建筑物沉降数据处理要求、流程、关键点等，按照设计图纸及现场情况，设置10个沉降观测点，用数字1到10分别对其标号，对建筑物进行30期的沉降观测。

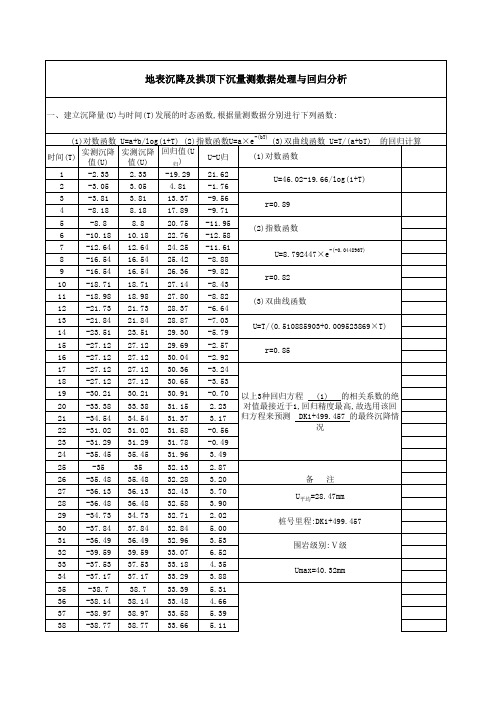
采动地表下沉时间序列的曲线拟合研究
地表下沉是指地表相对于某一基准面的位移，通常使用测站或卫星测量的高程数据来表示地表下沉的情况。

地表下沉可能由多种因素引起，包括构造活动、水文过程、岩土力学过程等。

在研究地表下沉时间序列的过程中，通常会对测量的地表下沉数据进行曲线拟合，以便于分析和理解地表下沉的规律。

曲线拟合是一种数学方法，它通过调整曲线的参数使得曲线能够尽可能地拟合数据，以便于对数据进行分析和预测。

在曲线拟合过程中，通常会使用最小二乘法或其他优化方法来调整曲线的参数，使得曲线与数据的误差最小。

常用的曲线拟合方法包括线性拟合、多项式拟合、指数拟合、对数拟合、幂函数拟合等。

根据数据的特点，可以选择合适的曲线拟合方法来进行拟合。

在研究地表下沉时间序列的过程中，可以使用曲线拟合方法来分析地表下沉的变化趋势和周期性等特点，并利用曲线拟合方法来预测地表下沉的未来变化情况。

例如，如果数据呈现出明显的线性趋势，则可以使用线性拟合方法来拟合数据，并利用拟合曲线的斜率来预测地表下沉的未来变化情况。

如果数据呈现出周期性的变化趋势，则可以使用多项式拟合或其他方法来拟合数据，并利用拟合曲线的周期性特点来预测地表下沉的未来变化情况。

在进行曲线拟合时，需要注意数据的质量和准确性，同时要考虑曲线拟合的精度和可
靠性。

此外，在利用曲线拟合结果进行预测时，也要注意曲线拟合的局限性，考虑其他可能影响地表下沉的因素，避免因忽略其他因素而导致预测结果的误差。