黄浦新王牌 春季周末小班 高中物理同步提高课程

尹JA老师小学奥数
黄浦小学培训黄浦新王牌小学补习
寒假提高班趣味奥数典型应用教学计划
课程开设目标：本次课程的开设主要是面向三年级和四年级没有奥数基础，或者之前只是短暂学习过奥数却并没有系统学习的中低年级学生。

为学生打开一面奥数神奇的大门，利用课余时间，集中训练出现频率最高的一些奥数知识点，主要分计算、应用题、几何、逻辑四大模块。

同时也是为了给春季班做一个衔接和过度，以训练思维，培养兴趣，做好过度为目的。

当然之前学习过这些知识的同学，如果当时掌握的不是特别好，也可以利用课余的时间，进行巩固和提高。

第一讲曲线与方程知识梳理1.曲线方程的概念一般地，如果曲线C 与方程()0,=y x F 之间有以下两个关系：①曲线C 上的点的坐标都是方程()0,=y x F 的解；②以方程()0,=y x F 的解为坐标的点都在曲线C 上。

则称方程()0,=y x F 是曲线C 的方程，曲线C 是方程()0,=y x F 的曲线.【析】（1）曲线本质上是点的集合，是满足某种性质的点的全体，也就是我们所说的轨迹； （2）曲线方程的概念体现了几何元素—点，与代数元素—方程之间的对应关系，关系①②两者构成曲线方程概念，缺一不可；（3）曲线方程概念建立的意义在于，使得我们得以用代数手段来研究几何问题. 2.求曲线方程的一般步骤：（1）建立坐标系；（2）设曲线上的任意一点的坐标为()y x ,；（3）根据曲线上点的坐标满足的条件列出关系等式；（4）用坐标y x ,表示这个等式，并化简；（5）证明化简后方程的解为坐标的点都在曲线上. 3.求曲线方程的一般方法：通常有“直接法”、“相关点法”、“参数法”等，后面将通过例题说明.4.曲线的交点：两条曲线()()0,,0,:211==y x F y x F C 的交点，就是方程组()()⎩⎨⎧==0,0,21y x F y x F 的解.题型示例例1、已知ABC ∆的A ∠、B ∠、C ∠的对边分别为a 、b 、c ，且c a >，a 、c 、b 三边成等差数列，2=AB ，求顶点C 的轨迹方程.例2、（1）已知ABC ∆中，90=∠C ，()0,2-A ，()4,3B ，求顶点C 的轨迹方程；（2）已知点()0,6A ，B 是曲线()1122=-+y x 上的动点，延长BA 到P ，使AB PA =，求动点P 的轨迹方程；例3、（1）在ABC ∆中，已知点()0,3A ，B 、C 在y 轴上运动，且保持2=BC ，求ABC ∆的外心轨迹方程.（2）已知A 、B 是抛物线2x y =上的两点，且满足0=⋅OB OA ，求AB 的中点轨迹方程.例4、已知直线l 经过点()2,0P ，且与圆2522=+y x 交于A 、B 两点，求AB 的中点M 的轨迹方程.例5.（1）如果两条曲线方程是()()0,,0,:211==y x F y x F C ，()00,y x P 是它们的交点，证明：对于任意常数λ，方程()()0,,21=+y x F y x F λ所表示的曲线也经过点P .（2）求经过两直线0143:,0:21=+-=-y x l y x l 的交点，并过点()1,1-P 的直线方程； （3）求经过曲线0322=-++y x y x 和03322=++y y x 的交点的直线方程.拓展练习一、填空题1、已知直线1-=ax y 与x y =2仅有一个公共点，则实数._________=a 2、若动点()y x P ,到直线2-=x 与点()0,2F 的距离相等，则P 点的轨迹方程为_______________________. 3、直线()2,0,12≠≠∈=-+a a R a aya x 与x 轴、y 轴交点的中点的轨迹方程为___________________.4、ABC ∆的顶点()()0,3,0,3B A -，顶点C 在直线5=+y x 上，则ABC ∆的重心轨迹方程为________________.5、设动直线x l ⊥轴，且与曲线1222=+y x 交于A 、B 两个点，P 是l 上满足1=⋅PB PA 的点，则点P 的轨迹方程为______________________.6、（上海08年高考题）曲线C 是平面内与两个定点()0,11-F 和()0,12F 的距离的积等于常数()12>a a 的点的轨迹，给出下列三个结论：①曲线C 过坐标原点；②曲线C 关于坐标原点对称；③若P 在曲线C 上，则21PF F ∆的面积不大于221a .其中正确命题是____________. 二、选择题1、方程()()0122=-+-xy y x 表示的曲线是（ ）A.一条直线和一条双曲线B.两条双曲线C.两个点D.以上答案都不对2、设过点()y x P ,的直线分别与x 轴的正半轴和y 轴的正半轴交于A 、B 两点，点Q 与P 关于y 轴对称，O 为坐标原点，若PA BP 2=，且1=⋅AB OQ ，则P 点轨迹方程是（ ）A.()0,0123322>>=+y x y x B.()0,0123322>>=-y x y x C.()0,0132322>>=-y x y x D.()0,0132322>>=+y x y x三、解答题1、求两条直线022:1=+-my x l 及042:2=-+m y mx l 的交点P 的轨迹方程.2、设P 是圆2522=+y x 上的动点，点D 是P 在x 轴上的投影，且PD MD 54=. （1）当P 在圆上运动时，求M 的轨迹C 的方程； （2）求过点()0,3且斜率为54的直线l 被C 所截得的线段AB 的长度.3、已知抛物线2:x y C =及直线2:-=x y l ，自C 上任意点P 作直线l 的垂线，垂足为Q ，PQ 的中点为M ，求M 的轨迹方程.4、已知与圆()()111:22=-+-y x C 相切的直线l 交x 轴、y 轴于A 、B 两点，O 为坐标原点，且a OA =，()2,2>>=b a b OB . （1）求AB 的中点轨迹方程； （2）求AOB ∆的面积的最小值.5、已知动点M 到定点()0,2-F 与定直线21-=x 的距离之比为2. （1）求动点M 的轨迹C 的方程；（2）若过点()1,0E 的直线与曲线C 在y 轴左侧交于不同的两点A 、B ，点()0,2-P 满足()PB PA PN +=21，求直线PN 在y 轴上的截距（与y 轴交点纵坐标）的取值范围.参考答案例1、以AB 为x 轴，AB 中垂线为y 轴建立坐标系，则()()0,1,0,1B A -，设()y x C ,，b c a ,, 成等差数列，c b a 2=+∴，()()4112222=+-+++∴y x y x ，化简得124322=+y x .()()222211,,y x y x b a c a ++>+-∴>∴> ，即0<x ，而C 不在x 轴上，所以2-≠x ，C ∴点轨迹方程为()2,0124322-≠<=+x x y x .（2）例2、（1）解法一：设()y x C ,，则()()4,3,,2--=+=y x BC y x AC ，0,=⋅∴⊥BC AC BC AC ，即()()()0432=-+-+y y x x ，化简得0422=--+y x y x ；解法二：C 在以AB 为直径的圆上，414522=+=AB ，圆心⎪⎭⎫⎝⎛2,21，C ∴的轨迹方程为()222241221⎪⎪⎭⎫ ⎝⎛=-+⎪⎭⎫ ⎝⎛-y x . （3）设()()00,,,y x B y x P ，A AB PA ∴=, 为PB 中点，()()1112122026220000=--+-⇒⎩⎨⎧-=-=⇒⎪⎪⎩⎪⎪⎨⎧+=+=∴y x y y x x y y x x ，即()()111222=++-y x ；例3、解法一：（直接法）设()y x P ,，则()()1,0,1,0+-y C y B ，()13,222+=+-∴=x y x PB PA ，化简得862-=x y .解法二：（参数法）设()t B ,0，则()t C +2,0，BA 中垂线方程为⎪⎭⎫⎝⎛--=-2332x t t y ，BC 的中垂线为1+=t y ，消去t 得862-=x y .例4、解法一：当AB 斜率不存在时，M 的坐标为()0,0，当AB 斜率存在时，设AB ：2+=kx y ，代入2522=+y x 并化简得()0214122=-++kx x k ，设()()2211,,,y x B y x A ，则()022122122221=-+⇒⎪⎩⎪⎨⎧+=+-=+=y y x kx y k k x x x ；解法二：设()y x M ,，()()2211,,,y x B y x A ，则()022202222525212121212121212122222121=-⋅+⇒=--⋅+++⇒⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=--+=+==+=+x y y x x x y y y y x x x y x x y y yy y x x x y x y x ，即0222=-+y y x .解法三：（定义法）M AB OM ∴⊥, 在以OP 为直径的圆上，即().1122=-+y x例4、（1）略；（2）设直线方程为()0143=-++-y x y x λ，将()1,1-P 代入得3-=λ，∴().01403143=-⇒=--+-y y x y x（3）049=-y x .拓展练习一、填空题 1、0或41-；2、x y 82=；3、()1,01≠≠=+x x y x ；4、533=+y x ； 5、3222=+y x 【析】设()()()y x P y x B t x A ,,,,,-，则()()1,,0,,022=-=⋅∴+=-=t y PB PA t y PB t y PA ，又1222=+t x ，消去t 得P 的轨迹方程为3222=+y x ； 6、②③【析】设()y x C ,，则()()2222211a y x y x =++⋅+-，①显然不对，将x -换x方程不变，②正确，221221sin 2121a PF F a S PF F ≤∠=∆，所以③正确. 二、选择题 1、C ；2、D. 三、解答题1、解法一：1l 过定点()0,2-M ，2l 过定点()0,2N ，当0≠m 时，mk 211=，m k 22-=，且2121,1l l k k ⊥∴-=⋅，设()y x P ,，则()()y x PN y x PM --=---=,2,,2，()()0222=+---∴y x x ，即422=+y x .P k ∴≠,01 不为()()24,0,222≠=+∴x y x .解法二：22+=x my ，当0=y 时2-=x ，点P 为()0,2-，当0≠y 时，yx m 22+=，代入2l 的方程得⇒=+⋅-+⋅+0222y x y x y x 422=+y x ，但2=x 时，⎩⎨⎧=-+=04442m y m my 无解，2≠∴x ，12,l l ∴的交点轨迹方程为()2422≠=+x y x .2、（1）设()()00,,,y x P y x M ，2545,45,542200=⎪⎭⎫⎝⎛+∴⎪⎩⎪⎨⎧==∴=y x y y xx PD MD ，即.1162522=+y x （2）将()354:+=x y l 代入1162522=+y x 并化简得0832=--x x ，()()()54125161221221221=-⎪⎭⎫ ⎝⎛+=-+-=x x y y x x AB .3、解法一：（参数法）设()()y x M t t P ,,,2，则()t x t y PQ --=-2:与2-=x y 联立得()()⎪⎪⎩⎪⎪⎨⎧-+=++=12112122t t y t t x Q Q ，由中点公式得⎪⎪⎩⎪⎪⎨⎧-+=++=21414321234122t t y t t x ，消去t得02106922=--+-y x y xy x .解法二：（相关点代入法）设()00,y x M ，则()00:x x y y MQ --=-与2-=x y 联立得⎪⎪⎩⎪⎪⎨⎧++-=-=+-=-=⇒⎪⎪⎩⎪⎪⎨⎧-+=++=1232112123212121121210000000000y x y y y y x x x x y x y y x x Q P Q P Q Q ，代入2x y =并化简得02106922=--+-y x y xy x .4、（1）AB 的方程为1=+b ya x ，即0=-+ab ay bx . l 与圆C 相切，122=+-+∴ba abb a ，即`()()222=--b a ，设AB 的中点为()y x M ,，则y b x a 2,2==，()()22222=--∴y x ， 即()()().1,12111>>=--y x y x （2）()()322322121+≥+-+-=-+==∆b a b a ab S AOB . 5、（1）设()y x M ,，则()122222222=-⇒=+++y x x yx ；（2）设()11,y x A 、()22,y x B ，NP 与y 轴交于()d Q ,0，设直线BA 的方程()01≠+=k kx y ，代入()1122-≤=-x y x 得()022122=---kx x k ，则()21012012018401221221222<<⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧>--=<-=+>-+=∆≠-k k x x k k x x k k k .()N PB PA PN ∴+=,21 为AB 的中点，则202210111,12k kx y k k x x x -=+=-=+=，由()()d N P k k kN ,0,0,2,11,122-⎪⎭⎫⎝⎛--三点共线得2222++-=k k d ，令()222++-=k k k f ，()k f 在()2,1上递减，()()()11222=<<-=∴f k f f ，所以.222>-<d d 或。

第一讲专题一 函数综合应用一．深刻理解函数的概念与性质函数的定义、函数的三要素（定义域、值域、对应法则）、反函数的定义及与原函数的关系、函数的四大性质（单调性、奇偶性、周期性、最值）时函数有关概念的重要内容,只有对这些概念做到准确、深刻理解，才能正确、灵活地加以运用. 例1、解答下列各题：（1）已知()()a ax x x f --=22log 是⎪⎭⎫⎝⎛-∞-21,上的减函数，则实数a 的取值范围是（ )（A ）[)+∞-,1 (B) ()+∞-,1 (C) ⎥⎦⎤⎢⎣⎡-21,1 (D) 以上答案都不对（2）设()122141+--=+x x f x x ，若()2=m f ，则().______=-m f（3）（09年山东高考题）定义在R 上的函数()f x 满足2log (1),0()(1)(2),0x x f x f x f x x -≤⎧=⎨--->⎩，则(2009)f 的值为【答】（ ）（A ）-1 (B) 0 (C) 1 (D) 2例2.函数()()()⎥⎦⎤⎢⎣⎡+-+-=2111log 22x a x a x f .（1）若()x f 的定义域为R ，求a 的范围； （2）若值域为[)+∞-,2，求a 的值.例3.已知函数()()()01,lg >>>∈-=+b a R k kb a x f xx的定义域为()+∞,0，是否存在这样的b a ,，使得()x f 在()+∞,1上取正值，且()4lg 3=f ？若存在求出b a ,的值，若不存在，请说明理由.二．数形结合解决数学问题是函数的显著特征之一借助于图像研究函数性质是研究函数的一种常用方法. 函数的几何特征与函数的数量特征紧密结合，有效地揭示了各类函数的定义域、值域、单调性、奇偶性、周期性等基本属性. 在解决数学问题时，利用图像的直观有助于理解题意，探寻解题思路，检验解题结果. 因此，既要从多角度观察图像，又要熟练掌握图像的平移变换、对称变换、翻折变换。

第1讲：匀速圆周运动的描述【课前演练】：例1．每年端午节，我国许多地方都要举行“龙舟”比赛，运动员用桨划船时，使人、船、桨一起前进的力是（）A、桨对水的作用力。

B、水对桨的作用力。

C、人对船的作用力。

D、水对船的浮力。

例2、关于一定质量的物体的运动和力的关系，下列说法中正确的是（）A、物体受到的合外力越大，加速度越大。

B、物体受到的合外力越大，速度越大。

C、物体从静止开始在外力作用下做直线运动，当合外力逐渐减小时，速度也逐渐减小。

D、物体原来做匀速直线运动，当合外力逐渐增大时，速度也一定逐渐增大。

例3、如图所示，一物体放在自动扶梯上，随自动扶梯匀速斜向下运动，则物体受到的力有（）A、1个。

B、2个。

C、3个。

D、4个。

例4、如图所示，与小车相对静止、悬挂于小车里的小球偏离竖直方向θ角，则小车的运动情况可能是（）A、向左加速运动。

B、向右加速运动。

C、向左减速运动。

D、向左匀速运动。

例5、如图所示，用斜向下的推力F推木箱，木箱恰好做匀速直线运动，则推力F与木箱所受的摩擦力的合力的方向一定是（）A．向下偏左。

B．向下偏右。

C．竖直向下。

D．水平向左。

例6、汽车甲沿着平直公路以速度v做匀速直线运动，当它路过某处时，该处有一辆汽车乙开始做初速度为零的匀加速直线运动去追赶甲车，根据上述的已知条件（）A、可求出乙车追上甲车时乙车的速度。

B、可求出乙车追上甲车时乙车所走的路程。

C、可求出乙车从启动到追上甲车所用的时间。

D、不能求出上述三者中的任何一个。

例7、力F1单独作用于一物体时，物体产生的加速度大小为a1＝2m/s2；力F2单独作用于同一物体时，该物体产生的加速度大小为a2＝4m/s2。

当F1和F2共同作用于该物体时，物体具有的加速度大小不可能．．．是（）A、2m/s2。

B、4m/s2。

C、6m/s2。

D、8m/s2。

例8.如图所示，在一辆表面光滑的小车上，质量分别为m1、m2的两个小球（m1＞m2）随车一起匀速运动。

八年级春季班教学计划
吴L老师
第四章机械和功
4.1，简单机械
1.杠杆的基础知识（教会学生能精准找出支点画出力和力臂）
2.杠杆的平衡条件（是教学的重点和难点，学生要能够找出最长力臂，求最小力）
3.杠杆的分类根据杠杆的动力臂和阻力臂的大小关系分为三类，学生要能够辨别常见的杠杆是属于哪类杠杆
4.机械功机械功率
5.机械能
第五章热与能
6.温度温标
7.期中复习
8热量比热容
9.内能
10.热机
提前学习初三学期的内容
第六章密度
11密度一
12密度二
13期末复习（一）
14期末复习（二）
春季课程第四章上课内容是在寒假的基础上进行提高，上课进度基本与学校同步，可以根据学生的具体情况在教学的难度和进度进行适度调整，若有家长和学生有宝贵的合理的意见或建议，可及时和教务人员或与我直接联系！。

高二物理新王牌小班教学提纲
同步加强复习课
1.法拉第电磁感应定律
2.感应电量的计算
3.与运动学与动力学结合的题目
4.电磁感应定律与能量转化
5.电磁感应与电路综合分析
6.解决电磁感应与电路综合问题的基本思路
7.交流电的产生及变化规律
8．正弦交流电的变化规律线框在匀强磁场中匀速转动．
9、最大值、平均值和有效值的应用
10.交流电的图象、
11、电感和电容对交流电的作用
12.理想变压器的构造、作用、原理及特征
13．理想变压器的理想化条件及其规律．
14.电压互感器
15.电能输送
16.期末复习
17. 期末复习
18．期末复习
19. 期末复习。

高一 第3讲 能和功（一）【知识点1】理解．．功的概念 功的概念：一个物体如果受到力的作用并在力的方向上发生了一段位移，这个力便对物体做了功。

做功的两个必要因素是：作用在物体上的力和物体在力的方向上发生的位移。

功的一般公式：cos Fs W θ 式中F 表示恒力的大小， s 表示位移的大小，θ表示力F 与位移s 之间的夹角。

F 可理解为一个力，对应的W 表示该力做的功；F 也可理解为合外力，则对应W 表示合外力对物体做的功。

功的单位：在国际单位制中功的单位是焦（J ） 1J=1N ﹒m正功和负功：当0≤θ<90°，cos θ>0, W=Fs cos θ>0,外力F 对物体做正功。

当θ=90°，cos θ=0, W=Fs cos θ=0 ，外力F 对物体不做功。

当90°<θ≤180°，cos θ<0, W =Fs cos θ< 0 ，外力F 对物体做负功。

功是标量。

功的正负不表示方向，正功表示动力作的功，负功表示阻力作的功。

【知识点2】知道．．功是能的转化的量度。

物体的运动形式是多种多样的，处于不同运动形式的物体具有不同形式的能。

能量的转化要通过做功来实现，功是能量转化的量度。

[巩固练习]1. 做功的两个必要因素是___________和_____________。

2. 放在粗糙水平地面上的物体，在20N 的水平拉力作用下，匀速运动20m ，则拉力做的功是________J ，摩擦力对物体做的功是________J ，重力对物体做的功是________J 。

弹力对物体做的功是_________J 。

合外力对物体做的功是_________J 。

3. 如图1-5-1中，物体在力F 的作用下，沿图示路径运动并通过一段距离s ，图中所给的θ角为已知，则力 F 对物体做的功W 分别为：(c)W =________。

图1-5-1 （a ）4. 起重机将质量为m 的木箱以加速度a 匀加速下降了h 高度，则木箱克服钢索拉力所做的功为____________。

第一讲复数的概念及运算知识梳理一、复数的有关概念1、复数的定义：我们把形如()R b a bi a ∈+,的数叫复数. 其中i 叫虚数单位，规定12-=i ，a 叫复数z 的实部，记作z Re ，b 叫复数z 的虚部，用z Im 表示.复数的分类：数()R b a bi a ∈+,()()()⎪⎩⎪⎨⎧=≠⎩⎨⎧=时为纯虚数虚数无理数有理数实数000a b b . 复数集用C 表示，实数集R 是复数集的真子集，即R C .2、几个重要概念（1）复数相等：R d c b a ∈,,,，则d b c a di c bi a ==⇔+=+且.（2）共扼复数：设复数()R b a bi a z ∈+=,，把复数bi a -叫复数z 的共扼复数，记为bi a z -=.（3）复平面：用直角坐标系表示复数的平面叫复平面.复数()R b a bi a z ∈+=,与点()b a Z ,及向量OZ 一一对应，22b a OZ +=叫复数的模. 设复数dic z bi a z +=+=21,在复平面内对应的点分别为21,Z Z ，则21,Z Z 间的距离为()()222121d c b a Z Z z z d -+-==-=二、复数的运算（1）加减法：()()()()i d b c a di c bi a ±+±=+±+； （2）乘法：()()()()i bc ad bd ac di c bi a ++-=+⋅+；（3）除法：()()()()2222d c adbc d c bd ac di c di c di c bi a di c bi a +-+++=-⋅+-⋅+=++. 【注】有关i 的运算：1,,1,4342414=-=-==+++n n n n i i i i i i，()i i 212±=±.（4）几个重要结论：对于复数()R b a bi a z ∈+=,，有①22b a z z +==；②2z z z =⋅；③2121z z z z ⋅=⋅，2121z z z z =； ④2121z z z z ±=±，2121z z z z ⋅=⋅，2121z zz z =⎪⎪⎭⎫⎝⎛基础练习一、填空题 1、设集合{}{}{}{}{}纯虚数虚数，有理数，复数，实数=====B A Q C R ,，{}无理数=M ，则().____________;_____;____;___;=====R M C B A B A A R A R C2、若()()()R y x i y i x ∈-+=+-,3112，则._________,==y x3、已知复数i z i z 21,221+=+=在复平面内对应的点分别为B A ,，判断向量AB 对应的复数所对应的点在第_________象限.4、若z 是纯虚数，且31=-z ，则._____=z5、若()52-=+i z ，则._______42=+z z6、(05天津高考）若复数)(213R a iia ∈++是纯虚数，则a 的值为_______.二、选择题1、“0=a ”是“复数()R b a bi a z ∈+=,是纯虚数”的（ ） A.充分非必要条件 B.必要非充分条件C.充要条件D.既非充分又飞必要条件 2、有下列命题： ①复数i i +->+11；②若复数di c yi x +=+，则c x =且d y =；③若21,z z 为复数，则02221=+z z 是01=z 且02=z 的充要条件；④虚数集是复数集的真子集. ⑤复数z 为实数的充要条件是0Im =z 其中正确的命题是（ ） A.②③ B.②④⑤ C.①②③④ D.④⑤ 3、已知C z z ∈21,，则21z z =是21z z =的（ ） A.充分非必要条件 B.必要非充分条件C.充要条件D.既非充分又飞必要条件 4、（上海高考题）设复数iim z 212+-=（i R m ,∈为虚数单位）在复平面内的点不可能位于（ ）A. 第一象限B.第二象限C. 第三象限D. 第四象限题型示例例1、当实数m 分别取什么值时，复数()i m m m m m z 653222++++-+=是（1）实数；（2）虚数；（3）纯虚数.例2.已知复数z 满足i z z -=-3，求复数z 的模.例3.设复数z 在复平面内对应的点为Z ，则满足下列条件的Z 的集合是什么图形？并画出其图形.（1）1Re =z ；（2）5=z ；（3）13=-i z ；（4）i z z -=-1例4.复数z 满足1=z 且i z ±≠，求证：R zz∈+21.例5.(05年上海高考）证明：在复数范围内，方程iiz i z i z +-=+--+255)1()1(2无解.拓展练习一、 填空题1、若()[)()πθθθ2,01tan 2cos ∈-+i 是纯虚数，则.________________=θ 2、若()()R m x i m m x x ∈=++++,022，则._____,__________==m x3、设{}{}C z z z Q C z z z P ∈-==∈+==,|,,|ωωωω，则._______=Q P4、已知()()()()i a a a z i a a a z 223,2162221+-+-=-+--=，其中R a ∈. 若21z z =，则._______=a5、（04年上海春季高考）若复数，2)1(=+i z 则z 的实部为_______.6、若i z +=1，且i z z baz z -=+-++1122，则._____1 2 =b a 7、已知()()410232232143ii i z -⎪⎪⎭⎫ ⎝⎛+--=，则.______=z8、若复数21=z 且21z z ≠，则.______22121=⋅--z z z z9、（08年上海高考题）设复数z 满足i z i z i z ++=++-1,2则的最大值是_______.二、选择题1、若R y x ∈,，()()()22,2i y x xy Q yi x yi x P -+=-⋅+=，则Q P ,的大小关系是（ ） A.Q P > B.Q P ≥ C.Q P ≤ D.不能确定2. （08年上海高考题）已知C z ∈，且i i z ,122=--为虚数单位，则i z 22-+的最小值是（ ）A. 2B.3C.4D.53.设复平面上复数21,z z 对应的点分别为B A ,，2121z z z z +=-，线段AB 的中点M 对应的复数是i 43+，则=+2221z z （ ）A.10B.20C.100D.200三、解答题1、当a 取何值时，复数()()()R a i a a a a z ∈+-+-+=67222. （1）是实数；（2）是纯虚数；（3）i z 428-=.2、已知()z z z f -+=1，且()i z f 310+=-，求复数z .3、(04年上海高考）已知复数i z i z +=-=θθsin ,cos 21，求21z z ⋅的最大值和最小值。

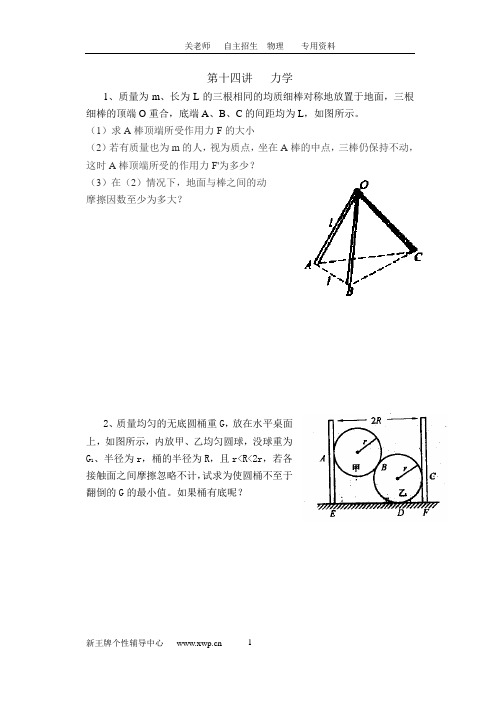
第十四讲力学1、质量为m、长为L的三根相同的均质细棒对称地放置于地面，三根细棒的顶端O重合，底端A、B、C的间距均为L，如图所示。

（1）求A棒顶端所受作用力F的大小（2）若有质量也为m的人，视为质点，坐在A棒的中点，三棒仍保持不动，这时A棒顶端所受的作用力F'为多少？（3）在（2）情况下，地面与棒之间的动摩擦因数至少为多大？2、质量均匀的无底圆桶重G，放在水平桌面上，如图所示，内放甲、乙均匀圆球，没球重为G1、半径为r，桶的半径为R，且r<R<2r，若各接触面之间摩擦忽略不计，试求为使圆桶不至于翻倒的G的最小值。

如果桶有底呢？3、如图所示，AB杆以恒定的角速度绕A点转动，并带动套在水平杆OC上的小环M运动。

运动开始时，AB杆在竖直位置，则运动中小环M的加速度将（A）逐渐增大（B）先减小后增大（C）先增大后减小（D）逐渐减小4、将一个小球从某点以初速度v0竖直向上抛出，当小球落回该抛出点时的速率为v1，已知小球在运动过程中受到的空气阻力大小与小球的速度大小成正比，求小球从抛出到落回原处所用的时间。

5、如图，将半径为R，质量为M，表面光滑的半径放在光滑的水平面上，在其正上方置于一质量为m的小滑块。

当小滑块从顶端无初速地下滑后，在图示的θ角位置处开始脱离半圆，已知cosθ=0.7，求M/m=?6、如图，两个质量分别为m1和m2的木块A、B用一劲度系数为k的轻弹簧连接，放在光滑的水平面上，A紧靠墙。

今用力推B块，使弹簧压缩x0，然后释放。

已知m1=m，m2=3m，求（1）释放后A、B两滑块速度相等时瞬时速度的大小（2）弹簧的最大伸长量7、如图甲所示，汽车沿倾角为α的斜坡，以恒定速率v0行驶，并且用一条长为L的轻绳拉动位于水平面上的一个质量为m的小车，若不计小车与路面的摩擦力，求当轻绳与水平面成α角时绳中张力。

8、如图，在光滑的水平面上有一带有光滑圆弧轨道的斜面，质量为m，圆弧轨道半径为R，圆心角为600,；一质量也为m的物体以v0向斜面运动。

第一讲四 三角比与三角函数4.1三角比定义1. 若扇形的周长为12,当扇形面积最大时,其圆心角大小为______2. 已知θ与θ9为终边相同角,将θ顺时针旋转2π为一个钝角,则______=θ3. 已知角α的顶点在原点，始边与x 轴的正半轴重合，终边经过点(P -，则sin 2tan αα-的值为________4. 已知角α的终边经过点)0)(12,5(≠-a a a P ，且0sin <α,则ααcos sin +的值为5. 已知a a +-=11sin θ，aa +-=113cos θ，若θ是第二象限角，则实数=a _____ 6. 已知角α的顶点在坐标原点，始边与x 轴的正半轴重合，角的终边经过点)3(y P ，-，且0)(43sin ≠=y y α，则αcos =_______ 7. 动点P 从点)0,1(出发，在单位圆上逆时针旋转α角，到点)322,31(-M ，已知角β的始边在x 轴的正半轴，顶点为(0,0)，且终边与角α的终边关于x 轴对称，则下面结论正确的是 （ ）A. 12arccos ,3k k Z βπ=-∈B. 12arccos ,3k k Z βπ=+∈C. 12arccos ,3k k Z βππ=+-∈D. 12arccos ,3k k Z βππ=++∈8. 已知）2,0(π∈x ，求证：x x x tan sin <<4.2 同角三角比恒等变换1. 若4sin ,tan 05θθ=->，则cos θ= 2. 若31)sin(=+απ，)0,2(πα-∈，则=αtan __________。

3. 已知3(,2),cot 2,2παπαα∈=-则sin = 4. 设παα<<≠=0),0cos t t （，则αtan 等于( )(A)t t 21- (B) t t 21-- (C) ±t t 21- (D) ±21tt -5. 已知ααcos 4sin 3-=，则ααα222cos 1cos sin +-=_______6. 已知)0(,51cos sin πααα<<=+，则ααsin cos -=________7. 化简得=⋅+⋅+⋅ααααααααcsc sec cos sin 2cot cos tan sin 22_______8. 是否存在实数k 和锐角α，使得sin α、cos α是方程012442=-+-k kx x 的两个根？若存在，求出k 和α的值；若不存在，请说明理由?4.3诱导公式1. 已知53)3sin(=-x π，则=-)65cos(x π_________2. 已知31)3sin(-=+απ，则αsin =_______3. 对任意的R θ∈，以下与sin 2πθ⎛⎫-⎪⎝⎭的值恒相等的式子为 （ ） A. sin 2πθ⎛⎫+ ⎪⎝⎭B. cos 2πθ⎛⎫+ ⎪⎝⎭C. ()cos 2πθ-D. 3sin 2πθ⎛⎫+ ⎪⎝⎭4. 已知方程)4cos(2)3sin(παπα-=-，则)sin()23sin(2)2cos(5)sin(ααπαπαπ----+-=_____5. 已知31cos =α，且02<<-απ，则αααππαtan )cos()2sin()cot(⋅-+⋅--=_______ 6. 化简：)()cos()sin(])1cos[(])1sin[(Z k k k k k ∈+⋅--+⋅++θπθπθπθπ=_______7. 已知2)cos()sin()(++++=βπαπx b x a x f ,若1)2012(=f ,则=)2013(f _______ 8. 是否存在），（），，（，、πβππαβα022∈-∈，使等式),2cos(2)sin(3βπαπ-=- )cos(2)cos(3βπα+-=-同时成立？若存在，求出βα、的值；若不存在，请说明理由？4.4 两角和差公式1. 已知π3(,π),sin ,25αα∈=则πtan()4α+=__ _．2.若02πα<<，02πβ-<<，1cos()43πα+=， cos()42πβ-= 则cos()2βα+= ( )A B ． C D ．-3. 若()350,sin ,sin 2513παβπααβ<<<<=+=，则cos β= . 4. 已知3πβα=+,则____tan tan 3tan tan =++βαβα5. 已知0sin sin sin ,0cos cos cos =++=++γβαγβα,则)cos(βα-=_____6. 已知m x =-)6cos(π，则=-+)3cos(cos πx x ________7. 若53)cos(51cos(=-=+βαβα，）,则=⋅βαtan tan ______ 8. 平面直角坐标系xoy 中，以ox 轴为始边作两个锐角α,β，它们的终边分别与单位圆相交于A 、B 两点，已知A 、B 的横坐标分别为10．则tan(αβπ+-)的值为_______4.5 两倍角公式1. 已知,2)4tan(=+πx 则xx2tan tan 的值为__________2. 设θθθ2,54cos ,53sin 则-==的终边所在的象限是 3. 设πx 20<≤,且x x x cos sin 2sin 1-=-,则x 的取值范围为______4. 已知21)4tan(=+απ，则ααα2cos 1cos 2sin 2+-=_______5. 角α的终边经过直线02=+y x 与曲线y =的交点，则cos 2()πα-=___________6. 已知ααcos 31sin -=，则ααπ2cos )4sin(-的值等于7. 化简：)2sin 1lg()]4cos(2lg()2sin21tan lg(cos 2x x x x x +--+-+⋅π=______ 8. 已知a =︒110tan ，求︒50tan 的值。

浦东最好的补习班浦东高中补习班新王牌高三物理彭J老师分子动浦东最好的补习班浦东高中补习班新王牌高三物理彭j老师分子动19.上部带有挡板的圆柱形气缸，内壁高度为d。

如图所示，气缸储存一定质量的气体，由无厚度和质量的活塞关闭。

开始时，活塞距离底部D/2，外部大气压力为1.0×105Pa，温度27℃，发现：(1)当气体温度升高到100℃时，乙活塞离底部的高度是多少？(2)当气体温度升高到500℃时，气体的压强是多少？20.质量可忽略的活塞在上端有开口的立式气缸中关闭一定量的理想气体。

铁砂堆积在活塞上，如图所示。

最初，活塞放置在气缸内壁的固定挡圈上。

气柱高度为H0，压力等于大气压力P0。

现在慢慢加热煤气。

当气体温度上升时△ t=60K时，活塞（和铁砂）开始离开挡圈并上升。

继续加热，直到气柱高度为H1=1.5h0。

然后，在保持温度不变的情况下，逐渐清除铁砂，直到清除所有铁砂后，气柱高度变为h2=1.8h0，并计算此时的气体温度（不包括活塞与气缸之间的摩擦）。

21、如图所示，截面积为s的汽缸a与容器b用一个带阀门k的细管相连通。

开始时阀门关闭，容器b内是真空的，汽缸a内被封闭空气的压强为p，温度为t1，活塞离开汽缸底部的高度为h。

打开阀门后，活塞下降，若将a、b内气体的温度一起升高到t2，活塞上升到离开汽缸底部高度4h/5处；若保持气体的温度为t1不变，取走活塞上的砂袋c，活塞同样也上升到离开汽缸底部4h/5处。

试求：（1）容器体积B.（2）砂袋质量。

22、如图所示，圆柱形汽缸竖直放置，汽缸内有质量m为150g的活塞，活塞与汽缸壁封闭良好，其上方放一质量m为50g的小木块，开始时活塞被销子k销于位置ⅰ（如实线所示，离缸底12cm)，此时汽缸内被封闭气体的压强为2×105pa，温度为360k。

外界大气压强为1×105pa。

现拔去销子k，活塞和小木块一起开始向上运动，当它们上升8cm到达位置ⅱ时（如虚线所示），汽缸内气体的温度为300k。