北京市2001中考数学试题分类解析 专题8 平面几何基础

[中考12年]连云港市2001-2012年中考数学试题分类解析专题08平面几何基础一、选择题1. （2001年江苏连云港3分）在比例尺1∶n的某市地图上，规划出一块长5cm、宽2cm的矩形工业园区，则该园区的实际面积是【】（单位：平方米）（A）n1000（B）2n1000（C）10n （D）210n2. （2001年江苏连云港3分）下列四个命题中的真命题是【】（A）同位角相等，则它们的平分线互相垂直（B）内错角相等，则它们的平分线互相垂直（C）同旁内角互补，则它们的平分线互相垂直（D）同旁内角相等，则它们的平分线互相垂直3. （2002年江苏连云港3分）下面给出四个命题，其中假命题是【】A．两条直线被第三直线所截，同位角相等B ．不相等的两角不是对顶点C ．平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧D ．以已知线段AB 为弦的圆的圆心的轨迹是线段AB 的垂直平分线4. （2004年江苏连云港3分）下列图案中，既是中心对称又是轴对称的图案是【 】A ．B ．C ．D ．5. （2005年江苏连云港3分）如图，直线1l ∥2l ，3l ⊥4l ．有三个命题：①︒=∠+∠9031；②︒=∠+∠9032；③42∠=∠．下列说法中，正确的是【 】（A ）只有①正确 （B ）只有②正确 （C ）①和③正确 （D ）①②③都正确6. （2006年江苏连云港3分）下列图案中，不是．．中心对称图形的是【】A、 B、 C、 D、7. （2006年江苏连云港3分）多边形的内角和不可能．．．为【】A、180°B、680°C、1080°D、1980°8. （2008年江苏连云港3分）已知AC为矩形ABCD的对角线，则图中1∠一定不相等∠与2的是【】A． B． C．D．9. （2010年江苏连云港3分）下列四个多边形：①等边三角形；②正方形；③正五边形；④正六边形．其中，既是轴对称图形又是中心对称图形的是【】A．①② B．②③ C．②④ D．①④10. （2011年江苏连云港3分）小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解．”小华根据小明的提示作出的图形正确的是【】A．B．C．D．11.（2012年江苏连云港3分）下列图案是轴对称图形的是【】A． B． C． D．12.（2012年江苏连云港3分）如图，将三角尺的直角顶点放在直线a上，a∥b，∠1＝50°，∠2＝60°，则∠3的度数为【】A．50° B．60° C．70° D．80°二、填空题1. （2004年江苏连云港3分）如图，两平面镜OA与OB之间的夹角为110°，光线经平面镜OA反射到平面镜OB上，再反射出去，其中∠1=∠2，则∠1的度数为▲ 度．2. （2005年江苏连云港3分）已知一个五边形的4个内角都是100，则第5个内角的度数是▲ ．3. （2006年江苏连云港3分）如图，∠BAC=30°，AB=10。

2001-2012年江苏无锡中考数学试题分类解析汇编（12专题）专题8：平面几何基础和向量一、选择题1. （江苏省无锡市2003年3分）三角形的周长小于13，且各边长为互不相等的整数，则这样的三角形共有【】A. 2个B. 3个C. 4个D. 5个【答案】B。

【考点】三角形三边关系。

【分析】根据三角形的两边之和大于第三边以及三角形的周长小于13，则其中的任何一边不能超过5，因此画树状图如下：可知，满足两边之和大于第三边，两边之差小于第三边的三个数有三组：2，3，4；2，4，5；3，4，5。

则这样的三角形共有三个。

故选B。

2. （江苏省无锡市2004年3分）下面给出的是一些产品的图案，从几何图形的角度看，这些图案既是中心对称图形又是轴对称图形的是【】A、 B、 C、 D、【答案】C。

【考点】中心对称图形，轴对称图形，生活中的旋转现象。

【分析】根据轴对称图形与中心对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合；中心对称图形是图形沿对称中心旋转180度后与原图重合。

因此，A、不是轴对称图形，也不是中心对称图形；B、不是轴对称图形，也不是中心对称图形；C、是轴对称图形，也是中心对称图形；D、不是轴对称图形，是中心对称图形。

故选C。

3.（江苏省无锡市2006年3分）在下面四个图案中，如果不考虑图中的文字和字母，那么不是轴对称图形的是【】【答案】B。

【考点】轴对称图形。

【分析】根据轴对称图形两部分沿对称轴折叠后可重合的概念可知，A、C、D都是轴对称图形，B不是轴对称图形，故选B。

4（江苏省无锡市2007年3分）下面四个图案中，是旋转对称图形的是【】Ａ．Ｂ．Ｃ．Ｄ．【答案】D。

【考点】旋转对称图形【分析】根据旋转图形的定义可知，A、B、C不是旋转对称图形；D、是旋转对称图形。

故选D。

5.（江苏省无锡市2008年3分）下面四个图案中，是轴对称图形但不是旋转对称图形的是【】A． B． C． D．【答案】D。

【考点】轴对称图形，旋转对称图形。

2001-2012年上海市中考数学试题分类解析汇编（12专题）专题8：平面几何基础和向量一、选择题2.（上海市2008年Ⅱ组4分）计算32a a -r r的结果是【 】A ．aB ．a rC ．a -D ．a -r【答案】B 。

【考点】向量的计算。

【分析】根据向量计算的法则直接计算即可：32=a a a -r r r。

故选B 。

3.（上海市2008年Ⅱ组4分）如图，在平行四边形ABCD 中，如果AB a =u u u r r ，AD b =u u u r r，那么a b +r r 等于【 】 A ．BD u u u rB ．AC u u u rC ．DB u u u rD ．CA uu u r【答案】B 。

【考点】向量的几何意义。

【分析】根据向量的意义，=a b AC +r r u u u r。

故选B 。

4.（上海市2009年4分）下列正多边形中，中心角等于内角的是【 】 A ．正六边形 B ．正五边形C ．正四边形C ．正三边形【答案】C 。

【考点】多边形内角与外角。

【分析】正n 边形的内角和可以表示成02180n -⋅（），则它的内角是等于02180n n-⋅（），n 边形的中心角等于0360n ，根据中心角等于内角就可以得到一个关于n 的方程：002180360n n n-⋅=（），解这个方程得n =4，即这个多边形是正四边形。

故选C 。

5.（上海市2009年4分）如图，已知AB CD EF ∥∥，那么下列结论正确的是【 】A ．AD BC DF CE =B ．BC DFCE AD =C ．CD BCEF BE= D ．CD ADEF AF=【答案】A 。

【考点】平行线分线段成比例。

【分析】已知AB CD EF ∥∥，根据平行线分线段成比例定理，得AD BCDF CE=。

故选A 。

6.（2012上海市4分）在下列图形中，为中心对称图形的是【 】 A ． 等腰梯形 B ． 平行四边形C ． 正五边形D ． 等腰三角形【答案】B 。

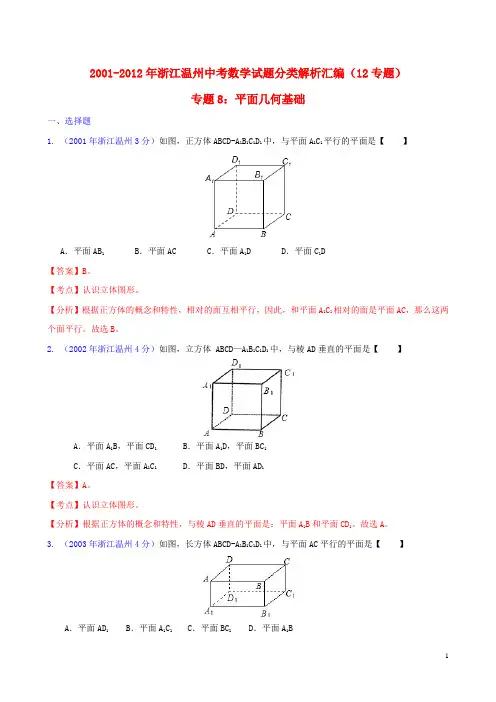
2001-2012年浙江温州中考数学试题分类解析汇编（12专题）专题8：平面几何基础一、选择题1. （2001年浙江温州3分）如图，正方体ABCD-A1B1C1D1中，与平面A1C1平行的平面是【】A．平面AB1 B．平面AC C．平面A1D D．平面C1D【答案】B。

【考点】认识立体图形。

【分析】根据正方体的概念和特性，相对的面互相平行，因此，和平面A1C1相对的面是平面AC，那么这两个面平行。

故选B。

2. （2002年浙江温州4分）如图，立方体 ABCD—A1B1C1D1中，与棱AD垂直的平面是【】A．平面A1B，平面CD1 B．平面A1D，平面BC1C．平面AC，平面A1C1 D．平面BD，平面AD1【答案】A。

【考点】认识立体图形。

【分析】根据正方体的概念和特性，与棱AD垂直的平面是：平面A1B和平面CD1。

故选A。

3. （2003年浙江温州4分）如图，长方体ABCD-A1B1C1D1中，与平面AC平行的平面是【】A．平面AD1 B．平面A1C1 C．平面BC l D．平面A1B【答案】B。

【考点】认识立体图形。

【分析】根据正方体的概念和特性，相对的面互相平行，因此，和平面AC相对的面是平面A1C1，那么这两个面平行。

故选B。

4. （2004年浙江温州4分）下面给出的四条线段中，最长的是【】(A) a (B) b (C) c (D) d【答案】D。

【考点】比较线段的长短。

【分析】通过观察比较：d线段长度最长。

故选D。

5. （2004年浙江温州4分）高斯用直尺和圆规作出了正十七边形，如图, 正十七边形的中心角∠AOB的度数近似于【】(A) 11° (B) 17° (C) 21° (D) 25°【答案】C。

【考点】正多边形和圆。

【分析】正多边形一定有外接圆，且每条边所对的中心角相等，因此360°÷17≈21°。

故选C。

6. （2005年浙江温州4分）如图，正方体ABCD－A1B1C1D1中，与平面A1C1平行的平面是【】A、平面AB1B、平面ACC、平面A1DD、平面C1D【答案】B。

广州市2001-2012年中考数学试题分类解析专题8：平面几何基础一、选择题1. （2002年广东广州3分）如图，若C是线段AB的中点，D是线段AC上的任一点（端点除外），则【】（A）AD·DB＜AC·CB（B）AD·DB=AC·CB（C）AD·DB＞AV·CB（D）AD·DB与AC·CB大小关系不确定2. （2004年广东广州3分）下列图形中，不是中心对称图形是【】A．矩形 B．菱形 C．正五边形 D．正八边形3. （2006年广东广州3分）如图，AB∥CD，若∠2=135°，那么∠l的度数是【】．(A)30° (B)45° (C)60° (D)75°【答案】B。

【考点】平角的定义，平行的性质。

【分析】如图，∵AB∥CD，若∠2=135°，∴∠3=135°。

∵∠1＋∠3=1800，∴∠l=1800－1350=450。

故选B。

4. （2006年广东广州3分）已知四组线段的长分别如下，以各组线段为边，能组成三角形的是【】．(A)l，2，3 (B)2，5，8 (C)3，4，5 (D)4，5，105. （2007年广东广州3分）下列立体图形中，是多面体的是【】A．B．C．D．6. （2007年广东广州3分）下列命题中，正确的是【】A．对顶角相等 B．同位角相等 C．内错角相等 D．同旁内角互补【答案】A。

【考点】命题和定理，对顶角的性质，四线八角性质。

【分析】根据同位角、内错角相等或同旁内角互补的条件必须是两直线平行形成的四线八角。

故选项B、C、D错误，故选A。

7. （2007年广东广州3分）下列各图中，是轴对称图案的是【】A． B． C． D．8. （2007年广东广州3分）小明由A点出发向正东方向走10米到达B点，再由B点向东南方向走10米到达C点，则正确的是【】A．∠ABC=22.5° B．∠ABC=45° C．∠ABC=67.5° D．∠ABC=135°9. （2008年广东广州3分）把下列每个字母都看成一个图形，那么中心对成图形有【】 O L Y M P I CA 1个B 2个C 3个D 4个【答案】B。

[中考12年]盐城市2001-2012年中考数学试题分类解析专题8：平面几何基础一、选择题1. （2001年江苏盐城4分）下列命题中，假命题是【】A.和已知线段两端点距离相等的点的轨迹，是这条线段的垂直平分线B.一组对边平行且对角线相等的四边形是矩形C.平行四边形是中心对称图形D.任意三角形都有内接圆2. （2002年江苏盐城4分）如图所示，光线L照射到平面镜I上，然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=550，∠γ=750，则∠β为【】A、500B、550C、600D、650【答案】D。

【考点】跨学科问题，镜面对称，三角形的内角和定理。

【分析】根据入射光线与水平线的夹角等于反射光线与水平线的夹角，三角形的内角和是180°求解：∠β所在的顶点处是一个平角为180°，α，γ经过反射后，与β所在的顶点处的一个角组成三角形的内角和180°，即180°-2β+α+γ=1800。

∴2β=∠α＋∠γ。

∴∠β=（550＋750）÷2=650。

故选D。

3. （2002年江苏盐城4分）下列四个命题：①如果两个点到一条直线的距离相等，那么过这两点的直线与已知直线平行；②函数y =3x中，y随x的增大而减小；③x2与2x1都是最简二次根式；④“同旁内角互补，两直线平行”的逆命题是真命题。

其中，不正确的命题个数是：【】A、1B、2C、3D、44. （2003年江苏盐城3分）一个正多边形它的一个外角等于与它不相邻的内角的14，则这个多边形是【】A．正十二边形 B．正十边形 C．正八边形 D．正六边形5. （2003年江苏盐城3分）下列四个命题：①三个角对应相等的两个三角形是全等三角形②到已知角两边距离相等的点的轨迹，是这个角的角平分线③用全等的正三角形，可以进行平面镶嵌④圆既是轴对称图形，又是中心对称图形．其中错误的命题有【】A．1个 B．2个 C．3个 D．4个6. （2004年江苏盐城3分）某正方形园地是由边长为1的四个小正方形组成,现要在园地上建一个花坛(阴影部分),使花坛面积是园地面积的一半,以下图中设计不合要求的是【】A. B. C. D.【答案】B。

2001-2012年江苏苏州中考数学试题分类解析汇编（12专题）专题8：平面几何基础和向量一、选择题1.（江苏省苏州市2003年3分）在△ABC中，若AB=9，BC=6，则第三边CA的长度的取值范围是【】A. 3＜CA＜9B. 6＜CA＜9C. 9＜CA＜15D. 3＜CA＜15【答案】D。

【考点】三角形三边关系【分析】根据三角形两边之和大于第三边，两边之差小于第三边的三边关系，即可求得：9－6 ＜CA ＜C9＋6，即 3＜CA＜15。

故选D。

2.（江苏省苏州市2004年3分）观察下列中国传统工艺品的花纹，其中轴对称图形是【】A. B. C. D.【答案】A。

【考点】轴对称图形。

【分析】根据轴对称图形两部分沿对称轴折叠后可重合的概念，观察图形可知图形A是轴对称图形。

故选A。

3.（江苏省苏州市2006年3分）如图，如果直线m是多边形ABCDE的对称轴，其中∠A=1300，∠B=1100．那么∠BCD的度数等于【】A. 400B.500C．600 D.700【答案】C。

【考点】轴对称的性质，多边形内角和定理。

【分析】根据对称的性质，找出相等的角，再根据五边形的内角和即可求解：由轴对称性质可知：∠E=∠A=130°，∠D=∠B=110°，∴∠BCD=540°－130°×2－110°×2=60°。

故选C。

4.（江苏省苏州市2006年3分）如图，给出了过直线外一点作已知直线的平行线的方法，其依据是【】A. 同位角相等，两直线平行B.内错角相等，两直线平行C.同旁内角互补，两直线平行D.两直线平行，同位角相等【答案】A。

【考点】平行线的判定。

【分析】作图时保持∠1=∠2，则可判定两直线平行：∵∠1=∠2，∴a∥b（同位角相等，两直线平行）。

故选A。

5.（江苏省苏州市2007年3分）如图，MN为⊙O的弦，∠M=50°，则∠MON等于【】A．50° B．55° C．65° D．80°【答案】D。

2001-2012年江苏泰州中考数学试题分类解析汇编（12专题）专题8：平面几何基础一、选择题2.（2001江苏泰州4分）①若不等式()a 2x 2a <--的解集为x 1>-，则a 2<。

②若α、β，则以α、β为根的一元二次方程为2x +3x+2=0。

③方程(x+3的解为x=3±。

④用反证法证明“三角形中至少有一个内角不小于600”。

第一步应假设三角形中三个内角都小于600。

以上4条解答，正确的条数为【 】。

A.0B. 1C. 2D. 3【答案】C 。

【考点】解不等式，非负数的性质，一元二次方程的根，解无理方程，反证法。

【分析】根据相关知识逐一判断：①当a 2<时，原不等式化为2a x a 2>--，即x 1>-；当a 2>时，原不等式化为2a x a 2<--，即x 1<-。

∴若不等式()a 2x 2a <--的解集为x 1>-，则a 2<。

∴结论正确。

②∵α、β，∴+3=02=0αβαβ-- ，，即+=3=2αβαβ ，。

∴根据一元二次方程根与系数的关系知，以α、β为根的一元二次方程为2x 3x+2=0-。

∴结论错误。

③∵当x=3-时，方程(x+3无意义，∴结论错误。

④结论正确。

∴正确的条数为2条。

故选C 。

3.（江苏省泰州市2002年4分）等腰三角形一边长为4，一边长9，它的周长是【 】A 、17B 、22C 、17或22D 、13【答案】B 。

【考点】等腰三角形的性质，三角形的构成条件。

【分析】分底边是4和底边是两种情况讨论：当底边是4时：三边是4，9，9，则周长是22；当底边是9时：三边是：4，4，9，因为4+4＜9不能构成三角形。

∴等腰三角形的周长为22。

故选B 。

4.（江苏省泰州市2002年4分）下列图形中是中心对称图形的是【 】A 、B 、C 、D 、【答案】C 。

【考点】中心对称图形，【分析】根据中心对称图形是图形沿对称中心旋转180度后与原图重合的概念和各图形的特点即可求解：A 、是轴对称图形；B 、有五个角，但有旋转，所以既不是轴对称图形也不是中心对称图形；C 、即是轴对称图形，又是中心对称图形；D 、是轴对称图形。

2001-2012年某某某某中考数学试题分类解析汇编（12专题）专题8：平面几何基础一、选择题1. （某某2002年3分）正五边形的内角是【】A、180ºB、360ºC、540ºD、720º【答案】C。

【考点】多边形内角和定理。

【分析】利用多边形的内角和为（n－2）•180°即可解决问题：（n－2）•180°=（5－2）×180°=540°。

故选C。

2.（某某2003年5分）已知三角形的两边a=3，b=7，第三边是c，且a<b<c，则c的取值X围是【】A、4<c<7B、7<c<10C、4<c<10D、7<c<13【答案】B。

【考点】三角形三边关系。

【分析】根据三角形的三边关系：第三边＞两边之差4，＜两边之和10，根据a＜b＜c即可得c的取值X 围：答：根据三角形三边关系可得4＜c＜10，∵a＜b＜c，∴7＜c＜10。

故选B。

3.（某某2004年3分）下列图中：①线段；②正方形；③圆；④等腰梯形；⑤平行四边形是轴对称图形，但不是中心对称图形有【】A、1个B、2个C、3个D、4个【答案】A。

【考点】中心对称和轴对称图形。

【分析】根据轴对称图形与中心对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合；中心对称图形是图形沿对称中心旋转180度后与原图重合。

结合线段、正方形、圆、等腰梯形、平行四边形的性质，根据轴对称图形和中心对称图形的概念作答：①，②，③既是轴对称图形又是中心对称的图形；④只是轴对称图形，但不是中心对称图形；⑤只是中心对称图形。

故选A。

4.（某某2005年3分）图所列图形中是中心对称图形的为【】A B C D【答案】C。

【考点】中心对称图形。

【分析】中心对称图形是图形沿对称中心旋转180度后与原图重合。

因此，A、是轴对称图形，不是中心对称图形；B、有五个角，但有旋转，所以既不是轴对称图形也不是中心对称图形；C、即是轴对称图形，又是中心对称图形；D、是轴对称图形，不是中心对称图形。

【中考12年】浙江省绍兴市2001-2012年中考数学试题分类解析专题08平面几何基础选择题1. （2004年浙江绍兴4分）4张扑克牌如图（1）所示放在桌面上，小敏把其中一张旋转180°后得到如图（2）所示，那么她所旋转的牌从左数起是【】A．第一张B．第二张C．第三张D．第四张2. （2004年浙江绍兴4分）已知∠AOB=30°，点P在∠AOB内部，P1与P关于OB对称，P2与P 关于OA对称，则P1，O，P2三点所构成的三角形是【】A．直角三角形B．钝角三角形C．等腰三角形D．等边三角形【答案】D。

【考点】轴对称的性质，等边三角形的判定。

【分析】根据轴对称的性质可知，OP1=OP2=OP，∠P1OP2=60°，∴△P1OP2是等边三角形。

故选D。

3. （2005年浙江绍兴4分）学校篮球场的长是28米，宽是【】（A）5米（B）15米（C）28米（D）34米【答案】B。

【考点】数学常识。

【分析】学校篮球场的长是28米，宽应小于28米，选项中只有15米和5米小于28米，而5米作为篮球场的宽度来说显然太小。

故选B。

4. （2005年浙江绍兴4分）“数轴上的点并不都表示有理数，如图中数轴上的点P”，这种说明问题的方式体现的数学思想方法叫做【】（A）代入法（B）换元法（C）数形结合（D）分类讨论5. （2006年浙江绍兴4分）吋是电视机常用规格之一，1吋约为拇指上面一节的长，则7吋长相当于【】A．课本的宽度B．课桌的宽度C．黑板的高度D．粉笔的长度【答案】A。

【考点】数学常识。

【分析】拇指上面一节的长约为3cm左右，则7时长约为21cm左右，相当于课本的宽度。

故选A。

6. （2006年浙江绍兴4分）若有一条公共边的两个三角形称为一对“共边三角形”，则图中以BC为公共边的“共边三角形”有【】A．2对B．3对C．4对D．6对7. （2007年浙江绍兴4分）下列名人中：①鲁迅；②姚明；③刘徽；④杨利伟；⑤高斯；⑥贝多芬；⑦陈景润．其中是数学家的为【】A．①③⑤B．②④⑥C．③⑤⑦D．④⑤⑥【答案】C。

江苏省宿迁市2001-2012年中考数学试题分类解析专题08 平面几何基础一、选择题1. （2001年江苏宿迁4分）一个角的平分线与这个角邻补角的平分线组成的角是【】A、平角B、钝角C、直角D、锐角2. （2004年江苏宿迁4分）如图，直线a、b被直线c所截，若a//b，∠1＝1300 ，则∠2等于【】A .300 B. 400 C. 500 D. 6003. （2004年江苏宿迁4分）已知一辆小轿车车牌号的后两个数字组成了一个中心对称图形，且这两个数字不相同，则这两个数字的和是【】A. 2B.12C. 15D.164. （2005年江苏宿迁3分）如图，AB∥CD，则图中∠1、∠2、∠3关系一定成立的是【】A．∠1＋∠2＋∠3＝180° B．∠1＋∠2＋∠3＝360°C．∠1＋∠3＝2∠2 D．∠1＋∠3＝∠25. （2006年江苏宿迁4分）下列图案中，不是轴对称图形的是【】6. （2007年江苏宿迁3分）如图，直线a∥b ,∠2=95°，则∠1等于【】A.100°B. 95°C. 99°D.85°7. （2007年江苏宿迁3分）如图，在△ABC中，AB=a，AC=b，BC边上的垂直平分线DE交BC、BA分别于点D、E，则△AEC的周长等于【】A. a＋bB.a－bC.2a＋bD.a＋2b8. （2008年江苏宿迁3分）下列图形中既是轴对称图形又是中心对称图形的是【】Ａ．正六边形Ｂ．正五边形Ｃ．平行四边形Ｄ．等腰三角形二、填空题1. （2001年江苏宿迁4分）如图，张村和李庄在河(用直线L表示)的同岸，现要在河边修一个泵站，分别向张村、李庄送水，请在河边确定泵站的位置，使所用的水管最短，(在L 上作出点A，用于表示泵站的位置，作图工具不限)2. （2001年江苏宿迁4分）下面四个命题：①y=kx(k<0)函数的函数值y随x的增大而减小；②分式的分子和分母都乘以同一个不等于零的整式，分式的值不变；③被开方数不相同的二次根式，一定不是同类二次根式；④对于方程ax2+bx+c=0，若b2－4ac>0,则该方程一定有两个不相等的实数根。