Increasing Solution Density by Dominated Relaxation

凝聚态物理英语Condensed matter physics is a branch of physics that deals with the macroscopic and microscopic properties of matter, specifically the behavior of solids and liquids. It is a highly interdisciplinary field that explores the quantum mechanical properties of matter in bulk. This field of study has led to numerous technological advancements and has greatly impacted our understanding of the physical world.One of the key concepts in condensed matter physics is the study of phase transitions. Phase transitions occur when a material changes from one state to another, such as from a solid to a liquid or from a liquid to a gas. These transitions are characterized by changes in the material's physical properties, such as density, conductivity, and magnetization. Understanding the mechanisms behind phase transitions is essential for developing new materials with novel properties and applications.Another important area of research in condensed matter physics is the study of quantum phenomena in solids. Quantum mechanics describes the behavior of particles on the atomic and subatomic levels, and in condensed matter physics, these principles are applied to understand the interactions between atoms in solids. Quantum phenomena in solids can lead tounique properties such as superconductivity, where materials exhibit zero resistance to electrical current, and magnetism, where materials exhibit magnetic properties due to the alignment of electron spins.Condensed matter physics also plays a crucial role in the development of new materials for various technologies. Researchers in this field work to understand the properties of materials at the atomic level and how they can be manipulated to create materials with specific properties. This knowledge has led to the development of new materials for applications in electronics, energy storage, and medical devices.In recent years, there has been a growing interest in the study of topological materials in condensed matter physics. Topological materials are materials that exhibit unique electronic properties due to their topological structure, which is determined by the arrangement of atoms in the material. These materials have the potential to revolutionize electronics and computing by enabling the development of new types of electronic devices with improved performance and efficiency.Overall, condensed matter physics is a diverse and dynamic field of study that continues to push the boundaries of our understanding of the physical world. Through the study of phasetransitions, quantum phenomena, and novel materials, researchers in this field are continually expanding our knowledge of matter and developing new technologies that have the potential to transform society.In conclusion, condensed matter physics is a fascinating and important field of study that has a profound impact on our understanding of the physical world and on technological advancements. Researchers in this field continue to make significant contributions to science and technology, and the future of condensed matter physics holds great promise for exciting new discoveries and innovations.。

城市规划专业外语第一篇：城市规划专业外语Urban Planning and the Contradictions of Sustainable Development城市规划与可持续发展的矛盾In the coming years planners face tough decisions about where they stand on protecting the green city, promoting the economically growing city, and advocating social justice.Conflicts among these goals are not superficial ones arising simply from personal preferences.Nor are they merely conceptual, among the abstract notions of ecological, economic, and political logic, nor a temporary problem caused by the untimely confluence of environmental awareness and economic recession.Rather, these conflicts go to the historic core of planning, and are a leitmotif in the contemporary battles in both our cities and rural areas, whether over solid waste incinerators or growth controls, the spotted owls or nuclear power.And though sustainable development aspires to offer an alluring, holistic way of evading these conflicts, they cannot be shaken off so easily.This paper uses a simple triangular model to understand the divergent priorities of planning.在未来几年规划面临艰难的抉择，他们站在保护绿色城市，促进城市经济增长，并倡导社会正义。

聚丙烯酰胺稀溶液的分子模拟刘艳艳1陈攀科1罗健辉2周歌1,*江波1,*(1四川大学化学学院,绿色化学与技术教育部重点实验室,成都610064;2中国石油勘探开发研究院,北京100083)摘要：聚丙烯酰胺(PAM)是一类重要的线性水溶性聚合物,具有“百业助剂”之称,因此对其溶液性质的研究意义重大.在溶液质量浓度约为1g ·mL -1的基础上,分别构建了含有不同水分子数的溶液模型.采用分子动力学(MD)方法模拟分析了不同温度下非离子型的聚丙烯酰胺(PAM -H)和阴离子型的聚丙烯酰胺(HPAM)在纯水溶液及含不同质量分数NaCl 的水溶液中的回旋半径(R g ).结果发现,不同温度下PAM -H 和HPAM 的抗盐性能的模拟结果与实验数据基本吻合,水分子数不同的溶液模型所得模拟结果趋势没有明显变化,为了提高模拟效率,选取含有2000个水分子的溶液模型分析HPAM 链中氧负离子及氧原子的径向分布函数,从微观结构模拟说明了HPAM 水溶液粘度随NaCl 质量分数增加而减小,且HPAM 比PAM -H 具有较好的增粘效果及较差的抗盐性能的原因.关键词：分子动力学;聚丙烯酰胺;溶液性质;回旋半径;径向分布函数中图分类号：O645;O641Molecular Simulation of Dilute Polyacrylamide SolutionsLIU Yan -Yan 1CHEN Pan -Ke 1LUO Jian -Hui 2ZHOU Ge 1,*JIANG Bo 1,*(1Key Laboratory of Green Chemistry and Technology,Ministry of Education,College of Chemistry,Sichuan University,Chengdu610064,P.R.China ;2Research Institute of Petroleum Exploration and Development of PetroChina,Beijing 100083,P.R.China )Abstract ：Polyacrylamide (PAM)applied to various fields is an important class of linear water -soluble polymers.Therefore,it is of great significance to study the solution properties of PAM.We constructed solution models containingdifferent amounts of water molecules with a mass concentration of about 1g ·mL ing molecular dynamics (MD)simulations we calculated the radius of gyration (R g )for non -ionic PAM (PAM -H)and anionic PAM (HPAM)in pure water and in aqueous solutions with different mass fractions of NaCl.We discussed their behaviors at different temperatures.We found that the salt tolerance of the polyacrylamides from the simulation agreed with the experimental results at different temperatures.Furthermore,the simulation results for all the solution models containing a different amount of water molecules basically showed a similar trend.Considering computational efficiency,the solution model containing 2000water molecules was selected for our study.The radial distribution functions (RDF)for the oxygen ions and oxygen atoms of the HPAM chain were investigated in NaCl solution model containing 2000water molecules.The reduced viscosity of HPAM solutions with increasing NaCl mass fractions and a better thickening ability as well as poor salt tolerance compared to PAM -H were explained considering their microstructures as determined by RDF.Key Words ：Molecular dynamics;Polyacrylamide;Solution property;Radius of gyration;Radial distribution function[Article]物理化学学报(Wuli Huaxue Xuebao )Acta Phys.-Chim.Sin .,2010,26(11)：2907-2914聚丙烯酰胺(PAM)是一种线性的水溶性聚合物[1].由于其分子链的柔顺性和分子形状(即链构象)的易变性,以及具有高极性、易形成氢键和高反应活性的酰胺基,使得聚丙烯酰胺具有许多极有价值的November Received:July 5,2010;Revised:August 5,2010;Published on Web:September 16,2010.*Corresponding authors.JIANG Bo,Email:jiangbo@;Tel:+86-28-85418112.ZHOU Ge,Email:zhougekk@;Tel:+86-28-85418112.The project was supported by the National Natural Science Foundation of China (20904035).国家自然科学基金(20904035)资助项目鬁Editorial office of Acta Physico -Chimica Sinica2907Acta Phys.-Chim.Sin.,2010Vol.26应用性能,易通过接枝或交联得到支链或网状结构的多种改性.因此,聚丙烯酰胺类聚合物应用广泛,享有“百业助剂”之称.然而,对于最初的聚丙烯酰胺产品——丙烯酰胺均聚物(非离子型聚丙烯酰胺, PAM-H)和水解聚丙烯酰胺(阴离子型聚丙烯酰胺, HPAM),其性能不能完全满足应用需求.PAM-H易发生水解而具有阴离子型负电性,且它们分子上的—COO-对盐极其敏感,在高温、高矿化度、高剪切环境下,会导致水溶液粘度大幅度下降,不能适应高温、高矿化度抽藏驱油和钻井方面的要求.因此必须对最初的聚丙烯酰胺产品进行改性,来提高其耐温、耐盐、抗剪切性能.在聚电解质溶液中,离子基团的静电斥力引起链的扩张,使特性粘数和粘度增大;外加小分子电解质可屏蔽离子基团的静电作用,减小链尺寸,使特性粘数和粘度减小[1-3].因此,可以通过测定聚合物溶液的特性粘数或粘度来研究及预测丙烯酰胺类聚合物的性能(耐温、耐盐、抗剪切等). Yahaya等[4]引入N-苄基丙烯酰胺单体对聚丙烯酰胺进行疏水改性,同时测试其水溶液在不同高分子浓度、盐浓度、温度及剪切率下的表观粘度变化.结果发现,疏水基团在丙烯酰胺均聚物中的引入可以明显提高其增粘性,且随溶剂条件及剪切率的变化具有很好的稳定性,尤其在盐溶液中的特性粘数值要大于水溶液中的值.实际上,关于丙烯酰胺类聚合物改性及其溶液性能研究的实验文献国内外已有很多[2-7],从微观结构研究丙烯酰胺类聚合物的性质也备受关注[8-10],而这些传统的方法实验周期较长,且消耗较大的人力、物力、财力[11].计算机模拟技术[12]对高分子稀溶液的研究能够获得高分子溶液的热力学性质(高分子-溶剂体系的混合熵、混合热和混合自由能)、动力学性质(高分子溶液的粘度、高分子在溶液中的扩散和沉降)以及聚合物的分子量和分子量分布、高分子在溶液中的形态和尺寸、高分子链段间及链段与溶剂分子间的相互作用、高分子稀溶液的流变性质以及聚合溶液中的磁性等;同样也可以获得高分子浓溶液的性质.所以,我们可以用计算机模拟技术来研究聚合物分子结构在不同溶剂和温度下的变化,可以直观了解聚合物溶液宏观性质的本质,指导聚合物的改性及合成,缩短新材料的开发周期,弥补传统实验方法的不足,具有一定的环保意义.由于计算能力和研究尺度的限制,聚丙烯酰胺类聚合物稀溶液的模拟研究不多,但仍有一些关于高分子溶液性质模拟研究的文献报道[13-22],为我们进行此方面的研究提供了基础,如Tung等[18]通过分子动力学模拟技术研究了溶剂的种类对无规聚甲基丙烯酸甲酯(a-PMMA)链在溶液中的动力学性质的影响,构建了不同种类a-PMMA溶液,对均方末端距<R2>、均方回转半径<S2>以及聚合物链的非球面率<R2>/<S2>等聚合物链动力学性质进行了模拟分析.因此,本文进行了PAM-H和HPAM稀溶液的性质初探,分别构建了含不同水分子数的溶液模型,采用分子动力学(MD)方法首先研究了PAM-H和HPAM在不同水溶液模型中的回旋半径(R g)受NaCl 质量分数和温度的影响变化,从中确定稀溶液模型的体系,同时进行了径向分布函数(RDF)g(r)分析,从微观结构解释说明了PAM-H和HPAM的宏观性质,从而为以后更深入的研究、改性聚丙烯酰胺及其分子设计奠定基础.1计算方法的提出及模拟方法1.1特性粘数的理论计算特性粘数[η]指分子链在指定盐水中形成水动力学体积的特征参数.它与聚合物的结构、分子量大小和分子形态有关,在热、酸碱、盐等因素作用下,溶液中聚合物的分子尺寸会发生很大变化,从而导致聚合物溶液的特性粘数发生变化.理论上引入一个可以表征分子尺寸的参数———回旋半径(R g).特性粘数与回旋半径之间的关系如下[23-24]:[η]=63/2Φ(R g)3/M(1)式中,M为聚合物的摩尔质量,Φ=10πN A/3,N A为阿佛加德罗常数.本文通过Materials Studio(MS)4.2软件计算得到回旋半径(R g),由R g的变化趋势可看出[η]的变化趋势.1.2模拟方法模拟使用由美国Accelrys公司开发的Materials Studio4.2软件,采用amorphous cell模块的construction分别添加不同的NaCl分子数到充满一定数目的H2O分子和一个聚合物分子链的立方元胞中,construction中的目标密度(target density of the final configurations)是指模型的溶液密度,由模型含有的所有原子质量及其体积计算得到,立方元胞的体积由所含水的密度(1g·mL-1)和个数计算,模型体积元胞参数(cell parameters)随目标密度变化而自动生成,这样就得到了溶液模型的初始结构.关于溶液密度的确定,由于本文构建的是聚合物稀溶液模型,而实际稀溶液的密度近似认为接近2908No.11刘艳艳等：聚丙烯酰胺稀溶液的分子模拟水的密度(约为1g·mL-1),因此本文所设定的目标密度能够保证高分子链周围水的质量浓度约为1g·mL-1;同时由于构建的溶液模型浓度很低,其高分子链之间的作用力比高分子链与溶剂分子间的作用力小得多,因此可以忽略高分子链间的作用力,即构建模型时只选择一条高分子链是相对合理的.为了避免以后进行分子动力学模拟时,溶液模型的能量陷入低能势阱中而无法达到动力学平衡,需先用smartminimizer方法进行至少2次5000步能量优化(步长设为1fs),直到初始结构能量最小化,然后在一定温度(298、308、318、328或338K)下进行450ps分子动力学模拟,其中先进行50ps NPT(等温等压系综,系统的粒子数N、温度T和压力P恒定)动力学平衡(p=0.0001GPa),再进行400ps NVT(正则系综,系统的粒子数N、体积V和温度T恒定)分子动力学计算,然后对最后200ps分子动力学轨迹采用amorphous cell模块中的analysis来获得回旋半径R g,之后采用forcite模块中的analysis来进行径向分布函数分析.图1(a)显示了含原子数最多的溶液模型(298K时,NaCl质量分数为0.4%的HPAM-3500溶液模型,此溶液模型表示符号中,“-”前表示模型中的聚合物种类,“-”后表示模型中的水分子数,文中所有溶液模型符号均按此规则表示)在NPT系综下的能量随模拟时间的变化,在模拟时间约为50ps时溶液模型就达到平衡,因此上述选取50ps NPT平衡时间是合理的;然后取此模型50ps NPT动力学所保存的最后一个模型,继续采用NVT系综进行动力学计算所得的能量随模拟时间的变化始终保持平衡(如图1(b)所示）,这说明本文所采用的方法合理.在298K下的溶液模型分别进行了600ps、1ns和2 ns的分子动力学模拟,所得模拟结果与450ps的结果很相似.为了提高模拟工作效率,本文选取450ps 的分子动力学模拟.以上能量优化和分子动力学模拟是在PCFF力场[25-27]下运行的.Soldera[26]用PCFF 力场模拟分析了两条聚甲基丙烯酸甲酯链的立构规整度及聚丙烯酸甲酯的能量,Dai等[27]用PCFF力场模拟预测了甘油-水二元低温防护剂的玻璃化转变温度,两者都得到了较好的分子动力学模拟效果.而且PCFF力场[25]适用于聚合物、有机和无机材料、大约20种金属、碳水化合物、液体、核酸的内聚能、力学性质、压缩性质、热容、弹性常数等.因此,本文采用PCFF力场是合理的.同时,Bishop[28]和Pan[29]等已经研究了被溶剂包围的单链高分子溶液体系,模拟分析了低聚合度高分子链的动力学平衡性质,如相关函数、回旋半径、末端距、扩散系数等,结果发现可以通过低聚合度高分子链来研究实际高分子的重要性质.因此,本文首先分别构建一条聚合度为50的无规PAM-H分子链和一条聚合度为50的水解度为25%的无规HPAM分子链(如图2所示),之后将PAM-H分子链嵌入到含有1000、1500、2000、3000或3500个水分子的立方元胞中,并保证整个元胞成电中性的情况下,分别添加不同个数的Na+和Cl-.图3所示为298图1不同系综下,0.4%(w,质量分数)NaCl的HPAM-3500模型能量随模拟时间的变化Fig.1Energy of the model as a function of simulation time under different ensembles for the HPAM-3500 model with0.4%(w,mass fraction)NaCl y in HPAM-y model(or PAM-H-y model)is the number of watermolecules.图2PAM-H(a)和HPAM(b)的结构Fig.2Structures of PAM-H(a)and HPAM (b)2909Acta Phys.-Chim.Sin.,2010Vol.26K 时,含有2000个水分子的HPAM 溶液模型(HPAM -2000).所有构建元胞的离子或分子均采用smart minimizer 方法进行5000步的能量最小化.构建立方元胞时采用周期性边界条件(PBC)[30],即以立方元胞为中心,周围有26个相邻镜像立方元胞,以达到利用较少粒子进行宏观性质模拟的目的,这不仅使粒子所受到的力和宏观样品中本体粒子所受到的力一样,而且可以节省CPU 计算总时间.这是由于模拟体系越大,所需分子动力学模拟的CPU 总时间越长.由于实际溶液中相距较远的粒子之间相互作用很小,可忽略,因此,本文采用截断半径1nm,即忽略1nm 以外的粒子对其中心粒子的相互作用能.聚合度为50的水解度为25%的无规HPAM 分子链的溶液模型的构建及方法同上.本文对优化后的高分子溶液体系,用discover 模块运行分子动力学模拟,同时记录模拟轨迹.模拟温度分别为298、308、318、328和338K,恒温方法采用Andersen 方法[21,31],积分步长为1fs,即每隔1fs 各质点就会有新的坐标和速度,每隔0.5ps 保存一次分子轨迹和坐标,以便以后计算分析,且每个模型重复三次上述过程,所得分析结果为三次平均值(每组数据偏差在5%以内).2结果与讨论2.1盐质量分数和温度对PAM -H 和HPAM 回旋半径的影响分别通过对含1000、1500、2000、3000和3500个水分子的溶液模型所得回旋半径值的比较,发现随水分子数的增加,不同模型所得结果趋势没有很大的偏差,本文从中选取具有代表意义的含1000或3500个水分子的溶液模型进行讨论(如表1所示).2.1.1盐对PAM -H 和HPAM 回旋半径的影响线性聚合物的回旋半径是线性高聚物的特征参数,它直接反映线性高分子链的构象,而链的构象又影响聚合物固态和溶液的许多性质,因此用计算机模拟高分子回旋半径是一项有意义的工作.表1列出本文所构聚合物溶液模型经能量优化、动力学模拟以及分析后的各参数及不同温度下的聚合度均为50的PAM -H 和HPAM 在不同溶液模型中的回旋半径值.由表1发现,各溶液模型中,当没有盐(NaCl)存在时,在不同温度下各高分子链的回旋半径值基本是最大的.即有盐存在情况下,普通的聚丙烯酰胺类产品的回旋半径减小(尤其是HPAM),且随盐质量分数的增加聚丙烯酰胺类产品的回旋半径基本依次减小,HPAM 的回旋半径减小趋势更显著,由方程(1)可知,[η]与R g 3/M 成正比,即特性粘数也随盐质量分数的增加而减小;在没有盐存在情况下,HPAM的回旋半径明显比PAM -H 的高.据实验数据[1]可得,普通的聚丙烯酰胺类产品的主要水化基团—COO -抗盐能力较差,在水溶液中由于它的水化作用和静电排斥作用,使分子主链伸展,有着较大的回旋半径,故特性粘数较大;而在盐溶液中,由于盐离子特别是高价盐离子的存在很大程度上容易破坏水化层,放出自由水,减弱了—COO -基团沿分子主链的排斥作用,使其分子主链蜷曲,回旋半径减小,特性粘数明显下降[1-3].综上所述,模拟的HPAM 回旋半径在盐存在情况下是明显减小的,且随盐质量分数的增加回旋半径减小,即此现象的模拟结果与实验结果[1-3]基本相吻合;且在没有盐存在情况下,HPAM 的回旋半径明显比PAM -H 的回旋半径高,这是由于模拟的HPAM 中含有—COO -基团,而模拟的PAM -H 中不含有此基团,因此模拟的HPAM 的回旋半径比PAM -H 大,其溶液粘度比PAM -H 的溶液图3未含有(a)和含有(b)2%NaCl 的HPAM -2000溶液模型Fig.3HPAM -2000solution models without (a)and with (b)2%NaCl(a)(b)2910No.11刘艳艳等：聚丙烯酰胺稀溶液的分子模拟粘度高,即同一分子量范围,HPAM比PAM-H具有更好的增粘效果,但HPAM抗盐性能比PAM-H差,此模拟结果同样与实验结果相一致[1].2.1.2温度对PAM-H和HPAM回旋半径的影响据实验资料[1]可知,普通PAM类产品的溶液粘度随温度的升高而降低,这是由于温度升高使分子链降解,其中包括高分子主链的断裂和主链与侧基连接键的断裂,前者使产品的分子量降低,部分或全部失去高分子性质,后者降低产品的亲水性,然而这需要的活化能比较高,一般200-220℃以上才发生[1].然而对于没有发生降解的PAM产品,在溶液中由于温度升高容易引起高分子主链单键的内旋转而引起构象的变化,从而导致高分子链尺寸增大,回旋半径增大,分子量越大回旋半径增加得越显著,相反,分子量越小回旋半径增加得越平缓[23-24].总体而言,在没有降解的情况下(200℃以下),PAM-H和HPAM溶液的粘度随温度的增加会有所增加.而对于模拟情况,考虑到高分子链节数只有50,相对实际PAM-H产品分子量极小,回旋半径随温度的增加会有所增加,但会非常平缓,如表1中所示,我们发现,各溶液模型中的高分子链的回旋半径随温度的变化不是很稳定,但数据点基本平均分布在趋势线的两侧,因此,图4中均用趋势线来描述数据的发展趋势.从图4中发现,有些系列的回旋半径总体趋向是随温度的增高而增大,如图4(a,c,d)中所示;而有些系列的回旋半径总体趋势是随温度的升高而降低,如图4(a,b,d)中所示.而上述实验结论[23-24]是回旋半径随温度的升高应平缓增加,即模拟数据与实验结论有些偏差,这意味着:如果想得到精确的变化趋势平缓的模拟数据(如此处回旋半径随温度的变化数据),需优化模拟方法,这将在以后更加系统地研究PAM-H和HPAM溶液性能时进行考察.综上所述,对于不同溶液模型,水分子数增加没有明显改变模拟结果的趋势,但是从含有1000个水分子到含有3500个水分子的溶液模型,其所含有的原子个数从3502增加到11002,而原子个数越多,模拟所需时间越长,从考虑计算效率的角度来看,我们应考虑在模拟结果趋势没有明显改变的前提下,选取原子数相对较少的模型.对于含有1000或1500个水分子的溶液模型,在以后研究pH值对PAM-H 和HPAM溶液的影响时,按实际比例所能在模型中添加的H+、OH-的个数太少,对于含有3000或3500个水分子的溶液模型,其原子个数达到了104数量级,体系太大,所需时间太长.综合考虑,本文确定了溶液模型中水分子数为2000.2.2HPAM溶液模型的径向分布函数分析由上述可知,PAM-H和HPAM的回旋半径随盐质量分数的增加会有不同程度的减小,从而导致溶液粘度减小.本节将以2000个水分子的模型为例,从微观结构验证上述观点.表1PAM-H和HPAM各溶液模型的参数及其在不同温度下的回旋半径值(R g)Table1Parameters for solution models and radius of gyration(R g)for PAM-H and HPAM at2911Acta Phys.-Chim.Sin.,2010Vol.26图5298K HPAM -2000模型中不同NaCl 质量分数下O --H 2O(a)和O -H 2O(b)径向分布函数图Fig.5Radial distribution functions of O --H 2O (a)and O -H 2O (b)of HPAM -2000model with different massfractions of NaCl at 298K径向分布函数g (r )是反映流体微观结构特征的物理量[32-33],其表示在距离某一设定中心原子A 为r 处,某一设定原子B 的数目密度与B 的平均数目密度的比值,即:g (r )=d N ρ4πr2(2)式中,d N 表示与中心的距离为r →r +d r 间的分子数目,ρ表示原子B 的平均数目密度.已有研究者[32-33]通过径向分布函数来研究离子水化作用,即通过离子-水径向分布函数的第一峰的大小来判断离子水化的强弱,且一般采用阴离子与水中的氢做径向分布函数.本文通过径向分布函数研究了在298K 下的不同NaCl 质量分数(w =0%、1%、2%)的HPAM 溶液模型微观结构.图5(a)和5(b)分别是溶液模型中w Na C l(%)w Na C l(%)图4不同NaCl 质量分数下各溶液模型中的回旋半径-温度关系图Fig.4Radius of gyration for PAM -H or HPAM as a function of temperature with different mass fractions of NaClsolution model:(a)PAM -H -1000;(b)HPAM -1000;(c)PAM -H -3500;(d)HPAM -35002912No.11刘艳艳等：聚丙烯酰胺稀溶液的分子模拟高分子链上的氧负离子(O-)-水径向分布函数g O--H(r)和氧原子(O)-水径向分布函数g O-H(r).从图5(a)可知,不同NaCl质量分数下,HPAM分子链上的O--H2O 径向分布函数均在0.16nm处出现第一峰值,其峰值随NaCl质量分数的增加分别为1.46、1.37、1.09,这说明NaCl加入到HPAM的水溶液中,确实破坏了高分子链中O-的水化层,放出自由水,有去水化作用,且随着NaCl质量分数的增加去水化作用增强,从而减弱了—COO-基团沿分子主链的排斥作用,使其分子主链蜷曲,回旋半径依次减小(如图6所示),从图3中也可以看出HPAM尺寸变化;而对于高分子链中O的水化作用可以从图5(b)看出,O-H2O径向分布函数均在0.18nm处出现第一峰值,其峰位置相对O--H2O径向分布函数发生右移,且其峰值随NaCl质量分数的增加分别为0.571、0.569、0.561,这表示O的水化作用很弱,与O-相比可以忽略不计,且NaCl质量分数的增加对其影响不大,这也从微观角度说明了上述HPAM比PAM-H具有较好的增粘效果及较差的抗盐性能的原因.3结论在保证溶液模型中高分子链周围水分子的质量浓度约为1g·mL-1的基础上,构建含有不同水分子数的PAM-H和HPAM溶液模型,MD方法模拟计算了其在不同温度和不同NaCl质量分数下的回旋半径,还模拟分析了部分模型的径向分布函数,结果发现,不同温度下PAM-H和HPAM的回旋半径随NaCl质量分数变化的模拟结果与实验结果在趋势上基本一致,且随着水分子数的增加,各溶液模型的模拟结果趋势没有明显的改变,考虑到模拟工作效率,我们确定了含有2000个水分子的溶液模型体系.同时,对含有2000个水分子的溶液模型作了进一步研究,模拟分析了HPAM在不同盐质量分数水溶液的径向分布函数,从微观角度分析了HPAM水溶液粘度随盐质量分数增加而减小,且HPAM比PAM-H具有较好的增粘效果及较差的抗盐性能的内在原因,这也进一步证明了我们研究工作的合理性.因此,在以后的研究工作中,我们将在此基础上,进一步完善模拟方法,尤其对变化趋势平缓的性能研究,如模拟不同高分子回旋半径随温度的变化,需进一步优化模拟方法,从而对PAM-H和HPAM溶液进行更准确、更深入的研究,使模拟结果能更好地说明解释实验现象,以便更好地指导实验工作.References1Fang,D.B.;Guo,R.W.;Ha,R.H.Acrylamide polymer.Beijing: Chemical Industry Press,2006:1-86[方道斌,郭睿威,哈润华.丙烯酰胺聚合物.北京:化学工业出版社,2006:1-86]2Gong,H.J.;Xin,X.;Xu,G.Y.;Wang,Y.J.Colloids Surf.A-Physicochem.Eng.Asp.,2008,317:5223Fang,D.B.;Guo,R.W.;Zhou,S.G.;Zhang,X.C.CIESC Journal, 1966,47:645[方道斌,郭睿威,周少刚,张曦晨.化工学报,1966,47:645]4Yahaya,G.O.;Ahdab,A.A.;Ali,S.A.;Abu-Sharkh,B.F.;Hamad,E.Z.Polymer,2001,42:33635Volpert,E.;Selb,J.;Candau,F.Polymer,1998,39:10256Ye,L.;Luo,K.F.;Huang,R.H.Eur.Polym.J.,2000,36:17117McCormick,C.L.;Nonaka,T.;Johnson,C.B.Polymer,1988,29: 7318Zhang,Y.B.;Wu,C.;Fang,Q.;Zhang,Y.X.Macromolecules, 1996,29:24949Klucker,R.;Munch,J.P.;Schosseler,F.Macromolecules,1997, 30:383910Qiu,X.P.;Zhang,X.R.;Ding,M.T.Chem.J.Chin.Univ.,1995, 16(8):1321[邱星屏,张雪蓉,丁马太.高等学校化学学报,1995,16(8):1321]11Zhu,W.P.Plastics Science and Technology,2002,(5):23 [朱伟平.塑料科技,2002,(5):23]12Chen,P.F.;Zhang,L.H.China Adhesives,2007,6:52[陈鹏飞,张丽华.中国胶黏剂,2007,6:52]13Yuan,S.L.;Xu,G.Y.;Cai,Z.T.Colloid Polym.Sci.,2003,281(1):6614Zeng,Q.H.;Yu,A.B.;Lu,G.Q.Prog.Polym.Sci.,2008,33(2): 19115Dalakogloua,G.K.;Karatasosa,K.;Lyulin,S.V.;Lyulin,A.V.图6298K时,HPAM-2000模型中HPAM回旋半径-NaCl质量分数关系图Fig.6Radius of Gyration for HPAM as a function ofthe mass fractions of NaCl at298K in the HPAM-2000model2913Acta Phys.-Chim.Sin.,2010Vol.26Mater.Sci.Eng.B,2008,152:11416Le,T.C.;Todd,B.D.;Daivis,P.J.;Uhlherr,A.J.Chem.Phys., 2009,130:07490117Drew,P.M.;Adolf,D.B.Soft Matter,2005,1:14618Tung,K.L.;Lu,K.T.;Ruaan,R.C.;Juin,J.Y.Desalination, 2006,192:38019Kairn,T.;Daivis,P.J.;Matin,M.L.;Snook,I.K.Int.J.Thermophys.,2004,25(4):107520Liu,Y.M.;Li,G.Z.;Song,W.K.;Wang,J.J.Acta Phys.-Chim.Sin.,2006,22(12):1456[刘永明,李桂芝,宋万坤,王进军.物理化学学报,2006,22(12):1456]21Tao,C.G.;Feng,H.J.;Zhou,J.;Lü,L.H.;Lu,X.H.Acta Phys.-Chim.Sin.,2009,25(7):1317[陶长贵,冯海军,周健,吕玲红,陆小华.物理化学学报,2009,25(7):1317]22Shao,Q.;Lü,L.H.;Lu,X.H.;Wei,M.J.;Zhu,Y.D.;Shen,W.F.Acta Phys.-Chim.Sin.,2009,25(3):583[邵庆,吕玲红,陆小华,魏明杰,朱育丹,沈文枫.物理化学学报,2009,25(3):583] 23Rubinstein,M.;Colby,R.Polymer physics.Oxford:Oxford University Press,2002:Chapter2724He,M.J.;Chen,W.X.;Dong,X.X.Polymer physics.Shanghai: Fudan University Press,2007:15-73[何曼君,陈维孝,董西侠.高分子物理.上海:复旦大学出版社,2007:15-73]25Sun,H.;Mumby,S.J.;Maple,J.R.;Hagler,A.T.J.Am.Chem.Soc.,1994,116:297826Soldera,A.Polymer,2002,43:426927Li,D.X.;Liu,B.L.;Liu,Y.S.;Chen,C.L.Cryobiology,2008, 56:11428Bishop,M.;Kalos,M.H.;Frisch,H.L.J.Chem.Phys.,1979,70: 129929Pan,R.;Liu,X.K.;Zhang,A.M.;Gu,p.Mater.Sci.,2007, 39:88730Yang,X.Z.Molecular simulation and polymer materials.Beijing: Science Press,2002:43[杨小震.分子模拟与高分子材料.北京:科学出版社,2002:43]31Andersen,H.C.J.Chem.Phys.,1980,72:238432Zhou,J.;Zhu,Y.;Wang,W.C.;Lu,X.H.;Wang,Y.Y.;Shi,J.Acta Phys.-Chim.Sin.,2002,18(3):207[周健,朱宇,汪文川,陆小华,王延儒,时均.物理化学学报,2002,18(3):207] 33Zhou,J.;Lu,X.H.;Wang,Y,R.;Shi,J.CIESC Journal,2000,51: 143[周健,陆小华,王延儒,时均.化工学报,2000,51:143]2914。

材料科学与工程基础（英文）_南京航空航天大学中国大学mooc课后章节答案期末考试题库2023年1.The driving force for steady-state diffusion is the __________.答案:concentration gradient2.Diffusion coefficient is with the increasing diffusion temperature.答案:exponentially increased;3.Due to , alloys are usually than pure metals of the solvent.答案:solid solution strengthening, stronger;4.The finer the grains, the larger the , and .答案:strength, hardness, toughness;5.With plastic deformation,the increase of dislocationdensity will result in .答案:higher strength;6.In general, Brinell Hardness test is to measure thematerial’s hardness.答案:relatively softer7.Yield strength is corresponding to the occurrenceof deformation.答案:noticeable plastic8.Strain Hardening is also named as .答案:work hardening9.Vacancy diffusion is usually interstitial one.答案:slower than10.Edge and screw dislocations differ in what way?答案:angle between Burgers vector and line direction.11. A ____ may form when impurity atoms are added to a solid, in which case theoriginal crystal structure is retained and no new phases are formed.答案:solid solution12.One explanation for why graphite powder acts so well as a “solid lubricant”is .答案:carbon atoms in graphite are covalently bonded within planar layers but have weaker secondary bonds between layers13.Substitutional atom (impurity) is an example of ______.答案:point defect14.Interstitial solid solution belongs to .答案:finite solid solution;15.The atomic packing factor for FCC is .答案:0.7416.The coordination number of BCC crystal structure is .答案:817.The crystal structure of Cu is ?答案:FCC18.How many atoms does the face centered cubic unit cell contain?答案:Four19.If the electron configuration of Fe is 1s2 2s2 2p6 3s2 3p6 3d6 4s2, then theelectron configurations for the Fe3+ is 1s2 2s2 2p6 3s2 _____.答案:3p6 3d520.Bonds in most metals are referred to as ______.答案:Non-directional21.Covalent bonding occurs as a result of _________ sharing.答案:electron22.Which of the following is NOT an example of primary bonding?答案:Van der Waals23.Atomic weight (A) of an element corresponds to the weighted average of theatomic masses of the atom’s naturally occurring ___________.答案:isotopes24.The point on a phase diagram where the maximum number of allowablephases are in equilibrium is .答案:eutectic point25.Sterling silver (92.5%Ag/7.5%Cu) is an example of ___________.答案:Solid solution26.Engineering stress-strain curve and true stress-strain curve are equal up to .答案:Yeild point27.Among thefollowingtypical transformations of austenite in steels,____________transformation is diffusionless.答案:martensitic28.The heat-treatable aluminum alloy can be strengthened by .答案:Both of above29.In the as-quenched state, martensite is very hard and so brittle that a heattreatment known as must be accomplished sequently.答案:tempering30.During heat treatment of steel, austenite transforms into martensite by .答案:quenching31.Which of the following plane has the highest planar density for fcc.答案:(111)32.Which of the following describes recrystallization?答案:Diffusion dependent with no change in phase composition33.Heating the cold-worked metal progresses in three stages: .答案:recovery, recrystallization, grain growth;34.Strength is increased by making dislocation motion .答案:difficult35.The boundary above which only liquid phase exist is called _________.答案:liquidus36.We have an annealed carbon steel which has hardness of 150HBS. Supposewe know the hardness of Pearlite is 200HBS and the hardness of Ferrite is 80HBS, determine the carbon amount of this steel.答案:0.45%37.The maximum solubility of C in γ-austenite - solid solution is .答案:2.1438.In a plain steel that contains 0.2 percentage carbon, we should expect: .答案:a 25% pearlite and 75% pro-eutectoid ferrite39. A copper-nickel alloy is high-temperature heat treated; the diffusion of Cuinto Ni and Ni into Cu regions is referred to as _____________________.答案:Inter-diffusion40.The phase diagram of Sn-Pb alloy is called .答案:Eutectic phase diagram。

PCR常见问题分析及对策(无扩增产物、非特异性扩增、拖尾、假阳性)问题1：无扩增产物现象：正对照有条带，而样品则无原因:1.模板:含有抑制物，含量低2.Buffer对样品不合适3.引物设计不当或者发生降解4.反应条件：退火温度太高，延伸时间太短对策:1.纯化模板或者使用试剂盒提取模板DNA或加大模板的用量2.更换Buffer或调整浓度3.重新设计引物（避免链间二聚体和链内二级结构）或者换一管新引物4.降低退火温度、延长延伸时间问题2：非特异性扩增现象：条带与预计的大小不一致或者非特异性扩增带原因：1.引物特异性差2.模板或引物浓度过高3.酶量过多4.Mg2+浓度偏高5.退火温度偏低6.循环次数过多对策：1.重新设计引物或者使用巢式PCR2.适当降低模板或引物浓度3.适当减少酶量4.降低镁离子浓度5.适当提高退火温度或使用二阶段温度法6.减少循环次数问题3：拖尾现象：产物在凝胶上呈Smear状态。

原因：1.模板不纯2.Buffer不合适3.退火温度偏低4.酶量过多5.dNTP、Mg2+浓度偏高6.循环次数过多对策：1.纯化模板2.更换Buffer3.适当提高退火温度4.适量用酶5.适当降低dNTP和镁离子的浓度6.减少循环次数问题4：假阳性现象：空白对照出现目的扩增产物原因：靶序列或扩增产物的交*污染对策：1.操作时应小心轻柔，防止将靶序列吸入加样枪内或溅出离心管外；2.除酶及不能耐高温的物质外，所有试剂或器材均应高压消毒。

所用离心管及加样枪头等均应一次性使用。

3.各种试剂最好先进行分装，然后低温贮存PCR产物的电泳检测时间一般为48h以内，有些最好于当日电泳检测，大于48h后带型不规则甚致消失。

假阴性，不出现扩增条带PCR反应的关键环节有①模板核酸的制备，②引物的质量与特异性，③酶的质量及，④PCR循环条件。

寻找原因亦应针对上述环节进行分析研究。

模板：①模板中含有杂蛋白质，②模板中含有Taq酶抑制剂，③模板中蛋白质没有消化除净，特别是染色体中的组蛋白，④在提取制备模板时丢失过多，或吸入酚。

饱和液相密度英文The density of a saturated liquid phase is an important parameter that characterizes the physical properties of a substance. It is defined as the mass per unit volume of the saturated liquid at a given temperature and pressure. The density of a substance is an extensive property, meaning that it varies depending on the amount of the substance present. Here, we will explore the concept of density in the context of saturated liquids and discuss its significance in various fields.Saturated liquids are liquids that are in equilibrium with their own vapor phase at a specific temperature and pressure. This means that any further increase in temperature or decrease in pressure would cause the liquid to start evaporating. The density of a saturated liquid depends on several factors, including the molecular weight and size of the substance, as well as the temperature and pressure conditions.In chemical engineering, the density of saturated liquids is a crucial parameter for designing and operating processes involving fluid flow, such as distillation and extraction. Knowledge of the density helps determine the required equipment sizes, pumping requirements, and flow rates. For example, in distillation columns, the density of the saturated liquid feed stream affects the liquid hold-up and the residence time of the components, which in turn influence separation efficiency.In the field of thermodynamics, the density of saturated liquids is essential for calculations involving heat transfer, phase equilibrium, and property estimation. For instance, the density of saturatedliquid water is used in the formulation of thermodynamic models like the Peng-Robinson or Soave-Redlich-Kwong equations of state. These equations are widely employed in process simulators to predict phase behavior and properties.The density of saturated liquids is also significant in environmental sciences, particularly in studies related to hydrology and groundwater flow. The density of groundwater determines its buoyancy and how it interacts with other subsurface materials. This information is crucial for understanding the movement and transport of contaminants in groundwater systems and designing remediation strategies.In the petroleum industry, density measurements of saturated liquid hydrocarbons are indispensable for exploration, production, and refining operations. The density of crude oil, for instance, provides vital information for estimating reserves, determining quality parameters, and designing storage and transportation facilities. Furthermore, the density of various liquid hydrocarbon fractions helps in the calculation of physical properties like viscosity and thermal conductivity.In conclusion, the density of saturated liquids plays a fundamental role in a wide range of disciplines and industries. Its understanding and accurate measurement are crucial for process design, thermodynamic calculations, environmental studies, and the petroleum industry. The density of a saturated liquid is influenced by various factors, including the molecular characteristics of the substance, temperature, and pressure conditions. Therefore, obtaining precise density values is essential for predicting andoptimizing the behavior of saturated liquid phases in different applications.。

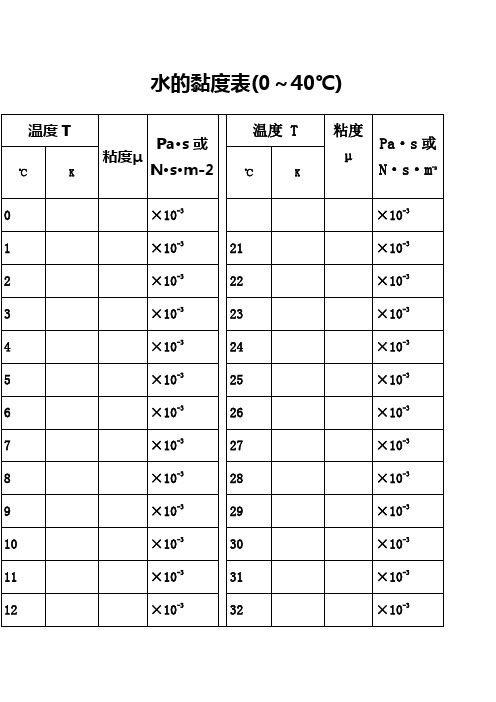
水的黏度表(0～40℃)水的物理性质F3??? Viscosity decreases with pressure(at temperatures below 33°C)Viscous flow occurs by molecules moving through the voids that exist between them. As the pressure increases, the volume decreases and the volume of these voidsreduces, so normally increasing pressure increases the viscosity.Water's pressure-viscosity behavior [534] can be explained by the increased pressure (up to about 150 MPa) causing deformation, so reducing the strength of the hydrogen-bonded network, which is also partially responsible for the viscosity. This reduction in cohesivity more than compensates for the reduced void volume. It is thus a direct consequence of the balance between hydrogen bonding effects and the van der Waals dispersion forces [558] in water; hydrogen bonding prevailing at lower temperatures and pressures. At higher pressures (and densities), the balance between hydrogen bonding effects and the van der Waals dispersion forces is tipped in favor of the dispersion forces and the remaining hydrogen bonds are stronger due to the closer proximity of the contributing oxygen atoms [655]. Viscosity, then, increases with pressure. The dashed line (opposite) indicates the viscosity minima.The variation of viscosity with pressure and temperature has been used as evidence that the viscosity is determined more by the extent of hydrogen bonding rather than hydrogen bonding strength.Self-diffusion is also affected by pressure where (at low temperatures) both the translational and rotational motion of water anomalously increase as the pressure increases.。

Urban environments are complex ecosystems,where human activities interact with natural elements to create a unique living space.Here are some key aspects to consider when writing an essay on city environments:1.Urban Planning:Discuss the importance of thoughtful urban planning in creating sustainable and livable cities.Mention how zoning laws,green spaces,and public transportation systems contribute to a citys environment.2.Pollution:Address the various forms of pollution found in urban areas,such as air pollution from vehicle emissions,noise pollution from traffic and construction,and light pollution from excessive artificial lighting.3.Green Spaces:Highlight the role of parks,gardens,and other green spaces in improving air quality,providing recreational areas,and enhancing the aesthetic appeal ofa city.4.Sustainable Practices:Explore the implementation of sustainable practices in urban areas,such as recycling programs,energyefficient buildings,and the use of renewable energy sources.5.Transportation:Discuss the impact of different modes of transportation on the urban environment,including the benefits and drawbacks of cars,public transit,cycling,and walking.6.Population Density:Consider how high population density in cities can lead to overcrowding,strain on resources,and social issues,but also the potential for vibrant, diverse communities.7.Economic Factors:Examine the relationship between economic development and the urban environment,including the role of industry,commerce,and the job market in shaping a citys landscape.8.Cultural Impact:Reflect on how the cultural identity of a city influences its environment,from architectural styles to local customs and traditions.9.Challenges and Solutions:Identify some of the major challenges faced by urban environments,such as climate change,resource scarcity,and social inequality,and propose potential solutions or strategies for mitigation.10.Future Outlook:Conclude with thoughts on the future of urban environments,considering technological advancements,demographic shifts,and the potential for creating smarter,greener cities.When writing your essay,ensure that you provide specific examples to support your points,and use a logical structure to organize your thoughts.Remember to cite credible sources if you are drawing from research or expert opinions.。

a rXiv:q uant-ph/03394v216M ay23Collisional decoherence reexamined Klaus Hornberger and John E.Sipe ∗Universit¨a t Wien,Institut f¨u r Experimentalphysik,Boltzmanngasse 5,1090Wien,Austria (Dated:Apil 17,2003)Abstract We re-derive the quantum master equation for the decoherence of a massive Brownian particle due to collisions with the lighter particles from a thermal environment.Our careful treatment avoids the occurrence of squares of Dirac delta functions.It leads to a decoherence rate which is smaller by a factor of 2πcompared to previous findings.This result,which is in agreement with recent experiments,is confirmed by both a physical analysis of the problem and by a perturbative calculation in the weak coupling limit.PACS numbers:03.65.Yz,03.65.Ta,03.75.-bI.INTRODUCTIONA classic result of decoherence theory is the rapid decay in the off-diagonal matrix el-ements in the coordinate representation of the density operatorρ(R1,R2;t)of a massive Brownian particle suffering collisions with the lighter particles of a thermal bath.Early cal-culations by Joos and Zeh[1]were improved by later authors,and the result of Gallis and Fleming[2]seems to be the most widely quoted[3].Theyfind,in the limit of an infinitely massive Brownian particle,that∂ρ(R1,R2;t)m dˆn1dˆn2equation derivations undertaken in,e.g.,quantum optics.In thefirst calculation wefind(2) withε=1.In the second wefind(2)withε=1and f(qˆn2,qˆn1)replaced by f B(qˆn2,qˆn1), thefirst Born approximation to that scattering amplitude.This is precisely what would be expected,since the second calculation requires the assumption of weak interaction;it thus serves to confirm theε=1result of thefirst.Neither of these is the most elegant or general calculation one could imagine;thefirst is rather cumbersome,and the second would be neater if generalized to second quantized form[5].But thefirst has the advantage of displaying the physics of decoherence in an almost pictorial way,while allowing a calculation involving the full scattering amplitude.And the second,in its simple form,establishes a clear connection with the usual approach to decoherence through the master equation approach common in quantum optics.Totally separate in their approaches,we feel that together they are a convincing demonstration thatε=1.These two calculations are presented in sections II and IV below.In section III we return to the traditional derivation and highlight its inherent shortcomings.We show how it should be modified by using a simple physical argument,which leads to a replacement rule for the occurring square of a Dirac delta function.This treatment then also yields the resultε=1. Our concluding remarks are presented in section V.II.SCATTERING CALCULATIONTo set our notation we begin with a review of the standard approach used to calculate collisional decoherence.However,we also wish to point out the difficulties that can arise in its application,so we begin in a more detailed way than is normally done.To apply scattering theory in a careful way one has to begin with an asymptotic-in state |φm |ψ ,a normalized ket that is the direct product of a Brownian particle ket|φm and abath particle ket|ψ .The asymptotic-in ket is the result of the evolution of a product ket |φ(−∞)m |ψ(−∞) at t=−∞to t=0under the Hamiltonian that describes the free evolution of both particles,without interaction.The effect of the two-particle scattering operator S on this asymptotic-in state,S(|φm |ψ ),then produces the asymptotic-out state.When evolved from t=0to t=∞by the non-interacting Hamiltonian,the asymptotic-out stateyields the actual state at t=∞that evolves from|φ(−∞)m |ψ(−∞) at t=−∞under the influence of the full Hamiltonian.FIG.1:Sketched are the wave packets associated with|φm and|ψ at t=0.In configuration(a) the state|φm |ψ could be taken as both an asymptotic-in state and an initial state at t=0;for configuration(b)that would not be possible.In general,of course,|φm |ψ does not describe the actual ket at t=0that evolves from |φ(−∞)m |ψ(−∞) at t=−∞,because the evolution of that actual ket involves the particle interaction.But if the kets|φm and|ψ are such that the(short-range)interaction between the particles has not yet had an effect(e.g.,Fig.1a but not Fig.1b),then|φm |ψ can be taken as the actual ket at t=0as well as the asymptotic-in ket.We only consider kets|φm and|ψ of this form below.We now turn to the impending collision of a bath particle characterized by|ψ and a Brownian particle described by a reduced density operator at t=0given by a convex sum of projectors|φm φm|,ρin= m p m|φm φm|= d R1d R2|R1 ρo(R1,R2) R2|,with probabilities p m>0, p m=1.Here the|R1,2 label position eigenkets of the Brownian particle,andρo(R1,R2)= m p m R1|φm φm|R2 (3) its position representation.Thenρtotalin=ρin⊗|ψ ψ|(4) can be considered both as the full initial(at t=0)density operator,and the full asymptotic-in density operator.The full asymptotic-out density operator is thenρtotal out =Sρtotalin S†= d R1d R2S(|R1 |ψ )ρo(R1,R2)( ψ| R2|)S†.To determine terms such as S(|R |ψ )it is useful tofirst consider the effect of the S operator on direct products|P |p of eigenkets|P of the Brownian particle momentum and eigenkets |p of the bath particle momentum.Since the total momentum commutes with the Soperator the scattering transformation can be reduced to a one-particle problem,with S(|P |p )= d q|P−q |p+q m∗M P+q|S o|m∗M P ,where the matrix element here is that of the one-particle scattering operator S o corre-sponding to the two-body interaction acting in the Hilbert space of the bath particle,and m∗=mM/(m+M)is the reduced mass.In the limit that the Brownian particle is much more massive than the bath particle,M≫m,this reduces toS(|P |p )→ d q|P−q |p+q p+q|S o|por,moving to a position representation for the Brownian particle,S(|R |p )= d q|R e−i q·R/ |p+q p+q|S o|p= d q|R |p+q p+q|e−i p·R/ S o e i p·R/ |p=|R e−i p·R/ S o e i p·R/ |p ,where p is the momentum operator for the bath particle,and so for general states|ψS(|R |ψ )=|R e−i p·R/ S o e i p·R/ |ψ≡|R ψR ,whereψR =e−i p·R/ S o e i p·R/ |ψ ,and thusρtotal= d R1d R2|R1 ψR1 ρo(R1,R2) ψR2 R2|.outis not thefinal density operator at t=∞,but only the asymptotic-out density Althoughρtotaloutoperator,it evolves to thefinal density operator through the non-interacting Hamiltonian, and overlaps of the form ψR2|ψR1 will be preserved during this free evolution.So thefinal reduced density operator for the Brownian particle at t=∞isρfinal= d R1d R2|R1 ψR2|ψR1 ρo(R1,R2) R2|≡ d R1d R2|R1 ρ(R1,R2) R2|,whereρ(R 1,R 2)= ψR 2|ψR 1 ρo (R 1,R 2).(5)As is well understood,decoherence arises because the bath particle becomes entangled with the Brownian particle and the two (asymptotic-out)states ψR 2 and ψR 1 resulting from scattering interactions associated with the same bath ket |ψ and different position eigenkets|R 2 and |R 1 can have negligible overlap even for |R 2−R 1|small.The change of the Brownian particle’s reduced density operator by a single collision is ∆ρ(R 1,R 2)≡ρ(R 1,R 2)−ρo (R 1,R 2)= ψR 2|ψR 1 −1 ρo (R 1,R 2).(6)It involves overlap terms of the form ψR 2|ψR 1 = ψ|e −i p ·R 2/ S †o e −i p ·(R 1−R 2)/ S o e i p ·R 1/ |ψ = ψ|S †2S 1|ψ =tr bath S †2S 1|ψ ψ| ,(7)where the operators S j =e −i p ·R j / S o e i p ·R j /(8)for j =1,2are translated scattering operators.We introduce corresponding T j operators according toS j =1+i T j ,(9)and using the unitarity of the S j ,which follows immediately because S o is unitary,we findS †2S 1=1+T †2T 1−12T †2T 2+i 2 T 2+T †2and so ψR 2|ψR 1 =1+ ψ|A|ψ ,(10)where A =T †2T 1−12T †2T 2+i 2T 2+T †2 .Thus the change in the Brownian particle reduced density operator is∆ρ(R1,R2)= ψ|A|ψ ρo(R1,R2)(11)The general strategy is to evaluate the matrix element ψ|A|ψ by inserting complete sets of momentum eigenstates,ψ|A|ψ = d q1d q2 ψ|q2 q2|A|q1 q1|ψ ,(12) determine q2|A|q1 ,and then perform the momentum eigenstate integrals.Writing S o= 1+i T o as well,and using the relations(8)and(9)wefindq2|A|q1 =e i(q1·R1−q2·R2)/ q2|T†o e i p·(R2−R1)/ T o|q1 (13)−1e i(q1−q2)·R2/ q2|T†o T o|q12i+δ(E2−E1)f(q2,q1),(14)2π mwhere f(q2,q1)is the scattering amplitude,we can identifyq2|T o|q1 =1f(q2,q1),2π q2where E i=q2i/(2m).Now in the traditional calculations[1,2,3]one calculates∂ρ(R1,R2)/∂t by considering the change∆ρ(R1,R2)in a time∆t due to collisions with bath particles that would pass in the neighborhood of the Brownian particle,taking the distribution of their velocities from the assumed thermal equilibrium of the bath.To calculate∆ρ(R1,R2)from one of these bath particles,a box-normalized momentum eigenstate, |q is used in place of a localized ket|ψ .Unlike the|φm |ψ states we introduced above,the|φm |q obviously cannot be considered either as asymptotic-in states or as the actual states at t=0since the |q are delocalized.Nonetheless,the traditional approach seems to simplify the calculation because, as is clear from(12),only diagonal elements q|A|q are required if the limit of an infinite boxis taken.But from the expression(13)for q2|A|q1 it is clear that,when a resolution over a complete set of momentum states|q′ is inserted between T†o and T o and the expression(15) for the matrix elements of T o is used,the diagonal elements q|A|q involve the square of Dirac delta functionsδ(q−q′).To evaluate these the“magnitude”ofδ(0)must be somehow set.This is done by relating it to an original normalization volume of the box.While not implausible,such a protocol is certainly not rigorous and is open to question.To avoid the necessity of this kind of maneuver we will employ bath states|ψ that are normalized and localized,as is required by a strict application of scattering theory.Before addressing the full calculation for a bath in thermal equilibrium we consider scattering involving a single state|ψ .A.Scattering of a single bath ketFrom the equations(12)and(13)for ψ|A|ψ in terms of q2|A|q1 it is clear that we require integrals of the formI1= d q1d q2u(q1,q2) q2|T o+T†o|q1 ,(16)I2(R)= d q1d q2u(q1,q2) q2|T†o e i p·R/ T o|q1 ,which we work out in Appendix A for an arbitrary function u(q1,q2)of the two momentum variables.Wefind that we can write these expressions exactly asI1= d q ˆq⊥d∆u(q−∆2)M1(q,∆)(17) andI2(R)= dˆn d q ˆq⊥d∆u(q−∆2)e i Q·R/ M2(q,ˆn,∆),(18) The integration over q covers all momentum space,while∆is a two dimensional momentum vector ranging over the plane perpendicular to q;ˆn is a unit vector with dˆn the associated solid angle element.Moreover,M1(q,∆)=12,q−∆2,q+∆4π2 2Q2)f(Q,q−∆FIG.2:For this as both the total asymptotic-inwithQ=ˆn 4.(21) With these formulas in hand we can address the expression for ψ|A|ψ once|ψ is specified. To do this,we take the bath particle wave function r′|ψ to be a Gaussian wave packet centered at r o in position and p o in momentum,r′|ψ =e i p o·(r′−r o)/√√2 q−∆πb2 3/2e i∆·r o/ e−∆2/(4b2)e−|q−p o|2/b2.We now assume that this wave packet is located far enough away from the regions of space where an initial density operator(3)is concentrated,and with an average momentum directed towards the Brownian particle such that the combined density operator(4)can be taken both as an initial density operator at t=0,and as the asymptotic-in density operator (see Fig.2).Then using the expressions above wefindψ|A|ψ = 1whereB(ˆn,q,∆)=e i q·(R1−R2)/ e i Q·(R2−R1)/ e−i∆·(r o−2e−i∆·(r o−R1)/ e−∆2/(4b2)M2(q,ˆn,∆)−12 e−i∆·(r o−R1)/ −e−i∆·(r o−R2)/ e−∆2/(4b2)M1(q,∆),and where we have put2.(23) The Gaussian functions will keep∆within about b of zero and q within about b of p o.We now assume that the central momentum p o is much greater in magnitude than its variance, p o≫b,and hence q≫b for all q that make a significant contribution;we also assume that the scattering amplitude varies little over the momentum range b.Then we can putM1(q,∆)≈14π2 2|f(qˆn,q)|2.Once these approximation are made the integral over∆of the three terms in B(ˆn,q,∆) can be done immediately.The integral over∆of thefirst term is not so simple because∆still appears in Q.In the exponential we have phase factors that vary asQ·(R2−R1)q2+∆2=qˆn·(R2−R1)8 q+...Thefirst correction term is of orderb2|R2−R1|(q/b)(24) Since q≫b this term will still be much smaller than unity even if the distance between the two positions of the Brownian particle is several widths of the wave packet.We assume that|R2−R1|is indeed such this quantity is much less than unity.Then we can replace the phase by its leading order expansionQ·(R2−R1) ,in the exponentials of thefirst two integrals,and the integration over∆can be done as well.These are two dimensional integrals over a plane perpendicular to q,and so they are of the form ˆq⊥d∆e−i∆·(r o−R),where we have used the fact that ab= and introducedexp − R2−(ˆq·R)2 /a2Γq(R)=A r o(q),(26)(πb2)3/2whereA r o(q)=Γq(r o−(Γq(r o−R1)+Γq(r o−R2)) dˆn|f(qˆn,q)|222πi+R.Moreover,since the integral in(26)restricts q to within a distance of about b of p o,in(27)we can replace q by p o in the scattering amplitudes and in the phase,using the assumption already made thatthey vary little over a range of b;we can also replace theΓq functions by correspondingΓpo functions.The integral in(26)can then be done,and using(11)wefind∆ρ(R1,R2)=−ρo(R1,R2)Γp(r o−oe−ℓ2/a2R)=FIG.3:A configuration where a≫R=|R1−R2|;ℓ=e−βp2/(2m)(29)ΩprovidedΩis much larger than the cube of the thermal de Broglie wave lengthλ= m.(30) The usual convex decomposition of(29)in terms of the delocalized energy eigenstates is the obvious one and,aside from the freedom in choosing orthogonal states from among adegenerate set,it is the only one in terms of orthogonal states.But a host of others can also found.A particularly convenient set of convex decompositions for our problem at hand can be obtained by usinge−βp2/(2m)= ¯β 2πm/ˆβ 3/2e−¯β(p−p)2/(2m)(31) which holds as long asˆβand¯βare both positive and11¯β+ ArrayΩ d pˆµ(p)|ψrp ψrp|,(32) whereˆµ(p)= ˆββ 3/4e−¯β(p−p)2/(4m)|r (34)=¯λ3/2e−¯β(p−p)2/(4m)|r ,are characterized by the length scale¯λ= m,(compare with (30)).One then immediately finds r ′|ψrp =2√¯λ3/2e i p ·(r ′−r )/ e −2π|r ′−r |2/¯λ2(35)so the wave packet |ψrp is centered at r and has an average momentum p .Indeed,it is of the Gaussian form used in the preceding section with minimal uncertainties,b ≡2m =k B ¯T2m =k B ˆT2m +(δp x )22.We see that in the class (32,33)of convex decompositions of ρbath a part of the thermal kinetic energy is associated with the size of the wave packets themselves,while the rest resides inthe motion of the centres of the wave packets.If we take ˆT→0then the wave packets are essentially all at rest characterized by a size ¯λ→λ,which is the thermal de Broglie wavelength.On the other hand,for ˆT≫¯T the wave packets are much larger than the thermal de Broglie wavelength,and essentially all the thermal kinetic energy is associated with the expectation value of the momenta of the wave packets;we have p 2 2mp 2ˆµ(p )d p =33k B ˆT1.Assumptions and choices1.We neglect initial correlations,taking the initial full density operator at t=0to be adirect product of a Brownian particle density operator and a density operator for the bath particles in thermal equilibrium,ρtotal(t=0)=ρo⊗ρbath.(36) 2.We assume that the density of bath particles is much less thanλ−3;then the issue ofparticle degeneracy does not matter and we may consider the density operator of the total bath to be just the product of density operators for individual particles.Thus we can calculate effects‘particle by particle’.We choose a volumeΩmuch larger than any other volume of interest.3.We use a convex decomposition ofρbath for a single bath particle of the type describedabove,with¯T≪T such thatˆT≈Tand thereforeb2≪ p2 .(37) This renders b sufficiently small so that the variation in scattering amplitudes over the momentum spread of a wave packet is negligible for essentially all of the wave packets in the convex decomposition.4.The value of¯T should also be small enough that the neglect of the variation of thescattering amplitudes in the integral(22)is justified,and that we can use the approx-imation of neglecting terms on the order of(24)above.For the latter we needb2q|R2−R1|≪1Now for typical wave packets the average momentum p,and hence q,will be of the order of mv wp=|R2−R1|= 8π λ≪1,vwpand sinceˆT≈T this reduces to¯T≪|R2−R1|5.We choose a coarse-graining time∆t sufficiently large thatv wp∆t≫a,(38)v wp∆t≫|R2−R1|.That is,a typical packet travels a distance much greater than its width and much greater than the distance between the two decohering sites during the coarse graining ing the expressions for v wp and a above,andˆT≈T,thefirst condition readsT∆t≫R(recall(23);see Fig.4).Of course,some of these will completely miss the Brownian particle,but none have had a collision with it in the past.For a given p we refer to this region of space as R(p).Returning to the wave packets,note that those with central positions r close to the R1 or R2of interest will initially be overlapping with regions of space for whichρo(R1,R2)is non-vanishing;here any talk of a collision is inappropriate,since at initiation,at t=0,the Brownian and bath particle would immediately be strongly interacting.This is an artifactΩ ψrp|A|ψrp ,where we assume that the inclusion of the problematic class of wave packets identified above will not lead to serious ing the result(26)from our scattering calculation above, we have∆ρ(R1,R2)=nρo(R1,R2) d pˆµ(p) R(p)d r d q e−|q−p|2/b2But this is not necessary.We can simply note that,by virtue of(37),ˆµ(p)will vary little over the range b that e−|q−p|2/b2peaks and falls.Hence we can replaceˆµ(p)byˆµ(q)and R(p)by R(q),and immediately do the integral over p to yield∆ρ(R1,R2)=nρo(R1,R2) d qˆµ(q) R(q)d r A r(q).Since the only r dependence is in theΓq,see(25),one can now do the r integral for each fixed q,putting d r=d r⊥dr ,where r refers to the distance in the direction−q.Since the integration over r⊥is unrestricted in the region R(q)we haveR(q)d r⊥Γq(r⊥−R⊥i)=1=R1,R2,orfor R∆t,mand so wefind∆ρ(R1,R2)ˆµ(q) dˆn e i(q−qˆn)·(R1−R2)/ −1 |f(qˆn,q)|2.mFinally,we recall thatˆT≈T and therefore putˆµ(q)≈µ(q),whereµ(q)= β,(41)4πand hence on a coarse grained time scale wefind(1,2)withε=1.III.THE TRADITIONAL APPROACH:A REMEDYWe showed in the preceding section how the problem of evaluating a squared Dirac function can be circumvented by expressing the thermal state of the bath particles in an over-complete,non-orthogonal basis of Gaussian wave packets(see Eq.(32)).However,it iscertainly reasonable to explore the possibility of using the standard diagonal representation of the thermal bath density operator,which facilitates the formal calculation considerably. After all,all the representations ofρbath are equally valid and should yield the same master equation provided the calculation is done in a correct way.It is therefore worthwhile to search for a way to deal properly with such an ill-defined object as the“square”of a delta distribution function.In this section we show how a proper evaluation of the diagonal momentum basis matrix elements can be implemented.This leads to an alternate derivation of the master equation (1,2),and allows us to highlight the origin of the problem plaguing earlier workers and to discuss further implications.However,rather than attempting a mathematically rigorous formulation,we base our presentation on a simple physical argument.Our point is that such an argument can lead to a prescription for correctly evaluating improper products of Dirac delta functions,although this differs from previous naive treatments.A.A single collisionLet us consider again the action of a single scattering event on the Brownian particle in position representationρo(R1,R2)and in the limit of a large mass.It follows from the discussion in section II that after the collision it differs merely by a factor from the initial Brownian state,ρ(R1,R2)=η(R1,R2)ρo(R1,R2)(42) which is given byη(R1,R2)=tr bath{e−i p R2/ S†o e i p(R2−R1)/ S o e i p R1/ ρbath},(43) (see Eqs.(5)and(7)).In section II only pure statesρbath=|ψ ψ|of the bath particle were considered,but the reasoning is immediately generalized to mixed states.The factorη(R1,R2)may be called the decoherence function,since it describes the ef-fective loss of coherence in the Brownian state which arises from disregarding the scattered bath particle.The normalization ofρbath impliesη(R1,R2)=1(44)lim|R1−R2|→0which means that the collision does not change the position distribution of the Brownian point particle,ρ(R,R)=ρo(R,R).On the other hand,possible quantum correlationsbetween increasingly far separated points will vanish,since a collision may be viewed as a position measurement of the Brownian particle by the bath which destroys superpositions of distant locations:lim|R1−R2|→∞η(R1,R2)=0(45) This complete loss of coherence implies that the collision took place with a probability of one.It could be realized,in particular,by taking the incoming bath particle state to be a momentum eigenket in a box centered on one of the scattering sites.In thermal equilibrium the density operator(29)of the bath particle can be written asρbath=λ3Ω p∈PΩµ(p) |p p|,(46) with the normalized momentum distribution function(40)atβ=1/(k B T).The |p are momentum eigenkets normalized with respect to the bath volumeΩ,|p =(2π )3/2(2π )3/2,(49) which satisfyp|p′ =δ(p−p′)and span the full space, d p|p p|=I.(50)Since the bath state(46)is diagonal in the momentum representation,an explicit expres-sion for the decoherence function(43)is readily obtained:η(R1,R2)→ d pµ(p) p|e−i p·R2/ S†o e i p·(R2−R1)/ S o e i p·R1/ |p= d pµ(p) 1− p|T†o T o |p +e i p·(R1−R2)/ p|T†o e i p·(R2−R1)/ T o |p= d pµ(p) 1−(2π )3Ω p∈PΩ→ d p.In the second line we introduced the operator T o=i(1−S o)and used the unitarity of S o,i(T o−T†o)=−T†o T o,as in section II and in[2,3].The last line follows after inserting a complete set of states (50)and noting the relation(47).The expression in square brackets in(51)should be well-defined andfinite.However, it involves two arbitrarily large quantities,the“quantization volume”Ω,which stems from the normalization of the bath particle,and the squared amplitude of the T o-operator with respect to(improper)momentum kets.The simple matrix element is given by the expression (15)p′|T o|p =δ(p−p′)|R1−R2|→∞.Therefore the limit(45)allows to specify the unknown function g(p)in(53).One obtainsg(p)=Ωσ(p)p2withσ(p)= dˆn f(pˆn,p) 2the total cross section for scattering at momentum p.Formally,this means that one should treat the expression involving the squaredδ-function and scattering amplitude asδ(p−p′)f(p′ˆn,p) 2→Ω∆t=−n d pµ(p)p∂tρ(R1,R2)=−F(R1−R2)ρ(R1,R2).(55) with F given by(2),again withε=1.C.InterpretationIt is clear that the derivation of the decoherence function(43)does not hold rigorously even for volume-normalized(47)momentum states,since their amplitude is uniform in spaceand they cannot be considered as asymptotic-in or asymptotic-out states.Nonetheless, the fact that one obtains the“correct”master equation by using the diagonal momentum representation(46)indicates that it can be reasonable,at least in a formal sense,to extend the applicability of(43)to volume-normalized momentum eigenstates.Then the appearance of the total cross section in the appropriate replacement rule(54) has a clear physical interpretation.The squared matrix element of the T o operator with respect to two orthogonal proper states may be viewed as the probability for a transition between the states due to a collision.The appropriate normalization of the probability necessary in the limit of improper states is then effected by the appearance of the total cross sectionσ(p)in(54),which is absent in the usual naive treatments of the squared delta function.This point of view is confirmed by the fact that the rule(54),which was derived from a simple physical argument(45),implies a conservation condition.Integrating(54)we have (2π )3=1(56)p2σ(p)and hence,using(50)and switching to volume-normalized states,p|T o T†o |p →1.(57) Inserting the identity(48)yieldsp′∈PΩ p′|T o |p 2→1.(58)This is reminiscent of the situation of a multi-junction in mesoscopic physics[8],or of the scattering offa quantum graph[9],where one defines a transition matrix T mn=|t mn|2 which connects afinite number of incoming and outgoing channels.There the t mn are the transmission amplitudes between the incoming and outgoing states and the currentconservation impliesm T mn=1with T mn=|t mn|2,in analogy to(58).The fact that the conservation relation(58)has no meaningful equivalence in the contin-uum limitΩ→∞is closely connected to the difficulty of evaluating the squared scattering amplitude in the momentum representation.It suggests that the diagonal representation ofρbath can be used in a rigorous formulation of the master equation only if the transition of going from a discrete to a continuous set of bath states is delayed until after the square of the scattering matrix element is evaluated.A calculation along this line,albeit in a perturbative framework,is presented in the following section.IV.WEAK-COUPLING CALCULATIONWe now consider an approach that is totally different from the derivation in Section II. Instead of performing a scattering calculation,we obtain a master equation for the reduced density operator from a weak coupling approximation that is very similar to the analyses of quantum optics.Again the assumption of a low density of bath particles will allow us to calculate the effect of the bath particles one particle at a time,so we begin with our Brownian particle and a single bath particle restricted to a box of normalization volumeΩ. While we will take the limitΩ→∞in the course of the calculation,we can do it in such a way that products of Dirac delta functions never appear.In the absence of any interaction between the particles the Hamiltonian readsH o=P22m,where m and M are the bath and Brownian particle masses and p and P are their momentum operators.The normalized eigenstates of H o are direct products |P |p ,where |p is given by(47)with(49),and similarlyR |P =e i P·R/ Ω.(59) The values of p and P are restricted to a discrete set,p,P∈PΩ,so that the wave functions respect periodic boundary conditions.Our full Hamiltonian is thenH=H o+V(r−R),where r and R are respectively the bath and Brownian particle position operators,and V describes the interaction.In the interaction picture the full density operator evolves according toρtotal I (t)=U(t)ρtotalI(0)U†(t),(60)。

Consideration of Orowan strengthening effect in particulate-reinforced metal matrix nanocomposites:A model for predicting their yield strengthZ.Zhang,D.L.Chen*Department of Mechanical and Industrial Engineering,Ryerson University,350Victoria Street,Toronto,Ont.,Canada M5B 2K3Received 28October 2005;received in revised form 17November 2005;accepted 8December 2005Available online 18January 2006AbstractAn analytical model for predicting the yield strength of particulate-reinforced metal matrix nanocomposites has been developed.The strengthening effects involving (i)Orowan strengthening effect,(ii)enhanced dislocation density due to the residual plastic strain caused by the difference in the coefficients of thermal expansion between the matrix and particles,and (iii)load-bearing effect have been taken into account in the model.The prediction is in good agreement with the experimental data reported in the literature.Ó2006Acta Materialia Inc.Published by Elsevier Ltd.All rights reserved.Keywords:Metal matrix nanocomposites;Yield strength;Orowan strengthening;Load-bearing effect;Enhanced dislocation density strengthening1.IntroductionNanocrystalline materials form an exciting area of mate-rials research because bulk materials with grain sizes of less than 100nm have properties that are not seen in their microcrystalline counterparts [1,2].However,nanostruc-tured materials generally suffer from insufficient ductility and reduced toughness compared with the conventional microcrystalline materials.On the other hand,metal matrix nanocomposites (MMNCs)are most promising in produc-ing balanced mechanical properties between nano-and micro-structured materials,i.e.,enhanced hardness,Young’s modulus,0.2%yield strength,ultimate tensile strength and ductility [3–9],due to the addition of nano-sized reinforcement particles into the matrix.To facilitate the development of MMNCs,it is necessary to develop constitutive relationships that can be used to predict the bulk mechanical properties of MMNCs as a function of the reinforcement,matrix,and processing con-ditions.In the past few years,some modeling work [10–13]has been done in this regard.Fan et al.[10]proposed a generalized law of mixture by using a rigorous continuum mechanics analysis and an equivalent microstructural transformation approach.He et al.[11]and Holtz et al.[12]qualitatively explained their results using Fan et al.’s model.Lurie et al.[13]developed a continuum mechanics model by consideration of interactions between the nano-particles and the matrix.However,in order to use the con-tinuum mechanics approach the authors [10–13]tried to modify the interface between the matrix and reinforcement particles.The difficulty with the continuum approach is that it ignores the influence of particles on the microme-chanics of deformation and strengthening mechanisms,such as the location of particles,grain size,and dislocation density [14].That is to say,the strengthening mechanisms or the types of MMNCs,which are the key factors in dom-inating the mechanical behavior,especially the yield strength,were not fully considered.In the meantime,Ramakrishnan [15]proposed an analytical model for pre-dicting the yield strength of the microsized particulate-rein-forced metal matrix composite (MMCs),using a composite sphere model for the intra-granular type of MMCs and1359-6462/$-see front matter Ó2006Acta Materialia Inc.Published by Elsevier Ltd.All rights reserved.doi:10.1016/j.scriptamat.2005.12.017*Corresponding author.Tel.:+14169795000x6487;fax:+14169795265.E-mail address:dchen@ryerson.ca (D.L.Chen).Scripta Materialia 54(2006)1321–1326incorporating two improvement parameters associated with the dislocation strengthening of the matrix and the load-bearing effect of the reinforcement.This model,repre-senting an incorporation of both continuum and microme-chanics approaches,has been used to predict the low-cycle fatigue life of discontinuous reinforced MMCs[16,17]. However,Ramakrishnan’s model was applicable only for MMCs containing microsized particles.The objective of this investigation was to model and predict the yield strength of the intra-granular type of MMNCs,which represents one of the most important aspects of the nanocomposite strengthening mechanisms and effects.By considering the strengthening mechanisms of MMNCs,and incorporating Ramakrishnan’s model and the Orowan strengthening effect,an analytical model for predicting the yield strength of particulate-reinforced MMNCs has been proposed.The theoretical predictions based on this model were found to be in good agreement with the experimental data reported in the literature.2.Model developmentDue to the excellent mechanical properties,MMNCs have attracted the interest of many researchers.A lot of work has been done involving different synthesis methods, structures,mechanical properties,and strengthening mech-anisms of MMNCs.Since the strengthening mechanisms of MMNCs are fundamental to the development of the pres-ent model,they arefirst summarized as follows.2.1.Orowan strengthening mechanismOrowan strengthening,caused by the resistance of closely spaced hard particles to the passing of dislocations, is important in aluminium alloys.It is widely acknowl-edged,however,that Orowan strengthening is not signifi-cant in the microsized particulate-reinforced MMCs, because the reinforcement particles are coarse and the interparticle spacing is large.Furthermore,since the rein-forcement is often found to lie on the grain boundaries of the matrix,it is unclear whether the Orowan mechanism can operate at all under these circumstances[18].For melt processed MMCs with the usually-used particles of5l m or larger,Orowan strengthening has indeed been pointed out to be not a major factor[14].In contrast,due to the pres-ence of highly-dispersed nanosized reinforcement particles (smaller than$100nm)in a metal matrix,Orowan strengthening becomes more favourable in MMNCs.It has been well established that the presence of a dispersion offine($100nm)insoluble particles in a metal can consid-erably raise the creep resistance,even for only a small volume fraction(<1%),due to the fact that Orowan bowing is necessary for dislocations to bypass the particles[18].For composites containingfine particles,strengthening is often explained by the Orowan mechanism[7,19–21].Shao et al.[7]explained the improved hardness in the nanocom-posite Ni/Al2O3films by using the Orowan dislocation bowing mechanism.Thilly et al.[21]observed Orowan loop mechanism and used it to simulate the good mechanical properties of Cu/Nb nanocomposites.It is noted that ther-mal stresses around the nanoparticles are large enough to cause plastic deformation in the matrix and dislocation loops around the vicinity of the nanoparticles[22,23].In addition,secondary processing,such as extrusion,is used to synthesize MMNCs.It is clear that plastic deformation has occurred during synthesis of MMNCs and Orowan loops are expected to exert a back stress on dislocation sources[24].Therefore,it is necessary to take into consider-ation the Orowan strengthening in the modeling of MMNCs.2.2.Enhanced dislocation density strengthening mechanismIn MMNCs,the increased interfacial area between the reinforcement and matrix contributes to the enhanced mechanical properties due to the nanosized particles.Also because of the thermal mismatch between the reinforce-ment and the matrix,which are in the thermal equilibrium only at the temperature at which they are brought into contact during the process,on cooling from the processing temperature thermal stresses around the nanoparticles large enough to cause plastic deformation are generated in the matrix,especially in the interface region[25].These stresses reduce quickly with increasing distance from the boundary,which can generate small defects such as dislo-cations in the close vicinity of nanosized particles[23]. The presence of a high dislocation density near the inter-face between the matrix and reinforcement particles has been experimentally observed[26,27].2.3.Load-bearing effect of the reinforcement strengthening mechanismDue to the nanosize of the reinforcement particles and the sound synthesizing methods,there is a strong cohesion at the atomic level between the matrix and particles,i.e., the nanosized particles are directly bonded to the matrix [28–30].In general,the yield strength of a composite material is the stress required to operate dislocation sources and is governed by the presence and magnitude of all the obsta-cles that restrict the motion of dislocations in the matrix. For MMCs,Ramakrishnan[15]proposed an analytical model to predict the yield strength by incorporating a mod-ified shear lag model(continuum mechanics approach)and an enhanced dislocation density model(micromechanics strengthening approach),r myc¼r ymð1þf lÞð1þf dÞ;ð1Þwhere r mycis the yield strength of the MMCs,r ym is the yield strength of the monolithic matrix,f l is the improvement factor associated with the load-bearing effect of the rein-forcement,f d is the improvement factor related to the1322Z.Zhang,D.L.Chen/Scripta Materialia54(2006)1321–1326dislocation density in the matrix,caused by the thermal mismatch between the matrix and the reinforcement particles.As stated above,for MMNCs Orowan strengthening mechanism should be taken into consideration.When several strengthening effects are simultaneously present,one way would be to use the rules of addition of the strengthening contributions,e.g.,by Lilholt [31].In this investigation Ramakrishnan’s approach [15]is considered,since it was shown that both additive and synergistic effects could be taken into account.Thus,the yield strength of particulate-reinforced MMNCs,r yc ,may be expressed as,r yc ¼r ym ð1þf l Þð1þf d Þð1þf Orowan Þ;ð2Þwhere f Orowan is the improvement factor associated with Orowan strengthening of the nanoparticles.For particu-late-reinforced composites the general expression for f l is [15,16,32],f l ¼0:5V p ;ð3Þwhere V p is the volume fraction of the reinforcement nano-particles.f d has been expressed to be [33],f d ¼kG m b ffiffiffiq p =r ym ;ð4Þwhere G m is the shear modulus of the matrix,b is the Bur-gers vector of the matrix,k is a constant,approximately equal to 1.25,q is the enhanced dislocation density which is assumed to be entirely due to the residual plastic strain developed due to the difference in the coefficients of thermal expansion (D CTE)between the reinforcement phase and the matrix during the post-fabrication cooling.For equiaxed particulates the following expression was reported [34],q ¼12D a D TV pbd p ð1ÀV p Þ;ð5Þwhere d p is the particle size,D a is the difference in thecoefficients of the thermal expansion,D T is the difference between the processing and test temperatures.The improvement factor f Orowan related to the Orowan strengthening of nanoparticles introduced in Eq.(2)can be expressed as,f Orowan ¼D r Orowan =r ym ;ð6Þwhere D r Orowan has been described by the Orowan–Ashby equation [24],D r Orowan ¼0:13G m b ln r;ð7Þwhere r is the particle radius,r =d p /2,and k is the interpar-ticle spacing,expressed as [16,35],k %d p12V p 13À1"#.ð8ÞSubstituting Eqs.(3)–(8)into Eq.(2)and considering D T =T process ÀT test ,D a =a m Àa p ,one can derive the fol-lowing equation for the yield strength of MMNCs,r yc ¼ð1þ0:5V p Þr ym þA þB þABr ym;ð9ÞA ¼1:25G m bffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi12ðT process ÀT test Þða m Àa p ÞV pbd p ð1ÀV p Þs ;ð9a ÞB ¼0:13G m b d p 1p1À1 ln d p 2b .ð9b ÞFig.1presents the analytical results of the effect of thevolume fraction (V p )on the yield strength based on Eq.(9)for different sizes of reinforcement nanoparticu-lates (d p ).The data for the nano-Al 2O 3particulate-reinforced magnesium nanocomposites tested at room temperature [8,36]are used:r ym =97MPa,E m =42.8GPa,m =0.3,G m =E m /[2(1+m )]=16.5GPa,b =0.32nm,a m =28.4·10À6(°C)À1,a p =9.0·10À6(°C)À1,T process =300°C,T test =20°C,and d p =20,30,40,50,70and 100nm.Two trends can be seen from Fig.1:(i)a higher vol-ume fraction of nanoparticles leads to a higher yield strength;(ii)the nanoparticle size has a strong effect on the yield strength.A small volume fraction of nanoparticu-lates of less than 0.06can significantly improve the yield strength of MMNCs.3.Verification of the model and discussionThe yield strength predicted via the present model,i.e.,Eq.(9),in a nano-Al 2O 3particulate-reinforced magnesium nanocomposite as a function of nanoparticle size can be seen in Fig.2.Clearly,the nanoparticle size has a signifi-cant effect on the yield strength when the volume fraction is slightly higher,e.g.,V p P 0.01.Another important point is that the improvement in the yield strength of the MMNCs becomes very strong when the nanoparticle size is smaller than about 100nm.This is in agreement withZ.Zhang,D.L.Chen /Scripta Materialia 54(2006)1321–13261323the experimental results[8,36],and provides a theoretical support to the terminology of nanotechnology, e.g., defined by the US National Science Foundation[37],where ‘‘...The novel and differentiating properties and functions are developed at a critical length scale of matter typically under100nm...’’is specified.Most researchers[9,14]in the area of nanocomposites have also done their research by controlling the nanoparticle size below100nm.Thus, 100nm is the critical size for nanoparticulate-reinforced MMNCs to produce excellent mechanical properties,com-pared to the counterpart of microparticulate-reinforced MMCs.Good agreement between the present model prediction, based on Eq.(9),and the experimental data is observed and shown in Fig.3.It is seen that the present model can be used to better predict the yield strength than Rama-krishnan’s model[15],thus indicating that Orowan strengthening effect should be taken into account in MMNCs.Since the tensile bar contained rod shaped Al2O3nanoparticles[8],the strengthening effect of such a rod shape should be higher than the spherical one[24].In our model all nanoparticles were assumed to be spherical. This is probably why our model slightly underestimates thefirst two experimental data.On the other hand,with increasing volume fraction of the reinforcement particles, the probability of forming the processing-induced voids becomes higher,leading to a degradation of the yield strength[38].This would be the main reason why the third experimental value was somewhat lower than our model prediction,because in the present model no porosity was considered within the nanocomposites.To further verify our model,another comparison between the present model prediction and the experimental data reported in Ref.[39]is shown in Fig.4,where the effect of the particle shape related to Orowan strengthening is also considered[24,39].The following data for the Y2O3-reinforced titanium nanocomposites tested at room tem-perature are used:r ym=330MPa[39];G m=44.8GPa, b=0.29nm[40];a m=11.9·10À6(°C)À1[41],a p= 9.3·10À6(°C)À1[42],T process=827°C for A1,B1,C1,D1 and900°C for A2,B2,C2,and d p=2,10,9,13,40,10 and30nm[39].On the basis of the values of the weight fraction given in Ref.[39],the following converted values of volume fraction V p=0.25,0.38,0.59,0.59,0.27,0.41 and0.54%are utilized.Again,good agreement between the model prediction for the minimum sized reinforcement particles and the experimental data is seen in Fig.4,where a combined effect1324Z.Zhang,D.L.Chen/Scripta Materialia54(2006)1321–1326of the variation in the volume fraction of nanoparticles, thermomechanical treatment,and microstructure has been taken into consideration.The above comparison between the present model prediction and the experimental data corroborates that it is necessary to consider Orowan strengthening in MMNCs. Fig.5shows an example of the comparison among the three improvement factors(f l,f d,f Orowan)as a function of the volume fraction of nanoparticles with a size of50nm in nano-Al2O3particulate-reinforced Mg nanocomposites. It is also seen that Orowan strengthening plays a significant role in MMNCs,while the load-bearing effect becomes very small.4.Conclusions(1)A model for predicting the yield strength of intra-granular type of metal matrix nanocomposites (MMNCs)is proposed on the basis of the strengthen-ing effects characterized by the modified shear lag model,enhanced dislocation density model,and the Orowan strengthening effect.(2)It is shown that the yield strength of MMNCs isgoverned by the size and volume fraction of nanopar-ticles,the difference in the coefficients of thermal expansion between the matrix and nanoparticles, and the temperature change after processing.(3)The present model indicates that100nm is a criticalsize of nanoparticles to improve the yield strength of MMNCs,below which the yield strength increases remarkably with decreasing particle size.(4)The proposed model shows excellent agreement withthe experimental data reported in the literature,indi-cating that it is necessary to consider Orowan strengthening in MMNCs.AcknowledgementsThe authors would like to thank thefinancial support provided by the Natural Sciences and Engineering Re-search Council of Canada(NSERC),and the Premier’s Re-search Excellence Award(PREA).References[1]Gleiter H.Mechanical properties and deformation behavior ofmaterials having ultra-fine microstructure.Dordrecht:Kluwer Aca-demic;1993.p.3–35.[2]Mago MJ.Mechanical properties and deformation behavior ofmaterials having ultra-fine microstructure.Dordrecht:Kluwer Aca-demic;1993.p.361–80.[3]Sekino T,Niihara K.Nanostruct Mater1995;6:663–6.[4]Hwang S,Nishimura C,McCormick PG.Scripta Mater2001;44:2457–62.[5]Audebert F,Prima F,Galano M,Tomut M,Warren PJ,Stone IC,et al.Mater Trans2002;43:2017–25.[6]Lu L,Lai M,Liang pos Sci Technol2004;64:2009–14.[7]Shao I,Vereecken PM,Chien CL,Searson PC,Cammarata RC.JMater Res2002;17:1412–8.[8]Hassan SF,Gupta M.Mater Sci Technol2004;20:1383–8.[9]Li XC,Yang Y,Cheng XD.J Mater Sci2004;39:3211–2.[10]Fan Z,Tsakiropoulos P,Miodownik AP.J Mater Sci1994;29:141–50.[11]He L,Allard LF,Ma E.Scripta Mater2000;42:517–23.[12]Holtz RL,Provenzano V.Nanostruct Mater1997;8:289–300.[13]Lurie S,Belov P,Volkov-Bogorodsky D,Tuchkova putMater Sci2003;28:529–39.[14]Lloyd DJ.Int Mater Rev1994;39:24–46.[15]Ramakrishnan N.Acta Mater1996;44:69–77.[16]Zhang Q,Chen DL.Scripta Mater2004;51:863–7.[17]Zhang Q,Chen DL.Int J Fatigue2005;27:417–27.[18]Clyne TW,Withers PJ.An introduction to metal matrix compos-ites.Cambridge:Cambridge University Press;1993.[19]Hazzledine PM.Scripta Metall Mater1992;26:57–8.[20]Huang H,Bush MB,Fisher GV.Key Eng Mater1997;127–31:1191–8.[21]Thilly L,Ve´ron M,Ludwig O,Lecouturier F.Mater Sci Eng A2001;309–310:510–3.[22]Thilly L,Ve´ron M,Ludwig O,Lecouturier F,Peyrade JP,Aske´nazyS.Philos Mag A2002;82:925–42.[23]Choi SM,Awaji H.Sci Tech Adv Mater2005;6:2–10.[24]Dieter GE.Mechanical metallurgy.third ed.New York(NY):Mc-Graw-Hill;1986.p.212–20.[25]Vaidya RU,Chawla pos Sci Technol1994;50:13–22.[26]Dunand DC,Mortensen A.Mater Sci Eng A1991;144:179–88.[27]Arsenault RJ,Shi N.Mater Sci Eng1986;81:175–87.[28]Liu HZ,Wang AM,Wang LH,Ding BZ,Hu ZQ.J Mater Res1997;12:1187–90.[29]Zhang HY,Maljkovic N,Mitchell BS.Mater Sci Eng A2002;326:317–23.[30]Liu HZ,Wang AM,Wang LH,Lou TP,Ding BZ,Hu ZQ.Nanostruct Mater1997;9:225–8.[31]Lilholt H.In:in:Proc of the4th Riso Int Symp on Metall MaterSci.Denmark,Roskilde:Riso National Laboratory;1983.p.381–92.[32]Nardone VC,Prewo KM.Scripta Metall1986;20:43–8.[33]Hansen N.Acta Metall1977;25:863–9.[34]Taya M,Arsenault RJ.Metal matrix composites—thermomechanicalbehavior.New York(NY):Pergamon Press;1989.[35]Meyers MA,Chawla KK.Mechanical behaviour of materials.Sad-dle River(NJ):Prentice Hall;1999.p.492–4.[36]Srikanth N,Hassan SF,Gupta M.J Compos Mater2004;38:2037–47.Z.Zhang,D.L.Chen/Scripta Materialia54(2006)1321–13261325[37]Available from:/home/crssprgm/nano/omb_nifty50.htm.[38]Tham LM,Su L,Cheng L,Gupta M.Mater Res Bull1999;34:71–9.[39]Castro V,Leguey T,Munˇoz A,Monge MA,Pareja R.Mater Sci EngA2005;A400–1:345–8.[40]Callister WD.Materials science and engineering—an introduction.sixth ed.New York(NY):John Wiley and Sons;2003.[41]Bever MB.Encyclopedia of materials science and engineering.NewYork(NY):Pergamon Press;1986.p.1059.[42]Kingery WD.Introduction to ceramics.second ed.New York(NY):John Wiley and Sons;1976.p.595.1326Z.Zhang,D.L.Chen/Scripta Materialia54(2006)1321–1326。

密度梯度离心的英文Density Gradient Centrifugation.Density gradient centrifugation is a powerful technique used in biochemistry and molecular biology to separate particles based on their density. This method exploits the difference in density between the particles and the surrounding medium, allowing for the efficient purification and fractionation of complex mixtures. In this article, we will explore the principles, applications, and advantages of density gradient centrifugation.Principles of Density Gradient Centrifugation.Density gradient centrifugation relies on theprinciples of sedimentation and buoyancy. When a particleis placed in a liquid medium, it experiences a force called the sedimentation force, which is proportional to the mass of the particle and the square of the centrifugal force. On the other hand, the buoyancy force, which opposes thesedimentation force, is proportional to the volume of the particle and the density of the medium.In density gradient centrifugation, a sample is layered on top of a gradient medium, which is typically a solution containing substances with gradually increasing density. When centrifuged, the particles in the sample migrate through the gradient medium based on their sedimentation and buoyancy forces. Particles with higher density sediment faster and migrate towards the bottom of the tube, while particles with lower density migrate slower and remain towards the top. This results in the formation of distinct bands within the gradient, each containing particles of similar density.Applications of Density Gradient Centrifugation.Density gradient centrifugation finds applications in various fields of biochemistry and molecular biology. Here are some examples:1. Cell Fractionation: Density gradient centrifugationis commonly used to separate different cellular compartments, such as mitochondria, lysosomes, and peroxisomes. By using gradients of sucrose or other dense media, these organelles can be purified based on their density differences.2. Virus Purification: Density gradient centrifugation is a crucial step in the purification of viruses. Virus particles can be separated from cellular debris and other contaminants by centrifuging them through a gradient of cesium chloride or sucrose. This method allows for the isolation of highly purified virus preparations.3. Protein Purification: Density gradient centrifugation can be employed to purify proteins based on their density. For instance, gradient media such as iodixanol or percoll can be used to separate proteins from each other or from contaminants. This technique is especially useful in purifying proteins from complex mixtures, such as cell lysates or serum.4. Nucleic Acid Purification: Density gradientcentrifugation is also used to purify nucleic acids, such as DNA and RNA. By centrifuging nucleic acid samples through gradients of cesium chloride or other dense media, impurities can be removed, and the nucleic acids can be recovered in high purity.Advantages of Density Gradient Centrifugation.Density gradient centrifugation offers several advantages over other separation techniques:1. High Resolution: Density gradient centrifugation allows for the separation of particles with closely related densities. The gradual increase in density within the gradient medium provides a continuous separation environment, enabling the formation of distinct bands even for particles with slight differences in density.2. Gentle Separation: Compared to other centrifugation techniques, density gradient centrifugation is relatively gentle on the particles being separated. The gradual density change within the gradient minimizes the shearforces acting on the particles, reducing the risk of damage or aggregation.3. High Purity: Density gradient centrifugation can achieve high purity separations, as the particles migrate through the gradient based solely on their density. This minimizes the co-sedimentation of contaminants and allows for the isolation of highly purified fractions.4. Scalability: Density gradient centrifugation can be scaled up or down depending on the sample volume and the desired resolution. This flexibility allows for the separation of both small and large samples, making it suitable for a wide range of applications.Conclusion.Density gradient centrifugation is a powerful technique for separating particles based on their density. By exploiting the principles of sedimentation and buoyancy, it allows for the efficient purification and fractionation of complex mixtures. With its high resolution, gentleseparation, and high purity, density gradient centrifugation finds applications in various fields of biochemistry and molecular biology, including cell fractionation, virus purification, protein purification, and nucleic acid purification.。

密度增量（density increment）”论证下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!密度增量（density increment）论证引言随着城市化进程的加速和人口增长的不断推进，城市发展面临着日益严峻的挑战。

2021年第49卷第1期—35 —石油机械CHINA PETROLEUM MACHINERYV钻井技术与装备A扶正器安放设计与套管居中度分析*郑睿I 江乐I 杨晨2李勇I 李炜彳周士杰°(1.中国石油集团工程技术研究院有限公司2.中国石油集团川庆钻探工程有限公司长庆固井公司3.中国石油塔里木油田分公司4.中石油江汉机械研究所有限公司)郑睿，江乐，杨晨，等.扶正器安放设计与套管居中度分析.石油机械，2021, 49 (1)： 35-40.摘要：套管居中程度对固井质量影响很大，合理设计扶正器安放位置有利于提高套管居中度。

为此，首先建立了套管居中度的数学模型，用于计算扶正器处和扶正器间套管的居中度，然后分析了井斜角、安放间距和套管内外液体密度差对套管居中度的影响规律。

研究结果表明：随着井斜角的增大，套管居中度降低；扶正器间距的增加会增大井斜角对居中度的影响；随着扶正器外 径的增大，套管居中度提高；随着套管内外液体密度差异的增大，套管居中度提高；井斜角越大，套管内外液体密度差产生的浮力对居中度的改善作用越明显。

最后利用C#程序语言编制了扶正器 安放设计与套管居中度分析软件。

用该软件对磨溪-X 井进行扶正器安放设计，三开4 285~4 614 m 井段共需安放24个刚性扶正器，居中度满足67%的要求；对塔里木油田固探-X 井进行居中度分析，模拟数据与实测数据的平均误差为14. 14%0研究结果对于大斜度井固井质量的提高具有重要意义。

关键词：套管扶正器；居中度；井斜角；安放间距；C#语言中图分类号：TE925 文献标识码：A DOI ： 10. 16082/j. cnki. issn. 1001-4578. 2021. 01. 005Installation Design of Centralizers and Analysis of Casing Central DegreeZheng Rui 1 Jiang Le 1 Yang Chen 2 Li Yong 1 Li Wei 3 Zhou Shijie 4(1. CNPC Engineering Technology 1? & Z) Company Limited ； 2. Changqing Well Cementing Company , CNPC Chuanqing DrillingEngineering Company Limited ； 3. PetroChina Tarim Oilfield Company ； 4. Jianghan Machinery Research Institute Limited Company ofCNPC)Abstract : Casing central degree has a great influence on cementing quality , and designing the installation po ­sition of centralizer reasonably is favorable to increase casing central degree ・ In this paper , the mathematical model of casing central degree is established to calculate the casing central degree at the position of centralizer and be ­tween centralizers. Then, the influence laws of hole deviation angle , installation spacing and fluid density differ ­ence between inside and outside the casing are analyzed. The results show that casing central degree decreases with the increase of hole deviation angle. The influence of hole deviation angle on central degree increases with the in ­crease of centralizer spacing. Casing central degree increases with the increase of centralizer OD. Casing central degree increases with the increase of the fluid density difference between inside and outside the casing. The larger the hole deviation angle is , the more greatly the central degree is improved by the buoyancy force generated due tothe fluid density difference between inside and outside the casing. Finally , the software for the installation design of centralizers and the analysis of casing central degree is developed by using C# language. This software is applied tothe installation design of centralizers in Well Moxi-X. 24 rigid centralizers are totally needed in the third section*基金项目：国家科技重大专项“提高大型体积压裂条件下固井质量与井筒完整性新技术” (2016ZX05022005)；中国石油天然气集团 有限公司重大工程专项“固井设计仿真监控系统升级与关键技术研发”(2018E-2103)。

82 | 城市研究Evolution Characteristics of High-density Cities' Park Construction in China's Mainland from 1996 to 2019中国大陆高密度城市公园建设水平演变特征分析*——从1996年到2019年徐吉羽 刘志强 余 慧 洪亘伟 XU Jiyu, LIU Zhiqiang, YU Hui, HONG Genwei高密度城市的人口与绿地矛盾日益突出，准确研判其公园建设水平的时空演变规律对新型城镇化建设有重要意义。

以人口密度和经济密度综合表征城市密度，在我国2019年266个地级及以上城市基础上，遴选出当年的26个高密度城市，并以此为研究单元探究1996—2019年高密度城市公园建设水平的演变特征。

从时序来看，公园建设态势为“快速提升—增速减缓—稳步推进”，建设模式以公园个数的增加引领公园规模、公园密度的高速发展。

从城市类型来看，经济密度是影响高密度进程速度和公园建设基础的重要因素，而人口密度的影响逐渐加强；“人口、经济密度极高”型、“高密度进程较快”型公园建设“主增个数，辅增规模”；“人口、经济密度双高”型、“高密度进程平稳”型公园配置最为协调。

提出“重密度、重配置”“重系统、重需求”“重低碳、重效能”等发展对策，以期为“公园城市”背景下高密度城市的绿色、可持续发展提供有益探索。

The contradiction between population and green space is increasingly prominent in high-density cities, so it is of greatsignificance to accurately study the spatial-temporal evolution of park construction in high-density cities. Based on the comprehensive representation of urban density by population density and economic density, 26 high-density cities have been selected from 266 prefecture-level and above cities in 2019 to explore the evolution characteristics of urban park construction level from 1996 to 2019. The results show that from the temporal perspective, the trend of park construction changes from rapid improvement to slow-down growth and to steady progress, and the construction pattern leads to the rapid development of park scales and park densities with the increase of park amounts. From the perspective of different city types, economic density is an important factor affecting the speed of high-density process and the foundation of park construction, and population density plays an increasingly important role. "High population and economic density" cities' and "rapid development" cities' park construction mainly increase in number and also increase in scale. Park construction in "high population and economic density" cities and "steady progress" cities are the most coordinated. To provide beneficial exploration for the green and sustainable development of high-density cities under the background of "park city", the development countermeasures emphasizing "density and configuration", "system and demand", and "low-carbon and efficiency" are put forward.高密度城市；公园建设水平；演变；人口密度；经济密度；中国high-density city; park construction level; evolution; population density; economic density; China文章编号 1673-8985（2022）06-0082-07 中图分类号 TU984 文献标志码 A DOI 10.11982/j.supr.20220611摘 要Abstract 关 键 词Key words 作者简介徐吉羽苏州科技大学建筑与城市规划学院硕士研究生刘志强（通信作者）苏州科技大学建筑与城市规划学院硕士生导师，教授，*******************基金项目：国家自然科学基金面上项目“基于空间计量分析的中国市域建成区绿地率空间分异的格局、演变及其机理研究”（编号51778389）；江苏省2021年普通高校研究生科研创新计划基金（编号KYCX21_3058）；江苏高校“青蓝工程”、江苏省企业研究生工作站（苏州园林设计院有限公司）和江苏高校品牌专业建设工程二期项目（风景园林）、“十四五”江苏省重点学科（风景园林学）资助。

制氢吸附剂硅胶的密度英文回答：The density of silica gel, an adsorbent for hydrogen, is a critical property in various applications, including hydrogen storage, purification, and separation. The density of silica gel can vary depending on its physical form, porosity, and surface chemistry.Amorphous silica gel, the most common form used as a hydrogen adsorbent, typically has a density in the range of 1.9-2.2 g/cm³. Its porous structure and high surface area contribute to its low density. The density of silica gel can be increased by densification processes, which involve compressing or sintering the material.The density of silica gel is also influenced by its porosity. Higher porosity corresponds to lower density, as the pores occupy a significant volume within the material. The surface chemistry of silica gel, particularly thepresence of surface hydroxyl groups, can also affect its density.In summary, the density of silica gel used as a hydrogen adsorbent typically ranges from 1.9 to 2.2 g/cm³. This value can vary depending on the physical form, porosity, and surface chemistry of the material.中文回答：硅胶作为氢气吸附剂的密度，是一个在包括储氢、提纯和分离在内的各种应用中至关重要的特性。

Optimizing Semiconductor Fluid Handling Solutions with 3M Science.3M™ Dyneon™ FluoroplasticsHigh purity material solutionsto help protect chip purityand increase yieldAdvancing semicon.Enhancing lives.From the Internet of Things and trends in 5G, to virtual reality and self-driving vehicles, the growing demand for ever smaller, faster, and more powerful devices has never been greater. 3M brings decades of science-based expertise to a range of raw materials and fluid-handling solutions for chip manufacturing, helping innovators across the industry meet their demand and shape the future of the semiconductor industry.3M ™ Fluoroplastics for fluid handling. Purity. Precision. Performance.As our lives and our devices become increasinglyinterconnected, advances in technology are pushing the limits of integrated circuits and chip design. At 3M, we produce ultra high purity PFA and PTFE materials that help enable the parts, equipment, and critical fluid delivery systems manufacturers need to maximize performance and yield.At our fingertips and all around us, smart devices have revolutionized how the world connects—and how we connect with our world. 3M science helps the products, equipment and fluid-handling systems the semiconductor industry needs today to create the chips of tomorrow.Semicon chip fabrication presents unique fluid-handling challenges, such as harsh cleaning and etching chemicals, high heat, and the need for handling ultra-pure water. Process contamination reduces reliability. As requirements get stricter, chip fabricators rely more than ever on the right materials. 3M ™ Fluoroplastics helpmanufacturers protect against contamination, corrosion and leaching—minimizing downtime and enhancing equipment performance.Challenges around optimizingfluid handling systems3M is a trusted partner serving industries around the world. Our decades of experience in fluoroplastic design andmanufacturing, backed by extensive purity and application knowledge, make 3M ultra high purity PFA and PTFE an excellent choice for semicon fluid handling applications.Our customers across the entire semicon value chain benefit from bench-to-bench 3M support,including material testing expertise and application insights.Reliable solutions backed by 3M scienceOur semicon material solutions start with 3M ™ Fluoroplastics, but they’re built on industry and application expertise. 3M raw materials,including ultra high purity PFA and PTFE, are engineered to maintain purity and integrity in some of the toughest conditions and manydemanding chemical delivery system environments. Our semicon experts help innovators across the value chain tailor 3M material solutions to better serve their customers’ needs and testing requirements.Semicon solutions from end to endChemicalManufacturersTubing & Component Manufacturers A handle on high-purity fluid handlingMax performance and chip yield come from minimum contamination and corrosion. Throughout the fabrication process, 3M ™ Fluoroplastics deliver critical fluids like etching chemicals and ultra pure water so fabs can push the limits of their semiconductor chip and integrated device design. • PFA tubing and piping • PFA valves and fittings • PTFE gaskets and seals • Anti-static PFA• PTFE and PFA sheets • PTFE and PFA films• PFA drums and containers• PFA and PTFE tanks and vessel liners • PFA dip tubes and dispense systemsTanks and Containment LinersChemical Distribution SystemsFour Value Chain Sectors Semifinished GoodsUsed primarily for its extremeresistance to chemical attack, broad temperature range, and transparency relative to PTFE, PFA, is meltprocessable through extrusion and injection molding. Its thermoplastic behavior allows vastly higherproductivity when manufacturing injection-molded parts.3M ™Dyneon ™Ultra High Purity PFA is engineered to withstand some of the toughest conditions while maintaining purity and integrity. Every lot is tested to meet the SEMI C90 standard, guaranteeing quality and consistency that enable ultra high-purity tubing and components needed in the semicon industry.PFAPFA ApplicationsTubing Wafer Carriers Pumps FittingsValvesLinings BasinsWafer CarriersLiningsPumpsGasketsFiltersA fully fluorinated plastic withapplications in nearly every industry, PTFE is an indispensable problem solver. Its low permeability and coefficient of friction, wide service temperature range, universal chemical resistance, and long service life make it ideal for manufacturing compression molded semifinished parts.3M ™ Dyneon ™ PTFE is engineered for technical excellence and reliability in low volume end useapplications such as liners and wafer baths.3M ™ Dyneon ™ TFM ™ Modified PTFE offers a modified PTFE polymer structure that provides enhanced properties including low surfaceroughness and improved mechanical properties.PTFEPTFE ApplicationsWhich raw material is right for your application?At 3M, we apply science in collaborative ways to enhance lives daily. Our skilled researchers at service labs around the globe continue to develop and improvefluoroplastics for semicon. Our applications specialists are here to help you select and handle materials to ensure the smoothest transition into your manufacturing process.While we produce premier raw materials, 3M expertise is deeply involved throughout the semiconvalue chain, including SEMI standards testing and troubleshooting every step of the way. As a global company, we have application engineers and testing capabilities around the world. Our material experts are available to apply extensive research and development catered towards the semiconductor industry—delivering solutions to the toughest challenges.3M ™ Fluoroplasticsare only the beginningA global partner for the world of semiconInvested in the advancement of semiconWarranty, Limited Remedy, and Disclaimer: Many factors beyond 3M’s control and uniquely within user’s knowledge and control can affect the use and performance of a 3M product in a particular application. User is solely responsible for evaluating the 3M product and determining whether it is fit for a particular purpose and suitable for user’s method of application. User is solely responsible for evaluating third party intellectual property rights and for ensuring that user’s use of 3M product does not violate any third party intellectual property rights. Unless a different warranty is specifically stated in the applicable product literature or packaging insert, 3M warrants that each 3M product meets the applicable 3M product specification at the time 3M ships the product. 3M MAKES NO OTHER WARRANTIES OR CONDITIONS, EXPRESS OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, ANY IMPLIED WARRANTY ORCONDITION OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE OR ANY IMPLIED WARRANTY OF NON-INFRINGEMENT OR ANY IMPLIED WARRANTY OR CONDITION ARISING OUT OF A COURSE OF DEALING, CUSTOM OR USAGE OF TRADE. If the 3M product does not conform to this warranty, then the sole and exclusive remedy is, at 3M’s option, replacement of the 3M product or refund of the purchase price.Limitation of Liability: Except where prohibited by law, 3M will not be liable for any loss or damages arising from the 3M product, whether direct, indirect, special, incidental or consequential, regardless of the legal theory asserted, including warranty, contract, negligence or strict liability.Technical Information: Technical information, recommendations, and other statements contained in this document or provided by 3M personnel are based on tests or experience that 3M believes are reliable, but the accuracy or completeness of such information is not guaranteed. Such information is intended for persons with knowledge and technical skills sufficient to assess and apply their own informed judgment to the information. No license under any 3M or third party intellectual property rights is granted or implied with this information.3M Dyneon and TFM are trademarks of 3M Company. Used under license.Please Recycle. Printed in USA. © 3M 2022. All rights reserved. Issued: 01/20223M Advanced Materials Division 3M CenterSt. Paul, MN 55144 USAP hone 1-800-367-8905Web /SemiFluidHandling。

强化机理英语There are several mechanisms that can be used to strengthen materials. These mechanisms include:1. Strain hardening (also known as work hardening or cold working): This mechanism involves deforming the material through processes such as rolling, forging, or stretching. The deformation introduces dislocations in the crystal structure, which impede the movement of other dislocations, making it harder for the material to deform further.2. Grain size reduction: By refining the grains in a material, their boundaries act as barriers to dislocation movement, effectively increasing the strength of the material. This can be achieved through processes such as cold working, heat treatment, or severe plastic deformation.3. Solid solution strengthening: By adding alloying elements to a material, the atomic size difference between the matrix and the alloying element can create strain fields around the alloying element atoms, hindering dislocation motion and increasing material strength.4. Precipitation hardening: This mechanism involves forming small precipitates within the material through either solution heat treatment or aging. The precipitates impede dislocation motion and enhance the material's strength.5. Transformation strengthening: Some materials can undergo phase transformations, such as martensitic transformation, whichresults in a significant increase in strength due to the formation of a new phase with a different crystal structure.6. Texture strengthening: The orientation of grains in a material can be controlled through processes such as rolling, drawing, or extrusion, creating an anisotropic microstructure that enhances strength in specific directions.7. Polymorphous strengthening: Certain materials can undergo a polymorphic phase transformation when subjected to high pressure or temperature, leading to an increase in their mechanical properties.These mechanisms can be used individually or in combination to achieve desired material properties, depending on the specific application and material requirements.。