指数函数基础填空题(含答案)

练习题一,选择题1.下列函数是指数函数的是（）A.y = -2xB. y = 2x+,C. y = 2_xD. y=l x2.函数y =@—2尸在R上为增函数，则a的取值范围是（）A. a>0 且a7^1B. a>3C. a<3D. 2<a<33.函数y=厂2+1@〉0, a^l)的图象必经过点( )A. (0,1)B. (1,1)C. (2,0)D. (2,2)4.f(x)=|jl|x|, xGR,那么班0是()A.奇函数且在（0, + <-）上是增函数B.偶函数且在（0, + 8）上是增函数C.奇函数且在（0, + 8）上是减函数D.偶函数且在（0,5.方程广「命的解为（）A. 2B. -2C. -1D. 16.方程4^=令的解为()A. 2B. -2C. -1D. 17.某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个）。

经过3个小时，这种细菌由1个nJ繁殖成（）A.511 个B.512 个C.1O23 个D1024 个8.在统一平面直角坐标系中，函数/（兀）8. 设a,b,c,d 都是不等于1的正数，y = a\y = h\y = c\y = d x 在同一•处标系中的图像如图所示，则a,b,c,d 的10. y= 0.3戶的值域是( )4. (-oo,0) B.[l,+x) C.(0,l] 0.(- oo,l]11. 当xe[-l,l]时函数/(x) = 3v -2的值域是()A. --,1 B\-1,1] C. 1,- D.[0,l3 3 2 2 1 1 | £ 512. 化简(/沪)(—3决质)十(丄，沪)的结果 ( ) A . 6a B • -a C . -9a D . 9a 2设指数函数/(x) = a x (a > 0卫主1),则下列等式中不正确的是(0,1] B • (04) C • (0,+o>)13. 14. f(nx) = [f(x)]n (n e Q) f(xyy=[f(x)]n {f(y)Y (n G N") 函数 y = (x-5)°4-(x-2p{x \ x 5,x 工 2} B . {x\x > 2}{x\x>5} D . {x\2< x < 5^x > 5}15. 函数/(x) = 2-,A 1的值域是16. 若指数函数y = (a + \)x 在(—oo, + 00)上是减函数，那么(A 、 0 < a < IB 、 -l<a <0C 、D 、 a <-11&函数/(x) = 2V , g(x) = x + 2,便.f(x) = g(x)成立的x 的值的集合() A 、是0 B 、有且只有一个元索C 、有两个元素D 、有无数个元素19.下列关系式中正确的是（ ）9 （ 1 \3 （ 1 \3 （ \ \3 A.-<2_L5 < 丄 B.- < - 3 \2 J（2 丿 \ 2> (1 < 1 \3 (1、 1 r 1 \i c. 2-1-5 < 1 —< A D.2 15 < - < 1 （2丿a二,填空题1. 两数y=pa"—1的定义域是（ — 8, 0],则实数a 的取值范围为 _________2. 函数 f （x ）=（*）_l, xe [ — 1, 2]的值域为 _______ ・3. 函数/（兀）=G 沏+1（。

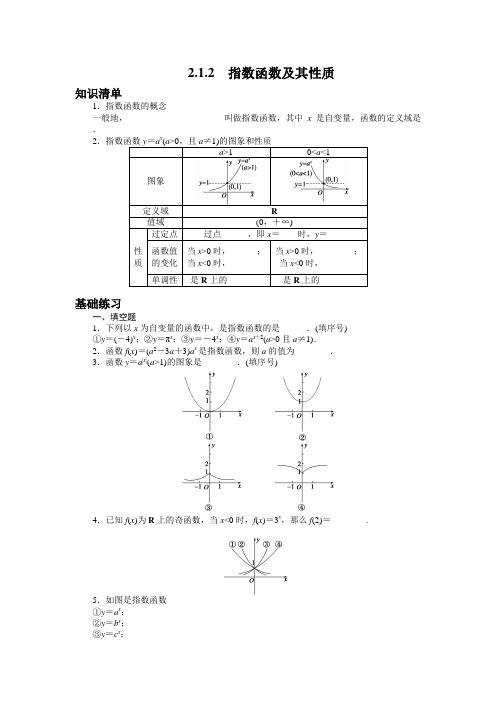
2.1.2 指数函数及其性质知识清单1．指数函数的概念一般地，______________________叫做指数函数，其中x 是自变量，函数的定义域是____．2．指数函数y ＝a x (a >0，且a ≠1)的图象和性质a >1 0<a<1图象定义域 R 值域 (0，＋∞)性 质 过定点过点______，即x ＝____时，y ＝____函数值 的变化 当x >0时，______； 当x <0时，________ 当x >0时，________； 当x <0时，________单调性是R 上的________是R 上的________基础练习一、填空题1．下列以x 为自变量的函数中，是指数函数的是______．(填序号)①y ＝(－4)x ；②y ＝πx ；③y ＝－4x ；④y ＝a x ＋2(a >0且a ≠1)． 2．函数f (x )＝(a 2－3a ＋3)a x 是指数函数，则a 的值为________． 3．函数y ＝a |x |(a >1)的图象是________．(填序号)4．已知f (x )为R 上的奇函数，当x <0时，f (x )＝3x，那么f (2)＝________.5．如图是指数函数 ①y ＝a x ； ②y ＝b x ； ③y ＝c x ；④y ＝d x 的图象，则a 、b 、c 、d 与1的大小关系是________．6．函数y ＝(12)x －2的图象必过第________象限．7．函数f (x )＝a x 的图象经过点(2,4)，则f (－3)的值为____．8．若函数y ＝a x －(b －1)(a >0，a ≠1)的图象不经过第二象限，则a ，b 需满足的条件为________．9．函数y ＝8－23－x (x ≥0)的值域是________． 二、解答题10．比较下列各组数中两个值的大小：(1)0.2－1.5和0.2－1.7； (2)1314⎛⎫⎪⎝⎭和2314⎛⎫⎪⎝⎭； (3)2－1.5和30.2.11．2000年10月18日，美国某城市的日报以醒目标题刊登了一条消息：“市政委员会今天宣布：本市垃圾的体积达到50 000 m 3”，副标题是：“垃圾的体积每三年增加一倍”．如果把3年作为垃圾体积加倍的周期，请你完成下面关于垃圾的体积V (m 3)与垃圾体积的加倍的周期.(1) (2)根据报纸所述的信息，你估计3年前垃圾的体积是多少？ (3)如果n ＝－2，这时的n ，V 表示什么信息？(4)写出n 与V 的函数关系式，并画出函数图象(横轴取n 轴)． (5)曲线可能与横轴相交吗？为什么？12．定义运算a ⊕b ＝⎩⎪⎨⎪⎧a (a ≤b )b (a >b )，则函数f (x )＝1⊕2x 的图象是________．(填序号)13．定义在区间(0，＋∞)上的函数f (x )满足对任意的实数x ，y 都有f (x y )＝yf (x )． (1)求f (1)的值；(2)若f (12)>0，解不等式f (ax )>0.(其中字母a 为常数)．能力提升一、填空题1．设P ＝{y |y ＝x 2，x ∈R }，Q ＝{y |y ＝2x ，x ∈R }，则P 、Q 的关系为________． 2．函数y ＝16－4x 的值域是________．3．函数y ＝a 在[0,1]上的最大值与最小值的和为3，则函数y ＝2ax －1在[0,1]上的最大值是________．4．若函数f (x )＝3x ＋3－x 与g (x )＝3x －3－x 的定义域均为R ，则下列命题正确的是________．(填序号)①f (x )与g (x )均为偶函数；②f (x )为偶函数，g (x )为奇函数； ③f (x )与g (x )均为奇函数；④f (x )为奇函数，g (x )为偶函数．5．函数y ＝f (x )的图象与函数g (x )＝e x ＋2的图象关于原点对称，则f (x )的解析式为________． 6．已知a ＝1335-⎛⎫ ⎪⎝⎭，b ＝1235-⎛⎫⎪⎝⎭，c ＝1243-⎛⎫ ⎪⎝⎭，则a ，b ，c 三个数的大小关系是________．7．春天来了，某池塘中的荷花枝繁叶茂，已知每一天新长出荷叶覆盖水面面积是前一天的2倍，若荷叶20天可以完全长满池塘水面，当荷叶刚好覆盖水面面积一半时，荷叶已生长了________天．8．已知函数f (x )是定义在R 上的奇函数，当x >0时，f (x )＝1－2－x ，则不等式f (x )<－12的解集是________．9．函数y ＝2212x x-+⎛⎫ ⎪⎝⎭的单调递增区间是________．二、解答题10．(1)设f (x )＝2u ，u ＝g (x )，g (x )是R 上的单调增函数，试判断f (x )的单调性； (2)求函数y ＝2212x x --的单调区间．11．函数f (x )＝4x －2x ＋1＋3的定义域为[－12，12]．(1)设t ＝2x ，求t 的取值范围； (2)求函数f (x )的值域．12．函数y ＝2x －x 2的图象大致是________．(填序号)13．已知函数f (x )＝2x－12x ＋1.(1)求f [f (0)＋4]的值；(2)求证：f (x )在R 上是增函数；(3)解不等式：0<f (x －2)<1517.知识清单1．函数y ＝a x (a >0，且a ≠1) R 2.(0,1) 0 1 y >1 0<y <1 0<y <1 y >1 增函数 减函数 基础练习 1．②解析 ①中－4<0，不满足指数函数底数的要求，③中因有负号，也不是指数函数，④中的函数可化为y ＝a 2·a x ，a x 的系数不是1，故也不是指数函数． 2．2解析 由题意得⎩⎪⎨⎪⎧a 2－3a ＋3＝1，a >0且a ≠1，解得a ＝2. 3．②解析 该函数是偶函数．可先画出x ≥0时，y ＝a x 的图象，然后沿y 轴翻折过去，便得到x <0时的函数图象．4．－19解析 当x >0时，－x <0，∴f (－x )＝3－x ，即－f (x )＝(13)x ，∴f (x )＝－(13)x .因此有f (2)＝－(13)2＝－19.5．b <a <1<d <c解析 作直线x ＝1与四个指数函数图象交点的坐标分别为(1，a )、(1，b )、(1，c )、(1，d )，由图象可知纵坐标的大小关系． 6．二、三、四解析 函数y ＝(12)x 的图象上所有的点向下平移2个单位，就得到函数y ＝(12)x －2的图象，所以观察y ＝(12)x －2的图象可知．7.18解析 由题意a 2＝4，∴a ＝2.f (－3)＝2－3＝18.8．a >1，b ≥2解析 函数y ＝a x －(b －1)的图象可以看作由函数y ＝a x 的图象沿y 轴平移|b －1|个单位得到．若0<a <1，不管y ＝a x 的图象沿y 轴怎样平移，得到的图象始终经过第二象限；当a >1时，由于y ＝a x 的图象必过定点(0,1)，当y ＝a x 的图象沿y 轴向下平移1个单位后，得到的图象不经过第二象限．由b －1≥1，得b ≥2.因此，a ，b 必满足条件a >1，b ≥2. 9．[0,8)解析 y ＝8－23－x ＝8－23·2－x ＝8－8·(12)x＝8[1－(12)x ]．∵x ≥0，∴0<(12)x ≤1，∴－1≤－(12)x <0，从而有0≤1－(12)x <1，因此0≤y <8.10．解 (1)考察函数y ＝0.2x . 因为0<0.2<1，所以函数y ＝0.2x 在实数集R 上是单调减函数．又因为－1.5>－1.7，所以0.2－1.5<0.2－1.7.(2)考察函数y ＝(14)x .因为0<14<1，所以函数y ＝(14)x 在实数集R 上是单调减函数．又因为13<23，所以1314⎛⎫ ⎪⎝⎭>2314⎛⎫ ⎪⎝⎭1.(3)2－1.5<20，即2－1.5<1；30<30.2，即1<30.2，所以2－1.5<30.2.11．解 (1)由于垃圾的体积每3年增加1倍，24年后即8个周期后，该市垃圾的体积是50 000×28＝12 800 000(m 3)．(2)根据报纸所述的信息，估计3年前垃圾的体积是50 000×2－1＝25 000(m 3)．(3)如果n ＝－2，这时的n 表示6年前，V 表示6年前垃圾的体积． (4)n 与V 的函数关系式是V ＝50 000×2n ，图象如图所示．(5)因为对任意的整数n,2n >0，所以V ＝50 000×2n >0，因此曲线不可能与横轴相交． 12．①解析 由题意f (x )＝1⊕2x＝⎩⎪⎨⎪⎧1， x ≥0；2x ， x <0.13．解 (1)令x ＝1，y ＝2，可知f (1)＝2f (1)，故f (1)＝0.(2)设0<x 1<x 2，∴存在s ，t 使得x 1＝(12)s ，x 2＝(12)t ，且s >t ，又f (12)>0，∴f (x 1)－f (x 2)＝f [(12)s ]－f [(12)t ]＝sf (12)－tf (12)＝(s －t )f (12)>0，∴f (x 1)>f (x 2)．故f (x )在(0，＋∞)上是减函数． 又∵f (ax )>0，x >0，f (1)＝0， ∴0<ax <1，当a ＝0时，x ∈∅，当a >0时，0<x <1a ，当a <0时，1a<x <0，不合题意．故x ∈∅.综上：a ≤0时，x ∈∅；a >0时，不等式解集为{x |0<x <1a}．能力提升 1．Q P解析 因为P ＝{y |y ≥0}，Q ＝{y |y >0}，所以Q P . 2．[0,4)解析 ∵4x >0，∴0≤16－4x <16， ∴16－4x ∈[0,4)． 3．3解析 函数y ＝a x 在[0,1]上是单调的，最大值与最小值都在端点处取到，故有a 0＋a 1＝3，解得a ＝2，因此函数y ＝2ax －1＝4x －1在[0,1]上是单调递增函数，当x ＝1时，y max ＝3. 4．②解析 f (－x )＝3－x ＋3x ＝f (x )，g (－x )＝3－x －3x ＝－g (x )．5．f (x )＝－e －x －2解析 ∵y ＝f (x )的图象与g (x )＝e x ＋2的图象关于原点对称，∴f (x )＝－g (－x )＝－(e －x ＋2)＝－e －x －2. 6．c <a <b解析 ∵y ＝(35)x 是减函数，－13>－12，∴b >a >1.又0<c <1，∴c <a <b . 7．19解析 假设第一天荷叶覆盖水面面积为1，则荷叶覆盖水面面积y 与生长时间的函数关系为y ＝2x －1，当x ＝20时，长满水面，所以生长19天时，荷叶布满水面一半． 8．(－∞，－1)解析 ∵f (x )是定义在R 上的奇函数， ∴f (0)＝0.当x <0时，f (x )＝－f (－x )＝－(1－2x )＝2x －1.当x >0时，由1－2－x <－12，(12)x >32，得x ∈∅；当x ＝0时，f (0)＝0<－12不成立；当x <0时，由2x －1<－12，2x <2－1，得x <－1.综上可知x ∈(－∞，－1)． 9．[1，＋∞)解析 利用复合函数同增异减的判断方法去判断．令u ＝－x 2＋2x ，则y ＝(12)u 在u ∈R 上为减函数，问题转化为求u ＝－x 2＋2x 的单调递减区间，即为x ∈[1，＋∞)．10．解 (1)设x 1<x 2，则g (x 1)<g (x 2)．又由y ＝2u 的增减性得()12g x<()22g x ，即f (x 1)<f (x 2)， 所以f (x )为R 上的增函数．(2)令u ＝x 2－2x －1＝(x －1)2－2， 则u 在区间[1，＋∞)上为增函数．根据(1)可知y ＝2212x x --在[1，＋∞)上为增函数． 同理可得函数y 在(－∞，1]上为单调减函数．即函数y 的增区间为[1，＋∞)，减区间为(－∞，1]．11．解 (1)∵t ＝2x 在x ∈[－12，12]上单调递增，∴t ∈[22，2]．(2)函数可化为：f (x )＝g (t )＝t 2－2t ＋3，g (t )在[22，1]上递减，在[1，2]上递增，比较得g (22)<g (2)． ∴f (x )min ＝g (1)＝2， f (x )max ＝g (2)＝5－2 2.∴函数的值域为[2,5－22]． 12．①解析 当x →－∞时，2x →0，所以y ＝2x －x 2→－∞， 所以排除③、④.当x ＝3时，y ＝－1，所以排除②.13．(1)解 ∵f (0)＝20－120＋1＝0，∴f [f (0)＋4]＝f (0＋4)＝f (4)＝24－124＋1＝1517.(2)证明 设x 1，x 2∈R 且x 1<x 2， 则22x>12x>0,22x－12x>0，∴f (x 2)－f (x 1)＝212121212121x x x x ---++ ＝()()()21212222121x x x x -++>0，即f (x 1)<f (x 2)，所以f (x )在R 上是增函数．(3)解 由0<f (x －2)<1517得f (0)<f (x －2)<f (4)，又f (x )在R 上是增函数，∴0<x －2<4，即2<x <6，所以不等式的解集是{x |2<x <6}．。

指数函数题型学霸总结四（含答案）阳光老师：祝你学业有成一、选择题（本大题共12小题，共60.0分）1.函数是指数函数，则有A. 或B.C. D. ，且【答案】C【解析】【分析】本题主要考查的是指数函数的概念，直接结合指数函数底数大于0且不等于1，前面系数为1，求解即可．【解答】解：由指数函数的概念，得，解得或当时，底数是1，不符合题意，舍去；当时，符合题意．故选C．2.若函数是指数函数，则a的取值范围是A. B. ，且C. D.【答案】B【解析】【试题解析】【分析】本题主要考查指数函数的定义，属于基础题．利用指数函数的定义中对底数的要求，列出不等式组，求解即得．【解答】解：因为函数是指数函数，得：，化简得故选B．3.有下列函数：；；；其中指数函数的个数是A. 0B. 1C. 2D. 3【答案】B【解析】【分析】本题考查指数函数的表达式和定义，属于基础题．根据指数函数的定义和表达式的要求即可得解．【解答】解：形如，且的函数称为指数函数，只有是指数函数．故选B．4.已知函数，若，则A. B. 0 C. D.【答案】C【解析】【试题解析】【分析】本题主要考查函数值的计算，属于基础题．发现是解题的关键．【解答】解：因为，所以，又，那么．故选C．5.下列各函数中是指数函数的是A. B. C. D.【答案】D【解析】【分析】本题考查了指数函数及其性质的相关知识，试题难度容易．根据指数函数的概念即可判断结果．【解答】解：根据指数函数的定义，且，可知只有D项正确，故选D．6.若函数在R上单调递减，则实数a的取值范围是A. B. C. D.【答案】C【解析】【分析】本题主要考查指数函数的单调性，属于基础题．根据指数函数的单调性，可知，解得实数a的取值范围．【解答】解：函数，在R上单调递减，则，解得，实数a的取值范围是．故选C．7.已知常数，函数经过点、，若，则a的值为A. 2B. 4C. 6D. 8【答案】B【解析】【分析】本题主要考察指数与指数幂的运算，考查运算求解能力，属于基础题．将p，q直接带入，计算即可求解得到答案．【解答】解：因为，，，，即，所以，所以，又因为，所以，又因为，所以，故选B．8.已知函数则A. 2B.C. 0D.【答案】B【解析】【分析】本题考查了函数定义域与值域、分段函数的相关知识，试题难度容易【解答】解：，．9.如图所示，面积为8的平行四边形OABC的对角线AC与BO交于点E，且若指数函数且的图象经过点E，B，则a等于A. B. C. 2 D. 3【答案】A【解析】【分析】本题考查了指数函数及其性质的相关知识，试题难度一般【解答】解：设点，则由已知可得点，，．因为点E，B在指数函数的图象上，所以所以，所以舍去或．10.下列图象中，可能是二次函数及指数函数的图象的是A. B.C. D.【答案】A【解析】【试题解析】【分析】本题主要考查指数函数的图象及性质、二次函数的图象及性质，属于基础题．指数函数在R上单调递减，则，可得，二次函数的图象与x轴的交点为、，结合选项即可判断．【解答】解：由指数函数的图象可知，指数函数在R上单调递减，则，，二次函数的图象与x轴的交点为、，只有选项A符合题意．故选A．11.函数与的图象关于A. 原点对称B. x轴对称C. y轴对称D. 直线对称【答案】C【解析】【分析】本题考查了函数的周期性和对称性、函数图象的变换平移、对称、伸缩、翻折变换的相关知识，试题难度较易【解答】解：设点为函数的图象上任意一点，则点为的图象上的点．因为点与点关于y轴对称，所以函数与的图象关于y轴对称，故选C．12.已知定义在R上的函数满足，且当时，，则A. 0B.C. 18D.【答案】C【解析】【分析】本题考查函数的周期性，涉及指数的运算，属于基础题．由题意可得函数为周期为2的周期函数，可得，代值计算可得．【解答】解：定义在R上的函数满足，函数为周期为2的周期函数，又当时，，，故选：C．二、填空题（本大题共14小题，共70.0分）13.指数函数的值域是__________．【答案】【解析】【分析】本题考查求函数值域的方法，考查指数函数的性质，解题的关键是将复杂函数化为基本函数，属于基础题．根据题意可知，函数，若令，于是可得y 转化为关于t的二次函数，根据指数函数的性质可知，结合二次函数的单调性还可得到在上函数单调递增，于是不难得到，对该不等式式求解，即可得到原函数的值域．【解答】解：令，则，因为该二次函数在上递增，所以，即原函数的值域为．故答案为．14.若函数且在区间上的最大值与最小值之和为3，则实数a的值为________．【答案】2【解析】【分析】本题考查指数函数的性质，属基础题，难度不大．讨论底数a的大小，利用指数函数的单调性求解即可．【解答】解：当时，函数在区间上单调递增，的最大值为a，最小值为，，解得，当时，函数在区间上单调递减，的最大值为，最小值为a，，解得舍，综上所述：．故答案为2．15.函数的定义域为________．【答案】【解析】【分析】本题考查了函数定义域与值域、指数方程与指数不等式的相关知识，试题难度容易【解答】解：依题意得，，得，得，得．则函数的定义域为．故答案为．16.已知函数且在区间上的函数值恒小于2，则a的取值范围是________．【答案】【解析】【分析】本题考查指数函数的性质，属于基础题．分类讨论，由指数函数的单调性得最值，求a的取值范围．【解答】解：当时，函数且在区间上单调递增，最大值为，由题意，所以，当时，函数且在区间上单调递减，最大值为，由题意，所以，则a的取值范围是故答案为17.若指数函数的图象经过点，则，．【答案】；【解析】【分析】本题考查了指数函数及其性质的相关知识，试题难度较易【解答】解：设且．因为的图象经过点，代入得，解得或舍去，所以，所以．18.若指数函数的图象经过点，则．【答案】【解析】【分析】本题考查了指数函数及其性质的相关知识，试题难度容易【解答】解：设且，由于其图象经过点，所以，解得或舍去，因此，故．19.已知，若，求的值．【答案】解：，若，则．所以．【解析】本题考查了指数与指数幂的运算的相关知识，试题难度一般20.已知函数是指数函数，且，则__________．【答案】 5x【解析】【分析】本题主要考查指数函数，由得，，解得即可．【解答】解：设x，且．由，得，，x．故答案为．21.若函数且的图象过点，则________．【答案】【解析】【分析】本题考查了指数函数及其性质的相关知识，试题难度容易【解答】解：由于函数图象过点，则，解得，故．22.已知直线与函数，，，的图象依次相交于点A，B，C，D，则这四点按从上到下的顺序排列是________．【答案】C，D，B，A【解析】【分析】本题考查指数函数的图象和性质，根据底数对指数函数图象的影响，在同一坐标系中画出题中四个函数的图象，即得到四个点的顺序．【解答】解：根据在第一象限内，底数越大指数函数的图象越靠近y轴，在同一坐标系中画出函数，，，的图象如下图：由图象得：这四个点从上到下的排列次序是：C，D，B，A．23.已知函数与的图象关于y轴对称，则．【答案】【解析】【分析】本题考查指数函数，涉及图象的对称变换和指数幂的运算，属于基础题．利用图象关于y轴对称的函数的解析式的关系将x换成，求得的解析式，然后代入运算化简即得．【解答】解：函数与的图象关于y轴对称，，．故答案为．24.以下是三个变量，，随变量x变化的函数值表：x1234567824816326412825614916253649640123其中关于x呈指数函数变化的函数是________．【答案】【解析】【分析】本题考查对数函数、指数函数与幂函数的增长差异．解题时要认真审题，注意指数函数的性质的合理运用．观察题中表格，可以看出，三个变量、、都是越来越大，但是增长速度不同，其中变量的增长速度最快，画出它们的图象图略，可知变量呈指数函数变化．【解答】解：观察题中表格，可知，三个变量，，都是越来越大，但是增长速度不同，增长速度最快，画出它们的图象，可知呈指数函数变化．25.函数是指数函数，则_______【答案】【解析】【分析】本题考查指数函数的定义，比较容易根据指数函数的定义，先确定a的值，再求．【解答】解：函数是指数函数，则，解得．所以，．所以，．故答案为．26.给定下列函数：；；，且；；；；；其中是指数函数的有________填序号【答案】解：指数函数为，很显然为二次函数，为指数函数，底数不一定大于0，故不是指数函数，底数小于0，不是指数函数，是指数函数，不是指数函数，是指数型函数，不是指数函数，不是指数函数，故答案为【解析】此题考查指数函数的定义，属于基础题．根据指数函数的定义进行求解即可．三、解答题（本大题共4小题，共48.0分）27.已知指数函数满足，定义域为R的函数是奇函数．确定和的解析式；判断函数的单调性，并用定义证明；若对于任意，都有成立，求a的取值范围．【答案】解：设且，，，，，是定义域为R的奇函数，，即，解得．经检验，当时，为奇函数，是定义在R上的减函数，证明如下：任取，，，则．，，又，，，，是定义在R上的减函数；，且为奇函数，，所以，因为，所以成立，设，，由对勾函数的单调性可知，函数在单调递增，在上单调递减，所以当时，有最大值为，所以．【解析】本题考查了函数的奇偶性和单调性，本题难度适中，属于较难题．利用指数函数过定点和函数为奇函数，得到关于参数的方程，解方程得到本题结论；利用函数单调性的定义加以证明，得到本题结论；利用函数的奇偶性和单调性，将原不等式转化为相应自变量的比较，利用对勾函数的单调性得到本题结论．28.某镇现在人均一年占有粮食，如果该镇人口平均每年增长，粮食总产量平均每年增长，那么x年后若人均一年占有y kg粮食，求y关于x的函数解析式．【答案】解：设该镇现在人口数量为M，则该镇现在一年的粮食总产量为360M kg．1年后，该镇粮食总产量为，人口数量为，则人均一年占有粮食为，2年后，人均一年占有粮食为，，x年后，人均一年占有粮食为，即所求函数解析式为【解析】本题考查了函数模型的应用的相关知识，试题难度较易29.用描点法在同一平面直角坐标系中画出与的图象．在的条件下，分别计算并比较与，与，与的值，从中你得到什么结论？【答案】解：作，的图象如下，，，；，；，；故；即与的图象关于y轴对称．【解析】本题主要考查了指数函数的图象及其性质，属于较易题．结合指数函数的图象，利用描点法作，的图象．可求得；；；从而可判断．30.已知不相等的两个实数a，b满足，判断实数a，b的大小关系．【答案】解：画出，的图像如图所示：，当a，b同为负时，，当a，b同为正时，，当a，b不同号时，不存在，综上所述，答案：当或．【解析】本题主要考查了指数函数的图像与性质，属于较易题画出图像，由图像可得结果．。

高一数学指数运算及指数函数试题一．选择题1．若xlog 23=1，则3x+9x的值为（B）A．3B．6C．2D．解：由题意x=，所以3x==2，所以9x=4，所以3x+9x=6故选B2．若非零实数a、b、c满足，则的值等于（B）A．1B．2C．3D．4解答：解：∵，∴设=m，a=log5m，b=log2m，c=2lgm，∴==2lgm（log m5+log m2）=2lgm•log m10=2．故选B．3．已知，则a等于（）A．B．C． 2 D． 4解：因为所以解得a=4故选D4．若a＞1，b＞1，p=，则a p等于（）A．1B．b C．l og b a D．a log b a解：由对数的换底公式可以得出p==log a（log b a），因此，a p等于log b a．故选C．5．已知lg2=a，10b=3，则log125可表示为（C）A．B．C．D．解：∵lg2=a，10b=3，∴lg3=b，∴log125===．故选C．6．若lgx﹣lgy=2a，则=（C）A．3a B．C．a D．解：∵lgx﹣lgy=2a，∴lg﹣lg=lg﹣lg=（lg﹣lg）=lg=（lgx﹣lgy）=•2a=a；故答案为C．7．已知函数，若实数a，b满足f（a）+f（b﹣2）=0，则a+b= A．﹣2 B．﹣1 C．0D．2解：f（x）+f（﹣x）=ln（x+）+ln（﹣x+=0∵f（a）+f（b﹣2）=0∴a+（b﹣2）=0∴a+b=2故选D．8．=（）A．1B．C．﹣2 D．解：原式=+2×lg2+lg5=+lg2+lg5=+1=，故选B．9．设，则=（）A．1B．2C．3D．4解：∵，∴==（）+（）+（）==3故选C10．，则实数a的取值区间应为（C）A．（1，2）B．（2，3）C．（3，4）D．（4，5）解：=log34+log37=log328∵3=log327＜log328＜log381=4∴实数a的取值区间应为（3，4）故选C．11．若lgx﹣lgy=a，则=（A）A．3a B．C．a D．解：=3（lgx﹣lg2）﹣3（lgy﹣lg2）=3（lgx﹣lgy）=3a故选A．12．设，则（）A．0＜P＜1 B．1＜P＜2 C．2＜P＜3 D．3＜P＜4 解：=log112+log113+log114+log115=log11（2×3×4×5）=log11120．∴log1111=1＜log11120＜log11121=2．故选B．13．已知a，b，c均为正数，且都不等于1，若实数x，y，z满足，则abc的值等于（A）A．1B．2C．3D．4解：∵a，b，c均为正数，且都不等于1，实数x，y，z满足，∴设a x=b y=c z=k（k＞0），则x=log a k，y=log b k，z=log c k，∴=log k a+log k b+log k c=log k abc=0，∴abc=1．故选A．14．化简a2•••的结果是（C）A．a B．C．a2D．a3解：∵a2•••=a2•••==a2，故选C15．若x，y∈R，且2x=18y=6xy，则x+y为（）A．0B．1C．1或2 D．0或2解：因为2x=18y=6xy，（1）当x=y=0时，等式成立，则x+y=0；（2）当x、y≠0时，由2x=18y=6xy得，xlg2=ylg18=xylg6，由xlg2=xylg6，得y=lg2/lg6，由ylg18=xylg6，得x=lg18/lg6，则x+y=lg18/lg6+lg2/lg6=（lg18+lg2）/lg6=lg36/lg6=2lg6/lg6=2．综上所述，x+y=0，或x+y=2．故选D．16．若32x+9=10•3x，那么x2+1的值为（D）A．1B．2C．5D．1或5解：令3x=t，（t＞0），原方程转化为：t2﹣10t+9=0，所以t=1或t=9，即3x=1或3x=9所以x=0或x=2，所以x2+1=1或5故选Dx x2A．﹣2＜a＜2 B．C．D．解；令t=2x，则t＞0若二次函数f（t）=t2﹣at+a2﹣3在（0，+∞）上有2个不同的零点，即0=t2﹣at+a2﹣3在（0，+∞）上有2个不同的根∴解可得，即故选D18．若关于x的方程=3﹣2a有解，则a的范围是（A）A．≤a＜B．a≥C．＜a＜D．a＞解：∵1﹣≤1，函数y=2x在R上是增函数，∴0＜≤21=2，故0＜3﹣2a≤2，解得≤a＜，故选A．二．填空题19．，则m=10．解：由已知，a=log2m，b=log5m．∴+=log m2+log m5=log m10=1∴m=10故答案为：10．20．已知x+y=12，xy=9，且x＜y，则=．解：由题设0＜x＜y∵xy=9，∴∴x+y﹣2==12﹣6=6x+y+2==12+6=18∴=，=∴=故答案为：21．化简：=（或或）．解：====．故答案为：（或或）．22．=1．解：===1．故答案为：1．23．函数在区间[﹣1，2]上的值域是[，8]．解：令g（x）=x2﹣2x=（x﹣1）2﹣1，对称轴为x=1，∴g（x）在[﹣1，1]上单调减，在[1，8]上单调递增，又f（x）=2g（x）为符合函数，∴f（x）=2g（x）在[﹣1，1]上单调减，在[1，，2]上单调递增，∴f（x）min=f（1）==；又f（﹣1）==23=8，f（2）==1，∴数在区间[﹣1，2]上的值域是[，8]．故答案为：[，8]．24．函数的值域为（0，8]．解：令t=x2+2|x|﹣3==结合二次函数的性质可得，t≥﹣3∴，且y＞0故答案为：（0，8]．25．函数（﹣3≤x≤1）的值域是[3﹣9，39]，单调递增区间是（﹣2，+∞）．．解：可以看做是由y=和t=﹣2x2﹣8x+1，两个函数符合而成，第一个函数是一个单调递减函数，要求原函数的值域，只要求出t=﹣2x2﹣8x+1，在[1，3]上的值域就可以，t∈[﹣9，9]此时y∈[3﹣9，39]函数的递增区间是（﹣∞，﹣2]，故答案为：[3﹣9，39]；（﹣2，+∞）三．解答题26．计算：（1）；（2）．解：（1）==（2）===2+2﹣lg3+lg2+lg3﹣lg2+2=627．（1）若，求的值；（2）化简（a＞0，b＞0）．解：（1）∵，∴x+x﹣1=9﹣2=7，x2+x﹣2=49﹣2=47，∴==3×6=18，∴==．（2）∵a ＞0，b ＞0，∴====．28．已知函数f （x ）=4x ﹣2x+1+3． （1）当f （x ）=11时，求x 的值；（2）当x ∈[﹣2，1]时，求f （x ）的最大值和最小值．解：（1）当f （x ）=11，即4x ﹣2x+1+3=11时，（2x ）2﹣2•2x ﹣8=0 ∴（2x ﹣4）（2x +2）=0 ∵2x ＞02x +2＞2，∴2x ﹣4=0，2x =4，故x=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分） （2）f （x ）=（2x ）2﹣2•2x +3 （﹣2≤x ≤1） 令∴f （x ）=（2x ﹣1）2+2当2x =1，即x=0时，函数的最小值f min （x ）=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）当2x =2，即x=1时，函数的最大值f max （x ）=3﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）29．已知函数||22)(x x x f -=. （1）若2)(=x f ，求x 的值；（2）若0)()2(2≥+t mf t f t 对于]2,1[∈t 恒成立，求实数m 的取值范围。

新课程必修第一册《指数函数与对数函数》基础测试题及答案解析时间：120分钟 满分：150分一、选择题(本大题共8小题，每小题5分，共40分) 1．若a<12，则化简42a －12的结果是( )A .2a －1B ．－2a －1C .1－2aD ．－1－2a2．函数y ＝lg x ＋lg (5－3x)的定义域是( )A ．[0，53) B ．[0，53] C ．[1，53)D ．[1，53]3．若a>1，则函数y ＝a x与y ＝(1－a)x 2的图象可能是下列四个选项中的( )4．函数f(x)＝ln(x ＋1)－2x的零点所在的大致区间是( )A ．(1,2)B ．(0,1)C ．(2，e)D ．(3,4)5．若0<a<1，在区间(－1,0)上函数f(x)＝log a (x ＋1)是( )A ．增函数且f(x)>0B ．增函数且f(x)<0C ．减函数且f(x)>0D ．减函数且f(x)<06．已知函数f(x)＝⎩⎪⎨⎪⎧log 3x ，x>02x， x≤0，则f(f(19))等于( )A ．4B .14C ．－4D ．－147．函数f(x)＝4x＋12x 的图象( )A ．关于原点对称B ．关于直线y ＝x 对称C ．关于x 轴对称D ．关于y 轴对称8．下列式子中成立的是( )A ．log 0.44<log 0.46B ．1.013.4>1.013.5C ．3.50.3<3.40.3D ．log 76<log 67二、多项选择题(本大题共4小题，每小题5分，共20分) 9．下列函数中，是奇函数且存在零点的是( )A ．y ＝x 3＋x B ．y ＝log 2x C ．y ＝2x 2－3D ．y ＝x |x |10．下列说法正确的是（ ） A ．函数()1f x x=在定义域上是减函数 B ．函数()22xf x x =-有且只有两个零点 C ．函数2xy =的最小值是1D ．在同一坐标系中函数2xy =与2xy -=的图象关于y 轴对称11．若函数1xy a b =+-(0a >,且1a ≠)的图像经过第一、三、四象限，则下列选项中正确的有（ ） A ．1a >B ．01a <<C ．0b >D ．0b <12．定义运算a ⊕b ＝⎩⎪⎨⎪⎧a ，a ≥b ，b ，a ＜b ，设函数f (x )＝1⊕2－x，则下列命题正确的有( )A ．f (x )的值域为[1，＋∞)B ．f (x )的值域为(0,1]C ．不等式f (x ＋1)＜f (2x )成立的范围是(－∞，0)D ．不等式f (x ＋1)＜f (2x )成立的范围是(0，＋∞) 二、填空题(本大题共4小题，每小题5分，共20分)13. 函数()()2lg lg x f x x =-的零点为________. 14．函数f(x)＝ax －1＋3的图象一定过定点P ，则P 点的坐标是________．15．如果函数y ＝log a x 在区间[2，＋∞)上恒有y>1，那么实数a 的取值范围是________．16.若函数f (x )＝log a x (a ＞0，且a ≠1)在⎣⎢⎡⎦⎥⎤12，4上的最大值为2，最小值为m ，函数g (x )＝(3＋2m )x 在[0，＋∞)上是增函数，则a ＋m ＝______. 三、解答题(本大题共6小题，共70分) 17．(10分)(1)计算：(－3)0－120＋(－2)－2－1416-；(2) 设log a 2＝m ，log a 3＝n ，求a 2m ＋n的值；18．(12分)(1) log 49－log 212＋5lg210-.(2)12lg 25lg 2lg ++()1lg 0.01+－； 19．(12分)设函数f(x)＝2x＋a 2x －1(a 为实数)．(1)当a ＝0时，若函数y ＝g(x)为奇函数，且在x>0时g(x)＝f(x)，求函数y ＝g(x)的解析式；(2)当a<0时，求关于x 的方程f(x)＝0在实数集R 上的解． 20．(12分)已知函数f (x )＝log ax ＋1x －1(a >0且a ≠1)， (1)求f (x )的定义域；(2)判断函数的奇偶性和单调性．21．(12分)已知－3≤12log x ≤－32，求函数f (x )＝log 2x 2·log 2x4的最大值和最小值．22．(12分) 已知函数2328()log 1mx x nf x x ++=+． （Ⅰ）若4,4m n ==，求函数()f x 的定义域和值域；（Ⅱ）若函数()f x 的定义域为R ，值域为[0,2]，求实数,m n 的值．答案及解析：一、单选题1．C [∵a <12，∴2a －1<0.于是，原式＝41－2a2＝1－2a .]2．C [由函数的解析式得：⎩⎪⎨⎪⎧lg x ≥0，x >0，5－3x >0，即⎩⎪⎨⎪⎧x ≥1，x >0，x <53.所以1≤x <53.]3．C [∵a >1，∴y ＝a x在R 上是增函数，又1－a <0，所以y ＝(1－a )x 2的图象为开口向下的抛物线．] 4．A f(1)＝ln2－2＝ln 2e 2<ln1＝0，f(2)＝ln3－1＝ln 3e>ln1＝0，所以函数f(x)＝ln(x ＋1)－2x的零点所在的大致区间是(1,2)．5．C [当－1<x <0，即0<x ＋1<1，且0<a <1时，有f (x )>0，排除B 、D.设u ＝x ＋1，则u 在(－1,0)上是增函数，且y ＝log a u 在(0，＋∞)上是减函数，故f (x )在(－1,0)上是减函数．]6．B [根据分段函数可得f (19)＝log 319＝－2，则f (f (19))＝f (－2)＝2－2＝14.]7．D 易知f(x)的定义域为R ，关于原点对称．∵f(－x)＝4－x＋12－x ＝1＋4x2x ＝f(x)，∴f(x)是偶函数，其图象关于y 轴对称．8．D [A 选项中由于y ＝log 0.4x 在(0，＋∞)单调递减， 所以log 0.44>log 0.46；B 选项中函数y ＝1.01x在R 上是增函数， 所以1.013.4<1.013.5；C 选项中由于函数y ＝x 0.3在(0，＋∞)上单调递增， 所以3.50.3>3.40.3；D 选项中log 76<1，log 67>1，故D 正确．] 二、多选题9．解析：选AD A 中，y ＝x 3＋x 为奇函数，且存在零点x ＝0，与题意相符；B 中，y ＝log 2x 为非奇非偶函数，与题意不符；C 中，y ＝2x 2－3为偶函数，与题意不符；D 中，y ＝x |x |是奇函数，且存在零点x ＝0，与题意相符． 10．解析：对于A ，()1f x x=在定义域上不具有单调性，故命题错误； 对于B ，函数()22xf x x =-有三个零点，一个负值，两个正值，故命题错误；对于C ，∵|x |≥0，∴2|x |≥20＝1，∴函数y ＝2|x |的最小值是1，故命题正确；对于D ，在同一坐标系中，函数y ＝2x 与y ＝2﹣x 的图象关于y 轴对称，命题正确.故选CD 11．解析：因为函数1xy a b =+- (0a >,且1a ≠)的图像经过第 一、三、四象限，所以其大致图像如图所示:由图像可知函数为增函数，所以1a >.当0x =时，110y b b =+-=<，故选AD.12．解析：选AC 由函数f (x )＝1⊕2－x，有f (x )＝⎩⎪⎨⎪⎧1，1≥2－x，2－x ，1＜2－x，即f (x )＝⎩⎪⎨⎪⎧2－x，x ＜0，1，x ≥0，作出函数f (x )的图象，如图所示，根据函数图象得f (x )的值域为[1，＋∞)，故A 正确，B 错误；若不等式f (x ＋1)＜f (2x )成立，由函数图象知，当2x ＜x ＋1＜0即x ＜－1时成立，当⎩⎪⎨⎪⎧2x ＜0，x ＋1≥0即－1≤x ＜0时也成立．所以不等式f (x ＋1)＜f (2x )成立时，x ＜0.故C 正确，D 错误．故选A 、C. 三、填空题13. 解析：由题知：()2lg lg 0x x -=，得(l g 1g )l 0x x -＝，∴lg 0x =或lg 1x =，∴1x =或10x =.故答案为：1x =或10x = 14．(1,4)解析 由于函数y ＝a x恒过(0,1)，而y ＝ax －1＋3的图象可看作由y ＝a x的图象向右平移1个单位，再向上平移3个单位得到的，则P 点坐标为(1,4)． 15．(1,2)解析 当x ∈[2，＋∞)时，y >1>0，所以a >1，所以函数y ＝log a x 在区间[2，＋∞)上是增函数，最小值为log a 2，所以log a 2>1＝log a a ，所以1<a <2.16.解析：当a ＞1时，函数f (x )＝log a x 是正实数集上的增函数，而函数f (x )＝log a x 在⎣⎢⎡⎦⎥⎤12，4上的最大值为2，因此有f (4)＝log a 4＝2⇒a ＝2，所以m ＝log 212＝－1，此时g (x )＝x 在[0，＋∞)上是增函数，符合题意，因此a ＋m ＝2－1＝1；当0＜a ＜1时，函数f (x )＝log a x 是正实数集上的减函数，而函数f (x )＝log a x 在⎣⎢⎡⎦⎥⎤12，4上的最大值为2，因此有f ⎝ ⎛⎭⎪⎫12＝log a 12＝2⇒a ＝22，所以m ＝log 224＝－4，此时g (x )＝－5x 在[0，＋∞)上是减函数，不符合题意. 答案：1 17．解 (1)原式＝1－0＋1－22－()1442-＝1＋14－2－1＝1＋14－12＝34.(2) ∵log a 2＝m ，log a 3＝n ， ∴a m ＝2，a n＝3. ∴a 2m ＋n＝a 2m ·a n ＝(a m )2·a n ＝22·3＝12.18．解 (1) 原式＝log 23－(log 23＋log 24)＋2lg 510＝log 23－log 23－2＋25＝－85.(2) ()11222lg 252100.1-⎡⎤⨯⨯⨯⎢⎥⎣⎦()172227lg 521010lg 102⎛⎫=⨯⨯⨯==⎪⎝⎭；19．解 (1)当a ＝0时，f (x )＝2x－1， 由已知g (－x )＝－g (x )，则当x <0时，g (x )＝－g (－x )＝－f (－x )＝－(2－x－1) ＝－(12)x＋1，由于g (x )为奇函数，故知x ＝0时，g (x )＝0， ∴g (x )＝⎩⎪⎨⎪⎧2x－1， x ≥0－12x＋1， x <0.(2)f (x )＝0，即2x＋a2x －1＝0，整理，得：(2x )2－2x＋a ＝0， 所以2x＝1±1－4a 2，又a <0，所以1－4a >1，所以2x＝1＋1－4a2， 从而x ＝log 21＋1－4a2.20．解 (1)要使此函数有意义，则有⎩⎪⎨⎪⎧x ＋1>0x －1>0或⎩⎪⎨⎪⎧x ＋1<0x －1<0，解得x >1或x <－1，此函数的定义域为 (－∞，－1)∪(1，＋∞)，关于原点对称． (2)f (－x )＝log a －x ＋1－x －1＝log a x －1x ＋1＝－log ax ＋1x －1＝－f (x )． ∴f (x )为奇函数．f (x )＝log a x ＋1x －1＝log a (1＋2x －1)，函数u ＝1＋2x －1在区间(－∞，－1)和区间(1，＋∞)上单调递减． 所以当a >1时，f (x )＝log a x ＋1x －1在(－∞，－1)，(1，＋∞)上递减； 当0<a <1时，f (x )＝log ax ＋1x －1在(－∞，－1)，(1，＋∞)上递增． 21．解 ∵f (x )＝log 2x2·log 2x4＝(log 2x －1)(log 2x －2) ＝(log 2x )2－3log 2x ＋2＝(log 2x －32)2－14，∵－3≤12log x ≤－32.∴32≤log 2x ≤3. ∴当log 2x ＝32，即x ＝22时，f (x )有最小值－14；当log 2x ＝3，即x ＝8时，f (x )有最大值2.22．(1)解 （Ⅰ）若4,4m n ==，则232484()log 1x x f x x ++=+，由2248401x x x ++>+，得到2210x x ++>，得到1x ≠-，故定义域为{}1x x ≠-．令224841x x t x ++=+，则2(4)840t x x t --+-= 当4t =时，0x =符合．当4t ≠时，上述方程要有解，则2644(4)0,t t ⎧∆=--≥⎨≠⎩，得到04t ≤<或48t <≤，又1x ≠-，所以0t ≠，所以08t <≤，则值域为3(,log 8]-∞．（Ⅱ）由于函数()f x 的定义域为R ，则22801mx x nx ++>+恒成立，则06440m mn >⎧⎨-<⎩，即016m mn >⎧⎨>⎩，令2281mx x nt x ++=+，由于()f x 的值域为[0,2]，则[1,9]t ∈，而 2()80t m x x t n --+-=，则由644()()0,t m t n ∆=---≥解得[1,9]t ∈ ，故1t =和9t =是方程644()()0t m t n ---=即2()160t m n t mn -++-=的两个根，则10169m n mn +=⎧⎨-=⎩，得到55m n =⎧⎨=⎩，符合题意．所以5,5m n ==．。

指数问题测试题及答案一、选择题1. 下列哪个表达式表示2的3次方？A. 2^3B. 2×3C. 3^2D. 2+3答案：A2. 计算2的5次方的结果是多少？A. 32B. 25C. 16D. 10答案：A3. 如果3的x次方等于27，那么x的值是多少？A. 3B. 4C. 6D. 9答案：A二、填空题4. 指数法则中，任何数的0次方等于______。

答案：15. 如果a^m = a^n，那么m等于______。

答案：n6. 指数运算中，底数相同，指数相加的法则是a^(m+n) = ______。

答案：a^m × a^n三、简答题7. 解释什么是指数函数，并给出一个例子。

答案：指数函数是一种数学函数，其中一个变量的幂等于另一个变量。

例如，y = 2^x，这是一个指数函数，其中2是底数，x是指数。

8. 描述如何计算5的4次方，并给出结果。

答案：5的4次方是将5自身乘以4次，即5 × 5 × 5 × 5 = 625。

四、计算题9. 计算下列表达式的值：(a) 4^3(b) (2^2)^3答案：(a) 4^3 = 4 × 4 × 4 = 64(b) (2^2)^3 = 4^3 = 4 × 4 × 4 = 6410. 如果8^x = 2^12，求x的值。

答案：由于8 = 2^3，我们可以将8^x写成(2^3)^x = 2^(3x)。

因此，2^(3x) = 2^12，所以3x = 12，解得x = 4。

五、证明题11. 证明对于任何正数a和b，a^b × b^a总是大于或等于a^a × b^b。

答案：由于a和b都是正数，我们可以应用AM-GM不等式（算术平均值-几何平均值不等式），即对于任意的正数x和y，有(x + y)/2 ≥ √(xy)。

将x设为a^b，y设为b^a，我们得到：(a^b + b^a)/2 ≥ √(a^b × b^a)两边同时平方，得到：(a^b + b^a)^2/4 ≥ a^b × b^a展开左边，得到：a^(2b) + 2a^b × b^a + b^(2a) ≥ 4a^b × b^a简化得到：a^(2b) - 2a^b × b^a+ b^(2a) ≥ 0这可以重写为：(a^b - b^a)^2 ≥ 0由于平方总是非负的，所以上述不等式成立。

指数函数习题新泰一中闫辉一、选择题1．以下函数中指数函数的个数是( ).①②③④A．0 个B．1 个C．2 个D．3 个2．假设，，那么函数的图象必然在〔〕A．第一、二、三象限 B ．第一、三、四象限C．第二、三、四象限D．第一、二、四象限3．，当其值域为时，的取值范围是〔〕A． B ．C．D．4．假设，，以下不等式成立的是〔〕A． B ． C ． D ．5．且，，那么是〔〕A．奇函数 B ．偶函数C．非奇非偶函数 D ．奇偶性与有关6．函数〔〕的图象是〔〕7．函数与的图象大体是().8．当时，函数与的图象只可能是〔〕9．在以以下图象中，二次函数与指数函数的图象只可能是〔〕10．计算机本钱不断降低 , 假设每隔 3 年计算机价格降低 , 现在价格为 8100 元的计算机 , 那么 9 年后的价格为 ( ).A．2400 元 B．900 元C．300 元D．3600 元二、填空题1．比较大小：〔1〕；〔2〕______ 1 ；〔3〕______2．假设，那么的取值范围为 _________．3．求函数的单调减区间为__________．4．的反函数的定义域是__________．5．函数的值域是__________．6．的定义域为, 那么的定义域为 __________.7．当时,, 那么的取值范围是 __________. 8．时，的图象过定点 ________ ．9．假设, 那么函数的图象必然不在第 _____象限 .10．函数的图象过点, 又其反函数的图象过点 (2,0),那么函数的剖析式为 ____________.11．函数的最小值为 ____________.12．函数的单调递加区间是 ____________.13．关于的方程有两个实数解 , 那么实数的取值范围是 _________.14．假设函数〔且〕在区间上的最大值是14，那么等于_________．三、解答题1．按从小到大排列以下各数：，，，，，，，2．设有两个函数与，要使〔 1〕；〔 2〕，求、的取值范围．3．, 试比较的大小.4．假设函数是奇函数，求的值．5．，求函数的值域．6．解方程：〔1〕；〔2〕．7．函数〔且〕〔1〕求的最小值；〔2〕假设，求的取值范围．8．试比较与的大小,并加以证明.9．某工厂从年到年某种产品的本钱共下降了19%，假设每年下降的百分率相等，求每年下降的百分率10．某工厂今年 1 月、 2 月、 3 月生产某产品分别为 1 万件、 1.2 件、 1.3 万件，为了估测今后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产量与月份数的关系，模拟函数可以采纳二次函数或函数〔其中、、为常数〕，四月份该产品的产量为 1.37 万件，请问用以上哪个函数作为模拟函数较好？请说明原由．11．设，求出的值．12．解方程．参照答案：一、1．B 2．A 3．D4．B5．A 6．B 7．D8．A 9．A 10．A二、 1．〔 1〕〔2〕〔3〕2．3．4．〔0，1〕5．6．7 ．8．恒过点〔 1，3〕 9 ．四 10 ．11．12．13．14．或三、 1．解：除以外，将其余的数分为三类：〔1〕负数：〔2〕小于 1 的正数：，，〔3〕大于 1 的正数：，，在〔 2〕中，；在〔 3〕中，；综上可知说明：对几个数比较大小的详尽方法是：〔1〕与 0 比，与 1 比，将所有数分成三类：，，，〔2〕在各样中两两比2．解：〔 1〕要使由条件是，解之得〔2〕要使，必定分两种情况：当时，只要，解之得；当时，只要，解之得或说明：假设是与比较大小，平时要分和两种情况考虑．3．4．解：为奇函数，，即，那么，5．解：由得，即，解之得，于是，即，故所求函数的值域为6．解：〔 1〕两边同除可得，令，有，解之得或，即或，于是或〔2〕原方程化为，即，由求根公式可获取，故7．解：〔 1〕，当即时，有最小值为〔2〕，解得当时，；当时，．8．当时,>,当时,>.9．解：设每年下降的百分率为，由题意可得，，，故每年下降的百分率为 10%10．解：设模拟的二次函数为，由条件，，，可得，解得又由及条件可得，解得下面比较，与的差，比的误差较小，从而作为模拟函数较好11．解：故12．解：令，那么原方程化为解得或，即或〔舍去〕，习题二1.求不等式 a2 x 7a4x1( a 0 ，且 a1) 中 x 的取值范围．x2.. 指数函数y b的图象以以下图，求二次函数 y ax2bx 的极点的横坐标的取值范围．ay1o x3. 函数f ( x)a x〔a0 ，且 a 1〕关于任意的实数x ，y都有〔〕Ａ． f (xy) f ( x) f ( y)Ｂ． f (xy ) f ( x) f ( y)Ｃ． f ( x y) f (x) f ( y)Ｄ． f (x y) f (x) f ( y)4. 假设(1)x(1) x，那么 x 满足〔〕23Ａ． x 0Ｂ． x0 Ｃ． x≤ 0Ｄ． x ≥ 0 5. (1) (a a 1) 23，求 a3 a 3；(2) a2 x 2 1，求 a3x aa x a 3xx；(3) x31 a ，求 a22ax 3x 6的值．6.函数 f (x) a x〔a0 ，a1〕在2，2 上函数值总小于 2，求实数 a 的取值范围．7 函数 f ( x)a x a x〔 a0， a1〕，且 f (1)3，那么 f(0) f (1) f (2)的值是．8. 假设关于x的方程22x2x ga a10 有实根，试求 a 的取值范围．9.当 a0 且 a 1 时，函数 f ( x)a x2 3 必过定点．10.设 y1a3x1， y2a2x其中 a0 ，且 a 1 ．确定x为何值时，有：〔１〕 y1y2；〔２〕 y1y2．11 当a0时，函数 y ax b 和 y b ax的图象是〔〕y y１１x xO OＡＢy y１１O xOxＣＤ12.函数 y f x的图象与 y2x的图象关于 x 轴对称，那么f x 的表达式为．13.假设函数 Fx12gf x x0是偶函数，且f x 不恒等于 0，那么f x 为〔〕2x1Ａ．奇函数Ｂ．偶函数Ｃ．可能是奇函数，也可能是偶函数Ｄ．非奇非偶函数14. 函数 f x 2x1，g x 1 x2，构造函数 F x 定义以下：当 f x ≥ g x 时， F x f x ；当f xg x 时， F xg x ，那么 F x 〔〕Ａ．有最大值 1，无最小值 Ｂ．有最小值 0，无最大值Ｃ．有最小值 1，无最大值Ｄ．无最小值，也无最大值15. 当 x 0 时，函数 f xa 2x1，那么实数 a 的取值范围是1 的值总大于 ．16. 函数f x 满足对任意实数x 1x 2 有 f x 1f x 2 且 f x 1 x 2f x 1 gf x 2 假设写出一个满足这些条件的函数那么这个函数可以写为．习题三一、选择题〔每题4 分，共计 40 分〕1．以下各式中成立的一项为哪一项〔〕A ． ( n) 713n 7 m 7 B ．3933 C ．4 x 3 y 3( x y) 4 D ．12( 3)4 33m211 11 52．化简 (a 3 b 2 )( 3a 2 b 3) (1a 6b 6 ) 的结果3A ． 9aB ．aC ． 6aD ． 9a 2 3．设指数函数f ( x) a x ( a 0, a1) ，那么以低等式中不正确 的是．．．A ． f ( x +y )= f(x ) · f ( y )B ． f 〔 xy 〕 f ( x)f ( y)C ． f ( nx)[ f ( x)] n (nQ )D ． [ f (xy)] n[ f ( x)] n ·[f ( y)] n5)01 4．函数 y(x( x 2)2〔〕〔〕( n N )〔〕A ． { x | x 5, x 2}B ． { x | x 2}C ． { x | x 5}D ． { x | 2 x 5或 x 5}5．假设指数函数ya x 在 [ －1,1] 上的最大值与最小值的差是 1，那么底数 a 等于〔〕A ．5 1 B ．5 1 C ．5 1 D ．1522226．方程 a |x| x 2 (0a 1) 的解的个数为〔〕A. 0 个个C. 2个D. 0个或 1个7．函数 f (x) 2|x|的值域是〔〕A ． (0,1]B ． (0,1)C ． (0, )D ． R2 x1, x 08．函数 f (x)1，满足 f ( x)1的 x 的取值范围〔〕x 2 , x 0A ． ( 1,1)B ． ( 1, )C ． { x | x 0或 x 2}D． { x | x 1或 x1}9． f (x)e x e x〔〕，那么以下正确的选项是2A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数 D．偶函数，在 R 上为减函数10．函数 y( 1) x 2 x 2得单调递加区间是〔 〕2C ．[ 1,2]D ． [ 1,1]A ．( , 1]B ．[2,)22二、填空题〔每题 4 分，共计 28 分〕11． a2 ,b 2 ，那么实数 a 、b 的大小关系为 ．12：不用计算器计算272 100.12927233 037=___________．481x 2813．不等式3 2 x 的解集是 __________________________ ．314． n2, 1,0,1,2,3 ，假设 ( 1)n( 1)n，那么 n ___________ ．251 x 2ax2 x a 215．不等式1恒成立，那么 a 的取值范围是．2216．定义运算：aa (a b)2 x的值域为 _________________b(a，那么函数 f x 2xb b)17. 以以下图的是某池塘中的浮萍延长的面积( m 2 ) 与时间 t ( 月 ) 的关系 : y a t , 有以下表达 :① 这个指数函数的底数是 2；y/m 2 ② 第 5 个月时 , 浮萍的面积就会高出30m 2 ；8③ 浮萍从 4m 2 延长到 12m 2需要经过1.5 个月；④ 浮萍每个月增加的面积都相等；⑤ 假设浮萍延长到2m 2、 3m 2 、 6m 24所经过的时间分别为 t 1 、 t 2 、 t 3 ，那么t 1t 2t 3 .21其中正确的选项是．0 1 2 3t/ 月三、解答题：〔 10+10+12=32 分〕18． aa 17 ，求以下各式的值:3 31122〔 1〕a1 a1 ； 〔 2〕 a 2a 2 ； 〔 3〕 a 2 a 2 ( a 1) .a2a 219. 函数y a 2 x2a x1(a1)在区间[－1，1]上的最大值是14，求a的值.20. 〔 1〕 f ( x)2m 是奇函数，求常数 m 的值；3x1〔 2〕画出函数 y | 3x 1 | 的图象，并利用图象答复：k 为何值时，方程 | 3x 1| k 无解？有一解？有两解？参照答案一、选择题〔 4*10=40 分〕题号 1 2 3 4 5 6 7 8 9 10答案BADDCCADAC二、填空题〔 4*7=28 分〕11. a b ；； 13. { x | x 4或 x2} ； 14.－1或 215.(-2, 2)； 16.(0,1]17.①②⑤三、解答题：〔 10+10+12=32 分〕111118．解 : 〔1〕原式 (a2)3(a 2 )3( a2a 2 )(a a 11)a a18 。

指数函数习题及答案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】指数函数习题一、选择题1．定义运算ab＝，则函数f(x)＝12x的图象大致为( )2．函数f(x)＝x2－bx＋c满足f(1＋x)＝f(1－x)且f(0)＝3，则f(b x)与f(c x)的大小关系是( )A．f(b x)≤f(c x)B．f(b x)≥f(c x)C．f(b x)>f(c x)D．大小关系随x的不同而不同3．函数y＝|2x－1|在区间(k－1，k＋1)内不单调，则k的取值范围是( ) A．(－1，＋∞)B．(－∞，1)C．(－1,1) D．(0,2)4．设函数f(x)＝ln[(x－1)(2－x)]的定义域是A，函数g(x)＝lg(－1)的定义域是B，若AB，则正数a的取值范围( )A．a>3 B．a≥3C．a> D．a≥5．已知函数f(x)＝若数列{a n}满足a n＝f(n)(n∈N*)，且{a n}是递增数列，则实数a的取值范围是( )A．[，3) B．(，3)C．(2,3) D．(1,3)6．已知a>0且a≠1，f(x)＝x2－a x，当x∈(－1,1)时，均有f(x)<，则实数a 的取值范围是( )A．(0，]∪[2，＋∞)B．[，1)∪(1,4]C．[，1)∪(1,2]D．(0，)∪[4，＋∞)二、填空题7．函数y＝a x(a>0，且a≠1)在[1,2]上的最大值比最小值大，则a的值是________．8．若曲线|y|＝2x＋1与直线y＝b没有公共点，则b的取值范围是________．9．(2011·滨州模拟)定义：区间[x1，x2](x1<x2)的长度为x2－x1.已知函数y＝2|x|的定义域为[a，b]，值域为[1,2]，则区间[a，b]的长度的最大值与最小值的差为________．三、解答题10．求函数y＝211．(2011·银川模拟)若函数y＝a2x＋2a x－1(a>0且a≠1)在x∈[－1,1]上的最大值为14，求a的值．12．已知函数f(x)＝3x，f(a＋2)＝18，g(x)＝λ·3ax－4x的定义域为[0,1]．(1)求a的值；(2)若函数g(x)在区间[0,1]上是单调递减函数，求实数λ的取值范围．指数函数答案1.解析：由ab＝得f(x)＝12x＝答案：A2.解析：∵f (1＋x )＝f (1－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2. 又f (0)＝3，∴c ＝3.∴f (x )在(－∞，1)上递减，在(1，＋∞)上递增． 若x ≥0，则3x ≥2x ≥1，∴f (3x )≥f (2x )． 若x <0，则3x <2x <1，∴f (3x )>f (2x )． ∴f (3x )≥f (2x )． 答案：A3.解析：由于函数y ＝|2x －1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k －1，k ＋1)内不单调，所以有k －1<0<k ＋1，解得－1<k <1. 答案：C4.解析：由题意得：A ＝(1,2)，a x －2x >1且a >2，由AB 知a x －2x >1在(1,2)上恒成立，即a x －2x －1>0在(1,2)上恒成立，令u (x )＝a x －2x －1，则u ′(x )＝a x ln a －2x ln2>0，所以函数u (x )在(1,2)上单调递增，则u (x )>u (1)＝a －3，即a ≥3. 答案：B5.解析：数列{a n }满足a n ＝f (n )(n ∈N *)，则函数f (n )为增函数， 注意a 8－6>(3－a )×7－3，所以，解得2<a <3. 答案：C6.解析：f (x )<x 2－a x <x 2－<a x ，考查函数y ＝a x 与y ＝x 2－的图象， 当a >1时，必有a －1≥，即1<a ≤2， 当0<a <1时，必有a ≥，即≤a <1， 综上，≤a <1或1<a ≤2. 答案：C7.解析：当a >1时，y ＝a x 在[1,2]上单调递增，故a 2－a ＝，得a ＝.当0<a <1时，y ＝a x 在[1,2]上单调递减，故a －a 2＝，得a ＝.故a ＝或. 答案：或8.解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线|y |＝2x ＋1与直线y ＝b 的图象如图所示，由图象可得：如果|y |＝2x ＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]． 答案：[－1,1]9.解析：如图满足条件的区间[a ，b ]，当a ＝－1，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－1，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：110.解：要使函数有意义，则只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1.∴函数的定义域为{x |－4≤x ≤1}．令t ＝－x 2－3x ＋4，则t ＝－x 2－3x ＋4＝－(x ＋)2＋，∴当－4≤x ≤1时，t max ＝，此时x ＝－，t min ＝0，此时x ＝－4或x ＝1. ∴0≤t ≤.∴0≤≤.∴函数y ＝2341()2x x --+[，1]．由t ＝－x 2－3x ＋4＝－(x ＋)2＋(－4≤x ≤1)可知，当－4≤x ≤－时，t 是增函数， 当－≤x ≤1时，t 是减函数． 根据复合函数的单调性知：y ＝1()2[－4，－]上是减函数，在[－，1]上是增函数．∴函数的单调增区间是[－，1]，单调减区间是[－4，－]．11.解：令a x ＝t ，∴t >0，则y ＝t 2＋2t －1＝(t ＋1)2－2，其对称轴为t ＝－1.该二次函数在[－1，＋∞)上是增函数．①若a >1，∵x ∈[－1,1]，∴t ＝a x ∈[，a ]，故当t ＝a ，即x ＝1时，y max ＝a 2＋2a －1＝14，解得a ＝3(a ＝－5舍去)． ②若0<a <1，∵x ∈[－1,1]，∴t ＝a x∈[a ，]，故当t ＝，即x ＝－1时， y max ＝(＋1)2－2＝14. ∴a ＝或－(舍去)． 综上可得a ＝3或.12.解：法一：(1)由已知得3a ＋2＝183a ＝2a ＝log 32. (2)此时g (x )＝λ·2x －4x ， 设0≤x 1<x 2≤1，因为g (x )在区间[0,1]上是单调减函数，所以g (x 1)－g (x 2)＝(2x 1－2x 2)(λ－2x 2－2x 1)>0恒成立，即λ<2x 2＋2x 1恒成立．由于2x 2＋2x 1>20＋20＝2，所以实数λ的取值范围是λ≤2. 法二：(1)同法一．(2)此时g (x )＝λ·2x －4x ，因为g (x )在区间[0,1]上是单调减函数，所以有g ′(x )＝λln2·2x －ln4·4x ＝ln2[－2·(2x )2＋λ·2x ]≤0成立． 设2x ＝u ∈[1,2]，上式成立等价于－2u 2＋λu ≤0恒成立． 因为u ∈[1,2]，只需λ≤2u 恒成立， 所以实数λ的取值范围是λ≤2.。

指数函数练习题一、选择题1. 下列函数中，哪一个函数是指数函数？A. y = 2xB. y = x^2C. y = 3^xD. y = log2xA. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 若指数函数f(x) = 2^x的图象向右平移1个单位，得到新函数g(x)，则g(x)的表达式为？A. g(x) = 2^(x+1)B. g(x) = 2^(x1)C. g(x) = 2^x + 1D. g(x) = 2^x 1二、填空题1. 指数函数的一般形式为______，其中底数a满足______。

2. 若f(x) = 3^x，则f(0) =______，f(1) =______。

3. 已知指数函数f(x) = a^x（a > 0且a ≠ 1）的图象过点(2,9)，则a =______。

三、解答题1. 判断下列函数是否为指数函数，并说明理由：（1）y = 5^(2x)（2）y = (1/2)^x（3）y = 4^x + 12. 已知指数函数f(x) = 2^x，求f(x)在x = 1处的切线方程。

3. 讨论指数函数f(x) = a^x（a > 0且a ≠ 1）的单调性，并说明理由。

4. 已知指数函数f(x) = 3^x，求证：对于任意实数x1、x2（x1 < x2），都有f(x1) < f(x2）。

5. 设指数函数f(x) = a^x（a > 0且a ≠ 1），若f(1) = 3，f(2) = 9，求f(x)的表达式。

四、综合题1. 已知指数函数f(x) = 2^x和g(x) = 4^x，求证：f(x)和g(x)的图象关于y轴对称。

2. 设指数函数f(x) = a^x（a > 0且a ≠ 1），若f(x)的图象经过点(1, 2)，求f(x)在x = 0处的切线方程。

3. 已知指数函数f(x) = 2^x，求证：对于任意实数x，都有f(x) > 0。

指数函数、对数函数基础练习题一、选择题1、设5.1348.029.0121,8,4-⎪⎭⎫⎝⎛===y y y ，则 ( )DA. 213y y y >> B 312y y y >> C 321y y y >> D 231y y y >> 2、如果lgx =lga +3lgb －5lgc ，那么（ ）CA ．x =a +3b －cB ．cabx 53=C ．53cab x = D ．x =a +b 3－c 33、设函数y =lg(x 2－5x )的定义域为M ，函数y =lg(x －5)+lg x 的定义域为N ，则（ ）CA ．M ∪N=RB ．M=NC ．M ⊇ND ．M ⊆N4、下列函数图象正确的是（ ）BA B C D 5、下列关系式中，成立的是 （ ）AA ．10log 514log 3103>⎪⎭⎫⎝⎛>B ． 4log 5110log 3031>⎪⎭⎫⎝⎛>C ． 03135110log 4log ⎪⎭⎫⎝⎛>>D ．0331514log 10log ⎪⎭⎫⎝⎛>>6、函数)10(|log |)(≠>=a a x x f a 且的单调递增区间为 ( )DA (]a ,0B ()+∞,0C (]1,0D [)+∞,1 二、填空题7、函数)2(log 221x y -=的定义域是 ，值域是 .(][)2,112 --， [)+∞,0；8、若直线y=2a 与函数）且1,0(|1|≠>-=a a a y x的图象有两个公共点，则a 的取值范围是 .210<<a 9、函数），且10(≠>=a a a y x在[]21，上的最大值比最小值大2a，则a 的值是__ 2321或10、函数 在区间 上的最大值比最小值大2，则实数 =___．或 ；11、设函数)1(log 2-=x y ，若[]2,1∈y ，则∈x []3,5 12、已知||lg )(x x f =，设)2(),3(f b f a =-=，则a 与b 的大小关系是 a b >三、解答题13、比较下列比较下列各组数中两个值的大小：（1）6log 7，7log 6； （2）3log π，2log 0.8； （3）0.91.1， 1.1log 0.9，0.7log 0.8； （4）5log 3，6log 3，7log 3． 解：（1）∵66log 7log 61>=， 77log 6log 71<=，∴6log 7>7log 6； （2）∵33log log 10π>=， 22log 0.8log 10<=，∴3log π>2log 0.8． （3）∵.91.11.11>=，1.1 1.1log 0.9log 10<=，0.70.70.70log 1log 0.8log 0.71=<<=，∴0.91.1>0.7log 0.8> 1.1log 0.9．（4）∵3330log 5log 6log 7<<<， ∴5log 3>6log 3>7log 3．14、设x ，y ，z ∈R +，且3x =4y =6z . 求证：yx z 2111=-; 证明：设3x=4y=6z=t . ∵x ＞0，y ＞0，z ＞0，∴t ＞1，lg t ＞0，6lg lg ,4lg lg ,3lg lg log 3tz t y t t x ==== ∴yttttxz21lg 24lg lg 2lg lg 3lg lg 6lg 11===-=-.15、若8log 3p =，3log 5q =，求lg 5．解：∵8log 3p =， ∴)5lg 1(32lg 33lg 33log 2-==⇒=p p p ， 又∵ q ==3lg 5lg 5log 3，∴ )5lg 1(33lg 5lg -==pq q ， ∴ pq pq 35lg )31(=+ ∴ pqpq3135lg +=．16、设a>0，xx e a a e x f +=)(是R 上的偶函数. （1） 求a 的值；（2） 证明：)(x f 在()+∞,0上是增函数.（1）解 依题意，对一切R x ∈有)()(x f x f -=，即.x x x x ae aee a a e +=+1所以011=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-x x e e a a 对一切R x ∈成立，由此得到01=-a a ， 即，12=a ，又因为a>0，所以a=1（2）证明 设,021x x <<()()()()212112212121211111121x x x x x x x x x x x x x x e e e e e e e e e e e x f x f +++--=⎪⎭⎫ ⎝⎛--=-+-=- 由0,0.,1221>->x x x x 得0,11221>->+x x x x e e e()()().,0)(,021上是增函数在即+∞<-∴x f x f x f17、已知函数)(log )1(log 11log )(222x p x x x x f -+-+-+=. (1)求函数f (x )的定义域；(2)求函数f (x )的值域. 解：(1)函数的定义域为(1，p ).(2)当p ＞3时，f (x )的值域为(－∞，2log 2(p +1)－2)；当1＜p ≤3时，f (x )的值域为(－∞，1+log2(p +1)).18、求函数y =log 22x ·log 24x(x ∈［1,8］)的最大值和最小值. 【解】 令t =log 2x ,x ∈［1,8］,则0≤log 2x ≤log 28即t ∈［0,3］∴y =(log 2x －1)(log 2x －2)=(t －1)(t －2)=t 2－3t +2=(t －23)2－41t ∈［0,3］∴当t =23,即log 2x =23,x =223=22时，y 有最小值=－41.当t =0或t =3，即log 2x =0或log 2x =3,也即x =1或x =8时，y 有最大值=2.教。

指数与指数函数练习题（1）1. 化简的结果是（）A.−2B.−2C.−2D.−22. 下列各函数中，值域为(0, +∞)的是（）A.y=2−x2 B.y=√1−2x C.y=x2+x+1 D.y=31x+13. 函数y=1sin x−x的一段大致图象是（）A. B.C. D.4. 函数f(x)=(12)x的值域是（）A.(0, +∞)B.(−∞, +∞)C.(0, 1)D.(1, +∞)5. 若函数f(x)＝a|2x−4|(a>0, a≠1)，满足f(1)=19，则f(x)的单调递减区间是（）A.(−∞, 2] B.[2, +∞) C.[−2, +∞) D.(−∞, −2]6. 如图是二次函数f(x)=x 2−bx +a 的部分图象，则函数g(x)=ln x +f′(x)的零点所在的区间是( )A.(14，12) B.(1, 2)C.(12，1)D.(2, 3)7. 奇函数f(x)在(−∞, 0)上单调递减，且f(2)=0，则不等式f(x)>0的解集是( ) A.(−∞, −2)∪(0, 2) B.(−∞, 0)∪(2, +∞) C.(−2, 0)∪(0, 2)D.(−2, 0)∪(2, +∞)8. 若2x ＝7，2y ＝6，则4x−y 等于（ ）A. B. C. D.9. 已知a >0，则2√a⋅√a 23=( )A.a 65B.a 56C.a −56D.a 5310. 下列运算结果中，一定正确的是（ ） A.a 3⋅a 4＝a 7 B.(−a 2)3＝a 6C.√a 88=aD.√(−π)55=−π11. 若函数(a >0，且a ≠1)是指数函数，则下列说法正确的是（ ）A.a ＝8B.f(0)＝−3C.D.a ＝4E.f(2)＝1612. 若a ＝log 20.5，b ＝20.5，c ＝0.52，则a ，b ，c 三个数的大小关系是（ ）A.a <b <cB.b <c <aC.a <c <bD.c <a <b13. 若函数f(x)=(a −1)x 是指数函数，则实数a 的取值范围是________．14. 函数f(x)=a x +3的图象一定过定点P ，则P 点的坐标是________．15. ＝________；＝________．16. 函数y =−a x−2+1(a >0且a ≠1)的图象必经过点________；17. 已知函数f(x)=a⋅2x −12x +1的图象经过点(1,13)．（1）求a 的值；（2）求函数f(x)的定义域和值域．18. 求值：（1）；（2）已知2a ＝5b ＝m ，且，求实数m 的值．19. （1）计算：0.064−13−(−57)0+[(−2)3]−43+16−0.75； 19.（2）化简：•(a 23−1−12−12⋅b13√a⋅b 5620. 请根据给出的函数图象指出函数的极值点和最大（小）值点．21. 已知(a>0，且a≠1)．（1）讨论函数f(x)和g(x)的单调性．（2）如果f(x)<g(x)，那么x的取值范围是多少？22. 已知函数y＝a（）|x|+b的图象过原点，且无限接近直线y＝2但又不与该直线相交．（1）求该函数的解析式，并画出图象；（2）判断该函数的奇偶性和单调性．参考答案与试题解析 指数与指数函数练习题（1）一、 选择题 （本题共计 9 小题 ，每题 5 分 ，共计45分 ） 1.【答案】 B【考点】有理数指数幂的运算性质及化简求值 【解析】 此题暂无解析 【解答】 此题暂无解答 2.【答案】 A【考点】指数函数的定义、解析式、定义域和值域 【解析】 此题暂无解析 【解答】 解：对于A ，y =2−x 2=(√22)x的值域为(0, +∞)；对于B ，因为1−2x ≥0， 所以2x ≤1，x ≤0，y =√1−2x 的定义域是(−∞,0]， 所以0<2x ≤1， 所以0≤1−2x <1，所以y =√1−2x 的值域是[0,1)．对于C ，y =x 2+x +1=(x +12)2+34的值域是[34,+∞)； 对于D ， 因为1x+1∈(−∞,0)∪(0,+∞)，所以y =31x+1 的值域是(0,1)∪(1,+∞)． 故选A ． 3.【答案】 A【考点】函数的图象与图象的变换 【解析】根据函数的奇偶性和特殊值即可判断． 【解答】f(−x)=−1sin x−x=−f(x)，∴y＝f(x)为奇函数，∴图象关于原点对称，∴当x＝π时，y=−1π<0，4.【答案】A【考点】指数函数的定义、解析式、定义域和值域【解析】根据指数函数的图象与性质，即可得出f(x)的值域是什么．【解答】解：∵函数f(x)=(12)x是指数函数，定义域是R，∴f(x)的值域是(0, +∞)．故选：A．5.【答案】B【考点】指数函数的单调性与特殊点【解析】由f(1)=19，解出a，求出g(x)＝|2x−4|的单调增区间，利用复合函数的单调性，求出f(x)的单调递减区间．【解答】由f(1)=19，得a2=19，于是a=13，因此f(x)＝(13)|2x−4|．因为g(x)＝|2x−4|在[2, +∞)上单调递增，所以f(x)的单调递减区间是[2, +∞)．故选：B．6.【答案】C【考点】二次函数的性质函数零点的判定定理【解析】由二次函数图象的对称轴确定b的范围，据g(x)的表达式计算g(12)和g(1)的值的符号，从而确定零点所在的区间．【解答】解：∵f(x)=x2−bx+a，结合函数的图象可知，二次函数的对称轴，12<x =b2<1 ∴ 1<b <2∴ f ’(x)=2x −b∴ g(x)=ln x +f′(x)=ln x +2x −b 在(0, +∞)上单调递增且连续 ∵ g(12)=ln 12+1−b <0， g(1)=ln 1+2−b =2−b >0，∴ 函数g(x)=ln x +f′(x)的零点所在的区间是(12,1).故选C . 7.【答案】 A【考点】其他不等式的解法 函数单调性的性质【解析】根据奇函数的性质求出f(−2)=0，由条件画出函数图象示意图，结合图象即可求出不等式的解集． 【解答】解：∵ f(x)为奇函数，且f(2)=0，在(−∞, 0)是减函数， ∴ f(−2)=−f(2)=0，f(x)在(0, +∞)内是减函数， ∴ 在(−∞,0)上，f(x)>0的解为(−∞,2), 在(0,+∞)上，f(x)>0的解为(0,2).∴ 不等式f(x)>0的解集为(−∞, −2)∪(0, 2). 故选A ． 8. 【答案】 D【考点】有理数指数幂的运算性质及化简求值 【解析】 此题暂无解析 【解答】 此题暂无解答 9.【答案】 B【考点】有理数指数幂的运算性质及化简求值 【解析】利用有理数指数幂的运算性质求解． 【解答】2√a⋅√a23=a 2a 12⋅a 23=a 2a 76=a 56，二、 多选题 （本题共计 3 小题 ，每题 5 分 ，共计15分 ） 10.【答案】 A,D【考点】有理数指数幂的运算性质及化简求值 【解析】根据有理数指数幂的运算法则计算． 【解答】A 选项a 3⋅a 4＝a 3+4＝a 7，正确；B 选项(−a 2)3＝−a 6，错误；C 选项当a ≥0时，√a 88=a ，当a <0时，√a 88=−a ，错误； D 选项√(−π)55=−π，正确． 11.【答案】 A,C【考点】指数函数的定义、解析式、定义域和值域 【解析】 此题暂无解析 【解答】 此题暂无解答 12.【答案】a ＝log 20.5＜0，b ＝20.5＞1，0＜c ＝0.52＜1，则a ＜c ＜b ，则选：C 【考点】指数函数的图象与性质 【解析】根据对数函数以及指数函数的性质求出a ，b ，c 的大小即可． 【解答】a ＝log 20.5<0，b ＝20.5>1，0<c ＝0.52<1， 则a <c <b ， 则选：C ．三、 填空题 （本题共计 4 小题 ，每题 5 分 ，共计20分 ） 13.【答案】(1, 2)∪(2, +∞) 【考点】指数函数的定义、解析式、定义域和值域 【解析】根据指数函数的定义，底数大于0且不等于1，求出实数a 的取值范围． 【解答】解：∵ 函数f(x)=(a −1)x 是指数函数， ∴ {a −1>0a −1≠1，解得a>1且a≠2；∴实数a的取值范围是(1, 2)∪(2, +∞)．故答案为：(1, 2)∪(2, +∞)．14.【答案】(0, 4)【考点】指数函数的单调性与特殊点【解析】此题暂无解析【解答】解：f(x)=a x+3的图象可以看作把f(x)=a x的图象向上平移3个单位而得到，且f(x)=a x一定过点(0, 1)，则f(x)=a x+3应过点(0, 4).故答案为：(0, 4).15.【答案】6,【考点】有理数指数幂的运算性质及化简求值【解析】此题暂无解析【解答】此题暂无解答16.【答案】(2, 0)【考点】指数函数的图象与性质【解析】结合指数函数过(0,1)点，结合题目条件，即可得出答案．【解答】令x−2=0，解得x=2当x=2时，y=−a2−2+1=0∴函数y=−a x−2+1(a>0且a≠1）图象过的定点为(2,0)答案：（20）四、解答题（本题共计 6 小题，每题 11 分，共计66分）17.【答案】【考点】函数的定义域及其求法函数的值域及其求法【解析】此题暂无解析【解答】 此题暂无解答 18. 【答案】原式＝＝＝99；因为2a ＝5b ＝m ，所以a ＝log 2m ，b ＝log 5m ，所以，所以．【考点】有理数指数幂的运算性质及化简求值 【解析】（1）直接利用有理数指数幂及根式的运算性质求解即可；（2）先利用指数式和对数式的互化，表示出a ，b 的值，然后利用对数的运算性质求解即可． 【解答】原式＝＝＝99；因为2a ＝5b ＝m ，所以a ＝log 2m ，b ＝log 5m ，所以，所以．19. 【答案】原式＝0.4−1−1+2−4+2−3=52−1+116+18=2716． 原式=a−13b 12⋅a −12⋅b 13a 16⋅b 56=a−13−12−16⋅b12+13−56=a −1=1a ．【考点】有理数指数幂的运算性质及化简求值【解析】（1）利用指数幂的运算性质即可得出．（2）利用指数幂的运算性质即可得出．【解答】原式＝0.4−1−1+2−4+2−3=52−1+116+18=2716．原式=a −13b 12⋅a −12⋅b 13a 16⋅b 56=a −13−12−16⋅b 12+13−56=a −1=1a ． 20.【答案】A ．函数的极大值点为x 2，极小值点为x 1，x 3，最大值点为a ，x 2，最小值点为x 3，B ．函数的极大值点为x 1，x 3极小值点为x 2，最大值点为x 1，最小值点为b ，C ．函数的极大值点为x 1，极小值点为x 2，最大值点为b ，最小值点为a【考点】函数的图象与图象的变换【解析】根据函数极值，最值与图象的关系进行判断即可．【解答】A ．函数的极大值点为x 2，极小值点为x 1，x 3，最大值点为a ，x 2，最小值点为x 3，B ．函数的极大值点为x 1，x 3极小值点为x 2，最大值点为x 1，最小值点为b ，C ．函数的极大值点为x 1，极小值点为x 2，最大值点为b ，最小值点为a 21.【答案】 当0<a <1时，>1，则f(x)＝a x 在R 上单调递减，g(x)＝．当a >2时，0<，则f(x)＝a x 在R 上单调递增，g(x)＝．因为f(x)<g(x)，即a x <，即a x <a −x ，当0<a <7时，不等式即为x >−x ；当a >1时，不等式即为x <−x ，综上，当0<a <3时，+∞)，当a >1时，不等式的解集为(−∞．【考点】函数单调性的性质与判断利用导数研究函数的单调性【解析】此题暂无解析【解答】此题暂无解答22.【答案】根据题意，函数y＝a（）|x|+b的图象过原点，则有7＝a+b，则a＝−b，又由f(x)的图象无限接近直线y＝−2但又不与该直线相交，则b＝2，又由a+b＝6，则a＝−2，则f(x)＝−2×（）|x|+2，其图象如图：根据题意，f(x)＝−7×（）|x|+3，其定义域为R，有f(−x)＝−2×（）|x|+2＝f(x)，则f(x)是偶函数，又由f(x)＝，f(x)在(0, +∞)上为增函数，0)上为减函数．【考点】函数的图象与图象的变换函数奇偶性的性质与判断分段函数的应用【解析】此题暂无解析【解答】此题暂无解答。

A 基础练习2.1.2指数函数（1时） 1．下列函数是指数函数的是( ) A ．y ＝－2xB ．y ＝2x ＋1 C ．y ＝2－x D ．y ＝1x【解析】 y ＝2－x＝⎝⎛⎭⎫12x，符合指数函数的定义，故选C.【答案】 C 2．函数y ＝(a －2)x 在R 上为增函数，则a 的取值范围是( )A ．a>0且a ≠1B ．a>3C ．a<3D ．2<a<3【解析】 由指数函数单调性知，底数大于1时为增函数，∴a －2>1，∴a>3，故选B. 【答案】 B 3．已知a ＝5－12，函数f(x)＝a x ，若实数m 、n 满足f(m)>f(n)，则m 、n 的大小关系为________．【解析】 ∵a ＝5－12∈(0,1)， 故a m >a n ⇒m<n. 【答案】 m<n4．已知指数函数f(x)的图象过点(2,4)，求f(－3)的值．【解析】 设指数函数f(x)＝a x (a>0且a ≠1)，由题意得a 2＝4，∴a ＝2，∴f(x)＝2x ， ∴f(－3)＝2－3＝18.B 综合应用一、选择题(每小题5分，共20分) 1．函数y ＝a x －2＋1(a>0，a ≠1)的图象必经过点( )A ．(0,1)B ．(1,1)C ．(2,0)D ．(2,2)【解析】 由于函数y ＝a x 经过定点(0,1)，所以函数y ＝a x－2经过定点(2,1)，于是函数y ＝a x －2＋1经过定点(2,2)．【答案】 D2．f(x)＝⎝⎛⎭⎫12|x|，x ∈R ，那么f(x)是( ) A ．奇函数且在(0，＋∞)上是增函数 B ．偶函数且在(0，＋∞)上是增函数 C ．奇函数且在(0，＋∞)上是减函数 D ．偶函数且在(0，＋∞)上是减函数 【解析】因为函数f(x)= |x|= 图象如右图． 由图象可知答案显然是D. 【答案】 D3．下列四个函数中，值域为(0，＋∞)的函数是( )A ．y ＝21x B ．y ＝2x －1C ．y ＝2x ＋1D ．y ＝⎝⎛⎭⎫122－x【解析】 在A 中，∵1x ≠0，∴21x≠1，即y ＝21x的值域为(0,1)∪(1，＋∞)．在B 中，2x －1≥0，∴y ＝2x －1的值域为[0，＋∞)． 在C中，∵2x >0，∴2x ＋1>1.∴y ＝2x ＋1的值域为(1，＋∞)． 在D 中，∵2－x ∈R ，∴y ＝⎝⎛⎭⎫122－x>0. ∴y ＝⎝⎛⎭⎫122－x 的值域为(0，＋∞)．故选D.【答案】 D 4．方程4x －1＝116的解为( ) A ．2 B ．－2 C ．－1 D ．1 【解析】 ∵4x －1＝116＝4－2，∴x －1＝－2，∴x ＝－1.故选C. 【答案】 C二、填空题(每小题5分，共10分) 5．函数y ＝a x －1的定义域是(－∞，0]，则实数a 的取值范围为________．【解析】 由a x －1≥0，得a x ≥1＝a 0，因为x ∈(－∞，0]，由指数函数的性质知0<a<1.【答案】 (0,1)6．函数f(x)＝⎝⎛⎭⎫13x－1，x ∈[－1,2]的值域为________．【解析】 函数y ＝⎝⎛⎭⎫13x 在区间[－1,2]上是减函数，所以⎝⎛⎭⎫132≤⎝⎛⎭⎫13x ≤⎝⎛⎭⎫13－1，即19≤⎝⎛⎭⎫13x ≤3， 于是19－1≤f(x)≤3－1，即－89≤f(x)≤2.【答案】 [－89，2]三、解答题(每小题10分，共20分) 7．已知函数f(x)＝a x －2(x ≥0)的图象经过点⎝⎛⎭⎫4，19，其中a>0且a ≠1. (1)求a 的值；(2)求函数y ＝f(x)(x ≥0)的值域． 【解析】 (1)函数图象过点⎝⎛⎭⎫4，19， 所以a 4－2＝19＝⎝⎛⎭⎫132，∴a ＝13，(2)f(x)＝⎝⎛⎭⎫13x －2(x ≥0)， 由x ≥0，得x －2≥－2， ∴0<⎝⎛⎭⎫13x －2≤⎝⎛⎭⎫13－2＝9，∴函数y ＝f(x)(x ≥0)的值域为(0,9]． 8．画出下列函数的图象，并说明它们是由函数f(x)＝2x 的图象经过怎样的变换得到的．(1)y ＝2x －1；(2)y ＝2x ＋1；(3)y ＝2|x|； (4)y ＝－2x .【解析】 如图所示．y=2x-1的图象是由y=2x 的图象向右平移1个单位得到；y=2x+1的图象是由y=2x 的图象向上平移1个单位得到；y=2|x|的图象是由y=2x 的y 轴右边的图象和其关于y 轴对称的图象组成的；y=-2x 的图象与y=2x 的图象关于x 轴对称．9．(10分)函数f(x)＝a x (a>0，且a ≠1)在区间[1,2]上的最大值比最小值大a2，求a的值．【解析】 (1)若a>1，则f(x)在[1,2]上递增，∴a 2－a ＝a 2，即a ＝32或a ＝0(舍去)．(2)若0<a<1，则f(x)在[1,2]上递减， ∴a －a 2＝a 2，即a ＝12或a ＝0(舍去)，综上所述，所求a 的值为12或32.2.1.2指数函数（2时） A 基础练习1．已知集合M ＝{－1,1}，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪12<2x ＋1<4，x ∈Z ，则M ∩N 等于( ) A ．{－1,1} B ．{－1} C ．{0} D ．{－1,0} 【解析】 因为N ＝{x|2－1<2x ＋1<22，x ∈Z }，又函数y ＝2x 在R 上为增函数， ∴N ＝{x|－1<x ＋1<2，x ∈Z } ＝{x|－2<x<1，x ∈Z }＝{－1,0}． ∴M ∩N ＝{－1,1}∩{－1,0}＝{－1}．故选B.【答案】 B2．设14<⎝⎛⎭⎫14b <⎝⎛⎭⎫14a<1，那么( )A ．a a <a b <b aB ．a a <b a <a bC ．a b <a a <b aD ．a b <b a <a a【解析】 由已知及函数y ＝⎝⎛⎭⎫14x是R 上的减函数， 得0<a<b<1.由y ＝a x (0<a<1)的单调性及a<b ，得a b <a a .由0<a<b<1知0<a b <1.∵⎝⎛⎭⎫a b a <⎝⎛⎭⎫a b 0＝1.∴a a <b a.故选C. 也可采用特殊值法，如取a ＝13，b ＝12.【答案】 C3．已知函数f(x)＝a －12x ＋1，若f(x)为奇函数，则a ＝________.【解析】 解法1：∵f(x)的定义域为R ，又∵f(x)为奇函数，∴f(0)＝0，即a －120＋1＝0.∴a ＝12.解法2：∵f(x)为奇函数，∴f(－x)＝－f(x)，即a －12－x ＋1＝12x ＋1－a ，解得a ＝12.【答案】 124．函数y ＝2－x 2＋ax －1在区间(－∞，3)内递增，求a 的取值范围．【解析】 对u ＝－x 2＋ax －1＝－⎝⎛⎭⎫x －a 22＋a 24－1，增区间为⎝⎛⎦⎤－∞，a 2，∴y 的增区间为⎝⎛⎦⎤－∞，a2，由题意知3≤a2，∴a ≥6. ∴a 的取值范围是a ≥6. B 综合应用一、选择题(每小题5分，共20分) 1．设y 1＝40.9，y 2＝80.48，y 3＝(12)－1.5，则( )A ．y 3>y 1>y 2B ．y 2>y 1>y 3C ．y 1>y 2>y 3D ．y 1>y 3>y 2 【解析】 y 1＝40.9＝21.8，y 2＝80.48＝21.44，y 3＝(12)－1.5＝21.5，∵y ＝2x 在定义域内为增函数， 且1.8>1.5>1.44， ∴y 1>y 3>y 2. 【答案】 D2．若⎝⎛⎭⎫142a ＋1<⎝⎛⎭⎫143－2a，则实数a 的取值范围是( )A.⎝⎛⎭⎫12，＋∞B.()1，＋∞ C ．(－∞，1) D.⎝⎛⎭⎫－∞，12 【解析】 函数y ＝⎝⎛⎭⎫14x在R 上为减函数，∴2a ＋1>3－2a ，∴a>12.故选A.【答案】 A3．设函数f(x)定义在实数集上，它的图象关于直线x ＝1对称，且当x ≥1时，f(x)＝3x －1，则有( )A ．f(13)<f(32)<f(23)B ．f(23)<f(32)<f(13)C ．f(23)<f(13)<f(32)D ．f(32)<f(23)<f(13)【解析】 因为f(x)的图象关于直线x ＝1对称，所以f(13)＝f(53)，f(23)＝f(43)，因为函数f(x)＝3x －1在[1，＋∞)上是增函数，所以f(53)>f(32)>f(43)，即f(23)<f(32)<f(13)．故选B.【答案】 B4．如果函数f(x)＝(1－2a)x 在实数集R 上是减函数，那么实数a 的取值范围是( )A ．(0，12)B ．(12，＋∞)C ．(－∞，12)D ．(－12，12)【解析】 根据指数函数的概念及性质求解．由已知得，实数a 应满足⎩⎪⎨⎪⎧1－2a>01－2a<1，解得⎩⎪⎨⎪⎧a<12a>0，即a ∈(0，12)．故选A.【答案】 A二、填空题(每小题5分，共10分) 5．设a>0，f(x)＝e x a ＋ae x (e>1)，是R 上的偶函数，则a ＝________.【解析】 依题意，对一切x ∈R ，都有f(x)＝f(－x)，∴e x a ＋a e x ＝1ae x ＋ae x ， ∴(a －1a )(e x －1e x )＝0.∴a －1a ＝0，即a 2＝1.又a>0，∴a ＝1. 【答案】 16．下列空格中填“>、<或＝”． (1)1.52.5________1.53.2，(2)0.5－1.2________0.5－1.5.【解析】 (1)考察指数函数y ＝1.5x . 因为1.5>1，所以y ＝1.5x 在R 上是单调增函数．又因为2.5<3.2，所以1.52.5<1.53.2. (2)考察指数函数y ＝0.5x .因为0<0.5<1，所以y ＝0.5x 在R 上是单调减函数．又因为－1.2>－1.5，所以0.5－1.2<0.5－1.5.【答案】 <，<三、解答题(每小题10分，共20分) 7．根据下列条件确定实数x 的取值范围：a<⎝⎛⎭⎫1a 1－2x(a>0且a ≠1)．【解析】 原不等式可以化为a 2x －1>a 12，因为函数y ＝a x (a>0且a ≠1)当底数a 大于1时在R 上是增函数；当底数a 大于0小于1时在R 上是减函数，所以当a>1时，由2x －1>12，解得x>34；当0<a<1时，由2x －1<12，解得x<34.综上可知：当a>1时，x>34；当0<a<1时，x<34.8．已知a>0且a ≠1，讨论f(x)＝a －x 2＋3x ＋2的单调性．【解析】 设u ＝－x 2＋3x ＋2＝－⎝⎛⎭⎫x －322＋174， 则当x ≥32时，u 是减函数，当x ≤32时，u 是增函数．又当a>1时，y ＝a u 是增函数，当0<a<1时，y ＝a u 是减函数，所以当a>1时，原函数f(x)＝a －x 2＋3x ＋2在⎣⎡⎭⎫32，＋∞上是减函数，在⎝⎛⎦⎤－∞，32上是增函数．当0<a<1时，原函数f(x)＝a －x 2＋3x ＋2在⎣⎡⎭⎫32，＋∞上是增函数，在⎝⎛⎦⎤－∞，32上是减函数．9．(10分)已知函数f(x)＝3x ＋3－x . (1)判断函数的奇偶性；(2)求函数的单调增区间，并证明．【解析】 (1)f(－x)＝3－x ＋3－(－x)＝3－x＋3x ＝f(x)且x ∈R ，∴函数f(x)＝3x ＋3－x是偶函数．(2)由(1)知，函数的单调区间为(－∞，0]及[0，＋∞)，且[0，＋∞)是单调增区间．现证明如下：设0≤x 1<x 2，则f(x 1)－f(x 2)＝3x 1＋3－x 1－3x 2－2－x 2＝3x 1－3x 2＋13x 1－13x 2＝3x 1－3x 2＋3x 2－3x 13x 13x 2＝(3x 2－3x 1)·1－3x 1＋x 23x 1＋x 2.∵0≤x 1<x 2，∴3x 2>3x 1，3x 1＋x 2>1， ∴f(x 1)－f(x 2)<0，即f(x 1)<f(x 2)， ∴函数在[0，＋∞)上单调递增， 即函数的单调增区间为[0，＋∞)．。

指数函数基础练习题一、选择题1. 若 f(x) = 2^x，则 f(3) 的值为：A. 2B. 4C. 8D. 162. 若 g(x) = 5^x，则 g(0) 的值为：A. 0B. 1C. 5D. 103. 若 h(x) = (1/3)^x，则 h(2) 的值为：A. 1/9B. 1/6C. 1/3D. 9/14. 若 k(x) = 10^x，则 k(-1) 的值为：A. 0.1B. 1C. 10D. 1005. 若 p(x) = e^x，则 p(1) 的值为：A. 1B. eC. e^2D. e^-1二、填空题1. 若 f(x) = 2^x，解方程 f(x) = 64，x 的值为 _______。

2. 若 g(x) = 5^x，解不等式 g(x) < 1，x 的取值范围为 _______。

3. 若 h(x) = (1/4)^x，解不等式 h(x) > 16，x 的取值范围为 _______。

4. 若 k(x) = 10^x，解方程 k(x) = 1000，x 的值为 _______。

5. 若 p(x) = e^x，解方程 p(x) = 5，x 的值约为 _______（保留两位小数）。

三、计算题1. 计算 f(2) + f(0) + f(-1) 的值。

2. 计算 g(3) - g(2) 的值。

3. 计算 h(1/2) + h(1/3) 的值。

4. 计算 k(-2) - k(0) 的值。

5. 若指数函数 f(x) = a * b^x，已知 f(0) = 3，f(2) = 27，求 a 和 b 的值。

四、解答题1. 将函数 f(x) = 4 * 2^x 的图像完整地画在坐标系中，并标出至少三个点的坐标。

2. 设函数 f(x) = 3 * 5^x，求函数 f(x) 的反函数，并说明反函数的定义域和值域。

3. 证明：指数函数 f(x) = b^x （其中 b > 0 且b ≠ 1）的图像经过点(0, 1)。

第讲指数函数时间：年月日刘老师学生签名：一、兴趣导入二、学前测试1．在区间上为增函数的是（ B ）A ． B． C． D．2．函数是单调函数时，的取值范围( A ）A． B ． C ． D．3．如果偶函数在具有最大值,那么该函数在有（ A ）A．最大值 B ．最小值 C ．没有最大值 D．没有最小值4．函数，是（ B ）A．偶函数 B ．奇函数 C．不具有奇偶函数 D ．与有关5．函数在和都是增函数，若，且那么（ D )A． B． C． D ．无法确定6．函数在区间是增函数，则的递增区间是（ B ）A． B． C． D．12三、方法培养☆专题1：指数函数的定义一般地，函数x y a =(a ＞0且a ≠1）叫做指数函数,其中x 是自变量,函数的定义域为R 。

例1指出下列函数那些是指数函数:（１）4x y =(２）x y 4=(３)4xy -= (４))4(-=xy (５）π=y x（6）x y 24=（7）xxy =（８）)1,21(()12≠>=-a a y a x解析：利用指数函数的定义解决这类问题。

解：(１），（５），（８）为指数函数变式练习11函数2(33)x y a a a =-+⋅是指数函数，则有（）Ａ．ａ＝１或ａ＝２ Ｂ．ａ＝１ Ｃ．ａ＝２ Ｄ．ａ＞０且1≠a 答案：C 2. 计算:105432)(0625.0833416--+++π; 解：（1）105432)(0625.0833416--+++π =（425)21+（827)31+（0。

062 5）41+1-21=（25）2×21+（23）313⨯+（0。

5）414⨯+21=25+23+0。

5+21 =5;☆专题2：指数函数的图像与性质一般地，指数函数y=a x在底数a ＞1及0＜a ＜1这两种情况下的图象和性质如下表所示:a ＞1 0＜a ＜1 图象3性质 ①定义域：R ②值域：（0，+∞）③过点（0，1),即x=0时y=1④在R 上是增函数，当x ＜0时,0＜y ＜1;当x ＞0时，y ＞1 ④在R 上是减函数，当x ＜0时，y＞1；当x ＞0时,0＜y ＜1在同一坐标系中作出y=2x和y=（21）x 两个函数的图象，如图2—1-2-3。

课时提升作业十六指数函数的图象及性质一、选择题(每小题5分,共25分)1.下列各函数中,是指数函数的是( )A.y=(-3)xB.y=-3xC.y=3x-1D.y=【解析】选D.由指数函数的定义知选项A中底数-3<0,不符合要求;选项B中系数为-1,不符合要求;选项C中,指数位置为x-1,不符合要求;只有选项D符合要求.【补偿训练】下列函数中指数函数的个数为( )①y=;②y=;③y=2x+3;④y=a x(a>0且a≠1,x≥0);⑤y=1x;⑥y=-1;⑦y=.A.1B.2C.4D.5【解析】选A.利用指数函数的定义可判断只有y=是指数函数.2.(2016·菏泽高一检测)若函数y=a x-(b+1)(a>0,a≠1)的图象在第一、三、四象限,则有( )A.a>1且b<0B.a>1且b>0C.0<a<1且b>0D.0<a<1且b<0【解析】选 B.由函数的图象在第一、三、四象限可知,此函数应为递增的,故a>1,又过定点(0,-b),此点应在y轴的负半轴上,则-b<0,即b>0.【补偿训练】指数函数y=a x与y=b x的图象如图所示,则( )A.a<0,b<0B.a<0,b>0C.0<a<1,b>1D.0<a<1,0<b<1 【解析】选C.指数函数在底数大于1时单调递增,底数大于0小于1时单调递减,因而选C.3.(2016·大庆高一检测)函数y=2+a x-2(a>0且a≠1)的图象恒过定点,它的坐标为( )A.(2,2)B.(2,3)C.(-2,2)D.(3,2)【解析】选B.令x=2,得y=2+a0=3,所以函数y=2+a x-2的图象恒过定点(2,3).【补偿训练】已知对不同的a值,函数f(x)=2+a x-1(a>0,且a≠1)的图象恒过定点P,则P点的坐标是( )A.(0,3)B.(0,2)C.(1,3)D.(1,2)【解析】选C.令x-1=0,得x=1,此时f(x)=2+1=3,所以图象恒过定点(1,3).4.指数函数y=f(x)的图象过点(1,3),则f(f(1))= ( )A.3B. 9C. 27D.【解析】选C.设f(x)=a x(a>0,a≠1),则a1=3,即a=3,所以f(x)=3x.所以f(1)=3,f(f(1))=f(3)=27.【延伸探究】若本题条件改为“指数函数y=f(x)的图象过点(-1,3)”,则f(f(1))的值又如何求解?【解析】设f(x)=a x(a>0,a≠1),则a-1=3,所以a=,所以f(x)=,则f(1)=,则f=,故f(f(1))=f=.5.(2016·广州高一检测)下列函数中,值域为(0,+∞)的是( )A. y=B.y=C.y=D.y=【解析】选B.易知C值域为[0,+≦),A值域为{y|y>0且y≠1},D值域为[0,1).二、填空题(每小题5分,共15分)6.(2016·大连高一检测)指数函数y=(2-a)x在定义域内是减函数,则a的取值范围是________.【解析】由题意可知,0<2-a<1,即1<a<2.答案:1<a<27.当x>0时,函数y=(a-8)x的值域恒大于1,则实数a的取值范围是________.【解析】当0<a-8<1即8<a<9时,函数y=(a-8)x在(0,+≦)上单调递减,则当x>0时,(a-8)x<(a-8)0=1不符合题意,当a-8>1即a>9时,函数y=(a-8)x在(0,+≦)上单调递增,则当x>0时,(a-8)x>(a-8)0=1符合题意,所以实数a的取值范围是a>9.答案:a>98.(2016·天津高一检测)函数y=a x在[0,1]上的最大值和最小值的和为3,则a的值等于.【解题指南】对a分类讨论,分为a>1和0<a<1两种情况分别表述出最大值和最小值计算.【解析】当a>1时,y min=a0=1;y max=a1=a,由1+a=3,所以a=2.当0<a<1时,y max=a0=1,y min=a1=a.由1+a=3,所以a=2矛盾,综上所述,有a=2.答案:2三、解答题(每小题10分,共20分)9.求下列函数的定义域和值域:(1)y=.(2)y=5-x-1.【解析】(1)要使函数y=有意义,只需1-x≥0,即x≤1,所以函数的定义域为{x|x≤1}.设y=3u,u=,则u≥0,由函数y=3u在[0,+≦)上是增函数,得y≥30=1,所以函数的值域为{y|y≥1}.(2)函数y=5-x-1对任意的x∈R都成立,所以函数的定义域为R.因为5-x>0,所以5-x-1>-1,所以函数的值域为(-1,+≦).10.已知函数f(x)=a x-1(x≥0)的图象经过点,其中a>0且a≠1.(1)求a的值.(2)求函数y=f(x)+1(x≥0)的值域.【解析】(1)因为函数f(x)=a x-1(x≥0)的图象经过点,所以a2-1=a=.(2)由(1)得f(x)=(x≥0),函数为减函数,当x=0时,函数取最大值2,故f(x)∈(0,2],所以函数y=f(x)+1=+1(x≥0)∈(1,3],故函数y=f(x)+1(x≥0)的值域为(1,3].一、选择题(每小题5分,共10分)1.已知函数f=2x+a的图象不过第二象限,那么常数a的取值范围是( )A.(-1,+∞)B.(-∞,-1]C.[-1,+∞)D.(-∞,1)【解析】选B.函数y=2x图象向下平移1个单位后图象过原点(0,0),不过第二象限.再向下平移,仍然不过第二象限,即把y=2x图象向下至少平移1个单位,所得函数y=2x+a图象就满足条件,由向下平移图象的变换法则,知a≤-1.2.(2016·福州高一检测)设函数f(x)=若f(x)是奇函数,则g(2)的值是( )A.-B.-4C.D.4【解析】选A.设x>0,则-x<0,由于f(x)是奇函数,则f(x)=-f(-x)=-2-x=-.故g(x)=-,则g(2)=-=-.【延伸探究】把本题中的条件“若f(x)是奇函数”改为“若f(x)是偶函数”,其他条件不变,试求g(2)的值.【解析】设x>0,则-x<0,由于f(x)是偶函数,则f(x)=f(-x)=2-x=.故g(x)=,则g(2)==.二、填空题(每小题5分,共10分)3.(2015·山东高考)已知函数f(x)=a x+b(a>0,a≠1)的定义域和值域都是[-1,0],则a+b=________ .【解析】当a>1时,函数f(x)单调递增,则无解;当0<a<1时,函数f(x)单调递减,则解得故a+b=-.答案:-4.已知函数f(x)=ab x+c(b>0,b≠1),x∈[0,+∞),若其值域为[-2,3),则该函数的一个解析式可以为f(x)=________.【解析】因为f(x)=ab x+c(b>0,b≠1),x∈[0,+≦),其值域为[-2,3), 所以当x=0时,f(0)=a+c=-2,当x→+≦时,b x→0,f(x)→c=3,解得a=-5,c=3,0<b<1,所以f(x)=-5+3(满足0<b<1的b均可).答案:-5+3(满足0<b<1的b均可)三、解答题(每小题10分,共20分)5.(2016·济南高一检测)设f(x)=3x,g(x)=.(1)在同一平面直角坐标系中作出f(x),g(x)的图象.(2)计算f(1)与g(-1),f(π)与g(-π),f(m)与g(-m)的值,从中你能得到什么结论?【解析】(1)函数f(x),g(x)的图象如图所示:(2)f(1)=31=3,g(-1)==3;f(π)=3π,g(-π)==3π;f(m)=3m,g(-m)==3m.从以上计算的结果看,两个函数当自变量取值互为相反数时,其函数值相等,即当指数函数的底数互为倒数时,它们的图象关于y轴对称. 【拓展延伸】指数函数图象的记忆口诀多个图形像束花,(0,1)这点把它扎.撇增捺减无例外,底互倒时y轴夹.x=1为判底线,交点纵标看小大.重视数形结合法,横轴上面图象察.6.已知函数f(x)=a x+b的图象过点(1,3)和(0,2).(1)试确定函数f(x)的解析式.(2)若关于x的方程|f(x)-2|=m有两个不同解,求实数m的取值范围. 【解题指南】(1)把点的坐标代入函数解析式,列出方程组求出a,b 的值即可.(2)根据题意,方程有两个不同的解,即h(x)=|f(x)-2|与g(x)=m的图象有两个交点,求出m的取值范围即可.【解析】(1)因为函数f(x)=a x+b的图象过点(1,3)和(0,2),所以解得a=2,b=1,所以f(x)=2x+1.(2)因为关于x的方程|f(x)-2|=m有两个不同的解,即|2x-1|=m有两个不同解,设h(x)=|2x-1|,g(x)=m,画出图象如图所示,由图象知,当0<m<1时,h(x)与g(x)的图象有两个交点, 所以对应方程有两个不同的解,所以所求实数m的取值范围是{m|0<m<1}.。

指数函数一、选择题(共29题，题分合计145分)1.指数函数y =f (x )的反函数的图象过点（2，-1），则此指数函数为A.xy )21(= B.x y 2= C.x y 3= D.xy 10=2.下列f (x )=(1+a x )2xa-⋅是A.奇函数B.偶函数C.非奇非偶函数D.既奇且偶函数3.函数y =2xxee --的反函数是A.奇函数且在(0，+∞)上是减函数B.偶函数且在(0，+∞)上是减函数C.奇函数且在(0，+∞)上是增函数D.偶函数且在(0，+∞)上是增函数4.若函数y =3+2x -1的反函数的图像经过P 点，则P 点坐标是A.（2，5）B.（1，3）C.（5，2）D.（3，1）5.已知0<a <1,b <-1,则函数y=a x+b 的图像必定不经过A.第一象限B.第二象限C.第三象限D.第四象限6.如图，当a ≠0时，函数y ax b =+和y b ax=的图象只可能是7.图中的曲线是指数函数的图象，已知a 的值分别取2，34，103，51，则相应于曲线C 1，C 2，C 3，C 4的a 依次为103,51,2,34.A 51,103,34,2.B34,2,51,103.C2,34,103,51.D8.已知函数xa y )1(22-=是定义域上的减函数，则字母a 的取值范围是A.0＜a ＜1B.21<<a C.－1＜a ＜1 D.－1＜a ＜09.已知三个数M =0.32－0.32，P =0.32－3.2，Q =3.2－0.32，则它们的大小顺序是A.M ＜P ＜QB.Q ＜M ＜PC.P ＜Q ＜MD.P ＜M ＜Q10.如果a ，b ，c 都是小于1的正数，且x ∈(－∞，0)，a x ＜b x ＜c x，则A.a ＜b ＜cB.c ＜a ＜bC.b ＜c ＜aD.c ＜b ＜a11.已知f (x )是偶函数，且x >0时，xx f 10)(=时，则x <0时，f (x )等于 A.10x B.10-x C.-10x D.-10-x12.若指数函数xa y =在[－1,1]上的最大值与最小值的差是1，则底数a 等于 A.251+B.251+- C. 251±D.215±13.下列函数中，值域是(0，+∞)的是A.y =132+-x x B.y =2x +3 x ∈(0，+∞)C.y =x 2+x +1D.y =x3114.当x ∈[0，+∞]时，下列函数中不是增函数的是A.y =x +a 2x -3B.y =2xC.y =2x 2+x +1D.y =｜3- x ｜15.已知p>q >1,0<a <1,则下列各式中正确的是A.a 0>a qB.p a >q aC.a -p <a -qD.p -a >q -a16.若-1<x <0，那么下列各不等式成立的是A.2-x <2x <0.2xB.2x <0.2x <2-xC.0.2x <2-x <2xD.2x <2-x <0.2x17.函数y=(a 2-1)-x与它的反函数在（0，+∞）上都是增函数，则a 的取值范围是A.1<｜a ｜<2B. ｜a ｜<2且｜a ｜≠1C.｜a ｜>2D. ｜a ｜>118.函数f （x ）=(a 2-1)x在R 上是减函数，则a 的取值范围是A.1>a B.2<a C.a<2 D.1<2<a19.一批设备价值a 万元，由于使用磨损，每年比上一年价值降低b%，则n 年后这批设备的价值为A.na(1-b%)B.a(1-nb%)C.a [(1-(b%))]nD.a(1-b%)n20.如果01<<a 且x x 121>>,则下列不等式中正确的是A.x x aa12< B.a a x x 12< C.a a x x12> D.ax x a12>21.下列四个命题中,真命题的是A.y =2x +1和22κ=y 都是指数函数 B.指数函数y =a x的最小值是0C.对任意的R ∈x ,都有3x >2xD.函数y =a x 与xa y )1(=的图象关于y 轴对称 22.要得到函数xy 212-=的图象，只需将指数函数xy ⎪⎭⎫ ⎝⎛=41的图象 A.向左平行移动1个单位 B.向右平行移动1个单位C.向左平行移动21个单位 D.向右平行移动21个单位23.某种细菌在培养过程中，每20分钟分裂一次（一个分裂为2个），经过3个小时，这种细菌由1个可繁殖成A.511个B.512个C.1023个D.1024个24.函数y =2x与y =x 2的图象的交点个数是A.0个B.1个C.2个D.3个25.设指数函数f (x ) = a x(a ＞0，a ≠1)，则下列等式中不正确的是A. f (x +y )=f (x )·f (y))()(.B y f x f y x f =-）（)()]([)(.C Q ∈=n x f nx f n)()]([·)]([)(.D *N ∈=n y f x f xy f nn n26.若函数xa y )1(2-=在),(+∞-∞上为减函数，则a 满足A.1<a B.21<<aC.21<<aD.21<<a27.已知镭经过100年剩留原头质量的95.76%,设质量为1的镭经过x 年后的剩留量为y ,则x , y 之间的函数关系是A.1009576.0x y = B.xy 1009576.0= C.xy )1009576.0(= D.1000424.01x y -=28.四个函数221221xy y y x y x x==⎪⎭⎫ ⎝⎛==，，，A.定义域都是RB.图象都不在x 轴下方C.在(0，+∞)上都是增函数D.图象都过点(0，1)29.函数f(x )的图像与函数g (x )=(21)x的图像关于直线y =x 对称，则f (2x -x 2)的单调减区间为A.（0，1）B.[1，+∞）C.（-∞，1］D.[1，2）二、填空题(共18题，题分合计71分)1.函数y =3232x-的单调递减区间是 .2.将三个数317.02.032,3.1,5.1⎪⎭⎫ ⎝⎛-按从小到大的顺序排列_________________________.3.当a ＞0且a ≠1时，函数f (x )=ax －2－3必过定点 .4.函数y =3x-21的定义域是 ，值域是 .5.函数y =axx 22-(0＜a ＜1)的定义域是 ，单调递增区间是 .6.若a 23<a2,则a 的取值范围是 .7.函数y =(31)1822+--x x(-31≤≤x )的值域是 _____ .8.直线x=a (a >0)与函数y =(31)x ,y =(21)x ,y =2x ,y =10x的图像依次交于A 、B 、C 、D 四点，则这四点从上到下的排列次序是 .9.若f (52x -1)=x -2,则f (125)= .10.已知f (x )=2x ,g (x )是一次函数，记F （x ）=f [g (x )],并且点（2，41）既在函数F （x ）的图像上，又在F -1（x ）的图像上，则F （x ）的解析式为 .11.函数2131xy -⎪⎭⎫ ⎝⎛=的定义域是 ， 值域是 .12.若函数m y x +=+15的图象不经过第二象限，则m 的取值范围是_________.13.已知－1<a <0，则三个数331,,3a a a由小到大的顺序是_______________.14.已知函数f (x )的定义域是（1，2），则函数f (2x)的定义域是 .15.若点⎪⎭⎫ ⎝⎛41,2既在函数bax y +=2的图象上， 又在它的反函数的图象上，则a =b = .16.已知函数f (x )的图象关于y 轴对称，函数g (x )的图象关于原点对称，且f (x )+ g (x )=10x则f (x )= g(x )= ______ .17.函数y =m 2x+2m x-1(m >0且m ≠1)，在区间[-1，1]上的最大值是14，则m 的值是 . 18.满足()22xxxx>的正数x 的取值范围是 .三、解答题(共40题，题分合计440分)1.求函数y x =-311的定义域及值域.2.求函数y x x =≠-3212()的反函数.3.0<a <1,解关于x 的不等式a1322+-x x >a522-+x x .4.若函数y =4x-3·2x+3的值域为[1，7]，试确定x 的取值范围.5.讨论函数y x x =⎛⎝ ⎫⎭⎪-+12223的增减性.6.解方程：(1)4225.04=-+x x(2)273.291=---xx(3)24322+-=x x7.说明指数函数xy 3=的图象经过怎样的变换，可以得到函数2311+⎪⎭⎫ ⎝⎛=+x y 的图象，并画出它们的图象.8.(1)判断函数2)(xxaa x f -+=和2)(xx aa x g --=（其中1,0≠>a a ）的奇偶性;(2)证明指数函数x a y =可以表示为一个偶函数与一个奇函数的和．9.一种产品的成本原来是1万元，近几年来，由于大搞技术创新，降低了能耗，使得该产品的成本每年平均比上一年降低11%，试画出成本随时间变化的函数图象，并从图上求出多少年后，该产品成本降为原来的一半以下．10.设函数|2|2--=x y(1)画出函数的图象；(2)根据图象指出函数的单调区间．11.已知n ∈N *，f (n )= n ·0.9 n，比较f (n )与f (n +1)的大小，并求f (n )的最大值.12.已知气压与高度的指数函数成比例，越往高处气压越低，以至接近于0。