2012~2015年武警部队院校招生统考士兵本科及士官高等职业技术教育《数学》真题及详解【圣才出品】

武警士兵考军校军考模拟题：数学部分（六）武警士兵考军校军考模拟题：数学部分（六）关键词：武警考军校军考模拟题京忠教育军考数学武警考试资料x2y231（2021-21）（12分）已知椭圆C:2?2?1(a?b?0)的离心率是，直线l:y?x?2ab3与原点为圆心，以椭圆C的短半轴长为半径的圆相切. （1）求椭圆C的方程；（2）设椭圆C的左焦点为F1，右焦点F2，直线l1过点F1且垂直于椭圆的长轴，动直线l2垂直于l1于点P，线段PF2的垂直平分线交l2于点M，求点M的轨迹方程.x2y2??1一个焦点的最短弦长为 2（2021-14）过椭圆43x2y2??1，3（2021-7）已知椭圆E的方程为左焦点为F1，如果椭圆E上的一点P到F1的259距离为2，M是线段PF1的中点，O为坐标原点，则OM= （） A.4 B.2 C.223 D.8 24（2021-12）以双曲线x?4y?4的中心为顶点，右焦点为焦点的抛物线方程是 5（2021-14）抛物线的顶点坐标在坐标原点，焦点是椭圆x?2y?8的一个焦点，则此抛物线的焦点到准线的距离为6（2021-13）顶点在原点，准线方程是x=2的抛物线的方程是7（2021-20）（11分）已知双曲线16x?9y?144，F1,F2是两个焦点，点P在双曲线上，且满足PF1PF2的值. 1?PF2?32，求?F2222x2y2?1过点(?32,2)，则该双曲线的焦点为 8（2021-15）若双曲线2?a49（2021-22）（13分）双曲线C的中心在坐标原点，顶点为A(0,2)，A点关于一条渐近线的对称点为B(2,0)，斜率为2且过点B的直线L交双曲线C与M，N两点. （1）求双曲线C的方程；（2）计算MN的值.10（2021-10）已知以原点为中心的双曲线的一条准线方程为x?5，离心率e?5，则5该曲线的标准方程为（）x2?y2?1 A.4x?y?1 B.422y2?1 C.x?4y?1D.x?4222x2y2x2y2611（2021-8）已知双曲线2?2?1(a?b?0)的离心率是，则椭圆2?2?1的离abab2心率是（） A.1223 B. C. D. 23222x2y212（2021-15）已知抛物线y?8x的准线过双曲线2?2?1(a?0,b?0)的一个焦点，ab且双曲线的离心率为2,则该双曲线的方程为213（2021-22）（12分）抛物线与直线y?4x与直线y?2x?k相交，截得的弦长为35，求k的值.x2y2314（2021-21）（12分）已知椭圆C:2?2?1(a?b?0)的离心率是，直线l:y?x?2ab3与原点为圆心，以椭圆C的短半轴长为半径的圆相切. （1）求椭圆C的方程；（2）设椭圆C的左焦点为F1，右焦点F2，直线l1过点F1且垂直于椭圆的长轴，动直线l2垂直于l1于点P，线段PF2的垂直平分线交l2于点M，求点M的轨迹方程.15（2021-22）（13分）双曲线C的中心在坐标原点，顶点为A(0,2)，A点关于一条渐近线的对称点为B(2,0)，斜率为2且过点B的直线L交双曲线C与M，N两点. （1）求双曲线C的方程；（2）计算MN的值.16（2021-21）14分）已知椭圆C经过点A(1,)，两焦点坐标分别为(?1,0),(1,0). （1）求椭圆C的方程；（2）E，F是椭圆上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值.32x2y25217（2021-22）（13分）已知椭圆2?2?1(a?b?0)点P(a,a)在椭圆上.ab52（1）求椭圆的离心率；（2）设点A为椭圆的左顶点，O为坐标原点，若点Q在椭圆上且满足AQ?AO，求直线OQ的斜率.18（2021-5）百米决赛有6 名运动员A、B、C、D、E、F参赛，每个运动员的速度都不同，则远动员A比运动员F先到终点的比赛结果共（） A.360种 B.240种 C.120种 D.48种19（2021-4）用数字1,2,3,4,5组成没有重复数字的数，则可以组成的六位数的个数为（） A.720 B.240 C.120 D.60020（2021-6）甲、乙、丙三位同学选修课程，从4门课程中，甲选修2门，乙、丙各选修3门，则这三位同学不同的选修方案共有（） A.48种 B.36种 C.96种 D.192种21（2021-8）名士兵拍成一排，其中甲乙两个必须排在一起的不同排法有（） A.720种 B.360种 C.240种 D.120种22（2021-6）如果把4名干部分配到3个中队，每个中队至少要分配一名干部，那么不同的分配方法有（） A.45种 B.36种 C.27种 D.9种23（2021-6）从4名男生和3名女生中选出3人，分别从事三项不同的工作，若这3人中至少有1名女生的选派方法有（） A.108种 B.186种 C.216种 D.270种24（2021-7）在50件产品中有4件次品，从中任意抽取5件，至少有3件事次品的抽法共有（）A.5种B.4140种C.96种D.4186种25（2021-7）我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中，有5架舰载机准备看舰，如果甲，乙二机必须相邻，丙，丁不能相邻，那么不同的着舰方法有（） A.24种 B.18种 C.12种 D.48种 26（2021-11）过(a?b)20的展开式中第4r项与第r+2项的系数相等，则r= 27（2021-12）在(x?18)的展开式中，x5的系数为 2x28（2021-12）在(2x?18)的展开式中，常数项为3xn29（2021-13）已知(1?2n)的展开式中，二项式系数和为64，则它的二项展开式的中间项是30（2021-13）(2x?31（2021-13）(x?3110)的展开式中，常数项是 22x13x)18的展开式中含x15的项的系数为 12x32（2021-14）在(x?)8的展开式中常数项为33（2021-14）(x?110)的展开式中，x4的系数为 2x34（2021-21）（10分）已知8支球队中有3支弱队，以抽签的方式将8支球队分为A，B两组，每组4支，求：（1）3支弱队分在同一组的概率; （2）A组中至少有两支弱队的概率.35（2021-22）（13分）甲、乙、丙三位毕业生，同时应聘一个用人单位，其中甲被选中的概率是231，乙被选中的概率是，丙被选中的概率是，各自是否被选中相互独立. 543（1）求三人都被选中的概率；（2）求只有两人被选中的概率.36（2021-17）（10分）已知一个口袋中有大小、质地相同的8个球，其中有4个红球和4个黑球，现在从中任取4个球. （1）求取出的球的颜色相同的概率；（2）若取出的红球数不少于黑球数，则可获得奖品，求获得奖品的概率.37（2021-20）（10分）甲乙两人各射击一次，击中目标的概率分别是击是否击中目标之间相互独立，每人各次射击是否击中相互独立. （1）求甲射击4次，至少有1次击中目标的概率；23和，假设两人射34（2）求两人射击4次，甲恰好击中目标2次，且乙恰好击中目标3次的概率.38（2021-18）（12分）某项选拔共有四轮考核，每轮设有一个问题，能正确回答问题者进入下一轮考核，否则即被淘汰，已知选手甲能正确回答第一、二、三、四轮问题的概率分别为4321,,,，且各轮问题能否正确回答互不影响. 5555（1）求选手甲进入第四轮才被淘汰的概率；（2）求选手甲至多进入第三轮考核的概率.39（2021-20）（14分）已知在3支不同编号的枪中有2支已经试射校正过，1支未经试射校正，某射手若使用其中校正过的枪，每次射击击中目标的概率为每次射击击中目标的概率为4，若使用没有校正的枪，51，假设没几是否击中之间相互没有影响. 5（1）若该射手用这2支已经校正过的枪各射击一次，求目标被击中的概率；（2）若该射手用这3支枪各射击一次，求目标至多被射中一次的概率.40（2021-16）（10分）战士小张考政治、语文、数学、外语4门课程，各课程考试成绩之间相互独立，其各门课程合格的概率分别为（1）求小张一门都不合格的概率；（2）求小张恰好有三门课程合格的概率.41（2021-20）（10分）袋中有大小相同的6个球，其中有4个红球，2个白球. （1）若任取3个球，求至少有一个白球的概率；（2）若有放回的取球3次，求恰好有1个白球的概率.4231,,,. 5342感谢您的阅读，祝您生活愉快。

考试大纲第一章集合与简易逻辑1.了解集合的意义及其表示方法；了解空集、全集、子集、交集、并集、补集的概念及其表示方法；了解符号属于、不属于、包含、不包含、等于的含义，并能正确运用它们表示元素与集合、集合与集合的关系。

2.了解逻辑连词“或”、“且”、“非”的含义；理解四种命题及其相互关系；掌握充分条件、必要条件与充要条件的意义。

第二章函数1.理解函数的概念，会求一些常见函数的定义域。

2.了解函数的单调性和奇偶性的概念，掌握判断一些简单函数的单调性和奇偶性的方法。

3.了解反函数的概念及互为相反数的函数图像间的关系，会求一些简单函数的反函数。

4.理解正比例函数、反比例函数、一次函数的概念，掌握它们的图像和性质，会求它们的解析式。

5.理解二次函数的概念，掌握它的图像和性质；会求二次函数的解析式及最大值或最小值；能运用二次函数的知识解决有关问题。

6.理解幂函数的概念，掌握幂函数的图像和性质。

7.理解分数指数幂的概念，掌握有理指数幂的运算性质；掌握指数函数的概念、图像和性质。

8.理解对数的概念，掌握对数的运算性质；掌握对数函数的概念、图像和性质。

9.能够运用函数的性质、指数函数和对数函数的性质解决一些简单的实际问题。

第三章数列1.理解数列的概念，了解数列通项公式和递推公式的意义，会根据数列的通项公式写出数列的任意项，会根据数列的递推公式写出数列的前几项。

2.理解等差数列、等差中项的概念，掌握等差数列的通项公式与前n项和的公式，并能解决简单的实际问题。

3.理解等比数列、等比中项的概念，掌握等比数列的通项公式与前n项和的公式，并能解决简单的实际问题。

第四章不等式1.理解不等式的性质及其证明。

2.掌握两个正数的算术平均数不小于几何平均数定理，并会解决一些简单的实际问题。

3.掌握用分析法、综合法和比较法证明简单的不等式。

4.会解一元一次不等式、一元一次不等式组和可化为一元一次不等式组的不等式，会解一元二次不等式，会表示不等式或不等式组的解集。

2012年武警部队院校招生统一考试综合试题物理部分（共60分，45分钟）一、单项选择题：（共20分，每小题4分）1．下列物理量中，属于矢量的是（ ）A ．电流强度B ．速度C ．功率D ．动能2．下列关于惯性的说法中，正确的是（ ）A ．只有物体静止时，才具有惯性B ．只有物体做匀速直线运动时，才具有惯性C ．只有物体运动状态改变时，才具有惯性D ．物体处于任何运动状态时都具有惯性3. 如图1所示，一根轻质弹簧的劲度系数为100N/m ，把弹簧竖直悬挂，重为2N 的物体挂在弹簧的下端保持静止，则弹簧的伸长量为（ ）A ．0.02mB ．50mC ．200mD ．0.2m4．在真空中有两个点电荷，它们之间的静电力为F 。

如果保持它们之间的距离不变，将它们各自所带的电荷量减小到原来的一半，那么它们之间静电力的大小等于（ ）A ．4FB ．2FC ．2FD ．4F5.如图2所示电场中实线表示电场线，一带正电粒子沿虚线轨迹由M 向N 运动，若不计重力，下列关于电场力做功和电势能变化正确的是（ ）A ．电场力做正功，带电粒子的电势能增加B ．电场力做正功，带电粒子的电势能减少C ．电场力做负功，带电粒子的电势能增加D ．电场力做负功，带电粒子的电势能减少 二、填空题（共20分，每小题4分）6.我国成功发射了自行研制的 “神舟七号”宇宙飞船，首次进行了宇航员的太空行走，飞船顺利返回地面，这是我国航天事业的一个新的里程碑。

当飞船在环绕地球的轨道上飞行时，所需的向心力由地球对它的__ _________提供；此时飞船中的航天员处于______ ______（选填“超重”或“失重”）状态。

7．如图3所示，在水平路面上一运动员驾驶摩托车跨越壕沟，壕沟两侧的高度差为0.8m ，水平距离为8 m ，则运动员跨过壕沟的初速度至少为（取g=10m/s 2）8．如图4所示，在光滑水平面上，一质量为m 的小球在绳的拉力作用下做半径为r 的匀速圆周运动，小球运动的线速度为v ，则绳的拉力F 大小为 .9．某汽车的质量为5000kg ，发动机的额定功率为36kW ，在水平公路上匀速行驶时所受阻力为2400N ，则汽车行驶中能达到的最大速图1 图3 图4度为 m/s ；此汽车以额定功率启动，速度达到v =10m/s 时的加速度大小为 . m/s 2。

二〇一五年武警部队院校招生统一考试士兵本科数学真题与详解一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项符合题目要求．1．已知全集为R ，集合{|13}{0246}A x x B =-<=≤，，，，，则A B 等于（ ） A ．{02}， B ．{102}-，， C ．{|02}x x ≤≤ D ．{|12}x x -≤≤ 2．在等比数列{}n a 中，已知31815243⋅⋅=a a a ，则3911=a a （ ）A ．3B ．9C ．27D ．813．设232555322555a b c ===（），（），（），则、、a b c 的大小关系是（ ）A ．>>b c aB ．>>a b cC ．>>c a bD ．>>a c b4．不等式1021x x -+≤的解集是（）A ．11]2（，- B ．11]2[，- C ．112（-，)[，）∞-+∞D ．112（-，][，）∞-+∞5．复数Z 满足12i Z i +=（），则复数Z 在复平面内对应的点在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．一排9个座位坐了3个三口之家，若每家人坐在一起，则不同的坐法种数为（ ）A ．33!⨯B ．333!⨯（）C ．43!（）D ．9! 7．若l 、m 、n 是互不相同的空间直线， α、β是不重合的平面，则下列命题中为真命题的是（ ）A ．若α⊥l ，∥βl ，则β⊥aB ．若β⊥a ，α⊂l ，则β⊥lC ．若⊥l n ，⊥m n ，则∥l mD ．若a β∥，α⊂l ，β⊂n ，则∥l n8． 将边长为a 的正方形ABCD 沿对角线AC 折起，使=BD a ，则三棱锥D -ABC 的体积为（ ）A ．36aB ．312aC 3D 39．过坐标原点且与点1）的距离都等于1的两条直线的夹角为（ ）A ．090B ．045C ．030D ．06010．已知点23A -（，）在抛物线2:2=C y px 的准线上，记C 的焦点为F ，则直线AF 的斜率为（ ）A ．43-B ． 1-C ．34-D ．12-二、填空题：本大题共5小题，每小题5分，共25分． 11．若函数2143（）=-++kx f x kx kx 的定义域为R ，则实数k 的取值范围是_______．12．已知向量a 、b 满足0⋅=a b ，||1||2a b ==，，则|2|a b -= _______．13． 若[]sin 242θθππ∈=，，，则sin θ=_______． 14．在5611（）（）-+-x x 的展开式中，含3x 的项的系数是_______． 15．椭圆2244+=x y 长轴上一个顶点为A ，以A 为直角顶点作一个内接于椭圆的等腰直角三角形，该三角形的面积是_______．三、解答题：本大题共7小题，共75分．解答应写出文字说明、证明过程或演算步骤． 16．(本小题满分10分，（1）和（2）分别为6分和4分)已知函数21（）=-x f x 的反函数为1（）-f x ，4()log (31)=+g x x （1）用定义证明 1（）-f x 在定义域上的单调性； （2）若1f x g x -≤（）（），求x 的取值集合D ． 17．(本小题满分10分，其中（1）和（2）各5分)在ABC △中，内角A B C ，，所对的边分别为a b c ，，，已知sin a c B C -，．（1）求cos A 的值； （2）求cos 26A π-（）的值． 18．(本小题满分10分，其中（1）和（2）分别为4分和6分)已知{}n a 是递增的等差数列，24a a ，是方程2560-+=x x 的根． （1）求{}n a 的通项公式；（2）求数列{}2n na 的前n 项和． 19．(本小题满分10分，（1）和（2）分别为4分和6分)已知向量cos sin cos sin 0a b ααβββα==<<<π（，），（，），． （1）若||2-=a b ，求证：⊥a b ；（2）设01c =（，），若+=a b c ，求α和β的值．20．(本小题满分10分，（1）和（2）分别为4分和6分)骰子（六个面上分别标以数1,2,3,4,5,6）每抛掷一次，各个面上的概率均等．（1）连续抛掷2次，求向上的数之和为6的概率；（2）连续抛掷5次，求向上的数为奇数恰好出现3次的概率．21．(本小题满分12分，（1）和（2）分别为5分和7分)如图，在四棱锥-PDC底面ABCD，P ABCD中，底面ABCD是正方形，侧面⊥PD DC PDC E是PC的中点．=∠=，，90（1）求证：∥PA平面EDB；（2）若⊥PB平面EFD．EF PB于点F，求证⊥22．(本小题满分13分，其中（1）和（2）分别为5分和8分)双曲线C的中心在坐标原点，右焦点为0），渐近线为=y．（1）求双曲线C的标准方程；（2）设直线:1A B两点，则当k为何值时，以AB为直径的圆=+l y kx与双曲线C交于、过原点？〖答案与详解〗一、选择题 1.【答案】A【详解】集合{|13}{0246}A x x B =-<=≤，，，，，则=A B {02}，． 【点评】考查集合的交集运算．（详见《军考突破》中1-1-10） 2.【答案】B【详解】根据等比数列性质，由31815243⋅⋅=a a a ，得5583=a ，83=a ，则329971197811119a a a a a a a a a ====（）． 【点评】考查等比数列的性质．（详见《军考突破》中3-3-4） 3.【答案】D【详解】由25x y =（）为减函数且3255>，得32552255b c =<=（）（），再由250y x x =>（）为增函数且3255>，得22553255a c =>=（）（），所以、、a b c 的大小关系是>>a c b ．另法：将232555322555a b c ===（），（），（），同时5次方，得5253523928245255125525a b c ======（），（），（），显然有55545208125125125a cb =>=>=， 则、、a bc 的大小关系是>>a c b ． 【点评】考查函数的单调性．（详见《军考突破》中2-5-5） 4.【答案】A【详解】不等式1021x x -+≤的零点为112、-，用根轴法（零点分段法）如图：解集是11]2（，-． 【点评】考查分式不等式解法，涉及序轴标根法．（详见《军考突破》中6-3-1） 5.【答案】A【详解】复数Z 满足12i Z i +=（），即2222212222111121i i i i i i Z i i i i i --+=====+++--（）（）（），则复数Z 对应点为11（，），是在复平面内的一象限．【点评】考查复数的运算．（详见《军考突破》中9-2-3）6.【答案】C【详解】第一步，分别将每一家捆绑，有33!（）种方法；第二步，再将三个全排列，有3!种方法．所以每家人坐在一起，则不同的做法为43!（）． 【点评】考查排列问题的基本计算方法—捆绑法．（（详见《军考突破》中7-1-4）中）7.【答案】A【详解】根据两平面垂直的判定定理，由α⊥l ，∥βl ，能够推出β⊥a ．【点评】考查平面与平面垂直的判定．（详见《军考突破》中10-2-3）． 8.【答案】D【详解】由题意，如图在三棱锥-D ABC 中，側棱长===DA DC BD a，====OA OB OC OD ，从而可知高为OD ,底面积212∆=ABC S a ，则三棱锥D-ABC 的体积为231132=⨯=V a ．【点评】考查三棱锥的体积的求法．（详见《军考突破》中10-4-2）9．【答案】D【详解】如下图,过坐标原点且与点1的距离都等于1的两条直线的夹角为00223060∠=∠=⨯=AOB AOP ．【点评】考查从圆外一点出发的圆的两条切线的夹角．（详见《军考突破》中11-2-3） 10．【答案】C 【详解】由题意，抛物线2:2=C y px 的准线方程为：2=-x ，所以C 的焦点为20F （，），直线AF 的斜率为033224k -==---（）．【点评】考查抛物线的准线方程与焦点坐标，以及过两点的斜率公式．（详见《军考突破》中12-3-3） 二、填空题 11．【答案】304k <≤ 【详解】∵函数2143（）=-++kx f x kx kx 的定义域为R ，∴0=k 或204120k k k ≠⎧⎨∆=-<⎩（），∴304k <≤． 【点评】考查函数的定义域的求法．（详见《军考突破》中2-5-1） 12．【答案】【详解】∵向量a 、b 满足0⋅=a b ，||1,||2==a b ，∴22|2|4422-=+-⋅=a b a b a b ． 【点评】考查向量模的求法．（详见《军考突破》中5-1-6） 13．【答案】34【详解】由[]sin 242θθππ∈=，，，∴sin cos sin cos θθθθ+=-=∴1113sin 2224θ====（（（． 【点评】考查三角恒等式的应用变形．（详见《军考突破》中4-2-2）14．【答案】30-【详解】展开式中含有3x 的项为：333333356102030（-）（-）+=--=-C x C x x x x ，∴含3x 的项的系数为30-．【点评】考查二项展开式的通项．（详见《军考突破》中7-2-2） 15．【答案】1625【详解】如图，设等腰直角三角形∆AMN 的底边20MN t t =>（），则椭圆2244+=x y 上点N 的坐标为2t t -（，），从而有22244t t -+=（），解得45=t ，所以∆AMN 的面积是21625=t ．【点评】考查椭圆的标准方程及顶点坐标，以及三角形的面积公式．（详见《军考突破》中12-1-4） 三、解答题 16．【详解】（1）函数21（）=-x f x 的值域为1+∞（-，）， 由21=-x y ，解得2log 1x y =+（），∴12log 11f x x x -=+>-（）（）（）． 任取121-<<x x ，111122122221()log 1log 1log 1x f x f x x x x --+-=+-+=+（）（）（）． ∵121-<<x x∴12011<+<+x x ， ∴121011+<<+x x ． ∴1221log 01+<+x x ，可得1112f x f x --<（）（）， 故1（）-f x 在定义域1+∞（-，）上为单调增函数． （2）∵1f x g x -≤（）（），即2log 1x +（）4log 31x +≤（），即2log 1x +（）4log 31x +≤（） ∴210310131x x x x +>⎧⎪+>⎨⎪++⎩≤（），解之得01x ≤≤，∴x 的取值集合为[01]，=D ．【点评】考查反函数和函数的单调性及对数不等的解法．（详见《军考突破》中2-5-5，2-5-7，6-3-4） 17．【详解】（1）在ABC △中，由正弦定理sin sin =b cB C，及已知条件sin =B C可得=b又∵,-=a c ∴2=a c由余弦定理222222cos 2+-===b c a A bc ． （2）在ABC △中，由（1）知cos =A，可得sin =A又221cos 22cos 114=-=-=-A A ．sin 22sin cos 2===A A A ∴cos 2cos2cos sin 2sin 666A A A πππ-=⋅+⋅（）1142=-=【点评】考查正弦定理与余弦定理．（详见《军考突破》中4-5-1、4-5-2） 18．【详解】 （1）方程2560-+=x x 的两根为1223x x ==， 由题意得2423a a ==，设等差数列{}n a 的公差为d ，则42122-==a a d ∴211222122n a a n d n n =+-=+-⨯=+（）（）． （2）设数列{}2nn a 的前n 项和为n S ，由（1）知1222++=n n n a n ． 23134122222①+++=++++n n n n n S 34121341222222②++++=++++n n n n n S ①-②得3412131112242222（）+++=++++-n n n n S 34123111242222（）+++=++++-n n n 34123111242222（）+++=++++-n n n 34123111242222（）+++=++++-n n n ∴1422++=-n n n S ． 【点评】考查由n S 求n a 和裂项相消法求数列的前n 项的和．（详见《军考突破》中3-4-1、3-4-7） 19．【详解】（1）由题意2||2-=a b ，即22（）-=a b∴22-22⋅+=a a b b∵向量cos sin a αα=（，），cos sin b ββ=（，）0βα<<<π，．∴2222=||||11=2++=+a b a b ∴0⋅=a b ，∴⊥a b ．（2）∵cos sin a b αα+=+（，）cos sin ββ=（，)cos cos sin sin αβαβ++=（，）01)（，∴cos cos 0sin sin 1αβαβ+=⎧⎨+=⎩∴cos cos sin sin 1αβαβ=-⎧⎨+=⎩∵0βα<<<π ∴1sin sin 2αβαβ=π-⎧⎪⎨==⎪⎩∴566αβππ==，． 【点评】考查向量平行及向量的数量积的运算．（详见《军考突破》中5-1-6、5-1-8）20．【详解】（1）设A 表示事件“抛掷2次，求向上的数之和为6”向上的数之和为6的结果有(1，5)、(2，4)、(3，3)、(4，2)、(5，1)5种 连续抛掷2次总的结果共有6×6=36种，∴5A 36（）=P ． （2）设B 表示事件“抛掷5次，求向上的数为奇数恰好出现3次”． 每次抛掷向上的数为奇数和偶数的概率都是12可看作5次独立重复试验中，事件“向上的数为奇数” 恰好出现3次． 则3325511105B 3C 1223216P P ==⨯⨯-==（）（）（）（）． ∴连续抛掷5次，向上的数为奇数恰好出现3次的概率为516． 【点评】考查独立重复试验的概率．（详见《军考突破》中8-1-6） 21．【详解】（1）在正方形ABCD 中，连接AC 交BD 于O ，连接EO. 因为ABCD 是正方形，所以O 为AC 的中点. 又因为E 为PC 的中点，所以EO//PA.∵⊄PA 平面EDB ，⊂EO 平面EDB ，∴∥PA 平面EDB ．（2）∵平面⊥PDC 平面ABCD ，且平面PDC 平面=ABCD CD ， 在平面ABCD 中，⊥BC DC∴⊥BC 平面PDC ， 又∵⊂DE 平面PDC ，∴⊥BC DE又∵=PD DC ，E 是PC 的中点， ∴⊥PC DE在平面PBC 中，，=BC PC C∴⊥DE 平面PBC ， ∴⊥PB DE又∵⊥EF PB ，且在平面EFD 中，，=DE EF E∴⊥PB 平面EFD ．【点评】考查平面与平面平行和直线与平面垂直的判定．（详见《军考突破》中10-2-2、10-2-3） 22．【详解】（1）由题意可知bc a==，∵222+=a b c∴22113a b ==，，∴双曲线的标准方程为2231-=x y ． （2）由22131=+⎧⎨-=⎩y kx x y得223220k x kx ---=（）由230-≠k 且0∆>，得<k ≠k ，设1122A x y B x y （，），（，） ∵以AB 为直径的圆过原点， ∴⊥OA OB ，∴0⋅=OA OB ，即12120+=x x y y 又∵1212222233k x x x x k k +=-=--，∴2121212121111y y kx k x k x x k x x =++=+++=（）（）（）∴22103+=-k ，解得1=±k ．故当1=±k 时，以AB 为直径的圆过原点．【点评】考查双曲线的标准方程和直线与双曲线相交的问题．（详见《军考突破》中12-2-4、12-4-5）。

军队院校招生文化科目统考士兵高中《数学》考前点题卷一[单选题]1.设集合U＝{1，2，3，4），M＝{1，2，3}，N＝{2，3（江南博哥），4}，则C U（M∩N）＝()。

A.{1，2}B.{2，3}C.{2，4}D.{1，4}参考答案：D参考解析：M∩N＝{2，3}，C U（M∩N）＝{1，4}.[单选题]2.已知下列命题：（1）如果a，b是两条直线，且a∥b，那么a平行于经过b的任何平面。

（2）如果直线“和平面a满足a∥α，那么a与α内的任何直线平行。

（3）如果直线a，b和平面a满足a∥a，b∥a，那么a∥b.（4）如果直线a，b和平面α满足a／／b，a／／α，b?α，那么b／／α。

其中正确的命题的个数为()。

A.0B.1C.2D.3参考答案：B参考解析：对于（1），有可能a在经过b的某个平面内.对于（2）a与α内的某些直线异面.对于（3），直线a，b平行，相交，异面都有可能；（4）是正确的.[单选题]3.已知a＝1og30.8，b＝1og25，c＝0.32，则()。

A.a＜b＜cB.b＜a＜cC.a＜c＜bD.c＜b＜a参考答案：C参考解析：a＝1og30.8＜0，b＝1og25＞1og22＝1，c＝0.32∈（0，1）.[单选题]4.已知平面向量a＝（3，－1），b＝（x，3），a⊥b，则x的值为()。

A.－3B.－1C.1D.3参考答案：C参考解析：.[单选题]5.已知双曲线的渐近线相互垂直，则双曲线的离心率为()。

A.B.C.D.参考答案：A参考解析：（－）＝－1，所以a2＝b2，所以a：b：c＝1：1：，所以e＝＝.[单选题]6.已知正项数列{a n}的各项均不相等，且，则下列各不等式中一定成立的是()。

A.B.C.D.参考答案：B参考解析：由条件知{a n}为等差数列，[单选题]7.若直线x－2y＋1＝0过圆x2＋y2－ax＋6y－1＝0的圆心，则实数a 的值为()。

A.10B.14C.－10D.－14参考答案：D参考解析：由于圆心坐标为（，－3），所以a＝－14.[单选题]8.椭圆上的一点P到左焦点的距离为1，则它到相对应准线的距离为()。

2012年武警部队院校招生统考士兵本科及士官高等职业技术教育《数学》真题及详解参考公式：一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的，把该项的代号写在题后的括号内．1．若复数（i为虚数单位）是纯虚数，则实数a＝（）．A．±1B．－1C．0D．1【答案】A【解析】，由纯虚数的定义可得2．在△ABC中，a，b，c分别是角A，B，C的对边，且，则△ABC一定是（）．A．等边三角形B．直角三角形C．等腰直角三角形D．无法确定【答案】B【解析】根据余弦的倍角公式得故该三角形为直角三角形．3．设，则m、n、p的大小关系是（）．A．n＞m＞pB．m＞p＞nC．m＞n＞pD．p＞m＞n【答案】D【解析】因为，所以函数为单调递减函数，又因为，则．4．在等差数列{a n}中，，则数列{a n}的前9项之和S9等于（）．A．66B．99C．144D．297【答案】B【解析】因为a n为等差数列，则也为等差数列，则所以数列{a n}的前9项之和S9为5．已知集合，则P的子集共有（）．A．2个B．4个C．6个D．8个【答案】B【解析】集合的交集取公共部分，即故含有2个元素的子集个数为个．6．若函数在[2，＋∞）上的最小值为－2，则实数m的值为（）．A．1B．－1C．－2D．－3【答案】C【解析】此函数的对称轴为，则函数在[2，＋∞）上单调递增，当x＝2时，取最小值，即7．在50件产品中有4件次品，从中任意抽取5件，至少有3件是次品的抽法共有（）．A．5种B．4140种C．96种D．4186种【答案】D【解析】当5件产品中有3件次品时，则有种抽法；当5件产品中有4件次品时，则有种抽法，所以共有种抽法．8．已知双曲线的离心率是，则椭圆的离心率是（）．【答案】C【解析】由双曲线的离心率公式得则椭圆的离心率为二、填空题：本大题共7小题，每小题5分，共35分，把答案填在题中横线上．9．已知，则＝________．【答案】1【解析】依题意有则10．＝________．【答案】【解析】11．已知向量＝________．【答案】【解析】，则。

201*年武警部队院校招生统一考数学试题201*年武警部队院校招生统一考数学试题密：号封考线内不要答题：名姓201*年武警部队院校招生统一考试数学试题（本试卷共三大题，总分值150分，考试时间150分钟）一、选择题：本大题共8小题，每题5分，共40分。

在每题给出的四个选项中，只有一个符合题目要求的，把该项的写在题后的括号内。

1．已知集合M＝x|2x2,xR，N＝x|x1,xR，则M∩N等于（）A.（1，2）B．（-2，1）C．D．（-∞，2）2．sin585°的值为（）A.222B.C.232D.323．设Sn是等差数列an的前n项和，已知a23，a611，则S7等于（）A.13B.35C.49D.634．抛物线x24y的焦点坐标是（）A.（0,1）B.（1,0）C.（0，-1）D.（-1,0）5．a,b,cR，以下命题正确的选项是（）A.aba2b2B.abacbcC.abacbcD.ab11ab6．已知向量a(1,2),b(x,4)，若a∥b，则ab等于（）A.－10B.－6C.0D.67．双曲线y29x2161的准线方程是（）A169916x5Bx5Cy5Dy5．高三（一）班学生要安排毕业晚会的4个音乐节目，2个舞蹈节目和1个曲艺节目的演第1页（共2页）出挨次，要求两个舞蹈节目不连排，则不同排法的种数是()A．1800B．3600C．4320D．5040二、填空题：本大题共7小题，每题5分，共35分，把答案填在题中横线上。

9．sin33cos27cos33sin27.10．过点A（2，3）且平行于直线x2y30的直线方程为____________.11．甲、乙两个人投篮，他们投进蓝的概率分别为25，12现甲、乙两人各投篮1次则两个人都投进的概率是12．在长方体ABCDA1B1C1D1中，已知AB3，AA1=1，则异面直线BA1与CC1所成的角为_____________.13．i是虚数单位，5i2i=D1C1A1B1 14.函数f(x)x1x1的定义域是DC15．正方体的内切球与外接球的半径之比为AB三、解答题：本大题共6小题，共75分，解同意写出文字说明，证明过程或演算步骤。

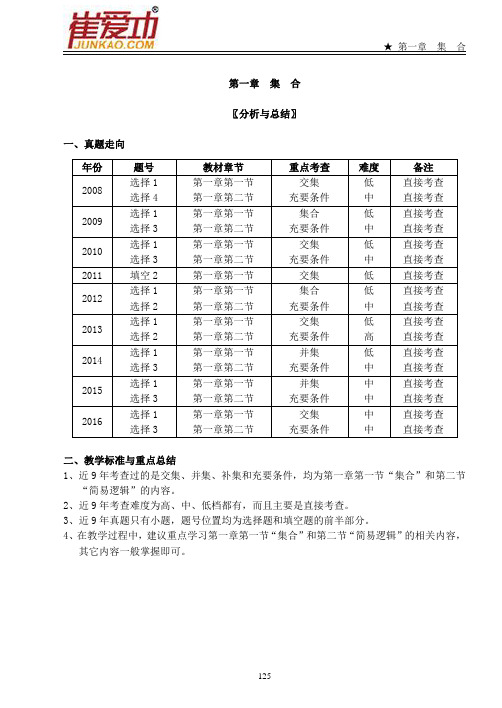
第一章集合〖分析与总结〗一、真题走向二、教学标准与重点总结1、近9年考查过的是交集、并集、补集和充要条件，均为第一章第一节“集合”和第二节“简易逻辑”的内容。

2、近9年考查难度为高、中、低档都有，而且主要是直接考查。

3、近9年真题只有小题，题号位置均为选择题和填空题的前半部分。

4、在教学过程中，建议重点学习第一章第一节“集合”和第二节“简易逻辑”的相关内容，其它内容一般掌握即可。

〖军考真题〗1．（2008军考真题选择1）已知集合{|10R}P x x x x =-∈≥（），，1{|0R}1Q x x x =>∈-，，则P Q 等于（ ）A ．∅B ．{|1R}x x x ∈≥，C ．{|1R}x x x >∈，D ．{|10R}x x x x <∈≥或，2．（2008军考真题选择4）设ππ22αβ∈-，（，），那么“αβ<”是“tan tan αβ<”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件3．（2009军考真题选择1）设R 为实数集，若A 为全体正实数的集合，{2112}B =--，，，，则下列结论正确的是（ ） A ．{21}A B =-- ，B ．0A B =-∞R （）（，）ðC ．0A B =+∞ （，）D ．{21}A B =--R （），ð 4．（2009军考真题选择3）条件||p x x =：，条件2q x x -≥：，则p 是q 的（ ） A ．充分不必要条件 B ．必要不充分C ．充要条件D ．既不充分也不必要条件5．（2010军考真题选择1）若集合{|23}A x x =-≤≤，{|1Q x x =<-或4}x >，则A B = （ ）A ．{|3x x ≤或4}x >B ．{|13}x x -<≤C ．{|34}x x <≤D ．{|21}x x -<-≤ 6．（2010军考真题选择3）0a <是方程2210ax x ++=至少有一个负根的（ ） A ．必要不充分条件 B ．充分不必要条件 C ．充分必要条件 D ．既不充分也不必要条件 7．（2011军考真题填空2）若{R |||3}{R |21}x A x x B x =∈<=∈>，，则A B = ． 8．（2012军考真题选择1）设全集5={|0}x U x ∈Z ≤≤，集合{13}A =，，{|B y y x ==，}x A ∈，则集合U U AB = （）（）痧（ ） A ．{0245}，，， B ．{045}，，C ．{245}，，D ．{45}，9．（2012军考真题选择2）设a 、b 都是实数，则“22lg 1lg 1a b +<+（）（）”是“a b <”的（ ）A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件10．（2013军考真题选择1）已知集合{|10R}P x x x x =-∈≥（），，1{|0R}1Q x x x =>∈-，， 则P Q 等于（ ）A ．∅B ．{|1R}x x x ∈≥，C ．{|1R}x x x >∈，D ．{|1x x ≥或0R}x x <∈， 11．（2013军考真题选择2）已知0A B C ≠ ，则“A 、B 、C 三者符号相同”是“方程22Ax By C +=表示椭圆”的（ ）A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件12．（2014军考真题选择1）已知集合{101}P =-，，，{|}Q x x ab a b P a b ==∈≠，，且，则 P Q 等于（ ）A ．{01}，B ．{10}-，C ．{101}-，，D ．{11}-，13．（2014军考真题选择3）“12x >且22x >”是“124x x +>且124x x >”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要14．（2015军考真题选择1）设集合2{5log 3}P a =+，（），集合{}Q a b =，，若{2}P Q = ，则P Q = （ ）A ．{124}，，B ．{125}，，C ．{123}，，D ．{235}，，15．（2015军考真题选择3）“k h =”是“直线2y x =+与圆222x k y h -+-=（）（）相切”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件16．（2016军考真题选择1）已知集合1{R |||2}{R |25}2x A x x B x =∈<=∈<< ，，则A B = （ ）A ．{R |22}x x ∈-<<B ．{R |12}x x ∈-<<C ．2{R |2log 5}x x ∈-<<D ．2{R |1log 5}x x ∈-<< 17．（2016军考真题选择3）已知集合{1}{123}A a B ==，，，，，则“3a =”是“A B ⊆”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件〖真题详解〗1．【答案】C【详解】由10x x -≥（），得1x ≥或0x ≤；由101x >-，得1x >，即Q P ⊆， 得{|1R}P Q Q x x x ==>∈ ，．【点评】本题考查解不等式和集合的运算（详见《军考突破》中1-1-10、6-3-1）． 2．【答案】C 【详解】函数tan y x =在区间ππ22-（，）上是增函数，αβ<tan tan αβ⇔<． 【点评】本题考查的是正切函数的单调性以及充要条件的判定（详见《军考突破》中4-3-3、1-2-3）． 3．【答案】D【详解】∵{|0}A x x =>，0{|}A x x =R ≤ð，∴{21}A B =--R （），I ð． 【点评】本题考查集合的交、并、补运算．（详见《军考突破》中1-1-10、1-1-11、1-1-12） 4．【答案】A 【详解】p ：||0x x x =⇔≥；q ：20x x x -⇔≥≥或1x -≤，∴p q ⇒，q /⇒p ． 【点评】本题涉及不等式的化简，重点考查充要条件的判定．（详见《军考突破》中1-2-3） 5．【答案】D【详解】{|21}A B x x =-<- ≤．034211-2-4-3-【点评】本题考查集合的交集运算．（详见《军考突破》中1-1-10） 6．【答案】B【详解】0a <时，用根与系数的关系定理可知方程2210ax x ++=有一个负根，一个正根．0a =时，方程2210ax x ++=有一个负根12x =-．这就表明0a <是方程2210ax x ++=有一个负根的充分非必要条件．【点评】要注意考虑特殊情况，这是做选择题的首选方法，本题也可分析出方程至少有一个负根的充要条件，但是作为选择题不是最好的方法．（详见《军考突破》中2-2-3） 7．【答案】{|03}x x <<【详解】{|33}{|0}A x x B x x =-<<=>，，所以{|03}A B x x =<< ．【点评】本题涉及绝对值不等式、指数不等式的解法，重点考查集合的交集运算（详见《军考突破》中1-1-10、6-3-1、6-3-4）． 8．【答案】D【详解】{012345}{13}{02}U A B ，，，，，，，，，=== ∴{0245}{1345}U U A B ，，，，，，，==痧∴{45}U U AB （）（），=痧． 【点评】本题考查集合的交、补运算．（详见《军考突破》中1-1-10、1-1-12） 9．【答案】D【详解】先化简2222111111||||ga gb a b a b +<+⇔+<+⇔<（）（） 又||||a b <不能推出a b <，a b <不能推出||||a b <．【点评】本题涉及对数的运算，重点考查充要条件．（详见《军考突破》中1-2-3） 10．【答案】C【详解】{|1P x x =≥或0R}x x ∈≤，，{|1R}Q x x x =>∈，，则{|1R }P Q x x x =>∈ ，． 【点评】考查集合的交集运算，涉及一元二次不等式以及分式不等式解法（详见《军考突破》中1-1-10、6-3-1）． 11．【答案】C 【详解】“方程22Ax By C +=表示椭圆”⇔“A 、B 、C 三者符号相同，且A B ≠”，所以“A 、B 、C 三者符号相同”⇐“方程22Ax By C +=表示椭圆”，而“A 、B 、C 三者符号相同”/⇒“方程22Ax By C +=表示椭圆”， 故“A 、B 、C 三者符号相同”是“方程22Ax By C +=表示椭圆”的必要不充分条件． 【点评】考查命题充分性必要性的判定，涉及椭圆的标准方程（详见《军考突破》中1-2-3、8-1-4）． 12．【答案】C【详解】{10}Q =-，，则{101}P Q =- ，，． 【点评】考查集合的并集运算（详见《军考突破》中1-1-11）．13．【答案】A【详解】充分性显然成立，若15x =，212x =，满足124x x +>且124x x >，但不满足12x >且22x >，故必要性不成立．【点评】考查命题的充分性和必要性的判断（详见《军考突破》中1-2-3）． 14．【答案】B【详解】据题设2log 321a a +=⇔=（）∴2b = {52}{12}P Q ==，，，，∴{125}P Q = ，，【点评】考查集合的并集运算（详见《军考突破》中1-1-11）．15．【答案】A【详解】直线2y x =+与圆222x k y h -+-=（）（）相切⇔圆心到直线的距离等于半径，即|2|2k h =-+=所以k h =或40k h -+=．【点评】考查命题的充分性和必要性的判断（详见《军考突破》中1-2-3）． 16．【答案】B【详解】∵{R |||2}={22}A x x x x =∈<-<< ，1{R |25}2x B x =∈<< 2log 51{222}x x -=<< 2{1log 5}x x =-<<，∴A B = {R |12}x x ∈-<< ．【点评】本题考查集合的交集运算．（详见《军考突破》中1-1-10） 17．【答案】A【详解】∵3a A B =⇒⊆，但3/A B a ⊆⇒=，所以“3a =”是“A B ⊆”的充分不必要条件．【点评】考查命题的充分性和必要性的判断（详见《军考突破》中1-2-3）．。

2014年武警部队院校招生统考士兵本科及士官高等职业技术教育《数学》真题及详解参考公式：一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项符合题目要求．1．设集合，则S∩T＝（）．A．[－4，＋∞）B．（－2，＋∞）C．（－2，1]D．[－4，1]【答案】C【解析】交集取公共部分，故．2．在复平面内，复数的对应点位于（）．A．第一象限B．第二象限C．第三象限D．第四象限【答案】B【解析】分子分母同乘（2＋i）得对应的点为（－1，2），位于第二象限．3．已知f（x）是奇函数，g（x）是偶函数，且，则g(1)＝（）．A．1B．2C．3D．4【答案】C【解析】根据奇偶函数的性质有，则联立已知条件解得4．记等比数列｛a n｝的前n项积为，若，则＝（）．A．256B．1C．81D．16【答案】D【解析】设等比数列，则所以前8项积为5．下列选项中，使不等式成立的x的取值范围是（）．A．（－1，0）B．（－∞，－1）C．（0，1）D．（1，＋∞）【答案】B【解析】由得；由得，取两者交集得．6．在锐角△ABC中，角A、B所对的边长分别为a、b，若，则角A 等于（）．【答案】C【解析】依题意有，由三角形的正弦定理，得因为是锐角△ABC，所以角A等于．7．我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中，有5架舰载机准备着舰，如果甲、乙二机必须相邻着舰，而丙、丁不能相邻着舰，那么不同的着舰方法有（）．A．24种B．18种C．12种D．48种【答案】A【解析】先将甲、乙全排列，有种；再将其捆绑在一起，看成一个，和戊全排列，有种；由于丙、丁不能相邻，因此将它们插空，有种，故共有8．两个圆锥有等长的母线，而它们的侧面展开图恰好拼成一个圆，若它们的侧面积之比为1:2，则它们的高之比为（）．【答案】A【解析】两圆锥侧面积分别为由得：；依题意有，即所以两个圆锥高之比为9．平面α∥平面β的一个充分条件是（）．A．存在一条直线a，a∥α，a∥βB．存在一条直线a，a⊂α，a∥βC．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥αD．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α【答案】D【解析】A项，当直线a平行于两平面的交线时，有a∥α，a∥β；B项，此时若两平面相交，只要使直线a平行于它们的交线即可；C项，此时若两平面相交，只要使直线a和b 同时平行于它们的交线即可；D项，因为两直线a，b异面，由a⊂α，b⊂β，a∥β，b∥α可推出a∥β．10．直线3x＋y－3＝0与6x＋my＋1＝0平行，则它们之间的距离为（）．A．4B．C．D．【答案】B【解析】两直线平行，可得m＝2，由两平行直线间的距离公式可得二、填空题：本大题共5小题，每小题5分．共25分．11．设f（x）是以2为周期的函数，且当时，，则f（－1）＝________．【答案】－1【解析】由题意知，．12．设等比数列{a n}的前n项和为S n，若S6:S3＝1:2，则S9:S3＝________．。

【数学答案与详解】一．单项选择（每小题4分，共36分）1．D【详解】在每个集合包含a 、b 时，c 、d 、e 三个元素可任选0、1、2、3个，于是问题等价于集合{c 、d 、e }的子集的个数，即共有23=8个；故选D 。

2．C【详解】A ．f （x ）=12x ，f （y ）=12y ，f （x+y ）=12()x y +，不满足f （x+y ）=f （x ）f （y ），故A 错；B ．f （x ）=x 3，f （y ）=y 3，f （x+y ）=（x+y ）3，不满足f （x+y ）=f （x ）f （y ），故B 错；C ．f （x ）=3x ，f （y ）=3y ，f （x+y ）=3x+y ，满足f （x+y ）=f （x ）f （y ），且f （x ）在R 上是单调增函数，故C 正确；D ．f （x ）=1()2x ，f （y ）=1()2y ，f （x+y ）=1(2x y +，满足f （x+y ）=f （x ）f （y ），但f （x ）在R 上是单调减函数，故D 错。

故选C 。

3．A【详解】若log 2a ＞log 2b ＞0，则a ＞b ＞1，故“a ＞b ＞1”是“log 2a ＞log 2b ＞0”的充要条件，故选A ．4．A【详解】∵f′（x ）=12x 2﹣2ax ﹣2b ，又因为在x=1处有极值，∴a+b=6，∵a ＞0，b ＞0，∴292a b ab +⎛⎫≤= ⎪⎝⎭，当且仅当a=b=3时取等号，所以ab 的最大值等于9；故选A 。

5．B【详解】设椭圆的方程为：22221x y a b +=，直线l 经过椭圆的一个顶点和一个焦点，则直线方程为：1x y c b +=，椭圆中心到l 的距离为其短轴长的14，2b =，4=b 2（2211c b +），∴223b c =，2223a c c-=，∴e=12c a =；故选B 。

6．C【详解】∵S n 为等差数列{a n }的前n 项和，a 4+a 5=24，S 6=48，∴1113424656482a d a d a d +++=⎧⎪⎨⨯+=⎪⎩，解得a 1=﹣2，d=4，∴{a n }的公差为4；故选C 。

军队院校士官高等职业技术教育招生考试：2022数学真题模拟及答案(1)共728道题1、设甲：x＝1，乙：x2＝1，则（）．（单选题）A. 甲是乙的必要条件，但不是乙的充分条件B. 甲是乙的充分必要条件C. 甲是乙的充分条件，但不是乙的必要条件D. 甲既不是乙的充分条件，也不是乙的必要条件试题答案：C2、已知全集，设集合，则＝（）．（单选题）A. {1，5，8}B. {1，3，5，7，8}C. {1，3，5，7}D. {3，5，7，8}试题答案：A3、下面可以得出，α∥β的条件是（）．（单选题）A. 平面α内有三点A、B、C到平面β的距离相等B. 平面γ∩α＝a，γ∩β＝b，且a∥bC. 存在直线l，使l⊥α，l⊥βD. 存在直线l，使l∥α，l∥β试题答案：C4、设，那么“α＜β”是“tanα＜tanβ”的（）．（单选题）A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件试题答案：C5、在等腰三角形ABC中，A是顶角，且，则cosB＝（）．（单选题）A.B.C.D.试题答案：A6、函数在某区间上是减函数，这区间可以是（）．（单选题）A.B.C.D.试题答案：A7、复数的模是（）．（单选题）A. 0B.C.D. 1试题答案：D8、若集合A满足，则集合A的个数是（）．（单选题）A. 4B. 7C. 8D. 10试题答案：B9、垂直于直线y＝x＋1且与圆相切于第一象限的直线方程是（）．（单选题）A.B.C.D.试题答案：A10、已知点A（4，3）和点B（0，－1），则线段AB的垂直平分线方程为（）．（单选题）A. x－2y＋3＝0B. x＋2y－3＝0C. x－y＋3＝0D. x＋y－3＝0试题答案：D11、若θ为第一象限角，且sinθ－cosθ＝0，则sinθ＋cosθ＝（）．（单选题）A.B.C.D.试题答案：A12、若，则（）．（单选题）A. sin θ＞cos θB. cos θ＜cos2θC. sin θ＜sin 2θD. sin θ＞sin2θ试题答案：C13、圆台上、下底面积分别为π，4π，侧面积为6π，这个圆台的体积是（）．（单选题）A.B.C.D.试题答案：D14、对于命题p和q，若“p且q”为真命题，则下列四个命题：①p或非q是真命题；（单②p且非q是真命题；③非p且非q是假命题；④非p或q是假命题，其中真命题是（）．选题）A. ①②B. ③④C. ①③D. ②④试题答案：C15、已知，则下列不等式中成立的是（）．（单选题）A.B.C.D.试题答案：C16、已知数列{a n}满足，则当n≥1时，a n等于（）．（单选题）A. 2nB.C.D.试题答案：D17、方程x2＋xy＝x的曲线是（）．（单选题）A. 一个点B. 一条直线C. 两条直线D. 一个点和一条直线试题答案：C18、成立的（）．（单选题）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既非充分也非必要条件试题答案：A19、下列各组平行线中，距离等于2的是（）．（单选题）A. 2x－7y＋8＝0与2x－7y－6＝0B. 2x＋3y－8＝0与2x＋3y＋18＝0C. 3x＋4y＝10与3x＋4y＝0D. y＝x与3y－3x＋5＝0试题答案：C20、已知成等比数列，则a的值为（）．（单选题）A. 3B. 4或－2C. 3或－3D. －3试题答案：B21、有100张卡片（从1号到100号），从中任取1张，取到的卡号是7的倍数的概率为（）．（单选题）A.B.C.D.试题答案：A22、的展开式中的常数项是（）．（单选题）A. －20B. －160C. 160D. 20试题答案：B23、函数的定义域是（）．（单选题）A. （－∞，－1]∪[1，＋∞）B. （－1，1）C. （－∞，－1）∪（1，＋∞）D. [－1，1]试题答案：C24、在△ABC中，A＝60°，，则此三角形有（）解．（单选题）A. 一个B. 两个C. 无解D. 无法确定．试题答案：C25、方程组的解集是（）．（单选题）A. {（3，4）}B. {（4，3）}C. {（3，4），（4，3）}D.试题答案：C26、已知二次函数有最小值－1，则a的值为（）．（单选题）A. 2B. －2C. 2或－2D. 以上答案都不对试题答案：A27、设定义在R上的函数f（x）＝x|x|，则f（x）（）．（单选题）A. 既是奇函数，又是增函数B. 既是偶函数，又是增函数C. 既是奇函数，又是减函数D. 既是偶函数，又是减函数试题答案：A28、以点A（－5，4）为圆心，且与x轴相切的圆的标准方程是（）．（单选题）A.B.C.D.试题答案：A29、已知角α的终边通过点（5，12），则＝（）．（单选题）A.B.C.D.试题答案：B30、与点P（－1，2）距离为的直线方程是（）．（单选题）A. 2x＋y－10＝0或2x＋y－6＝0B. 3x＝2或3y＝2C. y＝8或x＝8D. 4x＋3y＝0或4x＋3y－4＝0试题答案：D31、等差数列{}，已知那么的值等于（）．（单选题）A. aB. 2aC. 3aD. 4a试题答案：B32、4本不同的书中挑选3本分别发给3位同学每人1本，不同的挑选方法共有（）．（单选题）A. 种B. 种C. 种D. 种试题答案：B33、已知25与实数m的等比中项是1，则m＝（）．（单选题）A.B.C. 5D. 25试题答案：A34、已知直线，mx＋4y－2＝0与2x－5y＋n＝0互相垂直，垂足为（1，P），则m—n ＋P的值为（）（单选题）A. 24B. 20C. 0D. －4试题答案：B35、函数的定义域是（）．（单选题）A. 一1＜x＜1B. x＞1或x＜－1C. 0＜z＜1D. {－1，1}试题答案：D36、已知集合，则M、N的关系是（）．（单选题）A.B.C. M＝ND. M与N无包含关系试题答案：A37、三个数a，b，c不全为0只需（）．（单选题）A. a，b，c都不是0B. a，b，c中最多有一个是0C. a，b，c中只有一个是0D. a，b，c中至少有一个不是0试题答案：B38、（）．（单选题）A. 2B.C.D. －2试题答案：C39、已知R为圆的半径，则弧长为的圆弧所对的圆心角等于（）．（单选题）A. 135°C. 145°D.试题答案：B40、已知a＝（3，x），b＝（7，12），并且a⊥b，则x＝（）．（单选题）A.B.C.D.试题答案：A41、已知数列的前n项和，则此数列（）．（单选题）A. 是等差数列B. 是等比数列C. 从第二项起是等比数列D. 从第二项起是等差数列试题答案：D42、函数y＝2x＋1的反函数为（）．（单选题）A.B.C.D.试题答案：B43、已知O为坐标原点，点A，B的坐标分别为（a，0），（0，a），a是正常数，点P在线段AB上，且，则的最大值是（）．（单选题）B. 2aC. a2D. 3a试题答案：C44、由平面直角坐标系中坐标轴上的点所组成的集合是（）．（单选题）A.B.C.D.试题答案：D45、（1＋x）9的展开式中系数最大的项（）．（单选题）A. 只有一项，是126x5B. 只有一项，是126x6C. 有两项，是126x5和126x6D. 有两项，是126x4和126x5试题答案：D46、在的展开式中，a≠0，x3的系数是x4的系数与x2的系数的等差中项，那么a的值（）．（单选题）A. 只有1个，是B. 只有1个，是C. 有两个，是和D. 有两个，是和试题答案：D47、已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此棱锥的体积为（）．（单选题）A.B.C.D.试题答案：A48、如下图所示，M、N分别是空间四边形ABCD的边AB、CD的中点，连结MN，则下列说法中正确的是（）．（单选题）A. AC＋BD＝2MNB. AC＋BD＞2MNC. AC＋BD＜2MND. 以上结论都有可能成立试题答案：B49、某铁路线上一共有40个大小车站，铁路局要为这条线准备（）种不同的车票，售出车票共有（）种票价．（单选题）A. 40B. 80C. 780D. 1560试题答案：D50、已知以x为未知数的方程x2－（k＋1）x＋k＝0，那么（）．（单选题）A. 对于任何实数k，方程都没有实数根B. 对于任何实数k，方程都有实数根C. 对于某些实数k，方程有实数根；对于其他实数k，方程没有实数根D. 方程是否有实数根无法确定试题答案：B51、同时满足（1），（2）若a∈M，则6－a∈M的非空集合时有（）．（单选题）A. 16个B. 15个C. 7个D. 6个试题答案：C52、顶点在原点，准线方程是x＝2的抛物线方程是（）．（单选题）A.B.C.D.试题答案：B53、复数z满足，则z等于（）．（单选题）A.B.C.D.试题答案：D54、Rt△ABC的两直角边BC＝3，AC＝4，PC⊥平面ABC，且，则点P到斜边的距离为（）．（单选题）A.B. 3D.试题答案：B55、设全集．则＝（）．（单选题）A. {－6，0，5，8}B.C.D.试题答案：D56、两个数的等差中项为20，等比中项为12，那么这两个数为（）．（单选题）A. 18，22B. 9，16C. 4，36D. 16，24试题答案：C57、以等腰直角三角形斜边上的高为棱将其折成直二面角后，两直角边的夹角为（）．（单选题）A. 60°B. 45°C. 90°D. 30°试题答案：A58、设是反比例函数，且f（－2）＝4，则函数的解析式为（）．（单选题）A.C.D.试题答案：D59、空间四个点，每三个点都不共线，过其中三个点作平面，共可作（）平面．（单选题）A. 1个B. 2个C. 3个D. 4个试题答案：D60、过点A（4，1），并且在x轴、y轴上的截距之和为10的直线方程是（）．（单选题）A. x＋4y＋8＝0和x＋4y－5＝0B. x＋y－8＝0和x＋y＋5＝0C. x＋4y－8＝0和x＋y－5＝0D. x＋4y－5＝0和x＋y＋8＝0试题答案：C61、如果方程x2＋ky2＝2表示焦点在y轴上的椭圆，那么实数k的取值范围是（）．（单选题）A. （0，＋∞）B. （0，1）C. （1，＋∞）D. （0，2）试题答案：B62、下列函数中，既是偶函数，又在区间[0，3]内为减函数的是（）．（单选题）A. y＝cosxB. y＝log2xC. y＝x2－4D.试题答案：A63、设，则等于（）．（单选题）A. 0B. 64C. －64D. 128试题答案：D64、已知集合，则M、N的关系是（）．（单选题）A.B.C. M＝ND. M与N无包含关系试题答案：A65、若a，b∈R，则使|a|＋|b|＞1成立的充分条件是（）．（单选题）A.B.C. a≥1D. b＜－1试题答案：D66、若圆x2＋y2＝c与直线x＋y＝1相切，则c＝（）．（单选题）A.B. 1C. 2D. 4试题答案：A67、某地区高中分三类，A类学校共有学生2000人，B类学校共有学生3000人，C类学校共有学生4000人，若采取分层抽样的方法抽取900人，则A类学校中的学生甲被抽到的概率为（）．（单选题）A.B.C.D.试题答案：A68、设是反比例函数，且f（－2）＝4，则函数的解析式为（）．（单选题）A.B.C.D.试题答案：D69、cos38°cos7°－cos83°sin38°的值是（）.（单选题）A.B.C.D.试题答案：A70、设有不同的直线a、b和不同的平面α、β、γ，给出下列三个命题：①若a∥α，b∥α，则a∥b；②若a∥α，a∥β，则α∥β；③若a⊥γ，β⊥γ，则α∥β．其中正确的个数是（）．（单选题）A. 0B. 1C. 2D. 3试题答案：A71、在等差数列中，已知公差，且，则（）．（单选题）A. 85B. 145C. 110D. 90试题答案：A72、的解集是（）．（单选题）A.B.C.D.试题答案：C73、设i为虚数单位，那么的值等于（）．（单选题）A. 1B. －1C. iD. －i试题答案：C74、将函数的图像按向量a经过一次平移后得到y＝x2的图像，则a等于（）．（单选题）A. （2，－1）B. （－2，1）C. （－2，－1）D. （2，1）试题答案：A75、＝（）.（单选题）A.B.C. sin2αD.试题答案：C76、在△ABC中，三个角满足2A＝B＋C，且最大边长与最小边长分别是方程3x2－27x ＋32＝0的两根，则△ABC的外接圆半径是（）．（单选题）A.B. 14C.D.试题答案：C77、在等比数列{a n}中，a2＝1，a4＝4，则a7＝（）．（单选题）A. 30B. 31D. 33试题答案：C78、已知△ABC中，，那么BC等于（）．（单选题）A.B.C.D.试题答案：A79、由平面直角坐标系中坐标轴上的点所组成的集合是（）．（单选题）A.B.C.D.试题答案：D80、log23与log94两数的等比中项为（）．（单选题）A. 1B. －1C. ±1D. 不存在试题答案：C81、sin330°＝（）．（单选题）A.B.D.试题答案：B82、圆心为（1，－2），半径为的圆在x轴上截得的弦长为（）．（单选题）A. 8B. 6C.D.试题答案：A83、在a与b（b≠A）两数之间插入n个数，与a，b组成等差数列，则该数列公差为（）．（单选题）A.B.C.D.试题答案：B84、—个棱锥的各条棱都相等，那么这个棱锥必定不是（）．（单选题）A. 三棱锥B. 四棱锥C. 五棱锥D. 六棱锥试题答案：D85、若向量a＝（1，m），b＝（－2，4），且a·b＝－10，则m＝（）．（单选题）A. －4B. －2C. 1D. 4试题答案：B86、已知，且，则＝（）.（单选题）A.B.C.D.试题答案：A87、在△ABC中，A＞B是sinA＞sinB成立的（）.（单选题）A. 充分条件B. 必要非充分条件C. 充要条件D. 既不充分又不必要条件试题答案：C88、已知一个球的体积为，则它的表面积为（）．（单选题）A. 4πB. 8πC. 16πD. 24π试题答案：C89、已知平面向量a＝（1，1），b＝（1，－1），则两向量的夹角为（）．（单选题）A.B.C.D.试题答案：D90、如果直线l，m与平面α，β，γ满足：l＝β∩γ，l∥α，和m⊥γ，那么必有（）．（单选题）A. α⊥γ且l⊥mB. α⊥γ且m∥βC. m∥β且l⊥mD. α∥β且α⊥γ试题答案：A91、设集合M＝{x|x≥－3}，N＝{x|x≤1}，则M∩N＝（）．（单选题）A. RB. （－∞，－3]∪[1，＋∞）C. [－3，1]D.试题答案：C92、圆柱的底面积是πa，轴截面面积等于b，则圆柱的母线长是（）．（单选题）A.B.C.D.试题答案：B93、若A＞0，B＞0，C＜0，那么直线Ax＋By＋C＝0一定经过（）．（单选题）A. 第一、三象限B. 第一、二、四象限C. 第二、三象限D. 第二、三、四象限试题答案：B94、已知集合A＝{1，2，3，4}，B＝{x|－1＜x＜3}，则A∩B＝（）．（单选题）A. {0，1，2}B. {1，2}C. {1，2，3}D. {1，0，1，2}试题答案：B95、若直线l与平面M平行，则在平面M内与l垂直的直线（）．（单选题）A. 有无数条B. 只有一条C. 只有两条D. 不存在试题答案：A96、函数的周期是（）（单选题）A.B.C.D.试题答案：C97、已知，那么tan α的值等于（）．（单选题）A.B.C.D.试题答案：A98、要得到的图像，只需将函数y＝sin2x的图像（）．（单选题）A. 向右平行移动B. 向左平行移动C. 向右平行移动D. 向左平行移动试题答案：D99、设S n是等比数列{a n}的前n项和，若a2·a3＝2a1，且a4与2a7的等差中项为，则S ＝（）．（单选题）A. 35B. 33C. 29D. 31试题答案：D100、数列{a n}是公差不为0的等差数列，且a1，a3，a7为等比数列{b n}的连续三项，则数列{b n}的公比为（）．（单选题）A.B. 4C. 2D.试题答案：C101、直线x cosθ＋ysinθ＋a＝0与直线xsinθ－ycosθ＋b＝0的位置关系是（）．（单选题）A. 平行B. 垂直C. 相交但不垂直D. 无法确定，与θ，a，b的取值有关试题答案：B102、设x，y∈R，则不等式x＞Y与都成立的充要条件是（）．（单选题）A. xy＞0B. x＞0，y＜0C. xy＜0D. xy≠0试题答案：B103、已知数列，那么它的第5项的值等于（）．（单选题）A.B.C.D.试题答案：D104、正三棱锥的侧面积是底面积的2倍，那么侧面与底面所成的二面角的平面角是（）．（单选题）A. 30°B. 60°C. 45°D. 无法确定试题答案：B105、的倒数第3项是（）．（单选题）A.B.C.D.试题答案：C106、正六边形中，由任意三个顶点连线构成的三角形的个数为（）．（单选题）A. 6B. 20C. 120D. 720试题答案：B107、下列函数中，为奇函数的是（）．（单选题）A. y＝－x3B. y＝x3－2C.D.试题答案：A108、已知抛物线C：y2＝4x的焦点为F，直线y＝2x－4与C交于A，B两点，则cos ∠AFB＝（）．（单选题）A.B.C.D.试题答案：D109、若，且，则的最小值是（）．（单选题）A. 24B. 36C. 48D. 60试题答案：C110、已知点A（1，2），B（2，3），C（－2，5），则△ABC的三个内角中（）．（单选题）A. ∠A＝90oB. ∠B＝90oC. ∠C＝90oD. 没有直角试题答案：A111、经过两条直线2x－3y－1＝0和x－y＝0的交点，且垂直于直线2x－3y－1＝0的直线方程为（）．（单选题）A. 3x＋2y＋5＝0B. 2x＋3y＋5＝0C. 3x－2y＋5＝0D. 2x－3y＋5＝0试题答案：A112、下列四个条件中，在空间能确定一个平面的是（）．（单选题）A. 一条直线和一点B. 两条垂直直线C. 三个点D. 两条平行直线试题答案：D113、函数的定义域是（）．（单选题）A.B.C.D.试题答案：D114、两条异面直线是指（）．（单选题）A. 两条不相交的直线B. 两条不平行的直线C. 不在同一平面内的两条直线D. 不在任何一个平面内的两条直线试题答案：D115、函数的反函数为（）．（单选题）A. y＝x＋1（x∈R）B. y＝x－1（x∈R）C.D.试题答案：D116、已知a，b是异面直线，a⊥平面M，b⊥平面N，则平面M，N的关系是（）．（单选题）A. 相交B. 平行C. 重合D. 不确定试题答案：A117、sin330°＝（）．（单选题）A.B.C.D.试题答案：B118、关于x的不等式x2－2ax－8a2＜0（a＞0）的解集为（x1，x2），且x2－x1＝15，则A等于（）.（单选题）A.B.C.D.试题答案：A119、从10名理事中选出3名常务理事，共有可能的人选（）．（单选题）A. 120组B. 240组C. 600组D. 720组试题答案：A120、在二面角的一个面内有一点，它到棱的距离是到另一个平面的距离的2倍，则此二面角的平面角为（）．（单选题）A. 30°B. 45°C. 60°D. 90°试题答案：A121、函数的反函数是（）．（单选题）A.B.C.D.试题答案：D122、设甲：x＝1，乙：x2－3x＋2＝0，则（）．（单选题）A. 甲是乙的必要条件，但不是乙的充分条件B. 甲是乙的充分条件，但不是乙的必要条件C. 甲不是乙的充分条件，也不是乙的必要条件D. 甲是乙的充分必要条件试题答案：B123、下列关系式中，θ可能满足的关系式是（）.（单选题）A.B.C.D.试题答案：C124、设命题p：关于x的不等式ax2＋bx＋c＞0与Ax2＋Bx＋C＞0的解集相同；命题．则命题q是p的（）．（单选题）A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件试题答案：D125、已知－个等差数列的首项为1，公差为3，那么该数列的前5项和为（）．（单选题）A. 35B. 30C. 20D. 10试题答案：A126、在等差数列{a n}中，已知公差，且，则等于（）．（单选题）A. 120B. 145C. 150D. 170试题答案：B127、4位战士和2位班长并坐一排合影留念，若两位班长不相邻，则所有不同坐法的种数为（）．（单选题）A.B.D.试题答案：A128、椭圆25x2＋16y2＝1的焦点坐标是（）．（单选题）A.B.C.D.试题答案：D129、复数的值等于（）．（单选题）A. iB. －iC. 1D. －1试题答案：A130、已知的三个顶点分别为A（－3，4），B（－2，1），C（1，6），那么顶点D的坐标是（）．（单选题）A. （0，－9）B. （－9，0）C. （0，9）D. （9，0）试题答案：C131、已知tan α＝5，则sin α cos α＝（）．（单选题）A.C.D.试题答案：D132、已知成等比数列，则a的值为（）．（单选题）A. 3B. 4或－2C. 3或－3D. －3试题答案：B133、函数的图象是图中的（）．（单选题）A.B.C.D.试题答案：B134、在的展开式中x7项的系数是（）．（单选题）A. －14B. 14C. －56D. 56试题答案：A135、已知点A（1，2），B（3，4），C（5，0），则△ABC一定是（）．（单选题）A. 等腰直角三角形B. 等边三角形C. 等腰三角形D. 直角三角形试题答案：C136、如果三角形的顶点为A（－1，2），B（4，3），C（－2，5），那么它的面积为（）．（单选题）A. 4B. 8C. 16D. 24试题答案：B（单137、圆x2＋y2＝1沿x轴的正方向平移，使之与直线相切，则需平移向量a为（）．选题）A. （1，0）B.C. （2，0）D.试题答案：B138、10名学生中要选出3名代表，一共有（）种不同的选法．（单选题）A. 120B. 240C. 600D. 720试题答案：A139、设函数ｙ＝f（x）的定义域为[a，b]，其中b＞－a＞0，那么F（x）＝f（x）＋f（－x）的定义域为（）．（单选题）A. [a，－a]B. [－b，b]C. [a，b]D. [－b，－a]试题答案：A140、若直线按向量a平移得到直线，则a（）．（单选题）A. 只能是（0，2）B. 只能是（2，6）C. 只能是（0，2）或（2，6）D. 有无数个试题答案：D141、复数等于（）．（单选题）A. iB. －iC.D.试题答案：A142、直线y＝kx＋b（k≠0），关于直线x＋y＝0对称的直线方程为（）．（单选题）A. x＋ky＋b＝0B. x＋ky－b＝0C. x－ky－b＝0D. x－ky＋b＝0试题答案：D143、设等比数列{a n}的公比q＝2，前n项的和为，则＝（）．（单选题）A.B. 4C. 2D.试题答案：A144、正方体ABCD-A′B′C′D′的棱长是2，点A′到直线BD的距离d为（）．（单选题）A.B.C.D.试题答案：A145、的反函数是（）．（单选题）A.B.C.D.试题答案：C146、直线ax＋2y－1＝0与x＋（a－1）y＋2＝0平行，则a等于（）．（单选题）A.B. 2C. －1D. 2或－1试题答案：D147、函数的定义域是（）．（单选题）A.B.C.D. （其中）试题答案：C148、下列函数中，为减函数的是（）．（单选题）A. y＝x3B. y＝sinxC. y＝－x3D. y＝cosx试题答案：C149、向量a的模为10，它与x轴正方向的夹角为150°，则它在x轴上的投影为（）．（单选题）A.B. 5C. －5D.试题答案：A150、椭圆与的关系为（）．（单选题）A. 有相等的长轴B. 有相等的焦距C. 有相等的焦点D. 有相同的准线试题答案：B151、已知直线l1，l2的斜率是方程6x2＋x－1＝0的两个根，那么l1与l2所成的角是（）．（单选题）A. 15oB. 30oC. 45oD. 60o试题答案：C152、已知函数，则f（2）等于（）．（单选题）A.B. 2C. 1D.试题答案：C153、＝（）．（单选题）A.B.C.D.试题答案：A154、已知数列{a n}是等比数列，如果，且，则等于（）．（单选题）A. 8C. 32D. 48试题答案：B155、展开式中的常数项为（）．（单选题）A. 1B.C.D.试题答案：D156、函数的反函数是（）．（单选题）A.B.C.D.试题答案：B157、在复平面内，复数对应的点位于（）．（单选题）A. 第一象限B. 第二象限C. 第三象限D. 第四象限试题答案：B158、若，且a∥b，则锐角为（）．（单选题）A. 30°C. 60°D. 75°试题答案：B159、展开式中的第四项是（）．（单选题）A. 20B. 15C. 10D. 18试题答案：A160、已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半，且AB＝BC ＝CA＝2，则球面面积是（）．（单选题）A.B.C.D.试题答案：D161、的值为（）．（单选题）A. －1B. 0C.D. 1试题答案：A162、设函数，则f（1）＝（）．（单选题）A. 2B. log339C. 1D. log315试题答案：A163、已知直线l⊥平面α，直线m平面β，有下面四个命题：其中正确的两个命题是（）．（单选题）A. ①与②B. ③与④C. ②与④D. ①与③试题答案：D164、两条异面直线所成的角为θ．则θ的取值范围是（）．（单选题）A.B.C.D.试题答案：B165、甲、乙两人下棋，甲胜的概率为40％，甲不输的概率为90％，则甲、乙两人下成和棋的概率为（）．（单选题）A. 60％B. 30％C. 10％D. 50％试题答案：D166、如果圆锥的轴截面是正三角形，底面积是2π，则它的侧面积是（）．（单选题）A. 2πB. 10πC. 6πD. 4π试题答案：D167、下列函数中，为偶函数的是（）．（单选题）A. y＝3x2－1B. y＝x3－3C. y＝3xD. y＝log3x试题答案：A168、数列共有（）项．（单选题）A. 2003－1993B. 2003－（1993＋1）C. 2003－（1993－1）D. 以上都不对试题答案：C169、两排座位，第一排有3个座位，第二排有5个座位，若8个学生入座，不同坐法的种数是（）．（单选题）A.B.C.D.试题答案：D170、下列命题是复合命题的是（）．（单选题）A. 12是6的倍数B. 12比5大C. 四边形ABCD不是矩形D. a2＋b2＝c2试题答案：C171、从单词“equation”中选取5个不同的字母排成一排，含有“qu”（其中“qu”相连且顺序不变）的不同排法有（）种．（单选题）A. 120B. 480C. 720D. 840试题答案：B172、在的二项展开式中，的系数为（）．（单选题）A.B.C.D.试题答案：C173、已知等比数列{a n}的公比为2，S4＝1，则S8＝（）．（单选题）A. 15B. 17C. 19试题答案：B174、已知a＝（3，－1），b＝（－2，5），则3a－2b＝（）．（单选题）A. （2，7）B. （13，－7）C. （2，－7）D. （13，13）试题答案：B175、如图，从甲地到乙地有三条路可通，从乙地到丙地有四条路可通，从甲地到丁地有两条路可通，从丁地到丙地有四条路可通，而从甲地直接到丙地有三条路可通，则从甲地走到丙地，一共可有（）种不同的走法．（单选题）A. 16B. 99C. 23D. 288试题答案：C176、抛物线y2＝－4x的准线方程为（）．（单选题）A. x＝－1B. x＝1C. y＝1D. y＝－1试题答案：B（单177、一个等比数列，前n项之和为48，前2n项之和为60，那么前3n项之和为（）．选题）A. 63C. 87D. 108试题答案：A178、已知sinα＜0，cosα＞0，则在（）.（单选题）A. 第一或第二象限B. 第二或第四象限C. 第一或第四象限D. 第三或第四象限试题答案：B179、设i为虚数单位，那么的值等于（）．（单选题）A. 1B. －1C. iD. －i试题答案：C180、二次函数的图像与x轴的交点坐标为（）．（单选题）A. （－2，0）和（1，0）B. （－2，0）和（－1，0）C. （2，0）和（1，0）D. （2，0）和（－1，0）试题答案：A181、已知α为钝角，β为锐角，且，则等于（）．（单选题）A. 7C.D.试题答案：D182、复数的值等于（）．（单选题）A. 1B. －1C. iD. －i试题答案：D183、设圆，若0＜a＜1，则原点O（）．（单选题）A. 在圆上B. 在圆外C. 在圆内D. 与圆C的位置不确定试题答案：B184、直线2x－2y＋3＝0被曲线截得的线段中点到原点的距离是（）．（单选题）A.B.C.D. 29试题答案：B185、已知的展开式中各项系数的和等于512，那么n＝（）．（单选题）A. 10C. 8D. 7试题答案：B186、在△ABC中，如果C＝90o，a＝6，B＝30o，那么c－b等于（）．（单选题）A. 1B. －1C.D.试题答案：C187、△ABC的三个顶点为，则△ABC为（）三角形．（单选题）A. 锐角B. 直角C. 钝角D. 斜脚试题答案：B188、已知双曲线C：的焦距为10，点P（2，1）在C的渐近线上，则C的方程为（）．（单选题）A.B.C.D.试题答案：A189、两直线之间的距离是（）．（单选题）B.C.D. 不能确定试题答案：C190、（1＋x）9的展开式中系数最大的项（）．（单选题）A. 只有一项，是126x5B. 只有一项，是126x6C. 有两项，是126x5和126x6D. 有两项，是126x4和126x5试题答案：D191、已知向量a＝（2，4），b＝（m，－1），且a⊥b，则实数m＝（）．（单选题）A. 2B. 1C. －1D. －2试题答案：A192、设a，b，c为任意向量，m∈R，则下列不等式不一定成立的是（）．（单选题）A.B.C.D.试题答案：D。

士兵军校考试|大专毕业生士兵专升本文化科目统一考试数学考试大纲考试目标与要求理解函数的概念，会求函数的定义域和值域;掌握极限的四则运算法则;深刻理解导数概念及其几何意义，掌握导数的四则运算及复合函数、隐函数的求导法则。

理解原函数的概念，会求一元函数的不定积分和定积分;会求可分离变量的微分方程、一阶线性微分方程和二阶常系数齐次线性微分方程的解;能运用一元函数微分和积分学的有关知识，判断函数的单调性和曲线的凹凸性，会求函数的极值和最值，会用定积分计算平面图形的面积。

张为臻博客考试分值与时间大专生士兵专升本文化考试总成绩满分为600分，其中科学知识综合150分(其中高等数学50分)。

6月7日下午15:00—17:30：大专毕业生士兵科学知识综合共150分钟。

考试试卷结构题型分布：单项选择题：共5小题，每小题4分，共20分。

填空题：共5小题，每小题2分，共10分。

计算题：共2小题，每小题5分，共10分。

证明题：10分。

试卷结构：客观题(单项选择题，占40%);主观题(填空题、计算题、证明题，占60%)。

准维教育军队考试网考试范围与要求一、函数与极限(一)函数1、理解函数的概念，掌握函数的两大要素，会求函数的定义域;2、了解函数的单调性、奇偶性、有界性和周期性，并会讨论函数的这些性质;3、了解符合函数的概念，能熟练分析符合函数的符合过程;4、熟悉基本初等函数的性质和图形;5、了解分段函数的概念，并能画出简单分段函数的图形;6、会分析简单实际问题中的变量关系，并建立其函数关系式。

(二)极限1、了解极限的“ε—N”“ε—δ”定义，对定义中“任给”“存在”要具体理解。

了解函数极限与函数左、右极限的关系及差别。

2、掌握极限四则运算法则，了解极限存在的两个准则(夹逼准则和单调有界准则)，会用准则判断极限的存在性;3、会用两个重要极限公式求极限;4、了解无穷小与无穷大的概念、无穷小与函数极限的关系，掌握无穷小的比较以及等价无穷小在求极限中的应用。

- 70 -二〇一二年军队院校招生文化科目统一考试士兵高中数学真题与详解一、选择题（本题共36分有9个小题，每个小题都给出代号为A 、B 、C 、D 的四个结论，其中只有一个结论是正确的，将正确的结论代号写在答题纸指定位置上，选对得4分，选错、不选或多选一律得0分） 1．设全集{|05}U x x =∈Ζ≤≤，集合{13}A =，，{|}B y y x x A ==∈，，则集合 U U A B =（）（）（ ） A ．{0245}，，，B ．{045}，，C ．{245}，，D ．{45}，2．设a 、b 都是实数，则“22lg 1lg 1a b +<+（）（）”是a b <“”的（ ） A ．充要条件B ．充分不必要条件C．必要不充分条件D ．既不充分也不必要条件 3．设sin14cos1461a b c =+=。

，，a b c 、、的大小关系是（ ） A ．a b c <<B ．a c b <<C ．b c a <<D ．b a c <<4．已知||10||12a b ==，，且13365a b =-（）（），则向量a 与b 的夹角是（ ）A ．60 B ．105 C ．120 D ．1355．AB 是过抛物线2x y =的焦点的弦，且||4AB =，则AB 的中点到直线10y +=的距离是（ ）A ．52B ．114C ．2D ．36．设n S 是等差数列{}n a 的前n 项和，若5359a a =，则95SS =（ ） A ．12B ．2C ．1-D ．17．在ABC △中，三个角满足2A B C =+，且最大边长与最小边长分别是方程2327320x x -+=的两根，则ABC △的外接圆半径是（） AB ．14CD ．1438．已知过球面上A B C 、、三点的截面和球心的距离等于球半径的一半，且1AB AC BC ===，则球面面积为（ ） A ．49π B ．169πC ．πD ．23- 71 -9．已知函数cos sin 4f x f x x π'=+（）（），则4f π（）的值为（ ）A ．1B ．1- C 1D 1二、填空题（本题共32分有8个小题，每个小题4分，只要求给出结果，并将结果写在答题纸指定位置上）1．若函数1x f x x g x x e ϕ=+==（），（）（），则函数1{[]}g f x ϕ-（）的定义域是 ．2．设00xy >>，是3x 与3y 的等比中项，则11x y+的最小值为 ．3．不等式|1|122x -≤（）的解集为 ．4．已知sin sin sin 0cos cos cos 0αβγαβγ++=++=，，则cos βγ-（）的值等于 ． 5．已知数列2{log 1}n a n *-∈Ν（）（）为等差数列，且1235a a ==，，则213211lim n a a a a →∞++⋅⋅⋅+--（11n na a +-）= ． 6．若圆C 的圆心与点21P -（，）关于直线1y x =+对称，直线34110x y +-=与圆C 相交于A B 、两点，且||6AB =，则圆C 的方程为 ． 7．81x x -（）的展开式中，4x 的系数与41x的系数之差是 ． 8．从4个红球和5个白球中任取3个球，至少有一个红球的取法共有______种（用数字作答）． 三、计算题（本题共16分有2个小题）1．（本小题6分）解方程：1lg 8221lg5x x ++=-（）（）． 2．（本小题10分）设26cos 2f x x x =（）． （1）求f x （）的最大值及最小正周期；- 72 -（2）若锐角α满足3f α=-（）4tan 5α的值， 四、（12分）已知数列{}n a 是首项11a >，公比0q >的等比数列，设2log n n b a n *=∈N （），且13513560b b b b b b ++==，．（1）求数列{}n a 的通项公式； （2）设{}n b 的前n 项和为n S ，当1212n S S S n++⋅⋅⋅+最大时，求n 的值． 五、（12分）将编号为1234、、、的贺卡随意地送给编号为1234、、、的四位老师，要求每师都得到一张贺卡，记与贺卡编号相同的老师的个数为ξ． （1）求随机变量ξ的概率分布； （2）求ξ的数学期望．六、（12分）已知函数21ln 2f x x x =+（）． （1）求函数f x （）在区间1e [，]上的最大值和最小值； （2）证明：在区间1+∞（，）上，函数f x （）的图象在函数323g x x =（）的图象的下方．- 73 -七、（16分）如图所示，12l l ，是互相垂直的异面直线，MN 是它们的公垂线段，点A B 、在1l 上点C 在2l 上，AM MB MN ==． （1）证明AC NB ⊥；（2）若60ACB ∠=，求NB 与平面ABC 所成角的余弦值．ABCMNl 1l 2八、（14分）已知椭圆2222:10x y C a b a b+=>>（），短轴的一个端点到右焦点的（1）求椭圆C 的方程；（2）设直线l 与椭圆C 交A B 、两点，坐标原点O 到直线l 求三角形AOB 面积的最大值．- 74 -〖答案与详解〗一、选择题 1．【答案】D【详解】∵={012345}{13}{02}U A B ==，，，，，，，，，，∴{0245}U A =，，，，U B ={1345}，，，．∴{45}U U A B =（）（），． 【点评】考查集合的交、补运算．（详见《军考突破》中1-1-10、1-1-12） 2．【答案】D 【详解】先化简2222lg 1lg 111||||a b a b a b +<+⇔+<+⇔<（）（）． 又||||a b <不能推出a b <，a b <不能推出||||a b <．【点评】本题涉及对数的运算，重点考查充要条件．（详见《军考突破》中1-2-3） 3．【答案】B 【详解】2cos142sin5922a+=（），61b，60c = ∵sin x 在02π（，）递增，∴a c b <<．【点评】本题涉及辅助角公式，特殊角的三角值，重点考查正弦函数的单调性．（详见《军考突破》中4-2-3） 4．【答案】C 【详解】1333||||cos 1012cos 36555a b a b a b a b =<>=⨯⨯<>=-（）（），，∴1cos 2a b <>=-，，则向量a b ，夹角为120．【点评】考查利用数量积求向量的夹角．（详见《军考突破》中5-1-6）5．【答案】B141-y104，），焦点弦AB 中点M ，准线14y =-- 75 -易知111'=2222MM AA BB AF FB AB '''+=+==（）（） 所以M 到1y =-的距离为3311'2444MM '+=+=． 【点评】考查抛物线定义及梯形中位线的应用．（详见《军考突破》中8-3-1）6．【答案】D 【详解】∵19159553959522a a a a S a S a ++====（）（）， ∴955533995515599S a a S a a ==⨯==（）． 【点评】考查等差数列前n 项和公式及性质．（详见《军考突破》中3-2-5） 7．【答案】C 【详解】∵2A B C =+∴360A A B C A =++= 据题意，不妨设b a c ≤≤∴3293b c bc +=，且=据余弦定理2222222cos60349a b c bc b c bc b c bc =+-=+-=+-=（）∴7a =据正弦定理2sin a R A =即72sin60R=，得R =． 【点评】本题涉及三角形内角和一元二次方程根与系数关系，重点考查正弦定理，余弦定理．（详见《军考突破》中5-2-1、5-2-2） 8．【答案】B【详解】如图 球心为O 半径R ，过A B C 、、的截面圆心为H ，半径r ∵ABC △为正三角形 ∴23rAH =⨯=在Rt OHA △中，OA R AH =，∴2222R R =+（）得23R = ∴21649S R =π=π球． 【点评】本题涉及正三角形的外接圆半径的求法，球心与截面圆心垂直截面圆，重点考- 76 -考查球的表面积公式．（详见《军考突破》中9-4-3） 9．【答案】A ． 【详解】cos sin 4f x f x x π'=+（）（）求导得sin cos 4f x f x x π''=-+（）（）令444x f f πππ''==-，（）（解得14f π'=（） ∴1cos sin f x x x =+（）∴114f π==（．【点评】本题的核心问题是求得4f π'（）．因而需要对函数求导，求导数注意到4f π'（）为常数．（详见《军考突破》中13-1-3） 二、填空题 1．【答案】0+∞[，）【详解】由1ln x x e x x ϕϕ-=⇒=（）（）∴11{}{1}ln 1g f x g x g x ϕϕ--=+=+=[（）]（）[（）]定义域满足：ln 10110x x x +⇔+⇔≥≥≥（） ∴定义域是0+∞[，） 【点评】本题涉及求定义域，解对数不等式，反函数求法．重点考查复合函数的求法．（详见《军考突破》中2-5-1-2） 2．【答案】4【详解】据题设2003331x y x y x y >>=⇔+=，，（）111x y x y xy xy++==由均值不等式11144x y xy xy =+⇒≥≤≥．由1x y x y+=⎧⎨=⎩得12x y ==．当且仅当12x y ==时，11x y+最小值为4． 【点评】本题涉及等比中项，指数运算．重点考查利用均值不等式求最值．（详见《军考突破》中6-1-2） 3．【答案】{|11}x x x -=≤或【详解】原式22|1|211111112210x x x x x x x -⎧--⎪⇔⇔-⇔⇔-=⎨-⎪⎩≥≤≤≥（）（）（）或． 故原不等式解集为{|11}x x x -=≤或．【点评】考查指数不等式的解法．（详见《军考突破》中2-3-4） 4．【答案】12-- 77 -【详解】据题设sin sin sin cos cos cos βγαβγα+=-⎧⎨+=-⎩平方相加得2222sin 2sin sin sin cos 2cos cos cos 1ββγγββγγ+++++=（）（） 化简得1cos2βγ-=-（） 【点评】考查同角三角函数公式及和角差角的余弦公式．（详见《军考突破》中4-1-8、4-2-1） 5．【答案】1 【详解】数列2{log 1}n a -（）为等差数列，首项2log 311-=（），公差2log 511211d =--=-=（） ∴2log 111112n n n a n n a -=+-⋅=⇒-=（）（）11222212n n n n n n a a ++-=-=-=（） ∴1112nn n a a +=-（）∴122132111111112lim lim[]1122212nn n n n a a a a a a →∞→∞+++⋅⋅⋅+=++⋅⋅⋅+==----（）（）（）（） 【点评】考查等差数列的通项公式和等比数列的前n 项和，重点考查数列的极限．（详见《军考突破》中3-2-3、3-2-5）6．【答案】22118x y ++=（）【详解】设圆C 的圆心00C x y （，）∵00C x y （，）与21P -（，）关于1y x =+对称 ∴0000001102112122y x x y y x -⎧=-⎪=⎧+⎪⇒⎨⎨=-+-⎩⎪=+⎪⎩∴01C -（，），01C （，）到34110x y +-=距离3d =∴半径r ==C 的方程为22118x y ++=（）【点评】本题涉及两点关于直线对称，点到直线距离，圆的弦长的求法，重点考查待定系数法求圆的方程．（详见《军考突破》中7-2-1） 7．【答案】0 【详解】88218811r r r r r rr T C x C x x --+=-=-（）（） 令8242r r -=⇒= ∴4x 系数为222881C C -=（） 令8246r r -=-⇒=∴41x 系数为666881C C -=（） ∴4x 与41x 系数之差26880C C -= 【点评】考查二项式定理的通项公式．（详见《军考突破》中10-2-2） 8．【答案】74【详解】从9个球中任取3球的方法数为39C ，取3球无红球的方法数为35C ，所以至少有- 78 -一个红球的取法数为339574C C -=．【点评】考查组合数的知识，当正面情况较复杂时，需用间接法求解．（详见《军考突破》中10-1-3） 三、计算题1．【详解】原方程化作12lg 822lg10lg52lg 2lg 2x x x x ++=-==（）（）∴12822x x ++=令2x y = 所以2280y y --=解得24y y =-=和，∴22x =-（无解）24x =，∴2x =代入原方程检验知，2x =是原方程的根．【点评】本题涉及对数运算，一元二次方程，指数方程．重点考查对数方程的解法．（详见《军考突破》中2-3-3、2-4-4）2．【详解】（1）21cos 26cos 2622xf x x x x +==（）3cos223x x =+233x π=-+（）∴fx （）最大值是3，最小正周期是π． （2）∵32333f ααπ=--+=-（）（）∴sin 213απ-=-（）∵α为锐角∴523212ααππ-=-⇒=π∴4tan tan 53απ=【点评】本题涉及三角中降幂公式，辅助角公式，简单三角方程求解．重点考查正弦型函数的性质．（详见《军考突破》中4-2-3、4-3-4） 四、【详解】（1）据题设11n n a a q -=，又1221212log log log 1log n n n b a a q a n q -===+-（）∴{}n b 为等差数列，1211log 01b a a =>>（）由135336362b b b b b ++=⇒=⇒=由135500b b b b =⇒= ∴14b =1121132122164log 41612log 2log log 12a b a a b a q q =⎧===⎧⎧⎧⎪⇒⇒⇒⎨⎨⎨⎨=+=-=⎩⎩⎩⎪⎩∴115111622n n nn a a q ---===（）（2）522log log 25n n n b a n -===-1459222n n n b b n n n n S ++--===（）（）（）则92n S nn -= 记2129491929117212222244n n nn S S S n T n n n -+---=++⋅⋅⋅=++⋅⋅⋅==-+（）- 79 -若n T 最大，当且仅当1748.5124n =-=-（）∵n *∈Ν ∴89n =，或【点评】本题涉及等比数列通项，等差数列定义，通项前n 项和以及解方程知识，重点考查离散型二次函数的最值的求法．（详见《军考突破》中3-3-3、3-2-5） 五、【详解】（1）设老师编号与贺卡编号相同的个数为ξ，则0124ξ=，，，1ξ=（恰有1个老师与卡号相同）先从4个老师中人选1个，方法有14C 种． （例如设1号老师获1号卡）其余3人共有2种获卡方法（见1ξ=图表）据分步计数原理，共有142C ⨯种方法，而4个老师每人得1个贺卡，共有44A 种方法据等可能事件的概率144428124C P A ξ⨯===（） 2ξ=（恰有2个老师与卡号相同）先从4个老师中任选2个，方法有24C 种（例如设1，2号老师与卡号相同）其余2人有1种获卡方法（见2ξ=表）据分步计数原理，共有241C ⨯种方法．而4个老师每人得1个贺卡，共有44A 种方法，据等可能事件的概率244416224C P A ξ⨯===（） 4ξ=（恰有4个老师与卡号相同）只有1种方法（见4ξ=表）而4个老师每人得1个贺卡，共有44A 种方法据等可能事件的概率4411424P A ξ===（） 0ξ=我们也可以如上分析，直接得出9024Pξ==（）若用分布列的性质 861901124124242424P P P P ξξξξ==-=+=+==-++=（）（（）（）（））（）ξ分布列：★ 军考5年真题详解汇编- 80 -（2）86191240124242424Eξ=⨯+⨯+⨯+⨯=（） 【点评】考查古典概率的求法，重点考查了排列组合的运用和具体情况的表格分析．（详见《军考突破》中11-2-2） 六、【详解】（1）21ln 2f x x x =+（）求导1f x x x'=+（） ∵1x e ∈[，] ∴0f x '>（），则1f x e （）在[，]∴1f f x f e ≤≤（）（）（）即211122f x e +≤≤（）． ∴f x （）在1e [，]上最大值是2112e +，最小值是12（2）在1+∞（，）上，f x （）在323g x x =（）的图象下方．1f x g x x ⇔<∈+∞（）（）（，）恒成立2312ln 123x x x x ⇔+<∈+∞（，）恒成立 2312ln 0123x x x x ⇔+-<∈+∞（，）恒成立 考察函数2312ln 123h x x x x x =+-∈+∞（）（，）32221211212x x x x x h x x x x x x-++-++'=+-==（）（）（） ∵1x ∈+∞（，）∴2010210x x x x >-<++>，， ∴0h x '<（），∴h x （）在1+∞（，） 所以12110236h x h <=-=-<（）（）即2312ln 023x x x +-< 1x ∈+∞（，）恒成立 故原命题正确．【点评】考查利用导数求函数的最值．（详见《军考突破》中13-2-3） 七、【详解】（1）证明：∵12l l ⊥ ∴CN AB ⊥ ∵MN 是12l l ，公垂线 ∴CN MN ⊥∴CN 垂直于平面ABN 又BN ABN ⊂平面 ∴CN BN ⊥ ∵MA MB MN == ∴ABN △是Rt △且BN AN ⊥由于BN AN BN CN ⊥⊥，所以BN CAN ⊥平面★ 二〇一二年数学真题与详解- 81 -又AC CAN ⊂平面∴BN AC AC BN ⊥⊥即ABCMNHl 1l 2（2）在Rt ABN △中，∵MA MB MN AB =⊥，∴NA NB =从而CA CB =（射影相等则斜线相等）又60ACB ∠=，∴ABC △是正三角形连CM ，过N 作NH MC H ⊥于，连BH AB MN AB CM ⊥⊥， ∴AB CMN ⊥平面∴AB NH ⊥∴NH ABC ⊥平面∴NBH ∠是BN 和平面ABC 所成的角． 设1MA MB MN===，则CM =在Rt CMN △中，1CM MN ==，∴cos CMN ∠= 在RtMHN △中，sin 1NH MN CMN =∠==在Rt NHB △中，90NHB BN NH ∠===，∴sin cos NH NBH NBH BN ∠==⇒∠=即NB与平面ABC 所成角的余弦值为 【点评】考查了直角三角形斜边中线性质，直线与平面垂直的判定，线面垂直的性质，射影定理，重点考查直线与平面所成角的定义和求解方法．（详见《军考突破》中9-3-2） 八、【详解】（1）据题意1a c e c ab a ⎧=⎧⎪==⎪⎪⇒=⎨⎨⎪⎪==⎩⎪⎩2213x y +=（2）设直线l 方程为x my n =+ ····································································· ①★ 军考5年真题详解汇编- 82 -O 到l22433n m =⇔=+ 将①代入椭圆方程得，2223230m y mny n +++-=（）（） 设21122121222333mn n A x y B x y y y y y m m --+==++（，）（，）， 弦长212|||1AB y y m =-=+）∵22433n m =+∴||AB = 当且仅当22113233m m =-⇒=-+（）时，||AB 最大为2 此时AOB S △最大为1332222=又当直线l 斜率为0时，l 方程为y =（不妨）代入椭圆方程得x =∴||AB =弦∴1333224AOB S ==<△所以三角形AOB 【点评】本题涉及椭圆性质，待定系数法求椭圆方程，点到直线的距离，弦长公式，二次函数的最值，三角形面积公式．重点考查利用换元法求二次函数的最值．（详见《军考突破》中8-4-2）。

二〇一五年武警部队院校招生统一考试士兵本科数学真题与详解一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项符合题目要求.1.已知全集为R ,集合{|13}{0246}A x x B =-<=≤,,,,,则 A B 等于( )A .{02},B .{102}-,,C .{|02}x x ≤≤D .{|12}x x -≤≤2.在等比数列{}n a 中,已知31815243⋅⋅=a a a ,则3911=a a ( ) A .3 B .9 C .27 D .813.设232555322555a b c ===(),(),(),则、、a b c 的大小关系是( )A .>>b c aB .>>a b cC .>>c a bD .>>a c b4.不等式1021x x -+≤的解集是()A .11]2(,-B .11]2[,-C .112(-,)[,)∞-+∞D .112(-,][,)∞-+∞ 5.复数Z 满足12i Z i +=(),则复数Z 在复平面内对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限6.一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为( )A .33!⨯B .333!⨯()C .43!() D .9!7.若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是( )A .若α⊥l ,∥βl ,则β⊥aB .若β⊥a ,α⊂l ,则β⊥lC .若⊥l n ,⊥m n ,则∥l mD .若a β∥,α⊂l ,β⊂n ,则∥l n8. 将边长为a 的正方形ABCD 沿对角线AC 折起,使=BD a ,则三棱锥D -ABC 的体积为( ) A .36aB .312aC 3D 39.过坐标原点且与点1)的距离都等于1的两条直线的夹角为( )A .090B .045C .030D .06010.已知点23A -(,)在抛物线2:2=C y px 的准线上,记C 的焦点为F ,则直线AF 的斜率为( )- 107 -A .43-B .1-C .34-D .12-二、填空题:本大题共5小题,每小题5分,共25分. 11.若函数2143()=-++kx f x kx kx 的定义域为R ,则实数k 的取值范围是_______. 12.已知向量a、b满足0⋅=a b ,||1||2a b == ,,则|2|a b -=_______. 13.若[sin 242θθππ∈=,,sin θ=_______. 14.在5611()()-+-x x 的展开式中,含3x 的项的系数是_______.15.椭圆2244+=x y 长轴上一个顶点为A ,以A 为直角顶点作一个内接于椭圆的等腰直角三角形,该三角形的面积是_______.三、解答题:本大题共7小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分10分,(1)和(2)分别为6分和4分)已知函数21()=-x f x 的反函数为1()-f x ,4()log (31)=+g x x (1)用定义证明1()-f x 在定义域上的单调性;(2)若1f xg x -≤()(),求x 的取值集合D .17.(本小题满分10分,其中(1)和(2)各5分)在ABC △中,内角A B C ,,所对的边分别为a b c ,,,已知sin a c B C -==,. (1)求cos A 的值; (2)求cos 26A π-(的值. 18.(本小题满分10分,其中(1)和(2)分别为4分和6分)已知{}n a 是递增的等差数列,24a a ,是方程2560-+=x x 的根. (1)求{}n a 的通项公式;(2)求数列{}2n na的前n 项和.19.(本小题满分10分,(1)和(2)分别为4分和6分)已知向量cos sin cos sin 0a b ααβββα==<<<π(,),(,),.(1)若||-=a b ⊥ a b ; (2)设01c =(,),若+=a b c ,求α和β的值.- 108 -20.(本小题满分10分,(1)和(2)分别为4分和6分)骰子(六个面上分别标以数1,2,3,4,5,6)每抛掷一次,各个面上的概率均等. (1)连续抛掷2次,求向上的数之和为6的概率;(2)连续抛掷5次,求向上的数为奇数恰好出现3次的概率. 21.(本小题满分12分,(1)和(2)分别为5分和7分)如图,在四棱锥-P ABCD 中,底面ABCD 是正方形,侧面⊥PDC 底面ABCD ,090,,=∠=PD DC PDC E 是PC 的中点.(1)求证:∥PA 平面EDB ;(2)若⊥EF PB 于点F ,求证⊥PB 平面EFD .22.(本小题满分13分,其中(1)和(2)分别为5分和8分)双曲线C 的中心在坐标原点,右焦点为),渐近线为=y . (1)求双曲线C 的标准方程;(2)设直线:1=+l y kx 与双曲线C 交于、A B 两点,则当k 为何值时,以AB 为直径的圆过原点?- 109 -〖答案与详解〗一、选择题 1.【答案】A【详解】集合{|13}{0246}A x x B =-<=≤,,,,,则= A B {02},. 【点评】考查集合的交集运算.(详见《军考突破》中1-1-10) 2.【答案】B 【详解】根据等比数列性质,由31815243⋅⋅=a a a ,得5583=a ,83=a , 则329971197811119a a a a a a a a a ====(). 【点评】考查等比数列的性质.(详见《军考突破》中3-3-4) 3.【答案】D【详解】由25x y =(为减函数且3255>,得32552255b c =<=()(,再由250y x x =>()为增函数且3255>,得22553255a c =>=()(,所以、、a b c 的大小关系是>>a c b .另法:将232555322555a b c ===(((,同时5次方,得5253523928245255125525a b c ======(,(,(),显然有55545208 125125125a cb =>=>=, 则、、a bc 的大小关系是>>a c b . 【点评】考查函数的单调性.(详见《军考突破》中2-5-5) 4.【答案】A【详解】不等式1021x x -+≤的零点为112、-,用根轴法(零点分段法)如图:解集是11]2(,-.【点评】考查分式不等式解法,涉及序轴标根法.(详见《军考突破》中6-3-1) 5.【答案】A【详解】复数Z 满足12i Z i +=(),即2222212222111121i i i i i i Z i i i i i --+=====+++--()()(),则复数Z 对应点为11(,),是在复平面内的一象限. 【点评】考查复数的运算.(详见《军考突破》中9-2-3)6.【答案】C【详解】第一步,分别将每一家捆绑,有33!()种方法;第二步,再将三个全排列,有3!种方法.所以每家人坐在一起,则不同的做法为43!().【点评】考查排列问题的基本计算方法—捆绑法.((详见《军考突破》中7-1-4)中)- 110 -7.【答案】A【详解】根据两平面垂直的判定定理,由α⊥l ,∥βl ,能够推出β⊥a .【点评】考查平面与平面垂直的判定.(详见《军考突破》中10-2-3).8.【答案】D【详解】由题意,如图在三棱锥-D ABC 中,側棱长===D A D CBD a ,====OA OB OC OD ,从而可知高为OD ,底面积212∆=ABC S a ,则三棱锥D-ABC 的体积为231132=⨯=V a .【点评】考查三棱锥的体积的求法.(详见《军考突破》中10-4-2)9.【答案】D【详解】如下图,过坐标原点且与点1的距离都等于1的两条直线的夹角为00223060∠=∠=⨯=AOB AOP .【点评】考查从圆外一点出发的圆的两条切线的夹角.(详见《军考突破》中11-2-3) 10.【答案】C【详解】由题意,抛物线2:2=C y px 的准线方程为:2=-x ,所以C 的焦点为20F (,),直线AF 的斜率为033224k -==---().【点评】考查抛物线的准线方程与焦点坐标,以及过两点的斜率公式.(详见《军考突破》中12-3-3) 二、填空题11.【答案】304k <≤- 111 -【详解】∵函数2143()=-++kx f x kx kx 的定义域为R ,∴0=k 或204120k k k ≠⎧⎨∆=-<⎩(), ∴304k <≤.【点评】考查函数的定义域的求法.(详见《军考突破》中2-5-1) 12.【答案】【详解】∵向量a 、b 满足0⋅= a b ,||1,||2== ab,∴|2|-== a b【点评】考查向量模的求法.(详见《军考突破》中5-1-6) 13.【答案】34【详解】由[sin 242θθππ∈=,,,∴s i n c o s 1s i n 2i n θθθθ+=-=-∴1113sin 2224θ====(((. 【点评】考查三角恒等式的应用变形.(详见《军考突破》中4-2-2)14.【答案】30-【详解】展开式中含有3x 的项为:333333356102030(-)(-)+=--=-C x C x x x x ,∴含3x 的项的系数为30-.【点评】考查二项展开式的通项.(详见《军考突破》中7-2-2) 15.【答案】1625【详解】如图,设等腰直角三角形∆AM N 的底边20MN t t =>(),则椭圆2244+=x y 上点N 的坐标为2t t -(,),从而有22244t t -+=(),解得45=t ,所以∆AM N 的面积是21625=t .【点评】考查椭圆的标准方程及顶点坐标,以及三角形的面积公式.(详见《军考突破》中12-1-4) 三、解答题 16.【详解】- 112 -(1)函数21()=-x f x 的值域为1+∞(-,), 由21=-x y ,解得2log 1x y =+(), ∴12log 11f x x x -=+>-()()(). 任取121-<<x x ,111122122221()log 1log 1log 1x f x f x x x x --+-=+-+=+()()(). ∵121-<<x x∴12011<+<+x x , ∴121011+<<+x x . ∴1221log 01+<+x x ,可得1112f x f x --<()(), 故1()-f x 在定义域1+∞(-,)上为单调增函数.(2)∵1f xg x -≤()(),即2log 1x +()4log 31x +≤(),即2log 1x +()4log 31x +≤() ∴210310131x x x x +>⎧⎪+>⎨⎪++⎩≤(),解之得01x ≤≤,∴x 的取值集合为[01],=D . 【点评】考查反函数和函数的单调性及对数不等的解法.(详见《军考突破》中2-5-5,2-5-7,6-3-4) 17.【详解】 (1)在ABC △中,由正弦定理sin sin =b cB C,及已知条件sin =B C 可得=b 又∵,-=ac ∴2=ac由余弦定理222222cos 2+-===b c a A bc .(2)在ABC △中,由(1)知cos=A sin =A又221cos22cos 114=-=-=-A A .sin 22sin cos 2===A A A- 113 -∴cos 2cos2cos sin 2sin 666A A A πππ-=⋅+⋅()1142=-= 【点评】考查正弦定理与余弦定理.(详见《军考突破》中4-5-1、4-5-2)18.【详解】(1)方程2560-+=x x 的两根为1223x x ==, 由题意得2423a a ==,设等差数列{}n a 的公差为d ,则42122-==a a d ∴211222122n a a n d n n =+-=+-⨯=+()().(2)设数列{}2n n a 的前n 项和为nS ,由(1)知1222++=n n n a n . 23134122222①+++=++++ n n n n n S 34121341222222②++++=++++ n n n n n S①-②得3412131112242222()+++=++++- n n n n S 34123111242222(+++=++++- n n n 34123111242222(+++=++++- n n n 34123111242222(+++=++++- n n n ∴1422++=-n n n S . 【点评】考查由n S 求n a 和裂项相消法求数列的前n 项的和.(详见《军考突破》中3-4-1、3-4-7) 19.【详解】(1)由题意2||2-=a b ,即22()-= a b∴22-22⋅+= a a b b∵向量cos sin a αα=(,),cos sin b ββ= (,)0βα<<<π,. ∴2222=||||11=2++=+ a b a b ∴0⋅= a b ,∴⊥ a b .- 114 -(2)∵cos sin a b αα+=+(,)cos sin ββ=(,)cos cos sin sin αβαβ++=(,)01)(, ∴cos cos 0sin sin 1αβαβ+=⎧⎨+=⎩∴cos cos sin sin 1αβαβ=-⎧⎨+=⎩∵0βα<<<π∴1sin sin 2αβαβ=π-⎧⎪⎨==⎪⎩∴566αβππ==,. 【点评】考查向量平行及向量的数量积的运算.(详见《军考突破》中5-1-6、5-1-8)20.【详解】(1)设A 表示事件“抛掷2次,求向上的数之和为6”向上的数之和为6的结果有(1,5)、(2,4)、(3,3)、(4,2)、(5,1)5种连续抛掷2次总的结果共有6×6=36种,A 36()=P . (2)设B 表示事件“抛掷5次,求向上的数为奇数恰好出现3次”. 每次抛掷向上的数为奇数和偶数的概率都是12可看作5次独立重复试验中,事件“向上的数为奇数”恰好出现3次.则3325511105B 3C 1223216P P ==⨯⨯-==()()(. ∴连续抛掷5次,向上的数为奇数恰好出现3次的概率为516. 【点评】考查独立重复试验的概率.(详见《军考突破》中8-1-6) 21.【详解】(1)在正方形ABCD 中,连接AC 交BD 于O ,连接EO. 因为ABCD 是正方形,所以O 为AC 的中点. 又因为 E 为PC 的中点,所以EO//PA.∵⊄PA 平面EDB ,⊂EO 平面EDB ,∴∥PA 平面EDB .- 115 -(2)∵平面⊥PDC 平面ABCD ,且平面 PDC 平面=ABCD CD , 在平面ABCD 中,⊥BC DC ∴⊥BC 平面PDC , 又∵⊂DE 平面PDC , ∴⊥BC又∵=PD DC ,E 是PC 的中点, ∴⊥PC DE在平面PBC 中,,= BC PC C∴⊥DE 平面PBC , ∴⊥PB DE又∵⊥EF PB ,且在平面EFD 中,,= DE EF E∴⊥PB 平面EFD .【点评】考查平面与平面平行和直线与平面垂直的判定.(详见《军考突破》中10-2-2、10-2-3) 22.【详解】 (1)由题意可知bc a==,∵222+=a b c ∴22113a b ==,,∴双曲线的标准方程为2231-=x y . (2)由22131=+⎧⎨-=⎩y kx x y 得223220k x kx ---=() 由230-≠k 且0∆>,得<k ≠k , 设1122A x y B x y (,),(,) ∵以AB 为直径的圆过原点,OA OB ,- 116 -∴0⋅=OA OB ,即12120+=x x y y 又∵1212222233k x x x x k k +=-=--, ∴2121212121111y y kx k x k x x k x x =++=+++=()()() ∴22103+=-k ,解得1=±k . 故当1=±k 时,以AB 为直径的圆过原点. 【点评】考查双曲线的标准方程和直线与双曲线相交的问题.(详见《军考突破》中12-2-4、12-4-5)。