信号与系统大作业

1试分别指出以下波形是属于哪种信号？

题图1-1

1-2 试写出题1-1 图中信号的函数表达式。

1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示，试作出下列各信号的波形图，并加以标注。

题图1-3

⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)

⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)

2

⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)

2

1- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。

题图1-4

⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)

2

⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)

⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)

1- 5 已知信号x(5 2t )的波形如题图1-5 所示，试作出信号x(t)的波形图，并加以标注。

题图1-5

1- 6 试画出下列信号的波形图：

1

⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)

2

1

⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )

1-7 试画出下列信号的波形图：

⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]

⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)

⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)

信号与系统专题练习题

一、选择题

1．设当t 〈3时，x(t)=0，则使)2()1(t x t x -+-=0的t 值为 C 。 A t>-2或t>-1 B t=1和t=2 C t>—1 D t 〉-2

2．设当t 〈3时，x （t)=0，则使)2()1(t x t x -⋅-=0的t 值为 D 。 A t>2或t 〉-1 B t=1和t=2 C t>—1 D t>—2

3．设当t<3时，x(t ）=0，则使x （t/3)=0的t 值为 C 。 A t>3 B t=0 C t<9 D t=3

4．信号)3/4cos(3)(π+=t t x 的周期是 C 。A π2 B π C 2/π D π/2 5．下列各表达式中正确的是 B

A. )()2(t t δδ= B 。 )(21)2(t t δδ= C. )(2)2(t t δδ= D 。 )2(21

)(2t t δδ=

6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B . A 线性时不变系统 B 线性时变系统 C 非线性时不变系统 D 非线性时变系统 7。 已知 系统的激励e(t ）与响应r （t)的关系为:)()(2t e t r = 则该系统为 C .

A 线性时不变系统

B 线性时变系统

C 非线性时不变系统

D 非线性时变系统

8。 ⎰∞

-=t d ττ

τ

τδ2sin )

( A 。 A 2u （t ） B )(4t δ C 4 D 4u （t) 10. dt t t )2(2

信号与系统习题集

第一章作业

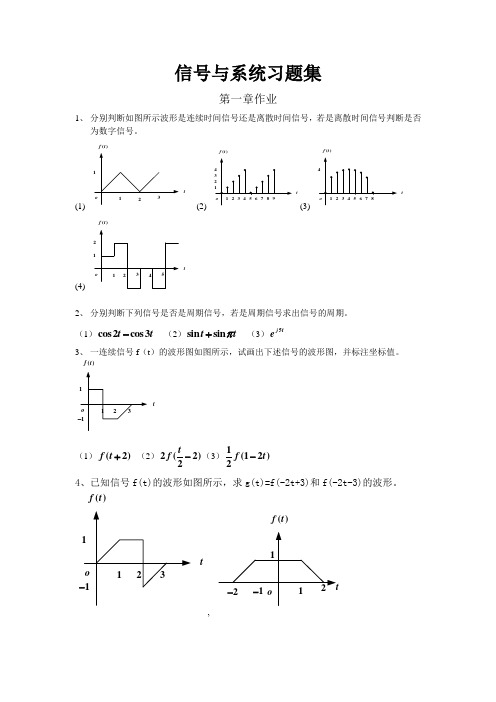
1、 分别判断如图所示波形是连续时间信号还是离散时间信号，若是离散时间信号判断是否

为数字信号。

(1)

t

()

f t (2) t

()

f t

(3) t

()

f t

(4) t

()

f t

2、 分别判断下列信号是否是周期信号，若是周期信号求出信号的周期。 （1）cos 2cos 3t t - （2）sin sin t t π+ （3）5j t

e

3、 一连续信号f （t ）的波形图如图所示，试画出下述信号的波形图，并标注坐标值。

t

()

f t

（1）(2)f t + （2）2(2)2t f -（3）

1

(12)2

f t

- 4、已知信号f(t)的波形如图所示，求g(t)=f(-2t+3)和f(-2t-3)的波形。

t

()

f t

,

()

f t

5、写出如图所示的各波形的函数式。

（1）t

()

f t

（2）t

()

f t

-

6、画出下列各时间函数的波形。

（1）[](1)(2)t u t u t ---，（2）[]

(1)(2)(2)t u t u t u t ---+- （3）[]

(3)()(2)t u t u t --- 7、求下列函数值。 （1）2()()t

d r t

e u t dt

-⎡⎤=

⎣⎦，（2）3()()t r t e t δ-= （3）()cos ()4

r t t t dt π

δ∞

-∞

=

-

⎰

，（4）2()()(1)t

r t t e t dt δ∞

--∞

=+-⎰, ( 5 ) 3'()()t r t e t δ=

8、画出下列系统的仿真框图。

()()

3()2()dr t de t r t e t dt dt

信号与系统练习题（带答案）

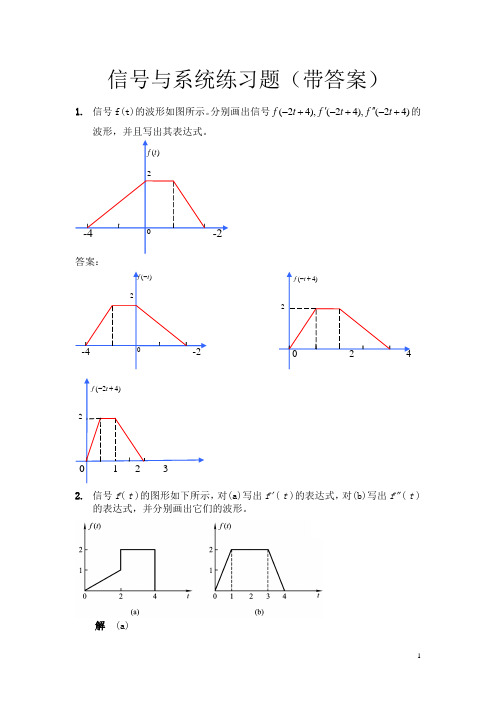
1. 信号f(t)的波形如图所示。分别画出信号(24),(24),(24)f t f t f t '''-+-+-+的

波形，并且写出其表达式。

答案：

2. 信号f ( t )的图形如下所示，对(a)写出f ' ( t )的表达式，对(b)写出f " ( t )

的表达式，并分别画出它们的波形。

解 (a)

20,2

1≤≤t

f ' (t

)= δ(t -2)， t = 2

-2δ(t -4)， t = 4

(b) f " (t ) = 2δ(t ) - 2δ(t -1)-2δ(t -3)+2δ(t -4)

3. 已知f(5-2t)的波形如图所示，试画出f(t)的波形。

52

:()(2)(2)(52)

5

2522

5

2

:(52)(2)(2)()

f t f t f t f t t t

f t f t f t f t −−−→−−−→-−−−→---=-∴-→-→→ 压缩反转平移

左移

反转

拉伸

分析（）右移

求解过程

55

[52()]2,22

t t t t -+=-∴+ 以代替

而求得－2t ，即f(5-2t)左移

(52)(2)f t f t -−−−→-时移

由

（2）反转：f(-2t)中以-t 代替t ，可求得f(2t),表明f(-2t)的波形 以t ＝0的纵轴为中心线对褶，注意()t δ是偶数，故

11

2()2()22

t t δδ--=+

(2)(2)f t f t -−−−→反褶

由

（3）尺度变换：以1

2

t 代替f(2t)中的t ，所得的f(t)波形将是f(2t)波形在时

间轴上扩展两倍。

4. 求序列{}12[]1,2,1,0,1,2[][1cos()][]2f n n f n n u n π

第一章 信号与系统

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。 （2）∞<<-∞=-t e

t f t

,)( （3）)()sin()(t t t f επ=

（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k

ε= （10）)(])1(1[)(k k f k

ε-+=

解：各信号波形为

（3）)()sin()(t t t f επ=

（4）)(sin )(t t f ε=

（5）)(sin )(t r t f =

（7）)(2)(k t f k ε=

（10）)(])1(1[)(k k f k ε-+=

1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）

)]7()()[6

sin(

)(--=k k k k f εεπ

（12）

)]()3([2)(k k k f k

---=εε 解：各信号波形为

（1）)2()1(3)1(2)(-+--+=t t t t f εεε

（2）

)2()1(2)()(-+--=t r t r t r t f

（5）

)2()2()(t t r t f -=ε

（8）

)]5()([)(--=k k k k f εε

第一章 信号与系统

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。 （2）∞<<-∞=-t e

t f t

,)( （3）)()sin()(t t t f επ=

（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k

ε= （10）)(])1(1[)(k k f k

ε-+=

解：各信号波形为

（3）)()sin()(t t t f επ=

（4）)(sin )(t t f ε=

（5）)(sin )(t r t f =

（7）)(2)(k t f k ε=

（10）)(])1(1[)(k k f k ε-+=

1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）

)]7()()[6

sin(

)(--=k k k k f εεπ

（12）

)]()3([2)(k k k f k

---=εε 解：各信号波形为

（1）)2()1(3)1(2)(-+--+=t t t t f εεε

（2）

)2()1(2)()(-+--=t r t r t r t f

（5）

)2()2()(t t r t f -=ε

（8）

)]5()([)(--=k k k k f εε

（11）

)]7()()[6

第一章 信号与系统

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。 （2）∞<<-∞=-t e

t f t

,)( （3）)()sin()(t t t f επ=

（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k

ε= （10）)(])1(1[)(k k f k

ε-+=

解：各信号波形为

（3）)()sin()(t t t f επ=

（4）)(sin )(t t f ε=

（5）)(sin )(t r t f =

（7）)(2)(k t f k ε=

（10）)(])1(1[)(k k f k ε-+=

1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）

)]7()()[6

sin(

)(--=k k k k f εεπ

（12）

)]()3([2)(k k k f k

---=εε 解：各信号波形为

（1）)2()1(3)1(2)(-+--+=t t t t f εεε

（2）

)2()1(2)()(-+--=t r t r t r t f

（5）

)2()2()(t t r t f -=ε

（8）

)]5()([)(--=k k k k f εε

1、 若系统的输入f (t)、输出y (t) 满足()3()4t y t e f

t -=，则系统为 线性的 （线性的、非线性

的）、 时变的 （时变的、时不变）、 稳定的 （稳定的、非稳定的）。

2、 非周期、连续时间信号具有 连续 、非周期频谱；周期、连续时间信号具有离散、非周期 频谱；

非周期、离散时间信号具有 连续 、周期频谱；周期、离散时间信号具有离散、 周期 频谱。 3、 信号f(t)的占有频带为0-10KHz,被均匀采样后,能恢复原信号的最大采样周期为 5×10-5 s . 4、 )100()(2

t Sa t f =是 能量信号 （功率信号、能量信号、既非功率亦非能量信号）。 5、 ()2cos()f t t =+是 功率信号 （功率信号、能量信号、既非功率亦非能量信号）。 6、 连续信号f(t)=sint 的周期T 0= 2π ,若对f(t)以fs=1Hz 进行取样，所得离散序列f(k)=

sin(k) ,该离散序列是周期序列？ 否 。

7、 周期信号2sin(/2)()j n t

n n f t e n ππ+∞

=-∞

=

∑，此信号的周期为 1s 、直流分量为 2/π 、频率为5Hz 的谐波分量的幅值为 2/5 。 8、 f (t) 的周期为0.1s 、傅立叶级数系数**033555

32F F F F F j --=====、其余为0。试写

出此信号的时域表达式f (t) = 5 + 6 cos ( 60 π t ) - 4 sin (100 π t ) 。 9、 f (k) 为周期N=5的实数序列，若其傅立叶级数系数()205=F ()5

大作业

第一章

基本题

计算卷积积分：

s(t)=f1 (t)*f2(t)

f1(t)=sinπt[u(t)-u(t-1)],f2(t)=(t-1)+δ(t+2)

解：s(t)=sin（t-1）[u(t-1)-u(t-2)]+sin(t+2)[u(t+2)-

u(t+1)]= f1(t-1)+f1(t+2)

综合题

已知f(t)和h(t)波形如下图所示，请计算卷积f(t)*h(t)，并画出f(t)*h(t)波形。

详细步骤如下：

第二章

基本题

描述某系统的微分方程为 y”(t) + 4y’(t) + 3y(t) = f(t) 求当f(t) = 2e-2t，t≥0；y(0)=2，y’(0)= -1时的解

解: (1) 特征方程为λ2 + 4λ+ 3 = 0 其特征根λ1=–1，λ2=–2。齐次解为

y h(t) = C1e -t + C2e -3t

当f(t) = 2e–2 t时，其特解可设为

y p(t) = Pe -2t

将其代入微分方程得

P*4*e -2t + 4(–2Pe-2t)+3Pe-t =2e-2t

解得 P=2

于是特解为 y p(t) =2e-t

全解为： y(t) = y h(t) + y p(t) = C1e-t+ C2e-3t + 2e-2t

其中待定常数C1,C2由初始条件确定。

y(0) = C1+C2+ 2 = 2，

y’(0) =–2C1–3C2–1=–1

解得 C1 =1.5，C2 =–1.5

最后得全解y(t)=1.5e – t –1.5e – 3t +2 e –2 t ,t ≥0 综合题

如图系统，已知

一、题目

1.已知信号f(t)=sin(20πt)+sin(80πt)，用如图所示的采样频率为fs=100Hz，大小为1的信号对其进行采

样，使用MATLAB编程，

（1）绘制采样后的信号时域上的波形图；

（2）对采样后的信号进行频谱分析，画出其幅度谱；

（3）要从采样信号中恢复出原始信号f(t)，在MATLAB中设计滤波器，画出滤波后的幅度谱；

（4）将信号f(t)加载到载波信号s(t)=cos(500πt)上，画出调制后信号的波形图和幅度谱。

二、原理

1、信号的采样

“取样”就是利用从连续时间信号f(t)中“抽取”一系列离散样本值的过程。这样得到的离散信号称为取样信号。采样信号f(t)可以看成连续信号f(t)和取样脉冲序列s(t)的乘积。其中取样脉冲序列s(t)也称为开关函数。如果其各脉冲间隔时间相同，均为Ts，就称为均匀取样。Ts称为取样周期，fs=1/Ts 称为取样频率或取样率，ωs=2πfs=2π/Ts称为取样角频率。

如果f(t)↔F(jω)，s(t)↔S(jω)，则由频域卷积定理，得取样信号fs(t)的频谱函数为

本题的取样脉冲序列s(t)是周期为Ts=0.01s的冲激函数序列δTs，也就是冲激取样。而冲激序列δTs（这里T=Ts，Ω=2π/Ts=ωs）的频谱函数也是周期冲激序列，即

2、采样定理

所谓模拟信号的数字处理方法就是将待处理模拟信号经过采样、量化和编码形成数字信号，再利用数字信号处理技术对采样得到的数字信号进行处理。

一个频带限制在(0,fc)Hz的模拟信号m(t)，若以采样频率fs≥2fc对模拟信号m(t)进行采样，得到最终的采样值，则可无混叠失真地恢复原始模拟信号m(t)。

《信号与系统》第二版(郑君里著)课后答案下载《信号与系统》第二版内容提要

第七章离散时间系统的时域分析

7.1 引言

7.2 离散时间信号——序列

7.3 离散时间系统的数学模型

7.4 常系数线性差分方程的求解

7.5 离散时间系统的单位样值(单位冲激)响应

7.6 卷积(卷积和)

7.7 解卷积(反卷积)

习题

第八章 z变换、离散时间系统的z域分析

8.1 引言

8.2 z变换定义、典型序列的z变换

8.3 z变换的收敛域

8.4 逆z变换

8.5 变换的基本性质

8.6 z变换与拉普拉斯变换的'关系

8.7 利用z变换解差分方程

8.8 离散系统的系统函数

8.9 序列的傅里叶变换(DTFT)

8.10 离散时间系统的频率响应特性

习题

第九章离散傅里叶变换以及其他离散正交变换 9.1 引言

9.2 傅里叶变换的离散性与周期性

9.3 从离散傅里叶级数到离散傅里叶变换

9.4 离散傅里叶变换的性质

9.5 离散傅里叶变换与z变换的关系

9.6 快速傅里叶变换(FFT)

9.7 离散傅里叶变换的应用

9.8 沃尔什变换及其应用举例

9.9 离散余弦变换(DCT)

习题

第十章模拟与数字滤波器

10.1 引言

10.2 无源一端口模拟网络综合

10.3 无源二端口模拟网络综合

10.4 模拟滤波器的逼近

10.5 模拟滤波器的频率变换与元件变换 10.6 无限冲激响应(IIR)数字滤波器

10.7 有限冲激响应(FIR)数字滤波器

10.8 RC有源滤波器

10.9 开关电容滤波器(SCF)

习题

第十一章反馈系统

11.1 引言

11.2 反馈系统的基本特性及其应用

《信号与系统》学习报告

《信号与系统》学习报告

姓名：

班级：

学号：

⼀、概述

在从事科学研究过程中，科学家们借助⼀定的⼯具⼿段或通过⼀定的思维⽅式不断发现新现象、新事物，提出新理论、新观点。科学家们揭⽰事物内在规律的“过程”被学者们提炼、总结为了“科学研究⽅法”。

“科学研究⽅法”的存在有利于学术规范的形成，有利于各门学科的可持续发展。从科研⾓度来讲，科学研究⽅法的优劣直接影响着科学研究的效果和效率；从学术⾓度来讲，科学研究⽅法的理解有助于对该学科的深⼊探讨。

《信号与系统》这门课程在介绍信号与系统分析的基本知识和⽅法的同时，实际上反映了许多科学研究的思维⽅法和规律[1]。因此，通过对这门课的知识内容所⽤“科学研究⽅法”的讨论和分析，学习科学家们建⽴模型、分析问题的思维⽅式和⼿段是⾮常有必要的。

傅⾥叶变换与拉普拉斯变换是《信号与系统》这门课程的核⼼内容，也是处理数学问题和⼯程问题不可或缺的理论⼯具。本⽂主要分析在傅⾥叶变换及拉普拉斯变换的研究过程中所涉及的科学研究⽅法。

⼆、科学研究的⽅法

我们主要举例探讨以下三种科学研究⽅法或思想：

（1）“变换”概念的引⼊：类⽐于空间变换、正交分解的思想；

（2）“傅⾥叶变换”的引⼊：改变观察问题的参照系；

（3）从傅⾥叶变换推⼴到拉普拉斯变换：将局部规律推⼴到全局。

三、在课本内容中的体现与应⽤

1.类⽐思想

有时⼈们说，科学的解释在于产⽣⼀种还原，将⼀个疑难的不熟悉的现象还原为我们已经熟悉的事实和原理[2]。⽐如玻尔的氢原⼦模型与⾏星绕⽇轨道、波动理论与⽔波的传播，将不熟悉的理论模型“类⽐于”某个熟悉的现象。在某些特定的情况

信号与系统试题库及答案

信号与系统试题库及答案，共22页

1.下列信号的分类办法不正确的是（A ）：

A 、数字信号和离散信号

B 、确定信号和随机信号

C 、周期信号和非周期信号

D 、因果信号与反因果信号

2.下列说法正确的是（D ）：

A 、两个周期信号x(t)，y(t)的和x(t)+y(t)一定是周期信号。

B 、两个周期信号x(t)，y(t)的周期分离为2和，则其和信号

x(t)+y(t) 是周期信号。

C 、两个周期信号x(t)，y(t)的周期分离为2和，其和信号x(t)+y(t)是周期信号。

D 、两个周期信号x(t)，y(t)的周期分离为2和3，其和信号x(t)+y(t)是周期信号。

3.下列说法不正确的是（D ）。

A 、普通周期信号为功率信号。

B 、时限信号(仅在有限时光区间不为零的非周期信号)为能量信号。

C 、ε(t)是功率信号；

D 、et 为能量信号;

一、填空（每空1分，共15分）

1、离散信号基本运算有

；；；四种。

2、拉氏变换中初值定理、终值定理分离表示为

)(lim )0(S SF f S ∞→=，；)(l i m )(0S SF f S →=∞ 。

3、延续系统的分析办法有

时域分析法；频域分析法和

复频域分析法。这三种分析办法，其输入与输出表达式分离是

y(t)=h(t)*f(t); Y(jω)= H(jω)?. F(jω); Y(s)= H(s)?. F(s)

集美高校2022—2022学年第2学期信号与系统试卷及答案

一、推断题(共9分，每题1.5分，对的打“V ”，错的打“X ”)。

1、一个信号的脉冲持续时光越小，它的频带宽度也就越小。（× ）

1-8 试判断下列信号中哪些为能量信号，哪那些为功率信号，或者都不是。

方法二：

由已知条件知道：当12(0)5,(0)3y y ==时的零输入响应为

12333(0)5(0)3(0)5(23)3(42)229,0t

t

t

t

t

t

x x x y y y e

e

e

e

e

e

t ------=+=++-=+>

以（1）为例按照定义说明线性、时不变性和因果性。

线性：设112212[]2[],[]2[];[][][]k k y k f k y k f k f k f k f k αβ===+

121212[]2{[][]}2[]2[][][]k

k

k

y k f k f k f k f k y k y k αβαβαβ=+=+=+

属于线性；

时不变性：

100001[]{[]}2[][]2

[][]

k

k k y k T f k k f k k y k k f k k y k -=-=--=-≠

因果性：[]2[]k y k f k =，输出不超前输入，因此为因果系统。

第二章

第三章

（1） 解：微分方程的特征方程为：2

320s s ++=，特征根1,21,2s =--

齐次解形式为：2(),0t t h y t Ae Be t --=+>

输入信号()()f t u t =，特解为(),0p y t C t =>，'()''()0p p y t y t ==。

将特解及其导数代入微分方程：0+0+2C=1，C=1/2，特解为()1/2,0p y t t =>。 全解形式为： 2()()()1/2,0t t h p y t y t y t Ae Be t --=+=++>，2'()2t t y t Ae Be --=-- 代入初始条件：(0)1/21,'(0)21y A B y A B =++==--=

《信号与系统》课程习题与解答

第三章习题

(教材上册第三章p160-p172)

3-1～3-3,3-5,3-9,3-12,3-13,3-15～3-17,3-19,3-22,3-24,3-25,3-29,3-32

第三章习题解答

3-2 周期矩形信号如题图3-2所示。 若：

求直流分量大小以及基波、二次和三次谐波的有效值。

解：直流分量

⎰⎰--=⨯==

22223

01105)(1τ

τv Edt dt t f T a T

T

f(t)为偶函数，∴

0=n b

)

(2cos )(222T n Sa T E tdt n t f T a n πττωττ⎰-==

)

(21T n Sa T E a F n n πςτ== 基波 =1a )

1.0s i n (20

)(2πππττ=T Sa T E

有效值 39

.11.0sin 22021≈=ππa

二次谐波有效值 32

.122

≈a

三次谐波有效值 21

.12

3≈a

3-3 若周期矩形信号)(1t f 和 )(2t f 波形如题图3-2所示，)(1t f 的参数为s μτ5.0=，

s T μ1=，E=1V ；)(2t f 的参数为s μτ5.1=，s T μ3=，E=3V ，分别求：

（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3） )(1t f 和 )(2t f 的基波幅度之比； （4） )(1t f 基波与)(2t f 三次谐波幅度之比。

解：（1）)(1t f s μτ5.0= s T μ1= E=1V 谱线间隔：

1073 20211

单项选择题

1、

设是信号的傅里叶变换，的波形如图所示，则等于（）。

1.4pi

2.2pi

3.6pi

4.0

2、完整表示对理想滤波器的逼近，可以采用（）

1.误差容限图

2.阻带最小衰减

3.对模拟与数字滤波器要区别对待

4.通带内最大误差

3、冲激函数的单边（下限规定为从0-时刻开始）拉氏变换为

1.js

2.0

3.s

4.1

4、下列滤波器中，通带最平坦的是（）

1.巴特沃思

2.贝塞尔滤波器

3.椭圆滤波器

4.切比雪夫

5、等于（）

1. F. 1

2.0

3.e^-5

4.e^-1

6、（）

1.f(-1)

2.f(1)

3.0

4.f(0)

7、已知信号x(t)的傅里叶变换为，则信号y(t)的频谱

为（）。

1.R(w)cos(w)

2.R(w)/2

3.R(w/2)

4.R(w)

8、关于抽样，下列说法错误的是（）

1. E. 理想的冲激采样可表示零阶保持抽样，二者的频谱变化是一致的。

2.时域抽样，频域会产生周期延拓

3.频域抽样，时域会产生周期延拓

4.由时域抽样可知，序列的频谱是周期连续的频谱

9、已知，则等于（）

1.2pi

2.0

3.1/2

4.1

10、周期信号的波形如图所示，则其傅里叶级数中含有（）。

1.正弦分量与余弦分量

2.直流分量与正弦分量

3.奇次谐波分量

4.直流分量与余弦分量

11、从S域到Z域的映射中，为保证映射前后滤波器的稳定性不变，则应满足

（）

1.s域左半平面映射到z域的单位圆内，虚轴到单位圆外

2.s域左半平面映射到z域的单位圆外，虚轴到单位圆内

3.s域左半平面映射到z域的单位圆外部，虚轴到单位圆

4.s域左半平面映射到z域的单位圆内，虚轴到单位圆