22.3实际问题与一元二次方程1作业设计

22.3 实质问题与二次函数第 1课时教课目标：1．使学生掌握用待定系数法由已知图象上一个点的坐标求二次函数y＝ ax2的关系式。

2.使学生掌握用待定系数法由已知图象上三个点的坐标求二次函数的关系式。

3．让学生体验二次函数的函数关系式的应用，提升学生用数学意识。

要点难点：要点：已知二次函数图象上一个点的坐标或三个点的坐标，分别求二次函数y＝ ax2、y＝ ax2＋b x ＋ c 的关系式是教课的要点。

难点：已知图象上三个点坐标求二次函数的关系式是教课的难点。

教课过程：一、创建问题情境如图，某建筑的屋顶设计成横截面为抛物线型( 曲线 AOB)的薄壳屋顶。

它的拱高AB 为4m，拱高 CO为 0.8m。

施工前要先制造建筑模板，如何画出模板的轮廓线呢?分析：为了画出吻合要求的模板，平时要先建立合适的直角坐标系，再写出函数关系式，而后依据这个关系式进行计算，放样画图。

以下列图，以AB的垂直均分线为y 轴，以过点 O 的 y 轴的垂线为 x 轴，建立直角坐标系。

这时，屋顶的横截面所成抛物线的极点在原点，对称轴是 y 轴，张口向下，所以可设它的函数关系式为：y ＝ ax2 (a＜ 0) (1)AB因为 y 轴垂直均分AB，并交 AB于点 C，所以 CB2＝ 2(cm) ，又 CO＝ 0.8m，所以点 B ＝的坐标为 (2 ，－ 0.8) 。

因为点 B 在抛物线上，将它的坐标代人(1) ，得－0.8＝a×22所以a＝－0.2所以，所求函数关系式是y＝－ 0.2x 2。

二、引申拓展问题 1：能不可以以A点为原点， AB所在直线为x 轴，过点 A 的 x 轴的垂线为y 轴，建立直角坐标系 ?让学生认识建立直角坐标系的方法不是独一的，以 A 点为原点， AB所在的直线为x 轴，过点 A 的 x 轴的垂线为y 轴，建立直角坐标系也是可行的。

问题 2，若以 A 点为原点， AB所在直线为x 轴，过点 A 的 x 轴的垂直为y 轴，建立直角坐标系，你能求出其函数关系式吗?分析：按此方法建立直角坐标系，则 A 点坐标为 (0 ， 0) ，B 点坐标为 (4 ， 0),OC 所在直线为抛物线的对称轴，所以有AC＝CB， AC＝2m， O点坐标为 (2 ； 0． 8) 。

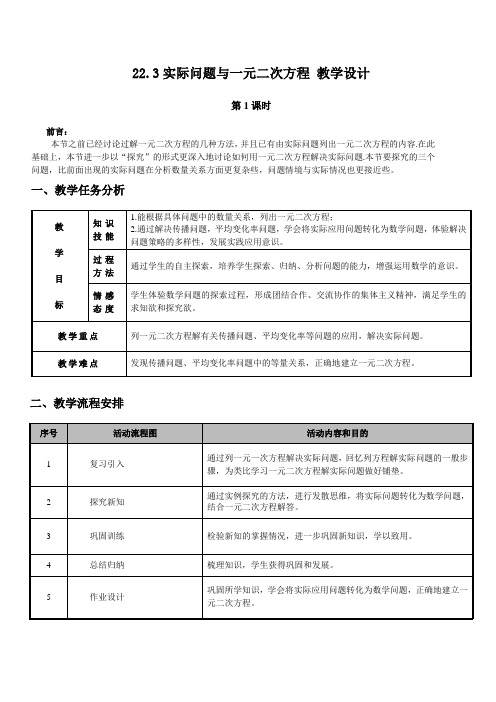
6000元，随着生产技术的进步，现在生产1吨甲种药品的成本是3000元，生产1吨乙种药品的成本是3600元，哪种药品成本的年平均下降率较大？(1)如何理解年平均下降额与年平均下降率？它们相等吗？(2)若设甲种药品年平均下降率为x，则一年后，甲种药品的成本下降了________元，此时成本为________元；两年后，甲种药品下降了________元，此时成本为________元．(3)增长率(下降率)公式的归纳：设基准数为a，增长率为x，则一月(或一年)后产量为a(1±x)；二月(或二年)后产量为a(1±x)2；n月(或n年)后产量为a(1±x)n；如果已知n月(n年)后总产量为M，则有下面等式：M＝a(1±x)n.(4)对甲种药品而言根据等量关系列方程为：________________.活动1创设情境1．长方形的周长________，面积________，长方体的体积公式________．2．如图所示：(1)一块长方形铁皮的长是10 cm，宽是8 cm，四角各截去一个边长为2 cm 的小正方形，制成一个长方体容器，这个长方体容器的底面积是________，高是________，体积是________．(2)一块长方形铁皮的长是10 cm，宽是8 cm，四角各截去一个边长为x cm 的小正方形，制成一个长方体容器，这个长方体容器的底面积是________，高是________，体积是________．活动2自学教材第20页～第21页探究3，思考老师所提问题要设计一本书的封面，封面长27 cm，宽21 cm，正中央是一个与整个封面长宽比例相同的矩形，如果要使四周的彩色边衬所占面积是封面面积的四分之一，上下边衬等宽，左右边衬等宽，应如何设计四周边衬的宽度(精确到0.1 cm)．(1)要设计书本封面的长与宽的比是________，则正中央矩形的长与宽的比是________．(2)为什么说上下边衬宽与左右边衬宽之比为9∶7？试与同伴交流一下．(3)若设上、下边衬的宽均为9x cm，左、右边衬的宽均为7x cm，则中央矩形的长为________cm，宽为________cm，面积为________cm2.(4)根据等量关系：________，可列方程为：________.(5)你能写出解题过程吗？(注意对结果是否合理进行检验．)(6)思考如果设正中央矩形的长与宽分别为9x cm和7x cm，你又怎样去求上下、左右边衬的宽？活动3变式练习如图所示，在一个长为50米，宽为30米的矩形空地上，建造一个花园，要求花园的面积占整块面积的75%，等宽且互相垂直的两条路的面积占25%，求路的宽度．答案：路的宽度为5米．作业布置教材第21－22页习题21.3第2－7题．课堂总结．列一元二次方程解应用题的步骤：审、设、找、列、解、答．最后要检验根是否符合实际．．传播问题解决的关键是传播源的确定和等量关系的建立．．若平均增长(降低)率为x，增长(或降低)前的基准数是a，增长(或降低)n 次后的量是b，则有：a(1±x)n＝b(常见n＝2)．．成本下降额较大的药品，它的下降率不一定也较大，成本下降额较小的药品，它的下降率不一定也较小．．利用已学的特殊图形的面积(或体积)公式建立一元二次方程的数学模型，并运用它解决实际问题的关键是弄清题目中的数量关系．．根据面积与面积(或体积)之间的等量关系建立一元二次方程，并能正确解方程，最后对所得结果是否合理要进行检验．。

22．3 实际问题与二次函数第1课时几何图形的最大面积1．经历数学建模的基本过程，能分析实际问题中变量之间的二次函数关系．2．会运用二次函数求实际问题中的最大值或最小值．3．能应用二次函数的性质解决图形中最大面积问题．一、情境导入孙大爷要围成一个矩形花圃．花圃的一边利用足够长的墙，另三边用总长为32米的篱笆恰好围成．围成的花圃是如图所示的矩形ABCD.设AB边的长为x米，矩形ABCD 的面积为S平方米．当x为何值时，S有最大值？并求出最大值．二、合作探究探究点：最大面积问题【类型一】利用二次函数求最大面积小李想用篱笆围成一个周长为60米的矩形场地，矩形面积S(单位：平方米)随矩形一边长x(单位：米)的变化而变化．(1)求S与x之间的函数关系式，并写出自变量x的取值范围；(2)当x是多少时，矩形场地面积S最大最大面积是多少解析：利用矩形面积公式就可确定二次函数．(1)矩形一边长为x，则另一边长为60－2x2，从而表示出面积；(2)利用配方法求出顶点坐标．解：(1)根据题意，得S＝60－2x2·x＝－x2＋30x.自变量x的取值范围是0＜x＜30.(2)S＝－x2＋30x＝－(x－15)2＋225，∵a＝－1＜0，∴S有最大值，即当x＝15(米)时，S最大值＝225平方米．方法总结：二次函数与日常生活的例子还有很多，体现了二次函数这一数学模型应用的广泛性．解决这类问题关键是在不同背景下学会从所给信息中提取有效信息，建立实际问题中变量间的二次函数关系．【类型二】利用二次函数判断面积取值成立的条件(2014·江苏淮安)用长为32米的篱笆围一个矩形养鸡场，设围成的矩形一边长为x米，面积为y平方米．(1)求y关于x的函数关系式；(2)当x为何值时，围成的养鸡场面积为60平方米？(3)能否围成面积为70平方米的养鸡场？如果能，请求出其边长；如果不能，请说明理由．解析：(1)先表示出矩形的另一边长，再利用矩形的面积公式表示出函数关系式；(2)已知矩形的面积，可以转化为解一元二次方程；(3)求出y的最大值，与70比较大小，即可作出判断．解：(1)y＝x(16－x)＝－x2＋16x(0＜x ＜16)；(2)当y＝60时，－x2＋16x＝60，解得x1＝10，x2＝6.所以当x＝10或6时，围成的养鸡场的面积为60平方米；(3)方法一：当y＝70时，－x2＋16x＝70，整理得：x2－16x＋70＝0，由于Δ＝256－280＝－24＜0，因此此方程无实数根，所以不能围成面积为70平方米的养鸡场．方法二：y＝－x2＋16x＝－(x－8)2＋64，当x ＝8时，y有最大值64，即能围成的养鸡场的最大面积为64平方米，所以不能围成70平方米的养鸡场．方法总结：与面积有关的函数与方程问题，可通过面积公式列出函数关系式或方程．【类型三】最大面积方案设计施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM 为12米．现以O 点为原点，OM 所在直线为x 轴建立直角坐标系(如图所示)．(1)直接写出点M 及抛物线顶点P 的坐标；(2)求出这条抛物线的函数关系式； (3)施工队计划在隧道门口搭建一个矩形“脚手架”CDAB ，使A 、D 点在抛物线上，B 、C 点在地面OM 上．为了筹备材料，需求出“脚手架”三根木杆AB 、AD 、DC 的长度之和的最大值是多少，请你帮施工队计算一下．解：(1)M (12，0)，P (6，6)．(2)设这条抛物线的函数关系式为y ＝a (x －6)2＋6，因为抛物线过O (0，0)，所以a (0－6)2＋6＝0，解得，a ＝－16，所以这条抛物线的函数关系式为：y ＝－16(x －6)2＋6，即y ＝－16x 2＋2x .(3)设OB ＝m 米，则点A 的坐标为(m ，－16m 2＋2m )，所以AB ＝DC ＝－16m 2＋2m .根据抛物线的轴对称，可得OB ＝CM ＝m ，所以BC ＝12－2m ，即AD ＝12－2m ，所以l ＝AB ＋AD ＋DC ＝－16m 2＋2m ＋12－2m －16m 2＋2m ＝－13m 2＋2m ＋12＝－13(m －3)2＋15.所以当m ＝3，即OB ＝3米时，三根木杆长度之和l 的最大值为15米．三、板书设计教学过程中，强调学生自主探索和合作交流，引导学生设计有助于学生设计表格，经历计算、观察、分析、比较的过程，直观地看出变化情况.。

22.3 实际问题与一元二次方程223 实际问题与一元二次方程在我们的日常生活和工作中，一元二次方程有着广泛的应用。

它不仅仅是数学课本上的一个知识点，更是解决许多实际问题的有力工具。

比如说，在农业生产中，农民伯伯需要规划田地的种植面积。

假设一块矩形田地，长比宽多 10 米，面积为 500 平方米。

我们就可以设这块田地的宽为 x 米，那么长就是 x ＋ 10 米。

根据矩形面积等于长乘宽，可列出方程 x(x ＋ 10) ＝ 500，通过求解这个一元二次方程，就能算出田地的长和宽，从而更好地进行种植规划。

再比如，在商业领域，一家商店计划销售某种商品。

已知该商品的进价为每件 30 元，售价为每件 50 元时，每天能卖出 200 件。

如果售价每提高 1 元，每天的销量就会减少 10 件。

为了获得每天 2240 元的利润，商品的售价应该定为多少呢？我们可以设售价提高了 x 元，那么单件利润就是 50 ＋ x 30 ＝ 20 ＋ x 元，每天的销量就是 200 10x 件。

根据利润等于单件利润乘以销售量，可得到方程（20 ＋ x)（200 10x)＝ 2240。

解这个方程，就能得出合适的售价，帮助商家制定最优的销售策略。

还有在建筑工程中，要建造一个靠墙的矩形花坛。

如果墙的长度为20 米，花坛的面积需要达到 100 平方米。

设花坛平行于墙的一边长为x 米，那么垂直于墙的一边长就是(100 ／x)米。

因为花坛有一边靠墙，所以花坛的周长为 x ＋ 2(100 ／ x)米。

考虑到材料成本的限制，总周长不能超过 40 米，就可以列出一元二次方程 x ＋ 2(100 ／ x) ＜＝ 40，通过求解这个方程，就能确定花坛边长的合理取值范围，从而在保证美观和实用的前提下，有效地控制成本。

在几何图形问题中，也常常会用到一元二次方程。

例如，一个直角三角形的两条直角边相差 3 厘米，面积为 6 平方厘米。

设较短的直角边为 x 厘米，那么较长的直角边就是 x ＋ 3 厘米。

22.3 实际问题与二次函数（第一课时） 教学设计一、内容和内容解析1.内容本节课是人教版《义务教育教科书•数学》九年级上册（以下统称“教材”）第二十二章“二次函数”22.3 实际问题与二次函数（第一课时），内容包括：利用二次函数解决抛掷问题与几何图形最值．2.内容解析二次函数是描述现实世界变量之间关系的重要数学模型，将实际问题中的变量关系转化为二次函数后，就可以利用二次函数的图象和性质加以解决，其关键是从实际问题中抽象出数学模型．本节课是在学生学习二次函数的图象和性质的基础上，借助于二次函数的图象研究二次函数的最小(大)值，并运用这个结论解决相关的实际问题．以现实生活为背景，通过对投掷、跳水、跳远、拱桥、隧道等抛物线的探究，建立合理的平面直角坐标系，利用待定系数法确定二次函数的表达式是解决此类问题的关键．通过探究矩形面积与矩形一边长两个变量之间的关系，让学生体会运用函数观点解决实际问题的作用，初步体验建立函数模型的过程和方法．基于以上分析，确定本节课的教学重点是：从实际问题中抽象出二次函数关系并运用二次函数的最小(大)值解决实际问题．二、目标和目标解析1.目标1)会求二次函数y ＝ax 2＋bx ＋c 的最小(大)值．2)能够从实际问题中抽象出二次函数关系，并运用二次函数及性质解决最小(大)值等实际问题． 2.目标解析达成目标1）的标志是：学生会借助于二次函数的图象得到在二次函数顶点处取得最小(大)值的结论，理解当x ＝－2ba时，函数有最小(大)值244ac b a －．达成目标2）的标志是：学生通过经历探索具体问题中数量关系和变化规律的过程，进一步体验如何从实际问题中抽象出二次函数模型，结合实际问题研究二次函数，将二次函数的最小(大)值的结论和已有知识综合运用来解决实际问题．三、教学问题诊断分析学生已经学习了二次函数的定义、图象和性质，学习了列方程、不等式和函数解决实际问题，这为本节课的学习奠定了基础．但运用二次函数的知识解决实际问题要求学生能选取适当的用来描述变量之间关系的函数分析问题和解决问题，对学生来说，要完成这一过程难度较大．基于以上分析，本节课的教学难点是：将实际问题抽象出数学模型，并利用二次函数解决实际问题．四、教学过程设计（一）复习巩固[问题]通过配方，写出下列抛物线的开口方向、对称轴、顶点坐标、说出两个函数的最大值、最小值分别是多少？1）y=6x2+12x 2）y=－4x2+8x－10师生活动：教师提出问题，学生回答．【设计意图】复习回顾二次函数y＝ax2＋bx＋c的图象特征和性质，为本节课学习利用二次函数解决抛掷问题与几何图形最值进行铺垫．（二）探究新知【问题】从地面竖直向上抛出一小球，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是h=30t－5t2（0≤t≤6）．小球的运动时间是多少时，小球最高？小球运动中的最大高度是多少？师：这个问题研究的是哪两个变量之间的关系？生：小球运动的高度h和小球运动的时间t两个变量之间的关系．师：结合题目内容，你觉得小球的运动时间与小球的高度有什么样的关系？生：小球运动的高度随小球的运动时间的变化而变化．师：小球的运动时间是多少时，小球最高呢？生：结合已学二次函数知识回答问题.师生活动：教师引导学生，得出如下结论：画出函数的图像h=30t－5t2（0≤t≤6），可以看出这个函数图象是一条抛物线的一部分。