2012-2017年高考文科数学真题汇编：基本初等函数学生版

全国卷2010----2017文科数学高考真题-------函数（2017新课标3）7．函数2sin 1x y x x =++的部分图像大致为 12．已知函数211()2(e e )x x f x x x a --+=-++有唯一零点，则a =A ．12-B ．13C ．12D ．11621．（12（1（2（2017A ．(1421．（12（1）讨论的单调性；（2）当0x ≥时，()1f x ax ≤+，求a 的取值范围.（2017新课标1）8．函数sin21cos x y x=-的部分图像大致为A ．B ．C ．9A ．f C ．y =14．曲线21．（12（1（2（2016新课标3）（7）已知4213332,3,25a b c ===，则(A)b a c << (B)a b c << (C)b c a << (D)c a b <<（16）已知()f x 为偶函数，当0x ≤时，1()e x f x x --=-，则曲线()y f x =在点(1,2)处的切线方程是_________.（21）（本小题满分12分）设函数()ln 1f x x x =-+．（I ）讨论()f x 的单调性；（II ）证明当(1,)x ∈+∞时，11ln x x x-<<； （x（2016（ (12)x 1,y 1），(x 2,(20)(((（2016新课标1）（8）若a >b >0，0<c <1，则（A ）log a c <log b c （B ）log c a <log c b （C ）a c <b c （D ）c a >c b（9）函数y =2x 2–e |x |在[–2,2]的图像大致为（A ）（B ）（C（12（A （21（（2015DA 运动,记BOP ∠12.A ．1,13⎛⎫ ⎪⎝⎭B ．()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C ．11,33⎛⎫-⎪⎝⎭D ．11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭ 二、填空题：本大题共4小题,每小题5分,共20分13.已知函数()32f x ax x =-的图像过点（-1,4）,则a =．16.已知曲线ln y x x =+在点()1,1处的切线与曲线()221y ax a x =+++相切,则a =．21.（本小题满分12分）已知()()ln 1f x x a x =+-.（I ）讨论()f x 的单调性；（II ）当()f x 有最大值,且最大值大于22a -时,求a 的取值范围.（2015（A （12a =()（A ）1-1421.（I （II （201415．偶函数)(x f y =的图像关于直线2=x 对称，3)3(=f ，则)1(-f =________．（2014新课标1）5.设函数)(),(x g x f 的定义域为R ，且)(x f 是奇函数，)(x g 是偶函数，则下列结论中正确的是A.)()(x g x f 是偶函数B.)(|)(|x g x f 是奇函数C.|)(|)(x g x f 是奇函数D.|)()(|x g x f 是奇函数12.已知函数32()31f x ax x =-+，若()f x 存在唯一的零点0x ，且00x >，则a 的取值范围是 ()2,+∞（B ）()1,+∞（C ）(),2-∞-（D ）(),1-∞-15.21.0 （1）求（2（2014f (9)=()A.－21.（1（2（2013（A ）a ＞c ＞b （B ）b ＞c ＞a （C ）c ＞b ＞a （D ）c ＞a ＞b11.已知函数f(x)=32x ax bx c +++,下列结论中错误的是（）（A ）∃0x R ∈,f(0x )=0 （B ）函数y=f(x)的图像是中心对称图形（C ）若0x 是f(x)的极小值点，则f(x)在区间（-∞,0x ）单调递减 （D ）若0x 是f （x ）的极值点，则'f (0x )=012.若存在正数x 使2x （x-a ）＜1成立，则a 的取值范围是（）（A ）（-∞，+∞）（B ）(-2,+∞)(C)(0,+∞)(D)（-1，+∞）（Ⅱ）讨论()f x 的单调性，并求()f x 的极大值。

第二部分 基本初等函数(2012年安徽卷理)（2）下列函数中，不满足：(2)2()f x f x =的是（ ）()A ()f x x = ()B ()f x x x =- ()C ()f x x =+1 ()D ()f x x =-【解析】选C()f x kx =与()f x k x =均满足：(2)2()f x f x =得：,,A B D 满足条件（2012年上海卷文）6、方程14230x x +--=的解是（2012年上海卷文）9、已知()y f x =是奇函数，若()()2g x f x =+且(1)1g =，则(1)g -=（2012年天津卷理）（4）函数3()=2+2x f x x -在区间(0,1)内的零点个数是 （A ）0 （Ｂ）1 （Ｃ）2 （Ｄ）34．B【命题意图】本试题主要考查了函数与方程思想，函数的零点的概念，零点存在定理以及作图与用图的数学能力.，即(0)(1)<0f f ⋅且函数()f x B 正确.． 1()2xy =1. (2012年福建卷理设函数⎩⎨⎧=为无理数为有理数x x x D ,0,1)(，则下列结论错误的是（ ）A ．)(x D 的值域为}1,0{B ．)(x D 是偶函数C ．)(xD 不是周期函数 D ．)(x D 不是单调函数 (2012年安徽文) （3）（2l o g 9）·（3log 4）=（A ）14（B ）12（C ） 2 （D ） 4 【解析】选D23lg 9lg 42lg 32lg 2log 9log 44lg 2lg 3lg 2lg 3⨯=⨯=⨯=(2012年安徽文)(13)若函数()|2|f x x a =+的单调递增区间是),3[+∞，则a =________. 【解析】_____a =6- 由对称性：362a a -=⇔=-（2012年山东卷理） 3 设a ＞0 a ≠1 ，则“函数f(x)= a x在R 上是减函数 ”，是“函数g(x)=(2-a) 3x 在R 上是增函数”的A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件解析：p ：“函数f(x)= a x在R 上是减函数 ”等价于10<<a ；q ：“函数g(x)=(2-a) 3x 在R上是增函数”等价于02>-a ，即,20<<a 且a ≠1，故p 是q 成立的充分不必要条件. 答案选A 。

11、（2016年山东）已知函数f(x )的定义域为R.当x ＜0时，f(x )=x 3-1；当-1≤x ≤1时，f(-x )= —f(x )；当x ＞12时，f(x +12)=f(x —12).则f(6)=（ D ） （A ）-2 （B ）-1 （C ）0 （D ）212、（2016年天津）已知)(x f 是定义在R 上的偶函数，且在区间)0,(-∞上单调递增，若实数a 满足)2()2(|1|->-f f a ，则a 的取值范围是（ C ）（A ）)21,(-∞（B ）),23()21,(+∞-∞Y （C ）)23,21( （D ）),23(+∞13、（2016年全国I 卷）若a>b>0，0<c<1，则（ B ）（A ）log a c <log b c （B ）log c a <log c b （C ）a c <b c （D ）c a >c b 14、（2016年全国I 卷高考）函数y =2x 2–e |x |在[–2,2]的图像大致为（ D ）（A ）（B ）（C ）（D ）15、（2016年全国II 卷）下列函数中，其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是（ D ）（A ）y =x （B ）y =lg x （C ）y =2x （D ）1y x=16、（2016年全国III 卷）已知4213332,3,25a b c ===，则（ A ）(A) b a c << (B)a b c <<(C) b c a << (D) c a b <<17、（2016年江苏）函数y =232x x --的定义域是 []3,1- .18、（2016年江苏）设f （x ）是定义在R 上且周期为2的函数，在区间[ −1,1)上，,10,()2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中.a ∈R 若59()()22f f -= ，则(5)f a 的值是 25- . 19、（2016年四川高考）若函数f （x ）是定义R 上的周期为2的奇函数，当0<x<1时，f （x ）=x 4，则f （25-）+f （2）= -2 。

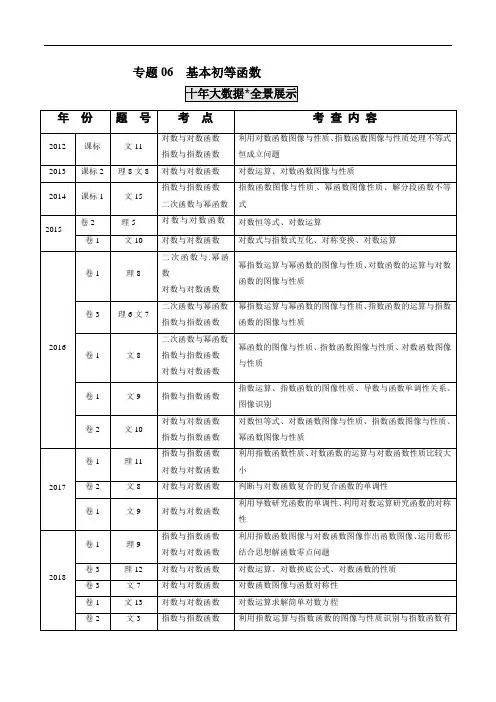
专题06 基本初等函数指数函数图像与性质、幂函数图像性质、解分段函数不等式二次函数与幂函数对数与对数函数二次函数与幂函数2021年高考仍将重点考查指数与指数函数、对数与对数函数这两个考点，考查利用指数运算、对数运算、及利用指数函数的图像与性质、对数函数图像与性质比较大小、处理单调性、解不等式等问题，难度为中档题．十年试题分类*探求规律考点20 指数与指数函数1．（2020北京卷6】已知函数12)(--=x x f x，则不等式()0f x >的解集是 （ ）A ．()1,1-B ．()(),11,-∞-+∞C ．()0,1D ．()(),01,-∞+∞【答案】C【解析】不等式()0f x >化为21,xx 在同一直角坐标系下作出y=2x ，y=x+1的图象（如图），得不等式()0f x >的解集是(0,1)，故选C ．【答案】B 【解析】当0<x 时，因为0--<xxe e ，所以此时2()0--=<x xe ef x x，故排除A ．D ；又1(1)2=->f e e，故排除C ，选B ．3．（2017新课标Ⅰ）设,,x y z 为正数，且235x y z ==，则A ．235x y z <<B ．523z x y <<C ．352y z x <<D ．325y x z <<【答案】D 【解析】设235x y z k ===，因为,,x y z 为正数，所以1k >，则2log x k =，3log y k =，5log z k =，所以22lg lg 3lg 913lg 23lg lg8x k y k =⨯=>，则23x y >，排除A 、B ；只需比较2x 与5z ，22lg lg 5lg 2515lg 25lg lg 32x k z k =⨯=<，则25x z <，选D ． 4．（2016年全国I 卷）函数2||2x y x e =-在[–2，2]的图像大致为A ．B ．C ．D ．【答案】D 【解析】∵2||2x y x e =-是偶函数，设2||2x y x e =-，则222(2)228f e e =⨯-=-，所以0(2)1f <<，所以排除A ，B ；当02x 时，22x y x e =-，所以4x y x e '=-，又()4xy e ''=-，当0ln4x <<时，()0y ''>，当ln42x <<时，()0y ''<，所以4xy x e '=-在(0,ln 4)单调递增，在(ln 4,2)单调递减，所以4xy x e '=-在[0,2]有14(ln 41)y '--，所以4x y x e '=-在[0,2]存在零点ε，所以函数22x y x e =-在[0,)ε单调递减，在(,2]ε单调递增，排除C ，故选D ．5．（2017北京）已知函数1()3()3x xf x =-，则()f xA ．是奇函数，且在R 上是增函数B ．是偶函数，且在R 上是增函数C ．是奇函数，且在R 上是减函数D ．是偶函数，且在R 上是减函数 【答案】A 【解析】11()3()(3())()33xx x x f x f x ---=-=--=-，得()f x 为奇函数， ()(33)3ln 33ln 30x x x x f x --''=-=+>，所以()f x 在R 上是增函数．选A ．6．（2015四川）设,a b 都是不等于1的正数，则“333a b >>”是“log 3log 3a b <”的A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件 【答案】B 【解析】由指数函数的性质知，若333a b ，则1a b ，由对数函数的性质，得log 3log 3a b ；反之，取12a，13b ，显然有log 3log 3a b ，此时01b a ，于是333a b ，所以“333ab”是log 3log 3a b <的充分不必要条件，选B ．7．（2015山东）设函数31,1()2,1x x x f x x -<⎧=⎨⎩≥，则满足()(())2f a f f a =的a 的取值范围是A ．2[,1]3B ．[0,1]C ．2[,)3+∞ D ．[1,)+∞ 【答案】C 【解析】由()(())2f a f f a =可知()1f a ≥，则121aa ≥⎧⎨≥⎩或1311a a <⎧⎨-≥⎩，解得23a ≥．8．（2014安徽）设3log 7a =， 1.12b =， 3.10.8c =，则A ．c a b <<B ．b a c <<C ．a b c <<D ．b c a <<【答案】B 【解析】∵32log 71a >=>， 1.122b =>， 3.10.81c =<，所以b a c <<．9．（2014浙江）在同意直角坐标系中，函数的图像可能是【答案】D 【解析】当1a >时，函数()(0)af x x x =>单调递增，函数()log a g x x =单调递增，且过点(1，0)，由幂函数的图象性质可知C 错；当01a <<时，函数()(0)af x x x =>单调递增，函数()log a g x x =单调递减，且过点(1，0)，排除A ，又由幂函数的图象性质可知C 错，因此选D ．10．（2012天津）已知122a =，0.212b -⎛⎫= ⎪⎝⎭，52log 2c =，则,,a b c 的大小关系为A ．c b a <<B ．c a b <<C ．b a c <<D ．b c a <<【答案】A 【解析】因为122.02.022)21(<==-b ，所以a b <<1，14log 2log 2log 25255<===c ，所以a b c <<，选A ． 11．（2015江苏）不等式224x x-<的解集为_______．【答案】(1,2)-【解析】由题意得：2212x x x -<⇒-<<，解集为(1,2)-．12．（2012山东）若函数在[1,2]-上的最大值为4，最小值为m ，且函数上是增函数，则a ＝ ．【答案】【解析】 当时，有，此时，此时为减函数，不合题意．若，则，故，检验知符合题意．考点21 对数与对数函数1．（2020全国Ⅰ文8）设3log 42a =，则4a-=（ ）A ．116 B ．19 C ．18D ．16 x x g x x x f a a log )(),0()(=≥=()(0,1)x f x a a a =>≠()(14g x m =-[0,)+∞141a >214,a a m -==12,2a m ==()g x =01a <<124,a a m -==11,416a m ==【答案】B 【解析】由3log 42a =可得3log 42a =，∴49a =，∴有149a-=，故选B ． 2．（2020全国Ⅰ理12）若242log 42log a ba b +=+，则（ ）A ．2a b >B ．2a b <C ．2a b >D ．2a b <【答案】B【思路导引】设2()2log x f x x =+，利用作差法结合()f x 的单调性即可得到答案．【解析】设2()2log x f x x =+，则()f x 为增函数，∵22422log 42log 2log a b ba b b +=+=+， ∴()(2)f a f b -=2222log (2log 2)a b a b +-+=22222log (2log 2)b bb b +-+21log 102==-<， ∴()(2)f a f b <，∴2a b <．∴2()()f a f b -=22222log (2log )a b a b +-+=222222log (2log )b b b b +-+=22222log b b b --， 当1b =时，2()()20f a f b -=>，此时2()()f a f b >，有2a b >；当2b =时，2()()10f a f b -=-<，此时2()()f a f b <，有2a b <，∴C 、D 错误，故选B ．3．（2020全国Ⅱ理9）设函数()ln 21ln 21f x x x =+--，则()f x （ ）A ．是偶函数，且在1,2⎛⎫+∞⎪⎝⎭单调递增 B ．是奇函数，且在11,22⎛⎫-⎪⎝⎭单调递减 C ．是偶函数，且在1,2⎛⎫-∞-⎪⎝⎭单调递增 D ．是奇函数，且在1,2⎛⎫-∞-⎪⎝⎭单调递减 【答案】D 【解析】由()ln 21ln 21f x x x =+--得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭，关于坐标原点对称，又()()ln 12ln 21ln 21ln 21f x x x x x f x -=----=--+=-，()f x ∴为定义域上的奇函数，可排除AC ；当11,22x ⎛⎫∈-⎪⎝⎭时，()()()ln 21ln 12f x x x =+--， ()ln 21y x =+在11,22⎛⎫- ⎪⎝⎭上单调递增，()ln 12y x =-在11,22⎛⎫- ⎪⎝⎭上单调递减，。

学科教师辅导教案授课日期及时段2018 年 月历年咼考试题集锦 直线和圆2 21. （2012辽宁文）将圆x +y -2x-4y+仁0平分的直线是（ ）(A) x+y -仁0 ( B ) x+y+3=0 (C ) x-y+1=0 ( D ) x-y+3= 02. （2012浙江文）设a € R ,则“ a = 1 ”是“直线l 1: ax+2y=0与直线丨2： x+（a+1）y+4=0平行的（）A 充分不必要条件B 必要不充分条件C 充分必要条件3. (2014 湖南文)若圆 G ：x 2+y 2=1 与圆 C 2: x 2 + y 2-6x-8y+m = 0 外切，则 m=()C.9D.-11. . 2 2 , - 2 2 、.4. (2012山东文)圆(x+2) +y =4与圆(x —2) +(y-1) =9的位置关系为(7. （2013安徽文）直线x+2y —5+亦=0被圆x 2+y 2 —2x —4y =0截得的弦长为（ ）（A ） 1 （B ） 2 （C ） 4（D ） 4、；68. （2014安徽文）过点P （-后,-1）的直线I 与圆x 2+y 2 =1有公共点，则直线I 的倾斜角的取值范围是（）JinnJiA.（0, ]B.（0, ]C.[0, ]D. [0,]63 6 39. （2012福建文）直线X ，3y -2 =0与圆x 2 y^4相交于 代B 两点，则弦 AB 的长度等于（）A . 2 5B . 2 3C . 、3D . 110 （2012广东文）在平面直角坐标系 xOy 中，直线3x+4y —5=0与圆x 2+y 2=4相交于 代B 两点，学员姓名 咼二辅导科目授课老师课时数2h次课D 既不充分也不必要条件A.21B.19 (A)[-3, -1](B) [-1,3](C) [-3,1]C 的方程是a 取值范围是（（A ）内切 （B ）相交 （C ）外切 （D ）相离则弦AB的长等于（）(A) 3^3(B)2J3（c）,l(D)-11. (2013陕西文) 已知点 2 2M(a,b)在圆O:x y=1夕卜，则直线ax + by = 1与圆O的位置关系是（) （A）相切（B）相交（C）相离（D）不确定12.（2014浙江文）已知圆x 2 2y 2x _2y a =:0截直线x y 2：=0所得弦的长度为4，则实数a的值为( )A. -2B.-4 C. -6 D. -813. （2013天津文）已知过点P（2,2）的直线与圆（x—1）2+ y2= 5相切，且与直线ax—y + 1 = 0垂直，则a等于22. (2015北京文)圆心为1,1且过原点的圆的方程是(25.(2013新标2文)在平面直角坐标系 xOy 中，已知圆P 在x 轴上截得线段长为 2.2,在y 轴上截得线段长 为2 3.(1)求圆心P的轨迹方程；(2)若P 点到直线y = x 的距离为宁，求圆P 的方程.26 . (2013陕西理)已知动圆过定点 A(4,0), 且在y 轴上截得的弦 MN 的长为8. (I )求动圆圆心的轨迹 C 的方程；2 2 A . x -1 y -1 i ； =12 2.x 1 y 1 i ； =12 2C ・ X 1 y 1 i ； =22 2.x_1 y-1 =223. (20XX 年广东理)平行于直线 2x y ^0且与圆x 2 y^5相切的直线的方程是()A . 2x-y 、5=0 或 2x-y- 5=0 B. 2x y 5 = 0 或 2x y -，5 = 0C.2x-yD. 2x y 5=0 或 2x y-5 = 024.( 20XX 年新课标 2 文)已知三点A(1,0), B(0, . 3),C(2, 3),则厶ABC 外接圆的圆心到原点的距离为A.5 B 「21 C.2、53334D.- 32 227.（2014新标1文）已知点P （2,2），圆C : x y -8y =0，过点P 的动直线l 与圆C 交于代B 两点，线 段AB 的中点为M , O 为坐标原点.（I ）求M 的轨迹方程；（II ）当|OP|=pM|时，求丨的方程及APOM 的面积。

2.3基本初等函数(I)【必考内容要求】2．指数函数（1） 了解指数函数模型的实际背景.（2） 理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算.（3） 理解指数函数的概念及其单调性，掌握指数函数图像通过的特殊点，会画底数为2，3，10，1/2，1/3的指数函数的图像．（4） 体会指数函数是一类重要的函数模型.3．对数函数（1） 理解对数的概念及其运算性质，知道用换底公式将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用.（2） 理解对数函数的概念及其单调性，掌握对数函数图像通过的特殊点，会画底数为2，10，1/2的对数函数的图像．（3） 体会对数函数是一类重要的函数模型；（4）了解指数函数 xy a =与对数函数log a y x =互为反函数（a ＞0且a ≠1）.4．幂函数（1）了解幂函数的概念. （2）结合函数y x =，2y x =，3y x =，1y x =,12y x =的图像，了解它们的变化情况. 【高考试题汇编】一、选择题(共4题)1.【2012年新课标卷理10】已知函数；则的图像大致为（ ）【解析】选得：或均有 排除1()ln(1)f x x x=+-()y f x=B ()ln(1)()1()010,()00()(0)0xg x x x g x xg x x g x x g x g '=+-⇒=-+''⇒>⇔-<<<⇔>⇒<=0x >10x -<<()0f x <,,A C D2.【2012年新课标卷文11】当0<≤12时，，则a 的取值范围是 （A ）(0，22)（B ）(22，1) （C ）(1，2) （D ）(2，2) 【命题意图】本题主要考查指数函数与对数函数的图像与性质及数形结合思想，中档题.【解析】由指数函数与对数函数的图像知，解得，故选A. 3.【2013年新课标卷2理】设a=log 36,b=log 510,c=log 714,则（A ）c ＞b ＞a （B ）b ＞c ＞a （C ）a ＞c ＞b (D)a ＞b ＞c4.【2013年新课标卷2文】设3log 2a =，5log 2b =，2log 3c =，则（ ）（A ）a c b >> （B ）b c a >> （C ）c b a >> （D ）c a b >>【答案】D【解析】因为321log 21log 3=<，521log 21log 5=<，又2log 31>，所以c 最大。

基本初等函数11．（2012年高考（安徽文））23log 9log 4⨯=（ ）A ．14B ．12C ．2D ．4 22．（2012年高考（广东理））(函数)下列函数中,在区间()0,+∞上为增函数的是（ ）A ．()ln 2y x =+ B．y =C ．12xy ⎛⎫= ⎪⎝⎭D ．1y x x=+33．（2012年高考（重庆））设函数2()43,()32,x f x x x g x =-+=-集合{|(())0},M x R f g x =∈>{|()2},N x R g x =∈<则MN 为 （ ）A ．(1,)+∞B ．(0,1)C ．(-1,1)D ．(,1)-∞44．（2012年高考（天津））下列函数中,既是偶函数,又在区间(1,2)内是增函数的为（ ）A ．cos 2y x =B ．2log ||y x =C ．2x xe e y --=D ．31y x =+55．（2012年高考（四川））函数(0,1)x y a a a a =->≠的图象可能是66．（2012年高考（山东））函数1()ln(1)f x x =+（ ） A ．[2,0)(0,2]- B ．(1,0)(0,2]- C ．[2,2]-D ．(1,2]-77．（2012年高考（广东））(函数)下列函数为偶函数的是（ ）A ．sin y x =B ．3y x =C ．x y e = D．y =88．（2012年高考（安徽文））设集合{3213}A x x =-≤-≤,集合B 是函数lg(1)y x =-的定义域;则A B =（ ）A ．(1,2)B ．[1,2]C ．[,)12D ．(,]1299．（2012年高考（四川理））函数1(0,1)x y a a a a=->≠的图象可能是1010．（2012年高考（江西理））下列函数中,与函数定义域相同的函数为 （ ）A ．y=1sin xB ．y=1nxxC ．y=xe xD ．sin xx二、填空题1111．（2012年高考（上海））方程03241=--+x x的解是_________.1212．（2012年高考（陕西））设函数发0,()1(),0,2x x f x x ìï³ïï=íï<ïïïî,则((4))f f -=_____ 1313．（2012年高考（北京））已知()(2)(3)f x m x m x m =-++,()22x g x =-.若,()0x R f x ∀∈<或()0g x <,则m 的取值范围是________.1414．（2012年高考（北京））已知函数()lg f x x =,若()1f ab =,则22()()f a f b +=_________.1515．（2012年高考（上海春））函数224log ([2,4])log y x x x=+∈的最大值是______.1616．（2012年高考（江苏））函数x x f 6log 21)(-=的定义域为____.三、解答题1717．（2012年高考（上海文理））已知函数)1lg()(+=x x f .(1)若1)()21(0<--<x f x f ,求x 的取值范围;(2)若)(x g 是以2为周期的偶函数,且当10≤≤x 时,有)()(x f x g =,求函数)(x g y =])2,1[(∈x 的反函数.基本初等函数参考答案一、选择题 1)【解析】选D23lg 9lg 42lg 32lg 2log 9log 44lg 2lg 3lg 2lg 3⨯=⨯=⨯= 2)（2012年高考（广东理））(函数)下列函数中,在区间()0,+∞上为增函数的是（ ）A ．()ln 2y x =+ B ．y =C ．12xy ⎛⎫= ⎪⎝⎭D ．1y x x=+解析:A.()ln 2y x =+在()2,-+∞上是增函数.3)．（2012年高考（重庆文））设函数2()43,()32,x f x x x g x =-+=-集合{|(())0},M x R f g x =∈>{|()2},N x R g x =∈<则MN 为 （ ）A ．(1,)+∞B ．(0,1)C ．(-1,1)D ．(,1)-∞【答案】:D 【解析】:由(())0f g x >得2()4()30g x g x -+>则()1g x <或()3g x >即321x -<或323x ->所以1x <或3log 5x>;由()2g x <得322x -<即34x <所以3log 4x <故(,1)MN =-∞4)（2012年高考（天津文））下列函数中,既是偶函数,又在区间(1,2)内是增函数的为（ ）A ．cos 2y x =B ．2log ||y x =C ．2x xe e y --=D ．31y x =+【解析】函数xy 2log =为偶函数,且当0>x时,函数x x y 22log log ==为增函数,所以在)2,1(上也为增函数,选B.5)（2012年高考（四川文））函数(0,1)x y a a a a =->≠的图象可能是[答案]C[解析]采用特殊值验证法.函数(0,1)x y a a a a =->≠恒过(1,0),只有C 选项符合.6)（2012年高考（山东文））函数1()ln(1)f x x =++（ ） A ．[2,0)(0,2]- B ．(1,0)(0,2]-C ．[2,2]-D ．(1,2]-解析:要使函数)(x f 有意义只需⎩⎨⎧≥-≠+040)1ln(2x x ,即⎩⎨⎧≤≤-≠->220,1x x x ,解得21≤<-x ,且0≠x .答案应选B.7)（2012年高考（广东文））(函数)下列函数为偶函数的是（ ）A ．sin y x =B ．3y x =C ．x y e =D ．y =:D.()()f x f x -===.8)（2012年高考（安徽文））设集合{3213}A x x =-≤-≤,集合B 是函数lg(1)y x =-的定义域;则A B =（ ）A ．(1,2)B ．[1,2]C ．[,)12D ．(,]12【解析】选D {3213}[1,2]A x x =-≤-≤=-,(1,)(1,2]B A B =+∞⇒=9)（2012年高考（四川理））函数1(0,1)x y a a a a=->≠的图象可能是[答案]C[解析]采用排除法.函数(0,1)x y a a a a =->≠恒过(1,0),选项只有C 符合,故选C.10)（2012年高考（江西理））下列函数中,与函数定义域相同的函数为 （ ）A ．y=1sin xB ．y=1nxxC ．y=xe xD ．sin xxD【解析】函数y =的定义域为()(),00,-∞+∞,而答案中只有sin xy x=的定义域为()(),00,-∞+∞.故选D.二、填空题11)（2012年高考（上海文））方程03241=--+x x的解是_________.[解析]0322)2(2=-⋅-x x ,0)32)(12(=-+x x ,32=x ,3log 2=x .12)（2012年高考（陕西文））设函数发0,()1(),0,2x x f x x ³=íï<ïïïî,则((4))f f -=_____解析:41(4)()162f --==,((4))(16)4f f f -==13)（2012年高考（北京文））已知()(2)(3)f x m x m x m =-++,()22x g x =-.若,()0x R f x ∀∈<或()0g x <,则m 的取值范围是________.【解析】首先看()22x g x =-没有参数,从()22x g x =-入手,显然1x <时,()0g x <,1x ≥时,()0g x ≥,而对,()0x R f x ∀∈<或()0g x <成立即可,故只要1x ∀≥时,()0f x <(*)恒成立即可.当0m =时,()0f x =,不符合(*),所以舍去;当0m >时,由()(2)(3)0f x m x m x m =-++<得32m x m --<<,并不对1x ∀≥成立,舍去;当0m <时,由()(2)(3)0f x m x m x m =-++<,注意20,1m x ->≥,故20x m ->,所以30x m ++>,即(3)m x >-+,又1x ≥,故(3)(,4]x -+∈-∞-,所以4m >-,又0m <,故(4,0)m ∈-,综上,m 的取值范围是(4,0)-.14)（2012年高考（北京文））已知函数()lg f x x =,若()1f ab =,则22()()f a f b +=_________.【解析】()lg ,()1f x x f ab ==,lg()1ab ∴=2222()()lg lg 2lg()2f a f b a b ab ∴+=+==15)（2012年高考（上海春））函数224log ([2,4])log y x x x=+∈的最大值是___5___.16)（2012年高考（江苏））函数x x f 6log 21)(-=的定义域为____.1266000112log 0log 620<x >x >x >x x x x -≥≤≤⎧⎧⎧⎪⎪⇒⇒⎨⎨⎨⎩⎪⎪⎩⎩三、解答题18．（2012年高考（上海文理））已知函数)1lg()(+=x x f .(1)若1)()21(0<--<x f x f ,求x 的取值范围;(2)若)(x g 是以2为周期的偶函数,且当10≤≤x 时,有)()(x f x g =,求函数)(x g y =])2,1[(∈x 的反函数.[解](1)由⎩⎨⎧>+>-01022x x ,得11<<-x .由1lg )1lg()22lg(0122<=+--<+-x x x x 得101122<<+-x x 因为01>+x ,所以1010221+<-<+x x x ,3132<<-x .由⎩⎨⎧<<-<<-313211x x 得3132<<-x (2)当x ?[1,2]时,2-x ?[0,1],因此)3lg()2()2()2()(x x f x g x g x g y -=-=-=-==由单调性可得]2lg ,0[∈y .因为y x 103-=,所以所求反函数是x y 103-=,]2lg ,0[∈x_s 12__。

A ．45B ．35C ．25D ．15【答案】C 【解析】从5支彩笔中任取2支不同颜色彩笔的取法有红黄、红蓝、红绿、红紫、黄蓝、黄绿、黄紫、蓝绿、蓝紫、绿紫，共10种，其中取出的2支彩笔中含有红色彩笔的取法有红黄、红蓝、红绿、红紫，共4种，所以所求概率P ＝410＝25.故选C.5．(2017·山东文)如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位：件)．若这两组数据的中位数相等，且平均值也相等，则x 和y 的值分别为( A )A ．3,5B ．5,5C ．3,7D ．5,76．（2014上海文）某校高一、高二、高三分别有学生1600名、1200名、800名，为了解该校高中学生的牙齿健康状况，按各年级的学生数进行分层抽样，若高三抽取20名学生，则高一、高二共抽取的学生数为 707．（2013福建理）某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分为6组：[40,50), [50,60), [60,70), [70,80), [80,90), [90,100)加以统计，得到如图所示的频率分布直方图，已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为（ B ） A ．588 B ．480 C ．450 D ．1208．(2017·全国Ⅰ文)如图，正方形ABCD 内的图形来自中国古代的太极图．正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是( B )A ．14B ．π8C ．12D ．π49．（2014江苏）为了了解一片经济林的生长情况，随机抽测了其中60株树木的底部周长（单位：cm ），所得数据均在区间[80130]，上，其频率分布直方图如图所示，则在抽测的60株树木中，有 株树木的底部周长小于100 cm ．【答案】2410.（2015北京文）某校老年、中年和青年教师的人数见下表，采用分层抽样的方法调查教师的身体状况，在抽取的样本中，青年教师有320人，则该样本的老年教师人数为（ ）A ．90B ．100C ．180D ．300 类别 人数老年教师 900 中年教师 1800青年教师 1600 合计4300【答案】C11.（2015年广东文）已知样本数据1x ，2x ，⋅⋅⋅，n x 的均值5x =，则样本数据121x +，221x +，⋅⋅⋅，21n x +的均值为 ．考12.（2015年福建理）为了解某社区居民的家庭年收入所年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表： 收入x （万元） 8.28.610.011.311.9支出y （万元）6.27.58.08.59.8根据上表可得回归直线方程ˆˆˆybx a =+ ，其中ˆˆˆ0.76,b a y bx ==- ，据此估计，该社区一户收入为15万元家庭年支出为( )A ．11.4万元B ．11.8万元C ．12.0万元D ．12.2万元 【答案】B13、（2016年北京）从甲、乙等5名学生中随机选出2人，则甲被选中的概率为（A ）15 （B ）25 （C ）825 （D ）925【答案】B14、（2017年新课标Ⅱ）从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )A.110B.15C.310D.25D 【解析】如下表所示,表中的点的横坐标表示第一次取到的数,纵坐标表示第二次取到的数:1 2 3 4 5 1 (1,1) (1,2) (1,3) (1,4) (1,5) 2 (2,1) (2,2) (2,3) (2,4) (2,5) 3 (3,1) (3,2) (3,3) (3,4) (3,5) 4 (4,1) (4,2) (4,3) (4,4) (4,5) 5(5,1)(5,2)(5,3) (5,4)(5,5)共有25种情况,满足条件的有10种,所以所求概率为1025＝25. 15、（2016年山东）某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20)， [20，22.5)，[22.5,25)，[25，27.5)，[27.5，30).根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是（ D ） （A ）56（B ）60（C ）120（D ）14016、（2016年天津）甲、乙两人下棋，两人下成和棋的概率是21，甲获胜的概率是31，则甲不输的概率为（ A ）（A ）65（B ）52 （C ）61 （D ）3117、（2016年全国I 卷）为美化环境，从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中，余下的2种花种在另一个花坛中，则红色和紫色的花不在同一花坛的概率是（ C ）（A ）13（B ）12（C ）23（D ）5618、（2016年全国II 卷）某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒.若一名行人来到该路口遇到红灯，则至少需要等待15秒才出现绿灯的概率为（ B ） （A ）710 （B ）58 （C ）38 （D ）31019、（2016年全国III 卷）某旅游城市为向游客介绍本地的气温情况，绘制了一年中月平均最高气温和平均最低气温的雷达图。

学科教师辅导教案学员姓名年级高三辅导科目数学授课老师课时数2h 第次课授课日期及时段2018 年月日：—：历年高考试题集锦（文）——解三角形1．（2017 新课标Ⅲ文）△ABC 的内角A，B，C 的对边分别为a，b，c，已知 C=60°，b= 6 ，c=3，则A=___。

2．(2012 广东文 ) 在ABC 中，若 A 60 , B 45 ,BC 3 2 ，则 AC ( )(A) 4 3 (B) 2 3 (C) (D)3．（2013 湖南）在锐角中ABC ，角 A, B 所对的边长分别为a,b . 若2a sin B 3b,则角A等于（）A． B ． C ． D ．12 6 4 34．(2013 湖南文 )在ABC 中，角 A，B 所对的边长分别为a，b. 若 2asinB= 3 b，则角 A 等于（）A.或3 23B.或434C. D.3232 a b 2 C5．(2014 江西理 ) 在ABC 中，内角A,B,C 所对应的边分别为a, b, c, ，若 c ( ) 6, , 则3ABC 的面积（）9 3 3 3A.3B.C.D. 3 32 26．（2014 江西文）在在ABC 中，内角 A,B,C 所对应的边分别为a, b, c, ，若3a 5b ，则2 2 2sin B sin A2sin A的值为（）A. 191B. C.13D.7257．（2017 新课标 1 文）11．△ABC 的内角A、B、C 的对边分别为a、b、c。

已知 sin B sin A(sin C cosC ) 0 ，a=2，c= 2 ，则C=A ．π12B．πππC．D．6 4 3新优学教育辅导教案第1 页（共 8 页）2 sin 2 sin 28．（2012 上海）在ABC 中，若 sin A B C ，则ABC 的形状是（）A．锐角三角形B．直角三角形C．钝角三角形D．不能确定9.（2013 天津理）在△ ABC 中，∠ ABC ＝π，AB＝2，BC＝3，则 sin ∠BAC 等于( )4A. 1010 B. 10 3 105 C. 10D.55π10.( 2013 新标 2 文) △ABC 的内角 A，B，C 的对边分别为a，b，c，已知 b＝2，B ＝，c＝6 π，则△ABC 4的面积为 ( )A．2 3＋2 B. 3＋1 C．2 3－2 D. 3－111、(2013 新标1 文) 已知锐角ABC 的内角 A,B,C 的对边分别为a,b, c，223cos A cos 2A 0 ，a 7，c 6 ，则b （）（A）10 （B）9 （C）8 （D） 512．（2013 辽宁）在△ABC 中，内角 A，B，C 的对边分别为a，b，c.若 asin Bcos C＋csin BcosA＝1 2b ，且 a＞b，则∠ B＝( )ππ2π5πA.6 B.3 C. 3 D.613．（2013 山东文）△ABC 的内角 A，B，C 所对的边分别为a，b，c.若 B＝2A，a＝1，b＝3，则 c ＝( )A．2 3 B．2 C. 2 D．114．（2013 陕西）设△ABC的内角 A, B, C 所对的边分别为a, b, c, 若 b cosC c cos B asin A , 则△ABC的形状为(A) 锐角三角形(B) 直角三角形(C) 钝角三角形(D) 不确定15、（2016 年新课标Ⅰ卷文）△ABC的内角 A、B、C的对边分别为a、b、c.已知 a 5 ，c 2，cos 2A ，3 则 b=（A） 2 （B） 3 （C）2 （D）316、（2016 年新课标Ⅲ卷文）在△ABC 中，πB = ，BC 边上的高等于13B C ,则sinA =4（A） 310 （B）1010（C）55（D）31010网 ZXXK]17、（2016 年高考山东卷文）△ABC 中，角 A，B，C 的对边分别是a，b，c，已知2 2b= c,a = 2b (1- sin A) ,新优学教育辅导教案第2 页（共 8 页）则 A=（A）3π（B）4 π（C）3π（D）4π618、2016 年高考北京卷文)在△ABC 中，2A ，a= 3 c，则3bc=_________.19、（2016 年高考新课标Ⅱ卷文）△ABC 的内角 A，B，C 的对边分别为a，b，c，若cos4 5A ，cosC ，5 13a=1，则 b=____________.20．（2013 安徽）设ABC 的内角 A, B,C 所对边的长分别为a, b,c 。