迁移性——竖直平面内的圆周运动

竖直平面内的圆周运动及实例分析说明：竖直平面内的圆周运动一般是变速圆周运动(带电粒子在匀强磁场中运动除外)，运动的速度大小和方向在不断发生变化，运动过程复杂，合外力不仅要改变运动方向，还要改变速度大小，所以对此要根据牛顿第二定律的瞬时性解决问题：在变速圆周运动中，虽然物体在各位置受到的向心力分别产生了物体通过各位置的向心加速度，但向心力公式仍是适用的．但要注意，对于物体做匀速圆周运动的情况，只有在物体通过最高点和最低点时，向心力才是合外力．一般不研究任意位置的情况，只研究特殊的临界位置──最高点和最低点。

同时，还可以向学生指出：此问题中出现的对支持面的压力大于或小于物重的现象，是发生在圆周运动中的超重或失重现象．一、教学目标： 1.知识与技能：（1）理解匀速圆周运动是变速运动；（2）进一步理解向心力的概念；（3）掌握竖直平面内最高点和最低点的圆周运动。

2.过程与方法：通过对竖直平面内特殊点的研究，培养学生观察能力、抽象概括和归纳推理能力。

3.情感态度价值观：渗透科学方法的教育。

二、重点难点：教学重点：分析向心力来源． 教学难点 ：实际问题的处理方法．向心力概念的建立及计算公式的得出是教学重点，也是难点。

通过生活实例及实验加强感知，突破难点。

三、授课类型：习题课 四、上课过程： （一）、情景引入： （二）、两类模型——轻绳类和轻杆类(1)轻绳模型：一轻绳系一小球在竖直平面内做圆周运动.小球能到达最高点(刚好做圆周运动)的条件是小球的重力恰好提供向心力，即mg ＝m rv 2，这时的速度是做圆周运动的最小速度v min ＝ . （绳只能提供拉力不能提供支持力）.类此模型：竖直平面内的内轨道，竖直（光滑）圆弧内侧的圆周运动，水流星的运动（水流星在竖直平面内作圆周运动过最高点的临界条件），过山车运动等，A O(2)轻杆模型：一轻杆系一小球在竖直平面内做圆周运动，小球能到达最高点(刚好做圆周运动)的条件是在最高点的速度 . （杆既可以提供拉力，也可提供支持力或侧向力.）①当v ＝0 时，杆对小球的支持力 小球的重力； ②当0<v <gr 时，杆对小球的支持力 于小球的重力； ③当v ＝gr 时，杆对小球的支持力 于零； ④当v >gr 时，杆对小球提供 力.类此模型：汽车过凸形拱桥，小球在竖直平面内的（光滑）圆环内运动，小球套在竖直圆环上的运动等。

竖直平面内的圆周运动释疑一、竖直平面内的圆周运动的特点竖直平面内的圆周运动一般是变速圆周运动，其合外力一般不指向圆心， 它产生两个方向的效果：因此变速圆周运动的合外力不等于向心力，只是在半径方向的分力F 1提供向心力．但在最高点和最低点时合外力沿半径指向圆心，全部提供向力，这类问题经常出现临界状态． 二、圆周运动的临界问题竖直平面内的圆周运动一般是变速圆周动物，其合外力一般不指向圆心，但在最高点和最低点时合外力沿半径指向圆心，全部提供向力，这类问题经常出现临界状态，下面对临界状态进行分析：1．没有物体支撑的小球，在竖直平面内做圆周运动过最高点，如图所示：①临界速度0v ：小球运动在最高点时，受的重力和弹力方向都向下，当弹力等于零时，向心力最小，仅由重力提供．由牛顿运动定律知mg=m Rv 2，得小球过圆周轨道最高点的临界速度为0v =gR ，它是小球能过圆周最高点的最小速度．【疑问】：为什么在最高点的速度为0v =gR 就刚好做完整的圆周运动？②当mg<m Rv 2，即v>gR ，小球能过圆周的最高点，此时绳和轨道分别对小球产生拉力和压力．③当mg>m Rv 2，即v<gR ，小球不能过圆周的最高点，小球在达到最高点之前就已经脱离了圆轨道．设小球在C 点脱离圆周，球将沿圆周的内侧向上做斜上抛运动．小球脱离圆周的临界条件是弹力为零．【疑问】：为什么会在C 点脱离轨道呢？做斜上抛运动的轨迹一定在圆的内部吗？【释疑】：两个疑问一个例题解答【例题】如图所示，一光滑的半径为R 的半圆形轨道固定在水平面上，一个质量为m 的小球以某一速度冲上轨道，最终小球将要从轨道口飞出．（1）如小球刚好能从D 点飞出，则小球在经过B 点时的速度大小至少为多少？ （2）如小球刚好从C 点飞出（脱离轨道），则小球在C 点的速度大小为多少？【分析】：（1）在最高点仅由重力提供向心力可求得gR B =υ，即为所求。

竖直平面内的圆周运动及实例分析竖直平面内的圆周运动一般是变速圆周运动(带电粒子在匀强磁场中运动除外)，运动的速度大小和方向在不断发生变化，运动过程复杂，合外力不仅要改变运动方向，还要改变速度大小，所以一般不研究任意位置的情况，只研究特殊的临界位置──最高点和最低点。

一、两类模型——轻绳类和轻杆类1．轻绳类。

运动质点在一轻绳的作用下绕中心点作变速圆周运动。

由于绳子只能提供拉力而不能提供支持力，质点在最高点所受的合力不能为零，合力的最小值是物体的重力。

所以：（1）质点过最高点的临界条件：质点达最高点时绳子的拉力刚好为零，质点在最高点的向心力全部由质点的重力来提供，这时有，式中的是小球通过最高点的最小速度，叫临界速度；（2）质点能通过最高点的条件是；（3）当质点的速度小于这一值时，质点运动不到最高点高作抛体运动了；（4）在只有重力做功的情况下，质点在最低点的速度不得小于，质点才能运动过最高点；（5）过最高点的最小向心加速度。

2．轻杆类。

运动质点在一轻杆的作用下，绕中心点作变速圆周运动，由于轻杆能对质点提供支持力和拉力，所以质点过最高点时受的合力可以为零，质点在最高点可以处于平衡状态。

所以质点过最高点的最小速度为零，（1）当时，轻杆对质点有竖直向上的支持力，其大小等于质点的重力，即；（2）当时，；（3）当，质点的重力不足以提供向心力，杆对质点有指向圆心的拉力；且拉力随速度的增大而增大；（4）当时，质点的重力大于其所需的向心力，轻杆对质点的竖直向上的支持力，支持力随的增大而减小，；（5）质点在只有重力做功的情况下，最低点的速度，才能运动到最高点。

过最高点的最小向心加速度。

过最低点时，轻杆和轻绳都只能提供拉力，向心力的表达式相同，即，向心加速度的表达式也相同，即。

质点能在竖直平面内做圆周运动（轻绳或轻杆）最高点的向心力最低点的向心力，由机械能守恒，质点运动到最低点和最高点的向心力之差，向心加速度大小之差也等于。

竖直平面内的圆周运动规律总结竭诚为您提供优质文档/双击可除竖直平面内的圆周运动规律总结篇一：竖直平面内的圆周运动及实例分析竖直平面内的圆周运动及实例分析竖直平面内的圆周运动一般是变速圆周运动(带电粒子在匀强磁场中运动除外)，运动的速度大小和方向在不断发生变化，运动过程复杂，合外力不仅要改变运动方向，还要改变速度大小，所以一般不研究任意位置的情况，只研究特殊的临界位置──最高点和最低点。

一、两类模型——轻绳类和轻杆类1．轻绳类。

运动质点在一轻绳的作用下绕中心点作变速圆周运动。

由于绳子只能提供拉力而不能提供支持力，质点在最高点所受的合力不能为零，合力的最小值是物体的重力。

所以：（1）质点过最高点的临界条件：质点达最高点时绳子的拉力刚好为零，质点在最高点的向心力全部由质点的重力来提供，这时有通过最高点的条件是，式中的是小球通过最高点的最小速度，叫临界速度；（2）质点能；（3）当质点的速度小于这一值时，质点运动不到最高点高作抛体运动了；，质点才能运动过最高点；（5）过最（4）在只有重力做功的情况下，质点在最低点的速度不得小于高点的最小向心加速度。

2．轻杆类。

运动质点在一轻杆的作用下，绕中心点作变速圆周运动，由于轻杆能对质点提供支持力和拉力，所以质点过最高点时受的合力可以为零，质点在最高点可以处于平衡状态。

所以质点过最高点的最小速度为零，（1）当时，轻杆对质点有竖直向上的支持力，其大小等于质点的重力，即；（2）当时，；（3）当而增大；（4）当随的增大而减小，，质点的重力不足以提供向心力，杆对质点有指向圆心的拉力；且拉力随速度的增大时，质点的重力大于其所需的向心力，轻杆对质点的竖直向上的支持力，支持力；（5 ）质点在只有重力做功的情况下，最低点的速度。

，向心加速度的表达，才能运动到最高点。

过最高点的最小向心加速度过最低点时，轻杆和轻绳都只能提供拉力，向心力的表达式相同，即式也相同，即。

质点能在竖直平面内做圆周运动（轻绳或轻杆）最高点的向心力最低点的向心力，由机械能守恒，向心加速度大小之差也等于。

竖直平面内的圆周运动 一、分析圆周运动要注意以下几个问题1、 首先要明确物体做圆周运动的圆轨道在哪里?圆心在哪里?2、对物体进行正确的受力分析，确定向心力。

由牛顿运动定律可知，有力才会有加速度。

产生向心加速度的力称做向心力，向心力一般是由合力提供，在具体问题中也可以是由某个实际的力提供，如拉力、重力、摩擦力等。

3、确定圆周运动各物理量之间的关系描述圆周运动的物理量主要是线速度、角速度、轨道半径、周期和向心加速度。

4、要注意虽然圆周运动向心加速度公式a=rv 2是从匀速圆周运动推出的，但是它也适用于非匀速圆周运动情况，可以是瞬时关系。

二、竖直平面内圆周运动应用实例分析（一）汽车过桥分析汽车匀速率过凸形桥和凹形桥两种情况，主要分析汽车在拱形桥最高点和凹形桥最低点对桥面的压力情况。

（1）汽车匀速过凸形路面时在最高点，重力mg 和地面支持力的合外力是使物体做圆周运动的向心力：mg N m v R-=2通过公式可以看出：汽车过拱形桥时，处于失重状态；且当汽车的速度增大时，对地面的压力在逐渐的减小，若汽车刚要脱离路面，此时，N=0， v gR =（2）汽车匀速过凹形最低点时N mg m v R N mg m v R-==+22，即车处于超重状态。

例1、如图所示，汽车质量为1.5×104kg ，以不变的速率先后驶过凹形桥面和凸形桥面，桥面圆弧半径为15 ｍ，如果桥面承受的最大压力不得超过2.0×105 N ，汽车允许的最大速率是多少?汽车以此速率驶过桥面的最小压力是多少?（ｇ＝10 m/s 2）解析：首先要确定汽车在何位置时对桥面的压力最大，汽车经过凹形桥面时，向心加速度方向向上，汽车处于超重状态；经过凸形桥面时，向心加速度方向向下，汽车处于失重状态，所以当汽车经过凹形桥面的最低点时如图2，汽车对桥面的压力最大。

当汽车经过凹桥面最低点时，设桥面支持力为1N F ，由牛顿第二定律有Rv m mg F N 21=- 要求51100.2⨯≤N F N解得允许的最大速度v m ＝7.07 m/s由上面的分析可知，汽车经过凸桥顶点时对桥面的压力最小，设为2N F .如图所示由R v m F mg m N 22=-解得52100.1⨯=N F N. 由牛顿第三定律知， 2N F 与2N F ′等值反向.（二）轻绳模型和轻杆模型这类问题的特点是：物体做圆周运动的速率是时刻变化的，先从简单的开始研究，只研究小球通过最高点和最低点时绳子或杆的受力情况。

竖直平面内的圆周运动模型1.引言圆周运动一直是物理学的重要研究课题之一，它被广泛应用于各种机械和电子设备中。

而本文将聚焦于竖直平面内的圆周运动模型。

竖直平面内的圆周运动模型有哪些特点？如何用公式描述这种运动模型？这是本文将要介绍的内容。

2.竖直平面内的圆周运动模型特点竖直平面内的圆周运动模型是指，物体在竖直方向上运动时同时还在平面内做圆周运动。

它有如下几个特点：2.1 运动轨迹竖直平面内的圆周运动模型的轨迹形式是狭义螺旋线。

物体沿着这条曲线不断前进。

2.2 运动速度初始速度指向切线方向，所有速度的大小相等，运动速度与运动方向始终相切。

2.3 运动加速度圆周运动的加速度有两部分：径向加速度和切向加速度。

径向加速度的大小为：a_r= \frac{v^2}{r}切向加速度的大小为：a_t= \frac{dv}{dt}= \frac{d}{dt}(v\Deltat)=v\frac{d}{dt}\Delta t2.4 运动周期竖直平面内的圆周运动模型的运动周期与它的初速度和半径有关系。

如果初始速度为v_0，半径为r，则运动周期为：T= \frac{2\pi r}{v_0}3.公式描述竖直平面内的圆周运动模型可以用如下公式来描述：x= r \cos (\omega t)y= r \sin (\omega t)z= v_0 t其中，x和y分别表示物体在平面内的坐标；z表示物体在竖直方向的坐标；r表示圆的半径，\omega表示物体在平面内的角速度，角速度的大小为：\omega= \frac{v_0}{r}4.总结竖直平面内的圆周运动模型是一种特殊的、复杂的运动模型。

它的轨迹形式为狭义螺旋线，初始速度指向圆弧的切线方向，所有速度的大小相等，运动速度与运动方向始终相切。

圆周运动的加速度有两部分：径向加速度和切向加速度。

径向加速度的大小为v^2/r，切向加速度的大小为v\frac{d}{dt}\Delta t。

竖直平面内的圆周运动模型的周期与初始速度和半径有关系，其周期为T= \frac{2\pi r}{v_0}。

竖直平面内的圆周运动专题一、竖直平面内的圆周运动的特点竖直平面内的圆周运动一般是变速圆周运动，其合外力一般不指向圆心， 它产生两个方向的效果：因此变速圆周运动的合外力不等于向心力，只是在半径方向的分力F 1提供向心力．但在最高点和最低点时合外力沿半径指向圆心，全部提供向力，这类问题经常出现临界状态． 二、圆周运动的临界问题竖直平面内的圆周运动一般是变速圆周动物，其合外力一般不指向圆心，但在最高点和最低点时合外力沿半径指向圆心，全部提供向力，这类问题经常出现临界状态，下面对临界状态进行分析：1． 没有物体支撑的小球（绳类约束）讨论在竖直平面内做圆周运动过最高点的情况，如图所示：①临界速度0v ：小球运动在最高点时，受的重力和弹力方向都向下，当弹力等于零时，向心力最小，仅由重力提供．由牛顿运动定律知mg=m Rv 2，得小球过圆周轨道最高点的临界速度为0v =gR ，它是小球能过圆周最高点的最小速度．②当mg<m Rv 2，即v>gR ，小球能过圆周的最高点，此时绳和轨道分别对小球产生拉力和压力．③当mg>m Rv 2，即v<gR ，小球不能过圆周的最高点，小球在达到最高点之前就已经脱离了圆轨道．小球脱离圆周的临界条件是弹力为零．【例题1】如图所示，一质量为0.5kg 的小球，用0.4m 长的细线拴住在竖直面内作圆周运动，求：（1）当小球在圆上最高点速度为4m/s 时，细线的拉力是多少？（2）当小球在圆上最低点的速度为6m/s ，细线的拉力是多少？（g=10m/s 2）练1.用长为l 的细线拴一个小球使其绕细线的加一端在竖直平面内做圆周运动，当球通过圆周的最高点时，细线受到的拉力等于球重的2倍，已知重力加速度为g ，则球此时的速度大小为___ ，角速度大小为_ _，加速度大小为_ __。

2． 有物体支撑的小球（杆类约束）讨论在竖直平面内做圆周运动的情况，如图所示．①临界速度0v ：由于轻杆或管状轨道对小球有支撑作用，因此小球在最高点的速度可以为零，不存在“掉下来”的情况．小球恰能达到最高点的临界速度0v =0．②小球过最高点时，所受弹力情况：A ．小球到达最高点的速度v=0，此时轻杆或管状轨道对小球的弹力N=mg ．B ．当小球的实际速度v>gR 时，产生离心趋势，要维持小球的圆周运动，弹力方向应向下指向圆心，即轻杆对小球产生竖直向下的拉力，管状轨道对小球产生竖直向下的压力，因此N F =m Rv 2-mg ，所以弹力的大小随v 的增大而增大。

高中物理：竖直面内圆周运动的4类问题，帮你归纳！
竖直面内的圆周运动是曲线运动的重点知识，也是重要的物理模型，更是高考中的重点考查内容之一。

重力场中竖直面内的圆周运动是典型的非匀速圆周运动，对于物体在竖直平面内做圆周运动的问题，中学物理一般只研究物体通过最高点和最低点时的情况，并且高考中涉及圆周运动的知识大多是临界问题，其中竖直面上线球模型、杆球模型、轨道模型、管道模型中圆周运动的临界问题出现的频率非常高，出题的方式既可以是计算题也可以是选择题，对考生的能力要求较高。

下面我们分类进行讨论：
总之，在分析做圆周运动的物体时，关键是要根据题意，明确物体所在的位置需要的向心力，再通过受力分析找出应提供的向心力，要维持这点的圆周运动，必须满足提供的向心力等于所需要的向心力。

▍ 来源：综合网络。

竖直平面内小球圆周运动问题的探究小球圆周运动是物理学里最基本的运动之
首先，我们来讨论竖直平面内小球圆周运动的概念。

在物理学里，我们把竖直平面内小球圆周运动的运动方式称为“直
线运动”。

在直线运动中，小球沿着一条直线，以恒定的速度
不断地前进。

接下来，我们来看看竖直平面内小球圆周运动的物理原理。

圆周运动是一种力学运动，它受到惯性力和外力的影响。

在竖直平面内，小球受到重力的影响，重力会使小球绕着一个圆弧运动，这就是小球圆周运动。

最后，让我们来看看竖直平面内小球圆周运动的一些应用。

在实际应用中，小球圆周运动可以用来模拟太阳系里行星的运动，也可以用来模拟水滴下落的运动，甚至还可以用来模拟风力发电机的运动。

竖直平面内的圆周运动速度变化1. 引言大家好！今天我们来聊聊一个有趣的话题，那就是竖直平面内的圆周运动。

听起来好像有点复杂，但其实就是我们在生活中经常遇到的那些事情，比如过山车、旋转木马，甚至是我们小时候玩的“转转乐”。

相信我，别跑，咱们慢慢聊，这里面可有不少好玩的知识等着你呢！2. 圆周运动的基本概念2.1 什么是圆周运动？首先，咱得弄明白什么叫圆周运动。

简单说，就是物体沿着一个圆形轨迹转动的运动方式。

就像咱们在广场上转圈，转得头晕脑胀，但还是不想停下来。

圆周运动在咱们的生活中无处不在，就像空气一样，虽然看不见，但却无时无刻不在影响着我们。

2.2 速度的变化说到圆周运动，咱得提到一个关键词，那就是“速度”。

在圆周运动中，速度可不是什么固定不变的东西。

咱常说“人无千日好，花无百日红”，同样，在转动的过程中，速度也是忽高忽低的。

比如，过山车在下坡的时候，速度就像开了挂一样，而在上坡时，又慢得像蜗牛，真是让人心情大起大落，刺激得不行。

3. 竖直平面内的速度变化3.1 高点与低点的对比想象一下，你坐在过山车的高点，周围一片风景如画，心里还想着“哇，这儿真不错！”可是，下一秒，过山车开始下滑，那速度就上来了，瞬间感觉像是被风吹到了天上去，真是心惊肉跳。

这里的秘密在于重力。

重力就像是一个不太好相处的朋友，给你推了一把，让你突然加速。

在高点时，速度慢，重力的拉力小，而在低点时，速度快，重力的作用显得尤为明显，真是让人叫绝的物理现象！3.2 动能与势能的转化再说说动能和势能。

动能就是你跑得快时的感觉，而势能就像你站在高处，准备跳下去的那种忐忑。

过山车上升时，势能增加，动能减少；而当它下滑时，势能减少，动能增加，完美的循环！这就好比咱们的人生，有时候得攒点势能，才能在关键时刻大放异彩。

4. 生活中的应用4.1 趣味的应用你知道吗，很多运动员在比赛时都在利用这种速度变化。

比如说，跳水运动员在跳跃前要先蓄势待发，等到一跃而下的时候，速度瞬间提升，那才叫一个帅气。

竖直平面内的圆周运动释疑一、竖直平面内的圆周运动的特点竖直平面内的圆周运动一般是变速圆周运动，其合外力一般不指向圆心， 它产生两个方向的效果：因此变速圆周运动的合外力不等于向心力，只是在半径方向的分力F 1提供向心力．但在最高点和最低点时合外力沿半径指向圆心，全部提供向力，这类问题经常出现临界状态． 二、圆周运动的临界问题竖直平面内的圆周运动一般是变速圆周动物，其合外力一般不指向圆心，但在最高点和最低点时合外力沿半径指向圆心，全部提供向力，这类问题经常出现临界状态，下面对临界状态进行分析：1．没有物体支撑的小球，在竖直平面内做圆周运动过最高点，如图所示：①临界速度0v ：小球运动在最高点时，受的重力和弹力方向都向下，当弹力等于零时，向心力最小，仅由重力提供．由牛顿运动定律知mg=m Rv 2，得小球过圆周轨道最高点的临界速度为0v =gR ，它是小球能过圆周最高点的最小速度．【疑问】：为什么在最高点的速度为0v =gR 就刚好做完整的圆周运动？②当mg<m Rv 2，即v>gR ，小球能过圆周的最高点，此时绳和轨道分别对小球产生拉力和压力．③当mg>m Rv 2，即v<gR ，小球不能过圆周的最高点，小球在达到最高点之前就已经脱离了圆轨道．设小球在C 点脱离圆周，球将沿圆周的内侧向上做斜上抛运动．小球脱离圆周的临界条件是弹力为零．【疑问】：为什么会在C 点脱离轨道呢？做斜上抛运动的轨迹一定在圆的内部吗？【释疑】：两个疑问一个例题解答【例题】如图所示，一光滑的半径为R 的半圆形轨道固定在水平面上，一个质量为m 的小球以某一速度冲上轨道，最终小球将要从轨道口飞出．（1）如小球刚好能从D 点飞出，则小球在经过B 点时的速度大小至少为多少？ （2）如小球刚好从C 点飞出（脱离轨道），则小球在C 点的速度大小为多少？【分析】：（1）在最高点仅由重力提供向心力可求得gR B =υ，即为所求。

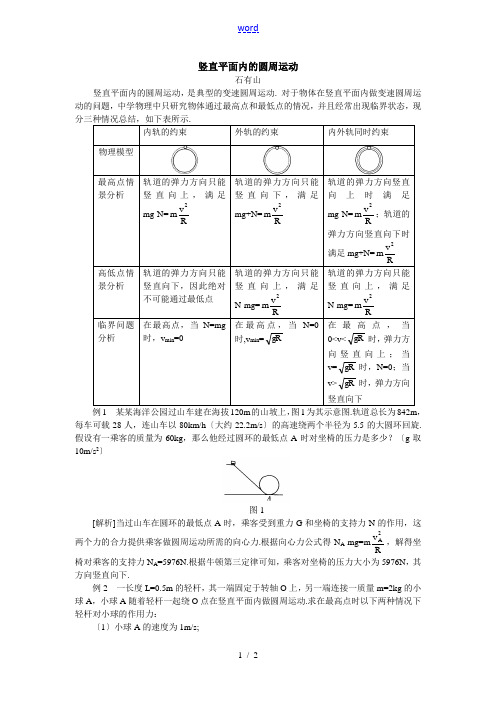
竖直平面内的圆周运动石有山竖直平面内的圆周运动，是典型的变速圆周运动. 对于物体在竖直平面内做变速圆周运动的问题，中学物理中只研究物体通过最高点和最低点的情况，并且经常出现临界状态，现分三种情况总结，如下表所示.内轨的约束外轨的约束内外轨同时约束物理模型最高点情景分析轨道的弹力方向只能竖直向上，满足mg-N=R v m 2轨道的弹力方向只能竖直向下，满足mg+N=Rv m 2轨道的弹力方向竖直向上时满足mg-N=Rv m 2；轨道的弹力方向竖直向下时满足mg+N=Rv m 2高低点情景分析 轨道的弹力方向只能竖直向下，因此绝对不可能通过最低点 轨道的弹力方向只能竖直向上，满足N-mg=R v m 2 轨道的弹力方向只能竖直向上，满足N-mg=Rv m 2临界问题分析 在最高点，当N=mg 时，v min =0 在最高点，当N=0时,v min =gR 在最高点，当0<v<gR 时，弹力方向竖直向上；当v=gR 时，N=0；当v>gR 时，弹力方向竖直向下例1 某某海洋公园过山车建在海拔120m 的山坡上，图1为其示意图.轨道总长为842m ，每车可载28人，连山车以80km/h 〔大约22.2m/s 〕的高速绕两个半径为5.5的大圆环回旋.假设有一乘客的质量为60kg ，那么他经过圆环的最低点A 时对坐椅的压力是多少？〔g 取10m/s 2〕图1[解析]当过山车在圆环的最低点A 时，乘客受到重力G 和坐椅的支持力N 的作用，这两个力的合力提供乘客做圆周运动所需的向心力.根据向心力公式得N A -mg=m Rv 2A ，解得坐椅对乘客的支持力N A =5976N.根据牛顿第三定律可知，乘客对坐椅的压力大小为5976N ，其方向竖直向下.例2 一长度L=0.5m 的轻杆，其一端固定于转轴O 上，另一端连接一质量m=2kg 的小球A ，小球A 随着轻杆一起绕O 点在竖直平面内做圆周运动.求在最高点时以下两种情况下轻杆对小球的作用力：〔1〕小球A 的速度为1m/s;〔2〕小球A 的速度为4m/s.〔g 取10m/s 2〕图2[解析]在最高点，当杆对小球的弹力为零时 v=s m 5gL /〔1〕v=1m/s<5m/s ，弹力方向竖直向上且满足mg-N=m L v 2，代入数据得N=16N.〔2〕v=4m/s>5m/s ，弹力方向竖直向下且满足mg+N=m Lv 2，代入数据得N=44N.[点评]杆约束的圆周运动相当于内外轨同时约束的圆周运动，在最高点时，弹力的方向可以竖直向上，也可以竖直向下.解此题时要充分利用没有弹力这一分界点的速度.。