实验五__函数

实验五 用matlab 求二元函数的极值1．计算二元函数的极值对于二元函数的极值问题,根据二元函数极值的必要和充分条件,可分为以下几个步骤: 步骤1.定义二元函数),(y x f z =.步骤2.求解方程组0),(,0),(==y x f y x f y x ,得到驻点.步骤3.对于每一个驻点),(00y x ,求出二阶偏导数22222,,.z z z A B C x x y y ∂∂∂===∂∂∂∂ 步骤4. 对于每一个驻点),(00y x ,计算判别式2B AC -,如果02>-B AC ,则该驻点是极值点,当0>A 为极小值, 0<A 为极大值;如果02=-B AC ,需进一步判断此驻点是否为极值点; 如果02<-B AC 则该驻点不是极值点.2．计算二元函数在区域D 内的最大值和最小值设函数),(y x f z =在有界区域D 上连续，则),(y x f 在D 上必定有最大值和最小值。

求),(y x f 在D 上的最大值和最小值的一般步骤为：步骤1. 计算),(y x f 在D 内所有驻点处的函数值；步骤2. 计算),(y x f 在D 的各个边界线上的最大值和最小值；步骤3. 将上述各函数值进行比较，最终确定出在D 内的最大值和最小值。

3．函数求偏导数的MATLAB 命令MATLAB 中主要用diff 求函数的偏导数,用jacobian 求Jacobian 矩阵。

可以用help diff, help jacobian 查阅有关这些命令的详细信息例1 求函数32824-+-=y xy x z 的极值点和极值. 首先用diff 命令求z 关于x,y 的偏导数>>clear; syms x y;>>z=x^4-8*x*y+2*y^2-3;>>diff(z,x)>>diff(z,y)结果为ans =4*x^3-8*yans =-8*x+4*y即.48,843yxyzyxxz+-=∂∂-=∂∂再求解方程，求得各驻点的坐标。

实验六 经验分布函数图形的绘制与演示6.1 实验原理设()F x 是总体X 的分布函数，12,,,n X X X "是来自总体X 的简单随机样本．对任意一个实数x ，定义函数#()(),i n X x F x x n≤=−∞<<∞. (6.1) 其中#()i X x ≤表示样本分量12,,,n X X X "中小于或等于x 的个数，或者说，()n F x 是事件“X x ≤”发生的频率．易见)(x F n 满足分布函数的性质（单增、有界、右连续等），故)(x F n 为一分布函数，称)(x F n 为总体X 的经验分布函数．由格列汶科定理知lim sup ()()0 1.n n x P F x F x →∞−∞<<∞⎛⎞−==⎜⎟⎝⎠该定理说明)(x F n 在整个实数轴上以概率1均匀收敛于()F x ．当样本容量n 充分大时，经验分布函数)(x F n 可以作为总体分布函数()F x 的一个良好的近似，这是数理统计学中以样本推断总体的理论依据．当给定样本值1212(,,,)(,,,)n n X X X x x x =""时，若将12,,,n x x x "从小到大排序：(1)(2)()n x x x ≤≤≤"，得到有序样本)()2()1(,,,n x x x "，由定义(6.1)知，)(x F n 的形式为(1)()(1)()0,,(),,1,2,,1,1,.n k k n x x k F x x x x k n nx x +<⎧⎪⎪=≤<=−⎨⎪>⎪⎩" (6.2)这就是根据样本观测值得到的经验分布函数的具体形式．6.2 实验目的及要求理解经验分布函数的构成，经验分布函数是样本的函数，随着样本观测值的变化而变化，通过实验学习经验分布函数图形的绘制方法和动态演示过程．具体要求为1. 任意产生一组随机样本，对该样本从小到大排序；2. 利用排序后的样本作经验分布函数图形；3. 让样本动态变化，观察相应的经验分布函数图形的变化，写出实验体会．6.3 实验过程为了说明经验分布函数图形的绘制和动态演示过程，我们通过一个实例来进行讲解． 例6.1 在Excel 中随机产生一个服从均匀分布(1,6)U 的，样本容量=4n 的随机样本．如图6.1，在单元格A2中输入产生均匀分布(1,6)U 随机数命令“=1+5*RAND( )”，再将其拖放填充至A5，就可在单元格区域A2:A5中产生了4个样本观测值1234,,,x x x x ，每按一次F9键，这些随机数都会发生变化，这为我们进行动态演示带来方便，这里1 3.82,x =2 2.81,x =3 1.32,x = 4 4.44x =. 接着我们把观测值1234,,,x x x x 从小到大排序，在单元格区域B2:B5中分别使用命令“=SMALL($A$2:$A$5, k)” (k=1,2,3,4) 得到顺序样本观测值：(1)(2)(3)(4)1.32, 2.81, 3.82, 4.44x x x x ====.在此基础上，我们可以利用条件语句和散点图绘制经验分布函数的图形．由(6.2)可知，此时经验分布函数的表达式为0, 1.32,0.25, 1.32 2.81,()0.5 2.81 3.82,0.75, 3.82 4.44,1,4.44.n x x F x x x x <⎧⎪≤<⎪⎪=≤<⎨⎪≤<⎪≥⎪⎩(6.3)图6.1 样本容量n= 4的样本观测值及其对应的经验分布函数图在单元格C2内输入起始值0，点击【编辑】/【填充】/【系列】，在出现的对话框中如图6.2输入相应选项，就可以在单元格区域C2:C702中顺序产生0，0.01，0.02，…，7共703个自变量x 的取值序列．图6.2 产生自变量x 的取值序列对于单元格区域C2:C702中任意一个单元格中x 的取值，其右侧（D 列）对应的单元格内为相应经验分布函数)(x F n 的值，)(x F n 的值按公式（6.3）来计算，具体计算公式为“(1)(2)(3)(4)IF(,0,IF(,0.25,IF(,0.5,IF(,0.75,1))))x x x x x x x x =<<<<”.例如，单元格D2内的计算公式就应为“=IF(C2<$B$2, 0, IF(C2<$B$3, 0.25, IF(C2<$B$4, 0.5, IF(C2<$B$5, 0.75, 1))))”.再利用拖放填充功能将单元格D2内的计算公式复制到整个单元格区域D2:D702中，就自动计算出所有)(x F n 的取值．最后，利用单元格区域C2:C702中自变量x 的取值和D2:D702中经验分布函数)(x F n 的值画出散点图，经过修饰调整后如图 6.1. 图中每一条水平线段右端的空心点可这样画出，鼠标右击图形中任一数据点，在弹出对话框中选择【设置数据系列格式】，再在弹出对话框中选【数据标记选项】/【内置】，类型选择“○”，大小选5磅，就可得出图6.1的效果．注意：最后一个数据点(7, 1)的“数据点格式”要改成实心点，以体现经验分布函数右连续的性质．只要双击最后一个数据点，在弹出对话框中选【数据标记填充】/【纯色填充】，颜色选“深蓝色”即可．6.4 讨论经验分布函数(6.2)可以看成服从离散均匀分布(1)(2)()111n x x x n n n ⎛⎞⎜⎟⎜⎟⎜⎟⎝⎠"" 的随机变量X 的分布函数．但要注意)()2()1(,,,n x x x "只是顺序统计量(1)(2)(),,,n X X X "的一组取值，而后者随着样本12,,,n X X X "的不同而随机变化的．上面设计的这个实验恰好能反映这种随机变化过程，每按一次F9键，1234,,,x x x x 发生一次变化，(1)(2)(3)(4),,,x x x x 也随之发生相应变化，经验分布函数的图形6.1也随之发生动态变化，这就给我们留下生动而直观的印象，加深对经验分布函数)(x F n 的理解．。

1大学数学实验 实验报告 | 2014/4/5一、 实验目的1、学习用Matlab 软件数值求解线性代数方程组，对迭代法的收敛性和解的稳定性作初步分析；2、通过实例学习用线性代数方程组解决简化问题。

二、 实验内容项目一：种群的繁殖与稳定收获：种群的数量因繁殖而增加，因自然死亡而减少，对于人工饲养的种群（比如家畜）而言，为了保证稳定的收获，各个年龄的种群数量应维持不变。

种群因雌性个体的繁殖而改变，为方便起见以下种群数量均指其中的雌性。

种群年龄记作k=1,2,…,n ,当年年龄k 的种群数量记作x k ，繁殖率记作b k （每个雌性个体1年的繁殖的数量），自然存活率记作s k （s k =1−d k ，d k 为1年的死亡率），收获量记作ℎk ，则来年年龄k 的种群数量x ̌k 应该为x ̌k =∑b k n k=1x k , x ̌k+1=s k x k −ℎk , (k=1,2,…,n -1)。

要求各个年龄的种群数量每年维持不变就是要求使得x ̌k =x k , (k=1,2,…,n -1).(1) 如果b k , s k 已知，给定收获量ℎk ，建立求各个年龄的稳定种群数量x k 的模型（用矩阵、向量表示）.(2) 设n =5,b 1=b 2=b 5=0,b 3=5,b 4=3,s 1=s 4=0.4,s 2=s 3=0.6,如要求ℎ1~ℎ5为500,400,200,100,100，求x 1~x 5.(3) 要使ℎ1~ℎ5均为500，如何达到？问题分析：该问题属于简单的种群数量增长模型，在一定的条件（存活率，繁殖率等）下为使各年龄阶段的种群数量保持不变，各个年龄段的种群数量将会满足一定的要求，只要找到种群数量与各个参量之间的关系，建立起种群数量恒定的方程就可以求解出各年龄阶段的种群数量。

模型建立：根据题目中的信息，令x ̌k =x k ，得到方程组如下：{x ̌1=∑b k nk=1x k =x 1x ̌k+1=s k x k −ℎk =x k+1整理得到：{−x 1∑b k nk=1x k =0−x k+1+s k x k =ℎk2 大学数学实验 实验报告 | 2014/4/52写成系数矩阵的形式如下：A =[b 1−1b 2b 3s 1−100s 2−1…b n−1b n0000⋮⋱⋮000000000⋯00−10s n−1−1]令h =[0, ℎ1,ℎ2,ℎ3,…,ℎn−2,ℎn−1]Tx =[x n , x n−1,…,x 1]T则方程组化为矩阵形式：Ax =h ，即为所求模型。

楚 雄 师 范 学 院2006—2007学年 第二 学期期末考试试卷 《数学实验》（A ）卷评分标准答题要求：１、写出各实验的ＭＡＴＬＡＢ求解命令或程序２、除绘图题外，写出各实验的实验结果一、完成以下实验（每个实验5分，共20分）。

实验一 曲线绘图1．抛物线232y x x =++解：clear;x=-2:0.1:2;y=x.^2+3*x+2;plot(x,y) 5分2．内摆线332cos ,2sin x t y t ==解：clear;t=linspace(0,2*pi);x=2*cos(t).^3;y=2*sin(t).^3;plot(x,y) 5分实验二 极限与导数3．求极限2121lim 11x x x →⎛⎫- ⎪--⎝⎭解：clear;syms x;s=limit(2/(x^2-1)-1/(x-1),x,1)s =-1/2 5分4．求函数(ln y x x =阶导数解：syms x;y=x*log(x+sqrt(1+x^2))-sqrt(1+x^2);dy=diff(y,x,1)dy=log(x+(1+x^2)^(1/2))+x*(1+1/(1+x^2)^(1/2)*x)/(x+(1+x^2)^(1/2))-1/(1+x^2)^(1/2)*x 5分二、完成以下实验（每个实验5分，共20分）。

实验三 级数5．求出()()ln 1f x x =+马克劳林展开式的前５项解：clear;syms x;y=log(1+x);f=taylor(y,0,5)f =x-1/2*x^2+1/3*x^3-1/4*x^4 5分６．求级数11(1)(2)n n n n ∞=++∑的和解：clearsyms ns=1/(n*(n+1)*(n+2));symsum(s,n,1,inf)ans =1/4 5分实验四 积分７．计算积分145sin dx x -⎰解：clear;syms x;s=int(1/(4-5*sin(x)),x)s =1/3*log(tan(1/2*x)-2)-1/3*log(2*tan(1/2*x)-1)5分８．选用一种计算数值积分的方法，求数值积分210x e dx -⎰解：法1 复化梯形求积公式x=0:0.01:1;y=exp(-x.^2);s1=trapz(x,y)s1 = 0.7468 5分法2 复化抛物线求积公式先编写M-函数文件function y=ex08(x)y=exp(-x.^2);保存后，在命令 命令运行指令：s2=quad('ex08',0,1)s2 =0.7468法3 牛顿-科兹求积公式s3=quadl('ex08',0,1)s3 =0.7468三、完成以下实验（每个实验5分，共20分）。

第五次实验题目-第七章函数教学目标31.一元二次方程的系数：a、b、c由主函数输入，编写函数求方程的根。

#include <stdio.h>#include <math.h>void root(double a, double b, double c){ double delta,x1,x2,m,n;if (fabs(a) <= 1e-6){if (fabs(b) <= 1e-6)puts("Not an equation");elseprintf("x=%.2lf",-c/b);return;}else{delta=b*b - 4*a*c;m = -b / (2*a);n = sqrt(fabs(delta)) / (2*a);x1 = m + n;x2 = m - n;if (fabs(delta) <= 1e-6)printf("x1=%.2lf, x2=%.2lf", x1, x1);else if (delta < 0)printf("x1=%.2lf+%.2lfi, x2=%.2lf-%.2lfi",m,n,m,n);elseprintf("x1=%.2lf, x2=%.2lf", x1, x2);}}int main( ){ double a,b,c;scanf("%lf%lf%lf",&a,&b,&c);root(a,b,c);return 0;}教学目标32.输入一串字符，统计其中英文字母的个数，编写统计英文字母个数的函数。

#include<stdio.h>int numberOfLetter(char str[]) {int i=0;int num = 0;//统计字母个数while (str[i]!=’\0’) {if ((str[i]>='A'&& str[i]<='Z')||( str[i]>='a'&& str[i]<='z')) num++;i++;}return num;}int main( ) {char str[100];int letterNum;printf("Enter a string: ");gets(str);letterNum = numberOfLetter(str);printf("Number of letters is %d.\n", letterNum);return 0;}教学目标33. 求100以内所有素数的和。

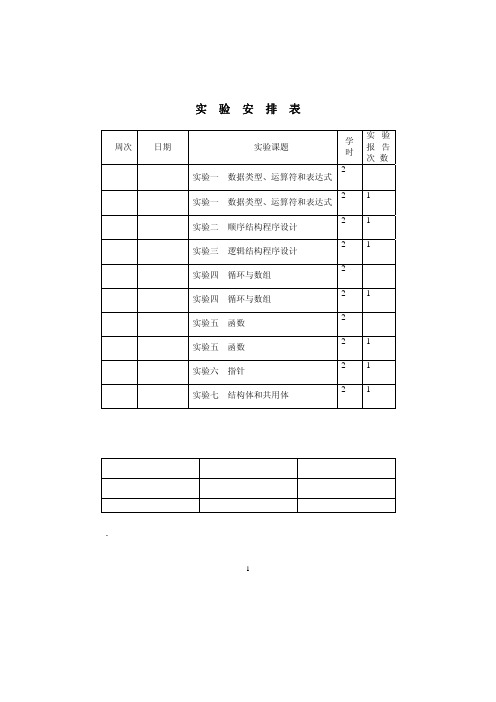
合肥师范学院实验报告册2013 / 201 学年第1 学期系别计算机科学与技术系实验课程高级语言程序设计专业班级姓名学号指导教师《高级语言程序设计》实验 班级： 学号： 姓名：-1-实验一 ——VC 工作环境及顺序结构程序设计一、实验目的1. 熟悉VC++的运行环境，掌握运行一个C 程序的基本步骤，包括编辑、编译、连接和运行；2. 理解顺序结构程序方式；3. 了解常用数据类型的输入输出方法；4. 了解C 程序的基本框架，能编写简单的C 程序，了解程序调试；二、实验预习内容在认真阅读教材及实验指导书的基础上，上机前请预习以下内容，并在空白处填写相应的步骤或命令。

1. 输入并运行一个简单、正确的程序。

输入编程示例 “Hello ，World ！”程序，即： # inc lude “stdio.h” int main(void) {printf("Hello ，World ！\n"); return 0; }1) 参考实验指导书P223～P233，学习C 程序的编辑、编译、运行，熟悉VC++6.0的基本界面操作。

2) 修改本例，使用printf （）输出自己的个性化签名，保存到文件ex1_1.c 中。

2. 程序改错题：# include stdio.h int mian(void) {printf( Welcome to You! \n" ) return 0;1) 分析本程序段中哪些地方存在错误？请标记出来，并给出修改意见。

2) 输入上面程序（或打开error1_2.c ），学习程序调试。

3. 程序阅读题：1) 请分析下面程序（ex1_3.c ）运行结果是什么？ # include <stdio.h> int main(void){ char c1,c2 ; c1=97; c2=98; printf( "c1=%c,c2=%c \n", c1, c2 ); printf( "c1=%d,c2=%d \n", c1, c2 ); return 0; } 运行结果是： 2) 若将程序第4，5行改为c1=197；c2=198；运行结果又如何？并简单分析。

实验五二阶网络函数的模拟一实验目的1 掌握求解系统响应的一种方法——模拟解法。

2 研究系统参数变化对响应的影响。

二原理说明1 为了求解系统的响应，需建立系统的微分方程，一些实际系统的微分方程可能是一个高阶微分方程或者是一个微分方程组，它们的求解是很费时间甚至是困难的。

由于描述各种不同系统（如电系统，机械系统）的微分方程有惊人的相似之处，因而可以用电系统来模拟各种非电系统，并进一步用基本运算单元获得该实际系统响应的模拟解。

这种装置又称为“电子模拟计算机”。

应用它能较快地求解系统的微分方程，并能用示波器将求解结果显示出来。

在初学这种方法时不妨以简单的二阶系统为例（本实验就是如此），其系统的微分方程为：y”+a1y’+a0y=x方框图如图5-1所示：图5-1 二阶网络函数方框图实际装置如图5-2所示。

图5-2实验线路图由模拟电路可得模拟方程为：⎢⎢⎢⎢⎢⎢⎣⎡-=--=--=--=-===dt dVo C R Vn Vb dt dVb C R Vq Va Rw Vb Vm R Vm Vi Rw Va Vh R Vh Vo Vn Vq Vm Vh 24,1322,110,0, 只要适当的选定模拟装置的元件参数，可得模拟方程和实际系统的微分方程完全相同。

本模拟实验的电路中：R1= R2= R3= R4=10k ΩRw1= Rw2=10k ΩC1=C2=0.1uF由上式可得： Vb Va Vo Vi -+=根据电路整理可得："'214324Vo C C R R Vo C R Vo Vi ⋅⋅⋅⋅+⋅⋅+=将电阻和电容参数代入则有： "6'31010Vo Vo Vo Vi --++=3 、实际系统响应的变化范围可能很大，持续时间可能很长，但是运算放大器输出电压是有一定限制的，大致在±10伏之间。

积分时间受RC 元件数值限制也不能太长，因此要合理的选择变量的比例尺度My 和时间的比例尺Mt ，使得Vy=MyY ，t M =M t t ，式中Y 和t 为实验系统方程中的变量和时间，V y 和t M 为模拟方程中的变量和时间。

一、概述Python是一种直观、易学、功能强大的计算机编程语言，广泛应用于Web开发、数据分析、人工智能等领域。

本文将介绍Python程序设计的8个实验内容，帮助读者深入了解和掌握Python编程技能。

二、实验一：基础语法1. 学习Python的基本语法，包括变量、数据类型、运算符等。

2. 编写一个简单的Python程序，实现对用户输入的数字进行排序并输出结果。

三、实验二：条件控制和循环1. 掌握Python的条件控制语句，如if-else和switch-case。

2. 熟练运用循环结构，包括for循环和while循环。

3. 编写一个Python程序，实现对用户输入的数字进行判断，输出是否为素数。

四、实验三：函数1. 学习Python函数的定义和调用。

2. 掌握参数传递和返回值的用法。

3. 编写一个Python程序，实现计算两个数的最大公约数和最小公倍数的函数，并进行调用测试。

五、实验四：列表和元组1. 了解Python中列表和元组的概念和用法。

2. 编写一个Python程序，实现对列表和元组的增删改查操作，并输出结果。

六、实验五：字典和集合1. 掌握Python中字典和集合的特点和用法。

2. 编写一个Python程序，实现对字典和集合的遍历和操作，并输出结果。

七、实验六：文件操作1. 学习Python文件的打开、读取和写入操作。

2. 编写一个Python程序，从文件中读取数据并进行处理，然后将结果写入新文件。

八、实验七：异常处理1. 理解Python中异常的概念和分类。

2. 编写一个Python程序，模拟发生异常并进行处理，保证程序正常运行。

九、实验八：面向对象编程1. 学习Python面向对象编程的相关知识，包括类、对象、继承等。

2. 编写一个简单的Python程序，实现一个基本的面向对象应用，并进行测试。

十、结语通过以上8个实验内容的学习，读者可以系统地了解和掌握Python程序设计的基础知识和技能，为进一步深入学习和应用Python打下坚实的基础。

数学与统计学院实验报告实验项目名称所属课程名称实验类型实验日期班级学号姓名成绩附录1：源程序x 34Log3x54Log1xx4 3218x4Log x14x4Log x2ArcTan32Tan x625Sinh355 3239120023ArcTan35523ArcTan33910.1x2If Re x20Im x20, 0.0999445SinIntegral 1.x20.1x2,Integrate Sin0.1t0.1x20.1t0.1x2,t,0,1,Assumptions Re x20Im x2032Erf411428Erf22Erfi4114428附录2：实验报告填写说明1．实验项目名称：要求与实验教学大纲一致。

2．实验目的：目的要明确，要抓住重点，符合实验教学大纲要求。

3．实验原理：简要说明本实验项目所涉及的理论知识。

4．实验环境：实验用的软、硬件环境。

5．实验方案（思路、步骤和方法等）：这是实验报告极其重要的内容。

概括整个实验过程。

对于验证性实验，要写明依据何种原理、操作方法进行实验，要写明需要经过哪几个步骤来实现其操作。

对于设计性和综合性实验，在上述内容基础上还应该画出流程图、设计思路和设计方法，再配以相应的文字说明。

对于创新性实验，应注明其创新点、特色。

6．实验过程（实验中涉及的记录、数据、分析）：写明具体实验方案的具体实施步骤，包括实验过程中的记录、数据和相应的分析。

7．实验结论（结果）：根据实验过程中得到的结果，做出结论。

8．实验小结：本次实验心得体会、思考和建议。

9．指导教师评语及成绩：指导教师依据学生的实际报告内容，给出本次实验报告的评价。

实验五：遗传算法求解函数最值问题实验一、实验目的使用遗传算法求解函数在及y的最大值。

二、实验内容使用遗传算法进行求解，篇末所附源代码中带有算法的详细注释。

算法中涉及不同的参数，参数的取值需要根据实际情况进行设定，下面运行时将给出不同参数的结果对比。

定义整体算法的结束条件为，当种群进化次数达到maxGeneration时停止，此时种群中的最优解即作为算法的最终输出。

设种群规模为N，首先是随机产生N个个体，实验中定义了类型Chromosome表示一个个体，并且在默认构造函数中即进行了随机的操作。

然后程序进行若干次的迭代，在每次迭代过程中，进行选择、交叉及变异三个操作。

1.选择操作首先计算当前每个个体的适应度函数值，这里的适应度函数即为所要求的优化函数，然后归一化求得每个个体选中的概率，然后用轮盘赌的方法以允许重复的方式选择选择N个个体，即为选择之后的群体。

但实验时发现结果不好，经过仔细研究之后发现，这里在x、y 取某些值的时候，目标函数计算出来的适应值可能会出现负值，这时如果按照把每个个体的适应值除以适应值的总和的进行归一化的话会出现问题，因为个体可能出现负值，总和也可能出现负值，如果归一化的时候除以了一个负值，选择时就会选择一些不良的个体，对实验结果造成影响。

对于这个问题，我把适应度函数定为目标函数的函数值加一个正数，保证得到的适应值为正数，然后再进行一般的归一化和选择的操作。

实验结果表明，之前的实验结果很不稳定，修正后的结果比较稳定，趋于最大值。

2.交叉操作首先是根据交叉概率probCross选择要交叉的个体进行交叉。

这里根据交叉参数crossnum进行多点交叉，首先随机生成交叉点位置，允许交叉点重合，两个重合的交叉点效果互相抵消，相当于没有交叉点，然后根据交叉点进行交叉操作，得到新的个体。

3.变异操作首先是根据变异概率probMutation选择要变异的个体。

变异时先随机生成变异的位置，然后把改位的01值翻转。

c语⾔程序设计教程（第2版）课后题及模拟题参考答案c语⾔程序设计教程（第2版）课后题及模拟题参考答案习题1 (4)1-1 填空题 (4)1-2 思考题 (4)1-3 编程题 (5)习题2 (6)2-1 单选题 (6)2-2 思考题 (6)习题3 (7)3-1 选择题 (7)3-2 填空题 (7)3-3 编程题 (8)习题4 (11)4-1单选题 (11)4-2填空题 (11)4-3 编程题 (11)习题5 (16)5-1单选题 (16)5-2填空题 (16)5-3 编程题 (16)习题6 (22)6-1单选题 (22)6-2填空题 (22)习题7 (25)7-1单选题 (25)7-2填空题 (25)7-3 编程题 (25)习题8 (26)8-1单选题 (26)8-2填空题 (26)8-3 编程题 (26)习题9 (30)9-1单选题 (30)9-2填空题 (30)9-3 编程题 (30)习题10 (38)10-1单选题 (38)10-2填空题 (38)10-3 编程题 (38)习题11 (41)11-1单选题 (41)11-2填空题 (41)习题12 (42)12-1单选题 (42)12-2 填空题 (42)实验1 熟悉Visual C++6.0可视化集成开发环境 (43)实验2 顺序结构程序设计 (43)实验3 选择结构程序设计 (43)实验4 循环结构程序设计 (44)实验5 函数 (47)实验6 数组 (54)实验7 指针 (58)实验8 结构体和共⽤体 (61)实验9 ⽂件 (63)实验10 综合编程 (64)模拟试卷（⼀）参考答案 (65)模拟试卷（⼆）参考答案 (67)习题11-1 填空题1. 函数2. 主函数main(),主函数main()3. 主函数main()4. 函数⾸部，函数体5. {, }6. /*, */7. 顺序结构，选择结构，循环结构8. .c, .obj, .exe1-2 思考题1. 结构化程序设计是指：为使程序具有⼀个合理的结构以保证程序正确性⽽规定的⼀套如何进⾏程序设计的原则。

高中数学实验及仪器一览表实验目的本实验旨在帮助高中数学学生通过实际操作，加深对数学理论的理解和应用能力的提高。

实验一: 测量与图形- 实验目标：学会使用测量工具进行各种测量和绘制图形。

- 所需仪器：直尺、量角器、经纬仪。

- 实验步骤：根据教师指导，进行长度、角度和坐标的测量，并使用这些数据绘制对应的图形。

实验二: 几何图形的性质- 实验目标：通过实践，掌握几何图形的性质和相互关系。

- 所需仪器：直尺、量角器、平行直线及垂直平分器。

- 实验步骤：根据教师指导，进行各种几何图形的构造，并观察它们的性质和特点。

实验三: 函数与方程- 实验目标：通过实验，深入理解函数与方程的概念，并掌握它们之间的关系。

- 所需仪器：直尺、画纸、函数绘图器。

- 实验步骤：根据教师指导，通过实际绘制函数图像和解方程的方法，验证函数与方程之间的联系。

实验四: 统计与概率- 实验目标：通过收集和分析实际数据，了解统计和概率的基本概念和应用。

- 所需仪器：数据采集工具、计算器。

- 实验步骤：根据教师指导，收集一组数据，并进行数据处理、统计和概率计算，从而得出结论。

实验五: 三角函数与解三角形- 实验目标：通过实践运用三角函数和三角形解析，提高对三角学的理解和应用能力。

- 所需仪器：三角函数表、解三角形仪器。

- 实验步骤：根据教师指导，使用三角函数表和解三角形仪器，解决一系列三角函数和三角形的相关问题。

实验六: 矩阵与向量- 实验目标：通过实际计算和运用矩阵与向量相关概念，加深对它们的理解和应用。

- 所需仪器：计算器、纸张。

- 实验步骤：根据教师指导，进行矩阵和向量的基本运算，并解决与矩阵和向量相关的实际问题。

以上为高中数学实验及仪器一览表，希望能够帮助学生们更好地进行实践学习，并提高数学能力。

实验五 氨基甲酸铵分解压的测定 （多相化学反应平衡常数和热力学函数的测定）一、实验目的1．测定氨基甲酸铵的分解压力，并求得反应的标准平衡常数和有关热力学函数。

2．了解真空泵的构造原理和使用方法以及获得低真空度的方法。

3．掌握大气压力计的构造原理，使用方法以及气压计读数的校正方法。

二、基本原理氨基甲酸铵的分解可用下式表示：NH 2COONH 4(固)＝2NH 3(气)＋CO 2(气)设反应中气体为理想气体，则其标准平衡常数K 可表示为：K ＝P P P P K CO NH p 232)(（1）式中3NH P 和2CO P 分别表示某温度下NH 3和CO 2的平衡分压，P 为标准压力。

设平衡总压为P ，则3NH P ＝P32（2）2CO P ＝P 31（3）代入式（1），得到p K ＝322743132P P P P P P （4）因此测得一定温度下的平衡总压后，即可按式（4）算出此温度的反应平衡常数。

氨基甲酸铵分解是一个热效应很大的吸热反应，温度对平衡常数的影响比较灵敏。

但当温度变化范围不大时，按平衡常数与温度的关系式，可得C RTH Kmln （5）式中m 为该反应的标准摩尔反应热，R 为摩尔气体常数，C 为积分常数。

根据式（5），只要测出几个不同温度下的 P K ，以 P K ln 对1/T 作图，由所得直线的斜率即可求得实验温度范围内的m 。

利用如下的热力学关系式：K RT G m ln （6）mm m S T G （7） 还可计算反应的标准摩尔吉氏函数变化m G 和标准摩尔熵变m S 等。

本实验用静态法测定氨基甲酸铵的分解压力。

三、仪器及试剂恒温槽一套、等压计、大气压力计、DPC—2B 型数字式低真空测压仪、三通活塞、二通活塞、真空泵、氨基甲酸铵，实验装置如图６-１。

四、实验步骤1．从气压计上读出大气压和室温，将大气压进行仪器误差和温度误差校正。

2．恒温槽及数字式低真空测压仪的调节使用。