固体线膨胀系数的测量

固体线膨胀系数的测定实验报告
目录
1. 实验目的
1.1 实验原理
1.1.1 线膨胀系数的概念
1.1.2 线膨胀系数的计算公式
1.2 实验器材
1.3 实验步骤
1.4 实验结果分析
1.5 实验结论
实验目的
通过测定固体线膨胀系数的实验，掌握固体在温度变化下的膨胀规律，了解物体在不同温度下的变化情况。

实验原理
线膨胀系数的概念
线膨胀系数是一个物体在单位温度变化下长度变化的比例系数，通常
表示为α。

线膨胀系数的单位为℃^-1。

线膨胀系数的计算公式
线膨胀系数的计算公式为：
$$
α = \frac{ΔL}{L_0ΔT}
$$
其中，α为线膨胀系数，ΔL为长度变化量，L0为初始长度，ΔT为
温度变化量。

实验器材
1. 物体（例如金属杆）
2. 尺子
3. 温度计
4. 烧杯
5. 热水
实验步骤
1. 测量物体的初始长度并记录为L0。

2. 将物体放入热水中，让其温度升高。

3. 使用温度计测量热水的温度变化ΔT。

4. 测量物体在热水中的长度变化量ΔL。

5. 根据公式计算出线膨胀系数α。

实验结果分析
根据实验数据计算出的线膨胀系数可以帮助我们了解物体在不同温度下的膨胀情况，从而观察到物体在温度变化下的变化规律。

实验结论
通过本次实验，我们成功测定了固体线膨胀系数，并对物体在温度变化下的膨胀规律有了更深入的了解。

这对于工程领域的材料选择和设计具有重要意义。

固体线膨胀系数的测定-回复
固体线膨胀系数是指单位长度（或面积）的物体温度升高时的长度（或面积）增加的比例。

固体线膨胀系数的测定可以通过以下步骤进行：
1. 准备测量装置：选用适合该物体的长度计和温度计等测量仪器，并确保测器的准确度。

2. 准备样品：选择所需的物体样品，保证样品的形状和尺寸符合实验要求。

3. 热平衡：将样品和测量仪器置于恒温浴中，达到热平衡状态。

4. 记录初始参数：记录下样品的长度、温度、环境温度等参数。

5. 加热：将恒温浴温度逐步提高，记录下不同温度下样品的长度、温度、环境温度等参数。

6. 数据处理：根据实验数据，计算出相邻温度下样品长度变化量与样品长度的比例，即固体线膨胀系数。

需要注意的是，在测量过程中要保证实验条件的恒定和精确，尽量避免误差。

另外，不同物质的固体线膨胀系数会随温度变化而发生变化，因此在实验中需根据具体情况进行调整。

实验三 固体线膨胀系数的测量【实验目的】1．了解热膨胀现象。

2．测量固体线膨胀系数。

【实验仪器】EH-3型热学实验仪，铜棒，铁棒，千分表。

【实验原理】大部分物质在一定温度范围内都呈现“热胀热缩”的宏观现象。

就晶体状固体模型而言，这是因为物质中相邻粒子间的平均距离随温度的升高而增大引起的。

两相邻粒子间的势能是它们之间距离的函数，其关系可用势能曲线描绘如图3-1。

在一定的温度下，粒子在其平衡位置r o 附近做热振动，具有一定的振动能量E 。

由于势能曲线的非对称性，热振动时的平均距离r 大于平衡距离r o 。

若温度升高（T 1、T 2），振动能量增加（E 1、E 2），则两原子之间的平均距离也增大（r 1、r 2），随之固体的体积膨胀。

因此，热膨胀现象是物体的势能曲线的非对称特性的必然结果。

固体的任何线度（长度、宽度、厚度、直径等）随温度的变化，都称为线膨胀。

对于各向同性的固体，沿不同方向的线膨胀系数相同；对于各向异性的固体，沿不同的晶轴方向，其线膨胀系数不同。

实验表明，原长度为L 的固体受热后，其相对伸长量正比温度的变化，即： αt L L ∆=∆ 式中，比例系数a 称为固体的线膨胀系数，对于一种确定的固体材料，它是一个确定的常数。

设温度在0℃时，固体的长度为L 0，当温度升高时，其长度为L t 。

t L L L t α=-00 （3-1） L t = L 0（1+αt ）。

（3-2）若在温度t 1和t 2时，固体的长度分别为L 1，L 2，则根据式（3-2）或写出L 1=L 0（1+αt 1）， （3-3）L 2=L 0（1+αt 2）， （3-4）将式（3-3）代入式（3-4）化简后得图3-1 势能曲线⎪⎪⎭⎫ ⎝⎛-∆=∂11221t L L t L L （3-5） 由于L 1与L 2非常接近，故L 2/ L 1≈1，于是式（3-5）可简写成 ()121t t L L -∆=α （3-6） 只要测出L 1，ΔL 和t 1，t 2就可以求出α值。

75实验八 固体线膨胀系数的测量一般物体都具有热胀冷缩的特性，这是由于物体内的粒子运动会随温度改变，当温度上升时，粒子的振动幅度加大，令物体膨胀；但当温度下降时，粒子的振动幅度便会减小下来，使物体收缩。

因此在日常生活生产中要注意“热胀冷缩”效应所产生的负面影响。

但水（0-4℃）、锑、铋、镓和青铜等物质，受热时收缩，遇冷时会膨胀，恰与一般物体特性相反。

【预习思考题】1.如何检验铜棒两端已被顶住？2.为什么要在加热之前读出千分表的初读数？【实验目的】1.了解热膨胀现象。

2.测量固体线膨胀系数。

【实验原理】大部分物质在一定温度范围内都呈现“热胀热缩”的宏观现象。

就晶体状固体模型而言，这是因为物质中相邻粒子间的平均距离随温度的升高而增大引起的。

固体的任何线度（长度、宽度、厚度、直径等）随温度的变化，都称为线膨胀。

对于各向同性的固体，沿不同方向的线膨胀系数相同；对于各向异性的固体，沿不同的晶轴方向，其线膨胀系数不同。

实验表明，原长度为L 的固体受热后，其相对伸长量正比温度的变化，即：αt LL∆=∆ 式中，比例系数α称为固体的线膨胀系数，对于一种确定的固体材料，它是一个确定的常数。

设温度在0℃时，固体的长度为L 0，当温度升高到t ℃时，其长度为L t ，则t L L Ltα=-0（1）76L t = L 0（1+αt） （2）若在温度t 1和t 2时，固体的长度分别为L 1，L 2，则根据式（2）可写出L 1=L 0（1+αt 1）， （3） L 2=L 0（1+αt 2）， （4）将式（3）代入式（4）化简后得⎪⎪⎭⎫ ⎝⎛-∆=11221t L L t L Lα （5） 由于L 1与L 2非常接近，故L 2/ L 1≈1，于是式（5）可简写成()121t t L L-∆=α （6）可见，只要测出L 1、ΔL 和t 1，t 2就可以求出α值。

【实验仪器】EH-3型热学实验仪（示意图见实验十）、铜棒、游标卡尺、千分表。

固体线膨胀系数的测定[实验目的]1、测量两种金属杆的线膨胀系数。

2、进一步使用光杠杆测定固体长度的微小变化。

3、初步掌握温度测量的要领。

[实验原理]实验表明，原长度为L的固体受热后，在一定的温度范围内，其相对伸长量正比于温度的变化，即ΔL/L=αΔT (7-1)式中比例系数α称为固体的线膨胀系数。

对于一种确定的固体材料，在一定温度范围内，它是常数，材料不同，α的值也不同。

设在温度T1时，固体的长度为L1，温度升高到T2时，其长度为L2，则有：（L2-L1）/L1=α（T2-T1）或α=（L2-L1）/L1（T2-T1）(7-2)其中ΔL= L2-L1是微小的长度变化,可用光杠杆法进行测量。

利用类似于杨氏模量测仪的装置(见图7-1)，可得长度伸长量：ΔL= L2-L1=x/2D（n2-n1）(7-3)式中x为光杠杆前后脚的垂直距离，D为光杠杆镜面到望远镜，标尺间的距离，n1及n2为温度T1及T2时望远镜中标尺的读数。

代入式（7-2）得α= x（n2-n1）/2D L1（T2-T1）（7-4）如果测得L1、T2、T1、n1、n2、x及D，便可从式（7-4）求出α值。

[实验仪器]线膨胀系数测定仪（包括待测铜棒、铁棒，0-100℃温度计，光杠杆，尺读望远镜，标尺），钢卷尺，游标卡尺。

[实验内容]测定铜棒和铁棒的线膨胀系数（两者实验步骤相同）（1）测量金属杆的长度L1并把它装入加热管道内。

（2）小心地把温度计插入加热管的被测棒孔内，记下加热前的温度T1。

（3）将光杠杆三个构成等腰三角形的尖脚放在白纸上轻轻地按一下，得到三个支点的位置。

通过作图量出等腰三角形的高X，然后将光杠杆放在平台上，使它的顶点脚放在金属杆的上端。

（4）调整光杠杆的位置，以及望远镜的位置和焦距，使得在望远镜中能清楚地看到标尺的刻度（调整方法同实验五），记下加热前标尺的读数n1。

（5）接通加热开关，要求测一组n-T值，作出n-T曲线，由曲线求α，并和附录附表8所载的标准值比较之。

固体线热膨胀系数的测定
固体的线热膨胀系数是描述固体在温度变化下长度变化的物理量。

测定固体线热膨胀系数的方法有几种常用的实验方法，其中包括：线膨胀测量法：这是最常用的方法之一。

它通过测量材料在不同温度下的长度变化来确定线热膨胀系数。

实验中，可以使用一个恒温器将样品加热或冷却到不同温度，并使用一个精密测量仪器（如游标卡尺）测量样品长度的变化。

根据测得的数据，可以计算出线热膨胀系数。

光学干涉法：这种方法利用光学干涉原理来测量固体在不同温度下的长度变化。

实验中，可以使用一束激光或白光通过材料，然后通过干涉现象来观察和测量样品表面上形成的干涉条纹。

根据干涉条纹的移动情况，可以计算出线热膨胀系数。

管道法：这种方法适用于较长且细长的材料（如管道）。

实验中，可以将样品放置在一个管道中，并通过在管道内流动的液体或气体来控制样品的温度。

通过测量管道的长度变化和温度变化，可以计算出线热膨胀系数。

需要注意的是，在进行固体线热膨胀系数测定时，应尽量减小实验误差，并根据具体材料和实验条件选择合适的方法。

此外，还应遵循实验安全操作规范，并确保实验设备和仪器的准确性和精度。

大学物理仿真实验报告固体线膨胀系数的测量院系名称：土木建筑学院专业班级：姓名：学号：固体线膨胀系数的测量一、实验目的1． 了解研究和测量热膨胀系数的意义及其应用。

2． 学习用光杠杆法测量微小长度变化。

3． 学习测量金属棒的线膨胀系数。

二、实验原理1． 材料的热膨胀系数各种材料热胀冷缩的强弱是不同的，为了定量区分它们，人们找到了表征这种热胀冷缩特性的物理量---线胀系数和体胀系数。

线膨胀是材料在受热膨胀时，在一维方向上的伸长。

在一定的温度范围内，固体受热后，其长度都会增加，设物体原长为 L ，由初温1t 加热至末温t 2，物体伸长了ΔL,则有上式表明，物体受热后其伸长量与温度的增加量成正比，和原长也成正比。

比例系数αl 称为固体的线胀系数。

体膨胀是材料在受热时体积的增加，即材料在三维方向上的增加。

体膨胀系数定义为在压力不变的条件下，温度升高1K 所引起的物体体积的相对变化，用αv表示。

即一般情况下，固体的体胀系数αv为其线胀系数的3倍，即αv=3αl ，利用已知的αl ，我们可测出液体的体胀系数αv。

2． 线胀系数的测量线膨胀系数是选用材料时的一项重要指标。

实验表明，不同材料的线胀系数是不同的，塑料的线胀系数最大，其次是金属。

殷钢、熔凝石英的线胀系数很小，由于这一特性，殷钢、石英多被用在精密测量仪器中。

表1.2.1-1给出了几种材料的线胀系数。

人们在实验中发现，同一材料在不同的温度区域，其线胀系数是不同的，例如某些合金，在金相组织发生变化的温度附近，会出现线胀系数的突变。

但在温度变化不大的范围内，线胀系数仍然是一个常量。

因此，线胀系数的测量是人们了解材料特性的一种重要手段。

在设计任何要经受温度变化的工程结构（如桥梁、铁路等）时，必须采取措施防止热胀冷缩的影响。

例如，在长的蒸气管道上，可以插入一些可伸缩的接头或插入一段U 型管；在桥梁中，可将桥的一端固牢在桥墩上，把另一端放在滚轴上；在铁路上，两根钢轨接头处要留有间隙等。

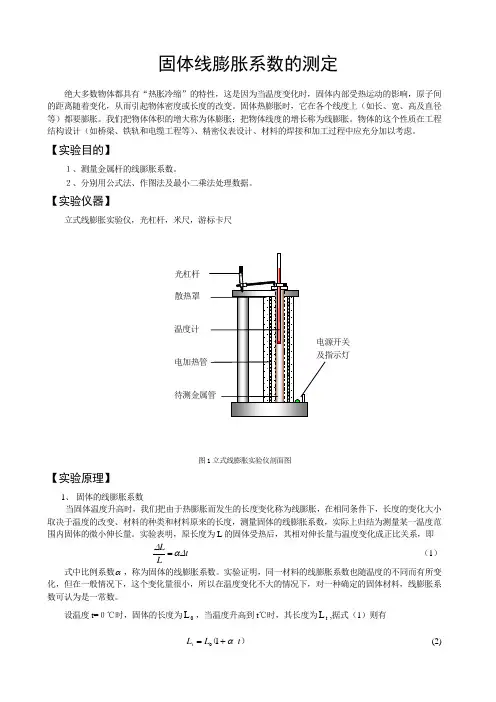
固体线膨胀系数的测定绝大多数物体都具有“热胀冷缩”的特性，这是因为当温度变化时，固体内部受热运动的影响，原子间的距离随着变化，从而引起物体密度或长度的改变。

固体热膨胀时，它在各个线度上（如长、宽、高及直径等）都要膨胀。

我们把物体体积的增大称为体膨胀；把物体线度的增长称为线膨胀。

物体的这个性质在工程结构设计（如桥梁、铁轨和电缆工程等）、精密仪表设计、材料的焊接和加工过程中应充分加以考虑。

【实验目的】１、测量金属杆的线膨胀系数。

２、分别用公式法、作图法及最小二乘法处理数据。

【实验仪器】立式线膨胀实验仪，光杠杆，米尺，游标卡尺图1立式线膨胀实验仪剖面图【实验原理】1、 固体的线膨胀系数当固体温度升高时，我们把由于热膨胀而发生的长度变化称为线膨胀，在相同条件下，长度的变化大小取决于温度的改变、材料的种类和材料原来的长度，测量固体的线膨胀系数，实际上归结为测量某一温度范围内固体的微小伸长量。

实验表明，原长度为L 的固体受热后，其相对伸长量与温度变化成正比关系，即t LL∆α∆= （1） 式中比例系数α，称为固体的线膨胀系数。

实验证明，同一材料的线膨胀系数也随温度的不同而有所变化，但在一般情况下，这个变化量很小，所以在温度变化不大的情况下，对一种确定的固体材料，线膨胀系数可认为是一常数。

设温度t=０℃时，固体的长度为0L ，当温度升高到t ℃时，其长度为t L ,据式（1）则有）（t L L t α+=10 (2)如果在温度为t １和t ２时（设t １＜t ２），金属杆长度分别为Ｌ１和Ｌ２，根据公式（2 ）可导出101(1)L L t α=+ (3)202(1)L L t α=+ (4)将式（3）代入式（4）化简后得：）（1122112t L L t L L L --=α (5) 因L 2与L 1非常接近，故1/12≈L L ,于是可将式（5）写成）（12112t t L L L --=α (6)但我们注意到，在α的表达式中，12L L L -=∆为一微小伸常量，不能直接测量，这里我们用光杠杆法测量。

固体线膨胀系数的测定大多数固体材料内部分子热运动的剧烈程度与物体的温度有关，故而都遵从热胀冷缩的规律。

固体的体积随温度升高而增大的现象称为热膨胀。

固体热膨胀时，它在各个线度上（如长、宽、高、直径等）都要膨胀，我们把物体线度的增长称为线膨胀；将体积的增大称为体膨胀。

若固体在各方向上热膨胀规律相同时，可以用固体在一个方向上的线膨胀规律来表征它的体膨胀，所以线膨胀系数是很多工程技术中选材料的重要技术指标。

在道路、桥梁、建筑等工程设计、精密仪器仪表设计、材料的焊接、加工等领域都必须考虑该参数的影响。

线膨胀系数的测量方法有很多种，包括：光杠杆法、千分表法、读书显微镜法、光学干涉法、组合法等，本实验采用千分表法测金属线膨胀系数，用FD-LEB 线膨胀系数测定仪进行测量。

一、实验目的1.学习测量固体线膨胀系数的方法；2.掌握用千分表测量微小长度变化的方法；3.练习作图法处理实验数据的方法；4.分析影响测量精度的因素。

二、实验原理固体受热后的长度L 和温度t 之间的关系为：)1(20 +++=t t L L βα (1)式中L 0为温度t=0℃时的长度， βα、是和被测物质有关的数值很小的常数，而β以后的各系数和α相比甚小，所以常温下可以忽略，则上式可写成：)1(0t L L α+= (2)式中α就是固体的线膨胀系数，其物理意义为温度每升高一度时物体的伸长量与它在零度时的长度比，单位是摄氏度分之一。

如果在温度t 1和t 2时，金属杆的长度分别为L 1和L 2，则有：)1(101t L L α+= (3) )1(202t L L α+= (4) 联立(3)、(4)式可得：)(1122112t L L t L L L --=α。

由于L 2与L 1相差微小，1/12≈L L 所以上式可近似写为tL L ∆∆=1α。

式中12L L L -=∆是固体当温度变化12t t t -=∆时相对应的伸长量。

该式通常可简单表示为：t L L ∆∆=α。