贵州专版2019中考数学总复习第一轮考点系统复习第4章三角形第6节锐角三角函数及其应用课件
- 格式:ppt
- 大小:5.43 MB
- 文档页数:40


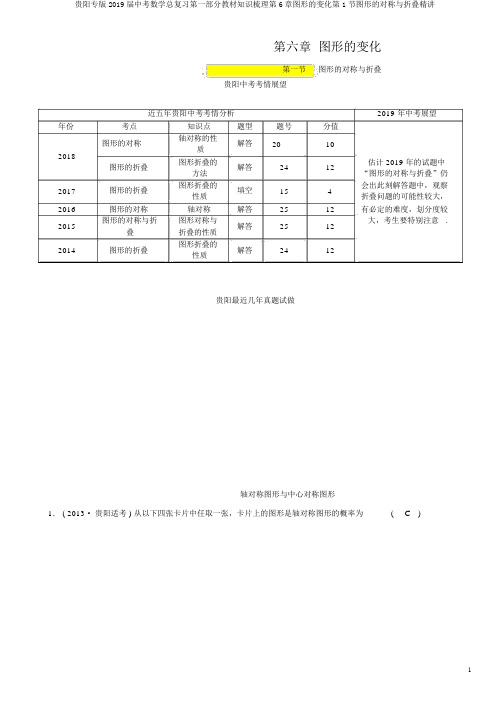
第六章图形的变化第一节图形的对称与折叠贵阳中考考情展望近五年贵阳中考考情分析2019 年中考展望年份考点知识点题型题号分值图形的对称轴对称的性解答2010质2018图形折叠的估计 2019 年的试题中图形的折叠解答2412方法“图形的对称与折叠”仍2017图形的折叠图形折叠的填空154会出此刻解答题中,观察性质折叠问题的可能性较大,2016图形的对称轴对称解答2512有必定的难度,划分度较2015图形的对称与折图形对称与解答2512大,考生要特别注意 .叠折叠的性质2014图形的折叠图形折叠的解答2412性质贵阳最近几年真题试做轴对称图形与中心对称图形1. ( 2013·贵阳适考 ) 从以下四张卡片中任取一张,卡片上的图形是轴对称图形的概率为(C)113A.4B.2C.4D.1图形的对称与折叠叠,点 C 的对应点为C′.(1)若点 C′恰好落在对角线 BD上时, BC′= ____ ;(2)若点 C′恰好落在线段 AB的垂直均分线上时,求 CE的长;(3)若点 C′恰好落在线段 AD的垂直均分线上时,求 CE的长.解:(1)BC′= BD-DC′= BD-DC = 10 - 6 = 4. 故应填: 4;(2)如图①,连接 CC′.∵点 C′在 AB的垂直均分线上,∴点 C′在 DC 的垂直均分线上.∴CC′= DC′= DC.∴△ DCC′是等边三角形.∴∠ CDC′= 60° . ∴∠ CDE=∠ C′DE=30°.∴DE=2CE.设 CE= x,则 DE= 2x.在 Rt△CDE中,由勾股定理,得(2x) 2- x2= 62.∴x= 2 3,即 CE的长为 2 3;(3)作 AD的垂直均分线,交 AD于点 M,交 BC于点 N.①当点 C′在矩形内部时,如图②.∵点 C′在 AD的垂直均分线上,∴DM= 4.设 CE= y,则 NE= 4- y,EC′= y.在 Rt△ENC′中,(4-y)2+(6-25) 2= y2,∴ y= 9- 3 5,即 CE的长为 9-35;图②图③②当点 C′在矩形外面时,如图③.同①的方法可得MC′= 2 5.∴C′ N=6+2 5.设 CE= z,则 EN= z- 4.在 Rt△ENC′中,由勾股定理,得(z - 4) 2+ (6 + 25) 2= z2.∴z= 9+ 3 5,即 CE=9+ 3 5.综上所述,点 C′恰好落在线段AD的垂直均分线上时, CE的长为 9- 35或 9+3 5.贵阳中考考点清单轴对称图形与轴对称轴对称图形轴对称图形定义假如两个图形对折后,这两个图形能够完整重合,那么我们就说这两个图形成轴对假如一个图形沿着某条直线对折后,直线称,这条直线叫做对称轴 .两旁的部分能够完整重合,那么这个图形就叫轴对称图形,这条直线叫做对称轴.性质对应点所连的线段被对称轴垂直均分.对应线段相等AB=① __ AC__AB=A′B′,BC=B′C′, AC=A′C′对应角相等∠B=∠C ∠A=② __∠A′ __ ,∠ C=∠ C′,∠ B=∠ B′(1)轴对称图形是一个拥有特别形状的图(1) 轴对称是指两个图形的差别形,只对一个图形而言;地点关系,一定涉及两个图(2)对称轴不必定只有一条 .形; (2) 只有一条对称轴 .(1) 沿对称轴翻折,两个图(1)沿对称轴对折,两部分重合;形重合;关系(2)假如把轴对称图形沿对称轴分成“两个(2) 假如把两个成轴对称的图形”,那么这“两个图形”就关于这条直图形拼在一起,看作一个整线成轴对称 .体,那么它就是一个轴对称图形 .温馨提示1.常有的轴对称图形:等腰三角形、矩形、菱形、正方形、圆.2.折叠的性质:折叠的本质是轴对称,折叠前后的两图形全等,对应边和对应角相等.3.凡是在几何图形中出现“折叠”这个字眼时,第一反应即存在一组全等图形,其次找出与要求几何量相关的条件量.(1)与三角形联合:①若涉及直角,则优先考虑直角三角形的性质( 勾股定理及斜边上的中线等于斜边的一半) ,若为含特别角的直角三角形,则应利用其边角关系计算;②若涉及两边( 角) 相等,则利用等腰三角形的相关性质计算,若存在60°角,则利用等边三角形性质进行相关计算,一般会作出高线构造特别角的直角三角形进行求解;③若含有中位线,则需利用中位线的地点及数目关系进行量的代换.(2)与四边形联合:①与平行四边形、矩形、菱形、正方形联合,常常会利用其特别性质求解;②若为一般的四边形,则可经过构造特别的三角形或四边形求解.中心对称图形与中心对称中心对称图形中心对称图形定义假如一个图形绕某一点旋转180°后能与它自己重合,我们心对称,这个点叫做它们的对称中心.性质对应线段相等,对应角相等 .对应点点 A与点 C,点 B与点 D.点 A与点 A′,点 B与点 B′,点 C与点 C′.对应线段AB= CD, AD= BC A B =A′B′,④ __BC__=B′C′, AC =A′C′对应角∠A=∠ C,∠A=∠ A′,∠ B=∠ B′,∠ C=∠ C′⑤ __∠B__=∠D差别中心对称图形是指拥有某种特征中心对称是指两个图形的关系 .的一个图形.把中心对称图形的两部分看作联系“两个图形”,则这“两个图形”成中心对称.把成中心对称的两个图形看作一个“整体”,则“整体”是一此中心对称图形 .规律总结常有的中心对称图形:平行四边形、矩形、菱形、正方形、正六边形、圆等.中考典题精讲精练轴对称图形与中心对称图形例 1以下汽车标记中既是轴对称图形又是中心对称图形的是(C)【分析】正确判断一个图形是不是轴对称图形和中心对称图形,要依据定义进行判断.A.是轴对称图形,不是中心对称图形,故此选项不吻合题意;B.既不是轴对称图形,也不是中心对称图形,故此选项不吻合题意;C.既是轴对称图形,也是中心对称图形,故此选项吻合题意;D.是轴对称图形,不是中心对称图形,故此选项不吻合题意.1. ( 2018·永州中考 ) 誉为全国第三大露天碑林的“浯溪碑林”,摩崖上铭刻着500 多方古今名家碑文,此中悬针篆文拥有较高的历史意义和研究价值.下边四个悬针篆文文字显然不是轴对称图形的是(C)2. ( 2018·衡阳中考 ) 以下生态环保标记中,是中心对称图形的是(B)图形的对称与折叠例 2如图,在矩形纸片ABCD中, AB= 4,AD= 12,将矩形纸片折叠,使点 C 落在 AD边上的点M处,折痕为PE,此时 PD= 3.(1)求 MP的值;(2)在 AB边上有一个动点 F,且不与点 A,B 重合.当 AF 等于多少时,△ MEF的周长最小?(3)若点 G, Q 是 AB 边上的两个动点,且不与点 A, B 重合, GQ=2. 当四边形 MEQG的周长最小时,求最小周长值. ( 计算结果保留根号 )【分析】(1) 依据折叠的性质和矩形的性质,得PD= PH= 3, CD= MH= 4,∠ H=∠ D=90°,而后利用勾股定理可计算出MP的值;(2) 作点 M关于 AB的对称点M′,连接M′E交 AB 于点 F,利用两点之间线段最短可得点 F 即为所求,过点E 作 EN⊥AD,垂足为 N,求出 AM, AM′的值,再证明 ME=MP,接着利用勾股定理计算出 MN,可得 NM′的值,而后证明△ AFM′∽△ NEM′,可利用相似比计算出AF;(3) 由 (2) 知点M′是点M 关于AB 的对称点,在EN 上截取ER= 2,连接M′R交 AB 于点G,再过点 E 作EQ∥RG,交 AB 于点 Q,易得QE= GR,而 GM=GM′,于是MG+QE=M′R,利用两点之间线段最短可得此时MG+ EQ最小,于是四边形 MEQG的周长最小,在Rt△ M′RN 中,利用勾股定理计算出 M′R,易得四边形 MEQG的最小周长.(2) 如图①,作点M关于 AB的对称点M′,连接M′E交 AB于点 F,点 F 即为所求,∴ AM=AM′=4.过点 E 作 EN⊥AD,垂足为N, ME=MP= 5.2 2在 Rt△ENM中,MN=ME-EN=3,∴NM′=11.由△AFM′∽△ NEM′,得AM′=AF16 NM′. ∴AF= .NE1116∴当 AF=11时,△ MEF的周长最小;(3)如图②,由 (2) 知点 M′是点 M关于 AB 的对称点.在 EN上截取 ER= 2,连接 M′R交 AB于点 G,再过点 E 作 EQ∥RG,交 AB于点 Q,易得 QE=GR.又∵ GM= GM′,则 MG+ EQ=M′G+ GR=M′R最小.∴四边形MEQG的周长最小,此时 M′R=11 2+ 22= 5 5,∴四边形MEQG的最小周长值是 7+5 5. ,3. ( 2018·资阳中考 ) 如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,A.12 cm B.16 cm C.20 cm D.28 cm4. ( 2014·贵阳中考) 如图,将一副直角三角板拼放在一起获得四边形ABCD,此中∠ BAC= 45°,∠ ACD=30°,点 E 为 CD边上的中点,连接AE,将△ ADE 沿 AE 所在直线翻折获得△ AD′E,D′ E 交 AC 于点 F, AB=62 cm.(1)AE 的长为 ____cm;(2)试在线段 AC上确立一点 P,使得 DP+ EP的值最小,并求出这个最小值;(3)求点 D′到 BC的距离.解: (1) ∵∠ BAC= 45°,∠ B= 90°,∴ AB= BC= 6 2.∴AC=12. ∵∠ ACD= 30°,∠ DAC= 90° .∴CD=8 3. ∵点 E 为 CD边上的中点,1∴AE=2CD= 4 3. 故应填: 4 3;(2)∵ Rt△ADC中,∠ACD=30°,∴∠ ADC= 60° .∵ E 为 CD边上的中点,∴DE= AE.∴△ ADE为等边三角形.∴△ AD′ E 为等边三角形.∴∠ AED′=60° .∵∠ EAC=∠ DAC-∠ EAD= 30°,∴∠ EFA= 90°,即 AC所在的直线垂直均分线段ED′,∴点 E, D′关于直线AC对称.连接 DD′交 AC于点 P,此时 DP+ EP值为最小,且DP+ EP=DD′.∵△ ADE是等边三角形,AD= AE= 4 3,1∴DD′= 2×2AD× 3=12,即 DP+ EP 最小值为 12 cm;(3)连接 CD′, BD′,过点 D′作 D′G⊥BC于点 G.∵AC 垂直均分线段 ED′,∴ AE=AD′, CE=CD′.∵AE=EC,∴ AD′= CD′= 4 3.∴△ ABD′≌△ CBD′ ( SSS).∴∠ D′ BG= 45° . ∴ D′ G= GB.设 D′G长为 x cm,则 CG长为 (62- x) cm.在 Rt△GD′C中,x2+(62- x) 2= (43) 2,解得 x1=3 2-6, x2= 3 2+6( 不合题意,舍去) .∴点 D′到 BC的距离为 (3 2-6) cm.。
