组合光实验

有关“水球光学”的实验现象
当航天员往水球中打入一个气泡，因为在太空中浮力已经消失了，所以气泡不会向上飘，而是老老实实待在水球中，水球因此被气泡变为了两部分，中间是空气，气泡周围是水。

这个时候整个水球就变成了两个透镜，外圈成为了一个凸透镜，所以呈现出一个倒立的像，内圈相当于变成了两个凹透镜的组合，这个时候又出现了一个正立的像。

因此可以在水球中同时看到一正一倒的两个像。

实验原理：
在地面上，水珠受到地球引力作用，呈现上小下大形状。

在太空中，由于微重力环境，水珠在表面张力作用下呈现透明圆球，球形水珠相当于两个组合在一起的凸透镜，光线通过它发生两次折射，从而形成一个倒立的人像；当在水球中注入一个气泡时，光线通过它发生四次折射，从而在形成一个正立的人像，其中倒立的像是光线在水球中两次折射的结果，正立的像是光线射入气泡四次折射的结果，这都是光的折射原理引起的光学现象。

闪光融合实验报告摘要：本实验旨在研究并分析闪光融合现象的产生原理和影响因素，并探讨其在实际应用中的潜在价值。

通过改变不同实验条件下的光源、材料和环境等因素，我们对闪光融合现象进行了详细观察和记录，并对实验结果进行了分析和总结。

实验结果表明，闪光融合具有明显的光学特性和应用潜力，为光电器件和光学技术领域带来了新的机遇和挑战。

引言：闪光融合是一种斑块间视觉融合的现象，常见于光学仪器和设备中，并且已经在一些新兴技术领域得到广泛应用。

其产生原理主要与光源的光度、光谱特性、材料的反射和折射性质、环境光等因素有关。

通过对这些因素进行控制和调节，可以实现不同程度的闪光融合效果。

因此，研究闪光融合现象对于光学技术和应用的发展具有重要意义。

材料与方法：在本实验中，我们选择了一种常见的闪光融合材料，并利用光学仪器观察和记录了不同实验条件下的闪光融合现象。

实验过程中，我们采用了以下步骤和方法：1. 准备工作：清洁实验仪器并保证环境光的稳定性。

2. 选择合适的光源：通过改变光源的光度和光谱特性，观察闪光融合效果的变化。

3. 材料选择：选择不同性质和特点的材料，观察和比较其闪光融合现象。

4. 实验记录：使用摄像设备和实时监测软件记录实验数据，并尽可能准确的描述和分析实验结果。

结果与讨论：通过实验观察和数据记录，我们发现闪光融合现象受多种因素的影响。

首先，光源的光度和光谱特性对闪光融合效果具有重要影响。

当光源光度较高、光谱分布较宽时，闪光融合现象较为明显。

其次，材料的反射和折射特性也对闪光融合效果产生显著影响。

不同的材料可呈现出不同的闪光融合效果，这与其光学特性有关。

最后，环境光也会对闪光融合现象产生一定的影响。

较强的环境光会削弱或干扰闪光融合效果。

基于以上研究结果，我们认为闪光融合现象具有广泛的应用潜力。

例如，在光电器件领域，可以利用闪光融合现象来提高光源亮度和颜色效果，进一步改进显示器和照明设备的性能。

此外，在光学技术领域，闪光融合也为相机镜头设计、光学仪器校准等方面提供了新的探索方向。

一、稳态法测物体的导热系数1.什么叫稳定导热状态？如何判断实验达到了稳定导热状态？稳定导热状态：盘A与盘C温度不随时间变化，B盘的导热速率等于C盘的散热速率判断实验达到稳定导热状态：一定时间内（如10min）盘C的温度变化不超过0.2℃. 2．待测样品盘是厚一点好还是薄一点好？薄一点好，这样可以减少样品盘侧面的热量损失，可以近似认为该盘热量仅由接触面传递，减少误差3.导热系数的测量公式成立的前提条件是什么？（1）盘B的厚度足够小，使得可以近似地认为盘B的侧面没有热量损失。

（2）加热盘，样品盘，散热盘均为理想的圆柱状/（3）热电偶的插头与盘A盘B紧密接触，能正确显示其温度（4）盘A与盘C都是热的良导体做的（5）样品盘与散热盘和发热盘紧密接触，中间没有热量损失（6）外界环境较稳定二、偏振与双折射1.自然光、线偏振光、椭圆偏振光的定义？自然光——在垂直于光的振动方向上等概率的包含各个横向光振动，各光振动彼此独立，无固定相位联系。

线偏振光——光矢量方向不变，大小随相位变化，在垂直于光波传播方向的平面上光矢量端点的轨迹是一条直线。

椭圆偏振光——光矢量随时间做有规律的变化，光矢量的末端在垂直于传播的方向上的轨迹是椭圆2.怎样用实验方法来区分自然光，线偏振光，椭圆偏振光？用偏振片进行观察啊：○若光强随偏振片的转动没有变化，这束光是自然光或者圆偏振光，这时，在偏振片之前放置1/4玻片，再转动偏振片。

如果强度仍没变化则是自然光：如果出现两次消光，则是圆偏振光，因为1/4玻片可以把圆偏振光变为线偏振光○如果用偏振片观察时，光强随偏振片的转动但没有消失，则这束光是部分偏振光或椭圆偏振光。

这时可以将偏振片停留在透射光强最大的位置，在偏振片前插入1/4玻片，使玻片的光轴与偏振片的投射方向平行，再次转动偏振片若出现两次消光，即为椭圆偏振光；若还是不出现消光，则为部分偏振光。

○如果随偏振片的转动出现两次消光，则这束光是线偏振光3.如何获得圆偏振光和椭圆偏振光线偏振光经过1/4玻片时，当偏振光的电矢量振动方向和玻片的光轴呈45°角时，得到圆偏振光。

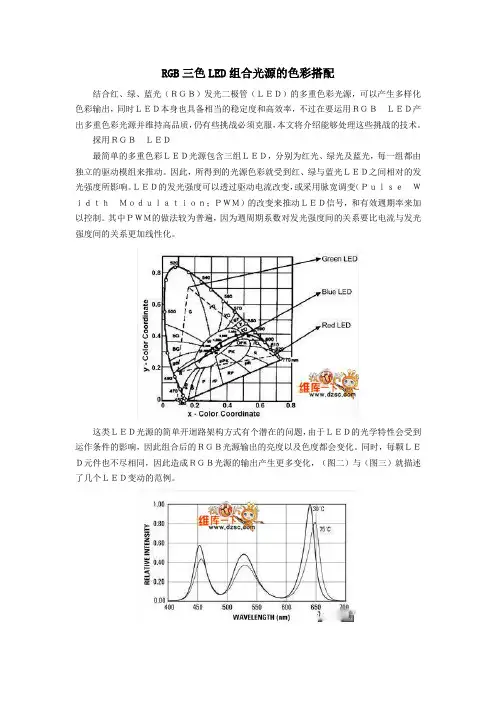
RGB三色LED组合光源的色彩搭配结合红、绿、蓝光（ＲＧＢ）发光二极管（ＬＥＤ）的多重色彩光源，可以产生多样化色彩输出，同时ＬＥＤ本身也具备相当的稳定度和高效率，不过在要运用ＲＧＢＬＥＤ产出多重色彩光源并维持高品质，仍有些挑战必须克服，本文将介绍能够处理这些挑战的技术。

採用ＲＧＢＬＥＤ最简单的多重色彩ＬＥＤ光源包含三组ＬＥＤ，分别为红光、绿光及蓝光，每一组都由独立的驱动模组来推动。

因此，所得到的光源色彩就受到红、绿与蓝光ＬＥＤ之间相对的发光强度所影响。

ＬＥＤ的发光强度可以透过驱动电流改变，或采用脉宽调变（ＰｕｌｓｅＷｉｄｔｈＭｏｄｕｌａｔｉｏｎ；ＰＷＭ）的改变来推动ＬＥＤ信号，和有效週期率来加以控制。

其中ＰＷＭ的做法较为普遍，因为週周期系数对发光强度间的关系要比电流与发光强度间的关系更加线性化。

这类ＬＥＤ光源的简单开迴路架构方式有个潜在的问题，由于ＬＥＤ的光学特性会受到运作条件的影响，因此组合后的ＲＧＢ光源输出的亮度以及色度都会变化。

同时，每颗ＬＥＤ元件也不尽相同，因此造成ＲＧＢ光源的输出产生更多变化，（图二）与（图三）就描述了几个ＬＥＤ变动的范例。

一个解决方式是使用光学反馈来产生一个闭回路系统，其基本的设置包含一个记录ＬＥＤ光源亮度的光感测器，以及依光感测器测量结果来调整光源输出的控制方法，这将可以让ＬＥＤ光源的亮度在每颗ＬＥＤ变化时维持稳定，也就是虽然各个零件各有变化，但总合维持不变。

在（图四）中，标记为２２的积分电路可以输出一个受到光二极管（１１ａ）上光量控制的电压，这个电压与ＶＳＥＴ比较，比较器的输出能控制计数器数值的增加或减少，计数器的输出则是用来推动一个数字模拟转换器（３７），进而控制ＬＥＤ的驱动电流。

另一个更先进的光学反馈方式则是采用三色光感测器，通常包含三个独立的光感测器以及上方的三色滤镜，让这类光感测器能够记录色彩资讯而不只是亮度，这将可以进一步控制红、绿与蓝光ＬＥＤ的发光强度比，这个功能相当关键，因为它让ＲＧＢ光源的亮度与色度得以控制，而ＡＳＳＰ则在三色光学反馈设计上扮演了重要的角色。

一、实验目的1. 理解组合光学的基本原理和实验方法。

2. 掌握组合光学元件（如透镜、棱镜、光栅等）的特性和应用。

3. 通过实验验证组合光学元件的成像规律和光学特性。

4. 提高动手能力和实验技能。

二、实验原理组合光学是指利用多个光学元件（如透镜、棱镜、光栅等）组合起来实现特定光学功能的技术。

本实验主要研究以下几种组合光学元件的特性和应用：1. 透镜组合：利用透镜的组合实现成像、放大、缩小等功能。

2. 棱镜组合：利用棱镜的组合实现光的折射、反射、分光等功能。

3. 光栅组合：利用光栅的组合实现光的衍射、干涉等功能。

三、实验仪器与材料1. 实验仪器：- 光具座- 平行光管- 成像透镜- 棱镜- 光栅- 分光计- 滤光片- 待测样品2. 实验材料：- 白光光源- 红光光源- 绿光光源- 蓝光光源四、实验内容与方法1. 透镜组合实验：- 将平行光管产生的平行光照射到成像透镜上，观察成像情况。

- 改变成像透镜与平行光管之间的距离，观察成像大小和位置的变化。

- 利用成像透镜组合实现放大、缩小等功能。

2. 棱镜组合实验：- 将白光光源通过棱镜，观察光的色散现象。

- 将红光光源通过棱镜，观察光的折射和反射现象。

- 利用棱镜组合实现光的分光、偏振等功能。

3. 光栅组合实验：- 将白光光源通过光栅，观察光的衍射现象。

- 将红光光源通过光栅，观察光的干涉现象。

- 利用光栅组合实现光的衍射、干涉等功能。

五、实验结果与分析1. 透镜组合实验：- 通过实验观察到，当成像透镜与平行光管之间的距离增大时，成像大小减小，位置向远离透镜的方向移动。

- 通过实验验证了成像透镜的成像规律，即物距与像距的关系。

2. 棱镜组合实验：- 通过实验观察到，白光通过棱镜后会发生色散，形成七色光带。

- 通过实验验证了棱镜的色散特性，即不同颜色的光在棱镜中折射角不同。

3. 光栅组合实验：- 通过实验观察到，白光通过光栅后会发生衍射，形成明暗相间的衍射条纹。

一、实验目的1. 了解光学套件的基本原理和组成部分；2. 掌握光学实验的基本操作方法；3. 通过实验，加深对光学知识的理解和应用能力；4. 培养学生的实验操作技能和团队合作精神。

二、实验器材1. 光学套件：包括透镜、光栅、滤光片、反射镜、折射镜、光纤等；2. 光具座、光源、测量工具、实验记录本等。

三、实验内容1. 透镜成像实验；2. 光栅衍射实验；3. 光纤通信实验；4. 光学元件组合实验。

四、实验步骤1. 透镜成像实验（1）将实验器材摆放在光具座上，调整光源方向，使光线垂直照射到实验台上；（2）将透镜放置在实验台上，调整透镜位置，观察透镜成像情况；（3）记录不同物距下的成像情况，分析透镜成像规律。

2. 光栅衍射实验（1）将实验器材摆放在光具座上，调整光源方向，使光线垂直照射到实验台上；（2）将光栅放置在实验台上，调整光栅角度，观察光栅衍射情况；（3）记录不同光栅角度下的衍射条纹，分析光栅衍射规律。

3. 光纤通信实验（1）将实验器材摆放在光具座上，调整光源方向，使光线垂直照射到实验台上；（2）将光纤连接到实验器材上，调整光纤角度，观察光纤通信情况；（3）记录不同光纤角度下的通信效果，分析光纤通信原理。

4. 光学元件组合实验（1）将实验器材摆放在光具座上，根据实验要求组合光学元件；（2）调整光学元件位置，观察组合后的光学系统效果；（3）记录不同组合方式下的光学系统性能，分析光学元件组合原理。

五、实验报告1. 实验报告格式：（1）实验名称、实验日期、实验班级、实验人数；（2）实验目的、实验原理；（3）实验器材、实验步骤；（4）实验数据、实验结果分析；（5）实验心得体会。

2. 实验报告内容：（1）实验目的和原理：简要介绍实验目的、实验原理及实验过程中涉及的光学知识；（2）实验器材和步骤：详细描述实验过程中所使用的器材和操作步骤；（3）实验数据：记录实验过程中观察到的数据，如物距、像距、衍射条纹等；（4）实验结果分析：分析实验数据，得出实验结论，验证实验原理；（5）实验心得体会：总结实验过程中的收获和体会，提出改进建议。

汽车前组合灯、后组合灯环境可靠性试验试验大纲参考广州广电计量检测股份有限公司机动车零部件检测试验室是CNAS认可实验室，福特、大众、标致雪铁龙（神龙）、日产、本田等国际著名汽车公司和上海汽车、奇瑞、吉利、广汽、比亚迪、福田、江淮等民族自主品牌车企的认可实验室，可以为汽车灯具企业提供从产品研发验证到ccc/e-mark/dot认证到一致性生产控制的全程技术服务。

广州广电计量检测股份有限公司通过卓越的质量保证服务，协助通用、福特、大众、法雷奥等知名整车企业和零部件企业质量技术不断进步。

汽车是由多达几千个电子零部件组成的复杂产品，特别是随着汽车产业的发展，控制电子部分、娱乐多媒体电子部分、导航及车载通信等等越来越多，使车辆复杂程度不断加大。

而这些电子零部件产品可靠性十分重要，直接决定了整车的安全及运行可靠性。

特别是严苛的环境(运输过程、存放、工作中、气候等等)，都在考验着汽车电子产品的可靠性。

本文简单整理出汽车前组合灯、后组合灯环境可靠性试验试验条件，以提供给广大客户参考。

（本文只例举介绍部分测试项目条件参考，具体测试要求由各大车厂提供）3 试验项目3.1外观试验3.2分界面试验3.3工作湿度试验3.4存放湿度范围试验3.5加热老化试验3.6防尘试验3.7浸没试验3.8配光性能试验3.9振动试验3.10腐蚀试验3.11接触力试验3.12表面涂层相容性试验3.13耐温性试验3.14灯泡试验3.15盐雾试验3.16防水试验4 试验设备和试样如果没有另外说明,所要求的各种试验装置可按照所指定的试验方法,试验技术条件、标准和法定技术要求来执行。

4.1试验设备各种试验设施和设备应处于良好工作状态,应具有可靠的核校验标签。

4.1.1总则：用于安装试样的支架和夹具电源：直流30V／10A，电压和电流是可调节的电压表的测量范围为直流0.2V，2V，20V，和200V，最低精度等级为0.5。

4.1.2耐热性加热老化冷热交变温热试验箱在室温230C±50C相对温度80％的条件试验室中进行试验湿度范围：－400C～900C温度的允许精度：±30C4.1.3振动试验，采用符合GB2423、10试验要求振动试验机上进行。

牛顿环实验探究光的干涉现象的产生原因光的干涉现象一直以来都是物理学中一个引人注目的研究领域。

牛顿环实验是其中的经典实验之一，通过观察牛顿环的形成与变化，可以深入了解光的干涉现象以及其产生的原因。

本文将介绍牛顿环实验的原理、实验装置以及实验结果，以便更好地理解光的干涉现象。

一、实验原理牛顿环实验是利用光的干涉现象来研究光的属性的一种实验方法。

光的干涉现象是指两束或多束光波叠加形成的干涉图样。

其中，牛顿环实验主要研究的是光的薄膜干涉，即光在介质表面的反射和透射导致的干涉。

当一束平行光通过一块凸透镜的表面时，光线会发生折射，形成从凸透镜和介质表面反射的光线叠加。

这种叠加会导致光的干涉现象的发生。

牛顿环实验中使用的是凸透镜和平凸玻璃片的组合，通过调节凸透镜和玻璃片之间的距离，可以观察到一系列的明暗相间的环形图样，即牛顿环。

二、实验装置牛顿环实验主要由以下几部分组成：凸透镜、平凸玻璃片、光源、光屏以及调节装置。

1. 凸透镜：实验中使用的凸透镜具有较大的曲率半径，常用的是半径为50 cm的凸透镜。

凸透镜的位置和调焦会影响到实验结果，需视实验需要进行调整。

2. 平凸玻璃片：平凸玻璃片是指两面均为平面的凸透镜，与凸透镜配合使用。

它与凸透镜之间的空气层会导致光的反射和透射，从而形成牛顿环。

3. 光源：光源需要保持稳定且均匀的光强，以确保实验结果的准确性。

常用的光源有白炽灯、氙灯等。

4. 光屏：光屏用于接收和观察光的干涉图样。

光屏放置在凸透镜和平凸玻璃片之间，适当调整位置可以获得更清晰的实验结果。

5. 调节装置：为了实现精确的调节，一些实验仪器配备了微调节装置，如千分尺等，这些装置可以帮助实验者准确地控制凸透镜和平凸玻璃片之间的距离。

三、实验结果在牛顿环实验中，通过凸透镜和平凸玻璃片的组合，并在透镜和玻璃片之间适当调节距离，就可以观察到一系列明暗相间的环状图案，即牛顿环。

牛顿环的特点是中心明亮逐渐过渡到暗环，再逐渐过渡到明环。

测交实验自由组合定律测交实验是物理学中用来研究光的折射现象的实验之一，通过这个实验可以得到光线在两种介质界面上的折射规律。

其中，测交实验自由组合定律是指在介质界面上，光线的入射角、出射角和折射率之间的关系。

本文将详细介绍测交实验自由组合定律及其应用。

1. 测交实验简介测交实验通常使用一块透明的玻璃板和一束直射的光线进行。

当光线从一个介质（如空气）斜射入光密介质（如玻璃板）时，会发生折射现象。

通过观察光线的入射角和出射角的关系，可以得出折射定律。

2. 折射定律折射定律是描述光线在介质界面上折射现象的基本规律。

在测交实验中，折射定律可以表示为：光线的入射角和出射角的正弦之比等于两种介质的折射率之比。

数学表达式如下：n1sinθ1 = n2sinθ2其中，n1和n2分别是两种介质的折射率，θ1和θ2分别是光线在两种介质中的入射角和出射角。

根据折射定律，我们可以计算出光线在不同介质中的传播情况。

3. 测交实验自由组合定律测交实验自由组合定律是在折射定律的基础上推导出来的。

它是指在同一介质中，光线通过两个界面的折射时，光线的入射角和出射角之间的关系。

根据测交实验自由组合定律，当光线通过两个界面的折射时，两个入射角之和等于两个出射角之和。

数学表达式如下：θ1 + θ3 = θ2 + θ4其中，θ1和θ2为光线相对于第一个界面的入射角和出射角，θ3和θ4为光线相对于第二个界面的入射角和出射角。

4. 应用举例测交实验自由组合定律在实际应用中具有重要意义，如在光学设备设计、材料研究和光信号传输等领域。

例如，在光纤通信中，光纤作为一种常见的光信号传输介质，其内部有多个介质界面。

当光线通过光纤的一段时，根据测交实验自由组合定律，可以确定光线的入射角和出射角，从而设计合适的折射结构，以实现高效的光信号传输。

另外，测交实验自由组合定律也可用于光学器件的设计中。

例如，透镜是一种常见的光学器件，通过调节透镜的曲率和折射率，可以控制光线经过透镜后的方向和聚焦效果。

用三棱镜把太阳光分成七色光实验作文《用三棱镜把太阳光分成七色光实验》作文一小朋友们，你们知道吗？有一个特别神奇的实验，可以把太阳光分成七种颜色呢！今天，阳光特别好，我决定来做这个有趣的实验。

我先找到了一个三棱镜，它看起来就像一块透明的小三角。

我拿着三棱镜走到太阳下面，哇！当阳光透过三棱镜的时候，神奇的事情发生啦！在墙上出现了一条像彩虹一样的光带。

红色在最上面，就像我最爱吃的苹果的颜色。

接着是橙色，像橙子的颜色。

黄色像香蕉一样明亮，绿色像小草一样清新。

蓝色像大海一样深，靛色有点像蓝莓的颜色，紫色就像我漂亮的裙子。

这七种颜色组合在一起，真是太漂亮啦！就像一个神奇的魔法，让我看到了太阳的秘密。

小朋友们，你们也快来试试这个有趣的实验吧！作文二嘿，小伙伴们！今天我要给你们讲讲我做的一个超好玩的实验——用三棱镜把太阳光分成七色光。

我跑到院子里，让阳光照在三棱镜上。

一瞬间，一道彩色的光出现在了墙上。

我仔细一看，红色最先出现，那是我玩具车的颜色。

然后是橙色，跟我妈妈做的橙汁颜色好像呀。

黄色像我画画用的蜡笔，绿色像树叶的颜色。

蓝色就像天空，靛色不太常见，但是也很漂亮。

紫色是我最喜欢的颜色之一，就像我头上的发夹。

这个实验太有趣啦，感觉我像一个小科学家！你们也快来试试，说不定会有新发现哟！《用三棱镜把太阳光分成七色光实验》作文一小朋友们，我要告诉你们一个特别神奇的事情！今天我做了一个实验，用三棱镜把太阳光分成了七种颜色。

我在阳台上，拿着三棱镜，阳光照过来的时候，我看到了好多颜色。

有红色，就跟我过年穿的新衣服一个色。

橙色呢，像我吃的橘子。

黄色像我书包上的五角星。

绿色像公园里的小草。

蓝色像我爸爸给我买的蓝色气球。

还有靛色和紫色，也都特别好看。

这些颜色组合在一起，就像一条漂亮的彩带。

我开心极了，感觉自己发现了一个大秘密。

你们也快去试试吧，一定也会觉得很神奇！作文二小伙伴们，我做了一个超级酷的实验！太阳出来的时候，我拿着三棱镜开始玩。

光的偏振实验马吕斯定律光的偏振实验马吕斯定律光的偏振是指光波振动方向的特性。

在物理学中，马吕斯定律是描述光的偏振性质的基本定律之一。

本文将介绍光的偏振实验以及马吕斯定律的原理与应用。

一、光的偏振实验光的偏振实验是通过一系列实验来观察和测量光波在通过偏振器材料时的偏振现象。

常用的偏振实验方法包括偏振片实验、旋光仪实验等。

1. 偏振片实验偏振片是一种特殊的光学材料，可以选择允许特定振动方向的光通过。

在偏振片实验中，我们可以通过两块偏振片的组合来观察光的偏振现象。

通常，将第一块偏振片设置为偏振器，通过旋转它的角度，可以改变光波通过的偏振方向。

随后，将第二块偏振片作为分析器，用于观察通过的光的强度。

根据分析器的角度，我们可以观察到光的透射光强度的变化。

2. 旋光仪实验旋光仪是一种常用的光学仪器，用于测量物质的旋光性质。

旋光性是指物质对偏振光的旋转效应。

在旋光仪实验中，通过旋转样品槽里的物质，可以观察到经过样品后偏振光旋转的现象。

二、马吕斯定律的原理马吕斯定律是法国科学家马吕斯在1808年提出的，该定律描述了光在通过各向同性材料（无论是吸收还是反射）时的偏振性质。

根据马吕斯定律，当一束不偏振光从一个均匀各向同性介质（例如空气、玻璃等）射入时，经过该介质后的光将成为线偏振光。

具体来说，假设光波的振动方向与入射面垂直，那么经过介质后，与入射面垂直的振动方向会被选择性地减弱，而平行于入射面的振动方向则会保持不变。

马吕斯定律的实质是光的振动方向在介质中受到选择性的吸收和减弱，从而导致光的偏振现象。

三、马吕斯定律的应用马吕斯定律在生活和科学研究中有着广泛的应用。

1. 偏振片根据马吕斯定律的原理，偏振片可以选择性地通过特定方向的光波，使其成为偏振光。

这种特性被广泛应用于摄影、光学仪器、偏振显微镜等领域。

2. 偏振光的产生与检测马吕斯定律的原理可以通过适当的实验装置来产生和检测偏振光。

例如，通过透镜和线性偏振片的组合，可以用于研究偏振光与物质的相互作用，有助于了解材料的光学性质。

一种工业视觉相机组合光源的制作方法引言工业视觉相机在现代制造业中发挥着重要的作用。

而光源作为工业视觉系统的关键组成部分之一，对于影像质量和检测效果起到至关重要的作用。

本文介绍了一种制作工业视觉相机组合光源的方法，该方法可以有效改善相机检测的准确性和稳定性。

背景传统的工业视觉相机光源往往由单一光源组成，其输出光线呈现较为单一的光谱和强度。

然而，在实际应用中，工业视觉系统往往需要对不同材料、颜色和形状的物体进行检测和识别。

因此，单一光源的局限性在一定程度上限制了工业视觉系统的应用范围和检测效果。

方法1. 光源选取为了制作一种具有更高灵活性和适应性的工业视觉相机组合光源，我们需要选择适合的光源组件。

常见的光源组件包括白色LED、红外LED、激光等。

根据实际需要，选择合适的光源组件进行制作。

2. 光源控制电路设计为了控制光源的亮度、颜色和模式等参数，我们需要设计光源控制电路。

电路设计需要根据所选光源的电气参数和控制要求进行，可以采用模拟电路或数字电路，以实现对光源的精确控制。

3. 光源组合设计在确定了光源和控制电路后，我们需要设计光源组合方式。

光源的组合方式可以根据实际需求采用并联或串联的方式，以实现不同颜色、强度和分布情况的光线输出。

4. 光源安装和调试完成光源组合的设计后，我们需要根据实际应用需求进行灯光的安装和调试。

在安装过程中，需要注意光源的位置、角度和距离等参数，以确保光线的聚焦和均匀分布。

5. 工业相机与光源的连接完成光源的安装后，需要将工业相机与光源进行连接。

连接方式可以选择光纤传输或线缆传输，根据实际需求选择合适的传输方式。

实验与结果我们通过上述的制作方法，成功制作了一种工业视觉相机组合光源。

在实际应用中，我们对该组合光源进行了测试和评估。

结果表明，相比传统的单一光源，该组合光源在物体检测和识别方面具有更好的效果和稳定性。

通过调整光源的组合方式和控制参数，我们可以获得更多样化的光线输出，满足不同场景下的工业视觉需求。

杨氏双缝干涉实验原理
杨氏双缝干涉实验是一种实验性的光学实验，通过变换激光源的频率和波长，来测量
和计算物体的物理参数。

它的原理和实验方法是根据 1887 年由电磁学家马克斯·吕
多·杨发表的经典实验，又称“双缝镜实验”，以及其后续发展所构建出来的。

最初，它
被用来测量光波的波长，后来发展为一种被用来测量和理解物理参数的实验方法。

它的原理可以概括如下：将一束激光光束从一个板条经过反射，首先在第一个双面反
射镜（称为双缝镜）之前分割，然后分别发射到第二个双面反射镜的两个平行的缝之间，
然后再被反射回第一个双面反射镜，最终分别被两个双面反射镜反射出来，成为一列平行
光束经过一定的距离后，可以交叉组合成一个新的信号结构。

这个新的信号结构取决于原
始激光光束的激光频率，以及两个双面反射镜之间的距离。

根据交叉组合信号结构的明暗
度变化，我们可以确定对应的激光波长以及两个双面反射镜之间的距离。

杨氏双缝干涉实验可以通过改变激光源的频率和波长以及两个双面反射镜之间的距离，来用于测量和计算物体的物理参数，例如块体的折射率、反射率、衍射率，覆盖物折射层
的厚度，介质的厚度，电极的间距，裂纹的深度和折射率等。

由于其原理简单、变量可调，并能够灵敏地检测物体的物理参数，因此杨氏双缝干涉实验在物理学，材料科学，光学和
化学等领域中应用非常广泛。

基于声光组合测量的水下构筑物表面缺陷三维可视化方法研究在科技的大海中，我们如同勇敢的探险家，不断探索未知的领域。

今天，我要与大家分享的是一项创新的研究——基于声光组合测量的水下构筑物表面缺陷三维可视化方法。

首先，让我们想象一下，如果我们的眼睛能够穿透水面，看到水下世界的每一个角落，那将是多么神奇的体验。

然而，现实往往比想象更加复杂。

在水下环境中，由于光线的折射和散射，我们的视线常常受到限制。

这就像在浓雾中寻找路标一样困难。

因此，我们需要一种方法，能够像灯塔一样照亮我们的道路，帮助我们清晰地看到水下构筑物的表面情况。

这种方法就是声光组合测量技术。

它结合了声波和光线的优势，通过声波探测物体的形状和位置，再利用光线进行精细的成像。

这就像是在黑暗中点燃了一支蜡烛，虽然光芒微弱，但却足以照亮我们前行的路。

然而，仅仅照亮道路还不够，我们还需要将这些信息转化为三维图像。

这就需要我们运用计算机图形学的知识，将收集到的数据进行建模和渲染。

这个过程就像是雕刻家在塑造雕像一样，需要耐心和技巧。

在这个过程中，我们遇到了许多挑战。

首先是数据的收集和处理。

由于水下环境的复杂性，我们收集到的数据往往充满了噪声和干扰。

这就需要我们像侦探一样，从海量的信息中找出有用的线索。

其次是三维建模的技术难题。

如何将二维的数据转化为三维的图像，这需要我们具备深厚的数学和物理知识。

然而，正是这些挑战，激发了我们的创新精神。

我们不断尝试新的方法和技术，希望能够找到最佳的解决方案。

就像攀登者面对陡峭的山峰一样，虽然路途艰辛，但山顶的风景却值得我们付出一切努力。

最后，我想说，这项研究不仅仅是一项技术的突破，更是一种科学精神的体现。

它告诉我们，无论面对多大的困难和挑战，只要我们有勇气和决心，就一定能够找到解决的办法。

正如古人所说：“山重水复疑无路，柳暗花明又一村。

”在科学的探索之路上，我们永远不会停止前进的脚步。

在未来的日子里，我相信这项技术将会得到更广泛的应用和发展。