初中几何导角问题

初中数学解几何题方法总结数学几何题在初中阶段是我们经常遇到的题型。

解几何题需要运用几何知识和推理能力，同时还需要一些解题技巧。

下面是对初中数学解几何题的一些方法总结。

1. 观察图形特点：在解几何题时，我们首先要观察图形的特点，包括图形的形状、对称性和相等的边或角等。

通过观察图形特点，我们可以获得一些有用的信息，从而更好地解题。

2. 利用几何定理：几何学有一些重要的定理，如皮亚诺定理、勾股定理、正弦定理和余弦定理等。

在解题时，我们可以运用这些定理来分析和推导出有关的几何关系，从而解决几何题。

3. 利用相似性：相似三角形是解几何题常用的方法之一。

如果两个三角形的对应角相等，且对应边成比例，那么这两个三角形是相似的。

通过相似性的性质，我们可以求解未知边或角的值。

4. 利用三角函数：在解三角形的几何题中，我们经常需要用到三角函数。

正弦、余弦和正切函数可以帮助我们求解三角形内的边长和角度。

在运用三角函数时，我们需要根据题目给出的条件，选择合适的三角函数关系式进行计算。

5. 运用推理和演绎：解几何题的过程中，推理和演绎是非常重要的。

通过逻辑推理和演绎，我们可以根据题目给出的条件，推导出所需的结果。

合理运用推理和演绎，可以在解几何题时事半功倍。

6. 假设和反证法：在解决一些复杂的几何题时，我们可以采用假设和反证法。

假设一些未知条件或结果，然后根据已知条件进行推导和证明。

通过反证法，我们可以反向推导出题目所求的结果，从而解决几何题。

7. 利用图形辅助线：当我们遇到难题时，可以尝试在图形中加入一些辅助线。

通过合理的辅助线可以将题目转化为易于解决的几何问题。

图形辅助线是解几何题的有效方法之一，可以帮助我们更好地理解和解决问题。

除了以上方法，还有一些解几何题的技巧需要我们注意：1. 画图准确：在解几何题时，我们需要准确地画出图形，尽量按照题目给出的条件和要求进行绘制。

画图准确对于解答几何题是很重要的。

2. 简化计算：在计算过程中，我们可以利用一些简化计算的技巧。

几何导角基础技巧一．常见几何导角模型1.外角性质（小旗模型）如图（a ）：B A BCD ∠+∠=∠由 180=∠+∠+∠ACB B A 和180=∠+∠ACB BCD 得： B A BCD ∠+∠=∠2.“飞镖”模型如图（b ）：ACD A ABD BDC ∠+∠+∠=∠证明思路：延长BD 交AC 于点E ，在CDE ∆和ABE ∆中，由BEC A ABD ∠=∠+∠和BDC ACD BEC ∠=∠+∠得： ACD A ABD BDC ∠+∠+∠=∠3.“8”字模型如图（c ）：D C B A ∠+∠=∠+∠证明思路：由180=∠+∠+∠AOB B A ， 180=∠+∠+∠COD D C ，COD AOB ∠=∠可得，D C B A ∠+∠=∠+∠。

4.“内角平分线”模型点P 是ABC ∠和ACB ∠的角平分线的交点。

如图（d ）：A P ∠+=∠2190 证明思路：由“飞镖”模型可得：ACP ABP A P ∠+∠+∠=∠再利用角平分线的性质可得：）（A ACP ABP ∠-=∠+∠ 18021，进而可得：A P ∠+=∠2190 5.“内外平分线”模型点P 是ABC ∠和外角ACD ∠的角平分线的交点如图（e ）：A P ∠=∠21 证明思路：由“小旗”模型可得：P PBC PCD ∠+∠=∠，A PBC A ABC PCD ∠+∠=∠+∠=∠22即可得出：A P ∠=∠216.“外角平分线”模型点P 是外角CBF ∠和外角BCE ∠的角平分线的交点如图（f ）：A P ∠-=∠2190证明：)(180PCB PBC P ∠+∠-=∠)E F (21180CB BC ∠+∠-=)2(21180ACB ABC A ∠+∠+∠-=)180(21180+∠-=AA ∠-=2190技巧与方法三角形中倒角技巧及角分线重要结论几何倒角技巧：1.三角形内角和：三角形的内角和为180°2.三角形外角定理：三角形的外角等于与之不相邻的两个内角之和3.角平分线：角的角平分线把这个角分为两个完全相等的角4.直角三角形：直角三角形两锐角互余5.平行线：平行线的性质6等腰三角形：三角形等边对等角，底角相等7.四边形内角和：四边形内角和为360°8.三角形两大基本模型：“8字”模型和“飞镖”模型的角度关系9.方程思想：设角度为未知数，利用上述倒角技巧找出等量关系。

初中数学知识点几何与三角函数的关系几何学与三角函数是初中数学中两个重要的知识点。

它们之间存在着密切的联系与相互依赖关系。

本文将详细探讨几何与三角函数之间的关系及其应用。

一、几何中的角与三角函数在几何中，角是一个基本概念，它是由两条射线共同确定的，起始于同一个点，但末端方向不同。

角可以分为锐角、直角、钝角、平角四种类型。

而在三角函数中，角也是一个重要的概念。

通过引入单位圆的概念，我们可以定义正弦、余弦和正切等三个基本三角函数。

其中，正弦函数sin(x)定义为对于任意角x，y坐标值等于单位圆上对应点的纵坐标；余弦函数cos(x)定义为对于任意角x，x坐标值等于单位圆上对应点的横坐标；正切函数tan(x)定义为tan(x) = sin(x)/cos(x)。

二、几何中的三角比在几何中，我们常常遇到需要求解三角形的边长或角度的问题。

这时，三角比的概念就会派上用场。

在任意三角形ABC中，我们定义正弦比、余弦比和正切比如下：正弦比sinA = 边对边A/斜边，余弦比cosA = 边对边A/斜边，正切比tanA = 边对边A/边对边B。

三、几何与三角函数的应用几何与三角函数的关系在实际问题中有着广泛的应用。

以下列举几个典型的应用：1. 三角形的面积公式通过几何中面积公式与三角函数的关系，我们可以推导出三角形的面积公式。

对于任意三角形ABC，其面积S等于底边乘以高的一半，即S = (1/2) * AB * h，而高h可以表示为h = BC * sinA，故三角形的面积公式可以进一步简化为S = (1/2) * AB * BC * sinA。

2. 三角函数查表在实际计算中，我们往往会遇到无法直接计算出三角函数值的情况。

这时，我们可以利用三角函数表进行查表计算。

通过查表，我们可以快速得到特定角度对应的三角函数值，从而简化计算过程。

3. 三角函数在三角形相似中的应用在几何中，相似三角形是一个重要的概念。

而在相似三角形的定理中，三角函数也起到了至关重要的作用。

七年级平行线中的求角度问题技巧全文共四篇示例，供读者参考第一篇示例：平行线中的求角度问题是中学几何学习中的重要内容，也是学生们较为关注的难点之一。

在七年级阶段，学生们开始接触平行线及其相关概念，如同位角、内错角、同旁内角等。

要想顺利解决平行线中的求角度问题，首先需要掌握基本的平行线性质，然后灵活运用各种角度间的关系和性质，通过观察图形，巧妙运用角度规律，逐步深入解决问题。

下面将介绍七年级平行线中求角度问题的解题技巧。

一、掌握基本的平行线性质在解决平行线中的求角度问题时，首先要明确以下几条基本平行线性质：1. 同位角相等：同位角是指两条直线被一条截线分成的相对的对应角，它们的大小相等。

掌握以上几条基本的平行线性质，可以快速推导出很多角度之间的关系，为解题提供便利。

二、观察图形，找到已知信息在解决平行线中的求角度问题时，要先仔细观察图形，寻找已知信息，明确题目要求。

有时候，题目中已经给出了一些角度的大小或者角度之间的关系，这些信息是解题的关键。

只有先了解已知信息，才能有针对性地解题。

三、灵活运用角度间的关系和性质在解决平行线中的求角度问题时，要灵活运用各种角度间的关系和性质，例如同位角、内错角、同旁内角等，根据题目条件构建方程，推导出未知角度的大小。

要注意在运用角度性质时，要保持逻辑清晰，不要遗漏任何可能的角度关系。

四、根据题目要求作答，注意单位问题在解决平行线中的求角度问题后，要根据题目要求给出最终的答案。

要注意单位问题，有时题目要求给出的是度数或者比例关系，要保持统一单位，并注意标注解题过程，使得解答清晰易懂。

五、多练习，巩固技巧要通过大量的练习来巩固求角度的解题技巧，熟练掌握平行线中的角度性质，不断提高解题能力。

通过反复练习，逐渐提高解题的速度和准确性，达到熟练运用平行线角度性质的目的。

第二篇示例：平行线是几何学中常见的概念，指在同一个平面上，不相交且方向相同的两条直线。

对于七年级的学生来说，理解和运用平行线的性质非常重要，尤其是在求解求角度问题时。

《角》教学设计一、学习目标根据六年级学生的认知水平及学习经验，按照新课程理念的目标要求，特制定以下学习目标：知识目标：1、学生通过实际生活中对角的理解建立起几何中角的概念，并能理解角的两个定义方法．2、学生学会角的各种表示方法。

3、学生学会角的度量及度、分、秒的转换。

能力目标：通过在图片、实例中找角，增强学生应用数学的意识，培养学生观察、探究、抽象、概括的能力以及把实际问题转化为数学问题的能力。

初步会用运动、变化的观点看待几何图形，初步形成辩证唯物主义观点。

情感目标：通过实际操作，体会角在实际生活中的应用，培养学生积极参与数学学习活动的热情和对数学的好奇心与求知欲。

二、教材分析1、教材的地位和作用：角是一个重要而基本的几何图形之一，有关角的概念和性质，表示方法、画法、计算等，都是重要的几何基础知识，是学习后续图形与几何知识以及其他数学知识的必备的知识基础。

在小学阶段，学生对于角已经有了初步的感性认识，认识很粗浅，有必要在初中阶段进一步学习，逐步提高到理性认识。

本节内容为鲁教版《数学》六年级下册第五章第3节第一课时角的表示与度量。

本节内容是学生在学习了直线、射线、线段及对角的概念已有粗浅的认识的基础上进一步认识角。

本节课的学习将为后面学习角的比较与运算建立基础，同时又对今后的几何学习有重要的作用。

2、教学内容及教材处理本节课主要内容是进一步认识角的意义，了解角的表示方法及掌握角的不同单位及简单转换。

在教学安排上通过生活中角的图形例子引入，进而由直观到抽象出角的数学图形，然后引导学生从静态和动态两方面归纳出角的定义。

对比角的几种表示方法，学会表示各种不同的角。

在角的单位的教学中，通过学生熟知的时钟的时、分、秒的转换帮助学生认识度、分、秒的概念及相互之间的转换。

三、教学重难点分析重点：角的定义、表示法及角的度量单位。

难点：角的表示方法的选择与角的单位转换。

四、学情分析针对初一年级学生基础薄弱，知识水平参差不齐的情况，本节课在师生合作的教学模式下注重引导启发相结合，注重讲解与训练相结合。

几何导角基础技巧
一．常见几何导角模型
1.外角性质（小旗模型）
如图（a ）：B A BCD ∠+∠=∠
由 180=∠+∠+∠ACB B A 和 180=∠+∠ACB BCD 得：
2.“飞镖”模型
如图（b ）：ACD A ABD BDC ∠+∠+∠=∠
证明思路：
延长BD 交AC 于点E ，在CDE ∆和中，
BDC ACD ∠=∠+得：”字模型
D C ∠+∠=
180=∠AOB ，
COD AOB ∠=∠
D C ∠+。

“内角平分线”模型
的角平分线的交点。

A ∠+2
190 证明思路：由“飞镖”模型可得：
再利用角平分线的性质可得：
，进而可得：P +=∠2
190 “内外平分线”模型
的角平分线的交点
A ∠2
1 点P 是外角CBF ∠和外角BCE ∠的角平分线的交点
如图（f ）：A P ∠-=∠2
190 证明：)(180PCB PBC P ∠+∠-=∠
技巧与方法
三角形中倒角技巧及角分线重要结论
几何倒角技巧：
1.三角形内角和：三角形的内角和为180°
2.三角形外角定理：三角形的外角等于与之不相邻的两个内角之和
3.角平分线：角的角平分线把这个角分为两个完全相等的角
4.直角三角形：直角三角形两锐角互余
5.平行线：平行线的性质
6等腰三角形：三角形等边对等角，底角相等
7.四边形内角和：四边形内角和为360°
8.三角形两大基本模型：“8字”模型和“飞镖”模型的角度关系
9.方程思想：设角度为未知数，利用上述倒角技巧找出等量关系。

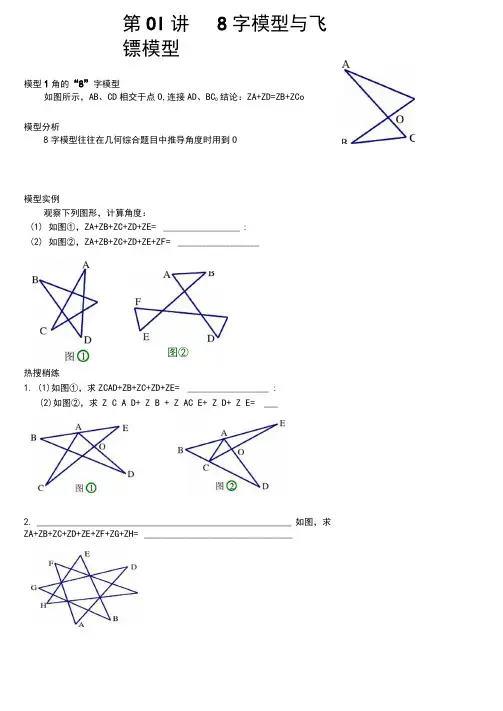
第Ol讲8字模型与飞镖模型模型1角的“8”字模型如图所示，AB、CD相交于点O,连接AD、BC O 结论：ZA+ZD=ZB+ZCo模型分析8字模型往往在几何综合题目中推导角度时用到O模型实例观察下列图形，计算角度：(1)如图①，ZA+ZB+ZC+ZD+ZE= ________________ :(2)如图②，ZA+ZB+ZC+ZD+ZE+ZF= _________________热搜梢练1.(1)如图①，求ZCAD+ZB+ZC+ZD+ZE= _________________ :(2)如图②，求Z C A D+ Z B + Z AC E+ Z D+ Z E= ___2. ________________________________________________ 如图，求ZA+ZB+ZC+ZD+ZE+ZF+ZG+ZH= _______________________________图②模型2角的飞镖模型如图所示，有结论：ZD=ZA+ZB+ZCo模型分析飞镖模型往往在几何综合题目中推导角度时用到a模型实例如图，在四边形ABCD中，AM、CM分别平分ZDAB和ZDCB, AM与CM交于W 探究ZAMC与ZB、ZD间的数量关系。

热搜精练1._________________________________________如图，ΛRZA+ZB+ZC+ZD+ZE+ZF=2.__________________________________ 如图，求ZA+ZB+ZC+ZD=C F模型3边的“8”字模型如图所示，AC、BD相交于点O,连接AD、BC O 结论：AC+BD>AD+BCoD模型实例如图，四边形ABCD的对角线AC、BD相交于点0。

求证：(1) AB+BC+CD+AD>AC+BD:(2) AB+BC+CD+AD<2AC+2BD.模型4边的飞镖模型如图所示有结论：AB+AC>BD+CD.模型实例如图，点O为三角形内部一点。

初中二年级几何学习技巧理解角的对顶角与同旁内角的性质与计算方法几何学习是数学学科中的一部分，对于初中二年级的学生来说，掌握几何知识是非常关键的。

而在几何学习中，理解角的对顶角与同旁内角的性质以及计算方法是必不可少的。

本文将为大家介绍一些关于角的对顶角与同旁内角的知识，以及一些提高学习效果的技巧。

1. 对顶角的性质与计算方法对顶角是指两条直线相交所形成的两对相对的角。

对顶角有以下性质：（1）对顶角相等：当两条直线相交时，所形成的对顶角是相等的。

这是一个重要的性质，在计算角的时候需要加以运用。

计算对顶角的方法一般有两种：利用已知的角度求解未知的角度，以及利用其他已知条件求解对顶角。

（2）利用已知的角度求解未知的角度：当我们已知某个角的度数时，可以利用对顶角相等的性质来求解另一个角的度数。

例如，已知角A的度数为30°，则角B的度数也为30°（因为对顶角相等）。

（3）利用其他已知条件求解对顶角：有时候我们无法直接得知某个角的度数，但可以利用其他已知条件来推导出对顶角的度数。

例如，已知两条直线平行，角A的度数为50°，则与角A对顶的角B的度数也为50°（因为平行线之间的对顶角相等）。

2. 同旁内角的性质与计算方法同旁内角是指两条平行线被一条横截线所截所形成的内角。

同旁内角也有以下性质：（1）同旁内角相等：当两条平行线被一条横截线所截时，所形成的同旁内角是相等的。

这个性质可以帮助我们计算角的度数。

计算同旁内角的方法与计算对顶角的方法类似。

利用已知角度求解未知角度以及利用其他条件求解同旁内角都是常用的计算方法。

例如，已知两条平行线被一条横截线所截，角A的度数为70°，则与角A同旁内的角B的度数也为70°（因为同旁内角相等）。

3. 学习几何的技巧与方法除了掌握角的对顶角与同旁内角的性质与计算方法，还有一些学习几何的技巧与方法可以帮助我们提高学习效果。

（1）掌握基本概念：在学习几何之前，先要掌握各种几何基本概念，如点、线、面等。

七年级北师大版上册动角问题解题技巧全文共四篇示例，供读者参考第一篇示例：七年级北师大版上册动角问题解题技巧在初中数学中，动角问题是一个比较常见的问题类型。

而在七年级北师大版上册中，也会涉及到一些关于动角的问题。

对于初学者来说，可能会觉得动角问题比较难以理解和解决。

但只要掌握了一些基本的解题技巧，就能够轻松地解决这类问题。

接下来，我们就来总结一下关于七年级北师大版上册动角问题的解题技巧。

一、理解动角的概念在解动角问题之前，首先要理解动角的概念。

动角指的是一个角绕着一个点旋转而形成的角度。

在解题时，通常会涉及到两个或多个角度的关系，并且需要根据这些角度的变化来进行计算。

对于动角的概念要有清晰的理解。

二、掌握角度的转化关系在解动角问题时，通常需要将一个角度的度数转化为另一个角度的度数。

在七年级北师大版上册中，通常会涉及到角度的换算，比如将角度转化为弧度，或者将弧度转化为角度。

需要熟练掌握这些角度的转化关系，才能够正确地解答问题。

三、利用几何关系解题在解动角问题时，还可以运用一些几何关系来帮助解题。

比如利用三角形、四边形等几何图形的性质，来推导出一些角度的关系。

通过画图、分析几何图形，可以更直观地理解问题，并找到解题的思路。

四、灵活运用三角函数在解动角问题时，三角函数也是一个很重要的工具。

利用三角函数的关系，可以帮助我们计算角度的大小，并解决一些复杂的问题。

在七年级北师大版上册中，可能会涉及到正弦、余弦、正切等三角函数的应用，因此需要熟练掌握这些三角函数的定义和性质。

五、多练习掌握解题技巧是需要不断练习的。

只有通过大量的练习，才能够熟练地运用这些技巧解决问题。

在练习时，可以选择一些相关的题目进行练习，逐步提高自己的解题能力。

动角问题在初中数学中是一个比较重要的问题类型。

通过理解动角的概念、掌握角度的转化关系、利用几何关系、灵活运用三角函数以及多练习，就能够轻松地解决七年级北师大版上册动角问题。

希望以上的解题技巧能够帮助到大家，加油！第二篇示例：动角问题是初中数学中一个非常基础但又非常重要的概念，几乎贯穿了整个初中数学的学习过程。