力学例题习题作业

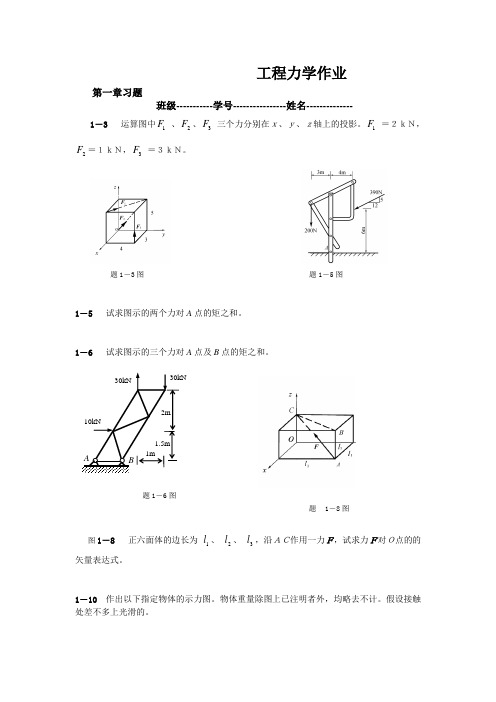
工程力学作业第一章习题班级-----------学号----------------姓名--------------1－3 运算图中1F 、2F 、3F 三个力分别在ｘ、ｙ、ｚ轴上的投影。

1F ＝２ｋＮ，2F ＝１ｋＮ，3F ＝３ｋＮ。

题1－3图 题1－5图1－5 试求图示的两个力对A 点的矩之和。

1－6 试求图示的三个力对A 点及B 点的矩之和。

题1－6图题 1－8图图1－8 正六面体的边长为 1l 、 2l 、 3l ，沿ＡＣ作用一力Ｆ，试求力Ｆ对Ｏ点的的矢量表达式。

1－10 作出以下指定物体的示力图。

物体重量除图上已注明者外，均略去不计。

假设接触处差不多上光滑的。

10kN30kN1m1.5m 2m30kNABF(a)圆轮(b)梁AB(g)梁AB 、CD 及联合梁整体B(e)吊桥AB题1-10图第二章习题班级-----------学号----------------姓名--------------2-5图示混凝土管搁置在倾角为30O的斜面上，用撑架支承，水泥管子重量F Q=5kN。

设A、B、C处均为铰接，且AD=DB，而AB垂直于斜面。

撑架自重及D、E处摩擦不计，求杆AC及铰B的约束力。

题2－5图2—10结构如图2—15所示。

M=1.5kN·m，a=0.3m，求铰A和铰C的反力。

各杆重均不计。

题2－10图班级-----------学号----------------姓名--------------2-11 滑道摇杆机构受两力偶作用，在图示位置平稳。

1OO ＝OA ＝０.２ｍ，1M ＝200Ｎ·ｍ，求另一力偶矩2M 及O ，O 1两处的约束力〔摩擦不计〕。

题2－11图第三章习 题 班级-----------学号----------------姓名--------------3-6 在水平的外伸梁上作用一力偶，其力偶矩M =60kN ·m 。

在C 点作用一铅垂载荷F P =20kN 。

波动(习题课后作业)1. 传播速度为200m/s, 频率为50Hz 的平面简谐波, 在波线上相距为0.5m 的两点之间的相位差是( D )(A) π/3 (B) π/6 (C) π/2 (D) π/4 解: λ=u/λ=200/50=4(m) Δφ=(2π/λ)Δx =(2π/4)⨯0.5=π/42. 图为沿X 轴正向传播的平面余弦横波在某一时刻的波形图, 图中P 点距原点1m, 则波长为( C )(A) 2.75m (B) 2.5m (C) 3m (D) 2.75m Y(cm) 解: 设波表达式为)2 cos(ϕλπω+-=x t A y x =0处 3) cos(2=+=ϕωt yv =－2ωsin(ωt+φ)<0即23) cos(=+ϕωt ,sin(ωt+φ)>0 得6 πϕω=+t所以t 时刻的波形分布函数为)26cos(2x y λππ-=P 点t 时刻的位移 0)26cos(2=-=λππy P 点t 时刻的速度 0)26sin(2>--=λππωv32O P X得)26cos(=-λππ0)26sin(<-λππ226πλππ-=-∴ λ = 3m3. 一横波沿X 轴负方向传播, 若t 时刻波形曲线如图所示, 在t+T/4时刻原X 轴上的1、2、3三点的振动位移分别是( B ) (A) A 、0、-A (B) -A 、0、A (C) 0、A 、0 (D) 0、-A 、04. 两个相干波源S 1和S 2, 相距L=20m, 在相同时刻, 两波源的振动均通过其平衡位置, 但振动的速度方向相反, 设波速u=600m/s, 频率ν=100Hz, 试求在S 1和S 2间的连线上因干涉产生最弱点的所有位置(距S 1的距离).解: 已知φ1–φ2=π, 设S1为原点，在S 1和S 2连线间任取一点P ，其坐标为x∙∙xS 2∙S 1 L=20m L –xPxLx x L x r -=--=∆2)(r ∆--=∆λπϕϕϕ221)2(2L x --=λππ)(6100600m u===νλxx 32326)220(3ππππππ-++=-⨯+=x 3235ππ-=干涉减弱条件 πϕ)12(+=∆k πππ)12(3235+=-k x 即 得 ),2,1,0(31 ±±=-=k k x 因200≤≤x 即 20310≤-≤k 解得 31319≤≤-k 所以,1 ,2 ,3 ,4 ,5 ,6------=k )(1 , 4 , 7 , 10 , 13 , 16 , 19 m x =∴。

第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。

（）2．在理论力学中只研究力的外效应。

（）3．两端用光滑铰链连接的构件是二力构件。

（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。

（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。

（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。

（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。

（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

（）二、选择题1．若作用在A点的两个大小不等的力F1和F2，沿同一直线但方向相反。

则其合力可以表示为。

①F1－F2；②F2－F1；③F1＋F2；2．作用在一个刚体上的两个力F A、F B，满足F A=－F B的条件，则该二力可能是。

①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。

③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。

3．三力平衡定理是。

①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。

4．已知F1、F2、F3、F4为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形，由此。

①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。

5．在下述原理、法则、定理中，只适用于刚体的有。

①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。

三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。

2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。

初三力学练习题例题题目一：力的合成与分解问题描述：一位小学生正沿直线行走，他向东方施加了15牛的力和向南方施加了20牛的力。

求小学生总的合力大小和方向。

解答：根据力的合成原理，可以通过向量法求解该问题。

首先，将15牛的力表示为向东方的力，记作F1 = 15N。

将20牛的力表示为向南方的力，记作F2 = 20N。

接下来，我们需要将这两个力进行合成，即求出其合力F。

根据向量加法原理，可以将F1和F2相加得到合力F。

根据平行四边形法则，可以得到合力F与F1和F2之间的关系：F = √(F1² + F2² + 2F1F2cosθ)其中，θ为F1与F2之间的夹角。

由题可知，F1 = 15N，F2 = 20N。

由于F1向东方，F2向南方，因此，F1与F2之间夹角为90°，cos90° = 0。

带入公式计算：F = √(15² + 20² + 2×15×20×0)= √(225 + 400 + 0)= √625= 25N得到小学生的合力大小为25牛。

接下来，求小学生合力的方向。

根据向量加法原理，可以得到合力的方向与F1和F2的方向相同。

即小学生总的合力方向向东南方向。

因此，小学生总的合力大小为25牛，方向为东南方向。

题目二：牛顿第二定律问题描述：一个质量为2千克的物体在水平方向上施加了一个30牛的力，与物体相接触的水平地面摩擦系数为0.3。

求物体的加速度和摩擦力大小。

解答：根据牛顿第二定律，物体的加速度a与施加在物体上的合力F和物体的质量m之间的关系为：F = ma。

根据题目可知，物体的质量m = 2千克，施加在物体上的合力F = 30牛。

将已知值带入公式计算：a = F / m= 30 / 2= 15m/s²得到物体的加速度为15米/秒²。

接下来，计算摩擦力的大小。

根据摩擦力公式，摩擦力Ff与物体所受的法向力Fn和摩擦系数μ之间的关系为：Ff = μFn。

第一章质点运动学例1、质点沿x轴正向运动，加速度a=-kv，k为常数。

设从原点出发时速度为v0，求运动方程x=x(t)与速度—位移关系v=v(x)。

例2、已知斜抛运动的抛射角为θ，初速度为v0。

求其轨迹方程。

例3、如图，小船在绳子的匀速v0牵引下运动，已知h。

求θ位置时船的速度与加速度大小。

（两种方法）例4、有一轮以匀角速ω旋转，一质点自轮心沿水平轮轴以匀速v0向轮边移动。

求质点的轨迹方程，以及t时刻质点的速度和加速度大小。

*例5、一只狼沿着半径为R的圆形岛边缘按逆时针方向匀速跑动，当狼经过某点时，一只猎犬以相同的速率从岛中心出发追逐狼。

设追逐过程中犬、狼、岛中心始终在一直线上，求猎犬的轨迹和追上狼时的位置。

*例6、（上海高考题改编）下图为平静海面上拖船A、B拖着驳船C运动的示意图。

已知A、B的速度分别沿缆绳CA、CB方向，且A、B、C不共线。

以下说法正确的是（）（多选）（A）C的速度大小可能介于A、B的速度大小之间（B）C的速度一定不小于A、B的速度（C）C的速度方向可能在CA、CB的夹角之外（D）C的速度方向一定在CA、CB的夹角之内**例7、已知点P0(l,0)处有一小船，以长为l的线，拉着小船从原点向上走，小船沿着绳运动，PQ为P点切线，Q点恒在y轴上。

（1）以图中θ为参数，求P点的轨迹方程。

（曳物线）（2）若Q 点以匀速u 向上运动，求θ位置处P 点的加速度。

练习题1、一质点沿x 轴运动，其速度—时间关系为⎪⎭⎫ ⎝⎛+=t t v 6sin 23ππ，式中各量均取国际单位。

已知当t =0时质点在x =-2m 处。

求：（1）2s 时质点的位置；（2）0s 至2s 质点的位移；（3）0s 和2s 两时刻质点的加速度。

2、一质点以初速度v 0=5i 开始离开原点，其运动加速度为a =-i -j 。

求：（1）质点到达x 坐标最大值时的速度；（2）上述时刻质点的位置。

3、如图所示，长为l 的棒的一端A 靠在墙上，另一端B 搁在地面上，A 端以恒定速率u 向下运动。

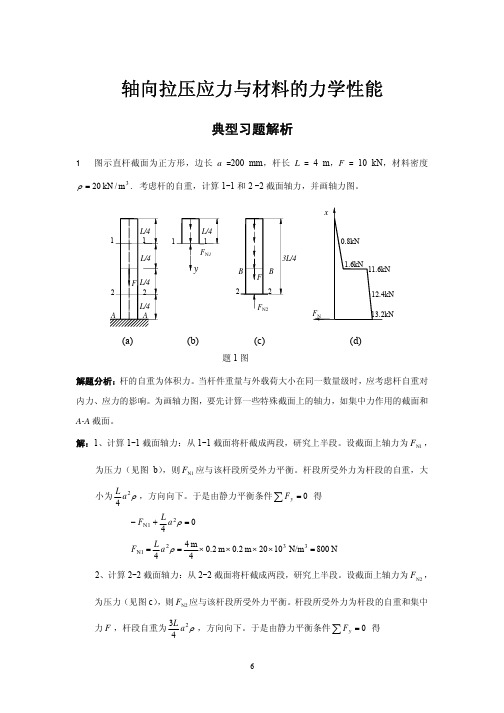
例题分析1土的物理性质和工程分类1.1 某完全饱和粘性土的含水量为40%ω=，土粒的相对密度s2.7d =，试按定义求土体的孔隙比e 和干密度d ρ。

解：设土粒的体积3s 1cm V =，则由下图所示的三相指标换算图可以得到：土粒的质量 s s w 2.7g m d ρ== 水的质量 w s 0.4 2.7 1.08g m m ω==⨯=孔隙的体积 3wv w w1.08cm m V V ρ===孔隙比 v s 1.08 1.081V e V ===； 干密度 3s s d v s 2.7 1.3g cm 1 1.08m m V V V ρ====++. 1.2 试证明下式 ()s w 1r n S nωγγ-=解：从基本指标的基本定义出发，w s m m ω=，s s w s m V γγ=，v Vn V=,将这些基本指标的定义式代入到上面等式的右边，可以得到：()w s v ss s w w r vw w v vw (1)1m m Vg n m V V m VS V n V V Vωγγργ⨯⨯⨯--====⨯ 1.3 某砂土试样，通过试验测定土粒的相对密度s 2.7d =，含水量9.43%ω=，天然密度31.66g cm ρ=，已知砂样处于最密实状态时干密度3dmax 1.62g cm ρ=，处于最疏松状态时干密度3dmin 1.45g cm ρ=。

试求此砂样的相对密实度r D ，并判断砂土所处的密实状态。

解：设土粒的体积3s 1cm V =，则通过三相图可以计算土粒的质量：s s w 2.7g m d ρ==；水的质量：w s 0.0943 2.70.255g m m ω==⨯=； 土样的质量：s w 2.955g m m m =+= ；天然状态下砂样体积：32.9551.78cm 1.66mV ρ===；天然状态下砂样的孔隙比：v s s s 0.780.781V V V e V V -====dmax1.62ρ处于最密实状态下砂样孔隙比：v s s s 0.670.671V V V e V V -==== 处于最疏松状态下砂样体积：3sdmin2.71.86cm 1.45m V ρ=== 处于最疏松状态下砂样孔隙比：v s s s 0.860.861V V V e V V -==== 相对密实度：max r max min 0.860.780.420.860.67e e D e e --===-- r 0.670.33D >> 所以处于中密状态。

力学综合习题及答案．．A．力的作用点 C．力的方向 D．力的单位（参考答案与试题解析一．选择题3．（2014•郴州）在以“力”为主题的辩论赛中，正方和反方提出了许多观点，小明把他们的观点归纳整理如下表．你．C D．，5．（2013•枣庄）图是描述地球上不同位置的人释放手中石块的四个示意图，图中的虚线表示石块下落的路径，则．C D．6．（2014•十堰）如图，分别在A、B、C处用同样大小的力推门，可以感受到在A点用力容易把门推开．这说明力的作用效果与下列哪个因素有关？（）7．（2013•永安市模拟）小华用矿泉水瓶做验证实验（如图）：他用水平力轻轻推动底部时，瓶子沿桌面平稳地移动；当用水平力轻推瓶盖时，瓶子翻了．他验证的是力的作用效果与（）8．如图所示，用大小相同的力，以不同的方向作用于塑料尺的同一点，塑料尺弯曲的程度不同．此现象表明影响力作用效果的因素是力的（）9．（2014•山西）2014年世界杯足球赛正在巴西进行．小伟和小梁运用所学物理知识对比赛中的一些现象进行分析，下列说法中全部正确的一组是（）①踢球时．脚感到疼是因为物体间力的作用是相互的②踢出去的足球能继续向前飞行是由于惯性③足球在空中飞行时受到重力和向前的推力④空中飞行的足球，若它所受的力全部消失它将立即停止⑤足球在空中飞行过程中．运动状态发生改变二．填空题（共9小题）10．（2013•沁阳市模拟）我们生活在地球上，重力无处不在．如工人师傅在砌墙时，常常利用重垂线来检验墙身是否竖直，这充分利用了重力的方向是竖直向下的这一原理；玩具“不倒翁”被扳倒后会自动起来，这是因为它的重心低的缘故．11．（2013•江永县二模）物体受到的重力的方向总是竖直向下的，建筑工人利用这个原理来检查所砌的墙是否符合要求，具体的做法是用细绳吊一个重物在墙边，当看到墙线与绷直的细线平行时，就达到要求了．12．（2013•天津）一座平直的跨海大桥全长1.6km，桥头立着如图所示的两个标志牌．如果一辆匀速行驶的载重汽车恰好达到两标志牌的最大限定值，该车通过桥中央时对桥面的压力为3×105N，通过该桥的时间为0.04 h．（g取10N/kg，车长不计）求出时间．v===0.04h13．（2012•南充）如果用g表示重力与质量的比值，则一个质量为m的物体受到的重力G=mg．它受到的重力方向总是竖直向下．14．（2014•深圳二模）请在图中画出小球所受力的示意图．15．（2013•鞍山模拟）请在图中画出铁锁松手后运动到A位置时的受力示意图（不计空气阻力）．16．（2014•十堰）滑板车是中学生喜爱的玩具之一．用脚蹬地，滑板车会沿地面向前运动，这说明力的作用是相互的．如果不再蹬地，滑板车的速度会越来越慢，最后停下来，这是因为它在运动中受到阻力，这表明力可以改变物体的运动状态．滑板车静止时，受到的一对平衡力是人与车自身的重力和地面的支持力．17．（2014•厦门）今年端午节，全国首创的“龙舟拔河赛”在集美龙舟池举行．龙舟靠划桨获得动力．若甲船战胜乙船，则甲船的动力大于乙船的动力，甲船拉乙船的力等于乙船拉甲船的力．（均选填“大于”、“小于”或“等于”）18．（2014•北海）如图所示，打网球时，击球瞬间网球迅速被压扁并反弹出去，这说明力既可以改变物体形状又可以改变物体运动状态；在球被压扁的同时球拍的拉线也弯曲了，这说明力的作用是相互的．。

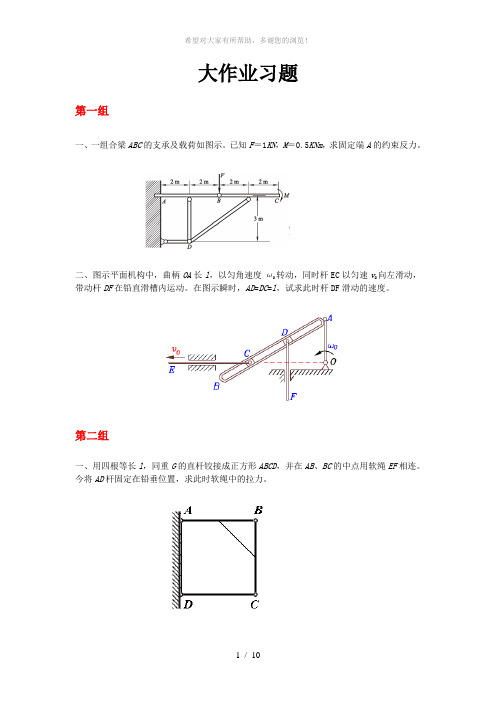
大作业习题第一组一、一组合梁ABC的支承及载荷如图示。

已知F＝1KN，M＝0.5KNm，求固定端A的约束反力。

二、图示平面机构中，曲柄OA长l，以匀角速度ω0转动，同时杆EC以匀速v O向左滑动，带动杆DF在铅直滑槽内运动。

在图示瞬时，AD=DC=l，试求此时杆DF滑动的速度。

第二组一、用四根等长l，同重G的直杆铰接成正方形ABCD，并在AB、BC的中点用软绳EF相连。

今将AD杆固定在铅垂位置，求此时软绳中的拉力。

二、一半径为r的半圆形凸轮，与长均为r的曲柄O1A、O2B相连，又与长为r的杆OC光滑接触。

曲柄O1A、O2B以相同的角速度分别绕其支座在图示平面内转动，并始终保持平行。

图示瞬时，OC杆与凸轮最高点接触，试求：（1）OC杆的角速度；（2）OC杆的角加速度。

第三组一、平面构架如图所示。

已知物块重W，DC=CE=AC=CB=2l，R=2r=l。

试求支座A、E处的约束力及BD杆所受的力。

二、平面机构如图所示。

套筒B与CB杆相互垂直并且刚连，CB杆与滚子中心C点铰接，滚子在车上作纯滚动，小车在水平面上平动。

已知：半径r=h=10cm，CB=4r。

在图示位置时，=60°，OA杆的角速度=2rad/s，小车的速度u=10m/s。

试求该瞬时滚子的角速度。

第四组一、图示平面机构，各构件自重均不计。

已知：OA=20cm，O1D=15cm，q=30°，弹簧常数k=100N/cm。

若机构平衡于图示位置时，弹簧拉伸变形d=2cm，M1=200N·m，试求使系统维持平衡的M2。

二、机构如图，已知：OA=2b；在图示瞬时，OB=BA，f=60°，q=30°，∠A=90°，OA的角速度为。

试求此瞬时套筒D相对BC的速度。

第五组一、图示来而结构由杆AB及弯杆DB组成，P=10N，M=20N·m，L=r=1m，各杆及轮自重不计，求固定支座A及滚动支座D的约束反力及杆BD的B端所受的力。

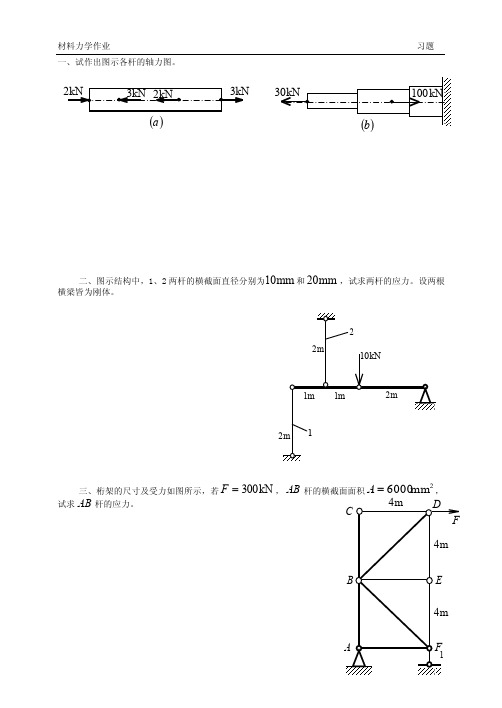
一、试作出图示各杆的轴力图。

二、图示结构中，1、2两杆的横截面直径分别为mm 10和mm 20，试求两杆的应力。

设两根横梁皆为刚体。

三、桁架的尺寸及受力如图所示，若kN 300=F ，AB杆的横截面面积2mm 6000=A ，试求AB 杆的应力。

()a四、在图示简易吊车中，BC 为钢杆，AB 为木杆。

木杆AB 的横截面面积21cm 100=A ，许用应力[]MPa 71=σ；钢杆BC 的横截面面积22cm 6=A ，许用应力[]MPa 1602=σ。

试求许可吊重[]F 。

五、在低碳钢拉伸实验用的力与变形曲线及应力应变曲线中分别标出p F 、s F 、b F 和p σ、s σ、b σ，并回答在εσ-曲线中的p σ、s σ、b σ是否是构件中的真实应力，如果不是请另绘出强化阶段与颈缩阶段真实应力曲线的大致形状。

六、像矿山升降机钢缆这类很长的拉杆，应考虑其自重的影响。

设材料单位体积的重量为γ，许用应力为[]σ。

钢缆下端所受拉力为F ，且钢缆截面不变。

试求钢缆的允许长度及其总伸长。

钢缆横截面面积为A 。

B七、图示结构中，AB 为刚体，杆1、杆2、杆3的材料和横截面面积均相同，在杆AB 的中点C 作用铅垂方向的载荷F，试计算C 点的水平位移和铅垂位移。

已知：kN20=F ，2321mm 100====A A A A ，mm 1000=l ，GPa 200=E 。

八、设横梁ABC D 为刚体。

横截面面积为2mm 36.76的钢索绕过无摩擦的滑轮。

设kN 20=P ，试求钢索内的应力和C九、图示结构中，AB 为刚体，1、2杆的抗拉（压）刚度均为EA 。

试求两杆的轴力。

十、图示杆系的两杆同为钢杆，GPa200=E ，C 061105.12-⨯=α。

两杆的横截面面积同为2cm 10=A 。

若AC 杆的温度降低C 200，而AB杆的温度不变，试计算两杆的轴力。

十一、图示支架中的三根杆件材料相同，杆1的横截面面积为2mm 200，杆2的横截面面积为2mm 300，杆3的横截面面积为2mm 400。

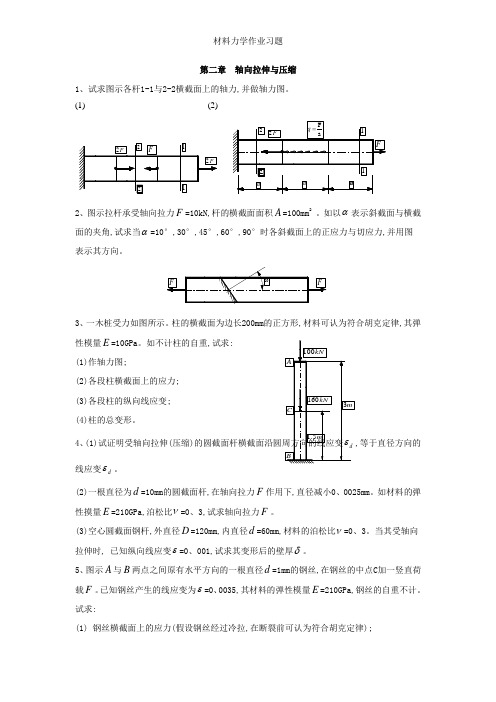
第二章 轴向拉伸与压缩1、试求图示各杆1-1与2-2横截面上的轴力,并做轴力图。

(1) (2)2、图示拉杆承受轴向拉力F =10kN,杆的横截面面积A =100mm 2。

如以α表示斜截面与横截面的夹角,试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力与切应力,并用图表示其方向。

3、一木桩受力如图所示。

柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。

如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力; (3)各段柱的纵向线应变;(4)柱的总变形。

4、(1)试证明受轴向拉伸(压缩)等于直径方向的线应变d ε。

(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0、0025mm 。

如材料的弹性摸量E =210GPa,泊松比ν=0、3,试求轴向拉力F 。

(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0、3。

当其受轴向拉伸时, 已知纵向线应变ε=0、001,试求其变形后的壁厚δ。

5、图示A 与B 两点之间原有水平方向的一根直径d =1mm 的钢丝,在钢丝的中点C 加一竖直荷载F 。

已知钢丝产生的线应变为ε=0、0035,其材料的弹性模量E =210GPa,钢丝的自重不计。

试求:(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律);(2) 钢丝在C点下降的距离∆;(3) 荷载F的值。

6、简易起重设备的计算简图如图所示、一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。

试问在提起重量为P=15kN的重物时,斜杆AB就是否满足强成,钢的许用应力]度条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。

已知材料的许用应力[σ=170MPa,试选择杆AB,AD的角钢型号。

第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

a a9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数 ，a = 2m 。

a a a 10kN/m12、求图示结构E 点的竖向位移。

EI = 常数 。

l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m 3m 3m14、求图示刚架B 端的竖向位移。

ql15、求图示刚架结点C 的转角和水平位移，EI = 常数 。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝常数。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI＝常数。

18、求图示刚架中D点的竖向位移。

E I = 常数。

qll l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。

l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。

ll21、求图示结构B点的竖向位移，EI = 常数。

(A) L A L B , E kA E kB.(B) L A L B , E kA E kB.(C) LAL B , E kA E kB・开始时转台以匀角速度3o 转动，此时有一质量为 m 的人站在转台中心，随后人沿半径向3解题示例 例题5— 5如图5—9所示。

弹簧的质量忽略不计，而倔强系数k 11.6牛顿/米。

绳子 质量忽略不计且不可伸长。

滑轮的半径 R 10厘米，绕其抽转动的转动惯量 I 0.01千 克.米2。

空气阻力不计，求质量 m 1千克的物体从静 止开始（此时弹簧 无伸长）落下h 1米时的速度大小 （v h ）。

F lf l己知2k 11.6N/m ， R 10cm ， I 0.01kg m ， h 1m ， m 1kg 求V h 例题5 一 6 一均匀棒长l 0.4米，质量M 1千克，可绕通过其 上端O 的水平轴转动，质量 m 0.01千克的弹片以速度 v 200 米/秒射入棒中，射入处离 O 点为0.3米（图5-11 ）。

求棒与弹片 一起转动时的角速度 ，及转过的角度 。

已知I 、M 、m 、弹片射入处 求、 角动量与刚体转动练习题 一.选择题 1.人造地球卫星绕地球做椭圆轨道运动，卫星轨道近地点和远地点分别为 和Ek 分别表示对地心的角动量及其动能的瞬时值，则应有B85—*11A 和B 。

用L(D ) L A L B , E kA E kB ・ 解：由角动量守恒 因为势能 E pA E pB E kA E kB答案：（C ）L A L B 由机械能守恒,2.由一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动, 转动惯量为J外跑去，当人到达转台边缘时，转台的角速度为3.如图所示，一静止的均匀细棒，长为 L 、质量为M ，可绕通过棒的端点且垂直于棒长的光滑固定轴 0在水平面内转动，转动惯量为1/3 ML2. 一质量为m 、速率为v 的子弹4. 关于力矩有以下几种说法：（1 ）对某个定轴而言，内力矩不会改变刚体的角动量。

第一章 绪论思 考 题1) 现代力学有哪些重要的特征？2) 力是物体间的相互作用。

按其是否直接接触如何分类？试举例说明。

3) 工程静力学的基本研究内容和主线是什么？ 4) 试述工程力学研究问题的一般方法。

第二章刚体静力学基本概念与理论习题2-1 求图中作用在托架上的合力F R 。

2-2 已知F 1=7kN ，F 2=5kN, 求图中作用在耳环上的合力F R 。

2-3 求图中汇交力系的合力F R 。

习题2-1图12030200N F4560F 习题2-2图2-4 求图中力F 2的大小和其方向角α。

使 a )合力F R =1.5kN, 方向沿x 轴。

b)合力为零。

2-5二力作用如图，F 1=500N 。

为提起木桩，欲使垂直向上的合力为F R =750N ，且F 2力尽量小，试求力F 2的大小和α角。

2-6 画出图中各物体的受力图。

(b)x453=30N =20N=40N A x45600N 2=700N0N 习题2-3图 (a )F 1习题2-4图F 12习题2-5图(b)(a )2-7 画出图中各物体的受力图。

(c)(d)(e)(f) (g) 习题2-6图(a)ACD2-8 试计算图中各种情况下F 力对o 点之矩。

(b)(d)习题2-7图P(d)(c)(a ) CA2-9 求图中力系的合力F R 及其作用位置。

2-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。

习题2-8图习题2-9图( a )1F 3 ( b )F 3F 2( c)1F /m( d )F 32-11 图示悬臂梁AB 上作用着分布载荷，q 1=400N/m ，q 2=900N/m, 若欲使作用在梁上的合力为零，求尺寸a 、b的大小。

第三章 静力平衡问题习 题3-1 图示液压夹紧装置中，油缸活塞直径D=120mm ，压力p =6N/mm 2，若α=30︒, 求工件D 所受到的夹紧力F D 。

( b )q ( c )习题2-10图B习题2-11图3-2 图中为利用绳索拔桩的简易方法。

第一章静力学公理与受力分析(1）一．是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。

（)2、作用于刚体上三个力的作用线汇交于一点，该刚体必处于平衡状态。

（）3、刚体是真实物体的一种抽象化的力学模型，在自然界中并不存在。

( ）4、凡是受两个力作用的刚体都是二力构件。

（）5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。

（）二．选择题1、在下述公理、法则、原理中,只适于刚体的有（）①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三．画出下列图中指定物体受力图。

未画重力的物体不计自重,所有接触处均为光滑接触。

整体受力图可在原图上画。

)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体)- 1 -)e(杆AC、CB、整体)f(杆AC、CD、整体四．画出下列图中指定物体受力图。

未画重力的物体不计自重，所有接触处均为光滑接触.多杆件的整体受力图可在原图上画。

)a(球A、球B、整体)b(杆BC、杆AC、整体- 2 -- 3 -第一章 静力学公理与受力分析(2）一．画出下列图中指定物体受力图。

未画重力的物体不计自重,所有接触处均为光滑接触。

整体受力图可在原图上画。

WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体)d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体- 4 -- 5 -第二章 平面汇交和力偶系一．是非题1、因为构成力偶的两个力满足F = — F ',所以力偶的合力等于零。

（ )2、用解析法求平面汇交力系的合力时，若选用不同的直角坐标系，则所求得的合力不同。

力学考试例题：
1. 一根质量为2kg的木棒，长为1m，一端固定，让其自由旋转。

问：木棒的质心和转动中心是否重合？如果重合，请说明理由。

如果不重合，请计算它们之间的距离。

2. 一辆汽车以速度v在平直路面上行驶，突然发现前方有一障碍物，司机紧急刹车。

假设汽车刹车时受到的阻力是恒定的，求汽车从开始刹车到停止所用的时间。

设汽车的质量为m，刹车时受到的阻力为kmg（其中k为常数）。

3. 一根长度为L的均匀细杆，一端固定在光滑水平轴上，自由旋转。

初始时，杆与水平轴线成一角度θ。

问：当杆以角速度ω旋转时，其质心和转动中心之间的距离是多少？
4. 一辆质量为M的汽车在平直路面上行驶，其上装载了一质量为m的货物。

汽车受到的阻力与其速度成正比，即f = kv（其中k 为常数）。

当汽车以速度v匀速行驶时，突然货物从车上滑下。

求货物滑下后，汽车的运动状态和最终速度。

5. 一根质量分布均匀的细杆，一端固定在光滑水平轴上，自由旋转。

初始时，杆与水平轴线成一角度θ。

问：当杆以角速度ω旋转时，其转动惯量是多少？。