Stimulus Properties of PMMA Effect of Optical Isomers and Conformational Restriction
- 格式:pdf
- 大小:151.09 KB
- 文档页数:5

Heat-resistant PMMA photonic crystal films with bright structural colorBingtao Tang *,Cheng Wu,Tao Lin,Shufen ZhangState Key Laboratory of Fine Chemicals,Dalian University of Technology,Dalian 116024,PR Chinaa r t i c l e i n f oArticle history:Received 4July 2013Received in revised form 8August 2013Accepted 13August 2013Available online 26August 2013Keywords:Polymethylmethacrylate Methacrylic acid Photonic crystal film Structural color Heat-resistantGlass transition temperaturea b s t r a c tWeak heat resistance of polymethylmethacrylate (PMMA)photonic crystal films has been the major challenge for its applications in displays or paints.This paper presents heat-resistant PMMA photonic crystal films with a bright structural color that are produced by using a simple preparation strategy.In this strategy,the heat resistance was controlled and remarkably improved by introducing methacrylic acid as comonomer together with methyl methacrylate.The mechanism of improving heat resistance was characterized by using scanning electron microscopy and differential scanning calorimetry.Three-dimensional ordered structures are produced,directly forming photonic crystal films that are highly heat-resistant and have a bright structural color.These two properties are signi ficant for applications in displays or paints.Crown Copyright Ó2013Published by Elsevier Ltd.All rights reserved.1.IntroductionPhotonic crystals are one class of functional materials with a periodicity in dielectric constant,which can control and manipu-late light [1e 7].The ability of the crystals to control and manipulate light is important for their applications in full-color displays,paints,photonic paper,switches,modulators,and filters [8e 10].Among various technical applications,the direct conversion of light to color (structural color)has received signi ficant attention because of its unique characteristics such as energy conservation.Considering their unique characteristics,arti ficial structural color films made through colloidal crystallization self-assembly,dielectric layer stacking,and direct lithographic patterning have received consid-erable attention in recent years [11].In contrast to the expensive and non-scalable technologies of dielectric layer stacking and direct lithographic patterning,colloidal crystallization self-assembly is most frequently used in making photonic crystals because raw materials are easily obtained,and self-assembly is quite simple [11].Among the materials used for producing photonic crystals through colloidal crystallization self-assembly,polymethylmethacrylate (PMMA),which is weather resistant,durable,and chemically sta-ble,is of great signi ficance [12e 16].Sotomayor Torres et al.successfully used PMMA beads to obtain photonic crystal structural color films by drying the spread latex;the film typically appears iridescent in the visible range [17].Zhu et al.obtained P(NIPAm-co -MAA)hydrogel photonic crystal microparticles with inverse-opal structure by a combination of micro fluidic and templating methods,which can respond to pH simultaneously due to the ex-istence of MAA functional groups [18].Chen et al.loaded Cd 0.4Zn 0.6S nanocrystals on the surface of PS-co -PMAA microspheres.The ob-tained hybrids of integrating electronic con finement and photonic con finement,opened promising avenues in the design and con-struction of next-generation photoelectric devices based on pho-tonic crystals [19].Gu et al.prepared PMMA inverse opals,which could be stretched nearly 100%with diffraction peak blue-shifting across the whole visible spectrum [20].However,the tuning color was not reversible because of the plastic deformation of the PMMA sheet [21].Simultaneously,emulsion polymerization is a commonly used method of obtaining polymer microspheres from the free radical polymerization of vinyl monomers [22e 24].Copolymerization with functional monomers could achieve effec-tive modi fication of polymer,which is of great signi ficance to speci fic applications.Methacrylic acid (MAA)is typically used as comonomer to modify polymer such as polymethylmethacrylate (PMMA)and polystyrene (PSt).Robin et al.successfully encapsu-lated ZnO nanoparticles by P(MMA-MAA).MAA units of the ob-tained copolymer shell acted as a coupling agent,which then grafted onto polypropylene [25].*Corresponding author.Tel.:þ8641184986267;fax:þ8641184986264.E-mail address:tangbt@ (B.Tang).Contents lists available at ScienceDirectDyes and Pigmentsjournal h omepage:www.elsevier.co m/locate/dyepig0143-7208/$e see front matter Crown Copyright Ó2013Published by Elsevier Ltd.All rights reserved./10.1016/j.dyepig.2013.08.012Dyes and Pigments 99(2013)1022e1028The persistence of photonic crystal structural color is crucial for its actual application in full-color displays,paints,and photonic paper.Once the periodic array is destroyed,the structural color will disappear.Therefore,the periodic arrays of photonic crystals should have high structural stability even under unstable environments.Among various external factors,temperature is very important because system temperature will increase as a result of the large thermal energy generated during solar radiation or laser irradiation [26e 28].However,PMMA has poor heat resistance because of its low glass transition temperature,which ranges from 40 C to 100 C [29e 31],which severely limits the application of PMMA photonic crystal films.In this report,heat-resistant photonic crystal structural color films were fabricated by assembling microspheres of methyl methacrylate (MMA)and methacrylic acid (MAA)through a vertical-lifting process.Three-dimensional ordered structures are achieved to form polymer crystal films that have a bright structural color.The introduction of MAA improves the heat resistance of photonic crystal films because copolymer has high spatial structure stability and temperature resistance [32].Therefore,heat-resistant PMMA structural color films that have a bright structural color are obtained.2.Experimental 2.1.MaterialsMMA,MAA,and potassium peroxydisulfate (initiator)were purchased from Sinopharm Chemical Agent Company (Shanghai,China).All chemical reagents were used as received and without further puri fication.2.2.Preparation of PMMA microspheresThe following were gradually added to a 250ml three-necked flask:150ml deionized water,8.7g MMA,and a certain amount of MAA.After the mixture was heated to 80 C in a water bath under a N 2gas atmosphere,0.080g of initiator was added.Five hours later,the microsphere emulsion from the copolymerization of MAA and MMA was obtained.2.3.Preparation and characterization of photonic crystal films 25ml emulsion of PMMA spheres was poured into a 25ml beaker,and then the beaker was placed in a Coater with Heatment (SYDC-100H DPI,SAN-YAN Instrument Co.Ltd.,Shanghai).Glass slides were used as a substrate,and the pulling rate was set to 1m m/s.The whole process was carried out at 25 C.Glass slides were immersed in chromic acid lotion for 12h and washed carefully before being used.A Nanoparticle Size and Zeta Potential Measurement (Zetasizer Nano Series Nano-ZS90,Malvern,UK)were used to measure the hydrodynamic sizes and zeta potential of the particles.Optical photographs of the films were taken by using a Nikon digital camera.Scanning electron micrographs (SEM)were taken by using Nova NanoSEM 450to observe the surface microstructures of the photonic crystal films.All the samples were coated with gold beforeTable 1Effect of MAA concentration on particle size and size distribution of PMMA particles.MAA (wt%)Z-Ave (nm)a PDIZp (mV)D hD a 02862540.02À35.310.33142700.03À34.318.73483010.05À38.725.63803290.05À40.3aD h :Hydrodynamic size of these microspheres measured by nanoparticle size measurement.D a :Actual measured diameters from theSEM.Fig.1.SEM images of copolymer microspheres with varying MAA contents.(a)Pure PMMA,(b)10.3wt%,(c)18.7wt%,(d)25.6wt%.B.Tang et al./Dyes and Pigments 99(2013)1022e 10281023observation.The re flection spectra of the films,which ranged from 400nm to 800nm,were measured by using a Hitachi U-4100spectrophotometer.Differential scanning calorimetry (DSC)was performed in a nitrogen atmosphere by using an American TA In-struments 910S DSC thermal analyzer from À20 C to 200 C at a heating rate of 5 C/min.FTIR spectroscopic analyses of the film samples were conducted in transmission mode by using a Thermo Scienti fic Nicolet 6700FTIR spectrometer.3.Results and discussionPMMA microspheres were prepared through the method of emulsion copolymerization.Table 1shows the effect of MAA con-tent on particle size and size distribution of PMMA particles.Monodisperse particles that have MAA content that varies between 0wt%and 25.6wt%are obtained.The hydrodynamic size of these microspheres increases monotonically from 286nm to 380nm.The actual measured diameters from the SEM results are 254,270,301,and 329nm,which are smaller than the hydrodynamic size.Poly-dispersity index (PDI)of the obtained microspheres ranges from 0.02to 0.05,and the corresponding zeta potential ranges from À34.3mV to À40.3mV.PDI and zeta potential results indicate that a stable monodispersed emulsion is prepared [33].After vertical-lifting assembly,the three-dimensional ordered structures were achieved.Fig.1shows the SEM images of the microstructure of photonic crystal films with varying MAAcontents.The uniformly-sized beads are arranged in an orderly array.The size of the microspheres increases along with the increasing amount of MAA.The three-dimensional ordered struc-ture can be further con firmed through the re flection spectra of polymer films in Fig.2.All films with 0,10.3,18.7,and 25.6wt%MAA show sharp re flectance peaks at wavelengths of 557,608,680,and 721nm.On the macro vision,structural color changes from green to red,as indicated in Fig.3.Bright structural colors are achieved because of an ordered structure (Fig.1).Compared with pure PMMA film,films with MAA show lower re flectance.It possibly results from the increase of PDI.As shown in Table 1,PDI increased from 0.02to 0.05when MAA was added.The increased PDI in-dicates that size distribution of microspheres turns wider and consequently leads to the reduction of re flectance.According to Bragg ’s law,the stop band and the color of a three-dimensional periodic structure can be explained by using the following equation:l ¼2d ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffin 2Àsin 2qq (1)where n is the effective refractive index of materials;d is the dis-tance between the crystalline planes in the (111)direction and is related to the polymer sphere diameter D by d ¼ffiffiffiffiffiffiffiffi2=3p D for theface-centered cubic (fcc)structure;and q ¼10 is the angle ofincident light.In addition,the effective refractive index n is deter-mined by the filling ratio (f )of the microparticles as follows:n ¼ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffin 2p f þn 2b ð1Àf Þq (2)where f ¼0.74is the filling ratio for the polymer in the fcc structure.n p and n b denote the refractive index of the polymer and back-ground materials,respectively.If the position of the stop band is within the visible range,the films display colors.The peak position of the stop band and the color of the crystal films depend on the relative filling ratio and the diameter of the polymer spheres.Here,n p ¼1.48and n b ¼n air ¼1,and the calculated peak positions of the stop bands for the photonic crystal films made of polymer spheres that are 254,270,301,and 329nm in diameter are 563,602,671,and 716nm,respectively.These values roughly match the experi-mental peak positions of 557,608,680,and 721nm,as shown in Fig.2.The FTIR spectrum can provide valuable information about the structure of the materials,which means that it can clearly reveal the copolymerization of MMA and MAA.For an accurate re flectionFig.2.Re flection spectra of films with varying MAA contents.(a)Pure PMMA,(b)10.3wt%,(c)18.7wt%,(d)25.6wt%.Fig.3.Photographs of polymer films with varying MAA contents.(a)Pure PMMA,(b)10.3wt%,(c)18.7wt%,(d)25.6wt%.B.Tang et al./Dyes and Pigments 99(2013)1022e 10281024of carboxy hydroxyl group in copolymers,we chose the paraffin paste method to avoid the interference of water contained in KBr. FTIR spectra for PMMA with varying MAA contents are shown in Fig.4a.The one on the top of Fig.4a is the curve of pure PMMA;it does not show the O e H bond at3253cmÀ1.This peak becomes stronger with increased MAA(Fig.4a).The broad peak at 2840cmÀ1to2970cmÀ1is caused by the paraffin.However, carbonyl group stretching peaks of carboxylic acid and carboxylic ester overlap completely at1730cmÀ1.To distinguish between the carboxy carbonyl group and the ester carbonyl group,we used Na2CO3as the basic reagent and tested the FTIR spectra after regulating the emulsion to pH9.At this moment,carboxylic acid exists in the form of carboxylic salt.Fig.4b shows the spectra,the one on the top is the curve of pure PMMA, and it displays only the C]O bond at1722cmÀ1.However,the copolymer(Fig.4b)also exhibits C]O stretches at1566cmÀ1, which indicates the presence of carboxylic salt.In summary,the O e H bond at3253cmÀ1in Fig.4a and the C]O bond at1566cmÀ1in Fig.4b proves the copolymerization of MMA with MAA.Heat resistance is an important property for polymers.To date, all reported photonic crystalfilms of PMMA have poor heat resis-tance because of their low glass transition temperature(T g).The DSC analysis(Fig.5a)shows that the glass transition temperatureof Fig.5.DSC curves(a)and the corresponding T g(b)of samples with varying MAAcontents.Fig.6.SEM images of PMMA photonic crystalfilms with18.7wt%MAA under various temperature.Rt:Roomtemperature.Fig.4.FTIR spectra of PMMA with varying MAA contents.(a)Spectra used infrared paraffin paste method,(b)Spectra after regulating pH.B.Tang et al./Dyes and Pigments99(2013)1022e10281025PMMA particles is improved when MAA is used.Pure PMMA has a heat flow change at 94.1 C,which corresponds to the T g of PMMA [34].Nevertheless,the photonic crystal films with 18.7wt%MAA shows a much higher T g at about 145 C (Fig.5a),which is higher than that of pure PMMA by about 50 C.The difference is ascribed to the con finement of intercalated PMMA chains [35]and demon-strates that the copolymer has better heat resistance than pure PMMA.As we can see in Fig.5b,a small amount of MMA can in-crease the T g of the polymer dramatically.Increasing the amount of MAA has little in fluence on T g when the copolymer contains more than 18.7wt%MAA.Photonic crystal structural colors are closely related to their periodicity order [36].Once the periodicity order is destroyed by heat,the structural color disappears.SEM was used toobserveFig.7.Photographs of photonic crystal films with 18.7wt%MAA under various temperature.Rt:Roomtemperature.Fig.8.SEM images of pure PMMA photonic crystal films under various temperature.Rt:Roomtemperature.Fig.9.Photographs of pure MMA photonic crystal films under various temperature.Rt:Room temperature.B.Tang et al./Dyes and Pigments 99(2013)1022e 10281026surface microstructure changes in these photonic crystal films during heating.As shown in Fig.6,the beads of PMMA photonic crystal films with 18.7wt%MAA are arranged uniformly with voids.However,as a result of the increasing temperature,microspheres deform,and voids shrink gradually after exceeding the T g of co-polymers.The effective refractive index decreases at the same time.As a result,the structural color fades,as indicated in Fig.7.When the temperature reaches 180 C,the voids disappear,which then results in the disappearance of color.Pure PMMA films show similar properties,while the microspheres ’deformation temperature is much lower.As we can see in Figs.8and 9,the microspheres deform into hexagons and the structural color of photonic crystal films disappears when the heating temperature reaches 100 pared with the pure PMMA films,copolymer photonic crystal films are more heat-resistant.The heat resistance of photonic crystal films can be identi fied by measuring the peak intensity at different temperatures.Fig.10shows the peak intensity of pure PMMA film and PMMA films with 10.3,18.7,and 25.6wt%MAA.For the pure PMMA film,the intensity decreases rapidly when the temperature increases to 90 C (Fig.10),and the intensity decreases to almost zero when the temperature is only 104 C.The re flectance peak intensity of the PMMA photonic crystal films with 18.7wt%MAA does not vary signi ficantly before the temperature increases to 160 C,which means that the close-packed structure is stable.Moreover,the in-tensity decreases dramatically to zero when the temperature is184 C,which can be attributed to the damage in the spherical structure.This decrease is due primarily to the reduced magnitude of the optical dielectric contrast,which is proportional to re flection intensity [37].Compared with the pure PMMA photonic crystal films,the heat resistance of the copolymer photonic crystal films that contain 18.7wt%MAA improves dramatically.The heat resistance of PMMA films was further proved by reversible temperature changes.Thermal cycling tests of PMMA photonic crystal films with 18.7wt%MAA were carried out,and the results of a 12-cycle test were shown in Fig.11.The samples are heated to 160 C every time,and peak intensity changes only little after 12cycles.The results also show that the films exhibit high heat resistance.In addition,the heat resistant PMMA film is man-ufactured in large-scale (Fig.12),which meets requirements for practical applications,especially serving as painting materials.4.ConclusionsIn summary,the heat resistance of PMMA films that have a bright structural color is dramatically improved by using meth-acrylic acid as a comonomer.The mechanism of improving the heat resistance of PMMA was investigated.PMMA photonic crystal films with 18.7wt%MAA could resist high temperatures up to 160 C.And the peak intensity changes only little after thermal cycling tests,which indicates that the films have high heat resistance.In addition,not only are the materials cheap and the preparation process simple and feasible,but the obtained PMMA photonic crystal films also display brilliant visual color under natural lighting conditions.This study offers a new approach for generating highly heat-resistant and brilliant photonic crystal films,which will accelerate their application in daily life.AcknowledgmentsThis work was supported by the National Natural Science Foundation of China (21276042),the National Science and Tech-nology Pillar Program (2013BAF08B06),Jiaogai Foundation of DUT (JGXM201224),Fundamental Research Funds for theCentralFig.10.Re flectance peak intensity of photonic crystal films with varying MAA contents at differenttemperature.Fig.11.Thermal cycling tests of PMMA photonic crystal films with 18.7wt%MAA.Fig.12.Photograph of PMMA photonic crystal films with 18.7wt%MAA manufactured in large-scale.B.Tang et al./Dyes and Pigments 99(2013)1022e 10281027Universities of China(DUT13LK35),and Program for Liaoning Excellent Talents in University(LJQ2013006).References[1]Kim SH,Lee SY,Yang SM,Yi GR.Self-assembled colloidal structures for pho-tonics.NPG Asia Mater2011;3:25e33.[2]Wu ZL,Gong JP.Hydrogels with self-assembling ordered structures and theirfunctions.NPG Asia Mater2011;3:57e64.[3]Joannopoulos JD,Villeneuve PR,Fan S.Photonic crystals.Solid State Commun1997;102:165e73.[4]González-Urbina L,Baert K,Kolaric B,Pérez-Moreno J,Clays K.Linear andnonlinear optical properties of colloidal photonic crystals.Chem Rev 2011;112:2268e85.[5]Hinterholzinger FM,Ranft A,Feckl JM,Ruhle B,Bein T,Lotsch BV.One-dimensional metal-organic framework photonic crystals used as platforms for vapor sorption.J Mater Chem2012;22:10356e62.[6]Chen YC,Geddes JB,Yin L,Wiltzius P,Braun PV.X-ray computed tomographyof holographically fabricated three-dimensional photonic crystals.Adv Mater 2012;24:2863e8.[7]Khunsin W,Amann A,Kocher-Oberlehner G,Romanov SG,Pullteap S,Seat HC,et al.Noise-assisted crystallization of opalfilms.Adv Funct Mater2012;22: 1812e21.[8]Arsenault AC,Puzzo DP,Manners I,Ozin GA.Photonic-crystal full-colourdisplays.Nat Photonics2007;1:468e72.[9]Campbell M,Sharp DN,Harrison MT,Denning RG,Turberfield AJ.Fabricationof photonic crystals for the visible spectrum by holographic lithography.Nature2000;404:53e6.[10]Han T,Liu YG,Wang Z,Wu Z,Wang S,Li S.Simultaneous temperature andforce measurement using Fabry-Perot interferometer and bandgap effect of a fluid-filled photonic crystalfiber.Opt Express2012;20:13320e5.[11]Kim H,Ge J,Kim J,Choi S,Lee H,Lee H,et al.Structural colour printing using amagnetically tunable and lithographicallyfixable photonic crystal.Nat Pho-tonics2009;3:534e40.[12]Ge J,Yin Y.Responsive photonic crystals.Angew Chem Int Ed2011;50:1492e522.[13]Shen W,Li M,Ye C,Jiang L,Song Y.Direct-writing colloidal photonic crystalmicrofluidic chips by inkjet printing for label-free protein b Chip 2012;12:3089e95.[14]Kimura T,Kawai T,Sakamoto Y.Magnetic orientation of poly(ethylene tere-phthalate).Polymer2000;41:809e12.[15]Pursiainen OL,Baumberg JJ,Winkler H,Viel B,Spahn P,Ruhl T.Nanoparticle-tuned structural color from polymer opals.Opt Express2007;15:9553e61.[16]Müller M,Zentel R,Maka T,Romanov SG,Sotomayor Torres CM.Dye-con-taining polymer beads as photonic crystals.Chem Mater2000;12:2508e12.[17]Müller M,Zentel R,Maka T,Romanov SG,Sotomayor Torres CM.Photonic crystalfilms with high refractive index contrast.Adv Mater2000;12:1499e503. [18]Wang J,Hu Y,Deng R,Liang R,Li W,Liu S,et al.Multiresponsive hydrogelphotonic crystal microparticles with inverse-opal ngmuir 2013;29:8825e34.[19]Yan L,Yu Z,Chen L,Wang C,Chen S.Controllable fabrication of nanocrystal-loaded photonic crystals with a polymerizable macromonomer via the CCTP ngmuir2010;26:10657e62.[20]Liu Z,Xie Z,Zhao X,Gu ZZ.Stretched photonic suspension array for label-freehigh-throughput assay.J Mater Chem2008;18:3309e12.[21]Zhao Y,Xie Z,Gu H,Zhu C,Gu Z.Bio-inspired variable structural color ma-terials.Chem Soc Rev2012;41:3297e317.[22]Van Gruijthuijsen K,Rufier C,Phou T,Obiols-Rabasa M,Stradner A.Light andneutron scattering study of PEG-oleate and its use in emulsion ngmuir2012;28:10381e8.[23]Han YK,Yih JN,Chang MY,Huang WY,Ho KS,Hsieh TH,et al.Facile synthesisof aqueous-dispersible nano-PEDOT:PSS-co-MA core/shell colloids through spray emulsion polymerization.Macromol Chem Phys2011;212:361e6. [24]Xia H,Wang Q,Qiu G.Polymer-encapsulated carbon nanotubes preparedthrough ultrasonically initiated in situ emulsion polymerization.Chem Mater 2003;15:3879e86.[25]De Rancourt Y,Couturaud B,Mas A,Robin JJ.Synthesis of antibacterial sur-faces by plasma grafting of zinc oxide based nanocomposites onto poly-propylene.J Colloid Interface Sci2013;402:320e6.[26]Synnefa A,Santamouris M,Livada I.A study of the thermal performance ofreflective coatings for the urban environment.Sol Energy2006;80:968e81.[27]Takebayashi H,Moriyama M.Surface heat budget on green roof and highreflection roof for mitigation of urban heat island.Build Environ2007;42: 2971e9.[28]Ihara I,Yamada H,Takahashi M.Two-dimensional monitoring of surfacetemperature distribution of a heated material by laser-ultrasound scanning.J Phys Conf Ser2011;278:012022.[29]Kopesky ET,McKinley GH,Cohen RE.Toughened poly(methyl methacrylate)nanocomposites by incorporating polyhedral oligomeric silsesquioxanes.Polymer2006;47:299e309.[30]Ash BJ,Siegel RW,Schadler LS.Glass-transition temperature behavior ofalumina/PMMA nanocomposites.J Polym Sci Part B Polym Phys2004;42: 4371e83.[31]Grohens Y,Brogly M,Labbe C,David MO,Schultz J.Glass transition ofstereoregular poly(methyl methacrylate)at ngmuir1998;14: 2929e32.[32]Yu GU,Dy JT,Enriquez EP.Opacity of P(MMA-MAA)-PMMA composite latexsystem with varying MAA concentration.Philipp J Sci2011;140:221e30. [33]Wong S,Kitaev V,Ozin GA.Colloidal crystalfilms:advances in universalityand perfection.J Am Chem Soc2003;125:15589e98.[34]Zhang Y,Wang X,Liu Y,Song S,Liu D.Highly transparent bulk PMMA/ZnOnanocomposites with bright visible luminescence and efficient UV-shielding capability.J Mater Chem2012;22:11971e7.[35]Matsubara K,Watanabe M,Takeoka Y.A thermally adjustable multicolorphotochromic hydrogel.Angew Chem Int Ed2007;46:1688e92.[36]Seago AE,Brady P,Vigneron JP,Schultz TD.Gold bugs and beyond:a review ofiridescence and structural colour mechanisms in beetles(Coleoptera).J R Soc Interface2009;6:S165e84.[37]Bertone JF,Jiang P,Hwang KS,Mittleman DM,Colvin VL.Thickness depen-dence of the optical properties of ordered silica-air and air-polymer photonic crystals.Phys Rev Lett1999;83:300e3.B.Tang et al./Dyes and Pigments99(2013)1022e1028 1028。
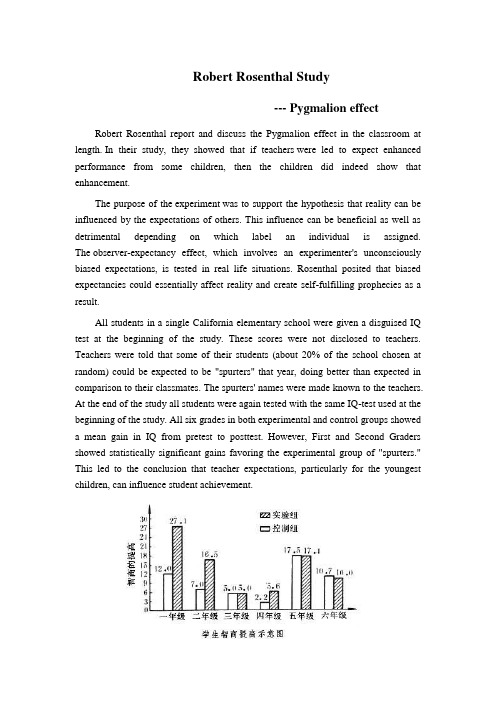
Robert Rosenthal Study--- Pygmalion effectRobert Rosenthal report and discuss the Pygmalion effect in the classroom at length. In their study, they showed that if teachers were led to expect enhanced performance from some children, then the children did indeed show that enhancement.The purpose of the experiment was to support the hypothesis that reality can be influenced by the expectations of others. This influence can be beneficial as well as detrimental depending on which label an individual is assigned. The observer-expectancy effect, which involves an experimenter's unconsciously biased expectations, is tested in real life situations. Rosenthal posited that biased expectancies could essentially affect reality and create self-fulfilling prophecies as a result.All students in a single California elementary school were given a disguised IQ test at the beginning of the study. These scores were not disclosed to teachers. Teachers were told that some of their students (about 20% of the school chosen at random) could be expected to be "spurters" that year, doing better than expected in comparison to their classmates. The spurters' names were made known to the teachers. At the end of the study all students were again tested with the same IQ-test used at the beginning of the study. All six grades in both experimental and control groups showed a mean gain in IQ from pretest to posttest. However, First and Second Graders showed statistically significant gains favoring the experimental group of "spurters." This led to the conclusion that teacher expectations, particularly for the youngest children, can influence student achievement.。

Crystalline structures in ultrathin poly(ethylene oxide)/poly(methylmethacrylate)blend filmsMingtai Wang *,Hans-Georg Braun *,Evelyn MeyerInstitute of Polymer Research Dresden,Hohe Strasse 6,D-01069Dresden,Germany Received 26May 2003;received in revised form 2June 2003;accepted 10June 2003AbstractAmorphous poly(ethylene oxide)/poly(methyl methacrylate)(PEO/PMMA)blend films in extremely constrained states are meta-stable and phase separation of fractal-like branched patterns happens in them due to heterogeneously nucleated PEO crystallization by diffusion-limited aggregation.The crystalline branches are viewed flat-on with PEO chains oriented normal to the substrate surface,upon increasing PMMA content the branch width remains invariant but thickness increases.It is revealed that PMMA imposes different effects on PEO crystallization,i.e.the length and thickness of branches,depending on the film composition.q 2003Elsevier Science Ltd.All rights reserved.Keywords:Crystallization;Poly(ethylene oxide);Surface pattern1.IntroductionEven though polymer crystallization has been exten-sively studied during the past decades [1,2],the crystal-lization in ultrathin films is a new topic in this field.Special enthalpic and entropic factors at polymer/substrate interface cause the organization of polymer chains in ultrathin films to deviate from their bulk states [3–6],and substrate adsorption effect,due to which polymer chains form stable loops dangling in the direction perpendicular to the substrate surface,reduces the thermodynamic potential of hetero-geneous nucleation for crystallization [7].Studying the crystallization in ultrathin polymer films has offered a possibility to reveal polymer chain organization during crystallization in real space [8–15].However,observation of crystalline morphology has mainly been done in ultrathin films containing only one polymer,and branched structures due to non-equilibrium crystallization by a diffusion-limited aggregation (DLA)process are always the case in the films of a thickness less than 10nm,as shown by the terrace structures with fingers [8,9],the finger-like [10–13]and fractal-like [15]patterns.In forming these structures,heterogeneous nucleation is necessary and polymer chains fold without influence of other polymers and by a stem length of 7–13nm.In this report we show the crystalline structures in ultrathin poly(ethylene oxide)/poly(methyl methacrylate)(PEO/PMMA)blend films and the effects on PEO crystallization imposed by PMMA.2.ExperimentalPolyethylene glycol standard (M w ¼6000;M w =M n ¼1:03)from Fluka and PMMA standard (M w ¼4200;M w =M n ¼1:06)from Polymer Standards Services (PSS,Germany)were used as received to prepare PEO/PMMA blend films.The radius of gyration,R g ;of a polymer chain is calculated by R g ¼ðNb 2=6Þ1=2;where N is the degree of polymerization and b the average statistical segment length.For b PMMA ¼0:69nm [16],the R g of the PMMA chain is 1.77nm.According to the data in literature [17],the b PEO and R g of the PEO chain are calculated to be 0.70and 3.30nm,respectively.Au films of 100nm thickness were prepared by thermal evaporation (rate 0.1nm/s)of gold on the glass slides primed with a Cr adhesive layer of 3nm thickness.PEO/PMMA blend films were dip-coated on the Au films from chloroform solutions (totally 1mg/ml)at an average lifting rate of 1.90mm/s.The coated polymer layers (given a refractive index of 1.5)0032-3861/03/$-see front matter q 2003Elsevier Science Ltd.All rights reserved.doi:10.1016/S0032-3861(03)00492-0Polymer 44(2003)5015–5021/locate/polymer*Corresponding authors.Tel.:þ49-351-4658633;fax:þ49-351-4658284.E-mail addresses:mingtaiwang@ (M.Wang),braun@ipfdd.de (H.G.Braun).had a thicknessðDÞof2–3.0nm within the tested composition range(0–50%PMMA,by weight).For D# R g of the longest component(PEO),thefilms can be defined as extremely constrained two-dimensional ones[16,18].To provide defined areas for studying crystallization by means of scanning electron microscopy(SEM)and atomic force microscopy(AFM),an newly-coatedfilm wasfirst scratched once with a razor blade after drying in the air for 15min,and then put immediately into a vacuum(in SEM sample chamber,ca.1026h Pa)to crystallize for about17h. For grazing incidence reflection infrared(GIR-IR)spec-troscopy,thefilms that had been dried in the air for15min were crystallized in the vacuum for24h without scratching. The temperature in the vacuum chamber was estimated by ambient temperatures to be21–228C.In vacuum condition the moisture influence on crystallization was eliminated.Film thickness was measured on an ELX-02C ellips-ometer(DRE GmbH,Germany;He–Ne laser source 632.8nm,708angle of incidence)in15–20min after coating when thefilm was still amorphous.GIR-IR spectra were recorded in vacuum on an IFS66V/S spectrometer (Bruker Co.),using a grazing incidence external reflection stage(from SPECAC,incident angle808C)at a resolution of4cm21and1000scans and a bare Aufilm as reference. Optical microscopy(OM)observation was done on a light microscope(Zeiss/Sis,Germany)in dark-field mode in ambient conditions.SEM and AFM studies of the samples were performed immediately after crystallization,as described previously[15].3.ResultsAs a typical blend system containing amorphous and semi-crystalline components,PEO/PMMA blend in bulk state has been studied by different means,such as differential scanning calorimetry(DSC)[19],nuclear magnetic resonance(NMR)[20],small-angle X-ray scatter-ing(SAXS)and small-angle neutron scattering(SANS)[21] and microscopy[22].In general,PEO and PMMA are miscible in melt and amorphous states resulting in a single concentration-dependent glass transition[23],addition of PMMA reduces the crystal growth rate[24,25]and crystal-linity[22,26]of PEO.The growth and melting of crystal lamellae of PEO spherulites in thin PEO/PMMAfilms have been revealed by hot-stage AFM[27].Recently,Ferreiro and co-workers[28]reported that the crystalline mor-phology in thin PEO/PMMAfilms(ca.200nm thick)can be tuned byfilm composition to get circular spherulites(50–100%PEO),seaweed morphology(40–50%PEO),sym-metric dendrites(30–40%PEO)and fractal structures(15–25%PEO).They also presented the growth dynamics of the symmetric dendrites with a focus on their growth pulsations [29],but how thefilm morphology is tuned by adding PMMA still remains unclear.In spite of the above extensive studies,we,to our knowledge,are still lacking the observation on the crystalline morphology in ultrathin PEO/PMMAfilms.3.1.SEM and OM observationsAfter crystallization in vacuum for several hours(e.g. 17–18h),the blendfilms are decorated by branched structures stemming from the scratch line(Fig.1).The branched structures clearly resemble the fractals formed in electrodeposition[30,31]and bacterial growth[32].Fractal formation proceeds theoretically by DLA process[33,34]. Crystalline structures reminiscent of DLA process have been observed in ultrathin PEOfilms,for example,the finger-like pattern in PEO monolayers[10,11].Reasonably, the fractal-like structures here are related to PEO crystal-lization in the blendfilms by DLA process.Note that SEM observations of the freshfilms showed that the PEO/PMMA films were homogeneous,but the pure PEOfilm was dispersed with some PEO dots(ca.1m m in diameter and6–7nm in height)that should be due to de-wetting of PEO on the substrate duringfilm formation because of the weak interaction between the Au surface and PEO[35];the non-scratchedfilms were not found branched structures for at least1h when kept in the vacuum.The branch growth depends strongly onfilm composition (Fig.1).Generally,both main branches and sub-branches became shorter with PMMA content.The branches were very long in90/10(¼PEO/PMMA)film,and the substrate surface was covered mainly by the branches stemming from the scratch line(Fig.1(b));but the branches in75/25film were much shorter than those in90/10film and a large structureless area appeared in front of the branches(Fig. 1(c)).Further increasing PMMA content to40%,the branches along the scratch line became much shorter and a much larger structureless areas resulted in front of them (Fig.1(d)).In PEOfilm,the branches stemming from PEO dots were much longer than these from the scratch line,the substrate surface was mainly covered by the branches nucleated by PEO dots which should crystallize prior to the branch growth because of their higher thickness[11].The scratch line was created for two purposes,to act as heterogeneous nucleation for crystallization and to provided defined areas for studying crystallization.Under an optical microscope,90/10film was observed to show,in about 3min after scratching with a needle(228C,33%relative humidity),the contrast change in the zones along the scratch line,indicating the starting of crystallization;however,we didn’tfind evidently the crystal growth in75/25film for 25min after scratching.Therefore,the branched structures here were not a direct result of scratching[36],and the scratch line acted as a surface defect to nucleate polymer chains.In the case of50/50film,where the branches were normally very short,a fortuitous long branched structure was found stemming from the scratch line,as shown in Fig.2.SEM revealed that the long structure grew actually alonga defect zone on the Au surface,which shows that theM.Wang et al./Polymer44(2003)5015–5021 5016structureless areas in front of the branches along the scratch line (Figs.1(d)and 2)consist of amorphous PMMA and PEO but the crystallization in them needs further hetero-geneous nucleation.The crystallization in the films (Fig.1)did take place in vacuum.On one hand,the time interval between the finish of scratching and the start of SEM vacuumization was very short (within ca.1min).On the other hand,if branch growth had finished before putting the film into the vacuum the branches should mainly stem from the scratch line and those nucleated by PEO dots should be much shorter in PEO film (Fig.1(a)).3.2.GIR-IR measurementsFig.3shows the GIR-IR spectra of the ultrathin films.Detailed assignments of IR vibrations of PEO [35,37]and PMMA [38]have been described by pared with the isotropic spectrum of bulk PMMA,the stretching band of methacrylate side group at 1100–1300cm 21is greatly enhanced relative to the C y O vibration at 1734cm 21in the ultrathin PMMA film,indicating that the film has more methoxy groups oriented normal to the Au surface than carbonyl groups and that PMMA is physically adsorbed onto the substrate due to interaction of the polarmethoxyFig.1.SEM images of the fractal-like structures in ultrathin PEO/PMMA films of different blend compositions,(a)100/0,(b)90/10,(c)75/25and (d)60/40.The scale bar of 10m m is for all images.The samples were crystallized for 17h.Fig.2.A SEM image of the fractal-like structures in ultrathin PEO/PMMA film of 50/50composition.The branches along the scratch line are normally very short in this sample (Inset).This image mainly shows a long branched structure stemming from the scratch line,which grew actually along a defect zone.The sample was crystallized for 17.5h.Fig.3.GIR-IR spectra of the ultrathin films crystallized for 24h.The traces correspond to the weight ratios of PEO/PMMA marked on the curves.SEM verified that the crystallization in blend films started from surface defects (e.g.dust particles).M.Wang et al./Polymer 44(2003)5015–50215017and carbonyl groups with the Au surface[38].Reasonably, PMMA prevented PEO from de-wetting during the co-deposition of them from solution[35],resulting in homogeneous blendfilms.The spectra of PEO at different temperatures[35,37] show that the intensity of the CH2wagging vibration of PEO at1342cm21is sensitive to the conformation order,which can be used to evaluate crystallization process[26].With respect to the CH2stretching vibration at around2888cm21 that is mainly attributed to PEO component,the change in the intensity of PEO band at1342cm21with PMMA content indicates that a higher PMMA content leads to a lower crystallinity of PEO in thefilm.As PMMA content is $40%the blendfilms are mainly amorphous.Only bands with transition dipole moments parallel(k)to PEO chain axis(1342,1242,1107and963cm21)[35,37] are intensively observed in the GIR-IR spectra of ultrathin PEO and90/10films.In the spectrum of75/25film,the vibrations of k bands are still evident while they are much weaker than the90/10and PEO cases.In thefilms with PMMA content$40%the vibration signals of PEO crystals are very weak(1342cm21)and non-evident(963cm21)for the crystal branches in them were too short to be easily detected by the GIR-IR scans,but the orientation of the crystallized PEO chains in them can be reasonably inferred by the results of the90/10and75/25films since thefilms crystallized in the same condition.Thus,the PEO chains in the crystals formed in the studiedfilms orient perpendicular to substrate surface and the branches are viewedflat-on, because in GIR-IR measurements only the transition dipole moment components normal to substrate surface can be observed.3.3.AFM resultsAFM measurements were performed to get the branch thickness,as shown in Fig.4.In the PEOfilm,the branches had a homogeneous thickness of8^1nm(Fig.4(a)). However,the branch thickness in the blendfilms verified with PMMA content,namely,4^1nm in90/10film(Fig. 4(b)),6^1nm in75/25film(Fig.4(c))and10^1nm in 60/40and50/50films(Fig.4(d)).For PMMA phases may segregate beside the branches(refer to latter discussion),the actual branch thickness may be somewhat larger than the measured data in the blendfilms,particularly in those containing a high PMMA content.Notice that the branches in60/40and50/50films had a similar thickness by the AFM data(Fig.4(d)),but the branches in the50/50film may actually be thicker than those in60/40film because more PMMA can segregate beside the branches in50/50film.As the branch growth mainly proceeds laterally and the PEO chains within the crystals take exclusively a confor-mation with chain axes perpendicular to substrate surface, one branch formed in thefilms studied here is reasonably a crystal lamella viewedflat-on and its thickness is related to the stem length of PEO chain folds within it.In pure PEO film the thickness of such branches is a direct measure of chain folding states[11,12,15].The thickness of8^1nm (Fig.4(a))infers that PEO chains fold4times when without influence of PMMA,as the length L of the fully extended crystalline PEO chain is37nm according to L¼ðM PEOn=M EO nÞ£0:2783nm[39].Even though the exact folding states of PEO chains in blendfilms,particularly as afilm contains a high PMMA content,are hard to obtain from the AFM data(Fig.4(c)and(d))because of the possible discrepancy between the actual and measured values of the branch thickness,the tendency towards higher branches when increasing PMMA content will not be altered.Therefore,from the composition dependence of branch thickness one would get an evaluation of PMMA influences on the organization of PEO chains during crystallization.4.DiscussionThe amorphous PEO/PMMA blendfilms are obtained by constrained geometry and only meta-stable,phase separ-ation of fractal-like branched patterns happens in them due to heterogeneously nucleated PEO crystallization by DLA process.The PEO chains in the crystals come from the amorphous blend areas ahead of them[10–12,15],where PEO and PMMA are mixed.Results show that increasing PMMA content to more than10%leads to a remarkable retardation effect of PMMA on the branch length,and only the PEO chains near the heterogeneous nucleation sites in films with PMMA content$40%can crystallize so that the films are mainly amorphous(Figs.1–3).In bulk state,the blends with PMMA content higher than,70%are completely amorphous[19,22,40].This indicates that the retardation effect of PMMA on PEO crystallization is dramatically enhanced by constrained geometry in the ultrathinfilms.Crystallization in the blendfilms involves the general features revealed in ultrathin PEO[10–12,15]and other polymer[8,9,14]films,namely,requiring necessary hetero-geneous nucleation,chain orientation normal to substrate surface and branched structures related to DLA process. Therefore,the crystal growth in the blendfilms obeys the basic principles in ultrathin polymerfilms,for example,the growth process is controlled by chain diffusion.It is believed that the retardation effect of PMMA on the branch growth is to reduce the transport property(mobility)of PEO chains in our cases,because upon increasing PMMA the mobility of PEO chains can be strongly reduced[20]and the system will become more rigid[22].SEM and AFM provide detailed structural information on the crystals.These data contain several interesting features.First,as PMMA content was changed from10to 40%,the branch thickness increased strikingly from4^1 to10^1nm.Second,the branches in90/10film were much thinner than those in PEOfilm.Finally,the branchM.Wang et al./Polymer44(2003)5015–5021 5018width (ca.0.20m m)in the blend films was independent of PEO/PMMA ratio,but smaller than that of the branches formed in the PEO film.As mentioned previously,the branch thickness is directly related to the chain folding during crystallization and can give an access to the information on the organization of PEO chains under PMMA influence.The thickness of the crystalline branches is determined by the kinetics of chain deposition at crystal growth fronts in diffusion-controlled growth process [11,12,15].A lowered chain deposition rate,which was achieved by evaluating crystallization temperature ðT c Þ[11]and by reducing the polymer concentration in diffusion field [15],has been proved in ultrathin PEO films to favor the growth of thicker branches.Reiter and Sommer [11,12]showed that the thickness of crystal lamellae increases with crystallization temperature.They argued that at a high deposition rate (large undercooling)the molecules attached to the crystal have less time to stretch out and are thus in a state of relatively low internal chain order (folded state);in contrast,if the crystals grow slowly,the attached molecules have more time to relax towards the fully extended form of lowest free energy by rearrangements at the crystal surface.Our previous results [15]showed that,as a result of the reduction of chain availability in the diffusion field,the chain deposition rate (or probability)at crystal growth fronts becomes small and the deposited polymer chains have a high probability to rearrange themselves to a state near equilibrium.In our opinion,the increase in branch thickness with PMMA content in the blend films results from the lowered chain deposition rate by adding PMMA (Fig.4(b)–(d)).PMMA has a high glass transition temperature ðT g Þ;but PEO have a low one.As a consequence of mixing thesetwoFig.4.AFM images of the fractal-like structures in ultrathin PEO/PMMA films of different blend compositions,(a)100/0,(b)90/10,(c)75/25(c)and (d)60/40.The inset to (d)is for 50/50film.The samples were crystallized for 17h and measured by means of non-contact AFM immediately after being taken out of the vacuum chamber;the scanned areas were near scratch line.All the branches were nucleated by the scratch lines,except for those in the left side of image (a)that were nucleated by a PEO dot.M.Wang et al./Polymer 44(2003)5015–50215019miscible polymers,the amorphous phase T g increases as theconcentration of PMMA increases[23],resulting in a morerigid crystallization system with a more reduced mobility ofPEO chains.The reduction of PEO chain mobility willinevitably lower the chain deposition rate at crystal growthfronts,leading to an easier relaxation of the deposited chainstowards the extended state and further higher branches asdescribed elsewhere[11,15].In a blend consisting of a semi-crystalline polymer andan amorphous one the equilibrium melting pointðT m80Þdepends on composition,increasing amorphous concen-tration will depress T m80[24,41,42].One question may arise,concerning whether the origin of the increase in branchthickness with PMMA content comes from the decrease inthe effective undercooling D TðD T¼T m802T cÞat whichcrystallization occurs.T m80in PEO/PMMA blends decreaseswith increase of PMMA content in the blends[24,41],butthe decreases is slight and only a maximum depression ofca.2.58C was observed[24].In spite of the depression ofT m80;moreover,the crystalline thickness in PEO/PMMA blends is independent of composition[21,41],but increaseswith T c:The equilibrium melting pointðT o mÞof the pure PEO used in this study was ca.648C,which was obtained byreferring to the data of a similar PEO(M w¼6000;M w=M n¼1:03;from Fluka Co.)in literature[24].There is no reason to believe that the increase in branch thickness with increasing PMMA content in our cases results mainly from the decrease in the effective undercooling,of which the contribution would be very faint if it could not be completely ruled out because the T c in our experiments was about428C below the T o m of the pure PEO.Interestingly,the branches in90/10film were muchthinner than those in PEOfilm(Fig.4(a)and(b)),whichshould not be caused by the PMMA segregating beside thebranches in the blendfilm because PMMA content wasrather low.A slow deposition rate of PEO chains at growthfronts favors the formation of higher branches,whereas afast deposition rate will result in thinner branches[11,15].Itis clear that the crystallization was accelerated in90/10filmas compared with that in PEOfilm.The crystal growth wasalso found to be enhanced in90/10blend of PEO/isotactic-PMMA(i-PMMA)when compared to the pure PEO,ratherthan being disrupted,this phenomenon was considered torelate to the immiscibility between PEO and i-PMMA[25].Therefore,two competitive effects may be imposed byPMMA on PEO crystallization depending on thefilmcomposition,to retard the crystallization by reducing themobility of PEO chains and to accelerate the crystallizationby probably de-mixing,where the latter effect is dominantas PMMA concentration is low but the former one will beenhanced by increasing PMMA content(Fig.4).As shown previously[15],a surface-tension effect,which favors the minimized interface area of crystal growthfronts,is coming into effect with the reduction in depositionrate of chains and the deposited chains will occupy a highestnumber of nearest neighbors at the growth fronts.With this consideration,one might expect a broadening of branches as the deposition rate reduces with increasing PMMA content. However,the branch width(ca.0.20m m)in the blendfilms is independent offilm composition and generally smaller than that in PEOfilm(Figs.1and4).No external factors could impose influences on the branch width in our experiments,except for the presence of PMMA in the system.On the other hand,the width difference between the branches in the blend and PEOfilms could not result from the two competitive effects imposed by PMMA in that the branch width did not changed with increasing PMMA content.The possible origin of the small and constant branch width in blendfilms lies in the laterally excluded PMMA phases from the crystals,which can be rationalized by the fact that the‘impurities’(PMMA)segregate away from the growth front and between the growing lamellae during the growth of PEO spherulites in thin PEO/PMMA films[27]and by the invariant crystalline lamellar thickness and increasing small-angle long period of crystalline phases with addition of PMMA[21,41].The deposition of PEO chains at the side faces of branches can be prevented by the excluded PMMA phases,but this will not be the case in the PEOfilm.5.ConclusionThe results presented in this study show the crystalline morphology in ultrathin PEO/PMMA blendfilms.The blendfilms in extremely constrained states are amorphous and meta-stable,and phase separation in them follows a fractal-like branched pattern due to heterogeneously nucleated PEO crystallization by DLA process.The crystal branches are viewedflat-on with polymer chains oriented normal to the substrate surface;the PEO chains in the crystalline branches come from the amorphous blend areas ahead of them.The branch width in blendfilms is independent of thefilm composition,which relates to the laterally excluded PMMA phases from the crystals.The presence of PMMA influences strikingly the branch length and thickness by imposing two competitive effects on the PEO crystallization,to accelerate and to retard the crystal-lization,depending on thefilm composition.The acceler-ated crystallization,probably by de-mixing between PEO and PMMA,leads to thinner and longer crystal branches; the retardation effect of PMMA,which results in thicker and shorter crystal branches,is attributed to reducing the mobility of PEO chains in the system. AcknowledgementsThe authors thank the DFG for supporting this work (priority program‘Wetting and structure formation at surfaces’).M.Wang acknowledges the Alexander von Humboldt Foundation for a research fellowship.M.Wang et al./Polymer44(2003)5015–5021 5020References[1]Bassett BC.Principles of polymer morphology.Cambridge:Cam-bridge University Press;1981.[2]Strobl G.The physics of polymers.Berlin:Springer;1996.[3]Despotopoulou MM,Miller RD,Rabolt JF,Frank CW.J Polym Sci:Part B:Polym Phys1996;34:2335–49.[4]Despotopoulou MM,Frank CW,Miller RD,Rabolt JF.Macromol-ecules1996;29:5797–804.[5]Frank CW,Rao V,Despotopoulou MM,Pease RFW,Hinsberg WD,Miller RD,Rabolt JF.Science1996;273:912–5.[6]Theodotou DN.Molecular modeling of polymer surfaces andpolymer/solid interfaces.In:Sanchez IC,editor.Physics of polymer surfaces and interfaces.Butterworth-Heinemann:Boston;1992.p.139–62.[7]Ebengou RH.J Polym Sci:Part B:Polym Phys1997;35:1333–8.[8]Sakai Y,Imai M,Kaji K,Tsuji M.J Cryst Growth1999;203:244–54.[9]Sakai Y,Imai M,Kaji K,Tsuji M.Macromolecules1996;29:8830–4.[10]Reiter G,Sommer JU.Phys Rev Lett1998;80:3771–4.[11]Reiter G,Sommer JU.J Chem Phys2000;112:4376–83.[12]Sommer JU,Reiter G.J Chem Phys2000;112:4384–93.[13]Reiter G,Castelein G,Sommer JU.Phys Rev Lett2001;86:5918–21.[14]Zhang F,Liu J,Huang H,Du B,He T.Eur Phys J E2002;8:289–97.[15]Wang M,Braun HG,Meyer E.Macromol Rapid Commun2002;23:853–8.[16]Tanaka K,Takahara A,Kajiyama T.Macromolecules1996;29:3232–9.[17]Chen EQ,Lee SW,Zhang A,Moon BS,Mann I,Harris FW,ChengSZD,Hsiao BS,Yeh F,von Merrewell E,Grubb DT.Macromolecules 1999;32:4784–93.[18]Tanaka K,Yoon JS,Takahara A,Kajiyama T.Macromolecules1995;28:934–8.[19]Liau WB,Chang CF.J Appl Polym Sci2000;76:1627–36.[20]Schantz S.Macromolecules1997;30:1419–25.[21]Russell TP,Ito H,Wignall GD.Macromolecules1988;21:1703–9.[22]Martuscelli E,Silvestre C,Addonizio ML,Amelino L.MakromolChem1986;187:1557–71.[23]Liberman SA,Gomes AS,Macchi EM.J Polym Sci:Polym Chem Ed1984;22:2809–15.[24]Alfonso GC,Russell TP.Macromolecules1986;19:1143–52.[25]John E,Ree T.J Polym Sci:Part A:Polym Chem1990;28:385–98.[26]Li X,Hsu SL.J Polym Sci:Polym Phys Ed1984;22:1331–42.[27]Pearce R,Vancso GJ.J Polym Sci:Part B:Polym Phys1998;36:2643–51.[28]Ferreiro V,Douglas JF,Warren JA,Karim A.Phys Rev E2002;65:042802.[29]Ferreiro V,Douglas JF,Warren J,Karim A.Phys Rev E2002;65:051606.[30]Matsushita M,Sano M,Hayakawa Y,Honjo H,Sawada Y.Phys RevLett1984;53:286–9.[31]Matsushita M,Hayakawa Y,Sawada Y.Phys Rev A1985;32:3814–6.[32]Ben-Jacob E.Contemporary Phys1997;38:205–41.[33]Witten TA,Sander LM.Phys Rev Lett1981;47:1400–3.[34]Sander LM.Nature1986;322:789–93.[35]Hoffmann CL,Rabolt JF.Macromolecules1996;29:2543–7.[36]Hobbs JK,Humphris ADL,Miles MJ.Macromolecules2001;34:5508–19.[37]Yoshihara T,Tadokoro H,Murahashi S.J Chem Phys1964;41:2902–11.[38]Lenk TJ,Hallmark VM,Rabolt JF,Ha¨ussling L,Ringsdorf H.Macromolecules1993;26:1230–7.[39]Kovacs AJ,Straupe C.J Cryst Growth1980;48:210–26.[40]Parizel N,Laupreˆtre F,Monnerie L.Polymer1997;38:3719–25.[41]Cimmino S,Pace ED,Martuscelli E,Silvestre C.Makromol Chem1990;191:2447–54.[42]Rim PB,Runt JP.Macromolecules1984;17:1520–6.M.Wang et al./Polymer44(2003)5015–50215021。

植物病原体检测和主机防御NBS-LRR蛋白Brody J DeYoung and Roger W InnesDepartment of Biology, Indiana University, Bloomington, Indiana 47405, USA.摘要核苷酸结合位点富含亮氨酸重复(NBS-LRR)家族属于植物蛋白用于病原体检测。
像哺乳动物的NOD- LRR蛋白'传感器'检测细胞内保守的病原相关分子模式,植物NBS-LRR蛋白检测病原体相关的蛋白质,最经常的效应分子负责的病原体毒力。
许多致病蛋白质的检测通过植物NBS-LRR蛋白间接从修改毒性蛋白造成宿主上的靶蛋白。
然而,一些NBS-LRR蛋白质直接结合病原菌的蛋白质。
以修改宿主蛋白或病原体的蛋白在植物NBS-LRR蛋白中的氨基末端和LRR结构域的构象变化。
这种构象的改变被认为是促进促进NBS结构域中ADP向ATP的转化,这样激活下游信号,由一个未知机制,导致病原体的抵抗作用。
植物缺乏脊椎动物适应性免疫靠什么来应对病原体。
至成功检测和抵御病原体,植物必须完全依赖于稳定的编码基因在基因组中。
虽然病原体检测的确切机制不同,植物,如动物,使用两个不同的防御系统,以识别和应对病原体的挑战,病原相关分子模式(PAMPS),如细菌鞭毛确认脂多糖和真菌疫的纤维素结合结构激发蛋白质,由植物跨膜受体,激活基础防御,第一道防线病原体想起先天免疫在脊椎动物中。
在植物和动物据推测生物的“军备竞赛”正在发生,使病原体已取得PAMP触发免疫逃避机制,通过不断变化的效应修改状态在宿主细胞的分子,从而绕过或破坏的第一行防线。
植物进化反击,蛋白质,检测特异性效应分子,一个机制,称为“效应触发免疫到第二行的金额防线。
植物效应触发免疫更像是哺乳动物适应性免疫该病原体的效应,而不是保守的元素,如的PAMPs,特别是认可。
但是,在哺乳动物适应性免疫的情况不一样,在植物宿主中效应触发免疫编码的每一个细胞中的特异性决定有机体。

杨欧,张晓湘,徐小涵,等. 抗氧化型壳聚糖/大豆蛋白复合食用膜的制备与应用[J]. 食品工业科技,2024,45(6):210−218. doi:10.13386/j.issn1002-0306.2023050177YANG Ou, ZHANG Xiaoxiang, XU Xiaohan, et al. Preparation and Application of Antioxidative Chitosan/Soybean Protein Isolate Composite Edible Membrane[J]. Science and Technology of Food Industry, 2024, 45(6): 210−218. (in Chinese with English abstract).doi: 10.13386/j.issn1002-0306.2023050177· 包装与机械 ·抗氧化型壳聚糖/大豆蛋白复合食用膜的制备与应用杨 欧,张晓湘,徐小涵,孙 玥,梁 进,李雪玲,李梅青,张海伟*(安徽农业大学茶与食品科技学院,农业农村部江淮农产品精深加工与资源利用重点实验室,安徽省特色农产品高值化利用工程研究中心,安徽合肥 230036)摘 要:以壳聚糖和大豆分离蛋白为复合膜基材,天然抗氧化剂为活性物质,制备具有抑制脂质氧化且可食用的活性保鲜膜。
通过膜的机械性能、微观结构、物理性质与抗氧化性能,优化添加抗氧化剂的种类及浓度,并分析复合膜对核桃油贮藏保质效果。
结果表明,8种天然抗氧化剂添加均显著提高了复合膜的阻氧性能(P <0.05),其中虾青素、葡萄籽提取物、维生素C 添加后使得油脂过氧化值减少约80%,且保持良好的机械性能。
当虾青素添加浓度为0.3%时,复合膜表现最佳性能,抗拉强度为6.546 MPa ,断裂伸长率为69.962%,DPPH 自由基清除能力为80.1%,水蒸气渗透率为1.21 g∙mm/m 2∙h∙kPa ;扫描电子显微镜显示膜表面平整光滑、规则、均匀;红外光谱分析显示成膜材料间均具有良好的相容性;差示扫描热量仪分析表明虾青素复合膜的热焓值最高,达到233.940 J/g ,热稳定性最好。

Modeling of morphology evolution in the injection moldingprocess of thermoplastic polymersR.Pantani,I.Coccorullo,V.Speranza,G.Titomanlio* Department of Chemical and Food Engineering,University of Salerno,via Ponte don Melillo,I-84084Fisciano(Salerno),Italy Received13May2005;received in revised form30August2005;accepted12September2005AbstractA thorough analysis of the effect of operative conditions of injection molding process on the morphology distribution inside the obtained moldings is performed,with particular reference to semi-crystalline polymers.The paper is divided into two parts:in the first part,the state of the art on the subject is outlined and discussed;in the second part,an example of the characterization required for a satisfactorily understanding and description of the phenomena is presented,starting from material characterization,passing through the monitoring of the process cycle and arriving to a deep analysis of morphology distribution inside the moldings.In particular,fully characterized injection molding tests are presented using an isotactic polypropylene,previously carefully characterized as far as most of properties of interest.The effects of both injectionflow rate and mold temperature are analyzed.The resulting moldings morphology(in terms of distribution of crystallinity degree,molecular orientation and crystals structure and dimensions)are analyzed by adopting different experimental techniques(optical,electronic and atomic force microscopy,IR and WAXS analysis).Final morphological characteristics of the samples are compared with the predictions of a simulation code developed at University of Salerno for the simulation of the injection molding process.q2005Elsevier Ltd.All rights reserved.Keywords:Injection molding;Crystallization kinetics;Morphology;Modeling;Isotactic polypropyleneContents1.Introduction (1186)1.1.Morphology distribution in injection molded iPP parts:state of the art (1189)1.1.1.Modeling of the injection molding process (1190)1.1.2.Modeling of the crystallization kinetics (1190)1.1.3.Modeling of the morphology evolution (1191)1.1.4.Modeling of the effect of crystallinity on rheology (1192)1.1.5.Modeling of the molecular orientation (1193)1.1.6.Modeling of theflow-induced crystallization (1195)ments on the state of the art (1197)2.Material and characterization (1198)2.1.PVT description (1198)*Corresponding author.Tel.:C39089964152;fax:C39089964057.E-mail address:gtitomanlio@unisa.it(G.Titomanlio).2.2.Quiescent crystallization kinetics (1198)2.3.Viscosity (1199)2.4.Viscoelastic behavior (1200)3.Injection molding tests and analysis of the moldings (1200)3.1.Injection molding tests and sample preparation (1200)3.2.Microscopy (1202)3.2.1.Optical microscopy (1202)3.2.2.SEM and AFM analysis (1202)3.3.Distribution of crystallinity (1202)3.3.1.IR analysis (1202)3.3.2.X-ray analysis (1203)3.4.Distribution of molecular orientation (1203)4.Analysis of experimental results (1203)4.1.Injection molding tests (1203)4.2.Morphology distribution along thickness direction (1204)4.2.1.Optical microscopy (1204)4.2.2.SEM and AFM analysis (1204)4.3.Morphology distribution alongflow direction (1208)4.4.Distribution of crystallinity (1210)4.4.1.Distribution of crystallinity along thickness direction (1210)4.4.2.Crystallinity distribution alongflow direction (1212)4.5.Distribution of molecular orientation (1212)4.5.1.Orientation along thickness direction (1212)4.5.2.Orientation alongflow direction (1213)4.5.3.Direction of orientation (1214)5.Simulation (1214)5.1.Pressure curves (1215)5.2.Morphology distribution (1215)5.3.Molecular orientation (1216)5.3.1.Molecular orientation distribution along thickness direction (1216)5.3.2.Molecular orientation distribution alongflow direction (1216)5.3.3.Direction of orientation (1217)5.4.Crystallinity distribution (1217)6.Conclusions (1217)References (1219)1.IntroductionInjection molding is one of the most widely employed methods for manufacturing polymeric products.Three main steps are recognized in the molding:filling,packing/holding and cooling.During thefilling stage,a hot polymer melt rapidlyfills a cold mold reproducing a cavity of the desired product shape. During the packing/holding stage,the pressure is raised and extra material is forced into the mold to compensate for the effects that both temperature decrease and crystallinity development determine on density during solidification.The cooling stage starts at the solidification of a thin section at cavity entrance (gate),starting from that instant no more material can enter or exit from the mold impression and holding pressure can be released.When the solid layer on the mold surface reaches a thickness sufficient to assure required rigidity,the product is ejected from the mold.Due to the thermomechanical history experienced by the polymer during processing,macromolecules in injection-molded objects present a local order.This order is referred to as‘morphology’which literally means‘the study of the form’where form stands for the shape and arrangement of parts of the object.When referred to polymers,the word morphology is adopted to indicate:–crystallinity,which is the relative volume occupied by each of the crystalline phases,including mesophases;–dimensions,shape,distribution and orientation of the crystallites;–orientation of amorphous phase.R.Pantani et al./Prog.Polym.Sci.30(2005)1185–1222 1186R.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221187Apart from the scientific interest in understandingthe mechanisms leading to different order levels inside a polymer,the great technological importance of morphology relies on the fact that polymer character-istics (above all mechanical,but also optical,electrical,transport and chemical)are to a great extent affected by morphology.For instance,crystallinity has a pro-nounced effect on the mechanical properties of the bulk material since crystals are generally stiffer than amorphous material,and also orientation induces anisotropy and other changes in mechanical properties.In this work,a thorough analysis of the effect of injection molding operative conditions on morphology distribution in moldings with particular reference to crystalline materials is performed.The aim of the paper is twofold:first,to outline the state of the art on the subject;second,to present an example of the characterization required for asatisfactorilyR.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221188understanding and description of the phenomena, starting from material description,passing through the monitoring of the process cycle and arriving to a deep analysis of morphology distribution inside the mold-ings.To these purposes,fully characterized injection molding tests were performed using an isotactic polypropylene,previously carefully characterized as far as most of properties of interest,in particular quiescent nucleation density,spherulitic growth rate and rheological properties(viscosity and relaxation time)were determined.The resulting moldings mor-phology(in terms of distribution of crystallinity degree, molecular orientation and crystals structure and dimensions)was analyzed by adopting different experimental techniques(optical,electronic and atomic force microscopy,IR and WAXS analysis).Final morphological characteristics of the samples were compared with the predictions of a simulation code developed at University of Salerno for the simulation of the injection molding process.The effects of both injectionflow rate and mold temperature were analyzed.1.1.Morphology distribution in injection molded iPP parts:state of the artFrom many experimental observations,it is shown that a highly oriented lamellar crystallite microstructure, usually referred to as‘skin layer’forms close to the surface of injection molded articles of semi-crystalline polymers.Far from the wall,the melt is allowed to crystallize three dimensionally to form spherulitic structures.Relative dimensions and morphology of both skin and core layers are dependent on local thermo-mechanical history,which is characterized on the surface by high stress levels,decreasing to very small values toward the core region.As a result,the skin and the core reveal distinct characteristics across the thickness and also along theflow path[1].Structural and morphological characterization of the injection molded polypropylene has attracted the interest of researchers in the past three decades.In the early seventies,Kantz et al.[2]studied the morphology of injection molded iPP tensile bars by using optical microscopy and X-ray diffraction.The microscopic results revealed the presence of three distinct crystalline zones on the cross-section:a highly oriented non-spherulitic skin;a shear zone with molecular chains oriented essentially parallel to the injection direction;a spherulitic core with essentially no preferred orientation.The X-ray diffraction studies indicated that the skin layer contains biaxially oriented crystallites due to the biaxial extensionalflow at theflow front.A similar multilayered morphology was also reported by Menges et al.[3].Later on,Fujiyama et al.[4] investigated the skin–core morphology of injection molded iPP samples using X-ray Small and Wide Angle Scattering techniques,and suggested that the shear region contains shish–kebab structures.The same shish–kebab structure was observed by Wenig and Herzog in the shear region of their molded samples[5].A similar investigation was conducted by Titomanlio and co-workers[6],who analyzed the morphology distribution in injection moldings of iPP. They observed a skin–core morphology distribution with an isotropic spherulitic core,a skin layer characterized by afine crystalline structure and an intermediate layer appearing as a dark band in crossed polarized light,this layer being characterized by high crystallinity.Kalay and Bevis[7]pointed out that,although iPP crystallizes essentially in the a-form,a small amount of b-form can be found in the skin layer and in the shear region.The amount of b-form was found to increase by effect of high shear rates[8].A wide analysis on the effect of processing conditions on the morphology of injection molded iPP was conducted by Viana et al.[9]and,more recently, by Mendoza et al.[10].In particular,Mendoza et al. report that the highest level of crystallinity orientation is found inside the shear zone and that a high level of orientation was also found in the skin layer,with an orientation angle tilted toward the core.It is rather difficult to theoretically establish the relationship between the observed microstructure and processing conditions.Indeed,a model of the injection molding process able to predict morphology distribution in thefinal samples is not yet available,even if it would be of enormous strategic importance.This is mainly because a complete understanding of crystallization kinetics in processing conditions(high cooling rates and pressures,strong and complexflowfields)has not yet been reached.In this section,the most relevant aspects for process modeling and morphology development are identified. In particular,a successful path leading to a reliable description of morphology evolution during polymer processing should necessarily pass through:–a good description of morphology evolution under quiescent conditions(accounting all competing crystallization processes),including the range of cooling rates characteristic of processing operations (from1to10008C/s);R.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221189–a description capturing the main features of melt morphology(orientation and stretch)evolution under processing conditions;–a good coupling of the two(quiescent crystallization and orientation)in order to capture the effect of crystallinity on viscosity and the effect offlow on crystallization kinetics.The points listed above outline the strategy to be followed in order to achieve the basic understanding for a satisfactory description of morphology evolution during all polymer processing operations.In the following,the state of art for each of those points will be analyzed in a dedicated section.1.1.1.Modeling of the injection molding processThefirst step in the prediction of the morphology distribution within injection moldings is obviously the thermo-mechanical simulation of the process.Much of the efforts in the past were focused on the prediction of pressure and temperature evolution during the process and on the prediction of the melt front advancement [11–15].The simulation of injection molding involves the simultaneous solution of the mass,energy and momentum balance equations.Thefluid is non-New-tonian(and viscoelastic)with all parameters dependent upon temperature,pressure,crystallinity,which are all function of pressibility cannot be neglected as theflow during the packing/holding step is determined by density changes due to temperature, pressure and crystallinity evolution.Indeed,apart from some attempts to introduce a full 3D approach[16–19],the analysis is currently still often restricted to the Hele–Shaw(or thinfilm) approximation,which is warranted by the fact that most injection molded parts have the characteristic of being thin.Furthermore,it is recognized that the viscoelastic behavior of the polymer only marginally influences theflow kinematics[20–22]thus the melt is normally considered as a non-Newtonian viscousfluid for the description of pressure and velocity gradients evolution.Some examples of adopting a viscoelastic constitutive equation in the momentum balance equations are found in the literature[23],but the improvements in accuracy do not justify a considerable extension of computational effort.It has to be mentioned that the analysis of some features of kinematics and temperature gradients affecting the description of morphology need a more accurate description with respect to the analysis of pressure distributions.Some aspects of the process which were often neglected and may have a critical importance are the description of the heat transfer at polymer–mold interface[24–26]and of the effect of mold deformation[24,27,28].Another aspect of particular interest to the develop-ment of morphology is the fountainflow[29–32], which is often neglected being restricted to a rather small region at theflow front and close to the mold walls.1.1.2.Modeling of the crystallization kineticsIt is obvious that the description of crystallization kinetics is necessary if thefinal morphology of the molded object wants to be described.Also,the development of a crystalline degree during the process influences the evolution of all material properties like density and,above all,viscosity(see below).Further-more,crystallization kinetics enters explicitly in the generation term of the energy balance,through the latent heat of crystallization[26,33].It is therefore clear that the crystallinity degree is not only a result of simulation but also(and above all)a phenomenon to be kept into account in each step of process modeling.In spite of its dramatic influence on the process,the efforts to simulate the injection molding of semi-crystalline polymers are crude in most of the commercial software for processing simulation and rather scarce in the fleur and Kamal[34],Papatanasiu[35], Titomanlio et al.[15],Han and Wang[36],Ito et al.[37],Manzione[38],Guo and Isayev[26],and Hieber [25]adopted the following equation(Kolmogoroff–Avrami–Evans,KAE)to predict the development of crystallinityd xd tZð1K xÞd d cd t(1)where x is the relative degree of crystallization;d c is the undisturbed volume fraction of the crystals(if no impingement would occur).A significant improvement in the prediction of crystallinity development was introduced by Titoman-lio and co-workers[39]who kept into account the possibility of the formation of different crystalline phases.This was done by assuming a parallel of several non-interacting kinetic processes competing for the available amorphous volume.The evolution of each phase can thus be described byd x id tZð1K xÞd d c id t(2)where the subscript i stands for a particular phase,x i is the relative degree of crystallization,x ZPix i and d c iR.Pantani et al./Prog.Polym.Sci.30(2005)1185–1222 1190is the expectancy of volume fraction of each phase if no impingement would occur.Eq.(2)assumes that,for each phase,the probability of the fraction increase of a single crystalline phase is simply the product of the rate of growth of the corresponding undisturbed volume fraction and of the amount of available amorphous fraction.By summing up the phase evolution equations of all phases(Eq.(2))over the index i,and solving the resulting differential equation,one simply obtainsxðtÞZ1K exp½K d cðtÞ (3)where d c Z Pid c i and Eq.(1)is recovered.It was shown by Coccorullo et al.[40]with reference to an iPP,that the description of the kinetic competition between phases is crucial to a reliable prediction of solidified structures:indeed,it is not possible to describe iPP crystallization kinetics in the range of cooling rates of interest for processing(i.e.up to several hundreds of8C/s)if the mesomorphic phase is neglected:in the cooling rate range10–1008C/s, spherulite crystals in the a-phase are overcome by the formation of the mesophase.Furthermore,it has been found that in some conditions(mainly at pressures higher than100MPa,and low cooling rates),the g-phase can also form[41].In spite of this,the presence of different crystalline phases is usually neglected in the literature,essentially because the range of cooling rates investigated for characterization falls in the DSC range (well lower than typical cooling rates of interest for the process)and only one crystalline phase is formed for iPP at low cooling rates.It has to be noticed that for iPP,which presents a T g well lower than ambient temperature,high values of crystallinity degree are always found in solids which passed through ambient temperature,and the cooling rate can only determine which crystalline phase forms, roughly a-phase at low cooling rates(below about 508C/s)and mesomorphic phase at higher cooling rates.The most widespread approach to the description of kinetic constant is the isokinetic approach introduced by Nakamura et al.According to this model,d c in Eq.(1)is calculated asd cðtÞZ ln2ðt0KðTðsÞÞd s2 435n(4)where K is the kinetic constant and n is the so-called Avrami index.When introduced as in Eq.(4),the reciprocal of the kinetic constant is a characteristic time for crystallization,namely the crystallization half-time, t05.If a polymer is cooled through the crystallization temperature,crystallization takes place at the tempera-ture at which crystallization half-time is of the order of characteristic cooling time t q defined ast q Z D T=q(5) where q is the cooling rate and D T is a temperature interval over which the crystallization kinetic constant changes of at least one order of magnitude.The temperature dependence of the kinetic constant is modeled using some analytical function which,in the simplest approach,is described by a Gaussian shaped curve:KðTÞZ K0exp K4ln2ðT K T maxÞ2D2(6)The following Hoffman–Lauritzen expression[42] is also commonly adopted:K½TðtÞ Z K0exp KUÃR$ðTðtÞK T NÞ!exp KKÃ$ðTðtÞC T mÞ2TðtÞ2$ðT m K TðtÞÞð7ÞBoth equations describe a bell shaped curve with a maximum which for Eq.(6)is located at T Z T max and for Eq.(7)lies at a temperature between T m(the melting temperature)and T N(which is classically assumed to be 308C below the glass transition temperature).Accord-ing to Eq.(7),the kinetic constant is exactly zero at T Z T m and at T Z T N,whereas Eq.(6)describes a reduction of several orders of magnitude when the temperature departs from T max of a value higher than2D.It is worth mentioning that only three parameters are needed for Eq.(6),whereas Eq.(7)needs the definition offive parameters.Some authors[43,44]couple the above equations with the so-called‘induction time’,which can be defined as the time the crystallization process starts, when the temperature is below the equilibrium melting temperature.It is normally described as[45]Dt indDtZðT0m K TÞat m(8)where t m,T0m and a are material constants.It should be mentioned that it has been found[46,47]that there is no need to explicitly incorporate an induction time when the modeling is based upon the KAE equation(Eq.(1)).1.1.3.Modeling of the morphology evolutionDespite of the fact that the approaches based on Eq.(4)do represent a significant step toward the descriptionR.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221191of morphology,it has often been pointed out in the literature that the isokinetic approach on which Nakamura’s equation (Eq.(4))is based does not describe details of structure formation [48].For instance,the well-known experience that,with many polymers,the number of spherulites in the final solid sample increases strongly with increasing cooling rate,is indeed not taken into account by this approach.Furthermore,Eq.(4)describes an increase of crystal-linity (at constant temperature)depending only on the current value of crystallinity degree itself,whereas it is expected that the crystallization rate should depend also on the number of crystalline entities present in the material.These limits are overcome by considering the crystallization phenomenon as the consequence of nucleation and growth.Kolmogoroff’s model [49],which describes crystallinity evolution accounting of the number of nuclei per unit volume and spherulitic growth rate can then be applied.In this case,d c in Eq.(1)is described asd ðt ÞZ C m ðt 0d N ðs Þd s$ðt sG ðu Þd u 2435nd s (9)where C m is a shape factor (C 3Z 4/3p ,for spherical growth),G (T (t ))is the linear growth rate,and N (T (t ))is the nucleation density.The following Hoffman–Lauritzen expression is normally adopted for the growth rateG ½T ðt Þ Z G 0exp KUR $ðT ðt ÞK T N Þ!exp K K g $ðT ðt ÞC T m Þ2T ðt Þ2$ðT m K T ðt ÞÞð10ÞEqs.(7)and (10)have the same form,however the values of the constants are different.The nucleation mechanism can be either homo-geneous or heterogeneous.In the case of heterogeneous nucleation,two equations are reported in the literature,both describing the nucleation density as a function of temperature [37,50]:N ðT ðt ÞÞZ N 0exp ½j $ðT m K T ðt ÞÞ (11)N ðT ðt ÞÞZ N 0exp K 3$T mT ðt ÞðT m K T ðt ÞÞ(12)In the case of homogeneous nucleation,the nucleation rate rather than the nucleation density is function of temperature,and a Hoffman–Lauritzen expression isadoptedd N ðT ðt ÞÞd t Z N 0exp K C 1ðT ðt ÞK T N Þ!exp KC 2$ðT ðt ÞC T m ÞT ðt Þ$ðT m K T ðt ÞÞð13ÞConcentration of nucleating particles is usually quite significant in commercial polymers,and thus hetero-geneous nucleation becomes the dominant mechanism.When Kolmogoroff’s approach is followed,the number N a of active nuclei at the end of the crystal-lization process can be calculated as [48]N a ;final Zðt final 0d N ½T ðs Þd sð1K x ðs ÞÞd s (14)and the average dimension of crystalline structures can be attained by geometrical considerations.Pantani et al.[51]and Zuidema et al.[22]exploited this method to describe the distribution of crystallinity and the final average radius of the spherulites in injection moldings of polypropylene;in particular,they adopted the following equationR Z ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi3x a ;final 4p N a ;final 3s (15)A different approach is also present in the literature,somehow halfway between Nakamura’s and Kolmo-goroff’s models:the growth rate (G )and the kinetic constant (K )are described independently,and the number of active nuclei (and consequently the average dimensions of crystalline entities)can be obtained by coupling Eqs.(4)and (9)asN a ðT ÞZ 3ln 24p K ðT ÞG ðT Þ 3(16)where heterogeneous nucleation and spherical growth is assumed (Avrami’s index Z 3).Guo et al.[43]adopted this approach to describe the dimensions of spherulites in injection moldings of polypropylene.1.1.4.Modeling of the effect of crystallinity on rheology As mentioned above,crystallization has a dramatic influence on material viscosity.This phenomenon must obviously be taken into account and,indeed,the solidification of a semi-crystalline material is essen-tially caused by crystallization rather than by tempera-ture in normal processing conditions.Despite of the importance of the subject,the relevant literature on the effect of crystallinity on viscosity isR.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221192rather scarce.This might be due to the difficulties in measuring simultaneously rheological properties and crystallinity evolution during the same tests.Apart from some attempts to obtain simultaneous measure-ments of crystallinity and viscosity by special setups [52,53],more often viscosity and crystallinity are measured during separate tests having the same thermal history,thus greatly simplifying the experimental approach.Nevertheless,very few works can be retrieved in the literature in which(shear or complex) viscosity can be somehow linked to a crystallinity development.This is the case of Winter and co-workers [54],Vleeshouwers and Meijer[55](crystallinity evolution can be drawn from Swartjes[56]),Boutahar et al.[57],Titomanlio et al.[15],Han and Wang[36], Floudas et al.[58],Wassner and Maier[59],Pantani et al.[60],Pogodina et al.[61],Acierno and Grizzuti[62].All the authors essentially agree that melt viscosity experiences an abrupt increase when crystallinity degree reaches a certain‘critical’value,x c[15]. However,little agreement is found in the literature on the value of this critical crystallinity degree:assuming that x c is reached when the viscosity increases of one order of magnitude with respect to the molten state,it is found in the literature that,for iPP,x c ranges from a value of a few percent[15,62,60,58]up to values of20–30%[58,61]or even higher than40%[59,54,57].Some studies are also reported on the secondary effects of relevant variables such as temperature or shear rate(or frequency)on the dependence of crystallinity on viscosity.As for the effect of temperature,Titomanlio[15]found for an iPP that the increase of viscosity for the same crystallinity degree was higher at lower temperatures,whereas Winter[63] reports the opposite trend for a thermoplastic elasto-meric polypropylene.As for the effect of shear rate,a general agreement is found in the literature that the increase of viscosity for the same crystallinity degree is lower at higher deformation rates[62,61,57].Essentially,the equations adopted to describe the effect of crystallinity on viscosity of polymers can be grouped into two main categories:–equations based on suspensions theories(for a review,see[64]or[65]);–empirical equations.Some of the equations adopted in the literature with regard to polymer processing are summarized in Table1.Apart from Eq.(17)adopted by Katayama and Yoon [66],all equations predict a sharp increase of viscosity on increasing crystallinity,sometimes reaching infinite (Eqs.(18)and(21)).All authors consider that the relevant variable is the volume occupied by crystalline entities(i.e.x),even if the dimensions of the crystals should reasonably have an effect.1.1.5.Modeling of the molecular orientationOne of the most challenging problems to present day polymer science regards the reliable prediction of molecular orientation during transformation processes. Indeed,although pressure and velocity distribution during injection molding can be satisfactorily described by viscous models,details of the viscoelastic nature of the polymer need to be accounted for in the descriptionTable1List of the most used equations to describe the effect of crystallinity on viscosityEquation Author Derivation Parameters h=h0Z1C a0x(17)Katayama[66]Suspensions a Z99h=h0Z1=ðx K x cÞa0(18)Ziabicki[67]Empirical x c Z0.1h=h0Z1C a1expðK a2=x a3Þ(19)Titomanlio[15],also adopted byGuo[68]and Hieber[25]Empiricalh=h0Z expða1x a2Þ(20)Shimizu[69],also adopted byZuidema[22]and Hieber[25]Empiricalh=h0Z1Cðx=a1Þa2=ð1Kðx=a1Þa2Þ(21)Tanner[70]Empirical,basedon suspensionsa1Z0.44for compact crystallitesa1Z0.68for spherical crystallitesh=h0Z expða1x C a2x2Þ(22)Han[36]Empiricalh=h0Z1C a1x C a2x2(23)Tanner[71]Empirical a1Z0.54,a2Z4,x!0.4h=h0Zð1K x=a0ÞK2(24)Metzner[65],also adopted byTanner[70]Suspensions a Z0.68for smooth spheresR.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221193。

Advanced Optical Properties of
Materials
随着科学技术的不断发展,材料科学也在不断的进步中,特别是光学材料。
随着人们对光的认识日益深入,对光学材料的要求也越来越高。
光学材料的最主要特性是它的光学性能,其中不乏一些现代先进的光学特性。
一、色变效应
色变效应是指材料在不同光照条件下颜色的变化。
银石墨烯是一种新型的色变材料,在光的作用下,在低波长光照下高透过率,红外光照下低透过率。
这种颜色变化可用来制备智能光学器件。
二、荧光效应
荧光效应是指材料在受到激发后在某些波长下发出荧光光谱。
荧光材料广泛应用于生物医药检测、紫外线检测等领域。
例如,氧化钆蛋白是一种荧光材料,具有很快的响应速度和高的灵敏度。
它可以广泛应用于微生物检测、环境污染检测等领域。
三、电致变色效应
电致变色效应是指材料在电场作用下,颜色的变化。
这种效应被广泛应用于信息显示、太阳能电池等领域。
例如,铁氰化铁是一种电致变色材料,可以广泛应用于电致变色太阳能电池的制备。
四、光子晶体效应
光子晶体效应是指材料在受到特定波长的光照射时会发生厚度对波长的选择性反射。
这种效应可被应用于光通信、光电子器件等领域。
例如,聚苯乙烯是一种光子晶体材料,可以用来制备窄波长滤光器、超光速光学器件等。
总之,现代先进的光学特性是材料科学持续发展的产物,其中每一个特性都对应着特定的应用领域,具有巨大的应用价值。
未来,将有越来越多的先进光学特性被发现和应用。

实 验 技 术 与 管 理 第37卷 第10期 2020年10月Experimental Technology and Management Vol.37 No.10 Oct. 2020ISSN 1002-4956 CN11-2034/TDOI: 10.16791/ki.sjg.2020.10.012不同浓度氯化钾对小鼠海马神经元膜电位的影响刘爱丽,谌 辉(天津医科大学 生物医学工程与技术学院,天津 300070)摘 要:基于静息膜电位对维持细胞正常状态的重要性,研究不同浓度氯化钾对小鼠海马神经元膜电位的影响。
利用全细胞膜片钳技术,记录4种氯化钾浓度(2.5、5、7.5、10 mmol/L )下海马神经元膜电位的变化,以及动作电位的发放情况。
实验结果表明,随着氯化钾浓度的增高,膜电位不断发生去极化;并且在7.5和10 mmol/L 浓度时可诱发动作电位,10 mmol/L 浓度时诱发动作电位的频率明显升高(P <0.05);与7.5 mmol/L 组相比,10 mmol/L 浓度KCl 诱发动作电位的幅值减小(P <0.01),最大上升斜率显著降低(P <0.01),最大下降斜率增大(P <0.05),而到达顶峰时长没有差异。
实验过程中,随着氯化钾浓度的升高,神经元兴奋性不断增强。
关键词:氯化钾;海马神经元;膜电位;动作电位;膜片钳中图分类号:R-332 文献标识码:B 文章编号:1002-4956(2020)10-0042-04Effect of different concentrations of potassium chloride onmembrane potential of hippocampal neurons in miceLIU Aili, SHEN Hui(School of Biomedical Engineering, Tianjin Medical University, Tianjin 300070, China)Abstract: Based on the importance of resting membrane potential in maintaining the normal state of cells, this paper studies the effect of different concentrations of potassium chloride on membrane potential of hippocampal neurons in mice. The whole cell patch clamp technology is used to record the changes of membrane potential and action potential of hippocampal neurons under four concentrations of potassium chloride (2.5, 5, 7.5, 10 mmol/L). The results show that with the increase of KCl concentration, the membrane potential is depolarized continuously, the action potential can be induced at 7.5 and 10 mmol/L, and the frequency of action potential induced by 10 mmol/L of KCl is significantly increased (P <0.05). Compared with 7.5 mmol/L group, the amplitude of action potential evoked by 10 mmol/L of KCl concentration is decreased (P <0.01), the maximum rising slope is significantly decreased (P <0.01), and the maximum decline slope is increased (P <0.05), but there is no difference in the duration of reaching the peak. During the experiment, the excitability of neurons is continuously enhanced with the increase of potassium chloride concentration.Key words: potassium chloride; hippocampal neuron; membrane potential; action potential; patch clamp由于细胞膜两侧离子的不均匀分布,导致膜两侧存在一定的电位差,称为膜电位(membrane potential )[1]。

Investigating the Properties ofPlasmasPlasma is one of the four fundamental states of matter, alongside solid, liquid, and gas. Unlike the other three, plasma is not commonly found on Earth, but rather in the universe at large. Despite its rarity, however, plasma plays a key role in many natural phenomena, such as lightning, auroras, and even the sun. In human-made devices, such as plasma TVs and fluorescent bulbs, plasma is used to create light. Because of its unique properties, plasma is also used in a variety of scientific experiments and industrial processes. In this article, we will explore the properties of plasma and some of the ways in which it is used.What is Plasma?Plasma is a gaseous state of matter in which the atoms or molecules are ionized, or stripped of their electrons. This creates a cloud of positively charged ions and negatively charged electrons. Because of the presence of charged particles, plasma is electrically conductive and can be influenced by magnetic fields. Plasma can be generated in many ways, such as heating a gas to high temperatures or applying a high voltage or electric current to a gas.Properties of PlasmaPlasma has several unique properties that set it apart from the other states of matter. One of these is its ability to conduct electricity. Because plasma is made up of ions and free electrons, it can carry electric current. This property is utilized in devices like plasma TVs, which use a gas discharge to create light.Another property of plasma is its ability to be manipulated by magnetic fields. This property is used in fusion research, where magnetic fields are used to contain and control the plasma in order to create fusion reactions.Plasma also has properties that make it useful in industrial processes. For example, plasma can be used to clean surfaces by breaking down contaminants and producing free radicals that react with the surface. This process, called plasma cleaning, is used in the semiconductor industry to prepare surfaces for the deposition of thin films.Applications of PlasmaPlasma has numerous applications in science and technology. One of the most well-known applications is in plasma TVs, which use a gas discharge to create the colored pixels on the screen. Plasma is also used in welding, where it is used to heat and melt metals to create a bond.In the field of energy, plasma is being investigated as a potential source of fusion energy. Fusion reactions release energy by fusing atomic nuclei together, which can then be harnessed to generate electricity. However, creating and controlling the high-temperature plasma needed for fusion is a significant scientific and engineering challenge.Plasma is also used in the medical field, where it is used to sterilize medical equipment and treat a variety of medical conditions. Plasma can be used to break down cancer cells, kill bacteria and viruses, and promote wound healing.ConclusionPlasma is an important and fascinating state of matter that has numerous applications in science and technology. Understanding the properties of plasma is crucial to many scientific fields, from fusion research to plasma cleaning. As our understanding of plasma continues to grow, so too will our ability to harness its power for a range of applications.。

Designation:D 4000–01An American National StandardStandard Classification System forSpecifying Plastic Materials 1This standard is issued under the fixed designation D 4000;the number immediately following the designation indicates the year of original adoption or,in the case of revision,the year of last revision.A number in parentheses indicates the year of last reapproval.A superscript epsilon (e )indicates an editorial change since the last revision or reapproval.This standard has been approved for use by agencies of the Department of Defense.1.Scope *1.1This standard provides a classification system for tabu-lating the properties of unfilled,filled,and reinforced plastic materials suitable for processing into parts.N OTE 1—The classification system may serve many of the needs of industries using plastic materials.The standard is subject to revision as the need requires;therefore,the latest revision should always be used.1.2The classification system and subsequent line callout (specification)is intended to be a means of identifying plastic materials used in the fabrication of end items or parts.It is not intended for the selection of materials.Material selection should be made by those having expertise in the plastics field after careful consideration of the design and the performance required of the part,the environment to which it will be exposed,the fabrication process to be employed,the inherent properties of the material not covered in this document,and the economic factors.1.3This classification system is based on the premise that plastic materials can be arranged into broad generic families using basic properties to arrange the materials into groups,classes,and grades.A system is thus established which,together with values describing additional requirements,per-mits as complete a description as desired of the selected material.1.4In all cases where the provisions of this classification system would conflict with the referenced ASTM specification for a particular material,the latter shall take precedence.N OTE 2—When using this classification system the two-letter,three-digit suffix system applies.N OTE 3—When a material is used to fabricate a part where the requirements are too specific for a broad material callout,it is advisable for the user to consult the supplier to secure callout of the properties to suit the actual conditions to which the part is to be subjected.1.5This standard does not purport to address all of the safety concerns,if any,associated with its use.It is the responsibility of the user of this standard to establish appro-priate safety and health practices and determine the applica-bility of regulatory limitations prior to use.2.Referenced Documents 2.1ASTM Standards:D 149Test Method for Dielectric Breakdown V oltage and Dielectric Strength of Solid Electrical Insulating Materials at Commercial Power Frequencies 2D 150Test Methods for A-C Loss Characteristics and Permittivity (Dielectric Constant)of Solid Electrical Insu-lating Materials 2D 256Test Method for Determining the Izod Pendulum Impact Resistance of Notched Specimens of Plastics 3D 257Test Methods for D-C Resistance or Conductance of Insulating Materials 2D 395Test Methods for Rubber Property—Compression Set 4D 412Test Methods for Vulcanized Rubber and Thermo-plastic Rubbers and Thermoplastic Elastomers—Tension 4D 471Test Method for Rubber Property—Effect of Liq-uids 4D 495Test Method for High-V oltage,Low-Current,Dry Arc Resistance of Solid Electrical Insulation 2D 569Method for Measuring the Flow Properties of Ther-moplastic Molding Materials 5D 570Test Method for Water Absorption of Plastics 3D 573Test Method for Rubber—Deterioration in an Air Oven 4D 575Test Methods for Rubber Properties in Compression 4D 618Practice for Conditioning Plastics and Electrical Insulating Materials for Testing 3D 624Test Method for Tear Strength of Conventional Vulcanized Rubber and Thermoplastic Elastomers 4D 635Test Method for Rate of Burning and/or Extent and Time of Burning of Self-Supporting Plastics in a Horizon-tal Position 3D 638Test Method for Tensile Properties of Plastics 3D 648Test Method for Deflection Temperature of Plastics Under Flexural Load 31This classification system is under the jurisdiction of ASTM Committee D20on Plastics and is the direct responsibility of Subcommittee D20.94on Government/Industry Standardization (Section D20.94.01).Current edition approved March 10,2001.Published June 2001.Originally published as D 4000–st previous edition D 4000–00a.2Annual Book of ASTM Standards ,V ol 10.01.3Annual Book of ASTM Standards ,V ol 08.01.4Annual Book of ASTM Standards ,V ol 09.01.5Discontinued —See 1994Annual Book of ASTM Standards ,V ol 08.01.1*A Summary of Changes section appears at the end of this standard.Copyright ©ASTM International,100Barr Harbor Drive,PO Box C700,West Conshohocken,PA 19428-2959,United States.NOTICE: This standard has either been superseded and replaced by a new version or discontinued.Contact ASTM International () for the latest information.D695Test Method for Compressive Properties of Rigid Plastics3D706Specification for Cellulose Acetate Molding and Extrusion Compounds3D707Specification for Cellulose Acetate Butyrate Molding and Extrusion Compounds3D747Test Method for Apparent Bending Modulus of Plastics by Means of a Cantilever Beam3D785Test Method for Rockwell Hardness of Plastics and Electrical Insulating Materials3D787Specification for Ethyl Cellulose Molding and Extru-sion Compounds3D789Test Methods for Determination of Relative Viscos-ity,Melting Point,and Moisture Content of Polyamide (PA)3D790Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materi-als3D792Test Method for Density and Specific Gravity(Rela-tive Density)of Plastics by Displacement3D883Terminology Relating to Plastics3D955Test Method for Measuring Shrinkage from Mold Dimensions of Molded Plastics3D1003Test Method for Haze and Luminous Transmittance of Transparent Plastics3D1149Test Method for Rubber Deterioration—Surface Ozone Cracking in a Chamber4D1203Test Methods for V olatile Loss from Plastics Using Activated Carbon Methods3D1238Test Method for Flow Rates of Thermoplastics by Extrusion Plastometer3D1248Specification for Polyethylene Plastics Molding and Extrusion Materials3D1434Test Method for Determining Gas Permeability Characteristics of Plastic Film and Sheeting6D1435Practice for Outdoor Weathering of Plastics3D1499Practice for Filtered Open-Flame Carbon-Arc Ex-posures of Plastics3D1505Test Method for Density of Plastics by the Density-Gradient Technique3D1525Test Method for Vicat Softening Temperature of Plastics3D1562Specification for Cellulose Propionate Molding and Extrusion Compounds3D1600Terminology for Abbreviated Terms Relating to Plastics3D1693Test Method for Environmental Stress-Cracking of Ethylene Plastics3D1709Test Methods for Impact Resistance of Plastic Film by the Free-Falling Dart Method3D1784Specification for Rigid Poly(Vinyl Chloride)(PVC) Compounds and Chlorinated Poly(Vinyl Chloride) (CPVC)Compounds3D1822Test Method for Tensile-Impact Energy to Break Plastics and Electrical Insulating Materials3D1898Practice for Sampling of Plastics7D1929Test Method for Ignition Properties of Plastics3D2116Specification for FEP-Fluorocarbon Molding and Extrusion Materials3D2137Test Methods for Rubber Property—Brittleness Point of Flexible Polymers and Coated Fabrics4D2240Test Method for Rubber Property—Durometer Hardness4D2287Specification for Nonrigid Vinyl Chloride Polymer and Copolymer Molding and Extrusion Compounds3D2288Test Method for Weight Loss of Plasticizers on Heating3D2565Practice for Operating Xenon Arc-Type Light-Exposure Apparatus With and Without Water for Exposure of Plastics8D2583Test Method for Indentation Hardness of Rigid Plastics by Means of a Barcol Impressor8D2584Test Method for Ignition Loss of Cured Reinforced Resins8D2632Test Method for Rubber Property—Resilience by Vertical Rebound4D2843Test Method for Density of Smoke from the Burn-ing or Decomposition of Plastics8D2863Test Method for Measuring the Minimum Oxygen Concentration to Support Candle-Like Combustion of Plastics(Oxygen Index)8D2951Test Method for Resistance of Types III and IV Polyethylene Plastics to Thermal Stress-Cracking8D3012Test Method for Thermal Oxidative Stability of Propylene Plastics,Using a Biaxial Rotator8D3029Test Methods for Impact Resistance of Flat,Rigid Plastic Specimens by Means of a Tup(Falling Weight)9 D3294Specification for PTFE Resin Molded Sheet and Molded Basic Shapes8D3295Specification for PTFE Tubing8D3296Specification for FEP-Fluorocarbon Tube8D3350Specification for Polyethylene Plastics Pipe and Fittings Materials8D3418Test Method for Transition Temperatures of Poly-mers by Thermal Analysis8D3595Specification for Polychlorotrifluoroethylene (PCTFE)Extruded Plastic Sheet and Film8D3638Test Method for Comparative Tracking Index of Electrical Insulating Materials10D3713Test Method for Measuring Response of Solid Plastics to Ignition by a Small Flame11D3801Test Method for Measuring the Comparative Extin-guishing Characteristics of Solid Plastics in a Vertical Position8D3892Practice for Packaging/Packing of Plastics8D3895Test Method for Oxidative-Induction Time of Poly-olefins by Differential Scanning Calorimetry86Annual Book of ASTM Standards,V ol15.09.7Discontinued—See1997Annual Book of ASTM Standards,V ol08.01.8Annual Book of ASTM Standards,V ol08.02.9Discontinued—See1994Annual Book of ASTM Standards,V ol08.02.Re-placed by Test Methods D5420and D5628.10Annual Book of ASTM Standards,V ol.10.02.11Discontinued—See1999Annual Book of ASTM Standards,V ol08.02.D3915Specification for Poly(Vinyl Chloride)(PVC)and Chlorinated Poly(Vinyl Chloride)(CPVC)Compounds for Plastic Pipe and Fittings Used in Pressure Applications8 D3935Specification for Polycarbonate(PC)Unfilled and Reinforced Material8D3965Specification for Rigid Acrylonitrile-Butadiene-Styrene(ABS)Compounds for Pipe and Fittings8D3985Test Method for Oxygen Gas Transmission Rate Through Plastic Film and Sheeting Using a Coulometric Sensor6D4020Specification for Ultra-High-Molecular-Weight Polyethylene Molding and Extrusion Materials8D4066Specification for Nylon Injection and Extrusion Materials8D4067Specification for Reinforced and Filled Polyphe-nylene Sulfide Injection Molding and Extrusion Materials8 D4101Specification for Propylene Plastic Injection and Extrusion Materials8D4181Specification for Acetal(POM)Molding and Extru-sion Materials8D4203Specification for Styrene-Acrylonitrile(SAN)In-jection and Extrusion Materials8D4216Specification for Rigid Poly(Vinyl Chloride(PVC) and Related Plastic Building Products Compounds8D4329Practice for Operating Light and Water Apparatus (Fluorescent UV Condensation Type)for Exposure of Plastics12D4349Specificaton for Polyphenylene Ether(PPE)Mate-rials12D4364Practice for Performing Accelerated Outdoor Weathering of Plastics Using Concentrated Natural Sun-light12D4396Specification for Rigid Poly(Vinyl Chloride)(PVC) and Related Plastic Compounds for Nonpressure Piping Products12D4441Specification for Aqueous Dispersions of Polytet-rafluorethylene12D4474Specification for Styrenic Thermoplastic Elastomer Injection Molding and Extrusion Materials(TES)12D4507Specification for Thermoplastic Polyester(TPES) Materials13D4549Specification for Polystyrene Molding and Extru-sion Materials(PS)12D4550Specification for Thermoplastic Elastomer-Ether-Ester(TEEE)12D4617Specification for Phenolic Compounds(PF)12D4634Specification for Styrene-Maleic Anhydride Mate-rials(S/MA)12D4673Specification for Acrylonitrile-Butadiene-Styrene (ABS)Molding and Extrusion Materials12D4745Specification for Filled Compounds of Polytet-rafluoroethylene(PTFE)Molding and Extrusion Materi-als12D4812Test Method for Unnotched Cantilever Beam Im-pact Strength of Plastics12D4894Specification for Polytetrafluoroethylene(PTFE) Granular Molding and Ram Extrusion Materials12D4895Specification for Polytetrafluoroethylene(PTFE) Resins Produced from Dispersion12D4976Specification for Polyethylene Plastics Molding and Extrusion Materials12D5021Specification for Thermoplastic Elastomer–Chlori-nated Ethylene Alloy(TECEA)12D5046Specification for Fully Crosslinked Elastomeric Al-loys(FCEAs)12D5138Specification for Liquid Crystal Polymers(LCP)12 D5203Specification for Polyethylene Plastics Molding and Extrusion Materials from Recycled Post-Consumer HDPE Sources12D5279Test Method for Measuring the Dynamic Mechani-cal Properties of Plastics in Torsion12D5420Test Method for Impact Resistance of Flat,Rigid Plastic Specimen by Means of a Striker Impacted by a Falling Weight(Gardner Impact)12D5436Specification for Cast Poly(Methyl Methacrylate) Plastic Rods,Tubes,and Shapes12D5628Test Method for Impact Resistance of Flat,Rigid Plastic Specimens by Means of a Falling Dart(Tup or Falling Weight)12D5676Specification for Recycled Polystyrene Molding and Extrusion Materials12D5990Classification System for Polyketone Injection and Extrusion Materials(PK)12D6339Specification for Syndiotactic Polystyrene Molding and Extrusion(SPS)12D6358Classification System for Poly(Phenylene Sulfide) Injection Molding and Extrusion Materials Using ISO Methods12D6360Practice for Enclosed Carbon-Arc Exposures of Plastics12D6457Specification for Extruded and Compression Molded Rod and Heavy-Walled Tubing Made from Poly-tetrafluoroethylene(PTFE)12D6585Specification for Unsintered Polytetrafluoroethyl-ene(PTFE)Extruded Film or Tape12E29Practice for Using Significant Digits in Test Data to Determine Conformance with Specifications14E84Test Method for Surface Burning Characteristics of Building Materials15E96Test Methods for Water Vapor Transmission of Mate-rials16E104Practice for Maintaining Constant Relative Humidity by Means of Aqueous Solutions17E162Test Method for Surface Flammability of Materials Using a Radiant Heat Energy Source15F372Test Method for Water Vapor Transmission of Flex-ible Barrier Materials Using an Infrared Detection Tech-nique612Annual Book of ASTM Standards,V ol08.03.13Discontinued—See1998Annual Book of ASTM Standards,V ol08.03. Replaced by Specification D5927.14Annual Book of ASTM Standards,V ol14.02. 15Annual Book of ASTM Standards,V ol04.07. 16Annual Book of ASTM Standards,V ol04.06. 17Annual Book of ASTM Standards,V ol11.03.2.2Federal Standard:18Department of Transportation Federal Motor Vehicle Safety Standard No.3022.3Underwriters Laboratories:19UL94Standards for Tests for Flammability for Parts in Devices and Appliances2.4IEC and ISO Standards:20IEC 93Recommended Methods of Tests for V olume and Surface Resistivities of Electrical Insulation Materials IEC 112Recommended Method for Determining the Com-parative Tracking Index of Solid Insulation Materials Under Moist ConditionsIEC 243Recommended Methods of Test for Electrical Strength of Solid Insulating Materials at Power Frequen-ciesIEC 250Recommended Methods for the Determination of the Permittivity and Dielectric Dissipation Factor of Electrical Insulation Materials at Power,Audio,and Radio Frequencies Including Metre WavelengthsIEC 60695-11-10:Fire Hazard Testing—Part 11-10:Test Flames—50W Horizontal and Vertical Flame Tests ISO 62Plastics—Determination of Water AbsorptionISO 75-1Plastics—Determination of Temperature of De-flection Under Load—Part 1:General PrinciplesISO 75-2Plastics—Determination of Temperature of De-flection Under Load—Part 2:Plastics and EboniteISO 178Plastics—Determination of Flexural Properties of Rigid PlasticsISO 179Plastics—Determination of Charpy Impact Strength of Rigid MaterialsISO 180Plastics—Determination of Izod Impact Strength of Rigid MaterialsISO 294-4Plastics—Injection Moulding of Test Specimens of Thermoplastic Materials—Part 4:Determination of Moulding ShrinkageISO 527–1Plastics—Determination of Tensile Properties—Part 1:General PrinciplesISO 527-2Plastics—Determination of Tensile Properties—Part 2:Test Conditions for Moulding and Extrusion PlasticsISO 604Plastics—Determination of Compressive Proper-tiesISO 868Plastics—Determination of Indention Hardness by Means of a Durometer (Shore Hardness)ISO 877Plastics—Determination of Resistance to Change Upon Exposure Under Glass to DaylightISO 974Plastics—Determination of the Brittleness Tem-perature by ImpactISO 1183Plastics—Methods for Determining the Density and Relative Density of Non-Cellular PlasticsISO 2039-2Plastics—Determination of Hardness—Part 2:Rockwell HardnessISO 3795Road Vehicles,Tractors,and Machinery for Agriculture and Forestry—Determination of Burning Be-havior of Interior MaterialsISO 4577Plastics—Polypropylene and Propylene—Copolymers—Determination of Thermal Oxidative Sta-bility in Air-Oven MethodISO 4589Plastics—Determination of Flammability by Oxygen IndexISO 4607Plastics—Method of Exposure to Natural Weath-eringISO 4892Plastics—Methods of Exposure to Laboratory Light SourcesISO 4892–4Plastics—Methods of Exposure to Laboratory Light Sources—Part 4:Open-flame Carbon-arcISO 6603-1Plastics—Determination of Multiaxial Impact Behavior of Rigid Plastics—Part 1:Falling Dart Method ISO 6721-1Plastics—Determination of Dynamic Mechani-cal Properties—Part 1:General PrinciplesISO 6721-2Plastics—Determination of Dynamic Mechani-cal Properties—Part 2:Torsion-Pendulum Method ISO 11357-1Plastics—Differential Scanning Calorimetry—Part 1:General principles ISO 11357-3Plastics—Differential Scanning Calorimetry—Part 3:Determination of Temperature and Enthalpy of Melting and Crystallization18Available from Superintendent of Documents,ernment Printing Office,Washington,DC 20402.19Available from Underwriters Laboratories,Inc.,Publication Stock,333Pfingsten Rd.,Northbrook,IL 60062.20Available from American National Standards Institute,11W.42nd St.,13th Floor,New York,NY10036.TABLE1Standard Symbols for Generic Families With Referenced Standards and Cell TablesStandard Symbol Plastic Family Name ASTM A Standard Suggested Reference Cell Tables forMaterials Without an ASTM Standard BUnfilled Filled ABA acrylonitrile-butadiene-acrylate EABS acrylonitrile-butadiene-styrene D3965D4673AMMA acrylonitrile-methyl methacrylate EARP aromatic polyester(see LCP)ASA acrylonitrile-styrene-acrylate ECA cellulose acetate D706CAB cellulose acetate butyrate D707CAP cellulose acetate proprionate E DCE cellulose plastics,general E DCF cresol formaldehyde H HCMC carboxymethyl cellulose ECN cellulose nitrate E DCP cellulose propionate D1562CPE chlorinated polyethylene FCPVC chlorinated poly(vinyl chloride)D4396,D1784,D5260,D3915,D4216CS casein H HCTA cellulose triacetate E DEC ethyl cellulose D787E DE-CTFE ethylene-chlorotrifluoroethylene copolymer D3275EEA ethylene-ethyl acrylate FEMA ethylene-methacrylic acid FEP epoxy,epoxide H HEPD ethylene-propylene-dieneEPM ethylene-propylene polymer F D ETFE ethylene-tetrafluoroethylene copolymer D3159EVA ethylene-vinyl acetate FFCEA fully crosslinked elastomeric alloy D5046FEP perfluoro(ethylene-propylene)copolymer D2116FF furan formaldehyde D3296H HIPS impact polystyrene(see PS)LCP liquid crystal polymer D5138MF melamine-formaldehyde H HPA polyamide(nylon)D4066PAEK polyaryletherketone D__PAI polyamide-imide D5204G G PARA polyaryl amidePB polybutene-1FPBT poly(butylene terephthalate)(see TPES)PC polycarbonate D3935PCTFE polymonochlorotrifluoroethylene D1430,D3595PDAP poly(diallyl phthalate)H HPE polyethylene D1248,D4976,D3350,D4020,D5203PEBA polyether block amidePEEK polyetheretherketonePEI polyether-imide D5205PEO poly(ethylene oxide)D__PESV polyether sulfonePET poly(ethylene terephthalate),general(see TPES)PETG glycol modified polyethylene terephthalate comonomer(see TPES)PF phenol-formaldehyde D4617PFA perfluoro alkoxy alkane D3307PI polyimide G GPIB polyisobutylene FPK polyketone D5990PMMA Poly(methyl methacrylate)D788,D5436DPMP poly(4-methylpentene-1)FPOM polyoxymethylene(acetal)D4181POP polyphenylene oxide(see PPE)PP poly(propylene plastics)D4101PPA polyphthalamide D5336PPE polyphenylene ether D4349PPOX poly(propylene oxide)PPS poly(phenylene sulfide)D4067,D6358PPSU poly(phenyl sulfone)G GPS polystyrene D4549,D5676PSU polysulfone D6394PTFE polytetrafluoroethylene D3294,D3295,D4441,D4745,D4894,D4895,D6457,D6585PUR polyurethane F DTABLE1ContinuedStandard Symbol Plastic Family Name ASTM A Standard Suggested Reference Cell Tables forMaterials Without an ASTM Standard BUnfilled Filled PVAC poly(vinyl acetate)F D PVAL poly(vinyl alcohol)F DPVB poly(vinyl butyral)F DPVC poly(vinyl chloride)D2287F D PVDC poly(vinyl idene chloride)F D PVDF poly(vinyl idenefluoride)D3222PVF poly(vinylfluoride)F D PVFM poly(vinyl formal)F DPVK poly(vinylcarbazole)F DPVP poly(vinyl pyrrolidone)F DSAN styrene-acrylonitrile D4203SB styrene-butadiene E DSI silicone plastics G GS/MA styrene-maleic anhydride D4634SMS styrene-methylstyrene E DSPS syndiotactic polystyrene D6339TECEA thermoplastic elastomer-chlorinated ethylene alloy D5021TEEE thermoplastic elastomer,ether-ester D4550TEO thermoplastic elastomer-olefinic D5593TES thermoplastic elastomer-stryenic D4474TPE thermoplastic elastomer(see individual material)TPES thermoplastic polyester(general)D4507TPU thermoplastic polyurethane D5476UF urea-formaldehyde H HUP unsaturated polyester D__VDF vinylidenefluoride D5575A The standards listed are those in accordance with this classification.D__indicates that a standard is being developed by the subcommittee responsible.B Cell Tables A and B have been reserved for the referenced standards and will apply to unfilled andfilled materials covered in those standards.3.Terminology3.1Definitions—The definitions used in this classification system are in accordance with Terminology D883.4.Significance and Use4.1The purpose of this classification system is to provide a method of adequately identifying plastic materials in order to give industry a system that can be used universally for plastic materials.It further provides a means for specifying these materials by the use of a simple line call-out designation. 4.2This classification system was developed to permit the addition of property values for future plastics.5.Classification5.1Plastic materials shall be classified on the basis of their broad generic family.The generic family is identified by letter designations as found in Table1.These letters represent the standard abbreviations for plastics in accordance with Termi-nology D1600.N OTE4—For example:PA=polyamide(nylon).5.1.1The generic family is based on the broad chemical makeup of the base polymer.By its designation,certain inherent properties arespecified.TABLE 3Suffix Symbols and Requirements ASymbol CharacteristicAColor (unless otherwise shown by suffix,color is understood to be natural)Second letter A =does not have to match a standardB =must match standardThree-digit number 001=color and standard number on drawing002=color on drawingBFluid resistanceSecond letter A =reference fuel A,ASTM D 471,aged 70h at 2362°CB =reference fuel C,ASTM D 471,aged 70h at 2362°C C =ASTM #1oil,ASTMD 471,aged 70h at 10062°C D =IRM 902oil,ASTM D 471,aged 96h at 10062°CE =IRM 903oil,ASTM D 471,aged 70h at 10062°CF =Distilled water,ASTM D 471,aged 70h at 10062°CThree digit number is obtained from Suffix Table 1.It indicates change in hardness,tensile strength,elongation,and volume.Example:BC 132specifies that material,after aging in ASTM #1oil for 70h at 100°C,can have changed no more than 2Shore D points,5%tensile strength,15%elongation,and 5%in volume.CMelting point—softening pointSecond letter B =ASTM D 1525,load 10N,Rate A (Vicat)C =ASTMD 1525,load 10N,Rate B (Vicat)D =ASTM D 3418(Transition temperature DSC/DTA)(ISO 11357-1and 11357-3)G =ISO 306,load 10N,heating rate 50°C/h (Vicat)H =ISO 306,load 10N,heating rate 120°C/h (Vicat)I =ISO 306,load 50N,heating rate 50°C/h (Vicat)J =ISO 306,load 50N,heating rate 120°C/h (Vicat)K =ASTM D 1525,load 50N,Rate A (Vicat)L =ASTM D 1525,load 50N,Rate B (Vicat)Three-digit number =minimum value°C EElectricalSecond letter A =dielectric strength (short-time),ASTM D 149(IEC 243)Three-digit number 3factor of 0.1=kV/mm,minB =dielectric strength (step by step),ASTM D 149(IEC 243)Three-digit number 3factor of 0.1=kV/mm,minC =insulation resistance,ASTMD 257(IEC 93)Three-digit number 3factor of 1014=V ,minD =dielectric constant at 1MHz,ASTM D 150,max (IEC 250)Three-digit number 3factor of 0.1=valueE =dissipation factor at 1MHz,ASTM D 150,max (IEC 250)Three-digit number 3factor of 0.0001=valueF =arc resistance,ASTM D 495,minThree-digit number =valueG =volume resistivity,ASTM D 257(IEC 93)Three-digit number 3factor of 1014=V -cm,minH =comparative tracking index,ASTM D 3638,ac frequency,50Hz,0.1%ammonium chloride (IEC 112)Three-digit number =V,minJ =volume resistivity,ASTM D 257(IEC 93),V -cmK =surface resistivity,ASTM D 257(IEC 93),V (per square)First digit indicates:1=minimum requirement 2=maximum requirementFinal two digits indicate the exponential value of the base 10Example:EJ206specifies a maximum volume resistivity of 106V -cm FFlammabilitySecond letter A =ASTM D 635(burning rate)(IEC 60695-11-10)000=to be specified by userB =ASTM D 2863(oxygen index)(ISO 4589)Three-digit number =value %,maxC =ASTMD 1929,Procedure A (flash-ignition)TABLE 2Reinforcement-Filler A Symbols B and TolerancesSymbol MaterialToleranceC Carbon and graphite fiber-reinforced 62percentage points G Glass-reinforced62percentage pointsL Lubricants (for example,PTFE,graphite,silicone,and molybdenum disulfide)depends upon material and process—to be specified.M Mineral-reinforced62percentage pointsRCombinations of reinforcements and fillers63percentage points (based on the total reinforcements or fillers,or both)A Ash content of filled or reinforced materials may be determined using Test Method D 2584where applicable.BAdditional symbols will be added to this table asrequired.Symbol CharacteristicThree-digit number=value,°C,minD=ASTM D1929,Procedure B(self-ignition)Three-digit number=value,°C,minE=ASTM D3713000=to be specified by userF=ASTM D3801000=to be specified by userG=ASTM E162First two digits indicate minimum specimen thickness00to be specified05 3.00mm010.25mm06 6.00mm020.40mm079.00mm030.80mm0812.70mm04 1.60mm09>12.70mmThird digit indicates theflame spread115max5100max225max6150max350max7200max475max8>200H=E84000=to be specified by userJ=FMVSS302(ISO3795)000=to be specified by userK=density of smoke,ASTM D2843000=to be specified by userL=UL94(IEC60695-11-10)First digit indicates minimum specimen thicknessMolding Materials Thin Filmsmmµm0to be specified to be specified10.2525.020.4050.030.8075.04 1.60100.05 2.50125.06 3.00150.07 6.00175.0812.70200.09>12.70>200.0Second digit indicates type offlame test1=Vertical(94V)1=Horizontal(94H)3=125mmflame(94-5V)4=Vertical thin materials(94VTM)Third digit indicates theflame rating0=(94V/94VTM)0-refer to UL941=(94V/94VTM)1-refer to UL942=(94V/94VTM)2-refer to UL943=(94HB)1-burn rate<40mm/min4=(94HB)2-burn rate<75mm/min5=(94-5V)A no holes on plaques6=(94-5V)B with holes on plaques7=(94foam)1refer to UL948=(94foam)2refer to UL949=(94foam)H refer to UL94G Specific gravitySecond letter A=ASTM D792(tolerance60.02)(ISO1183Method A)B=ASTM D792(tolerance60.05)(ISO1183Method A)C=ASTM D792(tolerance60.005)(ISO1183Method A)D=ASTM D1505(tolerance60.02)E=ASTM D1505(tolerance60.05)F=ASTM D1505(tolerance60.005)H=ASTM D792/D1505(max)L=ASTM D792/D1505(min)Three-digit number3factor of0.010=requirement valueH Heat resistance,properties at temperatureSecond letter A=heat aged for70h at10062°C,ASTM D573B=heat aged for70h at15062°C,ASTM D573C=heat aged for70h at20062°C,ASTM D573Three-digit number is obtained from Suffix Table1.It indicates change in hardness,tensile strength,elongation and volume.Second letter D=tested at10062°CE=tested at12562°CF=tested at15062°CThree-digit numbers obtained from Suffix Table2.It indicates tensile strength,elongation,and tear strength.。

CHAPTER 2BASIC PLASMA EQUATIONS AND EQUILIBRIUM2.1INTRODUCTIONThe plasma medium is complicated in that the charged particles are both affected by external electric and magnetic fields and contribute to them.The resulting self-consistent system is nonlinear and very difficult to analyze.Furthermore,the inter-particle collisions,although also electromagnetic in character,occur on space and time scales that are usually much shorter than those of the applied fields or the fields due to the average motion of the particles.To make progress with such a complicated system,various simplifying approxi-mations are needed.The interparticle collisions are considered independently of the larger scale fields to determine an equilibrium distribution of the charged-particle velocities.The velocity distribution is averaged over velocities to obtain the macro-scopic motion.The macroscopic motion takes place in external applied fields and in the macroscopic fields generated by the average particle motion.These self-consistent fields are nonlinear,but may be linearized in some situations,particularly when dealing with waves in plasmas.The effect of spatial variation of the distri-bution function leads to pressure forces in the macroscopic equations.The collisions manifest themselves in particle generation and loss processes,as an average friction force between different particle species,and in energy exchanges among species.In this chapter,we consider the basic equations that govern the plasma medium,con-centrating attention on the macroscopic system.The complete derivation of these 23Principles of Plasma Discharges and Materials Processing ,by M.A.Lieberman and A.J.Lichtenberg.ISBN 0-471-72001-1Copyright #2005John Wiley &Sons,Inc.equations,from fundamental principles,is beyond the scope of the text.We shall make the equations plausible and,in the easier instances,supply some derivations in appendices.For the reader interested in more rigorous treatment,references to the literature will be given.In Section2.2,we introduce the macroscopicfield equations and the current and voltage.In Section2.3,we introduce the fundamental equation of plasma physics, for the evolution of the particle distribution function,in a form most applicable for weakly ionized plasmas.We then define the macroscopic quantities and indicate how the macroscopic equations are obtained by taking moments of the fundamental equation.References given in the text can be consulted for more details of the aver-aging procedure.Although the macroscopic equations depend on the equilibrium distribution,their form is independent of the equilibrium.To solve the equations for particular problems the equilibrium must be known.In Section2.4,we introduce the equilibrium distribution and obtain some consequences arising from it and from thefield equations.The form of the equilibrium distribution will be shown to be a consequence of the interparticle collisions,in Appendix B.2.2FIELD EQUATIONS,CURRENT,AND VOLTAGEMaxwell’s EquationsThe usual macroscopic form of Maxwell’s equations arerÂE¼Àm0@H@t(2:2:1)rÂH¼e0@E@tþJ(2:2:2)e0rÁE¼r(2:2:3) andmrÁH¼0(2:2:4) where E(r,t)and H(r,t)are the electric and magneticfield vectors and wherem 0¼4pÂ10À7H/m and e0%8:854Â10À12F/m are the permeability and per-mittivity of free space.The sources of thefields,the charge density r(r,t)and the current density J(r,t),are related by the charge continuity equation(Problem2.1):@rþrÁJ¼0(2:2:5) In general,J¼J condþJ polþJ mag24BASIC PLASMA EQUATIONS AND EQUILIBRIUMwhere the conduction current density J cond is due to the motion of the free charges, the polarization current density J pol is due to the motion of bound charges in a dielectric material,and the magnetization current density J mag is due to the magnetic moments in a magnetic material.In a plasma in vacuum,J pol and J mag are zero and J¼J cond.If(2.2.3)is integrated over a volume V,enclosed by a surface S,then we obtain its integral form,Gauss’law:e0þSEÁd A¼q(2:2:6)where q is the total charge inside the volume.Similarly,integrating(2.2.5),we obtaind q d t þþSJÁd A¼0which states that the rate of increase of charge inside V is supplied by the total currentflowing across S into V,that is,that charge is conserved.In(2.2.2),thefirst term on the RHS is the displacement current densityflowing in the vacuum,and the second term is the conduction current density due to the free charges.We can introduce the total current densityJ T¼e0@E@tþJ(2:2:7)and taking the divergence of(2.2.2),we see thatrÁJ T¼0(2:2:8)In one dimension,this reduces to d J T x=d x¼0,such that J T x¼J T x(t),independent of x.Hence,for example,the total currentflowing across a spatially nonuniform one-dimensional discharge is independent of x,as illustrated in Figure2.1.A generalization of this result is Kirchhoff’s current law,which states that the sum of the currents entering a node,where many current-carrying conductors meet,is zero.This is also shown in Figure2.1,where I rf¼I TþI1.If the time variation of the magneticfield is negligible,as is often the case in plasmas,then from Maxwell’s equations rÂE%0.Since the curl of a gradient is zero,this implies that the electricfield can be derived from the gradient of a scalar potential,E¼Àr F(2:2:9)2.2FIELD EQUATIONS,CURRENT,AND VOLTAGE25Integrating (2.2.9)around any closed loop C givesþC E Ád ‘¼ÀþC r F Ád ‘¼ÀþC d F ¼0(2:2:10)Hence,we obtain Kirchhoff’s voltage law ,which states that the sum of the voltages around any loop is zero.This is illustrated in Figure 2.1,for which we obtainV rf ¼V 1þV 2þV 3that is,the source voltage V rf is equal to the sum of the voltages V 1and V 3across the two sheaths and the voltage V 2across the bulk plasma.Note that currents and vol-tages can have positive or negative values;the directions for which their values are designated as positive must be specified,as shown in the figure.If (2.2.9)is substituted in (2.2.3),we obtainr 2F ¼Àre 0(2:2:11)Equation (2.2.11),Poisson’s equation ,is one of the fundamental equations that we shall use.As an example of its application,consider the potential in the center (x ¼0)of two grounded (F ¼0)plates separated by a distance l ¼10cm and con-taining a uniform ion density n i ¼1010cm 23,without the presence of neutralizing electrons.Integrating Poisson’s equationd 2F d x 2¼Àen i eFIGURE 2.1.Kirchhoff’s circuit laws:The total current J T flowing across a nonuniform one-dimensional discharge is independent of x ;the sum of the currents entering a node is zero (I rf ¼I T þI 1);the sum of voltages around a loop is zero (V rf ¼V 1þV 2þV 3).26BASIC PLASMA EQUATIONS AND EQUILIBRIUMusing the boundary conditions that F ¼0at x ¼+l =2and that d F =d x ¼0at x ¼0(by symmetry),we obtainF ¼12en i e 0l 22Àx 2"#The maximum potential in the center is 2.3Â105V,which is impossibly large for a real discharge.Hence,the ions must be mostly neutralized by electrons,leading to a quasi-neutral plasma.Figure 2.2shows a PIC simulation time history over 10210s of (a )the v x –x phase space,(b )the number N of sheets versus time,and (c )the potential F versus x for 100unneutralized ion sheets (with e /M for argon ions).We see the ion acceleration in (a ),the loss of ions in (b ),and the parabolic potential profile in (c );the maximum potential decreases as ions are lost from the system.We consider quasi-neutrality further in Section 2.4.Electric and magnetic fields exert forces on charged particles given by the Lorentz force law :F ¼q (E þv ÂB )(2:2:12)FIGURE 2.2.PIC simulation of ion loss in a plasma containing ions only:(a )v x –x ion phase space,showing the ion acceleration trajectories;(b )number N of ion sheets versus t ,with the steps indicating the loss of a single sheet;(c )the potential F versus x during the first 10210s of ion loss.2.2FIELD EQUATIONS,CURRENT,AND VOLTAGE 2728BASIC PLASMA EQUATIONS AND EQUILIBRIUMwhere v is the particle velocity and B¼m0H is the magnetic induction vector.The charged particles move under the action of the Lorentz force.The moving charges in turn contribute to both r and J in the plasma.If r and J are linearly related to E and B,then thefield equations are linear.As we shall see,this is not generally the case for a plasma.Nevertheless,linearization may be possible in some cases for which the plasma may be considered to have an effective dielectric constant;that is,the “free charges”play the same role as“bound charges”in a dielectric.We consider this further in Chapter4.2.3THE CONSERVATION EQUATIONSBoltzmann’s EquationFor a given species,we introduce a distribution function f(r,v,t)in the six-dimensional phase space(r,v)of particle positions and velocities,with the interpret-ation thatf(r,v,t)d3r d3v¼number of particles inside a six-dimensional phasespace volume d3r d3v at(r,v)at time tThe six coordinates(r,v)are considered to be independent variables.We illus-trate the definition of f and its phase space in one dimension in Figure2.3.As particles drift in phase space or move under the action of macroscopic forces, theyflow into or out of thefixed volume d x d v x.Hence the distribution functionaf should obey a continuity equation which can be derived as follows.InFIGURE2.3.One-dimensional v x–x phase space,illustrating the derivation of the Boltzmann equation and the change in f due to collisions.time d t,f(x,v x,t)d x a x(x,v x,t)d t particlesflow into d x d v x across face1f(x,v xþd v x,t)d x a x(x,v xþd v x,t)d t particlesflow out of d x d v x across face2 f(x,v x,t)d v x v x d t particlesflow into d x d v x across face3f(xþd x,v x,t)d v x v x d t particlesflow out of d x d v x across face4where a x v d v x=d t and v x;d x=d t are theflow velocities in the v x and x directions, respectively.Hencef(x,v x,tþd t)d x d v xÀf(x,v x,t)d x d v x¼½f(x,v x,t)a x(x,v x,t)Àf(x,v xþd v x,t)a x(x,v xþd v x,t) d x d tþ½f(x,v x,t)v xÀf(xþd x,v x,t)v x d v x d tDividing by d x d v x d t,we obtain@f @t ¼À@@x(f v x)À@@v x(fa x)(2:3:1)Noting that v x is independent of x and assuming that the acceleration a x¼F x=m of the particles does not depend on v x,then(2.3.1)can be rewritten as@f @t þv x@f@xþa x@f@v x¼0The three-dimensional generalization,@f@tþvÁr r fþaÁr v f¼0(2:3:2)with r r¼(^x@=@xþ^y@=@yþ^z@=@z)and r v¼(^x@=@v xþ^y@=@v yþ^z@=@v z)is called the collisionless Boltzmann equation or Vlasov equation.In addition toflows into or out of the volume across the faces,particles can “suddenly”appear in or disappear from the volume due to very short time scale interparticle collisions,which are assumed to occur on a timescale shorter than the evolution time of f in(2.3.2).Such collisions can practically instantaneously change the velocity(but not the position)of a particle.Examples of particles sud-denly appearing or disappearing are shown in Figure2.3.We account for this effect,which changes f,by adding a“collision term”to the right-hand side of (2.3.2),thus obtaining the Boltzmann equation:@f @t þvÁr r fþFmÁr v f¼@f@tc(2:3:3)2.3THE CONSERVATION EQUATIONS29The collision term in integral form will be derived in Appendix B.The preceding heuristic derivation of the Boltzmann equation can be made rigorous from various points of view,and the interested reader is referred to texts on plasma theory, such as Holt and Haskel(1965).A kinetic theory of discharges,accounting for non-Maxwellian particle distributions,must be based on solutions of the Boltzmann equation.We give an introduction to this analysis in Chapter18. Macroscopic QuantitiesThe complexity of the dynamical equations is greatly reduced by averaging over the velocity coordinates of the distribution function to obtain equations depending on the spatial coordinates and the time only.The averaged quantities,such as species density,mean velocity,and energy density are called macroscopic quantities,and the equations describing them are the macroscopic conservation equations.To obtain these averaged quantities we take velocity moments of the distribution func-tion,and the equations are obtained from the moments of the Boltzmann equation.The average quantities that we are concerned with are the particle density,n(r,t)¼ðf d3v(2:3:4)the particlefluxG(r,t)¼n u¼ðv f d3v(2:3:5)where u(r,t)is the mean velocity,and the particle kinetic energy per unit volumew¼32pþ12mu2n¼12mðv2f d3v(2:3:6)where p(r,t)is the isotropic pressure,which we define below.In this form,w is sumof the internal energy density32p and theflow energy density12mu2n.Particle ConservationThe lowest moment of the Boltzmann equation is obtained by integrating all terms of(2.3.3)over velocity space.The integration yields the macroscopic continuity equation:@n@tþrÁ(n u)¼GÀL(2:3:7)The collision term in(2.3.3),which yields the right-hand side of(2.3.7),is equal to zero when integrated over velocities,except for collisions that create or destroy 30BASIC PLASMA EQUATIONS AND EQUILIBRIUMparticles,designated as G and L ,respectively (e.g.,ionization,recombination).In fact,(2.3.7)is transparent since it physically describes the conservation of particles.If (2.3.7)is integrated over a volume V bounded by a closed surface S ,then (2.3.7)states that the net number of particles generated per second within V ,either flows across the surface S or increases the number of particles within V .For common low-pressure discharges in the steady state,G is usually due to ioniz-ation by electron–neutral collisions:G ¼n iz n ewhere n iz is the ionization frequency.The volume loss rate L ,usually due to recom-bination,is often negligible.Hencer Á(n u )¼n iz n e (2:3:8)in a typical discharge.However,note that the continuity equation is clearly not sufficient to give the evolution of the density n ,since it involves another quantity,the mean particle velocity u .Momentum ConservationTo obtain an equation for u ,a first moment is formed by multiplying the Boltzmann equation by v and integrating over velocity.The details are complicated and involve evaluation of tensor elements.The calculation can be found in most plasma theory texts,for example,Krall and Trivelpiece (1973).The result is mn @u @t þu Ár ðÞu !¼qn E þu ÂB ðÞÀr ÁP þf c (2:3:9)The left-hand side is the species mass density times the convective derivative of the mean velocity,representing the mass density times the acceleration.The convective derivative has two terms:the first term @u =@t represents an acceleration due to an explicitly time-varying u ;the second “inertial”term (u Ár )u represents an acceleration even for a steady fluid flow (@=@t ;0)having a spatially varying u .For example,if u ¼^xu x (x )increases along x ,then the fluid is accelerating along x (Problem 2.4).This second term is nonlinear in u and can often be neglected in discharge analysis.The mass times acceleration is acted upon,on the right-hand side,by the body forces,with the first term being the electric and magnetic force densities.The second term is the force density due to the divergence of the pressure tensor,which arises due to the integration over velocitiesP ij ¼mn k v i Àu ðÞv j Àu ÀÁl v (2:3:10)2.3THE CONSERVATION EQUATIONS 31where the subscripts i,j give the component directions and kÁl v denotes the velocity average of the bracketed quantity over f.ÃFor weakly ionized plasmas it is almost never used in this form,but rather an isotropic version is employed:P¼p000p000p@1A(2:3:11)such thatrÁP¼r p(2:3:12) a pressure gradient,withp¼13mn k(vÀu)2l v(2:3:13)being the scalar pressure.Physically,the pressure gradient force density arises as illustrated in Figure2.4,which shows a small volume acted upon by a pressure that is an increasing function of x.The net force on this volume is p(x)d AÀp(xþd x)d A and the volume is d A d x.Hence the force per unit volume isÀ@p=@x.The third term on the right in(2.3.9)represents the time rate of momentum trans-fer per unit volume due to collisions with other species.For electrons or positive ions the most important transfer is often due to collisions with neutrals.The transfer is usually approximated by a Krook collision operatorf j c¼ÀXbmn n m b(uÀu b):Àm(uÀu G)Gþm(uÀu L)L(2:3:14)where the summation is over all other species,u b is the mean velocity of species b, n m b is the momentum transfer frequency for collisions with species b,and u G and u L are the mean velocities of newly created and lost particles.Generally j u G j(j u j for pair creation by ionization,and u L%u for recombination or charge transfer lossprocesses.We discuss the Krook form of the collision operator further in Chapter 18.The last two terms in(2.3.14)are generally small and give the momentum trans-fer due to the creation or destruction of particles.For example,if ions are created at rest,then they exert a drag force on the moving ionfluid because they act to lower the averagefluid velocity.A common form of the average force(momentum conservation)equation is obtained from(2.3.9)neglecting the magnetic forces and taking u b¼0in theÃWe assume f is normalized so that k f lv ¼1.32BASIC PLASMA EQUATIONS AND EQUILIBRIUMKrook collision term for collisions with one neutral species.The result is mn @u @t þu Ár u !¼qn E Àr p Àmn n m u (2:3:15)where only the acceleration (@u =@t ),inertial (u Ár u ),electric field,pressure gradi-ent,and collision terms appear.For slow time variation,the acceleration term can be neglected.For high pressures,the inertial term is small compared to the collision term and can also be dropped.Equations (2.3.7)and (2.3.9)together still do not form a closed set,since the pressure tensor P (or scalar pressure p )is not determined.The usual procedure to close the equations is to use a thermodynamic equation of state to relate p to n .The isothermal relation for an equilibrium Maxwellian distribution isp ¼nkT(2:3:16)so thatr p ¼kT r n (2:3:17)where T is the temperature in kelvin and k is Boltzmann’s constant (k ¼1.381Â10223J /K).This holds for slow time variations,where temperatures are allowed to equilibrate.In this case,the fluid can exchange energy with its sur-roundings,and we also require an energy conservation equation (see below)to deter-mine p and T .For a room temperature (297K)neutral gas having density n g and pressure p ,(2.3.16)yieldsn g (cm À3)%3:250Â1016p (Torr)(2:3:18)p FIGURE 2.4.The force density due to the pressure gradient.2.3THE CONSERVATION EQUATIONS 33Alternatively,the adiabatic equation of state isp¼Cn g(2:3:19) such thatr p p ¼gr nn(2:3:20)where g is the ratio of specific heat at constant pressure to that at constant volume.The specific heats are defined in Section7.2;g¼5/3for a perfect gas; for one-dimensional adiabatic motion,g¼3.The adiabatic relation holds for fast time variations,such as in waves,when thefluid does not exchange energy with its surroundings;hence an energy conservation equation is not required. For almost all applications to discharge analysis,we use the isothermal equation of state.Energy ConservationThe energy conservation equation is obtained by multiplying the Boltzmannequation by12m v2and integrating over velocity.The integration and some othermanipulation yield@ @t32pþrÁ32p uðÞþp rÁuþrÁq¼@@t32pc(2:3:21)Here32p is the thermal energy density(J/m3),32p u is the macroscopic thermal energyflux(W/m2),representing theflow of the thermal energy density at thefluid velocityu,p rÁu(W/m3)gives the heating or cooling of thefluid due to compression orexpansion of its volume(Problem2.5),q is the heatflow vector(W/m2),whichgives the microscopic thermal energyflux,and the collisional term includes all col-lisional processes that change the thermal energy density.These include ionization,excitation,elastic scattering,and frictional(ohmic)heating.The equation is usuallyclosed by setting q¼0or by letting q¼Àk T r T,where k T is the thermal conduc-tivity.For most steady-state discharges the macroscopic thermal energyflux isbalanced against the collisional processes,giving the simpler equationrÁ32p u¼@32pc(2:3:22)Equation(2.3.22),together with the continuity equation(2.3.8),will often prove suf-ficient for our analysis.34BASIC PLASMA EQUATIONS AND EQUILIBRIUMSummarySummarizing our results for the macroscopic equations describing the electron and ionfluids,we have in their most usually used forms the continuity equationrÁ(n u)¼n iz n e(2:3:8) the force equation,mn @u@tþuÁr u!¼qn EÀr pÀmn n m u(2:3:15)the isothermal equation of statep¼nkT(2:3:16) and the energy-conservation equationrÁ32p u¼@@t32pc(2:3:22)These equations hold for each charged species,with the total charges and currents summed in Maxwell’s equations.For example,with electrons and one positive ion species with charge Ze,we haver¼e Zn iÀn eðÞ(2:3:23)J¼e Zn i u iÀn e u eðÞ(2:3:24)These equations are still very difficult to solve without simplifications.They consist of18unknown quantities n i,n e,p i,p e,T i,T e,u i,u e,E,and B,with the vectors each counting for three.Various simplifications used to make the solutions to the equations tractable will be employed as the individual problems allow.2.4EQUILIBRIUM PROPERTIESElectrons are generally in near-thermal equilibrium at temperature T e in discharges, whereas positive ions are almost never in thermal equilibrium.Neutral gas mol-ecules may or may not be in thermal equilibrium,depending on the generation and loss processes.For a single species in thermal equilibrium with itself(e.g.,elec-trons),in the absence of time variation,spatial gradients,and accelerations,the2.4EQUILIBRIUM PROPERTIES35Boltzmann equation(2.3.3)reduces to@f @tc¼0(2:4:1)where the subscript c here represents the collisions of a particle species with itself. We show in Appendix B that the solution of(2.4.1)has a Gaussian speed distribution of the formf(v)¼C eÀj2m v2(2:4:2) The two constants C and j can be obtained by using the thermodynamic relationw¼12mn k v2l v¼32nkT(2:4:3)that is,that the average energy of a particle is12kT per translational degree offreedom,and by using a suitable normalization of the distribution.Normalizing f(v)to n,we obtainCð2p0d fðpsin u d uð1expÀj2m v2ÀÁv2d v¼n(2:4:4)and using(2.4.3),we obtain1 2mCð2pd fðpsin u d uð1expÀj2m v2ÀÁv4d v¼32nkT(2:4:5)where we have written the integrals over velocity space in spherical coordinates.The angle integrals yield the factor4p.The v integrals are evaluated using the relationÃð10eÀu2u2i d u¼(2iÀ1)!!2ffiffiffiffipp,where i is an integer!1:(2:4:6)Solving for C and j we havef(v)¼nm2p kT3=2expÀm v22kT(2:4:7)which is the Maxwellian distribution.Ã!!denotes the double factorial function;for example,7!!¼7Â5Â3Â1. 36BASIC PLASMA EQUATIONS AND EQUILIBRIUMSimilarly,other averages can be performed.The average speed vis given by v ¼m =2p kT ðÞ3=2ð10v exp Àv 22v 2th !4p v 2d v (2:4:8)where v th ¼(kT =m )1=2is the thermal velocity.We obtainv ¼8kT p m 1=2(2:4:9)The directed flux G z in (say)the þz direction is given by n k v z l v ,where the average is taken over v z .0only.Writing v z ¼v cos u we have in spherical coordinatesG z ¼n m 2p kT 3=2ð2p 0d f ðp =20sin u d u ð10v cos u exp Àv 22v 2th v 2d v Evaluating the integrals,we findG z ¼14n v (2:4:10)G z is the number of particles per square meter per second crossing the z ¼0surfacein the positive direction.Similarly,the average energy flux S z ¼n k 1m v 2v z l v in theþz direction can be found:S z ¼2kT G z .We see that the average kinetic energy W per particle crossing z ¼0in the positive direction isW ¼2kT (2:4:11)It is sometimes convenient to define the distribution in terms of other variables.For example,we can define a distribution of energies W ¼12m v 2by4p g W ðÞd W ¼4p f v ðÞv 2d vEvaluating d v =d W ,we see that g and f are related byg W ðÞ¼v (W )f ½v (W ) m (2:4:12)where v (W )¼(2W =m )1=2.Boltzmann’s RelationA very important relation can be obtained for the density of electrons in thermal equilibrium at varying positions in a plasma under the action of a spatially varying 2.4EQUILIBRIUM PROPERTIES 3738BASIC PLASMA EQUATIONS AND EQUILIBRIUMpotential.In the absence of electron drifts(u e;0),the inertial,magnetic,and fric-tional forces are zero,and the electron force balance is,from(2.3.15)with@=@t;0,en e Eþr p e¼0(2:4:13) Setting E¼Àr F and assuming p e¼n e kT e,(2.4.13)becomesÀen e r FþkT e r n e¼0or,rearranging,r(e FÀkT e ln n e)¼0(2:4:14) Integrating,we havee FÀkT e ln n e¼constorn e(r)¼n0e e F(r)=kT e(2:4:15)which is Boltzmann’s relation for electrons.We see that electrons are“attracted”to regions of positive potential.We shall generally write Boltzmann’s relation in more convenient unitsn e¼n0e F=T e(2:4:16)where T e is now expressed in volts,as is F.For positive ions in thermal equilibrium at temperature T i,a similar analysis shows thatn i¼n0eÀF=T i(2:4:17) Hence positive ions in thermal equilibrium are“repelled”from regions of positive potential.However,positive ions are almost never in thermal equilibrium in low-pressure discharges because the ion drift velocity u i is large,leading to inertial or frictional forces in(2.3.15)that are comparable to the electricfield or pressure gra-dient forces.Debye LengthThe characteristic length scale in a plasma is the electron Debye length l De.As we will show,the Debye length is the distance scale over which significant charge densities can spontaneously exist.For example,low-voltage(undriven)sheaths are typically a few Debye lengths wide.To determine the Debye length,let us intro-duce a sheet of negative charge having surface charge density r S,0C/m2into an。

静电纺丝薄膜的孔隙率表征英文回答:Poreosity is a critical parameter for characterizing electrospun thin films. It refers to the percentage of void space or empty volume within the film. It is an important factor to consider in various applications such as filtration, tissue engineering, and drug delivery, as it affects the permeability, porosity, and mechanical properties of the film.There are several methods to determine the poreosity of electrospun thin films. One commonly used technique is the mercury intrusion porosimetry (MIP). MIP involves immersing the film in a mercury-filled chamber and applying increasing pressure to force the mercury into the pores. The pressure required for mercury intrusion is then measured, and the pore size distribution and total pore volume can be calculated. This method provides information on both the size and distribution of the pores within thefilm.Another method is the bubble point test. In this test, a liquid is forced through the film and the pressure at which bubbles start to form is recorded. This pressure is known as the bubble point pressure and is related to the pore size and pore connectivity of the film. By measuring the bubble point pressure, one can determine the average pore size and the extent of pore interconnectivity within the film.In addition to these techniques, there are alsoindirect methods to estimate the poreosity of electrospun thin films. For example, scanning electron microscopy (SEM) can be used to analyze the surface morphology of the film and provide qualitative information about the pore structure. Image analysis software can then be used to quantify the poreosity based on the SEM images.中文回答:孔隙率是表征静电纺丝薄膜的关键参数之一。

Progress in Polymer Science 35 (2010) 1350–1375Contents lists available at ScienceDirectProgress in PolymerSciencej o u r n a l h o m e p a g e :w w w.e l s e v i e r.c o m /l o c a t e /p p o l y s ciRecent advances in graphene based polymer compositesTapas Kuilla a ,Sambhu Bhadra b ,Dahu Yao a ,Nam Hoon Kim c ,Saswata Bose d ,Joong Hee Lee a ,d ,∗a BIN Fusion Research Team,Department of Polymer &Nano Engineering,Chonbuk National University,Jeonju,Jeonbuk 561-756,Republic of Koreab School of Polymers and High Performance Materials,The University of Southern Mississippi,118College Drive #10076,Hattiesburg,MS 39406-0001,USAc Department of Hydrogen and Fuel Cell Engineering,Chonbuk National University,Jeonju,Jeonbuk 561-756,Republic of Korea dDepartment of BIN Fusion Technology,Chonbuk National University,Jeonju,Jeonbuk 561-756,Republic of Koreaa r t i c l e i n f o Article history:Received 8March 2010Received in revised form 13July 2010Accepted 21July 2010Available online 27 July 2010Keywords:GrapheneGraphene modification Polymer composites Mechanical properties Electrical conductivitya b s t r a c tThis paper reviews recent advances in the modification of graphene and the fabrication of graphene-based polymer nanocomposites.Recently,graphene has attracted both academic and industrial interest because it can produce a dramatic improvement in properties at very low filler content.The modification of graphene/graphene oxide and the utilization of these materials in the fabrication of nanocomposites with different polymer matrixes have been explored.Different organic polymers have been used to fabricate graphene filled polymer nanocomposites by a range of methods.In the case of modified graphene-based polymer nanocomposites,the percolation threshold can be achieved at a very lower filler loading.Herein,the structure,preparation and properties of polymer/graphene nanocomposites are discussed in general along with detailed examples drawn from the scientific literature.© 2010 Elsevier Ltd. All rights reserved.Contents 1.Introduction ........................................................................................................................13512.Graphene............................................................................................................................13522.1.Discovery of graphene (1352)Abbreviations:AFM,atomic force microscopy;CNT,carbon nanotubes;CNF,carbon nanofiber;CCl 4,carbon tetrachloride;CTEs,coefficient of thermalexpansions;CVD,chemical vapor deposition;S-CCG,chemically converted graphene;CHCl 3,chloroform;CMG,chemically modified graphene;Cryo-TEM,cryogenic transmission electron microscopy;DCM,dichloro methane;DMSO,dimethyl sulfoxide;DSC,differential scanning calorimetry;DMA,dynamic mechanical analysis;DMTA,dynamic mechanical thermal analysis;EELS,electron energy loss spectroscopy;EMI,electromagnetic interference; ,elec-trical conductivity;ESEM,environmental scanning electron microscopy;xGnP,exfoliated graphite nanoplatelet;FLG,few layer graphene;GNS,graphene nanosheets;EVA,ethylene vinyl acetate;EG,expanded graphite;FG,foliated graphite;FT-IR,fourier transform infra red;GPa,gigapascal;T g ,glass transition temperature;GO,graphite oxide;HMPA,hexamethylphosphoramide;HDPE,high density polyethylene;IR,infra red;GNP IL ,ionic-liquid-functionalized graphene;KMG,KOH treated GO;LDH,layered double hydroxide;LM,light microscopy;LLDPE,linier low density polyethylene;e //,loss factor;MPa,mega-pascal;MMA,methyl methacrylate;NMP,N-methylpyrrolidone;DMF,N,N -dimethylformamide;DMAc,N,N -dimethylacetamide;ODA,octadecylamine;PETI,phenylethynyl-terminated polyimide;PANI,polyaniline;PPS,poly(phenylene sulfide);PNIPAAm,poly(N-isopropylacrylamide);PSS,poly(sodium 4-styrenesulfonate);PVA,poly(vinyl alcohol);PS,polystyrene;PMMA,poly(methyl methacrylate);PI,polyimide;PET,poly(ethylene terepthalate);PE-g-MA,polyethylene grafted maleic anhydride;PP,polypropylene;PVC,poly(vinyl chloride);PA6,polyamide;SIS,poly(styrene-b -isoprene-b -styrene);PS,polystyrene;PU,polyurethane;PVDF,poly(vinylidene fluoride);PEDOT,poly(3,4-ethyldioxythiophene);PB −,pyrenebutyrate;PBA,pyrene butyric acid;SEM,scanning electron microscopy;SiO 2,silicaSiCsilicon carbide;SWNTs,single wall carbon nanotubes;SDS,sodium dodecyl sulfate;SDBS,sodium dodecyl benzene sulfonate;E /or G /,storage modulus;SSSP,solid-state shear pulverization;SPANI,sulfonated polyaniline;THF,tetrahydrofuran;TMEDA,tetramethylethylenediamine;TCNQ,7,7,8,8-tetracyanoquinodimethane;TGA,thermogravimetric analysis;TPU,thermoplastic polyurethane;XRD,X-ray diffraction.∗Corresponding author at:BIN Fusion Research Team,Department of Polymer &Nano Engineering,Chonbuk National University,Jeonju,Jeonbuk 561-756,Republic of Korea.Tel.:+82632702342;fax:+82632702341.E-mail address:jhl@chonbuk.ac.kr (J.H.Lee).0079-6700/$–see front matter © 2010 Elsevier Ltd. All rights reserved.doi:10.1016/j.progpolymsci.2010.07.005T.Kuila et al./Progress in Polymer Science35 (2010) 1350–137513512.2.Synthesis and structural features of graphene (1352)2.3.Surface modification of graphene (1352)2.3.1.Chemical modification of graphene (1353)2.3.2.Electrochemical modification of graphene (1356)2.3.3.–interaction (1357)3.Polymer/graphene nanocomposites (1358)3.1.Preparation methods of polymer/graphene nanocomposites (1358)3.1.1.In situ intercalative polymerization (1358)3.1.2.Solution intercalation (1359)3.1.3.Melt intercalation (1359)3.2.Graphenefilled different polymer composites (1360)3.2.1.Epoxy/graphene nanocomposites (1360)3.2.2.Polystyrene/graphene nanocomposites (1360)3.2.3.Polyaniline/graphene nanocomposites (1362)3.2.4.Nafion/graphene nanocomposites (1364)3.2.5.PVA/graphene nanocomposites (1364)3.2.6.PU/graphene nanocomposites (1365)3.2.7.PVDF/graphene nanocomposites (1366)3.2.8.Poly(3,4-ethyldioxythiophene)/graphene nanocomposites (1368)3.2.9.Polyethylene terephthalate/graphene nanocomposites (1368)3.2.10.Polycarbonate/graphene nanocomposites (1369)4.Conclusions (1369)Acknowledgements (1370)References (1371)1.IntroductionThefield of nanoscience has blossomed over the last twenty years,and the importance for nanotechnology will increase as miniaturization becomes more important in areas,such as computing,sensors,biomedical and many other applications.Advancements in these disciplines depend largely on the ability to synthesize nanoparti-cles of various materials,sizes and shapes,as well as to assemble them efficiently into complex architectures [1].Currently,nanomaterials have an enormous range of applications owing to their structural features.However, material scientists are examining materials with improved physicochemical properties that are dimensionally more suitable in thefield of nanoscience and technology.In this regard,the discovery of graphene and graphene-based polymer nanocomposites is an important addition in the area of nanoscience,playing a key role in modern science and technology[2].The discovery of polymer nanocomposites by the Toyota research group[3]has opened a new dimension in thefield of materials science.In particular,the use of inorganic nanomaterials asfillers in the preparation of polymer/inorganic composites has attracted increasing interest owing to their unique properties and numerous potential applications in the automotive,aerospace,con-struction and electronic industries[4–11].Thus far,the majority of research has focused on polymer nanocom-posites based on layered materials of a natural origin,such as a montmorillonite type of layered silicate compounds or synthetic clay(layered double hydroxide)[5–17]. However,the electrical and thermal conductivity of clay minerals are quite poor[18–20].In order to overcome these shortcomings,carbon-based nanofillers,such as carbon black,EG,CNT,and CNF have been introduced to the preparation of polymer nanocomposites[21–47].Among these,CNTs have proven to be very effective as conductivefillers[22,33–39].The only drawback of CNTs as a nanofiller is their higher production cost[48]. Therefore,the mass production of CNT based functional composite materials is very difficult.As Nicholas A.Kotov wrote in his review in Nature[49]“When carbonfibers just won’t do,but nanotubes are too expensive,where can a cost-conscious materials scientist go tofind a practical conductive composite?The answer could lie with graphene sheets”.Graphene is considered a two-dimensional carbon nanofiller with a one-atom-thick planar sheet of sp2bonded carbon atoms that are densely packed in a honeycomb crystal lattice.It is regarded as the“thinnest material in the universe”with tremendous application potential[50,51].Graphene is predicted to have remarkable properties,such as high thermal con-ductivity,superior mechanical properties and excellent electronic transport properties[52–56].These intrinsic properties of graphene have generated enormous interest for its possible implementation in a myriad of devices [57].These include future generations of high speed and radio frequency logic devices,thermally and electrically conducting reinforced nanocomposites,ultra-thin carbon films,electronic circuits,sensors,and transparent and flexible electrodes for displays and solar cells[57–71]. Graphene,as a nanofiller,may be preferred over other conventional nanofillers(Na-MMT,LDH,CNT,CNF,EG,etc.) owing to high surface area,aspect ratio,tensile strength (TS),thermal conductivity and electrical conductivity, EMI shielding ability,flexibility,transparency,and low CTE[52–56,72].Table1gives a comparative chart on the mechanical,thermal and electrical properties of graphene with CNT,steel,plastic,rubber andfiber.The tensile strength of graphene is similar or slightly higher than CNT, but much higher than steel,Kevlar,HDPE and natural rub-ber.The thermal conductivity of graphene is higher than1352T.Kuila et al./Progress in Polymer Science35 (2010) 1350–1375Table1Properties of graphene,CNT,nano sized steel,and polymers.Materials Tensile strength Thermal conductivity(W/mk)at room temperature Electrical conductivity(S/m)ReferencesGraphene130±10GPa(4.84±0.44)×103to(5.30±0.48)×1037200[73–84] CNT60–150GPa35003000–4000[35,85–88] Nano sized steel1769MPa5–6 1.35×106[89,90] Plastic(HDPE)18–20MPa0.46–0.52Insulator[91–93] Rubber(natural rubber)20–300.13–0.142Insulator[94,95] Fiber(Kevlar)3620MPa0.04Insulator[96,97]all these materials.The electrical conductivity of graphene is also higher than these materials except for steel[73–97].The superior properties of graphene compared to polymers are also reflected in polymer/graphene nanocom-posites.Polymer/graphene nanocomposites show superior mechanical,thermal,gas barrier,electrical andflame retardant properties compared to the neat polymer [2,44–47,98–101].It was also reported that the improve-ment in mechanical and electrical properties of graphene based polymer nanocomposites are much better in com-parison to that of clay or other carbonfiller-based polymer nanocomposites[2,98–101].Although CNTs show compa-rable mechanical properties compared to graphene,still graphene is a better nanofiller than CNT in certain aspects, such as thermal and electrical conductivity(Table1) [73–97].However,the improvement in the physicochem-ical properties of the nanocomposites depends on the distribution of graphene layers in the polymer matrix as well as interfacial bonding between the graphene layers and polymer matrix.Interfacial bonding between graphene and the host polymer dictates thefinal properties of the graphene reinforced polymer nanocomposite.Pristine graphene is not compatible with organic polymers and does not form homogeneous composites.In contrast,graphene oxide sheets are heavily oxygenated graphene(bearing hydroxyl,epoxide,diols,ketones and carboxyls functional groups)that can alter the van der Waals interactions sig-nificantly and be more compatible with organic polymers [68,102–106].There are also some additional carbonyl and carboxyl groups located at the edge of the sheets,which makes graphene oxide sheets strongly hydrophilic,allow-ing them to readily swell and disperse in water[107,108]. For this reason,GO has attracted considerable attention as a nanofiller for polymer nanocomposites.However,GO sheets can only be dispersed in aqueous media,which are incompatible with most organic polymers.In addition, unlike graphene,graphene oxide is electrically insulating, which makes it unsuitable for the synthesis of conducting nanocomposites.The surface modification of graphene is an essential step for obtaining a molecular level dispersion of individual graphene in a polymer matrix.The electri-cal conductivity of the resulting nanocomposites can be increased by the chemical reduction of GO,presumably by restoring the graphitic network of sp2bonds[2].2.Graphene2.1.Discovery of grapheneGraphene is the basic structural unit of some car-bon allotropes,including graphite,carbon nanotubes and fullerenes(Fig.1).It is believed to be composed of ben-zene rings stripped of their hydrogen atoms.The rolling up of graphene along a given direction can produce a car-bon nanotube.A zero-dimensional fullerene can also be obtained by wrapping-up graphene[109,110].In1940,it was established theoretically that graphene is the building block of graphite[111].In2004,Geim and co-workers at Manchester University successfully identified single lay-ers of graphene and other2-D crystals[112]in a simple tabletop experiment,which were previously considered to be thermodynamically unstable and could not exist under ambient conditions[113,114].The promising mechani-cal,electrical,optical,thermal and magnetic properties of graphene have“led to the creation of a new and exciting ‘laboratory’for the study of fundamental science.”2.2.Synthesis and structural features of grapheneGraphene can be prepared using four different meth-ods[84].Thefirst is chemical vapor deposition(CVD)and epitaxial growth,such as the decomposition of ethylene on nickel surfaces[115,116].The second is the microme-chanical exfoliation of graphite,which is also known as the‘scotch tape’or‘peel-off’method[112,117].The third method is epitaxial growth on electrically insulating sur-faces,such as SiC,and the fourth is the solution-based reduction of graphene oxide[84,118].Graphene is a single layer of carbon atoms packed densely in a honeycomb crystal lattice.The carbon-carbon bond(sp2)length in graphene is approximately0.142nm [119–121].Depending on the research group,the graphene layer thickness ranges from0.35to1nm relative to the SiO2substrate[122].Novoselov et al.measured platelet thicknesses of1–1.6nm[112].2.3.Surface modification of graphenePristine graphene materials are unsuitable for interca-lation by large species,such as polymer chains,because graphene as a bulk material has a pronounced tendency to agglomerate in a polymer matrix[106,123].It is likely that oxidation followed by chemical functionalization will facilitate the dispersion and stabilize graphene to prevent agglomeration[123,124].The functional groups attached to graphene can be small molecules[105,125–127]or polymer chains[128–130].The chemical functionalization of graphene is a particularly attractive target because it can improve the solubility and processability as well as enhance the interactions with organic polymers[131,132]. Considerable work has been carried out on the amination, esterification[104,132],isocyanate modification[133],andT.Kuila et al./Progress in Polymer Science 35 (2010) 1350–13751353Fig.1.Graphene (top left)is a honeycomb lattice of carbon atoms.Graphite (top right)can be viewed as a stack of graphene layers.Carbon nanotubes are rolled-up cylinders of graphene (bottom left).Fullerenes (C60)are molecules consisting of wrapped graphene through the introduction of pentagons on the hexagonal lattice (Reproduced with permission from Neto et al.[110]).polymer wrapping [128–130]as routes for the functional-ization of graphene.The electrochemical modification of graphene using ionic liquids has also been reported [48].The general approaches for preparing organo-modified graphene are as follows.2.3.1.Chemical modification of grapheneThis method is based on the modified Hummers method [134].Initially,graphite oxides are generally prepared from naturally occurring graphite.After oxidation,several chemical methods to obtain soluble graphene have been examined,including the reduction of graphite oxide (GO)in a stabilization medium [135],covalent modification by the amidation of the carboxylic groups [131,132],non-covalent functionalization of reduced graphene oxide [128–130],nucleophilic substitution to epoxy groups [105],and dia-zonium salt coupling [136].2.3.1.1.Reduction of graphite oxide (GO)in a stabilization medium.Park et al.[135]reported a simple route for the preparation of a homogeneous aqueous suspension of chemically modified graphene with good electrical conduc-tivity.In this method,the precursor graphene oxide was first dispersed in water followed by the addition of an aque-ous KOH solution (Fig.2).According to Park et al.,KOH,a strong base,can confer a large negative charge through reactions with the reactive hydroxyl,epoxy and carboxylic acid groups on the graphene oxide sheets,resulting in extensive coating of the sheets with negative charges and K +ions.The addition of hydrazine monohydrate to KOH-treated graphene oxide produces a homogeneous suspension of hKMG,which can remain stable for at least 4months.Recently,Li et al.prepared stable aqueous colloids of graphene sheets through the electrostatic stabilization of graphite [84].This discovery enabled the development of a facile approach to the large scale production of aque-ous graphene dispersions without the need for polymeric or surfactant stabilizers.2.3.1.2.Covalent modification of graphene.For the prepa-ration of organomodified graphene oxide/graphene,most studies followed a covalent modification technique.Differ-ent organic amines,alkyl lithium reagents,isocyanates,and diisocyanate compounds have been used for this purpose1354T.Kuila et al./Progress in Polymer Science35 (2010) 1350–1375Fig.2.A simple route for the preparation of a homogeneous aqueous suspension of graphene sheets from graphite stack:(a)graphite stack is oxidized to separate the individual layers of graphene oxide (GO),(b)GO is dispersed in water and treated with aqueous KOH solution to obtain KOH modified oxidized graphene (KMG)and finally (c)KMG is reduced using hydrazine to produce hydrazine reduced KOH modified graphene (hKMG)in the form of stable aqueous dispersion of individual graphene sheets.[131–133,137].These surface modifying agents reduce the hydrophilic character of graphene oxide sheets by forming amide and carbamate ester bonds with the carboxyl and hydroxyl groups,respectively [133].Niyogi et al.[132]reported an amide coupling reac-tion between the carboxyl acid groups of graphene oxides and octadecylamine (ODA).Thionyl chloride was used to activate the COOH groups in the presence of N,N -dimethylformamide (DMF)under reflux conditions.ODA-modified GO had a solubility of 0.5mg ml −1in THF,and was also soluble in CCl 4and 1,2-dichloroethane.Soluble graphene layers have also been prepared by react-ing graphite fluoride with alkyl lithium reagents [131].Vacuum-dried graphite fluoride and tetramethylethylene-diamine (TMEDA)were dissolved in hexane at 0◦C in an ice bath.An alkyl-lithium reagent was then added drop wise and stirred for 3days to produce functionalized graphene (Fig.3).IR spectral studies confirmed the covalent attach-ment of alkyl chains to the graphene layers [131].Xu et al.modified the surface of graphene via the cova-lent attachment of a porphyrin ring on the GO surfaces [138].Thionyl chloride was used to activate the carboxylic acid group in the presence of porphyrin using DMF as a sol-vent.Fig.4shows a schematic diagram for the modification of graphene via the covalent attachment of a porphyrin ring on to the GO surfaces.Organic isocyanates were added to a GO dispersion in anhydrous DMF and allowed to react with GO for a spe-cific period of time.The reaction was then quenched by adding methylene chloride,and the modified graphene was washed and dried [133].The isocyanate compound was attached to the hydroxyl and carboxyl groups of GO via the formation of carbamate and amide function-alities,respectively.Fig.5shows a schematic diagram of the formation of carbamate and amide functionali-ties.Isocyanate-modified graphene oxide readily forms a stable colloidal dispersion in all polar aprotic solvents,such as DMF,N-methylpyrrolidone (NMP),dimethyl sul-foxide (DMSO)and hexamethylphosphoramide (HMPA).The modification of GO with diisocyanate compounds was recently reported [137].The preparatory method was sim-ilar to isocyanate modification.However,there was an additional step.The diisocyanate treated graphene oxide was reduced by hydrazine monohydrate at 80◦C for 48h.The building blocks of the GO sheets were crosslinked to form lamellar porous structures via a reaction of diiso-cyanate with the carboxyl and hydroxyl groups on both sides of the sheets.2.3.1.3.Non-covalent functionalization of graphene.The reduction of a stable aqueous dispersion of exfoliated graphite oxide nanoplatelets with hydrazine hydrateT.Kuila et al./Progress in Polymer Science35 (2010) 1350–13751355Fig.3.Production of functionalized graphene layers from graphitefluoride and alkyl lithium reagent.Annealing of functionalized graphene produces 3-dimensional graphite.(Reproduced from Worsley et al.by permission of Elsevier Science Ltd.,UK[131]).resulted in the formation of aggregates[130].The precip-itated materials could not be re-dispersed,even after a prolonged ultrasonic treatment in water in the presence of surfactants,such as SDS and TRITON X-100.In order to overcome this problem,the reduction was carried out in the presence of polymer/polymeric anions,resulting in a stable polymer-grafted dispersion of graphene[130].Stable aqueous dispersions of graphitic nanoplatelets were prepared by coating reduced graphite oxide nanoplatelets with an amphiphilic polymer,poly(sodium 4-styrenesulfonate)(PSS)[130].In2008,an aqueous dispersion of graphene was prepared from expanded graphite using7,7,8,8-tetracyanoquinodimethane(TCNQ)anion as a stabilizer.This could provide a facile route for producing high quality water soluble and organic solvent soluble graphene sheets for a range of applications [139].It was suggested that TCNQ anions adsorb on the graphene sheets,which stabilizes them in water.The TCNQ-stabilized graphene sheets could be re-dispersed in water,DMF and dimethyl sulfoxide(DMSO).Xu et al.[140] reported the preparation of stable aqueous dispersions of graphene sheets using a water soluble pyrene derivative, 1-pyrenebutyrate(PB−),as a stabilizer because the pyrene moiety has been reported to have strong affinity to the basal plane of graphite via-stacking[141,142].For this, an alkaline solution of pyrene butyric acid(PBA)wasFig.4.Schematic showing the modification of graphene via the covalent attachment of a porphyrin ring on to the GO surfaces.The–NH2groups of prophyrene ring are covalently bonded to the carboxyl group of graphene by the amide linkage.Thionyl chloride was used to activate the carboxylic acid group in the presence of porphyrin in DMF.(Reproduced from from Xu et al.by permission of Wiley-VCH,Germany[138]).1356T.Kuila et al./Progress in Polymer Science35 (2010) 1350–1375Fig.5.Schematic showing the modification of GO using organic isocyanate in DMF medium.Scheme shows the reactions of isocyanate group with different functional groups of GO.Isocyanates react with the hydroxyl (left oval)and carboxyl groups (right oval)of graphene oxide sheets to form carbamate and amide functionalities,respectively (Reproduced from Stankovich et al.by permission of Elsevier Science Ltd.,UK [133]).reacted with a GO dispersion followed by reduction with hydrazine monohydrate at 80◦C for 24h.Both the modi-fied and reduced GO dispersed well in water and showed an electrical conductivity of 2×102S m −1.Homogeneous aqueous dispersions of reduced exfoliated graphite oxide in the presence of sulfonated polyaniline (SPANI)have been reported [128].The successful reduction of GO was confirmed by electrical conductivity measurements.The conductivity of the composite film was 30S m −1,which is similar to that of the reduced GO sheets reported in the literature [140].2.3.1.4.Nucleophilic substitution.Aliphatic amine-modified GO was prepared by a reaction of amine with an aqueous dispersion of GO [105].Nucleophilic substitution occurs on the epoxy groups of GO [143].For the small chain primary amine,C n H 2n +1NH 2(n =2,4,8,12),grafting was completed at room temperature.On the other hand,for long chain aliphatic amines (octadecylamine),the reaction mixture was heated under reflux for 24h.However,the later GO derivatives were dispersed more easily in organic solvents.X-ray diffraction (XRD)showed that the interlayer distance of the amine intercalated GO derivatives depends on the amine chain lengths and their orientation relative to the layers.According to Bourlinos et al.,the tilted orientation is more likely to be due to the hydrophilic nature of the layers [105].Bourlinos et al.[105]also reported amino acid modified graphene.In this case,an alkaline solution of amino acids was used to modify GO.Nucleophilic attack of the –NH 2end group on the epoxide groups of GO occurs,suggesting that the amino acid molecules adopt a flat orientation in the interlayer zone of GO.2.3.1.5.Diazonium salt coupling.Graphene (S-CCG)sheets wrapped chemically with sodium dodecyl benzene sul-fonate (SDBS)were obtained by the reduction of graphene oxide with hydrazine and functionalized by a treatment with aryl diazonium salts [136].Thefunctionalized graphene could be dispersed readily in N,N -dimethylformamide (DMF),N,N -dimethylacetamide (DMAc)and 1-methyl-2-pyrrolidinone (NMP)up to 1mg/mL with minimal sedimentation.Cryogenic trans-mission electron microscopy (Cryo-TEM)revealed the existence of individual sheets and a few multiple sheet structures of SDBS-coated graphene Thermogravimetric analysis showed that the thermal stability of functional-ized CCG was significantly higher than that of neat GO but lower than that of S-CCG.The degree of functionalization calculated from these weight losses was estimated to be ∼1functional group in 55carbon atoms.The chemical modifi-cation of epitaxial graphene by the covalent attachment of aryl groups to the basal carbon atoms was reported [125].Epitaxial graphene grown on SiC wafers was modified chemically with aryl groups via the formation of cova-lent bonds to the conjugated carbon atoms [118,125,144].The grafting of aryl groups was confirmed by FT-IR spec-troscopy.Nitrophenyl-functionalized epitaxial graphene exhibited some new bands at 1565and 1378cm −1,which correspond to the symmetric and asymmetric stretching modes of NO 2.2.3.2.Electrochemical modification of grapheneGraphite was treated electrochemically to produce a colloidal suspension of chemically modified graphene (CMG)[48].Fig.6shows a schematic diagram of the exper-imental set up.A commercial graphite electrode was used as the cathode,which was immersed in a phase-separated mixture of water and imidazolium-based ionic liquids.A constant potential of 10–20V was applied across the electrodes.After 30min electrochemical reaction,ionic liquid functionalized graphene (GNP IL )sheets originating from the graphite anode precipitated.Ultrasonication of dried GNP IL in DMF resulted in a homogeneous dispersion (1mg ml −1).The average length and width of the GNP IL were 700and 500nm,respectively,as evidenced from the TEM images.AFM image analysis revealed the thickness of GNP IL to be ∼1.1nm.。

鲨鱼表皮的仿生原理对人类的作用英语作文全文共3篇示例,供读者参考篇1The biomimetic principles of shark skin and their implications for humansIntroductionSharks are one of the most fascinating creatures in the ocean, known for their sleek bodies and powerful swimming abilities. One of the key features that contributes to their efficiency in the water is their unique skin. Shark skin is covered with tiny scales called dermal denticles, which have a structure that is now being studied and replicated for various human applications. This process is known as biomimicry, where engineers and scientists draw inspiration from nature to design innovative solutions to human problems.The structure of shark skinDermal denticles are small, tooth-like structures that cover the skin of sharks. These denticles are aligned in a specific pattern that reduces drag and turbulence as the shark swims through the water. The scales have a shape that resembles tinytooth-like structures, with ridges that run parallel to the flow of water and tiny riblets that break up the boundary layer, reducing friction. This unique design allows sharks to move efficiently through the water, enabling them to reach high speeds and maneuver quickly.Applications for human technologyThe biomimetic properties of shark skin have inspired researchers to develop new technologies and materials for human use. One of the most significant applications is in the field of aerodynamics, where the design of aircraft and vehicles is being improved to reduce drag and increase efficiency. By mimicking the structure of shark skin, engineers have been able to design surfaces that are more hydrodynamic and produce less noise, leading to improved performance and fuel efficiency.Another area where shark skin biomimicry is being applied is in the development of antimicrobial surfaces. The unique pattern of shark scales has been found to inhibit the growth of bacteria and pathogens, making it an ideal inspiration for creating surfaces that are resistant to microbial contamination. These antimicrobial materials have the potential to be used in healthcare settings, food processing facilities, and other critical environments where cleanliness is essential.Furthermore, the properties of shark skin are being harnessed for the development of new materials that can be used in underwater equipment and marine structures. By replicating the design of shark scales, researchers have been able to create coatings that reduce biofouling and corrosion, improving the durability and performance of underwater devices. These materials have the potential to revolutionize the marine industry by providing solutions that are more sustainable and environmentally friendly.Implications for sustainability and conservationIn addition to the technological advancements that have resulted from studying shark skin, there are also important implications for sustainability and conservation. By understanding and appreciating the intricate design of shark skin, we can gain a greater appreciation for the importance of preserving these magnificent creatures and their habitats. As sharks are facing increasing threats from overfishing and habitat destruction, it is crucial to recognize the value of their unique adaptations and the role they play in maintaining the balance of marine ecosystems.Furthermore, the development of biomimetic technologies that are inspired by shark skin can contribute to efforts toprotect the environment and reduce our impact on the planet. By designing materials and products that are more efficient, durable, and environmentally friendly, we can create a more sustainable future for ourselves and future generations. The study of shark skin serves as a powerful reminder of the incredible diversity and ingenuity of nature, and the importance of preserving and learning from the natural world.ConclusionThe biomimetic principles of shark skin have opened up a world of possibilities for human innovation and sustainability. By studying and replicating the unique structure of shark scales, researchers have developed new technologies and materials that have the potential to revolutionize industries and improve the quality of human life. Furthermore, the study of shark skin serves as a poignant reminder of the interconnectedness of all living things and the importance of protecting and conserving the natural world. As we continue to explore and learn from the wonders of nature, we can unlock new solutions to the challenges we face and create a more harmonious relationship with the planet.篇2Title: The Biomimetic Principle of Shark Skin and its Impact on HumanityIntroductionIn recent years, biomimicry, the practice of imitating natural biological processes in technology and design, has gained popularity as a sustainable and innovative solution to various challenges faced by humanity. One of the most fascinating examples of biomimicry is the replication of shark skin in various products and applications. The unique properties of shark skin have inspired scientists and engineers to develop materials and technologies that offer numerous benefits to human society. This essay will explore the biomimetic principle of shark skin and its impact on humanity.The Biomimetic Principle of Shark SkinShark skin is covered with millions of tiny, tooth-like scales called dermal denticles. These scales have a riblet structure that reduces drag and turbulence in water, allowing sharks to swim faster and more efficiently. This unique surface texture has inspired the development of biomimetic materials that can be used in a wide range of applications, from swimwear and sports equipment to airplanes and ships.Impact on HumanityThe biomimetic principle of shark skin has had a significant impact on humanity in various fields:1. Sports and Recreation: The biomimetic design of shark skin has been incorporated into swimsuits, wetsuits, and sports equipment to enhance performance. Athletes wearing shark skin-inspired gear have reported improved speed, agility, and endurance, leading to better results in competitions.2. Transportation: The riblet structure of shark skin has been used to design more aerodynamic vehicles, such as airplanes, trains, and cars. By reducing drag and turbulence, these vehicles can achieve higher speeds and greater fuel efficiency, contributing to a more sustainable transportation system.3. Medical Technology: The anti-bacterial properties of shark skin have inspired the development of biomimetic materials for medical devices, such as implants and wound dressings. These materials can prevent infections and promote faster healing, improving the effectiveness of medical treatments.4. Environmental Conservation: The biomimetic design of shark skin has raised awareness about the importance of preserving marine biodiversity. By studying and mimicking thenatural adaptations of sharks, scientists and engineers can develop sustainable solutions to protect and conserve ocean ecosystems.ConclusionThe biomimetic principle of shark skin has revolutionized various industries and has the potential to transform human society in the future. By harnessing the unique properties of shark skin, scientists and engineers can develop innovative materials and technologies that offer sustainable solutions to complex challenges. The impact of biomimicry extends beyond practical applications and serves as a reminder of the wonders of nature and the importance of preserving biodiversity for future generations.篇3The Bio-Inspired Principles of Shark Skin and Their Impact on HumansIntroductionSharks have roamed the oceans for over 400 million years, making them one of the Earth's oldest and most successful species. One of the key factors contributing to their longevity and efficiency as predators is their unique skin structure. Sharkskin is covered in tiny tooth-like scales called dermal denticles, which have inspired scientists to develop innovative technologies with applications in various fields. This article will explore the bio-inspired principles of shark skin and their potential impact on humans.Bio-Inspired DesignThe surface of shark skin is covered in thousands of tiny dermal denticles, which are shaped like miniature teeth. These denticles have a unique structure with riblets that run parallel to the shark's body, reducing drag and turbulence as water flows over the skin. This design helps sharks move through the water with minimal resistance, making them swift and efficient predators.Scientists have replicated the structure of shark skin to develop biomimetic materials that have a wide range of applications. For example, the riblet design has been incorporated into the design of swimsuits and wetsuits, reducing drag and improving the performance of competitive swimmers. In addition, shark-inspired coatings have been developed for ships and submarines to reduce fuel consumption and increase speed by up to 10%. These innovations have the potential torevolutionize industries such as sports, transportation, and defense.Medical ApplicationsThe unique properties of shark skin have also inspired medical researchers to develop innovative solutions for healthcare. The antibacterial properties of shark skin have been studied and replicated to create antibacterial coatings for medical devices and implants, reducing the risk of infections in patients. In addition, the riblet structure of shark skin has been used to design bandages and wound dressings that promote faster healing by reducing friction and preventing bacterial growth.Furthermore, researchers are exploring the potential of shark skin-derived materials in regenerative medicine. The collagen fibers in shark skin have been found to have high tensile strength and durability, making them ideal for tissue engineering and wound healing applications. By harnessing the regenerative properties of shark skin, scientists aim to develop advanced therapies for tissue repair and regeneration.Environmental ImpactIn addition to their applications in technology and medicine, the bio-inspired principles of shark skin have the potential to address environmental challenges such as pollution and climate change. The development of shark-inspired materials for water filtration and desalination could provide sustainable solutions for clean water access in developing countries. Furthermore, the use of shark-inspired coatings in renewable energy technologies such as wind turbines and solar panels could increase efficiency and reduce environmental impact.ConclusionThe bio-inspired principles of shark skin have the potential to revolutionize various industries and address pressing global challenges. By understanding and replicating the unique structure and properties of shark skin, scientists are developing innovative technologies with applications in sports, healthcare, and environmental sustainability. As we continue to explore the capabilities of shark-inspired materials, we may unlock new opportunities for improving human health, protecting the environment, and advancing technology.。


聚酰亚胺薄膜的红外透过率英文回答:Polyimide (PI) films are known for their excellent thermal stability, mechanical strength, and electrical insulation properties. However, their infrared (IR) optical properties are also of great importance in various applications, such as infrared sensors, optical windows,and thermal management devices. The IR transmittance of PI films is a key factor that determines their performance in these applications.The IR transmittance of PI films depends on several factors, including the wavelength of the incident radiation, the thickness of the film, and the chemical composition and molecular structure of the polymer. In general, PI films exhibit good IR transmittance in the near-infrared (NIR)and mid-infrared (MIR) regions. However, theirtransmittance decreases significantly in the far-infrared (FIR) region due to the absorption of radiation by thepolymer chains.The IR transmittance of PI films can be tailored by modifying the chemical composition and molecular structure of the polymer. For example, the incorporation of fluorine atoms into the polymer chain can enhance the IR transmittance in the FIR region. This is because fluorine atoms have a strong electronegativity, which reduces the absorption of radiation by the polymer chains.In addition to chemical modification, the IR transmittance of PI films can also be improved by controlling the film thickness. Thinner films typically exhibit higher IR transmittance than thicker films. This is because the absorption of radiation is proportional to the thickness of the film.The IR transmittance of PI films is a critical property that determines their performance in various applications. By understanding the factors that affect the IR transmittance of PI films, it is possible to design and fabricate films with tailored optical properties forspecific applications.中文回答:聚酰亚胺(PI)薄膜以其优异的热稳定性、机械强度和电绝缘性能而闻名。

张文莉,罗银,顾瑶佳,等. 柚子皮不溶性膳食纤维的提取工艺优化及特性分析[J]. 食品工业科技,2024,45(8):208−215. doi:10.13386/j.issn1002-0306.2023050336ZHANG Wenli, LUO Yin, GU Yaojia, et al. Optimized Extraction Conditions and Characteristics Analysis of Insoluble Dietary Fiber from Pomelo Peel[J]. Science and Technology of Food Industry, 2024, 45(8): 208−215. (in Chinese with English abstract). doi:10.13386/j.issn1002-0306.2023050336· 工艺技术 ·柚子皮不溶性膳食纤维的提取工艺优化及特性分析张文莉,罗 银,顾瑶佳,王 颖,刘星雨,蔡文博,刘恩岐*(徐州工程学院食品与生物工程学院,江苏徐州 221018)摘 要:为获得复合酶法制备柚子皮不溶性膳食纤维的制备工艺及其吸附特性,实验以柚子皮为原料,采用正交试验优化提取柚子皮不溶性膳食纤维(IDF ),并对其特性进行研究。
结果表明,料液比1:40 g/mL 、淀粉酶的添加量0.6%、淀粉酶的酶解时间90 min 、木瓜蛋白酶的添加量0.2%、木瓜蛋白酶的酶解时间30 min 为最佳提取条件,该条件下柚子皮IDF 得率为55.07%。
柚子皮IDF 的膨胀力、持水力、持油力和阳离子交换能力分别为2.84±0.09 mL/g 、12.54±0.11 g/g 、1.54±0.02 g/g 和0.36±0.04 mmol/g 。
此外,体外吸附研究表明,柚子皮IDF 对葡萄糖、胆固醇、胆酸钠的吸附能力分别为0.13±0.003 mmol/g 、12.27±0.020 mg/g 和53.25±0.100 mg/g 。
Pharmacology Biochemistry and Behavior, Vol. 64, No. 2, pp. 449–453, 1999© 1999 Elsevier Science Inc.Printed in the USA. All rights reserved0091-3057/99/$–see front matterPII S0091-3057(99)00060-X449Stimulus Properties of PMMA: Effect of Optical Isomers and Conformational RestrictionRICHARD YOUNG,MALGORZATA DUKAT,LUCA MALMUSI AND RICHARD A.GLENNONDepartment of Medicinal Chemistry, School of Pharmacy, Virginia Commonwealth University,Richmond, VA 23298-0540YOUNG,R.,M.DUKAT,L.MALMUSI AND R.A.GLENNON. Stimulus properties of PMMA: Effect of optical iso-mers and conformational restriction. PH ARMACOL BIOCH EM BEH AV 64 (2) 449–453, 1999.— para -Methoxymetham-phetamine (PMMA), a structural hybrid of two central stimulants, lacks stimulant properties but behaves in a manner similar to that of MDMA [ N -methyl-1-(3,4-methylenedioxyphenyl)-2-aminopropane]. PMMA has been established as a training drug in drug discrimination studies, and in the present investigation we sought to determine which optical isomer of PMMA is primarily responsible for its stimulus effects. Because PMMA is a conformationally flexible molecule, it was also of interest to determine what conformation is most important for its actions., Accordingly, we prepared and examined S ( ϩ )PMMA, R ( Ϫ )PMMA, and conformationally restricted forms of PMMA: PMMA-AT, TIQ-1, and TIQ-2. S ( ϩ )PMMA (ED 50 ϭ 0.32mg/kg) was found to be at least as potent as PMMA (ED 50 ϭ 0.41 mg/kg), whereas R ( Ϫ )PMMA failed to result in complete stimulus generalization. An aminotetralin-like conformation, as found in PMMA-AT (ED 50 ϭ 0.29 mg/kg), seems to better account for the actions of PMMA than a tetrahydroisoquinoline-like conformation because TIQ-1 and TIQ-2 failed to result in stimulus generalization. The results of the present study further support the concept that PMMA and MDMA share con-siderable similarity with respect to their stimulus properties in animals except that PMMA lacks the amphetaminergic stimu-lant component of action associated with MDMA.© 1999 Elsevier Science Inc.PMMA para - Methoxymethamphetamine MDMA MethamphetamineStimulantsAminotetralinsDrug discrimination TetrahydroisoquinolinesBOTH methamphetamine and para -methoxyamphetamine(PMA) are phenylalkylamine central stimulants; para -meth-oxymethamphetamine (PMMA) is a hybrid structure of methamphetamine and PMA (7) (see Fig. 1 for chemical structures). Surprisingly, however, PMMA lacks appreciable central stimulant activity. For example, PMMA is not a loco-motor stimulant in mice, and PMMA produces Ͻ20% (ϩ)am-phetamine-appropriate responding in rats trained to discrimi-nate (ϩ)amphetamine from saline vehicle (6). PMMA also bears a close structural resemblance to the controlled sub-stance analog MDMA (“Ecstasy”; “XTC”) or N - methyl-1-(3,4-methylenedioxyphenyl)-2-aminopropane. An MDMA stimulus has been demonstrated to generalize to PMMA, and PMMA was found to be three times more potent than MDMA (5). PMMA itself has been used as a training drug in drug discrimination studies (7). The PMMA stimulus failed to generalize to (ϩ)amphetamine; however, the PMMA stimu-lus did generalize to MDMA and, again, PMMA was three times more potent than MDMA (7). Because MDMA pos-sesses some amphetamine-like stimulant character, PMMA has been proposed to be a “cleaner” MDMA-like agent than MDMA itself (7); that is PMMA lacks the amphetaminergiccentral stimulant character of MDMA. We have been investi-gating the structure–activity relationships for PMMA-like ac-tivity, and in the present study we address two specific ques-tions: (a) are the stimulus effects of PMMA stereoselective or stereospecific, and (b) what is the preferred conformation for PMMA-like stimulus action. Accordingly, we prepared the two optical isomers of PMMA, S (ϩ)PMMA and R (Ϫ)PMMA, and three conformationally restricted analogs of PMMA (Fig. 1).Once prepared, these compounds were examined in animals trained to discriminate PMMA from vehicle.METHODThe animals employed in this investigation were previ-ously trained to discriminate PMMA, and are those used in an earlier study; their training has been reported (7). The ani-mals were housed individually and during the entire course of the study, the animals’ body weights were maintained at 80%of their free-feeding body weights. In their home cages, the animals were allowed drinking water ad lib. Briefly, the six male Sprague–Dawley rats used in the study were originally trained (15-min training session) to discriminate the intraperi-Requests for reprints should be addressed to Dr. R. A. Glennon, Virginia Commonwealth University, Medical College of Virginia, School of Pharmacy, Department of Medical Chemistry, Box 540 MCV Station, Richmond, VA 23928-0540.450YOUNG ET AL.toneal injections (15-min presession injection interval) of 1.25mg/kg of PMMA from vehicle (sterile 0.9% saline) under a variable interval 15-s schedule of reward (i.e., sweetened milk) using standard two-lever operant chambers (7). For half of the animals, the left lever was designated the drug-appro-priate lever, whereas the situation was reversed for the re-maining animals. Daily training sessions were conducted with PMMA, and learning was assessed during an initial 2.5-min nonreinforced (extinction) session followed by a 12.5-min training session. Data collected during extinction sessions in-cluded response rates (i.e., resp/min) and number of re-sponses on the drug-appropriate lever (expressed as a percent of total responses).Tests of stimulus generalization were conducted to deter-mine if the PMMA stimulus would generalize to the following agents: S (ϩ)PMMA, R(Ϫ)PMMA, PMMA-AT, TIQ-1, and TIQ-2. During this phase of the study, maintenance of the PMMA–saline discrimination was ensured by continuation of the training sessions on a daily basis (except on a generaliza-tion test day; see below). On 1 of the 2 days before a generali-zation test, half of the animals would receive PMMA and half would receive saline; after a 2.5-min extinction session, train-ing was continued for 12.5 min. Animals not meeting the orig-inal criteria (i.e., Ͼ80% of total responses on the drug-appro-priate lever after administration of training drug, and Ͻ20%of total responses on the same lever after administration of saline) during the extinction session were excluded from the immediately subsequent generalization test session. Duringthe investigations of stimulus generalization, test sessions were interposed among the training sessions. The animals were allowed 2.5 min to respond under nonreinforcement conditions; the animals were then removed from the operant chambers and returned to their home cages. An odd number of training sessions (usually five) separated any two generali-zation test session. Doses of the test drugs were administered in a random order, using a 15-min presession injection inter-val, to groups of four to six rats. If a particular dose of a chal-lenge drug resulted in disruption of behavior (i.e., no respond-ing), only lower doses would be evaluated in subsequent weeks. Stimulus generalization was considered to have oc-curred when the animals, after a given dose of challenge drug,made у80% of their responses on the PMMA-appropriate le-ver. Animals making fewer than five total responses during the 2.5-min extinction session were considered as being dis-rupted, and were not used in calculating mean percent PMMA-appropriate responding and mean responses per minute. Where stimulus generalization occurred, ED 50 values were calculated by the method of Finney (2). The ED 50doses are doses at which the animals would be expected to make 50% of their responses on the drug- appropriate lever.DrugsPMMA H Cl was previously prepared in our laboratories (6). The individual optical isomers of PMMA were prepared from the isomers of para-methoxyamphetamine (PMA) (9).FIG.1.Chemical structures showing the structural relationships between methamp-phetamine (Methamph), para -methoxyamphetamine (PMA), para -methoxymeth-amphetamine (PMMA), N -methyl-1-(3,4-methylene-dioxyphenyl)-2-aminopropane (MDMA), the two optical isomers of PMMA—S (ϩ)PMMA and R (Ϫ)PMMA—the aminotetralin analog of PMMA (PMMA-AT), and the tetrahydroisoquinoline analogs of PMMA (TIQ-1 and TIQ-2).STIMULUS PROPERTIES OF PMMA 451S ( ϩ )PMA H Cl was allowed to react with methyl chlorofor-mate in the presence of triethylamine to afford the intermedi-ate carbamate, which was subsequently reduced with lithium aluminum hydride in dry tetrahydrofuran. The crude product was isolated, converted to its HCl salt, and recrystallized from an absolute ethanol/anhydrous ether mixture to afford the de-sired product in 31% overall yield as a white cryatalline prod-uct; m.p. 203–205Њ C, [␣] 25 ϩ 13.0 Њ (H 2 O). The R ( Ϫ )isomer of PMMA H Cl was prepared in the same manner from R (Ϫ)PMA except that ethyl chloroformate was used as the acylating agent; the product was obtained as a white crystal-line solid in 55% yield, m.p. 205–207 Њ C, [ ␣ ] 25 Ϫ 13.1 Њ (H 2O).Both products were homogeneous as evidenced by thin-layer chromatography; proton magnetic resonance spectral data were consistent with the assigned structures, and both isomers analyzed correctly for C, H, and N to within 0.4% of theory (Atlantic Microlab, Norcross, GA).7-Methoxy-1,2,3,4-tetrahydroisoquinoline HCl (TIQ-1) was prepared by condensation of 3-methoxy-benzaldehyde with aminacetaldehyde dimethylacetal followed by catalytic reduc-tion under acidic conditions in a manner similar to that re-ported for the synthesis of related tetrahydroisoquinolines (8). The crude product was converted to its HCl salt and re-crystallized from absolute ethanol to give the desired productFIG.2.Upper panel: Results of stimulus generalization studies with PMMA, S (ϩ)PMMA,and R (Ϫ)PMMA in PMMA-trained animals. Lower panel: Results of stimulus generalization studies with conformationally restricted analogs of PMMA: PMMA-AT, TIQ-1, and TIQ-2; the dose–response curve for PMMA is reproduced in the lower panel for purpose of comparison.452YOUNG ET AL. as white crystals; m.p. 230–231ЊC [lit (1) m.p. 233–234ЊC].TIQ-1 was methylated using formaldehyde and sodium cy-anoborohydride to afford TIQ-2 as an HCl salt in 81% yieldafter recrystallization from an absolute ethanol/anhydrousether mixture; m.p. 201–202ЊC [lit (3) m.p. 201–202ЊC].(Ϯ)N-Methyl-2-amino-6-methoxytetralin H Cl (PMMA-AT)was prepared following a literature procedure (4) to give thedesired product as a white solid; m.p. 169–170ЊC [lit (4) m.p.172–174ЊC].Solutions of all drugs were made fresh daily in 0.9% sterilesaline, and all agents were administered via intraperitonealinjection in a 1.0 ml/kg injection volume. All doses refer tothe weight of the salt.RESULTSA dose–response curve for PMMA is shown in Fig. 2 (ra-cemic PMMA ED50ϭ 0.41 mg/kg; 95% CL ϭ 0.18–0.93 mg/kg). Saline produced 4% PMMA-appropriate responding(data not shown). Mean response rate after administration ofthe training dose of PMMA was 12.5 (SEM Ϯ1.8) responsesper minute, and after administration of saline was 12.3 (SEMϮ1.0) responses per minute. Dose–effect response rate datafor each compound are shown in Table 1 and are calculated aspercent of PMMA (based on the training dose of PMMA) re-sponses per minute. Administration of doses of S(ϩ)PMMAresulted in stimulus generalization (ED50) ϭ 0.32 mg/kg;95% CL ϭ 0.15–0.68 mg/kg) (Fig. 2). Administration ofR(Ϫ)PMMA resulted in the animals making a maximum of62% of their responses on the PMMA-appropriate lever at 1mg/kg; administration of 1.25, 1.50, and 1.75 mg/kg resulted inthe animals making (with number of animals responding/number of animals administered drug) 54% (4 of 5), 51% (3of 5), and 43% (3 of 5) of their responses on the drug-appro-priate lever. Administration of higher doses of R(Ϫ)PMMAresulted in disruption of the animals’ behavior. The animals’response rates after administration of the PMMA isomerswere similar to the response rate obtained after administra-tion of the training dose of PMMA except for a 26% declinein response rates after administration of 1.75 mg/kg ofR(Ϫ)PMMA (Table 1).Administration of PMMA-AT resulted in stimulus gener-alization (ED50ϭ 0.29 mg/kg; 95% CL ϭ 0.14–0.64 mg/kg)(Fig. 2); at the highest dose of PMMA-AT (1.25 mg/kg) theanimals’ response rates were reduced to 53% of the PMMAresponse rate (Table 1). The PMMA stimulus failed to gener-alize to either TIQ analog (Fig. 2). TIQ-1 produced a maxi-mum of 57% PMMA-appropriate responding at 8.0 mg/kg; atthis dose, only three of five animals made Ͼ5 responses dur-ing the entire 2.5-min extinction session, and the responserate of the responding animals was reduced by 78% (Table 1).TIQ-2 resulted in a maximum of 26% PMMA- appropriateresponding at 2.0 mg/kg; 4.0 mg/kg resulted in 9% PMMA-appropriate responding (42% reduction in response rates),and higher doses resulted in disruption of behavior.DISCUSSIONThe present results suggest that the PMMA stimulus maybe stereospecific in that only one of the two optical isomers ofPMMA resulted in complete PMMA-stimulus generalization.S(ϩ)PMMA (ED50ϭ 0.32 mg/kg) was at least as potent as (Ϯ)PMMA (ED50ϭ 0.41 mg/kg), whereas R(Ϫ)PMMA re-sulted only in partial generalization. These results are consis-tent with the observation that S(ϩ)MDMA (ED50ϭ 0.48 mg/ kg) is more potent than (Ϯ)MDMA (ED50ϭ 1.32 mg/kg) in PMMA-trained animals, and that R(Ϫ)MDMA results only in partial (68%) generalization (7). Thus, PMMA not only produces stimulus effects similar to those of MDMA (7), like MDMA the stimulus effects of PMMA may be stereospecific in PMMA-trained animals and the S(ϩ)isomer is the active isomer in both cases.Multiple conformations of phenylalkylamines are possible. Two possibilities include an aminotetralin-like conformation and a tetrahydroisoquinoline-like conformation (8). We have previously demonstrated that the actions of MDMA are asso-ciated more with an aminotetralin-like conformation than with a tetrahydroisoquinoline-like conformation (8). Others (10) have also demonstrated that aminotetralin and related analogs of MDMA retain MDMA-like actions. Hence, we ex-pected that PMMA-like activity would also be more associ-ated with an aminotetralin than tetrahydroisoquinoline con-formation. Indeed, the aminotetralin analog of PMMA, PMMA-AT (ED50ϭ 0.29 mg/kg), is at least as potent as PMMA (ED50ϭ 0.41 mg/kg) itself. In contrast, neither tet-TABLE1MEAN RESPONSE RATE DATA FOR RACEMIC PMMA,ITSOPTICAL ISOMERS,AND THREE CONFORMATONALLY RESTRICTED PMMA ANALOGS(PMMA-AT,TIQ-1,AND TIQ-2)CompoundDose(mg/kg)n/N*Response Rate†(as a % of PMMA resp/min) (ϩ)PMMA 1.256/6100%0.756/686%0.506/678%0.256/687%0.106/6101%Saline 1 ml/kg6/698%S(ϩ)PMMA0.655/5102%0.605/5106%0.255/5121%0.105/5104%R(Ϫ)PMMA 1.753/574%1.503/598%1.254/595%1.005/595%0.504/591%0.255/5101%PMMA-AT 1.254/553%0.755/551%0.505/577%0.255/576%0.105/585%TIQ-18.003/522%6.004/530%4.004/570%2.504/558%1.254/575%0.754/596%TIQ-2 4.005/558%2.004/589%1.254/578%0.754/470%Response rates for each compound were calculated as percent of the PMMA (1.25 mg/kg) response rate.*n/N = Number of animals responding/number of animals admin-istered drug.†Data collected during a 2.5–min extinction session.STIMULUS PROPERTIES OF PMMA453rahydroisoquinoline analog resulted in stimulus generaliza-tion. TIQ-1 produced a maximum of 57% PMMA-appropri-ate responding, whereas TIQ-2 produced a maximum of 26% PMMA-appropriate responding. Consistent with what was seen with MDMA, the aminotetralin conformation of PMMA appears to account for its stimulus actions .In conclusion, the stimulus effects of PMMA are primarily associated with the S(ϩ)isomer of PMMA, and an aminote-tralin rather than tetrahydroisoquinoline conformation better explains its actions. In these respects, PMMA behaves like MDMA.ACKNOWLEDGEMENTSThis work was supported in part by PHS Grant DA 01642.REFERENCES1.Bobbitt, J. M.; McNew, O.; Khanna, K. L.; Eberman, R.: Synthesisof isoquinolines III. A new synthesis of 1,2,3,4-tetrahydroisoquin-olines. J. Org. Chem. 30:2247–2250; 1965.2.Finney, D.: Probit analysis. London: Cambridge University Press;1952.3.Fritsch, P.: Ueber subsituirte Isochinoline und deren Tetrahydro-derivate; Synthese des Hydrastinins. Justus Liebig’s Ann. Chem.286:1–26; 1985.4.Kanao, M.; Hashizume, T.; Ichikama, Y.; Irie, K.; Isoda, S.: Spas-molytic agents. 2. 1,2,3,4- tetrahydro-2-naphthylamine derivatives.J. Med. Chem. 25:1358–1363; 1982.5.Glennon, R. A.; H iggs, R.: Investigation of MDMA-relatedagents in rats trained to discriminate MDMA from saline. Phar-macol. Biochem. Behav. 43:759–763; 1992.6.Glennon, R. A.; Ismaiel, A. M.; Martin, B.; Poff, D.; Sutton,M.: A preliminary investigation of PMMA, the 4-methoxy ana-log of methamphetamine. Pharmacol. Biochem. Behav. 31:9–13; 1988.7.Glennon, R. A.; Young, R.; Dukat, M.; Cheng, Y.: Initial charac-terization of PMMA as a discriminative stimulus. Pharmacol. Bio-chem. Behav. 57:151–158; 1997.8.Malmusi, L.; Dukat, M.; Young, R.; Teitler, M.; Darmani, N. A.;Ahmad, B.; Smith, C.; Glennon, R. A.: 1,2,3,4-Tetrahydroisoquin-oline and related analogs of the phenylalkylamine designer drug MDMA. Med. Chem. Res. 6:412–426; 1996.9.Nichols, D. E.; Barfknecht, C. F.; Rusterholz, D. B.; Benington,F.; Morin, R. D.: Asymmetric synthesis of enantiomers of psy-chotomimetic amphetamines. J. Med. Chem. 16:480–483; 1973. 10.Nichols, D. E.; Oberlender, R.: Structure activity relationships ofMDMA-like substances. In: Ashgar, K.; De Souza, E., eds. Pharma-cology and toxicology of amphetamine and related designer drugs.Washington, DC: US Government Printing Office; 1989:1–29.。