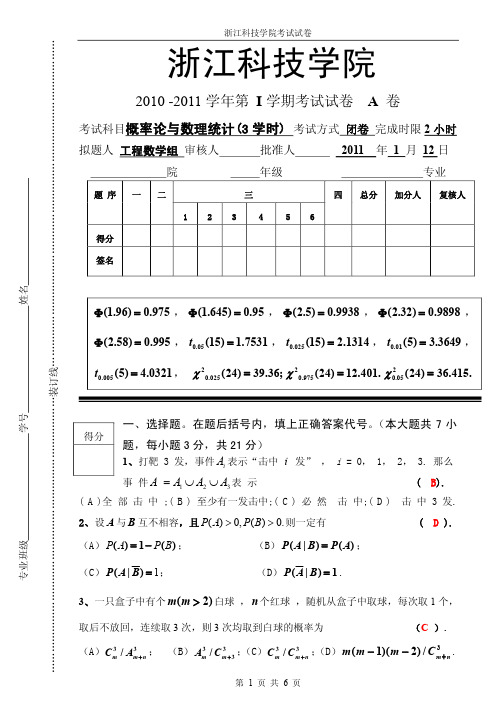
浙江科技学院11-12-1微积分试卷A卷

2007-2008学年第一学期考试试卷A 卷一、填空题(每题4分，共20分)1、515155⎛⎫ ⎪--⎝⎭； 2、18； 3、5； 4、1±，± 5、2A 二、选择题（每小题4分，共20分）1、C ；2、D ；3、B ；4、A ；5、B 三、解答题（本题共48分）1、（8分）解： D 1,2,3,4i c c i +=111111111111x x x x x x x ---+-----……………2分1c x ÷1111111111111111x x x x ---+----- …………………4分4,1,2,3i r r i -=0000000001000x x x x (5)分1423,r r r r ↔↔1000000000000x x x x………7分 ==4x …………………8分2、由**28(2)8A BA BA E E A BA E=-→-=……….2分，因2,A =-故A 可逆，11*2,A A A A --==-………….3分，从而*1*11118(2)8(2)8(2)8[2()]4(),B E A A A AA A A E A E A E -----=-=-=-=+=+其中113122222014()012,0021002246048002A E A E B -⎛⎫- ⎪-⎛⎫⎪⎪+=-→+=- ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭-⎛⎫ ⎪=- ⎪ ⎪⎝⎭………….7分……………… 8分. 3、（6分）证及解：由245A A E O -+= →(3)(7)26A E A E E O +-+=，…………………2分 故1(5)[(7)]26A E A E E +--=， …………………4分 故3A E +可逆，…………………5分 且11(3)(7).26A E A E -+=-- ……………………….6分 4、（10分）解：1123010411216410122132871000001161200000A ---⎛⎫⎛⎫⎪⎪--⎪ ⎪=−−−→ ⎪ ⎪-⎪⎪----⎝⎭⎝⎭行变……………5分 与原方程组同解的方程组为1343423441(,221x x x x x x x x =--⎧⎨=--+⎩为自由未知量)令*3451201,1(1,1,0,0)T x x x x x η===→=-=→=- …………7分与导出组同解的方程组为134342344(,22x x x x x x x x =-⎧⎨=--⎩为自由未知量)，…6分令341211,0,4,2(4,2,0,0)T x x x x ξ==→==-→=-，又令341220,1,1,2(1,2,0,1)T x x x x ξ==→=-=-→=-， …….…9分则2*12121141122,(,)010001i i i k k k k k R ηηξ=-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪=+=++∈ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑ ……10分5、（10分）解：123123123101(,,)(,,)(,,)012102A αααεεεεεε⎛⎫⎪== ⎪ ⎪⎝⎭ ， ……1分123123123111(,,)(,,)(,,)011001B βββεεεεεε⎛⎫⎪== ⎪ ⎪⎝⎭， ……………2分则1123123(,,)(,,)A B βββααα-=， …………………4分1(,)(,)A B E A B -−−−→行变，求出1221231110P A B -⎛⎫⎪== ⎪ ⎪--⎝⎭，……………8分6、（14分）解：320500200,()031(5)(2)(4)002013A f A A E λλλλλλλ-⎛⎫⎪==-=-=--- ⎪ ⎪-⎝⎭， A →的特征值为1232,4, 5.λλλ=== ……………4分当12λ=时，13001002011011011000A A E ⎛⎫⎛⎫ ⎪ ⎪=-=→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，11111100p ξ⎛⎫⎛⎫⎪⎪=-→=- ⎪⎪ ⎪⎪⎝⎭⎭ ， ………………………6分 当24λ=时，21001004011011,011000A A E ⎛⎫⎛⎫⎪ ⎪=-=-→- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭22001111p ξ⎛⎫⎛⎫⎪⎪=→= ⎪⎪ ⎪⎪⎝⎭⎭，……8分 当35λ=时，30000105021001,012000A A E ⎛⎫⎛⎫⎪ ⎪=-=-→ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭3310,0p ξ⎛⎫⎪== ⎪ ⎪⎝⎭，………………………10分令123001(,,)00P p p p ⎛⎫ ⎪ ⎪⎪==⎪⎪⎪⎪⎭，则P 为正交矩阵，………………12分 从而x Py =为正交变换，故222123123(,,)245f x x x y y y =++………………14分 四、（6分）证法一：易证两向量组122331,,αααααα+++与 123,,ααα等价，则其秩相等，从而命题得证． 证法二:充分性见P89例6,下证必要性.记112223331,,.βααβααβαα=+=+=+令1122330,k k k ααα++=即123123123123()()()0,222k k k βββββββββ-++--++++=亦123112321233()()()0,k k k k k k k k k βββ+-+-+++-+=因123,,βββ线性无关,则123123123000,0k k k k k k k k k k k k +-=⎧⎪-++=→===⎨⎪+-=⎩故123,,ααα线性无关.。

浙江理工大学2011—2012学年第2学期 《高等数学A2》期末试卷（A ）卷承诺人签名： 学号： 班级： （本试卷共四页）一、选择题（本题共6小题，每小题4分，满分24分） 1. 函数()()224,y x y x y x f ---=的极值为（ ）A .极大值为8B ．极小值为0C .极小值为8D .极大值为02.二元函数(,)f x y 在点00(,)P x y 处 ①连续；②两个偏导数连续；③可微；④两个偏导数都存在，那么下面关系正确的是（ ）A ．③①④ B. ③②① C. ③④① D. ②③①3. 曲线222x y z z x y -+=⎧⎨=+⎩在点（1，1，2）处的一个切线方向向量为（ ）. A. （-1，3，4） B.（3，-1，4） C. （-1，0，3） D. （3，0，-1） 4. 设⎰⎰σ=+Dy x d e I 22, 4:22≤+y x D , 则=I （ ）A.)1(24-πe B. )1(24-πe C. )1(4-πe D. 4e π 5. 设∑是球面2222x y z R ++=，则222dSx y z ∑++⎰⎰＝（ ） A. 24R π B. 4π C. 2R π D. π6. 若1(1)n n n a x ∞=-∑在1x =-处收敛，则此级数在2x =处（ ）． A. 条件收敛 B. 绝对收敛 C. 发散 D. 敛散性不能确定二、填空题（本题共5小题，每小题4分，满分20分）1. 曲面xy z =上点M 处的法线垂直于平面52=--z y x ，则M 的坐标是 ;2. 设22z xy u -=，则u 在)1,1,2(-处的方向导数的最大值为 ;3. 交换积分顺序，有()=⎰⎰--221,y y ydx y x f dy______________________ ;4. 设椭圆L：13422=+y x 的周长为l，则⎰=+Lds y x 2)23( ;5. 设()f x 是周期为2的周期函数，它在区间(1,1]-的定义为210()01x f x x x -<≤⎧=⎨<≤⎩，则()f x 的傅里叶级数在1x =收敛于 .三、解答题（本题共6小题，每小题6分，满分36分）1．求过点M （4,-3,1）且与两直线：326-==zy x 和⎩⎨⎧=+-=+-+022012z x z y x 都平行的平面方程．2. 设(,)sin x z f xy y y =+，其中f 具有二阶连续偏导数，求2,z zx x y∂∂∂∂∂．3. 将函数1()f x x=展开为3x -的幂级数，并求收敛域.4. 计算⎰⎰⎰Ωz y x xy d d d ，其中Ω是由柱面122=+y x 及平面0,0,1===y x z 所围成且在第一卦限内的区域.5. 求曲线积分22(2)(sin )Lxy dx x y dy --+⎰，其中L 是沿曲线1y =0，1）到点（2，1）的弧段.6. 计算曲面积分2y dzdx zdxdy ∑+⎰⎰，其中∑是球面2224(0)x y z z ++=≥的上侧.四、综合题（本题共2小题，每小题8分，满分16分）1. 验证2232(38)(812)y x y xy dx x x y ye dy ++++在整个 xoy 平面内是某一函数(,)u x y 的全微分,并求这样的一个(,)u x y .2. 求幂级数115n n n n x ∞-=∑的收敛域、和函数以及数项级数15n n n∞=∑的和.五、证明题（4分）设∑∞=12n n a 收敛，证明级数1nn a n ∞=∑绝对收敛.一、选择题（本题共6小题, 每小题4分，满分24分）1．A; 2．D ; 3．A; 4．C; 5．B ； 6.B 二、填空题（本题共5小题, 每小题4分，满分20分）1. (-1,2,-2);2. ;3.()()⎰⎰⎰⎰----+11111012,,x xdy y x f dxdy y x f dx ;4. 12l ;5.32三、解答题（本题共6小题，每小题6分，满分36分）1. 1(6,2,3)s =-,2121(2,1,4)201i j ks =-=----, ………2分取平面的法向量为12623(11,30,2)214i jkn s s =⨯=-=-----………2分所以平面方程为：11(4)30(3)(1)0x y z --++--=，即1130135x y z -+-=…2分2.121211()0z f y f yf f x y y∂''''=⋅+⋅+=+∂, ……………2分 2111122212222211[()][()]z x xf y f x f f f x f x y y y y y∂''''''''''=+⋅+⋅--+⋅+⋅-∂∂ 111222231.x f xyf f f y y''''''=+-- .………4分3.解：)3(31)(-+=x x f =)33(1131-+⋅x , ……………2分因为∑∞=+=-011)1(n n n xx ，)1,1(-∈x , 所以∑∞=-⋅-=-+⋅)33(31)1()33(1131n n n x x =∑∞=+--01)3()31()1(n n n n x , 其中1331<-<-x ，即60<<x . ……………3分 当0=x 时，级数为∑∞=031n 发散；当6=x 时，级数为∑∞=⋅-031)1(n n 发散,故x 1=∑∞=+--01)3()31()1(n n n n x ，)6,0(∈x . ………1分 4. 解：如图，选取柱面坐标系,此时⎪⎩⎪⎨⎧≤≤≤≤≤≤,10,2π0,10:r z θΩ所以π112000d d d d d cos sin d xy x y z r r r r z θθθΩ=⋅⋅⎰⎰⎰⎰⎰⎰ ………3分=⎰⎰r r d d 2sin 213102πθθ=814)42cos (142π0=⋅-r θ. ………3分 5. 解：令22P x y =-，2(sin )Q x y =-+,则2,Py∂=-∂1,Q x ∂=-∂ ………2分 选择:1BA y =由B （2，1）到A （0，1）,则由格林公式得原式2(2L Bx y+=-⎰⎰………2分22()(2)(sin )AB DQ Pdxdy x y dx x y dy x y∂∂=--+--+∂∂⎰⎰⎰22(2)Ddxdy x dx =-+-⎰⎰⎰2208(2)423Ddxdy x dx π=-+-=-+-⎰⎰⎰. ………2分6. 解：补上221:0 (4)z x y ∑=+≤下侧。

⎩ 1 21 2一、单项选择题（每题 3 分，共计6 ⨯ 3 = 18 分）1. 设二阶常系数线性齐次微分方程 y "- 2 y '+ y = 0 ，则方程的通解为（）．A. (C + C )exB. (C + C x )ex12C. x (C e x + C e - x)⎧ y 2 + z 2 = 4 2. 空间曲线Γ ： ⎨x = 0A ． x 2 + y 2 + z 2= 4 C ． x 2 - y 2 + z 2= 412D ． C e x+ C e - x绕 z 轴旋转而得到的旋转曲面方程是（ ）．B ． x 2 + y 2 - z 2= 4 D ． x 2+ y 2+ z 2= 23. 函数 z = f (x , y ) 的偏导数 f x '(x , y ), f y '(x , y ) 在点(x 0 , y 0 ) 处存在是函数在该点可微分的（）．A ．充分必要条件B ．充分条件C ．必要条件D ．既不充分也不必要4. 设 I 1 =⎰⎰(x + y )2d σ, I 2 = ⎰⎰(x + y )3d σ，其中积分区域 D 是由 x 轴， y 轴 DD与直线 x + y = 1所围成，则（）．A. I 1 > I 2B. I 1 < I 2C. I 1 = I 2D. 不能比较5. 设曲线积分⎰(axy 3 - y 2cos x ) d x + (1 + by sin x + 3x 2 y 2) d y 与路径无关，L则a ,b = （）．A ．1, -2B ． -2, 2C ． 2, 2D ． 2, -26. 若级数∑ a n n =1(x - 2)n在 x = -2 处收敛，则此级数在 x = 5 处（ ）．∞ 成绩：姓名：班级：学号：考试方式：闭卷学分：4课程编号：CK0M02B03 课程名称：高等数学A 试卷编号：A 卷 科技学院第二学期期末考试试题y a0 1 A ．发散 B ．条件收敛 C ．绝对收敛 D ．收敛性不确定二、填空题（每小题 3 分，共计6 ⨯ 3 = 18 分） 1．方程 y ' + y ' = x 2+ 1特解的形式是()．2→→2．已知向量 a = (4, m ,1) 与 b = (2,3,n ) 平行，则m =（），n =（ ）．y3. 设函数 z = e x ，则全微分dz =()．4.． 将二次积分 ⎰xdx ⎰ 2f (x , y )dy 的积分次序变换成先 x 后 y 的二次积分（）．5.设平面曲线 L 为上半圆周 y =，则⎰sin(x 2 + y 2 ) d s =（）．L∞n6．当| a |（）时，级数∑( ) n =1 收敛．三、计算题 1（每小题 6 分，共计 8×6＝48 分）1.求曲面 z = x 2 + 2y 2上点M (2,1,6) 处切平面方程及法线方程．2. 设2sin( x + 2 y - 3z ) = x + 2 y - 3z 确定隐函数 z = z (x , y ) ，求∂z + ∂z ．∂x ∂y3. 设函数 z=f (xy , y 2) ，且 f 具有连续偏导数，求偏导数 ∂z ∂x ∂z 与全微分dz ． ∂y4.计算二重积分⎰⎰(x + y ) d x d y ，其中 D 是由曲线 y = x 2 与曲线 y = 4x 2D（ x ≥ 0 ）以及 y = 1所围成的有界闭区域．5. 求由抛物面2z = x 2 + y 2与平面 z = 2 所围立体的体积．6.计算曲线积分 ⎰xy d x + (x + y ) d y ，其中 L 是由曲线 x = 与 y = x 2 所围L成的闭曲线的逆时针方向．4 - x 2， 2n =0n !n =0 ⎩ 1 21 21∞n17. 判别级数∑(-1) ln(n +100) 的敛散性，如果收敛，是绝对收敛还是条件收敛？8. 将函数 f (x ) =15 - x展开成 x - 2 的幂级数，并求收敛区间． 四、计算题 2（每小题 5 分，共计 5×2＝10 分）1. 求球面 x 2+ y 2+ z 2= 4 含在圆柱面 x 2+ y 2= 2x 内部的曲面面积．∞n x∞12n2. 已知幂级数∑ x n =0 五、综合题（6 分）= e ，求幂级数∑(2n )! x 的收敛域以及和函数．→→→设一力场 F = ( y 2 + 1) i + (x 2+ y ) j ，有一质点在此力场中沿曲线 y = ax 2 自 点O (0,0) 移动到点 A (1, a ) ，求a 的值使力场所作的功为最小．参考答案一、单项选择题（每题 3 分，共计6 ⨯ 3 = 18 分）1. 设二阶常系数线性齐次微分方程 y "- 2 y '+ y = 0 ，则方程的通解为（ B ）．A. (C + C )exB. (C + C x )ex12C. x (C e x + C e - x)⎧ y 2 + z 2 = 4 2. 空间曲线Γ ： ⎨x = 0A ． x 2+ y 2+ z 2= 412D ． C e x+ C e - x绕 z 轴旋转而得到的旋转曲面方程是（ A ）．B ． x 2 + y 2 - z 2= 40 1 212 00 y C ． x 2 - y 2 + z 2= 4D ． x 2 + y 2 + z 2= 23. 函数 z = f (x , y ) 的偏导数 f x '(x , y ), f y '(x , y ) 在点(x 0 , y 0 ) 处存在是函数在该点可微分的（ C）．A ．充分必要条件B ．充分条件C ．必要条件D ．既不充分也不必要4. 设 I 1 =⎰⎰(x + y )2d σ, I 2 = ⎰⎰(x + y )3d σ，其中积分区域 D 是由 x 轴， y 轴 DD与直线 x + y = 1所围成，则（ A ）．A. I 1 > I 2B. I 1 < I 2C. I 1 = I 2D. 不能比较5. 设曲线积分⎰(axy 3 - y 2cos x ) d x + (1 + by sin x + 3x 2 y 2) d y 与路径无关，L则a ,b = （ D ）．A ．1, -2B ． -2, 2C ． 2, 2D ． 2, -26. 若级数∑ a n n =1(x - 2)n在 x = -2 处收敛，则此级数在 x = 5 处（ C ）．A ．发散B ．条件收敛C ．绝对发散D ．收敛性不确定二、填空题（每小题 3 分，共计6 ⨯ 3 = 18 分）1．方程 y ' + y ' = x 2+ 1特解的形式是( 2y * = x (a x 2 + a x + a ) )．→ →1 2．已知向量 a = (4, m ,1) 与 b = (2,3,n ) 平行，则m = （ 6 ）， n = （）．2y3.设函数 z = e x，则全微分dz =(e x(- y x 2 dx + 1 dy ))．x4.． 将二次积分⎰xdx ⎰ 2f (x , y )dy 的积分次序变换成先 x 后 y 的二次积分（ ⎰dy⎰2 yf (x , y )dx ）．∞ 2a5.设平面曲线 L 为上半圆周 y∞1 n，则⎰sin(x 2 + y 2 ) d s =（ 4πsin 4 ）．L6．当| a |（ > 1）时，级数∑( ) n =1 收敛．三、计算题 1（每小题 6 分，共计 8×6＝48 分）1.求曲面 z = x 2 + 2y 2上点M (2,1,6) 处切平面方程及法线方程．解：因为 z = f (x , y ) = x 2+ 2 y2切平面法向量n = (2x , 4 y , -1) |M = (4, 4, -1) 2 分所以切平面方程为4(x - 2) + 4( y -1) - (z - 6) = 0 ，即4x + 4 y - z = 64 分法线方程为x - 2= y - 1 =z - 66 分4 4 -12.设2sin( x + 2 y - 3z ) = x + 2 y - 3z 确定隐函数 z = z (x , y ) ，求∂z + ∂z． ∂x ∂y解：设函数 F (x , y , z ) = 2sin(x + 2 y - 3z ) - x - 2 y + 3z ，则F x = 2cos(x + 2 y - 3z ) - 1 ， F z = -6cos(x + 2 y - 3z ) + 3F y = 4cos(x + 2 y - 3z ) - 2 ， 3 分∂z 2cos(x + 2 y - 3z ) - 1 1 所以∂x = 3(2cos(x + 2 y - 3z ) - 1) = 3， 4 分∂z 2(2cos(x + 2 y - 3z ) - 1) 2 ∂y = 3(2cos(x + 2 y - 3z ) - 1) = 3 ， 5 分∂z ∂z 于是 ∂x + ∂y= 1 ．6 分y 1 1 2 1 2 2 y 13.设函数 z =f (xy , y 2) ，且 f 具有连续偏导数，求偏导数 ∂z ∂x ∂z与全微分dz ．∂y解 ： ∂z= yf '，∂z= xf ' + 2 yf '，4 分∂x 1∂y1 2dz = yf 'dx + (xf ' + 2yf ')dy6 分4.计算二重积分⎰⎰(x + y ) d x d y ，其中 D 是由直线 y = x 2 与直线 y = 4x 2D（ x ≥ 0 ）以及 y = 1所围成的有界闭区域． 解：使用直角坐标计算，⎰⎰(x + y ) d x d y = ⎰d y ⎰ D2(x + y ) d x4 分= ⎰1⎡ 1 x 2 + yx ⎤d y0 ⎢⎣2 ⎦⎥ y 2= ⎰ ( 3 y + 1 3y 2) d y = 31 ． 6 分0 8 2 80 5.求由抛物面2z = x 2 + y 2与平面 z = 2 所围立体的体积．解：所围立体在 xoy 面的投影区域为 D : x 2+ y 2≤ 4 ，1 分则立体的体积为A =1 ⎰⎰(x2 + y 2 )dxdy3 分D=1 ⎰⎰ρ3d ρd θ D=1⎰2πd θ⎰ 2ρ3d ρ52 0 0= 4π．6 分6.计算曲线积分 ⎰xy d x + (x + y ) d y ，其中 L 是由曲线 x = 与 y = x 2 所围Lyy ， 分x 1 n =0n =0n =0x 成的闭曲线的逆时针方向．解：利用格林公式计算，这里 P = xy ,Q = x + y ，则1 分⎰ xy d x + (x + y ) d y = ⎰⎰(1 - x ) d x d y3 分LD= ⎰0(1 - x ) d x ⎰x 2 d y5 分13( - x 2- x 2+ x 3 ) d x 0⎡ 2 3⎢ x 2- 1 x 3 - 2 5 x 2+ 1 ⎤111 x 4 ⎥ =． 6 分⎣ 3 3 5 4 ⎦ 0 60∞n1 7. 判别级数∑(-1) ln(n +100) 的敛散性，如果收敛，是绝对收敛还是条件收敛？∞ 1 ∞ 1 解： 因为正项级数∑ln(n +100) > ∑ n +100 ， n =0∞1 n =0 ∞1由级数∑ n + 100 发散，知级数∑ln(n +100) 发散，2 分n =0∞nn =01又交错级数∑(-1) ln(n +100) 满足条件：1） lim1= 0 ，n →∞ln(n +100)2） 1 > 1ln(n +100) ln(n +101)， 4 分∞n1 所以交错级数∑(-1) ln(n +100) 收敛，∞n1 于是级数∑(-1) ln(n +100) 条件收敛．6 分8. 将函数 f (x ) =15 - x展开成 x - 2 的幂级数，并求收敛区间． = n =0= ⎰xyn !n =0 - + + 211 1解：因为 f (x ) == 5 - x3(1 - 2 分x 2) 31 x -2 ( x - 2) 2 = [1 + + + ( x - 2) n 4 分3 3 32 3 n= ∑ n =0(x - 2)n 3n +1求收敛区间，从< 1中解出-1 < x < 5 6 分四、计算题 2（每小题5 分，共计 5×2＝10 分）1. 求球面 x 2+ y 2+ z 2= 4 含在圆柱面 x 2+ y 2= 2x 内部的曲面面积． 解：该部分曲面在 xoy 平面上的投影域为D ： x 2 + y 2 ≤ 2 x ， 1 分则d A=x d y =x d yx d y 3 分于是A = 4⎰⎰D πd x d y2 cos θ= 4⎰ πd θ⎰ρ2= 8(π- 2) = 16π．5 分3∞n x∞12n2. 已知幂级数∑ x n =0∞= e ，求幂级数∑(2n )! x 12n的收敛域以及和函数．解：先求出幂级数∑(2n )! x的收敛域，因为∞ x - 23n =0] -n ! n !⎰lim x 2n +2⋅ (2n )! = limx = 0 ， n →∞ (2n + 2)! x2n n →∞ (2n + 2)(2n +1)所以收敛域为(-∞, +∞) ，2 分x∞1n1 2131n又e =∑ xn =0= 1+ x + x 2! + x + + x 3! n ! + ， x ∈(-∞, +∞)- x ∞1 n 12 1 3( -1) n n e = ∑ (-x ) n =0 = 1- x + x 2! - x + +3! x + ， x ∈(-∞, +∞) n ! 4 分上面两式相加除以 2 即得1 (e x + e - x ) = 1 + 1 x2 + 1 x 4 + 1x 6 + ∑ 1 x 2n ． 5 分2 2! 4! 6! 五、综合题（6 分）→→→n =0 (2n )!设一力场 F = ( y 2 + 1) i + (x 2+ y ) j ，有一质点在此力场中沿曲线 y = ax 2 自点O (0,0) 移动到点 A (1, a ) ，求a 的值使力场所作的功为最小． 解：据第二类曲线积分的物理应用知，W (a ) = ⎰( y 2 +1)dx + (x 2 + y )dy2 分L= 1(a 2 x 4 + 1)dx + (x 2 + ax 2 )2axdx=12 43a 2 5a (a +1) 4 1⎰0(a x + 2a (a + 1)x + 1)dx = [ x +5 2x ] 0a 2 a 2 + a 7 2 a = + = a + + 1， 4 分5 2 10 2对W (a ) 求导，得 W '(a ) = 7 a + 1 ，令W '(a ) = 0 ，得a = - 5，5 2 又W "(a ) = 7 > 0 ，所以当a = - 514时，力场所作的功为最小．6 分5 14∞ 2。

浙江大学2007-2008学年春季学期 《微积分Ⅱ》课程期末考试试卷一 、填空题（每小题5分.共25分.把答案填在题中横线上） 1.点M （1,－1, 2）到平面2210x y z -+-=的距离d = . 2.已知2a =,3b =,3a b ⋅=,则a b += . 3.设(,)f u v 可微.(,)yxz f x y =,则dz = .4.设()f x 在[0.1]上连续.且()f x ＞0, a 与b 为常数.()}{,01,01D x y x y =≤≤≤≤,则()()()()Daf x bf y d f x f y σ++⎰⎰= .5.设(,)f x y 为连续函数.交换二次积分次序2220(,)x x dx f x y dy -=⎰⎰.二 、选择题（每小题5分.共20分.在每小题给出的四个选项中只有一个是符合题 目要求的.把所选字母填入题后的括号内）6.直线l 1:155121x y z --+==-与直线l 2:623x y y z -=⎧⎨+=⎩的夹角为 （A ）2π . （B ）3π . （C ）4π . （D ）6π. [ ] 7.设(,)f x y 为连续函数.极坐标系中的二次积分cos 2d (cos ,sin )d f r r r r πθθθθ⎰⎰可以写成直角坐标中的二次积分为（A）100(,)dy f x y dx ⎰⎰ （B）100(,)dy f x y dx ⎰⎰（C）10(,)dx f x y dy ⎰⎰（D）10(,)dx f x y dy ⎰⎰[ ]8.设1, 02()122, 12x x f x x x ⎧≤≤⎪⎪=⎨⎪-≤⎪⎩ ()S x 为()f x 的以2为周期的余弦级数.则5()2S -=（A ）12. （B ）12-. （C ）34. （D ）34-. [ ] ＜9.设,)(0,0),(,)0, (,)(0,0),x y f x y x y ≠==⎩则(,)f x y 在点O (0,0)处（A ）偏导数存在.函数不连续 （B ）偏导数不存在.函数连续（C ）偏导数存在.函数连续 （D ）偏导数不存在.函数不连续 [ ] 三、解答题10.（本题满分10分）求曲线L ：2222222393x y z z x y⎧++=⎪⎨=+⎪⎩在其上点M （1.－1.2）处的切线方程与法平面方程.11.（本题满分10分）设F 可微.z 是由F (x y -,,)0y z z x --=确定的可微函数.并设23F F ''≠.求z zx y∂∂+∂∂. 12.（本题满分10分）设D 是由曲线3y x =与直线y x =围成的两块有界闭区域的并集.求2[e sin()]d xDx y σ++⎰⎰. 13.（本题满分10分）求空间曲线L ：222920335x y z x y z ⎧+-=⎨++=⎩上的点到xOy 平面的距离最大值与最小值.14.（本题满分10分）设平面区域D ={}(,)01,01x y x y ≤≤≤≤.计算二重积分22 1 d Dx y σ+-⎰⎰.15.（本题满分5分）设当y ＞0时(,)u x y 可微.且已知222222(,)()(2)y x du x y xy dx x y y dy x y x y=++-++++. 求(,)u x y .浙江大学2007－2008学年春季学期《微积分II 》课程期末考试试卷答案一、填空题（每小题5分.共25分） 1．231421=-++=d .2．22()()2496a b a b a b a b a b +=+⋅+=++⋅=++=3．()()dy xy f x x f dx y y f yx f dz x y x y 121211ln ln --'+⋅'+'+⋅'=4．()()()()()()()()⎰⎰⎰⎰++=++=D Dd x f y f x bf y af d y f x f y bf x af I σσ. ()()⎰⎰+=+=+=∴Db a I b a d b a I 21,2σ.5．()()2220111,,x x dx f x y dy dy f x y dx --=⎰⎰⎰⎰或 ()0111,dy f x y dx -⎰⎰或 ()1101,dy f x y dx -⎰⎰.二、选择题（每小题5分.共20分） 6．选（B ）.l 1的方向向量{}1,2,1-.l 2的方向向量{}2,1,1--.{}{}3,2163662,1,11,2,1cos πθθ===--⋅-=.7．选（D ）. 积分区域(){}0,,22≥≤+=y x y x y x D .化成直角坐标后故知选（D ）.8．选（C ）. 511111113()()()((0)(0))(1)222222224S S S f f -=-==-++=+=.9．选（A ）. ()()0000,0lim0,0,00x y x f f x→-''===.偏导数存在. 取kx y =.()4411lim,lim kk kk kx x f x x +=+=→→随k 而异.所以不连续．三、解答题（10～14每题10分.15题5分.共55分） 10．由L .视x 为自变量.有⎪⎩⎪⎨⎧=-+=++.0226,0264dx dz z dx dy y x dx dz z dx dy y x 以()()2,1,1,,-=z y x 代入并解出dxdzdx dy ,.得 87,45==dx dz dx dy . 所以切线方程为87245111-=+=-z y x .法平面方程为()()()57112048x y z -+++-=.即0127108=-++z y x .11．133212232332,,1y x z z F F F F F F F F z z z z x F F F y F F F x y F F ''''''''--+∂∂∂∂=-=-=-=-+==''''''''∂-+∂-+∂∂-.12．D 在第一象限中的一块记为D 1.D 在第三象限中的一块记为D 2.()()()()⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+++++=++2122122sin sin sin D D DD x D x x d y x d y x d e d e d y x eσσσσσ.32222312101xx x x x xxxD D e d e d dx e dy dx e dy σσ-+=+⎰⎰⎰⎰⎰⎰⎰⎰ ()()()()222210103333011x x x x x x e dx xx e dx x x e dx xx e dx -=-+-=-+-⎰⎰⎰⎰()2111130021()112x u u u u x x e dx e du ue du e ue e e e =-=-=---=--=-⎰⎰⎰()()()()3312101sin sin sin sin x x xxD D x y d x y d dx x y dy dx x y dy σσ-+++=+++⎰⎰⎰⎰⎰⎰⎰⎰()()()()103301cos cos cos cos x x x x dx x x x x dx -⎡⎤⎡⎤=-+-+-+-+⎣⎦⎣⎦⎰⎰ ()()()()13301cos cos cos cos 0x x x x dx x x x x dx ⎡⎤⎡⎤=-+-+++-+=⎣⎦⎣⎦⎰⎰ 所以.原式2-=e .13．L 上的点到平面xoy 的距离为z .它的最大值点.最小值点与2z 的一致.用拉格朗日乘数法.设()()()53329,,,,2222-+++-++=z y x zy x z z y x F μλμλ.求偏导数.并令其为零有：20F x x λμ∂=+=∂.1830F y x λμ∂=+=∂. 2430F z z z λμ∂=-+=∂.22920Fx y z x∂=+-=∂ . 3350Fx y z μ∂=++-=∂ ． 解之得两组解()()1215,,(1,,1);,,(5,,5)33x y z x y z ==--. 所以当31,1==y x 时.1=z 最小；当35,5-=-=y x 时.5=z 最大.14．将分成如图的两块.41的圆记为D 1.另一块记为D 2()⎰⎰⎰⎰--=-+DD d y x d y x 1222211σσ+()⎰⎰-+2122D d y x σ ()()()σσσd y x d y x d y xD DD ⎰⎰⎰⎰⎰⎰-+--++--=11111222222()()()()1222211122220211211211()43343D Dx y d x y d d r rdr dy xy dx πσσθππ=--++-=-++-=+-+=-⎰⎰⎰⎰⎰⎰⎰⎰15．由()222222,()(2)y x du x y xy dx x y y dy x y x y =++-++++.有222xy y x y x u ++=∂∂.从而知()()y y x y x y x u ϕ++=2221arctan,.又由y y x yx x y u 2222+++-=∂∂.推知 ()22222221()xx y x y y x y y x x y y ϕ-'++=-++++. ()()22,y y y y C ϕϕ'==+所以.()2221,arctan2x u x y x y y C y =+++. 注：若用凑的办法亦可：222222()(2)y x xy dx x y y dy x y x y++-++++()()22222211221()ydx xdy ydx xdy xy ydx xdy ydy d xy dy x x y y y--=+++=++++ ()221(arctan)2x d xy y y =++ 所以.()C y y x y x y x u +++=22221arctan,． ()()u f u F ='．浙江大学2006–2007学年春季学期 《 微积分Ⅱ 》课程期末考试试卷开课学院： 理学院 考试形式：闭卷 考试时间： 年 月 日 所需时间：120 分钟 考生姓名： _____学号： 专业： ________一、 填空题（每小题5分.满分30分） 1． 直线63321-==+z y x 在平面0522=--+z y x 上的投影直线方程为.2． 数量场2),,(zye z y x g x +=在)0,3,1(P 点的梯度为 .=u函数)ln(),,(22z y x z y x f ++=在P 点沿u的方向导数为 .3． 设ϕϕ,),2,3(),,(f y x x u u x f z+== 具有二阶连续偏导数.则=∂∂∂yx z 2.4． 设}1,11|),{(3≤≤≤≤-=y x x y x D.则=+⎰⎰+Dy xy x e y x x d d )(222.5． 已知曲面1=z y x 与椭球面193222=++z y x 在第一卦限内相切.则切点坐标为 .公共切平面方程为.6． 设函数⎪⎩⎪⎨⎧<≤<≤=121,210,)(2x x x x x f .∑∞=+=10cos 2)(n n x n a a x S π.其中,2,1,0,d cos )(210==⎰n x x n x f a n π.则.)27(=S二、 （满分10分）求直线 ⎩⎨⎧=-++=-+-022012z y x z y x 绕x 轴旋转一周所得的旋转曲面方程.1002 22dd x yex y.三、（满分10分）计算⎰⎰-四、 (满分15分)已知),(y x z z =由方程013=++zxe z y 确定.试求1022==∂∂y x x z.五、 （满分15分）设平面),,(,1:z y x d y x =+π为曲线⎪⎩⎪⎨⎧=++=++014222z y x z y x 上的点),,(z y x 到平面π的距离.求),,(z y x d 的最大.最小值 .六、 (满分15分)如图是一块密度为ρ（常数）的薄板的平面图形（在一个半径为R 的半圆直 径上拼上一个矩形.矩形的另一边为h ）,已知平面图形的形心位于原点(0, 0). 试求：1. 长度 h ；2.薄板绕x 轴旋转的转动惯量.七、 (满分5分) 求证:当0,1≥≥s t 时.成立不等式 s e t t t ts +-≤ln .参考解答：一．1．⎩⎨⎧=--+=+-0522043z y x z y x ； 2. 21},0,,3{e e ；3. )3(2))(3(2222122222122212ϕϕϕϕϕϕ''+''⋅'+'+'⋅'⋅''+'''f f f ； 4.;32 5. ;03313,3,1,31=-++⎪⎭⎫⎝⎛z y x 6. 83.二．直线：t z t y t x -=-==1,1,曲面上点→),,(z y x P 直线上点00000001,1),,,(x z x y z y x -=-=22222020220)1()1(,,x x z y z y z y x x -+-=+⇒+=+=则旋转曲面方程：222)1(2x z y -=+三．⎰⎰10222d d xy ex y -⎰⎰⎰-==--212212220142)d 41(d d y y e x e y 2y yy2120202020221d d d d 212212212212212------=-+=+=⎰⎰⎰⎰e y e ey y e e y y e yy y y y四．,1)1,0(-=z ,032=∂∂++∂∂⋅x z xe e x z z y z z ex z y x 3110-=∂∂∴== ,02632222222=∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+⎪⎪⎭⎫ ⎝⎛∂∂⋅+∂∂⋅x z xe x z xe x z e x z z y x z z y z z z 2102294ex zy x =∂∂∴== 五．|1|21),,(-+=y x z y x d )14()()1(2222-++++++-+=z y x z y x y x L μλ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-++='=±===++='==+='-==⇒≠=++-+='=⇒==++-+='014,01302,002)1(20,002)1(22223231221z y x L z y x z y x L x z L xz x y y y x L x y x L z y xμλμλμμλλμμλ，无解最小距离：2236),,(323131-=-d .最大距离：2236),,(323131+=--d六．形心：01,0=⇒==⎰⎰⎰⎰DDxdxdy xdxdyx y σ即0d cos d d d 220=⋅+⎰⎰⎰⎰---ππθθRhRRr r r y x xR h R h R 320312)21(232=⇒=⋅+-⋅ ⎰⎰=Dxdxdy y I 2302202)832(d θsin d d d 22R R h r r r y y x RhRR πθππ+=⋅+=⎰⎰⎰⎰--- 七．设0)0,1(,ln ),(=-+-=F ts e t t t s t F s.ln ,0),(t s e t t e s t F s s s ==⇒=-=' 且对固定的1>t . 当,0),(,ln 0<'<<s t F t s s 当,0),(,ln >'>s t F t ss所以.t s ln =取得最小值且为0.则 0),(≤s t F .即s e t tt ts +-≤ln1、已知22(,)yf x y x y x +=-,则=),(y x f _____________.2、已知,则=⎰∞+--dx e x x21___________.π=⎰∞+∞--dx e x 23、函数22(,)1f x y x xy y y =++-+在__________点取得极值. 4、已知y y x x y x f arctan )arctan (),(++=,则=')0,1(x f ________.5、以x e x C C y 321)(+=(21,C C 为任意常数)为通解的微分方程是____________________. 6 知dxexp ⎰∞+- 0)1(与⎰-ep x x dx11ln 均收敛,则常数p 的取值范围是( c ).(A) 1p > (B) 1p < (C) 12p << (D) 2p >7 数⎪⎩⎪⎨⎧=+≠++=0 ,0 0,4),(222222y x y x y x x y x f 在原点间断,是因为该函数( b ).(A) 在原点无定义 (B) 在原点二重极限不存在 (C) 在原点有二重极限,但无定义(D) 在原点二重极限存在,但不等于函数值 8、若2211x y I +≤=⎰⎰,22212x y I ≤+≤=⎰⎰,22324x y I ≤+≤=⎰⎰,则下列关系式成立的是( a).(A)123I I I >> (B)213I I I >> (C)123I I I << (D)213I I I <<9、方程xe x y y y 3)1(596+=+'-''具有特解( d ). (A) b ax y += (B) x e b ax y 3)(+= (C) x e bx ax y 32)(+= (D) x e bx ax y 323)(+=10、设∑∞=12n na收敛.则∑∞=-1)1(n nna ( d ).(A) 绝对收敛 (B) 条件收敛 (C) 发散 (D) 不定 一、填空题(每小题3分,共15分)1、2(1)1x y y -+. 2、、)32,31(-. 4、1. 5、"6'0y y y -+=. 11、求由23x y =,4=x ,0=y 所围图形绕y 轴旋转的旋转体的体积.解：32y x =的函数为23,0x y y =>。

微积分试题 (A 卷)一. 填空题 (每空2分,共20分)1. 已知,)(lim 1A x f x =+→则对于0>∀ε，总存在δ>0，使得当时，恒有│ƒ(x )─A│< ε。

2. 已知2235lim2=-++∞→n bn an n ，则a = ，b = 。

3. 若当0x x →时，与 是等价无穷小量，则=-→ββα0limx x 。

4. 若f (x )在点x = a 处连续，则=→)(lim x f ax 。

5. )ln(arcsin )(x x f =的连续区间是 。

6. 设函数y =ƒ(x )在x 0点可导，则=-+→hx f h x f h )()3(lim000______________。

7. 曲线y = x 2＋2x －5上点M 处的切线斜率为6，则点M 的坐标为 。

8. ='⎰))((dx x f x d 。

9. 设总收益函数和总成本函数分别为2224Q Q R -=，52+=Q C ，则当利润最大时产量Q 是 。

二. 单项选择题 (每小题2分,共18分) 1. 若数列{x n }在a 的邻域（a -,a +）内有无穷多个点，则（ ）。

(A) 数列{x n }必有极限，但不一定等于a (B) 数列{x n }极限存在，且一定等于a(C) 数列{x n }的极限不一定存在 (D) 数列{x n }的极限一定不存在 2. 设11)(-=x arctgx f 则1=x 为函数)(x f 的（ ）。

(A) 可去间断点 (B) 跳跃间断点 (C) 无穷型间断点 (D) 连续点 3. =+-∞→13)11(lim x x x（ ）。

(A) 1 (B) ∞ (C)2e (D) 3e4. 对需求函数5p eQ -=，需求价格弹性5pE d -=。

当价格=p （ ）时，需求量减少的幅度小于价格提高的幅度。

(A) 3 (B) 5 (C) 6 (D) 105. 假设)(),(0)(lim ,0)(lim 0x g x f x g x f x x x x ''==→→；在点0x 的某邻域内(0x 可以除外)存在，又a 是常数，则下列结论正确的是（ ）。

浙江大学2004-2005学年秋冬季学期《微积分》课程期末考试试卷一、填空题1．1lim()xx x e x →-= .2．设()f x 可导，2(cos )f x y x =则d d yx= . 3．ln (0)xy x x=>的值域范围为 . 4．3121x x -=⎰5．设,arcsin x y t⎧⎪=⎨=⎪⎩则22d d y x = . 6．当0x →时，20cos d 2x tx e t t x --⎰与B Ax 等价无穷小，则常数A = ，B = .二、计算题1.求221d .22x x x x +++⎰ 2．已知(0),(),f a f b π==且()f x ''连续，求[]0()()sin d f x f x x xπ''+⎰.3．求2+∞⎰.4．求曲线sin (0)y x x π=≤≤与x 轴围成的平面图形分别绕x 轴和y 轴旋转一周所得的旋转体体积x V 和y V .5．在曲线段 2(08)y x x =≤≤上, 求一点2(,)P a a 使得过P 点的切线与直线0,8y x ==所围成的三角形的面积最大．三、求幂级数2021!n n n x n ∞=+∑的收敛区间以及在收敛区间上的和函数，并求级数0212!nn n n ∞=+∑的和.四、证明若2,e a b e <<<则2224ln ln ()b a b a e ->-⋅ 五、已知sin 0()0x e x x F x xa x ⎧≠⎪=⎨⎪=⎩为连续函数.（1）求常数a ； （2）证明()F x 的导函数连续.浙江大学2004-2005学年秋冬学期《微积分》课程期末考试试卷答案一、填空题1．2110ln()lim()lim x x x x x x e x e x e →→--=1002ln()1lim lim 22()x x x x e x e x x e x x e e e →→---===．2. 22(cos )d (cos )[2(cos )(cos )sin ln ]d f x y f x x f x f x x x x x'=-⋅． 3． (1,]e-∞ ．4.3121x x -+⎰．111x x x --=+⎰⎰12x x =⎰， 令sin x t =222222001312sin cos td 2sin (1-sin t)d 2()224228t x t x πππππ===⋅-⋅⋅=⎰⎰.5.由x =d d x t = a r c s i n y t =，d d y t =d 1d y x t =-，2221d d yt x==．6. 由洛必达法则20100cos d cos 12lim lim x tx B B x x x e t t x e x xAx ABx-→→----=⎰， 2323310[1()][1()]12!3!2!lim B x x x x x o x o x xABx-→++++-+--=， 其中：232331(),cos 1()2!3!2!xx x x e x o x x o x =++++=-+33101()3lim 1B x x o x ABx -→-+==, 得13,13B AB -=⎧⎪⎨=-⎪⎩，即1,412A B =-=. 二、计算题 1.22221221d d d 22221(1)x x x x x x x x x x ++=-++++++⎰⎰⎰=2ln(22)arctan(1)x x x C ++-++．2.[]00()()sin d ()sin d ()sin d f x f x x x f x x x f x x x πππ''''+=+⎰⎰⎰()sin d sin d ()f x x x x f x ππ'=+⎰⎰00()sin d sin ()()cos d f x x x xf x f x x x πππ''=+-⎰⎰00()sin d cos ()()sin d f x x x xf x f x x x πππ=--⎰⎰=a b +.3.221x +∞+∞=-⎰⎰21arcsinx +∞=-=6π . 4. 22sin d 2x V x x πππ==⎰,2002sin d 2cos 2cos d 2y V x x x x x x x πππππππ==-+=⎰⎰．5. 解:（1）过点2(,)P a a 的切线方程为 22()y a a x a -=-， 令0y =，得22()a a x a -=-，得2a x =， 令8x =，得222(8)16y a a a a a =+-=-，令221()(8)(16)(8)222a aS a a a a =--=-，213()(8)2(8)()(8)(8)22222a a a aS a a '=-+--=-- ，令()0S a '=，得163a =，16a =（舍）．1333()(8)(8)1622222a a S a a ''=----=- ，16316()1680323S ''=⋅-=-<，所以，当163a =时，三角形面积最大．三、因为 2220102121()!(1)!!n n n n n n n x x x n n n ∞∞∞===+=+-∑∑∑2220()2!n x n x x e n ∞==+∑222222(21)x x x x e e e x =+=+，所以2220021212(221)5!!n n n n n n e e n n ∞∞==++==⋅+=∑∑．四、 设 2()ln ,()f x x g x x ==，在[,]a b 上由柯西定理，有 222ln ln ln 2,b a e a b e b a ξξξ-=<<<<- .再令2ln 1ln (),()0()x xx x e x x x ϕϕ-'==<<,故()x ϕ单调下降，得222(),()x e x e e ϕ><<，有2ln 2e ξξ>,得2224ln ln ()b a b a e ->-. 五、 (1）因为 0sin lim1x x e xx→=， 所以1a =． (2）0sin 1(0)lim x x e xx F x→-'=20sin lim x x e x x x→-= 00sin cos 12cos lim lim 122x x x x x e x e x e x x →→+-===， 所以，2(s i n c o s )s i n,0;()1,0.x x x x e x e x e x x F x x x ⎧+-≠⎪'=⎨⎪=⎩而 20sin cos sin limx x x x xe x xe x e xx →+-02cos lim 12x x xe x x →==,所以 ()F x '在(,)-∞+∞上是连续的．浙江大学2005-2006学年秋冬学期《微积分》课程期末考试试卷一、 计算题1.已知抛物线2y ax bx c =++过点(1,2)，且在该点的曲率圆方程为22151()(),222x y -+-=则a = ,b = ,c =2.设12()sin d x f x t t =⎰，则(1) 10()d f x x =⎰ ；(2) 1()lim1x f x x →=- 3.若011lim ,2a x x →=则a = 4.当x = 时，函数2x y x =⋅取得极小值.5.曲线arctan y x =在横坐标为1的点处的切线方程为 *6.已知01(cos sin ),(0,2),2n n n xa a nxb nx x ππ∞=-=++∈∑则5b = （此题不作要求）二、求极限1.0sin tan lim tan (1)ln(1)x x x x x e x →--- 2. 21sin 0lim(cos )xx x → 三、求导数1.设函数()x x y =由sin 0y x x -+=所确定，求22d d ,d d x xy y2.设sin arctan ,ln(x t t y t =-⎧⎪⎨=+⎪⎩ 求22d d ,d d y y x x 3.设()arccot xy x e =-()y x '. 四、求积分 1.21d (1)(1)x x x ++⎰．2.x ．3.1321(x x x -+⎰． 4.20sin 2d 1cos xxx xπ+⎰．五、设曲线21:1(01),C y x x =-≤≤x 轴和y 轴所围区域被曲线22:(0)C y ax a =>分为面积相等的两部分，试求常数a .六、将函数12()arctan 12x f x x -=+展开成x 的幂级数，并求级数0(1)21nn n ∞=-+∑的和.七、设()f x 在(,)a +∞内可导，且lim (),x f x a →∞'=证明：()limx f x a x→∞=．浙江大学2005-2006学年秋冬学期《微积分》课程期末考试试卷答案 一、计算题1. 由2y ax bx c =++，有2,2y ax b y a '''=+=，得112,2,2x x a b c y a b y a =='''++==+=由曲率圆方程22151()(),222x y -+-=两边求导，152()2()022x y y '-+-=，得1,21x y y =='=，5222()02x y y y y ''''++-=，得1,24x y y ==''=根据2y ax bx c =++与曲率圆22151()(),222x y -+-=在点(1,2)有相同的,,y y y '''；得到 24,21,2a a b a b c =⎧⎪+=⎨⎪++=⎩， 所以有2,3,3a b c ==-=.2. （1）11120()d (sin d )d xf x x t t x =⎰⎰⎰＝111220sin d sin d xx t t x x x +⎰⎰12201=sin d 2x x ⎰ =12011cos (1cos1)22x -=- ． （2）1211sin d ()limlim 11xx x t tf x x x →→=--⎰21sin lim sin11x x →-==-. 3. 因为，当0x →时2112x, 所以200112lim ,2a x x x x →→==得 2a = . 4. ()2x y x x =⋅,()22ln 2x x y x x '=+,令()0,22ln 20x x y x x '=+=，解得 1ln 2x -=， 由于2()2ln 22ln 22ln 22ln 2(2ln 2)x x x x y x x x ''=++=+， 当1ln 2x =-时，1()0ln 2y -''>，所以当1ln 2x -=时，()2x y x x =⋅取到极小值．5. 因为, 21111arctan ,,,arctan1124x x y x y y y x π==''=====+， 所以，切线方程为 1(1)24y x π=-+. 6. 515b =．二、求极限1. 0sin tan lim tan (1)ln(1)x x x x x e x →---=30sin (cos 1)cos lim x xx x x→--，注：当0x →时1,ln(1)x e x x x --- , 20cos 11lim2x x x →-==-． 2. 因为 ,21sin 0lim(cos )xx x →=2cos 11cos 1sin 0lim[1(cos 1)]x x xx x -⋅-→+- ，而 20cos 11limsin 2x x x →-=-，1cos 1lim[1(cos 1)]x x x e -→+-=， 所以 11sin2lim(cos )xx x e-→=．三、求导数1. 对方程sin 0y x x -+=两边关于y 求导数,注意到()x x y =,有 d d 1cos 0d d x x x y y -+=,得 d d xy =11cos x-, 222d 1d()d()(cos )d d 1-cos d d d (1-cos )y xx x yx yy y x '--===3sin (1cos )x x -=-. 2. 2d 1sin arctan ,cos d 1x x t t t t t=-=-+, ln(y t =，d d y t =d d d d d yy t x t==, 222d d (1)cos 1yxt t =⎡⎤+-⎣⎦．3.111()arccot arccot [ln ln(1)]arccot ln(1)222xx x x x x y x e e e e e x e =---+=-++，2211()122(1)12(1)x x x x x x xe e e y x e e e e '=--+=--++++. 四、 １.21d (1)(1)x x x ++⎰=22111()d 2111x x x x x -++++⎰ 2111ln 1ln(1)arctan 242x x x C =+-+++. 2. (令15x t =)x =145315d t t t t +⎰=11215d 1t t t +⎰ =9753215()d 1tt t t t t t t -+-+-+⎰ =108642211111115[ln(1)]1086422t t t t t t C -+-+-++=28242231551515153155151515ln(1)282422x x x x x x C -+-+-++.3.1321(x x x -+⎰11x x -=⎰22202sin cos d t t t π=⎰ 注：令sin x t =22202sin (1sin )d t t t π=-⎰1312()224228πππ=⋅-⋅⋅=.4. 20sin 2d 1cos x x x x π+⎰=220dcos 1cos x x xπ-+⎰=20dln(1cos )x x π-+⎰ 2200ln(1cos )ln(1cos )d x x x x ππ=-+++⎰＝22(cos )ln 2(1)2d 1n nn x x n ππ+∞=-+-⋅⋅+∑⎰1201(1)ln 2cos d n nn x x n ππ-∞=-=-+∑⎰ 12201(1)ln 22cos d n n n x x n ππ-∞=-=-+⋅∑⎰=11(1)(21)!!ln 22(2)!!2n n n n n ππ-∞=---+⋅⋅⋅∑.五、由 221,y x y ax⎧=-⎪⎨=⎪⎩得交点0x =, 311212002(1)d ()33x S S x x x +=-=-=⎰，022310012[(1)]d ()33x x a S x ax x x x +=--=-=⎰，由12S S =，得212323=⋅， 所以 3a =.六、由12()arctan 12x f x x -=+， 2221()2(1)4,142n n nn f x x x x ∞=-'==--<+∑， 210(1)4()()d (0)2421n n x n n f x f x x f xn π∞+=-'=+=-+∑⎰， 当12x =时，210(1)41024212n n n n n π∞+=-=-+∑， 得 0(1)214nn n π∞=-=+∑.七、解法一：由洛必达法则, ()()lim lim 1x x f x f x a x →+∞→+∞'==.解法二：① 若0a =，由lim ()0x f x →+∞'=，按定义知0ε∀>，10x ∃>，当1x x >时，恒有()2f x ε'<．1(,)b x ∀∈+∞，当x b >时，有()()()2f x f b f x b x b εξ'-=-<-，由于()()()()2f x f b f x f b x b ε-≤-<-，有()()2f x f b x b ε≤+-，再取2x b >，使得2()2f b x ε<，当2x x >时， 有2()()()()()()2222x bf b x b f b f x f x f b f b x x x x x x εεεεε---+=<+<+<+=， 所以，()lim0x f x x→+∞=． ② 若0a ≠，由lim ()x f x a →+∞'=，则有 lim [()]0x f x ax →+∞'-=， 设()()F x f x ax =-，有lim ()0x F x →+∞'=，由①知，()()limlim 0x x F x f x axx x→+∞→+∞-==，得证．浙江大学2006-2007学年秋冬学期《微积分》课程期末考试试卷一、求导数或微积分（1）设sin43(arctan 2)ln 2x y x x =++，求d d yx .（2）设22d ,sin()d t ts x e s y t s s -==-⎰⎰，求t =d d y x 及22d d y x .（3）设()y y x =是由方程210x y e x xy +---=确定的x 的可导函数，求0d x y =. 二、求积分（4）求60x ⎰.（5）求2arctan d xxe x e ⎰. （6）求1+∞⎰.三、求极限 （7）求3012cos lim[()1]3x x x x →+-. （8）设()f a ''存在，()0f a '≠，求11lim[]()()()()x af a x a f x f a →-'--.（9）设1121)1))nn n u n n n ⎡⎤=+++⎢⎥⎣⎦（（（1，求lim n n u →∞. 四、选择题（10）设2620arcsin d ,(1)d xt t t e t αβ==-⎰⎰，则0x →时 [ ]（A ）αβ与是同阶但不等价无穷小. （B ）αβ与是等价无穷小. （C ）αβ是的高价无穷小. （D ）βα是的高价无穷小. （11）设级数1n n a ∞=∑收敛，则下述结论不正确的是[ ]（A ）11()n n n a a ∞+=+∑必收敛. （B ）2211()n n n a a ∞+=-∑必收敛.（C ）2211()n n n a a ∞+=+∑必收敛. （D ）2211()n n n a a ∞+=-∑必收敛.（12）设1,0,()()()d ,0,x x e x f x F x f t t x x -⎧≤==⎨>⎩⎰，则()0F x x =在处[ ]（A ）极限不存在 （B ）极限存在，但不连续（C ）连续但不可导 （D ）可导（13）设()y f x =为连续函数，除点x a =外，()f x 二阶可导，()y f x ''=的图形如图， 则() [ ]y f x =（A ）有一个拐点，一个极小值点，一个极大值点. （B ）有二个拐点，一个极小值点，一个极大值点. （C ）有一个拐点，一个极小值点，二个极大值点. （D ）有一个拐点，二个极小值点，一个极大值点.五、（14）设曲线2y ax =(0,x ≥常数0)a >与曲线21y x =-交于点A ，过坐标原点O 和点A 的直线与曲线2y ax =围成一平面形D ．(I) 求D 绕x 轴旋转一周所成的旋转体体积()V a ；（II ）求a 的值使()V a 为最大.六、（15）将函数21()arctan ln(1)2f x x x x =-+在0x =处展开成泰勒级数（即麦克劳林级数）并指明成立范围.七、（16）设0,x >证明2()(4)(2)20x x f x x e x e =---+<．浙江大学2006-2007学年秋冬学期《微积分》课程期末考试试卷答案一、求导数或微分(1） sin 4sin 4122d 14cos 4ln sin 46(arctan 2)d 14x x y x x x x x x x x -=⋅+⋅++． (2) 由 20d ts x e s -=⎰，得2d d t xe t -=，由20sin()d ty t s s =-⎰，令t s u -=，得0220sin d sin d tty u u u u =-=⎰⎰，得2d sin d y t t =，所以222d d sin ,d d t t y ye t e x x π==，2222222222(sin )d 2sin 2cos d t t t tt t e t y te t te t x e e--'+== 22222(sin cos )t te t t =+, 22d d t y x π=．(3) 由 210x y e x xy +---=及0x =，得0y =，对方程 210x y e x xy +---= 两边取微分有(d d )2d (d d )0x y e x y x x y y x ++--+=， 将0x =，0y =代入，得 0d d x y x ==．二、求积分 （4）解66x x =⎰⎰6x =⎰ （令33sin x t -=）2227(1sin )cos cos d t t t t ππ-=+⎰22012754cos d 54222t t πππ==⋅⋅=⎰．（5）解 令x e t =，2arctan d xxe x e ⎰＝3arctan d t t t ⎰211arctan d 2t t =-⎰ 2221arctan 1[d ]2(1)t t t t t =--+⎰ 2221arctan 11[d d ]21t t t t t t =--++⎰⎰ 21arctan 1[arctan ]2t t C t t=-+++ 21arctan [arctan ]2x x xxe e e C e-=-+++． （6）解t =，1+∞⎰202d 1t t +∞+⎰02arcta n t π+∞==. 三、求极限 (7) 解 3012cos lim[()1]3xx x x →+- 2cos ln()3301lim [1]x x x e x +→=- 注2cos ln()32cos [1ln(),(0)]3xx x e x x ++-→ 2012cos limln()3x xx →+= 201cos 1lim ln(1)3x x x →-=+ 注[cos 1cos 1ln(1),(0)33x x x --+→] 201cos 11lim ()36x x x →-==． (8) 解 11lim[]()()()()x af a x a f x f a →-'--()()()()lim ()()(()())x a f x f a f a x a f a x a f x f a →'---='-- ＝()()lim()(()())()()()x af x f a f a f x f a f a f x x a →''-'''-+-2()()()lim ()(()())2(())()()x a f x f a f a x a f a f x f a f a f a f x x a→''-''-=='-'''+-． （9）解 由 112[1)1))]nn n u n n n =+++（（（1， 取11ln ln(1)n n i i u n n==+∑,则 11100011limln lim ln(1)ln(1)d ln(1)d 2ln 211n n n n i i x u x x x x x n n x →∞→∞==+=+=+-=-+∑⎰⎰,所以 2ln 214lim n n u e e-→∞==． 四、（10）解：因为262000arcsin d limlim (1)d xx x t t te tαβ→→=-⎰⎰注：由洛必达法则2222331arcsin 3lim 1x x x x xe -→⋅=- 注：221,(0)x e x x -→ 22320231arcsin 1lim33x x x x x →==⋅， 所以，αβ与是同阶但不等价无穷小，则选 A ． （11）解：（A ） 因为11111()nn n n n n n aa a a ∞∞∞++===+=+∑∑∑11212n n n n n n a a a a ∞∞∞====+=+∑∑∑，而1nn a∞=∑收敛，所以11()n n n a a ∞+=+∑必收敛，（B ）因为222222222221122311211()n n n n n n n a a a a a a a a a a a ∞++++=-=-+-++-+-=∑，所以2211()n n n a a ∞+=-∑必收敛．（C ）因为2212345221111()n n n n n n n a a a a a a a a a a ∞∞++==+=+++++++=-∑∑所以2211()n n n a a ∞+=+∑必收敛,（D ）221234522112()(1)n n n n n n n n a a a a a a a a a ∞∞++==-=-+-++-+=-∑∑未必收敛，例如 1(1)n n n ∞=-∑收敛， 但221(1)nn n n a n ∞∞==-=∑∑发散，则结论不正确的是D ，本题选Ｄ（12）解：由1,0,()()()d ,0,x x e x f x F x f t t x x -⎧≤==⎨>⎩⎰，则 11121,0,()11,02x t x x t e dt e e x F x e dt e x x ----⎧=-≤⎪=⎨⎪=-+>⎩⎰⎰，即 112,0,()11,02x e e x F x e x x --⎧-≤⎪=⎨-+>⎪⎩， 因为 12101lim ()lim(1)12x x F x e x e ++--→→=-+=-， 11lim ()lim()1x x x F x e e e ----→→=-=- 所以 ()F x 在0x =处连续．因为 2012(0)lim 0x x F x++∆→∆'==∆， 01(0)lim 1xx e F x-∆-∆→-'==∆，(0)(0)F F +-''≠所以，()F x 在0x =不可导，所以选Ｃ． （13）如图，在点(,0)b 处，左边0y ''>，右边0y ''<，而点(,0)b 处0y ''=，所以点(,0)b 为曲线的拐点； 同理，在点(0,)d 处，左边0y ''<，右边0y ''>，而点(0,)d 处0y ''=，所以点(0,)d 为曲线的拐点； 在点(,0)c 处，左边0y '<，右边0y '>，而点(,0)c 处0y '=，所以点x c =为函数的极小值点； 在点(,0)a 处，左边0y '>，右边0y '<，而点(,0)a 处0y '=，所以点x a =为函数的极大值点， 所以，曲线有二个拐点，一个极小值点，一个极大值点. 选（B ）五、解：由22,1y ax y x ⎧=⎪⎨=-⎪⎩求得交点)1a A a +（如图）， 直线OA 的方程y x =． （Ｉ） 旋转体体积 ()Va 2224()d 1a x a x x aπ=-+⎰=25/2215(1)a a π⋅+， （II ）53222552(1)(1)d ()22d 15(1)a a a a V a a a π+-+=⋅+ 27/2(4)15(1)a a a π-=+．在0a >处有唯一驻点4a =，当04a <<时d ()0d V a a >， 当4a >时，d ()0d V a a<, 故4a =为唯一极大值点，为最大值点．六、（15）解：由21()arctan ln(1)2f x x x x =-+21()arctan ,(),1f x x f x x'''==+展开之，20()(1),(1,1)n n n f x x x ∞=''=-∈-∑，两边积分，得212100(1)(1)()(0),(1,1)2121n n n n n n f x f x x x n n ∞∞++==--''=+=∈-++∑∑，再次两边积分，得220(1)()(0)(21)(22)nn n f x f x n n ∞+=-=+++∑220(1),(1,1)(21)(22)nn n x x n n ∞+=-=∈-++∑． 右边级数在1x =±处收敛，左边函数在1x =±处连续，所以成立范围可扩大到闭区间[1,1]-． 七、（16）证法1：由2()(4)(2)2x x f x x e x e =---+2(0)0,()(1)(1),2xx x f f x e x e '==---(0)0f '=2221()()44x x x xx f x e xe xe e ''=-=-．而当0x >时2114x e >>，所以当0x >时()0f x ''<， 于是知，当0x >时，()0f x '<，从而知，当0x >时，()0f x <. 证法2：由证法一，有 2211()(0)(0)()()022f x f f x f x f x ξξ''''''=++=< 证法3：由2()(1)(1)2xx x f x e x e '=---()1()2x x xx e x ξ='⎡⎤=--⎣⎦()02xe ξξ=-<，所以()0f x <．注：设()(1)x g x x e =-，在[,]2xx 上的拉格郎日中值定理，有()2(1)(1)1(),222xx x x x x x e x e x e x x ξξ='⎡⎤---=--<<⎣⎦ ．浙江大学2007-2008学年秋冬学期《微积分》课程期末考试试卷一、(每小题6分)（1）设4cos 1tan 5ln 2x x y x e x π=++，求d d y x .（2）设由参数式22ln(1)x t ty t t ⎧=+⎨=-+⎩，确定了y 为x 的函数()y y x =，求曲线()y y x =的凹、凸区间及拐点坐标（区间用x 表示，点用(,)x y 表示）.（3）求210sin lim()x x x x→（4）求(2)]x x →+∞+二、(每小题6分) （5）求21d (1)x x x +⎰.（6）求arcsin d xxe x e⎰. （7）求230d x xe x +∞-⎰.三、（第(8)-(11)小题每小题8分，第(12)小题6分） （8）（8分） 设()y y x =是由32210y xy x x ++-+=及(1)0y =所确定，求131()d lim (1)x x y t tx →-⎰.（9）（8分）设2()231x f x x x =-+，试将()f x 展开成x的幂级数，并求()(0)(1)n f n ≥.（10）（8分） 设常数0a >，讨论曲线y ax =与2ln y x =在第一象限中公共点的个数. （11）（8分） 设0a <，曲线2y ax bx =+当01x ≤≤时0y ≥.又已知该抛物线与x 轴及直线1x =所围成的图形的面积13D =，试确定常数a 与b 使该图形绕x 轴旋转一周而成的旋转体体积V 最小.（12）（6分） 设()f x 在区间(0,1)内可导，且()f x M '≤（M 为常数）证明：① 级数1111(()())22n n n f f ∞+=-∑绝对收敛； ② 1lim ()2n n f →∞存在.四、选择题（四选一，每小题4分）（13）设()()(),()()()f x u x v x g x u x v x =+=-，并设0lim ()x u x →与0lim ()x v x →均不存在，则下列结论正确的是 [ ]（A ）若0lim ()x f x →不存在，则0lim ()x g x →必存在.（B ）若0lim ()x f x →不存在，则0lim ()x g x →必不存在.（C ）若0lim ()x f x →存在，则0lim ()x g x →必不存在.（D ）若0lim ()x f x →存在，则0lim ()x g x →必存在.（14）曲线1ln(1)(1)x y e x x =++-的渐近线的条数 [ ]（A ）4条 （B ）3条. （C ）2条. （D ）1条.（15）设2122()lim 1n n n x x xf x x -→∞++=+，则()f x 的不连续点的个数为 [ ] （A ）0个 （B ）1个. （C ）2个. （D ）多于2个. （16）设()f x [,]a b 上可导，且()0,()0,f a f b ''><下述结论不正确的是[ ] （A ）至少存在一点0(,)x a b ∈使0()()f x f a >； （B ）至少存在一点0(,)x a b ∈使0()()f x f b >； （C ）至少存在一点0(,)x a b ∈使0()0f x '=；（D ）至少存在一点0(,)x a b ∈使01()(()())2f x f a f b =+．（17）设0(1,2,)n a n >=，下列结论正确的是[ ]（A ）若存在0N >，当n N >时均有11n n a a +<，则1n n a ∞=∑必收敛. （B ）若存在0N >，当n N >时均有11n n a a +>，则1n n a ∞=∑必发散. （C ）若1n n a ∞=∑收敛.则必存在0N >，当n N >时必有11n na a +<， （D ）若1n n a ∞=∑发散.则必存在0N >，当n N >时必有11n na a +>．浙江大学2007-2008学年秋冬学期《微积分》课程期末考试试卷答案一、(每小题6分)（1）24cos 4cos d 5cos sec 54(sin ln )d 2x x x x y xx e x e x x x x x =++-． （2）由22x t t =+，d 2(1)d x t t =+，ln(1)y t t =-+，d d 1y t t t =+，2d d 2(1)y tx t =+， 224d 1d 2(1)y tx t -=+，令 22d 0d y x =， 得 1t = 当11t -<<时，22d 0d yx> 曲线凹；当1t >时，22d 0d yx< 曲线凸，当1t =时，对应拐点．换成,x y ，当13x -<<时， 曲线()y y x =凹； 当3x >时， 曲线当()y y x =凸，点(3,1ln 2)-为拐点．（3）解 因为2211sin ln()00sin lim()lim xxx x x x x ex→→= ，而22001sin 1sin limln lim ln(11)x x x x x x x x→→=+-，201sin lim (1)x x x x →=- 注sin sin ln(11)1,(0)x xx x x+--→ 3200sin cos 11lim lim 36x x x x x x x →→--===-， 所以 21160s i n l i m ()x x xe x-→=．（4）lim (2))xx →+∞+2lim (1)]x x x→+∞=+222sin 2(1(1))limx x x ++-+=22sin 24()limx x x --=sin 42lim 1x x --==- ．二、 （5）22111d ()d (1)(1)x x x x x x x -=-+++⎰⎰ =1ln ln 1x x C x--+++．（6） 方法1：令 arcsin x e t =，则cos sin ,ln sin ,d d sin x te t x t x t t===2arcsin cos d d sin x x e t tx t e t=⎰⎰1d()sin t t =-⎰ 1d sin sin t t t t =-+⎰ ln csc cot sin t t t C t =-+-+arcsin ln x x x e e e e C ---=-+-+，或写成arcsin ln 1x x e e x C -=--++．方法2：令 x e t =，则1ln ,d d ,(0)x t x t t t==>2arcsin arcsin 1d d arcsin d x xe t x t t e t t==-⎰⎰⎰arcsin t t =-+arcsin tt=-+arcsin 1ln t C t t =--++arcsin ln 1x x e e x C -=+-．（7）2232200011d d d 22x x tx ex x e x te t +∞+∞+∞---==⎰⎰⎰001[d ]2t t te e t +∞+∞--=-+⎰011[]22t e +∞-=-=．三、（8）解 由32210y xy x x ++-+=，1lim ()0x y x →=两边关于x 求导数，有23220y y xy y x ''+++-=，得222()3x yy x y x--'=+，1lim ()0x y x →'=， 222(3)(2)(22)(61)()(3)y x y x y yy y x y x ''+-----+''=+，1lim ()2x y x →''=-． 由洛必达法则，1321111()d ()()()1limlimlim lim (1)3(1)6(1)63x x x x x y t ty x y x y x x x x →→→→'''====----⎰． （9）解：()(21)(1)xf x x x =--1111121112x x x x-=-=+---- 0(2)nn n n x x ∞∞===-+∑∑1(21),2n n n x x ∞==-<∑ ()(0)(21)!,1n n f n n =-≥（10）解：令()2ln f x ax x =-，有2()f x a x'=-，令()0f x '=，得2x a=，22()f x x''=，由于()0f x ''>，所以22()22ln f a a=-为()f x 的唯一极小值，为最小值.以下讨论最小值的符号.①若222ln 0a->，即2a e >时，()0f x >，()f x 无零点，两曲线无公共点；②若2a e=，则当且仅当a e =时，()0f x =，()f x 有唯一零点，两曲线在第一象限中相切；③若20a e <<，有2()0f a<时，有因0lim ()x f x +→=+∞，lim ()x f x →+∞=+∞， 所以在区间2(0,)a 与2(,)a+∞内，()f x 各有至少一个零点，又因为在这两个区间中()f x 分别是严格单调的，所以()f x 正好有两个零点，即两曲线在第一象限中有且仅有两个交点． （11）解：因0a <，且当01x ≤≤时，0y ≥，所以如下图1211()d 323b ax bx x a +=+=⎰，所以312a b =-， 221220()d ()523a ab b V ax bx x ππ=+=++⎰21()51030b b π=-+，d 1()d 1015V b b π=-+，22d d 15V bb π=，令d 0d V b =，32b =，2232d 0d b V b=>，为唯一极小值，故32b V=为最小值，此时53,42a b =-=．（12）① 由拉格朗日中值定理 1111111111()()()()()()222222n n n n n n f f f f M ξξ++++''-=-=≤， 而1112n n ∞+=∑收敛，所以，1111[()()]22n n n f f ∞+=-∑绝对收敛；② 111()()22n n S f f +=-,因为lim n n S →∞存在，所以1lim ()2n n f →∞存在．四、 （13）解 （A ）若0lim ()x f x →不存在，则0lim ()x g x →必存在.不正确，例如 211(),()u x v x x x ==， 221111(),()f x g x x x x x=+=-， 此时0lim ()x f x →不存在，0lim ()x g x →也不存在．（B ）若0lim ()x f x →不存在，则0lim ()x g x →必不存在.不正确，例如 11(),()u x v x x x ==，2(),()0f x g x x==，此时0lim ()x f x →不存在，0lim ()0x g x →=存在．（C ）若0lim ()x f x →存在，则0lim ()x g x →必不存在.假设0lim ()x g x →存在，由()()2()f x g x u x +=，得0lim ()x u x →存在，与已知矛盾，所以结论正确．（D ）若0lim ()x f x →存在，则0lim ()x g x →必存在.由上述（Ｃ），说明0lim ()x g x →必存在不正确．所以结论正确的是Ｃ，本题选Ｃ． （14）解，因为11lim[ln(1)](1)x x e x x →++=∞-，1lim[ln(1)](1)x x e x x →++=∞-,有铅垂渐近线（0,1x x ==）2条，因为1lim[ln(1)]0(1)x x e x x →-∞++=-，有水平渐近线（0y =）1条，又因为 2()1l n (1)l i m l i m []1,1(1)xx x f x e a x x x x→+∞→-∞+=+==-,1lim[()]lim[ln(1)](1)x x x f x ax e x x x →+∞→+∞-=++--lim[ln (1)]lim[ln ln(1)]x x x x x x e e x e e x --→+∞→+∞=+-=++-lim ln(1)0x x e -→+∞=+=,有斜渐近线（y x =）1条，所以本题共有4条渐近线，选A.（15）解22122,1,3,1,2()lim 11,121,1,n n n x x x x x x x f x x x x x-→∞⎧+<⎪⎪=⎪++⎪==⎨+-=-⎪⎪⎪>⎪⎩， 则()f x 的不连续点(1,1x x =-=)的个数为2个所以选C. （16）解 取2()4,[1,1],1,1,()3,()3f x x x a b f a f b =-∈-=-===,当(1,1)x ∈-时()3f x >,()2,()2,()2f x x f a f b '''=-==-,满足题目条件:（A ）至少存在一点0(,)x a b ∈使0()()f x f a >，成立, （B ）至少存在一点0(,)x a b ∈使0()()f x f b >；成立, （C ）至少存在一点0(,)x a b ∈使0()0f x '=；成立,（D ）至少存在一点0(,)x a b ∈使01()(()())2f x f a f b =+．不成立. 所以本题选D（17）解 （A ）不成立,例如11n n ∞=∑,满足当1n >时 111n n a n a n +=<+, 但11n n∞=∑发散, （B ）成立,若存在0N >，当n N >时均有111,n n n na a a a ++>>， 则必有lim 0n n a →∞≠ 则1n n a ∞=∑必发散.（C ）不成立, 例如 21(1)2n n n ∞=-+∑收敛，但不存在0N >，当n N >时必有11n n a a +<， （D ）不成立,例如 11n n ∞=∑发散,但则存在0N >，当n N >时有111n na n a n +=<+．浙江大学2008-2009学年秋冬学期《微积分》课程期末考试试卷一、求导数或微分(每小题6分)（1）设sin 3(cos )(arcsin 2)x y x x e π=++，求d y .（2）设由参数式3arctan 16x t t y t t=++⎧⎨=+⎩，所确定的函数()y y x =在1t =-处的一阶导数d d yx , 及二阶导数22d d yx.二、求极限(每小题6分)（3）011lim()1x x x e →--, （4）lim x(5)21lim(sin cos )x x x x x →+.三、求积分(每小题6分)（6） 221ln d (1)x x x x x x -+-⎰, （7）11(2)x x x -+⎰, （8）已知2d 2x ex +∞-=⎰，求0xx -+∞⎰．四、(每小题6分)（9）试将函数12()arctan 12xf x x-=+展开成x 的幂级数，并写出此展开式成立的开区间. （10）求幂级数1!nnn n x n∞=∑的收敛半径及收敛区间，并讨论收敛区间端点处级数的敛散性. 五、(每小题8分)（11） 求由方程3222220y y xy y x -++-=确定的函数()y y x =的极值,并问此极值是极大值还是极小值,说明理由．（12）求由曲线2y x =与2y x =+围成的图形绕水平线4y =旋转一周所生成的旋转体体积V .（13）设()f x 在[0,1]上连续，(0)0f =，并设()f x 在0x =处存在右导数(0)1f +'=，又设0x +→时，220()()d ()d x x F x x f u u u u =-⎰⎰与n Ax 为等价无穷小，求常数n 及A 的值．六、(每小题8分)（14）设()f x 在闭区间[,]a b 上连续，(,)a b 内可导， （Ｉ）叙述并证明拉格朗日中值定理；（II ）如果再设()()f a f b =,且()f x 不是常数,试证明至少存在一点(,)a b ξ∈,使()0f ξ'>．（15）设n 为正整数，24021()d d 1nx x e t F x e t t t -=++⎰⎰（I ）试证明：函数()F x 有且仅有一个（实）零点（即()0F x =有且仅有一个实根），并且是正的，记此零点n x ；（II ）试证明级数21n n x ∞=∑收敛．浙江大学2008-2009学年秋冬学期《微积分》课程期末考试试卷答案一、求导数或微分(每小题6分)（1）sin 2d [(cos )(cos ln cos tan sin )6(arcsin 2)x y x x x x x x x =-+．（2）222d 2d ,3(2)d 1d x t y t t t t +==++，21d d 3(1),6d d t y y t x x =-=+=222222d d()d 66(1)d 2d d 21yy t t t x t x x t t +===+++， 221d 4d t y x =-=-．二、求极限(每小题6分)（3）00111lim()lim 1(1)x x x x x e xx e x e →→---=-- 注1,0x e x x -→ 201lim x x e xx →--= 011lim 22x x e x →-==． （4）limlim x x =lim2x ==-．(5)21201ln(sin cos )lim(sin cos )lim xx x x x x x x x x e →→++=，而22001ln(1sin cos 1)limln(sin cos )lim x x x x x x x x x x→→++-+= 20sin cos 11lim 2x x x x x →+-==， 注：ln(1sin cos 1)sin cos 1,0x x x x x x x ++-+-→所以，21lim(sin cos )x x x x x →+=三、求积分（6） 222111ln d ()ln d (1)(1)x x x x x x x x x x -+=+--⎰⎰ 1ln d ln ln d()1x x x x =--⎰⎰ 21ln 1ln d 21(1)x x x x x x =-+--⎰ 21ln 11ln ()d 211x x x x x x =-+---⎰ 21ln ln ln 1ln 21x x x x C x =-+--+-． （7）112211(2)(24x x x x x x x x --+=++⎰⎰110x x =⎰ 令sin x t =22210sin cos d t t t π=⎰222010sin (1sin )d x x x π=-⎰131510()224228πππ=⋅-⋅⋅=．(8)2(1xxx e -+∞+∞-=--⎰⎰0]xx -+∞=--⎰2024d xu u e u -+∞+∞-==⎰⎰四、（9）12()arctan12xf x x -=+， 221(12)(2)(12)2()12(12)1()12x x f x x x x +---'=-+++ 22422814x x -==-++ 21212012(4)(1)2,2n n n n n x x x ∞∞++===--=--<∑∑， 12120()(0)(1)2d x n n n n f x f x x ∞++==+-∑⎰12121011(1)2,4212n n n n x x n π∞+++==+-<+∑．（10）记!n nn a n =，由11(1)!11(1)limlim lim lim !1(1)(1)n n n n n n n n n nnn a n n n a n en n++→∞→∞→∞→∞++====++． 所以，收敛半径R e =，收敛区间为(,)e e -，在x e =±处，级数成为1!()nnn n e n∞=±∑， 考察!n n n n u e n =，有111(1)n n n u eu n+=>+， 所以lim 0n n u →∞≠，并且也有lim(1)0n n n u →∞-≠，所以在x e =±处，该级数都发散．（11）由3222220y y xy y x -++-=, 求导有2(6421)220y y x y y x '-+++-=,令0y '=,得y x =与3222220y y xy y x -++-=联立,有3222(21)0x x x x x x -+=-+=,解之得唯一解0x =.相应地有0y =, 此时的确可由2(6421)220y y x y y x '-+++-=解出y ',故0x =为驻点. 再有 222()6421x yy y y x -'''=-++ 2222(6421)(22)2()(6421)(6421)y y x y x y y y x y y x ''-++----++=-++． 以0x y ==,及0y '=代入,得20y ''=>,故当0x =时, y 为极小值,极小值0y =.（12）由2,2y x y x ⎧=⎨=+⎩得交点(1,1),(2,4)-，则由上图22221[(4)(4(2)]d V x x x π-=---+⎰2241(1249)d x x x x π-=+-+⎰235211108[1223]55x x x x ππ-=+-+=．(13)220000()d ()d ()lim lim x x n nx x x f u u u uF x Ax Ax++→→-=⎰⎰22201()2()d ()2lim x n x xf x x f u u x x Anx+-→+=⎰2201200()()2limlim (1)x n n x x f u duf x xAnx An n x++--→→==-⎰ 2302()lim (1)n x f x An n x +-→=-25202()(0)lim (1)n x f x f An n x x+-→-=- 按题意, 0()lim 1n x F x Ax +→=,又220()(0)lim (0)1x f x f f x++→-'==, 若5n >则25202()(0)lim (1)n x f x f An n x x+-→--为∞, 若5n <则25202()(0)lim 0(1)n x f x f An n x x +-→-=-为,均与题意不符,故 5n =，于是25202()(0)1lim (1)10n x f x f An n x x A +-→-=-⨯,所以110A =． (14)(I)略,(II)设存在0(,)x x a b =∈,使0()0,f x >在区间0[,]a x 上用拉格郎日中值定理,存在0(,)(,)a x a b ξ∈⊂使得00()()()0f x f a f x aξ-'=>-, 如果存在0(,)x a b ∈,使0()0,f x <在区间0[,]x b 上用拉格郎日中值定理类似可证． (15) (I) 24021()d d 1nx xe t F x e t t t -=++⎰⎰，2014021(0)d d 01t F e t t t -=+<+⎰⎰， 2140211()d d 01e tn F e t t nt -=+>+⎰⎰，24()01nxx nx ne F x ee -'=+>+，故知存在唯一的n x 使 1()0,0n n F x x n =<<．(II) 因为 221nx n <,211n n∞=∑收敛， 故21nn x∞=∑收敛．。

浙江工商大学2011/2012学年第二学期期中考试试卷解答一、填空题(每小题2分,共20分)1.设y y x x y f 22+=⎟⎠⎞⎜⎝⎛(0>x ,0>y ),则=)(x f 0,12>+x xx . 解 由11122+⎟⎠⎞⎜⎝⎛=+⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎠⎞⎜⎝⎛x y y x x y f 知x x xx f 22111)(+=+=,0>x . 2.)1arcsin(arcsin2y yx z −+=的定义域是},20|),{(22y x y y y x ≤≤−≤<. 解 欲使函数有意义,必须⎪⎩⎪⎨⎧≤−≤−≠≤≤−1110,1122y y y x ,即.⎩⎨⎧≤<≤≤−2022y y x y 3.定积分的值是∫−+22||)d e |(|x x x x 4.解====. ∫−+22||)d e |(|x x x x ∫∫−−+22||22d e d ||x x x x x 0d 22+∫x x 22|x 44.设,则= xy xy z e cos e −=z d .解 ==,由变量x z y y xy xy xy ⋅⋅+⋅e e sin e )e sin 1(e xy xy y +y x ,的轮换性,知 =.y z )e sin 1(e xy xy x +所以 =z d y z x z y x d d +=. )d d )(e sin 1(e y x x y xy xy ++5.交换积分次序:∫∫∫∫−+3123010d ),(d d ),(d 2xx y y x f x y y x f x =∫∫−123d ),(d y yx y x f y .解 根据所给二次积分得名积分限画出积分区域:x31O1D 2D 2xy =23xy −=y故∫∫∫∫−+312301d ),(d d ),(d 2x x y y x f x y y x f x===∫∫∫∫+21d d ),(d d ),(D D y x y x f y x y x f ∫∫+21d d ),(D D y x y x f ∫∫−1023d ),(d yyx y x f y .6.已知,则=∫−=πd cos )()(x x x f x x f )(x f 2+x .解 设,则A x x x f =∫πd cos )(A x x f −=)(.A =====.∫−πd cos )(x x A x ∫−πdsin )(x A x ∫−−ππ00d sin |sin )(x x x A x π0|cos 0x +2−故2)2()(+=−−=x x x f . 7.已知⎟⎟⎠⎞⎜⎜⎝⎛+=y x g xy f z )(,,f g 均可导,则y z∂∂=g y x f x ′−′2. 解y z ∂∂=2)()(y x y x g x xy f −⋅′+⋅′=g y x f x ′−′2. 8.设∫=4d sin ln πx x I ,∫=40d cot ln πx x J ,∫=40d cos ln πx x K ,则,I J ,K 的大小关系是J K I <<.解 由题设知反常积分、J 皆收敛.由定积分的几何意义知I 0<k ;由反常积分值的几何意义知0<I ,;而0>J I K J −=,故有J K I <<. 9.若0→x 时,是的同阶无穷小,则=∫−x x t t sin 0d tan n x n 6.解 由nx x x x tt ∫−→sin 0d tan lim=10)cos 1()sin tan(lim−→−⋅−n x nx x x x =10)cos 1()sin (lim−→−⋅−n x nx x x x =12302161lim −→⋅n x nx x x =c ≠0 知,即51=−n 6=n .10.点是函数的极)0,1()(2)(),(22222y x y x y x f −−+= 小 值点. 解 ,. x x y x f x 42)(222−⋅+=y y y x f y 42)(222+⋅+= 验证知0)0,1()0,1(==y x f f ,即是的驻点.)0,1(),(y x f 在点处,,)0,1(8|)4412()0,1()0,1(22=−+==y x f A xx )0,1(|8)0,1(xy f B xy ==0=,,因为,8|)4124()0,1()0,1(22=++==y x f C yy 02<−AC B 0>A ,所以是极小值点.)0,1(二、单项选择题(每小题2分,共10分)1.函数⎪⎩⎪⎨⎧=+≠+++=0 ,20 ,)(2sin ),(22222222y x y x y x y x y x f 在点处(). )0,0(D(A )无定义 ()无极限 ()有极限但不连续 ()连续 B C D 解 由)0,0(22sin lim )(2sin lim ),(lim022222200)0,0(),(f t tt y x y x y x f t y x y x y x ===++=+→→→→+知在点处连续. ),(y x f )0,0(2.若∫−=xt x t x x f 0d )sin(d d )(,则等于()(x f A ). (A ) ()x sin −B 1cos −x (C ) ()x sin D x sin 1−解∫∫−=−−0d sin d )sin(xx u u ux t tx t ,. x x u u x f x sin )1()sin(d sin )(0−=−⋅−−=′⎟⎠⎞⎜⎝⎛=∫−3.曲线,x y ln =a y ln =,(b y ln =b a <<0)以及轴所围成图形的面积为(y C ).(A )()(∫b ax x ln ln d ln B ∫b ax xe e d e C )()∫b ayy ln ln d e D ∫b ax x e e d ln 解 4.,由,∫∫=Dxy I σd D x y =22−=x y 所围,则化为二次积分后的结果是(). B O xyxy ln =aln bln A(A )(B ) ∫∫+=422d d y y y xy x I ∫∫−+=2122d d y y x xy y I (C )∫∫∫∫−−+=41210d d d d x x x xy xy x y xy x I(D )∫∫−+=2122d d y y y xy x I 解 Oxy1−2xy =22−=x y5.下列结论正确的是(). D (A )∫∞++1)1(d x x x与∫+10)1(d x x x都收敛 ()B ∫∞++1)1(d x x x与∫+10)1(d x x x都发散(C )∫∞++1)1(d x x x发散,∫+10)1(d x x x收敛 ()D ∫∞++1)1(d x x x收敛,∫+10)1(d x x x发散解 由于111)1(1+−=+x x x x ,则2ln 1ln d 111)1(d 11=+=⎟⎠⎞⎜⎝⎛+−=+∞+∞+∞+∫∫x xx x x x x x ,∞=+=+∫1101ln )1(d x x x x x , 所以∫∞++1)1(d x x x 收敛,∫+10)1(d x x x发散. 三、计算题(1)(每小题5分,共20分) 1.设⎪⎪⎩⎪⎪⎨⎧<+≥+=0 ,e 110 ,12)(x x x xx f ,计算.∫−−51d )1(x x f 解 ∫−−51d )1(x x f t x =−1∫−42d )(t t f =∫∫+++−4002d 12de 11t t t t t , 而 ∫−+02d e 11t t =∫−+−02d )e1e 1(t t t == 02|)e 1ln()2(0−+−−−t )e 1ln(2ln 22−++−=,2ln )e 1ln(2−+ ∫+40d 12t t t u t =+12∫⋅−312d )1(21u u u u =)13(21|61313−−u =310. 所以3102ln )e 1ln(d )1(251+−+=−∫−x x f . 2.确定,,c 的值,使得a b c tt t xax x b x =+−∫→d )1ln(sin lim 30(0≠c ).解 由题设:0d )1ln(lim 30=+∫→x b x t t t ,即0d )1ln(03=+∫b t t t ,而0)1ln(3≠+tt ,故. 0=b 由c xx xa t t t x ax x x x =+−=+−→→∫)1ln(cos lim d )1ln(sin lim 30030,而0lim )1ln(lim3030==+→→x x xx x x ,故 01)cos (lim 0=−=−→a x a x ,即1=a .=c 2121lim )1ln(cos 1lim d )1ln(sin lim 32030030=⋅=+−=+−→→→∫xx x xx x t t t x x x x x x . 综上,1=a ,0=b ,21=c .212ln Oxyxy e =D3.计算∫∫−=2ln 02e d 1ed xy y x I yxy. 解 =I ∫∫−Dy xyy x y d d 1e =∫∫−21ln 0d 1e d y y xyx y y =∫∫⋅−21ln 0)d(e 111d yxy y xy y y y =∫==⋅−21ln 0d |e 111y yy yx x xy y =∫−⋅−21ln d )1(e 111y yy y y y =∫−⋅−21ln d )1(e 111y y y yy y=∫−⋅−21d )1(111y y y y y y ==. 21|ln y 2ln 4.已知)sin ,2(x y y x g z −=,g 具有二阶连续偏导数,求yx z∂∂∂2. 解 x z ∂∂=x y g g cos 221⋅+⋅=21cos 2g x y g ⋅+,yx z ∂∂∂2=]sin )1([cos cos ]sin )1([2222121211x g g x y g x x g g ⋅+−⋅+⋅+⋅+−⋅=2221211cos sin cos )cos sin 2(2g x x y g x g x y x g ⋅+⋅+⋅−+−.四、计算题(2)(每小题6分,共24分)1.计算∫−4321d )1(arcsin x x x x.解 原式=∫−4321d 1arcsin x xx x =∫−43212d )(1arcsin 2x x x =∫4321arcsin d arcsin 2x x=4321)(arcsin x =224()3(ππ−=1442π.2.设,其中由方程2e ),,(yz z y xf x =),(y x z z =0=+++xyz z y x 确定,求)1,1,0(−′x f .解 方程0=+++xyz z y x 两边对x 求偏:01=+++x x xyz yz z ,解得xyyzz x ++−=11.==),,(z y x f x ′x x x z z y yz ⋅⋅+2e e 2xyyz z y yz x x ++−⋅⋅+1)1(2e e 2,)1,1,0(−′x f =1.3.计算,其中积分区域是在第一象限的部分. ∫∫−Dy x y x d d ||122≤+y x xOy122=+y x x y =1D 2D 解 原式=y x x y y x y x D D ∫∫∫∫−+−21d d )(d d )( =∫∫∫∫−+−241401d )cos sin (d d )sin cos (d πππθθθθθθr r r r r r r r =∫∫∫∫⋅−+⋅−12241240d d )cos (sin d d )sin (cos r r r r πππθθθθθθ=1032410340|31|)sin cos (|31|)cos (sin r r ⋅−−+⋅+πππθθθθ =312312−+−=3)12(2−. 4.计算,其中.∫=ax x f I 0d )(∫−−=x a y a y y x f 0)2(d e )(解法1 ===I ∫′−a ax x f x x xf 00d )(|)(∫−⋅−−−−ax a a x a x x 0)](2)[(d )1(e 0∫−a x a x x 0d e 2122 =∫−−−a x a x a 022)d(e 2122=axa 0|e 2122−−=)e 1(212a −−=)1(e 212−a . 解法2 ===I ∫∫−−a x a y a y y x 0)2(d e d ∫∫−−a y a y a y x y 0)2(d e d ∫−−a y a y y y a 0)2(d )(e =∫−−a y ay y ay 022)2(d e 212=a y ay 02|e 212−=)1(e 212−a . 五、应用题(每小题8分,共16分)1.生产某种产品需要A ,,三种原料,而且产量与B C A ,,原料的用量B C x ,,有以下关系:,已知三种原料售价分别为(万元),今用(万元)购买原料,问如何进料才能使产量最大？y z yz x Q 2005.0=3,2,12400解 问题为求目标函数在约束条件yz x Q 2005.0=240032=++z y x 下的最大值. 作拉格朗日函数:,令)240032(005.0),,,(2−+++=z y x yz x z y x F λλ⎪⎪⎩⎪⎪⎨⎧=−++==+==+==+=024*********.002005.0001.022z y x F y x F z x F xyz F z y x λλλλ, 解得唯一驻点1200=x ,300=y ,200=z .由问题的实际意义,当A ,,三种原料分别购买1200,300,200单位时,产量最大.B C2.求由23x y ≥与所确定的平面图形的面积以及该平面图形绕轴旋转而成的旋转体的体积.422=+y x S y y V4=解 S =∫−−−1122d )34(x x x =∫∫−−102102d 32d 42x x x xtx sin 2=10360|332d cos 2|cos |22x t t t −⋅∫π=332d )2cos 1(46−+∫πt t =32)|2sin 216(40−+ππt =3332+π. =y V ∫∫−−102102d 32d 42x x x x x x ππ=1041022|432)4(d 4x x x ππ−−−−∫ =23|)4(3210232ππ−−⋅−x =23)833(32ππ−−−=ππ235316−. 或 =y V ∫∫−+23230d )4(d 3y y y y ππ=233302|)314(|213y y y −+⋅ππ =πππ3331623−+=ππ235316−. 六、证明题(每小题5分,共10分)1.设在上可导,且)(x f ],[b a 0)(=a f ,证明:2)(2|d )(|a b M x x f b a −≤∫,|)(|max x f M b x a ′=≤≤. 证 由拉格朗日中值定理:))(()()()(a x f a f x f x f −′=−=ξ,x a <<ξ,b x a ≤≤.根据定积分的性质:=2|d )(|∫bax x f ≤∫b ax x f d |)(|∫−′b ax a x f d )(|)(|ξ≤∫−b ax a x M d )(=b aa x M |)(22−=2)(2a b M−. 2.证明:由方程0,=⎟⎠⎞⎜⎝⎛x z x y F 所确定的函数),(y x z z =满足z yzy x z x=∂∂+∂∂,其中具有一阶连续偏导数.F 证法1 2221xz F x y F F x −⋅+−⋅=,x F F y 11⋅=,x F F z12⋅=,则 221xF zF yF F F x zz x +=−=∂∂, 21F F F F y z z y −=−=∂∂.所以z F yF F zF yF y z y x z x=−+=∂∂+∂∂21221. 证法2 方程0,=⎟⎠⎞⎜⎝⎛x z x y F 分别对x ,y 求偏导得 012221=⋅−⋅⋅+−⋅x z x z F x yF x , 0121=⋅+⋅x z F x F y . 解得221xF zF yF z x +=和21F Fz y −=.所以 z F yF F zF yF y z y x z x =−+=∂∂+∂∂21221.。

浙江科技学院2013-2014学年第二学期考试试卷 A 卷考试科目 复变函数与积分变换 考试方式 闭 完成时限 2小时 拟题人 工程数学组 审核人 批准人 2014年 6 月 日参考答案及评分标准一、填空题（每小题3分，共15分）1. 32,0,1,2,4k k ππ-+=±± 2．i ± 3．24． 1+ei 5．1(1)!n - 二、选择题（每小题3分，共12分） 1. C 2. B 3. A 4. D三、计算题（每小题8分，共56分）1解： ln(23)ln 23arg(23)i i i i -+=-++-+ （4分）13ln13(arctan )22i π=+- （8分）2．解：322i z e π=-= ()230,1,2n i z n ππ+⋅== （4分）故：方程320z +=共有三个根，分别为：)1,2± （8分）3. 解：在C 的内部作两条分别包含0=z 与1-=z 的光滑简单闭曲线1C 与2C ，使1C ，2C 与C 满足复连通区域的柯西定理的条件，于是有⎰⎰⎰+++=+21333)1()1()1(C zC z C z dz z z e dz z z e dz z z e ，(4分)而i z e i dz z z e z z C zπ=⎪⎪⎭⎫ ⎝⎛+π=+=⎰2)1(2)1(0331,1135!22)1(2--=π-=⎥⎥⎦⎤⎢⎢⎣⎡"⎪⎪⎭⎫ ⎝⎛π=+⎰ie z e i dz z z e z zC z. (6分)故i e dz z z e Czπ-=+-⎰)52()1(13. (8分) 4.解：当01z <<时01111()()(1)(2)2122nn n o n zf z z z z z z ∞∞====-=-+----∑∑11(1)2nn n z ∞+==-∑ （4分） 当12z <<时11111()(1)(2)212(1)(1)2f z z z z z z z-==-=------- 1012n n n n o n z z+∞+∞+===--∑∑ （8分）5.解:法一：原式22Re ()295z iz iz i s f z iz πππ=-=-===- （8分）法二： 解：2()9zf z z=-在2z ≤上解析，由cauchy 积分公式，有 222229(9)()z z z z dz dz z z i z i ==-==-++⎰⎰2295z iz i z ππ=-⋅=- （8分）6. 解：因为)(z f 在1=z 没有定义，更不解析，所以1=z 是)(z f 的奇点， （1分）在+∞<-<10z 内，展开)(z f 为洛朗级数：+-+---=-53)1(!51)1(!311111sinz z z z ∑∞=+-+-=012)1()!12(1)1(n n n z n ， （4分）有无穷多负幂项，故1=z 是)(z f 的本性奇点. （6分） 并且11,11sin Re =⎥⎦⎤⎢⎣⎡-z s （8分）7. 解： 对方程两边取拉氏变换，[][][]t L y L y L =+''. --------------- ------------- ---- ---------2分令()[]()s Y t y L =，则，()()2'21)0()0(ss Y y sy s Y s =+-- …… …… .3分 对方程整理并且解出()s Y ：()()2221211+-++=s s s s s Y -------------- -- 6分 对方程求拉氏逆变换， 从而()t t t t y sin 2cos -+=. - --------------- 8分四、综合题（本大题共2小题,第1小题8分, 第2小题9分，共17分） 1. 解: 222,2x y u x y xy u x y u y x =-+⇒=+=-+2222220u uu x y∂∂⇒+=-=⇒∂∂是调和函数. （3分）(,)(,)(0,0)(0,0)(,)()(2)(2)x y x y y x v x y u dx u dy c y x dx x y dy c =-++=-+++⎰⎰()(2)xy x dx x y dy c =-+++⎰⎰22222x y xy c =-+++ （6分） 22221()()(2)222x y f z u iv x y xy i xy ⇒=+=-++-+++ 211(2)22i z i =-+ （8分）2. 解：设2422(),109z z f z z z -+=++则()f z 在Im 0z >内有两个一级极点 123,z i z i ==， （4分）371Re ((),3),Re ((),),4816i is f z i s f z i ++==- （8分） 因此，根据留数定理有24223712().10948166z z i i dz i z z ππ+∞-∞-+++=-=-++⎰（9分）。

微积分试卷及答案4套微积分试题(A卷)一.填空题(每空2分,共20分)1.已知$\lim\limits_{x\to1^+}f(x)=A$，则对于$\forall\epsilon>0$，总存在$\delta>0$，使得当$x\to1^+$时，恒有$|f(x)-A|<\epsilon$。

2.已知$\lim\limits_{n\to\infty}\dfrac{a_n^2+bn+5}{n^2+3n-2}=2$，则$a=1$，$b=3$。

3.若当$x\to x_0$时，$\alpha$与$\beta$是等价无穷小量，则$\lim\limits_{x\to x_0}\dfrac{\alpha-\beta}{\beta}=0$。

4.若$f(x)$在点$x=a$处连续，则$\lim\limits_{x\toa}f(x)=f(a)$。

5.函数$f(x)=\ln(\arcsin x)$的连续区间是$(0,1]$。

6.设函数$y=f(x)$在$x$点可导，则$\lim\limits_{h\to0}\dfrac{f(x+3h)-f(x)}{h}=3f'(x)$。

7.曲线$y=x^2+2x-5$上点$M$处的切线斜率为6，则点$M$的坐标为$(-1,2)$。

8.$\dfrac{d(xf'(x))}{dx}=xf''(x)+2f'(x)$。

9.设总收益函数和总成本函数分别为$R=24Q-2Q^2$，$C=Q+5$，则当利润最大时产量$Q=6$。

二.单项选择题(每小题2分,共18分)1.若数列$\{x_n\}$在$a$的$\epsilon$邻域$(a-\epsilon,a+\epsilon)$内有无穷多个点，则（B）数列$\{x_n\}$极限存在，且一定等于$a$。

2.设$f(x)=\arctan\dfrac{2}{x-1}$，则$x=1$为函数$f(x)$的（A）可去间断点。

2022年浙江科技学院计算机科学与技术专业《数据结构与算法》科目期末试卷A（有答案）一、选择题1、下列排序算法中，占用辅助空间最多的是（）。

A.归并排序B.快速排序C.希尔排序D.堆排序2、n个结点的完全有向图含有边的数目（）。

A.n*nB.n(n+1)C.n/2D.n*(n-1)3、某线性表中最常用的操作是在最后一个元素之后插入一个元素和删除第一个元素，则采用（）存储方式最节省运算时间。

A.单链表B.仅有头指针的单循环链表C.双链表D.仅有尾指针的单循环链表4、已知有向图G=(V，E)，其中V={V1，V2，V3，V4，V5，V6，V7}， E=｛<V1，V2>，<V1，V3>，<V1，V4>，<V2，V5>，<V3，V5>， <V3，V6>，<V4，V6>，<V5，V7>，<V6，V7>｝，G 的拓扑序列是（）。

A.V1，V3，V4，V6，V2，V5，V7B.V1，V3，V2，V6，V4，V5，V7C.V1，V3，V5，V2，V6，V7D.V1，V2，V5，V3，V4，V6，V75、下列关于AOE网的叙述中，不正确的是（）。

A.关键活动不按期完成就会影响整个工程的完成时间B.任何一个关键活动提前完成，那么整个工程将会提前完成C.所有的关键活动提前完成，那么整个工程将会提前完成D.某些关键活动若提前完成，那么整个工程将会提前完成6、下列关于无向连通图特性的叙述中，正确的是（）。

Ⅰ．所有的顶点的度之和为偶数Ⅱ．边数大于顶点个数减1 Ⅲ．至少有一个顶点的度为1A．只有Ⅰ B．只有Ⅱ C．Ⅰ和Ⅱ D．Ⅰ和Ⅲ7、下列叙述中，不符合m阶B树定义要求的是（）。

A．根结点最多有m棵子树 B．所有叶结点都在同一层上C．各结点内关键字均升序或降序排列 D．叶结点之间通过指针链接8、设X是树T中的一个非根结点，B是T所对应的二叉树。

2011-2012学年第一学期期末高等数学A1考试试卷一．选择题(每小题3分，共18分)1. 微分方程xy y ′=+是( )。

(A) 可分离变量方程； (B) 齐次方程；(C) 一阶线性方程； (D) 伯努利方程。

2．若()f x 的导函数为sin x ，则()f x 的一个原函数( )。

(A ) 1sin x +； (B ) 1sin x −； (C ) 1cos x +； (D ) 1cos x −。

3．已知()0411cos 2xf t dt x ⎡⎤−=−⎣⎦∫，则()0f ′=( )。

(A) 2； (B)21e −； (C) 1； (D) 1e −。

4．阿基米德螺线()0a a ρθ=>相应于θ从0变到π2的一段弧与极轴所围成图形的面积为( )。

(A)2212a d ππθθ−∫； (B)220122a d πθθ∫； (C)222012a d πθθ∫； (D)22012a d πθθ∫。

5．通解为212x x x y C e C e xe −=++的微分方程是 ( )。

(A) 23x y y y xe ′′′−−=； (B) +23x y y y e ′′′−=；(C) +23x y y y xe ′′′−= ； (D) 23x y y y e ′′′−−=。

6．设()y f x =是方程240y y y ′′′−+=的一个解，若()00f x >，且0()0f x ′=，则()f x 在0x 处 ( )。

(A) 取得极大值； (B) 取得极小值；(C) 某邻域内单调增加； (D) 某邻域内单调减少。

二．填空题(每小题3分，共18分)1．函数(y C x C =−为任意常数）是微分方程1xy y ′′′−= ，（在“通解、特解、解”中选择一个答案）。

2．抛物线2y ax bx c =++在处，曲率最大。

3．=∫。

4．设()f x 的一个原函数是ln xx，则()d x f x x ′∫=。

湖北汽车工业学院微积分(一)(下)考试卷（ 2011-2012-2）一、（本题满分21分，每小题3分）填空题： 1．='⎰]sin [20x tdt 2sin 2x x ．2．过点)3,2,1(-且与平面0144=-++z y x 平行的平面方程为 044=+++z y x .3．设yx z =，则 =dz xdy x dx yx y y ln 1+- .4．⎰⎰+-=Ddxdy y x I )432(，其中D }4),{(22≤+=y x y x ，则=I π16 .5．微分方程)1)(1(22y x y --='的通解为C x y +-=2)1(arcsin .6．平面曲线2x y =与x y =所围成的平面图形绕x 轴旋转一周所得旋转体体积为15/2π . 7．设数项级数∑∞=1n nu收敛且和为s ，则级数∑∞=++11)(n n nu u的和为12u s - ．二、（本题满分21分，每小题3分）选择填空题（请将所选答案填入题号前的方括号内）： 【B 】1. 设)(x f 在),(+∞-∞内连续,)(x F 是)(x f 在),(+∞-∞内的一个原函数，0≠c ，则dx c x f ba⎰+)(等于)(A )()(c a F c b F ---. )(B )()(c a F c b F +-+.)(C )()(c b F c a F ---. )(D )()(c b F c a F +-+.【C 】2．设)2,1,3(--=a ，)1,2,1(-=b ，则⨯ 等于)(A 3. )(B 7. )(C )7,1,5(. )(D )7,1,5(-. 【A 】3．下列级数中条件收敛的是)(A ∑∞=+-111)1(n nn . )(B ∑∞=+-1211)1(n nn .)(C ∑∞=--11)107()1(n nn . )(D ∑∞=-151)1(n n n .【A 】4. 下列微分方程中是齐次方程的是)(A dx y x ydx xdy 22-+=. )(B x y y x y sin 2=+'.)(C y y x y ln sin ='. )(D x x y y sec tan =-'．【D 】5. 设)(x f 在]1,0[上连续且满足1)()(1-=⎰dt t f x x f ，则⎰1)(dx x f 等于)(A 1 . )(B 2. )(C 1-. )(D 2-．【C 】6. 设x y y x D ≤≤≤+≤0,41:22，则二重积分=⎰⎰σd xyDarctan)(A2163π . )(B 2323π. )(C 2643π. )(D 21283π． 【C 】7. 函数x x f /1)(=的在1=x 点处的幂级数展开式为)(A ∑∞=--0)1()1()(n nnx x f ＝, 11<<-x ． )(B ∑∞=-0)1()(n n x x f ＝, 20<<x ．)(C ∑∞=--0)1()1()(n nnx x f ＝，20<<x ． )(D ∑∞=--1)1()1()(n n n x x f ＝，20<<x ．三、计算下列各题（共3284=⨯分）1． 设函数),(y x z z =由方程z y x z y x ++=++222确定，证明：y x yzx z x z z y -=∂∂-+∂∂-)()(． [证] 方程z y x z y x ++=++222两边对x 求导得xzx z zx ∂∂+=∂∂+122， 解得z x x z 2112--=∂∂，由字符轮换性知zy y z 2112--=∂∂，于是 y x zy x z z x z y y z x z x z z y -=---+---=∂∂-+∂∂-2112)(2112)()()(. 2 ．计算dx xx ⎰--11241．[解] 原式dx xx ⎰-=102412. dt ttt t x ⎰⋅=04cos cos sin 2sin πdt t ⎰=204sin 2π83221432ππ=⋅⋅⋅= 3．判别正项级数nx nn n21sin 2∑∞=的敛散性 ． [解] n n n n nx n u 2sin 22≤=， 设n n n v 2=，121221lim lim 11<=⋅+=+∞→+∞→n n v v n n n nn n ，于是级数∑∞=12n n n 收敛.从而原级数∑∞=12sin 2n nnx n收敛. 4．某工厂生产甲种产品x 件乙种产品y 件的总利润函数为22222040),(y xy x y x y x L ---+=设备的最大产出力为15=+y x ，求x 与y 为何值时利润最大？ 解：作 )15(222040),(22-++---+=y x y xy x y x y x F λ …令 ⎪⎩⎪⎨⎧=-+==+--==+--=015),,(02220),,(02440),,(y x y x F y x y x F y x y x F x x λλλλλλ得 10=x ，5=y ．于是当这两种产品分别生产10件与5件的时候利润最大 ． 四．（8分）交换二次积分⎰⎰=101y xy dx e dy I 的次序并计算．【解】dx e dx I x xy⎰⎰=210 dx xe x y y xy ⎰===1002| ⎰=-=10.21)(dx x xe x 五、（8分）求微分方程2212)1(xx xy y x -=+'+的通解.解：方程变形为：2221)1(12x x xx xy y -+=++' 通解为： ])([)()(C dx e x Q e y dxx p dx x p +⎰⎰=⎰-]1)1([12221222C dx exx x edxx xdxx x+⎰⋅-+⎰=++-⎰]1)1([1)1(221)1(2222C dx exx x ex x d x x d +⎰⋅-+⎰=++++-⎰]1[11]1)1([22)1ln(22)1ln(22C dx xxx C dx e x x x e xx+-+=+⋅-+=⎰⎰++- 11]12)1([1122222+--=+---+=⎰x x C C xx d x 法二：221])1[(x x y x -='+ 通解为 C x y x +--=+221)1(六、（10分）求幂级数n n x n )11(1-∑∞=的收敛域与和函数，并求级数nn n n 211⋅-∑∞=的和．解：收敛域为)1,1(-)(1)1-(1)(1111x S x x n x x x n x S n n nn n n --=-==∑∑∑∞=∞=∞=n x x S n n ∑∞==11)(， x x n x x S n n n n -=='='-∞=∞=∑∑11)()(1111 )1l n ()(1x x S --=，于是 )1l n (1)(x xxx S -+-=． 2ln 1)21(-=S ，2ln 1)21(211-==⋅-∑∞=S n n nn ．湖北汽车工业学院 微积分A2考试试卷（2013~2014~2 A 卷）一、（本题满分21分，每小题3分）单项选择题（请将所选答案填入答题卡的指定位置）：【 B 】1. 设)4,1,1(-=a ，),0,2(λ=b ，且b a ⊥，则=λ)(A 2-． )(B21． )(C 2． )(D 21-． 【 B 】2．极限=+-→→22101limy x xyy x)(A 0． )(B 1． )(C 1-．)(D21． 【 C 】3．设⎰⎰+=xyx dx e dt t f y x F 112)(),(,则xF ∂∂为)(A )(xy f ． )(B 22)(x xe xy yf +． )(C )(xy yf ． )(D 22)(x xe xy f +．【 D 】4．二次积分dy y x f dx x x ⎰⎰-2010),(=)(A ρρθρθρθπd f d ⎰⎰1020)sin ,cos (． )(B ρρθρθρθθπd f d ⎰⎰cos 020)sin ,cos (．)(C ρρθρθρθπd f d ⎰⎰120)sin ,cos (． )(D ρρθρθρθθπd f d ⎰⎰cos 020)sin ,cos (．【 B 】5．已知2)(,3)2(20==⎰dx x f f ，则⎰'20)(dx x f x =)(A 10． )(B 4． )(C 6． )(D 1．【 C 】6．若级数)0(1≠∑∞=n n n u u 收敛，则级数∑∞=11n nu)(A 绝对收敛． )(B 条件收敛． )(C 发散． )(D 无法确定．【 D 】7．函数xx f -=31)(，则)(x f 的麦克劳林展开式为：)(A ∑∞==03)(n n nx x f ，(1<x )．)(B ∑∞==13)(n n nx x f ，(3<x )．)(C ∑∞=+=013)(n n n x x f ，(1<x )． )(D ∑∞=+=013)(n n nx x f ，(3<x )．二、（本题满分21分，每小题3分）填空题：1．过点)3,2,1(M 且与平面05532=++-z y x 平行的平面方程为11532=+-z y x ．或0)3(5)2(3)1(2=-+---z y x2．设}42),{(22≤+≤=y x y x D ，则⎰⎰Ddxdy =π2．3．交换二重积分⎰⎰=2010),(x dy y x f dx I 的次序，则I =⎰⎰11),(ydx y x f dy ．4．⎰∞+141dx x=3/1．5．已知yx e z +=2，则dz =)2(2dy dx e y x ++．6．=+⎰-223)sin 1(dx x 4．7．微分方程yx dx dy 232=的通解是Cx y +=32．三、（本题满分8分）设函数),(y x z z =由方程0e =-xyz z 所确定，求x z ∂∂与yz∂∂． [解] 令xyz z y x F z -=e ),,(，则yz F x -='， xz F y -='， xy F z z -='e ．从而有xy yz F F x z z z x -=''-=∂∂e ，xyxzF F y z zz y -=''-=∂∂e ． 四、（本题满分8分）曲线2xy =与直线0,3==y x 围成一个平面图形，①求此平面图形的面积；②求图形绕x 轴旋转一周所生成的旋转体的体积． [解] 90331)1(332===⎰x dx x A ）（2 dx x dV 22)(π=，于是πππ524351035304===⎰x dx x V ．五、(本题满分8分) 判定级数∑∞=-13)1(n n nn是否收敛，若收敛，指出是绝对收敛还是条件收敛． [解] 令nn n n nn u 33)1(=-=， 由于131331lim lim11<=+=+∞→+∞→n n n n n n n u u ， 所以正项级数∑∞=13n n n 收敛，从而∑∞=-13)1(n n n n 绝对收敛．六、（本题满分8分）求微分方程x x x y y sin =+'满足初始条件0==πx y 的特解． [解] 此方程为一阶线性微分方程，其中 x x P 1)(=，xx x Q sin )(= 其通解为])([)()(C dx e x Q e x dxx P dx x P +⎰⎰=⎰-]sin [11C dx e xx e dxx dxx +⎰⎰=⎰-)sin (1C xdx x x x +⋅=⎰)sin (1⎰+=C xdx x )cos (1C x x+-=由初值条件0==πx y 可得1-=C ，故特解为)1(cos 1)1cos (1+-=--=x xx x y ．七、（本题满分8分）计算二重积分⎰⎰-Dydxdy e ，其中D 为直线x y y x =1=0=,,所围的区域． [解]（X 型） ⎰⎰⎰⎰--=1102xyDy dy e dx dxdy e⎰⎰----=-=1111)()(dx e e dy e x xy110121----=--=e e ex．（Y 型）⎰⎰⎰⎰--=y yDy dx dy e dxdy e12)(111⎰⎰-----==dy e yedy ye y yy101121)(----=+-=e ee y．八、（本题满分8分）求函数324),(223+-+-=y xy x x y x f 的极值．［解］ 令⎩⎨⎧=-='=+-=',022,02832y x f y x x f y x 得唯一)2,2(,)0,0(，又86-=''x f xx，2=''xy f ，2-=''yy f ，于是 在点)0,0(处，2,2,8-==-=C B A ，则0122)2)(8(22>=---=-B AC 且08<-=A ，所以函数),(y x f 在)0,0(处有极大值3)0,0(=f ． 在点)2,2(处，2,2,4-===C B A ，则0122)2(422<-=--⋅=-B AC ，所以)2,2(不是函数),(y x f 的极值点．九、（本题满分10分）求级数∑∞=--11)1(n nn nx 的收敛域与和函数． [解] 易求得1=R ，且当1=x 时级数∑∞=--111)1(n n n 收敛，当1-=x 时级数∑∞=-11n n发散. 因此∑∞=--11)1(n nn nx 的收敛域是]1,1(-. 在区间)1,1(-内，设=)(x S ∑∞=--11)1(n nn nx ，则 x x x n x n x x S n n n n n n n n n n n +=-=-='-='⎥⎦⎤⎢⎣⎡-='∑∑∑∑∞=-∞=--∞=-∞=-11)()1()()1()1()(111111111 所以 )1ln(11)(0x dx x x S x+=+=⎰，11≤<-x .湖北汽车工业学院 微积分考试试卷（ 2014—2015—2）一、（本题满分21分，每小题3分）单项选择题（请将所选答案填入题号前的方括号内）：[ A ] 1．⎰=xdt t x f 0cos )(，则=')0(f（A ）1． （B ）0． （C ）1-． （D ）2π． [ D ] 2．设y x z 2=，则=∂∂22xz（A ）xy 2． （B ）x ． （C ）x 2． （D ）y 2．[ B ] 3．已知平面区域D 为222≤+y x ，则=+⎰⎰Dd y xσ)2(2（A ）π． （B ）π4． （C ）π3． （D ）0． [ C ] 4．由曲线x e y =与直线1=x 及直线2=x 所围图形的面积为（A ）e ． （B ）1-e ． （C ）e e -2． （D ）2e ． [ D ] 5．下列级数中收敛的是（A ）∑∞=+1131n n ． （B ）∑∞=+121n n n． （C ）∑∞=11cos n n n ． （D ）∑∞=+12n nn n．[ A ] 6．设),(y x z z =由方程022=--+z z xy y 所确定，则=∂∂yz（A ）122++z x y ． （B ）12+z y． （C ）122++-z x y ． （D ）12+-z y．[ C ] 7．微分方程0=-'y y 的通解为（A ）c x y +=． （B ）．x ce y 2= （C ）x ce y =． （D ）x e y =．二、（本题满分21分，每小题3分）填空题（请将正确答案填入题后相应横线上）1．=-+→→12lim1xy xy y x 0 ．2．设向量}1,3,2{-=→a 与向量},1,0{k a -=→垂直，则=m -3 ． 3．设xy y z sin =，则=dz dy xy xy xy dx xy y )cos (sin cos 2++． 4．设220(,)x I dx f x y dy =⎰⎰，则交换积分次序后=I 422(,)y I dy f x y dx =⎰⎰ ．5．=+⎰-dx x x 1121 0 ．6．过点)2,1,3(-且与平面052=+-+z y x 平行的平面方程为012=+-+z y x ．7．幂级数∑∞=⋅-12)1(n nn n n x 的收敛域为 (2,2]-．【温馨提示】请将下面解题过程直接写在各题相应空白处 三、（本题满分8分）设)ln 1ln(y x z ++=，求),1(e xz∂∂，),1(e yz ∂∂．解 由y x x z ln 11++=∂∂，yy x y z 1ln 11⋅++=∂∂ 所以31ln 111),1(=++=∂∂e x z e故(1,)11111ln 3e z ye e e∂=⋅=∂++四、（本题满分8分）计算定积分dx x x ⎰+412解 令12+=x t ，则212-=t x ，tdt dx =原式=tdttt ⋅⋅-⎰312121dt t )1(21312⎰-==103 五、（本题满分8分）计算二重积分⎰⎰+=Ddxdy y x I )(，其中积分区域D 是由直线x y =及曲线2x y =所围成的区域．解 积分区域D 为：10≤≤x ，x y x ≤≤2 画图 故⎰⎰+=xxdy y x dx I 2)(1⎰+=1022]21[(dx y xy xx⎰--=10432)2123(dx x x x 10543]1014121[x x x --==203六、（本题满分8分）求函数364),(22+-++=y x y x y x f 的极值．解 由⎩⎨⎧=-==+=062042y f x f y x 得点)3,2(-，又2==xx f A ，0==xy f B ，2==yy f C ，故在点)3,2(-处,2=A ,0=B ,2=C 042<-=-AC B ，且0>A所以)3,2(-为极小值点，极小值为10)3,2(-=-f七、（本题满分8分）求幂级数∑∞=++01)2(n n x n 的收敛域及和函数．解 由ρ123lim||lim 1==++=∞→+∞→n n a a n nn n ，故1ρ1==r ， 且幂级数在1±=x 处均发散，故收敛域为)1,1(-设=)(x s ∑∞=++01)2(n n xn =∑∞=+'02)(n n x)(02'=∑∞=+n n x)1(2'-=x x =22)1(2x x x --，1||<x 八、（本题满分8分）判断级数∑∞=-1241n nn 的敛散性．解 由=+∞→nn n u u 1lim 1441)1(l i m 212-⋅-++∞→n n n n n 141<= 故由正项级数的达朗贝尔判别法知级数收敛- 九、（本题满分10分）求微分方程xx x y y cos =+'的通解． 解 次微分方程为一阶线性微分方程 且x x p 1)(=，xxx Q cos )(= 则])([)()(C dx e x Q ey dx x p dxx p +=⎰⎰⎰-]cos [11C dx e x xe dxxdx x +=⎰⎰⎰- ]cos [ln ln C dx e xx ex x +=⎰- ]cos [1C xdx x xx +⋅=⎰ )(sin 1C x x+= -湖北汽车工业学院微 积 分 (一)（下） 考 试 卷（ 2014-2015-2 ）一、（本题满分21分，每小题3分）选择填空题（请将所选答案填入题号前的方括号内）： 【B 】1. 平面曲线2x y =与2y x =所围成的平面图形的面积为)(A21. )(B 31. )(C 32. )(D 43. 【C 】2．设)1,2,4(=，),2,2(k -=，若a 与b 相互垂直，则k 等于)(A 0. )(B 2-. )(C 3. )(D 4.【A 】3．设0≠a 为常数，则级数∑∞=-02)1(n n n)(A 绝对收敛． )(B 条件收敛． )(C 发散． )(D 敛散性无法判断．【A 】4. 积分⎰-=222sin ππxdx I 等于)(A2π. )(B 4π. )(C 8π. )(D 16π. 【B 】5. 设函数)1(),(-+=y x xy y x f 在点)31,31(处)(A 取极大值 . )(B 取极小值. )(C 不取极值. )(D 在该点不可微． 【D 】6. 设yx z =，则dz 等于)(A dy x xdx x dz y y +=ln . )(B ydy x xdx x dz y y ln ln +=. )(C dy x dx yx dz y y +=-1. )(D xdy x dx yx dz y y ln 1+=-． 【B 】7. 函数xx f -=21)(的马克劳林展开式的第三项为 )(A 222x . )(B 322x . )(C 222x -. )(D 322x -．二、（本题满分21分，每小题3分）填空题：1．=+⎰-112)sin (dx x e x x32． 2．过点)1,2,3(且与平面0132=++-z y x 平行的平面方程为0232=-+-z y x .3．设),(y x z z =是由方程z e z y x +=+22所确定的隐函数，则=dz )(12ydy xdx e z++ . 4．设⎰⎰+=Ddxdy y x f I )(22，其中D 是由曲线122=+y x ，直线x y =及y 轴所围成的第一象限的平面图形，则I 的极坐标系下的二次积分为:=I rdr r f d ⎰⎰1024)(ππθ．5．微分方程dx y dy x 221)1(-=+的满足条件1)0(=y 的特解为2arctan arcsin π+=x y .6．设数项级数∑∞=1n n u 的前n 项的和为1+=n n s n ，则级数的通项=n u )1(1+n n ． 7. 计算=⎰→2arctan limx tdt x x 21.三、 （8分）计算dx xx ⎰---11221． 解：22arcsin22212110112112112π==---=--⎰⎰⎰---x dx xx dx xdx xx ．四、（8分） 设函数)ln 1ln(y x z ++=，求),1(e xz ∂∂，),1(e yz∂∂．解：y x x z ln 11++=∂∂，)ln 1(1y x y x z ++=∂∂， 31),1(=∂∂e xz ，eyz e 31),1(=∂∂． 五、（8分）求微分方程x e x x yy )1(1+=+-'的通解. 解：方程变形为：xe x y x y =+-+'2)1(1 即 x e x y ='+)1(，C e x y x +=+1，通解为：))(1(C e x y x ++=．．六、（8分）判别级数∑∞=-+++-131322)1()1(n n n n n 的敛散性，并指出是绝对收敛还是条件收敛．解：332)1()1(31+++-=-n n n u n n ，取21n v n =，∑∞=121n n收敛，． +∞<=+++=∞→∞→21332)1(lim lim 32n n n n v u n nn n ，． 于是原级数收敛，且为绝对收敛。