3-2向量组的线性相关性

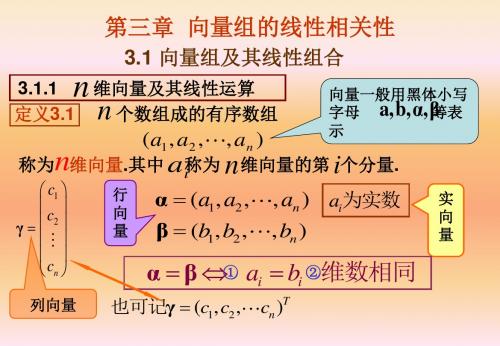
3.向量组的线性相关性与线性方程组的解§3.1 线性方程组解的判定1.定理3.1:n 元线性方程组AX=b ，其中A=(a 12a 12a 1n a 21a 22a 2na m1a m2a mn),x=( x 1x 2??x n ) ,b=( b 1b 2??b m )(1)无解的充要条件是R(A)＜R(A,b)；(2)有惟一解的充要条件是R(A)=R(A,b)=n ，(3)有无穷多解的充要条件是R(A)=R(A,b)＜n.注：(1)R(A,b)先化为行阶梯形，判别。

有解时再化为行最简形求解。

(2)R(A)=m 时，AX=b 有解。

(3)R(A)=r 时，有n-r 个自由未知量，未必是后面n-r 个。

2.定理3.2:n 元线性方程组AX=0(1)有惟一解（只有零解）的充要条件是R(A)=n ； (2)有无穷多解(有非零解)充要条件是R(A)＜n .注：(1)m ＜n,AX=0必有非零解。

3.定理3.3:矩阵方程AX=B 有解的充要条件是R(A)=R(A,B) 求解线性方程组例1. {4x 1+2x 2?x 3=23x 1?x 2+2x 3 =1011x 1+3x 2 =8例2. {2x 1+x 2?x 3+x 4 =14x 1+2x 2?2x 3+x 4=22x 1+x 2 ?x 3?x 4 =1例3. 求解齐次线性方程组{3x 1+ 4x 2?5x 3+ 7x 4 =02x 1?3x 2+3x 3? 2x 4 =04x 1+11x 2?13x 3+16x 4=07x 1?2x 2+ x 3+ 3x 4 =0例4.写出一个以X=C 1(2?310)+C 2(?2401)为通解的齐次线性方程组。

例5（每年）.（1）λ取何值时，非齐次线性方程组{ λx 1+x 2+x 3=1x 1+λx 2+x 3=λx 1+x 2+λx 3=λ2（1）有惟一解；（2）无解；（3）有无穷多组解？并在有无穷多组解时求出通解.（2）非齐次线性方程组{x 1+x 2+2x 3=02x 1+x 2+ax 3=13x 1+2x 2+4x 3=b当a,b 取何值时，（1）有惟一解；（2）无解；（3）有无穷多组解？并求出通解.例5(12/13学年).设A=(λ110λ?1011λ), b=(a11),已知Ax=b 存在两个不同的解：(1)求λ,a;(2)求Ax=b 的通解。

向量组线性相关性向量组线性相关性是数学中一个重要的概念，它可以在许多应用中使用，包括统计和线性代数。

它表明了两个变量是如何相互影响的，并且可以用来解释不同情况下变量之间的线性关系。

因此，了解这个概念对推断变量之间的关系非常重要。

在这篇文章中，我们将详细讨论向量组线性相关性的定义、特性和应用。

首先，我们将介绍什么是向量组，包括它的结构、特性和如何表示。

接下来，我们将讨论线性相关性的定义，它的两个重要特性，即相关系数和回归线。

最后，我们将讨论向量组线性相关性的应用，特别是在统计学中，它可以用来推断和预测数据集之间的关系。

首先，让我们来看看什么是向量组。

它是一组由单位矢量组成的数值，它们被称为标量。

向量组由坐标轴上的点组成，这些点的特性取决于它们的大小和关系。

例如，在二维空间中，每一个矢量都可以用它的横坐标和纵坐标来表示，这两个坐标是矢量的分量。

此外，矢量的大小是按照它们两个坐标的积来表示的，这个大小可以用简单的乘法计算，也可以用更复杂的三角函数计算。

其次，我们来讨论线性相关性。

线性相关性是指在两个变量之间存在线性关系的能力。

它可以用相关系数来表示。

相关系数是一个指标，表示两个变量的相关性。

它的值介于-1和1之间，-1表示完全负相关，1表示完全正相关，0表示无关。

因此，通过计算相关系数，可以了解两个变量之间的线性关系。

此外，另一个重要的线性相关性特性是回归线。

回归线是一条拟合两个变量之间线性关系的直线，它可以用来推测两个变量之间的关系。

通过画出回归线，可以更清楚地了解两个变量之间的关系，例如它们之间是线性相关还是非线性相关。

最后，我们来看看向量组线性相关性的应用。

它主要应用于统计学，用来推断和预测数据集之间的关系。

它也可以用来了解变量之间的线性依赖性，以及变量的趋势及其变化。

此外，它还可以用来帮助预测未来，因为它可以用来推断不同数据集之间的相关性。

总之，向量组线性相关性是一个非常重要的概念，它可以帮助我们了解变量之间的关系，推断不同数据集之间的关系，以及预测未来。

第3章n维向量和线性方程组向量是线性代数的重点内容之一，也是难点，对逻辑推理有较高的要求。

本章从研究向量的线性关系（线性组合、线性相关与线性无关）出发，然后讨论向量组含最多的线性无关向量的个数，即引出向量组的秩和最大无关组，最后，应用向量空间的理论研究线性方程组的解的结构。

无论是证明、判断、还是计算，关键在于深刻理解本章的基本概念，搞清楚其相互关系，并会灵活应用。

3. 1 n维向量及其运算定义（n维向量）由数域F中的n个数a-i,a2/ , a n组成的有序数组-■ - ( a i, a2, , a n)a2耳一称为数域F上的一个n维向量，前者称为行向量，后者称为列向量，其中a1, a2 / ,a n称为向量的分量（或坐标）。

分量是实（复）数的向量称为实（复）向量。

如果没有特殊的声明，以下所讨论指数域F上的向量。

行向量可以看成行矩阵，列向量看成列矩阵，向量的运算规定按矩阵的运算法则进行。

以下讨论的向量，再没有指明是行向量还是列向量时，都当作列向量。

设有向量■■ = （a i,a2,…，a n），- - （b1 ,b2 / , b n ）则向量相等的定义为- a i = b i （i=1,2,…,n）向量的加法定义为a + P =（a i +b i a? +b2 …a* +b n T数乘向量的定义为k：（「k）二（ka i,ka2, ,ka n）T向量的加法以及数乘运算统称为向量的线性运算，它满足下列8条运算规律（其中：■,'-,为n维向量，k,l为常数）：（1）二：+：= ：+=；)( :• - ) ( - )；(3)存在零向量0= ( 0,0，…，0 ) T，使得〉+0= ;(4)存在:-的负向量-二=(_a i,_a2,…，-a n)T,使得〉+ (-二)=0；(5)仁• = ：•；(6)k(l ： )=(kl):-;(7)k(: + 1 )=k +k :;(8)(k+l)用=k : +1 :;如果记矩阵A = (a j )m n的第j列向量为：a i ja2jQ j = : , (j=1,2,…,n)貝一则由向量的线性运算，可将方程组Ax=b写成下列形式：论一：* - X2J2…'x n J n二 b而齐次线性方程组A X=0则可写成向量形式：Xv 1 ■ X2： 2 …• X n： n = 03. 2向量组的线性相关性定义(线性组合)设宀，：^，…，〉m是一组n维向量，k1, k2/ ,k m是一组常数，则称向量kr 1 k2： 2 k m： m为向量〉1,〉2,i,〉m的一个线性组合，并称k1,k2 / , k m为该线性组合的系数。

由3个2维向量组成的向量组线性相关3个2维向量组线性相关是指，一组由3个2维向量组成的向量之间存在线性关系，即它们的线性组合可以表示为它们的标量积。

3个2维向量组线性相关是比较常见的，它们可以用投影和变换来实现，也可以用线性代数的方法来分析。

首先，我们简单地介绍一下什么是一个2维向量。

2维向量就是一条直线，由长度和方向（也可以称为角度）组成。

在数学中，它可以被表示为一个有两个分量的有序对，即（x,y）。

其中的x和y分量分别表示向量的横向长度和纵向长度。

其中，x为横向长度，即从原点（（0，0））沿着向量右侧的长度；y为纵向长度，即从原点（（0，0））沿着向量上部的长度。

接下来，我们可以用数学语言来描述什么是3个2维向量组线性相关。

假设，给定一组3个2维向量，即：A（x1，y1），B（x2，y2），C（x3，y3）。

若这3个2维向量之间存在线性关系，即，它们的线性组合可以用标量积来表示，则称这3个向量组线性相关。

如果这3个2维向量组中存在2个或2个以上的向量平行，则该组向量不存在线性相关性，只有当所有3个2维向量都不能表示为两个或两个以上的向量的线性组合时，才可以称为线性相关。

此外，3个2维向量组线性相关可以用几种方式来实现和分析。

投影法是一种比较简单的方法，它将3个2维向量映射到一个新的空间中，以形成一个新的“坐标系”，由新的“坐标系”可以更容易地确定3个2维向量之间的线性关系。

另一种是变换法，利用线性代数，将3个2维向量变换到一个新的基准空间，并利用新的基准空间来检验3个2维向量之间的线性关系。

最后，我们来看下3个2维向量组线性相关在实际中的一些应用。

由于3个2维向量构成的空间是一个简单的，它在很多领域都有应用。

比如在科学研究领域，它可以用来描述粒子的线性组合、在几何分析领域，它可以用来解决复杂的角度关系问题等；又如在技术制造方面，它可以用来表示组件的定位关系；在信息技术领域，它可以用来描述向量之间的线性关系等。