当前位置：文档之家 › 第7章应力状态和强度理论(答案)

第7章应力状态和强度理论(答案)

  • 格式：doc
  • 大小：562.00 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

材料力学带答疑

材料力学带答疑

第七章应力和应变分析强度理论1.单元体最大剪应力作用面上必无正应力答案此说法错误（在最大、最小正应力作用面上剪应力一定为零；在最大剪应力作用面上正应力不一定为零。

拉伸变形时，最大正应力发生在横截面上，在横截面上剪应力为零；最大剪应力发生在45度角的斜截面上，在此斜截面上正应力为σ/2。

）2. 单向应力状态有一个主平面，二向应力状态有两个主平面答案此说法错误（无论几向应力状态均有三个主平面，单向应力状态中有一个主平面上的正应力不为零；二向应力状态中有两个主平面上的正应力不为零）3. 弯曲变形时梁中最大正应力所在的点处于单向应力状态答案此说法正确（最大正应力位于横截面的最上端和最下端，在此处剪应力为零。

）4. 在受力物体中一点的应力状态，最大正应力作用面上切应力一定是零答案此说法正确（最大正应力就是主应力，主应力所在的面剪应力一定是零）5.应力超过材料的比例极限后，广义虎克定律不再成立答案此说法正确（广义虎克定律的适用范围是各向同性的线弹性材料。

）6. 材料的破坏形式由材料的种类而定答案此说法错误（材料的破坏形式由危险点所处的应力状态和材料的种类综合决定的）7. 不同强度理论的破坏原因不同答案此说法正确（不同的强度理论的破坏原因分别为：最大拉应力、最大线应变、最大剪应力、形状比能。

）二、选择1.滚珠轴承中，滚珠与外圆接触点为应力状态。

A：二向； B：单向C：三向D：纯剪切答案正确选择C（接触点在铅垂方向受压，使单元体向周围膨胀，于是引起周围材料对接触点在前后、左右方向的约束应力。

）2.厚玻璃杯因沸水倒入而发生破裂，裂纹起始于。

A：内壁 B：外壁 C：内外壁同时 D：壁厚的中间答案正确选择：B （厚玻璃杯倒入沸水，使得内壁受热膨胀，外壁对内壁产生压应力的作用；内壁膨胀使得外壁受拉，固裂纹起始于外壁。

）3. 受内压作用的封闭薄壁圆筒，在通过其壁上任意一点的纵、横两个截面中。

A：纵、横两截面均不是主平面； B：横截面是主平面、纵截面不是主平面；C：纵、横二截面均是主平面； D：纵截面是主平面，横截面不是主平面；答案正确选择：C （在受内压作用的封闭薄壁圆筒的壁上任意取一点的应力状态为二向不等值拉伸，其σx =pD/4t、σy=pD/2t。

材料力学 第07章 应力状态分析与强度理论

材料力学 第07章 应力状态分析与强度理论
2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时，导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= －txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心，CD（CD'） 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx－ sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

材料力学 第七章 应力状态和强度理论

材料力学 第七章 应力状态和强度理论

y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。

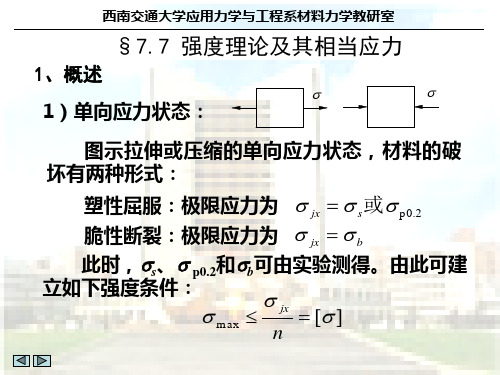
第7章-应力状态和强度理论03

第7章-应力状态和强度理论03

3）最大切应力理论(第三强度理论)
假设最大切应力max是引起材料塑性屈服的因 素，则：
max jx
对低碳钢等塑性材料，单向拉伸时的屈服是 由45°斜截面上的切应力引起的，因而极限应力 jx可由单拉时的屈服应力求得，即：
jx
因为： max
ss
2
常数
s1 s 3
对图示平面应力状态，不能分别用
s max [s ]
max [ ]
来建立，因为s与之间会相互影响。 研究复杂应力状态下材料破坏的原因，根据一 定的假设来确定破坏条件，从而建立强度条件，这 就是强度理论的研究内容。
4）材料破坏的形式 常温、静载时材料的破坏形式大致可分为： • 脆性断裂型： 例如： 铸铁：拉伸、扭转等； 低碳钢：三向拉应力状态。 • 塑性屈服型： 例如： 低碳钢：拉伸、扭转等； 铸铁：三向压缩应力状态。 可见：材料破坏的形式不仅与材料有关，还与 应力状态有关。


单拉： s r 4 3 s s s 由此可得： s
1
3 [ ] 0.577[s ] 0.6[s ]
s s 0.577s s
例：两端简支的工字钢梁承受荷载如图a所示。已 知材料（Q235钢）的许用应力为[s]=170MPa和[]= 100MPa。试按强度条件选择工字钢号码。
W 508 10 m
6
3
再按切应力强度条件进行校核。对28a号工 字钢，查表可得截面几何性质为：
I z 71.14 10 6 m 4
Iz S z ,max
d 0.85 10 m
2
24.62 10 2 m
中性轴处的最大切应力（纯剪应力状态）为：
max

材料力学第七章

材料力学第七章

若应力状态由主应力表示，并且在max 0 和 min 0 的情况下，则式（7-7） 成为
max min
max
min
2
1 3
2
进一步讨论，由式（7-4）和式（7-6）可知
tan
21
1 tan 20
上式表明1 与 0 之间有如下关系：
1
0
4
可见，切应力取得极值的平面与主平面之间的夹角为 45 。
若三个主应力中，只有一个主应力不等于零，这样的应力状态称为 单向应力状态。若三个主应力中有两个不等于零，称为二向应力状态或 平面应力状态。若三个主应力皆不为零，称为三向应力状态或空间应力 状态。
第二节 平面应力状态分析——解析法
一、斜截面上的应力
图 7-1 所示为平面应力状态的最一般情况。已知 x ， y ， xy 和 yx 。现 在研究图中虚线所示任一斜截面上的应力，设截面上外法向 n 与 x 轴的夹角 为 。
令 d /d 0 ，由式（7-1）可得
x
2
y
sin
2
xy
cos 2
0
解得
（7-3）
tan 20
2 xy x y
通过运算，可以得到斜截面上正应力的极值为
（7-4）
max min
x
y 2
x
2
y
2
2 xy
（7-5）
由式（7-4）可知， 取得极值的角0 有两个，二者相差 90 ，即最大正应 力 max 和最小正应力 min ，二者分别作用在两个相互垂直的截面上。当 0 ， 取得极值时，该斜截面上的切应力 0 ，即正应力就是主应力。
（a）
（b） 图7-6
例 7-4 悬臂梁受力如图 7-7（a）所示。试求截面 n n 上 A 点处的主应力 大小和方向，并按主平面画出单元体。

家电公司研发部资料材料力学习题答案(七)

家电公司研发部资料材料力学习题答案(七)

第七章 应力状态和强度理论7-1 围绕受力构件内某点处取出的微棱柱体的平面图如图所示，已知该点处于平面应力状态，AC 面上的正应力σ＝－14MPa ，切应力为零，试从平衡方程确定σx 和τx 值。

答：σx ＝37.9MPa ,τx ＝74.2MPa 解：利用公式求解x x x x x cos 2sin 222sin 2cos 22yyyαασσσσσατασστατα+-=+--=+代入数据得x x x x x 9292140.3430.94229200.940.3432σστστ+--=+⨯-⨯-=⨯+⨯σx ＝37.9MPa ,τx ＝74.2MPa7-2 试绘出图示水坝内A 、B 、C 三小块各截面上的应力（只考虑平面内受力情况）。

A: B: C:7-3 已知平面应力状态如图所示，已知σx ＝100MPa ，σy =40MPa,以及该点处的最大主应力σ1＝120MPa ，试用应力圆求该点处的τx 及另外两个主应力σ2，σ3和最大剪应力τmax。

答：MPa,60,0MPa,20max 32===τσσx τ＝40 MPa 解：由应力圆分析可得A BC题 7 - 2 图题 7 - 1 图111(100,),(40,),(,0)x x c D D C ττσ'-x 121004070MPa221207050MPa 705020MPayc c c r r σσσσσσσ++====-=-=∴=-=-=是平面应力状态3=0σ∴222x x 13max (100)40MPa120060MPa 22c r σττσστ∴=-+⇒=--===7-4 已知平面应力状态一点处互相垂直平面上作用有拉应力90MPa 和压应力50MPa ，这些面上还有剪应力，如果最大主应力为拉应力100MPa ，试求：(1) 上述面上的切应力； (2) 此平面上另一主应力； (3) 最大切应力平面上的正应力； (4) 最大切应力。

孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-应力状态和强度理论(圣才出品)

孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-应力状态和强度理论(圣才出品)
六、强度理论及其相当应力 强度理论是关于材料破坏规律的假设。材料破坏或失效的基本形式有两种： （1）脆性断裂：在没有明显的塑性变形情况下发生突然断裂的破坏形式； （2）塑性屈服：产生显著的塑性变形而使构件丧失正常的工作能力的破坏形式。 按照强度理论所建立的强度条件可统一写作：σr≤[σ]。常用强度理论分类及其主要内容 见表7-1-5。
一、应力状态概述（见表7-1-1） 表7-1-1 应力状态概述主要内容
二、平面应力状态的应力分析·主应力（见表7-1-2）
1 / 66
圣才电子书

十万种考研考证电子书、题库视频学习平台
表7-1-2 主应力主要内容
2 / 66
圣才电子书 十万种考研考证电子书、题库视频学习平台

三、空间应力状态的概念 对于受力物体内一点处的应力状态，最普遍的情况是所取单元体三对平面上都有正应力 和切应力，这种应力状态为一般的空间应力状态。在一般的空间应力状态中，有9个应力分 量，分别为正应力σx、σy、σz和切应力τxy、τyx、τxz、τzx、τyz、τzy，其中τxy＝τyx、τxz＝τzx、 τyz＝τzy。 四、应力与应变间的关系（见表7-1-3）
τA＝M2/Wp＝16×78.6/（π×0.023）Pa＝50MPa
σA＝M1/Wz＝32×39.3/（π×0.023）Pa＝50MPa
A 点单元体如图 7-2-2（d）所示。
图 7-2-2（d）
7-2 有一拉伸试样，横截面为 40mm×5mm 的矩形。在与轴线成 α＝45°角的面上 切应力 τ＝150MPa 时，试样上将出现滑移线。试求试样所受的轴向拉力 F 的数值。

B
=
FS 2Iz
( h2 4
−
y2)

7工程力学(下)—应力状态和强度理论1

7工程力学(下)—应力状态和强度理论1

σα =
σx +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
7.2 平面应力状态
对于斜截面的切线t参考轴列平衡方程为 对于斜截面的切线 参考轴列平衡方程为 ΣFt = 0, τ α d A − (σ x d A cos α ) sin α − (τ x d A cos α ) cos α + (σ y d A sin α ) cos α
σα =
σ x + σ y σ x −σ y
2 + 2
cos 2α −τ x sin 2α
τα =
σ x −σ y
2
sin2α +τ x cos2α
2 求正应力的极值
σ x −σ y dσ α = −2[ sin 2α + τ x cos 2α ] = 0 令: dα 2
比较可知, 极值正应力所在的平面, 比较可知 极值正应力所在的平面 就是切应力 τα为零的平面。这个切应力等于零的平面 叫做 为零的平面。这个切应力等于零的平面, 主平面, 主平面上的正应力, 叫做主应力。也就 主平面 主平面上的正应力 叫做主应力。 主应力 是说, 在通过某点的各个平面上, 是说 在通过某点的各个平面上 其中的最大正 应力和最小正应力就是该点处的主应力。 应力和最小正应力就是该点处的主应力。 表示主平面的法线n与 轴间的夹角 轴间的夹角, 以α0表示主平面的法线 与x轴间的夹角 由上式 可得 −2τ x tan 2α 0 = σ x −σ y
σ α = σ x cos 2 α + σ y sin 2 α − 2τ x sin α cos α
又由三角关系: 又由三角关系

材料力学 第七章 应力状态与强度理论

材料力学 第七章 应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明） 有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2

第七章应力状态习题答案

第七章应力状态习题答案

( 2 ）图解法作应力圆如题 7 . 4 图（ d 1）所示。应力圆与 σ 轴的两个交点的坐标，即是 σ 1 、 σ 3 的数 值。由 CDx ，顺时针旋转 2α 0 ，可确定主平面的方位。 CDx 的长度即为最大切应力的数值。主应力单 元体如题 7 . 4 图（d2）所示。
5
( e ）如题 7 . 4 图（ e ）所示。
τα =
σ x −σ y
2
⎛ 100 − 50 ⎞ sin 2α + τ xy cos 2α = ⎜ sin120D + 0 ⎟ MPa = 21.7 MPa 2 ⎝ ⎠
( 2 ）图解法 作应力圆如题 7 . 3 图（ cl ）所示。从图中可量得 Dα 点的坐标，此坐标便是 σ α 和 τ α 数值。 ( d ）如题 7 . 3 图（ d ）所示。
按照主应力的记号规定
σ 1 ＝4.7MPa， σ 2 ＝0， σ 3 ＝－84.7MPa
tan 2α 0 = − 2τ xy
σ x −σ y
=
=
−2 × 20 = −0.5 ， α 0 ＝－13.3° 0 + 80
τ max =
σ1 − σ 3
2
4.7 + 84.7 MPa = 44.7 MPa 2
。
1
斜截面 AB 与 x 平面的夹角 a2 = 105 ，其上应力 σ a2＝45MPa,τ a = 25 3MPa 。将这些数据代入斜截面
。
2
上应力公式中，对 AB 斜截面有
σx +σ y
2
+
σ x −σ y
2
cos 210。− τ xy sin 210。= 45 ①
σ x −σ y

材料力学第七章

材料力学第七章
2

x y
2
cos 2 x sin 2

x y
2
sin 2 x cos 2
补充例 题1
T
图示圆轴中，已知：圆轴直径d=100mm， 轴向拉 力F=500kN，外力矩Me=7kN· m。 求C点 =30°截面上的应力。
y T
y
F x
F
C
x
第7章
应力状态和强度理论
§7-1 概 述
低 碳 钢 拉 伸 试 验
铸 铁 拉 伸 试 验
低 碳 钢 扭 转 试 验
铸 铁 扭 转 试 验
1、一点处的应力状态
构件内一点处各截面方向上的应力的情况，称 为该点的应力状态。可由围绕该点的一个单元体面 上的应力表示。
目的：通过应力状态分析求出该点处的 max 、 max 及 其作用面，从而更好地进行强度分析。
30
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
分析轴向拉伸杆件的最大切应力的作用面，说 补充例 明低碳钢拉伸时发生屈服的主要原因。 题3
低碳钢拉伸时，其上任意一点都是单向应力状态。
x

x y
2

x y
2
cos 2 x sin 2

x
单元体如何取？ 在研究点的周围，取一个由三对互相垂直的平 面构成的六面体，该六面体的边长分别为无穷小量 dx、dy和dz，如下图所示。
y
dz dx dy x
z
单元体每个面上应力均布；每对相互平行面上的 性质相同的应力大小相等；可用截面法求任一截面上 的应力。
根据单元体的局部平衡：
y
n


y

材料力学习题册答案-第7章 应力状态

材料力学习题册答案-第7章 应力状态

第 七 章 应力状态 强度理论一、 判断题1、平面应力状态即二向应力状态，空间应力状态即三向应力状态。

(√)2、单元体中正应力为最大值的截面上，剪应力必定为零。

(√)3、单元体中剪应力为最大值的截面上，正应力必定为零。

(×) 原因：正应力一般不为零。

4、单向应力状态的应力圆和三向均匀拉伸或压缩应力状态的应力圆相同，且均为应力轴 上的一个点。

(×) 原因：单向应力状态的应力圆不为一个点，而是一个圆。

三向等拉或等压倒是为一个点。

5、纯剪应力状态的单元体，最大正应力和最大剪应力值相等，且作用在同一平面上。

(×) 原因：最大正应力和最大剪应力值相等，但不在同一平面上6、材料在静载作用下的失效形式主要有断裂和屈服两种。

(√)7、砖,石等脆性材料式样压缩时沿横截面断裂。

(×)8、塑性材料制成的杆件，其危险点必须用第三或第四强度理论所建立的强度条件来校核强度。

(×) 原因：塑性材料也会表现出脆性，比如三向受拉时，此时，就应用第一强度理论9、纯剪应力状态的单元体既在体积改变，又有形状改变。

(×) 原因：只形状改变，体积不变10、铸铁水管冬天结冰时会因冰膨胀被胀裂，而管内的冰不会被破坏，只是因为冰的强度比铸铁的强度高。

(×) 原因：铸铁的强度显然高于冰，其破坏原因是受到复杂应力状态 11．圆杆受扭时，杆内阁点处于纯剪切状态。

（√）12．受扭圆轴内最大拉应力的值和最大切应力的值相等。

(√)二、 选择题1、危险截面是（ C ）所在的截面。

A 最大面积B 最小面积C 最大应力D 最大内力2、关于用单元体表示一点处的应力状态，如下论述中正确的一种是( D )。

A 单元体的形状可以是任意的B 单元体的形状不是任意的，只能是六面体微元C 不一定是六面体，五面体也可以，其他形状则不行D 单元体的形状可以是任意的，但其上已知的应力分量足以确定任意方向面上的硬力 3、受力构件内任意一点，随着所截取截面方位不同，一般来说（ D ） A 正应力相同，剪应力不同 B 正应力不同，剪应力相同 C 正应力和剪应力均相同 D 正应力和剪应力均不同 4、圆轴受扭时，轴表面各点处于（ B ）A 单向应力状态B 二向应力状态C 三向应力状态D 各向等应力状态 5、分析处于平面应力状态的一点，说法正确的是（ B ）。

材料力学-07-应力分析和强度理论

材料力学-07-应力分析和强度理论

§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
1.斜截面上的应力 1.斜截面上的应力
y
σx
a
τ yx
τ xy
σx α
τa
n
τ xy
σa
dA
x
σy
n
τ yx
σy
t
t
∑F = 0
∑F =0
13
§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
tan 2α0 = − 2τ xy
σ x −σ y
由上式可以确定出两个相互垂直的平面， 由上式可以确定出两个相互垂直的平面，分别 为最大正应力和最小正应力所在平面。 为最大正应力和最小正应力所在平面。 所以，最大和最小正应力分别为： 所以，最大和最小正应力分别为：
σmax = σ x +σ y
2 1 + 2 − 1 2
单元体
单元体——构件内的点的代表物， 单元体——构件内的点的代表物，是包围被研究点的 ——构件内的点的代表物 无限小的几何体。 常用的是正六面体。 无限小的几何体。 常用的是正六面体。 单元体的性质—— 平行面上，应力均布； 单元体的性质——1) 平行面上，应力均布； —— 2) 平行面上，应力相等。 平行面上，应力相等。
2 2
σy
τ xy
α
60 − 40 60 + 40 = + cos(−60o ) + 30 sin(−60o ) 2 2
σx
= 9.02 MPa
τα =
σ x −σ y
2 60 + 40 = sin(−60o ) − 30 cos(−60o ) 2

第七章：应力状态、强度理论

第七章：应力状态、强度理论

s
2 2
s
2 3
2 s1s 2
s 3s 2
s1s 3 )
1 t 2 0 (t )2 2 0 0 t (t ))
2E
s1
1 t 2
E
G
E
21
)
§7–6 强度理论及其相当应力
强度理论：是关于“材料发生强度破坏或失效”的假设
材料的破坏形式： ⑴ 脆性断裂 如铸铁在拉伸和扭转时的突然断裂 ⑵ 塑性屈服 如低碳钢在拉伸和扭转时明显的塑性变形
sx
t 绕研究对象顺时针转为正；
y
txy
逆时针为正。
Ox
图1
s
sx
y
sy
ttxy
Ox 图2
设：斜截面面积为dA，由分离体平衡得：
Fn 0
n s dA (t xydAcos )sin (s xdAcos ) cos t (t yxdAsin ) cos (s ydAsin )sin 0
容器表面用电阻应变片测得环向应变 t =350×10-6，若已知容器平均 直径D=500 mm，壁厚=10 mm，容器材料的 E=210GPa，=0.25
试求:1.导出容器横截面和纵截面上的正应力表达式； 2.计算容器所受的内压力。
s1 sm
p p
p
x
l
图a
D
y
xp
AO
B
解：容器的环向和纵向应力表达式 1、轴向应力:(longitudinal stress) 用横截面将容器截开，受力如图b所示,根据平衡方程
第七章 应力状态和强度理论
§7–1 概述 §7–2 平面应力状态的应力分析.主应力 §7–3 空间应力状态的概念
§7–4 复杂应力状态下的应力 -- 应变关系 ——（广义虎克定律）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1
7.1已知应力状态如图所示（单位：MPa ），试求：
⑴指定斜截面上的应力； ⑵主应力；
⑶在单元体上绘出主平面位置及主应力方向； ⑷最大切应力。

解：100x MPa σ=200y MPa σ=
100x MPa τ=0
30α=-
（1）cos 2sin 2211.622
x y
x y
x
ασσσσ
σατα+-=
+
-=sin 2cos 293.32
x y
x MPa ασστατα-=+=
（2）max 261.82
x y
MPa σσσ+=
=
min 38.22x y
MPa σσσ+==
MPa 8.2611=σMPa 2.382=σ03=σ
（3）13
max 130.92
MPa σστ-==
7.2扭矩m kN T ⋅=5.2作用在直径mm D 60=的钢轴上，试求圆轴表面上任一点与母线成ο
30=α方向上的正应变。

设E=200GPa,0.3υ=。

解：表面上任一点处切应力为：
max 59P
T
MPa W τ=
= 表面上任一点处单元体应力状态如图
30sin 251MPa στα=-=-
120sin 251MPa στα=-=
()
00430301201
3.310E
εσυσ-=
-=⨯
2στ
τ
7.3用电阻应变仪测得空心钢轴表面某点与母线成ο
45方向上的正应变4
100.2-⨯=ε，已知转速min /120r ，G=80GPa ，试求轴所传
递的功率。

解：表面任一点处应力为
max 9550P
P
P T n W W τ==
max 9550
P W n
P τ∴=
纯剪切应力状态下，0
45斜截面上三个主应力为：1στ=20σ=3στ=-
由广义胡克定律 ()11311E E υ
εσυστ+=
-=
又()
21E G υ=+Q V 2G τε∴= 代入max 9550
P W n
P τ=
，得109.4P KW =
7.4图示为一钢质圆杆，直径mm D 20=，已知A 点与水平线成ο
60
方向上的正应变4
60101.4-⨯=ο
ε，E=200GPa ，0.3υ=，
试求荷载P 。

解：0P
A
σ=204D P πσ=⋅
斜截面上 02
060cos
4
σσσα==
2001503cos 4
σσσα==
由广义胡克定律
()
0006015060134E E
υεσυσσ-=
-= 将060043E εσυ
=
-代入2
04
D P πσ=⋅
解得P=36.2KN
ο
3
7.5在一槽形刚体的槽内放置一边长为mm 10的正立方钢块，钢块与槽壁间无孔隙，当钢块表面受kN 6的压力（均匀分布在上表面）时，试求钢块内任意点的主应力。

已知
33.0=μ。

解：坐标系如图所示 易知： 0x ε=0y σ=z P A
σ=- 由广义胡克定律
()1
x x y z E εσυσσ⎡⎤=
-+⎣
⎦
()1y y x z E
εσυσσ⎡⎤=-+⎣⎦ ()1
z z x y E
εσυσσ⎡⎤=-+⎣⎦ 解得 19.8x MPa σ=-0y σ=60z MPa σ=- 可知刚块内任一点的主应力为
10σ=219.8MPa σ=-360MPa σ=-
7.6试对铸铁零件进行强度校核。

已知：MPa t 30][=σ，
30.0=μ，危险点的主应力为：
MPa 29][1=σ，MPa 20][2=σ，MPa 20][3-=σ.
解：由题意，对铸铁构件应采用第一或第二强度理论 第一强度理论：[]129t MPa σσ=p
第二强度理论：()[]12329t MPa σμσσσ-+=p
Y
X
Z
故零件安全。

7.7圆杆如图所示，已知mm d 10=，Pd T 10
1
=，试求许用荷载P 。

若材料为：
⑴ 钢材，MPa 160][=σ； ⑵ 铸铁，MPa t 30][=σ。

解：此为拉扭组合变形，危险点全部在截面周线上，应力状态如图
2
4P P A d σπ=
=21610p
T P W d τπ==
（1） 钢材 由第三强度理论[]2234r σστσ=+≤，得P=9.8KN
（2） 铸铁 由第一强度理论[]2211
42
2
r t σ
σστσ=
+
+≤，得P=1.32KN 7.8某种圆柱形锅炉，平均直径为mm 1250，设计时所采用的工作内压为23个大气压，在工作温度下的屈服极限MPa s
5.182=σ，
若安全系数为8.1，试根据第三强度理论设计锅炉的壁厚。

解：设该锅炉为薄壁圆筒结构，壁厚为δ，由题意容器承受的内压为
230.1 2.3P MPa =⨯= （一个大气压=0.1MPa ）
由薄壁圆筒的特点，可认为圆筒横截面上无切应力，而正应力沿壁厚和圆周都均匀分布，于是得圆筒横截面上的正应力为
T
P
δ
δσ4π4π2pD D D p A F =⨯=='τ
5
圆筒径向截面（纵截面）上的正应力，单位长度圆筒中以纵截面取的分离体如图所示
()''221P N F F PD σδ==⨯⨯⨯=
得 ''
2PD
σδ
=
圆筒内壁上沿半径方向的正应力为 '''
P σ=-
故 12PD σδ=
24PD σδ=
3P σ=-由薄壁圆筒的特点，4PD
δ
远大于P ,可认为30σ=。

由第三强度理论[]3132s r PD
n
σσσσσδ=-=≤=， 解得14.2mm δ≥
7.9在矩形截面钢拉伸试样的轴向拉力KN F 20=时，测得试样中段B 点处与其轴线成030方向的
线应变为
4301025.30
-⨯=ε。

已知材料
的弹性模量a GP E 210=，试求泊松比。

解：0100F
MPa A
σ=
= 0
2030cos 75MPa σσα==0
20120cos 25MPa σσα==
由广义胡克定律
0030301201E
εσυσ⎡⎤=
-⎣⎦ 解得0.27υ=
7.10mm D 120=,mm d 80=的空心圆轴，两端承受一对扭转力偶矩e M ，如图所示。

在轴的中部表面A 点处，测得与其母线成045方向的线应变为445106.20
-⨯=ε。

已知材料的
D
弹性常数a GP E 200=，3.0=ν。

试求扭转力偶矩e M 。

解：A 点处切应力e P P
M T
W W τ=
= 应力状态及主应力单元体如图
1στ=，20σ=，3στ=-
()0
1134511E E
υεεσυστ+==
-= 代入相关数据，解得
10.9e M KN m =•。

相关主题