练习

一年级体育练习(可直接打印)以下是一些适合一年级学生的体育练，帮助他们发展身体素质和锻炼身体。

这些练可以在学校或家庭进行，无需特殊设备。

请教师或家长监督学生进行这些练，确保他们的安全和正确的执行。

热身运动在进行任何体育练之前，请确保学生进行适当的热身运动。

这些热身运动有助于预防运动伤害，并提高身体的柔韧性和血液循环。

- 跳绳：让学生跳绳2-3分钟，以提高心率和热身身体。

- 摇臂运动：让学生站直，双臂伸直放在身体两侧。

用力摇动双臂，每侧10次，以活动手臂肌肉。

- 踮脚尖走：让学生踮起脚尖，以小步跑的方式向前走，保持身体稳定，重复10次，以锻炼小腿肌肉。

跑步练跑步是锻炼心肺功能和增强体力的好方法。

以下是一些适合一年级学生的跑步练。

- 短跑：在操场或者指定地点，划定一段短跑的距离（例如50米），让学生进行短跑练。

鼓励他们全力冲刺，但在安全范围内。

- 长跑：为学生规划一段较长的跑步路线，例如操场一圈或者一条合适的步行道。

鼓励他们用合适的速度跑完这段距离，并逐渐增加跑步时间。

平衡练平衡练有助于培养学生的身体协调能力和稳定性。

- 单脚站立：让学生单脚站立，保持平衡的同时抬起另一只脚，保持10秒钟。

然后换脚进行练。

- 走直线：在地面上用粉笔或者绳子画一条直线，让学生沿直线走。

鼓励他们保持平衡和稳定，并尽量不离开直线。

球类练球类运动可以培养学生的手眼协调能力和团队合作能力。

- 投篮练：为学生提供一个合适的高度的篮球架，让他们进行投篮练。

可以使用合适大小的篮球或者软球进行投篮。

- 传球练：组织学生之间进行传球练。

可以使用足球、篮球或者其他适合的球进行练。

拉伸运动和冷却在结束体育练之前，学生需要进行适当的拉伸运动和冷却。

- 大腿拉伸：让学生用一只手抓住一只脚的脚踝，将脚后跟向臀部拉伸，保持10秒钟，然后换脚进行练。

- 拉伸手臂和肩膀：让学生伸直一只手臂，用另一只手臂扶住伸直的手臂肘部，然后轻轻向身体的反方向拉伸，保持10秒钟，然后换手进行练。

被动操1、扩胸运动：仰卧，双手握住宝宝双手的腕部，让宝宝握住家长的大拇指，两臂放于身体两侧。

第1拍将双手向外平展与身体成90°，掌心向上；第2拍两臂向胸前交叉。

2、弯臂运动：仰卧，双手握住宝宝双手的腕部，让宝宝握住家长的大拇指，两臂放于身体两侧。

第1拍将左臂肘关节前屈；第2拍将左肘关节伸直还原；第3、4拍换右手屈伸肘关节，还原。

3、绕臂运动：仰卧，双手握住宝宝双手的腕部，让宝宝握住家长的大拇指，两臂放于身体两侧。

第1-3拍将左臂弯曲贴近身体，以肩关节为中心，由内向外做回环动作，第4拍还原；第5-8拍换右手，动作相同。

4、伸臂运动：仰卧，双手握住宝宝双手的腕部，让宝宝握住家长的大拇指，两臂放于身体两侧。

第1拍两臂向外平展，掌心向上；第2拍两臂向胸前交叉；第3拍两臂上举过头，掌心向上；第4拍还原。

5、翘脚运动：仰卧，左手操作宝宝的左踝部，右手握住左足前掌。

第1拍将宝宝足尖向上，屈曲踝关节；第2拍足尖向下伸展踝关节；连续做8拍。

后8拍换右足，做伸展右踝关节动作。

（注意：伸屈时动作要求自然，切勿用力过猛。

）6、屈腿运动：仰卧，家长两手分别握住宝宝的两个膝关节下部。

第1拍屈宝宝左膝关节，使膝缩近腹部；第2拍伸直左腿；第3、4拍屈伸右膝关节。

左右轮流，模仿蹬车动作。

（注意：屈膝时稍帮助宝宝用力，伸直时动作放松。

）7、举腿运动：仰卧，两下肢伸直平放，家长两掌心向下，握住宝宝两膝关节。

第1、2拍将两下肢伸直上举90°，第3、4拍还原。

（注意：两下肢伸直上举时臀部不离开地垫，动作轻缓。

）8、翻身运动：仰卧并腿，两臂屈曲放在胸前，家长左手扶胸腹部，右手垫于宝宝背部。

第1、2拍轻轻地将宝宝从仰卧转为左侧卧，第3、4拍还原。

第5～8拍家长换手将宝宝从仰卧转为右侧卧，还原。

（注意：俯卧时宝宝的两臂自然地放在胸前，使头抬高。

）9、起坐运动：仰卧，家长双手握住宝宝双手，或用右手握住宝宝左手，左手按住宝宝双膝。

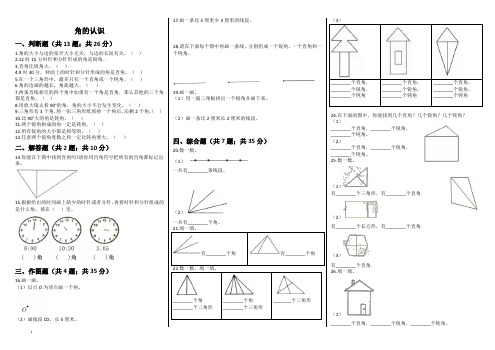
角的认识一、判断题（共13题；共26分）1.角的大小与边的张开大小无关，与边的长短有关。

（）2.12时15分时针和分针形成的角是锐角。

3.直角比锐角大。

（）4.9时30分，钟面上的时针和分针形成的角是直角。

（）5.在一个三角形中，最多只有一个直角或一个钝角。

（）6.角的边画的越长，角就越大。

（）7.两条直线相交的四个角中如果有一个角是直角，那么其他的三个角都是直角。

（）8.用放大镜去看90°的角，角的大小不会发生变化。

（）9.三角形有3个角，将一张三角形纸剪掉一个角后，还剩2个角。

（）10.比90°大的角是钝角。

（）11.两个锐角拼成的角一定是钝角．（）12.所有锐角的大小都是相等的。

（）13.任意两个锐角度数之和一定比钝角要大。

（）二、解答题（共2题；共10分）14.你能在下图中找到直角吗?请你用直角符号把所有的直角都标记出来。

15.根据给出的时间画上缺少的时针或者分针，再看时针和分针组成的是什么角，填在（）里。

三、作图题（共4题；共35分）16.画一画。

（1）以点O为顶点画一个角。

（2）画线段CD，长5厘米。

17.画一条比5厘米少3厘米的线段。

18.请在下面每个图中再画一条线，分别组成一个锐角、一个直角和一个钝角。

19.画一画。

（1）用一副三角板拼出一个锐角并画下来。

（2）画一条比2厘米长2厘米的线段。

四、综合题（共7题；共35分）20.数一数。

（1）一共有________条线段。

（2）一共有________个角。

21.填一填。

有________个角有________个角22.数一数，填一填。

________个角________个三角形________个角________个三角形_______个三角形________个直角，________个锐角，________个钝角________个直角，________个锐角，________个钝角________个直角，________个锐角，________个钝角24.在下面的图中，你能找到几个直角？几个锐角？几个钝角？（1）________个直角，________个锐角，________个钝角。

练习的反义词基本解释[释义](1) 基本义：(动)反复学习;以求熟练。

练习武艺。

(作谓语)(2) (名)为巩固学习效果而安排的作业等。

[构成]并列式：练+习[例句]练习题。

(作定语)交练习。

(作宾语)近义词实习、操练、操演、演习、老练、熟习、纯熟、练、熟练、进修、研习、学习反义词生疏英文翻译1.(反复学习) practise; practice2.(习题或作业等) exercise详细解释◎ 练习liànxí[practice;practise] 为了获得熟练技巧而经常进行某种动作练习大刀练习射击◎ 练习liànxí[exercise] 习题或作业(如一篇)拼音练习(1).操练;训练。

《三国志·魏志·张范传》：“士不素抚，兵不练习，难以成功。

”《北齐书·高昂传》：“ 敖曹所将部曲，练习已久。

” 元李文蔚《蒋神灵应》第一折：“开田畴，练习军士。

” 清黄遵宪《陆军官学校开校礼成》诗：“制胜非有他，所贵在练习。

”(2).反复学习，以求熟练。

《英烈传》第六八回：“你做父亲，不令练习女工，反事末务!”《老残游记》第七回：“当初传下这个拳法来的时候，专为和尚们练习了这拳，身体可以结壮，精神可以悠久。

” 老舍《月牙儿》十三：“我的字还需要练习。

”(3).熟悉谙习。

《晋书·胡毋辅之传》：“父原，练习兵马，山涛称其才堪边任。

”《北史·阎毗传》：“ 帝嗣位，盛修军器，以毗性巧，练习旧事，詔典其职。

” 宋司马光《赠卫尉少卿司马府君墓表》：“驾部君宽厚有守，练习法令，善为政吏，民不能欺。

”《明史·高拱传》：“ 拱练习政体，负经济才，所建白皆可行。

”。

根的判别式练习题一．填空题（共9小题）1．方程x2﹣5x﹣1＝0的根的判别式的值为．2．若关于x的方程x2﹣mx+m＝0有两个相等的实数根，则m的值为．3．已知关于x的一元二次方程x2﹣2x+k＝0有两个相等的实数根，则k的值为．4．若关于x的一元二次方程k2x2+（4k﹣1）x+4＝0有两个不同的实数根，则k的取值范围是．5．等腰三角形ABC的三条边长分别为4，a，b，若关于x的一元二次方程x2+（a+2）x+6﹣a＝0有两个相等的实数根，则△ABC的周长是．6．等腰△ABC中，BC＝8，AB、AC的长是关于x的方程x2﹣10x+m＝0的两根，则m的值是．7．如果恰好只有一个实数a是方程（k2﹣9）x2﹣2（k+1）x+1＝0的根，则k的值为．8．若方程x2+2（1+a）x+3a2+4ab+4b2+2＝0有实根，则＝9．已知双曲线y＝与直线y＝﹣x+1没有交点，则b的取值范围是．二．解答题（共5小题）10．已知关于x的一元二次方程．（1）求证：对于任意实数m，该方程总有两个不相等实数根；（2）如果此方程有一个根为0，求m的值．11．已知关于x的方程（k﹣2）x2﹣2x+1＝0有两个实数根．（1）求k的取值范围；（2）当k取最大整数时，求此时方程的根．12．已知关于x的一元二次方程2x2﹣3mx+m2+m﹣3＝0（m为常数）．（1）求证：无论m为何值，方程总有两个不相等的实数根：（2）若x＝2是方程的根，则m的值为．13．已知：关于x的一元二次方程x2﹣（3m+1）x+2m2+m＝0（1）求证：无论m取何值，这个方程总有实数根；（2）若△ABC的两边的长是这个方程的两个实数根，第三边的长为3，当△ABC为等腰三角形时，求m的值及△ABC的周长．14．已知关于x的方程x2﹣（k+2）x+2k＝0．（1）试说明：无论k取什么实数值，方程总有实数根．（2）若等腰△ABC的一边长a为1，另两边长b、c恰好是这个方程的两个实数根，求△ABC的周长？参考答案与试题解析一．填空题（共9小题）1．方程x2﹣5x﹣1＝0的根的判别式的值为29．【分析】根据方程的系数结合根的判别式，可得出Δ＝29，此题得解．【解答】解：∵a＝1，b＝﹣5，c＝﹣1，∴Δ＝b2﹣4ac＝（﹣5）2﹣4×1×（﹣1）＝29．故答案为：29．【点评】本题考查了根的判别式，牢记根的判别式Δ＝b2﹣4ac是解题的关键．2．若关于x的方程x2﹣mx+m＝0有两个相等的实数根，则m的值为0或4．【分析】根据方程的系数结合根的判别式Δ＝0，即可得出关于m的方程，解之即可求出m的值．【解答】解：∵关于x的方程x2﹣mx+m＝0有两个相等的实数根，∴Δ＝（﹣m）2﹣4×1×m＝0，解得：m1＝0，m2＝4，∴m的值为0或4．故答案为：0或4．【点评】本题考查了根的判别式，牢记“当Δ＝0时，方程有两个相等的实数根”是解题的关键．3．已知关于x的一元二次方程x2﹣2x+k＝0有两个相等的实数根，则k的值为2．【分析】由关于x的一元二次方程x2﹣2x+k＝0有两个相等的实数根，即可得判别式Δ＝0，继而可求得k的值．【解答】解：∵关于x的一元二次方程x2﹣2x+k＝0有两个相等的实数根，∴Δ＝b2﹣4ac＝（﹣2）2﹣4×1×k＝8﹣4k＝0，解得：k＝2，故答案为：2．【点评】此题考查了一元二次方程判别式的知识．此题比较简单，注意掌握一元二次方程有两个相等的实数根，即可得Δ＝0．4．若关于x的一元二次方程k2x2+（4k﹣1）x+4＝0有两个不同的实数根，则k的取值范围是且k≠0．【分析】根据一元二次方程的定义及根的判别列出不等式组求解即可．【解答】解：根据题意可知，．解得：且k≠0，故答案为：且k≠0．【点评】本题主要考查一元二次方程的定义及根的判别式，根据题意列出不等式组是解题的关键．5．等腰三角形ABC的三条边长分别为4，a，b，若关于x的一元二次方程x2+（a+2）x+6﹣a＝0有两个相等的实数根，则△ABC的周长是10．【分析】根据根的判别式的意义得到Δ＝（a+2）2﹣4（6﹣a）＝0，进而可由三角形三边关系定理确定等腰三角形的三边长，即可求得其周长．【解答】解：根据题意得Δ＝（a+2）2﹣4（6﹣a）＝0，解得a1＝﹣10（负值舍去），a2＝2，在等腰△ABC中，①4为底时，则b＝a＝2，∵2+2＝4，∴不能组成三角形；②4为腰时，b＝4，∵2+4＞4，∴能组成三角形，∴△ABC的周长＝4+4+2＝10．综上可知，△ABC的周长是10．故答案为：10．【点评】此题考查了根的判别式、等腰三角形的性质及三角形三边关系定理；在求三角形的周长时，不能盲目的将三边相加，而应在三角形三边关系定理为前提条件下分类讨论，以免造成多解、错解．6．等腰△ABC中，BC＝8，AB、AC的长是关于x的方程x2﹣10x+m＝0的两根，则m的值是25或16．【分析】等腰△ABC中，BC可能是方程的腰也可能是方程的底边，应分两种情况进行讨论．当BC是底边时，AB＝AC，则方程x2﹣10x+m＝0有两个相等的实根，即Δ＝0，即可得到关于m的方程，求得m的值；当BC是腰时，则方程一定有一个解是x＝8，根据一元二次方程的根与系数的关系即可求得另一边，即底边与m的值．【解答】解：在方程x2﹣10x+m＝0中，x1+x2＝10，当这两边是等腰三角形的腰时，有x1＝x2＝5，∴x1x2＝25＝m，当这两边的长有一边为8时，有8+x2＝10，∴x2＝2，m＝x1x2＝2×8＝16，∴m＝25或16．故答案为：25或16．【点评】本题考查了一元二次方程的根与系数的关系及等腰三角形中有两边相等的性质，关键掌握x1，x2是方程x2+px+q＝0的两根时，x1+x2＝﹣p，x1x2＝q．7．如果恰好只有一个实数a是方程（k2﹣9）x2﹣2（k+1）x+1＝0的根，则k的值为±3或﹣5．【分析】分原方程是一元一次方程和一元二次方程两种情况讨论即可得到答案．【解答】解：①当原方程是一个一元一次方程时，方程只有一个实数根，则k2﹣9＝0，解得k＝±3，②如果方程是一元二次方程时，则方程有两个相等的实数根，即Δ＝b2﹣4ac＝0，即：4（k+1）2﹣4（k2﹣9）＝0解得：k＝﹣5．故答案为±3或﹣5．【点评】本题考查了根的判别式，同时还考查了分类讨论思想，是一道好题．8．若方程x2+2（1+a）x+3a2+4ab+4b2+2＝0有实根，则＝﹣．【分析】由二次方程有实根，得到△≥0，即Δ＝4（1+a）2﹣4（3a2+4ab+4b2+2）≥0，通过代数式变形可得两个非负数的和小于或等于0，从而得到a，b的方程组，解方程组即可求出它们的比．【解答】解：∵方程有实根，∴△≥0，即Δ＝4（1+a）2﹣4（3a2+4ab+4b2+2）≥0，化简得：2a2+4ab+4b2﹣2a+1≤0，∴（a+2b）2+（a﹣1）2≤0，而（a+2b）2+（a﹣1）2≥0，∴a+2b＝0，a﹣1＝0，解得a＝1，b＝﹣，所以＝﹣．故答案为﹣．【点评】本题考查了一元二次方程ax2+bx+c＝0（a≠0，a，b，c为常数）根的判别式Δ＝b2﹣4ac．当Δ＞0，方程有两个不相等的实数根；当Δ＝0，方程有两个相等的实数根；当Δ＜0，方程没有实数根．同时考查了几个非负数和的性质以及代数式变形的能力．9．已知双曲线y＝与直线y＝﹣x+1没有交点，则b的取值范围是b＞．【分析】根据方程解析式，可以得到＝﹣x+1，即可转化为一个一元二次方程，利用判别式求出b的取值范围．【解答】解：因为双曲线y＝与直线y＝﹣x+1没有交点，即方程＝﹣x+1无解，去分母，得x2﹣x+b＝0，∴Δ＝b2﹣4ac＝（﹣1）2﹣4×1×b＝1﹣4b＜0，解得b＞．【点评】考查一元二次方程根的判别式和双曲线与直线的位置关系，同时考查综合应用能力及推理能力．二．解答题（共5小题）10．已知关于x的一元二次方程．（1）求证：对于任意实数m，该方程总有两个不相等实数根；（2）如果此方程有一个根为0，求m的值．【分析】（1）求出Δ＝1，即可证明方程总有两个不相等实数根；（2）把x＝0代入可得关于m的一元二次方程，即可解得答案．【解答】（1）证明：对关于x的一元二次方程，Δ＝[﹣（m﹣1）]2﹣4×（m2﹣2m）＝m2﹣2m+1﹣m2+2m＝1，∴Δ＞0，∴对于任意实数m，一元二次方程总有两个不相等实数根；（2）解：如果此方程有一个根为0，则×02﹣（m﹣1）×0+（m2﹣2m）＝0，∴m2﹣2m＝0，解得m＝0或m＝2，答：m的值为0或2．【点评】本题考查一元二次方程根的判别式及解一元二次方程，解题的关键是掌握根的判别式△与根个数的关系以及解一元二次方程的方法步骤，此题难度不大．11．已知关于x的方程（k﹣2）x2﹣2x+1＝0有两个实数根．（1）求k的取值范围；（2）当k取最大整数时，求此时方程的根．【分析】（1）根据二次项系数非零及根的判别式Δ≥0列出关于k的不等式组，求解即可．（2）由（1）中k的取值范围得出符合条件的k的值，代入原方程，求解即可．【解答】解：（1）∵关于x的方程（k﹣2）x2﹣2x+1＝0有两个实数根，∴，解得k≤3且k≠2．（2）由题意得，k＝3，当k＝3时，方程为x2﹣2x+1＝0，即（x﹣1）2＝0，解得x1＝x2＝1．【点评】本题考查一元二次方程，牢记：一元二次方程ax2+bx+c＝0（a≠0）的根的判别式为Δ＝b2﹣4ac，当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程无实根．12．已知关于x的一元二次方程2x2﹣3mx+m2+m﹣3＝0（m为常数）．（1）求证：无论m为何值，方程总有两个不相等的实数根：（2）若x＝2是方程的根，则m的值为．【分析】（1）根据根的判别式求出Δ＝（m﹣4）2+8，再根据根的判别式得出答案即可；（2）把x＝2代入方程，得出关于m的一元二次方程，再求出方程的解即可．【解答】（1）证明：2x2﹣3mx+m2+m﹣3＝0，Δ＝（﹣3m）2﹣4×2×（m2+m﹣3）＝9m2﹣8m2﹣8m+24＝m2﹣8m+24＝（m﹣4）2+8，因为不论m为何值，（m﹣4）2≥0，即Δ＞0，所以无论m为何值，方程总有两个不相等的实数根：（2）解：把x＝2代入方程2x2﹣3mx+m2+m﹣3＝0得：2×22﹣3m×2+m2+m﹣3＝0，整理得：m2﹣5m+5＝0，解得：m＝，故答案为：．【点评】本题考查了解一元二次方程，根的判别式，一元二次方程的解等知识点，能熟记根的判别式的内容和一元二次方程的解的定义是解此题的关键．13．已知：关于x的一元二次方程x2﹣（3m+1）x+2m2+m＝0（1）求证：无论m取何值，这个方程总有实数根；（2）若△ABC的两边的长是这个方程的两个实数根，第三边的长为3，当△ABC为等腰三角形时，求m的值及△ABC的周长．【分析】（1）根据方程的系数结合根的判别式，即可得出Δ＝（m+1）2≥0，由此可证出：无论m取何值，这个方程总有实数根；（2）分3为底边及3为腰长两种情况考虑：①当3为底边时，根据等腰三角形的性质可得出m的值，结合根与系数的关系可求出两根之和，由该值为负值可得出该结论不符合题意；②当3为腰长时，代入x＝3可求出m值，再利用根与系数的关系结合三角形的三边关系可求出△ABC的周长．综上即可得出结论．【解答】（1）证明：∵a＝1，b＝﹣（3m+1），c＝2m2+m，∴Δ＝[﹣（3m+1）]2﹣4（2m2+m）＝m2+2m+1＝（m+1）2≥0，∴无论m取何值，这个方程总有实数根；（2）解：设方程的两根为x1，x2．①当3为底边时，则两腰的长是方程的两根，∴Δ＝（m+1）2＝0，∴m＝﹣1，∴x1+x2＝3m+1＝3×（﹣1）+1＝﹣2＜0，∴此种情况不合题意，舍去；②当3为腰时，把x＝3代入方程x2﹣（3m+1）x+2m2+m＝0得：9﹣3（3m+1）+2m2+m＝0，解得m1＝1，m2＝3．当m＝1时，x1+x2＝3m+1＝4，△ABC的周长为7；当m＝3时，x1+x2＝3m+1＝10，此时腰长为3，底为7，∵3+3＜7，∴此种情况不合题意，舍去．综上所述：m的值为1，△ABC的周长为7．【点评】本题考查了根的判别式、根与系数的关系、一元二次方程的解、等腰三角形的性质以及三角形三边关系，解题的关键是：（1）牢记“当△≥0时，方程有实数根”；（2）分3为底边及3为腰长两种情况考虑．14．已知关于x的方程x2﹣（k+2）x+2k＝0．（1）试说明：无论k取什么实数值，方程总有实数根．（2）若等腰△ABC的一边长a为1，另两边长b、c恰好是这个方程的两个实数根，求△ABC的周长？【分析】（1）把一元二次方程根的判别式转化成完全平方式的形式，得出△≥0可知方程总有实数根；（2）根据等腰三角形的性质分情况讨论求出b，c的长，并根据三角形三边关系检验，综合后求出△ABC的周长．【解答】（1）证明：∵Δ＝b2﹣4ac＝（k+2）2﹣8k＝（k﹣2）2≥0，∴无论k取任意实数值，方程总有实数根；（2）解：分两种情况：①若b＝c，∵方程x2﹣（k+2）x+2k＝0有两个相等的实数根，∴Δ＝b2﹣4ac＝（k﹣2）2＝0，解得k＝2，∴此时方程为x2﹣4x+4＝0，解得x1＝x2＝2，∴△ABC的周长为5；②若b≠c，则b＝a＝1或c＝a＝1，即方程有一根为1，∵把x＝1代入方程x2﹣（k+2）x+2k＝0，得1﹣（k+2）+2k＝0，解得k＝1，∴此时方程为x2﹣3x+2＝0，解得x1＝1，x2＝2，∴方程另一根为2，∵1、1、2不能构成三角形，∴所求△ABC的周长为5．综上所述，△ABC的周长为5．。

击剑步伐练习题击剑是一项古老而优雅的运动，它融合了力量、速度和技巧。

准确的步伐是击剑运动的基础，它不仅能为选手提供战术优势，还能提高反应速度和身体协调性。

以下是几个针对击剑步伐的练习题，帮助你提高击剑技巧和整体水平。

练习一：前后步练习这个练习可以帮助你熟悉击剑的前后步移动。

做好准备姿势，将重心放在后脚，然后迈出一步，将前脚放在身体的中心。

然后反方向迈出一步，将重心转移到前脚。

重复这个动作，确保前后移动的步伐平稳流畅。

可以练习将前后步与击剑动作结合起来，例如进行冲刺攻击或后撤闪避。

练习二：侧步练习击剑比赛中，侧步是非常常见的动作，可以帮助选手避开对手的进攻并找到更好的进攻角度。

这个练习要求你迈出一步并向一侧移动，保持身体平衡和稳定。

确保侧步后还能够立即做出出击或防守的反应。

可以练习进行多次的侧步，逐渐提高速度和灵活性。

练习三：跳跃练习跳跃是击剑中的一种高难度技巧，它需要良好的身体协调性和爆发力。

在练习中，你可以设置一些小障碍物（例如横放的绳子），跳跃过它们。

这有助于提高你的爆发力和灵活性，并模拟真实比赛中需要跳跃的情况。

在跳跃的过程中保持身体平衡，并注意保护好手部和脚部。

练习四：方向转变练习这个练习要求你在击剑动作中迅速转换方向。

可以选择一个目标（例如一个标志牌或者图标）设在距离你几步的地方，然后利用上述步伐移动技巧快速地朝不同的方向移动和攻击。

这个练习旨在帮助你更好地掌握方向转变的技巧和节奏感，提高你在比赛中的反应速度和灵活性。

练习五：配合练习击剑是一项对手之间的交流运动，良好的配合是成功的关键。

在练习中，你可以与一位击剑伴侣进行对抗，通过模拟真实比赛中的情况来提高自己的技巧。

注意与伴侣之间的配合和协作，同时注意保护好自己和对方的安全。

这个练习可以帮助你更好地理解击剑动作和战术，并提高你在比赛中的整体实力。

通过这些击剑步伐练习题，你可以逐步提高你的击剑技巧和整体水平。

请记住，在进行练习时要确保安全，并与教练或有经验的击剑选手一起进行，以获得更好的指导和建议。

小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________。

1第一章1-1. 晶体与非晶体的本质区别是什么？单晶体为何有各向异性而实际金属表现为各向同性？（1）晶体中的质点在空间作有规则的排列，而非晶体内部的质点排列不规则 （2）因为不同的晶面及晶向上，原子的排列情况不同，所以晶体表现为各向异性，而实际金属是由很多方向各异的单晶体杂乱排列而成，所以整体表现为各向同性。

1-4. 铜和铁室温下的晶格常数分别为0.286n m 和0.3607n m ，求1c m 3铁和铜中的原子数。

1n m (n a n o m e t e r )=10--99m =10A (a n g s t r o n g ) 铜的晶格常数＝0.286 x 10--77c m 铁的晶格常数＝0.3607 x 10--77c m1c m 3铜的原子数＝3)710286.0(31cm x cm - x 4 ＝ 1.71x 10231c m 3 铁的原子数＝3)7103607.0(31cm x cm -x 2 = 4.26x 102221-5. 常见的金属晶体典型结构有哪几种？α－F e , γ－F e , C u , A l , N i , P b , C r , V , M o , M g , Z n , W 各属于何种晶体结构？面心立方结构、体心立方结构、密排六方结构 γ－F e , C u , A l , N i , P b - 面心立方结构 α－F e , C r , V , M o , W - 体心立方结构 M g , Z n - 密排六方结构1 作图表示立方晶系（211）、（112）、（210）、（321）、（223）、（236）晶面与[111]、[111]、[021]、[112]、[211]、[123]晶向。

解：如图所示。

（211）、（112）、（210）、（321）、（223）、（236）晶面：（211） （112） （210）1.2★作图表示立方晶系（211）、（112）、（210）、（321）、（223）、（236）晶面与[111]、[111]、[021]、[112]、[211]、[123]晶向。

1、二（1）班有男生22人，女生20人。

现在把他们平均分成7组，每组有多少人？1、饼干每箱56元，洗衣粉每袋4元。

妈妈拿着80元钱买了一箱饼干，余下的钱买洗衣粉，可以买几袋？2、一个加数是25，另一个加数比它多16，它们的和是多少？3、一个加数是25，另一个加数比它少16，他们的和是多少？4、76加上34与18的差，和是多少？5、23与37的和再减去15，差是多少？7、二（1）班有50位小朋友，老师买了7盒月饼，每盒8块，每人一块月饼够吗？如果不够，还差多少？8、二年级一班有152人，二班有138人，三班有147人。

医院要给我们二年级的学生注射疫苗，它们要准备多少个一次性注射器？9、数学书每包8本，共56元，语文书每本5元。

哪种书更便宜？便宜多少钱？10、丽丽写了6天大字，前5天每天写3张纸，最后一天练了4张纸，丽丽一共写了多少张纸？11、明明有18元钱，小灵有24元钱，小灵应该给明明多少元钱，两人的钱数才一样多？11、一桶油连桶重19千克，倒了一半油后，连桶重12千克。

倒掉了多少油？油桶里原来有多少千克油？12.小花将45只苹果平均分给9个小朋友，每人得到几只苹果？13.一串糖葫芦有5只山楂，7串糖葫芦一共有几只山楂？14.花园里有8盆月季花，一串红的盆数是月季花的5倍，一串红有几盆？15.阳光公园里有柳树28棵，银杏树7棵，柳树的棵数是银杏树的几倍？16. 二年级有40位学生，参加跳绳比赛的有16人，参加围棋比赛的有7人，剩下的是不参加比赛的，那不参加比赛的有几人？17.有7袋糖果，每袋9块，我吃了6块，还剩下几块？18.小明练书法，一张纸上只能写8个大字，如果要写50个大字，那么小明需要几张纸？19.有一堆苹果，不到50只，把这堆苹果平均分给7个人，还余下3只，这堆苹果有几只？20. 妈妈今年32岁，冬冬今年7岁，当妈妈50岁时，冬冬几岁？21. 小玲装糖，每袋糖一样多，已经装了8袋，桌上还剩4粒糖；如果装9袋，还缺3粒，每袋装几粒？一共有几粒糖？22、一、二、三年级一共修理椅子52把，一年级修理了20把，二年级修理了18把。

“我已开始练习开始慢慢着急着急这世界没有你已经和眼泪说好不哭泣但倒数计时的爱该怎么继续” ————经典摘录
《练习》刘德华
如果留下多一秒钟
可以减少明天想你的痛
我会愿意放下所有
交换任何一丝丝可能的占有
幸福只剩一杯沙漏
眼睁睁看着一幕幕甜蜜
不会再有原本平凡无奇的拥有
到现在竟像是无助的奢求
我已开始练习
开始慢慢着急
着急这世界没有你
已经和眼泪说好不哭泣
但倒数计时的爱该怎么继续
我天天练习
天天都会熟悉
在没有你的城市里
试着删除每个两人世界里
那些曾经共同拥有的一切美好和回忆
幸福只剩一杯沙漏
眼睁睁看着一幕幕甜蜜
不会再有原本平凡无奇的拥有
到现在竟像是无助的奢求
我已开始练习
开始慢慢着急
着急这世界没有你
已经和眼泪说好不哭泣
但倒数计时的爱该怎么继续
我天天练习
天天都会熟悉
在没有你的城市里
试着删除每个两人世界里
那些曾经共同拥有的一切美好和回忆
爱是一万公顷的森林
迷了路的却是我和你
不是说好一起闯出去
怎能剩我一人回去回去
我已开始练习
开始慢慢着急
着急这世界没有你
已经和眼泪说好不哭泣
但倒数计时的爱该怎么继续
我天天练习
天天都会熟悉
在没有你的城市里
试着删除每个两人世界里
那些曾经共同拥有的一切美好和回忆那些曾经共同拥有的一切美好和回忆。

力量素质练习题力量素质是运动员在各项体育运动中取得优异成绩所必须具备的基本素质之一。

通过合理的锻炼和训练，可以提高身体的力量素质，从而提升运动表现。

下面将介绍几个力量素质练习题，帮助读者了解如何进行力量素质的训练。

1. 俯卧撑俯卧撑是一种常见且有效的上肢力量训练动作。

正确的俯卧撑姿势是平躺在地面上，双脚紧贴地面，双手掌心向下与肩膀平齐，缓慢下降至胸部接触地面，再用力推起，保持身体挺直。

针对不同的训练目标，可以进行多种俯卧撑变体，如宽幅俯卧撑、窄幅俯卧撑、单臂俯卧撑等。

逐渐增加俯卧撑的次数和难度，可以有效训练上肢力量。

2. 深蹲深蹲是一种全身性的力量练习动作，主要锻炼下肢和核心力量。

正确的深蹲姿势是站立时双脚与肩同宽，双手自然下垂，保持上身挺直，然后屈膝下蹲，臀部下降至膝盖与地面平行或稍微低于平行位置，再用力站起。

在进行深蹲训练时，要注意保持膝盖与脚尖的方向保持一致，背部保持挺直，避免腰部过分前倾或后倾。

3. 提铃提铃是一种能够训练上肢力量和核心稳定性的练习动作。

可以使用哑铃、杠铃等道具进行练习。

站立时，双脚与肩同宽，双手握住铃的两侧，然后用力向上提起铃，使手臂伸直，再缓慢放下。

在进行提铃训练时，要确保动作的幅度适中，避免用力过度导致肌肉受伤。

4. 懒人伸展懒人伸展是一种用于锻炼核心力量的简单练习动作。

躺在地面上，屈膝保持双脚平放于地面，双臂伸直撑在地板上，使上半身离地，并保持平衡。

通过懒人伸展可以训练核心部位的力量和稳定性，同时也可以促进腹肌的发展。

通过以上介绍的力量素质练习题，运动员可以有针对性地进行力量素质的训练。

然而，重要的是要根据自身情况和目标制定训练计划，并在专业教练的指导下进行训练。

同时，合理的营养摄入和充足的休息也是提高力量素质的关键因素。

只有坚持科学训练，并注重全面发展，才能在运动中获得更好的成绩。

小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________。

幼儿园体育练习题培养孩子的运动技巧和体能运动在幼儿园阶段对于孩子的身体发展和整体素质的培养至关重要。

通过体育练习题的方式，可以有效地培养孩子的运动技巧和体能。

本文将探讨如何运用适合幼儿的体育练习题来促进孩子的运动发展。

一、动作练习1. 跳绳练习跳绳是一个简单而有效的运动方式，可以帮助孩子提高协调能力和爆发力。

在幼儿园中，可以设置跳绳练习的课程，让孩子们跟着教师一起练习。

比如，让孩子们先学会单脚跳和双脚跳，然后逐渐增加难度，如换脚跳、交叉跳等。

2. 球类运动球类运动不仅可以培养孩子们的手眼协调能力，还可以锻炼他们的反应能力和团队合作意识。

在幼儿园中，可以进行简单的投掷练习，如投篮、投球等，以及接球练习，如接球比赛等。

3. 徒手操练习徒手操是一种通过特定动作和节奏来提高孩子的灵活性、协调性和力量的运动方式。

可以设计一些简单的徒手操练习，如踏步操、摆臂操等，让孩子们通过模仿教师的动作来进行练习。

二、游戏活动1. 制定游戏规则在幼儿园中，可以通过制定一些有趣的游戏规则来培养孩子的运动技巧和体能。

比如，设置一个追逐游戏，让孩子们追赶快速移动的球，以提高他们的速度和敏捷性。

2. 平衡训练平衡是孩子们运动发展的基础，可以通过一些游戏活动来培养孩子们的平衡感。

比如，设置一个“走钢丝”游戏，让孩子们在练习中逐渐提高站立在细绳上的平衡能力。

3. 美术与体育的结合通过将美术与体育结合，可以更好地培养孩子们的创造力和运动技巧。

比如，可以让孩子们自由绘制一幅关于运动的画，并在画面中加入一些体操动作，让孩子们在创作中体验和学习更多的运动动作。

三、定期评估和反馈1. 设立考核体系为了更好地培养孩子的运动技巧和体能，幼儿园可以设立一套考核体系，对孩子们的运动表现进行评估。

比如，按照孩子的年龄和能力设置一些基本的技能测试，如跑步速度、跳绳次数等，以便及时发现孩子的进步和不足。

2. 给予积极的反馈在评估的基础上，教师应该及时给予孩子们积极的反馈和鼓励，让他们感受到自己的努力和进步。

小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________小学数学计算练习 2024-11-24姓名：___________ 座号：__________ 情况：___________。

语文练习题语文练习题(15篇)语文练习题1一.读一读，把不正确的字划去。

(百白)灵鸟(保宝)护(支枝)头(青轻)声伙(半伴)(吵少)闹二、连一连，再读一读。

快乐地灯光消灭旗帜热闹的歌唱明白田鼠明亮的市场挥动道理三、照样子把句子补充完整。

例：小黄莺唱歌。

(可爱的)小黄莺(快乐地)唱歌。

1、果园里的苹果熟了。

————————————————————2、小朋友做游戏。

————————————————————3.小鱼游来游去。

四、分苹果。

吹争踩吵追喝拍跑望捉()()()()表示眼的动作表示手的动作表示脚的动作表示口的动作语文练习题2一、在加粗字的正确读音下画横线。

1．鲸的祖先跟牛羊的祖先一样，生活在陆（lù lòu）地上。

2．不同种类的鲸，喷（pēn pèn）出的气形成的水柱也不一样。

3．如果听到什么声响，它们立即（jí jì）四散游开。

4．“吃音玻璃”就是消除（chū chú）噪音的能手。

5．假如空中没有灰尘，地面上的万物都将是湿漉漉（lǔ lù）的。

二、一锤定音（给加粗字选择正确的读音）。

娱乐（yú yù）选择（zé zhé）诵读（yǒng sòng）某种（mǎo mǒu）一锤定音（用“√”选择正确的读音）。

船cuán（）chuán（）坐zuò（）zhuò（）闪sǎn（）shǎn（）蓝lán（）nán（）降生jiàng（）xiáng（）模仿mé（）mó（）幻觉huàn（）yòu（）陶醉zhuì（）zuì（）霎时sà（）shà（）娇宠chǒng（）cǒng（）三、在正确读音下面画“_____”。

贮存（zhù chǔ）塑像（sù shù）挫折（cuō cuò）霎时（sà shà）消瘦（sòu shòu）镌刻（juān juàn）四、我会选（选择正确的答案填在括号里）。

韦达定理练习题一．填空题（共16小题）1．方程x2+x﹣1＝0的两根为x1、x2，则x1+x2的值为．2．已知实数x1，x2是方程x2+x﹣1＝0的两根，则x1x2＝．3．已知a，b是方程x2+x﹣3＝0的两个不相等的实数根，则ab﹣2022a﹣2022b的值是．4．设x1、x2是方程x2﹣mx＝0的两个根，且x1+x2＝﹣3，则m的值是．5．若m，n是方程x2+2021x﹣2022＝0的两个实数根，则m+n﹣mn的值为．6．一元二次方程x2﹣3x+1＝0的两个实数根为α、β，则αβ﹣α﹣β的值为．7．已知α，β是一元二次方程x2﹣x﹣9＝0的两个实数根，则代数式α2﹣2α﹣β+3的值为．8．设a、b为x2+x﹣2021＝0的两个实数根，则a3+a2+3a+2024b＝．9．已知x1，x2是方程x2﹣x﹣1＝0的根，则的值是．10．α、β是关于x的方程x2﹣x+k﹣1＝0的两个实数根，且α2﹣2α﹣β＝4，则k的值为．11．关于x的一元二次方程3x2﹣10x﹣17＝0的两个根分别为x1和x2，则＝．12．已知a，b是关于x的一元二次方程x2+（m+3）x﹣2＝0的两个不相等的实数根，且满足＝﹣1，则m的值是．13．已知m，n是方程x2+2x﹣5＝0的两个实数根，则mn+m+n＝．14．已知m，n是方程x2﹣3x＝2的两个根，则式子的值是．15．已知方程x2﹣2x﹣2＝0的两根分别为x1，x2，则x12﹣x22+4x2的值为．16．关于x的一元二次方程x2﹣kx+4＝0的两个实数根分别是x1、x2，且满足x12+x22﹣2x1﹣2x2﹣7＝0，则k的值为．二．解答题（共4小题）17．已知关于x的方程2x2+2kx+k﹣1＝0．（1）求证：无论k为何值，方程总有两个不相等实数根；（2）若x＝﹣1是该方程的一个根，求方程的另一个根．18．已知：关于x的一元二次方程x2﹣（2k+3）x+k2+3k+2＝0．（1）证明无论k取何值时方程总有两个实数根．（2）△ABC中，BC＝5，AB、AC的长是这个方程的两个实数根，求k为何值时，△ABC 是等腰三角形？19．已知关于x的方程x2﹣4mx+4m2﹣4＝0．（1）求证：此方程有两个不相等的实数根；（2）若此方程的两个根分别为x1，x2，其中x1＞x2，且x1＝3x2，求m的值．20．阅读材料并解决下列问题：材料1 若一元二次方程ax2+bx+c＝0（a≠0）的两根为x1、x2，则x1+x2＝﹣，x1x2＝．材料2 已知实数m，n满足m2﹣m﹣1＝0，n2﹣n﹣1＝0，且m≠n，求+的值．解：由题知m，n是方程x2﹣x﹣1＝0的两个不相等的实数根，根据材料1，得m+n＝1，mn＝﹣1，∴+＝＝＝＝﹣3．根据上述材料解决下面的问题：（1）一元二次方程5x2+10x﹣1＝0的两根为x1，x2，则x1+x2＝，x1x2＝．（2）已知实数m，n满足3m2﹣3m﹣1＝0，3n2﹣3n﹣1＝0，且m≠n，求m2n+mn2的值．（3）已知实数p，q满足p2＝7p﹣2，2q2＝7q﹣1，且p≠2q，求p2+4q2的值．参考答案与试题解析一．填空题（共16小题）1．方程x2+x﹣1＝0的两根为x1、x2，则x1+x2的值为﹣1．【分析】根据一元二次方程根与系数的关系直接可得答案．【解答】解：∵方程x2+x﹣1＝0的两根为x1、x2，∴x1+x2＝﹣1，故答案为：﹣1．【点评】本题考查一元二次方程根与系数的关系，解题的关键是掌握一元二次方程根与系数的关系．2．已知实数x1，x2是方程x2+x﹣1＝0的两根，则x1x2＝﹣1．【分析】根据根与系数的关系解答．【解答】解：∵方程x2+x﹣1＝0中的a＝b＝1，c＝﹣1，∴x1x2＝＝﹣1．故答案是：﹣1．【点评】此题主要考查了根与系数的关系，一元二次方程ax2+bx+c＝0（a≠0）的根与系数的关系为：x1+x2＝﹣，x1•x2＝．3．已知a，b是方程x2+x﹣3＝0的两个不相等的实数根，则ab﹣2022a﹣2022b的值是2019．【分析】由a，b是方程x2+x﹣3＝0的两个不相等的实数根，利用根与系数的关系即可求出两根之和和两根之积，代入代数式即可求解．【解答】解：∵a，b是方程x2+x﹣3＝0的两个不相等的实数根，∴a+b＝﹣1，ab＝﹣3．∴ab﹣2022a﹣2022b＝ab﹣2022（a+b）＝﹣3﹣2022×（﹣1）＝2019，故答案为：2019．【点评】此题主要考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．4．设x1、x2是方程x2﹣mx＝0的两个根，且x1+x2＝﹣3，则m的值是﹣3．【分析】直接利用根与系数的关系求解．【解答】解：根据根与系数的关系得x1+x2＝m，而x1+x2＝﹣3，所以m＝﹣3．故答案为：﹣3．【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．5．若m，n是方程x2+2021x﹣2022＝0的两个实数根，则m+n﹣mn的值为1．【分析】利用根与系数的关系可得出m+n＝﹣2021，mn＝﹣2022，再将其代入m+n﹣mn 中即可求出结论．【解答】解：∵m，n是方程x2+2021x﹣2022＝0的两个实数根，∴m+n＝﹣2021，mn＝﹣2022，∴m+n﹣mn＝﹣2021﹣（﹣2022）＝1．故答案为：1．【点评】本题考查了根与系数的关系，牢记“两根之和等于﹣，两根之积等于”是解题的关键．6．一元二次方程x2﹣3x+1＝0的两个实数根为α、β，则αβ﹣α﹣β的值为﹣2．【分析】根据根与系数的关系得到α+β＝3，αβ＝1，然后利用整体代入的方法计算．【解答】解：根据根与系数的关系得到α+β＝3，αβ＝1，所以αβ﹣α﹣β＝αβ﹣（α+β）＝1﹣3＝﹣2．【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，则x1+x2＝﹣，x1x2＝．7．已知α，β是一元二次方程x2﹣x﹣9＝0的两个实数根，则代数式α2﹣2α﹣β+3的值为11．【分析】利用一元二次方程的根及根与系数的关系可得出α2﹣α＝9，α+β＝1，再将其代入α2﹣2α﹣β+3＝α2﹣α﹣（α+β）+3中即可求出结论．【解答】解：∵α，β是一元二次方程x2﹣x﹣9＝0的两个实数根，∴α2﹣α﹣9＝0，α+β＝1，∴α2﹣α＝9，所以α2﹣2α﹣β+3＝α2﹣α﹣（α+β）+3＝9﹣1+3故答案为：11．【点评】本题考查了一元二次方程的根以及根与系数的关系，利用一元二次方程的根及根与系数的关系，找出α2﹣α＝9，α+β＝1是解题的关键．8．设a、b为x2+x﹣2021＝0的两个实数根，则a3+a2+3a+2024b＝﹣2024．【分析】先根据一元二次方程根的定义得到a2＝﹣a+2021，再用a表示a3得到a3＝2022a ﹣2021，所以原式变形为2024（a+b），接着根据根与现实的关系得到a+b＝﹣1，然后利用整体代入的方法计算．【解答】解：∵a为x2+x﹣2021＝0的根，∴a2+a﹣2021＝0，即a2＝﹣a+2021，∴a3＝a（﹣a+2021）＝﹣a2+2021a＝a﹣2021+2021a＝2022a﹣2021，∴a3+a2+3a+2024b＝2022a﹣2021﹣a+2021+3a+2024b＝2024（a+b），∵a、b为x2+x﹣2021＝0的两个实数根，∴a+b＝﹣1，∴a3+a2+3a+2024b＝2024×（﹣1）＝﹣2024．故答案为：﹣2024．【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根，则x1+x2＝﹣，x1x2＝．9．已知x1，x2是方程x2﹣x﹣1＝0的根，则的值是﹣1．【分析】利用根与系数的关系求出两根之和与两根之积，将所求式子通分并利用同分母分式的加法法则计算，把求出的两根之和与两根之积代入计算，即可求出值．【解答】解：∵x1，x2是方程x2﹣x﹣1＝0的根，∴x1+x2＝1，x1x2＝﹣1，∴＝＝＝﹣1．故答案为：﹣1．【点评】此题考查了一元二次方程根与系数的关系，熟练掌握根与系数的关系是解本题10．α、β是关于x的方程x2﹣x+k﹣1＝0的两个实数根，且α2﹣2α﹣β＝4，则k的值为﹣4．【分析】α2﹣2α﹣β＝α2﹣α﹣（α+β）＝4，然后根据方程的解的定义以及一元二次方程根与系数的关系，得到关于k的一元一次方程，即可解得答案．【解答】解：∵α、β是方程x2﹣x+k﹣1＝0的根，∴α2﹣α+k﹣1＝0，α+β＝1，∴α2﹣2α﹣β＝α2﹣α﹣（α+β）＝﹣k+1﹣1＝﹣k＝4，∴k＝﹣4，故答案是：﹣4．【点评】本题考查了一元二次方程的解以及根与系数的关系，掌握根与系数的关系是解题的关键．11．关于x的一元二次方程3x2﹣10x﹣17＝0的两个根分别为x1和x2，则＝．【分析】根据一元二次方程根与系数的关系可得，，再由进行求解即可．【解答】解：∵一元二次方程3x2﹣10x﹣17＝0的两根是x1，x2，∴，，∴．故答案是：．【点评】本题主要考查了一元二次方程根与系数的关系，解题的关键在于能够熟练掌握一元二次方程根与系数的关系．12．已知a，b是关于x的一元二次方程x2+（m+3）x﹣2＝0的两个不相等的实数根，且满足＝﹣1，则m的值是﹣5．【分析】根据根与系数的关系结合＝﹣1，即可得出关于m的方程，解之即可得出m的值，再由根的判别式Δ＞0，即可确定m的值．【解答】解：∵a，b是关于x的一元二次方程x2+（m+3）x﹣2＝0的两个不相等的实数根，∴a+b＝﹣（m+3），ab＝﹣2，∵＝﹣1，即＝＝﹣1，解得：m＝﹣5．∵原方程有两个不相等的实数根，∴Δ＝（m+3）2﹣4×（﹣2）＝（m+3）2+8＞0，∴m＝﹣5．故答案为：﹣5．【点评】本题考查了根与系数的关系以及根的判别式，根据根与系数的关系结合＝﹣1，找出关于m的方程是解题的关键．13．已知m，n是方程x2+2x﹣5＝0的两个实数根，则mn+m+n＝﹣7．【分析】根据根与系数的关系得到m+n＝﹣2，mn＝﹣5，然后利用整体代入的方法计算即可．【解答】解：根据题意得：m+n＝﹣2，mn＝﹣5，所以mn+m+n＝﹣5+（﹣2）＝﹣7．故答案为：﹣7．【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1•x2＝．14．已知m，n是方程x2﹣3x＝2的两个根，则式子的值是27．【分析】利用一元二次方程解的定义和根与系数的关系，采用整体代入求解．【解答】解：∵m，n是方程x2﹣3x＝2的两个根，∴m2＝3m+2，n2﹣2＝3n，m+n＝3，∴m3﹣10m+n＝m（3m+2）﹣10m+n＝3m2﹣8m+n＝3（3m+2）﹣8m+n＝m+n+6＝3+6＝9，n﹣＝＝＝3，原式＝9×3＝27．故答案为：27．【点评】本题考查了一元二次方程解的定义和根与系数的关系，利用整体思想代入求值是解题的关键．15．已知方程x2﹣2x﹣2＝0的两根分别为x1，x2，则x12﹣x22+4x2的值为4．【分析】利用一元二次方程解的定义得到x12＝2x1+2，x22＝2x2+2；然后由根与系数的关系求得x1+x2＝2；最后代入所求的代数式求值即可．【解答】解：∵方程x2﹣2x﹣2＝0的两根分别为x1，x2，∴x12＝2x1+2，x22＝2x2+2，x1+x2＝2．∴x12﹣x22+4x2＝（2x1+2）﹣（2x2+2）+4x2＝2（x1+x2）＝2×2＝4．故答案是：4．【点评】此题主要考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．16．关于x的一元二次方程x2﹣kx+4＝0的两个实数根分别是x1、x2，且满足x12+x22﹣2x1﹣2x2﹣7＝0，则k的值为5．【分析】由根与系数的关系可得：x1+x2＝k，x1x2＝4，再把已知的条件进行整理，整体代入运算即可求解．【解答】解：∵一元二次方程x2﹣kx+4＝0的两个实数根分别是x1、x2，∴x1+x2＝k，x1x2＝4，∵x12+x22﹣2x1﹣2x2﹣7＝0，∴（x1+x2）2﹣2x1x2﹣2（x1+x2）﹣7＝0，∴k2﹣2×4﹣2k﹣7＝0，整理得：k2﹣2k﹣15＝0，解得：k＝5或k＝﹣3，当k＝﹣3时，Δ＝32﹣4×1×4＝9﹣16＝﹣7＜0，则原方程无实数解，故k＝5．故答案为：5．【点评】本题主要考查根与系数的关系，解答的关键是熟记根与系数的关系并灵活运用．二．解答题（共4小题）17．已知关于x的方程2x2+2kx+k﹣1＝0．（1）求证：无论k为何值，方程总有两个不相等实数根；（2）若x＝﹣1是该方程的一个根，求方程的另一个根．【分析】（1）根据方程的系数结合根的判别式Δ＝b2﹣4ac，可得出Δ4（k﹣1）2+4＞0，由此可证出方程有两个不相等的实数根；（2）把x＝﹣1代入方程，求得k＝1，即可得出2x2+2x＝0，然后解方程即可求出方程的另一个根．【解答】（1）证明：Δ＝b2﹣4ac＝（2k）2﹣4×2×（k﹣1）＝4k2﹣8k+8＝4（k﹣1）2+4＞0，∴方程有两个不相等的实数根．（2）解：∵x＝﹣1是该方程的一个根，∴2﹣2k+k﹣1＝0，解得k＝1，∴方程为2x2+2x＝0，解得：x1＝﹣1，x2＝0，∴方程的另一个根为x＝0．【点评】本题考查了根与系数的关系以及根的判别式，解题的关键是：牢记“当Δ＞0时，方程有两个不相等的实数根”．18．已知：关于x的一元二次方程x2﹣（2k+3）x+k2+3k+2＝0．（1）证明无论k取何值时方程总有两个实数根．（2）△ABC中，BC＝5，AB、AC的长是这个方程的两个实数根，求k为何值时，△ABC 是等腰三角形？【分析】（1）表示出方程根的判别式，根据根的判别式的正负即可确定出方程根的情况；（2）由（1）得到AB≠AC，分AC＝BC与AB＝BC两种情况求出k的值即可．【解答】（1）证明：∵Δ＝[﹣（2k+3）]2﹣4×1×（k2+3k+2）＝1＞0，∴无论k取何值时方程总有两个实数根．（2）解：∵方程x2﹣（2k+3）x+k2+3k+2＝0的解为：x＝＝，即x1＝k+2，x2＝k+1，∵AB、AC是方程的两个实数根，∴AB≠AC，∵BC＝5，∴当k+2＝5，或k+1＝5时，△ABC是等腰三角形，∴k＝3或4，故当k为3或4时，△ABC是等腰三角形．【点评】此题考查了根与系数的关系，涉及的知识有：一元二次方程根与系数的关系，根的情况判断，以及等腰三角形的性质，熟练掌握运算法则是解本题的关键．19．已知关于x的方程x2﹣4mx+4m2﹣4＝0．（1）求证：此方程有两个不相等的实数根；（2）若此方程的两个根分别为x1，x2，其中x1＞x2，且x1＝3x2，求m的值．【分析】（1）求出一元二次方程根的判别式，判断Δ与0的关系．（2）利用一元二次方程根与系数的关系求出x1+x2与x1x2，再利用x1＝3x2形成关于m 的方程，然后求解即可．【解答】（1）证明：关于x的方程x2﹣4mx+4m2﹣4＝0，∵a＝1，b＝﹣4m，c＝4m2﹣4．∴Δ＝（﹣4m）2﹣4×1×（4m2﹣4）＝16＞0．∴此方程有两个不相等的实数根；（2）解：若此方程的两个根分别为x1，x2，由题意得，x1+x2＝4m，x1x2＝4m2﹣4．∵x1＝3x2，∴3x2+x2＝4m，即x2＝m，∴x1＝3m，∴3m•m＝4m2﹣4，即m2＝4，解得m＝±2．当m＝﹣2时，x1＝﹣6，x2＝﹣2．此时x1＜x2，不符合题意．∴m＝﹣2舍去故m的值为2．【点评】本题考查了一元二次方程根的判别式，及根与系数的关系，根据根与系数的关系及两个根的关系得到方程中有关参数的方程是解题的关键．20．阅读材料并解决下列问题：材料1 若一元二次方程ax2+bx+c＝0（a≠0）的两根为x1、x2，则x1+x2＝﹣，x1x2＝．材料2 已知实数m，n满足m2﹣m﹣1＝0，n2﹣n﹣1＝0，且m≠n，求+的值．解：由题知m，n是方程x2﹣x﹣1＝0的两个不相等的实数根，根据材料1，得m+n＝1，mn＝﹣1，∴+＝＝＝＝﹣3．根据上述材料解决下面的问题：（1）一元二次方程5x2+10x﹣1＝0的两根为x1，x2，则x1+x2＝﹣2，x1x2＝﹣．（2）已知实数m，n满足3m2﹣3m﹣1＝0，3n2﹣3n﹣1＝0，且m≠n，求m2n+mn2的值．（3）已知实数p，q满足p2＝7p﹣2，2q2＝7q﹣1，且p≠2q，求p2+4q2的值．【分析】（1）5x2+10x﹣1＝0中，a＝5，b＝10，c＝﹣1，则x1+x2＝﹣＝﹣2，x1x2＝＝﹣．（2）由题意m，n可以看作3x2﹣3x﹣1＝0的两个不等的实数根，由此可得结论；（3）由题意知p与2q即为方程x2﹣7x+2＝0的两个不等的实数根，由此可得结论．【解答】解：（1）在5x2+10x﹣1＝0中，a＝5，b＝10，c＝﹣1，∴x1+x2＝﹣＝﹣2，x1x2＝＝﹣．故答案为：﹣2，﹣；（2）∵m，n满足3m2﹣3m﹣1＝0，3n2﹣3n﹣1＝0，m≠n，∴m，n可以看作3x2﹣3x﹣1＝0的两个不等的实数根，∴m+n＝1，mn＝﹣，∴m2n+mn2＝mn（m+n）＝﹣×1＝﹣；（3）由题意知p与2q即为方程x2﹣7x+2＝0的两个不等的实数根，∴p+2q＝7，2pq＝2，∴p2+4q2＝（p+2q）2﹣4pq＝72﹣2×2＝45．【点评】本题考查根与系数的关系，解题的关键是掌握根与系数的关系，灵活运用所学知识解决问题．。