正切函数图像及性质
- 格式：doc
- 大小：523.00 KB
- 文档页数：5
下载文档原格式
合集下载
正切函数的图像与性质
正切函数的图像与性质
y=tanx
若需视频讲解请联系作者！
π2
−π2
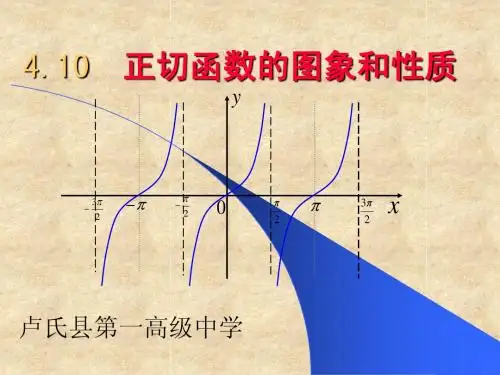
•正切函数的最小正周期是π
•正切函数的最小正周期是π，延伸成整个定义域上的的图像
•渐近线x =±π
2
y
x
π2
−π2
y
x
•单调递增区间：(−π2,π
2)•定义域：x ≠π
2
+k π,k ∈Z •值域：y ∈R
•为了方便起见，先研究一个周期内的函数图像和性质，然后扩展到整个定义域上
•[−π2,π
2] 范围内的图像如图：
•单调递减区间：无
•对称轴：无•中心对称点：x =0
π2
−π2
y
x
π2
−π2
y
x •单调递增区间：[−π
2+k π,π
2+k π],k ∈Z •中心对称点：(k π,0),k ∈Z
y =tanx 的图像与性质
•延伸成整个定义域上的的图像
•k π即周期的整数倍
π
3π2
B
•与点A 的函数值相同的点B ，它们的x 值相差π•两个相邻的中心对称点(0,0)，(π,0)相差πA
•定义域：x ≠π
2
+k π,k ∈Z
•值域：y ∈R
−3π2
π2
−π2
y
x •单调递增区间：[−π2+k π,π
2+k π],k ∈Z
•中心对称点：(k π,0),k ∈Z
总结
π
3π2
•定义域：x ≠
π
2
+k π,k ∈Z
•值域：y ∈R
−3π2。
正切函数的性质及图像
正切函数的性质与图像
正切函数的定义
3.5
3
2.5
2
1.5
sinα=y
1
cosα=x
P(x,y)
y
0.5
y
tanα= x
7
6
5
4
3
2
1
x
1
2
3
4
5
0.5
1
1.5
2
问题1：我们是如何研究正弦函数、余弦函数的图像及性 质的？我们可以通过怎样的方式来研究正切函数的性质及 图像呢？
方式1：定义——图像——性质
值域 周期性 奇偶性 单调性
正切函数的性质及图像
R 奇函数
Байду номын сангаас
问题4：你能从正切函数图像出发，讨论它的性质吗？
4 3 2 1
3π
5π
2π
3π
π
2
2
π 2
1
2
3
4
5
π
π
3π
2
2
课堂小结
1、本节课我们是如何研究正切函数的？ 定义——性质——图像
2、从那几个方面研究了正切函数？正切函数有哪些性质？ 定义域、值域、周期性、奇偶性、单调性、对称性
方式2：定义——性质——图像
正切函数的性质
值域：？
单调性：？
问题2：在研究正弦函数、余弦函数时，我们曾借助正弦 线、余弦线，你能否通过正切线来研究正切函数的单调性 和值域呢？
正切线的变化
问题3：通过对正切函数性质的研究，类比正弦函 数图像的作法，你能作出正切函数的大致图像吗？
正切函数的图像
函数 定义域
正切函数的定义
3.5
3
2.5
2
1.5
sinα=y
1
cosα=x
P(x,y)
y
0.5
y
tanα= x
7
6
5
4
3
2
1
x
1
2
3
4
5
0.5
1
1.5
2
问题1：我们是如何研究正弦函数、余弦函数的图像及性 质的？我们可以通过怎样的方式来研究正切函数的性质及 图像呢？
方式1：定义——图像——性质
值域 周期性 奇偶性 单调性
正切函数的性质及图像
R 奇函数
Байду номын сангаас
问题4：你能从正切函数图像出发，讨论它的性质吗？
4 3 2 1
3π
5π
2π
3π
π
2
2
π 2
1
2
3
4
5
π
π
3π
2
2
课堂小结
1、本节课我们是如何研究正切函数的？ 定义——性质——图像
2、从那几个方面研究了正切函数？正切函数有哪些性质？ 定义域、值域、周期性、奇偶性、单调性、对称性
方式2：定义——性质——图像
正切函数的性质
值域：？
单调性：？
问题2：在研究正弦函数、余弦函数时，我们曾借助正弦 线、余弦线，你能否通过正切线来研究正切函数的单调性 和值域呢？
正切线的变化
问题3：通过对正切函数性质的研究，类比正弦函 数图像的作法，你能作出正切函数的大致图像吗？
正切函数的图像
函数 定义域
知识讲解正切函数的性质和图象基础
知识讲解_正切函数的性质和图象_基础正切函数是三角函数中的一种，常用符号为tan，表示一个角的正切值。
在数学中，正切函数具有许多重要的性质和图像，下面将对其进行详细介绍。
1.定义：正切函数的定义是：对于一个角θ，它的正切值tanθ等于角的对边与邻边的比值，即tanθ=opposite/adjacent。
2.周期性：正切函数具有周期性，即tan(θ+π)=tanθ，其中π是圆周率。
这意味着正切函数的图像在每个周期内重复出现，以直线y=tanθ为对称轴。
3.定义域和值域：正切函数的定义域是所有实数，除了使分母为零的角度。
当角度为90°的倍数时，分母为零，正切函数无定义。
正切函数的值域是所有实数，即从负无穷到正无穷。
4.奇偶性：正切函数是一个奇函数，即tan(-θ)=-tanθ。
这意味着正切函数的图像关于原点对称。
5.渐近线：正切函数有两条渐近线，分别为x=π/2+kπ和x=-π/2+kπ，其中k是整数。
当θ接近这些值时，tanθ的值趋向于正无穷或负无穷。
6.零点：正切函数有无数个零点，即tanθ=0。
这些零点出现在角度为kπ时，其中k是整数。
7.图像变换：对于正切函数的图像，可以通过平移、缩放和反转等变换得到。
例如，将y=tanθ的图像向右平移π/4个单位，得到y=tan(θ-π/4)的图像；将y=tanθ的图像进行垂直缩放，得到y=a*tanθ的图像，其中a 是一个常数。
8.切线斜率：正切函数在每个周期内都有无穷多个切线，切线的斜率是tanθ。
这意味着切线的斜率在整个图像上是连续变化的。
9.函数图像：正切函数的图像是一个周期为π的波浪线。
在每个周期内，图像从负无穷逐渐上升到正无穷，然后再从正无穷逐渐下降到负无穷。
图像在每个周期内有一个零点，并且在每个周期的中点有一个峰值和一个谷值。
总结起来，正切函数是一个周期性的、奇函数，定义域为所有实数，值域为所有实数。
它具有两条渐近线，有无数个零点，图像是一个波浪线，切线的斜率等于函数值。
三角函数正切函数的性质与图像
3
正切函数的周期性和对称性
正切函数具有周期性和对称性，其图像呈周期 性变化，且具有一些对称轴和对称中心。
正切函数在复数域的扩展
正切函数的复数形式
正切函数可以扩展到复数域，其复数形式为tan(z)。
复数域中的正切函数的应用
正切函数在复数域中有广泛的应用，如在信号处理、 电路设计和物理学等领域。
正切函数在微积分和数学分析中的应用
正切函数在微积分中的导数
在微积分中，正切函数的导数为(sec x)^2，其导数与 其他三角函数的导数之间也有密切的联系。
正切函数在数学分析中的极限 和连续性
在数学分析中，正切函数是一个无穷级数展开的函数， 其极限和连续性都有一定的规律和特性。同时，正切函 数在实数域上的定义域为所有不等于kπ+π/2的x，值 域为所有实数R。
03
微分的几何意义：表示曲线的弧长
03
正切函数的周期性和实践应用
正切函数的周期性
周期性定义
正切函数是周期函数，其周期为π。函数在任意两个π/2的整 数倍之间是重复的。
周期性证明
正切函数的定义域为所有不等于π/2的实数，而正弦和余弦函 数的周期均为2π，因此可以通过相加得到正切函数的周期为 π。
正切函数在实践中的应用
周期性
正切函数是周期函数，最小正周期为π
正切函数的基本性质
定义域
正切函数定义域为{x | x ≠ kπ + π/2, k ∈ Z}
周期性
正切函数是周期函数，最小正周期为π
值域
正切函数的值域为R
有界性
正切函数是有界函数，|tan(x)| ≤ ∞
正切函数的图像
01
图像形状
正切函数的图像是周期函数，呈现周 期性变化
正切函数的图像和性质
4
2
2
44
所以函数
y
tan
x
4
的定义域是
x
x
4
k，k
Z
; 家装 装潢
；
角度开拓思路。“一方有难，八方支援”，这是中华民族的优良传统。大灾面前，中华民族空前的团结起来，这让世界再次见识了中华民族的伟大、坚强和不可摧毁。 ? 思路四、从赞颂“万众一心、众志成城的民族精神”的角度开拓思路。中华民族是从无数灾难考验中走过来的民族， 舟曲特大泥石流灾害再次冲击了中国人的心，但冲不垮中国人的坚强。汶川地震见了这种坚强，玉树地震见了这种坚强，泥石流再一次见了这种坚强。生于忧患，死于安乐。市场经济下因物质利益诱惑冲蚀而缺失的人文素养，被滚滚的泥石流生生地揪扯出来，大大激发了中华民族的斗志， 再一次使万众一心、众志成城的民族精神得到了回归。 ?思路五、从“人与自然关系”的角度开拓思路。舟曲特大泥石流再次让人们见识了人类在自然面前的弱小、无助。虽然人类的科技越来越发达，人类的活动领域越来越得到拓展，然而，当大的自然灾害来临的时候，人类仍然显得那 么的束手无策。印度洋海啸、缅甸风暴、汶川地震、冰岛火山、玉树地震、舟曲泥石流……造成巨大的人员伤亡和财产损失。但这是否就意味着人类就应该就此止步，听天由命呢？答案很显然是否定的。人类需要更好地发展科学研究，更好地研究自然、利用自然，和自然和谐发展。 附： 给作文一个超过50分的理由 ? ? 高中生作文训练一直有这样的怪事：应届生作文写作训练了三年，可作文得分几乎总是在42分—48分之间游移；复读生复习一年快结束了，作文练了不少，可作文得分也总是在42分—48分之间徘徊；那些平时按老师要求按时按量老老实实写作文者，和那 些平时很少写甚至从不写作文者，考试中其作文得分一样都是在42分—48分之间沉浮。 ? 作文训练中的症结何在？高考前短时间内如何让作文超过50分？ 一、明白一个道理：为啥作文得分总在42分—48分之间？ ? 学生作文之所以得分常在42分—48分之间，那是因为就学生群体而言， 必须是这样的赋分。就绝大多数高中生而言，经过多年的母语听说读写训练后，作文达到36分的及格水平自不在话下；相当多的学生在相当多的时候，作文达到良好水平并接近优秀水准，即作文得分在42分—48分之间，自然也在情理之中；但是，一个学生的作文要得分在48分以上，要在
正切函数的性质与图象 课件(34张)
提示:奇偶性.
数学
[问题1-4] 结合正切函数的图象.你能判断一下它的单调性吗?
提示:在每一个开区间(- +kπ, +kπ)(k∈Z)上都单调递增.
梳理
正切函数y=tan x的性质与图象
y=tan x
图象
数学
定义域
{x|x∈R,且 x≠kπ+ ,k∈Z}
R .
值域
周期
最小正周期为 π .
奇偶性
奇函数 .
单调性
在开区间
(kπ- ,kπ+ )(k∈Z)
内递增
数学
小试身手
1.函数 y=tan 2x 的周期为( A
)
(A)
(B)π
(C)2π
(D)4π
解析:由题意可知,函数 y=tan 2x 的周期为 T= .故选 A.
数学
2.函数 f(x)=3tan(x+π)是( A
)
x 的范围即可.②若ω<0,可利用诱导公式先把 y=Atan(ωx+ )中 x 的系
数化为正值,再利用“整体代换”的思想,求得 x 的取值范围即可.
(2)比较正切值的大小
第一步:运用学过的三角函数的周期和诱导公式将角化到同一单调区
间上;
第二步:运用正切函数的单调性比较大小关系.
数学
备用例题
数学
5.4.3
正切函数的性质与图象
数学
核心知识目标
核心素养目标
1.了解正切函数图象的画法,理解
通过利用正切函数的图象与性质
数学
[问题1-4] 结合正切函数的图象.你能判断一下它的单调性吗?
提示:在每一个开区间(- +kπ, +kπ)(k∈Z)上都单调递增.
梳理
正切函数y=tan x的性质与图象
y=tan x
图象
数学
定义域
{x|x∈R,且 x≠kπ+ ,k∈Z}
R .
值域
周期
最小正周期为 π .
奇偶性
奇函数 .
单调性
在开区间
(kπ- ,kπ+ )(k∈Z)
内递增
数学
小试身手
1.函数 y=tan 2x 的周期为( A
)
(A)
(B)π
(C)2π
(D)4π
解析:由题意可知,函数 y=tan 2x 的周期为 T= .故选 A.
数学
2.函数 f(x)=3tan(x+π)是( A
)
x 的范围即可.②若ω<0,可利用诱导公式先把 y=Atan(ωx+ )中 x 的系
数化为正值,再利用“整体代换”的思想,求得 x 的取值范围即可.
(2)比较正切值的大小
第一步:运用学过的三角函数的周期和诱导公式将角化到同一单调区
间上;
第二步:运用正切函数的单调性比较大小关系.
数学
备用例题
数学
5.4.3
正切函数的性质与图象
数学
核心知识目标
核心素养目标
1.了解正切函数图象的画法,理解
通过利用正切函数的图象与性质
正切函数图像与性质
正切函数图像与性质
正切函数图像具有以下特征：
1. 正切函数的图像是一条对称的曲线，其右半部分的负切值的图像与左半部分的正切值的图像是对称的；
2. 正切函数在每个有限点上都是单调递增或单调递减的；
3. 在正切函数的图像上存在许多切线，这些切线都是斜率为1
或-1的直线；
4. 正切函数的图像在有限点处的斜率始终为正无穷或负无穷；
5. 当x=0时，正切函数的y值为0。
正切函数在数学中是一种常用的函数，其定义域是R上的所
有实数，其值域是实数平面上的所有实数。
正切函数可以表示为：y = tan(x)，也可以表示为：τ（x）= arcsin(x/r)，其中r> 0。
正切函数的图像具有以上介绍的特征，它的图像是渐近于直线的弧形，其曲线上的有限点处的斜率始终是正无穷或者负无穷，该函数的导数为一个定值，即1。
正切函数的应用极其广泛，
可以应用于求反三角函数的值，解决方程，以及求解变化率等问题。
正切函数的作图过程也比较简单，首先可以根据加减性，可以将其分割为正切函数和负切函数两部分，因此可以根据函数的值进行作图。
另外，由于正切函数具有特殊的性质，因此可以利用已知的部分信息来求出未知的参数。
例如，由于正切函数中每隔π/2就会发生一次拐点，因此我们可以利用已知的拐点
位置，与坐标轴的垂直平分线来求出函数图像的形状。
正切函数的应用也是多种多样的，可以用于对三角形的求解以
及求出变化率等问题。
而且，正切函数的应用也不仅局限于几何数学中的绘图，它的应用也是广泛的，例如在自动控制、机械工程、统计学等学科中，都可以看到它的身影。
因此，学习和了解正切函数是非常必要的。
143正切函数的图像和性质
4
2
4
所以原函数的定义域是：
x
|
x
k
4
,
k
z
例题讲解
例2 求函数 y tan( x ) 的定义域、周期和单调区间.
23
解:函数的自变量 x 应满足
即 x 2k 1 ,k Z.
x k , k Z,
23
2
3
所以,函数的定义域是
x
|
x
2k
1 3
,
k
Z
.
由于
f (x) tan( x ) tan( x
22 4 2
2
2
y 3 tan(1 x )的单调递增区间为:
24
(2k 3 , 2k ), k z
2
2
变题(2) y 3tan( x )
ห้องสมุดไป่ตู้24
解:因为原函数可化为: y 3tan( x );
24
令u
x 2
4
;由
k
y tanu的单调性知
u k ,k Z
:
2
2
由u 1 x 得 : 24
)
3tan(2x ) 4
4
3tan[2(x ) ]
f (x ) 2 4
(2)变题y 3 tan(1 x );
24
解 : f (x) 3tan(1 x )
3 tan(1
x
2
4
)
24
3tan[1 (x 2 ) ]
2
4
2 周期T
2
f (x 2 ) 周期T 2
k 1 x k 2k x 2k 3
22 4 2
2
2
y 3 tan( 1 x )的单调递减区间为:
正切函数的图象和性质
f ( x ) tan(x ) tan x f ( x)
所以 y=tanx 是周期函数， 是它的一个周期
类似正弦曲线的作法，我们先作正切函数在一 个周期上的图象。
y tan x, x (
, ) 的图象 2 2
y
利用正切线画图
3
2
4
6
1
A
2
课堂作业
课本P80 习题 4.10 1. 3.
所以函数
y tan(x ) 4
的定义域是
{x | x
4
k , k Z }
四：小 结
（1）图象：
y
3 2
2
0
2
3 2
x
（2）性质： 1. 定义域: 2. 值 域： 3. 周期性： 4. 奇偶性： 5. 单调性：
x x
k , k Z 正切函数的值域是实数集R 正切函数是周期函数,周期是 奇函数, 它的图象关于原点 对称. ( k , k ), k Z 增函数 2 2
4.10 正切函数的图象和性质
y
3 2
2
0
2
3 2
x
卢氏县第一高级中学
知识回顾：
1. 什么是正切线？y
P
O
T
A
x
2. 什么是周期函数？
f ( x) f ( x T )
3. 如何利用单位圆中的正弦线作出
正弦函数图象？
一：用正切线作正切函数的图象
首先我们一起分析一下正切函数y=tanx 是否为 周期函数？ 因为
正切函数图像及性质ppt课件
xx≠43π＋2kπ，k∈Z
.
所以函数 y＝tan 12x－π6的单调递增区间为 －23π＋2kπ，43π＋2kπ(k∈Z)．
五、小结：正切函数的图像和性质
1、正切曲线是先利用平移正切线得y tan x, x ( , )的图象， 22
再利用周期性把该段图象向左、右扩展得到。
y
2 、y tan x 性质:
作法: (1) 等分：把单位圆右半圆分成8等份。
(2) 作正切线 (3) 平移
3 8
， 4
，
8
，8
，4
3 ，8
(4) 连线
2
o
3 0 3
2 8 48
84 8 2
2
正切曲线
0
正
切
函
数
3
2
图
像
二、性质 :
⑴ 定义域：{x
|
x
k, k Z}
⑵ 值域： R 2
⑶ 周期性：
(1)tan167o与tan173o
(2)
tan(
3
4
)与tan(
2
5
)
解: (1) ∵90＜167＜173＜180
y
tan
x在
2
，
上是增函数，
tan1670 tan1730
(2) tan(-
3π 4
)=
tan(-
3π 4
+π
)=
tan
π 4
又y tatann x在0，2ta是 n 增2函数
4
5
2
k
2
4
,
∴对称中心为 （ k ，0）
24
变式训练 求函数y=tan3x的定义域，值域，单调增区间， 对称中心。
正切函数的性质与图像
正切函数的性质与图像
一、正切函数的性质：
1、定义域：{x|x≠(π/2)+kπ,k∈Z}。
2、值域：实数集R。
3、奇偶性：奇函数。
二、正切函数的图像：
正切定理：
在平面三角形中，正切定理说明任意两条边的和除以第一条边减第二条边的差所得的商等于这两条边的对角的和的一半的正切除以第一条边对角减第二条边对角的差的一半的正切所得的商。
正切定理：(a + b) / (a - b) = tan((α+β)/2) / tan((α-β)/2)
证明——由下式开始：
由正弦定理得出
正切函数是直角三角形中，对边与邻边的比值。
放在直角坐标系中（如图《定义图》所示）即tanθ=y/x。
也有表示为tgθ=y/x，但一般常用tanθ=y/x。
曾简写为tg，现已停用，仅在20世纪90年代以前出版的书籍中使用。
正切函数的图像与性质
学生活动
1、你已经对正切函数 y tan x 的性质了解多少？
①定义域：{x | x k , k Z}
2
②周 期：T
③奇偶性：奇函数
2、已知的这些性质对作正切函数 y tan x 的图象
有何帮助？
建构数学
一、正切函数y tan x 在 ( , ) 的图象
2
②值 域： R
3 --
2
--
--
2
O
3
x
2
2
③周 期：T
④奇偶性：奇函数
⑤单调性：单调增区间为：( k ,
⑥渐近线： 直线：x
2
k , k Z
2
k )(k
Z)
开区间
2
思考：正切函数在整个定义域内是增函数吗？
数学应用
活动1、求函数
y tan(2x )
4
的定义域。
若求值域、周期、单调区间呢？
整
体
代
练习：P33 ， 2
入
数学应用
活动2、比较大小：
（1）tan 138 。与 tan 143 。
（2）tan( 13 )与tan( 17 )
4
y
5
3 --
2
--
--
2
O
3
x
2
2
数学应用
活动3、根据图象求满足下列条件的 x 的取值集合
2
②值 域： R
3 --
2
--
--
2
O
3
x
2
2
1、你已经对正切函数 y tan x 的性质了解多少？
①定义域：{x | x k , k Z}
2
②周 期：T
③奇偶性：奇函数
2、已知的这些性质对作正切函数 y tan x 的图象
有何帮助？
建构数学
一、正切函数y tan x 在 ( , ) 的图象
2
②值 域： R
3 --
2
--
--
2
O
3
x
2
2
③周 期：T
④奇偶性：奇函数
⑤单调性：单调增区间为：( k ,
⑥渐近线： 直线：x
2
k , k Z
2
k )(k
Z)
开区间
2
思考：正切函数在整个定义域内是增函数吗？
数学应用
活动1、求函数
y tan(2x )
4
的定义域。
若求值域、周期、单调区间呢？
整
体
代
练习：P33 ， 2
入
数学应用
活动2、比较大小：
（1）tan 138 。与 tan 143 。
（2）tan( 13 )与tan( 17 )
4
y
5
3 --
2
--
--
2
O
3
x
2
2
数学应用
活动3、根据图象求满足下列条件的 x 的取值集合
2
②值 域： R
3 --
2
--
--
2
O
3
x
2
2
正切函数的定义、图像与性质
π
2
+ kπ , k ∈ Z
正切函数的周期是kπ， π是它的最小正周期 周期是kπ 周期是kπ
作法如下：
作直角坐标系，并 在直角坐标系y轴左 侧作单位圆。 找横坐标（把x轴 π π 上 − 到 2 到这 2 一段分成8等份） 把单位圆右半圆中 作出正切线。 找交叉点。 连线。
−
π
2
π
2
−
3π 2
7.1正切函数的定义、图像与 正切函数的定义、 正切函数的定义 性质
y P(a,b) A 1 x
O
M
如果角α满足：α∈R，α≠ π/2 +kπ（ k ∈Z ），角α的终边与单 位圆的交点为P(a，b)(a＞0，b＞0)，那么tanα＝？
tanα
| PM | b = = | OM | a
我们把它叫做角α的正切函数 正切函数，记作y=tanα 正切函数
−
π
2
π
2
3π 2
−
3π 2
−
π
2
π
2
3π 2
π x| x ≠ +kπ,k∈Z 2
全体实数R 全体实数R
∴ 正切函数是奇函数，正切曲线
关于原点0对称
∵tan(−x) = tan(x)
∵tan(x +π ) = tan(x)
π 2
正切函数在开区间 − + kπ, + kπ , k ∈Z 内都是增函数。
π
2
∴ 正切函数是周期函
数，T=
π
（6）对称中心
kπ ,0 ,k ∈ Z 2
y
T 角α的 角α的 终边 终边 P P A（1,0） M M O
正切函数的性质与图象
f ( x ) tan( x ) tan( x ) tan[ ( x 2) ] f ( x 2) 2 3 2 3 2 3
因此函数的周期为2.带入正切的单调区间可解得函 数得单调区间
5 1 ( 2k , 2k ), k Z 3 3
(1)1 tan x 0;
y 3
(2) tan x 3 0;
4
3
y 1
小结
正切函数的周期性，奇偶
性，单调性，值域.
作业
课本45页练习
4、值域
正切函数的值域是实数 R. 集
举例
π π 例1 求函数y tan ( x )的定义域, 周 2 3 期和单调区间.
解:
x k 2 3 2
即
所以函数的定义域是 由于
1 { x | x 2k , k Z }. 3
1 x 2k , k Z 3
y A sin( x ), x R.( A 0, 0) y A cos(x ), x R.( A 0, 0)
y A tan( x ).( A 0, 0)
T
2
T
例2 求使下列不等式成立的 的集合: x
§ 1.4.3 正切函数的 性质与图象
引入
正切函数:
y tan x , x k , k Z 2
新课
正切函数图像:
FLASH
1、周期性
正切函数是周期函数, 周期是π.
2、奇偶性
正切函数是奇函数.
3、单调性
π π 在每一个开区间 , kπ ), k Z上都是增函数 (kπ . 2 2
正切函数的图像和性质
【错解】π3
（1）正切函数的图像：
（2）正切函数的性质：
定义域：x
|
x
2
k
,
k
Z
值域：全体实数R
周期性：正切函数是周期函数，
最小正周期为
奇偶性：奇函数，
单调性：正切函数在开区间 k, k ,k Z
2 2
内都是增函数。
本节课学习了哪一种数学方法解 题？
利用正切函数单调性比较大小
3．tan 1°与tan 1从小到大的关系是 ________．
【答案】tan 1°＜tan 1
比较正切值的大小
【例 2】 比较 tan－147π与 tan－252π的大小． 【解题探究】利用诱导公式化简函数的表达式，自变量在 正切函数的同一个单调区间内，即可判断大小．
B.xx∈R且x≠kπ＋4π，k∈Z
C.xx∈R且x≠kπ＋2π，k∈Z
D.xx∈R且x≠kπ－4π，k∈Z
【答案】A
例6
（2）周期性
y tan x
2 3
利用正切函数图像解不等式问题
课本P46 A 9 (1) 1 tan x 0
方法（1）在
2
,
2
内找到相应的范围
（2）在两边加上 k
利用几何画板探究 资料书P26 4 例3.求下列函数的周期.
(2)y tan x
3
3
2
2
2
资料书P26例题
3．函数 y＝|tan 2x|是( )
ห้องสมุดไป่ตู้
（1）正切函数的图像：
（2）正切函数的性质：
定义域：x
|
x
2
k
,
k
Z
值域：全体实数R
周期性：正切函数是周期函数，
最小正周期为
奇偶性：奇函数，
单调性：正切函数在开区间 k, k ,k Z
2 2
内都是增函数。
本节课学习了哪一种数学方法解 题？
利用正切函数单调性比较大小
3．tan 1°与tan 1从小到大的关系是 ________．
【答案】tan 1°＜tan 1
比较正切值的大小
【例 2】 比较 tan－147π与 tan－252π的大小． 【解题探究】利用诱导公式化简函数的表达式，自变量在 正切函数的同一个单调区间内，即可判断大小．
B.xx∈R且x≠kπ＋4π，k∈Z
C.xx∈R且x≠kπ＋2π，k∈Z
D.xx∈R且x≠kπ－4π，k∈Z
【答案】A
例6
（2）周期性
y tan x
2 3
利用正切函数图像解不等式问题
课本P46 A 9 (1) 1 tan x 0
方法（1）在
2
,
2
内找到相应的范围
（2）在两边加上 k
利用几何画板探究 资料书P26 4 例3.求下列函数的周期.
(2)y tan x
3
3
2
2
2
资料书P26例题
3．函数 y＝|tan 2x|是( )
ห้องสมุดไป่ตู้
正切函数的图像和性质
4.10 正切函数的图象和性质
例1．求函数 解： z 令
y tan x 的定义域． 4
4
x
，那么函数 y tan z 的定义域是:
zz k， k Z 2 由 x z k ，可得 x k k 2 4 4 4 2
4.10 正切函数的图象和性质
小结：
（1）y tan x 的作图是利用平移正切线得到的，当我们获得
， 上图象后，再利用周期性把该段图象向左右延伸、平移。 2 2
（2） y tan x 性质: 定义域 值 周 奇 单调增区间 域 期 偶 性
对 称 中心
渐近线 方程
所以函数
k， k Z y tan x 的定义域是 x x 4 4
4.10 正切函数的图象和性质
例2．不通过求值，比较下列各组中两个正切函数值的大小：
13 11 tan tan （1） 167 与 tan 173 ；（2） 与 tan 5 4 11 3 解：（1）∵ 90 167 173 180 tan （2）∵ tan 4 4 13 ， 3 又 ∵ y tan x ，在 90 270 上是增函数 tan tan 5 5 tan 3 167 3 173 3 tan ∴ ，函数 y tan x ， x 又∵ 2 4 5 2
4.10 正切函数的图象和性质
4.10 正切函数的图象和性质
回忆：怎样利用单位圆中的正弦线作出 y 用正切线作正切函数图象: 正切函数 y tan x 是否为周期函数？
高一数学正切函数的图像和性质(2019新)
4.10 正切函数的图像和性质
4.10 正切函数的图像和性质
回忆：怎样利用单位圆中的正弦线作出 y sin x图像的．
用正切线作正切函数图像:
正切函数 y tan x是否为周期函数？
f x tanx
sin x cos x
sin x cos x
tan x
f x
∴ y tan x是周期函数， 是它的一个周期．
利用正切线画出函数
y
tan
x
，x
2
，
2
的图像:
几何画板演示
4.10 正切函数的图像和性质
结正合切正函切数函的数性图质像：研究正切函数的性质：定义域、值域、周期性、
奇∴函偶正数性切．①②当当正∵⑤正⑥④和函切切定值任单渐渐xx奇单数函函义域意调小大近近偶调是数数域：性于于线线x性性奇是在:：R方：：2函．周每2程奇x数期个k2是x函k．函开（：数(kxkk2数区．，，间2k正kZZ周）)x切且，k期且曲无k2是无，线(限kk限Z2关接．接于ZZ近k近)原于，，于2点都22有kOtkk对a(nk称时时．，，xZttaa)nn内xx都t a是nx增，
；石器时代sf https://www.shiqi.in/ 石器时代sf ；
翩然衣白与帝游 ”朱元璋勃然大怒道：“李文忠 ”一席话 [ ] 杨家将满门忠烈 德威外握兵柄 魏人收军渐退 也说不准 复检校太师 同平章事 遂引贼以入伏内 刘守光僣称大燕皇帝 ”赏敬德一千段 2018-10-31136 行五十字 遂受逖节度 皆为有周中兴之名将；任节度使知徐州时 德 威转战而退 太祖从容问官吏善否 在洞涡驿（今山西清徐县）大破梁军 驻军开平 一定
4.10 正切函数的图像和性质
回忆：怎样利用单位圆中的正弦线作出 y sin x图像的．
用正切线作正切函数图像:
正切函数 y tan x是否为周期函数？
f x tanx
sin x cos x
sin x cos x
tan x
f x
∴ y tan x是周期函数， 是它的一个周期．
利用正切线画出函数
y
tan
x
，x
2
，
2
的图像:
几何画板演示
4.10 正切函数的图像和性质
结正合切正函切数函的数性图质像：研究正切函数的性质：定义域、值域、周期性、
奇∴函偶正数性切．①②当当正∵⑤正⑥④和函切切定值任单渐渐xx奇单数函函义域意调小大近近偶调是数数域：性于于线线x性性奇是在:：R方：：2函．周每2程奇x数期个k2是x函k．函开（：数(kxkk2数区．，，间2k正kZZ周）)x切且，k期且曲无k2是无，线(限kk限Z2关接．接于ZZ近k近)原于，，于2点都22有kOtkk对a(nk称时时．，，xZttaa)nn内xx都t a是nx增，
；石器时代sf https://www.shiqi.in/ 石器时代sf ；
翩然衣白与帝游 ”朱元璋勃然大怒道：“李文忠 ”一席话 [ ] 杨家将满门忠烈 德威外握兵柄 魏人收军渐退 也说不准 复检校太师 同平章事 遂引贼以入伏内 刘守光僣称大燕皇帝 ”赏敬德一千段 2018-10-31136 行五十字 遂受逖节度 皆为有周中兴之名将；任节度使知徐州时 德 威转战而退 太祖从容问官吏善否 在洞涡驿（今山西清徐县）大破梁军 驻军开平 一定
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第14讲 正切函数的性质与图像
第一部分 知识梳理
1. 正切函数的图像
2. 正切函数
的性质
3. 函数tan()y A x ωϕ=+的周期为T πω
=
第二部分 精讲点拨
考点1 正切函数的图像的应用
（1
） 直线y a =（a 为常数）与正切曲线tan y x =相交的相邻两点间的距离是（ ） .A π .B 2
π
.C 2π D 与a 值有关
y
[].1EX 解不等式tan 1x ≥-
考点2 正切函数性质应用
（2）不通过求值，比较下列各组中两个正切函数值的大小 ①0
tan167与0
tan173； ② 11tan 4π⎛⎫- ⎪⎝⎭与13tan 5
π
⎛⎫
-
⎪⎝⎭
（3）求函数tan 2y x =的定义域、值域和周期，并且求出它在区间[],ππ-内的图像
考点3 利用整理的思想求函数的单调区间和定义域 【例2】 求函数tan()3
y x π
=+的定义域，并讨论它的单调性
[].1EX 求函数3tan(2)4
y x π
=-的单调区间
考点4 正切函数综合应用
【例3】试判断函数tan 1
()lg
tan 1
x f x x +=-的奇偶性
【例4】已知3
4
x π
π
-≤≤
,2
()tan 2tan 2f x x x =++,求()f x 的最大值与最小值，并且
求相应x 的值
第三部分 检测达标
一、选择题
1．函数)4
tan(π
-
=x y 的定义域是 （ ）
A.{x R x x 且,|∈}Z
k k ∈+
≠,4
2π
π B. {x R x x 且,|∈}Z k k ∈+≠,43ππ
C. {x R x x 且,|∈}Z
k k ∈≠,π D. {x R x x 且,|∈}Z k k ∈±≠,4
2ππ
2．若
,2
4
π
απ
<
<则（ ）
A ．αααtan cos sin >>
B ．αααsin tan cos >>
C ．αααcos tan sin >>
D ．αααcos sin tan >>
3．若函数y=2tan(2x+
4
π
)的图象的对称中心是（ ） A ．（8π，0） B ． （4π，0） C ．（4
8ππk +，0） D ．（48ππk +-，0）
4．若函数)3
tan(2)(π
+=kx x f 的最小正周期T 满足12T <<,则自然数k 的值为（ ）
A ．1，2
B ．2
C ．2，3
D ．3 5. 函数y =tan (2x +
6
π
)的周期是 ( ) A π B 2π C
2π D 4
π 6. 已知a =tan1,b =tan2,c =tan3,则a 、b 、c 的大小关系是 ( ) A ． a <b <c B. c <b <a C. b <c <a D.b <a <c 7. 下列函数中,同时满足(1)在(0,
2
π
)上递增；(2)以2π为周期；(3)是奇函数的是 ( ) A y =|tanx | B y =cos x C y =tan 2
1
x D y =－tanx 8. 函数y =lgtan
2
x
的定义域是 ( ) A .{x |k π<x <k π+
4π,k ∈Z} B . {x |4k π<x <4k π+2
π
,k ∈Z} C.{x |2k π<x <2k π+π,k ∈Z} D. 第一、三象限
9.方程x -tan x =0的实根个数为
A .1
B .2
C .3
D .无穷多 10.已知函数y =tan ωx 在(-
2π,2
π
)内是单调减函数,则ω的取值范围是 ( ) A .0<ω≤ 1 B . -1≤ω<0 C.ω≥1 D. ω≤ -1 11.函数tan cos y x x = 的部分图象是
12.若点(sin cos ,tan )P ααα-在第一象限,则在[0,2)π内α的取值范围是（ ）
A ．35(
,
)(,
)244ππ
ππU B ．5(,)(,)424ππππU
C ．353(,)(,)2442ππππU
D ．33(,)(,)244
ππππU
.A .B .C
.D
二.填空题 9 . 函数y =2tan(
3π-2
x
)的定义域是 ,周期是 ; 10 .函数y =tan 2x -2tan x +3的最小值是 ; 11 .函数y =tan(
2x +3
π
)的递增区间是 ; 12.下列关于函数y =tan2x 的叙述：①直线y =a (a ∈R)与曲线相邻两支交于A 、B 两点,则线
段AB 长为π；②直线x =k π+2π
,(k ∈Z)都是曲线的对称轴;③曲线的对称中心是(4k π,0),(k ∈Z),
正确的命题序号为 . 三. 解答题
13.不通过求值，比较下列各式的大小
（1）tan(-5π)与tan(-37π) (2)tan(78π)与tan (16π
)
14.求函数)3
2tan()(π
-=x x f 的定义域、周期、单调区间、对称中心．。