人教版数学九年级上册 《切线长定理的相关计算》必考题型专项分类专题练习(专题分类练习 详细答案)
- 格式:docx
- 大小:334.60 KB
- 文档页数:18

专题11 切线定理(综合题)知识互联网易错点拨知识点1:切线的判定定理和性质定理1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.细节剖析:切线的判定方法:(1)定义:直线和圆有唯一公共点时,这条直线就是圆的切线;(2)定理:和圆心的距离等于半径的直线是圆的切线;(3)判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.(切线的判定定理中强调两点:一是直线与圆有一个交点,二是直线与过交点的半径垂直,缺一不可). 2.切线的性质定理:圆的切线垂直于过切点的半径.细节剖析:切线的性质:(1)切线和圆只有一个公共点;(2)切线和圆心的距离等于圆的半径;(3)切线垂直于过切点的半径;(4)经过圆心垂直于切线的直线必过切点;(5)经过切点垂直于切线的直线必过圆心.知识点2:切线长定理1.切线长:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. 细节剖析:切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段.2.切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.细节剖析:切线长定理包含两个结论:线段相等和角相等.3.圆外切四边形的性质:圆外切四边形的两组对边之和相等.知识点3:三角形的内切圆1.三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆.2.三角形的内心:三角形内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.细节剖析:(1)任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;(2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即(S 为三角形的面积,P 为三角形的周长,r 为内切圆的半径). (3) 三角形的外心与内心的区别:内心(三角形内切圆的圆心)三角形三条角平分线的交点(1)到三角形三边距离相等;(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB;(3)内心在三角形内部.一.选择题1.(2022•吉林一模)如图,△ABC内接于⊙O,AC为⊙O直径,过点B的切线交CA的延长线于点P.若∠P=32°,则∠ACB的度数是()A.29°B.30°C.31°D.32°【易错思路引导】连接OB,根据切线的性质可得∠OBP=90°,再根据直角三角形的两个锐角互余可得∠AOB=58°,然后利用圆周角定理进行计算即可解答.【规范解答】解:连接OB,∵PB与⊙O相切于点B,∴∠OBP=90°,∵∠P=32°,∴∠AOB=90°﹣∠P=58°,∴∠ACB=∠AOB=29°,故选:A.【考察注意点】本题考查了切线的性质,圆周角定理,三角形的外接圆与外心,熟练掌握切线的性质,以及圆周角定理是解题的关键.2.(2017秋•昆明期末)如图所示,在平面直角坐标系xOy中,⊙A半径为3,且点A的坐易错题专训标为(5,0),将⊙A沿x轴的负方向平移,使⊙A与y轴相切,则平移的距离为()A.2 B.5 C.8 D.2或8【易错思路引导】平移分在y轴的左侧和y轴的右侧两种情况写出答案即可.【规范解答】解:当⊙A位于y轴的右侧且与y轴相切时,平移的距离为2;当⊙A位于y轴的左侧且与y轴相切时,平移的距离为8.故选:D.【考察注意点】本题考查了切线的判定与性质,坐标与图形变化﹣平移,解题的关键是了解当圆与直线相切时,点到圆心的距离等于圆的半径.3.(2022春•沙坪坝区校级期中)如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,D 是⊙O上一点,连接BD,CD,∠BDC=30°,延长AB至点F,使得BF=AB,连接OF,过点B作BG⊥OF于点G,BG=2,则OC的长为()A.B.C.D.2【易错思路引导】连接OB,由切线的性质得出∠OBF=∠OBA=90,设OB=x,则AB=x,由锐角三角函数的定义得出,解得x=,则可得出答案.【规范解答】解:连接OB,∵∠BDC=30°,∴∠BOC=2∠BDC=60°,∵AB为⊙O的切线,∴AF⊥OB,∴∠OBF=∠OBA=90,设OB=x,则AB=x,∵BF=AB,∵BF=x,∵BG=2,∴OG==,∵∠FBG+∠GBO=90°,∠GBO+∠BOG=90°,∴∠FBG=∠BOG,∴cos∠FBG=cos∠BOG,∴,∴,解得x=,∴OB=OC=,故选:A.【考察注意点】本题考查了切线的性质,直角三角形的性质,勾股定理,锐角三角函数的定义,熟练掌握切线的性质是解题的关键.4.(2022•鼓楼区校级模拟)如图,AD是⊙O的直径,PA,PB分别切⊙O于点A,B,若∠BCD =α,则∠P的度数是()A.90°﹣2αB.90°﹣αC.45°D.2α【易错思路引导】连接OB,利用圆周角定理可得∠BOD=2α,然后利用切线的性质可得∠OAP=∠OBP=90°,从而利用四边形内角和可得∠P+∠AOB=180°,最后利用同角的补角相等即可解答.【规范解答】解:连接OB,∵∠BCD=α,∴∠BOD=2∠BCD=2α,∵PA,PB分别切⊙O于点A,B,∴∠OAP=∠OBP=90°,∴∠P+∠AOB=360°﹣∠OAP﹣∠OBP=180°,∵∠AOB+∠BOD=180°,∴∠P=∠BOC=2α,故选:D.【考察注意点】本题考查了切线的性质,圆周角定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.5.(2022•德阳)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,则下列结论:①∠BAD=∠CAD;②若∠BAC=60°,则∠BEC=120°;③若点G为BC的中点,则∠BGD=90°;④BD=DE.其中一定正确的个数是()A.1 B.2 C.3 D.4【易错思路引导】利用三角形内心的性质得到∠BAD=∠CAD,则可对①进行判断;直接利用三角形内心的性质对②进行判断;根据垂径定理则可对③进行判断;通过证明∠DEB =∠DBE得到DB=DE,则可对④进行判断.【规范解答】解:∵E是△ABC的内心,∴AD平分∠BAC,∴∠BAD=∠CAD,故①正确;如图,连接BE,CE,∵E是△ABC的内心,∴∠EBC=∠ABC,∠ECB=ACB,∵∠BAC=60°,∴∠ABC+∠ACB=120°,∴∠BEC=180°﹣∠EBC﹣∠ECB=180°﹣(∠ABC+∠ACB)=120°,故②正确;∵∠BAD=∠CAD,∴=,∴OD⊥BC,∵点G为BC的中点,∴G一定在OD上,∴∠BGD=90°,故③正确;如图,连接BE,∴BE平分∠ABC,∴∠ABE=∠CBE,∵∠DBC=∠DAC=∠BAD,∴∠DBC+∠EBC=∠EBA+∠EAB,∴∠DBE=∠DEB,∴DB=DE,故④正确.∴一定正确的①②③④,共4个.故选:D.【考察注意点】本题考查了三角形的内切圆与内心,圆周角定理,三角形的外接圆与外心,解决本题的关键是掌握三角形的内心与外心.6.(2022•临沭县二模)如图,在平面直角坐标系中,以M(2,3)为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,则AC的长为()A.4 B.C.D.6【易错思路引导】设⊙M与x轴相切于点D,连接MD,过点M作ME⊥AC,垂足为E,根据垂径定理可得AC=2AE,再利用切线的性质可得∠MDO=90°,然后根据点M的坐标可得ME=2,MA=MD=3,最后在Rt△AEM中,利用勾股定理进行计算即可解答.【规范解答】解:设⊙M与x轴相切于点D,连接MD,过点M作ME⊥AC,垂足为E,∴AC=2AE,∵⊙M与x轴相切于点D,∴∠MDO=90°,∵M(2,3),∴ME=2,MD=3,∴MA=MD=3,在Rt△AEM中,AE===,∴AC=2AE=2,故选:B.【考察注意点】本题考查了切线的性质,垂径定理,坐标与图形的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.二.填空题7.(2022•南关区校级模拟)如图,⊙O与△OAB的边AB相切,切点为B.将△OAB绕点B按顺时针方向旋转得到△O′A′B,使点O'落在圆O上,边A′B交线段AO于点C.若∠A =15°,⊙O的半径长为2,则BC的长为 2 .【易错思路引导】连接OO′,根据旋转可得△BOO'为等边三角形,进而可求出∠A'BO,再利用∠A=15°,可证明△BCO是等腰三角形,得到答案.【规范解答】解:如图,连接OO′,由题意得:BO=OO'=BO',∴△BOO'为等边三角形,∴∠OBO'=60°,∵AB与⊙O相切于点B,∴∠ABO=90°,∴∠A'BO'=90°,∴∠A'BO=∠A'BO'﹣∠OBO'=30°,∵∠A=15°∴∠AOB=90°﹣∠A=75°,∴∠BCO=180°﹣∠AOB﹣∠A'BO=75°,∴BC=BO=2,故答案为:2.【考察注意点】本题考查的是切线的性质、旋转变换的性质,掌握圆的切线垂直于经过切点的半径是解题的关键.8.(2022•香坊区校级开学)如图,在⊙O中,PA切⊙O于点A,PB切⊙O于点B,连接PO,若PA=,∠APB=60°,则线段PO的长为 2 .【易错思路引导】连接OA,根据切线长定理得到∠APO=∠APB=30°,根据切线的性质得到OA⊥PA,根据余弦的定义计算,得到答案.【规范解答】解:连接OA,∵PA切⊙O于点A,PB切⊙O于点B,∴OA⊥PA,∠APO=∠APB=30°,在Rt△PAO中,cos∠APO=,∴OP===2,故答案为:2.【考察注意点】本题考查的是切线的性质、切线长定理,熟记圆的切线垂直于经过切点的半径是解题的关键.9.(2022•南岗区三模)如图,△ABC内接于⊙O,BD为⊙O的切线,连接AD,若AD经过圆心O,且∠D=50°,则∠C的大小为70 度.【易错思路引导】连接OB,如图,根据切线的性质得到∠OBD=90°,再利用三角形外角性质计算出∠AOC=140°,然后根据圆周角定理计算∠C的度数.【规范解答】解:连接OB,如图,∵BD为⊙O的切线,∴OB⊥BD,∴∠OBD=90°,∵∠AOC=∠OBD+∠D=90°+50°=140°,∴∠C=∠AOC=×140°=70°.故答案为:70.【考察注意点】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.10.(2022•老河口市模拟)PA,PB是⊙O的切线,A,B是切点,点C是⊙O上不与A,B重合的一点,若∠APB=70°,则∠ACB的度数为55°或125°.【易错思路引导】根据切线的性质得到∠OAP=90°,∠OBP=90°,再根据四边形内角和得到∠AOB=110°,然后根据圆周角定理和圆内接四边形的性质求∠ACB的度数.【规范解答】解:∵PA,PB是⊙O的两条切线,∴OA⊥PA,OB⊥PB,∴∠OAP=90°,∠OBP=90°,∵∠APB=70°,∴∠AOB=360°﹣90°﹣90°﹣70°=110°,当点C在劣弧AB上,则∠ACB=∠AOB=55°,当点C′在优弧AB上,则∠AC′B=180°﹣55°=125°.则∠ACB的度数为55°或125°.故答案为:55°或125°.【考察注意点】本题切线的性质,圆周角定理和圆内接四边形的性质,解决本题的关键是掌握切线的性质.11.(2021•鹤峰县模拟)已知正方形ABCD边长为2,DE与以AB的中点为圆心的圆相切交BC于点E,求三角形DEC的面积 1.5 .【易错思路引导】根据已知可得DA与圆O相切于点A,EB与圆O相切于点B,设DE与圆O相切于点F,利用切线长定理可得DA=DF=2,EB=EF,然后设EB=EF=x,表示出DE,CE的长,最后在Rt△DEC中利用勾股定理进行计算即可解答.【规范解答】解:设∴DE与圆O相切于点F,∵四边形ABCD是正方形,∴∠OAD=∠OBC=∠C=90°,AB=BC=AD=CD=2,∵OA、OB是圆O的半径,∴DA与圆O相切于点A,EB与圆O相切于点B,∵DE与圆O相切于点F,∴DA=DF=2,EB=EF,设EB=EF=x,则EC=BC﹣EB=2﹣x,DE=DF+EF=2+x,在Rt△DEC中,DC2+CE2=DE2,∴22+(2﹣x)2=(2+x)2,解得:x=,∴EC=BC﹣EB=2﹣x=,∴三角形DEC的面积=EC•DC=××2=1.5,故答案为:1.5.【考察注意点】本题考查了切线的性质,正方形的性质,熟练掌握切线长定理是解题的关键.12.(2020秋•亭湖区校级月考)如图,正方形ABCD的边长为4,M为AB的中点,P是BC边上的动点,连接PM,以点P为圆心,PM长为半径作圆P,当圆P与正方形ABCD的边相切时,CP的长为 2.5或4﹣2.【易错思路引导】分两种情形分别求解:如图1中,当⊙P与直线CD相切时;如图2中当⊙P与直线AD相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形.【规范解答】解:如图1中,当⊙P与直线CD相切时,设PC=PM=x.在Rt△PBM中,∵PM2=BM2+PB2,∴x2=22+(4﹣x)2,∴x=2.5,∴CP=2.5;如图2中当⊙P与直线AD相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形.∴PM=PK=CD=2BM,∴BM=2,PM=4,在Rt△PBM中,PB==2,∴CP=BC﹣PB=4﹣2.综上所述,CP的长为2.5或4﹣2.故答案是:2.5或4﹣2.【考察注意点】本题考查切线的性质、正方形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.13.(2021秋•广丰区期末)已知点M(2.0),⊙M的半径为1,OA切⊙M于点A,点P为⊙M 上的动点,当P的坐标为(1,0),(3,0)(,)时,△POA是等腰三角形.【易错思路引导】根据题意画出图形分三种情况讨论:当点P在x轴上,PA=PO=1,OA =OP″=3,当点P是切点时,AO=AP=,进而可以解决问题.【规范解答】解:如图,当P的坐标为(1,0),(3,0),(,)时,△POA是等腰三角形.理由如下:连接AM,∵M(2.0),⊙M的半径为1,∴OM=2,AM=PM=1,∴OP=1,∵OA切⊙M于点A,∴∠MAO=90°,∴∠AOM=30°,∴∠AMO=60°,∴PA=AM=PM=1,∴OP=PA=1,∴P(1,0);当OA=OP′时,连接AP′交x轴于点H,∵OA切⊙M于点A,∴OP′切⊙M于点P′,∴∠P′OM=∠AOM=30°,∴∠AOP′=60°,∴△AOP′是等边三角形,∴AP′=OA===,∴OH=OA=,P′H=AP′=,∴P′(,);∵MA=MP″,∠AMO=60°,∴∠MAP″=∠MP″A=30°,∴∠AOP″=∠MP″A=30°,∴OA=OP″,∴P″(3,0).综上所述:当P的坐标为(1,0),(3,0),(,)时,△POA是等腰三角形.故答案为:(1,0),(3,0),(,).【考察注意点】本题考查了切线的性质,等腰三角形的判定与性质,勾股定理,等边三角形的判定与性质,坐标与图形性质,解决本题的关键是得到△AOP′是等边三角形.14.(2021•宁波模拟)如图,等腰△ABC中,AB=AC=5,BC=6,BD是腰AC上的高,点O 是线段BD上一动点,当半径为的⊙O与△ABC的一边相切时,OB的长为或.【易错思路引导】作AH⊥BC于点H,根据等腰三角形的性质可得HC的长,再利用三角函数可得DC,根据勾股定理得到BD的长,根据半径为的⊙O与△ABC的一边相切,分三种情况讨论根据相似三角形的性质求解即可得到结论.【规范解答】解:如图,作AH⊥BC于点H,∵AB=AC=5,BC=6,∴HC=3,∵∠AHC=90°,AC=5,∴cos C===,∴DC=,∴BD==,①⊙O与AC相切时,切点为D,∵半径为,∴OD=,∵BD=,∴OB=BD﹣OD=﹣=;②⊙O与BC相切时,切点为M,∴OM⊥BC,∴∠BMO=∠BDC=90°,∵∠MBO=∠DBC,∴△MBO∽△DBC,∴=,∴=,∴BO=;③⊙O与AB相切时,切点为N,∴ON⊥AB,∴∠BNO=∠BDA=90°,∵∠NBO=∠DBA,∴△NBO∽△DBA,∴=,∴=,∴BO=.当圆O与AB相切时,OB的长为,∵BD=,∵>,也就是说,圆O与AB相切,是圆心O在线段BD外即在直线BD上的时候,不符合题意,故答案只有两种情况,即圆O与AC,AB相切时.综上所述,AP的长为或.故答案为:或.【考察注意点】本题考查了切线的判定和性质,勾股定理,相似三角形的判定和性质,熟练正确切线的性质是解题的关键.三.解答题15.(2022•长清区二模)如图,⊙O是△ABC的外接圆,其切线AE与直径BD的延长线相交于点E,且∠ACB=60°.(1)求证:AE=AB;(2)若DE=2,求⊙O的半径.【易错思路引导】(1)连接OA,根据圆周角定理求出∠AOB=120°,从而利用等腰三角形的性质可得∠OBA=∠OAB=30°,然后根据切线的性质可得∠OAE=90°,从而利用三角形的外角可求出∠E=30°,最后根据等腰三角形的判定即可解答;(2)设⊙O的半径为r,然后根据含30度角的直角三角形可得OE=2OA,进行计算即可解答.【规范解答】(1)证明:连接OA,∵∠ACB=60°,∴∠AOB=2∠ACB=120°,∵OA=OB,∴∠OBA=∠OAB=30°,∵AE与⊙O相切于点A,∴∠OAE=90°,∴∠E=∠AOB﹣∠OAE=30°,∴∠E=∠OBA=30°,∴AB=AE;(2)设⊙O的半径为r,∵∠OAE=90°,∠E=30°,∴OE=2OA,∵DE=2,∴2+r=2r,∴r=2,∴⊙O的半径为2.【考察注意点】本题考查了切线的性质,含30度角的直角三角形,三角形的外接圆与外心,熟练掌握切线的性质,以及含30度角的直角三角形是解题的关键.16.(2022•内黄县二模)如图,在△ABC中,∠ABC=90°,∠BAC=30°,以AB为直径作⊙O,交AC于点D,过点D作⊙O的切线DM交BC于点M.(1)求证:CM=BM.(2)若AD=2,P为AB上一点,当PM+PD为最小值时,求AP的长.【易错思路引导】(1)连接OD,OM,先利用圆周角定理求出∠DOB=60°,再利用切线的性质可得∠ODM=90°,然后利用HL证明Rt△ODM≌Rt△OBM,从而利用全等三角形的性质可得∠DOM=∠BOM=30°,进而可得AC∥OM,即可解答;(2)连接DB,过点D作DE⊥AB,垂足为E,并延长交⊙O于点D′,连接D′M交AB于点P,连接DP,此时PM+PD的值最小,根据直径所对的圆周角是直角可得∠ADB=90°,从而在Rt△ADB中,求出DB,AB的长,再在Rt△ABC中,求出BC的长,从而求出BM的长,然后证明△DOB是等边三角形,再利用等腰三角形的三线合一性质求出OE的长,从而求出DE的长,最后证明8字模型相似三角形△MBP∽△D′EP,利用相似三角形的性质求出BP的长,进行计算即可解答.【规范解答】(1)证明:连接OD,OM,∵∠BAC=30°,∴∠DOB=2∠A=60°,∵DM与⊙O相切于点D,∴∠ODM=90°,∵∠ABC=90°,OD=OB,OM=OM,∴Rt△ODM≌Rt△OBM(HL),∴∠DOM=∠BOM=∠DOB=30°,∴∠A=∠BOM,∴AC∥OM,∵OA=OB,∴BM=CM;(2)连接DB,过点D作DE⊥AB,垂足为E,并延长交⊙O于点D′,则DE=D′E,∴点D与点D′关于AB对称,连接D′M交AB于点P,连接DP,此时PM+PD的值最小,∵AB是⊙O的直径,∴∠ADB=90°,∵AD=2,∠DAB=30°,∴BD=AD•tan30°=2×=2,∴AB=2BD=4,∴OA=OB=OD=AB=2,在Rt△ABC中,BC=AB•tan30°=4×=,∴CM=BM=BC=,∵∠DOB=60°,∴△DOB是等边三角形,∵DE⊥OB,∴OE=EB=OB=1,∴DE=OE=,∴DE=D′E=,∵∠D′EP=∠CBP=90°,∠MPB=∠EPD′,∴△MBP∽△D′EP,∴=,∴=,∴BP=,∴AP=AB﹣BP=,∴AP的长为.【考察注意点】本题考查了切线的性质,圆周角定理,垂径定理,轴对称﹣最短路线问题,含30度角的直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.17.(2022•衡阳)如图,AB为⊙O的直径,过圆上一点D作⊙O的切线CD交BA的延长线于点C,过点O作OE∥AD交CD于点E,连接BE.(1)直线BE与⊙O相切吗?并说明理由;(2)若CA=2,CD=4,求DE的长.【易错思路引导】(1)连接OD,理由切线的性质可得∠ODE=90°,然后利用平行线和等腰三角形的性质可得OE平分∠DOB,从而可得∠DOE=∠EOB,进而可证△DOE≌△BOE,最后利用全等三角形的性质即可解答;(2)设⊙O的半径为r,先在Rt△ODC中,利用勾股定理求出r的长,再利用(1)的结论可得DE=BE,最后在Rt△BCE中,利用勾股定理进行计算即可解答.【规范解答】解:(1)直线BE与⊙O相切,理由:连接OD,∵CD与⊙O相切于点D,∴∠ODE=90°,∵AD∥OE,∴∠ADO=∠DOE,∠DAO=∠EOB,∵OD=OA,∴∠ADO=∠DAO,∴∠DOE=∠EOB,∵OD=OB,OE=OE,∴△DOE≌△BOE(SAS),∴∠OBE=∠ODE=90°,∵OB是⊙O的半径,∴直线BE与⊙O相切;(2)设⊙O的半径为r,在Rt△ODC中,OD2+DC2=OC2,∴r2+42=(r+2)2,∴r=3,∴AB=2r=6,∴BC=AC+AB=2+6=8,由(1)得:△DOE≌△BOE,∴DE=BE,在Rt△BCE中,BC2+BE2=CE2,∴82+BE2=(4+DE)2,∴64+DE2=(4+DE)2,∴DE=6,∴DE的长为6.【考察注意点】本题考查了切线的判定与性质,直线与圆的位置关系,全等三角形的判定与性质,勾股定理,熟练掌握全等三角形的判定与性质,以及勾股定理是解题的关键.18.(2022•津南区一模)已知△ABC内接于⊙O,AB为⊙O直径,弦CD与AB相交于点E,∠BAC=36°.(Ⅰ)如图①,若CD平分∠ACB,连接BD,求∠ABC和∠CBD的大小;(Ⅱ)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若AE=AC,求∠P的大小.【易错思路引导】(Ⅰ)根据直径所对的圆周角是直角可得∠ACB=90°,再利用角平分线的定义可得∠ACD=∠DCB=45°,从而求出∠ABC的度数,然后根据同弧所对的圆周角相等可得∠A=∠D=36°,最后利用三角形的内角和定理进行计算即可解答;(Ⅱ)连接OC,OD,根据切线的性质可得∠ODP=90°,再利用等腰三角形的性质可得∠BAC=∠OCA=36°,∠ACB=∠ABC=72°,从而求出∠OCD的度数,然后再根据OD=OC,求出∠ODC的度数,最后利用三角形的外角求出∠DOC的度数,从而求出∠P的度数.【规范解答】解:(Ⅰ)∵AB为⊙O直径,∴∠ACB=90°,∵CD平分∠ACB,∴∠ACD=∠DCB=∠ACB=45°,∵∠BAC=36°,∴∠ABC=90°﹣∠BAC=54°,∵∠A=∠D=36°,∴∠CBD=180°﹣∠D﹣∠DCB=99°,∴∠ABC的度数为54°,∠CBD的度数为99°;(Ⅱ)连接OC,OD,∵DP与⊙O相切于点D,∴∠ODP=90°,∵OA=OC,∴∠BAC=∠OCA=36°,∵AE=AC,∠BAC=36°,∴∠ACB=∠ABC=72°,∴∠OCD=∠ACE﹣∠OCA=36°,∵OD=OC,∴∠ODC=∠OCD=36°,∴∠DOE=∠AEC﹣∠ODC=36°,∴∠P=90°﹣∠DOE=54°,∴∠P的度数为54°.【考察注意点】本题考查了切线的性质,等腰三角形的性质,圆周角定理,三角形的外接圆与外心,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.19.(2022•佛山模拟)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.(1)求证:BC是⊙O的切线;(2)若∠OFA=60°,半径为4,在圆O上取点P,使∠PDE=15°,求点P到直线DE的距离.【易错思路引导】(1)连接OD,利用角平分线的定义,同圆的半径相等,平行线的判定与性质和切线的判定定理解答即可;(2)利用分类讨论的思想方法分:①当点P在上时,PH的长为点P到直线DE的距离,②当点P在上时两种情形解答:①连接OD,OP,过点O作OM⊥DE于点M,过点P 作PN⊥OM于点N,利用等边三角形的判定与性质,圆周角定理,直角三角形的边角关系定理求得MN.即可得出结论;②连接OP,交DE于点H,则PH的长为点P到直线DE的距离,利用等腰三角形的性质和直角三角形的边角关系定理解答即可.【规范解答】(1)证明:连接OD,如图,∵AD平分∠BAC交BC于点D,∴∠OAD=∠CAD.∵OA=OD,∴∠ODA=∠OAD,∴∠ODA=∠CAD,∴OD∥AC,∴∠ODC+∠C=180°.∵∠C=90°,∴∠ODC=90°,∴OD⊥BC,∵OD是⊙O的半径,∴BC是⊙O的切线;(2)解:①当点P在上时,PH的长为点P到直线DE的距离,连接OD,OP,过点O作OM⊥DE于点M,过点P作PN⊥OM于点N,如图,∵OA=OF,∴∠OAF=∠OFA=60°,∵AD平分∠BAC,∴∠BAD=∠DAC=30°,∴∠EOD=60°,∵OE=OD,∴△ODE是等边三角形,∴DE=OE=4.∵OM⊥DE,∴DM=EM=2,∠EOM=∠EOD=30°,∴OM=2.∵∠PDE=15°,∴∠POE=30°,∴∠POM=∠POE+∠EOM=60°.∵PN⊥OM,∴ON=OP•cos60°=2,∴MN=OM﹣ON=2﹣2.∵PH⊥DE,OM⊥DE,PN⊥OM,∴四边形PHMN为矩形,∴PH=MN=2﹣2.∴点P到直线DE的距离为2﹣2;②当点P在上时,连接OP,交DE于点H,如图,∵∠EOP=2∠PDE,∠PDE=15°,∴∠EOP=30°.由①知:∠EOD=60°,∴∠EOP=∠EOD,即OP为∠EOD的平分线,∵OE=OD,∴OH⊥DE,∴PH的长为点P到直线DE的距离,∵OH=OD•cos30°=2,∴PH=OP﹣OH=4﹣2.综上,若∠PDE=15°,则点P到直线DE的距离为2﹣2或4﹣2.【考察注意点】本题主要考查了圆的切线的判定与性质,圆周角定理,平行线的判定与性质,角平分线的定义,等边三角形的判定与性质,特殊角的三角函数值,直角三角形的边角关系定理,矩形的判定与性质,利用分类讨论的思想方法解答是解题的关键.20.(2022•西青区二模)已知PA,PB分别与⊙O相切于点A,B,C为⊙O上一点,连接AC,BC.(Ⅰ)如图①,若∠APB=70°,求∠ACB的大小;(Ⅱ)如图②,AE为⊙O的直径交BC于点D,若四边形PACB是平行四边形,求∠EAC的大小.【易错思路引导】(Ⅰ)连接OA、OB,由PA,PB是⊙O的切线得∠OAP=∠OBP=90°,而∠APB=70°,根据四边形的内角和等于360°可以求出∠AOB=110°,再根据圆周角定理即可解决问题;(Ⅱ)连接CE,由AE为⊙O的直径得∠ACE=90°,然后根据圆周角定理、三角形内角和定理即可解决问题.【规范解答】解:(Ⅰ)如图①,连接OA、OB,∵PA,PB是⊙O的切线,∴PA⊥OA,PB⊥OB,∴∠OAP=∠OBP=90°,∵∠APB=70°,∴∠AOB=360°﹣90°﹣90°﹣70°=110°,∴∠ACB=∠AOB=55°,∴∠ACB的大小为55°;(Ⅱ)连接CE,AB,OB,∵AE为⊙O的直径,∴∠ACE=90°,∵四边形PACB是平行四边形,∴∠ACB=∠P,∴∠BCE=90°﹣∠P,∴∠BAE=∠BCE=90°﹣∠P,∵∠AOB=180°﹣∠P,∵OA=OB,∴∠OAB=∠ABO=(180°﹣∠AOB)=∠P,∴∠ACE=∠ACB+∠BCE=∠P+∠P=90°,∴∠P=60°,∴∠ACB=60°,∠BAE=∠BCE=30°,∵AC∥PB,∴=,∴∠EAC=30°.【考察注意点】本题考查圆的切线的性质定理、四边形的内角和等于360°、圆周角定理、三角形内角和定理及其推论等知识,根据切线的性质定理求得∠OAP=∠OBP=90°是解题的关键。
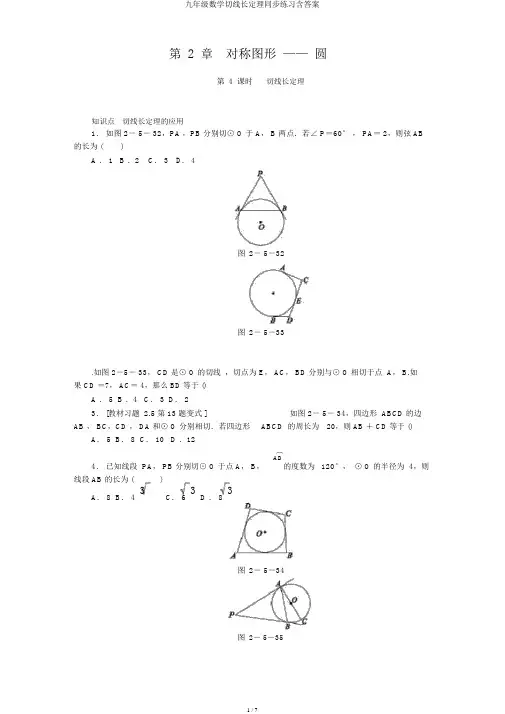
第 2 章 对称图形 —— 圆第 4 课时 切线长定理知识点 切线长定理的应用1. 如图 2- 5- 32,PA ,PB 分别切⊙ O 于 A , B 两点.若∠ P =60° , PA = 2,则弦 AB的长为 ()A . 1B .2C . 3D . 4图 2- 5-32图 2- 5-33.如图 2-5- 33, CD 是⊙ O 的切线 ,切点为 E , AC , BD 分别与⊙ O 相切于点 A , B.如果 CD =7, AC = 4,那么 BD 等于 ()A . 5B .4C . 3D . 23. [教材习题 2.5 第 13 题变式 ]如图 2- 5- 34,四边形 ABCD 的边AB , BC ,CD , DA 和⊙ O 分别相切.若四边形ABCD 的周长为 20,则 AB + CD 等于 ()A . 5B . 8C . 10D .12︵4. 已知线段 PA , PB 分别切⊙ O 于点 A , B ,AB120°, ⊙ O 的半径为 4,则的度数为 线段 AB 的长为 ()A . 8B . 43C . 6 3D . 83图 2- 5-34图 2- 5-35.如图 2-5- 35, PA, PB 是⊙ O 的切线,A , B 为切点, AC 是⊙ O 的直径,∠P= 40°,则∠ BAC 的度数为 ________.6.如图 2- 5- 36,PA , PB 分别切⊙ O 于点 A , B ,∠ AOP =50°,则∠PAB = ________°,∠ OPB= ________°.图2- 5-36图2- 5-377.如图 2- 5- 37,PA , PB, DE 分别切⊙ O 于点 A, B, C,若⊙ O 的半径为5, OP=13,则△ PDE 的周长为 ________.图2- 5-388.如图 2- 5- 38,P 是⊙ O 的直径 AB 的延长线上一点, PC, PD 分别切⊙ O 于点C,D. 若 PA = 6,⊙O 的半径为 2,则∠ CPD 的度数为 ________.9.如图 2- 5- 39,PA , PB 为⊙ O 的两条切线, A , B 为切点.若是⊙ O 的半径为5,∠OPA = 30°,求两条切线的夹角∠APB 的度数及切线PA 的长.图2- 5-39图 2- 5-40 10. [2016 ·梁溪区一模 ]AB = 4, AD = 5,AD , AB , BC 分别与⊙BC 于点 M ,切点为 N ,则 DM 的长为 (O 相切于点)如图2-5-40,在矩形ABCD 中,E,F, G,过点 D 作⊙ O 的切线交139 A. 34 13C. 39D. 2511.如图 2- 5- 41, PA, PB 是⊙ O 的切线, A , B 为切点, AC 是⊙ O 的直径,∠ ACB = 70°.求∠ P 的度数.图2- 5-4112.如图 2- 5- 42,△ ABC 的内切圆⊙ O 与 AC , AB , BC 分别相切于点D, E, F,且AB =5 cm, BC= 9 cm, AC = 6 cm,求 AE , BF 和 CD 的长.图2- 5-4213.如图 2- 5- 43, PA, PB 为⊙ O 的两条切线,切点分别为 A ,B ,直线 CD 切⊙ O 于点 E.(1)试试究△ PCD 的周长与线段 PA 的数量关系;(2)若∠ P=α,求∠ COD 的度数.图2- 5-4314.如图 2- 5- 44, AB 是⊙ O 的直径, AM , BN 分别切⊙ O 于点 A , B, CD 分别交AM , BN 于点 D ,C, DO 均分∠ ADC.(1)求证: CD 是⊙ O 的切线;(2)若 AD = 4, BC=9,求⊙ O 的半径 R.图2- 5-4415.如图 2- 5- 45, PA, PB 分别与⊙ O 相切于点 A , B,点 M 在 PB 上,且OM ∥ AP, MN ⊥ AP,垂足为 N.(1)求证: OM = AN ;(2)若⊙ O 的半径 R= 3, PB= 9,求 OM 的长.图2- 5- 45详解详析1. B2. C3. C4. B5. 20°[ 剖析 ]∵ PA,PB是⊙ O的切线,A,B为切点,1∴PA = PB,∴∠ BAP =∠ ABP =2×(180° - 40° )= 70° .由 PA 是⊙ O 的切线, A 为切点,AC 是⊙ O 的直径,得∠ PAC = 90°,∴∠ BAC =90° - 70°=20°. 6. 50 407. 24 [ 剖析 ]∵ PA,PB,DE分别切⊙ O于A,B,C三点,∴AD = CD , CE= BE , PA= PB,OA ⊥ PA.在Rt△ OAP 中,依照勾股定理,得 AP = 12,∴△ PDE 的周长为PD+ DE+ PE= PD+ AD + BE + PE= 2PA = 24.8. 60°[ 剖析 ] 连接 OC.∵ PA= 6,⊙O 的半径为2,∴OP= PA - OA =4.∵PC, PD 分别切⊙ O 于点 C,D ,∴∠ OPC=∠ OPD, OC⊥ PC.∵OP= 2OC,∴∠ OPC= 30°,∴∠ CPD=60° .9.解:连接 OA , OB,则 OA ⊥PA, OB ⊥ PB.∵OA = OB ,OP= OP,∴Rt△ OAP≌ Rt△ OBP ,∴∠ OPA=∠ OPB,∴∠ APB =2∠ OPA= 60° .在Rt△ AOP 中,可求得 OP= 2OA = 10,∴PA= OP2- OA 2=5 3.10. A [剖析 ] 如图,连接 OE, OF,ON , OG.在矩形 ABCD 中,∠ A =∠ B = 90°, CD = AB = 4.∵ AD , AB ,BC 分别与⊙ O 相切于点 E, F,G,∴∠ AEO =∠ AFO =∠ OFB=∠ BGO = 90°.又∵ OE= OF= OG,∴四边形AFOE ,四边形 FBGO 是正方形,∴AF = BF= AE = BG =2,∴DE = 3.∵ DM 是⊙ O 的切线,∴DN = DE =3, MN = MG ,∴CM =5- 2- MG = 3- MN.在Rt△ DMC 中, DM 2= CD2+ CM 2,∴ (3+ MN) 2= 42+ (3- MN) 2,4 4 13∴MN =3,∴ DM = 3+3=3.应选 A.11.解:连接 AB.∵AC 是⊙ O 的直径,∴∠ CBA = 90°,∴∠ BAC = 90° -∠ ACB = 20° .∵PA , PB 是⊙ O 的切线,∴PA = PB,∠ CAP= 90°,∴∠ PAB =90° - 20°= 70°.∵PA = PB,∴∠ PBA =∠ PAB = 70°,∴∠ P=180° -∠ PAB -∠ PBA = 40°.12.解:∵⊙ O 与△ ABC 的三边都相切,∴AE = AD ,BE = BF ,CD = CF.设AE = x cm, BF= y cm, CD=z cm,x+ y= 5,x=1,{y+z=9,) {y=4,)则 z+ x= 6,解得z= 5.即AE = 1 cm, BF= 4 cm, CD=5 cm.13.解: (1) △ PCD 的周长= 2PA. 原由以下:∵ PA , PB 分别切⊙ O 于点 A , B ,CD 切⊙ O 于点 E,∴PA = PB, AC = CE, BD = DE,∴△ PCD 的周长= PD+DE + PC+ CE= PB+ PA= 2PA ,即△ PCD 的周长= 2PA.(2)如图,连接 OA, OE, OB.由切线的性质,得OA⊥ PA,OB⊥PB,OE⊥ CD,BD=DE,AC=CE.∵OA = OE=OB ,易证△ AOC ≌△ EOC ,△EOD ≌△ BOD ,∴∠ AOC =∠ EOC,∠ EOD=∠ BOD ,11∴∠ COD =∠ EOC+∠ EOD= 2(∠ AOE +∠ BOE) = 2∠ AOB.∵∠ P=α,OA ⊥ PA, OB⊥PB ,∴∠ AOB = 180°-α,1∴∠ COD = 90°-2α.14 解: (1)证明:如图,过点 O 作 OE⊥ CD 于点 E.∵ AM 切⊙ O 于点 A,∴OA ⊥ AD.又∵ DO 均分∠ ADC ,∴OE= OA.∵ OA 为⊙ O 的半径,∴OE 是⊙ O 的半径,∴CD 是⊙ O 的切线.(2) 过点 D 作 DF⊥ BC 于点 F.∵ AM ,BN 分别切⊙ O 于点 A, B,∴AB ⊥ AD ,AB ⊥ BC,∴四边形 ABFD 是矩形,∴AD = BF , AB = DF.又∵ AD =4, BC = 9,∴ FC= 9- 4=5.∵AM ,BN , DC 分别切⊙ O 于点 A , B, E,∴ AD = DE ,BC= CE,∴CD = DE + CE=AD + BC = 4+9=13. 在 Rt△ DFC 中, CD2= DF2+ FC2,∴DF = CD2- FC2= 12,∴AB = 12,∴⊙ O 的半径 R 为 6.15.解: (1) 证明:如图,连接 OA ,则 OA ⊥PA.∵MN ⊥PA ,∴ MN ∥OA.∵OM ∥PA ,∴四边形ANMO 是平行四边形.又∵ MN ⊥ AP,∴?ANMO 是矩形,∴OM =AN.(2)如图,连接 OB,则 OB⊥ PB,∴∠ OBM =∠ MNP = 90° .∵四边形ANMO 是矩形,∴OA = MN.又∵ OA =OB ,∴OB = MN.∵OM ∥AP ,∴∠ OMB =∠ MPN ,∴△ OBM ≌△ MNP ,∴ OM = MP.设OM =x,则 MP= x, AN = x.∵PA = PB= 9,∴NP =9- x.在Rt△ MNP 中,有 x2= 32+ (9- x)2,解得 x= 5,即 OM = 5.。

切线的判定与性质及切线长定理(答案版)切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.注意:切线的判定方法:(1)定义:直线和圆有唯一公共点时这条直线就是圆的切线;(2)定理:和圆心的距离等于半径的直线是圆的切线;(3)判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.(切线的判定定理中强调两点:一是直线与圆有一个交点二是直线与过交点的半径垂直缺一不可).题型1:切线的判定-连半径证垂直1.如图AB为⊙O的直径AC平分∠BAD交⊙O于点C CD⊥AD垂足为点D.求证:CD是⊙O 的切线.【答案】证明:连接OC∵AC平分∠DAB∴∠DAC=∠BAC∵OC=OA∴∠BAC=∠ACO∴∠DAC=∠ACO∴OC∠AD∵CD∠AD∴OC∠DC∵OC过圆心O∴CD是∠O的切线.【解析】【分析】连接OC 根据角平分线的定义和等腰三角形的性质得出∠DAC=∠BAC 根据平行线的判定得出OC∠AD 根据平行线的性质得出OC∠DC 再根据切线的判定得出结论。
【变式1-1】如图在∠O中AB为直径BP为∠O的弦AC与BP的延长线交于点C 且AB=AC PE⊥AC于点E 求证:PE是∠O的切线.【答案】解:连接AP OP∵AB为∠O直径∴∠APB=90°即AP⊥BC又∵AB=AC∴点P是BC的中点又∵O是AB的中点∴OP是△ABC的中位线∴OP∠AC∴∠OPE=∠PEC又∵PE⊥AC∴∠PEC=90°∴∠OPE=90°∴OP⊥PE.∴PE是∠O的切线.【解析】【分析】连接AP OP 由AB为直径可知AP⊥BC结合AB=AC可得点P为BC的中点而O是AB的中点可得OP是△ABC的中位线可知OP∠AC 进而∠OPE=∠PEC 然后结合PE⊥AC可得OP⊥PE即可得到结论。
【变式1-2】如图D为∠O上一点点C在直径BA的延长线上且∠CDA=∠CBD.求证:CD是∠O 的切线.【答案】证明:连接OD∵AB为直径∴∠ADO+∠BDO=90°又∵∠CDA=∠CBD∴∠CDA=∠BDO∴∠ADC+∠ADO=90°∴OD⊥CD∴CD是∠O的切线.【解析】【分析】连接OD 由圆周角定理可得∠ADO+∠BDO=90° 由已知条件以及等腰三角形的性质可得∠CDA=∠BDO 进而得到∠ADC+∠ADO=90° 据此证明.题型2:切线的判定-作垂直证半径2.ΔABC为等腰三角形O为底边BC的中点腰AB与⊙O相切于点D.求证:AC是⊙O的切线.【答案】证明:过点O作OE∠AC于点E 连结OD OA∵AB与O相切于点D∴AB∠OD∵∠ABC为等腰三角形O是底边BC的中点∴AO是∠BAC的平分线∴OE=OD 即OE是O的半径∵AC经过O的半径OE的外端点且垂直于OE∴AC是O的切线。


2021年人教版数学九年级上册《切线长定理》同步专项练习卷一、选择题1.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )A.三条边的垂直平分线的交点B.三条角平分线的交点C.三条中线的交点D.三条高的交点2.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )A.4B.8C.4 3D.8 33.如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )A.15°B.30°C.60°D.75°4.把直尺和圆形螺母按如图所示放置在桌面上,∠CAB=60°,若量出AD=6 cm,则圆形螺母的外直径是( )A.12 cmB.24 cmC.6 3 cmD.12 3 cm5.如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于()A.50°B.60°C.70°D.70°6.如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为( )A.60° B.75° C.70° D.65°7.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA 的长为( )A.2 B. C. D.8.如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A=100°,∠C=30°,则∠DFE的度数是()A.55°B.60°C.65°D.70°9.如图,等边三角形ABC边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O半径为()A.2B.3C.4D.4﹣10.如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知CD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△CMN),则剪下的△CMN的周长是()A.9cmB.12cmC.15cmD.18cm11.如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F.给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是()A.0B.1C.2D.312.如图,等边△ABC的边长为2,⊙A的半径为1,D是BC上的动点,DE与⊙A相切于点E,DE 的最小值是()A.1B.C.D.2二、填空题13.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为.14.已知三角形的三边分别是5、12、13,则其内切圆的直径与外接圆的直径之比是.15.如图,PA、PB是⊙0的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC= .16.如图,PA,PB切⊙O于点A,B,点C是⊙O上的一点,且∠ACB=65°,则∠P= .17.如图,PA,PB分别切⊙O于A,B,并与⊙O的切线,分别相交于C,D,已知△PCD的周长等于8cm,则PA= cm;已知⊙O的直径是6cm,PO= cm.18.如图,已知点O是△ABC的内切圆的圆心,若∠BOC=124°,则∠A= ______ .三、解答题19.如图所示,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)PA的长;(2)∠COD的度数.20.如图所示,正方形ABCD的边长为4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆,再过点A作半圆的切线,与半圆切于点F,与CD交于点E,求△ADE的面积.21.如图,已知直线PA交⊙O于A,B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.(1)求证:CD为⊙O的切线;(2)若DC+DA=6,⊙O的直径为10,求AB的长.22.如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.(1)求证:∠A=∠BDC;(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.23.如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.(1)求证:AC是⊙O的切线;(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;(3)求证:CD=HF.参考答案1.答案为:B2.答案为:B.3.答案为:D.4.答案为:D.5.答案为:B6.答案为:D .7.答案为:B.8.答案为:C9.答案为:D.10.答案为:B11.答案为:C.12.答案为:B13.答案为:5.14.答案为:4:13.15.答案是:20°.16.答案为:50°.17.答案为:4,5.18.答案为:68°.19.解:(1)∵CA ,CE 都是⊙O 的切线,∴CA=CE.同理DE=DB ,PA=PB ,∴△PCD 的周长=PD +CD +PC=PD +BD +PC +CA=PB +PA=2PA=12,∴PA=6, 即PA 的长为6.(2)∵∠P=60°,∴∠PCE +∠PDE=120°,∴∠ACD +∠CDB=360°-120°=240°.∵CA ,CE ,DB ,DE 是⊙O 的切线,∴∠OCE=∠OCA=12∠ACD. ∠ODE=∠ODB=12∠CDB , ∴∠OCE +∠ODE=12(∠ACD +∠CDB)=120°,∴∠COD=180°-120°=60°.20.解:设DE=x cm ,则CE=(4-x)cm.∵CD ,AE ,AB 均为⊙O 的切线,∴EF=CE=(4-x)cm ,AF=AB=4 cm ,∴AE=AF +EF=(8-x)cm.在Rt △ADE 中,AE 2=AD 2+DE 2,即(8-x)2=42+x 2,解得x=3.∴S △ADE =12AD ·DE=12×4×3=6(cm 2). 21.解:(1)连接OC ,证∠DAC=∠CAO=∠ACO ,∴PA ∥CO ,又∵CD ⊥PA ,∴CO ⊥CD ,∴CD 为⊙O 的切线(2)过O 作OF ⊥AB ,垂足为F ,∴四边形OCDF 为矩形.∵DC +DA=6,设AD=x ,则OF=CD=6-x ,AF=5-x ,在Rt △AOF 中,有AF 2+OF 2=OA 2,即(5-x)2+(6-x)2=25, 解得x 1=2,x 2=9,由AD <DF 知0<x <5,故x=2,从而AD=2,AF=5-2=3,由垂径定理得AB=2AF=6.22.解:(1)如图,连接OD ,∵AB 为⊙O 的直径, ∴∠ADB=90°,即∠A+∠ABD=90°,又∵CD 与⊙O 相切于点D ,∴∠CDB+∠ODB=90°,∵OD=OB ,∴∠ABD=∠ODB ,∴∠A=∠BDC ;(2)∵CM 平分∠ACD ,∴∠DCM=∠ACM ,又∵∠A=∠BDC,∴∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,∵∠ADB=90°,DM=1,∴DN=DM=1,∴MN=.23.(1)证明:(1)如图,连接OE.∵BE⊥EF,∴∠BEF=90°,∴BF是圆O的直径,∴OB=OE,∴∠OBE=∠OEB,∵BE平分∠ABC,∴∠CBE=∠OBE,∴∠OEB=∠CBE,∴OE∥BC,∴∠AEO=∠C=90°,∴AC是⊙O的切线;(2)证明:∵∠C=∠BHE=90°,∠EBC=∠EBA,∴BEC=∠BEH,∵BF是⊙O是直径,∴∠BEF=90°,∴∠FEH+∠BEH=90°,∠AEF+∠BEC=90°,∴∠FEH=∠FEA,∴FE平分∠AEH.(3)证明:如图,连结DE.∵BE是∠ABC的平分线,EC⊥BC于C,EH⊥AB于H,∴EC=EH.∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,∴∠CDE=∠HFE,∵∠C=∠EHF=90°,∴△CDE≌△HFE(AAS),∴CD=HF,。

新人教版九年级数学上册24.2.2.3切线长定理习题要点感知1 经过圆外一点作圆的切线,这点和切点之间线段的长,叫做这点到圆的____.从圆外一点可以引圆的两条切线,它们的____相等,这一点和圆心的连线平分____.预习练习1-1 如图,PA,PB是⊙O的切线,切点分别是A,B,若PA=6 cm,则PB=____.1-2 如图,PA、PB是⊙O的切线,切点分别是A,B,若∠APB=60°,OA=2 cm,则OP=____.要点感知2 与三角形各边____的圆叫做三角形的内切圆,内切圆的圆心是____的交点,叫做三角形的____.三角形的内切圆只有____个,而圆的外切三角形有____个.预习练习2-1 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=____.知识点1 切线长定理1.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )A.4B.8C.43D.832.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )A.9B.10C.12D.143.(青海中考)如图,PA、PB切⊙O于点A、B,点C是⊙O上的一点,且∠ACB=65°,则∠P=____.4.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5 cm,求铁环的半径.知识点2 三角形的内切圆5.如图,点O 是△ABC 的内切圆的圆心,若∠BAC=80°,则∠BOC=( ) A.130° B.120° C.100° D.90°6.如图,在△ABC 中,点P 是△ABC 的内心,则∠PBC+∠PCA+∠PAB=____.7.已知在Rt △ABC 中,∠C=90°,AC=6,BC=8,则△ABC 的内切圆的半径为____.8.△ABC 的内切圆⊙O 与BC ,CA ,AB 分别相切于点D ,E ,F ,且AB=18 cm ,BC=28 cm ,CA=26 cm ,求AF ,BD ,CE 的长.9.一个钢管放在V 形架内,如图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN=60°,则OP=( ) A.50 cmB.253cmC.3350cm D.503 cm10.如图,若AB 、AC 分别切⊙O 于B 、C ,延长OB 到D 使BD=OB ,连接AD ,∠DAC=78°,则∠ADO 的度数为( ) A.56° B.39° C.64° D.78°11.(青岛中考)如图,AB 是⊙O 的直径,BD ,CD 分别是过⊙O 上点B ,C 的切线,且∠BDC=110°.连接AC ,则∠A 的度数是____.12.如图,已知⊙O 是边长为2的等边△ABC 的内切圆,则⊙O 的半径为____.13.如图,PA,PB 分别与⊙O 相切于点A,B ,⊙O 的切线EF 分别交PA,PB 于点E,F ,切点C 在弧AB 上,若PA 长为2,则△PEF 的周长是____14.如图所示,点I 为△ABC 的内心,点O 为△ABC 的外心,若∠BOC=140°,求∠BIC 的度数.15.(河南中考)如图,CD 是⊙O 的直径,且CD=2 cm ,点P 为CD 的延长线上一点,过点P 作⊙O 的切线PA 、PB ,切点分别为点A、B.(1)若∠APO=90°证明:△ACP是等腰三角形(2)填空:①当DP=____cm时,四边形AOBD是菱形;②当DP=____cm时,四边形AOBP是正方形.挑战自我16.(曲靖中考)如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,AC、PB的延长线相交于点D.(1)若∠1=20°,求∠APB的度数;(2)当∠1为多少度时,OP=OD,并说明理由.参考答案要点感知1 切线长.切线长,两条切线的夹角.预习练习1-1 6 cm.1-2 4 cm.要点感知2 都相切,三角形三条角平分线,内心.一,无数.预习练习2-1 如115°.1.B2.D3.50°4.设圆心为O,连接OA,OP.∵三角板有一个锐角为30°,∴∠PAO=60°.又∵PA与⊙O相切,∴∠OPA=90°.∴∠POA=30°.∵PA=5 cm,OP=53cm.即铁环的半径为53 cm. 5.A 6.90度. 7.2.8.根据切线长定理得 AE=AF ,BF=BD ,CE=CD. 设AF=AE=x cm , 则CE=CD=(26-x)cm , BF=BD=(18-x)cm. ∵BC=28 cm ,∴(18-x)+(26-x)=28.解得x=8.∴AF=8 cm ,BD=10 cm ,CE=18 cm.9.A10.C11.35°.12.331. 13.4.14.∵点O 为△ABC 的外心,∠BOC=140°, ∴∠A=70°.又∵点I 为△ABC 的内心,∴∠BIC=125°.15.(1)连接OA.∵PA 为⊙O 的切线, ∴∠OAP=90°. 在Rt △AOP 中,∠AOP=90°-∠APO=90°-30°=60°. ∴∠ACP=21∠AOP=21×60°=30°. ∴∠ACP=∠APO.∴AC=AP .∴△ACP 是等腰三角形.(2)1,2-1(提示:①当四边形AOBD 是菱形时,AO=AD=OD ,∠AOP=60°,而∠OAP=90°,∴OP=2OA=2,∴DP=OP-OD=2-1=1;②当四边形AOBP 是正方形时,OP=2OA=2,∴DP=OP-OD=2-1.) 挑战自我16.(1)∵PA 是⊙O 的切线, ∴∠PAO=90°.∵∠1=20°,∴∠BAP=90°-∠1=70°. 又∵PA 、PB 是⊙O 的切线,∴PA=PB. ∴∠BAP=∠ABP=70°.∴∠APB=180°-70°×2=40°.(2)当∠1=30°时,OP=OD.理由如下: 当∠1=30°时,由(1)知∠BAP=∠ABP=60°, ∴∠APB=180°-60°×2=60°.∵PA、PB是⊙O的切线,∴∠OPB=12∠APB=30°.又∵∠D=∠ABP-∠1=60°-30°=30°,∴∠OPB=∠D.∴OP=OD.。

切线长〔一〕填空1.:如图7-143,直线BC切⊙O于B点,AB=AC,AD=BD,那么∠A=____.∠2.:如图7-144,直线DC与⊙O相切于点C,AB为⊙O直径,AD⊥DC 于D,∠DAC=28°侧∠CAB=____.3.:直线AB与圆O切于B点,割线ACD与⊙O交于C和D4.:如图7-145,PA切⊙O于点A,割线PBC交⊙O于B和C两点,P=15°,∠ABC=47°,那么∠C=____.5.:如图7-146,三角形ABC的∠C=90°,内切圆O与△ABC的三边分别切于D,E,F 三点,∠DFE=56°,那么∠B=____.6.:如图7-147,△ABC内接于⊙O,DC切⊙O于C点,∠1=∠2,那么ABC为____三角形.7.:如图7-148,圆O为△ABC外接圆,AB为直径,DC切⊙O于C点,A=36°,那么∠ACD=.〔二〕选择8.:△ABC内接于⊙O,∠ABC=25°,∠ACB=75°,过A点作⊙O的切线交BC的延伸线于P,那么∠APB等于[ ]A.°;B.55°;C.50°;D.40°.9.:如图7-149,PA,PB切⊙O于A,B两点,AC为直径,那么图中与∠PAB相等的角的个数为[]A.1个;B.2个;C.4个;D.5个.10.如图7-150,四边形ABCD为圆内接四边形,AB是直径,MN切⊙O于C点,∠BCM=38°,那么∠ABC的度数是[]A.38°;B.52°;C.68°;D.42°.11.如图7-151,PA切⊙O于点A,PCB交⊙O于C,B两点,且PCB过点O,AE⊥BP交⊙O于E,那么图中与∠CAP相等的角的个数是[]A.1个;B.2个;C.3个;D.4个.〔三〕计算12.:如图7-152,PT与⊙O切于C,AB为直径,∠BAC=60°,AD为⊙O 一弦.求∠ADC与∠PCA的度数.13.:如图7-153,PA切⊙O于A,PO交⊙O于B,C,PD均分∠APC.求∠ADP的度数.14.:如图7-154,⊙O的半径OA⊥OB,过A点的直线交OB于P,交⊙O于Q,过Q引⊙O的切线交OB延伸线于C,且PQ=QC.求∠A的度数.15.:如图7-155,⊙O内接四边形ABCD,MN切⊙O于C,∠BCM=38°,AB为⊙O直径.求∠ADC的度数.16.:如图7-156,PA,PC切⊙O于A,C两点,B点17.:如图7-157,AC为⊙O的弦,PA切⊙O于点A,PC过O点与⊙O交于B,∠C=33°.求∠P的度数.18.:如图7-158,四边形ABCD内接于⊙O,EF切⊙O19.BA是⊙O的弦,TA切⊙O于点A,∠BAT=100°,点M在圆周上但与A,B不重合,求∠AMB 的度数.20.:如图7-159,PA切圆于A,BC为圆直径,∠BAD=∠P,PA=15cm,PB=5cm.求BD的长.21.:如图7-160,AC是⊙O直径,PA⊥AC于A,PB切⊙O于B,BEAC于E.假定AE=6cm,EC=2cm,求BD的长.22.:如图7-161所示,P为⊙O外一点,PA切⊙O于A,从PA中点M引⊙O割线MNB,∠PNA=138°.求∠PBA的度数.23.:如图7-162,DC切⊙O于C,DA交⊙O于P和B两点,AC交⊙O于Q,PQ为⊙O直径交BC于E,∠BAC=17°,∠D=45°.求∠PQC与∠PEC的度数.24.:如图7-163,QA切⊙O于点A,QB交⊙O于B25.:如图7-164,QA切⊙O于A,QB交⊙O于B和C26.:在图7-165中,PA切⊙O于A,AD均分∠BAC,PE均分∠APB,AD=4cm,PA=6cm.求EP的长.27.;如图7-166,PA为△ABC外接圆的切线,A为切点,DE∥AC,PE=PD.AB=7cm,AD=2cm.求DE的长.28.:如图7-167,BC是⊙O的直径,DA切⊙O于A,DA=DE.求∠BAE的度数.29.:如图7-168,AB为⊙O直径,CD切⊙O于CAE∠CD于E,交BC于F,AF=BF.求∠A的度数.30.:如图7-169,PA,PB分别切⊙O于A,B,PCD为割线交⊙O于C,D.假定AC=3cm,AD=5cm,BC=2cm,求DB的长.31.:如图7-170,ABCD的极点A,D,C在圆O上,AB的延伸线与⊙O 交于M,CB的延伸线与⊙O交于点N,PD切⊙O于D,∠ADP=35°,∠ADC=108°.求∠M的度数.32.:如图7-171,PQ为⊙O直径,DC切⊙O于C,DP交⊙O于B,交CQ延伸线于A,∠D=45°,∠PEC=39°.求∠A的度数.33.:如图7-172,△ABC内接于⊙O,EA切⊙O于A,过B作BD∥AE交AC延伸线于D.假定AC=4cm,CD=3cm,求AB的长.34.:如图7-173,△ABC内接于圆,FB切圆于B,CF⊥BF于F交圆于E,∠1=∠2.求∠1的度数.35.:如图7-174,PC为⊙O直径,MN切⊙O于A,PB⊥MN于B.假定PC=5cm,PA=2cm.求PB的长.36.:如图7-175,AD为⊙O直径,CBE,CD分别切⊙37.:如图7-176,圆内接四边形ABCD的AB边经过圆心,AD,BC的延伸线订交于E,过C点的切线CF⊥AE于F.求证:〔1〕△ABE为等腰三角形;〔2〕假定BC=1cm,AB=3cm,求EF的长.38.:如图7-177,AB,AC切⊙O于B,C,OA交⊙O于F,E,交BC于D.〔1〕求证:E为△ABC心里;〔2〕假定∠BAC=60°,AB=a,求OB与OD的长.〔四〕证明39.:在△ABC中,∠C=90°,以C为圆心作圆切AB边于F点,AD,BC 分别与⊙C切于D,E两点.求证:AD∥BE.40.:PA,PB与⊙O分别切于A,B两点,延伸OB到C,41.:⊙O与∠A的两边分别相切于D,E.在线段AD,AE〔或在它们的延伸线〕上各取一点B,C,使DB=EC.求证:OA⊥BC.⊥EC于H,AO交BC于D.求证:BC·AH=AD·CE.*43.:如图7-178,MN切⊙O于A,弦BC交OA于E,过C点引BC的垂线交MN于D.求:AB∥DE.44.:如图7-179,OA是⊙O半径,B是OA延伸线上一点,BC切⊙O于C,CD⊥OA于D.求证:CA均分∠BCD.45.:如图7-180,BC是⊙O直径,EF切⊙O于A点,AD⊥BC于D.求证:AB均分∠DAE,AC均分∠DAF.46.:如图7-181,在△ABC中,AB=AC,∠C=2∠A,以AB为弦的圆O与BC切干点B,与AC 交于D点.求证:AD=DB=BC.47.:如图7-182,过△ADG的极点A作直线与DG的延伸线订交于C,过G作△ADG的外接圆的切线二均分线段AC于E.求证:AG2=DG·CG.48.:如图7-183,PA,PB分别切⊙O于A,B两点,PCD为割线.求证:AC·BD=BC·AD.BC=BA,连结AC交圆于点E.求证:四边形ABDE是平行四边形.50.:如图7-185,∠1=∠2,⊙O过A,D两点且交AB,AC于E,F,BC切⊙O于D.求证:EF∥BC.51.:如图7-186,AB是半圆直径,EC切半圆于点C,BE⊥CE交AC于F.求证:AB=BF.52.:如图7-187,AB为半圆直径,PA⊥AB,PC切半圆于C点,CD⊥AB于D交PB于M.求证:CM=MD.〔五〕作图53.求作以线段AB为弦,所含圆周角为锐角∠α〔见图7-188〕的弧〔不写作法,写出、求作,答出所求〕.54.求作一个以α为一边,所对角为∠α,此边上高为h的三角形.55.求作一个以a为一边,m为此边上中线,所对角为∠α的三角形〔不写作法,答出所求〕.切线长定理及弦切角练习题(答案)〔一〕填空1.36° 2.28° 3.50°4.32°5.22° 6.等腰7.54°〔二〕选择8.C 9.D 10.B 11.C〔三〕计算12.30°,30°.13.45°.提示:连结AB交PD于E.只要证明∠ADE=∠AED,证明时利用三角形外角定理及弦切角定理.∠14.30°.提示:因为PQ=QC,所以∠QCP=∠QPC.连结OQ,那么知∠POQ与QCP互余.又∠OAQ=∠OQA与∠QPC互余,所以∠POQ=∠OAQ=∠OQA.而它们的和为90°〔因为∠AOC=90°〕.所以∠OAQ=30°16.°.提示:解法一连结AC,那么∠PAC=∠PCA.又∠P=45°,所以PAC=∠°.进而∠B=∠°.解法二连结OA,OC,那么∠AOC=180°-∠P=135°,所以17.24°.提示:连结OA,那么∠POA=66°.18.60°.提示:连结BD,那么∠ADB=40°,∠DBC=20°.设∠ABD=∠BDC〔因为AB//CD〕=x°,那么因∠B+∠D=180°,所以2x°+60°=180°,x°=60°,进而∠ADE=∠ABD=60°.19.100°或80°.提示:M可在弦AB对的两弧的每一个上.进而22.42°.提示:∠ABM=∠NAM.于是明显△ABM∽△NAM,NMP,所以△PMB∽△NMP,进而∠PBM=∠NPM.再由∠ABM=∠NAM,就有∠PBA=∠PBM+∠NAM=∠NPM+∠NAM=180°-∠PNA=42°.23.28°,39°.提示:连结PC.24.41°.提示:求出∠QAC和∠ACB的度数.25.100°.以DB=9.因为2DP=2×9,由此得DP2=9.又DP>0,所以DP=3,进而,DE=23=6〔cm〕.28.45°.提示:连结AC.因为DA=DE,所以∠ABE+∠BAE=∠AED=∠EAD=CAD+∠CAE,但∠ABE=∠CAD,所以∠BAE=∠CAE.因为∠BAE+∠CAE=90°,所以∠BAE=45°.29.60°.提示:解法一连结AC,那么AC⊥BC.又AF⊥CE,所以∠ACE=∠F.又DC切⊙O于C,所以∠ACE=∠B.所以∠F=∠B.因为AF=BF,所以∠BAF=∠B=∠F.所以∠BAF=60°.31.37°.提示:连结AC,那么∠M=∠ACN=∠CAD.32.17°.提示:连结PC,那么∠QPC+∠PBC=90°.45°=∠D=〔∠BPQ+∠QPC〕∠DCP=〔∠BPQ+∠QPC〕-∠PBC=[∠BPQ+〔90°-∠PBC〕]-∠PBC.所以2∠PBC-∠BPQ=45°.〔1〕又∠PBC+∠BPQ=39°,〔2〕进而∠PBC=28°,∠BPQ=11°.于是∠A=∠PBC-∠BPQ=17°.34.30°.提示:连结BE,由∠1=∠2,可推出∠EBF=∠ECB=∠EBC,而这三个角的和为90°,所以每个角为30°.36.60°.提示:连结OB,那么OB⊥CE,进而∠C=∠BOE=60°.37.〔1〕提示:连结OC,那么∠E=∠OCB=∠OBC=∠CDE,所以△ABE为等腰三角形.38.〔1〕提示:连结BE.只要证明∠ABE=∠DBE.〔四〕证明39.提示:AC,BC各均分∠A,∠B.想法证出∠A+∠B=180°.40.提示:连结OP,想法证出∠BPC=∠BPO.42.提示:在△BCE和△DAH中,∠BCE=∠DAH〔它们都与∠DCH互补〕.又A,D,C,H共圆,所以∠CEB=∠ACB=∠AHD,进而△BCE∽△DAH.这就得所要证明的比率式.43.提示:连结AC.先证明A,E,C,D四点共圆.由此得∠ADE=〔∠ACE=〕MAB,所以AB//DE.44.提示:证法一延伸AO交⊙O于点E,连结EC,那么∠BCA=∠E,且∠ACD=E.所以∠BCA=∠ACD.∠证法二连结OA,那么∠BCA与∠OCA互余;又∠ACD与∠OAC互余,而∠OCA=OAC,所以∠BCA=∠ACD.46.提示:由得∠A=36°,∠B=∠C=72°,∠DBC=∠A=36°,所以∠ABD=36°,进而AD=BD.又∠C=∠CDB=72°,所以BD=BC.47.提示:过A作CD的平行线交BC于H,那么AH=CG.而后证AG2=DG·AH=DG·CG.49.提示:因为BC=BA,所以∠A=〔∠C=〕∠D;又∠CED=∠DBF〔BF是AB的延伸线〕,所以它们的补角∠DEA=∠ABD.进而四边形ABDE是平行四边形.50.提示:连结DE,那么∠BDE=∠1=∠2=∠FED.所以EF//BC.51.提示:连结BC,那么∠ACB=90°=∠FCB.因为CE⊥BE,所以∠F=∠ECB.因为EC切半圆于C,所以∠ECB=∠A,所以∠A=∠F,所以AB=BF.52.提示:连结AC,BC并延伸BC交AP延伸线于点N.第一所以CM=MD.。

初中数学试卷马鸣风萧萧切线长定理习题1.在△ABC 中,AB=5cm BC=7cm AC=8cm, ⊙O 与BC 、AC 、 AB 分别相切于 D 、 E 、F ,则 AF=_____, BD=_______ 、CF=________第1题图 2题图2.已知PA 、PB 切⊙O 于A 、B ,∠APB=60º,PA=4,则⊙O 的半径为 。
3、如图,PA,PB,分别切⊙O 于点A,B,∠P=70°,∠C 等于 。
4.如图1,PA 、PB 分别切圆O 于A 、B 两点,C 为劣弧AB 上一点,∠APB=30°,则∠ACB=( ).A .60°B .75°C .105°D .120°3题图 4题图 5.圆外一点P ,PA 、PB 分别切⊙O 于A 、B ,C 为优弧AB 上一点,若∠ACB=a ,则∠APB=( )A .180°-aB .90°-aC .90°+aD .180°-2a 6.如图2,PA 、PB 分别切圆O 于A 、B ,并与圆O 的切线,分别相交于C 、D ,•已知PA=7cm ,则△PCD 的周长等于_________.7.已知:如图,从两个同心圆O 的大圆上一点A ,作大圆的弦AB 切小圆于C 点,大圆的弦AD 切小圆于E 点.求证:(1)AB=AD ; (2)DE=BC 。
B AC P O B A C POABCD E O123B AC D P O 8.如图,PA ,PB 为⊙O 的切线,A 、B 是切点,OP 与⊙O 交于C ,∠APB=60°,求证:OC=PC9、如图在△ABC 中,圆I 与边BC 、CA 、AB 分别相切于点D 、E 、F ,∠B =60°,∠C =70°,求∠EDF 的度数。
10.如图所示,EB 、EC 是⊙O 的两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E=46°,∠DCF=32°,求∠A 的度数.BA CED OF11.已知:Rt △ABC 中,∠ABC=90°,以AB 为直径的⊙O 交AC 于D ,过D 作⊙O 的切线DE ,交BC 于E ,求证:BE=CE .12.如图,PA 、PB 分别切圆O 于A 、B ,并与圆O 的切线,分别相交于C 、D ,•已知PA=7cm ,求△PCD 的周长.FE I DB ACPB C A O13.已知:如图,在三角形ABC中,内切圆O与△ABC的三边分别切于D,E,F三点,∠DFE=56°,求∠A得度数。


人教版九年级数学试题24.2.2 直线与圆的位置关系第1课时直线与圆的位置关系1.填表:直线与圆的位置关系图形公共点个数公共点名称圆心到直线的距离d与圆的半径r的关系直线的名称相交相切相离2.若直线a与⊙O交于A,B两点,O到直线a•的距离为6,•AB=•16,•则⊙O•的半径为_____.3.在△ABC中,已知∠ACB=90°,BC=AC=10,以C为圆心,分别以5,52,8为半径作图,那么直线AB与圆的位置关系分别是______,_______,_______.4.⊙O的半径是6,点O到直线a的距离为5,则直线a与⊙O的位置关系为()A.相离 B.相切 C.相交 D.内含5.下列判断正确的是()①直线上一点到圆心的距离大于半径,则直线与圆相离;②直线上一点到圆心的距离等于半径,则直线与圆相切;③直线上一点到圆心的距离小于半径,•则直线与圆相交. A.①②③ B.①② C.②③ D.③6.OA平分∠BOC,P是OA上任一点(O除外),若以P为圆心的⊙P与OC相离,•那么⊙P 与OB的位置关系是()A.相离 B.相切 C.相交 D.相交或相切7.如图所示,Rt△ABC中,∠ACB=90°,CA=6,CB=8,以C为圆心,r为半径作⊙C,当r 为多少时,⊙C与AB相切?8.如图,⊙O的半径为3cm,弦AC=42cm,AB=4cm,若以O为圆心,•再作一个圆与AC 相切,则这个圆的半径为多少?这个圆与AB的位置关系如何?9.如图所示,在直角坐标系中,⊙M的圆心坐标为(m,0),半径为2,•如果⊙M与y轴所在直线相切,那么m=______,如果⊙M与y轴所在直线相交,那么m•的取值范围是_______.10.如图,△ABC中,AB=AC=5cm,BC=8cm,以A为圆心,3cm•长为半径的圆与直线BC的位置关系是_______.11.如图,正方形ABCD的边长为2,AC和BD相交于点O,过O作EF∥AB,交BC于E,交AD于F,则以点B为圆心,2长为半径的圆与直线AC,EF,CD的位置关系分别是什么?12.已知⊙O的半径为5cm,点O到直线L的距离OP为7cm,如图所示.(1)怎样平移直线L,才能使L与⊙O相切?(2)要使直线L与⊙O相交,应把直线L向上平移多少cm?13.如图,Rt△ABC中,∠C=90°,AC=3,AB=5,若以C为圆心,r为半径作圆,•那么:(1)当直线AB与⊙C相切时,求r的取值范围;(2)当直线AB与⊙C相离时,求r的取值范围;(3)当直线AB与⊙C相交时,求r的取值范围.14.在南部沿海某气象站A测得一热带风暴从A的南偏东30•°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,•若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.答案:1.略 2.10 3.相离,相切,相交 4.C 5.C 6.A 7.r=24 58.r=1cm,•这个圆与AB相离 9.±2,-2<m<2 10.相切 11.相切,相交,相离12.(1)直线L向上平移2cm或12cm (2)大于2cm且小于12cm13.(1)r=2.4 (2)r<2.4 (3)r>2.4 14.B•市受影响,影响时间为4时15.(1)2 (2)8(3)①0<r<2时,没有;②r=2时,一个;③2<•r<8时,2个;④r=8时,3个;⑤r>8时,4个习题试解预习法检验预习效果的最佳途径数学学科有别于其他学科的一大特点就是直接用数学知识解决问题。

第3课时切线长定理一、选择题1.下列说法中,不正确的是 ( ) A.三角形的内心是三角形三条内角平分线的交点B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的内心到三角形的三边的距离相等2.给出下列说法:①任意一个三角形一定有一个外接圆,并且只有一个外接圆;②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.其中正确的有 ( )A.1个 B.2个 C.3个 D.4个3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( ) A.21 B.20 C.19 D.184.如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有 ( )A.1个 B.2个C.3个 D.4个4题图5题图6题图5.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( )A.三条中线的交点 B.三条高的交点C.三条角平分线的交点 D.三条边的垂直平分线的交点6.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )A.21 B.20 C.19 D.18二、填空题6.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.6题图 7题图 8题图7.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.PBAO8.如图,已知⊙O 是△ABC 的内切圆,∠BAC=50o,则∠BOC 为____________度. 三、解答题9. 如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长.10. 如图,PA 、PB 是⊙O 的两条切线,切点分别为点A 、B ,若直径AC= 12,∠P=60o,求弦AB 的长.11. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.(1)求∠APB 的度数;(2)当OA =3时,求AP 的长.12.已知:如图,⊙O 内切于△ABC ,∠BOC =105°,∠ACB =90°,AB =20cm .求BC 、AC 的长.13.已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.14.如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2 cm,AD=4 cm.(1)求⊙O的直径BE的长;(2)计算△ABC的面积.15.已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.(1)若AC=12cm,BC=9cm,求⊙O的半径r;(2)若AC=b,BC=a,AB=c,求⊙O的半径r.四、体验中考16.(2011年安徽)△ABC 中,AB =AC ,∠A 为锐角,CD 为AB 边上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( ) A .120° B .125° C .135° D .150°17.(2011年绵阳)一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60︒,则OP =( )A .50 cmB .253cmC .3350cm D .503cm 18. (2011年甘肃定西)如图,在△ABC 中,5cm AB AC ==,cos B 35=.如果⊙O 的半径为10cm ,且经过点B 、C ,那么线段AO = cm .17题图 18题图 19题图19. (2011年湖南怀化)如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且60=∠AEB ,则=∠P __ ___度.参考答案◆随堂检测1. C2. B (提示:②④错误)3. 760(提示:连接ID,IF ∵∠DEF=520∴∠DIF=1040∵D、F是切点∴DI⊥AB,IF⊥AC∴∠ADI=∠AFI=900∴∠A=1800-1040=760)4. 52 (提示:AB+CD=AD+BC)5. 1150 (提示:∵∠A=500∴∠ABC+∠ACB=1300∵OB,OC分别平分∠ABC,∠ACB ∴∠OBC+∠OCB=650∴∠BOC=1800-650=1150)◆课下作业 ●拓展提高1. D (提示:AD=AF,BD=BE,CE=CF ∴周长=821218⨯+⨯=)2. C3. D4. 解:∵AD,AE 切于⊙O 于D,E ∴AD=AE=20 ∵AD,BF 切于⊙O 于D,F ∴BD=BF 同理:CF=CE ∴C △ABC =AB+BC+AC=AB+BF+FC+AC=AB+BD+EC+AC=AD+AE=405. 解:连接BC ∵PA,PB 切⊙O 于A,B ∴PA=PB ∵∠P=600 ∴△ABC 是正三角形 ∵∠PAB=600∵PA 是⊙O 切线 ∴CA ⊥AP ∴∠CAP=900 ∴∠CAB=300 ∵直径AC ∴∠ABC=900 ∴cos300=ABAC∴AB=6. 解:(1)∵在△ABO 中,OA =OB ,∠OAB =30°∴∠AOB =180°-2×30°=120°∵PA 、PB 是⊙O 的切线∴OA ⊥PA ,OB ⊥PB .即∠OAP =∠OBP =90° ∴在四边形OAPB 中,∠APB =360°-120°-90°-90°=60°.(2)如图①,连结OP∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ,即∠APO =12∠APB =30° 又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP =tan 30OA°=7. 解:(1)连接OD ∴OD ⊥AC ∴△ODA 是Rt △设半径为r ∴AO=r+2 ∴(r+2)2—r 2=16 解之得:r=3 ∴BE=6(2) ∵∠ABC=900 ∴OB ⊥BC ∴BC 是⊙O 的切线 ∵CD 切⊙O 于D ∴CB=CD 令CB=x∴AC=x+4,BC=4,AB=x ,AB=8 ∵2228(4)x x +=+ ∴6x = ∴S △ABC =186242⨯⨯= ●体验中考 1. C2. A (提示:∠MPN=600可得∠OPM=300 可得OP=2OM=50)3.3(提示:连接OB ,易得:∠ABC=∠AOB ∴cos ∠AOB=cos ∠35=OBOA AO=)4. ∠P=600专项训练二概率初步一、选择题1.(徐州中考)下列事件中的不可能事件是( )A.通常加热到100℃时,水沸腾 B.抛掷2枚正方体骰子,都是6点朝上C.经过有交通信号灯的路口,遇到红灯 D.任意画一个三角形,其内角和是360°2.小张抛一枚质地均匀的硬币,出现正面朝上的可能性是( )A.25% B.50% C.75% D.85%3.(2016·贵阳中考)2016年5月,为保证“中国大数据产业峰会及中国电子商务创新发展峰会”在贵阳顺利召开,组委会决定从“神州专车”中抽调200辆车作为服务用车,其中帕萨特60辆、狮跑40辆、君越80辆、迈腾20辆,现随机从这200辆车中抽取1辆作为开幕式用车,则抽中帕萨特的概率是( )A.110B.15C.310D.254.(金华中考)小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )A.14B.13C.12D.345.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为( )A.12B.13C.14D.166.现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )A.13B.16C.19D.1127.分别转动图中两个转盘一次,当转盘停止转动时,两个指针分别落在某个数所表示的区域,则两个数的和是2的倍数或3的倍数的概率等于( )A.316B.38C.58D.1316第7题图第8题图8.(2016·呼和浩特中考)如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )A.16B.π6C.π8D.π5二、填空题9.已知四个点的坐标分别是(-1,1),(2,2),⎝ ⎛⎭⎪⎫23,32,⎝ ⎛⎭⎪⎫-5,-15,从中随机选取一个点,在反比例函数y =1x 图象上的概率是________.10.(黄石中考)如图所示,一只蚂蚁从A 点出发到D ,E ,F 处寻觅食物.假定蚂蚁在每个岔路口都可能随机选择一条向左下或右下的路径(比如A 岔路口可以向左下到达B 处,也可以向右下到达C 处,其中A ,B ,C 都是岔路口).那么,蚂蚁从A 出发到达E 处的概率是________.11.(贵阳中考)现有50张大小、质地及背面图案均相同的《西游记》任务卡片,正面朝下放置在桌面上,从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回,洗匀后再抽.通过多次试验后,发现抽到绘有孙悟空这个人物卡片的频率约为0.3.估计这些卡片中绘有孙悟空这个人物的卡片张数约为________.12.(荆门中考)荆楚学校为了了解九年级学生“一分钟内跳绳次数”的情况,随机选取了3名女生和2名男生,则从这5名学生中,选取2名同时跳绳,恰好选中一男一女的概率是________.13.(重庆中考)点P 的坐标是(a ,b ),从-2,-1,0,1,2这五个数中任取一个数作为a 的值,再从余下的四个数中任取一个数作为b 的值,则点P (a ,b )在平面直角坐标系中第二象限内的概率是________.14.★从-1,1,2这三个数字中,随机抽取一个数记为a ,那么,使关于x 的一次函数y =2x +a 的图象与x 轴、y 轴围成的三角形的面积为14,且使关于x 的不等式组⎩⎨⎧x +2≤a ,1-x ≤2a有解的概率为________.三、解答题15.(南昌中考)在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)先从袋子中取出m (m >1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A ,请完成下列表格:(2)先从袋子中取出m 个红球,再放入m 个一样的黑球并摇匀,随机摸出1个黑球的概率等于45,求m 的值.16.(菏泽中考)锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________; (2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________; (3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.17.(丹东中考)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;(2)若两人抽取的数字之和为2的倍数,则甲获胜;若抽取的数字之和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.18.一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,3,5,x,甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率稳定在它的概率附近,估计出现“和为8”的概率是________;(2)如果摸出的这两个小球上数字之和为9的概率是13,那么x的值可以取4吗?请用列表法或画树状图法说明理由;如果x的值不可以取4,请写出一个符合要求的x的值.参考答案与解析1.D 2.B 3.C 4.A 5.A 6.C 7.C8.B 解析:∵AB =15,BC =12,AC =9,∴AB 2=BC 2+AC 2,∴△ABC 为直角三角形,∴△ABC 的内切圆半径为12+9-152=3,∴S △ABC =12AC ·BC =12×12×9=54,S 圆=9π,∴小鸟落在花圃上的概率为9π54=π6.9.12 10.12 11.15 12.35 13.15 14.13 15.解:(1)4 2或3 (2)根据题意得6+m 10=45,解得m =2,所以m 的值为2. 16.解:(1)14 解析:第一道肯定能对,第二道对的概率为14,所以锐锐通关的概率为14;(2)16 解析:锐锐两次“求助”都在第二道题中使用,则第一道题对的概率为13,第二道题对的概率为12,所以锐锐能通关的概率为12×13=16;(3)锐锐将每道题各用一次“求助”,分别用A ,B 表示剩下的第一道单选题的2个选项,a ,b ,c 表示剩下的第二道单选题的3个选项,树状图如图所示.共有6种等可能的结果,锐锐顺利通关的只有1种情况,∴锐锐顺利通关的概率为16.17.解:(1)所有可能出现的结果如下表,从表格可以看出,总共有9种结果,每种结果出现的可能性相同,其中两人抽取相同数字的结果有3种,所以两人抽取相同数字的概率为13;(2)不公平.从表格可以看出,两人抽取数字之和为2的倍数有5种,两人抽取数字之和为5的倍数有3种,所以甲获胜的概率为59,乙获胜的概率为13.∵59>13,∴甲获胜的概率大,游戏不公平.2 3 52 2 23 2 5 2 3 2 3 3 3 5 3 52 53 5 5 518.解:(1)0.33(2)图略,当x 为4时,数字和为9的概率为212=16≠13,所以x 不能取4;当x =6时,摸出的两个小球上数字之和为9的概率是13.。
提技术·题组训练切线长定理1.如图 , 已知以直角梯形 ABCD的腰 CD为直径的半圆 O与梯形上底 AD,下底 BC以及腰 AB均相切, 切点分别是 D,C,E. 若半圆 O的半径为 2, 梯形的腰 AB为 5, 则该梯形的周长是 ()A.9B.10C.12D.14【分析】选 D.依据切线长定理 , 得 AD=AE,BC=BE,所以梯形的周长是 5×2+4=14.2. 如图 ,PA,PB 为☉ O 的切线 ,A ,B 分别为切点 , ∠APB=60° , 点 P 到圆心 O 的距离 OP=2,则☉ O 的半径为 ()A. B.1 C. D.2【分析】选 B. 连结 OA,∵PA为☉ O的切线 , ∴PA⊥OA,∵∠ APO=∠APB=30°,∴OA=2× =1,∴☉O的半径为 1.3.如图 , 从☉ O外一点 P 引圆的两条切线 PA,PB,切点分别是 A,B, 假如∠ APB=60°, 线段 PA=10,那么弦 AB的长是 ()A.10B.12C.5D.10【分析】选 A. ∵PA,PB都是☉ O的切线 , ∴ PA=PB,∵∠ APB=60°, ∴△ PAB是等边三角形 , ∴AB=PA=10.4.如图 ,AC 是☉ O 的直径 , ∠ ACB=60°, 连结 AB,过 A,B 两点分别作☉ O 的切线 , 两切线交于点P. 若已知☉ O的半径为 1, 则△ PAB的周长为.【解题指南】 (1) 由直径所对的圆周角是直角, 从而将问题转变到直角三角形中.(2)利用勾股定理和特别三角形的性质得出直角边 AB 的长 .(3)再联合切线的性质和切线长定理获得答案 .【分析】∵AC 是☉ O 的直径 , ∴∠ ABC=90° , ∠ BAC=30°,CB=1,AB=.∵AP 为切线, ∴∠CAP=90°, ∠PAB=60°.又∵ AP=BP,∴△ PAB为正三角形 , ∴周长为 3.答案: 35.如图 ,PA,PB 分别切☉ O于 A,B, 并与☉ O的切线 , 分别订交于 D,C, 已知 PA=7cm,则△ PCD的周长等于.]【分析】设 DC与☉ O的切点为 E, ∵PA,PB分别是☉ O的切线 , 且切点为 A,B,∴PA=PB=7cm;同理 , 可得 :DE=DA,CE=CB;则△ PCD的周长 =PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=14cm,故△PCD的周长是 14cm.答案 : 14cm【知识概括】切线长应用注意的双方面当多条直线与同一圆相切时 :(1) 注意简化 : 概括出现了几对切线长定理的基本图形 , 从而将复杂问题简单化 , 从而发现必需的数目关系 .(2) 注意联系 , 如圆心是几个角的角均分线的交点 .6. 如图 , 在直角梯形 ABCD中,AB∥ CD,以 AD为直径的☉ O切 BC于 E, 连结 OB,OC,尝试究 OB 与OC有何地点关系 ?【分析】∵AD为☉ O的直径 , 四边形 ABCD为直角梯形 , ∴AB,CD为☉ O的切线 .∵☉O与 BC相切,∴∠ ABO=∠CBO,∠DCO=∠BCO.∵AB∥ CD,∴∠ ABC+∠ BCD=180°.∴∠ OBE+∠OCE=90°. ∴∠ BOC=90°, 所以 OB⊥OC.三角形的内切圆及心里1.以下说法中 , 不正确的选项是 ()A.三角形的心里是三角形三条内角均分线的交点B.锐角三角形、直角三角形、钝角三角形的心里都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的心里到三角形的三边的距离相等【分析】选 C.A,B,D 都正确 , 经过半径外端而且垂直于半径的直线是圆的切线, 垂直于半径的直线不必定是圆的切线 .2.如图 , 正三角形的内切圆半径为 1, 那么这个正三角形的边长为 ()A.2B.3C. D.2[AD=CD,依据半径是1, 可知AO=2,【分析】选D.由于圆内切于正三角形, 如图, 连结AO及 OD,可知依据勾股定理, 得AD=, 所以AC=2.【知识概括】三角形的内切圆和心里(1)一个三角形有且只有一个内切圆 , 而一个圆有无数多个外切三角形 .(2)三角形的心里是三条角均分线的交点 , 所以 , 钝角三角形、直角三角形、锐角三角形的心里都在三角形的内部 , 三角形的心里到三边的距离相等 .3. 如图 , 在△ ABC中, 点 P 是△ ABC的心里 , 则∠ PBC+∠PCA+∠PAB=°.【分析】∵点 P 是△ ABC的心里 , ∴ PB均分∠ ABC,PA均分∠ BAC,PC均分∠ ACB,∴∠ PBC+∠PCA+∠PAB=90° .答案: 904.如图 , ☉ I 是△ ABC的内切圆, 切点分别为点 D,E,F, 若∠ DEF=52°, 则∠A=.【分析】连结 ID,IF,∵☉I是△ ABC的内切圆,∴I D⊥ AB,IF ⊥AC.又∵☉ I 中, ∠DIF=2∠DEF=104°, 四边形 DIFA 中 ,∠IDA=∠IFA=90°,∴∠ A=180°- ∠ DIF=76°.答案 : 76°5. 如图 , 已知☉ O是△ ABC的内切圆 , 切点为 D,E,F, 假如 AE=2,CD=1,BF=3,求内切圆的半径 r.【分析】∵☉O是△ ABC的内切圆 , 切点为 D,E,F, ∴AF=AE,EC=CD,DB=BF,∵A E=2,CD=1,BF=3,∴AF=2,EC=1,BD=3 ∴AB=BF+AF=5,BC=BD+DC=4,AC=AE+EC=3,∴△ ABC是直角三角形且∠ C=90°,∴(AB+BC+AC)r=AC× BC,即 6r=6,r=1.【错在哪?】作业错例讲堂实拍如图 , △ABC中, ∠ A=45° ,I是心里,则∠ BIC=° .(1) 错因:.(2)纠错 :.答案: (1) I是心里,不是外心,要理解心里和外心的差别.(2) ∵∠ A=45°, ∴∠ ABC +∠ACB=180°-45 °=135°, ∵I 是△ ABC的心里,∴∠ IBC= 1∠ABC,∠ICB=1∠ ACB,∴∠ IBC+∠ICB=1( ∠ABC+∠ ACB)=67.5°,∴∠ BIC=180°222-67.5 °=112.5 °.答案: 112.5。
第二十四章圆24.2.2.3 切线长定理培优训练卷一、选择题(共10小题,3*10=30)1.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( ) A.∠1=∠2 B.PA=PBC.AB⊥OP D.点C是OP的中点2.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )A.4 B.8C.4 3 D.8 33.如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( )A.50°B.65°C.100°D.130°4如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )A.15°B.30°C.60°D.75°5. 如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为( )A.(-2,3) B.(-3,2)C.(3,-2) D.(2,-3)6.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC=( )A.130°B.120°C.100°D.90°7.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )A.56°B.62°C.68°D.78°8.如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E,则△ADE和四边形EBCD周长之比为( )A.3∶4 B.4∶5C.5∶6 D.6∶79.如图,四边形ABCD的各边分别与⊙O相切于点E,F,G,H,且AB=16,CD=10,则此四边形ABCD的周长为( )A.50 B.52C.54 D.5610.如图,O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则( ) A.EF>AE+BF B.EF<AE+BFC.EF=AE+BF D.EF≤AE+BF二.填空题(共8小题,3*8=24)11. 如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是__________.12. 如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB 的度数为___________.13. 在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的周长为____________.14. 如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,OD.若∠ABC=40°,则∠BOD 的度数是______.15.如图,Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆半径r=_______.16.如图,AB,AC,CE都是⊙O的切线,B,D,E为切点,P为劣弧上一点,若∠A+∠C=110°,则∠BPE=___________.如图,AB是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为___________.18.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为_______.三.解答题(共7小题,46分)19.(6分) 为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5 cm,求铁环的半径.20. (6分) 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC =28 cm,CA=26 cm,求AF,BD,CE的长.21. (6分) 如图,AC⊥BC于点C,BC=4,AC=3,⊙O与直线AB,BC,CA均相切,求⊙O的半径.22. (6分) 如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O的半径为2,求∠CPD.23.(6分) 如图,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.(1)求PA的长;(2)求∠COD的度数.24.(8分) 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长是多少?25.(8分) 如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.(1)求证:BO⊥CO;(2)求BE和CG的长.参考答案1-5 DBADA 6-10 ACDBC11. 75°12. 135°13. 4π14. 70°15. 216. 55°17.48°18. 13 319. 解:设圆心为O,连接OA,OP.∵三角板有一个锐角为30°,∴∠PAO=60°.又∵PA与⊙O相切,∴∠OPA=90°,∴∠POA=30°,∵PA=5 cm,∴OA=10 cm,可求OP=5 3 cm,即铁环的半径为5 3 cm20. 解:根据切线长定理,得AE=AF,BF=BD,CE=CD.设AF=AE=x cm,则CE=CD=(26-x)cm,BF=BD=(18-x)cm.∵BC=28 cm,∴(18-x)+(26-x)=28,解得x=8,∴AF=8 cm,BD=10 cm,CE=18 cm21. 解:由切线长定理得BE=BF,CD=CF,AD=AE,连接OD,OF,则四边形DCFO为正方形,设OF=CD=x,则由BF=BE得BC+x=BA+AE=AB+3-x,∴4+x=5+3-x,∴x=2,∴⊙O的半径为222. 解:∵PA=6,⊙O的半径为2,∴PB=PA-AB=6-4=2,∴OP=4,∵PC、PD切⊙O于点C、D.∴∠OPC=∠OPD ,∴CO ⊥PC ,∴sin ∠OPC=2: 4 =0.5 ,∴∠OPC=30°,∴∠CPD=60°,23. 解:(1)由切线长定理可得CA =CE ,同理DE =DB ,PA =PB ,∴三角形PCD 的周长=PD +CD +PC =PD +PC +CA +BD =PA +PB =12,则PA 的长为6(2)连接OA ,OE ,OB ,∵∠P =60°,∴∠AOB =180°-∠P =120°,由切线长定理可得∠AOC =∠EOC =12∠AOE , ∠DOB =∠EOD =12∠EOB , ∴∠COD =∠EOC +∠EOD =12∠AOB =60° 24. 解:连接OD 、OE ,∵⊙O 是Rt △ABC 的内切圆,∴OD ⊥AB ,OE ⊥BC ,∵∠ABC=90°,∴∠ODB=∠DBE=∠OEB=90°,∴四边形ODBE 是矩形,∵OD=OE ,∴矩形ODBE 是正方形,∴BD=BE=OD=OE=4cm ,∵⊙O 切AB 于D ,切BC 于E ,切MN 于P ,NP 与NE 是从一点出发的圆的两条切线, ∴MP=DM ,NP=NE ,∴Rt △MBN 的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=4cm+4cm=8cm ,25. 解:(1)连接OE ,OF ,∵BE 切⊙O 于点E ,BC 切⊙O 于点F ,∴BE =BF ,OE ⊥AB ,OF ⊥BC ,则△BOE ≌△BOF ,∴∠EBO=∠FBO,同理∠FCO=∠GCO,又∵AB∥CD,∴∠ABC+∠DCB=180°,∴∠OBC+∠OCB=90°,∴BO⊥CO(2)易得Rt△BOF∽Rt△BCO,∴BO2=BF·BC,∵BO=6 cm,OC=8 cm,∴BC=10 cm,∴BE=BF=BO2BC=3610=3.6(cm),∵AB,BC,CD分别与⊙O相切,∴BE=BF=3.6 cm,CG=CF,∵CF=BC-BF=10-3.6=6.4(cm),∴CG=CF=6.4 cm。
第3课时切线长定理一、选择题1.下列说法中,不正确的是 ( ) A.三角形的内心是三角形三条内角平分线的交点B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的内心到三角形的三边的距离相等2.给出下列说法:①任意一个三角形一定有一个外接圆,并且只有一个外接圆;②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.其中正确的有 ( )A.1个 B.2个 C.3个 D.4个3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( ) A.21 B.20 C.19 D.184.如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有 ( ) A.1个 B.2个C.3个 D.4个4题图5题图6题图5.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( ) A.三条中线的交点 B.三条高的交点C.三条角平分线的交点 D.三条边的垂直平分线的交点6.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )PBAOA .21B .20C .19D .18 二、填空题6.如图,⊙I 是△ABC 的内切圆,切点分别为点D 、E 、F ,若∠DEF=52o,则∠A 的度为________.6题图 7题图 8题图7.如图,一圆内切于四边形ABCD ,且AB=16,CD=10,则四边形ABCD 的周长为________. 8.如图,已知⊙O 是△ABC 的内切圆,∠BAC=50o,则∠BOC 为____________度. 三、解答题9. 如图,AE 、AD 、BC 分别切⊙O 于点E 、D 、F ,若AD=20,求△ABC 的周长.10. 如图,PA 、PB 是⊙O 的两条切线,切点分别为点A 、B ,若直径AC= 12,∠P=60o,求弦AB 的长.11. 如图,PA 、PB 是⊙O 的切线,A 、B 为切点,∠OAB =30°.(1)求∠APB 的度数;(2)当OA =3时,求AP 的长.12.已知:如图,⊙O 内切于△ABC ,∠BOC =105°,∠ACB =90°,AB =20cm .求BC 、AC 的长.13.已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC 的面积S.14.如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2 cm,AD=4 cm.(1)求⊙O的直径BE的长;(2)计算△ABC的面积.15.已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°.(1)若AC=12cm,BC=9cm,求⊙O的半径r;(2)若AC=b,BC=a,AB=c,求⊙O的半径r.四、体验中考16.(2011年安徽)△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB 的度数是( )A .120°B .125°C .135°D .150°17.(2011年绵阳)一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60︒,则OP =( ) A .50 cm B .253cm C .3350cm D .503cm 18. (2011年甘肃定西)如图,在△ABC 中,5cm AB AC ==,cos B 35=.如果⊙O 的半径为10cm ,且经过点B 、C ,那么线段AO = cm .17题图 18题图 19题图19. (2011年湖南怀化)如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且ο60=∠AEB ,则=∠P __ ___度.参考答案◆随堂检测 1. C2. B (提示:②④错误)3. 760 (提示:连接ID,IF ∵∠DEF=520 ∴∠DIF=1040 ∵D 、F 是切点 ∴DI ⊥AB,IF ⊥AC∴∠ADI=∠AFI=900 ∴∠A=1800-1040=760) 4. 52 (提示:AB+CD=AD+BC)5. 1150 (提示:∵∠A=500 ∴∠ABC+∠ACB=1300 ∵OB,OC 分别平分∠ABC,∠ACB ∴∠OBC+∠OCB=650∴∠BOC=1800-650=1150) ◆课下作业 ●拓展提高1. D (提示:AD=AF,BD=BE,CE=CF ∴周长=821218⨯+⨯=)2. C3. D4. 解:∵AD,AE 切于⊙O 于D,E ∴AD=AE=20 ∵AD,BF 切于⊙O 于D,F ∴BD=BF 同理:CF=CE∴C △ABC =AB+BC+AC=AB+BF+FC+AC=AB+BD+EC+AC=AD+AE=405. 解:连接BC ∵PA,PB 切⊙O 于A,B ∴PA=PB ∵∠P=600 ∴△ABC 是正三角形 ∵∠PAB=600∵PA 是⊙O 切线 ∴CA ⊥AP ∴∠CAP=900 ∴∠CAB=300 ∵直径AC ∴∠ABC=900∴cos300=ABAC∴AB=6. 解:(1)∵在△ABO 中,OA =OB ,∠OAB =30°∴∠AOB =180°-2×30°=120°∵PA 、PB 是⊙O 的切线∴OA ⊥PA ,OB ⊥PB .即∠OAP =∠OBP =90° ∴在四边形OAPB 中,∠APB =360°-120°-90°-90°=60°.(2)如图①,连结OP∵PA 、PB 是⊙O 的切线∴PO 平分∠APB ,即∠APO =12∠APB =30° 又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP =tan 30OA°=7. 解:(1)连接OD ∴OD ⊥AC ∴△ODA 是Rt △设半径为r ∴AO=r+2 ∴(r+2)2—r 2=16 解之得:r=3 ∴BE=6(2) ∵∠ABC=900 ∴OB ⊥BC ∴BC 是⊙O 的切线 ∵CD 切⊙O 于D ∴CB=CD 令CB=x∴AC=x+4,BC=4,AB=x ,AB=8 ∵2228(4)x x +=+ ∴6x = ∴S △ABC =186242⨯⨯= ●体验中考 1. C2. A (提示:∠MPN=600可得∠OPM=300 可得OP=2OM=50)3.3连接OB ,易得:∠ABC=∠AOB ∴cos ∠AOB=cos ∠35=OBOA AO=)4. ∠P=600。
切线长练习一.选择题(1)若⊙O的切线长和半径相等,则两条切线所夹角的度数为()A.30°B.45°C.60° D.90°(2)若AB、AC分别切⊙O于B、C,延长OB到D使BD=OB,连AD,∠DAC=78°,则∠ADO=()A.56°B.39°C.64°D.78°(3)如图7—153,AB、AC切⊙O于B、C,AO交⊙O于D,过D作⊙O切线分别交AB、AC 于E、F,若OB=6,AO=10,则△AEF的周长是()A.10B.12C.14D.16(4)如图:AB、AC切⊙O于B、C,BC交OA于D,则图中的直角三角形共有()A.3B.4C.5D.6(5). 如图:△ABC与⊙O分别切于D、E、F,DE∥BC,AB=8,AD=5,则BC的长为()A.3B.6C.8D.无法求出二,填空题(1)已知⊙O的半径是4cm,点P和圆心O的距离为8cm,经过点P作⊙O的两条切线,则两条切线夹角为________度.(2)ABCD是⊙O的外切等腰梯形,若上底CD=4cm,圆的半径是3cm,则腰长为(3)作一个半径为2 cm的圆,使它与已知60°角的两边都相切,则圆心到角的顶点的距离是__________;(4)⊙O的半径为2,弦AB=23,过A、B两点的⊙O的切线相交于点P,PO与圆相交于C,则C到PA的距离是_______;(5)P A、PC分别切⊙O于A、C两点,B为⊙O上与A、C不重合的点,若∠P=50°,则∠AB C=_______.(6)已知:PA、PB分别切⊙O于点A和B,C为弧AB上一点,过C与⊙O相切的直线分别交PA、PB于点D和E,若PA=2cm,∠APB=60°则(1)△PDE的周长= (2)∠DOE= .三,解答题1. 已知如图:在△ABC中,∠ACB=Rt∠,⊙O的O点在BC上,且AB切⊙O于D,若OC∶CB=1∶3,AD=2.求BE的长.2.如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,再过A点作半圆的切线,与半圆相切于F点,与DC相交于E点.求:△ADE的面积.四.思考题在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8厘米,AD=24厘米,BC=26厘米,AB是⊙O的直径,动点P从点A开始沿AD边向点D以1厘米/秒的速度运动.动点Q从点C开始沿CB边向点B以3厘米/秒的速度运动,P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒,求:(1)t分别为何值时,四边形PQCD为平行四边形、等腰梯形?(2)t分别为何值时,直线PQ与⊙O相切、相交、相离?辅助线,如何添,找出规律凭经验。
《切线长定理的相关计算》必考经典题型专项分类专题练习(专题分类练习+详细解析)题型一:切线长定理与三角形问题1. 如图所示,PA,PB是☉O的切线,且∠APB=40°,下列说法不正确的是( )A.PA=PBB.∠APO=20°C.∠OBP=70°D.∠AOP=70°2. 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC,BC相切于点D,E.则AD为( )A.2.5B.1.6C.1.5D.13. 如图,半圆O与等腰直角三角形两腰CA,CB分别切于D,E两点,直径FG在AB 上,若BG=√2-1,则△ABC的周长为 .4.如图,PA,PB分别切圆O于点A,B,并与圆O的切线CD,分别相交于点D,C,已知△PCD的周长等于10cm,求PA.1. 如图,一圆内切于四边形ABCD,且BC=10,AD=7,则四边形的周长为( )A.32B.34C.36D.382. 如图,四边形ABCD中,AD∥BC,DC⊥AD,DC⊥BC,以CD为直径的半圆O与AD,BC 以及AB均相切,切点分别是点D,C,E.若半圆O的半径为2,AB长为5,则该四边形的周长是( )A.9B.10C.12D.143. 如图,AB,BC,CD分别与☉O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.(1)求证:BO⊥CO.(2)求BE和CG的长.1. 在直角坐标系中,☉O的半径为1,则直线y=-2x+√5与☉O的位置关系是( )A.相离B.相交C.相切D.无法确定2. 如图,在平面直角坐标系中,☉P与x轴分别交于A,B两点,点P的坐标为(3,-1),AB=2√3.若将☉P向左平移,则☉P与y轴相切时点P的坐标为 _.3. (1)已知,如图1,△ABC的周长为l,面积为S,其内切圆圆心为O,半径为r,求.证:r=2Sl(2)已知,如图2,△ABC中,A,B,C三点的坐标分别为A(-3,0),B(3,0),C(0,4).若△ABC内心为D.求点D的坐标.(3)与三角形的一边和其他两边的延长线相切的圆,叫旁切圆,圆心叫旁心.请求出条件(2)中的△ABC位于第一象限的旁心的坐标.1. 如图,一个钢管放在V 形架内,点O 为钢管的圆心.如果MP=10cm,∠MON=120°,则钢管的半径OM 的值为 ( )A.10√33cm B.10√3cm C.50√33cm D.5√3cm2. 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?” ( )A.3步B.5步C.6步D.8步3.如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB 处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E 两点,经测量发现AD 和BE 的长恰是方程x 2-25x+150=0的两根(单位:cm),则该自来水管的半径为________cm.4. 等腰Rt△ABC和☉O如图放置,已知AB=BC=1,∠ABC=90°,☉O的半径为1,圆心O与直线AB的距离为5.(1)若△ABC以每秒2个单位的速度向右移动,☉O不动,则经过多长时间△ABC的边与圆第一次相切?(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,☉O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?《切线长定理的相关计算》必考经典题型专项分类专题练习(专题分类练习+详细解析)题型一:切线长定理与三角形问题1. 如图所示,PA,PB是☉O的切线,且∠APB=40°,下列说法不正确的是( )A.PA=PBB.∠APO=20°C.∠OBP=70°D.∠AOP=70°【解析】选C.∵PA,PB是☉O的切线,且∠APB=40°,∴PA=PB,∠APO=∠BPO=20°,∠PAO=∠PBO=90°, ∴∠BOP=∠AOP=70°,∴C 是错误的.2. 如图,Rt △ABC 中,∠ACB=90°,AC=4,BC=6,以斜边AB 上的一点O 为圆心所作的半圆分别与AC,BC 相切于点D,E.则AD 为 ( )A.2.5B.1.6C.1.5D.1【解析】选B.连接OD,OE,OC,设OD=r,∵AC,BC 切☉O 于D,E, ∴∠ODC=∠OEC=90°,OD=OE, ∵S △AOC +S △BOC =S △ABC ,即12OD ·AC+12OE ·BC=12BC ·AC,12r ·4+12r ·6=12×6×4, r=2.4,AD=AC-r=1.6.3. 如图,半圆O 与等腰直角三角形两腰CA,CB 分别切于D,E 两点,直径FG 在AB 上,若BG=√2-1,则△ABC 的周长为 .【解析】如图,连接OD,OE,∵半圆O 与等腰直角三角形两腰CA,CB 分别切于D,E 两点,∴∠C=∠OEB=∠OEC=∠ODC=90°,∴四边形ODCE是矩形.∵OD=OE,∴四边形ODCE是正方形,∴CD=CE=OE.∵∠A=∠B=45°,∴△OEB是等腰直角三角形.设OE=r,则BE=r,∴OB=OG+BG=√2-1+r,∵OB=√2OE=√2r,∴√2-1+r=√2r,解得r=1.∴AC=BC=2r=2,AB=2OB=2×(1+√2-1)=2√2.∴△ABC的周长为:AC+BC+AB=4+2√2.4.如图,PA,PB分别切圆O于点A,B,并与圆O的切线CD,分别相交于点D,C,已知△PCD的周长等于10cm,求PA.【解析】设DC与☉O的切点为E.∵PA,PB分别是☉O的切线,且切点为A,B,∴PA=PB.同理,可得:DE=DA,CE=CB,则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10cm.∴PA=PB=5cm.题型二:切线长定理与多边形问题1. 如图,一圆内切于四边形ABCD,且BC=10,AD=7,则四边形的周长为( )A.32B.34C.36D.38【解析】选B.如图,根据切线长定理可知,AE=AH,BE=BF,CF=CG,DG=DH.所以AE+DG=AH+DH=AD,BE+CG=BF+CF=BC,所以AB+BC+CD+DA=AE+BE+BC+CG+DG+DA=2AD+2BC=2×7+2×10=34.2. 如图,四边形ABCD 中,AD ∥BC,DC ⊥AD,DC ⊥BC,以CD 为直径的半圆O 与AD,BC 以及AB 均相切,切点分别是点D,C,E.若半圆O 的半径为2,AB 长为5,则该四边形的周长是( )A.9B.10C.12D.14【解析】选D.根据切线长定理,得AD=AE,BC=BE,所以四边形ABCD 的周长是5×2+4=14.3. 如图,AB,BC,CD 分别与☉O 相切于E,F,G,且AB ∥CD,BO=6cm,CO=8cm. (1)求证:BO ⊥CO. (2)求BE 和CG 的长.【解析】(1)∵AB ∥CD, ∴∠ABC+∠BCD=180°.∵AB,BC,CD 分别与☉O 相切于点E,F,G, ∴BO 平分∠ABC,CO 平分∠DCB, ∴∠OBC=12∠ABC,∠OCB=12∠DCB,∴∠OBC+∠OCB=12(∠ABC+∠DCB)=12×180°=90°, ∴∠BOC=90°,∴BO ⊥CO. (2)连接OF,则OF ⊥BC, ∴Rt △BOF ∽Rt △BCO, ∴BF BO =BOBC . ∵在Rt △BOC 中, BO=6cm,CO=8cm, ∴BC=√62+82=10(cm), ∴BF 6=610, ∴BF=3.6cm,∵AB,BC,CD 分别与☉O 相切, ∴BE=BF=3.6cm,CG=CF, ∵CF=BC-BF=10-3.6=6.4(cm). ∴CG=CF=6.4cm.题型三:切线长定理与坐标问题1. 在直角坐标系中,☉O 的半径为1,则直线y=-2x+√5与☉O 的位置关系 是 ( ) A.相离B.相交C.相切D.无法确定【解析】选C.如图所示,过O 作OC ⊥直线AB,垂足为C, 直线AB 为y=-2x+√5. 令x=0,解得:y=√5; 令y=0,解得:x=√52, ∴A (√52,0),B(0,√5), 即OA=√52,OB=√5.在Rt △AOB 中,根据勾股定理得:AB=2+OB 2=52, 又S △AOB =12AB ·OC=12OA ·OB, ∴OC=OA·OB AB =√52×√552=1,又圆O 的半径为1,则直线y=-2x+√5与圆O 的位置关系是相切.2. 如图,在平面直角坐标系中,☉P 与x 轴分别交于A,B 两点,点P 的坐标为(3,-1),AB=2√3.若将☉P 向左平移,则☉P 与y 轴相切时点P 的坐标为 _.【解析】(2,-1)或(-2,-1)3. (1)已知,如图1,△ABC 的周长为l ,面积为S,其内切圆圆心为O,半径为r,求证:r=2Sl .(2)已知,如图2,△ABC 中,A,B,C 三点的坐标分别为A(-3,0),B(3,0),C(0,4).若△ABC 内心为D.求点D 的坐标.(3)与三角形的一边和其他两边的延长线相切的圆,叫旁切圆,圆心叫旁心.请求出条件(2)中的△ABC 位于第一象限的旁心的坐标.【解析】(1)连接OA,OB,OC,设△ABC 的三边分别为a,b,c 则: S=S △OAB +S △OBC +S △OAC =12(a+b+c)r=12l r. ∴r=(2)∵A(-3,0),B(3,0),C(0,4),∴AB=6,AC=BC=5.l =AB+AC+BC=16,S=12AB ·OC=12.由条件(1)得:r==2×1216=32,得D (0,32). (3)如图,设∠B 和∠C 的外角平分线交于点P,则点P 为旁心.∵∠MCB=2∠PCB=2∠CBA,∴∠PCB=∠CBA,∴CP ∥AB.过点P 分别作PE ⊥x 轴于E,PF ⊥CB 于F,则PF=PE=OC=4.在Rt △PFC 中,PC=PF sin∠PCF =PF sin∠CBO =445=5.∴P 点坐标为(5,4).即条件(2)中的△ABC 位于第一象限的旁心的坐标为(5,4).题型四:切线长定理与实际问题1. 如图,一个钢管放在V 形架内,点O 为钢管的圆心.如果MP=10cm,∠MON=120°,则钢管的半径OM 的值为 ( )A.10√33cmB.10√3cmC.50√33cmD.5√3cm【解析】选A.由题意可得OM ⊥MP,ON ⊥NP.∵∠MON=120°,∴∠MOP=60°,设OM=xcm,则OP=2xcm,在Rt △OPM 中,OM 2+MP 2=OP 2,即x 2+102=(2x)2,解得x=10√33,∴OM 的值为10√33cm. 2. 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?” ( )A.3步B.5步C.6步D.8步【解析】选A.3.如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB 处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E 两点,经测量发现AD 和BE 的长恰是方程x 2-25x+150=0的两根(单位:cm),则该自来水管的半径为________cm.【解析】连接OD,OE.解方程x 2-25x+150=0,得x 1=10,x 2=15,∴设AD=10,BE=15,半径为r,∴AB=AD+BE=25,∴(AD+r)2+(BE+r)2=AB 2,即(10+r)2+(15+r)2=252,解得:r=5.答案:54. 等腰Rt △ABC 和☉O 如图放置,已知AB=BC=1,∠ABC=90°,☉O 的半径为1,圆心O 与直线AB 的距离为5.(1)若△ABC以每秒2个单位的速度向右移动,☉O不动,则经过多长时间△ABC的边与圆第一次相切?(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,☉O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?【解析】(1)假设第一次相切时,△ABC移至△A′B′C′处,A′C′与☉O切于点E,连OE并延长,交B′C′于F.设☉O与直线l切于点D,连OD,则OE⊥A′C′,OD⊥直线l.由切线长定理可知C′E=C′D;设C′D=x,则C′E=x,易知C′F=√2x,∴√2x+x=1,则x=√2-1,∴CC′=BD-BC-C′D=5-1-(√2-1)=5-√2;∴△ABC运动的时间为5−√2秒.2(2)设经过t秒△ABC的边与圆第一次相切,设经过t秒△ABC的边与☉O第一次相切时,△ABC移至△A″B″C″处,☉O与BC所在直线的切点D移至D′处,A″C″与☉O切于点E,连OE并延长,交B″C″于F.∵CC″=2t,DD′=t,∴C″D′=CD+DD′-CC″=4+t-2t=4-t.由切线长定理得C″E=C″D′=4-t;又∵FC″=√2C″E=√2C″D′,而FC″+C″D′=FD′=1,∴(√2+1)C″D′=(√2+1)(4-t)=1,解得:t=5-√2.答:经过5-√2秒△ABC的边与圆第一次相切.学海迷津:数学学习十大方法1、配方法所谓配方,就是把一个解析式利用恒等变形的方法,把其中的某些项配成一个或几个多项式正整数次幂的和形式。