指数函数运算、图像及其性质

指数函数的图像是一条向上开口的曲线，通常表示为y=a^x（a>0，a≠1）。

指数函数的性质有：
1.在y 轴上的截距为1。

2.对于不同的指数函数，它们的图像形状是相同的，只有位置不同。

如果改变指数函数的
指数，则会改变函数的斜率，即函数图像会发生平移。

3.对于相同的指数函数，如果改变函数的系数，则会改变函数的尺度，即函数图像会发生
伸缩。

对数函数的图像是一条向右开口的曲线，通常表示为y=loga(x)（a>0，a≠1）。

对数函数的性质有：
1.在y 轴上的截距为0。

2.对于不同的对数函数，它们的图像形状是相同的，只有位置不同。

如果改变对数函数的
底数，则会改变函数的斜率，即函数图像会发生平移。

3.对于相同的对数函数，如果改变函数的系数，则会改变函数的尺度，即函数图像会发生
伸缩。

幂函数的图像可以是一条向上开口的曲线，也可以是一条向右开口的曲线，通常表示为y=x^n（n为常数）。

幂函数的性质有：
1.当n>0 时，幂函数的图像是一条向上开口的曲线。

2.当n<0 时，幂函数的图像是一条向右开口的曲线。

3.当n=0 时，幂函数的图像是一条水平直线。

4.幂函数的图像在y 轴上的截距为1。

5.对于不同的幂函数，它们的图像形状是相同的，只有位置不同。

如果改变幂函数的指数，
则会改变函数的斜率，即函数图像会发生平移。

6.对于相同的幂函数，如果改变函数的系数，则会改变函数的尺度，即函数图像会发生伸
缩。

指数函数图像及性质
指数函数图像的特征就是“J”形的曲线，它可用来表示水平和垂直运动的加速度和内能释放。

指数函数可以表示非常多种物理或生物学现象。

指数函数图像具有以下性质：
1. 指数函数图像以指数增长和指数衰减。

即曲线是从左向右张开的，以及从右向左收缩的。

2. 一般情况下，指数函数图像会通过坐标原点（0,0），如果不是，则说明指数函数图像是一条平行曲线。

3. 在每一个定义域，指数函数图像的斜率最大值为1，但是随着x的增加，它的斜率越来越小，趋近于0。

4. 在不同的定义域，指数函数图像的形状也有所不同，一般数学家会把它们分成“快速增长函数”和“减速函数”，其中前者的最大斜率大于1而后者的最大斜率小于1。

5. 对于指数函数图像，从右向左看斜率是负值，而从左向右看又会变成正值。

6. 有时候，指数函数图像会拐到右上或者右下方，这时候说明指数函数正在发挥它的作用。

7. 指数函数的绝对值有三种情况，即增加，减少和突然增加，这种情况受到外部因素的影响。

8. 指数函数图像在平行于y轴的负半轴上，其值会无限接近0，而在平行于y轴的正半轴上，其值会无限增长。

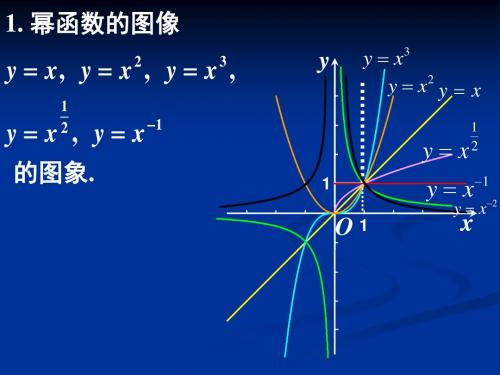
指数函数的概念及图像和性质指数函数的定义一般地，函数xy a =（a ＞0且a ≠1）叫做指数函数，其中x 是自变量，函数的定义域为R .我们在学习函数的单调性的时候，主要是根据函数的图象，即用数形结合的方法来研究. 先来研究a ＞1的情况下面我们通过用计算机完成以下表格，并且用计算机画出函数2xy =的图象再研究，0＜a ＜1的情况，用计算机完成以下表格并绘出函数1()2xy =的图象.x从图中我们看出12()2xxy y ==与的图象有什么关系?通过图象看出12()2xxy y y ==与的图象关于轴对称,实质是2x y =上的x ,y 点(-)x y x ,y y 1与=()上点(-)关于轴对称.2讨论：12()2xx y y ==与的图象关于y 轴对称，所以这两个函数是偶函数，对吗？②利用电脑软件画出115,3,(),()35x xx x y y y y ====的函数图象.问题：1：从画出的图象中，你能发现函数的图象与底数间有什么样的规律.从图上看x y a =（a ＞1）与xy a =（0＜a ＜1）两函数图象的特征.问题2：根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大（小）值、奇偶性.问题3：指数函数xy a =（a ＞0且a ≠1），当底数越大时，函数图象间有什么样的关系.x（1）在[,]xa b f x a 上,()=（a ＞0且a ≠1）值域是[(),()][(),()];f a f b f b f a 或 （2）若0,x f x f x x ≠≠∈则()1;()取遍所有正数当且仅当R; （3）对于指数函数()x f x a =（a ＞0且a ≠1），总有(1);f a = （4）当a ＞1时，若1x ＜2x ，则1()f x ＜2()f x ；x 例1 比较下列各题中两个数的大小： (1) 3 0.8 , 30.7 (2) 0.75-0.1, 0.750.1例2 (1)求使4x>32成立的x 的集合； (2)已知a 4/5>a2 ,求实数a 的取值范围.指数函数y=a x(a>0,a≠1)底数a对函数图象的影响，我们通过两个实例来讨论a>1和0<a<1两种情况。

指数函数对数函数与幂函数指数函数的性质与图像xx年xx月xx日CATALOGUE 目录•指数函数的定义与性质•对数函数的定义与性质•幂函数的定义与性质•指数函数、对数函数与幂函数的比较•指数函数、对数函数与幂函数的应用案例•总结与展望01指数函数的定义与性质指数函数的定义02指数函数：y=f(x)=a^x03a>0时，函数图像过一三象限；a<0时，函数图像过二四象限。

指数函数的性质函数图像恒过(0,1)点值域：R a>1时，函数为单调递增函数；0<a<1时，函数为单调递减函数奇偶性：当a>0时，为奇函数；当a=0时，既不是奇函数也不是偶函数；当a<0时，为偶函数指数函数的图像图像恒过(0,1)点当a>1时，函数的增长速度随着x的增大而逐渐加快；当0<a<1时，函数的增长速度随着x的增大而逐渐减慢。

a>1时，函数为单调递增函数，图像位于一三象限；0<a<1时，函数为单调递减函数，图像位于二四象限。

当a>1时，函数的最大值无限趋近于正无穷大；当0<a<1时，函数的最小值无限趋近于0。

02对数函数的定义与性质1 2 3自然对数：以数学常数e为底数的对数，记作ln(x)。

常用对数：以10为底数的对数，记作lg(x)。

底数为任意正数的对数，记作log(x)。

对数的运算性质log(a*b)=log(a)+log(b)；log(a/b)=log(a)-log(b)；log(a^n)=nlog(a)。

对数恒等式log(a/b)=log(a)-log(b)；log(a^n)=nlog(a)。

对数的运算律如果a>0且a不等于1，M>0，N>0，那么log(a)(MN)=log(a)M +log(a)N；log(a)(M/N)=log(a)M -log(a)N；log(a)M^n=nlog(a)M。

•对数函数的图像与性质：图像与x轴交点为1，当x>1时，函数值大于0；当0<x<1时，函数值小于0。

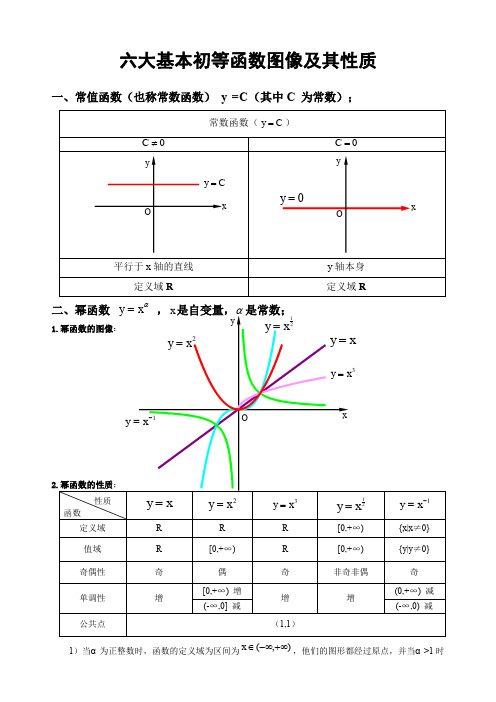
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2xy =3x y =21xy =1-=x y定义域 R RR [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时xyOxy =2x y =3x y =1-=x y 21xy =O=y xCy =Oxyy在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性 非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数 在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

指数函数的性质与图像
指数函数图像及性质如下：
1、a＞1，图像单调递增，走势是同为增函数时，底大近轴，对称性是底数互为倒数时，图像关于y轴对称。

2、0＜a＜1，图像单调递减，走势是同为减函数时，底小近轴，对称性是底数互为倒数时，图像关于y轴对称。

3、指数函数的自变量范围是（-∞，+∞），因变量范围是（0,+∞）；当指数函数自变量范围在（-∞，0）时，因变量输出范围为（0，1）。

指数函数的判定
在理解指数函数的概念时，应抓住定义的“形式”像y=2*3^x，y=2^1/x，y=3^根号x-2，y=(2^x)-1 等函数均不符合形式y=a^x(a>0，且a不等于1)，因此它们都不是指数函数。

指数函数的定义表达式中，在ax前的系数必须是数1，自变量x必须在指数的位置上，且不能是x的其他表达式，否则，就不是指数函数。

指数与对数函数的运算与性质指数与对数函数是高中数学中的重要概念，它们在数学和实际问题中都有广泛的应用。

本文将介绍指数与对数函数的运算规则和性质，帮助读者更好地理解和应用这两个函数。

一、指数函数的运算与性质指数函数的定义形式为y=a^x，其中a为常数且大于0且不等于1。

指数函数的运算规则包括以下几个方面：1. 指数相加规则当底数相同时，指数可以进行相加。

例如，对于指数函数y=2^x和y=2^y，可以得到y=2^(x+y)。

这个规则在计算指数函数的和或差时非常有用。

2. 指数相乘规则当底数相同时，指数可以进行相乘。

例如，对于指数函数y=2^x和y=2^y，可以得到y=(2^x)^y，进一步化简为y=2^(xy)。

这个规则在计算指数函数的乘积或幂次时非常有用。

3. 指数的负指数规则对于正实数a和整数m，有a^(-m)=1/(a^m)。

这个规则为计算负指数的指数函数提供了方便。

4. 指数为零规则对于任意正实数a，有a^0=1。

这个规则说明任何数的零次幂都等于1。

除了上述运算规则，指数函数还有以下几个性质：1. 指数函数的图像当底数a大于1时，指数函数呈现增长趋势；当底数a介于0和1之间时，指数函数呈现衰减趋势。

指数函数的图像通常是一条平滑的曲线。

2. 指数函数的性质指数函数的性质包括：对于任意正实数a，有a^x>0；当x1时，a^x2>a^x1。

二、对数函数的运算与性质对数函数的定义形式为y=loga(x)，其中a为常数且大于0且不等于1。

对数函数的运算规则包括以下几个方面：1. 对数的乘法规则loga(xy)=loga(x)+loga(y)。

这个规则为计算对数函数的乘积提供了方便。

2. 对数的除法规则loga(x/y)=loga(x)-loga(y)。

这个规则为计算对数函数的商提供了方便。

3. 对数的指数规则loga(x^m)=m*loga(x)。

这个规则为计算对数函数的幂次提供了方便。

除了上述运算规则，对数函数还有以下几个性质：1. 对数函数的图像对数函数的图像通常是一条平滑的曲线，且在x轴的正半轴上逐渐增加。

精选文档指数函数、对数函数、幂函数的图像与性质理解有理数指数幂的含义，掌握幂的运算；理解指数函数的观点，理解指数函数的单一性，掌握指数函数图象经过的特别点；理解对数的观点及其运算性质，理解对数函数的观点，理解对数函数的单一性，掌握对数函数图象经过的特别点。

认识指目标数函数y=a x与对数函数ylog a x 互为反函数〔a0,且a1〕。

认识幂函数的概11念。

联合函数y=x ，y=x 2，y=x 3，y ，y x 2的图象，认识它们的变化状况。

x要点指数、对数的运算性质；指数函数、对数函数的图像与性质的综合应用；幂函数图像的应用。

难点 指数函数、对数函数的图像与性质的综合应用，幂函数图像的应用。

方法建议第一回首指数、对数的运算性质；指数函数、对数函数的图像与性质等根底知识。

再经过经典例题的解析，帮助学生理解根底知识，加深对知识的认识和记忆。

再通过精题精练，使学生形成能力。

在例题和习题的选择上能够依据学生的实质状况进 行。

讲堂精讲例题 搭配讲堂训练题 课后作业程度及数目A 类 〔4 〕道 〔4 〕道 〔11 〕道B 类 〔3 〕道 〔3 〕道 〔10 〕道C 类 〔0〕道 〔0〕道 〔0〕道理解有理数指数幂的含义，掌握幂的运算；理解指数函数的观点，理解指数函数的单一性，掌握指数函数图象经过的特别点。

理解对数的观点及其运算性质。

理解对数函数的观点， 理解对数函数的单一性，掌握对数函数图象经过的特别点。

认识指数函数 y=a x 与对数函数y log a x 互为反函数〔 a 0,且a 1〕。

认识幂函数的观点。

联合函数 y=x ，y=x 2，y=x 3，1y1，yx 2的图象，认识它们的变化状况。

指数函数、对数函数在高中数学中据有十x分重要的地位，是高考要点考察的对象， 热门是指数函数、 对数函数的图象与性质的综合应用．同时考察分类议论思想和数形联合思想；多以选择、填空题的形式出现，有时会与其余知识联合在知识交汇点处命题。

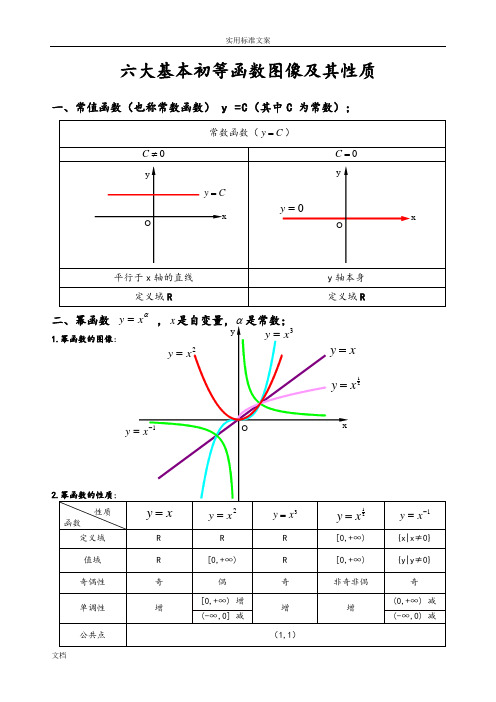
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性 非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数 在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

指数函数的图像和性质
指数函数是一种特殊函数，其定义域为实数集合R，值域也是实数集合R。

指
数函数的图像是一条弧线，朝右上方抛物线式延伸，底点在坐标原点处。

其图像如下所示：
指数函数具有以下性质：
一、指数函数是定义在实数集合上的单值函数，其图象是一条朝右上方延伸的
弧线，且在坐标原点处有底点，函数值随x增大而增大，函数图像上每一点到底点的距离都不变；
二、指数函数对任何正实数都有定义，指数函数f(x)=a^x（a为正实数）的图
谱具有单调性，当a的值不同时，指数函数的函数图象具有相似的特点；
三、指数函数具有不变性，不论x的取值范围如何，函数的函数图象仍不改变；
四、指数函数的切线斜率随着x的增大而增大；
五、指数函数的斜率在同一条线上增加或减少；
六、不论指数函数是升幂函数还是降幂函数，其图象都是从坐标原点开始，一
条朝右上方延伸的弧线。

以上就是指数函数的图像与性质，根据以上描述，指数函数的函数图像与以及
其性质可以得出：指数函数是从坐标原点开始，一条朝右上方延伸的弧线，有着单调性，不变性，切线斜率随着x的增大而增大等性质。

指数函数运算法则公式及性质
一般地，y=a^x函数(a为常数且以a>0，a≠1)叫做指数函数，函数的定义域是R。

接下来分享指数函数运算法则公式及性质。

指数函数运算法则
（1）a^m+n=a^m∙a^n；
（2）a^mn=(a^m)^n；
（3）a^1/n=^n√a；
（4）a^m-n=a^m/a^n。

指数函数的性质
(1)指数函数的定义域为R，这里的前提是a大于0且不等于1。

对于a不大于0的情况，则必然使得函数的定义域不连续，因此我们不予考虑，同时a等于0函数无意义一般也不考虑。

(2)指数函数的值域为(0，+∞)。

(3)函数图形都是上凹的。

(4)a>1时，则指数函数单调递增;若0<a<1，则为单调递减的。

(5)函数总是在某一个方向上无限趋向于X轴,并且永不相交。

(6)指数函数无界。

(7)指数函数是非奇非偶函数
(8)指数函数具有反函数，其反函数是对数函数。