高考数学第一轮复习：《直线与圆圆与圆的位置关系》(北师大版)

高考数学专题复习：直线与圆、圆与圆的位置关系一、单选题1．已知圆22:2440A x y x y +---=，圆22:2220B x y x y +++-=，则两圆的公切线的条数是（ ） A ．1条B ．2条C ．3条D ．4条2．已知点(,)P x y 是直线l ：40kx y -+=(0k >)上的动点，过点P 作圆C ：2220x y y =++的切线PA ，A 为切点，若||PA 最小为2时，圆M ：220x y my +-=与圆C 外切，且与直线l 相切，则m 的值为（ ）A ．2-B ．2C ．4D 23．在平面直角坐标系xOy 中，圆C 的方程为228150x y x +-+=，若直线2y kx =-上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值是（ ） A ．23-B ．13C ．43D ．24．已知直线10x my m -+-=被圆O ：224x y +=所截得的弦长为m =（ ）A ．1-B ．1C ．2D ．5．已知直线():10l mx y m R +-=∈是圆22:4210C x y x y +-++=的对称轴，过点()2,A m -作圆C 的一条切线，切点为B ，则AB 等于（ ）A ．4B ．C ．D ．36．设a ，b 为正数，若圆224210x y x y ++-+=关于直线10ax by -+=对称，则2a bab+的最小值为（ ） A ．9B ．8C ．6D ．107．已知圆221:4240C x y x y ++--=，2223311:222C x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭，则这两圆的公共弦长为（ ）A ．2B ．C ．2D ．18．设0r >，圆()()22213x y r -++=与圆2216x y +=的位置关系不可能是（ ） A ．相切B ．相交C ．内切或内含D ．外切或相离9．已知圆C ：()()22cos sin 3x y θθ-+-=交直线1y =-于A ，B 两点，则对于θ∈R ，线段AB 长度的最小值为（ ）A ．1B C D ．210．在同一平面直角坐标系下，直线ax by ab +=和圆222()()x a y b r -+-=（0ab ≠，0r >）的图象可能是（ ）．A ．B ．C ．D ．11．圆1C ：221x y +=与圆2C ：()224310x y k x y +++-=（k ∈R ，0k ≠）的位置关系为（ ）A ．相交B ．相离C ．相切D ．无法确定12．若直线:1l y kx =-与圆()()22:212C x y -+-=相切，则直线l 与圆()22:23D x y -+=的位置关系是（ ） A ．相交 B ．相切 C ．相离 D ．不确定二、填空题13．圆22230x y y ++-=被直线0x y k +-=分成两段圆弧，且较短弧长与较长弧长之比为1：3，则k =________.14．过原点且倾斜角为60︒的直线与圆2240x y y +-=相交，则直线被圆截得的弦长为_____.15．过点()2,0与圆22 A: 230x y x +--+=相切的直线方程为__________.16．若直线mx ＋2ny －4＝0（m ，n ∈R ）始终平分圆22420x y x y +--=的周长，则mn 的取值范围是________． 三、解答题17．已知以点()1,1A 为圆心的圆与直线1:220l x y ++=相切，过点()2,0B 的动直线l 与圆A 相交于M ､N 两点. （1）求圆A 的方程；（2）当4MN =时，求直线l 的方程.18．已知圆C ：222430x y x y ++-+=．（1）若直线l 过点(2,0)-且被圆C 截得的弦长为2，求直线l 的方程；（2）从圆C 外一点P 向圆C 引一条切线，切点为M ，O 为坐标原点，且PM PO =，求PM 的最小值．19．直线l ：y x =与圆C ：()()221316x y -+-=相交于A 、B 两点．（1）求平行于l 且与圆C 相切的直线方程； （2）求ABC 面积．20．已知圆C 过点()2,0R 、()4,2S -，且圆心C 在直线280x y --=上． （1）求圆C 的方程；（2）若点P 在圆C 上，O 为原点，()(),00A t t >，求tan POA ∠的最大值．21．已知圆C 的方程为226440x y x y ++-+=.（1）若直线:10l x y -+=与圆C 相交于M 、N 两点，求||MN 的长; （2）已知点()1,5P ，点Q 为圆C 上的动点，求||PQ 的最大值和最小值.22．已知直线:20l mx y m -+-=，C 的方程为22240x y x y +--=. （1）求证：l 与C 相交；（2）若l 与C 的交点为A 、B 两点，求OAB 的面积最大值.（O 为坐标原点）参考答案1．B 【分析】分别求得两圆的圆心坐标和半径，结合两圆的位置关系的判定方法，求得两圆的位置关系，即可求解. 【详解】由圆22:2440A x y x y +---=可化为22(1)(2)9x y -+-=， 可得圆心坐标为(1,2)A ，半径为3R =，由圆22:2220B x y x y +++-=可化为22(1)(1)4x y +++=， 可得圆心坐标为(1,1)B --，半径为2r，则圆心距为d AB == 又由5,1R r R r +=-=，所以R r AB R r -<<+， 可得圆A 与圆B 相交，所以两圆公共切线的条数为2条. 故选：B. 2．B 【分析】根据题意当CP 与l 垂直时，||PA 的值最小，进而可得2k =，再根据圆M 与圆C 外切可得0m >，根据圆M 与直线l 相切，利用圆心到直线的距离等于圆的半径，即可求出. m 的值.【详解】圆C 的圆心为(0,1)C -，半径为1，当CP 与l 垂直时，||PA 的值最小，此时点C 到直线l 的距离为d =，由勾股定理得22212+=，又0k >，解得2k =， 圆M 的圆心为(0,)2mM ，半径为||2m ， ∵圆M 与圆C 外切，∴||1|(1)|22m m+=--，∴0m >，∵圆M 与直线l 相切，∴|4|2m m -+=2m =， 故选:B 3．C 【分析】根据直线与圆的位置关系和点到直线的距离公式建立不等式，解之可得选项. 【详解】圆C 的标准方程为22(4)1x y -+=，半径1r =，当圆心(4,0)到直线2y kx =-的距离1d r ≤+时，满足题意，圆心在直线上的射影点即满足题意，故有2d =≤，解得403k ≤≤，即k 的最大值为43， 故选：C. 4．A 【分析】由于直线过定点(1,1)--P，而||OP =OP 垂直，从而由斜率的关系列方程可求出m 【详解】∵直线10x my m -+-=过定点(1,1)--P ，连接OP，则||OP ∴直线10x my m -+-=与OP 垂直，11m=-， ∴1m =-， 故选：A. 5．A 【分析】根据直线():10l mx y m R +-=∈是圆22:4210C x y x y +-++=的对称轴，则圆心在直线l 上，求得m ，由过点()2,A m -作圆C 的一条切线，切点为B ，利用勾股定理即可求得AB . 【详解】由方程224210x y x y +-++=得()()22214x y -++=，圆心为()2,1C -，因为直线l 是圆C 的对称轴，所以圆心在直线l 上，所以1m =，所以A 点坐标为()2,1-，则AC =4AB =.故选：A ． 6．A 【分析】求出圆的圆心坐标，得到,a b 的关系，然后利用基本不等式求解不等式的最值即可． 【详解】解：圆224210x y x y ++-+=，即()()22214x y ++-=，所以圆心为(2,1)-， 所以210a b --+=，即21a b +=，因为0a >、0b >，则2222(2)(2)2252229a b a b a b a b ab a ab ab abab+++++⋅===，当且仅当13b a ==时，取等号． 故选：A ． 7．C 【分析】先求出两圆的公共弦所在直线的方程，用垂径定理求弦长. 【详解】由题意知221:4240C x y x y ++--=，222:3310C x y x y ++--=，将两圆的方程相减，得30x y +-=，所以两圆的公共弦所在直线的方程为30x y +-=.又因为圆1C 的圆心为(2,1)-，半径3r =，所以圆1C 的圆心到直线30x y +-=的距离d ==所以这两圆的公共弦的弦长为222223222d .故选：C. 8．D 【分析】计算出两圆圆心距d ，并与两圆半径和作大小比较，由此可得出结论. 【详解】两圆的圆心距d 4r +，4r +，所以两圆不可能外切或相离．9．C 【分析】由题意圆C 的圆心C 在单位圆上，求出点C到直线1y =-的距离的最大值，根据圆的弦长AB =. 【详解】解：由圆C ：()()22cos sin 3x y θθ-+-=，知该圆的半径r =()cos ,sin C θθ在单位圆221x y +=上，∵原点O到直线1y =-12=，则点C 到直线1y =-的距离d 的最大值为13122+=，由AB =d 取最大值32时，线段AB故选：C ．10．D 【分析】根据直线的位置及圆心所在的象限判断参数a 、b 的符号，进而确定正确选项. 【详解】直线ax by ab +=在x ，y 轴上的截距分别为b 和a ，圆心横坐标为a ，纵坐标为b ． A ：由直线位置可得0b <，而由圆的位置可得0b >，不正确． B ：由直线位置可得0a >，而由圆的位置可得0a <，不正确． C ：由直线位置可得0a >，而由圆的位置可得0a <，不正确．D ：由直线位置可得0a >，0b <，而由圆的位置可得0a >，0b <，正确.11．A 【分析】求出两圆的圆心和半径，再求出两圆的圆心距，与两圆的半径和差比较可得结论 【详解】解：圆1C ：221x y +=的圆心1(0,0)C ，半径为11r =，由()224310x y k x y +++-=，得222325(2)()124x k y k k +++=+，所以圆2C 的圆心为23(2,)2C k k --，半径2r所以12121C C r r +=1>0k ≠）1，所以1221C C r r >-所以两圆相交． 故选：A 12．A 【分析】由直线l 与圆C 相切可构造方程求得k；分别在2k =2k =过比较圆心到直线距离与圆的半径之间大小关系可得位置关系. 【详解】由圆C 方程知其圆心()2,1C直线l 与圆C相切，=2k =由圆D 方程知其圆心()2,0D，半径r =∴圆心D 到直线l距离d =当2k =(()222233021d r+-=-=<+，即d r <，此时圆D 与直线l 相交；当2k =(()222233021d r --=-=<+，即d r <，此时圆D 与直线l 相交； 综上所述：圆D 与直线l 相交. 故选：A. 13．1或3- 【分析】由题意可知较短弧所对圆心角是90︒，此时圆心到直线0x y k +-==，再由点到直线的距离公式求解即可 【详解】由题意知，圆的标准方程为()2214x y ++=，较短弧所对圆心角是90︒，所以圆心()0,1-到直线0x y k +-==1k =或3k =-.故答案为：1或3- 14．【分析】由已知求出直线方程，将圆方程化为标准方程求出圆心和半径，然后求出圆心到直线的距离，再利用弦长、弦心距和半径的关系求出弦长 【详解】解：由题意得直线方程为tan60y x =︒0y -=， 由2240x y y +-=，得22(2)4x y +-=，则圆心为(0,2)，半径为2， 所以圆心(0,2)0y -=的距离为1d ==，所以所求弦长为=故答案为：15．x =2或)2y x =-. 【分析】 分斜率不存在和斜率存在两种情况讨论：斜率不存在时，直线l ：x =2与圆相切；斜率存在时，设其为k ，则直线l ：()2y k x =-，利用圆心到直线的距离等于半径，列方程求出k ，即可求出直线方程.【详解】圆22 A: 230x y x +--+=化为标准方程：()(22 11x y -+=，所以当过点()2,0的直线斜率不存在时，直线l ：x =2与圆相切；过点()2,0的直线斜率存在时，设其为k ，则直线l ：()2y k x =-，因为l 与圆A 相切，所以圆心到直线的距离等于半径，1=，解得：k =，此时l：)2y x =-. 故答案为：x =2或)2y x =-. 16．(,1]-∞【分析】 由题意得直线过圆心，进而得到2240m n +-=，所以mn 可转化为()2n n -，结合二次函数的值域即可求解.【详解】因为直线mx ＋2ny －4＝0（m ，n ∈R ）始终平分圆22420x y x y +--=的周长，所以直线经过圆心，又因为圆心为()2,1，则2240m n +-=，即2m n +=，因此2m n =-，所以()()2222111mn n n n n n =-=-+=--+≤，所以mn 的取值范围是(,1]-∞，故答案为：(,1]-∞.17．（1）()()22115x y -+-=；（2）2x =或0y =.【分析】（1）利用圆心到直线的距离求半径，即可得圆的方程；（2）首先考查直线斜率不存在的直线，判断是否满足4MN =，当直线的斜率存在时，设直线20kx y k --=，利用弦长公式求得斜率k ，即可得直线方程.【详解】解：（1）由题意可知，点A 到直线1l 的距离d =因为圆A 与直线1l 相切，则圆A 的半径r d ==所以，圆A 的标准方程为()()22115x y -+-=（2）①当直线l 的斜率不存在时因为直线l 的方程为2x =.所以圆心A 到直线l 的距离11d =.由（1）知圆的半径为r 4MN ==. 故2x =是符合题意的一条直线.②当直线l 的斜率存在时设直线l 的斜率为k ，则直线20kx y k --=圆心A 到直线l 的距离1d =因为22212MN d r ⎛⎫+= ⎪⎝⎭所以245+=，即()2211k k +=+，解得0k = 因此，直线l 的方程为0y =综上所述，直线l 的方程为2x =或0y =.18．（1）2x =-或3460x y -+=；（2． 【分析】（1）根据题意，由圆的方程分析圆的圆心与半径，分直线的斜率存在与不存在两种情况讨论，求出直线的方程，综合即可得答案；（2）根据题意，连接MC ，PC ，分析可得PMC △为直角三角形，即222||||||PM PC MC =-，设(,)P x y ，分析可得||MC ||||PM PO =，分析可得2222(1)(2)2x y x y ++--=+，变形可得P 的轨迹方程，据此结合直线与圆的方程分析可得答案．【详解】解：（1）222430x y x y ++-+=可化为22(1)(2)2x y ++-=．当直线l 的斜率不存在时，其方程为2x =-，易求得直线l 与圆C 的交点为(2,1)A -，()23B -，，2AB =，符合题意；当直线l 的斜率存在时，设其方程为(2)y k x =+，即20kx y k -+=，则圆心C 到直线l 的距离1d ，解得34k =． 所以直线l 的方程为3460x y -+=，综上，直线l 的方程为2x =-或3460x y -+=．（2）如图，PM 为圆C 的切线，连接MC ，PC ，则CM PM ⊥．所以PMC △为直角三角形．所以222PM PC MC =-．设点P 为(,)x y ，由（1）知点C 为(1,2)-，MC =PM PO =，P 的轨迹方程为2430x y -+=． 求PM 的最小值，即求PO 的最小值，也即求原点O 到直线2430x y -+=的距离，代入点到直线的距离公式可求得PM 的最小值d =19．（1）20x y -++或20x y -+-=；（2）【分析】（1）设切线方程为y x b =+，由切线定义求得b ，进而求得结果；（2）作CD AB ⊥，由点到直线距离公式求得CD ，再由弦长公式求得AB ，进而求得面积.【详解】（1）设切线方程为y x b =+，则圆心(1,3)C 到切线的距离4d r ==，解得2b =±所以切线方程为20x y -++或20x y -+-=；（2）作CD AB ⊥，垂足为D ，CD ==，∴AB ==∴1122ABC S AB CD =⋅=⨯△20．（1）()2244x y -+=；（2 【分析】 （1）根据垂径定理的逆定理可得弦RS 的垂直平分线过原点，又圆心C 在直线280x y --=上，联立直线方程即可得解；（2）根据题意知当OP 与圆相切时，tan POA ∠值最大，计算即可得解.【详解】（1）由20142RS k --==--，线段RS 中点坐标为(3,1)-， 所以线段RS 的垂直平分线为4y x =-，即40x y --=，由28040x y x y --=⎧⎨--=⎩可得圆C 的圆心为(4,0)，易得半径2r ，所以圆C 的方程为22(4)4x y -+=；（2）由圆心在x 轴正半轴上，由()(),00A t t >，所以OA 在正半轴上，由090POA <∠<，故当OP 和圆相切时，即P 为切点时POA ∠最大，此时tan POA ∠最大，tanPOA ∠=. 21．（1）2；（2）最大值为8，最小值为3.【分析】（1）先将圆的方程化为标准方程，得出圆心坐标和半径，求出圆心到直线l 的距离，由勾股定理可得答案.（2）先求出PC 的长度，由圆的性质可得PC r PQ PC r -≤≤+，从而得到答案.【详解】解：（1）圆C 的一般式方程为()()22329x y ++-=，即圆心()C 3,2-，半径3r =，所以圆心C 到直线l ：10x y -+=的距离d ==所以弦长 2MN ==；（2）5PC ，又3r =，所以max 8PQ PC r =+=，min 2PQ PC r =-=，即PQ 的最大值为8，最小值为3.22．（1）证明见解析；（2）5【分析】 （1）由题知直线l 过定点1,2，且为C 的圆心，故l 与C 相交；（2）由题知2AB r ==l 与直线OC 垂直时，O 到直线l 的距离最大，最大值为OC =.【详解】解：（1）由题知直线():21l y m x -=-，C 的标准方程为()()22125x y -+-=， 所以直线l 过定点1,2，为圆的圆心，所以直线过C 的圆心，故l 与C 相交；（2）由（1）知直线:20l mx y m -+-=过圆C 的圆心，C 的半径为r =所以2AB r ==所以当O 到直线l 的距离最大时，OAB 的面积取最大值，故当直线l 与直线OC 垂直时，O 到直线l 的距离最大，最大值为OC =所以OAB 的面积最大值为11522AB OC =。

第四节 直线与圆、圆与圆的位置关系授课提示：对应学生用书第359页[A 组 基础保分练]1．（2021·某某某某模拟）直线ax －by ＝0与圆x 2＋y 2－ax ＋by ＝0的位置关系是（ ） A ．相交 B ．相切 C ．相离 D ．不能确定解析：将圆的方程化为标准方程得⎝⎛⎭⎫x －a 22＋⎝⎛⎭⎫y ＋b 22＝a 2＋b 24，所以圆心坐标为⎝⎛⎭⎫a 2，－b 2，半径r ＝a 2＋b 22．因为圆心到直线ax －by ＝0的距离d ＝⎪⎪⎪⎪a 22＋b 22a 2＋b 2＝a 2＋b 22＝r ，所以直线与圆相切． 答案：B 2．（2021·某某质检）圆x 2＋y 2＝4与圆x 2＋y 2－4x ＋4y －12＝0的公共弦所在直线和两坐标轴所围成图形的面积为（ ） A ．1 B ．2 C ．4 D ．8 解析：由（x 2＋y 2－4）－（x 2＋y 2－4x ＋4y －12）＝0得公共弦所在直线的方程为x －y ＋2＝0，它与两坐标轴分别交于（－2，0），（0，2），所以直线和两坐标轴所围成图形的面积为12×2×2＝2． 答案：B 3．（2021·某某十四校二联）已知直线x －2y ＋a ＝0与圆O ：x 2＋y 2＝2相交于A ，B 两点（O 为坐标原点），且△AOB 为等腰直角三角形，则实数a 的值为（ ） A ．6或－ 6 B ．5或－ 5 C ． 6 D ． 5 解析：因为直线x －2y ＋a ＝0与圆O ：x 2＋y 2＝2相交于A ，B 两点（O 为坐标原点），且△AOB为等腰直角三角形，所以O 到直线AB 的距离为1，由点到直线的距离公式可得|a |12＋（－2）2＝1，所以a ＝±5． 答案：B 4．（2021·某某市第一次统考）直线l ：y ＝kx ＋1与圆O ：x 2＋y 2＝1相交于A ，B 两点，则“k ＝1”是“|AB |＝2”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件解析：依题意，注意到|AB |＝2＝|OA |2＋|OB |2等价于圆心O 到直线l 的距离等于22，即有1k 2＋1＝22，k ＝±1．因此，“k ＝1”是“|AB |＝2”的充分不必要条件． 答案：A 5．（2021·某某一中模考）圆C 1：（x ＋1）2＋（y －2）2＝4与圆C 2：（x －3）2＋（y －2）2＝4的公切线的条数是（ ） A ．1 B ．2 C ．3 D ．4解析：圆C 1：（x ＋1）2＋（y －2）2＝4的圆心为（－1，2），半径为2，圆C 2：（x －3）2＋（y －2）2＝4的圆心为（3，2），半径为2，两圆的圆心距|C 1C 2|＝（－1－3）2＋（2－2）2＝4＝2＋2，即两圆的圆心距等于两圆的半径之和，故两圆相外切，故公切线的条数为3． 答案：C 6．（2021·某某调研）已知直线l ：x ＋y －5＝0与圆C ：（x －2）2＋（y －1）2＝r 2（r ＞0）相交所得的弦长为22，则圆C 的半径r ＝（ ） A ． 2 B ．2 C ．2 2 D ．4 解析：法一：依题意，得圆C 的圆心坐标为（2，1），圆心到直线l 的距离d ＝|2＋1－5|1＋1＝2，因为弦长为22，所以2r 2－d 2＝22，所以r ＝2．法二：联立得⎩⎪⎨⎪⎧x ＋y －5＝0，（x －2）2＋（y －1）2＝r 2，整理得2x 2－12x ＋20－r 2＝0，设直线l 与圆C 的两交点分别为A （x 1，y 1），B （x 2，y 2），所以x 1＋x 2＝6，x 1x 2＝20－r 22，所以|AB |＝1＋k 2|x 1－x 2|＝2（x 1＋x 2）2－4x 1x 2＝22，所以r ＝2． 答案：B 7．（2021·某某天河模拟）已知圆C 的方程为x 2－2x ＋y 2＝0，直线l ：kx －y ＋2－2k ＝0与圆C 交于A ，B 两点，则当△ABC 面积最大时，直线l 的斜率k ＝_________．解析：由x 2－2x ＋y 2＝0，得（x －1）2＋y 2＝1，则圆的半径r ＝1，圆心C （1，0）， 直线l ：kx －y ＋2－2k ＝0与圆C 交于A ，B 两点， 当CA 与CB 垂直时，△ABC 面积最大，此时△ABC 为等腰直角三角形，圆心C 到直线AB 的距离d ＝22， 则有|2－k |1＋k 2＝22，解得k ＝1或7． 答案：1或7 8．（2021·某某六校联考）已知直线y ＝ax 与圆C ：x 2＋y 2－2ax －2y ＋2＝0相交于A ，B 两点，且△ABC 为等边三角形，则圆C 的面积为_________．解析：圆C ：x 2＋y 2－2ax －2y ＋2＝0可化为（x －a ）2＋（y －1）2＝a 2－1，因为直线y ＝ax 和圆C 相交，△ABC 为等边三角形，所以圆心C 到直线ax －y ＝0的距离为32·a 2－1，即d ＝|a 2－1|a 2＋1＝3（a 2－1）2，解得a 2＝7，所以圆C 的面积为6π．答案：6π9．已知圆M 过C （1，－1），D （－1，1）两点，且圆心M 在直线x ＋y －2＝0上． （1）求圆M 的方程；（2）设P 是直线3x ＋4y ＋8＝0上的动点，P A ，PB 是圆M 的两条切线，A ，B 为切点，求四边形P AMB 面积的最小值．解析：（1）设圆M 的方程为（x －a ）2＋（y －b ）2＝r 2（r ＞0），根据题意得⎩⎪⎨⎪⎧（1－a ）2＋（－1－b ）2＝r 2，（－1－a ）2＋（1－b ）2＝r 2，a ＋b －2＝0，解得a ＝b ＝1，r ＝2，故所求圆M 的方程为（x －1）2＋（y －1）2＝4．（2）由题意知，四边形P AMB 的面积为S ＝S △P AM ＋S △PBM ＝12（|AM |·|P A |＋|BM |·|PB |）．又|AM |＝|BM |＝2，|P A |＝|PB |，所以S ＝2|P A |，而|P A |2＝|PM |2－|AM |2＝|PM |2－4， 所以S ＝2|PM |2－4．因此要求S 的最小值，只需求|PM |的最小值，即在直线3x ＋4y ＋8＝0上找一点P ，使得|PM |的值最小，所以|PM |min ＝3，所以四边形P AMB 面积的最小值为2|PM |2－4＝25．10．已知圆O ：x 2＋y 2＝r 2（r ＞0）与直线3x －4y ＋15＝0相切． （1）若直线l ：y ＝－2x ＋5与圆O 交于M ，N 两点，求|MN |； （2）设圆O 与x 轴的负半轴的交点为A ，过点A 作两条斜率分别为k 1，k 2的直线交圆O 于B ，C 两点，且k 1k 2＝－3，试证明直线BC 恒过一点，并求出该点的坐标．解析：（1）由题意知，圆心O 到直线3x －4y ＋15＝0的距离d ＝159＋16＝3＝r ，所以圆O ：x 2＋y 2＝9．又圆心O 到直线l ：y ＝－2x ＋5的距离d 1＝54＋1＝5，所以|MN |＝29－d 21＝4．（2）证明：易知A （－3，0），设B （x 1，y 1），C （x 2，y 2），则直线AB ：y ＝k 1（x ＋3），由⎩⎪⎨⎪⎧y ＝k 1（x ＋3），x 2＋y 2＝9，得（k 21＋1）x 2＋6k 21x ＋9k 21－9＝0， 所以－3x 1＝9k 21－9k 21＋1，即x 1＝－3k 21＋3k 21＋1，所以y 1＝k 1（x 1＋3）＝6k 1k 21＋1，所以B ⎝ ⎛⎭⎪⎫3－3k 21k 21＋1，6k 1k 21＋1． 同理C ⎝ ⎛⎭⎪⎫3－3k 22k 22＋1，6k 2k 22＋1． 由k 1k 2＝－3得k 2＝－3k 1，将－3k 1代替k 2，可得C ⎝ ⎛⎭⎪⎫3k 21－27k 21＋9，－18k 1k 21＋9． 当3－3k 21k 21＋1≠3k 21－27k 21＋9，即k 1≠±3时，k BC ＝6k 1k 21＋1＋18k 1k 21＋93－3k 21k 21＋1－3k 21－27k 21＋9＝4k 13－k 21，k 1≠±3．从而直线BC ：y －6k 1k 21＋1＝4k 13－k 21⎝⎛⎭⎪⎫x －3－3k 21k 21＋1． 即y ＝4k 13－k 21⎣⎢⎡⎦⎥⎤x －3－3k 21k 21＋1＋9－3k 212（k 21＋1）， 化简得y ＝4k 13－k 21⎝⎛⎭⎫x ＋32． 所以直线BC 恒过一点，该点为⎝⎛⎭⎫－32，0． 当k 1＝±3时，k 2＝∓3，此时x B ＝－32＝x C ，所以直线BC 的方程为x ＝－32，过点⎝⎛⎭⎫－32，0． 综上，直线BC 恒过定点⎝⎛⎭⎫－32，0． [B 组 能力提升练]1．（2021·某某马某某模拟）在平面直角坐标系xOy 中，若圆C ：（x －3）2＋（y －a ）2＝4上存在两点A ，B 满足：∠AOB ＝60°，则实数a 的最大值是（ ） A ．5 B ．3 C ．7 D ．2 3 解析：根据题意，圆C 的圆心为（3，a ），在直线x ＝3上， 分析可得：当圆心距离x 轴的距离越远，∠AOB 越小，如图，当a >0时，圆心C 在x 轴上方，若OA ，OB 为圆的切线且∠AOB ＝60°，此时a 取得最大值，此时∠AOC ＝30°，有|OC |＝2|AC |＝4，即（3－0）2＋（a －0）2＝16，解得a ＝7，故实数a 的最大值是7． 答案：C 2．（2021·某某某某模拟）在平面直角坐标系xOy 中，圆C 经过点（0，1），（0，3），且与x 轴正半轴相切，若圆C 上存在点M ，使得直线OM 与直线y ＝kx （k >0）关于y 轴对称，则k 的最小值为（ ）A ．233B ． 3C ．2 3D ．4 3解析：如图，因为圆C 经过点（0，1），（0，3），且与x 轴正半轴相切， 所以圆心的纵坐标为2，半径为2，则圆心的横坐标为22－12＝3，所以圆心坐标为（3，2），设过原点与圆相切的直线方程为y ＝k 1x ，由圆心到直线的距离等于半径，得|3k 1－2|k 21＋1＝2，解得k 1＝0（舍去）或k 1＝－43．所以若圆C 上存在点M ，使得直线OM 与直线y ＝kx （k >0）关于y 轴对称，则k 的最小值为43．答案：D 3．（2020·高考全国卷Ⅰ）已知⊙M ：x 2＋y 2－2x －2y －2＝0，直线l ：2x ＋y ＋2＝0，P 为l 上的动点．过点P 作⊙M 的切线P A ，PB ，切点为A ，B ，当|PM |·|AB |最小时，直线AB 的方程为（ ）A ．2x －y －1＝0B ．2x ＋y －1＝0C ．2x －y ＋1＝0D ．2x ＋y ＋1＝0 解析：⊙M ：（x －1）2＋（y －1）2＝4， 则圆心M （1，1），⊙M 的半径为2． 如图，由题意可知PM ⊥AB ，∴S 四边形P AMB ＝12|PM |·|AB |＝|P A |·|AM |＝2|P A |，∴|PM |·|AB |＝4|P A |＝4|PM |2－4．当|PM |·|AB |最小时，|PM |最小，此时PM ⊥l ．故直线PM 的方程为y －1＝12（x －1），即x －2y ＋1＝0．由⎩⎪⎨⎪⎧x －2y ＋1＝0，2x ＋y ＋2＝0，得⎩⎪⎨⎪⎧x ＝－1，y ＝0，∴P （－1，0）． 又∵P A 与⊙M 相切，∴直线P A 的方程为x ＝－1（∵在⊙M 中，－1≤x ≤1）， ∴P A ⊥x 轴，P A ⊥MA ，∴A （－1，1）． 又直线AB 与l 平行，设直线AB 的方程为2x ＋y ＋m ＝0，将A （－1，1）的坐标代入2x ＋y ＋m ＝0，得m ＝1． ∴直线AB 的方程为2x ＋y ＋1＝0． 答案：D4．已知圆的方程为x 2＋（y －1）2＝4，圆心为C ，若过点P ⎝⎛⎭⎫1，12的直线l 与此圆交于A ，B 两点，则当∠ACB 最小时，直线l 的方程为（ ）A ．4x －2y －3＝0B ．x ＋2y －2＝0C ．4x ＋2y －3＝0D ．x －2y ＋2＝0解析：圆心坐标为（0，1），当弦长|AB |最小时，∠ACB 最小，此时直线AB 与PC 垂直，k l ＝－11－120－1＝2，所以直线l 的方程为y －12＝2（x －1），即4x －2y －3＝0．答案：A5．已知直线l ：x ＋ay －1＝0（a ∈R ）是圆C ：x 2＋y 2－4x －2y ＋1＝0的对称轴．过点A （－4，a ）作圆C 的一条切线，切点为B ，则|AB |＝_________．解析：由于直线x ＋ay －1＝0是圆C ：x 2＋y 2－4x －2y ＋1＝0的对称轴，所以圆心C （2，1）在直线x ＋ay －1＝0上，所以2＋a －1＝0，所以a ＝－1，所以A （－4，－1）．所以|AC |2＝36＋4＝40．又r ＝2，所以|AB |2＝40－4＝36．所以|AB |＝6． 答案：6 6．（2021·某某启东中学检测）已知圆C 1：（x －1）2＋（y ＋1）2＝1，圆C 2：（x －4）2＋（y －5）2＝9，点M ，N 分别是圆C 1，圆C 2上的动点，P 为x 轴上的动点，则|PN |－|PM |的最大值是_________．解析：圆C 1：（x －1）2＋（y ＋1）2＝1的圆心为C 1（1，－1），半径为1，圆C 2：（x －4）2＋（y －5）2＝9的圆心为C 2（4，5），半径为3．要使|PN |－|PM |最大，需|PN |最大，且|PM |最小，|PN |的最大值为|PC 2|＋3，|PM |的最小值为|PC 1|－1，故|PN |－|PM |的最大值是（|PC 2|＋3）－（|PC 1|－1）＝|PC 2|－|PC 1|＋4，设C 2（4，5）关于x 轴的对称点为C ′2（4，－5），|PC 2|－|PC 1|＝|PC ′2|－|PC 1|≤|C 1C ′2|＝（4－1）2＋（－5＋1）2＝5，故|PC 2|－|PC 1|＋4的最大值为5＋4＝9，即|PN |－|PM |的最大值是9． 答案：97．已知圆O ：x 2＋y 2＝9及点C （2，1）．（1）若线段OC 的垂直平分线交圆O 于A ，B 两点，试判断四边形OACB 的形状，并给出证明；（2）过点C 的直线l 与圆O 交于P ，Q 两点，当△OPQ 的面积最大时，求直线l 的方程． 解析：（1）四边形OACB 为菱形，证明如下：易得OC 的中点为⎝⎛⎭⎫1，12，设A （x 1，y 1），B （x 2，y 2），易得OC 的垂直平分线的方程为y ＝－2x ＋52，代入x 2＋y 2＝9，得5x 2－10x －114＝0，∴x 1＋x 22＝1，y 1＋y 22＝－2×1＋52＝12，∴AB 的中点为⎝⎛⎭⎫1，12，则四边形OACB 为平行四边形， 又OC ⊥AB ，∴四边形OACB 为菱形．（2）当直线l 的斜率不存在时，l 的方程为x ＝2，则P ，Q 的坐标为（2，5），（2，－5），∴S △OPQ ＝12×2×25＝25．当直线l 的斜率存在时，设l 的方程为y －1＝k （x －2）⎝⎛⎭⎫k ≠12， 即kx －y ＋1－2k ＝0⎝⎛⎭⎫k ≠12， 则圆心O 到直线l 的距离d ＝|1－2k |k 2＋1．由平面几何知识得|PQ |＝29－d 2， ∴S △OPQ ＝12×|PQ |×d ＝12×29－d 2×d ＝（9－d 2）d 2≤⎝ ⎛⎭⎪⎫9－d 2＋d 222＝92．当且仅当9－d 2＝d 2，即d 2＝92时，S △OPQ 取得最大值为92．∵25＜92，∴S △OPQ 的最大值为92，此时，令4k 2－4k ＋1k 2＋1＝92，解得k ＝－7或k ＝－1．故直线l 的方程为x ＋y －3＝0或7x ＋y －15＝0．[C 组 创新应用练]1．已知直线l ：x ＋y －1＝0截圆Ω：x 2＋y 2＝r 2（r ＞0）所得的弦长为14，点M ，N 在圆Ω上，且直线l ′：（1＋2m ）x ＋（m －1）y －3m ＝0过定点P ，若PM ⊥PN ，则|MN |的取值X 围为（ ）A ．[2－2，2＋ 3 ]B ．[2－2，2＋ 2 ]C ．[6－2，6＋ 3 ]D ．[6－2，6＋ 2 ]解析：由题意，2r 2－12＝14，解得r ＝2，因为直线l ′：（1＋2m ）x ＋（m －1）y －3m ＝0过定点P ，故P （1，1），设MN 的中点为Q （x ，y ），则OM 2＝OQ 2＋MQ 2＝OQ 2＋PQ 2，即4＝x 2＋y 2＋（x －1）2＋（y －1）2，化简可得⎝⎛⎭⎫x －122＋⎝⎛⎭⎫y －122＝32，所以点Q 的轨迹是以⎝⎛⎭⎫12，12为圆心，62为半径的圆，所以|PQ |的取值X 围为⎣⎢⎡⎦⎥⎤6－22，6＋22，|MN |的取值X 围为[6－2，6＋2]．答案：D2．已知从圆C ：（x ＋1）2＋（y －2）2＝2外一点P （x 1，y 1）向该圆引一条切线，切点为M ，且有|PM |＝|PO |（O 为坐标原点），则当|PM |取得最小值时点P 的坐标为_________． 解析：如图所示，圆C 的圆心为C （－1，2），半径r ＝2，因为|PM |＝|PO |，所以|PO |2＋r 2＝|PC |2，所以x 21＋y 21＋2＝（x 1＋1）2＋（y 1－2）2，即2x 1－4y 1＋3＝0．要使|PM |最小，只要|PO |最小即可．当直线PO 垂直于直线2x －4y ＋3＝0，即直线PO 的方程为2x ＋y ＝0时，|PM |最小，此时点P 即为两直线的交点，由⎩⎪⎨⎪⎧2x －4y ＋3＝0，2x ＋y ＝0，得⎩⎨⎧x ＝－310，y ＝35，故当|PM |取得最小值时，点P 的坐标为⎝⎛⎭⎫－310，35．答案：⎝⎛⎭⎫－310，35。

2008高考数学一轮复习 直线和圆的位置关系【知识概要】1、直线和圆位置关系的判定方法一是方程的观点，即把圆的方程和直线的方程联立成方程组，利用判别式Δ来讨论位置关系.①Δ＞0，直线和圆相交.②Δ=0，直线和圆相切.③Δ＜0，直线和圆相离.方法二是几何的观点，即把圆心到直线的距离d 和半径R 的大小加以比较.①d ＜R ，直线和圆相交.②d =R ，直线和圆相切.③d ＞R ，直线和圆相离.2、直线和圆相切，这类问题主要是求圆的切线方程.求圆的切线方程主要可分为已知斜率k 或已知直线上一点两种情况，而已知直线上一点又可分为已知圆上一点和圆外一点两种情况.3、直线和圆相交，这类问题主要是求弦长以及弦的中点问题.【基础训练】1、设m >0，则直线2（x +y ）+1+m =0与圆x 2+y 2=m 的位置关系为（ ）A.相切B.相交C.相切或相离D.相交或相切 解析：圆心到直线的距离为d =21m +，圆半径为m . ∵d －r =21m +－m =21（m －2m +1）=21（m －1）2≥0， ∴直线与圆的位置关系是相切或相离. 选C2、圆x 2＋y 2－4x +4y +6=0截直线x －y －5=0所得的弦长等于（ ） A.6 B.225 C.1 D.5 解析：圆心到直线的距离为22，半径为2，弦长为222)22()2(-=6.选A 3、圆x 2+y 2－4x =0在点P （1，3）处的切线方程为（ ）A x +3y －2=0B x +3y －4=0C x －3y +4=0D x －3y +2=0解法一：x 2+y 2－4x =0y =kx －k +3⇒x 2－4x +（kx －k +3）2=0.该二次方程应有两相等实根，即Δ=0，解得k =33. ∴y －3=33（x －1），即x －3y +2=0. 解法二：∵点（1，3）在圆x 2+y 2－4x =0上，∴点P 为切点，从而圆心与P 的连线应与切线垂直.又∵圆心为（2，0），∴1230--·k =－1.解得k =33，∴切线方程为x －3y +2=0.选D 4、由动点P 向圆122=+y x 引两条切线PB PA ,，切点分别为060,,=∠APB B A ，则动点P 的轨迹方程是 解析：由030,,,=∠∴∠⊥=APO AOB PO PA OA PB PA 平分 在230sin ,0==∆OAPO PAO Rt 中，设),(y x P ，则有422=+y x5、若直线y =x +k 与曲线x =21y -恰有一个公共点，则k 的取值范围是___________.解析：利用数形结合. 答案：－1＜k ≤1或k =－2【典型例题】例1、 已知圆x 2+y 2+x －6y +m =0和直线x +2y －3=0交于P 、Q 两点，且OP ⊥OQ （O 为坐标原点），求该圆的圆心坐标及半径.剖析：由于OP ⊥OQ ，所以k OP ·k OQ =－1，问题可解.解：将x =3－2y 代入方程x 2+y 2+x －6y +m =0，得5y 2－20y +12+m =0.设P （x 1，y 1）、Q （x 2，y 2），则y 1、y 2满足条件y 1+y 2=4，y 1y 2=512m +. ∵OP ⊥OQ ，∴x 1x 2+y 1y 2=0.而x 1=3－2y 1，x 2=3－2y 2，∴x 1x 2=9－6（y 1+y 2）+4y 1y 2.∴m =3，此时Δ＞0，圆心坐标为（－21，3），半径r =25. 评述：在解答中，我们采用了对直线与圆的交点“设而不求”的解法技巧，但必须注意这样的交点是否存在，这可由判别式大于零帮助考虑.例2、自点A （－3，3）发出的光线l 射到x 轴上，被x 轴反射，其反射光线所在的直线与圆x 2＋y 2－4x －4y ＋7＝0相切，求光线l 所在直线的方程.解：圆（x －2）2＋（y －2）2＝1关于x 轴的对称方程是（x －2）2＋（y ＋2）2＝1. 设l 方程为y －3＝k （x ＋3），由于对称圆心（2，－2）到l 距离为圆的半径1，从而可得k 1＝－43，k 2＝－34．故所求l 的方程是3x ＋4y －3＝0或4x ＋3y ＋3＝0. 例3、已知圆C ：（x －1）2＋（y －2）2＝25，直线l ：（2m +1）x +（m +1）y －7m －4=0 （m ∈R ）.（1）证明：不论m 取什么实数，直线l 与圆恒交于两点；（2）求直线被圆C 截得的弦长最小时l 的方程.剖析：直线过定点，而该定点在圆内，此题便可解得.（1）证明：l 的方程（x +y －4）+m （2x +y －7）=0.2x +y －7=0， x =3， x +y －4=0， y =1，即l 恒过定点A （3，1）.∵圆心C （1，2），｜AC ｜＝5＜5（半径），∴点A 在圆C 内，从而直线l 恒与圆C 相交于两点.（2）解：弦长最小时，l ⊥AC ，由k AC ＝－21， ∴l 的方程为2x －y －5=0.评述：若定点A 在圆外，要使直线与圆相交则需要什么条件呢？ 【方法归纳总结】1、有关直线和圆的位置关系，一般要用圆心到直线的距离与半径的大小来确定.2、当直线和圆相切时，求切线方程一般要用圆心到直线的距离等于半径，求切线长一般要用切线、半径及圆外点与圆心连线构成的直角三角形；与圆相交时，弦长的计算也要用弦心距、半径及弦长的一半构成的直角三角形.3、有关圆的问题，注意圆心、半径及平面几何知识的应用.4、在确定点与圆、直线与圆、圆与圆的位置关系时，经常要用到距离，因此，两点间的距离公式、点到直线的距离公式等应熟练掌握，灵活运用.【针对训练】1、圆1)3()1(22=++-y x 的切线方程中有一个是（ ）（A ）x －y ＝0 （B ）x ＋y ＝0 （C ）x ＝0 （D ）y ＝0解：直线ax+by=022(1)(1x y -+=与相切1=，由排除法， ∵m ∈R ，∴ 得选C,本题也可数形结合，画出他们的图象自然会选C,用图象法解最省事。

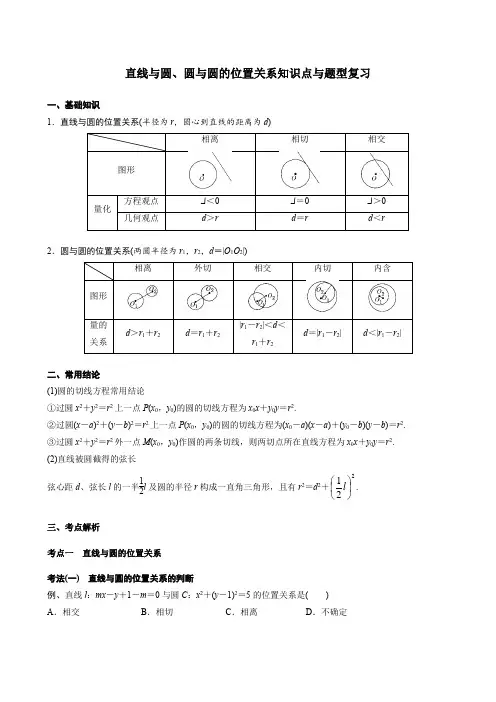
直线与圆、圆与圆的位置关系知识点与题型复习一、基础知识1．直线与圆的位置关系(半径为r ，圆心到直线的距离为d )Δ＜0 Δ＝0 Δ＞02．圆与圆的位置关系(两圆半径为r 1，r 2，d ＝|O 1O 2|)|r －r |＜d ＜二、常用结论(1)圆的切线方程常用结论①过圆x 2＋y 2＝r 2上一点P (x 0，y 0)的圆的切线方程为x 0x ＋y 0y ＝r 2.②过圆(x －a )2＋(y －b )2＝r 2上一点P (x 0，y 0)的圆的切线方程为(x 0－a )(x －a )＋(y 0－b )(y －b )＝r 2. ③过圆x 2＋y 2＝r 2外一点M (x 0，y 0)作圆的两条切线，则两切点所在直线方程为x 0x ＋y 0y ＝r 2. (2)直线被圆截得的弦长弦心距d 、弦长l 的一半12l 及圆的半径r 构成一直角三角形，且有r 2＝d 2＋221⎪⎭⎫⎝⎛l .三、考点解析考点一 直线与圆的位置关系 考法(一) 直线与圆的位置关系的判断例、直线l ：mx －y ＋1－m ＝0与圆C ：x 2＋(y －1)2＝5的位置关系是( ) A ．相交 B ．相切 C ．相离 D ．不确定[解题技法]判断直线与圆的位置关系的常见方法： (1)几何法：利用d 与r 的关系．(2)代数法：联立方程组，消元得一元二次方程之后利用Δ判断．(3)点与圆的位置关系法：若直线恒过定点且定点在圆内，可判断直线与圆相交．考法(二) 直线与圆相切的问题例、(1)过点P (2,4)作圆(x －1)2＋(y －1)2＝1的切线，则切线方程为( )A ．3x ＋4y －4＝0B ．4x －3y ＋4＝0C ．x ＝2或4x －3y ＋4＝0D ．y ＝4或3x ＋4y －4＝0 (2)已知圆C ：x 2＋y 2－2x －4y ＋1＝0上存在两点关于直线l ：x ＋my ＋1＝0对称，经过点M (m ，m )作圆C 的切线，切点为P ，则|MP |＝________.考法(三) 弦长问题例、(1)若a 2＋b 2＝2c 2(c ≠0)，则直线ax ＋by ＋c ＝0被圆x 2＋y 2＝1所截得的弦长为( ) A.12 B ．1 C.22D.2 (2)设直线y ＝x ＋2a 与圆C ：x 2＋y 2－2ay －2＝0相交于A ，B 两点，若|AB |＝23，则圆C 的面积为( ) A ．4π B ．2π C ．9π D ．22π跟踪练习：1．已知圆的方程是x 2＋y 2＝1，则经过圆上一点M ⎪⎪⎭⎫⎝⎛2222，的切线方程是________． 2．若直线kx －y ＋2＝0与圆x 2＋y 2－2x －3＝0没有公共点，则实数k 的取值范围是________．3．设直线y ＝kx ＋1与圆x 2＋y 2＋2x －my ＝0相交于A ，B 两点，若点A ，B 关于直线l ：x ＋y ＝0对称，则|AB |＝________.考点二 圆与圆的位置关系例、已知圆M ：x 2＋y 2－2ay ＝0(a ＞0)截直线x ＋y ＝0所得线段的长度是22，则圆M 与圆N ：(x －1)2＋(y －1)2＝1的位置关系是( )A ．内切B ．相交C ．外切D ．相离变式练习：1．若圆C 1：x 2＋y 2＝1与圆C 2：x 2＋y 2－6x －8y ＋m ＝0外切，则m ＝( )A ．21B ．19C ．9D ．－112.(变结论)若本例两圆的方程不变，则两圆的公共弦长为________．[解题技法]几何法判断圆与圆的位置关系的3步骤： (1)确定两圆的圆心坐标和半径长；(2)利用平面内两点间的距离公式求出圆心距d ，求r 1＋r 2，|r 1－r 2|； (3)比较d ，r 1＋r 2，|r 1－r 2|的大小，写出结论．课后作业1．若直线2x ＋y ＋a ＝0与圆x 2＋y 2＋2x －4y ＝0相切，则a 的值为( ) A ．±5 B ．±5 C ．3 D ．±32．与圆C 1：x 2＋y 2－6x ＋4y ＋12＝0，C 2：x 2＋y 2－14x －2y ＋14＝0都相切的直线有( ) A ．1条 B ．2条 C ．3条 D ．4条3．直线y ＝kx ＋3被圆(x －2)2＋(y －3)2＝4截得的弦长为23，则直线的倾斜角为( ) A.π6或5π6 B ．－π3或π3 C ．－π6或π6 D.π64．过点(3,1)作圆(x －1)2＋y 2＝r 2的切线有且只有一条，则该切线的方程为( ) A ．2x ＋y －5＝0 B ．2x ＋y －7＝0 C ．x －2y －5＝0 D ．x －2y －7＝05．若圆x 2＋y 2＋2x －6y ＋6＝0上有且仅有三个点到直线x ＋ay ＋1＝0的距离为1，则实数a 的值为( ) A ．±1 B ．±24 C ．± 2 D ．±326．过点P (1，－2)作圆C ：(x －1)2＋y 2＝1的两条切线，切点分别为A ，B ，则AB 所在直线的方程为( ) A ．y ＝－34 B ．y ＝－12 C ．y ＝－32 D ．y ＝－147．在平面直角坐标系xOy 中，直线x ＋2y －3＝0被圆(x －2)2＋(y ＋1)2＝4截得的弦长为________． 8．若P (2,1)为圆(x －1)2＋y 2＝25的弦AB 的中点，则直线AB 的方程为________． 9．过点P (－3,1)，Q (a,0)的光线经x 轴反射后与圆x 2＋y 2＝1相切，则a 的值为________．10．点P 在圆C 1：x 2＋y 2－8x －4y ＋11＝0上，点Q 在圆C 2：x 2＋y 2＋4x ＋2y ＋1＝0上，则|P Q |的最小值是________．11．已知圆C 1：x 2＋y 2－2x －6y －1＝0和圆C 2：x 2＋y 2－10x －12y ＋45＝0. (1)求证：圆C 1和圆C 2相交；(2)求圆C 1和圆C 2的公共弦所在直线的方程和公共弦长．12．已知圆C 经过点A (2，－1)，和直线x ＋y ＝1相切，且圆心在直线y ＝－2x 上． (1)求圆C 的方程；(2)已知直线l 经过原点，并且被圆C 截得的弦长为2，求直线l 的方程．提高练习1．过圆x 2＋y 2＝1上一点作圆的切线，与x 轴、y 轴的正半轴相交于A ，B 两点，则|AB |的最小值为( ) A. 2 B.3 C ．2 D ．32．在平面直角坐标系xOy 中，A 为直线l ：y ＝2x 上在第一象限内的点，B (5,0)，以AB 为直径的圆C 与直线l 交于另一点D .若AB ―→·CD ―→＝0，则点A 的横坐标为________． 3．已知圆C ：x 2＋(y －a )2＝4，点A (1,0)．(1)当过点A 的圆C 的切线存在时，求实数a 的取值范围； (2)设AM ，AN 为圆C 的两条切线，M ，N 为切点，当|MN |＝455时，求MN 所在直线的方程．。

第四节直线与圆、圆与圆的位置关系授课提示：对应学生用书第158页［基础梳理］1．直线与圆的位置关系与判断方法(1)几何法：利用圆心到直线的距离d与半径r的大小关系．①d〈r⇔直线与圆相交；②d＝r⇔直线与圆相切；③d〉r⇔直线与圆相离．(2)代数法：联立方程，消去x（或y)得一元二次方程，计算Δ＝b2－4ac.①Δ〉0⇔直线与圆相交；②Δ＝0⇔直线与圆相切；③Δ〈0⇔直线与圆相离．2．圆与圆的位置关系设圆O1：(x－a1）2＋(y－b1)2＝r错误!(r1〉0)，圆O2＋（y－b2＝r2方法位置关系几何法：圆心距d与r1，r2的关系代数法：两圆方程联立组成方程组的解的情况外离d〉r1＋r2无解外切d＝r1＋r2一组实数解续表相交｜r1－r2｜〈d〈r1＋r2两组不同的实数解内切d＝｜r1－r2｜(r1≠r2）一组实数解内含0≤d〈|r1－r2|(r1≠r2）无解位置关系内含内切相交外切外离公切线条数01234圆的方程两种设法技巧：（1）经过直线l：Ax＋By＋C＝0与圆x2＋y2＋Dx＋Ey＋F＝0的交点的圆的方程表示为（x2＋y2＋Dx＋Ey＋F）＋λ(Ax＋By＋C）＝0.（2）经过圆x2＋y2＋D1x＋E1y＋F1＝0与圆x2＋y2＋D2x＋E2y＋F2＝0的两个交点的圆的方程表示为x2＋y2＋D1x＋E1y＋F1＋λ(x2＋y2＋D2x＋E2y＋F2）＝0。

[四基自测]1．（基础点:直线与圆的位置关系）直线y＝x＋6与圆x2＋y2－2y－4＝0的位置关系为（)A．相离B．相切C．相交且不过圆心 D.相交过圆心答案：A2．(基础点：圆与圆的位置关系）两圆x2＋y2－2y＝0与x2＋y2－4＝0的位置关系是（）A．相交B．内切C．外切 D.内含答案：B3．（基础点：圆的弦长)直线l：3x－y－6＝0与圆x2＋y2－2x－4y＝0相交于A，B两点,则｜AB｜＝________．答案：104．（易错点:求圆的切线方程)已知直线l：y＝k(x＋错误!）和圆C：x2＋(y－1)2＝1，若直线l与圆C相切，则k＝________．答案：0或3授课提示：对应学生用书第158页考点一直线与圆的位置关系挖掘1直线与圆位置关系的判断/ 自主练透[例1](1）直线l：mx－y＋1－m＝0与圆C：x2＋（y－1)2＝5的位置关系是()A．相交B．相切C．相离D。

高考专题--直线与圆、圆与圆的位置关系本文介绍了高考数学中与直线和圆、圆和圆的位置关系相关的知识点。

首先讲解了直线与圆的位置关系，通过圆心到直线的距离公式，可以得到关于x或y的一元二次方程，通过判别式Δ可以判断相交、相切、相离的位置关系。

接着讲解了圆与圆的位置关系，通过圆心距和半径之间的关系，可以判断相离、外切、内含、内切的位置关系。

最后通过诊断自测，帮助读者巩固所学知识点。

本文旨在介绍高考数学中关于直线和圆、圆和圆的位置关系的知识点。

首先，我们研究了如何判断直线和圆的位置关系，通过圆心到直线的距离公式，我们可以得到一个关于x或y的一元二次方程，并通过判别式Δ来确定相交、相切、相离的位置关系。

接着，我们研究了如何判断圆和圆的位置关系，通过圆心距和半径之间的关系，我们可以确定相离、外切、内含、内切的位置关系。

最后，我们通过诊断自测来巩固所学知识点。

1.解析：根据题意，有以下两个公式：AB|=\sqrt{1+\frac{1}{k^2}(y_1-y_2)^2-4y_1y_2}1+k^2(x_1+x_2)^2-4x_1x_2根据公式进行计算即可。

2.解析：求过一点的圆的切线方程，需要先判断该点是否在圆上，如果在圆上，则切线有无数条；如果不在圆上，则切线有且只有一条。

斜率不存在的情况需要特别注意。

易错防范]1.求圆的弦长问题，需要注意应用圆的性质解题，即用圆心与弦中点连线与弦垂直的性质，可以用勾股定理或斜率之积为-1列方程来简化运算。

2.过圆上一点作圆的切线有且只有一条；过圆外一点作圆的切线有且只有两条，若仅求得一条，除了考虑运算过程是否正确外，还要考虑斜率不存在的情况，以防漏解。

基础巩固题组1.解析：将圆的方程化为标准方程，得到圆心坐标为(1,4)，根据点到直线的距离公式，将圆心到直线的距离代入公式，解出a的值即可。

答案：A2.解析：根据题意，可以得出该圆的圆心坐标为(1,0)，半径为r。

根据求解切线的公式，可以得到切线方程为2x+y-7=0.答案：B3.解析：将圆的方程化为标准方程，得到圆心坐标为(-1,1)，半径为2-a。

{北师大版}2020高考数学文科一轮复习课后练45《直线与圆圆与圆的位置关系》(建议用时：60分钟) A 组 基础达标一、选择题1．(2019·广州模拟)若一个圆的圆心为(0,1)，且该圆与直线y ＝x ＋3相切，则该圆的标准方程是( ) A ．x 2＋(y －1)2＝2 B ．(x －1)2＋y 2＝2 C ．x 2＋(y －1)2＝4D ．(x －1)2＋y 2＝42．(2019·昆明摸底调研)直线l ：x －y ＝0与圆C ：(x －2)2＋y 2＝6相交于A ，B 两点，则|AB |＝( ) A ．2 B ．4 C ． 2 D. 63．已知圆O 1的方程为x 2＋y 2＝4，圆O 2的方程为(x －a )2＋y 2＝1，如果这两个圆有且只有一个公共点，那么a 的所有取值构成的集合是( )A ．{1，－1}B ．{3，－3}C ．{1，－1,3，－3}D ．{5，－5,3，－3}4．已知直线l ：kx －y －3＝0与圆O ：x 2＋y 2＝4交于A ，B 两点，且OA →·OB →＝2，则k ＝( ) A ．2 B ．± 2 C ．±2 D ． 25．已知过原点的直线l 与圆C ：x 2＋y 2－6x ＋5＝0相交于不同的两点A ，B ，且线段AB 的中点坐标为D (2，2)，则弦长为( )A ．2B ．3C ．4D ．5 二、填空题6．(2019·南京模拟)在平面直角坐标系xOy 中，若直线ax ＋y －2＝0与圆C ：(x －1)2＋(y －a )2＝16相交于A ，B 两点，且△ABC 为直角三角形，则实数a 的值是________．7．(2019·兰州月考)点P 在圆C 1：x 2＋y 2－8x －4y ＋11＝0上，点Q 在圆C 2：x 2＋y 2＋4x ＋2y ＋1＝0上，则|PQ |的最小值是________．8．若⊙O ：x 2＋y 2＝5与⊙O 1：(x －m )2＋y 2＝20(m ∈R )相交于A ，B 两点且两圆在点A 处切线互相垂直，则线段AB 的长度是________．4 [由题意⊙O 1与⊙O 在A 处切线互相垂直，则两切线分别过另一圆圆心，∴O 1A ⊥OA ．三、解答题9．已知圆C经过点A(2，－1)，和直线x＋y＝1相切，且圆心在直线y＝－2x上．(1)求圆C的方程；(2)已知直线l经过原点，并且被圆C截得的弦长为2，求直线l的方程．10．(2018·河北邢台月考)已知圆C的方程为x2＋(y－4)2＝1，直线l的方程为2x－y＝0，点P在直线l上，过点P作圆C的切线PA，PB，切点为A，B.(1)若∠APB＝60°，求点P的坐标；(2)求证：经过A，P，C(其中点C为圆C的圆心)三点的圆必经过定点，并求出所有定点的坐标．B组能力提升1．已知两点A(－m,0)和B(2＋m,0)(m＞0)，若在直线l：x＋3y－9＝0上存在点P，使得PA⊥PB，则实数m 的取值范围是( )A．(0,3) B．(0,4)C．[3，＋∞)D．[4，＋∞)2．(2019·达州联考)若圆(x－3)2＋(y＋5)2＝r2有且只有两个点到直线4x－3y＝2的距离等于1，则半径r的取值范围是( )A．(4,6) B．(4,6]C ．[4,6)D ．[4,6]3．若直线x sin θ＋y cos θ＝1与圆x 2＋y 2－2x －2y cos θ＋cos 2θ＋1516＝0相切，且θ为锐角，则这条直线的斜率是________．4．(2018·江苏南通模拟)如图，在平面直角坐标系xOy 中，已知圆C ：x 2＋y 2－4x ＝0及点A (－1，0)，B (1,2)．(1)若直线l 平行于AB ，与圆C 相交于M ，N 两点，|MN |＝|AB |，求直线l 的方程；(2)在圆C 上是否存在点P ，使得|PA |2＋|PB |2＝12？若存在，求点P 的个数；若不存在，说明理由． 解析{北师大版}2020高考数学文科一轮复习课后练45《直线与圆圆与圆的位置关系》(建议用时：60分钟) A 组 基础达标一、选择题1．(2019·广州模拟)若一个圆的圆心为(0,1)，且该圆与直线y ＝x ＋3相切，则该圆的标准方程是( ) A ．x 2＋(y －1)2＝2 B ．(x －1)2＋y 2＝2 C ．x 2＋(y －1)2＝4D ．(x －1)2＋y 2＝4A [由于圆心为(0,1)，设该圆的标准方程是x 2＋(y －1)2＝r 2(r ＞0)，因为该圆与直线y ＝x ＋3相切，故r ＝|2|2＝2，故该圆的标准方程是x 2＋(y －1)2＝2.故选A ．]2．(2019·昆明摸底调研)直线l ：x －y ＝0与圆C ：(x －2)2＋y 2＝6相交于A ，B 两点，则|AB |＝( ) A ．2 B ．4 C ． 2 D. 6B [由题意知，圆C 的圆心为C (2,0)，半径为6，圆心C 到直线l 的距离为2，所以|AB |＝262－22＝4，故选B.]3．已知圆O 1的方程为x 2＋y 2＝4，圆O 2的方程为(x －a )2＋y 2＝1，如果这两个圆有且只有一个公共点，那么a 的所有取值构成的集合是( )A ．{1，－1}B ．{3，－3}C ．{1，－1,3，－3}D ．{5，－5,3，－3}C [因为两圆有且只有一个公共点，所以两个圆内切或外切，内切时，|a |＝1；外切时，|a |＝3，所以实数a 的取值集合是{1，－1,3，－3}．]4．已知直线l ：kx －y －3＝0与圆O ：x 2＋y 2＝4交于A ，B 两点，且OA →·OB →＝2，则k ＝( ) A ．2 B ．± 2 C ．±2 D ． 2 B [圆O ：x 2＋y 2＝4的圆心为(0,0)，半径为2， 设OA →与OB →的夹角为θ，则 2×2×cos θ＝2， 解得cos θ＝12，θ＝π3，∴圆心到直线l 的距离为2cos π6＝3，可得|－3|1＋k2＝3，解得k ＝± 2.]5．已知过原点的直线l 与圆C ：x 2＋y 2－6x ＋5＝0相交于不同的两点A ，B ，且线段AB 的中点坐标为D (2，2)，则弦长为( )A．2 B．3C．4 D．5A[将圆C：x2＋y2－6x＋5＝0，整理得其标准方程为(x－3)2＋y2＝4，∴圆C的圆心坐标为(3,0)，半径为2.∵线段AB的中点坐标为D(2，2)，∴|CD|＝1＋2＝3，∴|AB|＝24－3＝2.故选A．]二、填空题6．(2019·南京模拟)在平面直角坐标系xOy中，若直线ax＋y－2＝0与圆C：(x－1)2＋(y－a)2＝16相交于A，B两点，且△ABC为直角三角形，则实数a的值是________．－1[由题意知，圆C的半径是4，△ABC为直角三角形，则圆心C(1，a)到直线ax＋y－2＝0的距离为22，所以|a＋a－2|a2＋1＝22，解得a＝－1.]7．(2019·兰州月考)点P在圆C1：x2＋y2－8x－4y＋11＝0上，点Q在圆C2：x2＋y2＋4x＋2y＋1＝0上，则|PQ|的最小值是________．35－5[把圆C1、圆C2的方程都化成标准形式，得(x－4)2＋(y－2)2＝9，(x＋2)2＋(y＋1)2＝4.圆C1的圆心坐标是(4,2)，半径长是3；圆C2的圆心坐标是(－2，－1)，半径是2.圆心距d＝＋2＋＋2＝35＞5.故圆C1与圆C2相离，所以|PQ|的最小值是35－5.]8．若⊙O：x2＋y2＝5与⊙O1：(x－m)2＋y2＝20(m∈R)相交于A，B两点且两圆在点A处切线互相垂直，则线段AB的长度是________．4[由题意⊙O1与⊙O在A处切线互相垂直，则两切线分别过另一圆圆心，∴O1A⊥OA．又|OA|＝5，|O1A|＝25，∴|O1O|＝5.又A，B关于O1O所在直线对称，∴AB是Rt△OAO1斜边上高的2倍．∴|AB|＝2×5×255＝4.]三、解答题9．已知圆C经过点A(2，－1)，和直线x＋y＝1相切，且圆心在直线y＝－2x上．(1)求圆C的方程；(2)已知直线l 经过原点，并且被圆C 截得的弦长为2，求直线l 的方程． [解] (1)设圆心的坐标为C (a ，－2a )， 则a －2＋－2a ＋2＝|a －2a －1|2. 化简，得a 2－2a ＋1＝0，解得a ＝1. ∴C (1，－2)，半径r ＝|AC |＝－2＋－2＋2＝ 2.∴圆C 的方程为(x －1)2＋(y ＋2)2＝2.(2)①当直线l 的斜率不存在时，直线l 的方程为x ＝0， 此时直线l 被圆C 截得的弦长为2，满足条件．②当直线l 的斜率存在时，设直线l 的方程为y ＝kx ，由题意得|k ＋2|1＋k2＝1，解得k ＝－34， ∴直线l 的方程为y ＝－34x .综上所述，直线l 的方程为x ＝0或y ＝－34x .10．(2018·河北邢台月考)已知圆C 的方程为x 2＋(y －4)2＝1，直线l 的方程为2x －y ＝0，点P 在直线l 上，过点P 作圆C 的切线PA ，PB ，切点为A ，B .(1)若∠APB ＝60°，求点P 的坐标；(2)求证：经过A ，P ，C (其中点C 为圆C 的圆心)三点的圆必经过定点，并求出所有定点的坐标． [解] (1)由条件可得圆C 的圆心坐标为(0,4)，|PC |＝2，设P (a,2a )，则a 2＋a －2＝2，解得a ＝2或a ＝65，∴点P 的坐标为(2,4)或⎝⎛⎭⎫65，125.(2)设P (b,2b )，过点A ，P ，C 的圆即是以PC 为直径的圆，其方程为x (x －b )＋(y －4)(y －2b )＝0，整理得x2＋y 2－bx －4y －2by ＋8b ＝0，即(x 2＋y 2－4y )－b (x ＋2y －8)＝0.由⎩⎪⎨⎪⎧x 2＋y 2－4y ＝0，x ＋2y －8＝0，得⎩⎪⎨⎪⎧x ＝0，y ＝4或⎩⎨⎧x ＝85，y ＝165，∴该圆必经过定点(0,4)和⎝⎛⎭⎫85，165.B 组 能力提升1．已知两点A (－m,0)和B (2＋m,0)(m ＞0)，若在直线l ：x ＋3y －9＝0上存在点P ，使得PA ⊥PB ，则实数m 的取值范围是( )A ．(0,3)B ．(0,4)C ．[3，＋∞)D ．[4，＋∞)C [因为A (－m,0)，B (2＋m,0)(m ＞0)，所以以AB 为直径的圆的圆心为(1,0)，半径为1＋m ，即方程为(x －1)2＋y 2＝(1＋m )2.若直线l ：x ＋3y －9＝0上存在点P ，使得PA ⊥PB ， 则直线l 与圆有公共点． ∴|1－9|2≤1＋m ，解得m ≥3.] 2．(2019·达州联考)若圆(x －3)2＋(y ＋5)2＝r 2有且只有两个点到直线4x －3y ＝2的距离等于1，则半径r 的取值范围是( )A ．(4,6)B ．(4,6]C ．[4,6)D ．[4,6]A [由圆的标准方程得圆心坐标(3，－5)， 则圆心(3，－5)到直线4x －3y ＝2的距离d ＝|4×3－－－2|32＋42＝255＝5. 若圆(x －3)2＋(y ＋5)2＝r 2有且只有两个点到直线4x －3y ＝2的距离等于1，则满足d －1＜r ＜d ＋1，即4＜r ＜6，故选A ．]3．若直线x sin θ＋y cos θ＝1与圆x 2＋y 2－2x －2y cos θ＋cos 2θ＋1516＝0相切，且θ为锐角，则这条直线的斜率是________．－33 [圆x 2＋y 2－2x －2y cos θ＋cos 2θ＋1516＝0化为标准方程得(x －1)2＋(y －cos θ)2＝116，圆心为(1，cos θ)，半径为14，由题意得，圆心到直线的距离d ＝|1×sin θ＋cos 2θ－1|cos 2θ＋sin 2θ＝14，所以|sin θ－sin 2θ|＝14.因为θ为锐角，所以0＜sin 2θ＜sin θ＜1，sin 2θ－sin θ＋14＝0，解得sin θ＝12，故cos θ＝32，所以直线x sin θ＋y cos θ＝1的斜率k ＝－sin θcos θ＝－1232＝－33.]4．(2018·江苏南通模拟)如图，在平面直角坐标系xOy 中，已知圆C ：x 2＋y 2－4x ＝0及点A (－1，0)，B (1,2)．(1)若直线l 平行于AB ，与圆C 相交于M ，N 两点，|MN |＝|AB |，求直线l 的方程；(2)在圆C 上是否存在点P ，使得|PA |2＋|PB |2＝12？若存在，求点P 的个数；若不存在，说明理由．[解] (1)圆C 的标准方程为(x －2)2＋y 2＝4，所以圆心C (2,0)，半径为2.因为l ∥AB ，A (－1,0)，B (1,2)，所以直线l 的斜率为2－01－－＝1.设直线l 的方程为x －y ＋m ＝0，则圆心C 到直线l 的距离为d ＝|2－0＋m |2＝|2＋m |2.因为|MN |＝|AB |＝22＋22＝22，而|CM |2＝d 2＋⎝⎛⎭⎫|MN |22，所以4＝＋m 22＋2，解得m ＝0或m ＝－4，故直线l的方程为x －y ＝0或x －y －4＝0.(2)假设圆C 上存在点P ，设P (x ，y )，则(x －2)2＋y 2＝4，|PA |2＋|PB |2＝(x ＋1)2＋(y －0)2＋(x －1)2＋(y －2)2＝12，化简得x 2＋y 2－2y －3＝0，即x 2＋(y －1)2＝4.因为|2－2|＜－2＋－2＜2＋2，所以圆(x －2)2＋y 2＝4与圆x 2＋(y －1)2＝4相交，所以存在点P ，使|PA |2＋|PB |2＝12，点P 的个数为2.。