第十一章习题讲解

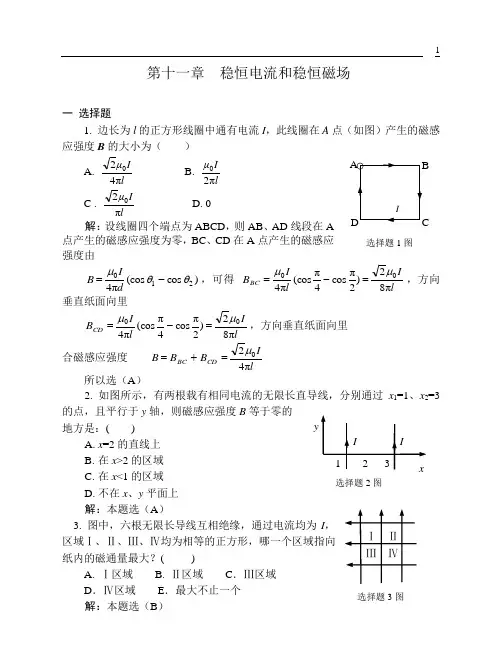
第十一章 稳恒电流和稳恒磁场一 选择题1. 边长为l 的正方形线圈中通有电流I ，此线圈在A 点（如图）产生的磁感应强度B 的大小为（ ）A. l I μπ420B. lIμπ20 C .lIμπ20 D. 0 解：设线圈四个端点为ABCD ，则AB 、AD 线段在A 点产生的磁感应强度为零，BC 、CD 在A 点产生的磁感应强度由)cos (cos π4210θθμ-=dIB ，可得 lIl IB BC π82)2πcos 4π(cosπ400μμ=-=，方向垂直纸面向里lI l I B CD π82)2πcos 4π(cos π400μμ=-=，方向垂直纸面向里合磁感应强度 lIB B B CD BC π420μ=+=所以选（A ）2. 如图所示，有两根载有相同电流的无限长直导线，分别通过x 1=1、x 2=3的点，且平行于y 轴，则磁感应强度B 等于零的地方是：( )A. x =2的直线上B. 在x >2的区域C. 在x <1的区域D. 不在x 、y 平面上 解：本题选（A ）3. 图中，六根无限长导线互相绝缘，通过电流均为I ，区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形，哪一个区域指向纸内的磁通量最大？( )A. Ⅰ区域B. Ⅱ区域 C ．Ⅲ区域D ．Ⅳ区域E ．最大不止一个解：本题选（B ）选择题2图Ⅰ Ⅱ Ⅲ Ⅳ 选择题3图选择题1图4. 如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知：（ ）A. ∮L B ·d l =0，且环路上任意一点B =0B. ∮L B ·d l =0，且环路上任意一点B ≠0C. ∮L B ·d l ≠0，且环路上任意一点B ≠0D. ∮L B ·d l ≠0，且环路上任意一点B =常量解：本题选（B ）5. 无限长直圆柱体，半径为R ，沿轴向均匀流有电流，设圆柱体内（r <R ）的磁感应强度为B i ，圆柱体外（r >R ）的磁感应强度为B e ，则有：（ ）A. B t 、B e 均与r 成正比B. B i 、B e 均与r 成反比C. B i 与r 成反比，B e 与r 成正比D. B i 与r 成正比，B e 与r 成反比解：导体横截面上的电流密度2πR IJ =，以圆柱体轴线为圆心，半径为r的同心圆作为安培环路，当r <R ，20ππ2r J r B i ⋅=⋅μ，20π2R IrB i μ=r <R ，I r B e ⋅=⋅0π2μ， rIB e π20μ=所以选（D ）6. 有三个质量相同的质点a 、b 、c ，带有等量的正电荷，它们从相同的高度自由下落，在下落过程中带电质点b 、c 分别进入如图所示的匀强电场与匀强磁场中，设它们落到同一水平面的动能分别为E a 、E b 、E c ，则（ ）A. E a <E b =E cB. E a =E b =E cC. E b >E a =E cD. E b >E c >E a解：由于洛伦兹力不做功，当它们落到同一水平面上时，对a 、c 只有重力做功， 则E a =E c ，在此过程中，对b 不仅有重力做功，电场力也要做正功，所以E b >E a =E c所以选（C ）7. 图为四个带电粒子在O 点沿相同方向垂直于磁力线射入均匀磁场后的偏转轨迹的照片，磁场方向垂直纸面向外，四个粒子的质量相等，电量大小也相等，则其中动能最大的带负电的粒子的轨迹是：( )A. OaB. ObC. Oc D . Od解：根据B F ⨯=v q ，从图示位置出发，带负选择题7图c dba B O• B× × × × × × Ea bc 选择题6图 选择题4图电粒子要向下偏转，所以只有Oc 、Od 满足条件，又带电粒子偏转半径Bqm R v=，22k 22qB m E R =∴，质量相同、带电量也相等的粒子，动能大的偏转半径大，所以选Oc 轨迹所以选（C ）8. 如图，一矩形样品，放在一均匀磁场中，当样品中的电流I 沿X 轴正向流过时，实验测得样品A 、A '两侧的电势差V A -V A '>0，设此样品的载流子带负电荷，则磁场方向为：（ ）A ． 沿X 轴正方向B ．沿X 轴负方向C ．沿Z 轴正方向D ．沿Z 轴负方向 解：本题选（C ）9. 长直电流I 2与圆形电流I 1共面，并与其一直径相重合如图（但两者间绝缘），设长直电流不动，则圆形电流将：（ ）A. 绕I 2旋转B. 向左运动C. 向右运动D. 向上运动E. 不动 解：圆形电流左半圆和右半圆受到长直电流安培力的方向均向右，所以圆形电流将向右运动所以选（C ）二 填空题1. 成直角的无限长直导线，流有电流I =10A ，在直角决定的平面内，距两段导线的距离都是a =20cm 处的磁感应强度B = 。

工程力学第十一章习题解答题目：一物体质量为10kg，在水平地面上以10m/s的初速度开始运动，若物体受到一个恒力F=20N的作用，且与运动方向相反，求物体在力作用下停止前所经过的距离。

解答过程：一、问题分析根据牛顿第二定律，力等于质量乘以加速度，即F=ma。

本题中，物体受到一个恒力F=20N的作用，且与运动方向相反，因此加速度a为负值。

我们需要求解物体在力作用下停止前所经过的距离。

二、解题步骤1. 求加速度a根据牛顿第二定律，F=ma，代入已知数据，得到加速度a：a = F/m = -20N / 10kg = -2m/s²2. 求物体停止前所经过的时间t由于物体初速度v0=10m/s，加速度a=-2m/s²，根据速度-时间关系式v=v0+at，我们可以求解物体停止前的时间t：0 = 10m/s - 2m/s² tt = 10m/s / 2m/s² = 5s3. 求物体在力作用下停止前所经过的距离s根据位移-时间关系式s=v0t + 1/2at²，代入已知数据，求解物体在力作用下停止前所经过的距离s：s = 10m/s 5s + 1/2 (-2m/s²) (5s)²s = 50m - 25ms = 25m三、答案验证根据动能定理，物体在运动过程中，动能的变化等于外力做的功。

物体从初始速度10m/s减速到0，动能变化为：ΔK = 1/2 m (v² - v0²) = 1/2 10kg (0 - 100m²/s²) = -500J外力做的功为：W = F s = 20N 25m = 500J由于动能变化等于外力做的功，所以我们的答案是正确的。

四、总结本题主要考查了牛顿第二定律、速度-时间关系式、位移-时间关系式和动能定理的应用。

通过求解加速度、时间和距离，我们得到了物体在力作用下停止前所经过的距离为25m。

第十一章 微分方程习题详解第十一章 微分方程 习 题 11—11．判断下列方程是几阶微分方程？（1）23d tan 3sin 1;d y y t t t t ⎛⎫=++ ⎪⎝⎭（2）(76)d ()d 0;x y x x y y -++=（3）2()20;x y yy x ''''-+= （4）422()0'''''++=xy y x y ．解 微分方程中所出现的未知函数导数（或微分）的最高阶数，叫做微分方程的阶．所以有：（1）一阶微分方程； （2）一阶微分方程； （3）三阶微分方程； （4）三阶微分方程． 2．指出下列各题中的函数是否为所给微分方程的解： （1）2'=xy y ，25=y x ；（2）0''+=y y ，3sin 4cos =-y x x ； （3）20'''-+=y y y ，2e =x y x ；（4）2()()20'''''-++-=xy x y x y yy y ，ln()=y xy ．解 （1）将10'=y x 代入所给微分方程的左边，得左边210=x 22()5x ==右边，故25=y x 是微分方程2'=xy y 的解．（2）将3cos 4sin '=+y x x ，3sin 4cos ''=-+y x x 代入所给微分方程的左边，得左边(3sin 4cos )(3sin 4cos )0=-++-==x x x x 右边，故3sin 4cos =-y x x 是微分方程0''+=y y 的解．（3）将2e =x y x ，22e e '=+x x y x x ，22e 4e e ''=++x x x y x x 代入微分方程的左边，得左边222(2e 4e e )2(2e e )e 2e 0=++-++=≠x x x x x x x x x x x x （右边），故2e =x y x 不是所给微分方程20'''-+=y y y 的解．（4）对方程ln()=y xy 的两边关于x 求导，得 1''=+y y x y，即 ''=+xyy y xy ．再对x 求导，得2()''''''''++=++yy x y xyy y y xy ，即2()()20'''''-++-=xy x y x y yy y ，故ln()=y xy 是所给微分方程的解．3．确定下列各函数关系式中所含参数，使函数满足所给的初始条件． （1）22-=x y C ， 05==x y ；（2）2120()e ,0==+=x x y C C x y ，01='=x y ．解 （1）将0=x ，5=y 代入微分方程，得220525=-=-C所以，所求函数为2225-=y x ．（2）222212122e 2()e (22)e '=++=++x x x y C C C x C C C x ，将00==x y，01='=x y 分别代入212()e =+x y C C x 和2122(22)e '=++x y C C C x ，得10=C ，21=C ，所以，所求函数为2e =x y x ．4．能否适当地选取常数λ，使函数e λ=x y 成为方程90''-=y y 的解．解 因为e λλ'=x y ，2e λλ''=x y ，所以为使函数e λ=x y 成为方程 90''-=y y 的解，只须满足2e 9e 0λλλ-=x x ，即2(9)e 0λλ-=x ．而e 0λ≠x ，因此必有290λ-=，即3λ=或3λ=-，从而当3λ=，或3λ=-时，函数33e ,e -==x x y y 均为方程90''-=y y 的解．5．消去下列各式中的任意常数12,,C C C ，写出相应的微分方程． （1）2;y Cx C =+ （2）()tan ;y x x C =+ （3）12e e ;x x xy C C -=+ （4）212()y C C x -=．解 注意到，含一个任意常数及两个变量的关系式对应于一阶微分方程；含两个独立常数的式子对应于二阶微分方程．（1）由2=+y Cx C 两边对x 求导，得'=y C ，代入原关系式2y Cx C =+，得所求的微分方程为2()''+=y xy y ．（2）由tan()=+y x x C 两边对x 求导，得2tan()sec ()'=+++y x C x x C ，即 2tan()tan ()'=++++y x C x x x C ．而tan()=+yx C x，故所求的微分方程为 2⎛⎫'=++ ⎪⎝⎭y y y x x x x ，化简得 22'=++xy y x y ．（3）由12e e -=+x x xy C C 两边对x 求导，得 12e e -'+=-x x y xy C C ，两边再对x 求导，得12e e -''''++=+x x y y xy C C ，可得所求的微分方程为2'''+=xy y xy ．（4）由212()-=y C C x 两边对x 求导，得122()'-⋅=y C y C ，将212()-=y C C x代，并化简得12'=-xy y C ，对上式两边再对x 求导，得22''''+=y xy y ，故第十一章 微分方程习题详解所求的微分方程为20'''+=xy y ．习 题 11—21．求下列微分方程的通解或特解：（1）ln 0;xy y y '-= （2）cos sin d sin cos d 0;x y x x y y += （3）22();y xy y y '''-=+ （4）(1)d ()d 0;x y x y xy y ++-= （5）23yy xy x '=-，01;x y == （6）22sin d (3)cos d 0x y x x y y ++=，16x y=π=． 解 （1）分离变量，得11d d ln =y x y y x，两端积分，得 ln(ln )ln ln =+y x C ，即 ln =y Cx ，所以原方程的通解为 e C x y =．注 该等式中的x 与C 等本应写为||x 与||C 等，去绝对值符号时会出现±号；但这些±号可认为含于最后答案的任意常数C 中去了，这样书写比较简洁些，可避开绝对值与正负号的冗繁讨论，使注意力集中到解法方面，本书都做这样的处理．（2）原方程分离变量，得cos cos d d sin sin =-y xy x y x，两端积分，得 ln(sin )ln(sin )ln =-+y x C ，即 ln(sin sin )ln ⋅=y x C ，故原方程的通解为 sin sin ⋅=y x C ．（3）原方程可化成 2d (1)2d -+=yx y x ，分离变量，得 212d d 1=-+y x y x ，两端积分，得 12ln(1)-=-+-x C y， 即 12ln(1)=++y x C是原方程的通解．（4）分离变量，得d d 11=+-y x y x y x ，两边积分，得 ln(1)ln(1)ln -+=+-+y y x x C ，即 e (1)(1)y x C y x -=+- 是原方程的通解．（5）分离变量，得2d d 31=-y y x x y ，两端积分，得2211ln(31)ln 62-=+y x C ， 即 211262(31)ex y C -=．由定解条件01==x y，知16(31)-=C ，即162=C ，故所求特解为 21112662(31)2x y e-=，即223312e -=x y ．（6）将方程两边同除以2(3)sin 0+≠x y ，得22cos d d 03sin +=+x yx y x y，两端积分，得 122cos d d 3sin +=+⎰⎰x yx y C x y ，积分后得 2ln(3)ln(sin )ln ++=x y C （其中1ln =C C ），从而有2(3)sin +=x y C ，代入初始条件16=π=x y，得 4sin 26π==C ．因此，所求方程满足初始条件的特解为 2(3)sin 2+=x y ，即 2arcsi 3n2y x =+． 2．一曲线过点0(2,3)M 在两坐标轴间任意点处的切线被切点所平分，求此曲线的方程． 解 设曲线的方程为()y y x =，过点(,)M x y 的切线与x 轴和y 轴的交点分别为(2,0)A x 及(0,2)B y ，则点(,)M x y 就是该切线AB 的中点．于是有22'=-yy x ，即xy y '=-，且(2)3=y ， 分离变量后，有11d d =-y x y x，积分得 ln ln ln =-y C x ，即 =C y x ．由定解条件23==x y ，有6=C ，故 6=y x为所求的曲线． 3．一粒质量为20克的子弹以速度0200v =（米/秒）打进一块厚度为10厘米的木板，然后穿过木板以速度180v =（米/秒）离开木板．若该木板对子弹的阻力与运动速度的平方成正比（比例系数为k ），问子弹穿过木板的时间．解 依题意有2d d =-vmkv t，0200==t v ， 即 21d d -=kv t v m，两端积分，得 10.02=+=+k kt C t C v m （其中20克＝0.02千克）， 代入定解条件0200==t v ，得1200=C ，故有200100001=+v kt ．第十一章 微分方程习题详解设子弹穿过木板的时间为T 秒，则2000.1d 100001Tt kt =+⎰200ln(100001)10000=+Tkt k 1ln(100001)50=+kT k， 又已知=t T 时，180==v v 米/秒，于是20080100001=+kT ，从而，0.00015=kT ，为此有 0.1ln(1.51)500.00015=+⨯T，所以0.10.0075ln 2.5=⨯T 0.000750.00080.9162≈=（秒）， 故子弹穿过木板运动持续了0.0008=T （秒）．4．求下列齐次方程的通解或特解：（1）0;xy y '- （2）22()d d 0;x y x xy y +-= （3）332()d 3d 0;x y x xy y +-= （4）(12e )d 2e (1)d 0;x x yyxx y y++-=（5）22d d yx xy y x=-，11;x y == （6）22(3)d 2d 0y x y xy x -+=， 01x y==．解 （1）原方程变形，得'=+y y x ，令=yu x，即=y ux ，有''=+y u xu ，则原方程可进一步化为'+=u xu u分离变量，得1d =u x x ，两端积分得ln(ln ln +=+u x C ，即u Cx ，将=yu x代入上式并整理，得原方程的通解为2y Cx ．（2）原方程变形，得22d d +=y x y x xy，即21d d x xy y x y ⎛⎫+ ⎪⎝⎭=． 令=yu x，即=y ux ，有''=+y u xu ，则原方程可进一步化为 21+'+=u u xu u， 即 1d d =u u x x ，两端积分，得 211ln 2=+u x C ，将=yu x代入并整理，得原方程的通解22(2ln )=+y x x C （其中12=C C ）．（3）原方程变形，得332d d 3+=y x y x xy ，即32d 1()d 3()+=y y x x y x ， 令=y ux ，有d d d d =+y uu x x x，则原方程可进一步化为 32d 1d 3++=u u u x x u ， 即 3231d d 12u u x u x=-，两端积分，得311ln(12)ln ln 22--=-u x C ， 即 23(12)-=x u C ，将=yu x代入上式并整理，得原方程的通解为 332-=x y Cx ．（4）显然，原方程是一个齐次方程，又注意到方程的左端可以看成是以xy为变量的函数，故令=x u y ，即=x uy ，有d d d d =+x u u y y y，则原方程可化为 d ()(12e )2e (1)0d +++-=u u uu yu y， 整理并分离变量，得2e 11d d 2e +=-+u uu y u y， 两端积分，得ln(2e )ln ln +=-+u u y C ，第十一章 微分方程习题详解即 2e +=u C u y ．将 =xu y代入并整理，得原方程的通解为 2e +=xy y x C ．（5）原方程可化为2d d ⎛⎫=- ⎪⎝⎭y y y x x x ． 令=yu x，有d d d d =+y u u x x x ，则原方程可进一步化为2d d +=-uu xu u x， 即 211d d -=u x u x ，两端积分，得 1ln =+x C u ，将=yu x代入，得 ln =+xx C y， 代入初始条件11==x y，得 1ln11=-=C ．因此，所求方程满足初始条件的特解为1ln =+xy x．（6）原方程可写成22d 1320d -+=x x x y y y．令=x u y ，即=x uy ，有d d d d =+x uu y y y，则原方程成为 2d 132()0d -++=uu u u yy， 分离变量，得221d d 1=-u u y u y，两端积分，得 2ln(1)ln ln -=+u y C ，即 21-=u Cy ，代入=xu y并整理，得通解 223-=x y Cy ．由初始条件01==x y，得1=-C ．于是所求特解为322=-y y x ．5．设有连结原点O 和(1,1)A 的一段向上凸的曲线弧OA ，对于OA 上任一点(,)P x y ，曲线弧OP 与直线段OP 所围成图形的面积为2x ，求曲线弧OA 的方程．解 设曲线弧的方程为()=y y x ，依题意有201()d ()2-=⎰xy x x xy x x ，上式两端对x 求导，11()()()222'--=y x y x xy x x ，即得微分方程4'=-yy x， 令=yu x，有d d d d =+y u u x x x ，则微分方程可化为d 4d +=-u u xu x ，即d 4d =-u x x， 积分得4ln =-+u x C ，因=yu x，故有 (4ln )=-+y x x C ．又因曲线过点(1,1)A ，故1=C ．于是得曲线弧的方程是(14ln )=+y x x ．6．化下列方程为齐次方程，并求出通解：（1）(1)d (41)d 0--++-=x y x y x y ； （2）()d (334)d 0+++-=x y x x y y ． 解 （1）原方程可写成d 1d 41-++=+-y x y x y x ， 令10410x y y x --=+-=⎧⎨⎩，解得交点为1=x ，0=y ．作坐标平移变换1=+x X ，=y Y ，有d d d d d(1)d ==+y Y Yx X X， 所以原方程可进一步化为d d 4-=+Y Y XX Y X（※） 这是齐次方程．设=Y u X ，则=Y uX ，d d d d =+Y u u X X X，于是（※）式可化为 1d d 41YY X Y X X-=⋅+， 即第十一章 微分方程习题详解d 1d 41-+=+u u u XX u ， 变量分离，得2411d d 41+=-+u u X u X， 两端积分，得2111ln(41)arctan(2)ln 22++=-+u u X C ， 即 22ln (41)arctan(2)⎡⎤++=⎣⎦X u u C 1(2)=C C ，将1==-Y y u X x 代入，得原方程的通解为 222ln 4(1)arctan1⎡⎤+-+=⎣⎦-yy x C x ． （2）原方程可写成d d 43()+=-+y x yx x y ， 该方程属于d ()d =++yf ax by c x类型，一般可令=++u ax by c ． 令=+u x y ，有d d 1d d =-y u x x，则原方程可化为 d 1d 43-=-u ux u， 即34d 2d 2-=-u u x u ，积分得 32ln 22+-=+u u x C ，将=+u x y 代入上式，得原方程的通解为32ln 2+++-=x y x y C ．习 题 11—31．求下列微分方程的通解：（1）22e -'+=x y xy x ； （2）23'-=xy y x ； （3）d tan 5d yx y x-=； （4）1ln '+=y y x x ； （5）2(6)d 2d 0-+=y x y y x ； （6）d 32d ρρθ+=． 解 （1） ()d ()d e ()e d -⎡⎤⎰⎰=+⎢⎥⎣⎦⎰p x x p x x y q x x C ()222d 2d e e e d e d x x x xx x x x C x x C ---⎛⎫⎰⎰=+=+ ⎪⎝⎭⎰⎰2221e e 2x x C x --=+． （2）原方程可化为3'-=y y x x， 故通解为33d d 3321e e d ---⎡⎤⎛⎫⎰⎰=+=-=-⎢⎥ ⎪⎝⎭⎣⎦⎰x x x x y x x C x C Cx x x ．（3）原方程可化为d cos 5cos d sin sin -=y x x y x x x， 故通解为cos cos d d sin sin 5cos e e d sin ⎛⎫- ⎪⎝⎭⎡⎤⎰⎰=+⎢⎥⎢⎥⎣⎦⎰x x x x x x x y x C x 25cos sin d sin 5sin x x x C C x x ⎡⎤=+=-⎢⎥⎣⎦⎰． （4）所给方程的通解为()11d d ln ln 1e ed ln d ln -⎡⎤⎰⎰=+=+⎢⎥⎣⎦⎰⎰x xx x x x y x C x x C x1(ln )ln ln -=-+=+C xx x x C x x x． （5）方程可化为 2d 6d 2x x y y y -=，即 d 31d 2x x y y y -=-，故通解为 33d d 1e e d 2-⎡⎤⎰⎰=-+⎢⎥⎢⎥⎣⎦⎰y yy y x y y C3211d 2y y C y ⎛⎫=-+ ⎪⎝⎭⎰312⎛⎫=+ ⎪⎝⎭y C y ． （6）()3d 3d 33e 2e d e 2e d θθθθρθθ--⎡⎤⎰⎰=+=+⎢⎥⎣⎦⎰⎰C C 33322e e e 33C C θθθ--⎛⎫=+=+ ⎪⎝⎭．2．求下列微分方程的特解： （1）d tan sec d yy x x x -=，00x y ==； （2）cos d cot 5e d x y y x x +=，24π==-x y ； （3）23d 231d y x y x x -+=，10x y ==．第十一章 微分方程习题详解解 （1）tan d tan d e sec e d -⎛⎫⎰⎰=⋅+ ⎪⎝⎭⎰x xx x y x x C ()lncos lncos e sec ed -=+⎰x xx x C()1sec cos d cos x x x C x=⋅+⎰cos +=x Cx， 代入初始条件0,0==x y ，得0=C ．故所求特解为 cos =xy x． （2） cot d cot d cos e 5e e d -⎛⎫⎰⎰=⋅+ ⎪⎝⎭⎰x x x x x y x C ()cos 15esin d sin xx x C x=⋅+⎰()cos 15e sin =-+x C x， 代入初始条件,42π==-x y ，得1C =，故所求特解为cos 15e sin -=xy x， 即 cos sin 5e 1+=x y x ．（3） 332323d d ee d ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭⎡⎤⎰⎰=+⎢⎥⎢⎥⎣⎦⎰x x x x x x y x C 22113ln 3ln e e d ⎛⎫-++ ⎪⎝⎭⎡⎤=+⎢⎥⎢⎥⎣⎦⎰x x xx x C 222211113332e 11e d ee d 2x x x x x x C x C x x --⎛⎫⎡⎤⎛⎫⎪=+=-+⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎣⎦⎪⎝⎭⎰⎰ 2221133311e e e 22x x x x x C Cx -⎛⎫=+=+ ⎪ ⎪⎝⎭，代入初始条件1,0==x y ，得12e=-C ，故所求特解为 21311e 2-⎛⎫=- ⎪ ⎪⎝⎭x x y ． 3．求一曲线的方程，这曲线通过原点，并且它在点(,)x y 处的切线斜率等于2+x y ． 解 设曲线方程为()=y y x ，依题意有2'=+y x y ，即2'-=y y x ．从而有()d de 2e d e2ed --⎛⎫⎰⎰=+=+ ⎪⎝⎭⎰⎰x x xxy x x C x x Ce (2e 2e )22e x x x x x C x C --=--+=--+． 由0=x ，0=y ，得2=C ．故所求曲线的方程为2(e 1)=--x y x ．4．设曲线积分2()d [2()]d +-⎰Lyf x x xf x x y 在右半平面（0>x ）内与路径无关，其中()f x 可导，且(1)1=f ，求()f x ．解 依题意及曲线积分与路径无关的条件，有2[2()][()]0∂-∂-=∂∂xf x x yf x x y，即 2()2()2()0'+--=f x xf x x f x ．记()=y f x ，即得微分方程及初始条件为112'+=y y x，11==x y ． 于是，)11d d22e e d -⎛⎫⎰⎰=+=+ ⎪⎝⎭⎰x xx x y x C x C23⎫=⎪⎭C x 代入初始条件 1,1==x y ，得13=C ，从而有 2()3=f x x5．求下列伯努利方程的通解：（1）2d ;d yx y xy x+= （2）42323;y y x y x '+=（3）4d 11(12);d 33y y x y x +=- （4）3d [(1ln )]d 0-++=x y y xy x x ． 解 （1）方程可以化为21d 11d --+=y y y x x． 令1-=z y ，则2d d d d -=-z y y x x ，即2d d d d -=-y z y x x ．代入方程，得d 11d -+=z z x x，即 d 11d -=-z z x x， 其通解为11d de (e )d ln -⎛⎫⎰⎰=-+=- ⎪⎝⎭⎰x xx x z x C Cx x x ，所以原方程的通解为1ln =-Cx x x y． （2）原方程化为41233d 23d --+=y yy x x x． 令13-=z y ，则43d 1d d 3d -=-z y y x x ，即43d d 3d d -=-y z y x x ．代入方程，得2d 233d -+=z z x x x，即2d 2d 3-=-z z x x x，第十一章 微分方程习题详解其通解为22d d 233e (e )d -⎡⎤⎰⎰=-+⎢⎥⎣⎦⎰x x x xz x x C2433()d ⎡⎤=-+⎢⎥⎣⎦⎰x x x C273337⎛⎫=- ⎪⎝⎭x C x ．所以原方程的通解为 12733337-=-yCx x ．（3）原方程化为4311(12)33--'+=-y y y x ．令3-=z y ，则43-''=-z y y ，于是原方程化为21z x z '-=-，其通解为d d 21e ()e d e ()e 21d x x x x z x C x x x C --⎡⎤⎰⎰⎡⎤=+=+⎢⎥⎣⎦⎣--⎦⎰⎰ e (21)e 21e x x xx C x C -⎡⎤=--+=--+⎣⎦，所以原方程的通解为 321e -=--+x y x C ．（4）原方程化为31(1ln )'-=+y y x y x ，即3211ln --'-=+y y y x x． 令2-=z y ，则32-''=-z y y ，则原方程化为22(1ln )'+=-+z z x x，其通解为 22d de 2(1ln )e d -⎡⎤⎰⎰=-++⎢⎥⎣⎦⎰x xx x z x x C222(1ln )d x x x x C -⎡⎤=-++⎣⎦⎰233221(1ln )d 33x x x x x C x -⎡⎤=-++⋅+⎢⎥⎣⎦⎰23322(1ln )39x x x x C -⎡⎤=-+++⎢⎥⎣⎦222(1ln )39x x x Cx -=-+++，所以原方程的通解为 2222(1ln )39--=-+++y x x x Cx ，或写成233242ln 93=--+x x x x C y ．习 题 11—41．求下列全微分方程的通解：（1）21d ()d 0;2xy x x y y ++= （2）3222(36)d (46)d 0;x xy x y x y y +++=（3）e d (e 2)d 0;y y x x y y +-= （4）(cos cos )sin sin 0x y x y y x y '+-+=． 解 （1）易知，=P xy ，21()2=+Q x y ．因为∂∂==∂∂P Q x y x ，所以原给定的方程为全微分方程．而21(,)0d ()d 2x yu x y s x t t =++⎰⎰22221111()2224x y y x y y =+=+，于是，所求方程的通解为221124+=x y y C ． （2）易知，2236=+P x xy ，3246=+Q y x y ．因为12∂∂==∂∂P Qxy y x， 所以原给定的方程为全微分方程．而2320(,)3d (46)d xyu x y s s t x t t =++⎰⎰34223x y x y =++， 于是，所求方程的通解为 34223++=x y x y C ．（3）易知，e y P =，e 2y Q x y =-．因为 e y P Qy x∂∂==∂∂，原方程为全微分方程．将原方程的左端重新组合，得2(e d e d )2d d(e )y y y x x y y y x y +-=-，于是，所求方程的通解为 2e y x y C -=．（4）原方程可化为(cos cos )d (sin sin )d 0x y x y y x y x ++-+=，易知，sin sin P y x y =-+，cos cos Q x y x =+．因为 sin cos P Qx y y x∂∂=-+=∂∂，原方程为全微分方程．方程的左端重新组合，得(cos d sin d )(cos d sin d )0x y y y x x y y x x ++-=， d(sin )d(cos )d(sin cos )0x y y x x y y x +=+=，于是，所求方程的通解为 sin cos x y y x C +=．第十一章 微分方程习题详解2．用观察法求出下列方程的积分因子，并求其通解：（1）2()d d 0;x y x x y =-+ （2）22(3)d (13)d 0y x y x xy y -+-=． 解 （1）用21x 乘方程，便得到了全微分方程 211d d 0⎛⎫+-= ⎪⎝⎭y x y x x ，将方程左端重新组合，得2d d d d 0-⎛⎫+=-= ⎪⎝⎭y x x y y x x x x ． 于是，通解为 -=yx C x． （2）原方程可化为232d 3d d 3d 0xy x y x y xy y -+-=，即232d d 3(d d )0xy x y y x xy y +-+=，用21y 乘方程，便得到了全微分方程 21d d 3(d d )0+-+=x x y y x x y y ， 221111d d 3d()d 3022x xy x xy y y ⎛⎫⎛⎫⎛⎫--=--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，于是，原方程的通解为21132--=x xy C y． 3．用积分因子法解下列一阶线性方程：（1）24ln xy y x '+=； （2）tan y y x x '-=． 解 （1）将原方程写成24ln '+=xy y x x， 此方程两端乘以2d 2eμ⎰==xx x 后变成224ln '+=x y xy x x ，即 2()4ln '=x y x x ，两端积分，得2224ln d 2ln ==-+⎰x y x x x x x x C ，于是，原方程的通解为 22ln 1=-+C y x x ． （2）方程两端乘以tan d e cos μ-⎰==x xx ，则方程变为cos sin cos '-=y x y x x x ，即 (cos )cos '=y x x x ，两端积分，得cos cos d sin cos ==++⎰y x x x x x x x C ，于是，原方程的通解为 tan 1cos =++Cy x x x．习 题 11—51．求下列微分方程的通解： （1）211y x ''=+； （2）e x y x '''=； （3）(5)(4)10y y x -=．解（1）1121d arctan 1'=+=++⎰y x C x C x ， ()212121arctan d arctan ln(1)2y x C x C x x x C x C =++=-+++⎰．（2）11e d e e ''=+=-+⎰x x x y x x C x C ，1212(e e )d e 2e x x x x y x C x C x C x C '=-++=-++⎰， 2112323(e 2e )d e 3e 2x x x x C y x C x C x C x x C x C =-+++=-+++⎰． （作为最后的结果，这里12C 也可以直接写成1C ）． （3）令(4)=z y ，则有d 10d -=z z x x，可知=z Cx ，从而有 44d d =yCx x ， 再逐次积分，即得原方程的通解53212345=++++y C x C x C x C x C ．2．求下列微分方程的通解：（1）;y y x '''=+ （2）0;xy y '''+= （3）310;y y ''-= （4）()3y y y ''''=+． 解 （1）令'=y p ，则'''=y p ，且原方程化为'-=p p x ．利用一阶线性方程的求解公式，得()d d 11e e d eed x x xxp x x C x x C --⎛⎫⎰⎰=+=+ ⎪⎝⎭⎰⎰()11e e e 1e x x x x x C x C --=--+=--+．第十一章 微分方程习题详解即11e x p x C =--+，再积分，得通解21121(1e )d e 2x x y x C x x x C C =--+=--++⎰．（2）令'=y p ，则'''=y p ，且原方程化为0'+=xp p ，分离变量，得d d =-p xp x，积分得 11ln ln ln =+p C x，即 1=C p x，再积分，得通解 112d ln ==+⎰C y x C x C x ．（3）令'=y p ，则d d ''=py py，且原方程化为 3d 10d -=py py， 分离变量，得 31d d =p p y y ，积分得 2121=-+p C y ，故'==y p ， 再分离变量，得d =±x ．由于||sgn()=y y y ，故上式两端积分，sgn()d =±⎰y x，即12sgn(=±+y C x C ，两边平方，得()221121-=+C y C x C ．（4）令'=y p ，则d d ''=p y py ，且原方程化为3d d =+ppp p y，即 2d (1)0d ⎡⎤-+=⎢⎥⎣⎦p p p y ． 若0≡p ，则≡y C ．≡y C 是原方程的解，但不是通解． 若0≡p ，由于p 的连续性，必在x 的某区间有0≠p ．于是2d (1)0d -+=pp y，分离变量，得2d d 1=+py p ，积分得 1arctan =-p y C ，即()1tan =-p y C ，亦即 ()1cot d d -=y C y x ．积分得()12ln sin ln -=+y C x C ．即 ()12sin e -=x y C C ，也可写成()21arcsin e =+x y C C ．由于当20=C 时，1=y C ，故前面所得的解≡y C 也包含在这个通解之内．3．求下列初值问题的解：（1）sin ''=+y x x ，(0)1=y ，(0)2'=-y ； （2）2(1)2'''+=x y xy ，(0)1=y ，(0)3'=y ； （3）2e y y ''=，(0)0=y ，(0)0'=y ； （4）()21'''+=y y ，(0)0=y ，(0)0'=y ．解 （1）易知，211cos 2'=-+y x x C ，3121sin 6=-++y x x C x C ．由初值条件(0)2'=-y ，知1201-=-+C ，得11=-C ；由(0)1=y ，知21000=-++C ，得21=C ．故特解为31sin 16=--+y x x x ．（2）令'=y p ，则'''=y p ，且原方程化为2(1)2'+=x p xp ，变量分离，得212d d 1=+x p x p x，两端积分，得 21(1)'==+y p C x ．再两端积分，得 3121()3=++y C x x C ．由初值条件(0)3y '=，有213(10)=+C ，解得，13=C ，由初值条件(0)1y =，有22113(00)3=+⋅+C ，解得，21=C ，故所给初值条件的微分方程的特解为 331=++y x x ．（3）令'=y p ，则d d py py ''=，且原方程化为 2d e d y ppy=，即2d e d y p p y =，第十一章 微分方程习题详解两端积分得22111e 22yp C =+． 代入初始条件(0)0=y ，(0)0y '=，得 112C =-，从而22111e 222y p =-，即22e 1y p =-，亦即 '=y ．分离变量后积分d =±⎰x ，即d -=⎰y x ，得2arcsin(e )-=+y x C ，代入初始条件(0)0y =，得2π=2C ．于是，符合所给初值条件的特解为 e sin -π⎛⎫=⎪2⎝⎭y x ， 即 lncos lnsec =-=y x x ．（4）令'=y p ，则d d py py''=，且原方程化为 2d 1d ppp y+=， 分离变量，得2d d 1pp y p =-，两端积分，得 211ln(1)2--=+p y C ， 代入初始条件(0)0y =，(0)0y '=，得 10=C ．从而，21ln(1)2=--y p ，即'==y p再分离变量，得d =±y x d =±y y x ．两端积分，得2arch(e )=±+y x C ，代入初始条件(0)0=y ，得20=C ，从而有满足所给初始条件的特解为arch(e )=±y x ，即e ch()ch()=±=y x x ，或写成 ln ch()=y x ．4．试求''=y x 的经过点(0,1)M 且在此点与直线112=+y x 相切的积分曲线． 解 由于直线112=+y x 在(0,1)M 处的切线斜率为12，依题设知，所求积分曲线是初值问题''=y x ，01==x y ，012='=x y 的解．由''=y x ，积分得2112'=+y x C ，再积分，得 21216=++y x C x C ，代入初始条件01==x y ，012='=x y ，解得 112=C ，21=C ，于是所求积分曲线的方程为 211162=++y x x ．5．对任意的0>x ，曲线()=y f x 上的点(,())x f x 处的切线在y 轴上的截距等于1()d xf t t x ⎰， 且()=y f x 存在二阶导数，求()f x 的表达式．解 设曲线的方程为()=y f x ，其中()=y f x 有二阶导数，则在点(,())M x f x 处的切线方程为()()()'-=-Y f x f x X x ，令0=X ，知切线在y 轴上的截距为()()'=-Y f x xf x ，据题意，有1()d ()()'=-⎰x f t t f x xf x x ，即20()()()d '-=⎰x xf x x f x f t t ． 两端求导，得2()()2()()()''''+--=f x xf x xf x x f x f x ，即[]()()0x f x xf x '''+=，已知0>x ，故有()()0f x xf x '''+=，令'=y p ，则'''=y p ，且原方程化为d 0d pp xx+=， 分离变量，得11d d =-p x p x，两端积分，得 1ln ln ln =-p C x ，即1'==C y p x．第十一章 微分方程习题详解再对两端积分，得12ln =+y C x C ，即12()ln =+f x C x C ．习 题 11—61．下列函数组中，在定义的区间内，哪些是线性无关的． （1）e x ，e ;x - （2）23sin x ，21cos ;x - （3）cos2x ，sin 2;x （4）ln x x ，ln x ． 解 （1）因为1e x y =，2e x y -=满足：212e e exx x y y -==≠常数， 所以函数组e x ，e x -是线性无关的．（2）因为213sin y x =，221cos y x =-满足：21223sin 31cos y x y x==-， 所以函数组23sin x ，21cos -x 是线性相关的．（3）因为1cos2y x =，2sin 2y x =满足：12cos2cot 2sin 2y x x y x==≠常数， 所以函数组cos2x ，sin 2x 是线性无关的．（4）因为1ln y x x =，2ln y x =满足：12ln ln y x x x y x==≠常数， 所以函数组ln x x ，ln x 是线性无关的．2．验证1cos y x ω=及2sin y x ω=都是方程20y y ω''+=的解，并写出该方程的通解． 证明 由1cos y x ω=，得1sin y x ωω'=-，21cos y x ωω''=-； 由2sin y x ω=，得1cos y x ωω'=，21sin y x ωω''=-． 可见，2sin 0i y x ωω''+= (1,2)i =，故1cos y x ω=及2sin y x ω=都是方程20y y ω''+=的解．又因为12cot y x y ω=≠常数，故1cos y x ω=与2sin y x ω=线性无关．于是所给方程的通解为 1212cos sin y y y C x C x ωω=+=+．3．验证21e x y =及22e x y x =都是微分方程24(42)0y xy x y '''-+-=的解，并写出该方程的通解．证明 由21e x y =，得212e x y x '=，221(24)e x y x ''=+； 由22e x y x =，得222(12)e x y x '=+，232(64)e x y x x ''=+． 因为2222221114(42)(24)e 42e (42)e 0x x x y xy x y x x x x '''-+-=+-⋅+-=； 22223222224(42)(64)e 4(12)e (42)e 0x x x y xy x y x x x x x x '''-+-=+-⋅++-=， 所以21e x y =及22e x y x =都是方程24(42)0y xy x y '''-+-=的解．又因为21y x y =≠常数，故21e x y =与22e x y x =线性无关，于是所给方程的通解为 21212()e x y y y C C x =+=+．4．若13y =，223y x =+，22e 3x y x =++都是方程()()()y P x y Q x y f x '''++=(()0)f x ≠的特解，当()P x ，()Q x ，()f x 都是连续函数时，求此方程的通解．解 因为221y y x -=，32e x y y -=，所以2x 及e x 都是方程()()()y P x y Q x y f x '''++=对应齐次方程的特解．又因为32221e xy y y y x -=≠-常数，所以21y y -与32y y -线性无关．因此，所给方程()()()y P x y Q x y f x '''++=的通解为212e 3x y C x C =++．习 题 11—71．求下列微分方程的通解．（1）40;y y '''-= （2）3100;y y y '''--= （3）960;y y y '''++= （4）0;y y ''+=（5）6250;y y y '''-+= （6）(4)5360''+-=y y y ．解 （1）所给方程对应的特征方程为240r r -=，解之，得10r =，24r =，所以原方程的通解为412e x y C C =+．（2）所给方程对应的特征方程为23100r r --=解之，得15r =，22r =-，所以原方程的通解为第十一章 微分方程习题详解5212e e x x y C C -=+．（3）所给方程对应的特征方程为29610r r ++=解之，得 1213r r ==-，所以原方程的通解为1312()ex y C C x -=+．（4）所给方程对应的特征方程为210r +=，解之，得 1i r =，2i r =-，所以原方程的通解为12cos sin y C x C x =+．（5）所给方程对应的特征方程为26250r r -+=，解之，得 134i r =-，234i r =+，所以原方程的通解为312e (cos 4sin 4)x y C x C x =+．（6）所给方程对应的特征方程为425360r r +-=，解之，得 1,22r =±，3,43i r =±，所以原方程的通解为221234e e cos3sin3x x y C C C x C x -=+++．2．求下列微分方程满足所给初始条件的特解： （1）00430,6,10==''''-+===x x y y y y y ； （2）00440,2,0==''''++===x x y y y y y ； （3）00250,2,5=='''+===x x y y y y ； （4）004130,0,3==''''-+===x x y y y y y ．解 （1）所给方程对应的特征方程为2430r r -+=，解之，得 11r =，23r =，所以原方程的通解为312e e x x y C C =+，从而，312e 3e x x y C C '=+，代入初始条件006,10x x y y =='==，得12126,310,C C C C +=⎧⎨+=⎩ 解得124,2,C C =⎧⎨=⎩ 故所求特解为34e 2e x x y =+．（2）所给方程对应的特征方程为24410r r ++=，解之，得 1,212r =-，所以原方程的通解为1212()ex y C C x -=+，从而，12211221211e ee 22x x x C C C x y ----'=-， 代入初始条件002,0x x y y =='==，得1122,10,2C C C =⎧⎪⎨-+=⎪⎩ 解得，122,1,C C =⎧⎨=⎩ 故所求特解为12(2)ex y x -=+．（3）所给方程对应的特征方程为2250r +=，解之，得 1,25i r =±，所以原方程的通解为12cos5sin5y C x C x =+，从而，125sin55cos5y C x C x '=-+，代入初始条件002,5x x y y =='==，得122,55,C C =⎧⎨=⎩ 解得，122,1,C C =⎧⎨=⎩ 故所求特解为2cos5sin5y x x =+．（4）所给方程对应的特征方程为24130r r -+=，解之，得 1,223i r =±，所以原方程的通解为212e (cos3sin 3)x y C x C x =+，从而，21221e [(23)cos3(23)sin3]x y C C x C C x '=++-，代入初始条件000,3x x y y =='==，得1120,233,C C C =⎧⎨+=⎩ 解得120,1,C C =⎧⎨=⎩ 故所求特解为2e sin3x y x =．3．设圆柱形浮筒，直径为0.5米，铅直放在水中，当稍向下压后突然放开，浮筒在水第十一章 微分方程习题详解中上下振动的周期为2秒，求浮筒的质量．解 设x 轴的正向铅直向下，原点在水面处．平衡状态下浮筒上一点A 在水平面处，又设在时刻t ，点A 的位置为()x x t =，此时它受到的恢复力的大小为21000||gV g R x ρ=π排水（R 是浮筒的半径），恢复力的方向与位移方向相反，故有21000mx g R x ''=-π，其中m 是浮筒的质量．记221000g R mωπ=，则得微分方程20x x ω''+=．其对应的特征方程为220r ω+=，解得1,2i r ω=±，故12cos sin sin()x C t C t A t ωωωϕ=+=+，A 1sin C Aϕ=． 由于振动周期22T ωπ==，故ω=π，即221000g R m π=π，从中解出浮筒的质量为 21000195gR m =≈π（千克）．习 题 11—81．求下列微分方程的特解*y 的形式（不必求出待定系数）． （1）2331;y y x ''-=+ （2）;y y x '''+= （3）2e ;x y y y '''-+= （4）23e ;x y y y -'''--= （5）32e ;x y y y x '''-+= （6）22(3)e ;x y y x x '''-=+- （7）276e sin ;x y y y x '''++= （8）245e sin ;x y y y x '''-+= （9）2222e cos ;x y y y x x '''-+= （10）22e sin x y y y x x '''-+=．解 （1）2()31f x x =+属于e ()λx m P x 型（其中，2()31m P x x =+，0λ=），对应齐次方程的特征方程为230r -=．易知，0λ=不是特征方程的根，所以特解*y 的形式为*2y Ax Bx C =++ （这里A 、B 和C 为待定系数）．（2）()f x x =属于e ()λx m P x 型（其中，()m P x x =，0λ=），对应齐次方程的特征方程为20r r +=．易知，0λ=是特征方程的一个单根，所以特解*y 的形式为*2()y x Ax B Ax Bx =+=+ （这里A 和B 为待定系数）．（3）()e x f x =属于e ()λx m P x 型（其中，()1m P x =，1λ=），对应齐次方程的特征方程为2210r r -+=，易知，1λ=是特征方程的二重根，所以特解*y 的形式为*2e x y Ax = （其中A 为待定系数）．（4）()e x f x -=属于e ()λx m P x 型（其中，()1m P x =，1λ=-），对应齐次方程的特征方程为2230r r --=，易知，1λ=-是特征方程的一个单根，所以特解*y 的形式为*e x y Ax -= （其中A 为待定系数）．（5）()e x f x x =属于e ()λx m P x 型（其中，()m P x x =，1λ=），对应齐次方程的特征方程为2320r r -+=，易知，1λ=是特征方程的一个单根，所以特解*y 的形式为*2()e ()e x x y x Ax B Ax Bx =+=+ （其中A 和B 为待定系数）．（6）2()(3)e x f x x x =+-是e ()λx m P x 型（其中，2()3m P x x x =+-，1λ=），对应齐次方程的特征方程为220r r -=，易知，1λ=是不是特征方程的根，所以特解*y 的形式为*2()e x y Ax Bx C =++ （其中A 、B 和C 为待定系数）．（7）2()e sin x f x x =属于[]e ()cos ()sin x l n P x x P x x λωω+型（其中2λ=，1ω=，()0l P x =，()1n P x =）．对应齐次方程的特征方程为2760r r ++=，易知，i 2i λω+=+不是特征方程的根，所以应设其特解为*2e (cos sin )x y A x B x =+ （其中A 、B 为待定系数）．（8）2()e sin x f x x =属于[]e ()cos ()sin x l n P x x P x x λωω+型（其中2λ=，1ω=，()0l P x =，()1n P x =）．对应齐次方程的特征方程为2450r r -+=，易知，i 2i λω+=+是特征方程的根，所以应设其特解为*2e [cos sin )]x y x A x B x =+ （其中A 和B 为待定系数）．（9）由2()2e cos xf x x x =属于[]e ()cos ()sin x l n P x x P x x λωω+型（其中2λ=，1ω=，()2l P x x =，()0n P x =），对应齐次方程的特征方程为2220r r -+=，易知，i 2i λω+=+不是特征方程的根，所以应设其特解为*2e [()cos ()sin )]x y Ax B x Cx D x =+++ （其中A 、B 、C 和D 为待定系数）．（10）()e sin x f x x x =属于[]e ()cos ()sin x l n P x x P x x λωω+型（其中1λ=，1ω=，()0l P x =，()n P x x =）．对应齐次方程的特征方程为2220r r -+=，易知，i 1i λω±=±是特征方程的根，所以应设其特解为[]*e ()cos ()sin )x y x Ax B x Cx D x =+++（其中A 、B 、C 和D 为待定系数）．2．求下列各微分方程的通解．（1）22e ;x y y y '''+-= （2）323e ;x y y y x -'''++= （3）369(1)e ;x y y y x '''-+=+ （4）e cos ''+=+x y y x ．解 （1）()2e x f x =是e ()λx m P x 型（其中，()2m P x =，1λ=），对应齐次方程的特征方第十一章 微分方程习题详解程为2210r r +-=，解得 112r =，21r =-，故对应齐次方程的通解为 1212e e x x Y C C -=+．因为1λ=不是特征方程的根，所以特解*y 的形式为*e x y A =，代入原方程得2e e e 2e x x x x A A A +-=．消去e x ，有1A =，即 *e x y =，故原方程的通解为1*212e e e x x x y Y y C C -=+=++．（2）()3e x f x x -=是e ()λx m P x 型（其中，()3m P x x =，1λ=-），对应齐次方程的特征方程为 2320r r ++=，解得 11r =-，22r =-，故对应齐次方程的通解为212e e x x Y C C --=+．因为1λ=-是特征方程的单根，所以特解*y 的形式为*2()e ()e x x y x Ax B Ax Bx --=+=+，代入原方程并消去e x -，得2(2)3Ax A B x ++=．比较系数，得32A =，3B =-，即 *233e 2x y x x -⎛⎫=- ⎪⎝⎭，故原方程的通解为 *22123e e 3e 2x x x y Y y C C x x ---⎛⎫=+=++- ⎪⎝⎭．（3）3()(1)e x f x x =+是e ()λx m P x 型（其中，()1m P x x =+，3λ=），对应齐次方程的特征方程为 2690r r -+=，解得 1,23r =，故对应齐次方程的通解为312()e x Y C C x =+．因为3λ=是特征方程的二重根，所以特解*y 的形式为*23323()e ()e x x y x Ax B Ax Bx =+=+，代入原方程并消去e x ，得621Ax B x +=+．比较系数，得16A =，12B =，即 *32311e 62x y x x ⎛⎫=+ ⎪⎝⎭，故原方程的通解为*33231211()e e 62x x y Y y C C x x x ⎛⎫=+=+++ ⎪⎝⎭．（4）原方程对应的齐次方程的特征方程为210r +=，解得1,2i r =±，故对应齐次方程的通解为。

第十一章冲突与冲突管理思考题1.什么是冲突？关于冲突有三种不同的观念，分别是什么？答：冲突是行为主体之间，由于目的、手段分歧而导致的对立状态。

人们对组织冲突的理解主要有三种不同的观点，按出现的先后顺序大致可划分为传统观念、人际关系观念和相互作用观念。

冲突的传统观念：认为冲突是群体内功能失调的结果，冲突都是消极的有害的，势必造成组织、群体、个人之间的不和、分裂和对抗，降低工作效率，影组织目标的实现。

因此，组织中领导者必须尽量减少冲突，最好是避免冲突。

冲突的人际关系观念:认为对于任何组织、群体和个人而言，冲突是不可避免的客观存在。

冲突既无法避免又不可能彻底消除，并且冲突的影响既有消极的一面，也有积极的一面，所以，应当接受冲突，对冲突加以控制和利用。

冲突的相互作用观念：认为冲突对于组织既有建设性、推动性的一面，也有破坏性、阻滞性的一面。

如果组织中没有冲突，过分融洽、安宁的组织或群体会失去生机、活力和创新精神。

相反，保持适当的冲突水平，可以促进组织变革，使组织保持旺盛的生命力。

不同的冲突类型会对组织产生不同的影响，也就影响着组织的管理水平和管理方式。

因此，要根据不同类型的冲突区别处理。

2.冲突的积极作用和消极作用分别有哪些？答：（1）冲突的积极作用①冲突解决的过程能够激发组织中的积极变革和创新。

有时候人们为了消除冲突，就必须要寻求改变现有方式和方法的途径。

这个寻求解决冲突的过程，不仅可以导致变革的创新，而且可以使得变革更容易为下属所接受，甚至达到员工的期望和要求。

②在决策的过程中有意地激发冲突，极有可提高决策的有效性。

在群体决策过程中，由于从众压力或由于个人领导者的权威控制了局面，或凝聚力强的群体为了获得内部一致性，而不愿考虑更多的备选方案，更倾向于获得群体内部一致的意见，就可能因方案未得到充分讨论而造成决策失误，如果以提出反对意见或提出多种不同看的方式来激发冲突，就可能提出更多创造性的方案，提高决策的正确性和有效性。

第十一章 几何光学通过复习后，应该:1.掌握单球面折射成像、共轴球面系统、薄透镜成像、薄透镜的组合、放大镜和显微镜;2.理解共轴球面系统的三对基点、眼的分辨本领和视力、近视眼、远视眼、散光眼的矫正;3.了解透镜像差、眼的结构和性质、色盲、检眼镜、光导纤维内窥镜。

11-1 一球形透明体置于空气中，能将无穷远处的近轴光线束会聚于第二个折射面的顶点上，求此透明体的折射率。

习题11-1附图（原11-2附图）解: 无穷远处的光线入射球形透明体，相当于物距u 为∞，经第一折射面折射，会聚于第二折射面的顶点，则v=2r（r 为球的半径），已知n 1 =1.0，设n 2 =n（即透明体的折射率），代入单球面折射成像公式，得rn r n 1.0-20.1=+∞ 解得n =2.0，即球形透明体的折射率。

11-2 在3m 深的水池底部有一小石块，人在上方垂直向下观察，此石块被观察者看到的深度是多少?（水的折射率n =1.33）习题11-2附图（原11-3附图）解: 这时水池面为一平面的折射面，相当于r 为∞，已知u =3m，n 1 =1.33，n 2 =1.0，观察者看到的是石块所成的像，设其像距为v ，应用单球面折射成像公式，得∞=+ 1.33-.010.1m 333.1v 解得v =-2.25m，这表明石块在水平面下2.25m 处成一虚像，即观察者看到的“深度”。

11-3 圆柱形玻璃棒（n =1.5）放于空气中，其一端是半径为2.0cm 的凸球面，在棒的轴线上离棒端8.0cm 处放一点物，求其成像位置。

如将此棒放在某液体中（n =1.6），点物离棒端仍为8.0cm，问像又在何处?是实像还是虚像?习题11-3附图 （a）【原11-5附图（a）】解: ①如本题附图（a）所示，已知n 1 =1.0，n 2 =1.5，u =8.0cm，r =2.0cm，代入单球面折射成像公式，得cm0.2 1.0-.515.1cm 0.80.1=+v得v =12cm，在玻璃棒中离顶点12cm 处成一实像。

第11章 供配电系统的运行和管理11-1．节约电能有何重要意义？答：节约电能的意义主要表现为：1．缓解电力供需矛盾。

节约电能可以节约煤炭、水力、石油等一次能源，使整个能源资源得到合理使用，缓解电力供需矛盾,并能减轻能源部门和交通运输部门的紧张程度。

2．节约国家的基建投资。

节约电能可以节约国家用于发电、输配电及用电设备所需要的投资，给整个国民经济带来很大的利益,有利于国民经济的发展。

3．提高企业的经济效益。

节约电能可以减少企业的电费开支，降低生产成本，积累资金，提高企业的经济效益。

4．推动企业用电合理化。

节约电能可以推动企业采用新技术、新材料、新设备、新工艺，加速设备改造和工艺改革，从而提高企业的经营管理水平，使企业生产能力得到充分发挥，促进企业生产水平的不断发展和提高。

11-2．什么叫负荷调整？有哪些主要调整措施？答：根据供电系统的电能供应情况及各类用户不同的用电规律，合理地安排各类用户的用点时间，以降低负荷高峰，填补负荷的低谷（即所谓的“削峰填谷”），充分发挥发、变电设备的潜能，提高系统的供电能力。

负荷调整的主要措施：①同一地区各厂的厂休日错开；②同一厂内各车间的上下班时间错开，使各个车间的高峰负荷分散；③调整大容量用电设备的用点时间，使它避开高峰负荷时间用电，做到各时段负荷均衡，从而提高了变压器的负荷系数和功率因数，减少电能的损耗。

④实行“阶梯电价+分时电价” 的综合电价模式。

“阶梯电价”全名为“阶梯式累进电价”，是指把户均用电量设置为若干个阶梯，随着户均消费电量的增长，电价逐级递增。

峰谷分时电价是指根据电网的负荷变化情况，将每天24小时划分为高峰、平段、低谷等时段，各时段电价不同，以鼓励用电客户合理安排用电时间，削峰填谷，提高电力资源的利用效率。

11-3．什么叫经济运行？什么叫变压器的经济负荷？答：经济运行是指整个电力系统的有功损耗最小，获得最佳经济效益的设备运行方式。

变压器的经济负荷S ec.T ，就是应满足变压器单位容量的综合有功损耗△P/S 为最小值的条件。

第十一章 光的衍射1． 波长为500nm 的平行光垂直照射在宽度为0.025mm 的单缝上，以焦距为50cm 的会聚透镜将衍射光聚焦于焦面上进行观察，求（1）衍射图样中央亮纹的半宽度；（2）第一亮纹和第二亮纹到中央亮纹的距离；（3）第一亮纹和第二亮纹的强度。

解：（1）零强度点有sin (1,2, 3....................)a n n θλ==±±± ∴中央亮纹的角半宽度为0aλθ∆=∴亮纹半宽度290035010500100.010.02510r f f m a λθ---⨯⨯⨯=⋅∆===⨯ （2）第一亮纹，有1sin 4.493a παθλ=⋅= 9134.493 4.493500100.02863.140.02510rad a λθπ--⨯⨯∴===⨯⨯ 21150100.02860.014314.3r f m mm θ-∴=⋅=⨯⨯==同理224.6r mm =（3）衍射光强20sin I I αα⎛⎫= ⎪⎝⎭，其中sin a παθλ= 当sin a n θλ=时为暗纹，tg αα=为亮纹 ∴对应 级数 α 0II0 0 11 4.493 0.047182 7.725 0.01694 . . . . . . . . .2． 平行光斜入射到单缝上，证明：（1）单缝夫琅和费衍射强度公式为20sin[(sin sin )](sin sin )a i I I a i πθλπθλ⎧⎫-⎪⎪=⎨⎬⎪⎪-⎩⎭式中，0I 是中央亮纹中心强度；a 是缝宽；θ是衍射角，i 是入射角（见图12-50） （2）中央亮纹的角半宽度为cos a iλθ∆=证明：(1))即可(2)令(sin sin ai πθπλ==± ∴对于中央亮斑 sin sin i aλθ-=3． 在不透明细丝的夫琅和费衍射图样中，测得暗条纹的间距为1.5mm ，所用透镜的焦距为30mm ，光波波长为632.8nm 。

第十一章长期负债及借款费用[题目答案分离版] 字体：大中小一、单项选择题1、符合资本化条件的资产所发生的借款费用在予以资本化时，要与资产支出相挂钩的是()。

A、专门借款利息B、专门借款的溢价摊销C、一般借款利息D、外币专门借款的汇兑差额【正确答案】C【答案解析】本题考核借款费用资本化的核算。

专门借款发生的借款费用不需要考虑资产支出。

【该题针对“借款费用的范围”知识点进行考核】【答疑编号10532857,点击提问】2、A公司于2012年2月1日经临时股东大会批准，决定建造一栋办公楼，为此于2012年2月15日向某银行申请贷款8 000万元；2012年3月1日工程动工兴建，并于当日领用自产建材一批，共计80万元；2012年4月1日，上述贷款获准发放到位，并于当日开始计息；2012年4月15日支付在建工程人员职工薪酬95万元。

除上述专门借款外，该项工程未占用其他借款；预计工期为2年。

不考虑其他因素，则该项工程借款费用开始资本化的时点为()。

A、2012年2月15日B、2012年3月1日C、2012年4月1日D、2012年4月15日【正确答案】C【答案解析】本题考核开始资本化时点的确定。

开始资本化时点需要同时满足为使资产达到预定可使用或可销售状态所必要的购建或生产活动已经开始、资产支出已经发生、借款费用已经发生三个条件。

【该题针对“借款费用的确认”知识点进行考核】【答疑编号10532856,点击提问】3、2012年1月1日，甲企业融资租入一台设备。

租赁资产原账面价值为35万元，合同规定每年年末支付10万元租金，租赁期为4年，承租人无优惠购买选择权，租赁开始日估计资产余值为4万元，承租人的母公司提供资产余值的担保金额为2万元，另外担保公司提供资产余值的担保金额为1万元。

在租赁开始日为安装设备支付工程承包商设备安装费15万元；按照合同约定从租赁期的第二年起，再按本项目营业收入的3%收取租金(假定2012年度本项目营业收入为1 000万元)，则最低租赁付款额为()万元。

第十一章 氧化还原反应1. 用离子电子法配平下列反应式：（1）PbO 2 + Cl - → Pb 2+ + Cl 2 （酸性介质） （2）Br 2 → BrO 3- + Br - （酸性介质） （3）HgS + NO 3- + Cl - → HgCl 42- + NO 2 + S （酸性介质） （4）CrO 42- + HSnO 2- → HSnO 3- + CrO 2- （碱性介质） （5）CuS + CN - + OH - → Cu(CN)43- + NCO- + S （碱性介质） 解：用离子电子法配平：（1）PbO 2 + Cl - → Pb 2+ + Cl 2 （酸性介质）PbO 2 + 4H + + 2e - = Pb 2+ + 2H 2O （还原） +）2Cl - = Cl 2 + 2e - （氧化）PbO 2 + 2Cl + 4H = Pb + Cl 2 +2H 2O （2）Br 2 → BrO 3- + Br - （酸性介质）×5）21Br 2 + e - = Br - （还原）+）×1）2Br 2 + 3 H 2O = BrO 3- + 5Br - + 6H + （氧化）3Br 2 + 3H 2O = BrO 3- + 5Br - + 6H +（3）HgS + NO 3- + Cl - → HgCl 42- + NO 2↑+ S （酸性介质） ×2）NO 3- + 2H + + e - = NO 2 + H 2O （还原） +） HgS + 4Cl - = HgCl 42- + S + 2e - （氧化）HgS + 2NO 3 + 4Cl + 4H = HgCl 4 + 2NO 2↑+ S +2H 2O（4）CrO 42- + HSnO 2- → HSnO 3- + CrO 2- （碱性介质） ×2）CrO 42- + 2H 2O + 3e - = CrO 2- + 4OH - （还原） +）×3）HSnO 2- + 2OH - = HSnO 3- + H 2O + 2e - （氧化）2CrO 4 + 3HSnO 2 + 4H 2O + 6OH = 3HSnO 3- + 2CrO 2- + 8OH - + 3H 2O 整理：2CrO 42- + 3HSnO 2- + H 2O = 3HSnO 3- + 2CrO 2- + 2OH -（5）CuS + CN - + OH - → Cu(CN)43- + NCO - + S （碱性介质） ×2）CuS + 4CN - + e - = Cu(CN)43- + S 2- （氧化） +） CN - + 2OH - = NCO - + H 2O + 2e - （还原）2CuS + 9CN - + 2OH - = 2Cu(CN)43- + NCO - + H 2O +2S 2-2. 用离子电子法配平下列电极反应： （1）MnO 4- → MnO 2 （碱性介质） （2）CrO 42- →Cr(OH)3 （碱性介质） （3）H 2O 2 → H 2O （碱性介质） （4）H 3AsO 4 → H 3AsO 3 （酸性介质） （5）O 2 → H 2O 2(aq) （酸性介质） 答：配平过程略。

第十一章短期经济波动模型：产品市场和货币市场的共同均衡1.决定总需求的重要因素有哪些？答案要点：收入水平和结构、供求水平的结构对应、消费、投资、净出口的大小、物价水平、利率水平、政府支出2.为什么价格水平的上升会提高利率？答案要点：在货币供给不变的条件下，价格水平上升意味着货币需求增大和实际货币存量的减少，为保持货币市场的均衡，就必须提高利率来抑制货币需求的增长。

3.为什么IS曲线向右下方倾斜？答案要点：在投资的预期收益不变情况下，利率下降意味着投资成本的减少和利润的增加，所以，企业会增加投资。

而增加投资需求就会增加产出和均衡收入。

这样，IS曲线就会表现出向右下方倾斜。

4.为什么LM曲线向右上方倾斜？答案要点：均衡收入提高增加了货币的交易需求，在货币供给不变的条件下，为保持货币市场的均衡，利率必须上升，以便抑制货币的投机需求。

于是，LM曲线就会表现出向右上方倾斜。

5.减少政府支出为什么会降低利率？答案要点：这会降低货币需求，在货币供给不变的情况下，为维持货币市场的均衡，利率必须降低。

6.增加货币供给为什么会降低利率？答案要点：货币供给增加会使货币市场失去原来的均衡，要恢复均衡就需要相应增大货币需求，为此，利率就会降低。

7.IS曲线和LM曲线为什么不能各自独立地决定均衡的国民收入和均衡的利率？答案要点：IS曲线涉及的利率是外生变量，必须由货币市场决定；LM曲线涉及的收入也是外生变量，必须由产品市场决定，所以他们都无法各自独立地决定均衡的国民收入和均衡的利率。

8.你认为IS▬LM模型是说明总需求的好模型吗？答案要点：该模型具有较简洁、直观、能大致说明宏观经济中总需求的优点和特征。

但其缺陷也是十分明显的，一是两条曲线的交点具有偶然性和不确定性，严重影响其说服力。

二是模型无法反映消费需求的情况。

三是该模型受限于其静态表现。

四是没有表现出凯恩斯所强调的投资需求的不确定性，表现的却是投资与利率的确定性关系。

第十一章：量子跃迁[1] 具有电荷q 的离子，在其平衡位置附近作一维简谐振动，在光的照射下发生跃迁，入射光能量密为)(ωρ，波长较长，求：（1）跃迁选择定则。

（2）设离子处于基态，求每秒跃迁到第一激发态的几率。

（解）本题是一维运动，可以假设电磁场力的方向与振动方向一致。

（1）跃迁选择定则：为确定谐振子在光照射下的跃迁选择定则，先计算跃迁速率，因为是随时间作交变的微扰，可以用专门的公式（12）（§11.4，P396）)(34//'2222k k kk kk r q W ωρπ→= （1）式中2'→k k r 应理解为谐振子的矢径的矩阵元的平方和，但在一维谐振子情形，→k k r /仅有一项2/k k x )(34//'2222k k k k kk x q W ωρπ = （2）根据谐振子的无微扰能量本征函数来计算这矩阵元dx x k k k ⎰∞∞-=)0('/ψ （3）式中)(2)(!)0(ax H k ax k kk πψ=，μω=a~446~ 要展开（3）式，可以利用谐振子定态波函数的递推公式：}212{1)0(1)0(1)0(+-++=k k k k k x ψψαψ （4） 代入（3），利用波函数的正交归一化关系：mn n xn dx δψψ=⎰)0(*)0( dxk k x k k kk k ⎰∞∞-+-++⋅=}212{1)0(1)0(1*)0(''ψψαψ1,1,''21121+-++=k k k k k k δαδα（5） 由此知道，对指定的初态k 来说，要使矢径矩阵元（即偶极矩阵元）不为零，末态'k 和初态k 的关系必需是：,1'-=k k 这时21,1'kk x x k k k α==- （6） ,1'+=k k 这时211,1'+==+k k x x k k k α因得结论：一维谐振子跃迁的选择定则是：初态末态的量子数差数是1。

习 题 十 一11-1 如图所示，在点电荷+Q 的电场中放置一导体球。

由点电荷+Q 到球心的径矢为r ，在静电平衡时，求导体球上的感应电荷在球心O 点处产生的场强E 。

[解] 静电平衡时，导体内任一点的场强为零，O 点的场强是点电荷+Q 及球面上感应电荷共同贡献的，由场强叠加原理有0Q 0='+=E E E r E E 20Q 4r Q πε-=-='11-2 一带电量为q 、半径为r 的金属球A ，放在内外半径分别为1R 和2R 的不带电金属球壳B 内任意位置，如图所示。

A 与B 之间及B 外均为真空，若用导线把A ，B 连接，求球A 的电势。

[解] 以导线把球和球壳连接在一起后，电荷全部分布在球壳的外表面上(或者说导体球的电荷与球壳内表面电荷中和)，整个系统是一个等势体，因此20B A 4R q U U πε==11-3 如图所示，把一块原来不带电的金属板B 移近一块已带有正电荷Q 的金属板A ，平行放置。

设两板面积都是S ，板间距为d ，忽略边缘效应，求：(1)板B 不接地时，两板间的电势差；(2)板B 接地时，两板间的电势差。

[解] (1) 由61页例1知，两带电平板导体相向面上电量大小相等符号相反，而相背面上电量大小相等符号相同，因此当板B 不接地，电荷分布为因而板间电场强度为 SQ E 02ε=电势差为 SQdEd U 0AB 2ε== (2) 板B 接地时，在B 板上感应出负电荷，电荷分布为B A-Q/2Q/2Q/2Q/2A B -QQ故板间电场强度为 SQ E 0ε=电势差为 SQdEd U 0AB ε==11-4 如图所示，有三块互相平行的导体板，上导体板到中间导体板的距离为5.0cm ，上导体板到下导体板的距离为8.0cm ，外面的两块用导线连接，原来不带电。

中间一块两面上带电，其面电荷密度之和为25m C 103.1-⨯=σ。

求每块板的两个表面的面电荷密度各是多少(忽略边缘效应)?[解] 因忽略边缘效应，可把三个导体板看作无限大平板，由例1知32σσ-= (1) 45σσ-= (2)忽略边缘效应，则导体板可看成无限大的，具有屏蔽性，在相邻导体板之间的电场只由相对于二表面上电荷决定。

第11章运算符重载一．单项选择题1．下列运算符中，运算符在C++中不能重载。

A．?： B．+ C． D．<=解：C++中不能被重载的运算符有：·，一，：：，?：。

本题答案为A。

2．下列运算符中，运算符在C++中不能重载。

A．&& B．[] C．：： D．new解：c++中不能被重载的运算符有：·，·+，：：，?：。

本题答案为c。

3．下列关于运算符重载的描述中，是正确的。

A．运算符重载可以改变操作数的个数B．运算符重载可以改变优先级C．运算符重载可以改变结合性D．运算符重载不可以改变语法结构解：运算符重载不能改变操作数的个数、运算符的优先级、运算符的结合性和运算程的语法结构。

本题答案为D。

4．友元运算符objl>obj2被C++编译器解释为。

A．operator>(objl，obj2) B．>(obj1，obj2)C．obj2．operator：>(obj1) D．objl．operator>(obj2)解：重载为友元函数的运算符的调用形式如下：operator<运算符>(<参数1>，<参数2>)等价于：<参数1><运算符><参数2>本题答案为A。

5．现需要对list类对象使用的逻辑运算符“==”重载，以下函数声明是正确的。

A、list & list：：operator==(const list &a)；B、list list：：operator==(const list &a)；C、bool & list：：operator==(const list &a)；D、bool list：：operator==(const list &a)；6. 以下类中分别说明了“+=”和“++”运算符重载函数的原型。

第11章课后习题答案11-1 解1）由公式可知：轮齿的工作应力不变，则则，若，该齿轮传动能传递的功率11-2解由公式可知，由抗疲劳点蚀允许的最大扭矩有关系：设提高后的转矩和许用应力分别为、当转速不变时，转矩和功率可提高69%。

11-3解软齿面闭式齿轮传动应分别验算其接触强度和弯曲强度。

（1）许用应力查教材表11-1小齿轮45钢调质硬度：210～230HBS取220HBS；大齿轮ZG270-500正火硬度：140～170HBS，取155HBS。

查教材图11-7，查教材图11-10 ,查教材表11-4取，故：（2）验算接触强度，验算公式为：其中：小齿轮转矩载荷系数查教材表11-3得齿宽中心距齿数比则：、，能满足接触强度。

（3）验算弯曲强度，验算公式：其中：齿形系数：查教材图11-9得、则：满足弯曲强度。

11-4解开式齿轮传动的主要失效形式是磨损，目前的设计方法是按弯曲强度设计，并将许用应力降低以弥补磨损对齿轮的影响。

（1）许用弯曲应力查教材表11-1小齿轮45钢调质硬度：210～230HBS取220HBS；大齿轮45钢正火硬度：170～210HBS，取190HBS。

查教材图11-10得,查教材表11-4 ，并将许用应用降低30%故（2）其弯曲强度设计公式：其中：小齿轮转矩载荷系数查教材表11-3得取齿宽系数齿数，取齿数比齿形系数查教材图11-9得、因故将代入设计公式因此取模数中心距齿宽11-5解硬齿面闭式齿轮传动的主要失效形式是折断，设计方法是按弯曲强度设计，并验算其齿面接触强度。

（1）许用弯曲应力查教材表11-1，大小齿轮材料40Cr 表面淬火硬度：52～56HRC，取54HRC。

查教材图11-10得，查材料图11-7得。

查教材表11-4 ，因齿轮传动是双向工作，弯曲应力为对称循环，应将极限值乘70%。

故（2）按弯曲强度设计，设计公式：其中：小齿轮转矩载荷系数查教材表11-3得取齿宽系数齿数，取齿数比齿形系数应将齿形系数较大值代入公式，而齿形系数值与齿数成反比，将小齿轮的齿形系数代入设计公式，查教材图11-9得因此取模数（3）验算接触强度，验算公式：其中：中心距齿宽，取满足接触强度。

第十一章企业发展能力分析习题解析（一）单项选择题1。

可以反映股东权益账面价值增加变化的指标是( ）。

A。

权益乘数B。

股东权益增长率C.产权比率D.三年资本平均增长率2。

下列项目中，不属于企业资产规模增加原因的是（）。

A.企业对外举债B。

企业实现盈利C.企业发放股利D.企业发行股票注:企业发放股利属于资产规模减少的原因。

3.如果企业某一种产品处于成长期，其销售增长率的特点是（ ).A.比值比较大B.与上期相比变动不大C。

比值比较小D。

与上期相比变动非常小4.下列指标中，不可以用来表示收益增长能力的指标是（）。

A.净利润增长率B.营业利润增长率C.销售增长率D.三年利润平均增长率5。

下列指标中，属于增长率指标的是（ )。

A。

产权比率B。

资本收益率C.不良资产比率D.资本积累率注：资本积累率即股东权益增长率或称之为净资产增长率。

（二）多项选择题1。

企业单项发展能力包括（）。

A.资产发展能力B.收益发展能力C.营业收入发展能力D.负债发展能力E。

股东权益发展能力2.股东权益增长率的大小直接取决于下列因素中的（）。

A.净资产收益率B.总资产周转率C。

总资产报酬率D.股东净投资率E。

权益乘数3。

可以用于反映企业发展能力的财务指标包括（）。

A。

资产增长率B.销售增长率C.资本积累率D。

净利润增长率E.营业利润增长率4.可以用来反映企业收益增长能力的财务指标有（）。

A。

净利润增长率B.销售增长率C.总资产报酬率D。

资本积累率E.营业利润增长率（三）判断题1.从长远的角度看,上市公司的增长能力是决定公司股票价格上升的根本因素。

（正确 )注：导致上市公司股票价格上升的因素包括资金供给、经济政策、经营绩效、市场信息等许多方面，但是长期来看，决定股票市价的根本因素只能是企业自身的生存、获利、发展情况，尤其是企业的增长能力的高低。

2.企业能否持续增长对投资者、经营者至关重要,但对债权人而言相对不重要，因为他们更关心企业的变现能力。