基于MATLAB的ADSP AR(2)模型的LMS 与 RLS 算法分析

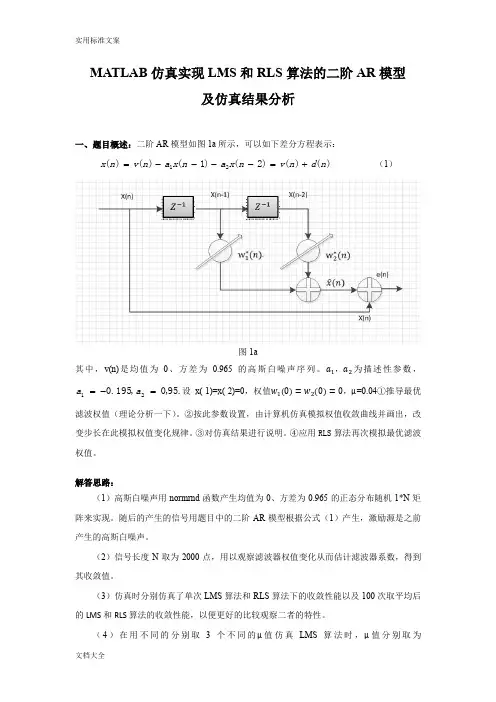
MATLAB 仿真实现LMS 和RLS 算法的二阶AR 模型及仿真结果分析一、题目概述：二阶AR 模型如图1a 所示，可以如下差分方程表示：)()()2()1()()(21n d n v n x a n x a n v n x +=----= （1）图1a其中，v(n)是均值为0、方差为0.965的高斯白噪声序列。

a 1，a 2为描述性参数，.95,0,195.021=-=a a 设x(-1)=x(-2)=0，权值w 1(0)=w 2(0)=0，μ=0.04①推导最优滤波权值（理论分析一下）。

②按此参数设置，由计算机仿真模拟权值收敛曲线并画出，改变步长在此模拟权值变化规律。

③对仿真结果进行说明。

④应用RLS 算法再次模拟最优滤波权值。

解答思路：（1）高斯白噪声用normrnd 函数产生均值为0、方差为0.965的正态分布随机1*N 矩阵来实现。

随后的产生的信号用题目中的二阶AR 模型根据公式（1）产生，激励源是之前产生的高斯白噪声。

（2）信号长度N 取为2000点，用以观察滤波器权值变化从而估计滤波器系数，得到其收敛值。

（3）仿真时分别仿真了单次LMS 算法和RLS 算法下的收敛性能以及100次取平均后的LMS 和RLS 算法的收敛性能，以便更好的比较观察二者的特性。

（4）在用不同的分别取3个不同的μ值仿真LMS 算法时，μ值分别取为0.001,0.003,0.006；用3个不同的λ值仿真RLS 算法时λ值分别取为1,0.98,0.94，从而分析不同步长因子、不同遗忘因子对相应算法收敛效果的影响。

二、 算法简介1．自适应算法的基本原理自适应算法的基本信号关系如下图所示：图 1b 自适应滤波器框图输入信号x(n)通过参数可调的数字滤波器后产生输出信号y(n)，将其与参考信号d(n)进行比较，形成误差信号e(n)。

e(n)通过某种自适应算法对滤波器参数进行调整，最终是e(n)的均方值最小。

当误差信号e(n)的均方误差达到最小的时候，可以证明信号y(n)是信号d(n)的最佳估计。

MATLAB 仿真实现LMS 和RLS 算法题目：序列x(n)有AR （2）模型产生：)()2()1()(21n w n x a n x a n x +-+-=，w(n)是均值为0、方差为1的高斯白噪声序列。

.7.0,4.121-==a a 用LMS 算法和RLS 算法来估计模型参数21,a a 。

按照课本第三章63页的要求，仿真实现LMS 算法和RLS 算法，比较两种算法的权值收敛速度，并对比不同u 值对LMS 算法以及λ值对RLS 算法的影响。

解答：1 数据模型（1）高斯白噪声用用randn 函数产生均值为0、方差为1的标准正态分布随机矩阵来实现。

随后的产生的信号用题目中的AR （2)模型产生，激励源是之前产生的高斯白噪声。

（2）信号点数这里取为2000，用2000个信号来估计滤波器系数。

（3）分别取3个不同的u 、λ值来分析对不同算法对收敛效果的影响。

其中u=[0.001,0.003,0.006]，lam=[1,0.98,0.94]。

2 算法模型2.1自适应算法的基本原理自适应算法的基本信号关系如下图所示：图 1 自适应滤波器框图输入信号x(n)通过参数可调的数字滤波器后产生输出信号y(n)，将其与参考信号d(n)进行比较，形成误差信号e(n)。

e(n)通过某种自适应算法对滤波器参数进行调整，最终是e(n)的均方值最小。

当误差信号e(n)的均方误差达到最小的时候，可以证明信号y(n)是信号d(n)的最佳估计。

2.2 LMS 算法简介LMS 算法采用平方误差最小的原则代替最小均方误差最小的原则，信号基本关系如下：1()()()()()()(1)()2()()(0,1,2,....1)N i i i y n w n x n i e n d n y n w n w n e n x n i i N μ-=-=-+=+-=-∑ 写成矩阵型式为：()()()()()()(1)()2()()T y n W n X n e n d n y n W n W n e n X n μ==-+=+ 式中，W(n) 为n 时刻自适应滤波器的权矢量，011()[(),(),....()]TN W n w n w n w n -=，N 为自适应滤波器的阶数；X( n) 为n 时刻自适应滤波器的参考输入矢量，由最近N 个信号采样值构成，()[(),(1),....(1)]TX n x n x n x n N =--+；d ( n) 是期望的输出值；e ( n) 为自适应滤波器的输出误差调节信号(简称失调信号) ；μ是控制自适应速度与稳定性的增益常数，又叫收敛因子或步长因子。

RLS和LMS自适应算法分析RLS（Recursive Least Squares）自适应算法和LMS（Least Mean Squares）自适应算法是常见的自适应滤波算法，在信号处理、通信系统等领域有广泛应用。

本文将对这两种算法进行详细分析比较，并对它们的优缺点进行评价。

首先，我们先介绍一下这两种算法的基本原理。

RLS算法是一种递归估计算法，通过估计系统的权值并逐步修正的方式逼近期望响应。

根据最小二乘估计准则，RLS算法通过最小化滤波器输出与期望响应之间的均方误差来更新权值。

该算法以过去的输入和期望响应作为参考，通过不断修正权值，逼近最佳解。

常用的RLS算法有全选信号算法、选择性部分信号退化算法等。

LMS算法则是一种基于梯度下降的迭代算法，通过不断修正权值，使得滤波器输出的均方误差逐渐减小。

该算法的优势在于计算简单、适合实时应用。

LMS算法通过使用当前输入和期望响应对滤波器权值进行更新，更新步长由算法的学习速率参数确定，步长过大会导致算法发散，步长过小会降低收敛速度。

接下来，我们以几方面来分析比较这两种算法。

1.性能比较：在滤波效果方面，RLS算法由于基于历史输入和期望响应进行计算，能够更好地估计权值，提高滤波性能。

而LMS算法则在计算简单、实现容易的基础上，性能相对较差。

在噪声较大的环境下，RLS算法的性能相对更为优秀。

2.计算复杂度：RLS算法需要存储历史输入和期望响应，并进行矩阵运算，因此计算复杂度较高。

而LMS算法只需要存储当前输入和期望响应，并进行简单的乘法和加法运算，计算复杂度较低。

在资源受限的环境下，LMS算法更加适用。

3.收敛速度：RLS算法在每次迭代时都通过递归方式重新计算权值，因此收敛速度较快。

而LMS算法只通过当前输入和期望响应更新权值，因此收敛速度较慢。

在需要快速适应的应用场景下，RLS算法更为适合。

4.算法稳定性：由于RLS算法需要存储历史输入和期望响应，内存消耗较大。

LMS和RLS算法应用及仿真分析
LMS算法（Least Mean Squares）是一种基于梯度下降策略的机器学
习算法，它主要应用于解决系统辨识、信号分类和数据拟合等问题。

LMS
算法是一种收敛率较高的优化算法，由于其算法简单、快速，因此在工业
中被广泛应用。

基本原理：LMS算法的基本原理是进行参数更新，以最小化残差平方
和（RSS）作为目标函数，从而改善结果的稳定性和准确性。

LMS算法的
另一个重要思想是，在学习过程中每次迭代都仅使用当前一个输入和相应
的输出。

因此，该算法不需要获得训练样本数据的完整集合，可以仅仅从
一个训练样本中获得有限的信息，并通过这种限定的信息进行迭代。

LMS算法的算法步骤：
（1）初始化参数θ；
（2）给定一个输入样本xn，根据当前的参数θ计算出预测输出ŷn；
（3）根据已知的真实输出dn，计算出当前的残差en；
（4）根据梯度下降法更新参数θ；
（5）重复2～4步，直到达到目标函数的收敛性。

仿真分析：
首先，使用Matlab仿真模拟LMS算法，以模拟实际的系统辨识任务。

LMS 和RLS 算法应用及仿真分析摘要：本文采用MATLAB 软件对LMS 和RLS 两种自适应均衡算法在回波抵消器中的应用进行仿真，分析收敛步长μ、抽头w 、遗忘因子λ 等参数对回波抵消器性能的影响，并对两种算法下的性能做出比较。

关键词：LMS ；RLS ；自适应；回波抵消1 引言进入90 年代后期，通过网络拨打长途电话即IP 电话开始盛行，由于发话端到受话端的延迟达100ms 以上，而人耳对大于50ms 的回声就能辨别出来，因此IP 电话的回声严重影响通话效果。

如何消除回声成为非常重要的问题，回波抵消器就是一个自适应辨识系统，它通过特定的算法辨识未知的目标系统，即回声路径。

本文采用LMS 和RLS 算法实现回波抵消，并对收敛步长μ、抽头w 、遗忘因子λ 等相关参数对回波抵消性能的影响进行了仿真分析，从而为一种通用的回波抵消技术的实际应用提供理论参考。

回波抵消算法原理图如图1 所示。

图1 回波抵消算法原理图 2 LMS 和RLS 算法概述最陡下降法（LMS ）和递归最小二乘算法（RLS ）是自适应滤波最常用，也是最基本的两种算法。

下面分别对LMS 和RLS 两种算法原理做简单介绍。

2.1 LMS 算法设J(n)是n 时刻均方误差，J(n+1)是n+1 时刻的均方误差，W(n)、W(n+1)分别是n 、n+1时刻M 维抽头权向量011()[()()...()]T M W n w n w n w n -= (1)为使J(n+1)<J(n) (2)W(n)必须按J(n)的负方向变化即(1)()W n W n J μ→→→+=-∇ (μ>0) (3)最后以U (n )*e (n )瞬时值代替统计平均，得到抽头权向量迭代式 *(1)()()()W n W n U n e n μ→→+=- (4)式中U(n)式n 时刻的输入向量[u(n) u(n-1) u(n-2)···u(n-M+1)]。

LMS及RLS自适应干扰抵消算法的比较LMS（Least Mean Square）和RLS（Recursive Least Squares）是两种常用的自适应滤波算法，用于干扰抵消。

它们在不同场景下有着不同的特点和适用性。

LMS算法是一种迭代算法，通过不断调整滤波器的权值来最小化误差信号的均方差。

它的优点是实现简单，计算量较小，适用于大多数实时应用。

它采用梯度下降法来更新权值，根据误差信号和输入信号的乘积来调整权值，使得误差不断减小。

然而，LMS算法有一个较大的问题，就是收敛速度较慢，因为它只基于当前样本进行权值更新，对数据的统计特性要求较高。

另外，LMS算法对噪声的功率估计不准确，容易导致性能退化。

与LMS算法相比，RLS算法是一种递推算法，通过不断更新逆协方差矩阵来获得最佳权值。

它的优点是收敛速度快，稳定性好，适用于非平稳环境下的信号处理。

RLS算法通过在线估计输入信号的统计特性，能够更准确地抵消干扰。

然而，RLS算法的计算量较大，实时性不如LMS算法，而且对初始参数的选择要求较高，误差传播的问题可能会导致性能下降。

虽然LMS算法和RLS算法在特点和适用性上存在差异，但在实际应用中，可以根据具体的场景选择合适的算法。

如果系统对实时性要求较高，并且希望实现简单，LMS算法是一个合适的选择。

如果系统需要更准确的干扰抵消，并且可以容忍一定的计算复杂度，RLS算法是一个更好的选择。

另外，也可以考虑将两种算法结合使用，利用它们各自的优点来提高干扰抵消的性能。

总结起来，LMS算法和RLS算法是两种常用的自适应干扰抵消算法。

LMS算法具有实现简单、计算量小的特点，适用于实时应用；RLS算法具有收敛速度快、稳定性好的特点，适用于非平稳环境下的信号处理。

在实际应用中可以根据具体的场景选择合适的算法，或者结合两种算法来提高干扰抵消的性能。

RLS和LMS自适应算法分析RLS (Recursive Least Squares) 和 LMS (Least Mean Squares) 是两种常见的自适应滤波算法。

它们在信号处理、通信系统和自适应控制等领域得到广泛应用。

本文将对这两种算法进行分析比较。

首先，我们来看看RLS算法。

RLS算法使用最小均方误差准则来自适应调整滤波器系数。

它利用递归方式计算出均方误差的最小值。

RLS算法基于Wiener-Hopf方程，通过解析方法来计算最优系数。

这种方法计算量较大，但是提供了更好的性能。

RLS算法根据观测数据和期望输出之间的误差信号来不断调整滤波器的权重，并且在递归过程中更新这些权重。

相比于LMS算法，RLS算法具有更快的收敛速度和更高的精度。

但是，RLS 算法也存在一些问题，比如计算复杂度高、存储要求大以及对噪声和系统不确定性敏感。

接下来，我们来看看LMS算法。

LMS算法是一种基于随机梯度下降的自适应算法。

在LMS算法中，滤波器的系数通过逐步调整以减小误差标准差。

LMS算法利用误差信号和输入信号之间的乘积来更新滤波器系数。

这种算法简单易于实现，计算复杂度低，并且对存储要求不高。

LMS算法适用于非平稳环境下的自适应滤波问题。

然而，LMS算法的收敛速度较慢，需要一定的迭代次数才能达到最优解，而且对于高阶滤波器，可能存在稳定性问题。

此外，LMS算法对输入信号的统计特性有一定的要求。

综上所述，RLS算法和LMS算法都是常见的自适应滤波算法，它们在不同的应用领域有不同的适用性和特点。

RLS算法在计算复杂度和存储要求上较高，但是具有更快的收敛速度和更高的精度。

LMS算法计算复杂度低，存储要求小，但是收敛速度较慢。

一般情况下，对于较小的系统和较简单的滤波器，可以使用LMS算法，而对于复杂的系统和高阶滤波器，可以使用RLS算法。

在实际应用中，需要根据具体的要求和约束来选择合适的算法。

此外，还可以根据实时计算需求和系统资源限制等因素，对RLS 和LMS算法进行优化和改进，如考虑快速RLS算法和正则化LMS算法等。

MATLAB 仿真实现LMS 和RLS 算法题目：序列x(n)有AR （2）模型产生：)()2()1()(21n w n x a n x a n x +-+-=，w(n)是均值为0、方差为1的高斯白噪声序列。

.7.0,4.121-==a a 用LMS 算法和RLS 算法来估计模型参数21,a a 。

按照课本第三章63页的要求，仿真实现LMS 算法和RLS 算法，比较两种算法的权值收敛速度，并对比不同u 值对LMS 算法以及λ值对RLS 算法的影响。

解答：1 数据模型（1）高斯白噪声用用randn 函数产生均值为0、方差为1的标准正态分布随机矩阵来实现。

随后的产生的信号用题目中的AR （2)模型产生，激励源是之前产生的高斯白噪声。

（2）信号点数这里取为2000，用2000个信号来估计滤波器系数。

（3）分别取3个不同的u 、λ值来分析对不同算法对收敛效果的影响。

其中u=[0.001,0.003,0.006]，lam=[1,0.98,0.94]。

2 算法模型2.1自适应算法的基本原理自适应算法的基本信号关系如下图所示：图 1 自适应滤波器框图输入信号x(n)通过参数可调的数字滤波器后产生输出信号y(n)，将其与参考信号d(n)进行比较，形成误差信号e(n)。

e(n)通过某种自适应算法对滤波器参数进行调整，最终是e(n)的均方值最小。

当误差信号e(n)的均方误差达到最小的时候，可以证明信号y(n)是信号d(n)的最佳估计。

2.2 LMS 算法简介LMS 算法采用平方误差最小的原则代替最小均方误差最小的原则，信号基本关系如下：1()()()()()()(1)()2()()(0,1,2,....1)N i i i y n w n x n i e n d n y n w n w n e n x n i i N μ-=-=-+=+-=-∑ 写成矩阵型式为：()()()()()()(1)()2()()T y n W n X n e n d n y n W n W n e n X n μ==-+=+式中，W(n) 为n 时刻自适应滤波器的权矢量，011()[(),(),....()]TN W n w n w n w n -=，N 为自适应滤波器的阶数；X( n) 为n 时刻自适应滤波器的参考输入矢量，由最近N 个信号采样值构成，()[(),(1),....(1)]TX n x n x n x n N =--+；d ( n) 是期望的输出值；e ( n) 为自适应滤波器的输出误差调节信号(简称失调信号) ；μ是控制自适应速度与稳定性的增益常数，又叫收敛因子或步长因子。

LMS与RLS算法程序LMS（最小均方）和RLS（递推最小二乘）是两种常见的自适应滤波算法，在信号处理和通信系统中被广泛应用。

本文将介绍LMS和RLS的基本理论原理，并给出相应的算法程序。

1.LMS算法LMS算法是一种最简单的自适应滤波算法，其基本原理是通过调整滤波器的权值，使得输出信号与期望信号的均方误差最小化。

LMS算法每次迭代都根据误差进行权值更新，可通过以下步骤实现：步骤1:初始化滤波器的权值w(n)=0；步骤2:输入一个样本x(n)；步骤3:计算滤波器的输出y(n)=w(n)^T*x(n)；步骤4:计算误差e(n)=d(n)-y(n)，其中d(n)为期望输出；步骤5:更新滤波器权值w(n+1)=w(n)+μ*e(n)*x(n)，其中μ为步长参数；步骤6:返回步骤2下面是一个简单的LMS算法的Python代码示例：```pythonimport numpy as npdef LMS(x, d, mu, iterations):N = len(x)w = np.zeros(N) # 初始化滤波器权值y = np.zeros(N) # 存储输出信号e = np.zeros(N) # 存储误差信号for n in range(iterations):y[n] = np.dot(w, x[n]) # 计算输出信号e[n]=d[n]-y[n]#计算误差信号w = w + mu * e[n] * x[n] # 更新权值return y, e, w#测试x = np.array([[1, 2, 3, 4, 5], [2, 3, 4, 5, 6]]) # 输入信号d = np.array([4, 7, 10, 13, 16]) # 期望输出mu = 0.01 # 步长参数iterations = len(x[0]) # 迭代次数y, e, w = LMS(x, d, mu, iterations)print("输出信号:", y)print("误差信号:", e)print("滤波器权值:", w)```2.RLS算法RLS算法是一种快速收敛的自适应滤波算法，它通过递推计算得到滤波器的权值更新，以减小均方误差。

LMS和RLS算法应用及仿真分析LMS（最小均方）算法和RLS（递归最小二乘）算法是两种经典的自适应滤波算法，广泛应用于各种实际场景中。

本文将介绍LMS和RLS算法的原理及其在实际应用场景中的应用，并进行仿真分析。

首先，我们来介绍LMS算法。

LMS算法是一种基于梯度下降法的自适应滤波算法，在信号处理中经常应用于滤波、降噪、系统辨识等领域。

其基本原理是通过不断调整滤波器的权值，使得滤波器的输出与期望输出之间的均方误差最小化。

LMS算法的核心是权值更新公式：w(n+1)=w(n)+μe(n)x(n)，其中w(n)表示第n次迭代的权值向量，μ为步长因子，e(n)为滤波器输出与期望输出之差，x(n)为输入信号。

LMS算法具有简单、易实现的特点，但收敛速度较慢，对信号的统计特性较为敏感。

LMS算法在实际应用中有着广泛的应用。

以自适应滤波为例，LMS算法可以用于消除信号中的噪声，提高信号的质量。

在通信系统中，LMS算法可以应用于自适应均衡，解决信道等效时延导致的传输误差问题。

除此之外，LMS算法还可以用于系统辨识、自适应控制等领域。

接下来，我们来介绍RLS算法。

RLS算法是一种基于递归最小二乘法的自适应滤波算法，广泛应用于信号处理、自适应滤波、波束形成等领域。

与LMS算法相比，RLS算法具有更快的收敛速度和更好的稳定性。

其核心思想是通过递归计算逆相关矩阵，从而得到滤波器的最优权值。

RLS算法的权值更新公式可以表示为：w(n+1)=w(n)+K(n)e(n)，其中K(n)为滤波器的增益向量，e(n)为滤波器输出与期望输出之差。

不同于LMS算法，RLS算法的步长因子时刻变化，可以根据需要进行调整，从而实现最优的权值更新。

RLS算法在实际应用中也有着广泛的应用。

例如，在通信系统中，RLS算法可以用于波束形成，提高信号的接收效果。

在自适应滤波中，RLS算法可以用于降低信号中的噪声。

此外，在自适应控制领域，RLS算法可以用于模型辨识、参数估计等问题。

中国网络大学CHINESE NETWORK UNIVERSITY 毕业设计(论文)院系名称：百度网络学院专业：百度学生姓名：百度学号：123456789指导老师：百度中国网络大学教务处制2019年3月1日前言自适应信号处理的理论和技术经过40 多年的发展和完善,已逐渐成为人们常用的语音去噪技术。

我们知道，在目前的移动通信领域中，克服多径干扰，提高通信质量是一个非常重要的问题，特别是当信道特性不固定时，这个问题就尤为突出，而自适应滤波器的出现，则完美的解决了这个问题。

另外语音识别技术很难从实验室走向真正应用很大程度上受制于应用环境下的噪声。

自适应滤波的原理就是利用前一时刻己获得的滤波参数等结果，自动地调节现时刻的滤波参数，从而达到最优化滤波。

自适应滤波具有很强的自学习、自跟踪能力，适用于平稳和非平稳随机信号的检测和估计。

自适应滤波一般包括3个模块：滤波结构、性能判据和自适应算法。

其中，自适应滤波算法一直是人们的研究热点，包括线性自适应算法和非线性自适应算法，非线性自适应算法具有更强的信号处理能力，但计算比较复杂，实际应用最多的仍然是线性自适应滤波算法。

线性自适应滤波算法的种类很多，有RLS自适应滤波算法、LMS自适应滤波算法、变换域自适应滤波算法、仿射投影算法、共扼梯度算法等[1]。

其中最小均方(Least Mean Square,LMS)算法和递归最小二乘(Recursive Least Square,RLS)算法就是两种典型的自适应滤波算法，它们都具有很高的工程应有价值。

本文正是想通过这一与我们生活相关的问题，对简单的噪声进行消除，更加深刻地了解这两种算法。

我们主要分析了下LMS算法和RLS算法的基本原理，以及用程序实现了用两种算法自适应消除信号中的噪声。

通过对这两种典型自适应滤波算法的性能特点进行分析及仿真实现，给出了这两种算法性能的综合评价。

1 绪论1.1课题背景与意义自适应噪声抵消( Adaptive Noise Cancelling，ANC) 技术是自适应信号处理的一个应用分支，其主要理论和框架由B.Widrow等在1975 年提出，经过三十多年的丰富和扩充，现在已经应用到了很多领域，比如车载免提通话设备，房间或无线通讯中的回声抵消( AdaptiveEcho Cancelling，AEC) ，在母体上检测胎儿心音，机载电子干扰机收发隔离等，都是用自适应干扰抵消的办法消除混入接收信号中的其他声音信号。

RLS和LMS自适应算法分析RLS（Recursive Least Squares）和LMS（Least Mean Square）是两种常用的自适应滤波算法，用于实时信号处理和系统辨识。

本文将对这两种算法进行详细的分析。

1.RLS算法：RLS算法是一种基于权值的算法，用于实时估计系统的参数。

其基本思想是通过最小化误差平方和，更新滤波器的权值。

具体算法步骤如下：a.初始化滤波器权值和协方差矩阵。

b.输入新的观测值，并计算滤波器输出。

c.根据观测值和滤波器输出的误差，更新滤波器的权值和协方差矩阵。

d.重复步骤b和步骤c，直到滤波器收敛。

RLS算法的优点是收敛速度快，能够较快地适应系统的变化。

同时，由于使用了协方差矩阵更新权值，能够更好地抑制噪声。

2.LMS算法：LMS算法是一种基于梯度下降的算法，也是一种最小均方误差（Mean Square Error，MSE）的自适应算法。

具体算法步骤如下：a.初始化滤波器权值。

b.输入新的观测值，并计算滤波器输出。

c.根据观测值和滤波器输出的误差，更新滤波器的权值。

d.重复步骤b和步骤c，直到滤波器收敛。

LMS算法的优点是计算简单，实现容易。

然而，由于是一种基于梯度下降的算法，其收敛速度相对较慢，并且对于高维信号处理时存在着性能损失的问题。

3.RLS算法与LMS算法的比较：a.计算复杂度：RLS算法的计算复杂度较高，需要对协方差矩阵进行计算和更新，而LMS算法的计算复杂度较低，只需要进行简单的权值更新。

b.收敛速度：RLS算法的收敛速度较快，能够较快地适应变化的系统；而LMS算法的收敛速度相对较慢。

c.稳定性：RLS算法对于数据的不确定性比较敏感，误差的扩散效应较小；而LMS算法存在着误差累积的问题。

根据相关应用需求，选择合适的自适应算法。

如果需要较快地适应系统的变化，并能较好地抑制噪声，可以选择RLS算法；而如果需要计算简单、实现容易，且对于系统的适应速度要求较低，可以选择LMS算法。

LMS与RLS自适应滤波算法对比研究
一、背景介绍
自适应滤波是现代通信和信号处理中非常重要的技术，它可以有效的
去除信号中的突发噪声，提取出有效的信号。

传统的滤波方法是基于给定
的滤波器参数来完成，无法适应环境变化，难以达到较好的过滤效果，所
以传统的滤波方法的性能不能满足视频真实环境下的实时过滤要求。

LMS
和RLS算法便是一种自适应滤波算法，它们能够适应复杂、随机的信号环境，以获取较高的滤波效率和单位突发噪声的抑制能力。

两者具有共同之处，又能够满足特定的应用需求，因此在信号处理方面有其特有的应用价值。

二、LMS算法介绍
LMS算法是由 Widrow和Hoff于1960年提出的一种自适应滤波算法，它是一种局部最小二乘法。

它通过一系列的参数更新，以实时的方式用最
小均方误差的原则，尽可能接近实时输入信号的期望值。

LMS算法速度快，不需要额外的矩阵求逆操作，而且只用到了一个小型矩阵，对于实时性能
要求高的应用是一个较好的选择。

三、RLS算法介绍
RLS算法是由Park和Kendall于1960年提出的一种自适应滤波算法，它实现了局部最小二乘估计。

与LMS算法不同的是，RLS算法引入了一个
状态变量，可以单独对待每一个输入信号，从而可以更新滤波器的参数，
以实现快速的收敛性。

前言自适应信号处理的理论和技术经过40 多年的发展和完善,已逐渐成为人们常用的语音去噪技术。

我们知道，在目前的移动通信领域中，克服多径干扰，提高通信质量是一个非常重要的问题，特别是当信道特性不固定时，这个问题就尤为突出，而自适应滤波器的出现，则完美的解决了这个问题。

另外语音识别技术很难从实验室走向真正应用很大程度上受制于应用环境下的噪声。

自适应滤波的原理就是利用前一时刻己获得的滤波参数等结果，自动地调节现时刻的滤波参数，从而达到最优化滤波。

自适应滤波具有很强的自学习、自跟踪能力，适用于平稳和非平稳随机信号的检测和估计。

自适应滤波一般包括3个模块：滤波结构、性能判据和自适应算法。

其中，自适应滤波算法一直是人们的研究热点，包括线性自适应算法和非线性自适应算法，非线性自适应算法具有更强的信号处理能力，但计算比较复杂，实际应用最多的仍然是线性自适应滤波算法。

线性自适应滤波算法的种类很多，有RLS自适应滤波算法、LMS自适应滤波算法、变换域自适应滤波算法、仿射投影算法、共扼梯度算法等[1]。

其中最小均方(Least Mean Square,LMS)算法和递归最小二乘(Recursive Least Square,RLS)算法就是两种典型的自适应滤波算法，它们都具有很高的工程应有价值。

本文正是想通过这一与我们生活相关的问题，对简单的噪声进行消除，更加深刻地了解这两种算法。

我们主要分析了下LMS算法和RLS算法的基本原理，以及用程序实现了用两种算法自适应消除信号中的噪声。

通过对这两种典型自适应滤波算法的性能特点进行分析及仿真实现，给出了这两种算法性能的综合评价。

LMS及RLS自适应干扰抵消算法的比较1 绪论1.1课题背景与意义自适应噪声抵消( Adaptive Noise Cancelling，ANC) 技术是自适应信号处理的一个应用分支，其主要理论和框架由B.Widrow等在1975 年提出，经过三十多年的丰富和扩充，现在已经应用到了很多领域，比如车载免提通话设备，房间或无线通讯中的回声抵消( AdaptiveEcho Cancelling，AEC) ，在母体上检测胎儿心音，机载电子干扰机收发隔离等，都是用自适应干扰抵消的办法消除混入接收信号中的其他声音信号。

LMS与RLS自适应滤波算法性能比较LMS(最小均方)自适应滤波算法和RLS(递推最小二乘)自适应滤波算法是两种常见的自适应滤波算法。

它们都可用于滤波器自适应参数的更新，以便满足所需的滤波器性能。

以下是对LMS和RLS自适应滤波算法性能进行比较的一些主要方面。

1.算法原理和复杂度LMS算法是一种梯度下降法，基于误差信号和输入信号的乘积构建更新过程。

它的更新过程简单，易于实现，并且具有较低的计算复杂度。

相比之下，RLS算法不仅考虑了误差信号和输入信号的乘积，还包括过去输出和输入信号的一些特定值，以构建更准确的更新过程。

这导致了更复杂的计算，因此RLS算法的计算复杂度较高。

2.收敛速度和稳定性LMS算法的收敛速度通常较慢，这是因为它只使用局部梯度信息来进行参数更新。

它可能需要更多的迭代次数才能达到所需的滤波器性能。

相反，RLS算法具有更快的收敛速度，这是因为它利用全局信息进行参数更新。

然而，RLS算法对计算误差更敏感，当计算误差较大时，参数更新可能会变得不稳定。

3.对突变信号的适应性LMS算法通常对突变信号有较好的适应性，这是因为它每次只使用部分信息进行参数更新。

当输入信号突然发生变化时，LMS可以相对更快地适应。

与之相反，RLS算法对突变信号的适应性较差，因为它更关注整个信号的统计特性。

当输入信号发生突变时，RLS可能需要更长的时间来重新估计滤波器参数。

4.计算复杂度由于LMS算法只使用局部信息进行参数更新，其计算复杂度较低。

通常，LMS算法的计算复杂度与滤波器长度成正比。

相反，RLS算法会使用全局信息进行参数更新，因此其计算复杂度较高。

通常情况下，RLS算法的计算复杂度与滤波器长度的平方成正比。

综上所述，LMS算法和RLS算法在性能方面有一些明显的区别。

LMS 算法适用于计算资源有限的应用，但它的收敛速度相对较慢。

相反，RLS 算法具有更快的收敛速度，但计算复杂度较高。

因此，对于不同的应用需求，可以选择适合的算法来实现自适应滤波器的性能优化。

自适应滤波LMS与RLS的matlab 实现MATLAB 仿真实现LMS 和RLS 算法的二阶AR 模型及仿真结果分析一、题目概述：二阶AR 模型如图1a 所示，可以如下差分方程表示：)()()2()1()()(21n d n v n x a n x a n v n x +=----= （1）图1a其中，v(n)是均值为0、方差为0.965的高斯白噪声序列。

a 1，a 2为描述性参数，.95,0,195.021=-=a a 设x(-1)=x(-2)=0，权值w 1(0)=w 2(0)=0，μ=0.04①推导最优滤波权值（理论分析一下）。

②按此参数设置，由计算机仿真模拟权值收敛曲线并画出，改变步长在此模拟权值变化规律。

③对仿真结果进行说明。

④应用RLS 算法再次模拟最优滤波权值。

解答思路：（1）高斯白噪声用normrnd函数产生均值为0、方差为0.965的正态分布随机1*N矩阵来实现。

随后的产生的信号用题目中的二阶AR模型根据公式（1）产生，激励源是之前产生的高斯白噪声。

（2）信号长度N取为2000点，用以观察滤波器权值变化从而估计滤波器系数，得到其收敛值。

（3）仿真时分别仿真了单次LMS算法和RLS算法下的收敛性能以及100次取平均后的LMS和RLS算法的收敛性能，以便更好的比较观察二者的特性。

（4）在用不同的分别取3个不同的μ值仿真LMS算法时，μ值分别取为0.001,0.003,0.006；用3个不同的λ值仿真RLS算法时λ值分别取为1,0.98,0.94，从而分析不同步长因子、不同遗忘因子对相应算法收敛效果的影响。

二、算法简介上式越旧的数据对()n ε的影响越小。

通过计算推导得到系数的迭代方程为：w (n )=w (n −1)+k (n )e ∗(n) （5）式(5)中，增量k(n)和误差e ∗(n)计算公式如下：(n 1)x(n)k(n)(n)T(n 1)x(n)T T x λ-=+- (6)e ∗(n )=d ∗(n )−x T (n )∗w(n −1)（7） 式（6）中T(n)= R̂−1(n )，也就是当前时刻自相关矩阵的逆。

§2.3.2 LMS 算法的自适应均衡的计算机仿真实现本小节我们来讨论基于LMS 算法的自适应均衡的计算机仿真实现。

当数据以低于2400比特/秒的速度传输时，ISI 相对较小，在调制解调器的运行中没有问题。

然而，对于高于2400比特/秒高速通信来说，在调制解调器中需要均衡器来校正信道失真[3]。

由于信道特性总的来说是未知的，且是时变的，因此需要用自适应算法进行自适应均衡。

图2.5描述了自适应滤波在自适应的信道均衡中的应用。

最初，传输一个已知的时间较短的训练序列，用LMS 算法来调整均衡器的系数。

在训练序列之后实际的数据序列{)(n y }被传输。

均衡器对信道特性的缓慢变化进行连续跟踪，从而对系数进行调整，用判定来代替已知的训练序列。

当判定误差较少时，这种方法有较好的效果[3]。

信道（a ）（b ）图2.5 数据传输系统中自适应均衡器的模型（1） 学习曲线特性的比较用于研究LMS 算法性能的自适应均衡系统仿真模型如图2.6所示。

数据发生器用于产生信道输入序列()y n 。

仿真时取()y n 为双极性信号。

()y n 一方面经信道传输后(信号为)(n x )由自适应均衡器进行均衡，均衡器的输出为)(ˆn y。

()y n 同时经延迟电路延迟后作为参考信号()d y n 。

自适应滤波器采用LMS 算法力图使()d y n 与)(ˆn y的均方误差2{|()|}E e n 取最小。

数据发生器信道延迟D自适应均衡器噪声发生器LMS ()h n ()()d y n y n D =-()x n ()y n ()v n ++()c n ()e n ()y n ()s n图2.6 研究自适应均衡器性能的系统仿真框图仿真时，信道采用升余弦脉冲响应来模拟[3][7]：20.51cos (2)1,2,30()n n W h n π+-==⎧⎧⎫⎡⎤⎪⎨⎬⎢⎥⎨⎣⎦⎩⎭⎪⎩其他 (2.3.14)该脉冲响应关于2=n 对称。